Página 10

Revisão dos conteúdos de anos anteriores

Para o capítulo 1: Conjuntos numéricos

Números naturais

O conjunto dos números naturais é representado por:

= {0, 1, 2, 3, 4, 5, reticências}

As reticências indicam que o conjunto é infinito.

Números inteiros

O conjunto dos números inteiros é representado por:

= {reticências, ‒3, ‒2, ‒1, 0, +1, +2, +3, reticências}

Para representar os números inteiros em uma reta numérica, traçamos uma reta r e sobre ela marcamos o ponto O, chamado origem, que corresponde ao número zero.

Usando a mesma unidade de medida de comprimento, assinalamos pontos consecutivos à direita da origem e, para cada ponto, fazemos corresponder um número inteiro positivo. O mesmo deve ser feito para representar pontos situados à esquerda da origem, que correspondem aos números inteiros negativos.

Teremos, então:

Esquema. Reta numérica r com os números menos 3. menos 2, menos 1, zero, mais 1, mais 2 e mais 3 representados por meio de pontos. Os números negativos estão representados por pontos de cor vermelha e os números positivos por pontos de cor verde. O ponto correspondente ao número zero tem a cor preta. Os pontos correspondentes a menos 3, menos e menos 1 estão identificados pelas letras F, E e D, respectivamente. Os pontos correspondentes a mais 1, mais 2 e mais 3 estão identificados pelas letras A, B e C, respectivamente. O ponto correspondente ao zero está identificado com a letra O. Abaixo dos pontos vermelhos, há uma seta vermelha para a esquerda indicando: sentido negativo. Abaixo dos pontos verdes, há uma seta verde para a direita indicando: sentido positivo.

1. No caderno, escreva os números naturais de cada item. Em seguida, escreva os números inteiros.

5; \frac{1}{5}; - 5; - \frac{1}{5}

b) ‒0,20; ‒2,0; ‒2,3; ‒1,2

c) ‒5; ‒3,0; 10; 12

\frac{5}{2}; 5,1; 6,3; \frac{8}{9}

2. Copie as retas em seu caderno e substitua por números os pontos indicados por letras:

Gráfico. Reta numérica dividida em 12 partes iguais por meio de 13 risquinhos. No terceiro risquinho está representada a letra C,. No quinto, sexto e sétimos risquinhos estão representados os números menos 1, 0 e 1 respectivamente e no décimo segundo risquinho está representada a letra A.

Gráfico. Reta numérica dividida em 6 partes iguais por meio de 7 risquinhos. No terceiro e quartos risquinhos estão representadas as letras X e Y, respectivamente. No sexto e sétimo risquinhos, estão representados os números menos 31 e menos 30, respectivamente.

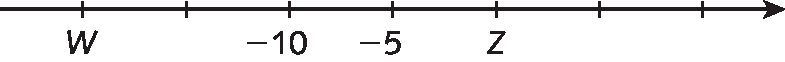
Gráfico. Reta numérica dividida em 6 partes iguais por meio de 7 risquinhos. No primeiro risquinho está representada a letra W. No terceiro, quarto e quinto risquinhos, estão representados os números menos 10, menos 5 e a letra Z, respectivamente.

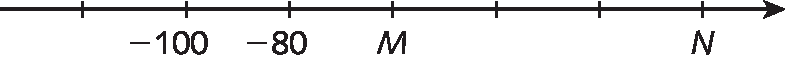
Gráfico. Reta numérica dividida em 6 partes iguais por meio de 7 risquinhos. No segundo, terceiro e quartos risquinhos estão representadas os números menos 100, menos 80 e a letra M, respectivamente. No sétimo risquinho, está representada a letra N.

3. Em seu caderno, indique se a afirmação é verdadeira (V) ou falsa (F).

a) ‒12 > 5

b) 12 > ‒5

c) ‒12 > ‒5

d) 12 > 5

Números racionais

O conjunto dos números racionais é representado por:

= \{\frac{a}{b}, sendo a e b números inteiros e b \neq 0\}

Podemos estabelecer uma correspondência entre os números racionais e os pontos na reta numérica. Vamos analisar alguns exemplos:

O ponto que corresponde ao número

- \frac{7}{4}

, que equivale a

- 1 \frac{3}{4}

, está localizado entre os pontos correspondentes aos números ‒2 e ‒1. Podemos dividir o segmento entre ‒2 e ‒1 em quatro partes iguais e marcar o ponto B, conforme mostramos a seguir.

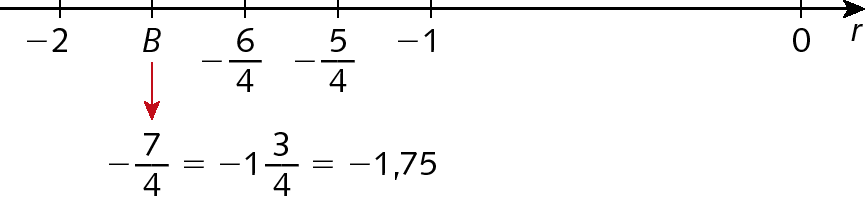
Esquema. Reta numérica r com os seguintes números e letras representados: menos 2, B, menos 6 quartos, menos 5 quartos, menos 1 e 0. Da letra B parte uma seta para baixo para a seguinte sentença matemática. Menos 7 quartos igual ao número misto menos 1 inteiro e 3 quartos que é igual a menos 1 vírgula 75.

4. Em seu caderno, indique quais afirmações são verdadeiras.

a) O número

- \frac{5}{7}

é racional, mas não é natural.

b) O número ‒7 é inteiro, mas não é racional.

c) O número 8,8 não é inteiro nem racional.

d) Os números ‒9 e 6,5 são racionais.

5. Em seu caderno, copie as sentenças e complete com os sinais >, < ou = para que elas sejam verdadeiras.

a) ‒12

b) 2,7

‒5

c) ‒2,2

‒2,1

d) ‒

\frac{1}{5}

- \frac{1}{2}

6. Estes números do quadro foram indicados por letras na reta numérica a seguir.

\frac{9}{4} \frac{1}{2} 4 \frac{9}{2}

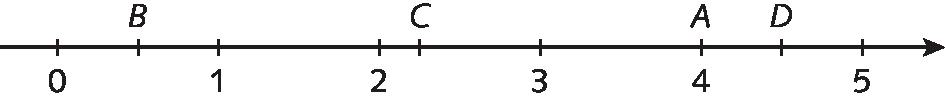
Gráfico. Reta numérica com os números de zero a 5 representados. No centro do trecho entre zero e 1, há um tracinho com a letra B acima. No trecho entre 2 e 3, há um tracinho próximo a 2 com a letra C acima. Acima do do número 4, a letra A. No centro do trecho entre 4 e 5, há um tracinho com a letra D acima.

Associe cada letra a um número do quadro.

Respostas e comentários

1. a) número natural: 5; números inteiros: 5 e ‒5

1. b) nenhum número natural; número inteiro: ‒2,0

1. c) números naturais: 10 e 12; números inteiros: todos os números

1. d) nenhum número natural; nenhum número inteiro

2. a) a → 6; C → ‒3

2. b) xis → ‒34; Y → ‒33

2. c) Z → 0; W → ‒20

2. d) M → ‒60; N → 0

3. a) F

3. b) V

3. c) F

3. d) V

4. itens a, d

5. a) <

5. b) >

5. c) <

5. d) >

A : 4; B : \frac{1}{2}; C : \frac{9}{4}; D : \frac{9}{2}

Revisão dos conteúdos de anos anteriores

Números naturais

A revisão a respeito dos números naturais e dos números inteiros foca nas representações (por meio de conjuntos e da reta numérica).

• Na atividade 1, os estudantes devem identificar os números naturais e, depois, os números inteiros em cada item. Se tiverem dificuldades, lembre-os de que todo número natural é inteiro, mas nem todo número inteiro é natural.

• Na atividade 2, os estudantes devem identificar a escala utilizada em cada reta numérica e os números correspondentes aos pontos indicados por letras. Caso tenham dúvidas, questione-os sobre a ordenação dos números representados na reta, levando-os a perceber que o menor número fica à esquerda do maior.

• A atividade 3 aborda a comparação entre dois números inteiros. Provavelmente os estudantes terão mais dificuldades no item c, no qual devem comparar números negativos. Se necessário, oriente-os a fazer essa comparação usando a reta numérica.

Números racionais

Com a intenção de ampliar a revisão dos conjuntos numéricos, o tema agora são os números racionais com o estudo da representação desses números por meio de conjuntos e da reta numérica.

• Na atividade 4, os estudantes devem identificar se os números são racionais ou não; além disso, nos itens a, b e c, devem identificar também se são números naturais ou números inteiros. Se eles tiverem dúvidas, explique-lhes que, em cada item, se houver algum trecho falso, toda a afirmação será considerada falsa.

• A atividade 5 envolve comparação de dois números racionais. Se os estudantes tiverem dificuldades, incentive-os a identificar a localização dos pontos correspondentes a estes números na reta numérica para fazer as comparações.

• A atividade 6 desenvolve a estimativa da a localização de pontos correspondentes a números racionais na reta numérica. Se os estudantes apresentarem dificuldades, na lousa, analise com a turma entre quais números inteiros está cada fração.

Página 11

Para o capítulo 2: Potenciação e radiciação

Potenciação de números racionais

Para um número racional a com expoente natural n maior que 1, definimos:

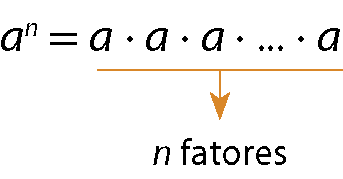
Esquema. a elevado a n igual, a vezes a vezes a vezes reticências, vezes a; Um fio laranja sai dos fatores dessa multiplicação e indica n fatores.

Para todo número racional a com expoente 1, temos: a1 = a

Considere os exemplos:

a) (‒2)1 = ‒2

b) (+0,5)1 = +0,5

{(\frac{7}{2})}^{1}

\frac{7}{2}

Para todo número racional a não nulo, com expoente igual a zero, temos: a0 = 1

Analise os exemplos:

a) (+18)0 = 1

{(– \frac{2}{5})}^{0}

= 1

c) (‒6,4)0 = 1

Se o expoente for um número par, a potência será um número positivo.

Analise os exemplos:

a) (+3)4 = (+3) ⋅ (+3) ⋅ (+3) ⋅ (+3) = +81

b) (‒5)2 = (‒5) ⋅ (‒5) = +25

{(- \frac{1}{3})}^{2} = (- \frac{1}{3}) \cdot (- \frac{1}{3}) = \frac{1}{9}

Se o expoente for um número ímpar, a potência terá o mesmo sinal da base.

Confira os exemplos:

a) (‒3)3 = (‒3) ⋅ (‒3) ⋅ (‒3) = ‒27

b) (+5)3 = (+5) ⋅ (+5) ⋅ (+5) = +125

c) (‒0,6)3 = (‒0,6) ⋅ (‒0,6) ⋅ (‒0,6) = ‒0,216

7. Sem realizar cálculos, responda em seu caderno: Quais destas potências têm resultado positivo?

a) (‒25)10

b) (+15)1

c) (300)12

d) (‒29)63

e) (‒0,25)9

{(\frac{15}{8})}^{15}

g) (‒0,36)0

h) (‒200,1)55

8. Em seu caderno, calcule as potências a seguir.

a) (‒6)4

b) (+6)3

c) (‒3)6

d) 26

e) (‒1,1)3

{(- \frac{1}{2})}^{3}

g) 0,34

{(\frac{1}{2})}^{5}

Raiz quadrada de números racionais

• Quando o índice da raiz é 2, podemos omiti-lo. Assim:

\sqrt[2]{100} = \sqrt{100}

• Os quadrados perfeitos são números racionais que podem ser escritos como potência de base racional e expoente 2. Os números 0; 0,01; 0,04; 0,09; 0,16; 0,25; 1; 4; 9; 16 e 25 são exemplos de quadrados perfeitos.

• A raiz quadrada de um quadrado perfeito é o número racional não negativo cujo quadrado é igual ao número dado.

Então:

\sqrt{0, 09}

= 0,3, pois (0,3)2 = 0,9.

• A raiz quadrada de zero é zero:

\sqrt{0} = 0

, pois 02 = 0

• A raiz quadrada de números racionais negativos não é um número racional, pois o quadrado de um número racional nunca é negativo. Por exemplo:

\sqrt{- \frac{1}{9}}

não é um número racional, pois não existe número racional que multiplicado por ele mesmo resulte em

-

\frac{1}{9}

• A raiz quadrada de um número que não é um quadrado perfeito não é um número racional. Por exemplo:

\sqrt{0,1}

não é um número racional, pois 0,1 não é um quadrado perfeito.

9. Calcule a raiz quadrada dos números a seguir.

\sqrt{64}

- \sqrt{81}

\sqrt{100}

- \sqrt{16}

\sqrt{49}

- \sqrt{4}

Respostas e comentários

7. itens a, b, c, f, g

8. a) +.1296

8. b) +216

8. c) +729

8. d) 64

8. e) ‒1,331

8. f)

- \frac{1}{8}

8. g) 0,0081

8. h)

\frac{1}{32}

9. a) 8

9. b) ‒9

9. c) 10

9. d) ‒4

9. e) 7

9. f) ‒2

Potenciação de números racionais

Esta revisão retoma potências em que a base é um número racional e o expoente é um número natural, assim como a análise do expoente (par ou ímpar) para identificar se o resultado será positivo ou negativo.

• Na atividade 7, destaque aos estudantes que é pedido no enunciado para não realizar os cálculos, uma vez que é necessário saber apenas se o resultado é positivo ou negativo, observando o sinal da base e o expoente de cada potência. Ao final da atividade, permita que eles calculem cada item para conferir as respostas.

• Na atividade 8, os estudantes devem calcular as potências dadas. Caso tenham dificuldades, oriente-os a escrever as potências como multiplicações sucessivas e a efetuá-las. Assim, devem realizar multiplicações de números racionais representados tanto na forma decimal quanto na fórma fracionária.

Raiz quadrada de números racionais

É retomada a ideia de raiz quadrada de números racionais para que, no capítulo 2 deste volume, este estudo possa ser ampliado para a raiz enésima de números reais.

Se possível, na lousa, forneça mais alguns exemplos de raízes quadradas de números racionais escritos tanto na fórma decimal quanto na fracionária.

• A atividade 9 envolve o cálculo de raízes quadradas de números racionais, que são também números inteiros. Acompanhe principalmente a resolução dos itens b, d e f, pois alguns estudantes podem se confundir com o cálculo de raízes quadradas de números racionais negativos e concluir que o resultado não é um número racional. Caso isso ocorra, destaque que cada radicando é positivo, o que possibilita o cálculo da raiz, devendo ser colocado o sinal de menos para o resultado desse cálculo.

Página 12

10. Associe cada item ao seu resultado:

\sqrt{0,0001}

\sqrt{1,44}

\sqrt{0,81}

\sqrt{0,25}

I. 1,2

II. 0,01

III. 0,5

IV. 0,9

11. Determine o valor das seguintes raízes.

\sqrt{\frac{4}{25}}

\sqrt{\frac{9}{64}}

- \sqrt{\frac{100}{4}}

\sqrt{\frac{1}{16}}

12. Copie em seu caderno apenas as afirmações verdadeiras.

a) 100 é quadrado perfeito.

b) 0 não é um quadrado perfeito.

c) A raiz quadrada de

\frac{35}{10}

é um número racional.

d) A raiz quadrada de 0,4 não é um número racional.

13. Determine os valores de W, X, Y e Z.

\sqrt{W} = 4

\sqrt{X} = 9

\sqrt{Y} = 8

\sqrt{Z} = 0, 2

Para o capítulo 3: Sistemas de equações do 1º grau

O plano cartesiano

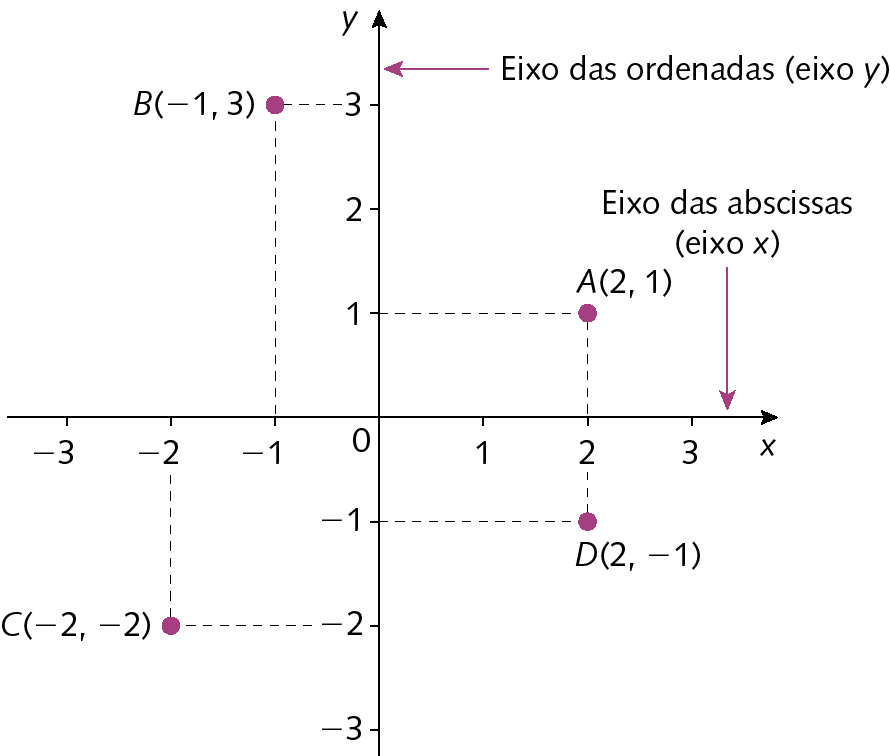
O plano cartesiano é composto de dois eixos, um horizontal e um vertical, chamados de eixo das abscissas (eixo x) e eixo das ordenadas (eixo y), respectivamente. Para representar um ponto no plano cartesiano, utilizamos um par ordenado.

• O ponto a(2, 1) tem abscissa x = 2 e ordenada y = 1.

• O ponto B(‒1, 3) tem abscissa x = ‒1 e ordenada y = 3.

• O ponto C(‒2, ‒2) tem abscissa x = ‒2 e ordenada y = ‒2.

• O ponto D(2, ‒1) tem abscissa x = 2 e ordenada y = ‒1.

Plano cartesiano. Retas numéricas perpendiculares que se intersectam no ponto 0. Na reta numérica horizontal estão representados os números menos 3, menos 2, menos 1, 0, 1, 2 e 3 e ela está identificada com a letra x. Há uma seta para ela com a indicação: Eixo das abcissas (eixo x). Na reta numérica vertical estão representados os números menos 3, menos 2, menos 1, 0, 1, 2 e 3 e ela está identificada com a letra y. Há uma seta para ela com a identificação: Eixo das ordenadas (eixo y). No plano cartesiano, está representado o ponto A que corresponde ao par ordenado (2,1). Do número 2 representado no eixo das abcissas, parte uma linha vertical tracejada. Do número 1 representado no eixo das ordenadas parte uma linha horizontal tracejada. As duas linhas tracejadas se encontram no ponto A. No plano cartesiano, está representado o ponto B que corresponde ao par ordenado (menos 1,3). Do número menos 1 representado no eixo das abcissas, parte uma linha vertical tracejada. Do número 3 representado no eixo das ordenadas parte uma linha horizontal tracejada. As duas linhas tracejadas se encontram no ponto B. No plano cartesiano, está representado o ponto C que corresponde ao par ordenado (menos 2, menos 2). Do número menos 2 representado no eixo das abcissas, parte uma linha vertical tracejada. Do número menos 2 representado no eixo das ordenadas parte uma linha horizontal tracejada. As duas linhas tracejadas se encontram no ponto C. No plano cartesiano, está representado o ponto D que corresponde ao par ordenado (2, menos 1). Do número 2 representado no eixo das abcissas, parte uma linha vertical tracejada. Do número menos 1 representado no eixo das ordenadas parte uma linha horizontal tracejada. As duas linhas tracejadas se encontram no ponto D.

14. Observe os pontos representados no plano cartesiano.

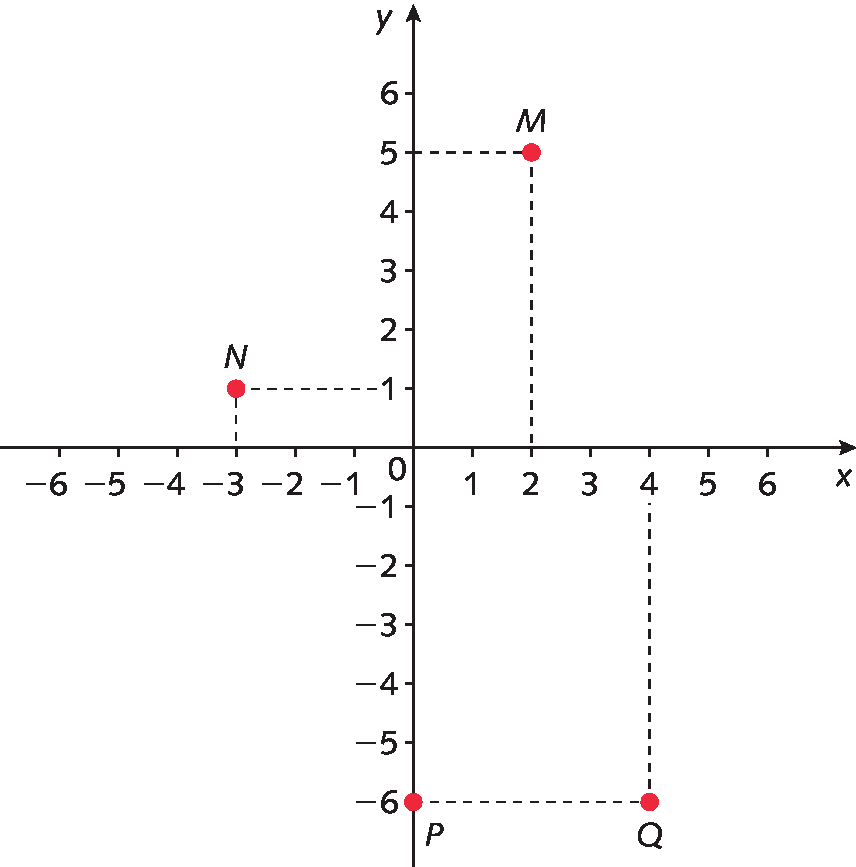
Em seu caderno, escreva as coordenadas de cada um deles.

15. Faça em seu caderno um plano cartesiano e nele represente estes pontos.

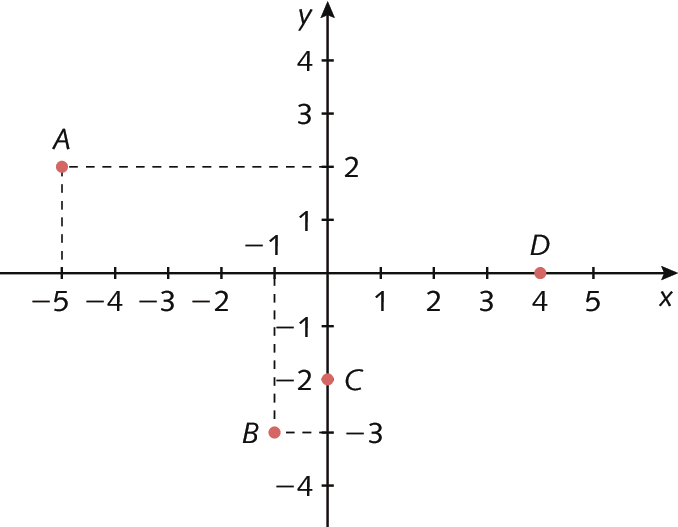
a) A(‒5, 2)

b) B(‒1, ‒3)

c) C(0, ‒2)

d) D(4, 0)

Para o capítulo 4: Ângulos e transformações geométricas

Ângulos

Ângulo é a união de duas semirretas de mesma origem, com uma das regiões do plano limitada por elas.

Respostas e comentários

10. a – dois; B – um; C – quatro; D – três

11. a)

\frac{2}{5}

11. b)

\frac{3}{8}

11. c)

- \frac{10}{2} = - 5

11. d)

\frac{1}{4}

12. itens a, d

13. a) 16

13. b) 81

13. c) 64

13. d) 0,04

14. M(2, 5); N(‒3, 1); P(0, ‒6); Q(4, ‒6)

15. Resposta em Orientações.

• A atividade 10 envolve apenas raízes de números racionais escritos na fórma decimal, então é importante observar como os estudantes realizam os cálculos desse tipo. Caso tenham dificuldades, peça-lhes que encontrem o quadrado dos números da 2ª coluna para confirmar a correspondência com os números da 1ª coluna.

• Na atividade 11, os radicandos estão na fórma fracionária. Assim, oriente os estudantes a calcular em cada item a fração que multiplicada por si mesma terá como resultado a fração dentro do radical. No item c, verifique se eles se lembram de colocar o sinal de menos após o cálculo da raiz.

• Ao resolver a atividade 12, os estudantes devem identificar se os números são ou não quadrados perfeitos. Note que até mesmo nos itens c e d essa identificação deve ser feita, pois, se

\frac{35}{10}

e 0,4 não são quadrados perfeitos, a raiz quadrada desses números não é um número racional. Se necessário, peça que façam os cálculos dos quadrados perfeitos que conhecem mais próximos dos números apresentados.

• Na atividade 13, os estudantes devem identificar o número correspondente à letra dentro de cada radical. Confira se eles notam que esse número é o quadrado do resultado da raiz quadrada.

O plano cartesiano

Nesse momento, a revisão é a respeito do plano cartesiano. Destaque para os estudantes como se representam os eixos, os pontos e como esse plano é dividido em 4 quadrantes. Os exemplos apresentados devem ser analisados por eles a fim de esclarecer esse tipo de representação.

• Para resolver a atividade 14, os estudantes devem identificar as coordenadas de cada um dos pontos indicados no plano cartesiano. Vale a pena destacar que a ordem das coordenadas é sempre a mesma: primeiro x e depois y. Por exemplo, as coordenadas (2, 1) e (1, 2) representam pontos diferentes.

• Na atividade 15, os estudantes devem construir um plano cartesiano e, em seguida, indicar nele cada um dos pontos. Procure acompanhar desde a construção do plano cartesiano para sanar eventuais dúvidas.

• Resposta da atividade 15:

Ilustração. Plano cartesiano com 4 pontos representados. Os pontos são A de abscissa menos 5 e ordenada 2, B de abscissa menos 1 e ordenada menos 3, C de abscissa zero e ordenada menos 2 e D de abscissa 4 e ordenada zero

Ângulos

Ao revisar o conceito de ângulo, apresente a definição, a principal unidade de medida de abertura de um ângulo (grau) e algumas classificações de ângulos com base na sua medida de abertura.

Página 13

Os lados de um ângulo são as semirretas que o determinam, e o vértice é a origem comum dessas semirretas.

Medida da abertura de um ângulo

Ao medir um ângulo, consideramos a abertura entre seus lados. Podemos utilizar como unidade de medida de ângulo o grau (grau).

Ângulo reto, ângulo agudo e ângulo obtuso

Ângulo reto: ângulo que tem medida de abertura igual a 90graus.

Ângulo agudo: ângulo que tem medida de abertura maior que 0grau e menor que 90graus.

Ângulo obtuso: ângulo que tem medida de abertura maior que 90graus e menor que 180graus.

A \hat{O} B

é reto,

C \hat{O} D

é agudo e

E \hat{O} F

é obtuso:

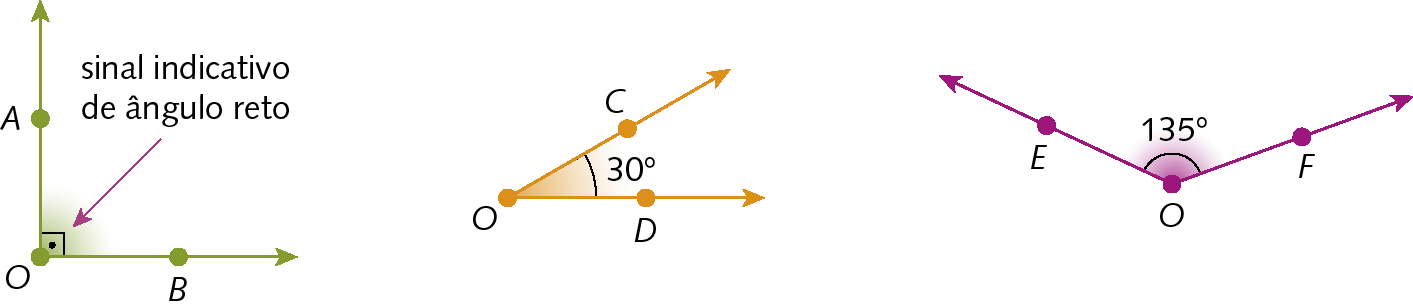
Figura geométrica. Ângulo AOB com abertura medindo 90 graus, Um lado do ângulo está na vertical e o outro na horizontal. Figura geométrica. Ângulo COD com abertura medindo 30 graus. Figura geométrica. Ângulo EOF com abertura medindo 135 graus.

Ângulos congruentes

Ângulos congruentes são ângulos que têm a mesma medida de abertura.

16. Em seu caderno, escreva se a afirmação é verdadeira (V) ou falsa (F).

a) A abertura de um ângulo reto mede 70graus.

b) Dois ângulos retos são sempre congruentes.

c) A medida de abertura de um ângulo obtuso é maior que 90graus.

d) A medida de abertura de um ângulo agudo é maior que 90graus.

17. Identifique os pares de ângulos congruentes e registre-os em seu caderno.

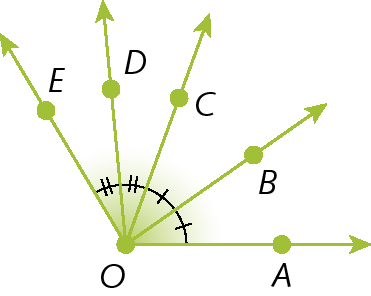
Figura geométrica, Ângulos com o mesmo vértice. AOB, BOC, COD e DOE. Os ângulos AOB e BOC têm a mesma medida de abertura. Os ângulos COD e DOE têm a mesma medida de abertura.

Transformações geométricas

Isometrias são transformações geométricas que preservam o formato e as medidas da figura original.

Translação é a isometria pela qual a figura é deslocada em determinada direção e sentido, mantendo uma mesma medida da distância entre cada um dos pontos da figura original e o correspondente da figura obtida.

Esquema. À esquerda uma figura marrom e outra preta. Abaixo delas uma seta indicando a direção, o sentido e a medida da distância em que serão transladadas. À direita, 2 cópias da mesma figura, indicando como a figura foi obtida a partir da figura original, após a translação. Há cotas indicando a medida da distância do deslocamento.

Rotação é a isometria pela qual uma nova figura é obtida a partir de um giro da figura original ao redor de um único ponto fixo. Esse ponto é chamado de centro de rotação.

Respostas e comentários

16. a) F

16. b) V

16. c) V

16. d) F

17.

E \hat{O} B e D \hat{O} C; C \hat{O} B e B \hat{O} A

• A atividade 16 envolve o conceito de ângulos congruentes e a distinção entre ângulo agudo, obtuso e reto. Em caso de equívocos, represente na lousa ângulos retos, agudos e obtusos com a medida de abertura indicada para que a turma classifique-os e, depois, identifique quais são ângulos congruentes.

• Com a resolução da atividade 17, é possível avaliar se os estudantes utilizam adequadamente a notação de ângulo, assim como se identificam ângulos congruentes. Caso tenham alguma dificuldade em identificar os ângulos congruentes, peça à turma que fale os pares que podem ser congruentes e represente-os na lousa para que os estudantes possam visualizá-los separadamente.

Transformações geométricas

Neste momento, são retomadas as isometrias: translação, rotação e reflexão (em relação a uma reta e em relação a um ponto). Caso tenha fácil acesso a algum computador com software de geometria dinâmica, podem-se complementar os exemplos de fórma mais dinâmica.

Página 14

Em uma rotação, o giro pode ser feito no sentido horário ou no sentido anti-horário, segundo certa medida da abertura de um ângulo.

Esquema. Figura que se parece com uma espiral. Há um ponto A em uma extremidade da figura e uma seta para este ponto indicando: centro de rotação. Á direita foi aplicado um giro na figura de 90 graus no sentido horário. A figura obtida ficou em destaque e a anterior ficou desfocada. Há uma seta para o centro de rotação indicando: giro de 90 graus. Á direita foi aplicado um giro na figura inicial de 180 graus no sentido horário. A figura obtida ficou em destaque e as figura inicial e a obtida na etapa anterior estão desfocadas. Há uma seta para o centro de rotação indicando: giro de 180 graus. Á direita foi aplicado um giro na figura inicial de 270 graus no sentido horário. A figura obtida ficou em destaque e as figura inicial e as obtidas nas etapas anteriores estão desfocadas. Há uma seta para o centro de rotação indicando: giro de 270 graus.

Reflexão é a isometria pela qual uma figura pode ser refletida, em um plano, de dois modos:

em relação a uma reta

em relação a um ponto

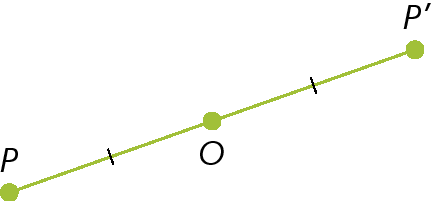
Ilustração. Pontos P e P linha simétricos em relação ao ponto O.

18. Observe as figuras a seguir.

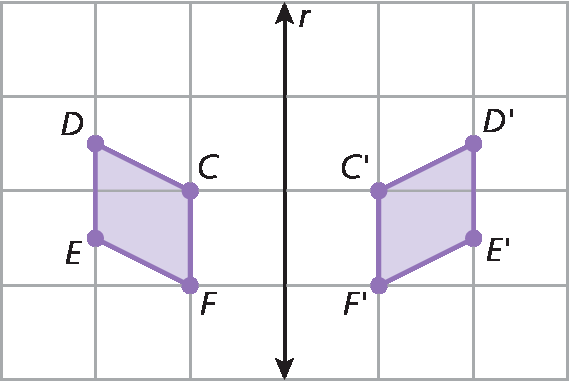
Figura geométrica. Malha quadriculada com uma reta r vertical no meio e de cada lado um quadrilátero roxo, O quadrilátero do lado esquerdo tem vértices nos pontos C, D, E e F e o do lado direito tem vértices nos pontos C linha, D linha, E linha e F linha. Eles são congruentes e estão a uma mesma medida de distância da reta r.

A figura a bê cê dê passou por uma transformação geométrica, originando a figura á′bit′centésimo′divisores de ′. Em seu caderno, responda:

a) Qual transformação foi feita?

b) O que é a reta r?

19. Usando uma folha quadriculada, copie as figuras e faça o que se pede em cada item.

a) A figura á bê cê dê é sofreu uma translação e o ponto E′ é o correspondente ao ponto ê. Represente a figura á′bit′centésimo′divisores de ′E′.

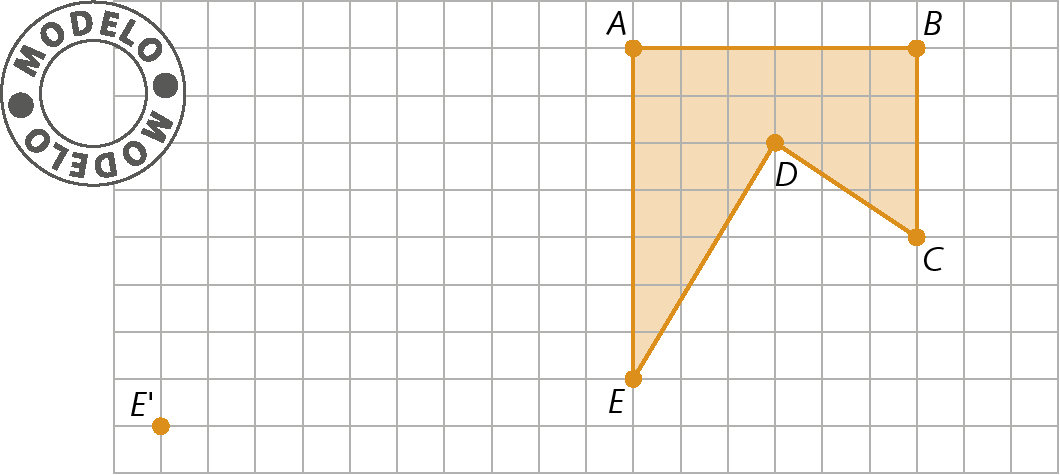
Ilustração. Símbolo de Modelo. Figura geométrica. Malha quadriculada com pentágono não convexo ABCDE representado do lado direito dela. Á esquerda do vértice E está representado o ponto E linha. Para chegar ao ponto E linha partindo do ponto E, é preciso descer um quadradinho para baixo e caminhar 10 quadradinhos para a esquerda.

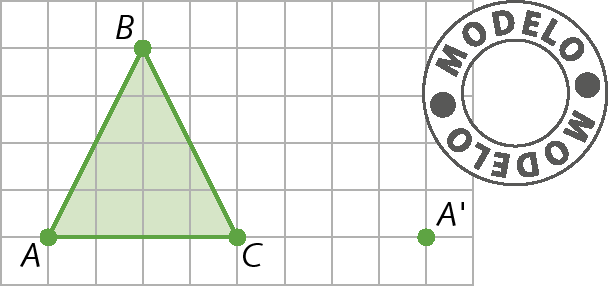
b) A figura á bê cê sofreu uma rotação e o ponto á′ é o correspondente ao ponto a. Represente a figura á′bit′centésimo′.

Figura geométrica. Malha quadriculada com triângulo ABC representado do lado esquerdo dela. Á direita do vértice C está representado o ponto A linha. Para chegar ao ponto A linha partindo do ponto C, é preciso caminhar 4 quadradinhos para a direita. Ilustração. Símbolo de Modelo.

Respostas e comentários

18. a) reflexão

18. b) eixo de simetria

19. a) Resposta em Orientações.

19. b) Resposta em Orientações.

• Na atividade 18, os estudantes devem identificar a transformação geométrica feita e o que representa a reta r. Caso tenham dúvidas no item a, na lousa, analise o que é uma translação, uma rotação e uma reflexão para levá-los a concluir que o quadrilátero á linha bê linha cê linha dê linhafoi obtido por uma reflexão em relação à reta r (eixo de simetria) do quadrilátero a bê cê dê.

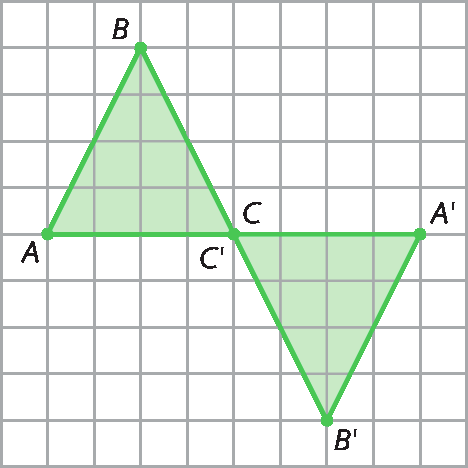
• Em cada item da atividade 19, os estudantes devem reproduzir a figura no caderno e, depois representar a figura obtida após realizar uma translação (item a) e uma rotação (item b). Caso tenham dúvidas, destaque que é fornecido apenas um vértice de cada figura que devem representar e que a partir dele, eles devem determinar os demais vértices. Em seguida, analise com a turma quais são as transformações geométricas em cada item: considerando u a unidade de medida de comprimento do lado de um quadradinho, há uma translação de 1 unidade para baixo e 10 unidades para a esquerda no item a e uma rotação de um giro de 180graus em relação ao ponto C no item b.

• Resposta do item a da atividade 19:

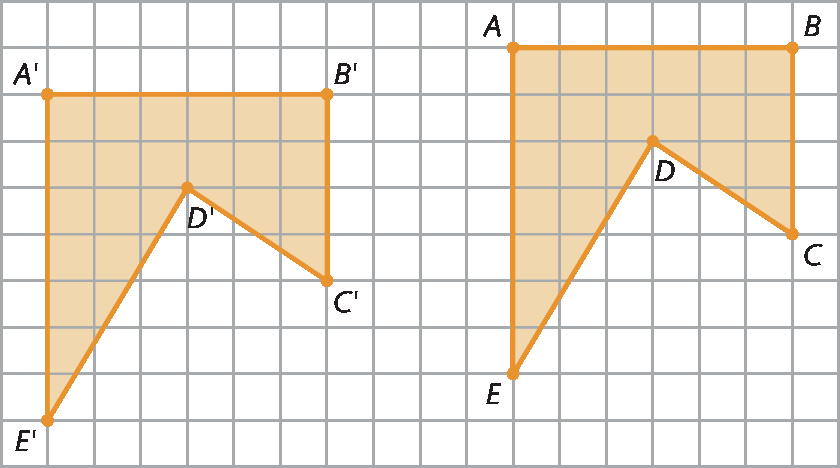
Figura geométrica. Malha quadriculada com a representação do pentágono não convexo ABCDE e sua translação A linha, B linha, C linha, D linha e E linha. A translação foi feita da direita para a esquerda e de cima para baixo. A medida do deslocamento é determinada pela diagonal do retângulo composto por 10 quadradinhos da malha dispostos lado a lado.

• Resposta do item b da atividade 19:

Figura geométrica. Malha quadriculada com a representação do triângulo ABC e sua rotação de 180 graus em torno do ponto C A linha, B linha e C linha,

Página 15

Para o capítulo 5: Polígonos

Elementos e medidas de um polígono

Podemos identificar os seguintes elementos no polígono á bê cê dê é:

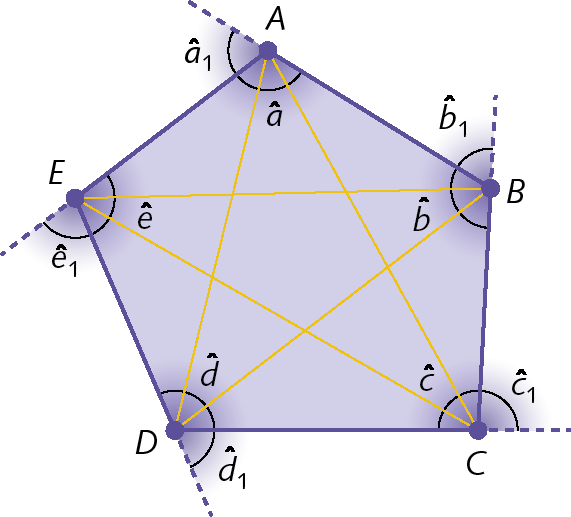
Figura geométrica. Pentágono ABCDE. Estão representados as suas diagonais e ângulos internos e externos.

• lados: segmentos de reta que formam o contorno do polígono (

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{E A}

);

• vértices: pontos de encontro de dois lados consecutivos (a, B, C, D, ê );

• diagonais: segmentos de reta que unem dois vértices não consecutivos (

\overline{A C}, \overline{A D}, \overline{B D},

\overline{B E}, \overline{C E}

);

• ângulos internos: ângulos formados por dois lados consecutivos (

\hat{a}, \hat{b}, \hat{c}, \hat{d}, \hat{e}

);

• ângulos externos: ângulos formados por um lado do polígono e pelo prolongamento do lado consecutivo a ele (

{\hat{a}}_{1}, {\hat{b}}_{1}, {\hat{c}}_{1}, {\hat{d}}_{1}, {\hat{e}}_{1}

Soma das medidas de abertura dos ângulos internos de um polígono

A soma das medidas de abertura dos ângulos internos de qualquer triângulo é sempre 180graus.

Para determinar a soma das medidas de abertura dos ângulos internos de qualquer polígono, traçamos todas as diagonais que partem de um único vértice, decompondo o polígono em triângulos, e multiplicamos a quantidade de triângulos por 180graus.

20. Em seu caderno:

• trace o polígono á bê cê dê é;

• trace uma diagonal;

• marque dois ângulos internos;

• marque um ângulo externo.

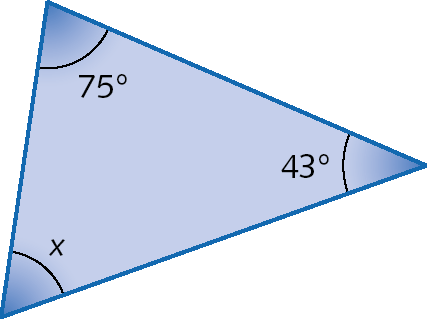
21. Para cada um dos polígonos a seguir, encontre o valor de x. Registre a resposta em seu caderno.

Figura geométrica. Triângulo cujas medidas das aberturas dos ângulos internos medem 75 graus, 43 graus e x.

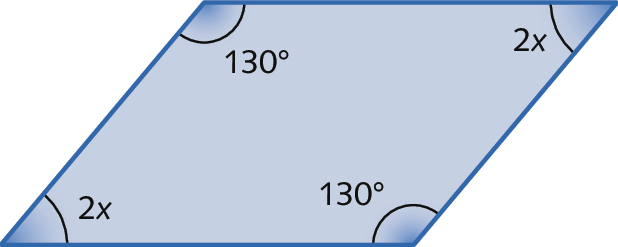
Figura geométrica. Quadrilátero. 2 ângulos internos opostos tem medidas de abertura iguais a 130 graus e os outros 2 ângulos opostos tem medidas de abertura iguais a 2x.

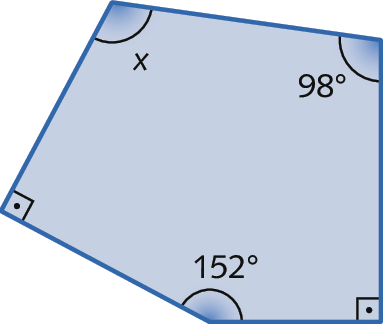
Figura geométrica. Pentágono com 2 ângulos internos retos e os outros 3 ângulos internos com aberturas medindo x, 98 graus e 152 graus.

Polígono regular

Um polígono é regular quando todos os ângulos internos têm mesma medida de abertura e todos os lados têm mesma medida de comprimento.

Ângulos internos de um polígono regular

Como os ângulos internos de um polígono regular têm a mesma medida de abertura, para descobrir a medida de abertura de cada ângulo interno de um triângulo equilátero, por exemplo, dividimos 180graus por 3, que resulta em 60graus.

Ângulos externos de um polígono regular

Os ângulos internos e externos dos polígonos são suplementares, ou seja, a soma das medidas de abertura de um ângulo interno e de um ângulo externo é 180graus.

Por isso, conhecendo a medida de abertura de um ângulo interno de qualquer polígono regular, podemos calcular a medida de abertura de um ângulo externo dele.

Respostas e comentários

20. Um exemplo de resposta está na seção Resoluções e comentários das atividades deste Manual do Professor.

21. a) x = 62graus

21. b) x = 25graus

21. c) x = 110graus

Elementos e medidas de um polígono

O foco desta revisão são os elementos que compõem um polígono e a soma das medidas de abertura dos ângulos internos de polígonos. É interessante apresentar alguns exemplos de polígonos na lousa para que a turma os decomponha em triângulos e determine a soma das medidas de abertura dos ângulos internos.

• A atividade 20 permite muitas respostas diferentes, uma vez que não estão determinadas as medidas de comprimento dos lados e as medidas de abertura dos ângulos internos do polígono á bê cê dê é. Circule entre os estudantes para observar se as respostas são coerentes com o enunciado e indique possíveis ajustes necessários. É importante notar se eles identificam que o polígono deve ser um pentágono por ter 5 vértices.

• Ao resolver a atividade 21, os estudantes relacionam cada polígono à respectiva soma das medidas de abertura dos ângulos internos para encontrar o valor de x. Se achar conveniente, pergunte aos estudantes se é possível conferir se o valor está correto. Espera-se que eles digam que basta substituir o valor encontrado nas respectivas medidas de abertura e efetuar a adição das medidas de abertura dos ângulos internos de cada polígono para verificar se encontraram a soma esperada.

Polígono regular

A revisão sobre polígono é ampliada para os polígonos regulares tanto no que se refere à definição quanto à questão dos ângulos internos e externos de um polígono regular.

Página 16

22. Qual dos polígonos seguintes é regular? Por quê?

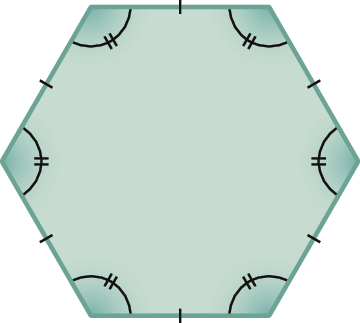
Figura geométrica. Hexágono com lados congruentes e ângulos internos congruentes.

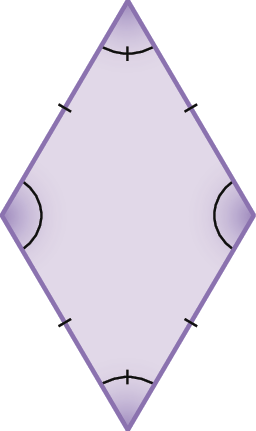
Figura geométrica. Losango. 2 ângulos opostos são agudos e os outros 2 ângulos opostos são obtusos.

23. Escreva no caderno, qual é o polígono regular cuja abertura de:

a) cada ângulo interno mede 90graus?

b) cada ângulo externo mede 120graus?

Para o capítulo 6: Probabilidade

Probabilidade

Um experimento aleatório é um acontecimento que conhecemos os resultados possíveis, mas não podemos assegurar qual será o resultado. Por não ser possível prever o resultado com exatidão, procuramos medir as chances, ou seja, determinar a probabilidade de certo resultado ocorrer.

A probabilidade de determinado resultado em um experimento aleatório é a razão entre o número de possibilidades favoráveis e o número total de possibilidades.

24. Em seu caderno, registre apenas as afirmações verdadeiras.

a) Quando lançamos uma "moeda honesta", há sempre mais chance de sair cara do que coroa.

b) No lançamento de um "dado honesto" de 6 faces, há a mesma chance de sair um número par e um número ímpar.

c) A probabilidade de sair um número maior que 6 em um "dado honesto" de 6 faces é igual a zero.

25. Em uma urna, há 12 fichas nas seguintes cores:

Figura geométrica. Retângulo dividido em 12 partes retangulares iguais, sendo 6 azuis, 3 vermelhas, 2 amarelas e 1 branca.

Ao retirar uma ficha dessa urna, sem olhar, qual é a probabilidade de ela ser da cor:

a) amarela?

b) vermelha?

c) azul?

d) branca?

Para o capítulo 7: Triângulos e quadriláteros

Triângulos

Triângulo é um polígono com três lados.

Principais elementos de um triângulo

• Vértices: a, B e C

• Lados:

\overline{A B}, \overline{A C} e \overline{B C}

• Ângulos internos:

\hat{A}, \hat{B} e \hat{C}

• Ângulos externos:

\hat{x}, \hat{y} e \hat{z}

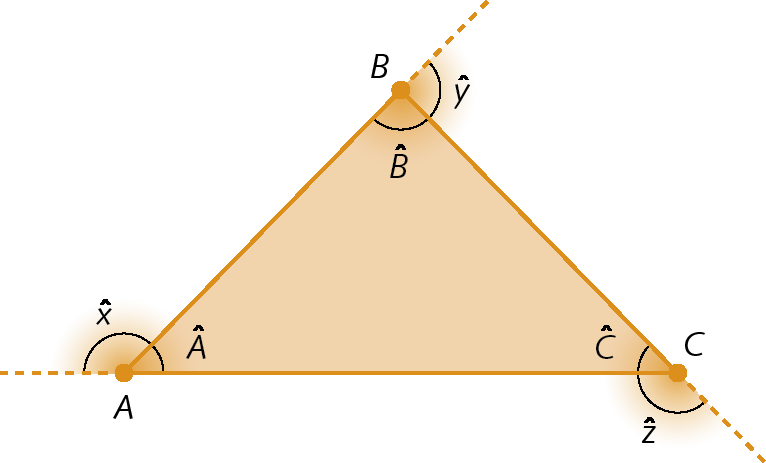
Figura geométrica. Triângulo ABC com os ângulos internos e externos indicados.

26. Em seu caderno, desenhe um triângulo PQR e indique todos seus ângulos internos.

27. Analise este triângulo.

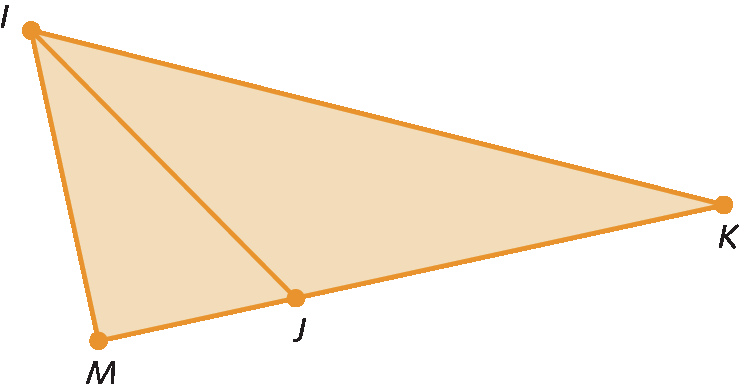
Figura geométrica. Triângulo IMK com um uma reta interna criando mais dois triângulos, IMJ e IJK.

Em seu caderno, indique as afirmações falsas (F) e as verdadeiras (V).

\hat{M}

é um ângulo interno do triângulo IMK.

\overline{M J}

é um lado do triângulo IMK.

I \hat{J} M

é um ângulo externo do triângulo IJK.

d) J é um vértice do triângulo IMK.

Respostas e comentários

22. Polígono do item a, pois todos os ângulos internos têm a mesma medida de abertura e todos os lados têm mesma medida de comprimento. O polígono do item b tem apenas todos os lados com a mesma medida de comprimento.

23. a) quadrado

23. b) triângulo equilátero

24. itens b, c

25. a)

\frac{2}{12} = \frac{1}{6}

25. b)

\frac{3}{12} = \frac{1}{4}

25. c)

\frac{6}{12} = \frac{1}{2}

25. d)

\frac{1}{12}

26. Um exemplo de resposta está na seção Resoluções e comentários das atividades deste Manual do Professor.

27. a) V

27. b) F

27. c) V

27. d) F

• Aproveite a realização da atividade 22 e enfatize com a turma que para um polígono ser regular não basta apenas que seus lados sejam congruentes ou que seus ângulos internos sejam congruentes. As duas condições devem estar satisfeitas simultaneamente.

• Na atividade 23, os estudantes devem identificar os polígonos regulares utilizando a medida de abertura de cada ângulo interno ou externo. Caso tenham dúvidas, peça que esbocem polígonos para observar quais atendem à condição de cada item.

Probabilidade

Nesta revisão, define-se experimento aleatório e probabilidade de um resultado em um experimento aleatório. Se possível, apresente alguns exemplos de situações, como sorteio de bolas numeradas ou lançamento de “dado honesto” ou “moeda honesta”, para que a turma calcule a probabilidade de alguns resultados ocorrerem.

• A atividade 24 pode ser respondida sem o cálculo de probabilidades, mas com a comparação entre as chances de ocorrer dois resultados. Em caso de dúvidas, auxilie os estudantes a fazer as relações, com questões do tipo: “Ao lançar uma ‘moeda honesta’, a chance de sair cara é maior, menor ou igual ao de sair coroa?” (Espera-se que respondam que é igual). “Quais são os possíveis resultados no lançamento de um ‘dado honesto’ numerado de 6 faces?” (Espera-se que respondam 1, 2, 3, 4, 5 ou 6).

• Com a resolução da atividade 25, espera-se que os estudantes coloquem em prática o cálculo de probabilidades. Para auxiliá-los, pode-se pedir a eles, inicialmente, que observem as fichas e respondam: “Qual é a cor com mais chance de ser sorteada? E a cor com menos chance?” (Espera-se que respondam, respectivamente, azul e branca). Após os cálculos, peça que retomem essas estimativas e confiram se as respostas estão de acordo com o esperado.

Triângulos

Com a intenção de aprofundar o estudo dos polígonos, o foco desta revisão serão os triângulos, especificamente seus elementos.

• Há infinitas representações de triângulos possíveis para a atividade 26, então é interessante que os estudantes façam comparações com as respostas de outros colegas para observar o que elas têm em comum e de diferente. Se necessário, proponha ajustes nas respostas, destacando principalmente que a figura deve ter três vértices, três lados e três ângulos internos.

• Na atividade 27, os estudantes devem identificar se o elemento citado em cada item corresponde ao triângulo indicado. Ao final da atividade, peça a alguns deles que expliquem oralmente por que determinada afirmação é falsa ou verdadeira; essas explicações poderão esclarecer eventuais dúvidas da turma.

Página 17

Quadriláteros

Quadrilátero é um polígono com quatro lados.

Paralelogramo é um quadrilátero que tem dois pares de lados paralelos.

Trapézio é um quadrilátero que tem apenas um par de lados paralelos.

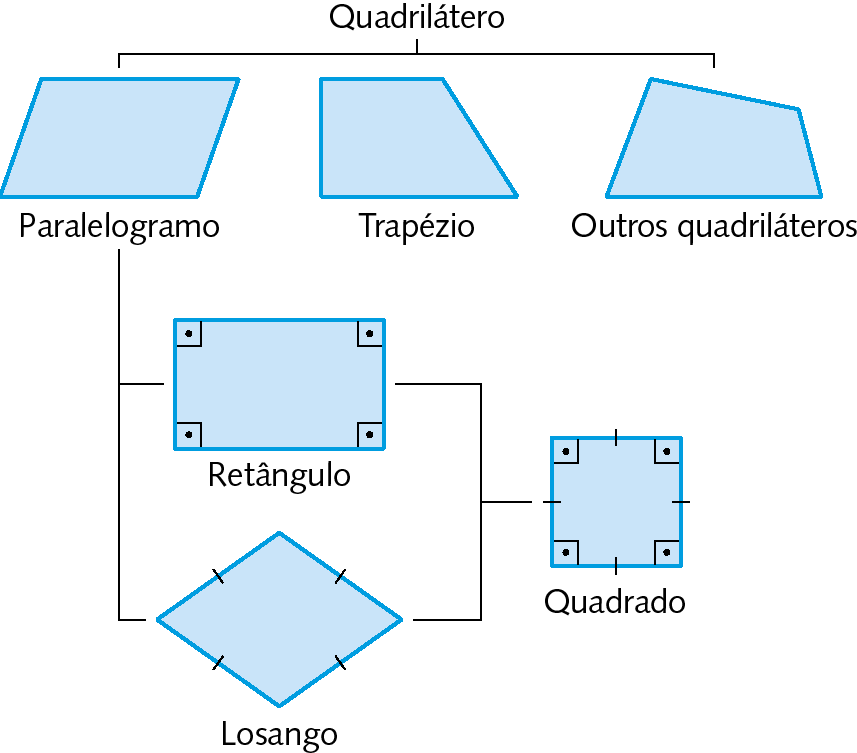
Esquema. No primeiro nível, aparece a representação de 3 quadriláteros. Da esquerda para a direita: um paralelogramo, um trapézio e um quadrilátero qualquer. Do paralelogramo partem fios para as representações de um retângulo e losango. Das representações do retângulo e losango partem fios rumo a representação de um quadrado.

28. Com o auxílio de régua e esquadro, classifique cada quadrilátero como paralelogramo, trapézio ou outro quadrilátero.

Figura geométrica. Quadrilátero com um par de lados paralelo.

Figura geométrica. Quadrilátero sem par de lados paralelos.

Figura geométrica. Quadrilátero com os 2 pares de lados paralelos.

Versão adaptada acessível

28. Desenhe em seu caderno três quadriláteros: um trapézio, um paralelogramo e um outro que não seja quadrilátero nem paralelogramo.

Orientação para acessibilidade

Respostas

Espera-se que os estudantes percebam que para o quadrilátero ser classificado como paralelogramo deve ter os dois pares de lados opostos paralelos e que para ser trapézio deve ter apenas um par de lados opostos paralelos. O outro quadrilátero que o estudante deve desenhar não pode ter nenhum par de lados opostos paralelos. Procure auxiliar seus estudantes nessa atividade.

29. Quais afirmações a seguir são verdadeiras?

a) Todo quadrado é um retângulo.

b) Todo retângulo é um losango.

c) Todo retângulo tem quatro ângulos com medida de abertura de 90graus.

d) Todo quadrado tem os quatro lados congruentes.

e) Alguns losangos têm lados com medidas diferentes.

f) Todo retângulo é um quadrado.

Para o capítulo 8: Área, volume e capacidade

Medida da área

Ao calcular a medida da área de polígonos, as medidas de comprimento consideradas devem estar na mesma unidade de medida.

Retângulo

medida do comprimento ou medida de comprimento da base

medida da largura ou medida de comprimento da altura

Figura geométrica. Retângulo. Letra b indicando a medida do comprimento e letra h indicando a medida do comprimento da altura. — Aretângulo = b ⋅ h

Quadrado

medida de comprimento do lado

Figura geométrica. Quadrado. Letra a indicando a medida do comprimento de cada lado. — Aquadrado = a ⋅ a = a2

Paralelogramo

medida de comprimento da base

medida de comprimento da altura relativa à base

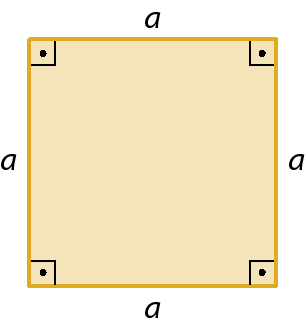
Figura geométrica. Paralelogramo ABCD. Está representado com uma linha tracejada uma das alturas do paralelogramo. Há uma cota horizontal com a letra b indicando a medida do comprimento da base e uma letra h ao lado da linha tracejada indicando a medida do comprimento da altura relativa à base. — Aparalelogramo = b ⋅ h

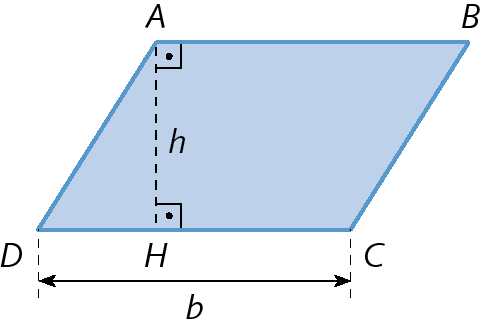
Triângulo

medida do comprimento da base

medida do comprimento da base

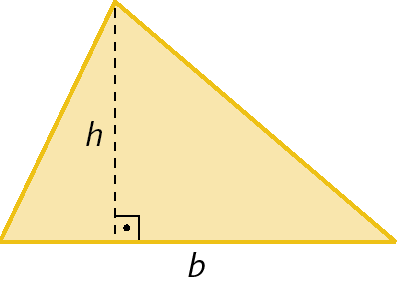
Atriângulo =

\frac{b \cdot h}{2}

Respostas e comentários

28. a) trapézio

28. b) outro quadrilátero

28. c) paralelogramo

28. d) trapézio

29. itens a, c, d

Quadriláteros

• Com base nos quadriláteros representados, a atividade 28 apresenta a classificação de cada um deles em paralelogramo, trapézio ou outro quadrilátero. Caso os estudantes tenham dificuldades, retome essas classificações baseando-se nas palavras deles.

• Na atividade 29, os estudantes devem avaliar afirmações sobre retângulos, losangos e quadrados, prestando atenção principalmente nos termos “todo” e “alguns”. Por exemplo, no item ê, eles podem considerar erroneamente que a afirmação é verdadeira; se isso ocorrer, destaque que a afirmação é falsa por causa do termo “alguns” e que seria verdadeira se fosse “Todo losango tem os quatro lados congruentes”.

Medida da área

Esta revisão é a respeito do cálculo das medidas de área de triângulos e dos quadriláteros mais conhecidos: retângulo, paralelogramo, trapézio e losango.

Página 18

Trapézio

medida de comprimento da base maior

medida de comprimento da base menor

medida de comprimento da altura

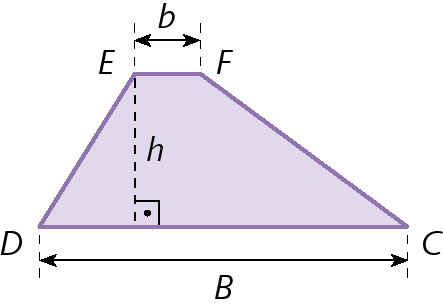
Atrapézio =

\frac{(B + b) \cdot h}{2}

Losango

medida de comprimento da diagonal maior

medida de comprimento da diagonal menor

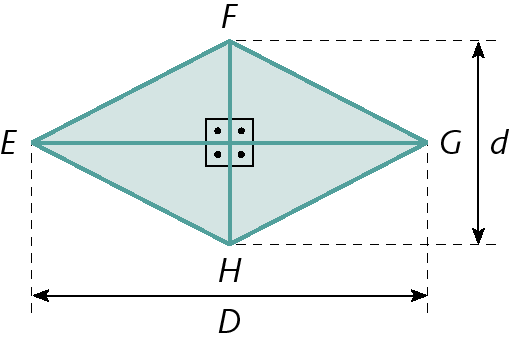
Alosango =

\frac{D \cdot d}{2}

30. Determine a medida da área dos seguintes polígonos:

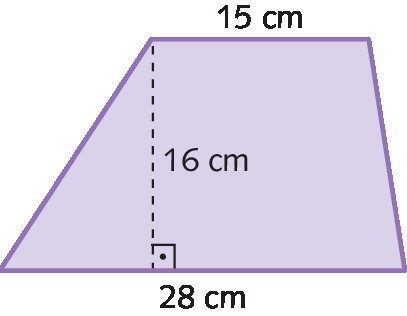
Figura geométrica. Trapézio cuja medida do comprimento da base maior é 28 centímetros, da base menor é 15 centímetros e da altura é 16 centímetros.

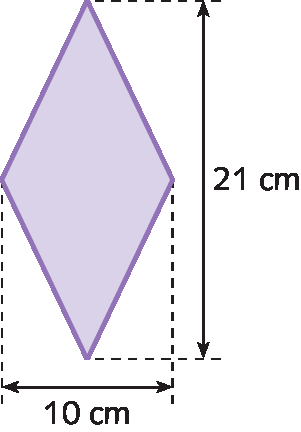
Figura geométrica. Losango cuja medida do comprimento da diagonal maior é 21 centímetros e a diagonal menor é 10 centímetros.

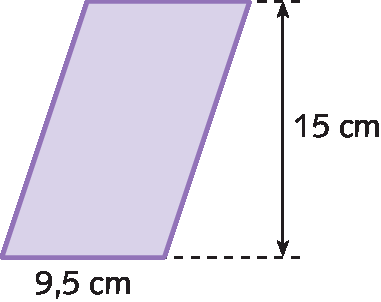
Figura geométrica. Paralelogramo cuja base mede 9 vírgula 5 centímetros de comprimento e tem altura medindo 15 centímetros de comprimento.

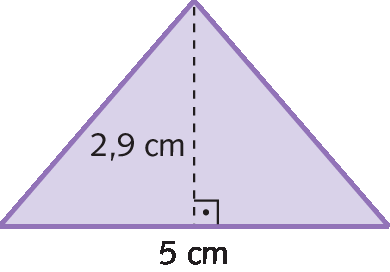
Figura geométrica. Triângulo cuja medida do comprimento da base é 5 centímetros e a da altura é 2 vírgula 9 centímetros.

Medida de volume

Ao calcular a medida de volume de sólidos geométricos, as medidas de comprimento consideradas devem estar na mesma unidade de medida.

Paralelepípedo reto-retângulo

A medida de volume de um paralelepípedo reto-retângulo é igual ao produto das medidas do comprimento (c), da largura (a) e da altura (h).

Vparalelepípedo = c ⋅ a ⋅ h

Cubo

O cubo é um caso particular de paralelepípedo, pois tem todas as arestas com a mesma medida de comprimento. Assim, para um cubo cuja medida de comprimento da aresta é a, temos:

Vcubo = a ⋅ a ⋅ a = a3

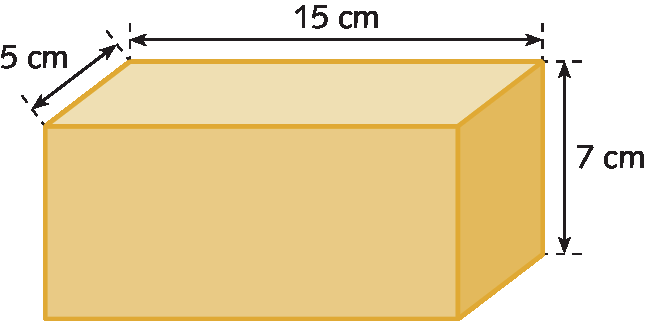
31. Qual é a medida de volume deste paralelepípedo?

Figura geométrica. Paralelepípedo laranja com 5 centímetros de largura, 15 centímetros de comprimento e 7 centímetros de altura.

32. Calcule a medida de volume do cubo de cada item, conhecendo a medida de comprimento da aresta (a):

a) a = 12 centímetros

b) a = 0,4 métro

c) a = 9 centímetros

Para o capítulo 9: Equações do 2º grau

Equações do 1º grau

Equação é uma sentença matemática expressa por uma igualdade que apresenta pelo menos um valor desconhecido representado por uma letra denominada incógnita.

• 3x + 5 = 2 é uma equação cuja incógnita é x.

• 5m ‒ 2 = 7n é uma equação cujas incógnitas são m e n.

• 4b ‒ 9 < 6 não é uma equação, pois não é uma igualdade.

Respostas e comentários

30. a) 344 centímetros quadrados

30. b) 105 centímetros quadrados

30. c) 142,5 centímetros quadrados

30. d) 7,25 centímetros quadrados

31. 525 centímetros cúbicos

32. a) .1728 centímetros cúbicos

32. b) 0,064 métros cúbicos

32. c) 729 centímetros cúbicos

• Na atividade 30, os estudantes devem calcular a medida da área de um trapézio (item a), um losango (item b), um paralelogramo (item c) e um triângulo (item d). Se eles tiverem dificuldades ajude-os a classificar o quadrilátero presente nos itens a, b e c e a identificar as medidas da base, altura, e diagonais conforme o polígono.

Medida de volume

Esta revisão retoma o cálculo da medida de volume de alguns sólidos geométricos: paralelepípedo reto-retângulo e cubo, que é um paralelepípedo reto-retângulo que tem todas as arestas congruentes. Se possível, apresente alguns exemplos dessas figuras para que a turma calcule a medida de volume delas.

• Nas atividades 31 e 32, os estudantes devem calcular a medida de volume de um paralelepípedo (atividade 31) e de três cubos (atividade 32). Destaque a necessidade de indicar a unidade de medida de volume ao apresentar as respostas.

Equações do 1º grau

Esta revisão retoma o conceito de equação e, mais especificamente, de equação do 1º grau por meio de exemplos. Além disso, aborda-se a ideia de incógnita, muito importante na definição de equação.

Página 19

• 5 + 13 = 2 ⋅ 9 não é uma equação, pois não tem incógnita.

Quando o maior expoente de uma incógnita em uma equação é 1, a denominamos equação do 1º grau.

• ‒1 ‒ 0,4x = 7 é uma equação de 1º grau.

• x2 + 1 = 0 não é uma equação de 1º grau.

33. Em seu caderno, indique quais sentenças a seguir são equações:

a) 3x + 5 = ‒0,4 + 2x

b) (‒1) ⋅ 32 = 10 ‒ 42

c) a + b + c =

\frac{10}{7}

d) 2x 2 ⩽ 52

34. Escreva, em seu caderno, quais são as afirmações verdadeiras.

a) 2m + 1 ≠ m é uma equação.

b) 35 = 2t ‒ 0,5 é uma equação de 1º grau.

c) 2m ‒ 9 + j = 4 é uma equação cujas incógnitas são m, j e 4.

d) As incógnitas da equação x 2 + y = a são x, y e a.

e) k 3 =

\frac{9}{8}

é uma equação, mas não de 1º grau.

Raiz de uma equação

Quando a incógnita de uma equação assume um valor que torna a sentença verdadeira, esse valor é chamado de raiz da equação.

Vamos considerar as equações 3x + 12 = 42 e 5x = ‒10. Para saber se o número 10 é raiz de uma delas, fazemos a substituição:

3x + 12 = 42

3 ⋅ 10 + 12 = 42

30 + 12 = 42

42 = 42

sentença verdadeira

Logo, 10 é raiz dessa equação.

5x = ‒10

5 ⋅ 10 = ‒10

50 = ‒10

sentença falsa

Logo, 10 não é raiz dessa equação.

O conjunto universo é formado por todos os números que uma incógnita pode assumir e é indicado por conjunto universo.

As raízes da equação que pertencem ao conjunto universo são as soluções dessa equação e formam seu conjunto solução, que é indicado por S.

No exemplo anterior, se considerarmos que a incógnita da equação 3x + 12 = 42 só assume valores naturais, temos conjunto universo =

. Como 10 é número natural e é raiz da equação, dizemos que ele é solução dessa equação e que o conjunto solução dessa equação é S = {10}.

35. Sendo conjunto universo =

, anote no caderno as equações cujo conjunto solução é S = {‒1}.

a) ‒3 = 5x ‒ 2x

b) 8x ‒ 10 = ‒2

c) 5x ‒ 14 = 12x

\frac{x}{2} - 2 = - \frac{5}{2}

36. Considere conjunto universo =

e a equação ‒8x + 23 = 23 + x. Qual dos conjuntos a seguir é o conjunto solução dessa equação?

a) S = {0}

b) S = {1}

c) S = {‒2}

d) S = {‒4}

Resolução de equações de 1º grau com uma incógnita

Quando duas equações têm o mesmo conjunto universo e as mesmas raízes, elas são chamadas de equações equivalentes.

Princípio aditivo das igualdades: quando adicionamos ou subtraímos uma mesma quantidade nos dois membros de uma equação, obtemos uma equação equivalente à primeira.

Princípio multiplicativo das igualdades: quando multiplicamos ou dividimos por um mesmo número não nulo os dois membros de uma equação, obtemos uma equação equivalente à primeira.

Para resolver uma equação, aplicamos os princípios aditivo e multiplicativo das igualdades, de modo a obter equações equivalentes mais simples que as iniciais, determinando, assim, as soluções da equação. Por exemplo:

6x ‒ 10 = 50, sendo conjunto universo =

6 x ‒ 10 + 10 = 50 + 10

6x = 60

\frac{6 x}{6}

\frac{60}{6}

x = 10

S = {10}

Respostas e comentários

33. itens a, c

34. itens b, d, ê

35. itens a, d

36. alternativa a

• Na atividade 33, os estudantes devem identificar quais sentenças são equações. Para ampliar a atividade, peça que expliquem oralmente por que os itens b e d não são equações. Espera-se que observem que, a sentença do item b, não apresenta incógnita e que a sentença do item d é uma desigualdade.

• Na atividade 34 os estudantes vão analisar afirmações relacionadas aos conceitos de equação, incógnita e equação de 1º grau. A cada item que os estudantes considerarem falso, peça que expliquem o erro da afirmação.

Raiz de uma equação

Esta retomada amplia o estudo das equações, focando especificamente o conceito de raiz de uma equação, sem ainda tratar da resolução de uma equação.

• Nas atividades 35 e 36, espera-se que os estudantes associem equações ao seu respectivo conjunto solução. Caso tenham dificuldades, oriente-os a substituir a incógnita de cada equação pelo número pertencente ao conjunto solução; se obtiverem uma igualdade, o conjunto solução corresponde à equação.

Resolução de equações de 1º grau com uma incógnita

Para finalizar a revisão acerca de equações de 1º grau, o foco agora é a resolução desse tipo de equação, explicando os princípios aditivo e multiplicativo das igualdades. Se achar necessário, apresente exemplos de equações para a turma resolver antes das atividades.

Página 20

37. Sabendo que conjunto universo =

, resolva estas equações no caderno.

a) 5x + 10 = ‒10

b) x ‒ 12 = 29

c) 2x = ‒2 + 6x

38. Para conjunto universo =

, identifique quais afirmações são verdadeiras.

a) O conjunto solução da equação 2x + 3 = ‒8 + x é S = ∅.

b) S = {10} é o conjunto solução da equação 9 + 5x = 5,9.

c) S = {12} é o conjunto solução da equação ‒48 = 3x ‒ 7x.

Para o capítulo 10: Grandezas e proporcionalidade

Razão e proporção

A razão entre dois números, a e bê, com b ≠ 0, nessa ordem, é dada por

\frac{a}{b}

Podemos expressar a razão na fórma de fração, de porcentagem ou de número decimal.

Exemplo:

Se uma pessoa gastou R$ 10,00dez reais com bebidas e R$ 50,00cinquenta reais com alimentos, podemos dizer que a razão entre o gasto com bebidas e comidas foi

\frac{10}{50}

, que equivale a

\frac{20}{100}

= 20% = 0,2.

Proporção é uma igualdade entre duas razões.

Exemplos:

\frac{3}{10} = \frac{9}{30}

\frac{6}{15} = \frac{4}{10}

Propriedade fundamental das proporções

Em toda proporção, o produto dos extremos é igual ao produto dos meios, ou seja, dados a, b, c e d racionais não nulos, com

\frac{a}{b} = \frac{c}{d}

, temos a ⋅ d = b ⋅ c.

Por exemplo, usando as proporções citadas anteriormente, temos que:

\frac{3}{10} = \frac{9}{30}

3 ⋅ 30 = 9 ⋅ 10

\frac{6}{15} = \frac{4}{10}

6 ⋅ 10 = 4 ⋅ 15

39. Observe este quadro com os valores das 3 peças que compõem um produto.

Peça	Valor
Peça 1	R$ 30,00
Peça 2	R$ 3,00
Peça 3	R$ 90,00
Total	R$ 123,00

Escreva em seu caderno:

a) a razão entre o valor da peça 1 e o da peça 2.

b) a razão entre o valor da peça 2 e o da peça 1.

c) a razão entre o valor da peça 3 e o total.

40. Quais pares de razões são proporções?

\frac{11}{9} e \frac{22}{18}

\frac{1}{3} e \frac{3}{8}

\frac{216}{600} e \frac{36}{100}

\frac{4}{7} e \frac{10}{11}

41. Determine o valor de x nas proporções sabendo que x é um número real diferente de zero.

\frac{2}{3} = \frac{10}{x}

\frac{8}{x} = \frac{4}{15}

\frac{x}{100} = \frac{13}{26}

Grandezas e proporcionalidade

Grandezas diretamente proporcionais

Duas grandezas são diretamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual à razão entre os valores correspondentes da segunda.

Grandezas inversamente proporcionais

Duas grandezas são inversamente proporcionais quando a razão entre dois valores quaisquer da primeira é igual ao inverso da razão entre os valores correspondentes da segunda.

Respostas e comentários

37. a) S = {‒4}

37. b) S = {41}

37. c) S =

\{\frac{1}{2}\}

38. itens a, c

39. a)

\frac{30}{3} = 10

39. b)

\frac{3}{30} = \frac{1}{10}

39. c)

\frac{90}{123} = \frac{30}{41}

40. itens a, c

41. a) x = 15

41. b) x = 30

41. c) x = 50

• Na atividade 37, os estudantes devem resolver as equações usando os princípios aditivo e multiplicativo das igualdades. Se observar algum equívoco, peça ao estudante que substitua na equação o valor encontrado e verifique se é mesmo raiz.

• A atividade 38 trabalha o reconhecimento de afirmações verdadeiras por meio da resolução de cada equação ou pela substituição dos números pertencentes aos conjuntos solução. No item a, ao resolver a equação, os estudantes devem obter x = −5,5 e identificar que esse número não pertence ao conjunto solução (conjunto dos números naturais); portanto, a equação dada não tem solução (ou raiz).

Razão e proporção

A partir da retomada das ideias de razão e proporção, são discutidas noções fundamentais para desenvolver o tema da proporcionalidade. Além disso, é apresentada a propriedade fundamental das proporções, muito importante no estudo desse tema.

• Na atividade 39, os estudantes devem encontrar as razões pedidas, sendo fundamental ter atenção à ordem em que os valores das grandezas são citados, já que a razão será diferente de acordo com a ordem.

• Para resolver as atividades 40 e 41, é preciso utilizar a propriedade fundamental das proporções, sendo que, na atividade 40, ela será utilizada para conferir se os pares de razões formam uma proporção e, na atividade 41, ela será utilizada para encontrar um dos números que faltam na proporção.

Grandezas e proporcionalidade

A partir da explicação dos dois tipos de relação proporcionais entre grandezas (direta e inversamente), é feita uma breve retomada do tema. Caso observe a necessidade, exponha alguns exemplos numéricos antes das atividades.

Página 21

42. Copie estes quadros no caderno e complete-os, considerando que as grandezas X e Y são diretamente proporcionais.

X	Y
5	12
10	24
2,5	6
15

X	Y
0,2	16
1
10	800
0,1	8

43. As grandezas M e N são inversamente proporcionais, conforme indicado neste quadro.

M	N
4	24
8	12
12	8
6	16

Qual será o valor de N quando M for 1?

Para o capítulo 11: Medidas de tendência central e pesquisa estatística

Médias

Muitas vezes, em uma pesquisa, podemos sintetizar as informações calculando a média aritmética ou a média aritmética ponderada e utilizar essas medidas para representar o conjunto de dados da pesquisa.

Acompanhe a situação.

Vamos analisar o quadro dos pontos obtidos por um estudante no vestibular:

Disciplina	Nota
Matemática	8
Redação	7
Inglês	5
História	9

Se a pontuação final for a média aritmética (em que todas as pontuações têm o mesmo peso), calculamos assim:

\frac{8 + 7 + 5 + 9}{4}

\frac{29}{4}

= 7,25

Se a pontuação final for a média ponderada considerando que Matemática tem peso 2, Redação tem peso 3 e as demais disciplinas, peso 1, calculamos assim:

\frac{2 \cdot 8 + 3 \cdot 7 + 1 \cdot 5 + 1 \cdot 9}{2 + 3 + 1 + 1} = \frac{51}{7} ≅ 7,3

44. Analise este quadro com preços de um mesmo produto encontrado em diferentes mercados.

Mercado	Preço (em reais)
Mercado 1	36,80
Mercado 2	42,90
Mercado 3	39,90
Mercado 4	31,80
Mercado 5	40,00

Calcule, em seu caderno, o preço médio desse produto.

45. Confira a pontuação que duas marcas de chocolate receberam de um cliente, considerando alguns critérios.

Critério	Marca A	Marca B
Preço (peso 2)	7	8
Sabor (peso 3)	8	7
Aroma (peso 1)	7	7

Em seu caderno, calcule a média ponderada para cada uma dessas marcas.

Respostas e comentários

42. Respostas em Orientações.

43. 96

44. R$ 38,28 trinta e oito reais e vinte e oito centavos

45. marca a: 7,5; marca B: 7,3

• Na atividade 42, espera-se que os estudantes identifiquem, em cada item, a relação entre os valores das grandezas X e Y para completar a célula com o valor que falta. Vale destacar que, em ambos os casos, as grandezas são diretamente proporcionais. Em caso de dúvida, oriente-os a usar a propriedade fundamental das proporções ou questione-os, por exemplo, no item b: “Por quanto eu devo multiplicar o 10 para obter 800?”. Espera-se que os estudantes respondam que é preciso multiplicar por 80, então aproveite para levá-los a perceber que em todas as linhas do quadro do item b o valor de Y corresponde ao produto do valor de X por 80.

Resposta do item a da atividade 42:

X	Y
5	12
10	24
2,5	6
15	36

Resposta do item b da atividade 42:

X	Y
0,2	16
1	80
10	800
0,1	8

• A atividade 43 apresenta um quadro de valores das grandezas M e N, inversamente proporcionais, para que os estudantes descubram o valor de N para um valor de M dado. Se eles tiverem dificuldades, faça questionamentos, como: “Quando o valor de M é 4, o valor de N é 24; quando o valor de M for 1, é esperado que o valor de N seja maior ou menor que 24?”. Nesse caso, como as grandezas são inversamente proporcionais e o valor de M diminuiu, de 4 para 1, necessariamente o valor de N aumentará e será maior que 24.

Médias

Nesta revisão, pretende-se focar as ideias de média aritmética e média aritmética ponderada. Se considerar adequado, faça juntamente com os estudantes os exemplos apresentados para que fique mais clara a diferença entre essas médias.

• Nas atividades 44 e 45, os estudantes devem calcular, respectivamente, média aritmética e média aritmética ponderada com base em dados apresentados em quadros. Se necessário, chame a atenção da turma para o fato de que, nas médias aritméticas ponderadas da atividade 45, o numerador corresponde à soma dos produtos da nota de cada critério pelo respectivo peso, e o denominador corresponde à soma dos pesos.

Página 22

Para o capítulo 12: Gráficos estatísticos

Gráficos

Gráfico de barras

Esse tipo de gráfico é utilizado principalmente para comparar informações. Podemos ter gráficos de barras verticais (exemplo a seguir) ou barras horizontais.

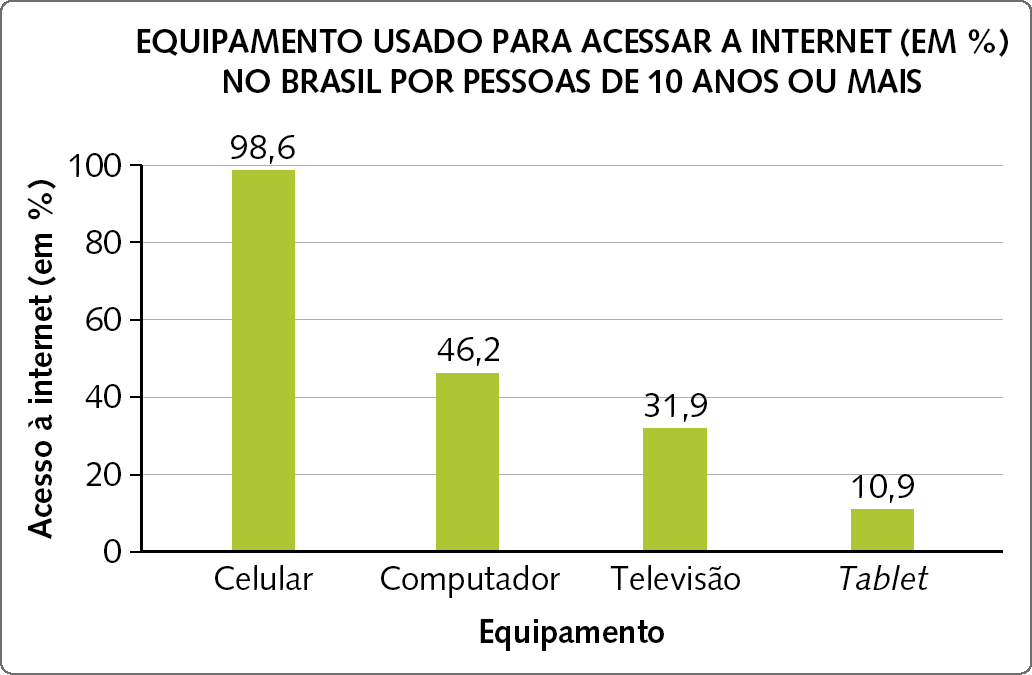
Dados obtidos em: https://oeds.link/0A3tBp. Acesso em: 4 julho 2022.

Gráfico de segmentos

Esse tipo de gráfico é usado quando queremos observar a variação de algum fato ao longo do tempo.

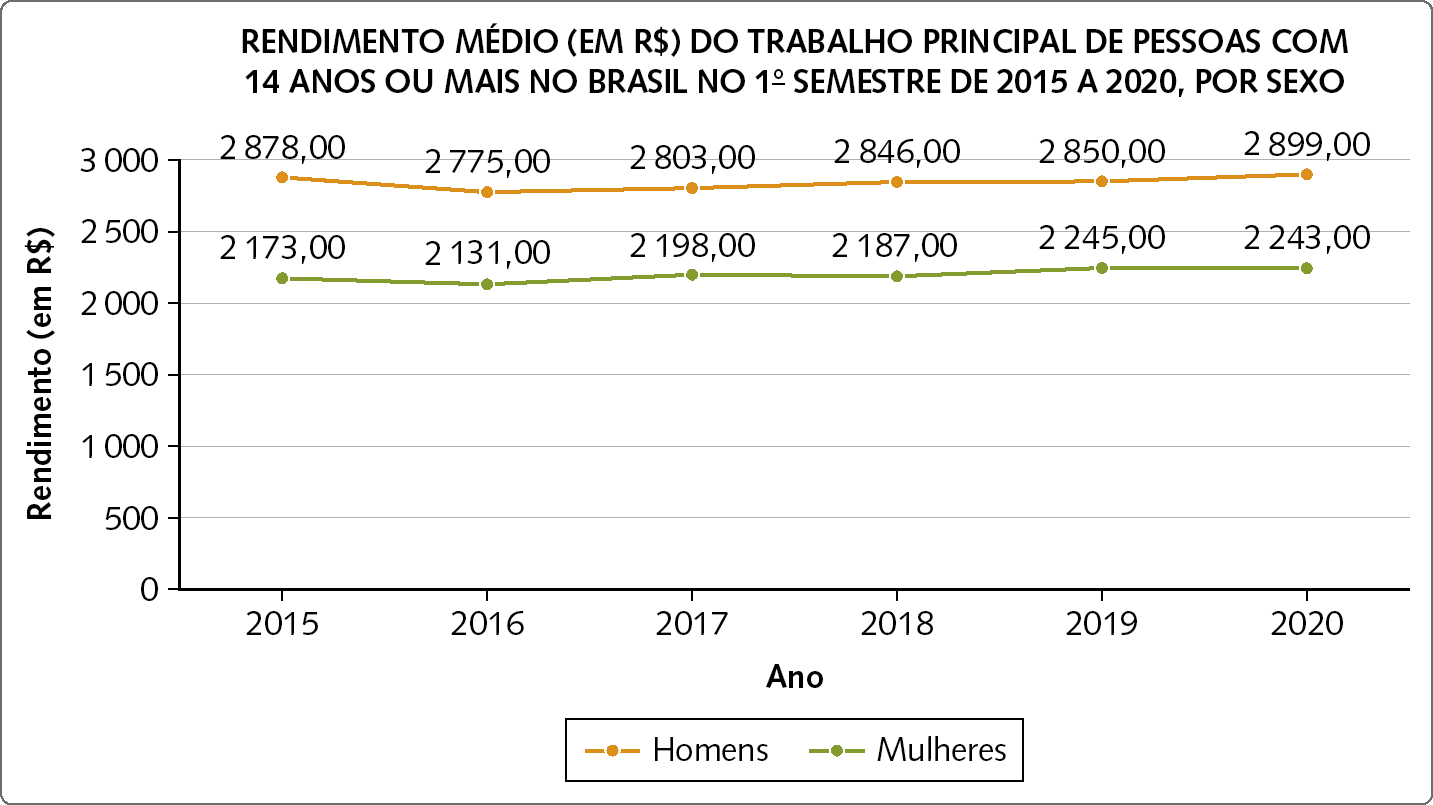
Dados obtidos em: https://oeds.link/LDPePJ. Acesso em: 4 julho 2022.

Gráficos de setores

Esse tipo de gráfico é usado quando queremos representar partes de um total.

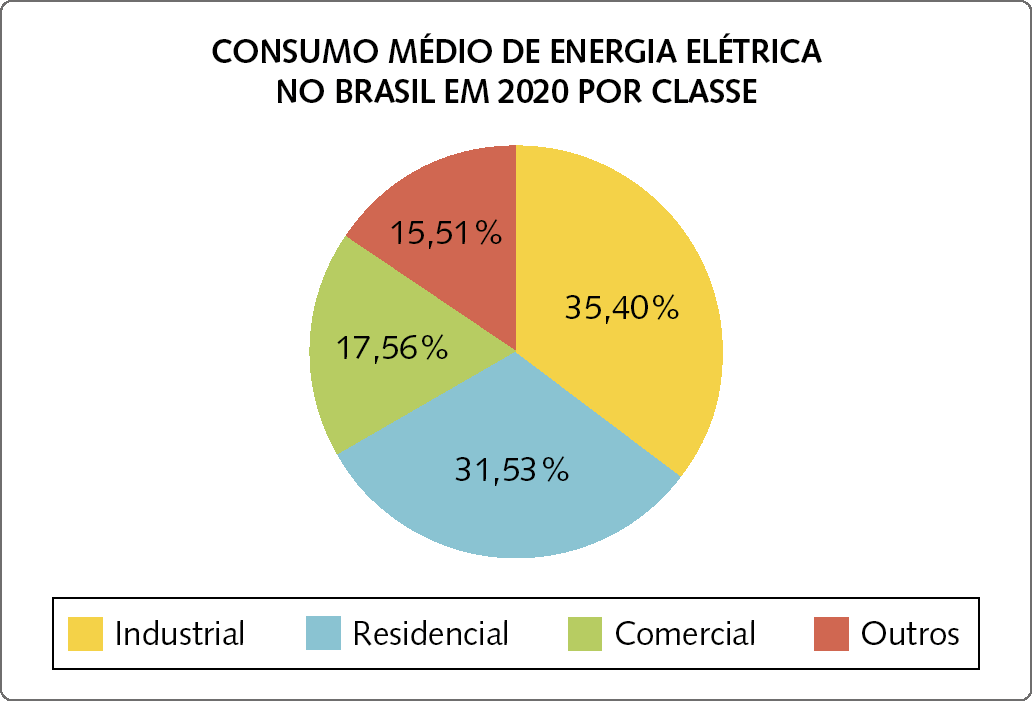
Gráfico de setores. Gráfico que mostra o CONSUMO MÉDIO DE ENERGIA ELÉTRICA NO BRASIL EM 2020 POR CLASSE. As categorias são: Industrial, Residencial, Comercial e Outros. Os consumos médio por categoria: Industrial: 35,40 por centos; Residencial: 31,53 por cento; Comercial: 17,56 por cento Outros: 15,51 por cento.

Dados obtidos em: https://oeds.link/1ZvWpg. Acesso em: 4 julho 2022.

46. O que é possível interpretar de cada gráfico dado como exemplo?

Respostas e comentários

46. Espera-se que os estudantes interpretem: do gráfico de barras, que o equipamento mais usado para acessar a internet é o celular; do gráfico de segmentos, que os salários das mulheres são muito menores que os salários dos homens; do gráfico de setores, que a maior parte do consumo de energia elétrica no Brasil é industrial, mas que o percentual do consumo residencial também é elevado.

Gráficos

Neste momento, é feita uma breve revisão dos principais tipos de gráficos estatísticos por meio de exemplos de gráficos construídos com base em dados reais.

• Na atividade 46, há mais de uma interpretação possível para cada gráfico; por isso, ao final da atividade, incentive os estudantes a compartilhar suas interpretações com as dos colegas, de modo a complementar e até mesmo refinar suas respostas.