Unidade 1
Capítulo 1 Conjuntos numéricos
Capítulo 2 Potenciação e radiciação
Capítulo 3 Sistemas de equações do 1º grau

Infográfico disponível em: https://oeds.link/rf7LPR. Acesso em: 4 jul. 2022.
As condições de vida e de trabalho são iguais para homens e mulheres? O que é possível afirmar com base no infográfico anterior? Ao final do estudo desta Unidade, você responderá a essa e a outras questões.
Respostas e comentários
Abertura da Unidade
Bê êne cê cê:
• Competências gerais 7 e 9 (as descrições estão na página seis).
• Competência específica 8 (a descrição está na página sete).
Objetivos:
• Motivar a turma a estudar os conteúdos da Unidade 1.
• Verificar os conhecimentos previamente adquiridos pelos estudantes sobre a interpretação de dados apresentados na fórma de porcentagem.
• Trazer à luz o problema da desigualdade de gênero.
Proponha aos estudantes que analisem os dados apresentados no infográfico e comentem sobre o que acharam mais importante. Após eles se manifestarem, informe que, na política, mesmo as mulheres sendo a maioria entre os eleitores brasileiros, elas ainda ocupam apenas uma pequena parte dos cargos eletivos. Em relação à ocupação de cargos gerenciais, eles devem perceber que, de cada 3 cargos gerenciais, aproximadamente 2 são ocupados por homens. Uma discussão mais ampla sobre a desigualdade de gênero será realizada na seção É hora de extrapolar proposta ao final desta Unidade e, por isso, você pode deixar para explorar os dados deste infográfico mais adiante.
As questões propostas favorecem o desenvolvimento das competências gerais 7 e 9 e da competência específica 8 da Bê êne cê cê, uma vez que promovem o diálogo e a argumentação com base em dados confiáveis.
No capítulo 1, será retomado o estudo dos conjuntos numéricos e será introduzido o conjunto dos números reais. Já, no capítulo 2, serão estudadas a potenciação e a radiciação e suas propriedades. Por fim, no capítulo 3, serão estudados os sistemas de equações do 1º grau com duas incógnitas.
Na seção É hora de extrapolar, os estudantes terão a oportunidade de pesquisar e analisar dados sobre a desigualdade de gênero. Na sequência, farão uma pesquisa sobre personalidades femininas de destaque. Por fim, eles vão planejar e produzir um podcast sobre a personalidade escolhida.
Capítulo 1 Conjuntos numéricos
Trocando ideias

O Brasil é o país em que mais caem raios no mundo. Segundo o Grupo de Eletricidade Atmosférica (ilá), são 78 milhões de raios todos os anos.

A probabilidade de uma pessoa ser atingida por um raio é de 0,000001, porém, se a pessoa estiver em uma área descampada, essa probabilidade aumenta para 0,001.
▸


Em dias chuvosos, o que devemos fazer para nos proteger dos raios? Converse com os colegas.
▸

Podemos afirmar que o número ..78000000 é um número inteiro? E racional?
▸

Podemos afirmar que os números 0,000001 e 0,001 são números inteiros? E racionais?
▸

Você conhece algum número que não seja racional? Qual?
Neste capítulo, vocês vão estudar os números irracionais. Antes, porém, vamos retomar alguns conceitos e propriedades dos conjuntos numéricos já estudados.
Respostas e comentários
Trocando ideias: primeiro item: resposta pessoal; segundo item: sim, o número ..78000000 é inteiro e racional; terceiro item: os números 0,000001 e 0,001 não são inteiros, mas são racionais; quarto item: respostas pessoais.
CAPÍTULO 1 – CONJUNTOS NUMÉRICOS
Trocando ideias
Bê êne cê cê:
• Competência geral 9 (a descrição está na página seis).
• Competências específicas 3 e 8 (as descrições estão na página sete).
Objetivos:
• Abordar sobre os cuidados que se deve ter, em dias chuvosos, para se proteger contra os raios.
• Levantar os conhecimentos previamente adquiridos pelos estudantes sobre os números inteiros e racionais.
• Levantar os conhecimentos prévios dos estudantes sobre os números irracionais.
Tema contemporâneo transversal:

Inicie a aula explicando à turma que raios são descargas elétricas de grande intensidade que conectam o solo e as nuvens de tempestade na atmosfera. Comente também sobre a diferença entre raio, relâmpago e trovão. Explique que os relâmpagos são todas as descargas elétricas geradas por nuvens de tempestades, que se conectam ou não ao solo. Já os raios são somente as descargas que se conectam ao solo. Os trovões, por sua vez, são os sons produzidos pelo rápido aquecimento e expansão do ar na região da atmosfera onde a corrente elétrica do raio circula.
Após esclarecer esses conceitos para a turma, discuta as probabilidades de uma pessoa ser atingida por um raio. É importante que eles percebam o quanto aumenta essa probabilidade quando a pessoa se encontra em uma área descampada. Diga que, ao ser atingida por um raio, a pessoa sofre queimaduras em diversas partes do corpo, podendo causar parada cardíaca e respiratória. Após esse momento inicial, proponha que conversem sobre a questão proposta no primeiro item. Espera-se que eles respondam que devem evitar ficar em áreas descampadas ou embaixo de árvores ou próximo a postes, cercas de arame, linhas férreas e topo de prédios, por exemplo.
O segundo e o terceiro item possibilitam levantar os conhecimentos adquiridos em anos anteriores sobre os números inteiros e racionais. Incentive-os a justificar suas respostas. Você pode ampliar a proposta e solicitar a alguns estudantes que deem exemplos de números que pertencem ao conjunto dos números inteiros e que pertencem ao conjunto dos números racionais. Espera-se também que eles reconheçam que todo número inteiro é um número racional, mas nem todo número racional é um número inteiro. Por fim, questione-os no último item sobre a existência de números que não sejam racionais e verifique se eles conhecem algum.
As questões incentivam a interação e o diálogo, o que favorece o desenvolvimento da competência geral 9 e a competência específica 8 da Bê êne cê cê. Além disso, os estudantes mobilizam conceitos das Unidades temáticas Números e Probabilidade e estatística, favorecendo, assim, o desenvolvimento da competência específica 3.

1 Números naturais
Para contar uma quantidade de objetos, pessoas, animais etcétera, usamos os números naturais. O conjunto dos números naturais representado por

é dado por:

= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, reticências}
O zero é o menor número natural. Todo número natural tem um sucessor; desse modo, dizemos que a sequência dos números naturais é infinita. Todo número natural, com exceção do zero, tem um antecessor.
Observe:

Os números naturais estão presentes em diversas situações e têm diferentes funções.
Podem indicar a posição de alguém em uma competição, a quantidade de objetos em um local, um número de telefone, um dia do mês no calendário etcétera.
Sequência numérica
Uma sequência numérica é uma sequência cujos elementos são números escritos em certa ordem. A sequência pode ser infinita, na qual usamos reticências para indicar que ela continua indefinidamente. Ou pode ser finita, na qual listamos todos os elementos. Cada um dos elementos da sequência é chamado de termo da sequência.
Podemos expressar algebricamente uma sequência numérica por meio da sua lei de formação, que é uma regra que mostra como a sequência progride ou é formada. Analise os exemplos.
a) Uma sequência infinita na qual á1 = 0 e án + 1 = ánícone de altura+ 3, para todo n inteiro positivo.
Para n = 1, temos: á1 + 1 = á1 + 3 ⇒ á2 = 0 + 3 = 3
Para n = 2, temos: á2 + 1 = á2 + 3 ⇒ á3 = 3 + 3 = 6
Para n = 3, temos: á3 + 1 = á3 + 3 ⇒ á4 = 6 + 3 = 9
Para n = 4, temos: á4 + 1 = á4 + 3 ⇒ á5 = 9 + 3 = 12
Essa lei de formação gera a sequência (0, 3, 6, 9, 12, reticências), que é a sequência de múltiplos de 3.
Respostas e comentários
Números naturais
Bê êne cê cê:
• Habilidades ê éfe zero oito ême ah um zero e ê éfe zero oito ême ah um um.
Objetivos:
• Recordar o conjunto dos números naturais.
• Identificar a regularidade de sequências numéricas e escrever algebricamente o padrão.
Justificativa
Recordar o conjunto dos números naturais é importante para que os estudantes possam avançar no estudo dos demais conjuntos numéricos e perceber como eles estão relacionados.
A identificação de regularidades de sequências numéricas e a escrita algébrica de padrões possibilitam o desenvolvimento das habilidades ê éfe zero oito ême ah um zero e ê éfe zero oito ême ah um um.
Mapeando conhecimentos
Pergunte aos estudantes: “O que são números naturais? Em que situações cotidianas eles são utilizados? O que é antecessor e sucessor de um número natural?”. Incentive a participação da turma.
Para as aulas iniciais
Recorde os conceitos mapeados na dinâmica inicial. Em seguida, escreva na lousa alguns números que são naturais e outros que não são. Depois, peça aos estudantes que identifiquem os números naturais e determinem o antecessor e o sucessor de cada um. Você também pode explorar os vários usos dos números naturais (contagem, medida, ordem e código).
Inicie o estudo dos números naturais retomando um pouco da história dos números. Comente que o zero foi o último algarismo a ser inventado, pois está relacionado à ideia de ausência, que demorou a ser compreendida. Por exemplo, como o número 102 possui uma centena, duas unidades e nenhuma dezena, lemos “cento e dois”, sem pronunciar a dezena ausente.
Sequência numérica
Introduza as notações á1, á2, á3, ..., utilizadas para representar os termos de uma sequência. Chame a atenção para o fato de que começamos por á₁, pois é o primeiro termo, sendo possível também a indicação do primeiro termo como á0.
(ê éfe zero oito ême ah um zero) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.
(ê éfe zero oito ême ah um um) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.
b) Uma sequência infinita na qual á1 = 0 e án + 1 = án + 7, para todo n inteiro positivo.
Para n = 1, temos: á1 + 1 = á1 + 7 ⇒ á2 = 0 + 7 = 7
Para n = 2, temos: á2 + 1 = á2 + 7 ⇒ á3 = 7 + 7 = 14
Para n = 3, temos: á3 + 1 = á3 + 7 ⇒ á4 = 14 + 7 = 21
Para n = 4, temos: á4 + 1 = á4 + 7 ⇒ á5 = 21 + 7 = 28
Essa lei de formação gera a sequência (0, 7, 14, 21, 28, ...), que é a sequência de múltiplos de 7.

Eventualmente são dados os primeiros termos de uma sequência, mas não a sua lei de formação, e, mesmo assim, podemos determinar os demais termos dessa sequência. Observe a situação a seguir.


Para expor ao professor a maneira como pensaram, os estudantes montaram este fluxograma.
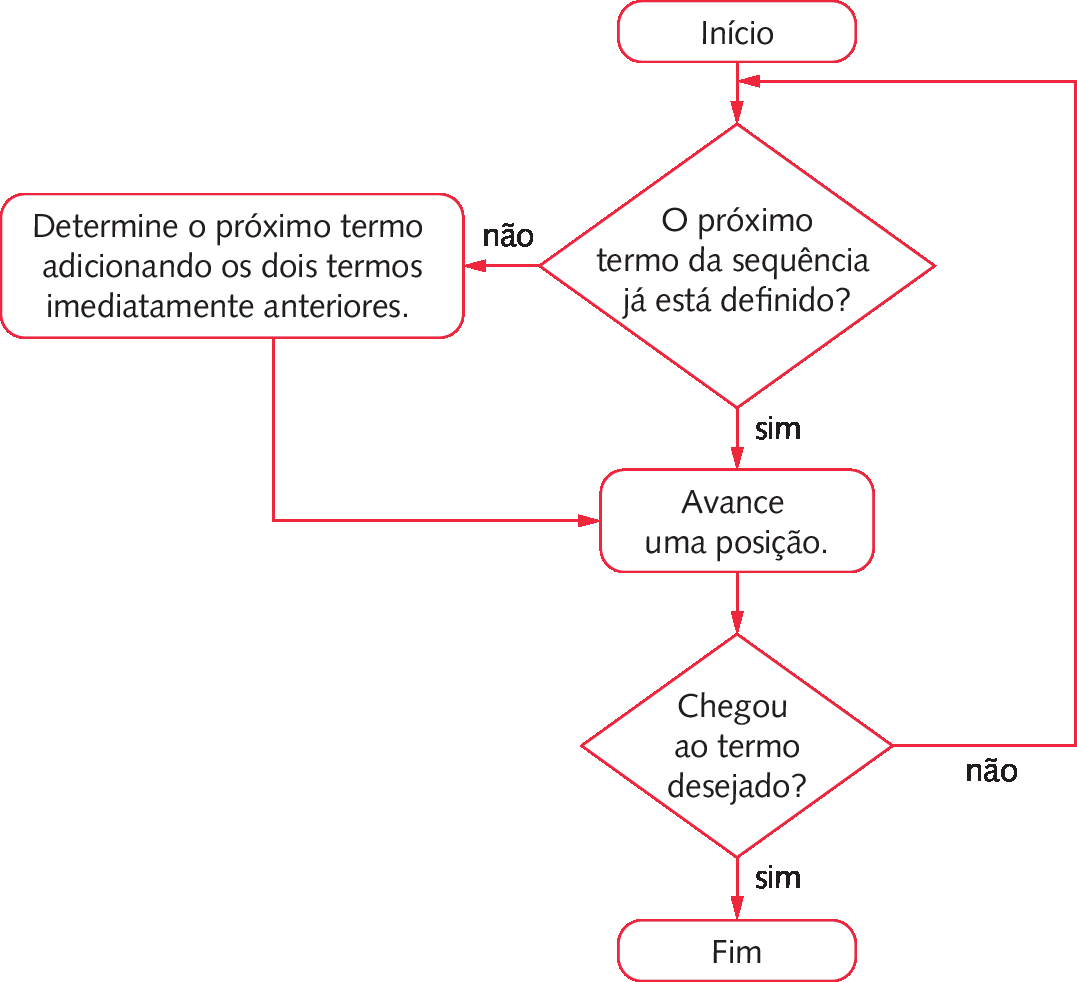
Após exporem o fluxograma para o professor, eles disseram que bastaria fazer o que é solicitado para determinar a sequência até o termo desejado.
▸ Usando o fluxograma, determine os 10 primeiros termos da sequência de Fibonacci.
Respostas e comentários
Item: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55
Comente que é possível ter uma sequência na qual a lei de formação seja independente do termo anterior, por exemplo, an = 2n, para n ⩾ 0, que é a sequência dos números naturais pares. Nesse caso, a fórmula é tida como a fórmula do termo geral da sequência.
Nas sequências apresentadas, a lei de formação é feita de tal fórma que cada valor da sequência é obtido em função do termo anterior ou dos termos anteriores.
Para a sequência de Fibonacci, se julgar pertinente, apresente a lei de formação utilizando as notações de sequências: para á₁ = 1, á₂ = 1 e n natural tal que n > 2. Assim, a lei de formação da sequência pode ser dada por an = an − 1 + an − 2 .
Atividades
Faça as atividades no caderno.
1. Escreva o antecessor e o sucessor de cada número.
a) 17
b) 999
c) .1000
d) .12989
2. Responda às questões no caderno.
a) Quais números naturais são maiores que o sucessor de 3 e menores que o antecessor de 10?
b) Existe algum número natural maior que o sucessor de 10 e menor que o antecessor de 3?
3. Em cada sequência numérica, determine os termos que faltam representados por

.
a) 2, 4, 6,

,

,

,
reticências , na qual a ₁ = 2, a indice de 2 = 4 e a indice de n = a n menos 2 + a ₙ ₋ ₁, em que n > 2
b) 1, 5, 9, 13, 17, 21,

,

,
reticências , na qual a ₁ = 1,
a indice de 2 = 5 e a n = a ₁ + (n menos 1) ⋅ (a n menos 1 menos a n menos 2 ), em que n > 2
4.


No caderno, escreva os cinco primeiros termos de uma sequência numérica recursiva e troque com um colega para que ele construa um fluxograma que determine a sequência até o 10º termo. Faça o mesmo com a sequência dele.

2 Números inteiros

No fim da tarde de determinado dia de julho, a medida de temperatura na cidade de São Joaquim (Santa Catarina) era 5 graus Célsius. No início da noite, essa medida de temperatura caiu 8 graus Célsius. Qual foi a medida de temperatura registrada após essa queda?
Para responder a essa pergunta, podemos fazer a seguinte subtração:
5 menos 8 = menos3
Isso significa que a medida da temperatura chegou a três graus Celsius abaixo de zero, sendo indicada por um número negativo (menos3). O menos3 é um exemplo de número inteiro.
O conjunto dos números inteiros representado por

é dado por:

= {reticências, menos5, menos4, menos3, menos2, menos1, 0, 1, 2, 3, 4, 5, reticências}
Observe que todo número natural é também um número inteiro. Todo número inteiro tem um sucessor e um antecessor; por exemplo, menos3 é o sucessor de menos4 e menos1 é o antecessor de 0.
Respostas e comentários
1. a) antecessor: 16; sucessor: 18
1. b) antecessor: 998; sucessor: .1000
1. c) antecessor: 999; sucessor: .1001
1. d) antecessor: .12988; sucessor: .12990
2. a) 5, 6, 7 e 8
2. b) não
3. a) 10; 16; 26
3. b) 25; 29
4. Respostas pessoais.
Resposta: abaixo de zero grau (menos2 graus Célsius)
• Para a atividade 2, sugira aos estudantes que façam uso da reta numérica para identificar os números.
Números inteiros
Objetivo:
Recordar o conjunto dos números inteiros.
Justificativa
Recordar o conjunto dos números inteiros é importante, dentre outras coisas, para que os estudantes percebam que todos os elementos do conjunto

são também elementos do conjunto

, ou seja,

⊂

. Além disso, permite avançar para o estudo dos demais conjuntos numéricos.
Mapeando conhecimentos
Pergunte aos estudantes: “O que são números inteiros? Em que situações cotidianas eles são utilizados? Qual é a relação entre os números inteiros e os números naturais? O que é oposto ou simétrico de um número inteiro?”. Incentive a participação da turma.
Para as aulas iniciais
Na seção Revisão dos conteúdos de anos anteriores, há uma revisão sobre os números naturais e inteiros. Peça aos estudantes que leiam essa revisão e façam as atividades 1, 2 e 3. Discuta cada uma das atividades com a turma e tire as dúvidas remanescentes.
Comente que o uso da letra

para representar o conjunto dos números inteiros se deve à palavra alemã Zahl, que significa “número”.
Explique que os números inteiros são formados pelos números naturais (inclusive o zero) e pelos números naturais acrescidos do sinal negativo, ou seja, são compostos de valores positivos, negativos e do elemento neutro zero. Chame a atenção para o fato de o zero ser o elemento neutro da adição.
Retome a ideia de extensão de conjuntos e de propriedade de fechamento, comentando que os inteiros são fechados para a adição, a subtração e a multiplicação e que, no entanto, é necessário estender o conjunto quando envolve a operação de divisão.
Se julgar adequado, apresente a representação dos conjuntos com a utilização de diagramas, mostrando que o conjunto dos naturais está inscrito, ou contido, no conjunto dos inteiros.
Se julgar conveniente, explore as notações e os subconjuntos de

:
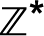
,
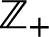
,
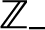
,
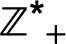
,
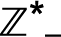
.
Atividades
Faça as atividades no caderno.
5. Considere os números a seguir e responda às questões.
5; menos8; 0; 14; menos100; 57; menos18;
Fração. 2 sobre 3.; menos0,4; menos1
a) Quais são números naturais?
b) Quais são números inteiros?
c) Todo número natural é um número inteiro?
6. Avalie as afirmações a seguir e copie as verdadeiras em seu caderno.
a) Há sempre um número inteiro entre dois números inteiros.
b) A diferença de dois números inteiros é sempre um número inteiro.
c) Existe número natural que não é número inteiro.
7. Escreva o que se pede:
a) os cinco menores números naturais ímpares;
b) os números inteiros negativos maiores que menos5;
c) três números inteiros menores que menos20;
d) os números naturais maiores que menos3 e menores que 7.
8. Responda às questões a seguir considerando a sequência dos números inteiros.
a) Qual é o sucessor de 100?
b) Qual é o sucessor de menos30?
c) Se n é um número inteiro, qual é a expressão que representa seu sucessor?
d) Se a é um número inteiro, qual é a expressão que representa seu antecessor?
9. O saldo bancário da conta de Pedro estava negativo em R$ 380,00trezentos e oitenta reais. Ele fez um depósito e o novo saldo passou a ser R$ 970,00novecentos e setenta reais. Qual foi o valor do depósito realizado por Pedro?
10. Considere a sequência dos números inteiros a seguir:
reticências, menos5, menos4, menos3, menos2, menos1, 0, 1, 2, 3, 4, 5, reticências
a) Há quantos números inteiros entre menos5 e 3?
b) Qual é o maior número inteiro negativo dessa sequência?
Respostas e comentários
5. a) 0, 5, 14, 57
5. b) menos100, menos18, menos8, menos1, 0, 5, 14, 57
5. c) sim
6. a) falsa
6. b) verdadeira
6. c) falsa
7. a) 1, 3, 5, 7 e 9
7. b) menos4, menos3, menos2 e menos1
7. c) Exemplo de resposta: menos21, menos22 e menos23
7. d) 0, 1, 2, 3, 4, 5 e 6
8. a) 101
8. b) menos29
8. c) n + 1
8. d) a menos 1
9. R$ 1.350,00mil trezentos e cinquenta reais
10. a) há sete números inteiros: menos4, menos3, menos2, menos1, 0, 1 e 2
10. b) menos1
• Na atividade 5, chame a atenção para o fato de que não é porque um número está na fórma de fração que não é inteiro ou natural. Dê exemplos de frações aparentes.
• A atividade 6 permite aos estudantes refletir sobre propriedades que valem em determinado conjunto, mas não em outro. Amplie essa atividade solicitando que, para as afirmações falsas, apresentem um contraexemplo.
• Na atividade 7, se julgar necessário, oriente os estudantes a usar a reta numérica. A ordenação numérica é um assunto com o qual os estudantes costumam ter dificuldades. Para pensar na ordenação, utilize exemplos sobre medidas de altura e profundidade, como os andares de um prédio, sobre saldos positivos e negativos ou até mesmo sobre as eras antes de Cristo (antes de Cristo) e depois de Cristo (Depois de Cristo).
• Na atividade 8, chame a atenção para o fato de que, para os números inteiros negativos, quanto mais próximo do zero, maior será o valor. Nos itens c e d, ressalte que a representação dentro do conjunto dos números inteiros é a mesma que teríamos se considerássemos o conjunto dos números naturais. A diferença está no intervalo a ser considerado.
• Explore a atividade 9, trazendo a ideia das operações com números inteiros. Reforce a compreensão das operações dentro desse conjunto, fugindo de regras decoradas.
• Na atividade 10, comente que o termo “entre” não considera os extremos. Se julgar pertinente, no item a, apresente a representação simbólica menos5 < x < 3.

3 Números racionais
Acompanhe a situação a seguir.
Uma peça de tecido medindo 75 metros de comprimento vai ser dividida em 10 partes iguais.

Quantos metros terá cada uma dessas partes?
Para responder a essa pergunta, podemos efetuar a divisão:
75 : 10 = 7,5
Portanto, cada uma dessas partes terá 7,5 metros de medida de comprimento.
Os números obtidos pela divisão de dois números inteiros, em que o divisor é diferente de zero, podem ser escritos na fórma de fração ou na fórma decimal. Confira estes exemplos:
a)
Sentença matemática. A fração 75 sobre 10 é igual a 7,5.b)
Sentença matemática. Menos 3 sobre 8 é igual a menos 0 vírgula 375.c)
Sentença matemática. 4 sobre 2 igual a 2d)
Sentença matemática. 13 sobre 3 é igual a 4 vírgula 333 reticência.e)
Sentença matemática. Menos 1 sobre 25 é igual a menos 0 vírgula 04.f)
Sentença matemática. Menos 45 sobre 9 é igual a menos 5.Números que podem ser escritos na fórma de fração, com numerador e denominador inteiros e denominador diferente de zero, são chamados de números racionais.
O conjunto dos números racionais é indicado por

e pode ser representado da seguinte maneira:

Observações
1. Todo número inteiro é um número racional, ou seja, pode ser escrito na fórma
Fração. a sobre b., em que ei e b são números inteiros e b ≠ 0. Analise estes exemplos.
a)
Sentença matemática. 3 é igual a a fração 3 sobre 1 é igual a fração 6 sobre 2 é igual a fração 9 sobre 3 é igual a fração 12 sobre 4.b)
Sentença matemática. Menos 5 é igual a fração menos 5 sobre 1 é igual a fração menos 20 sobre 4 é igual a fração menos 35 sobre 7.c)
Sentença matemática. Zero é igual a fração 0 sobre 1 é igual a fração 0 sobre 2 é igual a fração 0 sobre 3 é igual a fração 0 sobre 4.2. Os números racionais podem ser representados por pontos na reta numérica.

3. Entre dois números racionais quaisquer sempre existe outro número racional. Por exemplo, entre 1,4 e 1,6 há infinitos números racionais. Alguns deles são: 1,45; 1,48; 1,5; 1,52 e 1,555.
Respostas e comentários
Números racionais
Bê êne cê cê:
• Competências gerais 1, 3 e 4 (as descrições estão na página seis).
• Competência específica 1 (a descrição está na página sete).
• Habilidades ê éfe zero oito ême ah zero quatro e ê éfe zero oito ême ah zero cinco.
Objetivos:
• Recordar o conjunto dos números racionais.
• Resolver problemas que envolvam o cálculo de porcentagem.
• Identificar uma dízima periódica e obter sua fração geratriz.
Tema contemporâneo transversal:

Justificativa
O quociente de 2 números inteiros nem sempre é um número inteiro e por isso é importante ampliar o conjunto

, obtendo o conjunto

. Recordar o conjunto dos números racionais possibilita aos estudantes perceber a necessidade dessa ampliação e como os conjuntos numéricos estudados se relacionam.
Resolver problemas que envolvam porcentagens é útil para atuarmos em situações cotidianas e favorece o desenvolvimento da habilidade ê éfe zero oito ême ah zero quatro.
O estudo do conjunto dos números racionais traz à tona as dízimas periódicas e as frações geratrizes correspondentes a elas. Obter essas frações é importante para verificar que esses números são racionais e favorece o desenvolvimento da habilidade ê éfe zero oito ême ah zero cinco.
Mapeando conhecimentos
Proponha aos estudantes que identifiquem números racionais em jornais, revistas, embalagens ou folhetos. Depois, reúna-os em grupos para discutir o significado dos números encontrados e a maneira como foram representados. Por fim, questione se sabem definir números racionais e como se relacionam com os números naturais e os números inteiros.
Para as aulas iniciais
Peça aos estudantes que leiam a revisão sobre números racionais da seção Revisão dos conteúdos de anos anteriores e façam as atividades 4, 5 e 6. Discuta-as com a turma e tire as dúvidas remanescentes.
A observação 3 explora a ideia de densidade do conjunto

. Se achar oportuno, represente os números do exemplo na reta numérica para que os estudantes percebam que, entre 2 números racionais, sempre há um número racional, em um processo sem fim, independentemente do intervalo observado.
(ê éfe zero oito ême ah zero quatro) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.
(ê éfe zero oito ême ah zero cinco) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.
Representação decimal dos números racionais
Os números racionais na fórma de fração podem ser representados na fórma decimal.
Observe os exemplos a seguir.
a)
4 quintos igual a 4 dividido por 5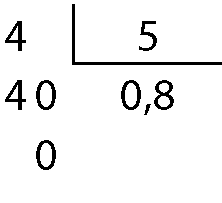
Portanto:
4 quintos igual a 0,8b)
7 décimos igual a 7 dividido por 10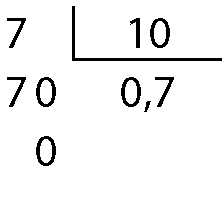
Portanto:
7 décimos igual a 0,7c)
22 oitavos igual a 22 dividido por 8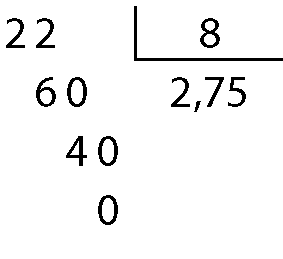
Portanto:
22 oitavos igual a 2,75d)
sete terços= 7 dividido por 3
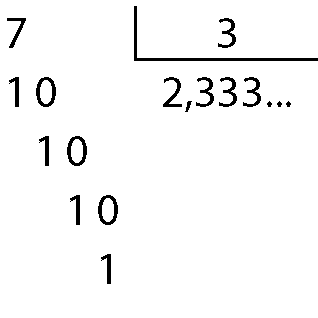
Portanto:
7 terços igual a 2,333 reticênciasNa divisão de 7 por 3, o algarismo 3 do quociente continuará se repetindo infinitamente. O número decimal 2,333reticências é uma dízima periódica e o algarismo 3 que se repete é chamado de período.
A dízima 2,333reticências é uma dízima periódica simples, pois o período (3) aparece logo após a vírgula. Podemos também representar a dízima 2,333reticências colocando um traço sobre o período, ou seja: 2,333reticências =
dízima periódica 2,3 de período 3Agora, observe um exemplo em que o período da dízima periódica se inicia a partir do algarismo da segunda casa decimal.
Sentença matemática. 29 sobre 90 é igual a 29 dividido por 90.
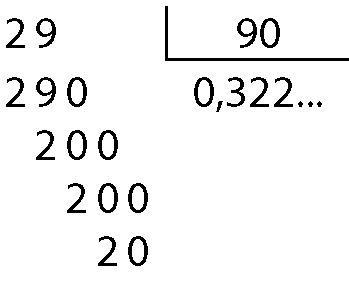
Portanto:
Sentença matemática. A fração 29 sobre 90 é igual a 0,0322 reticências.Na divisão de 29 por 90, o algarismo 2 do quociente continuará se repetindo infinitamente. O número decimal 0,3222reticências é uma dízima periódica e o período é o algarismo 2 (algarismo que se repete).
A dízima 0,3222reticências é uma dízima periódica composta, uma vez que, entre a vírgula e o período (2), existe uma parte não periódica, o algarismo 3.
Podemos representar a dízima 0,3222reticências por
dízima periódica 0,32 de período 32.
Respostas e comentários
Representação decimal dos números racionais
Se julgar conveniente, retome o algoritmo da divisão, sanando eventuais dúvidas, de modo que não se torne um obstáculo na aprendizagem dos números racionais. É importante que os estudantes compreendam o algoritmo, dando significado aos passos para executá-lo; por exemplo, ao efetuar 7 dividido por 10, precisamos colocar o algarismo 0 e a vírgula no quociente, pois, ao dividir 7 unidades por 10, não obtemos unidade.
Ao trabalhar a representação decimal dos números racionais, é importante que fique claro para os estudantes que tal representação será finita ou infinita periódica. Pode-se comentar com eles a possibilidade de decidir se a representação decimal de uma fração será finita ou infinita periódica sem ter que efetuar a divisão.
A representação decimal de uma fração será finita quando for possível obter uma fração equivalente à fração original cujo denominador seja uma potência de 10. Por exemplo, a representação decimal das frações,
Fração. 1 sobre 4.,
Fração. 1 sobre 25.e
Fração. 7 sobre 200.é finita, pois:
;
;
A representação decimal de uma fração será infinita e periódica quando não for possível obter uma fração equivalente à fração original cujo denominador seja uma potência de 10. Por exemplo, a representação decimal das frações
Fração. 1 sobre 7.,
Fração. 2 sobre 9.e
Fração. 7 sobre 11.é infinita e periódica. Nesse caso, proponha aos estudantes que tentem encontrar uma fração equivalente a essas, cujo denominador seja uma potência de 10 para que percebam que isso não é possível.
Outra caracterização para esse critério é a seguinte:
• se, ao decompor em fatores primos, o denominador da fração for somente potências de 2, de 5 ou de ambas, então a representação decimal da fração será finita;
• se, ao decompor em fatores primos, o denominador da fração for alguma potência com base diferente de 2 ou de 5, então a representação decimal da fração será infinita e periódica.
Comente sobre a dízima periódica composta, em que o número da parte decimal que não se repete é chamado de anteperíodo.

Um pouco de história
Faça a atividade no caderno.
Matemática e música
O matemático e filósofo grego Pitágoras (c.glossário 570 antes de Cristo-c.glossário 496 antes de Cristo) traçou uma ligação direta entre Matemática e música ao construir, com uma corda e dois cavaletes, um instrumento que ficou conhecido como “monocórdio de Pitágoras”. Com base em observações, ele percebeu que o som (as notas musicais) dependia da medida de comprimento da corda que o produzia.
A divisão da corda em medidas de comprimento diferentes possibilitou, posteriormente, a criação de uma escala com sete notas: dó, ré, mi, fá, sol, lá e si, que formam a escala pitagórica.
|
Dó |
Ré |
Mi |
Fá |
Sol |
Lá |
Si |
Dó |
|---|---|---|---|---|---|---|---|
|
1 |
|
|
|
|
|
|
|
Atividade

Com o auxílio de uma calculadora, escreva em seu caderno os números desse quadro na fórma decimal. Nas dízimas periódicas em que o período é maior do que a quantidade de dígitos mostrados na calculadora, escreva o valor aproximado com oito casas decimais.
Cálculo de porcentagem
Em nosso cotidiano, usamos porcentagem em diversas situações. Confira alguns exemplos.

Respostas e comentários
Um pouco de história: 1;
Sentença matemática. 8 sobre 9 igual a 0 vírgula 8 com período no 8.;
Sentença matemática. 64 sobre 81 é aproximadamente igual a 0 vírgula 79012347.;
Sentença matemática. 3 sobre 4 igual a 0 vírgula 75.;
Sentença matemática. 2 sobre 3 igual a 0 vírgula 6 com período no 6.;
Sentença matemática. 16 sobre 27 igual a 0 vírgula 592 com período no 592.;
Sentença matemática. 128 sobre 243 é aproximadamente igual a 0 vírgula 52674897.;
Sentença matemática. 1 sobre 2 igual a 0 vírgula 5.O boxe Um pouco de história trata da relação entre Matemática e música por meio do instrumento conhecido como “monocórdio de Pitágoras”. É importante que os estudantes observem que cada nota musical está associada a um número racional e reflitam como a Matemática está presente em diversas situações e áreas do conhecimento. Momentos como esse podem colaborar para o desenvolvimento das competências gerais 1, 3 e 4 e da competência específica 1.
Cálculo de porcentagem
No cálculo de porcentagens, se necessário, relembre a multiplicação com frações. Se achar interessante, explique também sobre o uso de decimais no cálculo de porcentagens.
Uma porcentagem indica a parte de um todo que contém 100 partes iguais. Por exemplo, representar 13% é o mesmo que se referir a 13 partes de 100 que formam o todo.
Uma porcentagem pode ser escrita na fórma de fração, ou seja, 13% pode ser escrito como
Fração. 13 centésimos..
Quando queremos calcular, de maneira rápida, o valor referente à porcentagem de um total, basta multiplicar a porcentagem (ou sua fração equivalente) pelo valor total. Analise os exemplos a seguir.
• Para calcular 13% de 730, basta multiplicar 730 por 13%, ou seja, multiplicar 730 por
Fração. 13 centésimos..
Sentença matemática. 730 vezes a fração 13 sobre 100 é igual a fração 9 mil 490 sobre 100 é igual 94 vírgula 9.
Dessa forma, concluímos que 13% de 730 é 94,9.
• No início do estudo foi citada a promoção de um carro. Podemos calcular o desconto de 20% concedido na compra do carro que custa R$ 20.000,00vinte mil reais da seguinte maneira:
Sentença matemática. 20 sobre 100 vezes 20 mil é igual a fração 400 mil sobre 100 é igual 4 mil.
Dessa forma, concluímos que o desconto é de R$ 4.000,00quatro mil reais e que o preço do carro será de R$ 16.000,00dezesseis mil reais após aplicado o desconto.
• Para determinarmos a porcentagem de desconto na promoção da televisão, comparamos o preço após o desconto com o preço inicial. Assim:
Sentença matemática. 600 sobre mil e 200 é igual a fração 50 sobre 100 é igual a 50 por cento.
Dessa forma, concluímos que a televisão realmente está sendo vendida pela metade do preço.
Agora, acompanhe a situação.
Marcos trabalha em uma empresa que compra e vende móveis usados. Para impulsionar as vendas, ele e a gerente prepararam um evento para a exposição dos móveis.


Respostas e comentários
As porcentagens estão presentes no dia a dia ao falarmos sobre compras à vista ou a prazo. Podemos sempre nos deparar com situações de descontos, acréscimos e juros. Converse com a turma a respeito dessas possibilidades. Pergunte aos estudantes se eles conseguem dar um exemplo em que perceberam o uso da porcentagem pelos responsáveis durante uma compra ou algum exemplo que eles mesmos tenham vivenciado. É comum encontrarmos cartazes e anúncios como “tudo na loja com até 50% de desconto”. Pergunte a eles se compreendem o papel da palavra “até” nesse contexto, verificando se entendem que não são todos os produtos que recebem essa porcentagem de desconto. Explique que, quando for necessário comprar um produto ou pagar por um serviço, é sempre interessante perguntarmos sobre descontos e sobre as condições do pagamento.
A situação que envolve a empresa na qual Marcos trabalha pode favorecer o desenvolvimento da habilidade EF08MA04.
Sugestão de atividade extra
Se julgar adequado, sugira aos estudantes que realizem mentalmente o cálculo das seguintes porcentagens:
• 1% de R$ 200,00duzentos reais;
• 5% de R$ 200,00duzentos reais;
• 10% de R$ 320,00trezentos e vinte reais;
• 10% de R$ 123,00cento e vinte e três reais;
• 25% de R$ 1.000,00mil reais;
• 30% de R$ 250,00duzentos e cinquenta reais;
• 12% de R$ 300,00trezentos reais.
Para fazer tudo em tempo hábil, Marcos resolveu dispor todos os valores em uma planilha eletrônica. Ele organizou os dados em 4 colunas, da seguinte maneira:
• Na primeira coluna (coluna a), ele colocou os valores pagos por cada móvel (valores de compra).
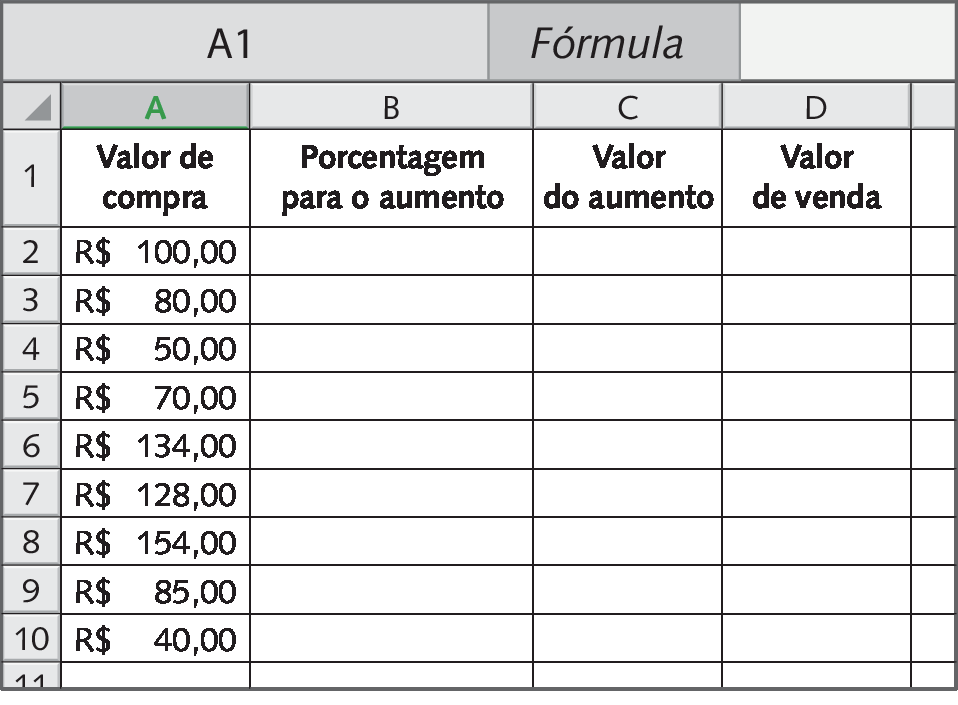
• Na segunda coluna (coluna B), ele colocou a porcentagem a ser aumentada em cada preço, conforme a gerente havia orientado, na célula B2 e arrastou-a para baixo até a célula B10. Assim, Marcos não precisou reescrever a mesma porcentagem nas outras células da coluna.
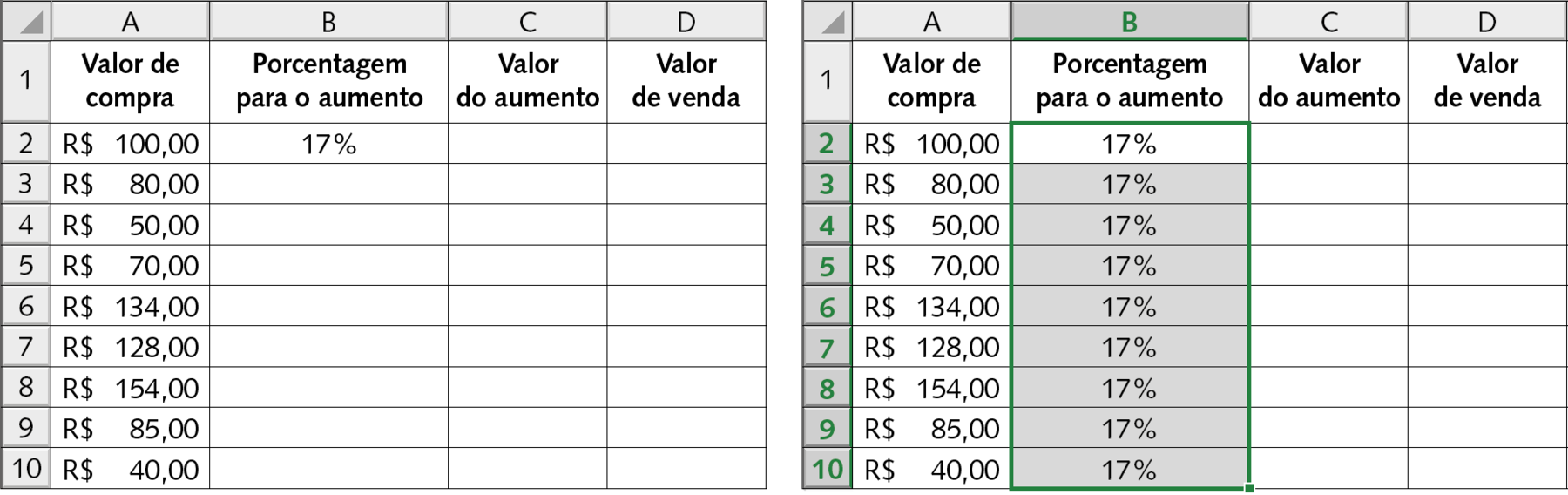
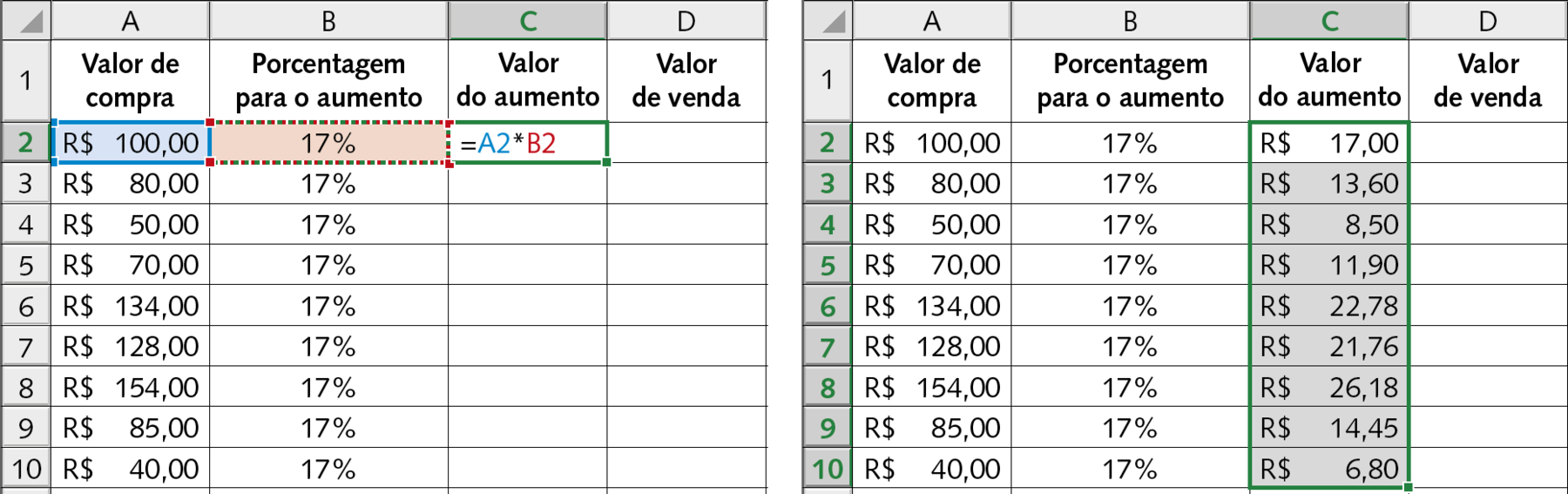
• Na terceira coluna (coluna C), ele multiplicou a porcentagem a ser aumentada pelo valor de compra e, assim, obteve o valor do aumento. Após montar a fórmula na célula C2, Marcos arrastou-a para baixo de modo a aplicar a mesma fórmula até a célula C10.
Respostas e comentários
Se possível, proponha outras atividades para serem resolvidas usando um software de planilha eletrônica. Comente que o sinal de multiplicação é dado pelo asterisco (*).
• Por último, na quarta coluna (coluna D), ele adicionou o valor de compra ao valor do aumento. Após montar a fórmula na célula D2, Marcos arrastou-a para baixo de modo a aplicar a mesma fórmula até a célula D10.
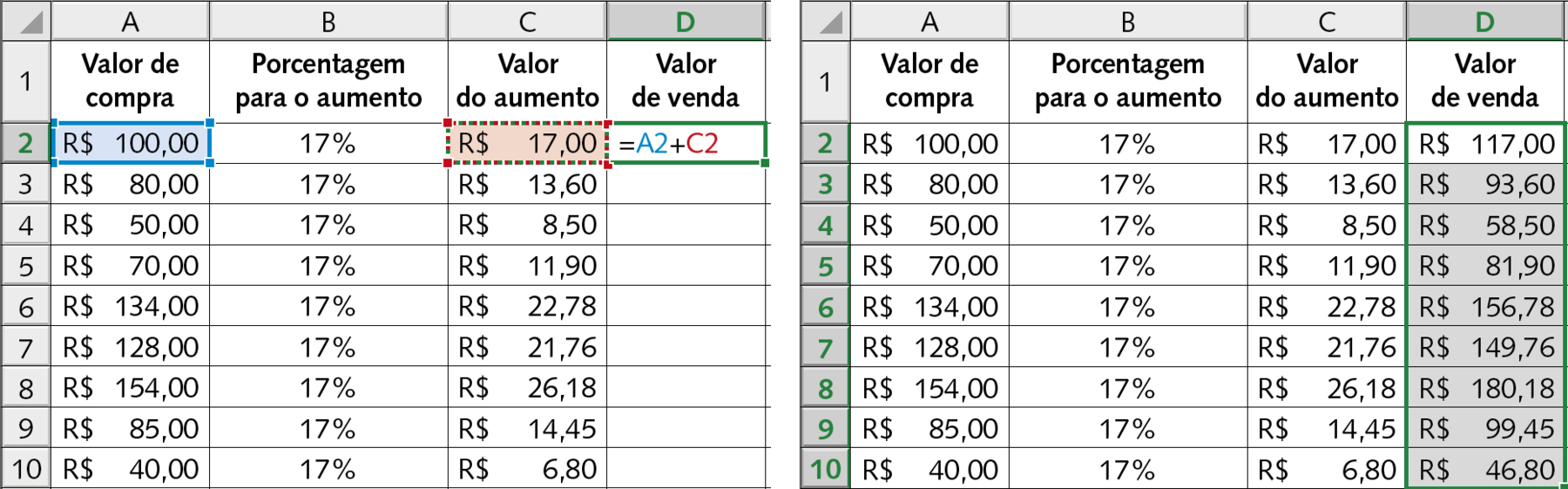
Dessa forma, Marcos conseguiu calcular o preço de venda dos novos móveis a tempo de expô-los no evento.
Atividades
Faça as atividades no caderno.
11. Avalie as afirmações a seguir e copie as verdadeiras em seu caderno.
a) Todo número inteiro é racional.
b) Todo número racional é inteiro.
c) Todo número racional é natural.
d) Entre dois números racionais existe sempre outro número racional.
•

Para as afirmações falsas, dê um exemplo que justifique tal classificação. Depois, converse com os colegas e o professor sobre os diferentes exemplos apresentados.
12. Indique um número situado entre:
a) 3,457 e 3,459;
b) 1,05 e 1,06.
•

Converse com o professor e os colegas para comparar os números indicados em cada caso e responda: Há somente uma resposta para cada item ou há infinitas respostas? Justifique.
13. Escreva, no caderno, a representação decimal de cada um dos números racionais a seguir.
a)
6 sobre 5b)
157 sobre 100c)
7 sobre 3d)
13 sobre 11e)
menos 5 sobre 8f)
menos 15 sobre 90g)
1 sobre 55h)
menos 3 sobre 4• Quais desses números racionais têm dízima periódica como representacão decimal?
Respostas e comentários
11. a) verdadeira
11. b) falsa; exemplo de justificativa: 0,1 é racional e não é inteiro.
11. c) falsa; exemplo de justificativa: 0,1 é racional e não é natural.
11. d) verdadeira
12. Há infinitas respostas.
12. a) Exemplo de resposta: 3,4588
12. b) Exemplo de resposta: 1,05213
13. a) 1,2
13. b) 1,57
13. c)
dízima periódica 2,3 de período 313. d)
dízima periódica 1,18 de período 1813. e) ‒0,625
13. f)
dízima periódica menos 0,16 de período 1613. g)
dízima periódica 0,018 de período 1813. h) ‒0,75
13. Item:
7 sobre 3;
13 sobre 11;
menos 15 sobre 90;
1 sobre 55Ao final da situação apresentada, discuta com os estudantes se seria possível obter o valor de fórma direta, sem necessidade das duas colunas centrais, concluindo sobre a possibilidade de se utilizar o fator 1,17.
• Para a atividade 11, pode ser interessante a utilização do diagrama para a representação dos conjuntos numéricos e a localização dos exemplos nesse diagrama.
Esta atividade permite aos estudantes refletir sobre propriedades que valem em determinado conjunto numérico, mas que não valem em outro.
• Para a atividade 12, item a, estimule os estudantes a pensar que existe uma infinidade de números, não somente o 3,458. Cite, como exemplo, os números 3,4571; 3,45711; 3,457111; e 3,4571111; e comente que poderíamos continuar indefinidamente apenas com o dígito 1 ou combinando outros. A mesma ideia se aplica ao item b.
14. Identifique o período das dízimas periódicas a seguir, classificando-as em simples ou compostas.
a) ‒3,4777reticências
b) 0,333reticências
c)
dízima periódica menos 0,05 de período 5d) ‒0,323232reticências
15. Um dos benefícios do trabalhador brasileiro é o décimo terceiro salário, pago pelos empregadores no fim do ano. Para quem trabalhou o ano inteiro, o valor a ser pago corresponde ao salário mensal e, para quem trabalhou menos de um ano, o valor a ser pago é proporcional à quantidade de meses trabalhados.
a) Se uma pessoa foi admitida em uma empresa no dia 1º de maio, quantos meses ela trabalhou nesse ano? Esse período corresponde a que fração de um ano?
b) Sabendo que o salário mensal dessa pessoa é R$ 2.514,50dois mil quinhentos e quatorze reais e cinquenta centavos, qual foi o valor do décimo terceiro salário recebido?
16.

Alguém queria determinar, usando uma calculadora, quanto gastaria ao pagar duas contas nos valores de R$ 329,18trezentos e vinte e nove reais e dezoito centavos e de R$ 2.231,11dois mil duzentos e trinta e um reais e onze centavos. Após apertar a tecla

, o resultado que apareceu no visor foi:

a) O resultado obtido está correto? Caso não esteja, explique o que pode ter acontecido.
b) Qual é o valor correto a pagar por essas duas contas?
17. Calcule a porcentagem dos valores a seguir.
a) 12% de 144
b) 25% de .1024
c) 1% de ..123587600
d) 24% de 72
18.


Retome a situação de Marcos, que compra e vende móveis usados. A gerente pediu a ele que elaborasse outra planilha, reproduzida a seguir.

a) Junte-se com um colega e comparem a situação de Marcos apresentada anteriormente com a da planilha anterior. Que semelhanças e diferenças vocês identificam?
b) Reproduzam, em uma planilha eletrônica, os valores de compra e a porcentagem para o aumento. Em seguida, obtenham o valor do aumento e o valor de venda para cada imóvel, em real, obtido com a venda desses três móveis.
Respostas e comentários
14. a) 7 (composta)
14. b) 3 (simples)
14. c) 5 (composta)
14. d) 32 (simples)
15. a) 8 meses;
8 sobre 12(ou fração equivalente)
15. b) R$ 1.676,33 mil seiscentos e setenta e seis reais e trinta e três centavos
16. a) não; exemplo de explicação: a pessoa se esqueceu de apertar a tecla

para indicar a vírgula no valor R$ 329,18trezentos e vinte e nove reais e dezoito centavos.
16. b) R$ 2.560,29 dois mil quinhentos e sessenta reais e vinte e nove centavos
17. a) 17,28
17. b) 256
17. c) ..1235876
17. d) 17,28
18. a) Resposta pessoal.
18. b) Resposta em Orientações.
• A atividade 15 permite aos estudantes compreender como é feito o cálculo do décimo terceiro salário, ainda que não seja parte de sua realidade. Sempre que possível, proponha situações envolvendo aspectos da educação financeira, pois, se bem escolhidas e exploradas, podem contribuir significativamente para a formação do estudante como cidadão.
• Na atividade 18, as células da coluna B do quadro devem ser preenchidas com o valor 23% , porcentagem de aumento. As células da coluna C representam o valor do aumento, isto é, 23% dos respectivos valores de compra, que estão na coluna a. Finalmente, as células da coluna D representam o valor de venda, que são obtidos adicionando o valor de compra com o valor de aumento. Temos, então, o seguinte quadro preenchido:
|
A |
B |
C |
D |
|
|---|---|---|---|---|
|
1 |
Valor de compra |
Porcentagem para o aumento |
Valor do aumento |
Valor de venda |
|
2 |
R$ 60,00 |
23% |
R$ 13,80 |
R$ 73,80 |
|
3 |
R$ 80,00 |
23% |
R$ 18,40 |
R$ 98,40 |
|
4 |
R$ 100,00 |
23% |
R$ 23,00 |
R$ 123,00 |

Lendo e aprendendo

Cai a expectativa de vida no Brasil
Indicador mostra quantos anos, em média, uma pessoa vive em determinado país
A expectativa de vida dos brasileiros caiu de 76,7 anos para 74,8 anos em 2020. A redução foi resultado do alto número de mortes por causa da côvid dezenóveno último ano. O indicador é o mais baixo desde 2013.
O número foi apontado em um estudo feito por uma equipe de pesquisadores da Faculdade de Saúde Pública da Universidade Harvard, em parceria com a Universidade Federal de Minas Gerais.
reticências
A expectativa de vida é um importante indicador social e de saúde. Esse número mostra o tempo que a população vive, em média. Outra fórma de entender esse número é imaginar que os bebês nascidos em 2020 irão viver, em média, quase dois anos a menos do que aqueles que nasceram em 2019. Os dados oficiais do Brasil ainda serão consolidados pelo IBGE.
Apesar de alguns outros países também terem tido muitas mortes, a queda da expectativa de vida não foi tão alta. Nos Estados Unidos, por exemplo, os americanos perderam 1,13 ano de expectativa de vida.
Como base de comparação, a mais alta expectativa de vida no mundo é a do Japão — 84,6 anos, e a mais baixa é a da República Centro-Africana — 53,3 anos.
CABRAL, M. C. Cai a expectativa de vida no Brasil. Qualé, São Paulo, edição 28, página 12, 3 a 17 de maio de 2021.
Atividades
1. Responda às questões no caderno.
a) Em que mês e ano a matéria anterior foi publicada?
b) O que é a expectativa de vida?
c) Qual era a expectativa de vida dos brasileiros em 2020? E em 2019?
d) Por que a expectativa de vida no Brasil caiu?
e) Qual era o país cuja população tinha a expectativa de vida mais alta em 2020? E o que tinha a expectativa de vida mais baixa?
2. Copie as afirmações no caderno e marque V para as verdadeiras e F para as falsas.
a) (

) Todos os números que aparecem no texto são números racionais.
b) (

) Os números 2013, 2019 e 2020 não são números racionais.
c) (

) Em 2020, a expectativa de vida da população do Japão superava a da população da República Centro-Africana em mais de 30 anos.
d) (

) No texto, não aparece nenhum número inteiro.
3. Em 2020, trabalhar de casa era uma das recomendações para se proteger da côvid dezenóve. Analise estes dados da pesquisa realizada pela FGV Social e responda as questões no caderno.

CABRAL, M. C. Cai a expectativa de vida no Brasil. Qualé, São Paulo, edição 28, página 12, 3 a 17 de maio de 2021.
a) Na sua opinião, o que os dados revelam?
b) Seus pais ou responsáveis tiveram que trabalhar durante a pandemia? Como eles fizeram para se proteger da côvid dezenóve?
Respostas e comentários
1. a) maio de 2021
1. b) É um indicador social e de saúde que mostra o tempo que a população de um determinado local vive, em média.
1. c) 74,8 anos; 76,7 anos.
1. d) Porque houve um alto número de mortes causadas pela Covid-19.
1. e) Japão; República Centro-Africana.
2. a) V
2. b) F
2. c) V
2. d) F
3. a) Resposta pessoal.
3. b) Respostas pessoais.
Lendo e aprendendo
Bê êne cê cê:
• Competência geral 7 (a descrição está na página seis).
• Competência específica 4 (a descrição está na página sete).
Objetivos:
• Desenvolver a competência leitora.
• Reconhecer números racionais e números inteiros.
• Ler e interpretar dados apresentados em um infográfico.
• Refletir sobre a oportunidade de se trabalhar em casa durante a pandemia e sobre os cuidados para se proteger contra a Covid–19.
Tema contemporâneo transversal:

Inicie o trabalho com esta seção, fazendo a leitura compartilhada do texto com os estudantes. Depois, converse com eles sobre a temática trazida pelo texto. O texto atribui a queda da expectativa de vida ao alto número de mortes causadas pela Covid-19, mas é importante salientar que vários fatores exercem influência direta, como: serviços de saneamento ambiental, alimentação, índice de violência, poluição, serviços de saúde, educação, entre outros. Portanto, a diminuição na expectativa de vida está diretamente associada a uma piora geral nas condições de vida da população. Após essa conversa inicial, peça aos estudantes que realizem as atividades propostas.
• Na atividade 1, os estudantes vão responder a algumas questões sobre o texto. Após terminarem, peça aos estudantes que se reúnam com um colega para conversar sobre o que responderam. Acompanhe as duplas e tire as possíveis dúvidas.
• A atividade 2 explora o que foi estudado sobre os conjuntos numéricos. Esse é o momento oportuno para verificar se eles apresentam dificuldades para reconhecer números inteiros ou números racionais. Incentive-os a justificar cada uma das respostas, sejam elas falsas ou verdadeiras.
• A atividade 3 convida os estudantes a interpretar dados estatísticos sobre quem conseguia trabalhar de casa em 2020. Embora a resposta do item a seja pessoal, espera-se que eles percebam que os dados apresentados revelam que trabalhar de casa era um privilégio para os mais ricos e os de maior escolaridade. Por incentivar os estudantes a argumentar com base em dados confiáveis, este item da atividade favorece o desenvolvimento da competência geral 7 e da competência específica 4 da Bê êne cê cê.
No item b, eles devem relatar exemplos que vivenciaram em suas famílias. Reserve um tempo da aula para que possam compartilhar suas respostas. Aproveite a oportunidade para falar sobre as demais recomendações que foram adotadas na época visando à proteção contra a côvid dezenóve.
Fração geratriz de uma dízima periódica
Podemos determinar a fração que gera uma dízima periódica. Essa fração é chamada de fração geratriz. Observe os exemplos a seguir.
a) Vamos determinar a fração geratriz da dízima 0,777reticências
Indicamos a dízima periódica 0,777reticências por x.
x = 0,777reticências

Multiplicamos os dois membros dessa igualdade por 10 para obter outro número com a mesma parte decimal.
10x = 7,777reticências

Subtraímos, membro a membro,

de

, eliminando a parte decimal.
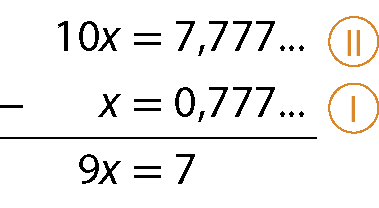
Assim:
Sentença matemática. x igual a 7 sobre 9.Portanto,
Fração. 7 sobre 9.é a fração geratriz de 0,777reticências
b) Vamos determinar a fração geratriz da dízima 4,151515reticências
Indicamos a dízima periódica 4,151515reticências por x.
x = 4,151515reticências

Multiplicamos os dois membros dessa igualdade por 100 para obter outro número com a mesma parte decimal.
100x = 415,151515reticências

Subtraímos, membro a membro,

de

, eliminando a parte decimal.
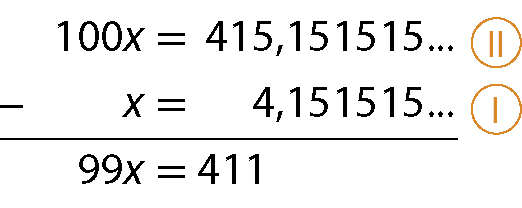
Assim:
Sentença matemática. x igual a 411 sobre 99.Portanto,
Fração. 411 sobre 99.é a fração geratriz de 4,151515reticências
c) Vamos determinar a fração geratriz da dízima 0,04777reticências
Indicamos a dízima periódica 0,04777reticências por y.
y = 0,04777reticências

Multiplicamos os dois membros dessa igualdade por 100 para obter uma dízima periódica simples.
100y = 4,777reticências

Multiplicamos os dois membros da igualdade

por 10 para obter outro número com a mesma parte decimal do segundo membro da igualdade

.
.1000y = 47,777reticências

Subtraímos, membro a membro,

de

, eliminando a parte decimal.
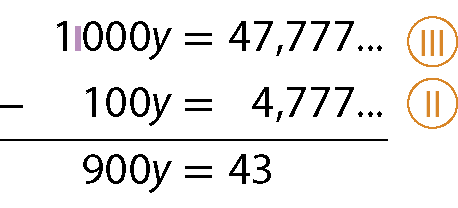
Assim:
Sentença matemática. y igual a 43 sobre 900.Portanto,
Fração. 43 sobre 900.é a fração geratriz de 0,04777reticências
Respostas e comentários
Fração geratriz de uma dízima periódica
Para explorar este tópico, verifique se há necessidade de rever ou sanar eventuais dúvidas relacionadas à multiplicação de decimais por potências de 10.
O processo de obtenção da fração geratriz de uma dízima periódica deve ser trabalhado de fórma cuidadosa para que os estudantes possam compreender o significado do que está sendo feito, e não apenas memorizar um processo que pode não fazer sentido para eles.
Atividades
Faça as atividades no caderno.
19. Determine a fração geratriz de cada uma das dízimas periódicas a seguir.
a)
dízima periódica 0,8 de período 8b) 3,151515reticências
c) 0,05222reticências
d) 0,007007007reticências
e) 2,4777reticências
f) 0,1444reticências
20.

Calcule mentalmente e registre no caderno os resultados de:
a) 5 + 0,777reticências
b) 8 + 0,333reticências
c) 0,6 + 0,222reticências
d) 1,5 + 0,555reticências
21. Efetue as operações a seguir.
a) 0,5 + 0,555reticências
b)
dízima periódica menos 2,7 de período 7⋅ 0,06
22.

Utilizando uma calculadora, determine o resultado de:
a) .8000 : .9000
b) 80 : 90
c) 16 : 18
d) 30 : 110
e) .3000 : .11000
f) 9 : 33
• Que regularidade você observou ao realizar essas divisões? Por que você acha que isso ocorreu?

4 Números irracionais
Luciano queria determinar o valor de
Sentenças matemáticas. Raiz quadrada de 2., ou seja, encontrar o número que elevado ao quadrado desse como resultado 2.
Inicialmente, ele verificou que
Sentenças matemáticas. Raiz quadrada de 2.é um número decimal situado entre 1 e 2.


A seguir, verificou que
Sentenças matemáticas. Raiz quadrada de 2.é um número decimal situado entre 1,4 e 1,5:
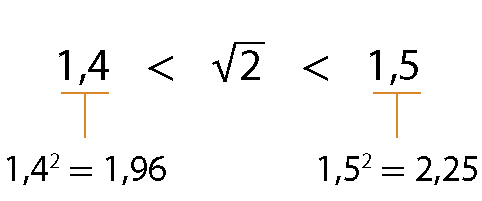
Luciano continuou buscando o valor de
Raiz quadrada de dois.e verificou que é um número situado entre 1,41 e 1,42.
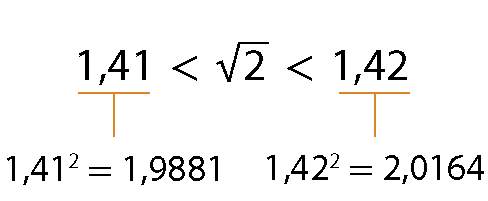
Ele avançou mais algumas etapas na busca da
Sentenças matemáticas. Raiz quadrada de 2., encontrando:
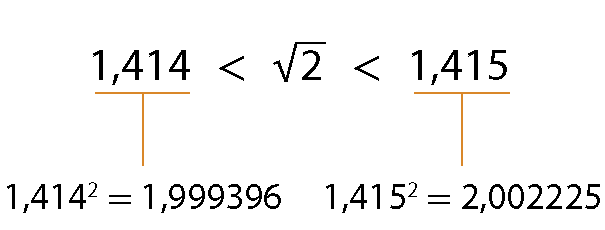
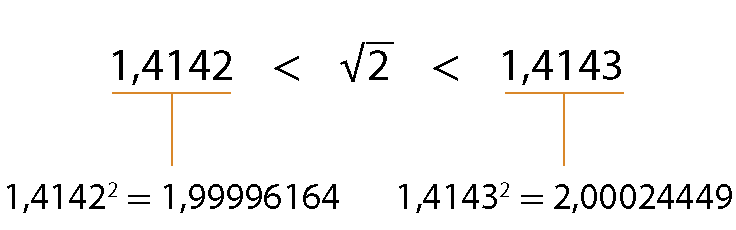
Luciano prosseguiu com esse raciocínio, mas não encontrou um número que, elevado ao quadrado, resultasse exatamente em 2. Desse modo, Luciano se perguntou:
Será que existe um número que, ao ser elevado ao quadrado, resulte em 2?
Respostas e comentários
19. a)
Fração. 8 sobre 9.19. b)
Fração 312 sobre 99.19. c)
Fração 47 sobre 900.19. d)
Fração. 7 sobre 999.19. e)
Fração 223 sobre 90.19. f)
Fração 13 sobre 90.20. a) 5,777reticências
20. b) 8,333reticências
20. c) 0,8222reticências
20. d) 2,0555reticências
21. a) 1,0555reticências
21. b) 0,1666reticências
22. a) 0,8888reticências
22. b) 0,8888reticências
22. c) 0,8888reticências
22. d) 0,272727reticências
22. e) 0,272727reticências
22. f) 0,272727reticências
22. Espera-se que os estudantes percebam que os itens a, b e c têm o mesmo resultado e que isso ocorre porque essas divisões, se fossem escritas na fórma de fração, seriam frações equivalentes. O mesmo ocorre com os itens d, ê e f.
• A atividade 20 explora o cálculo mental envolvendo números decimais. Atividades dessa mesma natureza contribuem para que os estudantes, aos poucos, ampliem seu repertório de estratégias de cálculo envolvendo esses e outros números.
Números irracionais
Objetivo:
Reconhecer os números irracionais como aqueles que apresentam representação decimal infinita e não periódica.
Justificativa
Os estudantes já se depararam com números cuja representação decimal é infinita e não periódica, por exemplo, no cálculo de raízes quadradas de números racionais que não são quadrados perfeitos. Reconhecer que números com essa característica pertencem a um conjunto próprio (conjunto dos números irracionais) consolida os conhecimentos adquiridos no que diz respeito aos conjuntos numéricos. Além disso, reconhecer a existência desse conjunto é um passo importante para que compreendam que o conjunto dos números reais é formado pelo conjunto dos números racionais e pelo conjunto dos números irracionais.
Mapeando conhecimentos
Escreva na lousa alguns números cuja representação decimal é infinita e não periódica e pergunte aos estudantes se os números que escreveu são racionais e o porquê. Ouça os argumentos deles. Caso algum estudante diga que algum dos números é racional, proponha que escreva o número na fórma
a sobre bcom a e b inteiros e b ≠ 0. Assim, ele deve perceber que esse número não pode ser escrito dessa fórma e, consequentemente, não é um número racional. Em seguida, peça aos estudantes que deem outros exemplos de números que não são racionais.
Para as aulas iniciais
Esclareça que não há um número irracional que também seja racional, simultaneamente. Proponha aos estudantes que façam uma pesquisa sobre os números irracionais. Depois, reserve um momento para que possam compartilhar o que pesquisaram.
Ao introduzir a noção de número irracional, explique aos estudantes a diferença entre a aproximação de um número irracional, por exemplo,
Sentenças matemáticas. Raiz quadrada de 2., dada por uma calculadora, e o próprio número
Sentenças matemáticas. Raiz quadrada de 2.. É fundamental oferecer aos estudantes um esclarecimento a respeito desse aspecto para que eles não confundam o número
Sentenças matemáticas. Raiz quadrada de 2.com uma de suas aproximações racionais, por exemplo, 1,414 ou 1,414214. Pesquisas mostram que é comum o estudante não diferenciar um número irracional de uma aproximação racional.
Após muitos cálculos e estudos, os matemáticos provaram que
Raiz quadrada de dois.não é racional, isto é, não pode ser expresso como decimal exato ou dízima periódica.
Números que têm infinitas casas decimais e não são periódicos são chamados de números irracionais.
Os matemáticos mostraram que existem infinitos números irracionais. Os números
Raiz quadrada de dois.,
Sentenças matemáticas. Raiz quadrada de 3.,
Raiz quadrada de cinco.,
Raiz quadrada de sete.,
Sentenças matemáticas. Raiz quadrada de 11.,
Sentenças matemáticas. Raiz quadrada de 13.,
Sentenças matemáticas. Raiz quadrada de 17.e seus simétricos são alguns exemplos de números irracionais.

Veja que interessante
Faça a atividade no caderno.
O número π (pi)
O número cujo valor corresponde ao quociente da medida do comprimento de qualquer circunferência pela medida de comprimento de seu diâmetro (dobro da medida de comprimento do raio), na mesma unidade, é chamado de número π (pi).
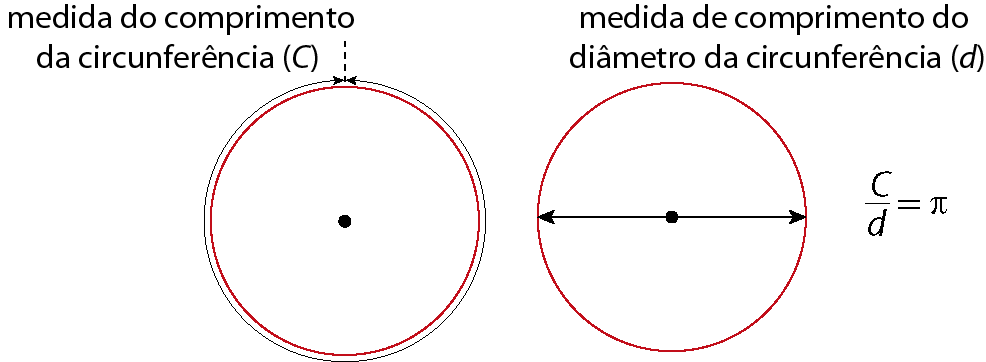
Determinar o valor de π foi, durante séculos, um desafio para os matemáticos. Eles provaram que o número π tem infinitas casas decimais e não apresenta período; portanto, é um número irracional. Confira a seguir o número π com 20 casas decimais.
3,14159265358979323846reticências
O número π causa um fascínio tão grande em determinadas pessoas que elas se dedicam a calcular mais e mais casas decimais. O professor Yasumasa Kanada, da Universidade de Tóquio, no Japão, é conhecido por bater vários recordes mundiais, entre 1981 e 2002, no cálculo de casas decimais do π. Nessa busca, em 2002, ele empregou um supercomputador durante mais de seiscentas horas, atingindo 1,241 trilhões de casas.
Em 2011, Shigeru Kondo, engenheiro japonês, obteve o número π com cêrca de 10 trilhões de casas decimais após usar um programa de computador que calcula trilhões de dígitos durante 371 dias, ou seja, mais de um ano.
Atividade
Os recordes de casas decimais do π são quebrados frequentemente. Por isso, pesquise qual é o recorde atual.
Atividades
Faça as atividades no caderno.
23. Escreva, em seu caderno, os números que são irracionais.
a) 0
b)
Raiz quadrada de dois.c) ‒3,14
d)
Raiz quadrada de cinco.e) 0,777reticências
f) π
g) 1,73
h) 0,54
i)
Raiz quadrada de quatro.j)
3 sobre novecentosk)
Menos Raiz quadrada de três.l)
Raiz quadrada de 4924.

Utilizando uma calculadora, determine, com aproximação de duas casas decimais, o valor de:
a)
Raiz quadrada de 2, fim da raiz, mais, raiz quadrada de 3.b)
pi menos 2 vezes raiz quadrada de 3.c)
Raiz quadrada de 2, fim da raiz, vezes raiz quadrada de 3.d)
Raiz quadrada de 3, fim da raiz, menos, raiz quadrada de 2.Respostas e comentários
Veja que interessante: Em abril de 2022, o recorde era da Universidade de Ciências Aplicadas de Graubünden, na Suíça, por determinar 62,8 trilhões de casas decimais de π em agosto de 2021.
23. itens b, d, f, k
24. a) 3,15
24. b) ‒0,32
24. c) 2,45
24. d) 0,32
Se julgar pertinente, explore um pouco mais a história dos números irracionais: ficou claro para os matemáticos que as frações não eram suficientes para medir todas as grandezas, mesmo que fossem positivas. Assim, na Antiguidade grega, ficou comprovado que, por exemplo, o lado de um quadrado é incomensurável com sua diagonal, ou seja, que não existe um segmento de reta, por menor que seja sua medida de comprimento, que possa servir de unidade de medida comum ao comprimento do lado e da diagonal de um mesmo quadrado de maneira que as medidas de ambos sejam múltiplos inteiros dessa unidade. Tal constatação, ao longo da história, acabou por provocar a introdução dos números irracionais e a ampliação do conjunto dos números racionais para o conjunto dos números reais. Se julgar adequado, proponha aos estudantes que façam uma pesquisa a respeito da descoberta da existência de segmentos de reta incomensuráveis e da crise que esse fato gerou na Matemática na Antiguidade. Oriente-os a buscar, principalmente, a contribuição de Eudoxo para a superação de tal crise e explorar a relação entre os segmentos de reta incomensuráveis e os números irracionais.
É importante comentar com os estudantes que existem infinitos números irracionais, assim como existem infinitos números naturais, inteiros e racionais. Para ajudá-los a se convencerem de tal fato, proponha que escrevam no caderno exemplos de números irracionais, tais como 0,1011011101111reticências, 0,1234567890070007reticências etcétera. Ajude os estudantes a perceber por que esses números são irracionais mostrando que não há período.
• Na atividade 24, calcule também o valor de
Sentenças matemáticas. Raiz quadrada de 5., comentando que o resultado não é o mesmo que
Raiz quadrada de 2, fim da raiz+
Raiz quadrada de 3.. Se achar interessante, calcule
Sentenças matemáticas. Raiz quadrada de 6., comentando que é igual ao produto
Raiz quadrada de 2, fim da raiz⋅
Raiz quadrada de 3..
Sugestão de atividade extra
Aproveitando a seção Veja que interessante sobre o número π, solicite aos estudantes que, em duplas, façam uma pesquisa a respeito da história desse número, visando aprofundar as informações tratadas no livro e perceber que vários conceitos matemáticos se desenvolveram ao longo do processo de busca pelo valor exato de π (enquanto se pensava que isso era possível) e de aproximações mais precisas.
25.

Com uma calculadora, determine o valor aproximado, com cinco casas decimais, de:
a)
raiz quadrada de 10b)
Sentença matemática. Abre parênteses a fração 4 sobre 3, fecha parênteses, elevado a 4c)
22 sobre 7.d)
Fração de numerador 13 vezes raiz quadrada de 146 e denominador 50e)
Raiz quadrada de 2, fim da raiz, mais, raiz quadrada de 3.f)
355 sobre 113.• Quais desses valores são mais próximos do valor de π?
26. Represente na reta numérica os números a seguir.
a)
Raiz quadrada de 2.b)
Menos raiz quadrada de 2.c)
2 vezes raiz quadrada de 2.d)
Menos 2 vezes raiz quadrada de 2.27. Coloque em ordem crescente os números a seguir.
Sentenças matemáticas. Raiz quadrada de 3; menos 1,2; a fração 10 sobre 3; 2 vezes raiz quadrada de 2; a fração 4 sobre 3; 0,5.

5 Números reais
Os números naturais e os números inteiros são também números racionais. Se juntarmos em um só conjunto os números racionais e os números irracionais, obteremos o conjunto dos números reais, cujo símbolo é

.
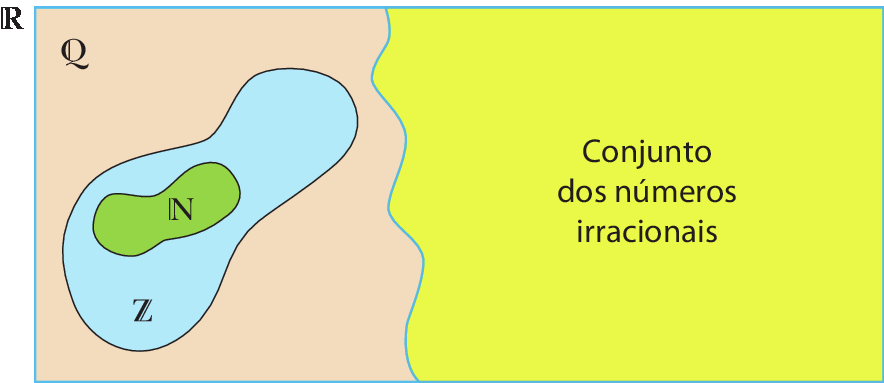
Portanto, todos os números que estudamos até agora pertencem ao conjunto dos números reais.
Atividades
Faça as atividades no caderno.
28. Analise estes números.
‒35;
Fração. Raiz quadrada de 3.;
Fração 40 sobre 5.; 1,222; π; 0,444reticências;
Menos raiz quadrada de 2.;
Fração 1 sobre 7.a) Quais deles são números naturais?
b) Quais deles são números inteiros?
c) Quais deles são números racionais?
d) Quais deles são números irracionais?
e) Quais deles são números reais?
f) Apresente-os em ordem crescente.
29. Dê um exemplo de:
a) número racional e não inteiro maior que 2;
b) número real e não racional maior que 3;
c) número inteiro e não natural maior que 4.
30. Escreva em seu caderno os números que pertencem ao conjunto dos números reais.
a)
0 sobre 5.b)
Raiz quadrada de 0.c) ‒0,005
d)
Raiz quadrada de 64.e)
Menos raiz quadrada de 36.f)
Raiz quadrada de 1.g) 11 111
h) ‒π
31. Em cada item, escreva três números:
a) inteiros maiores que ‒15 e menores que ‒11;
b) racionais maiores do que
Menos três sobre quatroe menores que
Menos um sobre dois.;
c) irracionais maiores que 1,3010010001;
• Apresente as respostas anteriores em ordem decrescente.
32. Avalie as sentenças a seguir e copie as verdadeiras no caderno.
a) Todo número inteiro é racional.
b) Todo número real é racional.
c) Toda dízima periódica é número racional.
d) Todo número irracional é real.
e) Todo número que tem infinitas casas decimais é irracional.
f) Todo número real é irracional.
g) O número zero é real, inteiro e racional.
Respostas e comentários
25. a) 3,16228
25. b) 3,16049
25. c) 3,14286
25. d) 3,14159
25. e) 3,14626
25. f) 3,14159
25.
355 sobre 113.e
Fração de numerador 13 vezes raiz quadrada de 146 e denominador 5026.
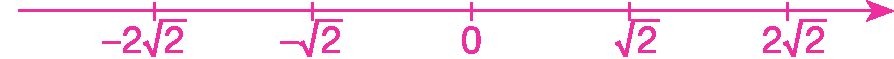
27. ‒1,2; 0,5 ;
4 terços;
Raiz quadrada de 3.;
2 vezes raiz quadrada de 2.;
10 terços28. a)
Fração 40 sobre 5.28. b) ‒35;
Fração 40 sobre 5.28. c) 1,222; 0,444...;
Fração. 1 sobre 7.;
Fração 40 sobre 5.; ‒35
28. d)
Menos raiz quadrada de 2.,
Raiz quadrada de 3., π
28. e) Todos são reais.
28. f) ‒35; ‒
Raiz quadrada de 2.;
Fração. 1 sobre 7.; 0,444reticências; 1,222;
Raiz quadrada de 3.; π;
Fração 40 sobre 5.29. a) Exemplo de resposta: 2,1
29. b) Exemplo de resposta: π
29. c) não existe
30. Todas as alternativas.
31. a) ‒14, ‒13 e ‒12
31. b) Exemplo de resposta:
Sentença matemática. menos 7 sobre 10.,
Sentença matemática. menos 6 sobre 10.,
Sentença matemática. menos 55 sobre 100.31. c) Exemplo de resposta:
Raiz quadrada de 2.,
Raiz quadrada de 3.,
Raiz quadrada de 531. Exemplo de resposta:
;
Raiz quadrada de 3.;
Raiz quadrada de 2.;
Sentença matemática. menos 55 sobre 100.;
Sentenças matemáticas. menos 6 sobre 10.;
Sentença matemática. menos 7 sobre 10.; ‒12; ‒13; ‒14
32. a) verdadeira
32. b) falsa
32. c) verdadeira
32. d) verdadeira
32. e) falsa
32. f) falsa
32. g) verdadeira
Números reais
Objetivo:
Compreender o conjunto dos números reais.
Justificativa
Compreender o conjunto dos números reais permite aos estudantes relacionarem todos os conjuntos numéricos estudados até aqui e efetuar qualquer adição, subtração, multiplicação e divisão com números reais (exceto a divisão por zero), bem como extrair a raiz quadrada de qualquer número positivo.
Mapeando conhecimentos
Copie o diagrama a seguir na lousa e peça aos estudantes que o reproduzam no caderno.
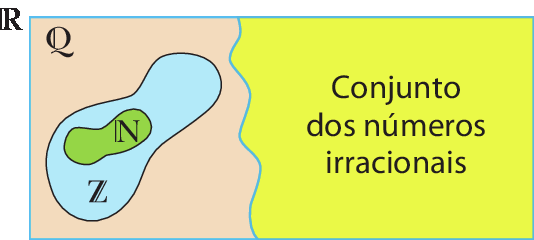
Depois, pergunte aos estudantes o que o
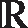
está representando nesse diagrama e se conhecem o significado desse símbolo. Espera-se que identifiquem que, reunindo o conjunto dos números racionais (

) com o conjunto dos números irracionais, obtemos um conjunto representado por
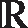
(conjunto dos números reais).
Aproveite também para fazer o seguinte questionamento: “Ao dispormos os números reais na reta numérica, ficam ‘buracos’ como ao dispormos os números racionais? Por quê?”.
Para as aulas iniciais
Retome o questionamento feito na dinâmica inicial e leve os estudantes a perceber que existe uma correspondência entre cada número real e cada ponto da reta numérica. Proponha na sequência que representem alguns números reais na reta numérica, utilizando aproximações para números irracionais quando necessário.
• Na atividade 31, item c, comente que o número 1,3010010001 é racional, mas que devem dar exemplos de números irracionais maiores do que este racional. Lembre-os de que os irracionais possuem infinitas casas decimais e não possuem período.
• A atividade 32 explora a relação entre os conjuntos numéricos. Se julgar pertinente, amplie a atividade solicitando a eles que justifiquem as alternativas falsas.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Números naturais
O conjunto dos números naturais é dado por:

= {0, 1, 2, 3, 4, reticências}
Todo número natural tem um sucessor e todo número natural, com exceção do zero, tem um antecessor.
Sequência numérica
É a sequência cujos elementos são números escritos em certa ordem. Cada elemento dela é chamado de termo da sequência.
A lei de formação é uma regra que mostra como a sequência progride ou é formada.
Por exemplo, na sequência (0, 3, 6, 9, 12, reticências), a lei de formação é á1 = 0 e án + 1 = 3 + án.
1. Escreva no caderno a afirmação verdadeira.
a) 9 é um número natural.
b) ‒5 é um número natural.
c)
Fração. 1 sobre 4.é um número natural.
2. Indique o antecessor e o sucessor dos números a seguir.
a) 211
b) 199
c) 300
3. No caderno, escreva os seis primeiros termos de uma sequência numérica na qual á1 = 2, á2 = 5 e án = án ‒ 2 + án ‒ 1, em que n > 2.
Números inteiros
O conjunto dos números inteiros é dado por:

= {reticências, ‒4, ‒3, ‒2, ‒1, 0, 1, 2, 3, reticências}
4. Escreva em seu caderno o que se pede.
a) Os números inteiros entre 7 e 12.
b) Os números inteiros entre ‒11 e ‒8.
5. Uma conta estava com saldo negativo de R$ 610,00seiscentos e dez reais. Após um depósito de R$ 3.200,00três mil duzentos reais, qual será o novo saldo?
Números racionais
O conjunto dos números racionais pode ser dado por:

Fração geratriz de uma dízima periódica
Na divisão de 7 por 3, o algarismo 3 do quociente 2,333reticências continuará se repetindo infinitamente; chamamos esse quociente de dízima periódica.
A fração que gera uma dízima periódica é chamada de fração geratriz. Por exemplo,
Fração. 7 sobre 9.é a fração geratriz de 0,777reticências
6. Quais números a seguir são racionais?
a) ‒4
b) 0
c)
Raiz quadrada de 3.d)
Fração. 1 sobre 4.7. Escreva a representação decimal de:
a)
Fração 1 sobre 2b)
Fração. 3 sobre 5.c)
Fração. 123 sobre 100.d)
Fração. Menos 10 sobre 9.8. Escreva a fração geratriz destas dízimas.
a)
Dízima. 0 vírgula 5 com período 5.b) 0,1333reticências
c) 1,232323reticências
d) 0,02444reticências
Números irracionais
Os números irracionais têm infinitas casas decimais e não são periódicos.
9. Escreva no caderno as sentenças verdadeiras.
a) 3,2 é um número racional
b)
Sentença matemática. Raiz quadrada de 16é um número irracional
c)
Menos Raiz quadrada de três.é um número inteiro
d)
Sentença matemática. Menos raiz quadrada de 7.é um número irracional
Números reais
A união do conjunto dos números racionais e dos conjunto dos números irracionais forma o conjunto dos números reais, cujo símbolo é

.
10. Analise os números a seguir.
Sentenças matemáticas. menos 12; raiz quadrada de 7; a fração 15 sobre 3; 1,88; pi; a fração 3 sobre 7.
• Agora, no caderno, indique a qual conjunto numérico cada um deles pertence (naturais, inteiros, racionais, irracionais e ou ou reais).
Respostas e comentários
1. a) Verdadeira
1. b) Falsa
1. c) Falsa
2. a) antecessor: 210; sucessor: 212
2. b) antecessor: 198; sucessor: 200
2. c) antecessor: 299; sucessor: 301
3. 2, 5, 7, 12, 19, 31
4. a) 8, 9, 10, 11
4. b) ‒10, ‒9
5. R$ 2.590,00 dois mil quinhentos e noventa reais
6. itens a, b, d
7. a) 0,5
7. b) 0,6
7. c) 1,23
7. d) ‒1,111reticências
8. a)
Resposta: 8. a) A fração 5 sobre 9.8. b)
Resposta: 8. b) A fração 12 sobre 90.8. c)
Resposta: 8. c) A fração 122 sobre 99.8. d)
Resposta: 8. d) A fração 22 sobre 900.9. a) V
9. b) F
9. c) F
9. d) V
10. –12 pertence aos conjuntos dos inteiros, racionais e reais;
Raiz quadrada de sete.pertence aos conjuntos dos irracionais e reais;
15 sobre 3.pertence ao conjunto dos naturais, inteiros, racionais e reais; 1,88 pertence ao conjunto dos racionais e reais;
Sentenças matemáticas. menos 12; raiz quadrada de 7; a fração 15 sobre 3; 1,88; pi; a fração 3 sobre 7.pertence ao conjunto dos irracionais e reais;
Três sobre setepertence ao conjunto dos racionais e reais.
Revisão dos conteúdos deste capítulo
Números naturais
• Na atividade 1, os estudantes devem identificar se os números 9, ‒5 e
Fração. 1 sobre 4.são números naturais. Espera-se que percebam que ‒5 é um número inteiro negativo e
Fração. 1 sobre 4.está escrito na fórma
Fração. a sobre b.com a e b inteiros e b diferente de zero. Logo, ‒5 e
Fração. 1 sobre 4.não são números naturais. Portanto, apenas a afirmação do item a é verdadeira.
• Na atividade 2, espera-se que os estudantes entendam que antecessores e sucessores correspondem, respectivamente, a números que “vêm imediatamente antes” e números que “vêm imediatamente depois” de um número natural estabelecido. Se achar necessário, antes da atividade, forneça alguns números naturais para a turma identificar seus antecessores e sucessores.
• A atividade 3 apresenta a lei de formação de uma sequência numérica para que os estudantes escrevam alguns termos. Verifique se eles notam que os dois primeiros termos foram dados e que só precisam identificar mais quatro termos, substituindo-os na lei de formação apresentada.
Números inteiros
• Na atividade 4, os estudantes devem identificar números inteiros em um intervalo numérico. Caso tenham dúvidas, destaque que o termo “entre” não considera os extremos do intervalo e incentive-os a utilizar a reta numérica, principalmente no item b.
• A atividade 5 explora a ideia de uma operação entre números inteiros negativos e positivos. Caso os estudantes apresentem dificuldades, retome a leitura do enunciado, destacando que o saldo inicial é negativo, ou seja, inicia-se a situação com −R$ 610,00seiscentos e dez reais.
Números racionais
• Na atividade 6, os estudantes devem identificar quais números são racionais. Se tiverem dúvidas, peça que tentem escrever cada número como uma fração cujo numerador e o denominador são números inteiros.
• As atividades 7 e 8 são complementares: na atividade 7, os estudantes identificam os números decimais correspondentes às frações; na atividade 8, identificam as frações correspondentes aos números decimais (nesse caso, dízimas periódicas). Se os estudantes tiverem dificuldades para escrever a fração geratriz correspondente a cada dízima periódica, com base em alguns exemplos, retome o processo utilizado, explicando-o passo a passo.
Números irracionais
• Na atividade 9, os estudantes devem identificar se alguns números são racionais, irracionais ou inteiros. Se considerarem que a afirmação do item b é verdadeira, pergunte-lhes se conhecem algum número cujo quadrado é igual a 16 e leve-os a perceber que
Sentença matemática. Raiz quadrada de 16.= 4.
Números reais
A atividade 10 explora a ideia de que os números reais equivalem à união de todos os outros conjuntos abordados; portanto, os estudantes devem identificar que todos os números fornecidos são números reais. Caso tenham dificuldades para indicar os números pertencentes aos outros conjuntos numéricos, retome as características de cada conjunto.
Glossário
- c.
- : abreviação do latim circa, que significa “por volta de”. Antes de um ano, indica que a data apontada é aproximada.
- Voltar para o texto