Página 76

Unidade 2

Capítulo 4 Ângulos e transformações geométricas

Capítulo 5 Polígonos

Capítulo 6 Probabilidade

Fotografia. Homem de cabelo curto, camisa listrada azul e calça clara com os braços levantados. À frente dele, mulher de cabelos grisalhos e camisa azul. À esquerda, dois homens em pé.

Segundo o Instituto Brasileiro de Geografia e Estatísca (í bê gê É), em 2019 os idosos brasileiros representavam 16,2% da população do país, e projeções indicavam que esse percentual dobrará em 2045.

Você conhece os direitos dos idosos? Na sua opinião, as pessoas viverem mais tempo significa que estão vivendo saudavelmente e tendo suas necessidades atendidas? Ao final desta Unidade, você responderá essas e outras questões.

Respostas e comentários

Abertura da Unidade

Bê êne cê cê:

• Competências gerais 7 e 9 (as descrições estão na página seis).

• Competência específica 8 (a descrição está na página sete).

Objetivos:

• Motivar a turma a estudar os conteúdos da Unidade 2.

• Conscientizar os estudantes sobre a importância de respeitar e valorizar os idosos.

Tema contemporâneo transversal:

Para iniciar a Unidade, pergunte qual é a ideia que eles têm a respeito do termo ”expectativa de vida”. Incentive-os a verbalizar o que pensam e a conversar entre si. Explique que esse é um conceito estatístico relacionado ao bem-estar da população. Se achar conveniente, apresente algum gráfico publicado pelo í bê gê É mostrando como a expectativa de vida dos brasileiros modificou-se nos últimos anos. Espera-se que eles percebam que a expectativa de vida dos brasileiros vem aumentando ao longo dos anos e que isso está relacionado a melhorias nas áreas da saúde, econômica, educação, saneamento básico, entre outras. Finalize dizendo que a área da Matemática responsável por essa análise é a Probabilidade e Estatística.

Convide-os a refletir sobre a outra questão proposta. Pergunte se eles conhecem o Estatuto do Idoso. Verifique depois se, na opinião deles, esses direitos garantem melhor qualidade de vida aos idosos e, consequentemente, um aumento da expectativa de vida.

As questões propostas favorecem o desenvolvimento das competências gerais 7 e 9 e da competência específica 8 de Matemática, uma vez que promovem o diálogo e a argumentação com base em dados confiáveis.

No capítulo 4, serão estudados ângulos, figuras geométricas e transformações geométricas. No capítulo 5, os objetos de estudo serão os polígonos, seus elementos e classificações. Por fim, no capítulo 6, serão aprofundadas as ideias de probabilidades.

Na seção É hora de extrapolar, os estudantes pesquisarão sobre os direitos dos idosos no Brasil e terão a oportunidade de analisar dados do Relatório Mundial de Envelhecimento e Saúde da OMS. Por fim, irão elaborar e apresentar uma cartilha sobre direitos dos idosos com sugestões de prevenções e cuidados para a população.

Sugestão de proposta para a promoção da saúde mental dos estudantes

A dança é uma atividade que faz bem ao corpo e à mente. Pode ser praticada por qualquer pessoa independentemente da idade, agilidade ou tipo de corpo. Além disso, é uma fórma de socialização. Considere firmar parceria com professores de outros componentes curriculares e implementar um projeto de dança na escola. Projetos como esse proporcionam momentos de diversão e convívio que contribuem para a melhoria da saúde psicológica.

Página 77

Capítulo 4 Ângulos e transformações geométricas

Trocando ideias

Considerada a mais antiga arte em cerâmica do Brasil e uma das mais antigas das Américas, a arte marajoara é o conjunto de artefatos, sobretudo em cerâmica, dos habitantes da Ilha de Marajó, no Pará.

Fotografia. Vasos cilíndricos de cerâmicas. Da esquerda para direita: vaso marrom com formas geométricas douradas e avermelhadas. Vaso branco com formas geométricas em formato de losangos e retângulos na cor vermelha e preta. Dois vasos de cor clara com padrões geométricos na cor marrom. — Grafismos presentes nas peças de cerâmica feitas por moradores locais da Ilha de Marajó.

▸

Reúna-se com três colegas e pesquisem sobre a arte marajoara. Depois, compartilhem com a turma o que tiverem encontrado.

▸

Que transformações geométricas você reconhece nos grafismos presentes nas peças de cerâmica marajoara anteriores?

Neste capítulo, vamos retomar e nos aprofundar em assuntos como ângulos e transformações geométricas.

Conheça mais

No site do Museu Paraense Emílio Goeldi, há um catálogo com diversos exemplares da cerâmica marajoara no livro digital Cerâmica marajoara: a comunicação do silêncio, de Lilian Bayma de Amorim.

Respostas e comentários

Trocando ideias: primeiro item: resposta pessoal; segundo item: exemplos de resposta podem ser translações, rotações e reflexões.

CAPÍTULO 4 – ÂNGULOS E TRANSFORMAÇÕES GEOMÉTRICAS

Trocando ideias

Bê êne cê cê:

• Competências gerais 2, 5, 6, 7 e 9 (as descrições estão na página seis).

• Competências específicas 3 e 8 (as descrições estão página sete).

Objetivos:

• Levantar os conhecimentos previamente adquiridos pelos estudantes sobre as transformações geométricas.

• Pesquisar sobre a arte marajoara.

Tema contemporâneo transversal:

Forme uma roda de conversa com os estudantes e comente que a Ilha de Marajó é a maior ilha fluviomarinha do mundo, cercada pelos rios Amazonas e Tocantins, e pelo Oceano Atlântico. Mostre a localização dessa ilha em um mapa e conte que os antigos marajoaras faziam vasilhas, chocalhos, potes, urnas funerárias, estatuetas, bonecas para crianças, cachimbos, porta-venenos para flechas etcétera Atualmente, moradores locais da ilha, produzem réplicas de várias peças, especialmente os vasos, para fins comerciais.

Em seguida, proponha que se organizem em grupos para realizar a pesquisa solicitada no primeiro item. Caso julgue oportuno, associe esse conteúdo ao componente curricular Artes, apresentando materiais que possam servir de fonte de consulta para eles ou planejar uma pesquisa na sala de informática. Outra possibilidade é solicitar que façam essa pesquisa em casa e reservar um tempo da aula seguinte para que possam conversar sobre o que pesquisaram. Momentos como esse contribuem para o desenvolvimento das competências gerais 2, 5, 6, 7 e 9 da Bê êne cê cê, uma vez que valorizam a manifestação artística dos marajoaras e a diversidade de saberes e vivências culturais, utilizam tecnologias digitais da informação para realizar a pesquisa, argumentam com base em informações confiáveis e exercitam o diálogo e a empatia. A competência específica 8 também tem o seu desenvolvimento favorecido por conta da interação promovida pela tarefa.

Na questão proposta no segundo item, os estudantes vão mobilizar o que estudaram sobre transformações geométricas em anos anteriores. Recorde com eles o que são grafismos e verifique se identificam translações, rotações e reflexões nos grafismos presentes nas cerâmicas da fotografia. É importante incentivá-los a explicar suas respostas. Você pode ampliar a proposta e solicitar que reproduzam algum desses grafismos ou que criem grafismos similares. Essa relação entre Matemática e Arte contribui para o desenvolvimento da competência específica 3 de Matemática.

Página 78

1 Ângulos

Duas semirretas de mesma origem determinam no plano duas regiões, que, nesta figura, estão destacadas com cores diferentes.

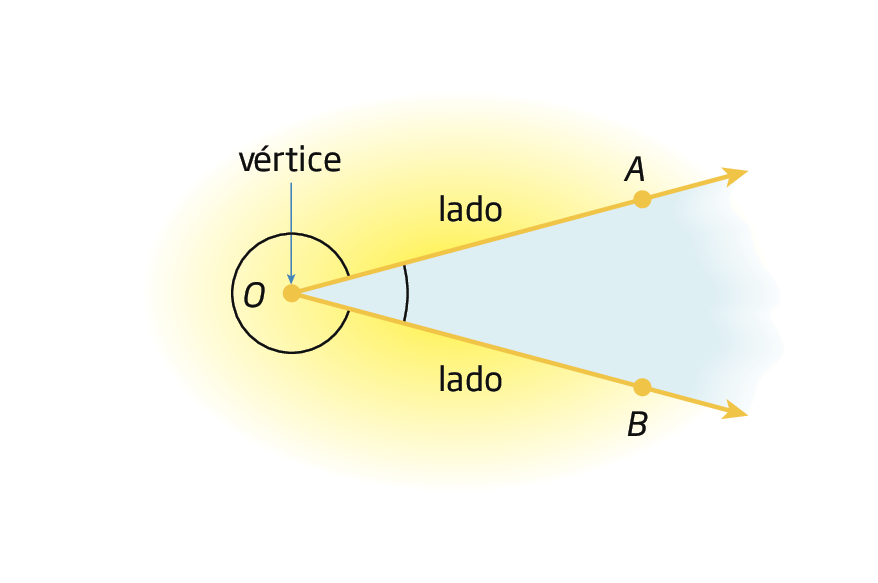
Figura geométrica. À esquerda, ponto O (vértice). De O parte um segmento de reta com ponto A (lado) e um segmento de reta com ponto B (lado). Destaque para ângulo externo ao redor de O.

As semirretas

\vec{O A}

\vec{O B}

determinam dois ângulos que podem ser indicados por

A \hat{O} B

Ângulo é a união de duas semirretas de mesma origem, com uma das regiões do plano limitada por elas.

Classificação de ângulos

De acordo com a medida da abertura, um ângulo pode ser classificado em:

• Ângulo nulo

Figura geométrica. Segmento de reta com ponto O na extremidade esquerda, o ponto A ao centro e à direita o ponto B.

m e d (A \hat{O} B) = 0 °

• Ângulo de uma volta

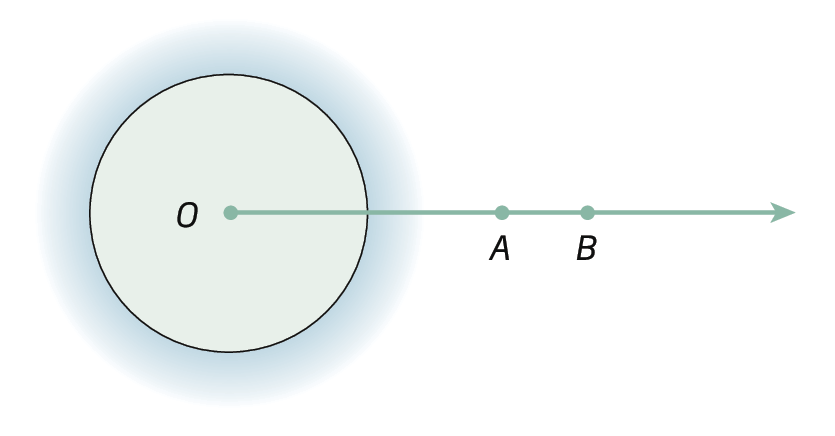
Figura geométrica. Segmento de reta com ponto O na extremidade esquerda, ponto A no centro e à direita o ponto B. Destaque para ângulo ao redor do ponto O, indicando uma volta completa.

m e d (A \hat{O} B) = 360 °

• Ângulo reto

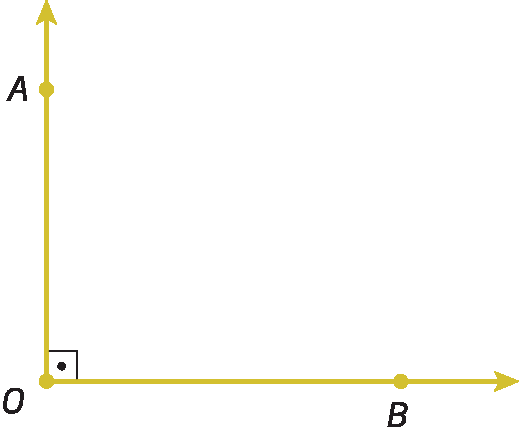
Figura geométrica. À esquerda há um ponto O. Partindo dele saem dois segmentos de reta, formando um ângulo de 90º entre eles. A abertura entre os segmentos está voltada para a parte superior direita. No segmento vertical há um ponto A e no horizontal, um ponto B.

m e d (A \hat{O} B) = 90 °

• Ângulo raso ou de meia-volta

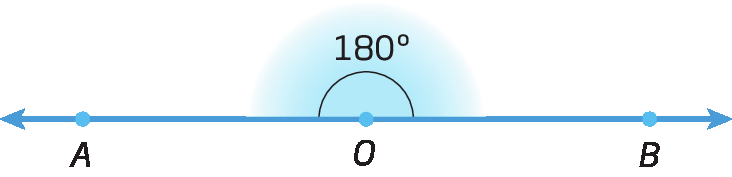
Figura geométrica. Segmento de reta com ponto O no centro, ponto A à esquerda e ponto B à direita. Destaque para ângulo de 180 graus ao redor de O.

m e d (A \hat{O} B) = 180 °

• Ângulo agudo

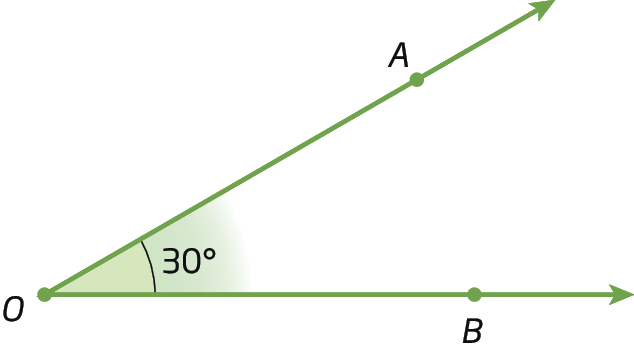
Figura geométrica. À esquerda há um ponto O. Partindo dele saem dois segmentos de reta, formando um ângulo de 30º entre eles. A abertura entre os segmentos está voltada para a parte superior direita. No segmento superior há um ponto A e no inferior, um ponto B.

0 ° < m e d (A \hat{O} B) < 90 °

• Ângulo obtuso

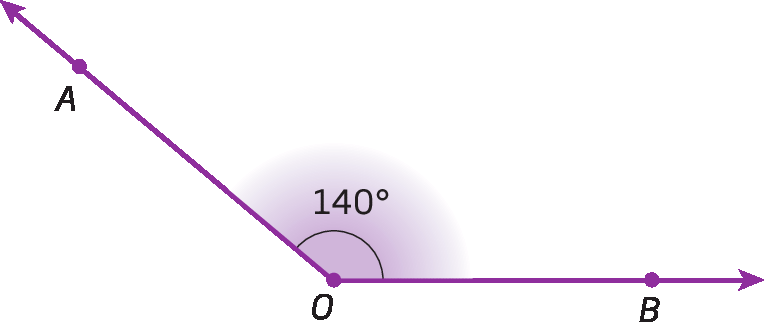
Figura geométrica. À esquerda há um ponto O. Partindo dele saem dois segmentos de reta, formando um ângulo de 140º entre eles. Um dos segmentos é oblíquo, inclinado para a esquerda e outro é horizontal. A abertura entre os segmentos está voltada para a parte superior direita. No segmento oblíquo há um ponto A e no horizontal, um ponto B.

90 ° < m e d (A \hat{O} B) < 180 °

Respostas e comentários

Ângulos

Bê êne cê cê:

Habilidade ê éfe zero oito ême ah um cinco.

Objetivos:

• Retomar o conceito e a classificação de ângulos.

• Reconhecer ângulos congruentes.

• Compreender o conceito de bissetriz de um ângulo.

• Compreender o conceito de mediatriz de um segmento de reta.

• Construir com régua e compasso ângulos cuja abertura mede 90graus, 60graus, 45graus e 30graus.

Justificativa

Retomar o conceito de ângulos e classificá-los é importante para que possam avançar no estudo de outros conceitos e procedimentos de Geometria.

O reconhecimento de ângulos congruentes é útil nas construções com régua e compasso e, também, no estudo da semelhança de figuras.

Os conceitos de bissetriz e mediatriz mobilizam os conhecimentos anteriores dos estudantes sobre retas, semirretas, segmentos de reta, ângulos e medidas de abertura de ângulos.

A construção com régua e compasso de ângulos ditos notáveis (90graus, 60graus, 45graus e 30graus) é importante no estudo futuro das razões trigonométricas (seno, cosseno, tangente etcétera).

Mapeando conhecimentos

Peça aos estudantes que construam um ângulo cuja abertura mede 60graus e com o auxílio de um transferidor tracem a semirreta que divide esse ângulo em dois ângulos com a mesma medida de abertura. Em seguida, pergunte: “Qual é a origem desta semirreta? Qual é a medida da abertura de cada ângulo formado? A semirreta que você traçou recebe um nome especial. Você sabe que nome é esse?”. Se achar oportuno, organize a turma de modo que realizem a tarefa considerando também ângulos cuja abertura mede 90graus e 30graus.

Proponha que tracem um segmento de reta, encontrem o ponto médio dele e tracem uma reta perpendicular ao segmento passando por esse ponto médio utilizando suas estratégias pessoais. Depois, pergunte: “Como podemos chamar essa reta?”.

Para as aulas iniciais

Na seção Revisão dos conteúdos de anos anteriores, retoma-se a medida da abertura de um ângulo, a classificação de ângulos e o conceito de ângulos congruentes. Peça aos estudantes que leiam essa revisão e façam as atividades 16 e 17.

Defina bissetriz e mediatriz. Peça que explorem as ferramentas “Bissetriz” e “Mediatriz” disponíveis no GeoGebra. A ideia é apenas se familiarizar com as ferramentas e com os conceitos.

Explique para a turma a notação de ângulo agudo, 0grau < medida de(

A \hat{O} B

) < 90graus: “a medida da abertura de

A \hat{O} B

está entre 0grau e 90graus, excluindo esses extremos do intervalo”. A mesma ideia vale para a notação de ângulo obtuso.

(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.

Página 79

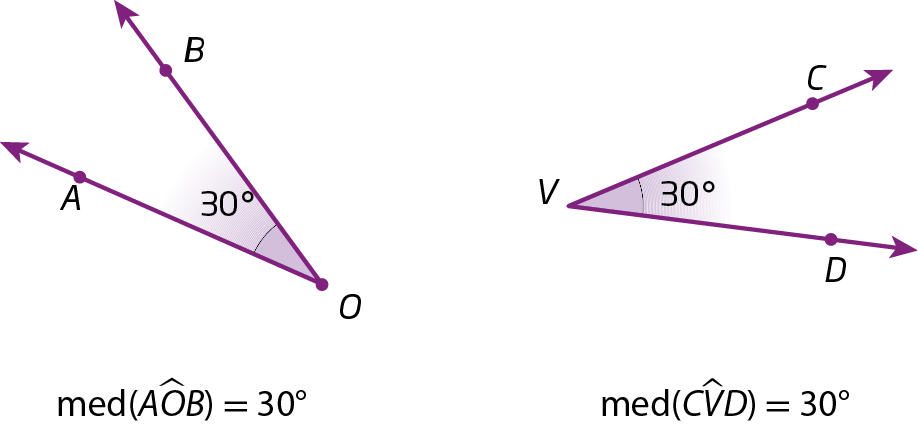
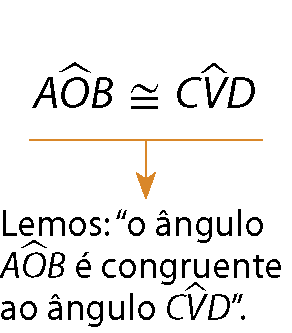
Ângulos congruentes

Dois ângulos são congruentes quando têm a mesma medida de abertura.

Ilustração. Duas ilustrações, uma ao lado da outra. À esquerda há um ponto O. Partindo dele saem dois segmentos de reta, formando um ângulo de 30 graus entre eles. A abertura entre os segmentos está voltada para a parte superior esquerda. No segmento superior há um ponto B e no inferior, um ponto A. Legenda: Medida de abertura do ângulo AOB, igual 30 graus.
À direita há um ponto V. Partindo dele saem dois segmentos de reta, formando um ângulo de 30 graus entre eles. A abertura entre os segmentos está voltada para a direita. No segmento superior há um ponto C e no inferior um ponto D.
Legenda: medida de abertura do ângulo CVD igual, 30 graus.

Esquema. Acima, À esquerda o ângulo AOB, à direita símbolo similar ao sinal de igual com símbolo similar ao acento tio acima e à direita o ângulo CVD. Abaixo de tudo, seta laranja apontando para a informação: Lemos o ângulo AOB é congruente ao ângulo CVD.

Atividades

Faça as atividades no caderno.

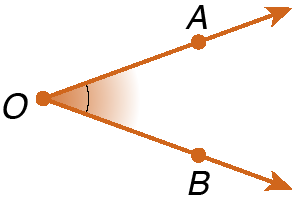
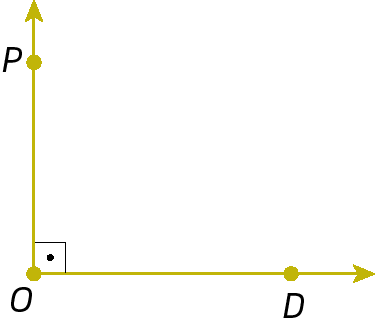
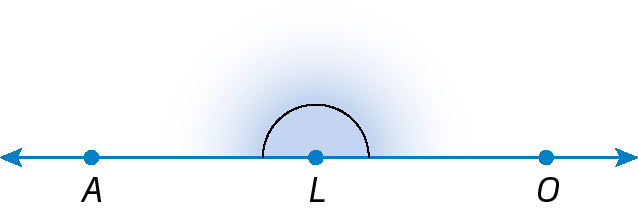
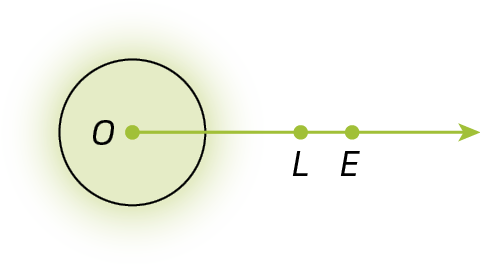
1. Classifique os ângulos a seguir em nulo, raso, de uma volta, reto, agudo ou obtuso.

Figura geométrica. À direita há um ponto O. Partindo dele saem dois segmentos de reta, formando um ângulo menor que 90º entre eles. A abertura entre os segmentos está voltada para a direita. No segmento superior há um ponto A e no inferior, um ponto B.

Figura geométrica. Segmento de reta com ponto A na extremidade esquerda, o ponto B ao centro e à direita o ponto C.

Figura geométrica. À esquerda há um ponto O. Partindo dele saem dois segmentos de reta, um deles está completamente na vertical e outro completamente na horizontal. A abertura entre os segmentos está voltada para a parte superior direita. No segmento vertical há um ponto P e no horizontal, um ponto D. Destaque para o menor ângulo entre os segmentos.

Figura geométrica. À esquerda há um ponto O. Partindo dele saem dois segmentos de reta, formando um ângulo maior que 90º entre eles. Um dos segmentos é oblíquo, inclinado para a esquerda e outro é horizontal. A abertura entre os segmentos está voltada para a parte superior direita. No segmento oblíquo há um ponto C e no horizontal, um ponto D.

Figura geométrica. Segmento de reta com ponto L no centro, ponto A à esquerda e ponto O à direita. Destaque para ângulo ao redor de L.

Figura geométrica. Segmento de reta com ponto O na extremidade esquerda, ponto L no centro e à direita o ponto E. Destaque para ângulo ao redor do ponto O, indicando uma volta completa.

2. Classifique cada ângulo destacado nos quadriláteros a seguir em agudo, reto ou obtuso.

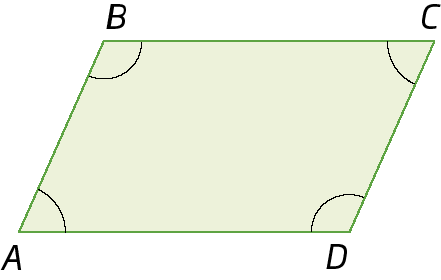
Figura geométrica. Paralelogramo ABCD. Segmento AB paralelo a CD, inclinados para a direita.

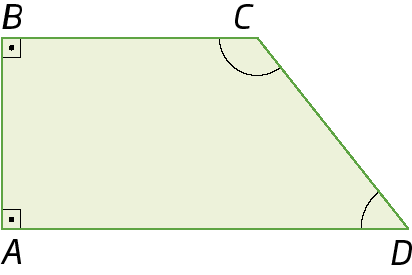
Figura geométrica. Trapézio ABCD com segmento AB completamente na vertical, segmento BC paralelo a AD e completamente na horizontal e segmento CD inclinado para a esquerda.

3. Determine o valor de a, sabendo que

A \hat{O} B

M \hat{N} P

são congruentes.

Figura geométrica. À esquerda, ponto O. De O, segmento de reta horizontal com ponto B. segmento de reta diagonal com ponto A. Em O, destaque para o ângulo dado por fração 2 a sobre 2 + 30 graus.

Figura geométrica. À esquerda, ponto N. De N partem o segmento de reta diagonal com ponto M e o segmento de reta diagonal com ponto P. Em N, destaque para o ângulo fração 3 a sobre 4 + 27 graus.

Respostas e comentários

1. a) ângulo agudo

1. b) ângulo nulo

1. c) ângulo reto

1. d) ângulo obtuso

1. e) ângulo raso

1. f) ângulo de uma volta

2. a) agudos:

\hat{C}

\hat{A}

; obtusos:

\hat{B}

\hat{D}

2. b) retos:

\hat{A}

\hat{B}

; agudo:

\hat{D}

; obtuso:

\hat{C}

Ângulos congruentes

Após abordar o conceito de ângulos congruentes, distribua para os estudantes uma folha com a representação de alguns polígonos como retângulos, triângulos equiláteros, hexágonos regulares etcétera Depois, peça que determinem as medidas das aberturas dos ângulos internos deles com o auxílio de um transferidor e identifiquem os ângulos congruentes.

• Na atividade 3, comente que, se dois ângulos são congruentes, as medidas das aberturas desses ângulos são iguais. Os estudantes devem chegar à seguinte sentença:

\frac{2 a}{3}

+ 30graus =

\frac{3 a}{4}

+ 27graus

12 ⋅

(\frac{2 a}{3} + 30 °)

= 12 ⋅

(\frac{3 a}{4} + 27 °)

8a + 12 ⋅ 30graus = 9a + 12 ⋅ 27graus

a = 36graus

Portanto, a = 36graus.

Página 80

Bissetriz de um ângulo

Na figura a seguir, a semirreta

\vec{O C}

, interna ao ângulo

A \hat{O} B

, divide

A \hat{O} B

em dois ângulos congruentes. Assim, a semirreta

\vec{O C}

é a bissetriz do ângulo

A \hat{O} B

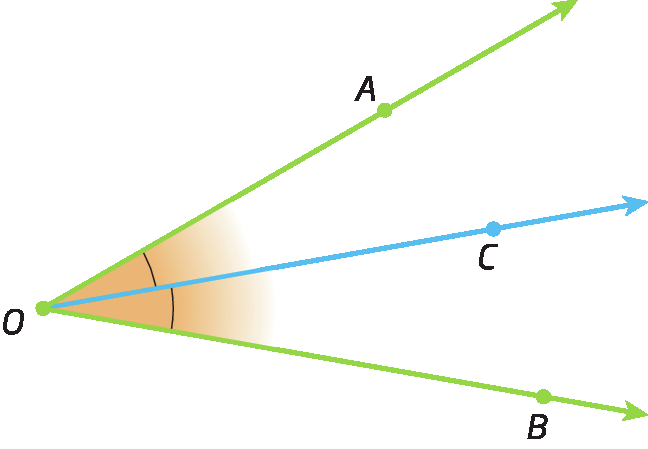
Figura geométrica. À esquerda, ponto O. De O, reta diagonal com ponto B. Reta diagonal com ponto A. Em O, reta (bissetriz) com ponto C.

A \hat{O} C ≅ C \hat{O} B

Bissetriz de um ângulo é a semirreta interna a esse ângulo com origem no vértice do ângulo que o divide em dois ângulos congruentes.

Construção geométrica da bissetriz de um ângulo

Para construir a bissetriz do ângulo

A \hat{O} B

, podemos realizar os seguintes passos.

Cuidado! Evite acidentes ao usar o compasso.

1º) Dado um ângulo

A \hat{O} B

, centramos o compasso em O e, com uma abertura qualquer, determinamos os pontos C e D sobre as semirretas

\vec{O A}

\vec{O B}

, respectivamente.

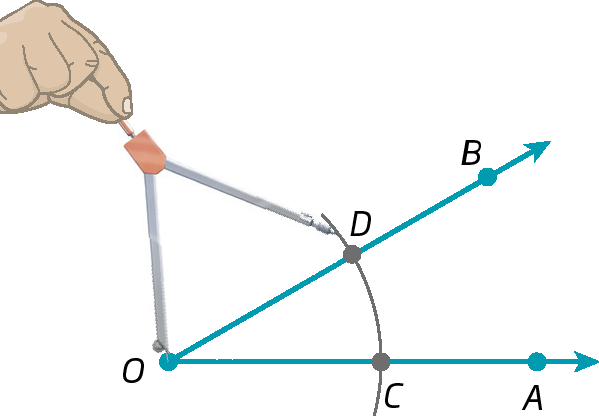
Ilustração. À esquerda, ponto O. De O, segmento de reta diagonal com ponto B e ponto D entre os pontos O e B. Segmento de reta horizontal com ponto A e ponto C entre os pontos O e A. Em O, destaque para a mão de uma pessoa com compasso aberto, ponta seca em O, traçando arco CD.

2º) Centramos o compasso em C e em D e traçamos arcos que se cruzam na região interna do ângulo, obtendo um ponto ê.

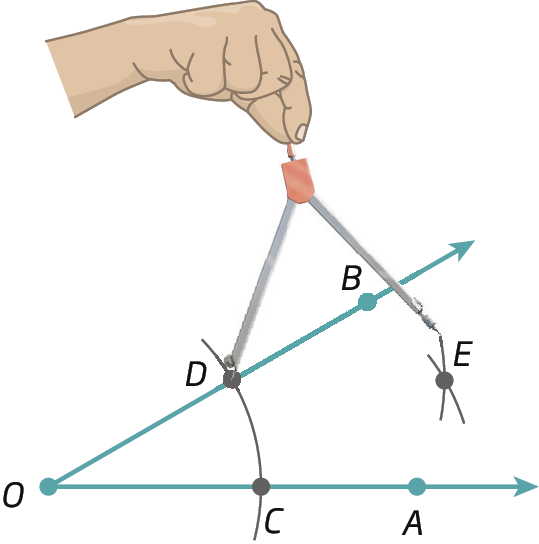
Ilustração. À esquerda, ponto O. De O, segmento de reta diagonal com ponto B e ponto D entre O e B. Reta horizontal com ponto A e ponto C entre O e A. Destaque para a mão de uma pessoa com compasso aberto com ponta seca em D traçando o ponto E no centro, entre as retas.

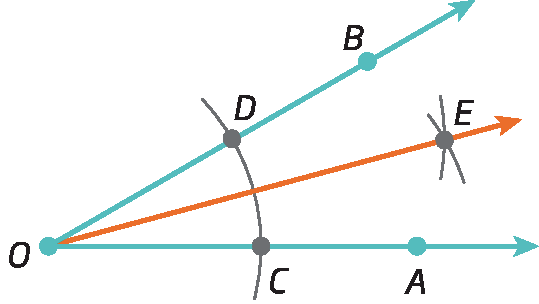
3º) Traçamos

\vec{O E}

determinando, assim, a bissetriz de

A \hat{O} B

Ilustração. À esquerda, ponto O. De O, reta diagonal com ponto B e ponto D entre O e B. Reta horizontal com ponto A e ponto C entre O e A. Destaque para a Bissetriz de O até ponto E entre retas A e B.

Tecnologias digitais em foco

Bissetriz

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para construir a bissetriz de um ângulo e realizar algumas investigações.

Construa

Siga os passos a seguir para construir a bissetriz de um ângulo.

1º) Construa um ângulo

A \hat{O} B

qualquer. Para isso, utilize a ferramenta

Ilustração. Botão quadrado com uma reta diagonal com dois pontos sobre ela.

e trace duas semirretas de mesma origem óh:

\vec{O A}

\vec{O B}

Respostas e comentários

Bissetriz de um ângulo

As justificativas para as construções geométricas não serão trabalhadas nesse momento. Entretanto, os passos da construção podem ser compreendidos pelos estudantes, bem como as propriedades que são consequências dessas construções. As justificativas de cada um dos passos serão trabalhadas em outros capítulos da coleção.

Por exemplo, a justificativa para o procedimento trabalhado aqui para a construção da bissetriz de um ângulo está no fato de que ODEC é um losango; nesse quadrilátero, as diagonais são bissetrizes dos ângulos internos do losango.

Também é possível justificar essa construção observando que ODC é um triângulo isósceles; nessa situação,

\overline{O E}

é a reta suporte da mediatriz e também da bissetriz do ângulo

C \hat{O} D

Você pode retomar e justificar a construção da bissetriz no capítulo 7, quando são estudados os triângulos e quadriláteros.

Tecnologias digitais em foco

Bê êne cê cê:

• Competência geral 5 (a descrição está na página seis).

• Competência específica 2 (a descrição está na página sete).

• Habilidade ê éfe zero oito ême ah um cinco.

Objetivo:

Construir a bissetriz de um ângulo utilizando o software GeoGebra ou outro software de geometria dinâmica.

Bissetriz

Se achar conveniente, mostre aos estudantes outro modo de construir a bissetriz de um ângulo qualquer.

1. Dado um ângulo

B \hat{O} C

qualquer, trace uma circunferência c de centro em O e raio com qualquer medida de comprimento.

2. Marque os pontos P em

\vec{O B}

e Q em

\vec{O C}

, intersecções dessas semirretas com a circunferência c.

3. Trace uma circunferência d de centro em P, e raio r com qualquer medida de comprimento.

4. Trace uma circunferência e de centro em Q, com mesma medida de comprimento de raio de d.

5. Marque o ponto D, uma das intersecções entre as circunferências d e e.

6. Trace a semirreta

\vec{O D}

, que é a bissetriz do ângulo

B \hat{O} C

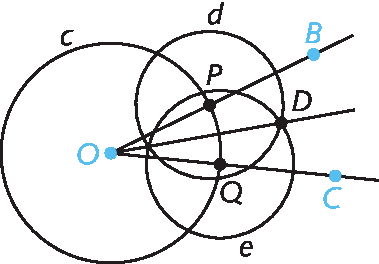
Figura geométrica. À esquerda, ponto O. De O, segmento de reta diagonal com ponto B . Segmento de reta diagonal com ponto C . Destaque para os pontos O, B e C, em azul. Circunferência c com centro em O, cortando os segmentos nos pontos P e Q. P entre O e B e Q entre O e C. Circunferência d com centro em P e circunferência e com centro em Q. Ponto D é um dos pontos de intercessão entre as circunferências d e e.

As atividades propostas nessa seção podem ser realizadas com qualquer software de geometria dinâmica. Na falta de acesso a computadores, a proposta pode ser adaptada para ser realizada com a utilização de papel e instrumentos de desenho (régua, compasso, transferidor etcétera).

Página 81

Tecnologias digitais em foco

2º) Siga o passo a passo da construção geométrica da bissetriz de um ângulo da página anterior e construa a bissetriz

\vec{O C}

do ângulo

A \hat{O} B

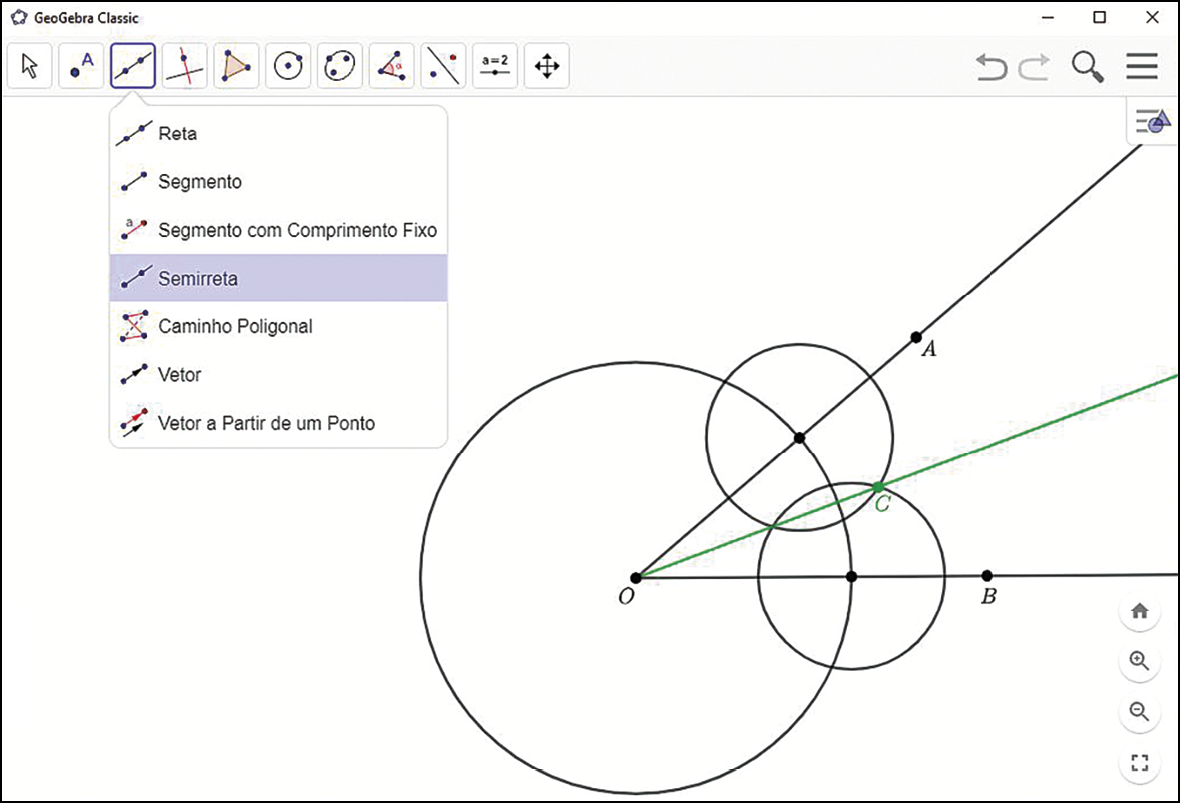
Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão com uma reta diagonal com dois pontos, aba selecionada: semirreta. Na tela abaixo, circunferência centrada no ponto O. À direita, duas circunferências com centro na fronteira da circunferência centrada em O, que se interseccionam em dois pontos, o ponto C é o ponto de interseção fora da circunferência centrada em O, o outro ponto de interseção está dentro da circunferência centrada em O. De O, reta horizontal com ponto B, localizado fora das circunferências e reta diagonal com ponto A, localizado fora das circunferências. Entre as retas, bissetriz passando pelo ponto C, destacada em verde.

Utilize a ferramenta

Ilustração. Botão quadrado com uma circunferência com um ponto no centro e um ponto na fronteira.

para construir circunferências que podem ter qualquer medida de comprimento do raio.

Utilize a ferramenta

Ilustração. Botão quadrado com uma reta diagonal com ponto central e um raio.

para construir circunferências que têm uma medida de comprimento do raio definida.

Explore

Faça o que se pede usando as ferramentas do GeoGebra.

a) Meça a abertura dos ângulos

C \hat{O} A

B \hat{O} C

. Em seguida, movimente os pontos móveis da construção. Que relação podemos identificar entre as medidas realizadas?

b) Marque um ponto D qualquer na semirreta

\vec{O C}

. Utilize a ferramenta

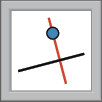
Ilustração. Botão quadrado com duas retas cruzadas.

e trace uma reta r, perpendicular a

\vec{O A}

passando por D, e uma reta s, perpendicular a

\vec{O B}

passando por D. Depois, marque ê e F, intersecções das perpendiculares com os lados do ângulo.

• O que as medidas de comprimento dos segmentos

\overline{D E}

\overline{D F}

representam?

c) Meça o comprimento desses segmentos. Em seguida, movimente o ponto D sobre a semirreta

\vec{O C}

. Que relação podemos identificar entre as medidas realizadas?

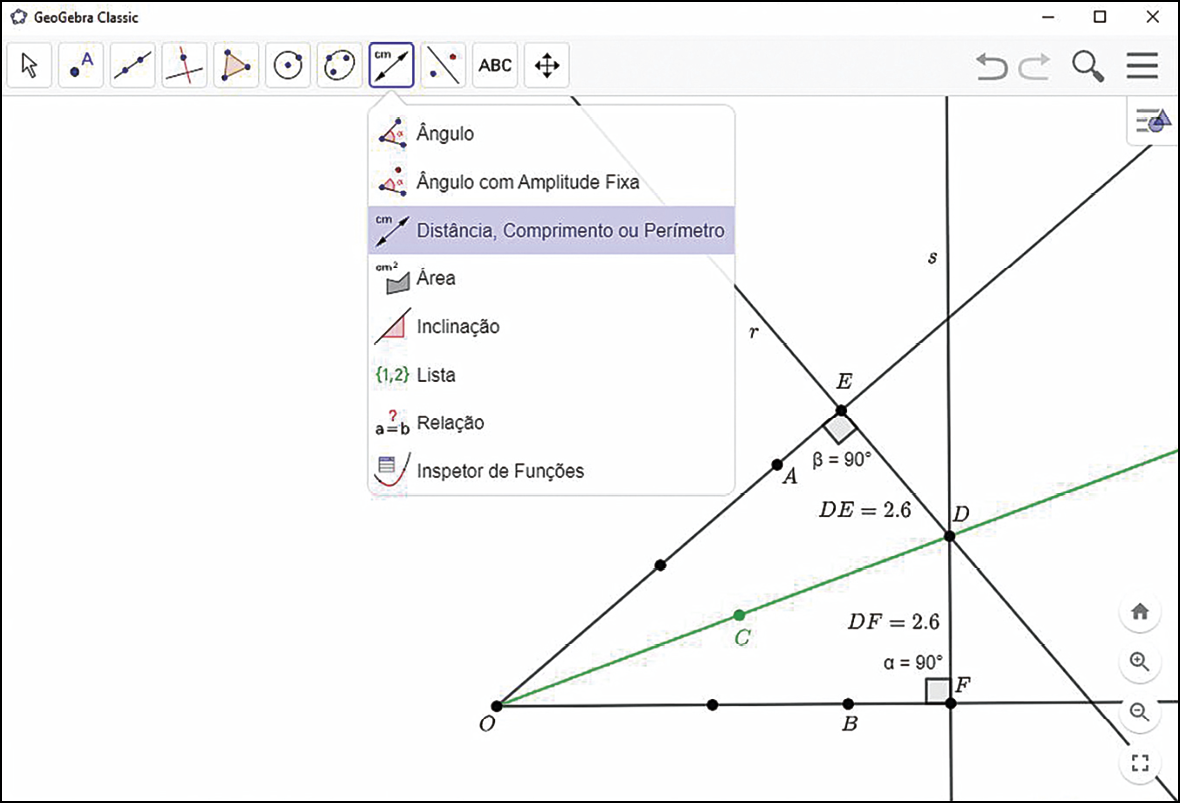
Ilustração. Software de geometria. Acima, botões de comandos. Destaque para botão com uma reta diagonal, aba selecionada: distância, comprimento ou perímetro. Na tela abaixo, semirreta horizontal com ponto sem rótulo e pontos B e F. Semirreta diagonal inclinada para a direita com ponto sem rótulo, ponto A e ponto E. Reta s formando um angulo alfa de 90º no ponto F, cortando a reta horizontal. Reta r, diagonal inclinada para a esquerda, cortando diagonal no ponto E, formando um ângulo beta de 90º e cortando a reta s no ponto D. Semirreta destacada em verde, saindo de O, entre as outras duas semirretas, cortando a reta s no ponto D e com ponto C entre os pontos O e D. Indicação que o segmento de reta DE mede 2.6 e segmento DF mede 2.6.

Observação

Note que nessa imagem “escondemos” algumas construções. Você pode fazer o mesmo clicando com o botão direito do mouse sobre a construção e desabilitando a opção “Exibir Objeto”. É interessante utilizar esse recurso e esconder alguns traçados, permitindo melhor visualização nas investigações.

Respostas e comentários

Explore: a) Elas são iguais.

b) Resposta: As medidas das distâncias entre o ponto D e a semirreta

\vec{O A}

e entre D e a semirreta

\vec{O B}

, respectivamente.

c) Espera-se que os estudantes percebam que dê ê = DF, ou seja, que as medidas das distâncias entre D e cada lado do ângulo são iguais.

No item a do Explore, os estudantes terão a oportunidade de verificar experimentalmente que a bissetriz de um ângulo é o lugar geométrico dos pontos do plano que estão à uma mesma medida de distância dos lados desse ângulo.

Página 82

Mediatriz de um segmento de reta

Na figura a seguir, a reta m é perpendicular ao segmento de reta

\overline{A B}

e passa pelo ponto M, ponto médio de

\overline{A B}

. O ponto médio de um segmento de reta é aquele que o divide em dois segmentos congruentes. Assim, m é mediatriz do segmento de reta

\overline{A B}

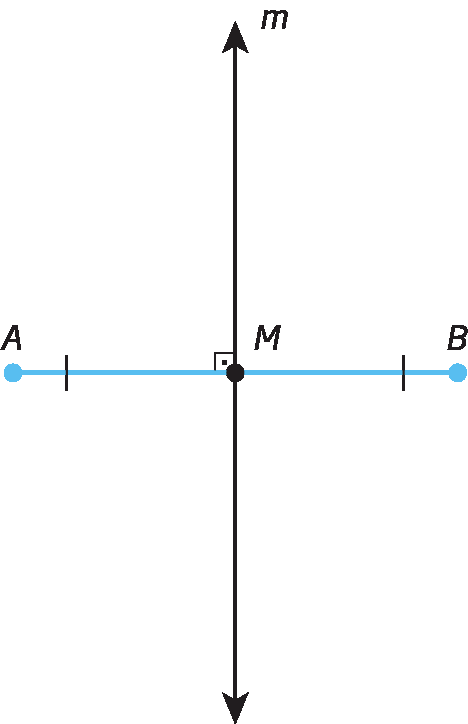
Figura geométrica. Segmento AB com ponto M no centro em destaque, azul. Em M, reta vertical m cruzando segmento AB.

Mediatriz é a reta perpendicular a um segmento de reta que passa pelo ponto médio desse segmento.

Observação

Podemos indicar a medida de comprimento de um segmento de reta

\overline{A B}

por

med (\overline{A B})

ou, simplesmente, por AB.

Construção geométrica da mediatriz de um segmento de reta

Para construir a mediatriz do segmento de reta

\overline{A B}

, podemos realizar os seguintes passos.

Cuidado! Evite acidentes ao usar o compasso.

1º) Dado um segmento de reta

\overline{A B}

, centramos o compasso em a e, com uma abertura maior que a metade do segmento de reta, traçamos um arco de circunferência.

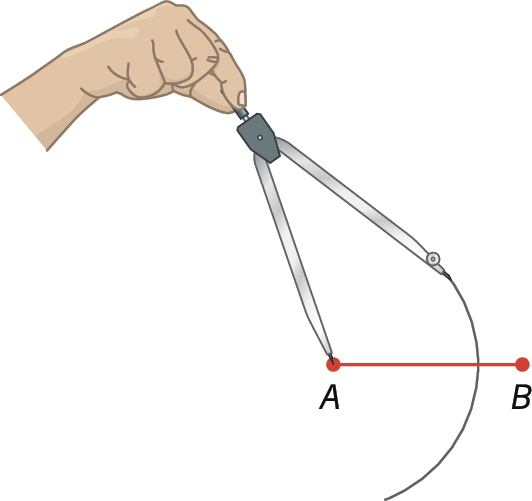
Ilustração. Segmento AB. Destaque para a mão de uma pessoa com compasso aberto com ponta seca em A, traçando arco próximo de B.

2º) Centramos o compasso em B e, com a mesma abertura, traçamos outro arco que cruze o primeiro. Com isso, obtemos os pontos C e D.

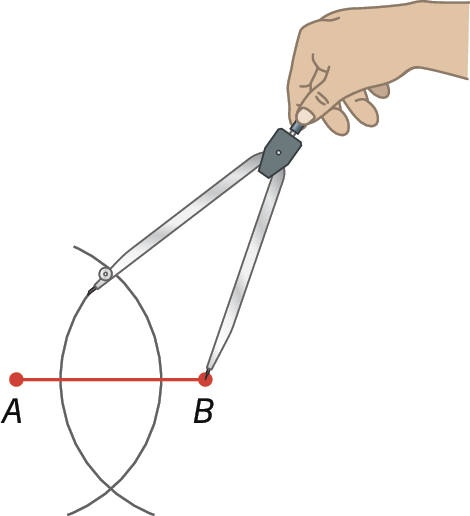
Ilustração. Segmento AB. Destaque para a mão de uma pessoa com compasso aberto, ponta seca em B traça arco próximo de A.

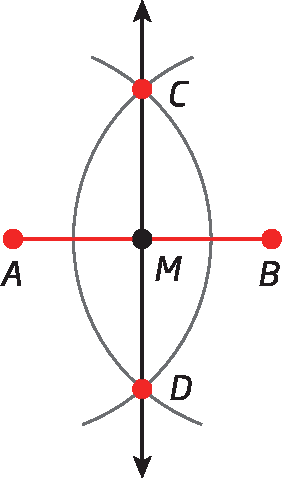
3º) Traçamos

\overset{\leftrightarrow}{C D}

determinando, assim, a mediatriz de

\overline{A B}

. Confira que M, intersecção de

\overline{A B}

com

\overset{\leftrightarrow}{C D}

, é o ponto médio do segmento de reta.

Ilustração. Segmento AB. No centro, reta vertical que intersecciona AC no ponto M . Acima da reta vertical, ponto C e abaixo, ponto D. Dois arcos que se interseccionam entre si e a reta nos pontos C e D. Um arco com abertura voltada para a direita e outro com abertura voltada para a esquerda.

Respostas e comentários

Mediatriz de um segmento

A definição de mediatriz cita duas propriedades: é perpendicular ao segmento e passa por seu ponto médio.

Também é possível definir a mediatriz em termos de um lugar geométrico, como veremos no tópico a seguir. O desenvolvimento dessa definição torna evidente as propriedades citadas.

Oriente os estudantes quanto aos cuidados no manuseio do compasso a fim de evitar acidentes.

Sugestão de atividade extra

Proponha a seguinte situação para os estudantes: “Dado um segmento de reta

\overline{A B}

, siga os mesmos passos para a construção da mediatriz desse segmento, mas utilize como abertura do compasso a medida do comprimento do segmento de reta

\overline{A B}

.”

Ao encontrarem as intersecções C e D, peça que liguem as extremidades do segmento a essas intersecções e pintem o interior das figuras, formando dois triângulos. Pergunte aos estudantes o que eles podem dizer em relação aos lados desses triângulos e ao segmento de reta

\overline{A B}

. Os estudantes devem perceber que os triângulos são equiláteros e as medidas de comprimento dos seus lados são iguais a AB.

Nessa atividade, os estudantes poderão constatar que a construção da mediatriz de um segmento de reta pode ser utilizada para representar triângulos isósceles (ou triângulos equiláteros que são casos particulares).

Essas propriedades serão retomadas no capítulo 7.

Página 83

Tecnologias digitais em foco

Mediatriz e ponto médio

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para construir a mediatriz e o ponto médio de um segmento de reta e realizar algumas investigações.

Construa

Siga os passos seguintes para construir a mediatriz e o ponto médio de um segmento de reta.

1º) Utilize a ferramenta

Ilustração. Botão quadrado com uma reta diagonal com dois pontos.

e construa um segmento de reta

\overline{A B}

2º) Siga o passo a passo do tópico Construção geométrica da mediatriz de um segmento de reta e construa a mediatriz m e o ponto médio M do segmento de reta

\overline{A B}

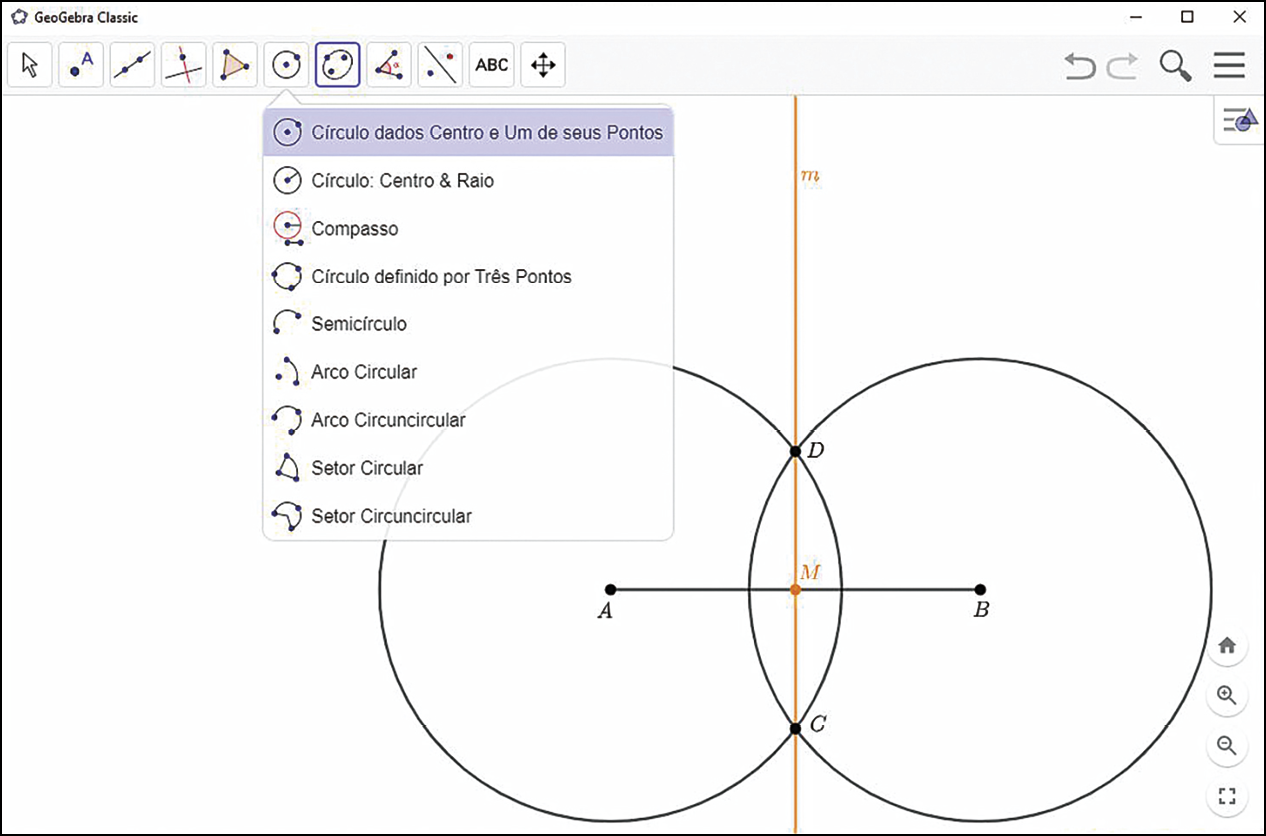
Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão circunferência com ponto no centro e na fronteira. Na tela abaixo, reta vertical m interseccionando ao meio o segmento AB no ponto M. Há duas circunferências de mesmo tamanho, uma centrada em A e outra em B, que se interseccionam nos pontos D e C, sendo que os pontos D e C estão sobre a reta m.

Explore

Faça o que se pede usando as ferramentas do GeoGebra.

a) Utilize a ferramenta

Ilustração. Botão quadrado com uma reta diagonal e cm ao lado.

e meça o comprimento dos segmentos de reta

\overline{A M}

\overline{M B}

. Depois, utilize a ferramenta

Ilustração. Botão quadrado com duas retas unidas à esquerda e ângulo alfa.

e meça a abertura dos ângulos formados entre m e o segmento de reta

\overline{A B}

. Por fim, movimente a construção por meio dos pontos móveis (a ê B). Que relação podemos identificar em relação às medidas obtidas?

b) Marque um ponto P qualquer sobre a reta m e, utilizando a ferramenta

, meça o comprimento dos segmentos de reta

\overline{A P}

\overline{P B}

. Depois, movimente o ponto P ao longo da reta m. Que relação podemos identificar?

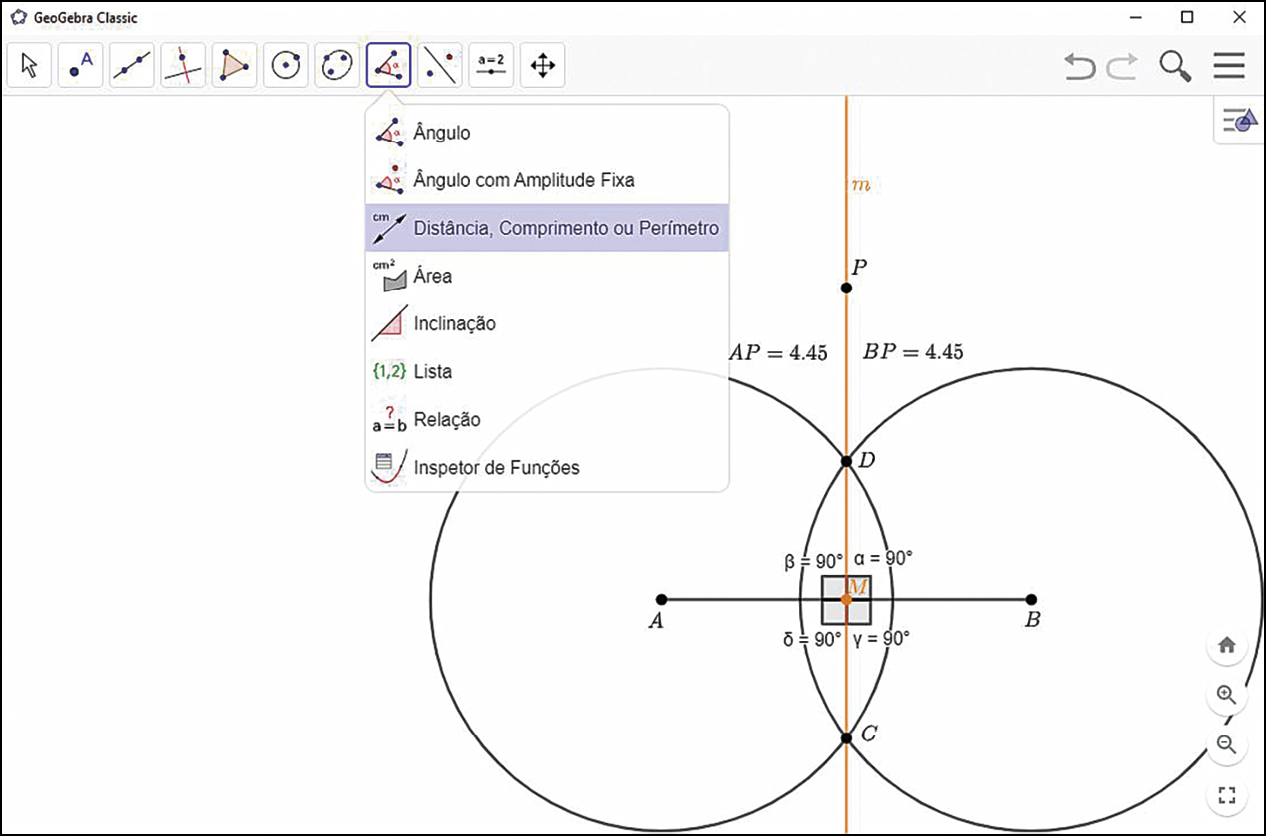
Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão com dois segmentos de reta unidos na sua origem e com marcação de um ângulo alfa no menor dos ângulos entre eles.
Aba selecionada: distância, comprimento ou perímetro. Na tela abaixo, reta vertical m em laranja, com ponto P sobre a reta e ponto M na intersecção com o segmento de reta AB. Há duas circunferências de mesmo tamanho, uma centrada no ponto A e outra no ponto B. As duas circunferências se interseccionam nos pontos C (superior) e D (inferior). Indicação das medidas: AP = 4.45. BP = 4.45. No centro, quatro ângulos retos, o ângulo alfa entre MB e MD, beta entre MD e MA, delta entre MA e MC e gama entre MC e MB.

Respostas e comentários

Explore: a) As medidas de comprimento dos segmentos de reta

\overline{A M} e \overline{M B}

são iguais e a abertura dos ângulos formados entre m e

\overline{A B}

mede 90graus.

b) Espera-se que os estudantes percebam que AP = BP independentemente da posição do ponto P.

Tecnologias digitais

em foco

Bê êne cê cê:

• Competência geral 5 (a descrição está na página seis).

• Competência específica 2 (a descrição está na página sete).

• Habilidade ê éfe zero oito ême ah um cinco.

Objetivo:

Construir a mediatriz e o ponto médio utilizando o software GeoGebra ou outro software de geometria dinâmica.

Mediatriz e ponto médio

Se achar conveniente, mostre aos estudantes outro modo de construir a mediatriz e o ponto médio.

1. Construa um segmento de reta

\overline{A B}

2. Trace uma circunferência c, de centro em A, passando por B.

3. Trace uma circunferência d, de centro em B, passando por A.

4. Marque os pontos C e D, intersecções das circunferências c e d.

5. Trace a reta mediatriz m passando pelos pontos C e D.

6. Marque o ponto médio M, intersecção da reta m com o segmento de reta

\overline{A B}

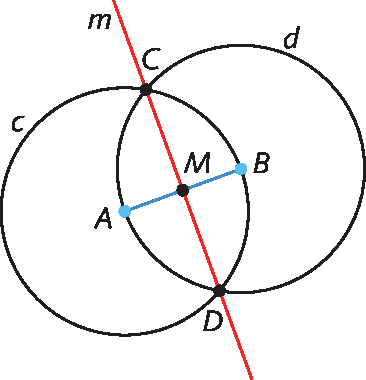
Figura geométrica. Duas circunferências de mesmo tamanho, circunferência c centrada em A e circunferência d centrada em B. Ponto M no centro do segmento AB. As circunferências se interseccionam nos pontos C (superior) e D (inferior). Reta m passando pelos pontos C, M e D.

Em Explore, os estudantes terão a oportunidade de verificar experimentalmente que mediatriz de um segmento é o lugar geométrico dos pontos do plano que estão à mesma medida de distância de seus extremos. Essa utilização da tecnologia digital para produzir conhecimento favorece o desenvolvimento da competência geral 5 e da competência específica 2 de Matemática.

Página 84

Atividades

Faça as atividades no caderno.

Cuidado! Evite acidentes ao usar o compasso nas atividades 6, 7, 11 e 12.

4. Nesta ilustração,

\vec{O B}

é a bissetriz de

A \hat{O} C

, e

\vec{O D}

é a bissetriz de

C \hat{O} E

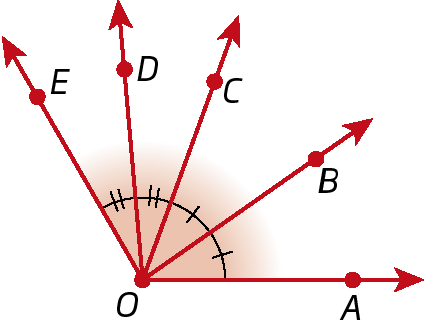
Figura geométrica. À esquerda, ponto O. Partindo de O, segmento de reta horizontal com ponto A e segmentos de retas diagonais: B, C, D, E. Marcação que o ângulo entre EÔD é igual ao ângulo DÔC e o ângulo entre CÔB é igual ao ângulo BÔA.

a) Qual é a medida da abertura de

A \hat{O} B

m e d (B \hat{O} C) =

35graus?

b) Qual é a medida da abertura de

C \hat{O} D

m e d (D \hat{O} E) =

25graus?

c) Qual é a medida da abertura de

D \hat{O} A

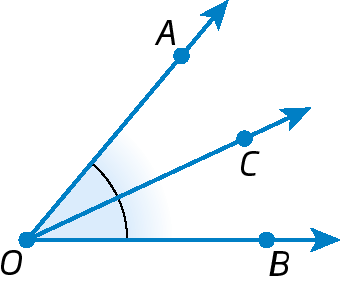
5. Na figura seguinte,

\vec{O C}

é a bissetriz de

A \hat{O} B

m e d (A \hat{O} C) = 25 °

. Determine as medidas da abertura de

A \hat{O} B

e de

B \hat{O} C

Figura geométrica. À esquerda, ponto O. Partindo de O, segmento de reta horizontal com ponto B e segmentos de retas diagonais: C e A. Indicação que o ângulo AÔC é igual CÔB.

6. Construa no caderno, com o auxílio de um transferidor, um ângulo cuja abertura meça 80graus. Em seguida, utilizando régua e compasso, determine a bissetriz desse ângulo e escreva a medida da abertura de cada ângulo obtido.

7. No caderno, utilizando régua e compasso:

a) construa um ângulo qualquer;

b) divida o ângulo em quatro ângulos congruentes.

8. Na figura seguinte,

\vec{O B}

é bissetriz de

A \hat{O} C

\vec{O D}

é bissetriz de

C \hat{O} E

m e d (A \hat{O} C) = 80 °

m e d (C \hat{O} E) = 60 °

. Determine

m e d (B \hat{O} D)

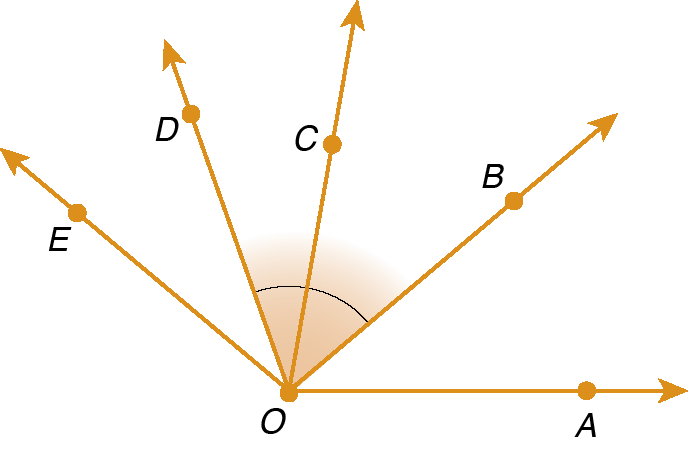
Ilustração. À esquerda, ponto O. Partindo de O, semirreta O A na horizontal e semirretas O B, O C, O D e O E da direita para a esquerda. Os pontos A, B, C, D e E não estão alinhados. Destaque para os ângulos B O C e C O D

9. Na figura a seguir, M é o ponto médio de

\overline{A B}

e N é o ponto médio de

\overline{B C}

m e d (\overline{A B}) = 10 c m

m e d (\overline{B C}) = 8 c m

, determine

m e d (\overline{M N}) .

Figura geométrica. Segmento com os pontos: A, M, B, N e C. A medida de A até B é 10 centímetros e de B até C é 8 centímetros.

10. Na figura seguinte, R, S e T são os pontos médios dos segmentos de reta

\overline{A B}

\overline{B C}

\overline{C D}

, respectivamente.

Figura geométrica. Segmento com os pontos: A, R, B, S, C, T e D. A medida A até B é 4 centímetros. A medida B até C é 2 centímetros e a medida C até D é 6 centímetros.

Determine:

a) a medida de comprimento de

\overline{R S}

;

b) a medida de comprimento de

\overline{S T}

;

c) a medida de comprimento de

\overline{S D}

;

d) a medida de comprimento de

\overline{R D}

11. Copie o segmento de reta

\overline{A B}

no caderno e, com o auxílio de um compasso, determine sua mediatriz.

Figura geométrica. Modelo. Segmento diagonal AB.

12. Copie o △ á bê cê no caderno e, com o auxílio de um compasso, trace as mediatrizes dos segmentos

\overline{A B}

\overline{B C}

\overline{A C}

Figura geométrica. Modelo. Triângulo ABC.

Respostas e comentários

4. a) 35graus

4. b) 25graus

4. c) 95graus

m e d (A \hat{O} B) = 50 °

;

m e d (B \hat{O} C) = 25 °

6. 40graus

7. Respostas pessoais.

8. 70graus

9. 9 centímetros

10. a) 3 centímetros

10. b) 4 centímetros

10. c) 7 centímetros

10. d) 10 centímetros

11. Resposta em Orientações.

12. Resposta em Orientações.

Nas atividades 6, 7, 11 e 12, oriente os estudantes quanto aos cuidados no manuseio do compasso a fim de evitar acidentes.

• Na atividade 7, sugira aos estudantes que construam, no item a, um ângulo com medida de abertura suficiente para que sua divisão em quatro ângulos congruentes não seja tão difícil de fazer. Para o item b, eles podem utilizar a construção da bissetriz três vezes: a primeira divide o ângulo em duas partes com a mesma medida de abertura, e as duas próximas devem dividir essas duas partes ao meio, resultando em quatro ângulos congruentes.

• Na atividade 11, caso seja necessário, retome a construção da mediatriz apresentada na página anterior, explicando o passo a passo.

Resposta da atividade 11:

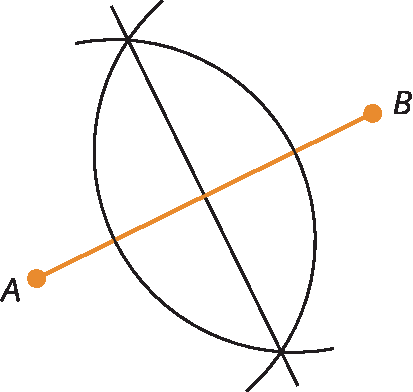
Figura geométrica. Segmento AB, uma reta corta o segmento ao meio e intersecciona dois arcos. Um arco com abertura para direita e outro para a esquerda. Os dois arcos tem intersecção entre si e a reta em dois pontos.

• Na atividade 12, os estudantes trabalham com a construção do circuncentro do triângulo. Ao construírem o ponto que é a intersecção das três mediatrizes, oriente-os a colocar a ponta-seca do compasso nesse ponto e a abrir o compasso até algum vértice do triângulo e que, assim, tracem uma circunferência. Depois, pergunte o que percebem com a construção. Incentive a turma a raciocinar sobre a propriedade da mediatriz. Comente que o ponto de intersecção pertence às três mediatrizes. Os estudantes devem associar essa propriedade à construção da circunferência, observando que todas medidas das distâncias do ponto de intersecção das mediatrizes aos vértices do triângulo são iguais entre si e numericamente iguais à medida do comprimento raio da circunferência que circunscreve o triângulo.

Resposta da atividade 12:

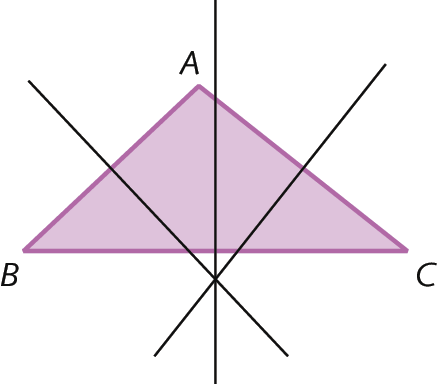
Figura geométrica. Triângulo ABC cortado pelas mediatrizes dos segmentos AB, BC e AC.

Página 85

Construção de ângulos com régua e compasso

A seguir, vamos verificar como podemos construir alguns ângulos com o auxílio de régua e compasso. Esses ângulos podem ser utilizados, por exemplo, na construção de figuras planas ou em transformações geométricas.

Cuidado! Evite acidentes ao usar o compasso.

Ângulo de medida da abertura de 60graus

Confira o passo a passo para a construção de um ângulo cuja medida de abertura é 60graus.

1º) Traçamos uma semirreta

\vec{O A}

. Centramos o compasso em óh e, com uma abertura qualquer, traçamos um arco, determinando em

\vec{O A}

o ponto B.

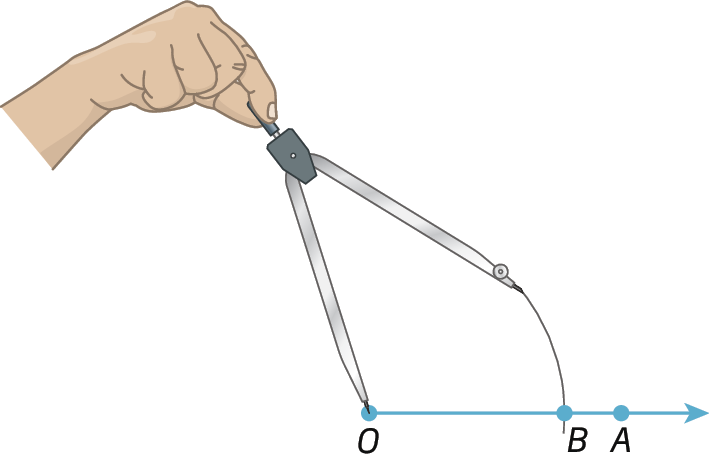
Ilustração. Semirreta com ponto O à esquerda, B e A à direita. Destaque para a mão de uma pessoa com compasso aberto com ponta seca em O, traça arco em B.

2º) Centramos o compasso em B e, com a mesma abertura, traçamos um arco cruzando o arco anterior, determinando o ponto C.

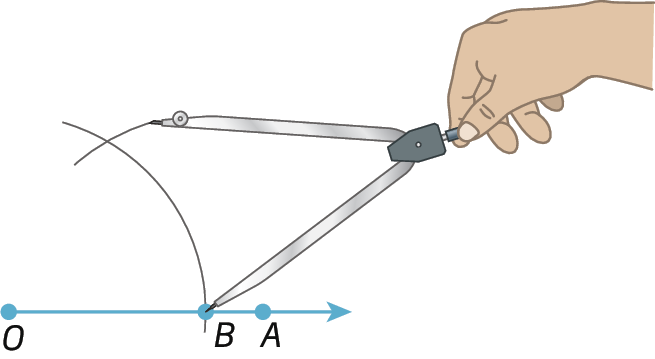
Ilustração. Semirreta com ponto O à esquerda, B e A à direita. Destaque para a mão de uma pessoa com compasso aberto com ponta seca em B, traça linha em arco, cruzando com o arco que passa por B.

3º) Traçamos

\vec{O C}

determinando, assim, o ângulo

B \hat{O} C

cuja abertura mede 60graus.

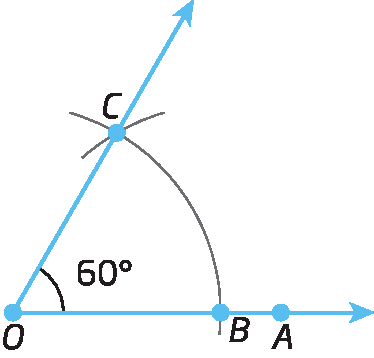
Ilustração. À esquerda, ponto O. De O, segmento de reta horizontal com ponto B e A e reta diagonal com ponto C. Ângulo em BC é 60 graus. Arco passando pelos pontos B e C, com concavidade virada para o ponto O.

Um ângulo cuja medida de abertura é 30graus pode ser construído traçando-se a bissetriz de um ângulo cuja abertura mede 60graus.

Tecnologias digitais em foco

Ângulo de medida da abertura de 60graus

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para construir um ângulo cuja abertura mede 60graus e realizar algumas investigações.

Construa

Siga os passos a seguir para construir um ângulo de medida da abertura de 60graus.

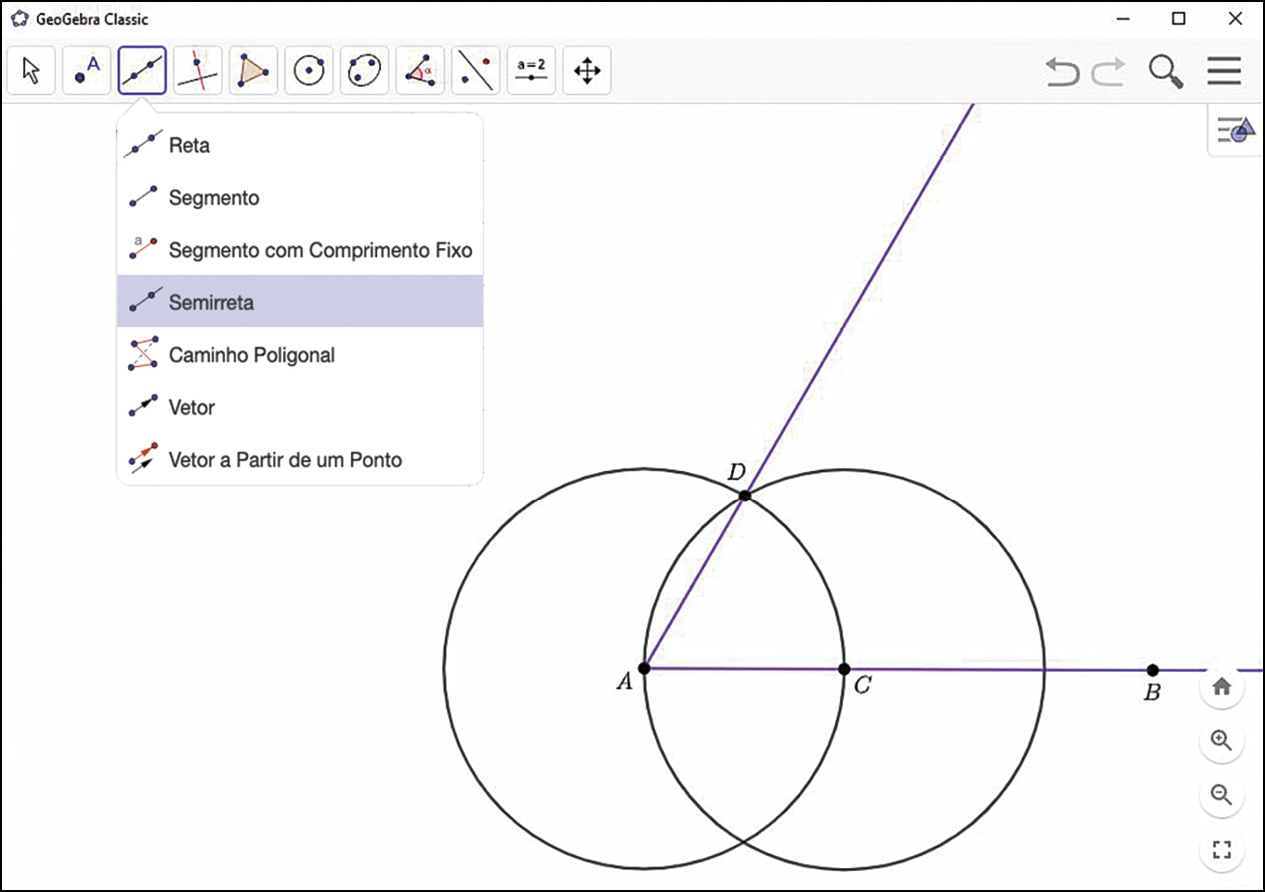
1º) Utilize a ferramenta

e construa uma semirreta

\vec{A B}

2º) Siga o passo a passo do início deste tópico e construa um ângulo

B \hat{A} D

cuja abertura mede 60graus.

Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão com uma reta diagonal com dois pontos sobre ela e aba selecionada: semirreta. Na tela, duas circunferências de mesmo tamanho. O ponto A é o centro da circunferência à direita e o ponto C da circunferência à esquerda. Elas se interseccionam no ponto D (superior) e em um ponto não rotulado (inferior). Semirreta horizontal partindo de A, passando pelos pontos C e B. Semirreta diagonal para cima, partindo de A e passando em D.

Respostas e comentários

Construção de ângulos com régua e compasso

Após explorar a construção do ângulo com abertura medindo 60graus, peça aos estudantes que proponham uma maneira de construir um ângulo com medida de abertura de 120graus. Eles podem obter esse ângulo construindo dois ângulos com abertura medindo 60graus consecutivos e adjacentes. Caso tenham dificuldades, oriente-os a construir o ângulo com abertura medindo 60graus e, em seguida, utilizar o lado construído (

\vec{O C}

da imagem) como se fosse a base utilizada no início da construção (

\vec{O A}

da imagem).

Oriente os estudantes quanto aos cuidados no manuseio do compasso a fim de evitar acidentes.

Tecnologias digitais em foco

Bê êne cê cê:

Habilidade ê éfe zero oito ême ah um cinco.

Objetivo:

Construir um ângulo com medida de abertura de 60graus utilizando o software GeoGebra ou outro software de geometria dinâmica.

Ângulo de medida de abertura medindo 60graus

Após os estudantes realizarem o 1º e o 2º passos, peça a eles que comparem os ângulos e as construções auxiliares. É importante que eles percebam que a medida do comprimento do raio das circunferências é irrelevante para a construção do ângulo, porém ambas devem ter a mesma medida de comprimento de raio.

Página 86

Tecnologias digitais em foco

Explore

a) Utilize a ferramenta

e meça a abertura do ângulo

B \hat{A} D

. Depois, movimente os pontos móveis. O que você pode concluir?

b) Utilize a ferramenta

Ilustração. Botão quadrado com um triângulo.

e construa o triângulo cujos vértices sejam os pontos a, C e D .

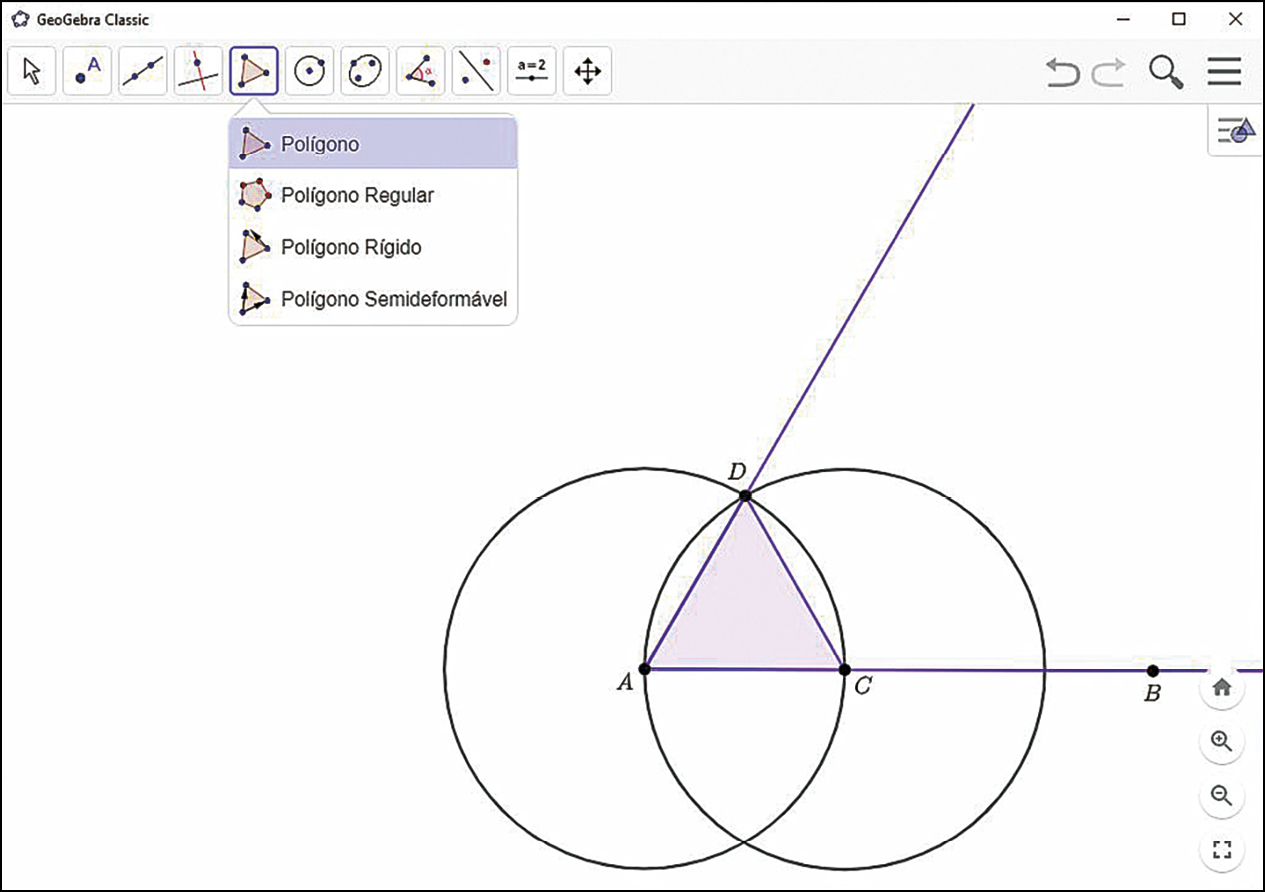
Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão com um triângulo e aba polígonos. Na tela, duas circunferências, a da direita com centro em A e a da esquerda com centro em C. Elas se interseccionam no ponto D (superior) e em um ponto não rotulado (inferior). Semirreta horizontal partindo de A , B passando por C e por B. Semirreta diagonal para cima, partindo de A e passando em D, ou seja, na intersecção das circunferências. Triângulo formado ACD.

Agora, utilize a ferramenta

e meça o comprimento dos lados desse triângulo. O que você pode concluir?

c) Por que podemos garantir que a abertura do ângulo construído mede 60graus?

Ângulo de medida da abertura de 90graus

Analise o passo a passo para a construção de um ângulo cuja medida de abertura é 90graus.

Cuidado! Evite acidentes ao usar o compasso.

1º) Traçamos a reta

\overset{\leftrightarrow}{A B}

. Centramos o compasso em a e, com uma abertura qualquer, traçamos um arco cruzando a reta

\overset{\leftrightarrow}{A B}

em dois pontos, determinando os pontos C e D.

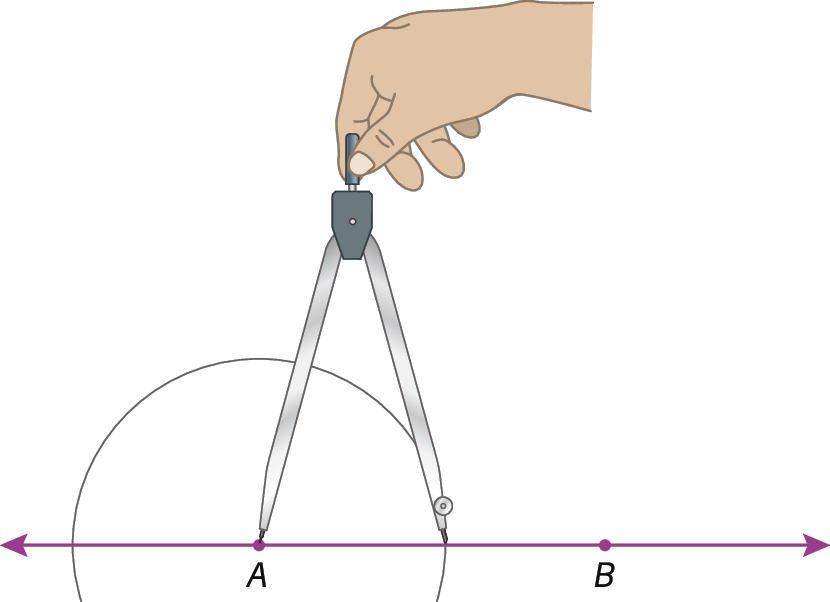
Ilustração. Reta com ponto A à esquerda e B à direita. Destaque para a mão de uma pessoa com compasso aberto com ponta seca em A traçando arco de um lado a outro do ponto, cruzando a reta.

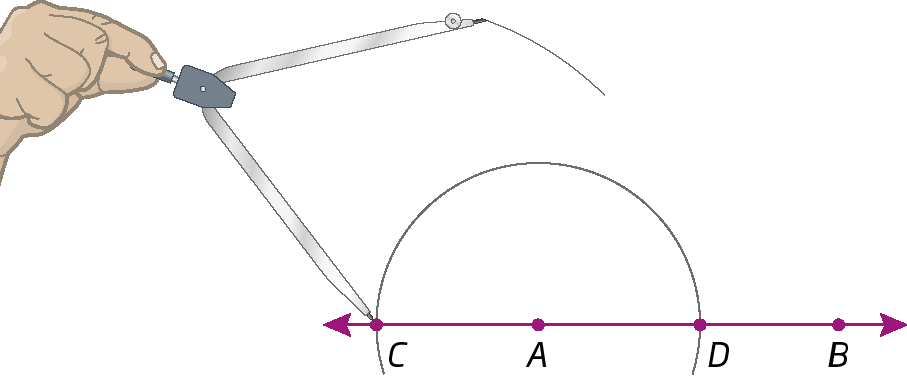
2º) Centramos o compasso em C e, com uma abertura maior que

\overline{C A}

, traçamos um arco.

Ilustração. Reta com ponto A à direita e B à esquerda. Semicircunferência centrada em A e cruzando a reta nos pontos C (à esquerda de A) e D (à direita de D). O ponto D fica entre A e B. Destaque para a mão de uma pessoa com um compasso aberto, ponta seca no ponto C, riscando um arco acima da circunferência.

Respostas e comentários

Explore: a) Espera-se que os estudantes concluam que a abertura do ângulo

B \hat{A} D

mede 60graus independentemente da medida de comprimento do raio das circunferências que foram traçadas na construção de

B \hat{A} D

b) Espera-se que os estudantes concluam que o triângulo á cê dê é um triângulo equilátero.

c) Porque o ângulo construído é um dos ângulos internos de um triângulo equilátero

e, portanto, sua abertura mede 60graus.

Em Explore, os estudantes terão a oportunidade de verificar que a medida da abertura do ângulo construído é igual a 60graus. Se achar oportuno, antes de propor o item b, verifique se eles conseguem encontrar um caminho para demonstrar que, de fato, o ângulo construído tem essa medida. Dê um tempo para que explorem a construção, as ferramentas do software e levantem hipóteses. Essa utilização da tecnologia digital para produzir conhecimento favorece o desenvolvimento da competência geral 5 e da competência específica 2 de Matemática.

Depois que os estudantes construírem o ângulo com abertura medindo 90graus, peça que construam um quadrado. Em seguida, eles devem determinar a bissetriz de algum dos ângulos retos do quadrado. Pergunte o que podem observar em relação a essa bissetriz. Espera-se que eles percebam que um pedaço da bissetriz coincide com a diagonal do quadrado.

Se julgar adequado, peça aos estudantes que construam os ângulos com abertura medindo 75graus e 105graus, que podem ser obtidos a partir dos algoritmos vistos anteriormente para a construção de ângulos e da bissetriz.

Página 87

3º) Centramos o compasso em D e, com a mesma abertura do passo anterior, traçamos um arco, cruzando o arco anterior e determinando o ponto ê.

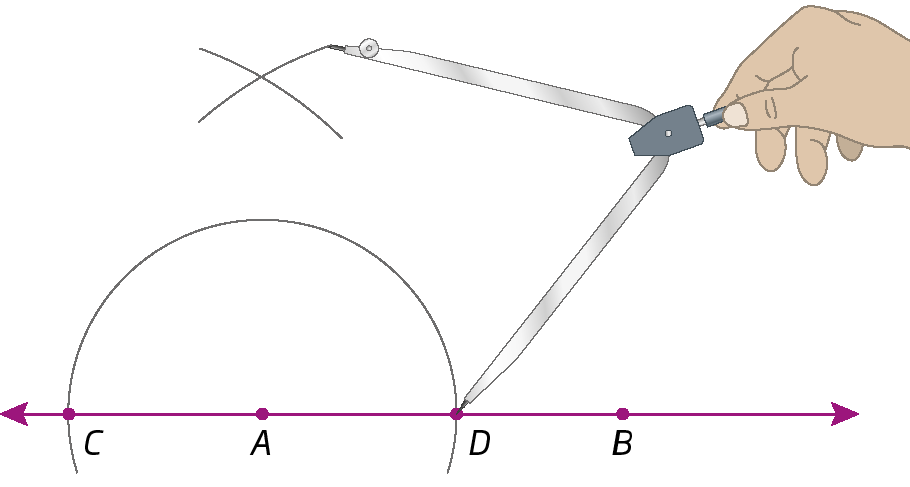
Ilustração. Reta com ponto A à esquerda e B à direita. Semicircunferência centrada em A e cruzando a reta nos pontos C (à esquerda de A) e D (à direita de D). O ponto D fica entre A e B. Destaque para a mão de uma pessoa com um compasso aberto, ponta seca no ponto D, riscando um arco acima da circunferência, cruzando com outro arco, acima do ponto A.

4º) Traçamos

\vec{A E}

determinando, assim, o ângulo

B \hat{A} E

,que mede 90graus.

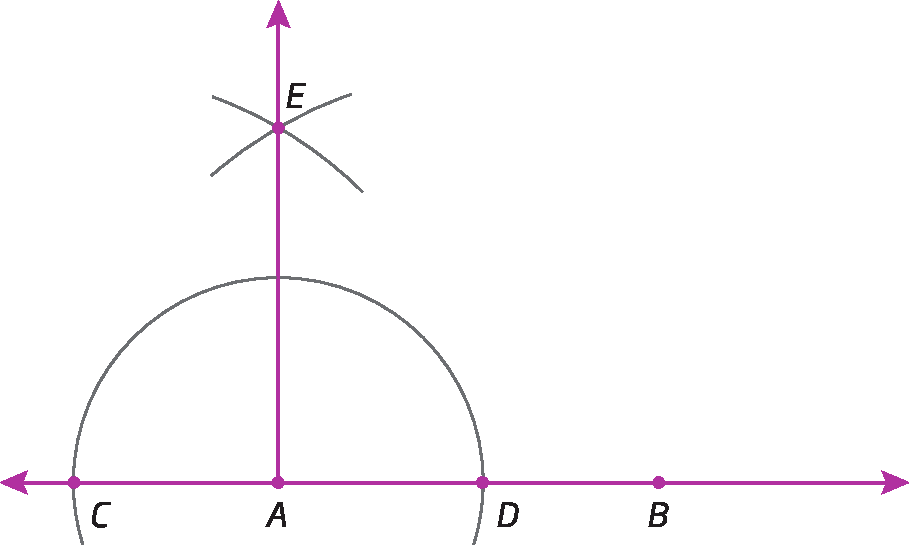
Observação

Na construção do ângulo de medida da abertura de 90graus, determinamos dois pontos (C e D) equidistantesglossário do vértice do ângulo (a) e, com isso, repetimos os mesmos passos da construção da mediatriz.

Um ângulo cuja medida de abertura é 45graus pode ser construído traçando-se a bissetriz de um ângulo reto.

Cuidado! Evite acidentes ao usar o compasso.

Retas paralelas

No 7º ano, construímos retas paralelas com o uso de esquadros. Agora, vamos estudar como construir retas paralelas usando régua e compasso.

1º) Traçamos a reta s e marcamos um ponto óh qualquer em s. Centramos o compasso em óh e traçamos um arco que intercepta s em a e em B.

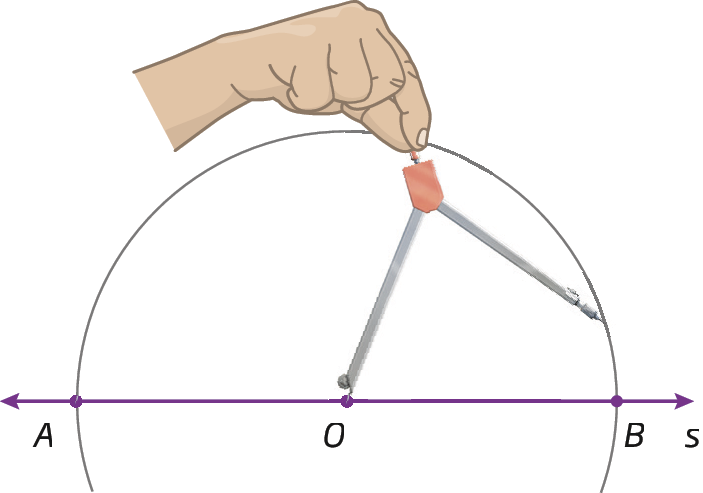
Ilustração. Reta s com ponto A à esquerda, B à direita e O no centro. Destaque para a mão de uma pessoa com compasso aberto, ponta seca em O traçando arco AB.

2º) Com centros em a e em B e uma abertura menor que

\overline{A B}

, traçamos arcos que interceptam o arco do passo anterior e determinamos os pontos M e N.

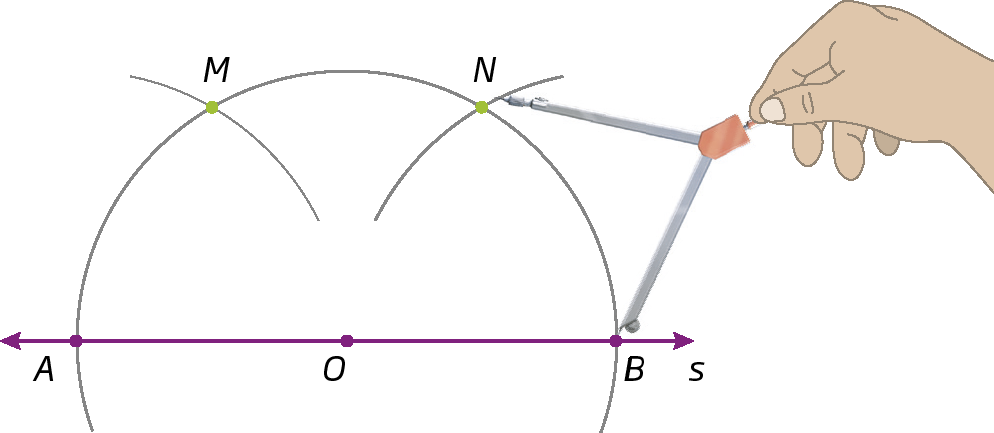
Ilustração. Reta s com ponto A à esquerda, B à direita e O no centro. Arco passando por A e B. Destaque para mão com compasso aberto, ponta seca no ponto B, traçando um arco que intersecciona o arco AB no ponto N. Ponto M é a intersecção de outro arco, similar ao primeiro, mas com referência ao ponto A.

3º) Traçamos t ⫽ s passando por M e por N.

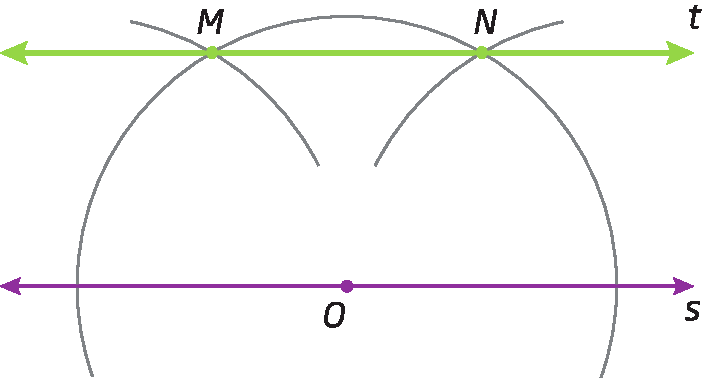
Ilustração. Reta s com ponto A à esquerda, B à direita e O no centro. Arco passando por A e B. Arco que intersecciona o arco AB no ponto N. Ponto M é a intersecção de outro arco, similar ao primeiro, mas com referência ao ponto A. Reta t passando pelos pontos M e N.

Respostas e comentários

Solicite aos estudantes que utilizem régua e compasso e reproduzam os passos para construir retas paralelas. Em seguida, desafie-os a utilizar essa construção para construir um retângulo qualquer e, depois, um quadrado.

A construção das retas paralelas se justifica pelo seguinte fato: esses passos são necessários para a construção de um trapézio isósceles, e sabemos que, no trapézio, as bases são segmentos de reta paralelos. Não deixe de retornar a essa construção quando forem abordados os trapézios no capítulo 7.

• Nas atividades 13 e 14 da página seguinte, para a construção do ângulo com abertura medindo 15graus e do ângulo com abertura medindo 90graus, os estudantes deverão utilizar as construções aprendidas até o momento e aplicar a construção da bissetriz. Na atividade 13, por exemplo, podem construir um ângulo com abertura medindo 60graus e sua bissetriz, obtendo dois ângulos com medida de abertura igual a 30graus. Em seguida, podem traçar a bissetriz de um desses ângulos, obtendo assim dois novos ângulos com abertura medindo 15graus. Para obter o ângulo com abertura medindo 90graus na atividade 14, eles podem construir dois ângulos adjacentes e consecutivos com abertura medindo 60graus e, em seguida, construir a bissetriz de um deles.

• Resposta da atividade 13 da página seguinte:

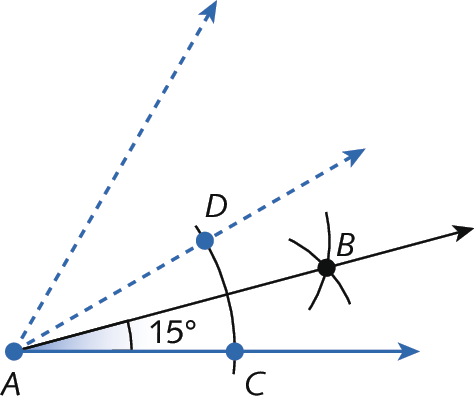
Figura geométrica. Ponto A à esquerda. Partindo de A, semirreta horizontal com ponto C e semirreta diagonal partindo de A, contendo ponto B. Ponto B é a intersecção de dois semi-arcos. Partindo de A, duas semirretas pontilhadas diagonais, acima do segmento AB. Arco cruzando a reta horizontal no ponto C e a reta pontilhada no ponto D.

• Resposta da atividade 14 da página seguinte:

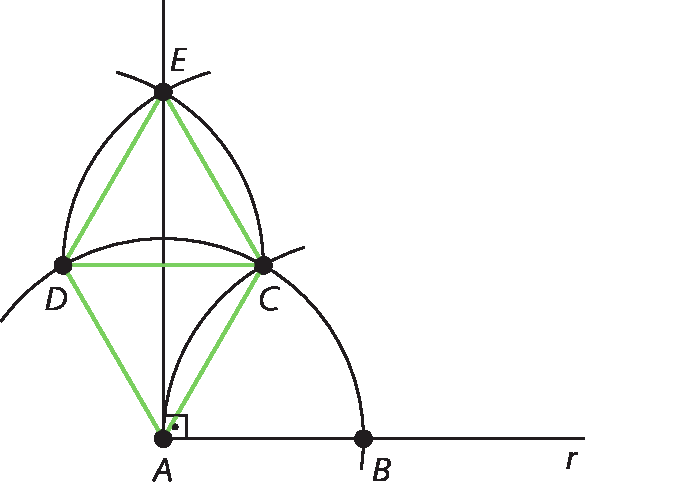
Figura geométrica. Reta r, ponto A à esquerda e B à direita, sobre a reta r. Partindo de A, reta formando um ângulo de 90º com a reta r, contendo o ponto E. Semicircunferência com centro em A. Sobre ela, à esquerda da reta perpendicular está o ponto D e à direita, o ponto C. Pedaço de semicircunferência centrada em B passando por A e por C. Pedaço de semicircunferência centrada em C passando por D e por E. Pedaço de semicircunferência centrada em D passando por C e por E. Destaque para os triângulos formados pelos pontos CDE e ACD.

• Na atividade 15, também da página seguinte, há mais de uma maneira de construir os ângulos apresentados. Por exemplo, para o ângulo com abertura medindo 150graus, o estudante pode construir um ângulo reto e, em seguida, construir um ângulo com abertura medindo 60graus adjacente ao ângulo reto (90graus + 60graus = 150graus). Outra fórma de construir esse ângulo é, a partir de um ângulo raso

B \hat{A} C

e, em seguida, construir um ângulo com abertura medindo 30graus (

D \hat{A} C

), consecutivo e não adjacente a

B \hat{A} C (180 ° - 30 ° = 150 °)

. Reforce para eles os cuidados ao manusear o compasso.

• Para a atividade 16 da página seguinte, caso os estudantes tenham dificuldade, comente que o ponto P deve ser considerado como um dos pontos obtidos no segundo passo da construção de uma reta paralela (M ou N), desta página. Alerte para os riscos em relação ao manuseio do compasso.

Página 88

Atividades

Cuidado! Evite acidentes ao usar o compasso nas atividades.

Faça as atividades no caderno.

13. No caderno, trace a semirreta

\vec{A C}

e construa o ângulo

B \hat{A} C

de medida da abertura de 15graus.

14. No caderno, construa um ângulo reto utilizando as construções passo a passo do ângulo de medida da abertura de 60graus e da bissetriz.

15. Dos ângulos de medida de abertura de 30graus, 45graus, 100graus, 125graus e 150graus, quais podem ser construídos com régua e compasso usando as construções que aprendemos até aqui? Construa, no caderno, aqueles que forem possíveis.

16. Desenhe, em seu caderno, uma reta r e um ponto P externo a essa reta. Em seguida, construa, com régua e compasso, uma reta s paralela à r, passando pelo ponto P.

2 Lugares geométricos

Você já brincou de caça ao tesouro? Analise a ilha e as pistas que levam ao local em que está localizado um baú camuflado.

Ilustração. Ilha com três andares. No topo, bandeiras 1 e 2 à esquerda, 3 e 4 no centro da ilha. No segundo andar, um rio. À esquerda da bandeira 1, árvore azul. Entre as bandeiras 3 e 4, árvore amarela. Na parte inferior, ao redor, mar e um barco. Abaixo papel amarelo enrolado nas laterais com as informações: Pista 1. A medida da distância do marco 1 ao baú é igual à medida da distância desse marco à árvore de copa azul. Pista 2. A medida da distância do marco 2 ao baú é igual à medida da distância do marco 4 ao baú. Pista 3. A medida da distância entre o baú e a trilha que passa somente pelo marco 3 é igual à medida da distância desse marco à árvore de copa amarela. Pista 4. A medida da distância do baú à trilha do marco 2 é igual à medida da distância do baú à trilha que passa pelos marcos 3 e 4.

Respostas e comentários

13. Resposta em Orientações.

14. Resposta em Orientações.

15. 30graus, 45graus e 150graus

16. Resposta pessoal.

Lugares geométricos

Bê êne cê cê:

Habilidade ê éfe zero oito ême ah um sete.

Objetivo:

Compreender a circunferência, a mediatriz, a bissetriz e a reta paralela como lugares geométricos.

Justificativa

Compreender a circunferência, a mediatriz, a bissetriz e a reta paralela como lugares geométricos possibilita aos estudantes ampliarem esses conceitos e aplicá-los na resolução de diferentes problemas cotidianos, o que favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um sete.

Mapeando conhecimentos

Explique aos estudantes o que é lugar geométrico. Depois, organize a sala em quatro grupos e atribua para cada um as seguintes tarefas:

Grupo 1: Definir a circunferência como lugar geométrico.

Grupo 2: Definir a bissetriz como lugar geométrico.

Grupo 3: Definir a mediatriz como lugar geométrico.

Grupo 4: Definir a reta paralela a uma reta dada como lugar geométrico.

Incentive os estudantes de cada grupo a desenhar, medir, experimentar e conjecturar. Reserve um momento para que os grupos possam compartilhar suas conclusões e como chegaram a elas.

Para as aulas iniciais

Espera-se que não tenham encontrado dificuldades em perceber que a circunferência é o lugar geométrico dos pontos do plano que equidistam de um ponto fixo (centro da circunferência).

Caso tenham apresentado dificuldades para definir a bissetriz, oriente-os a marcar um ponto qualquer P sobre a bissetriz e medir a distância entre ele e os lados do ângulo inicial. Destaque que, para medir essa distância, devem traçar um segmento de reta que ligue o ponto P ao lado do ângulo, formando um ângulo reto, e medir o comprimento desse segmento. Questione o que podem afirmar sobre as medidas de distância entre o ponto P e os lados do ângulo inicial.

Em relação à definição da mediatriz, sugira que marquem pontos na mediatriz e meçam a distância entre cada um desses pontos e as extremidades do segmento.

Por fim, para ajudá-los a definir a reta paralela, proponha que marquem pontos em uma das retas e meçam a distância entre cada um desses pontos e a outra reta.

(ê éfe zero oito ême ah um sete) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

Página 89

Com base nessas pistas, é possível determinar as regiões onde o baú está localizado. Para saber a localização exata do baú, é necessário decifrar as pistas.

Cada pista sugere uma propriedade das seguintes construções: circunferência, mediatriz, retas paralelas e bissetriz. A essas pistas damos o nome de lugar geométrico.

Lugar geométrico é a figura formada por todos os pontos do plano que têm em comum uma determinada propriedade.

Circunferência

Verifique este recorte da ilustração da ilha.

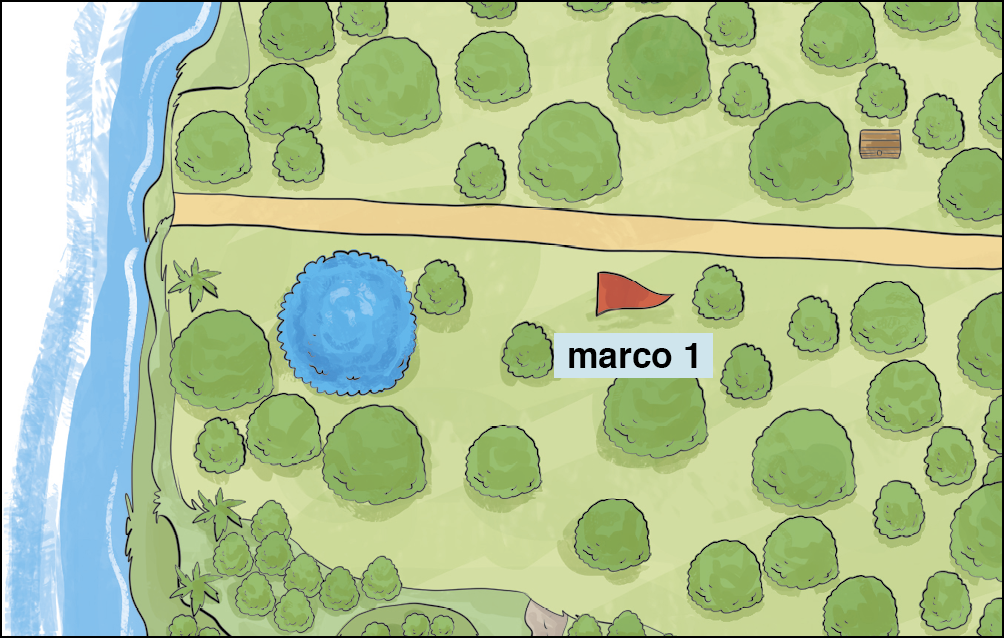
Ilustração. Destaque para trecho horizontal da ilha com bandeira do marco 1 com árvore de copa azul à esquerda.

A pista que será utilizada é a seguinte:

Ilustração. Papel amarelo enrolado nas laterais com as informações: Pista 1. A medida da distância do marco 1 ao baú é igual à medida da distância desse marco à árvore de copa azul.

Como sabemos a medida da distância do marco 1 à árvore, é possível delimitar uma linha em que seja possível encontrar o baú. Sabemos que na circunferência encontram-se todos os pontos do plano que mantêm a mesma medida da distância a partir do seu centro. Isso significa que o baú do tesouro está em algum lugar da circunferência.

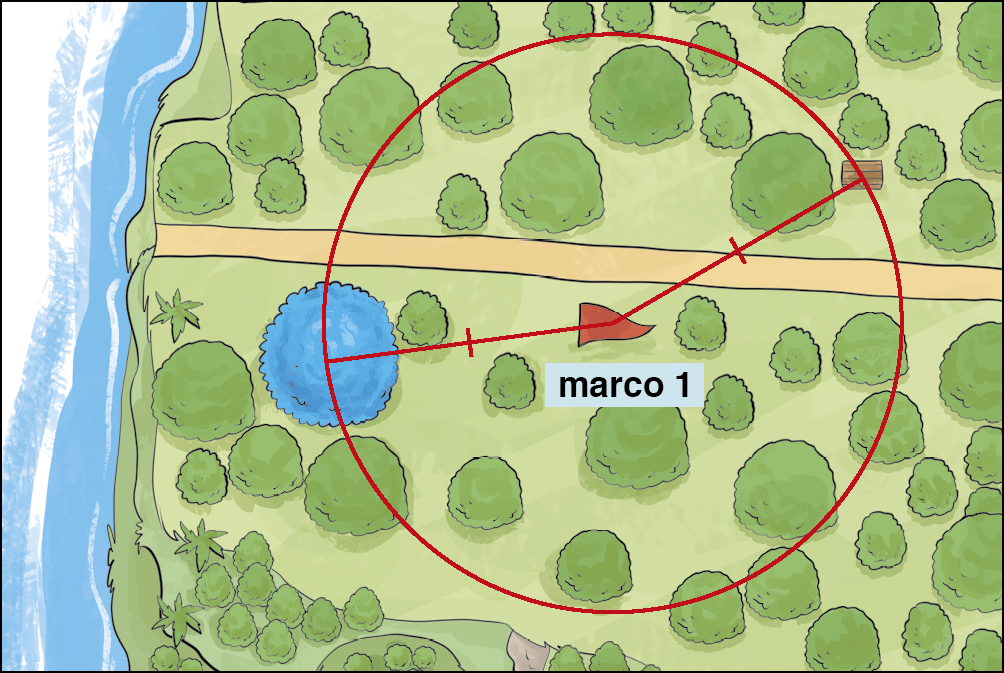
Ilustração. Destaque para trecho da ilha com bandeira do marco 1 com árvore de copa azul à esquerda. Circunferência ao redor do marco 1 passando pela árvore azul. Raio do marco 1 ao centro até a árvore azul e do marco 1 para direita.

Circunferência é o lugar geométrico dos pontos do plano que equidistam de um ponto fixo.

Clique no play e acompanhe a reprodução do Áudio.

Transcrição do áudio

Círculos nas plantações

Duração: 3:26min. Página: 89.

>> [LOCUTORA] Círculos nas plantações

Música de fundo.

>> [Pena]: Felipe, você sabe o que são agroglifos?

>> [Felipe] Agroglifos?! São aqueles círculos e símbolos nas plantações?

>> [Pena] Sim, exatamente isso! E você sabe como são feitos os agroglifos?

>> [Felipe] Ah! Certamente são feitos por aliens, né?

Som de nave espacial.

>> [Pena] Então, será que não tem outro jeito de fazer isso? Será que os alienígenas vão atravessar todo o Universo para vir aqui e ficar amassando trigo?

>> [Felipe] É, acho que não, né? Mas como é possível então fazer uma coisa dessas? A gente precisaria estar em uma nave espacial, porque os desenhos são enormes!

>> [Pena] Será? Você sabe traçar esses símbolos em um papel?

>> [Felipe] Sei, Pena. Basta usar um compasso. Com ele, dá para fazer essas curvas, bissetrizes. Existe toda uma gama de desenhos que podemos fazer com uma régua e um compasso. Mas, Pena, a gente não tem compassos gigantes para fazer círculos em plantações. Aonde você está querendo chegar?

>> [Pena] De fato, não temos compassos gigantes, mas, com um pouco de imaginação e técnicas matemáticas, nós podemos fazer a mesma coisa. Por exemplo, imagine que uma pessoa fique parada no meio de uma plantação, segurando a ponta de uma corda. Aí, uma segunda pessoa, a certa distância, segurando a outra ponta da corda e mantendo-a sempre esticada, caminhe ao redor da que está no centro. Ao andar em volta da outra, essa pessoa forma um círculo.

Efeito sonoro de ideia.

>> [Felipe] É verdade, Pena! Afinal, os passos da pessoa ao redor vão estar sempre a uma mesma distância da pessoa que estiver no centro, né?

>> [Pena] Exatamente! E, se ela vai amassando o trigo por onde ela passa, depois de completar uma volta terá formado um círculo ali!

>> [Felipe] E como ela amassa o trigo? Com os pés?

>> [Pena] Na verdade, ela pode usar uma tábua de madeira ou qualquer outro material um pouco maior. E, conforme o trigo vai sendo amassado, ele se prende no que já está no chão e não levanta mais.

>> [Felipe] Tá, Pena. O círculo eu até entendi, mas os agroglifos não são só círculos, são desenhos complexos, formas geométricas…

>> [Pena] Ora! Mas tudo o que você pode fazer no papel com compasso você pode fazer numa plantação, só dá um pouco mais de trabalho. Você tem de fato um compasso gigante, que é basicamente o uso de uma corda esticada na medida do raio que você quer desenhar. Inclusive, você sabia que em 1992 foi criada uma competição de agroglifos? Foi o primeiro e último “Concurso Internacional de Círculos na Plantação”, que aconteceu na Inglaterra. E, adivinha, foram os humanos que ganharam! Nenhum alienígena veio competir. Três engenheiros fizeram desenhos incríveis. Olha como eles foram espertos: usaram canos para amassar o trigo e escadas para fazer pontes na plantação e não deixar marcas erradas no chão, estragando o desenho. Então, Felipe, é bem possível que por trás desses desenhos todos exista um pessoal na verdade muito criativo e muito bom de matemática e geometria! E aí, você ainda acha que são os aliens que fazem os agroglifos?

>> [Felipe] Poxa, Pena, você me convenceu! É incrível o que dá para fazer com a geometria, né?

>> [Pena] Pois é, com geometria e criatividade!

Vinheta.

Créditos Os áudios inseridos neste conteúdo são da Free Sound e da Sonys. A trilha sonora “Royale” executada por George Lipe and Overtimes está disponível no YouTube.

Respostas e comentários

O estudo dos lugares geométricos, nesse momento, será feito de fórma intuitiva, a partir da definição de cada um deles dentro de um contexto. Assim, não vamos utilizar a linguagem matemática formal para comparar conjuntos de pontos do plano. Consequentemente, as demonstrações das propriedades de cada um dos lugares geométricos apresentados ficarão para estudos posteriores.

Circunferência

Ao apresentar a definição de circunferência como lugar geométrico, construa na lousa uma circunferência utilizando um giz preso a um barbante. Segure uma ponta do barbante no centro da circunferência e com a outra ponta, com o giz preso, risque a circunferência. Com o barbante preso, mostre que qualquer ponto da circunferência está à mesma medida da distância de seu centro (o ponto fixo), e essa medida da distância é determinada pela medida do comprimento do raio da circunferência (medida do comprimento do barbante).

Página 90

Mediatriz

Analise outro recorte feito a partir da ilustração da ilha.

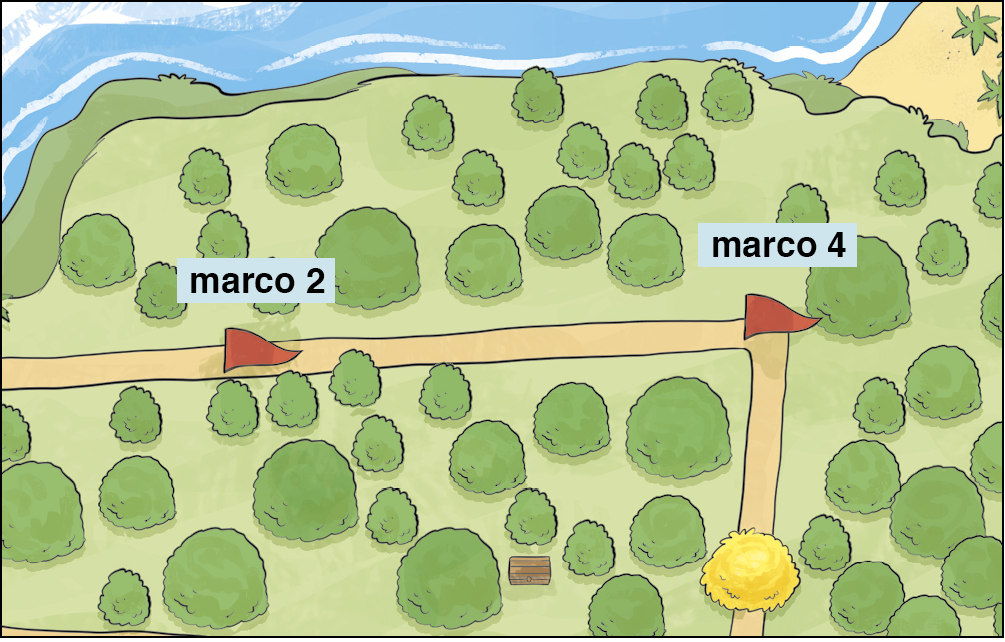
Ilustração. Destaque para trecho da ilha com bandeira do marco 2 à esquerda e à direita, marco 4 com árvore amarela abaixo do marco 4.

Vamos utilizar a seguinte pista:

Ilustração. Papel amarelo enrolado nas laterais com as informações: Pista 2. A medida da distância do marco 2 ao baú é igual à medida da distância do marco 4 ao baú.

Não sabemos a posição do baú, mas conhecemos a localização dos marcos 2 e 4; então, a partir do ponto médio do segmento de reta que une os marcos 2 e 4, as medidas de distância d são iguais.

A mediatriz é a reta perpendicular que passa pelo ponto médio, e é possível demostrar que, dado um ponto qualquer da mediatriz, a medida da distância entre esse ponto e uma das extremidades do segmento de reta (nesse caso, por exemplo, ponto que localiza o marco 2) é igual à medida da distância entre esse mesmo ponto e a outra extremidade do segmento de reta (ponto que localiza o marco 4).

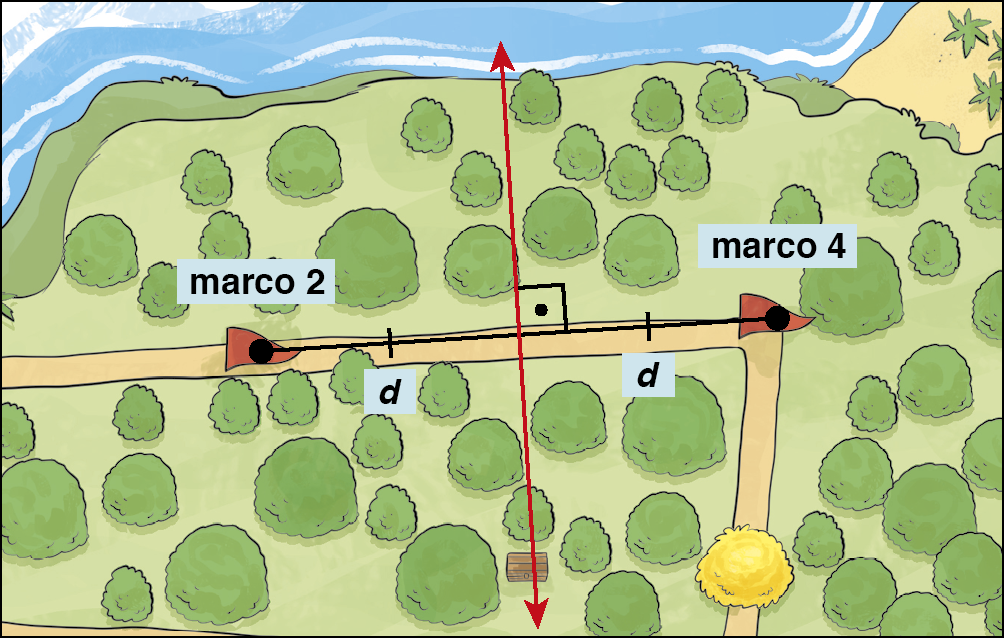
Ilustração. Destaque para trecho da ilha com bandeira do marco 2 à esquerda e à direita, marco 4 com árvore amarela abaixo do marco 4. Reta vertical entre marco 2 e marco 4 e segmento de reta horizontal do marco 2 ao marco 4. O ângulo entre as retas é 90º. Do marco 2 até a reta vertical, medida d e da reta vertical até marco 4, medida d.

Mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos fixos dados (extremidades de um segmento de reta).

Assim, o tesouro está em algum lugar da mediatriz, o que reduz as possibilidades de localização do baú aos pontos de intersecção entre a mediatriz e a circunferência.

Respostas e comentários

Mediatriz

Se julgar adequado, ao explicar a mediatriz como lugar geométrico, relembre os passos da construção da mediatriz por meio de circunferências, nas orientações da página 83. Faça, na lousa, a construção da mediatriz e coloque mais de um par de circunferências concêntricas, mostrando que as intersecções estão sobre a mediatriz do segmento cujas extremidades são os centros dessas circunferências.

Página 91

Retas paralelas

Confira outro recorte da ilustração da ilha.

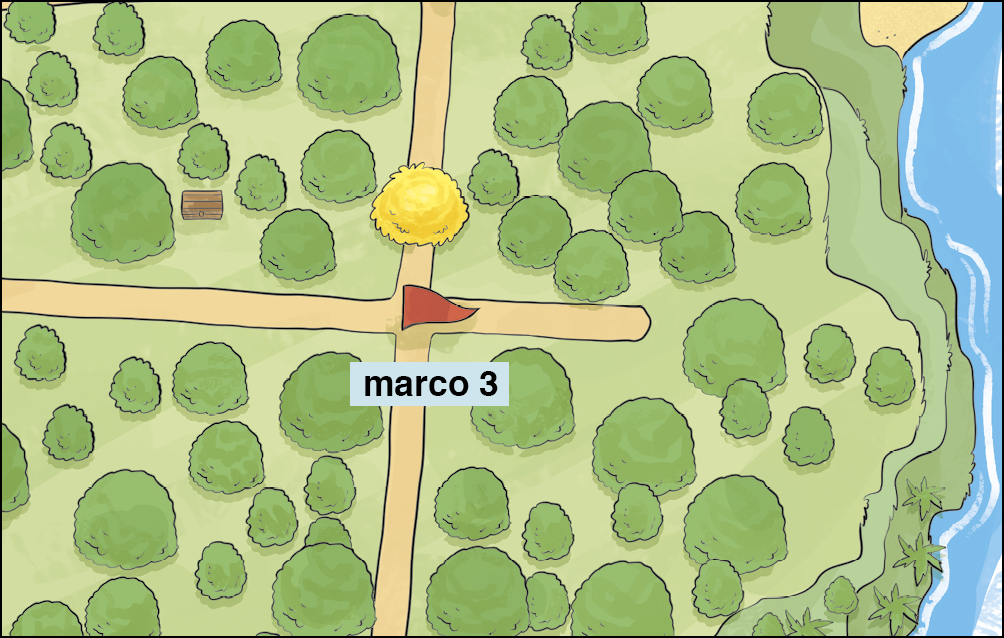
Ilustração. Destaque para trecho da ilha com bandeira do marco 3 e árvore amarela acima.

A pista que vamos utilizar diz:

Ilustração. Papel amarelo enrolado nas laterais com as informações: Pista 3. A medida da distância entre o baú e a trilha que passa somente pelo marco 3 é igual à medida da distância desse marco à árvore de copa amarela.

Como conhecemos a medida da distância h entre o marco 3 e a árvore de copa amarela, e o baú está à mesma medida da distância da trilha que contém apenas esse marco, podemos concluir que o baú está em uma reta paralela a essa trilha, passando pela árvore de copa amarela.

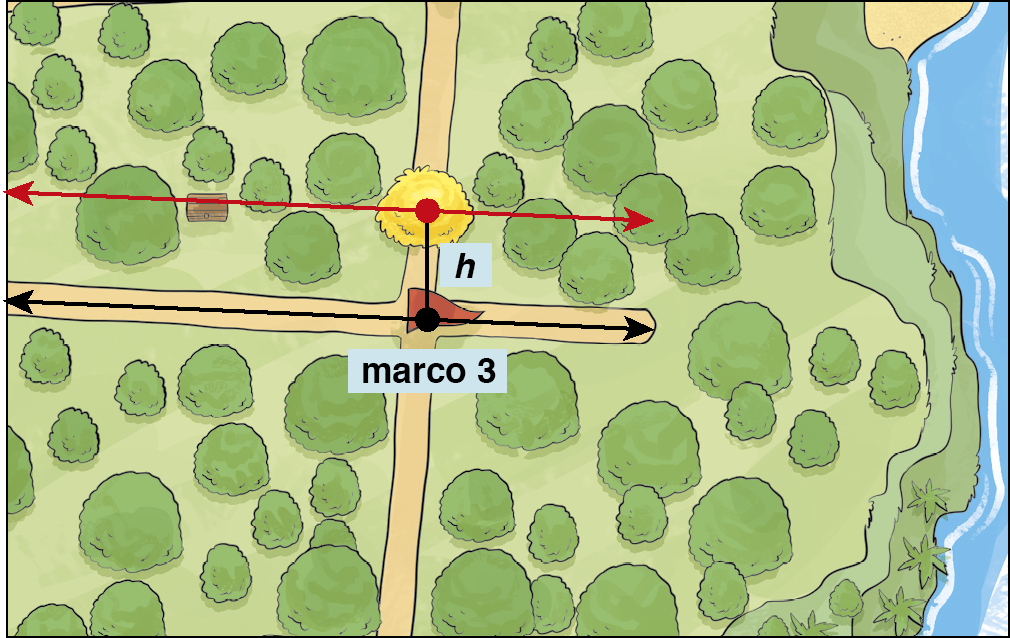
Ilustração. Destaque para trecho da ilha com bandeira do marco 3 e árvore amarela acima. Reta horizontal em marco 3 e acima, reta horizontal vermelha sobre árvore amarela. Do marco 3 até árvore amarela, medida h.

Reta paralela é o lugar geométrico dos pontos do plano que equidistam de uma reta dada.

Com essa pista, podemos garantir a localização exata do baú.

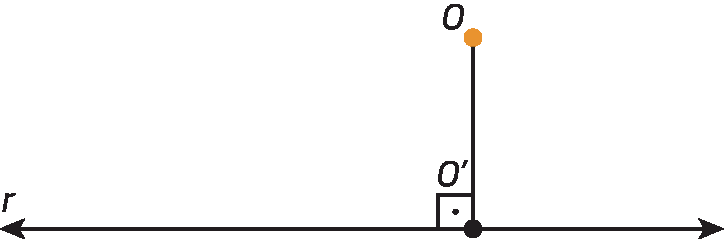
Observação

A medida da distância entre um ponto óh e uma reta r é dada pela medida de comprimento do segmento de reta perpendicular a r, com uma extremidade no ponto óh e a outra extremidade no ponto ó linha, na intersecção do segmento com a reta r.

Figura geométrica. Reta r na horizontal com ponto O linha. Acima de O linha, segmento formando um ângulo de 90º com a reta r, contendo o ponto O. — A medida da distância entre O e r é igual a óhó linha .

Respostas e comentários

Retas paralelas

Após apresentar o conceito de reta paralela como lugar geométrico, proponha aos estudantes que verifiquem experimentalmente que, a rigor, existem duas retas paralelas que satisfazem essa condição: uma em cada semiplano determinado pela reta em questão. Essa verificação pode ser feita utilizando instrumentos de desenho ou com o auxílio de um software de geometria dinâmica como o GeoGebra.

Página 92

Bissetriz

Verifique este último recorte da ilustração da ilha.

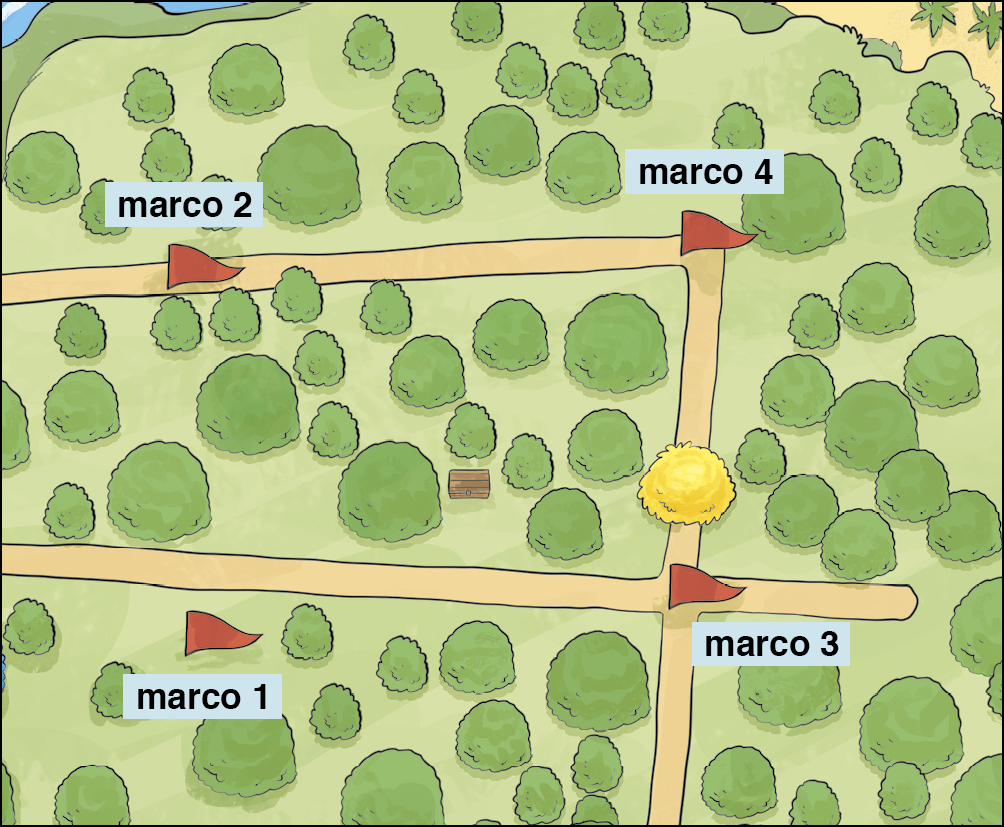
Ilustração. Destaque para trecho da ilha. Abaixo, à esquerda, bandeira com marco 1 e à direita, bandeira com marco 3. A cima, à esquerda, bandeira com marco 2 e à direita bandeira com marco 4.

A última pista traz a seguinte informação:

Ilustração. Papel amarelo enrolado nas laterais com as informações: Pista 4. A medida da distância do baú à trilha do marco 2 é igual à medida da distância do baú à trilha que passa pelos marcos 3 e 4.

Poderíamos ter utilizado essa pista antes de outras. Verifica-se que as semirretas (trilhas) que saem do marco 4 e passam pelos marcos 2 e 3 formam um ângulo e que um ponto qualquer da bissetriz desse ângulo tem a mesma medida de distância a cada lado do ângulo. Essa informação confirma a localização do baú.

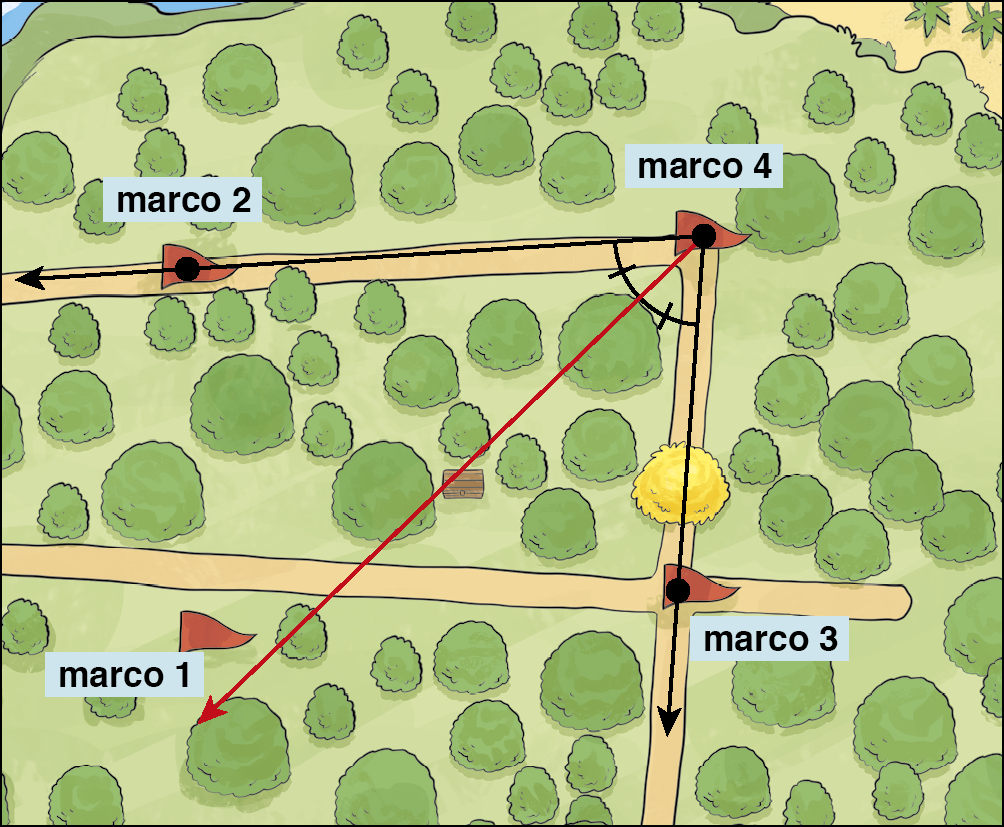
Bissetriz de um ângulo é o lugar geométrico dos pontos do plano que equidistam dos lados desse ângulo.

Respostas e comentários

Bissetriz

Pode não ser trivial para os estudantes compreenderem a bissetriz de um ângulo como uma semirreta com pontos que equidistam dos lados desse ângulo. Caso tenham dificuldade, construa a bissetriz de um ângulo na lousa.

Página 93

Note na ilustração a seguir a localização exata do baú.

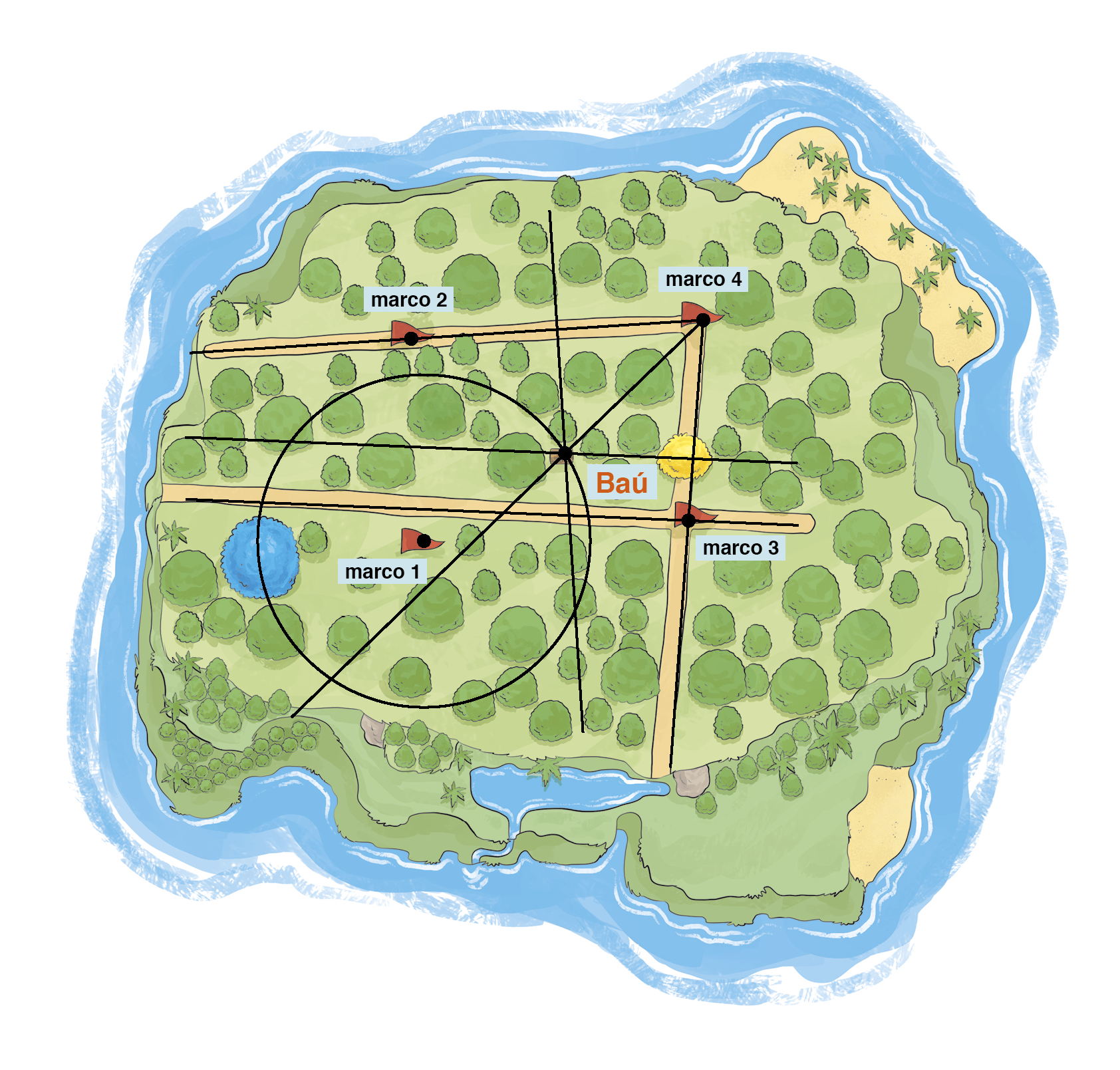
Ilustração. Destaque para topo da ilha. À esquerda, marco 1. Acima, marco 2. à direita, marco 3 e 4. Entre eles, árvore amarela. Do marco 4, reta horizontal para marco 2 e reta vertical para marco 3, bissetriz para marco 1 passando pelo baú . Circunferência passa pelo baú com centro no marco 1. Duas retas passando pelo baú e cruzando a circunferência.

Atividades

Faça as atividades no caderno.

17. O lugar geométrico dos pontos do plano que equidistam de dois pontos fixos é denominado:

a) semirreta.

b) ponto médio.

c) mediatriz.

d) bissetriz.

18. A afirmação a seguir é verdadeira? Justifique.

A medida da distância entre a rua das Américas e a dos Eucaliptos é a mesma em qualquer ponto, pois elas são paralelas.

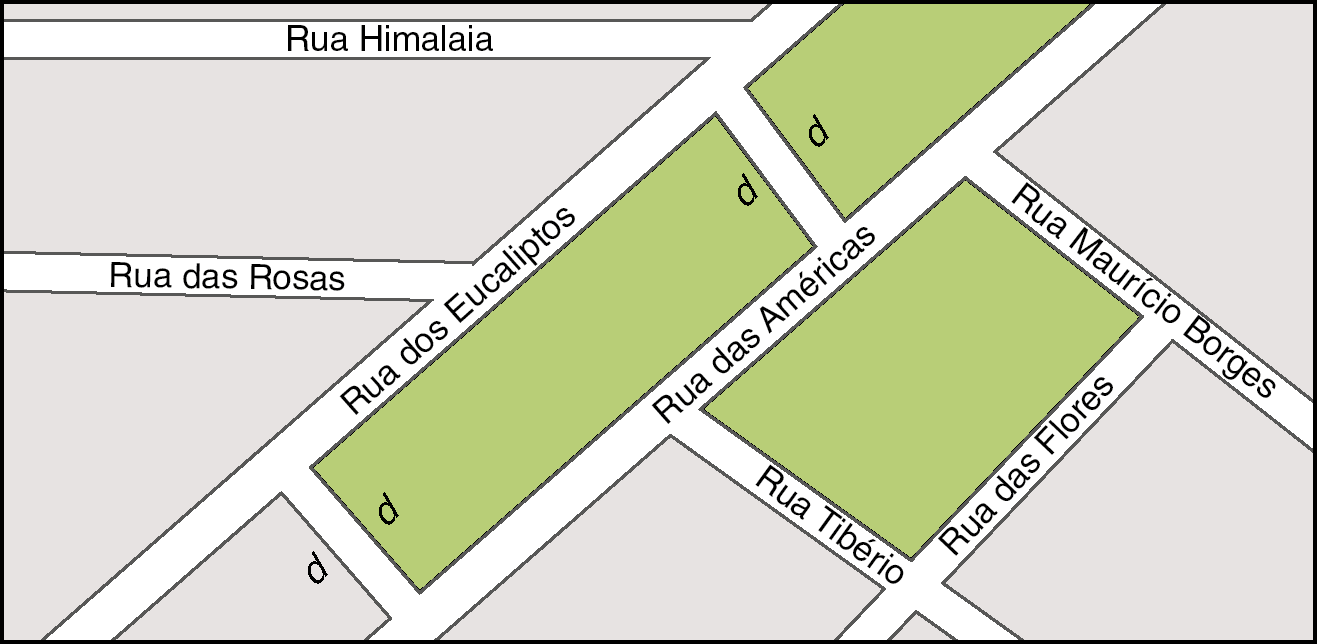
Ilustração. Guia de ruas. Na horizontal à esquerda, Rua Himalaia e Rua das Rosas, as duas cruzando a Rua dos Eucaliptos, na diagonal, inclinada para a direita. Rua das Américas também na diagonal, paralela a Rua dos Eucaliptos. Entre elas um quarteirão retangular, cuja lateral menor tem distância d. À direita, na diagonal inclinada para a esquerda, Rua Maurício Borges e Rua Tibério. Cruzando-as, na diagonal inclinada para a direita, Rua das Flores. — Imagem ilustrativa sem escala.

Respostas e comentários

17. alternativa c

18. Sim, pois as ruas são paralelas, e retas paralelas são o lugar geométrico do plano que mantém a mesma medida da distância de uma reta.

Sugestão de atividade extra

Após a realização da atividade 18, convide os estudantes a buscar, em mapas da região onde moram ou de alguma grande cidade brasileira, outros exemplos de ruas aparentemente paralelas e de ruas que parecem formar ângulos de medida de abertura iguais a 30graus, 45graus, 60graus e 90graus.

Os estudantes podem realizar uma brincadeira de caça ao tesouro utilizando esses mapas da mesma fórma que foi feito no início desse tópico. Peça que se reúnam em grupos de quatro estudantes e elaborem um mapa do tesouro com base no mapa e nas ruas escolhidas. O tesouro deve estar em uma posição que seja possível de identificar por meio de pistas com descrições geométricas. Oriente os grupos a trocarem as atividades, entregando apenas o mapa e as descrições. Dê algum tempo para que tentem localizar o tesouro, anotem em uma folha e destroquem os mapas, as folhas com a resposta e as instruções de localização do tesouro. Cada grupo deve avaliar se os colegas seguiram corretamente as instruções e se conseguiram localizar o tesouro a partir das pistas. Se algum grupo não conseguir encontrar o tesouro, analise a resolução e o próprio enunciado, esclarecendo eventuais dúvidas.

Página 94

19. Na figura a seguir, as mesas de madeira no centro são denominadas tribunas. Qual delas o palestrante deve ocupar para que esteja à mesma medida de distância de cada poltrona de uma mesma fileira da plateia?

Ilustração. Três bancadas uma ao lado da outra, sendo 1, 2 e 3. Ao redor, três fileiras, sendo: uma fileira com 31 cadeiras, uma fileira com 27 cadeiras e uma fileira com 23 cadeiras.

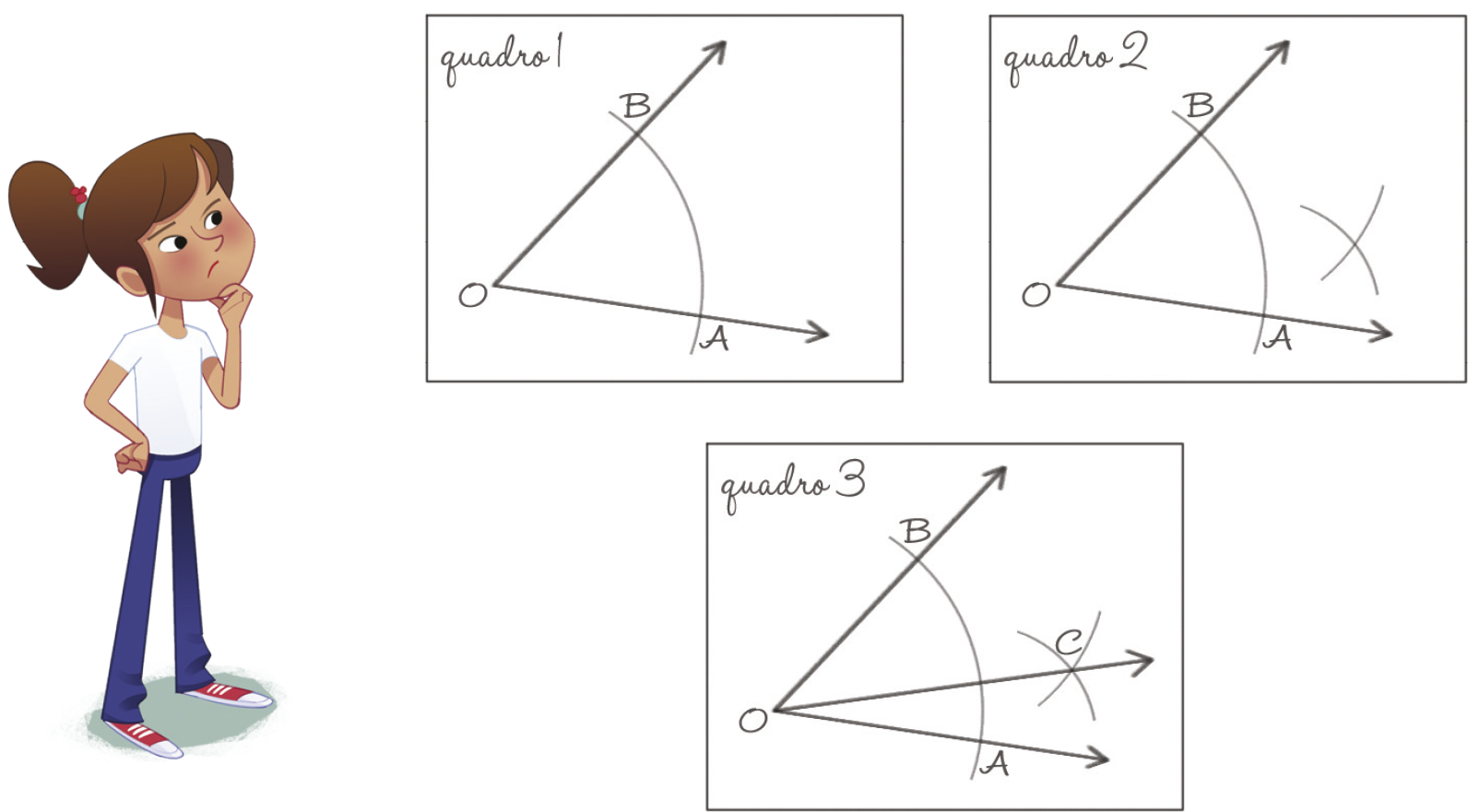
20. Mariana tentou construir a bissetriz do ângulo

A \hat{O} B

conforme os passos seguintes e percebeu, na última etapa, que a construção tinha um erro. Em qual quadro ocorreu o erro? Como Mariana deve corrigi-lo?

Ilustração. Menina branca de cabelo castanho comprido e preso, camiseta branca, calça azul e tênis vermelho e branco com expressão de quem está pensando, olhando para os quadros.

Ilustração. Quadro 1. À esquerda, ponto O. De O, reta diagonal com ponto A e reta diagonal com ponto B. Arco em AB.

Ilustração. Quadro 2. À esquerda, ponto O. De O, segmento de reta diagonal com ponto A e segmento de reta diagonal com ponto B. Arco em AB. Cruzamento de dois semi-arcos entre os segmento OB e OA.

Ilustração. Quadro 3. À esquerda, ponto O. De O, segmento de reta diagonal com ponto A e segmento de reta diagonal com ponto B. Arco em AB. Cruzamento no ponto C de dois semi-arcos entre os segmento OB e OA. Semirreta partindo de O e passando por C, de forma a dividir o ângulo AÔB de forma desigual.

3 Transformações geométricas

Isometrias são transformações geométricas que preservam o formato e as medidas da figura inicial, como translação, rotação e reflexão, que podemos encontrar na ilustração a seguir.

Ilustração. Sequência de seis figuras compostas por um hexágono laranja com seis losangos vermelhos dentro unidos no centro.

A figura obtida a partir de uma transformação geométrica é chamada de imagem dessa transformação.

Respostas e comentários

19. tribuna 2

20. O erro aconteceu no quadro 2. Para traçar os arcos que determinam o ponto C, a abertura do compasso deve ser a mesma.

Transformações geométricas

Bê êne cê cê:

• Competência específica 3 (a descrição está na página sete).

• Habilidade ê éfe zero oito ême ah um oito.

Objetivos:

• Retomar os conceitos de translação, rotação e reflexão.

• Reconhecer e construir figuras obtidas por composições de transformações geométricas.

Justificativa

Retomar os conceitos de translação, rotação e reflexão é importante para que os estudantes consolidem os conhecimentos previamente adquiridos e possam explorar as composições de transformações geométricas.

É possível reconhecer as composições de transformações geométricas em contextos diversos, o que possibilita aos estudantes verificar como a Matemática pode se relacionar com outras áreas do conhecimento, o que favorece o desenvolvimento da competência específica 3 de Matemática. O estudo dessas composições também amplia o repertório dos estudantes sobre esse conteúdo e contribui para o desenvolvimento da habilidade ê éfe zero oito ême ah um oito.

Mapeando conhecimentos

Reproduza, em papel ou arquivo eletrônico, algumas imagens de mosaicos construídos por translações, rotações e/ou reflexões de figuras; distribua as imagens entre os estudantes de cada grupo:

Ilustração. Retângulo com mosaico constituído de triângulos alaranjados e vermelhos e de quadrados amarelos. Dois padrões. No primeiro padrão, ao centro, um hexágono constituído de triângulos e na base de cada triângulo, um quadrado. No segundo padrão, ao centro um quadrado e em cada lateral um triângulo.
A figura é padrão 1, padrão 2 e finaliza com padrão 1.

Em seguida, peça aos grupos que identifiquem translações, rotações e/ou reflexões. Reserve um momento para que os grupos compartilhem seus mosaicos e descobertas.

Para as aulas iniciais

Na seção Revisão dos conteúdos de anos anteriores, retomam-se os conceitos de translação, rotação e reflexão em relação a uma reta e em relação a um ponto. Faça a leitura coletiva dessa revisão com a turma e proponha que realizem as atividades 18 e 19. Discuta essas atividades com a turma e tire as possíveis dúvidas.

Você também pode propor aos estudantes que retomem os mosaicos explorados na dinâmica inicial e investiguem a equivalência entre algumas transformações e composições de transformações.

(ê éfe zero oito ême ah um oito) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

Página 95

Translação

Translação é o deslocamento de uma figura dado por um vetor.

Um vetor (

) pode ser representado por um segmento orientado que indica a direção, o sentido e a medida da distância do deslocamento.

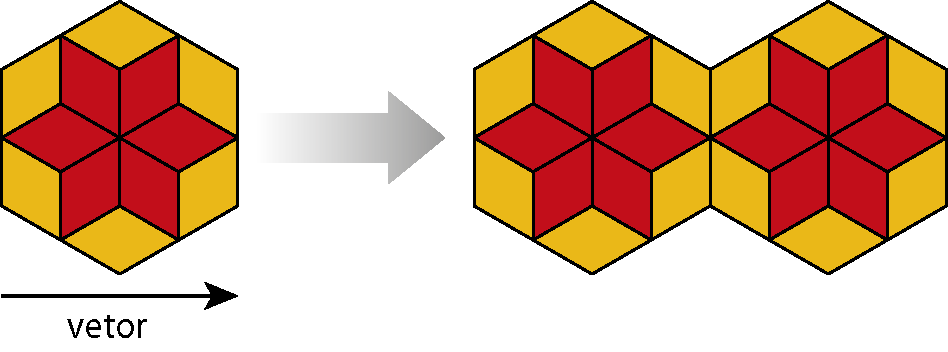
Ilustração. Figura composta por um hexágono laranja com seis losangos vermelhos dentro unidos no centro. Seta para direita na parte inferior: vetor. Ao lado, ilustração. Duas figuras compostas por um hexágono laranja com seis losangos vermelhos dentro unidos no centro.

Confira a seguir algumas translações de polígonos na malha quadriculada.

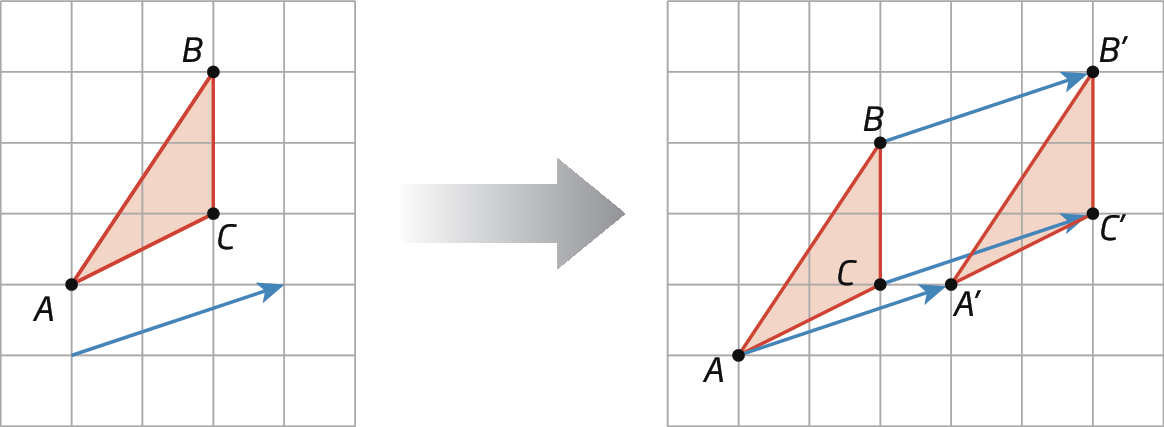
Figura geométrica. Malha quadriculada com triângulo ABC. Vetor diagonal para direita abaixo da figura. Ao lado, malha quadriculada com triângulo ABC. À direita, triângulo idêntico, porém deslocado, A linha, B linha, C linha. Há vetores indicando a translação dos pontos A para A linha, B para B linha e C para C linha.

O vetor (em azul) indica a direção, o sentido e a medida da distância do deslocamento. Note que cada ponto do triângulo foi transladado de acordo com o vetor. Assim, o triângulo á linha bê linha cê linha é a translação do triângulo á bê cê.

Verifique mais um exemplo de translação.

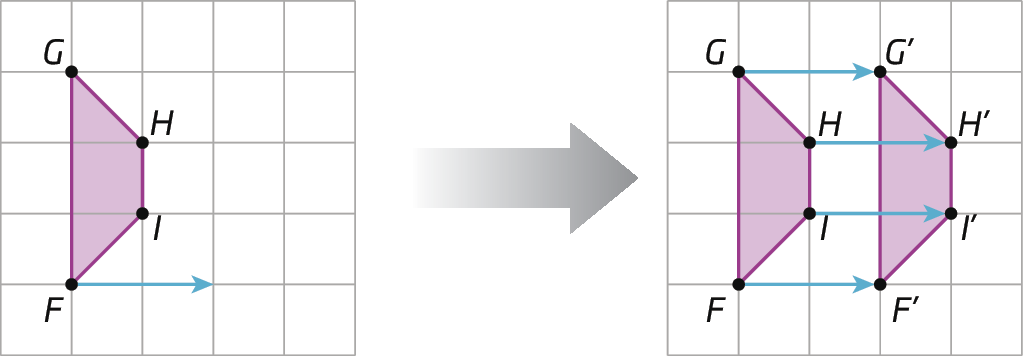
Figura geométrica. Malha quadriculada com trapézio GHIF. Vetor horizontal para direita abaixo da figura. Ao lado, malha quadriculada com triângulo trapézio GHIF. À direita, trapézio idêntico, porém deslocado, G linha, H linha, I linha, F linha. Há vetores indicando a translação dos pontos G para G linha, H para H linha, I para I linha e F para F linha.

Atividades

Faça as atividades no caderno.

21. Em uma malha quadriculada, copie estas figuras e as translade de acordo com o vetor.

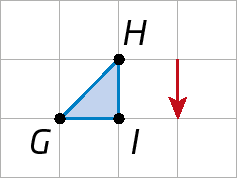
Figura geométrica. Malha quadriculada com triângulo azul G H I. Ao lado, seta vertical para baixo.

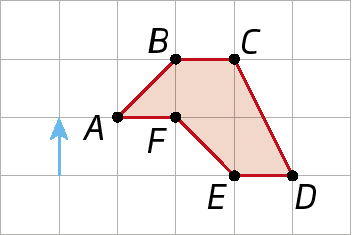
Figura geométrica. Malha quadriculada com figura laranja ABCDEF.

Respostas e comentários

21. a) Resposta em Orientações.

21. b) Resposta em Orientações.

Translação

Chame a atenção dos estudantes para o fato de que a translação consiste em deslocar, ou transportar, uma figura no plano, obtendo-se uma figura congruente à original. Após apresentar os exemplos desta página, você pode propor aos estudantes que, em uma folha de papel quadriculado, façam um desenho ou uma figura geométrica e o reproduzam em um local diferente do papel, realizando uma translação.

É importante também comentar que a representação de vetores se parece com a representação de semirretas. Enfatize com a turma que esses conceitos são diferentes.

• Resposta do item a da atividade 21:

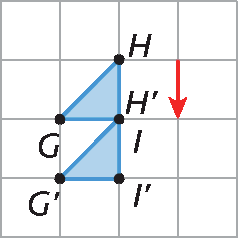
Figura geométrica. Malha quadriculada com triângulo GHI. Vetor vertical ao lado da figura, apontando para baixo. Na mesma malha, abaixo, triângulo idêntico, porém deslocado, G linha, H linha, I linha. O ponto I coincide com H linha. As figuras se interseccionam nesse único ponto.

• No item b da atividade 21, os estudantes podem estranhar o fato de as figuras se sobreporem na resposta. Explique que o deslocamento promovido pela translação não foi suficiente para que as figuras não se sobrepusessem e que a construção está correta.

Resposta do item b da atividade 21:

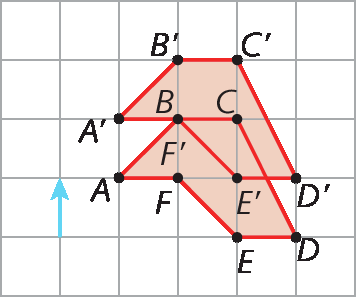
Figura geométrica. Malha quadriculada com figura geométrica de seis lados ABCDEF. Vetor vertical ao lado da figura, apontando para cima. Na mesma malha, acima, figura geométrica idêntica, porém deslocada, A linha, B linha, C linha, D linha, E linha e F linha. O ponto B coincide com F linha. As figuras tem intersecção, o ponto C está dentro da figura A linha, B linha, C linha, D linha, E linha, F linha e o ponto E linha está dentro da figura ABCDEF.

Página 96

Rotação

Rotação é o giro de uma figura em torno de um centro de rotação, em determinado sentido (horário ou anti-horário), segundo um ângulo de rotação.

A figura seguinte foi rotacionada a partir de um giro de 60graus no sentido horário. Sucessivas rotações de giro de 60graus nesse sentido produzem a figura em vermelho a seguir.

Ilustração. Um losango vermelho. Abaixo está escrito: centro de rotação. Seta para direita, indicando dois losangos unidos pelo lado. Abaixo está escrito: rotação de um giro de 60 graus no sentido horário. Seta para direita, indicando seis losangos unidos no centro. Abaixo está escrito: sucessivas rotações.

Na figura, o centro de rotação é um vértice do polígono, mas podemos escolher o centro de rotação em qualquer posição, inclusive externo ou interno à figura a ser rotacionada.

Cuidado! Evite acidentes ao usar o compasso.

Construção de uma rotação com transferidor e compasso

Podemos rotacionar uma figura utilizando um transferidor e um compasso.

Acompanhe os passos a seguir para obter a rotação de uma figura, dados o centro, a medida de abertura do ângulo e o sentido da rotação.

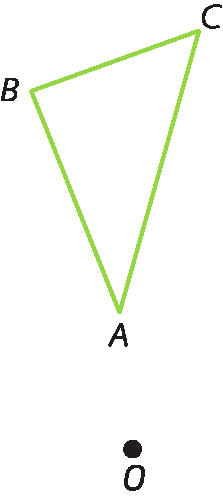
Ilustração. Triângulo ABC. Abaixo, ponto O.

• centro de rotação: óh

• medida da abertura do ângulo de rotação: 40graus

• sentido da rotação: anti-horário

1º) Centramos o compasso no ponto óh e traçamos um arco passando pelo ponto a, outro passando por B e um terceiro passando por C.

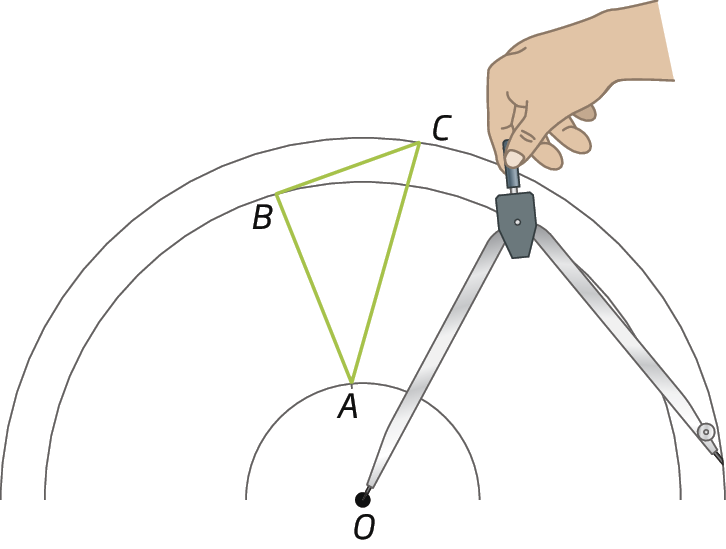
Ilustração. Triângulo ABC. Abaixo, ponto O. Destaque para a mão de uma pessoa traçando arco que passa sobre o ponto C e tem ponta seca em O. Há arcos de circunferência passando por B e A, centrados em O.

2º) Colocamos o centro do transferidor em óh e, alinhando o transferidor com

\overline{A O}

, marcamos 40graus; onde a medida de abertura do ângulo cruzar com o arco que passa pelo ponto a, marcamos o ponto á linha. Fazemos o mesmo com os pontos B e C, marcando os pontos bê linha e cê linha , atentando para o sentido do giro.

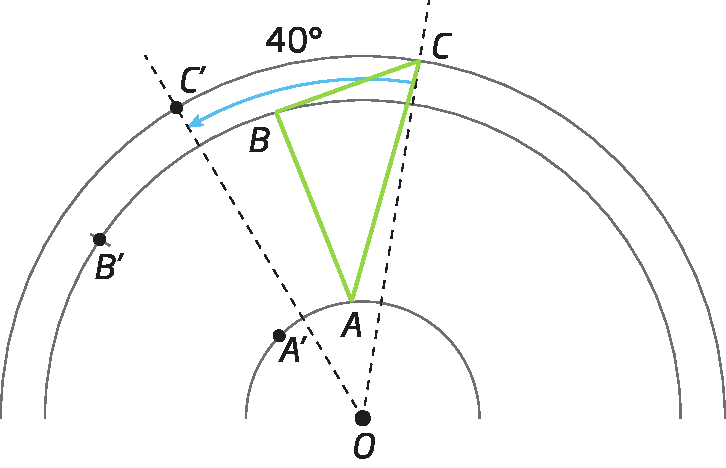
Ilustração. Triângulo ABC. Abaixo, ponto O. Arco passa sobre o ponto C. Há arcos de circunferência passando por B e A, centrados em O. Ponto A linha posicionado sobre o arco e a esquerda de A, ponto B linha posicionado sobre o arco e a esquerda de B, Ponto C linha posicionado sobre o arco e a esquerda de C. Duas semirretas pontilhadas, uma parte de O e passa por C e outra parte de O e passa por C linha. Em destaque o ângulo de 40 graus entre as linhas.

3º) Unimos os pontos á linha, bê linha e C ', obtendo a rotação do triângulo á bê cê de um ângulo de medida da abertura de 40graus no sentido anti-horário em torno do ponto óh.

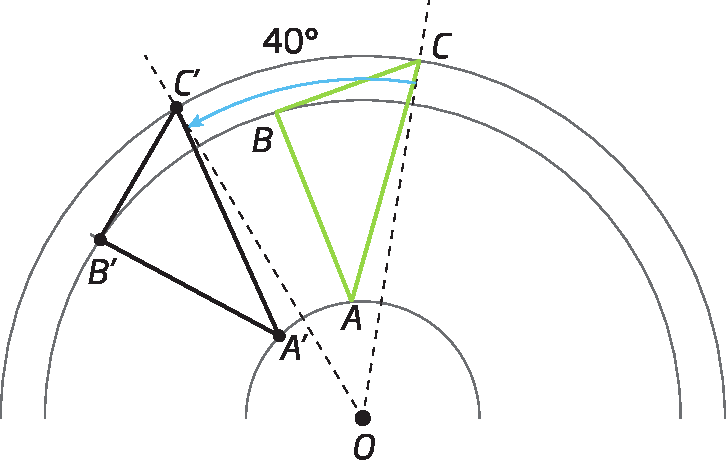
Ilustração. Triângulo ABC. Abaixo, ponto O. Um arco passa sobre o ponto C. Há arcos de circunferência passando por B e A, centrados em O. Ponto A linha posicionado sobre o arco e a esquerda de A, ponto B linha posicionado sobre o arco e a esquerda de B, Ponto C linha posicionado sobre o arco e a esquerda de C. Duas semirretas pontilhadas, uma parte de O e passa por C e outra parte de O e passa por C linha. Em destaque o ângulo de 40 graus entre as linhas. Triângulo formado por A linha, B linha e C linha.

Respostas e comentários

Rotação

É importante que os estudantes compreendam que para realizar uma rotação é necessário determinar um ponto (centro da rotação), a medida da abertura de um ângulo (ângulo da rotação) e um sentido (horário ou anti-horário).

Ao explorar a construção de uma rotação com transferidor e compasso, recomenda-se que você reproduza com a turma os passos descritos nesta página e vá tirando as dúvidas que possam surgir.

Oriente os estudantes quanto aos cuidados no manuseio do compasso a fim de evitar acidentes.

Sugestão de atividade extra

Antes de abordar o estudo sobre rotação, peça aos estudantes que pesquisem previamente o significado dessa palavra. Peça também que encontrem imagens que remetam a rotações na natureza ou em obras de arte. Os estudantes podem apresentar, por exemplo, imagens de algumas flores e frutos, como pétalas em torno de um centro, ou de um corte transversal de uma laranja. Explique que a rotação pode ser imaginada também em objetos de três dimensões, como os sólidos geométricos, a própria laranja ou, até mesmo, o planeta Terra. A rotação nesses casos se dá em torno de uma reta. Entretanto, o objeto de estudo serão as seções planas desses objetos, pois nesse momento nos concentraremos nas figuras planas. As imagens de exemplos podem ser obtidas em jornais, revistas ou impressas a partir da internet. Oriente os estudantes a colar as imagens no caderno, identificando o centro de rotação e justificando o motivo de acreditarem que as imagens apresentadas foram rotacionadas em torno de determinado ponto. Caso haja divergências entre o conceito e o que os estudantes apresentaram, explique os possíveis erros e esclareça eventuais dúvidas.

Página 97

Atividades

Faça as atividades no caderno.

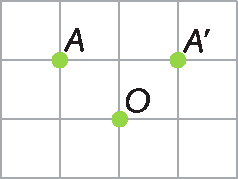
22. Em uma malha quadriculada, copie as figuras a seguir e obtenha as rotações de centro óh :

a) do ponto a, com um giro de 90graus, no sentido horário;

Figura geométrica. Malha quadriculada com ponto A na parte superior esquerda e ponto O na parte inferior direita.

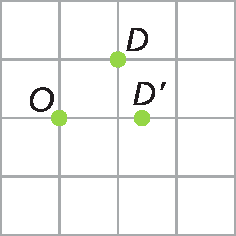
b) do ponto D, com um giro de 45graus, no sentido horário;

Figura geométrica. Malha quadriculada com ponto D na parte superior direita e ponto O na parte inferior esquerda.

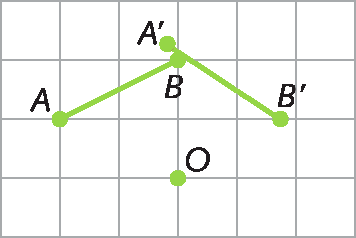
c) do segmento de reta

\overline{A B}

, com um giro de 60graus, no sentido horário.

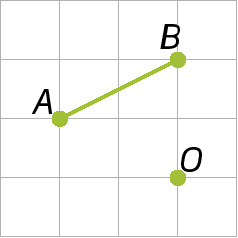
Figura geométrica. Malha quadriculada com ponto A na parte inferior esquerda e ponto O na parte superior direita formam segmento AB. Abaixo de B, ponto O.

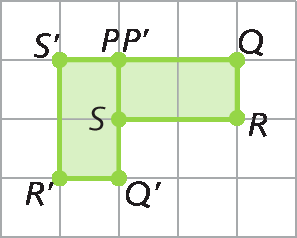
23. Copie as figuras seguintes em uma malha quadriculada e obtenha as rotações:

a) de centro P, no sentido horário, com uma rotação de um giro de 90graus;

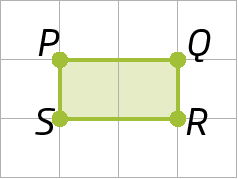
Figura geométrica. Malha quadriculada com retângulo verde PQRS.

b) de centro óh, no sentido anti-horário, com uma rotação de um giro de 180graus;

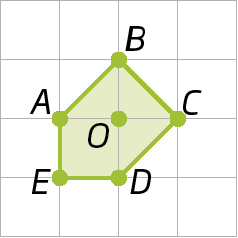
Figura geométrica. Malha quadriculada com figura verde ABCDE. No centro da figura, ponto O.

c) de centro P, no sentido anti-horário, com uma rotação de um giro de 45graus.

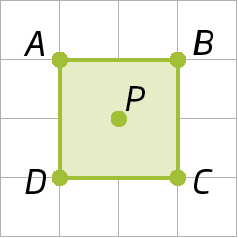
Figura geométrica. Malha quadriculada com quadrado verde ABCD. No centro da figura, ponto P.

Reflexão

Reflexão é a transformação geométrica que reflete todos os pontos de uma figura em relação a uma reta (simetria axial) ou a um ponto (simetria central), mantendo cada ponto da figura à mesma medida da distância do eixo de simetria ou do centro de reflexão, respectivamente.

Simetria axial

Reconhecemos a simetria axialglossário pela presença de um eixo de simetria. Uma figura pode ter mais de um eixo de simetria.

um eixo de simetria

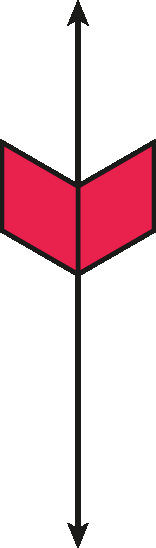
Figura geométrica. Dois losangos na vertical. No centro, reta vertical e reta horizontal entre os losangos. Abaixo está escrito: dois eixos de simetria.

dois eixos de simetria

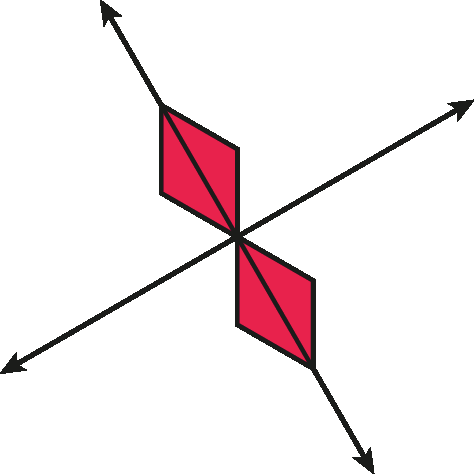
Figura geométrica. Hexágono composto por seis triângulos, dentro de cada um deles, um losango. Os losangos são unidos no centro. Seis retas cortam a figura, de forma a passar pelo centro do hexágono, laterais ou pelo meio do triângulo. Abaixo está escrito: vários eixos de simetria.

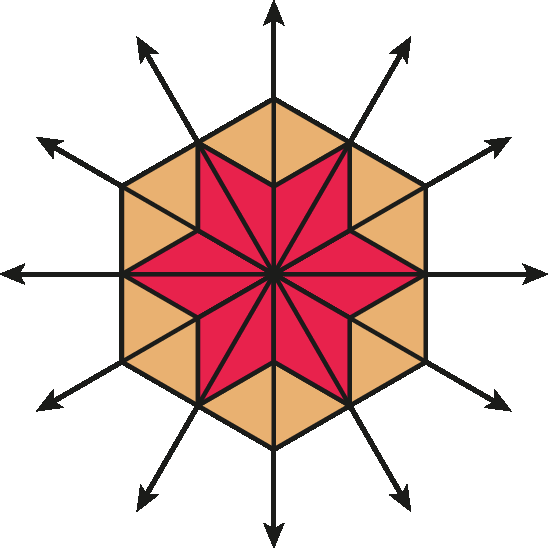
vários eixos de simetria

Respostas e comentários

22. a) Resposta em Orientações.

22. b) Resposta em Orientações.

22. c) Resposta em Orientações.

23. a) Resposta em Orientações.

23. b) Resposta em Orientações.

23. c) Resposta em Orientações.

Reflexão

Antes de iniciar a exploração do tópico, pergunte aos estudantes se já repararam em como é a escrita bombeiros ou ambulância na frente dos carros de emergência. Pergunte se conseguem explicar o motivo. Em seguida, peça que escrevam essas palavras no caderno e determinem sua reflexão, como na imagem a seguir.

Esquema. Eixo de simetria. Reta vertical ao centro. À esquerda, AMBULÂNCIA, BOMBEIROS. À direita, as mesmas palavras escritas de trás para frente.

Peça aos estudantes que voltem à página do Trocando ideias e observem os grafismos presentes nas peças de cerâmica feitas por moradores locais da Ilha de Marajó, a fim de identificar a presença de simetria axial. A imagem a seguir, destaque a presença de um eixo de simetria em um dos vasos.

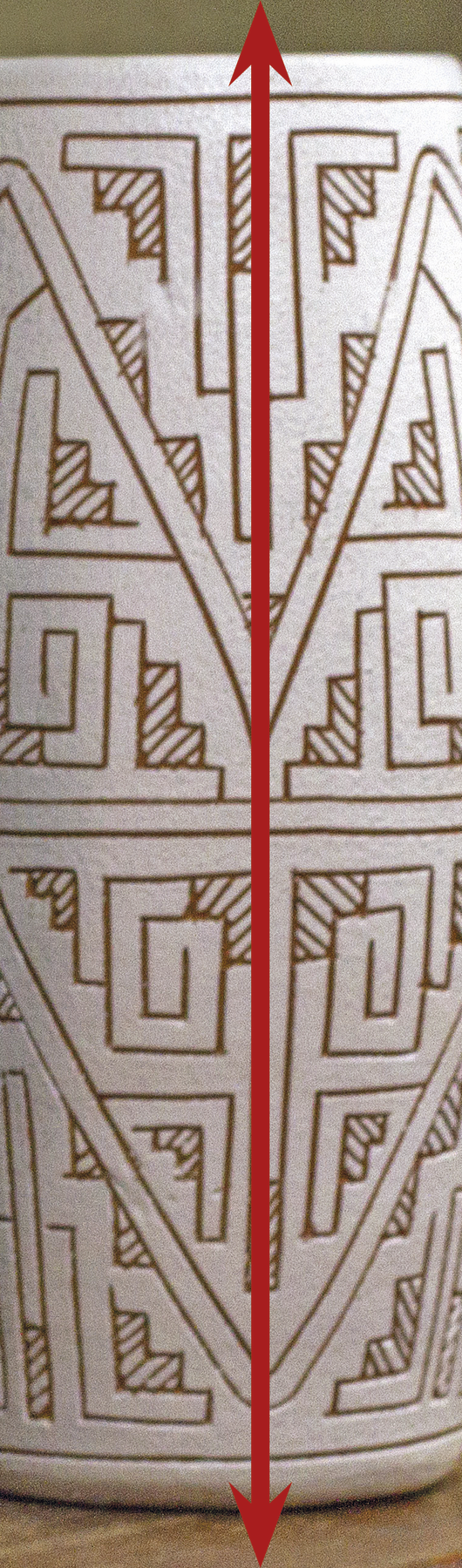
Fotografia. Vaso de cerâmica com desenhos geométricos. No centro, reta vertical.

• Respostas da atividade 22:

Figura geométrica. Malha quadriculada com ponto A na parte superior esquerda e ponto A linha ao lado. Abaixo, entre A e A linha, ponto O.

Figura geométrica. Malha quadriculada com ponto O no centro à esquerda e ponto D linha ao lado. Acima, ponto D.

Figura geométrica. Malha quadriculada com segmento AB inclinado para a direita e A linha B linha inclinado para a esquerda. Abaixo, ponto O.

• Respostas da atividade 23:

Figura geométrica. Malha quadriculada com retângulo verde na horizontal composta pelos pontos: PQRS. Na vertical, figura composta pelos pontos: P linha, Q linha, R linha, S linha. As figuras de interseccionam no segmento P linha S.

Figura geométrica. Malha quadriculada com figura verde composta pelos pontos: ABCDE. Sobre ela, figura composta pelos pontos A linha, B linha, C linha, D linha, E linha. No centro, ponto O. A coincide com C linha. B linha coincide com D. C coincide com A linha e D linha coincide com B.

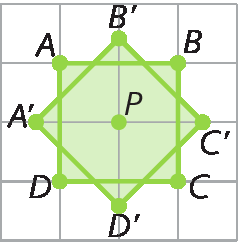
Ilustração. Malha quadriculada com quadrado verde composto pelos pontos: ABCD. Sobre ele, quadrado verde composto pelos pontos A linha, B linha, C linha, D linha. No centro, ponto P. As figuras são concêntricas, porém não se sobrepõem.

Página 98

Vamos representar o eixo de simetria pela reta r. Podemos determinar, em relação a esse eixo, a figura simétrica de um ponto, de um segmento de reta, de uma reta ou de uma figura plana qualquer.

Simetria de um ponto

Dois pontos distintos a e á linha são simétricos em relação a uma reta r se esta divide o segmento de reta

\overline{A A'}

perpendicularmente no seu ponto médio.

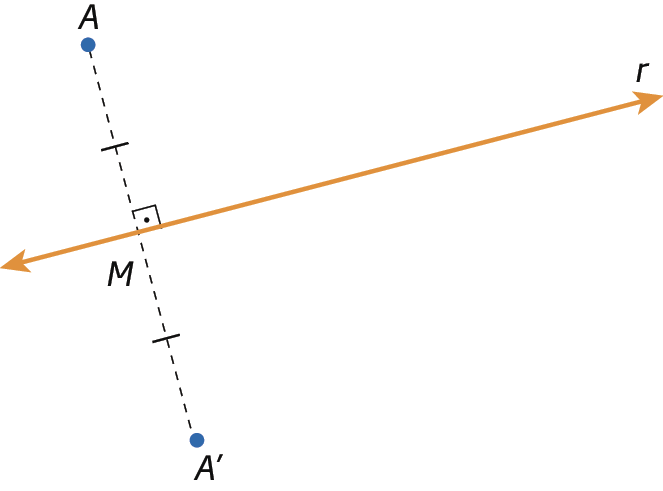
Figura geométrica. Reta diagonal r. Sobre ela, à esquerda, reta tracejada vertical A A linha formam ângulo reto na intersecção com a reta r, no ponto M.
Abaixo está escrito: A linha é simétrico de A em relação à reta r.

\overline{A M} ≅ \overline{A' M}

A‘ é simétrico de a em relação à reta r.

Simetria de um segmento de reta

Na figura a seguir, os pontos á linha e bê linha são, respectivamente, simétricos de a ê B em relação à reta r. Dizemos, então, que os segmentos

\overline{A B}

\overline{A' B'}

são simétricos em relação à reta r.

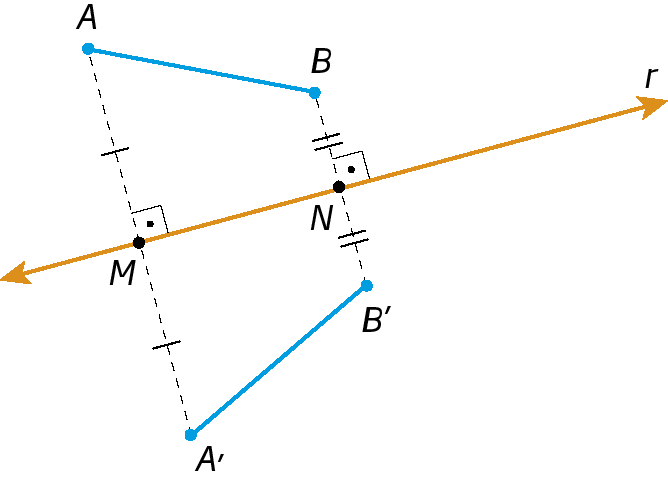
Figura geométrica. Reta diagonal r. Sobre ela, à esquerda, reta tracejada vertical A A linha formam ângulo reto no ponto M com reta r. À direita, reta tracejada B B linha formam ângulo reto no ponto N com reta r. Segmento AB e segmento A linha B linha. Indicação de que o segmento AM tem mesmo tamanho que M A linha e que BN tem mesmo tamanho que N B linha. Abaixo está escrito: Segmento A linha B linha é simétrico de AB em relação à reta r.

\overline{A M} ≅ \overline{A ’ M}

\overline{B N} ≅ \overline{B ’ N}

\overline{A' B'}

é simétrico de

\overline{A B}

em relação à reta r.

Simetria de uma reta

Os pontos a, B e C estão alinhados, assim como seus simétricos á linha, bê linha e cê linha . As retas

\overset{\leftrightarrow}{A B}

\overset{\leftrightarrow}{A' B'}

são simétricas em relação à reta r.

\overline{A M} ≅ \overline{A ’ M}

\overline{B N} ≅ \overline{B ’ N}

\overset{\leftrightarrow}{A' B'}

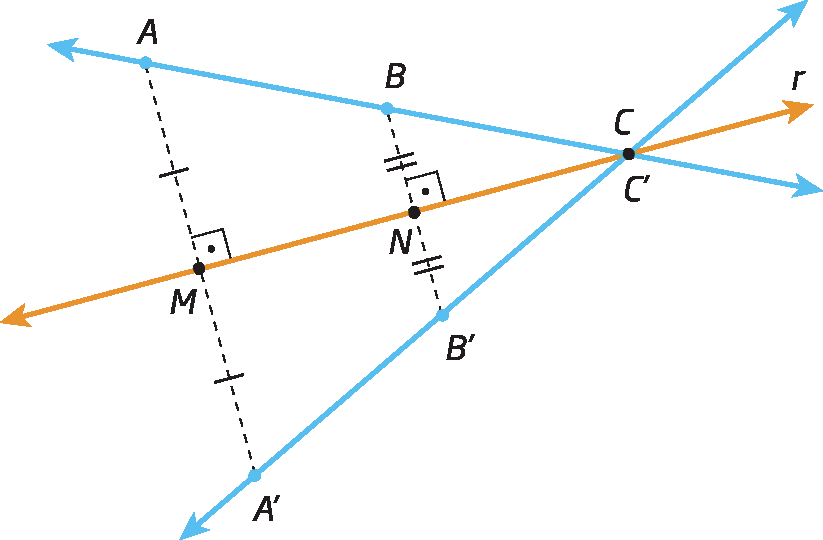
é simétrica de

\overset{\leftrightarrow}{A B}

em relação à reta r.

Respostas e comentários

Proponha aos estudantes que, em uma folha de papel quadriculado, representem o simétrico de um ponto, de um segmento de reta e de uma reta em relação a um eixo de simetria. Você pode propor essa atividade antes ou depois de abordar o conteúdo desta página. Se optar por propor antes, ele servirá para diagnosticar os conhecimentos previamente adquiridos por eles. Se optar por propor depois, a atividade servirá para aplicar o que foi estudado. Você também pode propor que a atividade seja realizada com o GeoGebra.

Página 99

Simetria de um círculo

Os centros óh e ó linha são simétricos em relação à reta r, e os círculos têm raios com a mesma medida de comprimento.

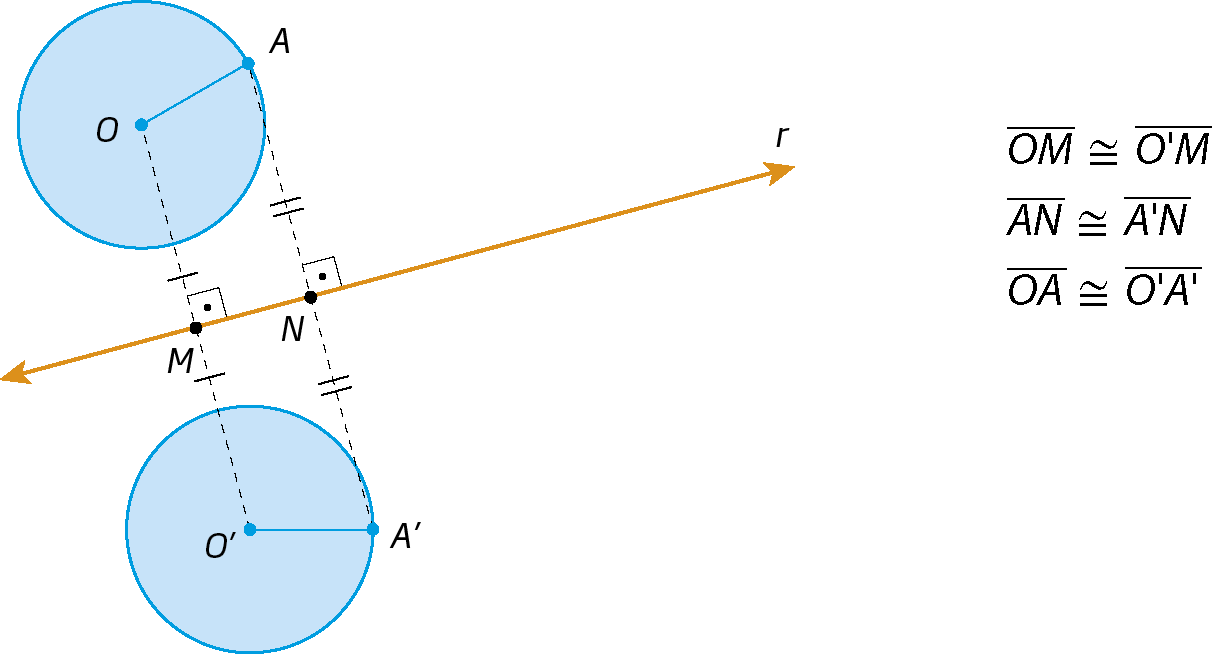
Figura geométrica. Reta diagonal r. Acima, circunferência com centro no ponto O. Abaixo, circunferência com centro no ponto O linha. Semirreta tracejada de O até O linha, interseccionando a reta r no ponto M, formando ângulo reto. À direita, ponto A sobre a fronteira da circunferência de centro O. Também à direita, ponto A linha sobre a fronteira da circunferência de centro O linha. Semirreta tracejada de A até A linha interseccionando a reta r no ponto N, formando ângulo reto. Indicação de que o segmento OM tem mesma medida do segmento M O linha e que o segmento AN tem mesma medida que N A linha.
Abaixo está escrito: O círculo de centro O linha e comprimento de raio medindo O linha A linha é simétrico do círculo de centro O e comprimento de raio medindo OA em relação à reta r. — O círculo de centro ó linha e comprimento de raio medindo O'A' é simétrico do círculo de centro óh e comprimento de raio medindo ó á em relação à reta r.

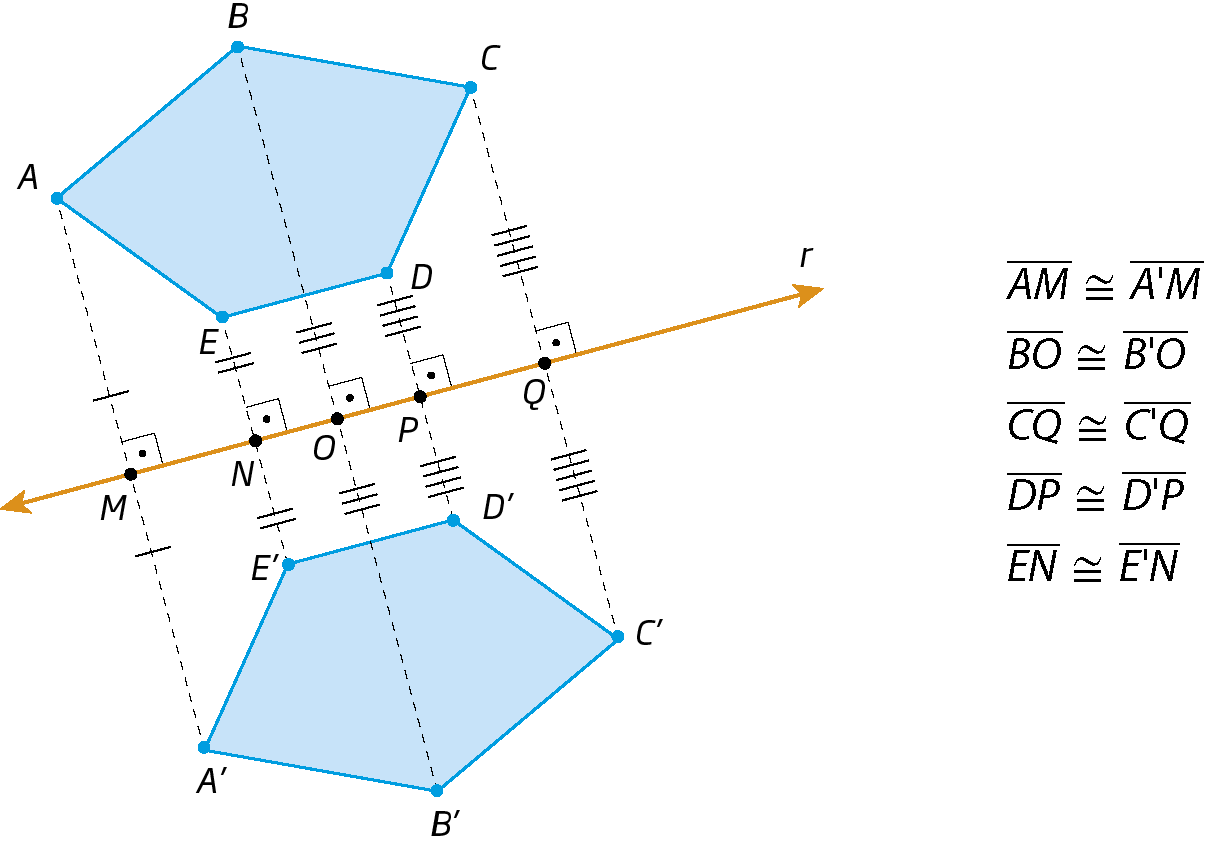
Simetria de um polígono

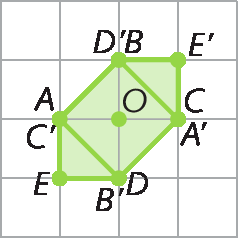
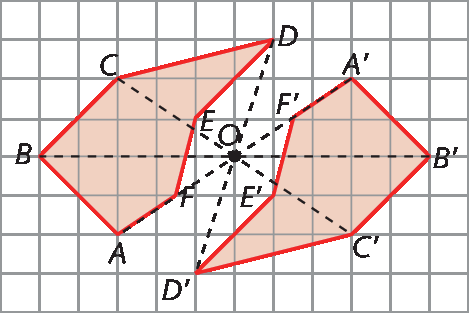
Na figura, note que os pontos á linha, bê linha, cê linha, dê linha e E ' são, respectivamente, simétricos de a, B, C, D e ê em relação à reta r. Dizemos que os polígonos á bê cê dê é e á linha bê linha cê linha dê linha é linha são simétricos em relação à reta r.

Figura geométrica. Reta diagonal r. Acima, pentágono ABCDE. Abaixo, pentágono A linha, B linha, C linha, D linha, E linha. Reta tracejada vai de A até A linha e intersecciona a reta r em M, formando ângulo reto, de forma que AM tenha mesmo tamanho que M A linha. Reta tracejada vai de B até B linha e intersecciona a reta r em O, formando ângulo reto, de forma que BO tenha mesmo tamanho que O B linha. Reta tracejada vai de C até C linha e intersecciona a reta r em Q, formando ângulo reto, de forma que CQ tenha mesmo tamanho que Q C linha. Reta tracejada vai de E até E linha e intersecciona a reta r em N, formando ângulo reto, de forma que EN tenha mesmo tamanho que N E linha. Reta tracejada vai de D até D linha e intersecciona a reta r em P, formando ângulo reto, de forma que DP tenha mesmo tamanho que P D linha.
Legenda: O polígono A linha B linha C linha D linha E linha é simétrico do polígono ABCDE em relação à reta r. — O polígono á linha bê linha cê linha dê linha é linha é simétrico do polígono á bê cê dê é em relação à reta r.

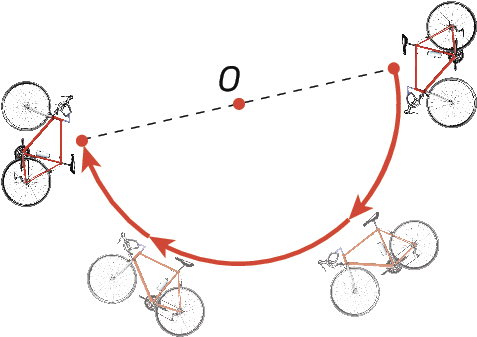
Simetria central

A simetria central é determinada em relação a um ponto denominado centro de simetria.

Essa transformação é equivalente a uma rotação de um giro de 180graus em qualquer sentido (horário ou anti-horário).

Esquema. Reta tracejada com ponto O no centro. Arco de uma semicircunferência, com setas da direita para a esquerda, apontando para a esquerda, com 4 bicicletas em volta.
Legenda: O ponto O é o centro de simetria. — O ponto óh é o centro de simetria.

Respostas e comentários

Após apresentar o simétrico de um polígono, pergunte aos estudantes: “O que podemos afirmar sobre os lados correspondentes dos polígonos á bê cê dê é e á linha bê linha cê linha dê linha é linha? E sobre os ângulos correspondentes? Quais são os pontos médios dos segmentos de reta

\overline{A A ’}

\overline{B B ’}

\overline{C C ’}

\overline{D D ’}

\overline{E E ’}

?”. Espera-se que eles respondam que os lados e os ângulos correspondentes dos polígonos á bê cê dê é e á linha bê linha cê linha dê linha é linha são congruentes e que os pontos médios de

\overline{A A ’}

\overline{B B ’}

\overline{C C ’}

\overline{D D ’}

\overline{E E ’}

são, respectivamente, M, O, Q, P e N.

Proponha que, em uma folha de papel quadriculado, representem um polígono e o seu simétrico em relação a uma reta. Caso julgue conveniente, proponha uma atividade similar com o GeoGebra.

Sugestão de leitura

No link indicado a seguir, há uma resposta de um professor de Física sobre o fenômeno da imagem refletida na superfície de um lago. Se achar pertinente, trabalhe essa questão com os estudantes, explicando a eles o que provoca o reflexo da montanha na água. Disponível em: https://oeds.link/PJppzl. Acesso em: 3 agosto 2022.

Página 100

Simetria de um ponto

O simétrico de um ponto M em relação a um ponto óh é o ponto M' tal que óh é o ponto médio do segmento

\overline{M M ’}

Figura geométrica. Segmento M M linha. No centro, ponto O.

\overline{M O} ≅ \overline{M' O}

M' é simétrico de M em relação ao ponto óh.

Simetria de um segmento de reta

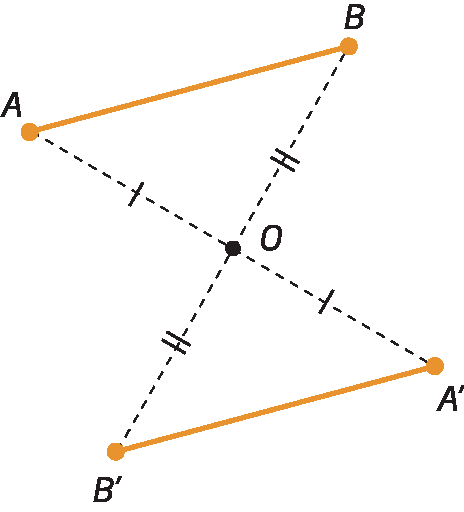
Figura geométrica. Segmento AB. Abaixo, segmento B linha, A linha. Entre os segmentos, ponto O. Diagonal vai de A até A linha e diagonal vai de B até B linha. Elas se cruzam em O. Tamanho de AO é igual ao de O A linha e o tamanho de BO é igual ao de B linha O.

\overline{A O} ≅ \overline{A ’ O}

\overline{B O} ≅ \overline{B ’ O}

\overline{A ’ B ’}

é simétrico de

\overline{A B}

em relação ao ponto óh.

Simetria de uma reta

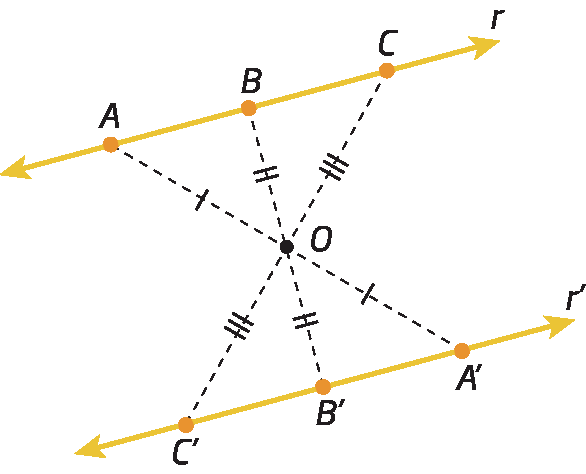
Figura geométrica. Reta r com segmento ABC. Abaixo, reta r linha com pontos C linha, B linha, A linha. Entre os segmentos, ponto O. Diagonal vai de A até A linha e diagonal vai de B até B linha e de C até C linha. Elas se cruzam em O. O tamanho dos segmentos AO e O A linha é igual, o tamanho de BO e O B linha é igual e o tamanho de CO e O C linha é igual.

\overline{A O} ≅ \overline{A ’ O}

\overline{B O} ≅ \overline{B ’ O}

\overline{C O} ≅ \overline{C ’ O}

érre linha é simétrica de r em relação ao ponto óh.

Simetria de um círculo

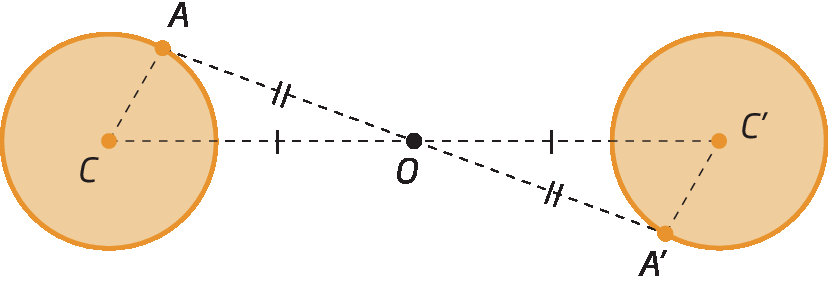
Figura geométrica. À esquerda, circunferência com ponto C no centro e A na extremidade superior. À direita, circunferência com ponto C linha no centro e A linha na extremidade inferior. Entre as circunferências, ponto O. Reta tracejada vai de C até C linha e de A até A linha. Elas se cruzam no centro em O. O segmento AO tem mesmo tamanho do segmento O A linha e o segmento CO tem o mesmo tamanho do segmento O C linha.

\overline{C O} ≅ \overline{C ’ O}

\overline{A O} ≅ \overline{A ’ O}

\overline{A C} ≅ \overline{A ’ C ’}

C e cê linha são simétricos em relação ao ponto óh, e os círculos têm raios com a mesma medida de comprimento, ou seja, os círculos são simétricos em relação ao ponto óh.

Simetria de um polígono

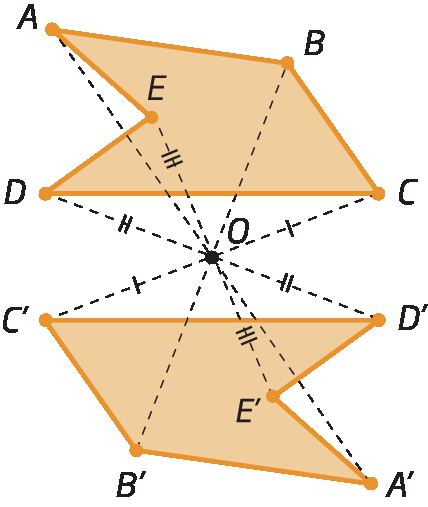
Figura geométrica. Acima, figura ABCDE. Abaixo, figura A linha, B linha, C linha, D linha, E linha. Entre as figuras, ponto O. Diagonal vai de A até A linha, diagonal vai de B até B linha, diagonal de C até C linha, diagonal de D até D linha e diagonal de E até E linha. Elas se cruzam no centro em O.
O segmento AO tem mesmao tamanho de O A linha, o segmento BO tem mesmo tamanho que O B linha, o segmento CO tem mesmo tamanho que O C linha, o segmento DO tem mesmo tamanho que O D linha, o segmento EO tem mesmo tamanho que O E linha.

\overline{A O} ≅ \overline{A ’ O}

\overline{B O} ≅ \overline{B ’ O}

\overline{C O} ≅ \overline{C ’ O}

\overline{D O} ≅ \overline{D ’ O}

\overline{E O} ≅ \overline{E ’ O}

O polígono á'bit'centésimo'divisores de 'E' é simétrico ao polígono á bê cê dê é em relação ao ponto óh.

Respostas e comentários

Proponha aos estudantes que, em uma folha de papel, representem o simétrico de um ponto, de um segmento de reta, de uma reta, de um círculo e de um polígono em relação a um ponto, denominado centro de simetria. Você pode propor essa atividade antes ou depois de abordar o conteúdo desta página. Se optar por propor antes, ele servirá para diagnosticar os conhecimentos previamente adquiridos por eles. Se optar por propor depois, a atividade servirá para aplicar o que foi estudado. Você também pode propor que a atividade seja realizada com o GeoGebra.

Após obterem o simétrico de um polígono, pergunte: “O que podemos afirmar sobre os lados correspondentes dos polígonos? E sobre os ângulos correspondentes?”. Se apresentarem dificuldades, oriente-os a realizar as medidas usando a régua e o transferidor, caso a atividade tenha sido feita em papel, ou por meio das ferramentas de medida do GeoGebra, se a atividade tenha sido feita nesse software.

Sugestão de atividade extra

Proponha a criação de painéis usando folhas de cartolina. Cada estudante deve ter uma folha de cartolina dividida ao meio. Peça que pesquisem imagens de mosaicos na internet e escolham alguma que tenha simetria. Utilizando canetas coloridas ou lápis de cor, peça para reproduzirem o padrão geométrico na parte superior da cartolina, preenchendo toda essa parte da folha. Na parte de baixo, oriente-os a explicar, por escrito, a fórma geométrica, o tipo de simetria e as transformações geométricas envolvidas na elaboração do painel. A explicação deve ser direcionada ao público em geral, pois os painéis podem ficar em exposição na escola.

Página 101

Lendo e aprendendo

Máscaras

As máscaras africanas tradicionais são um dos elementos da grande arte africana que mais evidentemente influenciou a Europa e a arte ocidental em geral no século vinte.

São representações ou manifestações de forças normalmente invisíveis, usadas em ritos agrários, funerários ou de iniciaçãoglossário , rememorando mitos e outras tradições, através de suas fórmas, movimentos, cores e materiais. Às vezes, as máscaras têm pouca semelhança com a aparência humana, para deixar claro que um indivíduo ao usá-las, introjeta um personagem do mundo sobrenatural, tornando visível a presença desse personagem no mundo natural e humano. Habitualmente, são consideradas máscaras apenas objetos faciais e os adornos de cabeça esculpidos, sem levar em conta o traje que os acompanha. Do ponto de vista africano, porém, a máscara é todo um conjunto: a máscara é o próprio mascarado quando se põe em movimento.

Museu Afro Brasileiro (MAFRO). Disponível em: https://oeds.link/mDJmis. Acesso em: 4 julho 2022.

Fotografia. Máscara em tom alaranjado com o rosto mais fino na parte inferior e boca pequena. Tem orelhas arredondadas e adorno na parte superior com linhas na testa. — Máscara tradicional utilizada em Camarões.

Fotografia. Máscara marrom com cabelos nas laterais, O rosto é arredondado com linhas na testa na parte inferior do rosto. — Máscara utilizada em cerimônias tradicionais na África do Sul.

Atividades

1. Responda às questões no caderno.

a) Em que ocasiões as máscaras africanas são utilizadas?

b) As máscaras africanas sempre têm aparência humana? Por quê?

c) O que é a máscara para os africanos?

2. Estas imagens foram criadas tomando como inspiração algumas máscaras africanas.

Ilustração. Dez máscaras diferentes. Máscara com a parte inferior mais fina, linhas na parte superior, olhos amarelos, traços e pontos nas bochechas e boca larga. Máscara com adorno pontiagudo na cabeça e linha vertical amarela no centro. Os olhos são caídos e tem brincos de argola. Máscara circular com faixa no centro e um olho de cada lado. Máscara comprida com linhas verticais no topo da cabeça. Olhos arredondados, um triângulo de ada lado do rosto e boca redonda. Máscara de cor preta com pontos azuis na testa. Olhos pequenos, brincos de argola e queixo estreito. Máscara com a parte superior arredondada com traços verticais e parte inferior fina, os olhos são arredondados com dois triângulos acima e dois abaixo dos olhos e boca pequena. Máscara com penas amarelas nas laterais. No centro da testa, um círculo com círculo amarelo dentro. Em cada lado do rosto, linhas amarelas e azuis. Máscara com duas hastes curvadas para cima na parte superior e quatro hastes curvadas para baixo na parte inferior. Faixa horizontal na testa e boca arredondada com linhas verticais e horizontais. Máscara circular com olhos redondos grandes e boca pequena. Traços verticais para cima e desenho no centro. Máscara comprida com faixa preta e dourada na parte superior no centro. Abaixo, olhos pequenos e boca em formato de losango.

a) Que tipo de simetria está presente nestas imagens? Justifique.

b) Em uma folha de papel sulfite, desenhe uma máscara inspirada em uma máscara africana, aplicando o que você aprendeu sobre as transformações geométricas no plano.

Reúna-se com os colegas e façam uma pesquisa sobre a influência da cultura africana na formação do povo brasileiro.

Respostas e comentários

1. a) Em ritos agrários, funerários ou de iniciação.

1. b) Não, porque, em alguns casos, ao utilizá-la, o indivíduo introjeta um personagem do mundo sobrenatural.

1. c) É o próprio mascarado quando se põe em movimento.

2. a) Simetria axial, pois em cada figura há um eixo de simetria.

2. b) Comentário em Orientações.

3. Comentário em Orientações.

Lendo e aprendendo

Bê êne cê cê:

• Competências gerais 6, 9 e 10 (as descrições estão na página seis).

• Competências específicas 3 e 8 (as descrições estão na página sete).

• Habilidade ê éfe zero oito ême ah um oito.

Objetivos:

• Desenvolver a competência leitora.

• Reconhecer a presença de simetria nas máscaras africanas.

• Pesquisar sobre a influência da cultura africana para a formação do povo brasileiro.

Temas contemporâneos transversais:

Inicie essa seção pedindo aos estudantes que leiam o texto individualmente e, depois, comente que as máscaras africanas são adereços utilizados em cerimônias e rituais e têm grande importância religiosa, mística e espiritual para diversos povos africanos. Nessas cerimônias, as máscaras têm como finalidade estabelecer contato com o mundo espiritual e com os deuses. Diga também que cada grupo étnico pode possuir diversas máscaras, cada uma delas com significados e utilizações diferentes.

Convém também reservar um tempo para analisar as fotografias da página. Deixe-os à vontade para verbalizar o que mais lhes chama a atenção e, aos poucos, incentive-os a identificar as simetrias presentes nelas. Se possível, exiba outros exemplos de máscaras africanas.

• Na atividade 1, os estudantes vão responder a algumas questões sobre o texto. Após terminarem, faça a correção oralmente. Você pode ampliar a proposta dessa atividade e solicitar aos estudantes que elaborem questões com base no texto. Depois, eles podem trocar as questões com um colega e responder às questões propostas por ele.

• A atividade 2 permite aos estudantes mobilizar o que estudaram sobre as transformações geométricas no plano. No item a, espera-se que eles reconheçam a simetria axial das imagens. Se necessário, mostre o eixo de simetria de cada uma delas. Já no item b, eles vão aplicar as transformações geométricas no plano para desenhar uma máscara inspirada em uma máscara africana. Se possível, firme uma parceria com o professor ou a professorade Arte para promover uma melhor experiência aos estudantes. A relação entre Matemática e Arte explorada na atividade favorece o desenvolvimento da competência específica 3 de Matemática.

• Na atividade 3, é solicitado aos estudantes que pesquisem sobre a influência da cultura africana na formação do povo brasileiro. O objetivo dessa atividade é mostrar que a cultura africana vai muito além das máscaras. Esse pode ser o momento oportuno para propor um projeto interdisciplinar em parceria com o professor de História. É importante que eles reconheçam que essa cultura tem influência na culinária, no aspecto religioso, na música, entre outros.

A temática do trabalho proposto busca a valorização da cultura africana, o que favorece o desenvolvimento da competência geral 6 da Bê êne cê cê. Além disso, os estudantes exercitam a empatia e o diálogo, o que contribui para o desenvolvimento das competências gerais 9 e 10 e da competência específica 8 de Matemática.

Página 102

Atividades

Faça as atividades no caderno.

Cuidado! Evite acidentes ao usar o compasso na atividade 25.

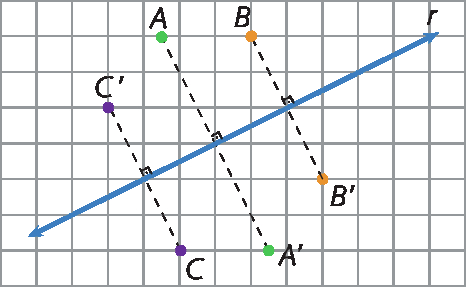
24. Em uma malha quadriculada, copie a figura seguinte. Depois, obtenha os pontos á linha, bê linha e cê linha simétricos aos pontos a, B e C em relação à reta r.

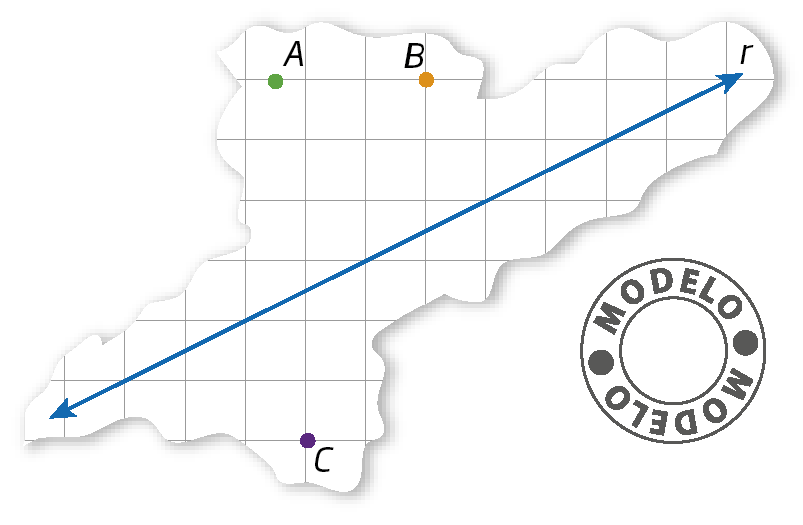
Figura geométrica. Modelo. Parte de uma malha quadriculada com reta r na diagonal. Na parte superior da malha, pontos A e B. Na parte inferior direita, ponto C.

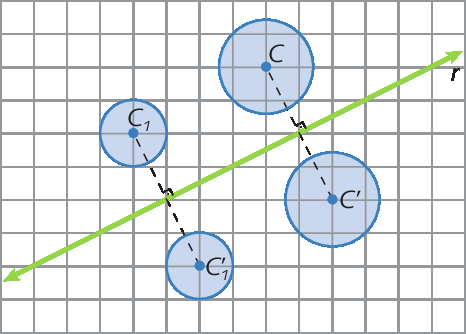
25. Em uma malha quadriculada, utilize o compasso para copiar os círculos seguintes. Depois, construa o simétrico de cada círculo em relação à reta r.

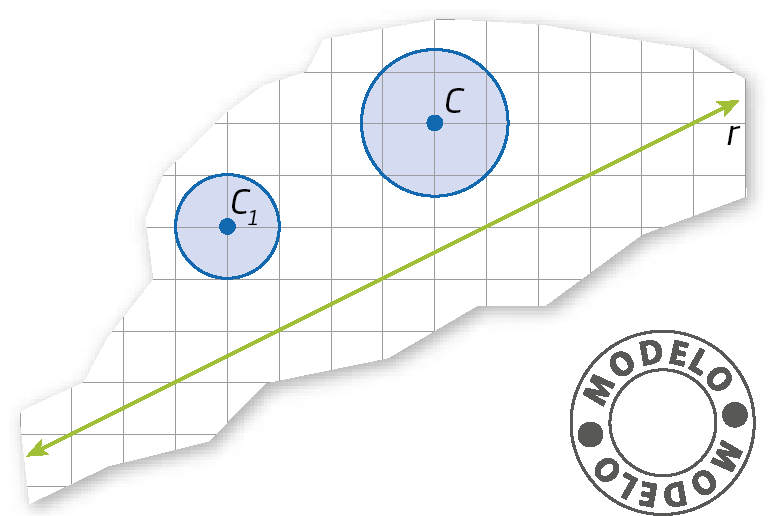
Figura geométrica. Modelo. Parte de uma malha quadriculada com reta r na diagonal. Na parte superior da malha, circunferência com centro C1 e circunferência maior com centro C.

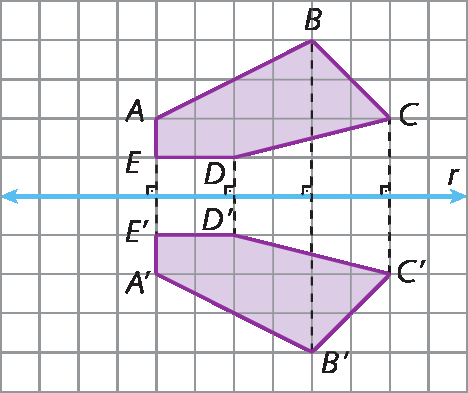
26. Em uma malha quadriculada, copie o polígono seguinte. Depois, construa o simétrico desse polígono em relação à reta r.

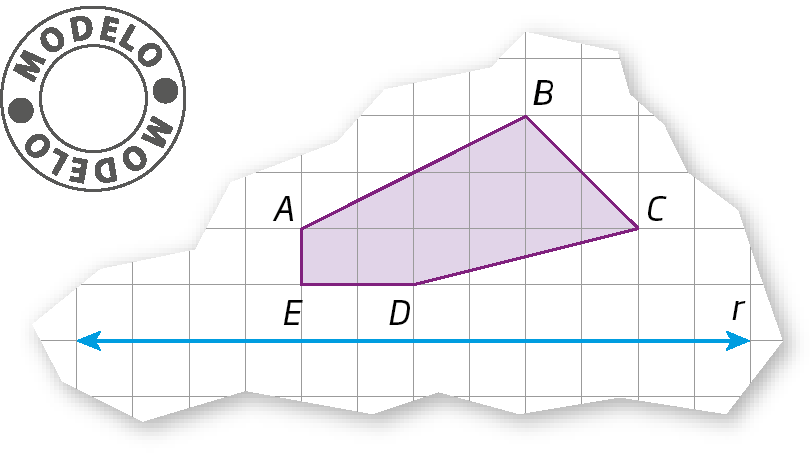
Figura geométrica. Modelo. Parte de uma malha quadriculada com reta r na horizontal. Acima da reta, figura rosa ABCDE.

27. Em uma malha quadriculada, copie a figura seguinte. Depois, construa o polígono á linha bê linha cê linha dê linha é linha éfe linha simétrico do polígono á bê cê dê é éfe em relação ao ponto óh.

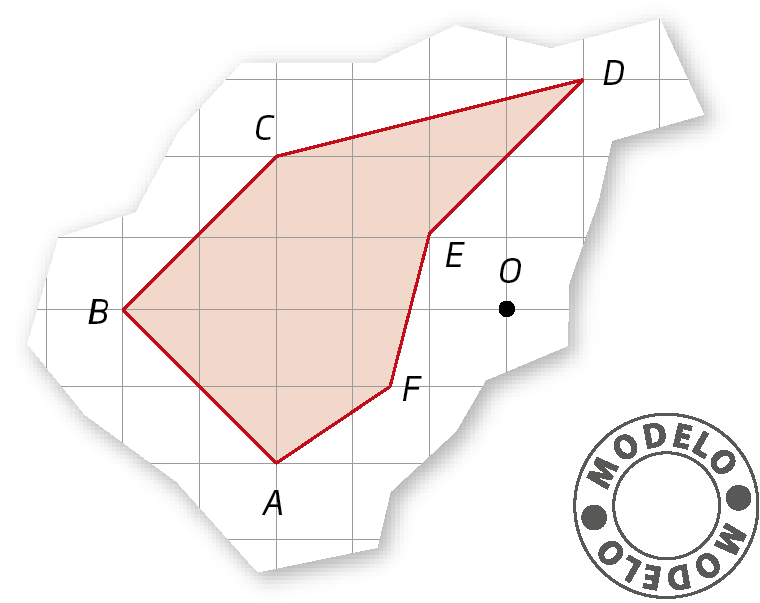
Figura geométrica. Modelo. Parte de uma malha quadriculada com figura laranja ABCDEF. À direita de E, posicionado fora da figura, ponto O.

Composição de transformações

Podemos compor transformações realizando as mesmas transformações geométricas sucessivas vezes, ou combinar transformações diferentes.

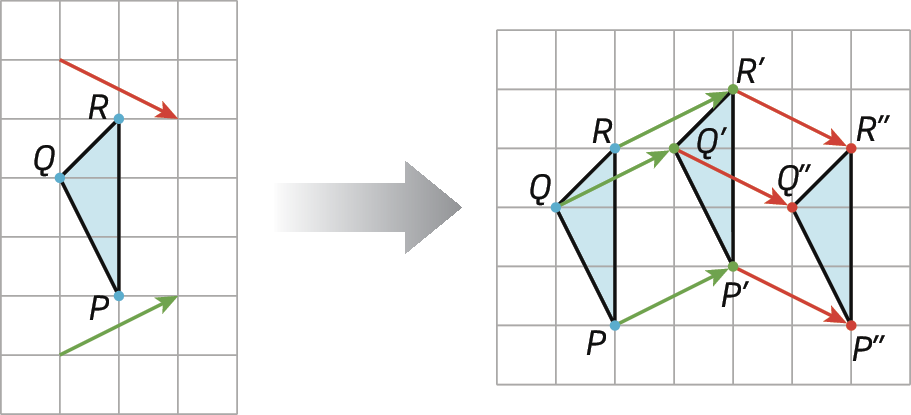
Composição de translações

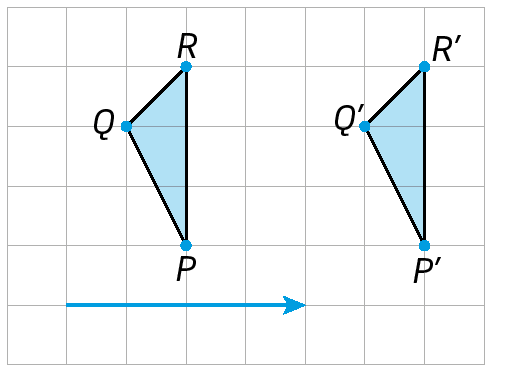
Esta figura mostra translações sucessivas. Transladamos o triângulo pê quê érre utilizando o vetor verde e sua imagem (triângulo P'Q'R'), utilizando o vetor vermelho.

A primeira translação leva o triângulo pê quê érre ao triângulo P'Q'R' e está representada pelo vetor verde. A segunda translação leva o triângulo P'Q'R' ao triângulo P"Q"R" e está representada pelo vetor vermelho.

Ilustração. Malha quadriculada com triângulo PQR. Acima, seta diagonal vermelha pontando para a lateral direita, para baixo. Abaixo, seta verde na diagonal para cima. Ao lado, malha quadriculada com triângulo PQR. Setas verdes na diagonal para cima, apontando para o triângulo P linha, Q linha, R linha, congruente ao triângulo PQR. Setas vermelhas na diagonal para baixo, apontando para a triângulo congruente P duas linhas, Q duas linhas, R duas linhas.

Respostas e comentários

24. Resposta em Orientações.

25. Resposta em Orientações.

26. Resposta em Orientações.

27. Resposta em Orientações.

Oriente os estudantes quanto aos cuidados no manuseio do compasso a fim de evitar acidentes.

• Resposta da atividade 24:

Figura geométrica. Malha quadriculada com reta r na diagonal. na parte superior da reta, os pontos, da esquerda para a direita, C linha, A e B. Na parte inferior, C, A linha e B linha. Segmentos tracejados formando um ângulo reto com a reta r: de C linha em C, de A a A linha, de B a B linha.

• Resposta da atividade 25:

Figura geométrica. Malha quadriculada com reta r na diagonal. Na parte superior da malha, circunferência com centro C1 e circunferência maior com centro C. Abaixo, circunferência C1 linha, idêntica a circunferência com centro em C1 linha, circunferência e C linha, idêntica a circunferência C. Segmento pontilhado ligando C1 a C1 linha, cruzando a reta r com um ângulo reto. Segmento pontilhado ligando C a C linha, cruzando a reta r com um ângulo reto.

• Resposta da atividade 26:

Figura geométrica. Malha quadriculada com reta r na horizontal. Acima da reta, figura ABCDE. Abaixo, figura A linha, B linha, C linha, D linha, E linha, idêntica a figura de cima, porém espelhada. Segmentos de reta pontilhados, cruzando a reta r com ângulo reto, A A linha, B B linha, C C linha, D D linha, E E linha.

• Resposta da atividade 27:

Figura geométrica. Malha quadriculada com figura ABCDEF. À direita, figura idêntica a primeira, mas virada para o outro lado, A linha, B linha, C linha, D linha, E linha e F linha. Ponto O no centro, entre as duas figuras. Segmentos pontilhados unindo os pontos e passando pelo ponto O, A A linha, B B linha, C C linha, D D linha, E E linha, F F linha.

Composição de transformações

As composições de transformações estão presentes em mosaicos e em diferentes obras de arte. É importante que os estudantes percebam que podemos compor as mesmas transformações sucessivas vezes ou combinar transformações diferentes. Ao apresentar os exemplos, peça aos estudantes que os reproduzam em uma folha de papel quadriculado ou que criem seus próprios exemplos inspirados nos exemplos do livro.

Página 103

Ao transladar o mesmo triângulo por outro vetor, como mostra o exemplo a seguir, podemos obter, diretamente, o resultado final da translação sucessiva feita anteriormente.

Figura geométrica. Malha quadriculada com triângulo PQR. Abaixo, seta horizontal para direita. Ao lado, triângulo semelhante P linha, Q linha e R linha.

Tecnologias digitais em foco

Composição de translações

Nesta seção, vamos verificar experimentalmente, por meio do GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, uma propriedade da composição de translações.

Construa

Siga os passos seguintes para transladar sucessivamente um polígono qualquer.

1º) Utilize a ferramenta

e construa um polígono qualquer. Pode ser, por exemplo, um triângulo á bê cê.

2º) Use a ferramenta

e construa dois vetores quaisquer.

3º) Clique na ferramenta

Ilustração. Botão quadrado com uma reta diagonal com dois pontos. Abaixo, seta diagonal.

. Depois, clique sobre o triângulo á bê cê e sobre o vetor vermelho. O polígono que aparecerá na tela (triângulo á linha bê linha cê linha ) é a imagem da translação pelo vetor vermelho.

4º) Clique na ferramenta

. Depois, clique sobre o triângulo á linha bê linha cê linha e sobre o vetor azul. O polígono que aparecerá na tela (triângulo á duas linhas bê duas linhas cê duas linhas ) é a imagem da translação pelo vetor azul.

Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão com uma reta diagonal e um ponto de cada lado, aba selecionada: translação por um vetor. Na tela abaixo, triângulo ABC com seta horizontal da esquerda para direita. Ao lado, triângulo A linha, B linha e C linha com seta diagonal para cima e seta maior diagonal para cima. Na parte superior, triângulo A duas linhas, B duas linhas e C duas linhas. Todos os triângulos são congruentes. — Neste exemplo, o triângulo A'B'C' foi obtido do triângulo á bê cê por meio da translação pelo vetor vermelho, e o triângulo á duas linhas bê duas linhas cê duas linhas foi obtido do triângulo á linha bê linha cê linha por meio da translação pelo vetor azul.

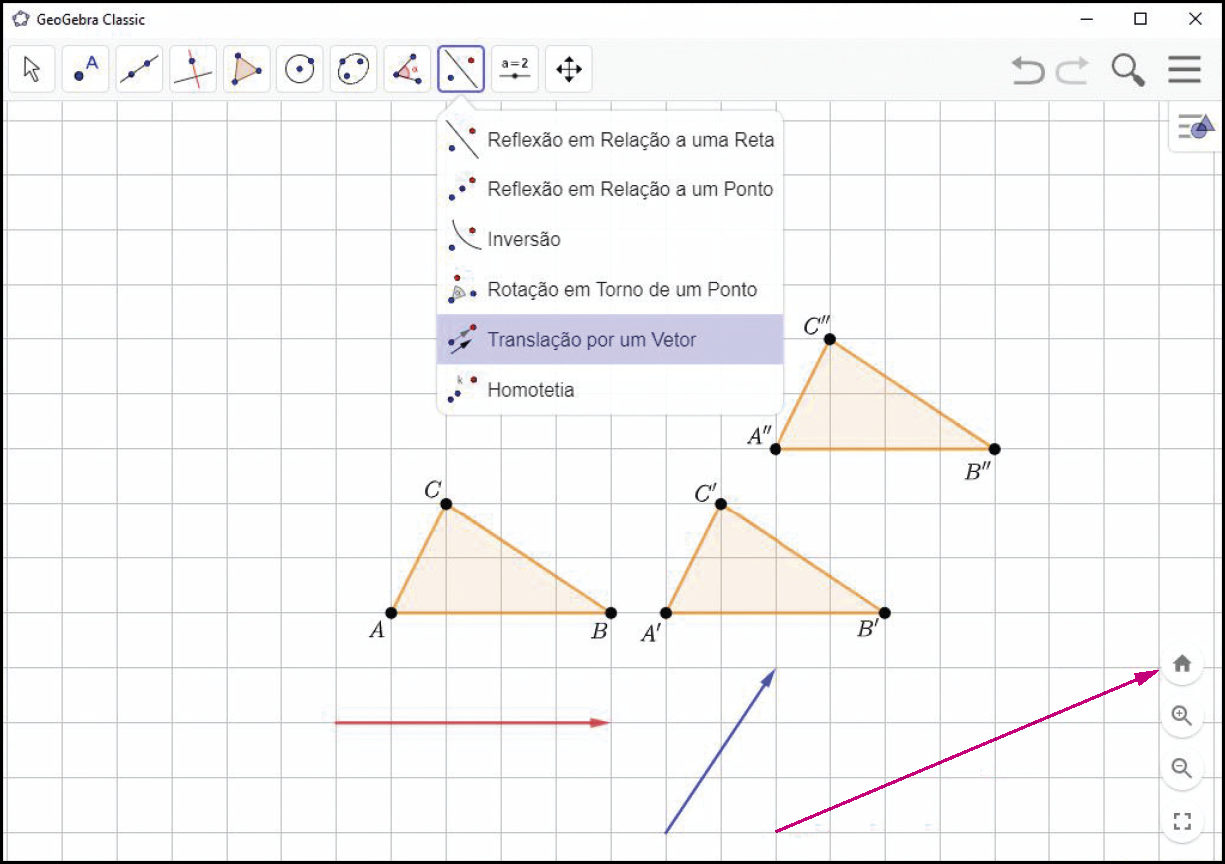
Explore

É possível obter o triângulo á duas linhas bê duas linhas cê duas linhas por meio de uma única translação do triângulo á bê cê. Descubra o vetor dessa translação e represente-o no GeoGebra.

Respostas e comentários

Explore: Resposta na imagem anterior.

Tecnologias digitais em foco

Bê êne cê cê:

Habilidade ê éfe zero oito ême ah um oito.

Objetivo:

Reconhecer e construir figuras obtidas por meio de composição de translações utilizando o software GeoGebra ou outro software de geometria dinâmica.

Composição de translações

No 1º passo, você pode orientar a cada estudante que construa um polígono diferente.

Ao lerem o comando do 2º passo é possível que alguns deles não se recordem do conceito de vetor. Caso isso ocorra, relembre que o vetor determina o sentido, a direção e a medida da distância do deslocamento da figura na translação.

É importante que realizem o 3º passo, observem e, só depois, realizem o 4º passo.

Em Explore, os estudantes terão a oportunidade de investigar a possibilidade de obter o polígono que é imagem da segunda translação diretamente do polígono construído no 1º passo. É importante incentivá-los a experimentar a comparar sua construção com a dos colegas e a dialogar.

Página 104

Composição de reflexões

Na figura a seguir, foram feitas duas reflexões em sequência do quadrilátero a bê cê dê: uma em relação à reta r e outra em relação à reta s.

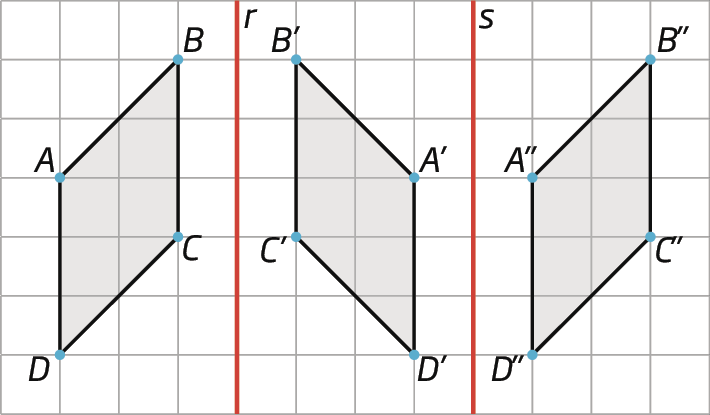
Figura geométrica. Malha quadriculada com paralelogramo ABCD. Reta vertical r. Paralelogramo A linha, B linha, C linha, D linha. Reta vertical s. Paralelogramo A duas linhas, B duas linhas, C duas linhas, D duas linhas. Os paralelogramos tem mesmas dimensões, porém sofreram reflexão.

Note que o quadrilátero á linha bê linha cê linha dê linha foi obtido do quadrilátero a bê cê dê a partir da reflexão em relação à reta r. Já o quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas foi obtido do quadrilátero á linha bê linha cê linha dê linha por meio da reflexão em relação à reta s.

A reflexão da figura á linha bê linha cê linha dê linha equivale uma translação da figura a bê cê dê.

Tecnologias digitais em foco

Composição de reflexões em relação a retas

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para explorar propriedades da composição de reflexões em relação a retas.

Construa

Siga os passos seguintes para refletir um polígono qualquer.

1º) Utilize a ferramenta

e construa um polígono qualquer. Pode ser, por exemplo, um quadrilátero a bê cê dê.

2º) Use a ferramenta

e construa uma reta r.

3º) Use a ferramenta

Ilustração. Botão quadrado com uma reta diagonal e um ponto sobre ela. Abaixo, reta paralela.

e construa uma reta s paralela à reta r.

4º) Clique na ferramenta

Ilustração. Botão quadrado com uma reta diagonal e um ponto de cada lado.

. Depois, clique sobre o polígono e sobre a reta r. O polígono que aparecerá na tela (quadrilátero á linha bê linha cê linha dê linha ) é a imagem da reflexão pela reta r.

5º) Clique na ferramenta

. Depois, clique sobre o quadrilátero á linha bê linha cê linha dê linha e sobre a reta s. O polígono que aparecerá na tela (quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas ) é a imagem da reflexão pela reta s.

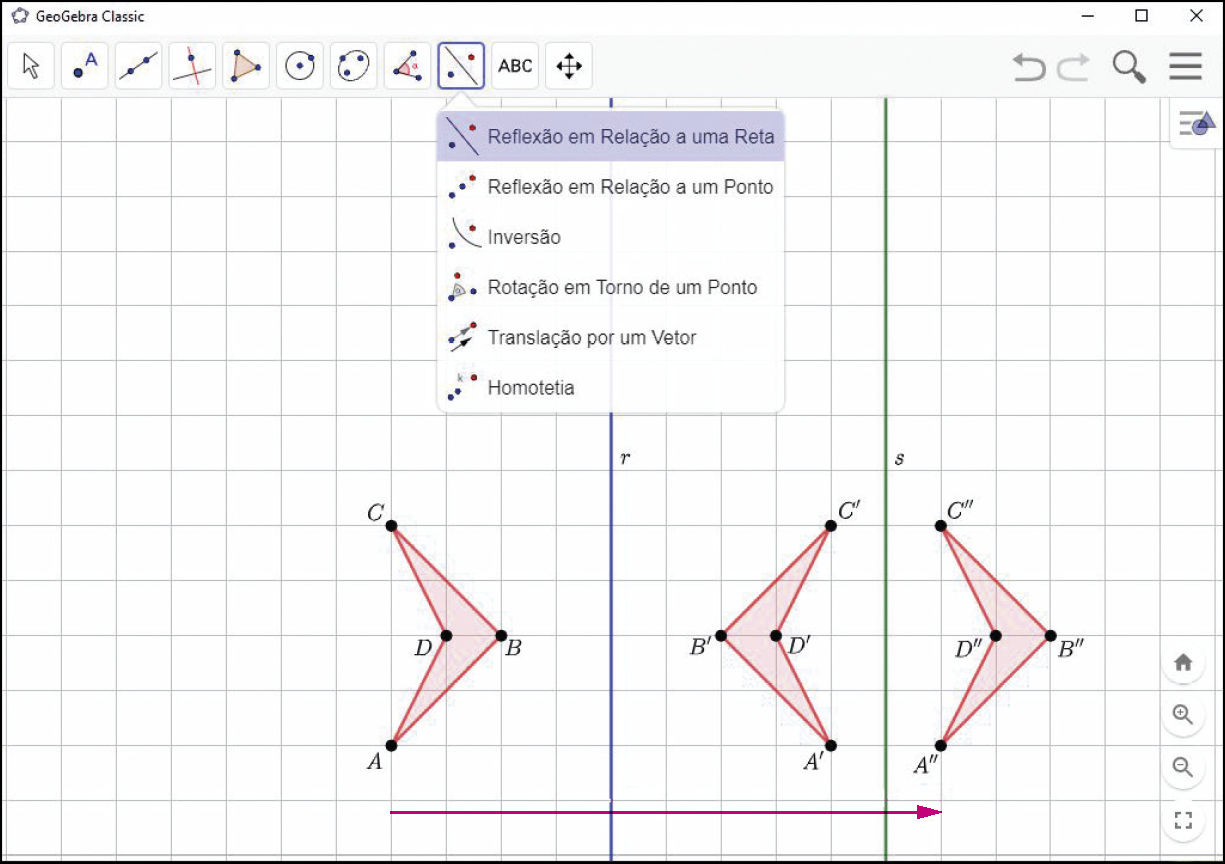
Respostas e comentários

Tecnologias digitais em foco

Bê êne cê cê:

Habilidade ê éfe zero oito ême ah um oito.

Objetivo:

Reconhecer e construir figuras obtidas por meio de composição de reflexões em relação a retas utilizando o software GeoGebra ou outro software de geometria dinâmica.

Composição de reflexões em relação a retas

No 1º passo, você pode orientar a cada estudante que construa um polígono diferente.

No 3º passo, eles vão construir uma reta s paralela a uma outra reta r. Embora esteja indicado o uso da ferramenta “Reta Paralela”, você pode incentivá-los a obter a reta s, utilizando procedimentos análogos ao da construção com régua e compasso da reta paralela. Esse pode ser um momento oportuno para verificar os conhecimentos previamente adquiridos pelos estudantes.

É importante que realizem o 4º passo, observem e, só depois, realizem o 5º passo.

Página 105

Tecnologias digitais em foco

Explore

a) É possível obter o quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas por meio de uma translação do quadrilátero a bê cê dê. Represente o vetor dessa translação no GeoGebra.

b) Faça o que se pede.

1º) Utilize a ferramenta

Ilustração. Botão quadrado com uma reta diagonal e outra na vertical, com um ponto sobre ela.

e trace uma reta que seja perpendicular às retas r e s e que intercepte r no ponto P e s no ponto Q.

2º) Utilize a ferramenta

e meça a distância entre as retas r e s.

3º) Utilize a ferramenta

e meça a distância entre os pontos a e A". Ao que corresponde essa medida? Movimente o quadrilátero a bê cê dê e verifique o que ocorre.

c) O que podemos afirmar em relação à medida de comprimento do vetor da translação que leva a bê cê dê a á duas linhas bê duas linhas cê duas linhas dê duas linhas?

d) E se as retas r e s não fossem paralelas? Seria possível obter o quadrilátero á duas linhas bê duas linhas cê duas linhas dê duas linhas por meio de uma única transformação geométrica do quadrilátero a bê cê dê? Investigue e escreva sua conclusão no caderno. Dica: Meça a abertura do ângulo formado pelas retas r e s.

Composição de rotações

Podemos rotacionar figuras sucessivamente em torno de um mesmo ponto ou em torno de pontos diferentes. Analise os exemplos a seguir.

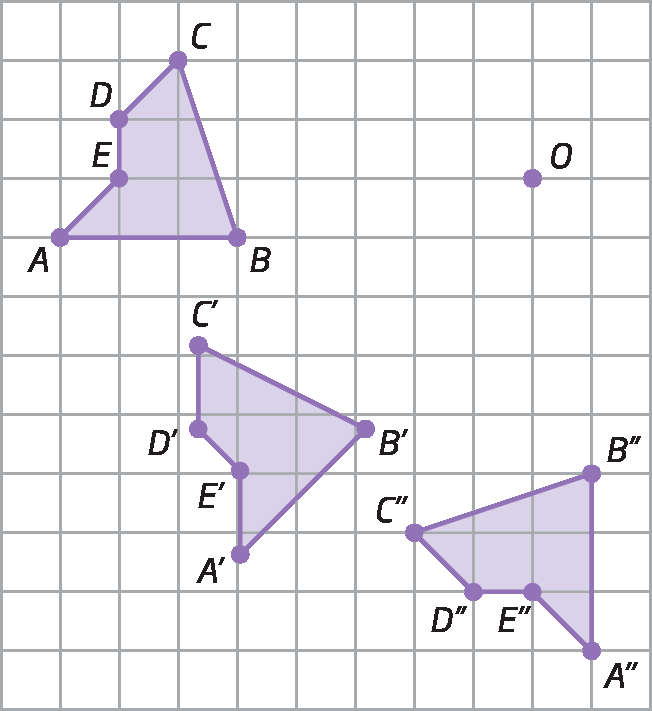
Figura geométrica. Malha quadriculada com figura roxa ABCDE. Abaixo, figura roxa A linha, B linha, C linha, D linha, E linha. Na parte inferior, figura roxa A duas linhas, B duas linhas, C duas linhas, D duas linhas, E duas linhas. À direita da figura ABCDEF, ponto O. As figuras tem mesmo formato e dimensões, porém estão em posições diferentes. — Note que o pentágono á linha bê linha cê linha dê linha é linha foi obtido do pentágono á bê cê dê é por meio de uma rotação, no sentido anti‑horário, de um giro de 45° ao redor do ponto óh, e que o pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas foi obtido do pentágono á linha bê linha cê linha dê linha é linha por meio de uma rotação, no sentido anti-horário, de um giro de 45graus ao redor do ponto óh.

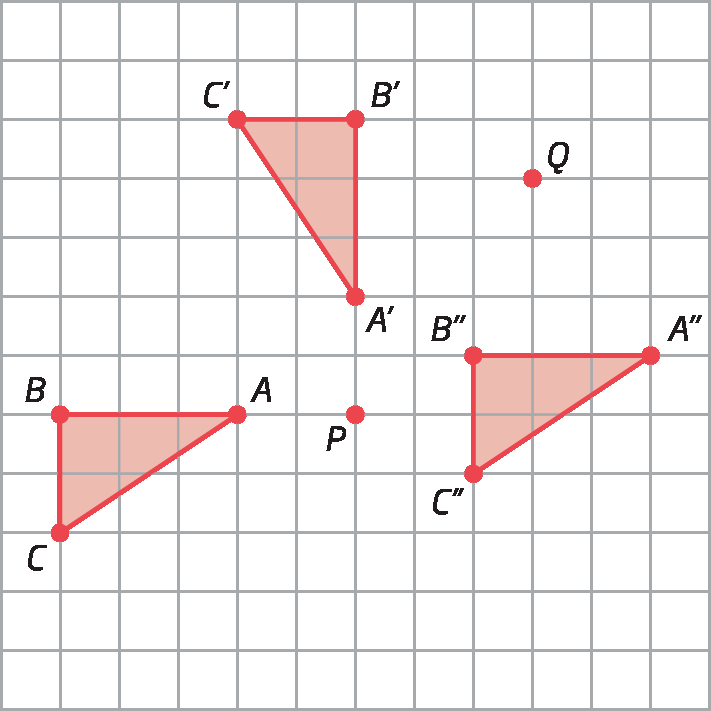
Figura geométrica. Malha quadriculada com triângulo vermelho ABC. Ao lado, triângulo vermelho A duas linhas, B duas linhas, C duas linhas. Acima, triângulo vermelho A linha, B linha, C linha. à direita, ponto Q. As figuras tem mesmo formato e dimensões, porém estão em posições diferentes. — Note que o triângulo á linha bê linha cê linha foi obtido do triângulo á bê cê por meio de uma rotação, no sentido horário, de um giro de 90graus ao redor do ponto P. Já o triângulo á duas linhas bê duas linhas cê duas linhas foi obtido do triângulo á linha bê linha cê linha por meio de uma rotação, no sentido horário, de um giro de 270graus ao redor do ponto Q.

Respostas e comentários

Explore: a) Resposta na imagem anterior.

b) Espera-se que os estudantes respondam que essa medida é igual ao dobro da medida da distância entre as retas r e s e que essa igualdade mantém‑se verdadeira com as movimentações.

c) Espera-se que os estudantes percebam que a medida do comprimento do vetor é igual ao dobro da medida da distância entre as retas r e s.

d) Espera-se que os estudantes percebam que, nesse caso, a reflexão sucessiva pelas retas r e s é equivalente a uma rotação no sentido anti-horário com centro no ponto de intersecção das retas e ângulo de medida da abertura igual ao dobro da medida da abertura do ângulo formado por r e s.

No item a do Explore, os estudantes terão a oportunidade de perceber que realizar duas reflexões sucessivas em relação a retas paralelas é o mesmo que realizar uma única translação. É importante incentivá-los a experimentar e levantar hipóteses.

No item d do Explore, eles vão verificar que, quando as retas não são paralelas, realizar duas reflexões sucessivas em relação a elas é o mesmo que realizar uma rotação no sentido anti-horário com centro no ponto de intersecção das retas e ângulo de medida de abertura igual ao dobro da medida da abertura do ângulo formado pelas retas. Proponha que façam esse item sem apresentar a dica. Se perceber que estão com dificuldades, dê a dica para eles. É importante que se sintam motivados para testar suas hipóteses e apresentar as conclusões.

Apresente os exemplos de composições de rotações para a turma. Se achar conveniente, proponha a eles que produzam outros exemplos, seja em papel quadriculado, seja no GeoGebra.

Página 106

Tecnologias digitais em foco

Composição de rotações em torno de um mesmo ponto

Nesta seção, vamos utilizar o GeoGebra ou outro software de geometria dinâmica que seu professor pode indicar, para explorar propriedades da composição de rotações em torno de um mesmo ponto.

Construa

Siga os passos seguintes para realizar rotações sucessivas de um polígono qualquer em torno de um mesmo ponto.

1º) Construa um polígono qualquer, utilizando a ferramenta

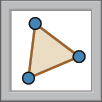
. Pode ser, por exemplo, um pentágono á bê cê dê é.

2º) Marque um ponto óh qualquer utilizando a ferramenta

Ilustração. Botão quadrado com a letra A e um ponto

. Esse ponto será o centro da rotação.

3º) Clique na ferramenta

Ilustração. Botão quadrado com dois segmentos de retas partindo do mesmo ponto, um ângulo alfa e dois pontos.

. Depois, clique sobre o polígono e sobre o ponto óh. Por fim, escolha a medida da abertura do ângulo e o sentido da rotação. O polígono que aparecerá na tela (pentágono á linha bê linha cê linha dê linha é linha ) é a imagem da rotação.

4º) Clique na ferramenta

. Depois, clique sobre o pentágono á linha bê linha cê linha dê linha é linha e sobre o ponto óh. Por fim, escolha a medida da abertura do ângulo. O sentido da rotação deve ser o mesmo do 3º passo. O polígono que aparecerá na tela (pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas ) é a imagem da rotação.

Ilustração. Software de geometria dinâmica. Acima, botões de comandos. Destaque para botão com dois segmentos de reta que partem do mesmo ponto e ângulo alfa entre elas, aba selecionada: rotação em torno de um ponto. Na tela abaixo, quadrilátero ABCD. Abaixo, quadrilátero A linha, B linha, C linha, D linha. Ao lado, quadrilátero A duas linhas, B duas linhas, C duas linhas, D duas linhas. À direita da figura ABCDE, ponto O. Todas as figuras tem mesmas dimensões e formato, porém estão em diferentes posições. — Nesse exemplo, o pentágono á linha bê linha cê linha dê linha é linha foi obtido do pentágono á bê cê dê é por meio de uma rotação, no sentido anti-horário, de um giro de 45graus ao redor do ponto óh, e o pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas foi obtido do pentágono á linha bê linha cê linha dê linha é linha por meio de uma rotação, no sentido anti‑horário, de um giro de 45graus ao redor do ponto óh.

Explore

a) É possível obter o pentágono á duas linhas bê duas linhas cê duas linhas dê duas linhas é duas linhas por meio de uma única transformação geométrica do pentágono á bê cê dê é? Se sim, descreva essa transformação.

b) O que a investigação feita por você, no item anterior, sugere?

Respostas e comentários

Explore: a) Sim; espera-se que os estudantes, após algumas investigações, percebam que o pentágono A"B"C"D"E' pode ser obtido do pentágono á bê cê dê é por meio de uma rotação, no sentido anti-horário, de um giro de 90graus ao redor do ponto óh.

b) Espera-se que os estudantes respondam que a investigação feita sugere que realizar duas rotações sucessivas, no mesmo sentido, uma com um giro de xgraus e outra com um giro de ygraus, em torno de um ponto O qualquer corresponde a realizar uma única rotação, no mesmo sentido das rotações anteriores, de um giro de (x + y)graus ao redor de óh.

Tecnologias digitais em foco

Bê êne cê cê:

Habilidade ê éfe zero oito ême ah um oito.

Objetivo:

Reconhecer e construir figuras obtidas por meio de composição de rotações em torno de um mesmo ponto utilizando o software GeoGebra ou outro software de geometria dinâmica.

Composição de rotações em torno de um mesmo ponto

No 4º passo do Construa, enfatize com a turma que a segunda rotação deve ser realizada no mesmo sentido que a segunda. Comente que a construção deles não deve ser igual à do exemplo apresentado na seção.

No Explore, a ideia é que eles façam experimentações e percebam que realizar duas rotações sucessivas, no mesmo sentido, uma com um giro de xgraus e outra com um giro de ygraus, em torno de um ponto O qualquer, corresponde a realizar uma única rotação no mesmo sentido das rotações anteriores, de um giro de (x + y)graus ao redor de O. Caso estejam com dificuldades, em vez de construírem um pentágono, proponha que construam um triângulo.

Página 107

Atividades

Faça as atividades no caderno.

28. Em uma malha quadriculada, copie a figura seguinte e a translade utilizando primeiro o vetor azul e, depois, o vetor verde.

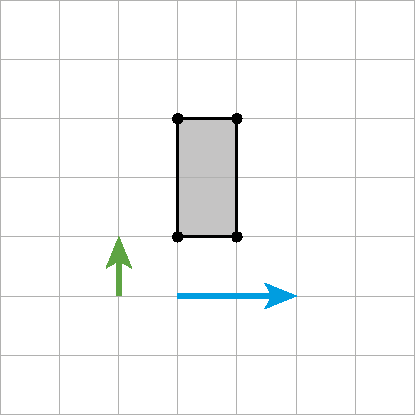
Figura geométrica. Malha quadriculada com figura composta por dois quadradinhos, um sobre o outro, e seta vertical para cima. Abaixo, seta da esquerda para direita.

29. Em uma malha quadriculada, copie novamente a figura da atividade 28 e a translade primeiro utilizando o vetor verde e, depois, o vetor azul.

30. Copie a figura a seguir em uma malha quadriculada e faça 3 rotações sucessivas em torno do ponto C, no sentido horário, com um giro de 90graus.

Figura geométrica. Malha quadriculada com triângulo ABC.

31.

Analise a figura a seguir.

Figura geométrica. Figura semelhante a seta verde para direita. Reta vertical. Seta verde virada para esquerda. Reta vertical. Seta verde virada para direita.

a) No caderno, elabore duas questões que possam ser respondidas observando as transformações geométricas.

b) Troque de caderno com um colega e responda às questões criadas por ele.

c) Analise as respostas do colega e dê um retorno a ele, dizendo o que ele respondeu corretamente e onde ele se equivocou.

Respostas e comentários

28. Resposta em Orientações.

29. Resposta em Orientações.

30. Resposta em Orientações.

31. a) Respostas pessoais.

31. b) Respostas pessoais.

31. c) Resposta pessoal.

• Compare as translações sucessivas das atividades 28 e 29 e discuta sobre o que acontece ao trocarmos a ordem das transformações. Pergunte aos estudantes se as figuras obtidas ao final são sempre iguais ou se em alguma situação obtemos figuras diferentes. Espera-se que eles percebam que o resultado pode ser diferente, dependendo da composição de transformações.

Resposta da atividade 28:

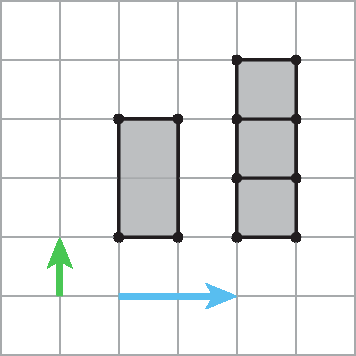
Ilustração. Malha quadriculada com figura composta por dois quadradinhos sobrepostos, seta vertical para cima. Abaixo, seta da esquerda para direita. Ao lado, figura composta por três quadradinhos sobrepostos.

Resposta da atividade 29:

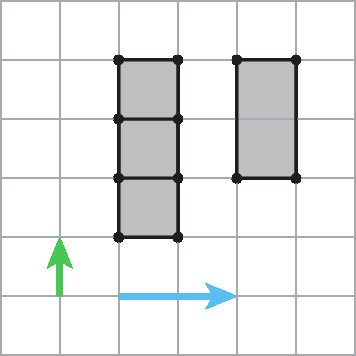
Figura geométrica. Malha quadriculada com figura composta por três quadradinhos sobrepostos à esquerda, seta vertical para cima. À direita, figura composta por dois quadradinhos sobrepostos. Abaixo, seta da esquerda para direita.

Resposta da atividade 30:

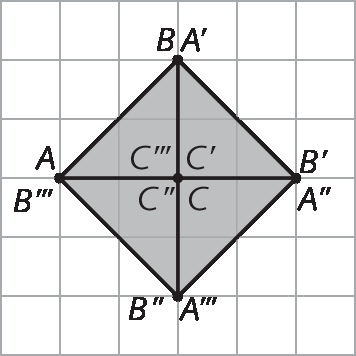
Figura geométrica. Malha quadriculada com quadrilátero dividido em quatro triângulos. Triângulo A, B e C três linhas. Triângulo A linha, B linha e C linha. Triângulo C, A duas linhas e A três linhas. Triângulo B duas linhas, C duas linhas e B três linhas. Os triângulos possuem dois lados em comum, formando um quadrado. No centro, o ponto C, que coincide com os pontos C linha, C duas linhas e C três linhas.

Página 108

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Ângulo

Ângulo é a união de duas semirretas de mesma origem, com uma das regiões do plano limitada por elas.

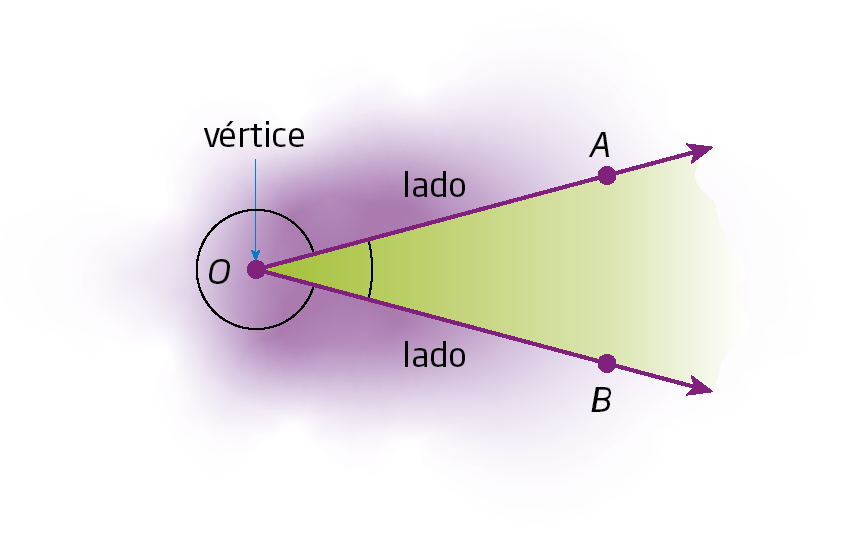
Classificação de ângulos

De acordo com a medida da abertura, um ângulo pode ser classificado em:

Ângulo nulo

Figura geométrica. Semirreta com ponto O à esquerda e ponto A no centro e ponto B à direita.

m e d (A \hat{O} B) = 0 °

Ângulo de uma volta

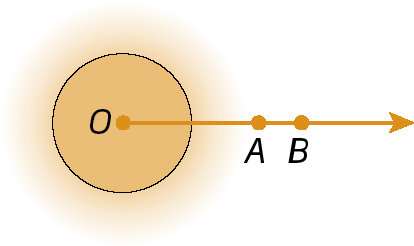
Figura geométrica. Semirreta com ponto O à esquerda e ponto A no centro. à direita, ponto B. Destaque para ângulo ao redor do ponto O, indicado uma volta completa.

m e d (A \hat{O} B) = 360 °

Ângulo reto

m e d (A \hat{O} B) = 90 °

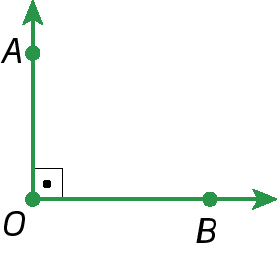
Ângulo raso ou de meia-volta

Figura geométrica. Reta com ponto A à esquerda, ponto B à direita e ponto O no centro. Destaque para ângulo de 180 graus ao redor de O.

m e d (A \hat{O} B) = 180 °

Ângulo agudo

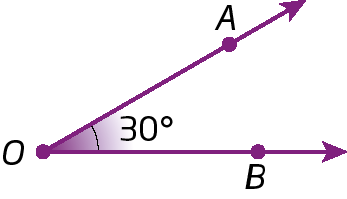
Figura geométrica. À esquerda, ponto O. De O, reta horizontal com ponto B. Reta diagonal com ponto A. Em O, ângulo de 30 graus.

0 ° < m e d (A \hat{O} B) < 90 °

Ângulo obtuso

Figura geométrica. Abaixo, ponto O. De O, reta diagonal para esquerda com ponto A. Reta horizontal com ponto B. Em O, ângulo de 140 graus.

90 ° < m e d (A \hat{O} B) < 180 °

1. Analise os ângulos seguintes e indique:

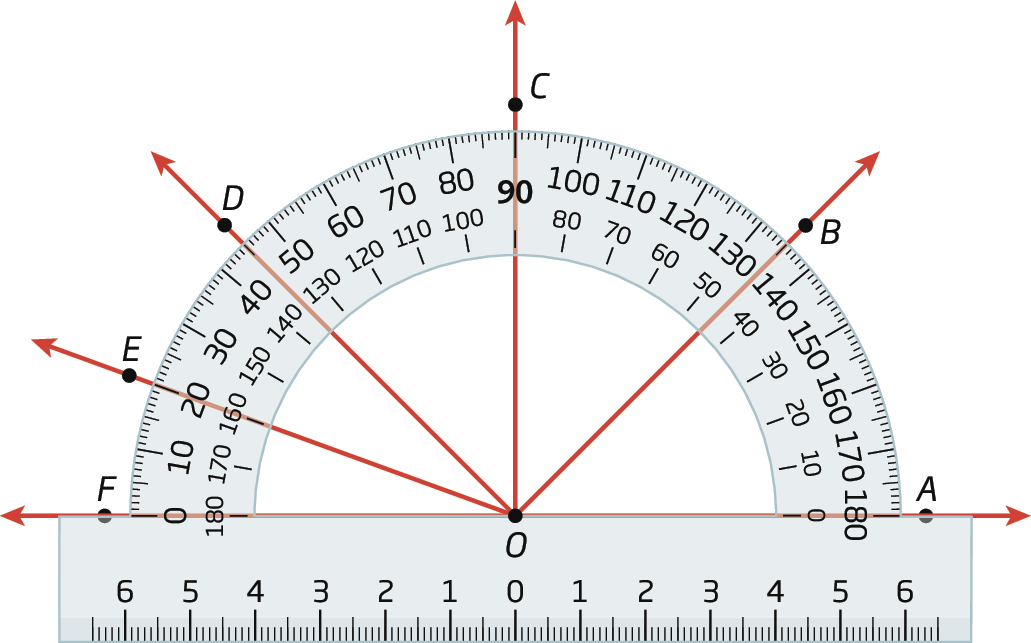
Figura geométrica. Na parte inferior, régua na horizontal com ponto O no centro. Acima, transferidor de 180 graus. De O, retas: A: 0 grau. B: 135 graus. C: 90 graus. D: 45 graus. E: 20 graus. F: 180 graus.

a) os ângulos agudos;

b) os ângulos obtusos;

c) o ângulo raso;

d) os ângulos retos.

Ângulos congruentes

Dois ângulos são congruentes quando têm a mesma medida de abertura.

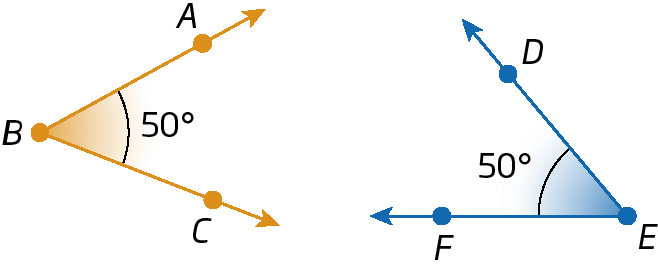
Figura geométrica. À esquerda, ponto B. De B, reta diagonal com ponto C. Reta diagonal com ponto A. Em O, ângulo de 50 graus.

Figura geométrica. À direita, ponto E. De E, reta diagonal com ponto D. Reta horizontal com ponto F. Em E, ângulo de 50 graus.

Os ângulos

A \hat{B} C

D \hat{E} F

são congruentes. Indicamos:

A \hat{B} C ≅ D \hat{E} F

Bissetriz de um ângulo

Bissetriz de um ângulo é a semirreta interna a esse ângulo com origem no vértice do ângulo que o divide em dois ângulos congruentes.

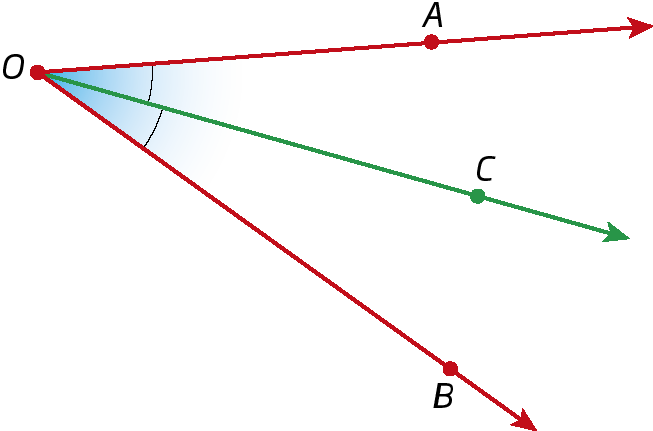
Figura geométrica. À esquerda, ponto O. De O, reta diagonal com ponto A. Reta diagonal com ponto B. Em O, bissetriz com ponto C.

A \hat{O} C ≅ C \hat{O} B

Respostas e comentários

1. a)

A \hat{O} B, B \hat{O} C, C \hat{O} D, C \hat{O} E, D \hat{O} E, D \hat{O} F e E \hat{O} F

1. b)

A \hat{O} D, A \hat{O} E, B \hat{O} E e B \hat{O} F

1. c)

A \hat{O} F

1. d)

A \hat{O} C, B \hat{O} D e C \hat{O} F

Revisão dos conteúdos deste capítulo

Ângulo

• Na atividade 1, os estudantes vão analisar alguns ângulos e identificar aqueles que são agudos (item a), obtusos (item b), raso (item c) e retos (item d). Este é o momento oportuno para verificar se compreenderam como se mede a abertura de ângulos com um transferidor e como podemos classificar ângulos de acordo com a medida da abertura. Também é importante verificar se, em cada item, os estudantes representam os ângulos de fórma correta.

Página 109

Mediatriz de um segmento

Mediatriz é a reta perpendicular a um segmento de reta que passa pelo ponto médio desse segmento.

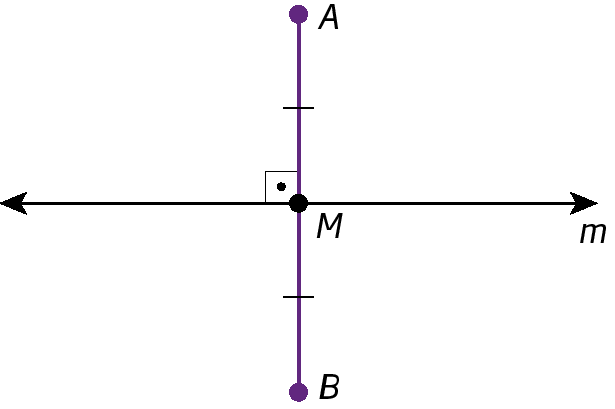
Figura geométrica. Reta m na horizontal. Sobre ela, segmento AB na vertical. As retas se cruzam em M no centro.

2. Nesta figura, a semirreta

\vec{O C}

é a bissetriz de

A \hat{O} B

m e d (A \hat{O} C) = 10 °

. Determine a medida da abertura do ângulo

A \hat{O} B

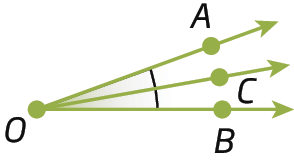
3. Em uma reta, tomamos os pontos a, B e C, nessa ordem, com A bê = 8 centímetros e BC = 10 centímetros. Sendo P o ponto médio de

\overline{A C}

, quanto mede o comprimento de

\overline{B P}

Lugares geométricos

Lugar geométrico é a figura formada por todos os pontos do plano que têm em comum uma determinada propriedade.

Circunferência

Circunferência é o lugar geométrico dos pontos do plano que equidistam de um ponto fixo.

Mediatriz

Mediatriz é o lugar geométrico dos pontos do plano que são equidistantes de dois pontos fixos dados (extremidades de um segmento de reta).

Retas paralelas

Reta paralela é o lugar geométrico dos pontos do plano que equidistam de uma reta dada.

Bissetriz

Bissetriz de um ângulo é o lugar geométrico dos pontos do plano que equidistam dos lados desse ângulo.

4. Para manter a horta, um jardineiro sugeriu a instalação de uma torneira de irrigação em um lugar que tenha a mesma medida da distância dos muros. Descreva, em seu caderno, os possíveis lugares em que a torneira pode ser instalada.

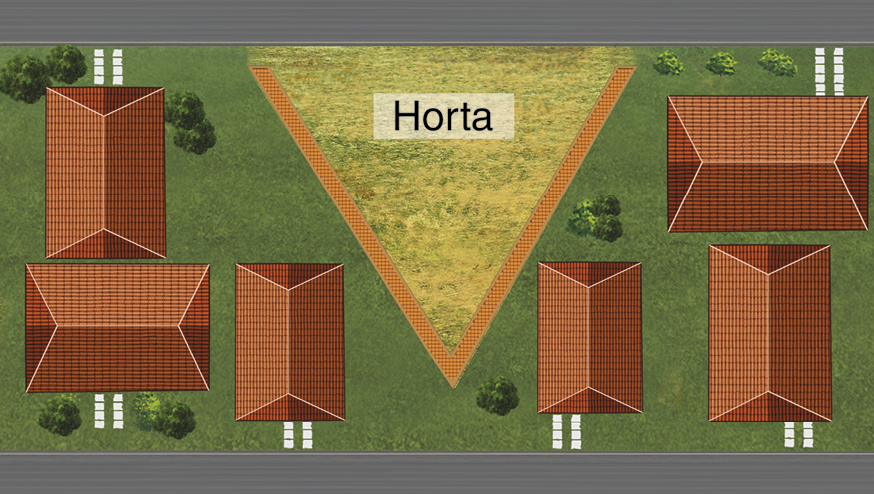
Ilustração. Área retangular gramada com horta representada por um triângulo virado para baixo no centro. Ao redor, seis construções.

Transformações geométricas

Translação é o deslocamento de uma figura dado por um vetor.

Rotação é o giro de uma figura em torno de um centro de rotação, em determinado sentido (horário ou anti-horário), segundo um ângulo de rotação.

Composição de transformações

Podemos compor transformações realizando as mesmas transformações geométricas sucessivas vezes, ou combinar transformações diferentes.

5. As transformações realizadas a seguir podem ser, na ordem apresentada:

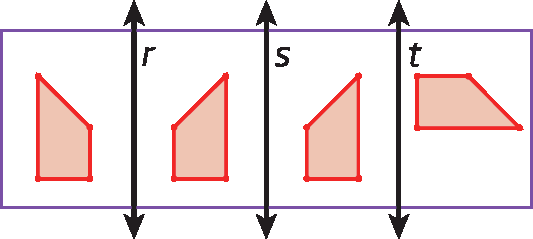
Figura geométrica. Trapézio laranja com lado menor para direita. Reta vertical r. Trapézio laranja com lado menor para esquerda. Reta vertical s. Trapézio laranja com lado menor para esquerda. Reta vertical t. Trapézio laranja com lado menor para cima. As figuras tem mesmas dimensões e tamanhos.

a) translação, reflexão e rotação.

b) reflexão, translação e rotação.

c) rotação, reflexão e translação.

d) reflexão, reflexão e translação.

Respostas e comentários

med (A \hat{O} B) = 20 °

3. 1 centímetro

4. Comentário em Orientações.

5. alternativa b

• Na atividade 2, é possível que alguns estudantes concluam erroneamente que

m e d (A \hat{O} B) = 5 °

. Isso pode acontecer caso não tenham se atentado à posição dos pontos na figura. Oriente-os a reproduzir a figura no caderno e indicar a medida da abertura do ângulo

A \hat{O} C

nela. Dessa fórma, os estudantes poderão perceber de maneira mais clara qual medida devem determinar.

• Caso tenham dificuldades para fazer a atividade 3, oriente-os a traduzir o enunciado por meio de uma figura, como a da referência a seguir.

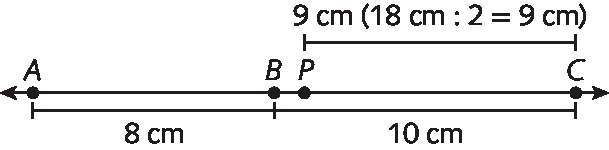
Ilustração. Reta com ponto A à esquerda e ponto C à direita. Na região central, pontos B e P. De C até B: 10 centímetros. De P até C, 9 centímetros (9 centímetros, abre parênteses 18 centímetros dividido por 2 = 9 centímetros, fecha parênteses). À esquerda de P, ponto B. De A até B, 8 centímetros.

Com base na figura, espera-se que os estudantes concluam que a medida do segmento de reta

\overline{B P}

é igual a 1 centímetro.

Lugares geométricos

• Faça a leitura coletiva do enunciado da atividade 4 com a turma e tire as eventuais dúvidas. Peça que observem a imagem e indiquem com o dedo os possíveis lugares em que a torneira pode ser instalada e por quê. Espera-se que eles concluam que a torneira deve ser instalada em qualquer ponto da bissetriz do ângulo formado pelos muros. Caso julgue necessário, proponha que reproduzam essa figura em papel vegetal e, depois, tracem a bissetriz do ângulo formado pelos muros do terreno. Peça também que confiram se a torneira, estando em qualquer ponto dessa bissetriz, resolve o problema de fato.

Transformações geométricas

• Na atividade 5, espera-se que os estudantes percebam que a figura inicial foi submetida a uma sucessão de transformações geométricas no plano. Para identificar se ocorreu reflexão, translação ou rotação, eles precisam observar a posição das figuras. Após identificarem a alternativa correta, incentive-os a justificar o porquê das alternativas a, c e d serem falsas. Isso pode ajudar os estudantes que apresentaram dificuldades ao realizar a atividade.

Glossário

equidistante: :tem a mesma medida de distância entre dois ou mais objetos (pontos, por exemplo).; Voltar para o texto

axial: : palavra derivada de axis, termo latino que significa “eixo”.; Voltar para o texto

rito de iniciação: : cerimônia (realização de uma tarefa ou ritual particular), que ocorre em muitas sociedades, para introduzir um novo membro.; Voltar para o texto