Página 110

Capítulo 5 Polígonos

Trocando ideias

origâmi é uma técnica japonesa de dobradura com a qual se constroem representações de determinados objetos ou seres sem cortar ou colar o papel.

Ilustração. Figuras feitas de origamis. Figura redonda vermelha e amarela com tiras, parecida com um catavento. Um sapo verde, um pássaro azul, um elefante marrom, figura redonda verde e azul com tiras, parecida com catavento, um avião vermelho e um barco azul. — Representações utilizando a técnica do origâmi.

▸

As partes de algumas das representações na foto anterior se parecem com polígonos. Que polígonos são esses?

▸ Siga os passos seguintes e construa a representação da cabeça de um leão.

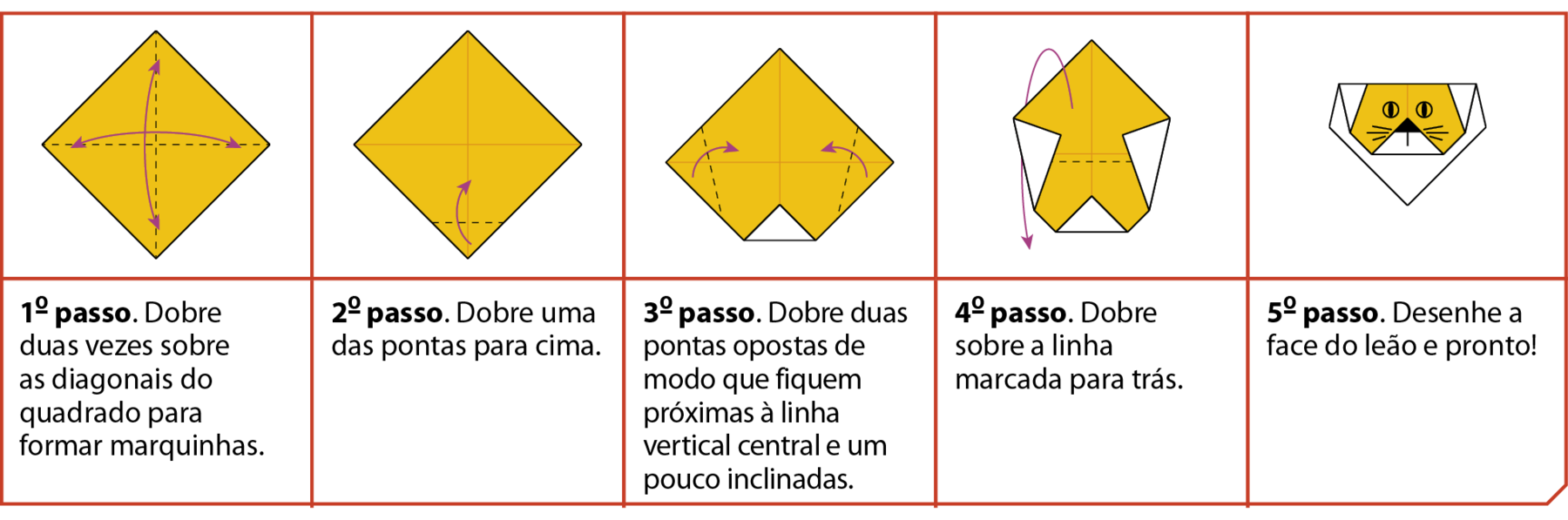
Quadro. Losango laranja com seta vertical e diagonal. 1º passo. Dobre duas vezes sobre as diagonais do quadrado para formar marquinhas. Losango com seta de baixo para cima na ponta inferior direita. 2º passo. Dobre uma das pontas para cima. Losango com a parte inferior dobrada e setas nas laterais de fora para dentro. 3º passo. Dobre duas pontas opostas de modo que fiquem próximas à linha vertical central e um
pouco inclinadas. Losango com a ponta inferior e laterais dobradas para dentro. Linha vertical e horizontal dentro. Seta de baixo para cima passando por trás da figura. 4º passo. Dobre sobre a linha marcada para trás. Rosto de um leão formado. 5º passo. Desenhe a face do leão e pronto

Neste capítulo, vamos ampliar o estudo dos polígonos, dando atenção às diagonais, aos ângulos internos e ângulos externos e aos polígonos regulares.

Respostas e comentários

Trocando ideias: primeiro item: triângulos, quadriláteros e pentágonos.

CAPÍTULO 5 – POLÍGONOS

Trocando ideias

Bê êne cê cê:

• Competências gerais 3, 6 e 9 (as descrições estão na página seis).

• Competência específica 8 (a descrição está na página sete).

Objetivos:

• Verificar se os estudantes reconhecem polígonos em objetos cotidianos.

• Verificar os conhecimentos prévios dos estudantes sobre o conceito de diagonal de um polígono.

• Introduzir a técnica do origami.

Inicie o trabalho com a seção Trocando ideias mostrando para a turma alguns exemplos concretos de origâmi ou de imagens de representações construídas utilizando essa técnica. Depois, esclareça que a inspiração dos origamistas (pessoas que se dedicam à arte do origâmi) está, principalmente, nos elementos da natureza e nos objetos cotidianos. Conte que o ato de dobrar o papel, para esses criadores, representa a transformação da vida, uma vez que, esse pedaço de papel, um dia, foi semente de uma planta que germinou, cresceu e se transformou em uma árvore. E que, depois, o homem transformou a planta em folhas de papel, cortando-as em quadrados e dobrando-as de diferentes maneiras para representar animais, plantas e outros objetos.

Convide-os a responder à primeira questão e verifique se reconhecem os triângulos e quadriláteros presentes em algumas partes das representações presentes nas fotografias. Caso tenham dificuldade, retome esses conceitos com eles. Você também pode aproveitar para questioná-los o porquê dos triângulos e quadriláteros serem considerados polígonos.

Para que realizem a atividade proposta no segundo item, você pode, se possível, distribuir papel dobradura para a turma ou pedir com antecedência que levem de casa. A atividade pode ser realizada em duplas caso julgue conveniente. No primeiro passo da construção, os estudantes vão se deparar com o conceito de diagonal. Esse é o momento oportuno para verificar o que sabem sobre esse conceito. Oriente-os durante toda a atividade. Após concluírem, exponha os trabalhos na sala ou em algum local da escola. A atividade pode ser feita em parceria com o professor ou a professora de Arte.

O tema dessa seção possibilita a valorização de uma manifestação artística oriental, o que contribui para o desenvolvimento das competências gerais 3 e 6 da Bê êne cê cê. Além disso, os estudantes são incentivados a exercitar o diálogo e a empatia, o que favorece o desenvolvimento da competência geral 9 e da competência específica 8.

Página 111

1 Polígonos

Observe o passo a passo que Lucas realizou utilizando um pedaço de papel retangular e uma tesoura de pontas arredondadas. A figura formada por Lucas após finalizada a dobradura se parece com um polígono.

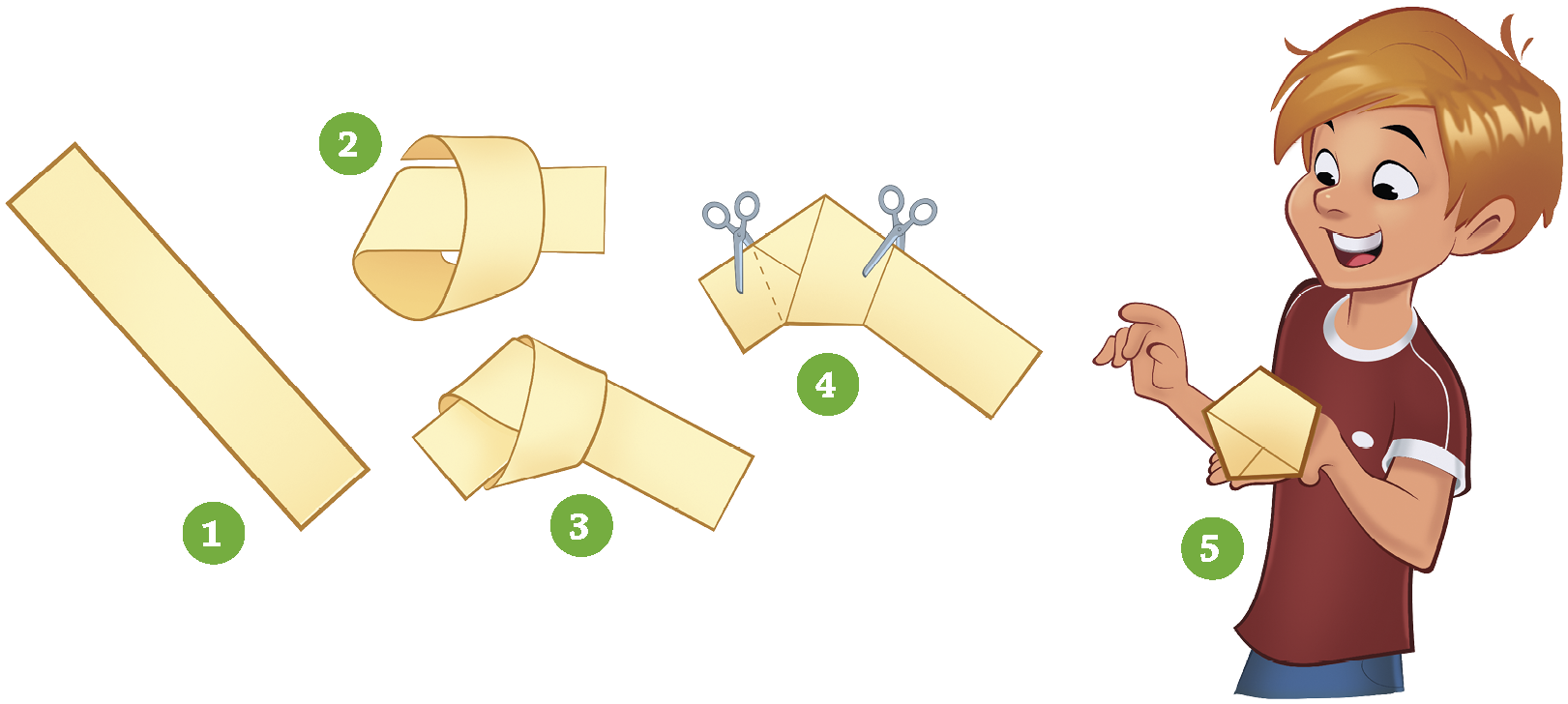
Ilustração. 1. Tira de papel retangular. 2. Papel com uma extremidade voltada para cima. 3. Papel com uma volta semelhante a um nó. 4. Destaque para tesoura dos dois lados recortando a sobra do papel. 5. Menino de cabelo castanho, camisa vermelha segura um modelo de polígono feito com dobraduras,

Um polígono pode ser convexo ou não convexo. Para ser convexo, é necessário que todos os segmentos de reta, com extremidades no interior do polígono, tenham todos os seus pontos situados no interior desse polígono.

Continuaremos a estudar somente os polígonos convexos e, para simplificar, vamos tratá-los simplesmente por polígonos.

Elementos de um polígono

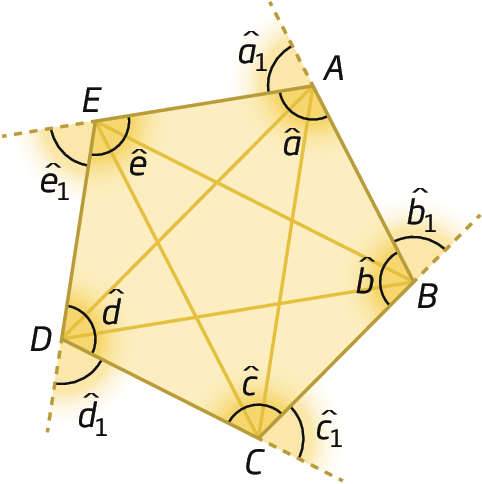
Observe o polígono á bê cê dê é a seguir:

Figura geométrica. Pentágono amarelo ABCDE. Dentro, cinco diagonais: AC, AD, BE, BD e CE. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1 e e1. Ângulos internos: a, b, c, d, e.

Sugestão de leitura

GENOVA, Carlos. origâmi : dobras, contas e encantos. São Paulo: Escrituras, 2008.

Além de apresentar origamis a serem confeccionados, o livro explora a importância de figuras geométricas na composição das dobraduras.

Podemos destacar alguns de seus elementos.

• Lados são os segmentos de reta que formam o contorno do polígono:

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} e \overline{E A}

• Vértices são os pontos que são extremidades dos lados do polígono: a, B, C, D e ê

• Diagonais são os segmentos de reta cujas extremidades são vértices que não pertencem a um mesmo lado do polígono:

\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E} e \overline{C E}

• Ângulos internos são os ângulos formados por dois lados consecutivos que contêm a região interna do polígono:

\hat{a}, \hat{b}, \hat{c}, \hat{d} e \hat{e}

• Ângulos externos são os ângulos formados pelo prolongamento de um dos lados do polígono e por seu lado adjacente e que não contêm a região interna do polígono:

{\hat{a}}_{1}, {\hat{b}}_{1}, {\hat{c}}_{1}, {\hat{d}}_{1} e {\hat{e}}_{1}

Respostas e comentários

Polígonos

Objetivos:

• Reconhecer polígonos.

• Identificar os elementos de um polígono.

Justificativa

No capítulo serão estudadas como se determina o número de diagonais de um polígono, a soma das medidas das aberturas dos ângulos internos e externos de um polígono e as propriedades dos polígonos regulares. Nesse âmbito, é importante que os estudantes reconheçam polígonos e identifiquem seus elementos (lados, vértices, diagonais, ângulos internos e ângulos externos).

Mapeando conhecimentos

Reproduza a atividade 20 da seção Revisão dos conteúdos de anos anteriores na lousa e peça aos estudantes que a façam. Esse é o momento oportuno para diagnosticar se sabem o que é um polígono e se identificam e até representam alguns de seus elementos, como diagonais, ângulos internos e ângulos externos. É importante que, ao final, as representações dos estudantes possam ser compartilhadas e discutidas.

Para as aulas iniciais

Faça a leitura compartilhada da revisão sobre elementos de um polígono presentes na seção Revisão dos conteúdos de anos anteriores. Depois, retome alguns dos polígonos representados pelos estudantes na dinâmica inicial para explorar a identificação de outros elementos, como lados e vértices.

Como os polígonos já foram objeto de estudo em anos anteriores, peça aos estudantes que escrevam uma definição e deem um exemplo de polígono convexo e não convexo. Espera-se que eles entendam um polígono como uma região plana delimitada por uma linha poligonal fechada. No caso de um polígono convexo, é necessário que todos os segmentos de reta, com extremidades no interior do polígono, tenham todos os seus pontos situados no interior desse polígono.

Retome os elementos de um polígono e destaque o fato de os ângulos externos serem suplementares aos ângulos internos.

Página 112

Nome dos polígonos

Um polígono é nomeado de acordo com o número de lados, que é igual ao número de ângulos internos. Observe o nome de alguns polígonos.

Número de lados	Nome do polígono
3	Triângulo
4	Quadrilátero
5	Pentágono
6	Hexágono
7	Heptágono
8	Octógono

Número de lados	Nome do polígono
9	Eneágono
10	Decágono
11	Undecágono
12	Dodecágono
15	Pentadecágono
20	Icoságono

Atividades

Faça as atividades no caderno.

1. Nas figuras a seguir, nomeie o polígono e identifique seus lados, vértices e diagonais.

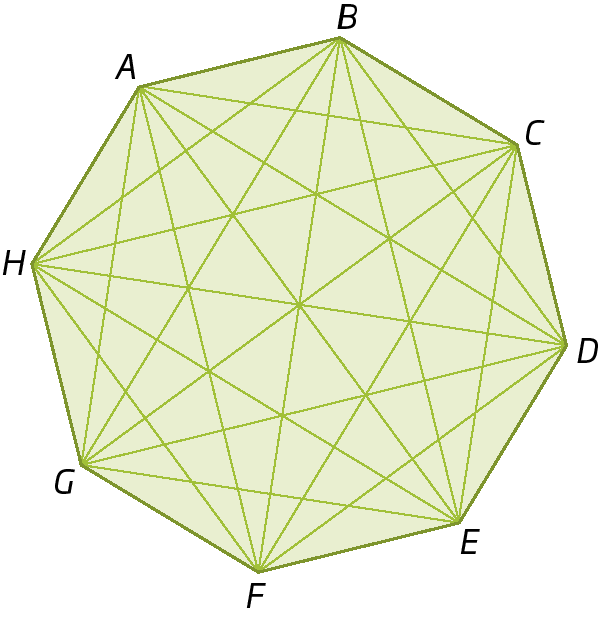
Octógono ABCDEFGH com as diagonais traçadas

2. Use uma régua e construa, em seu caderno, os polígonos seguintes.

a) pentágono á bê cê dê é;

b) octógono á bê cê dê é éfe gê agá;

c) quadrilátero a bê cê dê.

3. Responda às questões sobre um eneágono.

a) Quantos são seus ângulos internos?

b) Quantos são seus vértices?

4. Responda aos itens a seguir sobre um pentágono á bê cê dê é.

a) Quantos lados ele possui?

b) Quantas diagonais diferentes ele possui?

c) Identifique todas as suas diagonais.

5. A abertura do ângulo formado por dois lados consecutivos de um octógono mede 135graus. Qual é a soma das medidas das aberturas de todos os ângulos internos desse octógono, sendo todos eles congruentes?

Respostas

1. a) triângulo á bê cê

lados:

\overline{A B}, \overline{B C}, \overline{A C}

vértices: a, B, C

diagonais: não há

1. b) octógono á bê cê dê é éfe gê agá

lados:

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}, \overline{E F}, \overline{F G}, \overline{G H}, \overline{H A}

vértices: a, B, C, D, ê, F, G, H

diagonais:

\overline{A C}, \overline{A D}, \overline{A E}, \overline{A F}, \overline{A G}, \overline{B D}, \overline{B E}, \overline{B F}, \overline{B G}, \overline{B H}, \overline{C E}

\overline{C F}, \overline{C G}, \overline{C H}, \overline{D F}, \overline{D G}, \overline{D H}, \overline{E G}, \overline{E H}, \overline{F H}

2. a) Exemplo de resposta em Orientações.

2. b) Exemplo de resposta em Orientações.

2. c) Exemplo de resposta em Orientações.

3. a) 9

3. b) 9

4. a) 5

4. b) 5

4. c)

\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E} e \overline{C E}

5. .1080graus

Comentários

Sugestão de leitura

Para aprofundar os conhecimentos sobre polígonos, sugerimos a leitura do trabalho “Descobrindo a arte de construir polígonos”, que relata a realização de oficinas com estudantes de 8º ano com a temática de construção de polígonos.

Disponível em: https://oeds.link/yasa0K. Acesso em: 4 agosto 2022.

Nome dos polígonos

Explore a nomenclatura usada na classificação dos polígonos, relacionando os prefixos ao número de lados e de ângulos.

• Na atividade 2 é importante que os estudantes percebam que os polígonos representados não precisam ser regulares. Desse modo, solicite a eles que representem na lousa diferentes polígonos para cada item.

Exemplos de resposta da atividade 2.

Figura geométrica. Figura laranja ABCDE.

Figura geométrica. Octógono verde ABCDEFGH.

Figura geométrica. Paralelogramo azul ABCD.

• Nesse momento, a resolução da atividade 4 se dá de fórma intuitiva, sem a necessidade do uso de fórmulas ou de construção da figura propriamente dita.

• Do mesmo modo, para resolver a atividade 5, basta que os estudantes percebam que a soma das medidas da abertura dos ângulos internos é obtida adicionando 8 parcelas iguais a 135graus, ou seja, a soma é .1080graus.

Página 113

2 Diagonais de um polígono

O número de diagonais de um polígono varia de acordo com o número de lados que ele possui.

Analise o número de diagonais que partem do vértice a em cada polígono a seguir.

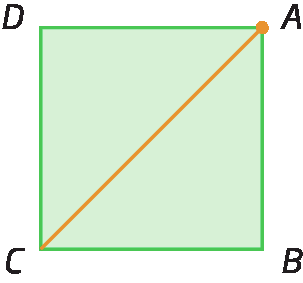
Figura geométrica. Quadrado verde ABCD com diagonal AC dentro. — 4 lados uma diagonal (4 menos 3 = 1)

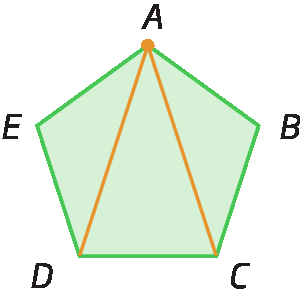
Figura geométrica. Pentágono verde ABCDE com diagonais de AC e AD — 5 lados duas diagonais (5 menos 3 = 2)

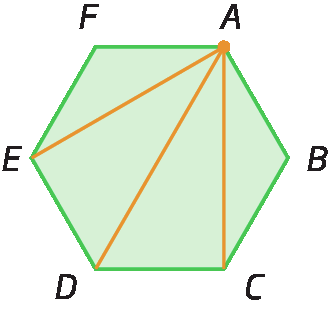
Figura geométrica. Hexágono verde ABCDEF com diagonais de AF, AD e AC — 6 lados 3 diagonais (6 menos 3 = 3)

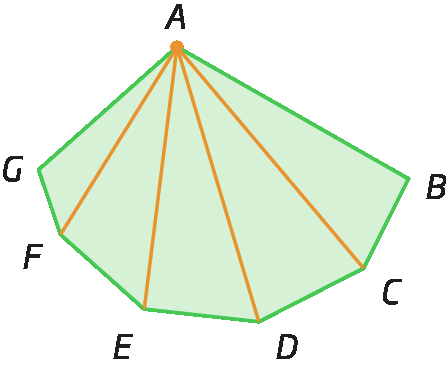
Figura geométrica. Heptágono verde ABCDEFG com diagonais de AF, AE, AD, AC, AB. — 7 lados 4 diagonais (7 menos 3 = 4)

Assim, se um polígono tem n lados, podemos traçar (n menos 3) diagonais a partir de cada vértice. E como esse polígono possui n vértices, então podemos traçar n ⋅ (n menos 3) diagonais. Porém, dessa fórma, estamos contando a mesma diagonal duas vezes. Por exemplo, no hexágono á bê cê dê é éfe anterior, partindo do vértice a, temos a diagonal

\overline{A C}

e, partindo do vértice C, temos a diagonal

\overline{C A}

, mas

\overline{A C}

\overline{C A}

determinam a mesma diagonal.

Logo, para determinar o número de diagonais (d ) de um polígono de n lados, fazemos:

d = \frac{n \cdot (n - 3)}{2}

Considere um outro exemplo.

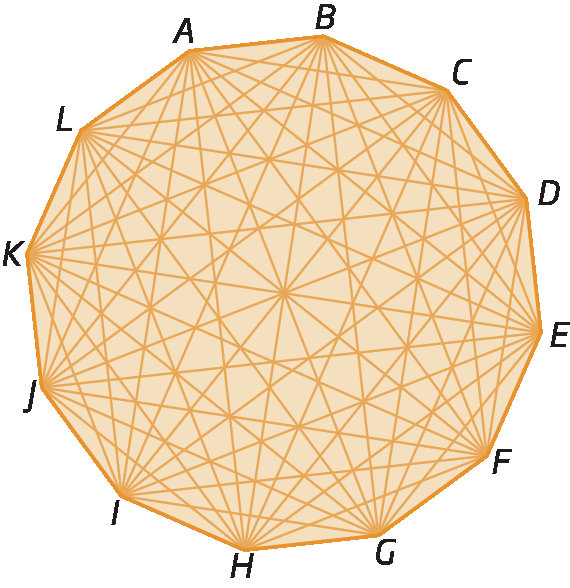
O dodecágono tem 12 lados. Vamos calcular o número de diagonais desse polígono.

n = 12

d = \frac{12 \cdot (12 - 3)}{2} = 54

Logo, o dodecágono tem 54 diagonais.

Figura geométrica. Dodecágono laranja ABCDEFGHIJKL com as diagonais traçadas dentro. — Representação de todas as diagonais de um dodecágono.

Respostas e comentários

Diagonais de um polígono

Objetivo:

Determinar o número de diagonais de um polígono.

Justificativa

Determinar o número de diagonais de um polígono mobiliza conhecimentos das unidades temáticas Geometria, Números e Álgebra e possibilita resolver diferentes problemas.

Mapeando conhecimentos

Peça aos estudantes que representem em uma folha de papel alguns polígonos, tracem todas as diagonais de cada um, contem essas diagonais e completem um quadro como o da referência seguinte:

Número de lados do polígono	4	5	6	8	10
Número de diagonais

Eles podem representar quantos e quais polígonos quiserem.

Em seguida, desafie-os a encontrar uma relação entre o número de diagonais e o número de lados de um polígono. Oriente-os a indicar o número de diagonais por d e o número de lados por n.

Para as aulas iniciais

Retome a dinâmica inicial e verifique quem conseguiu obter a relação entre d e n. Depois, oriente os estudantes que tiveram mais dificuldades. Peça que quantifiquem as diagonais que partem de um mesmo vértice, multipliquem essa quantidade pelo número de vértices e dividam o resultado final por 2 para eliminar as diagonais que foram contadas duas vezes. Por fim, peça que todos ampliem o quadro da dinâmica inicial, porém o número de diagonais deve ser preenchido com o uso da fórmula:

d = \frac{n (n - 3)}{2}

Caso a escola disponha de um laboratório de informática, prepare atividades para que, por meio da interação com um software de Geometria dinâmica, os estudantes possam construir os conhecimentos que serão formalizados posteriormente. Assim, em vez de dizer diretamente aos estudantes: “Se um polígono tem n lados, podemos traçar (n menos 3) diagonais a partir de cada vértice”, pode-se propor que cheguem a essa conclusão por meio da observação de regularidades ao utilizarem o software. Uma aula pautada no uso de ferramentas tecnológicas deve proporcionar aos estudantes a chance de serem os protagonistas de seu processo de aprendizagem.

Página 114

3 Ângulos internos e ângulos externos de um polígono

Soma das medidas das aberturas dos ângulos internos de um polígono

Analise o experimento feito por João para verificar que a soma das medidas das aberturas dos ângulos internos de um triângulo é 180graus.

Ilustração. Três quadros. 1. Triângulo ABC com ângulos a, b e c. 2. Destaque para uma tesoura recortando os ângulos do triângulo ABC. 3. Os ângulos a, b e c unidos. Ao lado, homem negro de cabelo preto e camisa vermelha diz: Primeiro, marquei, com cores diferentes, os ângulos internos do triângulo ABC. Na sequência, recortei o modelo de triângulo em 3 partes, em que cada parte continha um ângulo interno; e, por último,
coloquei os ângulos marcados lado a lado, de modo a torná-los adjacentes. Assim, obtive os 180 graus!

Traçando as diagonais que partem de um mesmo vértice, é possível decompor qualquer polígono em triângulos. Observe as figuras a seguir.

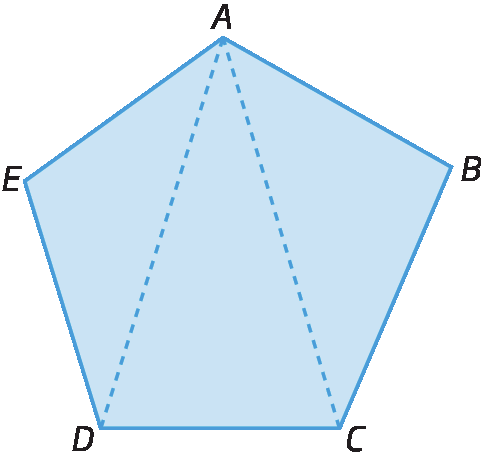
Figura geométrica. Pentágono azul ABCDE com diagonais de AC e AD. — O polígono de 5 lados foi decomposto em 3 triângulos.

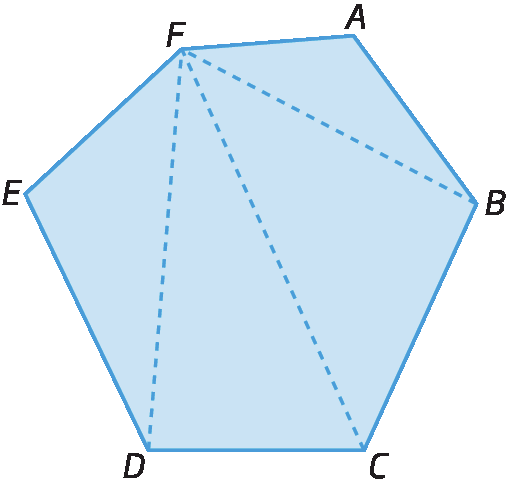
Figura geométrica. Hexágono azul ABCDEF com diagonais de FB, FC e FD. — O polígono de 6 lados foi decomposto em 4 triângulos.

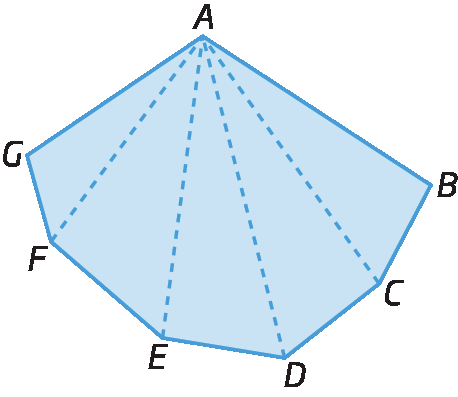
Figura geométrica. Heptágono azul ABCDEFG com diagonais de AC, AD, AE e AF. — O polígono de 7 lados foi decomposto em 5 triângulos.

Fixando um dos vértices de um polígono e traçando as diagonais que partem desse vértice, decompomos o polígono de n lados em (n – 2) triângulos.

Como a soma das medidas das aberturas dos ângulos internos de cada triângulo é 180graus, podemos afirmar que a soma das medidas das aberturas dos ângulos internos (Si ) de um polígono de n lados corresponde a:

Si = (n ‒ 2) ⋅ 180graus

Respostas e comentários

Ângulos internos e ângulos externos de um polígono

Objetivos:

• Determinar a soma das medidas das aberturas dos ângulos internos de um polígono.

• Determinar a soma das medidas das aberturas dos ângulos externos de um polígono.

Justificativa

Determinar a soma das medidas das aberturas dos ângulos internos e externos de um polígono, amplia os conhecimentos previamente adquiridos pelos estudantes sobre a soma das medidas das aberturas dos ângulos internos de um triângulo e mobiliza conhecimentos das unidades temáticas Geometria, Grandezas e Medidas e Álgebra.

Mapeando conhecimentos

Reproduza a atividade 21 da seção Revisão dos conteúdos de anos anteriores na lousa e peça aos estudantes que a façam. Esse é o momento oportuno para verificar se, para determinar o valor de x em cada item, eles utilizam o fato de que a soma das medidas das aberturas dos ângulos internos de um triângulo, de um quadrilátero e de um pentágono são iguais, respectivamente, a 180graus, 360graus e 540graus.

Para as aulas iniciais

Faça a leitura coletiva da revisão sobre a soma das medidas das aberturas dos ângulos internos de um polígono presente na seção Revisão dos conteúdos de anos anteriores. Depois, resolva a atividade 21 com a turma aplicando a relação Si = (n − 2) ⋅ 108graus e resolvendo as equações do 1º grau na incógnita x.

Sugestão de atividade extra

Organize os estudantes em duplas e peça a eles que recortem um pedaço de papel de modo que ele se pareça com um triângulo e que dobrem como sugerem as linhas pontilhadas da representação a seguir.

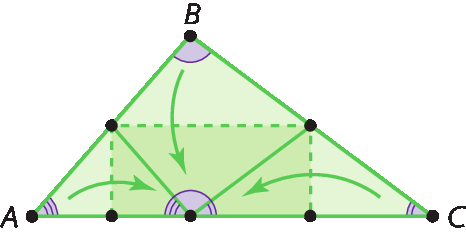
Figura geométrica.. Triângulo ABC. Há um ponto no centro de lada lado. No lado AC, um ponto no centro e um de cada lado. Retângulo verde tracejado com a junção dos ângulos a, b e c no ponto ao centro de AC.

Ao fazer isso, espera-se que os estudantes percebam que é possível construir um ângulo raso (de 180graus) justapondo os ângulos internos do triângulo. Com isso, eles podem verificar experimentalmente que a soma das medidas das aberturas dos ângulos internos do triângulo é igual a 180graus e, procedendo da mesma fórma com qualquer triângulo, podem concluir que essa é uma propriedade válida para todos os triângulos.

Página 115

Considere mais alguns exemplos.

a) Qual é a soma das medidas das aberturas dos ângulos internos de um hexágono?

n = 6

Si = (n ‒ 2) ⋅ 180graus

Si = (6 ‒ 2) ⋅ 180graus

Si = 4 ⋅ 180graus

Si = 720graus

A soma das medidas das aberturas dos ângulos internos de um hexágono é 720graus.

b) A soma das medidas das aberturas dos ângulos internos de um polígono é 900graus. Qual é esse polígono?

Si = 900graus

Si = (n ‒ 2) ⋅ 180graus

900graus = (n ‒ 2) ⋅ 180graus

\frac{900 °}{180 °} = \frac{(n - 2) \cdot 180 °}{180 °}

5 = n ‒ 2 ⇒ n = 7

Logo, o polígono é um heptágono.

Soma das medidas das aberturas dos ângulos externos de um polígono

Considere o hexágono á bê cê dê é éfe. Cada ângulo interno com o ângulo externo correspondente são adjacentes suplementares. Assim:

a + a1 = 180°

b + b1 = 180°

c + c1 = 180°

d + d1 = 180°

e + e1 = 180°

f + f1 = 180°

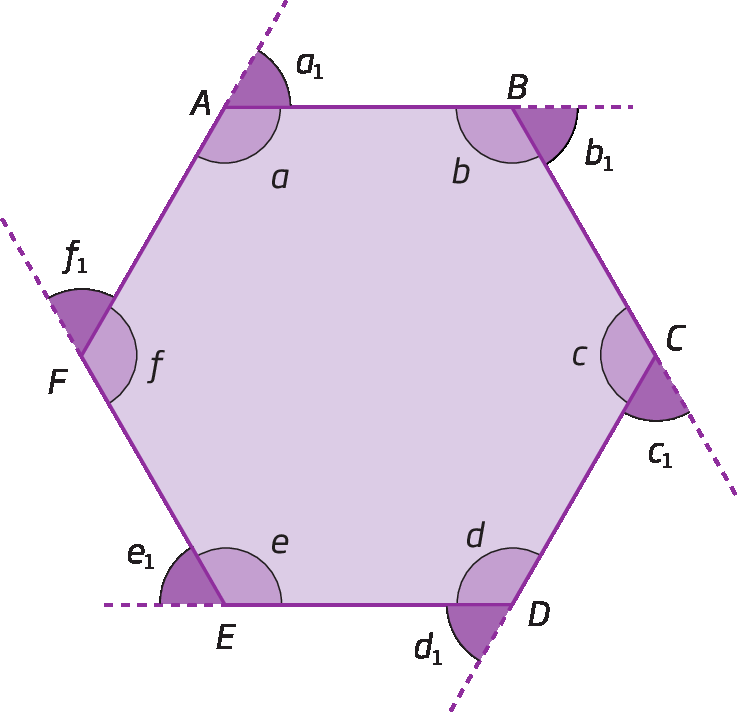
Figura geométrica. Hexágono roxo ABCDEF. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1, e1, f1. Ângulos internos: a, b, c, d, e, f.

Adicionando as medidas das aberturas de todos os ângulos, temos:

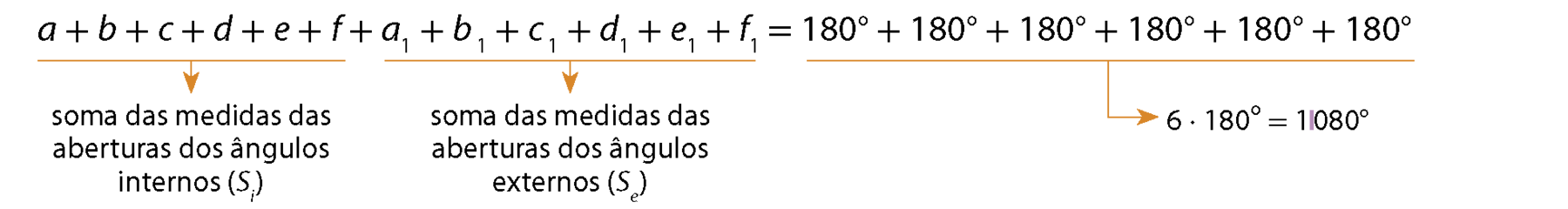
Sentença matemática com esquema. A mais b mais c mais d mais e mais f mais a1 mais b1 mais c1 mais d1 mais e1 mais f1 igual a 180 graus mais 180 graus 180 graus 180 graus 180 graus 180 graus. Seta para baixo saindo de a mais b mais c mais d mais e mais f: soma das medidas das aberturas dos ângulos internos abre parênteses, S i, fecha parênteses. Seta para baixo saindo de a1 mais b1 mais c1 mais d1 mais e1 mais f1: soma das medidas das aberturas dos ângulos externos, abre parênteses, S e, fecha parênteses. Seta para baixo saindo de 180 graus mais 180 graus 180 graus 180 graus 180 graus 180 graus: 6 vezes 180 graus igual a 1 080 graus.

Assim: Si + Se = .1080°. Como Si = (n ‒ 2) ⋅ 180° e n = 6, então:

(6 ‒ 2) ⋅ 180° + Se = .1080°

4 ⋅ 180° + Se = .1080°

720° + Se = .1080°

Se = 360°

Logo, a soma das medidas das aberturas dos ângulos externos do hexágono é 360graus.

Para qualquer polígono de n lados, temos:

Si + Se = n ⋅ 180°

(n ‒ 2) ⋅ 180° + Se = n ⋅ 180°

n ⋅ 180° ‒ 360° + Se = n ⋅ 180°

Se = 360°

Ilustração. Menino negro de camiseta azul e calça. Ele está deitado segurando um livro aberto e com a cabeça encostada na mochila, pensa: Realmente, quando adicionamos as medidas das aberturas de todos os ângulos do hexágono ABCDEF, obtivemos: Si + Se = 1080 graus. seta para baixo indicando 6 (número de lados do hexágono) vezes 180 graus.

Assim:

Em qualquer polígono, a soma das medidas das aberturas dos ângulos externos é 360graus.

Respostas e comentários

Em vez de apresentar diretamente a decomposição de polígonos em triângulos e, então, obter a expressão que permite determinar a soma das medidas das aberturas dos seus ângulos internos, é interessante que, por meio de investigações, os estudantes sejam levados a perceber, por si mesmos, essa possibilidade de decomposição e, a partir de tal ideia, chegar à expressão visada.

Soma das medidas das aberturas dos ângulos externos de um polígono

O fato de que a soma das medidas das aberturas dos ângulos externos de um polígono é igual a 360graus pode ser percebido pelos estudantes por meio de investigações realizadas com o auxílio de um software de Geometria dinâmica. Até mesmo a verificação indicada no livro de que cada ângulo interno e seu externo correspondente são adjacentes suplementares pode ser facilitada pela utilização do software.

Em outros momentos da vida escolar dos estudantes, quando aparecer a questão das medidas das aberturas dos ângulos de um polígono, eles saberão como determinar a soma das medidas das aberturas dos ângulos internos e também a soma das medidas das aberturas dos ângulos externos de um polígono de n lados. Assim, em vez de apresentar diretamente o resultado visado, peça a eles que obtenham, a partir dos conhecimentos já construídos, as expressões que permitem obter a medida da abertura de cada ângulo externo e de cada ângulo interno de um polígono regular de n lados.

Página 116

Veja que interessante

Faça as atividades no caderno.

Vamos fazer um experimento com os ângulos externos de um polígono?

Em uma folha de papel, desenhe um polígono qualquer e indique seus ângulos externos. Verifique o modelo.

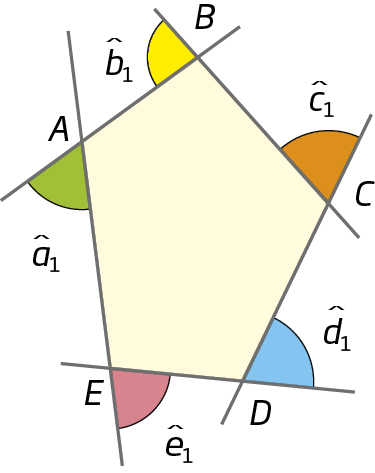
Figura geométrica. Pentágono ABCDE. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1, e1.

Em seguida, recorte, com uma tesoura de pontas arredondadas, cada um dos ângulos e una-os em torno de um dos vértices, de modo que se tornem adjacentes dois a dois.

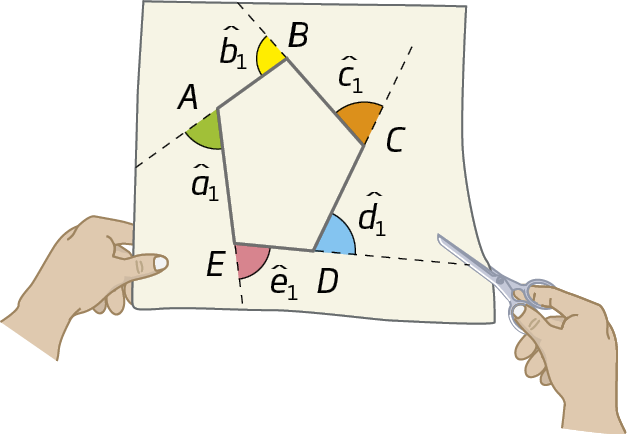
Ilustração. Folha de papel com pentágono ABCDE. Do lado externo de cada ponto, reta tracejada diagonal formando ângulos externos: a1, b1, c1, d1, e1. Destaque para a mão de uma pessoa com uma tesoura no papel.

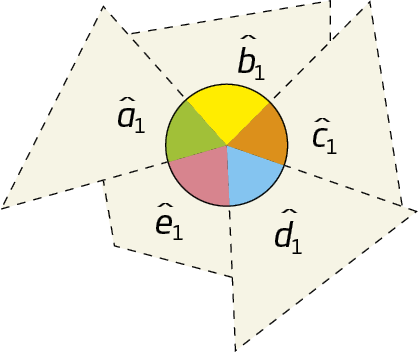
Ilustração. Formas triangulares com os ângulos recortados: a1, b1, c1, d1, e1 unidos no centro e formando um círculo.

Atividade

O que você pode verificar com esse experimento?

Atividades

Faça as atividades no caderno.

6. Determine o número de diagonais de um polígono de:

a) 5 lados;

b) 9 lados;

c) 15 lados;

d) 20 lados.

7. Determine a soma das medidas das aberturas dos ângulos internos dos polígonos a seguir.

a) Quadrilátero

b) Eneágono

c) Undecágono

d) Icoságono

8. Indique o nome dos polígonos cuja soma das medidas das aberturas dos ângulos internos é:

a) .1080graus

b) .1980graus

c) .2340graus

d) .1800graus

9. Em cada caso, calcule o valor de x, em grau.

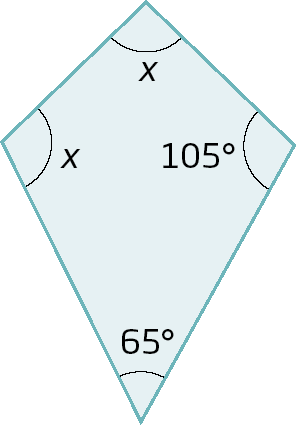
Figura geométrica. Quadrilátero com ângulos: x, x, 105 graus e 65 graus.

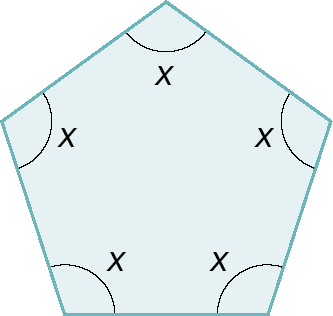
Figura geométrica. Pentágono com 5 ângulos x.

10. Determine o polígono que tem a soma das medidas das aberturas dos ângulos internos e a soma das medidas das aberturas dos ângulos externos iguais.

Respostas e comentários

Veja que interessante: Espera-se que os estudantes percebam que, com o experimento, verificamos que a soma das medidas das aberturas dos ângulos externos de um polígono é 360graus.

6. a) 5 diagonais

6. b) 27 diagonais

6. c) 90 diagonais

6. d) 170 diagonais

7. a) 360graus

7. b) .1260graus

7. c) .1620graus

7. d) .3240graus

8. a) octógono

8. b) polígono de 13 lados

8. c) pentadecágono

8. d) dodecágono

9. a) x = 95graus

9. b) x = 108graus

10. quadrilátero

Para realizar a atividade do boxe Veja que interessante, será preciso uma folha de papel sulfite, régua, lápis de cor e tesoura com pontas arredondadas para cada estudante.

Incentive os estudantes a representar polígonos convexos de n lados, de modo que possam verificar que a soma das medidas das aberturas dos ângulos externos é igual a 360graus.

Página 117

4 Polígonos regulares

Um polígono que tem todos os lados com a mesma medida de comprimento e todos os ângulos com a mesma medida de abertura é denominado polígono regular. Os polígonos a seguir são exemplos de polígonos regulares.

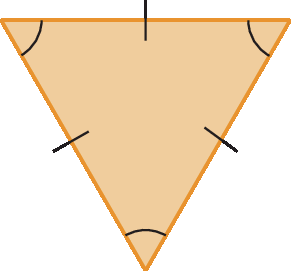
Figura geométrica. Triângulo com três lados e ângulos iguais. — triângulo equilátero

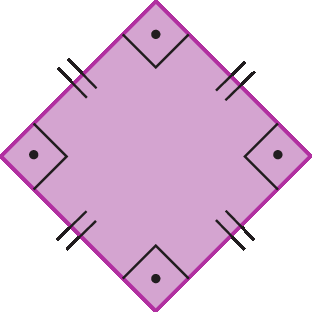
Figura geométrica. Quadrado com quatro lados e ângulos iguais. — quadrado

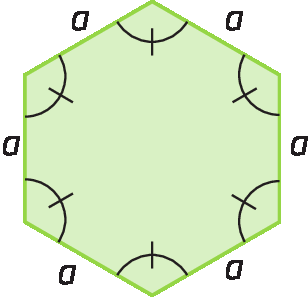
Figura geométrica. Hexágono com seis lados iguais, cada lado mede a. — hexágono regular

Medidas das aberturas do ângulo interno e do ângulo externo de um polígono regular

Em um polígono regular de n lados, indicando a medida da abertura do ângulo interno por ai e a medida da abertura do ângulo externo por ae , temos:

Sentença matemática. A i igual a s i dividido por n ou A i igual a, abre parênteses, n menos 2, fecha parênteses, vezes 180 graus, dividido por n.

Sentença matemática. A e igual a s e dividido por n ou A e igual a 360 graus dividido por n.

Agora, considere os exemplos a seguir.

a) Vamos determinar a medida da abertura do ângulo interno e a do ângulo externo de um decágono regular.

O decágono é o polígono que tem 10 lados.

Logo, n = 10. Assim:

a_{e} = \frac{S_{e}}{n} = \frac{360 °}{10} = 36 °

a_{i} = \frac{S_{i}}{n} = \frac{(n - 2) \cdot 180 °}{n} = \frac{(10 - 2) \cdot 180 °}{10} = 144 °

Logo, a medida da abertura do ângulo externo é 36graus e a medida da abertura do ângulo interno é 144graus.

Sugestão de leitura

SMOOTHEY, Marion. Atividades e jogos com quadriláteros. São Paulo: Scipione, 1998. (Coleção Investigação matemática).

Partindo de situações cotidianas, o livro traz desafios com fósforos, dobraduras e quebra-cabeças que ajudam a compreender conceitos como: quadriláteros, ângulos, diagonais, pontos e retas.

b) Vamos calcular o número de lados de um polígono regular cuja medida da abertura do ângulo interno é igual a 108graus.

Como

a_{i} = \frac{(n - 2) \cdot 180 °}{n}

, então:

108 ° = \frac{(n - 2) \cdot 180 °}{n}

108° ⋅ n = 180° ⋅ n ‒ 360°

72° ⋅ n = 360°

n = 5

Logo, o polígono tem 5 lados, ou seja, é um pentágono.

Respostas e comentários

Polígonos regulares

Bê êne cê cê:

• Competências gerais 2, 4 e 10 (as descrições estão na página seis).

• Competência específica 5 (a descrição está na página sete).

• Habilidades ê éfe zero oito ême ah um cinco e EF08MA16.

Objetivos:

• Compreender o conceito de polígono regular.

• Construir polígonos regulares com régua e compasso.

Justificativa

Compreender o conceito de polígono regular amplia os conhecimentos sobre polígonos adquiridos pelos estudantes. Já a construção de polígonos regulares com régua e compasso favorece o desenvolvimento da habilidade ê éfe zero oito ême ah um cinco.

Mapeando conhecimentos

Reúna os estudantes em grupos e distribua folhas de papel com alguns polígonos regulares representados nelas. Depois, peça que meçam os lados e as aberturas dos ângulos internos desses polígonos e verbalizem o que concluíram. Espera-se que eles reconheçam a congruência dos lados e dos ângulos internos de cada polígono. Depois, pergunte: “Como vocês fariam para determinar a medida da abertura de cada ângulo interno de um polígono regular?”. Deixe que investiguem e conjecturem. Caso ache necessário, dê como dica partir da fórmula da soma das medidas das aberturas dos ângulos internos de um polígono.

Para as aulas iniciais

Na seção Revisão dos conteúdos de anos anteriores, é retomado o conceito de polígono regular e como se determina a medida da abertura dos ângulos internos e externos de polígonos regulares. Faça a leitura coletiva dessa revisão com a turma. Depois retome a questão feita na dinâmica inicial e verifique se conseguiram concluir como se determina, de modo geral, a medida da abertura de cada ângulo interno de um polígono regular. Caso seja necessário, oriente-os a dividir a fórmula da soma das medidas das aberturas dos ângulos internos de um polígono pela quantidade de ângulos internos do polígono regular. Por fim, explore com eles as atividades 22 e 23.

(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.

(ê éfe zero oito ême ah um seis) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.

Página 118

Atividades

Faça as atividades no caderno.

11. Determine as medidas das aberturas dos ângulos internos e dos ângulos externos dos seguintes polígonos:

a) quadrilátero regular;

b) octógono regular;

c) eneágono regular;

d) icoságono regular.

12. Qual é o polígono regular cujas medidas das aberturas dos ângulos internos são iguais às medidas das aberturas dos ângulos externos?

13. Em um polígono regular, a medida da abertura do ângulo externo é 40graus. Quantos lados tem esse polígono?

14. Em um polígono regular, ai ‒ ae = 60graus. Qual é esse polígono?

Ângulo central de um polígono regular

Uma circunferência circunscrita a um polígono contém todos os vértices desse polígono. Nesse caso, podemos dizer também que o polígono está inscrito na circunferência.

Todo polígono regular pode ser inscrito em uma circunferência.

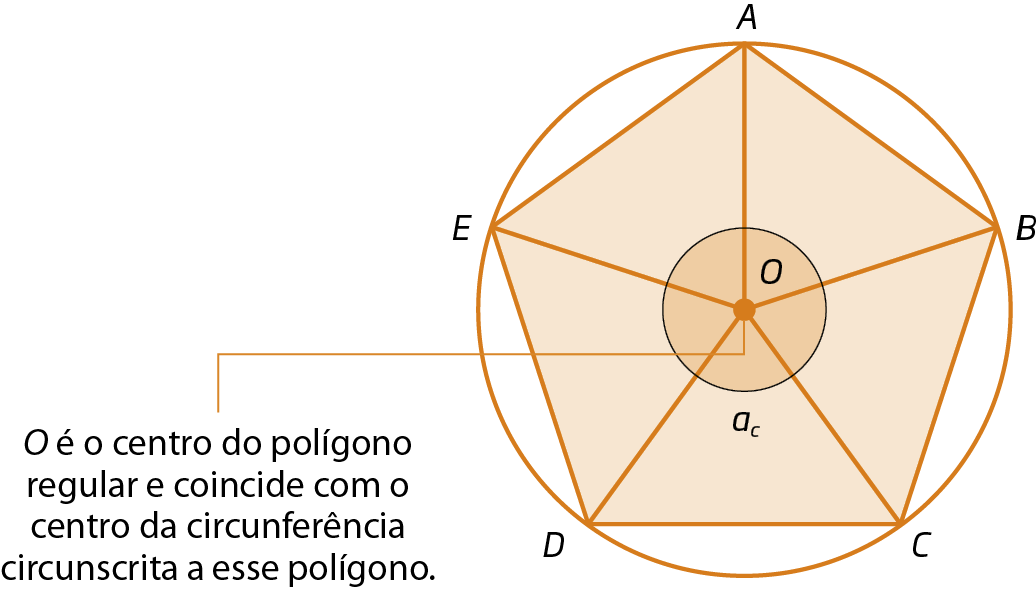
Denominamos ângulo central de um polígono regular aquele cujo vértice é o centro da circunferência e cujos lados passam por dois vértices consecutivos do polígono.

No pentágono regular á bê cê dê é a seguir, ac indica a medida da abertura do ângulo central.

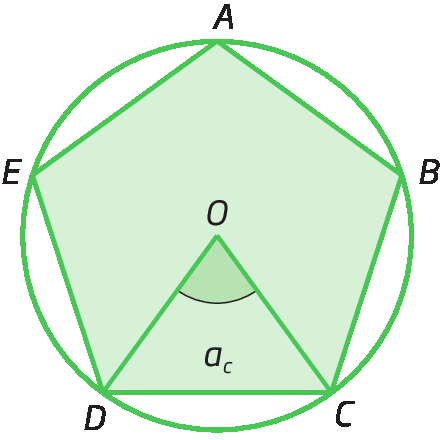
Figura geométrica. Circunferência com pentágono ABCDE inscrito, centro O, que é centro da circunferência. Está definido o triângulo OCD, o ângulo DOC está destacado e tem medida ac.

Sendo óh o centro de um polígono regular, a soma das medidas das aberturas de todos os ângulos centrais (ésse minúsculoc ) é 360graus (uma volta completa).

Sc = 360°

Figura geométrica. Circunferência circunscrita ao pentágono ABCDE laranja com centro em O. Há um outro círculo com centro em O, demarcando os ângulos centrais. Do centro O, tem-se uma reta diagonal para cada vértice do pentágono. De O sai uma seta para o texto: O é o centro do polígono regular e coincide com o centro da circunferência circunscrita a esse polígono

Logo, em um polígono de n lados, a medida da abertura do ângulo central é:

a_c =  

\frac{360 °}{n}

Respostas e comentários

11. a) ái = 90graus; áe = 90graus

11. b) ái = 135graus; áe = 45graus

11. c) ái = 140graus; áe = 40graus

11. d) ái = 162graus; áe = 18graus

12. quadrilátero regular ou quadrado

13. 9 lados

14. hexágono

Sugestão de leitura

Sugerimos a leitura do trabalho “O ensino de polígonos regulares por meio de materiais manipuláveis”, que tem como objetivo apresentar uma proposta do uso de materiais concretos para o ensino de polígonos regulares inscritos na circunferência. Se considerar adequado, faça as atividades propostas com os estudantes. Disponível em: https://oeds.link/yVqVnA. Acesso em: 4 agosto 2022.

Ângulo central de um polígono regular

Dizer que um polígono está inscrito em uma circunferência significa que todos os vértices desse polígono são pontos da circunferência.

Sugestão de atividade extra

A proposição “Todo polígono regular pode ser inscrito em uma circunferência.” pode ser reescrita em sua fórma condicional: “Se um polígono é regular, então pode ser inscrito em uma circunferência”. A sentença que chamamos de contrapositiva é construída assim: “Se um polígono não pode ser inscrito em uma circunferência, então ele não é regular”.

E se o polígono puder ser inscrito em uma circunferência, ele será regular com certeza? É o que veremos nesta atividade.

1. Divida a classe em duplas. Cada dupla deverá representar três circunferências em uma folha de papel. Peça aos estudantes que escolham grupos de quatro pontos, cinco pontos e seis pontos sobre as circunferências; um grupo sobre cada circunferência. Peça, então, que unam os pontos de modo a obterem polígonos.

2. Pergunte e deixe que discutam entre si: esses polígonos são regulares?

3. Finalmente, questione: Se todo polígono regular pode ser inscrito em uma circunferência, então todo polígono inscrito em uma circunferência é regular?

Essa atividade explora as implicações lógicas, as recíprocas e as contrapositivas.

Página 119

Construção de polígonos regulares com régua e compasso

Podemos construir polígonos regulares a partir do seu ângulo central. Acompanhe a seguir a construção de um triângulo equilátero e a de um quadrado.

Cuidado! Evite acidentes ao usar o compasso.

Triângulo equilátero

A medida da abertura do ângulo central do triângulo equilátero é igual a 120graus. Observe a sequência de passos para construí-lo.

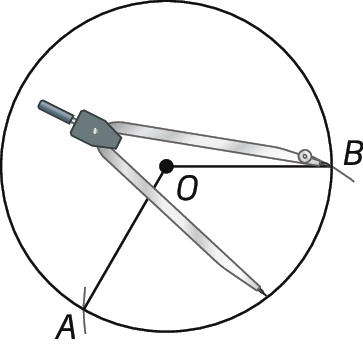
1º) Construímos uma circunferência de centro O com medida de comprimento de raio qualquer, e, com a mesma abertura do compasso, centrando-o em um ponto qualquer da circunferência, traçamos dois arcos, cruzando a circunferência em dois pontos, A e B. Construímos os segmentos de reta

\overline{A O} e \overline{O B}

, determinando o ângulo central

A \hat{O} B

Ilustração. Circunferência com ponto O no centro. De O, tem-se uma reta horizontal com ponto B e reta diagonal para baixo com ponto A. Compasso aberto entre A e B traça linha em B.

2º) Centrando o compasso em B e mantendo a sua abertura inicial, traçamos mais dois arcos consecutivos na circunferência, marcando o ponto C. Traçamos

\overline{O C}

, determinando os ângulos centrais

B \hat{O} C e A \hat{O} C

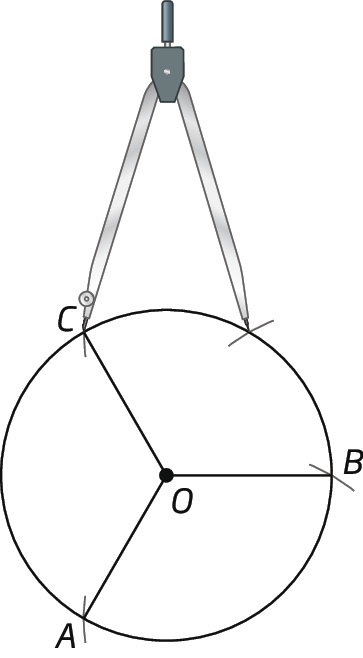
Ilustração. Circunferência com ponto O no centro. De O, tem-se reta horizontal com ponto B e reta diagonal para baixo com ponto A. Compasso aberto em C na reta de O e traça linha entre B e C.

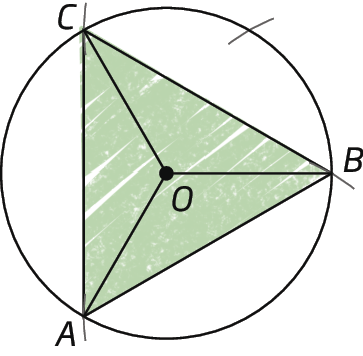
3º) Construímos os segmentos de reta

\overline{A B}, \overline{A C} e \overline{B C}

, formando, assim, o triângulo equilátero.

Ilustração. Circunferência com triângulo verde ABC e ponto O no centro.

Quadrado

A medida da abertura do ângulo central do quadrado é igual a 90graus. Observe a sequência de passos para construí-lo.

1º) Construímos uma circunferência de centro óh com medida de comprimento de raio qualquer. Traçamos um diâmetro, marcando os pontos a ê cê, intersecções do diâmetro com a circunferência.

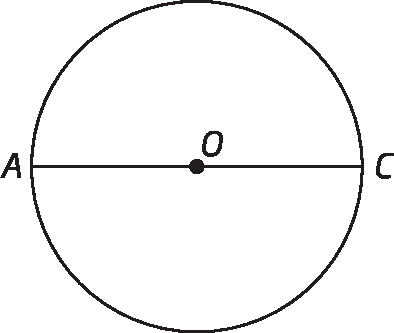
Ilustração. Circunferência com reta horizontal AC e ponto O no centro.

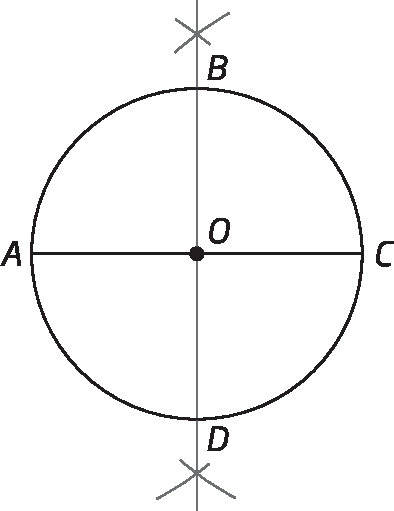
2º) Construímos uma reta perpendicular à

\overline{A C}

, passando por óh, marcando os pontos B e D, intersecção da reta perpendicular com a circunferência. Assim, determinamos 4 ângulos centrais com medida de abertura 90graus:

A \hat{O} B, B \hat{O} C, C \hat{O} D e D \hat{O} A

Ilustração. Circunferência com reta horizontal AC e ponto O no centro. Reta vertical BD passa em O.

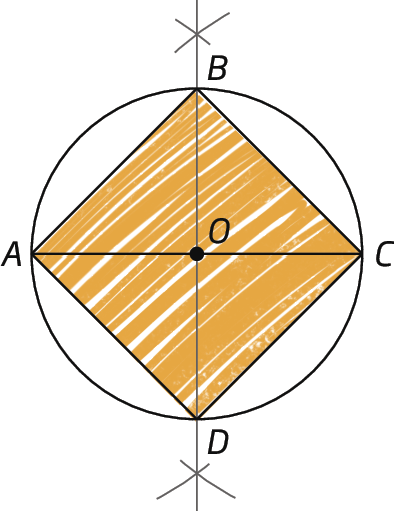
3º) Traçamos os segmentos de reta

\overline{A B}, \overline{B C}, \overline{C D} e \overline{D A}

, formando, assim, o quadrado.

Ilustração. Circunferência com reta horizontal AC e ponto O no centro. Reta vertical BD passa em O. As retas formam um losango laranja.

Observação

No capítulo 7, apresentaremos a justificativa para a validade das construções apresentadas nesta página.

Respostas e comentários

Antes de apresentar as construções do triângulo equilátero e do quadrado, propostas nesta página, verifique se os estudantes levantam hipóteses sobre essas construções. Para isso, pode-se propor algumas questões, como: “Em quantos pontos um quadrado inscrito intersecta a circunferência? E um triângulo equilátero? Como você faria para determinar esses pontos?”.

Oriente os estudantes quanto aos cuidados no manuseio do compasso a fim de evitar acidentes.

Sugestão de atividade extra

Após explorar as construções propostas nesta página, peça aos estudantes que, usando régua e compasso, construam outros polígonos regulares, como o hexágono regular. Algumas propostas de construções podem ser encontradas na dissertação “Polígonos construtíveis por régua e compasso: uma apresentação para professores da Educação Básica”, de Kelisson Ferreira de Lima.

Disponível em: https://oeds.link/bOoIdX. Acesso em: 4 agosto 2022.

Você poderá justificar a construção do triângulo equilátero depois que o hexágono regular for construído.

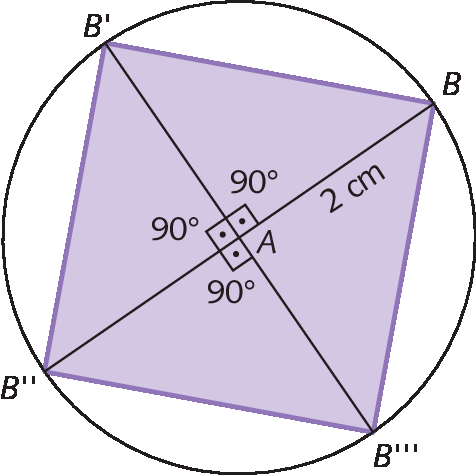
Quanto ao quadrado, a construção se justifica pelo fato de que, no quadrado, as diagonais são perpendiculares e são congruentes. Volte a essa construção quando os quadriláteros forem explorados.

Página 120

Atividades

Faça as atividades no caderno.

15. Calcule a medida da abertura do ângulo central de cada polígono regular.

a) hexágono;

b) decágono;

c) dodecágono;

d) icoságono.

16. Faça o que se pede.

a) Construa no caderno um triângulo equilátero inscrito em uma circunferência cujo raio mede 1,5 centímetro de comprimento.

b) Construa no caderno um quadrado inscrito em uma circunferência cujo raio mede 2 centímetros de comprimento.

17.

Observe as frases a seguir. Se as colocarmos na sequência correta, obteremos o passo a passo para construir um hexágono regular.

A. Construa um ângulo central cuja medida da abertura seja igual a 60graus.

B. Construa um ângulo central adjacente ao anterior.

C. Trace um segmento de reta consecutivo ao anterior, fechando o polígono.

D. Trace um segmento de reta unindo os pontos obtidos.

E. Marque a intersecção do último lado do ângulo construído com a circunferência.

F. Construa uma circunferência.

G. Trace o segmento de reta consecutivo ao anterior, unindo-o ao último ponto obtido.

H. Marque a intersecção dos lados do ângulo com a circunferência.

a) Reproduza o fluxograma a seguir em seu caderno e complete-o com as letras correspondentes a cada uma das frases anteriores. Note que, no fluxograma, há um grupo de passos que devem ser repetidos para obtermos o hexágono regular. Indique, no campo adequado, a quantidade de vezes que esse grupo deve ser repetido.

Fluxograma. Modelo. Início. Oito espaços para respostas. Fim. Do quinto ao oitavo espaço para resposta, (repita, espaço para resposta, vezes).

b) Utilizando a ideia anterior como referência, elabore, no caderno, um esquema com uma sequência de comandos para a construção de outro polígono regular.

c) Troque de caderno com um colega e tente construir o polígono conforme a orientação no esquema.

d) Discuta com o colega os fluxogramas elaborados, analisando se as instruções produziram o polígono desejado. Caso isso não tenha ocorrido, investiguem se houve falha no comando ou na sequência dos comandos inseridos no esquema.

Respostas e comentários

15. a) á_c = 60graus

15. b) á_c = 36graus

15. c) á_c = 30graus

15. d) á_c = 18graus

16. a) Exemplo de resposta em Orientações.

16. b) Exemplo de resposta em Orientações.

17. a) Resposta em Orientações.

17. b) Resposta pessoal.

17. c) Resposta pessoal.

17. d) Resposta pessoal.

Exemplo de respostas da atividade 16:

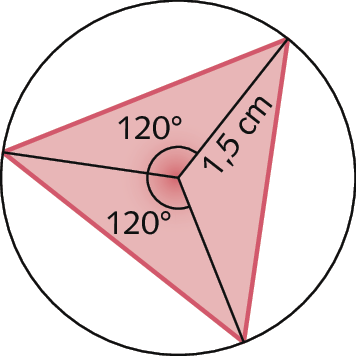
Figura geométrica. Circunferência com triângulo vermelho e três diagonais. A medida da diagonal é 1 centímetro e meio. As medidas de dois ângulos são: 120 graus e 120 graus.

Figura geométrica. Circunferência com quadrilátero roxo B, B linha, B duas linhas, B três linhas com duas diagonais que se cruzam no centro. A medida da diagonal é 2 centímetros. As medidas de três ângulos são: 90 graus, 90 graus e 90 graus.

• A atividade 17 estimula o raciocínio lógico, o pensamento computacional, a criatividade e a elaboração de questões pelos estudantes, favorecendo o desenvolvimento das competências gerais 2, 4 e 10 e da competência específica 5.

• Resposta do item a da atividade 17:

Fluxograma. Início. F, A, H, D, B, E, G, C. Fim. (B, E, G: repita 4 vezes).

Página 121

Revisão dos conteúdos deste capítulo

Faça as atividades no caderno.

Polígonos

Uma linha poligonal fechada simples com sua região interna fórma uma figura geométrica plana chamada polígono.

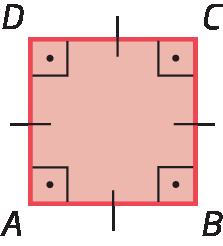
1. Dê o nome do polígono e identifique seus lados, vértices e diagonais.

Figura geométrica. Quadrilátero ABCD vermelho com os quatro lados iguais destacados e os quatro ângulos retos destacados.

2. Um heptágono possui:

a) quantos vértices?

b) quantos lados?

Diagonais de um polígono

O número de diagonais de um polígono varia de acordo com o número de lados que ele possui. Logo, para determinar o número de diagonais (d) de um polígono de n lados, fazemos:

d = \frac{n \cdot (n - 3)}{2}

3. Determine o número de diagonais de um polígono de:

a) 8 lados

b) 3 lados

Ângulos internos e ângulos externos de um polígono

Soma das medidas das aberturas dos ângulos internos de um polígono

A soma das medidas das aberturas dos ângulos internos (ésse minúsculoi) de um polígono de n lados corresponde a:

Si = (n ‒ 2) ⋅ 180°

Soma das medidas das aberturas dos ângulos externos de um polígono

Em qualquer polígono, a soma das medidas das aberturas dos ângulos externos é 360graus.

4. A soma das medidas das aberturas dos ângulos internos de um polígono é 720graus. Qual é esse polígono?

5. Determine a soma das medidas das aberturas dos ângulos internos de um pentágono.

Polígonos regulares

Um polígono que possui todos os lados com a mesma medida de comprimento e todos os ângulos com mesma medida de abertura é denominado polígono regular.

Medidas das aberturas do ângulo interno e do ângulo externo de um polígono regular

Em um polígono regular de n lados, indicando a medida da abertura do ângulo interno por ái e a medida da abertura do ângulo externo por áe , temos:

a_{i} = \frac{S_{i}}{n} ou a_{i} = \frac{(n - 2) \cdot 180 °}{n}

a_{e} = \frac{S_{e}}{n} ou a_{e} = \frac{360 °}{n}

Ângulo central de um polígono regular

Denominamos ângulo central de um polígono regular aquele cujo vértice é o centro da circunferência e cujos lados passam por dois vértices consecutivos do polígono.

Sendo óh o centro de um polígono regular, a soma das medidas das aberturas de todos os ângulos centrais (ésse minúsculoc ) é 360graus (uma volta completa).

S_c = 360°

Logo, em um polígono de n lados, a medida da abertura do ângulo central é:

a_{c} = \frac{360 °}{n}

6. A medida da abertura do ângulo interno de um polígono regular é o triplo da medida da abertura do seu ângulo externo. Qual é esse polígono?

Respostas e comentários

1. quadrado a bê cê dê; lados:

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D A}

vértices: a, B, C, D; diagonais:

\overline{A C}, \overline{B D}

2. a) 7

2. b) 7

3. a) 20

3. b) 0

4. hexágono

5. 540graus

6. octógono

Revisão dos conteúdos deste capítulo

Polígonos

• Na atividade 1, espera-se que os estudantes reconheçam o quadrilátero a bê cê dê como um quadrado, uma vez que todos os ângulos internos são retos e têm todos os lados com a mesma medida de comprimento. Depois, eles devem indicar os lados, os vértices e as diagonais. Verifique se reconhecem que os lados e as diagonais são segmentos de reta e se utilizam a notação correta.

• Na atividade 2, os estudantes devem se lembrar de que um heptágono é um polígono com 7 lados. Oriente-os a representar um heptágono qualquer no caderno para verificar que o número de lados é igual ao número de vértices.

Diagonais de um polígono

• A atividade 3 pode ser feita aplicando a relação

d = \frac{n \cdot (n - 3)}{2}

ou representando as diagonais de um polígono qualquer de oito lados e outro de três lados para depois contá-las. É importante que os estudantes tenham acesso a esses dois modos de resolução.

Ângulos internos e externos de um polígono

• As atividades 4 e 5 são realizadas por meio da aplicação da relação ésse minúsculoprimeiro = (n menos 2) ⋅ 180graus, em que ésse minúsculoprimeiro é a soma das medidas das aberturas dos ângulos internos do polígono e n é o número de lados. Após realizarem os cálculos, sugira que representem um pentágono e um hexágono qualquer em uma folha de papel, meçam as aberturas dos ângulos internos de cada um desses polígonos e, depois, adicionem essas medidas para verificar se obtém 540graus e 720graus, respectivamente. É possível que as somas obtidas por eles sejam próximas desses valores. Caso isso ocorra, comente sobre as possíveis razões: defeitos nos transferidores, falhas no processo de medição, entre outros.

Polígonos regulares

• A atividade 6 demanda que os estudantes traduzam o enunciado da atividade para a linguagem algébrica. Espera-se que eles escrevam a seguinte expressão: áprimeiro = 3 ⋅ á_e. Depois, oriente-os a organizar a medida das aberturas dos ângulos internos e externos de alguns polígonos regulares em um quadro até descobrir o polígono que atende às condições do enunciado.

Como 135graus = 3 ⋅ 45graus, o polígono regular que atende às condições do enunciado é o octógono.

Polígono regulares	ai	ae
Quadrado	90°	90°
Pentágono	108°	72°
Hexágono	120°	60°
Octógono	135°	45°