Revisão dos conteúdos de anos anteriores
Faça as atividades no caderno.
Para o capítulo 1: Potenciação e radiciação com números reais
Números racionais
Os números racionais (conjunto representado por

) podem ser escritos na fórma de fração, com numerador e denominador inteiros e denominador diferente de zero.
Os números naturais (conjunto representado por

) e os números inteiros (conjunto representado por

) são também números racionais.
Números irracionais
Os números irracionais têm infinitas casas decimais e não são periódicos. Os números
Sentença matemática. Raiz quadrada de 2.,
Sentença matemática. 2 vezes raiz quadrada de 3.,
Sentença matemática. Menos raiz quadrada de cinco.e π são exemplos de números irracionais.
Números reais
Se juntarmos em um só conjunto os números racionais e os números irracionais, obteremos o conjunto dos números reais, cujo símbolo é

.

1. Em seu caderno, indique as sentenças verdadeiras e as falsas.
a) 7,3 é um número irracional.
b)
Sentença matemática. Raiz quadrada de 12.é um número real.
c)
Sentença matemática. Fração menos 3 quartos.é um número irracional.
d) 0,333reticências é um número racional.
2. Escreva, em seu caderno, os números que não são racionais.
a)
Sentença matemática. Raiz quadrada de 16.b) 1,29
c)
Sentença matemática. Menos raiz quadrada de 3.d) menos7,777reticências
e)
Sentença matemática. Menos raiz quadrada de 81.f)
Sentença matemática. Fração dois sobre raiz quadrada de dois.g)
Sentença matemática. Fração 8, 21 avos.h)
Sentença matemática. 4 raiz quadrada de 2.Propriedades da potenciação
Considerando que a é um número real não nulo e que m e n são números inteiros, temos:
Produto de potências de mesma base:
Quociente de potências de mesma base:
Potência de uma potência:
Sentença matemática. Abre parênteses, a elevado a m, fecha parênteses, elevado a n, igual a a elevado a m vezes n.Potência de um produto:
Sentença matemática. Abre parênteses, a vezes b, fecha parênteses, elevado a m, igual a, a elevado a m vezes b elevado a m.Potência de um quociente:
Sentença matemática. Abre parênteses, a dividido por b, fecha parênteses, elevado a m, igual a, a elevado a m dividido por b elevado a m.3. Escreva, em seu caderno, em fórma de uma única potência:
a) 117 ⋅ 1112
b)
Sentença matemática. Abre parênteses, menos, fração 1 meio, fecha parênteses, elevado a 10, vezes, abre parênteses, menos fração 1 meio, fecha parênteses, elevado a 15.c) 3115 : 3114
d)
Sentença matemática. Abre parênteses, fração 3 quintos, fecha parênteses, elevado a 20, dividido, abre parênteses, fração 3 quintos, fecha parênteses, elevado a 12.4. Quais sentenças estão corretas? Anote-as em seu caderno.
a)
Sentença matemática. 3 elevado a 10 igual a 3 elevado a 8 mais 3 elevado a 2.b)
Sentença matemática. 5 elevado a 9 dividido por 5 elevado a 3 igual a 5 elevado a 3.c)
Sentença matemática. 7 elevado a 5 vezes 7 elevado a 6 igual 7 elevado a 11.d) 10012 : 10011 = 100
Raiz quadrada
A raiz quadrada de um número real positivo x é um número não negativo que, elevado ao quadrado, resulta em x.
Raiz quadrada exata
Os números 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121 e 144 foram obtidos de um produto de dois fatores iguais. Chamados quadrados perfeitos, esses números têm como raiz quadrada o fator que os originou.
Raiz quadrada aproximada
Quando um número real não negativo não é um quadrado perfeito, sua raiz quadrada não é exata, mas podemos obter um valor aproximado para ela. Vamos considerar como exemplo
Sentença matemática. Raiz quadrada de 150..
Para começar, procuramos entre quais quadrados perfeitos está o 150: entre 144 e 169.
Como
Sentença matemática. Raiz quadrada de 144 igual a 12.e
Sentença matemática. Raiz quadrada de 169 igual a 13.,
Sentença matemática. Raiz quadrada de 150.está entre 12 e 13.
Calculamos os quadrados de alguns números situados entre 12 e 13, com uma casa decimal:
12,12 = 146,41
12,22 = 148,84 (<150)
12,32 = 151,29 (>150)
Assim, 12,2 corresponde a uma aproximação de
Sentença matemática. Raiz quadrada de 150.com uma casa decimal.
5. Decomponha estes números em fatores primos e, se possível, determine a raiz quadrada exata de cada um deles.
a) 2 116
b) 625
c) 972
d) 784
6. Escreva entre quais quadrados perfeitos estão os seguintes números.
a) 51
b) 93
c) 190
d) 388
7. Agora, calcule a raiz aproximada dos números da atividade anterior com uma casa decimal.
a) 51
b) 93
c) 190
d) 388
Para o capítulo 2: Matemática financeira
Porcentagem
Uma porcentagem indica a parte de um todo que contém 100 partes iguais. Por exemplo, 27% representa 27 partes de 100 ao todo.
Uma porcentagem póde ser escrita na fórma de fração ou na fórma decimal:
Para calcular o valor referente à porcentagem de um total, multiplicamos a porcentagem (ou sua fração equivalente) pelo valor total.
8. Em seu caderno, calcule:
a) 42% de 50;
b) 16% de 160;
c) 60% de 32;
d) 95% de 8;
e) 120% de 68.
9. Um produto custa R$ 900,00novecentos reais. Calcule o novo valor caso esse produto tenha um:
a) aumento de 15%;
b) aumento de 10%;
c) desconto de 20%;
d) desconto de 1%.
Para o capítulo 3: Segmentos proporcionais e semelhança
Razão e proporção
A razão entre dois números, a e b, com b ≠ 0, nessa ordem, é dada por
Sentença matemática. Fração a sobre b..
Proporção é uma igualdade entre duas razões. Por exemplo,
Sentença matemática. 15 meios igual a 30 quartos..
Propriedade fundamental das proporções
Em toda proporção, dados a, b, c e d não nulos, com
Sentença matemática. a sobre b igual a c sobre d., temos a ⋅ d = b ⋅ c.
10. Aplicando a propriedade fundamental das proporções, identifique quais pares de razões são proporções.
a)
Sentença matemática. 5 quartos igual a 10 oitavos.b)
Sentença matemática. 1 terço igual a 2 quartos.c)
Sentença matemática. 18 terços igual a 6 sobre 1.d)
Sentença matemática. 7 quintos igual a 10, 14 avos.Para o capítulo 4: Fatoração e equações do 2º grau
Expressões algébricas
Uma expressão matemática formada por números e letras ou somente por letras é chamada de expressão algébrica.
Em expressões algébricas, as letras são chamadas de variáveis.
Valor numérico é o resultado das operações efetuadas em uma expressão algébrica após a substituição das variáveis por números.
Adição e multiplicação de termos algébricos
Cada parcela de uma expressão algébrica é um termo algébrico, que é formado por duas partes: a parte numérica, denominada coeficiente, e a parte com letras, denominada parte literal.
Para adicionar termos algébricos que têm a mesma parte literal, devemos adicionar os coeficientes e conservar a parte literal.
Para multiplicar dois termos algébricos, devemos:
• multiplicar os coeficientes numéricos entre si;
• multiplicar as partes literais entre si.
11. Determine o valor numérico de cada expressão algébrica considerando x = menos 1.
a) 45 + 43x
b)
Sentença matemática. Fração, numerador: 12x menos 1, denominador: 10x.c)
Sentença matemática. 2x ao quadrado menos x.12. Calcule as adições algébricas.
a) 6a menos 9b + 12b menos a
b)
Sentença matemática. Fração x sobre 2 mais fração x sobre 3 mais fração x sobre 6c) 2y menos 9 + 8y + 9
13. Determine os produtos algébricos.
a)
Sentença matemática. 22 vezes, abre parênteses, 9 mais 3x menos 2y, fecha parênteses.b)
Sentença matemática. a vezes b vezes, abre parênteses, meno 3b, fecha parênteses.c)
b sobre 4, fim da fração, vezes, abre parêntese, menos a sobre 3, fecha parêntese.Equação do 2º grau com uma incógnita
Equação é uma sentença matemática expressa por uma igualdade que apresenta pelo menos um valor desconhecido representado por uma letra denominada incógnita.
Uma equação do 2º grau na incógnita x pode ser reduzida a uma equação do tipo
ax ao quadrado mais bx mais c igual a zero., em que a, b e c são números reais, com a ≠ 0; chamamos a, b e c de coeficientes da equação do 2º grau.
Uma equação do 2º grau com uma incógnita, na fórma
ax ao quadrado mais bx mais c igual a zero., é considerada completa quando tem todos os coeficientes (a, b, c) diferentes de zero; quando b ou c ou os dois coeficientes são iguais a zero, dizemos que a equação do 2º grau
Sentença matemática. ax ao quadrado mais bx mais c igual a zero., na incógnita x, é incompleta.
14. Entre os itens a seguir, quais são equações do 2º grau? Nos casos afirmativos, escreva se a equação é completa ou incompleta.
a)
Sentença matemática. 5x ao quadrado mais x igual a zero.b)
Sentença matemática. Menos 5x ao quadrado mais 25 igual a zero.c) 2x + 13 = 0
d)
Sentença matemática. x ao quadrado sobre 2 mais x mais 1 igual a zero.15. Escreva, em seu caderno, uma equação do 2º grau seguindo as orientações de cada item:
a) completa com todos os coeficientes iguais a 5;
b) incompleta com a = 9 e b = menos1;
c) incompleta com a = 9 e c = menos1.
Raiz de uma equação do 2º grau
Raiz de uma equação é um número que, ao substituir a incógnita, torna a sentença verdadeira.
Por exemplo, vamos verificar se 0 e menos8 são raízes da equação
Sentença matemática. 2x ao quadrado menos 128 igual a zero..
Para x = 0:
menos 128 = 0

sentença falsa
Para x = menos8:
2 ⋅ 64 menos 128 = 0

sentença verdadeira
Logo, 0 não é raiz dessa equação e menos8 é raiz dessa equação.
16. Identifique as sentenças verdadeiras e as falsas.
a) 0 não é raiz da equação
Sentença matemática. 2x ao quadrado menos 5x igual a zero.b) 0 é raiz da equação
Sentença matemática. x ao quadrado mais x sobre 2 igual a zero.c) 1 é raiz da equação
Sentença matemática. x ao quadrado menos x mais 5 igual a zero.d) 2 não é raiz da equação
Sentença matemática. x ao quadrado menos 2x mais 1 igual a zero.17. Qual dos números é raiz da equação
Sentença matemática. x ao quadrado mais 2x menos 3 igual a zero.?
a) menos3
b) 0
c) 1
d) 2
Para o capítulo 5: Função afim
Representação da relação entre grandezas no plano cartesiano
É possível relacionar os valores de duas grandezas por meio de quadros e sentenças algébricas, mas também por meio de gráficos no plano cartesiano.
Para grandezas diretamente proporcionais, se os valores da grandeza do eixo das abscissas podem ser somente números naturais, o gráfico da relação entre os valores não é uma linha contínua, mas pontos alinhados; se os valores dessa grandeza podem ser qualquer número real, o gráfico é uma linha contínua.
Confira essa situação.
Para relacionar o número de ingressos e o valor total a pagar por esses ingressos, foi feito este quadro.
|
Número de ingressos (n) |
1 |
4 |
6 |
10 |
|---|---|---|---|---|
|
Total a pagar em R$ (t) |
20 |
80 |
120 |
200 |
Como as grandezas são diretamente proporcionais e o número de ingressos só póde ser um número natural, os valores das grandezas são representados como pontos alinhados no plano cartesiano.
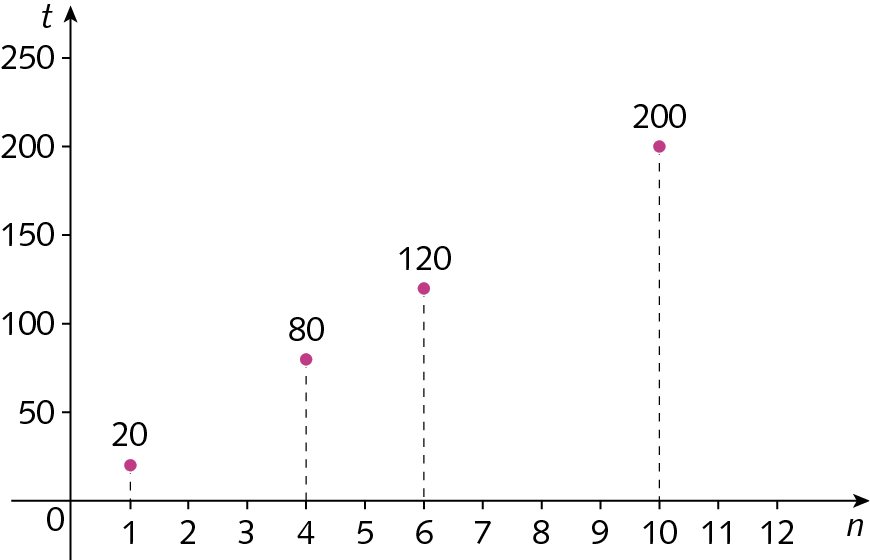
18. Considerando que os valores das grandezas são quaisquer números reais positivos ou nulos, relacione cada quadro com o respectivo gráfico.
A)
|
x |
0 |
5 |
10 |
15 |
|---|---|---|---|---|
|
y |
0 |
15 |
30 |
45 |
B)
|
x |
5 |
10 |
15 |
20 |
|---|---|---|---|---|
|
y |
2,5 |
5 |
7,5 |
10 |
C)
|
x |
2 |
3 |
4 |
5 |
|---|---|---|---|---|
|
y |
9 |
13,5 |
18 |
22,5 |
um)
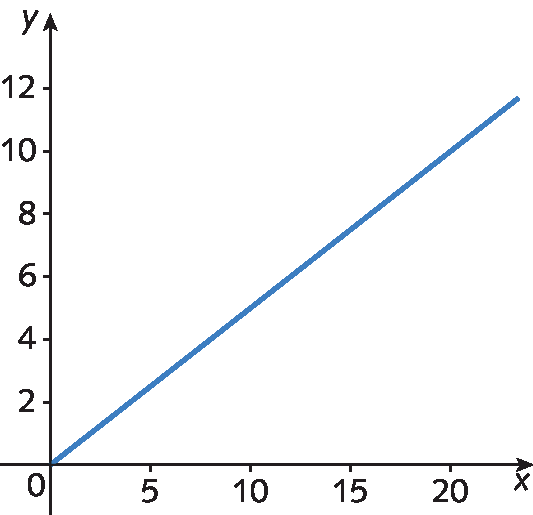
dois)
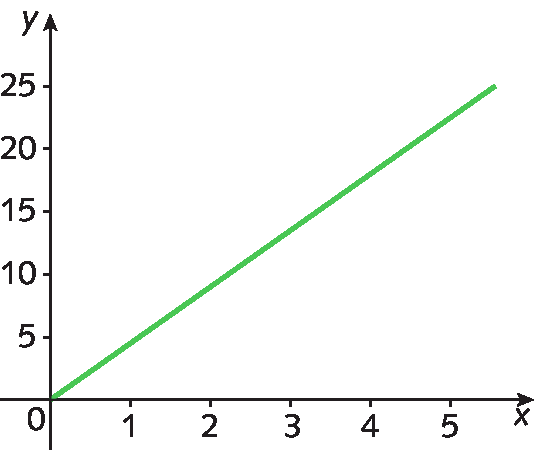
três)
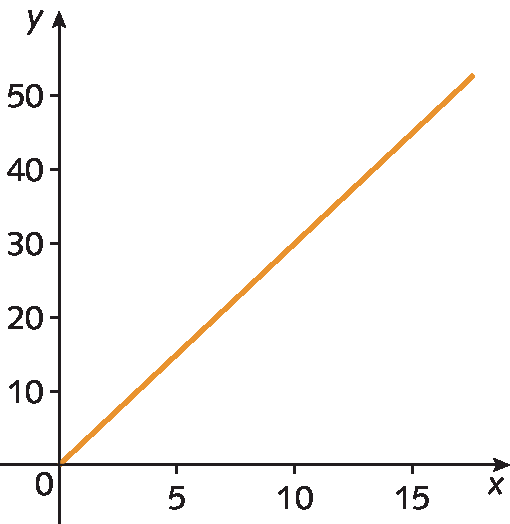
Para o capítulo 6: Função quadrática
Grandezas não proporcionais
Muitas situações no cotidiano envolvem grandezas que não têm proporcionalidade direta nem inversa entre elas.
Confira um exemplo dessas grandezas na situação a seguir.
Em um lançamento de 10 métros feito por um jogador de futebol, foram registradas as medidas da distância entre a bola e o jogador (representada por d) e da altura da bola (representada por h), em metro, no quadro a seguir.
|
d (m) |
0 |
2 |
5 |
10 |
|---|---|---|---|---|
|
h (m) |
0 |
1,6 |
2,5 |
0 |
Nessa situação, a relação entre as grandezas não é direta nem inversamente proporcional, mas é possível relacionar as medidas pela sentença algébrica
Sentença matemática. h igual a menos, fração, numerador: d ao quadrado, denominador: 10, fim de fração, mais d., em que d é um número real tal que 0 ⩽ dê ⩽ 10.
19. Este quadro apresenta as medidas de comprimento do lado de um quadrado (representadas por a), em centímetro, e as respectivas medidas de área da figura (representadas por y), em centímetro quadrado. Analise-o e, depois, faça o que se pede.
|
a (cm) |
1 |
2 |
3 |
4 |
|---|---|---|---|---|
|
y (cm2) |
1 |
4 |
9 |
16 |
a) Relacione essas medidas por meio de uma sentença algébrica.
b) Calcule a medida de área do quadrado cujo comprimento do lado mede 3,5 centímetros.
c) Calcule a medida de comprimento do lado do quadrado cuja área mede 64 centímetros quadrados.
Para o capítulo 7: Relações métricas no triângulo retângulo
Triângulo retângulo
Um triângulo retângulo é um polígono de três lados que tem um ângulo interno reto, ou seja, com medida de abertura de 90graus.
20. No caderno, represente a figura indicada em cada item ê, depois, decomponha-a em triângulos retângulos.
a) Um triângulo isósceles.
b) Um quadrado.
Para o capítulo 8: Circunferência, arcos e ângulos
Circunferência
Circunferência é a figura formada por todos os pontos de um plano que estão à mesma medida da distância de um ponto fixo desse plano. O ponto fixo é chamado centro da circunferência.
Nesta circunferência representada, o ponto O é o centro da circunferência.

a, B, C e D são alguns pontos da circunferência.
O raio é um segmento de reta que une o centro óh a um ponto qualquer da circunferência, como
Símbolo. Segmento de reta OA.,
Símbolo. Segmento de reta OB.e
Símbolo. Segmento de reta OC..
O diâmetro é um segmento de reta que tem duas extremidades na circunferência e que passa pelo centro da circunferência, como
Símbolo. Segmento de reta AB..
21. Analise esta circunferência de centro C e, no caderno, indique quais afirmações são verdadeiras.
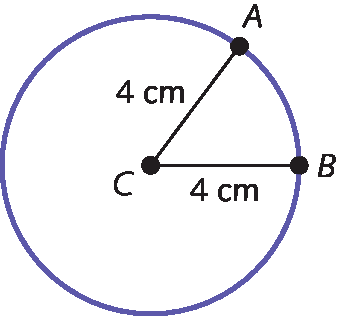
a) Os pontos a e B equidistam de C.
b) C é o centro dessa circunferência.
c) O segmento de reta
Símbolo. Segmento de reta BC.é raio da circunferência e sua medida de comprimento é 4 centímetros.
d) O segmento de reta
Símbolo. Segmento de reta AC.é diâmetro da circunferência e sua medida de comprimento é 8 centímetros.
Para o capítulo 9: Polígonos regulares
Um polígono regular tem todos os lados com a mesma medida de comprimento e todos os ângulos com a mesma medida de abertura.
Medidas das aberturas do ângulo interno e do ângulo externo de um polígono regular
Em um polígono regular de n lados, indicando a medida da abertura do ângulo interno por ái , a soma das medidas das aberturas dos ângulos internos por ésse minúsculoi , a medida da abertura do ângulo externo por áe e a soma das medidas das aberturas dos ângulos externos por ésse minúsculoe , temos:
ou
Sentença matemática. a i igual abre parênteses, n menos 2, fecha parênteses, vezes, 180 graus sobre n.e
ou
Sentença matemática. a e igual 360 graus sobre n.22. Em seu caderno, determine a medida da abertura do:
a) ângulo interno de um pentágono regular;
b) ângulo interno de um octógono regular;
c) ângulo externo de um decágono regular;
d) ângulo externo de um hexágono regular.
Ângulo central de um polígono regular
Todo polígono regular póde ser inscrito em uma circunferência. Ângulo central de um polígono regular é aquele cujo vértice é o centro da circunferência e cujos lados passam por dois vértices consecutivos do polígono.
Neste pentágono regular á bê cê dê é, ác é um dos ângulos centrais.
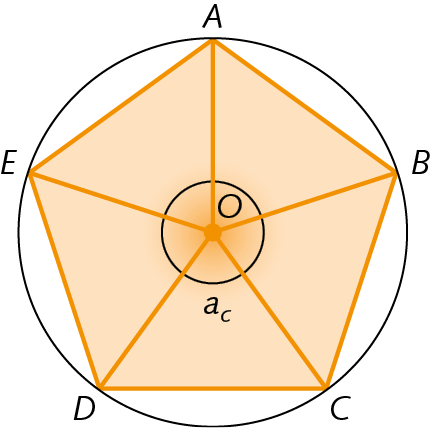
Sendo óh o centro de um polígono regular, a soma das medidas das aberturas de todos os ângulos centrais é 360graus (uma volta completa).
Em um polígono de n lados, a medida da abertura do ângulo central, indicada por ác , é:
23. Calcule, em seu caderno, a medida da abertura do ângulo central de um triângulo equilátero.
24. Em seu caderno, escreva a medida da abertura do ângulo
Símbolo. Ângulo GOH.do polígono regular inscrito na circunferência de centro óh a seguir.
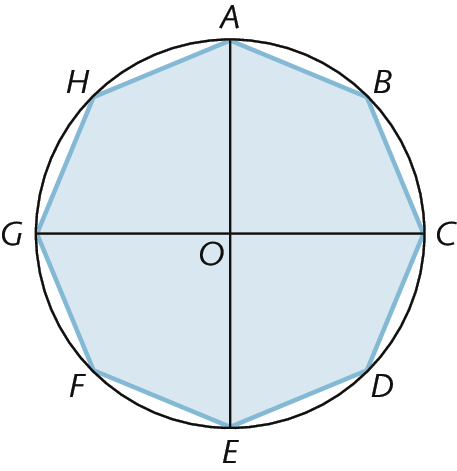
25. Qual destes polígonos é um polígono regular que tem a medida da abertura do ângulo central igual a 60graus?
a)

b)

c)

d)

Para o capítulo 10: Vistas ortogonais e volume
Medida de volume
A medida de volume de um paralelepípedo é obtida multiplicando-se as medidas de comprimento (a), largura (b) e altura (h).
Vparalelepípedo = a ⋅ b ⋅ h
26. Em seu caderno, copie este quadro e complete com as medidas que faltam. Considere as medidas de comprimento, altura e largura em centímetro e a medida de volume em centímetro cúbico.

|
Medida do comprimento |
Medida da altura |
Medida da largura |
Medida do volume |
|---|---|---|---|
|
2 |
6 |
120 |
|
|
0,5 |
0,2 |
0,3 |
|
|
1 |
5 |
30 |
|
|
2 |
2 |
2 |
Para o capítulo 11: Construção de gráficos estatísticos
Gráficos estatísticos
Gráfico de barras
Esse tipo de gráfico é utilizado principalmente para comparar informações. Podemos ter gráficos de barras verticais ou barras horizontais.
Gráfico de setores
Esse tipo de gráfico é usado quando queremos representar partes de um total.
Gráfico de segmentos
Esse tipo de gráfico é usado quando queremos analisar a variação de algum fato ao longo do tempo.
27. Na tabela a seguir, Brenda registrou as vendas de sua loja em 2023.
|
Produto |
Unidades vendidas |
|---|---|
|
A |
150 |
|
B |
200 |
|
C |
620 |
|
D |
400 |
Dados obtidos por Brenda em 2023.
Esses dados foram representados em dois gráficos diferentes:
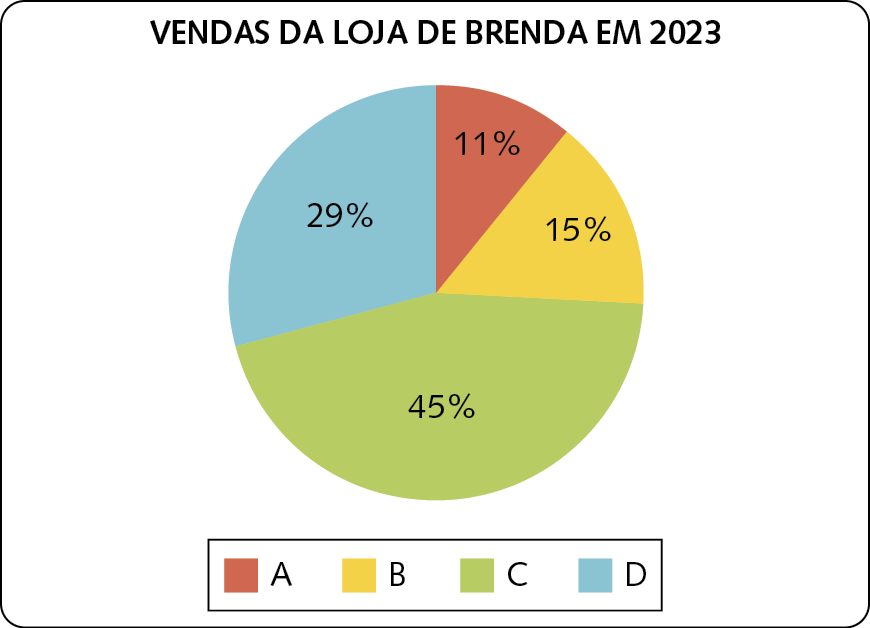
Dados obtidos por Brenda em 2023.
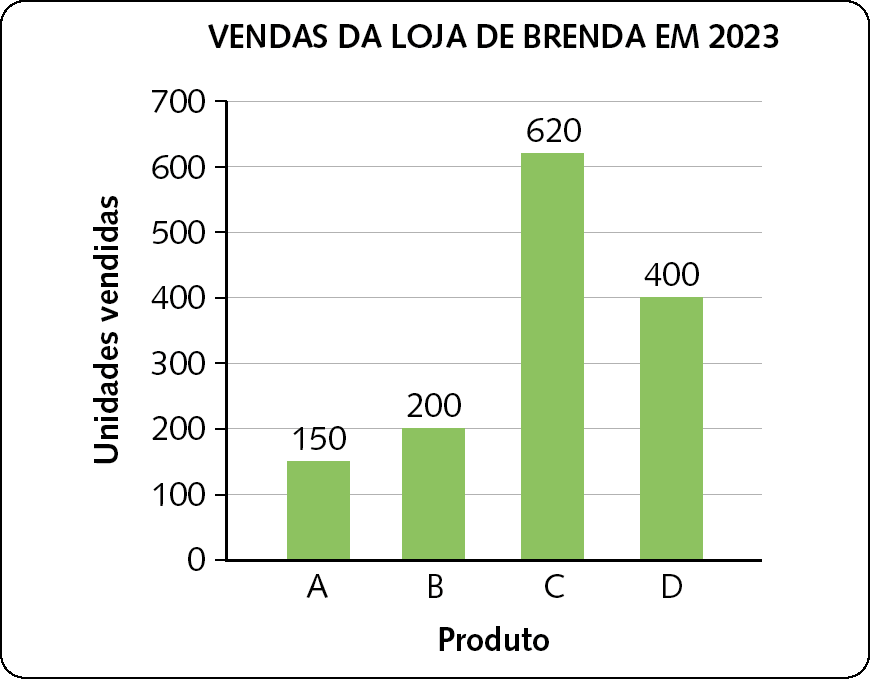
Dados obtidos por Brenda em 2023.
Em seu caderno, responda
a) Qual é o tipo de cada gráfico?
b) Qual desses gráficos é mais adequado a essa situação?
28. Em dezembro de 2023, Camila organizou as informações sobre uma exposição de arte e fez um gráfico para representar o número de visitantes por mês.
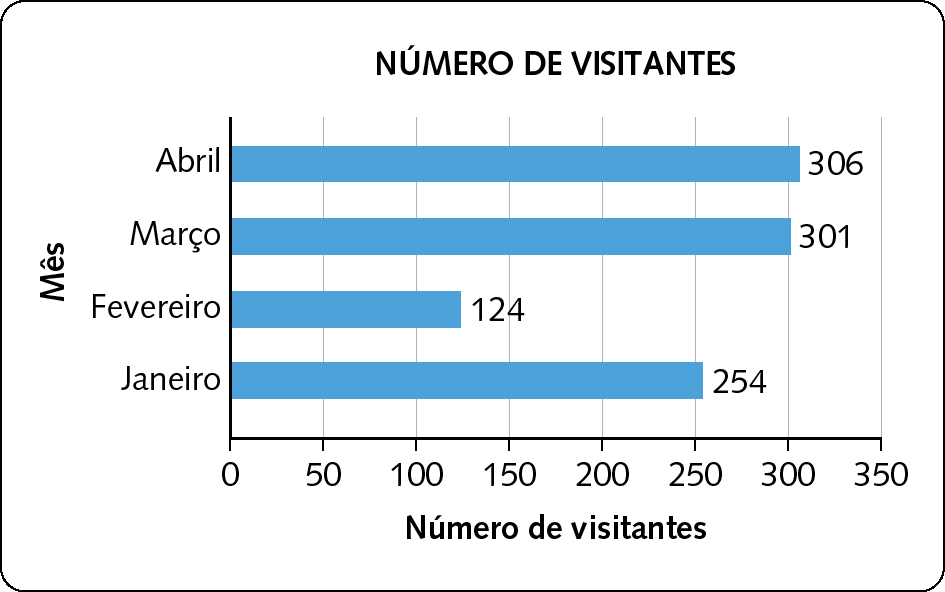
Dados obtidos por Camila em dezembro de 2023.
Em seu caderno, represente as informações desse gráfico em um gráfico de segmentos.
Para o capítulo 12: Probabilidade e estatística
Possibilidades
Um experimento aleatório é uma situação em que conhecemos os resultados possíveis, mas em que não podemos assegurar o resultado final.
O espaço amostral de um experimento aleatório é composto de todos os resultados possíveis no experimento.
Princípio multiplicativo
Considere que um acontecimento ocorra em duas etapas sucessivas, a e B. Se a ocorrer de m maneiras e se, para cada uma delas, B póde ocorrer de n maneiras, o número de maneiras em que o acontecimento póde ocorrer é
Sentença matemática. m vezes n..
Probabilidade
Um evento é qualquer subconjunto do espaço amostral.
A probabilidade P da ocorrência de um evento é uma medida que pode assumir um valor de 0 a 1 e é dada pela razão:
29. Para abrir um cadeado, usa-se uma senha de 4 dígitos.
a) Quantas possibilidades de senha existem?
b) Se a senha começar com 34, quantas possibilidades de senha existem?
c) Se a senha tiver apenas algarismos ímpares, quantas possibilidades de senha existem?
30. Uma urna tem 30 bolas, sendo 10 vermelhas, 5 roxas e as restantes, brancas.
Uma bola dessa urna é retirada ao acaso. Calcule, em seu caderno, a probabilidade de essa bola ser:
a) vermelha;
b) roxa;
c) branca.

Unidade 1
Capítulo 1 Potenciação e radiciação com números reais
Capítulo 2 Matemática financeira
Capítulo 3 Segmentos proporcionais e semelhança

O que é consumo consciente? Será que você consome de fórma consciente? O que podemos fazer para praticar o consumo consciente? Ao final desta Unidade, você responderá a essas e outras questões.
Parte 1
Capítulo 1 Potenciação e radiciação com números reais
Trocando ideias
Os fractais são figuras com autossimilaridade, ou seja, eles contêm, dentro de si, cópias menores deles mesmos; essas cópias, por sua vez, contêm cópias ainda menores e, assim, sucessivamente. Os fractais podem ser encontrados na natureza ou ser produzidos por equações matemáticas e programas de computador.

O triângulo de Sierpinski é um exemplo de fractal. Confira como ele póde ser construído.

▸

Qual é o número de triângulos com fundo preto presentes em cada uma das figuras anteriores? Como essas quantidades podem ser representadas na fórma de potência?
▸


Reúna-se com um colega e pesquisem em livros ou na internet outros exemplos de fractais. Depois, compartilhem com a turma o que encontraram.
Neste capítulo, vamos estudar a potenciação e a radiciação com números reais.

1 Números reais
O conjunto dos números reais é composto do conjunto dos números racionais e do conjunto dos números irracionais.
Um número racional póde ser escrito na fórma
Sentença matemática. Fração a sobre b., com a e b inteiros e b diferente de zero, e sua representação decimal póde ser um decimal exato ou uma dízima periódica. Um número irracional tem uma representação decimal infinita e não periódica.
Sugestão de leitura
GUELLI, Oscar. A invenção dos números. São Paulo: Ática, 1996. (Coleção Contando a história da Matemática).
O livro traz como surgiu a ideia de número, como os povos antigos contavam, como surgiram os números irracionais e muitas outras curiosidades sobre números.
Localização de um número real na reta numérica
Acompanhe esta situação.
A professora de Jean solicitou que a turma localizasse os pontos que representam os números
raiz quadrada de 3,
raiz quadrada de 4e
raiz quadrada de 5em uma reta numérica.
Jean traçou a reta numérica e, admitindo que
raiz quadrada de 4é igual a 2, já fez essa indicação como aparece a seguir.

Para localizar os pontos correspondentes aos números
raiz quadrada de 3e
raiz quadrada de 5, percebeu que não poderia fazer isso com exatidão. Então, como somente um quadrado perfeito tem raiz quadrada exata (
Sentença matemática. Raiz quadrada de 1 igual a 1.,
Sentença matemática. Raiz quadrada de 4 igual a 2.,
Sentença matemática. Raiz quadrada de 9 igual a 3.etcétera), Jean resolveu encontrar aproximações para
raiz quadrada de 3e
raiz quadrada de 5partindo dos quadrados perfeitos e, depois, fazendo aproximações melhores.
Analise como ele fez as aproximações.
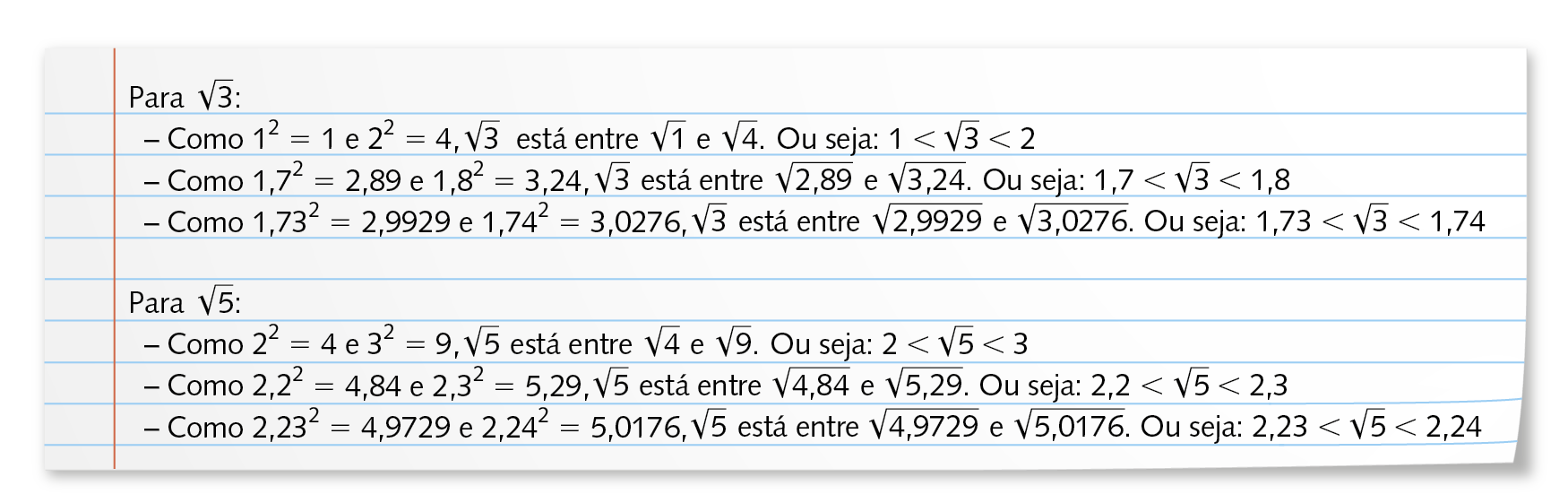
Com isso, ele fez a representação na reta numérica da seguinte fórma:

Observações
1. Ao fazer uma aproximação por tentativa e erro, póde ser necessário tentar alguns valores que sejam descartados. Por exemplo, para encontrar uma aproximação com uma casa decimal para
raiz quadrada de 3, é necessário calcular: 1,1elevado a 2 = 1,21; 1,2elevado a 2 = 1,44; 1,3elevado a 2 = 1,69; 1,4elevado a 2 = 1,96; 1,5elevado a 2 = 2,25; 1,6elevado a 2 = 2,56; 1,7elevado a 2 = 2,89; 1,8elevado a 2 = 3,24. Como 1,7elevado a 2 é o maior valor menor que 3 e 1,8elevado a 2 é o menor valor maior que 3, a aproximação mais exata para
raiz quadrada de 3com uma casa decimal está nesse intervalo.
2. Na situação de Jean, foram feitas aproximações de até duas casas decimais, mas poderiam ser feitas aproximações para um número maior ainda de casas decimais, uma vez que os números são irracionais, ou seja, têm uma representação decimal infinita e não periódica.
Representação geométrica de um número irracional
É possível representar, geometricamente, alguns números irracionais na reta numérica. Acompanhe a representação geométrica de
2 raiz quadrada de 2.
Considerando dois quadrados cujos lados medem 1 centímetro de comprimento, temos que a medida de área de cada um deles é 1 centímetro quadrado.
Recortando os dois quadrados por uma das diagonais, obtemos quatro triângulos. Com esses triângulos, podemos montar um novo quadrado com 2 centímetroselevado a 2 de medida de área.
Confira:
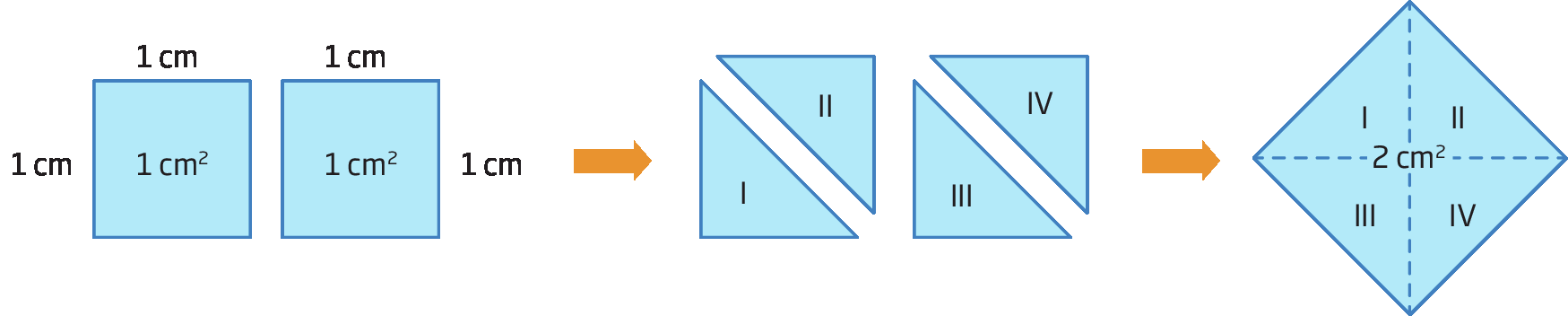
Um quadrado cujo comprimento do lado mede a tem medida de área aelevado a 2. Assim, um quadrado cuja área mede 2 centímetroselevado a 2 tem a medida de comprimento do lado que elevada ao quadrado tem como resultado 2 centímetros quadrados, ou seja,
raiz quadrada de 2, fim da raiz, centímetros.
Agora, podemos transportar, com o auxílio de um compasso, a medida de comprimento do lado do quadrado para a reta numérica e determinar os pontos
2 raiz quadrada de 2e seu simétrico,
Sentença matemática. Menos raiz quadrada de 2..
Cuidado! Evite acidentes ao usar o compasso.
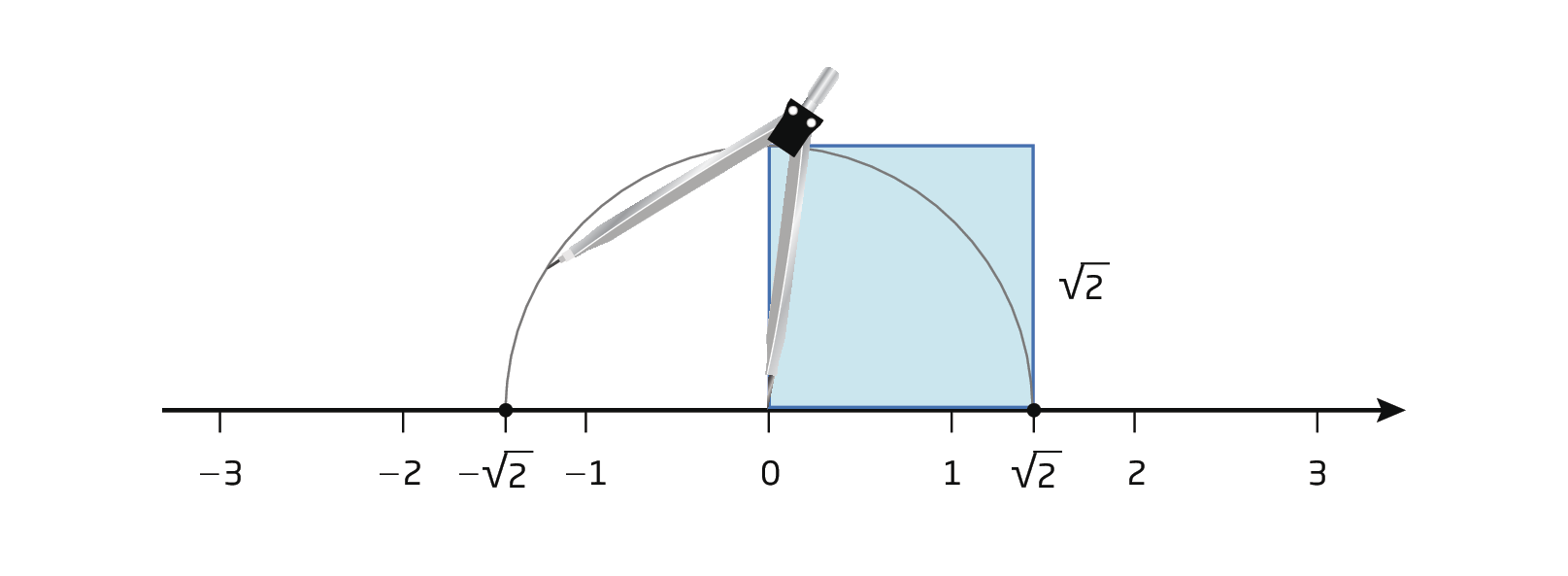
▸ Se posicionar a ponta-sêca sobre esses pontos determinados e mantiver a mesma abertura do compasso, que outros números você vai localizar na reta numérica? Esses números são irracionais?
Demonstração da irracionalidade de
Sentença matemática. Raiz quadrada de 2.Vamos supor que
2 raiz quadrada de 2seja um número racional. Assim, podemos representá-lo da seguinte maneira:
, sendo p e q números inteiros, com q diferente de zero, e sendo
Sentença matemática. Fração p sobre q.uma fração irredutível.
Elevando ao quadrado os dois lados da igualdade, temos:
Sentença matemática. Abre parênteses, raiz quadrada de 2, fecha parênteses, ao quadrado igual, abre parênteses, fração p sobre q, fecha parênteses, ao quadrado implica em, 2 igual a fração p ao quadrado sobre q ao quadrado, implica em, 2q ao quadrado igual a p ao quadrado.
• Como q é inteiro, então qelevado a 2 também é inteiro e 2qelevado a 2 é um número par, pois, multiplicando 2 por um número inteiro, obtemos um número par. Assim, pelevado a 2 é par.
• p também é par, pois um número par multiplicado por um número par resulta em um número par (quando multiplicamos um número ímpar por um número ímpar, obtemos um número ímpar).
Se p é par, podemos escrevê-lo como 2k, sendo k um número inteiro, diferente de zero.
Assim, temos:
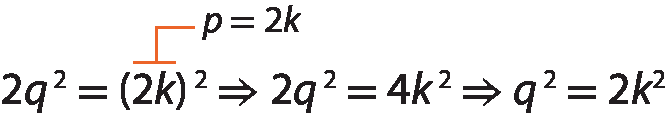
2kelevado a 2 é um número par, então qelevado a 2 é par e, consequentemente, q é par.
Mas, se p e q são números pares, então
Sentença matemática. Fração p sobre q.não é irredutível, o que contraria a suposição inicial. Assim, chegamos a um absurdo, ou seja,
2 raiz quadrada de 2não póde ser chamado de racional. Logo,
2 raiz quadrada de 2é irracional.
Atividades
Faça as atividades no caderno.
1. Localize os números a seguir em uma reta numérica. Se necessário, utilize aproximações.
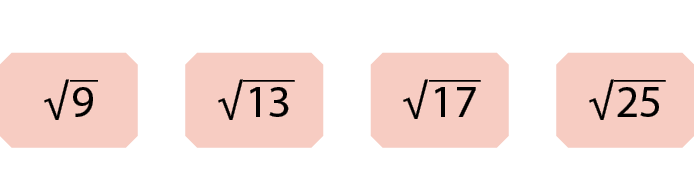
2. Verifique quais números são irracionais e quais não são.
a)
Sentença matemática. Raiz quadrada de 1.b)
2 raiz quadrada de 2c)
raiz quadrada de 3d)
raiz quadrada de 4e)
raiz quadrada de 53. Identifique quais afirmações são verdadeiras e quais são falsas.
a) Todo número em fórma de raiz é irracional.
b) A representação decimal de um número irracional é infinita e não periódica.
c)
Sentença matemática. Raiz quadrada de 120.é um número irracional.

2 Potência de um número real com expoente inteiro
Vamos determinar o valor da potência de um número real a quando o expoente inteiro for maior que 1, igual a 1, nulo ou negativo. Analise os casos a seguir.
• Expoente maior que 1

Confira alguns exemplos.
a)

b)

c)

d)

• Expoente 1
a elevado a 1 = a
Confira alguns exemplos.
a) 7elevado a 1 = 7
b)
Sentença matemática. Abre parênteses, menos fração 3 quintos, fecha parênteses, elevado a 1, igual a menos 3 quintos.c) (1,3756)elevado a 1 = 1,3756
d) (menos0,01)elevado a 1 = menos0,01
• Expoente zero, com base não nula
a elevado a 0 = 1, com a ≠ 0
Confira alguns exemplos.
a) 5elevado a 0 = 1
b)
Sentença matemática. Abre parênteses, menos 8 nonos, fecha parênteses, elevado a zero igual a 1.c) (101,54)elevado a 0 = 1
d) (menos0,0001)elevado a 0 = 1
• Expoente inteiro negativo, com base não nula
, com a ≠ 0 e menosn inteiro negativo
Confira alguns exemplos.
a)
Sentença matemática. 5 elevado a menos 1, igual a 1 quinto.b)
Sentença matemática. Abre parênteses, menos 7, fecha parênteses, elevado a menos 2 igual a, abre parênteses, menos 1 sétimo, fecha parênteses, ao quadrado, igual a 1 sobre 49.c)
Sentença matemática. Abre parênteses, menos 3 quartos, fecha parênteses, elevado a menos 1 igual a, menos 4 terços.d)
Sentença matemática. Abre parênteses, menos 2 terços, fecha parênteses, elevado a menos 3, igual a, abre parênteses, menos 3 meios, fecha parênteses, elevado a 3, igual a menos 27 oitavos.Observações
1. Quando a base é negativa, o sinal da potência é:
• positivo, se o expoente é par. Por exemplo:
(menos0,1)elevado a 2 = (menos0,1) ⋅ (menos0,1) = 0,01
• negativo, se o expoente é ímpar. Por exemplo:
Sentença matemática. Abre parênteses, menos 1 meio, fecha parênteses, elevado a 3, igual a, abre parênteses, menos 1 meio, fecha parênteses, vezes, abre parênteses, menos 1 meio, fecha parênteses, vezes, abre parênteses, menos 1 meio, fecha parênteses, igual a menos 1 oitavo.
2.

Logo: menos2elevado a 4 ≠ (menos2)elevado a 4

Atividades
Faça as atividades no caderno.
4. Calcule as potências a seguir.
a) 0elevado a 7
b) menos5elevado a 2
c) menos(1,2)elevado a 2
d) (menos5)elevado a 2
e) menos(0,3)elevado a 0
f)
Esquema. Sentença matemática. Abre parênteses, menos 2 terços, fecha parênteses, elevado a 3.g)
Esquema. Sentença matemática. Menos, abre parênteses, 2 quintos, fecha parênteses, elevado a 3.h)
Esquema. Sentença matemática. Abre parênteses, 1 inteiro e 2 terços, fecha parênteses, elevado ao quadrado.5. Calcule as potências de expoente negativo.
a) 7elevado a menos um
b)
Esquema. Sentença matemática. Abre parênteses, 1 quinto, fecha parênteses, elevado a menos 2.c)
Esquema. Sentença matemática. Abre parênteses, 5 nonos, fecha parênteses, elevado a menos 1.d)
Esquema. Sentença matemática. Abre parênteses, menos 3 oitavos, fecha parênteses, elevado a menos 1.e) (menos3)elevado a menos três
f) 10elevado a menos dois
g) (menos1)elevado a menos cinco
h)
Esquema. Sentença matemática. Abre parênteses, 1 centésimo, fecha parênteses, elevado a menos 1.6. No caderno, escreva cada item na fórma de potência com expoente inteiro negativo.
a)
Sentença matemática. Fração, numerador: 1, denominador: 10 elevado a 4.b)
Sentença matemática. Fração, numerador: 1, denominador: 5 elevado a 7.c)
Sentença matemática. Fração, numerador: 1, denominador: 2 elevado a 3.d)
Sentença matemática. Fração, numerador: 1, denominador: 7 elevado a 5.7. No caderno, escreva os números a seguir como potência de base 2.
a) 64
b)
Sentença matemática. Fração 1 sobre 32.c) 256
d)
Sentença matemática. Fração 1 sobre 64.8. Calcule o valor das expressões a seguir.
a) abre parêntesesmenos3fecha parênteseselevado a 2 + abre parêntesesmenos3fecha parênteseselevado a 3
b) menosabre parêntesesmenos2fecha parênteseselevado a 4 + abre parêntesesmenos2fecha parênteseselevado a 5 ⋅ 4elevado a menos três
c) abre parênteses4elevado a 0 : 4elevado a menos umfecha parênteses dividido por abre parênteses4elevado a menos um dividido por 4elevado a menos doisfecha parênteses
d)
Sentença matemática. Fração, numerador: abre parênteses, menos 1, fecha parênteses, elevado a 5, denominador: abre parênteses, menos 2, fecha parênteses, elevado amenos 2, mais, abre parênteses 0,1, fecha parênteses, elevado a menos 2.e)
Sentença matemática. Abre parênteses, menos 1 terço, fecha parênteses, ao quadrado, menos, abre parêntese, menos 1 terço, fecha parênteses, elevado a menos 2.Propriedades das potências com expoentes inteiros
Vamos estudar as propriedades do cálculo com potências de expoente inteiro e base real não nula.
• Produto de potências de mesma base
aelevado a ême ⋅ aelevado a n = a elevado a m mais n
Analise alguns exemplos.
a) 2elevado a 2 ⋅ 2elevado a 3 = abre parênteses2 ⋅ 2fecha parênteses ⋅ abre parênteses2 ⋅ 2 ⋅ 2fecha parênteses = 2elevado a 5 ou 2elevado a 2 ⋅ 2elevado a 3 = 2elevado a 2 mais 3 = 2elevado a 5
b)
Sentença matemática. Abre parênteses, 1 meio, fecha parênteses, elevado a menos 3, vezes, abre parênteses, 1 meio, fecha parênteses, elevado a menos 2 igual a, abre parênteses, 1 meio elevado a, menos 3 mais, abre parênteses, menos dois, fecha parênteses, fora do expoente, igual a, abre parênteses, 1 meio, fecha parênteses, elevado a menos 5.c) 5elevado a m menos 1 ⋅ 5² ⁺ ᵐ = 5elevado a m menos 1 mais 2 mais m = 5elevado a 2m mais 1
• Quociente de potências de mesma base
aelevado a ême : aelevado a n = aelevado a m menos n
Observe alguns exemplos.
a) 2elevado a 3 dividido por 2elevado a 2 =
Sentença matemática. Abre parênteses, 2 vezes 2 vezes 2, fecha parênteses, denominador: abre parênteses, 2 vezes 2, fecha parênteses.= 2 ou 2elevado a 3 dividido por 2elevado a 2 = 2elevado a 3 menos 2 = 2elevado a 1 = 2
b)
Sentença matemática. Fração, numerador: abre parênteses, 0 vírgula 3, fecha parênteses, elevado a 5, denominador: abre parênteses, 0 vírgula 3, fecha parênteses, elevado a 2, igual a, abre parênteses, 0 vírgula 3, fecha parênteses, elevado a 5 menos 2, igual a, abre parênteses, 0 vírgula 3, fecha parênteses, elevado a 3.c) 5elevado a menos dois dividido por 5elevado a menos quatro = 5elevado a menos 2 menos, abre parênteses, menos 4, fecha parênteses = 5elevado a menos 2 mais quatro = 5elevado a 2
d) 3elevado a 2m menos 1 dividido por 3elevado a 1 menos m = 3²ᵐ ⁻ ¹ ⁻ ⁽¹ ⁻ elevado a ême⁾ = 3elevado a 2m menos 1 menos 1 mais m = 3elevado a 3m menos 2
• Potência de potência
abre parêntesesa elevado a êmefecha parênteseselevado a n = a elevado a ême ⋅ elevado a n
Analise alguns exemplos.
a) abre parênteses2²)³ = abre parênteses2 ⋅ 2)³ = abre parênteses2 ⋅ 2fecha parênteses ⋅ abre parênteses2 ⋅ 2fecha parênteses ⋅ abre parênteses2 ⋅ 2fecha parênteses = 2elevado a 6 ou abre parênteses2²)³ = 2elevado a 2 ⋅ ³ = 2elevado a 6
b) abre parênteses10elevado a 5fecha parênteseselevado a menos dois = 10elevado a 5 ⋅ ⁽⁻²⁾ = 10 elevado a menos dez
c) abre parênteses2elevado a xisfecha parênteseselevado a xis ⁻ ¹ = 2elevado a xis ⋅ ⁽elevado a xis ⁻ ¹⁾ =
Sentença matemática. 2x ao quadrado menos x.• Potência de um produto ou de um quociente
abre parêntesesa ⋅ bfecha parênteseselevado a ême = a elevado a ême ⋅ b elevado a ême
abre parêntesesa dividido por bfecha parênteseselevado a ême = a elevado a ême dividido por b elevado a ême
Analise alguns exemplos.
a) abre parênteses3 ⋅ 5fecha parênteseselevado a menos dois = 3elevado a menos dois ⋅ 5elevado a menos dois
b)
Sentença matemática. Abre parênteses, 3 quintos, fecha parênteses, igual a fração, numerador: 3 elevado a menos 2, denominador: 5 elevado a menos 2.Observação
Atenção para as desigualdades a seguir, com bases reais não nulas e expoentes inteiros.
• aelevado a ême + aelevado a n ≠ aelevado a ême ⁺ ⁿ
• aelevado a ême menos aelevado a n ≠ aelevado a ême ⁻ ⁿ
•
Abre parênteses, a elevado a m, fecha parênteses, elevado a n, diferente de, a elevado a m elevado a n, com a, m e n ≠ 1
• abre parêntesesa + bfecha parênteseselevado a n ≠ aelevado a n + belevado a n, com a ≠ menosb; a, b e n ≠ 1
• abre parêntesesa menos bfecha parênteseselevado a n ≠ aelevado a n menos belevado a n, com a ≠ b

Veja que interessante
Faça as atividades no caderno.
Calculadora científica
A calculadora científica possibilita a resolução de cálculos básicos, fracionários, de porcentagem, científicos e estatísticos. Nos smartphones, como o da imagem, você póde usar uma calculadora científica escolhendo um aplicativo de calculadora que inclua essa funcionalidade.
Confira agora alguns exemplos de cálculos que utilizam as teclas

e

.
a) 2elevado a 3


b) 2elevado a menos três


c) abre parêntesesmenos2fecha parênteseselevado a menos três


d) 9elevado a 2


e) abre parêntesesmenos9fecha parênteseselevado a 2

Atividade
Analise as sequências de teclas de cada exemplo anterior e identifique os resultados que aparecem no visor de uma calculadora científica. Em seguida, se possível, utilize uma calculadora científica para conferir os resultados.
Atividades
Faça as atividades no caderno.
9. Aplique as propriedades e expresse os resultados na fórma de uma única potência.
a) 3elevado a 5 ⋅ 3elevado a menos dois
b) melevado a 5 ⋅ melevado a menos seis, com m ≠ 0
c) abre parênteses0,1fecha parênteseselevado a menos três ⋅ abre parênteses0,1fecha parênteseselevado a 3
10. Transforme as expressões em uma única potência.
a) abre parênteses5elevado a 2fecha parênteseselevado a menos quatro
b) abre parêntesesnelevado a menos cincofecha parênteseselevado a 4, com n ≠ 0
c) abre parênteses5elevado a 2fecha parênteseselevado a n
d)
Fração, numerador: x ao cubo, denominador: x elevado a menos 2, com x ≠ 0
11. Aplique as propriedades das potências de um produto ou de um quociente.
a) abre parênteses3 ⋅ 7fecha parênteseselevado a 4
b) abre parênteses2elevado a 4 ⋅ aelevado a menos trêsfecha parênteseselevado a menos um, com a ≠ 0
c) abre parêntesesaelevado a 3elevado a xis dividido por belevado a xis fecha parênteseselevado a menos quatro , com a ≠ 0 e b ≠ 0
12. Determine o valor das potências
2 ao cubo ao quadradoe (2elevado a 3)elevado a 2.
13. Escreva, na fórma fracionária, a expressão (3elevado a menos quatro)elevado a 5.
14. Sendo a = 10elevado a menos quatro, b = 10elevado a menos cinco e c = 10elevado a 3, determine:
a) a dividido por belevado a 2
b) a dividido por abre parêntesesb ⋅ cfecha parênteses
15. Simplifique cada expressão a seguir.
a)
Sentença matemática. Fração, numerador: x elevado a 10, abre parênteses, x ao quadrado, fecha parênteses, elevado a 4, denominador: x elevado a 23, fora do expoente, dividido por x ao quadrado., com x ≠ 0
b)
Sentença matemática. Fração, numerador: 5 elevado a , 3x menos 2, fora do expoente, vezes, 5 elevado a x menos 1, denominador: 5 elevado a x menos 5.
Veja que interessante
Faça as atividades no caderno.
Os prefixos mais conhecidos
Confira estas afirmações.
• A medida do comprimento do armário é 80 centímetros.
• Quero comprar 5 quilogramas de carne.
• A usina termoelétrica produzia 17 megawatts de energia.
As partes destacadas das palavras – centi, quilo e mega – são denominadas prefixos. Cada prefixo corresponde a uma potência de base 10.
Neste quadro estão os prefixo mais conhecidos.
|
Nome do prefixo |
Símbolo do prefixo |
Potência de base 10 correspondente ao prefixo |
Significado do prefixo na forma decimal |
|---|---|---|---|
|
tera |
T |
10 elevado a 12 |
1.000.000.000.000 (trilhão) |
|
giga |
G |
10 elevado a 9 |
1.000.000.000 (bilhão) |
|
mega |
M |
10 elevado a 6 |
1.000.000 (milhão) |
|
quilo |
k |
10 elevado a 3 |
1.000 (mil) |
|
hecto |
h |
10 elevado a 2 |
100 (cem) |
|
deca |
da |
10 elevado a 1 |
10 (dez) |
|
deci |
d |
10 elevado a -1 |
0,1 (décimo) |
|
centi |
c |
10 elevado a -2 |
0,01 (centésimo) |
|
mili |
m |
10 elevado a -3 |
0,001 (milésimo) |
|
micro |
μ |
10 elevado a -6 |
0,000001 (milionésimo) |
|
nano |
n |
10 elevado a -9 |
0,000000001 (bilionésimo) |
|
pico |
p |
10 elevado a -12 |
0,000000000001 (trilionésimo) |
Quando falamos sobre medida de armazenamento de dados, geralmente usamos o termo byte com as devidas variações de prefixo. No entanto, o bit é a menor unidade de medida de informação que póde ser armazenada ou transmitida; um conjunto de 8 bits corresponde a 1 byte (1 báite), que é a unidade-padrão de medida de armazenamento de dados.
Como a quantidade de informação armazenada utiliza o sistema binário (base 2), os fatores de multiplicação para a obtenção das unidades de medida são potências de 2. Analise alguns exemplos:
a) 1 quilobyte (cá bê) é igual a 2elevado a 10 báites ou 1 024 báites;
b) 1 megabyte (ême bê) é igual a 2elevado a 20 báites ou 1 048 576 báites;
c) 1 gigabyte (gê bê) é igual a 2elevado a 30 báites ou 1 073 741 824 báites.
Podemos utilizar potências de base 10 para expressar valores aproximados para os múltiplos do byte. Assim:
a) 1 quilobyte (cá bê) é aproximadamente igual a 1 000 báites ou 10elevado a 3 báites;
b) 1 megabyte (ême bê) é aproximadamente igual a 1 000 000 báites ou 10elevado a 6 báites;
c) 1 gigabyte (gê bê) é aproximadamente igual a 1 000 000 000 báites ou 10elevado a 9 báites.
Atividade
Compare os resultados de 2elevado a 10 e 10elevado a 3; 2elevado a 20 e 10elevado a 6; e 2elevado a 30 e 10elevado a 9. Verifique quão próximos estão.

Lendo e aprendendo

cinco gê no Brasil
Governo anuncia chegada da tecnologia para o ano que vem. Veja perguntas e respostas sobre a nova geração de internet móvel
O governo brasileiro anunciou para o ano que vem a chegada ao país do cinco gê. A nova geração de internet móvel, que já é utilizada em algumas partes do mundo, promete revolucionar diversos setores. Algumas pessoas, no entanto, criticam o fato de tanto dinheiro ser investido na nova tecnologia enquanto parte dos brasileiros não tem nenhum tipo de acesso à rede.
Há outras críticas? Quais os desafios para a implementação? O que vai mudar na prática? Quais são as vantagens tecnológicas? Verifique as respostas a essas e outras dúvidas:
O quatro gê vai acabar?
Não. Todas as outras gerações de internet vão continuar funcionando.
O que é o cinco gê?
É a nova tecnologia de rede de internet móvel, mais potente e veloz, com menor tempo de resposta dos comandos. É uma evolução do quatro gê. A letra “gê” significa geração, ou seja, mostra a evolução dessas tecnologias.
O que vai mudar na prática?
O engenheiro e mestre em tecnologia Eduardo Tude explica que a velocidade maior e a latênciaglossário menor vão permitir uma série de aplicações não suportadas pelo quatro gê. “Abre um leque grande de possibilidades”, diz.
Ele cita como exemplo a internet das coisas, não só com os celulares conectados, mas geladeiras, máquinas de lavar, televisores e uma infinidade de aparelhos eletrônicos. Cidades e casas inteligentes também poderão ser uma realidade. Testes com automóveis totalmente autônomos, inclusive, já estão avançados em várias partes do mundo. Outro setor que deve se beneficiar é o da saúde, com telemedicina e diagnósticos muito mais avançados, além de cirurgias feitas remotamente.
Ah, e claro, a vida de quem joga no celular também deve mudar bastante para melhor, por causa da velocidade do cinco gê.
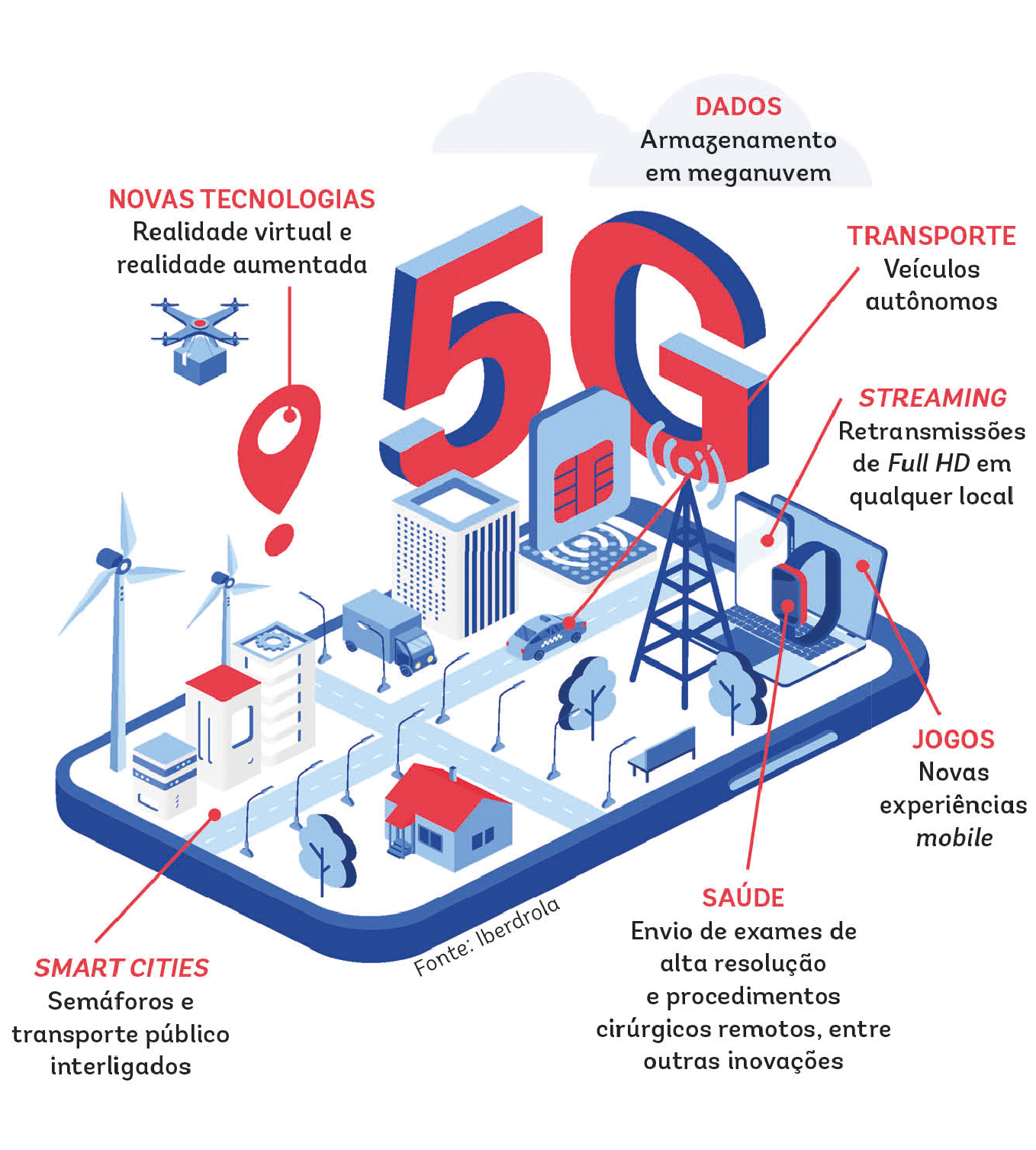
Lendo e aprendendo
[reticências]
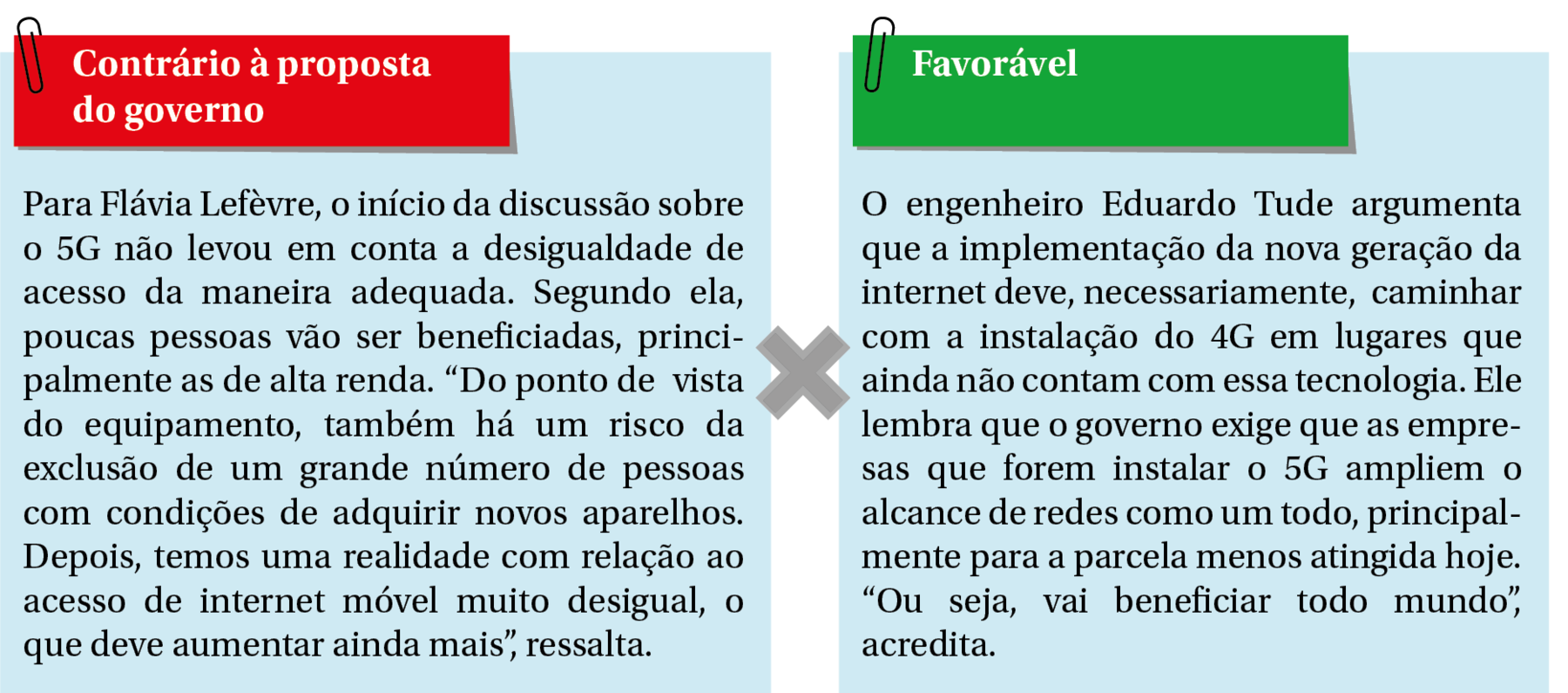
A polêmica da desigualdade
A principal delas diz respeito à desigualdade de acesso à internet no país. Apesar de crescente, pesquisa do í bê gê É mostrou que um em cada quatro brasileiros ainda não está conectado. De um lado, alguns acham que a proposta do governo para o cinco gê vai piorar esse cenário. Do outro, dizem que o modelo proposto para a implementação da nova tecnologia vai ajudar a diminuir essa diferença de conectividade. Verifique dois argumentos:
Qualquer celular terá acesso?
Não. Será preciso ter um aparelho compatível com a tecnologia cinco gê. Essa, inclusive, é outra crítica ao modelo, pois hoje o aparelho mais barato à venda que suporta a nova geração de internet custa por volta de três mil reais. Para Tude, no entanto, a tendência é que os preços diminuam com o tempo.
[reticências]
Como funciona?
Por meio de antenas que transmitem ondas (ou frequências) de rádio, assim como as outras redes móveis. A ideia é que as da nova rede sejam acopladas às já existentes. Claro, novas antenas também devem ser instaladas para alcançar distâncias maiores.
Qual é a diferença em relação ao quatro gê?
A velocidade da rede cinco gê póde chegar a 10 gigabytes por segundo, que póde ser até 100 vezes mais rápida do que a quatro gê. Isso significa, por exemplo, que um filme de alta definição poderá ser baixado em uma fração de segundos, o que leva cérca de uma hora com as redes quatro gê atuais.
Já a latência da tecnologia cinco gê deve ser entre 1 e 2 milissegundosglossário . No caso do quatro gê, esse intervalo é de 35 a 52 milissegundos. Outra diferença é que, com o cinco gê, será possível conectar mais dispositivos simultaneamente. Além disso, espera-se que a nova geração de internet seja mais sustentável, com uma redução de cérca de 90% do consumo de energia.
É fake!
Pouco depois do início da pandemia, uma mensagem circulou nas redes sociais dizendo que as ondas de transmissão do cinco gê poderiam “carregar” o vírus da côvid dezenóve, aumentando assim a transmissão da doença. Porém, não há uma evidência científica sobre isso. A Organização Mundial da Saúde (ó ême ésse), inclusive, já negou que os vírus possam viajar em ondas de rádio e redes móveis.
Lendo e aprendendo
Há risco para a saúde?
Algumas pessoas alertaram sobre a possibilidade de as ondas de frequência fazerem mal à saúde. De acôrdo com a ó ême ésse, a classificação de toda radiação de radiofrequência (da qual os sinais de celular fazem parte) é de “possivelmente cancerígenas”. Na prática, isso quer dizer que não há evidências concretas sobre o assunto. Para se ter uma ideia, comer legumes em conserva ou usar talco em pó, por exemplo, são classificados com o mesmo nível de risco. Já a ingestão de bebidas alcoólicas e o consumo de carne processada são classificados com riscos maiores.
A evolução da tecnologia
Fazer uma videochamada, mandar mensagem de texto, ouvir música, trabalhar... Hoje, podemos realizar inúmeras tarefas com nossos celulares. Mas nem sempre foi assim. Observe como tudo começou.
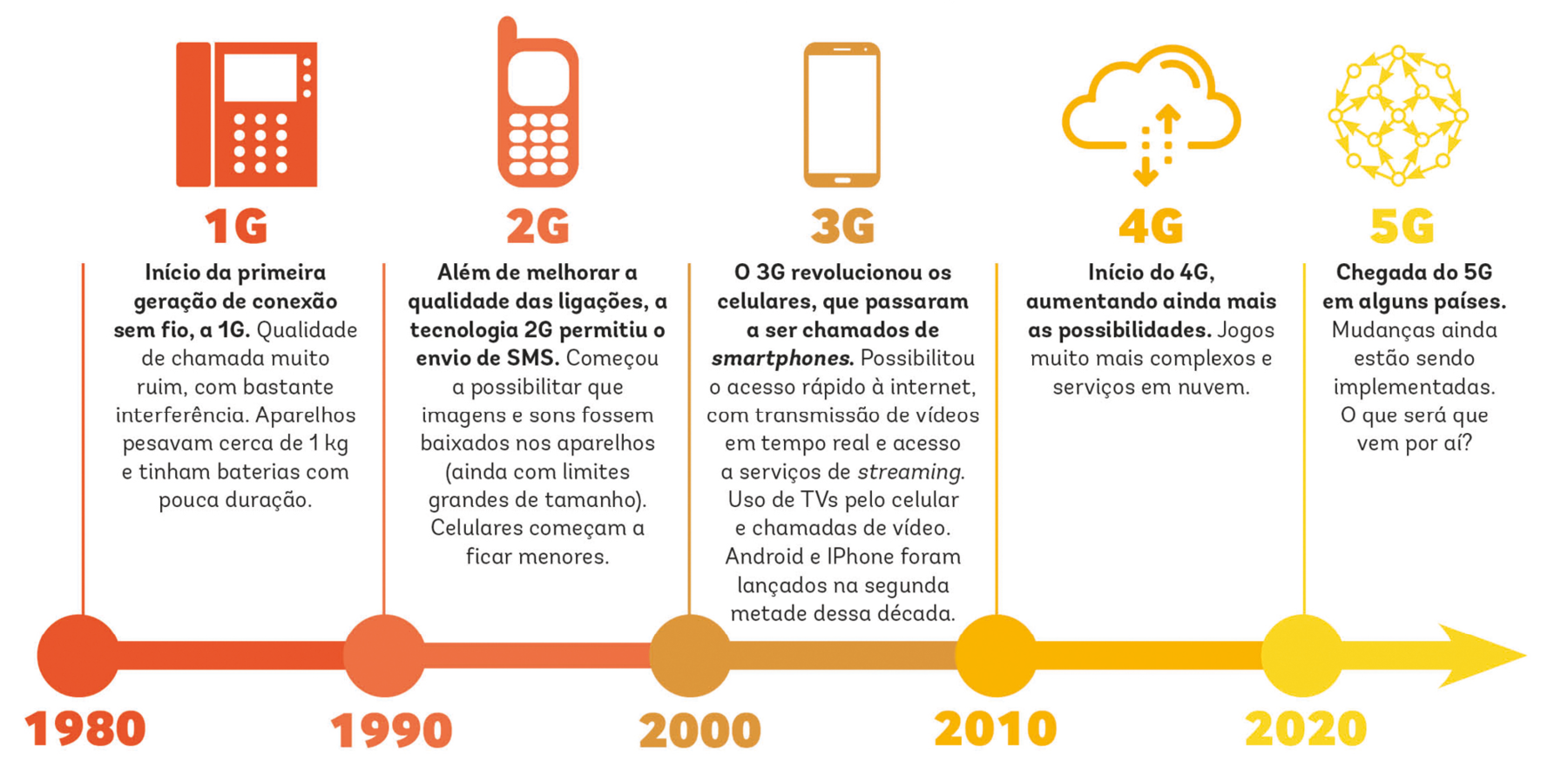
CABRAL, M. C. cinco gê no Brasil. Qualé, São Paulo, edição 38, p. 6-9, 1º a 15 de novembro de 2021.
Atividades
1. Responda às questões no caderno.
a) Em que mês e ano a matéria anterior foi publicada?
b) De acôrdo com o í bê gê É, qual era a porcentagem de brasileiros, em 2021, que não estava conectada à internet?
2. Qual é, aproximadamente, a medida de velocidade a que a rede cinco gê póde chegar?
Dica: bê é o símbolo utilizado para representar a unidade de medida báite.
a) 10elevado a 10 báites por segundo
b) 10elevado a 9 báites por segundo
c) 10elevado a 6 báites por segundo
d) 10elevado a onze báites por segundo
3. Em relação à polêmica que diz respeito à desigualdade de acesso à internet no país, você concorda com a opinião de Flávia Lefèvre ou com a de Eduardo Tude? Escreva um pequeno texto para justificar sua resposta.
4.


Vivemos em um mundo em que há muitas informações circulando. São tantas fontes e pessoas produzindo e compartilhando informação que fica difícil realmente saber o que é e o que não é verdade. Por isso se fala muito em fake news: publicações com informações comprovadamente falsas que costumam viralizar nas redes sociais. O texto apresenta um exemplo de fake news relacionado à chegada do cinco gê. Alguma vez você desconfiou de uma publicação divulgada na tê vê ou na internet? Você checou essa publicação? Como você fez para saber se era verdadeira ou falsa? Converse com os colegas sobre o assunto.
Notação científica
Números muito grandes ou muito próximos de zero podem ser escritos por meio de uma multiplicação da forma x ⋅ 10elevado a bê, em que:
• x pertence ao intervalo 1 < x < 10;
• b é um número inteiro.
Chamamos essa representação de notação científica. Confira alguns exemplos.
•
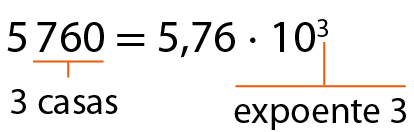
•
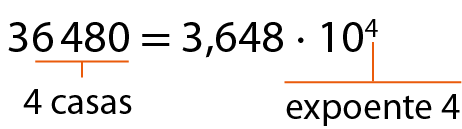
•
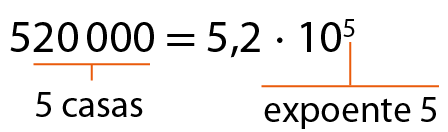
•
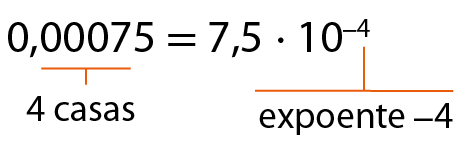
•
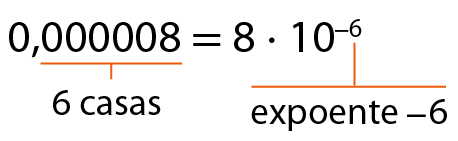
•
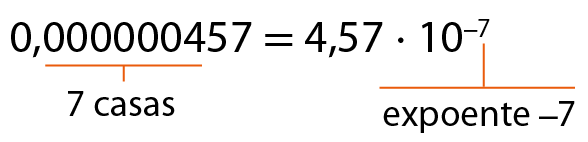
Analise, agora, alguns valores que usualmente representamos com notação científica.
a) Medida da distância aproximada da Terra ao Sol: ..150000000 quilômetros = 1,5 ⋅ 10elevado a 8 quilômetros;
b) Medida da velocidade da luz: .300000 quilômetros por segundo = 3 ⋅ 10elevado a 5 quilômetros por segundo
c) Medida aproximada de 1 ano-luz: ....9460000000000 quilômetros = 9,46 ⋅ 10elevado a 12 quilômetros;

d) Medida de comprimento do diâmetro da molécula da água: 280 picômetros = 0,000000000280 métro = 2,8 ⋅ 10elevado a menos dez métro;
e) Medida de comprimento do diâmetro de um elétron: 0,000000000000000001 métro = 1 ⋅ 10elevado a menos dezoito métro;
f) Femtossegundoglossário : 0,000000000000001 segundo = 1 ⋅ 10elevado a menos quinze segundo.
Atividades
Faça as atividades no caderno.
16. No caderno, escreva os números em notação científica.
a) .85700
b) ...945000000000
c) 0,0000002
d) ..13000000
e) ...1080000000
f) 0,00000000013
17. Uma pessoa adulta tem cérca de 5 litros de sangue. Em uma pessoa saudável, 1 milímetro cúbico de sangue possui, aproximadamente:
• 5 milhões de glóbulos vermelhos ou hemácias;
• 8 mil glóbulos brancos ou leucócitos.
Escreva, em notação científica, quantas hemácias e quantos leucócitos possui, aproximadamente, um adulto.
18. O físico italiano Avogadro (1776-1856) mostrou que, em 18 gramas de água, há cérca de 6,02 ⋅ 10elevado a 23 moléculas. No caderno, escreva em notação científica o número aproximado de moléculas contidas em 1 miligrama de água.
19.

Junte-se a um colega e escreva dois números conforme as indicações a seguir para que ele os reescreva em notação científica.
• O primeiro número deve ser da ordem do trilhão. Seu colega deverá arredondá-lo de fórma que, em notação científica, fique com duas casas decimais.
• O segundo número deve estar entre 0 e 1 e ter mais de cinco casas decimais após a vírgula. Seu colega deverá arredondá-lo de fórma que, em notação científica, fique com duas casas decimais.

3 Raiz enésima de um número real
Podemos escrever a raiz quadrada de um número real positivo como potência de expoente fracionário.
, em que m é inteiro
Confira alguns exemplos a seguir.
a)
Sentença matemática. Raiz quadrada de 64 igual a raiz quadrada de 64 elevado a 1, igual a, 64 elevado a 1 sobre 2.b)
Sentença matemática. Raiz quadrada de 77 igual a raiz quadrada de 77 elevado a 1, igual a, 77 elevado a 1 sobre 2.c)
Sentença matemática. Raiz quadrada de 7 ao cubo igual a raiz quadrada de 7 ao cubo, igual a, 7 elevado a 3 sobre 2.d)
Sentença matemática. 16 elevado a menos 1 sobre 2, igual, raiz quadrada de 16 elevado a menos 1, igual a, raiz quadrada de 1 sobre 16.A raiz enésima de um número real a, sendo n um número natural e n ⩾ 2, póde ser representada assim:
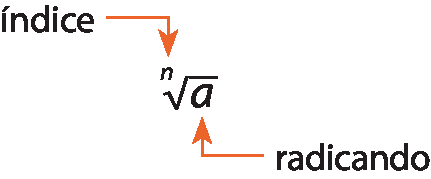
Analise os dois exemplos a seguir.
a)

b)
Sugestão de leitura
RAMOS, Luzia Faraco. Uma raiz diferente. São Paulo: Ática, 2001. (Coleção A descoberta da Matemática).
O livro une as questões das raízes familiares do jovem personagem à raiz diferente citada no título: raiz quadrada e raiz cúbica. Há também desafios e atividades para prender a atenção do leitor.
Observações
1. Podemos omitir o índice 2 da raiz quadrada. Assim:
•
Sentença matemática. Raiz quadrada de 16 igual a raiz de 16.•
Sentença matemática. Raiz quadrada de 25 igual a raiz de 25.•
Sentença matemática. Raiz quadrada de 49 sobre 169 igual a raiz de 49 sobre 169.2. Sendo n um número natural, com n ⩾ 2, temos:
Sentença matemática. Raiz enésima de zero igual a zero.3. O termo radical é também nome do símbolo
raiz quadrada de zero.
Atividades
Faça as atividades no caderno.
20. Como se leem os radicais a seguir?
a)
Sentença matemática. Raiz quadrada de 7.b)
raiz cúbica de 13c)
Sentença matemática. Raiz quarta de 17.d)
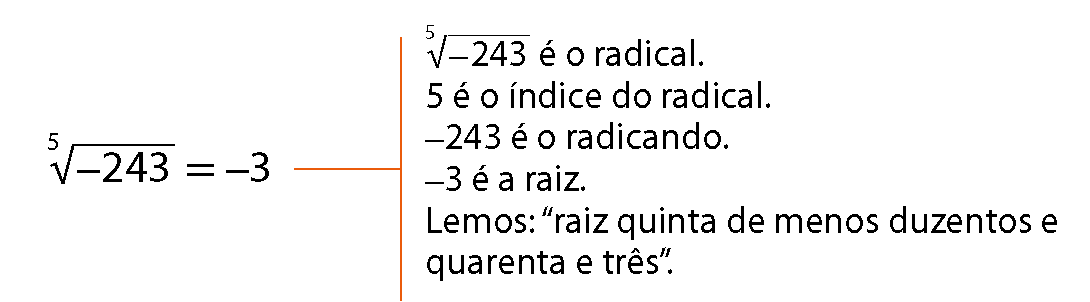
Sentença matemática. Raiz sexta de 42.21. Na expressão
Sentença matemática. Raiz cúbica de 343 igual a 7., identifique:
a) a raiz;
b) o radicando;
c) o radical;
d) o índice do radical.
22.

Escreva quatro radicais (dois racionais e dois irracionais). Em seguida, peça a um colega que identifique quais são racionais e quais são irracionais.
Determinação da raiz enésima de um número real
Na determinação da raiz enésima de um número real a, ou seja,
Sentença matemática. Raiz enésima de a., podem ocorrer os casos a seguir.
• 1º caso: a ⩾ 0 e n um número natural maior ou igual a 2.
Analise os exemplos a seguir.
a)
Sentença matemática. Raiz quadrada de 16 igual a 4, é o mesmo que, 4 ao quadrado igual a 16.b)
Sentença matemática. Raiz quarta de 81 igual a 3, é o mesmo que, 3 elevado a 4 igual a 81.c)
Sentença matemática. Raiz cúbica de 125 igual a 5, é o mesmo que, 5 elevado a 3 igual a 125.d)
Sentença matemática. Raiz quinta de 32 igual a 2, é o mesmo que, 2 elevado a 5 igual a 32.Sendo a um número real, a ⩾ 0 e n um número natural maior ou igual a 2, temos que
Sentença matemática. Raiz enésima de a.corresponde ao número real não negativo b, tal que belevado a n = a. Assim:
• 2º caso: a < 0 e n um número natural ímpar maior que 2.
Analise os exemplos a seguir.
a)
Sentença matemática. Raiz cúbica de menos 1000 igual a menos 10.b)
Sentença matemática. Raiz quinta de menos 1024 igual a menos 4.c)
Sentença matemática. Raiz cúbica de menos 27 igual a menos 3.Sendo a um número real, a < 0 e n um número natural ímpar maior que 2, temos que
Sentença matemática. Raiz enésima de a.corresponde ao número real negativo b, tal que b elevado a n = a. Assim:
• 3º caso: a < 0 e n um número natural par diferente de zero.
Como determinar
Sentença matemática. Raiz quadrada de menos 4.no conjunto dos números reais?
Sentença matemática. Raiz quadrada de menos 4.
não é um número real, pois nenhum número real elevado ao quadrado é igual a menos4.
Sendo a um número real, a < 0 e n um número natural par diferente de zero, temos que
Sentença matemática. Raiz enésima de a.não representa um número real.
Atividades
Faça as atividades no caderno.
23. Determine o valor de:
a)
Sentença matemática. Raiz quadrada de 100.b)
Sentença matemática. Raiz quarta de 256.c)
Sentença matemática. Mais ou menos, raiz quadrada de 25.d)
Sentença matemática. Menos raiz quadrada de 144.e)
Sentença matemática. Raiz cúbica de menos 8.f)
Sentença matemática. 3 vezes raiz quadrada de 16.24. Determine o valor das expressões a seguir.
a)
Sentença matemática. Menos raiz quadrada de menos 81, menos raiz cúbica de menos 27.b)
Sentença matemática. Raiz cúbica de 0 mais raiz cúbica de menos 1 mais raiz quadrada de 0 vírgula 25.25. Em cada caso, determine o valor de a.
a)
Sentença matemática. Raiz quadrada de a igual a 100.b)
Sentença matemática. Raiz cúbica de a igual a menos 6.c)
Sentença matemática. Raiz quarta de a igual a 5.26. Identifique os radicais que representam números reais.
a)
raiz quadrada de zerob)
Sentença matemática. Raiz quadrada de menos 1.c)
Sentença matemática. Raiz quadrada de 1.d)
Sentença matemática. Raiz cúbica de menos 1.e)
Sentença matemática. Raiz sexta de menos 1.f)
Sentença matemática. Raiz 16 de menos 1.27. Em cada caso, determine o valor de x.
a)
Sentença matemática. Raiz quadrada de 2x igual a 6., para x ⩾ 0
b)
Sentença matemática. Raiz cúbica de x mais 1 igual a 2., para x ⩾ menos1
c)
Sentença matemática. Raiz quadrada de x mais 2 igual a 5., para x ⩾ menos2
28. Sendo a = 64 e b = 36, determine:
Sentença matemática. Raiz quadrada de a mais raiz quadrada de b menos, abre parênteses, raiz quadrada de a mais b, fecha parênteses.
29. Determine o valor de x.
Sentença matemática. x igual a raiz quadrada de 21 mais, ainda dentro da raiz, raiz quadrada de 13 mais, ainda dentro das raízes, raiz quadrada de 7 mais, ainda dentro das raízes, raiz quadrada de 4, fecha todas as raízes.
Propriedades dos radicais
As propriedades dos radicais podem ser usadas na simplificação dos cálculos.
1ª propriedade
Analise as igualdades:


Substituindo dois em um, temos:
Sentença matemática. Raiz cúbica de 4 elevado a 3 é igual a 4.
Dados
aum número real e n um número natural, temos:
• se n é ímpar e maior que 2,
Sentença matemática. Raiz enésima de a elevado a n é igual a a.;
• se n é par, não nulo,
Sentença matemática. Raiz enésima de a elevado a n é igual ao módulo de a..
Confira mais alguns exemplos.
a)
Sentença matemática. Raiz quadrada de 13 ao quadrado, igual a módulo de 13, igual a 13.b)
Sentença matemática. Raiz quadrada de, abre parênteses, menos 2, fecha parênteses, ao quadrado, igual a, módulo de menos 2, igual a 2.c)
Sentença matemática. Raiz quinta de 32 igual a raiz quinta de 2 elevado a 5, igual a 2.d)
Sentença matemática. Raiz cúbica de, abre parênteses, menos 3, fecha parênteses, elevado a 3, igual a, menos 3.2ª propriedade
Analise as igualdades:


Igualando um a dois, temos:
Dados a e b números reais não negativos e n um número natural maior ou igual a 2, temos:
Confira mais alguns exemplos.
a)
Raiz quadrada de 3 vezes 7, fim da raiz, igual a raiz quadrada de 3, fim da raiz, vezes raiz quadrada de 7, fim da raizb)
Raiz quarta de 2 vezes 3 vezes 7, fim da raiz, igual a, raiz quarta de 2, fim da raiz, vezes raiz quarta de 3, fim da raiz, vezes raiz quarta de 7, fim da raizc)
Raiz cúbica de 5 vezes 17, fim da raiz, igual a, raiz cúbica de 5, fim da raiz, vezes a raiz cúbica de 17, fim da raizd)
Raiz quinta de 2 elevado a 3, vezes x, vezes, y elevado ao cubo, fim da raiz, igual a, raiz quinta de 2 ao cubo,fim da raiz, vezes a raiz quinta de x, fim da raiz, vezes a raiz quinta de y ao cubo, fim da raiz, com x ⩾ 0 e y ⩾ 0
3ª propriedade
Analise as igualdades:


Igualando um a dois, temos:
Dados a e b números reais não negativos, com b diferente de 0, e n um número natural maior ou igual a 2, temos:
Confira mais alguns exemplos.
a)
Sentença matemática. Raiz quadrada de 3 sobre 7 igual a raiz quadrada de 3 sobre a raiz quadrada de 7.b)
Sentença matemática. Raiz cúbica de, fração, numerador: a elevado a 5, denominador: b elevado a 3, igual a, fração, numerador: raiz cúbica de a elevado a 5, denominador: raiz cúbica de b elevado a 3, igual a, fração, numerador: raiz cúbica de a elevado a 5, denominador: b., com a ⩾ 0 e b > 0
c)
Sentença matemática. Raiz quinta de 5 sobre 17, igual a , fração, numerador: raiz cúbica de 5, denominador: raiz cúbica de 17.d)
Sentença matemática. Raiz quinta de, fração, numerador: a elevado a 3, denominador: 7b, igual a, fração, numerador: raiz quinta de a elevado a 3, denominador: raiz quinta de 7b., com a ⩾ 0 e b > 0
4 ª propriedade
Analise a igualdade:

Multiplicando o índice do radical e o expoente do radicando por 2, obtemos:

Igualando um a dois, temos:
Raiz cúbica de 5 elevado a 3, fim da raiz, igual a índice 3 vezes 2, radicando 5 elevado a 3 vezes 2, fim do expoente, fim da raiz
Glossário
- latência
- : tempo que demora para a transferência de informações dentro da rede. Por isso, quanto menor for essa medida, mais rápido vai chegar o pacote de dados de um ponto a outro.
- Voltar para o texto
- milissegundo
- : milésima parte do segundo.
- Voltar para o texto
- femtossegundo
- : unidade de medida de tempo que corresponde a 10elevado a menos quinze segundos.
- Voltar para o texto