Página 34

Parte 2

De modo inverso, podemos observar que:

\sqrt[6]{5^{6}} = \sqrt[6 : 2]{5^{6 : 2}} = \sqrt[3]{5^{3}} = 5

Dados a um número real não negativo, n um número natural maior ou igual a 2 e m e p números naturais diferentes de zero, temos:

\sqrt[n]{a^{m}} = \sqrt[n \cdot p]{a^{m \cdot p}}

Dados a um número real não negativo, n um número natural maior ou igual a 2 e m e p números naturais diferentes de zero, sendo p divisor comum a m e n, temos:

\sqrt[n]{a^{m}} = \sqrt[n : p]{a^{m : p}}

Confira mais alguns exemplos.

\sqrt[5]{2^{3}} = \sqrt[5 \cdot 2]{2^{3 \cdot 2}} = \sqrt[10]{2^{6}}

\sqrt{3^{25}} = \sqrt[2 \cdot 2]{3^{25 \cdot 2}} = \sqrt[4]{3^{50}}

\sqrt[8]{x^{6}} = \sqrt[8 : 2]{x^{6 : 2}} = \sqrt[4]{x^{3}}

, com x ⩾ 0

\sqrt[10]{b^{15}} = \sqrt[10 : 5]{b^{15 : 5}} = \sqrt{b^{3}}

, com b ⩾ 0

5ª propriedade

Analise as igualdades:

Sentença matemática. Raiz cúbica da raiz quadrada de 64 igual a, raiz cúbica de 8 igual a, 2.

Sentença matemática. Raiz sexta de 64 igual a, raiz sexta de 2 elevado a 6, igual a 2.

Igualando um a dois, temos:

\sqrt[3]{\sqrt{64}} = \sqrt[6]{64}

Dados a um número real não negativo e m e n números naturais maiores ou iguais a 2, temos:

\sqrt[m]{\sqrt[n]{a}} = \sqrt[m \cdot n]{a}

Confira mais alguns exemplos.

\sqrt{\sqrt[3]{3}} = \sqrt[2 \cdot 3]{3} = \sqrt[6]{3}

\sqrt[3]{\sqrt[5]{7}} = \sqrt[3 \cdot 5]{7} = \sqrt[15]{7}

\sqrt[5]{\sqrt[3]{2}} = \sqrt[15]{2}

\sqrt[4]{\sqrt{\sqrt[3]{5}}} = \sqrt[4]{\sqrt[6]{5}} = \sqrt[24]{5}

Atividades

Faça as atividades no caderno.

30. Determine o valor dos radicais.

\sqrt{7^{2}}

\sqrt[3]{11^{3}}

\sqrt{x^{2}}

\sqrt[5]{6^{5}}

\sqrt[3]{{(a + b)}^{3}}

\sqrt[3]{a^{3} \cdot b^{3}}

31. Decomponha o radicando em fatores primos e determine o valor dos radicais.

\sqrt{25}

\sqrt[4]{81}

\sqrt[8]{256}

\sqrt[3]{343}

\sqrt{121}

\sqrt[4]{625}

Página 35

32. Transforme os radicais em um produto de dois ou mais radicais.

\sqrt{5 \cdot 17}

\sqrt[4]{5 \cdot 7 \cdot 11}

\sqrt[5]{2 \cdot x^{4}}

, com x ⩾ 0

\sqrt[3]{10 \cdot 20}

\sqrt[3]{3 \cdot 7}

\sqrt[3]{7 \cdot a^{2} \cdot b}

, com a ⩾ 0 e b ⩾ 0

33. Transforme em um quociente de radicais.

\sqrt{\frac{5}{7}}

\sqrt[3]{\frac{7}{11}}

\sqrt[4]{\frac{10}{17}}

\sqrt[3]{\frac{a}{b}}

, com a ⩾ 0 e b > 0

\sqrt[5]{\frac{2 x}{5 y^{3}}}

, com x ⩾ 0 e y > 0

\sqrt[3]{\frac{8}{27}}

34. Simplifique os radicais, dividindo o índice do radical e o expoente do radicando por um mesmo número.

\sqrt[4]{3^{2}}

\sqrt[5]{7^{10}}

\sqrt[8]{7^{6}}

\sqrt[12]{2^{3} \cdot a^{6}}

, com a ⩾ 0

\sqrt[15]{5^{10}}

\sqrt[6]{a^{2} b^{2}}

, com a ⩾ 0 e b ⩾ 0

35. Decomponha os radicandos em fatores primos e, em seguida, simplifique os radicais.

\sqrt[8]{64}

\sqrt[10]{625}

\sqrt[20]{243}

\sqrt[14]{128}

36. Transforme em uma única raiz.

\sqrt{\sqrt{5}}

\sqrt[5]{\sqrt[2]{13}}

\sqrt[3]{\sqrt{7}}

\sqrt[5]{\sqrt[6]{11}}

\sqrt[3]{\sqrt{\sqrt[5]{4}}}

\sqrt{\sqrt{\sqrt{\sqrt{x}}}}

, com x ⩾ 0

37. Determine o valor do número natural x maior ou igual a 2 nas expressões a seguir.

\sqrt[15]{2^{10}} = \sqrt[x]{2^{2}}

\sqrt[6]{13^{9}} = \sqrt{13^{x}}

\sqrt[x]{\sqrt[3]{7}} = \sqrt[15]{7}

\sqrt[9]{6^{6}} = \sqrt[3]{6^{x}}

38. Transforme em um único radical.

\sqrt{3} \cdot \sqrt{5}

\sqrt[3]{7} \cdot \sqrt[3]{11}

\sqrt{2} \cdot \sqrt{5} \cdot \sqrt{7}

\sqrt[12]{5} \cdot \sqrt[12]{10}

\frac{\sqrt{12} \cdot \sqrt{15}}{\sqrt{8}}

\frac{\sqrt[3]{9} \cdot \sqrt[3]{10}}{\sqrt[3]{12} \cdot \sqrt[3]{15}}

\frac{\sqrt[6]{4} \cdot \sqrt{\sqrt[3]{10}}}{\sqrt[6]{120}}

39. Transforme em um único radical, escrevendo o radicando na fórma mais simples possível.

\frac{\sqrt{20}}{\sqrt{24}}

\frac{\sqrt[3]{10}}{\sqrt[3]{18}}

\frac{\sqrt[4]{30}}{\sqrt[4]{24}}

\frac{\sqrt[5]{16}}{\sqrt[5]{20}}

40. Identifique as sentenças verdadeiras.

\sqrt{\frac{a^{2}}{b^{2}}} = \frac{a}{b}

, com a ⩾ 0 e b > 0

\sqrt{a} + \sqrt{b} = \sqrt{a + b}

, com a ⩾ 0 e b ⩾ 0

\sqrt{a^{2} + b^{2}}

= a + b, com a ⩾ 0 e b ⩾ 0

\sqrt{a} \cdot \sqrt{a}

= a, com a ⩾ 0

\sqrt{a^{2} \cdot b^{2}}

= a ⋅ b, com a ⩾ 0 e b ⩾ 0

\sqrt{x^{2} - y^{2}} = \sqrt{x^{2}} - \sqrt{y^{2}}

= x menos y, com x ⩾ 0 e y ⩾ 0

Página 36

4 Operações com radicais

Adição e subtração de radicais

Na adição e na subtração com radicais, três casos podem ser considerados.

• 1º caso: Todos os radicais têm o mesmo índice e o mesmo radicando, ou seja, são semelhantes.

Efetuamos as adições e as subtrações dos fatores externos e mantemos o mesmo radical. Por exemplo:

3 \sqrt{3} - \sqrt{3} - 5 \sqrt{3} + \frac{\sqrt{3}}{2} = (3 ‒ 1 ‒ 5 + \frac{1}{2}) \sqrt{3} = ‒ \frac{5}{2} \sqrt{3}

• 2º caso: Todos os radicais podem ser reescritos como radicais semelhantes. Por exemplo:

\sqrt{180} + \sqrt{20} = \sqrt{2^{2} \cdot 3^{2} \cdot 5} + \sqrt{2^{2} \cdot 5} = 2 \cdot 3 \cdot \sqrt{5} + 2 \cdot \sqrt{5} = 6 \sqrt{5} + 2 \sqrt{5} = 8 \sqrt{5}

• 3º caso: Apenas alguns radicais são semelhantes.

Efetuamos as adições e as subtrações dos radicais semelhantes e repetimos os radicais não semelhantes. Por exemplo:

\sqrt{5} - 3 \sqrt{5} + \sqrt{10} + 3 \sqrt{2} - 4 \sqrt{5} = (\sqrt{5} - 3 \sqrt{5} - 4 \sqrt{5}) + \sqrt{10} + 3 \sqrt{2} = - 6 \sqrt{5} + \sqrt{10} + 3 \sqrt{2}

Observação

Preste muita atenção às desigualdades a seguir.

•

\sqrt{3} + \sqrt{2} \neq \sqrt{5}

•

2 + \sqrt{5} \neq 2 \sqrt{5}

•

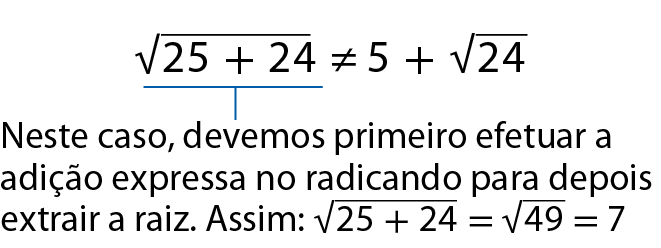
Esquema. Raiz quadrada de 25 mais 24 é diferente de 5 mais raiz quadrada de 24. Indicação saindo de 25 + 24: Neste caso, devemos primeiro efetuar a adição expressa no radicando para depois extrair a raiz. Assim: a raiz quadrada de 25 mais 24 é igual a raiz quadrada de 49 que é igual a 7.

Atividades

Faça as atividades no caderno.

41. Efetue as operações a seguir.

\sqrt{7} - 5 \sqrt{7} + 2 \sqrt{7}

2 \sqrt[5]{2} + \sqrt[5]{64}

2 \sqrt{16} + 3 \sqrt[3]{16} + 4 \sqrt[4]{16} + \sqrt[6]{16}

(3 \sqrt{2} + 7 \sqrt{3}) + (6 \sqrt{2} - 2 \sqrt{3})

\sqrt{32} - 2 \sqrt{12} - \sqrt{75} + 3 \sqrt{72}

42. Simplifique as expressões a seguir.

3 \sqrt[3]{2} - 7 \sqrt[3]{2} - 6 \sqrt[3]{2}

\sqrt{12} - \sqrt[4]{9} - \sqrt[6]{27} - \sqrt[8]{81}

2 \sqrt{150} - 4 \sqrt{54} + 6 \sqrt{24}

7 \sqrt{32} - 5 \sqrt{2} + \sqrt{8}

43. Determine a medida do perímetro das figuras.

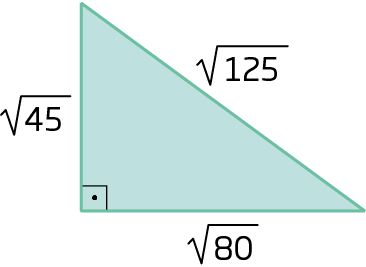
Ilustração. Triângulo retângulo, com a indicação do ângulo reto e lados, raiz quadrada de 45, raiz quadrada de 80 e hipotenusa raiz quadrada de 125.

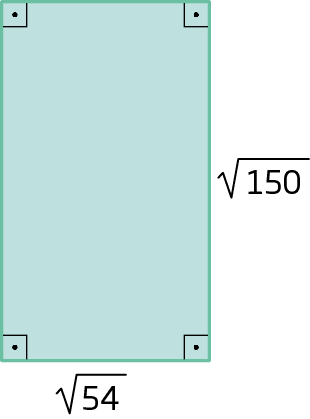
Ilustração. Retângulo, com a indicação dos 4 ângulos retos e lados raiz quadrada de 150 e raiz quadrada de 54.

44. Considerando, com aproximação de centésimos,

\sqrt{2} = 1, 41

\sqrt{3} = 1, 73

, determine o valor aproximado do número real y na fórma decimal, sendo:

y = \sqrt{200} + \sqrt{300} + \sqrt{800} + \sqrt{1 200}

Página 37

Multiplicação de radicais

No estudo da 2ª propriedade dos radicais, vimos que:

\sqrt{4 \cdot 9} = \sqrt{4} \cdot \sqrt{9}

Logo, podemos escrever:

\sqrt{4} \cdot \sqrt{9} = \sqrt{4 \cdot 9}

De fórma análoga, podemos ter:

\sqrt[3]{2} \cdot \sqrt[3]{7} = \sqrt[3]{2 \cdot 7} = \sqrt[3]{14}

\sqrt[5]{6} \cdot \sqrt[5]{11} = \sqrt[5]{6 \cdot 11} = \sqrt[5]{66}

\sqrt{5} \cdot \sqrt{6} = \sqrt{5 \cdot 6} = \sqrt{30}

\sqrt[3]{10} \cdot \sqrt[3]{12} = \sqrt[3]{10 \cdot 12} = \sqrt[3]{120}

2 \sqrt{5} \cdot \sqrt{7} \cdot 3 \sqrt{10} = (2 \cdot 3) \sqrt{5 \cdot 7 \cdot 10} = 6 \sqrt{350}

Se os radicais tiverem índices diferentes, devemos reduzi-los ao mesmo índice e, depois, efetuar a operação. Acompanhe o exemplo a seguir.

\sqrt{2} \cdot \sqrt[3]{5} = \sqrt[6]{2^{3}} \cdot \sqrt[6]{5^{2}} = \sqrt[6]{2^{3} \cdot 5^{2}} = \sqrt[6]{200}

Em alguns casos, podemos simplificar uma expressão que envolva radicais utilizando a propriedade distributiva. Seguem alguns exemplos:

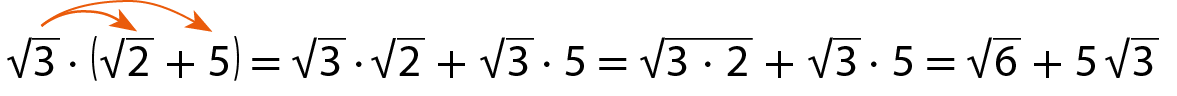
Esquema. Sentença matemática. Raiz quadrada de 3 vezes, abre parênteses, raiz quadrada de 2 mais 5, fecha parenteses. há duas setas saindo da raiz quadrada de 3, uma indo para raiz quadrada de 2 e outra para o 5. após o parênteses, igual a raiz quadrada de 3, vezes, raiz quadrada de 2, mais, raiz quadrada de 3 vezes 5 igual a, raiz quadrada de 3 vezes 2 mais raiz quadrada de 3 vezes 5 igual a, raiz quadrada de 6 mais 5 vezes raiz quadrada de 3.

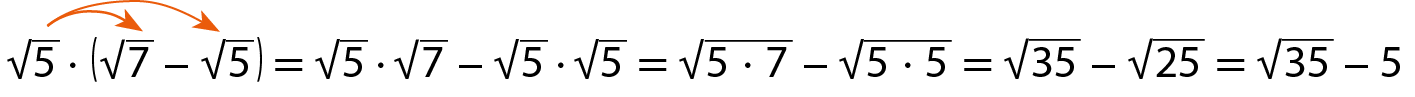
Esquema. Sentença matemática. Raiz quadrada de 5 vezes, abre parênteses, raiz quadrada de 7 menos raiz quadrada de 5, fecha parenteses. há duas setas saindo da raiz quadrada de 5, uma indo para raiz quadrada de 7 e outra para a raiz quadrada de 5. após o parênteses, igual a raiz quadrada de 5, vezes, raiz quadrada de 7, menos, raiz quadrada de 5 vezes raiz quadrada de 5, igual a raiz quadrada de 5 vezes 7 menos raiz quadrada de 5 vezes 5 igual a, raiz quadrada de 35 menos raiz quadrada de 25 igual a, raiz quadrada de 35 menos 5.

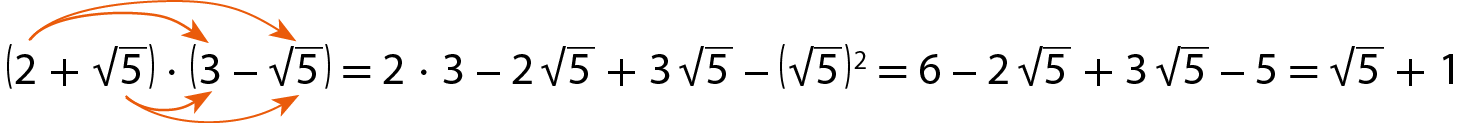
Esquema. Sentença matemática. Abre parênteses. 2 mais raiz quadrada de 5, fecha parênteses, vezes, abre parênteses, 3 menos raiz quadrada de 5. Há duas setas saindo do 2 indo até ao 3 e a raiz quadrada de 5 do outro parênteses, e duas setas saindo da raiz quadrada de 5 do primeiro parênteses, para o 3 e a raiz quadrada de 5 do segundo parênteses. Após o último parênteses, igual a 2 vezes 3 menos 2 vezes raiz quadrada de 5 mais 3 vezes raiz quadrada de 5 menos, abre parênteses, raiz quadrada de 5, fecha parênteses, ao quadrado, igual a 6 menos 2 raiz quadrada de 5 mais 3 vezes raiz quadrada de 5 menos 5 igual a raiz quadrada de 5 mais 1.

Atividades

Faça as atividades no caderno.

45.

Calcule mentalmente os produtos.

\sqrt{15} \cdot \sqrt{6}

3 \sqrt[5]{6} \cdot 4 \sqrt[5]{5}

\sqrt{2} \cdot \sqrt{\frac{1}{2}}

\sqrt[3]{7} \cdot \sqrt[3]{11}

3 \sqrt[3]{2} \cdot 2 \sqrt[3]{3}

\sqrt{10} \cdot \frac{\sqrt{10}}{10}

46. Determine a medida do perímetro e a medida da área de cada figura.

Ilustração. Retângulo de lados 3 raiz quadrada de 3 e 4 raiz quadrada de 3, com os 4 ângulos retos indicados.

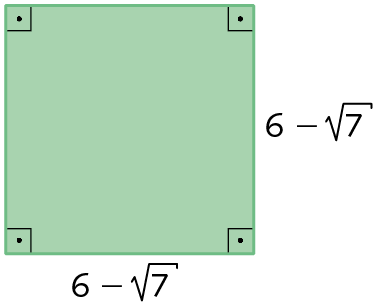
Ilustração. Quadrado de lado 6 menos rais quadrada de 7, com os 4 ângulos retos indicados.

47. Efetue as multiplicações a seguir.

\sqrt[5]{2} \cdot \sqrt[5]{3} \cdot \sqrt[5]{50}

3 \sqrt[3]{8} \cdot \frac{\sqrt[3]{3}}{8}

48. Determine os produtos a seguir.

\sqrt[3]{3} \cdot \sqrt{2}

\sqrt[4]{2} \cdot \sqrt{8}

\sqrt[4]{2^{3}} \cdot \sqrt[4]{2^{2}} \cdot \sqrt{2}

\sqrt[8]{5} \cdot \sqrt[6]{5}

\sqrt{10} \cdot \sqrt[5]{12} \cdot \sqrt[3]{30}

\sqrt[3]{0, 04} \cdot \sqrt[6]{625}

49. Aplicando a propriedade distributiva, determine os produtos a seguir.

\sqrt{7} \cdot (\sqrt{7} - 1)

(\sqrt{5} - 1) \cdot (\sqrt{5} + 3)

(\sqrt{3} - 2) \cdot (1 - \sqrt{3})

\sqrt{5} \cdot (\sqrt{2} + \sqrt{3})

(2 \sqrt{2} + 2) \cdot (2 - \sqrt{2})

\sqrt{2} \cdot (1 - \sqrt{2})