Página 38

Parte 3

Divisão de radicais

No estudo da 3ª propriedade dos radicais, vimos que:

\sqrt{\frac{4}{9}} = \frac{\sqrt{4}}{\sqrt{9}}

Logo, podemos escrever:

\frac{\sqrt{4}}{\sqrt{9}} = \sqrt{\frac{4}{9}}

De fórma análoga, podemos ter:

\frac{\sqrt[3]{17}}{\sqrt[3]{4}} = \sqrt[3]{\frac{17}{4}}

\frac{\sqrt[5]{3}}{\sqrt[5]{8}} = \sqrt[5]{\frac{3}{8}}

\sqrt{8} : \sqrt{2} = \frac{\sqrt{8}}{\sqrt{2}} = \sqrt{\frac{8}{2}} = \sqrt{4} = 2

\sqrt[3]{30} : \sqrt[3]{18} = \frac{\sqrt[3]{30}}{\sqrt[3]{18}} = \sqrt[3]{\frac{30}{18}} = \sqrt[3]{\frac{5}{3}}

Se os radicais tiverem índices diferentes, devemos reduzi-los ao mesmo índice e, depois, efetuar a operação. Acompanhe o exemplo:

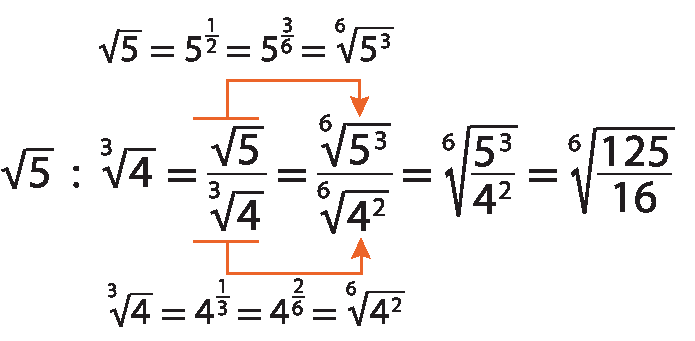
Esquema. Raiz quadrada de 5 dividido por raiz cúbica de 4 igual a, fração. numerador: raiz quadrada de 5, denominador: a raiz cúbica de 4, igual a, fração, numerador: raiz sexta de 5 ao cubo, denominador: raiz sexta de 4 ao quadrado, igual a, raiz sexta de 5 ao cubo sobre 4 ao quadrado, igual a, raiz sexta de 125 sobre 16. Há uma seta saindo do numerador da primeira fração indo até o numerador da segunda fração com a seguinte informação: raiz quadrada de 5 igual a, 5 elevado a 1 sobre 2, fora do expoente, igual a, 5 elevado a 3 sobre 6, fora do expoente, raiz sexta de 5 ao cubo. Há outra seta saindo do denominador da primeira fração indo até o denominador da segunda fração com a seguinte informação: raiz cúbica de 4 igual a, 4 elevado a 1 sobre 3, fora do expoente, igual a, 4 elevado a 2 sobre 6, fora do expoente, igual a raiz sexta de 4 ao quadrado.

Atividades

Faça as atividades no caderno.

50. Determine os quocientes a seguir.

\sqrt[3]{128} : \sqrt[3]{2}

\sqrt[5]{3^{5}} : \sqrt[5]{3^{2}}

\sqrt{\frac{10}{3}} : \sqrt{\frac{5}{6}}

8 \sqrt{75} : 4 \sqrt{3}

51. Efetue as divisões a seguir.

\sqrt[3]{8} : \sqrt{2}

\sqrt[8]{16} : \sqrt[12]{64}

\sqrt[4]{6} : \sqrt{2}

\sqrt[3]{10} : \sqrt{2}

\sqrt[5]{7} : \sqrt[6]{7}

\sqrt[4]{8} : \sqrt[8]{8}

Potenciação e radiciação de radicais

Potenciação de radicais

Analise os exemplos de potências a seguir:

(\sqrt{2})^{3} = \sqrt{2} \cdot \sqrt{2} \cdot \sqrt{2} = \sqrt{2 \cdot 2 \cdot 2} = \sqrt{2^{3}}

, então:

(\sqrt{2})^{3} = \sqrt{2^{3}}

(\sqrt[3]{5})^{4} = \sqrt[3]{5} \cdot \sqrt[3]{5} \cdot \sqrt[3]{5} \cdot \sqrt[3]{5} = \sqrt[3]{5 \cdot 5 \cdot 5 \cdot 5} = \sqrt[3]{5^{4}}

, então:

(\sqrt[3]{5})^{4} = \sqrt[3]{5^{4}}

Para efetuar a potenciação com um radical em que o radicando é um número real positivo, elevamos o radicando ao expoente dado.

Página 39

Dados a um número real positivo, m um número natural maior ou igual a 2 e n um número inteiro, temos:

{(\sqrt[m]{a})}^{n} = \sqrt[m]{a^{n}}

Confira mais alguns exemplos.

(\sqrt[]{5})^{3} = \sqrt{5^{3}} = \sqrt{5 \cdot 5^{2}} = 5 \sqrt{5}

(\sqrt[4]{7})^{8} = \sqrt[4]{7^{8}} = \sqrt[4]{7^{4}} \cdot \sqrt[4]{7^{4}} = 7 \cdot 7 = 7^{2} = 49

(\sqrt[3]{a b^{2}})^{4} = \sqrt[3]{{(a b^{2})}^{4}} = \sqrt[3]{a^{4} \cdot b^{8}} = \sqrt[3]{a \cdot a^{3} \cdot b^{2} \cdot b^{3} \cdot b^{3}} = a \cdot b \cdot b \cdot \sqrt[3]{a b^{2}} = a b^{2} \cdot \sqrt[3]{a b^{2}}

, com a e b números reais positivos

Radiciação de radicais

Analise as igualdades:

\sqrt[2]{\sqrt[3]{64}} = \sqrt[2]{4} = 2

\sqrt[6]{64} = 2

Como as duas expressões,

\sqrt[2]{\sqrt[3]{64}} e \sqrt[6]{64}

, são iguais a 2, então:

\sqrt[2]{\sqrt[3]{64}} = \sqrt[6]{64} = 2

Dados a um número real maior ou igual a zero e m e n números naturais maiores ou iguais a 2, temos:

\sqrt[m]{\sqrt[n]{a}} = \sqrt[m \cdot n]{a}

Confira mais alguns exemplos.

\sqrt[5]{\sqrt{7}} = \sqrt[5 \cdot 2]{7} = \sqrt[10]{7}

\sqrt[3]{\sqrt{\frac{125}{64}}} = \sqrt[3 \cdot 2]{\frac{5^{3}}{2^{6}}} = \frac{\sqrt[6]{5^{3}}}{\sqrt[6]{2^{6}}} = \frac{\sqrt{5}}{2}

Atividades

Faça as atividades no caderno.

52. Efetue as potenciações dos radicais a seguir.

(2 \sqrt[]{3})^{3}

(2 \sqrt[]{2})^{7}

(\sqrt[3]{a b^{}})^{4}

, em que a > 0 e b > 0

(2 \sqrt[7]{a^{5} b^{2}})^{3}

, em que a > 0 e b > 0

{(\frac{x}{y} \cdot \sqrt{\frac{y}{x}})}^{2}

, em que x > 0 e y > 0

(\sqrt[5]{y^{3}})^{2}

, em que y > 0

53. Escreva cada expressão como uma única raiz.

\sqrt[7]{\sqrt[4]{7}}

\sqrt{\sqrt[4]{512}}

54. Calcule o valor de cada uma das expressões a seguir.

(\sqrt[]{2^{}})^{6} + (2 \sqrt[]{3^{}})^{4} + (- 3 \sqrt[]{7^{}})^{2} + {(\sqrt{\frac{1}{2}})}^{‒ 2}

{(\sqrt[3]{\sqrt{64}})}^{2}

55. Identifique a alternativa correta.

A expressão

\frac{\sqrt{2} \cdot {(\sqrt[5]{2})}^{2}}{{(\sqrt[10]{2})}^{4}}

é igual a:

\sqrt[10]{2^{3}}

\sqrt[5]{2}

\sqrt{2}

\sqrt[10]{2^{4}}

\sqrt[5]{2^{3}}

Página 40

Racionalização de denominadores

Considere o número fracionário

\frac{5}{\sqrt{3}}

, cujo denominador é o número irracional

\sqrt{3}

Vamos multiplicar o numerador e o denominador por

\sqrt{3}

, obtendo uma fração equivalente:

Esquema. Sentença matemática. Fração, numerador, 5 vezes raiz quadrada de 3, denominador: raiz quadrada de 3 vezes raiz quadrada de 3, igual a fração, numerador: 5 raiz quadrada de 3, denominador: 3. Há uma indicação partindo da raiz quadrada de 3 do numerador da primeira fração e da raiz quadrada de 3 do numerador da primeira fração, escrito: Note que, raiz de 3 sobre raiz de 3 é igual a 1. Assim, ao multiplicarmos 5 sobre raiz de 3 por essa expressão, não alteramos seu valor.

O número fracionário obtido,

\frac{5 \sqrt{3}}{3}

, tem denominador racional.

A esse procedimento damos o nome de racionalização.

Para racionalizar o denominador de um número fracionário, devemos multiplicar o numerador e o denominador por um radical ou uma expressão com radical chamada fator racionalizante, a fim de obter uma fração equivalente com denominador racional.

A seguir, vamos estudar os principais casos de racionalização.

Ilustração. Homem de cabelo preto e jaleco branco. Em pé segurando um livro aberto, ele fala: A racionalização de denominadores permite a obtenção de uma fração equivalente que facilita o cálculo por aproximação.

• 1º caso: O denominador é um radical de índice 2.

Analise os exemplos a seguir

\frac{5}{\sqrt{2}}

Multiplicamos o numerador e o denominador por

\sqrt{2}

 , obtendo uma fração equivalente:

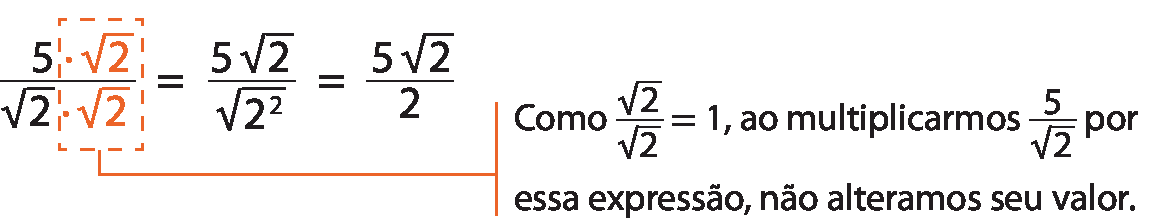
Esquema. Sentença matemática. Fração, numerador, 5 vezes raiz quadrada de 2, denominador: raiz quadrada de 2 vezes raiz quadrada de 2, igual a fração, numerador: 5 raiz quadrada de 2, denominador: raiz quadrada de 2 ao quadrado, igual a, fração, numerador: 5 raiz quadrada de 2, denominador: raiz quadrada de 2 ao quadrado, igual a, 5 raiz quadrada de 2 sobre 2.
Há uma indicação partindo da raiz quadrada de 2 do numerador da primeira fração e da raiz quadrada de 2 do denominador da primeira fração, escrito: Como raiz quadrada de 2 sobre raiz quadrada de 2 é igual a 1, ao multiplicarmos 5 sobre raiz quadrada de 2 por essa expressão, não alteramos seu valor.

\sqrt{\frac{4}{17}} = \frac{\sqrt{4}}{\sqrt{17}} = \frac{2}{\sqrt{17}}

Vamos multiplicar o numerador e o denominador por

\sqrt{17}

\frac{2 \cdot \sqrt{17}}{\sqrt{17} \cdot \sqrt{17}} = \frac{2 \sqrt{17}}{\sqrt{17^{2}}} = \frac{2 \sqrt{17}}{17}

\frac{3}{5 \sqrt{7}}

Vamos multiplicar o numerador e o denominador por

\sqrt{7}

\frac{3 \cdot \sqrt{7}}{5 \sqrt{7} \cdot \sqrt{7}} = \frac{3 \sqrt{7}}{5 \sqrt{7^{2}}} = \frac{3 \sqrt{7}}{5 \cdot 7} = \frac{3 \sqrt{7}}{35}

\sqrt{\frac{5}{11}} = \frac{\sqrt{5}}{\sqrt{11}}

Vamos multiplicar o numerador e o denominador por

\sqrt{11}

\frac{\sqrt{5} \cdot \sqrt{11}}{\sqrt{11} \cdot \sqrt{11}} = \frac{\sqrt{5} \cdot \sqrt{11}}{\sqrt{11^{2}}} = \frac{\sqrt{55}}{11}

Página 41

• 2º caso: O denominador é um radical de índice diferente de 2.

Analise os exemplos a seguir.

\frac{3}{\sqrt[3]{7}}

Multiplicamos o numerador e o denominador da fração por

\sqrt[3]{7^{2}}

\frac{3 \cdot \sqrt[3]{7^{2}}}{\sqrt[3]{7} \cdot \sqrt[3]{7^{2}}} = \frac{3 \sqrt[3]{7^{2}}}{\sqrt[3]{7^{3}}} = \frac{3 \sqrt[3]{7^{2}}}{7}

\frac{2}{\sqrt[5]{2^{3}}} = \frac{2 \cdot \sqrt[5]{2^{2}}}{\sqrt[5]{2^{3}} \cdot \sqrt[5]{2^{2}}} = \frac{2 \sqrt[5]{2^{2}}}{\sqrt[5]{2^{5}}} = \frac{2 \sqrt[5]{2^{2}}}{2} = \sqrt[5]{2^{2}}

• 3º caso: O denominador é uma adição ou uma subtração de dois termos, em que pelo menos um deles é uma raiz quadrada não exata (irracional).

Confira o seguinte produto:

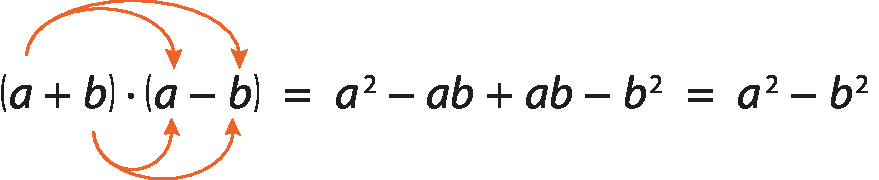
Esquema. Sentença matemática. Abre parênteses, a mais b, fecha parênteses, vezes, abre parênteses, a menos b, fecha parênteses, igual a, a ao quadrado menos ab mais ab menos b ao quadrado, igual a, a ao quadrado menos b ao quadrado. Da primeira expressão, saem duas setas laranjas saem de a e chegam em a e b da segunda expressão. Também saem duas setas de b que chegam em a e b da segunda expressão.

Utilizaremos esse resultado para racionalizar denominadores que se enquadram nesse caso. Analise os exemplos a seguir.

Como o denominador é uma adição de dois números irracionais

(\sqrt{2} + \sqrt{3})

, multiplicamos o numerador e o denominador dessa fração por

(\sqrt{2} - \sqrt{3})

. Assim:

\frac{5}{\sqrt{2} + \sqrt{3}}

\frac{5 \cdot (\sqrt{2} - \sqrt{3})}{(\sqrt{2} + \sqrt{3}) \cdot (\sqrt{2} - \sqrt{3})} = \frac{5 (\sqrt{2} - \sqrt{3})}{{(\sqrt{2})}^{2} - {(\sqrt{3})}^{2}} = 5 \cdot \frac{(\sqrt{2} - \sqrt{3})}{- 1} = - 5 (\sqrt{2} - \sqrt{3})

\frac{\sqrt{2}}{\sqrt{7} - \sqrt{5}} = \frac{\sqrt{2} \cdot (\sqrt{7} + \sqrt{5})}{(\sqrt{7} - \sqrt{5}) \cdot (\sqrt{7} + \sqrt{5})} = \frac{\sqrt{2 \cdot 7} + \sqrt{2 \cdot 5}}{{(\sqrt[]{7})}^{2} - {(\sqrt[]{5})}^{2}} = \frac{\sqrt{14} + \sqrt{10}}{7 ‒ 5} = \frac{\sqrt{14} + \sqrt{10}}{2}

Atividades

Faça as atividades no caderno.

56. Racionalize o denominador dos seguintes números.

\frac{7}{\sqrt{2}}

\frac{6}{\sqrt{2}}

\frac{1}{7 \sqrt[5]{8}}

\frac{1}{\sqrt[3]{7}}

57. Racionalize os denominadores dos seguintes números.

\frac{1}{\sqrt{3} + 1}

\frac{3}{5 ‒ \sqrt{7}}

\frac{4 \sqrt{3}}{\sqrt{2} + \sqrt{3}}

\frac{\sqrt{2} ‒ 1}{2 ‒ \sqrt{2}}

58. No caderno, identifique a alternativa que corresponde ao valor da expressão:

\frac{1}{\sqrt{2}} + \frac{1}{\sqrt{18}} ‒ \frac{1}{\sqrt{8}}

\frac{\sqrt{3}}{6}

\sqrt{12}

c) ‒

\frac{10}{\sqrt{288}}

‒ \frac{5 \sqrt{2}}{12}

\frac{5 \sqrt{2}}{12}