Parte 4
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Potência de um número real com expoente inteiro
Considere a um número real.
• Expoente maior que 1

• Expoente 1
aelevado a 1 = a
• Expoente zero, com base não nula
aelevado a 0 = 1, com a ≠ 0
• Expoente inteiro negativo, com base não nula
Sentença matemática. a elevado a menos n igual a 1 sobre a elevado a n, igual a abre parênteses, 1 sobre a, fecha parênteses, elevado a n.
, com a ≠ 0 e ‒n número inteiro negativo
Propriedades das potências com expoentes inteiros
Considere que a e b são números reais não nulos e que m e n são números inteiros.
• Produto de potências de mesma base
Sentença matemática. a elevado a n, vezes, a elevado a m igual a, a elevado a n mais m.
• Quociente de potências de mesma base
Sentença matemática. a elevado a n, dividido por, a elevado a m igual a, a elevado a n menos m.
• Potência de potência
Sentença matemática. abre parênteses, a elevado a n, fecha parênteses, elevado a m, igual a, a elevado a n vezes m.
• Potência de um produto ou de um quociente
Sentença matemática. abre parênteses, a vezes b, fecha parênteses, elevado a n, igual a, a elevado a n vezes b elevado a n.
Sentença matemática. abre parênteses, a dividido por b, fecha parênteses, elevado a n, igual a, a elevado a n dividido por b elevado a n.
1. Efetue as potências de números reais com expoentes inteiros.
a)
Sentença matemática. abre parênteses, menos 4, fecha parênteses, elevado a 0.
b)
Sentença matemática. abre parênteses, menos 4, fecha parênteses, elevado a 3.
c)
Sentença matemática. abre parênteses, menos 5 oitavos, fecha parênteses, elevado a menos 2.
d)
menos, abre parênteses, 0 vírgula 2, fecha parênteses, elevado a menos 3
2. Aplique as propriedades de potências e expresse os resultados na fórma de única potência.
a)
Sentença matemática. 3 elevado a 4 vezes 3 elevado a 2 vezes 3 elevado a 0.b)
Sentença matemática. Abre parênteses, 2 elevado a 8, dividido por, 2 elevado a 5, fecha parênteses, vezes 2 elevado a menos 3.
c)
Sentença matemática. Abre colchete, abre parênteses, 4 ao cubo, fecha parênteses, ao quadrado, fecha colchetes. dividido por 4 elevado a menos 5.
d)
Sentença matemática. Abre colchete, abre parênteses, menos 4, fecha parênteses, ao quadrado, vezes 2, fecha colchetes, elevado a 3.
3. Determine o valor das expressões numéricas.
a)
Sentença matemática. Abre colchete, abre parênteses, menos 4, fecha parênteses, elevado a 0 menos 3 elevado a 0 mais, abre parênteses, menos 2, fecha parênteses, elevado a 0, menos 1 elevado a 0, fecha colchetes. elevado a 10.b)
Sentença matemática. Abre parênteses, 2 vezes 3, fecha parênteses, ao quadrado, dividido por, abre parênteses, menos 1 meio, fecha parênteses, elevado a menos 2.c)
Sentença matemática. Abre parênteses, 3 elevado a 0, fecha parênteses, ao quadrado, vezes, abre parênteses, 2 ao quadrado, fecha parênteses, elevado a 0.d)
Sentença matemática. Abre parênteses, 0 elevado a 5, vezes 1 elevado a 4, fecha parênteses, elevado a 20, vezes, abre parênteses, 2 ao cubo vezes 3 ao quadrado, fecha parênteses, mais, abre parênteses, 4 elevado a 1 dividido por 5 elevado a zero, fecha parênteses, ao quadrado.Raiz enésima de um número real
Podemos escrever a raiz quadrada de um numero real positivo como potência de expoente fracionário.
, em que m é inteiro
Determinação da raiz enésima de um número real
Na determinação da raiz enésima de um numero real a, ou seja,
Sentença matemática. Raiz enésima de a., podem ocorrer os casos a seguir.
1º caso: a ⩾ 0 e n um número natural maior ou igual a 2. Por exemplo:
2º caso: a < 0 e n um número natural ímpar maior que 2. Por exemplo:
3º caso: a < 0 e n um número natural par diferente de zero.
Sendo a um número real, a < 0 e n um número natural par diferente de zero, temos que
Sentença matemática. Raiz enésima de a.não representa um número real.
4. Determine o valor das expressões numéricas.
a)
Sentença matemática. Raiz cúbica de 27 mais raiz quinta de menos 32 menos raiz décima de 1.
b)
Sentença matemática. Raiz cúbica de 343 menos raiz décima de 1024.
c)
Sentença matemática. Raiz quadrada de 25 menos raiz cúbica de 1000 mais raiz quinta de menos 1024.
d)
Sentença matemática. Raiz quadrada de 100 vezes raiz cúbica de menos 216.
e)
Sentença matemática. Fração, numerador: raiz quinta de menos 243, denominador: raiz sétima de menos 128.
Propriedades dos radicais
1ª propriedade
Dados a um número real e êne um número natural, temos:
• se êne é ímpar e maior que 2,
Sentença matemática. Raiz enésima de a elevado a n igual a a.;
• se êne é par, não nulo,
Sentença matemática. Raiz enésima de a elevado a n igual ao médulo de a..
2ª propriedade
Dados a e b números reais não negativos e n um número natural maior ou igual a 2, temos:
3ª propriedade
Dados a e b números reais não negativos, com
Sentença matemática. b diferente de zero., e n um número natural maior ou igual a 2, temos:
4ª propriedade
Dados a um número real não negativo, n um número natural maior ou igual a 2 e m e p números naturais diferentes de zero, temos:
Dados a um número real não negativo, n um número natural maior ou igual a 2 e m e p números naturais diferentes de zero, sendo p divisor comum a m e n, temos:
5ª propriedade
Dados a um número real não negativo e m e n números naturais maiores ou iguais a 2, temos:
5. Aplique as propriedades e determine os valores dos radicais.
a)
Sentença matemática. Raiz cúbica de menos 216.b)
Sentença matemática. Raiz sexta de, abre parênteses, 3 oitavos, fecha parênteses, elevado a 6.c)
Sentença matemática. Raiz quadrada da raiz quadrada de 1296.d)
Sentença matemática. Raiz quadrada de 8 vezes raiz quadrada de 6 vezes raiz quadrada de 3.e)
Fração, denominador: raiz quadrada da raiz quinta da raiz quadrada de 2 elevado a 4, fora das raízes, vezes, raiz quinta da raiz quarta de 2. Denominador: raiz quadrada da raiz décima de 32f)
Fração, denominador: raiz quadrada da raiz quadrada da raiz quadrada de 256, Denominador: raiz quadrada da raiz quarta de 7 elevado a 8Operações com radicais
Adição e subtração de radicais
1º caso: Todos os radicais têm o mesmo índice e o mesmo radicando, ou seja, são semelhantes. Efetuamos as adições e as subtrações dos fatores externos e mantemos o mesmo radical. Por exemplo:
2º caso: Todos os radicais podem ser reescritos como radicais semelhantes. Por exemplo:
3º caso: Apenas alguns radicais são semelhantes. Efetuamos as adições e as subtrações dos radicais semelhantes e repetimos os radicais não semelhantes. Por exemplo:
6. Efetue as adições e as subtrações a seguir.
a)
Sentença matemática. 3 raiz quadrada de 7 mais 4 raiz quadrada de 7 menos raiz quadrada de 7.b)
Sentença matemática. Raiz cúbica de 256 menos 2 raiz cúbica de 4.c)
Sentença matemática. Raiz quadrada de 54 mais 2 raiz quadrada de 6 menos raiz quadrada de 72.d)
Sentença matemática. Raiz quadrada de 8 menos raiz quadrada de 52 mais raiz quadrada de 18 menos raiz quadrada de 117.Multiplicação de radicais
• Se os radicais têm mesmo índice, basta usar a 2ª propriedade dos radicais. Por exemplo:
Sentença matemática. Raiz cúbica de 3 vezes raiz cúbica de 4 igual a raiz cúbica de 2 vezes 4 igual a raiz cúbica de 12.
• Se os radicais tiverem índices diferentes, devemos reduzi-los ao mesmo índice e, depois, efetuar a multiplicação. Por exemplo:
Sentença matemática. Raiz cúbica de 3 vezes raiz quadrada de 5 igual a raiz sexta de 3 ao quadrado vezes raiz sexta de 5 ao cubo igual a raiz sexta de 3 ao quadrado vezes 5 ao cubo igual a raiz cúbica de 1125.
• Em alguns casos, usamos a propriedade distributiva. Por exemplo:
a)
Sentença matemática. Raiz quadrada de 3, abre parênteses, raiz quadrada de 5 mais raiz quadrada de 7, fecha parênteses, igual a raiz quadrada de 3 vezes raiz quadrada de 5 mais raiz quadrada de 3 vezes raiz quadrada de 7 igual araiz quadrada de 3 vezes 5 mais raiz quadrada de 3 vezes 7 igual a raiz quadrada de 15 mais raiz quadrada de 21.
b)
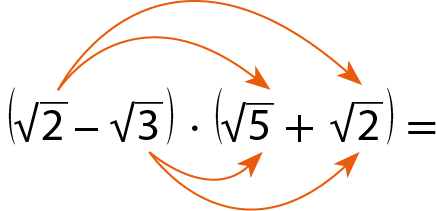
igual a raiz quadrada de 2 vezes raiz quadrada de 5 mais raiz quadrada de 2 vezes raiz quadrada de 2 menos raiz quadrada de 3 vezes raiz quadrada de 5 menos raiz quadrada de 3 vezes raiz quadrada de 2
igual a raiz quadrada de 10 mais raiz quadrada de 4 menos raiz quadrada de 15 menos raiz quadrada de 6
igual a 2 mais raiz quadrada de 10 menos raiz quadrada de 15 menos raiz quadrada de 6.
Divisão de radicais
• Se os radicais têm mesmo índice, basta usar a 3ª propriedade dos radicais. Por exemplo:
Sentença matemática. Raiz quadrada de 3 quintos igual a raiz quadrada de 3 sobre raiz quadrada de 5, é o mesmo que, raiz quadrada de 3 sobre raiz quadrada de 5 igual a raiz quadrada de 3 sobre 5.
• Se os radicais tiverem índices diferentes, devemos reduzi-los ao mesmo índice e, depois, efetuar a divisão. Por exemplo:
Sentença matemática. Raiz cúbica de 6 sobre raiz quadrada de 2, igual a, raiz sexta de 6 ao quadrado, sobre raiz sexta de 2 ao cubo, igual a raiz sexta de 6 ao quadrado sobre 2 ao cubo, igual a, raiz sexta de 36 sobre 8 igual a raiz sexta de 9 sobre 2.
7. Efetue as multiplicações e as divisões com radicais.
a)
Sentença matemática. Raiz quadrada de 7 vezes raiz quadrada de 5.b)
Sentença matemática. Fração, numerador: raiz cúbica de menos 8, denominador: raiz cúbica de 4.c)
Sentença matemática. Raiz quinta de 5 vezes raiz quadrada de 3.d)
Sentença matemática. Fração, numerador: raiz quarta de 3 sobre raiz cúbica de 6, fora da raiz, vezes, raiz quarta de 4.e)
4 abre parênteses, raiz quadrada de 10, fim da raiz, mais 1, fecha parêntesesf)
Sentença matemática. Abre parênteses, raiz quadrada de 7 menos raiz quadrada de 3, fecha parênteses, vezes, abre parênteses, raiz quadrada de 7 mais 2 raiz quadrada de 3, fecha parênteses.Potenciação e radiciação de radicais
Potenciação de radicais
Dados a um número real positivo, m um número natural maior ou igual a 2 e n um número inteiro, temos:
Radiciação de radicais
Dados a um número real maior ou igual a zero e m e n números naturais maiores ou iguais a 2, temos:
8. Efetue e simplifique quando possível as potenciações e as radiciações a seguir. Considere que a e b são números reais positivos.
a)
Sentença matemática. Abre parênteses, raiz quadrada de 3, fecha parênteses, elevado a 6.b)
Sentença matemática. Abre parênteses, raiz cúbica de 5, fecha parênteses, elevado a 2.c)
Sentença matemática. Abre parênteses, raiz quarta de b ao quadrado, fecha parênteses, elevado a 2.d)
Sentença matemática. Raiz quadrada da raiz cúbica de 5.e)
Sentença matemática. Raiz quadrada da raiz quadrada da raiz quadrada de a.f)
Sentença matemática. Raiz quadrada da raiz cúbica de b elevado a 9.Racionalização de denominadores
Quando temos uma fração com denominador irracional, multiplicamos o numerador e o denominador por um radical ou uma expressão com radical, a fim de obter uma fração equivalente com denominador racional.
1º caso: O denominador é um radical de índice 2. Por exemplo:
2º caso: O denominador é um radical de índice diferente de 2. Por exemplo:
3º caso: O denominador é uma adição ou uma subtração de dois termos, em que pelo menos um deles é uma raiz quadrada não exata (irracional). Por exemplo:
9. Racionalize os denominadores de cada uma das expressões a seguir.
a)
Sentença matemática. 5 sobre raiz quadrada de 5.b)
Sentença matemática. 1 sobre raiz cúbica de 2 ao quadrado.c)
Sentença matemática. Raiz quadrada de 3 sobre raiz quinta de 5.d)
Sentença matemática. 3 sobre raiz quadrada de 2, fora da raiz, menos 1.e)
Sentença matemática. Fração, numerador: raiz quadrada de 2, denominador: raiz quadrada de 3 mais raiz quadrada de 7.f)
Sentença matemática. Fração, numerador: 5 raiz quadrada de 3, denominador: 10 mais raiz quadrada 5.