Unidade 2
Capítulo 4 Fatoração e equações do 2º grau
Capítulo 5 Função afim
Capítulo 6 Função quadrática


Capítulo 4 Fatoração e equações do 2º grau
Trocando ideias

A Influenza é uma infecção viral aguda, que afeta o sistema respiratório e é de alta transmissibilidade. A Campanha Nacional de Vacina contra a Influenza ocorrida em 2021 tinha por objetivo prevenir o surgimento de complicações decorrentes da doença, óbitos, internações e sobrecarga nos serviços de saúde.

▸

A medida da área do cartaz oficial da campanha é de .2944 centímetros quadrados e o comprimento dos lados medem x e x + 18. Em seu caderno, escreva uma equação que possibilite determinar a medida do comprimento dos lados do cartaz oficial. O que você pode dizer sobre esta equação?
▸


Você sabe resolver a equação que obteve no item anterior? Se sim, explique aos colegas.
Neste capítulo, vamos estudar monômios, polinômios, fatoração e como resolver equações completas do 2º grau por fatoração e outros métodos.

1 Expressões algébricas, monômios e polinômios
Neste capítulo, retomaremos brevemente a ideia de expressões algébricas, a partir das quais estudaremos monômios e polinômios.
Expressões algébricas
Acompanhe a situação a seguir.
Uma fábrica produz embalagens de leite.

|
Quantidade de embalagens produzidas nos três primeiros meses de 2023 |
||
|
Sem defeito |
Com defeito |
|
|---|---|---|
|
Janeiro |
90 mil |
2,5 mil |
|
Fevereiro |
68 mil |
3,2 mil |
|
Março |
75 mil |
1,8 mil |
Dados obtidos pelo gerente comercial da fábrica nos três primeiros meses de 2023.
Cada embalagem sem defeito gera um ganho de x reais, e cada uma das defeituosas, um prejuízo de y reais. Observe, na tabela, a produção da fábrica nos três primeiros meses de 2023.
O gerente comercial concluiu que o lucro da fábrica, no 1º trimestre de 2023, poderia ser expresso da seguinte maneira:
(.90000 + .68000 + .75000) ⋅ x menos (.2500 + .3200 + .1800) ⋅ y = .233000x menos .7500y
A expressão .233000x menos .7500y é um exemplo de expressão algébrica e representa o lucro da fábrica no 1º trimestre de 2023.
Expressões algébricas são aquelas que indicam operações matemáticas que contêm números e letras ou somente letras.
Se o ganho com cada embalagem sem defeito fosse de R$ 0,26zero reais e vinte e seis centavos e o prejuízo com cada embalagem com defeito fosse de R$ 0,15zero reais e quinze centavos, o lucro no 1º trimestre de 2023 da fábrica seria de R$ 59.455,00cinquenta e nove mil quatrocentos e cinquenta e cinco reais, pois:
.233000 ⋅ R$ 0,26zero reais e vinte e seis centavos menos .7500 ⋅ R$ 0,15zero reais e quinze centavos = R$ 59.455,00cinquenta e nove mil quatrocentos e cinquenta e cinco reais
Nessa situação, empregamos letras (x e y) para representar os valores referentes ao ganho e ao prejuízo. Essas letras são denominadas variáveis da expressão.
Acompanhe outra situação.
Vamos determinar a expressão algébrica correspondente à medida da área da parte verde da figura a seguir.
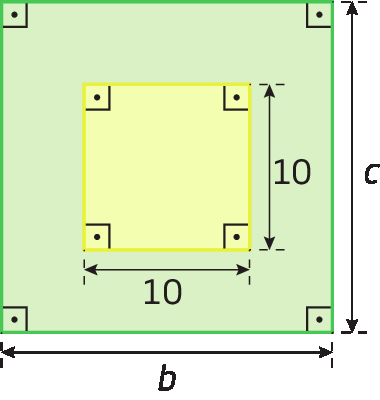
Aamarela = 10 ⋅ 10 = 10elevado a 2 = 100
Atotal = b ⋅ c
Averde = (Atotal) menos (Aamarela) = bc menos 100
Portanto, a medida da área da parte verde será representada pela expressão algébrica bc ‒ 100.
Atividades
Faça as atividades no caderno.
1. Determine uma expressão algébrica que representa a medida do perímetro de cada figura.
a)
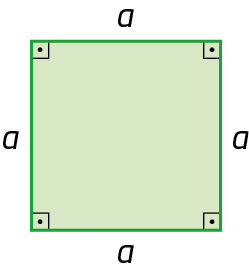
b)
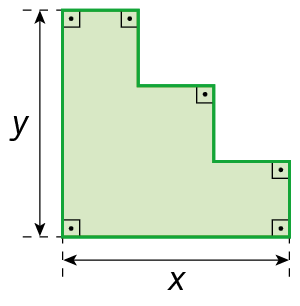
c)

d)

2. Responda, com uma expressão algébrica, às perguntas a seguir.
a) Quantos meses há em x anos?
b) Quantos anos há em y dias? (Considere o ano não bissexto.)
3. Qual é a expressão algébrica que representa a medida da área de cada figura?
a)
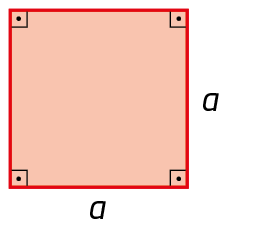
b)
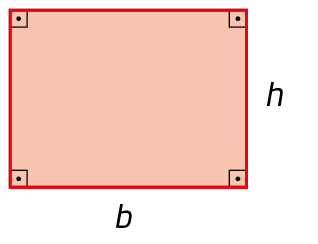
c)
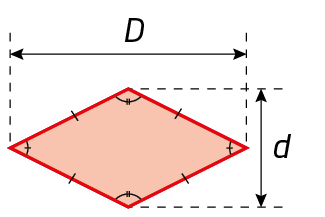
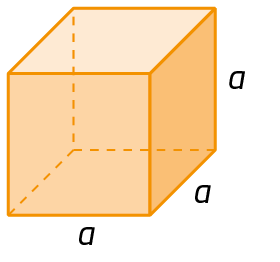
4. Qual é a expressão algébrica que representa a medida do volume de cada paralelepípedo representado a seguir?
a)
b)
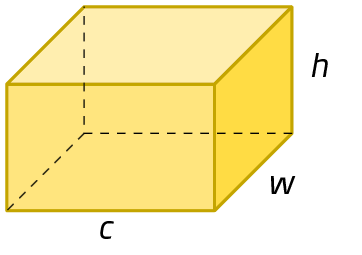
Monômio
Analise as expressões algébricas utilizadas em cada situação a seguir.
• A medida do perímetro de um quadrado cujo comprimento de cada lado mede a.
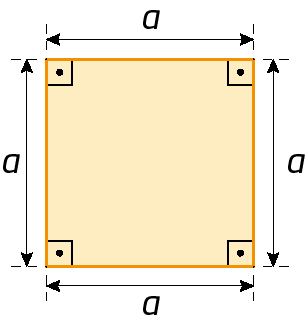
4 ⋅ a ou 4a
• A medida da área de um quadrado cujo comprimento de cada lado mede x.
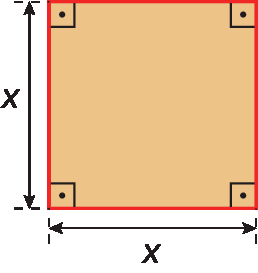
x ⋅ x ou xelevado a 2
• A medida do volume de um paralelepípedo retângulo cujos comprimento, largura e altura medem, respectivamente, a, b e c.
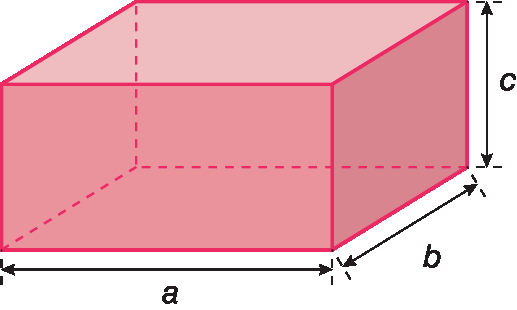
á bê cê
As expressões 4a, xelevado a 2 e á bê cê são exemplos de monômio.
Um monômio é um número ou uma expressão algébrica formada pela multiplicação de um número por uma ou mais letras. Essas letras devem sempre ser expressas na fórma de potência com expoentes naturais.
Observe, a seguir, alguns exemplos de monômios.
a) 16
b) x
c) a elevado a 3b elevado a 2
d)
Sentença matemática. fração 1 meio, x elevado a 3, fim do expoente, y elevado ao quadrado.e) menos5nelevado a 2
Em geral, podemos identificar duas partes nos monômios: o coeficiente e a parte literal.
• coeficiente: corresponde à parte numérica;
• parte literal: corresponde às variáveis, incluindo seus expoentes.
Observe os exemplos a seguir.




Observações
1. O monômio que tem coeficiente zero representa o número real zero e é chamado de monômio nulo. Analise os exemplos:
a) 0x ou 0
b) 0a elevado a 2b elevado a 3 ou 0
c) 0m elevado a 5n elevado a 4 ou 0
2. Todo número real é um monômio sem a parte literal. Observe os exemplos:
a) 12
b) menos5
c)
Fração 3 sobre 4.
d) menos0,6
3. Quando um monômio é formado apenas por uma variável ou por uma multiplicação de variáveis, o coeficiente é igual a 1. Por exemplo:
a) y ou 1y
b) x elevado a 3yz elevado a 2 ou 1x elevado a 3yz elevado a 2
c) xy ou 1xy
d) x elevado a 4z elevado a 3 ou 1x elevado a 4z elevado a 3
Atividades
Faça as atividades no caderno.
5. Escreva no caderno o coeficiente e a parte literal dos monômios.
a)
Sentença matemática. Fração 1 quinto, a elevado a 3, fim do expoente, b elevado a 4.b) menosa elevado a 2bc elevado a 3
c)
Sentença matemática. Fração 3 meios, x elevado a 3.d)
Sentença matemática. Menos 5 raiz de 3; m, n ao quadrado.e)
a ao quadrado vezes b ao cubo vezes c a quarta, tudo sobre 5.f) xis ípsilon zê
g) menosxis ípsilon
h)
Sentença matemática. Fração de numerador 4 pi, r elevado a 3, fim do expoente, e denominador 3.6. Identifique, entre as expressões algébricas a seguir, as que são monômios.
a) menos8
b) a + 2b
c)
Sentença matemática. Fração 5 sobre b.d) 16á bê cê
e) x elevado a 5
f)
Sentença matemática. Fração 2a sobre 3.g) menosá ípsilon
h) menosa + a elevado a 2
i) x elevado a 2y
j)
Sentença matemática. Fração de numerador x mais y e denominador 2.k) 1 000
l) menos0,06b

Converse com o professor e os colegas sobre o porquê de as outras expressões não serem classificadas como monômios.
7. Represente com um monômio o que se pede em cada item.
a) a medida da área do retângulo;
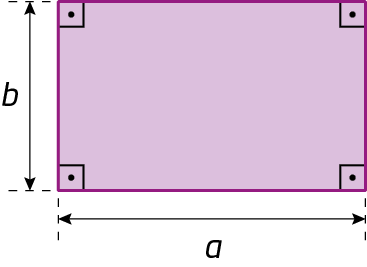
b) a medida do perímetro do hexágono regular;

c) a medida da área da parte pintada de azul da figura;
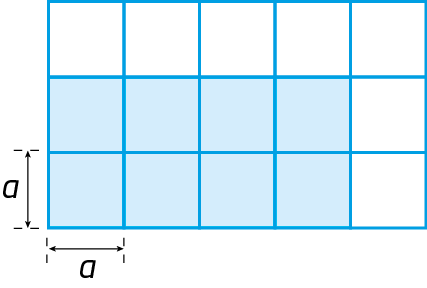
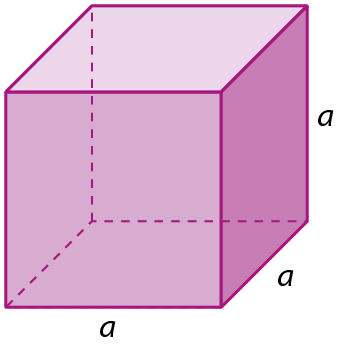
d) a medida do volume do cubo.
Monômios semelhantes
Monômios que apresentam a mesma parte literal são chamados monômios semelhantes.
Assim, são exemplos de monômios semelhantes:
a) 5a elevado a 3b elevado a 2 e
Menos meio vezes a ao cubo vezes b ao quadradob) 12,
raiz quadrada de 3e
menos 3 quartos
c)
Raiz quadrada de 2, fim da raiz, vezes a elevado a 5, fim do expoente, vezes b elevado ao quadrado.e
Menos fração 3 sétimos vezes a elevado a 5, fim do expoente, vezes b elevado ao quadrado.d) 3m elevado a 2n e
Menos 4 nonos vezes m ao quadrado vezes n.Observação
Observe atentamente os monômios a seguir.
a) 2x elevado a 4,
3 quartos vezes x elevado a 5.e ‒7x elevado a 6
b) 20a elevado a 2b elevado a 5 e
Menos 1 terço vezes a ao cubo vezes b elevado a 5.Em ambos os casos, a parte literal parece a mesma, mas perceba que os expoentes são diferentes. Tanto em um caso quanto no outro, os monômios não são semelhantes.
Atividades
Faça as atividades no caderno.
8. Identifique as alternativas que apresentam monômios semelhantes.
a) 6xelevado a 2 e menos5xelevado a 2
b) 15xy e 30x
c) menos8, 10 e menos15
d) 5belevado a 2 e menos7a
e)
Fração. Numerador, 30x ao quadrado, e denominador 41.e menos2xelevado a 2
f) 8melevado a 2n e 6mnelevado a 2
g)
x sobre 5e 6
h) xelevado a 2 e
1 sobre x ao quadrado.9. Escreva, no caderno, um monômio semelhante a:
Sentença matemática. Menos fração 2 terços, a elevado a 5, fim do expoente, b elevado a 7, fim do expoente, c elevado a 9.
10. Escreva, no caderno, dois monômios semelhantes cujos coeficientes sejam números inversos.
Adição e subtração de monômios
Uma expressão algébrica em que todos os monômios são semelhantes pode ser simplificada adicionando ou subtraindo os coeficientes. Analise os dois exemplos a seguir.
a) Qual é a expressão algébrica que representa a medida da área do retângulo á cê dê éfe?
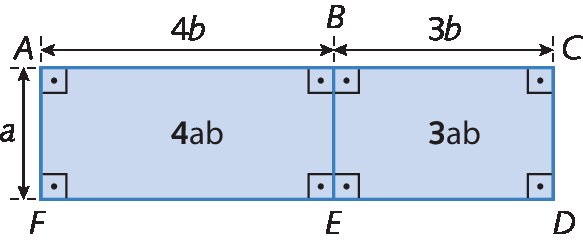
As expressões algébricas que representam as medidas das áreas dos retângulos á bê é éfe e BCDE são, respectivamente, 4A bê e 3A bê.
A medida da área do retângulo á cê dê éfe é obtida adicionando as medidas das áreas dos retângulos á bê é éfe e BCDE, ou seja, 4A bê + 3A bê. Acompanhe como podemos fazer esse cálculo:
4ab + 3ab = (4 + 3)ab = 7ab
Portanto, a medida da área do retângulo á cê dê éfe é representada pelo monômio 7A bê.
b) Sabendo que a medida da área do retângulo á cê dê éfe é representada pelo monômio 9xy, qual é a expressão algébrica que representa a medida da área do retângulo BCDE?
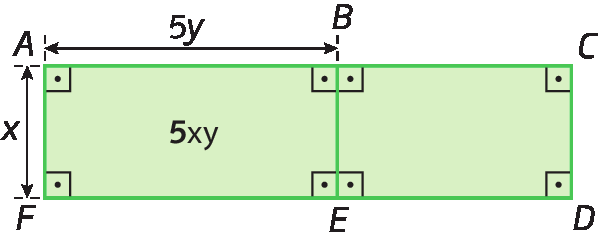
A medida da área do retângulo BCDE é obtida subtraindo da medida da área de á cê dê éfe a medida da área do retângulo á bê é éfe, ou seja, calculando 9xis ípsilon menos 5xis ípsilon. Acompanhe como podemos fazer esse cálculo.
9xy menos 5xy = (9 menos 5)xy = 4xy
Portanto, a medida da área do retângulo BCDE é representada pelo monômio 4xy.
Se uma expressão tem monômios semelhantes e não semelhantes, efetuamos a adição ou a subtração dos semelhantes e conservamos os demais. Nesse caso, dizemos que foi efetuada uma redução de termos semelhantes. Acompanhe os exemplos:


Atividades
Faça as atividades no caderno.
11. Observe a figura e responda às questões.
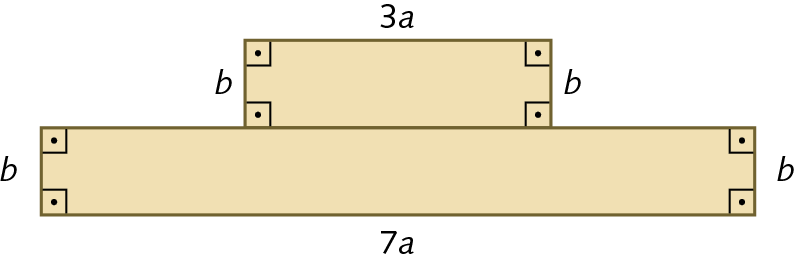
a) Que monômio representa a medida da área do retângulo um? E do retângulo dois?
b) Que monômio representa a medida da área total da figura?
c) Sendo a = 0,85 centímetro e b = 0,75 centímetro, qual é a medida da área total da figura?
12. Simplifique as expressões:
a) 5xy + 15xy menos 12xy + 2xy
b)
Sentença matemática. Abre parênteses, menos fração 1 sobre 3, fim da fração, xy, fecha parênteses, mais, abre parênteses, fração 4 sobre 9, fim da fração, xy, fecha parênteses, mais, abre parênteses, menos fração 1 sobre 9, fim da fração, xy, fecha parênteses.c) 9x elevado a 4y elevado a 3 menos 18x elevado a 4y elevado a 3 menos 10x elevado a 4y elevado a 3 + 2x elevado a 4y elevado a 3
13. Que monômio devemos adicionar à expressão menos3á bê cê para obter 5á bê cê?
14. Dada a expressão algébrica
Sentença matemática. Fração 4 sobre 3, fim da fração, x elevado ao quadrado, y menos fração 3 sobre 8, fim da fração, x elevado ao quadrado, y mais fração 4 sobre 9, fim da fração, x elevado ao quadrado, y menos fração 1 sobre 4, fim da fração, x elevado ao quadrado, y.
, determine o seu valor numérico para x = menos1 e y = 2.
Multiplicação de monômios
Inicialmente, vamos recordar que: a elevado a m ⋅ a elevado a n = a elevado a m ⁺ⁿ, sendo a um número real não nulo e m e n números inteiros. Agora, observe os exemplos a seguir.
a) Qual é a expressão algébrica que representa a medida da área do retângulo a bê cê dê?
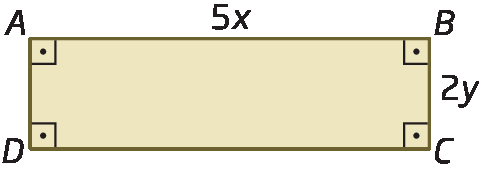
A medida da área do retângulo a bê cê dê é dada pela multiplicação dos monômios 5x e 2y:
5x ⋅ 2y = (5 ⋅ 2) ⋅ (x ⋅ y) = 10xy
Portanto, o monômio 10xy representa a medida da área desse retângulo.
b) Qual é a expressão algébrica que representaa medida do volume V do paralelepípedo reto-retângulo a seguir?
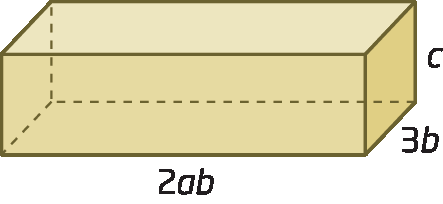
A medida do volume desse paralelepípedo reto-retângulo é determinada multiplicando-se os monômios 2ab, 3b e c:
2ab ⋅ 3b ⋅ c = (2 ⋅ 3 ⋅ 1) ⋅ (a ⋅ b ⋅ b ⋅ c) = 6abelevado a 2c
Portanto, o monômio 6abelevado a 2c representa a medida do volume desse paralelepípedo.
A multiplicação de monômios é efetuada multiplicando-se os coeficientes e as partes literais entre si. Observe mais alguns exemplos:

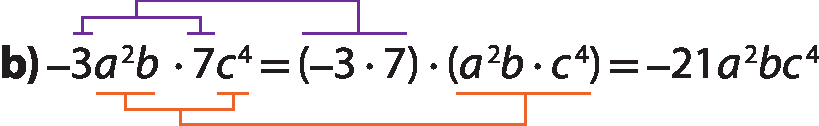
Atividades
Faça as atividades no caderno.
15. Determine os produtos.
a) x elevado a 7 ⋅ x elevado a 8
b) (+3x) ⋅ (menos8x)
c) (menos2x elevado a 2y) ⋅ (+7xy)
d) (+4ab elevado a 2) ⋅ (menos2abc)
16. Qual é o monômio que representa a medida da área de cada figura?
a)
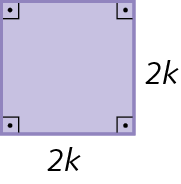
b)

17. Efetue as multiplicações.
a) x elevado a 2 ⋅ x elevado a 4 ⋅ x elevado a 13
b)
Sentença matemática. Abre parênteses, a fração 1 sobre 10, fim da fração, vezes yk, fecha parênteses, vezes, abre parênteses, a fração 10 sobre 7, fim da fração, vezes x, fecha parênteses, vezes, abre parênteses, 14z, fecha parênteses.c) (menos0,4a elevado a 2b) ⋅ (+0,01b) ⋅ (menos0,02a elevado a 2b elevado a 3)
d) (menos3mnp) ⋅ (+mp) ⋅ (menos18mn)
18. Sabendo que a ⋅ B = C + D, determine o monômio D, sendo a = 2x elevado a 2y elevado a 3, B = menos4xy e C = menos14x elevado a 3y elevado a 4.
19. Dê um exemplo de dois monômios tais que o seu produto seja 6p elevado a 3q.
20. Observe a figura e responda às questões.
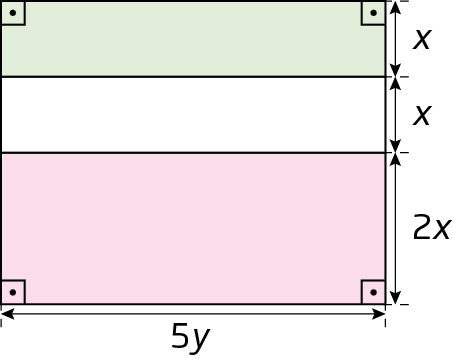
a) Qual é o monômio que representa a medida da área da parte verde da figura? E a medida da área da parte rosa?
b) Qual é o monômio que representa a medida da área total da figura?
Divisão de monômios
Inicialmente, vamos recordar que:
a elevado a m dividido por a elevado a n = a elevado a m ‒ ⁿ, sendo a um número real não nulo e m e n dois números inteiros.
Agora, acompanhe como podemos dividir monômios.
a)
Sentença matemática. Abre parênteses, 20 x elevado a 5, fecha parênteses, dividido por, abre parênteses, 4 x elevado a 3, fecha parênteses, é igual a fração 20 x elevado a 5 sobre 4 x elevado a 3, fim da fração, é igual a 5 x elevado a, início do expoente, 5 menos 3, fim do expoente, é igual a 5 x elevado ao quadrado.b)
Sentença matemática. Abre parênteses, menos fração 1 sobre 2, fim da fração, a elevado a 5, fim do expoente, b elevado ao quadrado, fecha parênteses, dividido por, abre parênteses, 3 a elevado a 3, fim do expoente, b, fecha parênteses, é igual a fração, início do numerador, menos fração 1 sobre 2, fim da fração, a elevado a 5, fim do expoente, b elevado ao quadrado, fim do numerador, início do denominador, 3 a elevado a 3, fim do expoente, b, fim do denominador, é igual a, abre parênteses, menos fração 1 sobre 2, fim da fração, dividido por 3, fecha parênteses, vezes, abre parênteses, fração, início do numerador, a elevado a 5, fim do expoente, b elevado a quadrado, fim do numerador, início do denominador, a elevado a 3, fim do expoente, b, fim do denominador, fecha parênteses, é igual a menos fração 1 sobre 6, fim da fração, a elevado a, início do expoente, 5 menos 3, fim do expoente, b elevado a, início do expoente, 2 menos 1, fim do expoente, é igual a menos fração 1 sobre 6, fim da fração, a elevado ao quadrado, b.c)
Sentença matemática. Abre parênteses, menos 30 x elevado a 4, fim do expoente, y elevado a 3, fim do expoente, z elevado ao quadrado, fecha parênteses, dividido por, abre parênteses, menos 6x, y elevado a 3, fim do expoente, z, fecha parênteses, é igual a fração, início do numerador, menos 30 x elevado a 4, fim do expoente, y elevado a 3, fim do expoente, z elevado ao quadrado, fim do numerador, início do denominador, menos 6x, y elevado a 3, fim do expoente, z, fim do denominador, é igual a 5 x elevado a, início do expoente, 4 menos 1, fim do expoente, y elevado a, início do expoente, 3 menos 3, fim do expoente, z elevado a, início do expoente, 2 menos 1, fim do expoente, é igual a 5 x elevado a 3, fim do expoente, z.A divisão de monômios com divisor diferente de zero é efetuada dividindo coeficiente por coeficiente e parte literal por parte literal.
Atividades
Faça as atividades no caderno.
21. Qual é o monômio que representa o resultado de cada divisão?
a) (16x elevado a 7) dividido por (4x elevado a 3)
b) (menos60a elevado a 5b elevado a 3) dividido por (menos15a elevado a 2b)
c) (menos125a elevado a 5b elevado a 3c elevado a 7) dividido por (menos25a elevado a 4b elevado a 3c elevado a 2)
d) (18x elevado a 5y elevado a 4) dividido por (‒9x elevado a 5y elevado a 3)
e)
abre parênteses, menos 3 quintos vezes x y vezes z ao quadrado, fecha parênteses, dividido por, abre parênteses, 0 vírgula 2 vezes y z, fecha parênteses.f) (0,2x elevado a 2y elevado a 4) dividido por (0,25xy elevado a 2)
g) (b elevado a 2m elevado a 2) dividido por (‒5bm)
h) (menos250x elevado a 3) dividido por (50x elevado a 3)
i) (18x elevado a 4) dividido por (3x elevado a 2)
j) (menos10x elevado a 3) dividido por (menos2x elevado a 2)
22. Responda às questões.
a) Por qual monômio devemos dividir
Sentença matemática. Fração 2 sobre 3, fim da fração, x elevado ao quadrado, y elevado a 3.para obter
Sentença matemática. Menos fração 1 sobre 5, fim da fração, xy .?
b) Qual é o monômio que, multiplicado por 10ab elevado a 3, tem como resultado 15a elevado a 2b elevado a 5?
c) Qual é o monômio que devemos multiplicar por menos2xy para obter
3 quartos vezes x ao quadrado vezes y ao cubo.?
23. Efetue as divisões a seguir.
a) (menos30a elevado a 4b elevado a 6) dividido por (menos6ab elevado a 5)
b) (x elevado a 4y elevado a 4z elevado a 4) dividido por (x elevado a 2y elevado a 3z elevado a 4)
c) (6x elevado a 6) dividido por (menos3xelevado a 4)
Polinômio
Acompanhe a situação.
Márcia faz salgados e doces, por encomenda, para vender.

Os salgados são vendidos a R$ 0,45zero reais e quarenta e cinco centavos a unidade, e os doces, a R$ 0,35zero reais e trinta e cinco centavos a unidade. Quanto Márcia cobrará por uma encomenda de x salgados e y doces?
Podemos representar o total, em reais, arrecadado com a venda dos salgados pelo monômio 0,45x e o total, em reais, arrecadado com a venda dos doces pelo monômio 0,35y. Assim, para representar o total, em reais, arrecadado pelas vendas de salgados e doces, devemos adicionar os monômios:

Expressões algébricas formadas por um monômio ou pela adição e ou ou subtração de monômios denominam-se polinômios.
Considere os exemplos a seguir.
a) 5x + 8 é um polinômio de dois termos, também chamado de binômio.
b) y elevado a 2 menos 7y + 10 é um polinômio de três termos, também chamado de trinômio.
c) a elevado a 3 + 5a elevado a 2b + 6ab elevado a 2 + b elevado a 3 é um polinômio de quatro termos.
Observações
1. Um polinômio cujos coeficientes são todos iguais a zero é denominado polinômio nulo. Por exemplo:
0x elevado a 3 + 0x elevado a 2 + 0x
2. Um monômio é um polinômio de um termo.
3. O termo do polimônio que não apresenta variáveis (letras) é chamado de termo independente. Nos exemplos anteriores, o termo independente do primeiro polinômio é 8 e o do segundo é 10. No exemplo do item c, não há termo independente.
Atividades
Faça as atividades no caderno.
24. Foram colocadas x caixas de laranjas e y caixas de maçãs em uma embarcação. Determine o polinômio que representa o total de frutas colocadas na embarcação, sabendo que cada caixa de laranjas contém 120 unidades e cada caixa de maçãs, 80 unidades.

25. Na figura a seguir, os lotes a, B e C têm medidas de áreas iguais. Determine um polinômio que expresse a medida da área de cada lote.
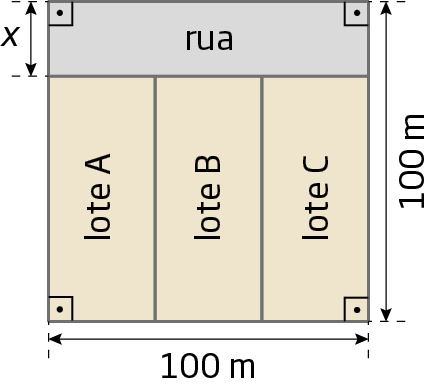
Grau de um polinômio
Considere o polinômio x elevado a 4y menos x elevado a 5y elevado a 3 + 3x elevado a 2yz e os termos que o compõe.
O grau de cada termo é dado pela soma dos expoentes da parte literal. Comprove:
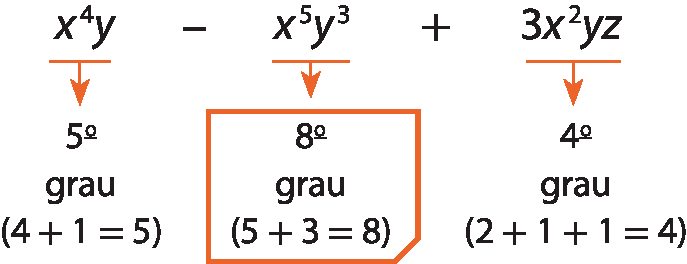
O grau de um polinômio é determinado pelo termo de maior grau.
Portanto, o polinômio x elevado a 4y menos x elevado a 5y elevado a 3 + 3x elevado a 2yz é do 8º grau, já que o termo de maior grau é xelevado a 5yelevado a 3.
Também é possível estabelecer o grau de um polinômio em relação a determinada variável. Nesse caso, o grau do polinômio corresponde ao maior expoente com que a variável figura em um dos termos não nulos do polinômio.
Observe alguns exemplos.
a) O polinômio x elevado a 4 menos 3x elevado a 2y elevado a 3 + 5x elevado a 3y é do 4º grau em relação a x e do 3º grau em relação a y.
b) O polinômio a elevado a 6b elevado a 4 + 10bc é do 6º grau em relação a a, do 4º grau em relação a b e do 1º grau em relação a c.
Atividades
Faça as atividades no caderno.
26. Determine o grau dos polinômios.
a) 5a elevado a 2 + b elevado a 3
b) 4x elevado a 2 + 2x elevado a 2y elevado a 3 + 5y elevado a 4
c) 5m elevado a 2 + 6mn + 4n elevado a 3
d) 16ab elevado a 3 + 7a elevado a 2 + 5b elevado a 2
e) menos7x elevado a 4y + x elevado a 2y menos 2x elevado a 3y elevado a 4
f) x elevado a 4y elevado a 2 menos 2xy elevado a 3
g) 4a elevado a 2b elevado a 3 + 5a elevado a 5
27. Determine o grau de cada polinômio em relação à variável x e à variável y, respectivamente.
a) 2x elevado a 2 + 5xy elevado a 3
b) x elevado a 5y menos x elevado a 3y elevado a 4
c) 2x elevado a 2y elevado a 2 menos 5x elevado a 3y
d) ax elevado a 3 menos bx elevado a 2 + 2abxy elevado a 2
e) 3x elevado a 2y + 5xy elevado a 2 menos y elevado a 4
f) x elevado a 2 + 2xy + y elevado a 3
Adição de polinômios
Observe os polígonos a bê cê dê e ême êne ó.
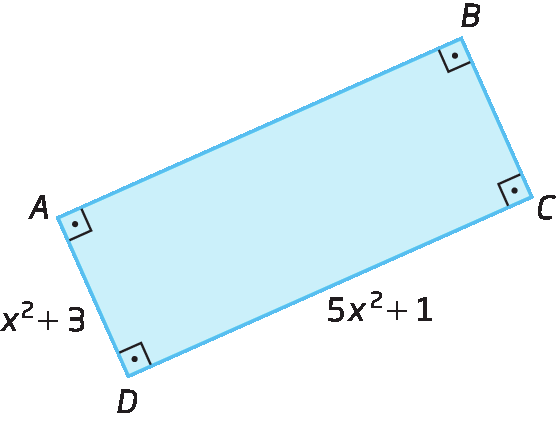
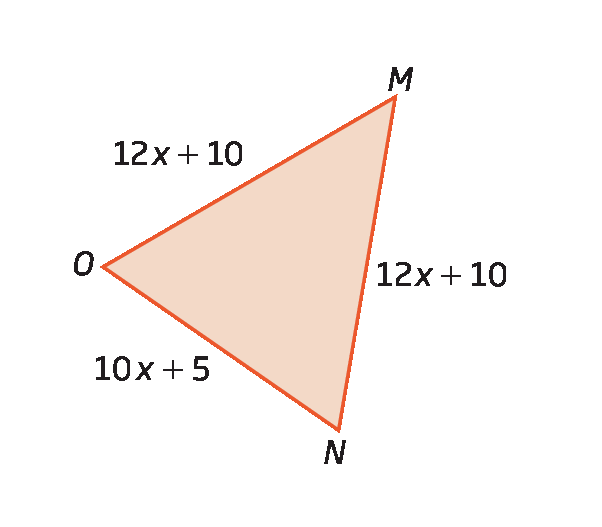
Sabendo que a bê cê dê representa um retângulo e ême êne ó, um triângulo isósceles, como podemos determinar a medida do perímetro de cada polígono?
Temos que as medidas dos comprimentos dos lados do retângulo a bê cê dê são indicadas por x elevado a 2 + 3 e 5x elevado a 2 + 1. Desse modo, podemos representar a medida do perímetro da seguinte maneira:
(x elevado a 2 + 3) + (5x elevado a 2 + 1) + (x elevado a 2 + 3) + (5x elevado a 2 + 1)
Agrupando os termos semelhantes e reduzindo-os, obtemos:
x elevado a 2 + 5x elevado a 2 + x elevado a 2 + 5x elevado a 2 + 3 + 1 + 3 + 1 = 12xelevado a 2 + 8
Assim, 12x elevado a 2 + 8 representa a medida do perímetro do retângulo a bê cê dê.
Agora, para determinar a medida do perímetro do triângulo isósceles ême êne ó, cujas medidas dos comprimentos dos lados são indicadas por 12x + 10, 12x + 10 e 10x + 5, fazemos:
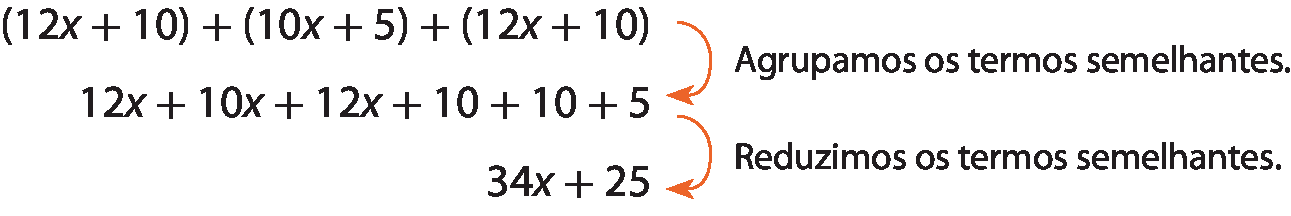
Logo, 34x + 25 representa a medida do perímetro do triângulo isósceles ême êne ó.
Observação
Quando adicionamos um polinômio a outro e obtemos como resultado um polinômio nulo, dizemos que eles são opostos. Por exemplo, o polinômio menosx elevado a 2 + 5x menos 4 é oposto ao polinômio x elevado a 2 menos 5x + 4, pois:
(menosx elevado a 2 + 5x menos 4) + (x elevado a 2 menos 5x + 4) = menosx elevado a 2 + x elevado a 2 + 5x menos 5x menos 4 + 4 = 0
Subtração de polinômios
Vamos determinar a diferença entre os polinômios 5x elevado a 3 menos 4x + 8 e 2x elevado a 3 + 6x elevado a 2 menos 2, ou seja:
(5xelevado a 3 menos 4x + 8) menos (2x elevado a 3 + 6x elevado a 2 menos 2)
Na subtração de polinômios, podemos adicionar o primeiro polinômio ao oposto do segundo. Assim:
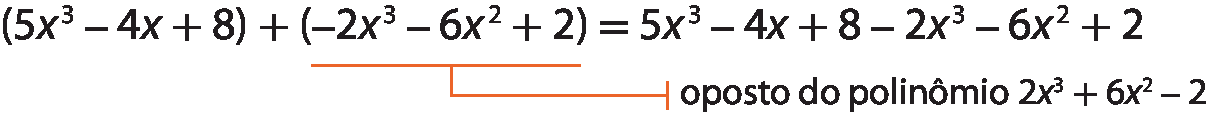
Agora, podemos agrupar os termos semelhantes e reduzi-los:
5x elevado a 3 menos 2x elevado a 3 menos 6x elevado a 2 menos 4x + 8 + 2 = 3x elevado a 3 menos 6x elevado a 2 menos 4x + 10
Portanto, 3x elevado a 3 menos 6x elevado a 2 menos 4x + 10 representa a diferença entre os polinômios 5x elevado a 3 menos 4x + 8 e 2x elevado a 3 + 6x elevado a 2 ‒ 2.
Atividades
Faça as atividades no caderno.
28. Efetue as operações reduzindo os termos semelhantes.
a) (menos3x elevado a 2 + 5x menos 8) + (6x elevado a 2 menos 4x menos 3)
b) (8ab menos 7bc + 3ac) + (menos5bc + 3ab menos ac)
c)
Sentença matemática. Abre parênteses, menos fração 3x sobre 2, fim da fração, menos fração y sobre 3, fim da fração, fecha parênteses, mais, abre parênteses, fração x sobre 5, fim da fração, menos fração y sobre 4, fim da fração, fecha parênteses, mais, abre parênteses, 2x mais y, fecha parênteses.d)
Sentença matemática. Abre parênteses, fração a sobre 2, fim da fração, mais b, menos 6, fecha parênteses, mais, abre parênteses, fração 2a sobre 3, fim da fração, mais 2b menos 5, fecha parênteses.29. Escreva no caderno, na fórma reduzida, o polinômio que representa a medida doperímetro da figura a seguir.

30. Em uma partida de tênis, Roberta deu x saques e acertou 45% deles. Luísa, sua adversária, deu y saques e acertou 60% menos 2. Nessas condições, determine o polinômio que representa a quantidade de saques que as duas acertaram juntas.
31. Dado o polinômio menosx elevado a 3 + 2x elevado a 2 menos 4x + 5, responda às questões.
a) Qual é o oposto desse polinômio?
b) Qual é o resultado da adição desse polinômio com seu oposto?
32. Efetue as operações reduzindo os termos semelhantes.
a) (6a elevado a 2 menos 7ab + 8b elevado a 2) menos (8ab + 5a elevado a 2 menos 7b elevado a 2)
b) (5x elevado a 3 menos 4x elevado a 2 + 6x + 8) menos (7x elevado a 3 + 8x elevado a 2 menos 10x)
c) (5m menos 2mn + 7n) menos (2m menos 8mn menos 10n)
d)
Sentença matemática. Abre parênteses, fração x sobre 3, fim da fração, mais fração xy sobre 2, fim da fração, menos fração y sobre 5, fim da fração, fecha parênteses, menos, abre parênteses, fração 3y sobre 2, fim da fração, menos fração 2xy sobre 5, fim da fração, mais fração x sobre 4, fim da fração, fecha parênteses.
e) (5x elevado a 2 menos 4x + 9) menos (8x elevado a 2 menos 6x + 3)
33. Sendo a = 6x elevado a 2 menos 3x menos 8, B = 5x elevado a 2 + 4x menos 3 e C = x elevado a 2 menos 10x, determine:
a) a menos B
b) B menos a
c) a + B menos C
d) a menos (B + C )
34. Determine o polinômio que, adicionado a 6a elevado a 2 menos 7ab + 8b elevado a 2 menos 5a elevado a 2b elevado a 2, tem como resultado 2ab menos a elevado a 2 + 2b elevado a 2 + 3a elevado a 2b elevado a 2.
Multiplicação de polinômios
Acompanhe a situação.
Na casa de Pedro, o escritório fica ao lado do quarto, conforme o esquema.
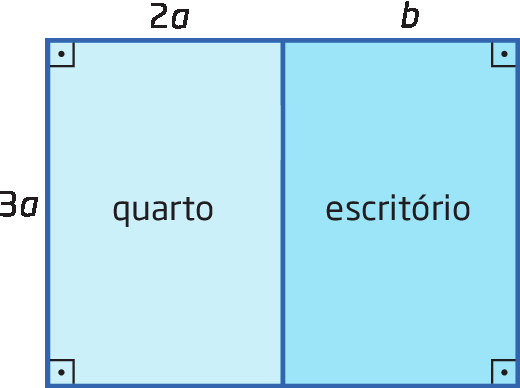
Que expressão algébrica representa a medida da área total desses dois cômodos?
Podemos determinar essa expressão algébrica de dois modos:
1º) Multiplicando a medida do comprimento pela medida da largura dos dois ambientes juntos.
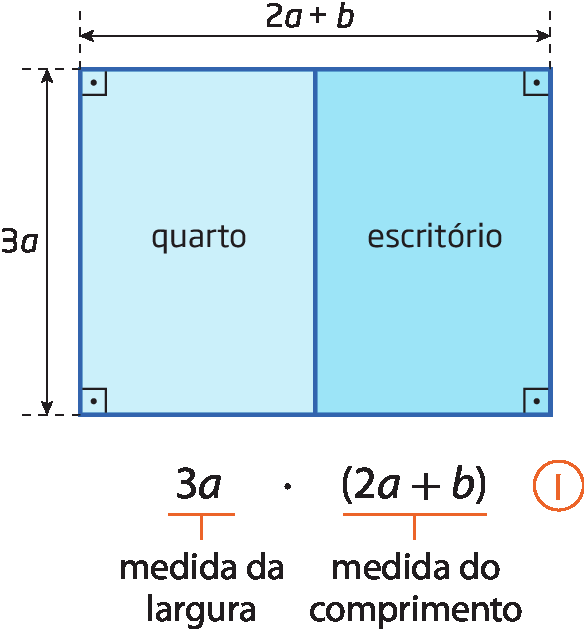
2º) Adicionando a medida da área do quarto e do escritório.
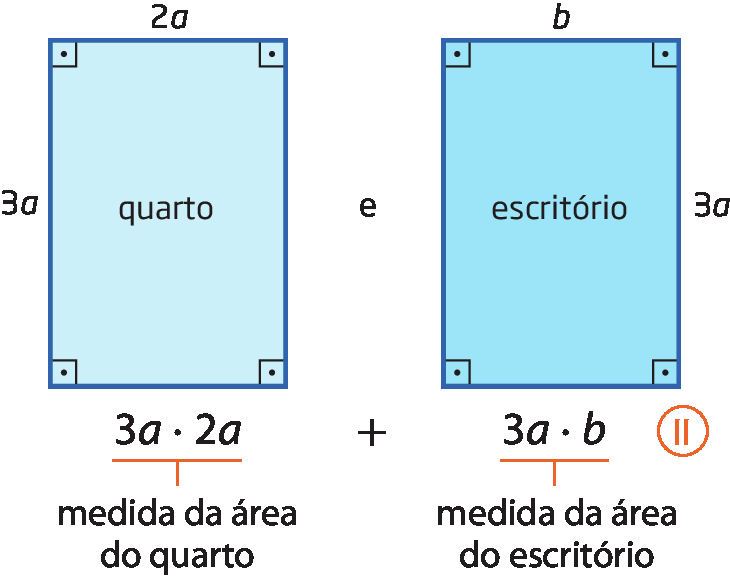
De um e dois, verificamos que 3a ⋅ (2a + b) = 3a ⋅ 2a + 3a ⋅ b. Observe que, ao aplicarmos a propriedade distributiva em 3a ⋅ (2a + b), obtemos 3a ⋅ 2a + 3a ⋅ b:
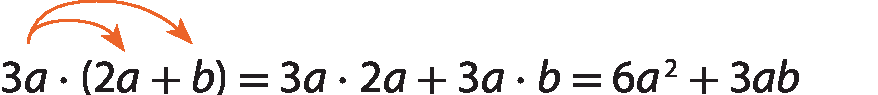
Portanto, o polinômio 6a elevado a 2 + 3ab representa a medida da área total desses cômodos.
Na multiplicação de um monômio por um polinômio, usamos a propriedade distributiva, multiplicando o monômio por todos os termos do polinômio e adicionando, em seguida, os resultados.
Acompanhe outra situação.
O esquema a seguir mostra as dimensões do apartamento de Luís.

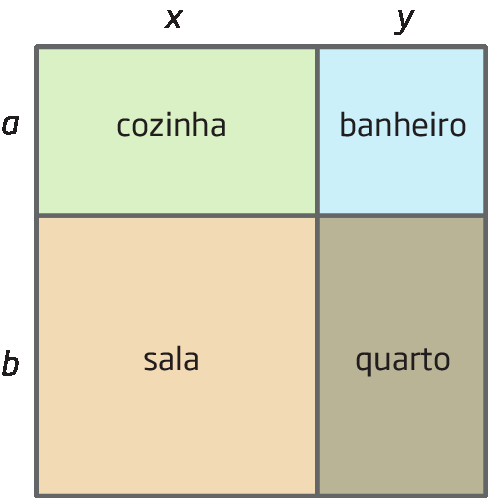
Considerando que todos os cômodos do apartamento são retangulares, que expressão algébrica póde representar a medida da área total do apartamento?
Podemos determinar a expressão algébrica da medida da área total de dois modos:
1º) Multiplicando as medidas da largura e do comprimento do apartamento.
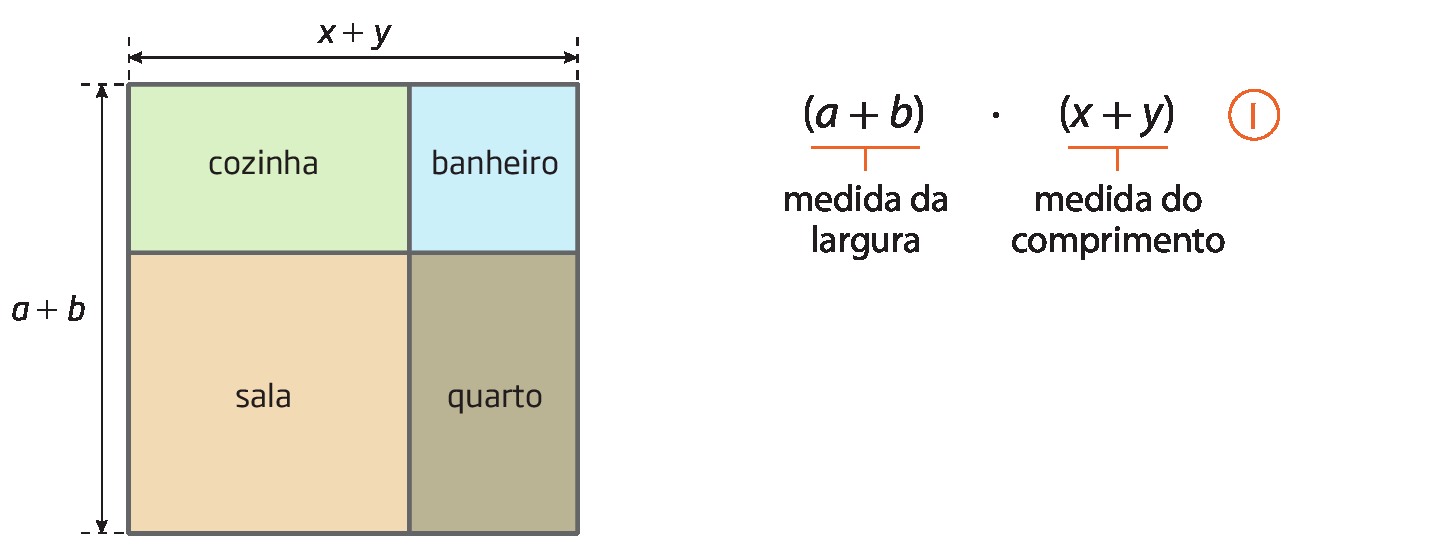
2º) Adicionando as medidas das áreas de cada um dos quatro cômodos.
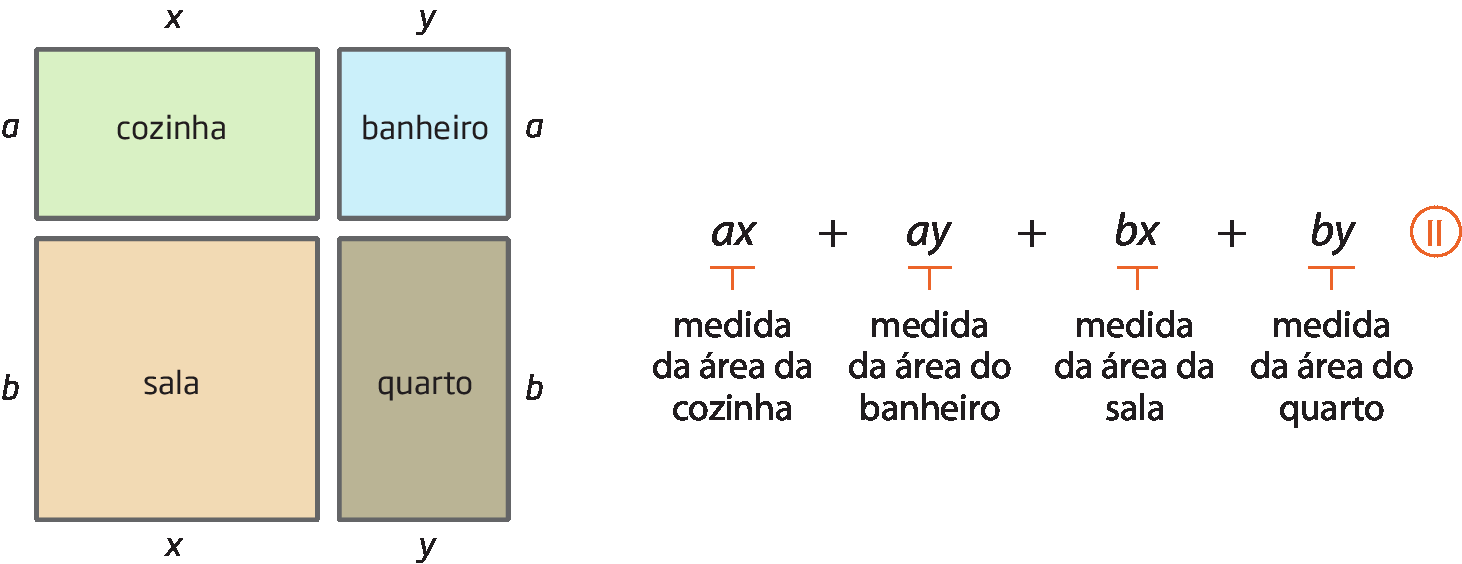
De um e dois, verificamos que (a + b) ⋅ (x + y) = ax + ay + bx + by. Observe que, aplicando a propriedade distributiva em (a + b) ⋅ (x + y), obtemos ax + ay + bx + by:
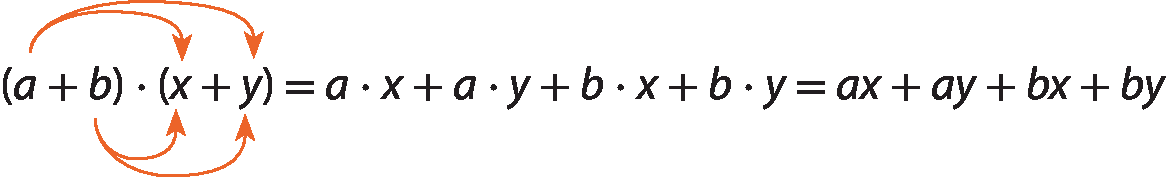
Portanto, o polinômio ax + ay + bx + by representa a medida da área total do apartamento.
Na multiplicação de dois polinômios, utilizamos a propriedade distributiva, multiplicando cada termo de um polinômio por todos os termos do outro, e, em seguida, adicionamos os novos termos obtidos.
Considere alguns exemplos.
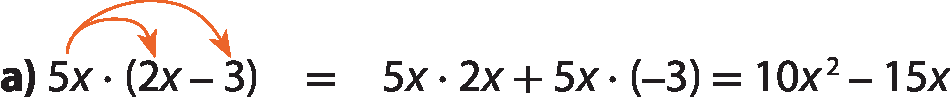
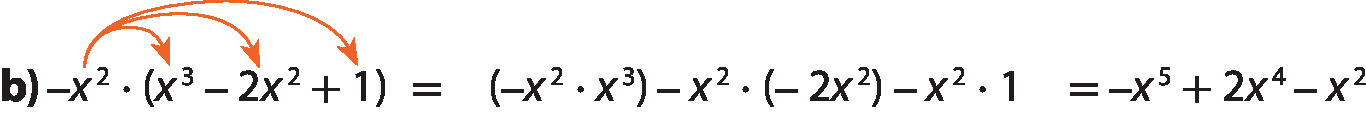
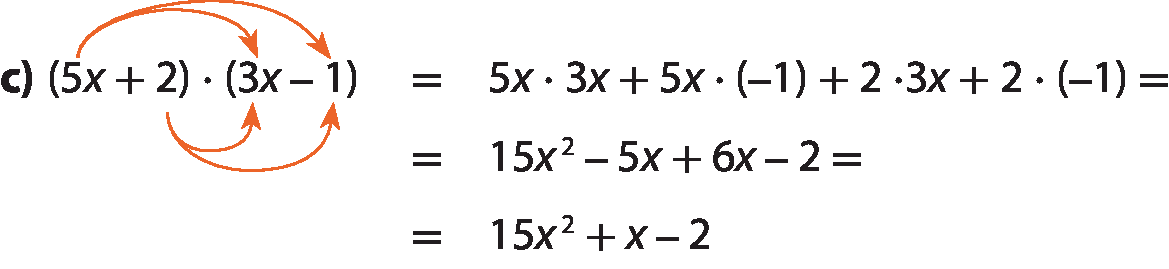
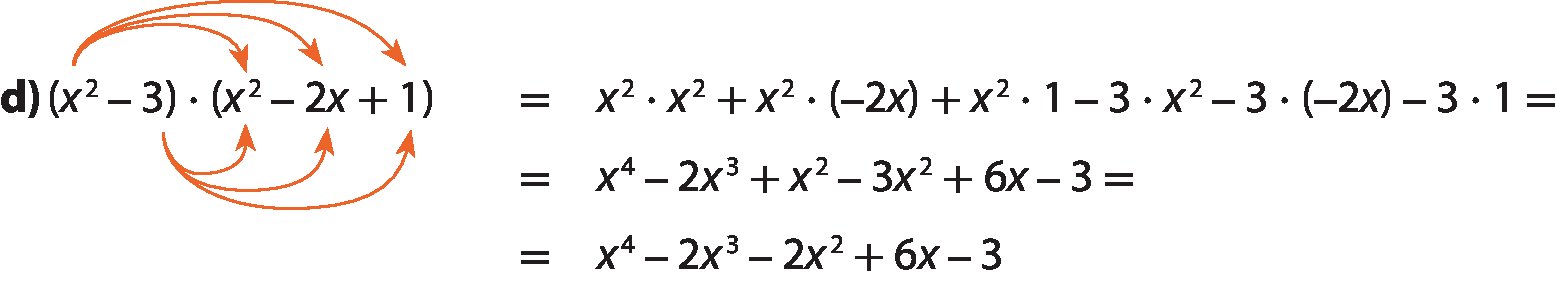
Atividades
Faça as atividades no caderno.
35. Efetue os produtos.
a) 5 ⋅ (6x menos 2)
b) m elevado a 2 ⋅ (m menos n)
c) (6a elevado a 2 + 10ab + b elevado a 2) ⋅
Abre parênteses, menos 3 quartos vezes a, fecha parênteses.d)
Sentença matemática. Fração de numerador a elevado ao quadrado, b, e denominador 2, fim da fração, vezes, abre parênteses, fração, b elevado ao quadrado, sobre 3, fim da fração, menos fração a elevado ao quadrado, sobre 4, fecha parênteses.36. Determine o polinômio que representa a medida da área do retângulo a seguir.

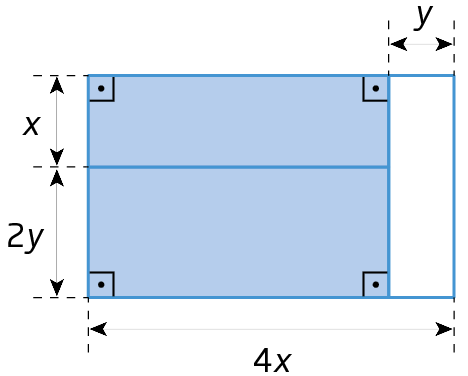
37. Qual é o polinômio que representa a medida da área da região azul da figura?
38. Efetue as operações reduzindo os termos semelhantes.
a) (3x + 2) ⋅ (x menos 3)
b) (3a elevado a 2 + 2a + 4) ⋅ (menosa menos 3)
c) (menos2x + 5) ⋅ (6x elevado a 2 + 4x + 3)
d) (5x elevado a 2 + 2x menos 1) ⋅ (x menos 3)
e) (a + b) ⋅ (a menos b)
39. Sendo a = x + 5, B = x elevado a 2 + 2x + 1 e C = 2x elevado a 2 menos 4, determine:
a) a ⋅ B
b) bê ⋅ cê
c) a ⋅ B ⋅ cê
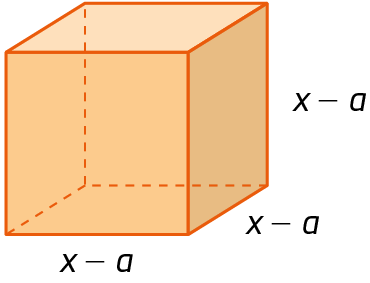
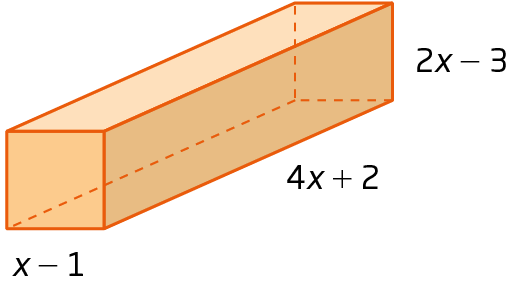
40. Determine o polinômio que representa a medida do volume de cada figura.
a)
b)
Divisão de polinômio por monômio
Considere o retângulo a bê cê dê e as expressões algébricas que representam a medida do comprimento da altura e a medida de sua área.

Medida da área do retângulo a bê cê dê: 12x elevado a 4 menos 8x elevado a 3 + 6x elevado a 2
Medida do comprimento da altura: 2x
Qual é a expressão algébrica que representa a medida do comprimento da base desse retângulo?
Para determinar a expressão que representa a medida do comprimento da base do retângulo a bê cê dê, temos que dividir o polinômio 12x elevado a 4 menos 8x elevado a 3 + 6x elevado a 2 (medida da área do retângulo) pelo monômio 2x (medida do comprimento da altura do retângulo).
Portanto, a medida do comprimento da base desse retângulo póde ser representada por 6x elevado a 3 menos 4x elevado a 2 + 3x.
O quociente de um polinômio por um monômio não nulo é obtido dividindo-se cada termo do polinômio pelo monômio e adicionando os novos termos obtidos.
Observe mais alguns exemplos de divisão de polinômios por monômios.
a)
Sentença matemática. Abre parênteses, 6 x elevado a 5, fim do expoente, mais 2 x elevado a 3, fecha parênteses, dividido por x, é igual a fração, 6 x elevado a 5, fim do expoente, sobre x, fim da fração, mais fração 2 x elevado a 3, fim do expoente, sobre x, fim da fração, é igual a 6 x elevado a, início do expoente, 5 menos 1, fim do expoente, mais 2 x elevado a, início do expoente, 3 menos 1, fim do expoente, é igual a 6 x elevado a 4, fim do expoente, mais 2 x elevado ao quadrado.b)
Sentença matemática. Abre parênteses, 24 x elevado ao quadrado, b elevado a 3, fim do expoente, menos 18 a elevado a 3, fim do expoente, b elevado a 4, fim do expoente, menos 6a, b elevado a 5, fim do expoente, fecha parênteses, dividido por 3a, b elevado a 3, fim do expoente, é igual a fração de numerador 24 a elevado ao quadrado, b elevado a 3, fim do expoente, e denominador 3a, b elevado a 3, fim do expoente, fim da fração, menos a fração de numerador 18 a elevado a 3, fim do expoente, b elevado a 4, fim do expoente, e denominador 3a, b elevado a 3, fim do expoente, fim da fração, menos a fração de numerador 6a, b elevado a 5, fim do expoente, e denominador 3a, b elevado a 3, fim do expoente, fim da fração, é igual a.= 8a elevado a 2 ⁻ ¹b elevado a 3 ⁻ elevado a 3 menos 6a elevado a 3 ⁻ ¹b elevado a 4 ⁻ elevado a 3 menos 2a elevado a 1 ⁻ ¹b elevado a 5 ⁻ elevado a 3 = 8a menos 6a elevado a 2b menos 2b elevado a 2
c)
Sentença matemática. Abre parênteses, 4 a elevado ao quadrado, b elevado a 3, fim do expoente, menos 2 a elevado a 3, fim do expoente, b elevado a 4, fim do expoente, fecha parênteses, dividido por, 6a, b elevado ao quadrado, é igual a fração de numerador 4 a elevado ao quadrado, b elevado a 3, fim do expoente, e denominador 6a, b elevado ao quadrado, fim da fração, menos a fração de numerador 2 a elevado a 3, fim do expoente, b elevado a 4, fim do expoente, e denominador 6a, b elevado ao quadrado, fim da fração, é igual a fração 2 sobre 3, fim da fração, a elevado a, início do expoente, 2 menos 1, fim do expoente, b elevado a, início do expoente, 3 menos 2, fim do expoente, menos a fração 1 sobre 3, fim da fração, a elevado a, início do expoente, 3 menos 1, fim do expoente, b elevado a, início do expoente, 4 menos 2, fim do expoente, é igual a fração 2 sobre 3, fim da fração, ab, menos a fração 1 sobre 3, fim da fração, a elevado ao quadrado, b elevado ao quadrado.Atividades
Faça as atividades no caderno.
41. Efetue as divisões.
a) (10x elevado a 6 + 12x elevado a 5) dividido por (2x elevado a 3)
b) (30a elevado a 2 + 60ab + 90b elevado a 2) dividido por (30)
c) (menos6ab + 9a elevado a 2b + 12ab elevado a 2) dividido por (3ab)
d)
Sentença matemática. Abre parênteses, fração 5 sobre 6, fim da fração, x elevado ao quadrado, menos fração, 3 sobre 4, fim da fração, x , fecha parênteses, dividido por, abre parênteses, menos fração 2 sobre 3, fim da fração, x, fecha parênteses.e) (m elevado a 5 + m elevado a 3) dividido por (menosm elevado a 2)
f) (m elevado a 2n elevado a 3 + mn elevado a 4 + m elevado a 5n elevado a 2) dividido por (menosmn)
42. O produto de um monômio por um polinômio é 20a elevado a 2b elevado a 5 + 30a elevado a 3b elevado a 7. Sendo o monômio 5a elevado a 2b elevado a 3, determine o polinômio.
43. A medida da área de um retângulo é representada por b elevado a 2x elevado a 2 + 2bx. Sendo bx a medida do comprimento da altura, determine a expressão algébrica que representa a medida do comprimento da base do retângulo.
44. Determine o quociente de 10x elevado a 2y elevado a 3 menos 20x elevado a 3y elevado a 5 + 30x elevado a 4y elevado a 6 pelos monômios:
a) 10xy
b) menos20xy elevado a 3
c) 5x elevado a 2y elevado a 2
d) menos10x elevado a 2y

2 Produtos notáveis
Quadrado da soma de dois termos
O quadrado da soma de dois termos, a e b, é indicado por (a + b)elevado a 2. Desenvolvendo esse produto, obtemos:
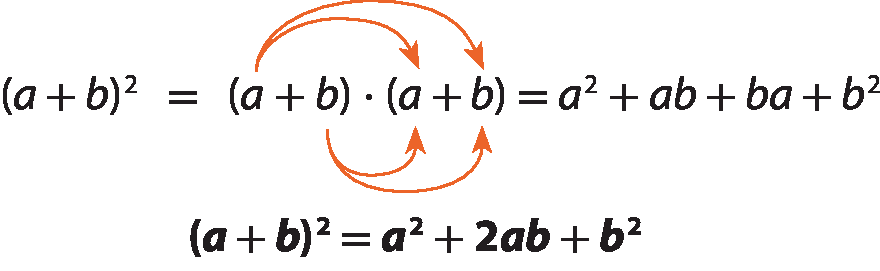
Ou seja:
O quadrado da soma de dois termos é igual ao quadrado do primeiro termo mais duas vezes o produto dos dois termos mais o quadrado do segundo termo.

Observe alguns exemplos.
a) (x + y) elevado a 2 = x elevado a 2 + 2xy + y elevado a 2
b)
Sentença matemática. Abre parênteses, a fração a sobre 5, fim da fração, mais 3b, fecha parênteses, elevado ao quadrado, é igual a, abre parênteses, fração a sobre 5, fecha parênteses, elevado ao quadrado, mais 2 vezes fração a sobre 5, fim da fração, vezes, 3b, mais abre parênteses, 3b, fecha parênteses, elevado ao quadrado, é igual a fração a elevado ao quadrado sobre 25, fim da fração, mais fração 6ab sobre 5, fim da fração, mais 9 b elevado ao quadrado.Representação geométrica
Vamos representar geometricamente o quadrado da soma de dois termos, a e b, que indicamos por (a + b)elevado a 2, admitindo os números a e b positivos.
Considere o quadrado a bê cê dê cuja medida do comprimento do lado é representada por a + b.
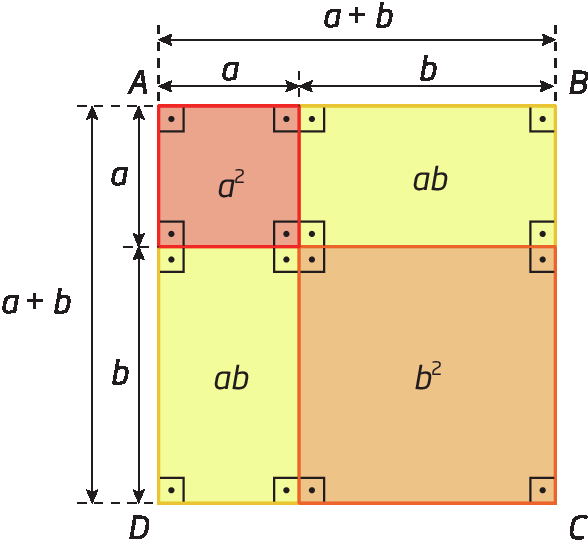
Determinando a medida da área a do quadrado de duas maneiras, obtemos:
•

•

Portanto, as expressões (a + b)elevado a 2 e a elevado a 2 + 2ab + b elevado a 2 representam a mesma medida de área, ou seja:
(a + b) elevado a 2 = a elevado a 2 + 2ab + b elevado a 2

Um pouco de história
Faça a atividade no caderno.
A Álgebra na Antiguidade
A Álgebra geométrica grega é apresentada de fórma muito interessante na obra Os elementos, de Euclides. No livro dois dessa obra, encontramos o conceito de produtos notáveis e, na proposição 4, o seguinte texto:


Nessa proposição, vemos como os problemas que envolviam Álgebra eram concebidos e apresentados na Antiguidade. O uso de figuras era extremamente importante para o melhor entendimento dos textos. Na figura a seguir estão representados os itens 1, 2 e 3 dessa proposição de Euclides, sendo:
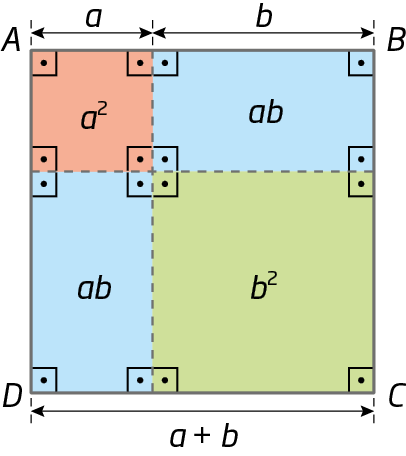
(1) o quadrado a bê cê dê;
(2) os quadrados de medida de áreas a elevado a 2 e b elevado a 2;
(3) os retângulos de medida de áreas A bê.
Atividade
Represente geometricamente o quadrado cuja medida da área é representada por xelevado a 2 +10x + 25.
Atividades
Faça as atividades no caderno.
45. Desenvolva algebricamente cada quadrado da soma de dois termos.
a) (x + 1)elevado a 2
b) (2x + 10)elevado a 2
c)
Sentença matemática. Abre parênteses, xy, mais a fração 1 sobre 3, fecha parênteses, elevado ao quadradod) (x + 5)elevado a 2
e) (xelevado a 5 + 2xelevado a 3)elevado a 2
f) (6 + x)elevado a 2
g) (2x + xy)elevado a 2
h) (xelevado a 2 + 1)elevado a 2
i) (x + 2y) elevado a 2
j)
Sentença matemática. Abre parênteses, x elevado a 3, fim do expoente, mais a fração 1 sobre 3, fecha parênteses, elevado ao quadrado46. Simplifique as expressões.
a) x ⋅ (2x menos 1) + x ⋅ (1 menos 3x)
b) (a + 5) ⋅ (a + 5) menos (a + 5)elevado a 2
c) y ⋅ (y + 2)) menos 2y ⋅ (3 menos y)
d) (2 + x)elevado a 2 menos (x + 2)elevado a 2
47. Dados os polinômios a = 2xelevado a 2 + 3 e B = xelevado a 2 + 4, determine:
a) Aelevado a 2
b) B elevado a 2
c) (a + B)elevado a 2
48.

Observe como Pedro utilizou a ideia de produtos notáveis para calcular o quadrado de 41:
41elevado a 2 = (40 + 1)elevado a 2 = 40elevado a 2 + 2 ⋅ 40 ⋅ 1 + 1elevado a 2 = 1 600 + 80 + 1 = 1 681
Agora, calcule mentalmente os quadrados e registre o raciocínio no caderno.
a) 12elevado a 2
b) 61elevado a 2
c) 33elevado a 2
d) 92elevado a 2
49. Sabendo que a elevado a 2 + b elevado a 2 = 34 e (a + b) elevado a 2 = 64, calcule o valor de 6ab, sendo a > 0 e b > 0.
50. Desenvolva o produto (x + 3y) elevado a 2 e justifique geometricamente.
51. Sendo (x + y)elevado a 2 = 256 e x elevado a 2 + y elevado a 2 = 136, determine xy.
52. Observe a figura a seguir e responda às questões.
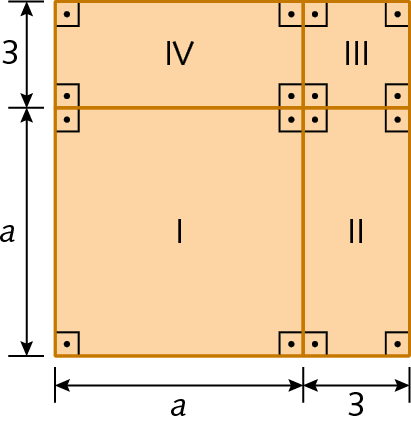
a) Qual é a expressão algébrica que representa a medida da área do quadrado maior?
b) Quais são as expressões algébricas que representam as áreas das figuras um, dois, três e quatro?
Quadrado da diferença de dois termos
O quadrado da diferença de dois termos, a e b, é indicado por (a menos b) elevado a 2. Desenvolvendo esse produto, obtemos:
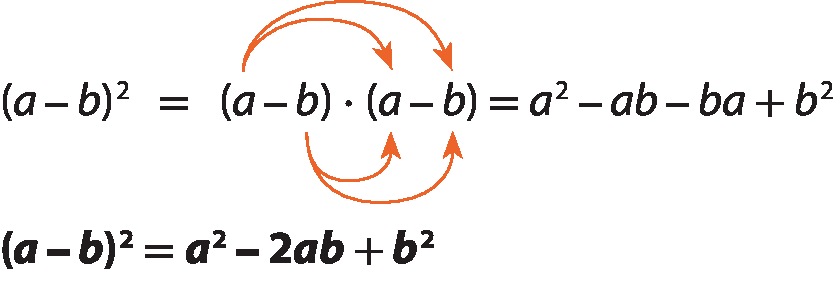
Ou seja:
O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo menos duas vezes o produto dos dois termos mais o quadrado do segundo termo.
Observe dois exemplos.
a) (x menos y)elevado a 2 = x elevado a 2 menos 2xy + y elevado a 2
b)
Sentença matemática. Abre parênteses, fração a sobre 3, fim da fração, menos 2b, fecha parênteses, elevado ao quadrado, é igual a, abra parênteses, fração a sobre 3, fecha parênteses, elevado ao quadrado, menos 2 vezes fração a sobre 3, fim da fração, vezes, 2b, mais, abre parênteses, 2b, fecha parênteses, elevado ao quadrado, é igual a fração a elevado ao quadrado sobre 9, fim da fração, menos a fração 4ab sobre 3, fim da fração, mais 4 b elevado ao quadrado.Representação geométrica
Considere o quadrado a bê cê dê, cuja medida dos comprimentos dos lados é indicada por a (figura 1). Vamos diminuir a medida do comprimento do lado e determinar o quadrado á bê linha cê linha dê linha, cuja medida do comprimento dos lados mede (a menos b) (figura 2). Observe:
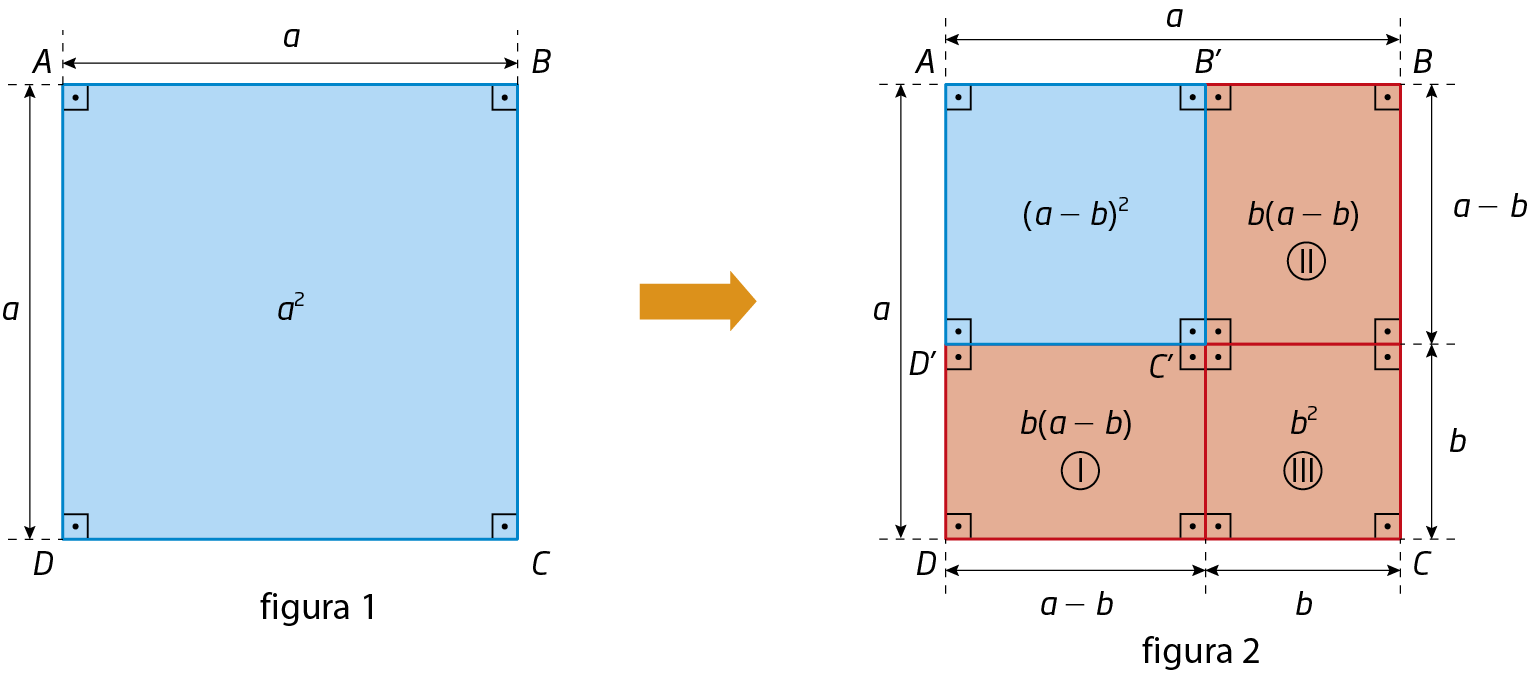
Determinando a medida da área A do quadrado de duas maneiras, obtemos:
•

•

Portanto, as expressões (a menos b)elevado a 2 e a elevado a 2 menos 2ab + b elevado a 2 representam a mesma medida de área, ou seja:
(a menos b)elevado a 2 = a elevado a 2 menos 2ab + b elevado a 2

Atividades
Faça as atividades no caderno.
53. Desenvolva algebricamente cada quadrado da diferença de dois termos.
a) (x menos 3)elevado a 2
b)
Sentença matemática. Abre parênteses, fração x sobre 3, fim da fração, menos 2, fecha parênteses, elevado ao quadrado.c) (9x elevado a 2 menos 2)elevado a 2
d) (x elevado a 3 menos y elevado a 3)elevado a 2
e) (x elevado a 2 menos y elevado a 2)elevado a 2
f) (menosx menos y)elevado a 2
g) (xy menos z)elevado a 2
h)
Sentença matemática. Abre parênteses, fração x sobre 2, fim da fração, menos fração y sobre 3, fecha parênteses, elevado ao quadrado.54.

Ana utilizou a ideia de produtos notáveis para calcular o quadrado de 16, observe como ela registrou:
16elevado a 2 = (20 menos 4)elevado a 2 = 20elevado a 2 menos 2 ⋅ 20 ⋅ 4 + 4elevado a 2 = 256
Agora, calcule mentalmente os quadrados e registre o raciocínio no caderno.
a) 17elevado a 2
b) 19elevado a 2
c) 14elevado a 2
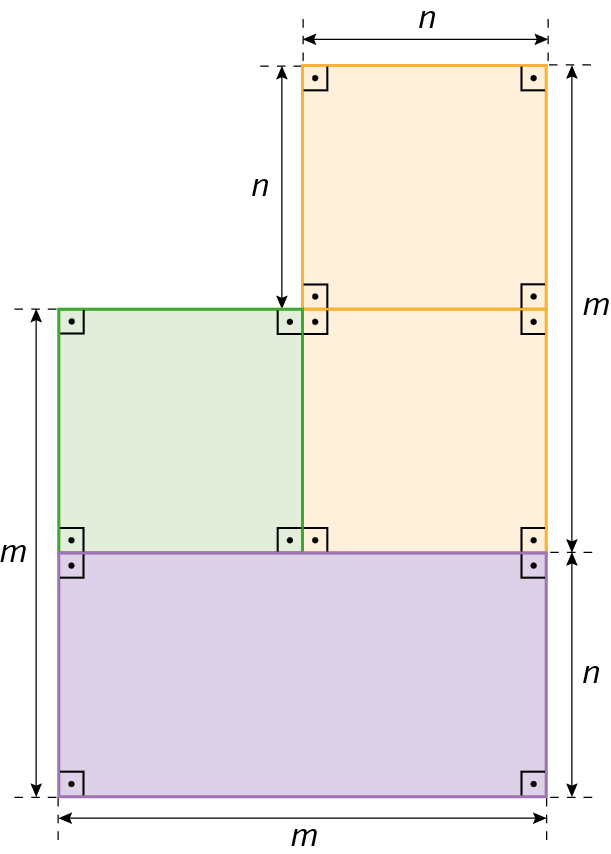
55. Qual é o polinômio que representa a medida da área do quadrado verde?
56. Sabendo que (a menos b)elevado a 2 = 16 e a elevado a 2 + b elevado a 2 = 106, calcule o valor de
Fração ab sobre 3., sendo a > 0 e b > 0.
57. Sabendo que a elevado a 2 + b elevado a 2 = 52 e A bê = 24, calcule o valor de (a menos b)elevado a 2.
58. A figura a seguir foi utilizada por um professor, em sala de aula, para mostrar a igualdade:
4ab + (a menos b)elevado a 2 = (a + b)elevado a 2 em que a e b são números positivos.
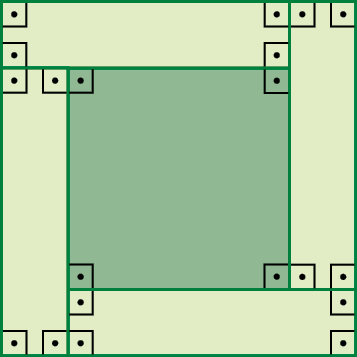
a) Copie a figura no caderno e indique os segmentos cuja medida do comprimento é indicada por a e b.
b)


Reúna-se com um colega e, juntos, mostrem que essa igualdade é verdadeira usando as medidas das áreas dos retângulos e dos quadrados. Depois, expliquem para o professor e os demais colegas da classe como vocês resolveram a atividade.
Produto da soma pela diferença de dois termos
O produto da soma pela diferença de dois termos, a e b, é indicado por (a + b) ⋅ (a menos b). Desenvolvendo esse produto, obtemos:
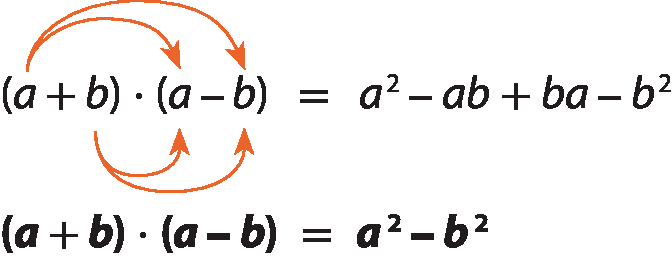
Ou seja:
O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
Observe alguns exemplos.
a) (x + y) ⋅ (x menos y) = x elevado a 2 menos y elevado a 2
b) (bx + 5) ⋅ (bx menos 5) = (bx)elevado a 2 menos (5)elevado a 2 = b elevado a 2x elevado a 2 menos 25
c)
Sentença matemática. Abre parênteses, fração k elevado ao quadrado sobre 3, fim da fração, mais 1, fecha parênteses, vezes abre parênteses, fração k elevado ao quadrado sobre 3, fim da fração, menos 1, fecha parênteses, é igual a, abre parênteses, fração k elevado ao quadrado sobre 3, fecha parênteses, elevado ao quadrado, menos, abre parênteses, 1, fecha parênteses, elevado ao quadrado é igual a fração k elevado a 4, fim do expoente, sobre 9, fim da fração, menos 1.Representação geométrica
Considere os quadrados a seguir.
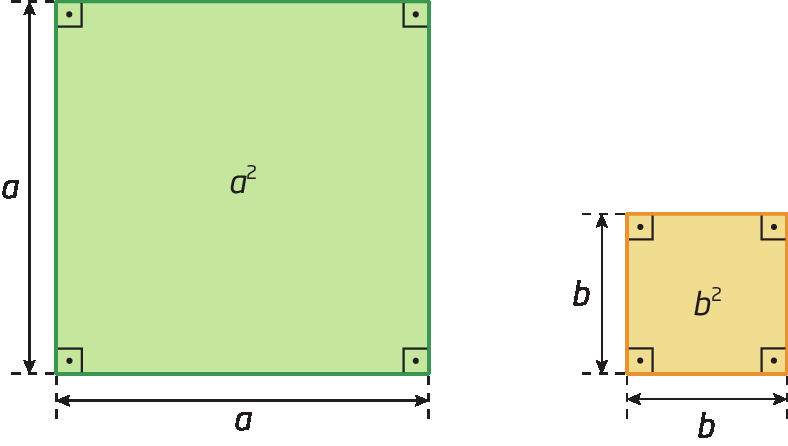
Retirando do quadrado verde uma superfície igual à do quadrado laranja, obtemos uma figura com medida de área a igual a a elevado a 2 menos b elevado a 2.
No retângulo obtido, temos:
• medida do comprimento da base: a menos b
• medida do comprimento da altura: a + b
• A = (a menos b) ⋅ (a + b)
Como as duas figuras têm a mesma medida de área, verificamos que: a elevado a 2 menos b elevado a 2 = (a + b) ⋅ (a menos b).
Atividades
Faça as atividades no caderno.
59. Desenvolva algebricamente os produtos.
a) (x + 1) ⋅ (x menos 1)
b) (3x + y) ⋅ (3x menos y)
c) (x + 5) ⋅ (x menos 5)
d) (2x + 5) ⋅ (2x menos 5)
60. Simplifique a expressão algébrica a seguir.
(x + 1)elevado a 2 + (x menos 1)elevado a 2 + 2(x + 1)(x menos 1)
61. Determine os produtos.
a)
Sentença matemática. Abre parênteses, x menos fração 1 sobre x, fecha parênteses, vezes, abre parênteses, x mais fração 1 sobre x, fecha parênteses.b)
Sentença matemática. Abre parênteses, x menos fração y sobre 3, fecha parênteses, vezes, abre parênteses, x mais fração y sobre 3, fecha parênteses.c) (x elevado a 2 + 1) ⋅ (x elevado a 2 menos 1)
d) (xy elevado a 2 menos z elevado a 2) ⋅ (xy elevado a 2 + z elevado a 2)
62.

Observe como Roberta calculou o produto de 41 por 39:
41 ⋅ 39 = (40 + 1) ⋅ (40 menos 1) = 40elevado a 2 menos 1elevado a 2 = 1 599
Agora, calcule mentalmente os produtos e registre o raciocínio no caderno.
a) 57 ⋅ 63
b) 52 ⋅ 48
c) 42 ⋅ 34
63.

Sabendo que a + b = 13 e aelevado a 2 menos belevado a 2 = 39, reúna-se com um colega e, juntos, determinem o valor de a. Depois, escrevam um texto explicando como vocês chegaram a esse valor. Apresentem o texto para o professor e os demais colegas da turma.

3 Fatoração
Podemos escrever o número 100 como o produto de dois ou mais números.
• 100 = 4 ⋅ 25
• 100 = 10 ⋅ 10
• 100 = 2 ⋅ 50
• 100 = 2 ⋅ 2 ⋅ 25
• 100 = 2 ⋅ 5 ⋅ 10
• 100 = 2 ⋅ 2 ⋅ 5 ⋅ 5
Nesses casos, escrevemos o número 100 na fórma fatorada.
Fatorar um número é escrevê-lo como o produto de dois ou mais fatores.
Além de números, podemos fatorar polinômios, isto é, escrevê-los como o produto de dois ou mais polinômios. Acompanhe o exemplo.
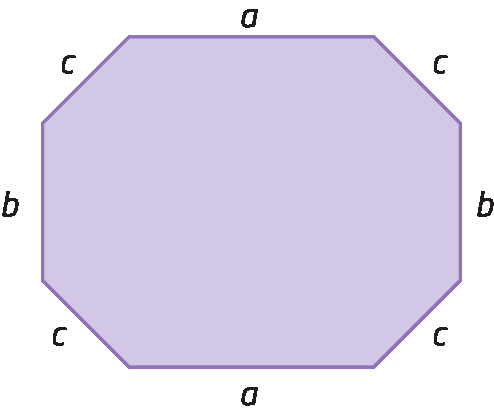
As medidas dos comprimentos dos lados do polígono são indicadas por a, b e c.
A medida de seu perímetro póde ser representada por:
a + a + b + b + c + c + c + c = 2a + 2b + 4c
Podemos também escrever esse polinômio da seguinte fórma:
2(a + b + 2c)
O polinômio 2(a + b + 2c) é uma fórma fatorada de 2a + 2b + 4c.
Agora, vamos estudar alguns processos utilizados para fatorar uma expressão algébrica.
Fatoração com um fator comum em evidência
A figura a seguir é formada por dois retângulos.
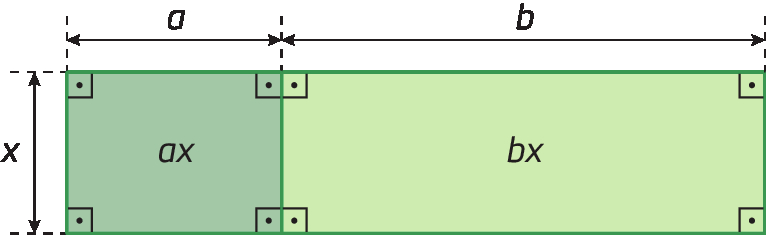
A medida da área total da figura póde ser obtida se adicionarmos as medidas das áreas dos retângulos que a compõem:
ax + bx
Também podemos determinar a medida da área dessa figura calculando a medida da área do retângulo cuja medida do comprimento da base é indicada por (a + b) e a medida do comprimento da altura é indicada por x:
x ⋅ (a + b)
Assim:
ax + bx = x(a + b)
O polinômio x(a + b) é uma fórma fatorada do polinômio ax + bx. Nesse caso, colocamos o fator comum (x) em evidência, obtendo uma fórma fatorada da expressão.
Observe alguns exemplos em que fatoramos alguns polinômios.
a)
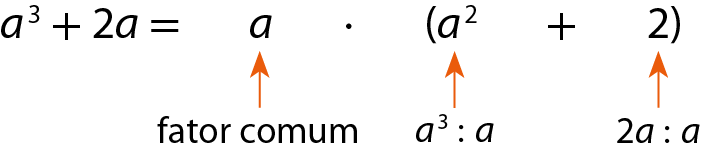
b)

c)
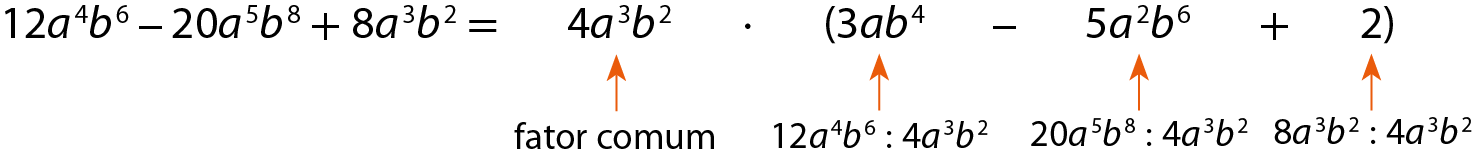
d)
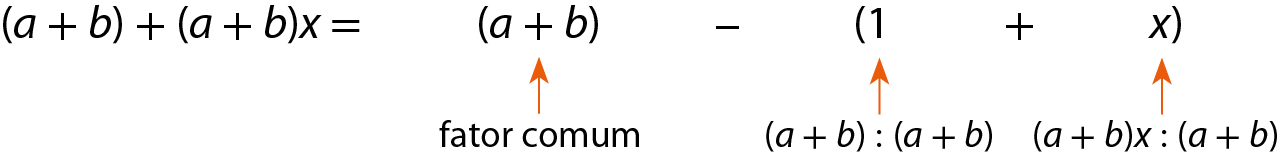
Atividades
Faça as atividades no caderno.
64. Escreva os números na fórma fatorada.
a) 36
b) 450
c) 120
d) 500
65. Colocando os fatores comuns em evidência, fatore:
a) ax + ay
b) 16x elevado a 2 + 20y elevado a 2
c) 5x + 15y menos 10z
d) menos5x elevado a 3y + 20x elevado a 2y elevado a 2
66. Fatore as expressões.
a) ax elevado a 3 + bx elevado a 2 menos cx
b) 12a elevado a 3x elevado a 2 + 6a elevado a 2x elevado a 3 menos 8ax elevado a 4
c)
Sentença matemática. Fração ab sobre 8, fim da fração, mais fração de numerador a elevado ao quadrado, b, e denominador 4, fim da fração, menos fração de numerador a, b elevado ao quadrado, e denominador 2.67. Escreva os polinômios a seguir na fórma de um produto:
a) x elevado a 5 + x elevado a 4 menos 2x elevado a 2
b) 6x + 3xy + 12xyz
c) 6x elevado a 2y menos 18xy elevado a 3
d) 15x elevado a 7 menos 3yx elevado a 4
Fatoração por agrupamento
Considere a figura a seguir.
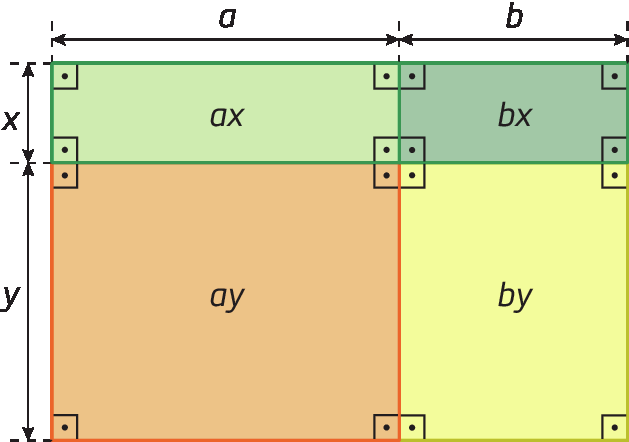
A medida da área total da figura póde ser obtida adicionando a medida das áreas dos retângulos menores:
ax + bx + ay + by
Ou póde ser obtida pelo cálculo da medida da área do retângulo cuja medida do comprimento da base é indicada por (a + b) e a medida do comprimento da altura é indicada por (x + y):
(a + b) ⋅ (x + y)
Assim:
ax + bx + ay + by = (a + b) ⋅ (x + y)
Podemos escrever ax + bx + ay + by na fórma (a + b) ⋅ (x + y), usando a fatoração:
(ax + bx) + (ay + by)

Agrupamos os termos com fatores comuns.
x(a + b) + y(a + b)

Colocamos o fator comum de cada grupo em evidência.
(a + b) ⋅ (x + y)

Colocamos o polinômio comum (a + b) em evidência.
Portanto, (a + b) ⋅ (x + y) é uma fórma fatorada do polinômio ax + bx + ay + by.
Observe alguns exemplos.
a) 3a menos 6y + ab menos 2by = 3a + ab menos 6y menos 2by =
= a(3 + b) ‒ 2y(3 + b) =
= (3 + b) ⋅ (a menos 2y)
b) x elevado a 4 + x elevado a 3 + x elevado a 2 + x = x elevado a 3(x + 1) + x(x + 1) =
= (x + 1) ⋅ (x elevado a 3 + x)
c) ax elevado a 2 menos abx + b elevado a 2 menos bx = ax(x ‒ b) + b(b menos x) =
= ax(x menos b) menos b(x menos b) =
= (x menos b) ⋅ (ax ‒ b)
d) mx elevado a 3 menos mx elevado a 2 + x elevado a 4 menos x elevado a 3 = mx elevado a 2(x menos 1) + x elevado a 3 (x menos1) =
= (x menos 1)(mx elevado a 2 + x elevado a 3) =
= (x menos 1)x elevado a 2(m + x) =
= x elevado a 2(x menos 1)(m + x)
Atividades
Faça as atividades no caderno.
68. Fatore as expressões por agrupamento.
a) xy + x menos 2y menos 2
b) 6x + 6y + ax + ay
c) 2x menos 2 + yx menos y
d) 2a + 2b + ax + bx
69. Fatore as expressões.
a) 7x + 7y + bx + by
b) ax menos ay menos bx + by
c) 6x elevado a 2 + 15x menos 4xy menos 10y
d) 2ax menos 2ay menos 3bx + 3by
70. Transforme as expressões em produtos.
a) 3(x menos 1) + a(x ‒ 1) + a elevado a 2(x menos 1)
b) ax + bx + ay + by + az + bz
c) (x + y)elevado a 2 menos 2(x + y)
d) ax menos a +
Fração. mx sobre 3, fim da fração, menos m sobre 3.71. Agrupe os termos das expressões e fatore-as.
a) ax menos ay + x menos y
b) abx elevado a 2 + aby elevado a 2 + cx elevado a 2 + cy elevado a 2
c) x elevado a 4 + 9x elevado a 3 menos 6x menos 54
d) ax menos 2ay + 5bx menos 10by + 11cx menos 22cy
Fatoração da diferença de dois quadrados
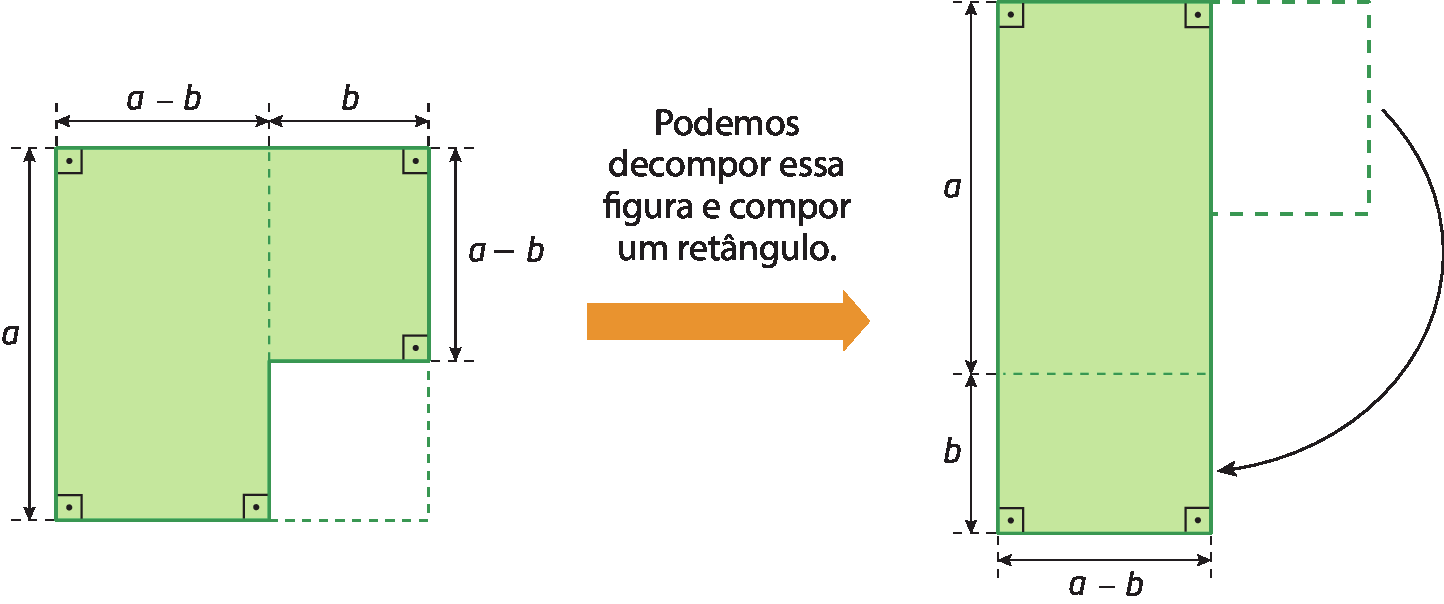
De um quadrado cuja medida do comprimento do lado é indicada por a, retirou-se um quadrado cuja medida do comprimento do lado é indicada por b, com b < a, obtendo a figura a seguir:
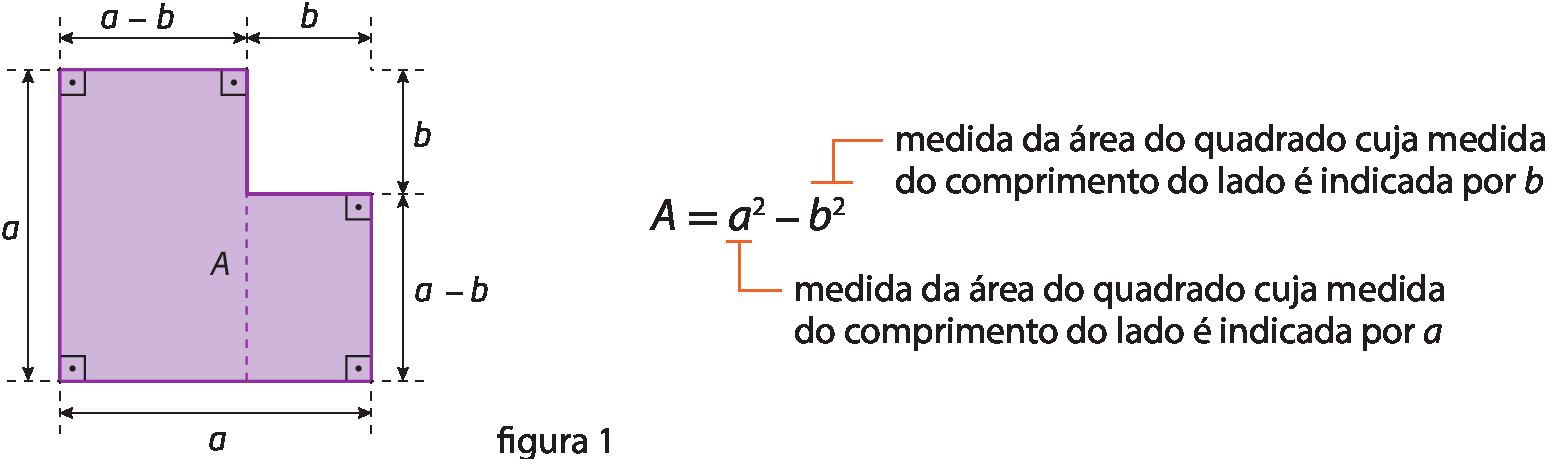
A medida da área da figura 1 é a elevado a 2 menos b elevado a 2, que corresponde a uma diferença de dois quadrados.
Podemos decompor a figura 1 conforme indicado a seguir (figura 2) e, depois, compor um retângulo (figura 3).
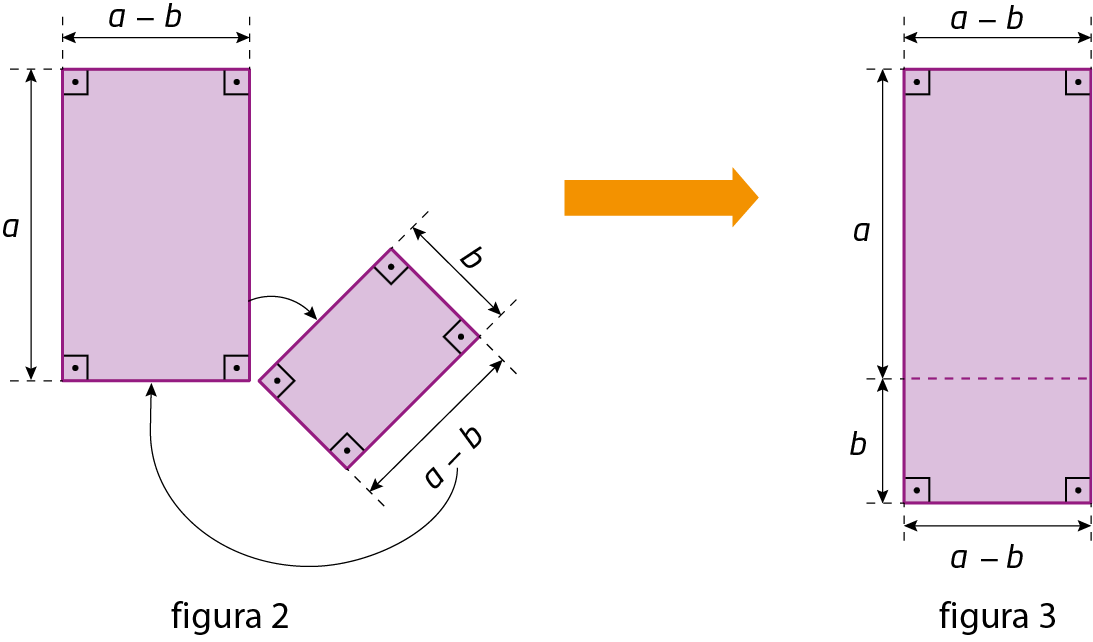
A medida da área da figura 1, representada por a elevado a 2 menos b elevado a 2, é igual à medida da área da figura 3, que póde ser representada por (a + b) ⋅ (a menos b).
Assim, justificamos geometricamente a igualdade:
a elevado a 2 menos b elevado a 2 = (a + b) ⋅ (a menos b)
Portanto, (a + b) ⋅ (a menos b) é uma fórma fatorada do polinômio aelevado a 2 menos b elevado a 2.
Observe alguns exemplos.
a)
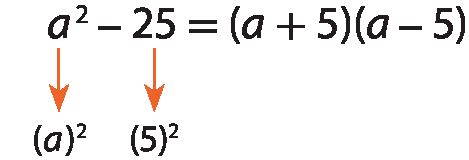
b)
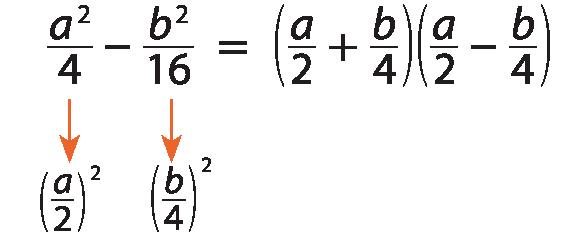
c)
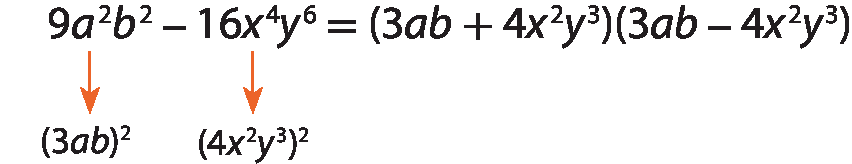
d)
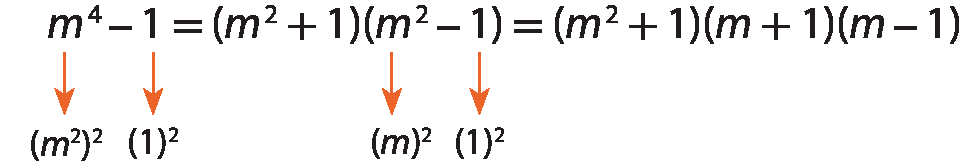
Atividades
Faça as atividades no caderno.
72. Fatore as expressões.
a) x elevado a 2 menos 49
b) 9a elevado a 2 menos 4b elevado a 2
c) 1 menos x elevado a 2
d) 4x elevado a 2 menos 25y elevado a 2
e) 4x elevado a 2 menos 25
f) x elevado a 2y elevado a 2 menos 1
g)
Sentença matemática. Fração x elevado ao quadrado sobre 4, fim da fração, menos fração 1 sobre 9.h)
Sentença matemática. x elevado ao quadrado menos fração 1 sobre x elevado a 4.73. Decomponha as expressões em produtos de fatores.
a) (x + y)elevado a 2 menos 1
b) 1 menos 9a elevado a 2
c) 4x elevado a 2 menos y elevado a 2
d) x elevado a 2 menos (y + 1)elevado a 2
74.

Roberto registrou o cálculo do produto de 21 por 19:
21 ⋅ 19 = (20 + 1) ⋅ (20 menos 1) = 20elevado a 2 menos 1elevado a 2 = 400 menos 1 = 399
Agora, calcule mentalmente os produtos e registre o raciocínio no caderno.
a) 81 ⋅ 79
b) 42 ⋅ 38
c) 101 ⋅ 99
75. Agrupe convenientemente os termos e fatore as expressões.
a) aelevado a 3 + aelevado a 2 menos 4a menos 4
b) aelevado a 2belevado a 2 menos aelevado a 2 menos belevado a 2 + 1
76.

A seguir temos como Melissa calculou a diferença dos quadrados dos números 100 e 90:
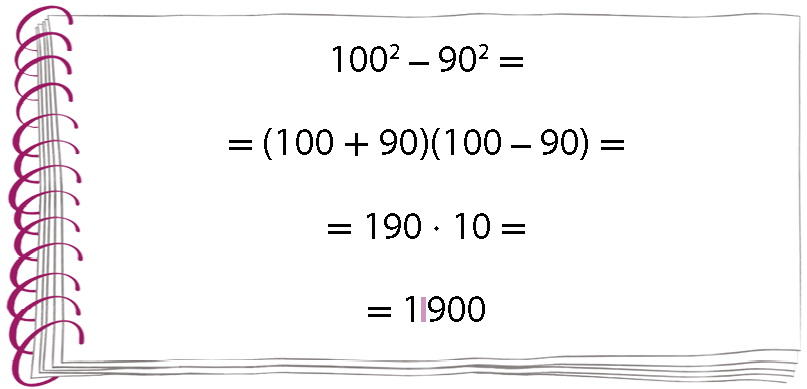
Agora, calcule da mesma fórma que Melissa:
a) 500elevado a 2 menos 400elevado a 2
b) .1000elevado a 2 menos 900elevado a 2
77. Demonstre, no caderno, que a soma de dois números inteiros e consecutivos é igual à diferença dos seus quadrados.
Fatoração do trinômio quadrado perfeito
Observe o quadrado cuja medida do comprimento do lado é indicada por a + b.
A medida da área desse quadrado póde ser indicada por:
a elevado a 2 + ab + ab + b elevado a 2 = a elevado a 2 + 2ab + b elevado a 2
ou
(a + b) ⋅ (a + b) = (a + b)elevado a 2
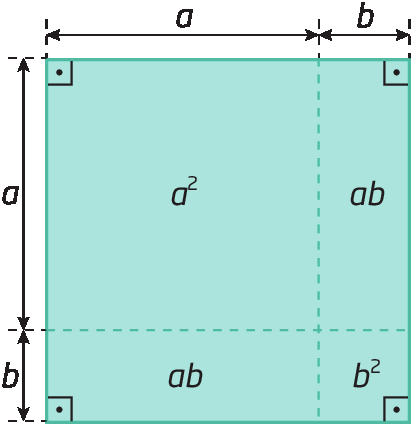
Verificamos, então, que:
a elevado a 2 + 2ab + b elevado a 2 = (a + b)elevado a 2
Portanto, a fórma fatorada de a elevado a 2 + 2ab + b elevado a 2 é (a + b)elevado a 2.
Vimos em produtos notáveis que:
(a ‒ b)elevado a 2 = a elevado a 2 ‒ 2ab + belevado a 2
Então:
a elevado a 2 menos 2ab + b elevado a 2 = (a menos b)elevado a 2
Portanto, a fórma fatorada de a elevado a 2 menos 2ab + b elevado a 2 é (a menos b)elevado a 2.
Observe os exemplos.
a) 4x elevado a 2 + 12x + 9 = (2x)elevado a 2 + 2 ⋅ (2x ⋅ 3) + 3elevado a 2 = (2x + 3)elevado a 2
b) 4melevado a 2nelevado a 2 menos 4mnc + c elevado a 2 = (2mn)elevado a 2 menos 2 ⋅ (2mn ⋅ c) + c elevado a 2 = (2mn menos c)elevado a 2
Atividades
Faça as atividades no caderno.
78. Fatore os polinômios.
a) x elevado a 2 + 6x + 9
b) x elevado a 2 menos 16x + 64
c) 9x elevado a 2 + 30xy + 25y elevado a 2
d) x elevado a 2 menos 2ax + a elevado a 2
e) 1 + 9m elevado a 2 menos 6m
f)
Fração 1 sobre 4a elevado a 2 menos 5ab + 25b elevado a 2
79. Quais dos polinômios a seguir são trinômios quadrados perfeitos?
a) a elevado a 2 + 6ab + 9b elevado a 2
b) a elevado a 2 + b +
Fração 1 sobre 4.c) 16x elevado a 2 menos 24xy + 9y elevado a 2
d) 4x elevado a 2 menos 4x + 1
80. Escreva a fórma fatorada dos polinômios.
a) x elevado a 2 menos 6x + 9
b) 1 menos 6x + 9xelevado a 2
c) x elevado a 2 menos 10x + 25
d) x elevado a 3 menos 2x elevado a 2 + x
e) x elevado a 4 + 2x elevado a 3 + x elevado a 2
f)
Fração 1 sobre 5.x 2 ‒
Fração 4 sobre cinco.x +
Fração 4 sobre 5.81. Escreva as expressões como um produto de polinômios.
a) a elevado a 2 + 2ab + b elevado a 2 menos c elevado a 2
b) (a elevado a 2 + b elevado a 2)elevado a 2 menos 4a elevado a 2b elevado a 2
c) (a elevado a 2 + b elevado a 2)elevado a 2 menos 2(a elevado a 2 + b elevado a 2) + 1
82. Considere um jardim com o formato de um quadrado de lado medindo x metros. Devem-se aumentar as dimensões em 2 metros, de acôrdo com a imagem.
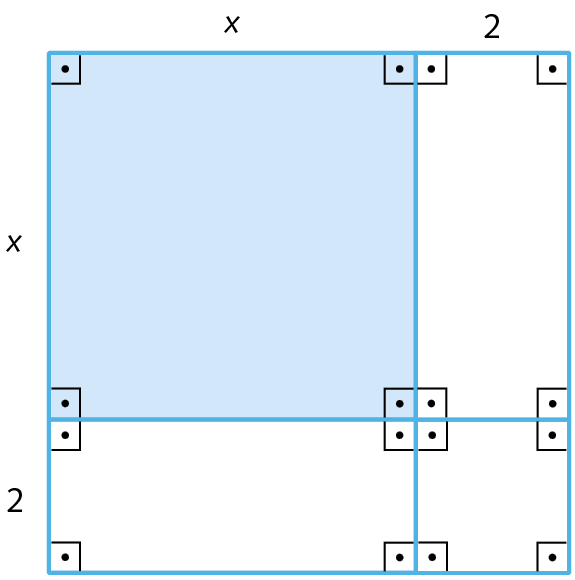
a) Indique, na fórma de um trinômio e na fórma fatorada, a nova medida de área do jardim.
b) Escreva uma expressão algébrica simplificada que indique a diferença entre as medidas de área nova e área antiga.
c) Se a diferença entre as medidas de área é de 42 métroselevado a 2, qual era aqui inicialmente a medida do lado do jardim?

4 Resolução de equações do 2º grau
Resolver uma equação do 2º grau significa encontrar as raízes dessa equação que pertencem ao conjunto universo dela.
Toda equação do 2º grau póde ser escrita na fórma axelevado a 2 + bx + c = 0, em que a, b e c são números reais e a ≠ 0.
• Quando todos os coeficientes (a, b e c) são diferentes de zero, dizemos que a equação é completa.
• Quando b ou c ou os dois coeficientes são iguais a zero, dizemos que a equação é incompleta.
Resolução de equações do 2º grau incompletas
Acompanhe a resolução de algumas equações de 2º grau incompletas.
a) Vamos resolver a equação 4xelevado a 2 menos 36 = 0, considerando U =

.
4xelevado a 2 menos 36 = 0
4xelevado a 2 menos 36 + 36 = 0 + 36

Adicionamos 36 a ambos os membros da equação.
4xelevado a 2 = 36
4xelevado a 2 dividido por 4 = 36 dividido por 4

Dividimos os dois membros por 4.
xelevado a 2 = 9
x é igual a raiz quadrada de 9 que é igual a 3.
ou
x é igual a menos raiz quadrada de 9 que é igual a menos 3.Como menos3 e 3 são raízes da equação e pertencem ao conjunto universo, então
Conjunto solução é igual a, abre chave, menos 3, 3, fecha chave..
b) Sendo U =

, vamos resolver a equação 2xelevado a 2 + 10 = 0.
2xelevado a 2 + 10 menos 10 = 0 menos 10

Subtraímos 10 de ambos os membros da equação.
2xelevado a 2 = menos10
2xelevado a 2 dividido por 2 = menos10 dividido por 2

Dividimos os dois membros por 2.
xelevado a 2 = menos5
Não existe número real que, elevado ao quadrado, seja igual a menos5. Portanto, S = ∅.
c) Agora, vamos resolver a equação
Sentença matemática. Menos 7 x elevado ao quadrado, é igual a 0., considerando U =

.
menos7xelevado a 2 dividido por menos7 = 0 dividido por menos7

Dividimos os dois membros por menos7.
xelevado a 2 = 0
x = menos0 = 0 ou x = +0 = 0
Como a equação tem duas raízes reais iguais a zero e 0 pertence ao conjunto universo, então
Conjunto solução é igual a, abre chave, 0, fecha chave..
Sugestão de leitura
GUELLI, Oscar. História da equação do 2º grau. São Paulo: Ática, 1999. (Coleção Contando a história da Matemática).
O livro conta a história das equações do 2º grau desde seu primeiro registro e passa pela evolução das representações até chegar ao uso de símbolos. Além disso, o livro traz vários desafios intrigantes para resolver.
d) Sendo U =

, vamos resolver
Sentença matemática. 2 x elevado ao quadrado menos 32 x, é igual a 0..
Uma fórma de resolver essa equação é colocar o fator comum 2x em evidência:
2x (x menos 16) = 0
Como o produto dos fatores 2x e (x menos 16) é zero, então pelo menos um deles é zero. Assim:
• 2xis = 0
xis = 0
ou
• (x menos 16) = 0
xis menos 16 = 0
xis = 16
Como 0 e 16 são raízes da equação e pertencem ao conjunto universo, então S = {0, 16}.
Atividades
Faça as atividades no caderno.
83. Resolva as equações considerando U =

.
a) x elevado a 2 menos 81 = 0
b) x elevado a 2 menos 3 = 0
c) x elevado a 2 + 24 = 0
d) 16x elevado a 2 menos 25 = 0
e) 5x elevado a 2 = 0
f) x elevado a 2 menos 5x = 0
g) menos2x elevado a 2 menos 10x = 0
h)
Sentença matemática. Fração 3 x elevado ao quadrado sobre 4, fim da fração, menos 5x, é igual a 0.i) 6x elevado a 2 = 5x
j) (x + 2)elevado a 2 = 4
84. Considerando U =

, resolva cada equação.
a) (2x menos 3)elevado a 2 + 12x = 9
b) x ⋅ (x + 2) = 4x
c) 3 ⋅ (x menos 2)elevado a 2 = 12
d)
Sentença matemática. 2 x elevado ao quadrado, menos fração 3 sobre 4, fim da fração, é igual a x elevado ao quadrado, mais fração 1 sobre 4.
85. Resolva as equações, considerando U =

.
a) 7m elevado a 2 + 3 = 8m elevado a 2 + 3
b)
Sentença matemática. Abre parênteses, fração x sobre 7, fim da fração, menos 11, fecha parênteses, vezes, abre parênteses, fração x sobre 7, fim da fração, mais 11, fecha parênteses igual a 0.86. O retângulo e o quadrado a seguir têm a mesma medida de área. Observe atentamente as figuras e responda às questões.
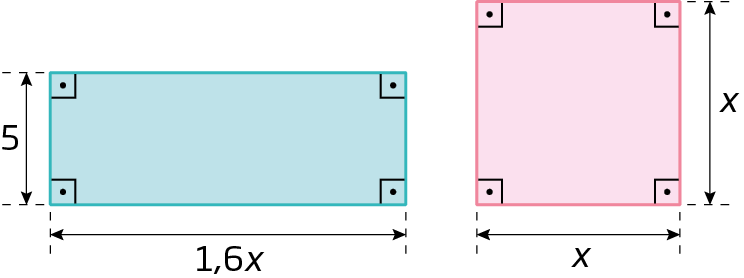
a) Qual é a medida do comprimento do lado do quadrado?
b) Qual é a medida do perímetro do quadrado? E o do retângulo?
c) Qual é a medida da área do retângulo e do quadrado?
87. Determine os possíveis valores de x em cada caso.
a) O quadrado de x é igual a 144.
b) O quadrado de x é igual a 169.
c) O dôbro do quadrado de x é igual ao triplo de x.
Resolução de equações do 2º grau completas
Mohammed ibn Musa al-Khowarizmi, matemático árabe do século nove, em seu livro Al-jabr Wa’l muqabalah, apresentou regras para encontrar as raízes positivas de equações do 2º grau. Em suas soluções, ele usava apenas palavras, sem empregar símbolos.
Uma das equações apresentadas e resolvidas por Al-Khowarizmi foi: x elevado a 2 + 10x = 39.
Como podemos encontrar as raízes dessa equação? A seguir, vamos estudar a resolução de equações do 2º grau completas, como a estudada por Al-Khowarizmi.

Resolução por fatoração
Vamos usar o que já foi estudado sobre fatoração e produtos notáveis para resolver algumas equações do 2º grau completas. Acompanhe alguns exemplos.
a) Vamos resolver a equação x elevado a 2 menos 10x + 25 = 0, considerando U =

.
Temos que xelevado a 2 menos 10x + 25 é um trinômio quadrado perfeito.

Assim:

Como (x menos 5)elevado a 2 = (x menos 5) ⋅ (x menos 5), temos:
(x menos 5) ⋅ (x menos 5) = 0
Os dois fatores da multiplicação são iguais e o produto dos fatores é zero, portanto:
(x menos 5) = 0 ⇒ x = 5
Como a equação tem duas raízes reais iguais a 5 e 5 pertence ao conjunto universo, então S = {5}.
b) Vamos resolver a equação 16x elevado a 2 + 24x = menos9, considerando U =

.
Adicionando 9 a ambos os membros da equação, obtemos:
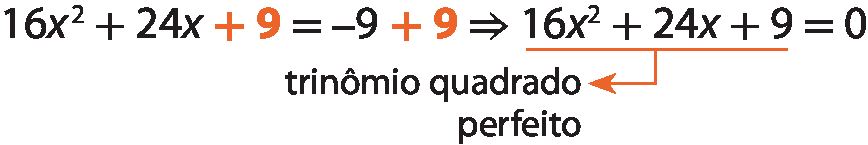
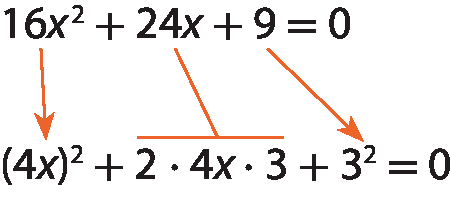

(4x + 3) ⋅ (4x + 3) = 0

Como (4x + 3)elevado a 2 = (4x + 3) ⋅ (4x + 3), temos:
(4x + 3) ⋅ (4x + 3) = 0
Os dois fatores da multiplicação são iguais e o produto dos fatores é zero, portanto:
(4x + 3) = 0
Sentença matemática. x é igual a menos fração 3 sobre 4.
Como a equação tem duas raízes reais iguais a
Menos fração 3 sobre 4e
Menos fração 3 sobre 4.pertence ao conjunto universo, então
Conjunto solução é igual a, abre chave, menos fração 3 sobre 4, fecha chave..
c) Agora, vamos determinar a raiz positiva da equação x elevado a 2 + 10x = 39, apresentada por Al-Khowarizmi.
Observe que o 1º membro da equação (x elevado a 2 + 10x) não é um trinômio quadrado perfeito. Para resolvê-la, devemos encontrar uma equação equivalente a ela, cujo 1º membro seja um trinômio quadrado perfeito.
Observe a explicação de Dênis sobre como ele determinou essa equação equivalente.
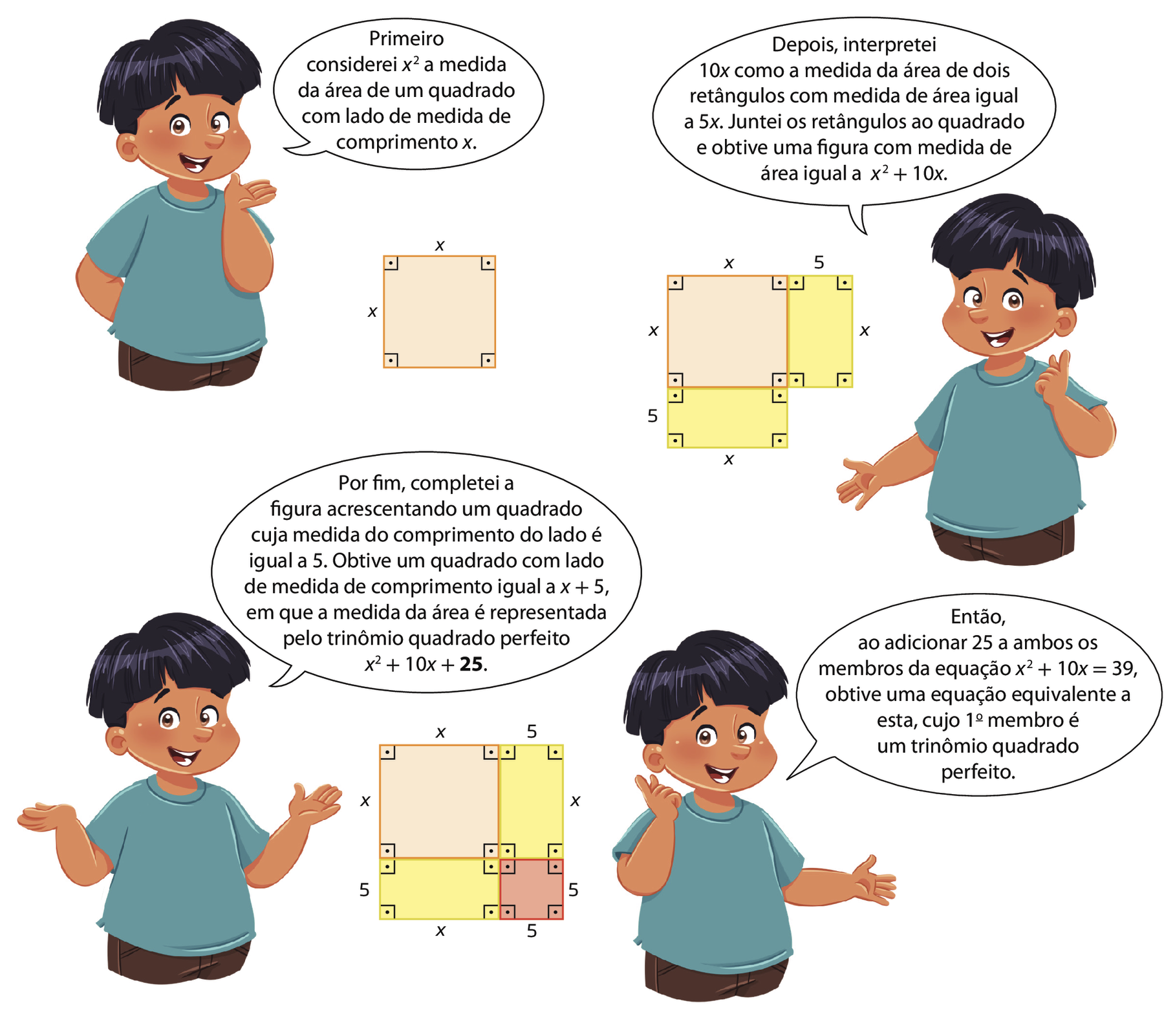
Agora, podemos resolver a equação inicial mais facilmente.
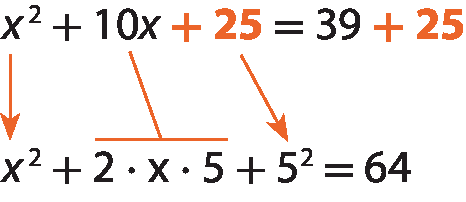
(x + 5)elevado a 2 = 64
x = 3
Portanto, 3 é a raiz positiva da equação x elevado a 2 + 10x = 39.

▸ Qual é a outra raiz da equação x elevado a 2 + 10x = 39? Por que essa raiz não poderia ser determinada pelo método de Al-Khowarizmi?
Fórmula de resolução de uma equação do 2º grau
Considerando a equação do 2º grau ax elevado a 2 + bx + c = 0, em que a, b e c são coeficientes reais com a ≠ 0, vamos obter, por meio da generalização do método de completar quadrados, uma fórmula para calcular suas raízes. Acompanhe:
1º) Multiplicamos ambos os membros da equação por 4a:
4a ⋅ (ax elevado a 2 + bx + c) = 0 ⋅ 4a
4a elevado a 2x elevado a 2 + 4abx + 4ac = 0
2º) Subtraímos 4ac de ambos os membros da equação:
4a elevado a 2x elevado a 2 + 4abx + 4ac menos 4ac = 0 menos 4ac
4a elevado a 2x elevado a 2 + 4abx = menos4ac
3º) Adicionamos b elevado a 2 a ambos os membros da equação:
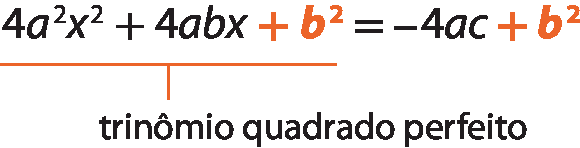
4a elevado a 2x elevado a 2 + 4abx + b² = ‒4ac + belevado a 2
4º) Fatoramos o 1º membro:
(2ax + b)elevado a 2 = b elevado a 2 ‒ 4ac
5º) Considerando b elevado a 2 ‒ 4ac ⩾ 0, extraímos a raiz quadrada dos dois membros:
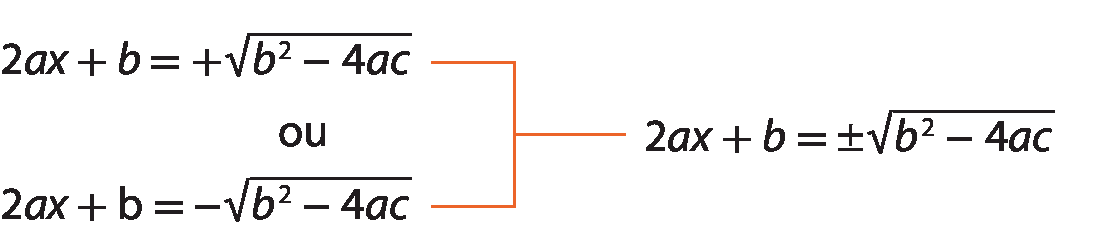
6º) Isolamos x:
Sentença matemática. 2ax é igual a menos b mais ou menos, início da raiz quadrada, b elevado ao quadrado menos 4 a c, fim da raiz.
Sentença matemática. x é igual a fração de numerador menos b mais ou menos, início da raiz quadrada, b elevado ao quadrado menos 4 a c, fim da raiz, e denominador 2a.
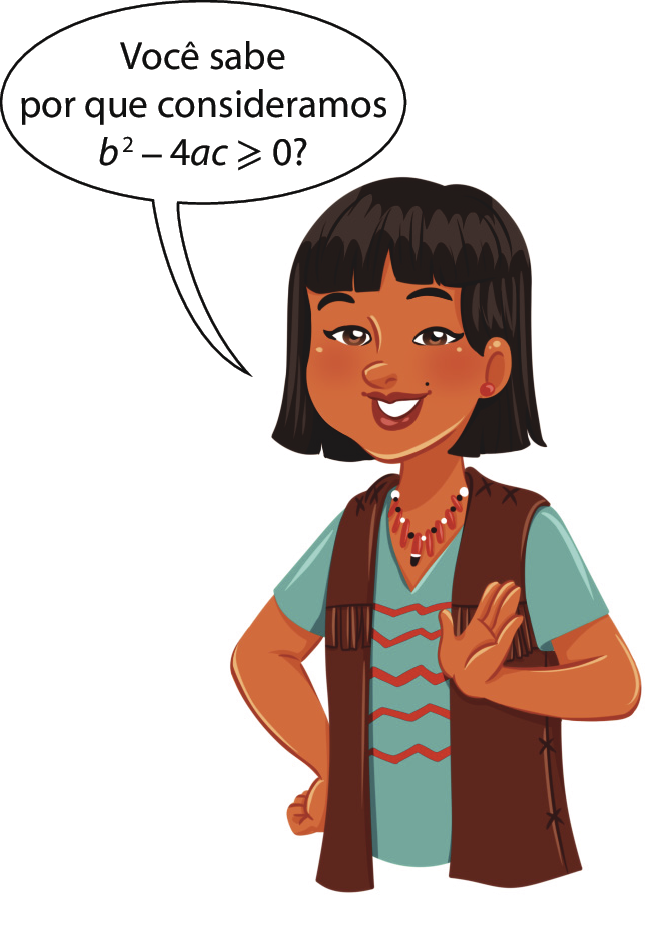
Assim, encontramos a fórmula resolutiva de equações do 2º grau ax elevado a 2 + bx + c = 0, em que a, b e c são números reais com a ≠ 0.
A fórmula resolutiva de equações do 2º grau é conhecida como fórmula de báscara, que permite determinar as raízes de uma equação quando conhecemos os seus coeficientes.
Assim, concluímos que as raízes da equação do 2º grau ax elevado a 2 + bx + c = 0 são:
e
Sentença matemática. x2 é igual a fração de numerador menos b menos, início da raiz quadrada, b elevado ao quadrado menos 4 a c, fim da raiz, e denominador 2a.Vamos resolver, por exemplo, a equação 7x elevado a 2 + 13x menos 2 = 0 considerando U =

.
Aplicando a fórmula resolutiva para a = 7, b = 13 e c = menos2, temos:
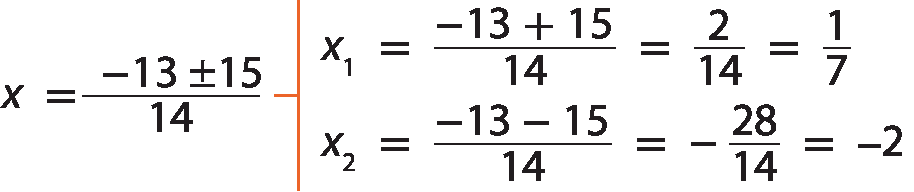
Como menos2 e
Fração 1 sobre 7.são raízes da equação e pertencem ao conjunto universo, então
Conjunto solução é igual a, abre chave, menos 2, fração 1 sobre 7, fecha chave..
Sugestão de leitura
ROSA, Ernesto. As mil e uma equações. São Paulo: Ática, 2008. (Coleção A descoberta da Matemática).
Kamal, améd e Najla descobrem um plano para assassinar o emir e desvendam os segredos das equações do 2º grau nessa história divertida e interessante que se passa nos reinos muçulmanos do século nove. No final do livro, há também um minialmanaque com desafios e enigmas para resolver.
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Fórmula de Bhaskara?
Duração: 4:17min. Página: 118.
>> [Locutora] Fórmula de Bhaskara?
Vinheta.
Fundo musical.
>> [Locutora] Hoje, vamos falar sobre um matemático de quem você provavelmente já ouviu falar: Bhaskara. Esse nome é familiar?
>> [Locutora] Caso não seja, só para você saber, quando alguém precisa resolver problemas com equações quadráticas, geralmente acaba usando uma fórmula que, popularmente aqui no Brasil, é conhecida como fórmula de Bhaskara.
>> [Locutora] Tá! Mas quem é esse moço? E por que damos o nome dele para tal fórmula?
>> [Locutora] Bhaskara nasceu na Índia e foi um dos mais importantes matemáticos do século XII. Também foi diretor do maior centro de pesquisas astronômicas e matemáticas da Índia, na época: o Observatório de Ujjain. Dentre os livros que escreveu, dois ficaram famosos: Lilavati e Bijaganita. O livro Bijaganita trata de álgebra e possui muitos problemas sobre equações lineares e quadráticas.
>> [Locutora] Diferente dos dias atuais, em que costumamos resolver equações por meio de letras e números, antigamente, os problemas, as regras e as soluções eram escritas com palavras. As fórmulas só apareceram muito tempo depois, por volta de 1 600 anos depois de Cristo.
>> [Locutora] Só como curiosidade, no livro Lilavati, do Bhaskara, existem problemas que foram enunciados de uma forma bem peculiar, com linguagem poética. [Tom animado] Isso mesmo! Veja um exemplo!
>> [Locutora] [Tom de narrativa] “Linda donzela de olhos resplandecentes, uma vez que entendeis o método de inversão correto, dizei-me: qual é o número que, multiplicado por 3, depois acrescido de três quartos do produto, depois dividido por 7, diminuído de um terço do quociente, multiplicado por si mesmo...” E por aí vai.
>> [Locutora] É importante destacar que, antes de Bhaskara, outros povos já conheciam, estudavam e resolviam equações quadráticas.
>> [Locutora] Mesopotâmicos, por volta de 1 700 anos antes de Cristo, já conheciam problemas com equações quadráticas. Os gregos, cerca de 300 anos antes de Cristo, também lidavam com essas equações, mas as resolviam de forma diferente, utilizando métodos geométricos. Os árabes, no século quatro [sic] depois de Cristo, também resolveram problemas que envolviam equações quadráticas, mas utilizavam um método chamado de completamento de quadrados.
Pausa com fundo musical.
>> [Locutora] Bhaskara, apesar de conhecer maneiras de resolver equações quadráticas, [tom enfático] não desenvolveu o método para a resolução da equação de segundo grau [tom enfático] e nem escreveu a fórmula como a conhecemos hoje! Mesmo porque as fórmulas surgiram mais de quatro séculos depois dele. Então, por que chamamos a fórmula para resolução da equação de segundo grau de fórmula de Bhaskara?
>> [Locutora] Pois é, o Brasil é o único país do mundo que relaciona essa fórmula ao nome desse importante matemático. A origem dessa associação é incerta, mas, a partir da década de 1960, o uso do termo “fórmula de Bhaskara” passou a ser comum no Brasil. Mas saiba que Bhaskara nada teve a ver com isso!
Fundo musical.
Vinheta.
Créditos
Todos os áudios inseridos neste conteúdo são da Free Sound.
Atividades
Faça as atividades no caderno.
88. Resolva as equações, considerando U =

.
a) x elevado a 2 + 5x + 6 = 0
b) 6x elevado a 2 menos x menos 2 = 0
c)
Sentença matemática. x elevado ao quadrado, menos 2 raiz de 5, fim da raiz, x, mais 4, é igual a 0.d) x elevado a 2 menos 14x + 49 = 0
89. A soma de um número real com seu quadrado é 42. Determine esse número.
90. Subtraindo o inverso de um número real qualquer (diferente de zero) desse mesmo número, obtemos
Fração 3 sobre 2.. Determine esse número.
91.


Com base no retângulo a seguir, elabore um problema sobre medidas de área no qual seja necessário encontrar o valor da incógnita x. Troque de problema com um colega. Conversem a respeito da resolução e verifiquem se os procedimentos efetuados foram adequados para encontrar a resposta. Caso tenham dúvidas, conversem com o professor.
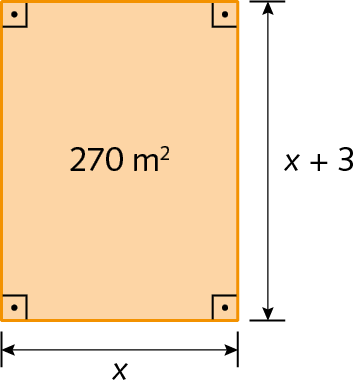
92.


Elabore um problema envolvendo a idade de duas pessoas. A equação que resolve o problema deve ser uma equação do 2º grau que póde ser resolvida por algum método de fatoração. Troque de problema com um colega. Em seguida, conversem a respeito da resolução e verifiquem se os procedimentos efetuados estavam corretos.
Discriminante
A expressão b elevado a 2 menos 4ac é chamada de discriminante da equação do 2º grau ax elevado a 2 + bx + c = 0 e é representada pela letra grega Δ (delta).
Então, a fórmula de báscara póde ser escrita assim:
Sentença matemática. x é igual a fração de numerador menos b mais ou menos raiz quadrada de delta, fim da raiz, e denominador 2a.
Analisando essa fórmula, podemos verificar se uma equação tem ou não raízes reais e obter uma relação entre os coeficientes e as raízes de uma equação do 2º grau.
• Quando Δ > 0,
Raiz quadrada de delta.é um número real e a equação possui duas raízes reais diferentes.
e
Sentença matemática. x2 é igual a fração de numerador menos b menos raiz quadrada de delta, fim da raiz, e denominador 2a.• Quando Δ = 0,
Raiz quadrada de delta.é nulo e a equação tem duas raízes reais iguais.
• Quando Δ < 0,
Raiz quadrada de delta.não é um número real, pois qualquer número real elevado ao quadrado é igual a um número positivo ou nulo. Dizemos, então, que a equação não tem raízes reais.
Para, por exemplo, determinar os valores de m em que a equação 3x elevado a 2 + 6x + m = 0 possui duas raízes reais, temos:
a = 3, b = 6 e c = m
Para que a equação tenha duas raízes reais diferentes, temos que ter Δ > 0. Portanto, como Δ = belevado a 2 ‒ 4ac, temos:

Assim, os valores de m devem ser menores que 3 para que a equação tenha duas raízes reais diferentes.
Observe que, se m = 3, a equação tem duas raízes reais iguais, e que, se m > 3, a equação não tem raízes reais.
Em outro exemplo, para determinar o valor de k para a equação xelevado a 2 menos2x + k = 0 sabendo que possui duas raízes reais e iguais. Nesse caso, sabemos que ∆ = 0.
a = 1, b = menos2 e c = k
(menos2)elevado a 2 menos 4 ⋅ 1 ⋅ k = 0
4 menos 4k = 0
4 = 4k
1 = k
Assim, k é igual a 1, para que a equação xelevado a 2 menos2x + k = 0 tenha duas raízes reais e iguais.
Atividades
Faça as atividades no caderno.
93. Calcule o discriminante e indique se a equação tem raízes reais.
a) x elevado a 2 menos 10x + 21 = 0
b) x elevado a 2 menos 2x + 1 = 0
c) 4x elevado a 2 menos 4x + 1 = 0
d) 3x elevado a 2 + 6x + 4 = 0
94. Determine o valor de p na equação x elevado a 2 menos 6x + p menos 5 = 0, de incógnita x, de modo que suas raízes:
a) sejam reais e iguais;
b) sejam reais e diferentes;
c) não sejam reais.
95. Determine o valor de k para que a equação 3x² ‒ 5x + 2k = 0 não tenha raízes reais.
96. Determine os valores de a em cada uma das equações a seguir, de modo que:
a) a equação x elevado a 2 menos 7x + a = 0 tenha duas raízes reais diferentes;
b) a equação x elevado a 2 menos ax + 9 = 0 tenha duas raízes reais iguais;
c) a equação x elevado a 2 menos 3x + a = 0 não tenha raízes reais.
fórma fatorada de uma equação do 2º grau
Considere a equação ax elevado a 2 + bx + c = 0, com a ≠ 0 e suas raízes:
Sentença matemática. x1 é igual a fração de numerador menos b menos, início da raiz quadrada, b elevado ao quadrado menos 4 a c, fim da raiz, e denominador 2a.e
Sentença matemática. x2 é igual a fração de numerador menos b menos, início da raiz quadrada, b elevado ao quadrado menos 4 a c, fim da raiz, e denominador 2a..
Adicionando e multiplicando as raízes da equação, obtemos:
•
Sentença matemática. x1 mais x2 é igual a fração de numerador menos b mais raiz quadrada de delta, fim da raiz, e denominador 2a, fim da fração, mais fração de numerador menos b menos raiz quadrada de delta, fim da raiz, e denominador 2a, fim da fração, é igual a fração de numerador menos b menos b mais raiz quadrada de delta, fim da raiz, menos raiz quadrada de delta, fim da raiz, e denominador 2a, fim da fração, é igual a fração menos 2b sobre 2a, fim da fração, é igual a menos fração b sobre a.
Colocando a em evidência no 1º termo da equação axelevado a 2 + bx + c = 0, temos:
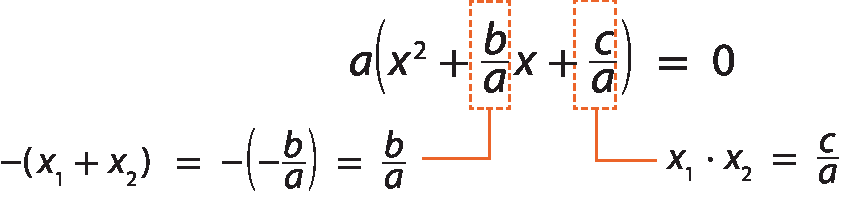
Assim:
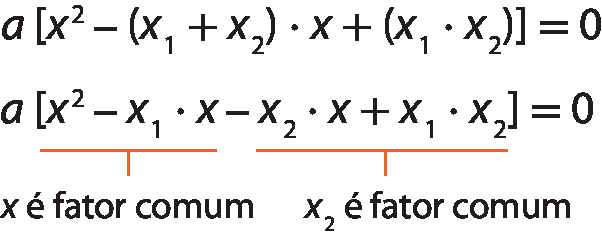
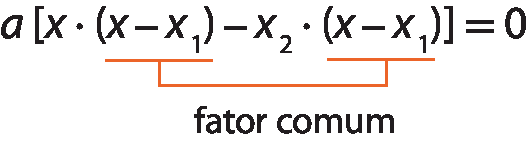
a ⋅ (x menos xis₁) ⋅ (x₁ menos xis₂) = 0
Portanto, a fórma fatorada da equação do 2º grau á xiselevado a 2 + bx + c = 0, cujas raízes são xis₁ e xis₂, é:
a ⋅ (x menos xis₁) ⋅ (x menos xis₂) = 0
Observe alguns exemplos:
a) Vamos escrever, na fórma fatorada, a equação xiselevado a 2 menos 5x + 6 = 0.
Temos que as raízes xis₁ e xis₂ da equação xiselevado a 2 menos 5x + 6 = 0 são 2 e 3, respectivamente.
Sendo a = 1, xis₁ = 2 e xis₂ = 3, a fórma fatorada de xiselevado a 2 menos 5x + 6 = 0 póde ser escrita como:
(x menos 2) (x menos 3) = 0
b) Vamos determinar uma equação do 2º grau cujas raízes sejam 3 e 4.
Usando a fórma fatorada para a = 1, temos:
(x menos 3)(x menos 4) = 0
Agora, aplicamos a propriedade distributiva:
xiselevado a 2 menos 4x menos 3x + 12 = 0
xiselevado a 2 menos 7x + 12 = 0
Logo, a equação procurada é xiselevado a 2 menos 7x + 12 = 0.
Atividades
Faça as atividades no caderno.
97. Obtenha a fórma fatorada das equações.
a) xiselevado a 2 menos 64 = 0
b) 2xiselevado a 2 menos 7x + 3 = 0
c) 4xiselevado a 2 menos 12x + 9 = 0
d) xiselevado a 2 + 2mx menos 3êmeelevado a 2 = 0
e) 3xiselevado a 2 menos 2xp +
Fração de numerador p elevado ao quadrado e denominador 3.= 0
98. Fatore os trinômios.
a) 2xiselevado a 2 menos 4x + 2
b) 8xiselevado a 2 menos 6x + 1
c) 6xiselevado a 2 + x menos 1
d) xiselevado a 2 + 5x menos 24
e)
Fração de numerador x ao quadrado e denominador 2, fim da fração, menos 3 meiosx menos 14
99. Determine uma equação do 2º grau que tenha:
a) duas raízes reais iguais a 7;
b) menos3 e 8 como raízes;
c) menos1 e menos5 como raízes e o coeficiente de xiselevado a 2 igual a 2;
d) nenhuma raiz real.
Resolução de problemas
Para resolver problemas que envolvam equações do 2º grau com uma incógnita, podemos:
um) encontrar a equação que representa matematicamente o problema;
dois) determinar as raízes da equação;
três) interpretar o valor das raízes, verificando a compatibilidade com os dados do problema, levando em consideração o universo em questão.
Podemos representar as etapas anteriores em um fluxograma:

Agora, acompanhe a resolução de alguns problemas utilizando uma equação do 2º grau.
Problema 1
Sebastião tem um terreno com as seguintes medidas: 26 métros de comprimento e 16 métros de largura.

Ele deseja aumentar a medida da área desse terreno para 816 métroselevado a 2, acrescentando faixas de mesma medida de comprimento de largura a um dos lados e ao fundo. Qual deve ser a medida do comprimento da largura dessas faixas?
Sabendo que a nova medida de área do terreno será 816 métroselevado a 2, escrevemos a seguinte equação:
(x + 16)(x + 26) = 816, com U =
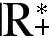
Observação
Como x, da equação anterior, corresponde à medida do comprimento da largura, temos que o conjunto universo da equação é U =
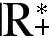
.
Resolvemos a equação para determinar a medida x, em metro:
(x + 16)(x + 26) = 816
x elevado a 2 + 26x + 16x + 416 = 816
x elevado a 2 + 42x menos 400 = 0
Resolvendo a equação, obtemos: x₁ = menos50 e x₂ = 8.
Como menos50 e 8 são raízes da equação, mas só 8 pertence ao conjunto universo, então S = {8}.
Logo, a medida do comprimento da largura das faixas é 8 métros.
Problema 2
Uma empresa de loteamento vai cercar três terrenos próximos, retangulares e de mesmas dimensões. A medida do comprimento é 20 métros maior que a medida da largura do terreno. Os três lotes têm, juntos, .8775 métroselevado a 2 de medida de área. Quais são as dimensões de cada lote?
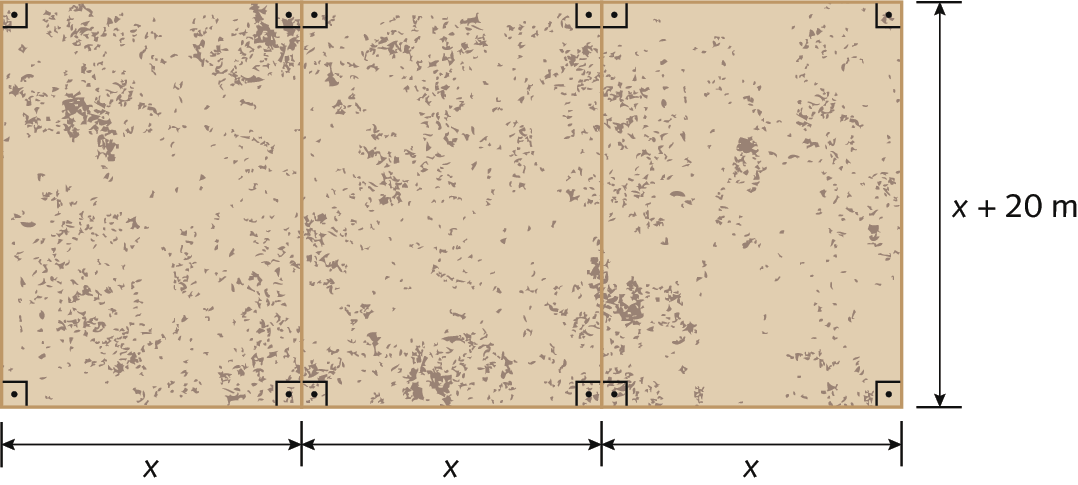
A equação que representa essa situação é:
3(x)(x + 20) = .8775, com U =
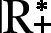
Resolvendo a equação para determinar a medida x em metro, temos:
3(x elevado a 2 + 20x) = 8 775
3x elevado a 2 + 60x = 8 775
3x elevado a 2 + 60x menos 8 775 = 0
É possível obter, a partir da equação, as raízes:
x1 é igual a 45.ou
x2 é igual a menos 65..
Como menos 65 e 45 são raízes da equação, mas só 45 pertence ao conjunto universo, então S = {45}.
Portanto, as dimensões de cada lote são 45 métros e 65 métros.
Atividades
Faça as atividades no caderno.
100. A metade do quadrado de um número inteiro positivo é igual ao dôbro desse número mais 6. Calcule-o.
101. O quadrado de um número natural é igual a seu dôbro adicionado com 24. Determine esse número.
102. O dôbro do quadrado de um número é igual ao produto desse número por 7, menos 3. Qual é o número?
103. O quadrado da idade de Camila subtraído da metade dessa idade é igual a 14 anos. Calcule a idade de Camila.
104. A soma dos quadrados de dois números inteiros positivos e consecutivos é 25. Calcule-os.
105. Determine a medida do comprimento do lado do quadrado em que o número que representa a medida da área excede o número que representa a medida do perímetro em 5.
106. Determine três números inteiros, positivos e consecutivos, tais que o quadrado do menor seja igual à diferença dos outros dois.
107. A medida da área da parte roxa da figura é 94 métroselevado a 2. Calcule a medida x em metro.
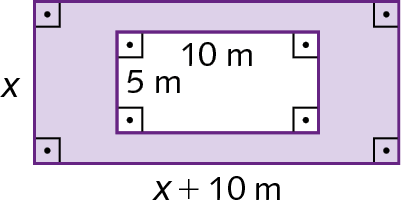

Veja que interessante
Faça as atividades no caderno.
Equações biquadradas
Perto do ano 2000 antes de Cristo, os babilônios não só resolviam as equações do 2º grau, como também discutiam a resolução de algumas equações de 3º grau e de um tipo especial de equação de 4º grau: as equações biquadradas.
De modo geral, uma equação na incógnita x é chamada de biquadrada quando póde ser escrita na fórma:
ax elevado a 4 + bx elevado a 2 + c = 0, com a ≠ 0
Um exemplo de equação biquadrada é x elevado a 4 menos 13x elevado a 2 + 36 = 0. Observe que podemos escrevê-la da seguinte fórma: (x elevado a 2)elevado a 2 menos 13x elevado a 2 + 36 = 0
Substituindo x elevado a 2 por uma incógnita auxiliar y, obtemos a equação: y elevado a 2 menos 13y + 36 = 0
Dessa fórma, reduzimos a equação biquadrada x elevado a 4 menos 13x elevado a 2 + 36 = 0 à equação do 2º grau y elevado a 2 menos 13y + 36 = 0 de incógnita y. Resolvendo essa equação, obtemos: y ₁ = 4 e y ₂ = 9. Como x elevado a 2 = y, temos:
• Para y = 4, temos x elevado a 2 = 4, ou seja, x = ±2
• Para y = 9, temos x elevado a 2 = 9, ou seja, x = ±3
Logo, as raízes da equação x elevado a 4 menos 13x elevado a 2 + 36 = 0 são menos3, menos2, 2 e 3.
Atividade
Resolva, no caderno, as seguintes equações biquadradas:
a) x elevado a 4 menos 5x elevado a 2 + 4 = 0
b) 2x elevado a 4 menos 16x elevado a 2 = 18

Resolvendo em equipe
Faça a atividade no caderno.
1. (ó bê ême) Qual é o valor da expressão ..20112011elevado a 2 + ..20112003elevado a 2 menos 16 × ..20112007?
a) 2 × 20112007elevado a 2
b) 2 × 20112003elevado a 2
c) 2 × 20112007
d) 2 × 20112003
e) 2 × 20112011elevado a 2
|
Interpretação e identificação dos dados |
• Analise as informações do enunciado e anote no caderno as que você julgar relevantes para a resolução do problema. |
|---|---|
|
Plano de resolução |
• Reescreva a expressão numérica dada, considerando 20.112.007 igual a x. |
|
Resolução |
• Junte-se a três colegas. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• Organizem a apresentação da resolução, explicitando cada etapa e justificando a escolha do número 20.112.007 como x. |
Revisão dos conteúdos deste capítulo
Produtos notáveis
Quadrado da soma de dois termos
Quadrado da diferença de dois termos
Produto da soma pela diferença de dois termos
1. Desenvolva os produtos notáveis.
a)
Sentença matemática. Abre parênteses, 3x mais 1, fecha parênteses, elevado ao quadrado.b)
Sentença matemática. Abre parênteses, 2m menos 5, fecha parênteses, elevado ao quadrado.c)
Sentença matemática. Abre parênteses, 6ab mais 1, fecha parênteses, vezes, abre parênteses, 6ab menos 1, fecha parênteses.d)
Sentença matemática. Abre parênteses, 5ab menos 7, fecha parênteses, elevado ao quadrado.e)
Sentença matemática. Abre parênteses, 2x mais 5, fecha parênteses, vezes, abre parênteses, 2x menos 5, fecha parênteses.2. Desenvolva os produtos notáveis e reduza os termos semelhantes.
a)
Sentença matemática. Abre parênteses, x mais 2y, fecha parênteses, elevado ao quadrado, mais, abre parênteses, 2x menos y, fecha parênteses, elevado ao quadrado.b)
Sentença matemática. 2, abre parênteses, m menos 2, fecha parênteses, elevado ao quadrado, menos, 3, abre parênteses, m mais 1, fecha parênteses, vezes, abre parênteses, m menos 1, fecha parênteses.c)
Sentença matemática. Abre parênteses, a mais b, fecha parênteses, elevado ao quadrado, menos, abre parênteses, a elevado ao quadrado mais b elevado ao quadrado, fecha parênteses.d)
Sentença matemática. Abre parênteses, 2a menos 3b, fecha parênteses, elevado ao quadrado, mais, abre parênteses, a menos 5b, fecha parênteses, abre parênteses, a mais 5b, fecha parênteses.3. Sendo
Sentença matemática. x elevado ao quadrado, mais y elevado ao quadrado, é igual a 56.e x ⋅ y = 22, qual é o valor de x + y?
4.

Utilize o quadrado da soma ou da diferença para calcular os quadrados a seguir.
a) 27elevado a 2
b) 43elevado a 2
c) 104elevado a 2
d) 297elevado a 2
5.

Utilize o produto da soma e da diferença de dois termos para resolver os produtos a seguir.
a) 95 ⋅ 105
b) 202 ⋅ 198
c) 54 ⋅ 46
d) 1 001 ⋅ 999
6. Observe a figura e responda.
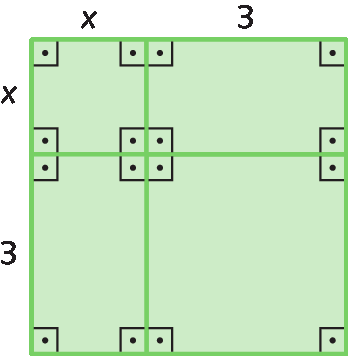
a) Quais expressões algébricas representam as medidas de área e do perímetro da figura?
b) Se x = 2 centímetros, determine as medidas de área e de perímetro.
Fatoração
Fatoração com um fator comum em evidência
Fatoração por agrupamento
Fatoração por diferença de dois quadrados
Fatoração do quadrado perfeito
7. Fatore as expressões e escreva o caso de fatoração utilizado.
a)
Sentença matemática. 7 x elevado ao quadrado, mais 7 y elevado ao quadrado.b)
Sentença matemática. x elevado ao quadrado, y elevado ao quadrado, menos 169, z elevado ao quadrado.c) 30 + 10x menos 12a menos 4ax
d)
5x ao quadrado menos x ao cubo.
e)
Sentença matemática. 16 a elevado ao quadrado, menos 8a, mais 1.8. Fatore as expressões algébricas:
a)
Sentença matemática. Abre parênteses, a mais 3, fecha parênteses, elevado ao quadrado, menos 9.b)
Sentença matemática. y, x elevado a 3, fim do expoente, menos, x, y elevado a 3.c)
Sentença matemática. y elevado a 3, fim do expoente, menos, y elevado ao quadrado, menos 9y, mais 9.d)
Sentença matemática. 12 x elevado ao quadrado, menos 48 y elevado ao quadrado.e)
Sentença matemática. 6 x elevado ao quadrado, menos 12x, mais 6.9.

Encontre os resultados das expressões numéricas a seguir, utilizando o caso de fatoração diferença de quadrados.
a) .2013elevado a 2 menos .2010elevado a 2
b) 475elevado a 2 menos 474elevado a 2
10. Complete as expressões algébricas, sabendo que elas representam quadrados perfeitos.
a)
Sentença matemática. 4 y elevado ao quadrado, mais quadrado cinza, mais 49.b)
Sentença matemática. Quadrado cinza menos 2m mais 1.c)
Sentença matemática. 9 n elevado ao quadrado, mais 6 n mais quadrado cinza.Resolução de equações do 2º grau
Resolução de equações do 2º grau incompletas
Observe como resolver algumas equações do 2º grau incompletas.
a) xelevado a 2 menos 4 = 0, considerando U =

.
xelevado a 2 = 4
Sentença matemática. x é igual a mais ou menos raiz de 4.
x = 2 ou x = menos2
Como menos2 e 2 são raízes da equação e pertencem ao conjunto universo, então
Conjunto solução é igual a, abre chave, menos 2, 2, fecha chave..
b) 2xelevado a 2 + 3 = 0, considerando U =

.
x ⋅ (2x + 3) = 0
x = 0 ou 2x + 3 = 0
2x = menos3
x igual a 3 sobre 2.
Como
Fração menos 3 sobre 2.e 0 são raízes da equação e pertencem ao conjunto universo, então
Conjunto solução é igual a, abre chave, fração menos 3 sobre 2, fim da fração, 0, fecha chave..
Resolução de equações do 2º grau completas
A fórmula resolutiva de equações do 2º grau axelevado a 2 menos bx + c = 0, em que a, b e c são números reais com a ≠ 0, é dada por:
Discriminantes
A expressão belevado a 2 ‒ 4ac é chamada de discriminante e representada pela letra grega
Delta..
Analisando a fórmula resolutiva, podemos verificar se uma equação tem ou não raízes reais e obter uma relação entre os coeficientes e as raízes (x₁ e x₂) de uma equação do 2º grau.
•
Esquema. Delta maior que 0. Seta para a direita com indicação: x1 é igual a fração de numerador menos b mais raiz quadrada de delta, fim da raiz, e denominador 2a, fim da fração, e x2 é igual a fração de numerador menos b menos raiz quadrada de delta, fim da raiz, e denominador 2a.•
Esquema. Delta igual a 0. Seta para a direita com indicação: x1 igual a x2 igual a fração menos b sobre 2a.• ∆ < 0 → não existem raízes reais.
11. Resolva as equações considerando U =

.
a)
Sentença matemática. x elevado ao quadrado menos 9 é igual a 0.b)
Sentença matemática. x elevado ao quadrado mais 8x, mais 15, é igual a 0.c)
Sentença matemática. m elevado ao quadrado, menos raiz de 2, fim da raiz, m, é igual a 0.d)
Sentença matemática. x elevado ao quadrado mais 10x, mais 25, é igual a 0.e)
Sentença matemática. x elevado ao quadrado menos 6x, menos 7 é igual a 0.f)
Sentença matemática. 16 y elevado ao quadrado menos 121 é igual a 0.g)
Sentença matemática. 3 x elevado ao quadrado mais 2x, mais 8, é igual a 0.12. Resolva as equações considerando U =

.
a)
Sentença matemática. Abre parênteses, x mais 4, fecha parênteses, elevado ao quadrado, mais, abre parênteses, x menos 4, fecha parênteses, elevado ao quadrado, é igual a 160.b) xelevado a 2 menos 11x = menos 28
c)
Sentença matemática. 4 x elevado ao quadrado mais 2x, mais 2, é igual a 1.d)
Sentença matemática. x elevado ao quadrado mais 7x, é igual a 35 menos 5x.13. A diferença entre o quadrado de um número e o seu triplo é igual a 10. Qual é esse número?
14. O quadrado de certo número diferente de zero é igual ao seu quádruplo. Que número é esse?
15. Uma empresa construirá um galpão em um terreno quadrado cuja medida, em metro, do comprimento do lado é indicada por y. Esse galpão será retangular com medidas de comprimento iguais a (y menos 30) métros e (y menos 40) métros. Sabe-se que a medida da área construída será de 1 200 métros quadrados. Qual deve ser a medida y em metro?
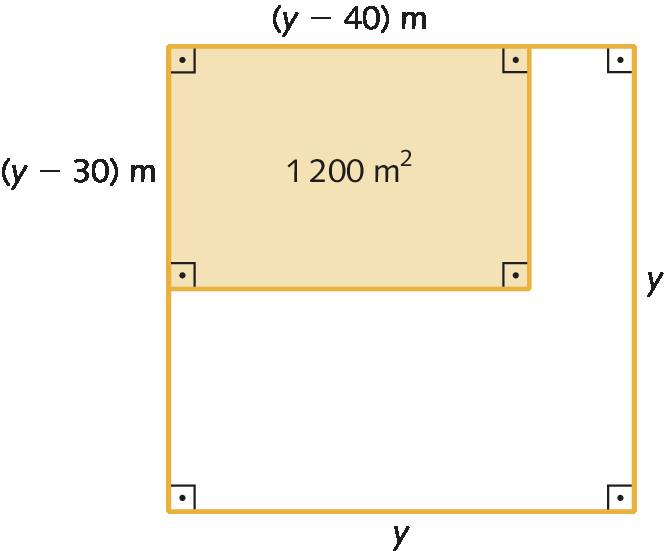
16. Determine o valor de p na equação xelevado a 2 + px + 4 = 0, para que ela tenha duas raízes reais e iguais.
17. Determine o valor de m na equação xelevado a 2 menos 6x + m = 0, para que a equação não apresente raízes reais.
18. Quais valores k póde assumir na equação x elevado a 2 menos 4x + k = 0, de fórma que a equação apresente duas raízes reais?