Capítulo 5 Função afim

Trocando ideias

A escala de Fahrenheit (grau éfe) é uma escala de medidas de temperatura em que 32 graus Farenrráite representam o ponto de fusão do gelo e 212 graus Farenrráite representam o ponto de ebulição da água pura sob pressão atmosférica padrão. Essa escala é muito usada em países de língua inglesa, principalmente nos Estados Unidos.

Fotografia. Termômetro de rua registrando 109 graus fahrenheit. O dia está ensolarado e há duas pessoas caminhando na rua, utilizando roupas leves e chapéu. — Termômetro registrando 109 graus Farenrráite em Seattle, Washington (Estados Unidos da América). Foto de 2021.

Podemos escrever a fórmula F = 1,8C + 32 para converter uma medida de temperatura C expressa em graus Celsius (ºC) para uma medida de temperatura F expressa em graus Fahrenheit (ºF).

▸

Quais são as medidas de temperatura de fusão do gelo e de ebulição da água em graus Celsius?

▸

Qual é a medida aproximada da temperatura registrada pelo termômetro da foto em graus Celsius?

▸

Em seu caderno, elabore um problema cuja resolução utilize a fórmula F = 1,8C + 32. Depois, troque de problema com um colega e resolva o problema proposto por ele.

Neste capítulo, vamos estudar a ideia de função e função afim.

Conheça mais

No Sistema Internacional de Unidades (ésse Í), a unidade-padrão de medida de temperatura é o kelvin (cá).

No site do Instituto Nacional de Metrologia, Qualidade e Tecnologia (in metro), é possível conferir uma versão traduzida do ésse Í.

Página 128

1 Ideia de função

Acompanhe a situação a seguir.

A Feira dos Caxixis é uma das feiras de artesanato mais antigas do Brasil e acontece uma vez ao ano na cidade de Nazaré das Farinhas, no estado da Bahia. Os caxixis são miniaturas de objetos em cerâmica produzidas na região.

Um dos expositores dessa feira vende cada um de seus caxixis a R$ 10,00dez reais. Quanto uma pessoa gastaria se ela comprasse duas peças? E se comprasse 3 peças? E se comprasse 5 peças?

Fotografia. Diversas esculturas de mulheres negras utilizando trajes africanos. — Feira de Caxixis, em Nazaré das Farinhas (Bahia). Foto de 2015.

Para responder a essas questões, podemos montar um quadro com a indicação de valor e de quantidade de peças.

Valor da compra de acordo com a quantidade de peças
Quantidade de peças	1	2	3	4	5	6
Valor (em R$)	10,00	20,00	30,00	40,00	50,00	60,00

Observe que cada quantidade de caxixis determina um valor a ser pago pelo cliente.

Quando isso ocorre, podemos dizer que o valor que o cliente vai pagar é dado em função da quantidade de peças.

Quando relacionamos duas grandezasglossário , dizemos que cada valor da primeira grandeza corresponde a um único valor da segunda grandeza e que a segunda grandeza é função da primeira.

Lei de formação da função

Quando temos uma relação em que uma grandeza é função de outra, a correspondência entre cada valor de uma grandeza e cada valor da outra póde ser expressa por uma sentença chamada lei de formação da função ou lei da função.

Na situação anterior, se indicarmos por y o valor, em real, a ser pago pelo cliente e por x a quantidade de peças, a lei da função será:

y = 10 ⋅ x, em que x é um número natural.

Variáveis

As grandezas envolvidas em uma relação em que uma é função da outra são chamadas de variáveis da situação apresentada. No caso da situação anterior, as variáveis são o valor, em real, e a quantidade de peças.

O valor a ser pago pelo cliente é a variável dependente, pois depende da quantidade de peças que ele deseja comprar.

A quantidade de peças é a variável independente, pois podemos escolher um valor para essa variável.

Página 129

Atividades

Faça as atividades no caderno.

1. Uma indústria produz embalagens biodegradáveis. Sua produção é de seiscentas unidades por hora.

a) Em 10 horas de trabalho, quantas embalagens biodegradáveis são produzidas?

b) Para produzir .4800 unidades de embalagens biodegradáveis, quantas horas são necessárias?

c) Podemos afirmar que a quantidade de embalagens biodegradáveis produzidas é função da medida do tempo de produção? Por quê?

d) No caderno, escreva uma lei que relacione a quantidade de embalagens biodegradáveis com a medida do tempo, em hora.

2. A medida da área (a) de um quadrado é dada em função da medida de comprimento (a) do seu lado. No caderno, escreva a lei dessa função e identifique a variável dependente e a variável independente.

A notação éfe de xis

Analise a afirmação de Teresa.

Ilustração. Idosa dentro de um carro azul. Ela diz: Meu carro consome 1 litro de combustível a cada 12 quilômetros rodados.

A quantidade de litros (q) de combustível consumido é função da medida da distância (x) percorrida. A lei dessa função é

q = \frac{x}{12}

, em que x é um número real positivo.

A função também póde ser representada por f; quando f varia em função de uma variável x, é o mesmo que escrevermos funçãoabre parênteses décimafecha parênteses. Assim, a função anterior poderia ser representada da seguinte fórma:

f

(x) = \frac{x}{12} (l e m o s: “ f d e x é i g u a l a \frac{x}{12} ”)

Nessa notação, x representa a medida da distância percorrida, em quilômetro, e funçãoabre parênteses décimafecha parênteses, a quantidade de litros de combustível consumido.

Valor de uma função

Na situação anterior, a quantidade de litros de combustível consumido de acôrdo com a medida da distância x percorrida, em quilômetro, foi representada por

f (x) = \frac{x}{12}

, em que x é um número real positivo.

Desse modo, para calcular a quantidade de litros de combustível consumido para o automóvel percorrer 108 quilômetros, basta substituir x por 108 na lei da função e efetuar a operação indicada:

f (108) = \frac{108}{12}

f (108) = 9

Isso significa que, quando x é igual a 108, o valor da função é 9.

Logo, o automóvel consumiu 9 litros de combustível para percorrer 108 quilômetros.

Página 130

Atividades

Faça as atividades no caderno.

3. A lei de formação de uma função função é funçãoabre parênteses décimafecha parênteses = 5x + 2. Calcule:

a) função(0)

b) função(menos1)

c) função(menos2)

d)

f (\frac{3}{4})

4. Dada a lei de uma função funçãoabre parênteses décimafecha parênteses = 5x menos 2, determine o valor de x de modo que:

a) funçãoabre parênteses décimafecha parênteses = 0

b) funçãoabre parênteses décimafecha parênteses = 3

c) funçãoabre parênteses décimafecha parênteses = menos10

d) funçãoabre parênteses décimafecha parênteses = 13

5. A lei de uma função função é

f (x) = \frac{1}{2} x - \frac{3}{4}

. Calcule:

a)

\frac{f (0) - f (1)}{f (2)}

b)

\frac{f (2) \cdot f (1)}{f (0)}

6. Ana elaborou o quadro a seguir.

x	0	$divisão de 1 sobre 16$	$divisão de 1 sobre 8$	$divisão de 1 sobre 4$
f(x)	0	$divisão de 1 sobre 8$	$divisão de 1 sobre 4$	$divisão de 1 sobre 2$

a) Qual é a lei de formação da função f que relaciona os valores da segunda e da primeira linha desse quadro?

b) Calcule o valor de funçãoabre parênteses décimafecha parênteses para

x = - \frac{1}{5}

.

c) Qual é o valor de x quando

f (x) = \frac{7}{2}

?

Representação gráfica de uma função

Cada número real tem um ponto correspondente na reta real e cada ponto da reta corresponde a um número real. Observe.

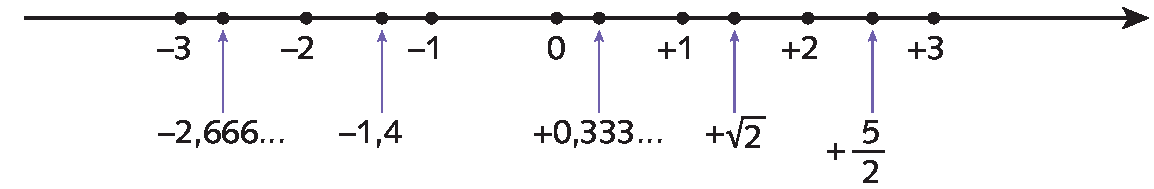
Gráfico. Reta numérica com os pontos: menos 3, menos 2,666, reticências, menos 2, menos 1,4, menos 1, 0, mais 0,333, reticências, mais 1, mais raiz quadrada de 2, mais 2, mais fração 5 sobre 2, mais 3.

Podemos ampliar essa noção, representando um par de números reais por pontos de um plano. Para isso, construímos um sistema de coordenadas cartesianas ou plano cartesiano.

Esse sistema consiste em duas retas reais perpendiculares (eixos), cujo ponto de intersecção corresponde à origem do sistema.

Gráfico. Plano cartesiano. Eixo x com marcações de menos 3 a 3. Eixo y com marcações de menos 3 a 3.

Temos que:

• o eixo x é chamado de eixo das abscissas;

• o eixo y é chamado de eixo das ordenadas;

• o ponto de coordenadas (0, 0) é a origem do plano cartesiano.

Página 131

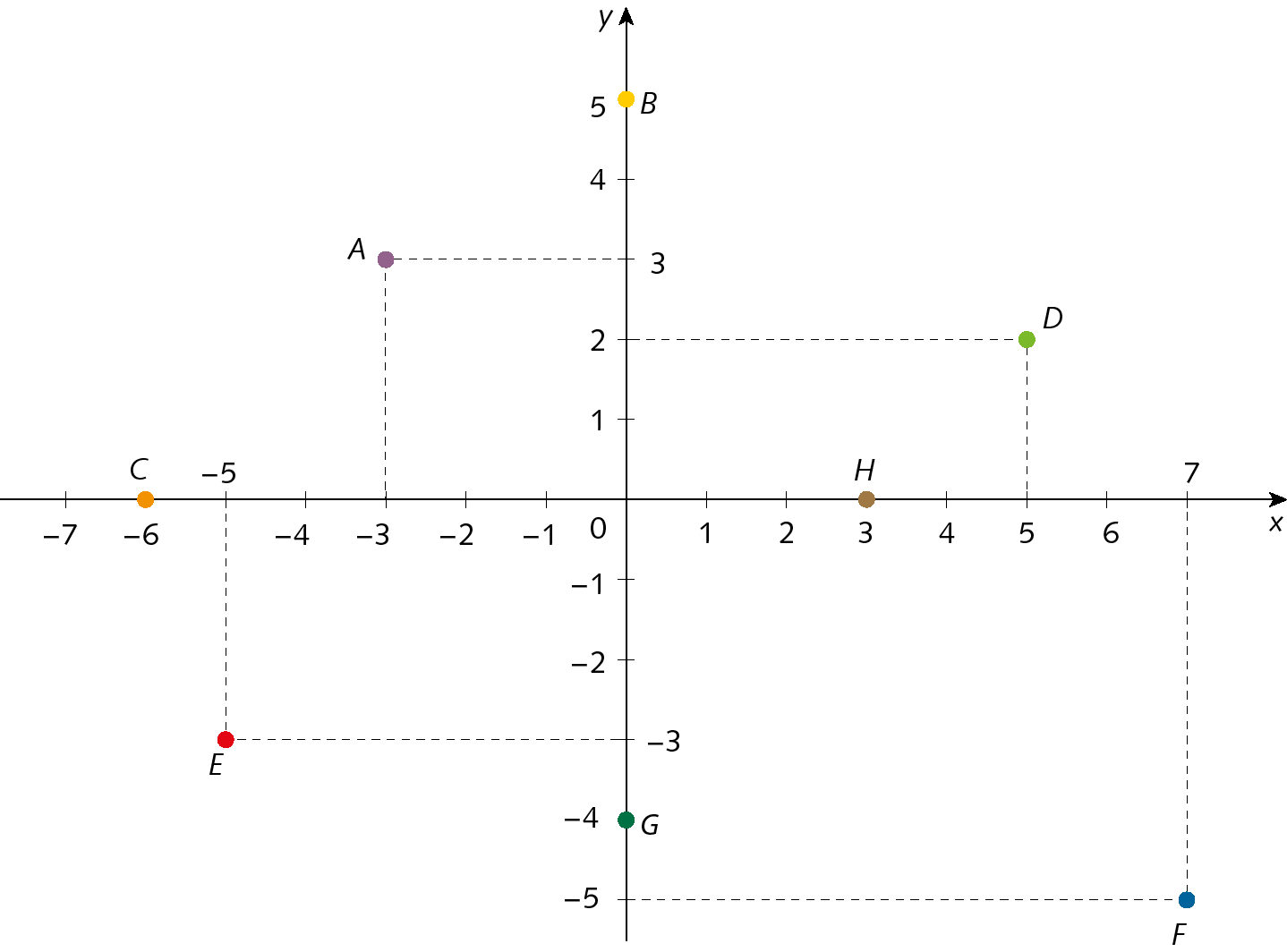
Observe como podemos representar os pontos a (menos3, 3); B (0, 5); C (menos6, 0); D (5, 2); ê (menos5, ‒3); F (7, menos5); G (0, menos4); e H (3, 0) no plano cartesiano.

Gráfico. Plano cartesiano. Alguns pontos coloridos estão indicados: ponto A lilás com coordenadas (menos 3, 3); ponto B amarelo com coordenadas (zero, 5); ponto C laranja com coordenadas (menos 6, zero); ponto D verde com coordenadas (5, 2); ponto E vermelho com coordenadas (menos 5, menos 3); ponto F azul com coordenadas (7, menos 5); ponto G verde com coordenadas (zero, menos 4);

Ilustração. Menino branco com cabelo castanho, cadeirante. A mão esquerda está segurando o suporte da roda e, a direita, está levantada com o dedo indicador levantado. Ele diz: Cada par ordenado (x, y) corresponde a um ponto de coordenadas x e y; e cada ponto corresponde a um par ordenado.

Toda situação que permite expressar uma grandeza em função da outra pode ser representada em um plano cartesiano na fórma de um gráfico. Acompanhe as situações a seguir.

Situação 1

A quantidade (q) de água desperdiçada por uma torneira gotejando lentamente é função da medida de tempo (t ). Analise alguns valores de q e t.

Quantidade de água desperdiçada por uma torneira gotejando lentamente
t (em minuto)	0	1	1,5	3
q (em mililitro)	0	7	10,5	21

Cada par ordenado pode ser representado por um ponto em um plano cartesiano. Nesse exemplo, o primeiro número do par ordenado indica a medida de tempo (em minuto), e o segundo número, a quantidade de água desperdiçada pela torneira (em mililitro).

Página 132

Gráfico. Eixo horizontal com a letra t e uma seta apontando com o texto "Indica a medida do tempo em que a torneira fica gotejando (em minuto)". Eixo vertical com a letra q e uma seta apontando com o texto "Indica o desperdício de água (em mililitros)". Os pontos com pares ordenados (0, 0); (1, 7); (1,5; 10,5) e (3, 21) estão indicados. Uma semirreta com origem em (0, 0) passa pelos demais pontos.

Ilustração. Mulher branca de cabelo castanho encaracolado, camisa listrada de verde e vermelho e jaleco branco. Está com a mão esquerda para trás e a direta levantada com o indicador apontando para o lado. Ela pergunta: Por que o gráfico parte da origem?

Note que os pontos obtidos estão alinhados. Isso acontece porque a quantidade de água desperdiçada é diretamente proporcional à medida do tempo que a torneira fica gotejando. Além disso, como a medida de tempo pode assumir qualquer valor real positivo ou nulo, o gráfico dessa função será uma linha contínua que parte da origem, passa pelos pontos (1, 7), (1,5; 10,5) e (3, 21), e continua indefinidamente.

▸ Qual é a lei da função que o gráfico representa?

Situação 2

Em uma planilha eletrônica, Beatriz descobriu uma maneira de calcular o inverso, com duas casas decimais, de qualquer número real, diferente de zero, inserido nela. Observe alguns números que Beatriz inseriu na planilha e os números correspondentes calculados.

Ilustração. Representação de uma planilha eletrônica. Primeira linha: Resultados obtidos pela planilha de acordo com os números inseridos. Segunda linha: Número inserido (x): menos 3; menos 1,5; 1; 1,5; 4. Terceira linha: Resultado (y): menos 0,33; menos 0,67; 1; 0,67; 0,25.

Cada par de números (número inserido, resultado) fórma um par ordenado (x, y), que pode ser representado por um ponto em um plano cartesiano.

Em seguida, Beatriz usou o mesmo programa em que fez a planilha e solicitou que fosse representado o gráfico da função que relaciona x e y.

Gráfico. Plano cartesiano. Eixo horizontal indicado pela letra x e uma seta apontando com o texto "Indica o inverso com duas casas decimais do número inserido por Beatriz.". Eixo vertical indicado pela letra y e uma seta indicando o texto "Indica o número inserido por Beatriz." Pontos indicados pelos pares ordenados: (menos 3, menos 0,33); e (menos 1,5; menos 0,67); e uma curva passando por estes dois pontos sem cruzar os eixos. Pontos indicados pelos pares ordenados: (1, 1); (1,5; 0,67); e (4; 0,25) e uma curva passando por estes pontos sem cruzar os eixos.

Ilustração. Menina branca de cabelo liso e loiro e camiseta colorida. Mão esquerda levantadas e mão direita espalmada. Ela fala: Como posso inserir qualquer número real, diferente de zero, na planilha, o gráfico dessa função é formado por linhas contínuas sem início nem fim.

▸ Qual é a lei da função que o gráfico representa?

Página 133

Situação 3

Uma loja vende Cê dês de acôrdo com o quadro a seguir.

Preço de acordo com a quantidade de CDs
Quantidade de CDs (n)	1	4	6	9
Preço (em R$) (p)	2,00	8,00	12,00	18,00

Nesse exemplo, também podemos representar os pares ordenados (n, p) em um plano cartesiano.

Note que o preço é diretamente proporcional à quantidade de Cê dês. Além disso, a quantidade de Cê dês só pode ser um número natural. Assim, no eixo das abscissas representamos apenas números naturais.

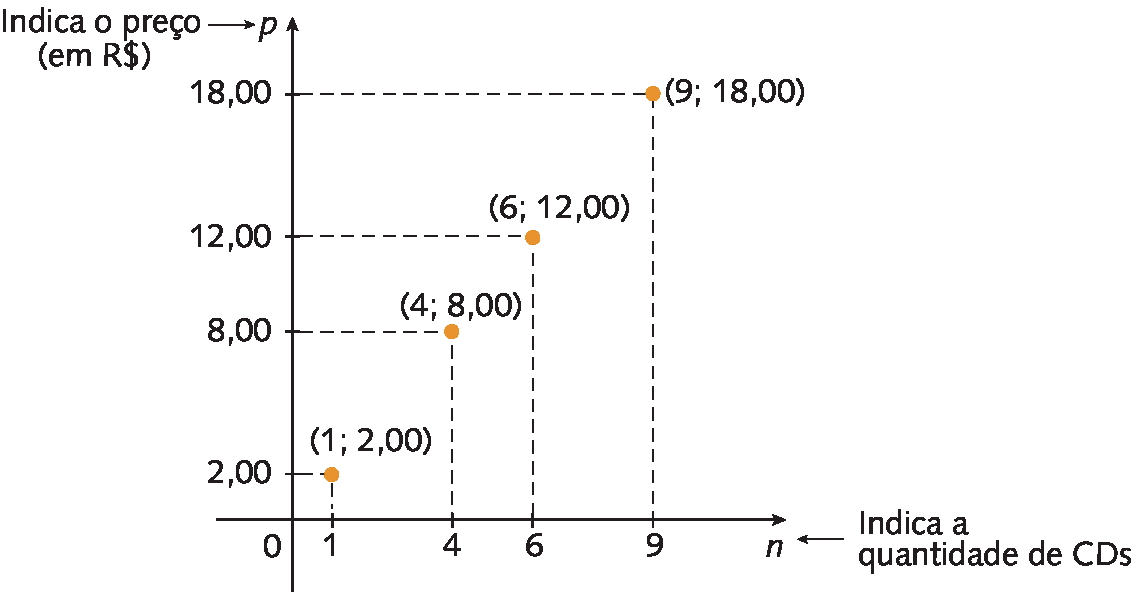
Gráfico. Eixo horizontal com letra n e uma seta apontando com o texto "indica a quantidade de CDs". Eixo vertical com a letra p e seta apontando com o texto "Indica o preço (em reais)". Os pontos com os seguinte pares ordenados estão indicados: (1; 2,00) (4; 8,00) (6; 12,00) (9; 18,00).

Ilustração. Menino branco de cabelo castanho e camiseta azul. Está de lado e com o indicador esquerdo apontado. Ele fala: Observe que os pontos representados no plano estão alinhados, porém não podemos uni-los com uma linha contínua.

▸ Qual é a lei da função que o gráfico representa?

Atividades

Faça as atividades no caderno.

7. Uma loja de fotografias está fazendo uma promoção para a impressão de fotos.

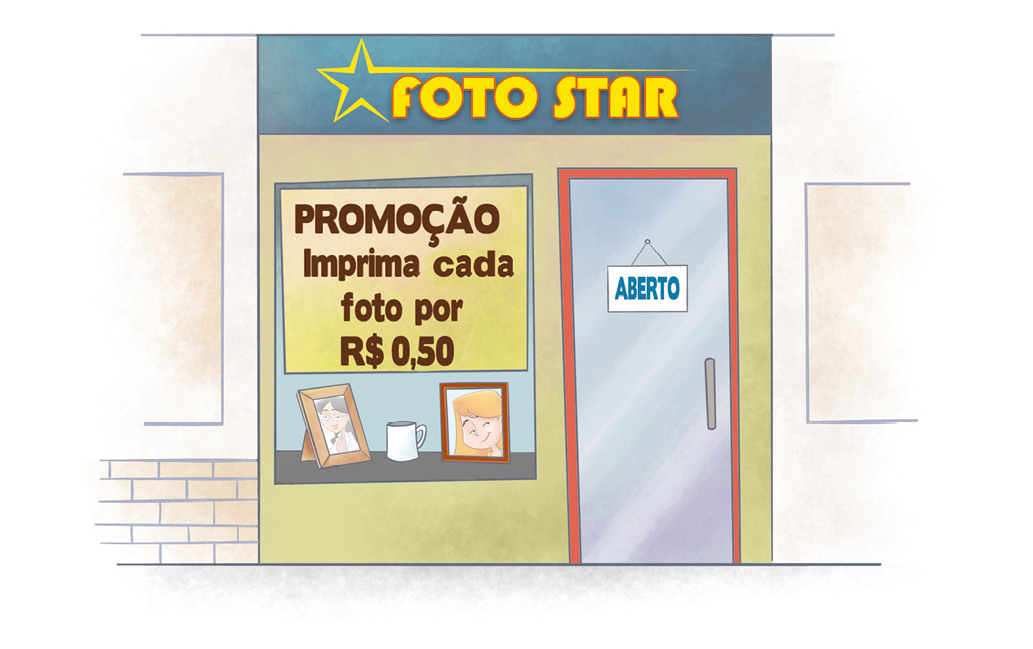
Ilustração. Frente Loja de fotografias com nome Foto Star. À esquerda, placa com o texto: PROMOÇÃO. Imprima cada foto por cinquenta centavos de real. Ao lado, porta com placa ABERTO.

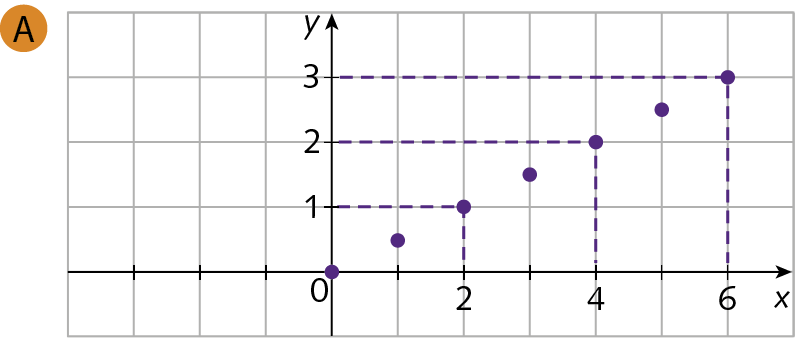
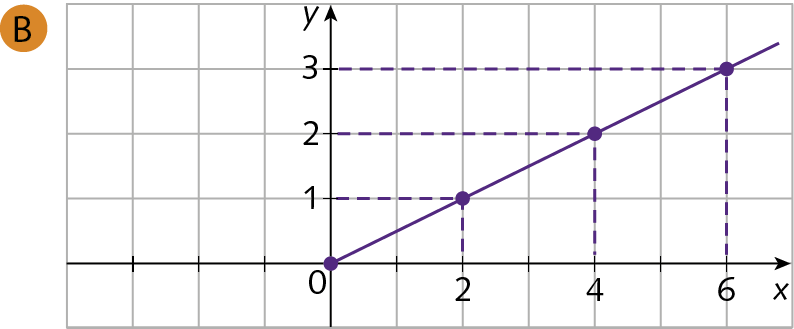
a) Qual é a lei da função que relaciona o preço (y) a pagar e a quantidade (x) de fotos impressas?

b) Qual dos gráficos a seguir corresponde à função encontrada no item a? Por quê?

Gráfico. Plano cartesiano em malha quadriculada. Os pontos com Pares ordenados a seguir estão indicados: (0, 0), (1, 1,5), (2, 1), (3, 2,5), (4, 2), (5, 2,5), (6, 3).

Gráfico. Plano cartesiano em malha quadriculada. Pontos indicados com os seguintes Pares ordenados: (0, 0), (2, 1), (4, 2), (6, 3). Semirreta sai da origem e passa pelos pontos.

8. Sejam x e y duas grandezas inversamente proporcionais. Sabe-se que, quando o valor de x é 3, o valor de y é 5. Determine a lei da função que relaciona o valor de y com o valor de x.

Página 134

9. Em Geografia, denomina-se densidade demográfica a medida expressa pela razão entre a população de uma região e a medida da área correspondente.

d = \frac{p}{a}

d

Ilustração. Seta alaranjada apontando para à direita.

densidade

p

população

a

medida da área

Densidade demográfica e medida da área são grandezas direta ou inversamente proporcionais? E as grandezas densidade demográfica e população?

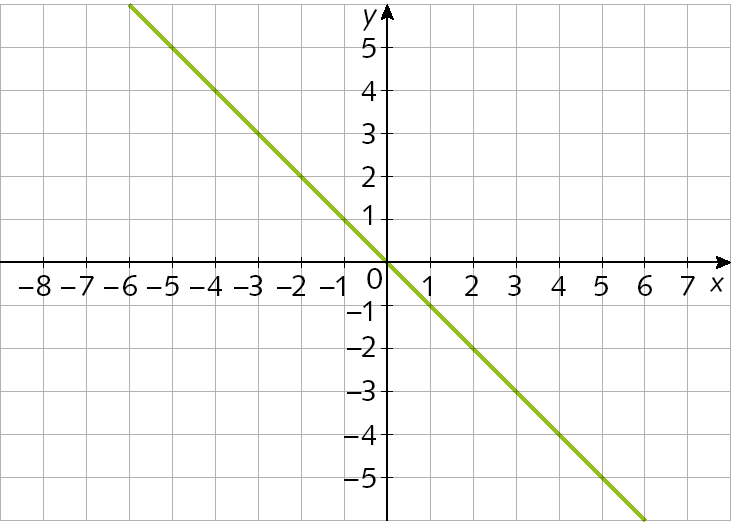
10. Qual dos gráficos seguintes pode representar a função f tal que

f (x) = \frac{2}{x}

, com x > 0.

a)

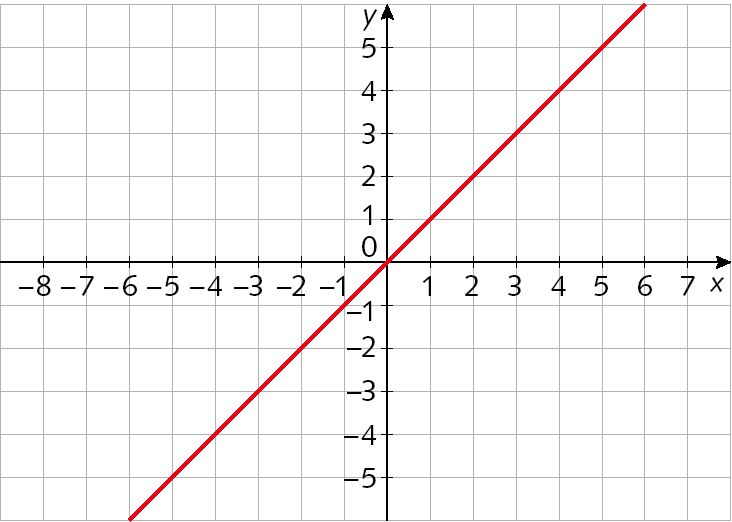
Gráfico. Plano cartesiano em malha quadriculada. Eixo x, pontos de menos 8 a 7. Eixo y, pontos de menos 5 a 5. Reta diagonal passa origem e pelo ponto (1,1).

b)

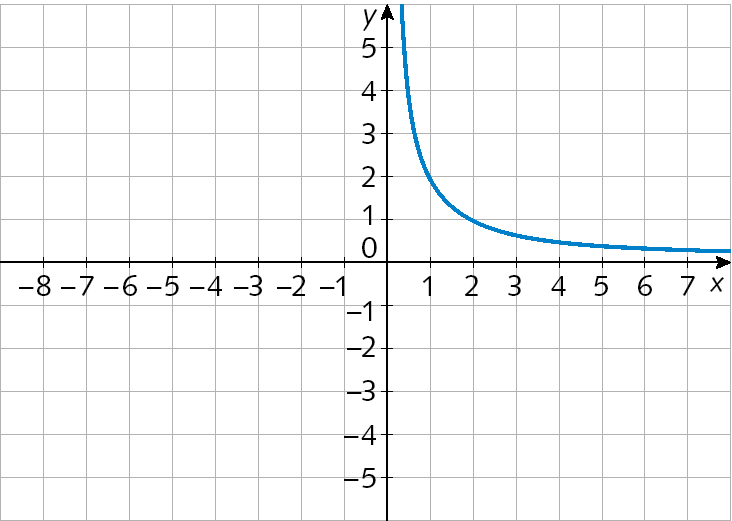
Gráfico. Plano cartesiano em malha quadriculada. Eixo x, pontos de menos 8 a 7. Eixo y, pontos de menos 5 a 5. Linha curvada para esquerda no primeiro quadrante.

c)

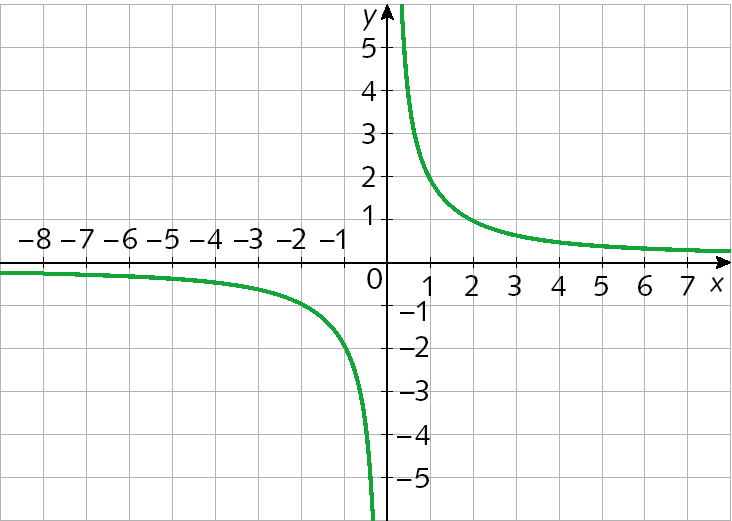
Gráfico. Plano cartesiano em malha quadriculada. Eixo x, pontos de menos 8 a 7. Eixo y, pontos de menos 5 a 5. Uma curva ilustrada no 3º quadrante e outra curva no primeiro quadrante.

d)

Gráfico. Plano cartesiano em malha quadriculada. Eixo x, pontos de menos 8 a 7. Eixo y, pontos de menos 5 a 5. Reta diagonal passa pela origem e pelo ponto (menos 1, 1).

Lendo e aprendendo

Ícone do tema FORMAÇÃO CIDADÃ. Ícone do tema SAÚDE.

Coronavírus e seu crescimento

Nos últimos meses, muito se tem ouvido falar a respeito do aumento do número de casos do novo coronavírus. E, em meio a tantas notícias sobre a pandemia, a expressão “crescimento exponencial” tornou-se bastante comum. Como todas as reportagens mostram, a expressão crescimento exponencial refere-se a um aumento acentuado no número de casos. [reticências]

Coronavírus é uma família de vírus que causam infecções respiratórias. Em dezembro de 2019, a Organização Mundial da Saúde (ó ême ésse) foi alertada sobre vários casos de pessoas infectadas pelo novo coronavírus na China, causador da doença côvid dezenóve. Com o fluxo internacional de pessoas, em pouco tempo o vírus se espalhou para o mundo e alcançou 189 países.

[reticências]

Página 135

Em epidemias de fácil contágio, como ocorre com o coronavírus, cada pessoa pode transmitir o vírus para diversas outras pessoas. Se toda a população for suscetível ao contágio e se cada infectado contagiar m novos casos em média, sendo m uma constante maior do que 1, o crescimento é exponencial.

Por exemplo, se cada indivíduo infectado transmite a doença para duas pessoas, m = 2, temos o seguinte esquema de propagação:

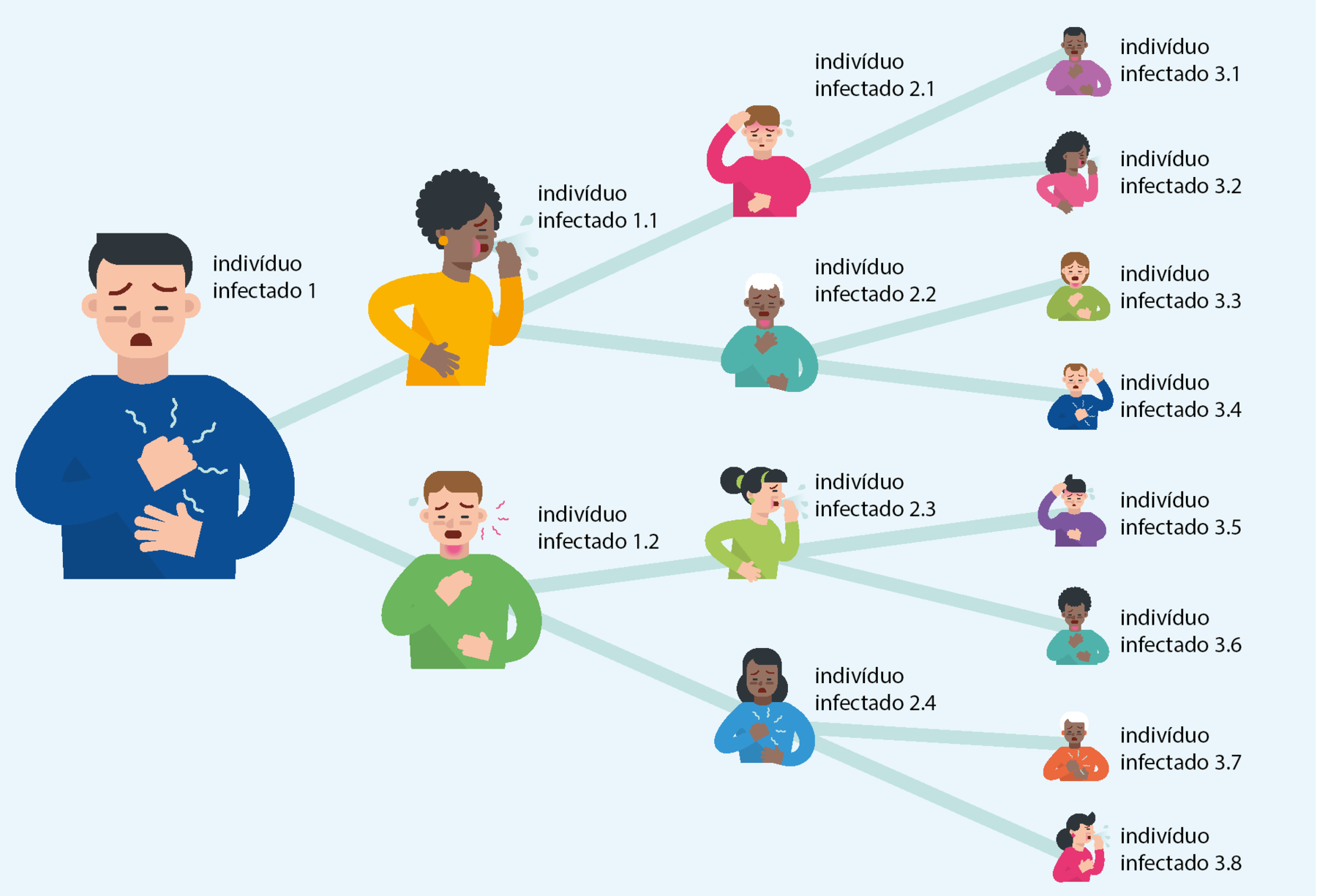
Esquema. Ilustração de um personagem homem branco com cabelo curto preto e blusa de frio azul com cota Indivíduo infectado 1. Dele saem dois fios para dois outros personagens: um para uma mulher negra de cabelo crespo curto e blusa de frio amarela com cota Indivíduo infectado 1.1 e outro para um homem branco com cabelo castanho e blusa de frio verde com a cota Indivíduo infectado 1.2. Do Indivíduo infectado 1.1 saem dois fios para outros dois personagens: um homem branco de cabelo castanho e blusa de frio rosa com cota Indivíduo infectado 2.1 e outro para um homem idoso negro de cabelo branco e blusa de frio azul clara com cota Indivíduo infectado 2.2. Do Indivíduo infectado 1.2, saem dois fios para outros dois personagens: um para uma mulher branca com cabelo preto preso e blusa de frio azul com cota Indivíduo infectado 2.3 e outra mulher negra com blusa de frio azul e cota Indivíduo infectado 2.4. Do indivíduo infectado 2.1 saem dois fios: um para um homem negro com blusa de frio lilás e cota Indivíduo infectado 3.1 e, outro, para uma mulher negra com cabelo preso e blusa de fio rosa com cota indivíduo infectado 3.2. Do Indivíduo infectado 2.2 saem dois fios, um para uma mulher de cabelo loiro preso e blusa de frio verde com cota Indivíduo infectado 3.3 e outro para um homem branco com cabelo castanho e blusa de frio azul com cota Indivíduo infectado 3.4. Do Indivíduo infectado 2.3 saem dois fios, um para mulher branca com cabelo preto preso e blusa de frio roxa com cota Indivíduo infectado 3.5 e outro para homem negro com cabelo crespo e blusa de frio verde com cota Indivíduo infectado 3.6. Do Indivíduo infectado 2.4 saem dois fios, um para mulher idosa negra com cabelo branco e blusa de frio laranja com cota Indivíduo infectado 3.7 e outro para mulher branca com cabelo preto preso e cota Indivíduo infectado 3.8.

Em notação matemática, o esquema desse exemplo fica função(t)=2elevado a t, em que t representa o tempo e função(t), o número de infectados no instante t [reticências].

Para saber a relação entre o tempo e o número de infectados, os matemáticos propõem modelos matemáticos que têm o objetivo de retratar a situação real.

[reticências]

É por meio dos resultados obtidos com os modelos matemáticos que os pesquisadores podem prever a eficiência do isolamento social e de medidas de proteção e a porcentagem de indivíduos que devem ser vacinados para erradicar uma doença. Desse modo, a Matemática ajuda o governo a tomar decisões mais assertivas em relação ao combate ao novo coronavírus.

PEREIRA, A. C.; TEODORO, G. S.; FERREIRA, R. E.; FILHO, H. G. F. Coronavírus e seu crescimento. Portal da Ciência, Universidade Federal de Lavras, 2 de dezembro de 2020. Disponível em: https://oeds.link/c5dVZl. Acesso em: 7 junho 2022.

Atividades

1. Responda às questões no caderno.

a) Quando o texto anterior foi publicado?

b) O que é coronavírus?

c) Qual é o nome da doença causada pelo novo coronavírus?

d) Como os modelos matemáticos podem ajudar a entender doenças epidemiológicas como a côvid dezenóve?

Página 136

Lendo e aprendendo

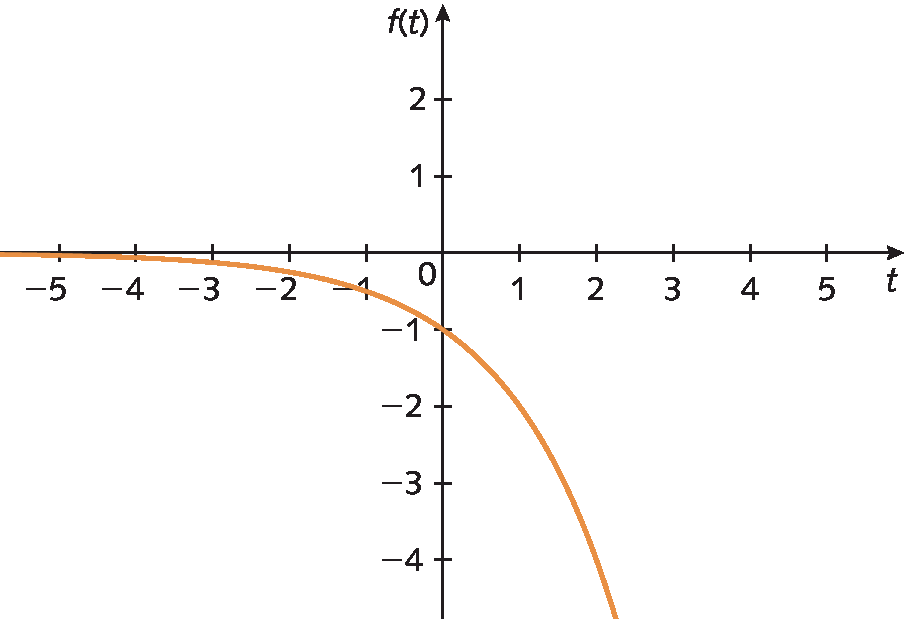
2. Qual destes gráficos é da função função(t) = 2elevado a t, em que t é um número real?

a)

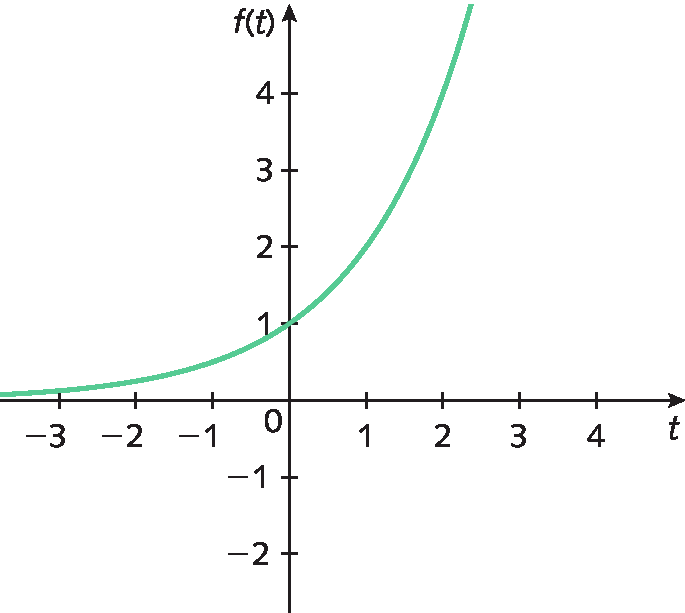
Gráfico. Eixo horizontal t, de menos 3 a 4. Eixo vertical f de t, de menos 2 a 4. Curva crescente pertencente ao segundo e primeiro quadrantes cortando o eixo vertical na ordenada 1.

b)

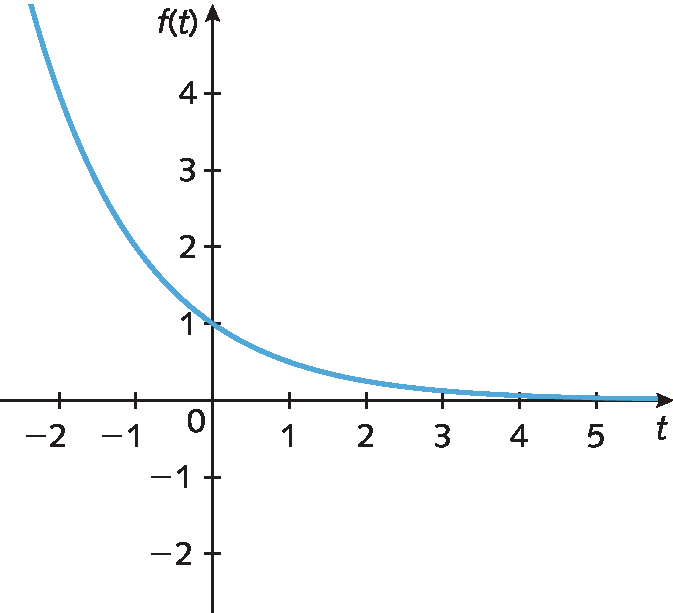
Gráfico. Eixo horizontal t de menos 2 a 5. Eixo vertical f de t de menos 2 a 4. Curva decrescente pertencente ao segundo e primeiro quadrantes, cortando o eixo vertical na ordenada 1.

c)

Gráfico. Eixo horizontal t de menos 5 a 5. Eixo vertical f de t de menos 4 a 2. Curva decrescente pertencente ao terceiro e quarto quadrantes, cortando o eixo vertical na ordenada menos um.

d)

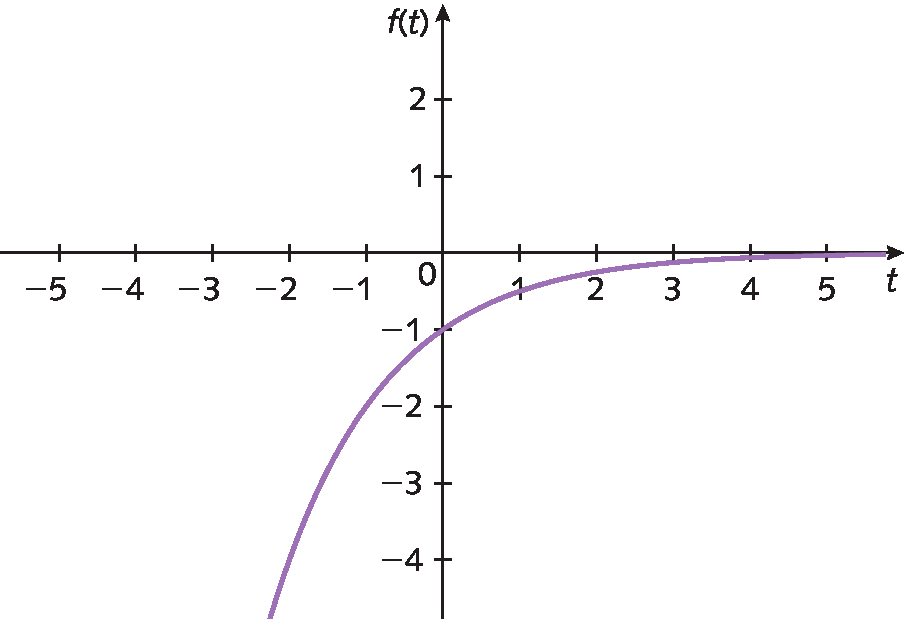
Gráfico. Eixo horizontal t, pontos de menos 5 a 5. Eixo vertical f de t, pontos de menos 4 a 2. Curva crescente pertencente aos terceiro e quarto quadrantes, cortando o eixo vertical na ordenada menos 1.

3. Em seu caderno, represente o gráfico da função descrita no texto.

4.

Os cientistas sabiam que, se nada fosse feito, a quantidade de pessoas infectadas com o novo coronavírus continuaria aumentando para números gigantescos. Para frear a transmissão do vírus, foi adotada uma série de medidas, entre elas o isolamento social. Muitas pessoas utilizaram as redes sociais para fazer um apêlo aos seus seguidores para não saírem de casa, enquanto outras fizeram o contrário e lembraram que nem todo mundo tinha o privilégio de se isolar. O que você pensa sobre o assunto? No caderno, escreva um pequeno texto com sua opinião. Depois, compartilhe seu texto e discuta o assunto com os colegas.

5. No período da pandemia de côvid dezenóve, foram publicadas diversas fake newsglossário sobre o assunto. Alguma vez você desconfiou de uma publicação divulgada na tê vê ou na internet? Você checou a fonte dessa publicação? Como você fez para saber se era verdadeira ou falsa?

2 Função afim

Acompanhe as situações a seguir.

Situação 1

Uma bomba retira água de uma cisterna e a lança em uma caixa‑d'água com vazão de 20 litros de água por minuto. O quadro a seguir mostra a relação da quantidade de litros de água despejada na caixa‑d'água em função da medida do tempo.

Página 137

Medida do tempo (x)	Quantidade de litros (y)
1 min	20 L
2 min	40 L
3 min	60 L
4 min	80 L

A lei da função que relaciona a quantidade de litros de água despejada (y) com a medida do tempo (x), em minuto, de funcionamento da bomba pode ser representada por:

y = 20x, em que x é um número real positivo maior ou igual a zero.

Note que os valores de y são diretamente proporcionais aos valores de x.

Situação 2

Mônica comprou um apartamento, ainda em construção, na cidade de Caruaru, em Pernambuco. Confira a planta baixa desse apartamento.

Ilustração. Mulher de cabelo castanho, camiseta verde e calça roxa. Ela fala: Esta planta baixa é uma representação em escala do apartamento que comprei.

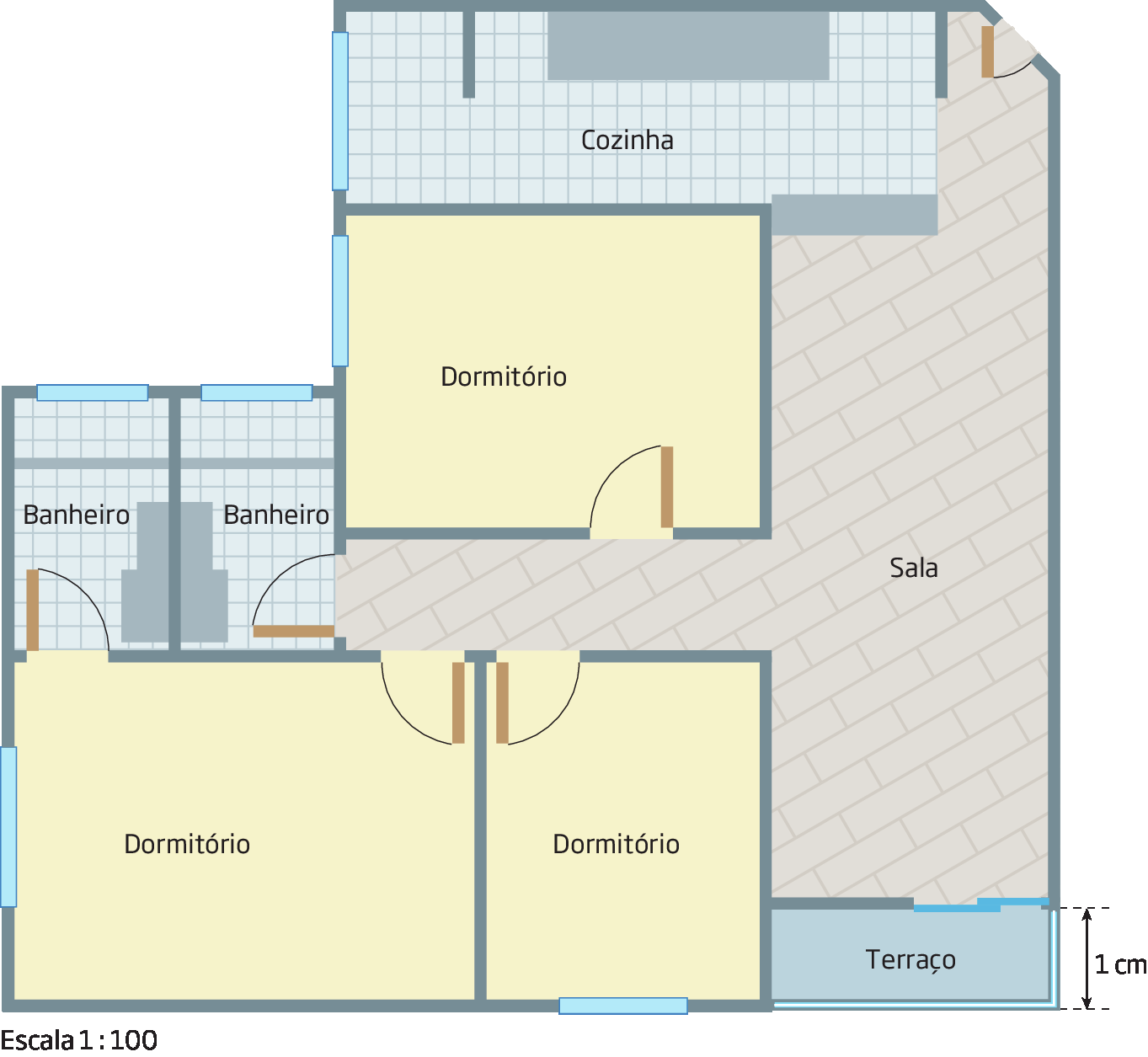
Ilustração. Planta de um apartamento dividido em cozinha, 3 dormitórios, sala, dois banheiros e terraço. Tem indicações das posições de portas e janelas. No canto inferior esquerdo há uma cota indicando a medida da largura do terraço como 1 centímetro. Abaixo Escala 1 para 100.

Escala é a razão entre a medida do comprimento que está na representação gráfica e a medida correspondente do comprimento real, expressos em uma mesma unidade de medida.

A planta baixa foi feita com escala de 1 dividido por 100 ou

\frac{1}{100}

(lemos: “1 para 100”). Isso significa que cada centímetro medido na planta corresponde a 100 centímetros de comprimento no local real, ou seja, a 1 métro na realidade.

Medida de comprimento na planta baixa (x)	Medida de comprimento real no apartamento (y)
1 cm	100 cm
2 cm	200 cm
3 cm	300 cm
4 cm	400 cm

Os valores de y são diretamente proporcionais aos valores de x. A lei da função que mostra a correspondência entre y e x é y = 100x, em que x é um número real maior ou igual a zero.

Página 138

Situação 3

Uma marcenaria fabrica mesas com medida da largura fixa de 1 métro e medida do comprimento variada.

Ilustração. Mesa retangular cujo tampo tem medida de 1 metro de largura por medida x de comprimento.

O quadro a seguir mostra a relação entre as medidas do comprimento e as medidas de perímetro das mesas fabricadas.

Medida do comprimento (x)	Medida do perímetro (y)
1 cm	4 cm
2 cm	6 cm
3 cm	8 cm
4 cm	10 cm
5 cm	12 cm

A medida do perímetro (y) dessa mesa é função da medida do comprimento (x) e pode ser expressa por:

y = 2x + 2, em que x é um número real positivo.

As leis das funções que correspondem às situações 1, 2 e 3 são do tipo y = ax + b, em que a e b são números reais.

Função afim é toda função função cuja lei pode ser escrita na fórma funçãoabre parênteses décimafecha parênteses = ax + b, em que a e b são números reais e x pode ser qualquer número real.

Observe alguns exemplos.

a) funçãoabre parênteses décimafecha parênteses = 2x + 5, em que a = 2 e b = 5

b) funçãoabre parênteses décimafecha parênteses = menos7x, em que a = menos7 e b = 0

Nos casos em que a ≠ 0 e b = 0, chamamos a função afim de função linear, que pode ser representada por funçãoabre parênteses décimafecha parênteses = ax.

c) funçãoabre parênteses décimafecha parênteses = menos5, em que a = 0 e b = menos5

Nos casos em que a = 0, chamamos a função afim de função constante.

d)

f (x) = \frac{x + 1}{3}

Essa lei também pode ser escrita assim:

f (x) = \frac{1 x}{3} + \frac{1}{3}

, em que

a = \frac{1}{3}

e

b = \frac{1}{3}

.

Observação

As leis a seguir não representam funções afins, pois não podem ser escritas na fórma y = ax + b, em que a e b são número reais.

• y = 2xelevado a 2 + 1

•

y = \frac{1}{x} ‒ 3

Página 139

Gráfico da função afim

O gráfico que representa uma função afim é sempre uma reta não perpendicular ao eixo x. Analise alguns exemplos.

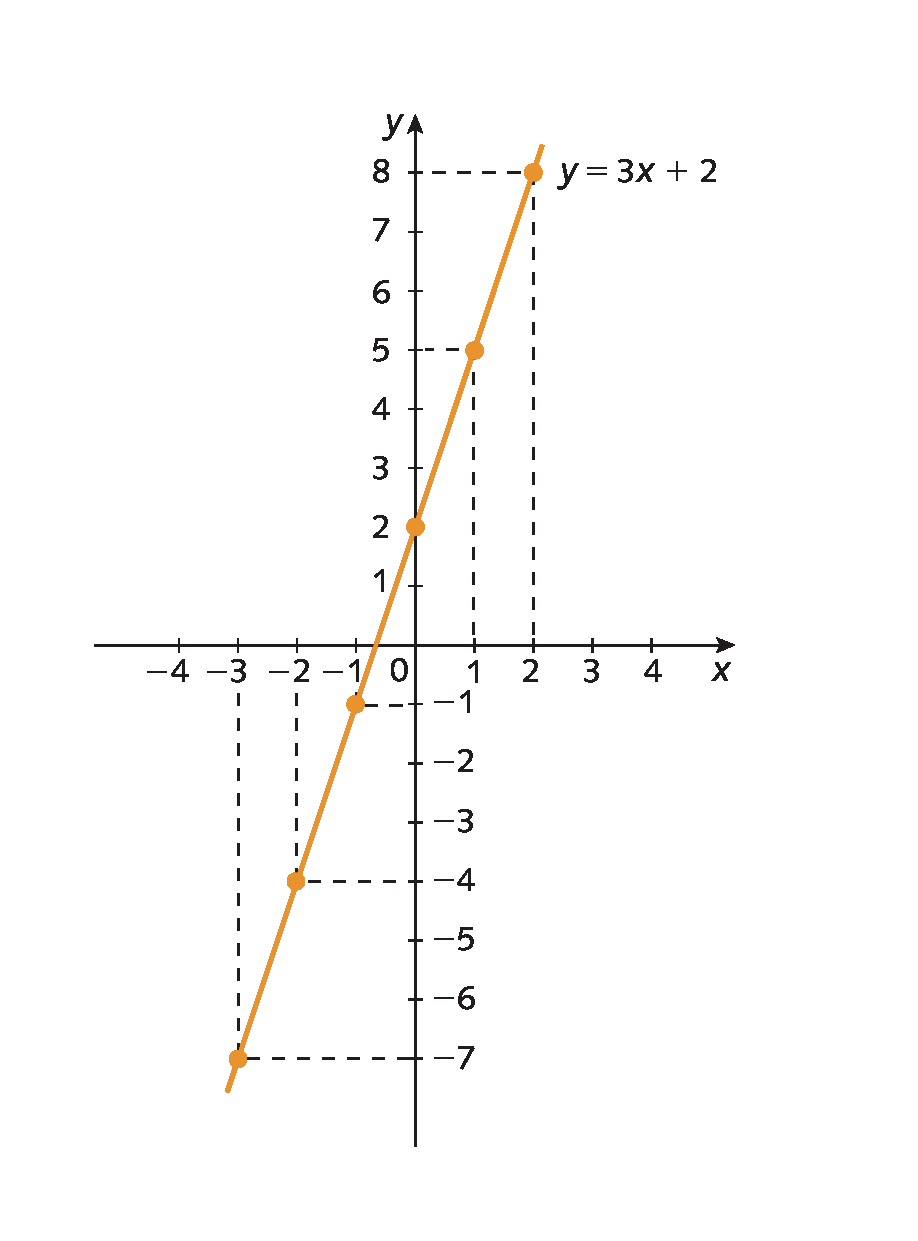
a) Vamos construir o gráfico da função função tal que funçãoabre parênteses décimafecha parênteses = 3x + 2, em que x é qualquer número real.

Inicialmente escolhemos valores arbitrários para x e calculamos os valores de y correspondentes para obter alguns pares ordenados.

Para x = menos3, temos: funçãoabre parênteses menos3fecha parênteses = 3 ⋅ abre parênteses menos3fecha parênteses + 2 = menos7

Para x = menos2, temos: funçãoabre parênteses menos2fecha parênteses = 3 ⋅ abre parênteses menos2fecha parênteses + 2 = menos4

Para x = menos1, temos: funçãoabre parênteses menos1fecha parênteses = 3 ⋅ abre parênteses menos1fecha parênteses + 2 = menos1

Para x = 0, temos: funçãoabre parênteses0fecha parênteses = 3 ⋅ 0 + 2 = 2

Para x = 1, temos: funçãoabre parênteses1fecha parênteses = 3 ⋅ 1 + 2 = 5

Para x = 2, temos: funçãoabre parênteses2fecha parênteses = 3 ⋅ 2 + 2 = 8

x	f (x) = y	(x, y)
−3	−7	(−3, −7)
−2	−4	(−2, −4)
−1	−1	(−1, −1)
0	2	(0, 2)
1	5	(1, 5)
2	8	(2, 8)

Representamos no plano cartesiano os pontos correspondentes aos pares ordenados encontrados e traçamos a reta que passa por esses pontos.

Gráfico. Eixo x de menos 4 a 4. Eixo y de menos 7 a 8. Pontos marcados com os seguintes pares ordenados: (menos 3, menos 7); (menos 2, menos 4); (menos 1, menos 1); (0, 2); (1, 5); (2, 8). Reta passando pelos pontos indicada por y igual a 3x mais 2.

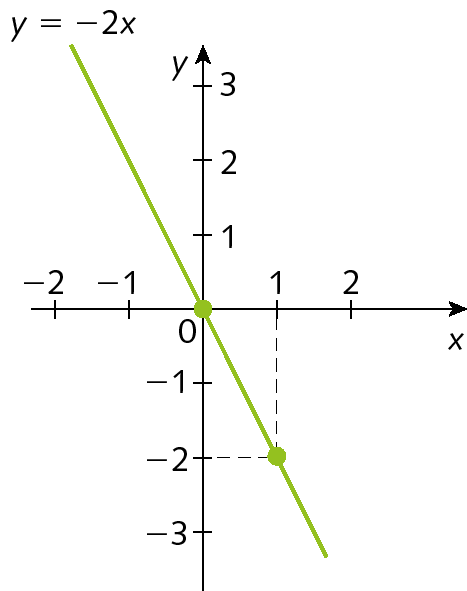
b) Vamos construir o gráfico da função g tal que g abre parêntesesxfecha parênteses = menos2x, em que x é qualquer número real.

Para x = 0, gabre parênteses0fecha parênteses = menos2 ⋅ 0 = 0

Para x = 1, gabre parênteses1fecha parênteses = menos2 ⋅ 1 = menos2

Gráfico. Eixo x, pontos de menos 2 a 2. Eixo y, pontos de menos 3 a 3. Reta passando pelos pontos de coordenadas (0, 0) e (1, menos 2). A reta está indicada como y igual a menos 2x

Ilustração. Menina de cabelo castanho escuro encaracolado, óculos e camiseta verde. Ela diz: Como o gráfico de uma função afim é sempre uma reta, precisamos conhecer apenas dois pontos para traçar seu gráfico. Ilustração. Menino de cabelo preto e camiseta lilás. A mão esquerda apoiada na cintura e a mão esquerda levantada. Ele fala: O gráfico de uma função linear é sempre uma reta que passa pelo ponto (0, 0), ou seja, pela origem do plano cartesiano.

Página 140

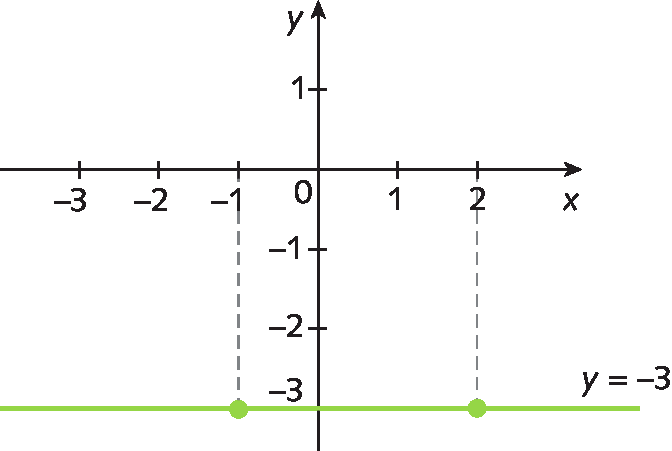
c) Vamos construir o gráfico de h, dada por h abre parêntesesxfecha parênteses = menos3, em que x é qualquer número real.

Gráfico. Plano cartesiano. Eixo x de menos 3 a 2 e eixo y de menos 3 a 1. Dois pontos indicados, cujos pares ordenados são (menos 1, menos 3) e (2, menos 3). Reta paralela ao eixo x passando pelos dois pontos e indicada por y igual a menos 3.

Ilustração. Menina branca com cabelo liso castanho. Ela veste uma regata verde, uma saia xadrez, bota rosa e tem uma blusa de frio amarrada na cintura. A mão esquerda está apoiada na cintura e a mão direita espalmada mais à frente. Ela diz: Observe que o valor de y sempre será igual a ‒3, independentemente do valor atribuído a x. Ao lado um menino asiático, branco com cabelo preto liso. Ele veste calça marrom, camiseta amarela, jaqueta e sapato preto. A mão esquerda está para trás e a direita levantada e espalmada. Ele diz: O gráfico de uma função constante sempre será uma reta paralela ao eixo x ou coincidente com o eixo x.

Atividades

Faça as atividades no caderno.

11. Identifique as leis de funções afim.

a) y = x menos 5

b) y = 4 menos 2x

c) y = 1

d) y = xelevado a 2 menos 5x + 6

e) y = menos4 menos x

f) y = xelevado a 2

12. Construa o gráfico das funções definidas pelas leis a seguir.

a) y = 2

b) y = 3x

c)

y = - \frac{2}{3} x

d) y = x + 3

e) y = 1 menos 2x

f)

y = \frac{1}{3} x - 2

13. O quadro a seguir relaciona a medida do tempo (t), em minuto, que uma válvula de saída de água fica aberta e a medida do volume (V), em litro, de água despejada na piscina.

t (em min)	V (em L)
1	60
2	120
3	180
4	240

De acôrdo com o quadro, responda às questões.

a) Qual é a lei da função que relaciona a medida do volume (V), em litro, de água despejada na piscina e a medida do tempo (t), em minuto, que a válvula fica aberta?

b) Qual é a quantidade de água contida no interior da piscina após 10 minutos?

c) Qual é a medida do tempo necessária para que a piscina fique com exatamente 900 litros?

14. Copie em seu caderno as afirmações verdadeiras.

a) Função afim é toda função cuja lei pode ser escrita na fórma y = ax + b, em que a e b são números reais e x pode ser qualquer número real.

b) A função f tal que

f (x) = \frac{2}{x}

é linear.

c) A função dada por

y = x \sqrt{2}

não é afim.

d) O gráfico da função dada por g abre parêntesesxfecha parênteses = 6 para qualquer x real é uma reta paralela ao eixo x.

e) O gráfico da função afim dada pela lei r abre parêntesesxfecha parênteses = menosx + 2 é uma reta que passa pela origem.

15. Construa, em um mesmo plano cartesiano, os gráficos das funções h, m, f, g, p e q e determine as coordenadas cartesianas do ponto de encontro, entre:

a) h abre parêntesesxfecha parênteses = x e m abre parêntesesxfecha parênteses = menosx

b) funçãoabre parênteses décimafecha parênteses = ‒x + 3 e g abre parêntesesxfecha parênteses = 2x menos 3

c)

p (x) = \frac{x}{2} + 1

e q abre parêntesesxfecha parênteses = x menos 1

Página 141

Zero de uma função afim

Em toda função função, cada valor de x em que funçãoabre parênteses décimafecha parênteses = 0 é chamado de zero da função.

O zero de uma função afim dada por y = ax + b, com a ≠ 0, será um único número x, tal que ax + b = 0. Resolvendo essa equação, obtemos

x = - \frac{b}{a}

.

Vamos, por exemplo, determinar o zero da função dada por y = 2x menos 2.

Quando y = 0, temos:

2x ‒ 2 = 0

2x = 2

x = 1

Portanto, 1 é o zero dessa função.

Graficamente, o zero de uma função afim funçãoabre parênteses décimafecha parênteses = ax + b, a ≠ 0, é a abscissa do ponto de intersecção do gráfico da função com o eixo x.

Observe o gráfico da função y = 2x menos 2.

x	y	(x, y)
0	−2	(0, −2)
1	0	(1, 0)

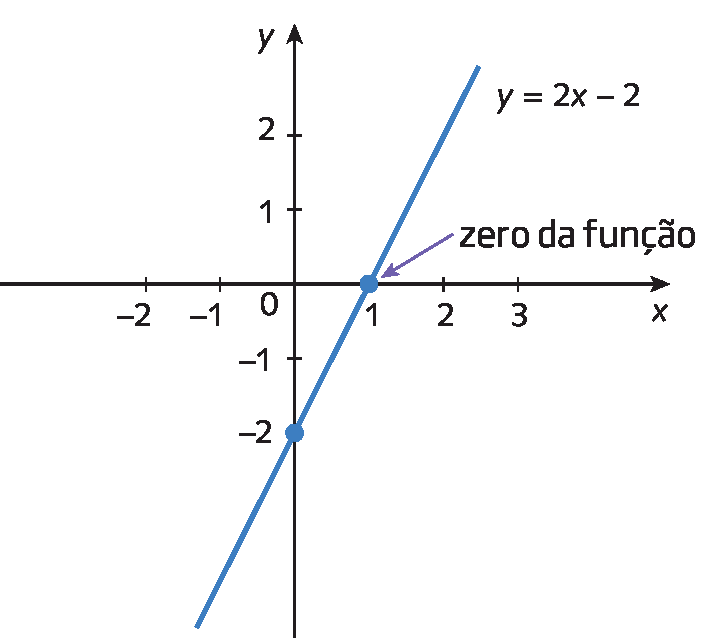
Gráfico. Plano cartesiano. Eixo x de menos 2 a 3. Eixo y de menos 2 a 2. Reta diagonal indicada por y igual a 2x menos 2. Corta o eixo y na ordenada menos dois e corta o eixo x na abscissa 1 com seta nesse ponto indicando 'zero da função'.

Como podemos observar no gráfico, a reta intercepta o eixo das abscissas no ponto (1, 0); dessa maneira, o valor 1 do eixo das abscissas é tido como zero da função.

Atividades

Faça as atividades no caderno.

16. Determine o zero destas funções afim.

a) y = menos4x + 8

b) y = menos3x menos 21

c) y = 2 menos 8x

d) y = 7 menos x

e) y = menos4x menos 64

f) y = menos6x + 18

g) y = 3x menos 9

h) y = 4x menos 20

17. Determine o valor de m para que o zero da função função tal que funçãoabre parênteses décimafecha parênteses = 3x + m menos 2 seja igual a 4.

18. Qual é a lei da função afim cujo zero é 1 e o seu gráfico passa pelo ponto (menos1, 2)?

Página 142

Variação de uma função afim

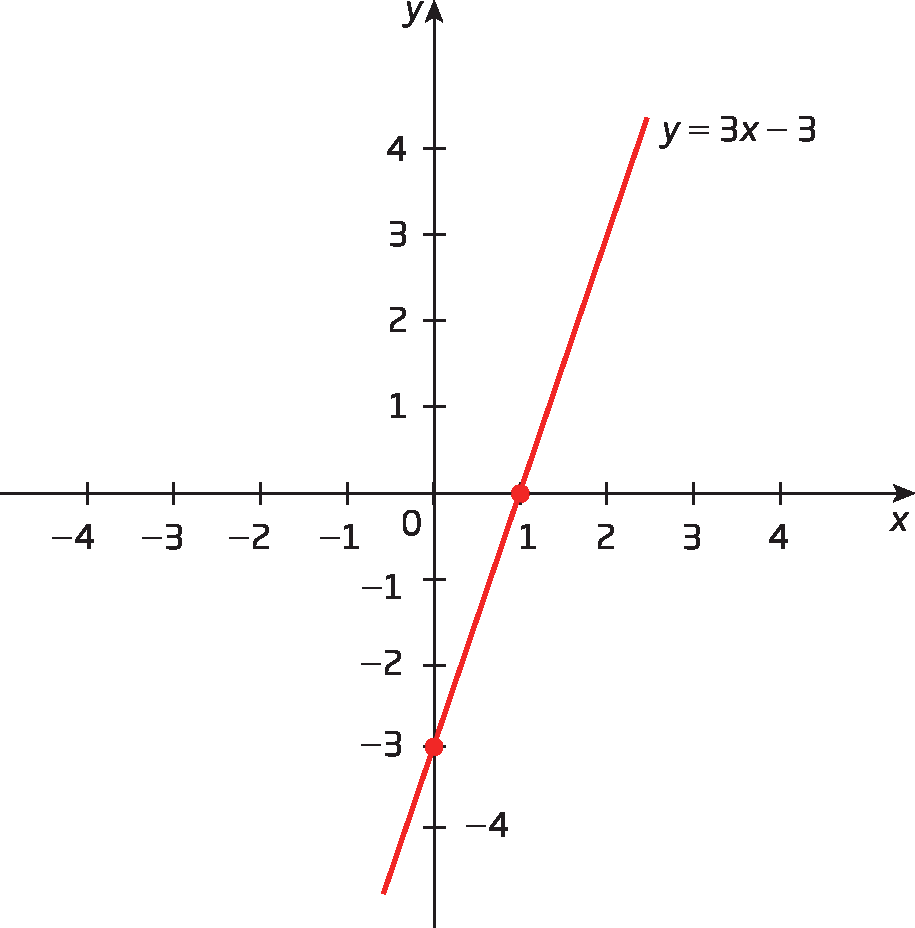
Observe os gráficos das funções dadas por y = 3x menos 3 e y = menosx + 2, em que x pode ser qualquer número real.

x	y	(x, y)
0	−3	(0, −3)
1	0	(1, 0)

Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 4, menos 3. menos 2, menos 1, 0, 1, 2, 3 e 4 e ele está rotulado como x. No eixo vertical estão indicados os números menos 4, menos 3. menos 2, menos 1, 0 1, 2 e 3 e ele está rotulado como y. No plano cartesiano estão indicados 2 pontos. O primeiro ponto tem coordenadas 0 e menos 3. O segundo ponto tem coordenadas 1 e 0. Está representada uma reta vermelha passando por estes dois pontos. À direita da reta, a sentença: y igual a 3x menos 3. — Aumentando o valor de x, o valor de y aumenta; por isso, dizemos que a função é crescente. Observe que na lei y = 3x menos 3, temos a = 3.

x	y	(x, y)
0	2	(0, 2)
2	0	(2, 0)

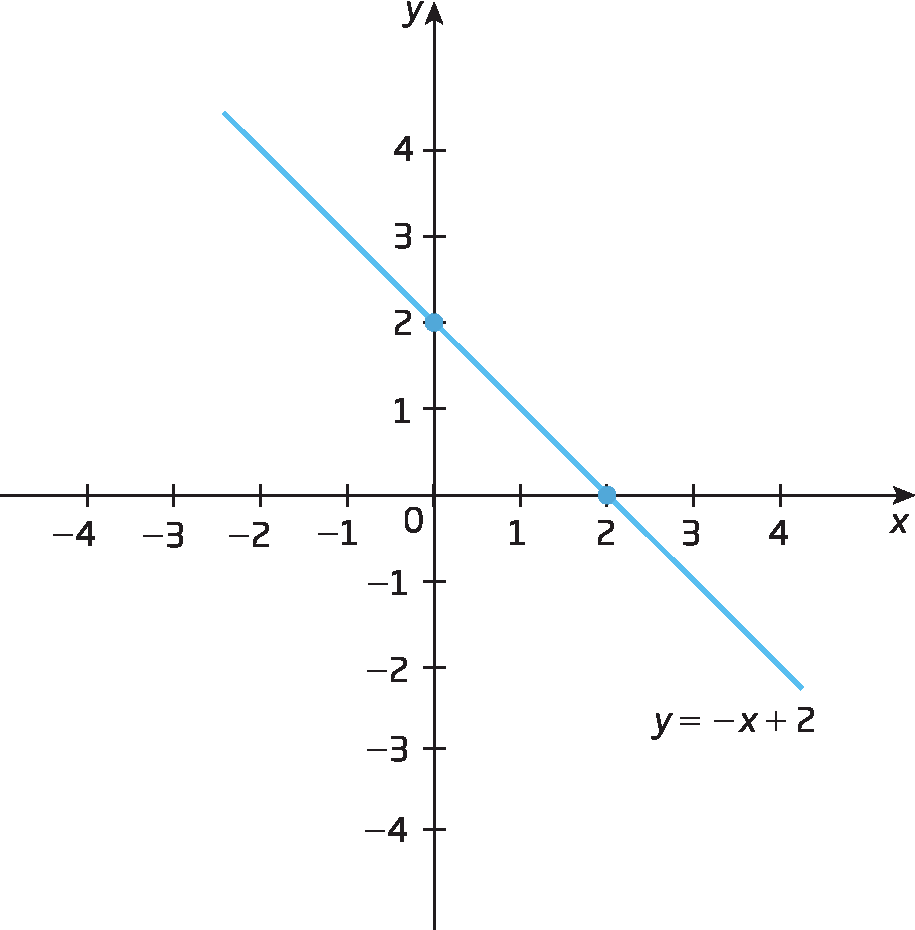
De modo geral, temos:

• uma função afim y = ax + b é crescente quando o coeficiente a é maior que zero (a > 0);

• uma função afim y = ax + b é decrescente quando o coeficiente a é menor que zero (a < 0).

Quando a = 0 em y = ax + b, a função é constante, pois, aumentando o valor de x, o valor de y não se altera.

Taxa de variação de uma função afim

A taxa de variação de uma função afim é a razão entre a variação de valores de y e a correspondente variação de valores de x, nessa ordem. Para encontrar a taxa de variação de uma função afim, precisamos conhecer dois pares ordenados que correspondam a pontos que pertençam à reta que é gráfico dessa função.

Seja (décimo₁, y₁) e (x₂, x₂) pontos que pertençam ao gráfico de uma função afim. Assim, a taxa de variação dessa função é dada por:

\frac{y_{2} - y_{1}}{x_{2} - x_{1}}

Página 143

Vamos determinar a taxa de variação da função y = 3x menos 3 por meio de seus pontos (0, menos3) e (1, 0):

\frac{0 ‒ (‒ 3)}{1 ‒ 0} = \frac{3}{1} = 3

▸ Considere outros pontos que pertençam à função y = 3x menos 3 e calcule a taxa de variação. O que você pode perceber?

Observação

A taxa de variação de uma função afim f, dada por funçãoabre parênteses décimafecha parênteses = ax + b, é constante para quaisquer dois pontos pertencentes à função considerados e, numericamente, é igual ao coeficiente a.

Estudo do sinal da função afim

Em uma função afim, podemos verificar para quais valores de x a função é positiva, para quais valores é negativa e para qual valor é nula.

Acompanhe os exemplos.

a) Vamos estudar o sinal da função afim: y = 2x + 5

A função é crescente, pois a = 2 (2 > 0).

O zero da função é

- \frac{5}{2}

.

Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 3. menos 2, menos 1, 0, 1 e 2 ele está rotulado como x. No eixo vertical estão indicados os números menos 2, menos 1, 0 1, 2, 3, 4 e 5 e ele está rotulado como y. No plano cartesiano estão indicados 2 pontos. O primeiro ponto tem coordenadas menos 5 meios e zero. O segundo ponto tem coordenadas 0 e 5. Está representada uma reta passando por estes dois pontos. À direita da reta, a sentença: y igual a 2x mais 5. Há uma seta apontando para a fração menos 5 meios, indicando: zero da função, abre parênteses, y igual a zero, fecha parênteses, A região abaixo da reta e acima do eixo x está destacada na cor azul. Nesta região, está a sentença y maior que zero. A região acima da reta e abaixo do eixo x está destacada na cor vermelha. Nesta região, está a sentença y menor que zero.

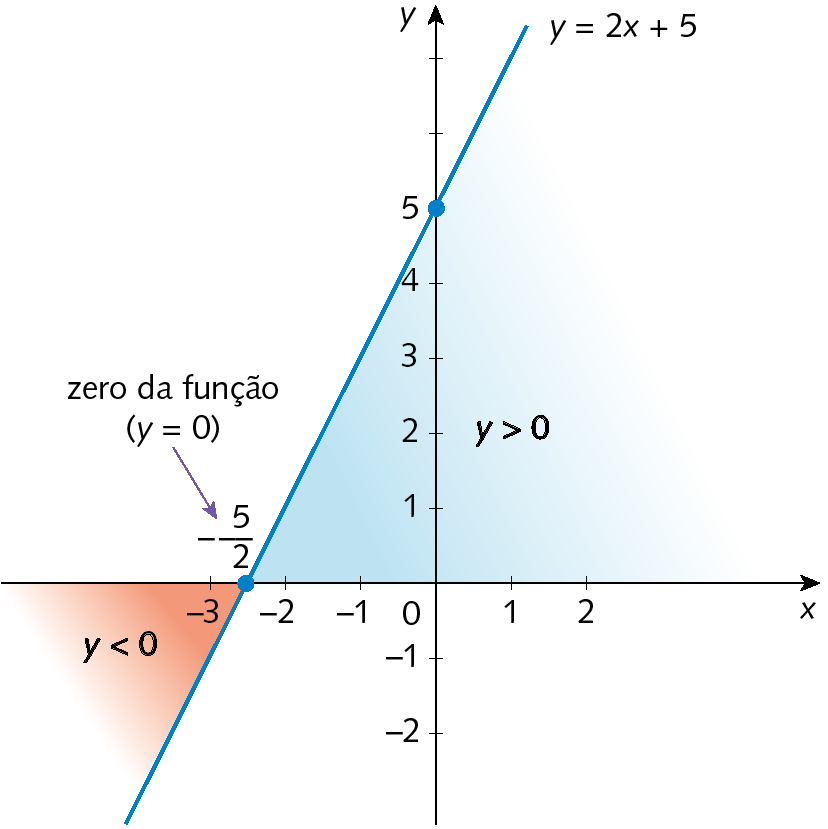
Observando o gráfico, verificamos que:

• para

x = - \frac{5}{2}

, a função é nula (y = 0);

• para

x > - \frac{5}{2}

, a função é positiva (y > 0);

• para

x < - \frac{5}{2}

, a função é negativa (y < 0).

b) Vamos estudar o sinal da função afim: y = menosx + 4

A função é decrescente, pois a = menos1 (menos1 < 0).

O zero da função é 4.

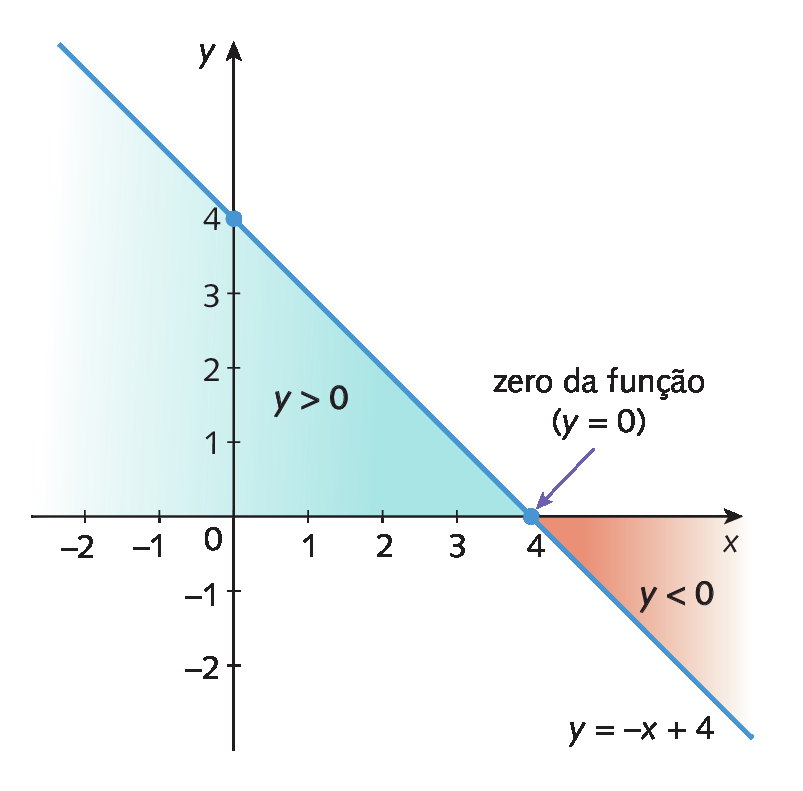
Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 2, menos 1, 0, 1, 2, 3 e 4 e ele está rotulado como x. No eixo vertical estão indicados os números menos 2, menos 1, 0 1, 2, 3 e 4 e ele está rotulado como y. No plano cartesiano estão indicados 2 pontos. O primeiro ponto tem coordenadas 0 e 4. O segundo ponto tem coordenadas 4 e 0. Está representada uma reta passando por estes dois pontos. À esquerda da reta, a sentença: y igual a menos x mais 4. Há uma seta apontando para o 4 do eixo x, indicando: zero da função, abre parênteses, y igual a zero, fecha parênteses, A região abaixo da reta e acima do eixo x está destacada na cor azul. Nesta região, está a sentença y maior que zero. A região acima da reta e abaixo do eixo x está destacada na cor vermelha. Nesta região, está a sentença y menor que zero.

Observando o gráfico, verificamos que:

• para x = 4, a função é nula (y = 0);

• para x < 4, a função é positiva (y > 0);

• para x > 4, a função é negativa (y < 0).

Página 144

Tecnologias digitais em foco

Gráfico da função afim

Nesta seção, vamos utilizar um software de construção de gráficos para investigar o que ocorre com o gráfico de uma função afim do tipo y = ax + b, conforme variamos os valores de a e b.

Construa

O gráfico de uma função afim é uma reta não perpendicular ao eixo x. No software, a construção desse gráfico pode ser feita determinando as coordenadas de dois pontos pertencentes a ele, marcando esses pontos no plano cartesiano e, por fim, traçando a reta que passa por esses pontos.

Um segundo modo de realizar essa construção é digitando a lei da função no campo apropriado e teclando Enter.

Escolha um desses modos indicados para fazer a construção de cada gráfico de função afim indicada nas investigações a seguir.

Explore

Vamos começar investigando o que ocorre com o gráfico de uma função afim do tipo y = x + b conforme variamos o valor de b.

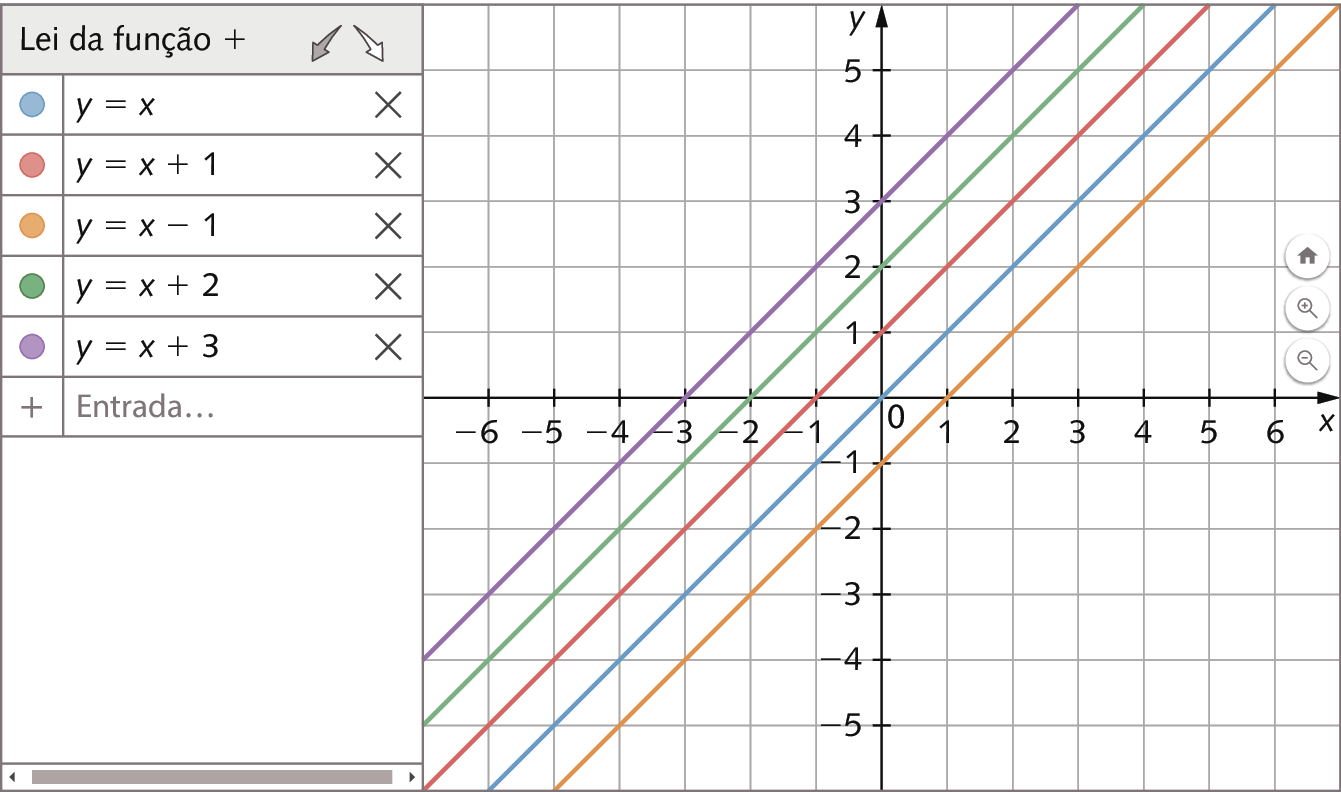
Ilustração. Reprodução da tela de um software de construção de gráficos. À esquerda, um quadro com leis de função.
Primeira linha: bolinha azul; y igual a x
Segunda linha: bolinha vermelha: y igual a x mais 1.
Terceira linha: bolinha laranja: y igual a x menos 1.
Quarta linha: bolinha verde: y igual a x mais 2.
Quinta linha: bolinha roxa: y igual a x mais 3.
Abaixo do quadro, um campo denominado Entrada.
Á direita do quadro uma região quadriculada com dois eixos perpendiculares. No eixo horizontal estão indicados os números menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5 e 6 e ele está rotulado como x.
No eixo vertical estão indicados os números menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0 1, 2, 3, 4 e 5 e ele está rotulado como y.
No plano estão representadas 5 retas paralelas: uma reta azul que passa pela origem, uma reta vermelha que passa pelos pontos de coordenadas menos 1, zero e zero, um; uma reta verde que passa pelos pontos de coordenadas menos 2, zero e zero, dois; uma reta roxa que passa pelos pontos de coordenadas menos 3, zero e zero, três e uma reta laranja que passa pelos pontos de coordenadas zero, menos 1 e um, zero.
As cores das retas têm correspondência com as cores das bolinhas do quadro do lado esquerdo.

a) Em um mesmo plano cartesiano, construa o gráfico das funções y = x e y = x + 1. O que você observou?

b) No mesmo plano cartesiano do item a, construa o gráfico das funções y = x menos 1, y = x + 2 e y = x + 3. Depois, compare o gráfico dessas funções com o gráfico de y = x. O que você observou?

c) O que as investigações anteriores sugerem em relação à posição da reta que é gráfico de uma função afim do tipo y = x + b, em que b é qualquer número real, e da reta que é gráfico de y = x?

Página 145

Tecnologias digitais em foco

Agora, vamos investigar o que ocorre com o gráfico de uma função afim do tipo y = ax conforme variamos o valor de a.

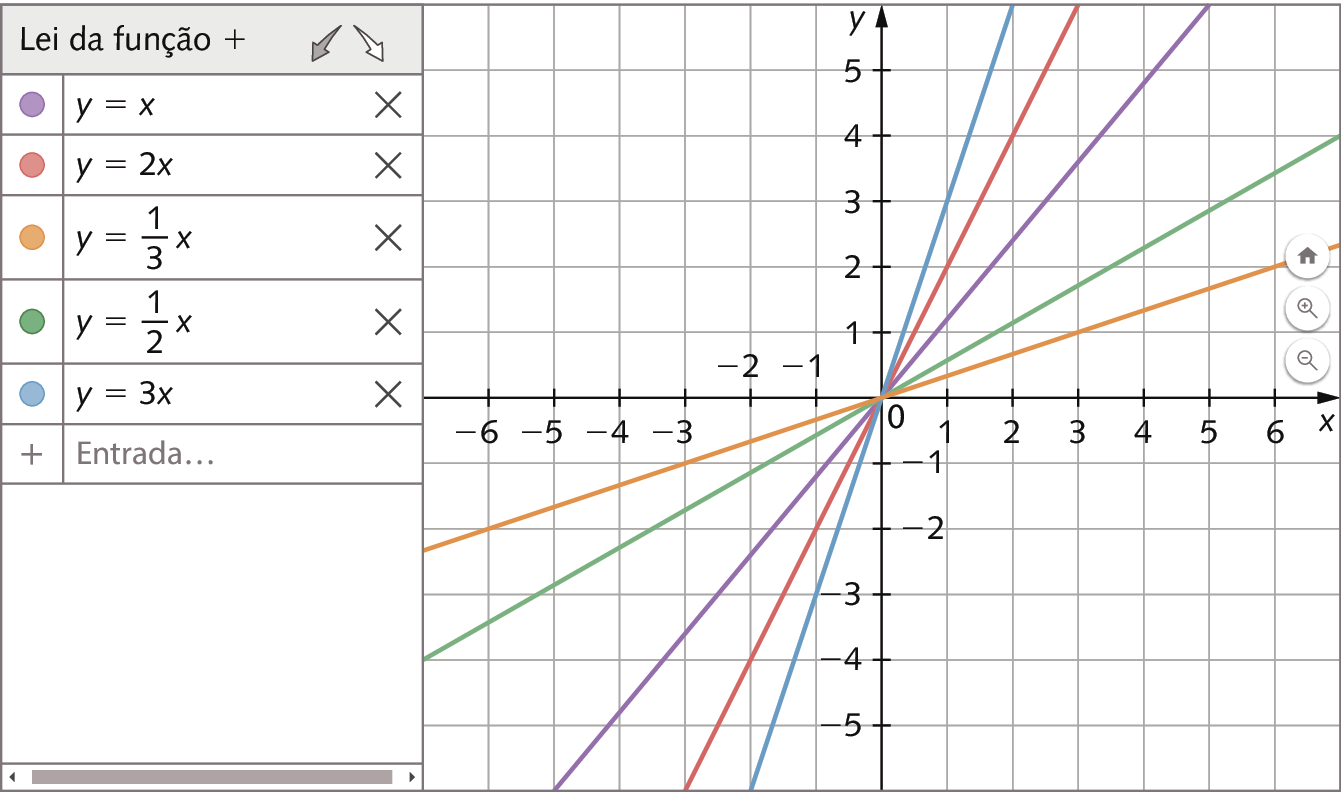
Ilustração. Reprodução da tela de um software de construção de gráficos. À esquerda, um quadro com leis de função. Primeira linha: bolinha roxa; y igual a x Segunda linha: bolinha vermelha: y igual a 2x. Terceira linha: bolinha laranja: y igual a um terço vezes x. Quarta linha: bolinha verde: y igual a meio vezes x, Quinta linha: bolinha azul: y igual a 3x. Abaixo do quadro, um campo denominado Entrada. Á direito do quadro uma região quadriculada com dois eixos perpendiculares,. No eixo horizontal estão indicados os números menos 6, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5 e 6 e ele está rotulado como x. No eixo vertical estão indicados os números menos 5, menos 4, menos 3, menos 2, menos 1, 0 1, 2, 3, 4 e 5 e ele está rotulado como y. No plano estão representadas 5 retas que se interceptam na origem. A reta roxa, passa pelo ponto de coordenadas um, um; a reta vermelha passa pelo ponto de coordenadas um, dois; a reta laranja passa pelo ponto de coordenadas três, um; a reta verde passa pelo ponto de coordenadas dois, um e a reta azul passa pelo ponto de coordenadas um, três. As corres das retas tem correspondência com as corres das bolinhas do quadro do lado esquerdo.

d) Em um mesmo plano cartesiano, construa o gráfico das funções y = x e y = 2x. O que você observou?

e) No mesmo plano cartesiano do item d, construa o gráfico das funções

y = \frac{1}{3} x

,

y = \frac{1}{2} x

e y = 3x. Depois, compare o gráfico dessas funções com o gráfico de y = x. O que você observou?

f) Em um mesmo plano cartesiano, construa os gráficos de y = x e y = menosx. O que você observou?

g) Dê três exemplos de pares de funções afim cujos gráficos sejam simétricos em relação ao eixo y.

h) Confira a seguir como Luana fez para construir o gráfico de y = 2x + 1 a partir do gráfico de y = x.

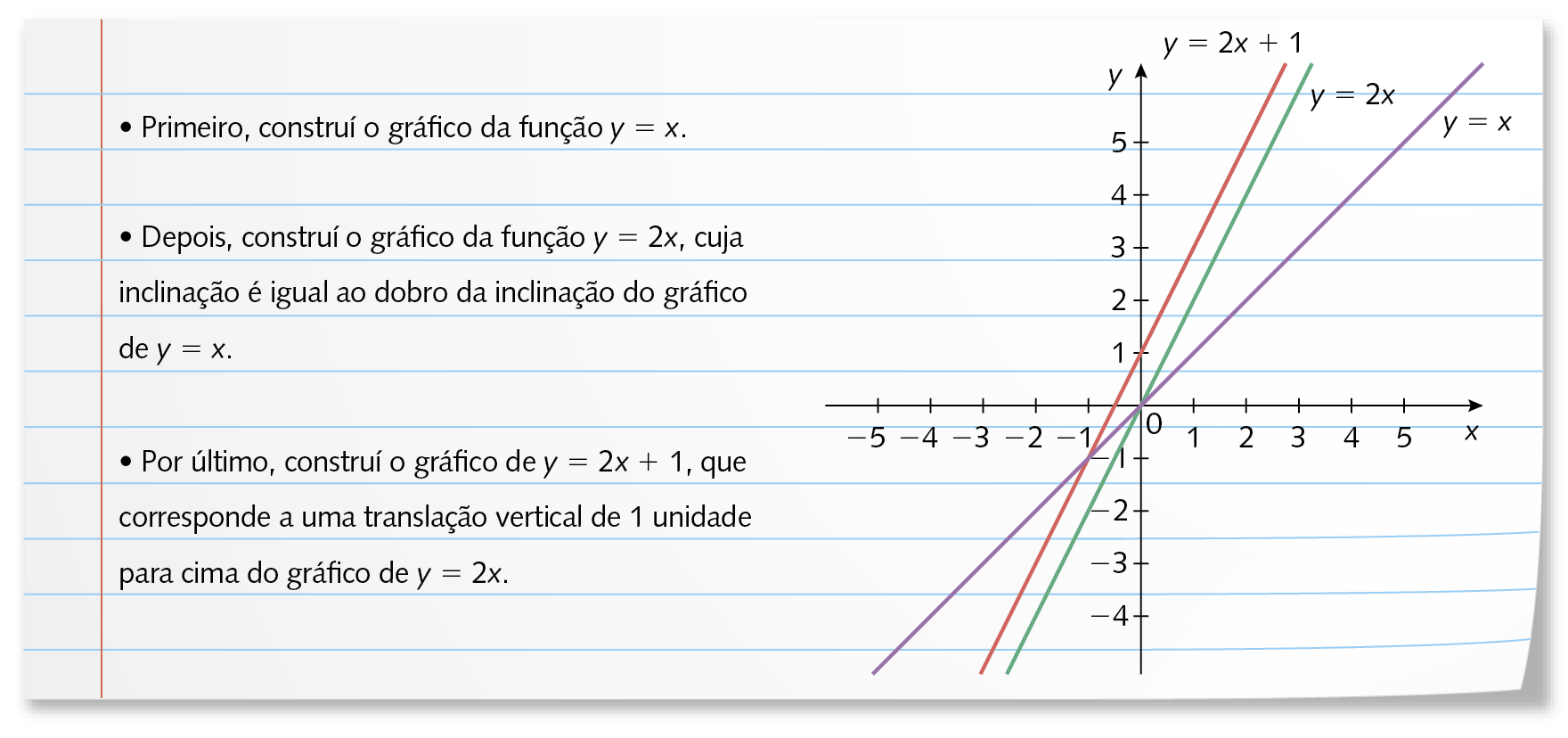
Ilustração. Á direita, gráfico com eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 5, menos 4, menos 3. menos 2, menos 1, 0, 1, 2, 3, 4 e 5 e ele está rotulado como x. No eixo vertical estão indicados os números menos 4, menos 3, menos 2, menos 1, 0 1, 2, 3, 4 e 5 e ele está rotulado como y. No plano cartesiano estão representadas 3 retas: uma verde que corresponde a função t igual a 2x, uma roxa que corresponde à função y igual a x e uma vermelha que corresponde à função y igual a 2x mais 1. Á esquerda, as informações: Primeiro, construí o gráfico da função y igual a x. Depois, construí o gráfico da função y igual a 2x, cuja inclinação é igual ao dobro da inclinação do gráfico de y igual x. Por último, construí o gráfico de y igual a 2x mais 1, que corresponde a uma translação vertical de 1 unidade para cima do gráfico de y igual a 2x.

Agora, faça como Luana e construa os gráficos de

y = \frac{1}{2} x + 2

e y = 3x menos 2 com base no gráfico de y = x.

Página 146

Atividades

Faça as atividades no caderno.

19. Construa o gráfico, localize o zero de cada uma das funções e classifique-as em crescente, decrescente ou constante.

a) funçãoabre parênteses décimafecha parênteses = 4x menos 20

b) funçãoabre parênteses décimafecha parênteses = 7x menos 21

c) funçãoabre parênteses décimafecha parênteses = menos4x + 1

d) funçãoabre parênteses décimafecha parênteses = x menos 3

20. Determine os valores reais de x que tornam a função positiva, negativa ou nula.

a) y = 2x menos 6

b) y = menos8 + x

c) y = menosx + 11

d) y = menos2x menos 4

21. Escreva no caderno a lei de uma função afim que tenha estas características:

• para x = 2, y = 0;

• para x < 2, y < 0;

• para x > 2, y > 0.

22. Generalize o estudo do sinal de uma função afim cuja lei é y = ax + b, crescente (a > 0). Depois, faça o mesmo para uma função afim decrescente.

3 Inequações

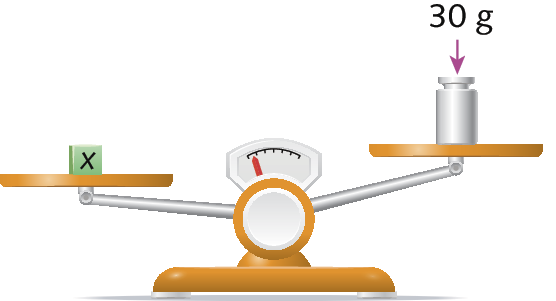
Na balança de dois pratos a seguir, podemos ver um abacaxi em um prato e no outro um peso de 60 gramas e três maçãs de mesma medida de massa.

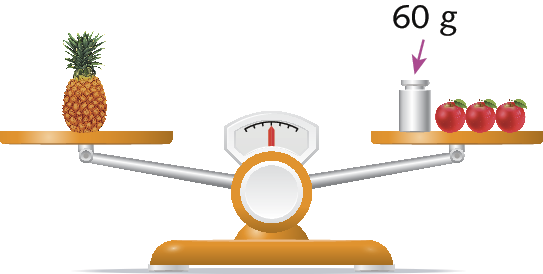
Ilustração. Balança de 2 pratos equilibrada. O prato da esquerda tem um abacaxi. O prato da direita tem um peso de 60 gramas e três maçãs idênticas.

Observe que os pratos dessa balança estão em equilíbrio, ou seja, há igualdade das medidas de massa contidas nos dois pratos.

Sabe-se que o abacaxi tem 300 gramas, mas a medida da massa das maçãs é desconhecida. Considerando que cada maçã tem x gramas, podemos representar essa igualdade na linguagem matemática pela seguinte equação:

300 = 60 + 3x

Agora, observe o que ocorre quando retiramos da balança uma das maçãs.

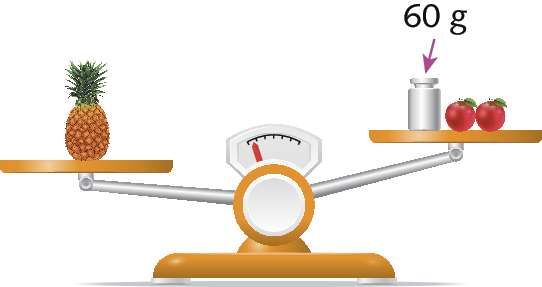
Ilustração. Balança de 2 pratos desequilibrada. O prato da esquerda está mais baixo que o prato da direita. O prato da esquerda tem um abacaxi. O prato da direita tem um peso de 60 gramas e duas maçãs idênticas.

Nesse caso, podemos verificar uma desigualdade das medidas de massa contidas nos dois pratos da balança. Essa desigualdade também pode ser representada na linguagem matemática:

300 > 60 + 2x

Página 147

Toda desigualdade que tenha pelo menos uma incógnita, com expoente maior ou igual a 1, é chamada de inequação. Considere alguns exemplos a seguir.

a) x + 5 > menos3x

b) xelevado a 2 menos 4 ⩽ 20

c) 12 + x ≠ 5x

d) x + y < 8

e) yelevado a 2 menos 2y ⩾ menos16

f) menos2x < 14

Uma inequação com uma incógnita é considerada do 1º grau quando o expoente da incógnita é igual a 1. Esse tipo de inequação pode ser escrito de uma das seguintes fórmas:

ax + b > 0

ax + b < 0

ax + b ⩾ 0

ax + b ⩽ 0

ax + b ≠ 0

sendo a um número real diferente de zero, b um número real qualquer e x a incógnita.

Observe os exemplos.

a) 3x > 6 (a incógnita é x )

b) 4y < 7 (a incógnita é y )

c) 2z ⩾ menos5 (a incógnita é z )

d) 3w ⩽ 9 (a incógnita é w )

Atividades

Faça as atividades no caderno.

23. Identifique, no caderno, os itens que apresentam uma inequação.

a) 3elevado a 2 + 1elevado a 2 = 10

b)

\frac{x}{3}

+ 1 < 0

c) 4x = menos12

d) 6x ≠ 0

e) 2x menos y > 5

f) 2x + 7 ⩽ 6x

24. Escreva no caderno uma inequação que represente cada uma das situações a seguir.

a) O dôbro de um número mais cinco é menor que oito.

b) A diferença entre um número e sua quinta parte é menor ou igual a quatro.

c) O quíntuplo de um número menos sua terça parte é menor que dois.

d) A diferença entre o triplo de um número e sua quarta parte é maior ou igual a sete.

25. A medida da distância entre duas estações de metrô é x quilômetros. Após percorrer 5 quilômetros, um trem está a menos da metade da medida da distância entre as duas estações. No caderno, escreva uma inequação que represente essa situação.

Fotografia. Vista da plataforma do metrô com algumas pessoas. Há portas de vidros antes do embarque e desembarque. À direita, escadas rolantes — Plataforma do metrô da estação Paulista em São Paulo (São Paulo). Foto de 2018.

26. Quais dos itens a seguir apresentam uma inequação do 1º grau com uma incógnita?

a) x + y > 4

b) x + 50 > 60

c) xiselevado a 2 + y > z

d) 60 > y

e) xelevado a 3 > x

f) 6w > 10 + w

g) 7a > a + b

h) c > 5c menos 10

Página 148

27. Observe esta balança e responda às questões.

Ilustração. Balança de 2 pratos desequilibrada. O prato da esquerda está mais baixo que o prato da direita. No prato da esquerda há um cubo com a letra x. No prato da direita há 5 pesos idênticos de 1 grama cada.

a) A desigualdade que melhor representa essa situação é x > 5 ou 5 > x ?

b) Se acrescentarmos 100 gramas a cada prato da balança, como poderemos representar a nova desigualdade?

Inequações equivalentes

Acompanhe as situações a seguir.

Situação 1

Esta balança está em desequilíbrio, pois a medida de massa contida no prato da esquerda é maior que a do prato da direita.

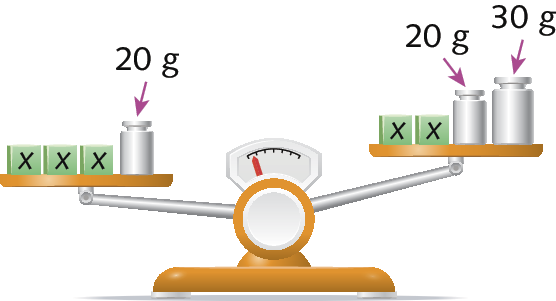
Ilustração. Balança de 2 pratos desequilibrada. O prato da esquerda está mais baixo que o prato da direita. No prato da esquerda há 3 cubos com a letra x e um peso de 20 gramas. No prato da direita há 2 cubos com a letra x, um peso de 20 gramas e um peso de 30 gramas.

Podemos representar a situação pela inequação 3x + 20 > 2x + 20 + 30.

Retirando 2

de cada prato da balança, ela continua em desequilíbrio e o prato da esquerda continua com maior medida de massa que o prato da direita.

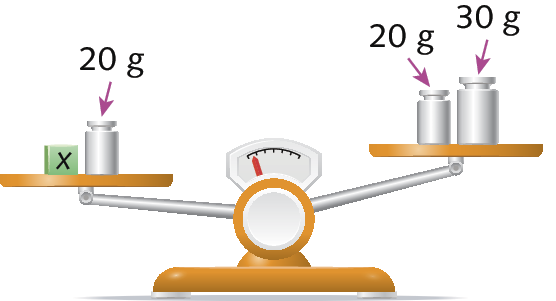
Podemos representar a situação da seguinte fórma:

3x + 20 menos 2x > 2x + 20 + 30 menos 2x,

ou seja,

x + 20 > 20 + 30

Retirando 20 gramas de cada prato, a balança ainda fica em desequilíbrio, e o prato da esquerda continua com maior medida de massa que o prato da direita.

Agora, podemos representar a situação da seguinte fórma:

x + 20 menos 20 > 20 + 30 menos 20,

ou seja,

x > 30

As inequações 3x + 20 > 2x + 20 + 30, x + 20 > 20 + 30 e x > 30 são equivalentes, ou seja, têm as mesmas soluções.

Em um mesmo conjunto universo, inequações que apresentam as mesmas soluções são chamadas de inequações equivalentes.

Quando adicionamos um mesmo número aos dois membros de uma inequação ou subtraímos um mesmo número dos dois membros de uma inequação, obtemos uma inequação equivalente à inequação dada. Esse é o princípio aditivo das desigualdades.

Página 149

Observe alguns exemplos.

a) 2x menos 5 > 7

2x menos 5 + 5 > 7 + 5

Ilustração. Seta alaranjada para à esquerda.

Adicionamos 5 unidades a cada membro.

2x > 12

As inequações 2x menos 5 > 7 e 2x > 12 são equivalentes.

b) 3x + 4 < 20

3x + 4 menos 4 < 20 ‒ 4

Subtraímos 4 unidades de cada membro.

3x < 16

As inequações 3x + 4 < 20 e 3x < 16 são equivalentes.

Situação 2

Esta balança está em desequilíbrio, e o prato da esquerda tem menor medida de massa. No prato da esquerda, foram colocados 2

de x gramas cada. No prato da direita, foram colocados 8

de 2 gramas cada.

Ilustração. Balança de pratos desequilibrada com 2 quadradinhos azuis no prato da esquerda, e 8 quadradinhos vermelhos no prato da direita. O prato da esquerda está um pouco acima do prato da direita. O ponteiro da balança aponta para a direita.

Podemos representar a situação por:

2x < 16

Retirando a metade da medida de massa de cada prato, a balança permanece desequilibrada e o prato da esquerda continua com menor medida de massa.

Ilustração. Balança de pratos desequilibrada com 1 quadradinho azul no prato da esquerda, e 4 quadradinhos vermelhos no prato da direita. O prato da esquerda está um pouco acima do prato da direita. O ponteiro da balança aponta para a direita.

Podemos representar a situação por:

\frac{2 x}{2} < \frac{16}{2}

x < 8

Portanto, 1

tem medida de massa menor que 8 gramas.

Quando multiplicamos ou dividimos os membros de uma inequação por um mesmo número diferente de zero, obtemos uma inequação equivalente à inequação dada. Esse é o princípio multiplicativo das desigualdades.

Observe este exemplo.

menos9 < 7x

menos9 · 4 < 7x · 4

Multiplicamos cada termo por 4.

menos36 < 28x

As inequações menos9 < 7x e menos36 < 28x são equivalentes.

Página 150

Observações

Ao multiplicar ou dividir os membros de uma desigualdade por um mesmo valor, é necessário estar atento ao sentido da desigualdade.

a) 2 > menos7

2 · 3 > menos7 · 3

Multiplicamos os dois membros da desigualdade por um número positivo.

6 > menos21

O sinal tem o mesmo sentido da desigualdade inicial.

b) 5 < 12

5 · (menos2) > 12 · (menos2)

Multiplicamos os dois membros da desigualdade por um número negativo.

menos10 > menos24

O sinal tem o sentido oposto ao da desigualdade inicial.

Por isso, ao multiplicar ou dividir os membros de uma inequação por um número negativo, é necessário inverter o sinal da desigualdade.

Analise estes exemplos.

a)

\frac{x}{5} ‒ 2 > 4

5 \cdot (\frac{x}{5} - 2) > 5 \cdot 4

Multiplicamos os membros por 5.

x menos 10 > 20

Mantemos o sinal da desigualdade, pois multiplicamos os dois membros da inequação por um número positivo.

As inequações

\frac{x}{5} ‒ 2 > 4

e x menos 10 > 20 são equivalentes.

b) menos3x < 8

\frac{- 3 x}{- 3} > \frac{8}{- 3}

Dividimos os dois membros da inequação por menos3, que é um número negativo; por isso, invertemos o sinal da desigualdade.

x > - \frac{8}{3}

As inequações ‒3x < 8 e

x > - \frac{8}{3}

são equivalentes.

Atividades

Faça as atividades no caderno.

28. Dada a inequação x < 15, é correto escrever: x menos 10 < 15 menos 10? Justifique sua resposta.

29. Considere a inequação menos7 < 5x. Obtenha inequações equivalentes a essa, fazendo o que se pede em cada item.

a) Multiplique os dois membros por 4.

b) Divida os dois membros da inequação obtida no item a por menos1.

c) Adicione menos3 aos dois membros da inequação obtida no item b.

d) Subtraia menos2 dos dois membros da inequação obtida no item c.

30. Sendo a < b, indique, no caderno, as sentenças verdadeiras.

a) a + 7 < b + 7

b)

\frac{a}{5} < \frac{b}{5}

c) 3a > 3b

d) a menos 10 < b menos 10

e) menos2a < menos2b

f) menosa > menosb

31. Se multiplicarmos os dois membros da desigualdade menos10x < menos12 por (menos1), que desigualdade obteremos?

Página 151

Resolução de uma inequação do 1º grau

Resolver uma inequação do 1º grau com uma incógnita significa determinar as soluções da inequação, ou seja, todos os números de determinado conjunto universo que, ao substituírem as incógnitas, tornam a sentença verdadeira. Esses números formam um conjunto chamado de conjunto solução, que indicamos pela letra S.

Para tanto, vale a fórma de resolução usada para as equações, aplicando, nesse caso, os princípios aditivo e multiplicativo das desigualdades.

Sendo U =

, vamos determinar o conjunto solução das inequações a seguir.

a) 3x menos 5 < 8

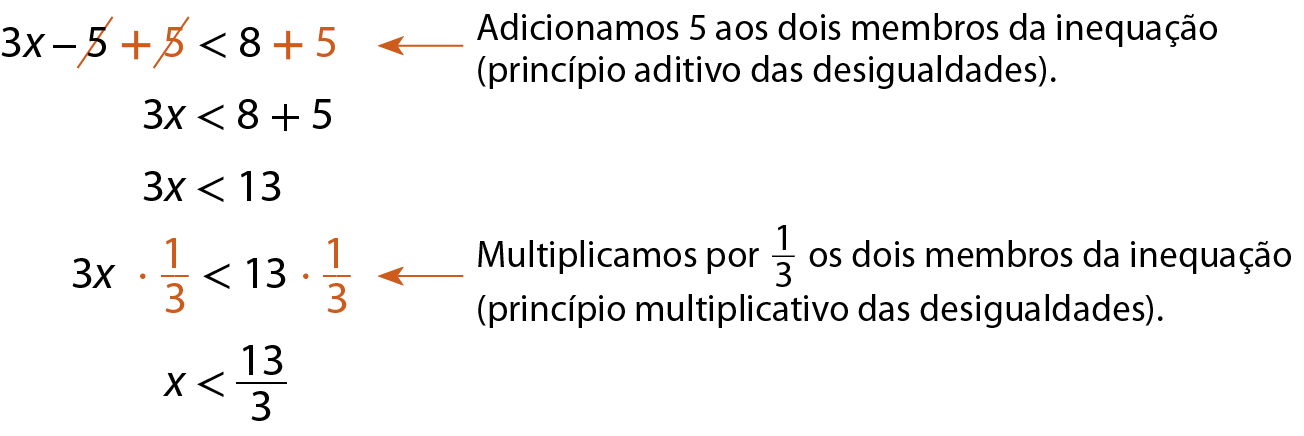
Sentença matemática. 3x menos 5 é menor que 8. Esquema. 3x menos 5 mais 5 é menor que 8 mais 5. À direita uma seta para a esquerda com a indicação: Adicionamos 5 aos dois membros da inequação (princípio aditivo das desigualdades). Em ambos os membros da desigualdade, a expressão ‘mais 5’ está em destaque. No primeiro membro da desigualdade, as expressões ‘menos 5’ e ‘mais 5’ estão com traço diagonal. Sentença matemática. 3x é menor que 8 mais 5.Sentença matemática. 3x é menor que 13.Esquema. 3x vezes fração 1 sobre 3 é menor que 13 vezes fração 1 sobre 3. À direita uma seta para a esquerda com a indicação: Multiplicamos por fração 1 sobre 3 os dois membros da inequação (princípio multiplicativo das desigualdades). Em ambos os membros da desigualdade, a expressão ‘vezes fração 1 sobre 3’ está em destaque. Sentença matemática. x é menor que fração 13 sobre 3.

A solução da inequação é o conjunto de todos os números racionais menores que

\frac{13}{3}

, ou seja,

S = \{x \in ℚ ∣ x < \frac{13}{3}\}

.

b) 10 menos 6x > menos2

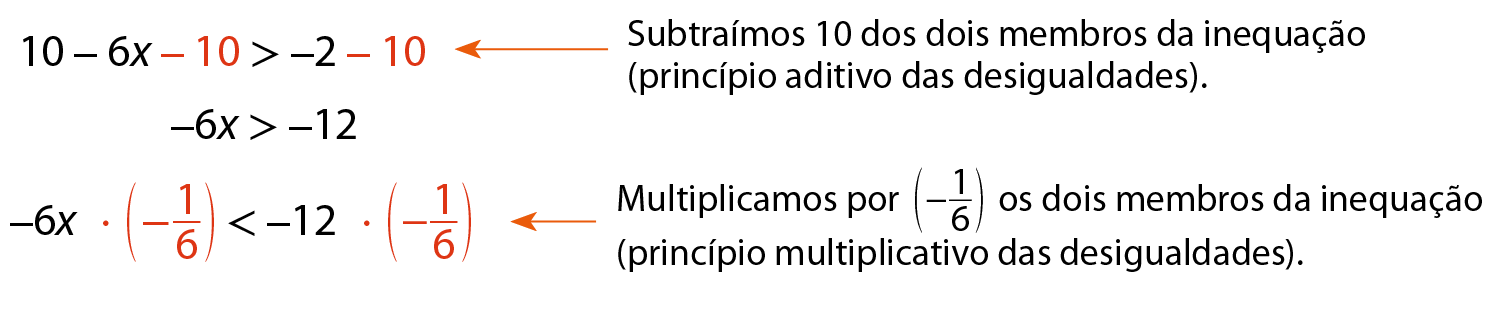
Esquema. 10 menos 6x, menos 10, é maior que menos 2 menos 10. À direita uma seta para a esquerda com a indicação: Subtraímos 10 dos dois membros da inequação (princípio aditivo das desigualdades). Em ambos os membros da desigualdade, a expressão 'menos 10' está em destaque. Sentença matemática. menos 6x é maior que menos 12.Esquema. menos 6x vezes, abre parênteses, menos fração 1 sobre 6, fecha parênteses, é menor que menos 12, vezes, abre parênteses, menos fração 1 sobre 6, fecha parênteses. À direita uma seta para a esquerda com a indicação: Multiplicamos por, abre parênteses, menos fração 1 sobre 6, fecha parênteses, os dois membros da inequação (princípio multiplicativo das desigualdades). Em ambos os membros da desigualdade, a expressão ‘vezes, abre parênteses, menos fração 1 sobre 6, fecha parênteses’ está em destaque.

x < 2

A solução da inequação é o conjunto de todos os números racionais menores que 2, ou seja, S = {x ∈

∣ x < 2}.

Atividades

Faça as atividades no caderno.

32. Sendo U =

, determine o conjunto solução das inequações.

a) (x + 2) + (x + 3) + (x + 4) ⩽ 1

b) 4 menos 2x > 3 menos 3x

c) x ‒ 5 ⩽ 1 menos x

d) x menos

\frac{1}{2}

<

\frac{5}{2}

+ 3x

33. Para quais números naturais a inequação

3 (x - \frac{1}{5}) + \frac{2 x}{3} < 8

é verdadeira?

34. Determine o maior valor inteiro para x que satisfaça a inequação

\frac{x - 10}{5} < 0

.

35. Qual é o número inteiro cujo triplo mais 5 é menor do que 2 e cuja terça parte mais 4 é maior do que 3?

36. Um retângulo tem 2y centímetros de medida do comprimento e y centímetros de medida da largura.Qual deve ser o menor valor inteiro de y, se a medida do perímetro do retângulo é maior que a medida do perímetro de um triângulo equilátero com 16 centímetros de medida de comprimento de lado?

Página 152

Comparando funções afim

Uma lanchonete vende dois tipos de suco natural. Vamos indicar a quantidade de litros de suco vendido pela letra x; o lucro será dado em função de x, em dezenas de reais.

O lucro obtido com a venda de suco de laranja, em dezenas de reais, pode ser representado pela função função, tal que funçãoabre parênteses décimafecha parênteses = 0,2x + 3.

Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números 0, 1, 2, 3, 4, 5, 6 e 7 e ele está rotulado como x. No eixo vertical estão indicados os números 0, 1, 2, 3, 4 e 5 e ele está rotulado como f de x. No plano cartesiano está representada uma reta laranja passando pelos pontos (0, 3) e (5, 4).

O lucro obtido com a venda de suco de uva, em dezenas de reais, pode ser representado pela função g, dada por g(x) = 0,6x + 1.

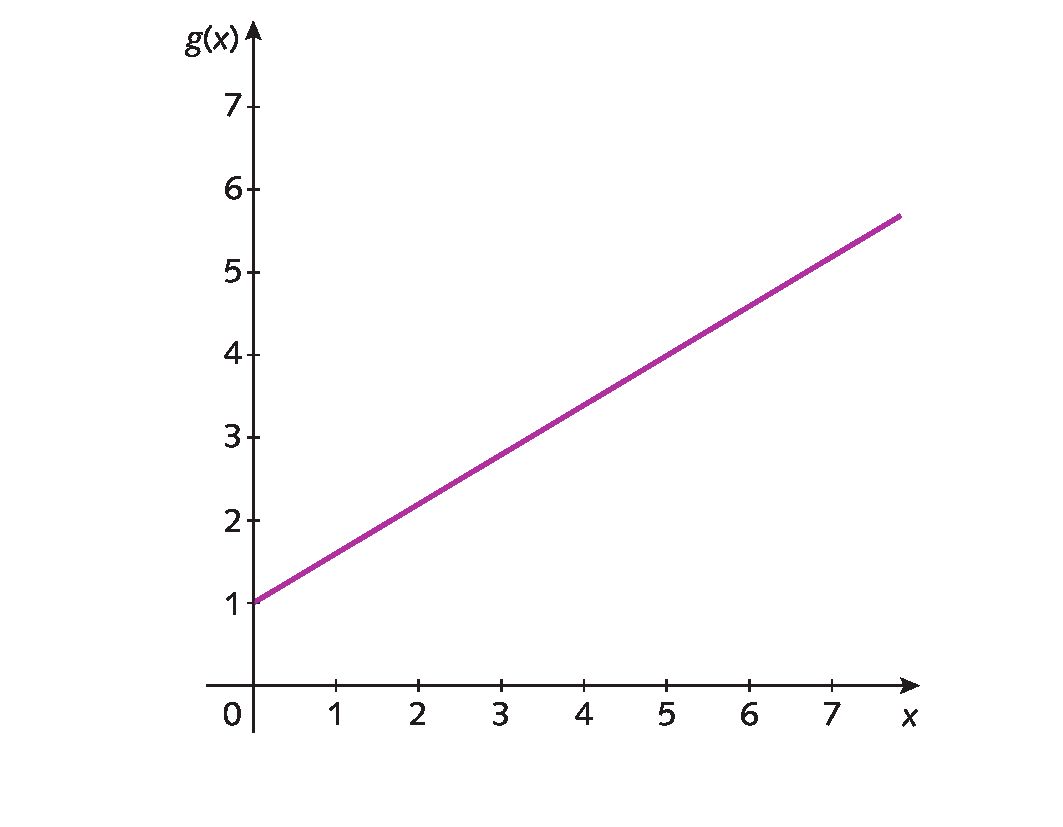
Podemos analisar a partir de qual momento a venda de um tipo de suco natural gera mais lucro para a lanchonete do que a venda do outro, observando os gráficos dessas funções:

Ilustração. Mulher de cabelo preto, camisa vermelha, jaleco branco e calça azul. Ela fala: Observe os coeficientes de x. Como 0 vírgula 6 maior que 0 vírgula 2, a função g cresce mais rápido do que a função f.

Página 153

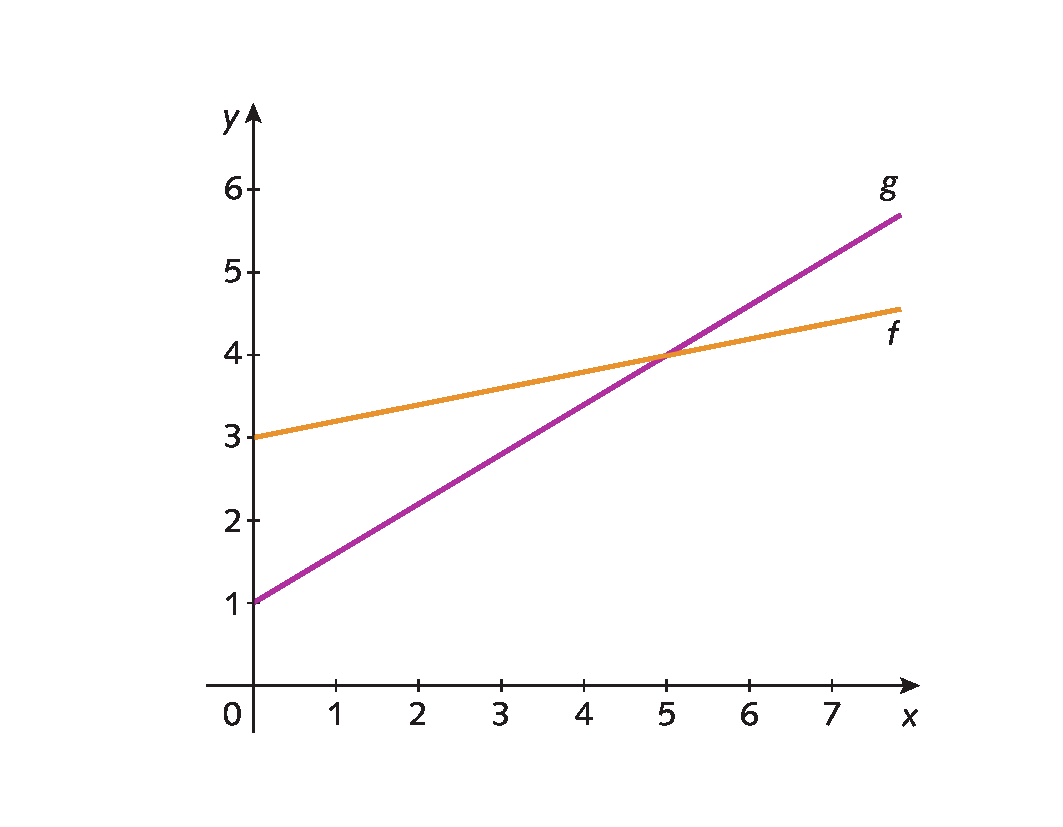
Analisando o gráfico, podemos perceber que, para algum valor de x, a venda de suco de uva é mais vantajosa do que a venda de suco de laranja. Para descobrir esse valor, podemos resolver a inequação gerada pela comparação das funções f e g. Assim:

g(x) > funçãoabre parênteses décimafecha parênteses

0,6x + 1 > 0,2x + 3

Resolvendo a inequação, encontramos x > 5. Isso significa que, acima de 5 litros de suco de uva vendidos, o lucro é maior do que aquele da venda da mesma quantidade de suco de laranja.

Atividades

Faça as atividades no caderno.

37. Determine os valores reais de x.

a) funçãoabre parênteses décimafecha parênteses > g(x), com funçãoabre parênteses décimafecha parênteses = 3x + 4 e g(x) = 2x + 2.

b) funçãoabre parênteses décimafecha parênteses < g(x), com funçãoabre parênteses décimafecha parênteses = 0,5x + 1 e g(x) = x.

c) h(x) ⩾ q(x), com h(x) = 20x + 5 e q(x) = 15x menos 5.

d) s (x) ⩽ t (x), com s (x) = 7x + 7 e t (x) = 2x + 2.

38. A seguir, temos as funções função e g , tais que:

• funçãoabre parênteses décimafecha parênteses = 2x menos 2

• g(x) = 0,5x + 1

a) Esboce no plano cartesiano o gráfico das duas funções.

b) Verifique a partir de qual valor atribuído a x teremos funçãoabre parênteses décimafecha parênteses > g(x).

39. Analise os gráficos das funções função e g.

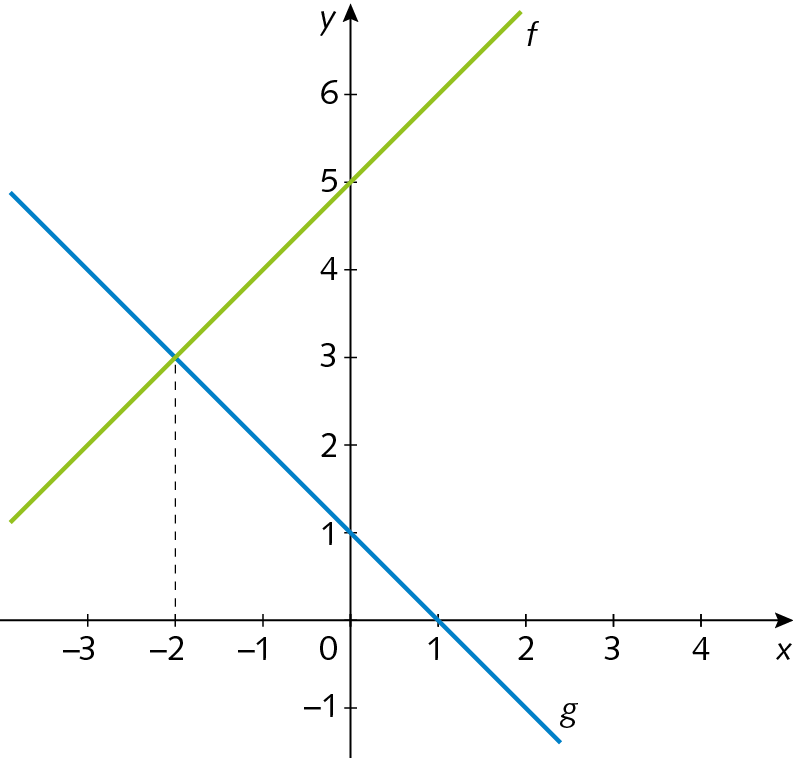
Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 3, menos 2, menos 1, 0, 1, 2, 3 e 4 e ele está rotulado como x. No eixo vertical estão indicados os números menos 1, 0, 1, 2, 3, 4, 5 e 6 e ele está rotulado como y. No plano cartesiano estão representadas duas retas que se interceptam no ponto (menos 2, 3): uma verde que corresponde à função f e passa pelo ponto (0, 5); e outra azul que corresponde à função g e passa pelo ponto (0, 1).

a) Para qual valor de x temos funçãoabre parênteses décimafecha parênteses = g(x)?

b) Qual é o conjunto solução da inequação funçãoabre parênteses décimafecha parênteses > g(x)?

c) Determine o conjunto solução da inequação g(x) ⩾ funçãoabre parênteses décimafecha parênteses.

40.

Elabore um problema no qual a solução envolva a comparação de duas funções. Uma deve ser uma função decrescente e a outra, uma função crescente. Utilize os gráficos das funções a seguir para se inspirar na situação a ser elaborada.

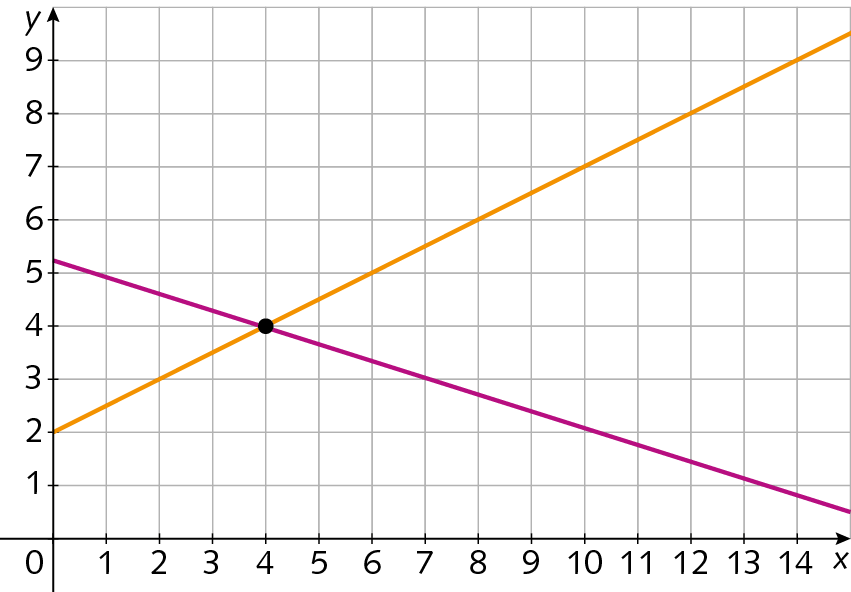
Gráfico. Malha quadriculada com eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 e 14 e ele está rotulado como x. No eixo vertical estão indicados os números 0, 1, 2, 3, 4, 5, 6, 7, 8, e 9 e ele está rotulado como y. No plano cartesiano estão representadas duas retas que se interceptam no ponto (4, 4): uma laranja que passa pelos pontos (0, 2), (2, 3), (6, 5), (8, 6), (10, 7), (12, 8) e (14, 9); e outra roxa passa pelo ponto (7, 3).

Troque a situação com um amigo e resolva aquela que ele propôs. Em seguida, discutam o resultado e verifiquem os procedimentos efetuados. Caso alguma dúvida persista, discuta com o professor.

41.

Dada a função função cuja lei é funçãoabre parênteses décimafecha parênteses = 3x + 2, elabore uma situação na qual x é um número natural. A partir da função e da situação que criar, esboce o gráfico da função, explicitando no contexto criado a variável dependente e a independente.

Página 154

Resolvendo em equipe

Faça a atividade no caderno.

(Etec) Um grupo de amigos, em visita a Aracaju, alugou um carro por dois dias.

A locação foi feita nas seguintes condições: R$ 40,00quarenta reais por dia e R$ 0,45zero reais e quarenta e cinco centavos por quilômetro rodado.

No primeiro dia, saíram de Aracaju e rodaram 68 quilômetros para chegar à Praia do Saco, no sul de Sergipe.

No segundo dia, também partiram de Aracaju e foram até Pirambu, no norte do estado, para conhecer o Projeto Tamar. Por uma questão de contrôle de gastos, o grupo de amigos restringiu o uso do carro apenas para ir e voltar desses lugares ao hotel onde estavam hospedados em Aracaju, fazendo exatamente o mesmo percurso de ida e volta. Nas condições dadas, sabendo que foram pagos R$ 171,80cento e setenta e um reais e oitenta centavos pela locação do carro, então o número de quilômetros percorrido para ir do hotel em Aracaju a Pirambu foi:

a) 68

b) 61

c) 50

d) 46

e) 34

Interpretação e identificação dos dados	• Analise as informações do enunciado e anote aquelas que você julgar relevantes para a resolução do problema. • No caderno, escreva a lei que relaciona o valor diário (V) a pagar em função da medida da distância (x) percorrida, em quilômetro. • Qual foi a medida da distância total percorrida na viagem de Aracaju à Praia do Saco? • Calcule o valor gasto na viagem de Aracaju à Praia do Saco.
Plano de resolução	• Qual foi o valor gasto na viagem de Aracaju a Pirambu? • O valor calculado no item anterior corresponde a quantos quilômetros percorridos? • Qual é a medida da distância entre Aracaju e Pirambu?
Resolução	• Forme dupla com um colega. • Mostre a ele seu plano de resolução e verifique se há ideias comuns entre vocês. • A dupla deverá discutir quais são as diferenças e as semelhanças de cada plano e escolher um deles para a execução do processo de resolução. Observação Resolvam o problema de maneira coletiva, mas façam o registro individualmente.
Verificação	• A dupla deve reler o problema e verificar se todas as condições do enunciado foram satisfeitas.
Apresentação	• A dupla deverá pesquisar informações relativas ao município de Pirambu (SE), como origem do nome, histórico, medida da área do município, população estimada, densidade demográfica etc.

Página 155

Revisão dos conteúdos deste capítulo

Ideia de função

Lei de formação da função

Quando temos uma relação em que uma grandeza é função de outra, a correspondência entre cada valor de uma grandeza e cada valor da outra pode ser expressa por uma sentença chamada lei de formação da função ou lei da função. Considere o exemplo:

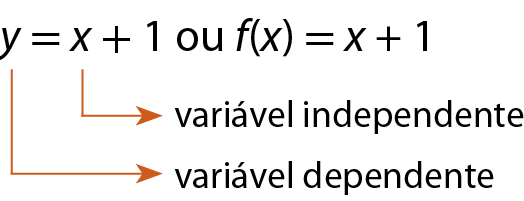
Esquema. y é igual a x mais 1 ou f de x é igual a x mais 1. Uma seta vermelha abaixo do y com os dizeres: variável dependente. Uma seta vermelha abaixo do x da primeira sentença com os dizeres: variável independente.

Valor de uma função

O valor da função funçãoabre parênteses décimafecha parênteses = x + 1 para x = 3 é igual a 4, pois:

função(3) = 3 + 1 = 4

1. A medida do perímetro (p) de um pentágono regular é dado em função da medida de comprimento x do seu lado.

a) Qual é a lei da função que relaciona p e x?

b) Qual será a medida de perímetro se x = 7,2 centímetros?

2. Sabe-se que a medida do comprimento (y) de certo retângulo está em função da medida da largura (x) e que a medida do comprimento excede a medida da largura em 5 unidades de medida de comprimento.

a) Qual é a lei da função que relaciona y e x?

b) Qual é a medida do comprimento do retângulo se a medida da largura for igual a 3,6 métros?

3. Um garçom ganha mensalmente R$ 1.200,00mil duzentos reais de salário mais uma comissão de 15% sobre todas as vendas feitas durante o mês. No mês em que o total de vendas no restaurante foi x, qual foi o salário S desse garçom?

4. A lei de formação de uma função f é dada por funçãoabre parênteses décimafecha parênteses = 2x + 9. Calcule:

a) função(‒2)

b) função(5)

c)

f (\frac{3}{2})

d) função(‒1) ⋅ função(0)

e)

\frac{f (- 3) + f (2)}{f (- \frac{1}{2})}

Função afim

Função afim é toda função f cuja lei pode ser escrita na fórma função(x) = ax + b, em que a e b são números reais e x pode ser qualquer número real.

Nos casos em que a ≠ 0 e b = 0, chamamos a função afim de função linear.

Nos casos em que a = 0, chamamos a função afim de função constante.

Gráfico da função afim

O gráfico que representa uma função afim é sempre uma reta não perpendicular ao eixo x. Vamos construir o gráfico de função(x) = x + 1.

x	f(x) = y	(x, y)
0	1	(0, 1)
−1	0	(−1, 0)

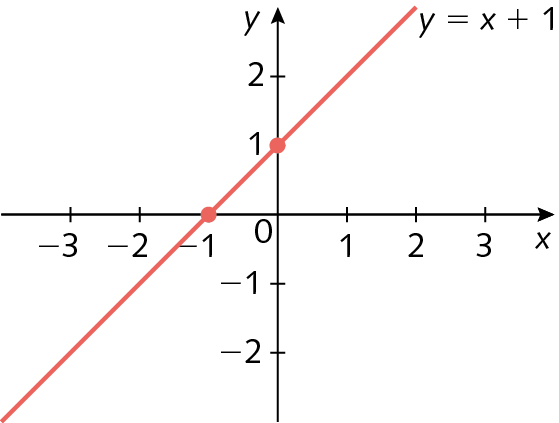
Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 3, menos 2, menos 1, 0, 1, 2 e 3 e ele está rotulado como x. No eixo vertical estão indicados os números menos 2, menos 1, 0, 1 e 2 e ele está rotulado como y. No plano cartesiano está representada uma reta que corresponde a y igual a x mais 1 e passa pelos pontos (menos 1, 0) e (0, 1).

O gráfico de uma função linear é sempre uma reta que passa pelo ponto (0, 0), ou seja, pela origem do plano cartesiano. Vamos construir o gráfico de g(x) = ‒2x.

x	g(x) = y	(x, y)
0	0	(0, 0)
1	−2	(1, −2)

Página 156

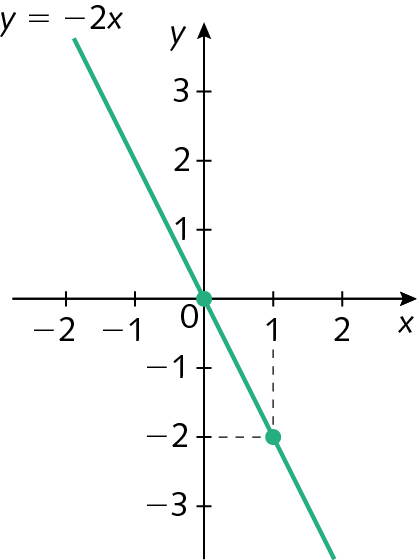
O gráfico de uma função constante sempre será uma reta paralela ao eixo x ou coincidente com o eixo x. Vamos construir o gráfico de h(x) = menos3.

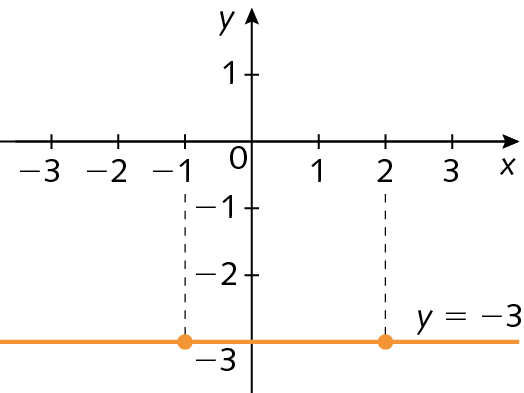
x	h(x) = y	(x, y)
−1	−3	(−1, −3)
2	−3	(2, −3)

Zero de uma função afim

Em toda função função, cada valor de x em que funçãoabre parênteses décimafecha parênteses = 0 é chamado de zero da função.

O zero de uma função afim dada por y = ax + b, com a ≠ 0, será um único número x, tal que ax + b = 0. Resolvendo essa equação, obtemos

x = ‒ \frac{b}{a}

Graficamente, o zero de uma função afim é a abscissa do ponto de intersecção do gráfico da função com o eixo das abscissas (eixo x).

5. Construa os gráficos destas funções afim.

a) y = 2x + 1

b) y = menos 3x + 2

c) y = x

d) y = menos 2x

e) y = 6

f) y = 5x menos 3

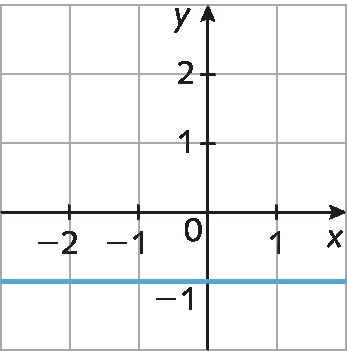
6. Analise os gráficos de funções afim a seguir e determine se representam uma função linear ou constante.

a)

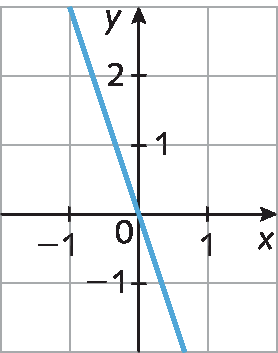
Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 1, 0 e 1 e ele está rotulado como x. No eixo vertical estão indicados os números menos 1, 0, 1 e 2 e ele está rotulado como y. No plano cartesiano está representada uma reta diagonal que passa pelo ponto (0, 0).

b)

Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 2, menos 1, 0 e 1 e ele está rotulado como x. No eixo vertical estão indicados os números menos 1, 0, 1 e 2 e ele está rotulado como y. No plano cartesiano está representada uma reta horizontal que passa pelos pontos (menos 2, menos 1), (menos 1, menos 1), (0, menos 1) e (1, menos 1).

7. Carlos revende capas de celular. Cada capa custa R$ 10,50dez reais e cinquenta centavos, e o frete é um valor fixo de R$ 23,00vinte e três reais. Determine:

a) a lei da função para o valor y a ser pago por Carlos para x capas de celular;

b) o valor a ser pago por Carlos para 120 capas de celular;

8. Dado o gráfico a seguir, determine:

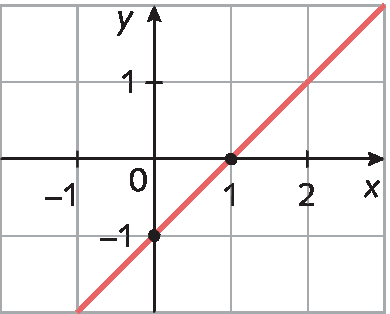
Gráfico. Eixo horizontal perpendicular a um eixo vertical. No eixo horizontal estão indicados os números menos 1, 0, 1 e 2 e ele está rotulado como x. No eixo vertical estão indicados os números menos 1, 0 e 1 e ele está rotulado como y. No plano cartesiano está representada uma reta que passa pelos pontos (0, menos 1), (1, 0) e (2, 1).

a) o par ordenado correspondente ao ponto de intersecção da reta com o eixo y;

b) o par ordenado correspondente ao ponto de intersecção da reta com o eixo x;

c) a lei de formação da função;

d) o zero da função.

9. Determine o zero destas funções considerando que x pode assumir qualquer valor real.

a) y = x + 3

b) y = menos 2x + 8

c) y = menos 5x

d) y = 2x + 5

Inequações

Toda desigualdade que tenha pelo menos uma incógnita, com expoente maior ou igual a 1, é chamada de inequação.

Inequações equivalentes

Em um mesmo conjunto universo, inequações que apresentam as mesmas soluções são chamadas de inequações equivalentes.

Pelo princípio aditivo das desigualdades, quando adicionamos um mesmo número aos dois membros de uma inequação ou subtraímos um mesmo número dos dois membros de uma inequação, obtemos uma inequação equivalente à inequação dada.

Pelo princípio multiplicativo das desigualdades, quando multiplicamos ou dividimos os membros de uma inequação por um mesmo número diferente de zero, obtemos uma inequação equivalente à inequação dada.

Ao multiplicar ou dividir os membros de uma inequação por um número negativo, é necessário inverter o sinal da desigualdade.

10. Resolva as inequações considerando U =

.

a) 7 menos 3 ⋅ ( 2x + 1 ) ⩽ menos x menos 11

b) 3 ⋅ (x menos 2) + 15 > 2 ⋅ (x + 1)

c) 5x menos 3 ⩽ 3 ⋅ (2x− 5)

d) 7x menos 1 > 12x + 7

Glossário

Grandeza: : Tudo aquilo que póde ser medido ou contado.; Voltar para o texto

Fake news: : Publicações com informações comprovadamente falsas que costumam viralizar nas redes sociais.; Voltar para o texto