Capítulo 6 Função quadrática
Trocando ideias
A Física é a ciência que estuda a natureza e seus fenômenos em seus aspectos mais gerais. Um dos propósitos da Física é estudar o movimento dos objetos: a trajetória, a rapidez com que se movem, a medida da distância percorrida em dado intervalo de tempo etcétera. Para isso são utilizadas funções matemáticas.
Alguns movimentos são retilíneos e uniformes e outros, como os movimentos balísticos, apresentam uma trajetória parabólica em que a medida de velocidade não é constante. Confira alguns exemplos de movimento balístico.

▸ A trajetória de uma pedra ao ser lançada no ar é dada pela função S = menostelevado a 2 + 10t, em que ésse indica a posição, em metros, da pedra no instante t em segundos.
a) Qual era a posição da pedra no instante t = 2 segundos? E no instante t = 4 segundos?
b)

Após quantos segundos a pedra atingirá o solo? Explique para a turma como você fez para chegar a essa conclusão.
Neste capítulo, vamos estudar o conceito de função quadrática, além de construir e analisar gráficos desse tipo de função.

1 Função quadrática
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
Acompanhe a situação a seguir.
Os gafanhotos são insetos que se alimentam principalmente de folhas. Eles têm pernas posteriores muito fortes, com as quais são capazes de dar grandes saltos.
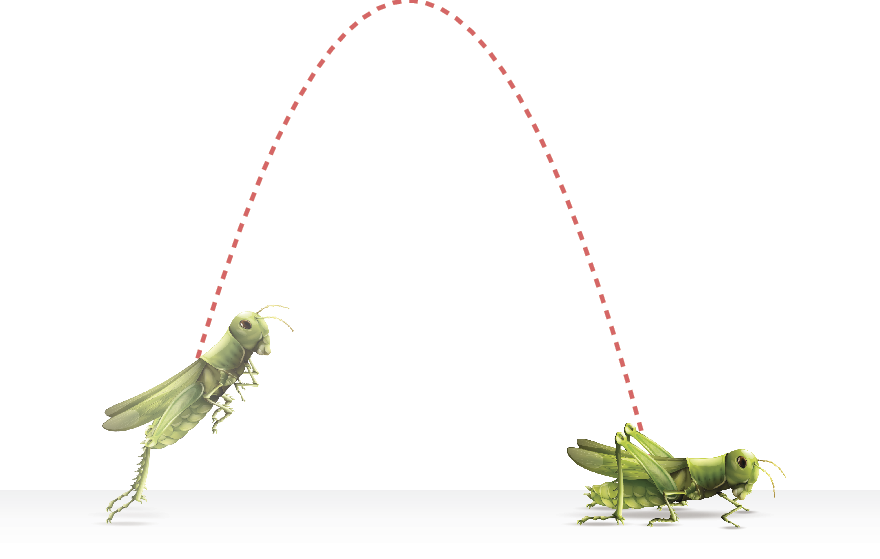
Um biólogo observou imagens dos movimentos de um gafanhoto e concluiu que, quando o inseto dava um pulo, a medida de sua altura agá, em metro, variava em função da medida do tempo tê, em segundo, pela lei:
h (t ) = menost elevado a 2 + 2t, em que t é um número real tal que 0 ⩽ t ⩽ 2
Essa função é um exemplo de função quadrática. Note que ela é do tipo y = axelevado a 2 + bx + c, com a = menos1, b = 2 e c = 0.
Função quadrática é toda função f cuja lei pode ser escrita na fórma f (x ) = ax elevado a 2 + bx + c, em que a, b e c são números reais, com a ≠ 0, e x pode ser qualquer número real.
Considere alguns exemplos.
a) f (x ) = 2x elevado a 2 + 16x + 30, em que a = 2, b = 16 e c = 30.
b) f (x ) = x elevado a 2 menos 16, em que a = 1, b = 0 e c = menos16.
c) f (x ) = 6x elevado a 2, em que a = 6, b = 0 e c = 0.
Atividades
Faça as atividades no caderno.
1. Considerando a função f, tal que f (x ) = ax elevado a 2 + bx + c, em que a ≠ 0, determine os valores dos coeficientes a, b e c nestas funções quadráticas.
a) f (x) = x elevado a 2 menos 25
b) f (x) = ‒3x elevado a 2 menos 6x + 9
c) f (x) = x elevado a 2 menos 18
d) f (x) = menos5x elevado a 2 + 13x
e) f (x) = x elevado a 2 menos 10x + 25
f) f (x) = 3xelevado a 2 menos 4x + 75
2. Sendo a função quadrática f definida por f (x) = 2x elevado a 2 menos 6, determine:
a) f (5)
b) f (0)
c) f (‒2)
d)
Sentença matemática. f, abre parênteses raiz quadrada de 11, fecha parênteses.3. Dada a função quadrática f definida por f (x ) = x elevado a 2 menos 5x + 6, para que valores de x tem-se f (x ) = 0?
4. Observe a figura a seguir. A medida da área (y) da figura é dada em função da medida de comprimento x indicada. Qual é a lei da função que relaciona x e y?
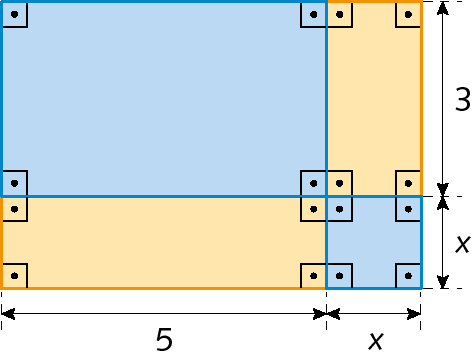
Gráfico da função quadrática
O gráfico de toda função quadrática é uma curva chamada parábola.
A parábola é uma curva geométrica que pode ser visualizada parcialmente quando um plano secciona a superfície de um cone (Figura 1) ou quando observamos a trajetória de uma bola lançada obliquamente (Figura 2).
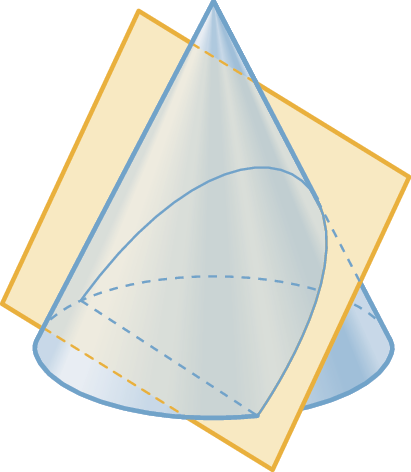

Para construir o gráfico de uma função quadrática, procedemos de maneira similar à da construção dos gráficos de funções afim. Acompanhe os exemplos a seguir.
a) Construção do gráfico da função quadrática f dada pela lei f (x ) = menosx elevado a 2 + 4x.
Inicialmente, escolhemos valores arbitrários para x e calculamos os valores de f(x) correspondentes para obter alguns pares ordenados.
|
x |
f (x) = y |
(x, y) |
|---|---|---|
|
−1 |
−5 |
(−1, −5) |
|
0 |
0 |
(0, 0) |
|
1 |
3 |
(1, 3) |
|
2 |
4 |
(2, 4) |
|
3 |
3 |
(3, 3) |
|
4 |
0 |
(4, 0) |
|
5 |
−5 |
(5, −5) |
Representamos no plano cartesiano os pontos correspondentes aos pares ordenados encontrados e unimos os pontos de modo a traçar a parábola que representa a função.
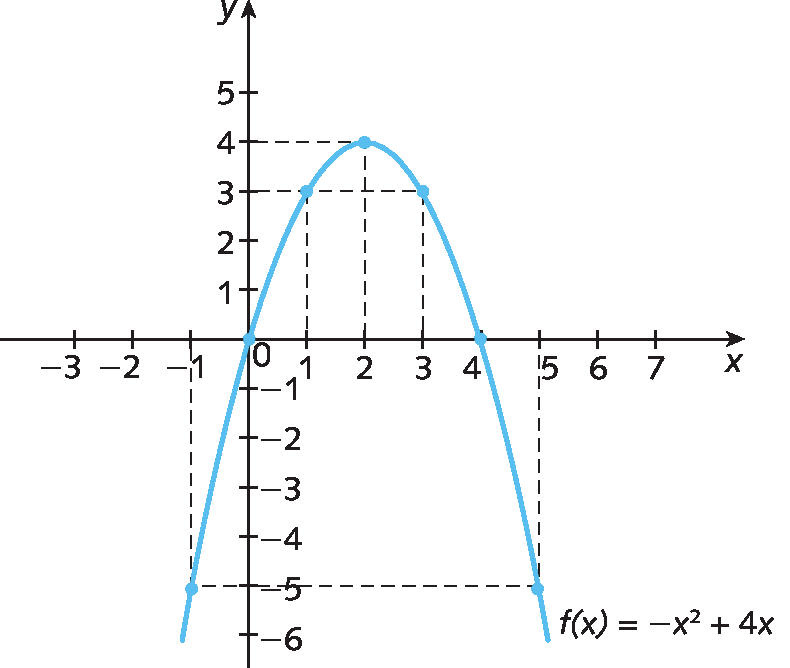
b) Construção do gráfico da função quadrática g dada pela lei g (x ) = x elevado a 2 + 2x menos 3.
|
x |
y |
(x, y) |
|---|---|---|
|
−3 |
0 |
(−3, 0) |
|
−2 |
−3 |
(−2, −3) |
|
−1 |
−4 |
(−1, −4) |
|
0 |
−3 |
(0, −3) |
|
1 |
0 |
(1, 0) |
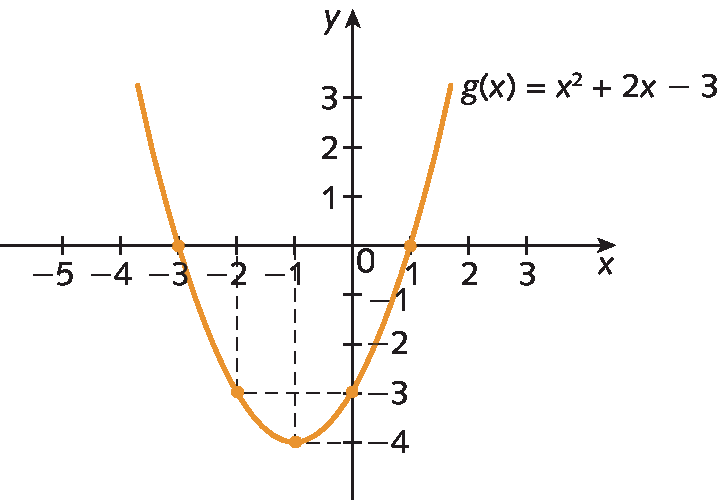
Concavidade da parábola
A parábola que representa o gráfico de uma função quadrática pode ter concavidade (abertura) voltada para cima ou para baixo.
Dada uma função quadrática de lei f (x ) = ax elevado a 2 + bx + c, quando:
• a > 0 , a parábola tem concavidade voltada para cima;
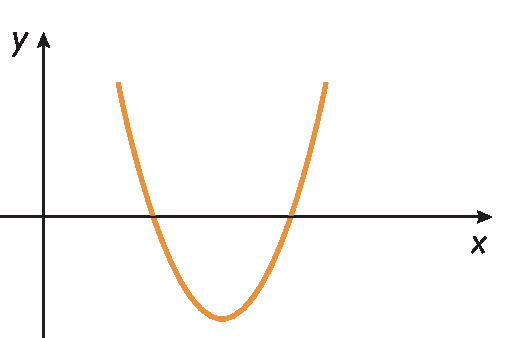
• a < 0 , a parábola tem concavidade voltada para baixo.
Analise alguns exemplos.
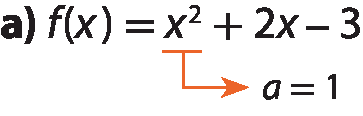
A parábola que representa f tem concavidade voltada para cima, pois 1 > 0.
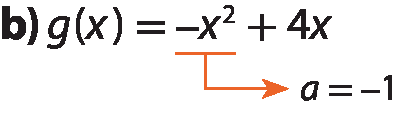
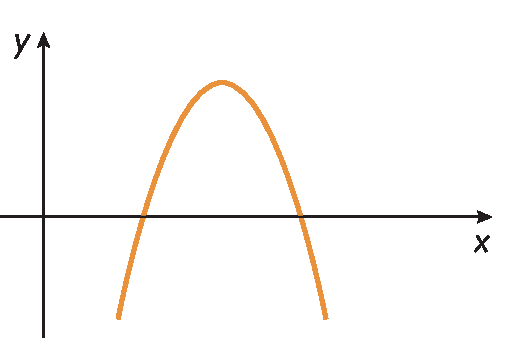
A parábola que representa g tem concavidade voltada para baixo, pois ‒‒1 < 0.
Atividades
Faça as atividades no caderno.
5. Considere estes dois gráficos.
Gráfico um
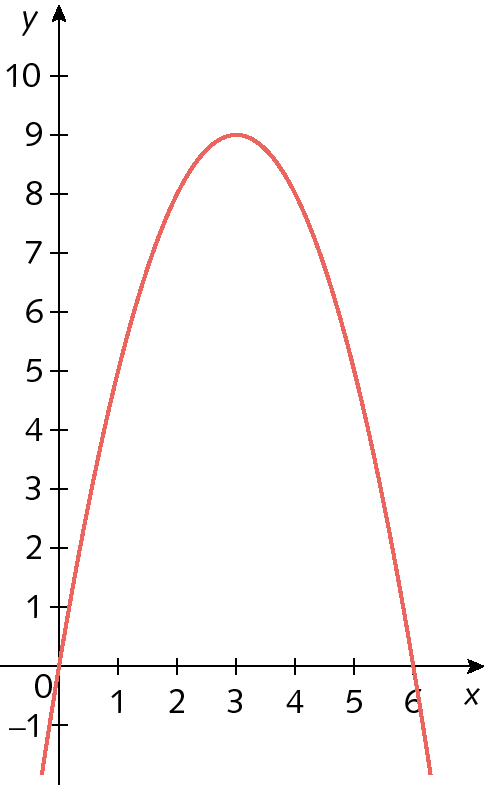
Gráfico dois
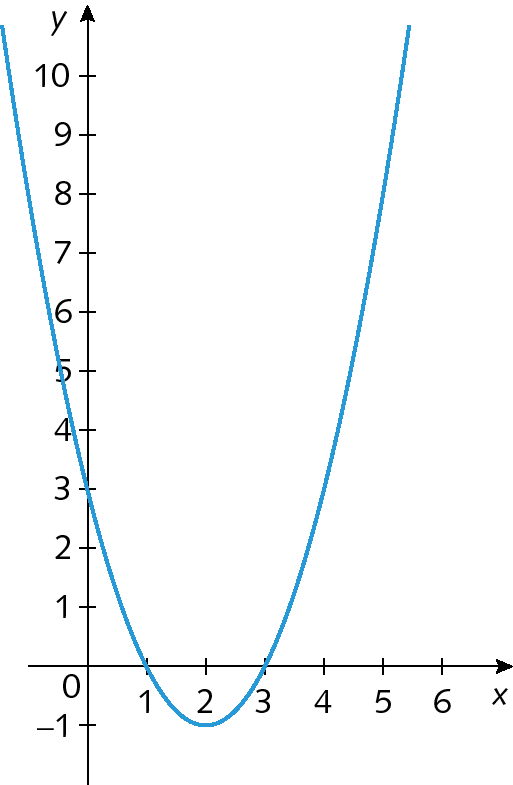
Sabendo que f(x) = xelevado a 2 menos 4x + 3 e g(x) = menosxelevado a 2 + 6x, qual função pode ser relacionada a cada um dos gráficos?
6. Das funções quadráticas a seguir, quais representam parábolas com concavidade voltada para cima?
a) y = ‒x elevado a 2 + x + 2
b) y = 2x elevado a 2
c) y = x elevado a 2 + 4x
d) y = x elevado a 2 + 2x + 5
e) y = menos3x elevado a 2 + 6
f) y = menos2x elevado a 2 + x + 3
g)
Sentença matemática. y igual a menos x elevado ao quadrado sobre 2, menos x.h)
Sentença matemática. y igual a, abre parênteses x sobre 7, mais 6, fecha parênteses, vezes abre parênteses -x mais 2, fecha parênteses.i)
Sentença matemática. y igual a, abre parênteses cinco nonos de x mais 3, fecha parênteses, elevado ao quadrado.7. Para que o gráfico da função f dada por f (x ) = (m menos 7)x elevado a 2 menos 3x menos 2 tenha a concavidade voltada para baixo, quais devem ser os valores de m?
8. Para que valores de p o gráfico da função
Sentença matemática. g, abre parênteses x, fecha parênteses, igual a abre parênteses p sobre 2 mais 3, fecha parênteses, vezes x elevado ao quadrado, menos raiz quadrada de 2 vezes x, mais 1.tem a concavidade voltada para baixo?
9. Após o lançamento de um projétil, verifica-se que a medida da altura (y ) alcançada por ele, em metro, é função da medida da distância percorrida na horizontal (x ), em metro, de acôrdo com a lei e o gráfico a seguir.
Sentença matemática. y igual ao oposto de x elevado ao quadrado sobre 900, mais dois terços de x.
, em que x é um número real tal que x ⩾ 0
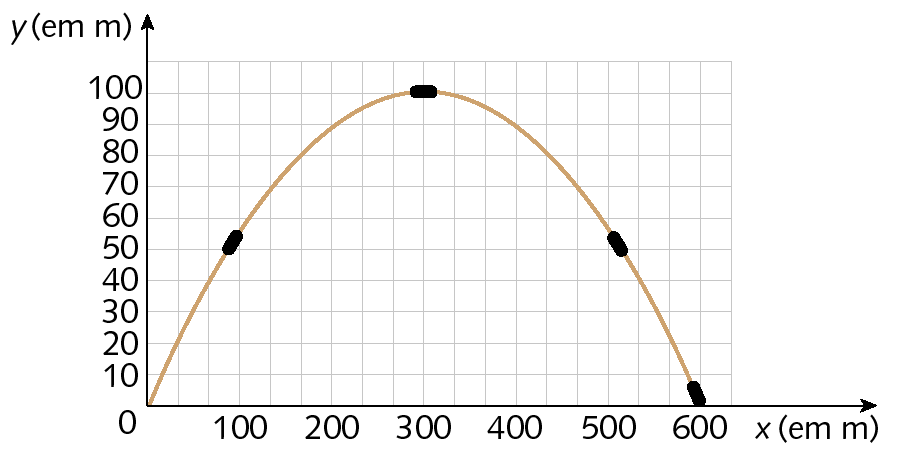
a) Copie o quadro no caderno substituindo cada

pelos valores correspondentes.

|
Medida da distância percorrida (em metro) |
Medida da altura |
|---|---|
|
100 |
|
|
200 |
|
|
100 |
|
|
400 |
|
|
600 |
0 |
b) Qual é a medida da altura máxima atingida pelo projétil?
c) Depois de quantos metros percorridos na horizontal o projétil atinge a medida da altura máxima?
d) Qual é a medida da distância total percorrida na horizontal pelo projétil após ser disparado?
Zeros de uma função quadrática
Para uma função f de lei f (x) = axelevado a 2 + bx + c, com a ≠ 0, denominamos zeros da função quadrática os valores de x tais que f (x) = 0.
Assim, na função f dada pela lei f (x) = x elevado a 2 + 2x menos 3:
• o número menos3 é zero da função, pois, para x = menos3, temos:
f(menos3) = (menos3)elevado a 2 + 2 ⋅ (menos3) menos 3 = 9 menos 6 menos 3 = 0
• o número 1 é zero da função, pois, para x = 1, temos:
f(1) = (1)elevado a 2 + 2 ⋅ 1 menos 3 = 1 + 2 menos 3 = 0
• o número 0 não é zero da função, pois, para x = 0, temos:
f(0) = (0)elevado a 2 + 2 ⋅ 0 menos 3 = 0 + 0 menos 3 = menos3
Determinação dos zeros de uma função quadrática
Para determinar os zeros da função definida por f (x ) = ax elevado a 2 + bx + c, com a ≠ 0, basta igualar a função a zero e encontrar as raízes reais da equação do 2º grau ax elevado a 2 + bx + c = 0.
Graficamente, os zeros da função quadrática (quando existem) correspondem às abscissas dos pontos de intersecção da parábola com o eixo x.
Acompanhe alguns exemplos.
a) Vamos determinar os zeros da função f dada por f (x ) = x elevado a 2 menos 5x + 6:
x elevado a 2 menos 5x + 6 = 0
delta = b elevado a 2 menos 4ac
delta = (‒5)elevado a 2 menos 4 ⋅ 1 ⋅ 6
delta = 25 menos 24
delta = 1
Sentença matemática. x igual à fração menos b mais ou menos raiz quadrada de delta, sobre 2 vezes a.
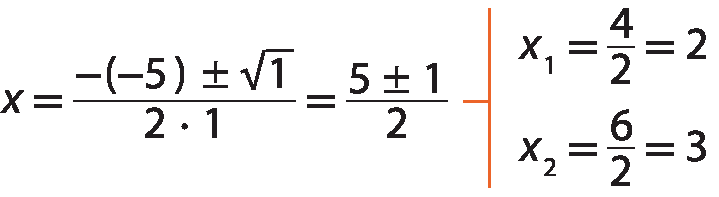
A equação x elevado a 2 menos 5x + 6 = 0 tem duas raízes reais diferentes: xindice 1 = 2 e xindice 2 = 3.
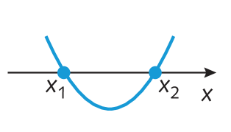
Assim, os zeros da função f dada por f (x ) = x elevado a 2 menos 5x + 6 são 2 e 3. Isso significa que o gráfico da função f intercepta o eixo x em dois pontos: (2, 0) e (3, 0). Analise o esboço do gráfico.
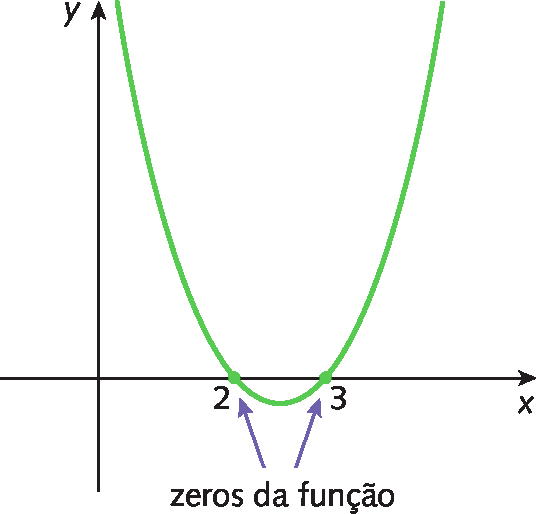

b) Vamos determinar os zeros da função g dada por g (x ) = menosx elevado a 2 + 2x menos 1:
menosx elevado a 2 + 2x menos 1 = 0
delta = b elevado a 2 menos 4ac
delta = 2elevado a 2 menos 4 ⋅ (‒1) ⋅ (‒1)
delta = 4 menos 4
delta = 0
Sentença matemática. x igual à fração menos b mais ou menos raiz quadrada de delta, sobre 2 vezes a.
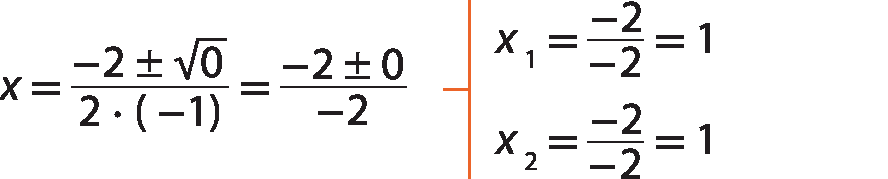
A equação menosx elevado a 2 + 2x ‒ 1 = 0 tem duas raízes reais iguais: xindice 1 = xindice 2 = 1
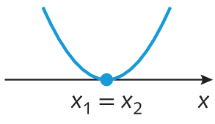
Assim, a função g dada por g (x ) = menosx elevado a 2 + 2x menos 1 tem um único zero igual a 1. Isso significa que o gráfico da função g intercepta o eixo x em um único ponto: (1, 0). Analise o esboço do gráfico.
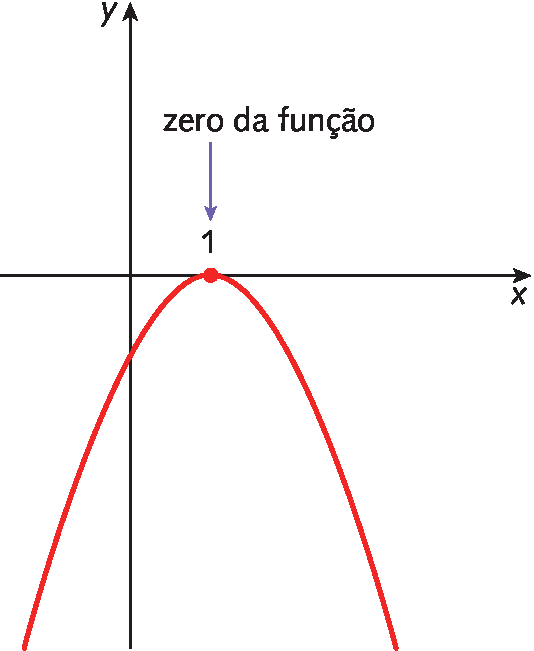

c) Vamos determinar os zeros da função h dada por h (x ) = x elevado a 2 + 2x + 3:
x elevado a 2 + 2x + 3 = 0
delta = 2elevado a 2 menos 4 ⋅ 1 ⋅ 3
delta = 4 menos 12
delta = menos8
Como delta < 0, a equação x elevado a 2 + 2x + 3 = 0 não tem raízes reais.
Assim, a função dada por h (x ) = x elevado a 2 + 2x + 3 não tem zeros reais.
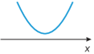
Isso significa que o gráfico da função agá não intercepta o eixo x. Analise o esboço do gráfico.
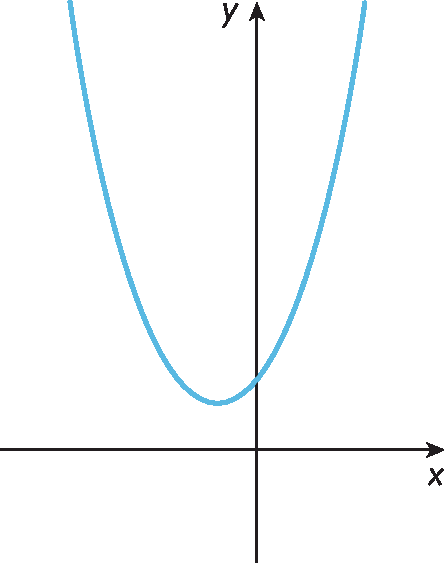

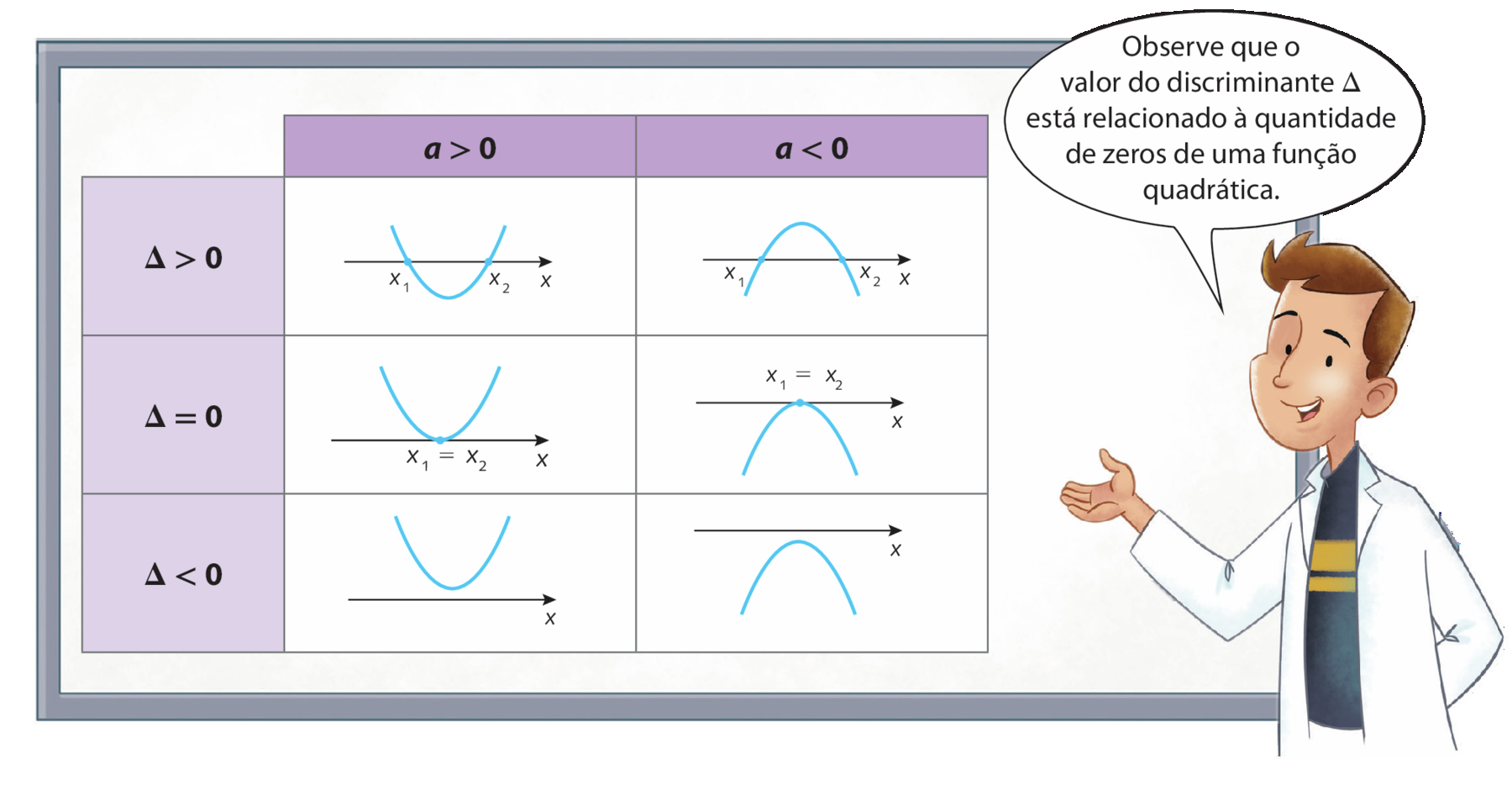
De modo geral, temos que:
• se delta > 0, a parábola intercepta o eixo das abscissas em dois pontos distintos;
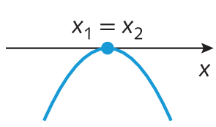
• se delta = 0, a parábola tangencia o eixo das abscissas em um único ponto;
• se delta < 0, a parábola não intercepta o eixo das abscissas.
Atividades
Faça as atividades no caderno.
10. Determine no caderno, se houver, os zeros das funções quadráticas definidas pelas leis a seguir.
a) y = 6x elevado a 2
b) y = x elevado a 2 menos 4
c) y = menosx elevado a 2 + 1
d) y = 5x elevado a 2 + 10x
e) y = menosx elevado a 2 + 2x menos 5
f) y = 3x elevado a 2 menos 5x + 2
g) y = menos9x elevado a 2 menos 6x menos 1
h) y = x elevado a 2 + 5x + 8
i) y = menos3x elevado a 2 + 2x ‒ 1
11. Determine as coordenadas dos pontos em que a parábola correspondente a cada função quadrática a seguir intercepta o eixo x.
a) y = menos3x elevado a 2 + 12x
b) y = x elevado a 2 menos 4
c) y = x elevado a 2 menos 8x + 15
12. Quais das afirmações a seguir são verdadeiras?
a) Uma função quadrática pode ter três zeros reais e distintos.
b) O gráfico de uma função quadrática dada por y = ax elevado a 2 + c não intercepta o eixo das abscissas quando 4ac > 0.
c) Os zeros da função g (x ) = ax elevado a 2 + bx, em que a ≠ 0, são 0 e
menos b sobre a..
d) O gráfico da função quadrática dada por p (x ) = ax elevado a 2 tangencia o eixo das abscissas no ponto (1, 0).
13. A trajetória de um projétil lançado é descrita pelo gráfico da função agá, tal que h (x ) = menosx elevado a 2 + 30x, no qual, em metro, h (x ) representa a medida da altura alcançada e x, a medida da distância percorrida na horizontal. Qual é a medida da distância percorrida pelo projétil ao atingir o solo?
14. Estes esboços são de gráficos de funções quadráticas do tipo f (x ) = ax elevado a 2 + bx + c, com a ≠ 0. Em cada caso, escreva no caderno se a é positivo ou negativo e se Δ é positivo, negativo ou nulo.
a)
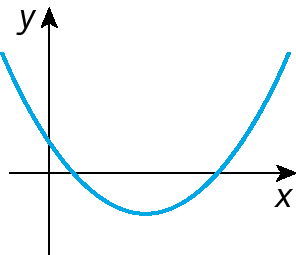
b)
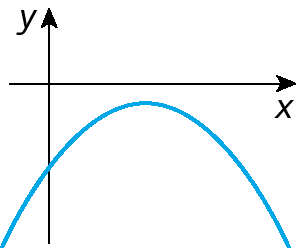
c)

d)
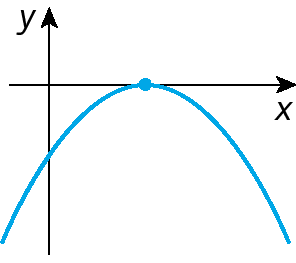
Cálculo das coordenadas do vértice da parábola
Observe nos exemplos a seguir que toda parábola tem um eixo de simetria e um vértice (V).
g(x ) = menosx elevado a 2 + 4x
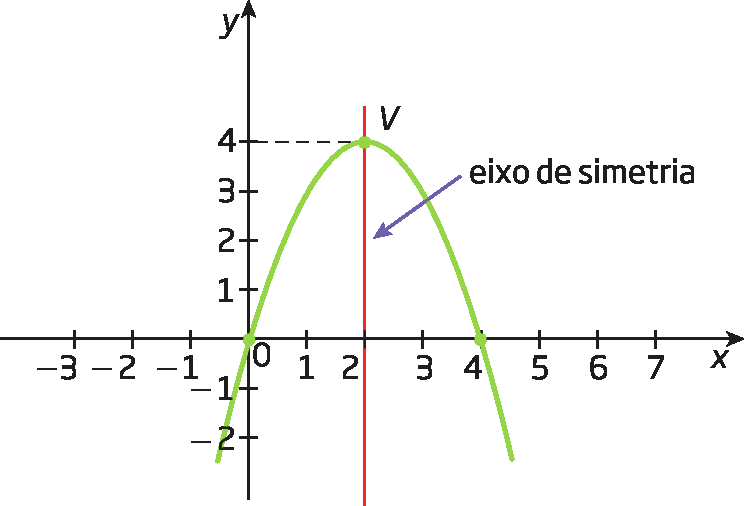
h(x ) = x elevado a 2 menos 2x menos 3
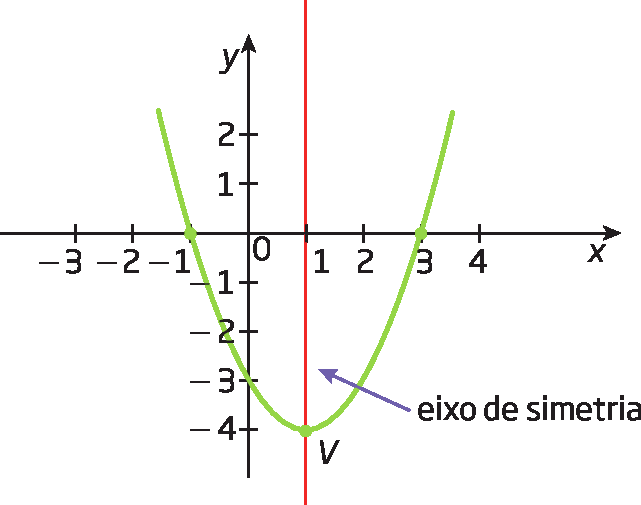
O vértice é a intersecção da parábola com o eixo de simetria.
Observe que nos dois casos a abscissa do vértice (décimoV) corresponde à metade da soma dos zeros da função
Abre parênteses, fração x1 mais x2 sobre 2, fecha parênteses.. E, para obter a ordenada do vértice (yV), basta substituir x por décimoV na lei da função e efetuar os cálculos.
Acompanhe como podemos calcular as coordenadas do vértice das parábolas que representam as funções g e h.
• Coordenadas do vértice da parábola que representa a função g:
Sentença matemática. x subscrito v igual à fração x1, mais x 2 sobre 2, igual à fração 0 mais 4 sobre 2, igual a 2.
yíndice V = g(xíndice V) = g(2) = menos(2)elevado a 2 + 4 ⋅ (2) = 4
Portanto, V(2, 4).
• Coordenadas do vértice da parábola que representa a função h:
Sentença matemática. x subscrito v igual à fração x1, mais x2 sobre 2, igual à fração menos 1 mais 3 sobre 2, igual a 1.
yíndice V = h(xíndice V) = h(1) = (1)elevado a 2 menos 2 ⋅ (1) menos 3 = menos 4
Portanto, V(1, menos 4).

Como toda parábola tem um eixo de simetria e um vértice V, podemos relacionar a abscissa do vértice da parábola que representa a função quadrática dada por f (x ) = ax elevado a 2 + bx + c aos coeficientes a e b.
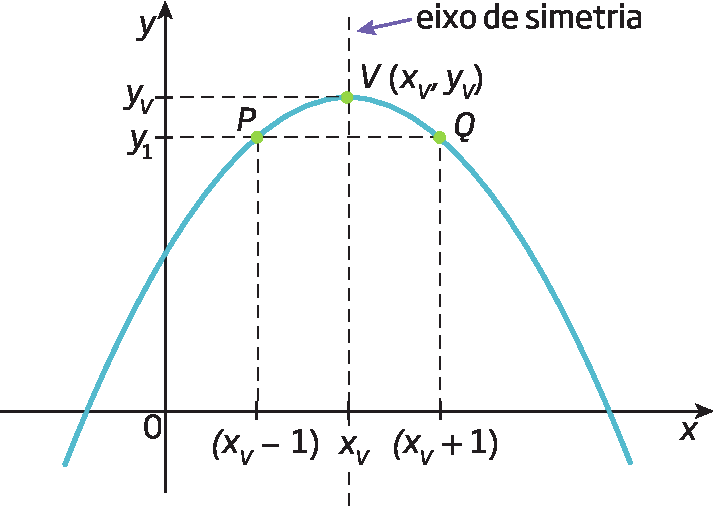

No gráfico da função quadrática f, as abscissas xíndice V menos 1 e xíndice V + 1 estão à mesma medida da distância de xíndice V e que f (xíndice V menos 1) = f (xíndice V + 1) = yindice 1. Dessa maneira, temos:
a(xíndice V menos 1)elevado a 2 + b(xíndice V menos1) + c = a(xíndice V + 1)elevado a 2 + b(xíndice V + 1) + c
a(xᵥ² menos 2xíndice V ⋅ 1 + 1) + b(xíndice V menos 1) + c = a(xᵥ² + 2xíndice V ⋅ 1 + 1) + b(xíndice V + 1) + c

menos2axíndice V ‒ b = 2axíndice V + b
menos4axíndice V = 2b

Lembre-se de que, conhecendo a abscissa décimoíndice V , a ordenada do vértice será yíndice V = f (xíndice V).
▸ Substitua décimoíndice V na lei da função quadrática e conclua que
y com índice v igual a menos delta sobre 4, em que delta = belevado a 2 menos 4ac.
Agora, acompanhe dois exemplos.
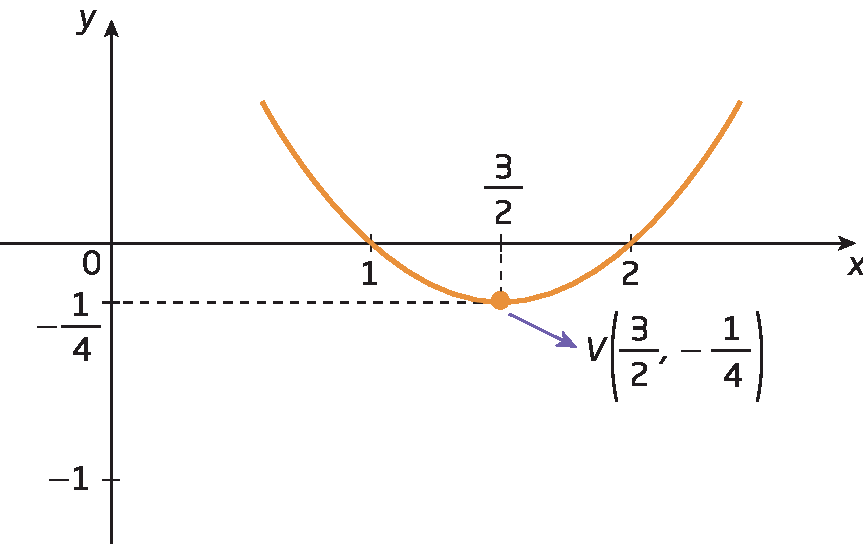
a) Vamos determinar as coordenadas do vértice da parábola correspondente ao gráfico da função quadrática p dada por p(x) = x elevado a 2 menos 3x + 2:
Sentença matemática. x subscrito v igual a menos b sobre 2a, igual à fração menos 3 sobre 2 vezes 1, igual a 3 sobre 2.
yV = p(xV) =
Sentença matemática. p, abre parênteses, 3 sobre 2, fecha parênteses.Sentença matemática. p, abre parênteses, 3 sobre 2, fecha parênteses, igual a, abre parênteses, 3 sobre 2, fecha parênteses, elevado ao quadrado, menos 3 vezes, abre parênteses, 3 sobre 2, fecha parênteses, mais 2.
Sentença matemática. p, abre parênteses, 3 sobre 2, fecha parênteses, igual a 9 sobre 4, menos 9 sobre 2, mais 2, igual a menos 1 sobre 4.
Portanto:
Sentença matemática. Par ordenado, V de abcissa 3 sobre 2 e ordenada menos 1 quarto..
b) Vamos determinar os valores de m e n para que o gráfico da função q dada por
Sentença matemática. q, abre parênteses x, fecha parênteses, igual a x elevado ao quadrado, menos mx, mais n sobre 2.tenha vértice V (1, 1):
A abscissa do vértice é dada por:
Sentença matemática. x subscrito v igual a menos b sobre 2a.. Então, para que xíndice V = 1, devemos ter:
Sentença matemática. sinal de menos para a fração, abre parênteses, menos m, fecha parênteses, sobre 2 vezes 1, igual a 1.
, ou seja: m = 2
Substituindo o valor de m na lei da função, obtemos:
Sentença matemática. q, abre parênteses x, fecha parênteses, igual a x elevado ao quadrado, menos 2x, mais n sobre 2.
Como xíndice V = 1 e yíndice V = 1, temos: q (1) = 1. Assim, podemos determinar o valor de n:
Sentença matemática. q, abre parênteses 1, fecha parênteses, igual a 1 elevado ao quadrado, menos 2 vezes 1, mais n sobre 2
Sentença matemática. 1 igual a 1 menos 2, mais n sobre 2, implica 2 igual a n sobre 2, implica n igual a 4.
Assim: m = 2 e n = 4.
Atividades
Faça as atividades no caderno.
15. Determine o valor de k para que o vértice da parábola, que é gráfico da função f tal que f (x ) = x elevado a 2 menos 8x + k, pertença ao eixo x.
16. Determine as coordenadas do vértice da parábola que representa cada função quadrática a seguir.
a) f (x ) = x elevado a 2 menos 4x + 3
b) f (x ) = menosx elevado a 2 + 6x menos 9
c) f (x ) = menosx elevado a 2 + 2x
d) f (x ) = x elevado a 2 + 2x + 3
e) f (x ) = x elevado a 2 menos x menos 2
f) f (x ) = 3x elevado a 2 menos 4x
17. A lei da função quadrática f correspondente ao gráfico a seguir é f (x ) = ax elevado a 2 + bx + 2. Determine a e b.

Construção do gráfico de uma função quadrática com base nas coordenadas do vértice
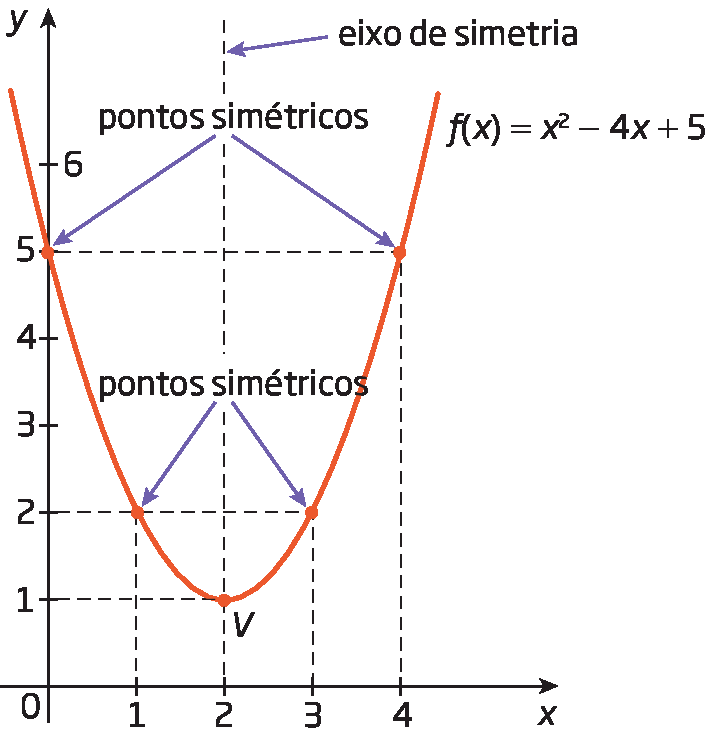
Analise como podemos construir o gráfico da função quadrática f dada por f (x ) = x elevado a 2 menos 4x + 5 com base nas coordenadas do vértice.
1º) Determinamos as coordenadas do vértice.
Sentença matemática. x subscrito v igual a menos b sobre 2a, igual a sinal de menos fração menos 4 sobre 2 vezes 1, igual a 2.
yíndice V = f(xíndice V) = (2)elevado a 2 menos 4 ⋅ (2) + 5 = 1
Assim, o vértice é o ponto V (2, 1).
2º) Determinamos valores para x que sejam simétricos em relação à abscissa do vértice e calculamos os valores de y correspondentes para obter alguns pares ordenados.
Nesse caso, vamos escolher valores para x que sejam simétricos em relação a xíndice V = 2.
|
x |
y |
(x, y) |
|
|---|---|---|---|
|
0 |
5 |
(0, 5) |
|
|
1 |
2 |
(1, 2) |
|
|
2 |
1 |
(2, 1) |
→ coordenadas do vértice |
|
3 |
2 |
(3, 2) |
|
|
4 |
5 |
(4, 5) |
3º) Marcamos no plano cartesiano os pontos correspondentes aos pares ordenados e traçamos a parábola que passa por esses pontos.
Atividades
Faça as atividades no caderno.
18. Construa no caderno o gráfico de cada função quadrática.
a) f (x ) = menosx elevado a 2
b) g (x ) = x elevado a 2 menos 9
c) h (x) = menosx elevado a 2 + 4
d) s (x ) = x elevado a 2 menos 4x
e) t (x ) = x elevado a 2 menos 6x + 10
f) u (x ) = menosx elevado a 2 + 4x ‒ 5
19. Construa o gráfico das funções quadráticas f e g, dadas pelas leis f (x ) = x elevado a 2 e g (x ) = ‒x elevado a 2 em um mesmo plano cartesiano. O que você pode perceber?
20. Construa o gráfico de cada função: f (x ) = x elevado a 2, b (x ) = x elevado a 2 menos 2, t (x ) = x elevado a 2 menos 1, h (x ) = x elevado a 2 + 1 e m (x ) = x elevado a 2 + 2. Depois, compare-os e analise como o valor de cê influencia o gráfico da função definida pela lei y = ax elevado a 2+ c.
Ponto de mínimo ou ponto de máximo de uma função quadrática
Acompanhe a situação a seguir.
Um goleiro chuta uma bola cuja trajetória pode ser representada pelo gráfico da função agá, dada pela lei h (x ) =
menos x ao quadrado sobre 20+ x, em que x indica a medida da distância horizontal percorrida, em metro, e h(x), a medida da altura que a bola alcançou, em metro. Qual é a medida da altura máxima atingida pela bola?
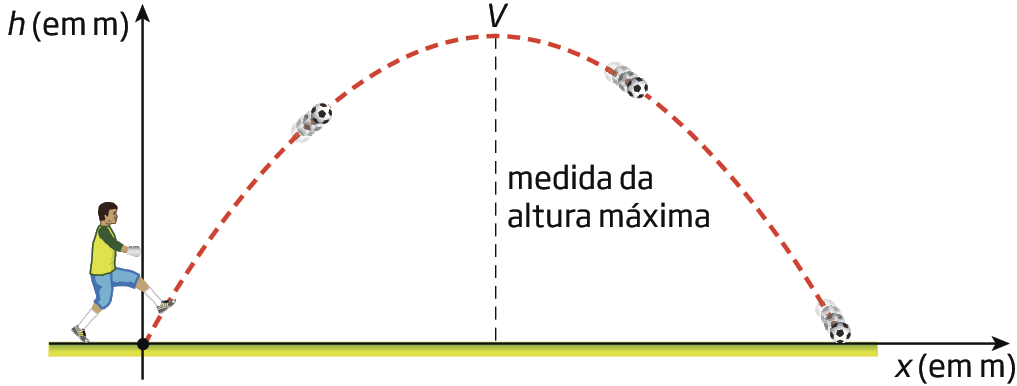
Perceba que o gráfico que representa a trajetória da bola é parte de uma parábola com a concavidade voltada para baixo e que a medida da altura máxima atingida pela bola corresponde à ordenada do vértice.
Vamos calcular xíndice V e yíndice V :
Sentença matemática. x subscrito v igual a menos b sobre 2a, igual a sinal de menos antes da fração 1 sobre 2 vezes o menos um sobre vinte.
, ou seja, xíndice V = 10;
Sentença matemática. y subscrito v, igual a, h, abre parênteses, x subscrito v, fecha parênteses, igual a h, abre parênteses, 10, fecha parênteses, igual a menos 10 elevado ao quadrado sobre 20, mais 10.
, ou seja, yíndice V = 5.
Portanto, a medida da altura máxima atingida pela bola é 5 metros.
Toda função quadrática tem um valor máximo ou um valor mínimo que corresponde à ordenada do vértice da parábola que a representa.
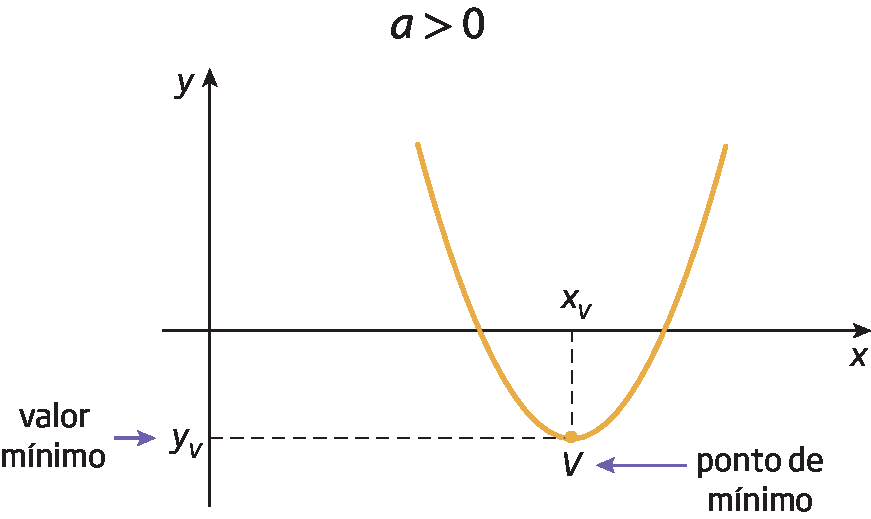
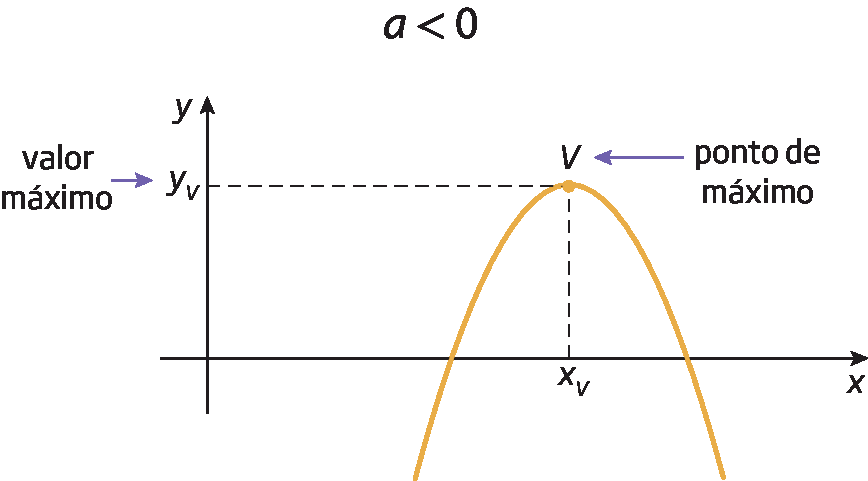
Para uma função quadrática f (x ) = ax elevado a 2 + bx + c, temos:
• se a > 0, a função tem valor mínimo, e o vértice é chamado ponto de mínimo;
• se a < 0, a função tem valor máximo, e o vértice é chamado ponto de máximo.
Atividades
Faça as atividades no caderno.
21. Em cada item, calcule o valor de x para que a função tenha um valor máximo.
a) f (x ) = menos2x elevado a 2 + 5x menos 2
b) f (x ) = menosx elevado a 2 + 11x menos 8
22. Verifique se as funções quadráticas admitem valor máximo ou valor mínimo e calcule esse valor.
a) f (x ) = x elevado a 2 menos 64
b) f (x ) = menos4x elevado a 2 + 4x menos 1
c) f (x ) = menosx elevado a 2 + 3x
d) f (x ) = x elevado a 2 menos x menos 6
e) f (x ) = menosx elevado a 2 + 5x menos 7
f) f (x ) = 2x elevado a 2 + 5x
23. Determine o valor de k para que a função definida porf (x ) = menos4x elevado a 2 + (k + 1)x + 2 admita valor máximo para x = 2.
24. Determine o valor de p na função dada por f (x ) = 3x elevado a 2 menos 2x + p, para que o valor mínimo seja
Sentença matemática. Fração 5 sobre 3..
25. Após o lançamento de uma bala por um canhão, verifica-se que a medida da altura (y), alcançada pela bala, em metro, é função da medida da distância horizontal percorrida (x), em metro, de acôrdo com a lei y = 100x – 2xelevado a 2, sendo 0 ⩽ x ⩽ 50.

Determine, em metro:
a) o alcance do lançamento;
b) a medida da altura máxima atingida pela bala.
26. A função g dada pela lei g(t) = televado a 2 menos 4t + 3 relaciona a medida da temperatura g, em grau Celsius, de uma câmara frigorífica e a medida do tempo t, em hora, em que permaneceu ligada.
a) Em quais momentos a medida da temperatura é igual a 0 grau Célsius?
b) Qual é a medida de temperatura mínima atingida?
27. Em certo país, houve uma epidemia provocada por um vírus. As estatísticas apontaram que, inicialmente, foram comprovados 280 mil casos de pessoas infectadas pelo vírus. Essa epidemia pode ser representada pela lei N(t) = 280 + 120t menos 10televado a 2, em que N(t) é o número de pessoas infectadas (em milhares) dado em função do número t de semanas decorridas. Imediatamente após a comprovação dos primeiros casos, teve início a vacinação em massa da população, a fim de controlar essa epidemia. O gráfico esboçado a seguir representa a situação desde o aparecimento do vírus até o seu combate.
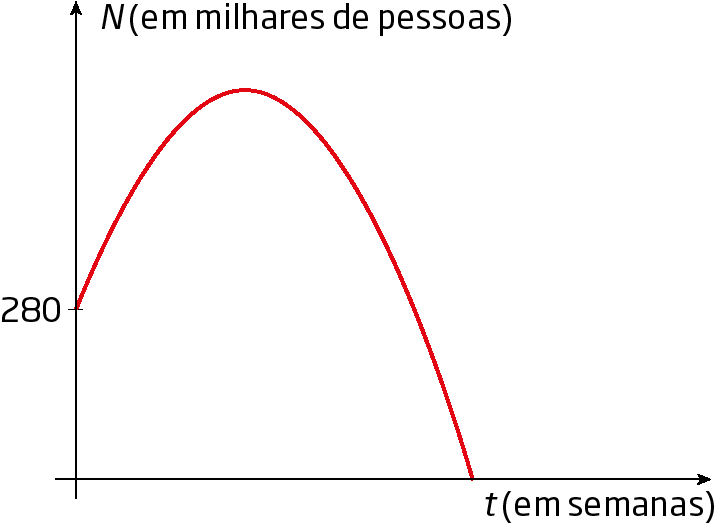
a) Qual foi a maior quantidade de pessoas infectadas nesse período?
b) Depois de quantas semanas essa epidemia foi controlada, isto é, o número de pessoas infectadas foi reduzido para zero?
28.


Elabore um problema em que haja um lançamento oblíquo de um objeto. Escolha o contexto que julgar mais interessante. A resolução do problema deve envolver uma função quadrática que determine a trajetória do objeto e a busca pela medida da altura máxima atingida na trajetória. Troque seu problema com um colega e resolva o que ele propôs. Discutam as estratégias e os procedimentos da resolução do problema. Se houver divergências, tentem esclarecer as dúvidas um do outro. Caso as dúvidas persistam, conversem com o professor.
29.


Em dupla, elaborem um problema no qual uma indústria produza determinado produto. Para isso, sigam as instruções a seguir. Depois, troquem o problema com outra dupla e resolvam.
• Considere x a quantidade do produto em milhares. O preço de custo é dado por uma função afim cê da fórma c(x) = ax + b, com a e bê reais positivos. E o preço de venda é dado por v(x) = kxelevado a 2 + mx + n, com cá, m e n reais e k ≠ 0.
• Uma das tarefas será determinar e esboçar o gráfico da função éle (lucro), em que L(x) = v (x) menos c (x). É importante que a parábola que representa a função éle tenha concavidade para baixo e uma das raízes seja zero.
• No gráfico, identifiquem o ponto que determina o lucro máximo em função da quantidade de produtos vendidos.
Revisão dos conteúdos deste capítulo
Função quadrática
Função quadrática é toda função f cuja lei pode ser escrita na fórma f(x) = axelevado a 2 + bx + c, em que a, b e c são números reais, com a ≠ 0
, e x pode ser qualquer número real.
1. Sendo a função quadrática f definida por f(x) = xelevado a 2 menos 3x + 2, determine:
a) f(menos1)
b) f(3)
c) f(0) + f(menos2)
d)
Sentença matemática. Fração f, abre parênteses 1, fecha parênteses, mais f abre parênteses 2, fecha parênteses, sobre f, abre parênteses 0, fecha parênteses.2. Dada a função f(x) = x elevado a 2 menos 4x + 3, determine o número real x tal que f(x) = 3.
3. Uma empresa de embalagens utiliza modelos retangulares de papelão com dimensões que medem x + 4 e x menos 3 para construir caixas. Determine a lei da função que representa a medida da área A(x) desses modelos de papelão em função de x.
4. Considere a figura a seguir.
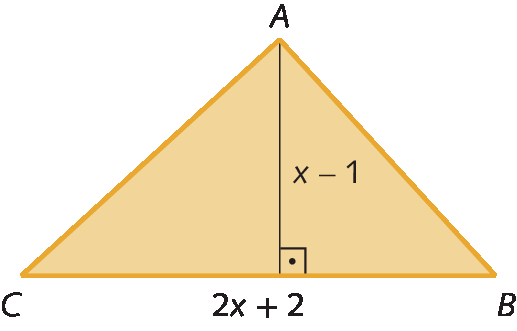
a) Determine a medida da área y do triângulo em função de x.
b) Calcule a medida da área em métroselevado a 2 para x = 7 métros.
Gráfico da função quadrática
O gráfico de toda função quadrática é uma curva chamada parábola.
Concavidade da parábola
A parábola que representa o gráfico de uma função quadrática pode ter concavidade (abertura) voltada para cima ou para baixo.
Dada uma função quadrática de lei f(x) = ax elevado a 2 + bx + c, quando:
• a > 0, a parábola tem concavidade voltada para cima;
• a < 0, a parábola tem concavidade voltada para baixo.
Zeros de uma função quadrática
Para uma função f de lei f(x) = axelevado a 2 + bx + c, com a ≠ 0, denominamos zeros da função quadrática os valores de x tais que f(x) = 0.
Seja delta = belevado a 2 menos 4ac, quando:
• delta > 0, a função tem dois zeros reais diferentes e a parábola intercepta o eixo das abscissas em dois pontos distintos;
• delta = 0, a função tem dois zeros reais iguais e a parábola tangencia o eixo das abscissas em um único ponto;
• delta < 0, a função não tem zeros reais e a parábola não intercepta o eixo das abscissas.
|
a > 0 |
a < 0 |
|
|---|---|---|
|
Δ > 0 |
|
|
|
Δ = 0 |
|
|
|
Δ < 0 |
|
|
Cálculo das coordenadas do vértice da parábola
V = (xíndice V, yíndice V)

5. Determine os valores de p para que o gráfico da função dada por
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a, abre parênteses, 2p mais 8, fecha parênteses, vezes x elevado ao quadrado, menos 5x, menos 13.tenha a concavidade voltada para cima.
6. Determine os valores de q para que o gráfico da função dada por
Sentença matemática. f, abre parênteses y, fecha parênteses, igual a, abre parênteses 5 menos 3 vezes q, fecha parênteses vezes y elevado ao quadrado, menos y, mais 8.tenha a concavidade voltada para baixo.
7. Para as funções quadráticas a seguir, determine os zeros da função.
a) f(x) = xelevado a 2 menos 8x + 7
b) f(x) = xelevado a 2 menos 36
c) f(x) = xelevado a 2 menos 3x
d) f(x) = menosxelevado a 2 menos 8x menos 16
8. Verifique, para cada função quadrática, se a parábola intercepta o eixo x em dois pontos distintos, se tangencia o eixo x ou se não intercepta o eixo x.
a)
Sentença matemática. y igual a x elevado ao quadrado, menos 6x, mais 5.
b)
Sentença matemática. y igual a menos x elevado ao quadrado, mais 6x, menos 16.
c)
Sentença matemática. y igual a menos x elevado ao quadrado, menos 2x, menos 1.
d)
Sentença matemática. y igual a x elevado ao quadrado, mais 6x, mais 8.
9. Determine as coordenadas do vértice da parábola que representa cada função quadrática.
a)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a x elevado ao quadrado, mais 4x, mais 1.b)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a, x elevado ao quadrado, menos 25.c)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a x elevado ao quadrado, menos 3x, mais 2.d)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a menos x elevado ao quadrado, menos 4x, menos 4.10. Esta parábola representa a função
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a, a vezes x elevado ao quadrado, mais bx, menos 3.. Determine a lei dessa função após calcular os coeficientes a e b.
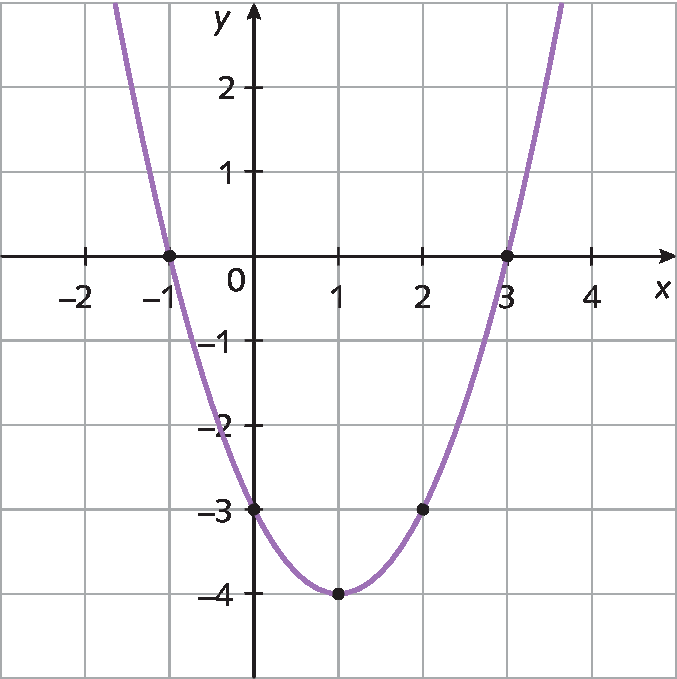
11. Sabendo que o vértice da parábola é V
Sentença matemática. Par ordenado V de abcissa 7 sobre 2 e ordenada menos 1 sobre 4., determine os coeficientes a e b da função quadrática
Sentença matemática. y igual a, a vezes x elevado ao quadrado, mais bx, mais 12.12. Para cada função quadrática a seguir, determine:
um. os zeros da função;
dois. o vértice;
três. o ponto em que a parábola corta o eixo das ordenadas;
quatro. o gráfico.
a)
Sentença matemática. y igual a x elevado ao quadrado, menos 8x, mais 15.b)
Sentença matemática. y igual ao oposto de x elevado ao quadrado, mais 10x, menos 24.c)
Sentença matemática. y igual a x elevado ao quadrado, menos 2x.d)
Sentença matemática. y igual a menos x elevado ao quadrado, mais 4.Ponto de mínimo ou ponto de máximo de uma função quadrática
Toda função quadrática tem um valor máximo ou um valor mínimo que corresponde à ordenada do vértice da parábola que a representa.
Para uma função quadrática f(x) = axelevado a 2 + bx + c, temos:
• se a > 0, a função tem valor mínimo, e o vértice é chamado ponto de mínimo;
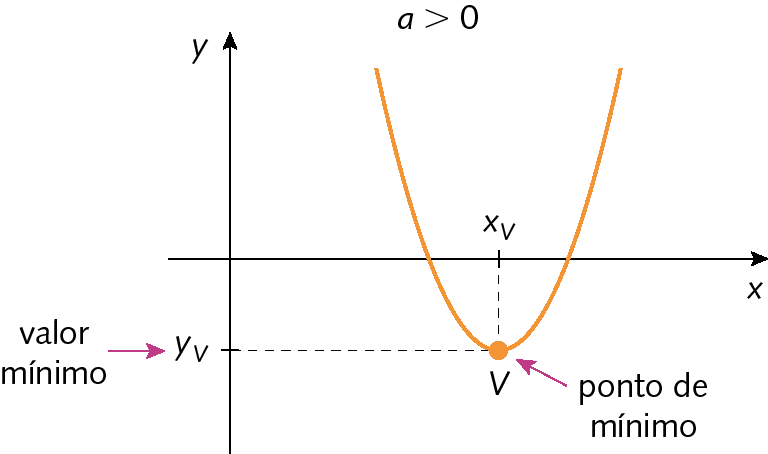
• se a < 0, a função tem valor máximo, e o vértice é chamado ponto de máximo.
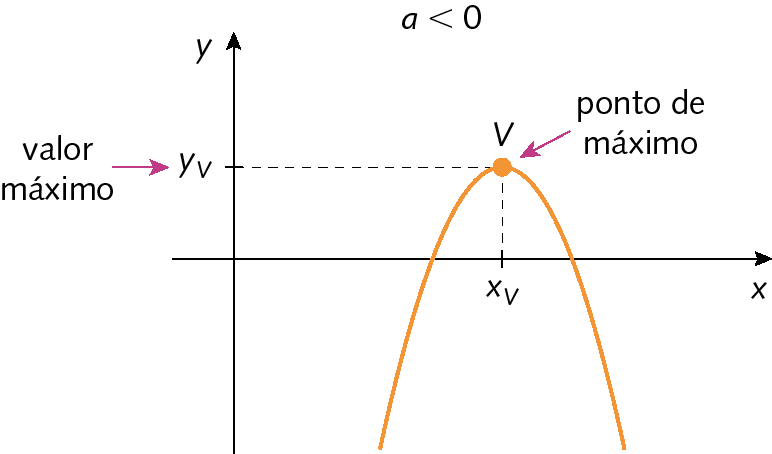
13. Verifique se as funções quadráticas admitem valor máximo ou valor mínimo e calcule esse valor.
a)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual ao oposto de x elevado ao quadrado, menos 6x, mais 7.b)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a menos x elevado ao quadrado, mais 121.c)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a x elevado ao quadrado, menos 20x.d)
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a x elevado ao quadrado, menos 12x, mais 36.14. Qual deve ser o valor de k para que a função definida por
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a menos 3 vezes x elevado ao quadrado, mais abre parênteses 2k mais 7, fecha parênteses vezes x, mais 2.admita valor máximo para x = 4?
15. Em uma companhia de transporte de ônibus, a receita de determinada viagem é dada por
Sentença matemática. f, abre parênteses x, fecha parênteses, igual a menos x elevado ao quadrado, mais 104x, mais 120., em que f(x) é a receita, em reais, e x é o número de passageiros para essa viagem. Determine:
a) o número de passageiros para atingir a receita máxima;
b) a receita máxima.
É hora de extrapolar
Faça as atividades no caderno.

Como as tecnologias influenciam a vida das pessoas?
A palavra “tecnologia” tem a sua origem no grego antigo téchne, que significa técnica, arte, ofício, e lôgos, que significa estudo de algo. Atualmente, a presença das tecnologias da informação e da comunicação na vida das pessoas é inegável, mas que outras tecnologias estão presentes em nosso cotidiano? E que tecnologias foram importantes para a história da humanidade?
Objetivos: Refletir sobre a influência das tecnologias; analisar dados sobre tecnologia nas ciências; pesquisar o funcionamento de inventos tecnológicos e produzir modelos para explicar o funcionamento de tais tecnologias.

Etapa 1: Reflexão sobre a influência das tecnologias no cotidiano e na história.
1. Reúnam-se em grupos e respondam às questões em seus cadernos.
a) Analisem a sentença “as tecnologias influenciam a humanidade”. Vocês concordam com ela? Por quê?
b) Quais tecnologias estão presentes atualmente na vida das pessoas?
c) Essas tecnologias são importantes? Por quê?
2. Segundo o dicionário eletrônico Uáis, tecnologia pode ser definida como:
1 teoria geral e/ou estudo sistemático sobre técnicas, processos, métodos, meios e instrumentos de um ou mais ofícios ou domínios da atividade humana (página exêmplo, indústria, ciência etcétera)
2 técnica ou conjunto de técnicas de um domínio particular
3 qualquer técnica moderna e complexa
a) Podemos dizer que a manufatura de ferramentas de pedra, a descoberta do fogo, a invenção da roda, as técnicas utilizadas na agricultura, os computadores e o mapeamento do dê êne á humano são exemplos de tecnologia?


b) Discutam e façam uma lista com 10 inventos tecnológicos que vocês consideram importantes para a história da humanidade.
c) Pesquisem na internet algumas informações sobre os inventos listados no item anterior e elaborem uma linha do tempo.
3. Apresentem a linha do tempo para a turma. Depois das apresentações, montem uma linha do tempo coletiva com todos os inventos tecnológicos escolhidos pelos grupos.
4. De que fórma a Matemática está presente nas tecnologias que utilizamos no dia a dia?

Etapa 2: Análise de dados sobre tecnologias nas ciências.
5. Leiam este texto e respondam à questão.
A ciência e a tecnologia alimentam-se uma à outra, impulsionando ambas para a frente. O conhecimento científico permite-nos desenvolver novas tecnologias, que muitas vezes nos permitem fazer novas observações sobre o mundo, que, por sua vez, nos permitem construir ainda mais conhecimento científico, que, em seguida, vai inspirar outra tecnologiareticências e assim por diante.
A ciência e a tecnologia em desenvolvimento acelerado. Saber Ciência: como a ciência realmente funciona, sem data Disponível em: https://oeds.link/O8rPrb. Acesso em: 22 julho 2022.
Vocês acham que o desenvolvimento de foguetes e satélites pode ser considerado exemplo de tecnologia que impulsiona a ciência? Por quê?
6. Vocês sabem como os foguetes funcionam? Existem experiências que mostram de fórma análoga, por meio de reações químicas, a propulsão dos foguetes construídos com garrafas péti, por exemplo.
Ao ser lançados, os foguetes do experimento chegam a determinada medida da altura e, como não continuam recebendo propulsão para se movimentar, começam a cair em algum momento. Esse movimento pode ser descrito por uma função quadrática.

Considerem o lançamento de um foguete cuja medida da altura h(x), em metros, pode ser descrita pela função agá, tal que h(x) = menosxelevado a 2 + 3x, em que x representa a medida do tempo a partir do lançamento, em segundos.
a) Em que momentos a medida da altura alcançada por esse foguete é de 2 metros?
b) Construa o gráfico da função agá, que representa o movimento desse foguete.
c) Em que momento esse foguete atinge a medida da altura máxima? Qual é essa medida de altura máxima?

Etapa 3: Pesquisa sobre inventos tecnológicos importantes e planejamento e produção de modelo explicativo.
7. Escolham um dos inventos tecnológicos marcados na linha do tempo elaborada na atividade 2. Façam uma pesquisa complementando as informações sobre o invento: como funciona, quando e quem o inventou e quais são as utilidades desse invento.
8. Vocês deverão construir um modelo do invento escolhido que ajude a explicar como ele funciona. Discutam no grupo quais materiais serão necessários para construí-lo. Deem preferência para as sucatas ou materiais reutilizáveis. Elaborem um planejamento, listando os materiais que serão utilizados e as divisões das tarefas entre os membros do grupo.
9. Construam o modelo do invento escolhido e elaborem um texto com as informações obtidas na pesquisa.

Etapa 4: Apresentação, análise e divulgação do modelo explicativo.
10. Estabeleçam uma parceria com outro grupo, para que mostrem o texto informativo e o modelo do invento tecnológico escolhido e façam uma apresentação explicando-o um para o outro. Façam uma leitura cuidadosa do texto, observem o modelo construído e escutem a apresentação, analisando a clareza das informações no texto e na apresentação e a qualidade do modelo.
11. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
12. Depois dos ajustes necessários, exibam o modelo para a turma e façam uma apresentação explicando como o invento tecnológico funciona, quando e por quem foi inventado e quais são os seus usos.
13. Por fim, organizem uma exposição dos modelos e dos textos elaborados para a comunidade escolar.

Etapa 5: Síntese do trabalho realizado.
14. Algumas questões que devem ser discutidas:
a) Quais tecnologias vocês utilizaram para realizar as atividades das etapas anteriores?
b) Quais tecnologias vocês acreditam que existirão daqui a dez anos? E daqui a cem anos?
15. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.