Unidade 3
Capítulo 7 Relações métricas no triângulo retângulo
Capítulo 8 Circunferência, arcos e ângulos
Capítulo 9 Polígonos regulares


O que você conhece sobre trânsito seguro? Você sabe o que significa a placa que aparece na imagem? Essa placa se parece com qual polígono? No fim desta Unidade, você responderá a essas e outras questões.
Capítulo 7 Relações métricas no triângulo retângulo
Trocando ideias

O metalúrgico é o profissional responsável pelos projetos de tratamento e de produção de metais e ligas metálicasglossário . Em seu dia a dia, ele precisa ler e interpretar projetos de peças tanto para fabricá-las como para conferir suas medidas.
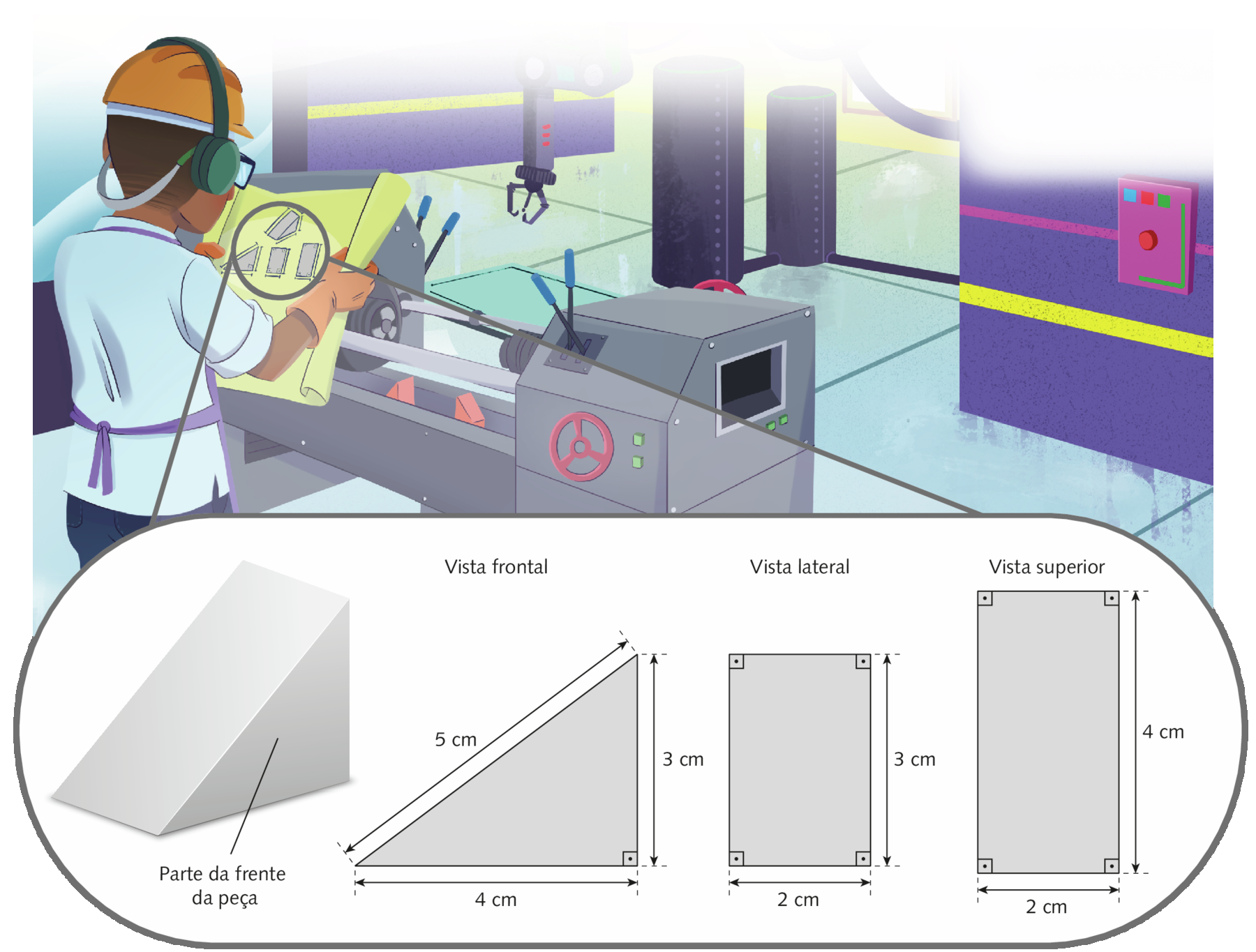
▸


Em sua opinião, por que é importante que profissionais como os metalúrgicos utilizem equipamentos de proteção individual? Converse com os colegas.
▸

Como podemos classificar o triângulo correspondente à vista frontal da peça? Por quê?
▸


Como as medidas de comprimento 3 centímetros, 4 centímetros e 5 centímetros dos lados da parte frontal da peça podem ser relacionadas? Converse com os colegas.
Neste capítulo, vamos estudar as relações métricas e trigonométricas de triângulos retângulos.

1 Projeções ortogonais
Considere um ponto P e uma reta r. Se traçarmos por P uma reta s perpendicular a r, obteremos na intersecção de s e érre um ponto pê linha, denominado projeção ortogonal do ponto P sobre a reta r.
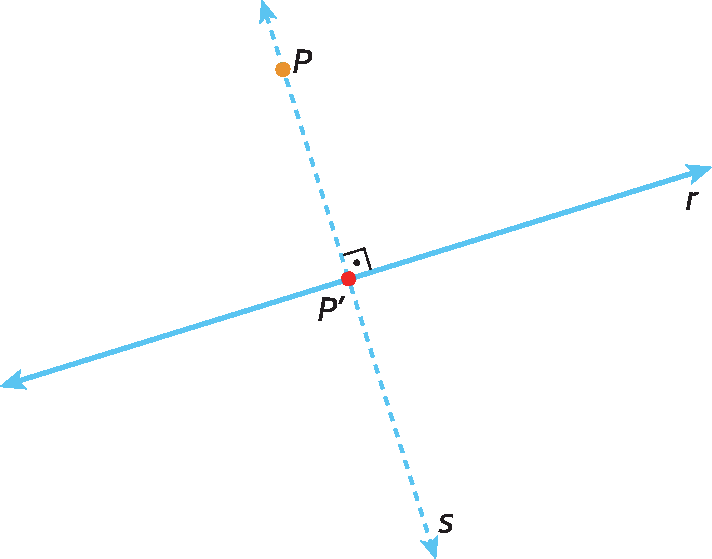
Quando o ponto P pertence à reta r, ele coincide com sua projeção ortogonal sobre ela.
Agora, considere um segmento de reta
A Be a reta r. Denominamos projeção ortogonal do segmento de reta
A Bsobre a reta r o conjunto das projeções ortogonais de todos os pontos do segmento de reta
A Bsobre r.

Logo,
segmento de reta A linha B linhaé a projeção ortogonal do segmento de reta
A Bsobre a reta r.
Atividades
Faça as atividades no caderno.
1. Copie as figuras no caderno e determine:
a) a projeção ortogonal do segmento de reta
E Fsobre a reta r ;

b) a projeção ortogonal do segmento de reta
C Dsobre a reta r .
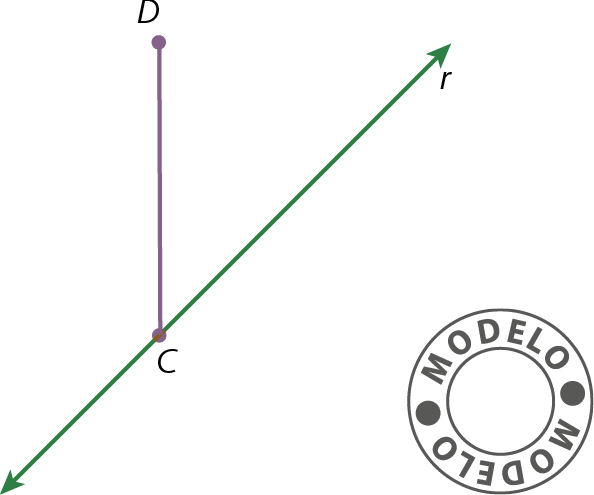
Versão adaptada acessível
1. Faça o que se pede em cada caso.
a) Represente uma reta r e um segmento de reta fora dela posicionado perpendicularmente a ela. Determine a projeção ortogonal desse segmento de reta sobre a reta r.
b) Represente uma reta r e um segmento de reta de modo que C pertença à essa reta e D esteja fora dela. Esse segmento não deve ser perpendicular à reta r. Determine a projeção ortogonal desse segmento de reta sobre a reta r.
2. Observe as figuras e determine:
a) a projeção ortogonal do segmento de reta
B Csobre
Reta AB.;

b) a projeção ortogonal do segmento de reta
A Bsobre
Reta BC.e a projeção ortogonal do segmento de reta
A Csobre
Reta BC.;
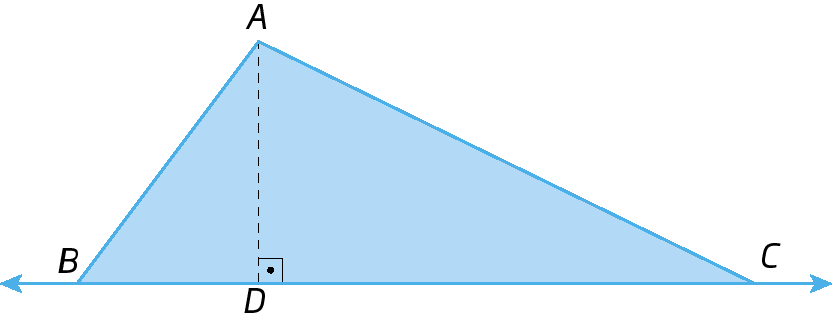
c) a projeção ortogonal do segmento de reta
A Csobre
Reta CB.;
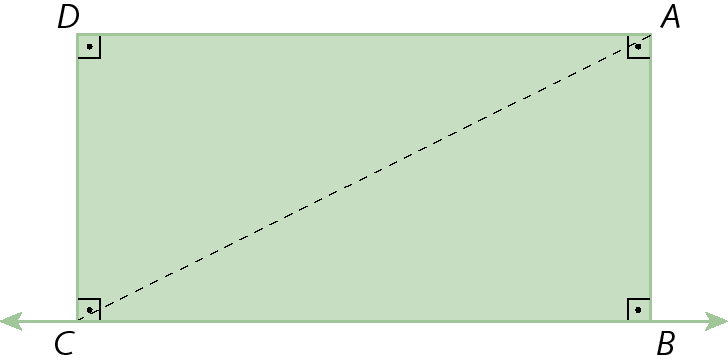
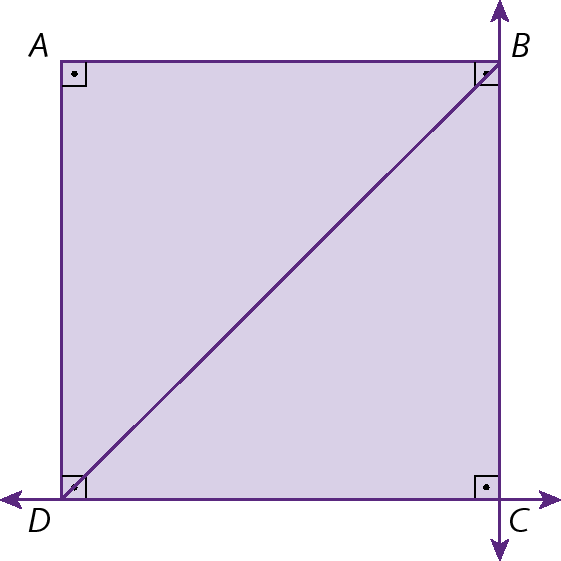
d) a projeção ortogonal do segmento de reta
A Dsobre
Reta DC.e a projeção ortogonal do segmento de reta
B Dsobre
Reta BC..

2 Triângulo retângulo
Em um triângulo retângulo, chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes a esse ângulo de catetos.
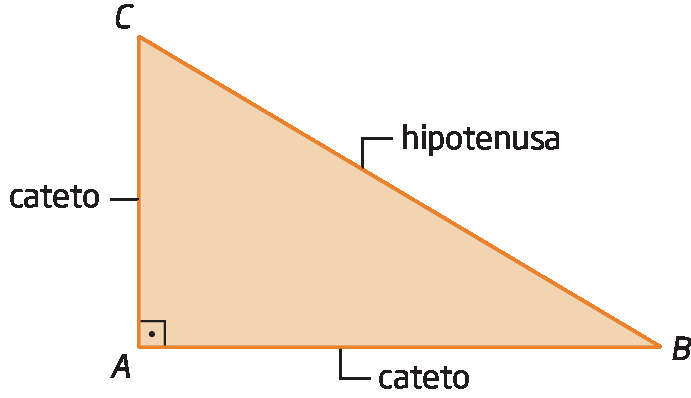
No triângulo retângulo á bê cê,
Segmento de reta CB.é a hipotenusa e
Segmento de reta AC.e
Segmento de reta ABsão os catetos.
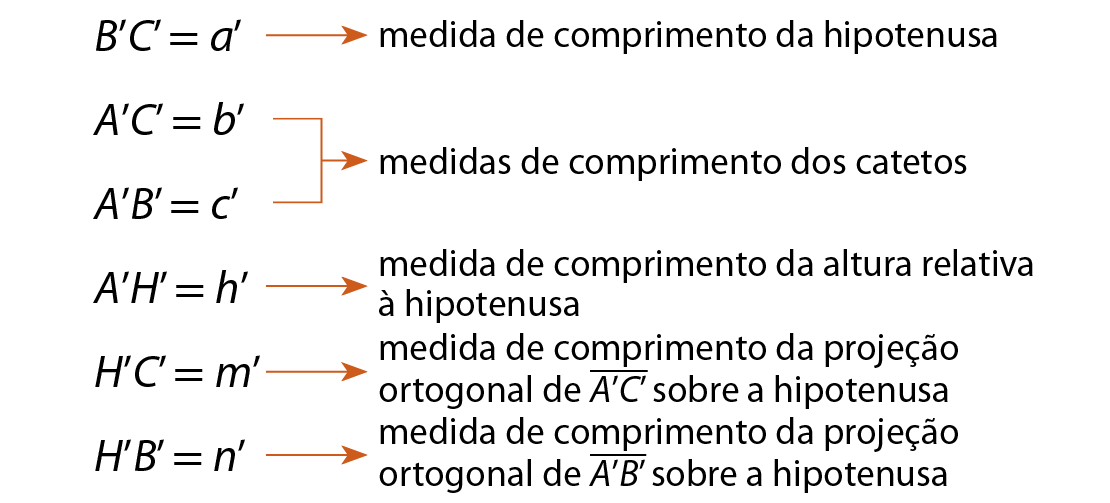
Elementos de um triângulo retângulo
Considere os triângulos retângulos á bê cê e a linha bê linha cê linha.
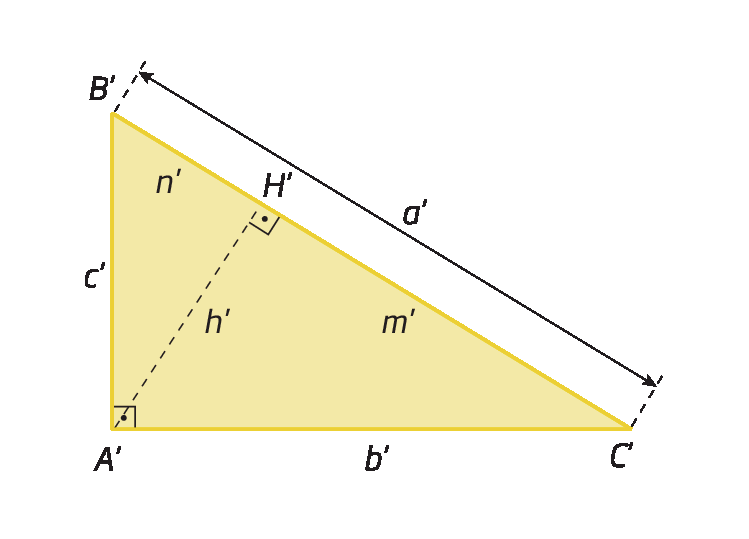
Representamos por letras minúsculas as medidas de comprimento dos segmentos de reta dos triângulos.
Assim:
• para o triânguloá bê cê, temos:
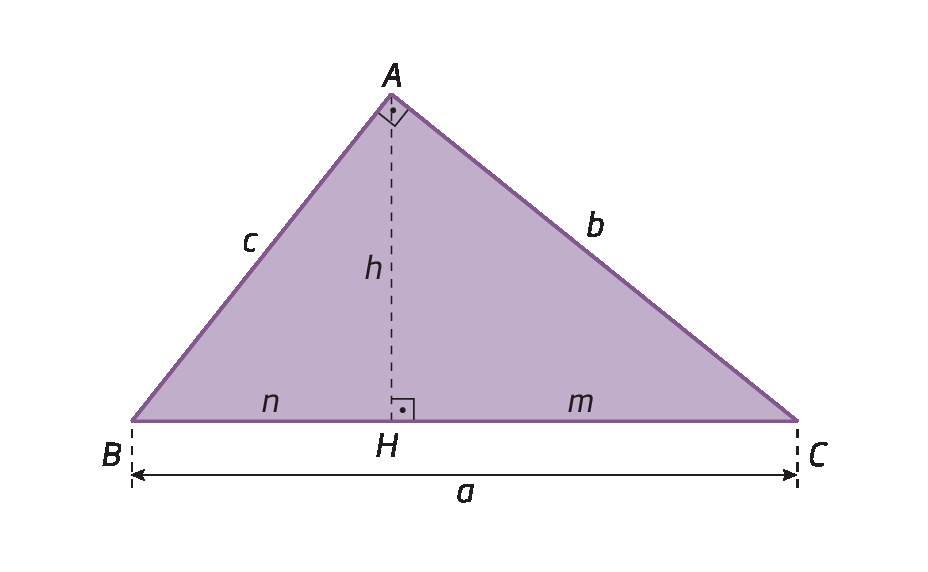
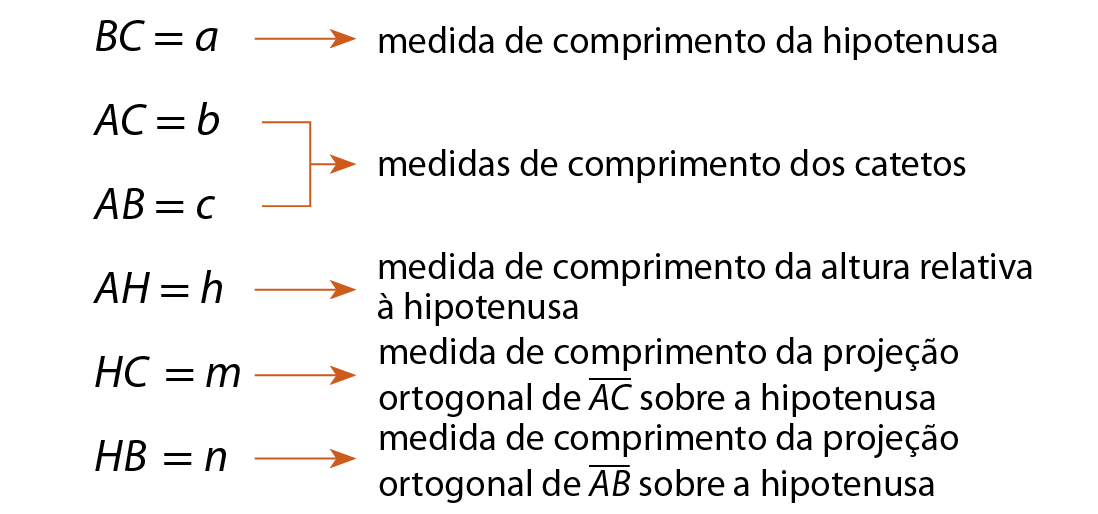
• para o triânguloa linha bê linha cê linha, temos:
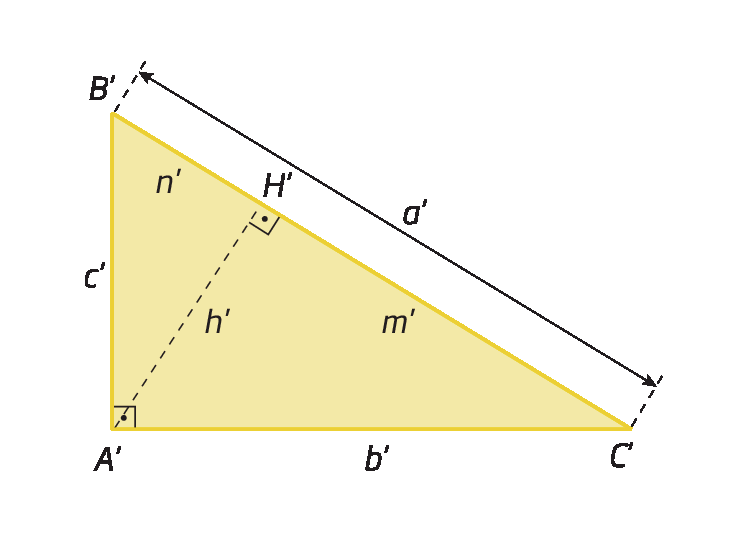
Relações métricas no triângulo retângulo
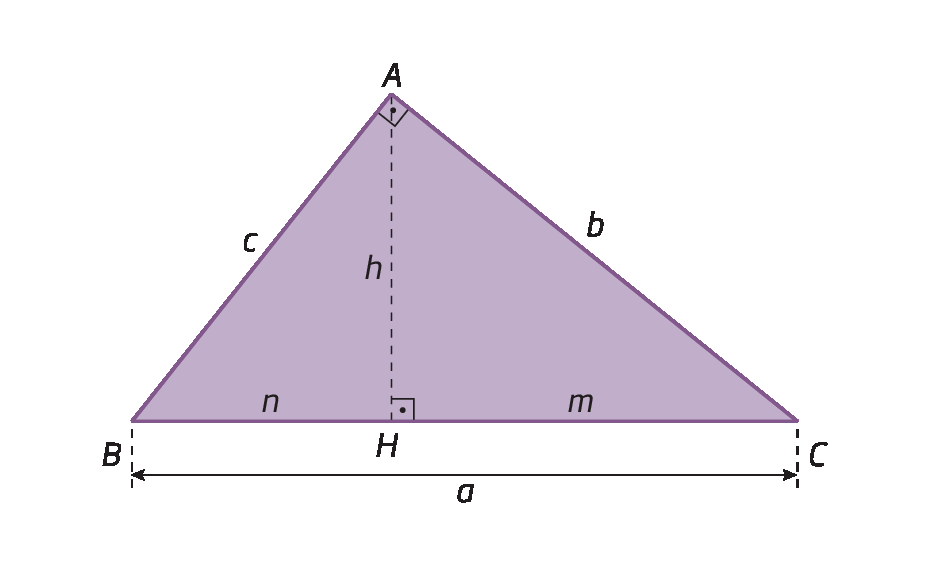
Considere o triângulo retângulo á bê cê.
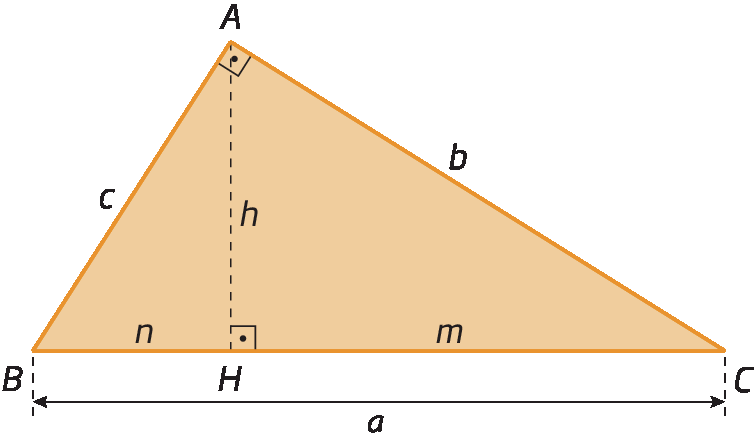
Traçando a altura
segmento de reta A Hrelativa à hipotenusa, podemos destacar três triângulos retângulos: triânguloá bê cê, triânguloagá bê á e triânguloagá á cê.
Vamos mostrar que esses triângulos são semelhantes entre si:
• triânguloá bê cê ∼ triânguloagá bê á
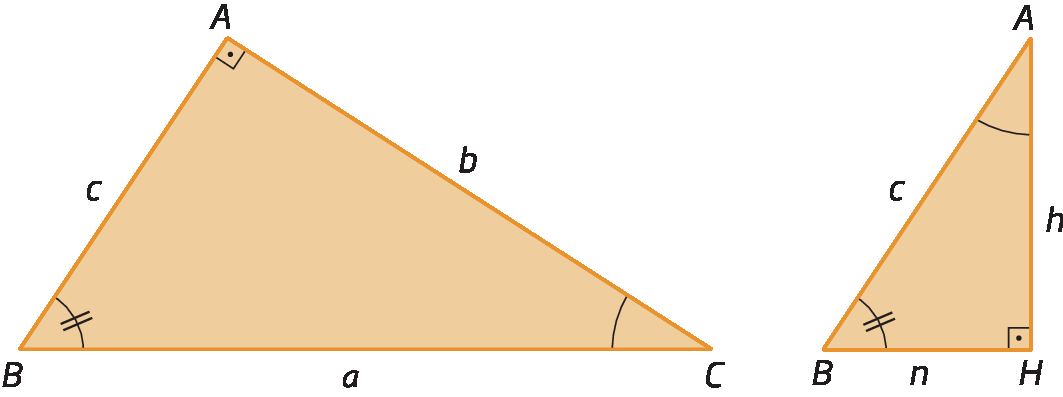
Observe que
Sentença matemática. Ângulo BAC é congruente ao ângulo BHA., pois são ângulos retos, e
Sentença matemática. Ângulo ABC é congruente ao ângulo HBA., pois são ângulos comuns aos dois triângulos.
Então, pelo caso á á, temos: triânguloá bê cê ∼ triânguloagá bê á.
• triânguloá bê cê ∼ triânguloagá á cê
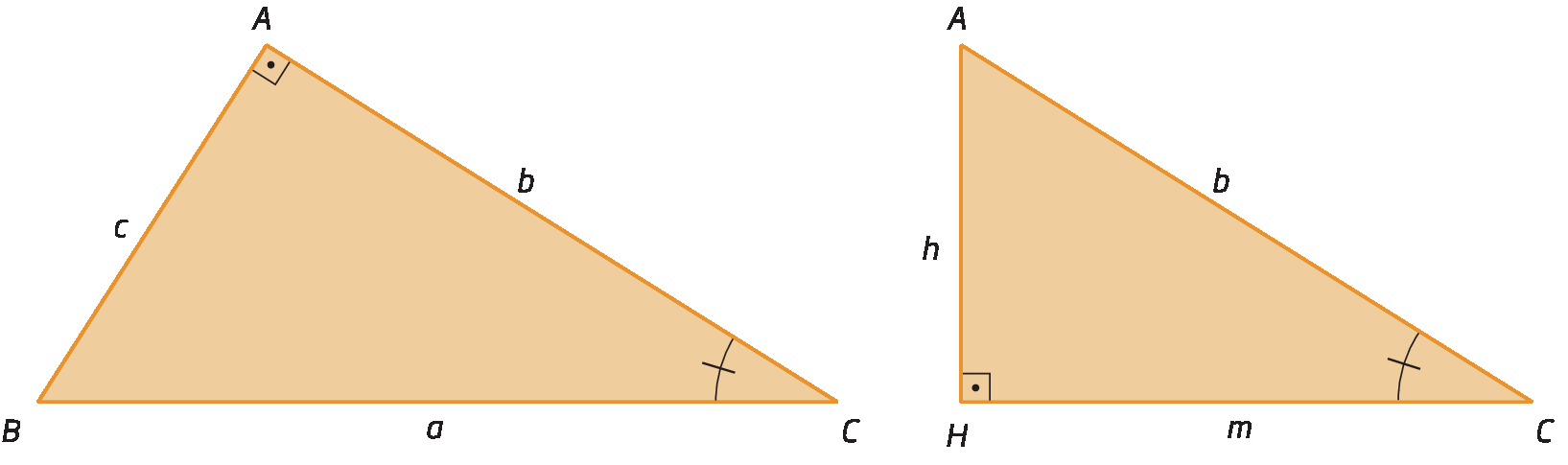
Observe que
Sentença matemática. Ângulo BAC é congruente ao ângulo AHC., pois são ângulos retos, e
Sentença matemática. Ângulo ACB é congruente ao ângulo HCA., pois são ângulos comuns aos dois triângulos.
Então, pelo caso á á, temos: triânguloá bê cê ∼ triânguloagá á cê.
Como triânguloá bê cê ∼ triânguloagá bê á e triânguloá bê cê ∼ triânguloagá á cê, podemos afirmar que: triânguloagá bê á ∼ triânguloagá á cê.
Portanto, os triângulos á bê cê, agá bê á e agá á cê são semelhantes entre si.
Em todo triângulo retângulo, a altura relativa à hipotenusa determina dois outros triângulos retângulos semelhantes entre si e também ao triângulo dado.
Em triângulos semelhantes, os lados correspondentes são proporcionais. Assim, podemos escrever as seguintes proporções em relação aos pares de triângulos:
• triânguloá bê cê e triânguloagá bê á
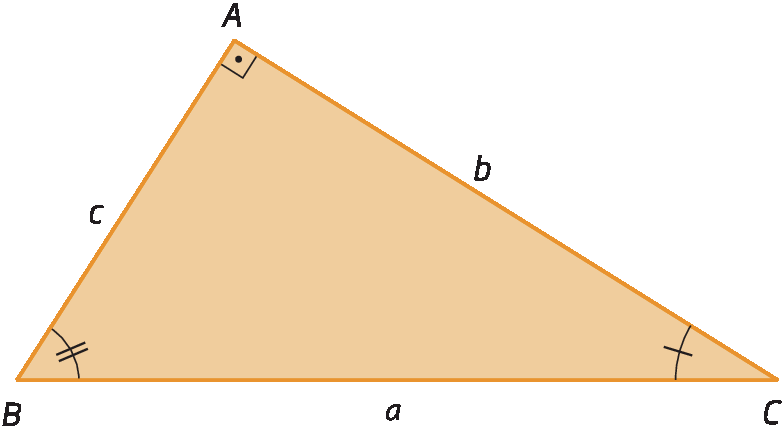
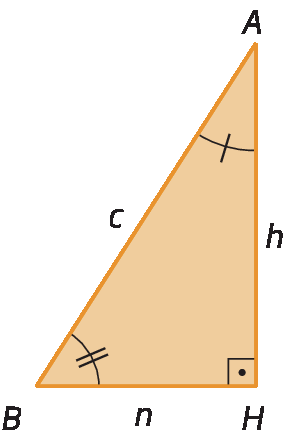
Como triânguloá bê cê ∼ triânguloagá bê á, então:

• triânguloá bê cê e triânguloagá á cê
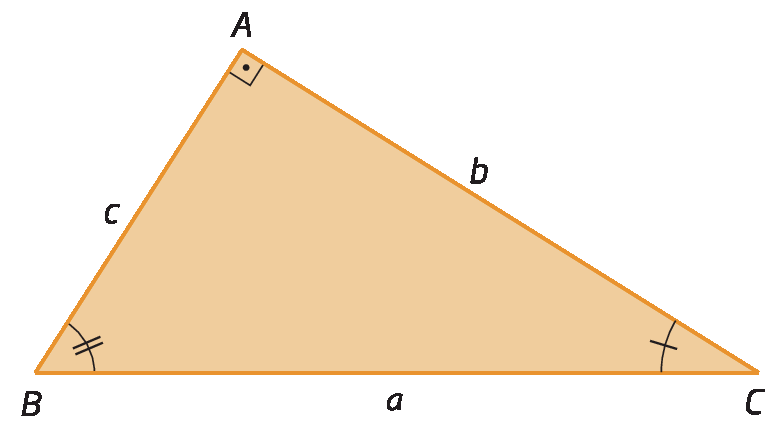
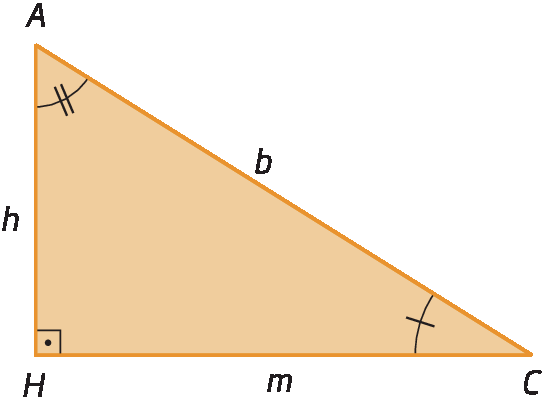
Como triânguloá bê cê ∼ triânguloagá á cê, então:

O quadrado das medidas de comprimento de cada um dos catetos é igual ao produto da medida de comprimento da hipotenusa pela medida de comprimento da projeção ortogonal do cateto considerado sobre a hipotenusa.
• triânguloagá bê á e triânguloagá á cê
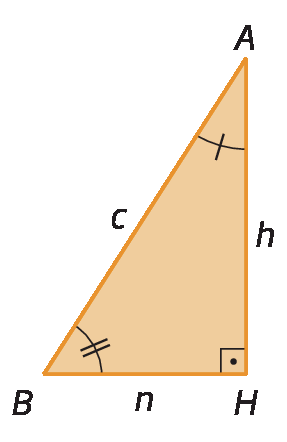
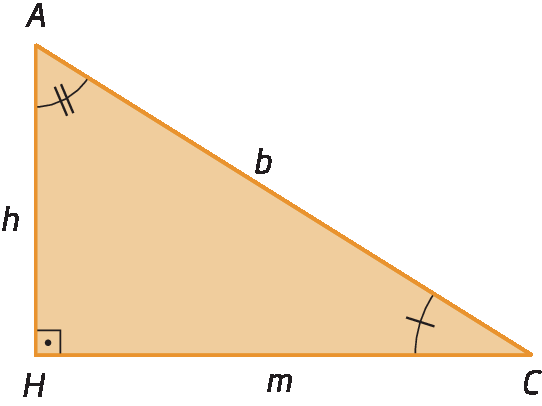
Como triânguloagá bê á ∼ triânguloagá á cê, então:

O quadrado da medida de comprimento da altura relativa à hipotenusa é igual ao produto das medidas de comprimento das projeções ortogonais dos catetos sobre a hipotenusa.
• triânguloá bê cê e triânguloagá ahC
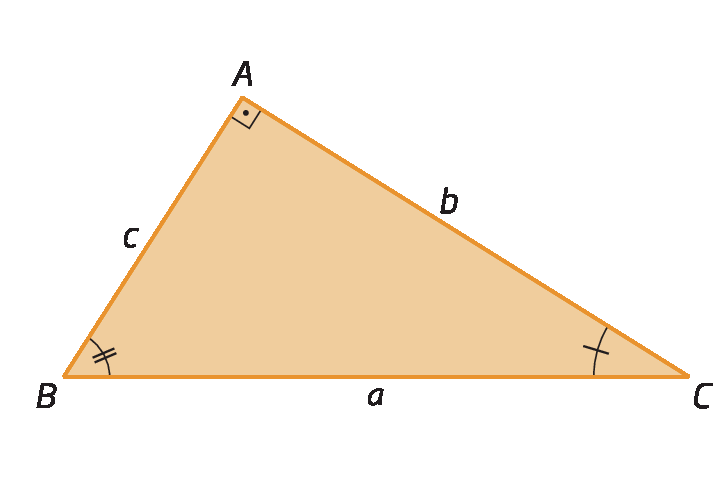
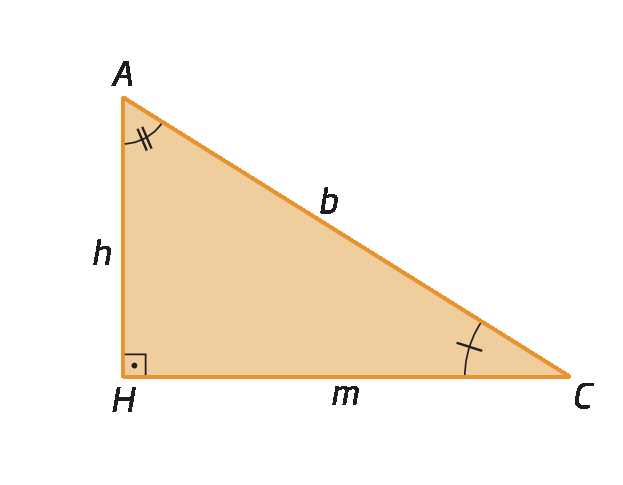
Como triânguloá bê cê ∼ triânguloagá ahC, então:

O produto das medidas de comprimento dos catetos é igual ao produto da medida de comprimento da hipotenusa pela medida de comprimento da altura relativa à hipotenusa.
Analise como podemos aplicar algumas relações métricas no triângulo retângulo.
a) O comprimento da hipotenusa do triângulo retângulo á bê cê mede 52 centímetros, e o comprimento da projeção ortogonal do maior cateto sobre ela mede 37 centímetros. Vamos determinar a medida de comprimento da altura relativa à hipotenusa.
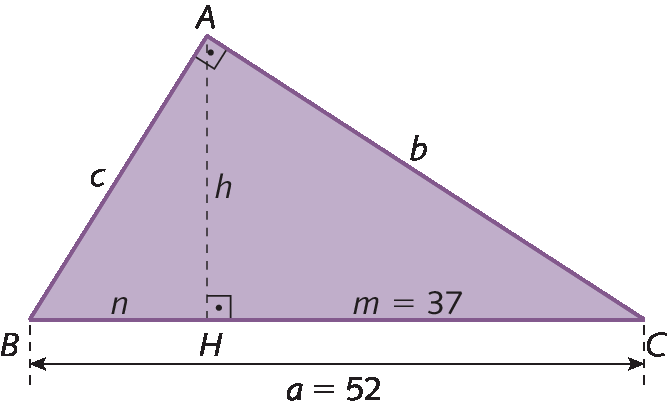
m + n = a ⇒ n = a ‒ m
Substituindo os valores dados:
n = 52 ‒ 37 = 15
Pela relação métrica helevado a 2 = m ⋅ n, temos:
helevado a 2 = 37 ⋅ 15 = 555
Como h > 0, temos:
Sentença matemática. h igual a raiz quadrada de 555, aproximadamente, 23,6.Portanto, o comprimento da altura relativa à hipotenusa mede aproximadamente 23,6 centímetros.
b) Vamos determinar a medida de comprimento da hipotenusa do triângulo retângulo á bê cê em que o comprimento do cateto
Segmento de reta AC.mede 24 centímetros, e o comprimento da sua projeção ortogonal sobre a hipotenusa (
Segmento de reta HC.), 13 centímetros.
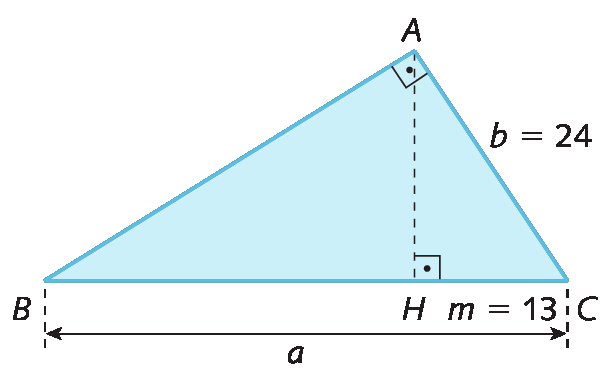
Considerando os dados apresentados, temos:
belevado a 2 = a ⋅ m
576 = a ⋅ 13
a é igual à 576 sobre 13, que é igual a 44,3
Portanto, o comprimento da hipotenusa
Segmento de reta BC.mede aproximadamente 44,3 centímetros.

3 Teorema de Pitágoras e aplicações
Na figura a seguir, representamos o triângulo retângulo á bê cê, cujos lados medem 3 u, 4 u e 5 u de comprimento, sendo u a unidade de medida de comprimento, e três quadrados construídos sobre cada um dos lados do triângulo.
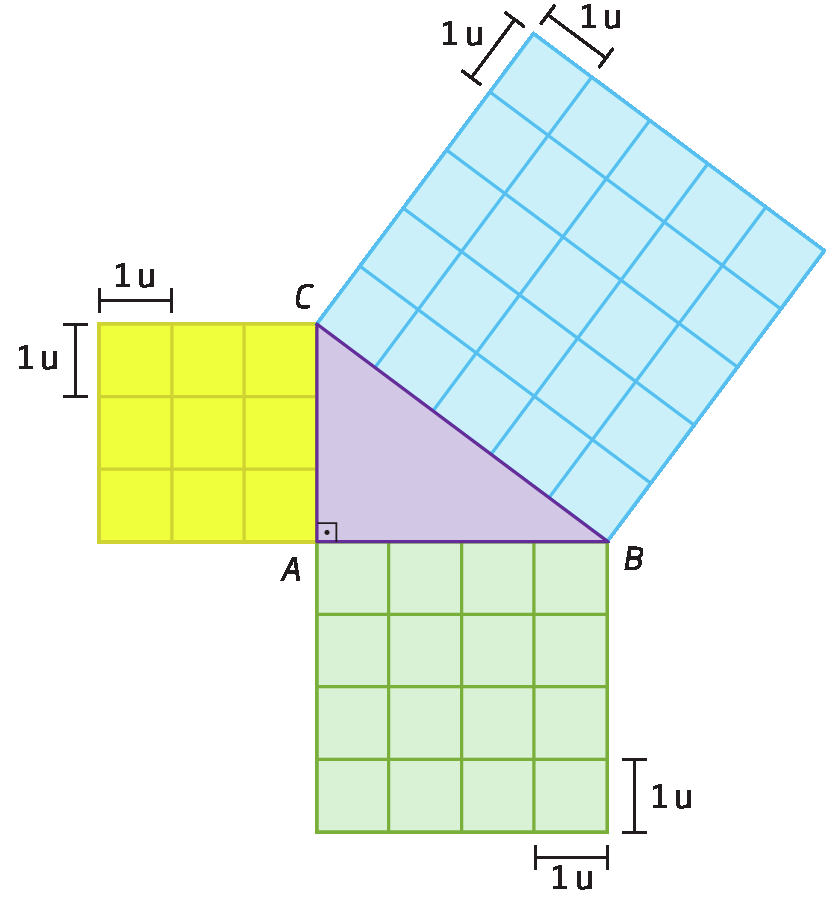
Esses quadrados estão divididos em quadradinhos com lados de medida uma unidade de comprimento, ou seja, cada um desses quadradinhos tem área medindo uma u². Portanto:
• a área do quadrado amarelo mede 9 unidadeselevado a 2;
• a área do quadrado verde mede 16 unidadeselevado a 2;
• a área do quadrado azul mede 25 unidadeselevado a 2.
Observe que a medida da área do quadrado azul corresponde à soma das medidas de área dos outros dois quadrados, pois:
25 unidadeselevado a 2 = 16 unidadeselevado a 2 + 9 unidadeselevado a 2
Associando essa relação às medidas de comprimento dos lados do triângulo á bê cê, temos:
25 unidadeselevado a 2 = 16 unidadeselevado a 2 + 9 unidadeselevado a 2 ⇒ (5 unidades)elevado a 2 = (4 unidades)elevado a 2 + (3 unidades)elevado a 2
Observe que o quadrado da medida de comprimento da hipotenusa é igual à soma dos quadrados das medidas de comprimento dos catetos.
Será que essa relação é válida para todos os triângulos retângulos? Vamos verificar!
Considere um triângulo retângulo á bê cê qualquer.
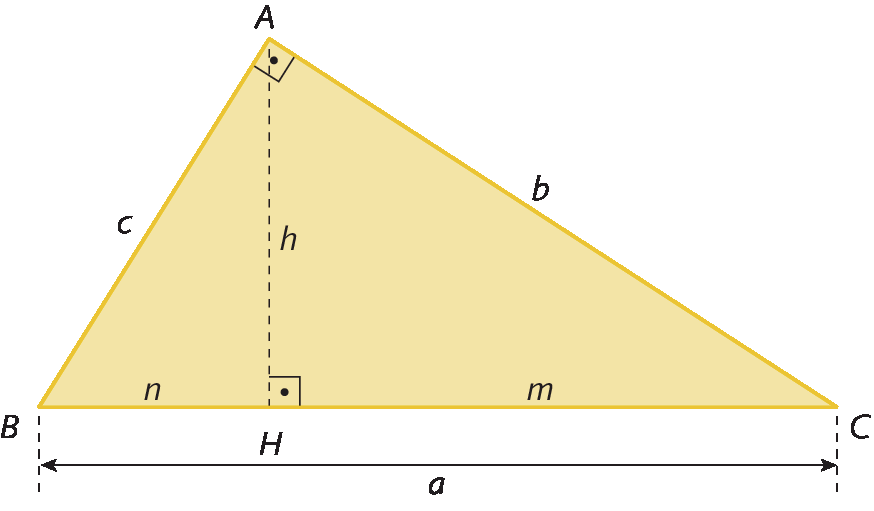
Temos que:
bêelevado a 2 = a ⋅ m e cêelevado a 2 = a ⋅ n
Adicionando as sentenças membro a membro, obtemos:
belevado a 2 + celevado a 2 = am + an
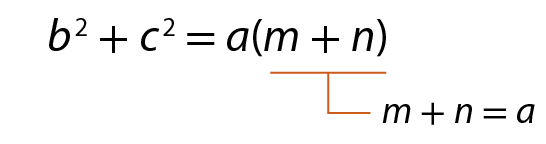
belevado a 2 + celevado a 2 = a ⋅ a
belevado a 2 + celevado a 2 = aelevado a 2

Assim, concluímos que:
Em todo triângulo retângulo, o quadrado da medida de comprimento da hipotenusa é igual à soma dos quadrados das medidas de comprimento dos catetos.
Essa é a relação métrica no triângulo retângulo mais conhecida, denominada teorema de Pitágoras.
Vamos realizar outra demonstração do teorema de Pitágoras. Podemos comparar as medidas de área de figuras geométricas. Para isso, considere o triângulo retângulo á bê cê a seguir.
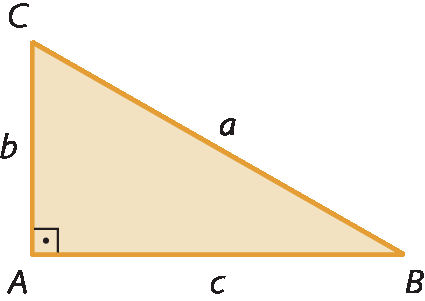
Precisamos demonstrar que aelevado a 2 = belevado a 2 + celevado a 2.
Isso será feito com base nas seguintes figuras.
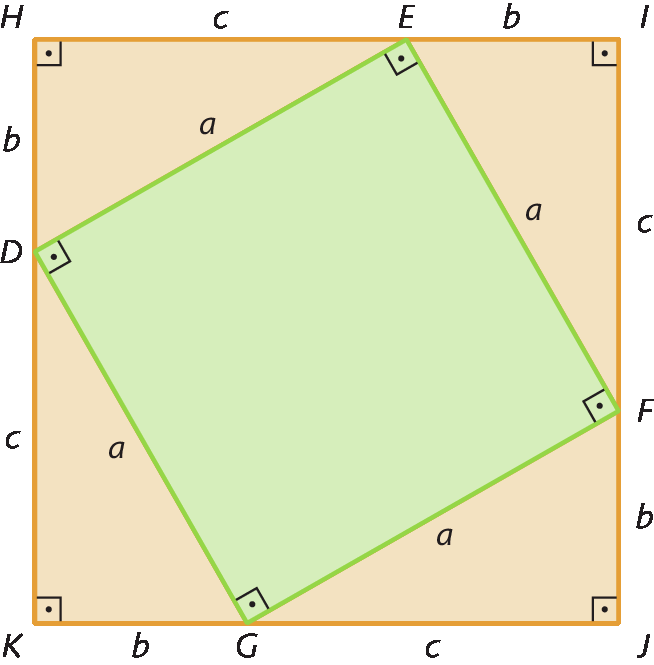
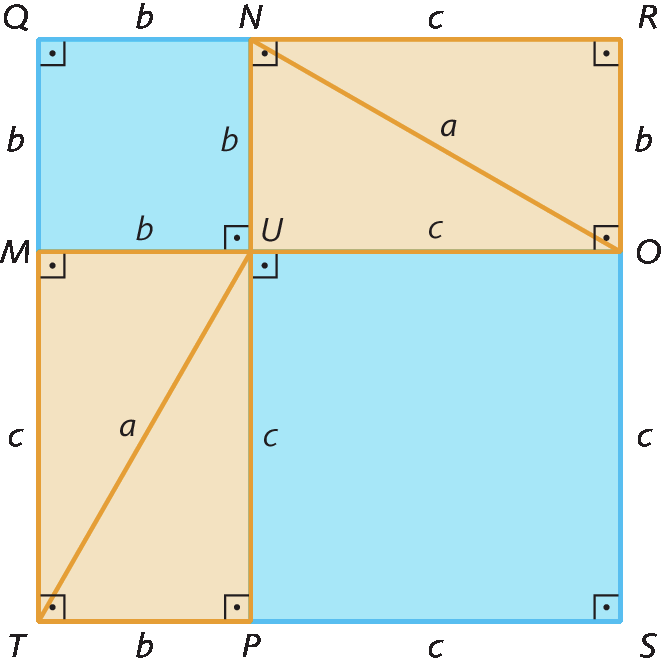
Os quadrados agá í jóta cá e kê érre ésse tê têm a mesma medida de área, pois seus lados têm a mesma medida de comprimento (b + c):
• a medida de área do quadrado agá í jóta cá é igual à soma da medida de área do quadrado dê é éfe gê e das medidas de área dos quatro triângulos, ou seja:
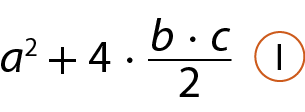
• a medida de área do quadrado kê érre ésse tê é igual à soma da medida de área do quadrado kê êne ú ême, da medida de área do quadrado ú ó ésse pê e das medidas de área dos quatro triângulos, ou seja:
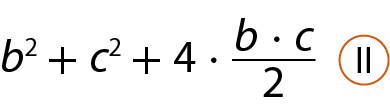
Como as medidas de área dos quadrados agá í jóta cá e kê érre ésse tê são iguais, podemos igualar

e

:
Sentença matemática. a ao quadrado mais 4 vezes fração com numerador b vezes c, e denominador 2, igual a b ao quadrado mais c ao quadrado mais 4, vezes fração com numerador b vezes c e denominador 2.
Subtraindo
4 vezes a fração com numerador b vezes c e denominador 2dos dois membros, temos:
aelevado a 2 = belevado a 2 + celevado a 2
Assim, demonstramos o teorema de Pitágoras.
Agora, vamos analisar um exemplo da aplicação do teorema de Pitágoras para determinar as medidas de comprimento desconhecidas de um triângulo retângulo.
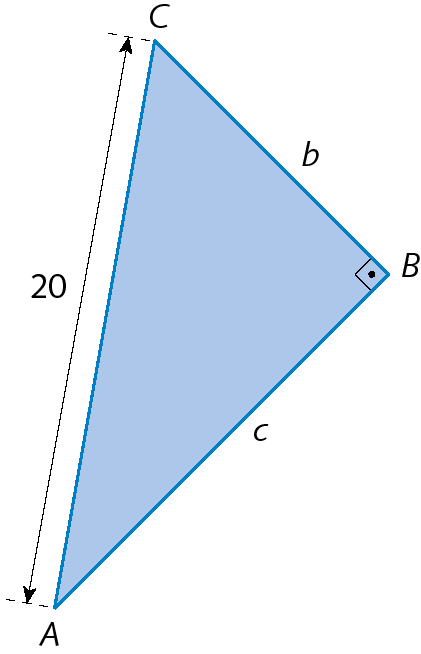
O comprimento da hipotenusa do triângulo retângulo á bê cê mede 20 centímetros, e a razão entre as medidas de comprimento dos catetos é
3 quartos. Vamos determinar as medidas de comprimento b e c, respectivamente, dos catetos
Segmento de reta BC.e
Segmento de reta BA..
Pelo teorema de Pitágoras, temos: 20elevado a 2 = belevado a 2 + celevado a 2 ⇒ 400 = belevado a 2 + celevado a 2

De acôrdo com o enunciado, sabemos que:
b sobre c é igual a 3 quartos, implica que, b ao quadrado sobre c ao quadrado, é igual a, 9 16 avos, implica que b ao quadrado é igual à fração 9 16 avos vezes c ao quadrado

Substituindo

em

, obtemos:
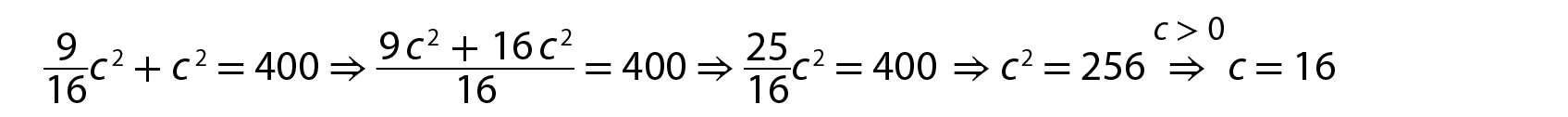
Como c = 16, então:
Esquema. b sobre c é igual a 3 quartos, implica que, b sobre 16 é igual a 3 quartos, implica que, b é igual a 12.
Portanto, os catetos medem 12 centímetros e 16 centímetros de comprimento.

Um pouco de história
Pitágoras
Pitágoras (aproximadamente 580 antes de Cristo-500 antes de Cristo) fundou a Escola Pitagórica, em Crotona (colônia grega situada ao sul da Itália), que constituía um centro de estudos de Matemática, Filosofia e Ciências Naturais. Como os ensinamentos eram orais e era costume atribuir todas as descobertas ao fundador da escola, várias delas foram atribuídas a Pitágoras, embora não se saiba ao certo se realmente foram realizadas por ele ou por outros membros do grupo.

Pitágoras é lembrado até hoje, principalmente pelo teorema que leva seu nome e estabelece uma relação entre as medidas de comprimento dos lados de um triângulo retângulo. Sabe-se, atualmente, que os babilônios, mais de um milênio antes de Pitágoras, já tinham conhecimento de tal relação para casos particulares, porém sua primeira demonstração póde ter sido dada por Pitágoras. Hoje são conhecidas cêrca de 370 demonstrações desse teorema.
Atividades
a) Identifique alguma superfície que se pareça com um triângulo retângulo em sua sala de aula ou em casa e verifique a validade do teorema de Pitágoras.
b)

Em grupo, pesquise outro modo de verificar ou demonstrar o teorema de Pitágoras.

Tecnologias digitais em foco
Verificando a validade do teorema de Pitágoras
Nesta seção, utilizaremos o GeoGebra, ou outro software de geometria dinâmica que seu professor indicar, para construir um triângulo e três quadrados sobre os lados desse triângulo e para comparar a medida de área do quadrado maior com a soma das medidas de área dos quadrados menores.
Construa
Siga os passos a seguir para construir um triângulo e três quadrados sobre os lados dele.
1º) Construa um triângulo á bê cê qualquer.
2º) Sobre o lado
A B, construa o quadrado á bê dê é externo ao triângulo.
3º) Da mesma maneira, construa o quadrado BCFG sobre o lado
Segmento de reta BC.e o quadrado á cê í agá sobre o lado
Segmento de reta AC..
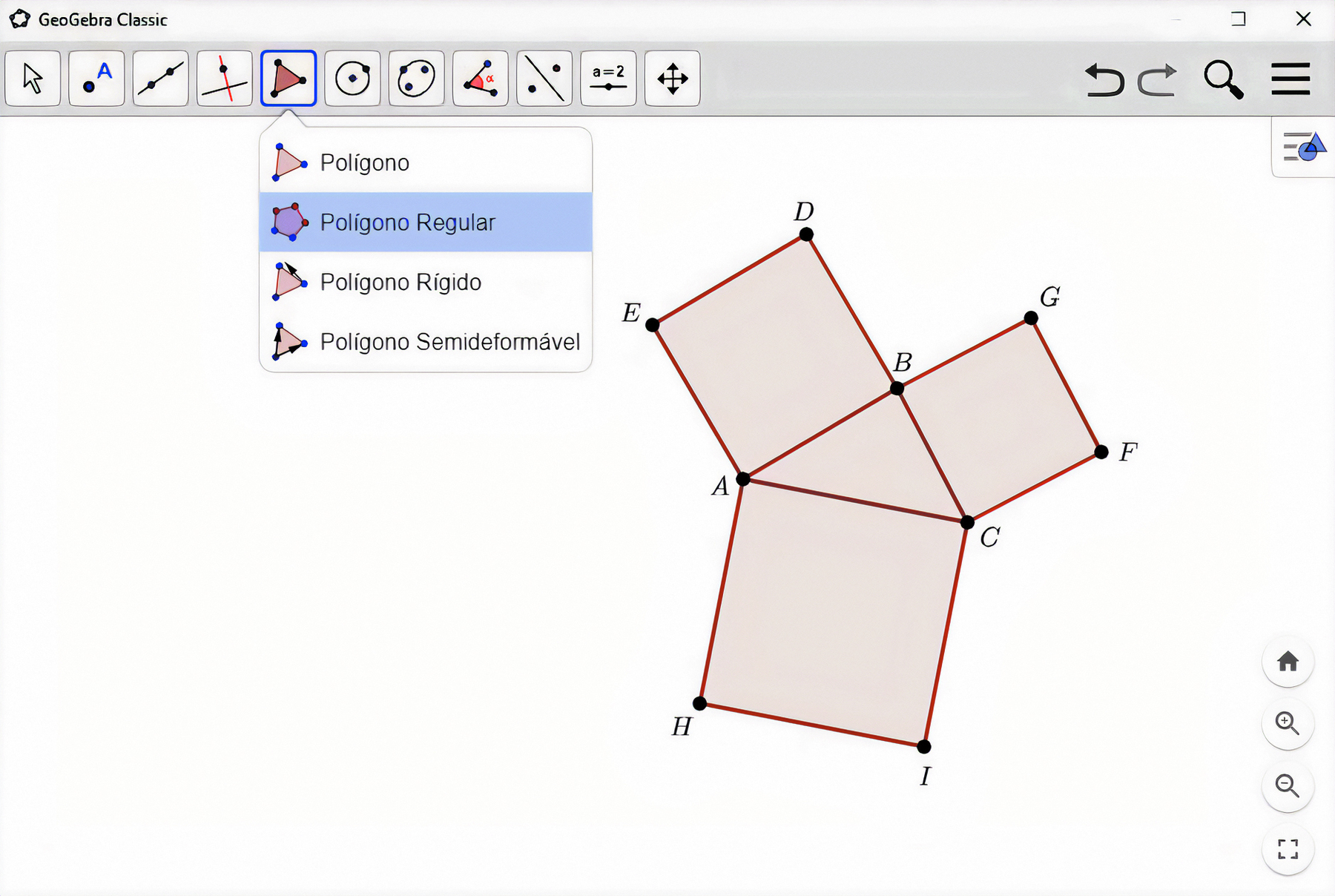
Explore
a) Meça as aberturas dos três ângulos internos do triângulo á bê cê e, usando a ferramenta

, determine as medidas de área dos quadrados á bê dê é, BCFG e á cê í agá. Movimente os vértices do triângulo construído de modo a obter um triângulo acutângulo. Compare a medida de área do quadrado maior com a soma das medidas de área dos quadrados menores. O que você observa?
b) Movimente, agora, os vértices do triângulo de modo a obter um triângulo obtusângulo. Compare a medida de área do quadrado maior com a soma das medidas de área dos quadrados menores. O que você observa?
c) Desta vez, movimente os vértices do triângulo de modo a obter um triângulo retângulo. Compare a medida de área do quadrado maior com a soma das medidas de área dos quadrados menores. O que você observa?
Atividades
Faça as atividades no caderno.
3. Determine o valor de x nos triângulos retângulos.
a)
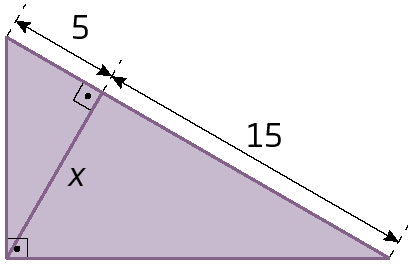
b)
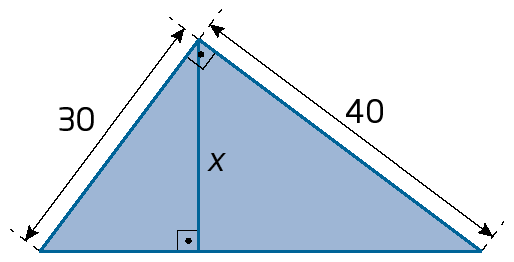
c)
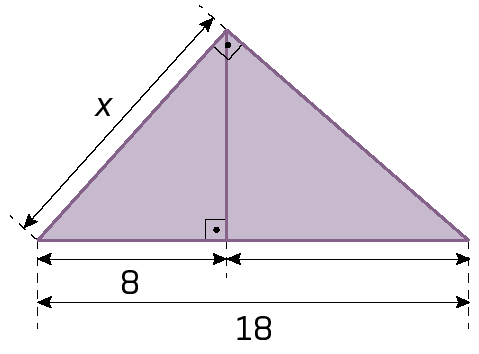
d)

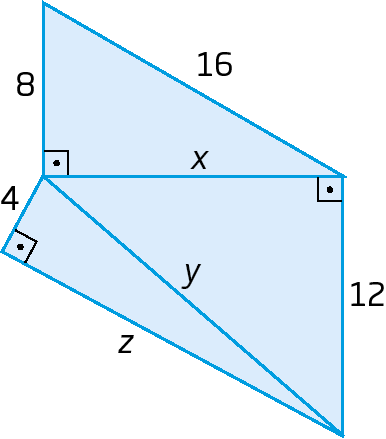
4. Determine os valores de x, y e z.
5. Em um triângulo retângulo, o comprimento da hipotenusa mede 40 métros, e o comprimento da altura relativa a ela, 19,2 métros. Calcule as medidas de comprimento dos catetos.
6. O comprimento de uma escada mede 4 métros e tem uma de suas extremidades apoiada no topo de um muro. A outra extremidade dista 2,4 métros da base do muro. Determine a medida da altura do muro.
7. Em um trapézio retângulo, as bases medem 16 centímetros e 4 centímetros de comprimento, respectivamente. O comprimento do maior lado não paralelo mede 13 centímetros. Quanto mede o perímetro do trapézio?
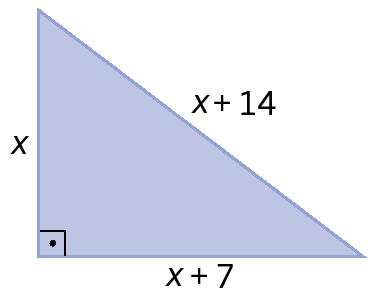
8. Determine as medidas de comprimento dos catetos e da hipotenusa deste triângulo retângulo, em metro.
9. O comprimento da hipotenusa de um triângulo mede 40 centímetros, e a razão entre as medidas de comprimento dos catetos é
3 quartos.
Calcule as medidas de comprimento dos catetos.
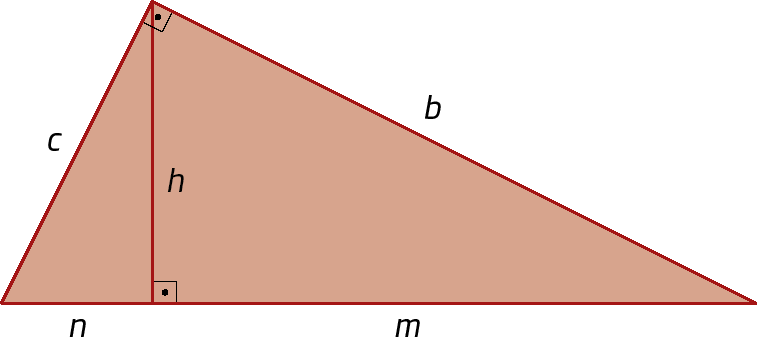
10. Neste triângulo retângulo, b é o dôbro de c. Determine
m sobre n.
11. Qual é a razão entre as medidas de comprimento da hipotenusa e de um cateto de um triângulo retângulo isósceles?
12. Uma empresa foi encarregada de construir uma piscina em um terreno. Como o terreno tinha formato irregular, só foi possível construir uma piscina com formato parecido com um triângulo com as seguintes características:
Medida de abertura do ângulo A é igual a 2 vezes medida de abertura do ângulo B, a é igual a 2 vezes raiz quadrada de 3 metrose b = 2 métros. Determine
Medida de abertura do ângulo A. Medida de abertura do ângulo B.e c.

Aplicações do teorema de Pitágoras
Agora, vamos estudar duas importantes aplicações do teorema de Pitágoras: uma no quadrado e outra no triângulo equilátero.
Diagonal de um quadrado
Considere este quadrado a bê cê dê, em que:
• a é a medida de comprimento do lado;
• d é a medida de comprimento da diagonal.
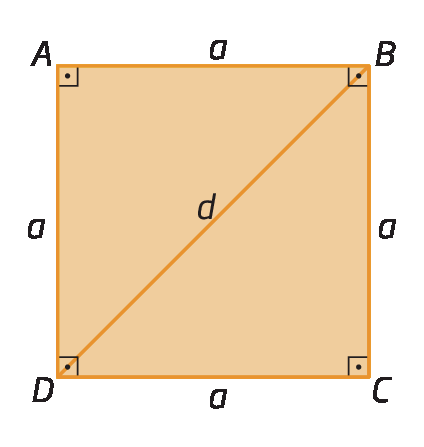
Observe que a diagonal
Segmento de reta BD.divide o quadrado a bê cê dê em dois triângulos retângulos congruentes (triângulobê á dê ≅ triângulobê cê dê).
Aplicando o teorema de Pitágoras no triângulo retângulo BCD, obtemos:
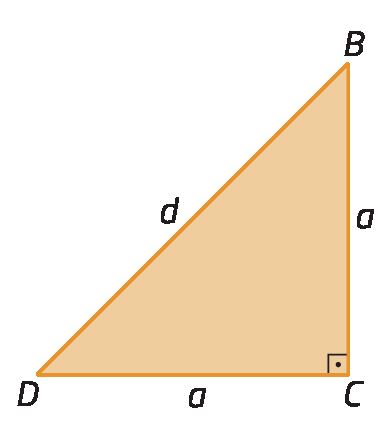
(BD )elevado a 2 = (CD )elevado a 2 + (BC )elevado a 2
delevado a 2 = aelevado a 2 + aelevado a 2
delevado a 2 = 2aelevado a 2
Como d > 0 e a > 0, temos:
d = a
Sentença matemática. Raiz quadrada de 2.Portanto, em um quadrado com lados de medida de comprimento x, a medida de comprimento da diagonal é x
Sentença matemática. Raiz quadrada de 2..
Altura de um triângulo equilátero
Considere este triângulo equilátero á bê cê, em que:
• a é a medida de comprimento do lado;
• h é a medida de comprimento da altura.
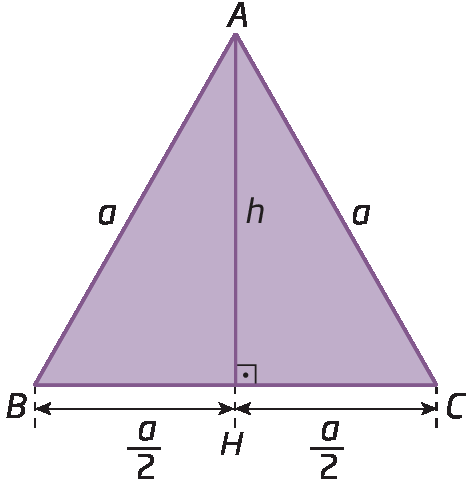
Observe que a altura
Segmento de reta AH.divide o triângulo equilátero á bê cê em dois triângulos retângulos congruentes (triânguloá bê agá ≅ triânguloá cê agá).
Aplicando o teorema de Pitágoras no triângulo retângulo á cê agá, obtemos:
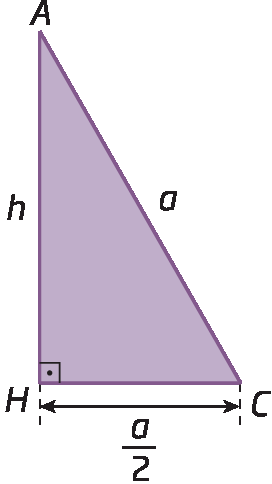
(AC )elevado a 2 = (AH )elevado a 2 + (CH )elevado a 2
h =
Esquema. Quadro com a expressão: h é igual a, fração de numerador a raiz quadrada de 3, e denominador 2.Portanto, em um triângulo equilátero com lados de medida de comprimento x, a medida de comprimento da altura é
a fração de numerador x raiz quadrada de 3 e denominador 2..
Atividades
Faça as atividades no caderno.
13. Determine a medida de comprimento da diagonal de um quadrado cujos lados medem 17 centímetros de comprimento.
14. Determine a medida de comprimento da diagonal de um quadrado com 400 centímetroselevado a 2 de medida de área.
15. O comprimento da diagonal de um quadrado mede 10 centímetros. Determine a medida de comprimento do lado desse quadrado.
16. Qual é a medida de comprimento da diagonal de um quadrado cujo perímetro mede 10
raiz quadrada de 2centímetros?
17. Qual é a medida de comprimento da diagonal de um retângulo cuja medida de comprimento x da altura tem um terço da medida de comprimento da base?
18. Determine a medida de comprimento da altura de um triângulo equilátero cujo comprimento do lado mede 8 centímetros.
19. O perímetro de um triângulo equilátero mede 12 centímetros. Determine a medida de comprimento da altura desse triângulo.
20. Quanto mede o perímetro de um triângulo equilátero cujo comprimento da altura mede 4
Sentença matemática. Raiz quadrada de 5.centímetros?
21. Mostre que a área do quadrado ê éfe gê agá mede (b ‒ c)elevado a 2.
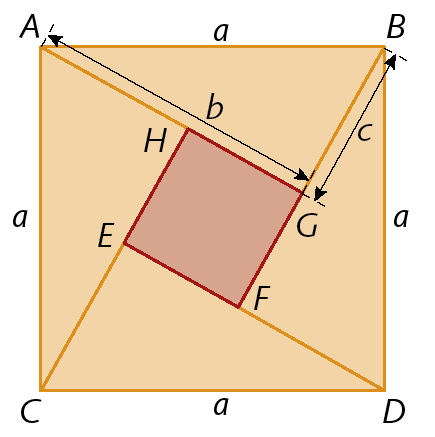
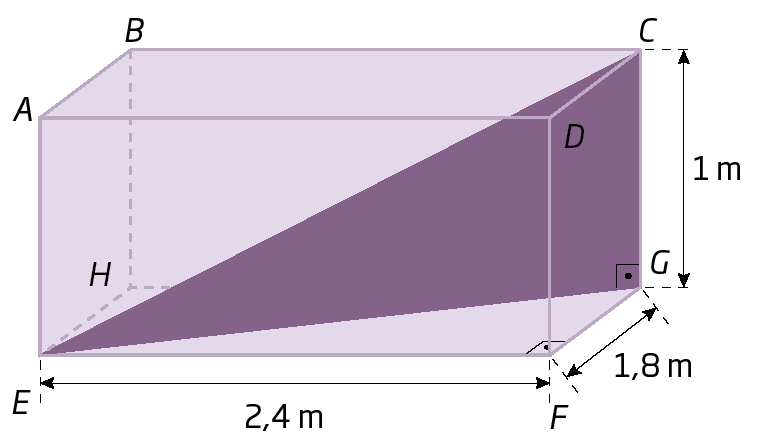
22. Observe o paralelepípedo reto-retângulo representado e calcule a medida de comprimento dos segmentos de reta
E G, e E C.
23.


Cada aresta deste cubo mede 2 centímetros de comprimento. Observe-o e faça o que se pede.
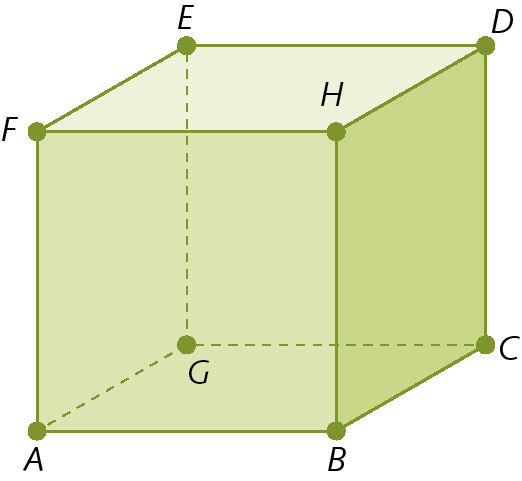
• No caderno, elabore duas questões relacionadas com a figura, sendo que pelo menos uma possa ser respondida utilizando o teorema de Pitágoras.
• Troque de caderno com um colega e responda às questões elaboradas por ele.
• Analise a resposta do colega e dê um retorno a ele, dizendo o que respondeu corretamente e em que pontos ele se equivocou.

4 Razões trigonométricas no triângulo retângulo
A palavra trigonometria vem do grego trígono, que significa “triangular”, e metria, que significa “medida”.
Entre os povos antigos, a Trigonometria surgiu como elemento de apôio na solução de problemas práticos de astronomia, agrimensura e navegação.
Hiparco (190 antes de Cristo-125 antes de Cristo) – astrônomo grego famoso por ter catalogado aproximadamente .1000 estrelas e calculado a medida da distância da Terra à Lua com erro inferior a 10% – teria sido o primeiro a utilizar as relações entre as medidas de comprimento dos lados e de abertura dos ângulos de um triângulo. É considerado o precursor da Trigonometria.
Atualmente, a Trigonometria tem vasta aplicação na topografia, na aviação e nos diversos ramos da engenharia.
Seno de um ângulo agudo
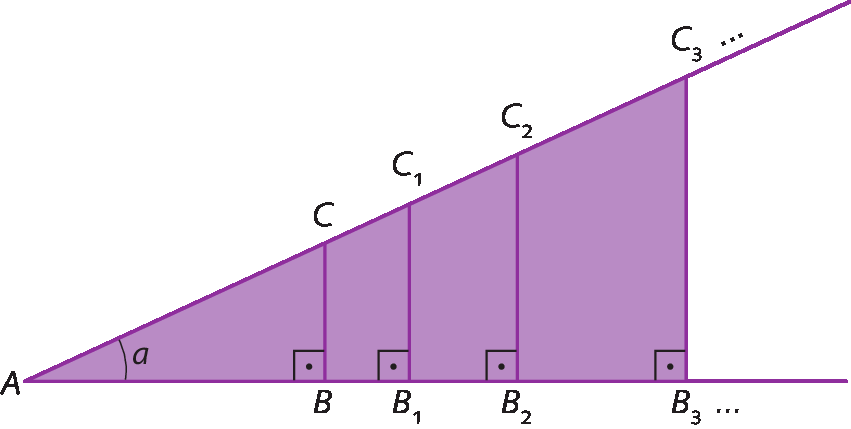
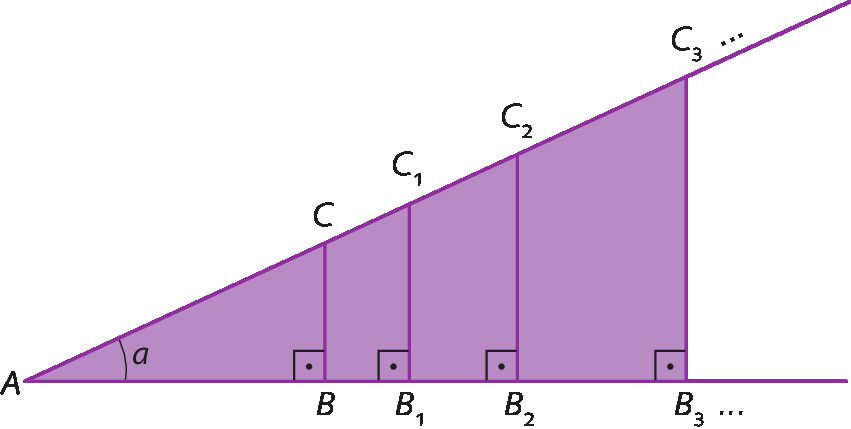
Considere os triângulos retângulos ABC, ABindice de 1Cindice de 1, ABindice de 2Cindice de 2 e ABindice de 3Cindice de 3.
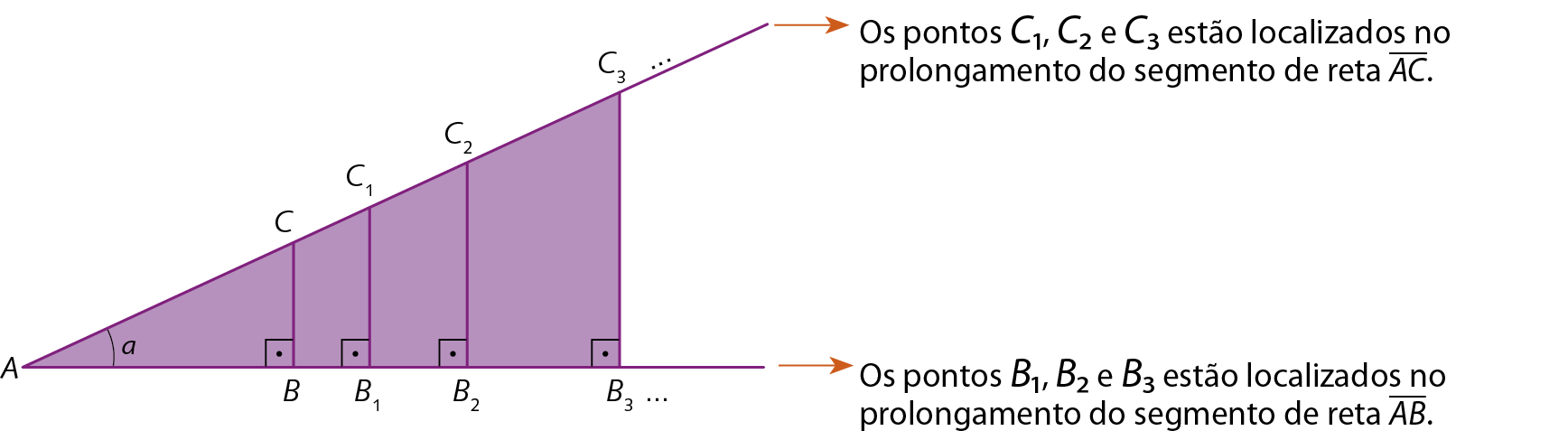
Os triângulos retângulos ABindice de 1Cindice de 1, ABindice de 2Cindice de 2 e ABindice de 3Cindice de 3 são semelhantes ao triângulo á bê cê, pois têm em comum o ângulo
Ae o ângulo reto (caso á á). Assim, podemos escrever:
• triânguloá bê cê ∼ triânguloABindice de 1Cindice de 1
Sentença matemática. AC, sobre AC 1, é igual a, BC, sobre, B 1, C1.
• triânguloá bê cê ∼ triânguloABindice de 2Cindice de 2
Sentença matemática. AC, sobre AC 2, é igual a, BC, sobre, B 2, C2.
• triânguloá bê cê ∼ triânguloABindice de 3Cindice de 3
Sentença matemática. AC, sobre AC 3, é igual a, BC, sobre, B 3, C3.
A partir disso, temos:
•
Sentença matemática. B1C1, sobre AC 1, é igual a, BC, sobre, AC.•
Sentença matemática. B2C2, sobre AC 2, é igual a, BC, sobre, AC.•
Sentença matemática. B3C3, sobre AC 3, é igual a, BC, sobre, AC.Observe que:
Sentença matemática. B1C1, sobre, AC1, é igual a, B2C2, sobre, AC2, é igual a, B3C3, sobre, AC3, é igual a, BC, sobre AC, é igual a, fração de numerador 'medida de comprimento do cateto oposto ao ângulo A' e denominador 'medida de comprimento da hipotenusa.'
Podemos traçar infinitos triângulos retângulos semelhantes ao triângulo á bê cê, com vértice a e lado oposto ao vértice A formado por segmento de reta paralelo a
Segmento de reta BC.com vértices situados nos prologamentos de
segmento de reta A B, e segmento de reta A C.
A razão que relaciona a medida de comprimento do cateto oposto ao ângulo
A.com a medida de comprimento da hipotenusa, em todos esses triângulos, é constante e recebe o nome de seno do ângulo de medida de abertura a. Assim:

Em todo triângulo retângulo, denominamos seno de um ângulo agudo a razão entre a medida de comprimento do cateto oposto a esse ângulo e à medida de comprimento da hipotenusa.
Confira mais um exemplo.
Vamos calcular o seno do ângulo
A.no triângulo retângulo á bê cê.
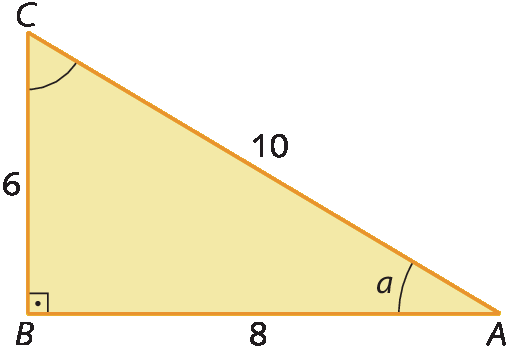

Cosseno de um ângulo agudo
Considere os triângulos retângulos á bê cê, abitindice de 1centésimoindice de 1, abitindice de 2centésimoindice de 2 e abitindice de 3centésimoindice de 3, já apresentados.
triânguloá bê cê ∼ triânguloABindice de 1Cindice de 1
triânguloá bê cê ∼ triânguloABindice de 2Cindice de 2
triânguloá bê cê ∼ triânguloABindice de 3Cindice de 3
Assim, podemos escrever:
•
Sentença matemática. A C, sobre A C 1, é igual a, A B, sobre, A B 1.•
Sentença matemática. A C sobre A C 2, é igual a, A B sobre A B 2.•
Sentença matemática. A C, sobre A C 3, é igual a, A B, sobre, A B 3.A partir disso, temos:
•
Sentença matemática. A B 1, sobre A C 1, é igual a, A B, sobre, A C.•
Sentença matemática. A B 2, sobre A C 2, é igual a, A B, sobre, A C.•
Sentença matemática. A B 3, sobre A C 3, é igual a, A B, sobre, A C.Observe que:
A razão que relaciona a medida de comprimento do cateto adjacente ao ângulo
Acom a medida de comprimento da hipotenusa, em todos esses triângulos, é constante e recebe o nome de cosseno do ângulo de medida de abertura a. Assim:

Em todo triângulo retângulo, denominamos cosseno de um ângulo agudo a razão entre a medida de comprimento do cateto adjacente a esse ângulo e à medida de comprimento da hipotenusa.
Analise mais alguns exemplos.
a) Vamos calcular o cosseno do ângulo
Ano triângulo retângulo á bê cê.
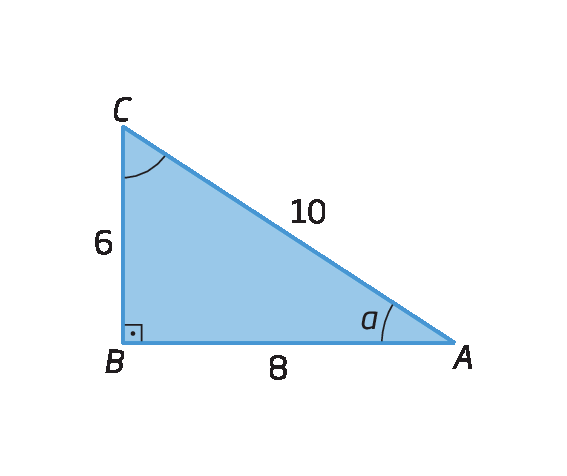

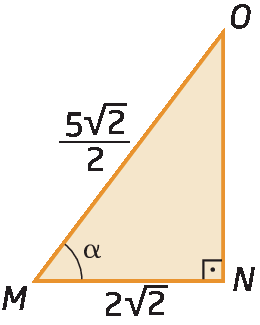
b) Vamos determinar o cosseno do ângulo
Mno triângulo retângulo ême êne ó.

Tangente de um ângulo agudo
Considere, mais uma vez, os triângulos retângulos ABC, AB₁C₁, ABindice de 2Cindice de 2 e ABindice de 3Cindice de 3, já apresentados.
triânguloá bê cê ∼ triânguloABindice de 1Cindice de 1
triânguloá bê cê ∼ triânguloABindice de 2Cindice de 2
triânguloá bê cê ∼ triânguloABindice de 3Cindice de 3
Assim, podemos escrever:
•
Sentença matemática. AB, sobre AB 1, é igual a, BC, sobre, B1C1.•
Sentença matemática. AB, sobre AB 2, é igual a, BC, sobre, B2 C2.•
Sentença matemática. A B sobre A B 3, é igual a, B C sobre B 3 C 3.A partir disso, temos:
•
Sentença matemática. B 1 C 1 sobre A B 1, é igual a, B C sobre A B.•
Sentença matemática. B 2 C 2 sobre A B 2, é igual a, B C sobre A B.•
Sentença matemática. B 3 C 3 sobre A B 3, é igual a, B C sobre A B.Observe que:
A razão que relaciona a medida de comprimento do cateto oposto ao ângulo
A.com a medida de comprimento do cateto adjacente ao ângulo
A., em todos esses triângulos, é constante e recebe o nome de tangente do ângulo de medida de abertura a. Assim:

Em todo triângulo retângulo, denominamos tangente de um ângulo agudo a razão entre a medida de comprimento do cateto oposto a esse ângulo e à medida de comprimento do cateto adjacente a esse ângulo.
Verifique mais alguns exemplos.
a) Vamos calcular a tangente do ângulo
A.no triângulo retângulo á bê cê.
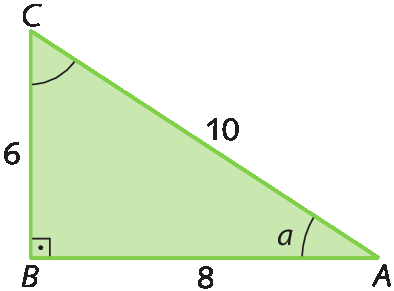

b) Com base no triângulo retângulo á bê cê, vamos determinar o seno, o cosseno e a tangente dos ângulos
B e C.
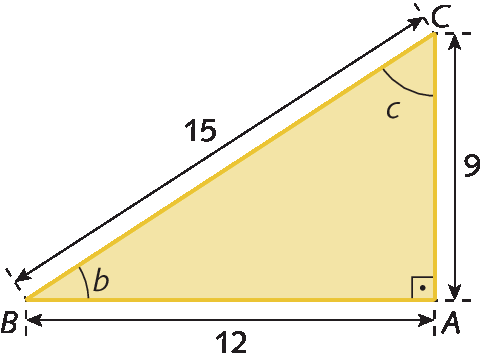
•
Sentença matemática. Seno de b, é igual a, AC sobre BC, é igual a 9 15 avos, é igual a 3 quintos.•
Sentença matemática. Cosseno de b, é igual a, AB sobre BC, é igual a 12 15 avos, é igual a 4 quintos.•
Sentença matemática. Tangente de b, é igual a, AC sobre AB, é igual a 9 12 avos, é igual a 3 quartos.•
Sentença matemática. Seno de c, é igual a, AB sobre BC, é igual a 12 15 avos, é igual a 4 quintos.•
Sentença matemática. Cosseno de c, é igual a, AC sobre BC, é igual a 9 15 avos, é igual a 3 quintos.•
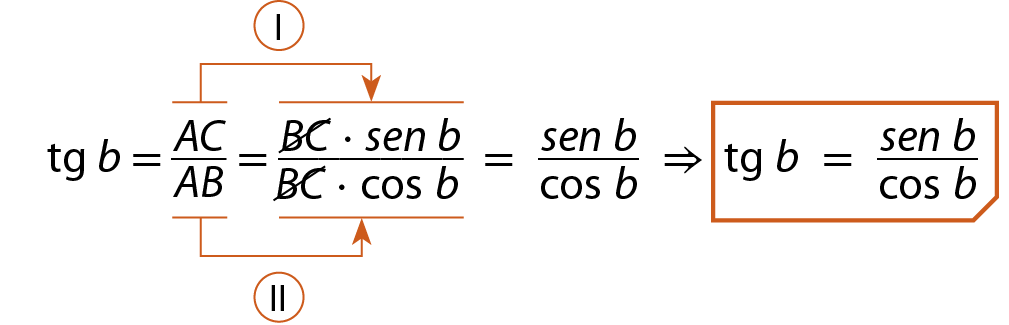
Sentença matemática. Tangente de c, é igual a, AB sobre AC, é igual a 12 nonos, é igual a 4 terços.A tangente de um ângulo agudo também póde ser obtida como a razão entre o seno e o cosseno desse ângulo. Dado um triângulo á bê cê qualquer, temos:
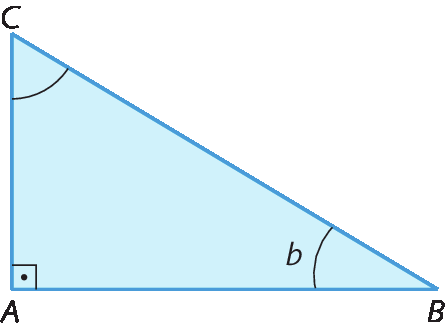
• seno de b =
fração A C sobre B C⇒ AC = BC ⋅ seno de b

• cosseno de b =
fração A B sobre B C⇒ AB = BC ⋅ cosseno de b

Como
Sentença matemática. Tangente de b igual a fração AC sobre A B, temos:
Atividades
Faça as atividades no caderno.
24. Determine as razões trigonométricas solicitadas em cada item.
a) seno de c, cosseno de b, tangente de b;

b) seno de b, cosseno de b, tangente de c;
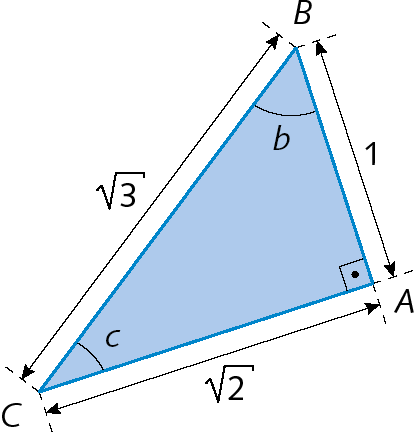
c) seno de b, cosseno de b, tangente de b;
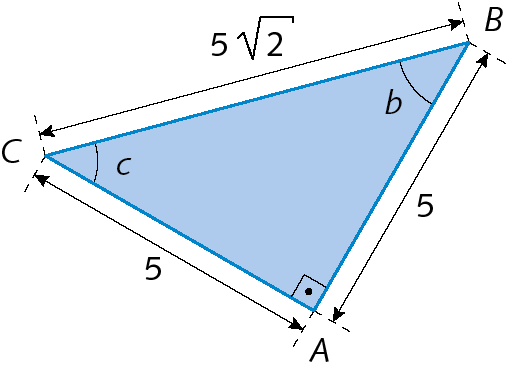
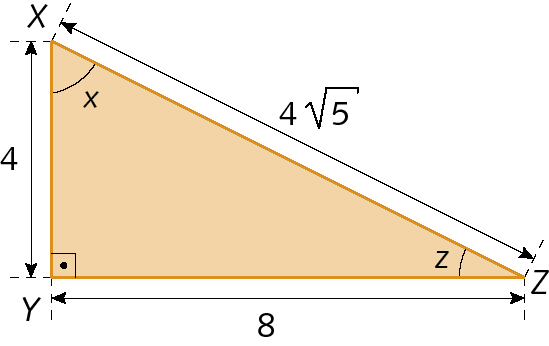
d) seno de x, cosseno de z, tangente de x;
e) seno de o, cosseno de p, tangente de p;
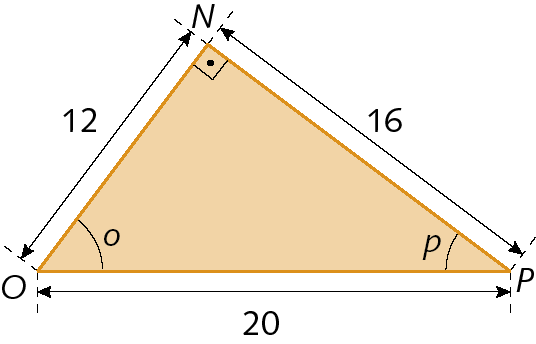
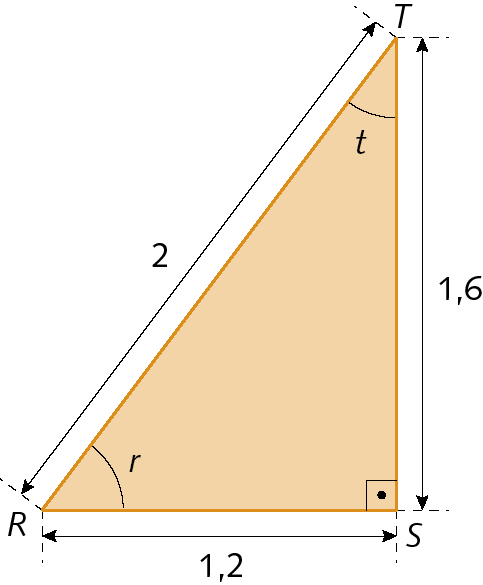
f) seno de r, cosseno de t, tangente de t.
25. A medida da inclinação de uma rampa corresponde à tangente do ângulo adjacente à base e oposto à altura dessa rampa.
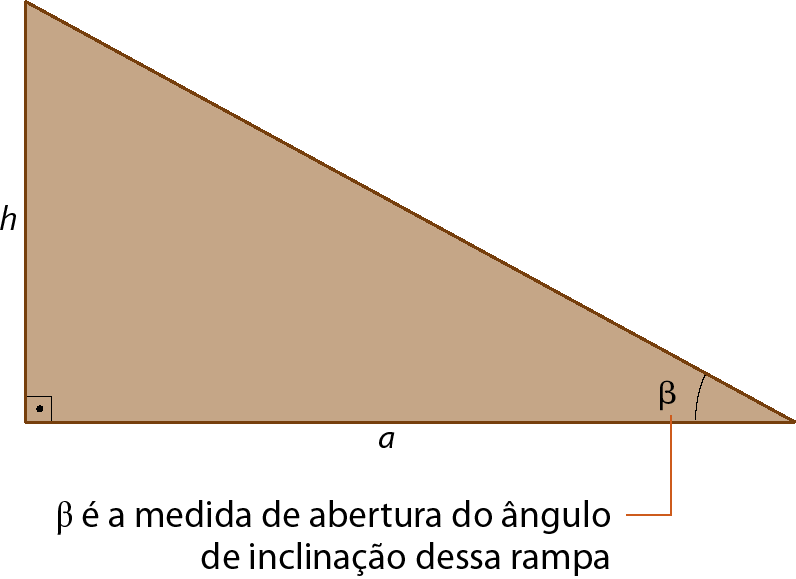
Assim, para calcular a medida da inclinação (tangente de β), devemos dividir a medida da altura da rampa (agá) pela medida do afastamento (a). Caso o resultado encontrado seja menor ou igual a 0,0833 (8,33%), a rampa é segura e segue os padrões de acessibilidade. Esse cálculo é necessário na construção de rampas de acesso para pessoas com deficiência de mobilidade.
Agora, com base nessa informação, responda:
a) Qual deve ser a medida da altura máxima de uma rampa que mede 2,5 métros de afastamento?
b) Qual deve ser a medida mínima de afastamento se uma rampa mede 25 centímetros de altura?
As razões trigonométricas dos ângulos de medidas de abertura de 30graus, 45graus e 60graus
Considere o quadrado a bê cê dê e o triângulo equilátero á bê cê a seguir.
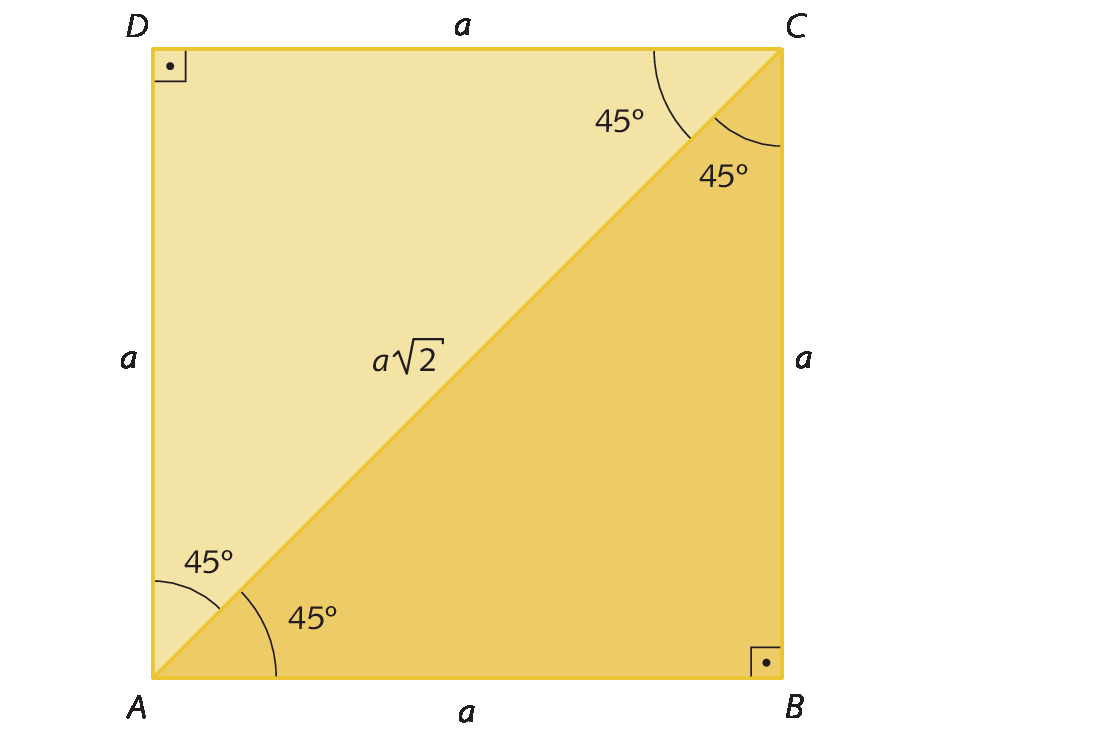
• medida de comprimento do lado do quadrado a bê cê dê: a
• medida de comprimento da diagonal do quadrado a bê cê dê:
Sentença matemática. a raiz quadrada de 2.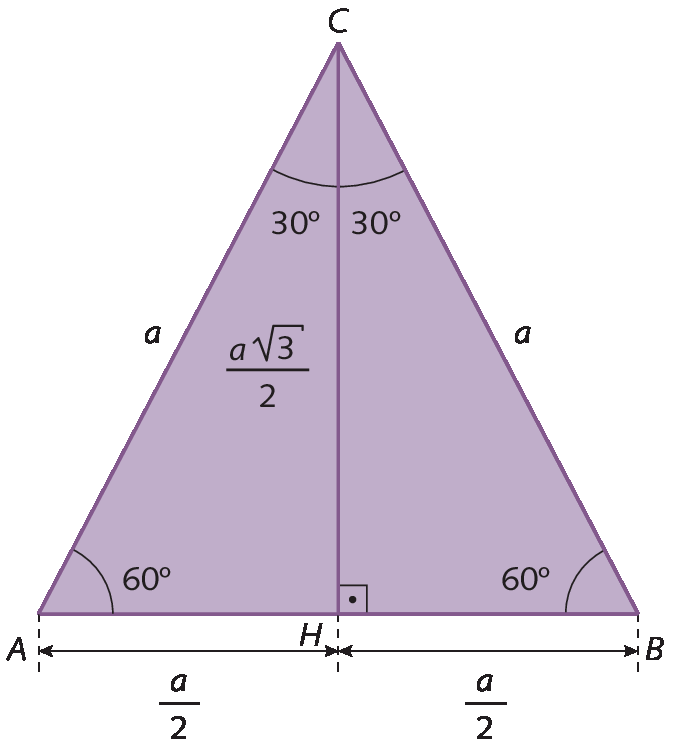
• medida de comprimento do lado do triângulo equilátero á bê cê: a
• medida de comprimento da altura do triângulo equilátero á bê cê:
fração de numerador a raiz quadrada de 3 e denominador 2As medidas de comprimento das diagonais de um quadrado e das alturas de um triângulo equilátero podem ser determinadas pelo teorema de Pitágoras.
Agora, vamos usar essas figuras para determinar o seno, o cosseno e a tangente dos ângulos de medidas de abertura de 30graus, 45graus e 60graus.
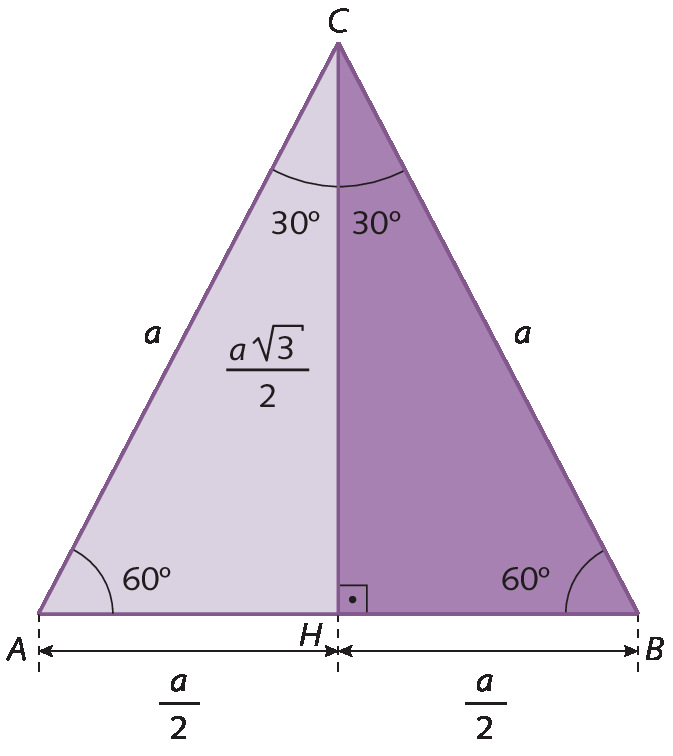
Seno, cosseno e tangente do ângulo de medida de abertura de 30graus
Observe o triânguloBHC e a aplicação das definições de seno, cosseno e tangente para o ângulo de medida de abertura de 30graus:
Seno, cosseno e tangente do ângulo de medida de abertura de 45graus
Observe o triânguloá bê cê e a aplicação das definições de seno, cosseno e tangente para o ângulo de medida de abertura de 45graus:

Seno, cosseno e tangente do ângulo de medida de abertura de 60graus
Observe o triânguloBHC e a aplicação das definições de seno, cosseno e tangente para o ângulo de medida de abertura de 60graus:


|
x |
30° |
45° |
60° |
|---|---|---|---|
|
sen x |
|
|
|
|
cos x |
|
|
|
|
tg x |
|
1 |
|
Analise mais alguns exemplos.
a) Vamos determinar o valor de x no triângulo retângulo á bê cê.
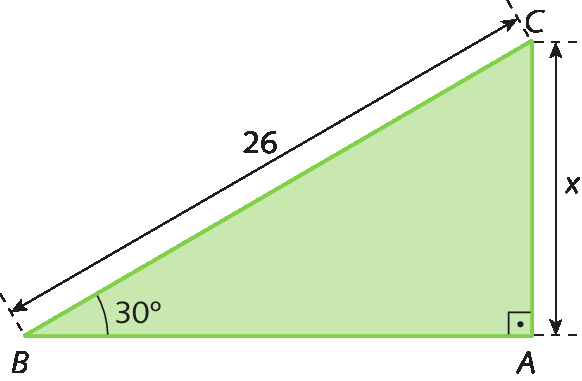
Sentença matemática. Seno de 30 graus, igual a, AC sobre CB.
Seno de 30 graus, igual, x 26 avos.
x = 26 ⋅ seno de 30graus
x, igual a, 26 vezes 1 meio, igual, 13.
Portanto, o valor de x é 13.
b) Dado o triânguloá bê cê, vamos determinar o valor de y.
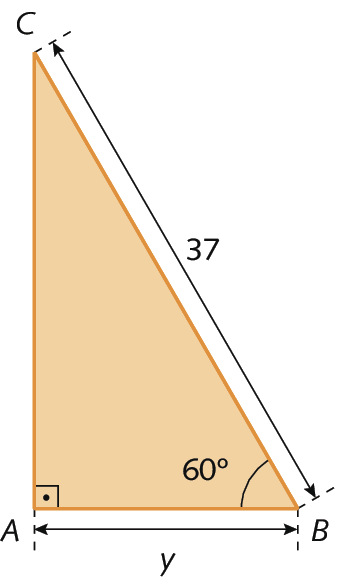
Sentença matemática. Cosseno de 60 graus, igual a, AB sobre BC.
cosseno de 60 graus, igual a, y 37 avos.
y = 37 ⋅ cosseno de 60graus
igual a, 37 vezes 1 meio, igual, 18 vírgula 5.
Portanto, o valor de y é 18,5.
c) Vamos determinar o valor de z para o triângulo retângulo á bê cê.
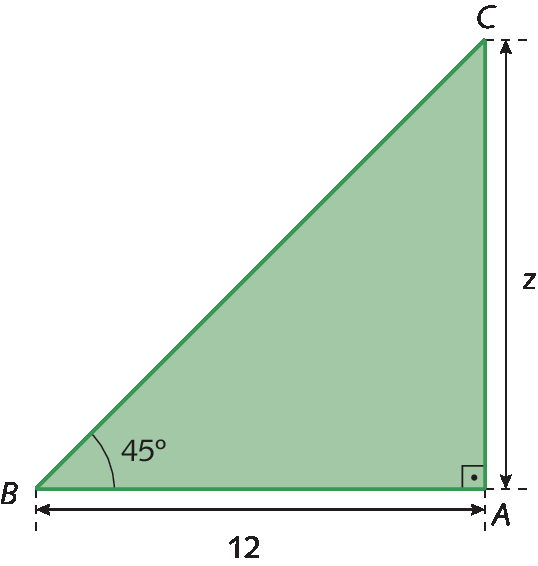
Sentença matemática. Tangente de 45 graus, igual a, AC sobre AB.
tangente de 45 graus, igual a, z 12 avos.
z = 12 ⋅ tangente de 45graus
z = 12 ⋅ 1 = 12
Portanto, o valor de z é 12.
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
26. Calcule o valor de x e y nestes triângulos retângulos.
a)
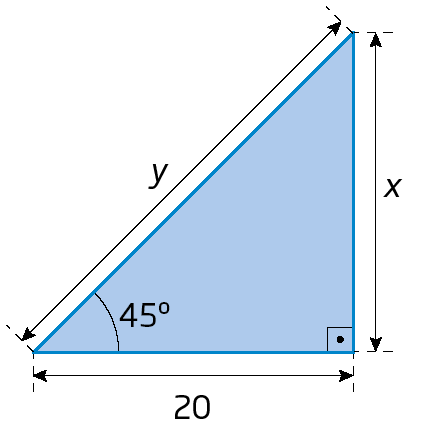
b)
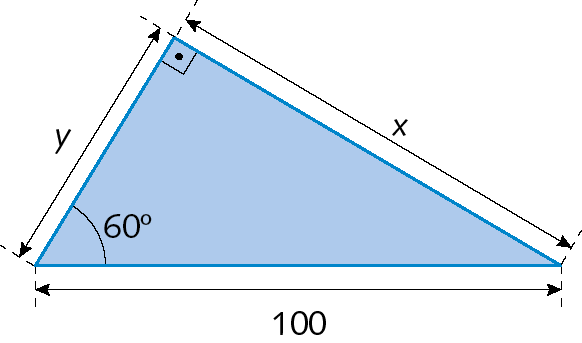
c)
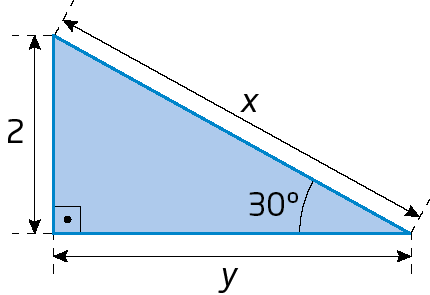
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
27. Determine o valor de m, n, h e x no triângulo retângulo a seguir.
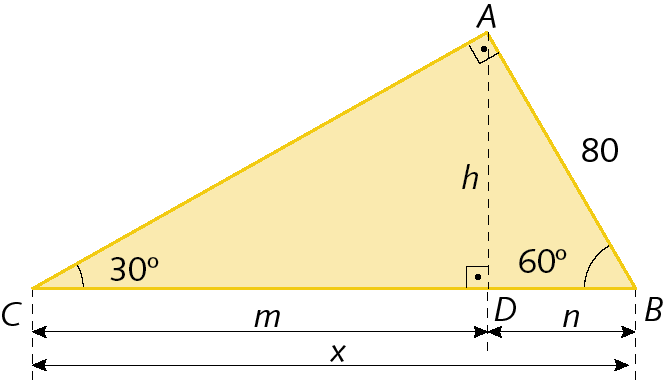
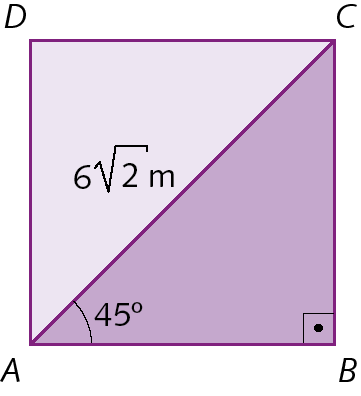
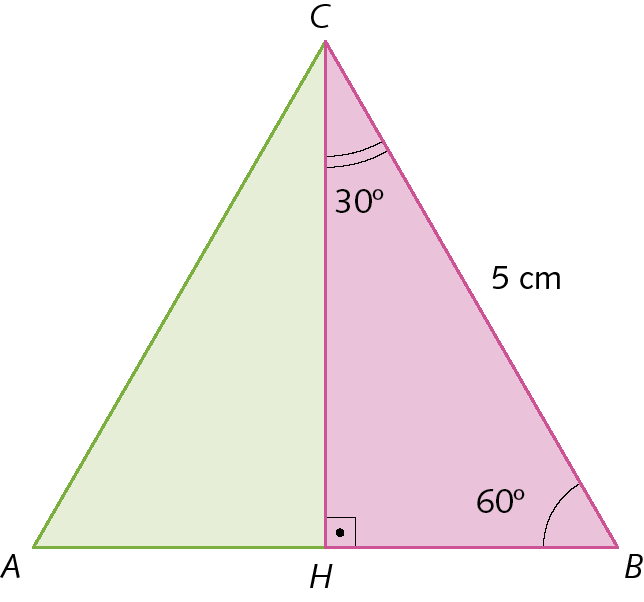
28. Calcule a medida de comprimento do lado
do quadrado a bê cê dê, em metro, e a medida de comprimento da altura
Segmento de reta CH.do triângulo á bê cê, em centímetro.
29. Determine a medida de comprimento h da altura deste triângulo retângulo.
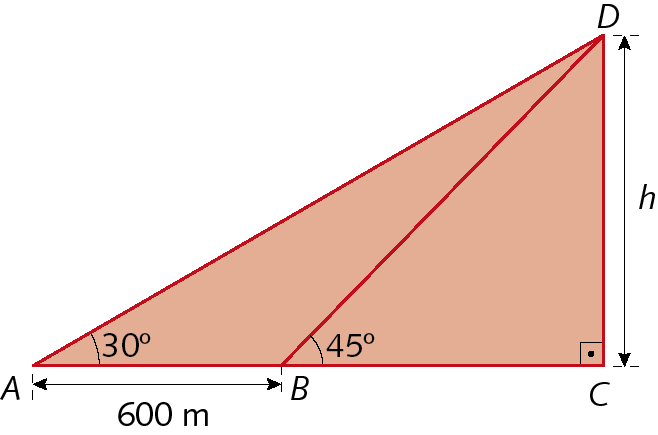
Tabela de razões trigonométricas
Na resolução de diversos problemas envolvendo razões trigonométricas, necessitamos dos valores do seno, do cosseno e da tangente de alguns ângulos com medidas de abertura diferentes de 30graus, 45graus e 60graus.
Por exemplo, o que você faria se precisasse do seno de 39graus para resolver um problema? Ou se precisasse do cosseno de 50graus? E da tangente de 81graus?
Por isso, há alguns séculos, matemáticos calcularam e organizaram os valores aproximados do seno, do cosseno e da tangente dos ângulos agudos cujas medidas de abertura variam de 1grau a 89graus.
Observe a seguir os valores com aproximação de milésimos.
|
x |
sen x |
cos x |
tg x |
|---|---|---|---|
|
1° |
0,017 |
1,000 |
0,017 |
|
2° |
0,035 |
0,999 |
0,035 |
|
3° |
0,052 |
0,999 |
0,052 |
|
4° |
0,070 |
0,998 |
0,070 |
|
5° |
0,087 |
0,996 |
0,087 |
|
6° |
0,105 |
0,995 |
0,105 |
|
7° |
0,122 |
0,993 |
0,123 |
|
8° |
0,139 |
0,990 |
0,141 |
|
9° |
0,156 |
0,988 |
0,158 |
|
10° |
0,174 |
0,985 |
0,176 |
|
11° |
0,191 |
0,982 |
0,194 |
|
12° |
0,208 |
0,978 |
0,213 |
|
13° |
0,225 |
0,974 |
0,231 |
|
14° |
0,242 |
0,970 |
0,249 |
|
15° |
0,259 |
0,966 |
0,268 |
|
16° |
0,276 |
0,961 |
0,287 |
|
17° |
0,292 |
0,956 |
0,306 |
|
18° |
0,309 |
0,951 |
0,325 |
|
19° |
0,326 |
0,946 |
0,344 |
|
20° |
0,342 |
0,940 |
0,364 |
|
21° |
0,358 |
0,934 |
0,384 |
|
22° |
0,375 |
0,927 |
0,404 |
|
23° |
0,391 |
0,921 |
0,424 |
|
24° |
0,407 |
0,914 |
0,445 |
|
x |
sen x |
cos x |
tg x |
|---|---|---|---|
|
25° |
0,423 |
0,906 |
0,466 |
|
26° |
0,438 |
0,899 |
0,488 |
|
27° |
0,454 |
0,891 |
0,510 |
|
28° |
0,469 |
0,883 |
0,532 |
|
29° |
0,485 |
0,875 |
0,554 |
|
30° |
0,500 |
0,866 |
0,577 |
|
31° |
0,515 |
0,857 |
0,601 |
|
32° |
0,530 |
0,848 |
0,625 |
|
33° |
0,545 |
0,839 |
0,649 |
|
34° |
0,559 |
0,829 |
0,675 |
|
35° |
0,574 |
0,819 |
0,700 |
|
36° |
0,588 |
0,809 |
0,727 |
|
37° |
0,602 |
0,799 |
0,754 |
|
38° |
0,616 |
0,788 |
0,781 |
|
39° |
0,629 |
0,777 |
0,810 |
|
40° |
0,643 |
0,766 |
0,839 |
|
41° |
0,656 |
0,755 |
0,869 |
|
42° |
0,669 |
0,743 |
0,900 |
|
43° |
0,682 |
0,731 |
0,933 |
|
44° |
0,695 |
0,719 |
0,966 |
|
45° |
0,707 |
0,707 |
1,000 |
|
46° |
0,719 |
0,695 |
1,036 |
|
47° |
0,731 |
0,682 |
1,072 |
|
48° |
0,743 |
0,669 |
1,111 |
|
49° |
0,755 |
0,656 |
1,150 |
|
50° |
0,766 |
0,643 |
1,192 |
|
51° |
0,777 |
0,629 |
1,235 |
|
52° |
0,788 |
0,616 |
1,280 |
|
53° |
0,799 |
0,602 |
1,327 |
|
54° |
0,809 |
0,588 |
1,376 |
|
55° |
0,819 |
0,574 |
1,428 |
|
56° |
0,829 |
0,559 |
1,483 |
|
57° |
0,839 |
0,545 |
1,540 |
|
58° |
0,848 |
0,530 |
1,600 |
|
59° |
0,857 |
0,515 |
1,664 |
|
60° |
0,866 |
0,500 |
1,732 |
|
61° |
0,875 |
0,485 |
1,804 |
|
62° |
0,883 |
0,469 |
1,881 |
|
63° |
0,891 |
0,454 |
1,963 |
|
64° |
0,899 |
0,438 |
2,050 |
|
65° |
0,906 |
0,423 |
2,145 |
|
66° |
0,914 |
0,407 |
2,246 |
|
67° |
0,921 |
0,391 |
2,356 |
|
68° |
0,927 |
0,375 |
2,475 |
|
69° |
0,934 |
0,358 |
2,605 |
|
70° |
0,940 |
0,342 |
2,747 |
|
71° |
0,946 |
0,326 |
2,904 |
|
72° |
0,951 |
0,309 |
3,078 |
|
73° |
0,956 |
0,292 |
3,271 |
|
74° |
0,961 |
0,276 |
3,467 |
|
75° |
0,966 |
0,259 |
3,732 |
|
76° |
0,970 |
0,242 |
4,011 |
|
77° |
0,974 |
0,225 |
4,332 |
|
78° |
0,978 |
0,208 |
4,705 |
|
79° |
0,982 |
0,191 |
5,145 |
|
80° |
0,985 |
0,174 |
5,671 |
|
81° |
0,988 |
0,156 |
6,314 |
|
82° |
0,990 |
0,139 |
7,115 |
|
83° |
0,993 |
0,122 |
8,144 |
|
84° |
0,995 |
0,105 |
9,514 |
|
85° |
0,996 |
0,087 |
11,430 |
|
86° |
0,998 |
0,070 |
14,301 |
|
87° |
0,999 |
0,052 |
19,081 |
|
88° |
0,999 |
0,035 |
28,636 |
|
89° |
1,000 |
0,017 |
57,290 |
Analise a seguir alguns exemplos do uso da tabela de razões trigonométricas.
|
x |
sen x |
cos x |
tg x |
|---|---|---|---|
|
31° |
0,515 |
0,857 |
0,601 |
|
32° |
0,530 |
0,848 |
0,625 |
|
33° |
0,545 |
0,839 |
0,649 |
|
34° |
0,559 |
0,829 |
0,675 |
|
35° |
0,574 |
0,819 |
0,700 |

a) Vamos localizar o valor aproximado do cosseno de 33graus.
Primeiro, localizamos 33graus e, então, na coluna “cosseno de x”, encontramos 0,839.
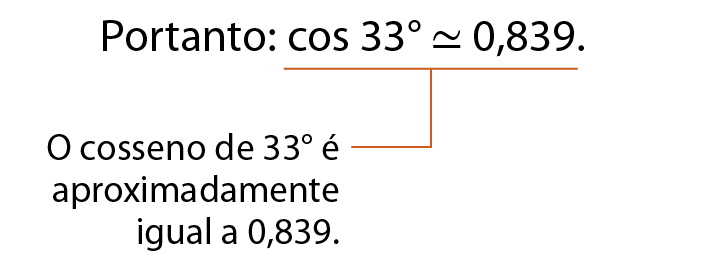
b) Vamos determinar a medida de abertura do ângulo cuja tangente é aproximadamente igual a 1,6.
Localizamos, na coluna “tangente de x”, o valor 1,6 e encontramos a medida de abertura do ângulo correspondente a esse valor.
|
x |
sen x |
cos x |
tg x |
|---|---|---|---|
|
56° |
0,829 |
0,559 |
1,483 |
|
57° |
0,839 |
0,545 |
1,540 |
|
58° |
0,848 |
0,530 |
1,600 |
|
59° |
0,857 |
0,515 |
1,664 |
|
60° |
0,866 |
0,500 |
1,732 |
Portanto, a medida de abertura do ângulo procurado é 58graus.
c) Qual é a medida de abertura do ângulo cujos seno e cosseno têm valores iguais?
Para responder a essa pergunta, localizamos, nas colunas “seno de x” e “cosseno de x”, valores iguais. Depois, encontramos a medida de abertura do ângulo correspondente a esses valores.
|
x |
sen x |
cos x |
tg x |
|---|---|---|---|
|
43° |
0,682 |
0,731 |
0,933 |
|
44° |
0,695 |
0,719 |
0,966 |
|
45° |
0,707 |
0,707 |
1,000 |
|
46° |
0,719 |
0,695 |
1,036 |
|
47° |
0,731 |
0,682 |
1,072 |
Portanto, a medida de abertura do ângulo procurado é 45graus.
Observação
A calculadora científica é um recurso útil e poderá ajudar no cálculo das razões trigonométricas dos ângulos.

Para a realização dos cálculos, utilize as teclas

para seno,

para cosseno e

para tangente e verifique se a calculadora científica está no modo DEG (grau = degree).
Vamos fazer um teste? Digite a sequência de teclas a seguir e confirme o resultado no visor.
•

•

•

Lembre-se de que calculadoras diferentes, por vezes, requerem distintos procedimentos para os cálculos.
Atividades
Faça as atividades no caderno.
30.

Utilizando uma calculadora científica ou a tabela de razões trigonométricas, determine, com aproximação de três casas decimais, os valores de:
a) seno de 17graus
b) cosseno de 2graus
c) tangente de 26graus
d) seno de 43graus
e) cosseno de 38graus
f) tangente de 50graus
g) cosseno de 14graus
h) tangente de 88graus
31. Utilizando a tabela de razões trigonométricas, determine a (em grau), sabendo que:
a) seno de a = 0,122
b) cosseno de a = 0,342
c) tangente de a = 0,7
d) seno de a = 0,829
e) tangente de a = 0,176
f) seno de a = 0,988
g) cosseno de a = 0,777
h) tangente de a = 1,732
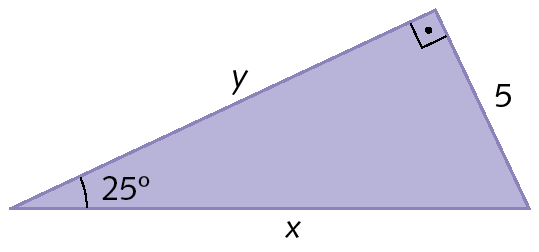
32. Calcule o valor de x e y nestes triângulos retângulos.
a)
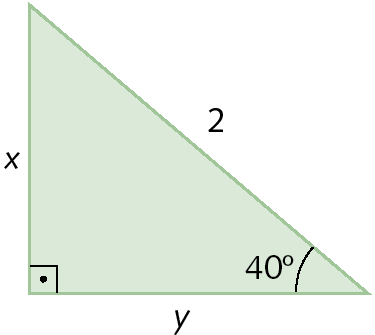
b)

5 Resolução de problemas
Neste tópico, vamos estudar alguns problemas que envolvem aplicações das razões trigonométricas estudadas.
Problema 1
De um posto de observação situado a 100 métros de um prédio, vê-se o ponto mais alto desse prédio sob um ângulo de medida de abertura de 44graus. Determine a medida da altura do prédio, sabendo que o posto está a 1 métro do solo. (Utilize: seno de 44graus = 0,70; cosseno de 44graus = 0,72; tangente de 44graus = 0,97.)
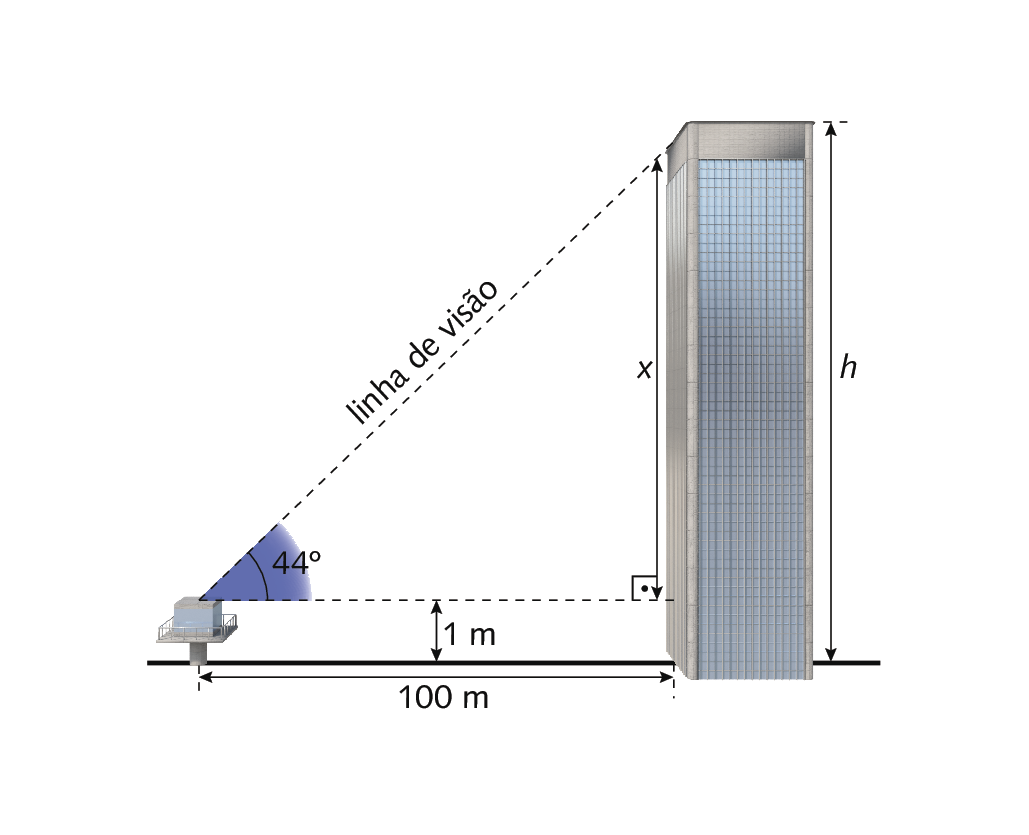
Como x corresponde à medida de comprimento do cateto oposto ao ângulo de medida de abertura de 44graus, podemos escrever:
Sentença matemática. Tangente de 44 graus é igual a x sobre 100 metros.
x = 100 métros ⋅ tangente de 44graus
x = 100 métros ⋅ 0,97
x = 97 métros
Então:
h = x + 1 métro
h = 97 métros + 1 métro = 98 métros
Portanto, a medida da altura do prédio é 98 métros.
Problema 2
Um avião, a uma medida da altura de .2000 métros, é visto por dois observadores que estão nos pontos a e B, sob ângulos de medidas de abertura de 28graus e 40graus, respectivamente. Qual é a medida da distância aproximada entre esses dois observadores? (Utilize: seno de 28graus = 0,47; cosseno de 28graus = 0,88; tangente de 28graus = 0,53; seno de 40graus = 0,64; cosseno de 40graus = 0,77; tangente de 40graus = 0,84.)
De acôrdo com o esquema a seguir, temos os triângulos retângulos BVC e á vê cê, com um dos catetos comum (
Segmento de reta VC.). A medida da distância entre os dois observadores é representada por x, que corresponde a uma parte da medida de comprimento do cateto
Segmento de reta AC.do triângulo á vê cê.
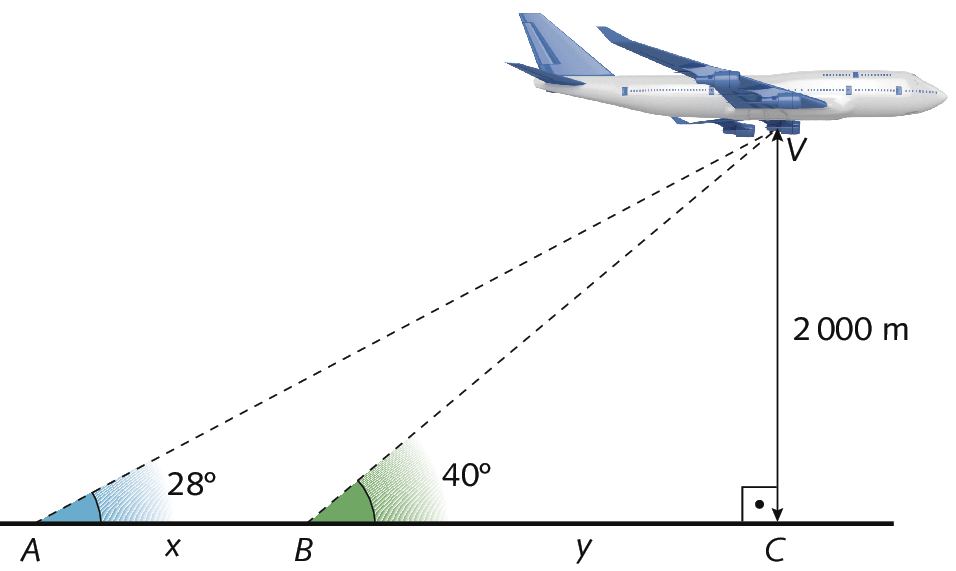
Do triângulo BVC, temos:
Tangente de 40 graus é igual a 2 mil metros, sobre y.
y é igual a fração de numerador 2 mil metros e denominador tangente de 40 graus
y é igual a 2 mil metros sobre 0,84. metros.
y ≃ .2380,95 métros
E, do triângulo á vê cê, temos:
t
tangente de 28 graus é igual a fração de numerador 2 mil metros e denominador x mais y
x mais y é igual a fração de numerador 2 mil metros e denominador tangente de 28 graus
x mais y é igual a fração de numerador 2 mil metros e denominador 0,53
x + y ≃ .3773,58 métros
x ≃ .3773,58 métros ‒ .2380,95 métros
x ≃ .1392,63 métros
Portanto, a medida da distância aproximada entre os dois observadores é .1392,63 métros.
Problema 3
Há situações em que não podemos utilizar uma trena para medir determinado comprimento, como a largura de um rio. Nesses casos, é comum utilizar um instrumento ótico chamado teodolito, que mede a abertura de um ângulo. Então, por meio da Trigonometria, é possível descobrir a medida desejada.
Observe esta situação representada. Determine a medida r da largura do rio.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
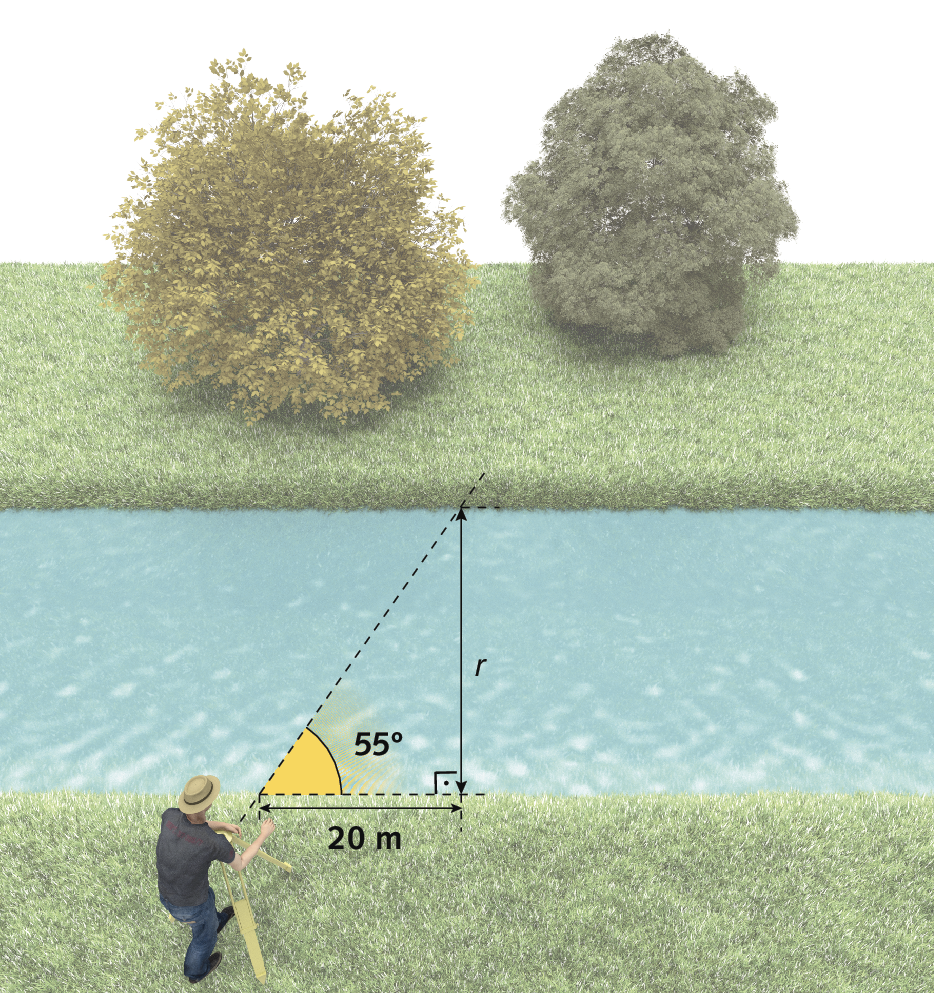
(Utilize: seno de 55graus = 0,82; cosseno de 55graus = 0,57; tangente de 55graus = 1,43.)
Do triângulo representado, temos:
Sentença matemática. Tangente de 55 graus é igual a r sobre 20 metros.
r = 20 métros ⋅ tangente de 55graus
r = 20 métros ⋅ 1,43 = 28,6 métros
Logo, a largura do rio mede 28,6 métros.
Atividades
Faça as atividades no caderno.
33. Um observador, distante 80 métros do mastro de uma bandeira, vê seu ponto mais alto sob o ângulo de medida de abertura de 38graus. A distância dos olhos dele ao chão mede 1,70 métro. Qual é a medida aproximada da altura do mastro?

34. Do alto de uma torre que mede 50 métros de altura, localizada em uma ilha, avista-se a praia sob um ângulo de medida de abertura de 45graus em relação à horizontal. Quanto mede a distância da torre à praia?
35. Observe o esquema e calcule a medida da distância (x) a que o garoto deve estar da tela.

36. Um foguete é lançado de uma rampa situada no solo, sob um ângulo de medida de abertura de 30graus. A que medida da altura estará o foguete após percorrer 8 quilômetros em linha reta?

37. Determine a medida do comprimento da sombra projetada por uma torre que mede
40 raiz quadrada de 3.métros de altura, sob ângulo de elevação de medida de abertura de 60graus em relação ao Sol.

38.

Uma das preocupações dos engenheiros de uma cidade litorânea é verificar as medidas das inclinações α, em relação à vertical, dos prédios situados na orla marítima. Essas inclinações podem ocorrer em razão de problemas nas fundações construídas sobre o solo arenosoglossário . Os valores aceitos, segundo os engenheiros, devem satisfazer esta condição: tangente de α ⩽ 0,052.
Reúna-se com um colega e determinem a medida da inclinação máxima aceita pelos engenheiros em um prédio situado à beira-mar.


6 Plano cartesiano
O plano cartesiano é composto de um eixo horizontal e um vertical, chamados de eixo das abscissas (eixo x) e eixo das ordenadas (eixo y), respectivamente, e podemos representar pontos ou polígonos em um plano.
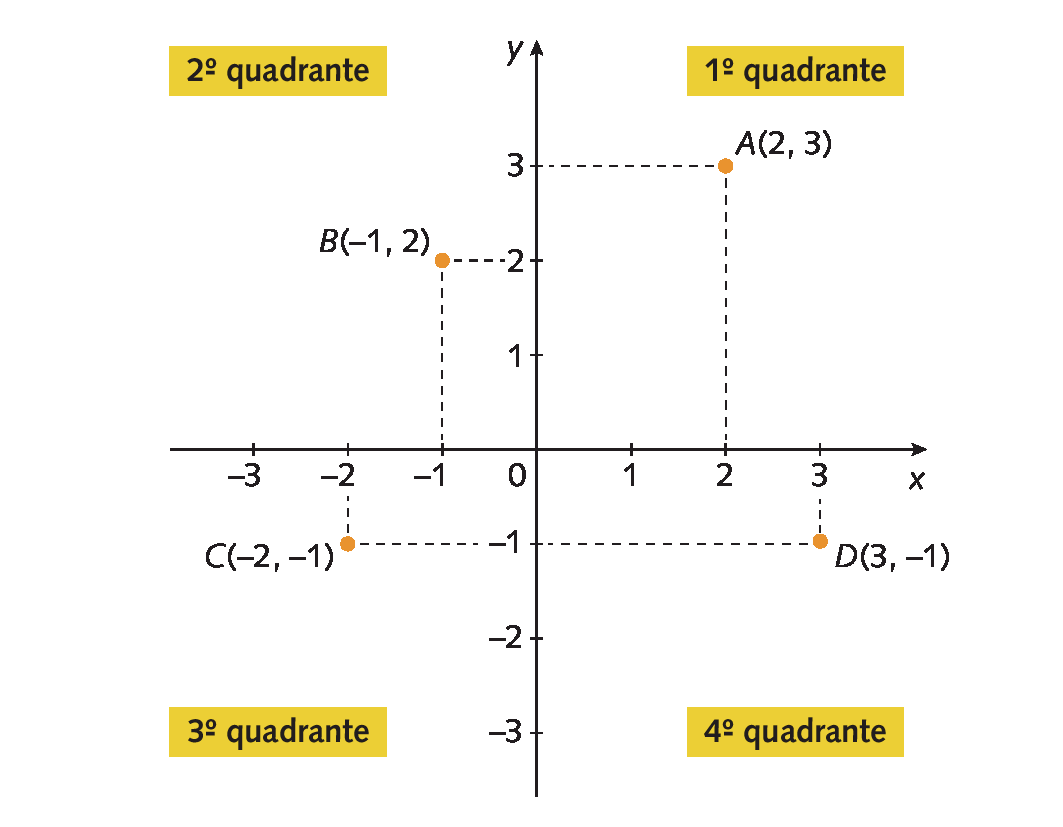
Analise a representação dos pontos a, B, C e D, cujos pares ordenados são (2, 3), (‒1, 2), (‒2, ‒1) e (3, ‒1), respectivamente.
Em um plano cartesiano:
• os pontos (x, y) do 1º quadrante têm abscissas e ordenadas positivas (x > 0 e y > 0);
• os pontos (x, y) do 2º quadrante têm abscissas negativas e ordenadas positivas (x < 0 e y > 0);
• os pontos (x, y) do 3º quadrante têm abscissas e ordenadas negativas (x < 0 e y < 0);
• os pontos (x, y) do 4º quadrante têm abscissas positivas e ordenadas negativas (x > 0 e y < 0).
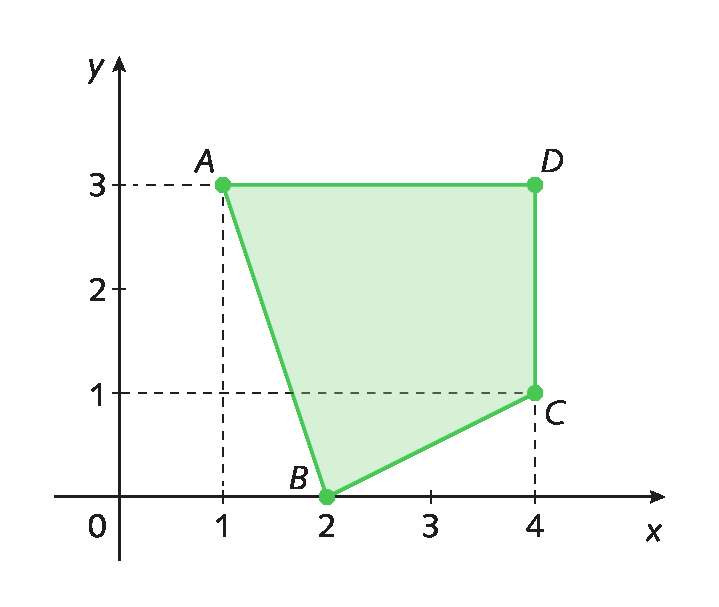
Observe, agora, o quadrilátero a bê cê dê representado no plano cartesiano. Os pontos a(1, 3), B(2, 0), C(4, 1) e D(4, 3) correspondem aos vértices do polígono.
Conhecendo as coordenadas dos vértices de um polígono, além de localizá-lo no plano cartesiano, podemos calcular as medidas de comprimento de seus lados.
Medidas de comprimento dos lados de um polígono
Continuando com o exemplo do quadrilátero a bê cê dê, verifique que:
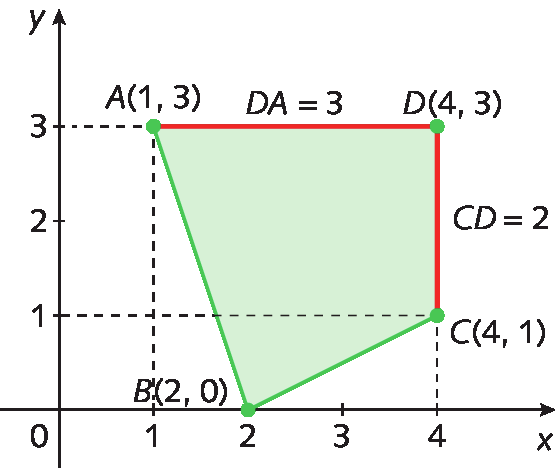
• as ordenadas dos pontos a e D têm o mesmo valor (3). Isso significa que o segmento de reta
D Aé paralelo ao eixo x;
• as abscissas dos pontos C e D, que determinam o lado
Segmento de reta CD., são iguais (4). Isso significa que
Segmento de reta CD.é paralelo ao eixo y.
Para determinar a medida de comprimento de
Segmento de reta DA.(paralelo ao eixo x), calculamos a diferença entre as abscissas dos pontos D e a:

Assim, a medida de comprimento de
D Aé 3 unidades de medida de comprimento.
Da mesma maneira, podemos determinar a medida de comprimento do lado
Segmento de reta CD.(paralelo ao eixo y), calculando a diferença entre as ordenadas dos pontos D e C:

Assim, a medida de comprimento de
Segmento de reta CD.é duas unidades de medida de comprimento.
Como os outros dois lados do quadrilátero (
Segmento de reta ABe
Segmento de reta BC.) não são paralelos aos eixos x e y, para determinar suas medidas de comprimento, podemos usar o teorema de Pitágoras.
Considere os pontos que determinam o lado
Segmento de reta AB, A(1, 3) e B(2, 0), e o ponto ê de coordenadas (1, 0), obtendo, assim, o triângulo retângulo á bê é, como indicado a seguir.
Nesse caso, temos:
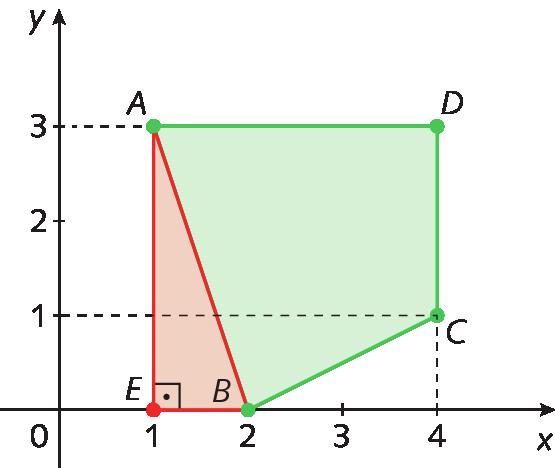
EA = 3 ‒ 0 = 3
BE = 2 ‒ 1 = 1
Aplicando o teorema de Pitágoras no triânguloá bê é, determinamos a medida de comprimento de
Segmento de reta AB.:
ABelevado a 2 = EAelevado a 2 + BEelevado a 2
ABelevado a 2 = 3elevado a 2 + 1elevado a 2 = 9 + 1 = 10
Sentença matemática. AB é igual raiz quadrada de 10.
Portanto, a medida de comprimento de
A Bé
raiz quadrada de 10unidades de medida de comprimento.
De modo análogo, determinamos a medida de comprimento de
Segmento de reta BC.. Para isso, consideramos os pontos B e C, o ponto F de coordenadas (4, 0) e o triângulo retângulo BCF. Assim:
CF = 1 ‒ 0 = 1
FB = 4 ‒ 2 = 2
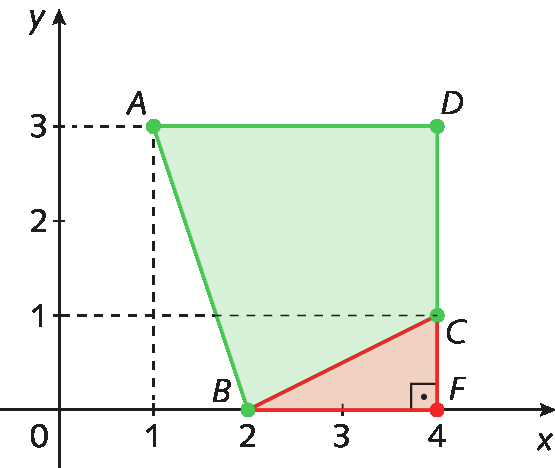
Aplicando o teorema de Pitágoras no triânguloBCF, determinamos a medida de comprimento de
Segmento de reta BC.:
BCelevado a 2 = CFelevado a 2 + FBelevado a 2
BCelevado a 2 = 1elevado a 2 + 2elevado a 2 = 1 + 4 = 5
Sentença matemática. BC é igual a raiz quadrada de 5.
Portanto, a medida de comprimento de
Segmento de reta BC.é
raiz quadrada de 5unidades de medida de comprimento.
Observações
1. Calcular a medida de comprimento do segmento de reta
A Bequivale a calcular a medida da distância entre os pontos a e B.
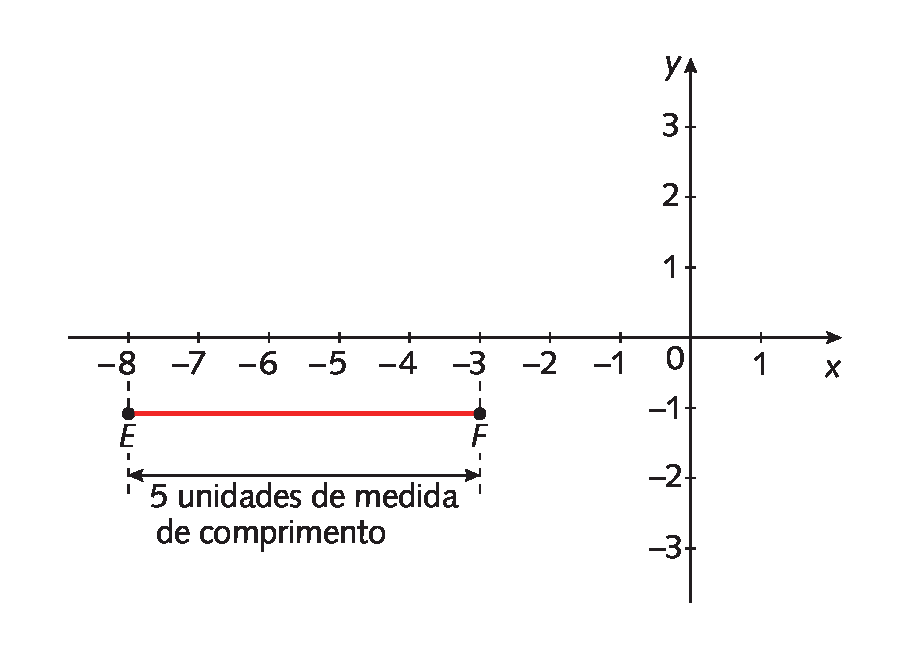
2. É importante lembrar que a medida da distância é dada em módulo; assim, para um segmento de reta
E Fde coordenadas ê(‒8, ‒1) e éfe(‒3, ‒1), a medida da distância entre os pontos ê e F é |‒8 ‒ (‒3)|, que resulta em 5 unidades de medida de comprimento.
Coordenadas do ponto médio de um segmento de reta
Acompanhe a situação a seguir.
Sejam os pontos a(1, 1) e B(5, 4) extremidades do segmento de reta de reta
A B. Vamos determinar as coordenadas (x, y) de M, o ponto médio de
A B.
Para auxiliar na resolução, vamos representar o segmento de reta
Segmento de reta ABno plano cartesiano e considerar o ponto C de coordenadas (5, 1), de modo a obter o triângulo retângulo ABC.
Consideramos M o ponto médio de
Segmento de reta AB, e o ponto D pertencente a
Segmento de reta AC., de modo que á ême dê seja um triângulo retângulo.
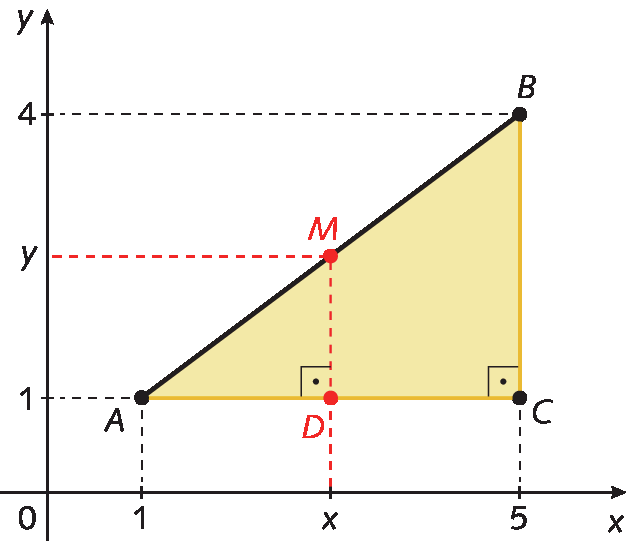
é paralelo ao eixo y.
é paralelo ao eixo y.
Observe que, como o ponto D pertence a
Segmento de reta AC., sua ordenada é 1, ao passo que sua abscissa é x, a mesma do ponto M, pois
Segmento de reta DM.é paralelo ao eixo y.
Pelo caso á á, com o ângulo reto e o ângulo
A.em comum, os triângulos á ême dê e á bê cê são semelhantes. Logo, as medidas de comprimento de seus lados são proporcionais. Desse modo, podemos escrever:
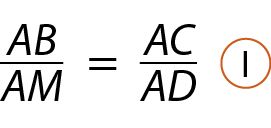
Como M é ponto médio de
Segmento de reta AB, então:
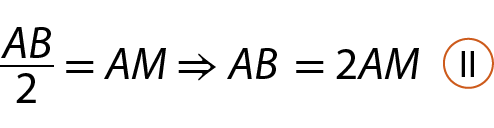
Substituindo

em

, obtemos:
Esquema. Razão. 2AM sobre AM é igual a AC sobre AD, implica que, AC é igual a 2AD.
Sabemos que: AC = 5 ‒ 1 e AD = x ‒ 1. Logo:
5 ‒ 1 = 2(x ‒ 1)
4 = 2x ‒ 2
x = 3
Para determinar y, podemos escrever:
Esquema. AB sobre AM é igual a BC sobre MD, implica que, 2 AM sobre AM, é igual a BC sobre MD, implica que, BC é igual a 2 MD.
Como BC = 4 ‒ 1 e MD = y ‒ 1, então:
4 ‒ 1 = 2(y ‒ 1)
3 = 2y ‒ 2
y = 2,5
Assim, concluímos que as coordenadas do ponto médio M são (3; 2,5).
Atividades
Faça as atividades no caderno.
39. Em cada caso, calcule a medida da distância entre os pontos a e B.
a)
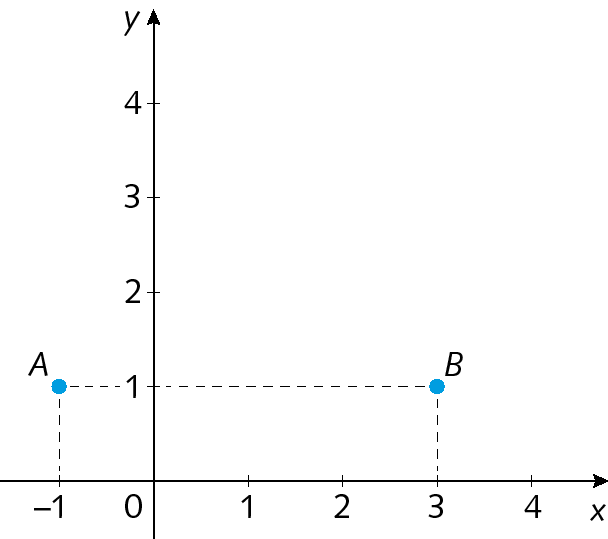
b)

c)

40. As coordenadas dos vértices do quadrilátero a bê cê dê são a(‒1, ‒1), B(‒1, 3), C(2, 3) e D(2, ‒1).
a) Represente esse quadrilátero em um plano cartesiano.
b) Como podemos classificar esse quadrilátero?
c) Calcule a medida de perímetro desse quadrilátero.
41. Determine a medida de comprimento da hipotenusa do triângulo retângulo a seguir.

42. Considere o quadrilátero a bê cê dê representado no plano cartesiano a seguir.
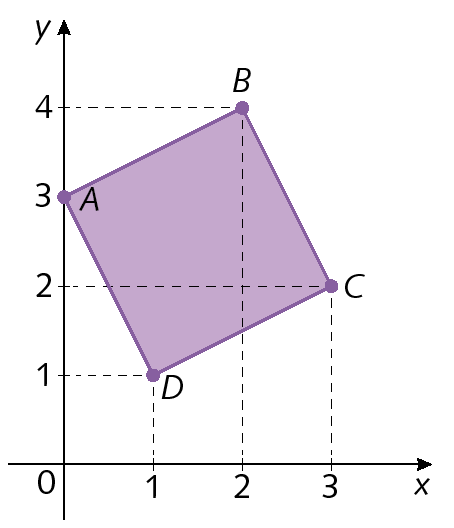
a) Quais são as coordenadas dos vértices desse quadrilátero?
b) Determine as medidas de perímetro e de área desse quadrilátero.
43. Em um plano cartesiano, represente:
• um ponto a distante 5 unidades de medida de comprimento do eixo das abscissas;
• um ponto B distante 5 unidades de medida de comprimento do eixo das ordenadas;
• um ponto C de coordenadas (5, 3);
• um ponto D de coordenadas (2, 5).
a) Que coordenadas a póde assumir de modo que a medida de comprimento do segmento de reta
A Dseja de 3 unidades de medida de comprimento?
b) Que coordenadas B póde assumir de modo que a medida de comprimento do segmento de reta
B Cseja de 6 unidades de medida de comprimento?
c) Que coordenadas os pontos a e B podem assumir de modo a obter um trapézio isósceles a bê cê dê?
44. Determine a medida da distância do ponto P(5, ‒dois):
a) à origem;
b) ao eixo das abscissas;
c) ao eixo das ordenadas.
45. Quais são as coordenadas do ponto médio de cada um dos segmentos de reta representados a seguir?
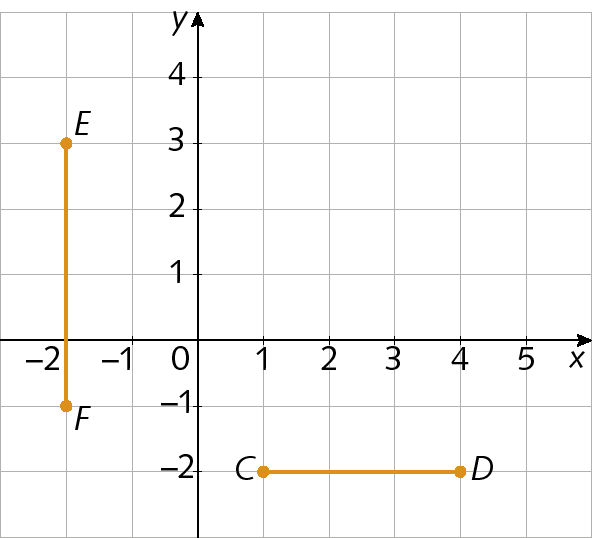
46.

Utilizando um software de geometria dinâmica, construa um quadrado a bê cê dê de modo que cada um de seus vértices esteja localizado em quadrantes diferentes de um plano cartesiano. Depois, responda:
a) Quantos quadrados podem ser construídos obedecendo essa indicação?
b) O que poderia ser acrescentado no enunciado do problema de modo que a construção do quadrado:
• tenha resposta única;
• tenha duas respostas possíveis;
• não tenha solução.
c)

Converse com um colega e comparem as alterações propostas no item b. Verifiquem se há mais de uma maneira de fazer essas alterações no enunciado.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Triângulo retângulo
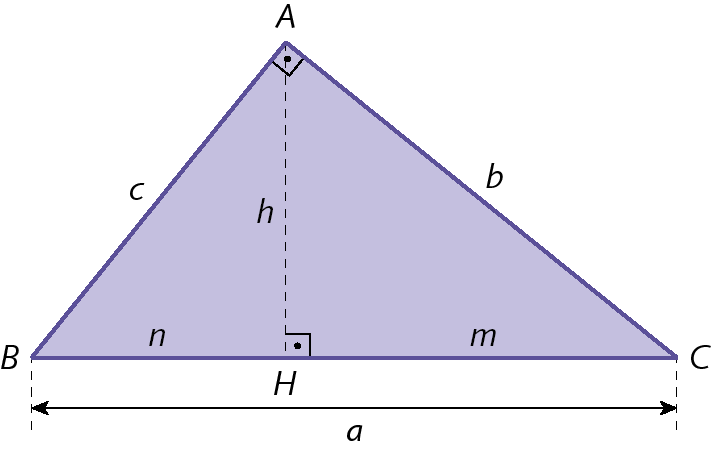
a → medida de comprimento da hipotenusa
b, c → medidas de comprimento dos catetos
h → medida de comprimento da altura relativa à hipotenusa
m, n → medidas de comprimento das projeções ortogonais dos catetos sobre a hipotenusa
Relações métricas no triângulo retângulo
1. Determine o valor desconhecido nos triângulos retângulos a seguir.
a)
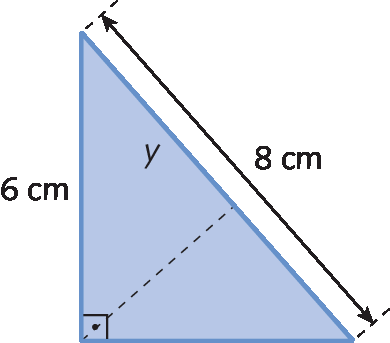
b)
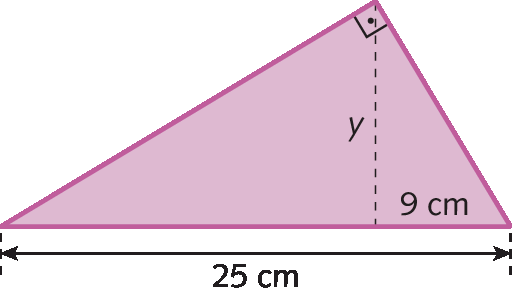
c)
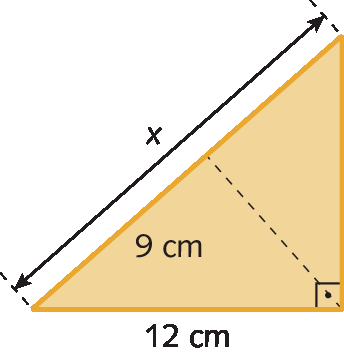
2. Sabendo que, em um triângulo retângulo, o comprimento da hipotenusa mede 25 centímetros e o comprimento de um dos catetos mede 7 centímetros, determine:
a) as medidas de comprimento das projeções ortogonais dos catetos sobre a hipotenusa;
b) a medida de comprimento do outro cateto;
c) a medida de comprimento da altura relativa à hipotenusa.
Teorema de Pitágoras e aplicações
Em todo triângulo retângulo, o quadrado da medida de comprimento da hipotenusa é igual à soma dos quadrados das medidas de comprimento dos catetos. Assim, seja a a medida de comprimento da hipotenusa e b e c as medidas de comprimento dos catetos, temos:
aelevado a 2 = belevado a 2 + celevado a 2
Aplicações do teorema de Pitágoras
Diagonal de um quadrado
Em um quadrado com lados de medida de comprimento x, a medida de comprimento da diagonal é
X raiz quadrada de 2..
Altura de um triângulo equilátero
Em um triângulo equilátero com lados de medida de comprimento x, a medida de comprimento da altura é
Sentença matemática. x raiz quadrada de 3, sobre 2..
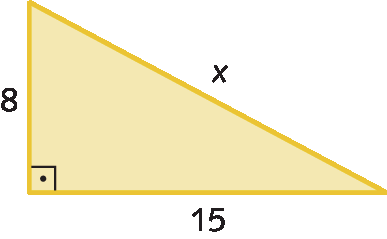
3. Calcule os valores de x e de y indicados nas figuras.
a)
b)
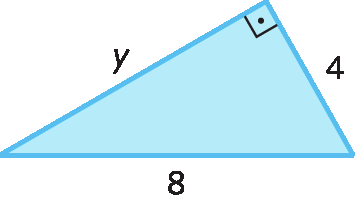
4. Uma escada de 2,5 métros de medida de comprimento é encostada em uma parede com o pé afastado 1,5 métro da parede. Quanto mede a altura que a escada atinge?
5. Calcule:
a) a medida de comprimento da diagonal de um retângulo, cujos lados medem 8 centímetros e 15 centímetros de comprimento;
b) a medida de comprimento da diagonal de um quadrado cujo lado mede 20 métros de comprimento;
c) a medida de comprimento da altura de um triângulo equilátero cujo lado mede 8 centímetros de comprimento.
Razões trigonométricas no triângulo retângulo
|
x |
30° |
45° |
60° |
|---|---|---|---|
|
sen x |
|
|
|
|
cos x |
|
|
|
|
tg x |
|
1 |
|
6. Determine o valor desconhecido nos triângulos retângulos a seguir:
a)
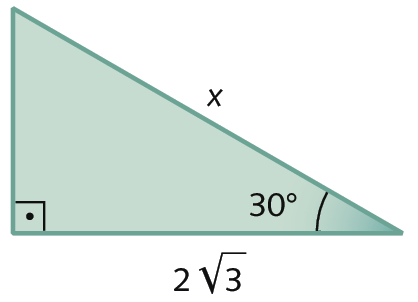
b)
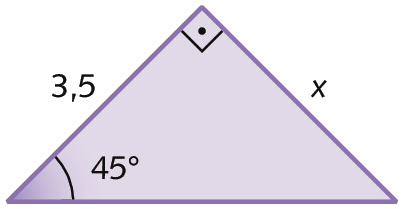
c)
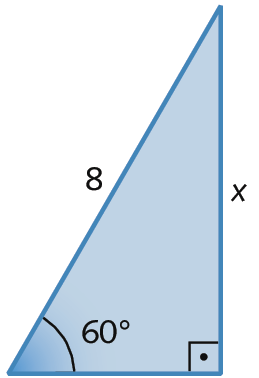
d)
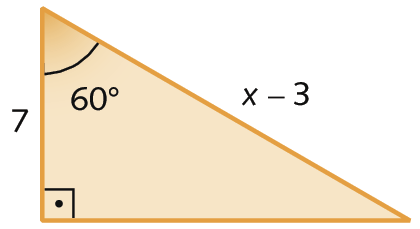
7. A pipa de Joaquim ficou presa em uma árvore. A linha da pipa ficou esticada, formando com o chão um ângulo de medida de abertura de 45graus. O comprimento da linha da pipa mede 8,5 métros. Determine a medida da altura da pipa em relação ao solo. (Utilize:
raiz quadrada de 2 é igual à 1,48. Um avião está a .1300 métros de medida de altura quando começa um movimento de descida para a pista de aterrissagem, em uma linha imaginária que fórma um ângulo de medida de abertura de 30graus com o solo. Qual será a medida da distância percorrida pelo avião até tocar o solo?
9. Observe o triângulo a seguir e determine:
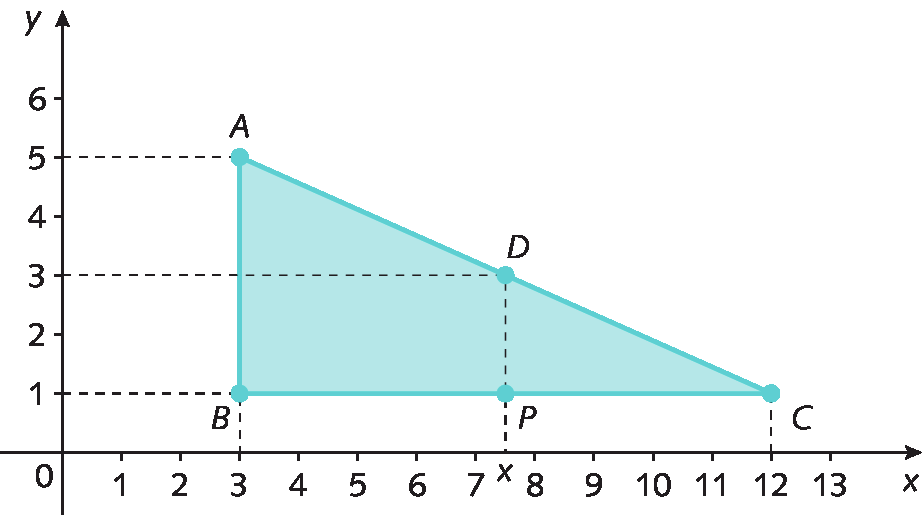
a) as coordenadas dos vértices;
b) as medidas de comprimento dos lados do triângulo em u, unidade de medida de comprimento;
c) a abcissa x do ponto médio D do lado
Segmento de reta AC..
Glossário
- Liga metálica
- : Mistura formada por dois ou mais elementos, sendo pelo menos um deles um metal.
- Voltar para o texto
- Solo arenoso
- : Tipo de solo com pouca umidade, com teor de areia superior a 70%.
- Voltar para o texto