Capítulo 8 Circunferência, arcos e ângulos
Trocando ideias
Wassily Wassilyevich Kandinsky (1866-1944) foi um artista russo. No início de sua carreira, retratou a arte popular russa e paisagens. No entanto, suas obras ganharam destaque quando ele se dedicou à arte abstrataglossário . Observe a seguir a reprodução de uma de suas obras.

▸


Na obra Composição oito, é possível notar figuras que se parecem com circunferências e arcos de circunferência. O que você sabe sobre essas figuras geométricas planas? Converse com os colegas.
▸

Reúna-se com um colega e pesquisem obras de arte em que é possível identificar figuras que se parecem com circunferências e arcos de circunferência. Depois, compartilhem com a turma o que encontraram.
Conheça mais
No site da Galeria Lenbachhaus de Munique (Alemanha), podem ser vistas diversas obras de candinsqui.
Neste capítulo, vamos ampliar os conhecimentos sobre circunferência e estudar arcos e ângulos central e inscrito a uma circunferência.

1 Circunferência
Analisamos uma obra de arte em que é possível identificar figuras que lembram circunferências.
Em Geometria:
Circunferência é a figura formada por todos os pontos de um plano que estão à mesma medida da distância de um ponto fixo desse plano. O ponto fixo é chamado de centro da circunferência.
Considere esta figura.
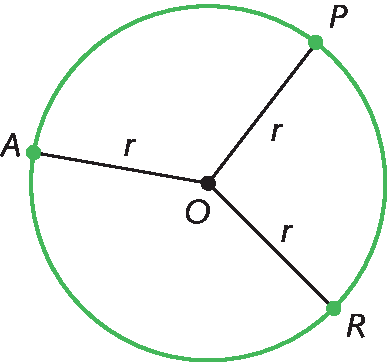
• O ponto óh é o centro da circunferência (ponto fixo).
• Os pontos a, P e R estão a uma medida de distância r do centro da circunferência (ponto óh), ou seja, são pontos da circunferência.
• Os segmentos de reta
OA,
OPe
ORsão raios da circunferência e têm medida de comprimento r.
Raio de uma circunferência
Temos que:
• raio é o segmento de reta que tem uma extremidade no centro da circunferência e a outra em qualquer ponto pertencente à circunferência;
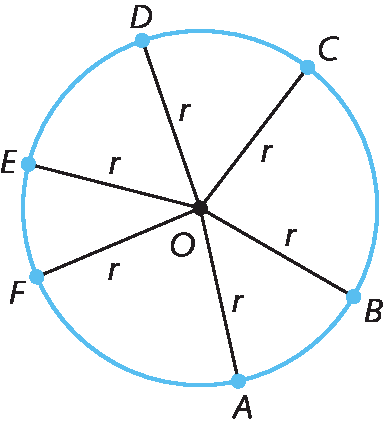
O: centro da circunferência
a, B, C, D, ê, F: pontos da circunferência
segmento de reta O A
,
segmento de reta O B,
segmento de reta O C,
segmento de reta O D,
segmento de reta O E,
segmento de reta O F: raios da circunferência
• em uma circunferência, podemos traçar infinitos raios e todos serão congruentes;
segmento OA é congruente ao segmento OB que é congruente ao segmento OC que é congruente ao segmento OD que é congruente ao segmento OE que é congruente ao segmento OF e assim por diante
OA = OB = OC = OD = OE = OF = ... = r
• quando duas circunferências têm raios com a mesma medida de comprimento, dizemos que as circunferências são congruentes.
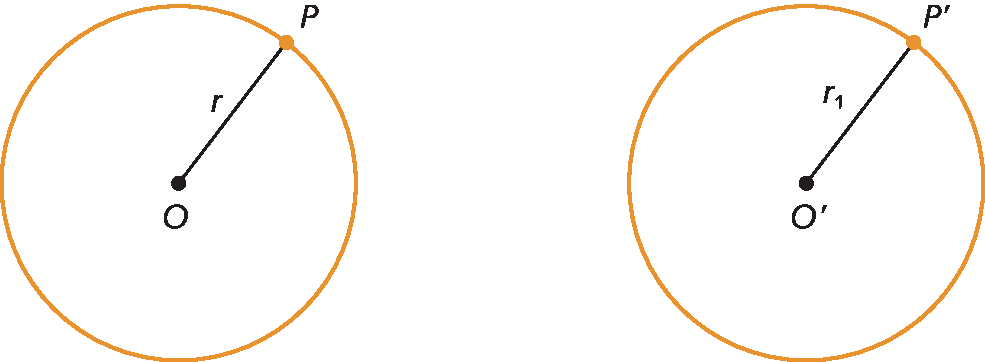
Temos:
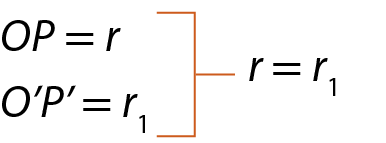
Como r = érre minúsculo₁, então a circunferência de centro O é congruente à circunferência de centro ó linha.
Corda e diâmetro de uma circunferência
A corda e o diâmetro são dois importantes elementos relativos a uma circunferência.
Corda é o segmento de reta com extremidades em dois pontos distintos de uma circunferência.
Considere a seguinte figura.
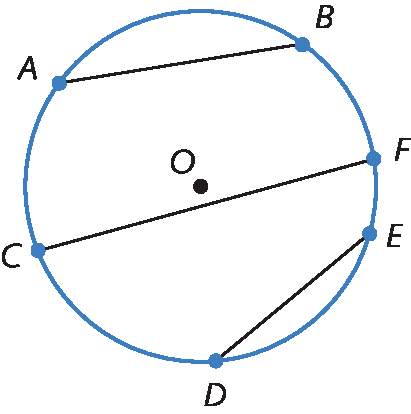
,
segmento de reta C Fe
segmento de reta D Esão exemplos de cordas da circunferência.
Diâmetro é o segmento de reta com extremidades em dois pontos distintos de uma circunferência, passando sempre pelo centro.
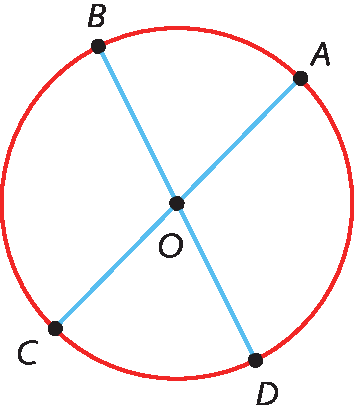
Na figura a seguir, os segmentos de reta
ACe
BDsão diâmetros da circunferência de centro O.
Podemos observar que, em uma circunferência qualquer com centro O e diâmetro com extremidades em A e P, temos:
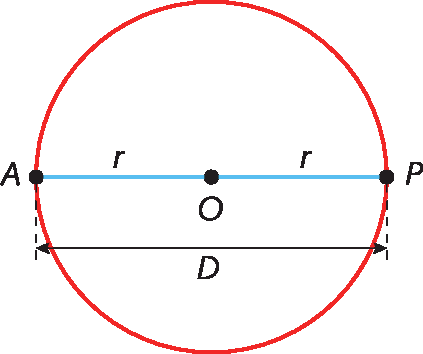
•
Segmento de reta AOé raio de medida de comprimento r;
•
Segmento de reta OPé raio de medida de comprimento r;
•
Segmento de reta APé diâmetro de medida de comprimento D.
Assim, verificamos que:
á pê = á ó + ó pê
D = r + r = 2r
Logo, a medida de comprimento do diâmetro (D) é igual ao dôbroda medida de comprimento do raio (r ).
Observações
1. O diâmetro é a maior corda da circunferência.
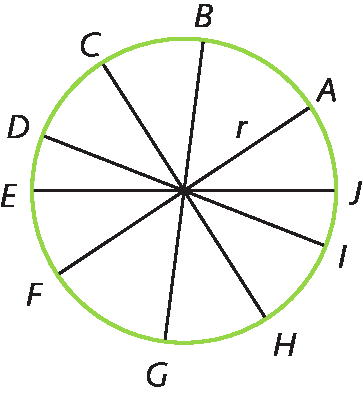
2. Em uma circunferência, podemos traçar infinitos diâmetros e todos serão congruentes. Nesta figura, temos:
AF = BG = CH = dê í = é jóta = ... = 2r
Atividades
Faça as atividades no caderno.
1. Na figura a seguir, o contorno do relógio se parece com uma circunferência. Considere que a medida de comprimento do diâmetro desse relógio é 40 centímetros.

a) Determine a medida de comprimento do raio desse relógio.
b) Identifique duas cordas na figura.
c) Identifique um diâmetro na figura.
d) Identifique um raio na figura.
2. Em uma circunferência, a medida de comprimento do diâmetro é 1,44 métro. Quanto mede o comprimento do raio dessa circunferência?
3. Copie os itens no caderno, substituindo cada

por uma palavra correspondente, tornando a sentença verdadeira.
a)

é o segmento de reta que une o centro a qualquer ponto da circunferência.
b) Em uma circunferência, podemos traçar infinitos

. Todos eles são

.
c) Duas circunferências são

quando os raios têm a mesma medida de comprimento.
d) A maior corda da circunferência é o

.
4. Observe a figura e responda às questões.
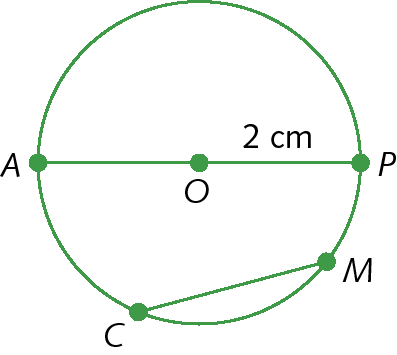
a) Qual é a medida de comprimento de
OP?
b) Qual é a medida de comprimento de
AP?
c) A medida de comprimento de
CMé maior que 4 centímetros ou menor? Justifique sua resposta.
5. Determine:
a) a medida de comprimento do diâmetro de uma circunferência cujo comprimento do raio mede 4,5 centímetros;
b) a medida de comprimento do raio de uma circunferência cujo comprimento do diâmetro mede 17 centímetros.
6. Observe a circunferência de centro O a seguir e responda às questões.
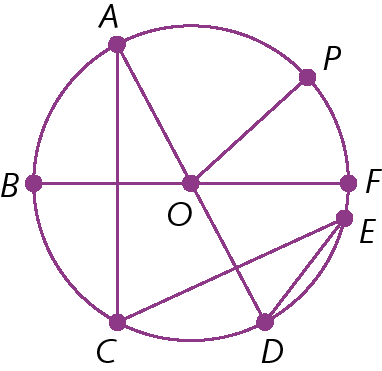
a) Quais são os segmentos de reta que representam os raios?
b) Quais são os segmentos de reta que representam as cordas?
c) Quais são os segmentos de reta que representam os diâmetros?
7. Considere a circunferência de centro óh e classifique o triângulo á ó bê quanto às medidas de comprimento dos lados. Depois, determine quanto medem as aberturas dos ângulos
ângulo OABe
ângulo OBA.

8. Considerando a circunferência de centro óh, mostre que as cordas
Segmento de reta ACe
Segmento de reta BDsão congruentes.


Lendo e aprendendo

Marte, o planeta vermelho
Em 2021, diversas missões espaciais pretendem estudar Marte. Veja o que já se sabe sobre o planeta vizinho da Terra e o que os cientistas ainda querem descobrir
Sondas enviadas para Marte
Agências espaciais dos Estados Unidos, Rússia, Índia, China, Europa e Emirados Árabes Unidos já enviaram sondas para analisar o planeta vizinho. Esses robôs tiram fotos, coletam amostras de solo e rochas, fazem medidas do território, entre outras funções. Além das sondas, cientistas estudam o planeta por meio da observação e de outras técnicas.
Os objetivos dos estudos são…
… reunir mais informações sobre a história, clima e formação de Marte. Acredita-se que o planeta vermelho possa nos ajudar a entender melhor como o Sistema Solar foi constituído e como os planetas passaram por transformações ao longo do tempo.
… descobrir se já existiram ou ainda existem seres vivos em Marte. Já se sabe que, no passado, o planeta tinha rios e lagos. Como a água é essencial para haver vida, isso póde ser uma pista de que Marte tenha abrigado fórmas de vida antigamente.
… estudar a possibilidade de, no futuro, enviar seres humanos para Marte. Até hoje, a humanidade só foi capaz de mandar sondas até o planeta vermelho.
Temperaturas médias
Terra: 14 graus Célsius
Marte: 63 graus Célsius
Diâmetro da Terra: .12755,66 quilômetros
Diâmetro de Marte: .6791,43 quilômetros
A Terra é o terceiro planeta mais próximo do Sol. Ela só fica atrás de Mercúrio e Vênus.
[reticências]
Ficha técnica
Posição no sistema solar: quarto planeta mais próximo do Sol.
Duração de um ano (tempo que leva para dar uma volta ao redor do Sol): equivalente a 687 dias terrestres.
Temperatura média: 63 graus Célsius.
Luas: Fobos e Deimos.
Fontes: Náza e Nature.
Marte, o planeta vermelho. Jornal Joca, número 165, página 7, 1 a 15 de março de 2021.
Atividades
Faça as atividades no caderno.
1. Copie as afirmações no caderno e marque V para as verdadeiras e F para as falsas.
a) (

) As sondas que foram enviadas para Marte já encontraram seres vivos.
b) (

) Seres humanos já foram enviados para Marte.
c) (

) Estudar Marte é importante para entender como o Sistema Solar foi constituído.
d) (

) A medida de comprimento do diâmetro da Terra é maior que a medida de comprimento do diâmetro de Marte.
2.

O diâmetro de uma esfera é o segmento de reta com extremidades em dois pontos distintos da esfera, passando sempre pelo centro. Supondo que os planetas Terra e Marte se parecem com uma esfera, use uma calculadora para determinar:
a) a medida de comprimento do raio da Terra;
b) a medida de comprimento do raio de Marte.
3.


Na sua opinião, qual é a importância de estudos como os que estão sendo realizados em Marte? Converse com os colegas.

2 Posições de um ponto em relação a uma circunferência
Observe a figura.
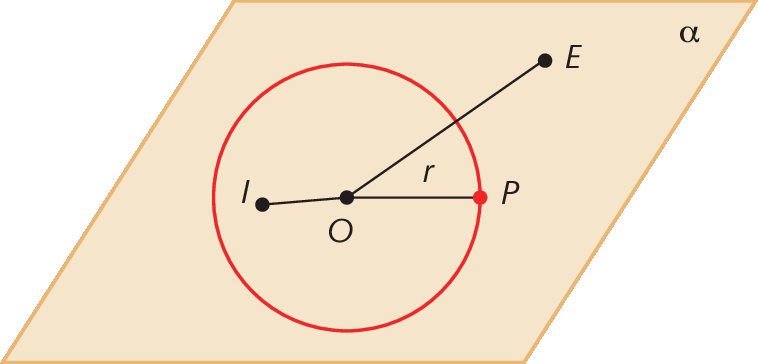
A circunferência está contida no plano α, e os pontos P, ê e ih desse plano são, respectivamente, pertencente, externo e interno à circunferência.
Dizemos que:
• considerando um ponto P e uma circunferência de centro óh, se a medida da distância entre O e P for igual à medida de comprimento do raio (ó pê = r), o ponto P pertence à circunferência;
• considerando um ponto ê e uma circunferência de centro óh, se a medida da distância entre O e ê for maior que a medida de comprimento do raio (ó é > r), o ponto ê é externo à circunferência;
• considerando um ponto ih e uma circunferência de centro óh, se a medida da distância entre O e ih for menor que a medida de comprimento do raio (ó í < r), o ponto ih é interno à circunferência.
Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso nas atividades 10 e 11.
9. Observe os pontos desta figura e indique:
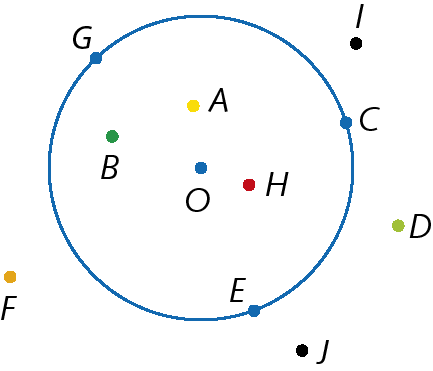
a) os pontos pertencentes à circunferência;
b) os pontos externos à circunferência;
c) os pontos internos à circunferência.
10. Desenhe, no caderno, uma circunferência com:
a) medida de comprimento do raio igual a 2 centímetros;
b) centro óh ;
c) pontos a, B e C pertencentes à circunferência;
d) pontos D, ê e F externos à circunferência;
e) pontos G, H, ih e J internos à circunferência.
11. Com uma régua, meça o comprimento dos raios érre minúsculo₁ e érre minúsculo₂ das circunferências C₁ e C₂, respectivamente. Em seguida, copie esta figura no caderno e desenhe:

• os pontos a, B e C, externos à C₂;
• os pontos D, ê e F, externos à C₁ e internos à C₂;
• os pontos G, H e ih, internos à C₁.
Agora, responda:
a) Todos os pontos de C₁ são internos à C₂?
b) Todos os pontos de C₂ são internos à C₁?
Versão adaptada acessível
9. Explique como podem ser identificados os pontos de uma circunferência, os pontos externos e os internos a ela. Você pode usar representações concretas, caso queira.

3 Posições de uma reta em relação a uma circunferência
Em relação à circunferência, uma reta póde ser: secante, tangente ou externa. A seguir, vamos estudar cada uma dessas possibilidades.
Reta secante
Uma reta é secante a uma circunferência quando corta a circunferência em dois pontos distintos.
A palavra secante vem de seccionar, que significa “cortar”.
Na figura a seguir, a reta s é secante à circunferência C de centro óh.
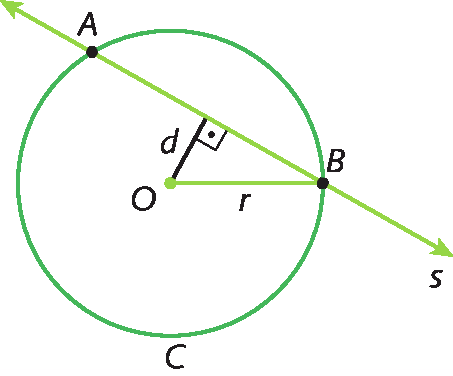
Observe que a medida da distância (d ) do centro (óh) à reta s é menor que a medida de comprimento do raio (r ):
d < r
Propriedade em relação à reta secante
Toda reta que passa pelo centro de uma circunferência e é perpendicular a uma secante passa pelo ponto médio da corda determinada por essa secante.
Analise a figura.
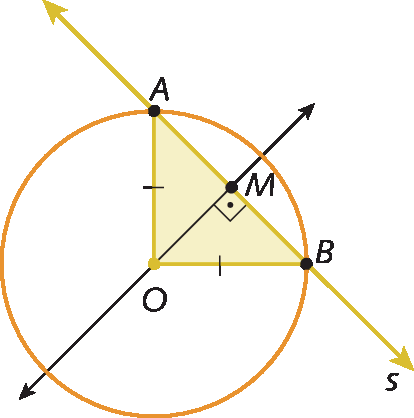
Temos
reta ABperpendicular a
reta OMe o triângulo á ó bê é isósceles, pois
segmentos OAe
segmentos OBsão raios da circunferência.
Então, pelo caso éle á áo , temos: triânguloá ó ême ≅ triângulobê ó ême
Assim: ême á = MB e, portanto, M é ponto médio de
segmento AB.
Reta tangente
Uma reta é tangente a uma circunferência quando tem apenas um ponto em comum com ela.
A palavra tangente vem de tanger, que significa “tocar”.
Na figura a seguir, a reta t é tangente à circunferência C₁, e a é denominado ponto de tangência (“ponto de contato”).

Observe que a medida da distância (d ) do centro (óh) à reta t é igual à medida de comprimento do raio (r):
d = r
Toda reta tangente a uma circunferência é perpendicular a um raio dessa circunferência no ponto de tangência.
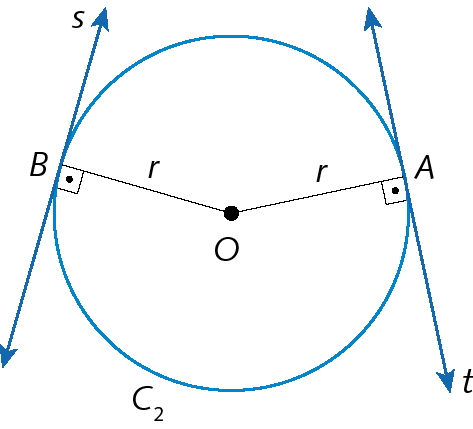
s é tangente à circunferência C2 e é perpendicular a
segmento OBem B.
t é tangente à circunferência C2 e é perpendicular a
segmento OAem a.
Reta externa
Uma reta é externa a uma circunferência quando não tem nenhum ponto em comum com ela.
Observe na figura a seguir que a reta k é externa à circunferência C.
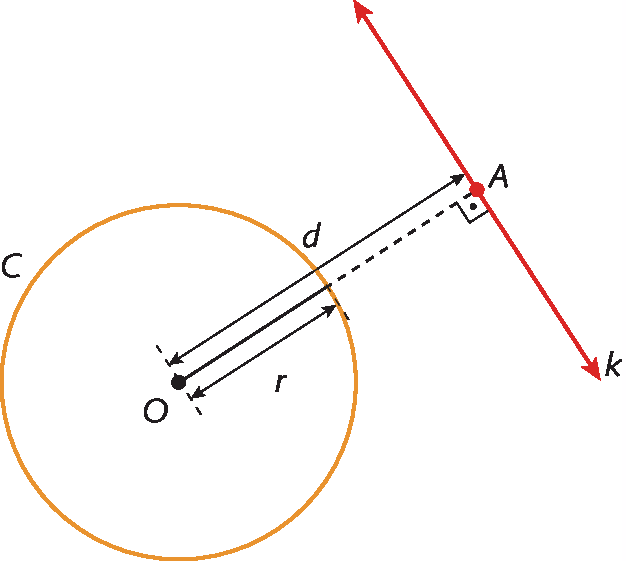
Note que a medida da distância (d ) do centro (óh) à reta k é maior que a medida de comprimento do raio (r):
d > r
Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso na atividade 12.
12. Represente, em seu caderno, um ponto P que dista 10 centímetros do centro óh de uma circunferência cujo comprimento do raio mede 5 centímetros. Depois, trace uma reta passando por P que seja:
a) tangente à circunferência;
b) secante à circunferência;
c) externa à circunferência.
13. Sendo d a medida da distância de uma reta t ao centro de uma circunferência, qual é a posição de t em relação a essa circunferência quando:
a) d = 8 e r = 7?
b) d = 6 e r = 9?
c) d = 10 e r = 10?
14. Em uma circunferência qualquer, toda reta perpendicular a um dos raios é tangente a essa circunferência? Justifique sua resposta.
15. Toda reta que fórma um ângulo reto com outra reta, que seja tangente a uma circunferência, passa pelo centro dessa circunferência? Justifique sua resposta.
16. Sabendo que o comprimento do raio de uma circunferência mede 10 centímetros, responda: A que medida da distância d do centro deveriam estar as retas r e s, paralelas, para que fossem, respectivamente, tangente e externa à circunferência?

4 Posições relativas de duas circunferências
De acôrdo com a posição relativa que apresentam, duas circunferências podem ser: tangentes exteriores, tangentes interiores, secantes, externas ou internas.
Para facilitar nosso estudo, vamos adotar as seguintes notações:
• O₁: centro da circunferência C₁;
• O₂: centro da circunferência C₂;
• d : medida da distância entre os centros O₁ e O₂;
• érre minúsculo₁: medida de comprimento do raio da circunferência C₁ ;
• érre minúsculo₂: medida de comprimento do raio da circunferência C₂;
• érre minúsculo₁ > érre minúsculo₂.
Circunferências tangentes exteriores
Duas circunferências são tangentes exteriores quando têm apenas um ponto comum e suas regiões internas não têm pontos comuns.
A medida da distância d entre os centros das duas circunferências tangentes exteriores é igual à soma das medidas de comprimento dos raios dessas circunferências.
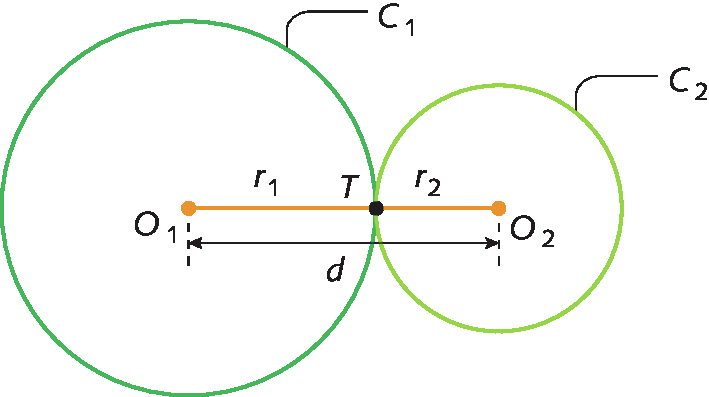
d = érre minúsculo₁ + érre minúsculo₂
T : ponto de tangência
Circunferências tangentes interiores
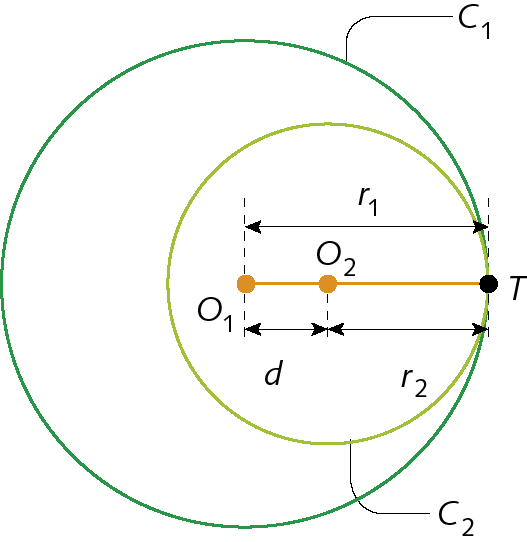
Duas circunferências são tangentes interiores quando têm apenas um ponto comum e uma é interna à outra.
A medida da distância d entre os centros das duas circunferências tangentes interiores é igual à diferença das medidas de comprimento dos raios dessas circunferências.
d = érre minúsculo₁ ‒ érre minúsculo₂
Circunferências secantes
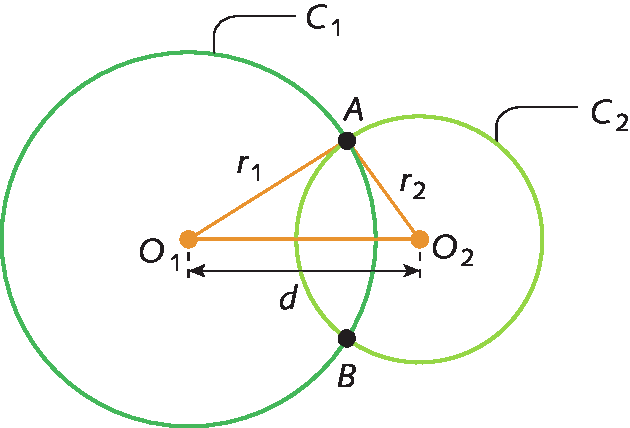
Duas circunferências são secantes quando têm dois pontos em comum.
Os pontos a e B são intersecções entre as circunferências. A medida da distância d entre os centros das duas circunferências secantes é dada pela seguinte desigualdade:
érre minúsculo₁ ‒ érre minúsculo₂ < d < érre minúsculo₁ + érre minúsculo₂
Circunferências externas
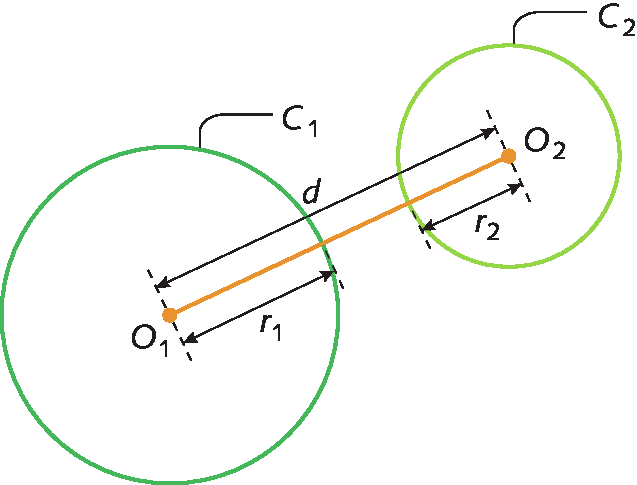
Duas circunferências são externas quando não têm ponto comum e suas regiões internas não têm pontos comuns.
A medida da distância d entre os centros das duas circunferências externas é maior que a soma das medidas de comprimento dos raios dessas circunferências.
d > érre minúsculo₁ + érre minúsculo₂
Circunferências internas
Duas circunferências são internas quando não têm ponto comum e uma é interna à outra.
A medida da distância d entre os centros das duas circunferências internas é menor que a diferença das medidas de comprimento dos raios dessas circunferências.
d < érre minúsculo₁ ‒ érre minúsculo₂
Observações
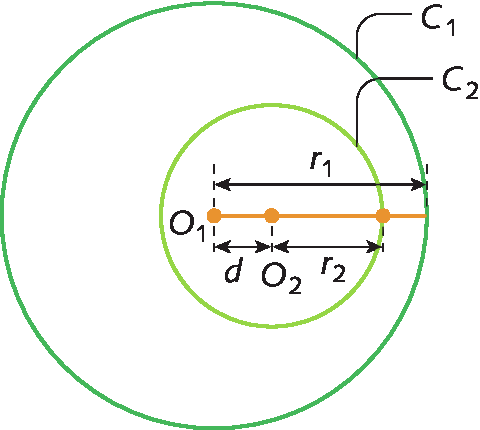
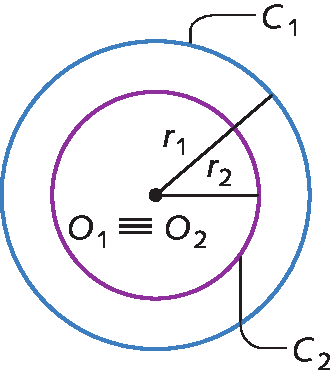
1. Quando duas ou mais circunferências têm o mesmo centro e uma é interna à outra, são denominadas circunferências concêntricas.

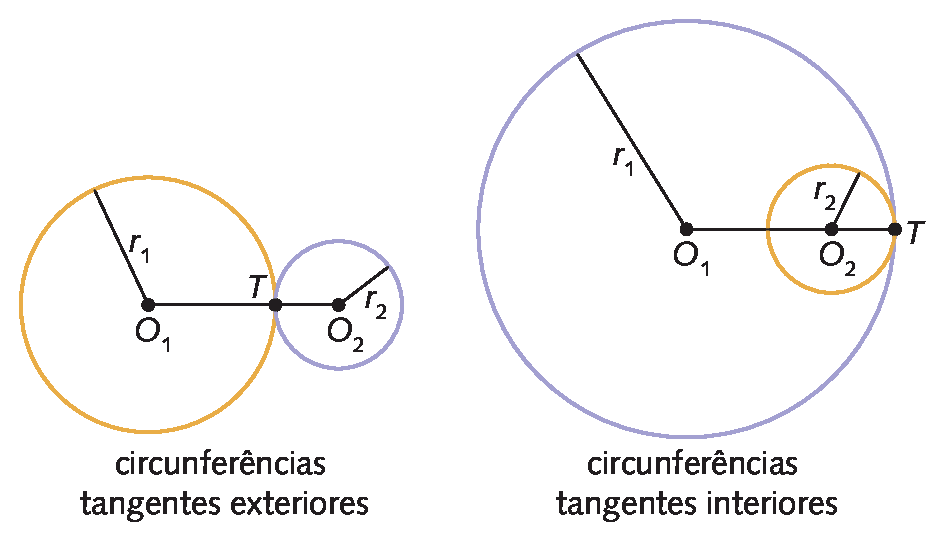
2. No caso das circunferências tangentes exteriores e das circunferências tangentes interiores, os centros O₁ e O₂ e o ponto de tangência T estão sempre alinhados.
Atividades
Faça as atividades no caderno.
17. Sendo érre minúsculo₁ e érre minúsculo₂ as medidas de comprimento dos raios de duas circunferências C1 e C2, respectivamente, e d a medida da distância entre os centros, determine as posições relativas em cada caso.
a) érre minúsculo1 = 2 centímetros, érre minúsculo2 = 5 centímetros e d = 10 centímetros
b) érre minúsculo1 = 4 centímetros, érre minúsculo2 = 2 centímetros e d = 2 centímetros
c) érre minúsculo1 = 3 centímetros, érre minúsculo2 = 7 centímetros e d = 10 centímetros
d) érre minúsculo1 = 3 centímetros, érre minúsculo2 = 10 centímetros e d = 4 centímetros
e) érre minúsculo1 = 5 centímetros, érre minúsculo2 = 5 centímetros e d = 8 centímetros
f) érre minúsculo1 = 6 centímetros, érre minúsculo2 = 4 centímetros e d = 9 centímetros
18. Determine a relação entre a medida da distância entre os centros (d ) e as medidas de comprimento dos raios de duas circunferências (érre minúsculo1 e érre minúsculo2, com érre minúsculo1 > érre minúsculo2) que são:
a) tangentes exteriores;
b) secantes;
c) externas;
d) concêntricas.
19. São dadas duas circunferências com medidas de comprimento dos raios érre minúsculo1 = 13 centímetros e érre minúsculo2 = 7 centímetros. Sendo d a medida da distância entre os centros dessas circunferências, quanto mede d para que essas circunferências sejam tangentes interiores?

20. Dadas duas circunferências, C1 e C2, com medidas de comprimento dos raios érre minúsculo1 e érre minúsculo2, identifique as afirmações verdadeiras a seguir, considerando d como a medida da distância entre os centros dessas circunferências.
a) As duas circunferências são concêntricas quando d = 0.
b) As duas circunferências, com érre minúsculo1 > érre minúsculo2, são secantes quando érre minúsculo1 ‒ érre minúsculo2 < d < érre minúsculo1 + érre minúsculo2.
c) As duas circunferências são tangentes quando têm dois pontos comuns.
d) As duas circunferências são externas quando d > érre minúsculo1 + érre minúsculo2.
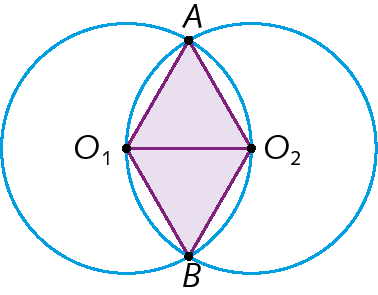
21. As circunferências da figura a seguir, de centros O1 e O2, têm raios medindo 2 centímetros de comprimento. Responda:
a) Quais são as medidas de comprimento de
segmento AO1e
segmento BO2?
b) Quanto mede o comprimento de cada lado do triângulo AO1O2?
c) Qual é a medida da abertura do ângulo
ângulo O1AO2?
d) Qual é o nome do quadrilátero AO2BO1?

5 Segmentos de reta tangentes
Observe a figura.
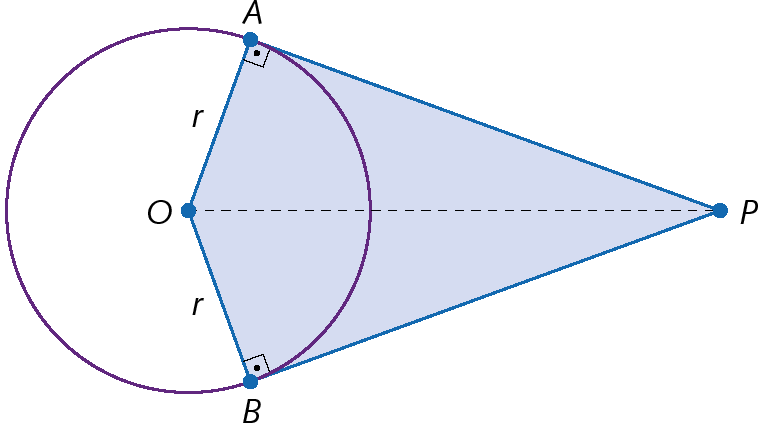
O ponto P é externo à circunferência de centro óh e cujo comprimento do raio mede r, e os segmentos de reta
PA e PBsão tangentes à circunferência.
Analisando os triângulos retângulos ó á pê e OBP, temos:
•
Segmento de reta OA é congruente ao segmento de reta OB

raios da circunferência
•
Segmento de reta OP é congruente ao segmento de reta OP
lado comum
•
medida do ângulo OAP é igual à medida do ângulo OBP que é igual a 90 grausPelo caso de congruência do triângulo retângulo, temos: △ó á pê ≅ △OBP
Portanto,
Segmento de reta PA é congruente ao segmento de reta PB.
Os segmentos de reta tangentes traçados de um mesmo ponto exterior a uma circunferência são congruentes.
Observação
Dois triângulos retângulos que têm a hipotenusa e um cateto respectivamente congruentes são congruentes.
Analise estes exemplos.
Vamos determinar o valor de x, sabendo que
Segmento de reta PAe,
Segmento de reta PB,
Segmento de reta QBe
Segmento de reta QCsão tangentes às circunferências.
a)
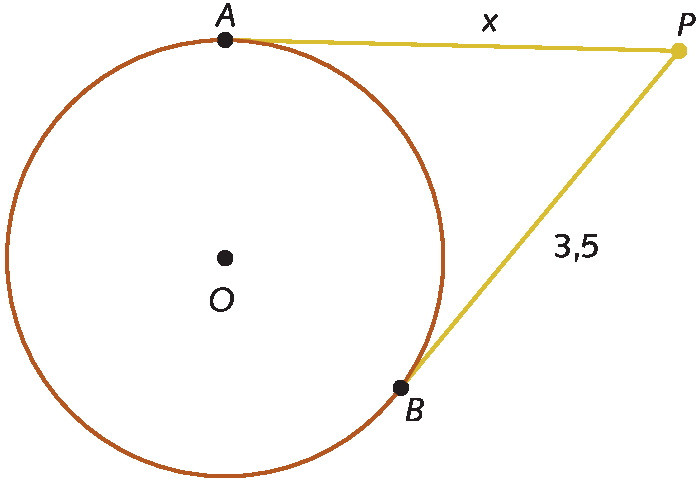
Temos: PA = PB
Logo:
x = 3,5
b)
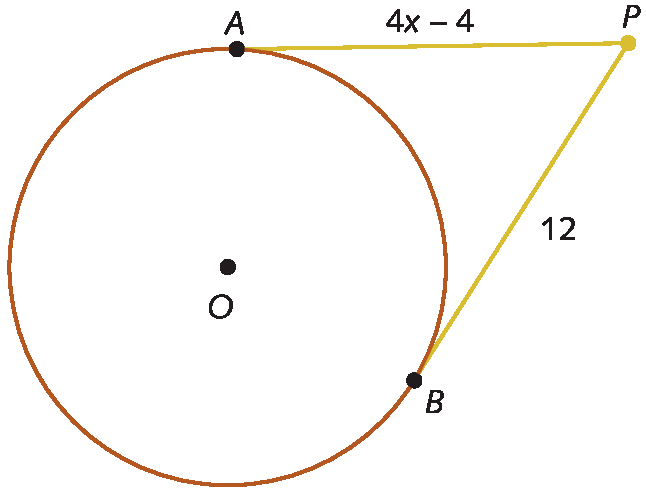
Temos: PA = PB
Logo:
4x ‒ 4 = 12
4x = 12 + 4
4x = 16
x = 4
c)
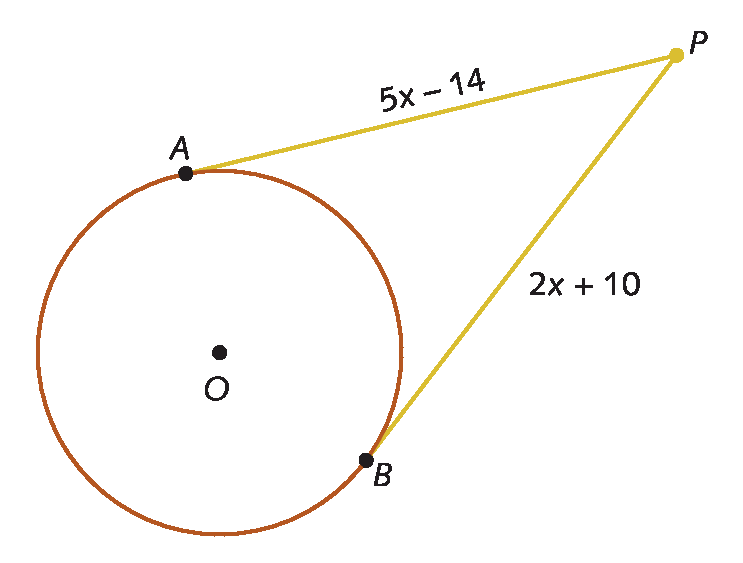
Temos: PA = PB
Logo:
5x ‒ 14 = 2x + 10
5x ‒ 2x = 10 + 14
3x = 24
x = 8
d)
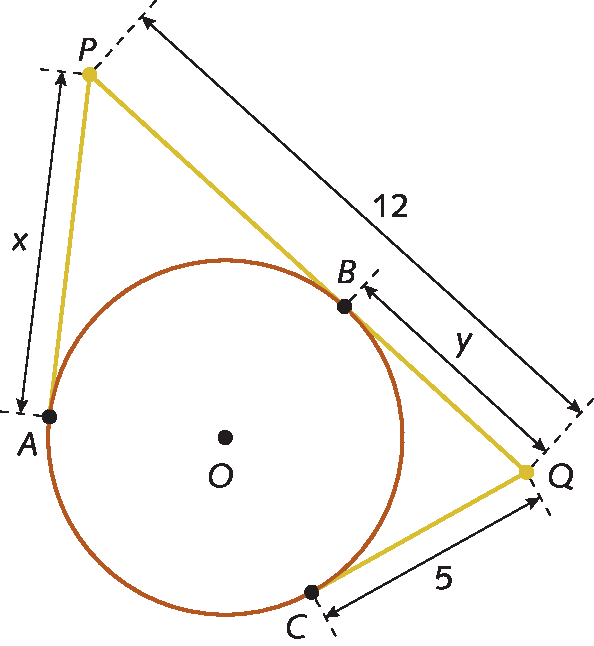
Como PA = PB, temos:
PB = x
Como QB = QC, temos: y = 5
Assim: PQ = PB + QB
12 = x + 5
x = 7
Polígonos circunscritos a uma circunferência
Um polígono está circunscrito a uma circunferência quando todos os seus lados são tangentes à circunferência.
Triângulo circunscrito
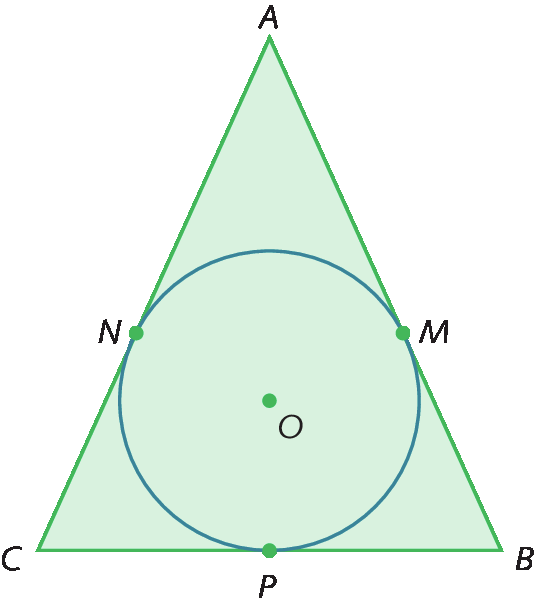
Confira esta figura.
O triânguloá bê cê está circunscrito à circunferência de centro óh, e os pontos M, N e P são os pontos de tangência.
Analise este exemplo.
Observe o triânguloá bê cê circunscrito à circunferência na figura a seguir. Vamos determinar o valor de x.
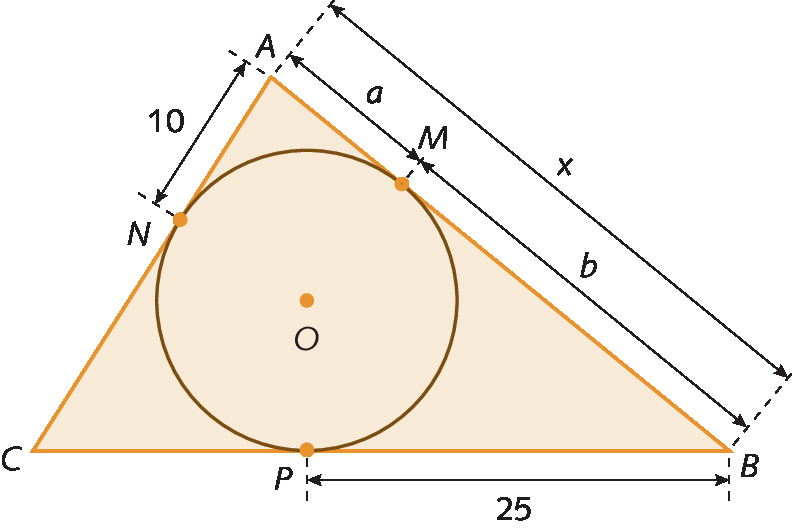
Como á êne = ei ém e MB = BP, temos:
á êne = a e BP = b
Então: a = 10 e b = 25
Sendo A bê = ei ém + MB, temos:
x = 10 + 25
x = 35
Quadrilátero circunscrito
Observe a figura a seguir.
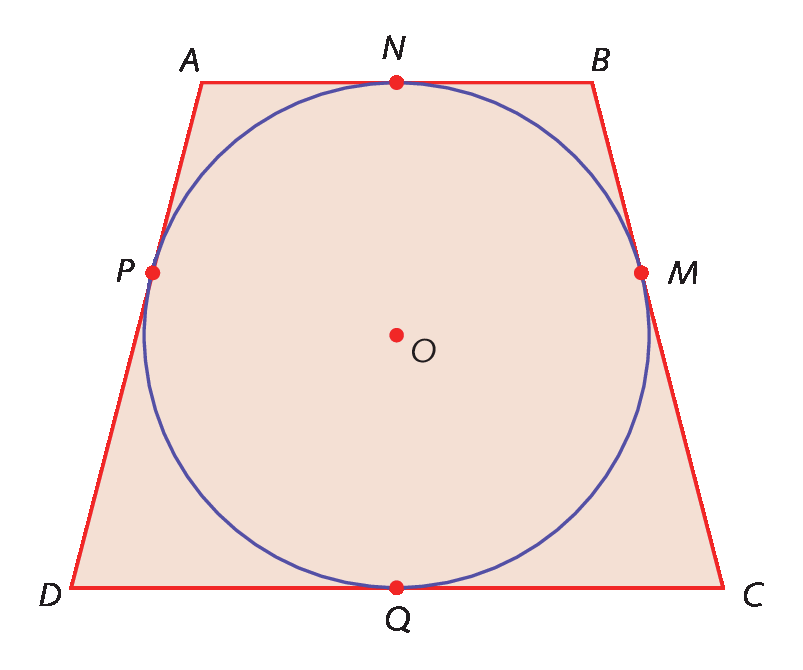
O quadrilátero a bê cê dê está circunscrito à circunferência de centro óh, e os pontos M, N, P e Q são pontos de tangência.
A soma das medidas de comprimento de dois lados opostos de um quadrilátero circunscritível a uma circunferência é igual à soma das medidas de comprimento dos outros dois.
Considere as medidas de comprimento x, y, z e w indicadas no quadrilátero a bê cê dê circunscrito à circunferência.
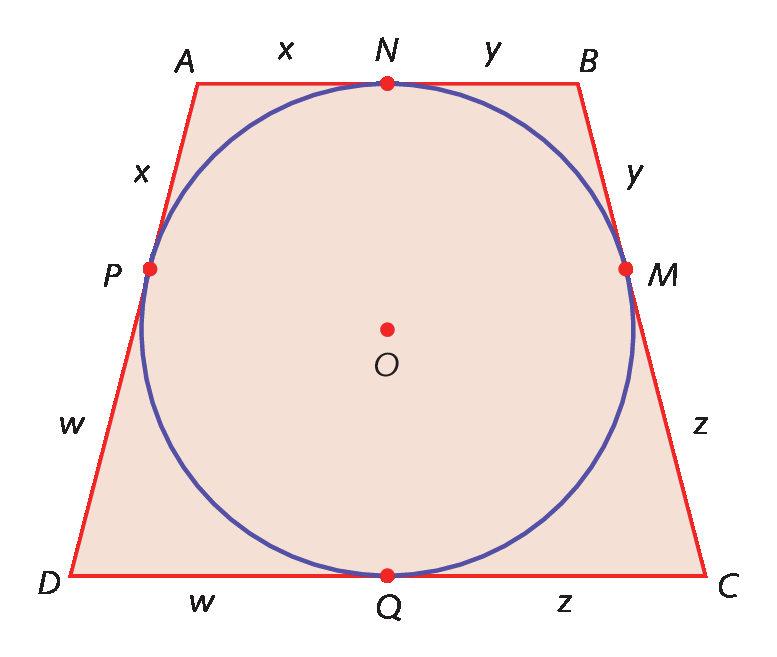
M, N, P e Q são pontos de tangência.
Como á êne = á pê = x, BM = BN = y, CQ = CM = z e DP = DQ = w, temos:
A bê + CD = x + y + z + w
á dê + BC = x + w + y + z
Logo:
A bê + CD = á dê + BC
Observações
1. A recíproca é verdadeira: em um quadrilátero, se a soma das medidas de comprimento de dois lados opostos é igual à soma das medidas de comprimento dos outros dois, o quadrilátero é circunscritível a uma circunferência.
2. Podemos dizer que os polígonos estão circunscritos às circunferências ou que as circunferências estão inscritas nos polígonos.
Atividades
Faça as atividades no caderno.
22. Determine o valor de x, sabendo que os segmentos de reta são tangentes às circunferências.
a)

b)

c)
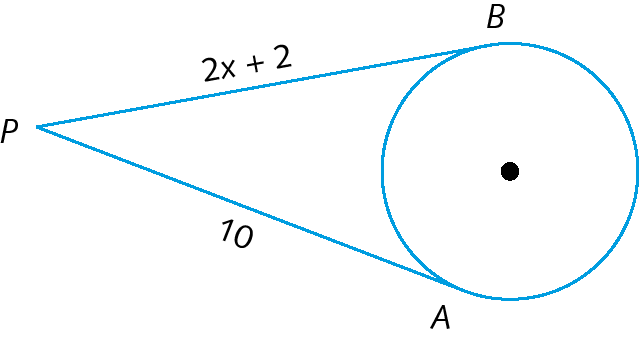
d)

23. Determine o valor de x nos casos a seguir.
a)
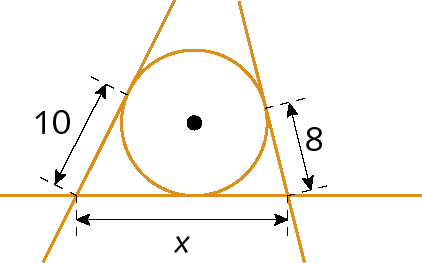
b)
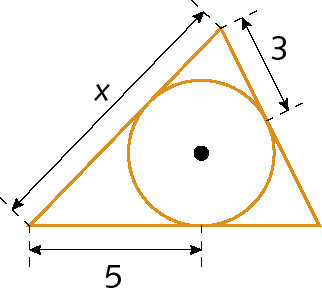
c)
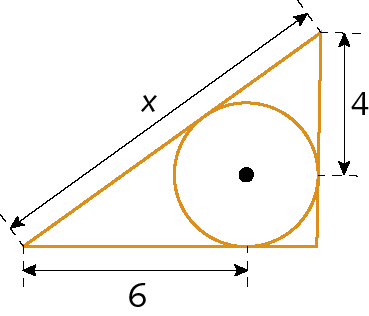
d)
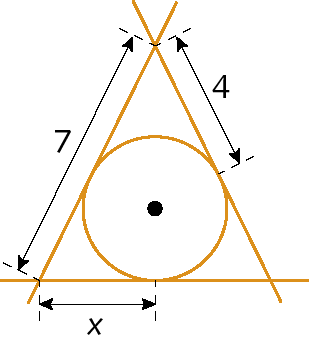
24. Determine o valor de x em cada caso.
a)
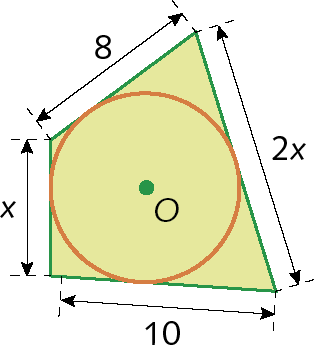
b)
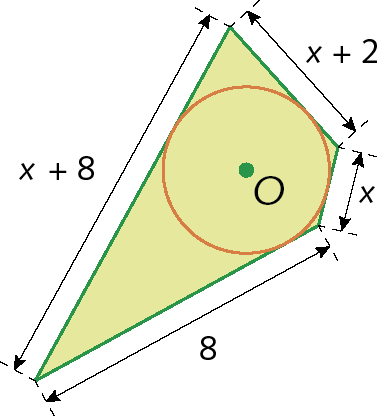
c)
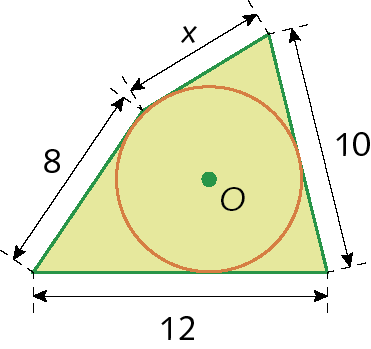
25. O ponto D é o ponto de tangência da circunferência inscrita com o lado
segmento ABdo triângulo á bê cê. Sabendo que á cê = 39 centímetros, A bê = 80 centímetros e BC = 89 centímetros, determine BD.
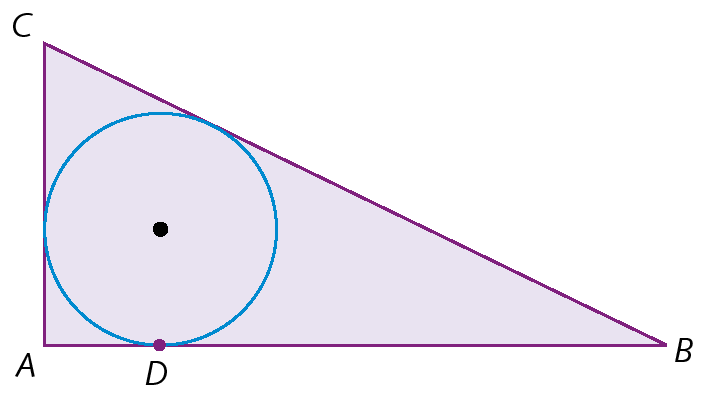
26. Na figura,
Reta PA,
Reta PBe
Reta DEsão tangentes à circunferência. Calcule a medida de perímetro do triângulo pê dê é, sendo pê á = 8 centímetros.

6 Arco de circunferência e ângulo central
Arco de circunferência
A parte da circunferência compreendida entre dois de seus pontos é denominada arco de circunferência.
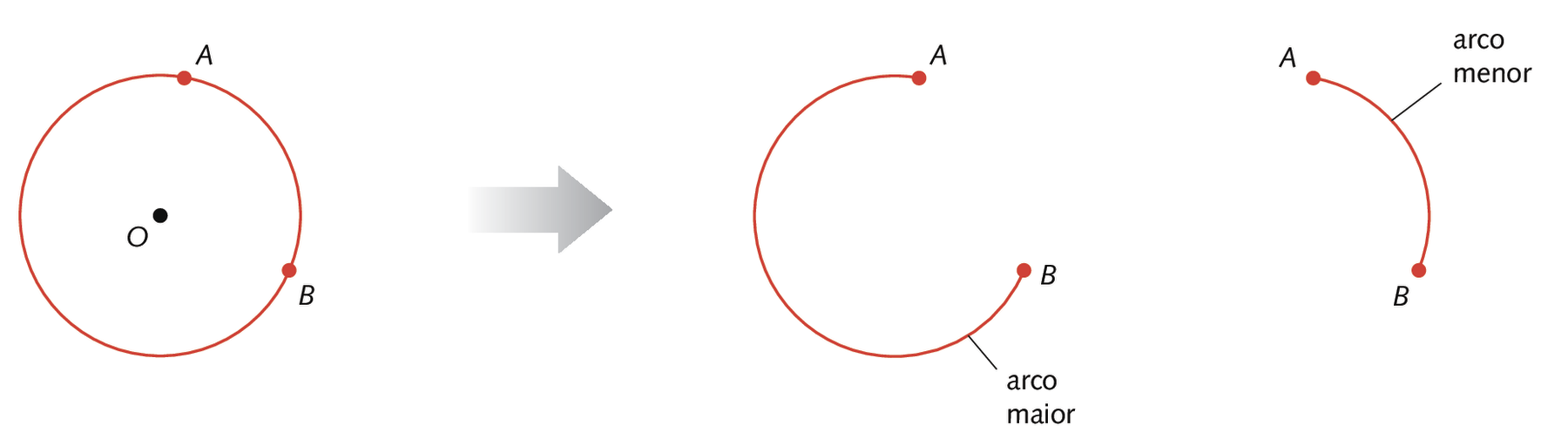
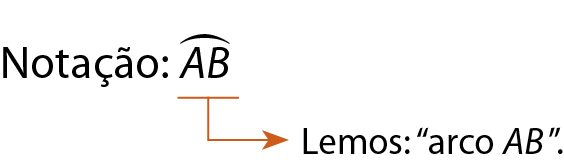
Chamamos os pontos a e B de extremos do arco
A B.
Para distinguir o arco menor do arco maior, indicamos
arco ABpara o menor e utilizamos mais um ponto da circunferência para o maior. Observe as figuras.

Notação:
arco AMB
Notação:
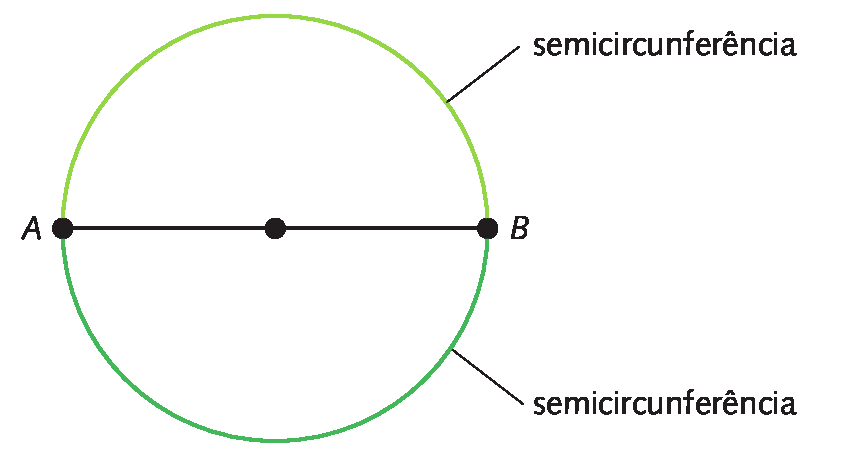
Arco A BQuando os extremos a e B do arco coincidem com as extremidades de um diâmetro, cada um dos arcos formados é denominado semicircunferência.
Ângulo central
O ângulo cujo vértice é o centro de uma circunferência é denominado ângulo central.
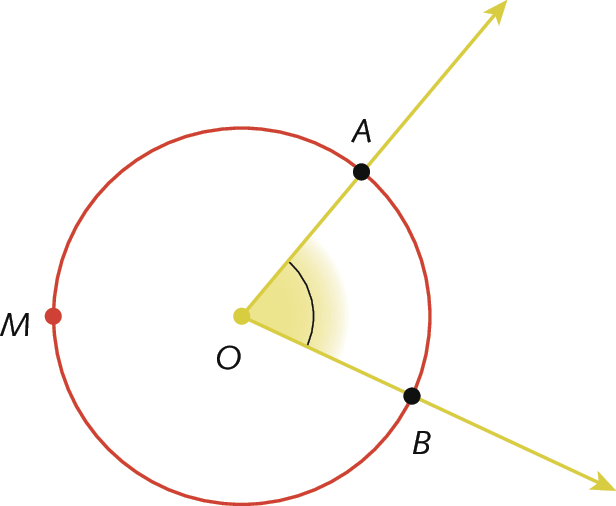
Observe na figura que
ângulo AOBé um ângulo central e
A Bé o arco correspondente.
Um arco póde ter medida angular ou medida de comprimento. Aqui usaremos apenas a medida angular, que indicaremos por medida do arco.
: ângulo central
: arco correspondente ao ângulo
A O BA medida da abertura do ângulo central é igual à medida do arco correspondente.
Assim:
Confira estes exemplos.
a) Vamos determinar a medida de
arco AMB.
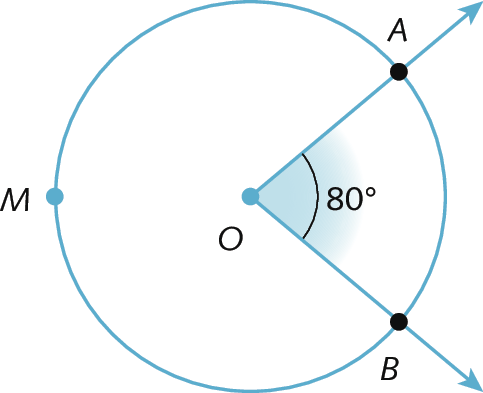
Como
medida do arco AB é igual à medida do Ângulo AOB, que é igual a 80 graus, temos:
medida do arco AMB é igual a 360 graus menos a medida do arco AB
medida do arco AMB é igual a 360 graus menos 80 graus
medida do arco AMB é igual a 280 graus
b) Observando a figura, vamos determinar as medidas de
arcos AB, AC, AD e AMD.
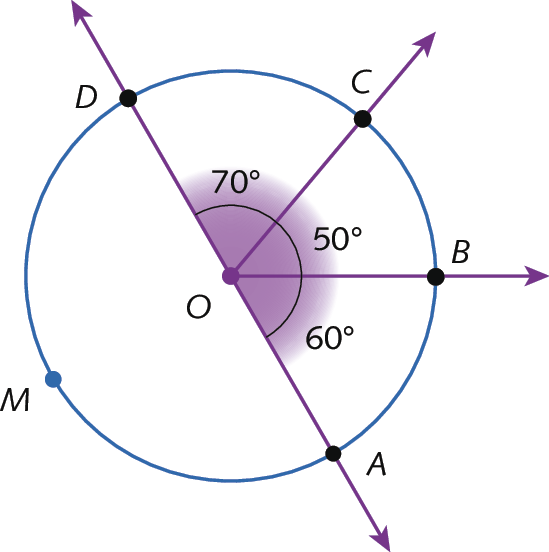
•
medida do arco AB é igual à medida do Ângulo AOB, que é igual a 60 graus•
medida do arco AC igual à medida do arco AB mais a medida do arco BCmedida do arco AC igual à medida do arco AB mais a medida do ângulo BOC
medida do arco AC igual a 60 graus mais 50 graus igual a 110 graus
•
medida do arco AD igual à medida do arco AC mais a medida do arco CDmedida do arco AD igual à medida do arco AC mais a medida do ângulo COD
medida do arco AD igual a 110 graus mais 70 graus igual a 180 graus
•
medida do arco AMB é igual a 360 graus menos a medida do arco ABmedida do arco AMD igual a 360 graus menos 180 graus igual a 180 graus
Atividades
Faça as atividades no caderno.
27. Dadas as figuras seguintes, determine as medidas dos arcos:
a)
arco MN,
arco NPe
arco MP
b)
arco BC,
arco ABe
arco AC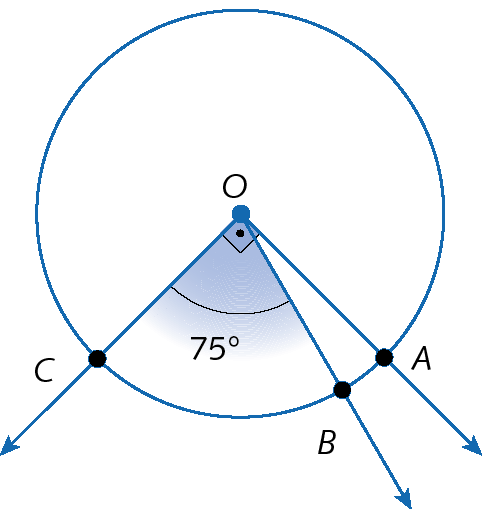
28. Quantos graus mede o arco
arco AMBda figura?

29. Em uma circunferência, os arcos
arco MNe
arco MANformam o giro de uma volta. Determine a medida de abertura x quando:
a)
medida do arco MAN igual a 3xe
medida do arco MN igual a x mais 30 grausb)
medida do arco MAN igual a x mais 120 grause
medida do arco MN igual a xc)
medida do arco MAN igual a 2x mais 80 grause
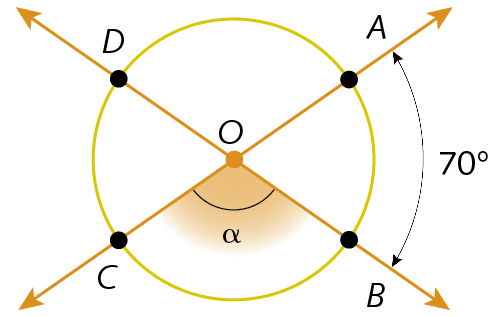
medida do arco MN igual a 3x sobre 230. Calcule a medida de abertura α de cada ângulo a seguir.
a)
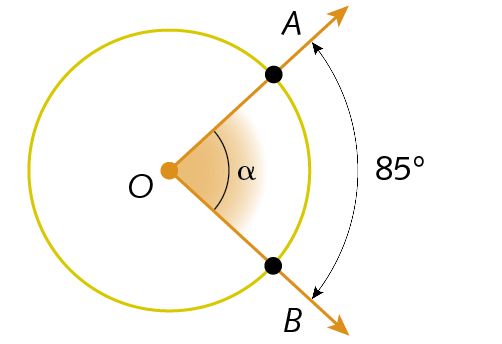
b)
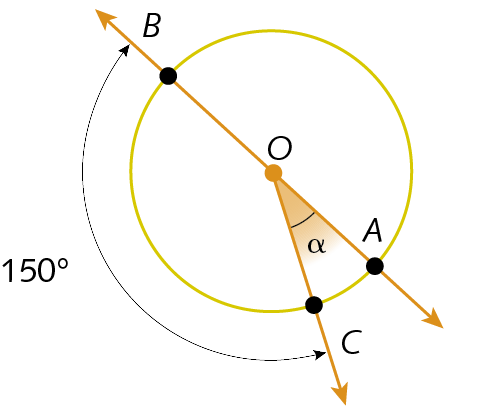
c)
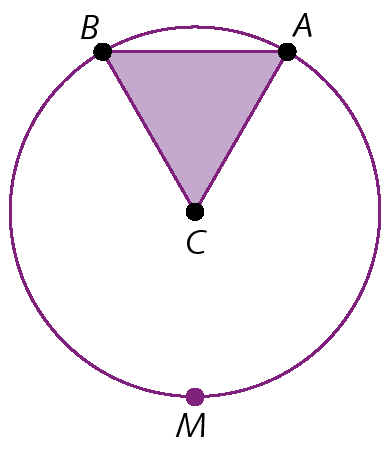
31. Nesta figura, o ponto C é o centro da circunferência e o triângulo á bê cê é equilátero. Qual é a medida do arco
arco AB?
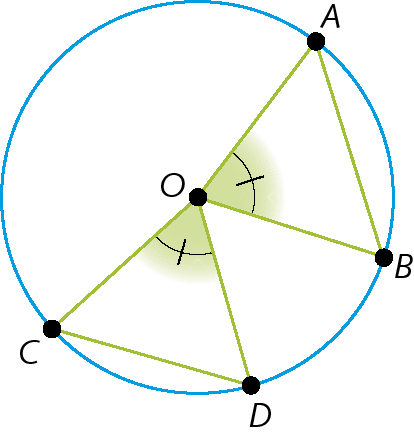
32. Prove que, em uma circunferência, ângulos centrais congruentes determinam cordas congruentes.

7 Ângulo inscrito
Ângulo inscrito a uma circunferência é todo ângulo cujo vértice é um ponto da circunferência e cujos lados são secantes a essa circunferência.
Podemos estabelecer uma relação entre a medida da abertura do ângulo inscrito e a medida do arco da circunferência por ele determinado.
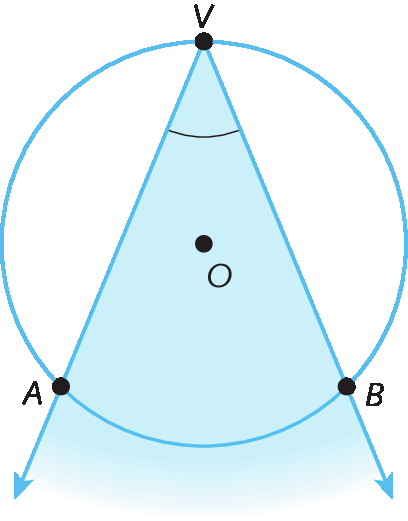
é um ângulo inscrito que determina o arco
A B na circunferência.

Tecnologias digitais em foco
Ângulos central e inscrito a uma circunferência
Nesta seção, utilizaremos o GeoGebra, ou outro software de geometria dinâmica que seu professor indicar, para construir um ângulo inscrito a uma circunferência e o ângulo central correspondente e para investigar a relação entre as medidas das aberturas desses ângulos.
Construa
Siga os passos a seguir para construir os ângulos.
1º) Construa uma circunferência C de centro óh.
2º) Marque três pontos distintos, a, B e V, na circunferência.
3º) Trace as semirretas
O A,
O B,
V Ae
V B.
O ângulo
ângulo AVBé um ângulo inscrito e
ângulo AOBé o ângulo central correspondente.
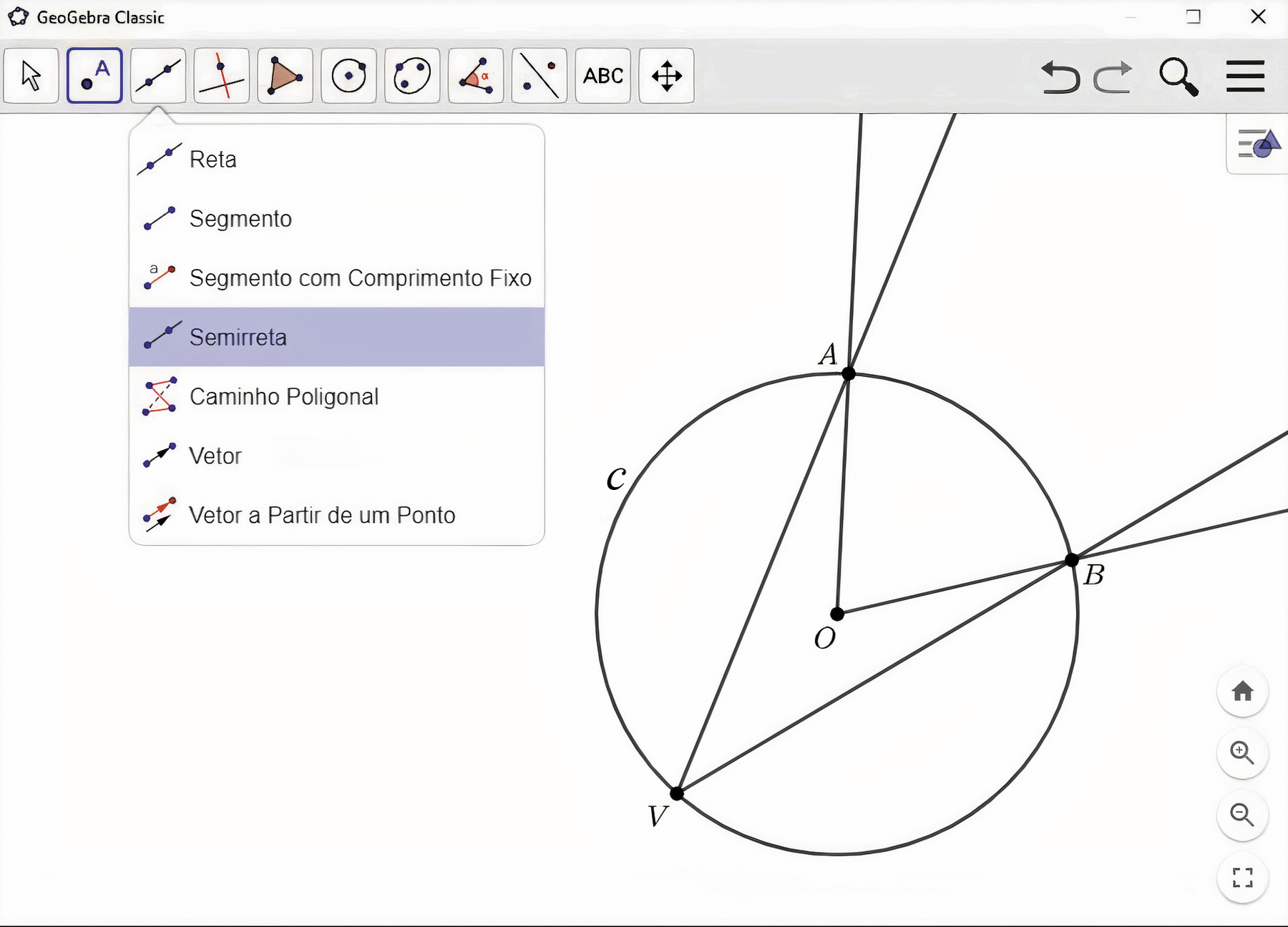
Explore
a) Meça as aberturas dos ângulos
A V Be
A O B. É possível perceber alguma relação entre essas medidas?
b) Movimente os pontos móveis da construção, modificando a configuração inicial. A relação observada é válida em diferentes configurações?
Nesta figura,
ângulo AVBé um ângulo inscrito e
segmento VBé um diâmetro da circunferência, sendo a a medida da abertura do ângulo inscrito
ângulo AVBe b a medida da abertura do ângulo central
ângulo AOB.
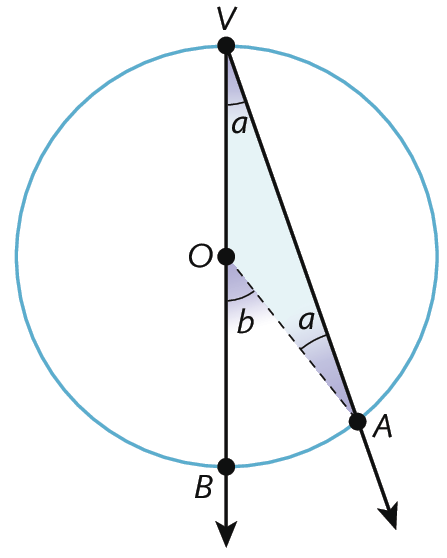
Como
segmento OVe
segmento OAsão raios da circunferência, o triângulo AOV é isósceles. Assim, os ângulos da base do triângulo AOV são congruentes:
No triângulo AOV, temos
medida ao ângulo VOA igual a 180 graus menos 2a, pois a soma das medidas das aberturas dos ângulos internos de um triângulo é 180graus. Observe que
ângulo VOAe
ângulo BOAformam um ângulo raso (estão sobre
semirreta VB), assim:

Logo:
A medida da abertura do ângulo inscrito em uma circunferência é a metade da medida do arco que ele determina na circunferência.
Esse resultado vale também para outras configurações, mas não faremos a demonstração disso aqui.
Analise estes exemplos.
a) Vamos determinar a medida de abertura x do ângulo nesta figura.
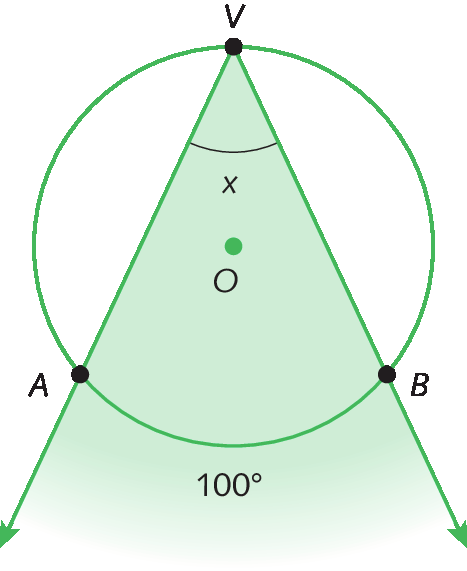
Como
medida do Ângulo AVB igual à medida do arco AB sobre 2, temos:
medida ao Ângulo AVB igual a 100 graus sobre 2
medida do ângulo A V B é igual a 50 graus
Portanto:
x é igual à medida do ângulo A V B, que é igual a 50 grausb) Nesta figura, qual é a medida de
arco AB?
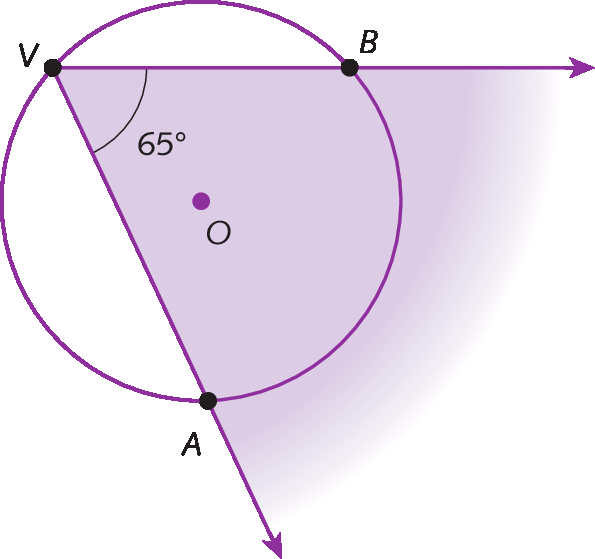
Como
medida do ângulo AVB igual à medida do arco AB, temos:
65 graus igual à medida ao arco AB sobre 2 implica que medida do arco AB igual a 65 graus vezes 2 implica que medida do arco AB é igual a 130 graus
c) Sabendo que a, B e C são pontos de uma circunferência e que a abertura do ângulo central
AOBmede 70graus, quais são as medidas de
Arco ABe da abertura do ângulo inscrito
ACB?
Como
medida do arco AB igual à medida do ângulo AOB, temos:
medida do arco igual a 70 graus
Como
medida do ângulo ACB igual à medida do arco AB sobre 2, temos:
medida ao ângulo ACB igual a 70 graus sobre 2
medida ao ângulo ACB igual 35 graus
Observações
1. O ângulo inscrito em uma semicircunferência é reto.
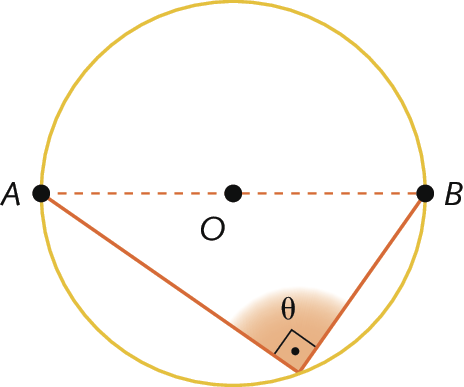
theta igual a medida do arco AB sobre 2 que é igual a 180 graus sobre 2 que é igual a 90 graus

2. Ângulos inscritos que determinam o mesmo arco são congruentes.
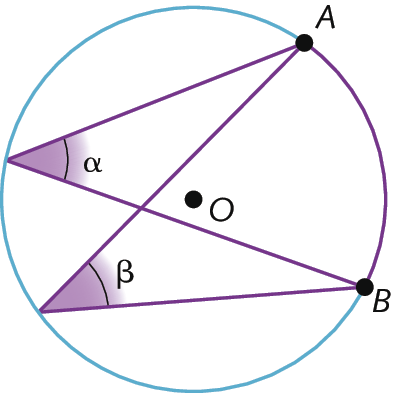
ângulo alfa igual ao ângulo beta igual à medida do arco AB sobre 2
Atividades
Faça as atividades no caderno.
33. Encontre o valor de α, em grau, em cada figura.
a)
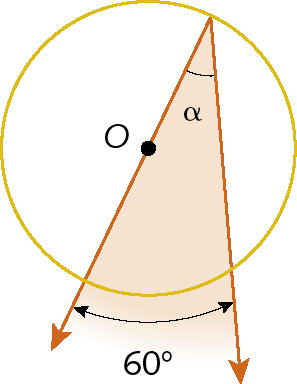
b)
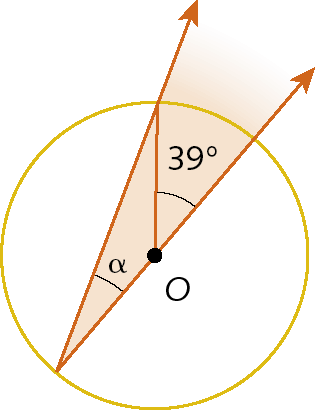
c)
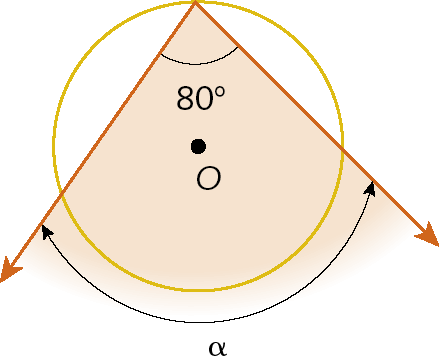
d)
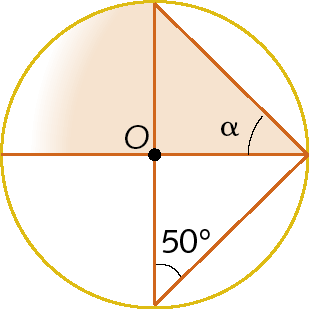
34. Um triângulo á bê cê está inscrito em uma circunferência, e o arco
arco ACmede 100graus. Calcule a medida da abertura do ângulo
ângulo CAB, sabendo que a abertura de
ângulo BCAmede 60graus.
35. Calcule a medida da abertura, em grau, dos ângulos assinalados.

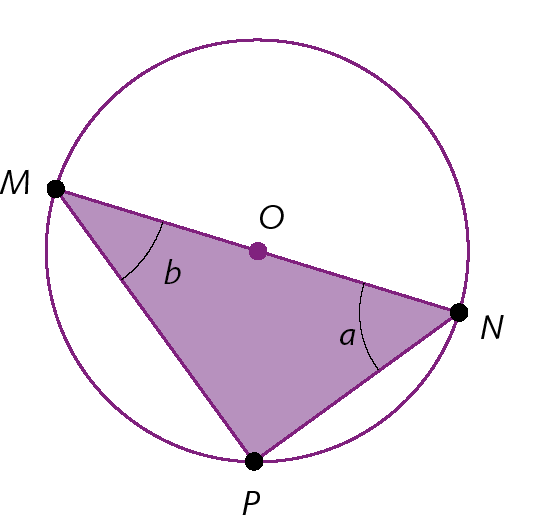
36. Determine a e b, em grau, na figura a seguir sabendo que a + 2b = 127graus.
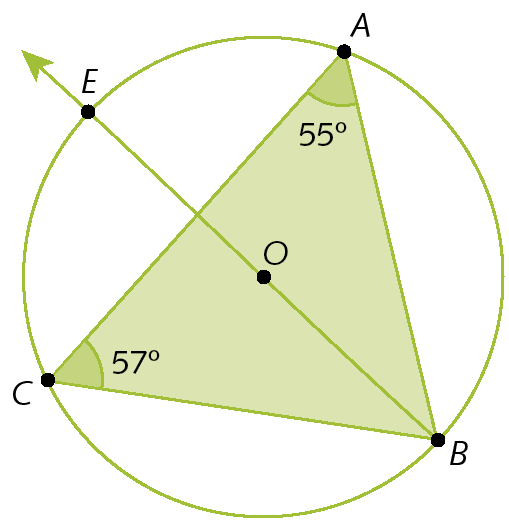
37. Sabendo que
semirreta BEé bissetriz de
ângulo ABC, determine a medida do arco
arco ECB.
38.

Utilizando um software de geometria dinâmica, faça uma construção geométrica de acôrdo com os passos a seguir.
1º) Construa uma circunferência C₁ de centro em a e raio
A B.
2º) Construa uma circunferência C₂ de centro em B e raio
A B.
3º) Marque C, uma das intersecções entre as circunferências C₁ e C₂.
4º) Trace a reta
Reta CA.
5º) Marque D, intersecção da circunferência C₁ com a reta
reta CA, D ≠ C.
6º) Trace a semirreta
semirreta AB.
7º) Trace a semirreta
Semirreta DB.
Agora faça o que se pede:
a) Utilizando as ferramentas do software, analise a construção realizada e indique a relação entre as medidas das aberturas dos ângulos
ângulo CABe
ângulo CDB.
b) No caderno, elabore uma questão sobre a construção realizada de maneira que um colega possa responder utilizando os recursos disponíveis no software de geometria dinâmica.
c)

Troque de caderno com um colega e responda à questão elaborada por ele. Em seguida, troquem as descobertas que fizeram com a construção e a investigação dos passos descritos.

Resolvendo em equipe
Faça a atividade no caderno.
Cuidado! Evite acidentes ao usar o compasso.
(ó bê mépi) Desenhe duas circunferências de mesmo centro, uma de raio medindo 1 centímetro e a outra de raio medindo 3 centímetros. Na região exterior à circunferência de 1 centímetro de raio e interior à de 3 centímetros de raio, desenhe circunferências que sejam, simultaneamente, tangentes às duas circunferências, como mostrado na figura dada.

a) Qual deve ser o raio dessas circunferências?
b) Qual é o número máximo dessas circunferências que podem ser desenhadas, sem que elas se sobreponham?
|
Interpretação e identificação dos dados |
• Analise as informações do enunciado e anote no caderno as que você julgar relevantes para a resolução do problema. |
|---|---|
|
Plano de resolução |
• Quais são as medidas das aberturas dos ângulos internos da figura encontrada no item anterior? |
|
Resolução |
• Junte-se a dois colegas. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• Apresentem a figura dada no problema e sua solução, construídas com régua e compasso, em uma folha de papel sulfite. |
Revisão dos conteúdos deste capítulo
Circunferência
Corda e diâmetro de uma circunferência
Sendo óh, centro da circunferência, temos:
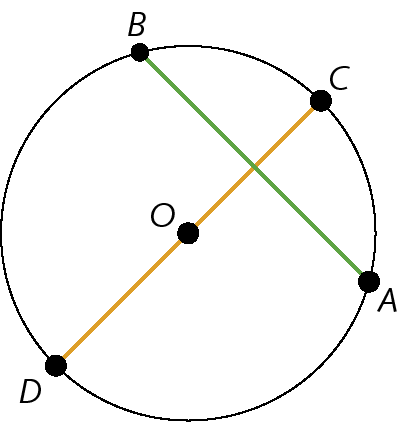
•
Segmento de reta ABe
Segmento de reta CDsão cordas;
•
Segmento de reta CDé um diâmetro;
•
Segmento de reta ODe
Segmento de reta OCsão raios.
Posições de uma reta em relação a uma circunferência
Em cada circunferência C, considere d a medida da distância da reta ao centro óh da circunferência e r a medida de comprimento do raio da circunferência.
Reta secante
Uma reta é secante a uma circunferência quando corta a circunferência em dois pontos distintos.

Nesse caso, temos: d < r
Reta tangente
Uma reta é tangente a uma circunferência quando tem apenas um ponto em comum com ela.

Nesse caso, temos: d = r
Reta externa
Uma reta é externa a uma circunferência quando não tem nenhum ponto em comum com ela.
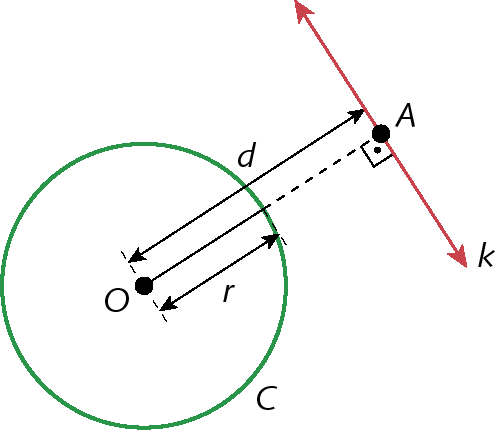
Nesse caso, temos: d > r
Posições relativas de duas circunferências
Nas circunferências C1 e C2, considere d a medida da distância entre O1 e O2 (respectivamente, centros das circunferências C1 e C2) e érre minúsculo1 e érre minúsculo2 as medidas de comprimento dos raios, respectivamente, das circunferências C1 e C2, tal que érre minúsculo1 > érre minúsculo2.
Circunferências tangentes exteriores
Duas circunferências são tangentes exteriores quando têm apenas um ponto comum e suas regiões internas não têm pontos comuns.
Nesse caso, temos:
d = érre minúsculo1 + érre minúsculo2
T: ponto de tangência

Circunferências tangentes interiores
Duas circunferências são tangentes interiores quando têm apenas um ponto comum e uma é interna à outra.

Nesse caso, temos:
d = érre minúsculo1 ‒ érre minúsculo2
T: ponto de tangência
Circunferências secantes
Duas circunferências são secantes quando têm dois pontos em comum.
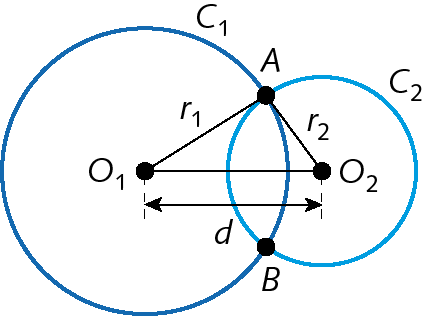
Nesse caso, temos:
érre minúsculo1 ‒ érre minúsculo2 < d < érre minúsculo1 + érre minúsculo2
A e B: intersecções entre as circunferências.
Circunferências externas
Duas circunferências são externas quando não têm ponto comum e suas regiões internas não têm pontos comuns.
Nesse caso, temos: d > érre minúsculo1 + érre minúsculo2

Circunferências internas
Duas circunferências são internas quando não têm ponto comum e uma é interna à outra.
Nesse caso, temos: d < érre minúsculo1 ‒ érre minúsculo2

1. Observe a figura e indique um segmento de reta que seja:
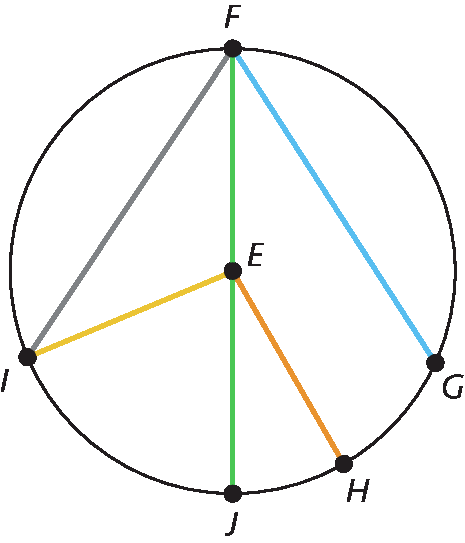
a) raio
b) corda
c) diâmetro
2. Considere uma circunferência de centro óh e raio de medida de comprimento r. Indicando por d a medida da distância entre uma reta e o centro da circunferência, determine a posição da reta em relação à circunferência para:
a) d = 4 centímetros e r = 4 centímetros;
b) d = 8 centímetros e r = 5 centímetros;
c) d = 11 centímetros e r = 16 centímetros;
d) d = 5 centímetros e r = 5 centímetros.
3. A medida da distância entre os centros de duas circunferências tangentes interiores é 7 centímetros. As medidas de comprimento dos raios são 2x ‒ 3 e x + 1. Qual é a medida de comprimento do raio de cada circunferência, considerando que o raio de maior medida de comprimento mede 2x ‒ 3?
4. Os centros de duas circunferências tangentes exteriores estão distantes 55 centímetros, e as medidas de comprimento dos raios são expressas por 3x + 1 e 5x ‒ 2. Qual é a medida de comprimento do raio de cada circunferência?
5. Qual é a posição relativa de duas circunferências cujos raios medem 7 centímetros e 4 centímetros de comprimento e a distância entre seus centros mede 10 centímetros?
Segmentos de reta tangentes
Os segmentos de reta tangentes traçados de um mesmo ponto exterior a uma circunferência são congruentes.
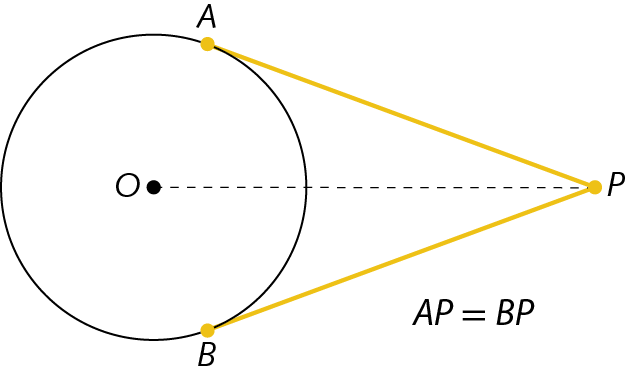
6. Determine o valor de x em cada caso sabendo que os segmentos de reta são tangentes às circunferências.
a)
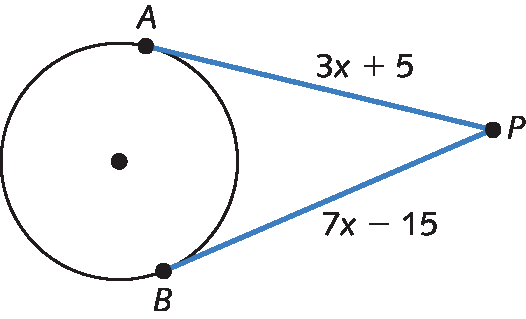
b)
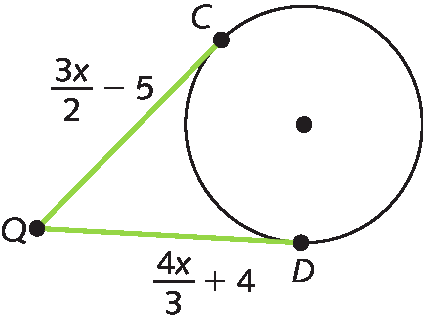
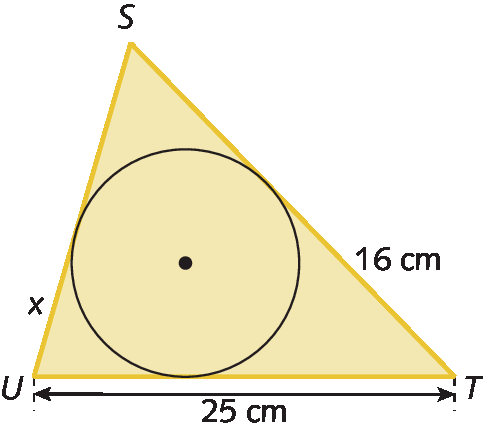
7. Em cada figura a seguir, temos uma circunferência inscrita em um triângulo. Determine as medidas de comprimento x.
a)
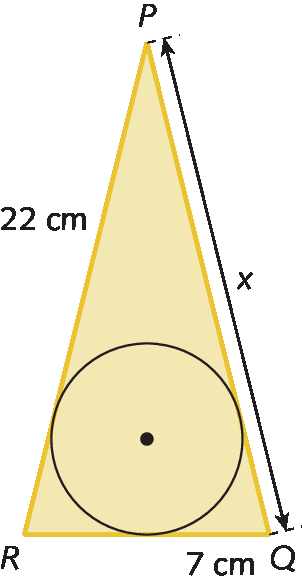
b)
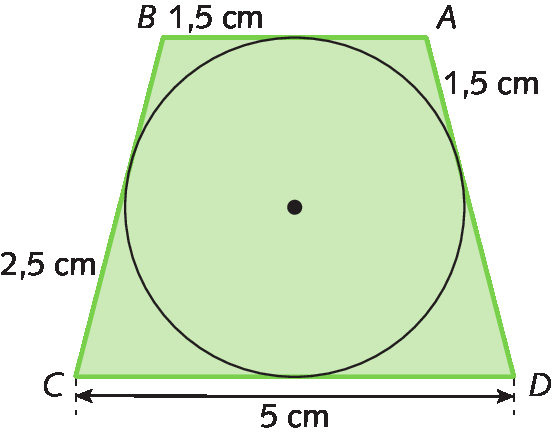
8. Calcule a medida de perímetro deste quadrilátero circunscrito à circunferência.
Arco de circunferência e ângulo central
Arco de circunferência
A parte da circunferência compreendida entre dois de seus pontos é denominada arco de circunferência.
Ângulo central
O ângulo cujo vértice é o centro de uma circunferência é denominado ângulo central.
A medida da abertura do ângulo central é igual à medida do arco correspondente.
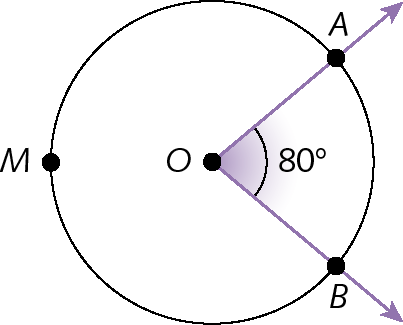
Como
medida do arco AB igual à medida do ângulo AOB, temos:
medida do arco AB igual a 80 graus
medida do arco AMB igual a 280 graus
Ângulo inscrito
Ângulo inscrito a uma circunferência é todo ângulo cujo vértice é um ponto da circunferência e cujos lados são secantes a essa circunferência.
A medida da abertura do ângulo inscrito em uma circunferência é a metade da medida do arco que ele determina na circunferência.

9. Determine a medida x, em graus, e a medida da abertura de cada ângulo central em destaque.
a)
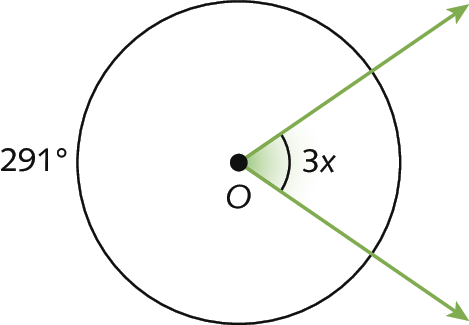
b)
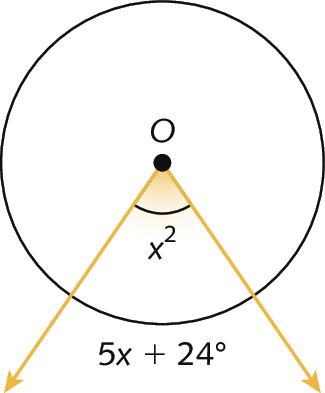
10. Determine as medidas x e y das aberturas dos ângulos nas circunferências a seguir.
a)
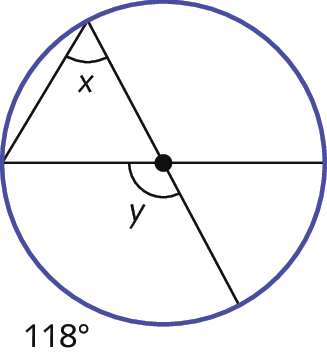
b)
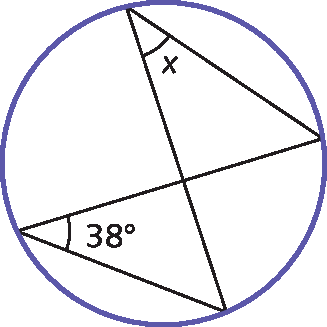
11. Se a medida da abertura de um ângulo inscrito em uma circunferência é 84graus e o arco da circunferência compreendido entre seus lados mede 5x + 8graus, qual é a medida da abertura x?
12. Qual é a medida x, em grau, nesta figura?
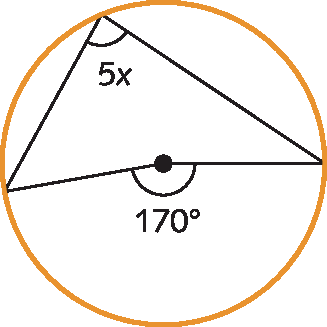
Glossário
- Arte abstrata
- : arte que não procura elaborar uma representação visual precisa da realidade.
- Voltar para o texto