Capítulo 9 Polígonos regulares
Trocando ideias
Os mosaicos são composições feitas com peças que se encaixam lado a lado. Eles costumam apresentar um padrão e podem ser encontrados em pisos, calçadas ou paredes.

As peças do mosaico anterior se parecem com hexágonos regulares, ou seja, hexágonos em que todos os lados têm a mesma medida de comprimento e todos os ângulos internos são congruentes. Esse mosaico é um exemplo de mosaico regular, pois suas peças se parecem com um só tipo de polígono regular.
Para a construção de mosaicos com peças que se parecem apenas com um tipo de polígono regular, é preciso que o número que expressa a medida da abertura do ângulo interno desse polígono seja um divisor de 360.
▸

É possível formar um mosaico em que todas as peças sejam iguais e quadradas? E um mosaico em que todas as peças sejam iguais e o formato delas seja de um triângulo equilátero? Por quê?
▸


É possível formar um mosaico em que todas as peças sejam iguais e o formato delas seja de um pentágono regular? Por quê? Converse com os colegas.
Neste capítulo, vamos estudar os polígonos regulares.

1 Polígonos
Um polígono é uma figura plana, definida por uma linha poligonal, fechada e simples com sua região interna.
Observe este polígono á bê cê dê é.
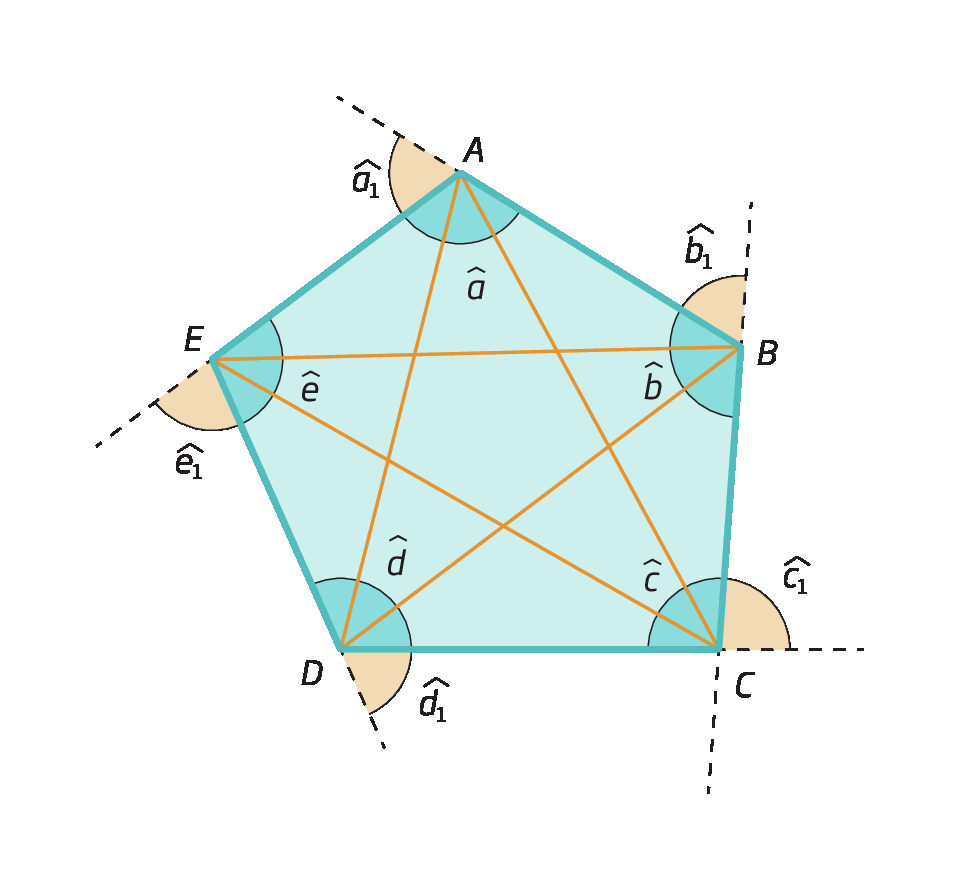
Podemos destacar os seguintes elementos desse polígono:
• lados: segmentos de reta que formam o contorno do polígono;
Segmento de reta AB
,
Segmento de reta BC,
Segmento de reta CD,
Segmento de reta DE,
Segmento de reta EA• vértices: pontos de encontro de dois lados consecutivos;
A, B, C, D, E
• diagonais: segmentos de reta cujas extremidades são dois vértices não consecutivos;
Segmento de reta AC
,
Segmento de reta AD,
Segmento de reta BD,
Segmento de reta BE,
Segmento de reta CE• ângulos internos: ângulos formados por dois lados consecutivos;
Ângulo A
,
Ângulo B,
Ângulo C,
Ângulo D,
Ângulo E• ângulos externos: ângulos formados por um lado do polígono e pelo prolongamento do lado consecutivo a ele.
Ângulo A1
,
Ângulo B1,
Ângulo C1,
Ângulo D1,
Ângulo E1
Polígonos inscritos e circunscritos a uma circunferência
Um polígono está inscrito em uma circunferência quando todos os vértices são pontos dessa circunferência. Observe os exemplos.
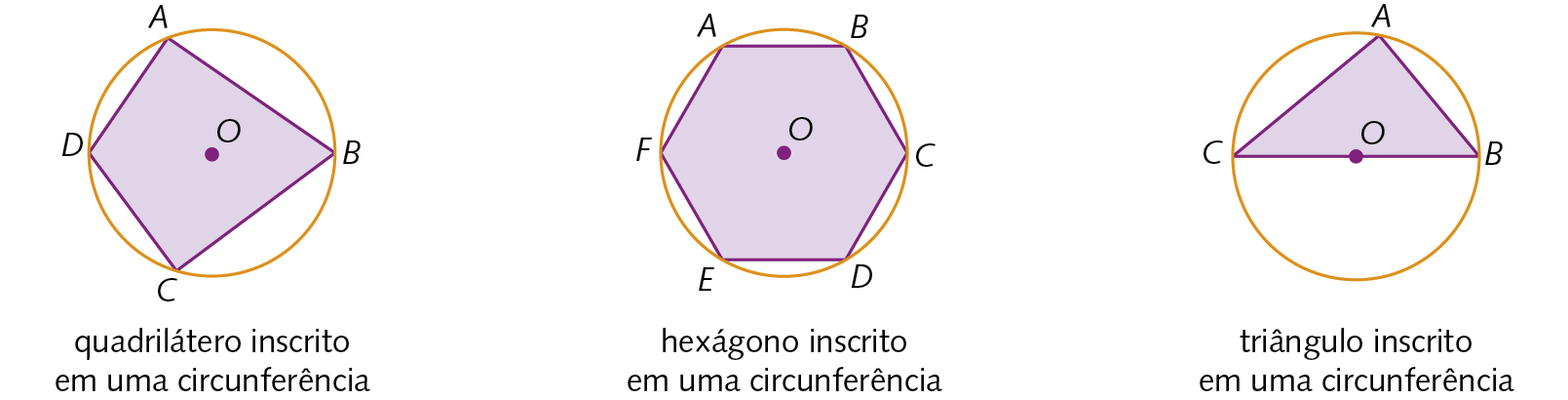
Podemos dizer que os polígonos estão inscritos nas circunferências ou que as circunferências circunscrevem os polígonos.
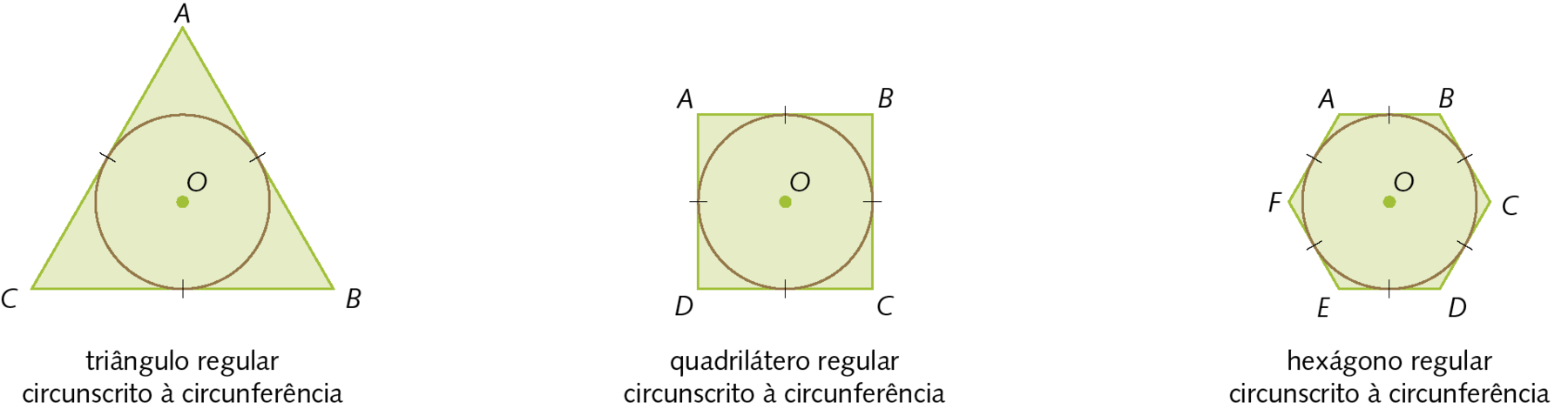
Um polígono está circunscrito a uma circunferência quando todos os lados são tangentes à circunferência. Analise os exemplos.
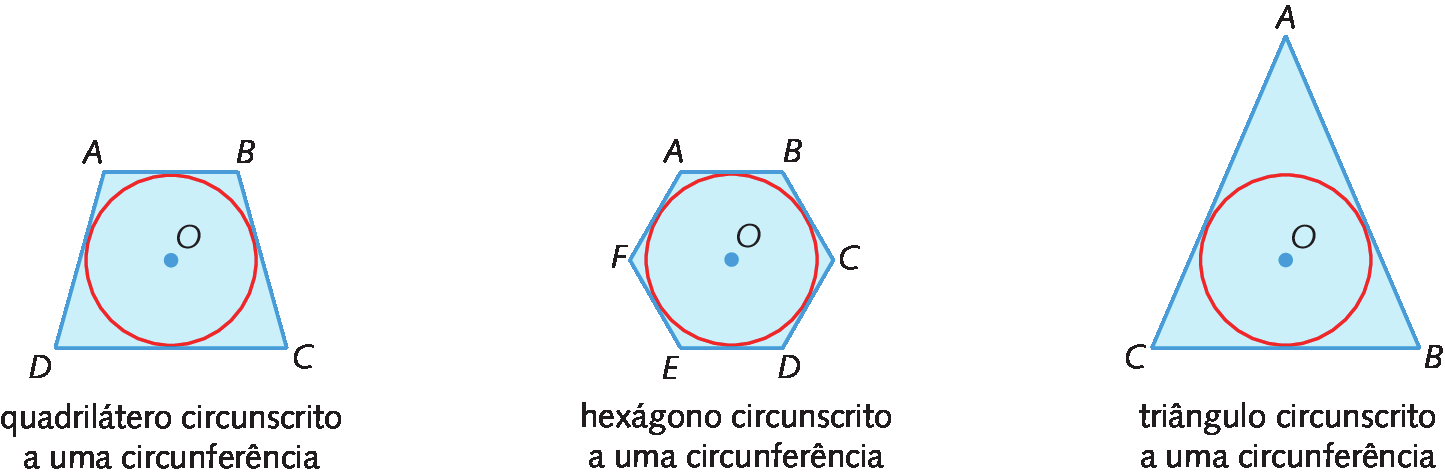
Nesse caso, podemos dizer que os polígonos estão circunscritos às circunferências ou que as circunferências estão inscritas nos polígonos.
Temos as seguintes propriedades para alguns polígonos inscritos em uma circunferência:
1ª propriedade
Todo triângulo inscrito em uma circunferência que tem um lado coincidente com o diâmetro da circunferência é retângulo.
Dado um triânguloá bê cê qualquer inscrito em uma circunferência, como o da figura, em que
BCé o lado do triânguloá bê cê que coincide com o diâmetro da circunferência, temos:

Assim:
Sentença matemática. Medida do ângulo A igual a 90 graus.Portanto, o triânguloá bê cê é retângulo.
2ª propriedade
Os ângulos opostos de um quadrilátero convexo inscrito em uma circunferência são suplementares.
Dado um quadrilátero convexo a bê cê dê qualquer inscrito em uma circunferência, conforme indicado na figura, temos:
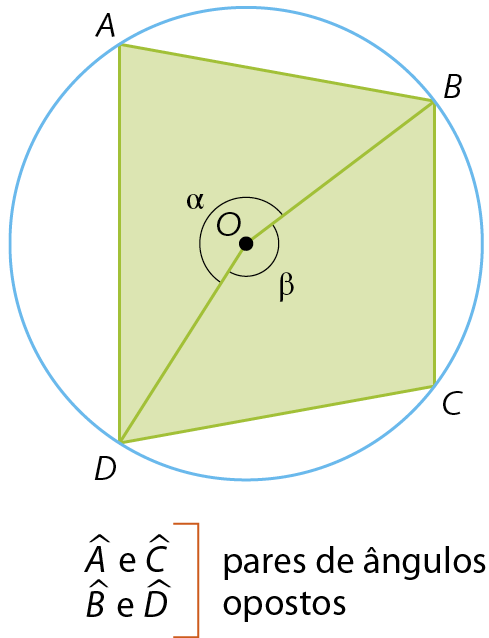
Sentença matemática. Medida do ângulo A igual a fração medida do arco BCD sobre 2 igual a fração beta sobre 2. Sentença matemática. Medida do ângulo C igual a fração medida do arco BAD sobre 2 igual a fração alfa sobre 2.
Sentença matemática. Medida do ângulo A mais medida do ângulo C igual a fração beta sobre 2 mais fração alfa sobre 2 igual a fração 360 graus sobre 2 igual a 180 graus.
Por analogia:
Sentença matemática. Medida do ângulo B mais medida do ângulo D igual a 180 graus.Logo:
Sentença matemática. Medida do ângulo A mais medida do ângulo C igual a medida do ângulo B mais medida do ângulo D igual a 180 graus.
Atividades
Faça as atividades no caderno.
1. Identifique os itens que apresentam um polígono inscrito em uma circunferência.
a)
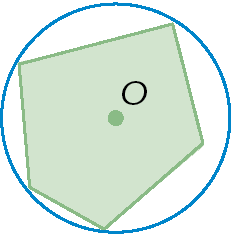
b)
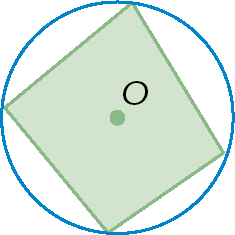
c)
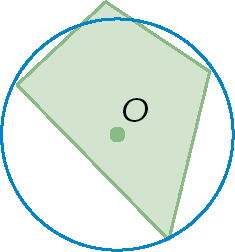
d)
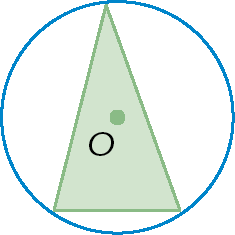
2. Identifique os itens que apresentam um polígono circunscrito à circunferência.
a)

b)
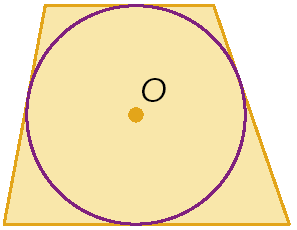
c)
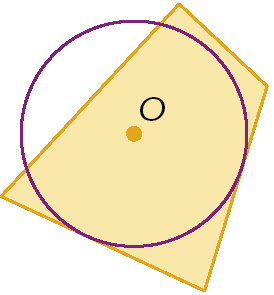
d)
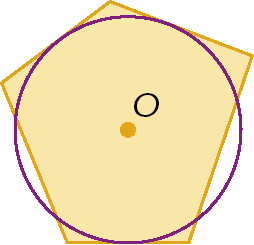
3. Sabendo que O é o centro das circunferências, determine o valor de x nas figuras.
a)
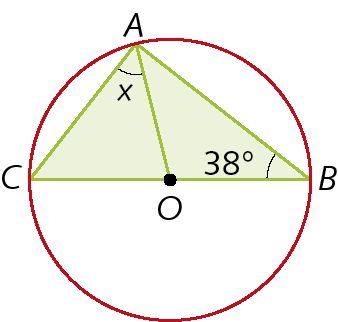
b)
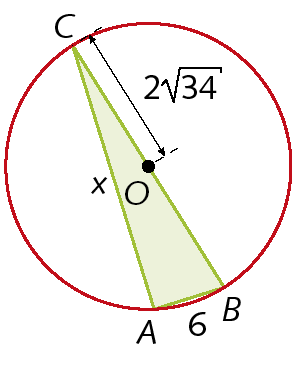
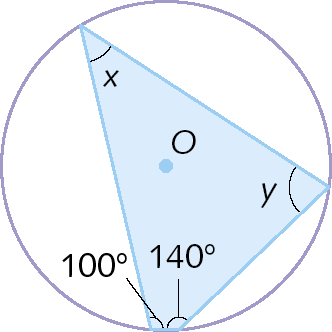
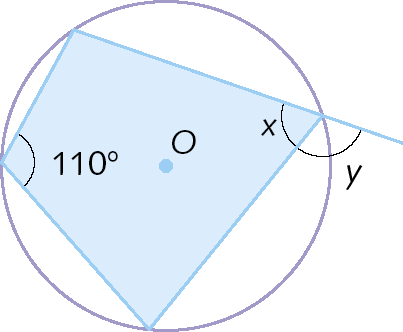
4. Determine as medidas x e y das aberturas dos ângulos nas figuras.
a)
b)
5.

Reúna-se com um colega, observem o quadrilátero a bê cê dê circunscrito a uma circunferência e façam no caderno o que se pede. Considere que x, y, z e w são as medidas de comprimento dos segmentos de reta com uma extremidade no vértice do quadrilátero e a outra extremidade no ponto de tangência do quadrilátero com a circunferência.
Considere que x, y, z e w são as medidas de comprimento dos segmentos de reta com uma extremidade no vértice do quadrilátero e a outra extremidade no ponto de tangência do quadrilátero com a circunferência.
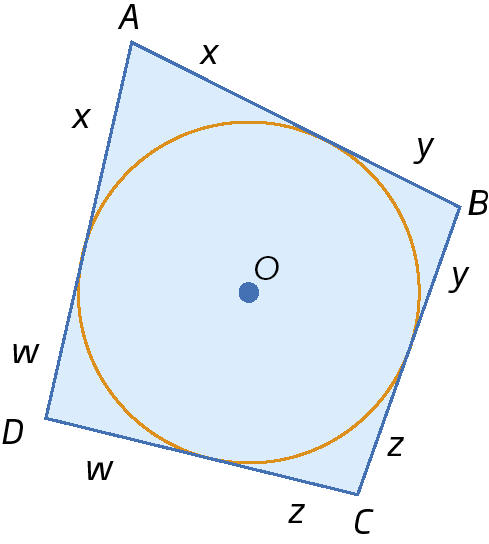
a) Escrevam as medidas de comprimento de
Lado AB,
lado B C,
lado C De
Lado DA.
b) Escrevam a soma das medidas de comprimento de
Lado ABe
Lado CD.
c) Escrevam a soma das medidas de comprimento de
Lado BCe
Lado DA.
d) O que vocês podem concluir sobre as somas das medidas de comprimento dos lados opostos de um quadrilátero circunscritível?
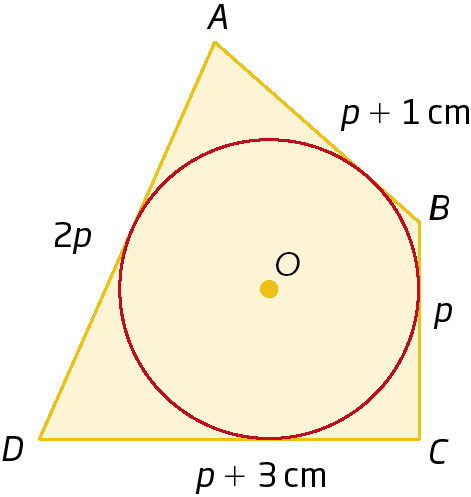
6. O quadrilátero a bê cê dê está circunscrito a uma circunferência. Determine a medida de comprimento p e a medida de perímetro desse quadrilátero.

2 Polígonos regulares
Um polígono regular é o polígono em que todos os lados têm a mesma medida de comprimento e todos os ângulos internos são congruentes, ou seja, quando o polígono é equiângulo e equilátero.
Observe o hexágono á bê cê dê é éfe.
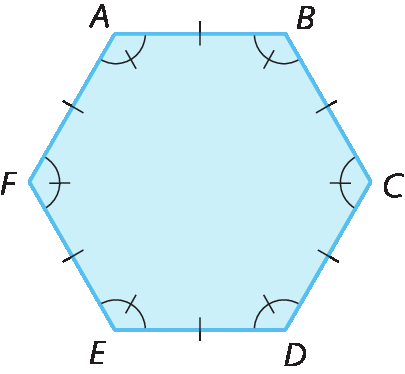
Esse polígono é regular, pois tem todos os lados congruentes e todos os ângulos congruentes, ou seja:
Observações
1. Os ângulos de um retângulo são todos congruentes, mas não podemos afirmar que seus lados são sempre congruentes. Logo, o retângulo é um polígono regular quando também for um quadrado.
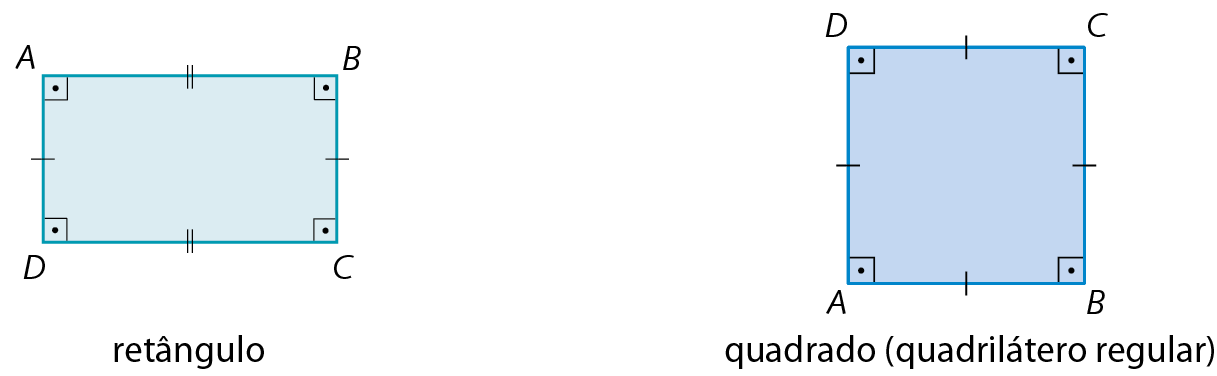
2. Os lados de um losango são todos congruentes, mas não podemos afirmar que seus ângulos são sempre congruentes. Logo, o losango é um polígono regular quando também for um quadrado.

Propriedades dos polígonos regulares
1ª propriedade
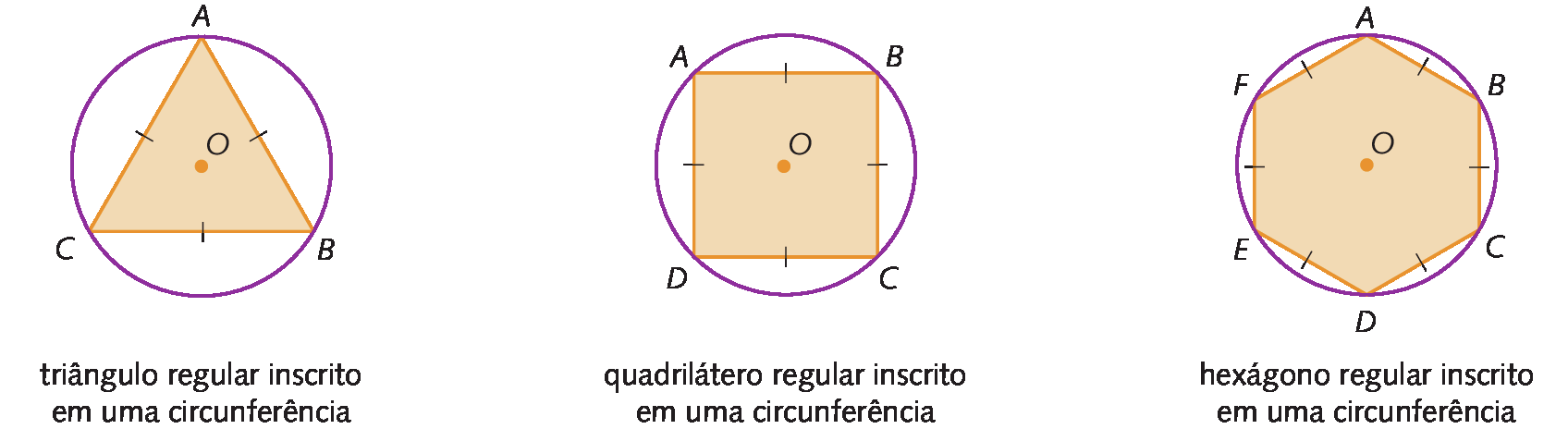
Todo polígono regular é inscritível em uma circunferência.
Para inscrever um polígono regular de n lados (n > 2) em uma circunferência, basta dividi‑la em n arcos congruentes e traçar todos os segmentos de reta que tenham como extremidades dois pontos consecutivos obtidos nessa divisão, determinando, assim, os lados do polígono.
Considere os exemplos.
2ª propriedade
Todo polígono regular é circunscritível a uma circunferência.
Para circunscrever um polígono regular de n lados (n > 2) a uma circunferência, basta dividi‑la em n arcos congruentes e traçar as tangentes nos pontos de divisão.
Confira os exemplos.
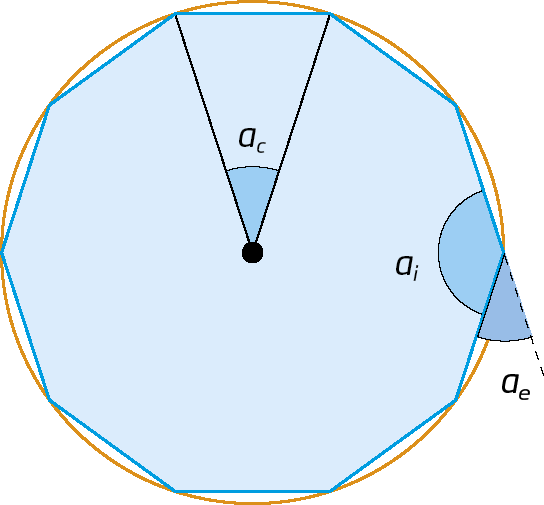
Elementos de um polígono regular
Vamos identificar os elementos de um polígono regular. Analise a figura.
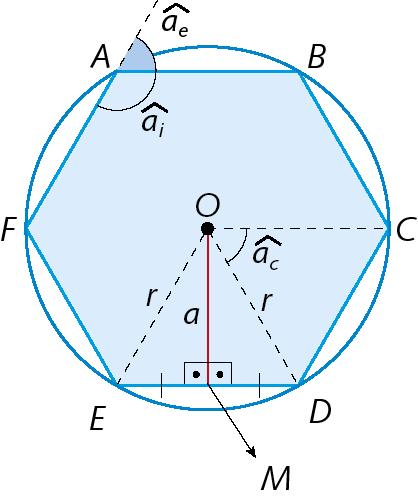
• O ponto óh é o centro do polígono e corresponde ao centro da circunferência circunscrita ao polígono.
• O raio da circunferência circunscrita (de medida de comprimento r ) é o raio do polígono:
Segmento de reta OC,
Segmento de reta OD,
Segmento de reta OE.
• O segmento de reta cujas extremidades são o centro e o ponto médio de qualquer lado do polígono é um apótema do polígono:
Segmento de reta OM., sendo M o ponto médio de
Lado DE.e OM = a.
• O ângulo que tem o vértice no centro e cujos lados contêm vértices consecutivos do polígono é um ângulo central
Ângulo AC:
Ângulo COD.,
Ângulo DOE.,
Ângulo BOC.,
Ângulo AOB.,
Ângulo AOF.,
Ângulo FOE..
• O ângulo formado por dois lados consecutivos do polígono é um ângulo interno
Ângulo AI.
• O ângulo externo
Ângulo AEé o suplemento do ângulo interno correspondente, ou seja: ai + ae = 180graus.
Vamos relembrar como determinar as medidas das aberturas dos ângulos central, interno e externo de um polígono regular.
• Ângulo central
A soma das medidas das aberturas dos ângulos centrais de um polígono regular é 360graus, ou seja, corresponde a uma volta completa. Logo, em um polígono regular de n lados, a medida da abertura do ângulo central é:
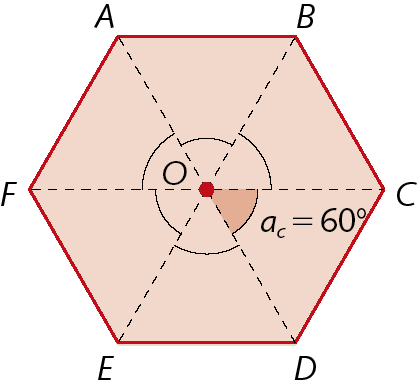
No hexágono á bê cê dê é éfe, a abertura do ângulo central mede 60graus, pois:
Sentença matemática. AC igual a fração 360 graus sobre 6 igual a 60 graus.• Ângulo interno
A partir de um único vértice, podemos decompor um polígono em triângulos e verificar que o número de triângulos é duas unidades menor que o número de lados. Como a soma das medidas das aberturas dos ângulos internos de um triângulo é 180graus, podemos afirmar que a soma das medidas das aberturas dos ângulos internos (Si ) de um polígono de n lados corresponde a:
ésse minúsculoi = (n ‒ 2) · 180graus
Assim, em um polígono regular de n lados, a medida da abertura do ângulo interno é:
No hexágono á bê cê dê é éfe, a abertura do ângulo interno mede 120graus, pois:
Sentença matemática. AI igual a fração, numerador, abre parênteses, 6 menos 2, fecha parênteses, vezes 180 graus, denominador 6, igual a 120 graus.• Ângulo externo
Como em um polígono o ângulo externo e o ângulo interno são suplementares, temos:
• a + a 1 = 180graus
• b + b 1 = 180graus
• c + c 1 = 180graus
• d + d 1 = 180graus
• e + e 1 = 180graus
• f + f 1 = 180graus
Calculando a soma das medidas das aberturas dos ângulos internos e externos, temos:

Então, em um polígono regular de n lados:
Si + Se = n ⋅ 180graus ⇒ (n ‒ 2) ⋅ 180graus + Se = n ⋅ 180° ⇒
⇒ n ⋅ 180graus ‒ 360graus + Se = n ⋅ 180graus ⇒ Se = 360°
Assim, em um polígono regular de n lados, a medida da abertura do ângulo externo é:
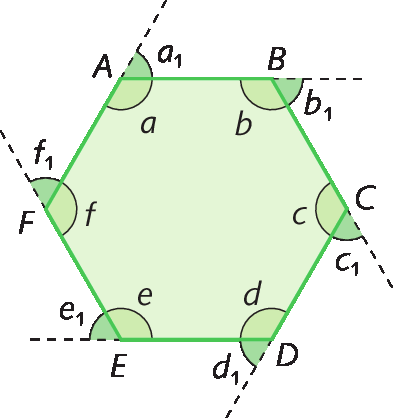
No hexágono á bê cê dê é éfe, a abertura do ângulo externo mede 60graus, pois:
Sentença matemática. AE igual a fração 360 graus sobre 6 igual a 60 graus.Construção de polígonos regulares com régua e compasso
Podemos construir alguns polígonos regulares a partir do seu ângulo central, como a construção de um triângulo equilátero.
Construção de um triângulo equilátero
1º) Traçamos uma circunferência qualquer e construímos um ângulo central de medida de abertura de 120°, marcando, na circunferência, os pontos A e B.
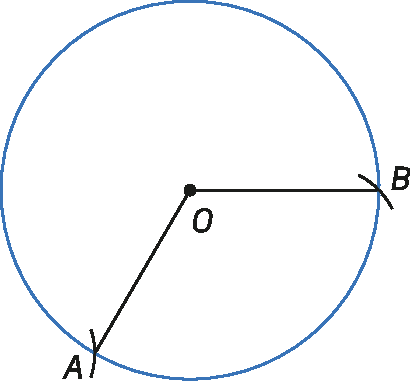
2º) Construímos outro ângulo central de mesma medida de abertura, adjacente ao primeiro, ao redor da circunferência, marcando o ponto C.
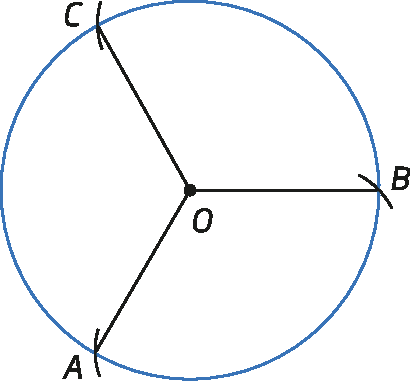
3º) Unimos os pontos a, B e C com segmentos de reta e obtemos o triânguloá bê cê.
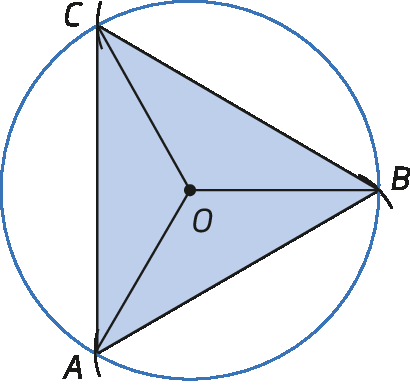
Note que, nessa construção, o polígono obtido está inscrito em uma circunferência.
Podemos construir outros polígonos regulares a partir do ângulo central, mas também podemos construir polígonos regulares a partir de um de seus lados.
Acompanhe, a seguir, a construção de um quadrado a partir de um de seus lados.
Construção de um quadrado
A partir do segmento de reta
ABdado, vamos construir um quadrado considerando esse segmento de reta como um de seus lados.

1º) Construímos uma reta perpendicular ao segmento de reta
Segmento de reta AB., passando por B, e, com o auxílio de um compasso, transportamos a medida de comprimento de
Segmento de reta ABpara a reta perpendicular, marcando o ponto C.
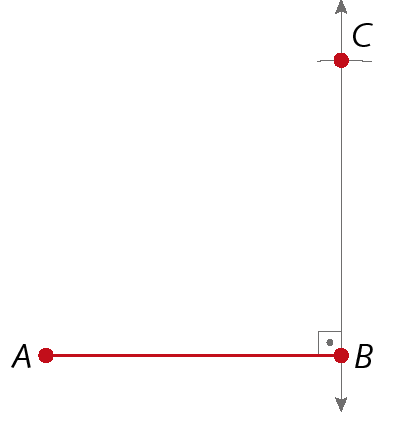
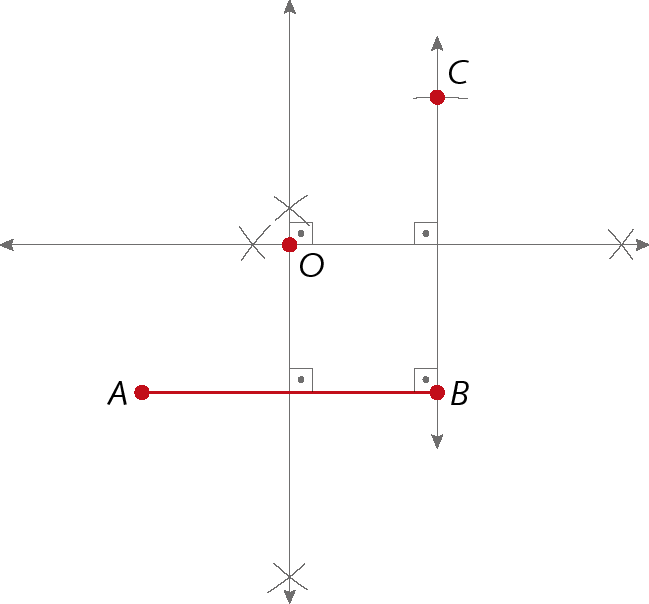
2º) Construímos as mediatrizes de
Segmento de reta ABe
Segmento de reta BC.e marcamos na intersecção das duas retas o ponto O.
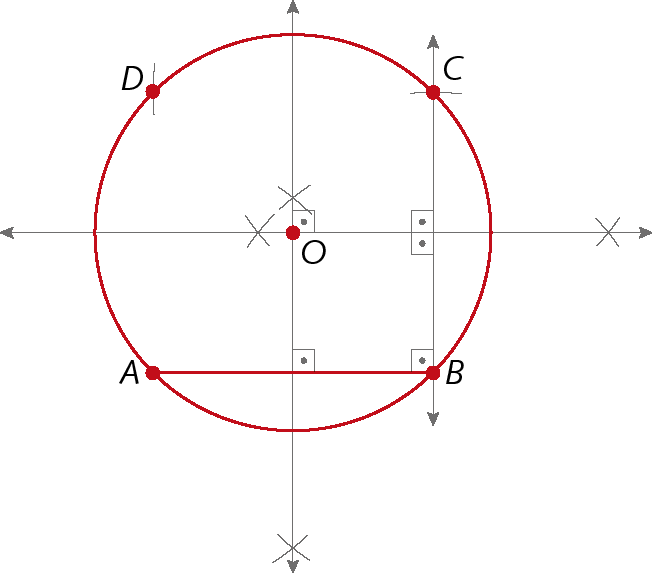
3º) Construímos uma circunferência de centro em O e raio
AOe, a partir do ponto C, transportamos a medida de comprimento do lado do quadrado, marcando o ponto D.
4º) Traçamos os segmentos de reta
BC,
CDe
ADdeterminando, assim, o quadrado ABCD.
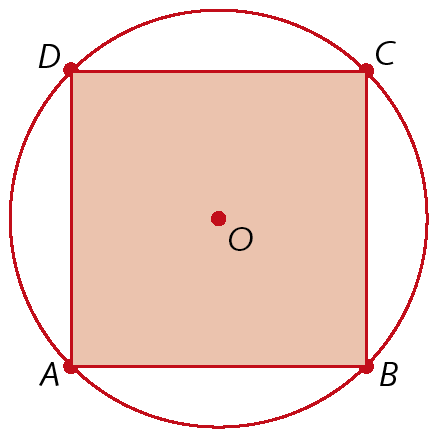
Observe que o quadrado construído está inscrito em uma circunferência de centro óh, obtido a partir do encontro das mediatrizes de dois lados do polígono.
Observação
O encontro das mediatrizes dos lados de um polígono é o circuncentro do polígono, centro da circunferência circunscrita a ele.
Construção de um polígono regular de en lados
Analise os passos descritos no esquema para construir polígonos regulares a partir de um lado conhecido.
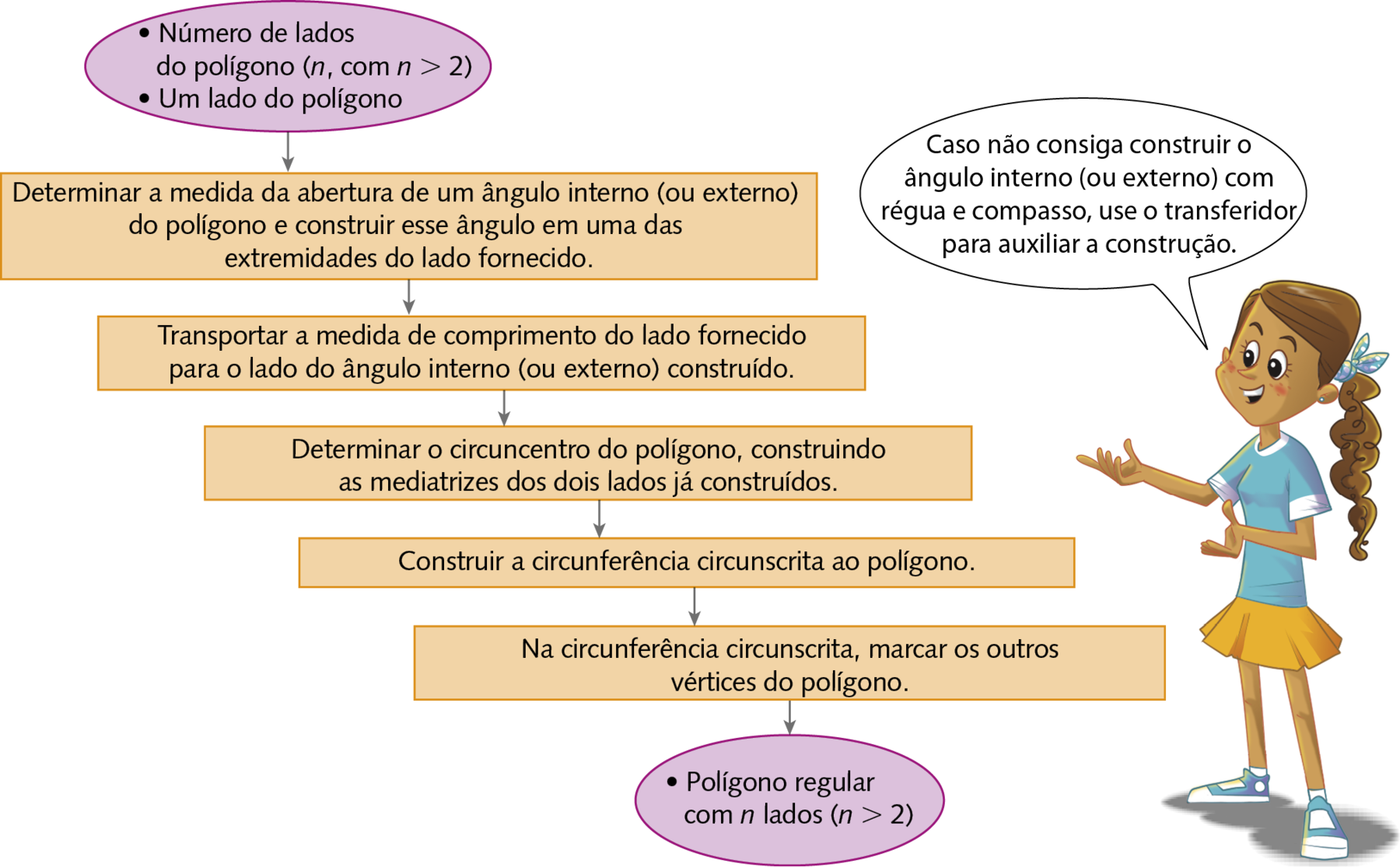
Observação
Desenhar um polígono regular com régua e compasso significa obtê-lo com o auxílio de intersecções feitas por segmentos de reta e circunferências desenhados com esses instrumentos.
O matemático alemão Carl Friedrich Gauss (1777-1855) provou que nem todo polígono regular póde ser desenhado com régua e compasso, como é o caso do heptágono regular. O que podemos obter é uma boa aproximação para esse polígono, que póde ser utilizada dependendo do objetivo. Observe uma aproximação dessa construção.
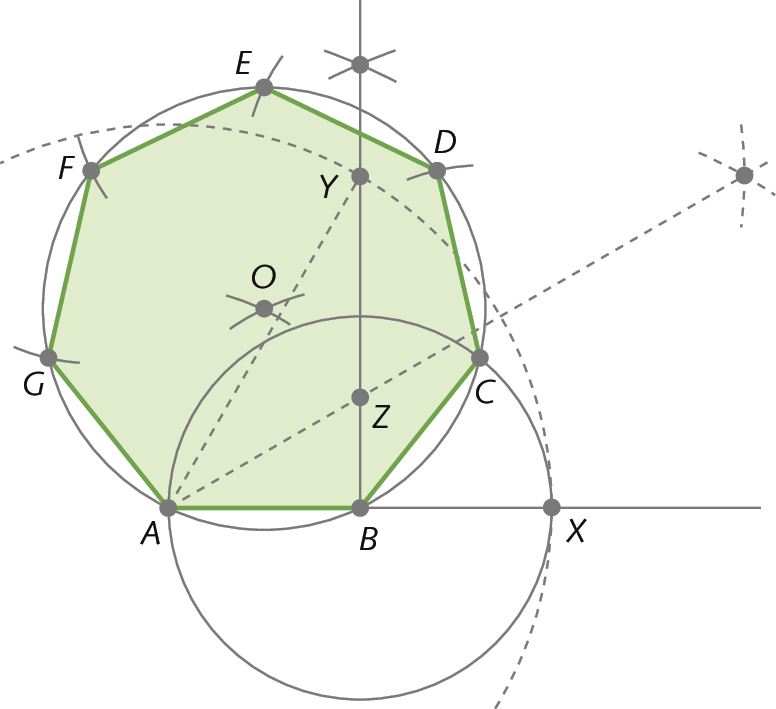
Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso nas atividades 8 e 15.
7. Quais das afirmações são verdadeiras?
a) Todo polígono regular é inscritível e circunscritível a uma circunferência.
b) Denomina‑se equiângulo um polígono que tem todos os ângulos congruentes.
c) O retângulo é um polígono regular.
d) Denomina‑se equilátero um polígono que tem todos os lados congruentes.
8. Desenhe, em seu caderno, um polígono regular qualquer, identificando:
a) o centro do polígono;
b) um ângulo central;
c) um raio;
d) um ângulo interno;
e) um apótema;
f) um ângulo externo.
9. Calcule as medidas das aberturas do ângulo central, do ângulo interno e do ângulo externo do decágono regular.
10. Calcule as medidas das aberturas do ângulo central, do ângulo interno e do ângulo externo do:
a) triângulo equilátero;
b) quadrado;
c) hexágono regular.
11. Determine o polígono regular cujas aberturas dos ângulos centrais medem:
a) 36graus;
b) 40graus;
c) 60graus;
d) 90graus;
e) 120graus.
12. Quantos lados tem um polígono regular cujas aberturas dos ângulos externos medem 24graus?
13. A abertura do ângulo interno de um polígono regular mede 135graus. Quanto mede a abertura do ângulo externo? Qual é esse polígono?
14. A soma das medidas das aberturas dos ângulos internos de um polígono regular é .1440graus. Quanto mede a abertura do ângulo externo desse polígono?
15. Trace um segmento de reta medindo 3 centímetros de comprimento e, a partir dele, desenhe um triângulo equilátero.
16.

A figura mostra um bloco de comandos realizado no TucaProg (software de programação visual).

Observe os comandos e responda às questões.
a) Esse bloco de comandos dá origem a qual polígono regular?
b) Em um polígono regular temos o ângulo central, o ângulo interno e o ângulo externo. Qual deles está representado no comando “Virar no sentido horário 45graus”?
c) Utilize o TucaProg para construir um tetracoságono regular (polígono com 24 lados).

3 Relações métricas nos polígonos regulares
Vamos estudar as relações entre as medidas de comprimento do lado, do apótema de um polígono regular e do raio da circunferência em que o polígono está inscrito.
Triângulo equilátero inscrito em uma circunferência
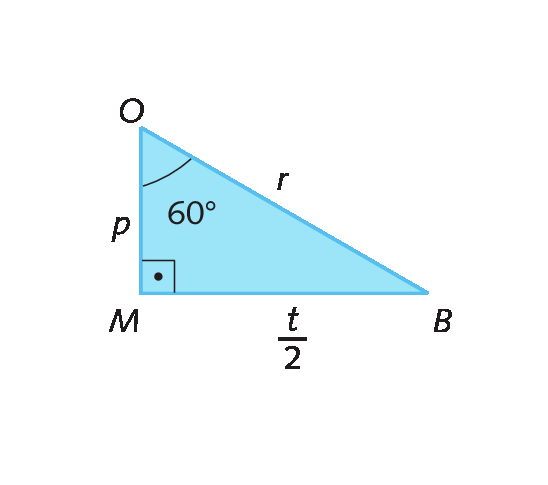
No triânguloá bê cê, temos:
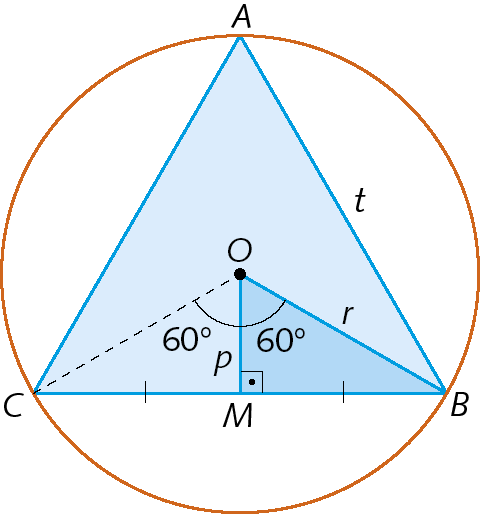
• t : medida de comprimento do lado do triângulo á bê cê;
• p : medida de comprimento do apótema do triângulo á bê cê (ó ême );
• r : medida de comprimento do raio da circunferência circunscrita ao triângulo á bê cê;

Agora, considerando o triângulo ô ême bê, determinamos as relações:

Quadrado inscrito em uma circunferência
No quadrado a bê cê dê, temos:
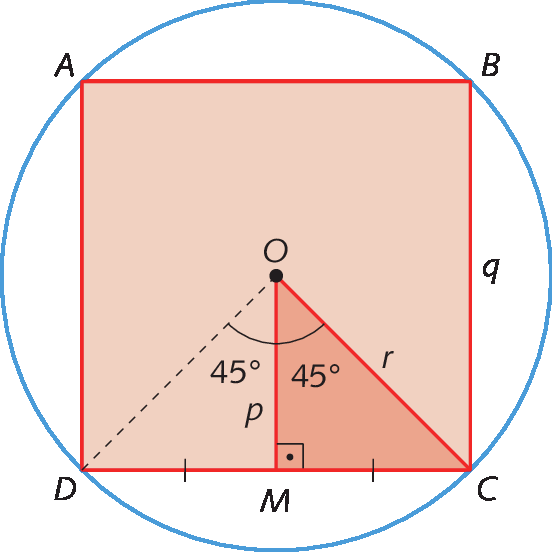
• q : medida de comprimento do lado do quadrado a bê cê dê;
• p : medida de comprimento do apótema do quadrado a bê cê dê (ó ême);
• r : medida de comprimento do raio da circunferência circunscrita ao quadrado a bê cê dê;

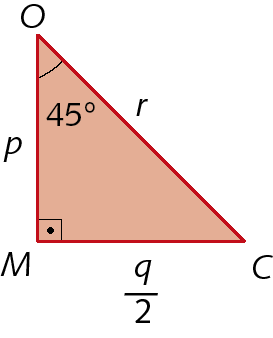
Agora, considerando o triângulo ó ême cê , determinamos as relações:


Hexágono regular inscrito em uma circunferência
No hexágono á bê cê dê é éfe, temos:
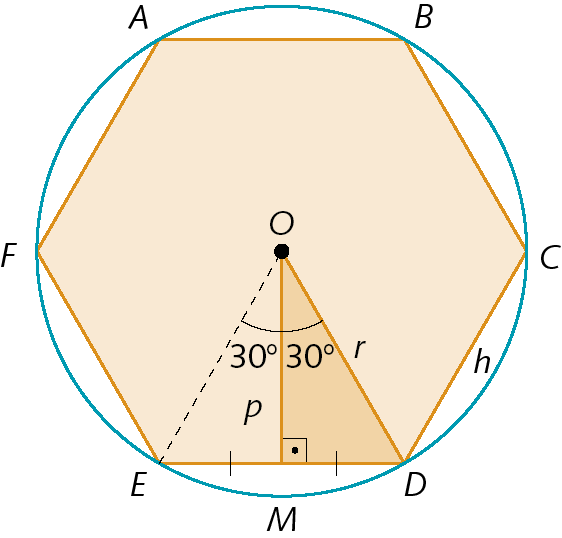
• h : medida de comprimento do lado do hexágono;
• p : medida de comprimento do apótema do hexágono;
• r : medida de comprimento do raio da circunferência circunscrita ao hexágono;

Considerando o triângulo ó ême dê, determinamos as relações:
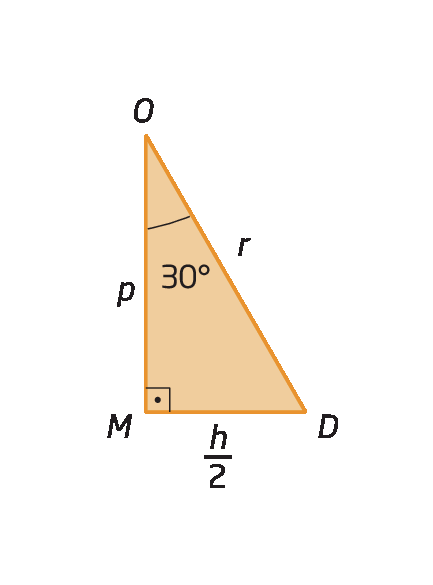

Confira estes exemplos.
a) Vamos determinar as medidas de comprimento do lado (q) e do apótema (p) de um quadrado inscrito em uma circunferência cujo comprimento do raio mede 10 centímetros.
Sentença matemática. Q igual a R raiz de 2 igual a 10 raiz de 2.
Sentença matemática. P igual a fração, numerador R raiz de 2, denominador 2, igual a fração, numerador 10 raiz de 2, denominador 2, igual a 5 raiz de 2.
Portanto, o comprimento do lado mede 10
Sentença matemática. Raiz de 2.centímetros e o comprimento do apótema mede
5 raiz de 2 centímetros..
b) Vamos determinar as medidas de comprimento do lado (t) e do apótema (p) de um triângulo equilátero inscrito em uma circunferência cujo comprimento do raio mede 12 centímetros.
Sentença matemática. T igual a R raiz de 3 igual a 12 raiz de 3.
Sentença matemática. P igual a fração R sobre 2 igual a fração 12 sobre 2 igual a 6.
Portanto, o comprimento do lado mede
12 raiz de 3 centímetros.e o comprimento do apótema mede 6 centímetros.
c) Agora, vamos determinar as medidas de comprimento do lado (h) e do apótema (p) de um hexágono regular inscrito em uma circunferência cujo comprimento do raio mede 8 centímetros.
h = r = 8
Sentença matemática. P igual a fração, numerador R raiz de 3, denominador 2, igual a fração, numerador 8 raiz de 3, denominador 2, igual a 4 raiz de 3.
Portanto, o comprimento do lado mede 8 cm e o comprimento do apótema mede
4 raiz de 3 centímetros..
Atividades
Faça as atividades no caderno.
17. Calcule as medidas de comprimento do lado e do apótema de um quadrado inscrito em uma circunferência cujo comprimento do raio mede 10 centímetros.
18. O perímetro de um quadrado inscrito em uma circunferência mede 40 centímetros. Determine a medida de comprimento do raio.
19. O comprimento do lado de um quadrado inscrito em uma circunferência mede 12 centímetros. Calcule a medida de comprimento:
a) do raio da circunferência que circunscreve o quadrado;
b) do apótema do quadrado.
20. O comprimento do lado de um quadrado inscrito em uma circunferência mede
6 raiz de 2 centímetros.. Determine a medida de comprimento do apótema desse quadrado.
21. Um quadrado está inscrito em uma circunferência cujo comprimento do raio mede 4 centímetros. Determine a medida:
a) de perímetro aproximado desse quadrado, usando
raiz de 2 igual a 1,41;
b) da área desse quadrado.
22. Calcule as medidas de comprimento do lado e do apótema de um triângulo equilátero inscrito em uma circunferência cujo comprimento do raio mede 8 centímetros.
23. O comprimento do lado de um triângulo equilátero mede 20 centímetros. Determine as medidas de comprimento do raio da circunferência circunscrita e do apótema.
24. O comprimento do apótema de um triângulo equilátero inscrito em uma circunferência mede 6 centímetros. Calcule a medida de comprimento do lado desse triângulo.
25. Calcule a medida de perímetro de um triângulo equilátero inscrito em uma circunferência cujo comprimento do raio mede
Sentença matemática. 10 raiz de 3.centímetros.
26. Calcule as medidas de comprimento do lado e do apótema de um hexágono regular inscrito em uma circunferência cujo comprimento do raio mede 12 centímetros.
27. O comprimento do apótema de um hexágono regular mede
5 raiz de 3 centímetros.. Determine a medida de perímetro do hexágono.
28. O comprimento do lado de um hexágono regular inscrito em uma circunferência mede 8 centímetros. Calcule as medidas de comprimento do raio da circunferência e do apótema do hexágono.
29. O comprimento da maior diagonal de um hexágono regular mede
12 raiz de 3 centímetros.. Calcule a medida de comprimento do apótema desse hexágono.
30. Com base no triângulo equilátero inscrito na circunferência, determine:
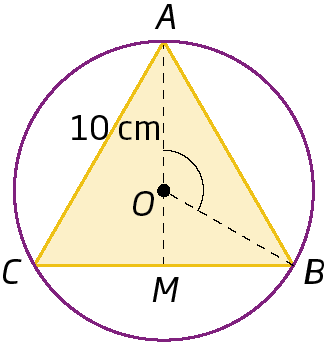
a) a medida de comprimento do segmento de reta
AB;
b) a medida de comprimento do segmento de reta
OM;
c) a medida da abertura do ângulo
AOB;
d) a medida de comprimento do segmento de reta
AM.
31. O comprimento do apótema de um hexágono regular inscrito em uma circunferência mede
6 raiz de 3 centímetros.. Determine a medida de comprimento do lado desse hexágono.
32. O comprimento do lado de um quadrado inscrito em uma circunferência mede
8 raiz de 3 centímetros.. Determine a medida de comprimento do apótema do hexágono regular inscrito na mesma circunferência.
33. Qual é a razão entre as medidas de comprimento do lado de um hexágono regular e do lado de um quadrado, nessa ordem (os dois estão inscritos na mesma circunferência)?
34. O comprimento do apótema de um hexágono regular inscrito em uma circunferência mede
12 raiz de 3 metros.. Determine a medida de comprimento:
a) da diagonal do quadrado inscrito nessa circunferência;
b) do apótema do triângulo equilátero inscrito nessa circunferência.
Polígonos regulares circunscritos
Considere os polígonos de n lados (na figura, n = 6), sendo um inscrito e outro circunscrito à circunferência cujo comprimento do raio mede r. Nessa figura, temos:
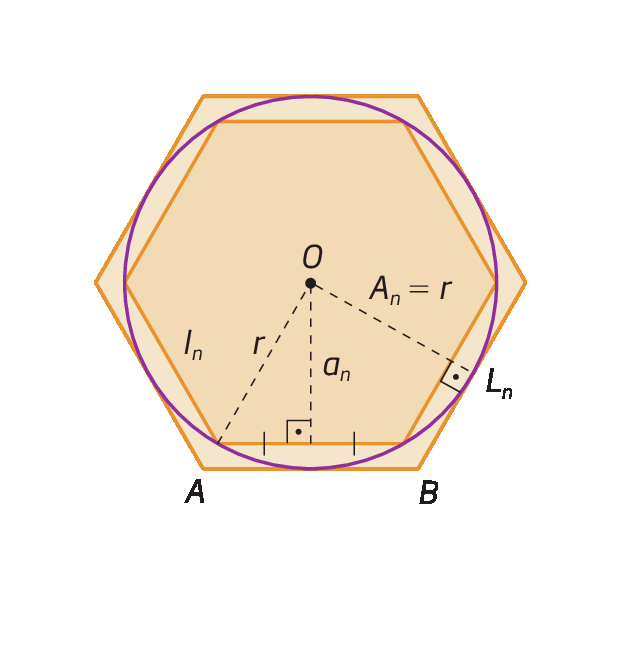
• quinquagésimon : medida de comprimento do lado do polígono regular inscrito;
• án : medida de comprimento do apótema do polígono regular inscrito;
• quinquagésimon : medida de comprimento do lado do polígono regular circunscrito;
• án : medida de comprimento do apótema do polígono regular circunscrito.
Como os polígonos inscrito e circunscrito à circunferência são semelhantes, podemos estabelecer a relação:

Acompanhe alguns exemplos.
a) Vamos calcular a medida de comprimento do lado de um triângulo equilátero circunscrito a uma circunferência cujo comprimento do raio mede 6 centímetros.
Precisamos das medidas de comprimento do apótema á₃ e do lado primeiro₃ do triângulo equilátero inscrito nessa mesma circunferência. Utilizando as relações estudadas
Sentença matemática. A minúsculo 3 igual a fração R sobre 2.e
Sentença matemática. L minúsculo 3 igual a R raiz de 3., obtemos estas medidas:
Sentença matemática. A minúsculo 3 igual a fração 6 sobre 2 igual a 3.
e
Sentença matemática. L minúsculo 3 igual a 6 raiz de 3..
Agora, substituindo os valores na proporção
Sentença matemática. Fração L minúsculo N sobre L maiúsculo N igual a fração A minúsculo N sobre R., temos:
Sentença matemática. Fração, numerador 6 raiz de 3, denominador L maiúsculo 3, igual a fração 3 sobre 6 implica que L maiúsculo 3 igual a 12 raiz de 3.
Portanto, o comprimento do lado do triângulo circunscrito a essa circunferência mede
12 raiz de 3 centímetros..
b) Vamos calcular a medida de comprimento do lado de um quadrado circunscrito a uma circunferência cujo comprimento do raio mede 10 centímetros.
As medidas de comprimento do apótema á₄ e do lado I₄ do quadrado inscrito nessa mesma circunferência se relacionam com a medida de comprimento do raio:
Sentença matemática. A minúsculo 4 igual a fração, numerador R raiz de 2, denominador 2, igual a fração, numerador 10 raiz de 2, denominador 2, igual a 5 raiz de 2.
Sentença matemática. L minúsculo 4 igual a R raiz de 2 igual a 10 raiz de 2.
Agora, substituindo os valores na proporção
Sentença matemática. Fração L minúsculo N sobre L maiúsculo N igual a fração A minúsculo N sobre R., temos:
Sentença matemática. Fração, numerador 10 raiz de 2, denominador L maiúsculo 4, igual a fração, numerador 5 raiz de 2, denominador 10, implica que L maiúsculo 4 igual a 20.
Portanto, o comprimento do lado do quadrado circunscrito a essa circunferência mede 20 centímetros.
Atividades
Faça as atividades no caderno.
35. Calcule a medida de comprimento do lado de um triângulo equilátero circunscrito a uma circunferência cujo comprimento do raio mede
2 raiz de 3 centímetros.36. Calcule a medida de comprimento do lado de um quadrado circunscrito a uma circunferência cujo comprimento do raio mede 8 centímetros.
37. Calcule a medida de comprimento do lado de um hexágono regular circunscrito a uma circunferência cujo comprimento do raio mede
4 raiz de 3 centímetros..
38. O perímetro de um hexágono regular inscrito em uma circunferência mede
24 raiz de 3 centímetros.. Calcule a medida de perímetro de um triângulo equilátero circunscrito a essa circunferência.
39.


Utilize um software de geometria dinâmica para realizar as construções a seguir:
• construa um pentágono regular á bê cê dê é;
• determine o centro óh do polígono;
• construa a circunferência de raio
OA;
• construa um pentágono regular éfe gê agá í jota circunscrito à circunferência;
• construa um apótema do pentágono menor.
a) Utilizando as ferramentas do software, meça o comprimento dos lados dos polígonos, o comprimento do apótema do polígono menor e o comprimento do raio da circunferência. Em seguida, com o auxílio de uma calculadora, verifique a validade da relação entre essas medidas.
b) Movimente os pontos do pentágono á bê cê dê é e observe o que acontece com a relação analisada no item a.
40.


Analise a construção.
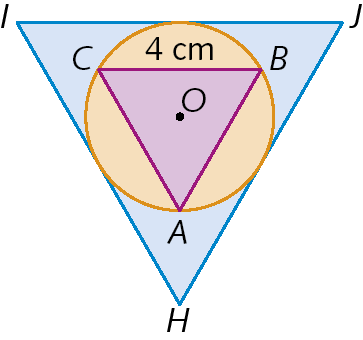
Considere que os triângulos agá é jota e á bê cê são equiláteros e BC = 4 centímetros.
• No caderno, elabore duas questões relacionadas com a figura.
• Troque de caderno com um colega e responda às questões elaboradas por ele. Em seguida, analise as respostas do colega e dê um retorno a ele, dizendo o que ele respondeu corretamente e em que pontos ele se equivocou.

Resolvendo em equipe
Faça a atividade no caderno.
(ó bê mépi) O polígono á bê cê dê é éfe é um hexágono regular. Os pontos M e N são pontos médios dos lados
AFe
BC, respectivamente. O hexágono ABNGHM é simétrico em relação à reta que passa por M e N.
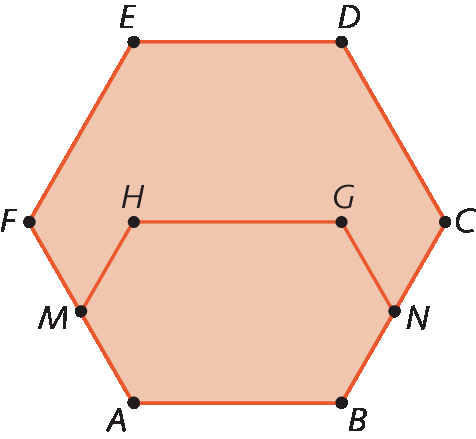
Qual é a razão entre as áreas dos hexágonos ABNGHM e á bê cê dê é éfe ?
a)
Fração 3 sobre 10.b)
Fração 4 sobre 11.c)
Fração 3 sobre 7.d)
Fração 7 sobre 15.e)
Fração 5 sobre 12.|
Interpretação e identificação dos dados |
• Analise as informações do enunciado e anote aquelas que você julgar relevantes para a resolução do problema. |
|---|---|
|
Plano de resolução |
• Os hexágonos ABCDEF e ABNGHM podem ser decompostos em triângulos equiláteros congruentes? |
|
Resolução |
• Junte‑se a um colega. |
|
Verificação |
• Releiam o problema e verifiquem se todas as condições do enunciado foram satisfeitas. |
|
Apresentação |
• Construam diversos triângulos equiláteros de cartolina. Utilizando apenas esses triângulos, componham novos polígonos, regulares ou não, e apresentem para os colegas. |
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Polígonos
Um polígono é uma figura plana, definida por uma linha poligonal, fechada e simples com sua região interna.
Polígonos inscritos e circunscritos a uma circunferência
Um polígono está inscrito em uma circunferência quando todos os vértices são pontos dessa circunferência.
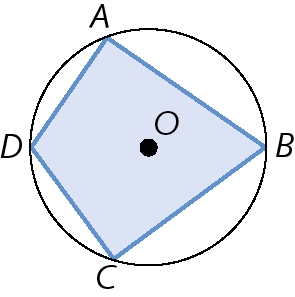
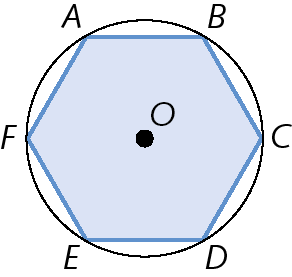
Um polígono está circunscrito a uma circunferência quando todos os lados são tangentes a circunferência.
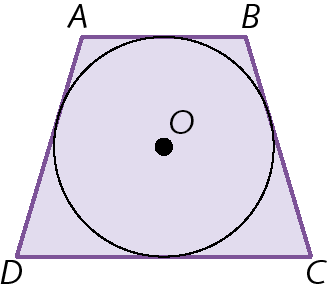
1ª propriedade: Todo triângulo inscrito em uma circunferência que tem um lado coincidente com o diâmetro da circunferência é retângulo.
2ª propriedade: Os ângulos opostos de um quadrilátero convexo inscrito em uma circunferência são suplementares.
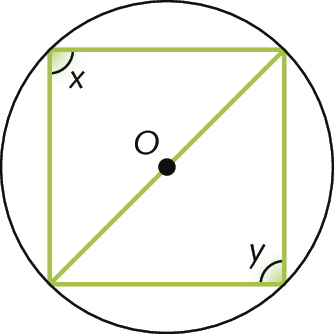
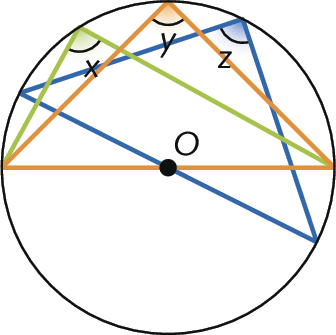
1. Determine as medidas x, y e z das aberturas dos ângulos desconhecidos nas circunferências.
a)
b)
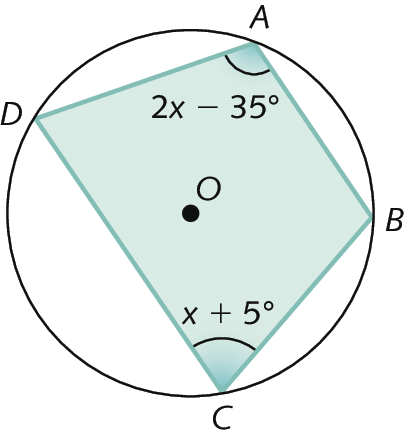
2. Sabendo que a bê cê dê é um quadrilátero inscrito na circunferência, determine a medida de abertura x.
Polígonos regulares
Um polígono regular é o polígono em que todos os lados têm a mesma medida de comprimento e todos os ângulos internos são congruentes, ou seja, quando o polígono é equiângulo e equilátero.
Propriedades dos polígonos regulares
1ª propriedade: Todo polígono regular é inscritível em uma circunferência.
2ª propriedade: Todo polígono regular é circunscritível a uma circunferência.
Elementos de um polígono regular
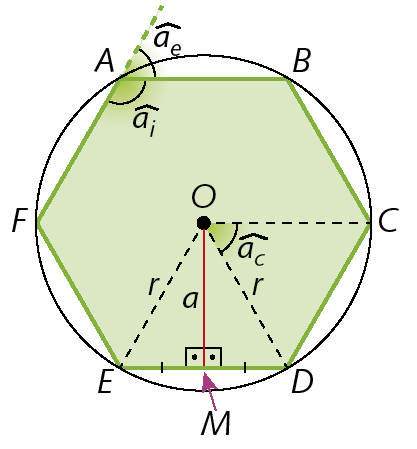
• O: centro do polígono e da circunferência
• r: medida de comprimento do raio do polígono e da circunferência circunscrita
• a: medida de comprimento do apótema (segmento de reta cujas extremidades são o centro e o ponto médio de qualquer lado do polígono)
• n: número de lados
•
Ângulo AC: ângulo central (ângulo que tem o vértice no centro e cujos lados contêm vértices consecutivos do polígono)
•
Ângulo AI: ângulo interno (ângulo formado por dois lados consecutivos do polígono)
•
Ângulo AE: ângulo externo (suplemento do ângulo interno correspondente)
Sentença matemática. AI mais AE igual a 180 graus.
3. Calcule a medida de abertura do ângulo central destes polígonos regulares:
a) pentágono;
b) octógono;
c) dodecágono (polígono de 12 lados);
d) polígono de 24 lados.
4. Sabendo que um pentadecágono regular tem 15 lados, determine:
a) a medida da abertura de cada ângulo interno;
b) a medida da abertura de cada ângulo externo;
c) a medida da abertura de cada ângulo central.
5. Sabendo que a soma das medidas das aberturas dos ângulos internos de um polígono regular mede .2880graus, determine quantos lados tem o polígono.
6. Se a abertura do ângulo externo de um polígono regular mede 18graus, quantos lados tem esse polígono?
7. Em um polígono regular, a medida da abertura do ângulo central é 40graus. Responda:
a) Quantos lados tem esse polígono?
b) Qual é a medida da abertura do ângulo interno?
c) Qual é a medida da abertura do ângulo externo?
8. Em um polígono regular, (3x + 36graus) representa a medida da abertura de um dos ângulos internos e (x ‒ 8graus) representa a medida da abertura do ângulo externo adjacente a esse ângulo interno.
a) Qual é a medida de abertura x?
b) Quantos lados tem esse polígono?
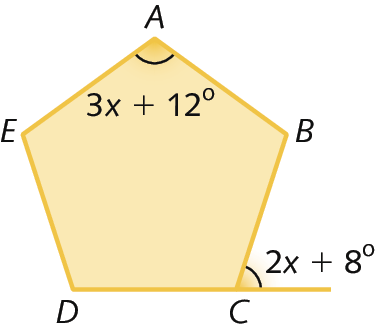
9. Calcule a medida de abertura x, sabendo que a figura é um pentágono regular.
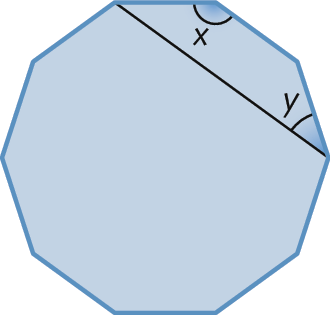
10. Este polígono regular é um decágono regular; determine as medidas x e y das aberturas dos ângulos.
Relações métricas nos polígonos regulares
Triângulo equilátero inscrito em uma circunferência
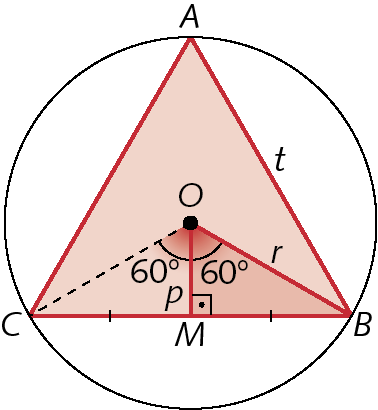
• t: medida de comprimento do lado do triângulo
• r: medida de comprimento do raio da circunferência circunscrita ao triângulo
• p: medida de comprimento do apótema do triângulo
Quadrado inscrito em uma circunferência
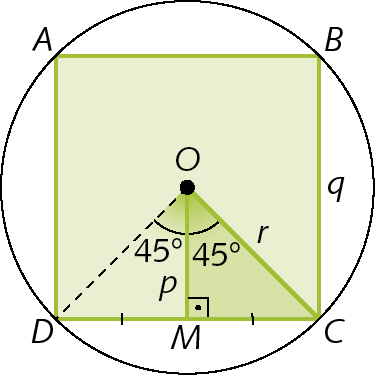
• q: medida de comprimento do lado do quadrado
• r: medida de comprimento do raio da circunferência circunscrita ao quadrado
• p: medida de comprimento do apótema do quadrado
Hexágono regular inscrito em uma circunferência
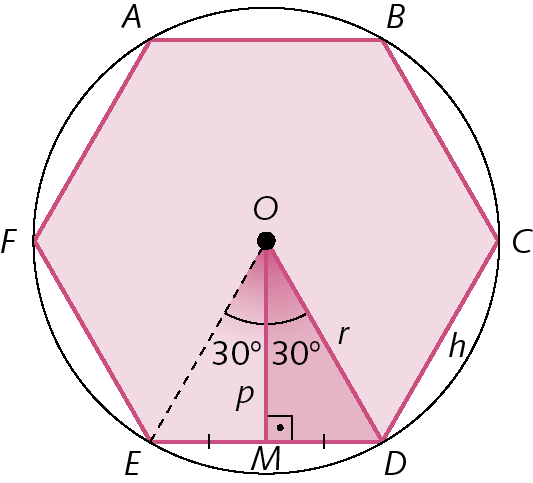
• h: medida de comprimento do lado do hexágono
• r: medida de comprimento do raio da circunferência circunscrita ao hexágono
• p: medida de comprimento do apótema do hexágono
h = r
11. Uma mesa circular tem como detalhe em seu tampo o desenho de um hexágono regular inscrito. Se o comprimento do raio do tampo mede
2 raiz de 3 metros, qual é a medida de perímetro do hexágono?
Dado:
Sentença matemática. Raiz de 3 igual a 1 vírgula 7..
12. Um quadrado a bê cê dê está inscrito em uma circunferência cujo comprimento do raio mede
8 raiz de 2 centímetros. Calcule:
a) a medida de comprimento do lado do quadrado;
b) a medida de comprimento do apótema do quadrado.
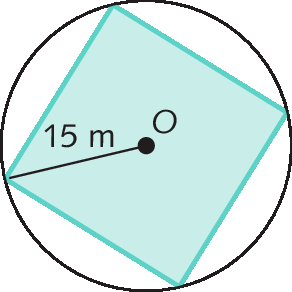
13. Determine a medida de perímetro e a medida da área do quadrado representado.
Use:
Sentença matemática. Raiz de 2 igual a 1 vírgula 4..
14. O comprimento do lado de um triângulo equilátero inscrito em uma circunferência mede 10 centímetros. Determine:
a) a medida de comprimento do raio da circunferência;
b) a medida de comprimento do apótema do triângulo.
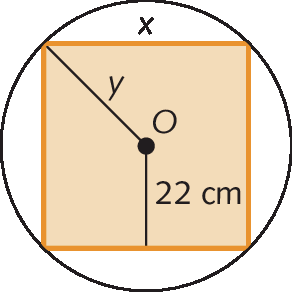
15. Determine as medidas de comprimento x e y na figura seguinte, sabendo que o quadrado está inscrito na circunferência.
Polígonos regulares circunscritos

• r: medida de comprimento do raio da circunferência
• n: número de lados
• ln: medida de comprimento do lado do polígono regular inscrito
• án: medida de comprimento do apótema do polígono regular inscrito
• Ln; medida de comprimento do lado do polígono regular circunscrito
• án: medida de comprimento do apótema do polígono regular circunscrito
16. Calcule a medida de comprimento do lado de um triângulo equilátero circunscrito a uma circunferência cujo comprimento do raio mede
4 raiz de 3 centímetros.
17. Calcule a medida de comprimento do lado de um quadrado circunscrito a uma circunferência cujo comprimento do raio mede 16 métros.
18. Calcule a medida de comprimento do lado de um hexágono regular circunscrito a uma circunferência cujo comprimento do raio mede
raiz de 3 centímetros.
É hora de extrapolar

Faça as atividades no caderno.
O que você conhece sobre trânsito seguro?
Diariamente, a maior parte da população brasileira transita em vias, seja como pedestre, ciclista, motorista ou passageiro e, infelizmente, as estatísticas apontam que os acidentes de trânsito estão entre as principais causas de óbito no país. Para que esses números diminuam, é importante que os cidadãos respeitem a legislação vigente e coloquem em prática ações para construir um trânsito mais seguro para todos.
Objetivos: Conhecer e entender o significado das placas de trânsito, analisar estatísticas de acidentes de trânsito e práticas para aumentar a segurança no trânsito e produzir placas para uma campanha pelo trânsito seguro.

Etapa 1: Conhecer e entender o significado das placas de trânsito.
1.
Reúna-se em grupo e respondam às questões em seus cadernos.
a) As placas de trânsito são importantes? Por quê?
b) O que são placas de regulamentação? Explique para que servem e dê cinco exemplos de placas desse tipo.
c) O que são placas de advertência? Explique para que servem e dê cinco exemplos de placas desse tipo.
2. As placas de regulamentação têm uma borda vermelha, preenchimento branco e formato circular, com exceção das placas:


a) Qual é o significado dessas placas e por que elas têm o formato diferente das outras placas de regulamentação? Caso necessário, pesquisem em sites especializados.
b) A placa A se parece com qual polígono? O que seria preciso verificar para saber se esta placa se parece com um polígono regular?
c) A regulamentação do Conselho Nacional de Trânsito (contrâm) recomenda que, nas vias urbanas, a placa B tenha o formato de triângulo equilátero com lado medindo 90 centímetros de comprimento e, ao ser colocada em suporte vertical, seja disposta de modo que a borda inferior fique a pelo menos 2 métros do solo.

Analise esta imagem e determine, em metro, a medida da altura total desta sinalização.
3. Analisem a placa e respondam às questões. Caso seja necessário, pesquisem em sites especializados.

a) Essa placa é de regulamentação ou de advertência?
b) Essa placa recebe o nome “área escolar”. Qual é a importância dessa sinalização?

Etapa 2: Análise de dados sobre a estatística do trânsito (acidentes) no Brasil.
4. Leiam o texto e respondam às questões.
Acidentes de trânsito: Mais de 1,35 milhão de pessoas perdem a vida, aponta ó ême ésse
[reticências]
De acôrdo com o “Global status report on road safety 2018”, lançado em dezembro de 2018, as mortes nas estradas continuam aumentando em todo o mundo e mais de 1,35 milhão de pessoas perdem a vida todos os anos em decorrência de acidentes de trânsito, o que significa que, em média, morre uma pessoa a cada 24 segundos. O documento revela ainda que as lesões causadas pelo trânsito são hoje a principal causa de morte de crianças e jovens entre 5 e 29 anos.
[reticências]
No Brasil, no ano de 2016, os dados também são lamentáveis: 3,5 crianças morreram por dia, ou seja, são 105 vidas perdidas em um mês. Conforme números compilados pelo Observatório Nacional de Segurança Viária (ONSV), juntamente com a Universidade Federal do Paraná (ú éfe pê érre), com informações do Sistema Datasus, foram registradas .1292 mortes de crianças entre zero e 14 anos naquele ano. Esta faixa etária representa 23% da população brasileira.
Observatório Nacional de Segurança Viária (ONSV), juntamente com a Universidade Federal do Paraná (UFPR), com informações do Sistema Datasus, foram registradas 1292 mortes de crianças entre zero e 14 anos naquele ano. Esta faixa etária representa 23% da população brasileira.
[reticências]
Em dezembro de 2018, audiência na Comissão de Viação e Transportes da Câmara dos Deputados destacou que a maioria dos acidentes de trânsito ocorre nos municípios, onde há excesso de motocicletas, pouca sinalização e, muitas vezes, falta um gestor específico de trânsito. A gestão do trânsito nos municípios foi apontada como o principal desafio para reduzir pela metade as mortes por acidentes no Brasil, por grupo de 100 mil habitantes, até 2028. A meta está prevista no Plano Nacional de Redução de Mortes e Lesões no Trânsito, que virou lei (Lei 13.614/18) em janeiro de 2018.[reticências]
Sociedade Brasileira de Medicina Tropical. Acidentes de trânsito: Mais de 1,35 milhão de pessoas perdem a vida, aponta OMS. Disponível em: https://oeds.link/BLPdTd. Acesso em: 29junho 2022.
a) Quais são as atitudes imprudentes que podem causar fatalidades no trânsito?
b) Que ações podem ser tomadas pelos cidadãos para diminuir as mortes no trânsito no Brasil?
c) Segundo a Organização Não Governamental Criança Segura, em 2018, 30% das mortes de crianças por acidente ocorreram no trânsito. Que medidas podem ser tomadas para diminuir esse percentual?
5. O governo da cidade de Seul, na Coreia do Sul, anunciou em 2016 a instalação da seguinte placa de trânsito em algumas vias da cidade.
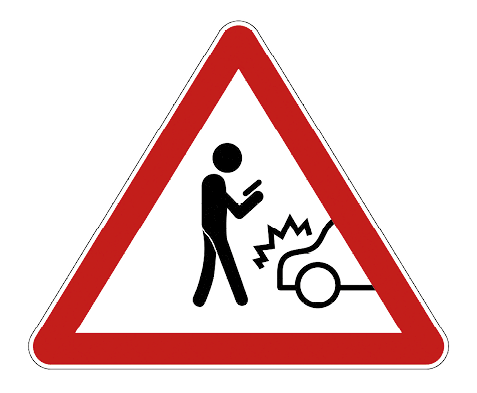
a) Qual é o objetivo da instalação dessa placa?
b) Seria interessante que a legislação brasileira adotasse uma placa semelhante no Brasil? Justifiquem.

Etapa 3: Pesquisar sobre direitos e deveres dos pedestres no trânsito e sobre dicas de como evitar acidentes.
6. O Código de Trânsito Brasileiro tem um capítulo destinado aos pedestres e condutores de veículos não motorizados. Pesquisem e façam uma lista dos direitos e dos deveres dos pedestres no trânsito.
7. Elaborem uma lista com dicas que motoristas, passageiros, ciclistas e pedestres podem utilizar para prevenir acidentes de trânsito.

Etapa 4: Confecção, análise das placas e realização de uma campanha pelo trânsito seguro.
8. Agora, cada grupo deverá confeccionar, utilizando ilustrações e textos:
• uma placa que transmite um direito ou um dever dos pedestres;
• uma placa contendo uma dica para prevenir acidentes de trânsito.
Essas placas deverão ter as características de uma placa de regulamentação ou de uma placa de advertência, dependendo do que vocês vão transmitir. Façam um esboço das placas para que os demais colegas da turma analisem a produção.
9. Disponibilizem os esboços das placas que serão elaboradas para que a turma analise a pertinência do desenho e o texto escolhido. Justifiquem a escolha do tipo de placa para cada caso: regulamentação ou advertência.
10. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
11. Determinem com a turma qual será o tamanho das placas, considerando que serão expostas para a comunidade escolar.
12. Depois dos ajustes necessários, confeccionem as placas e promovam uma campanha pelo trânsito seguro na comunidade escolar.

Etapa 5: Síntese do trabalho realizado.
13. Algumas questões que devem ser discutidas:
a)

Vocês consideram importante que todos tenham uma educação para o trânsito mesmo não sendo motoristas? Por quê?
b) Vocês acham que o conhecimento das dicas elaboradas na atividade 7 póde ajudar a prevenir acidentes?
14. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.