Unidade 4
Capítulo 10 Vistas ortogonais e volumes
Capítulo 11 Construção de gráficos estatísticos
Capítulo 12 Probabilidade e estatística


A roda de capoeira é uma manifestação cultural brasileira, herança africana que se difundiu por todo o Brasil, com elementos de arte marcial, esporte, cultura, dança e música.
Quais são as regras da capoeira? O que você conhece da cultura afro-brasileira? Qual era a porcentagem da população negra no Brasil de 2014 a 2019? Ao final desta Unidade, você responderá a essas e outras questões.
Capítulo 10 Vistas ortogonais e volume
Trocando ideias

O modelador 3 dê é o profissional que desenvolve a representação de objetos tridimensionais, por meio de softwares. Os modelos criados podem ser usados por cientistas, arquitetos, médicos e engenheiros. Além disso, muitos modeladores 3 dê trabalham para a indústria cinematográfica, de games ou no mercado publicitário.

▸

Reúna-se com um colega e, inspirados na imagem anterior, desenhem as projeções do paralelepípedo nos planos Alfa, Beta e gama
.
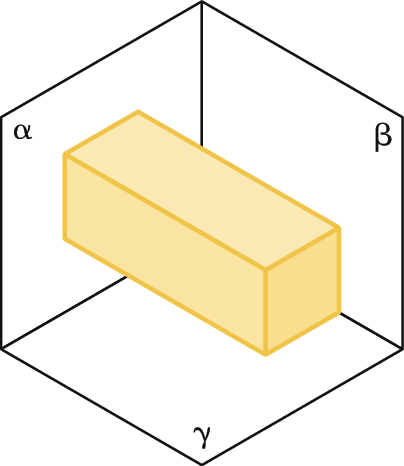
▸


Em sua opinião, qual é a importância do trabalho dos modeladores 3 dê para a Medicina? E para a Engenharia? Converse com os colegas.
Neste capítulo, vamos estudar as vistas ortogonais de figuras espaciais e as medidas de volume de prismas e cilindros retos.

1 Vistas ortogonais
Projeção ortogonal
Analise as projeções ortogonais de um ponto sobre uma reta e de um segmento de reta sobre uma reta.
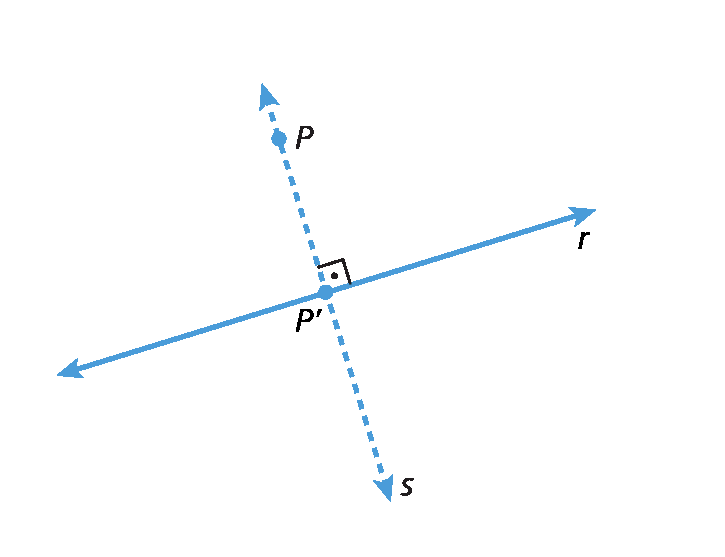
A projeção ortogonal do ponto P sobre a reta r é o ponto pê linha.
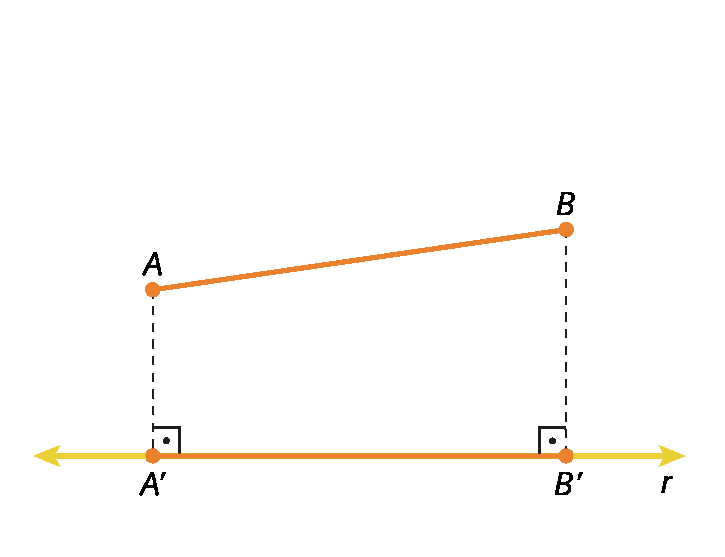
A projeção ortogonal do segmento de reta
Segmento de reta AB.sobre a reta r é o segmento de reta
Segmento de reta A linha B linha.Agora, vamos estudar as projeções ortogonais sobre um plano.
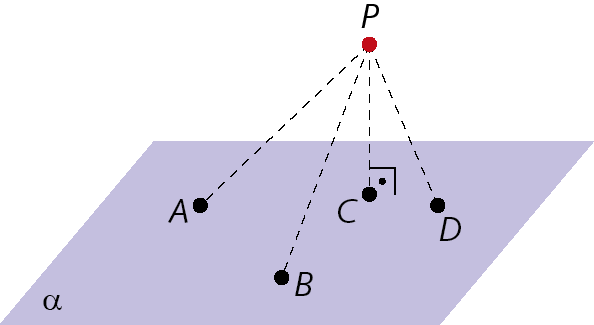
Considere o ponto P e o plano α representados a seguir.
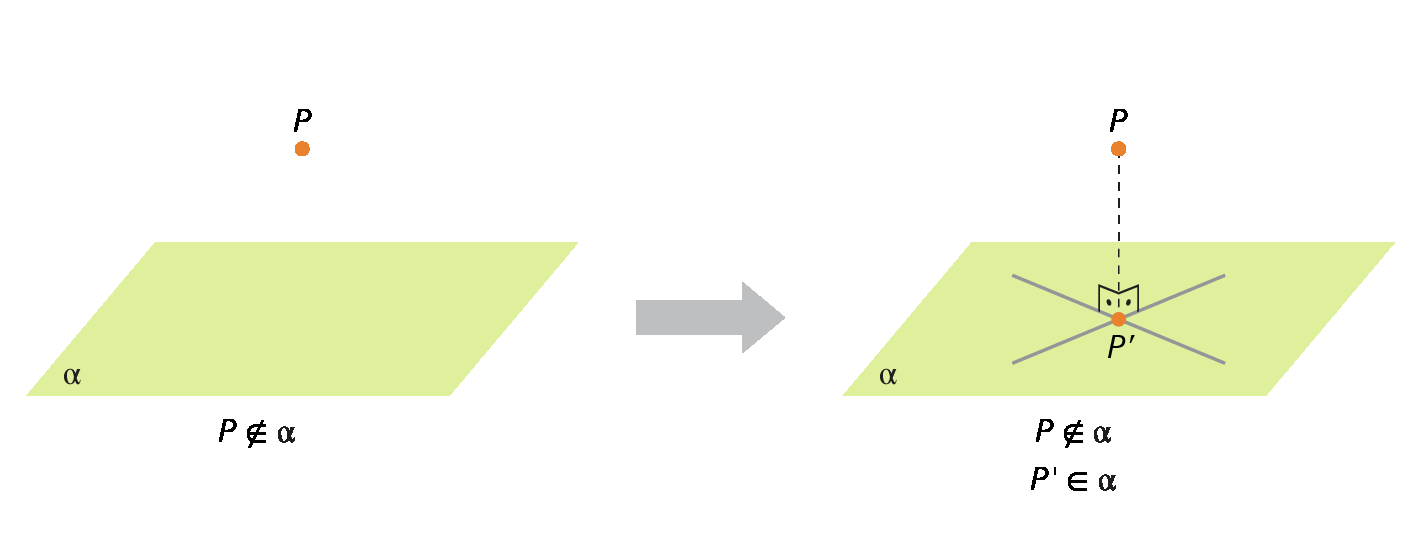
O ponto pê linha é a projeção ortogonal do ponto P sobre o plano α. Considerando uma reta perpendicular ao plano α, que contém o ponto P, o ponto pê linha é a intersecção dessa reta com o plano.
Projeção ortogonal de figuras sobre um plano
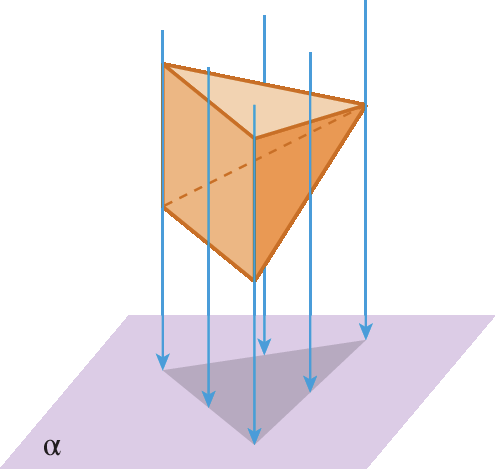
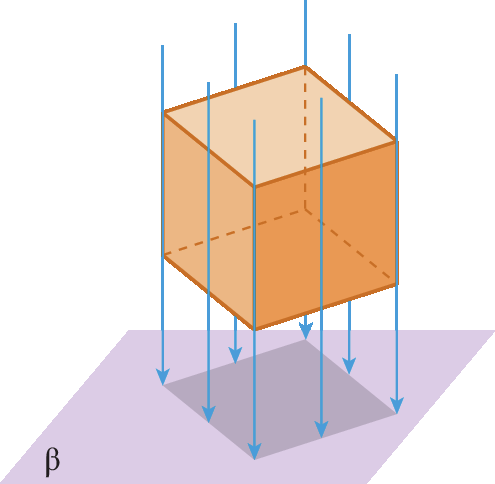
A projeção ortogonal de uma figura sobre um plano é o conjunto das projeções ortogonais de todos os pontos dessa figura sobre esse plano.
Considere alguns exemplos.
Atividades
Faça as atividades no caderno.
1. Identifique a projeção ortogonal do ponto P sobre o plano Alfa.
2. Que figura plana representa a projeção ortogonal do cilindro a seguir, nessa posição, sobre o plano Alfa?
3. Analise o exemplo anterior da projeção ortogonal da pirâmide sobre o plano Alfa. Ao mudar a posição dessa pirâmide, a projeção ortogonal sobre o plano sempre continuará sendo um triângulo? Explique sua resposta.
4. Represente, no caderno, a projeção ortogonal de um prisma de base hexagonal em relação a um plano Alfa. Considere que uma das faces do prisma esteja contida em um plano Beta paralelo a Alfa. Depois, responda:
a) A projeção ortogonal será sempre a mesma, independentemente da posição do prisma em relação ao plano?
b) Supondo que seja um prisma hexagonal regular e reto, se uma face lateral for paralela ao plano Alfa, que figura representará a projeção ortogonal do prisma sobre o plano Beta?
Vistas ortogonais
Carlos trabalha em uma metalúrgica. Para confeccionar algumas peças, ele usa as especificações que estão em um manual de instruções.

Estas são as imagens do manual de instruções.
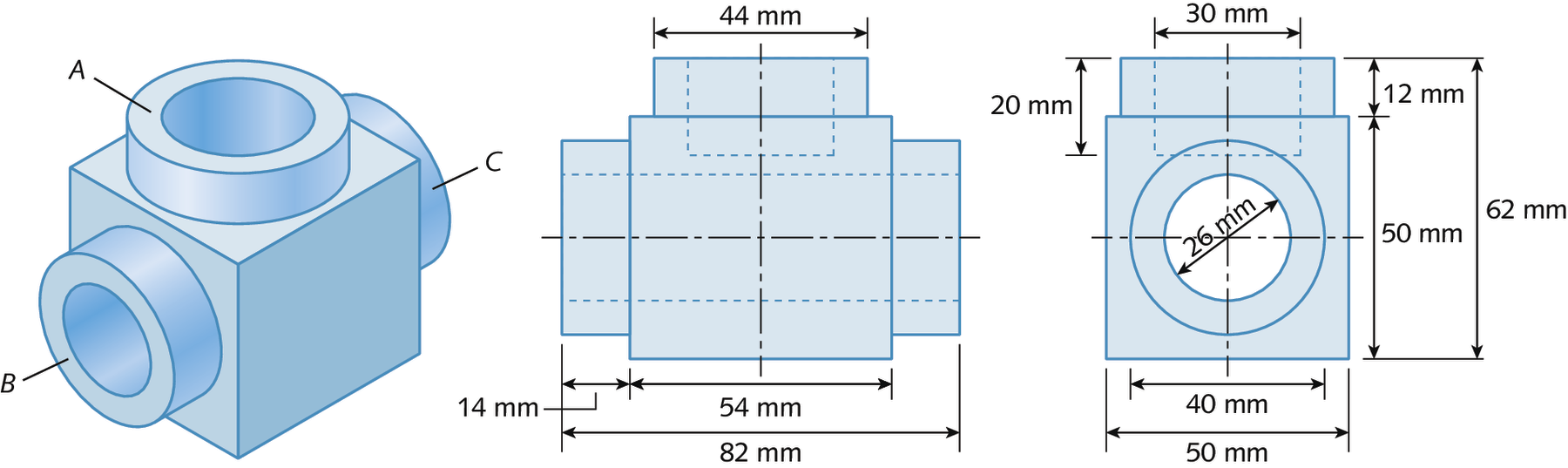
Neste exemplo, podemos identificar a imagem da peça a ser confeccionada e a representação de duas de suas vistas ortogonais. Essas vistas correspondem à projeção ortogonal da peça a dois planos distintos.
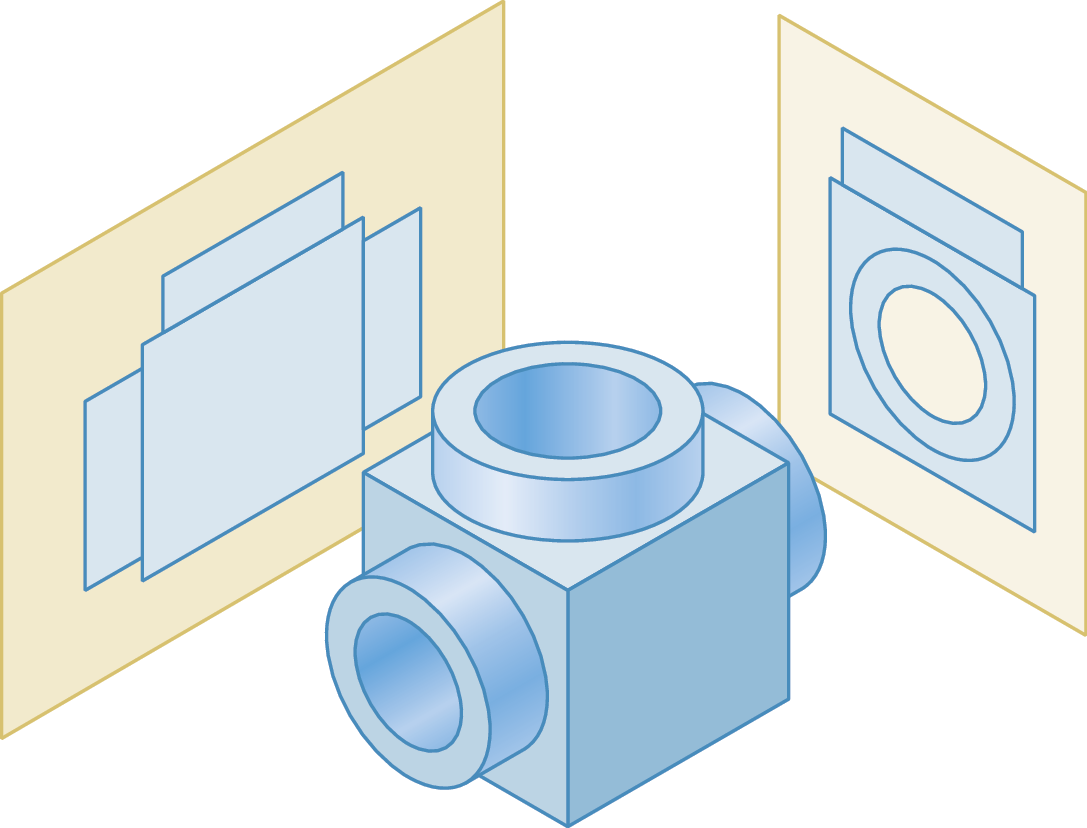
A projeção ortogonal de uma figura sobre um plano é chamada de vista ortogonal.
As vistas são obtidas em planos perpendiculares entre si e paralelos dois a dois. Nas ilustrações a seguir, temos a representação de um cubo e as projeções ortogonais de suas faces sobre os planos numerados de 1 a 6.
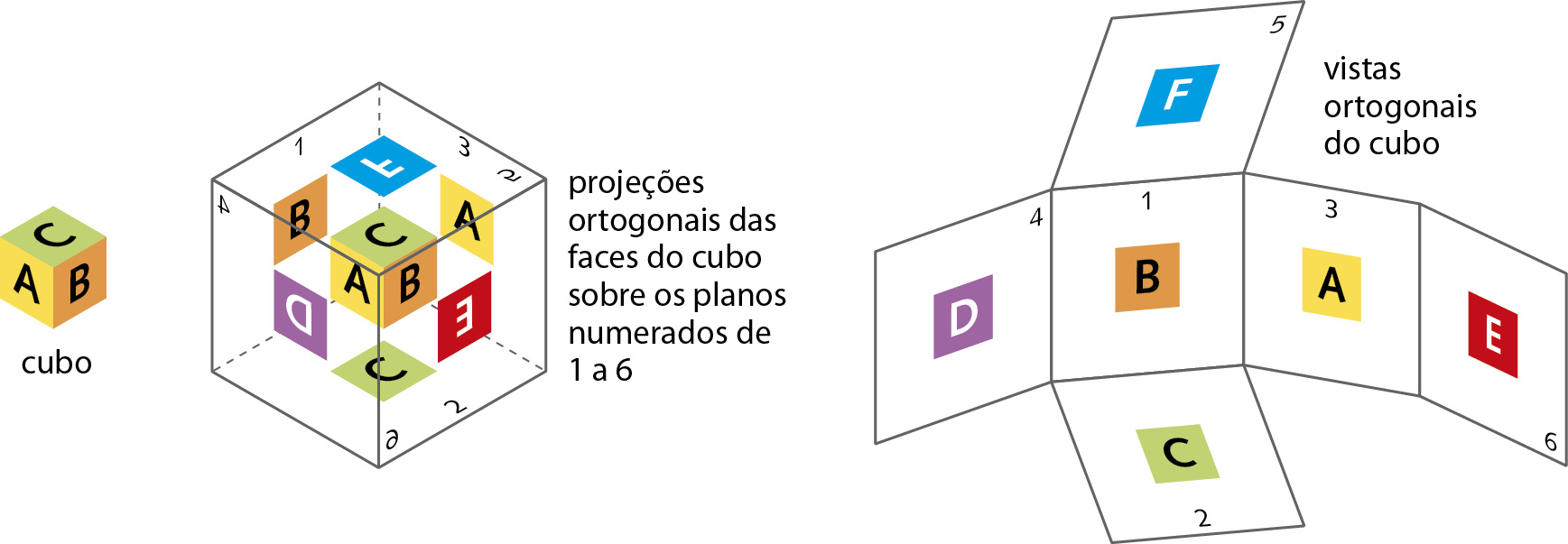
Neste caso, consideraremos a vista sobre o plano 1 como a vista frontal do cubo; logo, teremos seis vistas ortogonais do cubo: frontal (1), posterior (6), superior (2), inferior (5), lateral esquerda (3) e lateral direita (4).
Observações
1. Quando as arestas não são visíveis na vista ortogonal considerada, usamos linhas tracejadas para indicá-las. Considerando que a vista ortogonal da face laranja, na figura a seguir, corresponde à vista frontal da figura, temos:

Observe que a aresta
Segmento de reta AB., visível somente nas vistas superior e lateral esquerda, foi representada por uma linha tracejada nas vistas inferior e lateral direita.
2. Não existe uma regra para determinar a frente de uma figura e, consequentemente, sua vista frontal. Uma vez escolhida a frente, esta é tomada como referência para obtermos as outras vistas da figura.
Atividades
Faça as atividades no caderno.
5. Entre as imagens a seguir, qual não representa uma das vistas ortogonais da peça a seguir?
a)
b)

c)

d)

6. Represente, no caderno, as seis vistas ortogonais de cada um dos sólidos.
a)
b)
7. Márcia desenhou duas vistas ortogonais de uma peça de metal.
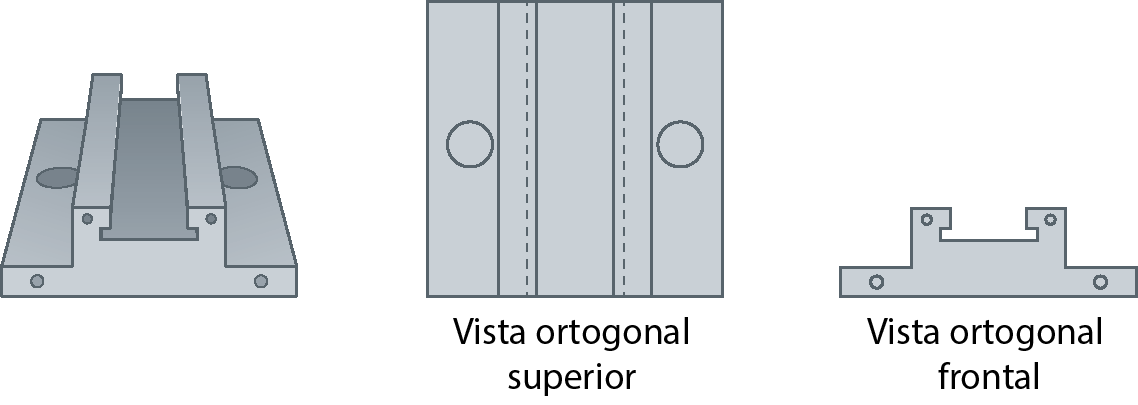
a) Desenhe, no caderno, uma possível vista lateral dessa peça.
b)

Há mais de um modo de desenhar essa vista? Converse com o professor e os colegas.
8. Considerando que a vista ortogonal da face verde, na figura a seguir, corresponde à vista frontal da figura, represente no caderno as vistas frontal, superior e lateral esquerda.

Depois, responda às questões.
a) Qual é a relação entre a vista ortogonal frontal e posterior, entre a vista ortogonal superior e inferior, e entre a vista ortogonal lateral esquerda e direita?
b) Para que, a partir das vistas, possamos imaginar a figura tridimensional, precisamos desenhar as seis vistas? Converse com o professor e os colegas.
Representação de figuras
Acompanhamos, anteriormente, como representar as vistas ortogonais de figuras não planas ou de objetos. Nesse momento, vamos estudar uma técnica para representar, no plano, uma figura ou um objeto a partir de suas vistas ortogonais.

Para fazer essa representação, não é necessário conhecer todas as vistas. Geralmente, são usadas três vistas ortogonais: lateral esquerda, superior e frontal.
Considere o exemplo.
A seguir, apresentamos três vistas ortogonais de uma figura não plana.
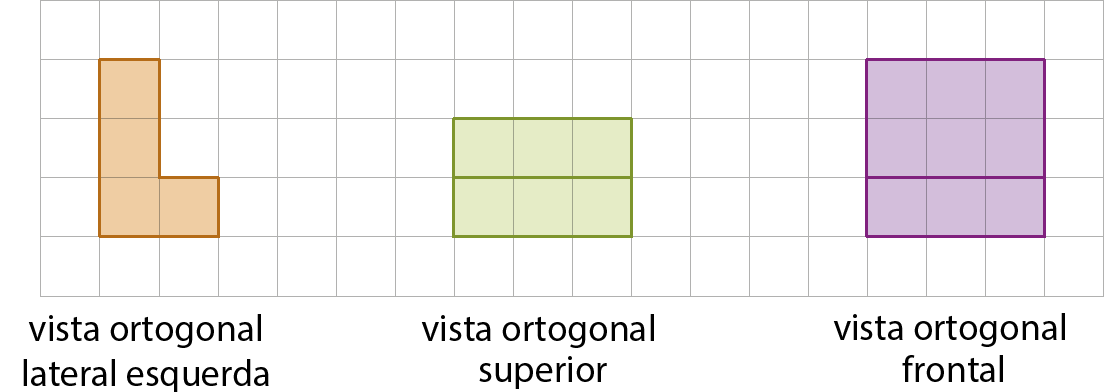
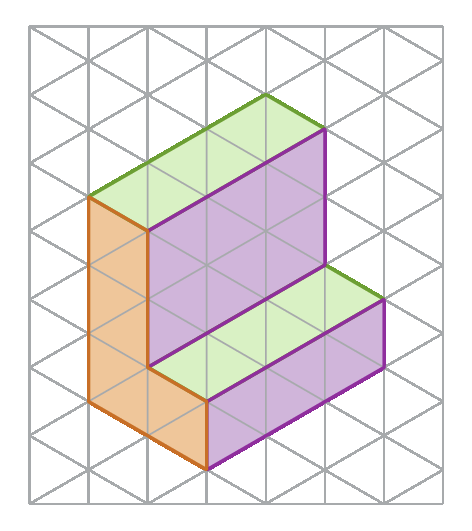
Vamos representar essa figura no plano, utilizando uma malha triangular. Nesse caso, considere, nas respectivas malhas, que o lado do quadradinho tem mesma medida de comprimento do lado do triângulo.
1º) Representamos a vista ortogonal lateral esquerda.
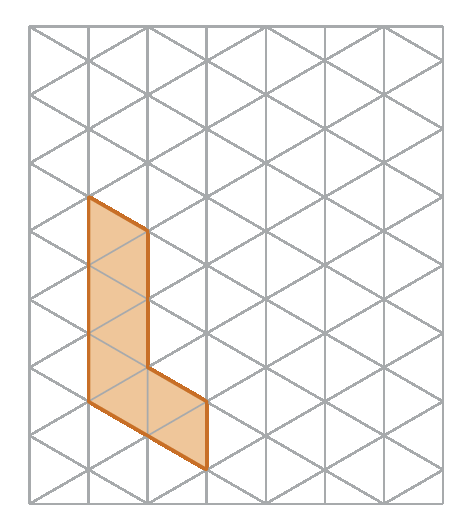
2º) Representamos a vista ortogonal superior.
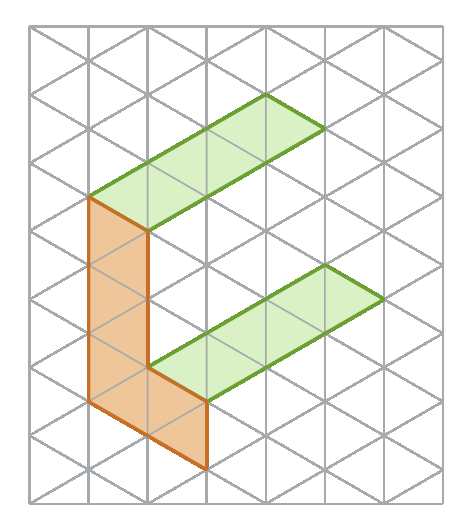
3º) Representamos a vista ortogonal frontal.
Atividades
Faça as atividades no caderno.
9. Em uma malha triangular, represente a figura correspondente a cada conjunto de vistas.
a)
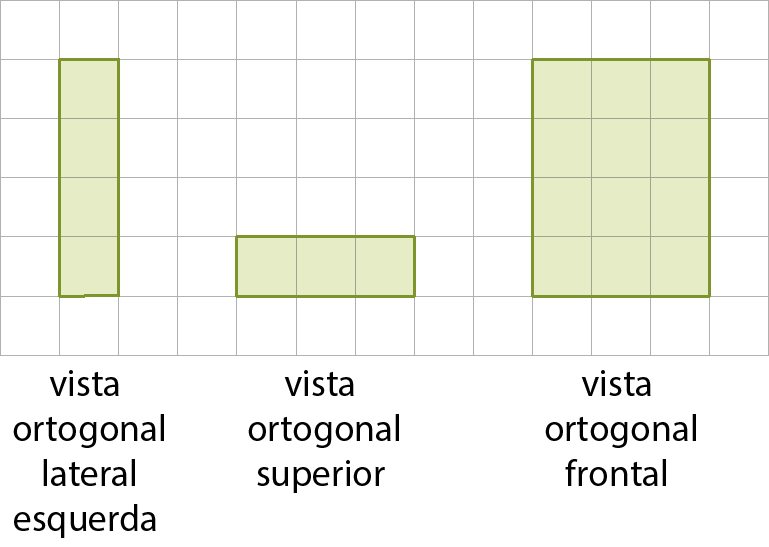
b)
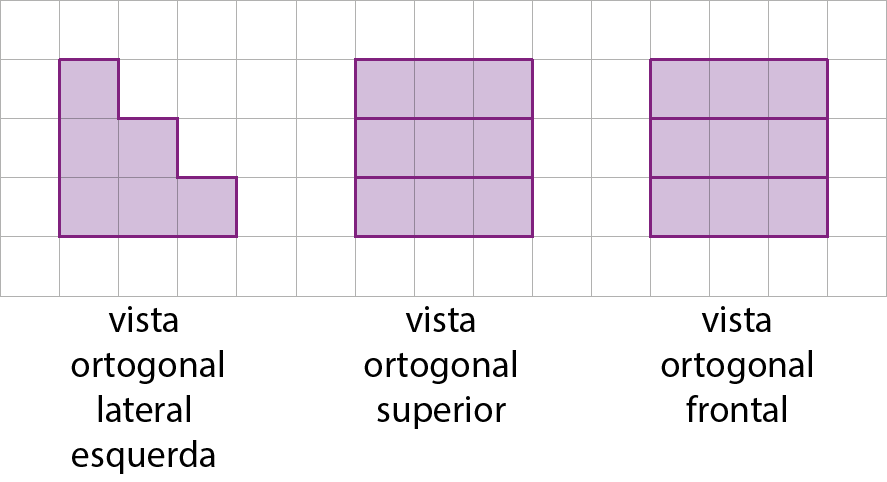
c)
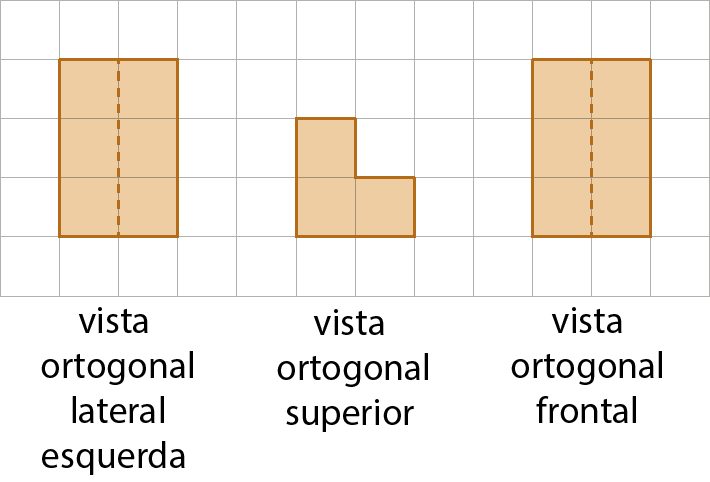
10. Associe cada conjunto de vistas ortogonais ao objeto correspondente.
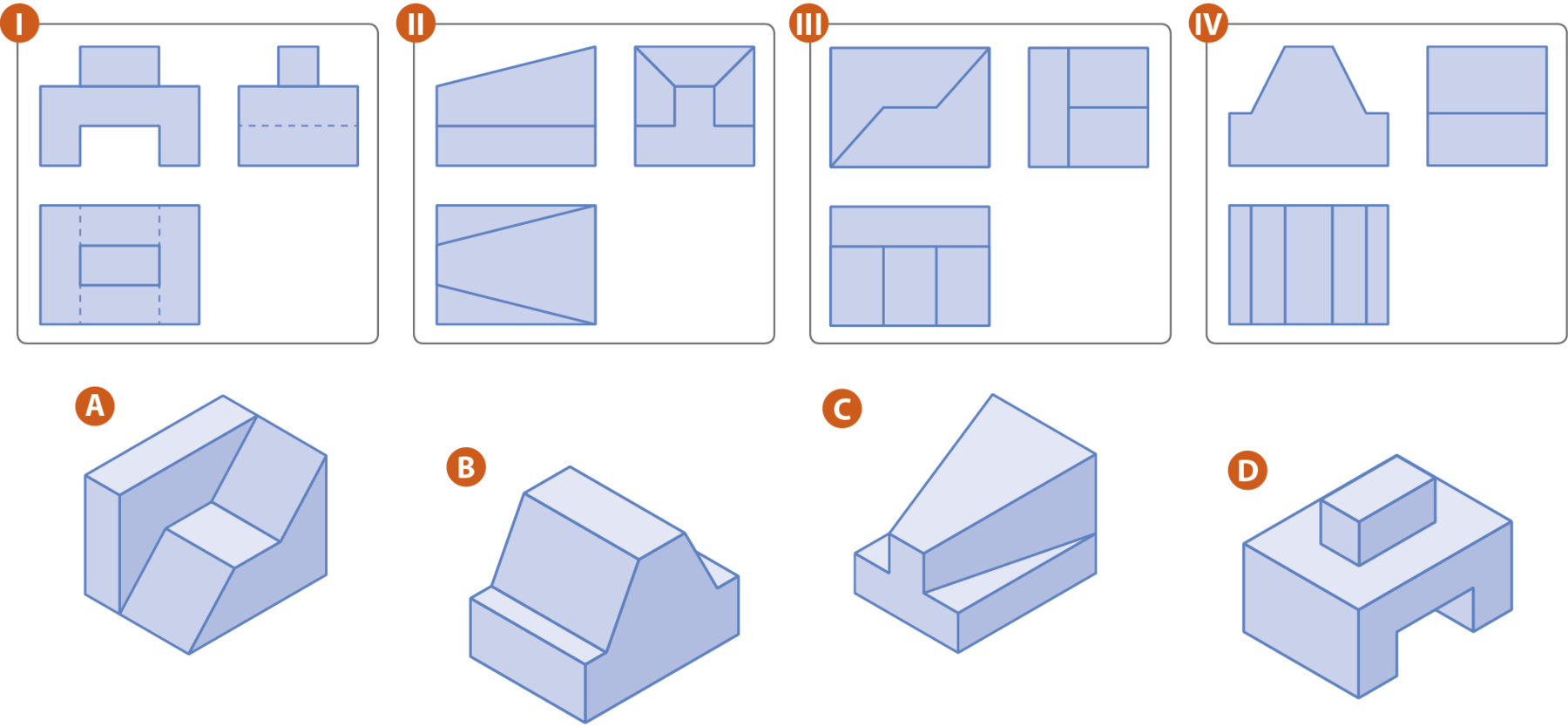
11.


Pense em um sólido geométrico e represente três vistas ortogonais dele. Peça a um colega que identifique o sólido geométrico a partir das vistas desenhadas.
12.


Imagine um objeto e represente, em uma malha quadriculada, as vistas ortogonais: frontal, superior e lateral esquerda. Depois, faça o que se pede.
a) Entregue seu desenho a um colega e peça a ele que represente seu objeto em uma malha triangular. Você também deverá representar o objeto que ele imaginou.
b) Depois, confiram os desenhos elaborados e verifiquem se as vistas ortogonais desenhadas estavam adequadas, permitindo a representação correta do objeto.

Veja que interessante
A perspectiva na arte
Houve um período em que as imagens eram retratadas sem a utilização de técnicas para criar a noção de profundidade e volume.

Com o passar do tempo, os artistas foram desenvolvendo e aperfeiçoando fórmas de retratar o aspecto da realidade em suas obras.
No século quinze, o escultor e arquiteto Filippo Brunelêsqui (1377-1446) percebeu que, ao olhar paisagens, construções ou outros elementos distantes, todas as linhas convergiam para um ponto no horizonte. Ele também percebeu que essas linhas marcavam a diminuição da medida de comprimento dos objetos quanto mais distantes se encontravam de nosso olhar. Esse ponto no horizonte é chamado ponto de fuga.
Com isso, foi desenvolvida uma perspectiva que se caracterizava pelo uso do ponto de fuga, para o qual converge uma série de linhas (linhas de fuga), tornando possível a representação de objetos tridimensionais.
Confira o seguinte desenho de um trabalho de Brunelêsqui e a construção finalizada.


Atividade

Pesquise obras de arte em que seja possível notar a presença de um ou mais pontos de fuga. Depois, compartilhe com um colega as obras que você encontrou e analise as obras dele enquanto ele analisa as suas.
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Matemática na Arquitetura
Duração: 11:10min. Página: 263.
>> [LOCUTORA] Matemática na Arquitetura
>> [LOCUTORA] A Matemática é essencial para a Arquitetura, servindo como base para criar as estruturas das construções. Além disso, serve como inspiração para as formas dos prédios e como ferramenta para calcular os custos das obras.
>> [LOCUTORA] Conversamos com o arquiteto David Moreno Sperling sobre a presença da Matemática no dia a dia dos arquitetos e a importância da Geometria e da perspectiva para esses profissionais. Também falamos sobre o papel da disciplina em questões importantes, como a preservação do meio ambiente.
>> [LOCUTORA] David já teve seu próprio escritório de Arquitetura e hoje dá aula para pós-doutorandos na Universidade de São Paulo.
>> [LOCUTORA] Oi, David. Você pode contar um pouco sobre como a Matemática apareceu, durante a sua graduação?
>> [DAVID MORENO SPERLING] No... no curso de graduação, ela... a Matemática, ela está presente desde o seu princípio, não é? Ela influencia as disciplinas que são posteriores, como as disciplinas de estruturas, de conforto ambiental, todas as disciplinas que nós chamamos técnicas, não é?, elas têm uma base tanto na Matemática, que considerando aí a Matemática não só a dimensão, a parte algébrica, mas também a parte geométrica, como também essas disciplinas têm uma... uma forte base na Física. Então, Matemática e Física, elas têm uma articulação, uma proximidade muito grande no curso de Arquitetura.
>> [LOCUTORA] Você poderia falar sobre como um arquiteto cria um projeto? De que maneira a Geometria auxilia no desenho de formas e de objetos em perspectiva?
>> [DAVID MORENO SPERLING] No campo do projeto e também da visualização das formas, não é?, é fundamental que utilizemos alguns desenhos, não é? E há alguns desenhos que comumente são chamados de plantas, de cortes, e há aqueles, que talvez estejam dentre os mais interessantes, que são chamadas [sic] de perspectivas, né? São aquelas que têm o poder de nos situar dentro de determinadas paisagens... ou de determinados espaços, como se nós estivéssemos dentro deles, né? Essa... essas perspectivas, elas estão dentro de um campo da Geometria, chamado geometria projetiva, e que estuda as relações entre os objetos reais e a sua imagem projetada ou, num certo sentido, como nós vemos as coisas. E aqui de... de início tem algo muito interessante, né?, que nos coloca a distinção entre o real e a percepção... e que, com certeza, traz reflexões muito importantes, não é?, entre o que é o real e a percepção. Então, nem sempre aquilo que é o real é aquilo que... como nós vemos, não é? Por exemplo, então, se citamos um trilho de trem, sabemos que ele é feito por duas linhas paralelas, não é? Isso é inegável. Por outro lado, dependendo da posição onde nós nos encontramos diante desse trilho, parece que essas duas linhas não são paralelas, mas elas são concorrentes, isto é, elas se encontrariam, né?, num ponto. Agora, um experimento interessante para fazermos em relação ao trilho do trem é imaginarmos uma imagem aérea desse mesmo trilho, não é?, que desconstrói rapidamente a primeira percepção. Então vejam só, se estamos posicionados no trilho, essas linhas parecem ser concorrentes e, se estamos sobrevoando esse trilho, na verdade elas recompõem a sua posição... na percepção de linhas paralelas. Então, nessas chamadas perspectivas cônicas, ou essas que têm um ponto de fuga, né?, que esse ponto para onde todas as linhas convergem, há uma relação direta entre distância e dimensão do que vemos. Significa aquilo que está mais perto é maior e aquilo que está mais distante é menor. Esses objetos com essa variação de percepção, né?, elas... na verdade, essa variação não está no objeto em si mesmo, mas na nossa percepção sobre esse objeto e que nós chamamos comumente de ilusão de ótica, não é? Há um campo das perspectivas na geometria projetiva que resolveu esse problema, vamos dizer assim, que são as chamadas perspectivas paralelas ou, então, as perspectivas cavaleiras, não é?, que, ao invés de representarem o mundo a partir desse ponto de fuga único, não é?, procura preservar a grandeza dos objetos. Então, são objetos que todos os seus lados, né?, preservam as suas dimensões, mas, num certo sentido, ao não privilegiarem, não é?, essa chamada ilusão de ótica, eles parecem um pouco estranhos para nós porque eles não se encaixam dentro desse cone visual ao qual estamos acostumados por conta da nossa percepção, não é?, e é uma percepção que, não só a Matemática estuda, mas novamente também a Física estuda a partir do campo da ótica.
>> [LOCUTORA] Conhecer bem os assuntos da Matemática ajuda a minimizar o impacto das obras no meio ambiente? Como?
>> [DAVID MORENO SPERLING] Claramente, a Arquitetura, ela está vinculada também com os impactos no meio ambiente. Talvez seja uma das atividades humanas que mais impactam o meio ambiente atualmente, não é? E a Matemática tem um papel-chave para pensarmos alguns aspectos vinculados a esses desafios. Então, por exemplo... dois exemplos acho que são significativos, não é? É... um vindo da necessidade do nosso entendimento tanto geométrico quanto algébrico das formas, e por outro, como na Arquitetura nós lidamos com formas que possuem matéria, elas estão sujeitas também às leis da Física, e as leis da Física que têm essa inter-relação com a... com a Matemática.
>> [DAVID MORENO SPERLING] Então vamos ver. No primeiro caso, nós podemos pensar numa obra que tenha uma maior área com menor gasto de material. Vamos pensar no seguinte: numa relação entre comprimento dos lados e a área de um polígono. Vamos imaginar o seguinte: se eu tenho um quadrado de lado 2, então, vamos fazer a somatória dos metros lineares de parede para fechar esse quadrado. Então, nós teríamos 2 + 2 + 2 + 2 igual a 8 metros lineares de parede. Vamos pensar, então, quais... qual é a área desse quadrado: lado 2, 2 x 2, nós temos 4 metros quadrados. Pois bem, vamos pensar, então, uma outra forma, uma forma que tenha os mesmos 8 metros lineares de parede. Por exemplo, um retângulo que é feito dos lados 1 + 3 + 1 + 3. Então, nós temos 8 metros lineares de parede. Por outro lado, se nós fizermos o cálculo da área desse retângulo, nós teremos o lado 3, de comprimento 3, e o lado de comprimento 1. Então, 3 x 1, nós temos 3 metros quadrados. Então, percebemos o seguinte: que, com os mesmos 8 metros lineares de parede, né?, nós podemos ter uma obra com mais área ou menos área. Vamos imaginar, então, que nós teríamos o mesmo gasto de tijolos para preencher essas paredes nos dois casos, mas, no primeiro caso, nós teríamos uma eficiência maior no seguinte sentido: eu tenho uma obra maior com o mes.... com o mesmo gasto de tijolo da obra... da segunda obra, que tem uma área menor.
>> [DAVID MORENO SPERLING] No segundo caso, não é?, esse que eu estava dizendo sobre a inter-relação da Matemática, com a Arquitetura e as leis da Física, exatamente porque as formas que produzimos na arquitetura, elas possuem matéria, não é?, há claramente inter-relações nas escolhas que os arquitetos fazem entre matérias, as formas e a posição no espaço que essa arquitetura... essas arquiteturas são posicionadas, né?, em relação, por exemplo, aos pontos cardiais e ventos predominantes, né? Essas relações, então, entre matéria, forma e posição no espaço, elas alteram claramente o conforto ambiental de uma edificação. Há formas e mesmo... relações entre formas, por exemplo, quando escolhemos relações entre poliedros, que facilitam o escoamento do vento, por exemplo. Então, nós podemos ter uma obra que tem um maior conforto ambiental e obras que têm menor conforto ambiental, exatamente por essas escolhas entre... e articulações, né?, vínculos entre materiais, formas e as posições no espaço.
>> [DAVID MORENO SPERLING] Isso se tratamos de arquitetura numa pequena escala, mas essas questões são válidas para escala urbana e estamos diante agora de fenômenos urbanos... é... fantásticos, mas ao mesmo tempo desafiadores e com sérios problemas, não é? Vamos pensar as grandes metrópoles e a necessidade de pensarmos em cidades mais compactas, não é?, que usam menos energia e requerem menores distâncias para os transportes.
>> [DAVID MORENO SPERLING] Então, como pensar, por exemplo, tanto em relação ao primeiro caso, não é?, de maiores áreas com menores gastos de material ou, no segundo caso, com conforto ambiental mais adequado, quando pensamos em termos de grandes metrópoles. Claramente, a questão da energia e de um menor uso de energia é chave para a nossa sobrevivência no planeta. Então, nesse sentido, a Matemática tem claros instrumentos para auxiliar os arquitetos nesses desafios.
Vinheta.
Créditos
Studio Núcleo de Criação

2 Medidas de volume
Agora, vamos estudar as medidas de volume de prismas e cilindros retos. Antes de iniciar esse estudo, é necessário relembrar as características dessas figuras geométricas.
Prismas e cilindros
Os prismas são poliedros com duas bases paralelas que são polígonos congruentes; as demais faces são paralelogramos.

Observações
1. O prisma de base retangular e faces também retangulares é denominado bloco retangular ou paralelepípedo reto-retângulo.
2. O cubo é o paralelepípedo reto-retângulo que tem todas as faces quadradas.
Os cilindros são corpos redondos que têm duas bases circulares congruentes.
Medida do volume de um paralelepípedo reto-retângulo
Para estudar a medida do volume dos outros prismas e dos cilindros, vamos relembrar o cálculo da medida do volume de um bloco retangular.
A medida do volume de um paralelepípedo reto-retângulo é calculada da maneira a seguir.

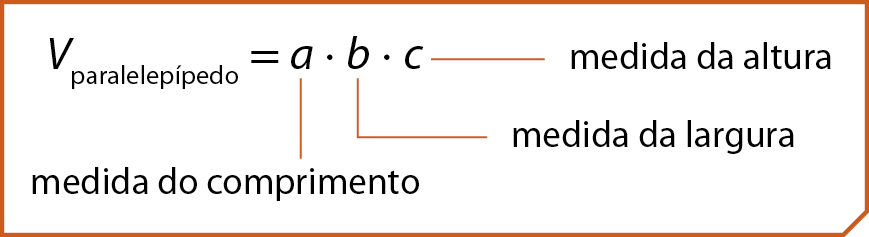
Considerando as medidas do comprimento (a) e da largura (b) como medidas das dimensões da base de um paralelepípedo reto-retângulo, podemos escrever:

Considere este exemplo.
Uma piscina, que tem o formato de um bloco retangular, ocupa uma área cuja medida é igual a 20 métros quadrados. Foi colocada água até 1,5 métro de medida de altura. Quantos litros de água foram colocados nessa piscina? (Lembre que 1 métro cúbico = .1000 litros)
vêpiscina = abase ⋅ h = 20 métros quadrados ⋅ 1,5 métro = 30 métros cúbicos
Como 1 métro cúbico = .1000 litros, temos:
30 métros cúbicos = .30000 litros
Portanto, foram colocados .30000 litros de água na piscina.
Medida do volume de um prisma triangular reto
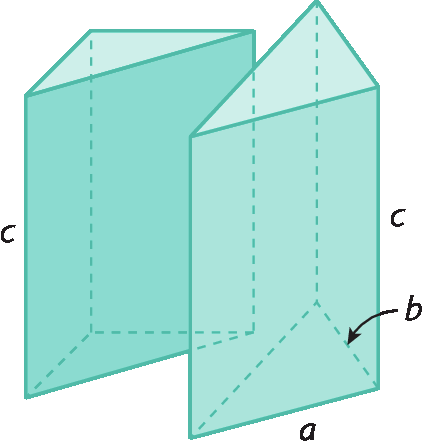
Considere que um paralelepípedo reto-retângulo, como o representado, foi decomposto em dois prismas triangulares idênticos, cujas bases são triângulos retângulos.
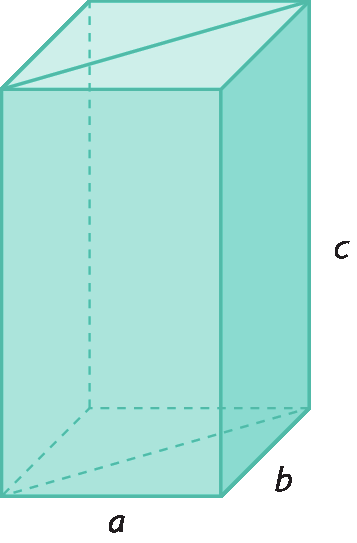
A medida do volume de um paralelepípedo reto-retângulo é calculada pelo produto:
Vparalelepípedo = a ⋅ b ⋅ c
Como esse paralelepípedo foi decomposto em dois prismas triangulares idênticos, a medida do volume de cada prisma triangular corresponde à metade da medida do volume do paralelepípedo.

A medida da área da base do paralelepípedo é igual a:
Abase do paralelepípedo = a ⋅ b
A medida da área da base de cada prisma triangular é metade da medida da área da base do paralelepípedo. Então:

De

e

, podemos escrever:
Vprisma triangular = A base do prisma triangular ⋅ c
Ou seja:

Medida do volume de um prisma reto
Qualquer prisma regular póde ser dividido em prismas triangulares idênticos. A quantidade de prismas triangulares formados será igual ao número de lados da base desse prisma regular.
Por exemplo, o prisma pentagonal regular póde ser decomposto em 5 prismas triangulares idênticos.
Logo, a medida do volume desse prisma póde ser calculada assim:
Vprisma pentagonal = 5 ⋅ Vprisma triangular

Observe que a medida da área da base do prisma pentagonal corresponde à soma das medidas das áreas das bases dos prismas triangulares, ou seja, A base do prisma pentagonal = 5 ⋅ A base do prisma triangular. Assim, podemos escrever:

Esse processo descrito para o prisma pentagonal regular póde ser adaptado para qualquer prisma reto.
De modo geral, a medida do volume de qualquer prisma reto póde ser calculada multiplicando-se a medida da área da base pela medida da altura.
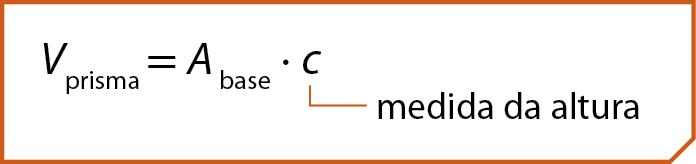
Acompanhe estes exemplos.
a) A altura do prisma triangular mede 10 centímetros, e a base é um triângulo equilátero cujo comprimento do lado mede 7 centímetros e o comprimento da altura mede 6centímetros.
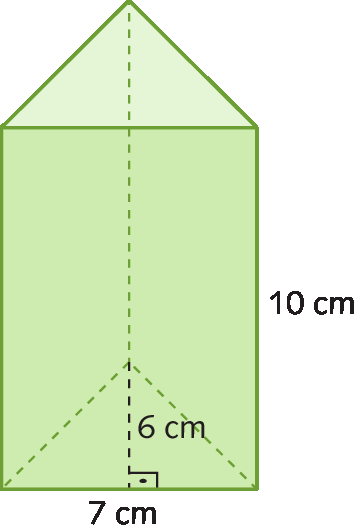
Qual é a medida do volume desse prisma?
Inicialmente, calculamos a medida da área da base:
Sentença matemática. A base igual a fração 7 centímetros vezes 6 centímetros sobre 2 igual a 21 centímetros quadrados.
Logo, a medida do volume do prisma é:
Vprisma = 21 centímetros quadrados ⋅ 10 centímetros = 210 centímetros cúbicos
b) Um prisma reto de base hexagonal regular tem 10 centímetros de medida de altura e base de medida de área igual a 15 centímetros quadrados.
Qual é a medida do volume desse prisma?
Vprisma = 15 centímetros quadrados ⋅ 10 centímetros = 150 centímetros cúbicos
Portanto, a medida do volume do prisma é 150 centímetros cúbicos.
Medida do volume de um cilindro reto
Ao dividir um círculo em n setores, sendo n um número muito grande, cada um dos setores circulares se aproxima do formato de um triângulo.
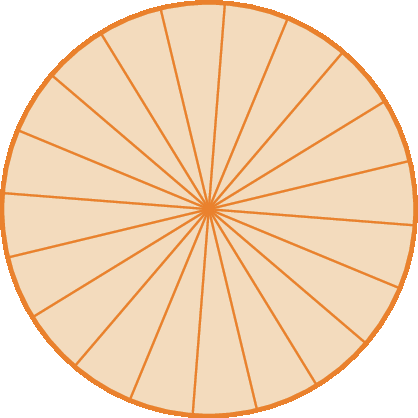
Do mesmo modo, dado um cilindro, a medida da área da sua base póde ser aproximada pela medida da área de n triângulos. Assim, a medida do volume de um cilindro reto poderá ser aproximada pela medida do volume de n prismas triangulares com a mesma medida da altura do cilindro.
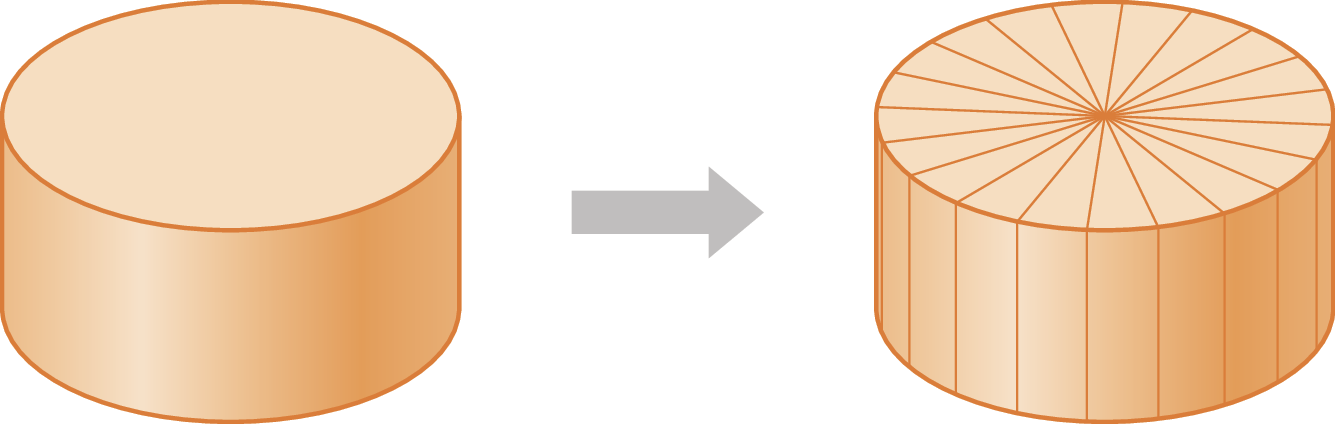
A medida do volume de um cilindro reto póde ser calculada multiplicando-se a medida da área da base pela medida da altura:

Acompanhe o exemplo.
Uma lata se parece com um cilindro reto, conforme mostra a imagem.
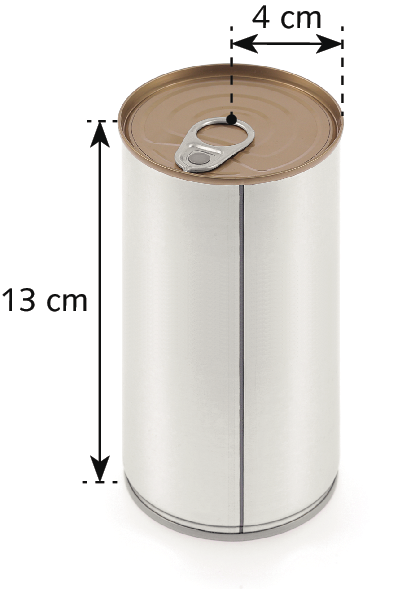
Sabendo que a medida da capacidade interna da lata corresponde a 90% da medida do volume total, quantos mililitros, aproximadamente, cabem nessa lata?
Inicialmente, calculamos a medida da área da base. Para isso, vamos considerar pi = 3,14:
Abase = pi ⋅ érre2 = 3,14 ⋅ (4 centímetros)2 = 3,14 ⋅ 16 centímetros quadrados = 50,24 centímetros quadrados
Logo, a área da base mede 50,24 centímetros quadrados.
Agora, determinamos a medida do volume da lata:
Vcilindro = Abase ⋅ c = 50,24 centímetros quadrados ⋅ 13 centímetros = 653,12 centímetros cúbicos
Portanto, o volume da lata mede 653,12 centímetros cúbicos.
Para determinar a medida da capacidade interna da lata, consideramos 90% da medida do volume total.
653,12 centímetros cúbicos ⋅ 0,9 = 587,808 centímetros cúbicos
Como 1 centímetro cúbico = 1 mililitro, concluímos que cabem aproximadamente 588 mililitros nessa lata.
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
13. Calcule a medida do volume dos seguintes paralelepípedos.
a)

b)

c)
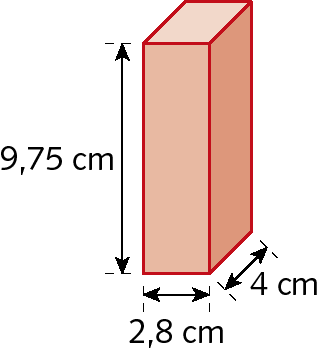
14. Calcule a medida do volume dos prismas a seguir.
a)

b) Considere que o triângulo da base é equilátero.
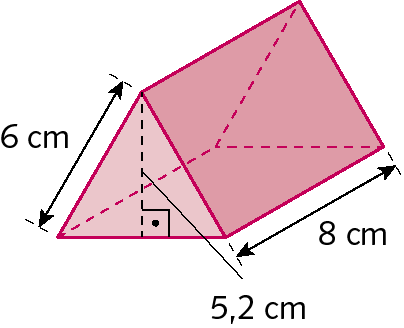
15. Considere um prisma octogonal regular, que foi decomposto em oito prismas triangulares idênticos. A medida da área da base desse prisma octogonal é 32 centímetros quadrados e a medida da altura é 5 centímetros.
a) Calcule a medida do volume do prisma octogonal.
b) Calcule a medida do volume de cada prisma triangular.
16. Considere os cilindros a seguir.
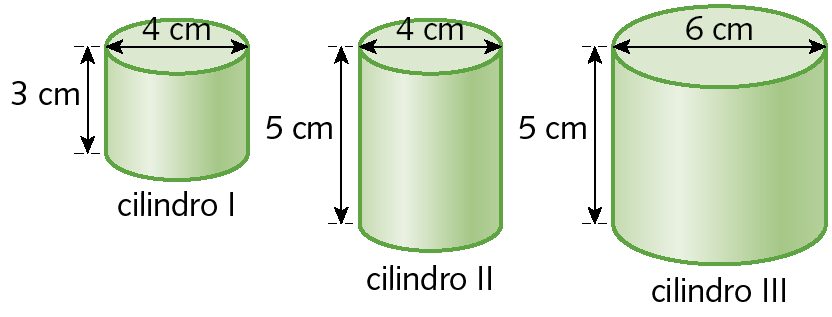
a) Sem efetuar os cálculos, indique qual dos cilindros tem maior medida de volume e qual tem menor medida de volume. Justifique sua resposta.
b) Calcule a medida do volume de cada um dos cilindros. Considere pi = 3,14.
17. Considere um prisma pentagonal reto em que a altura mede 5 centímetros e sua base é um pentágono regular cujo comprimento do lado mede 3 centímetros (considere que o comprimento do apótema mede 2,1 centímetros). Qual é a medida do volume desse prisma?
18. Neste recipiente, colocou-se água até
Ilustração. Dois terços.da medida de altura.
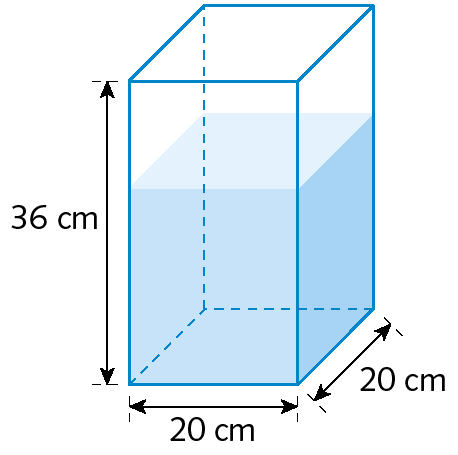
a) Qual é a medida do volume de água que foi colocada nesse recipiente?
b) Quantos mililitros de água ainda poderiam ser colocados nesse recipiente?
19. Márcia pretende embalar alguns bombons para entregar a um cliente. Ela já embalou, anteriormente, essa mesma quantidade em uma caixa cujo volume media 900 centímetros cúbicos. Para esses novos bombons, ela tem as seguintes caixas:

a) Considerando somente a medida do volume, Márcia poderá utilizar as caixas disponíveis? Justifique.
b) Além da medida do volume, o que Márcia poderia considerar na escolha da caixa?
c)

Indique uma informação que poderia ser acrescentada no enunciado, de modo que torne ambas as caixas inadequadas para Márcia.
20.


Elabore um problema envolvendo o cálculo da medida do volume de um cilindro reto qualquer. Escolha adequadamente o cilindro e suas medidas.
Em seguida, troque seu problema com o de um colega para que um resolva o problema criado pelo outro. Depois, confiram as resoluções e verifiquem se as informações contidas nos problemas foram suficientes para resolvê-los.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
Vistas ortogonais
A projeção ortogonal de uma figura sobre um plano é chamada de vista ortogonal.
Quando as arestas não são visíveis na vista ortogonal considerada, usamos linhas tracejadas para indicá-las, como a aresta
Segmento de reta AB.está indicada nas vistas inferior e lateral direita.
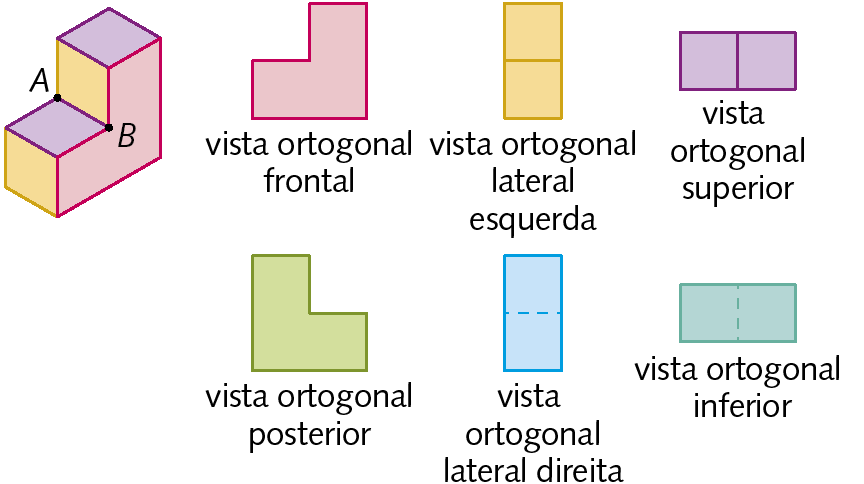
1. Considerando que a frente da figura é a face azul, represente a vista ortogonal superior, lateral esquerda e frontal destes sólidos geométricos.
a)
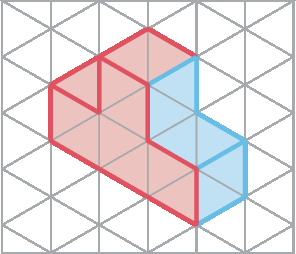
b)
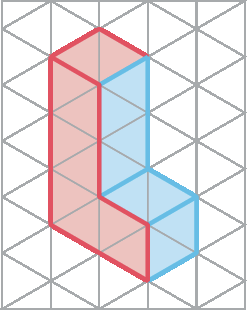
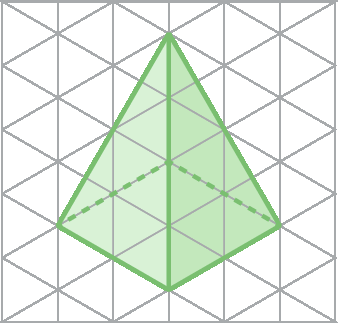
2. Represente a vista ortogonal frontal, lateral esquerda e superior desta pirâmide de base quadrada representada na malha triangular.
3. Escreva o poliedro que tenha as vistas ortogonais indicadas em cada item.
a)

b)

Medidas de volume
Medida do volume de um prisma reto
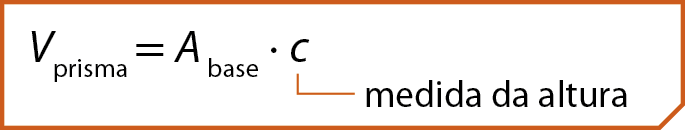
Medida do volume de um cilindro reto

4. Determine a medida do volume destes sólidos geométricos. Considere pi = 3,14.
a)
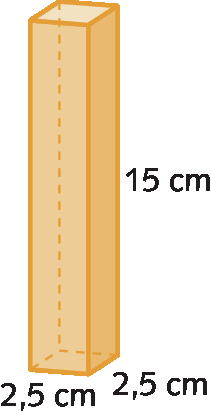
b)
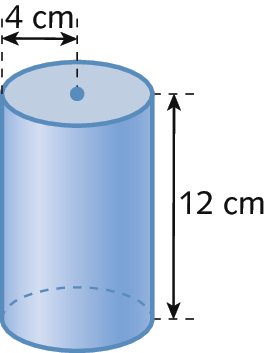
5. Quantos metros cúbicos de água são necessários para encher uma piscina retangular com 25 métros de medida do comprimento, 10 métros de medida da largura e 1,8 métro de medida da profundidade?
6. Um aquário tem o formato de um prisma de base triangular. Sabe-se que o triângulo da base é retângulo com catetos com medidas de comprimento de 50 centímetros e 40 centímetros e que a medida da altura do aquário é 20 centímetros. Determine:
a) a medida do volume do aquário em centímetros cúbicos;
b) quantos litros de água cabem nesse aquário. (Lembre-se: 1 litro = .1000 centímetros cúbicos)
7. Uma caixa-d’água cilíndrica será esvaziada completamente para limpeza. Ela tem 2,4 métros de medida de comprimento do diâmetro e 1 métro de medida da altura. Considerando pi = 3, determine:
a) a medida do volume da caixa-d’água em métro cúbico;
b) quantos litros de água cabem nessa caixa. (Lembre-se: 1 litro = .1000 centímetros cúbicos)
8. Calcule a medida do volume de um prisma de base hexagonal, sabendo que o hexágono da base é regular com lados medindo 3 centímetros de comprimento e que a medida da altura do prisma é 8 centímetros.