Capítulo 12 Probabilidade e estatística
Trocando ideias

Segundo dados do Instituto Brasileiro de Geografia e Estatística (í bê gê É), em 2020, homens e mulheres acima de 60 anos representavam aproximadamente 14,26% da população brasileira. Analise alguns dados sobre a população idosa no Brasil.
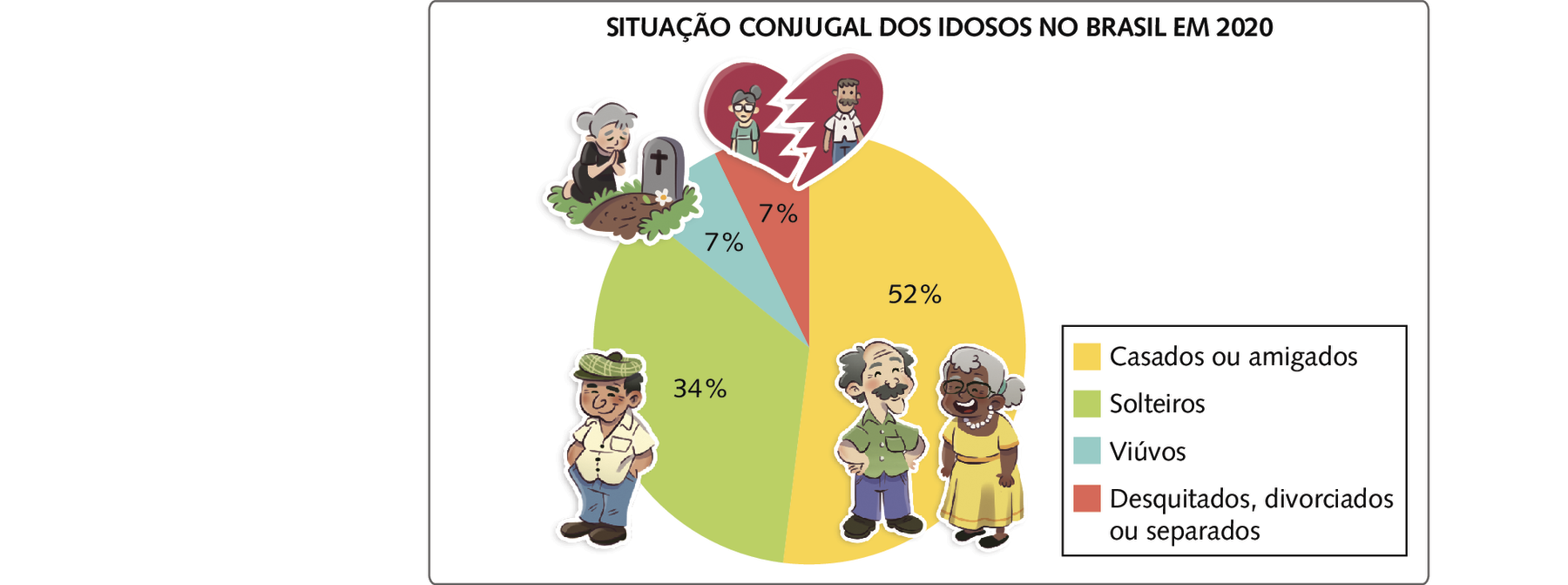
Dados obtidos em: BRASIL. Ministério da Mulher, da Família e dos Direitos Humanos. Fatos e números: idosos e família no Brasil. Brasília, Distrito Federal: Ministério da Mulher, da Família e dos Direitos Humanos, 2021. página 7.

Dados obtidos em: BRASIL. Ministério da Mulher, da Família e dos Direitos Humanos. Fatos e números: idosos e família no Brasil. Brasília, Distrito Federal: Ministério da Mulher, da Família e dos Direitos Humanos, 2021. página 7.
▸


Para coletar esses dados sobre os idosos, você acha que toda a população de idosos foi consultada? Por quê? Como você acha que os dados dessa pesquisa foram coletados? Converse com os colegas.
▸


Em sua opinião, que atitudes podem ser tomadas para evitar que os idosos sejam maltratados e desrespeitados? Converse com os colegas.
Neste capítulo, você vai aprofundar o estudo sobre o cálculo de probabilidades, além de planejar e executar pesquisas amostrais.

1 Probabilidade
A área da Matemática que estuda a chance de ocorrência de um evento é denominada teoria das probabilidades.
São várias as profissões que requerem conhecimentos de probabilidade. Em algumas, o profissional usa os conhecimentos relacionados a essa teoria para interpretar informações; em outras, é necessário fazer o cálculo de probabilidades e, com base nos resultados, tomar decisões.



Vamos relembrar alguns termos relacionados ao estudo de probabilidade. Para isso, considere a situação a seguir.

Como não é possível saber com exatidão o nome que será sorteado, essa situação é um exemplo de experimento aleatório.
O conjunto de todos os nomes fórma o espaço amostral. Chamamos de evento qualquer subconjunto do espaço amostral. Como todos os nomes têm a mesma chance de ser sorteados, chamamos o espaço amostral desse evento de espaço amostral equiprovável.
Outro exemplo de experimento aleatório é o lançamento de um "dado honesto" de seis faces.

Um possível evento é “sair o número 6” e o espaço amostral é formado pelos números 1, 2, 3, 4, 5 e 6.
Cálculo de probabilidade
Em uma urna giratória, há 100 bolinhas com as mesmas dimensões e as mesmas medidas de massa, numeradas de 1 a 100.

Cada bolinha tem a mesma chance de ser retirada. Qual é a probabilidade de se retirar, ao acaso, uma bolinha cujo número seja múltiplo de 5?
A probabilidade de um evento de espaço amostral equiprovável ocorrer, em um experimento aleatório, é a razão entre o número de elementos favoráveis a esse evento e o número de elementos do espaço amostral.
Nesse caso, os elementos do espaço amostral equiprovável são os números de 1 a 100; portanto, há 100 elementos.
Agora, vamos determinar os elementos que são favoráveis ao evento, ou seja, os números da sequência de 1 a 100 que são múltiplos de 5. Listando os elementos, temos:
5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100
Assim, determinamos que o evento é composto de 20 elementos.
Logo, a probabilidade de se retirar, ao acaso, uma bolinha cujo número seja múltiplo de 5 é:
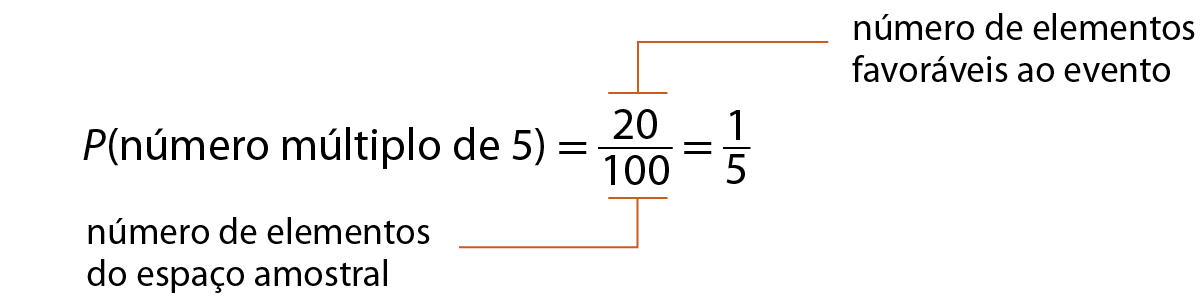
Concluímos que a probabilidade é
1 quinto. Também podemos representar por meio de uma porcentagem, que, nesse caso, é 20%.
Observação
A probabilidade é a medida da chance de ocorrência de um evento. Essa medida póde assumir um valor de 0 a 1.
• Se a probabilidade de um evento for igual a zero, dizemos que esse evento é impossível.
• Se a probabilidade de um evento for igual a um, dizemos que esse evento é certo.
Observe este exemplo.
Considerando a situação da urna giratória com 100 bolinhas numeradas de 1 a 100, qual é a probabilidade de se retirar, ao acaso, uma bolinha cujo número seja múltiplo de 2?
Nesse caso, o número de elementos favoráveis ao evento é 50, pois metade das bolinhas corresponde a números pares, ou seja, múltiplos de 2. Logo, a probabilidade é 50%, pois:
Atividades
Faça as atividades no caderno.
1. No lançamento de um “dado honesto” com as faces numeradas de 1 a 6, qual é a probabilidade de se obter, na face voltada para cima, um número de pontos menor que 5?
2. No sorteio de um tablet, foram entregues duzentas cartelas numeradas de 1 a 200. Ana recebeu as cartelas de números 78, 79, 80, 81, 82 e 83.

Sabendo que todos os números têm a mesma probabilidade de ser sorteados, qual é a probabilidade de Ana ganhar o tablet?
3. Em um saco, há 3 cartões azuis, 4 cartões amarelos, 8 cartões verdes e 5 cartões vermelhos, todos com as mesmas medidas das dimensões. Pretende-se retirar um cartão ao acaso.
a) Qual é a probabilidade de o cartão retirado ser amarelo?
b) Que cor de cartão tem maior probabilidade de ser retirada? Justifique.
c) Indique um evento que tenha 25% de probabilidade de ocorrência.
4.


Em dupla, elaborem uma situação de um experimento aleatório em que o evento:
a) tenha 25% de probabilidade de ocorrência;
b) tenha
1 décimode probabilidade de ocorrência;
c) seja impossível;
d) seja certo.
Eventos independentes e eventos dependentes
Eventos independentes
Dois "dados honestos", um azul e outro vermelho, serão lançados simultaneamente.

Vamos analisar dois eventos:
• evento a: sair o número 1 no dado vermelho;
• evento B: sair o número 3 no dado azul.
Considerando o lançamento simultâneo desses dados, vamos determinar o espaço amostral. Para isso, organizaremos as informações em um quadro.
|
Dado azul |
|||||||
|---|---|---|---|---|---|---|---|
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
Dado vermelho |
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
|
Observe que o espaço amostral é formado por 36 elementos, ou seja, há 36 resultados possíveis.
Há 6 possibilidades de sair o número 1 no dado vermelho, ou seja, de ocorrer o evento A. São elas:
(1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (1, 6)
Nesse caso, a probabilidade de sair o número 1 no dado vermelho é:
Também há 6 possibilidades de sair o número 3 no dado azul, ou seja, de ocorrer o evento B:
(1, 3); (2, 3); (3, 3); (4, 3); (5, 3); (6, 3)
Então, a probabilidade de sair o número 3 no dado azul é:
Observe que a ocorrência de um evento não interfere na ocorrência do outro. Por esse motivo, dizemos que são eventos independentes.
Agora, qual seria a probabilidade de os dois eventos acontecerem simultaneamente: sair o número 1 no dado vermelho e o número 3 no dado azul?
Vamos retomar o quadro com o espaço amostral e destacar as possibilidades referentes a cada evento.
|
Dado azul |
|||||||
|---|---|---|---|---|---|---|---|
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
Dado vermelho |
1 |
(1, 1) |
(1, 2) |
(1, 3) |
(1, 4) |
(1, 5) |
(1, 6) |
|
2 |
(2, 1) |
(2, 2) |
(2, 3) |
(2, 4) |
(2, 5) |
(2, 6) |
|
|
3 |
(3, 1) |
(3, 2) |
(3, 3) |
(3, 4) |
(3, 5) |
(3, 6) |
|
|
4 |
(4, 1) |
(4, 2) |
(4, 3) |
(4, 4) |
(4, 5) |
(4, 6) |
|
|
5 |
(5, 1) |
(5, 2) |
(5, 3) |
(5, 4) |
(5, 5) |
(5, 6) |
|
|
6 |
(6, 1) |
(6, 2) |
(6, 3) |
(6, 4) |
(6, 5) |
(6, 6) |
|
Observe que há somente uma possibilidade de os dois eventos acontecerem simultaneamente: (1, 3). Logo, a probabilidade P será:
A probabilidade P de dois eventos independentes ocorrerem simultaneamente também póde ser calculada multiplicando as probabilidades de cada evento ocorrer.
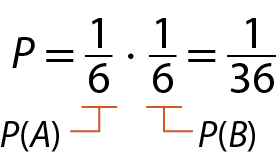
Acompanhe outro exemplo que aborda eventos independentes.
Na escola Prisma, há duas turmas de 9º ano. A professora de Arte sorteará, ao acaso, um estudante de cada turma para fazer uma apresentação de teatro.

A turma a tem 25 estudantes, sendo 15 meninas e 10 meninos. Já na turma B, há 24 estudantes, sendo 12 meninos e 12 meninas. Qual é a probabilidade de a professora sortear um menino da turma a e uma menina da turma B?
Os eventos “sortear um menino da turma a” e ”sortear uma menina da turma B” são independentes, pois a ocorrência de um evento não interfere na ocorrência do outro.
• Vamos determinar a probabilidade de sortear um menino da turma a (evento a):

• Agora, vamos calcular a probabilidade de sortear uma menina da turma B (evento B):

Como os eventos são independentes, a probabilidade será o produto entre a probabilidade de sortear um menino da turma a e a probabilidade de sortear uma menina da turma B. Assim, a probabilidade P de a professora sortear um menino da turma a e uma menina da turma B é:
Eventos dependentes
Em um recipiente, há 3 bolinhas verdes e 5 bolinhas amarelas, todas com as mesmas dimensões e as mesmas medidas de massa. Com os olhos vendados, uma pessoa vai retirar, ao acaso, uma bolinha. Depois, sem devolver a primeira bolinha ao recipiente, vai retirar uma segunda bolinha. Qual é a probabilidade de a primeira bolinha retirada ser verde e a segunda, amarela?
Vamos inicialmente calcular a probabilidade de a primeira bolinha ser verde:

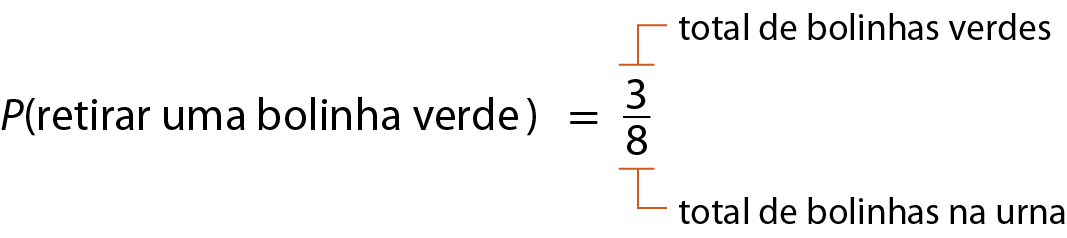
Agora, vamos calcular a probabilidade de a segunda bolinha ser amarela. Nesse caso, devemos considerar que uma bolinha verde foi retirada da urna; portanto, sobraram 7 bolinhas na urna: duas verdes e 5 amarelas. Logo:


Desse modo, a probabilidade P de a primeira bolinha ser verde e a segunda ser amarela é:
Nessa situação, observe que o primeiro evento (retirar uma bolinha verde) interfere na ocorrência do segundo evento (retirar uma bolinha amarela). Portanto, dizemos que são eventos dependentes.
Observação
Se alterarmos a situação e considerarmos que a primeira bolinha, após ser retirada, será devolvida ao recipiente para retirarmos a segunda bolinha, o que acontecerá?
Observe que o primeiro evento (retirar uma bolinha verde) não vai interferir na ocorrência do segundo evento (retirar uma bolinha amarela), pois a bolinha será devolvida. Com essa alteração, os eventos passaram a ser independentes.
Vamos, então, calcular a probabilidade de a primeira bolinha retirada ser verde e a segunda ser amarela, considerando que a primeira bolinha será devolvida à urna.
• P(a), ou seja, a probabilidade de a primeira bolinha ser verde:
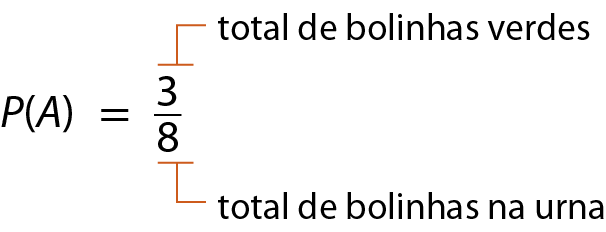
• P(B), ou seja, a probabilidade de a segunda bolinha ser amarela:
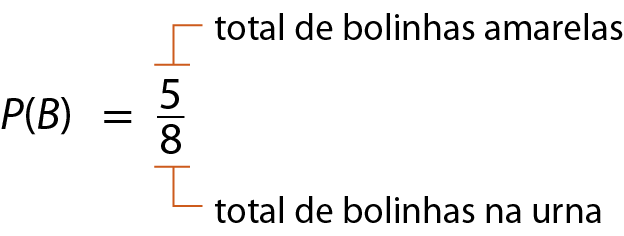
Assim, a probabilidade P de a primeira bolinha retirada ser verde e a segunda ser amarela é:
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Duração: 5:42min. Página: 294.
>> [LOCUTORA] Loteria
>> [LOCUTORA] Entrevistamos o jornalista Leonardo Sakamoto para falar sobre os boatos de fraude na loteria com base em argumentos matematicamente errados e a necessidade de se ter uma educação matemática para ler e interpretar as notícias. Leonardo é autor do artigo “Fraude na Mega-Sena: do deficit em Matemática, surge a teoria conspiratória”, no qual discute esses temas.
>> [LOCUTORA] No dia 23 de junho de 2018, depois do sorteio dos números 50, 51, 56, 57, 58 e 59 na Mega-Sena, uma parte da população brasileira ficou com a certeza de ter havido manipulação dos resultados. Segundo essas pessoas, seria impossível que um sorteio resultasse em uma sequência de números tão próximos, assim como a série 1, 2, 3, 4, 5 e 6, por exemplo. Por que, matematicamente, essas suspeitas de fraude não fazem sentido?
>> [ENTREVISTADO] Primeiro as pessoas desconhecem como funciona o sorteio da Mega-Sena, né? O sorteio da Mega, ela não é... as pessoas acham, “não, mas pera aí, o número 5 foi sorteado várias vezes, depois um outro número”. Não, primeiro que são sessenta bolas, né? E... a chance de qualquer uma dessas sessenta bolas ser escolhida em cada vez é absolutamente a mesma, né? Uma curiosidade é que umas das apostas mais frequentes na Mega-Sena é 1, 2, 3, 4, 5, 6. Então, tem muita... parte da sociedade reclama, mas parte da sociedade aposta nisso, né? Ao mesmo tempo, olha, a chance de você conseguir qualquer conjunto de seis números é absolutamente a mesma: 1, 2, 3, 4, 5, 6, de 12, 14, 48, 52, 59, é absolutamente a mesma. É uma em, aí vem um número bem grande, 50 063 860. Então, as pessoas desconhecem, primeiro, como funciona o sorteio e, segundo, desconhecem como funciona Estatística. Se a gente tivesse um ensino forte de Estatística, se as pessoas não cabulassem a aula de Estatística, Matemática, fica a dica, talvez percebessem, quando ficassem mais velhas e começassem a apostar na Mega-Sena, de [sic] que apostar na Mega-Sena não é uma questão de racionalidade, mas de fé.
>> [LOCUTORA] Por qual motivo você acha que as pessoas reagem com tamanha desconfiança diante de resultados dessa natureza?
>> [ENTREVISTADO] Primeiro, é não saber como funciona o sistema, como funciona a Estatística, como funciona o sorteio, tal... É... uma comparação é se você, hum, um avião sobrevoasse uma pequena vila da Idade Média, as pessoas achariam que aquilo é um anjo, né? Então, quando você desconhece a técnica, quando você desconhece a tecnologia, quando você não tem a informação, aquela informação ela é preenchida com alguma coisa, ela é preenchida com fantasia, ela é preenchida com conspiração. E vamos ser sinceros: o que que também é mais delicioso? O que que é mais agradável? O que que é mais, é, é gostoso de ser deglutido? O fato de que a Estatística prega peças ou o fato de que uma grande conspiração, formada por pessoas extremamente vis se apoderaram do sistema de... de sorteio e fizeram aqueles números, né? A segunda parte é mais interessante. Ah, mas não podem [sic] haver fraudes? Podem [sic] haver fraudes, mas a pergunta é, vamos usar a razão e fazer a pergunta contrária: se eu fosse fraudar a loteria, eu usaria 50, 51, 56, 57, 58, 59 ou usaria números mais distantes uns dos outros para não parecer que era fraude?
>> [LOCUTORA] Você considera importante uma educação matemática envolvendo Probabilidade e Estatística? Por quê?
>> [ENTREVISTADO] Olha, eu acho que é um dos pontos mais importantes da Matemática, exatamente porque isso impede que as pessoas sejam enganadas... né? Se as pessoas soubessem qual que é calcular ou entender qual que é a chance delas de conquistar determinado prêmio, de conseguir um emprego ou de entender a chance num concurso, as coisas mudariam. O ensino de Matemática, de Estatística, mas não apenas, mas outras questões correlatas, porcentagem, combinatória, permutação, tudo são, são... é, é essencial para o dia a dia. Um dos grandes problemas não é, disso tudo, não é a pessoa que não quer aprender, mas a pessoa não quer aprender muitas vezes porque o conhecimento é colocado diante dela de uma forma extremamente chata ou, [tom enfático] pior, extremamente desvinculada da realidade. As pessoas precisam entender para que que serve certa coisa na vida delas para poderem darem [sic] valor àquele conteúdo. Isso é a base de uma educação de qualidade. As pessoas precisam entender para que que serve aquilo. Então, para que que serve, por exemplo, você aprender Estatística? Em primeiro lugar, para não ser enganado na Mega-Sena; em segundo lugar, para não postar nas redes sociais teorias conspiratórias que nada têm a ver com a realidade. Mas, em terceiro lugar, em poder... é fundamental para poder ter subsídios para tomar decisões corretas na vida e no dia a dia, ou seja, aprender Estatística faz da gente não apenas um cidadão melhor, mas também uma pessoa menos enganada pela vida.
Vinheta.
Créditos
Studio Spectrum
Atividades
Faça as atividades no caderno.
5. Identifique se os eventos a seguir são independentes ou dependentes.
a) Uma indústria sabe que cérca de 5% dos parafusos fabricados têm defeitos. Um funcionário retirou ao acaso um parafuso de um lote a com 100 peças e outro parafuso de um lote B com duzentas peças para analisá-los. Qual é a probabilidade de ele ter retirado parafusos com defeito dos dois lotes?
b) Uma livraria vai sortear dois livros entre os clientes que preencheram um questionário sobre o atendimento da loja. No total, foram 500 questionários respondidos por clientes com 40 anos ou mais e 200 respondidos por clientes com menos de 40 anos. Qual é a probabilidade de o primeiro livro ser sorteado para um cliente com 40 anos ou mais e o segundo livro, para um cliente com menos de 40 anos?
6. Em uma caixa, há fichas numeradas de 1 a 100. Qual é a probabilidade de ser retirada inicialmente a ficha de número 5 e, depois, a ficha de número 58? Considere que a primeira ficha não foi devolvida à caixa.
7. Allan lançará duas "moedas honestas". Qual é a probabilidade de sair cara nas duas moedas se ele lançar:
a) uma moeda após a outra?
b) as moedas simultaneamente?
• Há diferença entre as probabilidades dos lançamentos de cada item? Justifique sua resposta.
8. Uma gincana terá 4 equipes: azul, verde, amarela e vermelha. Nas equipes azul e vermelha, há 15 participantes e, nas equipes verde e amarela, há 16 participantes.
a) A primeira prova será uma apresentação de teatro e a ordem de apresentação será definida por sorteio. Qual é a probabilidade de a ordem de apresentação ser: equipe amarela, equipe verde, equipe azul e equipe vermelha?
b) Em uma das provas, uma equipe será sorteada e, em seguida, um componente dessa equipe será sorteado. Rafaela está na equipe azul. Qual é a probabilidade de ela ser a primeira sorteada?
9. Uma empresa detectou que metade das 100 peças fabricadas em um setor estava com defeito. Essas 100 peças foram levadas para avaliação da equipe de contrôle de qualidade. Se essa equipe pegar, aleatoriamente, duas peças para avaliar, qual será a probabilidade de essas peças estarem com defeito?
10. Na escola Musicando, os estudantes de guitarra, violão e bateria estavam distribuídos desta maneira em 2023.
|
Guitarra |
Violão |
Bateria |
Total |
|
|---|---|---|---|---|
|
Homem |
20 |
15 |
10 |
45 |
|
Mulher |
14 |
12 |
15 |
41 |
|
Total |
34 |
27 |
25 |
86 |
Dados obtidos pela escola Musicando em 2023.
a) Se fosse realizado um sorteio para cada grupo de estudantes conforme o instrumento de estudo, qual seria a probabilidade de serem sorteados uma mulher que pratica guitarra, um homem que pratica violão e uma mulher que pratica bateria?
b) Se fossem realizados 3 sorteios agrupando todos os estudantes, sem separá-los por instrumento de estudo, qual seria a probabilidade de serem sorteados uma mulher que pratica guitarra, um homem que pratica violão e uma mulher que pratica bateria?
11.


Crie um experimento aleatório em que os eventos sejam dependentes e outro experimento em que os eventos sejam independentes. Depois, proponha a um colega que determine a probabilidade de cada um desses eventos enquanto você faz o mesmo para os eventos dele.

2 Pesquisa estatística
Em 2021, o í bê gê É divulgou a segunda edição do estudo Estatísticas de gênero: indicadores sociais das mulheres no Brasil com dados coletados de diversas fontes, como a Pesquisa Nacional por Amostra de Domicílios Contínua 2019 e o Tribunal Superior Eleitoral, em 2020.
Analise este infográfico com informações sobre esse estudo. %glossário
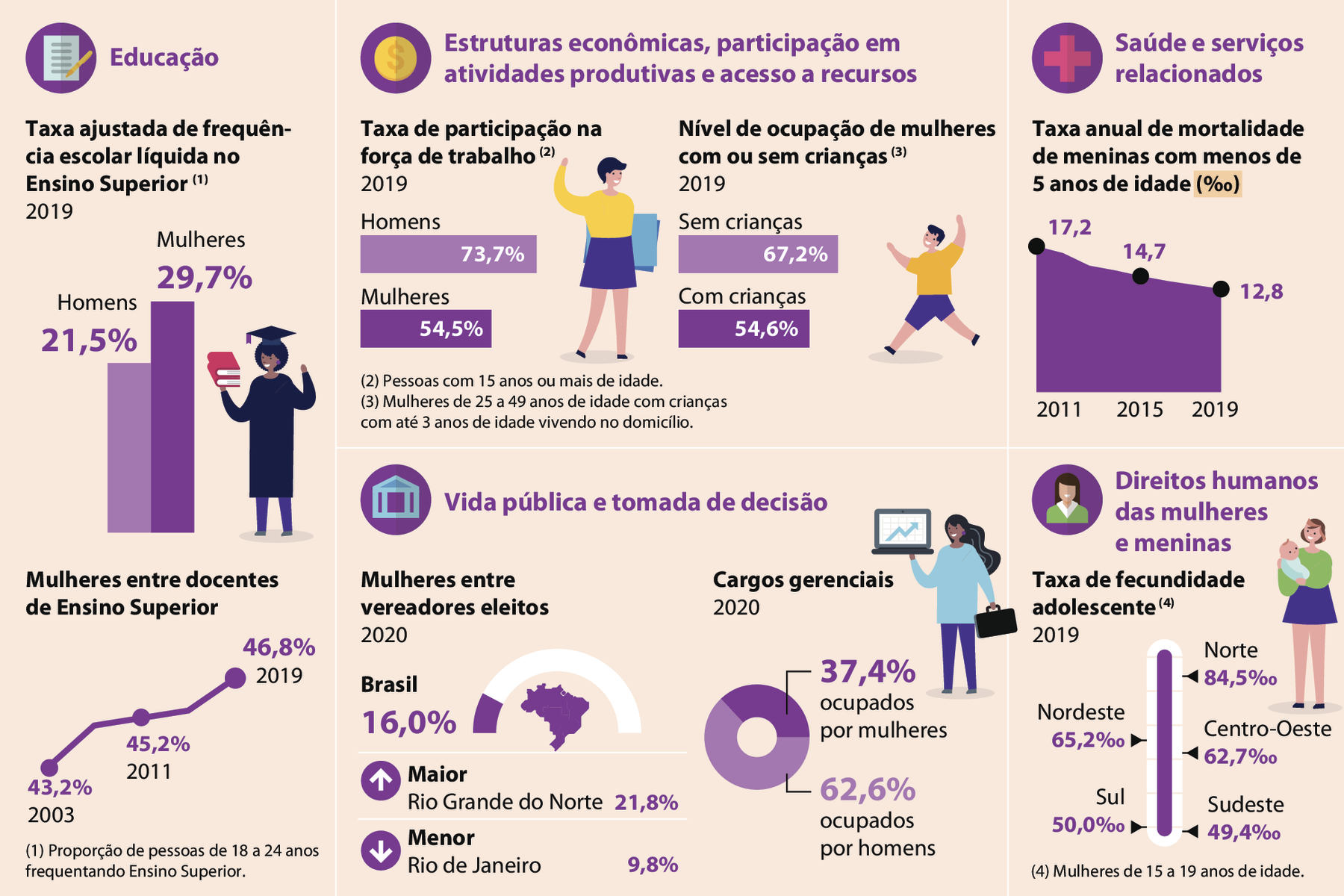
Dados obtidos em: í bê gê É. Diretoria de Pesquisas, Coordenação de População e Indicadores Sociais. Pesquisa Nacional por Amostra de Domicílios Contínua 2019. Rio de Janeiro: í bê gê É, 2020.
‰glossário
Estudos como esse são realizados por meio de técnicas e métodos estatísticos, que orientam as diferentes etapas do estudo: planejamento, coleta, organização, representação, análise, previsões e tomadas de decisão.
A Estatística está presente nas diferentes áreas de conhecimento e em nosso cotidiano, como nos noticiários, nas previsões do tempo, no estudo sobre a eficácia de medicamentos e em diferentes previsões e planejamentos de diversas áreas.
Neste momento, retomaremos os conceitos estudados em anos anteriores com o objetivo de orientar a compreensão e a realização de pesquisas estatísticas.
Planejamento de uma pesquisa estatística
Na realização de uma pesquisa estatística é comum passarmos pelas seguintes etapas de planejamento: problematização, definição da população ou amostra e realização da coleta dos dados.
Problematização
Uma investigação estatística parte da observação dos fenômenos e da identificação de um problema, o primeiro elemento a ser determinado em uma pesquisa. É com base nele que identificamos as perguntas a que queremos responder.
No exemplo apresentado, a investigação da pesquisa foi a desigualdade de gênero no Brasil, sendo elaboradas perguntas do tipo:
• Você frequenta as aulas da faculdade/universidade em que estuda?
• Você trabalha?
• Você tem filhos?
• Você ocupa cargo gerencial na empresa em que trabalha?
Observe que essas questões permitem coletar alguns dos dados apresentados no infográfico.
População e amostra
O conjunto formado por todos os elementos de uma pesquisa é denominado população ou universo estatístico. Quando uma pesquisa é realizada com todos os elementos de uma população, ela é denominada pesquisa censitária.
Entretanto, nem sempre é possível coletar dados de todos os elementos de um universo. Nesse caso, seleciona-se apenas uma parte da população, que chamamos de amostra.
Ao optar por uma pesquisa por amostragem (ou pesquisa amostral), a amostra deve ser escolhida de maneira conveniente e estratégica, para que seja possível extrair informações que representem a população como um todo.
Na escolha da amostra, devemos considerar algumas questões:
• Qual será o tamanho da amostra?
• Como essa amostra poderá ser selecionada?
• Que variáveis (qualitativa, quantitativa discreta ou contínua) devem-se considerar?
Por fim, devemos escolher a técnica de amostragem mais adequada: casual simples, sistemática ou estratificada. Cada uma com características que possam favorecer a representatividade da amostra, dependendo do cenário da pesquisa.
Atividades
Faça as atividades no caderno.
12. A diretoria de uma empresa pretende realizar um estudo sobre a satisfação de seus funcionários em relação à segurança no trabalho. Essa empresa tem 5 setores e 2 turnos de trabalho. Para essa pesquisa, será considerada uma amostra dos funcionários. Na sua opinião, que técnica de amostragem póde ser utilizada para determinar a amostra?
13.


Imagine que você vai realizar uma pesquisa com estudantes da sua escola para saber a opinião deles sobre os alimentos servidos. Em dupla, conversem sobre a problematização motivadora dessa pesquisa, elaborando perguntas que possam ser realizadas. Analisem se será uma pesquisa amostral ou censitária. Caso seja amostral, descrevam o tipo de amostragem a ser realizada. No fim, conversem com outra dupla para analisar as perguntas elaboradas e o tipo de pesquisa escolhido.
Coleta dos dados
As pesquisas estatísticas nos ajudam a responder a perguntas em diversos contextos. Vamos verificar como obter informações por meio de entrevistas e questionários. Acompanhe a situação.
A diretoria de uma escola quer saber a data de nascimento de todos os estudantes do 9º ano. Para isso, há duas opções: perguntar diretamente a cada um dos estudantes do 9º ano ou olhar a documentação que está nos arquivos dos estudantes.
Quando optam por perguntar diretamente a cada um dos elementos da amostra (nesse caso, aos estudantes), dizemos que a fonte é primária.
Ao optar por olhar a documentação, dizemos que a fonte é secundária.


Após definir a amostra e a fonte dos dados, a coleta poderá ser realizada por meio de entrevistas, questionários, fichas de observação ou outros instrumentos, conforme a variável escolhida.
Ao elaborar um questionário ou uma entrevista, dependendo da característica da variável, podemos ter perguntas abertas ou fechadas.
• Perguntas abertas: permitem qualquer tipo de resposta.
• Perguntas fechadas: geralmente são acompanhadas de alternativas para escolha. Nesse caso, póde-se deixar uma alternativa aberta, caso o entrevistado não encontre uma alternativa adequada.

Observação
Quando, em uma entrevista ou questionário, optamos por perguntas abertas, obtemos um resultado mais próximo do real, mas às vezes as respostas podem ser tão distintas entre si que dificultam sua organização.
Acompanhe a situação.
A professora de Giovana e Felipe pediu a eles que fizessem uma pesquisa sobre o tipo de filme preferido pelos colegas de classe. Confira o questionário que cada um elaborou.
Questionário de Giovana
|
Nome: |
|
Qual é o seu tipo de filme preferido? |
Questionário de Felipe
|
Nome: |
|
Qual é o seu tipo de filme preferido? |
Observe que Giovana deixou a pergunta em aberto, permitindo qualquer resposta. Já Felipe colocou algumas opções de resposta, o que facilitará a organização dos resultados.
Atividades
Faça as atividades no caderno.
14. Uma empresa pretende lançar um novo sabor de sorvete para vender a clientes adultos. Ela está em dúvida entre quatro sabores: goiaba, maracujá, acerola e manga. Para escolher o sabor, foi encomendada uma pesquisa.
a) Qual deve ser o público pesquisado?
b) Supondo que a pesquisa seja feita com uma amostra de 100 pessoas, que fatores devem ser levados em consideração?
c) O fato de o entrevistado consumir ou não sorvete deve ser considerado? E a frequência com que consome?
d) Monte um possível questionário para a realização dessa pesquisa.
15.


Retome as perguntas elaboradas na atividade 13, sobre a pesquisa da qualidade dos alimentos servidos na escola. Reflita com sua dupla sobre o tipo de perguntas feitas, se mudariam o tipo de pergunta ou incluíram novas. Depois, elabore um questionário com alguma pergunta fechada.
16.


Em grupo, você vai realizar uma pesquisa amostral com os estudantes de sua escola sobre o meio de transporte que utilizam para ir à escola. Definam a técnica de amostragem a ser utilizada, o tipo de perguntas e o questionário a ser aplicado. Depois, realize a coleta de dados. A análise será feita após os próximos tópicos.
Organização e representação
Um questionário com sugestões de respostas em alternativas nos ajuda a organizar os dados. Quando não estão apresentados dessa fórma, é preciso categorizá-los, ou seja, agrupar os elementos que têm a mesma propriedade.
Para isso, devemos considerar que todos os elementos devem estar em alguma categoria e que nenhum elemento deve aparecer em mais de uma categoria. Acompanhe um exemplo.
Apresentamos a lista de respostas que Gabriela obteve quando perguntou aos colegas qual era o lazer favorito deles em 2023.

Gabriela analisou as respostas e pensou em agrupá-las em duas categorias: atividades esportivas e outras atividades.

Após agrupá-los nessas categorias, Gabriela poderá representar esses dados em uma tabela e, depois, em diferentes gráficos. Por exemplo:
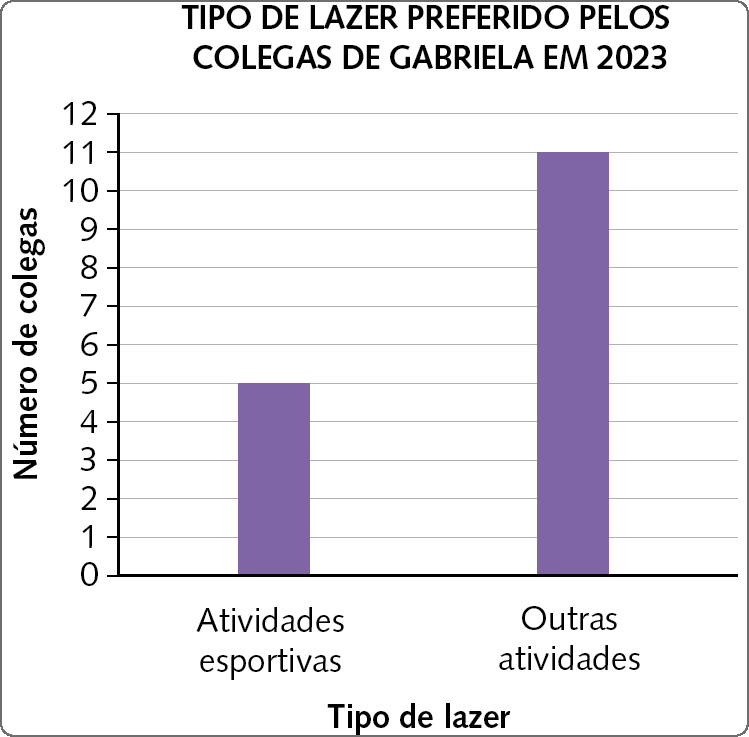
Dados obtidos por Gabriela em 2023.
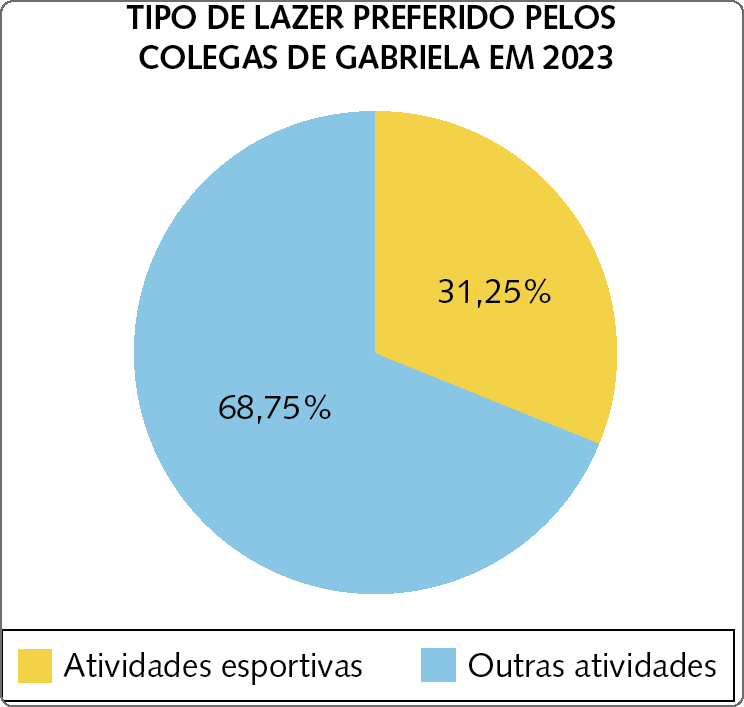
Dados obtidos por Gabriela em 2023.
Observe que os dois gráficos representam a mesma informação, mas de modos diferentes. No gráfico de barras, foram colocados os valores numéricos referentes ao número de colegas. Já no de setores, as informações foram colocadas em porcentagem.
Análise e conclusão
Assim como organizamos conjuntos de dados em tabelas e gráficos, também podemos sintetizar os dados utilizando as medidas de tendência central: moda, média e mediana. Elas são usadas para resumir ou representar um conjunto de dados, pois visam identificar um valor em torno do qual os dados tendem a se concentrar. Acompanhe a situação.
Mariana mediu a altura de todos os estudantes de sua turma e anotou os dados na lousa.

Depois, ela organizou os dados em ordem crescente e determinou algumas medidas:

• A moda corresponde ao valor de maior frequência e é usada para identificar a preferência em diferentes situações. Por esse motivo, póde ser aplicada em variáveis quantitativas ou qualitativas. Na situação, a moda é 1,56 métro, ou seja, é a medida da altura mais frequente na turma de Mariana.
• Já a mediana divide um conjunto de dados ordenado em duas partes iguais. Nesse exemplo, o termo central é 1,67 métro, o que significa que é possível dividir a turma em dois grupos com a mesma quantidade de estudantes, sendo um deles com 1,67 métro ou menos de medida da altura e o outro com 1,67 métro ou mais de medida da altura.
• A média é o quociente entre a soma dos valores observados e o número de observações. Essa medida sofre influência de todos os valores do conjunto de dados e nem sempre corresponde a um desses valores. Na situação observada, a média foi aproximadamente 1,648 métro.
Se analisarmos a média e a mediana juntas, podemos dizer que a maior parte dos estudantes da turma de Mariana tem medida da altura maior que a medida da altura média da turma.
Além dessas medidas, também temos a amplitude total, que é a diferença entre o valor máximo e o valor mínimo da variável. No exemplo dado, a amplitude total é 35 centímetros, o que indica que o estudante mais alto é 35 centímetros maior que o mais baixo.
No fim de uma pesquisa, precisamos voltar às questões de problematização e buscar respondê-las. Para isso, podemos montar um relatório com todas as informações coletadas, a representação e a análise dos dados e as respostas das questões iniciais.
Atividades
Faça as atividades no caderno.
17. Observe os dados de todos os funcionários da lanchonete Bom Lanche.
|
Sexo |
Salário |
Grau de escolaridade |
Anos de serviço |
|---|---|---|---|
|
Feminino |
3.000 |
Ensino Médio |
2 |
|
Feminino |
1.700 |
Ensino Médio |
1,5 |
|
Feminino |
3.750 |
Ensino Superior |
3 |
|
Masculino |
4.000 |
Ensino Superior |
4 |
|
Masculino |
2.500 |
Ensino Médio |
2 |
a) Qual é o salário médio dos funcionários dessa lanchonete?
b) Que medida de tendência central póde ser aplicada em relação às variáveis sexo e grau de escolaridade?
c) O que podemos dizer sobre a medida do tempo de serviço dos funcionários dessa lanchonete?
18. Uma empresa perguntou a opinião de 60 clientes em relação a um novo produto. Analise, no quadro, as notas, de 0 a 10, dadas pelos clientes.
|
5 |
8 |
10 |
6 |
7 |
3 |
4 |
5 |
6 |
7 |
|
4 |
9 |
10 |
7 |
8 |
9 |
10 |
3 |
4 |
1 |
|
5 |
5 |
8 |
6 |
3 |
7 |
8 |
8 |
9 |
10 |
|
3 |
10 |
5 |
7 |
5 |
6 |
7 |
8 |
2 |
5 |
|
8 |
8 |
4 |
7 |
5 |
6 |
1 |
2 |
9 |
4 |
|
9 |
3 |
4 |
5 |
8 |
4 |
3 |
5 |
9 |
1 |
a) Essas notas poderiam ser agrupadas em conceitos como: ruim, regular, bom e muito bom. Crie um critério para associar as notas a um desses conceitos.
b) Organize esses dados em uma tabela ou um gráfico, agrupando as notas de acôrdo com o conceito correspondente.
c) Determine a moda, a média e a mediana desse conjunto de dados. Depois, escreva uma conclusão sobre isso no caderno.
19. Organize, em tabelas e gráficos, os dados da sua pesquisa da atividade 16, sobre o meio de transporte utilizado pelos estudantes para irem à escola. Depois, determine medidas de tendência central e escreva no caderno uma conclusão sobre sua pesquisa.
20.


Realize uma pesquisa censitária ou por amostragem com os colegas de turma de algum tema relevante para o grupo. Elabore um questionário a ser aplicado, organize as informações em tabelas e gráficos, utilize as medidas de tendência central adequadas para a interpretação das informações, elabore um relatório com uma análise e sua conclusão sobre o tema pesquisado e, depois, apresente-o aos colegas de classe.
Revisão dos conteúdos deste capítulo
Faça as atividades no caderno.
Probabilidade
Um experimento aleatório é aquele em que conhecemos os resultados possíveis, mas não sabemos com exatidão qual deles vai ocorrer.
O conjunto de todos os resultados fórma o espaço amostral. Qualquer subconjunto do espaço amostral é chamado de evento.
Quando cada resultado tem a mesma chance de ocorrer, dizemos que o espaço amostral é equiprovável.
Cálculo de probabilidade
A probabilidade de um evento de espaço amostral equiprovável ocorrer, em um experimento aleatório, é a razão entre o número de elementos favoráveis a esse evento e o número de elementos do espaço amostral.
Eventos independentes
Quando a ocorrência de um evento não interfere na ocorrência do outro, temos eventos independentes.
Eventos dependentes
Quando um evento interfere na ocorrência de outro evento que ocorrerá, temos eventos dependentes.
1. Em uma urna, foram colocadas 25 bolinhas, sendo 16 azuis e 9 vermelhas, e foi retirada ao acaso uma bolinha.
a) Qual é a probabilidade de a bolinha retirada ser vermelha?
b) Qual é a probabilidade de a bolinha retirada ser azul?
c) Retirou-se uma bolinha azul e, sem repô-la, retirou-se outra bolinha ao acaso. Qual é a probabilidade de essa segunda bolinha ser azul?
2. No lançamento de um “dado honesto” de seis faces numeradas de 1 a 6, qual é a probabilidade de sair:
a) um número par?
b) um número menor que 5?
c) um número maior que 6?
3. Uma urna contém 50 cartões, numerados de 1 a 50. Ao retirar um cartão, ao acaso, qual é a probabilidade de sair:
a) um múltiplo de 4?
b) um divisor de 5?
c) um cartão com número maior que 30?
4. Para o lançamento de uma “moeda honesta” duas vezes consecutivas, determine a probabilidade de:
a) saírem duas faces diferentes;
b) sair pelo menos uma “cara”.
Pesquisa estatística
Planejamento de uma pesquisa estatística
O conjunto formado por todos os elementos de uma pesquisa é denominado população ou universo estatístico. Quando uma pesquisa é realizada com todos os elementos de uma população, ela é denominada pesquisa censitária.
Entretanto, nem sempre é possível coletar dados de todos os elementos de um universo. Nesse caso, seleciona-se apenas uma parte da população, que chamamos de amostra.
Ao optar por uma pesquisa por amostragem (ou pesquisa amostral), a amostra deve ser escolhida de maneira conveniente e estratégica, para que seja possível extrair informações que representem a população como um todo.
Organização e representação
Os dados de uma pesquisa podem ser organizados em algumas categorias e, depois, representados em uma tabela ou em diferentes gráficos.
Análise e conclusão
Assim como organizamos conjuntos de dados em tabelas e gráficos, também podemos sintetizar os dados utilizando as medidas de tendência central:
• moda: valor de maior frequência;
• mediana: termo central ou média aritmética dos dois termos centrais, quando os dados estão em ordem crescente ou decrescente;
• média: quociente entre a soma dos valores observados e o número de observações.
5. Um grupo de médicos pretende pesquisar a qualidade de sono dos adolescentes brasileiros. Esse grupo deve optar por uma pesquisa censitária ou amostral? Justifique.
6. Analise as medidas de massa dos jogadores do time de Jorge, obtidas por ele em 2023.
|
61 kg |
61 kg |
61 kg |
62 kg |
63 kg |
|
63 kg |
63 kg |
63 kg |
65 kg |
65 kg |
|
68 kg |
68 kg |
70 kg |
71 kg |
71 kg |
a) Organize os dados em uma tabela.
b) Construa um gráfico de barras verticais.
c) Calcule a média, a moda e a mediana.
7. Uma escola realizou uma pesquisa com os estudantes matriculados, na qual cada um deles apontou sua atividade cultural preferida. O resultado obtido foi representado nesta tabela.
|
Atividade cultural |
Quantidade de estudantes |
|---|---|
|
Teatro |
116 |
|
Cinema |
158 |
|
Show |
122 |
|
Contação de histórias |
74 |
|
Visita a museu |
90 |
Dados obtidos pela direção da escola em janeiro de 2024.
a) Determine a moda.
b) Construa um gráfico de barras horizontais.
c) Escreva no caderno três análises sobre as informações do gráfico.
8. Um parque fez um estudo sobre a idade de crianças visitantes no primeiro fim de semana de 2024, resultando no gráfico. Determine a média e a moda dos dados.
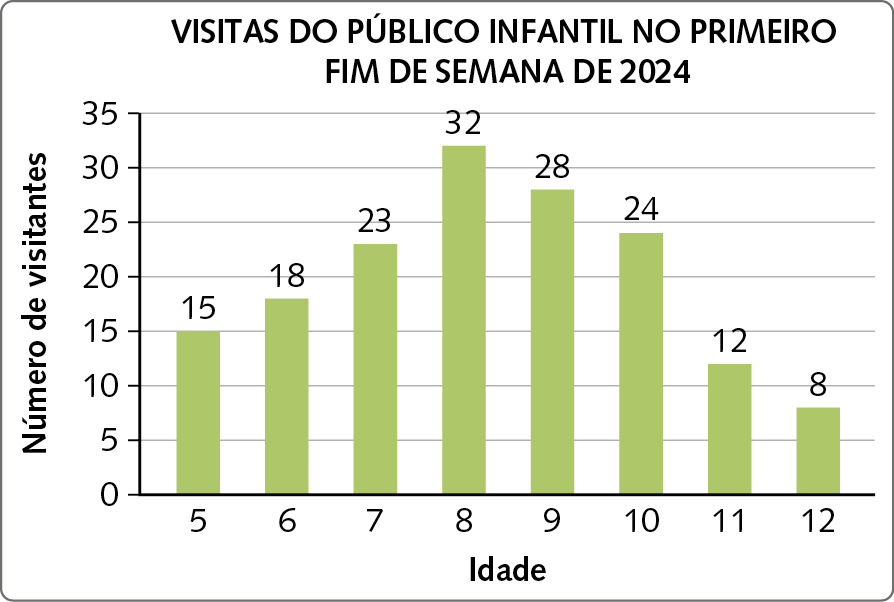
Dados obtidos pelo parque no primeiro fim de semana de 2024.
9. Uma empresa de uniformes tem 8 funcionários cujos salários, em reais, estão indicados a seguir:
|
5.200 |
3.780 |
2.370 |
2.370 |
|
1.180 |
1.180 |
1.180 |
1.180 |
a) Calcule a média, a mediana e a moda desses dados.
b) Se a empresa contratar um profissional especializado com um salário de .7480 reais, quais medidas de tendência central seriam alteradas?
10. Fábio anotou a seguir a medida de temperatura mínima de cada dia de uma semana.
|
Dia da semana |
Medida de temperatura mínima |
|---|---|
|
Domingo |
17 °C |
|
Segunda-feira |
18 °C |
|
Terça-feira |
17 °C |
|
Quarta-feira |
21 °C |
|
Quinta-feira |
19 °C |
|
Sexta-feira |
16 °C |
|
Sábado |
15 °C |
Dados obtidos por Fábio na primeira semana de 2024.
a) Construa um gráfico de segmentos com esses dados.
b) Determine a média, a mediana e a moda desses dados.
11. Este gráfico apresenta as notas da avaliação de Matemática do 4º bimestre de 2023 aplicada no 9º ano A pela professora Gabi. Sabendo que essa avaliação tinha valor de 0,0 a 10,0, responda:
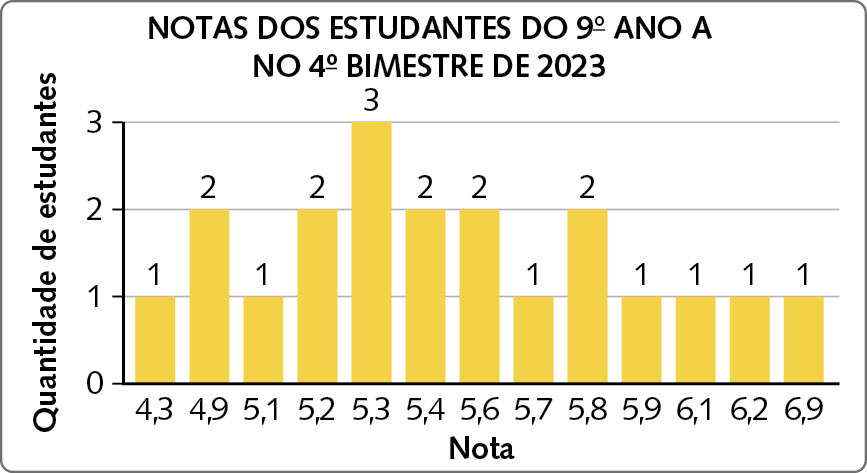
Dados obtidos pela professora Gabi no 4º bimestre de 2023.
a) Essa pesquisa é censitária ou amostral? Justifique.
b) Qual é o tamanho dessa população? Determine a média.
c) Determine a moda.
d) A qual conclusão podemos chegar com os dados dessa pesquisa?
É hora de extrapolar

Faça as atividades no caderno.
O que você conhece da cultura afro-brasileira?
Atualmente, negros e negras representam mais da metade da população brasileira e formam a maior população negra fóra da África. As manifestações da cultura afro-brasileira são constituintes da cultura brasileira e é de extrema importância que sejam de conhecimento de todos, assim como o estudo sobre personalidades negras importantes para o nosso país.
Objetivos: Analisar dados sobre a composição da população brasileira, pesquisar sobre a cultura afro-brasileira e sobre personalidades negras importantes para a história do Brasil e produzir um gibi que será exibido para a comunidade escolar.

Etapa 1: Análise de dados sobre a composição da população brasileira em relação à raça.
1. Reúnam-se em grupo, analisem a tabela e o gráfico produzidos com base nos dados sobre a composição da população brasileira segundo cor ou raça da Pesquisa Nacional de Amostra de Domicílios (Pnad), realizada no 3º trimestre de 2021 pelo í bê gê É.
|
Cor ou raça |
Número de habitantes (em milhares) |
|---|---|
|
Branca |
92.029 |
|
Preta |
20.030 |
|
Parda |
98.425 |
|
Amarela/indígena/sem declaração |
2.324 |
|
Total |
212.808 |
Dados obtidos em: https://oeds.link/hCjvGt. Acesso em: 17 junho 2022.
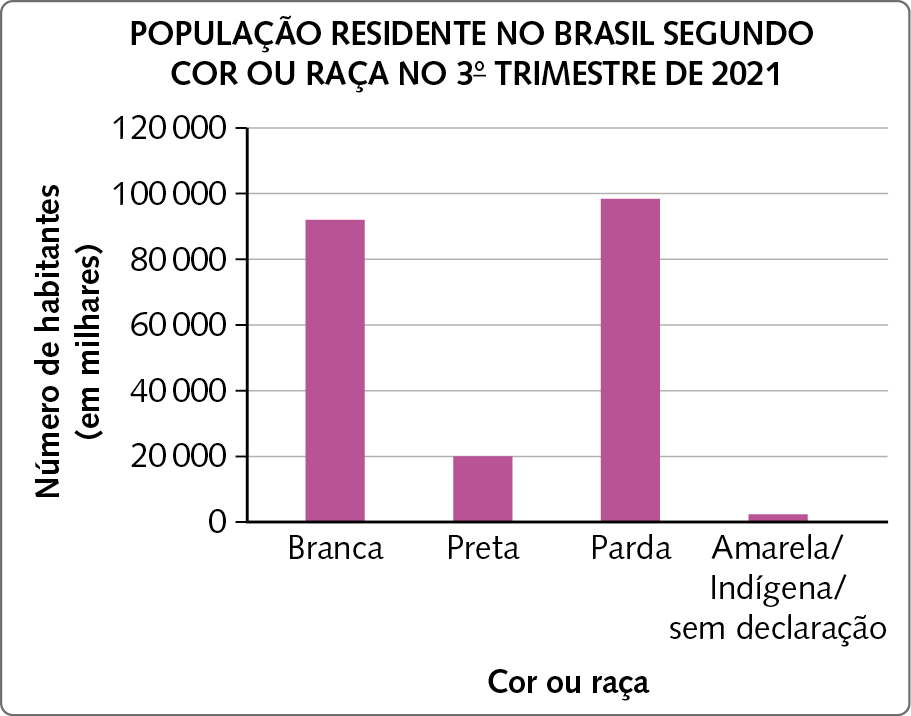
Dados obtidos em: https://oeds.link/hCjvGt. Acesso em: 17 junho 2022.
a) O gráfico de colunas é adequado para representar esses dados? Por quê?
b)

Com auxílio de uma calculadora, calcule que porcentagem cada categoria considerada na pesquisa representa da população.
c)

Utilizando um software de planilha eletrônica, construam um gráfico de setores sobre a composição da população brasileira segundo cor ou raça no 3º trimestre de 2021, de acôrdo com a pesquisa realizada pelo í bê gê É.
2. Leiam o texto e, com a análise dos dados apresentados a seguir, respondam às questões.
O í bê gê É (Instituto Brasileiro de Geografia e Estatística) usa preto como classificação de cor ou raça nas pesquisas de censo demográfico desde 1872, conforme Nota Técnica sobre o “Histórico da investigação sobre cor ou raça nas pesquisas domiciliares do í bê gê É”.
[reticências]
Para formar a classificação de negros, é comum que seja somada a população preta à população parda para a formação de um grupo. Portanto, usar o termo preto não é equivalente a usar a categoria negro, que póde incluir os pardos.
[reticências]
uól Vestibular. í bê gê É usa classificação de cor preta; grupo negro reúne pretos e pardos. São Paulo, 2013. Disponível em: https://oeds.link/5ytEO2. Acesso em: 17 junho 2022.
Analise os percentuais da população que se autodeclarou preta ou parda ao longo de vários anos na Pesquisa Nacional de Amostra de Domicílios, realizada pelo í bê gê É.
|
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
|---|---|---|---|---|---|---|
|
Preta |
7,3 |
7,7 |
8,2 |
8,6 |
9,3 |
9,4 |
|
Parda |
45,8 |
46,1 |
46,6 |
46,8 |
46,5 |
46,8 |
Dados obtidos em: https://oeds.link/C4V1fq. Acesso em: 17 junho 2022.
a) Calculem o percentual da população negra dos anos representados na tabela.
b) Que tipo de gráfico é o mais adequado para representar o percentual de negros no Brasil entre os anos de 2014 e 2019? Por quê?
c) Construam o gráfico escolhido no item b.

Etapa 2: Pesquisa sobre cultura afro-brasileira.
3. Considerando a definição de que a cultura afro-brasileira é todo tipo de manifestação cultural do Brasil que sofreu influência da cultura africana desde os tempos do Brasil colônia até a atualidade, façam uma lista das manifestações conhecidas por vocês que compõem a cultura afro-brasileira.
4. A capoeira é uma expressão cultural afro-brasileira de muita relevância. Em 2014, em Paris, a Roda de Capoeira recebeu da Unesco o título de Patrimônio Imaterial da Humanidade.

Sobre a capoeira, pesquisem e respondam:
a) A prática da capoeira foi proibida no Brasil por muitos anos, sendo liberada apenas na década de 1930. Como surgiu a capoeira e por que sua prática foi proibida?
b) Quais são as regras, os golpes, a música e os instrumentos usados na prática da capoeira?
5. O maracatu recebeu em 2014 o título de Patrimônio Cultural Imaterial do Brasil, dado pelo Iphan (Instituto do Patrimônio Histórico e Artístico Nacional).
Segundo o ifãn, o valor patrimonial do Maracatu Nação está na sua capacidade de comunicar características da cultura brasileira e carregar elementos fundamentais para a memória, a identidade e a formação da população afro-brasileira. Ainda segundo o Iphan, o Maracatu Nação é uma fórma de expressão que congrega relações comunitárias, e permite o compartilhamento de práticas, memórias e fortes vínculos com o sagrado.

a) O Maracatu é um ritmo típico de qual estado brasileiro?
b) Esta imagem mostra a alfaia, tipo de tambor utilizado para dar o ritmo no maracatu.

6. A cultura afro-brasileira se manifesta na música, na culinária, em religiões e em festividades. Escolham uma manifestação da cultura afro-brasileira para fazer uma pesquisa, em sites ou livros especializados, sobre as origens e as características dessa manifestação. Selecionem imagens para ilustrá-la.

Etapa 3: Pesquisa sobre personalidades negras importantes para a história do Brasil.
7. Observem as imagens. Vocês conhecem alguma dessas personalidades? Conversem entre si e com o professor e relatem o que sabem sobre cada uma delas.










8. Escolham uma das personalidades da atividade 7 e pesquisem a sua biografia. Selecionem algumas imagens para apresentar à turma.

Etapa 4: Confecção de histórias em quadrinhos.
9. Nesta etapa, vocês vão produzir histórias em quadrinhos sobre as pesquisas que fizeram. Para isso, deverão entender melhor esse gênero. Respondam às seguintes questões:
a) Quais histórias em quadrinhos vocês já leram?
b) Quais são as características das histórias em quadrinhos?
c) Que elementos tornam uma história em quadrinhos interessante?
10. Agora, produzam duas histórias em quadrinhos:
um. sobre a manifestação da cultura afro-brasileira selecionada (música, culinária, religiões e festividades);
dois. sobre a personalidade negra escolhida.
Incluam as informações obtidas nas pesquisas, considerando as características e os elementos interessantes desse gênero.

Etapa 5: Análise das histórias elaboradas e confecção dos gibis.
11. Disponibilizem as histórias em quadrinhos elaboradas pelo seu grupo para que os outros analisem a clareza das informações, a pertinência do título e as imagens utilizadas e para que deem dicas para deixar a leitura mais fluida e/ou interessante.
12. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
13. Façam os ajustes necessários, confeccionem dois gibis (impressos ou digitais), um com os quadrinhos sobre a cultura afro-brasileira e outro sobre as personalidades negras importantes para a história do Brasil, e os divulguem para a comunidade escolar.

Etapa 6: Síntese do trabalho realizado.
14. Algumas questões que devem ser discutidas:
a) Vocês consideram importante que a população brasileira tenha conhecimento sobre a cultura afro-brasileira? Por quê?
b) Vocês consideram que as histórias em quadrinhos são maneiras interessantes de divulgar conteúdo? Por quê?
15. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 4 e 5.
Glossário
- ‰
- : símbolo que representa a permilagem, que corresponde a uma fração de denominador .1000.
- Voltar para o texto