Capítulo 3 Segmentos proporcionais e semelhança


Trocando ideias
Durante a pandemia de coronavírus, o uso de máscaras de proteção era obrigatório, pois contribuía para que as pessoas pudessem se proteger e evitar a disseminação do sárs cóv dois, vírus que causa a côvid dezenóve.

▸

Além do uso de máscaras, que outras medidas de proteção foram adotadas para que as pessoas pudessem se proteger e evitar a disseminação do vírus da côvid dezenóve?
Analise os moldes de máscaras de proteção a seguir.
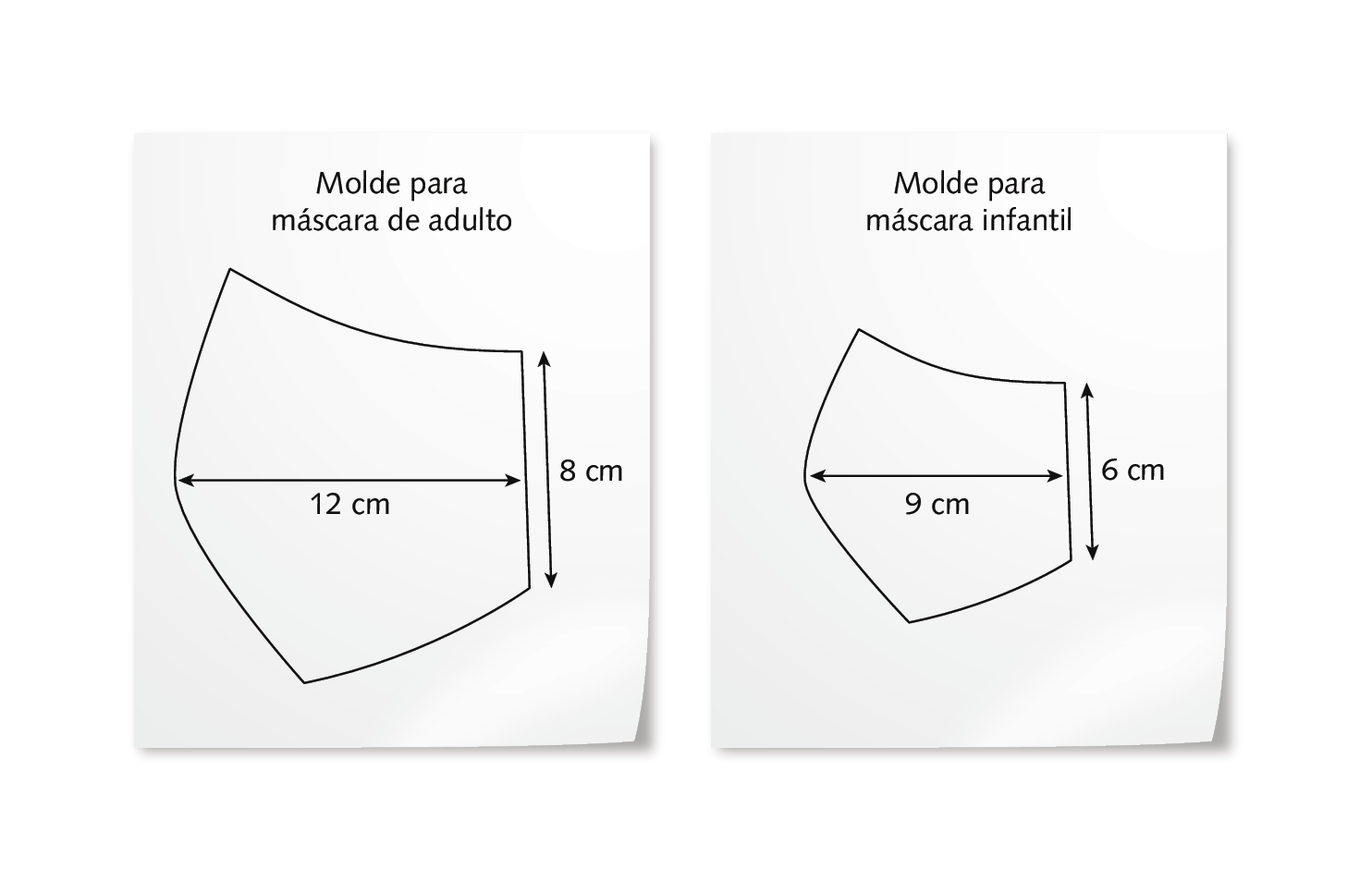
As figuras correspondentes a esses moldes são semelhantes porque as medidas das aberturas dos ângulos correspondentes são iguais, e as medidas de comprimento de quaisquer segmentos correspondentes são proporcionais.
▸ Qual é a taxa de redução do molde da máscara infantil em relação ao molde da máscara de adulto?
Neste capítulo vamos estudar o teorema de Tales e a semelhança entre figuras.
Respostas e comentários
Trocando ideias: primeiro item: Exemplos de resposta: vacinação, distanciamento social, lavagem das mãos, cobrir nariz e boca com o antebraço ao tossir ou espirrar, manutenção de ambientes limpos e ventilados etcétera; segundo item: 25%
CAPÍTULO 3 – SEGMENTOS PROPORCIONAIS E SEMELHANÇA
Trocando ideias
Bê êne cê cê:
• Competências gerais 6, 7 e 9 (as descrições estão na página seis).
• Competências específicas 2, 3 e 8 (as descrições estão na página sete).
Objetivos:
• Introduzir o conceito de semelhança de figuras.
• Conscientizar os estudantes sobre a importância das medidas de proteção que foram adotadas para evitar a disseminação do vírus da côvid dezenóve.
Temas contemporâneos transversais:


Comece a exploração desta seção Trocando ideias comentando com a turma que a covid-19, doença causada pelo coronavírus sárs cóv dois, é transmitida principalmente por meio do contato com pequenas gotículas que contêm o vírus e são expelidas por pessoas infectadas. Diga que essas gotículas entram em contato com as nossas vias aéreas fazendo com que o novo coronavírus se multiplique em nosso corpo. Portanto, o uso de máscaras é necessário como medida de proteção individual e coletiva. Nesse âmbito o seu uso é importante não só para a saúde como também é um ato de cidadania.
Convide os estudantes a responder à questão do primeiro item. Dê um tempo para que levantem todas as medidas de proteção que recordarem e registre-as na lousa. Essa dinâmica permite a eles valorizarem a diversidade de saberes e a fazer escolhas alinhadas ao exercício da cidadania. Além disso, ela possibilita a argumentação com base em fatos e promove o diálogo, criando o cenário favorável para que as competências gerais 6, 7 e 9 da Bê êne cê cê sejam desenvolvidas. A competência específica 8 também tem o seu desenvolvimento favorecido, uma vez que há interação e discussão de uma questão comum.
Proponha aos estudantes que comparem os moldes e descrevam o que observam. Espera-se que eles percebam que os moldes têm a mesma forma, mas tamanhos diferentes, ou, em outras palavras, que o molde para máscara infantil é uma redução do molde para máscara de adulto ou que o molde para máscara de adulto é uma ampliação do molde para máscara infantil. Depois, introduza o conceito de semelhança e peça que respondam à última questão. Caso tenham dificuldade, oriente-os a calcular a razão entre as medidas de comprimento correspondentes que estão explícitas. Eles devem perceber que esta razão é 0,75, o que indica que o molde para máscara infantil corresponde a 75% do tamanho do molde para máscara de adulto, ou seja, a taxa de redução foi de 25%.

1 Razão e proporção nos segmentos de reta
Modelismo é a arte de construir automóveis, aviões, trens, motos, navios etcétera. em miniatura.
Os modelos são semelhantes aos objetos reais, mas foram reduzidos obedecendo a uma razão.
Verifique as miniaturas a seguir.


O exemplo de uma razão utilizada pelos profissionais de modelismo é 1 dividido por 12, que corresponde à razão entre as medidas das dimensões do modelo construído e do objeto real. Essa razão indica que, se um comprimento do modelo mede a, então, no objeto real, o comprimento correspondente mede 12a.
A razão entre dois números a e b, com b ≠ 0, nessa ordem, é dada por ádividido porbit ou
Fração. a sobre b.. Lemos: “a está para b ”.
Se duas razões são iguais, temos uma proporção.
Proporção é uma igualdade entre duas razões.
Confira um exemplo.
As razões
Fração. dezoito décimos. Fração. vinte e sete quinze avosformam uma proporção:
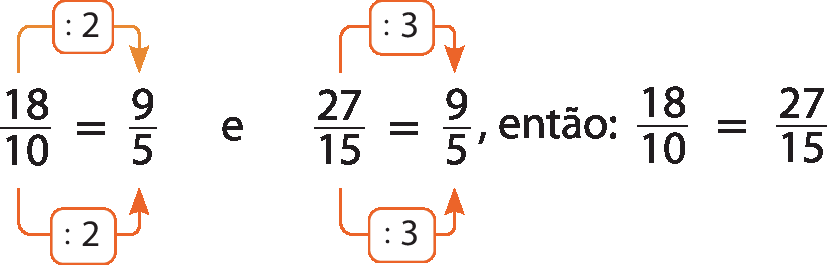
Podemos ler a proporção anterior da seguinte fórma:
“Dezoito está para dez assim como vinte e sete está para quinze”.
Respostas e comentários
Razão e proporção nos segmentos de reta
Objetivo:
Compreender o conceito de segmentos de reta proporcionais.
Justificativa
Compreender o conceito de segmentos de reta proporcionais é importante, dentre outras coisas, para entender e aplicar o teorema de Tales, que será estudado mais adiante neste mesmo capítulo.
Mapeando conhecimentos
Reproduza os segmentos de reta a seguir na lousa:
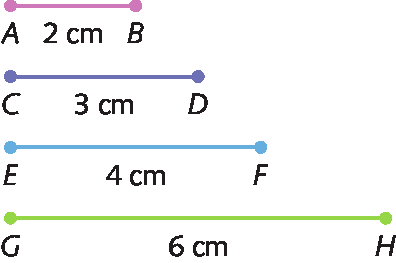
Depois, peça aos estudantes que determinem as razões
Sentença matemática. AB sobre CD.e
Sentença matemática. EF sobre GH.e verifique se percebem que as medidas desses segmentos de reta formam uma proporção, ou seja, que
Sentença matemática. AB sobre CD.=
Sentença matemática. EF sobre GH.=
Sentença matemática. dois terços. Você pode ampliar essa proposta e solicitar que representem segmentos de reta proporcionais no caderno e compartilhem com os colegas.
Para as aulas iniciais
Na seção Revisão dos conteúdos de anos anteriores são retomados os conceitos de razão e proporção. Faça a leitura coletiva desta revisão com a turma e explore com eles a atividade 10.
Você pode também explorar os segmentos de reta proporcionais feitos pelos estudantes na dinâmica inicial. Reproduza os segmentos de reta feitos por alguns deles na lousa e peça aos demais estudantes da turma que verifiquem se as medidas formam uma proporção.
Enfatize aos estudantes que, para o cálculo da razão, eles devem seguir a ordem em que os dados foram fornecidos. Assim:
• a razão entre os números 2 e 3 é
dois terços;
• a razão entre os números 3 e 2 é
Fração. três meios.
Na proporção
Sentença matemática. 18 sobre 10 igual a 27 sobre 15., os números 18 e 15 são denominados extremos e os números 10 e 27 são denominados meios.
Note que:
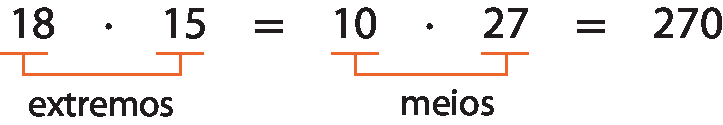
Essa propriedade é conhecida como propriedade fundamental das proporções.
Em toda proporção, o produto dos extremos é igual ao produtos dos meios, ou seja, dados a, b, c e d não nulos, com
Sentença matemática. a sobre b igual a c sobre d., temos a ⋅ d = b ⋅ c.
Atividades
Faça as atividades no caderno.
1. Determine, no caderno, a razão entre os números a seguir na ordem em que aparecem.
a) 8 e 10
b) menos2 e 3
c)
Sentença matemática. um meioe
Sentença matemática. 3 quartosd) 10 e 2
2. Aplicando a propriedade fundamental das proporções, verifique quais dos pares de razões a seguir formam uma proporção.
a)
Sentença matemática. cinco sextose
Sentença matemática. Seis quintosb)
Sentença matemática. menos, dez terçose
Sentença matemática. vinte sextosc)
Sentença matemática. doze quinze avose
Sentença matemática. quatro quintosd)
Sentença matemática. um meio sobre cincoe
Sentença matemática. três trinta avos.Razão entre segmentos de reta
Seja r a reta que passa pelos pontos distintos a e B.

Os pontos a e B e todos os demais entre eles formam um segmento de reta que é indicado por
Segmento AB. A medida de comprimento de um segmento de reta
Segmento ABé indicada por A bê ou med
abre parênteses, segmento AB, fecha parênteses..
A razão entre dois segmentos de reta corresponde à razão entre suas medidas de comprimento, considerando a mesma unidade de medida de comprimento.
Considere, por exemplo, os segmentos de reta
Segmento ABe
Segmento CD.

Como A bê = 30 milímetros e CD = 5 centímetros = 50 milímetros, temos a razão entre os segmentos de reta
Segmento ABe
Segmento CD:
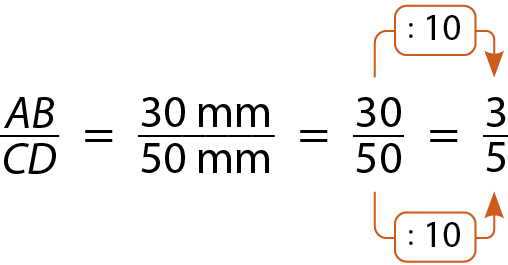
Logo, a razão entre esses segmentos de reta é
Sentença matemática. três quintos..
Respostas e comentários
1. a)
Sentença matemática. quatro quintos1. b)
Sentença matemática. menos, dois terços1. c)
dois terços1. d) 5
2. alternativas c, d
Razão entre segmentos de reta
Comente que, no exemplo, também se pode calcular a razão entre os segmentos
Segmento ABe
Segmento CD, usando a unidade de medida centímetro. Assim:
.
Ao medir o comprimento de um segmento de reta
segmento AB, comparamos quantas vezes uma unidade de medida de comprimento (1 milímetro, 1 centímetro, 1 métro, etcétera) cabe nessa medida.
Por exemplo, se usarmos 1 cm como unidade de medida, o comprimento desse segmento de reta mede a razão
AB sobre 1, centímetro..
Segmentos de reta proporcionais
Vamos considerar os segmentos de reta
Segmento AB, segmento CD, segmento EF, segmento GH,
Segmento AB, segmento CD, segmento EF, segmento GH,
Segmento AB, segmento CD, segmento EF, segmento GHe
Segmento AB, segmento CD, segmento EF, segmento GHe suas medidas de comprimento:
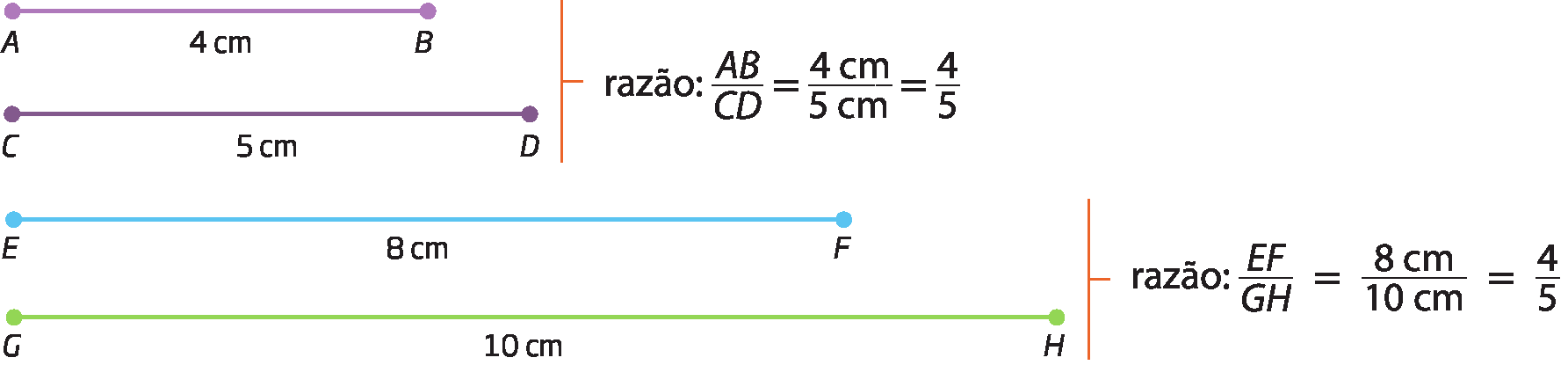
Como as razões obtidas são iguais, os segmentos de reta
Segmento AB, segmento CD, segmento EF, segmento GH,
Segmento AB, segmento CD, segmento EF, segmento GH,
Segmento AB, segmento CD, segmento EF, segmento GHe
Segmento AB, segmento CD, segmento EF, segmento GHformam, nessa ordem, uma proporção:
Atividades
Faça as atividades no caderno.
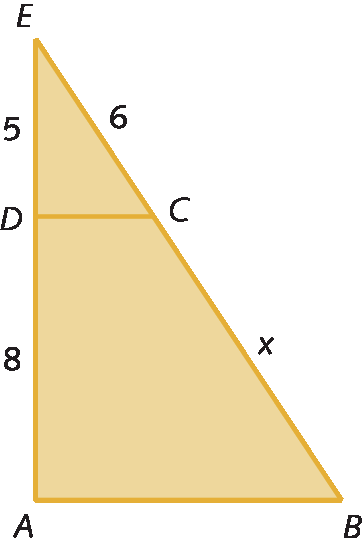
3. Determine a medida de comprimento x do segmento de reta
Segmento AB, sabendo que
Sentença matemática. AB sobre BC igual a 2 quintos.e BC = 20 centímetros.
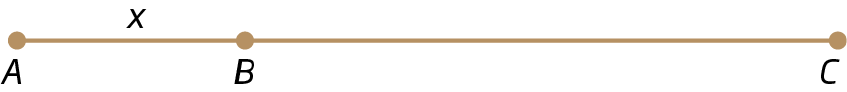
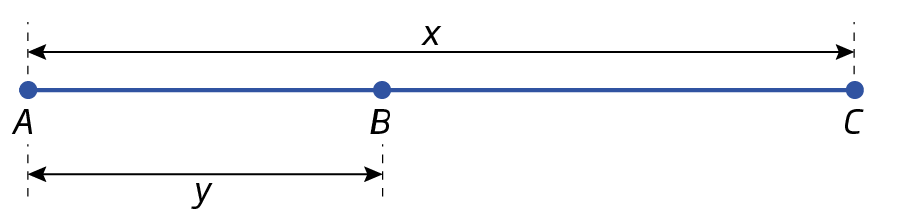
4. Dada a figura, determine as medidas de comprimento x e y, sabendo que
Sentença matemática. AB sobre AC igual a 3 sétimos.e BC = 16 centímetros.
5. Os segmentos de reta
Segmento de reta AB.,
Segmento de reta CD.,
Segmento de reta EF.e
Segmento de reta GH.formam, nessa ordem, uma proporção. Considerando que ê éfe = 3 centímetros, GH = 5 centímetros e AB + CD = 40 centímetros, determine A bê e CD.
6. A fotografia tem dimensões de 30 milímetros× 40 milímetros.

Queremos, com base nessa fotografia, reproduzir duas outras: uma com ampliação de 100% e outra com redução de 50%. Quais serão as medidas das dimensões das novas fotografias?

2 Teorema de Tales
Um feixe de retas paralelas é formado por duas ou mais retas de um mesmo plano que, consideradas duas a duas, são sempre paralelas.
Respostas e comentários
3. x = 8 centímetros
4. x = 28 centímetros; y = 12 centímetros
5. AB = 15 centímetros; CD = 25 centímetros
6. ampliação: 60 milímetros× 80 milímetros; redução: 15 milímetros× 20 milímetros
Segmentos de reta proporcionais
Se os estudantes estiverem com dificuldade na resolução das atividades, pergunte se a propriedade fundamental das proporções pode ser aplicada.
• A proporção obtida na atividade 5 é
AB sobre CD igual a EF sobre GH. Substituindo as medidas de comprimento temos:
Sentença matemática. AB sobre CD igual a 3 centímetros sobre 5 centímetros.Assim, aplicando a propriedade fundamental das proporções, obtemos (5 centímetros) ⋅ AB = (3 centímetros) ⋅ CD um. Como AB + CD = 40 centímetros dois, podemos isolar AB em dois e substituir em um:
(5 centímetros) ⋅ (40 centímetros ‒ CD) = (3 centímetros) ⋅ CD três.
Ao resolver três, obtemos CD = 25 centímetros e, substituindo em um, temos AB = 15 centímetros.
Teorema de Tales
Bê êne cê cê:
• Competência geral 1 (a descrição está na página seis).
• Competências específicas 1 e 2 (as descrições estão na página sete).
• Habilidades ê éfe zero nove ême ah um zero e ê éfe zero nove ême ah um quatro.
Objetivo:
Compreender o teorema de Tales.
Justificativa
Compreender o teorema de Tales é importante devido às diferentes aplicações na Geometria como, por exemplo, para dividir um segmento de reta em partes iguais e para demonstrar o teorema da bissetriz de um ângulo interno em um triângulo. Além disso, podemos aplicá-lo na resolução de diversos problemas.
Mapeando conhecimentos
Peça aos estudantes que, individualmente, representem três retas paralelas cortadas por duas transversais quaisquer e que meçam os segmentos de retas determinados por estas retas com o auxílio de uma régua. Depois, proponha que verifiquem se as medidas dos comprimentos dos segmentos de reta determinados sobre a primeira transversal são proporcionais às medidas de comprimento dos segmentos correspondentes determinados sobre a segunda transversal.
Para as aulas iniciais
Peça aos estudantes que compartilhem as conclusões a que chegaram na dinâmica inicial com toda a turma. Espera-se que eles percebam que um feixe de paralelas determina em duas transversais segmentos proporcionais.
• Antes de iniciar o conteúdo sobre o teorema de Tales, aproveite para retomar a ideia da Matemática como criação humana. Mencione que Tales foi um matemático grego. Nas próximas páginas, eles verão um pouco do trabalho que foi atribuído a ele. Explique que Tales é anterior a Euclides, mas este último recebe grande crédito por ter organizado os conhecimentos de Geometria na obra Os elementos. Esse tipo de conversa contribui para o desenvolvimento da competência geral 1 e da competência específica 1.
(EF09MA10) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal.
(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
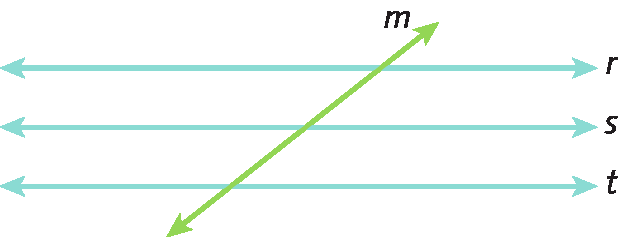
Uma reta que intercepta duas ou mais retas de um feixe de retas paralelas recebe o nome de transversal.
Na figura a seguir, a reta m é transversal ao feixe de retas paralelas formado pelas retas r, s e t.

Tecnologias digitais em foco
Teorema de Tales
Nesta seção, utilizamos o GeoGebra ou outro software de geometria dinâmica que seu professor indicar para construirmos um feixe de retas paralelas cortadas por duas transversais. Vamos verificar se os segmentos de reta determinados sobre uma transversal são proporcionais aos segmentos de reta determinados sobre a outra transversal.
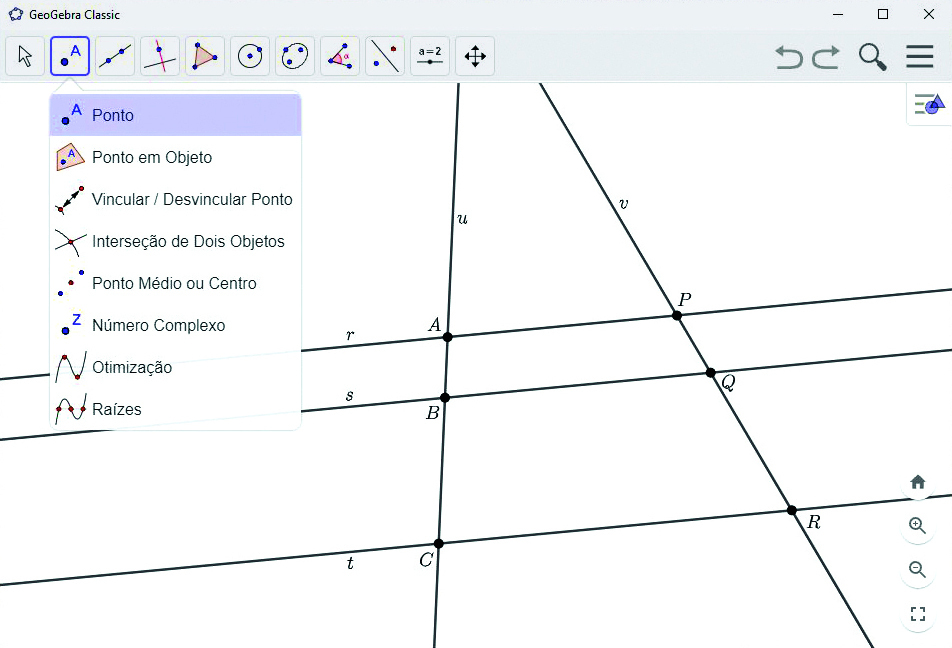
Construa
Siga os passos a seguir para construir as retas paralelas e as retas transversais.
1º) Construa uma reta r.
2º) Construa as retas s e t, paralelas à reta r.
3º) Construa duas retas, u e v, transversais ao feixe de retas paralelas construído nos passos anteriores.
4º) Marque os pontos a, B e C nas intersecções das retas r, s e t com a reta transversal u e os pontos P, Q e R nas intersecções das retas r, s e t com a reta transversal v.
Explore
a) Meça o comprimento dos segmentos
A B,
B C,
A C,
P Q,
Q Re
P Re, usando uma calculadora, determine as razões
Sentença matemática. AB sobre BC.,
Sentença matemática. PQ sobre QR.,
Sentença matemática. PQ sobre QR.e
Sentença matemática. PR sobre PQ..
b) Comparando as razões
AB sobre BCcom
PQ sobre QRe
AC sobre ABcom
PR sobre PQ, o que é possível verificar?
c) Movimente os pontos móveis, modificando a configuração inicial, e calcule novamente as razões. A relação que você percebeu continua sendo válida para diferentes configurações?
Respostas e comentários
Explore: a) Respostas pessoais.
b) Comparando as razões
AB sobre BCcom
PQ sobre QRe
AC sobre ABcom
PR sobre PQ, verificamos que elas são iguais, o que leva a conjecturar que, em um feixe de retas paralelas cortado por duas retas transversais, os segmentos de reta determinados sobre a primeira transversal são proporcionais a seus correspondentes determinados sobre a segunda transversal.
c) A relação verificada continua válida, independentemente da configuração apresentada.
Tecnologias digitais em foco
Bê êne cê cê:
• Competências gerais 2 e 5 (as descrições estão na página seis).
• Competência específica 2 (a descrição está na página sete).
• Habilidade ê éfe zero nove ême ah um quatro.
Objetivo:
Verificar experimentalmente o teorema de Tales.
Teorema de Tales
Nesta seção, os estudantes vão utilizar o GeoGebra ou um software de geometria dinâmica qualquer para construir um feixe de retas paralelas cortadas por duas transversais e verificar, experimentalmente, que as medidas dos comprimentos dos segmentos determinados sobre a primeira transversal são proporcionais às medidas dos comprimentos dos segmentos correspondentes determinados sobre a segunda transversal (teorema de Tales).
Oriente-os a realizar todos os passos do Construa. Ao final, peça que comparem a construção feita com a dos demais colegas.
O encaminhamento do Explore tem por objetivo levar os estudantes a verificar experimentalmente a validade do teorema de Tales. Deixe-os livres para trocar ideias e conjecturar sobre o assunto.
A proposta desta seção possibilita aos estudantes assumirem o papel de protagonistas do seu processo de aprendizagem na medida em que utilizam uma tecnologia digital para investigar e produzir conhecimento. Eles também argumentam e tem o raciocínio lógico estimulado. Por essas razões, as competências gerais 2 e 5 e a competência específica 2 têm o seu desenvolvimento favorecido.
(ê éfe zero nove ême ah um quatro) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.
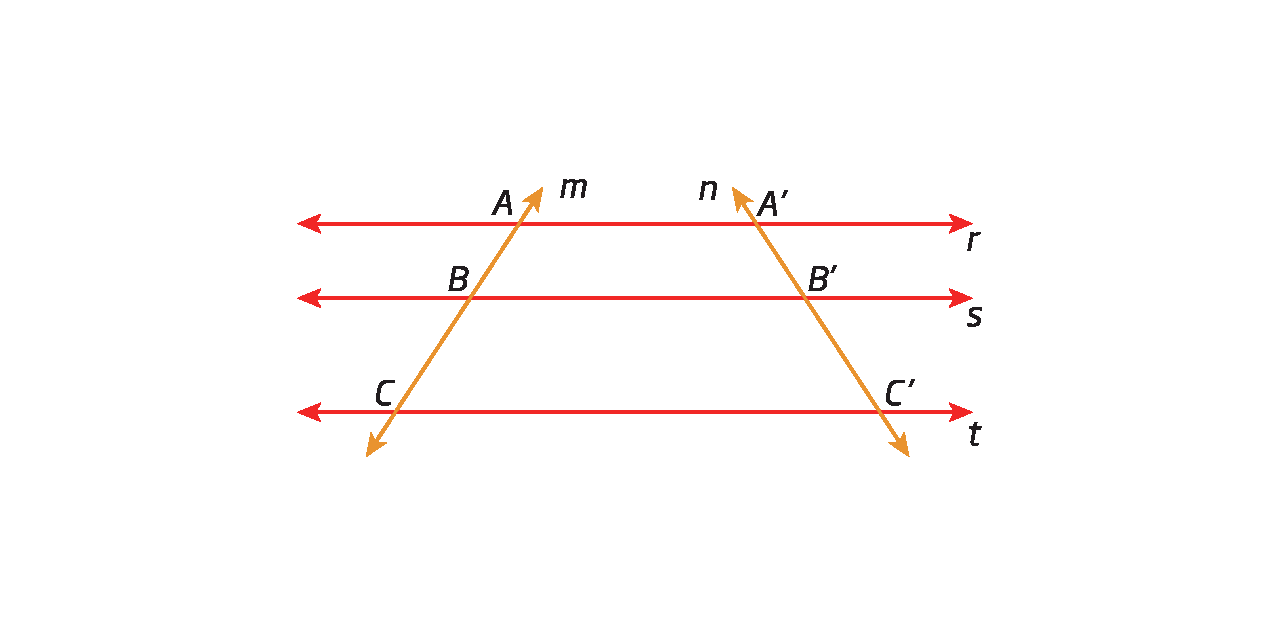
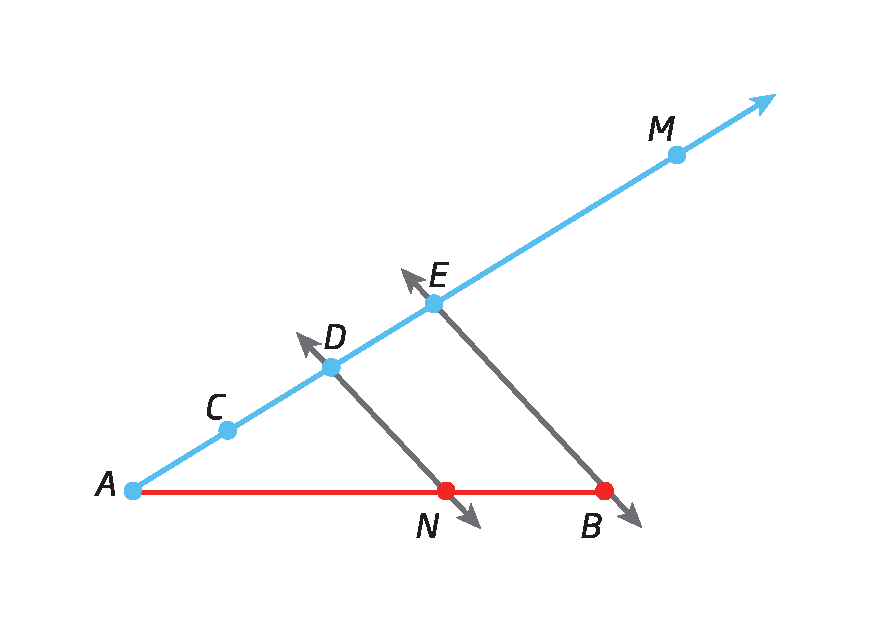
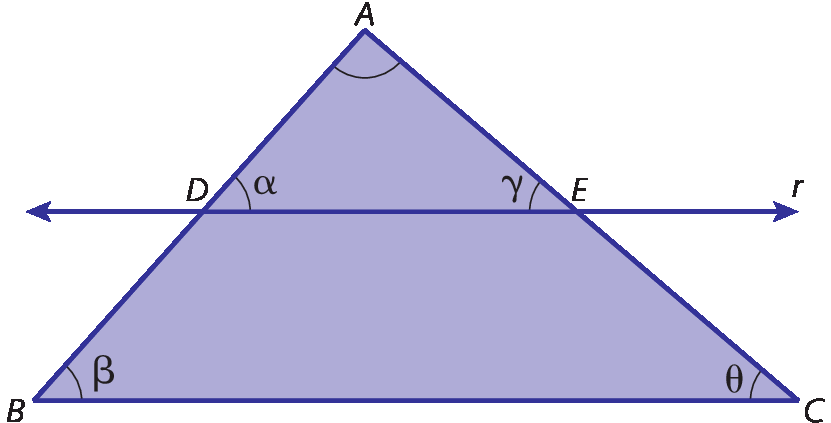
Agora, considere as retas paralelas r, s e t e as retas transversais m e n, no mesmo plano.
Sobre a reta m, temos os segmentos de reta
Segmento ABe
Segmento BC, congruentes entre si, e sobre a reta n, temos os segmentos de reta
Segmento de reta A linha, B linha.e
Segmento de reta B linha, C linha., conforme indicado a seguir.
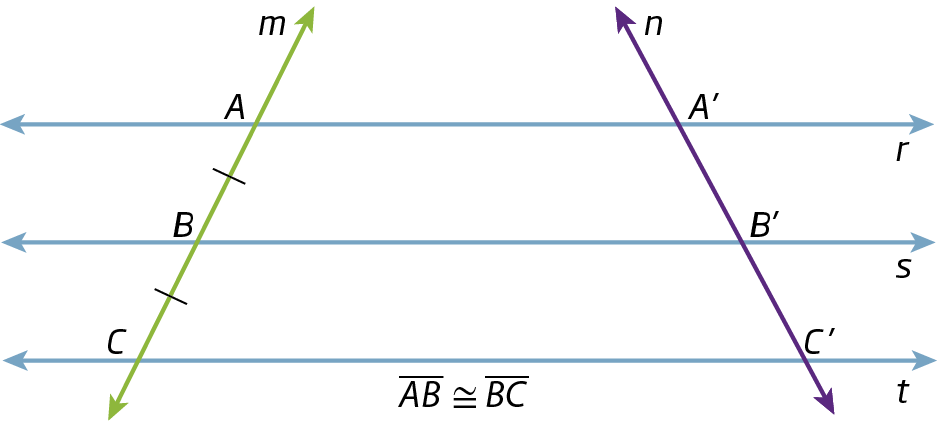
Vamos mostrar que, se
Segmento de reta AB congruente ao segmento de reta BC., então
Segmento de reta A linha B linha congruente ao segmento de reta B linha C linha..

Por á linha e bê linha, traçamos retas paralelas à reta transversal m, determinando os segmentos de reta
Segmento de reta A linha, M.e
Segmento de reta B linha, N.. Confira:
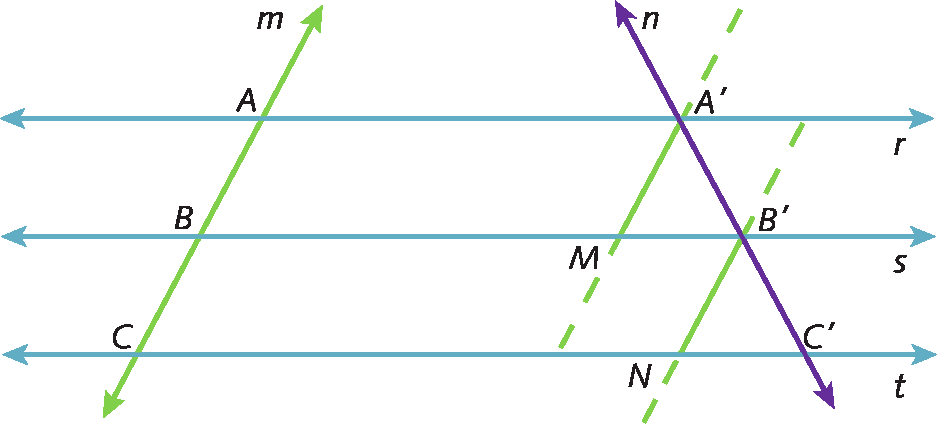
Como
Segmento de reta A linha M paralelo ao segmento de reta AB.e
Segmento de reta AA linha paralelo ao segmento de reta BM., AA'MB é um paralelogramo.
Como
Segmento de reta B linha N paralelo ao segmento de reta bc.e
Segmento de reta BB linha paralelo ao segmento de reta CN., BB’NC também é um paralelogramo.
Os lados opostos de um paralelogramo têm a mesma medida de comprimento, então:
Como
Segmento de reta AB congruente ao segmento de reta A linha M.,
Segmento de reta BC congruente ao segmento de reta B linha N.e
Segmento de reta AB congruente ao segmento de reta BC., temos:
Segmento de reta A linha M congruente ao segmento de reta B linha N.
E, considerando os triângulos á linha bê linhaM e bê linha cê linhaN, temos:
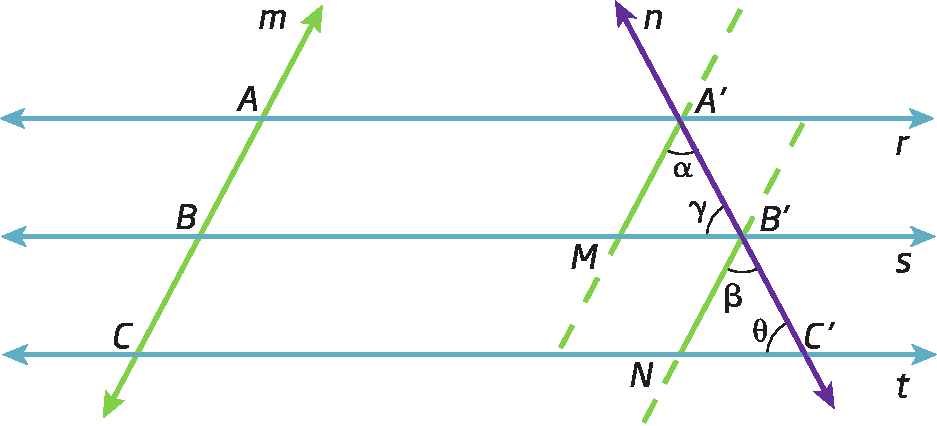
•
Segmento de reta A linha M congruente ao segmento de reta B linha N• Alfa = Beta

medidas de abertura dos ângulos correspondentes
• gama = teta

medidas de abertura dos ângulos correspondentes
Logo, △á linha bê linhaM ≅ △bê linha cê linhaN pelo caso LAá₀ (lado – ângulo – ângulo oposto).
Portanto,
Segmento de reta A linha B linha congruente ao segmento de reta B linha C linha., pois são lados correspondentes em triângulos congruentes.
Se um feixe de retas paralelas determinar segmentos de reta congruentes sobre uma transversal, esse feixe determinará segmentos de reta congruentes sobre qualquer outra transversal.
Respostas e comentários
Sugestão de leitura
Caso haja interesse em conhecer um pouco mais sobre os trabalhos de Tales de Mileto e a organização do conhecimento de Geometria por Euclides, sugerimos a leitura do artigo “Euclides, Geometria e fundamentos”, de Geraldo Ávila, a partir da página 199.
Observações
Vamos relembrar as relações entre os ângulos formados por duas retas paralelas cortadas por uma transversal.
1. Ângulos correspondentes são congruentes.
Sendo rparalelo s e t uma transversal, temos:
Símbolo. Ângulo a e ângulo bsão ângulos congruentes, e indicamos
Ângulo a congruente ao ângulo b..
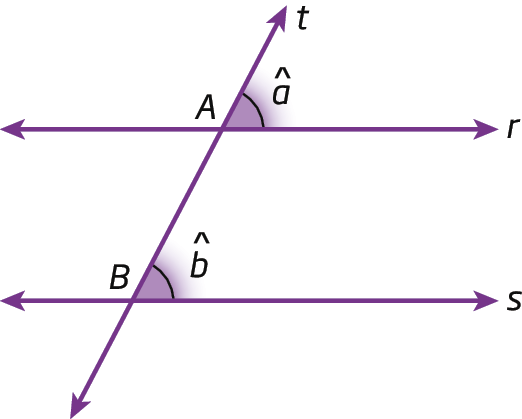
É possível demonstrar essa relação e, também, que para duas retas r e s cortadas por uma terceira reta t, se
Ângulo a congruente ao ângulo b., então rparalelo s, mas não faremos essas demonstrações aqui.
2. Ângulos alternos são congruentes.
Sendo rparalelo s e t uma transversal, temos:
•
Ângulo a congruente ao ângulo b.pois são ângulos correspondentes;
•
Ângulo d congruente ao ângulo a., pois são ângulos opostos pelo vértice (o.p.v.).
Logo,
Ângulo b congruente ao ângulo d.(ângulos alternos internos).
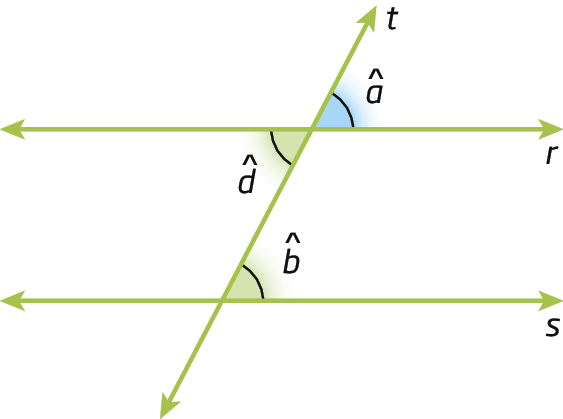
De maneira análoga, podemos verificar a congruência dos outros pares de ângulos alternos internos e dos pares de ângulos alternos externos.
3. Ângulos colaterais são suplementares.
Sendo rparalelo s e t uma transversal, temos:
•
Ângulo c congruente ao ângulo e., pois são ângulos alternos internos;
•
Sentença matemática. ângulo e, e ângulo bsão ângulos adjacentes suplementares.
Logo,
Sentença matemática. ângulo b, e ângulo csão suplementares (ângulos colaterais internos).
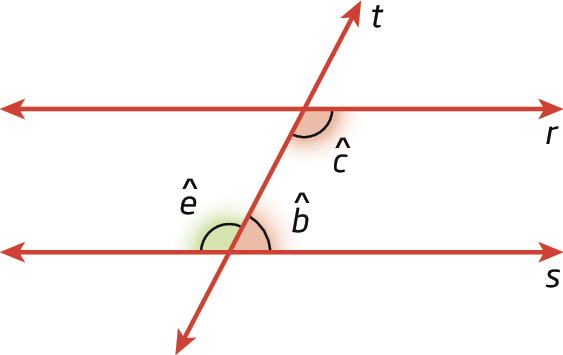
De maneira análoga, podemos verificar que os outros pares de ângulos colaterais internos e os pares de ângulos colaterais externos também são suplementares.
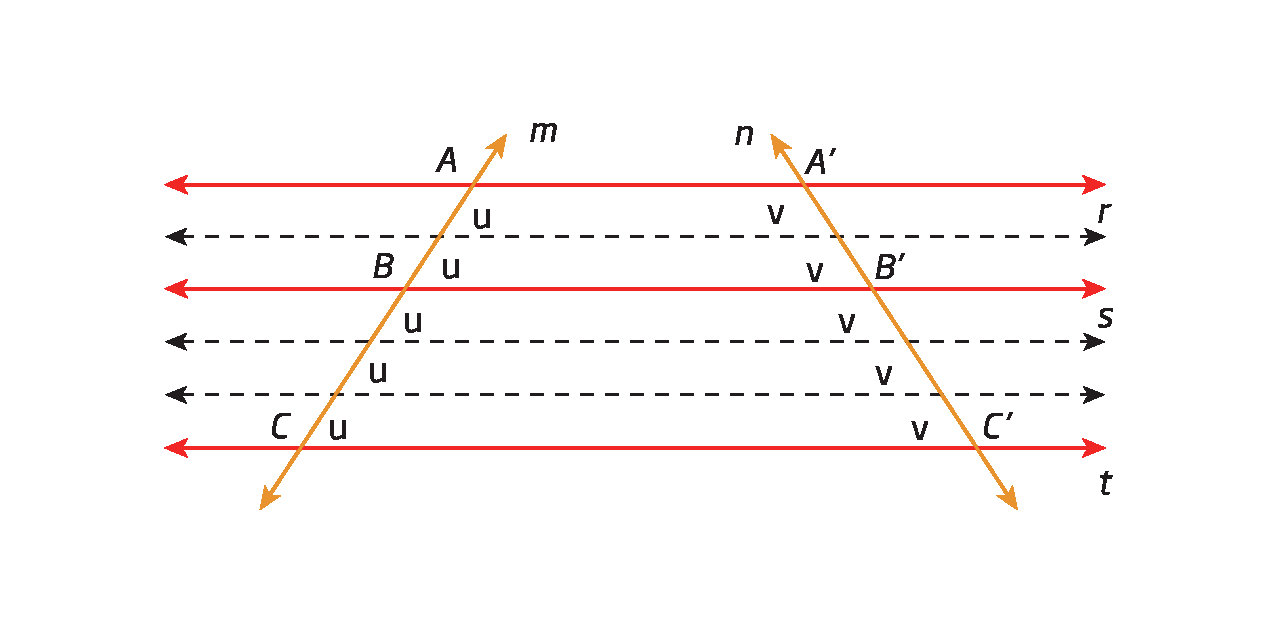
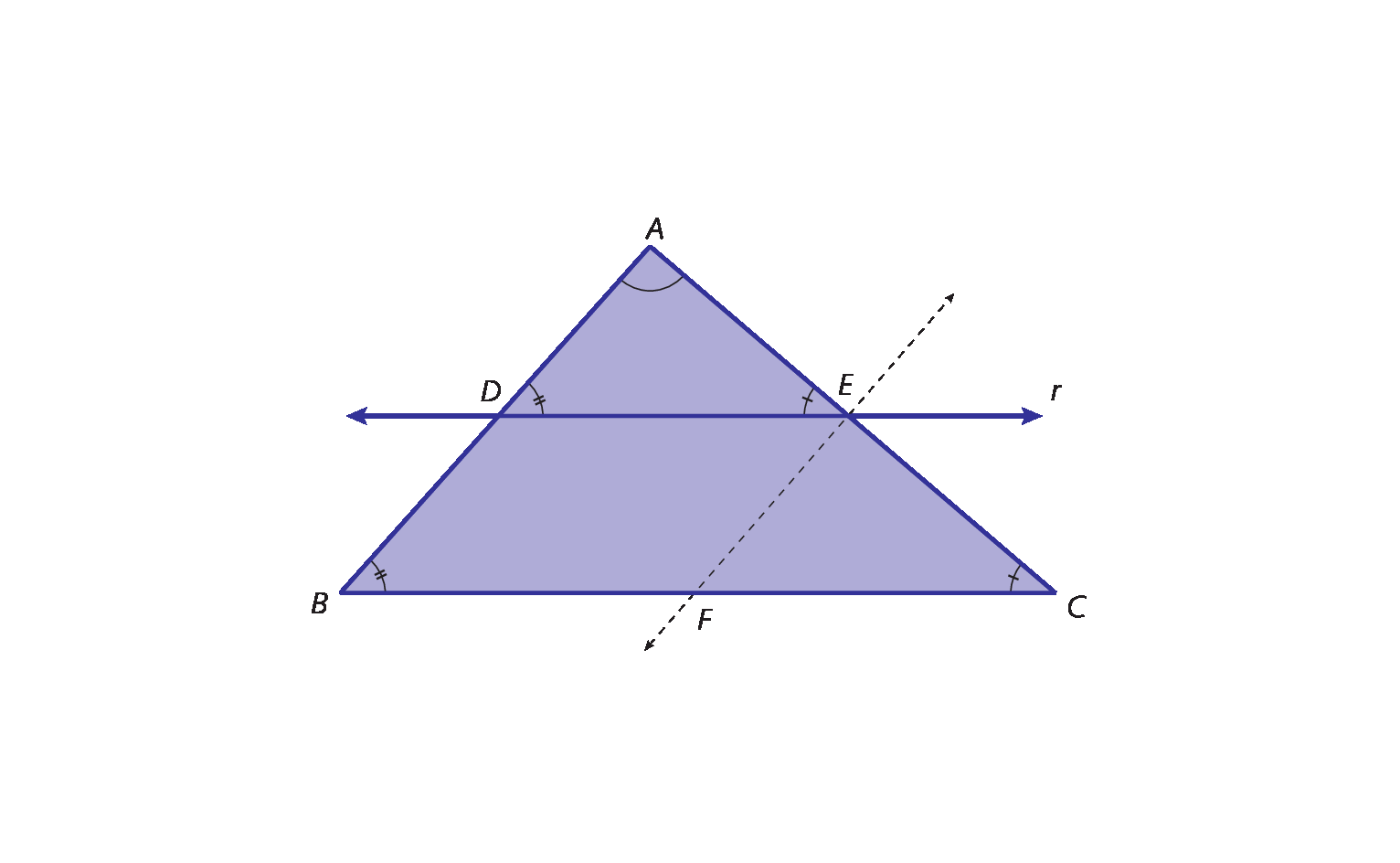
Agora, analise a figura a seguir em que rparalelo sparalelo t , m e n são retas transversais e A bê ≠ BC.
Vamos verificar a relação entre os segmentos de reta
Segmento AB,
Segmento BC,
Segmento de reta A linha, B linha.e
Segmento de reta B linha, C linha..
Vamos supor que possamos dividir
Segmento de reta AB.e
Segmento de reta BCem segmentos de reta de medida de comprimento 2u e 3u, respectivamente; a partir das retas r, s e t, traçamos retas auxiliares que dividem os segmentos de reta e, assim, temos A bê = 2u e BC = 3u.
Respostas e comentários
Verifique se os estudantes se recordam que dadas duas retas paralelas cortadas por uma transversal, os ângulos correspondentes são congruentes. Depois, questione-os se a recíproca desta afirmação é verdadeira. Dê um tempo para que levantem hipóteses. Depois, se julgar pertinente e perceber que os estudantes têm maturidade, demonstre que, dadas as retas r e s, cortadas por uma transversal t, se os ângulos de medidas Alfa e Beta forem congruentes, então as retas são paralelas.
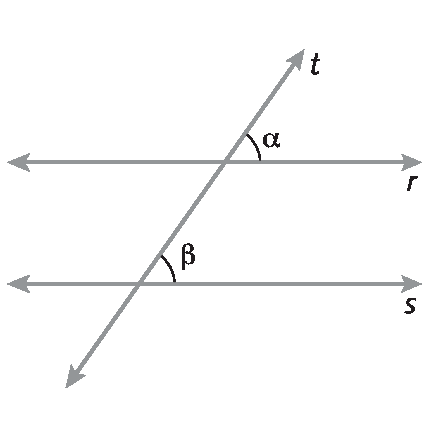
Vamos utilizar a demonstração por absurdo. Suponha que α e β são medidas de abertura de ângulos congruentes, mas, por absurdo, r e s não são retas paralelas. Então, na realidade, r e s se cruzam em algum ponto. Vamos indicar o ponto de intersecção de t com r por A, de t com s por B e de r com s por C.
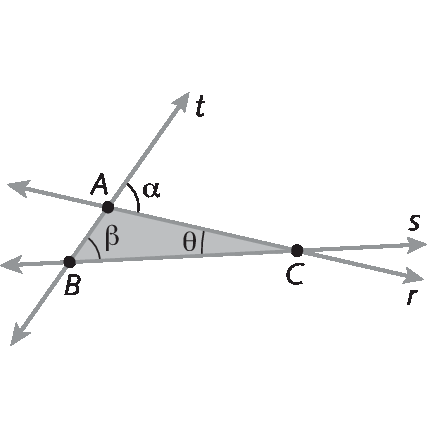
Temos um triângulo á bê cê, em que
Ângulo Amede 180graus ‒ Alfa ,
Ângulo Bmede β e
Ângulo Cmede teta. A soma das medidas das aberturas dos ângulos internos de um triângulo é 180graus, portanto,
medida do ângulo A mais medida do ângulo B mais medida do ângulo Cé igual a 180graus. Assim, (180graus ‒ Alfa ) + Beta + teta = 180graus, mas Alfa = Beta (por hipótese), portanto (180graus ‒ Alfa ) + Alfa + teta = 180graus, o que resulta em θ = 0grau. Isso é um absurdo, pois se á bê cê é um triângulo,
Ângulo Cdeve ter medida diferente de 0grau. O que nos permite concluir que, se as medidas das aberturas dos ângulos são iguais (Alfa = Beta), então as retas r e s são, necessariamente, paralelas.
Verifique se os estudantes conseguem deduzir as demonstrações das aberturas dos ângulos alternos e colaterais. Peça a eles que não consultem o livro e tentem argumentar de fórma convincente para mostrar a igualdade entre as medidas das aberturas desses ângulos.
Incentive os estudantes a deduzir as demonstrações e, dessa fórma, contribuir para o desenvolvimento da competência específica 2, além de favorecer o desenvolvimento da habilidade ê éfe zero nove ême ah um zero.
A demonstração foi particularizada para facilitar o entendimento dos estudantes. Avalie a conveniência de afirmar aos estudantes que os matemáticos demonstraram que o teorema é válido para medidas dos segmentos expressas por quaisquer números reais positivos.
Como o feixe de retas paralelas determina segmentos de reta congruentes sobre a transversal m, então também determinará segmentos de reta congruentes sobre a transversal n, assim:
Segmento de reta A linha B linha.e
Segmento de reta B linha C linha.são divididos em segmentos de reta de medida de comprimento v, sendo á linha bê linha = 2v e B'C' = 3v.
Então:
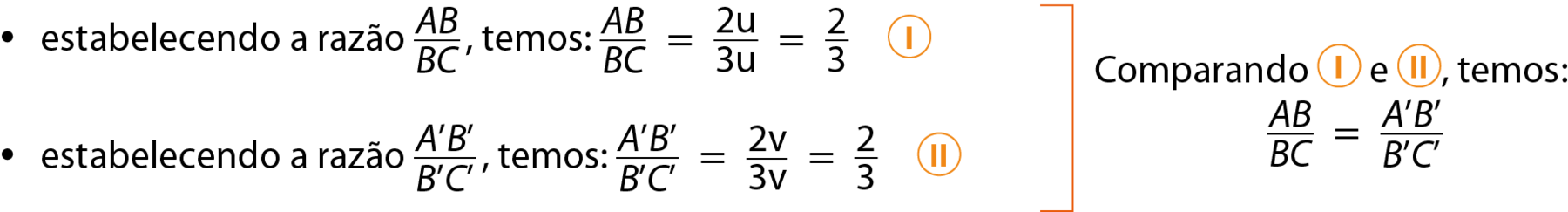
Logo,
Segmento ABe
Segmento BCsão proporcionais a
Segmento A'B'e
Segmento B'C'.
Segundo o teorema de Tales:
Se um feixe de retas paralelas é cortado por duas retas transversais quaisquer, m e n, os segmentos de reta determinados sobre m são proporcionais aos segmentos de reta correspondentes determinados sobre n.
Agora, confira este exemplo.
Um feixe de retas paralelas (r, s, t e u) determina sobre as transversais m e n os pontos a, B, C e D e os pontos á linha, bê linha, cê linha e dê linha. Sabendo que AB = 4 centímetros, BC = 5 centímetros, CD = 9 centímetros e A’D’ = 36 centímetros, vamos determinar á linha bê linha, bê linha cê linhae cê linha dê linha em centímetro.
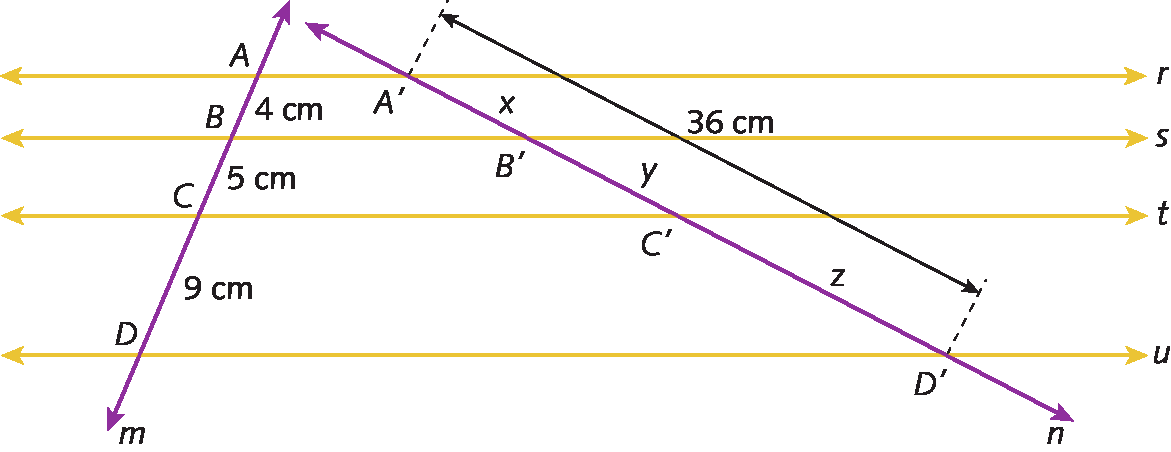
á dê = A bê + bê cê + cedê ⇒ á dê = 4 centímetros + 5 centímetros + 9 centímetros ⇒ á dê = 18 centímetros
Pelo teorema de Tales, temos:
Portanto, á linha bê linha = 8 centímetros, bê linha cê linha = 10 centímetros e cêlinhadêlinha = 18 centímetros.
Observação
Se não forem indicadas as unidades das medidas de comprimento de uma figura, consideramos todas as medidas dessa figura na mesma unidade.
Respostas e comentários
No estudo da divisão de segmentos de reta em partes proporcionais, será necessário retomar a construção de retas paralelas. Acompanhe a seguir a construção de uma reta paralela a uma reta s.
Centramos o compasso em O e traçamos um arco que intercepta s em A e B.
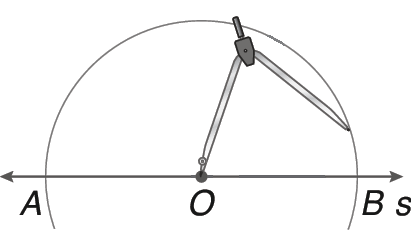
Com centros em A e B e a mesma medida de comprimento de raio, determinamos M e N.
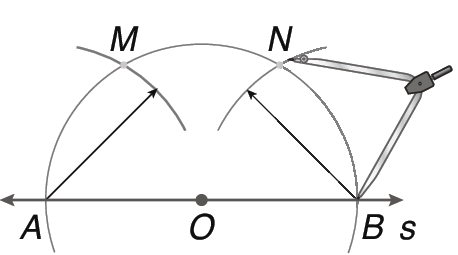
Traçamos t paralelo s, passando por M e N.
Alerte os estudantes sobre os riscos relacionados ao uso do compasso e oriente-os a tomar cuidado quanto ao uso deste instrumento.
Divisão de um segmento de reta em partes proporcionais
Uma das aplicações do teorema de Tales é a divisão de um segmento de reta em partes proporcionais.
Acompanhe o exemplo: dado o segmento de reta
Segmento de reta AB., vamos determinar um ponto N em
Segmento AB, tal que
AN sobre AB igual a 2 terços.
1º) Dado um segmento de reta
Segmento de reta AB., traçamos, com o auxílio de uma régua, uma semirreta
Semirreta AM.qualquer.
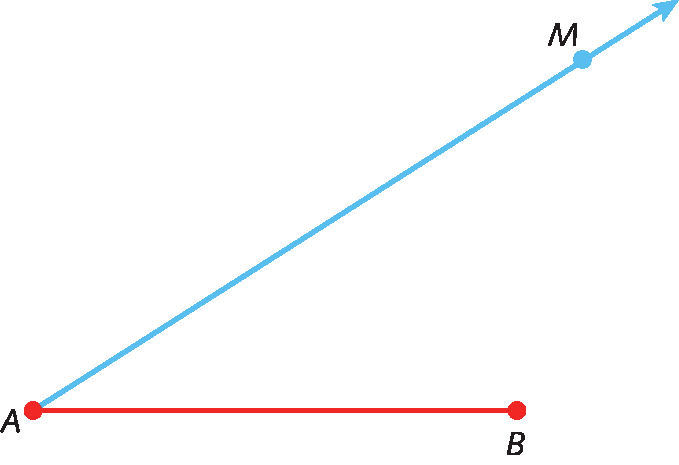
2º) Sobre a semirreta
Semirreta AM., marcamos três pontos (C, D e ê) de modo que á cê = CD = dê ê.
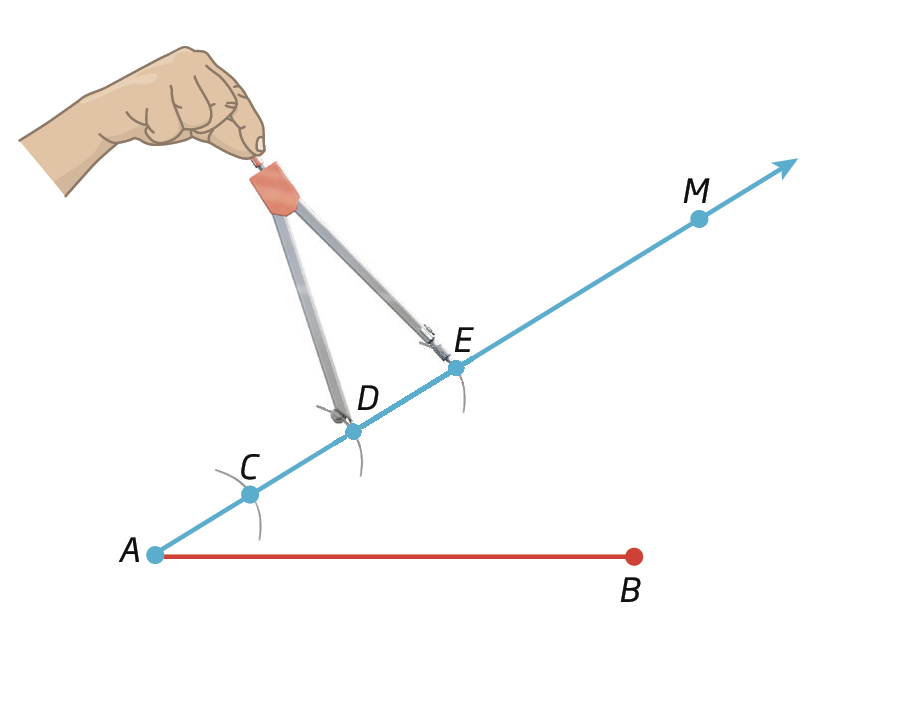
3º) Traçamos
Reta EB..
A seguir, traçamos uma paralela a
Reta EB., passando por D, que corta
Segmento de reta AB.em N.
Confira que:
Sentença matemática. AD sobre AE igual a 2 terços.e
Segmento ND paralelo ao segmento BEAssim, pelo teorema de Tales:
Dividimos, então,
Segmento de reta AB.em partes proporcionais.
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
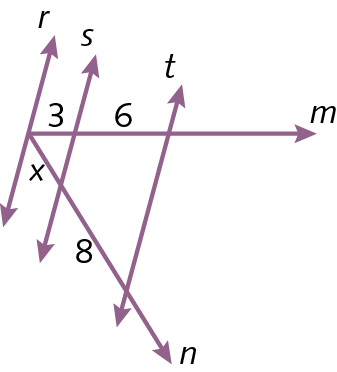
7. Sendo rparalelo sparalelo t, determine o valor de x.
a)
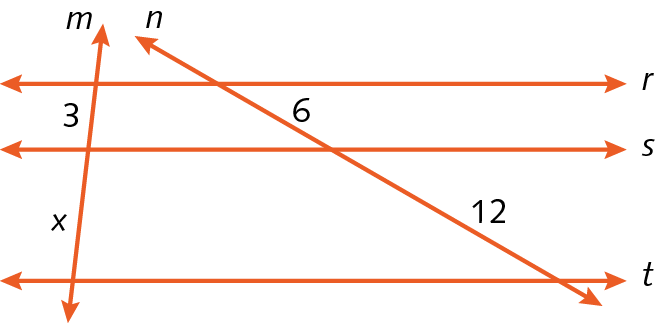
b)
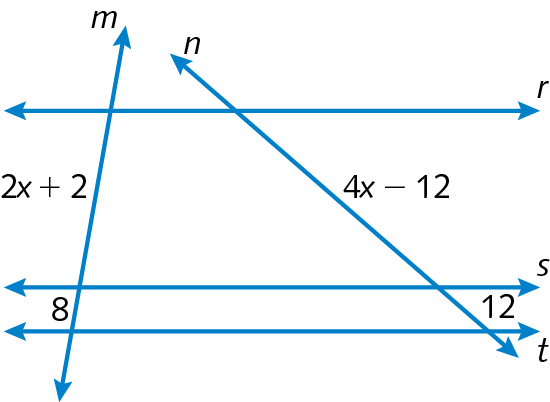
c)
8. Sendo aparalelo bparalelo cparalelo d, determine x, y e z.
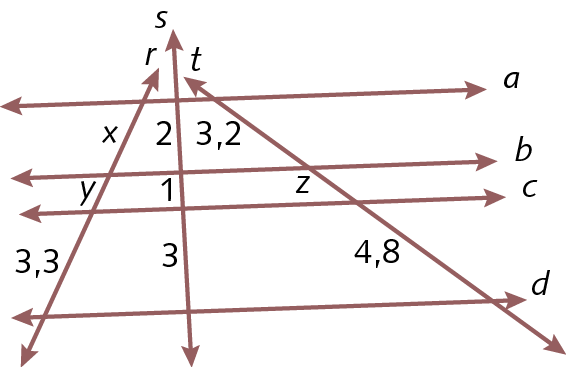
Respostas e comentários
7. a) x = 6
7. b) x = 15
7. c) x = 4
8. x = 2,2; y = 1,1; z = 1,6
Ao final da construção, converse com os estudantes que essa mesma ideia permite a divisão de um segmento de reta em n partes iguais. Se nessa construção, em particular, traçássemos uma reta paralela a
Segmento EBpassando por C, e marcássemos o ponto O, intersecção de
Segmento ABcom essa paralela, obteríamos
Segmento de reta AO congruente ao segmento de reta ON congruente ao segmento de reta NB., dividindo o segmento
Segmento de reta AB.em três partes com a mesma medida de comprimento.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
Cuidado! Evite acidentes ao usar o compasso na atividade 11.
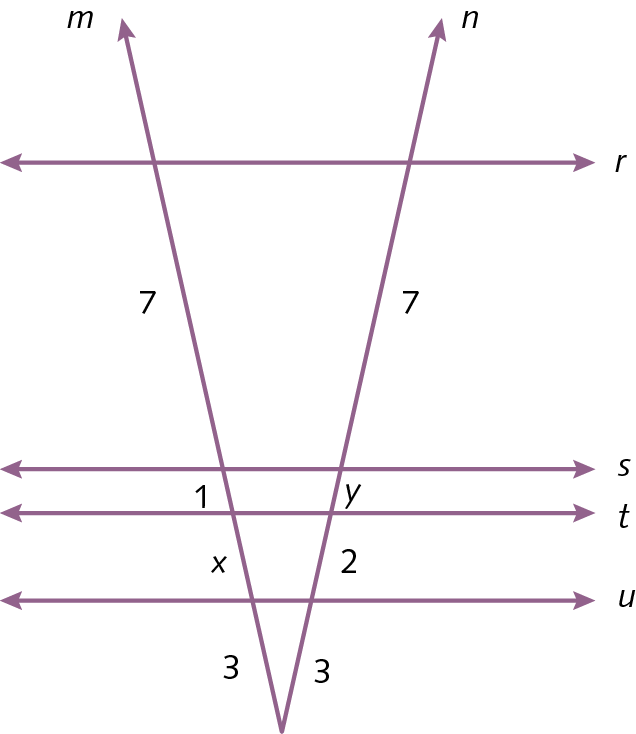
9. Considere rparalelo sparalelo tparalelo u. Calcule x e y.
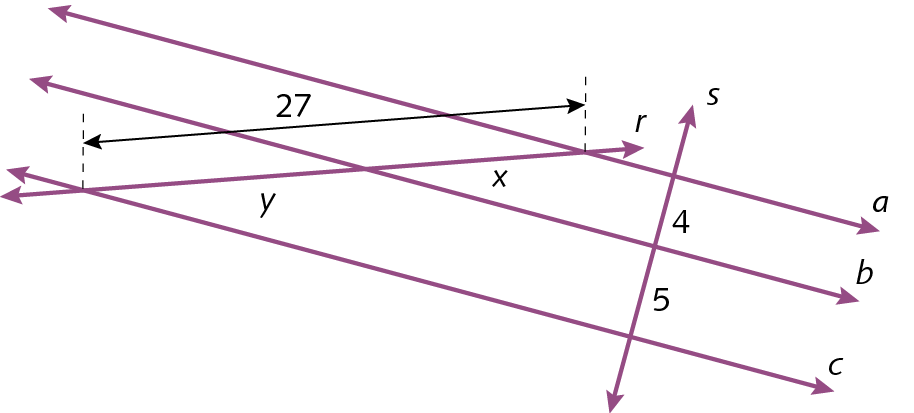
10. Sendo aparalelo bparalelo c, determine x e y.
a)
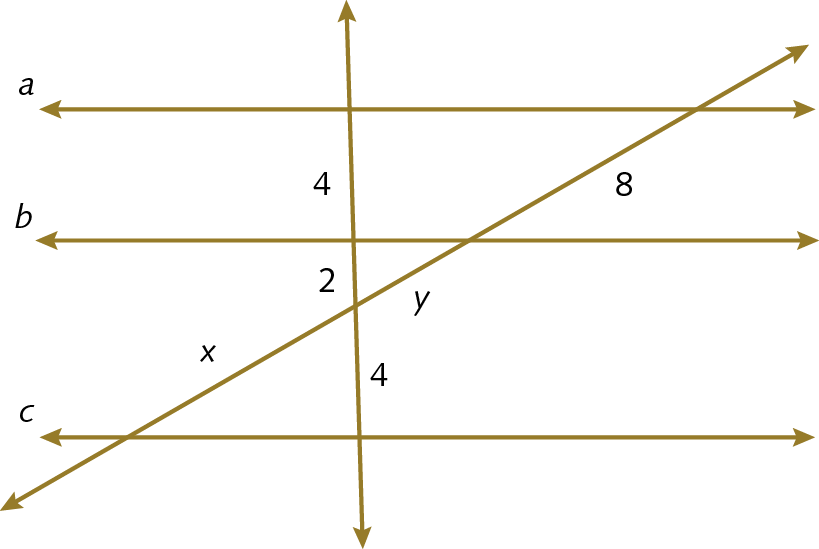
b)
11. Utilizando régua e compasso, reproduza, no caderno, o segmento de reta
Segmento de reta AB.a seguir. Em seguida, localize o ponto C nesse segmento de reta tal que
Sentença matemática. AC sobre AB igual a 3 quartos..

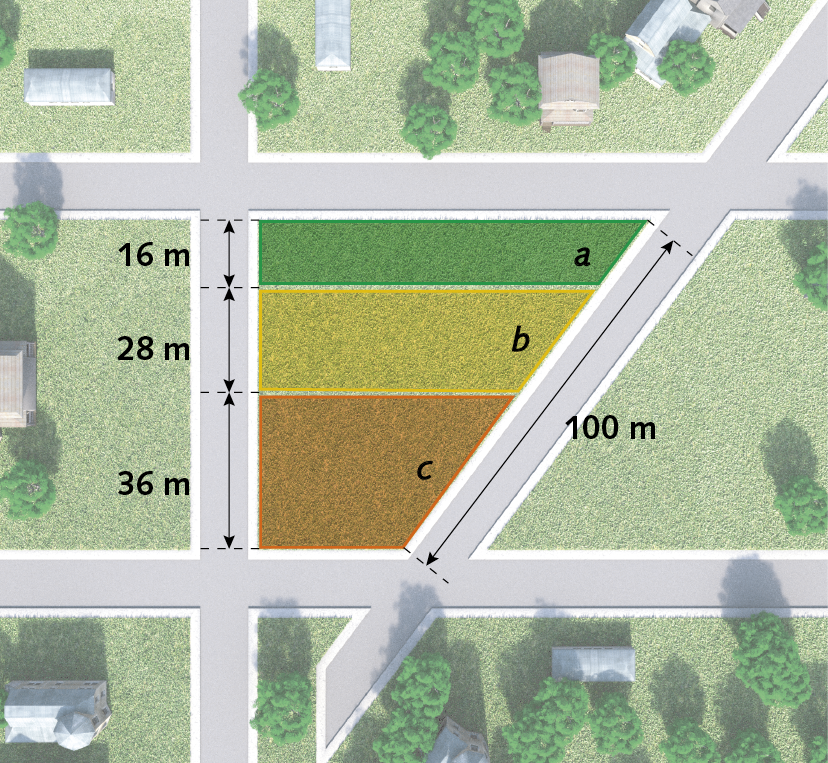
12. A figura apresenta três terrenos que ocupam uma quadra. Determine as medidas de comprimento a, b e c, em metro, sabendo que cada terreno tem um par de lados paralelos.
13. Considere que na figura:
• as retas
Símbolo. reta AA' e reta BB'e
Símbolo. reta AA' e reta BB'são paralelas entre si;
• as retas
Símbolo. reta BA' e reta CB'e
Símbolo. reta BA' e reta CB'são paralelas entre si;
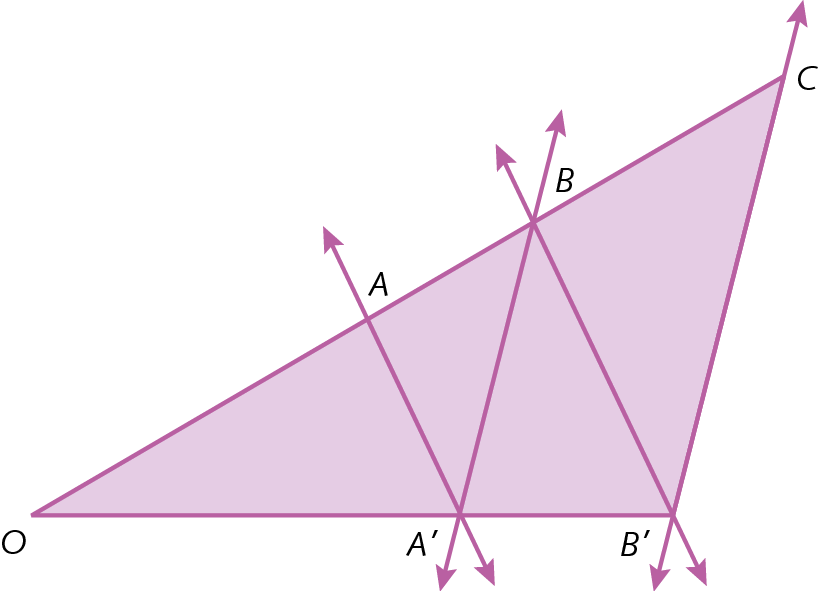
a) Aplicando o teorema de Tales para os triângulos ó áá linha e ó bêbê linha, escreva as relações entre as medidas dos comprimentos dos lados.
b) Aplicando o teorema de Tales para os triângulos ó bêá linha e ó cêbê linha, escreva as relações entre as medidas dos comprimentos dos lados.
c) Prove que
Sentença matemática. OB sobre OA igual a OC sobre OB..
Respostas e comentários
9. x = 2; y = 1
10. a) x = 12; y = 15
10. b) x = 8; y = 4
11. Resposta em Orientações.
12. a = 20 métros; b = 35 métros; c = 45 métros
13. a)
Sentença matemática. OA sobre OB igual a OA linha sobre OB linha.13. b)
Sentença matemática. OB sobre OC igual a OA linha sobre OB linha.
13. c) Aplicando a propriedade transitiva da igualdade nos resultados dos itens a e b, temos:
Sentença matemática. OA sobre OB igual a OB obre OC.Invertendo essas razões, temos:
Sentença matemática. OB sobre OA igual a OC obre OB.• A atividade 10 favorece o desenvolvimento de parte da habilidade ê éfe zero nove ême ah um quatro. Se os estudantes tiverem dificuldade, ajude-os a escrever as proporções para obter as medidas corretas.
• Na atividade 11, podemos iniciar traçando, com auxílio de uma régua, uma semirreta
Semirreta AMqualquer. Sobre a semirreta
Semirreta AM, com auxílio do compasso, marcamos quatro pontos (N, O, P e Q), de modo que NA = NO = OP = PQ.
Então, traçamos
Reta QBe, em seguida, uma paralela a
Reta QB, passando por P, determinando o ponto C em
Segmento ABde modo que
Sentença matemática. AQ sobre AP igual a 3 quartos., com
Segmento QB paralelo a segmento PC.
Por fim, pelo teorema de Tales, temos:
Sentença matemática. AP sobre AQ igual a AC obre AB igual 3 quartos..
Teorema de Tales nos triângulos
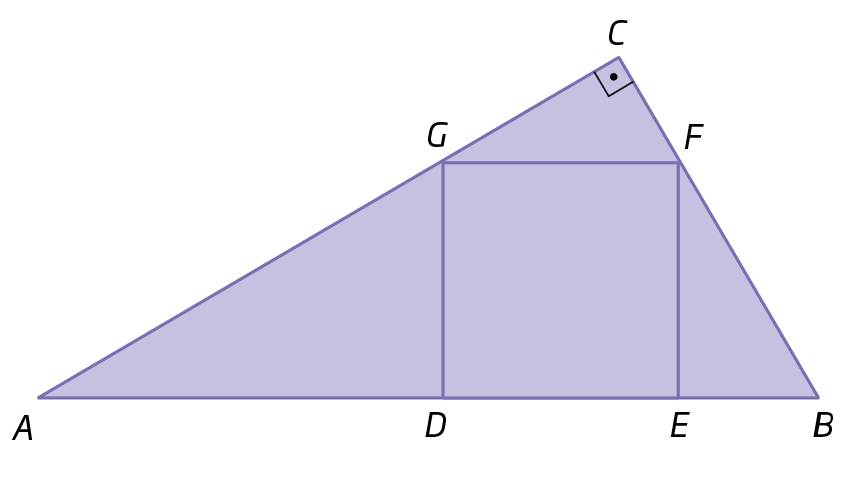
Analise o triângulo á bê cê, a reta s, paralela a t (reta suporte de
Segmento de reta BC.) que corta os lados
Segmento de reta AB.e
Segmento de reta AC., respectivamente, nos pontos M e N, e a reta r, paralela a s pelo ponto a.
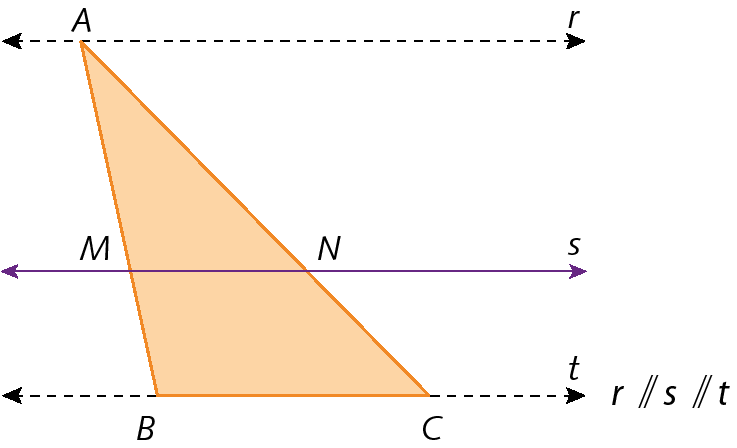
As retas r, s e t formam um feixe de paralelas.
Então, aplicando o teorema de Tales, temos:
Toda reta paralela a um lado de um triângulo determina, sobre os outros dois lados, segmentos de reta proporcionais.
Atividades
Faça as atividades no caderno.
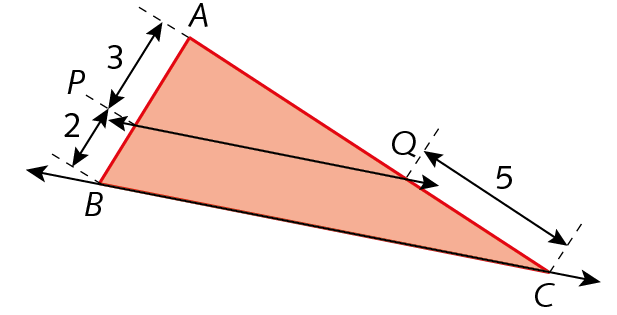
14. Na figura,
Reta PQ paralela a reta BC. Determine AQ.
15. Uma reta paralela ao lado
Segmento BCde um triângulo á bê cê determina os pontos D em
Segmento ABe ê em
Segmento AC. Sabendo que á dê = k, DB = k + 4, A Ê = 4 e ê cê = 6, determine a medida de comprimento do lado
Segmento ABdo triângulo.
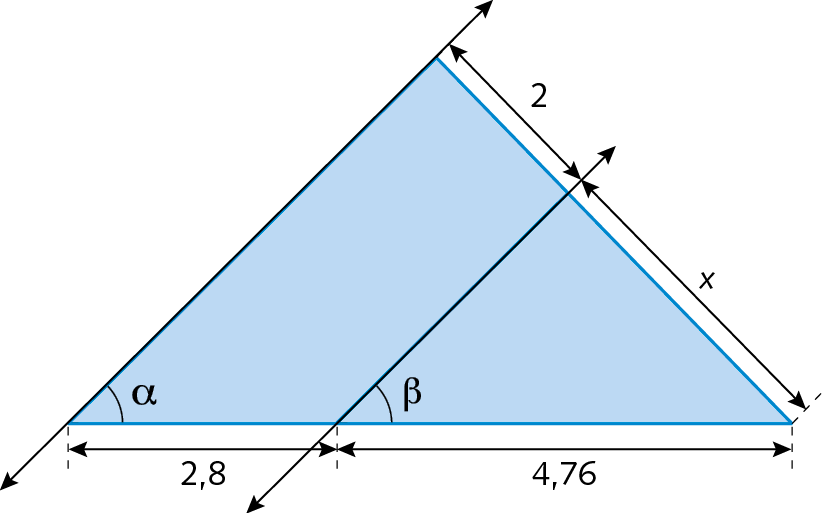
16. Determine o valor de x, sabendo que as medidas α e β das aberturas dos ângulos correspondentes são iguais.
Respostas e comentários
14. AQ = 7,5
15. A bê = 20
16. x = 3,4
• A atividade 14 envolve a aplicação do teorema de Tales nos triângulos. Este é o momento oportuno para verificar se os estudantes compreenderam a propriedade. Espera-se que para determinar AQ, eles escrevam a seguinte proporção:
Sentença matemática. 3 sobre 2 igual a AQ sobre 5.
• Caso tenham dificuldades para compreender o enunciado da atividade 15, oriente-os a fazer um esboço da situação.
• Na atividade 16, espera-se que os estudantes concluam que como α = β, então as retas representadas na figura são paralelas. Com base nisso, eles podem aplicar o teorema de Tales no triângulo e determinar x.

3 Semelhança
Figuras semelhantes
Confira os mapas que trazem as localizações dos pontos extremos do Brasil (norte – C, sul – D, leste – B, oeste – a) e das cidades de São Luís (Maranhão) e Salvador (Bahia).
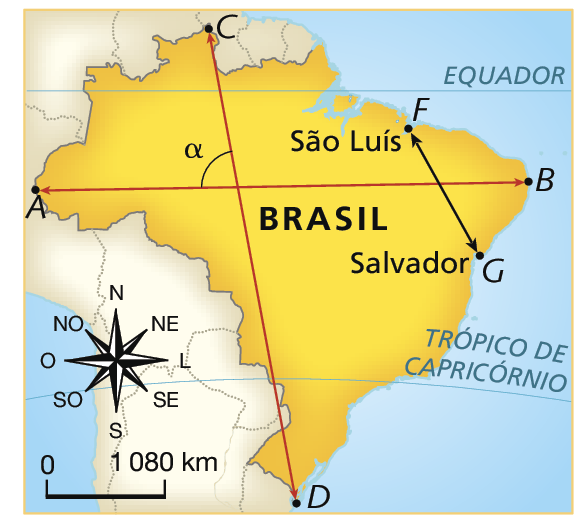
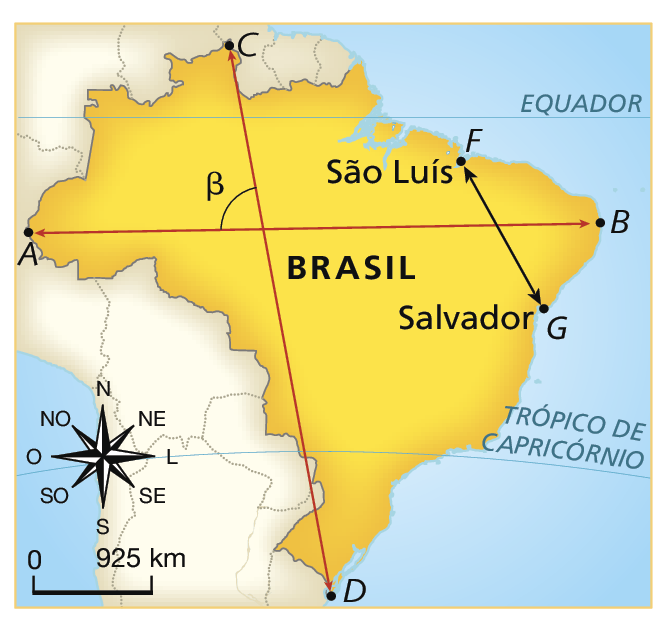
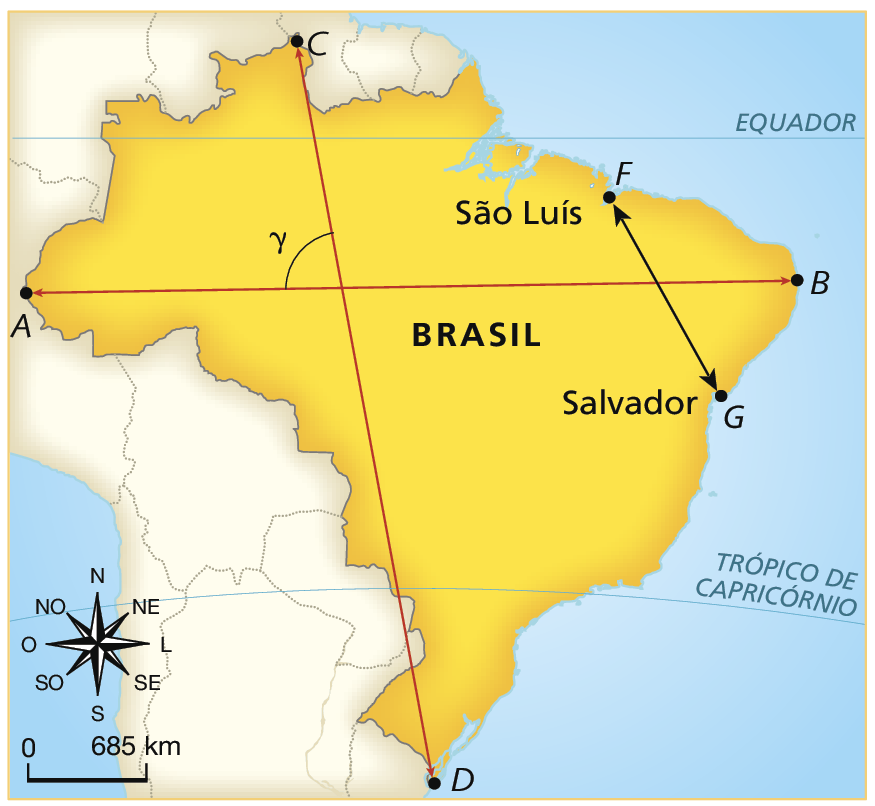
Elaborados com base em: í bê gê É. Atlas geográfico escolar. oitava edição Rio de Janeiro: í bê gê É, 2018. página 91.
As três imagens representam o mapa do Brasil; entretanto, note que os mapas têm a mesma fórma, mas tamanhos diferentes.
De acôrdo com os pontos apresentados, podemos identificar:
• A bê: medida da distância do ponto extremo oeste ao ponto extremo leste do Brasil;
• CD: medida da distância do ponto extremo norte ao ponto extremo sul do Brasil;
• FG: medida da distância entre os pontos que representam as cidades de São Luís e Salvador;
• Alfa , Beta e gama: medidas das aberturas dos ângulos formados pelos segmentos de reta
Segmento AB e segmento CD, respectivamente, no mapa um, no mapa dois e no mapa três.
Com o auxílio de uma régua e de um transferidor, podemos obter, em cada mapa, as medidas de comprimento dos segmentos de reta
Segmento AB e segmento FGe as medidas Alfa , Beta e gama das aberturas dos ângulos, obtendo os dados a seguir.
|
Mapa |
AB |
FG |
Medida da abertura do ângulo |
|---|---|---|---|
|
I |
4,2 cm |
1,2 cm |
α = 80° |
|
II |
4,9 cm |
1,4 cm |
β = 80° |
|
III |
6,3 cm |
1,8 cm |
γ = 80° |
Respostas e comentários
Semelhança
Objetivo:
Compreender o conceito de semelhança entre figuras.
Justificativa
Compreender o conceito de semelhança de figuras amplia os conhecimentos previamente adquiridos pelos estudantes sobre congruência de figuras e mobiliza o que estudaram sobre segmentos de reta proporcionais. Além disso, este conceito é importante para demonstrar o teorema de Pitágoras, que será estudado mais adiante.
Mapeando conhecimentos
Organize os estudantes em duplas e distribua para eles uma folha de papel quadriculado com as seguintes figuras representadas nela:
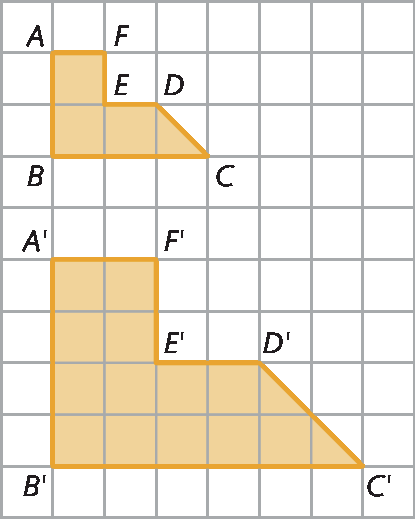
Em seguida, proponha as seguintes atividades:
1. Analise as medidas de abertura dos pares de ângulos internos
Angulo Ae
A linha,
Ângulo Be
B linha,
Ângulo Ce
C linha,
Ângulo De
D linha,
Ângulo Ee
E linhae
Ângulo Fe
F linha. O que você concluiu sobre elas, em cada par de ângulos correspondentes?
2. Observe agora os pares de lado
Segmento de reta A linha, B linha.e
Segmento AB,
Segmento de reta B linha, C linha.e
Segmento BC,
Segmento de reta C linha D linha.e
Segmento CD,
Segmento de reta D linha E linha.e
Segmento de reta DE.,
Segmento de reta E linha F linha.e
Segmento de reta EF.e
Segmento de reta F linha A linha.e
Segmento de reta FA.. Qual relação você encontrou entre as medidas de comprimento, em cada par de lados correspondentes?
Incentive a participação da turma.
Para as aulas iniciais
Retome a atividade da dinâmica inicial e discuta com a turma o modo como chegaram às respostas e faça as intervenções necessárias. Depois, pergunte aos estudantes o que são polígonos semelhantes e incentive-os a explicar utilizando vocabulário próprio. Aproveite a oportunidade para explorar polígonos que não são semelhantes. Incentive-os a justificar o porquê desses polígonos não serem semelhantes.
Oriente os estudantes a conferir as medidas do quadro utilizando régua e transferidor, alertando-os quanto a possíveis imprecisões dos instrumentos de medida.
Confira que, nesse exemplo, as figuras apresentam estas características:
• os ângulos correspondentes têm medidas das aberturas iguais;
• as medidas de comprimento dos segmentos de reta correspondentes são proporcionais.
4 vírgula 2 centímetros sobre 1 vírgula 2 centímetro igual a 3 vírgula 5; 4 vírgula 9 centímetros sobre 1 vírgula 4 centímetro igual a 3 vírgula 5; 6 vírgula 3 centímetros sobre 1 vírgula 8 centímetro igual a 3 vírgula 5; logo, AB sobre FG igual a 3 vírgula 5.
Dizemos que duas figuras são semelhantes quando as medidas das aberturas dos ângulos correspondentes são iguais e as medidas de comprimento dos segmentos de reta correspondentes são proporcionais.
Logo, podemos dizer que os mapas são semelhantes.
Sugestão de leitura
IMENES, L. M.; JAKUBOVIC, J. (Jakubo); LELLIS, M. Semelhança. São Paulo: Atual, 2005. (Coleção Pra que serve Matemática?).
Esse livro apresenta usos de semelhança no cotidiano. Além disso, traz curiosidades, jogos e charadas sobre o assunto.
Polígonos semelhantes
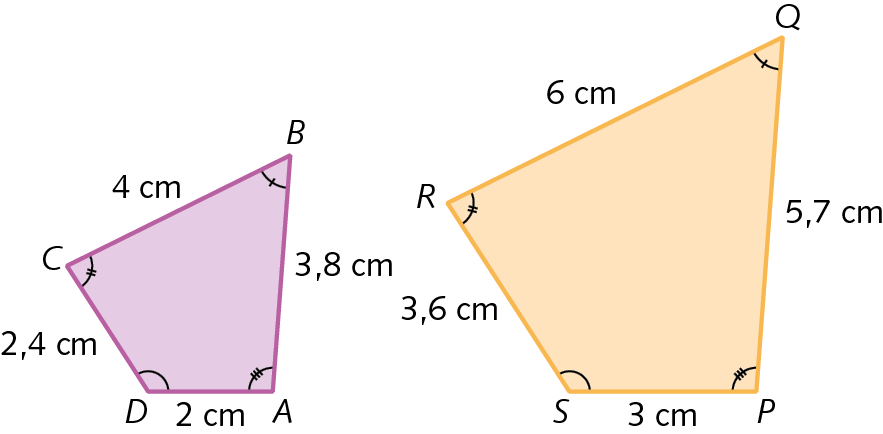
Considere os polígonos a bê cê dê e PQRS abaixo.
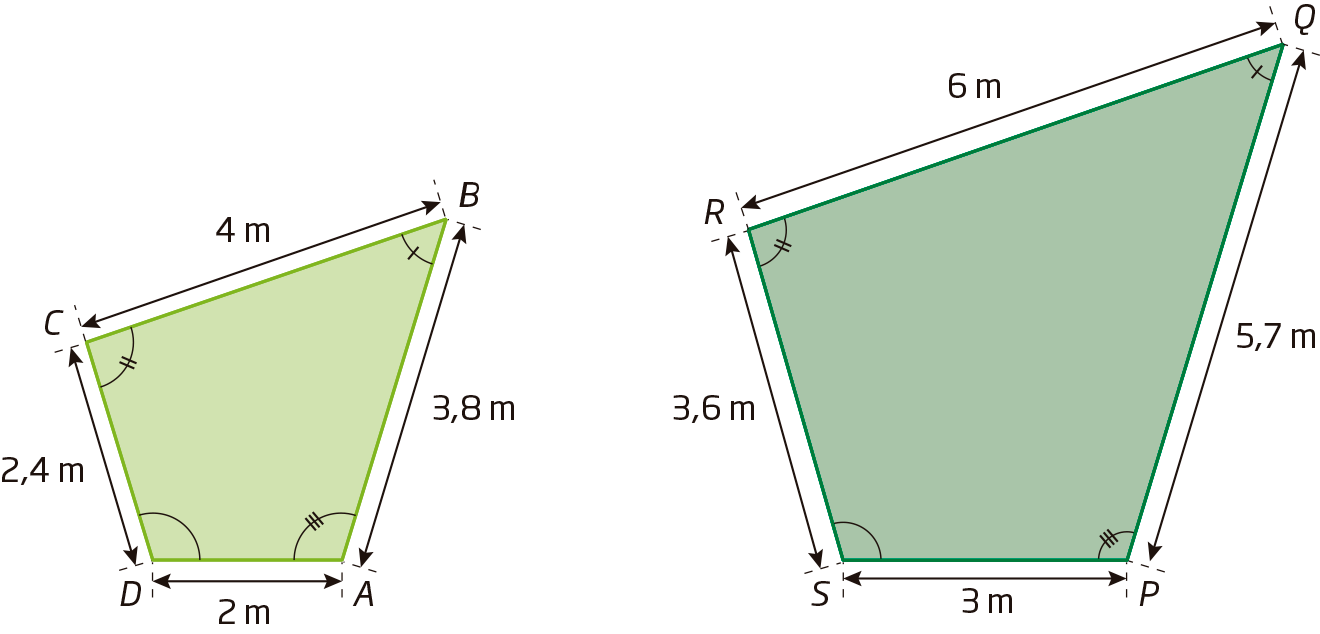
Comparando os polígonos, podemos identificar que:
• os ângulos correspondentes são congruentes;
Sentença matemática. Ângulo A congruente ao ângulo P
;
Sentença matemática. Ângulo B congruente ao ângulo Q;
Sentença matemática. Ângulo C congruente ao ângulo R;
Sentença matemática. Ângulo D congruente ao ângulo S• as medidas de comprimento dos lados correspondentes são proporcionais.
Sentença matemática. AB sobre PQ igual a BC sobre QR igual a CD sobre RS igual a DA sobre SP.
ou
Sentença matemática. 3 vírgula 8 metros sobre 5 vírgula 7 metros igual a 4 metros sobre 6 metros igual a 2 vírgula 4 metros sobre 3 vírgula 6 metros igual a 2 metros sobre 3 metros igual a 2 terços.Podemos dizer que os polígonos ABCD e PQRS são semelhantes e indicar:

Quando dois polígonos têm os ângulos correspondentes congruentes e as medidas de comprimento dos lados correspondentes são proporcionais, eles são denominados polígonos semelhantes.
A razão entre as medidas de comprimento dos lados correspondentes em polígonos semelhantes é denominada razão de semelhança ou coeficiente de proporcionalidade. Então, no exemplo da semelhança entre os polígonos a bê cê dê e PQRS, temos:
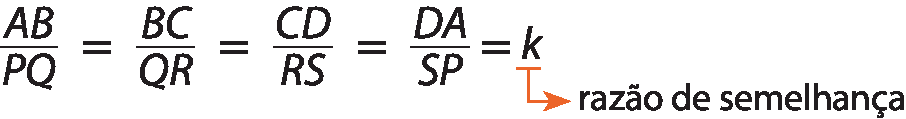
A razão de semelhança (k) nesse caso é
dois terços.
Respostas e comentários
Explique aos estudantes que duas figuras semelhantes podem ter o mesmo tamanho ou tamanhos diferentes. Quando têm as mesmas medidas dos lados correspondentes, podemos dizer que são também congruentes; se forem medidas diferentes, são apenas semelhantes. O caso particular em que as figuras são congruentes nos dá razão de semelhança (ou coeficiente de proporcionalidade) igual a 1. Para figuras apenas semelhantes, a comparação promovida pela razão de semelhança pode ser dada e analisada a partir de dois sentidos: da figura maior para a menor ou da menor para a maior. Se a razão de semelhança for um número entre 0 e 1, significa que a primeira figura tem medidas de comprimento correspondentes menores do que a segunda; decorre que o caso contrário nos dá um número maior que 1.
Agora, analise um exemplo em que precisamos determinar x, y e z, sabendo que os polígonos á bê cê dê é e éfe gê agá í jota são semelhantes.
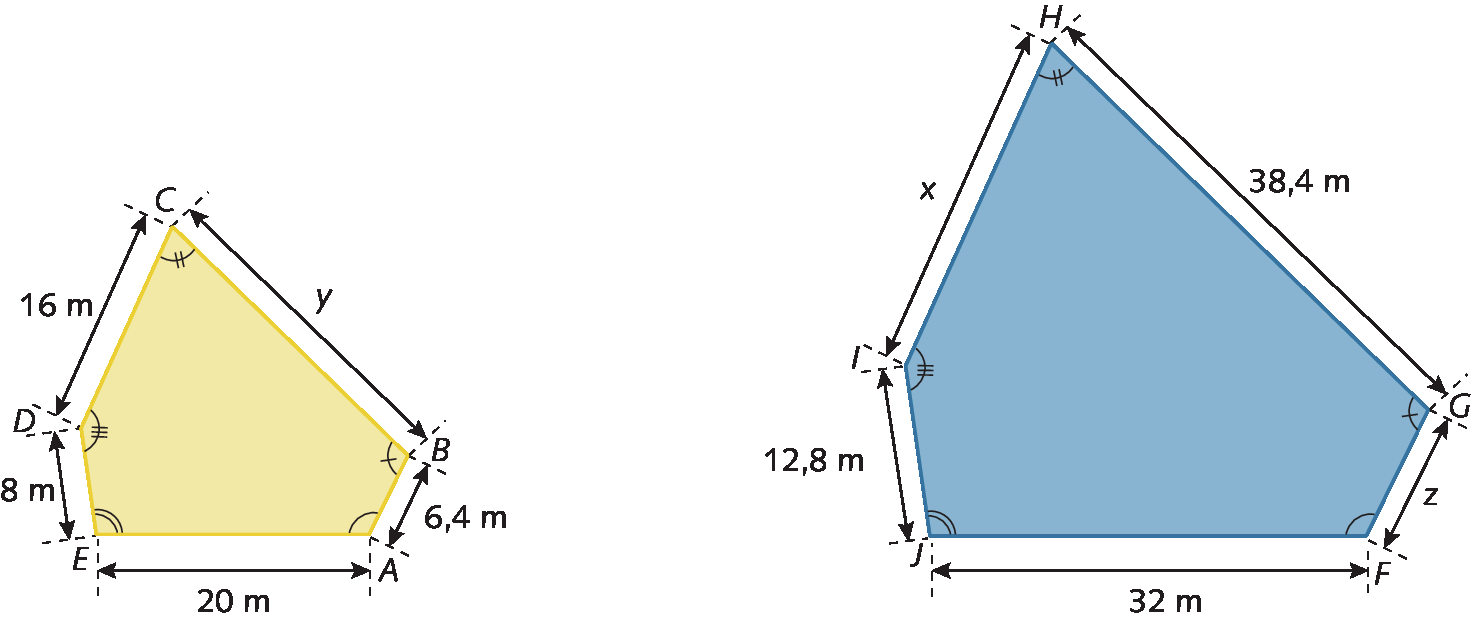
Inicialmente, determinamos a razão de semelhança k entre os dois polígonos, do polígono á bê cê dê é para o éfe gê agá í jota.
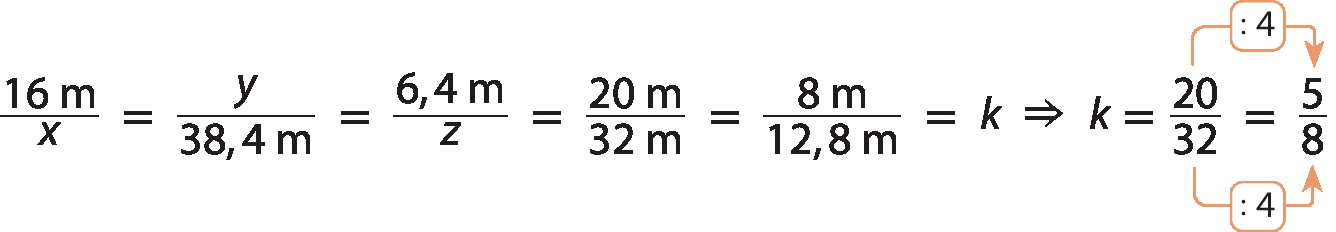
Em seguida, determinamos as medidas de comprimento x, y e z, em metro.
Sentença matemática. 16 metros sobre x é igual a 5 oitavos.
Sentença matemática. x igual a 16 metros vezes 8, tudo dividido por 5, igual a 25 vírgula 6 metros.
Sentença matemática. y sobre 38 vírgula 4 metros é igual a 5 oitavos.
Sentença matemática. y igual a 5 vezes 38 vírgula 4 metros, tudo dividido por 8, igual a 24 metros.
Sentença matemática. 6 vírgula 4 metros sobre z é igual a 5 oitavos.
Sentença matemática. z igual a 8 vezes 6 vírgula 4 metros, tudo dividido por 5, igual a 10 vírgula 24 metros.
Então, x = 25,6 métros, y = 24 métros e z = 10,24 métros.
Observação
Para se certificar de que dois polígonos são semelhantes, é preciso verificar as duas condições:
• os ângulos correspondentes devem ser congruentes;
• as medidas de comprimento dos lados correspondentes devem ser proporcionais.
Apenas uma das condições não é suficiente para garantir a semelhança entre polígonos. Por exemplo:
Respostas e comentários
Represente alguns polígonos na lousa e indique a medida do comprimento dos seus lados e as medidas das aberturas dos seus ângulos. Em seguida, peça aos estudantes que indiquem quais são semelhantes.
Atividades
Faça as atividades no caderno.
Cuidado! Evite acidentes ao usar o compasso na atividade 19.
17. Os polígonos a seguir são semelhantes? Justifique sua resposta.
a)
b)
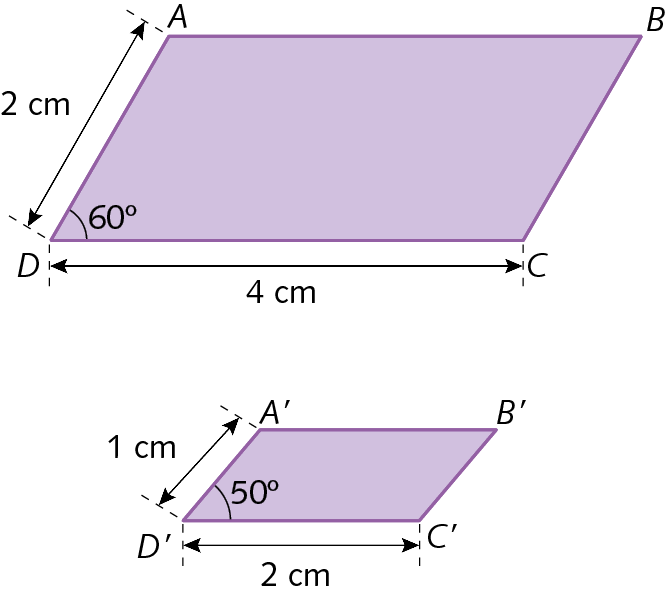
18. Em cada item, os polígonos são semelhantes. Determine os valores de x e de y.
a)
b)

19. Represente um triângulo semelhante ao triângulo á bê cê com razão de semelhança igual a
Fração. dois terços..

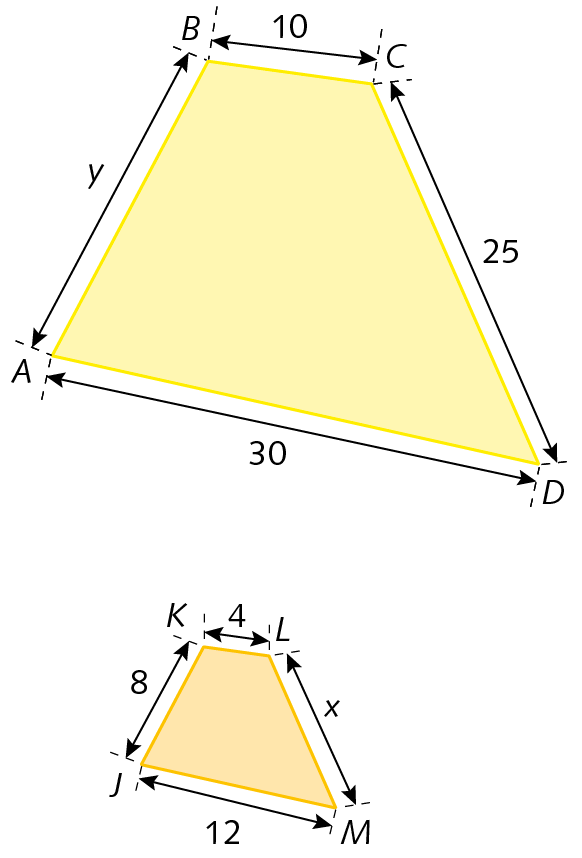
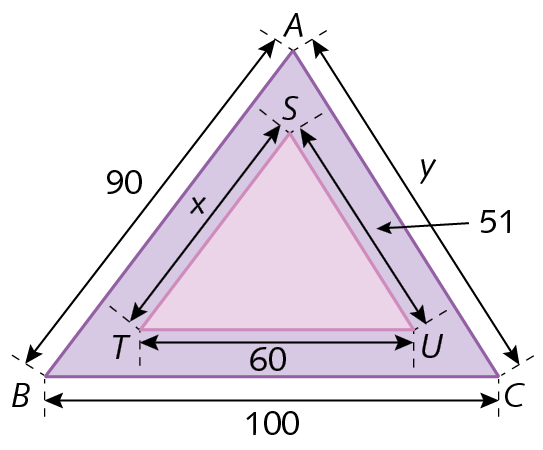
20. Em cada item, os triângulos á bê cê e STU são semelhantes. Determine os valores de x e de y.
a)
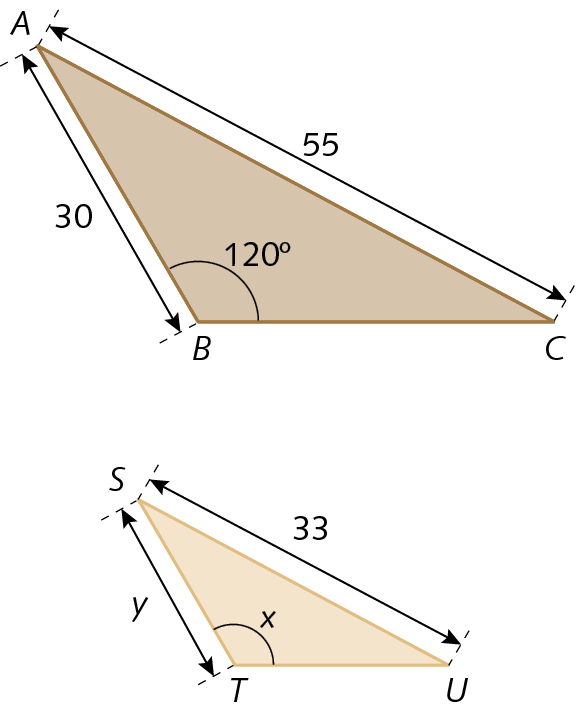
b)
Respostas e comentários
17. a) Sim, pois os ângulos correspondentes têm a mesma medida da abertura (90º) e a razão de semelhança é
5 sobre 2.
17. b) Não, pois os ângulos correspondentes têm medidas das aberturas diferentes.
18. a) x = 10; y = 20
18. b) x = 12; y = 27
19. Resposta em Orientações.
20. a) x = 54; y = 85
20. b) x = 120º; y = 18
• Na atividade 19, lembre os estudantes da construção de segmento proporcional.
Para que seja feita a construção do triângulo Abit’centésimo’ semelhante ao triângulo ABC, tal que
Sentença matemática. AB linha sobre AB igual a AC linha sobre AC igual a B linha C linha sobre BC igual a 2 terços., seguimos os seguintes passos:
• Traçamos, com o auxílio de uma régua, uma semirreta que passe por qualquer um dos lados do triângulo ABC. Neste caso, vamos escolher o lado
segmento ABpara traçar a semirreta
Semirreta AB.
• Sobre a semirreta
Semirreta AB, com auxílio do compasso, marcamos três pontos (N, O e P ), de modo que: NA = NO = OP.
• Traçamos uma reta
reta PCe uma nova reta paralela a
reta PCque passe pelo ponto O, determinando o ponto centésimo’ em
segmento AC, de modo que
AO sobre AP igual a 2 terços, com
Segmento PC paralelo a segmento OC. E, dessa forma, aplicando o teorema de Tales, temos:
Sentença matemática. AO sobre AP igual a AC linha sobre AC igual a 2 terços..
• Para finalizar a construção, podemos traçar uma reta
Reta B linha C linha., paralela à
reta BC. Segue do teorema de Tales que
Sentença matemática. AB linha sobre AB igual a 2 terços.. Assim, obtemos o triângulo Abit’centésimo’.

4 Triângulos semelhantes
Observe os triângulos á bê cê e FGH.
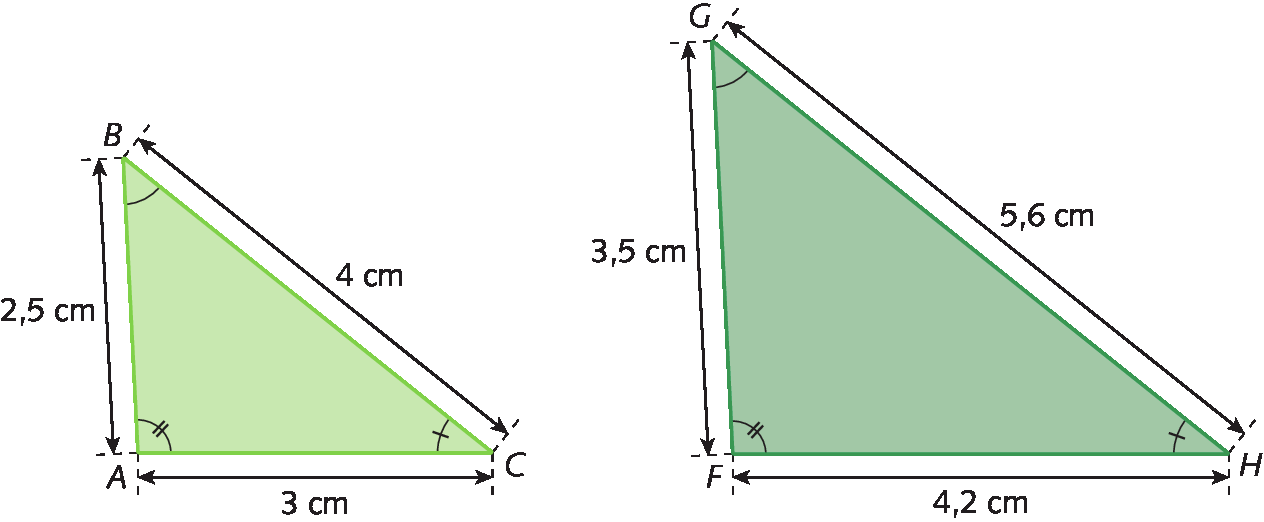
• Os ângulos correspondentes são congruentes:
Ângulo A congruente ao ângulo F,
Ângulo B congruente ao ângulo G,
Ângulo C congruente ao ângulo H.
• A razão entre as medidas de comprimento dos lados correspondentes é
Fração. cinco sétimos, pois:
Sentença matemática. 3 centímetros sobre 4 vírgula 2 centímetros igual a 2 vírgula 5 centímetros sobre 3 vírgula 5 centímetros igual a 4 centímetros sobre 5 vírgula 6 centímetros igual a 5 sétimos.
Podemos concluir que os triângulos ABC e FGH são semelhantes. Indicamos: △á bê cê ∼ △FGH
Dois triângulos são semelhantes quando os ângulos correspondentes são congruentes e as medidas de comprimento dos lados correspondentes são proporcionais.
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
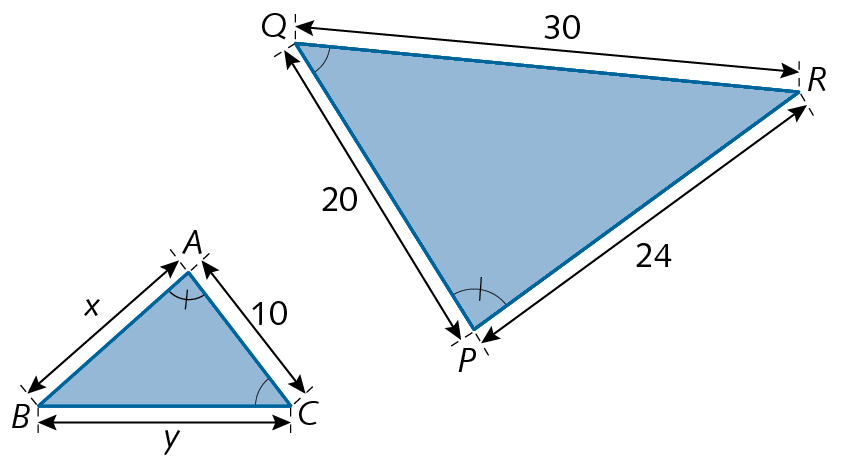
21. Os triângulos de cada item são semelhantes. Determine os valores de x e de y em cada caso.
a)
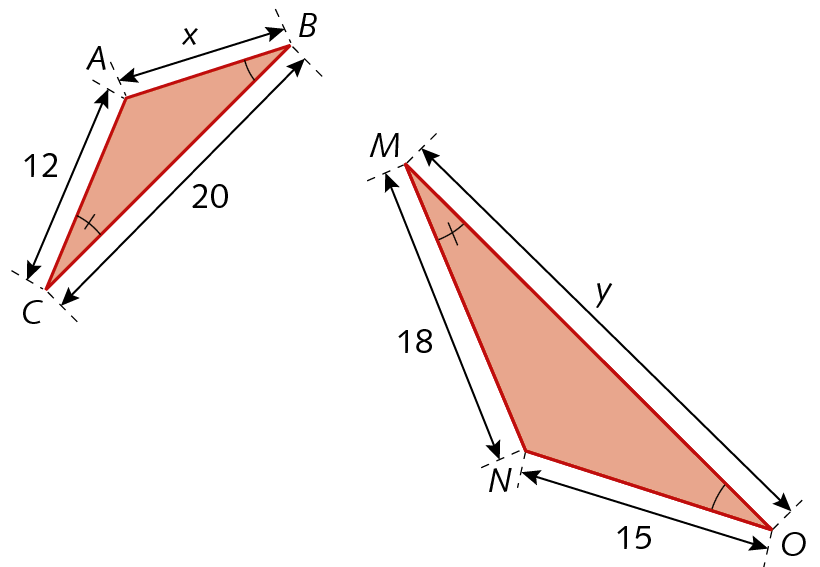
b)
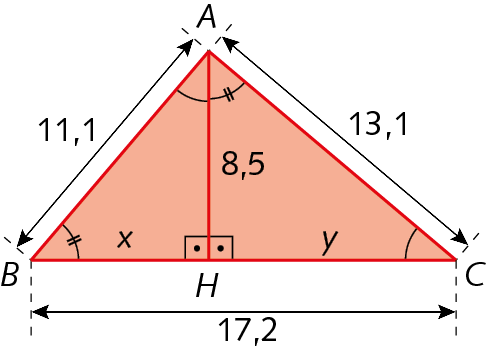
22. Calcule os valores aproximados de x e de y na figura, sabendo que a agá bê e CHA são triângulos semelhantes.
23. Calcule a medida da altura x de um poste, em metro, sabendo que o comprimento de sua sombra sobre o solo mede 8 métros no momento em que o comprimento da sombra de uma vara vertical de 3 métros mede 2 métros.

Respostas e comentários
21. a) x = 12; y = 15
21. b) x = 10; y = 30
22. x ≃ 7,2; y ≃
10
23. 12 métros
Triângulos semelhantes
Bê êne cê cê:
Habilidade ê éfe zero nove ême ah um dois.
Objetivos:
• Compreender o teorema fundamental da semelhança.
• Reconhecer triângulos semelhantes segundo cada um dos casos de semelhança.
Justificativa
O teorema fundamental da semelhança é imporante na resolução de diversos problemas envolvendo triângulos e, por esta razão, é importante compreendê-lo.
Reconhecer triângulos semelhantes, segundo cada um dos casos de semelhança, permite aos estudantes reconhecer que não é necessário conhecer a medida do comprimento de todos os lados nem a medida da abertura de todos os ângulos internos de dois triângulos para verificar se eles são semelhantes. Além disso, favorece o desenvolvimento da habilidade ê éfe zero nove ême ah um dois.
Mapeando conhecimentos
Pergunte aos estudantes: “Para verificar se dois triângulos são semelhantes é preciso conhecer a medida do comprimento de todos os lados e a medida da abertura de todos os ângulos internos dos dois triângulos?”. Incentive os estudantes a fazerem investigações e compartilharem as conclusões.
Para as aulas iniciais
Verifique as conclusões a que os estudantes chegaram. Se possível, explore alguns exemplos concretos com a turma.
Assim como as outras figuras planas, os triângulos semelhantes devem ter lados correspondentes proporcionais e ângulos correspondentes congruentes.
(EF09MA12) Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.
Teorema fundamental da semelhança
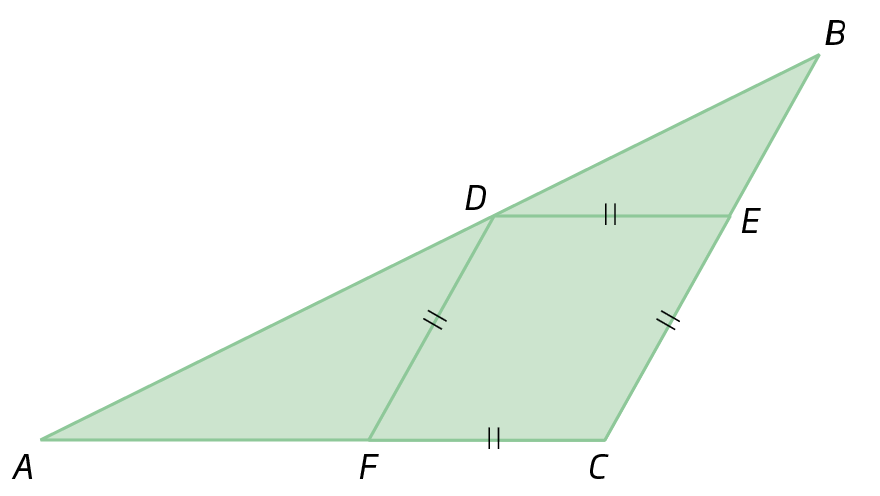
Considere um △á bê cê e uma reta r, paralela a
Segmento BC, que corta os lados
Segmento ABe
Segmento ACnos pontos D e ê, respectivamente, conforme a figura a seguir.
Vamos provar que os triângulos dê á é e bê á cê são semelhantes.
• Os ângulos internos correspondentes são congruentes, pois:
• o ângulo
BACé comum aos dois triângulos;
• os ângulos
ABCe
ADEsão correspondentes; logo, Alfa = Beta;
• os ângulos
ACBe
AEDsão correspondentes; logo, gama = teta.
• As medidas de comprimento dos lados correspondentes são proporcionais.
Se, pelo ponto ê, traçarmos
reta EFparalela a
Segmento AB, temos:
1
A D sobre A B, igual, A E sobre A C.

aplicação do teorema de Tales nos triângulos dê á é e bê á cê
2
A E sobre AC, igual, BF sobre BC.

aplicação do teorema de Tales nos triângulos cê ê éfe e CAB
3
Segmento D E congruente ao segmento B F.

lados opostos do paralelogramo DEFB
Substituindo BF por dê ê de 3 em 2, temos:
Sentença matemática. AE sobre AC igual a DE sobre BC.4
Comparando 1 e 4, temos:
AD sobre AB igual a AE sobre AC igual a DE sobre BCPortanto, os triângulos dê á é e bê á cê têm as medidas de comprimento dos lados correspondentes proporcionais. Assim, concluímos que os triângulos dê á é e bê á cê são semelhantes.
Segundo o teorema fundamental da semelhança:
Toda reta paralela a um lado de um triângulo que intercepta os outros dois lados em pontos distintos determina, com esses lados, um triângulo semelhante ao primeiro.
Respostas e comentários
Teorema fundamental da semelhança
Faça a leitura coletiva do texto com a turma. Se achar pertinente, desenvolva com eles a demonstração do teorema fundamental da semelhança. É importante que fique claro para a turma quais são as hipóteses e a tese.

Um pouco de história
Faça a atividade no caderno.
Nascido em Mileto (região atualmente pertencente à Turquia), o filósofo grego Tales foi considerado um dos sábios da Grécia e, para muitos historiadores, a Geometria demonstrativa teve início com ele. Além do teorema que recebe seu nome, é atribuída a ele, também, a demonstração de que as medidas das aberturas dos ângulos da base de um triângulo isósceles são iguais. Tales teria calculado a medida da altura das pirâmides, quando viveu no Egito, usando um método de triangulação, uma aplicação do teorema que recebeu seu nome. Um dos possíveis métodos usados por Tales teria sido aplicado da seguinte fórma:
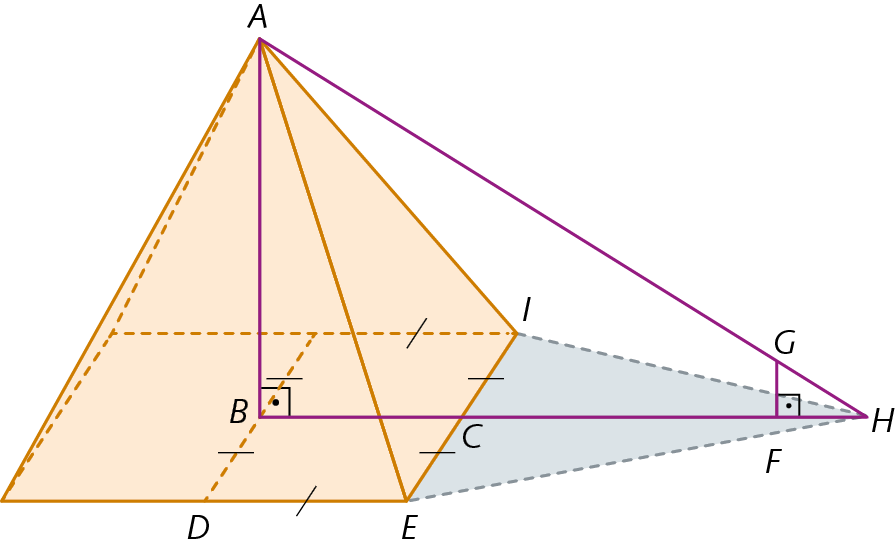
1º) Colocou uma estaca (representada por
segmento GF) na sombra da pirâmide sobre a perpendicular que passa no ponto médio (C) de um dos lados da base da pirâmide
segmento EI, de fórma que sua sombra terminasse no mesmo ponto (H) onde acabava a sombra da pirâmide.
2º) Mediu o comprimento de
segmento DE,
segmento CH,
segmento FHe
segmento GF. Como dê ê = BC, obteve a medida de comprimento de
segmento BH.
3º) Finalmente, calculou a medida da altura da pirâmide (representada por A bê), escrevendo a seguinte proporção:
(BH, FH e GF são medidas de comprimento conhecidas)
Atividade
Explique por que Tales pôde escrever essa proporção que o levou a obter a medida da altura da pirâmide.
Atividades
Faça as atividades no caderno.
24. Determine x e y nas figuras, sabendo que
segmento MN paralelo segmento BC.
a)
b)
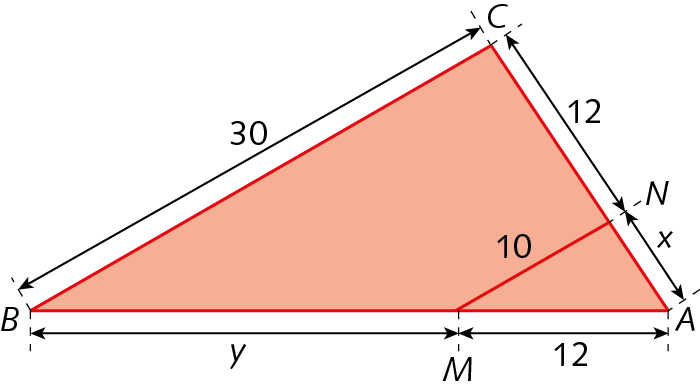
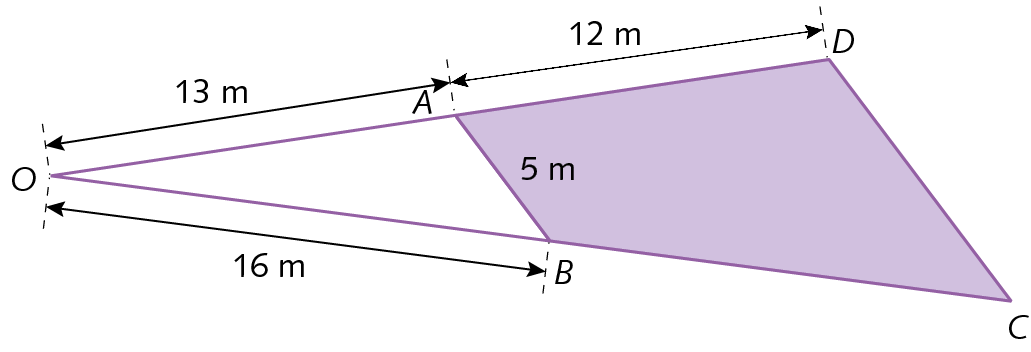
25. O formato de um pátio é representado pelo quadrilátero a bê cê dê, com
segmento AB paralelo segmento DC. Sabendo que A bê = 5 métros, á dê = 12 métros, ó á = 13 métros e ó bê = 16 métros, determine BC e DC.
Respostas e comentários
Um pouco de história: Resposta em Orientações.
24. a) x = 4; y = 12
24. b) x = 6; y = 24
25. BC =
Fração. 192 treze avosmétros; DC =
Fração. 125 treze avosmétros
Ao responder a questão proposta no boxe Um pouco de história, espera-se que os estudantes percebam que, pelo teorema fundamental da semelhança de triângulos, os triângulos ABH e GFH são semelhantes e, por isso, as medidas dos lados correspondentes são proporcionais. Assim, pode-se escrever:
Isso justifica por que Tales pôde escrever a proporção que o levou a obter a medida da altura da pirâmide.
• Na atividade 24, os estudantes vão aplicar o teorema fundamental da semelhança para determinar x e y nas figuras. Ajude-os a determinar as proporções caso tenham dificuldades. Reserve um momento para discutir os dois itens coletivamente.
• Na atividade 25, pergunte aos estudantes qual seria a medida do comprimento de
Segmento BCcaso AD = 6 métros. Espera-se que os estudantes percebam que a medida do comprimento de
Segmento BCseria igual à metade da encontrada anteriormente, ou seja,
96 treze avos metros.
Casos de semelhança de triângulos
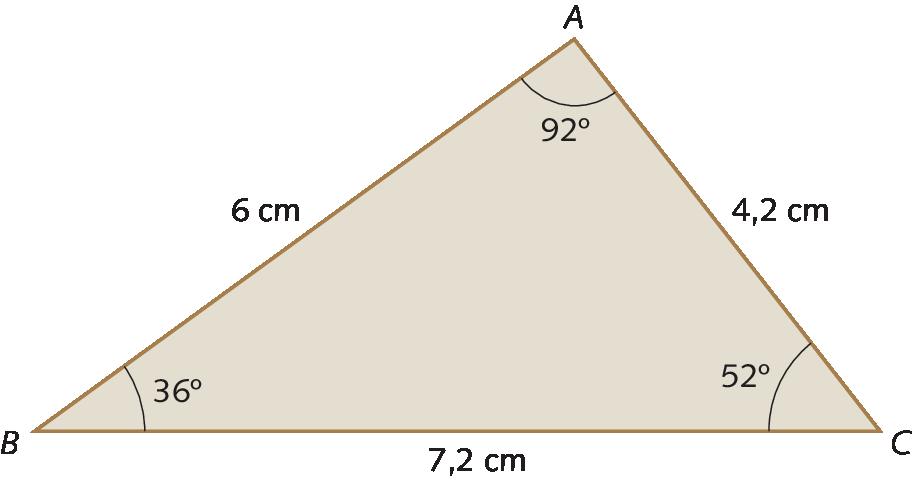
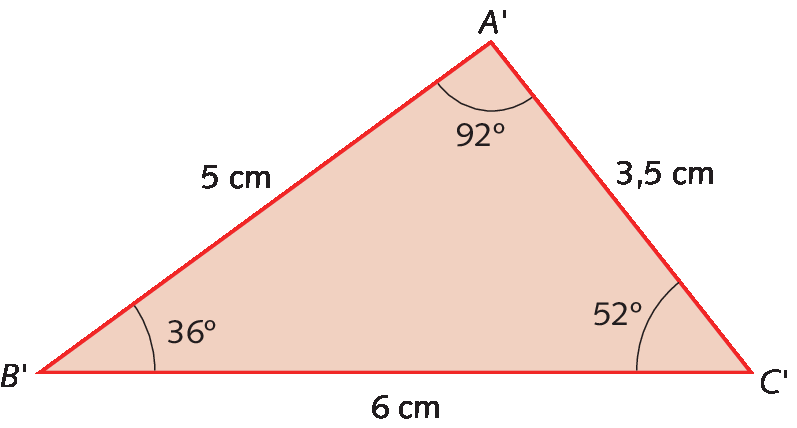
Vamos verificar se os triângulos á bê cê e a linha bê linha cê linha são semelhantes.
• Os ângulos internos correspondentes são congruentes.
medida do ângulo BAC igual a medida do ângulo B linha A linha C linha igual a 92 graus
medida do ângulo ABC igual a medida do ângulo A linha B linha C linha igual a 36 graus
medida do ângulo ACB igual a medida do ângulo A linha C linha B linha igual a 52 graus
• As medidas de comprimento dos lados correspondentes são proporcionais.
Sentença matemática. 6 centímetros sobre 5 centímetros igual a 7 vírgula 2 centímetros sobre 6 centímetros igual a 4 vírgula 2 centímetros sobre 3 vírgula 5 centímetros, que é igual a 6 quintos
Assim, concluímos que os triângulos á bê cê e á linha bê linha cê linha são semelhantes.
Existem três casos em que podemos verificar a semelhança entre triângulos conhecendo apenas alguns dos seus elementos.
1º caso: A A (Ângulo – Ângulo)
Se dois triângulos têm dois ângulos correspondentes congruentes, então esses triângulos são semelhantes.
Analise os triângulos á bê cê e á linha bê linha cê linha.
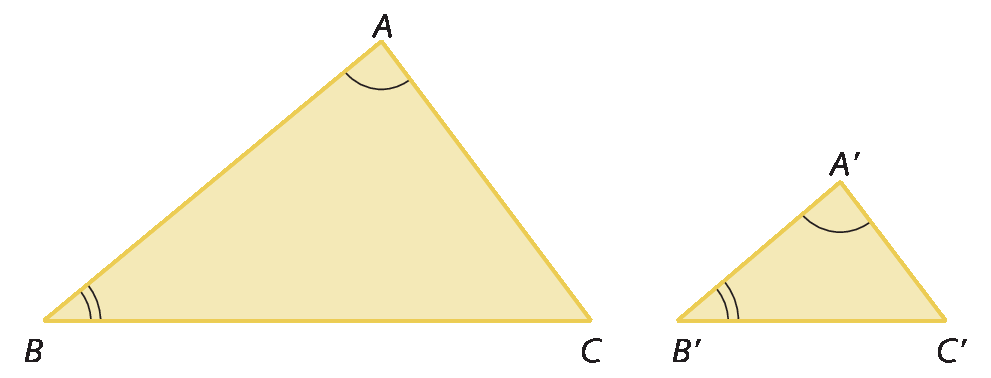
Como
Ângulo BAC congruente ao ângulo B'A'C'e
Ângulo ABC congruente ao ângulo A'B'C'', então: △á bê cê ∼ △á linha bê linha cê linha
2º caso: L A L (Lado – Ângulo – Lado)
Se dois triângulos têm as medidas de comprimento de dois pares de lados correspondentes proporcionais e os ângulos compreendidos por esses lados forem congruentes, então esses triângulos são semelhantes.
Analise os triângulos á bê cê e A'B'C'.
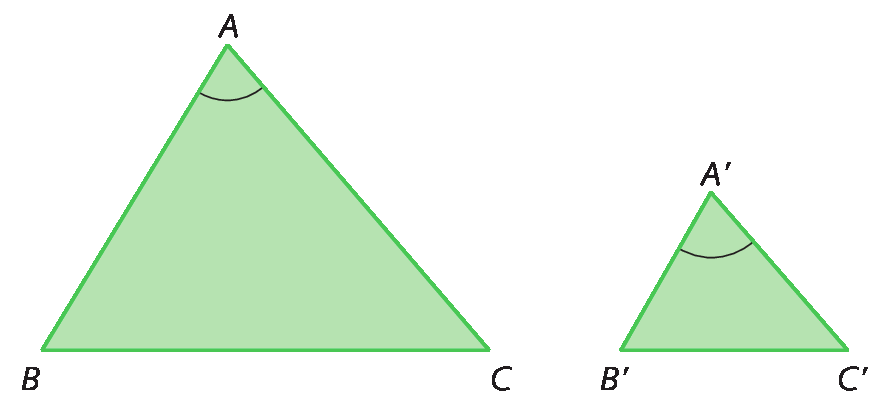
Se
Sentença matemática. AB sobre A linha B linha é igual a AB sobre A linha C linha.e como
Ângulo BAC congruente ao ângulo B linha A linha C linha., então: △á bê cê ∼ △á linha bê linha cê linha
Respostas e comentários
Caso considere interessante e tenha a oportunidade, antes de iniciar os trabalhos com os casos de semelhança de triângulos, apresente aos estudantes o vídeo sugerido a seguir. Depois, mostre os casos de semelhança entre triângulos e pergunte a eles qual foi o caso de semelhança utilizado na situação apresentada no vídeo. Se julgar adequado, peça aos estudantes que, em grupos, realizem a medição de algum objeto ou da construção da escola seguindo a estratégia que aprenderam.
Sugestão de vídeo
O vídeo “Medindo prédios com prato”, do canal Manual do Mundo, mostra como medir a altura de um prédio utilizando um prato e uma trena.
3º caso: L L L (Lado – Lado – Lado)
Se dois triângulos têm os três pares de lados correspondentes com medidas de comprimento proporcionais, esses triângulos são semelhantes.
Analise os triângulos á bê cê e á linha bê linha cê linha.
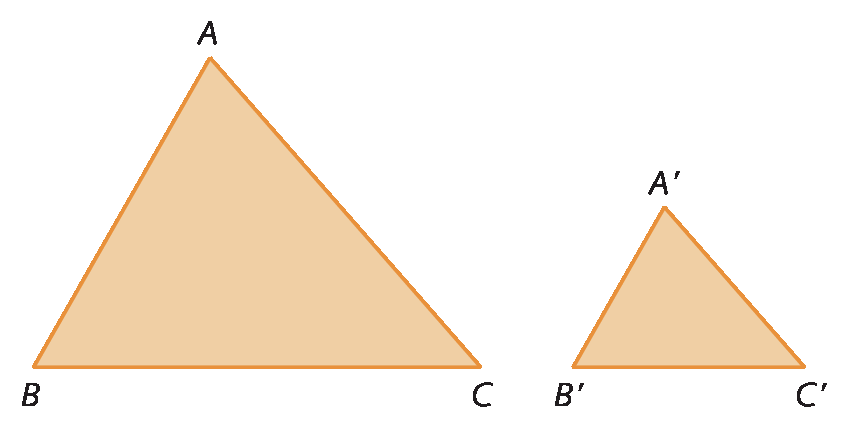
Como
AB sobre A linha B linha igual a AC sobre A linha C linha igual a BC sobre B linha C linha, então: △á bê cê ∼ △a linha bê linha cê linha
Atividades
Faça as atividades no caderno.
As imagens foram aplicadas sem respeitar a proporção real entre suas medidas.
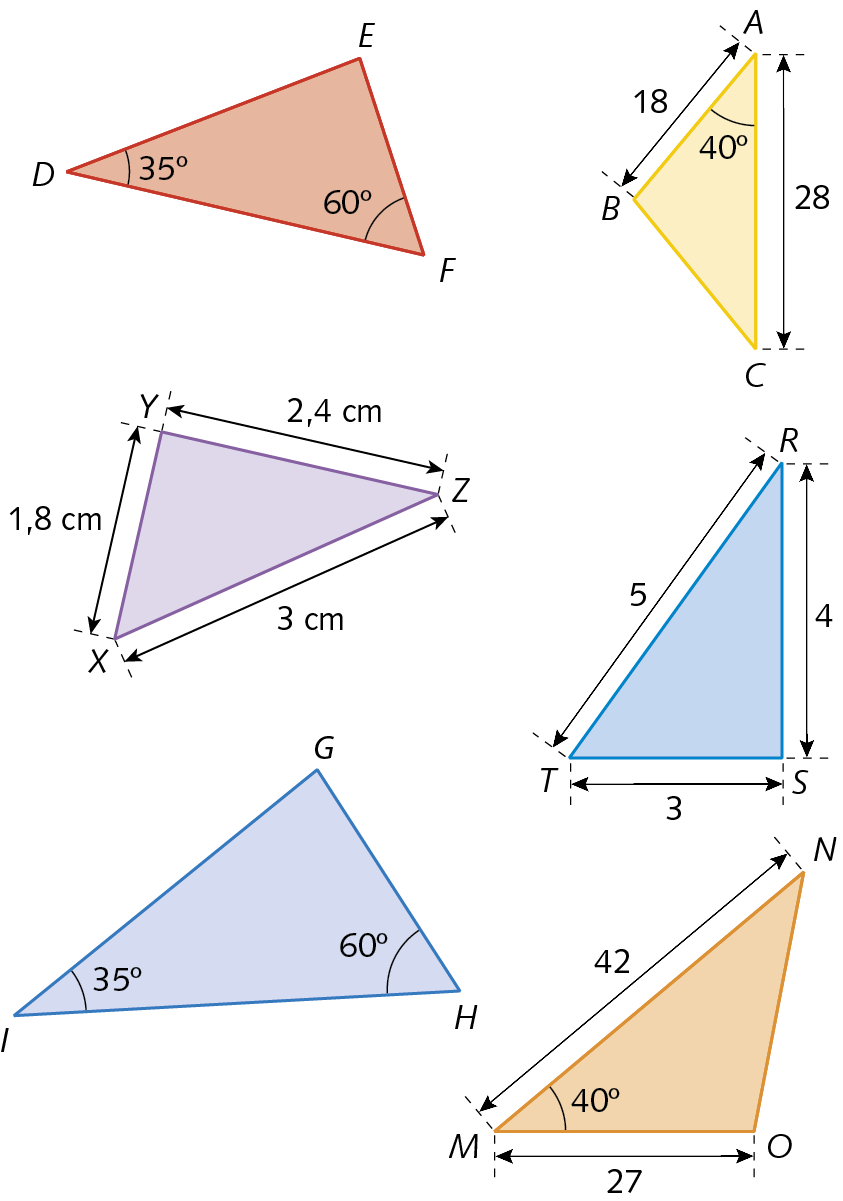
26. Identifique os pares de triângulos semelhantes, especificando o caso.
27. Sabendo que gê dê é éfe é um quadrado, responda: os triângulos ADG e GCF são semelhantes? Justifique sua resposta.
28. Identifique o caso de semelhança nos pares de triângulos semelhantes.
a)

b)
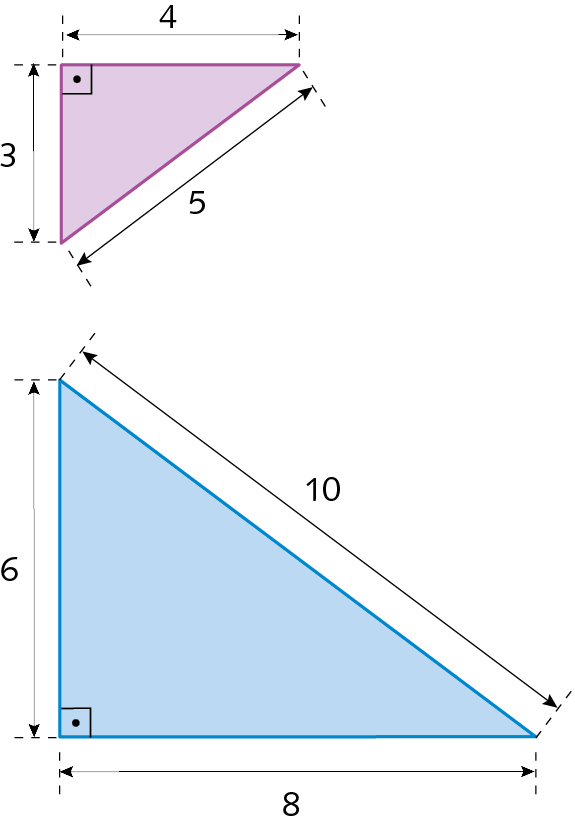
c)
Respostas e comentários
26. △ á bê cê ∼ △ ême ó êne (L A L); △ xis ípsilon zê ∼ △TSR (éle éle éle); △ dê ê éfe ∼ △ IGH (A A)
27. Sim. Comentários em Orientações.
28. a) L A L
28. b) L A L ou L L L
28. c) A A
• A atividade 27 incentiva a argumentação. Ajude-os a identificar os lados e ângulos correspondentes dos triângulos ADG e GCF. Como GDEF é um quadrado, temos:
Reta GF paralela à reta ABe
Ângulo ADGé um ângulo reto. Com base nisso, podemos concluir que
Medida do ângulo DAG igual medida do ângulo CGF, pois são ângulos correspondentes;
Medida do ângulo GDA igual medida do ângulo FCG, pois são ângulos retos. Portanto, pelo caso á á, △ADG ∼ △GCF.
29. Na figura, identifique dois triângulos semelhantes e o caso de semelhança correspondente, sabendo que o quadrilátero DECF é um losango.
30. Considere a figura a seguir.

a) Calcule a medida do comprimento da escada.
b) Os ângulos correspondentes são congruentes e os triângulos tem um lado com a mesma medida de comprimento?
c) Com base no item anterior, os triângulos são semelhantes?
31. Ronaldo notou que, em determinada hora do dia, o comprimento de sua sombra media 0,40 métro, enquanto o comprimento da sombra do prédio onde morava media 8 métros. Sabendo que Ronaldo mede 1,60 métro de altura, determine a medida da altura do prédio.

32.


Analise os triângulos a seguir.
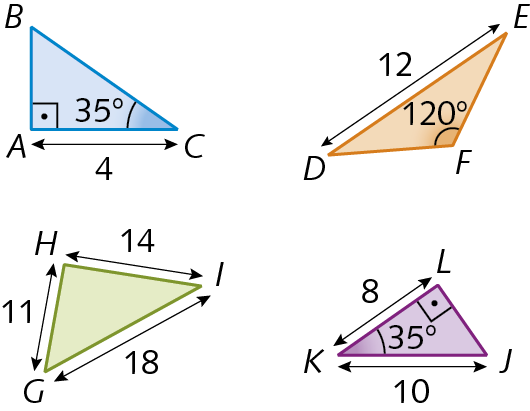
• No caderno, elabore um problema que possa ser resolvido a partir dos triângulos.
• Troque de caderno com um colega e resolva o problema elaborado por ele.
• Analise a resposta do colega e dê um retorno a ele, dizendo o que respondeu corretamente e em que pontos ele se equivocou.
33. Analise estes triângulos.
a) As medidas de comprimento dos lados correspondentes dos triângulos são proporcionais?
b) Um dos ângulos de cada triângulo tem a mesma medida de abertura?
c) Com base no item anterior, os triângulos são semelhantes?
Respostas e comentários
29. Exemplo de resposta:
△DBE ∼ △á bê cê (A A)
30. a) 5 métros
30. b) Resposta em Orientações.
30. c) Resposta em Orientações.
31. 32 métros
32. Respostas pessoais.
33. a) sim
33. b) sim
33. c) Resposta em Orientações.
• Na atividade 30, oriente os estudantes a fazer um esboço da situação como o representado a seguir:
Para realizar o item a, espera-se que apliquem o teorema de Tales:
2 vírgula 4 metros sobre 1 vírgula 6 metro igual a 3 metros sobre CQ
Assim, CQ = 2 métros
A medida do comprimento da escada é 5 métros, pois 3 métros + 2 métros = 5 métros.
• Resposta do item b da atividade 30:
Com base no esboço feito, os estudantes podem concluir mais facilmente que os ângulos correspondentes dos triângulos são congruentes, pois:
(ângulos retos)
(ângulo comum aos dois triângulos)
(pois a soma das medidas dos ângulos internos de um triângulo é 180º e a medida das aberturas dos outros dois ângulos internos correspondentes dos dois triângulos são iguais).
Os triângulos não têm lados correspondentes com a mesma medida de comprimento.
AB = 2,4 métros, BC = 1, 8 métro, CA = 3 métros, AP = 4 métros, PQ > 1,8 métro e QA = 5 métros.
• Resposta do item c da atividade 30:
Com base no item anterior, os triângulos são semelhantes pelo caso á á.
• Resposta do item c da atividade 33:
Espera-se que os estudantes respondam que os triângulos não são semelhantes, pois os ângulos que têm a mesma medida de abertura nos dois triângulos não estão compreendidos entre os lados que têm medidas de comprimento proporcionais.

Resolvendo em equipe
Faça a atividade no caderno.
(enêm) O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6 métros e 4 métros.
A figura representa a situação real na qual os postes são descritos pelos segmentos
Segmento ACe
Segmento BDe a haste é representada pelo segmento
segmento EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta
segmento AB. Os segmentos
segmento ADe
Segmento de reta BCrepresentam cabos de aço que serão instalados.
Qual deve ser o valor do comprimento da haste
representada pelo segmento EF?
a) 1 métro
b) 2 métros
c) 2,4 métros
d) 3 métros
e)
2 vezes raiz quadrada de 6, metros|
Interpretação e identificação dos dados |
• Analise as informações do enunciado e anote aquelas que você julgar relevantes para a resolução do problema. |
|
|---|---|---|
|
Plano de resolução |
• Monte as proporções relativas aos dois pares de triângulos semelhantes. |
|
|
Resolução |
• Reúna-se com dois ou três colegas. |
|
|
Verificação |
• O grupo deve reler o problema e verificar se todas as condições do enunciado foram satisfeitas. |
|
|
Apresentação |
• Cada grupo deverá elaborar uma síntese sobre os casos de semelhança de triângulos. Essa síntese poderá ser apresentada na forma de texto ou em um cartaz. Para cada um dos casos, inserir um exemplo que ilustre a explicação dada. |
Respostas e comentários
Resolvendo em equipe: alternativa c
Interpretação e identificação dos dados:
primeiro item: resposta pessoal
segundo item: Sim, os triângulos ABC e FBE são semelhantes pelo caso á á, pois ambos têm um ângulo reto e compartilham o ângulo
B.
terceiro item: ABD e AFE
Plano de resolução:
primeiro item:
Sentença matemática. FB sobre AB igual a EB sobre BC igual a FE sobre AC.;
Sentença matemática. AF sobre AB igual a AE sobre AD igual a FE sobre BD.segundo item:
Sentença matemática. AB igual a 5 meios vezes AF.terceiro item: Resolvendo o sistema, obtemos 2,4 métros para a medida de comprimento de
segmento EF.
Resolvendo em equipe
Bê êne cê cê:
• Competências gerais 1, 2 e 9 (as descrições estão na página seis).
• Competências específicas 1, 2 e 3 (as descrições estão na página sete).
A seção destaca as etapas selecionadas para encaminhar a resolução de problemas. Elas devem ser analisadas e discutidas com os estudantes. Além de favorecer o desenvolvimento das competências gerais 1, 2 e 9 e das competências específicas 1, 2 e 3, a seção permite a transferência de estratégias de resolução para outros contextos e situações.
Revisão dos conteúdos deste capítulo
Teorema de Tales
Um feixe de retas paralelas é formado por duas ou mais retas de um mesmo plano que, consideradas duas a duas, são sempre paralelas.
Uma reta que intercepta duas ou mais retas de um feixe de retas paralelas recebe o nome de transversal.
Se um feixe de retas paralelas é cortado por duas retas transversais quaisquer, m e n, os segmentos de reta determinados sobre m são proporcionais aos segmentos de reta correspondentes determinados sobre n.
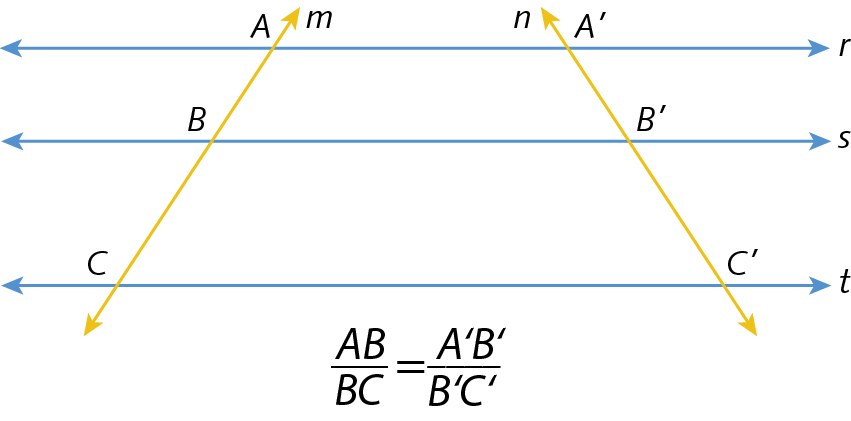
Teorema de Tales nos triângulos
Toda reta paralela a um lado de um triângulo determina, sobre os outros dois lados, segmentos de reta proporcionais.
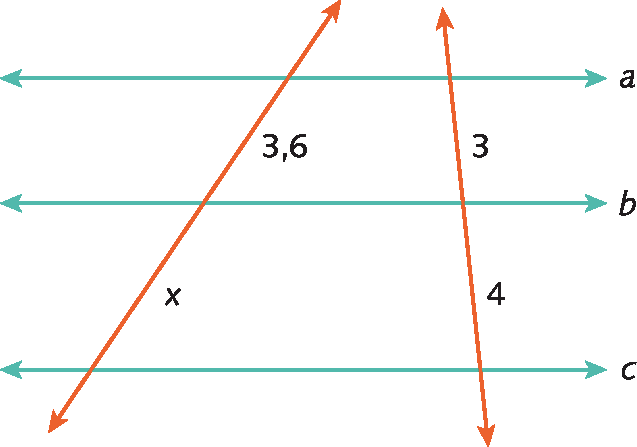
1. Determine os valores desconhecidos de x em cada caso, sabendo que a paralelo b paralelo c.
a)
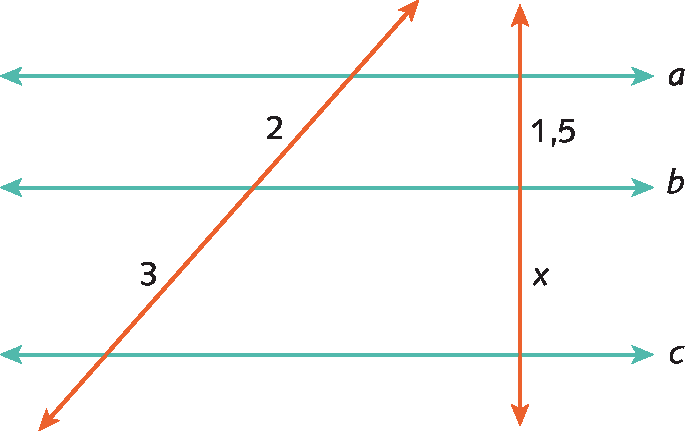
b)
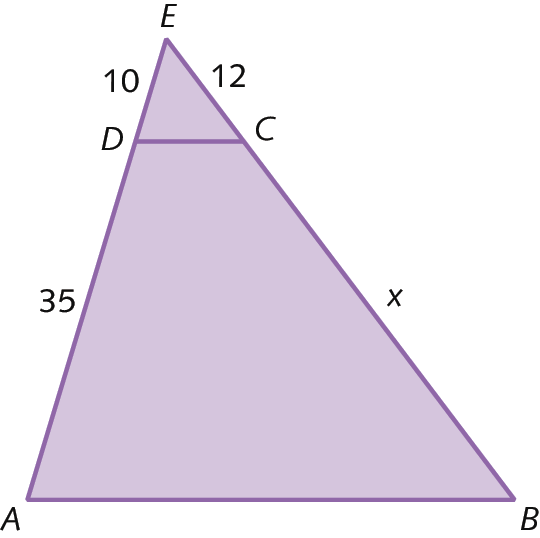
2. Determine o valor de x nos triângulos, sabendo que
Segmento AB paralelo ao segmento CD.
a)
b)
3. A figura a seguir representa três terrenos do bairro Recanto dos pássaros que se parecem com trapézios.
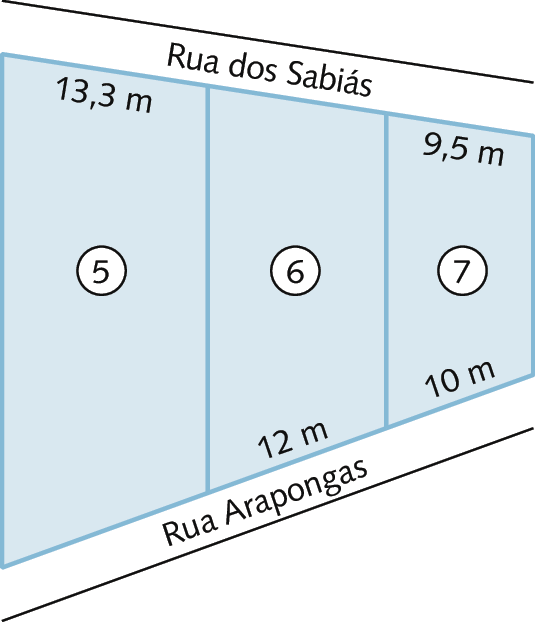
a) Marcelo é proprietário do lote 6 e pretende levantar um muro no fundo do terreno, na rua dos Sabiás. Qual deve ser a medida do comprimento desse muro?
b) O vizinho de Marcelo, no lote 5, pretende colocar um portão em toda a extensão da frente do terreno, na rua Arapongas. Qual deve ser a medida do comprimento do portão?
Respostas e comentários
1. a) x = 2,25
1. b) x = 4,8
2. a) x = 42
2. b) x = 9,6
3. a) 11,4 métros
3. b) 14 métros
Revisão dos conteúdos deste capítulo
Teorema de Tales
• A atividade 1 envolve a aplicação direta do teorema de Tales. Este é o momento oportuno para verificar se compreenderam e conseguem aplicar o teorema. Se achar necessário, apresente mais exemplos para a turma.
• A atividade 2 pode apresentar alguma dificuldade para os estudantes, uma vez que não está explícito o feixe de retas paralelas e as retas transversais. Oriente-os a reproduzir o triângulo de cada item no caderno e, depois, prolongar
Segmento AB,
Segmento CD,
segmento AEe
segmento BE.
• Na atividade 3, pergunte aos estudantes: “Qual informação fornecida no enunciado da atividade possibilita aplicar o teorema de Tales? Por quê?”. Espera-se que eles respondam que o fato dos terrenos serem parecidos com trapézios possibilita a aplicação do teorema de Tales, pois qualquer trapézio tem apenas um par de lados paralelo. Se achar conveniente, peça que reproduzam a figura no caderno, prolonguem os lados dos terrenos de modo a visualizar as retas e indiquem na figura onde será levantado o muro (item a) e onde o vizinho de Marcelo colocará o portão (item b).
Semelhança
Figuras semelhantes
Duas figuras são semelhantes quando as medidas dos ângulos correspondentes são iguais e as medidas dos segmentos correspondentes são proporcionais.
Polígonos semelhantes
Dois polígonos são semelhantes quando têm os ângulos correspondentes congruentes e as medidas de comprimento dos lados correspondentes são proporcionais.
;
Ângulo B congruente ao ângulo Q;
Ângulo C congruente ao ângulo R;
Ângulo D congruente ao ângulo S
4. Uma fábrica de tapetes está diminuindo as medidas das peças. Sabendo que as dimensões dos tapetes mediam 4 métros por 3 métros e que agora medem
Fração. dois quintosdisso, determine as medidas das dimensões dos tapetes atuais.
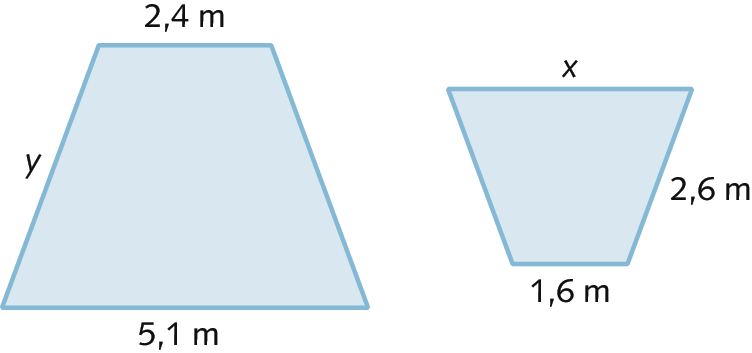
5. Considerando que o trapézio maior é uma ampliação do trapézio menor, determine as medidas de comprimento x e y.
Triângulos semelhantes
Dois triângulos são semelhantes quando os ângulos correspondentes são congruentes e as medidas de comprimento dos lados correspondentes são proporcionais.
Teorema fundamental da semelhança
Toda reta paralela a um lado de um triângulo que intercepta os outros dois lados em pontos distintos determinam, com esses lados, um triângulo semelhante ao primeiro.
Casos de semelhança de triângulos
1) á á (Ângulo – Ângulo):
Se dois triângulos têm dois ângulos correspondentes congruentes, então esses triângulos são semelhantes.
2) éle á éle (Lado – Ângulo – Lado):
Se dois triângulos têm as medidas de comprimento de dois pares de lados correspondentes proporcionais e os ângulos compreendidos por esses lados forem congruentes, então esses triângulos são semelhantes.
3) éle éle éle (Lado – Lado – Lado):
Se dois triângulos têm os três pares de lados correspondentes com medidas de comprimento proporcionais, esses triângulos são semelhantes.
6. Para descobrir a medida da altura do prédio em que mora, José utilizou a seguinte estratégia: mediu o comprimento da sombra do prédio e da sombra de sua filha no mesmo instante, obtendo, respectivamente, 8 métros e 60 centímetros. Como a filha de José mede 1,50 métro de altura, qual é a medida da altura do prédio?
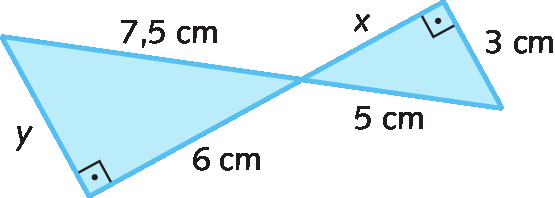
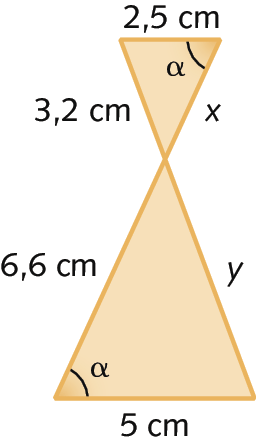
7. Nestes triângulos, identifique o caso de semelhança. Em seguida, calcule as medidas de comprimento desconhecidas, em centímetro.
a)
b)
Respostas e comentários
4. 1,6 métro por 1,2 métro
5. x = 3,4 métros e y = 3,9 métros
6. 20 métros
7. a) á á; x = 4 centímetros e y = 4,5 centímetros
7. b) á á; x = 3,3 centímetros e y = 6,4 centímetros
Semelhança
• Na atividade 5, os estudantes devem perceber que os trapézios estão em posições diferentes. Isso é importante para que considerem as medidas dos lados correspondentes corretamente.
Triângulos semelhantes
• Caso os estudantes tenham dificuldade para compreender a situação-problema da atividade 6, ajude-os a fazer um esboço dela.
• Na atividade 7, espera-se que os estudantes lembrem que ângulos opostos pelo vértice são congruentes. Para determinar as medidas de comprimento desconhecidas, verifique se identificam corretamente os lados correspondentes dos dois triângulos.
É hora de extrapolar
Faça as atividades no caderno.

Será que você consome de fórma consciente?
O ato de consumir está presente na rotina de todos nós, que diariamente consumimos recursos, produtos ou serviços. Diante da ação corriqueira de consumir, será que as pessoas refletem sobre o quê, como e quando consumir? Qual é a importância dessa reflexão?
Objetivos: Refletir sobre critérios para realizar uma compra; analisar dados sobre consumo consciente; pesquisar dicas para economizar e consumir de fórma consciente e produzir guias de bolso para ser distribuídos para a comunidade escolar.

Etapa 1: Pesquisa sobre preços e reflexão sobre critérios que podem ser usados no momento de consumir.
1. Junto à turma e ao professor, vocês deverão montar uma personagem, indicando as características: idade, sexo, profissão, estado civil, se tem filhos, o que gosta de fazer no tempo livre, o que gosta de assistir na televisão etcétera.
2. Em grupos, considerem que a personagem da atividade 1 peça ajuda para comprar e escolher uma televisão. Façam uma pesquisa, discutam as opções no grupo e decidam qual é a melhor escolha de compra para a personagem.
3. Apresentem as características do produto escolhido pelo seu grupo para a turma. Tragam as seguintes informações: marca e modelo, preço e fórma de pagamento. Expliquem quais foram os critérios utilizados para considerarem esse produto como a melhor escolha.
Após as apresentações, respondam:
a) Todos os grupos escolheram exatamente o mesmo produto? Por que vocês acham que isso ocorreu?
b) Algum grupo apresentou um critério que não havia sido usado? Se sim, vocês consideram esse critério relevante?
c) Ao comprar algum produto, vocês sempre realizam pesquisas para decidir qual é a melhor opção?
4. Analisem o anúncio de uma loja de carros.

a) Se uma pessoa comprar esse carro à vista, quanto ela pagará?
b) Qual será o valor das parcelas na opção 2?
c) Quanto uma pessoa pagará no total se escolher a opção 3?
d) Qual é a diferença entre o valor do carro no anúncio e o valor obtido no item c? Qual é o nome que se dá a essa diferença?
e) Se uma pessoa for adquirir esse carro, qual fórma de pagamento vocês acham que ela escolherá?

Etapa 2: Análise de dados sobre produção de lixo e pesquisa sobre consumo consciente.
5. Leiam o texto e respondam às questões.
Segundo dados do Panorama dos Resíduos Sólidos no Brasil 2020, a geração saiu de 66.700.000 de toneladas em 2010 para ..79100000 em 2019, uma diferença de 12.400.000 de toneladas. O mesmo estudo diz ainda que cada brasileiro produz, em média, 379,2 quilogramas de lixo por ano, o que corresponde a mais de 1 quilograma por dia. As informações foram coletadas e publicadas pela Associação Brasileira das Empresas de Limpeza Pública e Resíduos Especiais (abrélpe).
Dados obtidos em: https://oeds.link/RNAplf. Acesso em: 10 julho 2022.
a) Escreva em notação científica as medidas de massa apresentadas no texto.
b) Vocês contribuem para diminuir a quantidade de lixo gerada e favorecem a reciclagem? Se sim, como?
Respostas e comentários
1. Resposta pessoal.
2. Resposta pessoal.
3. a) Respostas pessoais.
3. b) Respostas pessoais.
3. c) Resposta pessoal.
4. Comentários em Orientações.
4. a) R$ 30.600,00 trinta mil seiscentos reais
4. b) R$ 750,00 setecentos e cinquenta reais
4. c) R$ 50.400,00 cinquenta mil quatrocentos reais
4. d) R$ 14.400,00quatorze mil quatrocentos reais; juro
4. e) Resposta pessoal.
5. a) ..66700000 = 6,67 ⋅ 107; ..79100000 = 7,91 ⋅ 107; ..12400000 = 1,24 ⋅ 107; 379,2 = 3,792 ⋅ 102
5. b) Respostas pessoais.
É hora de extrapolar
Bê êne cê cê:
• Competências gerais 2, 4, 7, 8, 9 e 10 (as descrições estão na página seis).
• Competências específicas 2, 4, 5, 6, 7 e 8 (as descrições estão na página sete).
Temas contemporâneos transversais:

A seção propõe o fechamento da Unidade por meio de um trabalho colaborativo que explora a pesquisa, a comunicação e a elaboração de um produto final (um guia de bolso), que será compartilhado com a comunidade escolar.
Com a finalidade de organizar o trabalho, a seção é dividida em etapas que promovem:
• Entendimento do contexto e dos objetivos do trabalho a ser realizado.
• Pesquisa coletiva.
• Elaboração, em grupo, do produto proposto.
• Apresentação e exposição do produto.
• Reflexão e síntese do trabalho.
As etapas de pesquisa e elaboração do produto podem ser realizadas extraclasse. Verifique o perfil dos estudantes e oriente-os com relação ao prazo, aos materiais e a outros aspectos necessários à realização do trabalho.
A seção também favorece o desenvolvimento das competências gerais 2, 4, 7, 8, 9 e 10 e das competências específicas de Matemática 2, 4, 5, 6, 7 e 8, procurando mobilizar conteúdos estudados nos capítulos que integram a unidade. Portanto, é recomendável trabalhar a seção depois de estudar os capítulos, mas, se preferir trabalhar as etapas da seção à medida que os capítulos forem estudados, atente para os conhecimentos prévios necessários.
Se achar conveniente, inicie uma discussão com a turma sobre o título da seção. É interessante verificar quais são as concepções dos estudantes sobre o que é consumir e o que é consumir de fórma consciente, questionando sobre o que e como eles (jovens) consomem.
Na etapa 1, caso não seja possível realizar a pesquisa em sites, peça aos estudantes que tragam folhetos de anúncios de lojas para que eles façam essa pesquisa.
• Na atividade 4, da etapa 1, os estudantes vão mobilizar o que aprenderam sobre porcentagem, juro e a ideia de desconto. No item a, espera-se que, os estudantes calculem R$ 36.000, 00trinta e seis mil reais ‒ 0,15 ⋅ R$ 36.000,00trinta e seis mil reais. No item b, verifique se os estudantes entendem o significado de “dar entrada” e, se for necessário, explique isso para a turma. Espera-se que eles concluam que nesta opção de pagamento, a pessoa paga R$ 18.000, 00dezoito mil reais no ato e precisa dividir a outra metade do valor em 24 parcelas. Assim, o valor de cada parcela dividindo R$ 18.000, 00dezoito mil reais por 24. No item c, os estudantes devem calcular 48 ⋅ R$ 1.050, 00mil cinquenta reais. Espera-se que eles percebam que a a diferença entre o valor obtido neste cálculo e o valor do carro no anúncio corresponde ao juro (item d). Converse com eles sobre por que essa opção de pagamento gera juros. Por fim, forme uma roda de conversa para discutir a questão proposta no item ê.
6. A produção de lixo é um dos fatores que deve ser considerado quando se pratica um consumo consciente. Pesquisem o que é o consumo consciente e elenquem outros fatores que devem ser considerados e dicas para praticá-lo.
7. Nas prateleiras de supermercados, é possível encontrar diversos produtos de limpeza em versões concentradas. Essas versões apresentam vantagens para o fabricante, o consumidor e o meio ambiente.
a) Identifiquem pelo menos três vantagens das versões concentradas de produtos. Vocês podem pesquisar na internet se acharem necessário.
b) Uma fábrica fará uma versão concentrada de um amaciante. A imagem a seguir mostra as medidas das dimensões da embalagem original e da embalagem da versão concentrada.

Considerando que a imagem da embalagem da versão concentrada é semelhante à imagem da embalagem original, determine a medida h da altura da embalagem da versão concentrada.

Etapa 3: Pesquisa sobre dicas para fazer boas compras e produção de guia de bolso sobre consumo.
8. É importante escolher cuidadosamente os produtos que consumimos e buscar fórmas de economizar. O Programa de Proteção e Defesa do Consumidor de São Paulo (procôn-ésse pê) disponibiliza diversos materiais com orientações para que os consumidores realizem boas compras e conheçam seus direitos. Escolham um dos temas a seguir e façam uma lista com as principais dicas para realizar boas compras ou com os direitos do consumidor. Complementem a pesquisa com informações de outras fontes, caso necessário.
• Tema 1: Brinquedo.
• Tema 2: Material escolar.
• Tema 3: Lazer, esporte e cultura.
• Tema 4: Supermercado.
• Tema 5: Eletroeletrônicos e eletrodomésticos.
• Tema 6: Direitos do consumidor.
9. A partir das informações coletadas, elaborem um guia de bolso com as principais informações obtidas sobre consumo consciente e as principais dicas sobre o tema escolhido. Os textos não devem ser extensos e o guia deve ser feito em formato digital ou em uma folha de tamanho a quatro, que será dobrada em duas ou três partes. Não esqueçam de planejar como os textos serão disponibilizados, pensando nas dobras e na facilidade de leitura por quem for utilizar o guia.


Etapa 4: Análise e distribuição dos guias elaborados.
10. Apresentem o guia elaborado pelo grupo para que a turma o analise e faça comentários em relação à clareza das informações e à diagramação dos textos.
11. Anotem as dúvidas, as opiniões e as sugestões dos colegas.
12. Depois dos ajustes necessários, façam cópias do guia e o distribuam para a comunidade escolar.


Etapa 5: Síntese do trabalho realizado.
13. Algumas questões devem ser discutidas.
a) Por que é importante que as pessoas consumam de maneira sustentável?
b) Vocês pretendem mudar algo na fórma como consomem produtos, serviços ou recursos? Se sim, como? Se não, por quê?
14. Redijam um texto que descreva o processo realizado pelo grupo nas etapas 3 e 4.
Respostas e comentários
6. Resposta em Orientações.
7. a) Algumas vantagens: redução do uso de materiais para a produção das embalagens; custos mais baixos para realizar o transporte; diminuição do uso de água e de produtos químicos na fabricação; facilidade de armazenamento nas casas; custo mais baixo para o consumidor.
7. b) 18,75 centímetros
8. Comentários em Orientações.
9. Comentários em Orientações.
Etapa 4: Comentários em Orientações.
13. a) Comentários em Orientações.
13. b) Respostas pessoais.
• A pesquisa proposta na atividade 6 da etapa 2 contribui para que os estudantes possam responder as questões propostas na abertura desta Unidade. Espera-se que eles concluam que consumo consciente é aquele que busca o equilíbrio entre a satisfação pessoal e a sustentabilidade global. Na sequência, forme uma roda de conversa com a turma e pergunte se eles consideram que consomem de fórma consciente e por quê. Depois, apresente para eles algumas ações que estão alinhadas ao consumo consciente, como: economizar papel, comprar somente o necessário, evitar adquirir mercadorias que têm muitas embalagens, levar a própria sacola no momento das compras, evitar o desperdício de alimentos, economizar água ao realizar as tarefas diárias, gastar menos combustível com o carro etcétera. Oriente-os a realizar a pesquisa em mídias, livros, revistas ou sites da internet.
• No item b da atividade 7, se achar oportuno, retome o conceito de semelhança e as estratégias para encontrar medidas em figuras semelhantes. Atribua outras medidas às embalagens (exemplos: largura e altura da tampa) e peça aos estudantes que encontrem a medida correspondente.
• Na atividade 8 da etapa 3, faça um levantamento para verificar qual tópico foi escolhido por cada grupo. Se houver repetições e algum tópico não for escolhido pelos grupos, converse com os estudantes para solicitar que troquem a temática, para que a pesquisa fique mais abrangente. Os temas 3, 4 e 6 favorecem o desenvolvimento da competência geral 8.
• Na atividade 9 da etapa 3, se for possível, disponibilize folhas de papel sulfite para que os estudantes possam fazer o planejamento, fazendo as dobras e anotando quais textos ficarão em cada parte da folha. Oriente-os a pensar em como será a capa do guia de bolso.
A etapa 4 apresenta-se como uma boa oportunidade para os estudantes interagirem e trocarem conhecimentos, o que favorece o desenvolvimento das competências gerais 8 e 9.
• No item a da atividade 13, espera-se que os estudantes citem, principalmente, a preservação do meio ambiente para a sociedade atual e para as gerações futuras.