CAPÍTULO 3 Estudando figuras geométricas

Observe a imagem e responda às questões no caderno.
a) Que figuras geométricas você identifica no grafismo da residência da fotografia?
b) Essas figuras são planas ou não planas?
c) O que mais chamou sua atenção nesses grafismos? Converse com o professor e os colegas.

Na fotografia, vemos a residência de Esther Mahlangu, artista nascida em 1935 e pertencente ao grupo étnico indebele, em Mpumalanga, África do Sul. Sua arte vem da herança artística dos indebele, que é passada de mãe para filha ao longo dos séculos; na cultura indebele, apenas as mulheres se dedicam aos grafismos e artesanatos.
Os grafismos são realizados a mão livre, sem medições ou esboços, baseados em um complexo sistema de sinais e símbolos.
1. Um pouco de história
Originalmente, Geometria foi o nome que os gregos deram à parte da Matemática que estudava a medida (metria) da terra (geo). Trata-se do ramo da Matemática em que são estudadas as figuras e suas características.
A origem da Geometria não é precisa porque não há registros escritos de épocas anteriores a 6000 anos antes de Cristo.
O historiador grego Heródoto (século cinco antes de Cristo) atribuiu aos egípcios a origem da Geometria, pois acreditava que ela tinha sido desenvolvida com a necessidade de fazer novas medições de terras depois de cada inundação provocada pelas cheias do rio Nilo.

Quando o rio Nilo transbordava, as demarcações de algumas propriedades desapareciam; assim que o rio voltava a seu leito normal, era preciso demarcar novamente os limites dessas terras. Esse trabalho era realizado pelos “estiradores de cordas” (agrimensores), que utilizavam os registros feitos antes das inundações e os conhecimentos que tinham de Geometria.
Alguns historiadores, porém, acreditam ser mais provável que os estudos geométricos tenham sido desenvolvidos pela classe sacerdotal egípcia, que, por ser privilegiada, dispunha de tempo para reflexões como essas.
A ideia mais aceita atualmente é a de que a Geometria tenha nascido tanto da necessidade de resolver problemas práticos como da observação e da reflexão sobre números, grandezas e formas.
Por volta de 300 antes de Cristo, o estudioso grego Euclides organizou todo o conhecimento geométrico desenvolvido até então em um texto didático chamado Os elementos. Por mais de dois milênios, foi o fundamento que orientou o ensino desse importante campo de estudo.

2. Figuras planas e não planas
Ao observar os objetos à nossa volta, percebemos que eles apresentam os mais variados formatos. Que formatos você reconhece nos brinquedos mostrados a seguir?
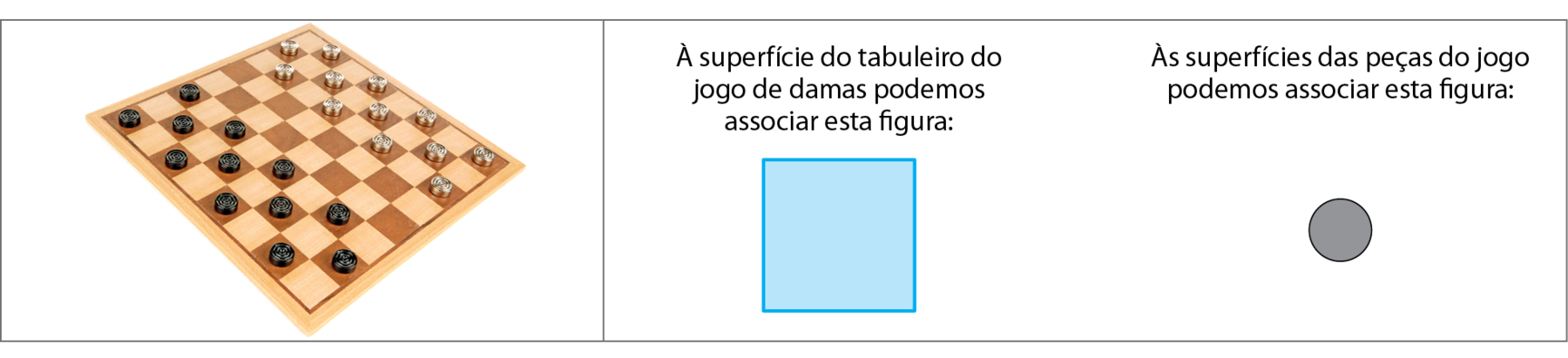
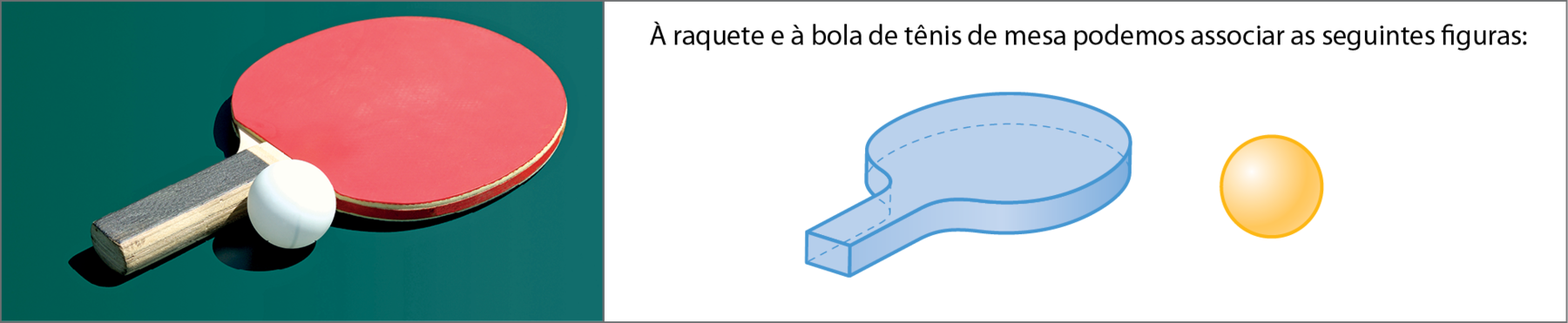
Os brinquedos mostrados são exemplos de objetos que têm características distintas. A cada um desses objetos, podemos associar diferentes figuras geométricas.
(As imagens não respeitam as proporções reais entre os objetos.)
Nos objetos representados, as superfícies do tabuleiro e das peças do jogo de damas dão a ideia de figuras geométricas plaanas, enquanto a raquete e a bola de tênis de mesa lembram figuras geométricas não plaanas. Acompanhe a explicação a seguir sobre figuras geométricas plaanas e não plaanas.

3. Os sólidos geométricos
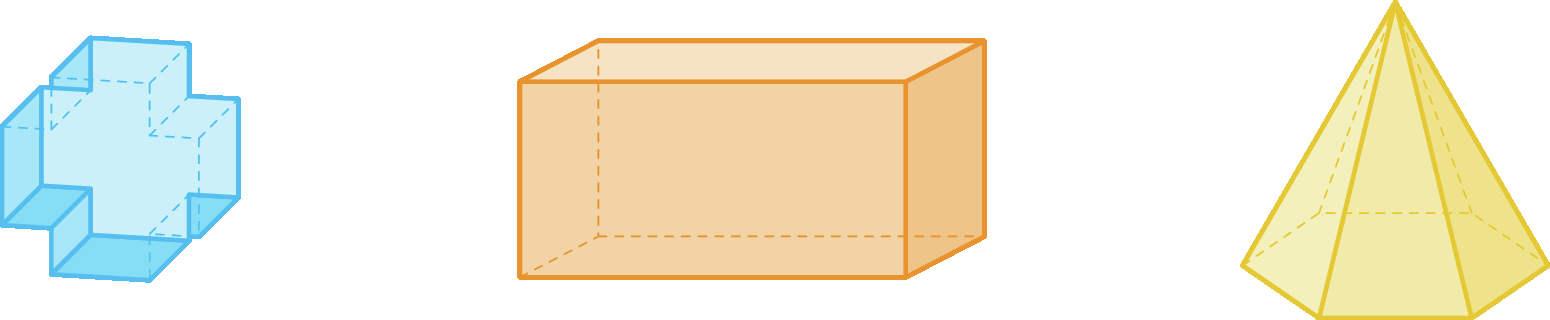
Algumas figuras geométricas não planas são chamadas sólidos geométricos.
Observe, nas fotografias a seguir, como as diferentes formas presentes nas obras de arte dão a ideia de sólidos geométricos.




(As imagens não respeitam as proporções reais entre os objetos.)
Corpos redondos e poliedros
Os sólidos podem ser organizados em grupos, como corpos redondos e poliedros. Essa organização considera a presença ou não de formas arredondadas.
|
Objetos com a forma de corpos redondos |
Objetos com a forma de poliedros |
|---|---|
|
|
|
(As imagens não respeitam as proporções reais entre os objetos.)
Os corpos redondos são sólidos geométricos que têm pelo menos uma parte com fórma arredondada. Observe alguns exemplos.

Os poliedros são sólidos geométricos que não têm fórma arredondada. Observe alguns exemplos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Para cada poliedro, desenhe uma figura plana que represente a parte da sua superfície vista de cima.
a)
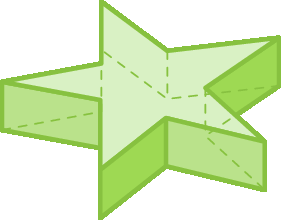
b)
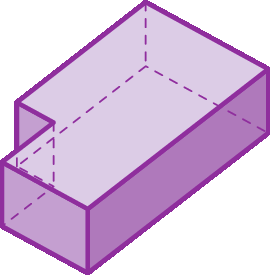
c)
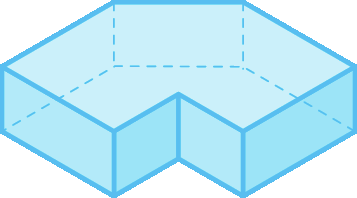
d)

2 Quais dos objetos a seguir dão ideia de um sólido? Quais dão ideia de um poliedro?

(As imagens não respeitam as proporções reais entre os objetos.)
3 Cada sólido representado a seguir é identificado por um número. Use essa identificação para classificar esses sólidos como corpo redondo ou poliedro. No caderno, construa um quadro para organizar as informações.
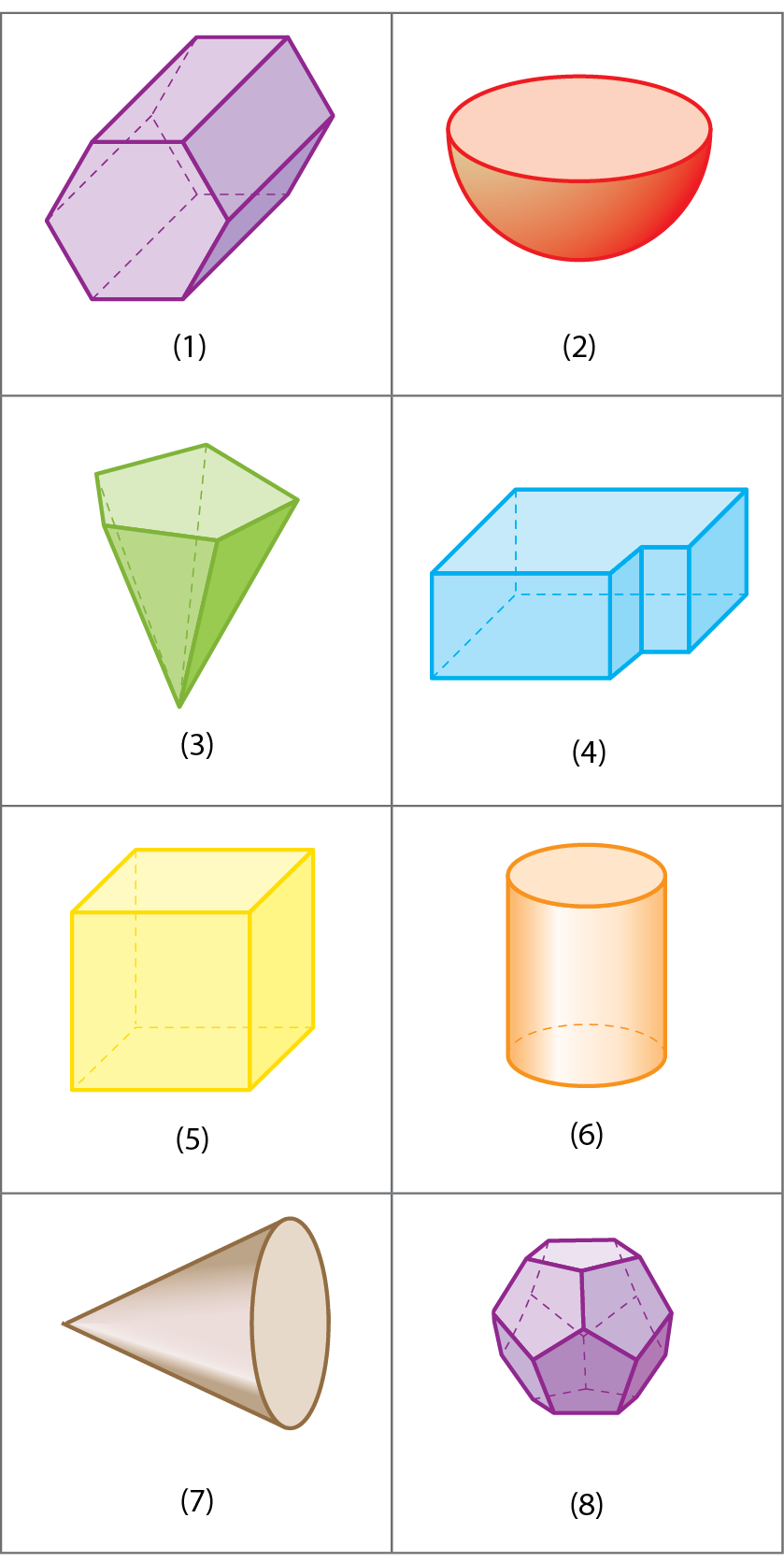
4 Observe o que Paulo e Pedro fizeram com copos descartáveis:
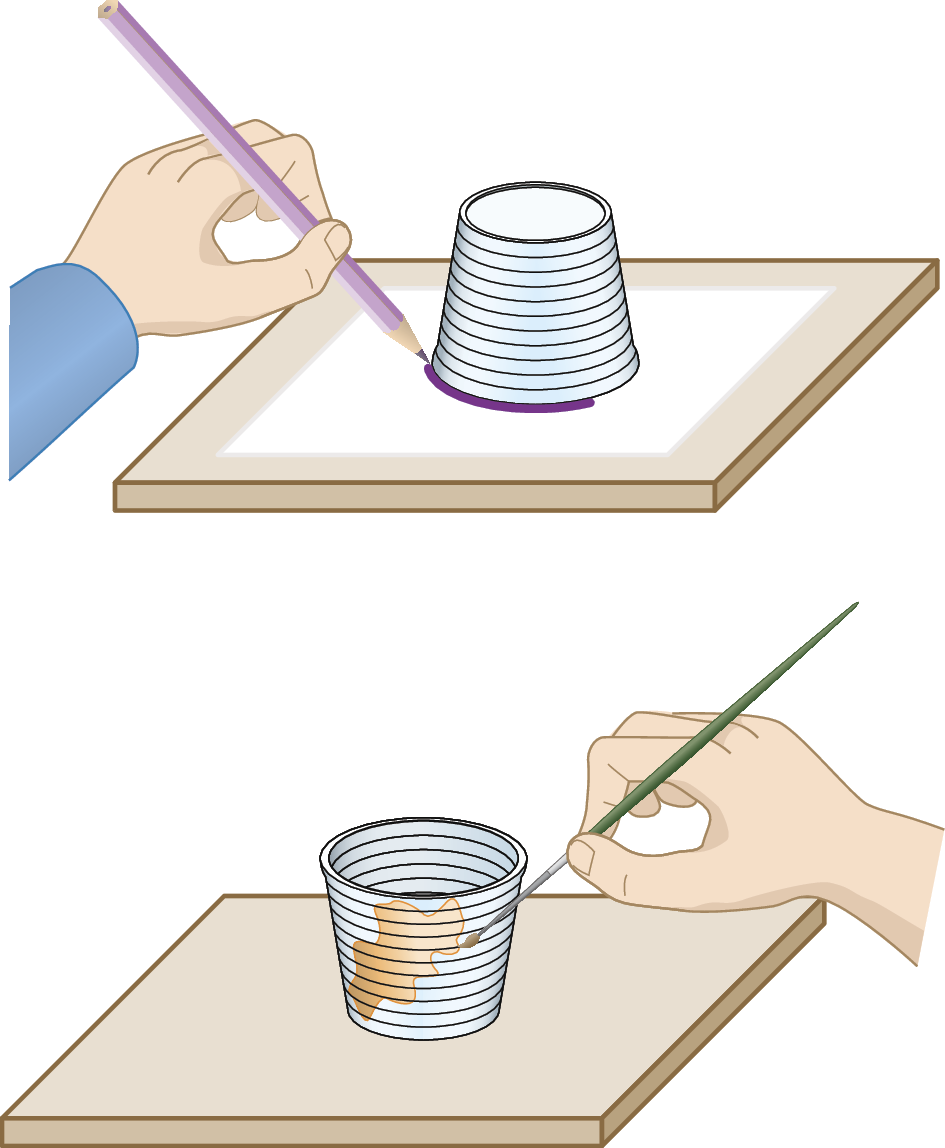
Paulo contornou com lápis a boca do copo sobre uma folha de papel. Pedro pintou toda a parte externa do copo com tinta guache.
a) Qual deles representou uma figura plana?
b) Pedro pintou a superfície de um poliedro?
5 Observe as imagens de um caranguejo e de sua sombra. Qual delas representa uma figura plana?

4. Conhecendo um pouco mais os poliedros
A palavra poliedro é uma composição de poli (muitas) com edro (faces). Portanto, poliedro significa “muitas faces”.
Elementos de um poliedro
Mariana usou um objeto com a fórma de um poliedro e carimbou todos os lados desse objeto em uma folha de papel esticada sobre a mesa, como representado na figura a seguir. Nessa folha, ficaram impressas figuras planas que representam as cinco faces do poliedro.

No objeto é possível observar uma linha comum entre duas faces. Essa linha é denominada aresta. O ponto de encontro de três ou mais arestas chama-se vértice.
No poliedro representado a seguir, as faces estão destacadas em azul; as arestas, em verde; e os vértices, em vermelho.
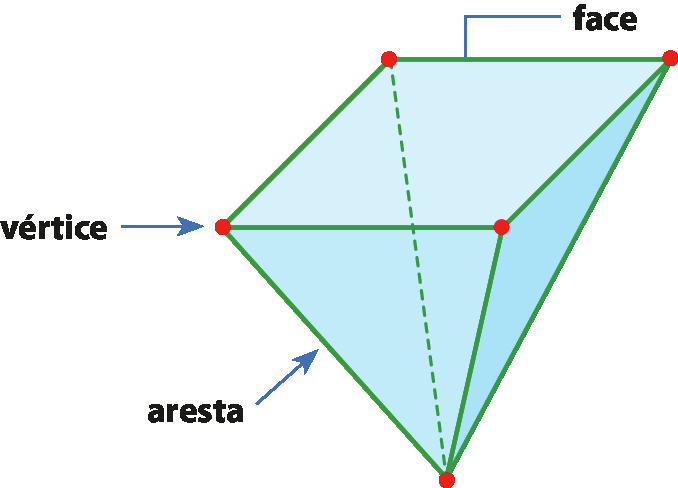
Esse poliedro tem:
• 5 faces;
• 8 arestas;
• 5 vértices.

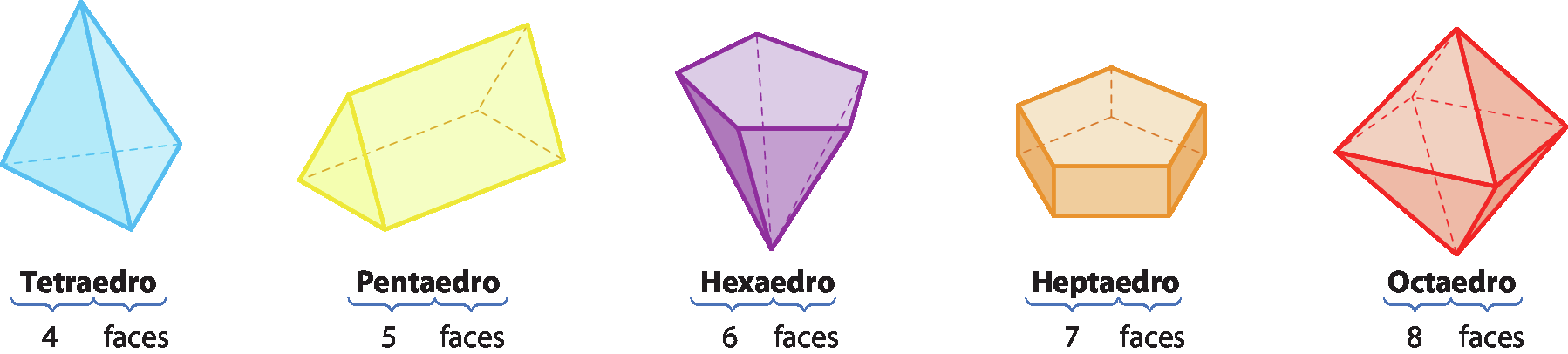
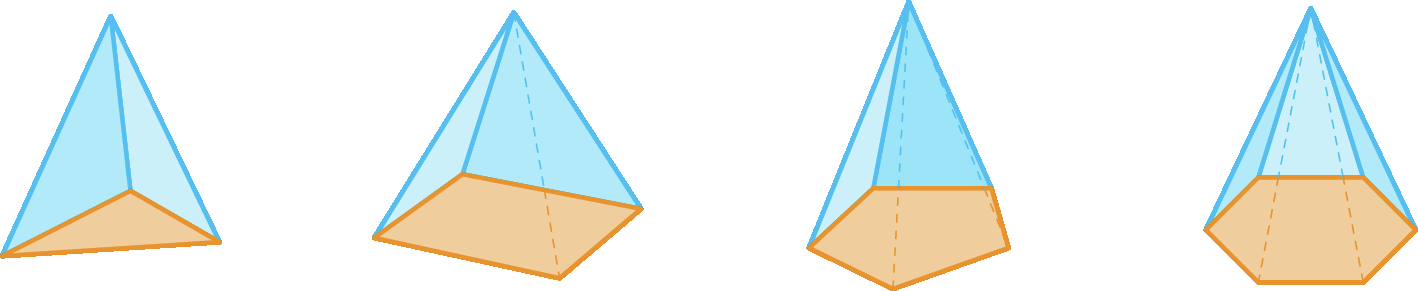
Nomeando poliedros
Os poliedros podem ser nomeados de acordo com o número de suas faces. Observe alguns exemplos.
Muitos poliedros apresentam o mesmo número de faces, mas não possuem a mesma forma. Os poliedros representados a seguir, por exemplo, apresentam o mesmo número de faces, porém têm formas diferentes.
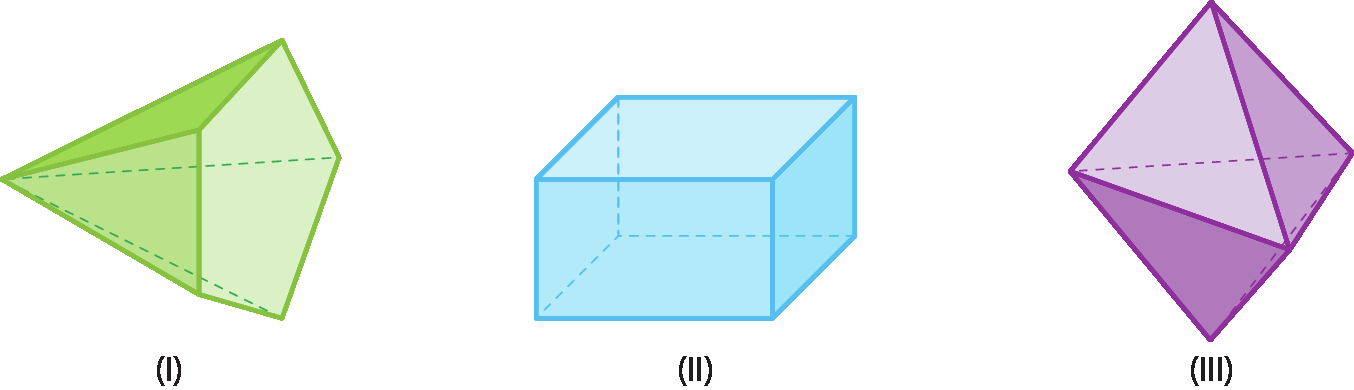
Observe que todos eles têm 6 faces, portanto são hexaedros, mas cada um possui uma fórma diferente. Alguns deles recebem nomes especiais:
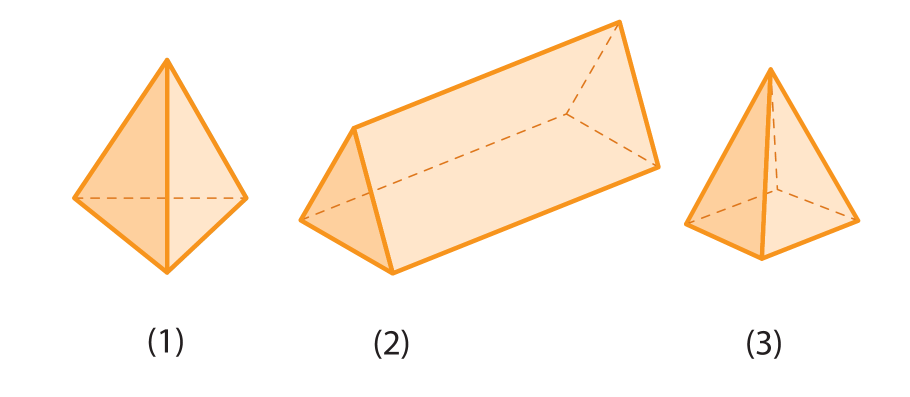
• o poliedro um é uma pirâmide;
• o poliedro dois é um prisma;
• o poliedro três não é pirâmide nem prisma.
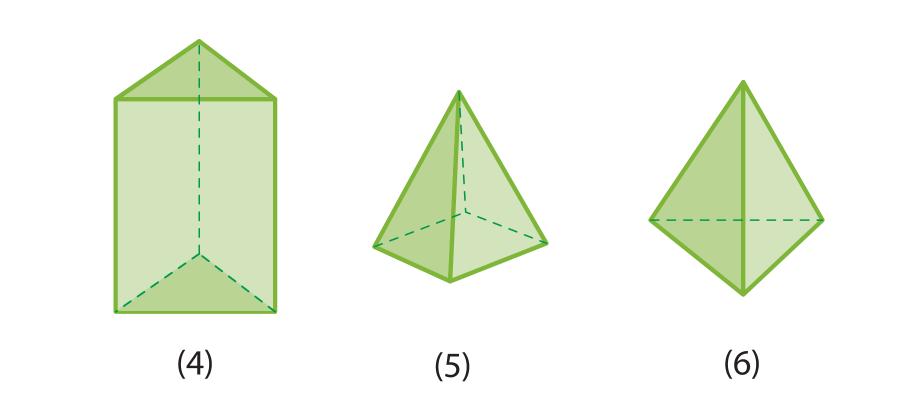
Prismas
Os poliedros representados a seguir são denominados prismas.
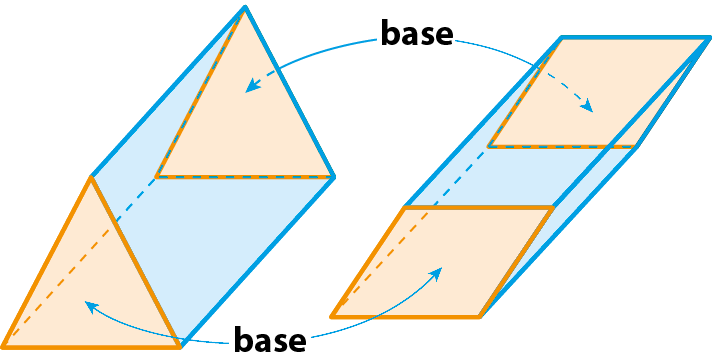
Nesses prismas, estão destacadas as faces chamadas de base; as demais são as faces laterais (que sempre são paralelogramos).
Observação
▶ No segundo prisma da esquerda para a direita, quaisquer duas faces opostas podem ser consideradas bases, e as demais são as faces laterais.
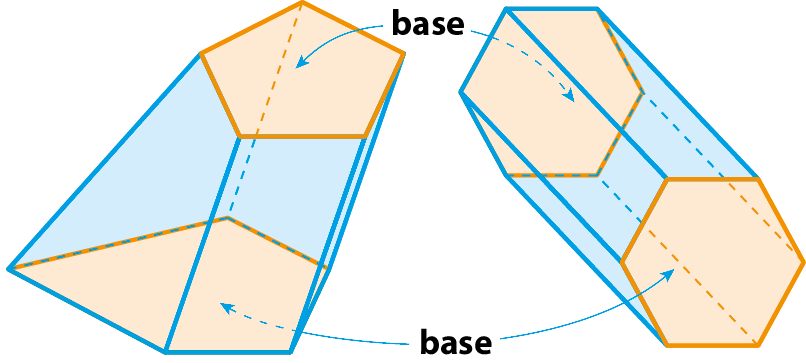
Pirâmides
Considere os poliedros a seguir, denominados pirâmides.
Nessas pirâmides, as faces coloridas de laranja são chamadas base; note que elas podem ter formas variadas. As faces coloridas de azul são as faces laterais, que são sempre triangulares.
Observação
▶ Na primeira pirâmide à esquerda, como todas as faces são triangulares, qualquer face pode ser considerada base, e as demais são as faces laterais.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
6 Em cada linha do quadro a seguir, descubra qual dos poliedros teve suas faces desenhadas.
|
Poliedros |
Faces |
|---|---|
|
|
|
|
|
|
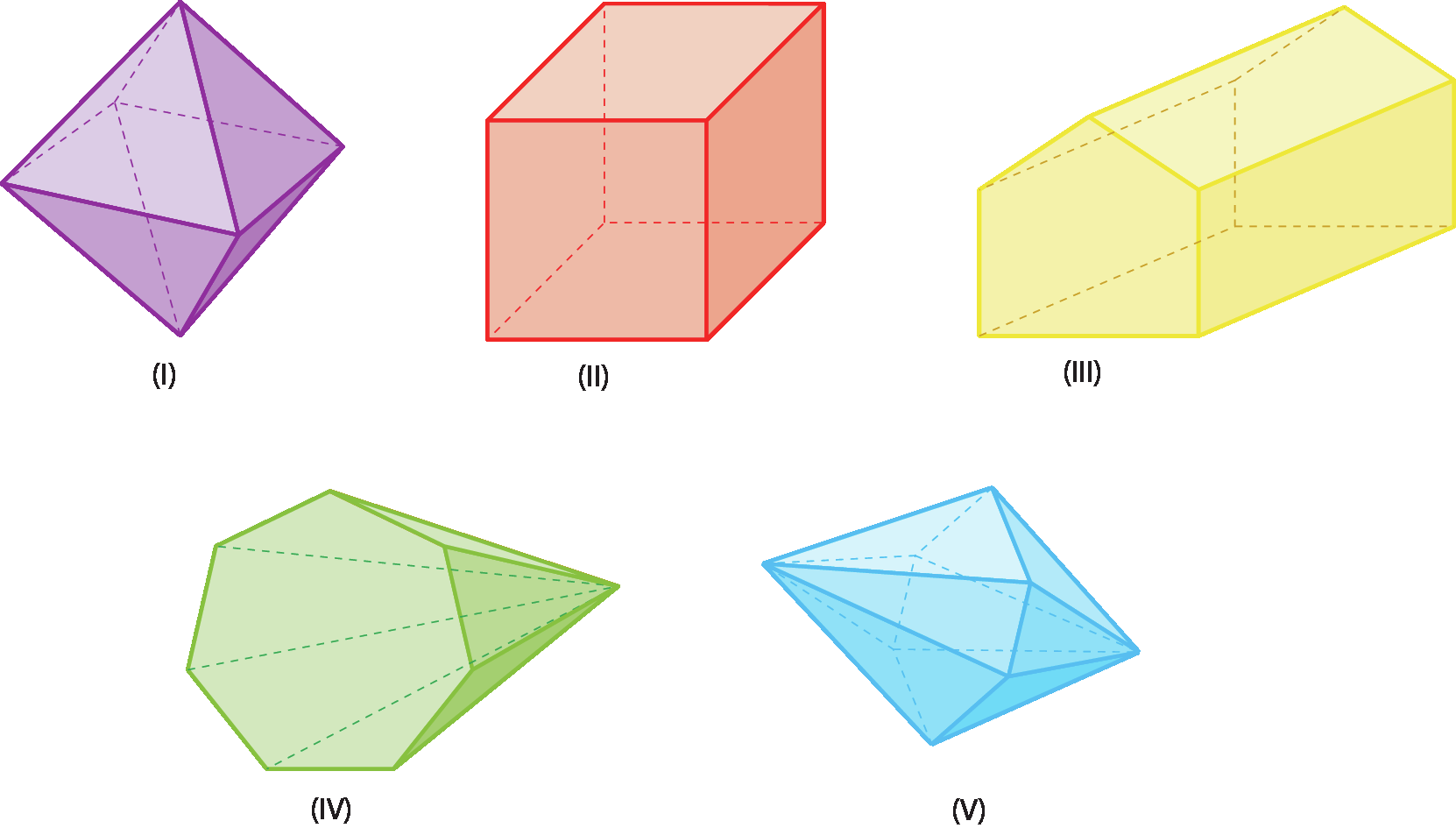
7 Construa no caderno um quadro como o modelo a seguir e complete-o contando o número de faces, de vértices e de arestas dos poliedros um, dois, três, quatro e cinco.

|
Poliedro |
Número de faces |
Número de vértices |
Número de arestas |
|---|---|---|---|
Versão adaptada acessível
7. Separe embalagens ou objetos que tenham a forma de poliedros, por exemplo, caixa de pasta de dentes, caixas de presente, embalagens de alimentos etc. Manipule essas embalagens de modo a identificar suas partes, como bicos, faces e contornos laterais. Com o auxílio do professor, identifique o que poderia ser associado a vértices, faces e arestas.
Conte o número desses elementos e faça um quadro indicando o nome do poliedro associado a cada objeto, e o número de faces, vértices e de arestas do poliedro.
8 Hora de criar – Pesquise e recolha embalagens de diferentes produtos (caixinhas poliédricas ou piramidais, tubos, cones, esferas etcétera). Com elas, construa uma maquete (prédio, trem, escada, pirâmide etcétera). Para cada embalagem usada, identifique o sólido geométrico que ela lembra. Para os poliedros usados, registre em um quadro quantos vértices, arestas e faces eles têm.
TRABALHANDO A INFORMAÇÃO
Interpretando um gráfico de barras
Para saber o número de domicílios com acesso à internet no Brasil, são feitos estudos anuais. O Centro Regional de Estudos para o Desenvolvimento da Sociedade da Informação (Cetic.br) realiza pesquisas anuais desde 2005, mapeando o acesso às tecnologias de informação e comunicação (internet, computadores, telefones celulares, televisão, entre outras) nos domicílios urbanos e rurais do país.
O gráfico de barras da imagem mostra os resultados obtidos em pesquisas como essa.

Observe que, nesse gráfico, o comprimento das barras corresponde à quantidade aproximada, em milhões, de domicílios com acesso à internet em cada ano.
A primeira barra, de baixo para cima, representa o número de domicílios em 2017 e registra o valor 42. Isso significa que, em 2017, 42 milhões de domicílios no Brasil tinham acesso à internet. As demais barras correspondem a dados de outros anos. Desse modo, fazemos a leitura de um gráfico de barras. O comprimento da barra representa a quantidade de vezes que cada informação foi observada na pesquisa.
Podemos fazer algumas interpretações analisando os dados desse gráfico. Por exemplo:
• 2017 foi o ano que apresentou o menor número de domicílios com acesso à internet.
• O período de 2018 a 2019 apresentou um aumento de 4 milhões de novos domicílios com acesso à internet (51 milhões ‒ 47 milhões = 4 milhões).
Pesquisas como essa são importantes para entender melhor algumas características da sociedade brasileira e ajudam os governos a desenvolver políticas públicas para atender às necessidades da população.
Assim, é possível identificar, por exemplo, se os domicílios rurais de determinado município não têm acesso à internet, ou em que regiões do país o acesso à internet precisa ser ampliado.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Com base no gráfico apresentado anteriormente, responda às questões a seguir.
a) Quantos domicílios tinham acesso à internet em 2020?
b) Considerando o aumento de domicílios com acesso à internet que ocorreu de um ano para o ano seguinte, qual é o período que apresenta o maior crescimento absoluto?
c) De quanto foi esse crescimento?
d) Considerando uma média de 2,8 moradores por domicílio, que estimativa se poderia fazer para a quantidade de pessoas com acesso à internet, no domicílio, em 2020?
2 Suponha que, em 2021, o número de domicílios com acesso à internet no Brasil tenha chegado a 71 milhões. Para representar essa informação no gráfico dado, devemos construir uma barra mais larga ou mais comprida do que as outras?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1

Desenhe diferentes figuras geométricas planas e escreva os nomes das que você souber. Converse com um colega para confrontar as respostas. Juntos, completem os nomes que faltarem. Se for necessário, peçam ajuda ao professor.
2

Com massa de modelar, construa algumas figuras geométricas não planas. Junte-se a um colega e conversem sobre as características dessas figuras. Registrem suas conclusões.
3 A figura a seguir mostra uma folha de zinco que, depois de ser curvada, soldada e fechada com tampa e fundo, deu origem a um recipiente.
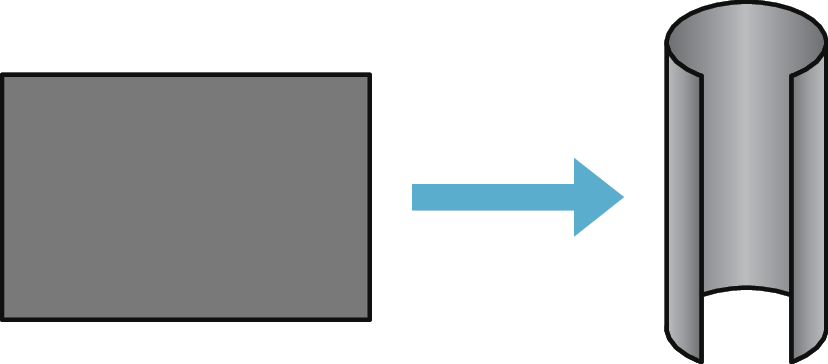
Esse recipiente tem a fórma de um corpo redondo ou de um poliedro?
4 Com massa de modelar, construa alguns modelos de poliedros, separando-os em três grupos: só prismas, só pirâmides e nem prismas nem pirâmides. Caso algum grupo fique sem elementos, construa o que faltar.
5

É possível uma pirâmide ter apenas 3 vértices? Por quê? Converse com um colega e comparem suas respostas.
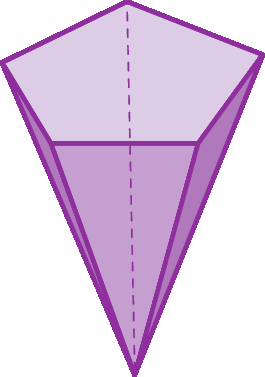
6 Determine o número de faces (F ), de vértices (V) e de arestas (A) destes poliedros:
a)
b)
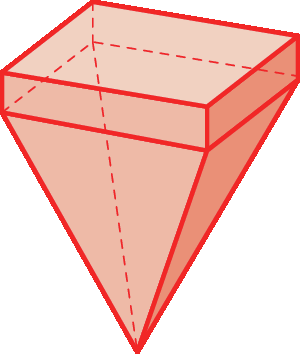
7

Junte-se a um colega e respondam às seguintes questões:
a) Se as bases de um prisma têm 7 vértices cada uma, quantas arestas tem esse prisma? E quantas faces laterais?
b) Se uma pirâmide tem 12 vértices, quantos lados tem sua base? Quantas faces laterais tem essa pirâmide? E quantas arestas?
c) Se uma pirâmide de 20 faces e um prisma têm o mesmo número de vértices, quantas faces tem o prisma?
8 Utilizando papelão ou outro papel de maior gramatura, copie e recorte a figura verde a seguir e tantas figuras rosa quantas forem necessárias para montar um modelo de pirâmide. Usando fita adesiva para colar as partes, construa esse modelo.
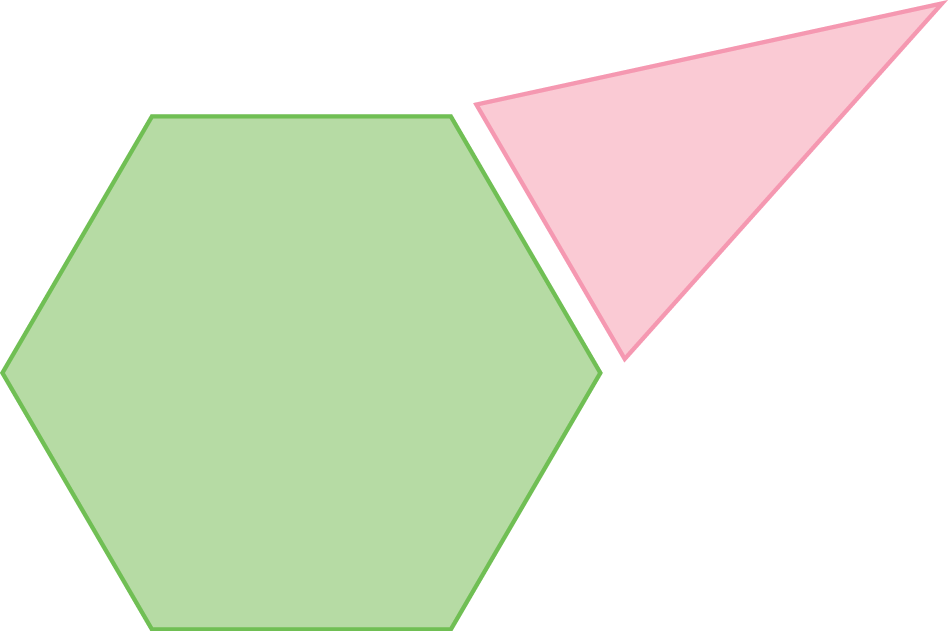
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
9 Do mesmo modo, utilizando papelão ou outro papel de maior gramatura, copie e recorte tantas figuras azuis e amarelas quantas forem necessárias para montar o modelo de um prisma. Usando fita adesiva para colar as partes, faça a construção solicitada.
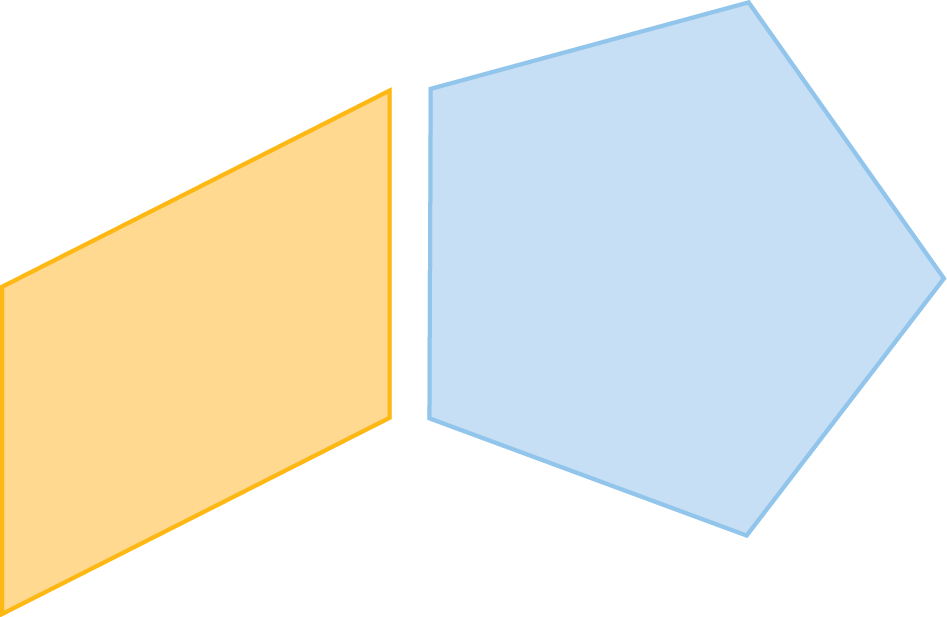
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Que objeto dá ideia de uma figura geométrica plana?
a) Bola de gude.
b) Caixa de sapato.
c) Cartão de visita.
d) Copo de plástico.

(As imagens não respeitam as proporções reais entre os objetos.)
2 Que objeto tem a fórma de corpo redondo?
a) Dado de 6 faces.
b) Livro com duzentas páginas.
c) Pilha.
d) Folha de papel sulfite.
3 Um tetraedro tem:
a) 5 faces.
b) 6 arestas.
c) 8 vértices.
d) 5 arestas.
4 Qual das figuras é uma pirâmide?
a)
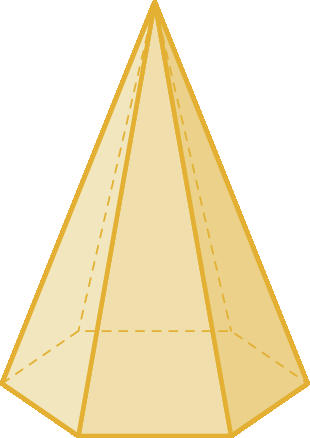
b)

c)
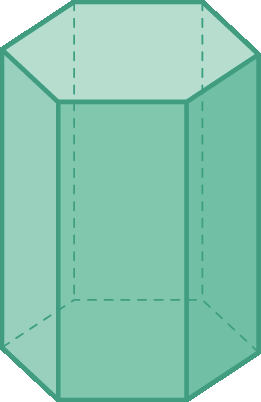
d)
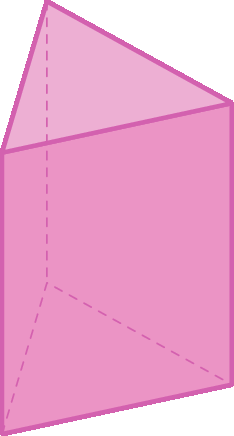
5 Um prisma de base triangular tem:
a) 3 faces.
b) 5 faces.
c) 6 faces.
d) 10 faces.
6 Se uma pirâmide possui 5 arestas na base, o número de vértices dela será:
a) 5.
b) 6.
c) 7.
d) 8.
7 Qual figura pode ser relacionada à sombra de um cone?
a)

b)

c)

d)

8 Analise a imagem do tambor a seguir.

Pode-se associar a fórma desse tambor a um:
a) poliedro.
b) prisma.
c) cilindro.
d) cone.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões.
a) Você estudou diferentes figuras geométricas. Como explicaria o que são figuras planas e não planas?
b) Que tipo de figura são os sólidos geométricos?
c) Dê exemplos de sólidos geométricos que têm pelo menos uma parte arredondada.
d) Que objetos do dia a dia têm a fórma de um poliedro? Cite três exemplos.
e) Quais são os elementos de um poliedro?
f) Dois poliedros que possuam 6 faces terão a mesma fórma? Justifique com dois exemplos.
g) Cite uma diferença entre um prisma de base quadrada e uma pirâmide de base quadrada.
DIVERSIFICANDO
Ampliar e reduzir
Existem algumas técnicas para ampliar e reduzir proporcionalmente um desenho ou uma figura. Um modo simples é dividir o desenho em quadradinhos, como se o tivéssemos colocado em uma malha quadriculada. Depois, basta copiar em outra malha quadriculada o mesmo número de quadradinhos – em tamanho maior, no caso de ampliação, e em tamanho menor, no caso de redução. Acompanhe um exemplo.
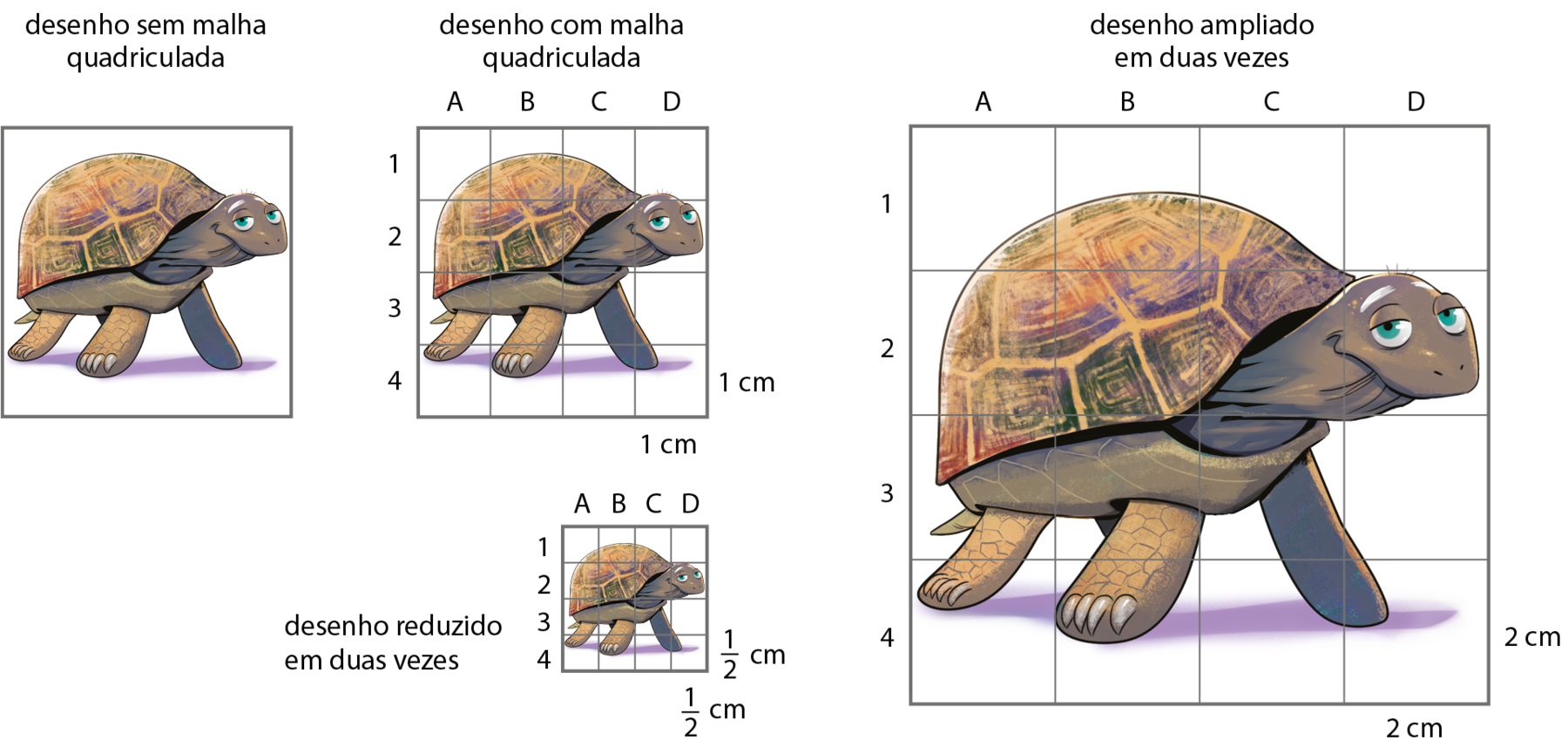
Observe que, para ampliar o desenho em duas vezes, o quadradinho cujo lado media 1 centímetro passou a ter lado medindo 2 centímetros no desenho novo. Para reduzir o desenho em duas vezes, o quadradinho passou a ter lado medindo
Fração. Um meio.centímetro no desenho novo, ou seja, a metade da medida do lado do quadradinho no desenho original. O número de quadradinhos é o mesmo; o que muda é o tamanho deles. Observe que os olhos da tartaruga, que no desenho original estavam na linha 2, coluna D, continuam nessa posição nos novos desenhos.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Mariana quer fazer os enfeites da própria festa com o tema folclore brasileiro. Ela pretende ampliar um desenho do curupira, depois colá-lo atrás da mesa do bolo em uma parede que mede 3 métros por 2 métros. Considerando as medidas indicadas no desenho original, qual será o tamanho máximo que o desenho ampliado de Mariana deverá ter ?

2 Mariana também quer reduzir o desenho para colocar nos pratinhos de doces, que medem 10 centímetros por 10 centímetros. No mínimo, em quantas vezes deve ser a redução?
3 Se Mariana usar a técnica de ampliação/redução descrita, qual poderá ser a medida do lado dos quadradinhos, em centímetro (com número natural), que ficarão sobre o desenho original?