
CAPÍTULO 4 Divisibilidade

Observe, leia e responda no caderno.
a) Qual operação devemos efetuar para verificar que o calendário Tzolkin compreende 260 dias?
b) No calendário Haab, de quantos dias era composto o Tun? E o Haab?
c) O total de dias do Haab é próximo do total anual de dias do calendário (gregoriano) que usamos?
d) Diferentes civilizações da Antiguidade desenvolveram meios para a contagem do tempo. Que necessidades cotidianas podem ter influenciado esse desenvolvimento? Converse com os professores e os colegas.
A mesoamericana civilização maia possuía conhecimentos avançados em astronomia e matemática. Os maias usavam um sistema matemático de base vigesimal (a contagem numérica era feita por múltiplos da sequência de zero a dezenove), no qual os números eram representados por símbolos.
Essa civilização também desenvolveu, por volta do século quatro antes de Cristo, seus medidores de tempo considerando a contagem vigesimal. Entre os vários calendários definidos estava o calendário Tzolkin, baseado no movimento de Vênus e na religiosidade maia e composto de 260 dias, sendo 13 períodos de 20 dias cada um.
Outro calendário, chamado Haab, era composto de um Tun e um Wayeb. O Tun continha 18 períodos (winal) de 20 dias (dia = k’in), e o Wayeb era um período de 5 dias de sacrifício em preparação para o novo Haab.
O uso simultâneo dos calendários Tzolkin e Haab contabilizava um ciclo completo, de 52 anos.
1. Múltiplos e divisores
Ana é artesã e o que mais gosta de fazer são pulseiras. Duas vezes por semana, Roberta vai ao ateliê da mãe para organizar as pulseiras em embalagens e colocá-las no mostruário.

•

Se Ana produzir 25 pulseiras, Roberta conseguiria organizá-las em embalagens com 5 unidades, sem sobrar nenhuma pulseira?
Para fazer essa organização, Roberta pode colocar 5 pulseiras em cada embalagem. Observe a notação que relaciona a quantidade de pulseiras e a quantidade de embalagens.

O número de pulseiras que Roberta anotou no caderno é o resultado da multiplicação do número de embalagens que ela já arrumou por 5 (quantidade de pulseiras em cada embalagem). Observe.
uma embalagem

1 ⋅ 5 = 5
duas embalagens

2 ⋅ 5 = 10
3 embalagens

3 ⋅ 5 = 15
4 embalagens

4 ⋅ 5 = 20
5 embalagens

5 ⋅ 5 = 25
e assim por diante.
Ao fazer essas multiplicações, Roberta verificou a quantidade de pulseiras que já colocou no mostruário.
Os números obtidos — 5, 10, 15, 20, 25, reticências — são denominados múltiplos de 5.
Um número natural é múltiplo de outro se for o resultado da multiplicação desse número por algum número natural.
Quando dividimos esses múltiplos por 5, obtemos resto zero, ou seja, a divisão é exata. Observe.
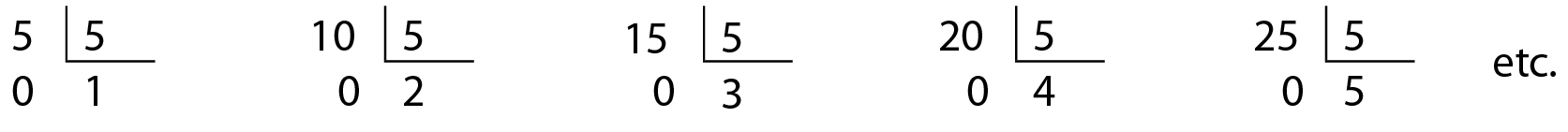
Considerando, por exemplo, a divisão 15 dividido por 5 = 3, dizemos que 15 é divisível por 5. Também podemos dizer que 5 é divisor ou fator de 15, pois a divisão de 15 por 5 é exata (tem resto zero).
Um número natural é divisível por outro quando a divisão do primeiro número pelo segundo é exata.
Em determinado dia, depois de organizar todo o material, Ana perguntou a Roberta quantas pulseiras havia no mostruário.

Ana tinha razão. Observe:
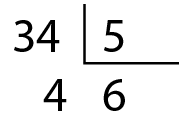
De fato, a divisão não é exata, pois tem resto 4. Nesse caso, dizemos que 34 não é divisível por 5 ou, ainda, que 5 não é divisor de 34. Por isso, 34 não é múltiplo de 5.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Identifique as sentenças verdadeiras, justificando sua resposta.
a) 35 é múltiplo de 7.
b) 180 é divisível por 40.
c) 7 é divisor de 42.
d) 24 é múltiplo de 144.
e) 252 é divisível por 12.
f) 10 é divisor de 5.
g) 69 é múltiplo de 31.
h) 510 é divisível por 34.
i) 17 é divisor de 34.
2 Dê pelo menos quatro exemplos de um número natural em cada item.
a) Múltiplo de 18.
b) Divisor de 18.
3 O número 724 é divisível por 8? Por quê?
4 O pai de Cauê cortou uma cenoura para dar a seu cãozinho. Começou com cortes do talo, desconsiderando a ponta, e finalizou cortando várias fatias, obtendo sempre a mesma quantidade de pedacinhos. Observe quantos pedacinhos ele obteve no primeiro corte.
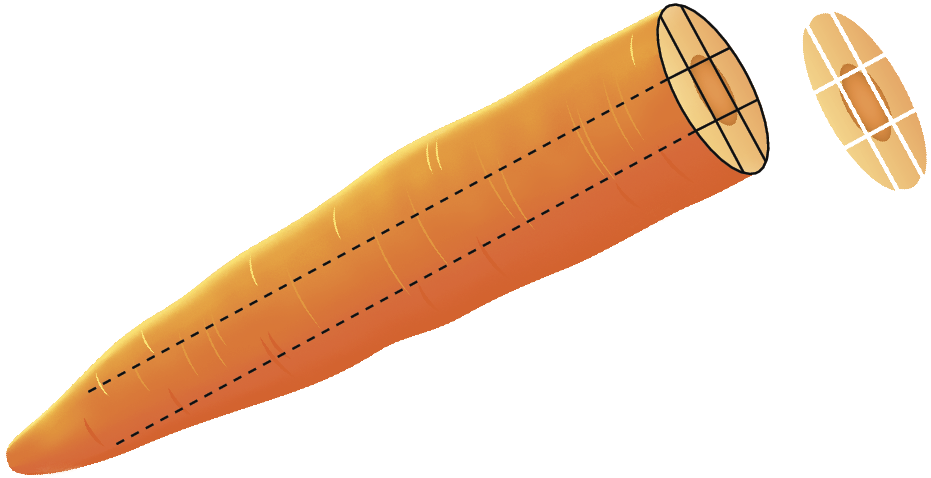
a) O número de pedacinhos de cada fatia é múltiplo de quais números?
b) Quantos pedacinhos serão obtidos em 12 fatias?
Os múltiplos de um número
Para encontrar um múltiplo de um número, basta multiplicá-lo por um número natural qualquer. Por exemplo, calculando 5 vezes 7, obtemos 35, que é múltiplo de 7. Com a sequência dos números naturais, podemos obter tantos múltiplos de 7 quantos quisermos:
0 ⋅ 7 = 0
1 ⋅ 7 = 7
2 ⋅ 7 = 14
3 ⋅ 7 = 21
4 ⋅ 7 = 28
5 ⋅ 7 = 35
e assim por diante.

Observe mais alguns exemplos.
a) Múltiplos de 8: 0, 8, 16, 24, 32, reticências
b) Múltiplos de 15: 0, 15, 30, 45, 60, reticências
c) Múltiplos de 22: 0, 22, 44, 66, 88, reticências
Observações
▶ Se n é um número natural diferente de zero, então:
• esse número tem infinitos múltiplos;
• zero é múltiplo desse número;
• esse número é múltiplo de si mesmo.
▶ O número zero constitui um caso especial. O zero é o único múltiplo de zero, pois qualquer número natural multiplicado por zero resulta em zero. No entanto, não podemos dizer que um número é divisível por zero, porque não existe divisão por zero.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
5 Quais são os números naturais múltiplos do número 1?
6 Determine os cinco primeiros múltiplos de:
a) 3;
b) 6;
c) 21;
d) sua idade.
7 Determine:
a) os múltiplos de 9 menores que 50;
b) os múltiplos de 6 maiores que 20 e menores que 50;
c) os múltiplos de 14 entre 40 e 90;
d) os múltiplos de 10 entre 12 e 50;
e) os múltiplos de 11 maiores que 66 e menores que 111.
8 A professora Mara pediu a um estudante que dissesse o menor múltiplo de 4 e que cada estudante seguinte dissesse um múltiplo de 4 em ordem crescente.

Assim, sem pular nenhum número, cada um dos 35 estudantes da turma teve sua vez de falar. Qual foi a resposta do décimo estudante? E a do vigésimo? E a do último?
9 Duas amigas estão disputando um jogo de desafios matemáticos. Para avançar as casas, é necessário acertar o enigma que está na carta sorteada.
Observe como Beatriz foi desafiada por Sofia.

Descubra você também quantas são as bolinhas da urna.
10 Em uma sala de aula, o número de estudantes presentes é múltiplo de 8. Esse número é maior que 30 e menor que 40. Quantos estudantes estão na sala?
11 Descubra o menor número que devemos adicionar a 90 para obter um múltiplo de 35.
12 Qual é o menor número que devemos subtrair de 90 para obter um múltiplo de 35?
13 Em 1705, Edmond Halley (1656-1742) previu que o cometa visto em 1531, 1607 e 1683 poderia ser visto novamente em 1759. Esse fato se comprovou e, anos depois, o cometa ganhou o nome do cientista. Admitindo que o período da órbita do cometa Halley é de 76 anos, qual será o primeiro ano do século vinte e um em que esse cometa voltará a ser visto?


14


Para obter múltiplos consecutivos de um número natural, precisamos multiplicar esse número por números naturais consecutivos.
Reúna-se com um colega e, usando uma calculadora, respondam às questões a seguir. Não se esqueçam de registrar os cálculos e as conclusões no caderno.
a) Obtenham dez múltiplos consecutivos de 2. Algum desses múltiplos termina em 1, 3, 5, 7 ou 9? Com quais algarismos esses múltiplos terminam?
b) Qualquer número natural que termina em 0, 2, 4, 6 ou 8 é múltiplo de 2? É divisível por 2?
c) Obtenham oito múltiplos consecutivos de 5. Com quais algarismos eles terminam?
d) Qualquer número natural que termina em 0 ou 5 é múltiplo de 5? É divisível por 5?
e) Obtenham seis múltiplos consecutivos de 10. Com que algarismo eles terminam?
f) Qualquer número natural que termina em 0 é múltiplo de 10? É divisível por 10?
15

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre múltiplos e divisores. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Os divisores de um número

Se você pensou no 12, por exemplo, já sabe que 12 é múltiplo de 12, porque 1 ⋅ 12 = 12. E deve ter obtido as divisões:

Como as divisões de 12 por 1 e de 12 por 12 são exatas, você deve ter concluído que 1 e 12 são divisores de 12. Isso ocorre com todos os números naturais diferentes de zero, ou seja:
Todo número natural diferente de zero tem como divisores o número 1 e ele mesmo.
Observe agora como Ivan e Natália fizeram para encontrar os outros divisores de 12.
Resolução de Ivan:

Resolução de Natália:

De acordo com as duas resoluções, concluímos que os divisores de 12 são: 1, 2, 3, 4, 6 e 12.
Observações
▶ O zero não é divisor de nenhum número natural n, não nulo, pois não há número natural que multiplicado por zero resulte em n.
▶ O maior divisor de um número natural diferente de zero é o próprio número.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
16 Responda às questões.
a) Que número é divisor de qualquer número natural?
b) Que número nunca é divisor de um número natural não nulo?
17 Determine os divisores de:
a) 11;
b) 18;
c) 25;
d) 90.
18 Quais são os divisores de 36 que também são divisores de 42? E qual é o maior dos divisores comuns a 36 e 42?
19 Você já reparou que os remédios são preparados para serem tomados a cada 6, 8 ou 12 horas? Por que não são sugeridas doses de 5 em 5 horas, por exemplo?

20 Lucas e Francisco confeccionaram fichas de cartolina contendo números naturais. Enquanto Lucas fez fichas usando os dez primeiros múltiplos de 15, Francisco escreveu todos os divisores de 120. As fichas foram embaralhadas com os números voltados para baixo. Beatriz pegou aleatoriamente, isto é, ao acaso, nove fichas com os números 8, 24, 30, 30, 40, 60, 75, 90 e 120.

a) Quantas fichas foram confeccionadas?
b) Alguma ficha que ficou em cima da mesa contém o mesmo número de alguma ficha que Beatriz pegou?
21 Míriam tem 90 fotografias para colar em seu álbum. Sabendo que cada página deve conter a mesma quantidade de fotografias, responda às questões.
a) Se o álbum tiver 15 páginas, quantas fotografias ela poderá colar em cada página?
b) Ela poderá colar 4 fotografias em cada página? Justifique sua resposta.
c) Quais serão as possíveis quantidades de fotografias de cada página se o álbum tiver mais de 10 e menos de 50 páginas?

22

Reúna-se com um colega, acompanhem o raciocínio e não se esqueçam de registrar as respostas e as conclusões.

a) 42 é um número divisível por 7 porque 42 = 6 ⋅ 7. E o número 28, é divisível por 7? Por quê?
b) Copiem a sentença a seguir substituindo o

pelo número que torna as igualdades verdadeiras.
(42 + 28) = (6 ⋅ 7 +

⋅ 7) = (6 +

) ⋅ 7
c) (42 + 28) é divisível por 7? Por quê?
d) Que propriedade da multiplicação foi usada na última igualdade do item b?
e) Escolham dois números divisíveis por 13. A soma desses números é divisível por 13? Por quê?
23

Hora de criar – Em duplas, cada integrante vai elaborar um problema que envolva os múltiplos e divisores, cuja resposta seja 8. Troquem de caderno para um avaliar o problema do outro. Depois, destroquem para corrigi-los, se necessário.
Pense mais um pouco...
FAÇA A ATIVIDADE NO CADERNO

Agora é sua vez!
Verifique se o número 28 também é perfeito. Justifique sua resposta.
PARA SABER MAIS
Sequências numéricas
Mateus organizou sua coleção de latas de alumínio. Observe como ele fez.

Contando de cima para baixo, obtemos, por meio da quantidade de latas de cada fileira, a seguinte sequência numérica:
1, 3, 5, 7, 9, 11
Cada termo (número) dessa sequência, a partir do segundo, é o anterior mais 2, ou seja:
3 = 1 + 2, 5 = 3 + 2, 7 = 5 + 2,
9 = 7 +2, 11 = 9 + 2
Quando podemos obter os termos de uma sequência usando os termos anteriores, temos uma sequência numérica recursiva.
Acompanhe mais alguns exemplos de sequências numéricas.
• 0, 2, 4, 6, 8, 10, 12, reticências Essa é a sequência dos números pares. Ela é infinita. Como 0 = 0 ⋅ 2, 2 = 1 ⋅ 2, 4 = 2 ⋅ 2, 6 = 3 ⋅ 2, e assim por diante, dizemos que cada termo dessa sequência é múltiplo de 2. Portanto, essa sequência também é conhecida como sequência dos múltiplos de 2. Ela é uma sequência crescente, pois cada número, a partir do segundo, é maior que o anterior. Note que, do segundo número em diante, cada termo pode ser obtido do anterior acrescentando 2. Essa é também uma sequência recursiva.
• Contando as latas de Matheus, das fileiras de baixo para cima, temos 11, 9, 7, 5, 3, 1. Essa sequência é decrescente e finita.
Note que, do segundo número em diante, cada termo pode ser obtido do anterior decrescendo 2. Essa é também uma sequência recursiva.
• 1, 24, 2, 12, 3, 8, 4, 6 Essa é a sequência dos divisores de 24. Ela é finita e, nessa ordem, não é crescente, nem decrescente, nem recursiva. Então, podemos notar que:

Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Determine a sequência:
a) dos números pares menores que 10;
b) dos divisores de 36;
c) dos múltiplos de 4.
2 Qual é a sequência dos números ímpares? Nessa sequência, qual é o termo anterior ao 91? E o posterior ?
3 Os termos de cada uma das sequências a seguir obedecem a certa ordem. Considerando essa ordem, determine o próximo termo.
a) 6, 11, 16, 21
b) 26, 22, 18, 14, 10
c) 3, 6, 12, 24, 48
4 Uma das atividades do famoso matemático Pitágoras era fazer cálculos usando pedrinhas. Um deles consistia em formar sequências numéricas como estas:

Como ele formava o 7elevado a 2 com as pedrinhas? E com a adição de números naturais?
5 Como você relaciona a sequência das latinhas de Mateus com a sequência das pedrinhas de Pitágoras para formar o 6elevado a 2?
2. Critérios de divisibilidade

Divisibilidade por 2
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
É verdade ou mentira na Internet?
[Filha]
Olha, pai, nosso ônibus chegou!
[Pai]
O que você tanto digita nesse celular, filha?
[Filha]
Só estou compartilhando algumas notícias com meus amigos, pai!
[Pai]
Não é melhor verificar primeiro se as notícias são verdadeiras?
[Filha]
Como eu faço isso?
[Pai]
Você pode seguir uma sequência de passos, usando um algoritmo!
[Filha]
O que é um algoritmo?
[Pai]
Como eu disse antes, é uma sequência de passos, de regras, para a resolução de um problema ou a realização de uma tarefa. Por exemplo, como você faz para saber se um número é par?
[Filha]
Ah, essa é fácil! Primeiro, eu divido esse número por 2. Então, se o resto for zero, significa que ele é divisível por 2 e, portanto, um número par. Se a divisão tiver resto diferente de 0, então o número não é divisível por 2 e, portanto, não é par.
[Pai]
Isso mesmo! Você acabou de descrever um algoritmo.
[Filha]
Sério?
[Pai]
E, se eu quiser saber se um número é múltiplo de 6, como eu faço?
[Filha]
Olha só, pai, vou fazer um desenho para te explicar.
Pelos critérios de divisibilidade que eu aprendi na escola, para um número ser múltiplo de 6, ou seja, divisível por 6, ele precisa ser par e divisível por 3 ao mesmo tempo.
O primeiro passo é verificar se ele é par. Se não for par, então não será múltiplo de 6. Mas, se for par, o próximo passo é verificar se é divisível por 3. Se ele não for divisível por 3, o número também não será múltiplo de 6; mas, se for divisível por 3, então, com certeza será múltiplo de 6.
Entendeu, pai?
[Pai]
Perfeitamente! Com seu desenho ficou bem fácil de entender! Aliás, o nome desse esquema que você desenhou é fluxograma!
[Filha]
Fluxograma?
[Pai]
Sim, essa representação gráfica que você desenhou no caderno, com a sequência de passos que devem ser seguidos para determinar se um número é múltiplo de 6,é chamada de fluxograma. Nesse caso, você usou setinhas para separar os passos e indicar sua sequência.
[Filha]
Que legal, pai! Mas… o que isso tem a ver com as notícias?
[Pai]
Quando recebemos uma notícia compartilhada ou fazemos uma busca na Internet, podemos seguir uma série de passos, usar um algoritmo, para saber se aquela notícia é verdadeira ou falsa.
Primeiro, é preciso prestar atenção à data da publicação, para evitar que uma notícia antiga seja compartilhada como atual.
Em seguida, podemos analisar se o texto foi criado para informar um acontecimento ou para influenciar e convencer as pessoas sobre determinado assunto. Uma notícia deve ser um texto informativo e imparcial, que não expressa opinião.
Depois, podemos analisar a linguagem, a forma como o texto é escrito. Notícias falsas costumam ter muitos erros gramaticais e de ortografia, além de usar adjetivos em excesso. Quando isso acontece, é melhor não compartilhar.
Seguimos para o próximo passo: devemos verificar a fonte. O texto, o vídeo ou a fotografia têm fonte? O autor é confiável e tem conhecimento para falar do assunto? Se não tiver fonte ou se não for confiável, então é melhor não compartilhar. Se for de fonte confiável, então podemos compartilhar com mais segurança.
[Filha]
Olha só, pai! Acabei de encontrar no site de uma universidade uma ferramenta desenvolvida por pesquisadores brasileiros para identificar fêique níus com 96% de precisão!
[Pai]
Que maravilha!
[Filha]
A ferramenta foi programada com um algoritmo para realizar a tarefa de identificar notícias falsas. Com essa sequência de passos, a plataforma identifica se um texto tem muitos adjetivos e erros gramaticais e de ortografia, que são comuns nas fêique níus.
Você só precisa copiar e colar o texto da notícia na ferramenta, que ela vai usar esse algoritmo para checar se o texto é falso ou não!
[Pai]
Que interessante! Ferramentas como essa são muito úteis e ajudam bastante! Agora você já sabe o que fazer quando ler uma notícia e quiser compartilhá-la com seus amigos, não é?
[Filha]
Sempre checar a fonte antes, questionando e buscando mais informações!
[Pai]
Isso mesmo! É preciso considerar também os fatos, não só as opiniões. Chegamos à escola! Boa aula, filha!
[Filha]
Obrigada, pai!
Todos os áudios inseridos neste conteúdo são da Freesound
Considere as divisões.
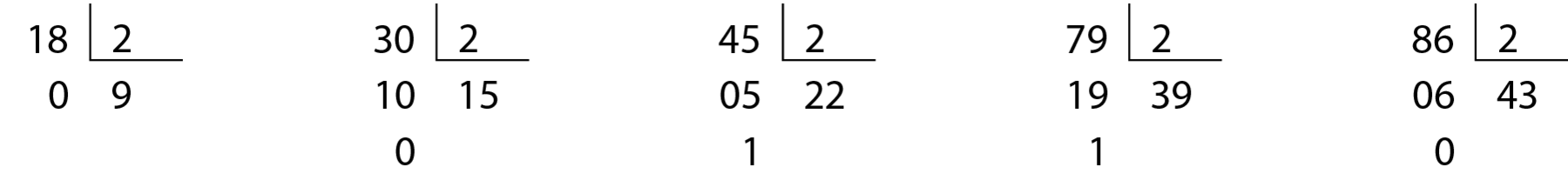
Observe que, quando dividimos números pares por 2, o resto é zero; quando dividimos números ímpares por 2, o resto é 1. Apresentamos apenas alguns exemplos, mas isso acontece sempre que dividimos um número natural por 2.
Observe outros exemplos.
a) .1798 é divisível por 2 e, portanto, é par.
b) .2005 não é divisível por 2 e, portanto, não é par.
c) 147 não é divisível por 2 e, portanto, não é par.
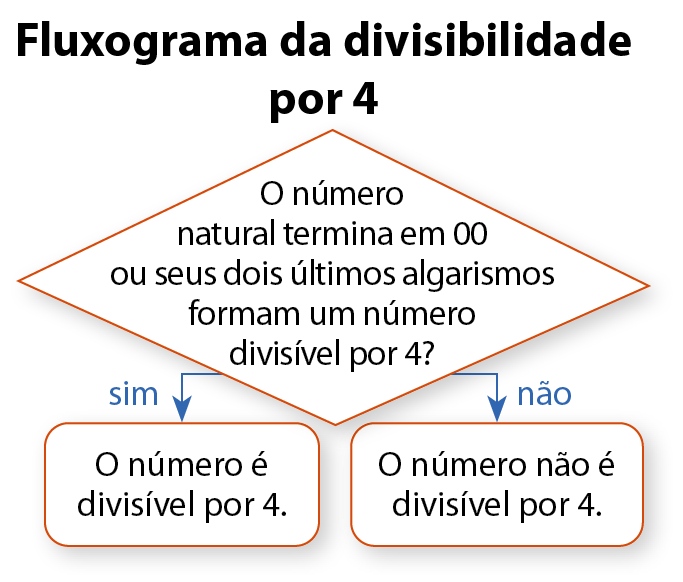
Uma maneira prática de representar um procedimento que apresenta etapas bem definidas é por meio de um esquema chamado fluxograma. O fluxograma ilustrado representa a divisibilidade por 2.
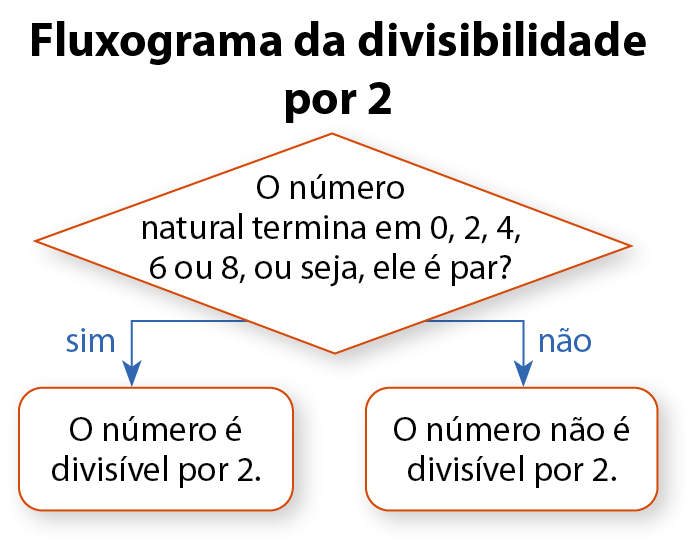
Um número natural é divisível por 2 somente quando é par.
Divisibilidade por 5
Considere as divisões.

Observe que 130, 75, 560 e .4015, que terminam em 5 ou em zero, são divisíveis por 5, enquanto os números 134 e .5107 não são. Esses são apenas alguns exemplos, mas isso acontece sempre.
Observe mais exemplos.
a) 110 é divisível por 5, pois termina em 0.
b) .1345 é divisível por 5, pois termina em 5.
c) 111 não é divisível por 5, pois não termina em 0 nem em 5.
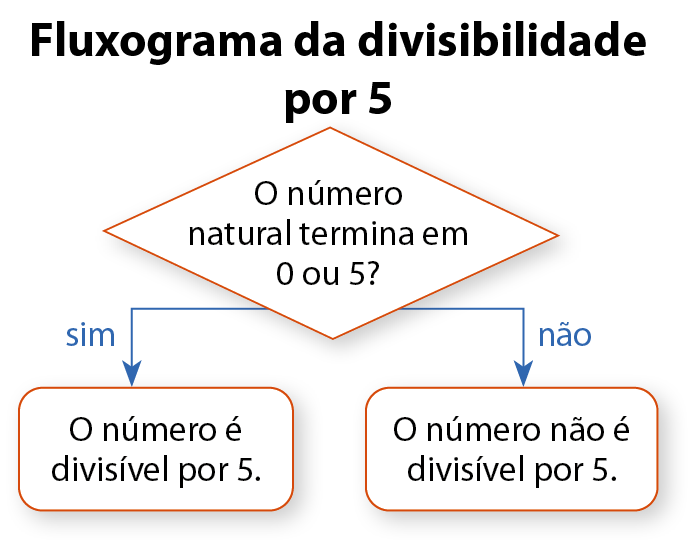
Um número natural é divisível por 5 somente quando termina em zero ou em 5.
Divisibilidade por 10
Considere as divisões.

Observe que 820, .4800 e .1230 são divisíveis por 10, mas os números 504 e 145 não são. Nessas divisões, somente os números que terminam em zero são divisíveis por 10. Apresentamos apenas alguns exemplos, mas isso acontece sempre.
Observe mais alguns exemplos.
a) 250 é divisível por 10, pois termina em zero.
b) .1370 é divisível por 10, pois termina em zero.
c) 827 não é divisível por 10, pois não termina em zero.
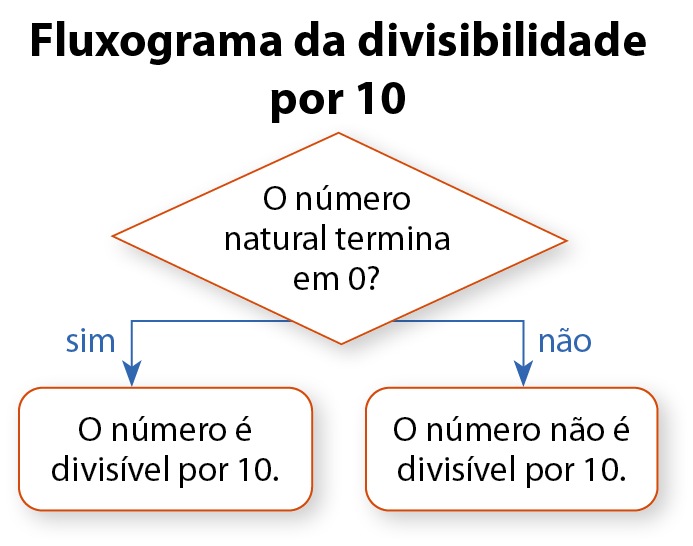
Um número natural é divisível por 10 somente quando termina em zero.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
24 Um número par pode ser divisível por 5? E um número ímpar pode ser divisível por 10? Justifique sua resposta.
25 Qual é o resto da divisão do número .98543 por 2? E por 5? E por 10?
26 Um edifício de 20 andares tem dois elevadores com defeito. Um deles só para nos andares pares; outro, só para nos andares cujo número é múltiplo de 5. Considerando o térreo o andar zero, em quais andares se pode pegar qualquer um desses dois elevadores?
27

Reúna-se com um colega, acompanhem o raciocínio e registrem as resoluções e as respostas no caderno.
a) 130 é divisível por 2 porque 130 = 65 ⋅ 2. E 130 é divisível por 5? Por quê?
b) Substituam os

pelos números que tornam as igualdades verdadeiras.
130 = 13 ⋅ (5 ⋅

) = 13 ⋅ (

⋅ 2) = 13 ⋅

c) 130 é divisível por (5 ⋅ 2 )? Por quê?
d) Todo número divisível por 2 também é divisível por 5? Explique.
e) Escolham um número que seja divisível por 2 e por 5. Ele é divisível por 10? Por quê?
28 Qual é o maior número de três algarismos que é divisível por 5? E qual é o maior deles divisível por 2? E por 10?
29

A escola de Elis realizou uma feira cultural.
a) Em um estande de Matemática, Elis propunha aos visitantes o seguinte desafio:

b) Em outro estande, um colega de Elis fazia outro desafio:

Junte-se a um colega e respondam a essas questões.
30

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre divisibilidade por 2, 5 ou 10. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Divisibilidade por 3
Vamos pesquisar. Na calculadora, escreva alguns números cuja soma dos valores absolutos dos algarismos é divisível por 3. Depois, escreva outros números cuja soma dos valores absolutos dos algarismos não é divisível por 3.

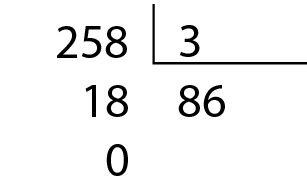
• 258 é divisível por 3;
• a soma dos valores absolutos dos algarismos do número 258 é 2 + 5 + 8 = 15, que é divisível por 3.
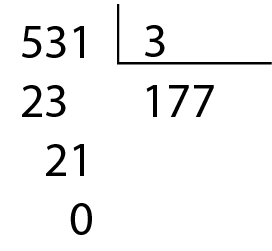
• 531 é divisível por 3;
• a soma dos valores absolutos dos algarismos do número 531 é 5 + 3 + 1 = 9, que é divisível por 3.
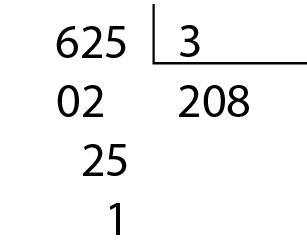
• 625 não é divisível por 3;
• a soma dos valores absolutos dos algarismos do número 625 é 6 + 2 + 5 = 13, que não é divisível por 3.
Observe outros exemplos.
a) 156 é divisível por 3
(1 + 5 + 6 = 12, que é divisível por 3).
b) .1370 não é divisível por 3
(1 + 3 + 7 + 0 = 11, que não é divisível por 3).
Além desses exemplos, sempre é verdade que:
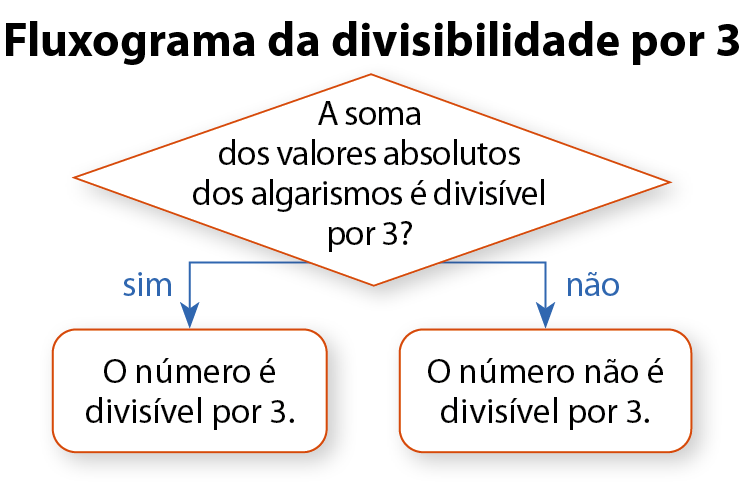
Um número natural é divisível por 3 somente quando a soma dos valores absolutos dos seus algarismos é divisível por 3.
Divisibilidade por 6
Observe os exemplos a seguir.
a) Já sabemos que o número 42 é divisível por 2 e por 3. Ele também é divisível por 6, pois 7 ⋅ 6 = 42.
b) O número 64 é divisível por 2, mas não é divisível por 3. Além disso, ele também não é divisível por 6, pois a divisão de 64 por 6 não é exata.
c) O número 75 é divisível por 3, mas não é divisível por 2. Ele também não é divisível por 6.
Além desses exemplos, sempre é verdade que:
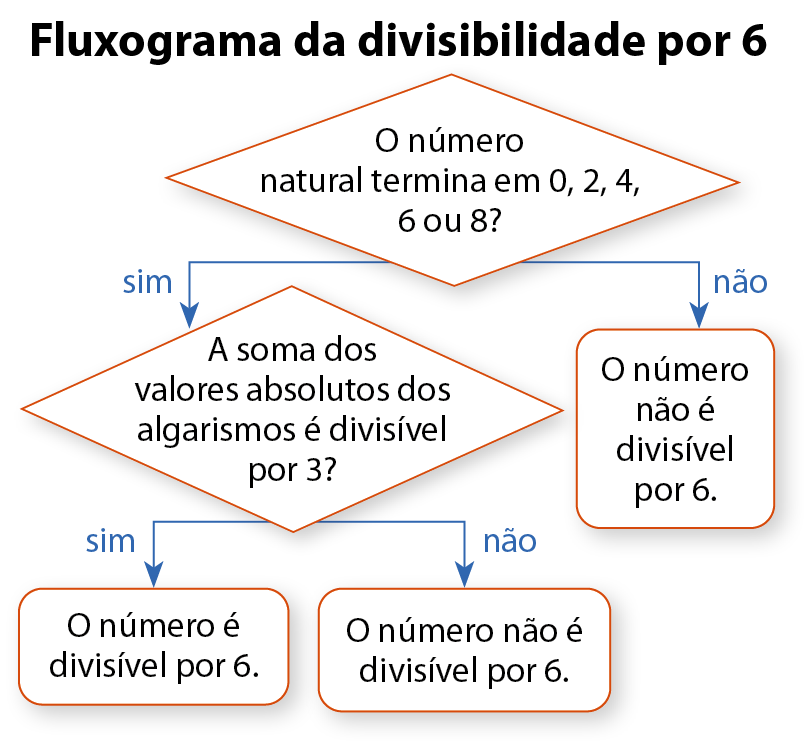
Um número natural é divisível por 6 somente quando é divisível por 2 e por 3.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
31 Dado o número 43

, determine quais algarismos podem ser colocados no lugar de

para que o número formado seja divisível:
a) por 2;
b) por 3;
c) por 6;
d) por 2 e não por 3;
e) por 3 e não por 6.
32 Determine para que valores de

o número 30.6

8 é:
a) divisível por 5;
b) divisível por 3.
Justifique suas respostas.
33 Um número é divisível por 15 quando ele é divisível por 3 e por 5. Quais dos números a seguir são divisíveis por 15?
• 135
• 320
• 363
• 510
• 480
34 Responda e justifique.
a) Se um número é múltiplo de 2, então ele é múltiplo de 6?
b) Se um número é múltiplo de 6, então ele é múltiplo de 2?
35 Em um show de prêmios foi apresentado a um dos candidatos o seguinte desafio:

Que resposta dá o prêmio à candidata?
Divisibilidade por 9
Considere as divisões.
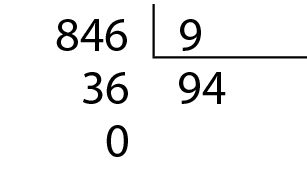
• 846 é divisível por 9;
• a soma dos valores absolutos dos algarismos do número 846 é 8 + 4 + 6 = 18, que é divisível por 9.
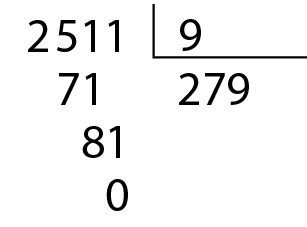
• .2511 é divisível por 9;
• a soma dos valores absolutos dos algarismos do número .2511 é 2 + 5 + 1 + 1 = 9, que é divisível por 9.
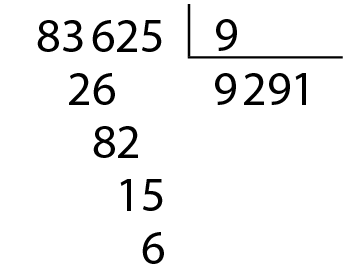
• .83625 não é divisível por 9;
• a soma dos valores absolutos dos algarismos do número .83625 é 8 + 3 + 6 + 2 + 5 = 24, que não é divisível por 9.
Observe outros exemplos.
a) .1566 é divisível por 9 (1 + 5 + 6 + 6 = 18, que é divisível por 9).
b) .2002 não é divisível por 9 (2 + 0 + 0 + 2 = 4, que não é divisível por 9).
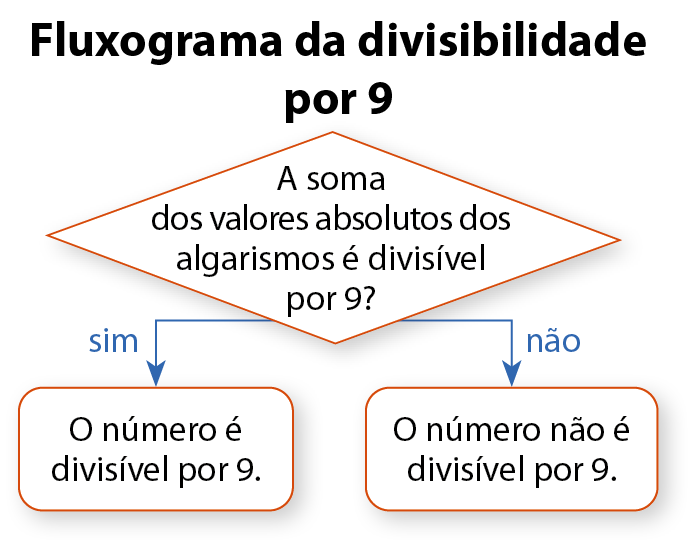
Apresentamos apenas alguns exemplos, mas sempre é verdade que:
Um número natural é divisível por 9 somente quando a soma dos valores absolutos dos seus algarismos é divisível por 9.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
36 Em uma gincana, a equipe vencedora seria aquela que apresentasse primeiro cinco números de três algarismos divisíveis por 9. A equipe amarela saiu na frente com o número 135, mas foi a azul que ganhou. Observe como a equipe azul aproveitou a pista da equipe amarela.

Descubra a estratégia da equipe azul e escreva os dois números que faltam.
37

Discuta as questões com um colega e respondam às perguntas a seguir. O número 567 é divisível por 9, pois 5 + 6 + 7 = 18, que é divisível por 9.
a) De quantas maneiras podemos escrever (5 + 6 + 7) apenas mudando a ordem dos algarismos? A soma continua sendo 18? Que propriedade da adição garante que a soma seja a mesma?
b) Quantos e quais números naturais de três algarismos diferentes, múltiplos de 9, podemos escrever com os algarismos 5, 6 e 7? Eles também são múltiplos de 3?
c) O número .3456 é divisível por 9? Quantos e quais são os números naturais de quatro algarismos diferentes, múltiplos de 9, formados por 3, 4, 5 e 6? Eles também são múltiplos de 3?
d) Se um número natural é divisível por 9, então também é divisível por 3?
Pense mais um pouco...
FAÇA A ATIVIDADE NO CADERNO

Vamos pesquisar curiosidades sobre a divisibilidade por 9.
1 Atribua a x e a y três pares de números com um algarismo, sendo x > y. Por exemplo, x = 7 e y = 2.
Para cada par de números, calcule a diferença dos números formados por xy e yx (exemplo: 72 e 27). A seguir, divida essa diferença por 9 e compare o resultado com x ‒ y. O que você pode concluir?

Compare a sua conclusão com a de um colega.
2 Atribua a x, a y e a z três ternos de números com um algarismo, sendo x > z (exemplo: x = 7, y = 8 e z = 2).
Para cada terno de números, calcule a diferença dos números formados por xis ípsilon zê e zê ípsilon xis. A seguir, divida essa diferença por 99 e compare o resultado com o número formado por algarismos dados por (x ‒ z) . O que você pode concluir? Compare a sua conclusão com a de um colega.
Divisibilidade por 4
Considere as divisões.
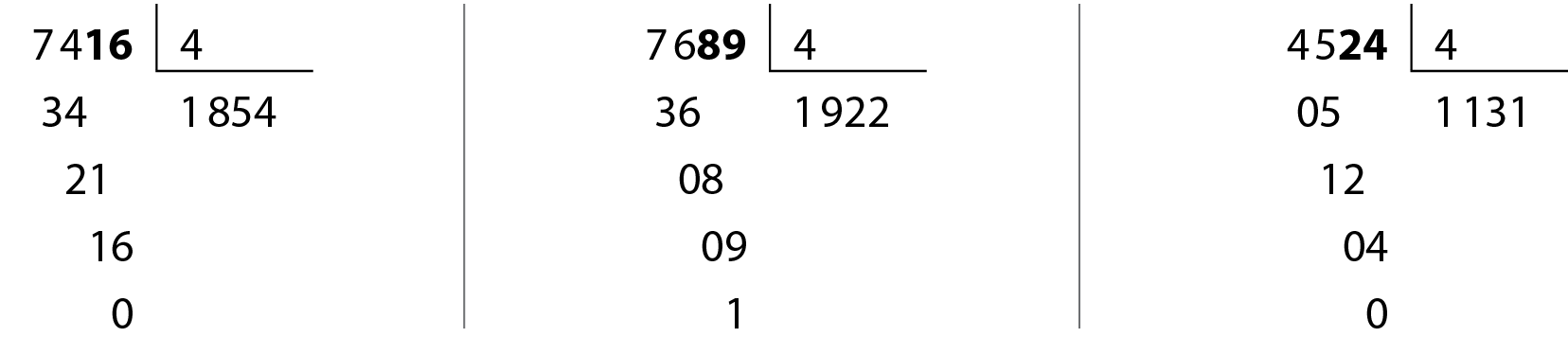
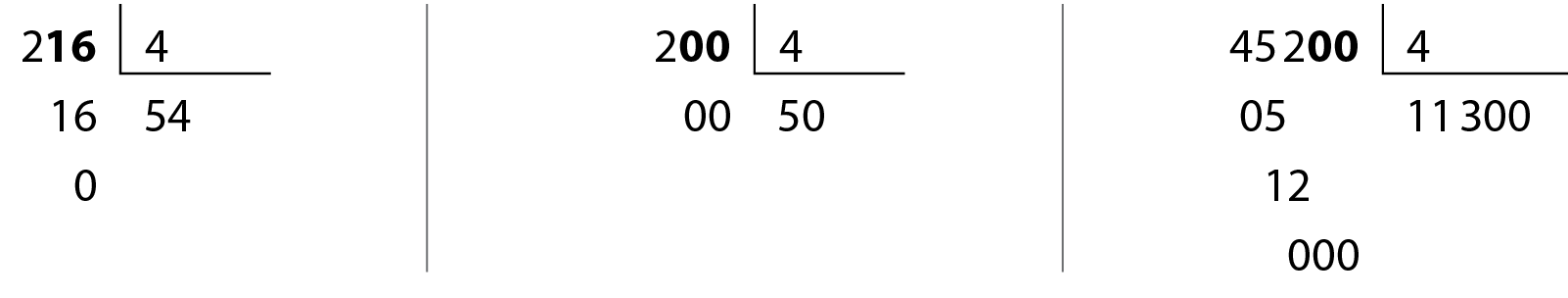
As divisões anteriores nos levam a concluir que:
• .7416, .4524 e 216 são divisíveis por 4. Verifique que 16 e 24 também são.
• .7689 não é divisível por 4. Verifique que 89 também não é.
• 200 e .45200 são divisíveis por 4 e terminam em 00.
Apresentamos apenas alguns exemplos, mas sempre é verdade que:
Um número natural é divisível por 4 somente quando termina em 00 ou quando o número formado por seus dois últimos algarismos à direita é divisível por 4.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Os rapazes 1, 2, 3 e 4 namoram uma das garotas a, B, C e D.
Observe atentamente os textos e as placas com o final dos números dos telefones e diga qual é o nome das quatro garotas e quem são seus respectivos namorados.


EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
38

Verifique mentalmente quais dos números a seguir são divisíveis por 4.
a) 932
b) .1040
c) 842
39 Em um restaurante, todas as mesas têm 4 lugares. É possível que a capacidade desse restaurante seja de 314 lugares? E de 308?
Justifique suas respostas.
40 Determine o menor número que somado a .5314 resulta em um número:
a) divisível por 2;
b) divisível por 3;
c) divisível por 4;
d) divisível por 5;
e) divisível por 6;
f) divisível por 9.
41 Qual é o menor número natural diferente de 1 que dividido por 3, 4 ou 5 dá resto 1?
42

Vimos que um número natural é divisível por 2 quando termina em 0 ou quando o número formado pelo último algarismo é divisível por 2. Também vimos que um número natural é divisível por 4, que é 2 ⋅ 2, quando termina em 00 ou quando o número formado pelos dois últimos algarismos é divisível por 4. Com um colega, escrevam vários números que terminam em 000 ou que o número formado pelos três últimos algarismos seja divisível por 8, que é 2 ⋅ 2 ⋅ 2.
a) Verifiquem que esses números são divisíveis por 8.
b) Elaborem o fluxograma da divisibilidade de um número natural por 8.
43

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre divisibilidade. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
3. Números primos
Existem números que têm somente dois divisores distintos (diferentes). O número 5 é um deles. Seus divisores são apenas o 1 e o 5.
Número primo é todo número que tem apenas dois divisores naturais distintos: o número 1 e o próprio número.
Por exemplo, os números 2, 3, 5, 7, 11, 13, reticências são números primos.
Existem também números naturais que têm mais de dois divisores distintos. O número 12 é um deles. Seus divisores são 1, 2, 3, 4, 6 e 12.
Todo número natural que tem mais de dois divisores distintos é chamado de número composto.
Por exemplo, os números 4, 9, 10, 15, 94 e 105 são números compostos.
O número 1 não é primo nem composto, pois tem um único divisor natural, que é ele mesmo.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
44 Classifique os números a seguir em primo ou composto.
a) 14
b) 11
c) 17
d) 21
e) 296
f) 37
45 Existe um número que é par e é primo ao mesmo tempo. Que número é esse? Existem outros números nessas condições?
46 Observe o calendário do mês de março de determinado ano.

a) Há algum domingo representado por um número primo? Em caso afirmativo, qual?
b) Quantos fins de semana (sábado e domingo, simultaneamente) existem nesse mês cujos dois dias são representados por números primos?
c) Qual dia da semana desse mês é representado por uma quantidade maior de números primos?
47 Existe algum múltiplo de 3 que seja primo? Em caso afirmativo, qual?
48 Existe algum múltiplo de 3, diferente de 3, que seja primo? Justifique sua resposta.
49 A soma dos algarismos de um número é 27. Esse número é primo? Por quê?
50 Qual é o menor número de dois algarismos que é primo? E qual é o maior?
51 Considere os números 7, 10, 35, 41, 75 e 77.
a) Determine todos os divisores de cada um desses números.
b) Construa uma tabela com duas colunas e sete linhas, registrando os números e as suas quantidades de divisores.
c) Construa um gráfico de colunas correspondente a essa tabela.
d) Qual desses números apresenta maior quantidade de divisores?
e) Entre os números apresentados, existem números primos? Em caso afirmativo, quais? Justifique.
52

Reúna‑se com um colega, leiam o texto a seguir e façam, no caderno, o que se pede.

Em 1742, da troca de cartas entre dois matemáticos, Christian Goldbach e Leonard Euler, surgiu a conjectura de Goldbach: “Todo número par, maior que dois, é a soma de dois primos”.
Observem alguns exemplos:
138 = 37 + 101; 974 = 313 + 661
a) Pesquisem em um dicionário e escrevam o significado da palavra conjectura.
b) Essa conjectura vale para os dez primeiros números pares maiores do que 2?
c) Mostrem que essa conjectura vale para o número 200. Agora respondam: Há mais de uma maneira de escrever o número 200 como soma de dois números primos?
d) Agora, cada um deve escolher um número par de três algarismos para o outro verificar essa conjectura.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO


Sabendo que Pedro tem mais de 20 anos e menos de 50 anos, descubra a idade dele hoje.
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Eratóstenes e os números primos
Duração: 5:38min. Página: 100.
>> [Locutor] Eratóstenes e os números primos
>> [Narrador] Antes de a ciência, tal como a conhecemos hoje, estar separada por áreas, os cientistas eram filósofos, astrônomos, físicos, matemáticos... [tom enfático] tudo ao mesmo tempo! Um desses pensadores foi Eratóstenes.
>> [Narrador] Eratóstenes nasceu no ano 276 antes de Cristo, na cidade de Cirene, na atual Líbia, e completou seus estudos em Atenas, na Grécia antiga. Era matemático, poeta, gramático, geógrafo, bibliotecário e astrônomo.
>> [Narrador] Ele foi o bibliotecário-chefe da [tom enfático] famosa Biblioteca de Alexandria e tornou-se conhecido por ser a primeira pessoa a calcular [tom enfático] corretamente a medida do comprimento da circunferência da Terra. É conhecido pelo Crivo de Eratóstenes, o primeiro método desenvolvido para encontrar números primos.
>> [Narrador] De acordo com esse método, para encontrar todos os números primos até 100, por exemplo, basicamente devemos escrever todos os números inteiros de 2 a 100 em um papel. O número 2 é o primeiro número primo da lista, então, o pintamos de verde.
>> [Narrador] Como próximo passo, pintamos de vermelho todos os múltiplos do número 2: o 4, o 6, o 8, o 10, o 12, e assim por diante.
>> [Narrador] Como todos esses números são divisíveis, também por 2, eles não são primos.
>> [Narrador] Seguimos o processo com o 3. Ele é primo, logo, o pintamos de verde e, depois, pintamos todos os seus múltiplos de vermelho.
>> [Narrador] Alguns já estarão pintados, como o 6, mas outros não, como o 9. Pintamos, então, o 9, o 15, e os demais múltiplos de 3.
>> [Narrador] O próximo número seria o 4, que já está pintado. Continuamos, então, com o 5, que é primo. E assim por diante...
>> [Narrador] Quando terminarmos, os números pintados de verde serão os primos.
>> [Narrador] Se antigamente os números primos já fascinavam o mundo com a sua estrutura particular, hoje eles são cruciais para os sistemas de segurança informática. A proteção dos nossos dados pessoais e de nossas contas bancárias [tom enfático] depende deles!
>> [Narrador] Mesmo atualmente, não existem técnicas computacionalmente eficientes para encontrar todos os números primos. Elas são variações daquele primeiro método elaborado por Eratóstenes.
>> [Narrador] Euclides demonstrou que existem infinitos números primos, e esse procedimento é eficiente para encontrar todos os primos menores do que um certo número.
>> [Narrador] Nosso problema hoje em dia é que, mesmo conhecendo muitos números primos, queremos sempre saber qual será o seguinte.
>> [Narrador] Aqui, a técnica é falha, pois não existe uma fórmula para encontrar números primos muito grandes.
>> [Narrador] O que fazemos, então, é procurar, número por número, todos os possíveis divisores de cada um.
>> [Narrador] Se, após testar um determinado número, o computador não encontrar nenhum divisor que não seja 1 e ele próprio, então, esse número pode ser considerado primo!
>> [Narrador] A isto se chama aplicar [tom enfático] força bruta computacional.
>> [Narrador] A dificuldade para encontrar novos números primos é [tom enfático] tão grande que essas descobertas tornaram-se muito raras e costumam até ser [tom enfático] noticiadas!
>> [Narrador] Um dos mais recentes números primos descobertos — e o [tom enfático] maior até então — foi encontrado em dezembro de 2018 e tem aproximadamente 25 milhões de dígitos. [Tom enfático] Dígitos!
>> [Narrador] Ele foi encontrado pelo projeto GIMPS, uma iniciativa aberta para qualquer um que deseje participar da busca por números primos.
>> [Narrador] Por conta dessa dificuldade, os números primos se tornaram tão importantes para os sistemas de segurança da informação.
>> [Narrador] Se eu tenho dois números primos grandes, é fácil calcular o produto deles. Mas se conheço apenas esse produto, é difícil encontrar os dois números primos que o geraram.
>> [Narrador] Esta é a base teórica do sistema de criptografia RSA, assim chamado graças às iniciais dos sobrenomes dos seus criadores: Rivest, Shamir e Adleman.
>> [Narrador] Esse sistema é um dos mais utilizados no mundo. Por meio dele, uma pessoa oferece abertamente a chave pública dela, composta pelo produto de dois números primos.
>> [Narrador] Isso pode acontecer por meio de um aplicativo de [tom enfático] conversa, por exemplo! Quem quiser enviar uma mensagem a ela usa esse número para criptografar seu recado.
>> [Narrador] Como só o dono da chave conhece os dois números primos originais em que ela se baseia, só ele pode utilizá-los para descriptografar e ler a mensagem que recebeu.
>> [Narrador] Se alguém mais quiser acessar essa mensagem, precisará primeiro encontrar os números primos que compõem a chave.
>> [Narrador] A ideia é que essa operação levaria tanto tempo que o conteúdo da mensagem já terá perdido a relevância quando ela for [tom enfático] finalmente decifrada!
Créditos
Studio Núcleo de Criação
Decomposição em fatores primos
Todo número natural composto pode ser decomposto em um produto de dois ou mais fatores diferentes de 1. Observe, por exemplo, algumas decomposições do número 36:

Vamos prosseguir, decompondo os fatores que são números compostos também em um produto de dois fatores, até que fiquem somente fatores primos:
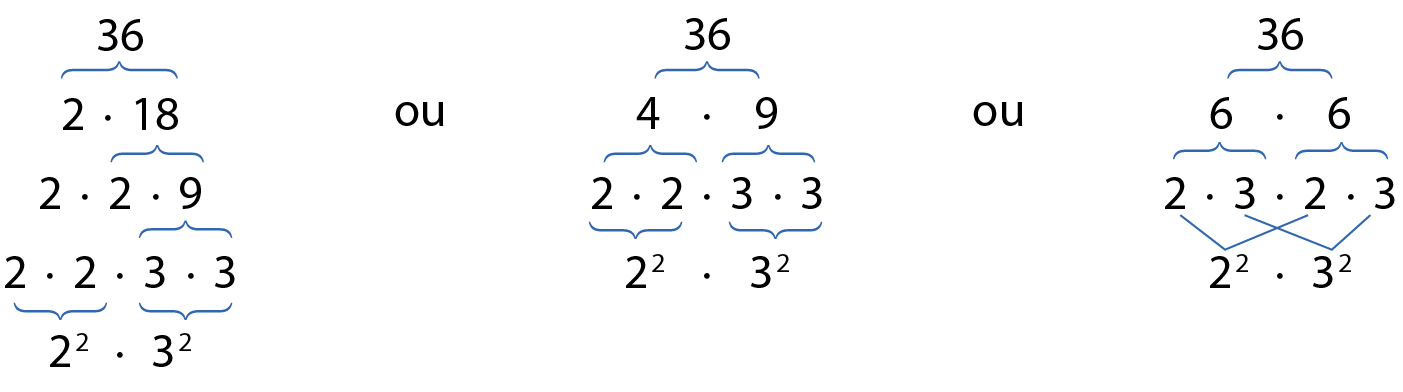
Quando um número está decomposto em um produto em que todos os fatores são números primos, dizemos que esse número está decomposto em fatores primos.
Portanto, o produto 2 elevado a 2 ⋅ 3 elevado a 2 é a decomposição em fatores primos do número 36.
Observe que pode haver diferentes maneiras de decompor um número natural em um produto de dois ou mais fatores, mas a decomposição em fatores primos é única.
Para efetuar a decomposição, pode‑se dividir o número dado pelo seu menor divisor primo. Depois, procede‑se da mesma maneira com o quociente obtido, até encontrar o quociente 1.
Acompanhe alguns exemplos de como decompor o número 60 em fatores primos:


Podemos escrever: 60 = 2 ⋅ 2 ⋅ 3 ⋅ 5 ou 60 = 2elevado a 2 ⋅ 3 ⋅ 5
Também podemos efetuar a decomposição do número 60 dos seguintes modos.
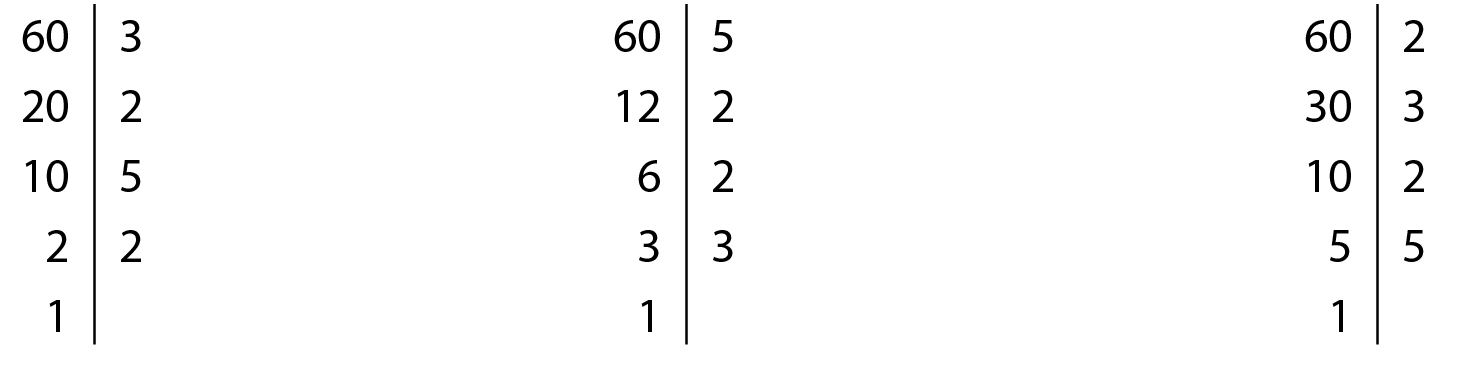
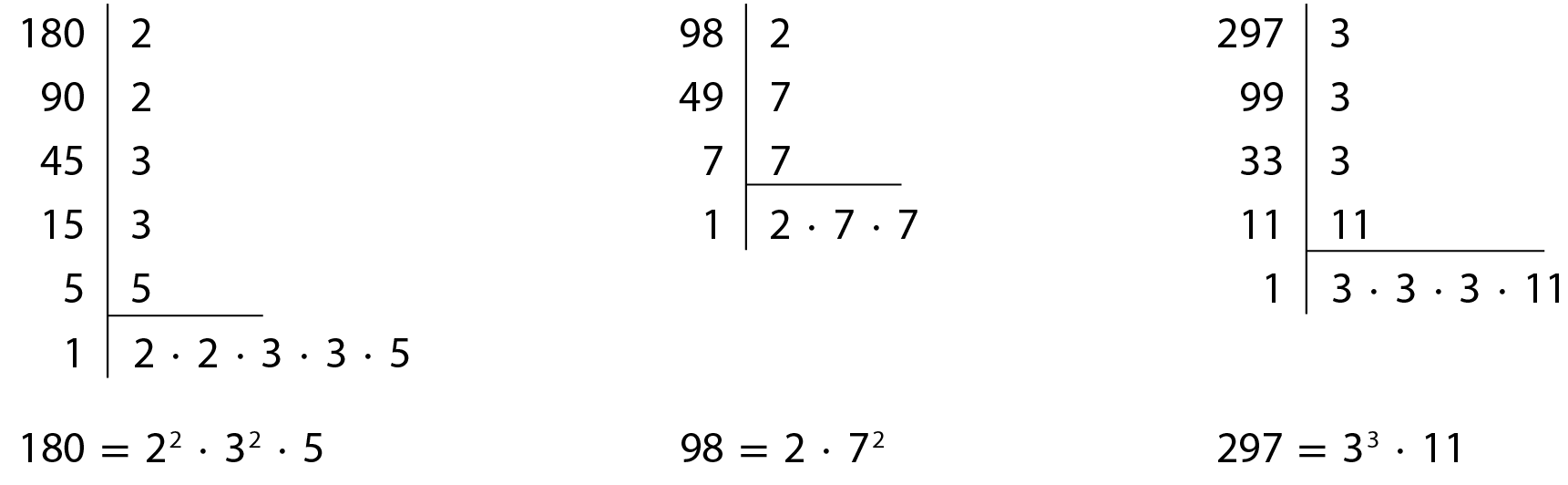
Agora, observe a decomposição em fatores primos dos números 180, 98 e 297.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
53 Determine o menor divisor primo de:
a) 64;
b) 75;
c) 85;
d) 49.
54 Decomponha os números a seguir em fatores primos.
a) 120
b) 144
c) 168
d) 225
e) 117
f) 125
55 Um número natural decomposto em fatores primos é representado assim: 2 elevado a 3 ⋅ 3 elevado a 2 ⋅ 7.
Que número é esse?
56 a = 2 ⋅ 3 ⋅ 11 e B = 2 elevado a 2 ⋅ 3 elevado a 2 ⋅ 5 são as decomposições de dois números naturais. Calcule A + B.
PARA SABER MAIS
ême dê cê e ême ême cê
Em uma escola, as turmas de 6º ano planejaram um evento que contou com a participação de todos os estudantes. O 6º ano a tem 42 estudantes, o 6º ano B, 36, e o 6º ano C tem 30. Cada turma formou suas equipes com o seguinte critério: todas as equipes tinham o mesmo número de estudantes e o maior número possível deles.
Para descobrir o número êne de estudantes de cada equipe, os organizadores pensaram assim:
êne tem de ser um divisor de 42, de 36 e de 30.
• divisores de 42: 1, 2, 3, 6, 7, 14, 21 e 42;
• divisores de 36: 1, 2, 3, 4, 6, 9, 12, 18 e 36;
• divisores de 30: 1, 2, 3, 5, 6, 10, 15 e 30.

Os divisores comuns a 42, 36 e 30 são 1, 2, 3 e 6. Assim, para terem o mesmo número de participantes, as equipes deveriam ter 1, 2, 3 ou 6 estudantes. Como o critério era o maior número possível, cada equipe deveria ter 6 estudantes, que é o maior divisor comum (ême dê cê) de 42, de 36 e de 30.
As irmãs Edi, Eni e Eti programaram os seus celulares para despertar às 7 horas, com repetição a cada 4, 6 e 8 minutos, respectivamente. Depois das 7 horas, quanto tempo se passou para os celulares voltarem a tocar juntos novamente?

Resolvemos essa questão considerando os múltiplos das repetições de cada uma delas.
• Edi: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, reticências
• Eni: 0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, reticências
• Eti: 0, 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, reticências
Os tempos de repetição comuns aos três celulares são: 24, 48, 72, reticências
Depois das 7 horas, os três celulares despertarão primeiro após 24 minutos, o menor múltiplo comum (ême ême cê) com exceção do zero.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
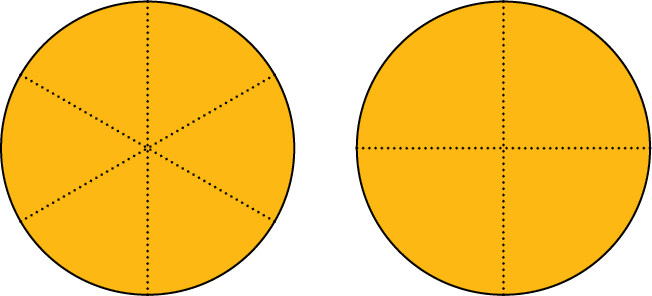
1 Liz comprou duas pizzas, uma cortada em seis pedaços iguais que lembram ângulos de 60°, a outra em pedaços iguais que lembram ângulos de 90°. Liz quer repartir as duas pizzas em pedaços de igual tamanho, o maior possível. Quantos graus deverá ter o ângulo que cada novo pedaço de pizza lembra?
2 As rodas a e bê fazem um “ploc” e partem em trilhos paralelos. A roda a faz um “ploc” a cada 6 centímetros, e a roda B, a cada 10 centímetros. Depois da partida, quantos centímetros elas andam até fazerem um “ploc” juntas novamente?

TRABALHANDO A INFORMAÇÃO
Construindo um gráfico de barras
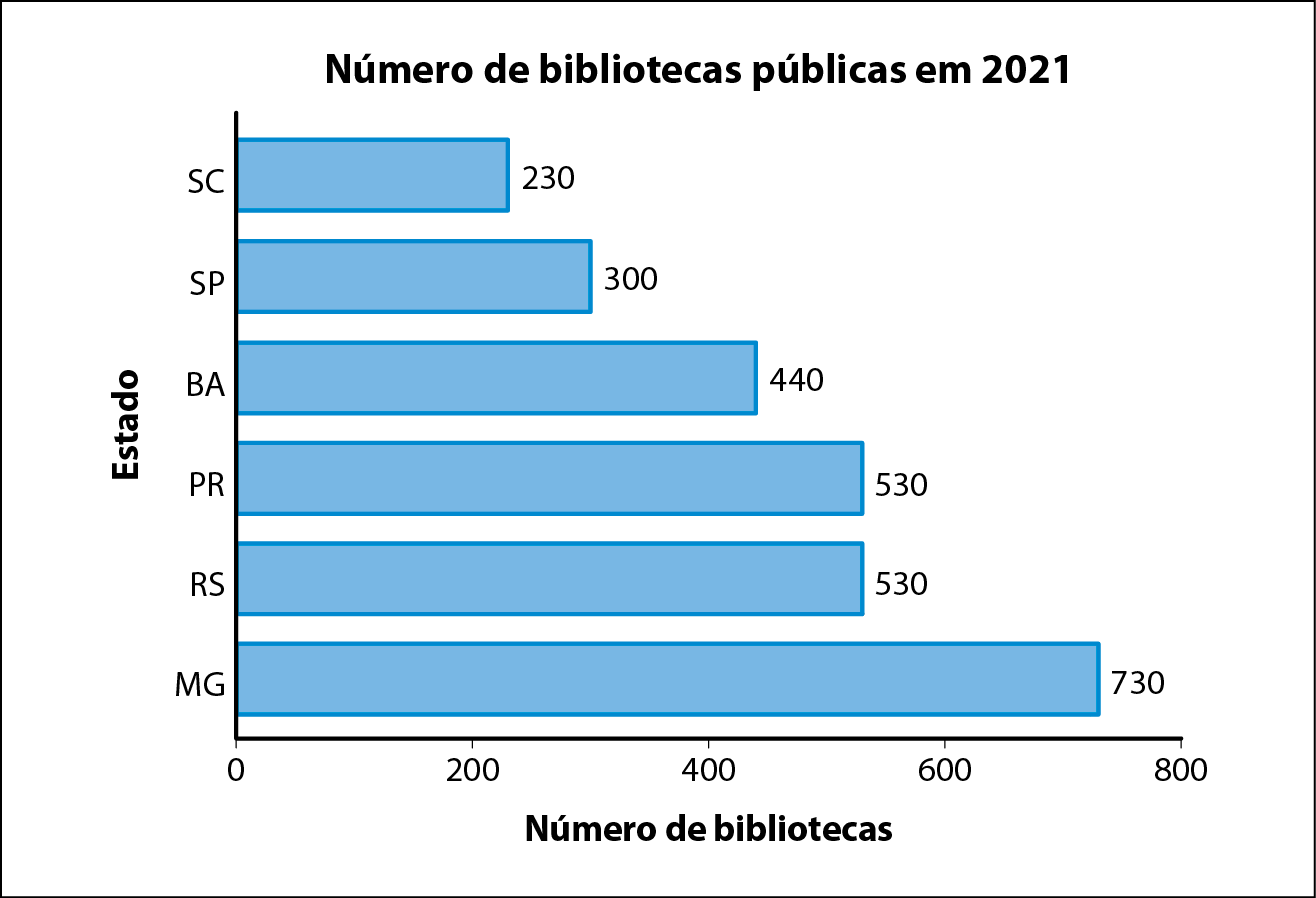
O Sistema Nacional de Bibliotecas Públicas (ésse êne bê pê) divulgou, em 2021, que em todo o Brasil havia .6057 bibliotecas. Note no quadro a seguir os seis estados que possuem o maior número de bibliotecas públicas com cadastro atualizado no sistema.
|
Estado |
Bibliotecas |
|---|---|
|
Minas Gerais |
727 |
|
Rio Grande do Sul |
534 |
|
Paraná |
527 |
|
Bahia |
443 |
|
São Paulo |
300 |
|
Santa Catarina |
233 |
Dados obtidos em: SISTEMA Nacional de Bibliotecas Públicas (ésse êne bê pê). Disponível em: https://oeds.link/IDONpH. Acesso em: 9 maio 2022.
Também é possível organizar e apresentar essas informações em um gráfico de barras. Para facilitar a construção do gráfico, vamos arredondar a quantidade de bibliotecas públicas de cada estado para a dezena mais próxima.
Para construir esse gráfico, com o auxílio de uma régua, adotamos os seguintes procedimentos:
• Traçamos uma linha horizontal, em que será registrada a quantidade de bibliotecas, e uma linha vertical, na qual serão indicados os estados.
• Escolhemos uma unidade de medida adequada de modo que caibam, na linha horizontal, os valores indicados na tabela, e outra unidade de medida de modo que caibam, na linha vertical, as larguras das barras. Para facilitar a leitura, convém que essas larguras sejam iguais.
• Traçamos as barras. A barra relativa a Minas Gerais deve ter comprimento de medida igual a 73 milímetros, pois esse estado possuía, aproximadamente, setecentas e trinta bibliotecas com cadastro atualizado em 2021. Da mesma fórma, a barra relativa ao estado de São Paulo deve ter comprimento medindo 30 milímetros, pois em 2021 havia trezentas bibliotecas em São Paulo. Assim, as barras relativas aos estados do Rio Grande do Sul, Paraná, Bahia e Santa Catarina devem ser construídas com 54 milímetros, 53 milímetros, 44 milímetros e 23 milímetros de medida de comprimento, respectivamente.
• Completamos o gráfico nomeando as linhas vertical e horizontal, chamadas de eixos, dando um título ao gráfico e indicando a fonte dos dados. Há gráficos de barras em que o eixo horizontal é omitido. Nesses casos, necessariamente, os valores são colocados à direita ou acima das respectivas barras.
Algumas interpretações podem ser feitas pela análise do gráfico:
• Em 2021, a Bahia tinha quase o dobro da quantidade de bibliotecas de Santa Catarina. Podemos afirmar isso porque o comprimento da barra referente ao estado da Bahia (44 milímetros) tem quase o dobro do comprimento da barra de Santa Catarina (23 milímetros).
• Entre os estados apresentados, o que tinha a menor quantidade de bibliotecas em 2021 era Santa Catarina.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Faça mais algumas interpretações do gráfico de barras apresentado anteriormente.
a) Quantas bibliotecas existiam no estado de São Paulo em 2021?
b) Em 2021, aproximadamente, quantas bibliotecas os estados de Santa Catarina e do Rio Grande do Sul tinham juntos?
c) E hoje, quantas bibliotecas existem no estado e no município em que você vive? Faça uma pesquisa na internet para responder.
2 O bibliotecário é o profissional que mantém organizados os dados relativos a empréstimos de livros. Observe no quadro quantos livros foram emprestados em uma biblioteca ao longo da semana.
|
Dia da semana |
Quantidade |
|---|---|
|
Segunda-feira |
12 |
|
Terça-feira |
15 |
|
Quarta-feira |
9 |
|
Quinta-feira |
18 |
|
Sexta-feira |
20 |
Dados obtidos das anotações do bibliotecário.
a) Em um gráfico de barras que represente os dados desse quadro, qual dia da semana deve ter a barra de maior comprimento? E qual dia deve ter a barra de menor comprimento?
b) Há alguma barra desse gráfico que deva ter o dobro do comprimento de outra barra? Em caso afirmativo, quais barras? Por quê?
c) Construa um gráfico de barras para representar os dados desse quadro.
3 Você tem o hábito de ler livros? E seus colegas? Faça uma pesquisa para obter essa informação.
a) Pergunte aos colegas quantos livros eles leram no ano passado e organize as informações coletadas em uma tabela.
b) Construa um gráfico de barras com os dados por quantidade de colegas e quantidade de livros lidos.
c) Compartilhe o resultado de sua pesquisa com o professor e os colegas da turma.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Na fila da bilheteria de um teatro, há menos de 50 pessoas. Contando essas pessoas de 6 em 6, sobram 3. Contando‑as de 7 em 7, também sobram 3. Quantas pessoas estão na fila?
2 Ana tem de 100 a 150 livros. Organizando‑os de 12 em 12, de 15 em 15 ou de 20 em 20, sempre resta um. Quantos livros Ana tem?
3

Verifique mentalmente se o número .34524 é divisível por 6. Justifique sua resposta.
4 Dê o menor número de três algarismos distintos:
a) divisível por 2;
b) divisível por 3;
c) divisível por 5;
d) divisível por 6.
5 Corrija as sentenças que são falsas.
a) O número 260 é divisível por 2, por 3 e por 5.
b) .2040 é divisível por 2, mas não é por 3.
c) .3065 é divisível por 5, mas não é por 3.
d) .18980 é divisível por 4, mas não é por 9.
6 Uma pessoa deseja efetuar, com o auxílio de uma calculadora, a divisão de um número por 36, mas a tecla 6 está com defeito. Como ela poderia fazer essa divisão?
7 Dividindo‑se um número por 10, restou 5.
a) Esse número é divisível por 2? Por quê?
b) Esse número é divisível por 5? Por quê?
8 Ari lê o número das placas antigas de automóveis: RIA‑8000, IRA‑5670, AIR‑4004 e RAI‑2600. Em qual dessas placas o número é divisível por:
a) .1000
b) 100
c) 10
9 Na abertura deste capítulo, falamos um pouco sobre os calendários maias. Para cada um dos 365 dias do Tzolkin, os maias contavam um período de 260 dias do Haab.
a) Após quantos dias haveria um Haab e um Tzolkin iniciando juntos?
b) Você consegue explicar por que o uso simultâneo dos calendários Tzolkin e Haab contabilizava um ciclo de 52 anos?

10 Usando uma calculadora em que a tecla 1 não funciona, como é possível efetuar a multiplicação de um número por 12?
11 Que algarismo deve ser colocado à esquerda de 283 para que se obtenha um número divisível por 9?
12

Alfredo pensou no número 518, trocou a ordem dos algarismos e obteve 815. Subtraindo o menor do maior, obteve 297.
a) Esse número é múltiplo de 9?
b) Agora, pense em um número e realize os mesmos passos do cálculo de Alfredo. O resultado da subtração em seu cálculo é divisível por 9?
13 Uma florista tem 100 rosas brancas e 60 rosas vermelhas. Ela pretende montar o maior número de ramalhetes que contenha, cada um, o mesmo número de rosas brancas e o mesmo número de rosas vermelhas.
a) Dessa fórma, qual é o maior número de ramalhetes que a florista poderá montar?
b) Quantas rosas brancas e quantas rosas vermelhas terá cada um desses ramalhetes?
14 Quando um número termina em 5, ele:
a) é divisível apenas por 5.
b) pode ser divisível por 2.
c) pode ser divisível por 3.
d) pode ser divisível por 10.
15 Para participar do campeonato estudantil de basquete foram inscritos menos de 50 estudantes. Formando‑se equipes de 7 estudantes, sobram 6. Formando‑se equipes de 9 estudantes, sobram 3. Nessas condições, se forem formadas equipes de 8 estudantes, quantas equipes seriam formadas?
16 (ú éfe ême gê) O número de três algarismos divisível ao mesmo tempo por 2, 3, 5, 6, 9, 11 é:
a) 330.
b) 66.
c) 676.
d) 990.
e) 996.
17 O ême dê cê de três números primos é:
a) o menor deles.
b) o maior deles.
c) o número 1.
d) o produto deles.
18 Determine o menor número que dividido por 12, por 15 e por 36 tem sempre resto igual a 2.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Em uma rodoviária há duas linhas de ônibus que se encaminham para destinos diferentes. Em uma dessas linhas, os veículos partem a cada 84 minutos e, na outra, a cada 165 minutos. Supondo que a primeira viagem dos veículos dessas linhas ocorra ao mesmo tempo, após quantos minutos haverá uma nova partida juntos?
a) .3350 minutos.
b) .4620 minutos.
c) .9900 minutos.
d) .13300 minutos.
2 O conjunto dos divisores comuns de 16 e 36 é representado por:
a) {0; 2; 4}.
b) {1; 2; 4}.
c) {2; 4; 8}.
d) {0; 2; 4; 8; 16}.
3 Qual é o menor número natural que devemos adicionar a 110 para obter um número que seja múltiplo de 13?
a) 7
b) 8
c) 9
d) 10
4 Uma sequência numérica é formada pelos divisores de 600. Pertencem a essa sequência os números:
a) 6 e 66.
b) 12 e .1200.
c) 25 e 125.
d) 40 e 150.
5 O conjunto dos múltiplos comuns de 8 e 12 pode ser representado por:
a) {0; 24; 48; 60; reticências}
b) {1; 2; 4; 8}
c) {0; 12; 24; 36; 48; reticências}
d) {8; 16; 24; 32; 40; reticências}
6 Todo número que termina em 0 ou em 5 é divisível por:
a) 2.
b) 4.
c) 5.
d) 10.
7 Uma fábrica precisa distribuir .16800 unidades de um produto. Para facilitar o transporte, elas são armazenadas em caixas com 10 unidades, que são transportadas em grupos de quatrocentas a quatrocentas e cinquenta unidades. Para fazer esse transporte, pretende-se usar a menor quantidade possível de veículos. Quantos veículos deverão ser usados?
a) 38 veículos.
b) 40 veículos.
c) 42 veículos.
d) 44 veículos.
8 Isa quebrou seu cofre de moedas de 1 real para comprar um presente de R$ 139,00cento e trinta e nove reais. Ao empilhá-las em montes de 16 ou 18 moedas, sobram sempre 9 moedas. Sabendo que Isa tem menos de R$ 200,00duzentos reais, podemos dizer que ela:
a) comprará o presente e ficará com 14 reais.
b) comprará o presente e ficará com 9 reais.
c) não comprará o presente, pois faltam 9 reais.
d) não comprará o presente, pois faltam 14 reais.
9 Qual é o maior número múltiplo dos números 6 e 9 que seja menor que 100?
a) 99
b) 90
c) 81
d) 72
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Existe algum número que é múltiplo de todos os números naturais? Justifique sua resposta.
b) Um número natural pode ter infinitos múltiplos; porém não podemos dizer o mesmo sobre seu número de divisores. Qual é o menor número de elementos que o conjunto de divisores de um número natural diferente de 1 pode ter?
c) Pense em um número entre 1 e 10. Multiplique o resultado por 9. Some os algarismos desse número. O resultado final foi 9, correto? Como você explica esse resultado? Funcionaria com números maiores que 10?
d) Quais são os critérios de divisibilidade que você aprendeu? Escreva um texto organizando essas informações.
e) Explique, com suas palavras, por que o algarismo 2 é o único número primo par.