ORIENTAÇÕES ESPECÍFICAS
Parte 1
O livro do 6º ano é composto de doze capítulos em que se desenvolvem as cinco Unidades Temáticas propostas pela Bê êne cê cê: Números, Álgebra, Geometria, Grandezas e medidas e Probabilidade e estatística, intercaladas e, sempre que possível, integradas, exploradas no corpo do texto explicativo e nas atividades.
A seguir, apresentamos sugestões de cronogramas para trabalhar com esses conteúdos em bimestre, trimestre e semestre com base nas organizações dos capítulos.
|
Capítulos |
Conteúdos |
Habilidades e competências da BNCC |
|||
|---|---|---|---|---|---|
|
1º semestre |
1º trimestre |
1º bimestre |
Capítulo 1 – Números |
• Emprego do número e suas diferentes funções; |
Habilidades: |
|
Capítulo 2 – Operações com números naturais |
• Comparação de números naturais; |
Habilidades: |
|||
|
Capítulo 3 – Estudando figuras geométricas |
• Origem da Geometria; |
Habilidades: |
|||
|
2º bimestre |
Capítulo 4 – Divisibilidade |
• Resolução de problemas que envolvam cálculos mentais ou escritos com números naturais; |
Habilidades: |
|
Capítulos |
Conteúdos |
Habilidades e competências da BNCC |
|||
|---|---|---|---|---|---|
|
1º semestre |
1º trimestre |
2º bimestre |
Capítulo 5 – Um pouco de Álgebra |
• Resolução de problemas que envolvam cálculos com números naturais; |
Habilidades: |
|
2º trimestre |
Capítulo 6 – Um pouco de Geometria plana |
• Entes primitivos: ponto, reta e plano e suas relações; |
Habilidades: |
||
|
Capítulo 7 – Números racionais na forma de fração |
• Noção de fração: parte/todo; |
Habilidades: |
|||
|
2º semestre |
3º bimestre |
Capítulo 8 – Operações com números racionais na forma de fração |
• Resolução de problemas que envolvam as ideias de múltiplo e de divisor no contexto de frações equivalentes e simplificação de frações nas operações com frações; |
Habilidades: |
|
Capítulos |
Conteúdos |
Habilidades e competências da BNCC |
|||
|---|---|---|---|---|---|
|
2º semestre |
3º trimestre |
3º bimestre |
Capítulo 9 – Números racionais na forma decimal e operações |
• Frações decimais e a representação na forma decimal dos números racionais; |
Habilidades: |
|
4º bimestre |
Capítulo 10 – Polígonos e Poliedros |
• Conceito e reconhecimento de linhas poligonais e de polígonos; |
Habilidades: |
||
|
Capítulo 11 – Comprimentos e áreas |
• Medidas de comprimento: unidades não padronizadas; |
Habilidades: |
|||
|
Capítulo 12 – Outras unidades de medida |
• Resolução de situações que envolvem estimativas e medidas; |
Habilidades: |
Considerações iniciais
Cada capítulo aborda objetos de conhecimento, entendidos como conteúdos, conceitos, processos, com a intenção de desenvolver as habilidades relacionadas a eles. Esses conhecimentos são articulados, retomados e ampliados a fim de proporcionar sua apropriação pelos estudantes, considerando a aprendizagem um processo contínuo e integrado.
Os conteúdos matemáticos são desenvolvidos de modo que as habilidades, as Unidades Temáticas, as competências e outras áreas do conhecimento se articulem e se relacionem, e são tratados na perspectiva das aprendizagens dos anos anteriores e posteriores. Assim, no livro do 6º ano do Ensino Fundamental, levamos em conta os objetivos de aprendizagem para o 5º ano, conforme proposto na Bê êne cê cê, visando preparar os estudantes para se apropriar dos conhecimentos previstos para o 7º ano.
A seguir, são feitas orientações didáticas sobre cada capítulo e o que se pretende que os estudantes desenvolvam neles.
Capítulo 1 — Números
• Objetivos do capítulo e justificativas
• Reconhecer os significados dos números naturais em diferentes contextos.
• Conhecer outros sistemas de numeração (egípcio e romano).
• Conhecer a origem do sistema de numeração indo-arábico.
• Compreender o sistema de numeração decimal, identificando o conjunto de regras e símbolos que o caracterizam.
• Praticar a leitura e a escrita dos números naturais.
• Comparar números naturais, assim como reconhecer sucessor e antecessor de qualquer um deles.
• Trabalhar com informações de embalagens.
Ao apresentar aos estudantes alguns dos sistemas de numeração desenvolvidos por diferentes civilizações, em diferentes períodos históricos, além das características desses sistemas, contribui-se para que os estudantes percebam a Matemática como uma ciência humana, fruto das necessidades de diferentes culturas, competência que deve ser trabalhada como explicitado na competência geral 1 e na competência específica 1.
Ao explorar o sistema de numeração indo-arábico como um conjunto de regras que permitem a escrita de qualquer número e compreender sua escrita e leitura, contribui-se para o desenvolvimento do letramento matemático e para que os estudantes adquiram ferramentas que os auxiliem na compreensão de mundo, uma vez que o uso de números está presente em diferentes contextos. Desse modo, contribuímos para o desenvolvimento das competências gerais 2 e 4 e da competência específica 4.
O trabalho proposto na seção Trabalhando a Informação proporciona aos estudantes um momento de reflexão sobre os tipos de informação contidos em embalagens e suas funções, o que propicia um trabalho com a competência geral 7 e o Tema Contemporâneo Transversal educação para o consumo.
A competência geral 7 e a competência específica 7 são trabalhadas na Abertura do capítulo que apresenta o projeto Mangues e o explora com questões que propiciam uma discussão de urgência social (preservação do meio ambiente). Já o desenvolvimento das competências gerais 9 e 10 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois permitem aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação às atividades propostas.
As diferentes atividades propostas contribuem para o desenvolvimento da competência específica 6, assim como as atividades em grupo contribuem para o desenvolvimento da competência específica 8.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah zero um) Comparar, ordenar, ler e escrever números naturais e números racionais cuja representação decimal é finita, fazendo uso da reta numérica.
(ê éfe zero seis ême ah zero dois) Reconhecer o sistema de numeração decimal, como o que prevaleceu no mundo ocidental, e destacar semelhanças e diferenças com outros sistemas, de modo a sistematizar suas principais características (base, valor posicional e função do zero), utilizando, inclusive, a composição e decomposição de números naturais e números racionais em sua representação decimal.
Neste capítulo, são desenvolvidos objetos de conhecimento da Unidade Temática Números. Nos conteúdos e atividades propostos, foram consideradas as aprendizagens dos anos iniciais do Ensino Fundamental, especialmente as do 5º ano, como a habilidade (ê éfe zero cinco ême ah zero um), relativa aos sistemas de numeração e aos números naturais.
Esse é o momento de ampliação dos conhecimentos desenvolvidos, na perspectiva de que a continuidade desse processo conduza o estudante a se apropriar das características do sistema de numeração decimal e da sequência dos números naturais, o que contribui para o desenvolvimento das habilidades (ê éfe zero seis ême ah zero um) e (ê éfe zero seis ême ah zero dois). Para isso, apresentam-se conceitos e atividades que conduzam os estudantes a reconhecer os principais aspectos dos números naturais: leitura, escrita e comparação.
Nessa exploração, espera-se que os estudantes mobilizem seus conhecimentos acerca das operações com números naturais, desenvolvidos nos anos anteriores, para a compreensão dos conteúdos estudados.
Além disso, ao ampliar os conhecimentos que os estudantes já têm sobre os números naturais, espera-se prepará-los para a apropriação de outros tipos de número e a ampliação dos conjuntos numéricos que serão estudados posteriormente, caso dos números inteiros, abordados no 7º ano do Ensino Fundamental, (ê éfe zero sete ême ah zero três).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
5. c) Seguindo os comandos da cartela, obtemos:

6. a) 1ª ordem corresponde às unidades, então o valor posicional é 7; 3ª ordem corresponde às centenas, então o valor posicional é 700.
6. b) 2ª ordem corresponde às dezenas, então o valor posicional é 50; 4ª ordem corresponde à unidade de milhar, então o valor posicional é .5000
7. a) Em .3765, o valor posicional do algarismo 3 é .3000.
7. b) Em ..32000000, o valor posicional do algarismo 3 é ..30000000.
8. Para escrever o menor número, as maiores ordens são preenchidas com os algarismos de menor valor. Como 056 = 56 tem apenas dois algarismos, 506 é o menor número possível. O maior número deve ser formado pelos algarismos de maior valor nas maiores ordens, portanto 986.
9. Os algarismos de menor valor são 0, 1 e 2; então, 102 é o menor número formado por 3 algarismos distintos.
14. Informe aos estudantes que alguns recibos ou cheques podem apresentar, além do valor referente ao dinheiro, números como número do recibo, data, número do banco, número da conta, número do CPF etcétera
O valor é de trinta e sete mil, trezentos e oitenta e cinco reais.
15. Aqui, usa-se a relação 1 milhão = ..1000000; dessa maneira:
15. a) 48 milhões = ..48000000
15. b) 110 milhões = ..110000000
16. a) O primeiro ponteiro está entre os algarismos 4 e 5, o segundo entre os algarismos 1 e 2, o terceiro entre os algarismos 7 e 8 e o quarto entre os algarismos 5 e 6. Logo, o número indicado é: .4175.
16. b) O primeiro ponteiro está entre os algarismos 8 e 9, o segundo entre os algarismos 9 e 0, o terceiro entre os algarismos 2 e 3 e o quarto entre os algarismos 1 e 2. Logo, o número indicado é: .8921.
17. Oriente os estudantes na representação dos medidores. Verifique se todos os algarismos foram representados corretamente.
19. Como os temas dos textos pesquisados podem ser variados, sugira que escolham temas que possam trazer curiosidades a serem compartilhadas entre os colegas. Escolha alguns desses textos para serem lidos na classe. Aproveite para avaliar a leitura em relação ao texto e aos números representados.
22. a) Nesse caso, ao considerar a expressão “maior que 5”, o estudante deve perceber que o número 5 não póde ser considerado. Assim, obtêm-se: 6, 7, 8, 9, 11 reticências
22. b) Ao indicar “menores ou iguais”, deve-se considerar o número 5: 0, 1, 2, 3, 4 e 5.
22. c) Como pede os números maiores que 5 e menores que 10, deve-se desconsiderar o 5 e o 10: 6, 7, 8 e 9.
22. d) Ao pedir números naturais entre 5 e 10, deve-se desconsiderar o 5 e o 10: 6, 7, 8 e 9.
22. e) Ao pedir os números de 5 a 10, devem-se considerar esses extremos; logo: 5, 6, 7, 8, 9 e 10.
24. O menor número natural de 3 algarismos é 100, e seu antecessor é 100 menos 1 = 99. O maior número natural de 4 algarismos é .9999, e seu sucessor é .9999 + 1 = .10000.
25. a) Na ilustração, Paulo está segurando placas com os algarismos 5, 7 e 9. Então, sua casa póde ter qualquer número formado por esses algarismos, ou seja: 579, 597, 759, 795, 957 ou 975.
25. b) Considerando que casas de menor numeração estão mais próximas do início da rua, a casa teria o número 579, que é o menor deles.
25. c) Considerando que casas de maior numeração estão mais próximas do fim da rua, a casa teria o número 975, que é o maior deles.
25. d) e) Para responder a essas questões, os estudantes deverão considerar o número de sua residência. Caso o local onde moram não tenha número de identificação, incentive-os a escolher outro número que tenha significado para eles, como o ano de nascimento ou de algum acontecimento que recordem.
26. Oriente os estudantes a definir uma escala adequada para a representação desses números.
27. Oriente os estudantes na elaboração das dicas e na troca de problemas para responder aos itens a e b. Esse tipo de atividade contribui para que eles possam trocar ideias e dúvidas sobre o conteúdo estudado.
Pense mais um pouco
Página 22
1. O capítulo vai da página 38 até 53, então são 53 menos 38 + 1 = 16 (16 páginas).
2. De 1 a 150, incluindo os extremos, obtemos:
• Números de 1 algarismo: de 1 a 9 → são 9 números → 9 algarismos
• Números de 2 algarismos: de 10 a 99 → são 90 números → 180 algarismos
• Números de 3 algarismos: de 100 a 150 → são 51 números → 153 algarismos
No total: 9 + 180 + 153 = 342 (342 algarismos).
3. a) Ao efetuar a subtração e, depois, não levar em conta a página inicial, Juliana cometeu um erro.
3. b) Da mesma maneira que Juliana, Alberto errou ao desconsiderar os números iniciais 10 e 100 dos dois últimos intervalos.
4. Ela imprimirá as páginas de 37 a 75, ou seja 75 menos 37 + 1 = 39 (39 páginas). Como são todos números de 2 algarismos, são necessários 78 algarismos para numerá-las (39 × 2 = 78).
Exercícios complementares
1. a) Seis mil, novecentos e trinta e sete: .6937
1. b) Dois milhões, quinhentos e trinta mil, setecentos e um: ..2530701
2. a) Os números são 167, 176, 617, 671, 716 e 761; portanto, o maior deles é 761.
2. b) O menor deles é 167.
2. c) O menor iniciando com 7 é 716.
2. d) O maior iniciando com 6 é 671.
3. a) Os números possíveis com essas restrições são 21, 42, 63 e 84. Logo, o número que é menor que 40 é o 21.
3. b) O número que é maior que 70 é o 84.
4. a) Para usar todos os algarismos, o número não póde iniciar com 0; dessa maneira, o menor número formado é ..1000223.
4. b) O maior número formado é ..3221000.
5. a) Arlete numerou com todos os números de 1 a 256. Nesse intervalo, existem:
• Números de 1 algarismo: 1 a 9 → 9 números → 9 algarismos
• Números de 2 algarismos: 10 a 99 → 90 números → 180 algarismos
• Números de 3 algarismos: 100 a 256 → 157 números → 471 algarismos
No total: 660 algarismos (9 + 180 + 471 = 660).
5. b) Nesse intervalo, os números com algarismo 2 são:
• Números de 1 algarismo: 2 → 1 vez
• Números de 2 algarismos:
Na unidade: 12, 22, 32, 42, reticências, 92 → 9 vezes
Na dezena: 20 a 29 → 10 vezes
• Números de 3 algarismos:
Na unidade: 102, 112, 122, 132, reticências, 212, 222, 232, 242, 252 → 16 vezes
Na dezena: 120 a 129, 220 a 229 → 20 vezes
Na centena: 200 a 256 → 57 vezes
No total: 113 vezes (1 + 9 + 10 + 16 + 20 + 57 = 113).
6. Lúcia – números de 2 algarismos: de 10 a 99 → 90 números.
Paula – números de 2 algarismos distintos: os 90 números anteriores, menos 11, 22, 33, 44, 55, 66, 77, 88 e 99, equivale à 81 números (90 menos 9 = 81).
Rogério – pares de dois algarismos são metade dos números de Lúcia → 90 dividido por 2 = 45 (45 números).
Renato – pares de dois algarismos distintos são os 45 de Rogério, menos 22, 44, 66 e 88 → 45 – 4 = 41 (41 números).
7. a) No texto, há o trecho “Um salário de ..4750000 cruzeiros reticências passou para .4750 cruzeiros reais”. Dessa maneira, o valor posicional do 7 era .700000 e passa a ser 700.
7. b) O valor posicional do 4 passa a ser .4000 e era ..4000000.
Verificando
1. Para representar o número .1493 no sistema de numeração romano, fazemos:
.1000 = ême 90 = xis cê
400 = cedê 3 = í í í
.1493 = ême cê dê xís cê í í í
No sistema de numeração egípcio, a flor de lótus representa .1000, uma corda enrolada representa 100, um calcanhar representa 10 e uma haste equivale a uma unidade, de fórma que a representação final será:

Alternativa d.
2. No número ..1085750, o valor posicional do algarismo 8 é .80000.
Alternativa c.
3. No número .95796, o algarismo 7 vale 700, ou seja, setecentas unidades.
Alternativa c.
4. Para escrever ...1050650001 por extenso, deve-se separar os números por classes: um bilhão, cinquenta milhões, seiscentos e cinquenta mil e um.
Alternativa c.
5. Vamos analisar cada uma das alternativas:
a) Falso, pois os algarismos de 0 a 9 são os 10 símbolos que compõem o sistema de numeração indo-arábico.
b) Falso, pois é um sistema de base 10.
c) Falso, pois o valor do número depende da posição dos algarismos, em um número.
d) Verdadeiro, há um símbolo para representar o zero: 0.
Alternativa d.
6. O sucessor será: ..1099099 + 1 = ..1099100.
Alternativa b.
7. O menor número formado terá os maiores algarismos nas primeiras ordens, e não póde iniciar por 0; portanto, será .2059.
Alternativa b.
8. Os valores maiores que 10 não incluem o próprio 10, mas a partir de seu sucessor:
{11, 12, 13, 14, 15, reticências}
Alternativa d.
9. O ponto A póde ser indicado como o ponto médio entre 20 e 100; logo, A = 60. Já a medida da distância de B a 100 corresponde a aproximadamente um terço da medida da distância de 100 a 130. Logo, B = 110.
Alternativa c.
Capítulo 2 — Operações com números naturais
• Objetivos do capítulo e justificativas
• Resolver situações-problema compreendendo diferentes significados das operações de adição, subtração, multiplicação, divisão, potenciação e radiciação que envolvem números naturais.
• Realizar cálculos relativos a operações com números naturais por meio de estratégias variadas, com compreensão dos processos nelas envolvidos.
• Reconhecer e usar as propriedades das operações de adição e multiplicação com números naturais.
• Resolver expressões numéricas que contenham operações com números naturais.
• Relacionar a potência com expoente natural a um produto reiterado de fatores iguais.
• Compreender e calcular a raiz quadrada exata, a raiz cúbica exata (e de outros índices) de um número natural.
• Arredondar números naturais para diferentes ordens.
• Perceber a utilidade dos arredondamentos para fazer estimativas.
• Iniciar a construção de tabelas como maneira de organizar, representar e interpretar dados.
• Ler, identificar e interpretar dados expressos em gráficos de colunas.
O trabalho com as quatro operações fundamentais, além da potenciação e da radiciação, por meio do estudo de suas propriedades, pelo uso de diferentes estratégias e por meio da resolução de problemas, favorece o desenvolvimento do letramento matemático. Desse modo, os objetivos explicitados contribuem para que os estudantes desenvolvam diferentes habilidades, como o uso de linguagem simbólica (formal e técnica), a compreensão leitora, a interpretação de informações e o desenvolvimento de um repertório para a resolução de diferentes situações-problema. Desse modo, contribuímos para o desenvolvimento das competências gerais 2 e 4 e da competência específica 2.
Os arredondamentos e as estimativas são ferramentas que favorecem o trabalho com a competência específica 2, que trata do desenvolvimento do raciocínio lógico, do espírito de investigação e da capacidade de produzir argumentos convincentes.
Na seção Para saber mais, ao trabalhar a multiplicação hindu, favorecemos o desenvolvimento da competência específica 1, da competência geral 1 e do Tema Contemporâneo Transversal diversidade cultural.
Situações-problema como a que trabalha a ideia retangular da multiplicação por meio da apresentação coreográfica com pessoas em cadeiras de roda na festa de recepção aos Jogos Paralímpicos de 2024, em Paris, despertam nos estudantes a reflexão sobre a importância da inclusão social e favorecem o desenvolvimento da competência específica 7.
Nas duas seções Trabalhando a informação, ao tratar de tabelas e gráficos, contribui-se para o desenvolvimento das competências específicas 4 e 6.
Ao contextualizar uma situação-problema com uma temática, que relata a queda da população de onças-pintadas em um parque nacional, orientamos a discussão sobre o Tema Transversal Contemporâneo educação ambiental e propiciamos o desenvolvimento da competência geral 7. Em outro momento, abordamos, por meio de matéria especializada do Conselho Federal de Medicina, a evolução do número de médicos no Brasil nos últimos cem anos, contribuindo para o trabalho com o Tema Contemporâneo Transversal saúde. Além dessa situação com a temática saúde, no exercício 52, da seção Exercícios propostos, solicitamos aos estudantes que pesquisem as informações contidas nas embalagens de produtos que consomem, fazendo-os refletir sobre essas informações e contribuir para o desenvolvimento da competência geral 8. Esse tema também é focado no exercício 21 com tabela de dados da FAO sobre a população mundial mal-nutrida. O desenvolvimento das competências gerais 9 e 10 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois permitem aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação às atividades propostas.
As diferentes atividades propostas contribuem para o desenvolvimento da competência específica 6, assim como as atividades em grupo contribuem para o desenvolvimento da competência específica 8. Já a proposta de Abertura propicia uma discussão de urgência social (preservação do meio ambiente), o que contribui para o desenvolvimento da competência específica 6.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah zero três) Resolver e elaborar problemas que envolvam cálculos (mentais ou escritos, exatos ou aproximados) com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.
(ê éfe zero seis ême ah três um) Identificar as variáveis e suas frequências e os elementos constitutivos (título, eixos, legendas, fontes e datas) em diferentes tipos de gráfico.
(ê éfe zero seis ême ah três dois) Interpretar e resolver situações que envolvam dados de pesquisas sobre contextos ambientais, sustentabilidade, trânsito, consumo responsável, entre outros, apresentadas pela mídia em tabelas e em diferentes tipos de gráficos e redigir textos escritos com o objetivo de sintetizar conclusões.
(ê éfe zero seis ême ah três três) Planejar e coletar dados de pesquisa referente a práticas sociais escolhidas pelos alunos e fazer uso de planilhas eletrônicas para registro, representação e interpretação das informações, em tabelas, vários tipos de gráficos e texto.
Neste capítulo serão aprofundados os conhecimentos acerca dos números naturais. Serão exploradas as operações entre eles, considerando a Unidade Temática Números, ampliando o que foi abordado no capítulo anterior e contribuindo para o desenvolvimento da habilidade (ê éfe zero sete ême ah zero três).
O estudo das quatro operações fundamentais toma por base os conhecimentos consolidados até o 5º ano do Ensino Fundamental e tem como foco aqueles que serão explorados no 7º ano, entre eles a resolução de problemas envolvendo operações com números inteiros (ê éfe zero sete ême ah zero quatro).
Ainda nessa Unidade Temática, são apresentadas as operações potenciação e radiciação com números naturais, conhecimentos que se articulam com aqueles a serem desenvolvidos no ano seguinte com relação aos números inteiros.
A Unidade Temática Álgebra articula-se com a Unidade Temática Números na seção Diversificando, na qual se aplica a propriedade aditiva da igualdade, considerando o cenário das aprendizagens do 5º ano (ê éfe zero cinco ême ah um zero).
A Unidade Temática Geometria é abordada na construção de algoritmo para resolver situações passo a passo, o que ocorre na seção Para saber mais, ao apresentar o procedimento da multiplicação hindu.
Interpretar gráficos de colunas e de barras e a abordagem proposta neste capítulo para a Unidade Temática Probabilidade e estatística contribuem para o desenvolvimento das habilidades (ê éfe zero seis ême ah três um) e (ê éfe zero seis ême ah três dois). Cabe observar que tais conhecimentos foram tratados no 5º ano (ê éfe zero cinco ême ah dois quatro), sendo agora ampliados e aprofundados na perspectiva de preparar os estudantes para, no ano seguinte, utilizarem gráficos para comunicar informações obtidas na realização de pesquisa (ê éfe zero sete ême ah três seis). A atividade proposta para que os estudantes realizem uma pesquisa contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah três três).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
1. A capacidade é dada pela adição do seu conteúdo com o que ainda se póde colocar até ficar cheia:
.35750 + .12250 = .48000. Na piscina cabem .48000 litros.
2. Os maiores números naturais menores que 3 e 5 são, respectivamente, 2 e 4, e como 2 + 4 = 6, encontramos o exemplo pedido.
3. A população do estado fóra da capital é de ..6052794, e a população da capital é de ..1115932; portanto, a população total do estado é de ..7168726, pois ..6052794 + ..1115932 = ..7168726.
4. Pela ilustração, observamos as seguintes distâncias (em quilômetro): A até B: 90; B até C: 153; C até D: 121; D até E: 239; E até A: 117, então:
4. a) 90 + 153 + 121 = 364; portanto, 364 quilômetros.
4. b) 117 + 239 = 356; portanto, 356 quilômetros.
4. c) 364 + 121 = 485; portanto, 485 quilômetros.
4. d) 153 + 121 + 239 = 513; portanto, 513 quilômetros.
5. O menor número natural maior do que 3 é o 4. Como 4 + 4 = 8 e 8 > 7, não é possível.
6. Ela pega o ônibus às 7 horas 10 minutos, demora 25 minutos no transporte e 11 minutos a pé, chegando à escola 7 horas 46 minutos (10 + 25 + 11 = 46).
7. Do texto: “Na primeira, o público pagante foi de .54321 pessoas, e o público não pagante foi de .3895 pessoas. Na segunda partida, a quantidade de pessoas aumentou: os pagantes foram .63247 pessoas, e os não pagantes, .5894 pessoas”.
7. a) Desse modo, na primeira partida compareceram .58216 torcedores (.54321 + .3895 = .58216) e, na segunda, .69141 espectadores (.63247 + .5894 = .69141).
7. b) O total de pessoas que assistiram aos jogos é de .127357 (.69141 + .58216 = .127357).
8. Todos os números com algarismos 2, 5 e 7 distintos são: 257, 275, 527, 572, 725, 752, e sua soma é .3108.
12. As propriedades mencionadas indicam que a ordem das parcelas não altera a soma (propriedade comutativa) e que podemos associar as parcelas de modos diferentes sem alterar a soma (propriedade associativa). Nos casos a seguir, a ideia é associar valores mais facilmente calculáveis, como os pares 5 + 5 = 6 + 4 = 7 + 3 = 10.
12. a) 73 + (15 + 5) = 73 + 20 = 93
12. b) 20 + (13 + 7) = 20 + 20 = 40
12. c) (18 + 12) + 61 = 30 + 61 = 91
12. d) 28 + 12 + 17 = (28 + 12) + 17 = 40 + 17 = 57
12. e) (15 + 5) + 9 = 20 + 9 = 29
12. f) (43 + 27) + 51 = 70 + 51 = 121
13. Mônica decompõe os números e depois os reagrupa para adicioná-los; observe:
13. a) (70 + 3) + (10 + 5) + 5 = (70 + 10) + (3 + 5 + 5) = 80 + 13 = 93
13. b) 20 + (10 + 3) + 7 = (20 + 10) + (3 + 7) = 30 + 10 = 40
13. c) (10 + 8) + (10 + 2) + (60 + 1) = (10 + 10 + 60) + (8 + 2 + 1) = 80 + 11 = 91
13. d) (20 + 8) + (10 + 7) + (10 + 2) = (20 + 10 + 10) + (8 + 7 + 2) = 40 + 17 = 57
13. e) (10 + 5) + 5 + 9 = 10 + (5 + 5 + 9) = 10 + 19 = 29
13. f) (40 + 3) + (50 + 1) + (20 + 7) = (40 + 50 + 20) + (3 + 1 + 7) = 110 + 11 = (100 + 10) + (10 + 1) = 100 + (10 + 10) + 1 = 121
14. Dados têm valores de 1 a 6, por isso as opções com soma 9 são duas: 3 e 6, 4 e 5.
15. a) No início da viagem, o hodômetro marcava .18540 quilômetros; depois de percorrer .1837 quilômetros na viagem, passará a marcar .20377 quilômetros (.18540 + .1837 = .20377).
15. b) Após percorrer .1400 quilômetros, passará a marcar .21777 quilômetros (.20377 + .1400 = .21777).
17. Cristina saiu de casa com 57 reais (5 × 10 + 3 × 1 + 2 × 2 = 50 + 3 + 4 = 57).
17. a) Ao todo, Cristina tem 57 reais (5 × 10 + 3 × 1 + 2 × 2 = 57). Pagando 35 reais no almoço, sobram 22 reais (57 – 35 = 22).
17. b) Ela precisa pagar exatamente 35 reais para não receber troco; póde fazer isso das seguintes maneiras: usando 3 cédulas de 10 reais, uma cédula de 2 reais e 3 moedas de 1 real ou 3 cédulas de 10 reais, duas cédulas de 2 reais e uma moeda de 1 real.
18. Usando a calculadora, obtém-se .67185 – .31846 = .35339; para conferir usando a operação inversa, deve-se efetuar .35339 + .31846 e observar que será igual a .67185.
19. A adição correspondente é a operação inversa:
19. a) .5812 – .4815 = 997 ⇒ 997 + .4815 = .5812
19. b) .72368 – .25586 = .46782 ⇒ .46782 + .25586 = .72368
20. 416 + 209 = 625, e duas subtrações que se póde associar são as operações inversas, ou seja, 625 – 209 = 416 e 625 – 416 = 209.
21. Podemos observar os valores na tabela, sempre em milhões.
• Ásia: em 2005, 554; em 2020, 418.
A diferença é de 136 milhões (554 – 418 = 136) a menos.
• América Latina e Caribe: em 2005, 52; em 2020, 60.
A diferença é de 8 milhões (60 – 52 = 8) a mais.
22. Não é possível efetuar a subtração nos números naturais se o minuendo for menor que o subtraendo. Assim:
22. a) 206 – 48 = 158
22. b) São valores iguais:
116 – 116 = 0
22. c) Impossível, pois 54 < 75.
22. d) São valores iguais:
91 – 91 = 0
22. e) Impossível, pois 13 < 23.
22. f) 67 – 49 = 18
23. Só é possível quando o minuendo for maior ou igual ao subtraendo.
24. Não podemos dizer isso. Observando o exemplo 10 – 5 ≠ 5 – 10 fica evidente que a subtração não é comutativa, pois a ordem da operação importa no resultado (e na possibilidade de efetuar a operação).
25. Resposta pessoal. Existem outras maneiras de fazer o cálculo proposto, por exemplo:
173 + 27 = (170 + 3) + (20 + 7) = (170 + 20) + (3 + 7) = 190 + 10 = 200
26. Temos uma subtração desconhecida

–

= 26
• Aumentar em 10 o subtraendo:

– (

+ 10) = 26 – 10 = 16
• Aumentar em 4 o minuendo: (

+ 4) –

= 26 + 4 = 30
• Aumentar ambos em 9 unidades: (

+ 9) – (

+ 9) = 26 + 9 – 9 = 26, não altera o resultado.
27. Deseja-se obter a diferença entre as quantidades de medalha, então a operação a ser efetuada é a subtração 30 – 20.
28. a) Do texto, “ao fazer uma jarra de limonada, coloquei 100 gramas de açúcar. Depois, coloquei mais 50 gramas. Experimentei e não estava boa. Resolvi acrescentar 250 gramas de açúcar”. Portanto, a quantidade total de açúcar é de 400 gramas (100 + 50 + 250 = 400).
28. b) Do texto, “o último acréscimo de açúcar deveria ter sido de apenas 150 gramas”. Como o acréscimo havia sido de 250 gramas, a quantidade a mais é de 100 gramas (250 – 150 = 100).
29. As operações são chamadas inversas quando indicam o processo contrário da operação de referência.
29. a)

– 12 = 20 ⇒

= 20 + 12 = 32
29. b)

+ 36 = 75 ⇒

= 75 – 36 = 39
29. c)

– 15 = 25 ⇒

= 25 + 15 = 40
29. d)

+ 98 = 231 ⇒

= 231 – 98 = 133
30. Posso utilizar a operação inversa para resolver, sabendo que o menor número de um algarismo é 1 e o maior é 9, o máximo e o mínimo valores para encontrar

são:
30. a) 100 –

= 1 ⇒

= 100 – 1 = 99 e 100 –

= 9 ⇒

= 100 – 9 = 91
Então,

póde ser 91, 92, 93, 94, 95, 96, 97, 98 e 99.
30. b) 108 –

= 1 ⇒

= 108 – 1 = 107 e 108 –

= 9 ⇒

= 108 – 9 = 99
Como

é um número de dois algarismos, póde ser 99.
30. c) 109 –

= 1 ⇒

= 109 – 1 = 108 e 109 –

= 9 ⇒

= 109 – 9 = 100
Como

é um número de dois algarismos, não há opção possível.
31. Resposta pessoal; elaboração de problema.
33. Como 2 + 8 = 10 e 5 + 5 = 10, póde ser mais fácil operar agrupando números cuja soma forme dezenas inteiras.
12 + 25 + 18 + 15 = 37 + 18 + 15 = 55 + 15 = 70
(12 + 18) + (25 + 15) = 30 + 40 = 70
34. A adição mental póde ser facilitada agrupando as ordens e procurando formar dezenas inteiras.
34. a) 11 + 37 + 9 = (11 + 9) + 37 = 20 + 37 = 57
34. b) (20 + 10) + (70 + 6) = (30 + 70) + 6 = 100 + 6 = 106
34. c) 54 + (20 + 3) + 7 = (54 + 20) + (3 + 7) = 74 + 10 = 84
34. d) (40 + 3) + 21 + 7 + (50 + 6) + 4 = = 40 + (3 + 7) + 50 + (6 + 4) + 21 = = 40 + 10 + 50 + 10 + 21 = 100 + 31 = 131
40. Nessa situação, receber um e-mail significa adicionar 1 à caixa de entrada, e apagar um e-mail significa subtrair 1.
40. a) Do texto, “acumulou 650 mensagens em um mês e deletou 288 delas. No mês seguinte, ele recebeu 740 novas mensagens e apagou .1000 mensagens”. Então a expressão será:
650 – 288 + 740 – .1000
40. b) Resolvendo a expressão do item a:
650 – 288 + 740 – .1000 = 362 + 740 – .1000 = = 1 102 – .1000 = 102
Portanto, cento e duas mensagens.
41. Nessa situação, subir indica adição e descer indica subtração na formulação da expressão.
41. a) Do texto, “depois de subir 455 metros de uma montanha, subiu mais 325 metros, porém escorregou e desceu 18 metros. Depois, ele tornou a subir 406 metros.”. Então a expressão será:
455 + 325 – 18 + 406
41. b) Resolvendo a expressão:
455 + 325 – 18 + 406 = 780 – 18 + 406 = = 762 + 406 = .1168
41. c) A alpinista está a .1168 métros da base da montanha.
42. Resposta pessoal.
43. a) A multiplicação nos permite descobrir o valor total de organizações retangulares, como é o caso da plantação de abacaxis enfileirados, efetuando 118 ⋅ 84.
43. b) Os números 118 e 84 são os fatores. O resultado se chama produto.
43. c) 118 ⋅ 84 = .9912; logo, .9912 pés de abacaxi.
44. Nesse caso, a multiplicação é a adição de parcelas iguais.
44. a) 4 parcelas 5 são equivalentes a 4 ⋅ 5.
44. b) 5 parcelas 2 são equivalentes a 5 ⋅ 2.
44. c) 3 parcelas 7 são equivalentes a 3 ⋅ 7.
44. d) duas parcelas a são equivalentes a 2 ⋅ a.
45. A figura é formada por um retângulo de 4 por 7 quadradinhos.
45. a) Será a soma das 4 linhas de quadradinhos:
7 + 7 + 7 + 7
45. b) Será a soma das 7 colunas de quadradinhos:
4 + 4 + 4 + 4 + 4 + 4 + 4
45. c) A multiplicação equivalente ao item a é 4 ⋅ 7 e ao item b é 7 ⋅ 4.
46. Larissa mora no 13º andar e está vindo do 4º andar, então precisa subir 9 lances de escada (13 – 4 = 9), cada um com 18 degraus; portanto, são 162 degraus (9 ⋅ 18 = 162).
47. Se qualquer um dos dois fatores de uma multiplicação for zero, o resultado (produto) também será zero.
48. Para efetuar uma multiplicação em que um dos fatores é potência de 10, pois basta acrescentar os “zeros” da potência em um dos outros fatores.
48. a) 5 ⋅ 10 = 50
48. b) 32 ⋅ 100 = .3200
48. c) 74 ⋅ .1000 = .74000
48. d) 42 ⋅ .10000 = .420000
49. a) 25 ⋅ 2 = 50
49. b) 25 ⋅ 200 = .5000
49. c) 5 ⋅ 60 = 300
49. d) 5 ⋅ 600 = .3000
49. e) 8 ⋅ 9 = 72
49. f) 80 ⋅ 90 = .7200
55. Um dado tem 6 opções de resultado, e uma moeda tem duas opções; por isso, o total de modos possíveis será de 12, pois 6 ⋅ 2 = 12.
56. Para a primeira faixa há 3 opções de cores. Tendo escolhido uma, para a segunda faixa haverá duas opções de cores e, escolhendo uma para essa faixa, para a terceira restará uma opção de cor. Assim, o total de maneiras possíveis é 6, pois 3 ∙ 2 ∙ 1 = 6.

57. Tendo 3 pares de tênis e 5 pares de meias, tenho 15 opções (3 ⋅ 5 = 15).
58. Primeira parte do trajeto tem duas opções (trem e ônibus) e a segunda parte tem 3 opções (metrô, carona, ônibus), totalizando 6 opções (2 ⋅ 3 = 6) de trajetos de ida e a mesma quantidade e opções para a volta. As opções são: trem-metrô, trem-carona, trem-ônibus, ônibus-metrô, ônibus-carona, ônibus-ônibus.
59. a) Nesse restaurante, há 3 tipos de sanduíche, 2 tipos de suco e 2 tipos de sobremesa, totalizando 12 opções de refeição (3 ⋅ 2 ⋅ 2 = 12).
59. b) Identificando as opções mais baratas em cada categoria, obtemos: cachorro-quente (R$ 5,00cinco reais), suco de limão (R$ 5,00cinco reais) e sorvete (R$ 5,00cinco reais).
60. Cada moeda tem as faces cara e coroa, obtidas sem dependência entre si, de modo que as opções ao lançar duas moedas são: cara e cara, cara e coroa, coroa e cara, coroa e coroa.
61. Resposta pessoal; elaboração e resolução de problemas.
62. O modo mais fácil de resolução depende das habilidades individuais; uma opção seria:
62. a) 36 ⋅ (25 ⋅ 4) = 36 ⋅ 100 = .3600
62. b) 5 ⋅ 45 ⋅ 2 = (5 ⋅ 2) ⋅ 45 = 10 ⋅ 45 = 450
62. c) 9 ⋅ 4 ⋅ 2 ⋅ 5 = 9 ⋅ 4 ⋅ (2 ⋅ 5) = 36 ⋅ 10 = 360
63. As propriedades da multiplicação são a comutatividade (a ordem dos fatores não altera o produto), a associatividade (podemos associar os fatores de modos diferentes sem alterar o produto) e a existência do elemento neutro (o número 1 é o elemento neutro da multiplicação); dessa maneira:
63. a) 2 ⋅ 17 ⋅ 5 = (2 ⋅ 5) ⋅ 17 = 10 ⋅ 17 = 170
63. b) 2 ⋅ 15 ⋅ 36 = (2 ⋅ 5) ⋅ (3 ⋅ 36) = 10 ⋅ 108 = .1080
63. c) 18 ⋅ 5 ⋅ 4 = (18 ⋅ 2) ⋅ (5 ⋅ 2) = 36 ⋅ 10 = 360
63. d) 2 ⋅ 38 ⋅ 5 = 38 ⋅ (2 ⋅ 5) = 38 ⋅ 10 = 380
63. e) 25 ⋅ 137 ⋅ 4 = (25 ⋅ 4) ⋅ 137 = 100 ⋅ 137 = .13700
63. f) 12 ⋅ 0 ⋅ 1 = 0
63. g) 14 ⋅ 20 ⋅ 10 = (14 ⋅ 2) ⋅ (10 ⋅ 10) = 28 ⋅ 100 = .2800
63. h) 12 ⋅ 1 ⋅ 10 = 12 ⋅ 10 = 120
63. i) 8 ⋅ 21 ⋅ 5 = (4 ⋅ 2) ⋅ (7 ⋅ 3) ⋅ 5 = (4 ⋅ 3 ⋅ 7) ⋅ (2 ⋅ 5) = 12 ⋅ 7 ⋅ 10 = 84 ⋅ 10 = 840
63. j) 75 ⋅ 1 ⋅ 4 = (25 ⋅ 3) ⋅ 4 = (25 ⋅ 4) ⋅ 3 = 100 ⋅ 3 = 300
64. A primeira impressora faz 12 cópias por minuto, a segunda imprime o triplo, ou seja, 36 cópias/minuto (12 ⋅ 3 = 36) e, portanto, 540 cópias em 15 minutos (36 ⋅ 15 = 540).
65. As roupas vendidas na loja foram as seguintes: em outubro, 84; em novembro, 168, pois 84 ⋅ 2 = 168; em dezembro, 504, pois 168 ⋅ 3 = 504. Portanto, no total do trimestre foram 756 peças de roupa (84 + 168 + 504 = 756).
70. Analisando cada caso:
70. a) verdadeira; como 1 é o elemento neutro da multiplicação, 6 ⋅ 1 = 6.
70. b) verdadeira; pela propriedade comutativa, a ordem dos fatores não altera o resultado da multiplicação.
70. c) verdadeira; pela propriedade distributiva, 6 ⋅ (7 + 4) é equivalente a 6 ⋅ 4 + 6 ⋅ 7.
70. d) falsa; pela propriedade distributiva, 10 ⋅ (x + 1) = 10 ⋅ x + 10 ⋅ 1 ≠ 10 ⋅ x.
70. e) falsa; qualquer multiplicação em que zero seja um dos fatores resulta em zero, 5 ⋅ 0 = 0.
71. A decomposição de um dos fatores em suas ordens e a propriedade distributiva são necessárias nessa resolução.
71. a) 5 ⋅ 15 = 5 ⋅ (10 + 5) = 5 ⋅ 10 + 5 ⋅ 5 = 50 + 25 = 75
71. b) 7 ⋅ 42 = 7 ⋅ (40 + 2) = 7 ⋅ 40 + 7 ⋅ 2 = 280 + 14 = 294
71. c) 3 ⋅ 25 = 3 ⋅ (20 + 5) = 3 ⋅ 20 + 3 ⋅ 5 = 60 + 15 = 75
71. d) 4 ⋅ 13 = 4 ⋅ (10 + 3) = 4 ⋅ 10 + 4 ⋅ 3 = 40 + 12 = 52
71. e) 7 ⋅ 93 = 7 ⋅ (90 + 3) = 7 ⋅ 90 + 7 ⋅ 3 = 630 + 21 = 651
71. f) 6 ⋅ 58 = 6 ⋅ (50 + 8) = 6 ⋅ 50 + 6 ⋅ 8 = 300 + 40 = 348
72. Resposta pessoal; elaboração e resolução de problemas.
73. Nessa elaboração, ao substituir os números por adições ou subtrações, estas precisam estar entre parênteses para que a resolução seja corretamente efetuada pelo colega.
85. Analisando as informações do enunciado, utilizando a propriedade, póde-se escrever:
dividendo = quociente ⋅ divisor + resto
Então:
• 42 = 7 ⋅ 6 + 0
• (42 + 1) = 7 ⋅ 6 + 1
O divisor é 6, e sabe-se que o resto de uma divisão entre dois números naturais sempre é menor que o divisor; portanto, o resto máximo será 5. Então, o valor máximo adicionado ao 42 é 5, pois: (42 + 5) = 7 ⋅ 6 + 5
86. Como o divisor é 32, o maior resto possível será 31, pois 32 – 1 = 31. Como: dividendo = quociente ⋅ divisor + resto, concluímos que 703 é o número procurado, pois 21 ⋅ 32 + 31 = 703.
87. O resto 8 é o maior possível; portanto, o divisor será 9, pois 8 + 1 = 9 e, assim, o quociente também é 9. Como dividendo = quociente ⋅ divisor + resto, 9 ⋅ 9 + 8 = 89.
88. Sem utilizar a tecla de divisão, póde-se efetuar a divisão com uma série de subtrações em que, inicialmente, o minuendo é o dividendo e o subtraendo é o divisor, que é então subtraído do resultado da operação anterior até não ser mais possível obter um número natural. Então, o quociente será a quantidade de subtrações efetuadas (a quantidade de vezes que apertou a tecla “igual”), e o resto será o último resultado parcial (que deve ser menor do que o divisor). Em uma sequência de operações iguais na calculadora, é possível apenas apertar a tecla “igual” para que se repita a última operação efetuada com o número que aparece no visor. Assim:
|
Teclas necessárias |
Sequência de resultados parciais |
Resultado da divisão |
|---|---|---|
|
|
31; 19; 7 |
Quociente 3; resto 7 |
|
|
221; 172; 123; 74; 25 |
Quociente 5; resto 25 |
|
|
626; 532; 438; 344; 250; 156; 62 |
Quociente 7; resto 62 |
|
|
138; 115; 92; 69; 46; 23; 0 |
Quociente 7; resto 0 |
93. Considerando a hierarquia das operações, efetuam-se primeiro multiplicações e divisões, e depois adições e subtrações, sempre na ordem em que aparecem. Quando há sinais de associação (parênteses, colchetes e chaves), resolvemos primeiro as operações neles contidas. Dessa maneira, obtemos:
93. a) 21 menos (32 menos 25) = 21 menos 7 = 14
93. b) 44 menos (4 ⋅ 9 menos 25) menos 12 = 44 menos (36 menos 25) menos 12 = 44 menos 11 menos 12 = 33 menos 12 = 21
93. c) 61 menos (54 menos 24 dividido por 4) = 61 menos (54 menos 6) = 61 menos 48 = 13
93. d) 25 menos {20 + [18 menos (13 + 10 dividido por 2)]} = 25 menos {20 + [18 menos (13 + 5)]} = 25 menos {20 + [18 menos 18]} = 25 menos {20 + 0} = 25 menos 20 = 5
93. e) 69 menos [26 + (67 menos 42)] = 69 menos [26 + 25] = 69 menos 51 = 18
93. f) 4 + [(55 menos 2 ⋅ 9) menos (40 dividido por 2 + 6)] = = 4 + [(55 menos 18) menos (20 + 6)] = = 4 + [37 menos 26] = 4 + 11 = 15 Associando os valores 14, 21, 13, 5, 18, 15 às letras do quadro N, U, M, E, R, O, forma-se a palavra número.
96. Substituindo os valores solicitados, por exemplo, 36 = 6 ⋅ 6 e 15 = 12 + 3 na expressão: 2 ⋅ 3 + 36 dividido por 6 + 3 ⋅ (15 menos 13) , obtemos: 2 ⋅ 3 + (6 ⋅ 6) dividido por 6 + 3 ⋅ [(12 + 3) menos 13]
Resolvendo a expressão, obtemos: 2 ⋅ 3 + (6 ⋅ 6) dividido por 6 + 3 ⋅ [(12 + 3) menos 13] = = 2 ⋅ 3 + 36 dividido por 6 + 3 ⋅ [15 menos 13] = = 2 ⋅ 3 + 36 dividido por 6 + 3 ⋅ 2 = 6 + 6 + 6 = 18
18 é o número de Ana.
97. A potenciação é uma multiplicação de fatores iguais, em que a base é o fator que se repete, e o expoente é o número de vezes que ele se repete.
97. a) duas repetições do 3 → 3elevado a 2
97. b) 3 repetições do 7 → 7elevado a 3
97. c) 4 repetições do 9 → 9elevado a 4
97. d) 6 repetições do 1 → 1elevado a 6
98. Análogo ao exercício anterior:
98. a) 10elevado a 3 são 3 fatores 10 → 10 ⋅ 10 ⋅ 10
98. b) 9elevado a 2 são 2 fatores 9 → 9 ⋅ 9
98. c) 8elevado a 4 são 4 fatores 8 → 8 ⋅ 8 ⋅ 8 ⋅ 8
98. d) 6elevado a 5 são 5 fatores 6 → 6 ⋅ 6 ⋅ 6 ⋅ 6 ⋅ 6
99. As potências de expoente 2 (ao quadrado) e as de expoente 3 (ao cubo) recebem nomes especiais. As potências com expoentes de outros valores são lidas com o número ordinal: quarta potência, quinta potência etcétera Dessa maneira:
99. a) quatro elevado à oitava potência.
99. b) treze elevado ao cubo.
99. c) duzentos e vinte elevado à sétima potência.
100. A potenciação é uma multiplicação de fatores iguais, em que a base é o fator que se repete, e o expoente é o número de vezes que ele se repete. Assim:
100. a) 5elevado a 3 = 5 ⋅ 5 ⋅ 5 = 25 ⋅ 5 = 125
100. b) 2elevado a 5 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32
100. c) 3elevado a 5 = 3 ⋅ 3 ⋅ 3 ⋅ 3 ⋅ 3 = 9 ⋅ 9 ⋅ 3 = 81 ⋅ 3 = 243
100. d) 4elevado a 5 = 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4 = 16 ⋅ 16 ⋅ 4 = 16 ⋅ 64 = .1024
100. e) 10elevado a 2 = 10 ⋅ 10 = 100
100. f) 10elevado a 6 = 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 ⋅ 10 = 100 ⋅ 100 ⋅ 100 = .10000 ⋅ 100 = ..1000000
101. É possível identificar que a sequência 3, 9, 27, 81 é 3elevado a 1, 3elevado a 2, 3elevado a 3, 3elevado a 4; portanto, o sexto termo da sequência seria 3elevado a 6 = 729.
102. Há sete caixas, cada caixa com sete compartimentos, e cada compartimento com sete embalagens. Então há 343 embalagens de ração, pois: 7elevado a 3 = 7 ⋅ 7 ⋅ 7 = 343
107. São quadrados perfeitos 100 = 10elevado a 2, 400 = 20elevado a 2 e 900 = 30elevado a 2.
108. Os números são: 169, 196, 619, 691, 916 e 961; desses, são quadrados perfeitos: 169 = 13elevado a 2, 196 = 14elevado a 2 e 961 = 31elevado a 2.
109. Testar com o número 7. Seu quadrado é 7elevado a 2 = 7 ⋅ 7 = 49 e o sucessor é 7 + 1 = 8. Adicionando 49 + 7 + 8 = 64. Como 64 = 8elevado a 2, é quadrado perfeito. É quadrado do sucessor do número escolhido.
110. A operação inversa da potenciação é a radiciação, que tem seu símbolo específico. Abaixo do símbolo de raiz está o radicando, e acima do símbolo está o índice, que indica qual é a raiz naquele caso (quadrada, cúbica, quarta etcétera). Raiz é o resultado da operação. Dessa maneira, em
Raiz quadrada de 64= 8 concluímos que:
110. a) O radicando é 64.
110. b) A raiz é 8.
110. c) O índice é 2 (na indicação da raiz quadrada, não é preciso escrever o índice 2).
111. O que justifica a igualdade na operação de raiz é a igualdade de potência inversa a ela; dessa maneira:
111. a)
Raiz quadrada de 100= 10 ⇔ 10elevado a 2 = 100
111. b)
Raiz cúbica de 343= 7 ⇔ 7elevado a 3 = 343
111. c)
Raiz quinta de 32= 2 ⇔ 2elevado a 5 = 32
111. d)
Raiz quarta de 1= 1 ⇔ 1elevado a 4 = 1
112. a) Como 7elevado a 2 = 49 ⇒
Raiz quadrada de 49= 7
112. b) Como 9elevado a 2 = 81 ⇒
Raiz quadrada de 81= 9
112. c) Como 11elevado a 2 = 121 ⇒
Raiz quadrada de 121= 11
112. d) Como 15elevado a 2 = 225 ⇒
Raiz quadrada de 225= 15
113. Substituir o valor de a em cada expressão e calcular.
113. a) a = 9 ⇒ 2 ⋅ a = 2 ⋅ 9 = 18; aelevado a 2 = 9elevado a 2 = 81;
Raiz quadrada de 9= 3
113. b) a = 25 ⇒ 2 ⋅ a = 2 ⋅ 25 = 50; aelevado a 2 = 25elevado a 2 = 625;
Raiz quadrada de 25= 5
113. c) a = 36 ⇒ 2 ⋅ a = 2 ⋅ 36 = 72; aelevado a 2 = 36elevado a 2 = 1 296;
Raiz quadrada de 36= 6
113. d) a = 100 ⇒ 2 ⋅ a = 2 ⋅ 100 = 200; aelevado a 2 = 100elevado a 2 = .10000;
Raiz quadrada de 100= 10
114. a) 3elevado a 2 + 4elevado a 2 = 25;
Raiz quadrada de 25= 5.
114. b) 6elevado a 2 + 8elevado a 2 = 100;
Raiz quadrada de 100= 10.
114. c) 9elevado a 2 + 12elevado a 2 = 225;
Raiz quadrada de 225= 15.
114. d) 12elevado a 2 + 16elevado a 2 = 400;
Raiz quadrada de 400= 20.
114. e) 5elevado a 2 + 12elevado a 2 = 169;
Raiz quadrada de 169= 13.
114. f) 10elevado a 2 + 24elevado a 2 = 676;
Raiz quadrada de 169= 26.
Para saber mais
Página 49
1. a)
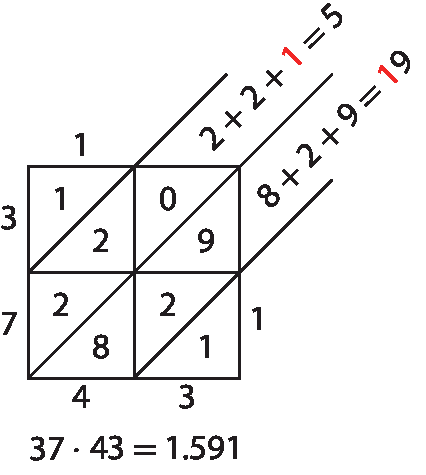
1. b)
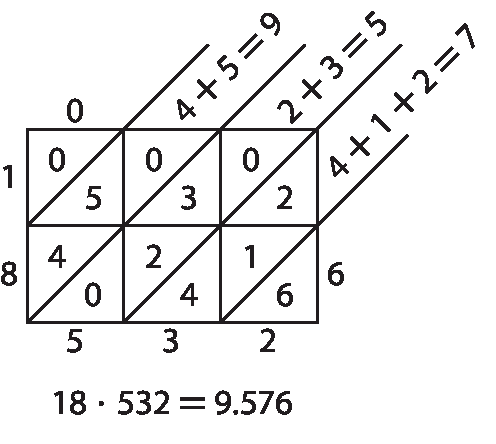
2. Escolhendo como exemplo 49 ⋅ 13, é possível efetuar das seguintes maneiras:
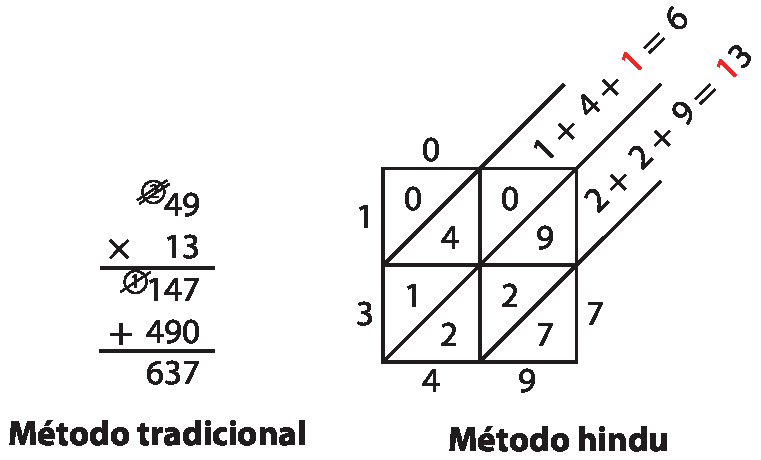
As duas maneiras de operar têm suas vantagens, podendo ser qualquer uma das duas considerada mais fácil.
Pense mais um pouco
Página 53
1. Escolhendo números de dois algarismos (números quaisquer): 19, 48, 75. Multiplicando por 101, obtemos: 19 ⋅ 101 = .1919; 48 ⋅ 101 = .4848; 75 ⋅ 101 = .7575. póde-se observar um padrão nas respostas, de repetição dos algarismos dos números escolhidos. Por isso:
1. a) 98 ⋅ 101 = .9898
1. b) 89 ⋅ 101 = .8989
2. Escolhendo números de três algarismos (números quaisquer): 197, 458, 765. Multiplicando por .1001, obtemos:
197 ⋅ .1001 = .197197
458 ⋅ .1001 = .458458
765 ⋅ .1001 = .765765
Pode-se observar um padrão nas respostas, de repetição dos algarismos dos números escolhidos. Por isso:
2. a) 356 ⋅ .1001 = .356356
2. b) 499 ⋅ .1001 = .499499
3. Usando as constatações feitas nos itens anteriores, é possível generalizar os resultados.
O valor da multiplicação dos números de dois algarismos por 101 tem sempre uma repetição desses algarismos nas suas ordens 3 e 4, sendo possível concluir A bê ⋅ 101 = a bê a bê.
O valor da multiplicação dos números de três algarismos por .1001 tem sempre uma repetição desses algarismos nas suas ordens 4, 5 e 6 (2ª classe, dos milhares), sendo possível concluir á bê cê ⋅ .1001 = abcabc.
Exercícios complementares
1. Arredondando para a dezena mais próxima:
1. a) 20 + 40 + 20 = 80
1. b) 30 + 40 + 80 = 150
1. c) 50 + 40 menos 20 + 20 = 90
1. d) 40 + 90 menos 60 menos 50 = 20
1. e) 60 menos 20 + 100 menos 30 = 110
2. Para elaborar a expressão que resolve esse problema, observe que uma compra significa subtração no saldo, e o pagamento de valores significa adição; dessa maneira: 50 menos 37 + 2 = 15
Logo, 15 reais.
3. A população total do estado é de ..4063614 habitantes, dos quais ..1933350 não moram na capital; então, a população da capital é de ..2130264 habitantes (..4063614 menos ..1933350 = ..2130264).
4. Para descobrir a idade no fim de 2027, é necessário descobrir quantos anos faltam até lá, efetuando uma subtração 2027 – [ano], e adicionar essa diferença na idade que a pessoa terá no fim do ano atual. Para saber em qual ano terá 33 anos, basta adicionar 33 ao seu ano de nascimento.
5. Há dois números, de modo que a menos b = 53; observar, por exemplo:
100 menos 47 = 53 ⇒ (100 + 1) menos (47 + 1) = 101 menos 48 = 53
Testando alguns pares de valores, é possível concluir que a diferença entre os sucessores é a mesma diferença entre os números. Nos outros volumes desta coleção será abordada a linguagem algébrica, ferramenta com a qual será possível justificar que a diferença entre os sucessores quaisquer é:
(a + 1) menos (b + 1) = a menos b
8. Observando o gráfico, concluímos:
8. a) O ano com mais matrículas é o com a barra mais alta, 2014.
8. b) Em 2015 havia uma.novecentas e dezesseis.112 matrículas, e em 2016 foram uma.oitocentas e cinquenta e nove.004, uma diminuição de .57108, pois ..1916112 menos ..1859004 = .57108.
8. c) Arredondando os valores para a unidade de milhar mais próxima, em 2015 havia uma.novecentas e dezesseis.000 e em 2016, uma.oitocentas e cinquenta e nove.000, uma diferença de .57000, pois ..1916000 menos ..1859000 = .57000.
9. O número natural é 21, pois 9 + (21 menos 15) ⋅ 2 = 9 + 6 ⋅ 2 = 9 + 12 = 21, e seu sucessor é 22, pois 21 + 1 = 22.
11. As informações do enunciado são: preço à vista .1590 reais, entrada 580 reais, parcela 360 reais, quantidade de parcelas 3. Portanto, o valor total do pagamento parcelado foi de .1660, pois 580 + 360 ⋅ 3 = 580 + .1080 = .1660. Dessa maneira, a diferença entre os preços é de 70 reais, pois .1660 menos .1590 = 70.
12. Entre 200 e 500, os quadrados perfeitos são 225, 256, 289, 324, 361, 400, 441 e 484, pois:
15elevado a 2 = 225
16elevado a 2 = 256
17elevado a 2 = 289
18elevado a 2 = 324
19elevado a 2 = 361
20elevado a 2 = 400
21elevado a 2 = 441
22elevado a 2 = 484
Verificando
1. Arredondando para a centena mais próxima,
.1758 + .2439 ⇒ .1800 + .2400 = .4200
Alternativa d.
2. Reorganizando os valores do 1º termo da igualdade, obtemos: .1400 + 553 + 37 = .1400 + (550 + 3) + 37 = .1400 + 550 + 40 = .1400 +

+ 40 ⇒

= 550.
Alternativa c.
3. Foram colocados .5337 itens, totalizando .6473 no estoque; então, a quantidade inicial em estoque era de .1136, pois .6473 menos .5337 = .1136.
Alternativa b.
4. Iniciando a simplificação da expressão, obtemos:
(980 menos 75) + 36 = 905 + 36.
Alternativa a.
5. Um conjunto de 510 latas precisará de 34 caixas, pois 510 dividido por 15 = 34.
Alternativa c.
6. Simplificando a expressão, obtemos: 10 menos 10 + (10 menos 10 + 10) menos 10 = 10 menos 10 + 10 menos 10 = 0
Alternativa a.
7. Escolhendo um sabor de sorvete entre 36 e um sabor de cobertura entre 7, consigo fazer duzentas e cinquenta e duas combinações (36 ⋅ 7 = 252) e 250 < 252 < 450.
Alternativa c.
8. Como divisão e multiplicação são operações inversas, o número

é tal que:

⋅ 14 = 518 ⇒

= 518 dividido por 14 = 37
Alternativa d.
9. Como potência e raiz são operações inversas, o número será 144, pois
Raiz quadrada de 144= 12 e 12elevado a 2 = 144.
Alternativa d.
10. Simplificando a igualdade e usando a propriedade da operação inversa, obtemos:
(27 + 14) ⋅

= 369 ⇒ 41 ⋅

= 369 ⇒

= 369 dividido por 41 = 9
Alternativa d.
11. Encontrar a tal que:
aelevado a 2 + 5 +
Raiz quadrada de a= 23
Testando os valores das alternativas, obtemos:
11. a) a = 9 ⇒ 9elevado a 2 + 5 +
Raiz quadrada de 9= 81 + 5 + 3 = 89 ≠ 23
11. b) a = 8 ⇒ 8elevado a 2 + 5 +
Raiz quadrada de 8= 64 + 5 +
Raiz quadrada de 8 = 69 +
Raiz quadrada de 8 ≠ 23
11. c) a = 4 ⇒ 4elevado a 2 + 5 +
Raiz quadrada de 4= 16 + 5 + 2 = 23
11. d) a = 3 ⇒ 3elevado a 2 + 5 +
Raiz quadrada de 3= 9 + 5 +
Raiz quadrada de 3= 14 +
Raiz quadrada de 3≠ 23
Alternativa c.
Capítulo 3 – Estudando figuras geométricas
• Objetivos do capítulo e justificativas
• Distinguir figuras planas de não planas, descrevendo algumas de suas características e estabelecendo relações entre elas.
• Classificar figuras não planas como corpos redondos e poliedros.
• Identificar e quantificar elementos de um poliedro: faces, vértices e arestas.
• Reconhecer prismas e pirâmides como poliedros e identificar suas bases.
• Associar o estudo de Geometria à Arquitetura e à História.
• Interpretar gráficos de barras.
• Explorar ampliação e redução de figuras com o uso de malhas quadriculadas.
Nós vivemos em um mundo tridimensional e, por esse motivo, nosso primeiro contato com a Geometria, ainda nos Anos Iniciais do Ensino Fundamental, acontece na análise de objetos tridimensionais, relacionando-os com representações planas de figuras observadas. Nesse sentido, nos Anos Finais vamos aprofundar esse estudo, verificando as características específicas dos corpos geométricos estudados.
Para classificar corpos geométricos em três dimensões como proposto, faz-se necessário construir uma argumentação plausível que distingua os objetos. Assim, este é um objeto muito próximo da competência específica 2 de Matemática, privilegiando a capacidade de construir argumentos convincentes para tal distinção.
Definidos os objetos geométricos de estudo e suas características, é importante que os estudantes consigam diferenciar cada elemento para que, no cotidiano, quando identificados, tais elementos possam servir de recursos para resoluções de problemas.
Os poliedros podem ser identificados em situações cotidianas, bem como suas bases, auxiliando os estudantes na resolução de problemas, sejam eles necessariamente matemáticos, sejam de implicação social.
A contextualização da Geometria no campo da História e da Arquitetura proporciona aos estudantes relações que favorecem a compreensão dos elementos geométricos estudados, tornando o estudo mais interessante e significativo para a turma. A Abertura do capítulo apresenta o grafismo e o artesanato africano que, passados de geração em geração, preservam a cultura e os conhecimentos historicamente construídos contemplando as competências gerais 1 e 3 e a competência específica 1.
As transformações geométricas fazem parte de estratégias de resolução de problemas pertinentes não só para a área de Matemática, mas onde se fizer necessária a ampliação ou a redução de figuras. Na Geografia, por exemplo, as escalas determinam o grau de ampliação/redução dos mapas a serem estudados. Assim, ao possibilitar o uso de processos e ferramentas matemáticas para modelar e resolver problemas em outras áreas de conhecimento, favorecemos o desenvolvimento da competência específica 5.
A seção Trabalhando a informação, que explora a evolução do acesso dos lares brasileiros à internet por meio da linguagem textual e gráfica, propicia o desenvolvimento da competência geral 4. Já o desenvolvimento das competências gerais 9 e 10 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois permitem aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação às atividades propostas.
As diferentes atividades propostas contribuem para o desenvolvimento da competência específica 6, assim como as atividades em grupo contribuem para o desenvolvimento da competência específica 8.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah zero três) Resolver e elaborar problemas que envolvam cálculos (mentais ou escritos, exatos ou aproximados) com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.
(ê éfe zero seis ême ah um sete) Quantificar e estabelecer relações entre o número de vértices, faces e arestas de prismas e pirâmides, em função do seu polígono da base, para resolver problemas e desenvolver a percepção espacial.
(ê éfe zero seis ême ah dois um) Construir figuras planas semelhantes em situações de ampliação e de redução, com o uso de malhas quadriculadas, plano cartesiano ou tecnologias digitais.
(ê éfe zero seis ême ah dois quatro) Resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento.
(ê éfe zero seis ême ah três um) Identificar as variáveis e suas frequências e os elementos constitutivos (título, eixos, legendas, fontes e datas) em diferentes tipos de gráfico.
(ê éfe zero seis ême ah três dois) Interpretar e resolver situações que envolvam dados de pesquisas sobre contextos ambientais, sustentabilidade, trânsito, consumo responsável, entre outros, apresentadas pela mídia em tabelas e em diferentes tipos de gráficos e redigir textos escritos com o objetivo de sintetizar conclusões.
Os conceitos e as atividades relacionados ao estudo de figuras geométricas planas e figuras geométricas não planas são o foco neste capítulo, desenvolvendo a Unidade Temática Geometria, envolvendo também os tópicos de características de sólidos e elementos de um poliedro, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah um sete). Vale ressaltar que atividades relacionadas a figuras geométricas foram desenvolvidas no 5º ano com (ê éfe zero cinco ême ah um seis) e (ê éfe zero cinco ême ah um sete), e sua retomada e ampliação pretendem consolidar esse conhecimento. Ainda na Unidade Temática Geometria, este capítulo traz, na seção Diversificando, a construção de figuras planas semelhantes em situações de ampliação e redução, aprofundando os conhecimentos abordados sobre esse tema no 5º ano com (ê éfe zero cinco ême ah um oito) e (ê éfe zero cinco ême ah dois quatro), contribuindo para o desenvolvimento das habilidades (ê éfe zero seis ême ah dois um) e (ê éfe zero seis ême ah dois quatro). Os conhecimentos desenvolvidos sobre leitura de dados expressos em tabela e gráficos, realizados no capítulo anterior, serão suporte para a articulação com a Unidade Temática Probabilidade e estatística neste capítulo, contribuindo para o desenvolvimento das habilidades (ê éfe zero seis ême ah três um) e (ê éfe zero seis ême ah três dois).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.
Trabalhando a informação
Página 79
1. É necessário observar as informações do gráfico: o comprimento da barra e o valor associado a ele a cada ano, considerando a informação do título de que os valores estão “em milhões”.
1. b) As diferenças de um ano para o outro, em milhões, são:
um) 2017 a 2018: 47 menos 42 = 5;
dois) 2018 a 2019: 51 menos 47 = 4;
três) 2019 a 2020: 62 menos 51 = 11. Portanto, a maior diferença ocorre de 2019 a 2020.
1. c) Conforme calculamos no item b, o crescimento de domicílios foi de 62 milhões menos 51 milhões = 11 milhões.
1. d) Em 2020 havia 62 milhões de domicílios com acesso à internet; considerando 2,8 moradores por domicílio, podemos estimar o total de pessoas com acesso à internet em 2,8 · 62 milhões = 174 milhões.
2. Uma barra mais comprida e de mesma largura que as demais, pois é o comprimento que determina, no eixo horizontal, o total de número de domicílios com acesso à internet.
Exercícios complementares
7. Para realizar esse exercício, perceba que sempre há o mesmo número de faces laterais e de arestas e vértices da base do sólido. Além disso, um prisma apresenta duas bases, e uma pirâmide sempre tem apenas uma base.
7. a) As bases do prisma têm 7 vértices cada; portanto, 7 arestas cada, além das 7 arestas unindo as bases, totalizando vinte e uma arestas (7 + 7 + 7 = 21). O prisma tem uma face lateral apoiada em cada aresta da base; portanto, são 7 faces laterais (7 · 1 = 7).
7. b) Uma pirâmide sempre tem 1 vértice fóra da base, e os demais vértices na base; então, havendo 12 vértices, são 12 menos 1 = 11 deles na base. Da mesma maneira, essa face tem 11 arestas, 11 faces laterais e 11 lados na figura plana que representa sua base. Além das arestas da base, há outras 11 unindo a base até o vértice fóra dela, totalizando vinte e duas arestas no sólido (11 + 11 = 22).
7. c) Uma pirâmide de 20 faces tem uma base e 19 faces laterais (20 menos 1 = 19), e, portanto, 19 vértices na base e 20 vértices no total (19 + 1 = 20). O prisma, então, tem os mesmos 20 vértices, sendo 20 dividido por 2 = 10 em cada base. Dessa maneira, o prisma tem 10 faces laterais e as duas bases, totalizando 12 faces (10 + 2 = 12).
8. A base (figura verde) tem 6 lados; portanto, são necessárias 6 faces laterais (figura rosa) para formar a pirâmide de base hexagonal.
9. A base (figura azul) tem 5 lados; portanto, são necessárias 5 faces laterais (figura laranja) e mais uma base para formar o prisma de base pentagonal.
Verificando
5. Um prisma de base triangular tem 9 arestas (3 + 3 + 3 = 9), 6 vértices (3 + 3 = 6) e 5 faces (3 + 2 = 5).
Alternativa b.
6. Uma pirâmide com 5 arestas na base tem 5 vértices na base e uma fóra dela, totalizando 6 vértices (5 + 1 = 6).
Alternativa b.
7. A base de um cone é um círculo e sua sombra também pode ter esse formato, mas não o formato de retângulo, pentágono ou hexágono.
Alternativa c.
8. O tambor de duas bases iguais pode ser associado a um corpo redondo chamado cilindro.
Alternativa c.
Capítulo 4 — Divisibilidade
• Objetivos do capítulo e justificativas
• Estabelecer entre os números naturais relações como “ser múltiplo de” e “ser divisor de”.
• Explorar sequências numéricas.
• Compreender e aplicar os critérios de divisibilidade por 2, 3, 4, 5, 6, 9 e 10.
• Compreender fluxogramas.
• Reconhecer e distinguir números primos de números compostos.
• Expressar números compostos por meio de sua decomposição de fatores primos.
• Interpretar e resolver problemas que envolvam as ideias de múltiplo e divisor.
• Desenvolver a noção de máximo divisor comum (ême dê cê) e a de mínimo múltiplo comum (ême ême cê).
• Construir gráficos de barras.
Além do processo operatório envolvido, estabelecer relações entre múltiplos e divisores está relacionado ao fato de que a multiplicação e a divisão são operações inversas. Esse é um importante aporte para que, a partir do 7º ano, sejam estabelecidas relações entre as operações ao resolver problemas envolvendo equações.
As sequências numéricas possibilitam o trabalho com cálculo mental para verificação destas e desenvolvem uma agilidade de raciocínio importante na busca de padrões e para a resolução de problemas. Fazendo a ponte entre a Aritmética e a Álgebra, a generalização de elementos de sequências, por meio de expressões algébricas, impõe para o estudante uma crescente habilidade de raciocínio e de uso da lógica, além de favorecer a aquisição da competência específica 2. Papel semelhante desempenham a construção com compreensão de algoritmos (entre outros, os critérios de divisibilidade) e de fluxogramas sobre relações matemáticas e destas sobre outras áreas. Esse rol de práticas e de conhecimentos subsidia o desenvolvimento da competência específica 6 e da competência geral 4.
Identificar números primos usando um quadro de números naturais, assim como o trabalho com arredondamentos e o uso de estimativas, possibilitam aos estudantes estabelecer relações entre os números naturais compostos, despertando o espírito de investigação, fortalecendo o cálculo mental e favorecendo a construção de estratégias operatórias com maior agilidade ao resolver problemas, o que é bem próximo da competência geral 2 e da competência específica 3.
As ideias operatórias devem ser exploradas tanto quanto os cálculos aritméticos, visto que a compreensão e a resolução de problemas que envolvam múltiplos e divisores podem ir além das operações inversas multiplicação e divisão, com os seus significados diversos.
O trabalho com frações equivalentes póde se tornar mais produtivo e ágil no uso das operações de adição e de subtração com frações ao calcularmos o mínimo múltiplo comum entre os denominadores das frações presentes na operação. Além disso, existem situações-problema que são resolvidas facilmente quando conceituamos máximo divisor comum e mínimo múltiplo comum, ampliando o leque de estratégias de resoluções que o estudante carrega consigo ao longo da Educação Básica, como apontado na competência geral 2.
Conforme indica a competência geral 4, o uso de recursos matemáticos para expressar e sintetizar ideias de diferentes áreas do conhecimento, incluindo a própria Matemática, torna a construção de gráficos de barras um fator importante para a recepção e a transmissão de informações pesquisadas ou apresentadas pela mídia e por outros meios digitais de informação.
Enfim, o empenho para alcançar os objetivos explicitados contribui para que os estudantes desenvolvam diferentes habilidades, como o uso de linguagem simbólica (formal e técnica), a compreensão leitora, a interpretação de informações e o desenvolvimento de um repertório para a resolução de diferentes situações-problema. Desse modo, contribuímos para o desenvolvimento das competências gerais 2 e 4 e da competência específica 2.
O trabalho proposto no exercício 14, da seção Exercícios propostos, que utiliza a calculadora como suporte para processo investigativo, contribui para o desenvolvimento da competência geral 5 e da competência específica 5.
As atividades a serem realizadas em grupos permitem aos estudantes exercitar diferentes habilidades socioemocionais ao trabalhar com colegas que podem ou não ter dificuldades ou facilidades em relação às atividades propostas. Dessa maneira, favorece-se o desenvolvimento das competências gerais 9 e 10 e da competência específica 8.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah zero três) Resolver e elaborar problemas que envolvam cálculos (mentais ou escritos, exatos ou aproximados) com números naturais, por meio de estratégias variadas, com compreensão dos processos neles envolvidos com e sem uso de calculadora.
(ê éfe zero seis ême ah zero quatro) Construir algoritmo em linguagem natural e representá-lo por fluxograma que indique a resolução de um problema simples (por exemplo, se um número natural qualquer é par).
(ê éfe zero seis ême ah zero cinco) Classificar números naturais em primos e compostos, estabelecer relações entre números, expressas pelos termos “é múltiplo de”, “é divisor de”, “é fator de”, e estabelecer, por meio de investigações, critérios de divisibilidade por 2, 3, 4, 5, 6, 8, 9, 10, 100 e 1000.
(ê éfe zero seis ême ah zero seis) Resolver e elaborar problemas que envolvam as ideias de múltiplo e de divisor.
(ê éfe zero seis ême ah três um) Identificar as variáveis e suas frequências e os elementos constitutivos (título, eixos, legendas, fontes e datas) em diferentes tipos de gráfico.
(ê éfe zero seis ême ah três dois) Interpretar e resolver situações que envolvam dados de pesquisas sobre contextos ambientais, sustentabilidade, trânsito, consumo responsável, entre outros, apresentadas pela mídia em tabelas e em diferentes tipos de gráficos e redigir textos escritos com o objetivo de sintetizar conclusões.
(ê éfe zero seis ême ah três três) Planejar e coletar dados de pesquisa referente a práticas sociais escolhidas pelos alunos e fazer uso de planilhas eletrônicas para registro, representação e interpretação das informações, em tabelas, vários tipos de gráficos e texto.
Neste capítulo, articulam-se todos os conhecimentos trabalhados nos capítulos anteriores que dizem respeito a Números. Assim, retomam-se atividades que envolvem as operações com números naturais na resolução de problemas, que compreendem as noções de múltiplos, divisores e critérios de divisibilidade. Além desses conteúdos, são abordados números primos, números compostos e decomposição de um número natural em fatores primos. Todos esses conhecimentos articulados constituem subsídios para os estudos sobre a Unidade Temática Números a serem desenvolvidos no 7º ano do Ensino Fundamental, dentre os quais destacamos múltiplos e divisores de um número natural (ê éfe zero sete ême ah zero um), e contribuem para o desenvolvimento das habilidades (ê éfe zero seis ême ah zero três), (ê éfe zero seis ême ah zero cinco) e (ê éfe zero seis ême ah zero seis). As Unidades Temáticas Números e Probabilidade e estatística articulam-se nas atividades apresentadas na seção Trabalhando a informação, com o objetivo de reconhecer elementos e interpretar informações expressas em tabelas e em gráficos de barras. Esse trabalho foi iniciado nos capítulos anteriores e é ampliado agora com a construção de gráficos de barras, contribuindo para o desenvolvimento das habilidades (ê éfe zero seis ême ah três um) e (ê éfe zero seis ême ah três dois). Já a proposta de pesquisa da atividade 3 contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah três três).
No capítulo apresentamos fluxogramas relacionados aos critérios de divisibilidade, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah zero quatro).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
6. Os múltiplos de um número são os valores resultantes da multiplicação desse número por um número natural. Por exemplo, os múltiplos de 3 são 3 ⋅ k, com k um número natural.
6. d) Os primeiros múltiplos da idade são 0, a própria idade, e a sua multiplicação por 2, 3 e 4.
7. a) Os múltiplos de 9 menores que 50 são 0, 9, 18, 27, 36 e 45. O próximo seria 9 ⋅ 6 = 54 > 50, mas é maior do que o limite estipulado.
7. b) O primeiro múltiplo de 6 maior do que 20 é 6 ⋅ 4 = 24. Em sequência, são múltiplos também os valores 30, 36, 42 e 48. O próximo múltiplo seria 6 ⋅ 9 = 54 > 50, mas já ultrapassa o máximo estipulado.
7. c) Os múltiplos de 14 entre 40 e 90 são 42, 56, 70, 84. O múltiplo anterior ao 42 é 14 ⋅ 2 = 28 < 40, enquanto depois do 84 é o valor 14 ⋅ 7 = 98 > 90.
7. d) Os múltiplos de 10 que estão no intervalo solicitado são 20, 30, 40, pois o intervalo “entre 12 e 50” não inclui os valores das extremidades, como o 50.
7. e) Os múltiplos de 11 entre 66 e 111 são 77, 88, 99 e 110, pois o intervalo não inclui as extremidades.
10. Observando os múltiplos de 8 entre 30 e 40, só há uma opção, 8 ⋅ 4 = 32.
Logo, 32 estudantes.
11. Queremos esse número x de modo que 90 + x seja múltiplo de 35, ou seja, algum desses: 0, 35, 70, 105, 140,reticências Como x deve ser o menor possível, 90 + x = 105 ⇒ x = 105 menos 90 = 15.
12. Análogo ao exercício 11, como quero 90 – x múltiplo de 35, 90 menos x = 70 ⇒ x = 20.
13. Seguindo as informações do texto, o cometa passou em 1 759, e isso se repete a cada 76 anos; portanto, ele passa nos anos 1 759 + 76 = 1835, 1835 + 76 = 1911, 1911 + 76 = 1987, 1987 + 76 = 2063. Como o século vinte e um começa no ano 2001, a resposta é ano 2063.
14. É possível encontrar uma sequência de múltiplos de um número de pelo menos dois modos. Usando o número 3 como exemplo: sabendo que os múltiplos são resultados da multiplicação de 3 por diversos números naturais, bastaria efetuar

etcétera para determinar os múltiplos de 3. Entre cada multiplicação, zerar o visor com a tecla

. Outra maneira, mais rápida, de calcular os múltiplos é por meio da adição sucessiva, ou seja, iniciando com o visor da calculadora zerado, teclar

para observar o primeiro múltiplo, em sequência para cada

pressionado, a operação vai se repetir e aparecerão no visor múltiplos consecutivos de 3.
14. a) Resposta possível: 10, 12, 14, 16, 18, 20, 22, 24, 26 e 28; não; 0, 2, 4, 6 ou 8.
14. b) Justificando para um dos valores, análogo para os outros. Um número natural que termina em 4 (algarismo 4 na unidade e qualquer quantidade de dezenas) póde ser escrito como “a4” = 10a + 4 = 2 ⋅ (5a + 2), é múltiplo de 2 para qualquer a. Da mesma maneira é divisível por 2, pois sua divisão é exata. Isso é válido para qualquer número com algarismo par na unidade.
14. c) Resposta possível: 10, 15, 20, 25, 30, 35, 40 e 45; 0 ou 5.
14. d) Um número que termina em 5 e tem uma quantidade qualquer de dezenas é “b5” = 10b + 5 = 5 ⋅ (2b + 1), ou seja, é sempre múltiplo de 5, e é divisível pois [5⋅ (2b + 1)] : 5 tem resto zero (e quociente 2b +1). Análogo para número terminado em zero, pois 5 ⋅ 2b é múltiplo e divisível por 5 (com quociente 2b).
14. e) Resposta possível: 10, 20, 30, 40, 50 e 60; 0.
14. f) Um número natural que termina em 0 é aspascê0” = 10 ⋅ c, que é múltiplo de 10 pela definição e também é divisível pois (10 ⋅ c) : 10 = c tem resto zero.
15. Respostas pessoais. Verifique se as condições dos problemas elaborados contemplam os conceitos abordados, e, se possível, sugira como poderiam ser enriquecidos.
16. a) Como o 1 é elemento neutro da divisão, qualquer número dividido por 1 é igual ao próprio número, de fórma que sempre há resto zero; o 1 é divisor de qualquer número natural.
16. b) Não é possível dividir nenhum número por zero; então, o zero nunca é divisor de um número.
17. a) Divisores de 11: 1, 11.
17. b) Divisores de 18: 1, 2, 3, 6, 9, 18.
17. c) Divisores de 25: 1, 5, 25.
17. d) Divisores de 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 45, 90.
18. Os divisores de 36 são 1, 2, 3, 4, 6, 9, 12, 18 e 36. Os divisores de 42 são 1, 2, 3, 6, 7, 14, 21, 42. Em comum, eles têm os divisores 1, 2, 3 e 6, e o maior deles é 6.
Observe que esta atividade antecipa, sem exigir conhecimento prévio do estudante, o conceito de máximo divisor comum, a ser trabalhado ainda neste capítulo.
19. A facilidade é um fator importante para a adesão ao tratamento com remédios contínuos; um componente disso é a possibilidade de administrar o tratamento no mesmo horário todos os dias. Como um dia tem 24 horas, para que isso ocorra, é necessário que sua posologia seja um divisor de 24 (1, 2, 3, 4, 6, 8, 12 ou 24), de modo que uma dose a cada 5 horas resultaria em dificuldade de acompanhamento do tratamento.
22. a) Como 42 é divisível por 7 (pois 42 = 6 ⋅ 7), então 42 : 7 = 6 tem resto zero. Fazendo de fórma análoga, como 28 = 7 ⋅ 4, então 28 : 7 = 4 com resto zero; logo, 28 é divisível por 7.
22. b) Como 28 = 4 ⋅ 7 e 42 = 6 ⋅ 7, póde-se escrever 42 + 28 = 6 ⋅ 7 + 4 ⋅ 7 = (6 + 4) ⋅ 7, então

= 4 nas duas ocorrências.
Do enunciado do item b, depreende-se que 7 é um fator de (42 + 28); logo, (42 + 28) é divisível por 7.
22. d) No item b, na última igualdade é utilizada a propriedade distributiva, que afirma que a expressão formada pela multiplicação, em que há um fator formado por uma soma ou diferença, como (6 + 4) ⋅ 7, é igual à multiplicação de cada uma das parcelas dessa soma, ou seja, nesse caso, 6 ⋅ 7 + 4 ⋅ 7.
22. e) Escolhendo os números 13 e 26 (pois 13 : 13 = 1, resto zero, e 26 : 13 = 2, resto zero), que são ambos divisíveis por 13. A soma 13 + 26 = 39 também é divisível por 13, pois 39 : 13 = 3, resto zero.
25. Como não é interessante efetuar a divisão inteira, vale procurar os divisores de 2, 5 e 10 mais próximos e menores do número .98543. Analisando: um número natural é divisível por 2 somente quando é par; portanto, .98542 é divisível por 2, então o resto da divisão .98543 : 2 será .98543 – .98542 = 1. Um número natural é divisível por 5 somente quando termina em zero ou em 5; portanto, .98540 é divisível por 5, e o resto de .98543 : 5 será .98543 – .98540 = 3. Um número natural é divisível por 10 somente quando termina em zero; da mesma fórma, .98540 é divisível por 10, e o resto de .98543 : 10 será .98543 – .98540 = 3.
27. a) Como 130 = 65 ⋅ 2 = 5 ⋅ (13 ⋅ 2); portanto, 130 é divisível por 5.
27. b) As igualdades de interesse são 130 = 13 ⋅ (5 ⋅

1) = 13 ⋅ (

2 ⋅ 2) = 13 ⋅

3. Podemos escrever 130 = 13 ⋅ (5 ⋅ 2) = 13 ⋅ 10; portanto,

1 = 2,

2 = 5 e

3 = 10.
27. c) Sim, é divisível, pois 130 = 13 ⋅ (5 ⋅ 2), ou seja, (5 ⋅2) é um dos fatores de 130.
27. d) Não, pois ter um fator 2 não implica ter um fator 5 na fatoração do valor.
27. e) O número 40 é divisível por 2 e por 5 ao mesmo tempo, pois 40 = 2 ⋅ 20 e 40 = 5 ⋅ 8. Ele também é divisível por 10, pois 40 = (2 ⋅ 5) ⋅ 4 = 10 ⋅ 4, isso acontece para qualquer número escolhido que seja divisível tanto por 2 como por 5.
28. O maior número de 3 algarismos é 999, porém para ser divisível por 5 deve ter os algarismos 0 ou 5 na ordem das unidades; portanto, o maior número de três algarismos que é divisível por 5 é 995. Já para ser divisível por 2, deve terminar em número par; portanto, o maior número de três algarismos divisível por 2 é 998. Para ser divisível por 10 deve terminar em 0; portanto, será 990.
29. a) Se um número é divisível por 10, então ele termina em 0. Assim, ele é par; portanto, divisível por 2. Além disso, pelo critério de divisibilidade por 5, podemos saber que ele também é divisível por 5.
29. b) Se um número natural termina em 2 zeros, ele é da fórma xis00, em que xis representa uma sequência de algarismos quaisquer. Assim, é possível dividir xis00 por 100 e obter o número natural definido pela sequência de algarismos dada por xis. Analogamente, se ele termina em 3 zeros, ele é da fórma xis000; é possível dividi-lo por .1000 e obtemos um número natural dado por xis.
30. Exemplo de resposta: Marcos anotou no caderno um número divisível por 2, Ana anotou outro número divisível por 5 e Emanuele anotou um terceiro número divisível por 10. Então, o produto entre os números que eles anotaram será divisível por 100? Resposta: Sim, será possível dividir o produto obtido por 2, depois por 5 e, ainda, por 10; assim, é possível dividi-lo por 2 ∙ 5 ∙ 10, isto é, por 100.
31. a) Considerando o número 43

.
Para ser divisível por 2 deve terminar em algarismo par; portanto, 0, 2, 4, 6 e 8.
31. b) Um número natural é divisível por 3 somente quando a soma dos valores absolutos dos seus algarismos é divisível por 3. Então, a soma 4 + 3 +

= 7 +

deve ser divisível por 3 (ser 3, 6, 9, 12, 15 etcétera). Como 7 > 3 e 7 > 6, a soma já é maior do que esses valores: 7 +

= 9 ⇒

= 2; 7 +

= 12 ⇒

= 5; 7 +

= 15 ⇒

= 8; 7 +

= 18 ⇒

= 11. Como

é formado apenas por um algarismo, 0 ⩽

⩽ 9, então o último valor não faz sentido. Assim, as opções para o último algarismo são 2, 5 e 8.
31. c) Um número natural é divisível por 6 somente quando é divisível por 2 e por 3. Dessa maneira, são opções as respostas em comum dos itens a e b, ou seja, 2 e 8.
31. d) São as respostas do item a que não são respostas do item b. Então, 0, 4 e 6.
31. e) Se é divisível por 3, mas não por 6, então não é por 2. São as respostas do item b que não são respostas do item a, ou seja, apenas o 5.
32. a) Não é possível, pois termina em 8, ou seja, não termina em 0 nem em 5.
32. b) Para 306

8 ser divisível por 3, 3 + 0 + 6 +

+ 8 = 17 +

também deve ser. Então 17 +

= 18 ⇒

= 1; 17 +

= 21 ⇒

= 4 e 17 +

= 24 ⇒

= 7. Então, as opções de algarismos são 1, 4 e 7.
33. Um número natural é divisível por 3 somente quando a soma dos seus algarismos é divisível por 3, e será divisível por 5 quando terminar em 0 ou 5; dessa maneira, são divisíveis por 15 os números 135, 510, 480 (itens a, d, e).
|
Item |
Testando por 3 |
É divisível por 3? |
Testando por 5 |
É divisível por 5? |
É divisível por 15? |
|---|---|---|---|---|---|
|
a) 135 |
1 + 3 + 5 = 9 |
Sim |
Termina em 5 |
Sim |
Sim |
|
b) 320 |
3 + 2 + 0 = 5 |
Não |
Termina em 0 |
Sim |
Não |
|
c) 363 |
3 + 6 + 3 = 12 |
Sim |
Termina em 3 |
Não |
Não |
|
d) 510 |
5 + 1 + 0 = 6 |
Sim |
Termina em 0 |
Sim |
Sim |
|
e) 480 |
4 + 8 + 0 = 12 |
Sim |
Termina em 0 |
Sim |
Sim |
36. Um número natural é divisível por 9 somente quando a soma dos valores absolutos dos seus algarismos é divisível por 9. Dessa maneira, não importa a posição dos algarismos, de fórma que, se 135 é divisível por 9, basta permutar (trocar de lugar) os algarismos para formar outros 5 números também divisíveis por 9: 153, 315, 351, 513 e 531. Sendo os últimos dois a resposta para esse problema, são os números que faltam.
37. O número 567 é divisível por 9, pois 5 + 6 + 7 = 18, que é divisível por 9.
37. a) A propriedade comutativa da adição permite alterar a ordem das parcelas; assim: 5 + 6 + 7 = 5 + 7 + 6 = 6 + 5 + 7 = 6 + 7 + 5 = 7 + 5 + 6 = 7 + 6 + 5 = 18. Há 6 maneiras de escrever alterando a ordem das parcelas, de modo que a soma será sempre 18.
37. b) São também 6 números diferentes: 567, 576, 657, 675, 756 e 765. Todos múltiplos de 9, como justificado no item a e múltiplos de 3, pois a soma dos algarismos é 18 = 3 ∙ 6, um múltiplo de 3.
37. c) O número .3456 é múltiplo de 9 pois 3 + 4 + 5 + 6 = 18, e 18 é múltiplo de 9. Da mesma maneira, é possível formar 24 números nessas condições. Como a soma dos algarismos de todos eles é 18, então também são divisíveis por 3.
37. d) Sim, pois se é divisível por 9, tem o fator 9 na sua composição, e por isso também terá o fator 3, uma vez que 9 = 3 ∙ 3.
38. Um número é divisível por 4 somente quando termina em 00 ou quando o número formado por seus dois últimos algarismos à direita é divisível por 4. Testando os valores:
38. a) 32 dividido por 4 = 8, resto 0; então, 932 é divisível por 4.
38. b) 40 dividido por 4 = 10, resto 0; então, .1040 é divisível por 4.
38. c) 42 dividido por 4 = 10, resto 2; então, 842 não é divisível por 4.
39. Como todas as mesas têm 4 cadeiras, a quantidade total de lugares deve ser divisível por 4. Testando: 314 → 14 dividido por 4 = 3, resto 2, não é divisível. 308 → 8 dividido por 4 = 2, é divisível. Então é possível que sejam 308 lugares.
41. Primeiro procurando o menor número natural divisível por 3, 4 e 5. Deve ser um número com fatores 3, 4 e 5; então, o menor é 3 ∙ 4 ∙ 5 = 60. Agora, como quero que tenha resto 1 na divisão por 3, 4 e 5, basta adicionar 60 + 1 = 61, que é o número procurado.
42. Um número divisível por 8 será da fórma 2 ∙ 2 ∙ 2 ∙ k = 8 ∙ k; então, escolhendo 5 números conforme solicitado pelo enunciado (terminar em 000 ou ser divisível por 8):
um) .1000; dois) .1008; três) .4016; quatro) .2456; cinco) .5000.
42. a) Verificando: um) .1000 : 8 = 125, é exata. dois) 1 008 dividido por 8 = 126, é exata. três) .4016 dividido por 8 = 502, é exata. quatro) .2456 dividido por 8 = 307, é exata. cinco) .5000 dividido por 8 = 625, é exata. São todas divisões exatas por 8; portanto, são todos valores divisíveis por 8.
42. b) Considerando os critérios apresentados, póde-se elaborar o fluxograma.
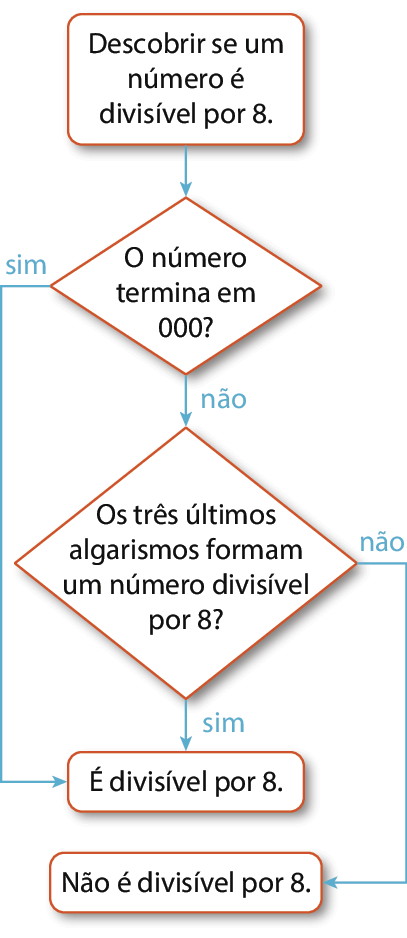
43. Exemplo de resposta: João anotou em uma folha um número e mostrou para Carina e para Ricardo. Ao ver o número, Carina disse que ele é divisível por 3 e Ricardo falou que é divisível por 5. João falou que ambos estão certos. Assim, é possível dizer que o número que João anotou é divisível por 15? Resposta: Sim, pois será possível dividir o número por 3 e, depois, por 5. Assim, é possível dividir por 3 ∙ 5, isto é, por 15.
44. Número primo é todo número que tem apenas dois divisores naturais distintos: o número 1 e o próprio número. Todo número natural que tem mais de dois divisores distintos é chamado de número composto. Dessa maneira:
44. a) Divisores de 14: 1, 2, 7 e 14. É composto.
44. b) Divisores de 11: 1 e 11. É primo.
44. c) Divisores de 17: 1 e 17. É primo.
44. d) Divisores de 21: 1, 3, 7 e 21. É composto.
44. e) Divisores de 296: 1, 2, 4, 8, 37, 74, 148 e 296. É composto.
44. f) Divisores de 37: 1 e 37. É primo.
45. Os divisores de 2 são 1 e 2, portanto ele é primo, além de ser par. Qualquer outro número par tem 2 como divisor; então, ele é o único número nessa condição.
46. c) Contando os primos por dia da semana nesse mês: domingo – 1 (dia 11); segunda – 2 (dias 5 e 19); terça – 1 (dia 13); quarta – 1 (dia 7); quinta – 1 (dia 29); sexta – 2 (dias 2 e 23); sábado – 3 (dias 3, 17, 31). Dessa maneira, sábado é o dia da semana representado pela maior quantidade de números primos.
47. Sabemos que um número primo é todo número que tem apenas dois divisores naturais distintos: o número 1 e o próprio número. Então, o único múltiplo de 3 que é primo é o próprio 3.
48. Não existe nenhum múltiplo de 3, diferente de 3, que seja primo, pois todo múltiplo de 3, diferente de 3, é divisível por 3.
49. Como a soma dos algarismos é 27, o número é divisível tanto por 3 como por 9; portanto, ele certamente não é primo.
50. Observando cada caso, o menor número de dois algarismos é 10, mas não é primo pois 2 e 5 também são seus divisores (além de 1 e dele mesmo). O próximo, 11, é primo pois só tem 1 e 11 como divisores. Já o maior número de dois algarismos é 99, que não é primo pois é divisível por 3 e 9, por exemplo. O 98 é par, e por isso é divisível por 2. O número 97, portanto, é o maior primo com dois algarismos, pois seus únicos divisores são 1 e 97.
51. a) Divisores de 7: 1, 7; divisores de 10: 1, 2, 5, 10; divisores de 35: 1, 5, 7, 35; divisores de 41: 1, 41; divisores de 75: 1, 3, 5, 15, 25, 75; divisores de 77: 1, 7, 11, 77.
51. b) A quantidade de divisores desses números é: 7 tem 2 divisores; 10 tem 4 divisores; 35 tem 4 divisores; 41 tem 2 divisores; 75 tem 6 divisores; 77 tem 4 divisores. A tabela é:
|
Números |
Quantidade de divisores |
|---|---|
|
7 |
2 |
|
10 |
4 |
|
35 |
4 |
|
41 |
2 |
|
75 |
6 |
|
77 |
4 |
Dados obtidos pelo estudante.
51. c) Oriente os estudantes na construção do gráfico. Eles podem utilizar uma malha quadriculada para a construção e assim, cada quadradinho da malha poderá representar um divisor. Desse modo, a barra referente ao número 7 seria formada por uma barra de 2 quadradinhos.
51. d) Entre esses números, o 75 tem a maior quantidade de divisores, com 6.
51. e) Entre os números apresentados, o 7 e o 41 têm apenas dois divisores distintos; logo, eles são números primos.
54. Decompondo os números apresentados em fatores primos, obtemos:
54. a) 120 = 2elevado a 3 · 3 · 5
54. b) 144 = 2elevado a 4 · 3elevado a 2
54. c) 168 = 2elevado a 3 · 3 · 7
54. d) 225 = 3elevado a 2 · 5elevado a 2
54. e) 117 = 3elevado a 2 · 13
54. f) 125 = 5elevado a 3
56. Calculando os valores de a, B e de A + B, obtemos:
A = 2 · 3 · 11 = 66
B = 2elevado a 2 · 3elevado a 2 · 5 = 180
A + B = 66 + 180 = 246
Para saber mais
Página 91
2. A sequência de números ímpares (que também é infinita) póde ser escrita como 1, 3, 5, 7, 9, 11, reticências; nessa sequência, o anterior ao 91 é 91 menos 2 = 89, e o posterior a ele é 91 + 2 = 93.
4. Observando a sequência das imagens dadas em que a quantidade de linhas e de colunas na disposição das pedrinhas é a base da potência de expoente 2, podemos concluir que Pitágoras formaria 7elevado a 2 dispondo as pedrinhas em 7 linhas e 7 colunas.
Trabalhando a informação
1. Fazendo a leitura do gráfico de barras, concluímos:
1. a) No estado de São Paulo, em 2021, havia trezentas bibliotecas públicas.
1. b) Nos estados de Santa Catarina e do Rio Grande do Sul, em 2021, havia 760 (230 + 530) bibliotecas públicas.
1. c) Resposta pessoal.
2. a) Em um gráfico de barras, o tamanho é proporcional à quantidade que a barra representa; por isso, a de maior comprimento é a que representa o dia com maior quantidade de empréstimos, ou seja, sexta-feira. A menor barra será do dia com menos empréstimos, que foi quarta-feira.
2. b) Na quarta-feira foram feitos 9 empréstimos, enquanto na quinta foram feitos 18, que é o dobro. Por isso, haverá uma barra com o dobro do comprimento da outra.
2. c)
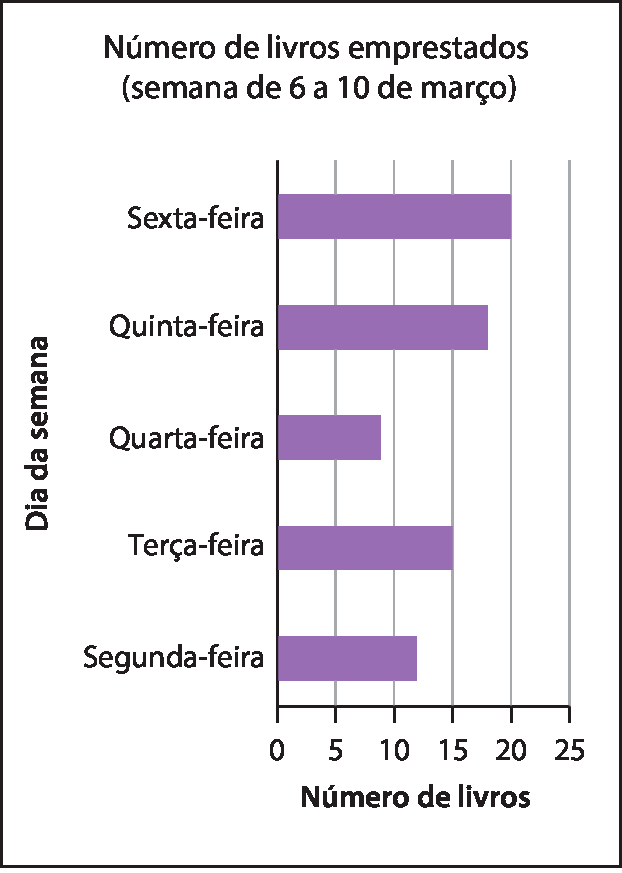
Dados obtidos das anotações do bibliotecário.
3. Resposta pessoal; deve ocorrer a elaboração de pesquisas e a organização de seus dados em gráficos e tabelas para compartilhamento de resultados. A pesquisa pode envolver quantidade de livros lidos, gêneros mais lidos, plataformas de leitura mais utilizadas, e o que mais suscitar interesse.
Exercícios complementares
2. A quantidade de livros de Ana é um a mais do que um número que seja múltiplo de 12, 15 e 20 ao mesmo tempo. De 100 a 150, os múltiplos de 12 são: 108, 120, 132, 144; os múltiplos de 15 são: 105, 120, 135, 150; os múltiplos de 20 são: 100, 120, 140. Entre esses valores, o único comum aos três é 120; portanto, Ana possui 120 + 1 = 121 livros.
3. Para um número ser divisível por 6, ele deve ser divisível por 2 e por 3 ao mesmo tempo. Como .34524 termina em 4, que é par, é divisível por 2. Para testar a divisibilidade por 3, é necessário adicionar os algarismos, 3 + 4 + 5 + 2 + 4 = 18. Como 18 é divisível por 3, .34524 também é. Dessa maneira, ele também é divisível por 6.
4. O menor número de três algarismos distintos é 102.
4. a) 102 é divisível por 2, pois termina em algarismo par.
4. b) A soma dos algarismos 1 + 0 + 2 = 3 é divisível por 3; por isso, 102 também é.
4. c) Para ser divisível por 5, o número deve terminar em 0 ou 5. Vamos observar cada sequência dos números de três algarismos distintos: 102 (não), 103 (não), 104 (não), 105 (sim, termina em 5 ou 0). Portanto, 105 é divisível por 5.
4. d) Pelos itens a e b, 102 é divisível por 2 e por 3, por isso é também por 6.
5. a) O número 260 é divisível por 2, pois termina em algarismo par, e por 5, pois termina em 0. 260 não é divisível por 3, pois 2 + 6 + 0 = 8, que não é divisível por 3.
5. b) .2040 é divisível por 2, pois termina em algarismo par, e também é divisível por 3, pois 2 + 0 + 4 + 0 = 6, que é divisível por 3.
5. c) Verdadeira, pois .3065 termina em 5, e a soma de seus algarismos é 3 + 0 + 6 + 5 = 14, que não é divisível por 3.
5. d) Verdadeira, pois .18980 é divisível por 4 pois 80 é divisível por 4. E não é divisível por 9, pois 1 + 8 + 9 + 8 + 0 = 26, e 26 não é divisível por 9.
6. Como 36 = 2elevado a 2 ∙ 3elevado a 2, dividir por esse valor é o mesmo que dividir por alguns de seus fatores, e depois dividir pelos outros, nesse caso com exceção do 6.
7. Todo número divisível por 10 termina em 0; portanto, o número do enunciado termina em 0 + 5 = 5.
7. a) O número termina em 5; logo, não é divisível por 2.
7. b) O número termina em 5; logo, é divisível por 5.
8. a) São divisíveis por .1000 os terminados em 000, ou seja, a 1ª.
8. b) São divisíveis por 100 os terminados em 00, ou seja, a 1ª e a 4ª.
8. c) São divisíveis por 10 os terminados em 0, ou seja, a 1ª, a 2ª e a 4ª.
9. a) É preciso encontrar o menor múltiplo comum entre 365 e 260.
|
365 |
260 |
|
730 |
520 |
|
1.095 |
780 |
|
1.460 |
1.040 |
|
1.825 |
1.300 |
|
2.190 |
1.560 |
|
2.555 |
1.820 |
|
2.920 |
2.080 |
|
3.285 |
2.340 |
|
3.650 |
2.600 |
|
4.015 |
2.860 |
|
4.380 |
3.120 |
|
4.745 |
3.380 |
|
5.110 |
3.640 |
|
5.475 |
3.900 |
|
5.840 |
4.160 |
|
6.205 |
4.420 |
|
6.570 |
4.680 |
|
6.935 |
4.940 |
|
7.300 |
5.200 |
|
7.665 |
5.460 |
|
8.030 |
5.720 |
|
8.395 |
5.980 |
|
8.760 |
6.240 |
|
9.125 |
6.500 |
|
9.490 |
6.760 |
|
9.855 |
7.020 |
|
10.220 |
7.280 |
|
10.585 |
7.540 |
|
10.950 |
7.800 |
|
11.315 |
8.060 |
|
11.680 |
8.320 |
|
12.045 |
8.580 |
|
12.410 |
8.840 |
|
12.775 |
9.100 |
|
13.140 |
9.360 |
|
13.505 |
9.620 |
|
13.870 |
9.880 |
|
14.235 |
10.140 |
|
14.600 |
10.400 |
|
14.965 |
10.660 |
|
15.330 |
10.920 |
|
15.695 |
11.180 |
|
16.060 |
11.440 |
|
16.425 |
11.700 |
|
16.790 |
11.960 |
|
17.155 |
12.220 |
|
17.520 |
12.480 |
|
17.885 |
12.740 |
|
18.250 |
13.000 |
|
18.615 |
13.260 |
|
18.980 |
13.520 |
|
19.345 |
13.780 |
|
19.710 |
14.040 |
|
20.075 |
14.300 |
|
20.440 |
14.560 |
|
20.805 |
14.820 |
|
21.170 |
15.080 |
|
15.340 |
|
|
15.600 |
|
|
15.860 |
|
|
16.120 |
|
|
16.380 |
|
|
16.640 |
|
|
16.900 |
|
|
17.160 |
|
|
17.420 |
|
|
17.680 |
|
|
17.940 |
|
|
18.200 |
|
|
18.460 |
|
|
18.720 |
|
|
18.980 |
9. b) .18980 dias é o equivalente a 52 anos (.18980 : 365 = 52) do calendário Tzolkin.
10. Multiplicar um número por 12 é o mesmo que multiplicá-lo por todos os fatores de 12: 12 = 22 ∙ 3; portanto, póde ser efetuado 4 ∙ 3, ou 6 ∙ 2, por exemplo.
11. Como 2 + 8 + 3 = 13, para ser divisível por 9 é preciso que o algarismo complete 18 = 9 ∙ 2 na soma, ou seja, será 18 – 13 = 5. Portanto, o número formado será .5283.
12. a) 297 é múltiplo de 9, pois 297 = 9 ∙ 33.
12. b) Resposta pessoal. O resultado da subtração é um número divisível por 9.
13. Com 100 rosas brancas e 60 rosas vermelhas distribuídas em arranjos de quantidades iguais:
13. a) O maior número de ramalhetes será o maior divisor comum de 100 e 60. Os divisores de 100 são: 1, 2, 4, 5, 10, 20, 25, 50 e 100. Os divisores de 60 são: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60. Então, o ême dê cê é 20. A florista póde fazer no máximo 20 ramalhetes iguais.
13. b) Serão 20 grupos, então 100 : 20 = 5 rosas brancas e 60 : 20 = 3 rosas vermelhas em cada.
14. Um número que termina em 5 é divisível por 5, mas não necessariamente apenas por ele. Ele não será divisível por 2, pois 5 é ímpar, nem por 10, pois não termina em zero. Ele póde ser divisível por 3, se a soma de seus algarismos for divisível por 3; por exemplo, 15, cuja soma mencionada é 1 + 5 = 6.
Alternativa c.
15. Formando equipes de 9, sobram 3, então podem ser: 3, 12, 21, 30, 39 ou 48 estudantes. Formando equipes de 7 estudantes, sobram 6, então podem ser 6, 13, 20, 27, 34, 41 ou 48 estudantes. Em comum às duas sequências, há o 48. Então, formando equipes de 8, serão 48 : 8 = 6 equipes.
16. Para ser divisível por 5 e por 2 ao mesmo tempo, ele deve terminar em zero, eliminando as alternativas b, c e e. Se for divisível por 9, já será por 3, e precisa que a soma dos algarismos seja múltipla de 9: o item a tem soma 3 + 3 + 0 = 6, e o item d tem soma 9 + 9 + 0 = 18, que é divisível. Testando o item d na divisibilidade por 11, obtemos: 990 : 11 = 90, resto 0, então é divisível por 11. Como é divisível por 2 e por 3, também será por 6.
Alternativa d.
17. Um número primo é sempre divisível apenas por 1 e por ele mesmo; portanto, o ême dê cê (maior divisor comum) entre eles será sempre 1.
Alternativa c.
18. Observando os primeiros múltiplos de 12, e os de 15 e os de 36, podemos perceber que o menor múltiplo comum entre eles é o 180. Então, o valor procurado será 180 + 2 = 182.
Verificando
1. Para resolver esse problema, é necessário encontrar o mínimo múltiplo comum entre os tempos dos ônibus, 84 e 165. Por isso, o ême ême cê será .4620; então, após essa quantidade de minutos os ônibus partirão novamente.
1. b) Oriente os estudantes a usar uma calculadora adicionando pela repetição do sinal “=”.
|
84 |
165 |
|
168 |
330 |
|
252 |
495 |
|
336 |
660 |
|
420 |
825 |
|
504 |
990 |
|
588 |
1.155 |
|
672 |
1.320 |
|
756 |
1.485 |
|
840 |
1.650 |
|
924 |
1.815 |
|
1.008 |
1.980 |
|
1.092 |
2.145 |
|
1.176 |
2.310 |
|
1.260 |
2.475 |
|
1.344 |
2.640 |
|
1.428 |
2.805 |
|
1.512 |
2.970 |
|
1.596 |
3.135 |
|
1.680 |
3.300 |
|
1.764 |
3.465 |
|
1.848 |
3.630 |
|
1.932 |
3.795 |
|
2.016 |
3.960 |
|
2.100 |
4.125 |
|
2.184 |
4.290 |
|
2.268 |
4.455 |
|
2.352 |
4.620 |
|
2.436 |
4.785 |
|
2.520 |
4.950 |
|
2.604 |
5.115 |
|
2.688 |
5.280 |
|
2.772 |
|
|
2.856 |
|
|
2.940 |
|
|
3.024 |
|
|
3.108 |
|
|
3.192 |
|
|
3.276 |
|
|
3.360 |
|
|
3.444 |
|
|
3.528 |
|
|
3.612 |
|
|
3.696 |
|
|
3.780 |
|
|
3.864 |
|
|
3.948 |
|
|
4.032 |
|
|
4.116 |
|
|
4.200 |
|
|
4.284 |
|
|
4.368 |
|
|
4.452 |
|
|
4.536 |
|
|
4.620 |
2. Os divisores de 16 são: 1, 2, 4, 8 e 16, e os divisores de 36 são: 1, 2, 3, 4, 6, 9, 12, 18 e 36. Então, o conjunto dos divisores comuns é {1, 2, 4}.
Alternativa b.
3. Queremos que 110 + x seja múltiplo de 13. Os múltiplos de 13 próximos de 110 são 104 e 117. Como quero adicionar um valor x, quero que 110 + x = 117 ⇒ 110 + x – 100 = 117 – 110 ⇒ x = 7.
Alternativa a.
4. Os divisores de 600 são 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, 40, 50, 60, 75, 100, 120, 150, 200, 300 e 600. Portanto, pertencem à sequência todos esses valores, em particular 40 e 150.
Alternativa d.
5. Os primeiros múltiplos de 8 são 0, 8, 16, 24, 32, 40, 48, reticências e os primeiros múltiplos de 12 são 0, 12, 24, 36, 48, reticênciasponto; dessa maneira, os múltiplos comuns podem ser representados pelo conjunto {0, 24, 48, reticências}.
Alternativa a.
6. Esse é o critério de divisibilidade por 5.
Alternativa c.
7. Há 16.oitocentas unidades para serem transportadas em caixas de 10 unidades, ou seja, são necessárias uma.seiscentas e oitenta caixas (.16800 : 10 = .1680). Elas são transportadas em grupos de quatrocentas a 450 unidades, ou 40 a 45 caixas por caminhão. Como .1680 é divisível por 40 e por 42, podem ser colocadas essas quantidades de caixas em cada veículo. Como queremos obter a menor quantidade de caminhões, escolhemos 42, totalizando 40 veículos (.1680 : 42 = 40).
Alternativa b.
8. Ao empilhar em montes de 16 moedas e sobrar 9, significa que Isa póde ter as seguintes quantidades de moedas: 25, 41, 57, 73, 89, 105, 121, 137, 153, 169 ou 185. No caso dos montes de 18 moedas com resto 9, significa que ela póde ter as seguintes quantidades: 27, 45, 63, 81, 99, 117, 135, 153, 171 ou 189. Em comum, as duas sequências têm o 153. Se Isa tem R$ 153,00cento e cinquenta e três reais, então ficará com R$ 153,00cento e cinquenta e três reais – R$ 139,00cento e trinta e nove reais = R$ 14,00quatorze reais.
Alternativa a.
9. Os maiores múltiplos de 9 menores que 100 são 99, 90, 81 e 72. Os múltiplos de 6 nessas condições são 96, 90, 84 e 78. O maior valor em comum é 90.
Alternativa b.

