Parte 5
Capítulo 9 — Números racionais na fórma decimal e operações
• Objetivos do capítulo e justificativas
• Ler, escrever e representar números racionais na fórma decimal.
• Reconhecer números racionais em diferentes contextos.
• Localizar números racionais na fórma decimal na reta numérica.
• Reconhecer que os números racionais podem ser expressos na fórma de fração e na fórma decimal, estabelecendo relações entre essas representações.
• Resolver e elaborar problemas que envolvam números racionais na fórma decimal, compreendendo os diferentes significados das operações entre esses números.
• Realizar cálculos que envolvam operações com números racionais na fórma decimal por meio de estratégias variadas.
• Resolver problemas que envolvam a ideia de porcentagem.
• Compreender o significado de média aritmética e aprender a calculá-la.
A representação decimal dos números racionais possibilita aos estudantes trabalhar com este campo numérico em diversos contextos, não só em distintas áreas do conhecimento como também em diferentes unidades temáticas da própria Matemática. No caso da representação de números racionais na fórma decimal sobre a reta, os estudantes se aproximam de indicações em instrumentos de medida de comprimento (régua, trena etcétera). Desse modo, os conteúdos trabalhados contribuem para o letramento matemático, favorecendo o desenvolvimento das competências específicas 3 e 4 e das competências gerais 2 e 4.
Na seção de abertura também exploramos a importância da vírgula por meio de um poema concreto, o que contribui para o desenvolvimento da competência geral 3 e da competência específica 6.
Os números racionais têm uma particularidade: o fato de poderem ser representados de diferentes maneiras, entre elas a representação fracionária e a decimal. Relacionar essas representações possibilita ao estudante compreender melhor o significado do número racional em questão no contexto em que ele está inserido. Assim, com múltiplas experiências, o conceito de número vai se consolidando.
Porcentagem é uma ideia que pode ser explorada em vários contextos, na própria Matemática e em outras áreas do conhecimento. Quando isso acontece, a compreensão sobre o conceito de porcentagem se amplia, dando significado ao que é estudado em sala de aula. É na resolução de problemas que a compreensão da porcentagem e a construção de estratégias de resolução de problemas ganham oportunidades.
O cálculo da média aritmética, explorado na seção Trabalhando a informação, foi relacionado a uma situação-problema sobre vendas, situação que contribui para o desenvolvimento da competência geral 6.
Outra temática explorada é o desperdício de alimentos, que contribui para o desenvolvimento da competência geral 7 e da competência específica 7.
O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diversas atividades a serem realizadas em grupos, pois possibilitam aos estudantes exercitar diferentes habilidades socioemocionais ao trabalhar com os colegas, interagindo de fórma cooperativa.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah zero um) Comparar, ordenar, ler e escrever números naturais e números racionais cuja representação decimal é finita, fazendo uso da reta numérica.
(ê éfe zero seis ême ah zero dois) Reconhecer o sistema de numeração decimal, como o que prevaleceu no mundo ocidental, e destacar semelhanças e diferenças com outros sistemas, de modo a sistematizar suas principais características (base, valor posicional e função do zero), utilizando, inclusive, a composição e decomposição de números naturais e números racionais em sua representação decimal.
(ê éfe zero seis ême ah zero sete) Compreender, comparar e ordenar frações associadas às ideias de partes de inteiros e resultado de divisão, identificando frações equivalentes.
(ê éfe zero seis ême ah zero oito) Reconhecer que os números racionais positivos podem ser expressos nas formas fracionária e decimal, estabelecer relações entre essas representações, passando de uma representação para outra, e relacioná-los a pontos na reta numérica.
(ê éfe zero seis ême ah um zero) Resolver e elaborar problemas que envolvam adição ou subtração com números racionais positivos na representação fracionária.
(ê éfe zero seis ême ah um um) Resolver e elaborar problemas com números racionais positivos na representação decimal, envolvendo as quatro operações fundamentais e a potenciação, por meio de estratégias diversas, utilizando estimativas e arredondamentos para verificar a razoabilidade de respostas, com e sem uso de calculadora.
(ê éfe zero seis ême ah um dois) Fazer estimativas de quantidades e aproximar números para múltiplos da potência de 10 mais próxima.
(ê éfe zero seis ême ah um três) Resolver e elaborar problemas que envolvam porcentagens, com base na ideia de proporcionalidade, sem fazer uso da “regra de três”, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.
(ê éfe zero seis ême ah três dois) Interpretar e resolver situações que envolvam dados de pesquisas sobre contextos ambientais, sustentabilidade, trânsito, consumo responsável, entre outros, apresentadas pela mídia em tabelas e em diferentes tipos de gráficos e redigir textos escritos com o objetivo de sintetizar conclusões.
Os números racionais na fórma decimal foram estudados no 4º e no 5º anos do Ensino Fundamental. Nesse momento, esses conhecimentos serão expandidos e aprofundados na perspectiva da construção de novos conhecimentos, o que favorece a sua apropriação pelos estudantes e os prepara para o detalhamento do estudo desse tema no 7º ano do Ensino Fundamental, no desenvolvimento das habilidades (ê éfe zero sete ême ah um zero), (ê éfe zero sete ême ah um um) e (ê éfe zero sete ême ah um dois). Assim, as atividades abordam conhecimentos relativos à notação decimal dos números racionais positivos, à ampliação do sistema de numeração decimal para as ordens decimais, à ordenação de números racionais na fórma decimal e à sua relação com pontos da reta numérica, às operações de adição, subtração, multiplicação, divisão e potenciação com números racionais na fórma decimal, ao cálculo de porcentagens na fórma decimal e ao uso da calculadora. Desse modo, os conteúdos trabalhados contribuem para o desenvolvimento das habilidades (ê éfe zero seis ême ah zero um), (ê éfe zero seis ême ah zero dois), (ê éfe zero seis ême ah zero sete) e (ê éfe zero seis ême ah zero oito).
As atividades propostas aos estudantes foram elaboradas com estratégias diferenciadas e com o objetivo de favorecer os desenvolvimentos das habilidades (ê éfe zero seis ême ah um zero), (ê éfe zero seis ême ah um um), (ê éfe zero seis ême ah um dois) e (ê éfe zero seis ême ah um três).
Nesse caso, as Unidades Temáticas Números e Probabilidade e estatística associam-se em atividades de cálculo de média aritmética. A atividade de coletar informações sobre os colegas para o cálculo de média contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah três dois).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações Didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
8. A malha toda representa 1 inteiro.
8. a) É uma malha de 20 × 50; logo, há .1000 quadradinhos, pois: 20 ⋅ 50 = .1000.
8. b) Em azul há 4 faixas de dimensões medindo 20 × 5, e um retângulo medindo 3 × 5; portanto, são 4 ⋅ 20 ⋅ 5 + 3 ⋅ 5 = 400 + 15 = 415; então, o número decimal que corresponde à parte pintada de azul é
415 milésimos= 0,415.
8. c) A parte não pintada de azul são os outros 585 quadradinhos (.1000 − 415 = 585), que representam
585 milésimos= 0,585.
9. Relacionando as frações decimais com as representações gráficas, obtemos:
9. a)
7 décimos, igual à, 7 vezes 1 décimos, igual à7 ⋅ 0,1 = 0,7
9. b)
3 décimos= 3 ⋅ 0,1 = 0,3
9. c)
18 centésimos igual à, 18 vezes 1 centésimo= 18 ⋅ 0,01 = 0,18
9. d)
4 centésimos= 0,04
9. e)
13 milésimos igual à, 13 vezes 1 milésimo= 13 ⋅ 0,001 = 0,013
9. f.
325 milésimos= 0,325
10. A leitura do número separa a parte inteira da parte decimal.
10. a) 30,06 → Trinta inteiros e seis centésimos.
10. b) 3,006 → Três inteiros e seis milésimos.
10. c) 0,036 → Trinta e seis milésimos.
10. d) 0,306 → Trezentos e seis milésimos.
10. e) 300,6 → Trezentos inteiros e seis décimos.
300 +
6 décimos, igual à 3006 décimos.
10. f) 0,36 → Trinta e seis centésimos.
11. a) 6,947 pode ser lido como seis inteiros e novecentos e quarenta e sete milésimos, ou seis vírgula novecentos e quarenta e sete.
11. b) 57,298 pode ser lido como cinquenta e sete inteiros e duzentos e noventa e oito milésimos, ou cinquenta e sete vírgula duzentos e noventa e oito.
12. Para responder a essa questão precisamos nos lembrar das propriedades utilizadas até aqui.
12. a) A vírgula separa a parte inteira da parte decimal: 10,45.
12. b) Como um centésimo é 0,01, então 75 centésimos é 0,75.
12. c) Um milésimo é 0,001; então, 25 milésimos é 0,025. A resposta final é 2,025.
12. d) Décimo de milésimo é
1 décimodo milésimo, ou seja, 0,0001, então 72 décimos de milésimos é 0,0072.
13. A resposta dessa atividade é pessoal. Ela vai depender dos textos selecionados.
17. Na comparação de números decimais, quando as partes inteiras forem iguais, devemos comparar as partes decimais. Como 7 = 7 e 5 décimos > 2 décimos, temos 7,5 > 7,2. Logo, o caminhão B pode transportar uma medida maior de massa.
18. Comparando os valores 58,6 e 58,570, como a parte inteira é igual, comparam-se 0,6 e 0,570.
Como 6 décimos > 5 décimos, temos 0,6 > 0,570; logo, 58,6 > 58,570. Portanto, Maria tem a maior medida de massa.
19. Os números naturais são inteiros não negativos, são números que não têm parte decimal (ou cuja parte decimal é igual a zero), então entre 12,3 e 17,1 existem os naturais 13, 14, 15, 16 e 17.
23. Mário efetuou 600 : .1000 e Maísa efetuou 600 : .10000.
23. a) No visor da calculadora deles aparecerá a fórma decimal do resultado da divisão; então, primeiro simplificando em fórma de fração e depois escrevendo como decimal, no caso de Mário será:
.
No visor da calculadora de Maísa aparecerá:
23. b) Tanto 0,6 como 0,06 têm zero unidades na parte inteira; então, comparam-se os décimos: 6 décimos > 0 décimo; então, 0,6 > 0,06. Portanto, 0,6 é maior.
24. Resposta pessoal, elaboração e resolução de problema.
29. Alinham-se as vírgulas e acrescentam-se zeros quando for necessário preencher as casas.
29. a) 0,4 − 0,325 = 0,075
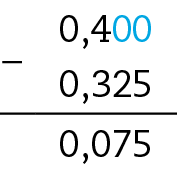
29. b) 1 − 0,275 = 0,725
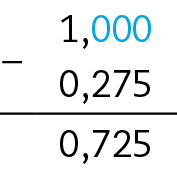
29. c) 5,6 − 4 = 1,6
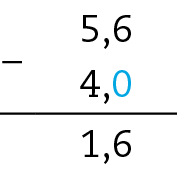
29. d) 12,36 − 8,634 = 3,726
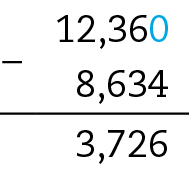
30. a) 0,075 + 0,325 = 0,4
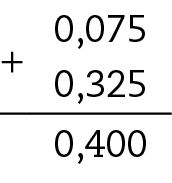
30. b) 0,725 + 0,275 = 1
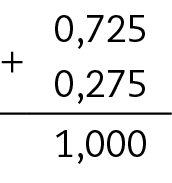
30. c) 1,6 + 4 = 5,6
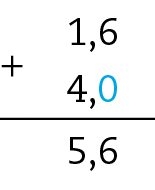
30. d) 3,726 + 8,634 = 12,36
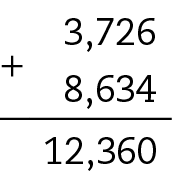
30. e) 0,4 − 0,075 = 0,325
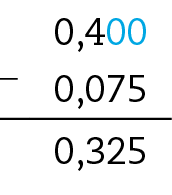
30. f) 1 − 0,725 = 0,275
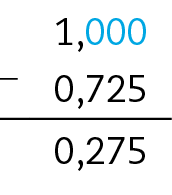
30. g) 5,6 − 1,6 = 4
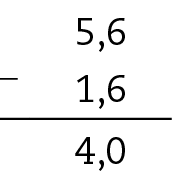
30. h) 12,36 − 3,726 = 8,634

32. a) 100,00 − 37,50 − 36,25 − 7,75 = 18,50
Logo, sobraram R$ 18,50dezoito reais e cinquenta centavos da quantia que a avó deu.
32. b) 100,00 − (37,50 + 36,25 + 7,75)
35. Calculando o valor de cada uma das expressões, obtemos:
35. a) 2,4 − (1,3 + 0,2) = 2,4 − 1,5 = 0,9
35. b) 2,4 − 1,3 + 0,2 = 1,1 + 0,2 = 1,3
35. c) 2,4 + (1,3 − 0,2) = 2,4 + 1,1 = 3,5
35. d) 2,4 + 1,3 + 0,2 = 3,7 + 0,2 = 3,9
Como 0,9 < 1,3 < 3,5 < 3,9, o item d tem o maior valor e o item a tem o menor valor.
36. Arredondam-se números com parte decimal menor do que 5 décimos para o inteiro anterior, e números com parte decimal igual ou maior do que 5 décimos são arredondados para o inteiro posterior. Dessa maneira:
36. a) 2,86 + 4,95 ≃ 3 + 5 = 8 e 2,86 + 4,95 = 7,81
36. b) 11,24 + 5,67 ≃ 11 + 6 = 17 e 11,24 + 5,67 = 16,91
36. c) 9,11 + 31,74 ≃ 9 + 32 = 41 e 9,11 + 31,74 = 40,85
36. d) 12,12 − 6,43 ≃ 12 − 6 = 6 e 12,12 − 6,43 = 5,69
36. e) 32,77 − 9,64 ≃ 33 − 10 = 23 e 32,77 − 9,64 = 23,13
36. f) 53,42 − 10,38 ≃ 53 − 10 = 43 e 53,42 − 10,38 = 43,04
37. Lendo os valores do gráfico, temos:
37. a) O número correspondente à barra desse ano é 257,8; portanto, em 2015 existiam 257,8 milhões de linhas ativas.
37. b) Em 2016 eram 244,1 milhões e em 2020 eram 234,1 milhões de linhas de telefone, uma diferença de 10 milhões (244,1 − 234,1 = 10).
37. c) Observar a maior e a menor barra, respectivamente 2015 e 2019.
47. Refazer as operações utilizando calculadora, lembrando de efetuar primeiro as multiplicações e depois as adições e subtrações.
47. a) 6,9 ⋅ 8,7 − 0,03 = 60,03 − 0,03 = 60
47. b) 14 − 15,6 ⋅ 0,84 = 14 − 13,104 = 0,896
47. c) 2,4 ⋅ (5 − 3,75) = 2,4 ⋅ 1,25 = 3
47. d) 4,6 ⋅ 5 − 12,36 = 23 − 12,36 = 10,64
47. e) 3,4 ⋅ 0,5 − 0,8 ⋅ 1,6 = 1,7 − 1,28 = 0,42
47. f) 12,78 − 4,3 ⋅ 2,6 = 12,78 − 11,18 = 1,6
48. Se 1 litro de etanol custa R$ 5,67cinco reais e sessenta e sete centavos, obtemos:
48. a) 45 litros custam 255,15 reais, pois 5,67 ⋅ 45 = 255,15.
48. b) Ele gastou R$ 5,67cinco reais e sessenta e sete centavos ⋅ 10 = R$ 56,70cinquenta e seis reais e setenta centavos, sendo possível efetuar cálculo mental simples pelo deslocamento da vírgula na representação decimal.
49. Na primeira loja, se cada metro custa R$ 0,85zero reais e oitenta e cinco centavos, 10 metros custarão R$ 8,50oito reais e cinquenta centavos. Na segunda loja, da fita prateada, ela gastou 8 ⋅ 0,9 =
fração, numerador 8 vezes 9, denominador 10= 7,2, ou seja, gastou R$ 7,20sete reais e vinte centavos, menos de 8 reais.
50. a) Os centavos no preço de cada livro eram 10; portanto, (10 ⋅ 3 = 30) 30 centavos na compra, que poderiam ter sido entregues para facilitar o troco. Dessa maneira, seu troco pode ser calculado por 100 + 0,3 − (3 ⋅ 20,1); portanto, 100,3 − 60,3 = 40; logo, 40 reais de troco.
50. b) As 4 notas de Maria totalizam R$ 50,00cinquenta reais (50 ⋅ 4 = 200). Como o caixa só tem notas de 10 reais e de 5 reais, o troco deve ser inteiro e múltiplo de 5. O troco atual da compra seria R$ 200,00duzentos reais − R$ 169,30cento e sessenta e nove reais e trinta centavos = R$ 30,70trinta reais e setenta centavos. Como o próximo múltiplo de 5 é 35, esse é o troco facilitado, sendo necessário completar com R$ 35,00trinta e cinco reais − R$ 30,70trinta reais e setenta centavos = R$ 4,30quatro reais e trinta centavos.
51. Um real tem 100 centavos; portanto:
51. a) São necessárias 20 moedas de R$ 0,05zero reais e cinco centavos (100 : 5 = 20) e 10 moedas de R$ 0,10zero reais e dez centavos (100 : 10 = 10) para obter 1 real.
51. b) É possível obter R$ 1,50um reais e cinquenta centavos com três moedas de dois modos: uma moeda de R$ 1,00um reais e duas moedas de 25 centavos (1,5 = 1,0 + 0,25 + 0,25) ou com três moedas de 50 centavos (1,5 = 0,5 + 0,5 + 0,5).
51. c) É possível obter 1 real de diferentes maneiras, por exemplo, reunindo: 20 moedas de 5 centavos; 10 moedas de 10 centavos; 4 moedas de 25 centavos; duas moedas de 50 centavos; uma moeda de 1 real; 10 moedas de 5 centavos e 5 moedas de 10 centavos; duas moedas de 25 centavos e uma moeda de 50 centavos; 5 moedas de 10 centavos e uma moeda de 50 centavos; 10 moedas de 5 centavos e duas moedas de 25 centavos etcétera
Se julgar conveniente, discorra sobre a necessidade de todos os cidadãos contribuírem para a circulação de moedas e sobre quanto é prejudicial o hábito de deixar as moedas guardadas, atrapalhando a circulação do dinheiro e dificultando a devolução de troco pelos comerciantes. O estudo dos diferentes modos de compor 1 real utilizando moedas é uma ação bem interessante, pois leva os estudantes a registrar relações numéricas que já utilizavam em situações cotidianas sem ter consciência.
52. a) Jonas tem 4 moedas de 25 centavos, 12 moedas de 5 centavos, 9 moedas de 50 centavos, vinte e duas moedas de 1 real e 11 moedas de 10 centavos. A expressão que representa essa quantia em reais é 4 ⋅ 0,25 + 12 ⋅ 0,05 + 9 ⋅ 0,5 + 22 ⋅ 1 + 11 ⋅ 0,1. Resolvendo essa expressão: 1 + 0,6 + 4,5 + 22 + 1,1 = 29,2. Então, Jonas tinha R$ 29,20vinte e nove reais e vinte centavos.
52. b) Jonas comprou o ingresso por R$ 22,00vinte e dois reais e a pipoca por R$ 5,50cinco reais e cinquenta centavos, então ficou com R$ 1,70um reais e setenta centavos (29,2 − 22 − 5,5 = 7,2 − 5,5 = 1,70).
59. Instrua os estudantes no uso da calculadora e relembre-os, se necessário, sobre a ordem das operações em expressões numéricas.
Com a calculadora, resolvendo na ordem apropriada, obtemos:
59. a) 10 : 16 + 16 : 10 = 0,625 + 1,6 = 2,225
59. b) 100 : 25 + 25 : 10 = 4 + 2,5 = 6,5
59. c) 10 : 8 − 2 : 5 + 4 = 1,25 − 0,4 + 4 = 4,85
61. No plano 1, o total pago pela TV não se altera, ele é dividido em 4 parcelas (uma entrada e as outras 3 a prazo). No plano 2, são 6 parcelas (uma entrada mais 5 a prazo), em que cada parcela tem o preço fixo de R$ 326,80trezentos e vinte e seis reais e oitenta centavos.
61. a) No plano 1, o valor de cada prestação é: .1774,40 : 4 = R$ 443,60quatrocentos e quarenta e três reais e sessenta centavos
61. b) No plano 2, o total pago é, em reais, 326,8 ⋅ 6 = .1960,8; portanto: R$ 1um reais.960,80novecentos e sessenta reais e oitenta centavos − R$ 1um reais.774,40setecentos e setenta e quatro reais e quarenta centavos = R$ 186,40cento e oitenta e seis reais e quarenta centavos.
Verifique se os estudantes utilizam corretamente a calculadora para efetuar as operações .1774,40 : 4 e .1774,40 : 5.
64. Aqui, é preciso prosseguir com a divisão até ter certeza do quociente com o número de casas decimais indicadas (nesse caso, uma casa). Na divisão com parte decimal, o resto dos inteiros é transformado em décimos (multiplicando a quantidade por 10) para que a divisão possa continuar. Para saber qual é a aproximação necessária, encontra-se uma casa a mais, se for um algarismo menor do que 4, arredonda-se para baixo; se for 5 ou maior, arredonda-se para cima.
64. a) 8 : 3 ≃ 2,7
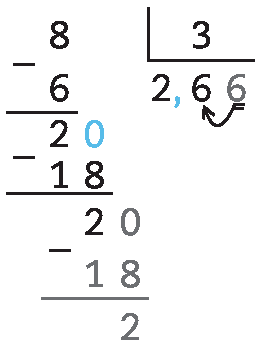
64. b) 142 : 21 ≃ 6,8
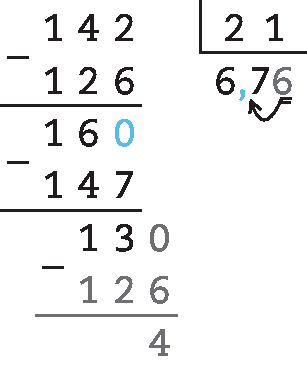
64. c) 158 : 6 ≃ 26,3
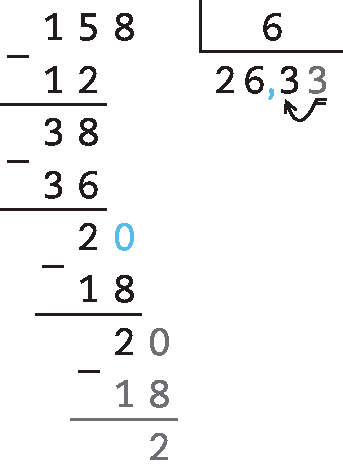
64. d) 53 : 9 ≃ 5,9
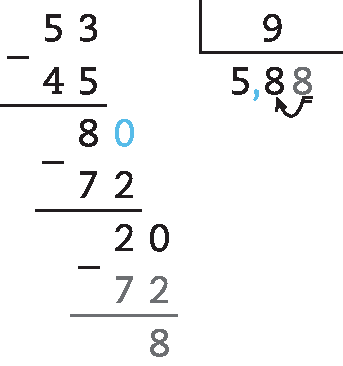
65. a) 76 : 3 ≃ 25,33
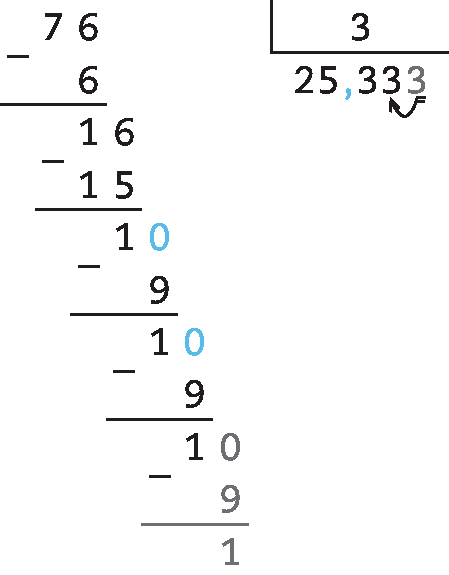
65. b) 58 : 6 ≃ 9,67
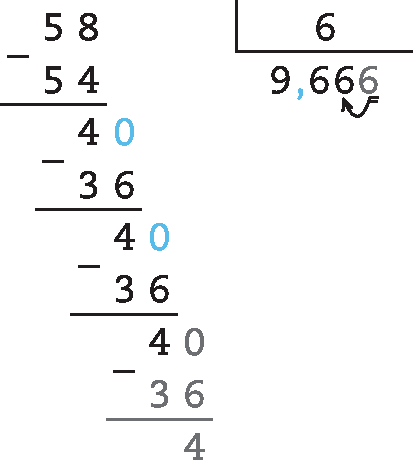
65. c) 45 : 8 ≃ 5,63
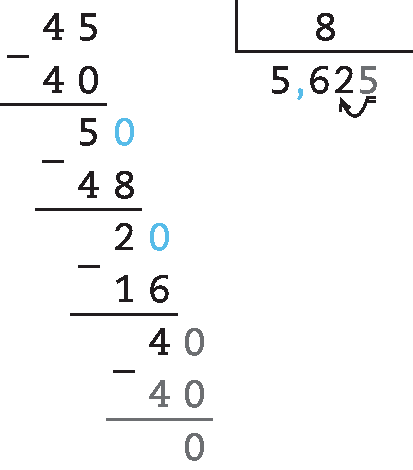
65. d) 243 : 17 ≃ 14,29
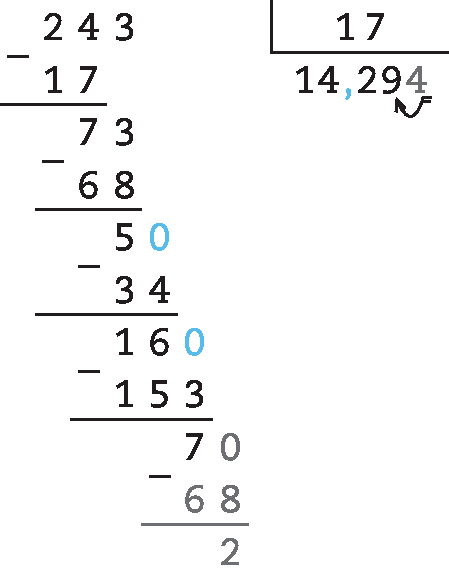
69. a) 25,46 : 6,7 = .2546 : 670 = 3,8
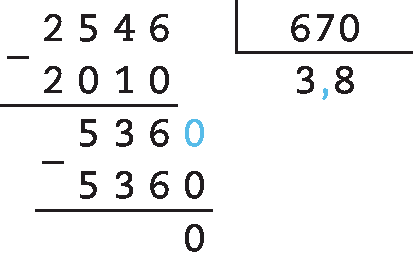
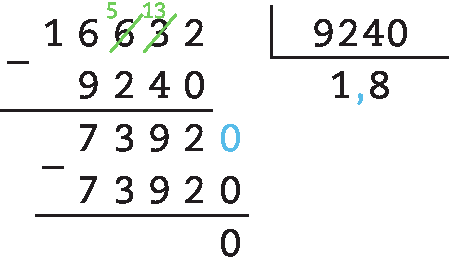
69. b) 1,6632 : 0,924 = .16632 : .9240 = 1,8
69. c) 124,976 : 8,56 = .124976 : 8,560 = 14,6

69. d) 0,09 : 0,36 = 9 : 36 = 0,25
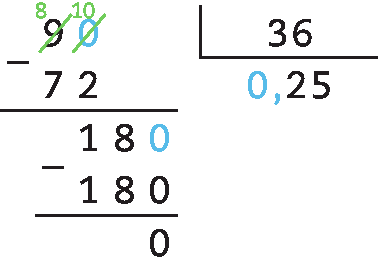
69. e) 203,82 : 15,8 = .20382 : .1580 = 12,9
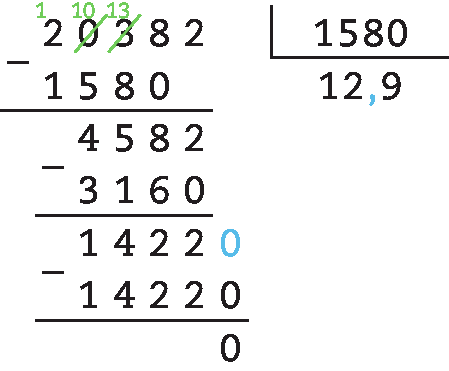
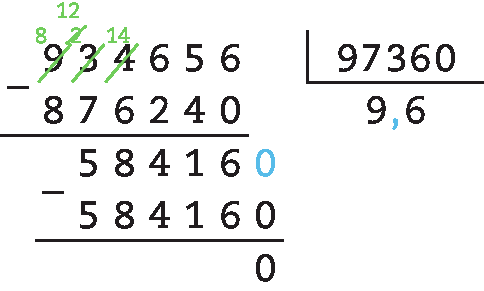
69. f) 93,4656 : 9,736 = .934656 : .97360 = 9,6
70. a) 7,4 : 6 = 74 : 60 ≃ 1,2
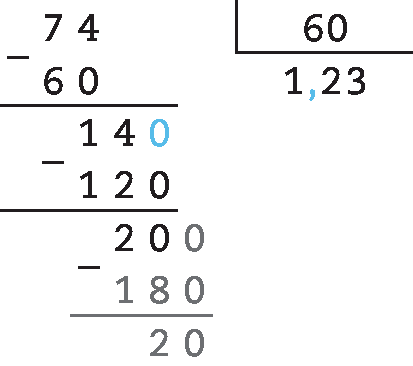
70. b) 2,5 : 0,3 = 125 : 3 ≃ 41,7
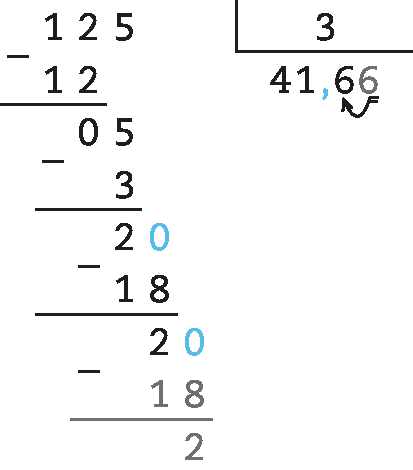
70. c) 9,4 : 2,1 = 94 : 21 ≃ 4,5
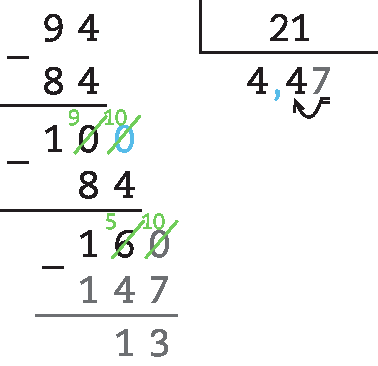
70. d) 85,6 : 9,6 = 856 : 96 ≃ 8,9
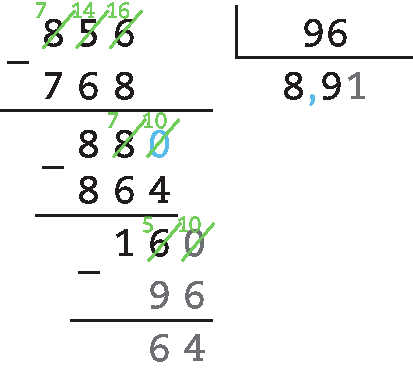
71. Aqui, o objetivo é obter um quociente com duas casas decimais.
71. a) 0,58 : 7 = 58 : 700 ≃ 0,08
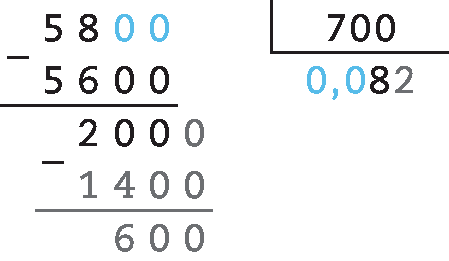
71. b) 10 : 0,9 = 100 : 9 ≃ 11,11
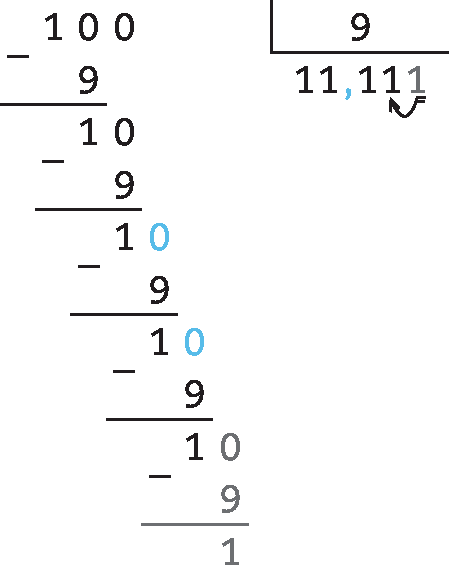
71. c) 0,25 : 0,7 = 25 : 70 ≃ 0,36
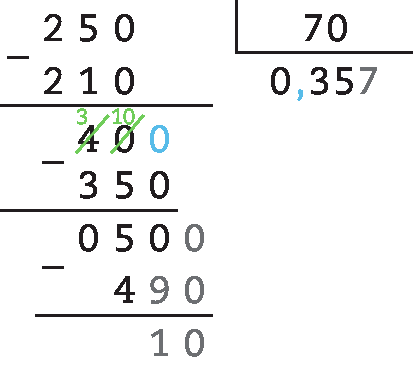
71. d) 45,6 : 9,2 = 456 : 92 ≃ 4,96
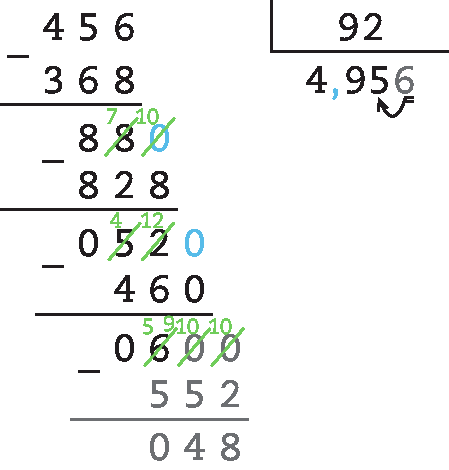
74. Como 43 : 8 = 5,375 e 25 : 4 = 6,25, obtemos:
74. a) 430 : 80 = (43 ⋅ 10) : (8 ⋅ 10) = 43 : 8 = 5,375
74. b) 4,3 : 0,8 =
43 décimos dividido por 8 décimos= 43 : 8 = 5,375
74. c) .4300 : 800 = (43 ⋅ 100) : (8 ⋅ 100) = 43 : 8 = 5,375
74. d) 0,43 : 0,08 =
43 centésimos dividido por 8 centésimos43 : 8 = 5,375
74. e) 250 : 40 = (25 ⋅ 10) : (4 ⋅ 10) = 25 : 4 = 6,25
74. f) 2,5 : 0,4 =
25 décimos dividido por 4 décimos= 25 : 4 = 6,25
74. g) .2500 : 400 = (25 ⋅ 100) : (4 ⋅ 100) = 25 : 4 = 6,25
74. h) 0,25 : 0,04 =
25 centésimos dividido por 4 centésimos= 25 : 4 = 6,25
75. Podem ser enchidas
30 0,5 avosgarrafas, ou seja, 60 garrafas, pois:
30 :
0,5, igual a, 30 dividido por 5 décimos, igual a, fração, numerador 30 vezes 10, denominador 5, igual a, fração, numerador 30 vezes 2, denominador 1, igual a 60.76. a) Pagando a prazo, são gastos 346 ⋅ 3 = .1038; então, Renata pagou 17 reais a mais, pois: .1038 − .1021 = 17
76. b) Ficando 7 dias, são gastos, em reais, cêrca de 148,29.
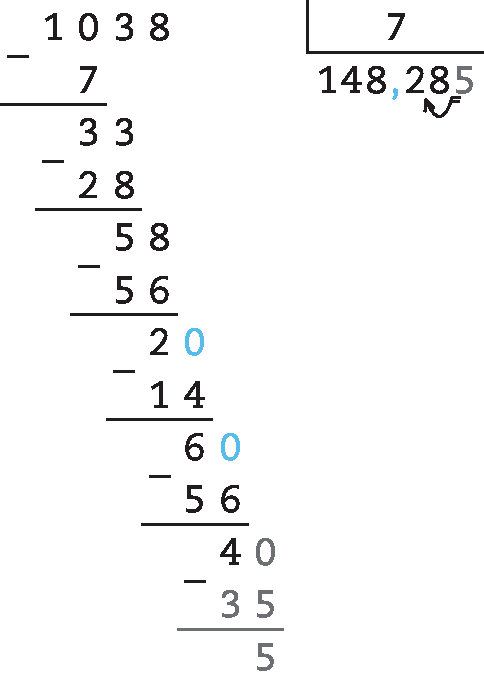
81.

84. Bruno diz que vai comprar 7 refrigerantes, 4 sucos e 5 lanches de metro.
84. a) A expressão que representa o que Bruno gastará é a soma das parcelas de cada item da compra, e cada parcela será a multiplicação entre a quantidade comprada e o preço unitário; dessa maneira, a expressão é: 7 ⋅ 6,25 + 4 ⋅ 8,12 + 5 ⋅ 47,75.
84. b) Resolvendo a expressão, obtemos:
7 ⋅ 6,25 + 4 ⋅ 8,12 + 5 ⋅ 47,75 =
= 43,75 + 32,48 + 238,75 = 314,98.
Logo, R$ 314,98trezentos e quatorze reais e noventa e oito centavos.
87. Verifique se os estudantes compreendem que a fórma abreviada troca a repetição dos algarismos e as reticências por um traço para indicar a dízima:
87. a) 0,222reticências =
0,2 com período 287. b) 0,531531531reticências =
0,531 com período 53187. c) 2,353535reticências =
2,35 com período 3587. d) 0,0222reticências =
0,02 com período 287. e) 0,56444reticências =
0,564 com período 487. f) 2,7212121reticências =
2,721 com período 2188. Avalie se os estudantes percebem que o período é formado pelos algarismos que se repetem na parte decimal de uma dízima periódica. Nessa notação, ele é indicado pela cópia antes das reticências.
88. a) 0,744reticências → o período é 4.
88. b) 2,45666reticências → o período é 6.
88. c) 0,2343434reticências → o período é 34.
88. d) 1,7525252reticências → o período é 52.
89. Simplificando a expressão:
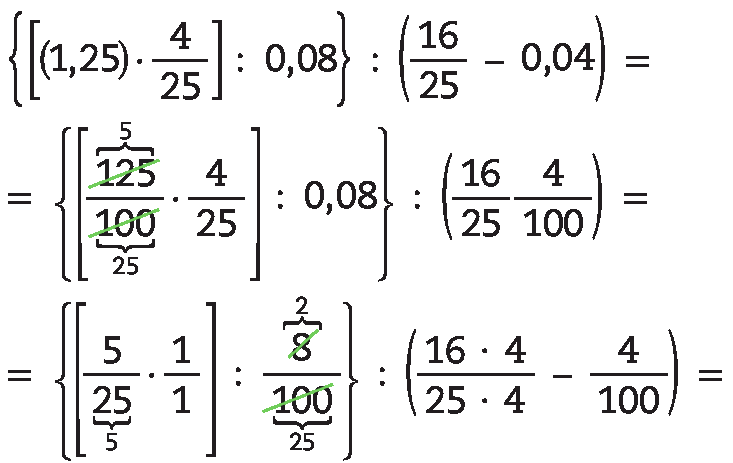
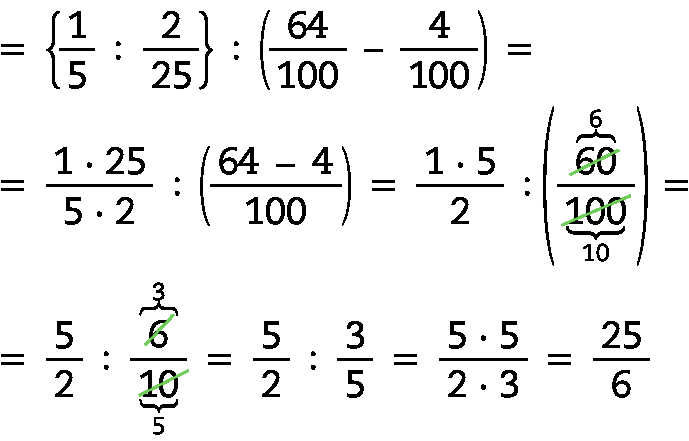
Alternativa a.
91. O enunciado propõe “em 2010, o Serviço de Estrangeiros e Fronteiras recebeu 24 mil pedidos de cidadania, em 2020 houve aumento de 141%”.
91. a) Então o valor procurado é a quantidade de pedidos em 2010 mais 141% dessa quantidade, ou seja, é 100% + 141% = 241% dos pedidos realizados em 2010.
Calculamos 241% de 24 mil:
= .57840 = 57,84
Logo, 57,84 mil brasileiros.
91. b) A diferença entre as quantidades de cidadanias solicitadas entre 2020 e 2010 é 57,84 mil − 24 mil = 33,84 mil.
Outra maneira de calcular é obtendo 141% da quantidade de cidadanias solicitadas em 2010, ou seja, 141% de 24 mil, que é dado por: 1,41 ⋅ .24000 = .33840 = 33,84
Logo, 33,84 mil brasileiros.
91. c) Resposta pessoal.
92. Analisando as informações do gráfico, temos:
92. a) A quantidade da população brasileira com mais de 60 anos em 2020 é 30,2 e a projeção para 2023 é 42,1. O aumento previsto, em porcentagem, é a relação
Fração. Numerador aumento absoluto, denominador porcentagem em 2020..
Portanto:
≃ 0,394 = 39,4%
92. b) Observar se, em algum conjunto de barras que representa cada faixa etária, a barra amarela (que representa 2020) é maior do que a laranja (que representa a projeção para 2030). Dessa maneira, observa-se projeção de diminuição entre os brasileiros de 0 a 19 anos e de 20 a 39 anos. A diminuição percentual é calculada como
Fração. Numerador porcentagem em 2020 menos porcentagem em 2030, denominador porcentagem em 2020..
Na primeira faixa etária, a diminuição foi de
Fração. Numerador 60 menos 57,2, denominador 60, igual a, 2,8 60 avos, igual a 0,046 com período 6.≃ 0,047 = 4,7%, e na segunda faixa etária foi de:
≃ 0,06569 ≃ 6,6%
92. c) A população total pode ser obtida pela soma da quantidade de cada faixa etária.
Em 2010, a população era de:
65,3 + 64,8 + 43,8 + 20,9 = 194,8 milhões.
Em 2020, a população era de:
60 + 68,5 + 53,1 + 30,2 = 211,8 milhões.
Em 2030, a projeção é que a população seja de:
57,2 + 64 + 61,5 + 42,1 = 224,8 milhões.
O aumento percentual, calculando como
, é:
• Entre 2010 e 2020:
≃ 0,08727 ≃ 8,7%
• Entre 2020 e 2030:
≃ 0,061379 ≃ 6,1%
92. d) Resposta pessoal.
Pense mais um pouco
Página 213
1. Os números digitados são: 4,1 (quatro inteiros e um décimo); 0,4 (quatro décimos); 0,032 (trinta e dois milésimos); 3,14 (três inteiros e catorze centésimos).
2. A maioria das calculadoras segue o padrão de numeração da língua inglesa, e por isso a vírgula é indicada por um ponto. Como o visor sempre começa zerado, quando o número é menor do que um inteiro (ou seja, começa com “0”), não é necessário apertar nenhuma tecla para indicar o primeiro zero, portanto é possível iniciar a digitação diretamente pela vírgula (

).
2. a) O número é 100 + 4 ⋅ 0,01 = 100,04. Portanto, a sequência de teclas será

.
2. b) O número é 21 ⋅ 0,001 = 0,021. Portanto, a sequência de teclas será

.
2. c) O número é 101 ⋅ 0,01 = 1,01. Portanto, a sequência de teclas será

.
2. d) O número é .2033 ⋅ 0,001 = 2,003. Portanto, a sequência de teclas será

.
3. a) Efetuar a divisão entre numerador e denominador:


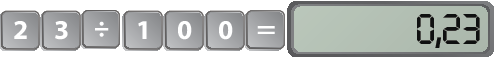
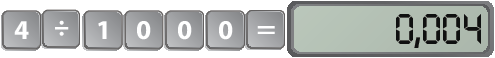






3. b) Em todos os cálculos do item a, a quantidade de zeros no denominador é a mesma de casas decimais da resposta obtida na calculadora. Dessa maneira, é possível realizar o procedimento prático de copiar o número do numerador e deslocar a vírgula por uma quantidade de casas igual à quantidade de zeros do denominador.
4. a) Aplicamos a quantidade de zeros do denominador como casas decimais do numerador:
4. b) Fazendo o caminho contrário, no denominador será colocada a potência de 10 com a quantidade de zeros igual à quantidade de casas decimais.
Página 227
1. Considerando os produtos 38,2 ⋅ 4 = 152,8 e 38,2 ⋅ 7 = 267,4, obtemos:
1. a) 38,2 ⋅ (4 ⋅ 10) = (38,2 ⋅ 4) ⋅ 10 = 152,8 ⋅ 10 = .1528 e 38,2 ⋅ 7 ⋅ 10 = 267,4 ⋅ 10 = .2674
1. b) (38,2 ⋅ 4) ⋅ 100 = 152,8 ⋅ 100 = .15280 e (38,2 ⋅ 7) ⋅ 10 = 267,4 ⋅ 100 = .26740
1. c) (38,2 ⋅ 4) ⋅ .1000 = 152,8 ⋅ .1000 = .152800 e (38,2 ⋅ 7) ⋅ .1000 = 267,4 ⋅ .1000 = .267400
2. Nesse caso, também se aplicam as propriedades da adição e da multiplicação.
2. a) 38,2 ⋅ 11 = 38,2 ⋅ (4 + 7) = 38,2 ⋅ 4 + 38,2 ⋅ 7 = 152,8 + 267,4 = 420,2
2. b) 38,2 ⋅ 3 = 38,2 ⋅ (7 − 4) = 38,2 ⋅ 7 − 38,2 ⋅ 4 = 267,4 − 152,8 = 114,6
2. c) 38,2 ⋅ 14 = 38,2 ⋅ 7 ⋅ 2 = 267,4 ⋅ 2 = 534,8
2. d) 38,2 ⋅ 8 = 38,2 ⋅ 4 ⋅ 2 = 152,8 ⋅ 2 = 305,6
2. e) 38,2 ⋅ 47 = 38,2 ⋅ (40 + 7) = 38,2 ⋅ 4 ⋅ 10 + 38,2 ⋅ 7 = 152,8 ⋅ 10 + 267,4 = .1528 + 267,4 = .1795,4
2. f) 38,2 ⋅ 74 = 38,2 ⋅ 7 ⋅ 10 + 38,2 ⋅ 4 = 267,4 ⋅ 10 + 152,8 = .2674 + 152,8 = .2826,5
Página 232
1. Efetuando na calculadora, em alguns itens é necessário utilizar as teclas de “adição à memória”

e “recuperar da memória”

:
1. a)

1. b)

1. c)

1. d)

1. e)

1. f.

1. g)

1. h)

1. i)

2. Efetuando na calculadora e escolhendo os números a = 2,2 e b = 1,1, ambos são não nulos e estão na fórma decimal; então, a : b = 2,2 : 1,1 = 2.
2. a) O dobro de a dividido pelo dobro de b é 2 ⋅ a : 2 ⋅ b = (2 ⋅ 2,2) : (2 ⋅ 1,1) = 4,4 : 2,2 = 2.
2. b) O triplo de a dividido pelo triplo de b é 3 ⋅ a : 3 ⋅ b = (3 ⋅ 2,2) : (3 ⋅ 1,1) = 6,6 : 3,3 = 2.
2. c) O quíntuplo de a dividido pelo quíntuplo de b é 5 ⋅ a : 5 ⋅ b = (5 ⋅ 2,2) : (5 ⋅ 1,1) = 11 : 5,5 = 2.
2. d) O sêxtuplo de a dividido pelo sêxtuplo de b é 6 ⋅ a : 6 ⋅ b = (6 ⋅ 2,2) : (6 ⋅ 1,1) = 13,2 : 6,6 = 2.
Perceba que todas essas divisões são iguais a a : b.
3. Quando se efetua uma divisão, ao multiplicar o divisor e o dividendo pelo mesmo fator diferente de zero não se altera o quociente (resultado) da divisão, ou seja, se k ≠ 0 ⇒ a : b = (k · a) : (k · b).
Página 235
Três triângulos

somam 8,4; então, cada um deles vale:

= 8,4 : 3 = 84 : 30 = 2,8
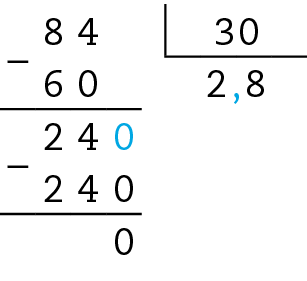
Dois triângulos

são equivalentes a um trapézio

(figura laranja); portanto, o trapézio é 2 ·

= 2 · 2,8 = 5,6. Como

+

= 6,8, temos

= 6,8 − 2,8 = 4. Temos

+

= 9,7; logo,

= 9,7 − 2,8 = 6,9. Por fim:
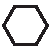
=

+

+

⇒

= 2,8 + 4 + 6,9 = 13,7. Então, os valores são: triângulo 2,8; trapézio 5,6; pentágono 6,9; hexágono 13,7.
Trabalhando a informação
1. Considerando os dados da tabela de faturamento por vendedor, se Carlos tivesse vendido R$ 23vinte e três reais.040,00quarenta reais, a média do faturamento passaria a ser:
=
=
Fração. Numerador 23.040 mais 33.500 mais 13.500, mais 21.000, mais 18.810, mais 28.400, denominador, 6.=
=
Fração. 138.250 sextos, igual a, 23.041,66 com período 6.≃ .23041,67
Como .23040 < .23041,67, Carlos estaria abaixo da média e não receberia o bônus.
2. A média de gastos de cada um pode ser calculada como
Fração.numerador total de gastos, denominador quantidade de meses.
Então, para Tiago:
Fração. Numerador 42 mais 43 mais 22 mais 80, denominador 4, igual à 187 quartos, igual à 46,75Para Clara:
Fração. Numerador 53 mais 52 mais 50 mais 40, denominador 4, igual à, 195 quartos, igual à 48,75.Como 48,75 > 46,75, de fato Tiago tinha razão.
3. a) A média de altura dos jogadores é calculada como
Fração. Numerador soma das alturas denominador quantidade de jogadoresEntão:
3. b) Há 3 jogadores com altura acima de 1,97 na equipe A, pois: 2,04 > 1,97; 2,01 > 1,97; 2,08 > 1,97; 1,90 < 1,97 e 1,82 < 1,97.
3. c) Há 2 jogadores com altura acima de 1,98 na equipe B, pois: 2,02 > 1,98; 2,01 > 1,98; 1,98 = 1,98; 1,96 < 1,98 e 1,93 < 1,98.
4. Resposta pessoal. Uma opção de resposta com dados fictícios é o cálculo da média da medida da altura:
= 1,475 ≃ 1,48
Cálculo da média da medida da massa:
Cálculo da média de idade (meses):
|
Medida da altura (m) |
Medida da massa (kg) |
Idade (meses) |
|
|---|---|---|---|
|
A |
1,60 |
50 |
158 |
|
B |
1,43 |
32 |
139 |
|
C |
1,55 |
47 |
150 |
|
D |
1,32 |
46 |
147 |
|
Média |
1,48 |
43,75 |
148,5 |
Dados fictícios.
Exercícios complementares
1. Verifique se os estudantes associam os números apresentados no termômetro a um intervalo de números de 35 a 42. Se necessário, pode-se propor a eles que representem a reta numérica e os números apresentados nos itens dessa atividade.
Para ler o termômetro representado, observa-se até onde se expande a coluna de mercúrio (líquido vermelho). Na escala, cada grau está dividido em 10 partes iguais por tracinhos menores, sendo o tracinho central um pouco maior, para facilitar a indicação de metade.
1. a) Essa temperatura está exatamente na metade entre 37 graus Célsius e 38 graus Célsius, ou seja, 37,5 graus Célsius.
1. b) Aqui, a temperatura está entre 38 graus Célsius e 39 graus Célsius, mas antes da metade, mais próximo dos 38 graus Célsius. O fim da barra vermelha está duas partes à direita dos 38 graus Célsius, ou seja, 38 graus Célsius + 0,2 grau Célsius = 38,2 graus Célsius.
1. c) Nessa ilustração, a marcação vermelha vai até um ponto que está entre 36 graus Célsius e 37 graus Célsius, mais próximo dos 37 graus Célsius. Contam-se duas partes entre a marcação e os 37 graus Célsius; portanto, a temperatura indicada é 37 graus Célsius − 0,2 grau Célsius = 36,8 graus Célsius.
2. Uma maneira de ler os números decimais é recitar a parte inteira e a parte decimal separadamente, citando as ordens como em “dois inteiros e cinco décimos”; outra maneira é ler os algarismos individualmente ou em pequenos grupos, fazendo a leitura explícita da vírgula, como em “dois vírgula cinco”.
2. a) Uma resposta possível é 3,79 (“três vírgula setenta e nove”); 1,102 (“um vírgula cento e dois”); 0,003 (“zero vírgula zero zero três”).
2. b)
1.251 centésimos= .1251 : 100 = 12,51
Lê-se doze inteiros e cinquenta e um centésimos.
2. c) Há 3 algarismos que não se repetem no número desejado; portanto, é um número formado por 3 algarismos. Como é um número menor que 0, o zero deve ser a parte inteira, e então há duas casas decimais (0,


). Colocando nessas casas decimais os algarismos 1 e 8, então as opções são 0,18 e 0,81, de modo que o maior número possível é 0,81. Lê-se zero vírgula oitenta e um.
2. d) Com os algarismos 5, 6 e 8 sem repetição posso formar um número de 3 algarismos. Como quero que esteja entre 6 e 7, será escrito como 6,


. As opções são 6,85 e 6,58; então, o número procurado é o maior deles, 6,85.
Lê-se seis vírgula oitenta e cinco.
3. Lembrando algumas relações:
;
1 centésimo igual a 1 sobre 100 igual a 0,01;
;
|
Item |
Parte inteira |
Parte decimal |
Representação por algarismos |
|---|---|---|---|
|
a |
4 |
5 décimos |
4,5 |
|
b |
0 |
39 centésimos |
0,39 |
|
c |
4 |
82 centésimos |
4,82 |
|
d |
6 |
45 milésimos |
6,045 |
|
e |
2 |
2 milésimos |
2,002 |
|
f |
0 |
125 décimos de milésimos |
0,0125 |
4. Para escrever uma fração na fórma decimal, basta dividir o numerador pelo denominador.
4. a)
32 sobre 10= 32 : 10 = 3,2
4. b)
475 sobre 100= 475 : 100 = 4,75
4. c)
21 sobre 1000= 21 : 1 000 = 0,021
4. d)
135 sobre 10= 135 : 10 = 13,5
4. e)
28 sobre 100= 28 : 100 = 0,28
4. f)
5 sobre 1000= 5 : 1 000 = 0,005
5. Para fazer essa transformação, lembrar aos estudantes que uma fração com denominador 1 é igual ao seu numerador.
5. a)
2,5 igual 2,5 sobre 1 igual a fração de numerador 2,5 vezes 10 e denominador 1 vezes 10 igual 25 sobre 105. b)
0,15 igual 0,15 sobre 1 igual a fração de numerador 0,15 vezes 100 e denominador 1 vezes 100 igual 15 sobre 1005. c)
2,37 igual a fração de numerador 2,37 vezes 100 e denominador 100 igual 237 sobre 1005. d)
4,125 igual a fração de numerador 4,125 vezes 1000 e denominador 1000 igual 4125 sobre 10005. e)
27,5 igual a fração de numerador 27,5 vezes 10 e denominador 10 igual 275 sobre 105. f)
0,3628 igual a fração de numerador 0,3628 vezes 10000 e denominador 10000 igual 3628 sobre 100005. g)
31,2 igual a fração de numerador 31,2 vezes 10 e denominador 10 igual 312 sobre 105. h)
0,02 igual a fração de numerador 0,02 vezes 100 e denominador 100 igual 0,02 sobre 1006. Zeros escritos à direita da parte decimal de um número não alteram o seu valor.
6. a) Sentença verdadeira: 2 décimos = 20 centésimos; então, 4,2 = 4,20.
6. b) Sentença verdadeira: 5,0 são cinco inteiros e zero décimo, o mesmo que 5.
6. c) Sentença verdadeira: 4 décimos = 40 centésimos = 400 milésimos; então, 5,4 = 5,40 = 5,400.
6. d) Sentença falsa: 5 centésimos ≠ 5 décimos; então, 3,05 ≠ 3,50.
6. e) Sentença falsa: 4 décimos ≠ 4 inteiros; então, 0,4 ≠ 4,0.
6. f) Sentença verdadeira: 0 centésimo = 0 décimo; então, 10,00 = 10,0.
7. Como 11 < 11,7 < 12; o menor número natural maior que 11,7 é o 12. Como 9 < 9,02 < 10; o maior número natural menor que 9,02 é 9.
8. A ordem crescente é do menor para o maior. Buscando identificar os menores valores entre os números 0,61; 1,3; 1,45; 0,2; 3,0; 0,99; inicia-se a comparação pela parte inteira. Como 0 < 1 < 3, temos:
0,2 menor que 0,61, menor que 0,99, menor que 1,3, menor que 1,45, menor que 3Entre os valores com a parte inteira igual a zero, comparam-se os décimos 2 < 6 < 9. Assim:
Nos valores cuja parte inteira é 1, comparam-se 3 < 4 ⇒
1,3 menor que 1,45Portanto, todos os valores em ordem crescente são escritos como 0,2 < 0,61 < 0,99 < 1,3 < 1,45 < 3,0. A representação na reta numérica é dada dividindo-se os inteiros em partes iguais (nesse caso, dividi-los por 100, transformando-os em centésimos, é uma boa alternativa) e identificando-se os valores de maneira proporcional.
9. O tanque do problema, conforme as informações na figura, está com
3 quartosde combustível. Como é um tanque de 75 litros, ele tem 56,25 litros, pois:
3 ⋅
75 sobre 4 igual 225 sobre 4= 225 : 4 = 56,25
10. a) 12,5 : 4,5 = 125 : 45 ≃ 2,8
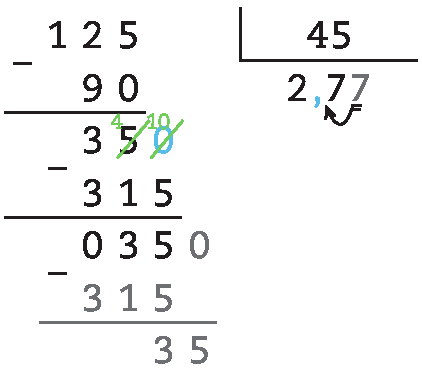
b) 15 : 7 ≃ 2,14
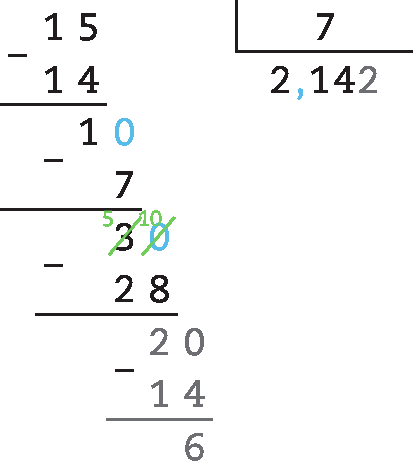
c) 45,6 : 13 = 456 : 130 ≃ 3,5
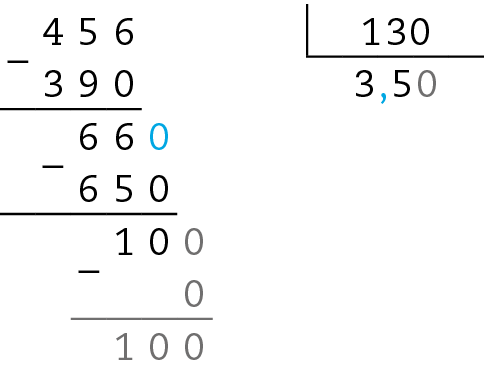
d) 18 : 2,3 = 180 : 23 ≃ 7,826

11. A caixa com 30 unidades custa R$ 22,50vinte e dois reais e cinquenta centavos; então, cada unidade sai por 75 centavos, pois:
22,5 : 30 = 225 : 300 = 0,75
12. Há 3 opções de pagamento para o fogão: à vista, em 6 parcelas (sem juros) ou em 16 parcelas (com juros).
12. a) Em 6 parcelas, o fogão custa o mesmo do pagamento à vista, R$ 609,90seiscentos e nove reais e noventa centavos.
12. b) Na modalidade de pagamento em 16 parcelas de R$ 55,23cinquenta e cinco reais e vinte e três centavos, o total pago é R$ 55,23cinquenta e cinco reais e vinte e três centavos ⋅ 16 = R$ 883,68oitocentos e oitenta e três reais e sessenta e oito centavos.
12. c) A diferença entre os preços é de R$ 883,68oitocentos e oitenta e três reais e sessenta e oito centavos − R$ 609,90seiscentos e nove reais e noventa centavos = R$ 273,78duzentos e setenta e três reais e setenta e oito centavos.
12. d) Como o preço à vista é igual ao preço do pagamento em 6 vezes, a diferença é o mesmo valor de R$ 273,78duzentos e setenta e três reais e setenta e oito centavos.
13. Acima de cada seta azul está escrita a operação que foi efetuada no primeiro número para resultar no segundo.
13. a) 5,6 ⋅ 10 = X = 56 X ⋅ 10 = Y = 56 ⋅ 10 = 560 Y ⋅ 10 = Z = 560 ⋅ 10 = .5600
13. b) X = 0,075 ⋅ 100 = 7,5 Y = 7,5 ⋅ 10 = 75 Z = 75 ⋅ 10 = 750
13. c) X = 538,5∶10 = 53,85 Y = 53,85∶10 = 5,385 Z = 5,385 ⋅ .1000 = 5.385
13. d) X = .17289 ∶ .1000 = 17,289 Y = 17,289 ⋅ 100 = .1728,9 Z = .1728,9 ⋅ 10 = 17.289
14. Quando o número de casas decimais for diferente na soma e na subtração, efetua-se a operação completando com zeros para alinhar a vírgula de todos os números.
14. a) 3,91 + 6,03 + 0,58 = 9,94 + 0,58 = 10,52
14. b) 5,2 − 3,216 = 5,200 − 3,216 = 1,984
14. c) 6,3 ⋅ 4,8 = 6,3 ⋅
48 sobre 100 igual a 3024 sobre 100= 30,24
14. d) 10 − 4,36 = 10,00 − 4,36 = 5,64
14. e)
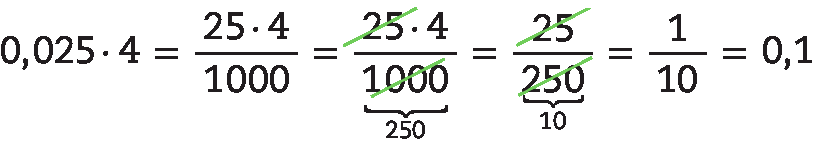
14. f) 25,44 : 5,3 = .2544 : 530 = 4,8
15. Resolvendo cada expressão, obtemos:
15. a) 3 ⋅ 1,36 + 12,22 = 4,08 + 12,22 = 16,3
15. b) (12 − 9,2) ⋅ (6 − 4,5 : 6) = 2,8 ⋅ (6 − 0,75) = 2,8 ⋅ 5,25 = 14,7
15. c) (3,1 − 2,8)3 ⋅ (4,5 − 2) : (4,25 − 3) = 0,33 ⋅ 2,5 : 1,25 = 0,027 ⋅ 2,5 : 1,25 = 0,0675 : 1,25 = 0,054
16. Efetuando-se a divisão 23 : 9, obtém-se o quociente
2,5 com um traço em cima do 5que é uma dízima periódica.
17. Usando a calculadora, obtemos:
17. a)

17. b)

17. c)

17. d)

17. e)

17. f)

Verificando
5. 10% de .8589 = 0,1 ⋅ .8589 = 858,9
Logo, o valor da comissão foi de R$ 858,90oitocentos e cinquenta e oito reais e noventa centavos.
Alternativa d.
8. 5, 5 ⋅ 1,4142 = 7,7781
Alternativa a.
10. 2,666reticências = 2 + 0,666... = 2 +
6 sobre 9=
24 sobre 9=
8 sobre 3Alternativa b.
Organizando
a) Espera-se que os estudantes indiquem que a vírgula é usada para separar a parte inteira da parte decimal de um número.
b) Sim, algumas frações expressam um número decimal exato, e outras, dízimas periódicas.
c) Primeiro devemos ler a parte inteira, se houver, e depois a parte decimal acompanhada da palavra milésimo ou milésimos.
d) Resposta possível: 2,1; 2,11; 2,111; 2,1111 e 2,11111.
e) Resposta possível: O zero na casa dos centésimos representa que não há centésimo nesse número; como esta seria a última casa, não é preciso representá-lo.
f) Deslocamos a vírgula para a direita, respectivamente, uma, duas, três, reticências, casas decimais.
g) Não é possível, visto que com 49 moedas teríamos R$ 12,25doze reais e vinte e cinco centavos, e com 50 moedas teríamos R$ 12,50doze reais e cinquenta centavos.
h) Sim. O quociente não se altera. O resto fica multiplicado pelo número.
Capítulo 10 — Polígonos e poliedros
• Objetivos do capítulo e justificativas
• Classificar figuras geométricas planas segundo critérios diversos, como: polígonos e não polígonos; paralelismo de lados; medidas de ângulos internos e de lados.
• Conceituar e classificar linhas poligonais e polígonos.
• Reconhecer e quantificar os elementos de um polígono: lados, vértices e ângulos internos.
• Classificar triângulos considerando a medida dos lados e a medida dos ângulos internos.
• Construir triângulos utilizando régua, transferidor e compasso.
• Classificar quadriláteros quanto ao paralelismo de seus lados.
• Classificar paralelogramos observando a presença de lados congruentes e ângulos internos retos.
• Conceituar par ordenado e representá-lo geometricamente.
• Associar pares ordenados de números a pontos do plano cartesiano do 1º quadrante.
• Localizar vértices de polígonos no plano cartesiano.
• Classificar poliedros de acordo com o número de faces.
• Identificar planificação da superfície de poliedros.
• Reconhecer semelhanças e diferenças entre prismas e pirâmides, identificando suas bases e faces laterais.
• Calcular probabilidade de um evento em experimento aleatório.
• Identificar variáveis e suas frequências quanto a dados organizados em tabela.
Neste capítulo, tratamos de polígonos e poliedros associando essas figuras geométricas abstratas a objetos do cotidiano. A ideia de classificação de polígonos parte do pressuposto de que estamos organizando elementos a partir de características comuns. O reconhecimento dessas características e dos elementos de um polígono possibilita a resolução de problemas relacionados ao estudo de polígonos. Para que esse objetivo seja alcançado é necessário explorar diversos tipos de polígono, com diferentes características, ampliando o repertório geométrico dos estudantes. Desse modo, contribuímos para o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2 e 3.
O uso de vários recursos para a construção de figuras geométricas possibilita a compreensão na prática de conceitos estudados muitas vezes apenas no âmbito teórico, sendo de suma importância que os estudantes tenham esse tipo de oportunidade. Este objetivo está relacionado à competência específica 5 e à competência geral 5.
Depois de estudar os princípios do plano cartesiano ainda nos Anos Iniciais do Ensino Fundamental, o estudante tem a oportunidade de definir o que é um par ordenado e sua representação geométrica. Quando trabalhamos pelo sistema de coordenadas, conseguimos explorar características específicas dos polígonos que, muitas vezes, só conseguiríamos fazer nos desenhos fóra do plano cartesiano se usássemos instrumentos de medida e construção, como régua e compasso, por exemplo. Assim, este objetivo se relaciona com as competências específicas 3, 5 e 6.
O trabalho com poliedros, neste capítulo, tem como objetivo ampliar os conceitos estudados nos Anos Iniciais do Ensino Fundamental. Ao relacionar os poliedros às planificações correspondentes e reconhecer suas características, desenvolve-se a capacidade de abstração e de resolução de problemas práticos do cotidiano, como o cálculo de volume.
Na seção Trabalhando a informação tratamos o conceito de probabilidade relacionado à fórma do cubo, associando as Unidades Temáticas Geometria e Probabilidade e estatística. O trabalho com probabilidade se faz necessário para que os estudantes compreendam o conceito de aleatoriedade. Ao propor a eles que façam um experimento, organizando as informações em tabelas, para depois calcular a probabilidade, contribuímos para o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2 e 3.
Na seção de abertura apresentamos uma obra de arte para que os estudantes possam fazer uma análise de suas características, o que contribui para o trabalho com a competência geral 3.
O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diferentes atividades a serem realizadas em grupos, pois possibilita aos estudantes exercitar diferentes habilidades socioemocionais ao trabalhar com os colegas, interagindo de fórma cooperativa.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah um seis) Associar pares ordenados de números a pontos do plano cartesiano do 1º quadrante, em situações como a localização dos vértices de um polígono.
(ê éfe zero seis ême ah um sete) Quantificar e estabelecer relações entre o número de vértices, faces e arestas de prismas e pirâmides, em função do seu polígono da base, para resolver problemas e desenvolver a percepção espacial.
(ê éfe zero seis ême ah um oito) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e classificá-los em regulares e não regulares, tanto em suas representações no plano como em faces de poliedros.
(ê éfe zero seis ême ah um nove) Identificar características dos triângulos e classificá-los em relação às medidas dos lados e dos ângulos.
(ê éfe zero seis ême ah dois zero) Identificar características dos quadriláteros, classificá-los em relação a lados e a ângulos e reconhecer a inclusão e a intersecção de classes entre eles.
(ê éfe zero seis ême ah dois um) Construir figuras planas semelhantes em situações de ampliação e de redução, com o uso de malhas quadriculadas, plano cartesiano ou tecnologias digitais.
(ê éfe zero seis ême ah dois dois) Utilizar instrumentos, como réguas e esquadros, ou softwares para representações de retas paralelas e perpendiculares e construção de quadriláteros, entre outros.
(ê éfe zero seis ême ah dois três) Construir algoritmo para resolver situações passo a passo (como na construção de dobraduras ou na indicação de deslocamento de um objeto no plano segundo pontos de referência e distâncias fornecidas etcétera).
(ê éfe zero seis ême ah dois quatro) Resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento.
(ê éfe zero seis ême ah três zero) Calcular a probabilidade de um evento aleatório, expressando-a por número racional (fórma fracionária, decimal e percentual) e comparar esse número com a probabilidade obtida por meio de experimentos sucessivos.
Os conhecimentos desenvolvidos ao longo do 5º ano do Ensino Fundamental acerca de polígonos, plano cartesiano e figuras geométricas não planas são, neste momento, retomados, ampliados e aprofundados. A perspectiva é de que o estudo das características de triângulos e quadriláteros e sua representação no plano cartesiano constituam embasamento necessário para que, durante o 7º ano, os estudantes investiguem e realizem transformações geométricas de polígonos no plano cartesiano (ê éfe zero sete ême ah um nove), entre outros assuntos.
Os conceitos e as atividades ligados à Unidade Temática Geometria, foco deste capítulo, são abordados em dois momentos. A primeira abordagem trata de tópicos de Geometria Plana − situação na qual se desenvolve a ideia de linha poligonal, de modo que os estudantes possam ampliar e consolidar a noção de polígono e de seus elementos −, promove o reconhecimento, a nomeação, a comparação e a classificação de triângulos e quadriláteros e trata da representação de vértices de polígonos no plano cartesiano. Algumas atividades exploram também a construção de triângulos com o uso de régua, compasso e transferidor e a análise de algumas de suas propriedades. Desse modo, contribuímos para o desenvolvimento das habilidades (EF06êmeA18), (EF06êmeA19), (EF06ême á20) e (EF06êmeA22). No exercício proposto 23, os estudantes devem construir um fluxograma com os passos a serem seguidos para a construção de triângulos usando régua e compasso, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah dois três).
A segunda abordagem insere-se nos estudos de figuras geométricas não planas. Nesse momento, espera-se que os estudantes quantifiquem e relacionem o número de vértices, de faces e de arestas de prismas e pirâmides ao polígono que determina suas bases, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah um sete).
O trabalho com plano cartesiano foi elaborado de modo que os estudantes associem pares ordenados a pontos do primeiro quadrante e posteriormente à representação de vértices de polígonos, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah um seis). Nos exercícios propostos 34 e 35, os estudantes devem construir figuras planas semelhantes com o apoio do plano cartesiano, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah dois um).
Algumas das atividades vinculam-se também a outras Unidades Temáticas, caso da seção Para saber mais, que apresenta o tema “Ladrilhamento” e trabalha a noção de área, relativa à Unidade Temática Grandezas e medidas, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah dois quatro). Já a seção Trabalhando a informação explora o tema “A probabilidade das cores”, situação na qual se trabalha o cálculo de probabilidades, relativo à Unidade Temática Probabilidade e estatística, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah três zero).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações Didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
1. Quando uma linha é formada apenas por segmentos de reta consecutivos e não colineares, ela é chamada de linha poligonal.
1. a) Não é, pois tem partes curvas.
1. b) É linha poligonal.
1. c) É linha poligonal.
1. d) Não é, pois tem partes curvas.
2. Linhas poligonais são abertas quando existem dois extremos que não estão conectados, e são fechadas quando não são abertas. Entre as fechadas, as linhas são simples quando não há cruzamentos entre segmentos, e são não simples quando há cruzamentos.
2. a) Todos os extremos estão conectados e não há cruzamento: linha fechada simples.
2. b) Todos os extremos estão conectados e há 2 cruzamentos: linha fechada não simples.
2. c) Há dois extremos na parte superior da figura que não estão conectados a outro segmento: linha aberta.
2. d) Há dois extremos na parte esquerda da figura que não estão conectados a outro segmento: linha aberta.
3. Uma região do plano é chamada de convéquica quando o segmento com extremos em quaisquer dois pontos da região está contido nessa região, isto é, tem todos os pontos nessa região. Por outro lado, uma região do plano é chamada de não convéquica se existem dois pontos pertencentes a ela que são extremos de um segmento que não está contido nessa região. Então:
3. a) Escolhendo como extremos do segmento de teste pontos próximos de cada um dos vértices à direita da figura, é possível notar que a região é não convéquica.
3. b) É convéquica.
3. c) Escolhendo como extremos do segmento de teste pontos próximos de cada um dos vértices à esquerda da figura, é possível notar que a região é não convéquica.
3. d) É convéquica.
10. Resposta possível:
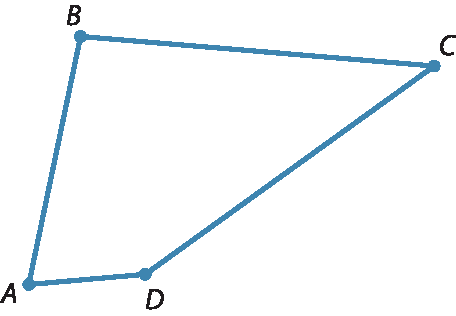
10. a) Esse polígono tem 4 vértices.
10. b) O polígono a bê cê dê tem como ângulos internos:
ângulo A B C,
ângulos BCD, CDE, EAB.
10. c) Esse polígono tem 4 lados:
Segmento AB, segmento BC, segmento CD e segmento DA.11. Um polígono de 3 vértices é um triângulo como á bê cê da imagem a seguir. Esse polígono não tem nenhuma diagonal.

12. Um polígono de 12 lados tem 12 vértices e 12 ângulos internos.
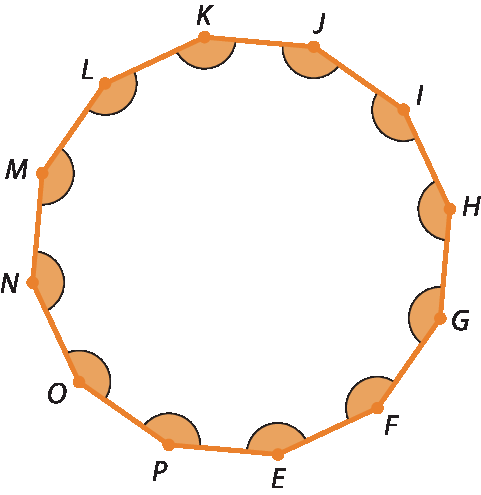
14. Em um polígono, o número de lados é igual ao número de ângulos internos.
14. a) Um hexágono tem 6 ângulos internos.
14. b) O polígono de 12 vértices e 12 lados é o dodecágono.
14. c) Um icoságono tem 20 lados; então, tem 20 vértices e 20 ângulos internos.
15. Há 5 equipes nesse torneio.
15. a) Foram disputadas 10 partidas ao todo. Se as equipes são A, B, C, D e ê, as partidas disputadas foram A − B; A − C; A − D; A − E; B − C; B − D; B − E; C − D; C − E; D − E.
15. b) Como há 5 equipes, o polígono que representa essa situação é o pentágono.
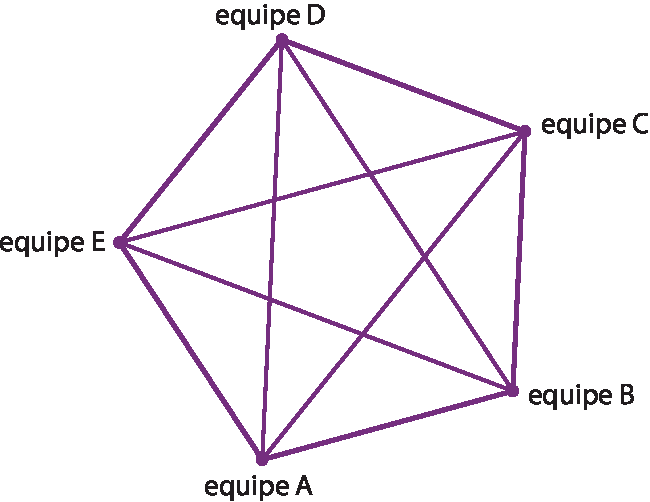
15. c) Em um pentágono em que os vértices representam as equipes, os lados e as diagonais, que ligam os vértices, representam as partidas.
15. d) Pelo desenho, basta contar a quantidade de diagonais e adicioná-la à quantidade de lados para obter o total de partidas.
19. a)
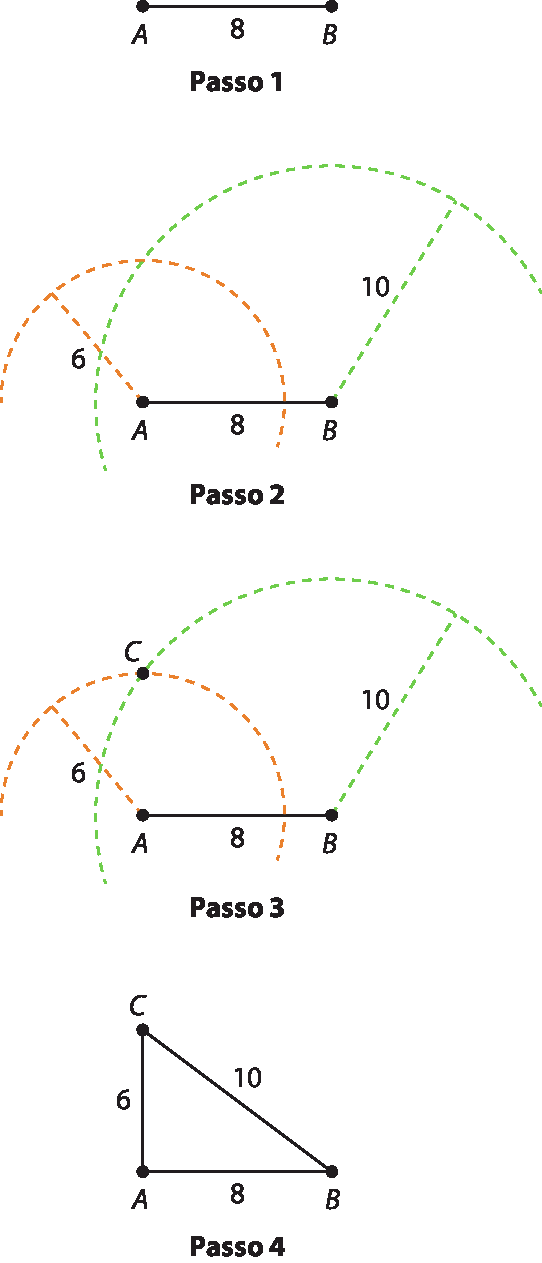
19. b)
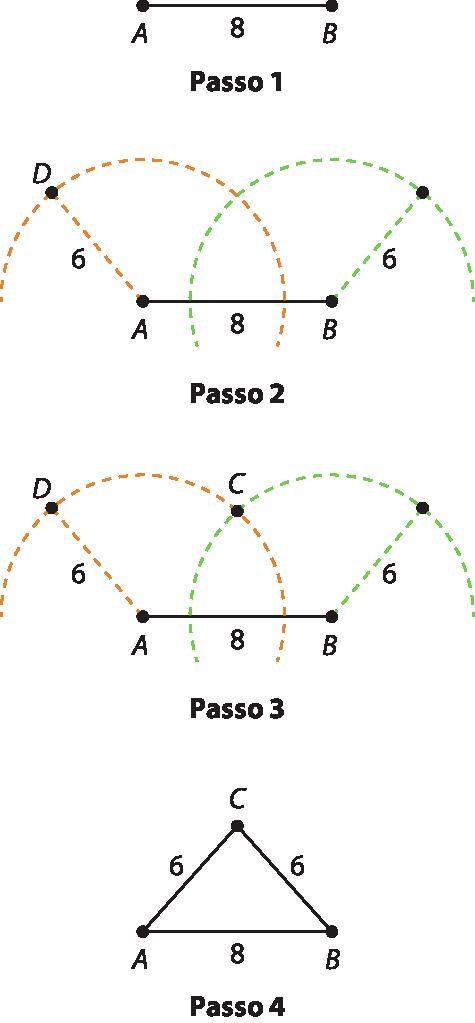
19. c)
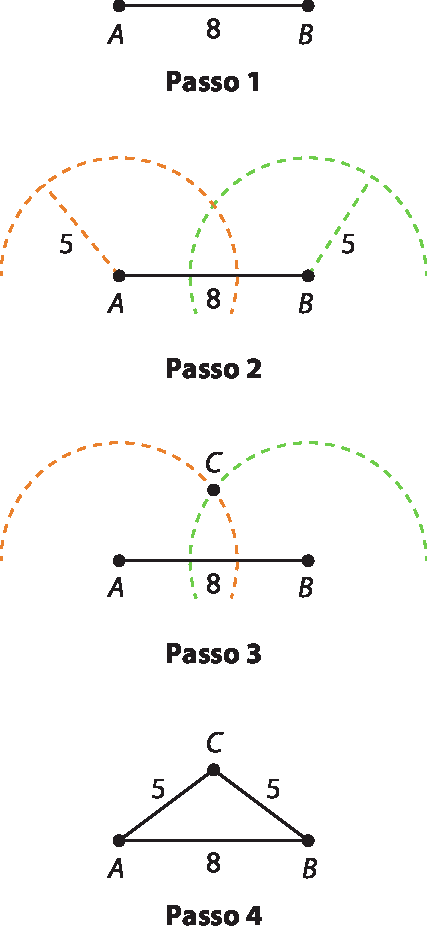
21. a)
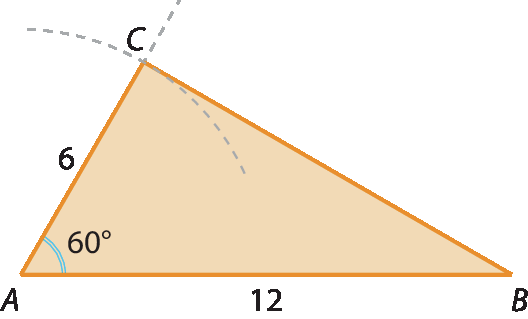
21. b)
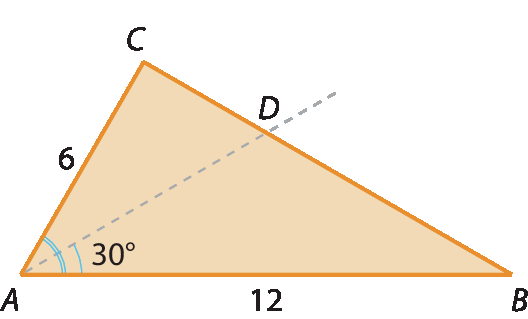
21. c) Medindo os segmentos nos triângulos construídos, é possível notar que sim, medida do
medida do segmento CD=
Fração. Numerador medida do segmento AD, denominador, 2.e medida do
medida do segmento ACFração. Numerador medida do segmento AB, denominador, 2.
.
21. d) Certifique-se de que os estudantes conseguem utilizar corretamente o transferidor para medir os ângulos desenhados; no exemplo, tem-se um posicionamento possível para encontrar medida do
ângulo A D B= 120graus.
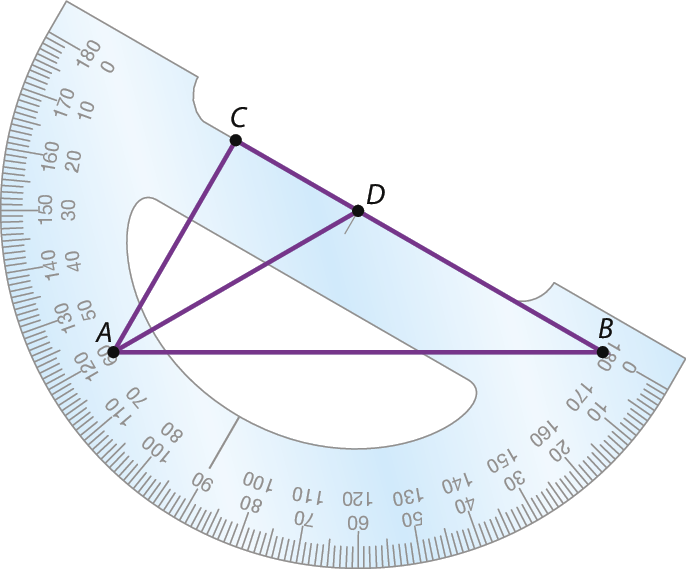
21. e) O triângulo á bê cê tem três lados com medidas de lado diferentes e um ângulo reto; é um escaleno retângulo. O triângulo á cê dê tem três lados com medidas de lado diferentes e um ângulo reto; é um escaleno retângulo. O triângulo á bê dê tem um ângulo obtuso e dois lados congruentes; é isósceles obtusângulo.
22. a)
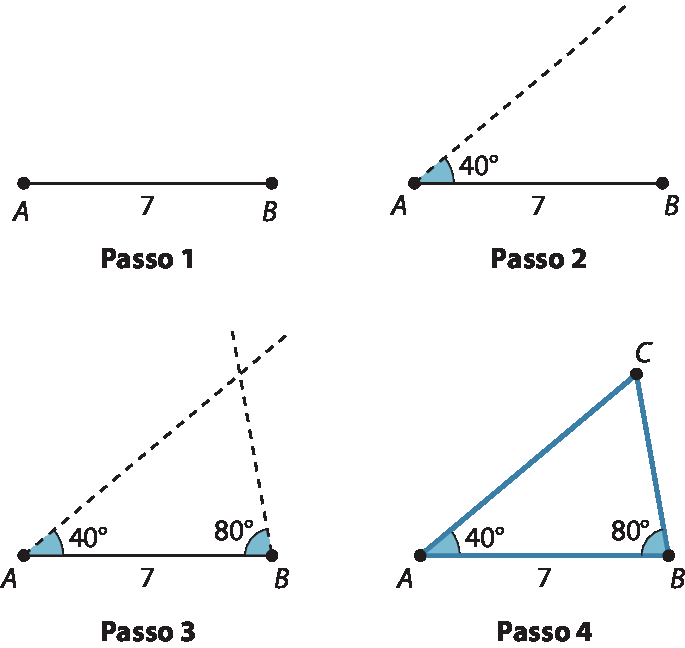
b)
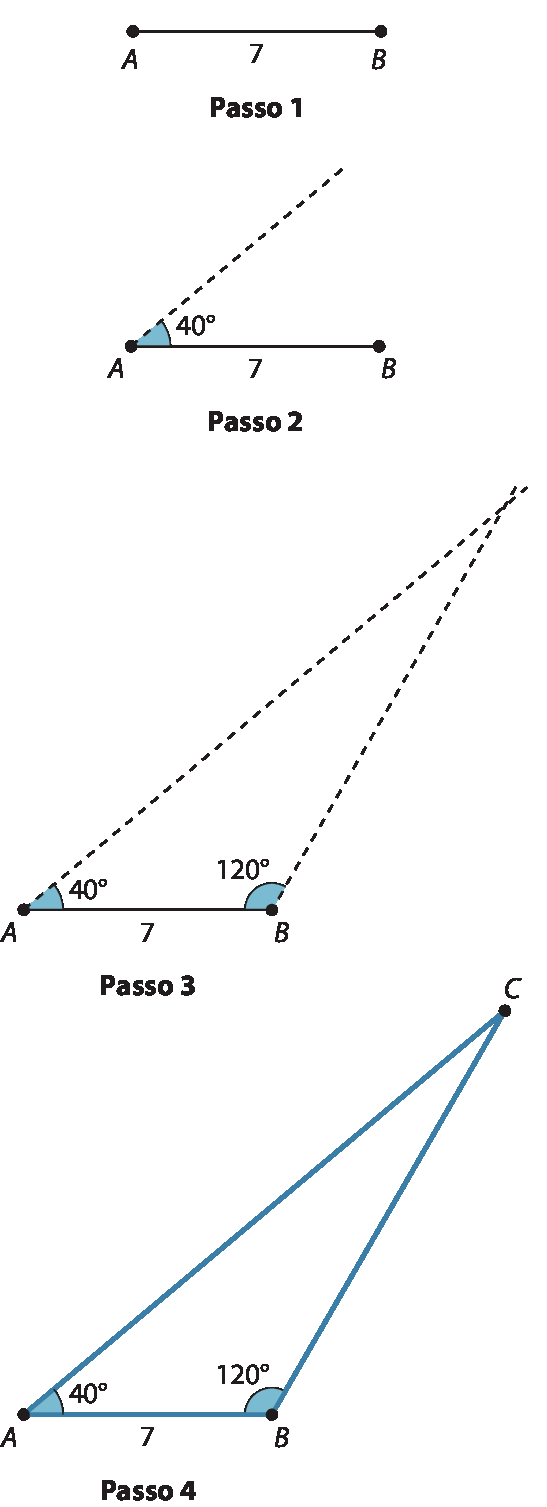
23. Considerando a construção de um triângulo quando são conhecidas as medidas de seus lados, um fluxograma possível é:
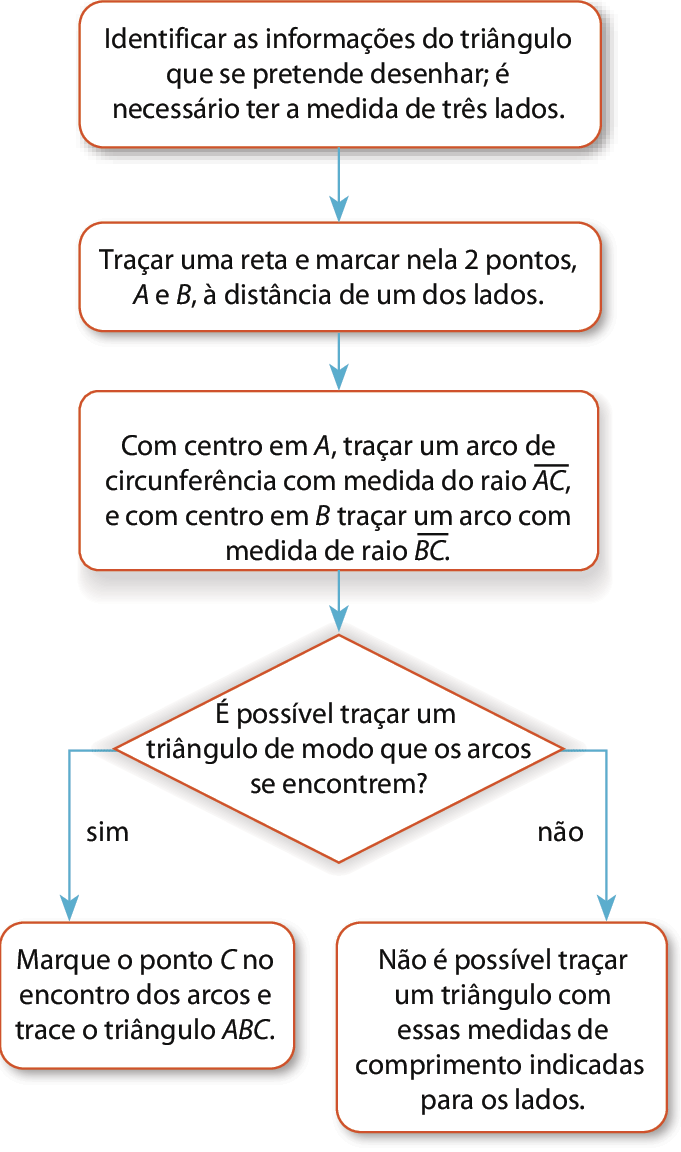
24. Polígonos de 4 lados são chamados de quadriláteros. Quadriláteros que têm apenas um par de lados paralelos são chamados de trapézios. Quadriláteros que têm dois pares de lados paralelos são chamados de paralelogramos. Observando as figuras e, nelas, os pares de lados que mantêm distância constante entre si, concluímos que há:
24. a) dois pares de lados paralelos; então, é paralelogramo;
24. b) um par de lados paralelos; então, é trapézio;
24. c) dois pares de lados paralelos; então, é paralelogramo;
24. d) um par de lados paralelos; então, é trapézio.
26. a) Falsa: nem todo losango tem quatro ângulos retos.
26. b) Falsa: apenas nos retângulos as diagonais são congruentes.
26. c) Verdadeira: todo quadrado tem quatro lados congruentes.
26. d) Verdadeira: um retângulo pode ser um exemplo de existência.
27.
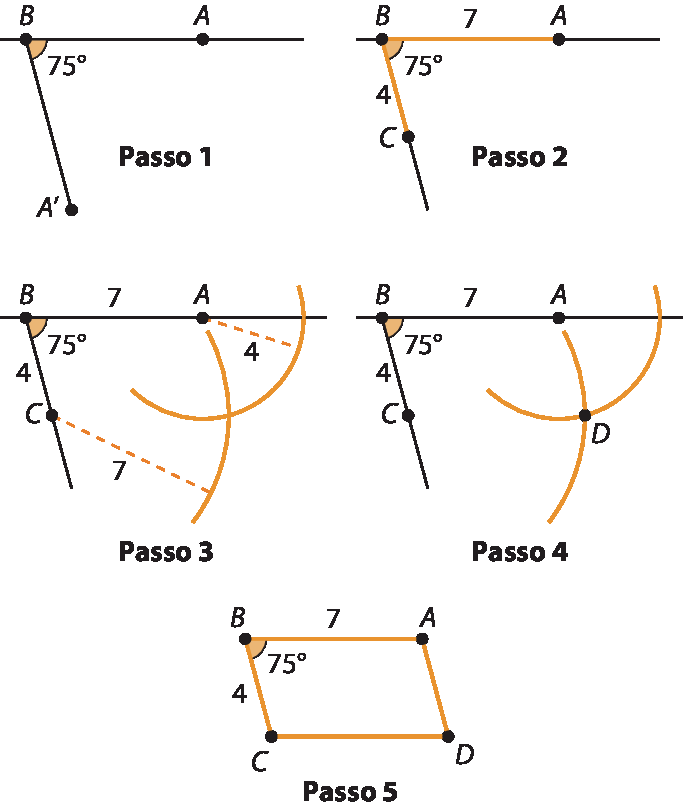
27. a) O polígono obtido é um paralelogramo.
27. b) Seria o mesmo que alterar a medida de comprimento de todos os lados para 6 centímetros; então, seria desenhado um losango.
27. c) Se a medida do ângulo interno fosse alterada para 90graus, seria desenhado um retângulo.
27. d) Fazendo todas as substituições, seria desenhado um quadrado de lado medindo 6 centímetros.
28. Resposta possível: escolhendo o quadrado, ele tem quatro ângulos de mesma medida (verdadeira) e tem três lados (falso).
31. a) a = 3
31. b) a = 0 e b = 1
31. c) a = 3 e b = 2
31. d) a = 2 e b = 8
31. e) a = 3 e b = 2
33. Respostas possíveis:
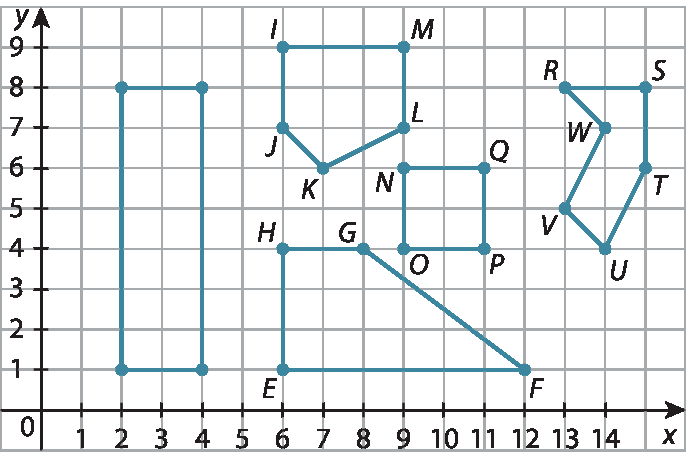
33. a) O retângulo a bê cê dê é formado pelos pontos A(2,1); B(4,1); C(4,8) e D(2,8).
33. b) O trapézio ê éfe gê agá é formado pelos pontos E(6,1); F(12,1); G(8,4) e H(6,4).
33. c) O losango êne ó pê quê é formado pelos pontos N(9,6); O(9,4); P(11,4) e Q(11,6).
33. d) O pentágono í jota cá éle ême é formado pelos pontos I(6,9); J(6,7); K(7,6); L(9,7) e M(9,9).
33. e) O hexágono érre ésse tê ú vê dábliu é formado pelos pontos R(13,8); S(15,8); T(15,6); U(14,4); V(13,5) e W(14,7).
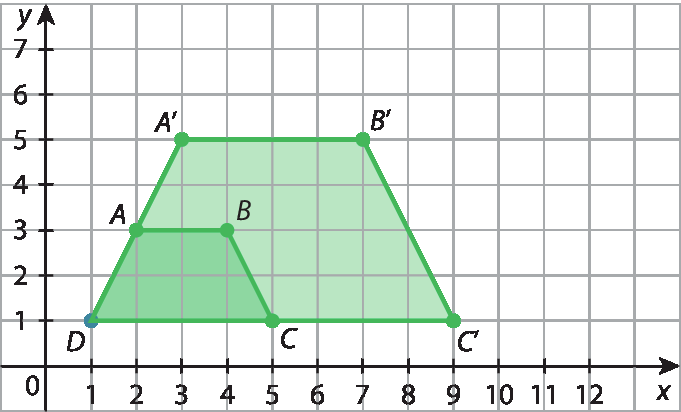
34. A representação do quadrilátero a bê cê dê e as representações possíveis para os quadriláteros ê éfe gê agá e í jota cá éle são reproduzidas a seguir.
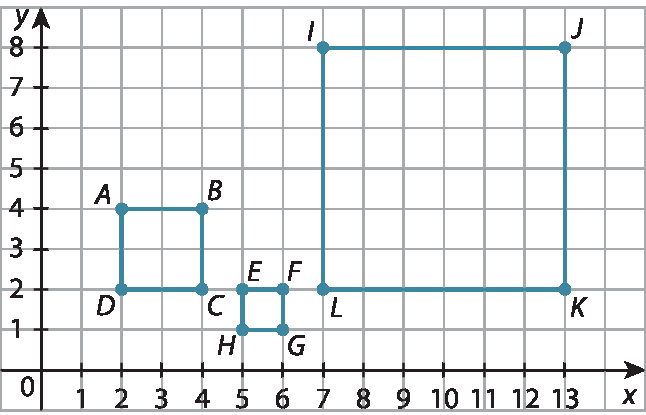
34. a) Nesse caso, as coordenadas dos vértices de ê éfe gê agá são E(5,2); F(6,2); G(6,1) e H(5,1); e de í jota cá éle são I(7,8); J(13,8); K(13,2) e L(7,2).
34. b) Como á bê linha cê linha dê linha tem todos os lados de medida de comprimento 1, é uma redução de a bê cê dê.
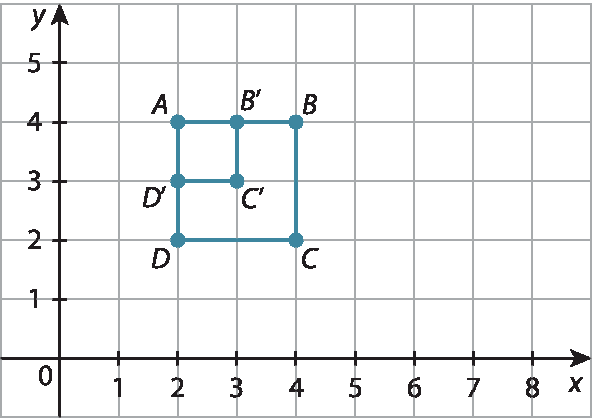
34. c) Todos os quadriláteros apresentados têm os seus quatro lados congruentes entre si, e com o transferidor é possível constatar que também todos os ângulos são congruentes e retos; dessa maneira, são quadrados.
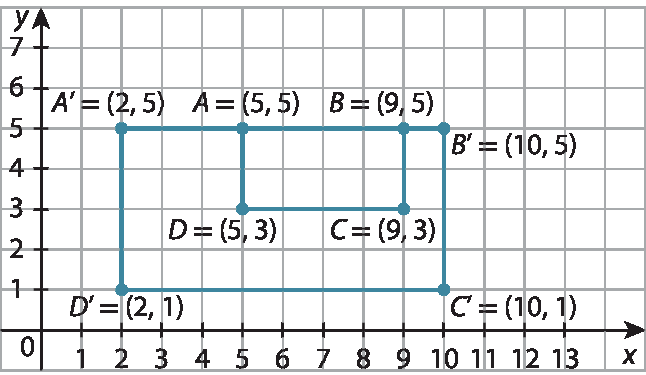
35. Como o lado
Segmento de reta ABdo retângulo tem medida de comprimento 4 unidades, a ampliação á linha bê linha cê linha dê linha deve ter medida de comprimento do lado
segmento A linha B linha8 unidades, assim como medida do
segmento A D= 2, então, medida do
segmento A linha D linha= 2 · 2 = 4. Como bê linha é (10, 5), então cê linha deve ser 4 unidades na vertical para baixo; então, a subtração de 4 unidades da ordenada resulta em cê linha = (10, 5 − 4) = (10, 1). O ponto A’ deve estar na horizontal para a esquerda 8 unidades, ou seja, subtrair 8 unidades da abscissa; então, á linha = (10 − 8, 5) = (2, 5). O ponto dê linha tem a mesma abscissa de á linha e a mesma ordenada de cê linha, então dê linha = (2, 1).
37. a) A quantidade de faces é a quantidade de polígonos que formam as planificações; já no caso das arestas e vértices, a planificação muitas vezes duplica suas representações.
A figura do item a tem base pentagonal, então 5 faces laterais mais uma base são 6 faces; há 5 arestas na base e 5 laterais, totalizando 10 arestas; no caso dos vértices, há 5 na base e mais 1 vértice superior, um total de 6.
A figura do item b é um cubo, um tipo de prisma com base em formato de quadrado; então, ele tem 4 faces laterais mais as duas bases, totalizando 6 faces (4 + 2 = 6); 4 arestas em cada base mais 4 na parte lateral da figura, então 12 arestas (4 + 4 + 4 = 12); e 4 vértices em cada face, então são 8 vértices (4 + 4 = 8).
Na figura do item c de base hexagonal, há 7 faces (6 + 1 = 7), 12 arestas (6 + 6 = 12) e 7 vértices (6 + 1 = 7).
A figura do item d pode ser compreendida como a união de um cubo (um tipo de pirâmide de base quadrada) e uma pirâmide de base quadrada por cima, de modo que uma face de cada se exclui, e 4 arestas e 4 vértices dessas formas são comuns. Por isso, a quantidade de faces do sólido desse item será
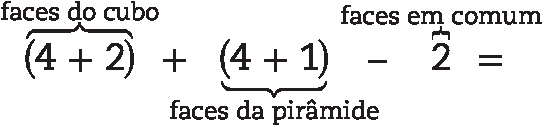
= 6 + 5 − 2 = 9
A quantidade de arestas será:
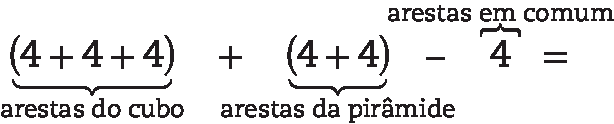
= 12 + 8 − 4 = 16
Além disso, a quantidade de vértices dessa figura é:
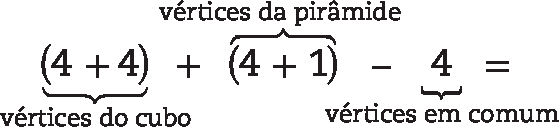
= 8 + 5 − 4 = 9
A figura do item e é um prisma com a base em formato hexagonal, então são 8 faces (6 + 2 = 8), 18 arestas (6 + 6 + 6 = 18) e 12 vértices (6 + 6 = 12).
37. b) Comparando, pode-se concluir que o número de arestas é sempre 2 a menos que a soma de vértices e faces, ou vê + éfe − 2 = a:
|
Figura |
Quantidade de vértices (V) |
Quantidade de faces (F) |
V + F |
Quantidade de arestas (A) |
|---|---|---|---|---|
|
a |
6 |
6 |
6 + 6 = 12 |
10 |
|
b |
8 |
6 |
8 + 6 = 14 |
12 |
|
c |
7 |
7 |
7 + 7 = 14 |
12 |
|
d |
9 |
9 |
9 + 9 = 18 |
16 |
|
e |
12 |
8 |
12 + 8 = 20 |
18 |
40. O total de arestas de um prisma pode ser dado por 3x, em que x é a quantidade de arestas relativas a cada base e, ainda, x é a quantidade de arestas relativas às faces laterais do prisma. Dessa maneira, como são 5 arestas na base (15 : 3 = 5), é um prisma de base pentagonal. Então, são 5 faces laterais mais duas bases, totalizando 7 faces (5 + 2 = 7). De modo semelhante, um prisma de 21 arestas tem uma base com 7 arestas (21 : 3 = 7), totalizando 9 faces (7 + 2 = 9).
41. Sim, existe, pois 39 é divisível por 3, uma vez que 3 + 9 = 12. Com vinte e duas arestas não é possível, pois 22 não é divisível por 3.
44. a) Há 3 na primeira pilha, duas na segunda e uma na última, totalizando 6 coleções, pois: 3 + 2 + 1 = 6.
44. b) Essa formação apresenta 3 pilhas de altura, 3 de comprimento e 3 de largura, totalizando 27 coleções, pois: 3 · 3 · 3 = 27.
45. a) O cubo com aresta de 2 centímetros é formado por 2 cubinhos de altura, 2 de comprimento e 2 de largura, totalizando 8 cubinhos, pois: 2 · 2 · 2 = 8.
45. b) Nesse caso, serão necessários 27 cubinhos, pois: 3 · 3 · 3 = 27.
46. É possível montar cubos com as planificações a e c; no caso do item b ocorreria a superposição de duas das faces (as primeiras das 2ª e 3ª linhas).
48. Uma pirâmide octogonal tem 8 vértices em sua base e um vértice onde ocorre o encontro de todas as faces laterais, totalizando 9 vértices, pois: 8 + 1 = 9. Em relação ao número de arestas, há 8 delas na base e 8 delas unindo a base ao vértice fóra dela, totalizando 16 arestas, pois: 8 + 8 = 16.
49. Uma pirâmide que tem 10 vértices tem uma base com 10 − 1 = 9 vértices (um eneágono); portanto, em relação ao número de arestas, há 9 + 9 = 18 delas e as faces são a base mais as faces laterais, totalizando 9 + 1 = 10.
Para saber mais
Página 258
1. a) Com um arame de 30 centímetros, é possível construir triângulos como estes:
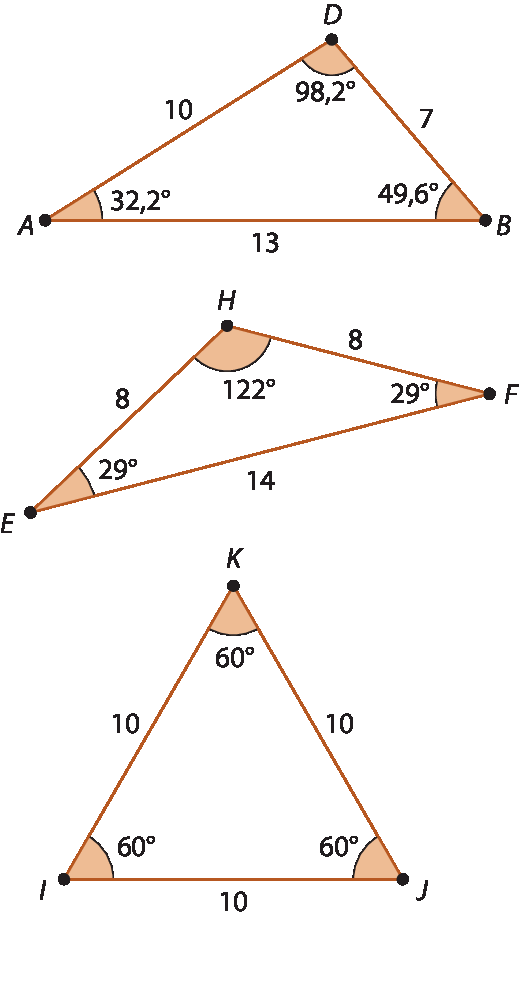
Adicionando as medidas de cada triângulo: 10 + 13 + 7 = 30; 8 + 8 + 14 = 30; 10 + 10 + 10 = 30. A medida do perímetro de todos os triângulos é igual à medida do comprimento do arame.
1. b) As medidas dos ângulos somam: 32,2graus + 98,2graus + 49,6graus = = 180graus; 29graus + 29graus + 122graus = 180graus; 60graus + 60graus + 60graus = 180graus.
Página 268
3. Completando o padrão dos azulejos, ilustrando-os a seguir com tons mais claros, é possível contar quantos faltam. No total são 21 alaranjados: 2 + 1 + 2 + 3 + 3 + 2 + 3 + 3 + 2 = 21; e 20 verdes: 2 + 1 + 2 + 2 + 2 + 2 + 3 + 3 + 3 = 20.
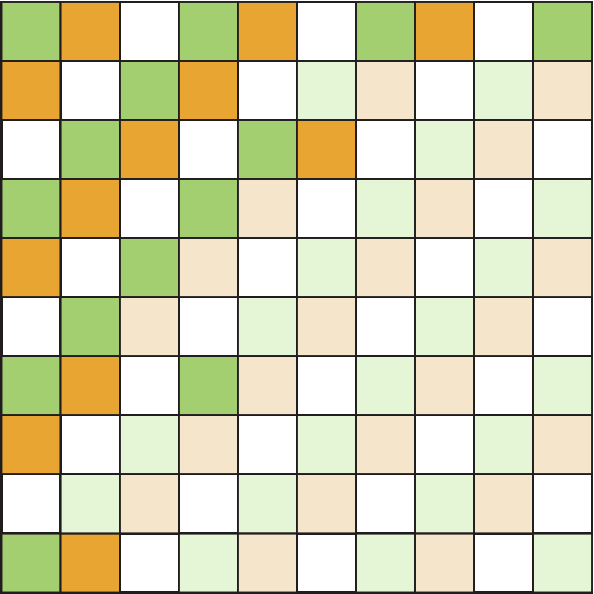
4. Para obter ladrilhamento utilizando apenas um mesmo tipo de região poligonal, deve ser possível unir cada um dos vértices da região poligonal a uma ou mais regiões poligonais e obter a soma das medidas dos ângulos internos relativos a esses vértices iguais a 360graus. Isso só ocorrerá com os triângulos equiláteros, hexágonos e quadrados.
Trabalhando a informação
Página 270
1. Há 30 fichas no total, de modo que são 4 azuis, 6 laranja e 5 vermelhas. Como a probabilidade é calculada como
fração: fichas daquela cor sobre total de fichas, então serão azuis:
; laranja:
6 sobre 30 igual fração de numerador 6 dividido por 6 e denominador 30 : 6 igual a 1 sobre 5; e vermelhas:
5 sobre 30 igual fração de numerador 5 dividido por 5 e denominador 30 : 5 igual a 1 sobre 6.
2. A seguir, um exemplo de resultados para compor a tabela de frequência.

Portanto, as frequências e probabilidades nesse caso são:
|
Face superior |
Frequência |
Probabilidade |
|---|---|---|
|
1 |
11 |
|
|
2 |
8 |
= |
|
3 |
14 |
= |
|
4 |
6 |
= |
|
5 |
11 |
|
|
6 |
10 |
= |
Exercícios complementares
1. A figura é composta de uma linha poligonal laranja-escura que delimita uma região no plano laranja-clara. A região externa ao polígono é representada em azul.
1. a) Os pontos que pertencem à linha são representados sobrepostos a ela; então, são A, B, C e D. Os pontos da região interior são P e M.
1. b) Traçando o segmento
PMé possível notar que ele não está totalmente contido na (dentro da) região poligonal; então, ela é não convéquica.
2. Desenhando:
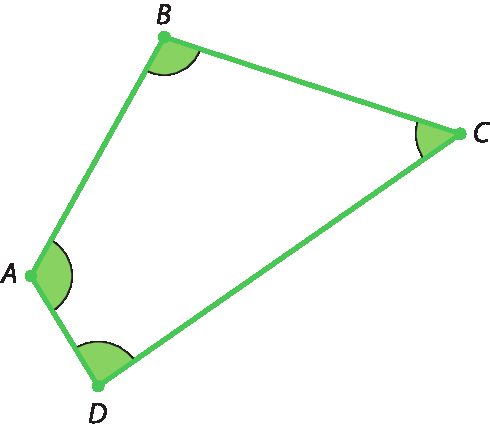
2. a) Esse polígono tem 4 ângulos internos, são eles:
ABC,
BCD, CD A, D A B.
2. b) O nome do polígono é a bê cê dê.
3. a) Quadriláteros que têm apenas um par de lados paralelos são chamados trapézios. Quadriláteros com dois pares de lados paralelos são chamados paralelogramos.
3. b) Um triângulo escaleno tem os três lados de medidas diferentes. Um triângulo equilátero tem os três lados de mesma medida.
4. Dobrando, é possível perceber que o ponto B e o ponto C se encontram.
4. a) Os lados
AB e ACsão congruentes, pois coincidem quando sobrepostos.
4. b) Os ângulos
Be
Csão congruentes pela mesma razão.
4. c) Como o triângulo tem dois lados com a mesma medida, é isósceles.
4. d) Os segmentos
BM e MCcoincidem quando dobrados, pois têm a mesma medida de comprimento.
4. e) Os ângulos
B M A e C M Asão congruentes e, juntos, formam um ângulo raso; portanto, ambos são retos.
5. a) As arestas de um prisma podem ser agrupadas em três setores, um em cada base e um deles unindo os vértices correspondentes das duas bases. Então, um prisma tem o triplo de arestas dos lados de sua base, por isso tem 9 lados na base e, assim, 27 arestas no total (9 + 9 + 9 = 27). Se a base tiver 10 lados, serão 30 arestas (3 ⋅ 10 = 30). Se a base tiver 11 lados, terá 33 arestas (11 ⋅ 3 = 33). Se a base tiver n lados, serão 3n arestas.
5. b) Nas pirâmides, há dois grupos de arestas, um na base e o outro nas faces laterais, unindo cada vértice da base com o vértice de fóra dela. Então, uma pirâmide tem o dobro de arestas dos lados de sua base; por isso tem uma base com 9 lados, e assim a pirâmide tem 9 + 9 = 18 arestas. Se a base tiver 10 lados, a pirâmide tem 10 ⋅ 2 = 20. Se a base tiver 11 lados, a pirâmide tem 11 ⋅ 2 = vinte e duas, e se a base tiver n lados, a pirâmide terá 2 ⋅ n = duasn arestas.
6. A primeira coordenada representa a posição horizontal, e a segunda, a posição vertical.
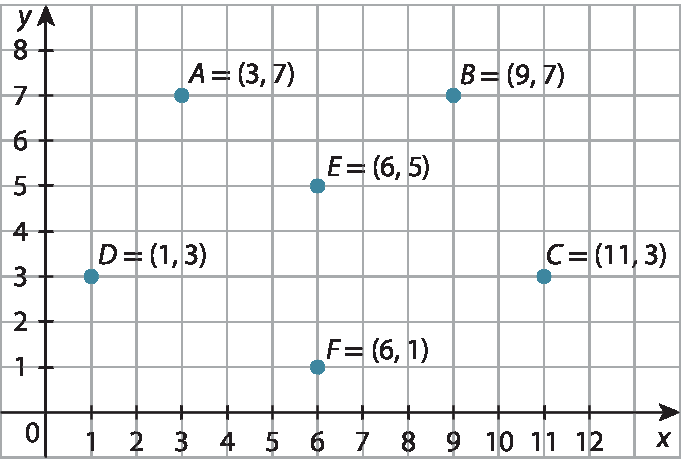
6. a) Traçando o quadrilátero a bê cê dê, forma-se um trapézio, pois
ABe
CDsão paralelos entre si. A característica é ter pelo menos um par de lados paralelos.
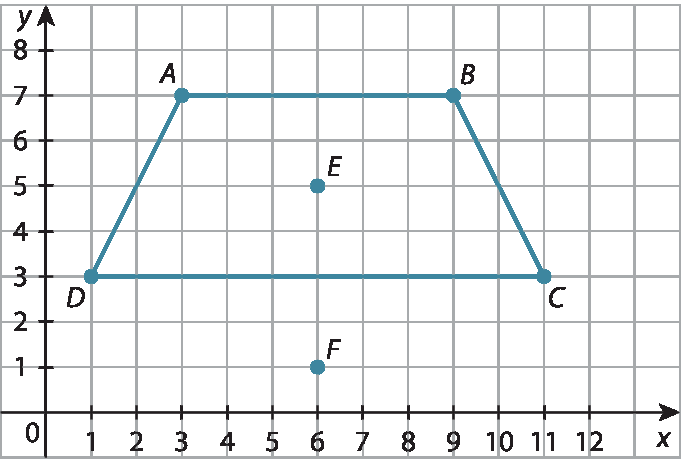
6. b) Respostas possíveis: são isósceles os triângulos á bê é, á bê éfe, dê cê é, DCF, EFC e EFD.
6. c) Os pontos são C, F, D e ê.
7. O trapézio original tem medidas A bê = 2, DC = 4, e a distância vertical de a até o segmento
DCé duas unidades. Como se deseja dobrar as medidas, ou seja, multiplicá-las por 2, então o trapézio ampliado será á linha bê linha = 2 ⋅ A bê = 2 ⋅ 2 = 4; dê linha cê linha = 2 ⋅ DC = 2 ⋅ 4 = 8 e a distância vertical de á linha até
D linha C linhaé 4 unidades pois 2 ⋅ 2 = 4.
Verificando
1. Ângulo é composto de diversos elementos, enquanto diagonal e lado são segmentos de reta; portanto, o único ponto é o vértice. De fato, o vértice é o ponto de encontro dos lados em um polígono.
Alternativa a.
2. ééquis é uma palavra grega que significa 6. O polígono de 6 lados é o hexágono.
Alternativa b.
3. Entre as classificações pela medida dos lados, equilátero é o triângulo que tem os seus lados com a mesma medida.
Alternativa b.
4. Um trapézio tem pelo menos um par de lados paralelos. Não é possível dizer quais são os ângulos e medidas dos lados.
Alternativa c.
5. Provavelmente, a resposta para esse exercício foi observada empiricamente diversas vezes pelos estudantes durante o desenvolvimento das atividades do capítulo. Um quadrilátero tem 4 vértices; um deles pode ligar-se com cada um dos outros 3, de modo que uma ligação é diagonal e as outras duas são lados. Para não contar duas vezes o número de diagonais (pois, por exemplo,
A Ce
C Asão o mesmo segmento), dividir o resultado por 2; então são duas diagonais:

Alternativa b.
6. Em um par ordenado, a primeira coordenada representa a posição no eixo horizontal e a segunda representa a posição no eixo vertical. A posição das coordenadas importa, e a origem do plano cartesiano é o ponto (0,0).
Alternativa b.
7. Deca é um prefixo que significa 10; portanto, um decaedro é um sólido de 10 faces.
Alternativa c.
8. Um dodecaedro tem 12 faces; portanto, esse dado tem 12 opções de resultado, sendo a probabilidade de sair um deles
1, 12 avos.
Alternativa d.
9. O prisma da imagem é reto, pois todas as suas faces laterais são retangulares, e tem a base em formato de hexágono, então é um prisma hexagonal reto.
Alternativa c.
10. Como a base é um quadrado, há 4 faces laterais triangulares, uma para cada lado da base.
Alternativa b.
Organizando
b) Toda linha poligonal fechada simples é denominada polígono.
c) Não. Um polígono é convéquiço quando a região interior determinada por ele é convéquiço.
d) Resposta pessoal.
g) Sim. Resposta pessoal.
Diversificando
1. Nessa atividade, oriente os estudantes na construção, auxiliando-os no planejamento quanto à necessidade ou não de incluir abas na planificação.
2.
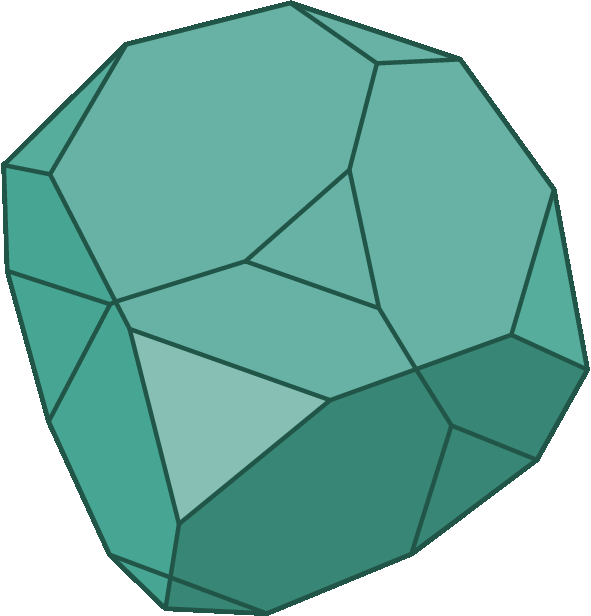
O cubo inicial tinha 6 faces e 6 vértices. As faces do cubo truncado serão octógonos no plano onde eram as faces do cubo original e triângulos onde eram os seus vértices. Então serão 6 faces octogonais e 8 faces triangulares.
3.
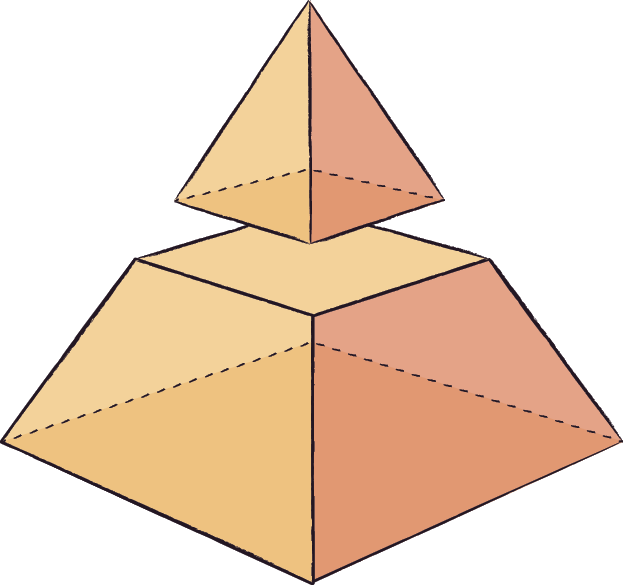
3. a) Nessa situação, o poliedro que contém o vértice é uma pirâmide de base quadrada.
3. b) O poliedro que contém o vértice tem 5 faces, sendo uma face quadrangular e 4 faces triangulares. O outro poliedro tem 6 faces quadrangulares.
Capítulo 11 — Comprimentos e áreas
• Objetivos do capítulo e justificativas
• Reconhecer as grandezas comprimento e área.
• Identificar unidades adequadas (padronizadas ou não) para expressar medidas de comprimento e de superfície e fazer uso da terminologia apropriada.
• Estabelecer conversões entre as unidades de medida mais usuais, para comprimento e área, em resolução de problemas.
• Obter medidas de comprimento por estimativas e aproximações.
• Calcular a medida do perímetro de polígonos.
• Calcular a medida de área de figuras plaanas pela decomposição e ou ou composição de figuras com áreas conhecidas, ou por meio de estimativas.
• Interpretar e desenhar planta baixa.
• Trabalhar com cálculo de áreas associado a medidas agrárias.
• Analisar e descrever mudanças que ocorrem na medida do perímetro e na medida da área de um quadrado com base na mudança da medida de seu lado.
• Determinar a medida da área de uma superfície retangular e, em particular, de uma superfície quadrada por meio das medidas de seus lados.
Entre as Unidades Temáticas da Matemática, Grandezas e medidas é a que tem relação direta com as demais e com outras áreas de conhecimento. Desse modo, o trabalho desenvolvido neste capítulo contribui para que o estudante possa conhecer e utilizar diferentes unidades de medida em situações de seu cotidiano. Desse modo, os conteúdos trabalhados contribuem para o desenvolvimento da competência geral 2 e das competências específicas 2, 3 e 6.
Inicialmente, apresentamos aos estudantes algumas unidades de medida de comprimento utilizadas em diferentes épocas, até a padronização pelo Sistema Internacional de Unidades, com o objetivo de mostrar a eles que a Matemática é uma ciência humana, fruto das necessidades e preocupações de diversas culturas e em distintos momentos históricos, contribuindo, assim, para o trabalho com a competência geral 1 e a competência específica 1.
Compreender as relações entre as unidades de medida padronizadas, de comprimento e de área, com seus múltiplos e submúltiplos, é uma ferramenta essencial para a resolução de diferentes situações-problema aplicáveis ao cotidiano. As atividades propostas ao longo do capítulo levam os estudantes a aplicar essas relações, o que contribui para o desenvolvimento da competência específica 6.
A relação entre as Unidades Temáticas Geometria e Grandezas e medidas está presente no estudo de perímetro e área, pois, para que o entendimento dessas grandezas seja concretizado, é importante que os estudantes tenham compreendido as características de diferentes figuras planas. Desse modo, o trabalho com essas grandezas contribui para o desenvolvimento da competência específica 3.
A composição e a decomposição de figuras planas para o cálculo de áreas fazem parte do processo de criação de estratégias para a resolução de problemas envolvendo áreas. Nesse sentido, esse objetivo está relacionado com a competência específica 2 e com a competência geral 2.
A leitura de plantas baixas é de aplicação social imediata para a compreensão de mapas de construções diversas, relacionando-se inclusive com o conceito de escala, ligado à ideia de proporcionalidade. Essa temática também se relaciona com o Tema Contemporâneo Transversal trabalho, o que contribui com o desenvolvimento da competência geral 6.
O exercício proposto 35 explora a análise de informações, em um gráfico de barras, sobre o desmatamento na Amazônia Legal, contribuindo para o trabalho com a competência geral 7 e com as competências específicas 4 e 7.
O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diversas atividades a serem realizadas em grupos, pois permitem que os estudantes exercitem diferentes habilidades socioemocionais ao trabalhar com os colegas, interagindo de fórma cooperativa.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah um dois) Fazer estimativas de quantidades e aproximar números para múltiplos da potência de 10 mais próxima.
(ê éfe zero seis ême ah um três) Resolver e elaborar problemas que envolvam porcentagens, com base na ideia de proporcionalidade, sem fazer uso da “regra de três”, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.
(ê éfe zero seis ême ah dois quatro) Resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento.
(ê éfe zero seis ême ah dois oito) Interpretar, descrever e desenhar plantas baixas simples de residências e vistas aéreas.
(ê éfe zero seis ême ah dois nove) Analisar e descrever mudanças que ocorrem no perímetro e na área de um quadrado ao se ampliarem ou reduzirem, igualmente, as medidas de seus lados, para compreender que o perímetro é proporcional à medida do lado, o que não ocorre com a área.
(ê éfe zero seis ême ah três dois) Interpretar e resolver situações que envolvam dados de pesquisas sobre contextos ambientais, sustentabilidade, trânsito, consumo responsável, entre outros, apresentadas pela mídia em tabelas e em diferentes tipos de gráficos e redigir textos escritos com o objetivo de sintetizar conclusões.
Neste capítulo, serão aprofundados os estudos relativos à Unidade Temática Grandezas e medidas, envolvendo as grandezas comprimento e área. Levam-se em conta os conhecimentos adquiridos no 5º ano do Ensino Fundamental (ê éfe zero cinco ême ah um nove) e (ê éfe zero cinco ême ah dois zero), aportes para a compreensão dos temas aqui tratados, que, por sua vez, visam preparar o estudante para o estudo sobre equivalência de áreas de figuras planas e cálculo de áreas por decomposição (ê éfe zero sete ême ah três um) e (ê éfe zero sete ême ah três dois), a ser desenvolvido no 7º ano.
Em relação aos conhecimentos que abrangem medidas de comprimento e de área, destacam-se o trabalho com situações-problema que envolvem unidades de medida padronizadas e não padronizadas, contribuindo para o desenvolvimento das habilidades (ê éfe zero seis ême ah um dois) e (ê éfe zero seis ême ah dois quatro).
O cálculo de áreas de figuras em malhas quadriculadas, a noção de planta baixa, medidas agrárias, o cálculo da área de superfícies retangulares e, em particular, de superfícies quadradas por meio de uma relação envolvendo medidas de seus lados contribuem para o desenvolvimento das habilidades (ê éfe zero seis ême ah dois quatro) e (ê éfe zero seis ême ah dois oito). Faz-se ainda análise e descrição de mudanças que ocorrem no perímetro e na área de um quadrado ao ampliar ou reduzir igualmente as medidas de seus lados, buscando o entendimento de que o perímetro é proporcional à medida do lado, o que não ocorre com a área. Esse trabalho se relaciona com a habilidade (é éfe seis ême á vinte e nove).
A Unidade Temática Números também é trabalhada neste capítulo, em atividades que abordam estimativas de áreas e cálculo de porcentagens, contribuindo para desenvolver a habilidade (ê éfe zero seis ême ah um três).
A conexão com a Unidade Temática Geometria se concretiza em atividades que promovem o reconhecimento de que perímetro e área são grandezas associadas a figuras geométricas planas, em particular a polígonos.
A leitura e a interpretação de dados apresentados em tabela, em gráfico de colunas e em gráfico de setores são exercitadas nas atividades que enfocam a Unidade Temática Probabilidade e estatística e contribuem com o desenvolvimento da habilidade (ê éfe zero seis ême ah três dois). Ressaltamos que tais conhecimentos representam a ampliação daqueles abordados no 5º ano do Ensino Fundamental, relativos à análise de dados apresentados em tabela e gráfico, que serão necessários para a construção de futuros conhecimentos sobre o planejamento e a realização de pesquisa, interpretação de dados para comunicá-los por meio de relatório escrito, tabelas e gráficos, além de interpretação e análise de dados apresentados em gráficos de setores, conhecimentos a serem adquiridos no 7º ano e que se relacionam com as habilidades (ê éfe zero sete ême ah três seis) e (ê éfe zero sete ême ah três sete).
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações Didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
7. Para responder a essa questão, relembre aos estudantes o modo como é comum referir-se a essas distâncias no cotidiano. Acompanhe os exemplos:
7. a) A distância de Natal a Recife é 285 quilômetros.
7. b) Uma folha A4 mede 21 centímetros de comprimento.
7. c) O celular lançado semana passada mede 8,8 milímetros de espessura.
10. Como Luís caminha durante 20 minutos, são .1200 segundos, pois: 20 ⋅ 60 = .1200. Como cada passo mede 70 centímetros, no total são: .1200 ⋅ 70 centímetros = .84000 centímetros = (.84000 : 100) métros = 840 métros.
11. A medida do palmo é 195 milímetros = (195 : .1000) métros = 0,195 métro. Como a janela mede 9 palmos, é o equivalente a 9 ⋅ 0,195 métro = 1,755 métro.
14. A medida de altitude do Pico da Neblina é .2995,3 métros, e a do Pico dos Três Estados é 2,665 quilômetros = (2,665 ⋅ .1000) métros = .2665 métros. Portanto, a diferença entre elas é:
.2995,3 métros − .2665 métros = 330,3 métros
15. a)
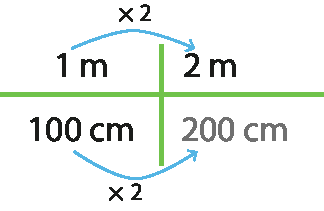
b)
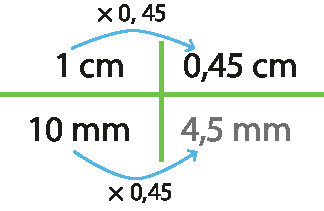
c)
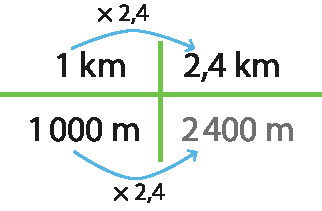
d)
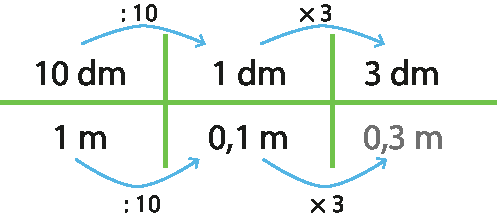
e)
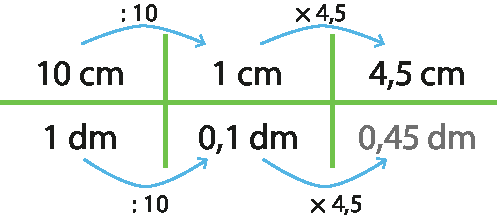
f)
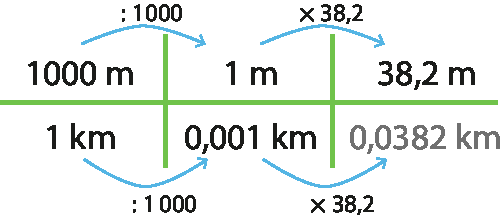
16. Como 380 centímetros = 3,8 métros, e o valor a pagar será a multiplicação do preço unitário pela quantidade comprada, será 2,5 ⋅ 3,8 = 9,5, ou seja, R$ 9,50nove reais e cinquenta centavos.
17. Uma milha marítima equivale a .1852 métros = (.1852 : .1000) quilômetros = 1,852 quilômetro. Como o navio percorreu 930 milhas, é o equivalente a 930 ⋅ 1,852 quilômetro = .1722,36 quilômetros.
18. Como 10 hectômetros = 1 quilômetro e .1000 métros = 1 quilômetro, a prova de natação percorre .1500 métros = (.1500 : .1000) quilômetros = 1,5 quilômetro e a prova de ciclismo percorre 400 hectômetros = (400 : 10) quilômetros = 40 quilômetros; então, a prova toda tem um percurso que mede: 1,5 quilômetro + 40 quilômetros + 10 quilômetros = 51,5 quilômetros
21. A medida do perímetro de um triângulo equilátero (todos os lados de mesma medida) cujo lado mede 7 centímetros é 3 ⋅ 7 centímetros = 21 centímetros. O triângulo isósceles (dois lados de mesma medida) com essa mesma medida de perímetro tem um lado medindo 8 centímetros. Existem duas possibilidades que devem ser consideradas: (um) 8 centímetros é a medida igual dos dois lados, e o terceiro lado tem outra medida m, ou (dois) um lado mede 8 centímetros e os outros dois medem um valor n igual entre eles. Como a medida do perímetro é a soma das medidas dos lados, é possível escrever:
(um) 8 + 8 + m = 21 ⇒ 16 + m = 21 ⇒ 16 + m − 16 = 21 − 16 ⇒ m = 5
(dois) 8 + n + n = 21 ⇒ 8 + 2n − 8 = 21 − 8 ⇒ 2n = 13 ⇒
⇒
2n sobre 2 igual 13 sobre 2⇒ n = 13 : 2 = 6,5
Então, as opções de triângulo isósceles nessas condições são: (um) dois lados medindo 8 centímetros e um lado medindo 5 centímetros e (dois) dois lados medindo 6,5 centímetros e um lado medindo 8 centímetros.
28. Utilizando o Sistema Internacinal de Unidades, temos:
28. a) quilômetro quadrado
28. b) centímetro quadrado
28. c) métro quadrado
28. d) métro quadrado
33. a)
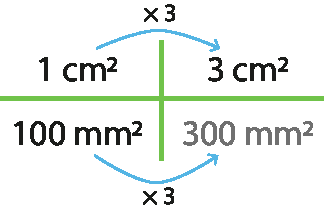
b)
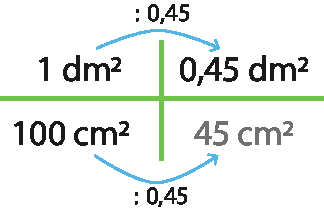
c)
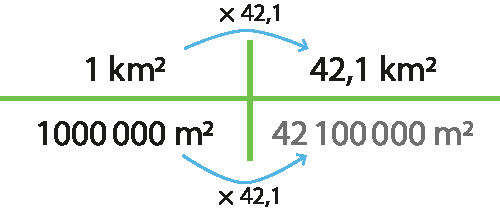
d)
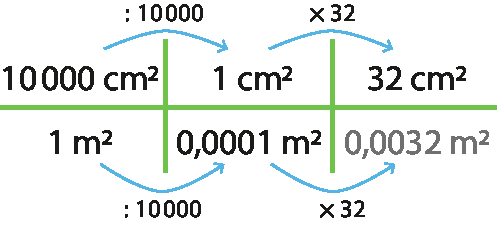
e)
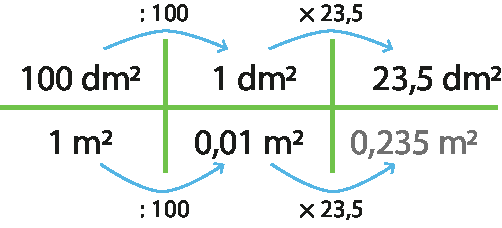
f)
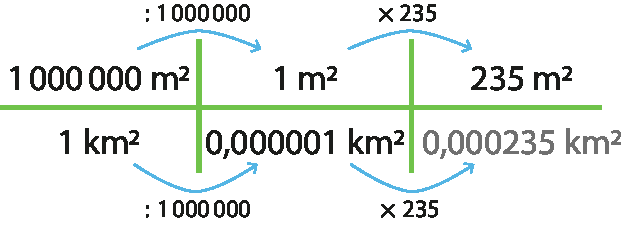
34. A área territorial do Brasil é de 8,5 milhões de quilômetros quadrados, com a distribuição por região indicada no gráfico de setor do enunciado. Então, calculando a área de cada região do país:
Norte
45,2% de 8,5 milhões = 45,2% ⋅ 8,5 milhões = =
fração de numerador 45,2 vezes 8,5 milhões e denominador 100=
fração de numerador 384,2 milhões e denominador 100= 3,842 milhões
Logo, aproximadamente 3,8 milhões de quilômetros quadrados.
Nordeste
18,2% de 8,5 milhões = 18,2% ⋅ 8,5 milhões = =
fração de numerador 45,2 vezes 8,5 milhões e denominador 100=
fração de numerador 384,2 milhões e denominador 100= 1,547 milhão
Logo, aproximadamente 1,5 milhão de quilômetro quadrado.
Centro-Oeste
18,9% de 8,5 milhões = 18,9% ⋅ 8,5 milhões = =
Numerador 18,9 vezes 8,5 milhões, denominador 100.=
160,65 milhões sobre 100.= 1,6065 milhão
Logo, aproximadamente 1,6 milhão de quilômetro quadrado.
Sudeste
10,9% de 8,5 milhões = 10,9% ⋅ 8,5 milhões = =
Numerador 10,9 vezes 8,5 milhões, denominador 100=
92,65 milhões sobre 100.= 0,9265 milhão
Logo, aproximadamente 0,9 milhão de quilômetro quadrado.
Sul
6,8% de 8,5 milhões = 6,8% ⋅ 8,5 milhões = =
Numerador 6,8 vezes 8,5 milhões, denominador 100.=
57,8 milhões sobre 100.= 0,578 milhão Logo, aproximadamente 0,6 milhão de quilômetro quadrado.
35. a) Observando o gráfico, temos que, em 2021, a Amazônia Legal teve a maior área desmatada e, em 2012, ela teve a menor área desmatada.
35. b) Calculando a diferença entre dois anos consecutivos: de 2009 a 2010 (diminuição), .7464 − .7000 = 464; de 2010 a 2011 (diminuição), .7000 − .6418 = 582; de 2011 a 2012 (diminuição), .6418 − .4571 = .1847; de 2012 a 2013 (aumento), .5891 − .4571 = .1320; de 2013 a 2014 (diminuição), .5891 − .5012 = 879; de 2014 a 2015 (aumento), .6207 − .5012 = .1195; de 2015 a 2016 (aumento), .7893 − .6207 = .1686; de 2016 a 2017 (diminuição), .7893 − .6947 = 946; de 2017 a 2018 (aumento), .7536 − .6947 = 589; de 2018 a 2019 (aumento), .10129 − .7536 = .2593; de 2019 a 2020 (aumento), .10129 − .10851 = 722; de 2020 a 2021 (aumento), .13235 − .10851 = .2384. Então, a maior diminuição ocorreu entre 2011 e 2012, e o maior aumento ocorreu entre 2020 e 2021.
35. c) Calcula-se a média para os dois períodos efetuando:
De 2009 a 2013 foi:
De 2017 a 2021 foi:
=
Então, em média, o desmatamento de 2009 a 2013 foi menor do que o de 2017 a 2021.
35. d) Depende do ano de nascimento do estudante. A soma das medidas das áreas desmatadas de 2016 a 2021 é .56561 quilômetros > .52000 quilômetros = 52 mil quilômetros; então, pessoas nesse ano ou antes responderiam que a medida da área desmatada é maior do que a medida da área do deserto.
35. e) Como a área do Atacama mede aproximadamente .105000 quilômetros quadrados, e a soma de área desmatada de 2009 a 2021 é .99154 quilômetros quadrados, o estudante teria de ter nascido antes de 2009 para responder sim a esse item, e seriam necessárias mais informações para responder com precisão; por isso, a resposta é pessoal, mas provavelmente será negativa.
38. A unidade de medida a refere-se ao are, que equivale a 100 métros quadrados. Dessa maneira, 1 hectare equivale a 100 ares; por isso, se o sítio tem 300 ares = (300 : 100) hectares = 3 hectares.
39. O alqueire tem sua medida equivalente em metros quadrados diferente em cada estado brasileiro. Na Bahia, 1 alqueire baiano equivale a .96800 métros quadrados.
100 alqueires baianos = (.96800 · 100) métros quadrados = ..9680000 métros quadrados é a extensão da fazenda em Maracás.
Como .10000 métros quadrados equivalem a 1 éctare, temos: ..9680000 métros quadrados = 968 hectares.
40. Como .10000 métros quadrados = 1 éctare, uma plantação de .35000 métros quadrados é equivalente a 1 ⋅ 3,5 hectares = 3,5 hectares. Como a safra média foi de .2760 quilogramas por hectare, o total produzido foi .2760 ⋅ 3,5 quilogramas = .9660 quilogramas.
41. 1 alqueire paulista equivale a .24200 métros quadrados.
1 alqueire mineiro equivale a .48400 métros quadrados.
84 ⋅ .24200 = ..2032800
48 ⋅ .48400 = ..2323200
Logo, a maior parte é mineira.
42. a) A medida da área total plantada é a soma da medida da área plantada em todas as regiões. Logo:
..3924343 + ..9458502 + ..12864432 + ..21550516 + ..30167264 = ..77965057 (..77965057 hectares)
42. b) O maior valor da coluna “medida de área” é ..30167264, correspondente à região Centro-Oeste. O menor valor é ..3924343, correspondente à região Norte.
42. c) Como .10000 métros quadrados equivalem a 1 éctare, temos 1 éctare = 0,01 quilômetro quadrado.
No Nordeste há ..9458502 hectares = .94585,02 quilômetros quadrados.
42. d) Uma resposta possível é a de que o território está ocupado com algo que não seja lavoura permanente, como a Floresta Amazônica.
45. a) A medida da área de uma superfície retangular é calculada efetuando-se (medida da base) · (medida da altura). O terreno tem 12,6 métros de frente (base) e 20 métros de fundo (altura), então a medida da área, em metros quadrados, será:
12,6 · 20 = 252
45. b) Como cada metro quadrado vale R$ 320,00trezentos e vinte reais, o terreno todo vale:
R$ 320,00trezentos e vinte reais · 252 = R$ 80.640,00oitenta mil seiscentos e quarenta reais
46. Desenho:
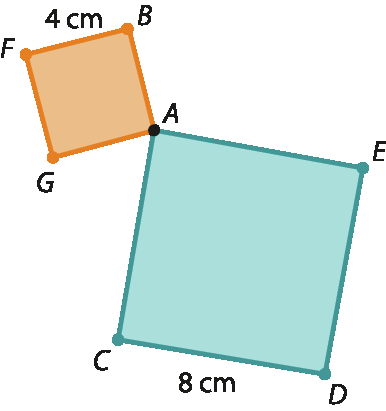
46. a) O quadrado á cê dê é tem lado de medida 8 centímetros, então a medida da área, calculada como (medida do lado)², é áACDE = (8 centímetros)2 = 64 centímetros quadrados; e o perímetro, que é a soma das medidas dos lados, é pêACDE = 4 · 8 centímetros = 32 centímetros. O quadrado ABFG tem medida de lado 4 cm; então, áABFG = (4 centímetros)2 = 16 centímetros quadrados e pêABFG = 4 · 4 centímetros = 16 centímetros.
46. b) Como pêACDE = 64 centímetros quadrados e áABFG = 16 centímetros quadrados, então o quadrado menor cabe 4 vezes no maior, pois 16 · 4 = 64.
46. c) Como observado no caso testado, dobrar a medida do lado dobra a medida do perímetro, mas quadriplica a medida da área.
47. O caminho percorrido pela formiga é equivalente ao perímetro do tampo da mesa; então, se éle é a medida do lado da mesa:
4 · éle = 5,2 métros ⇒
numerador 4 vezes L denominador 4 igual a 5,2 quartosmétros ⇒ éle = 5,2 : 4 métros = 1,3 métro
Por isso, a medida da área do tampo da mesa é (1,3 métro)2 = 1,69 métro quadrado.
51. Resposta pessoal. Um exemplo de desenho da parte externa de uma casa como essa:
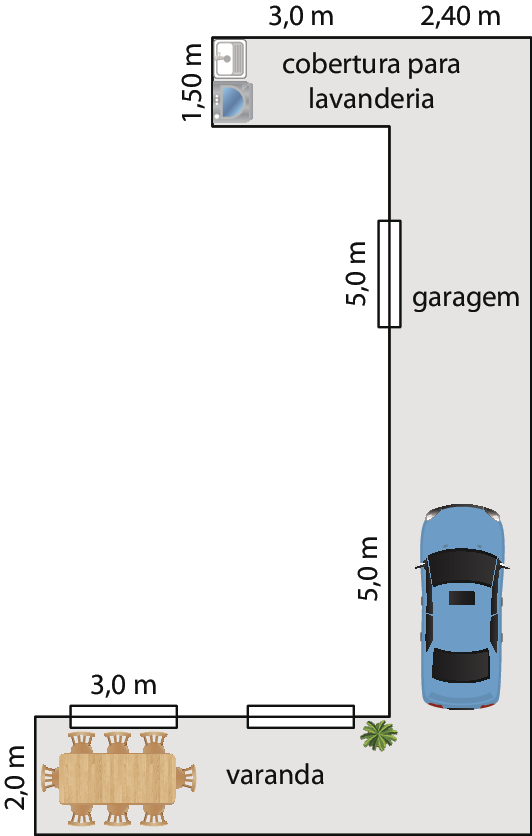
A medida da área total pode ser calculada pela expressão
e é 48,9 métros, pois: 2 · 6 + 4,5 + 13,5 · 2,4 = = 12 + 4,5 + 32,4 = 48,9
A medida do perímetro será 49,8 métros, pois: 2 + 3 + 3 + 5 + 5 + 3 + 1,5 + 3 + 2,4 + 1,5 + 5 + 5 + 2 + 2,4 + 3 + 3 = 49,8
Se ocorrer de a medida dos perímetros ser a mesma, não necessariamente a medida das áreas também será.
Exercícios complementares
1. Ele nasce com 35 centímetros, e aumenta 2 centímetros por mês por 3 meses e depois 1 centímetro por mês por 3 meses. Então, após 5 meses será 43 centímetros, pois:
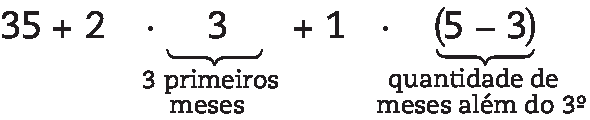
= 35 + 6 + 2 = 43
2. Um triângulo equilátero tem 3 lados de medidas iguais; então, 10,5 centímetros de medida de perímetro corresponde a 10,5 centímetros : 5 centímetros = 3,5 centímetros de medida de lado.
3. A medida do perímetro indica a quantidade de metros necessários para cercar o terreno com uma volta de arame. O perímetro do terreno da chácara de Luís mede, em metros:
250 + 220 + 125 + 220 + 125 = 940
Então, a medida de arame necessária para 10 voltas é:
10 · 940 métros = .9400 métros.
4. Já foram asfaltados 30% de 1,2 quilômetro. Assim:
· 1,2 quilômetro =
Numerador 30 vezes 1,2, denominador 100.quilômetro =
36 centésimosquilômetro = = 0,36 quilômetro = (0,36 · .1000) métro = 360 métros
5. O perímetro de um terreno quadrado de lado medindo 165 métros é 4 · 165 métros = 660 métros, que é a medida para o perímetro de um terreno de

de comprimento. É preciso que

> 0 por se tratar de uma medida de comprimento.
6. O campo tem área medindo 110 métros · 75 métros = .8250 métros quadrados, e cada saco pode gramar 50 métros quadrados : 10 = 5 métros quadrados. Então, são necessários .1650 sacos para gramar o terreno (.8250 : 5 = .1650).
Alternativa b.
7. O perímetro do retângulo tem medida 40 centímetros, e a medida de comprimento de um dos lados é 4 centímetros. Esse polígono tem dois pares de lados opostos de mesma medida de comprimento. Então, os outros lados desconhecidos serão: um medindo 4 centímetros (oposto ao que já era conhecido), o que significa que faltam 40 centímetros − 4 centímetros − 4 centímetros = 40 centímetros − 8 centímetros = 32 centímetros do perímetro; como os dois lados que faltam são opostos entre si, têm a mesma medida, que será 32 centímetros : 2 = 16 centímetros.
Alternativa d.
8. Contando os quadradinhos completos e aproximando a fração dos pedaços incompletos conforme o tamanho aparente, é possível aproximar a medida da área dessa figura para 33u.
9. A largura da rua mede 14 métros; como o vizinho da frente é responsável por metade, minha responsabilidade é 7métros da largura em frente à minha casa. Como o terreno mede 11 métros de frente, a medida da área asfaltada é 7 · 11 métros quadrados = 77 métros quadrados. Como o custo do asfalto é R$ 12,60doze reais e sessenta centavos por metro quadrado, o valor gasto é:
77 · R$ 12,60doze reais e sessenta centavos = R$ 970,20novecentos e setenta reais e vinte centavos
10. A lajota lisa custa R$ 0,50zero reais e cinquenta centavos e mede 20 centímetros por 20 centímetros e cobre uma área medindo 20 centímetros · 20 centímetros = 400 centímetros quadrados. Para cobrir a superfície de 48 métros quadrados = .480000 centímetros quadrados, serão necessárias .480000 : 400 = .1200 lajotas, gastando .1200 · R$ 0,50zero reais e cinquenta centavos = R$ 600,00seiscentos reais. A lajota decorada mede 10 centímetros por 12 centímetros e cobre uma área medindo 10 centímetros · 12 centímetros = 120 centímetros quadrados, sendo necessárias .480000 : 120 = .4000 lajotas, ou seja, gasto de .4000 · R$ 0,20zero reais e vinte centavos = R$ 800,00oitocentos reais. Então, a opção mais barata são as lajotas lisas, com um gasto de R$ 600,00seiscentos reais.
11. a) Se a área total mede 45 centímetros², sendo áa a área, em centímetro quadrado, da figura azul, então:
3 · 3 + áa = 45 ⇒ 9 + áa = 45 ⇒ 9 + áa − 9 = 45 − 9 ⇒ áa = 36
Como um dos lados mede 6 centímetros, então:
6 · xis = 36 centímetros ⇒
6x sobre 6 é igual a 36 centímetros sobre 6⇒ x = 6 centímetros
11. b) O perímetro da figura lilás mede pêl = 4 · 3 centímetros = 12 centímetros e o perímetro da figura azul mede pêa = 4 · 6 centímetros = 24 centímetros; portanto, a primeira é, sim, o dobro da segunda.
11. c) Como já visto, áa = 36 centímetros quadrados e calculando ál = (3 centímetros)2 = 9 centímetros quadrados. Uma não é o dobro da outra.
Verificando
1. Como a medida padronizada de polegada (í êne) é tal que 1 in = 2,54 centímetros, então 5,5 polegadas = 2,54 · 5,5 = 13,97 centímetros ≃ 14 centímetros.
Alternativa c.
2. 1 metro é equivalente a 100 centímetros; então, a unidade centímetro é adequada para medir objetos pequenos do cotidiano, como o comprimento de um lápis.
Alternativa d.
3. Como 1 métro = 100 centímetros = .1000 milímetros, então 1,5 métro = 150 centímetros = .1500 milímetros. Alternativa b.
4. O consultório é uma das salas dessa clínica médica e tem o formato de um trapézio, que mede 18 quadradinhos inteiros e mais duas metades de quadradinho, totalizando 19u de medida de área. Alternativa a.
5. O espelho tem formato de hexágono regular; então, tem 6 lados de mesma medida 25 centímetros. Assim, são necessários 6 · 25 centímetros = 150 centímetros de madeira para fazer a moldura.
Alternativa b.
6. 1 quilômetro = .1000 métros; então, a unidade de medida quilômetro é usada na medição de dimensões extensas, como a área de um país.
Alternativa a.
7. Como 100 métrosmétros² = 1 cmétroelevado a 2, a medida da área da folha de .62370 métrosmétros² é equivalente a (.62370 : 100) cmétros² = 623,7 cmétros².
Alternativa c.
8. Um alqueire goiano (a éle) equivale a .48400 métros quadrados, e um hectare (agá ah) equivale a .10000 métros quadrados. Como a região tem área medindo 435,6 hectares, é equivalente a (435,6 ⋅ .10000) métros quadrados = ..4356000 métros quadrados = 90 alqueires goianos.
Alternativa d.
9. A fórma desenhada tem lados equivalentes a 5 espaços e 4 espaços. Como cada espaço tem medida 3,5 centímetros, o retângulo tem medidas de lado 5 · 3,5 centímetros = 17,5 centímetros e 4 · 3,5 centímetros = 14 centímetros; portanto, a área mede 17,5 centímetros · 14 centímetros = 245 centímetros quadrados.
Alternativa c.
Capítulo 12 — Outras unidades de medida
• Objetivos do capítulo e justificativas
• Reconhecer as grandezas tempo, volume, capacidade e massa.
• Identificar unidades adequadas (padronizadas ou não) para medir essas grandezas, fazendo uso de terminologia própria.
• Obter medidas por meio de estimativas e aproximações.
• Estabelecer conversões entre as unidades de medida mais usuais para essas grandezas em resolução de problemas.
• Verificar a equivalência entre a capacidade de uma caixa cúbica de 1 decímetro de aresta e a capacidade de uma caixa de leite de 1 litro.
• Interpretar fluxogramas simples, identificando as relações entre os objetos representados.
• Organizar dados coletados por meio de pesquisa em uma tabela.
O trabalho com as unidades de medida de tempo se faz necessário para que os estudantes compreendam as relações entre hora, minuto e segundo. Neste capítulo exploramos essas relações por meio de situações contextualizadas, favorecendo o trabalho com a competência específica 6.
Do mesmo modo, o estudo das unidades de medidas padrão das grandezas volume, capacidade e massa e as relações com os múltiplos e submúltiplos são ferramentas para a resolução de problemas aplicadas ao cotidiano. Nesses casos, o trabalho com estimativas e aproximações proporciona uma vivência de levantamento de hipóteses e de confirmações que podem ser aplicadas em diferentes contextos. As atividades propostas ao longo do capítulo e a proposta da seção Para saber mais levam os estudantes a estabelecer essas relações, o que contribui para o desenvolvimento da competência geral 2 e das competências específicas 3 e 6.
A relação entre as Unidades Temáticas Geometria e Grandezas e medidas está presente no estudo da relação entre volume e capacidade. Dimensionar utensílios com capacidade de 1 litro se torna complexo pela variedade de formatos de produtos existentes no mercado com essa capacidade. Ter uma referência cúbica permite, inclusive, que as transformações de unidades de medida de capacidade e de volume se tornem mais compreensíveis.
A proposta da seção Trabalhando a informação “Fluxogramas como organizadores de tarefas” tem o objetivo de apresentar aos estudantes o fluxograma como um organizador de tarefas que pode ser aplicado em situações cotidianas, escolares ou relacionadas ao mundo do trabalho, contribuindo para o desenvolvimento das competências gerais 4 e 6 e da competência específica 6.
Já na seção Trabalhando a informação “Um projeto de pesquisa” propõe-se uma atividade relacionada à pesquisa estatística. Vivenciar todas as etapas desse processo oportuniza ao estudante compreender a seriedade de uma pesquisa e como podemos comparar e discutir os dados quando organizados em tabelas ou gráficos. Desse modo, a proposta de atividade contribui para o trabalho com a competência específica 4.
O exercício proposto 18 propõe uma reflexão ao uso consciente da água em situações do cotidiano, contribuindo para o trabalho com a competência geral 7 e com a competência específica 7. Também é apresentada uma situação de reflexão sobre o volume e a massa da mochila, contribuindo para o trabalho com a competência geral 8.
O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diversas atividades a serem realizadas em grupos, pois permitem que os estudantes exercitem diferentes habilidades socioemocionais ao trabalhar com os colegas, interagindo de fórma cooperativa.
• Habilidades trabalhadas no capítulo
(ê éfe zero seis ême ah zero quatro) Construir algoritmo em linguagem natural e representá-lo por fluxograma que indique a resolução de um problema simples (por exemplo, se um número natural qualquer é par).
(ê éfe zero seis ême ah um dois) Fazer estimativas de quantidades e aproximar números para múltiplos da potência de 10 mais próxima.
(ê éfe zero seis ême ah dois quatro) Resolver e elaborar problemas que envolvam as grandezas comprimento, massa, tempo, temperatura, área (triângulos e retângulos), capacidade e volume (sólidos formados por blocos retangulares), sem uso de fórmulas, inseridos, sempre que possível, em contextos oriundos de situações reais e/ou relacionadas às outras áreas do conhecimento.
(ê éfe zero seis ême ah três três) Planejar e coletar dados de pesquisa referente a práticas sociais escolhidas pelos alunos e fazer uso de planilhas eletrônicas para registro, representação e interpretação das informações, em tabelas, vários tipos de gráficos e texto.
(ê éfe zero seis ême ah três quatro) Interpretar e desenvolver fluxogramas simples, identificando as relações entre os objetos representados (por exemplo, posição de cidades considerando as estradas que as unem, hierarquia dos funcionários de uma empresa etcétera).
Os conhecimentos abordados neste capítulo também se referem à Unidade Temática Grandezas e medidas, oportunidade para desenvolver as ideias que envolvem medidas de tempo, de volume, de capacidade e de massa, contribuindo para o trabalho com a habilidade (ê éfe zero seis ême ah dois quatro). As conexões com outras Unidades Temáticas, no entanto, estão presentes nas diversas atividades propostas que compreendem medidas.
A relação com a Unidade Temática Números se estabelece na medida em que os conhecimentos construídos sobre números racionais (tanto na fórma de fração como na fórma decimal) possibilitam a resolução e a elaboração de problemas envolvendo grandezas e medidas como volume, capacidade e massa, com recurso a transformações entre unidades de medida. O trabalho com estimativas desenvolvido na seção Para saber mais favorece essa relação e contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah um dois).
A conexão com a Unidade Temática Álgebra aparece quando aplicamos as propriedades da igualdade em atividades que envolvem medidas de massa, por meio da análise de balança de dois pratos.
O vínculo com a Unidade Temática Geometria ocorre em atividades que promovem o reconhecimento do volume como grandeza associada a figuras geométricas não planas.
A conexão com a Unidade Temática Probabilidade e estatística se efetiva por meio de atividades de resolução de situações que apresentam dados de pesquisa e organização dos dados coletados em tabela e interpretação de gráfico de colunas, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah três três).
Além disso, o trabalho com fluxogramas favorece a associação da Matemática com outras áreas de conhecimento e com situações cotidianas, favorecendo o desenvolvimento da habilidade (ê éfe zero seis ême ah três quatro).
Além disso, conhecimentos apreendidos pelos estudantes ao longo do 5º ano do Ensino Fundamental relativos a grandezas e medidas favorecem a construção de novos conhecimentos, como os deste capítulo. Da mesma maneira, esses novos conhecimentos serão alicerces para outros, relativos à resolução e à elaboração de problemas envolvendo as mesmas grandezas, inseridos em variados contextos, a serem construídos durante o 7º ano.
• Comentários e resoluções
Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações Didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
3. Resposta pessoal. Ela depende das respostas à pesquisa realizada. Simulando algumas respostas, montamos a seguinte tabela:
|
Nome |
Cuidados pessoais |
Trabalhos escolares |
Lazer |
Outras atividades |
|---|---|---|---|---|
|
Gama |
10 |
6 |
2 |
6 |
|
Delta |
9 |
9 |
3 |
3 |
Dados fictícios.
6. É preciso determinar quantas pecinhas roxas compõem o sólido de cada item.
6. a) O sólido é formado por 6 pecinhas roxas; então, a medida de volume é 6u.
6. b) Esse sólido é formado por 4 pilhas, 3 delas com duas peças roxas e uma, ao fundo, com 4 peças, então 3 · 2 + 4 = 6 + 4 = 10, totalizando 10unidades de medida de volume.
7. a) No fundo da caixa estão dispostas 3 colunas de 5 dados, totalizando 15 dados por andar (3 · 5 = 15). Na parte ao fundo da representação é possível observar a indicação de que ainda cabem mais 2 andares de dados dispostos, totalizando 30 dados (15 · 2 = 30).
7. b) Observando as repartições nas duas faces graduadas da caixa, é possível concluir que as dimensões da caixa são 3 × 6 × 5; então, no total cabem 90 dados (3 · 6 · 5 = 90). Como na caixa já estão 5 dados, ainda cabem 85 dados (90 − 5 = 85).
8. Um cubo com aresta medindo 1 decímetro tem 1 decímetroelevado a 2 de medida de volume.
8. a) É preciso dobrar a medida da aresta do cubo inicial; então, serão necessários 8 cubos.
8. b) Como se deseja multiplicar por 3 a medida da aresta, serão necessários 27 cubos.
8. c) Serão necessários 125 cubos (5 · 5 · 5 = 125).
11. a) O litro é representado pela letra L: 8 éle
11. b) O quilolitro é cá éle, então: 5 cá éle.
11. c) O mililitro é ême éle, então: 80 ême éle.
16. a) O gráfico apresenta dados sobre a quantidade de água em 100 gramas de alguns alimentos. Entre os valores apresentados, a maior quantidade de água é relativa à alface.
16. b) 100 gramas de alface têm 0,096 litro de água e 100 gramas de espinafre têm 0,094 litro de água.
Então, a diferença é: 0,096 litro − 0,094 litro = 0,002 litro
16. c)
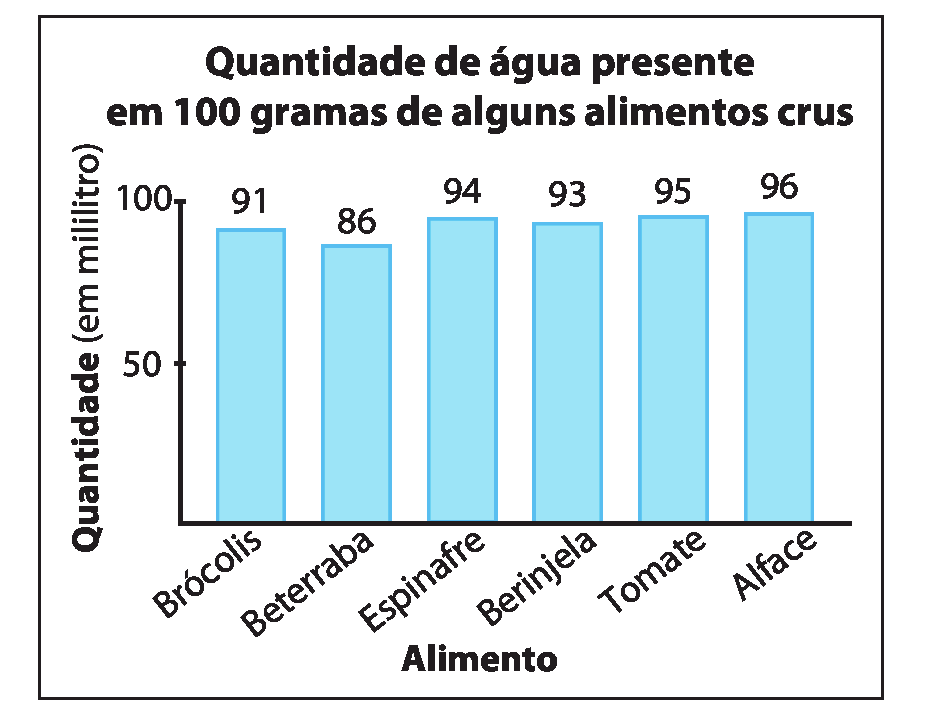
16. d) 1 quilolitro = .1000 litros
A quantidade de água em 100 gramas desses alimentos é sempre menor do que 0,1 litro = 1 decilitro. Portanto, o quilolitro (cá éle) não é a unidade adequada.
16. e) Em 100 gramas de brócolis, há 0,091 litro de água. Como 1 litro = .1000 mililitros, temos: 0,091 litro = (.1000 ⋅ 0,091) mililitro = 91 mililitros.
18. a) Do trecho, “Gotejando, uma torneira chega a desperdiçar 46 litros de água por dia.”; portanto, em 30 dias são desperdiçados 46 litros · 30 = .1380 litros, e em 365 dias são desperdiçados 46 litros · 365 = .16790 litros.
18. b) As orientações sobre consumo de água no banho são de que “no banho com chuveiro elétrico, em 15 minutos com o registro meio aberto, são gastos 45 litros de água. Se fecharmos o registro ao nos ensaboar e reduzirmos o tempo para 5 minutos, o consumo cairá para 15 litros”, então a economia com a mudança de atitude é 45 litros − 15 litros = 30 litros por banho. A economia em uma casa cujos moradores tomam 5 banhos por dia é 30 litros · 5 = 150 litros em um dia, por mês será 150 litros · 30 = .4500 litros. A quantidade de água economizada em um ano pode ser calculada de maneira aproximada efetuando-se:
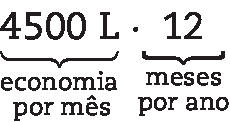
= .54000 litros ou, com maior precisão, efetuando-se: .54000 litros ou, com maior precisão, efetuando-se:
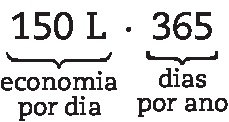
= .54750 litros
18. c) Do trecho, “Se uma pessoa escova os dentes em 5 minutos com a torneira não muito aberta, gasta 12 litros de água. Mas se molhar a escova e fechar a torneira enquanto escova os dentes e, ainda, enxaguar a boca com um copo de água, conseguirá economizar mais de 11,5 litros de água”. Então, a quantidade de água utilizada é:
12 litros − 11,5 litros = 0,5 litro = (0,5 · .1000) mililitro = 500 mililitros
18. d) Do trecho “Lavar calçada com a mangueira (a chamada ‘vassoura hidráulica’) traz grandes prejuízos. Em 15 minutos são perdidos 279 litros de água”. Então, em vez de utilizar 279 litros, são utilizados 60 litros, deixando de consumir 279 litros − 60 litros = 219 litros em cada lavagem. Em cinquenta e duas semanas, como é feita uma lavagem por semana, serão feitas cinquenta e duas lavagens, economizando 219 litros · 52 = .11388 litros. Se cada caixa-d’água tem capacidade medindo 500 litros, então são economizadas .11388 : 500 = vinte e duas vírgula setecentos e setenta e seis caixas-d’água, aproximadamente 23 caixas-d’água.
18. e) Resposta pessoal.
18. f) Resposta pessoal.
19. a) Uma garrafa de 350 mililitros de suco concentrado deve ser preparada com 8 partes de água para cada parte de suco. Então, se é utilizada uma garrafa de suco, são necessárias 8 garrafas de água, ou seja, são utilizados 350 mililitros de suco e são necessários 8 · 350 mililitros = .2800 mililitros de água, totalizando 350 mililitros + .2800 mililitros = .3150 mililitros = (.3150 : .1000) litro = 3,15 litros.
19. b) A metade da garrafa de suco concentrado contém 0,175 litro (350 : 2 = 175; portanto, 175 mililitros e 175 : .1000 = 0,175, em litro). O total de suco preparado é sempre a soma das partes de suco concentrado e água, ou seja, usando uma parte de suco concentrado, o resultado é um suco preparado com 9 partes (1 + 8 = 9). Então, para preparar 1,5 litro é necessário 1,5 litro : 9 ≃ 0,167 litro de suco concentrado, e, como 0,175 > 0,167, então é necessário menos do que a metade da garrafa. Para preparar 2 litros é necessário 2 litros : 9 ≃ 0,222 litro de suco, e, como 0,222 > 0,175, isso significa mais do que a metade da garrafa de suco concentrado.
20. O doce de leite é vendido em uma embalagem que tem medida de massa 400 gramas, mas a informação na embalagem abrevia a unidade de medida para “gr”, em vez de utilizar gê, que é a fórma padronizada pelo Sistema Internacional de Unidades.
21. Analisar os quadros considerando o número e a substância, escolhendo uma unidade de medida de massa plausível em cada caso, a partir da estimativa.
25. Como uma tonelada = .1000 quilogramas, temos:
1,5 tonelada = .1000 ⋅ 1,5 quilogramas = .1500 quilogramas
26. a) Como 1 quilograma = .1000 gramas, temos:
de 1 quilograma =
1 quartode .1000 gramas =
Fração. Numerador 1 vezes 1.000, denominador 4gramas = 250 gramas
26. b)
3 quartosde 1 quilograma = 3 ⋅
abre parênteses, 1 quarto de 1 quilograma, fecha parênteses= 3 ⋅ 250 gramas = 750 gramas
27. 20 pastilhas de 250 miligramas equivalem, em pastilhas, a: 20 · 250 miligramas = .5000 miligramas = (.5000 : .1000) gramas = 5 gramas.
28. O caminhão pode transportar até 9,6 t = (9,6 ·.1000) quilogramas = .9600 quilogramas.
28. a) 240 sacos de 50 quilogramas têm, juntos, medida de massa 240 · 50 quilogramas = .12000 quilogramas, e, como .12000 > .9600, o caminhão não pode transportar essa carga completa.
28. b) Como a carga máxima é .9600 quilogramas, isso é equivalente a .9600 : 50 = 192 (192 sacos).
29. O máximo é 3 miligramas por quilograma de medida de massa; então, um paciente de 60 quilogramas pode consumir no máximo 3 · 60 miligramas = 180 miligramas do analgésico. Como cada gota contém 5 miligramas, a dose máxima, em gotas, é 180 : 5 = 36.
30. A balança marcou a medida 0,875 quilograma = (0,875 · .1000) grama = 875 gramas, indicando que a medida da massa da refeição é 875 gramas − 350 gramas = 525 gramas. Como 1 quilograma = .1000 gramas custa R$ 44,00quarenta e quatro reais; então, 525 gramas custam (R$ 44,00quarenta e quatro reais : .1000) · 525 = R$ 0,044zero reais e quatro centavos · 525 = R$ 23,10vinte e três reais e dez centavos.
Exercícios complementares
3. a) Observando o gráfico, temos que, em 2010, a média era de 6 quilogramas.
3. b) A média é calculada pela soma do consumo de café no período dividida pela quantidade de anos, ou seja,
Fração. Numerador 5,8 mais 6,0 mais 6,1 mais 6,2 mais 6,4 mais 6,4 mais 6,2 mais 6,2, denominador 8 igual à=
=
49,3 oitavos, igual à 6,1625Aproximadamente 6,16 quilogramas.
3. c) Em 2011, a média era 6,1, e em 2012 passou a ser 6,2; como 6,1 < 6,2, a média aumentou. A diferença foi de 0,1 quilograma, pois 6,2 − 6,1 = 0,1.
3. d) Em 2015, o consumo foi de 6,2 quilogramas por habitante; então, .72000 habitantes consumiriam .72000 · 6,2 quilogramas = .446400 quilogramas.
4. Um cubo tem 12 arestas de mesma medida; então, se a soma de suas medidas é 64,8 centímetros, cada aresta tem medida de comprimento igual a: 64,8 ∶ 12 = 5,4 (5,4 centímetros). Sendo assim, o paralelepípedo formado tem duas arestas medindo 5,4 centímetros, e a terceira mede 5,4 centímetros ⋅ 3 = 16,2 centímetros.
4. a) A soma das medidas das arestas é: 4 ⋅ (5,4 + 5,4 + 16,2) centímetro = 4 ⋅ 27 centímetro = 108 centímetros.
4. b) Em um cubo, há 6 faces com mesma medida de área (5,4 centímetros)2 = 29,16 centímetros quadrados; então, a soma das medidas das áreas das faces é: 29,16 centímetros quadrados ⋅ 6 = 174,96 centímetros quadrados.
4. c) O paralelogramo tem 6 faces, sendo 4 delas retângulos medindo 5,4 centímetros × 16,2 centímetros e duas faces quadradas de lado medindo 5,4 centímetros. Então, a soma das medidas das áreas das faces, em centímetro quadrado, é: 4 ⋅ 5,4 ⋅ 16,2 + 2 ⋅ 5,42 = 349,92 + 2 ⋅ 29,16 = 349,92 + 58,32 = 408,24
5. A proveta da imagem contém líquido com volume medindo 250 mililitros = (240 : .1000) litro = 0,24 litro.
5. a) Como 10 decilitros (dê éle) é equivalente a 1 litro, a quantidade de líquido é 0,24 · 10 decilitro = 2,4 decilitros.
5. b) Como 100 centilitros (cê éle) é equivalente a 1 litro, a quantidade de líquido é 0,24 · 100 centilitro = 24 centilitros.
5. c) Como .1000 mililitros (ême éle) é equivalente a 1 litro, a quantidade de líquido é 0,24 · .1000 mililitro = 240 mililitros.
6. Como 10 mililitros = 1 centilitro, então 2,5 centilitros = (2,5 · 10) mililitro = 25 mililitros.
7. Considerando que uma tonelada = .1000 quilogramas, 1 quilograma = .1000 gramas e 1 grama = .1000 miligramas.
7. a) .54756 gramas = (.54756 : .1000) quilograma = 54,756 quilogramas
7. b) duas vírgula três toneladas = (2,3 · .1000) quilogramas = .2300 quilogramas
7. c)
Um meiotonelada = 0,5 tonelada = (0,5 ⋅ .1000) quilograma = 500 quilogramas = (500 ⋅ .1000) grama = .500000 gramas
7. d) 80 gramas = (80 · .1000) miligrama = .80000 miligramas
7. e) 15 gramas = (15 : .1000) quilograma = 0,015 quilograma
7. f)
3 quintosquilogramas = 0,6 quilograma = (0,6 ⋅ .1000)grama = 600 gramas
Verificando
1. Como 1 minuto = 60 segundos, temos:
565 segundos = (565 : 60) minuto ≃ 9,42 minutos
Alternativa a.
2. Trabalhando continuamente por esse período (das 8horas às 21horas45minutos) ela trabalhou por 21 horas 45 minutos − 8 horas = 13 horas 45 minutos = 13 horas +
3 quartoshoras. Recebendo R$ 25,90vinte e cinco reais e noventa centavos por hora, ela recebeu, no total, em reais:
· 25,9 +
3 quartos· 25,9 = 336,7 +
77,7 quartos= 336,7 + 19,425 = 356,125 ≃ 356,13
Alternativa d.
3. Contando a quantidade de cubos em cada sólido e multiplicando-a por vê, obtém-se o volume do sólido. (um) 4 cubos na horizontal, mais 3 empilhados ⇒ 4 vê + 3 vê = 7 vê; (dois) o sólido é composto de 3 andares, e há 9 cubos no primeiro, 4 cubos no segundo e 1 cubo no terceiro andar; portanto, 9 vê + 4 vê + 1 vê = 14 vê; (três) nos 3 andares desse sólido há 5, 3 e 1 cubos; então, o volume é 5 vê + 3 vê + 1 vê = 9vê.
Alternativa d.
4. Dos 2,5 mil litros produzidos, metade é engarrafado em embalagens de 330 mililitros = (300 : .1000) litro = 0,33 litro, ou seja, são 2,5 mil litros : 2 = 1,25 mil litro nessas embalagens e .1250 : 0,33 ≃ .3787,9 garrafas; arredondando para o inteiro anterior, são .3787.
Alternativa c.
5. O modo de preparo indica 1 copo de suco concentrado com 8 copos de água para o preparo. Então, com 220 mililitros de concentrado serão utilizados 220 mililitros · 8 = .1760 mililitros de água, um total de .1760 mililitros + 220 mililitros = .1980 mililitros = (.1980 : .1000) litro = 1,98 litro.
Alternativa b.
6. Como uma tonelada = .1000 quilogramas, temos: 14 toneladas = (14 · .1000) quilograma = .14000 quilogramas, então podem ser transportadas até 280 embalagens, pois: .14000 : 50 = .1400 : 5 = 280.
Alternativa c.
7. Como .1000 miligramas = 1 grama , temos: 360 grama = (360 ⋅ .1000) miligrama = .360000 miligramas. Como cada fármaco utiliza 3 miligramas, então podem ser produzidas .120000 unidades, pois: .360000 : 3 = .120000
Alternativa d.
8. Se 1,5 quilograma de ravióli usa 400 gramas de queijo, então 1 quilograma usa 400 gramas : 1,5 = .4000 gramas : 15 =
4000 gramas sobre 15 igual 800 sobre 3gramas de queijo. Então, para produzir 7,5 quilogramas de massa, são necessários:
=
=
Fração de numerador 6000 gramas dividido por 3, e denominador 3 dividido por 3 igual 2000 gramas sobre 1= .2000 gramas =
= (.2000 : .1000) quilogramas = 2 quilogramas
Alternativa b.
Sugestão de avaliação diagnóstica
Atividade 1
(ê éfe zero cinco ême ah zero um) Ler, escrever e ordenar números naturais até a ordem das centenas de milhar com compreensão das principais características do sistema de numeração decimal.
O quadro a seguir mostra a população estimada de cinco municípios brasileiros no ano de 2021, de acordo com o Instituto Brasileiro de Geografia e Estatística (í bê gê É).
|
Município (UF) |
População estimada em 2021 |
|---|---|
|
Anápolis (GO) |
396.526 |
|
Barreirinhas (MA) |
63.891 |
|
Castanhal (PA) |
205.667 |
|
Maringá (PR) |
436.472 |
|
Vila Velha (ES) |
508.655 |
Dados obtidos em: Instituto Brasileiro de Geografia e Estatística (í bê gê É): Estimativas da População. Disponível em: https://oeds.link/8gs6SU. Acesso em: 31 maio 2022.
a) Reproduza o eixo ordenado a seguir e escreva sobre ele o nome de cada um dos municípios apresentados no quadro, ordenando-os de acordo com a sua população.

b) Escreva por extenso a população de cada um desses municípios.
Respostas:
a) Barreirinhas − Castanhal − Anápolis − Maringá − Vila Velha
b) sessenta e três mil, oitocentos e noventa e um − duzentos e cinco mil, seiscentos e sessenta e sete − trezentos e noventa e seis mil, quinhentos e vinte e seis − quatrocentos e trinta e seis mil, quatrocentos e setenta e dois − quinhentos e oito mil, seiscentos e cinquenta e cinco
Resolução e comentários
Esta atividade avalia a leitura de números de até seis algarismos e sua ordenação na reta numérica. Observe quais estratégias os estudantes utilizam para ordená-los e peça-lhes que justifiquem seu raciocínio. Um estudante pode ter indicado a população de Barreirinhas, por exemplo, como a maior delas apenas por desatenção, ou por julgar que o maior algarismo inicial (6) indica o maior número.
O agrupamento dos algarismos de três em três deve-se ao fato de que, em geral, as pessoas são capazes de reconhecer três elementos agrupados em um simples relance, sem a necessidade de recorrer à contagem.
Observe também se os estudantes compreendem a escala utilizada para o eixo ordenado, na qual cada intervalo corresponde a 50 mil habitantes. É importante que eles reconheçam que essa escala possibilita a localização aproximada de um número. Como os dados para o número de habitantes apresentados no quadro encontram-se em intervalos diferentes, não há risco de confusão. Discuta com os estudantes como seria a ordenação de dois números que estão no mesmo intervalo, como .78754 e .78760. A proximidade desses números na escala apresentada torna mais difícil o reconhecimento de cada um deles no eixo ordenado. Nesse caso, para determinar qual desses números é o maior, é possível comparar algarismo a algarismo. Note que os três primeiros algarismos são os mesmos, mas que os algarismos das dezenas são diferentes para cada um dos números, o que possibilita concluir que .78760 é maior do que .78754, visto que 60 é maior do que 54.
Aproveite para perguntar aos estudantes sobre o valor posicional dos algarismos dos números apresentados. Por exemplo, qual é o valor posicional do algarismo 6 em cada um dos números? Ajude-os a identificar as diferentes ordens dos algarismos em um quadro e preencha esse quadro com eles. Depois, peça-lhes que expressem oralmente o valor posicional em cada caso. Por exemplo, no número .396526, um dos algarismos 6 tem o valor posicional .6000, enquanto o outro representa 6 unidades.
|
Centena de milhar |
Dezena de milhar |
Unidade de milhar |
Centena |
Dezena |
Unidade |
|---|---|---|---|---|---|
|
3 |
9 |
6 |
5 |
2 |
6 |
|
- |
6 |
3 |
8 |
9 |
1 |
|
2 |
0 |
5 |
6 |
6 |
7 |
|
4 |
3 |
6 |
4 |
7 |
2 |
|
5 |
0 |
8 |
6 |
5 |
5 |
Para escrever por extenso a população de cada um dos municípios, os estudantes devem reconhecer as diferentes ordens e identificar os valores correspondentes a elas. É possível que eles cometam erros. Ao analisar os números .508655 e .205667, por exemplo, pode ser que eles deixem ausente a ordem relacionada ao número zero.
Comente sobre as classes que formam cada grupo de três algarismos: classe das unidades simples e classe dos milhares.
É possível que estudantes com pouca compreensão dos princípios do sistema de numeração decimal escrevam respostas como “quinhentos e oito, seiscentos e cinquenta e cinco” e “duzentos e cinco, seiscentos e sessenta e sete”, em que grupos de três algarismos são lidos cada um como um número. Se verificar algum caso como esse, discuta como é determinado o valor posicional no sistema de numeração decimal, recorrendo, se possível, a recursos visuais, como o material dourado ou o ábaco.
Atividade 2
(ê éfe zero cinco ême ah zero dois) Ler, escrever e ordenar números racionais na fórma decimal com compreensão das principais características do sistema de numeração decimal, utilizando, como recursos, a composição e decomposição e a reta numérica.
Associe cada número com sua correspondente decomposição.
a) 3,50
b) 0,35
c) 0,035
d) 0,305
um3 décimos e 5 milésimos
dois35 milésimos
três3 décimos e 5 centésimos
quatro3 inteiros e 5 décimos
Resposta: a) quatro; b) três; c) dois; d) um
Resolução e comentários
O objetivo desta atividade é avaliar a compreensão dos estudantes em relação a composição, decomposição e leitura dos números na fórma decimal. É importante que eles compreendam que os algarismos à esquerda da vírgula representam a parte inteira e que aqueles à sua direita formam a parte fracionária: décimos, centésimos, milésimos etcétera Assim, é esperado que o número 3,50 ofereça menor dificuldade de identificação, pois é o único que apresenta parte inteira diferente de zero. Entretanto, como 0,50 pode ser lido como “cinquenta centésimos”, é importante que os estudantes reconheçam que 5 décimos (0,5) é o mesmo que 50 centésimos (0,50), para que associem o número 3,50 à decomposição “3 inteiros e 5 décimos”.
0,5 = 0,50 ou 0,5 =
5 décimos igual fração de numerador 5 vezes 10 e denominador 10 vezes 10 igual 50 centésimos= 0,50
Os outros três números podem trazer maior dificuldade, pois exigem a compreensão do valor das diferentes ordens decimais:
• o número 0,35 pode ser lido como “trinta e cinco centésimos” ou, na fórma decomposta, como “três décimos e cinco centésimos”;
• o número 0,035 pode ser lido como “trinta e cinco milésimos” ou, na fórma decomposta, como “três centésimos e cinco milésimos”;
• o número 0,305 pode ser lido como “trezentos e cinco milésimos” ou, na fórma decomposta, como “três décimos e cinco milésimos”.
Atividade 3
(ê éfe zero cinco ême ah zero três) Identificar e representar frações (menores e maiores que a unidade), associando-as ao resultado de uma divisão ou à ideia de parte de um todo, utilizando a reta numérica como recurso.
Três amigos compraram duas pizzas iguais. Que fração de uma pizza receberá cada um dos amigos?
Resposta:
2 terçosResolução e comentários
Para resolver essa atividade, o estudante pode recorrer diretamente à ideia de fração como uma divisão, efetuando 2 : 3 ou
2 terços, ou utilizar uma representação gráfica para obter a resposta correta. As duas pítsas são representadas por dois círculos, cada um deles divididos em 3 partes iguais. Assim, para que cada amigo receba a mesma porção de uma pítsa , eles devem receber 2 pedaços de uma pítsa com 3 pedaços no total, ou seja,
2 terçosde uma pítsa .
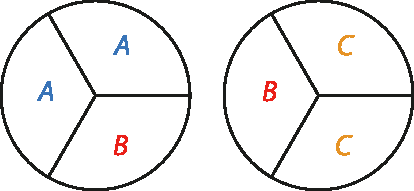
É possível que alguns estudantes, ao perceberem que a divisão de duas pítsas em três partes iguais só será possível se a pítsa for dividida em múltiplos de 3 partes, utilizem representações em que as pizzas sejam divididas em 6 partes iguais, 9 partes iguais etcétera Nesses casos, cada amigo receberá, respectivamente, 4 partes e 6 partes, o que representa
4 sextose
6 nonosde pítsa ; frações equivalentes à mesma fração irredutível
2 terços.
É importante ressaltar que, mesmo que alguns estudantes afirmem que um empecilho à resolução é a dificuldade em desenhar círculos e dividi-los em 3 partes iguais, mostre a eles que a fórma da figura não afeta a resolução. A pítsa pode ser representada por uma figura retangular, por exemplo, e a solução obtida será a mesma.
Atividade 4
(ê éfe zero cinco ême ah zero quatro) Identificar frações equivalentes.
Lucas gastou
2 quintosde suas economias com a compra de um computador. Sua irmã Marina registrou a fração desse gasto de um modo diferente. Qual das alternativas a seguir mostra um possível registro feito por Marina?
a)
3 sextos
b)
6, 15 avosc)
4 sétimos
d)
1 quarto
e)
3 décimosResposta: Alternativa b.
Resolução e comentários
É possível que alguns estudantes reconheçam que duas frações são equivalentes quando seus termos são multiplicados por um mesmo número inteiro positivo. Assim, eles perceberão que a fração
2 quintospode ter seus termos multiplicados por 3, obtendo a resposta
6, 15 avos.
Entretanto, é comum que outros estudantes recorram a outras representações. Por exemplo, desenhar cinco bolinhas e pintar duas delas de vermelho
abre parênteses 2 em 5 ou 2 quintos das bolinhas fecha parêntesese, depois, repetir a figura até que a fração obtida corresponda a uma das alternativas apresentadas.
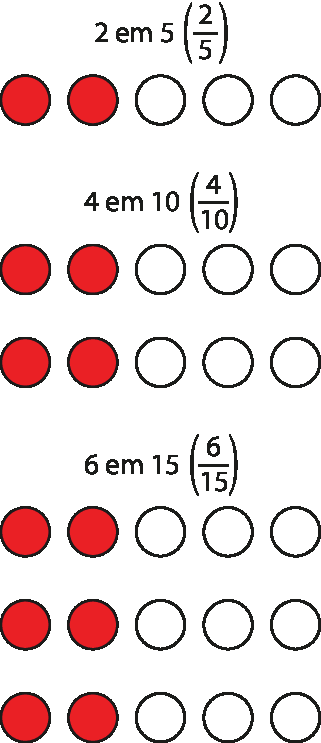
É importante observar se algum estudante escolheu uma das alternativas incorretas (a, c ou d), pois, nesse caso, é possível que, no lugar da multiplicação, o estudante tenha se equivocado e feito a adição de um número a cada um dos termos da fração. No item a, adicionou 1 a cada um dos termos de
2 quintos; no item c, adicionou 2; e no item d, subtraiu 1 de cada um dos termos. Um modo de fazê-los perceber o erro é desenhar dois retângulos iguais, um abaixo do outro, e pintar
2 quintosde um deles e
3 sextosdo outro, para que reconheçam visualmente o erro cometido.

Atividade 5
(ê éfe zero cinco ême ah zero cinco) Comparar e ordenar números racionais positivos (representações fracionária e decimal), relacionando-os a pontos na reta numérica.
Copie a reta numérica a seguir no caderno e marque sobre a reta os pontos correspondentes a cada um dos números: 0,25;
3 quartos;
4 quartos; 1,5.

Resposta:
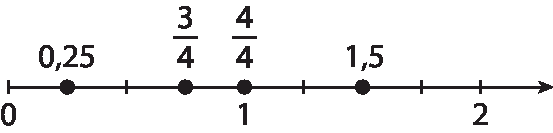
Resolução e comentários
A representação de uma fração na reta numérica exige a compreensão da ideia de parte de um todo e a convenção de que as partes correspondentes ao numerador da fração são contadas a partir do zero na reta numérica. Por exemplo, a fração
3 quartospoderia ser representada como qualquer uma das duas partes mostradas a seguir. Entretanto, apenas o ponto da extremidade do segmento da primeira figura representa o número
3 quartosna reta numérica.
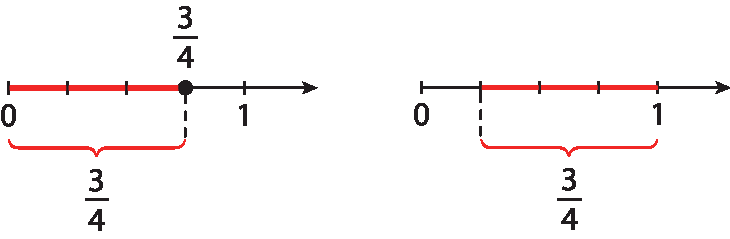
As frações aparentes, como
4 quartos, e as impróprias, como
6 quartos, apresentam, em geral, maior dificuldade para os estudantes, talvez pelo fato de o termo “fração” estar associado, na linguagem cotidiana, a partes de um todo que são menores do que esse todo.
Se você reconhecer essa dificuldade ao discutir as resoluções com os estudantes, diga a eles que a reta numérica é considerada infinita; portanto, qualquer quantidade de “quartos” maior do que uma unidade, ou seja, qualquer fração maior do que
1 quartotambém pode ser associada a um ponto dessa reta.
Atividade 6
(ê éfe zero cinco ême ah zero seis) Associar as representações 10%, 25%, 50%, 75% e 100% respectivamente à décima parte, quarta parte, metade, três quartos e um inteiro, para calcular porcentagens, utilizando estratégias pessoais, cálculo mental e calculadora, em contextos de educação financeira, entre outros.
Ao analisar a figura a seguir, Veridiana percebeu que 10% da figura corresponde à fração
1 décimo.

Assim, é correto afirmar que 75% correspondem a que fração?
a)
1 quintob)
1 oitavoc)
3 quartosd)
1, 25 avose)
1 meioResposta: Alternativa c.
Resolução e comentários
A fração correspondente à porcentagem 75% pode ser obtida simplificando a fração
75 centésimos, dividindo os termos da fração pelo mesmo número inteiro positivo. Isso pode ser feito diretamente ou em etapas:
ou:
Outro modo de obter rapidamente a fração correspondente é trabalhar com os estudantes a ideia de “metade da metade”: a metade de 100 é igual a 50, e a metade de 50 é igual a 25, de modo que 25 corresponde a um quarto de 100. Como 75 é o triplo de 25, conclui-se que 75% é igual a três quartos de 100%.
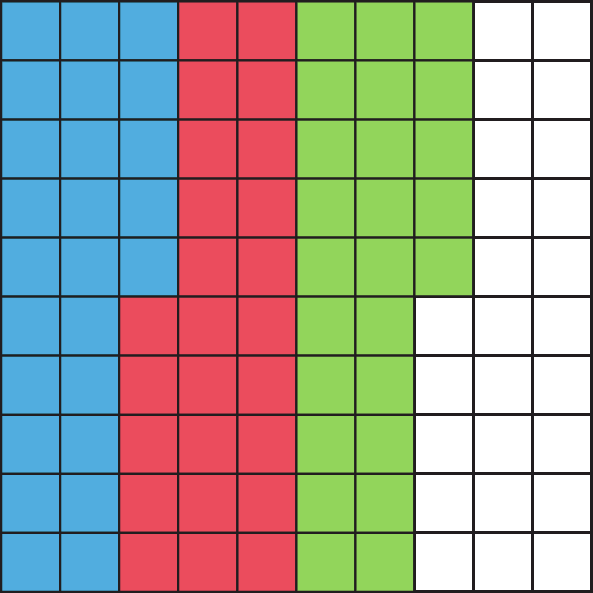
Outra possibilidade é estabelecer a relação entre frações, porcentagens e valores monetários utilizando moedas do nosso sistema monetário. Lembre os estudantes de que quatro moedas de 25 centavos totalizam 1 real.

Nos últimos anos, com a intensificação do uso de cartões eletrônicos para pagamentos, a circulação de moedas e o contato dos estudantes com elas têm diminuído, de modo que seu uso como apoio para o estudo da porcentagem traz benefícios também para o desenvolvimento do cálculo mental envolvendo valores monetários e para a comparação de valores em dinheiro.
Atividade 7
(ê éfe zero cinco ême ah zero sete) Resolver e elaborar problemas de adição e subtração com números naturais e com números racionais, cuja representação decimal seja finita, utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
César comprou um boné de R$ 26,00vinte e seis reais pagando ao vendedor com uma cédula de R$ 10,00dez reais, três cédulas de R$ 5,00cinco reais e uma de R$ 2,00dois reais. Ele recebeu de troco uma cédula de R$ 2,00dois reais e uma moeda de R$ 1,00um reais. Ao perceber o erro, ele devolveu ao vendedor um valor de modo que o troco fosse correto. Qual foi o valor devolvido por César?
Resposta: R$ 2,00dois reais
Resolução e comentários
Nesta atividade são avaliados a interpretação do enunciado, o reconhecimento da operação aritmética associada a cada etapa descrita e a realização correta dos cálculos. É esperado que os estudantes efetuem a seguinte operação: 10 + 5 + 5 + 5 + 2, obtendo 27. Em seguida, para saber o troco correto, basta efetuar 27 − 26, obtendo 1 como diferença. O troco recebido por César foi de R$ 3,00três reais (2 + 1 = 3), de modo que ele deve devolver ao vendedor R$ 2,00dois reais (3 − 1 = 2).
Discuta com os estudantes sobre a estratégia empregada por eles para realizar o cálculo 10 + 5 + 5 + 5 + 2 = 27, para saber se fazem o cálculo mental ou se recorrem à “conta armada”. É possível que o estudante seja inseguro quanto às suas habilidades de cálculo mental com adições básicas do tipo 5 + 2 + 1 e similares, mas, apesar de não haver problema quanto ao uso do algoritmo da adição para encontrar a soma, a dependência deste restringe o desenvolvimento das habilidades de cálculo mental e estimativa. No caso da subtração, observe se eles utilizam a ideia de “completar uma quantidade” ou a ideia de retirar. No primeiro caso, a subtração 27 − 26 pode ser efetuada completando a sequência dos números: vinte e seis, seguido de vinte e sete (assim a resposta é um). No segundo caso, 27 é pensado como 26 + 1, ou seja, ao subtrair 26 desse valor, subtrai-se 26 de 26, resultando em 0, e subtrai-se 1 de 0, resultando em 1.
Atividade 8
(ê éfe zero cinco ême ah zero oito) Resolver e elaborar problemas de multiplicação e divisão com números naturais e com números racionais cuja representação decimal é finita (com multiplicador natural e divisor natural e diferente de zero), utilizando estratégias diversas, como cálculo por estimativa, cálculo mental e algoritmos.
Para a construção de um trecho de 480 metros do sistema ferroviário de transporte público do Cariri, no Ceará, serão utilizados pares de peças de trilho de 6 metros de comprimento cada uma. Se cada peça custa R$ 150,00cento e cinquenta reais, quantos reais serão gastos com as peças para a construção desse trecho?
Resposta: R$ 24.000,00vinte e quatro mil reais
Resolução e comentários
O objetivo desta atividade é avaliar as habilidades de interpretação de texto e a atenção a todos os aspectos que condicionam a resolução e a execução correta do cálculo da multiplicação. Para determinar o número de peças necessárias, os estudantes devem utilizar a ideia de divisão “quantas vezes cabe”. Para saber quantas vezes 6 metros cabem em 480 metros, eles devem efetuar 480 : 6 = 80. Como as peças são usadas em pares (uma para cada lado do trilho), eles devem calcular o dobro de 80, ou seja, 2 ∙ 80 = 160. Se cada peça custa R$ 150,00cento e cinquenta reais, basta efetuar 160 ∙ 150 = .24000.
Observe o método utilizado pelos estudantes para efetuar a divisão, se eles aplicam o algoritmo convencional ou se utilizam a ideia de calcular quocientes parciais por estimativa e, ao final, adicioná-los. Nesse tipo de cálculo é possível que alguns estudantes obtenham, por exemplo, 480 : 6 = 8. Em casos como esse, pode-se conduzir a discussão por diversos caminhos. Considerando a operação inversa e a estimativa, comente com eles que, se 480 : 6 = 8, então 8 ∙ 6 seria igual a 480, o que não é correto, pois 8 ∙ 6 = 48, um resultado muito abaixo do esperado. Retomando as etapas do algoritmo da divisão, como 4 centenas não podem ser divididas em 6 partes iguais, em que cada parte seja ao menos igual a 1, então trocam-se 4 centenas por 40 dezenas, as quais adicionadas às 8 dezenas já existentes formam 48 dezenas. Esse raciocínio justifica a ação de selecionar os algarismos com um arco acima deles e efetuar 48 : 6.
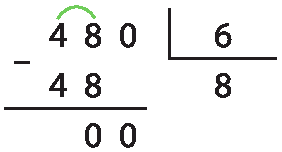
Como foram divididas 48 dezenas em 6 partes iguais, o resultado é 8 dezenas. Portanto, o primeiro algarismo do quociente representa a ordem das dezenas; assim, o número também terá um algarismo para as unidades. Registrando essas informações como indicado a seguir, o tipo de erro cometido no cálculo anterior tem menos possibilidade de ocorrer.
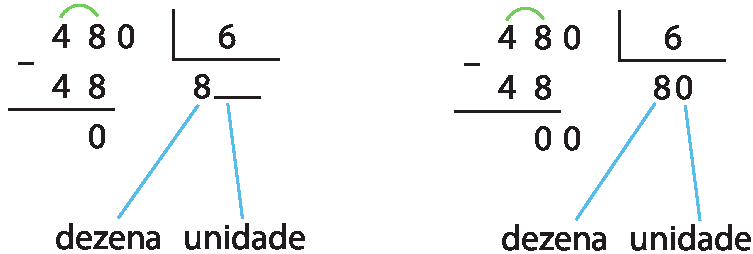
Ao dividir zero unidade por seis, o resultado é zero, completando o “espaço” destinado às unidades, portanto a resposta final é 80.
Atividade 9
(ê éfe zero cinco ême ah zero nove) Resolver e elaborar problemas simples de contagem envolvendo o princípio multiplicativo, como a determinação do número de agrupamentos possíveis ao se combinar cada elemento de uma coleção com todos os elementos de outra coleção, por meio de diagramas de árvore ou por tabelas.
Em uma sorveteria os clientes podem montar os próprios sorvetes escolhendo um sabor e o tipo de cobertura. De quantos modos é possível montar um sorvete, sabendo que há 6 sabores diferentes e 3 tipos de coberturas disponíveis?
Resposta: 18 modos diferentes.
Resolução e comentários
Esta atividade avalia a compreensão dos estudantes da ideia de “um para muitos”, que está associada ao raciocínio combinatório. Um erro comum pode ocorrer com a abordagem incorreta da natureza do problema, ao considerá-lo um problema do campo aditivo, fazendo 6 + 3 = 9 modos diferentes. Para ajudar os estudantes a compreender o problema, mostre-lhes que, ao escolher 1 sabor, por exemplo, morango, eles devem relacioná-lo com cada um dos 3 tipos de cobertura, obtendo 3 combinações diferentes.
Repetindo esse processo para cada um dos 6 sabores, conclui-se que é possível montar um sorvete de 18 modos diferentes (6 · 3 = 18).
Atividade 10
(ê éfe zero cinco ême ah um zero) Concluir, por meio de investigações, que a relação de igualdade existente entre dois membros permanece ao adicionar, subtrair, multiplicar ou dividir cada um desses membros por um mesmo número, para construir a noção de equivalência.
Vitória quer calcular mentalmente o resultado de 542 + 198. Qual dos processos a seguir pode facilitar o cálculo mental para Vitória e ainda fornecer o resultado correto da operação?
a) Adicionar 8 a cada uma das parcelas, obtendo 550 + 206. Depois, efetuar essa adição.
b) Adicionar duas unidades a 198, obtendo 200. Dividir 542 por 2, obtendo 271. Depois, calcular 200 + 271.
c) Adicionar duas unidades a 198, obtendo 200. Subtrair 2 unidades de 542, obtendo 540. Em seguida, calcular 200 + 540.
d) Subtrair duas unidades de cada parcela. Depois, calcular 540 + 196.
Resposta: Alternativa c.
Resolução e comentários
Com esta atividade é possível avaliar se os estudantes compreendem a relação de igualdade entre dois membros e a noção de equivalência. Primeiro, proponha a eles que calculem o resultado da operação 542 + 198, mentalmente ou com o auxílio de uma calculadora. Em seguida, eles devem escrever a igualdade relacionada a essa operação (542 + 198 = 740). Analisando cada uma das alternativas e efetuando as operações descritas em cada uma delas, é possível verificar se os estudantes compreendem que, para essa relação de igualdade ser mantida, é necessário que cada um dos membros da igualdade seja adicionado, subtraído, multiplicado ou dividido por um mesmo número.
Ao adicionar duas unidades a 198, obtendo 200, e subtrair duas unidades de 542, obtendo 540, a igualdade é mantida.
542 + 198 = 740
542 − 2 + 198 + 2 = 540 + 200 = 740
542 + 198 + 2 − 2 = 740 + 2 − 2
542 + 198 + 2 = 240 + 2
Atividade 11
(ê éfe zero cinco ême ah um um) Resolver e elaborar problemas cuja conversão em sentença matemática seja uma igualdade com uma operação em que um dos termos é desconhecido.
Renata passou o dia em uma feira de artes e artesanato expondo e vendendo aquarelas. Ela tinha certa quantia de dinheiro em sua carteira e, durante a manhã, comprou uma tapioca, pagando R$ 6,00seis reais. Nesse período ela também vendeu uma aquarela no valor de R$ 35,00trinta e cinco reais, e ficou com um total de R$ 50,00cinquenta reais na carteira.
Representando a quantia inicial de dinheiro na carteira de Renata por um quadradinho “

”, a igualdade que representa a situação descrita no texto é:
a)

+ 6 = 50 − 35
b)

− 6 + 35 = 50
c)

− 6 − 35 = 50
d)

+ 6 − 35 = 50
Resposta: Alternativa b.
Resolução e comentários
Esta atividade tem por objetivo avaliar o desenvolvimento das habilidades relacionadas ao pensamento algébrico dos estudantes. Para isso, eles devem interpretar a situação, relacionando as ações às operações aritméticas, e representá-la por meio de uma igualdade. Verifique se eles compreendem que a venda de um produto deve ser associada à adição e que a compra deve ser associada à subtração.
Um modo de facilitar a transcrição das ações descritas para a linguagem algébrica é utilizar esquemas com setas. As setas podem ser associadas com ações, facilitando a compreensão.
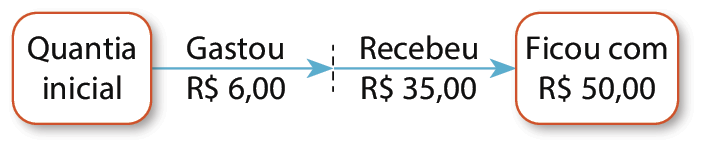
Em seguida, percorra cada etapa do diagrama anterior associando-a à linguagem matemática. A quantia inicial pode ser substituída pelo quadradinho “

”. Gastou R$ 6,00seis reais: significa que a quantia inicial foi diminuída de R$ 6,00seis reais; então, a expressão passou a ser

− 6. Considerando que Renata recebeu R$ 35,00trinta e cinco reais pela venda da aquarela, a expressão agora pode ser escrita como

− 6 + 35. Ao final das ações descritas, Renata ficou com R$ 50,00cinquenta reais na carteira; então, obtém-se a igualdade

− 6 + 35 = 50.
Para o desenvolvimento do pensamento algébrico dos estudantes, pode ser interessante utilizar recursos visuais que favoreçam a atribuição de significado aos conceitos e procedimentos. Uma possibilidade é utilizar o método de Singapura, em que as grandezas envolvidas são representadas por retângulos.
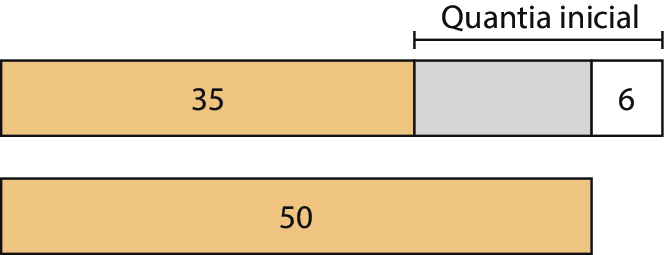
Observando que a quantia que sobrou após o pagamento de R$ 6,00seis reais adicionada a R$ 35,00trinta e cinco reais é um retângulo de mesma medida de comprimento do retângulo correspondente a R$ 50,00cinquenta reais, os estudantes podem perceber que (Quantia inicial) − 6 + 35 = 50.
Atividade 12
(ê éfe zero cinco ême ah um dois) Resolver problemas que envolvam variação de proporcionalidade direta entre duas grandezas, para associar a quantidade de um produto ao valor a pagar, alterar as quantidades de ingredientes de receitas, ampliar ou reduzir escala em mapas, entre outros.
Para uma receita de bolo de abacaxi, Jorge precisa de 6 ovos para fazer um bolo de 1 quilograma. Para fazer um bolo de 4,5 quilogramas para uma festa, Jorge deve aumentar a quantidade de todos os ingredientes da receita, incluindo os ovos. De quantos ovos ele precisa para fazer o bolo de 4,5 quilogramas?
Resposta: 27 ovos.
Resolução e comentários
A resolução desta atividade pode ser feita aplicando-se o conceito de proporcionalidade direta. Avalie se os estudantes compreendem que, ao aumentar a medida da massa do bolo, o número de ovos da receita também aumenta, assim como a quantidade de todos os outros ingredientes; ou seja, a receita inteira aumenta em 4,5 vezes. O aumento no número de ovos é proporcional ao aumento na quantidade de bolo. Caso algum estudante tenha mostrado dificuldade em entender a situação descrita no enunciado, a apresentação de um esquema pode ajudar.
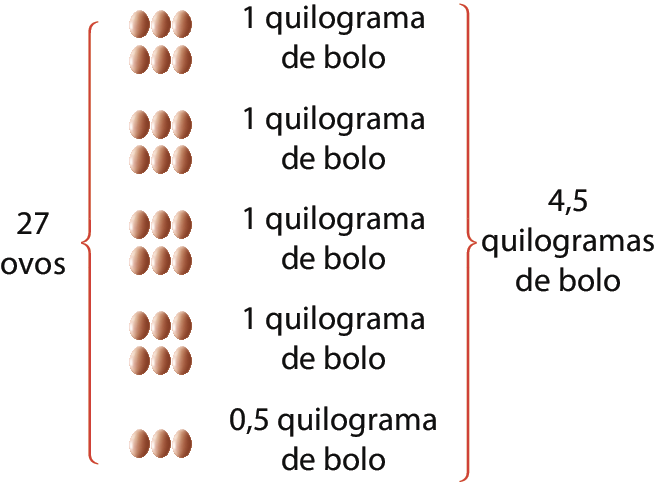
Assim como a medida da massa do bolo é multiplicada por 4,5 (4,5 · 1 = 4,5), o número de ovos também será multiplicado por 4,5; obtendo-se a quantidade 27 ovos (4,5 · 6 = 27).
Atividade 13
(ê éfe zero cinco ême ah um três) Resolver problemas envolvendo a partilha de uma quantidade em duas partes desiguais, tais como dividir uma quantidade em duas partes, de modo que uma seja o dobro da outra, com compreensão da ideia de razão entre as partes e delas com o todo.
Uma loja de canetas monta embalagens com duas canetas azuis e uma caneta preta. Se foram separadas 120 canetas para a montagem de embalagens para vender, quantas delas devem ser azuis e quantas devem ser pretas?
Resposta: 80 canetas azuis e 40 canetas pretas.
Resolução e comentários
Esta atividade permite uma grande variedade de estratégias de resolução, como tentativa e erro com o uso de quadros para a obtenção de aproximações sucessivas, ou a aplicação do conceito de proporcionalidade, entre outras. No primeiro caso, os estudantes podem escolher um valor inicial para o número de canetas pretas: 10, por exemplo. Determinam o número de canetas azuis, que deve ser o dobro do número de canetas pretas, e depois calculam o total de canetas, a fim de controlar os valores utilizados.
|
Canetas pretas |
Canetas azuis |
Total |
|---|---|---|
|
10 |
20 |
10 + 20 = 30 |
|
20 |
40 |
20 + 40 = 60 |
|
30 |
60 |
30 + 60 = 90 |
|
40 |
80 |
40 + 80 = 120 |
Dependendo do estudante, o número de tentativas necessárias para chegar à resposta pode ser menor; se ele perceber, por exemplo, que na 1ª tentativa a soma é 30, e que, como 120 = 4 · 30, multiplicar cada parcela por 4 resulta em 40 canetas pretas (4 · 10 = 40) e 80 canetas azuis (4 ∙ 20 = 80).
Uma solução que não exige tentativas pode ser obtida percebendo-se que, ao comprar uma embalagem com duas canetas azuis e uma caneta preta, são adquiridas 3 canetas. Assim, com 120 canetas podem ser montadas 40 embalagens para venda (120 : 3 = 40), nas quais haverá uma caneta preta em cada uma e 40 canetas pretas no total (40 · 1 = 40); duas canetas azuis em cada uma e 80 canetas azuis no total (40 ∙ 2 = 80).
Atividade 14
(ê éfe zero cinco ême ah um quatro) Utilizar e compreender diferentes representações para a localização de objetos no plano, como mapas, células em planilhas eletrônicas e coordenadas geográficas, a fim de desenvolver as primeiras noções de coordenadas cartesianas.
Karen mora em Araguaína (Tocantins), no ponto indicado pela letra K no mapa, e seu amigo Murilo mora em Gurupi (Tocantins), no ponto indicado pela letra M no mapa.
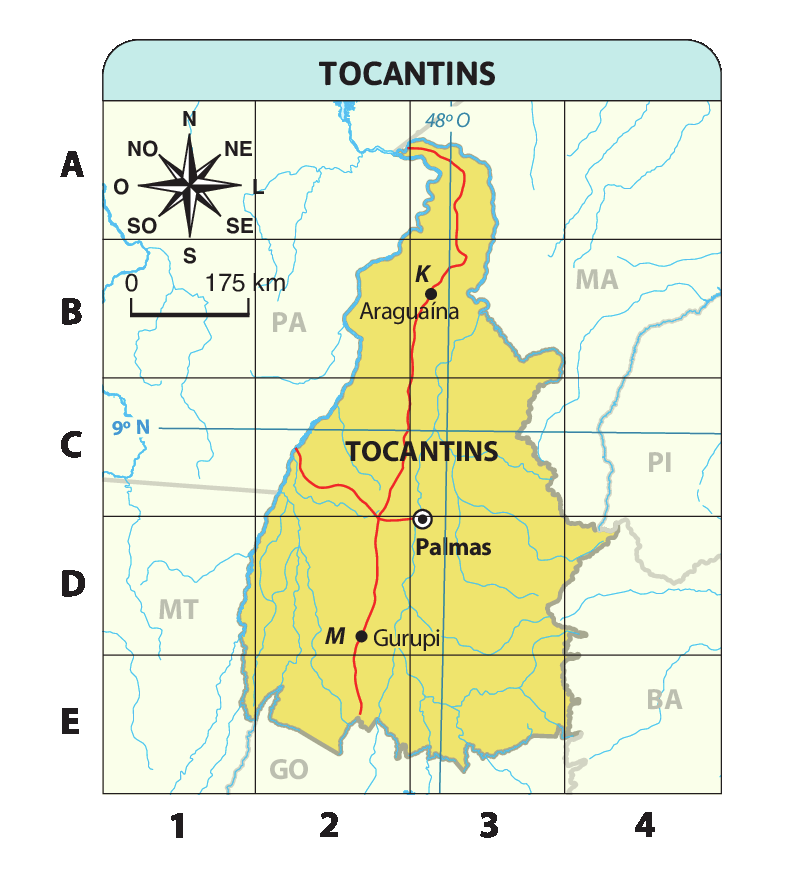
As localizações das residências de Karen e de Murilo podem ser dadas, respectivamente, por:
a) A2 e C3.
b) B3 e E2.
c) A3 e D3.
d) B2 e D2.
Resposta: Alternativa d.
Resolução e comentários
Para esta atividade não é esperado que os estudantes tenham muitas dificuldades, visto que são utilizadas letras para identificar uma das coordenadas, o que facilita a tarefa de obter a nomenclatura das células onde estão localizadas as cidades e residências dos amigos Karen e Murilo.
Assim, o objetivo é avaliar apenas a ideia que sustenta o uso de coordenadas cartesianas, ou seja, o cruzamento, ou intersecção, delas de modo a determinar a localização de um ponto em uma das células do mapa.
Note que, posteriormente, ao transpor a ideia para coordenadas cartesianas, o uso de duas coordenadas numéricas poderá trazer algumas dificuldades. É importante lembrar aos estudantes a convenção de que o primeiro número corresponde às coordenadas do eixo horizontal (coordenada xis), e o segundo número corresponde às coordenadas do eixo vertical (coordenada y).
Atividade 15
(ê éfe zero cinco ême ah um cinco) Interpretar, descrever e representar a localização ou movimentação de objetos no plano cartesiano (1º quadrante), utilizando coordenadas cartesianas, indicando mudanças de direção e de sentido e giros.
Um pequeno carrinho de contrôle remoto realiza um movimento que pode ser descrito com base no plano cartesiano a seguir.
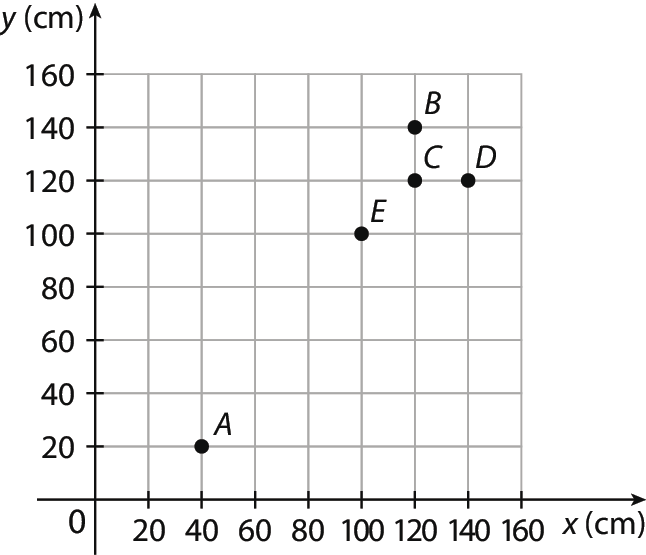
O carrinho sai do ponto a, anda 80 centímetros para cima, 20 centímetros para a direita, 20 centímetros para baixo, 80 centímetros para a direita, 40 centímetros para cima e 20 centímetros para a esquerda. Ao final do trajeto, o carrinho estará no ponto:
a) B.
b) C.
c) E.
d) D.
Resposta: Alternativa b.
Resolução e comentários
Com esta atividade é possível avaliar se os estudantes são capazes de identificar a representação da localização e da movimentação do carrinho no plano cartesiano. Verifique se eles reconhecem que as mudanças de direção e de sentido do movimento estão relacionadas às instruções para cima, para baixo, para a direita e para a esquerda.
O fato de o deslocamento do carrinho ser realizado ao longo da malha formada por linhas horizontais e verticais facilita a compreensão da atividade.
Atividade 16
(ê éfe zero cinco ême ah um seis) Associar figuras espaciais a suas planificações (prismas, pirâmides, cilindros e cones) e analisar, nomear e comparar seus atributos.
Observe a seguir a representação das planificações de quatro diferentes sólidos geométricos.
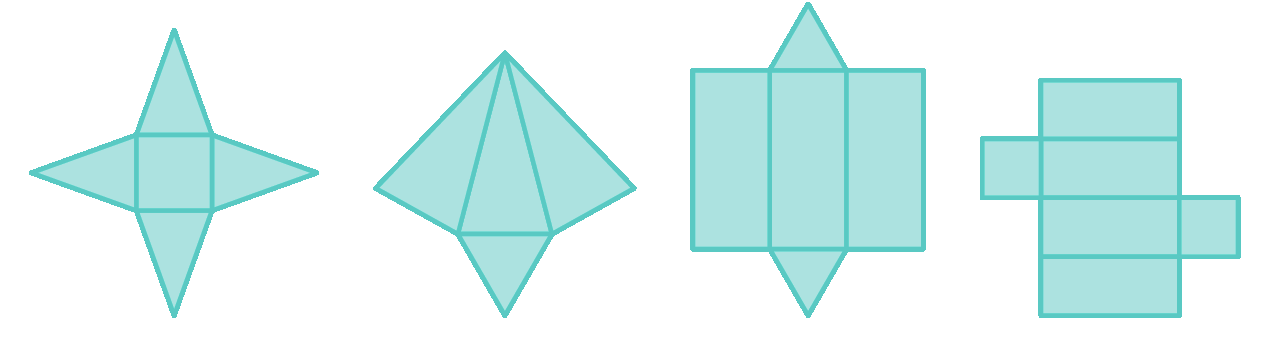
Qual dos sólidos a seguir não tem a sua planificação representada na figura anterior?
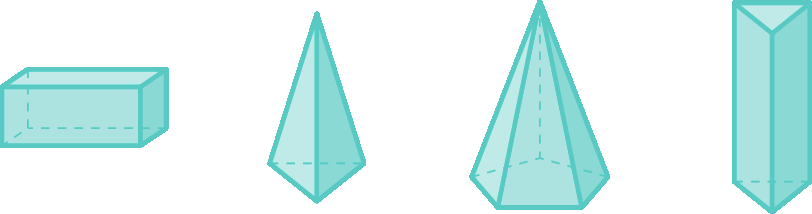
Resposta: A pirâmide de base pentagonal.
Resolução e comentários
Nesta atividade, os estudantes são avaliados em relação às suas habilidades de reconhecimento das características das figuras não planas e de identificação das representações de figuras não planas como figuras planas. Em situações como essa, eles podem ter dificuldades em compreender as convenções adotadas na representação de figuras não planas, como o recobrimento parcial de suas faces e a deformação causada pela representação em perspectiva. Assim, é possível que alguns estudantes tenham dificuldade em associar a figura do prisma de base triangular com a representação de sua planificação, pois as faces que são retangulares na planificação são retratadas como paralelogramos na representação em perspectiva. A pirâmide de base pentagonal pode ser erroneamente associada à planificação da pirâmide de base quadrada, pelo fato de ter muitos triângulos como faces laterais. Por esse motivo, se muitos dos estudantes apresentarem dificuldade em responder corretamente à atividade, pode ser interessante apresentar a eles modelos tridimensionais dos sólidos geométricos para que eles tenham a oportunidade de manipulá-los. Ao abrir, planificar e interagir com esses modelos, os estudantes podem observar as similaridades entre seus formatos, suas representações em perspectiva e suas planificações.
Atividade 17
(ê éfe zero cinco ême ah um sete) Reconhecer, nomear e comparar polígonos, considerando lados, vértices e ângulos, e desenhá-los, utilizando material de desenho ou tecnologias digitais.
Analise os polígonos a seguir e assinale a alternativa correta.
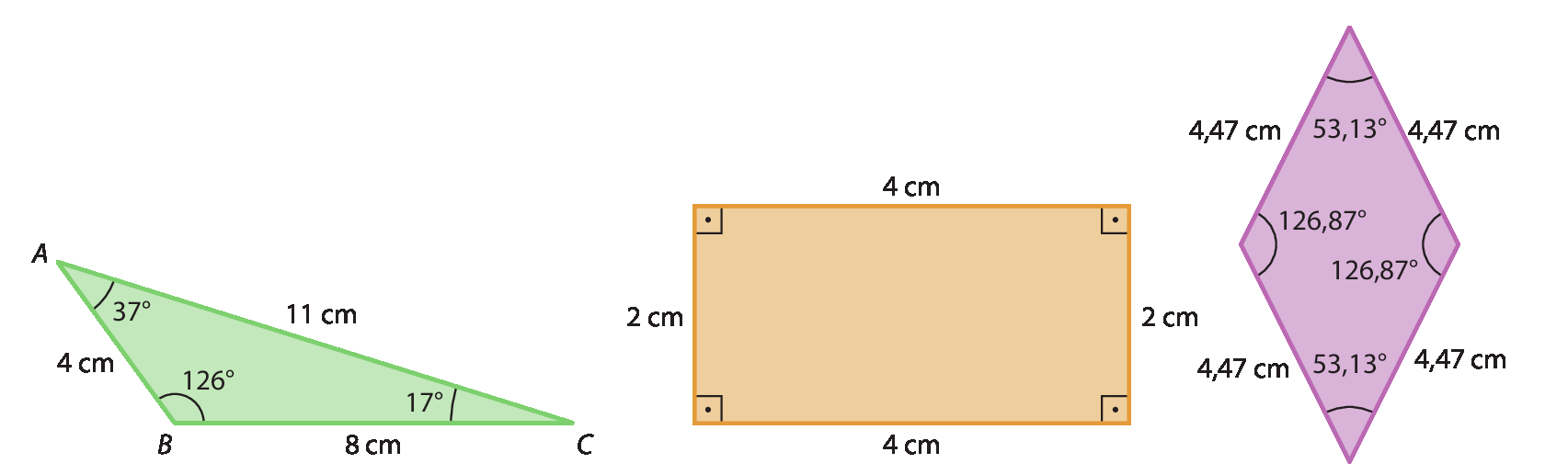
a) O número de lados de um polígono é sempre igual ao número de ângulos internos.
b) Se um polígono tem todos os ângulos internos de mesma medida, os seus lados também terão a mesma medida de comprimento.
c) O polígono cujos lados têm a mesma medida de comprimento também tem todos os seus ângulos internos de mesma medida.
d) O número de vértices de um polígono é igual ao dobro do seu número de lados.
Resposta: Alternativa a.
Resolução e comentários
Nesta atividade, os estudantes devem reconhecer os elementos dos polígonos e, com base neles, realizar as comparações indicadas nas alternativas apresentadas.
No caso do item b, se os estudantes tiverem a imagem mental apenas de um quadrado ou de um triângulo equilátero, por exemplo, a afirmação pode fazer sentido para eles. No entanto, ela está incorreta, considerando que se refere a polígonos de modo geral. Um contraexemplo à afirmação pode ser dado considerando a figura do retângulo: nela os ângulos são congruentes, mas os lados têm medidas de comprimento diferentes. No item c, o caso é similar ao anterior, mas eles podem recorrer à imagem do losango como contraexemplo da afirmação.
Apesar de as alternativas apresentadas não abordarem as medidas dos ângulos, pode-se aproveitar a discussão sobre as respostas dadas para sondar os conhecimentos dos estudantes sobre o assunto e discutir possíveis erros de compreensão. Por exemplo, uma interpretação equivocada é acreditar que, quanto mais distante do vértice estiver o “arco” que indica um ângulo, maior é a medida do ângulo, visto que a “abertura” é maior. Na figura a seguir, por exemplo, pode ser que eles identifiquem o ângulo
A O Bcomo sendo maior do que o ângulo
C O D, pois o arco
A Bé mais comprido do que o arco
C D.
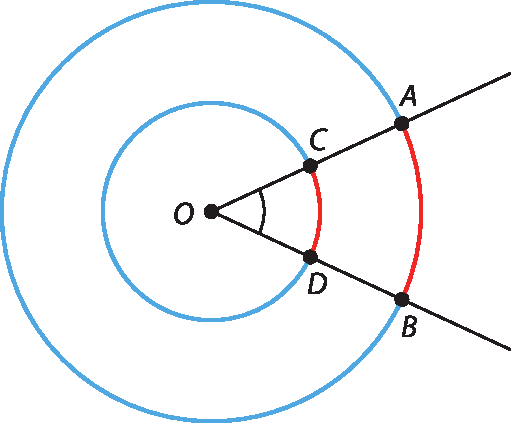
Atividade 18
(ê éfe zero cinco ême ah um oito) Reconhecer a congruência dos ângulos e a proporcionalidade entre os lados correspondentes de figuras poligonais em situações de ampliação e de redução em malhas quadriculadas e usando tecnologias digitais.
Sabendo que a figura 2 é uma ampliação da figura 1, assinale a alternativa correta.
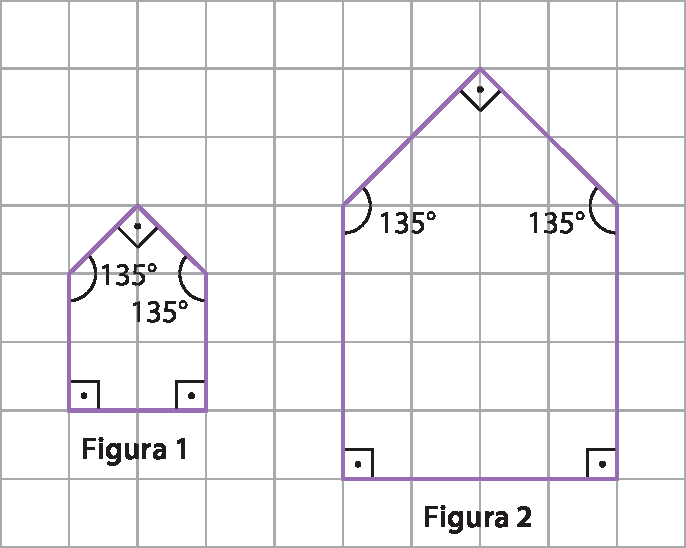
a) Ao ampliar uma figura, as medidas dos lados são multiplicadas por um mesmo valor, e as medidas dos ângulos também.
b) Em uma ampliação, as medidas dos ângulos não se alteram, e as medidas dos lados são multiplicadas por um mesmo valor.
c) Em uma ampliação, as medidas de cada lado são multiplicadas por valores diferentes.
d) Ao ampliar uma figura, as medidas dos lados não se alteram, e as medidas dos ângulos são multiplicadas por um mesmo valor.
Resposta: Alternativa b.
Resolução e comentários
Ao analisar a atividade, é provável que os estudantes tenham mais facilidade em reconhecer a relação entre as medidas dos lados da figura 1 e da figura 2 ampliada devido à possibilidade de efetuar a contagem do número de segmentos unitários (os lados dos quadradinhos da malha). Entretanto, a identificação de que os ângulos são congruentes exige a compreensão adequada do significado de ângulo, como comentado naatividade anterior, pois é possível que alguns estudantes considerem que a abertura de cada um dos ângulos na figura 1 é menor do que a abertura dos ângulos correspondentes na figura 2. Um modo de contornar essa dificuldade é pedir-lhes que peguem uma folha de papel sulfite e sobreponham o ângulo reto de qualquer um de seus cantos nos ângulos retos da figura 1 e da figura 2, para que façam uma comparação visual e reconheçam a congruência dos ângulos.
Atividade 19
(ê éfe zero cinco ême ah um nove) Resolver e elaborar problemas envolvendo medidas das grandezas comprimento, área, massa, tempo, temperatura e capacidade, recorrendo a transformações entre as unidades mais usuais em contextos socioculturais.
O Monte Everest, no Nepal, é conhecido como a montanha mais alta do planeta Terra, medindo .8849 metros de altitude. O Pico da Neblina, no norte do Amazonas, é o pico mais alto Brasil, medindo .2995 metros de altitude. Qual é a diferença entre a medida da altitude do Monte Everest e a medida da altitude do Pico da Neblina, em quilômetros?
Resposta: 5,854 quilômetros.
Resolução e comentários
Esta atividade avalia a habilidade dos estudantes de compreender o significado de diferentes unidades de medida, seu contexto de aplicação e as transformações entre as unidades de medida de comprimento mais usuais, o metro e o quilômetro. Para isso, eles devem lembrar que 1 quilômetro corresponde a .1000 metros, identificando, assim, que .5854 metros (.8849 − .2995 = .5854) corresponde a 5,854 quilômetros
5 mil 854 sobre mil igual 5,854.
Discuta com eles a importância de compreender a relação entre o metro e o quilômetro, duas das unidades de medida de comprimento mais utilizadas no dia a dia. Conhecer essas relações pode auxiliar, por exemplo, na leitura de mapas de cidades e de estradas.
Atividade 20
(ê éfe zero cinco ême ah dois zero) Concluir, por meio de investigações, que figuras de perímetros iguais podem ter áreas diferentes e que, também, figuras que têm a mesma área podem ter perímetros diferentes.
Reproduza no caderno a malha a seguir e desenhe:
a) dois polígonos com áreas de medidas iguais e perímetros de medidas diferentes;
b) dois polígonos com perímetros de medidas iguais e áreas de medidas diferentes.

Resposta possível:
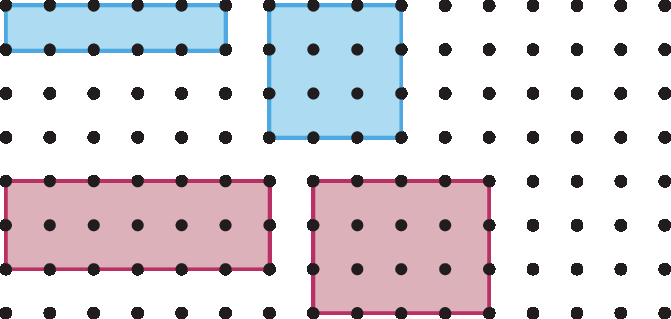
Resolução e comentários
Ao trabalhar com malhas pontilhadas, fique atento a um erro comum entre os estudantes ao calcular a medida do perímetro: para indicar a medida de comprimento do lado de um polígono, eles podem contar o número de pontos que formam esse lado, não o número de segmentos unitários contidos nele. Esse tipo de dificuldade pode, em muitos casos, revelar uma incompreensão do significado de medir um comprimento: a medida resulta da comparação do comprimento em análise com uma unidade de medida adotada como referência, como um segmento unitário medindo 1 centímetro ou 1 metro, por exemplo, e da determinação de quantas vezes o comprimento a ser medido contém esse segmento unitário de referência.
Os estudantes podem desenhar polígonos diversos, mas os retângulos oferecem a vantagem de servir como exemplo para as duas situações apresentadas. Para construir dois retângulos com perímetros de medidas iguais e com áreas de medidas diferentes, basta definir um valor, por exemplo, 12, e encontrar dois números cuja soma seja 6 (o semiperímetro). A partir dessa soma, alteram-se as parcelas da adição, adicionando uma ou duas unidades a uma delas e subtraindo o mesmo valor da outra:
2 + 4 = 6
3 + 3 = 6
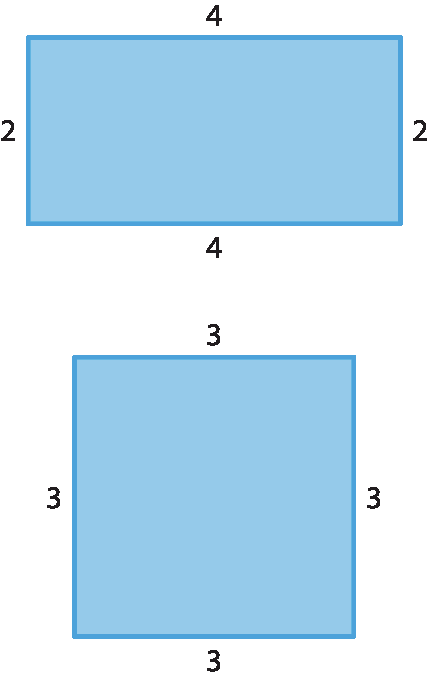
Assim, um dos retângulos tem área medindo 2 ∙ 4 = 8, e o outro tem área medindo 3 ∙ 3 = 9.
Para obter dois retângulos com áreas de medidas iguais e com perímetros de medidas diferentes, basta definir um número para a área que seja o resultado de pelo menos duas multiplicações distintas de dois números. Por exemplo, ao definir uma área de medida 18, pode-se efetuar 2 ∙ 9 = 18 e 3 ∙ 6 = 18. Ou seja, os lados de um dos retângulos medem 2 e 9, resultando em um perímetro de medida igual a 22. O outro retângulo tem lados medindo 3 e 6, resultando em um perímetro de medida igual a 18.
Atividade 21
(ê éfe zero cinco ême ah dois um) Reconhecer volume como grandeza associada a sólidos geométricos e medir volumes por meio de empilhamento de cubos, utilizando, preferencialmente, objetos concretos.
Considerando um cubinho como unidade de medida de volume, qual é o volume total da caixa ilustrada a seguir?
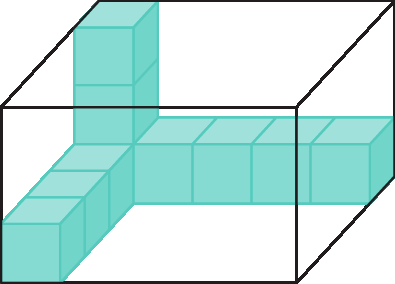
Resposta: setenta e duas unidades.
Resolução e comentários
Nesta atividade são avaliadas a percepção espacial dos estudantes e a compreensão deles de que as propriedades da multiplicação podem ser aplicadas para a obtenção do número de cubinhos correspondente ao volume da caixa. Um aspecto que pode levá-los a responder de maneira incorreta é o fato de o cubinho no cruzamento das fileiras estar oculto; assim, pode ser que os estudantes não o considerem no cálculo. É possível que eles calculem o total de cubinhos na primeira camada da base como 3 ∙ 5 = 15, e não o valor correto 4 ∙ 6 = 24. Como é possível formar 3 camadas como essa para preencher toda a caixa, o total de cubinhos correspondente ao volume total da caixa é 3 ∙ 24 = 72.
Outra possibilidade de resolução que pode levar ao erro consiste na contagem equivocada dos cubinhos que preencheriam o espaço vazio da caixa. Nesse caso, pode ser difícil desenhar os novos cubinhos para preencher a figura ou mesmo controlar a contagem dos cubinhos mentalmente, lembrando o posicionamento de cada um deles.
Atividade 22
(ê éfe zero cinco ême ah dois dois) Apresentar todos os possíveis resultados de um experimento aleatório, estimando se esses resultados são igualmente prováveis ou não.
Uma moeda é lançada duas vezes seguidas e, em cada lançamento, a face voltada para cima é registrada, como no exemplo a seguir, no qual ambos os lançamentos resultaram em “cara”.

Registre todos os possíveis resultados que podem ser obtidos no lançamento de duas moedas. Qual é o resultado mais provável: sair duas caras, duas coroas ou duas faces diferentes?
Resposta: Duas faces diferentes; uma face cara e outra face coroa (duas chances em 4).
CARA-CARA
CARA-COROA
COROA-CARA
COROA-COROA
Resolução e comentários
É comum que, para resolver esta atividade, os estudantes considerem que há somente 3 resultados possíveis: duas caras, duas coroas e uma cara com uma coroa. Nesse caso, eles concluirão que os eventos são igualmente prováveis. O erro resulta do fato de não considerarem a ordem em que as faces podem aparecer: cara seguida de coroa ou coroa seguida de cara.
É possível que alguns estudantes recorram a uma árvore de possibilidades, que apresenta a vantagem de representar visualmente a sequência possível de eventos.
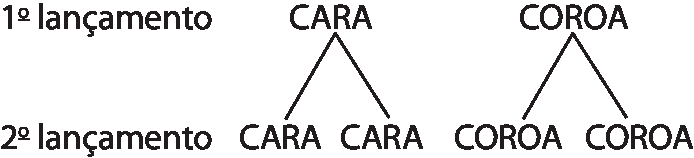
Apesar de ambas as abordagens anteriores para mapear todos os resultados possíveis no lançamento de uma moeda duas vezes seguidas possibilitarem a comparação entre os diferentes resultados, é importante considerar a possibilidade de ocorrência de outro tipo de erro comum relacionado a concepções intuitivas sobre a probabilidade de eventos sequenciais. A ideia de que o resultado do lançamento anterior da moeda influencia o resultado do lançamento seguinte. Nesse caso, é possível que os estudantes pensem que, se sair CARA no primeiro lançamento, no seguinte deve sair a outra face, COROA, porque CARA já saiu antes.
Isso ocorre frequentemente em outras situações. Por exemplo, em noticiários esportivos recorre-se frequentemente ao histórico dos resultados dos confrontos entre duas equipes para se projetar o favoritismo de uma delas, ignorando, por vezes, que tal comparação não faz sentido, se for considerado que muitas vezes os jogadores que participaram dos jogos anteriores não são mais os mesmos e que a partida não é um evento regido apenas pelas leis da aleatoriedade. Outro exemplo é a existência de sites na internet que mostram os números sorteados nas últimas edições de loterias. Novamente, o equívoco está em considerar que um número que não foi sorteado nos últimos 20 sorteios, por exemplo, tem maior probabilidade de ser sorteado em um novo sorteio, em relação a outros números, como se os sorteios tivessem memória.
Atividade 23
(ê éfe zero cinco ême ah dois três) Determinar a probabilidade de ocorrência de um resultado em eventos aleatórios, quando todos os resultados possíveis têm a mesma chance de ocorrer (equiprováveis).
No lançamento de um dado, qual é a probabilidade de sair o número 5?
a)
meiob)
um sextoc)
5 sextod)
um quintoResposta: Alternativa b.
Resolução e comentários
A atividade tem por objetivo avaliar a aplicação da definição de probabilidade como uma comparação entre o número de casos favoráveis e o total de casos possíveis em um evento equiprovável. No caso de um dado, há apenas um número 5 entre os seis números possíveis; logo, a probabilidade é de 1 em 6, ou
um sexto. Entretanto, não é incomum, em situações como essa, envolvendo valores numéricos (os números de 1 a 6 do dado), os estudantes considerarem que a probabilidade é de 5 em 6. É possível que, durante a discussão sobre as respostas, algum estudante discorde da solução dizendo que, se ele jogar um dado 6 vezes, nem sempre o número 5 sairá uma vez; então, a probabilidade não é igual a 1 em 6. Caso isso ocorra, explique-lhe que, à medida que jogamos o dado muitas vezes (centenas ou milhares de vezes), a probabilidade de sair o número 5 se aproxima de 1 em 6
um sexto. Assim, se julgar oportuno, combine com os estudantes que tragam um dado comum na aula seguinte, ou em uma data previamente combinada, para que cada um deles lance o dado cêrca de 30 vezes e registrem os resultados obtidos. Depois, compilem juntos os resultados na lousa e verifiquem se o número cinco saiu aproximadamente em um sexto dos lançamentos.
Atividade 24
(ê éfe zero cinco ême ah dois quatro) Interpretar dados estatísticos apresentados em textos, tabelas e gráficos (colunas ou linhas), referentes a outras áreas do conhecimento ou a outros contextos, como saúde e trânsito, e produzir textos com o objetivo de sintetizar conclusões.
As rampas de acesso são importantes para garantir o direito de pessoas em cadeiras de rodas de se locomoverem livremente pelos espaços públicos. O gráfico a seguir, chamado pictograma, mostra o número de rampas de acesso construídas ao longo de três anos em determinado município.

Qual das alternativas a seguir apresenta um título possível para uma reportagem sobre o tema?
a) Nos três últimos anos foram construídas 7 rampas de acesso no município.
b) A cada ano são construídas 40 novas rampas de acesso no município.
c) Há 70 rampas de acesso no município.
d) Nos últimos três anos foram construídas 70 novas rampas de acesso no município.
Resposta: Alternativa d.
Resolução e comentários
Nesta atividade, o objetivo é avaliar como os estudantes interpretam os dados representados em um gráfico, nesse caso, um pictograma. Além disso, é possível avaliar como os estudantes interpretam o texto para o título da notícia em cada alternativa. Caso algum estudante tenha assinalado a alternativa a, é provável que ele tenha considerado o total de 7 ícones, sem ter considerado a legenda do gráfico, que indica que cada ícone representa 10 rampas de acesso. A escolha da alternativa b pode indicar dificuldade de interpretação de texto ou do significado da variável indicada no eixo horizontal, o ano de construção da rampa. Nesse caso, seria importante discutir com o estudante os motivos de sua escolha, para que seja possível planejar uma intervenção adequada ao caso. Entre as alternativas incorretas, é possível que a alternativa c seja escolhida com maior frequência, devido ao fato de apresentar a quantidade correta de rampas indicadas no pictograma, 70. Entretanto, o gráfico não permite concluir que existem apenas 70 rampas de acesso na cidade, pois não se sabe quantas rampas já existiam antes do período mostrado no gráfico.
Atividade 25
(ê éfe zero cinco ême ah dois cinco) Realizar pesquisa envolvendo variáveis categóricas e numéricas, organizar dados coletados por meio de tabelas, gráficos de colunas, pictóricos e de linhas, com e sem uso de tecnologias digitais, e apresentar texto escrito sobre a finalidade da pesquisa e a síntese dos resultados.
Márcio entrevistou os moradores de 15 casas de seu bairro para saber quantas pessoas moram em cada uma delas. Ele registrou o resultado da maneira mostrada a seguir.
3 − 4 − 1 − 2 − 2 − 4 − 5 − 4 − 4 − 5 − 2 − 4 − 6 − 7 − 5
Reproduza o gráfico de colunas a seguir no caderno e complete-o de acordo com os dados obtidos por Márcio.
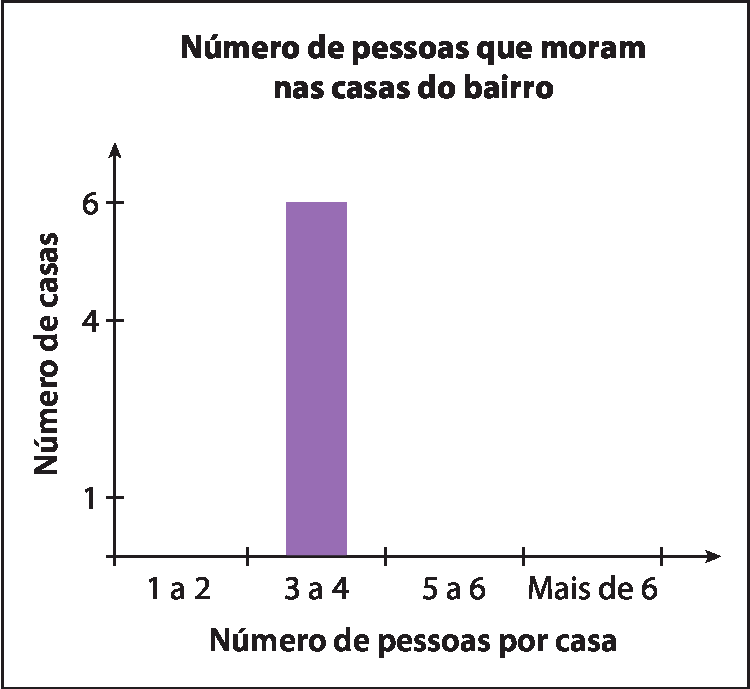
Resposta:
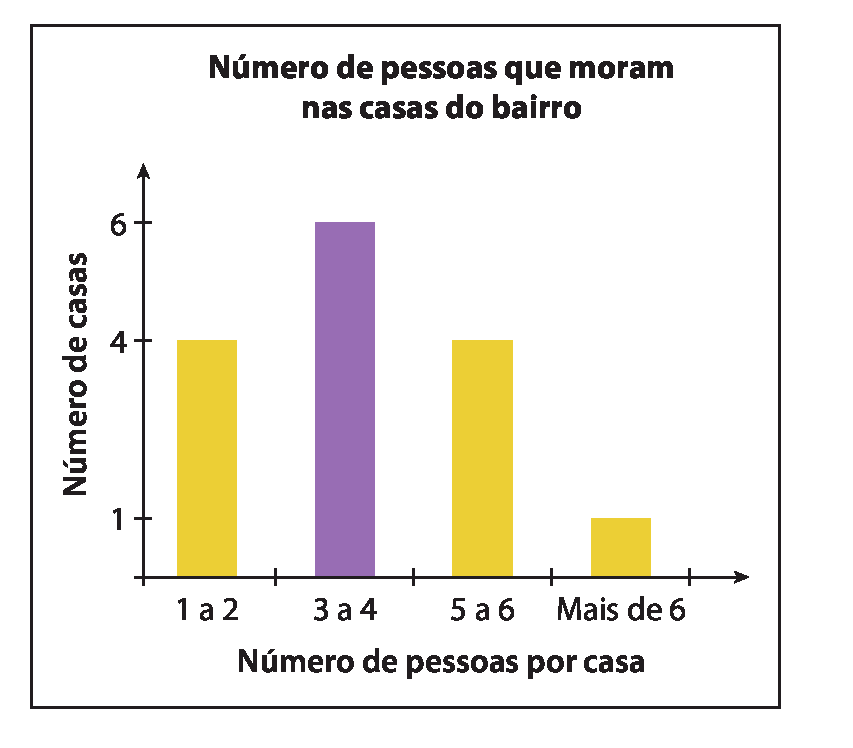
Resolução e comentários
Com esta atividade, espera-se que os estudantes compreendam que os dados devem ser agrupados de acordo com as indicações dadas no eixo horizontal. Eles devem realizar a contagem do número de casas para cada um dos intervalos apresentados no eixo horizontal, relacionados ao número de pessoas por casa. Em seguida, de acordo com os números obtidos, as colunas do gráfico podem ser construídas. Lembre-os de que as medidas das alturas das colunas devem ser proporcionais ao número de casas. Por exemplo, para o intervalo de 1 a 2 (número de pessoas por casa), existem 4 casas registradas por Márcio; então, podemos considerar que a medida da altura da coluna correspondente é 4 unidades. Para o intervalo de 3 a 4 existem 6 casas registradas; então, podemos considerar que a medida da altura da coluna correspondente é 6 unidades.
Se ocorrerem erros na contagem do número de casas para cada um dos intervalos, comente com os estudantes que, ao final da construção do gráfico, eles podem realizar a contagem de todos os valores correspondentes ao número de casas no eixo vertical, verificando, assim, se o resultado corresponde ao número total de casas pesquisadas, 15 (4 + 6 + 4 + 1 = 15). Dessa maneira, é possível minimizar os erros de contagem.