
CAPÍTULO 2 Operações com números naturais

Observe, leia e responda no caderno.
a) No total, quantas medalhas foram conquistadas pela delegação brasileira em 2020?
b) E quantas foram as medalhas conquistadas pelo atletismo? E pela natação?
c) Você conhece algum atleta medalhista dessa competição? Faça uma pesquisa e apresente o resultado aos colegas e professor.
Os Jogos Paralímpicos de Tóquio 2020, que ocorreram no período de 24 de agosto de 2021 a 5 de setembro de 2021, apresentaram exemplos de superação e humanismo. A delegação do Brasil, além de bater seu recorde de medalhas de ouro, igualou seu melhor desempenho histórico conquistado nos Jogos Paralímpicos do Rio 2016. No total, a delegação brasileira conquistou vinte e duas medalhas de ouro, 20 de prata e 30 de bronze. As medalhas foram obtidas em 14 modalidades das 20 em que o Brasil teve atletas inscritos.
O atletismo foi a modalidade que mais garantiu medalhas ao Brasil em Tóquio. Foram 8 de ouro, 9 de prata e 11 de bronze.
Respostas e comentários
a) setenta e duas medalhas.
b) O atletismo conquistou 28 medalhas (8 + 9 + 11 = 28). E a natação conquistou 23 medalhas (8 + 5 + 10 = 23).
c) Resposta pessoal.
Capítulo 2 - Operações com números naturais
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Este capítulo amplia os conhecimentos sobre números naturais do capítulo anterior e aprofunda o estudo das operações feito nos anos iniciais do Ensino Fundamental. Associamos as operações a situações cotidianas e mostramos seus diferentes significados. Também damos sentido às expressões numéricas vinculando-as a situações-problema. Iniciamos ainda o trabalho mais formal com a leitura e a interpretação de gráficos de colunas e de barras.
Ao explorar a situação presente na abertura aproveite para conversar com os estudantes sobre a inclusão e o papel de cada pessoa na sociedade. É importante que compreendam que a inclusão social é um processo que depende de uma sociedade livre de estereótipos e preconceitos, contribuindo para o desenvolvimento da competência geral 9 e do Tema Contemporâneo Transversal educação em direitos humanos. Comente que os Jogos Paralímpicos são o maior evento esportivo mundial envolvendo pessoas com deficiência, que ocorre há pelo menos cem anos. Mais informações sobre a história desses jogos podem ser obtidas em: REDE do esporte. Disponível em: https://oeds.link/IaGe38. Acesso em: 21 abril 2022.
No texto que acompanha a imagem, apresentamos informações sobre a delegação brasileira na disputa por medalhas em Tóquio. Com base nas informações, os estudantes devem responder às questões propostas para verificar a compreensão deles em relação à resolução de problemas de adição com números naturais.
Mais informações sobre a quantidade de medalhas obtidas nos Jogos Paralímpicos podem ser obtidas em: COMITÊ Olímpico Brasileiro. Disponível em: https://oeds.link/qdQBwk. Acesso em: 21 abril 2022.

Sugestão de leitura
Sugerimos a leitura do artigo:
MARQUES, RENATO F. R. A contribuição dos Jogos Paralímpicos para a promoção da inclusão social: o discurso midiático como um obstáculo. Revista USP, [sem local], número 107, página87-96, 2015. Identificador de Objeto Digital: 10.11606/issn.2316-9036.v0i107p87-96. Disponível em: https://oeds.link/eyPBjo. Acesso em: 21 abril 2022.
Neste artigo o autor propõe uma reflexão a respeito da maneira como atletas paralímpicos são retratados pela mídia durante os Jogos Paralímpicos e o produto dessa fórma de interação com os espectadores. Conclui-se que os atletas querem ser reconhecidos como pessoas produtivas e eficientes assim como qualquer outro cidadão.
1. Adição
Nos Jogos Paralímpicos de Tóquio 2020, a delegação brasileira conquistou 8 medalhas de ouro a mais do que nos Jogos Paralímpicos do Rio 2016, quando ficou com 14 dessas medalhas. A natação obteve seu melhor desempenho em toda a história dos jogos, com 8 medalhas de ouro, 5 de prata e 10 de bronze.
Em 2021, o nadador Daniel Dias foi eleito membro do Conselho dos Atletas do Comitê Paralímpico Internacional (IPC, na sigla em inglês). Nas quatro edições das Paralimpíadas em que competiu, conquistou 14 medalhas de ouro, 7 de prata e 6 de bronze.

Com base nas informações apresentadas, podemos descobrir, por exemplo, o total de medalhas conquistadas pelo nadador Daniel Dias nos Jogos Paralímpicos ao longo de sua carreira. Para isso, basta juntarmos as quantidades de medalhas de ouro, prata e bronze:
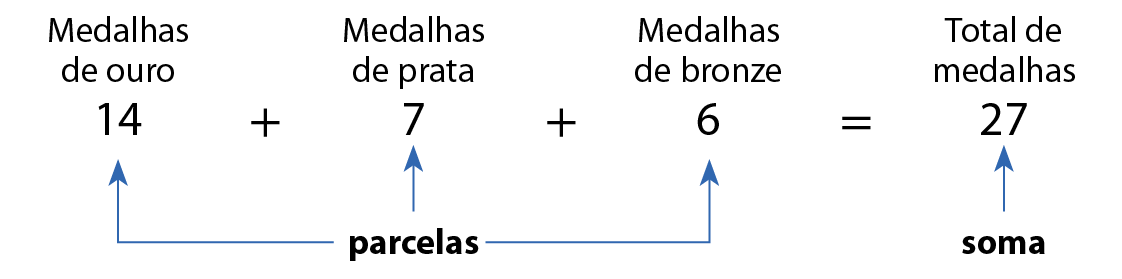
Portanto, Daniel manteve-se recordista com 27 medalhas nos Jogos Paralímpicos de Tóquio.
Na calculadora, fazemos essa adição da seguinte maneira:

Com os dados apresentados, podemos obter também outras informações. Se quisermos saber, por exemplo, a quantidade de medalhas de ouro conquistadas pelo Brasil nos Jogos Paralímpicos de Tóquio, devemos acrescentar à quantidade de medalhas de ouro conquistadas nos Jogos do Rio (14) a quantidade de medalhas conquistadas a mais em Tóquio (8):

Em uma calculadora, fazemos essa adição da seguinte maneira:

As ideias de juntar e acrescentar quantidades estão relacionadas à operação de adição.
Respostas e comentários
1. Adição
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico ampliamos o trabalho com a habilidade (ê éfe zero seis ême ah zero três) ao retomar as ideias de adição com números naturais, conceito estudado ao longo dos anos iniciais do Ensino Fundamental.
Para retomar e ampliar a operação de adição, mantivemos o contexto da abertura apresentando um texto sobre o nadador brasileiro Daniel Dias, que se consagrou nos Jogos Paralímpicos do Rio, em 2016, o maior medalhista da natação paralímpica da história da competição e manteve esse título nos Jogos Paralímpicos de Tóquio, 2020. Na adição que resulta o total de medalhas desse nadador, os estudantes retomam o significado de juntar associado a essa operação.
Se possível, peça aos estudantes que levem para a sala de aula calculadoras simples a fim de explorarem um pouco esse recurso em situações de adição.
Proponha aos estudantes novas situações que envolvam os significados de acrescentar ou juntar da adição para identificarem e resolverem, com ou sem o uso de calculadora. Em cada uma das adições efetuadas, retome com eles o significado de parcelas e soma em uma adição.

Sugestão de leitura
Para enriquecer o trabalho com números naturais e suas operações, sugerimos o livro:
PIRES, C. M. C. Números naturais e operações. São Paulo: Melhoramentos, 2013.
Neste livro a autora propõe uma reflexão sobre os caminhos percorridos no ensino de números e operações, retomando aspectos históricos e diferentes abordagens didáticas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Uma piscina está com .35750 litros de água. Colocando-se outros .12250 litros, ela ficará cheia. Quantos litros de água cabem nessa piscina?
2 Dados dois números naturais, em que um é menor que 3 e o outro é menor que 5, é possível a soma deles ser 6? Justifique sua resposta com um exemplo.
3 Segundo estimativa do Instituto Brasileiro de Geografia e Estatística (í bê gê É), estimada em 2021, o estado do Maranhão, sem considerar a capital, São Luís, tinha ..6052794 habitantes. Quantos habitantes tinha todo o estado do Maranhão, se São Luís tinha ..1115932 habitantes?

4 Na ilustração a seguir, está representada a distância rodoviária, em quilômetro, entre as cidades a, B, C, D e ê.
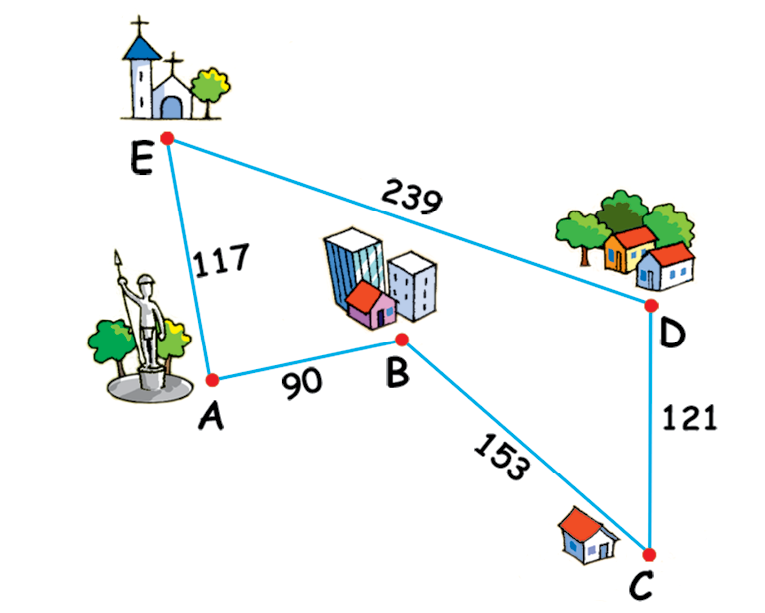
Quantos quilômetros percorre um automóvel que vai de:
a) a até D passando por B e C?
b) a até D passando por ê?
c) a até D passando por B e voltando até C?
d) B até ê passando por D?
5 É possível que a soma de dois números naturais maiores que 3 seja 7? Justifique.
6 Patrícia vai de ônibus para a escola. A viagem de ônibus dura cêrca de 25 minutos e ela ainda caminha mais 11 minutos a pé. Se ela pegar o ônibus às 7 horas e 10 minutos, a que horas ela deve chegar à escola?

7

Durante a decisão de um campeonato de futebol, foram realizadas duas partidas. Na primeira, o público pagante foi de .54321 pessoas, e o público não pagante foi de .3895 pessoas. Na segunda partida, a quantidade de pessoas aumentou: os pagantes foram .63247 pessoas, e os não pagantes, .5894 pessoas. Use uma calculadora para responder às questões a seguir.
a) Quantas pessoas compareceram à primeira partida? E à segunda?
b) Qual é o total de pessoas que assistiram a esses jogos?
8

Escreva no caderno todos os números com três algarismos distintos usando os algarismos 2, 5 e 7. Use uma calculadora para determinar a soma desses números.
9 Quero adicionar um número de um algarismo a um número de dois algarismos.
a) Para obter a soma 100, que pares de números posso escolher?
b) E para obter a soma 108? E para obter a soma 109?
10

Descubra uma maneira de determinar a soma .1893 + .5794 usando a calculadora, sabendo que a tecla 8 está quebrada.
11

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre adição com números naturais. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Respostas e comentários
1. .48000 litros.
2. Sim, pois: 2 + 4 = 6, em que 2 < 3 e 4 < 5.
3. ..7168726 habitantes.
4. a) 364 quilômetros.
4. b) 356 quilômetros.
4. c) 485 quilômetros.
4. d) 513 quilômetros.
5. Não, pois o menor número natural maior que 3 é 4, e, como 4 + 4 = 8, a soma é maior que 7.
6. Patrícia deve chegar à escola às 7 horas e 46 minutos.
7. a) .58216 pessoas; .69141 pessoas.
7. b) .127357 pessoas.
8. 257, 275, 527, 572, 725 e 752; .3108
9. a) 1 e 99; 2 e 98; 3 e 97; 4 e 96; 5 e 95; 6 e 94; 7 e 93; 8 e 92; 9 e 91
9. b) Para obter 108, é possível escolher apenas o par 9 e 99. Para obter 109, nenhum par é possível.
10. Resposta possível: .1493 + 400 + .5794
11. Resposta pessoal.
Exercícios propostos
Os exercícios propostos têm o objetivo de explorar as ideias da adição, juntar e acrescentar, em diferentes contextos.
As resoluções dos exercícios 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 2.
Nos exercícios 7 e 8 propomos o uso da calculadora para alguns cálculos. Aproveite esse momento para verificar se os estudantes fazem o uso correto desse instrumento reconhecendo a funcionalidade das diferentes teclas. Se considerar adequado, proponha que o cálculo seja realizado por meio do algoritmo usual e que a calculadora seja usada para conferência.
No exercício 9, o estudante precisará compreender que o enunciado restringe os números que podem ser parcelas da adição, já que um deles deverá ter um algarismo e o outro, dois algarismos. Como existem apenas dez números de um algarismo (0, 1, 2, 3, 4, 5, 6, 7, 8 e 9), para o item a, uma das possibilidades é testar cada um desses números para, então, encontrar seu par, observando que apenas o número zero não pode ser usado, pois teríamos 0 + 100, ou seja, uma das parcelas teria três algarismos. No item b, a única possibilidade de obter soma 108 é usar o maior número de um algarismo, ou seja, o número 9, para obter a seguinte adição: 99 + 9 = 108. No entanto, mesmo usando o maior número de um algarismo, não é possível obter a soma 109.
No exercício 10, para determinar .1893 + .5794, é preciso encontrar uma maneira de incluir a parcela 800 sem utilizar o algarismo 8. Essa parcela pode ser obtida, por exemplo, pela adição 400 + 400; logo, é possível escrever: .1493 + 400 + .5794. Incentive os estudantes a encontrarem outras decomposições para obter o número 800, chame alguns para ir até a lousa e escrever uma opção de resposta, desse modo, os estudantes perceberão que o exercício admite mais de uma resposta e ampliarão o repertório de estratégias de resolução do problema.
O exercício 11 tem como objetivo fazer com que os estudantes reflitam sobre o que aprenderam e que consigam elaborar uma situação-problema que apresente dados suficientes para responder a uma pergunta. Pode-se fazer um compilado dos problemas elaborados e propor aos estudantes que os resolvam em grupos, de modo a auxiliar os estudantes que tiverem dificuldades com o conteúdo estudado.
Esse exercício permite propor aos estudantes comparações entre os aspectos comuns e os divergentes do cotidiano deles, valorizando a contextualização. A escrita na aula de Matemática exerce papel importante na aprendizagem, pois os faz repensar e aprofundar os textos que produziram, registrar suas reflexões, percepções e o que descobriram sobre um conceito ou mesmo sobre uma situação vivida.
Para o professor, a produção escrita dá não apenas uma boa noção do que a turma aprendeu sobre o que foi desenvolvido nas aulas, mas também permite avaliar como os estudantes expressam suas ideias.
PARA SABER MAIS
Arredondar para fazer estimativas
Conhecer o valor exato de uma contagem nem sempre é tão importante. Em relação à população de um país, por exemplo, se dissermos que ela é de ..169799170 ou de 170 milhões, não estaremos mudando a ideia da quantidade de habitantes que queremos passar.
Nesse caso, dizemos que o número ..169799170 foi arredondado para 170 milhões.
É importante saber arredondar números, pois, em muitas situações do dia a dia, isso nos ajuda a fazer uma estimativa do resultado que queremos.
Arredondar um número significa trocá-lo por outro mais próximo de uma ordem escolhida. Por exemplo, ao comprar três produtos que custam 41, 28 e 19 reais, podemos arredondar esses números para 40, 30 e 20. Assim, é possível saber mais facilmente que o total a pagar é um valor próximo de 90 reais.
A fim de arredondar um número para determinada ordem, deve-se observar o primeiro algarismo que está à direita do algarismo da ordem escolhida: se for 0, 1, 2, 3 ou 4, mantém-se a ordem; se for 5, 6, 7, 8 ou 9, soma-se 1 ao algarismo da ordem escolhida.
Acompanhe exemplos de arredondamentos.
a) Para a dezena mais próxima: 36 → 40 75 → 80 183 → 180 552 → 550
b) Para a centena mais próxima: 236 → 200 657 → 700 .5418 → .5400 .7873 → .7900
c) Para o milhar mais próximo: .5982 → .6000 .24157 → .24000 .37539 → .38000 .44499 → .44000
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Em um posto de saúde, a enfermeira pediu a uma auxiliar que contasse quantas vacinas contra a gripe ainda havia nas três caixas. A auxiliar contou as vacinas de cada caixa e anotou em um papel:
617 + .1578 + 736
Para ter uma ideia do total de vacinas, a enfermeira fez um cálculo mental, arredondando as parcelas para a centena mais próxima. Observe como ela fez isso.

Verifique se o cálculo dela está correto.
2 Em uma loja, Lúcio fez uma estimativa para saber quanto pagaria por suas compras.

a) O que Lúcio fez para perceber o engano do vendedor?
b) Qual foi o valor da compra dele?
c)

Quando você precisa comprar mais de um item, costuma fazer estimativa do valor total antes de pagar? Os adultos com quem você mora costumam fazer isso? Na sua opinião, esse procedimento é importante? Por quê?
Respostas e comentários
1. 600 + .1600 + 700 = .2900; O cálculo dela está correto.
2. a) Estimou o total arredondando os números e fazendo um cálculo mental.
2. b) 121 reais.
2. c) Respostas pessoais.
Para saber mais
A seção constitui uma oportunidade para conversar com os estudantes sobre o uso de estimativas em diferentes situações cotidianas. Pergunte a eles se já fizeram uso deste recurso em alguma situação, por exemplo, para saber se o dinheiro disponível permitiria a compra de determinado produto ou para saber se acertou o resultado de uma operação proposta em uma atividade escolar.
É importante reforçar aos estudantes que, apesar do grande uso cotidiano de cálculos exatos, muitos deles com o uso de calculadora, diversas situações do dia a dia podem ser resolvidas por cálculos aproximados. Solicite a eles que deem exemplos de situações nas quais é comum fazer uso de estimativas.
Na resolução das atividades do Agora é com você!, perceba se ao fazerem o arredondamento, os estudantes fazem uso do cálculo mental como estratégia, uma vez que o arredondamento facilita os cálculos solicitados.
Na primeira atividade, a enfermeira do posto de saúde tinha a intenção de obter um número aproximado do total de vacinas. Para isso, fez arredondamento dos números para 600, .1600 e 700, chegando ao total de .2900. Com os arredondamentos, o resultado é suficiente para atender a algumas situações, por exemplo:
• saber se o total de vacinas é aproximadamente suficiente para atender aos usuários esperados naquele posto, tomando como base a quantidade média diária de atendimentos;
• conferir o custo aproximado de todas as vacinas, conhecendo seu preço unitário.
Aproveite a temática da atividade para conversar com os estudantes sobre a importância da vacinação para a saúde individual e como estratégia de saúde pública. Comente que a vacinação funciona como contrôle e prevenção de muitas doenças, que ao optarem por não se vacinar, os indivíduos colocam em risco sua saúde e a da comunidade. Conversas como essas contribuem para o trabalho com os Temas Contemporâneos Transversais saúde e vida familiar e social.
No item a da atividade 2 os estudantes devem perceber que ao fazer uma estimativa por arredondamentos, Lúcio conseguiu perceber que o vendedor se enganou em seus cálculos.
No item b, devem determinar o cálculo exato efetuando a adição: 19 + 38 + 64 = 121.
No item c devem refletir sobre o uso de estimativas em situações cotidianas, como a de compra de produtos. Espera-se que eles compreendam que tal procedimento é uma importante ferramenta para que o gasto fique dentro do esperado, contribuindo para o contrôle do orçamento familiar. Ao propor essa reflexão aos estudantes, contribuímos para o desenvolvimento do Tema Contemporâneo Transversal educação financeira.
Propriedades da adição
Para ir à escola, Carlos gasta, em média, 20 minutos andando e 25 minutos no ônibus. Para voltar da escola, ele gasta, em média, 25 minutos no ônibus e 20 minutos andando. Carlos leva mais tempo na ida ou na volta da escola?
Para saber, devemos adicionar os tempos gastos:
• Tempo gasto na ida: 20 + 25 = 45
• Tempo gasto na volta: 25 + 20 = 45
Em média, o tempo gasto é o mesmo, 45 minutos.
A ordem das parcelas não alterou a soma. Isso sempre ocorre quando adicionamos dois números naturais quaisquer. Trata-se da propriedade comutativa da adição, enunciada a seguir.
Em uma adição de dois números naturais, a ordem das parcelas não altera a soma.
Observe mais alguns exemplos.
a) 20 + 400 = 400 + 20
b) 130 + 500 = 500 + 130
Agora, observe dois modos de efetuar a adição 5 + 3 + 7.
1º) Efetua-se a adição das duas primeiras parcelas e adiciona-se ao resultado obtido a terceira parcela.

2º) Efetua-se a adição das duas últimas parcelas e adiciona-se ao resultado obtido a primeira parcela.

Ao associar as parcelas de modos diferentes, não houve alteração na soma. Isso sempre ocorre quando adicionamos três ou mais números naturais quaisquer. Trata-se da propriedade associativa da adição, enunciada a seguir.
Em uma adição de três ou mais números naturais quaisquer, podemos associar as parcelas de modos diferentes sem alterar a soma.
Observe mais alguns exemplos.
a)

b)
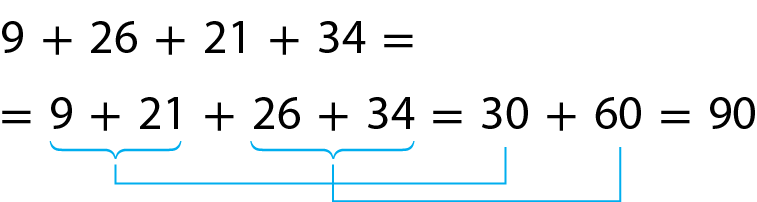
Agora, considere as seguintes adições:
• 5 + 0 = 0 + 5 = 5
• 0 + 7 = 7 + 0 = 7
• 53 + 0 = 0 + 53 = 53
Note que em todas essas adições há um número (o zero) que, em qualquer posição, não influi no resultado. Esse número é o elemento neutro da adição. A adição de um número natural qualquer com zero (ou vice-versa) é o próprio número. Trata-se de mais uma propriedade da adição: a existência do elemento neutro, enunciada a seguir.
O zero é o elemento neutro da adição.
Respostas e comentários
Propriedades da adição
Iniciamos o estudo das propriedades da adição ampliando as noções que os estudantes já trazem dos anos anteriores.
A propriedade do fechamento não foi considerada aqui porque não estamos realizando um estudo axiomático da teoria dos conjuntos.
Durante o trabalho com as propriedades, mostre na lousa situações em que os estudantes podem verificar quanto as propriedades da adição auxiliam no cálculo mental. Por exemplo, peça a eles que obtenham a soma da seguinte adição:
345 + 0 + 99 + 5 + 21
Discuta cada passagem a seguir com eles, de modo que percebam o que foi feito.
• Pela propriedade comutativa, podemos trocar a ordem das parcelas, convenientemente, já que a soma não é alterada: 345 + 0 + 99 + 5 + 21 = = 345 + 5 + 0 + 99 + 21
• Pela propriedade associativa, podemos associar as parcelas de maneira conveniente, pois a soma também não se altera: 345 + 0 + 99 + 5 + 21 = = 345 + 5 + 0 + 99 + 21 = = (345 + 5) + 0 + (99 + 21) = = 350 + 0 + 120
• Como o zero é o elemento neutro da adição, sabemos que 350 + 0 = 350, ou seja: 345 + 0 + 99 + 5 + 21 = = 345 + 5 + 0 + 99 + 21 = = (345 + 5) + 0 + (99 + 21) = = 350 + 0 + 120 = = 350 + 120 = 470
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
12

Efetue mentalmente estas adições. Para facilitar o cálculo, utilize as propriedades comutativa e associativa da adição. Registre no caderno como calculou.
a) 73 + 15 + 5
b) 20 + 13 + 7
c) 18 + 12 + 61
d) 28 + 17 + 12
e) 15 + 0 + 5 + 9
f) 43 + 51 + 27
13

Para calcular mentalmente, Mônica usa a decomposição dos números. Observe como ela faz:

Refaça os cálculos da atividade anterior aplicando a estratégia usada por Mônica.
14 Tatiana jogou dois dados, obtendo uma soma de 9 pontos. Quais são os possíveis pares de números para que ocorra essa soma?
15 Bruno mora em Uberlândia e vai viajar para Aracaju. Ele terá de percorrer .1837 quilômetros de carro. No painel do carro há um instrumento chamado hodômetro, que marca quantos quilômetros o veículo já percorreu. No início da viagem, o hodômetro marcava .18540 quilômetros.
a) Que número marcará o hodômetro quando Bruno chegar a Aracaju?
b) Durante a estadia em Aracaju, Bruno supõe que vai percorrer cêrca de .1400 quilômetros. Quanto deverá marcar o hodômetro quando ele iniciar a volta para casa?
16 Patrícia foi com seu pai comprar material escolar. Durante as compras, ela foi conferindo e anotando os preços dos produtos. Observe a lista de Patrícia:

O pai de Patrícia disse que não podia gastar mais de 60 reais. Ao ouvir isso, ela fez as contas mentalmente e disse que poderia comprar o apontador, que custava 3 reais, pois ainda restariam 7 reais.

O cálculo que Patrícia fez está correto? Explique por que ela pode fazer o cálculo dessa maneira.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Estude os vários caminhos possíveis para que, ao entrar pelo lugar indicado, você consiga chegar até a saída.
Você deve seguir pelas linhas azuis e pode andar em todas as direções, exceto voltar por onde veio. Ao passar por um número, você deve adicioná-lo ao total que já tem. Você só pode sair pelo lugar indicado quando a soma obtida for 37.
Descubra um caminho possível e indique-o pelos números que serão colocados na ordem de percurso.
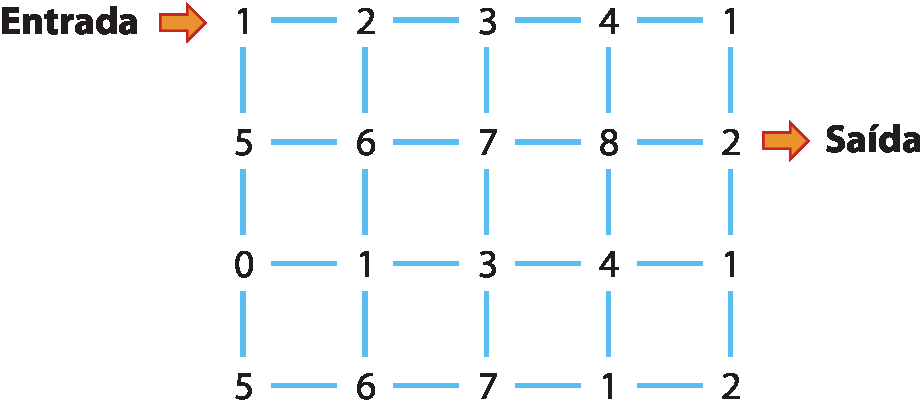
Respostas e comentários
12. a) 93
12. b) 40
12. c) 91
12. d) 57
12. e) 29
12. f) 121
13. a) 73 + 15 + 5 = (70 + 10) + (3 + 5 + 5) = 80 + 13 = 93
13. b) 20 + 13 + 7 = (20 + 10) + (3 + 7) = 30 + 10 = 40
13. c) 18 + 12 + 61 = (10 + 10 + 60) + (8 + 2 + 1) = 80 + 11 = 91
13. d) 28 + 17 + 12 = (20 + 10 + 10) + (8 + 7 + 2) = 40 + 17 = 57
13. e) 15 + 0 + 5 + 9 = 10 + (5 + 5 + 9) = 10 + 19 = 29
13. f) 43 + 51 + 27 = (40 + 50 + 20) + 3 + 1 + 7 = 110 + 11 = 121
14. 3 e 6, 4 e 5
15. a) .20377
15. b) .21777
16. Sim; ela usou a propriedade associativa da adição.
Pense mais um poucoreticências: 1, 5, 6, 7, 8, 4, 1, 2, 1 e 2
Exercícios propostos
Este bloco de exercícios explora a aplicação das propriedades da adição. Observe se os estudantes aplicam as propriedades estudadas de maneira conveniente, de modo a facilitar os cálculos. Compartilhe os diferentes procedimentos utilizados a fim de que eles possam comparar o que fizeram com o modo utilizado por outro colega e, assim, refletir sobre suas escolhas.
As resoluções dos exercícios 12 a 15 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 16, os estudantes devem perceber que a soma de Patrícia está certa, pois 9 + 14 + 21 + 6 = 50 e com mais 3 reais, o total seria de 53 reais. Para fazer o cálculo, Patrícia utilizou a propriedade associativa da adição, que diz que podemos associar as parcelas de modos diferentes sem alterar a soma. Espera-se que os estudantes percebam que a estratégia de Patrícia facilitou o cálculo.
Pense mais um poucoreticências
Na situação proposta nesta seção, o caminho pode ser descoberto por tentativa e erro. Um possível caminho deve passar pelos números 1, 5, 6, 7, 8, 4, 1, 2, 1 e 2, conforme indicado na figura a seguir.
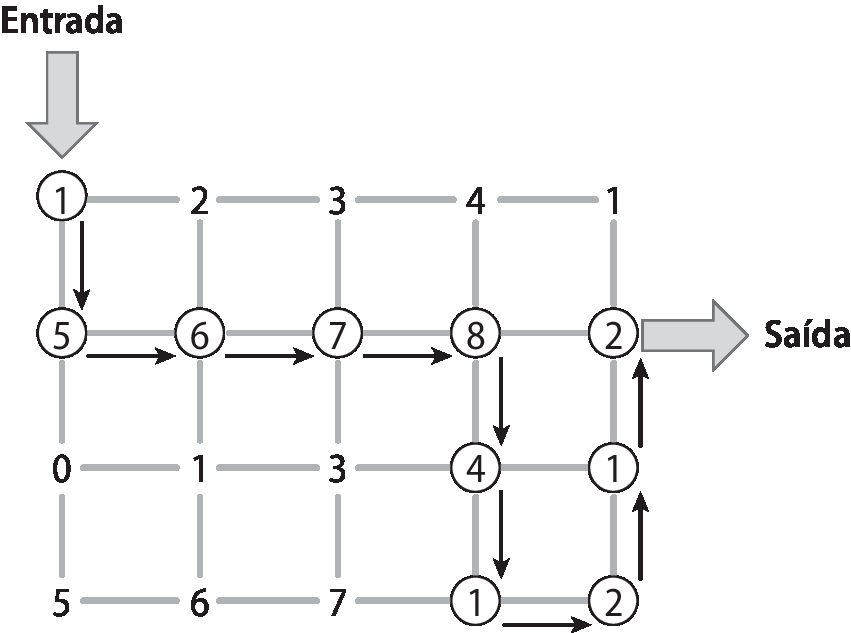
Outro caminho possível seria passar pelos números: 1, 5, 6, 7, 3, 7, 1, 4, 1 e 2.
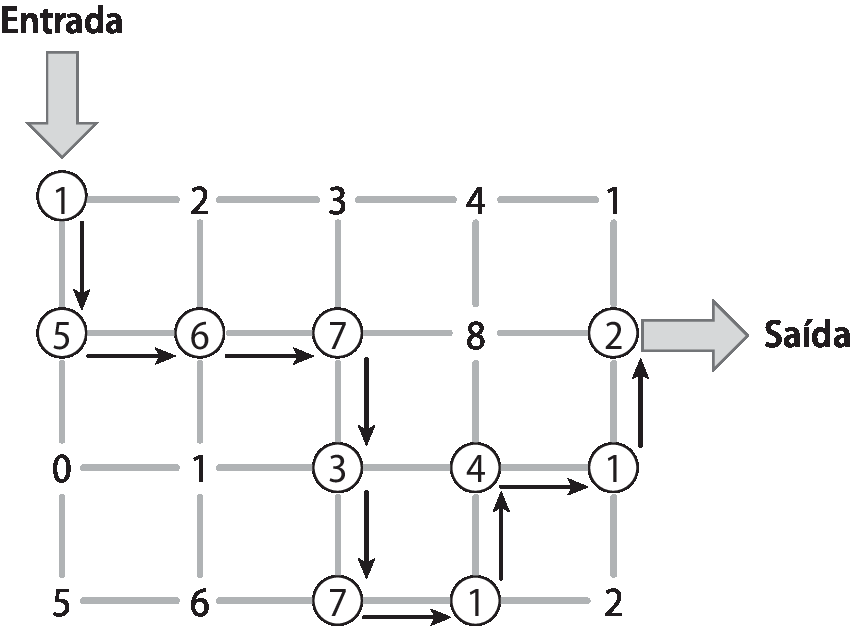
Incentive os estudantes a compartilhar as diferentes resoluções que encontrarem.
PARA SABER MAIS
Quadrado mágico
Quadrado mágico é um quadrado dividido em 4, 9, 16, 25 etcétera quadradinhos ocupados por números diferentes cuja soma dos números de qualquer linha, coluna ou diagonal tem um mesmo valor, que se chama soma mágica.
Os chineses chamavam o quadrado de lo-shu; na Figura 1, temos a representação de um quadrado mágico datado de 2850 antes de Cristo Na Figura 2, você encontra a transcrição para algarismos indo-arábicos.
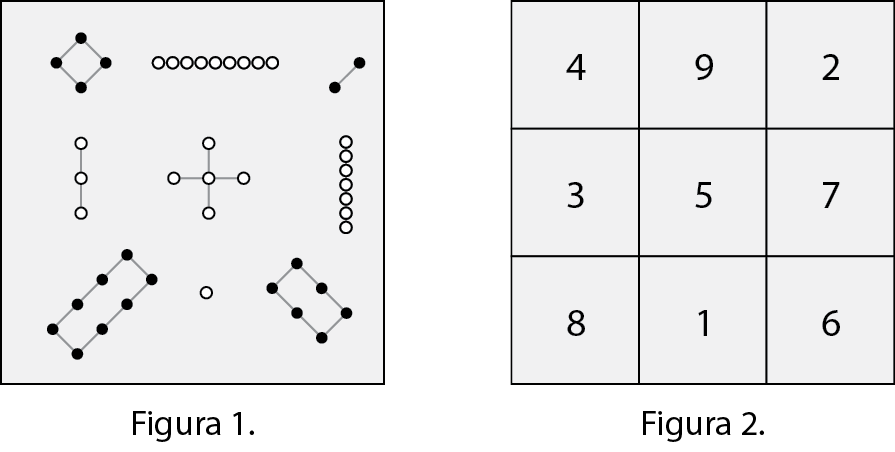
Esse é um quadrado mágico de ordem 3 (três linhas e três colunas), em que aparecem os números naturais de 1 a 9, cuja soma mágica é 15.
Com o passar do tempo, os quadrados mágicos ficaram conhecidos no Ocidente, tornando-se muito populares no século dezesseis. A presença do quadrado mágico nesse período mostrou-se tão significativa que o pintor alemão Albrechi Durrár (1471‑1528) o relatou em Melancolia um, gravura de 1514.
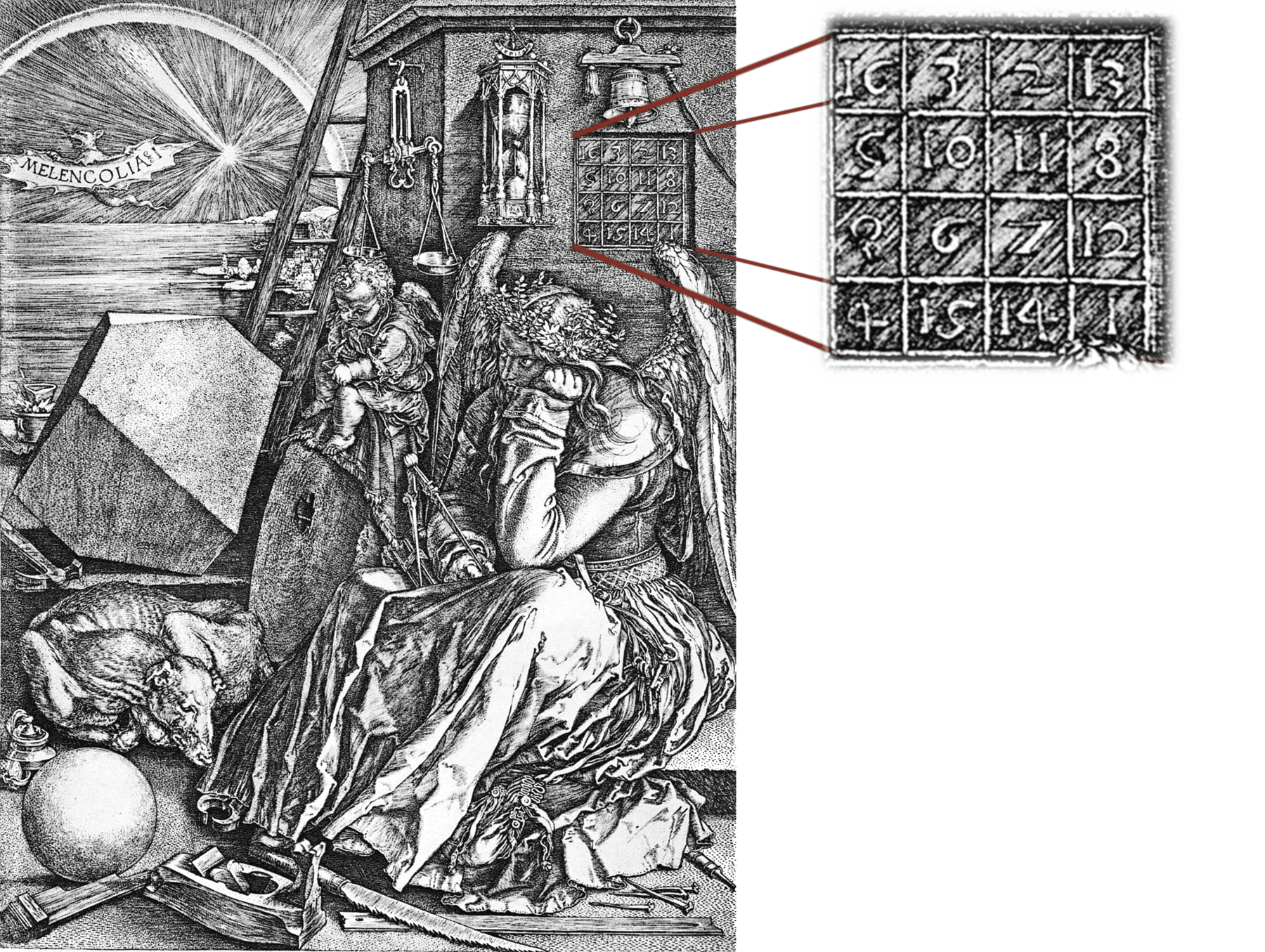
Alguns quadrados mágicos apresentam propriedades diferenciadas.
O quadrado hipermágico é aquele que pode ser decomposto em vários quadrados mágicos.
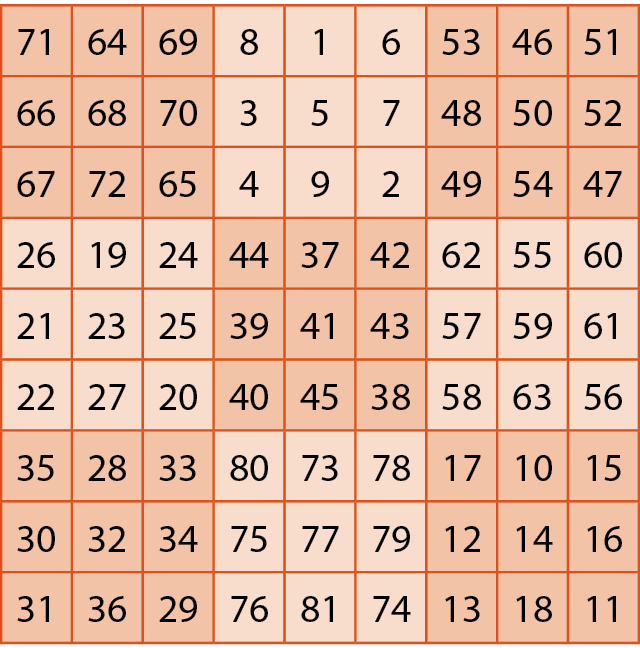
O quadrado ilustrado é hipermágico de ordem 9 e soma mágica 369. Ele pode ser decomposto em 9 quadrados mágicos de ordem 3.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Determine a soma mágica de cada um dos quadrados mágicos de ordem 3 obtidos a partir do quadrado hipermágico citado.
2 Escolha um dos quadrados cuja soma você calculou no exercício 1. Adicione 12 a cada número dele e verifique se o quadrado obtido ainda é mágico. Quanto aumentou a soma mágica?
3 Sabendo que, ao adicionar um mesmo número x a cada número de um quadrado mágico, fazemos a soma mágica aumentar 3 unidades, qual é o número x adicionado?
4 Usando os números 2, 3, 4, 5, 6, 7, 8, 9 e 10, construa um quadrado mágico de soma 18.
Respostas e comentários
1. 204; 15; 150; 69; 123; 177; 96; 231; 42
2. É. A soma mágica aumentou 36 unidades.
3. x = 1
4. Resposta possível:
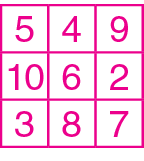
Para saber mais
O tema desta seção é um clássico dos jogos matemáticos: o quadrado mágico e o quadrado hipermágico. Além da aplicação do conhecimento matemático e da agilidade de raciocínio, os estudantes experimentam aqui o desafio de uma atividade lúdica que costuma ser muito proveitosa.
A seção pode ser trabalhada em duplas, desde a leitura do texto, que explora um pouco da história do quadrado mágico, até a realização das atividades propostas.
Ao explorar a gravura Melancolia um, apresentamos aos estudantes um exemplo de como a Matemática se relaciona com diferentes áreas do conhecimento, neste caso, com a Arte, contribuindo para o desenvolvimento da competência geral 3. O artista Albrechi Durrár desenvolveu máquinas para desenhar em perspectiva. Para saber mais sobre essas máquinas, sugerimos a leitura do seguinte trabalho:
MENEGUZZI, T. Os perspectógrafos de durrár na Educação Matemática: história, geometria e visualização. 2009. Dissertação (mestrado em Educação Científica e Tecnológica) – Universidade Federal de Santa Catarina, Florianópolis, 2009.
Antes das atividades propostas no Agora é com você!, peça a cada dupla que exponha os pontos do texto que acharam mais interessantes. Em seguida, os estudantes resolvem as questões e comparam os resultados obtidos com outra dupla, promovendo uma autocorreção entre eles. Fique atento para fazer as intervenções que achar necessárias no sentido de auxiliá-los nessa tarefa.
Na atividade 1, os estudantes devem encontrar 9 quadrados mágicos, com as seguintes somas:
um) 71 + 64 + 69 = 204;
dois) 8 + 1 + 6 = 15;
três) 53 + 46 + 51 = 150;
quatro) 26 + 19 + 24 = 69;
cinco) 44 + 37 + 42 = 123;
seis) 62 + 55 + 60 = 177;
sete) 35 + 28 + 33 = 96;
oito) 80 + 73 + 78 =231;
nove) 17 + 10 + 15 = 42.
Na atividade 2, considerando o quadrado mágico de soma 15, obtém-se:
8 + 12 = 20; 1 + 12 = 13; 6 + 12 = 18; 3 + 12 = 15; 5 + 12 = 17; 7 + 12 = 19; 4 + 12 = 16; 9 + 12 = 21 e 2 + 12 = 14.
Para verificar se o novo quadrado será mágico, devem obter a soma das linhas, colunas e diagonais e verificar se são iguais:
20 + 13 + 18 = 51; 15 + 17 + 19 = 51;
16 + 21 + 14 = 51; 20 + 15 + 16 = 51;
13 + 17 + 21 = 51; 18 + 19 + 14 = 51;
20 + 17 + 14 = 51; 18 + 17 + 16 = 51.
Antes a soma mágica era 15 e passou a ser 51, aumentando em 36 unidades (51 ‒ 15 = 36).
A resolução das atividades 3 e 4 estão no início deste Manual, nas orientações específicas do capítulo 2.
2. Subtração
Acompanhe estas situações.
Situação 1

Em apenas 20 anos, a população de onças-pintadas [diminuiu] no Parque Nacional do Iguaçu (PARNA Iguaçu), em Foz do Iguaçu, no Paraná, área que protege uma riquíssima biodiversidade da fauna e flora brasileiras. Segundo o Instituto para a Conservação dos Carnívoros Neotropicais (Pró-carnívoros), que trabalha com o monitoramento da espécie no Parque, as onças-pintadas foram reduzidas de 100 indivíduos para 20 indivíduos. reticências

Entre as ameaças para garantir a espécie viva na reserva, o Instituto aponta a falta de investimentos em estrutura e fiscalização, a caça predatória e de retaliação e a possibilidade de reabertura da Estrada do Colono.
Na Mata Atlântica, a estimativa é de que existam apenas duzentas e cinquenta onças-pintadas, maior felino do continente americano e maior predador terrestre do Brasil. A perda do hábitat reticências da espécie em razão do desmatamento para dar lugar a atividades agropecuárias ou pastagens nativas é crítica para o animal.
Fonte: WWF-BRASIL apoia monitoramento de onças-pintadas no Parque Nacional de Iguaçu. WWF-Brasil. 6 janeiro 2015. Disponível em: https://oeds.link/niV0el. Acesso em: 23 janeiro 2022.
Com os dados obtidos nesse texto, é possível descobrir quanto diminuiu a população de onças-pintadas do Parque Nacional do Iguaçu em 20 anos. Para isso, devemos tirar do total de indivíduos que existiam há 20 anos o total de indivíduos que existem hoje.

Logo, foram reduzidas 80 onças-pintadas.
Em uma calculadora, fazemos essa subtração da seguinte maneira:

Situação 2
Os oceanos abrigam a maior biodiversidade da Terra. O Registro Mundial de Espécies Marinhas é um banco de dados com a listagem dos seres conhecidos nos oceanos. Por enquanto, a lista soma .232588 espécies catalogadas, de um total de .239782 conhecidas.

Respostas e comentários
2. Subtração
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico ampliamos o trabalho com a habilidade (ê éfe zero seis ême ah zero três) ao retomar as ideias de subtração com números naturais, conceito estudado ao longo dos anos iniciais do Ensino Fundamental.
Na situação 1, que inicia o estudo da operação subtração, apresentamos um texto sobre a queda da população de onças-pintadas em um parque nacional. Faça a leitura do texto com os estudantes destacando as causas para essa queda, que são a caça predatória e a devastação da mata nativa. Aproveite para chamar a atenção dos estudantes para a necessidade de preservação do meio ambiente, tanto da fauna quanto da flora. Muitos animais foram extintos, ou estão em processo de extinção, como é o caso da onça-pintada. É uma oportunidade para discutir as causas da extinção dos animais, principalmente em função da destruição dos seus hábitats.
Deste modo, amplia-se o trabalho com o Tema Contemporâneo Transversal educação ambiental e com a competência geral 7.
Com as informações extraídas do texto, é possível descobrir quantas espécies o Registro Mundial de Espécies Marinhas ainda tem de catalogar para completar seu banco de dados. Para isso, devemos subtrair do total de espécies conhecidas o número de espécies já catalogadas:

Portanto, o Registro Mundial de Espécies Marinhas ainda tem de catalogar .7194 espécies.
Em uma calculadora, fazemos essa subtração da seguinte maneira:

Situação 3

Quantos médicos tem no Brasil?
De acordo com o estudo Demografia Médica Brasileira 2020, são 500 mil médicos no país [reticências].
Trata-se do maior quantitativo de médicos já registrado. Os dados apurados em 2020 são revelados em meio à maior crise da saúde mundial com a pandemia do novo coronavírus, [na qual] o médico e os demais profissionais da saúde estão na linha de frente.

Há 100 anos, em 1920 o número de médicos registrados era .14031.
Fonte: REVISAMED. Brasil tem 500 mil médicos, revela demografia 2020. 26 janeiro 2021. Disponível em: https://oeds.link/ETdjVy. Acesso em: 22 dez. 2021.
Para calcular quanto aumentou o número de médicos registrados no Brasil em um século, devemos comparar a quantidade relativa a 2020 com a quantidade relativa a 1920.

Portanto, o número de médicos registrados no Brasil aumentou, em um século, .485969.
Em uma calculadora, fazemos essa subtração da seguinte maneira:

As ideias de tirar, completar ou comparar estão relacionadas à subtração.
Respostas e comentários
Subtração
A retomada e a ampliação da subtração são feitas de modo similar ao da adição, com situações de contextos variados que destacam os significados associados a essa operação: tirar uma quantidade de outra, completar uma quantidade para atingir outra e comparar duas quantidades para obter a diferença entre elas.
Sugerimos que explore a subtração também com o uso de uma calculadora simples, pedindo aos estudantes que registrem no caderno o que fazem, nomeando os termos de cada subtração realizada: minuendo, subtraendo e resto (ou diferença).
Ao trabalhar com a situação 3, comente com os estudantes que, apesar do número de 500 mil médicos registrados, ainda faltam médicos em muitas unidades do Sistema Único de Saúde (SUS), é o que aponta a Demografia Médica do Brasil, realizada em 2020 pelo Conselho Federal de Medicina (CFM) em parceria com a Faculdade de Medicina da USP. Segundo esse estudo, a falta de médicos em determinados contextos envolve fatores distintos, desde aspectos demográficos e epidemiológicos da população, passando pelo financiamento e pelas relações entre público e privado no sistema de saúde, até a remuneração, carreira e condições de trabalho dos profissionais.
Ao conversar sobre essa realidade, contribui-se para o trabalho com o Tema Contemporâneo Transversal saúde.

Sugestão de leitura
Para ampliar a conversa sobre o tema da demografia médica, pode-se utilizar o seguinte material:
SCHEFFER, M. et al. Demografia Médica no Brasil 2020. São Paulo: Efe Eme Uspi, CFM, 2020. 312 página Disponível em: https://oeds.link/ibPaIa. Acesso em: 12 maio 2022.
Levantamento sobre as características e evolução da população de médicos no Brasil.
3. Adição e subtração
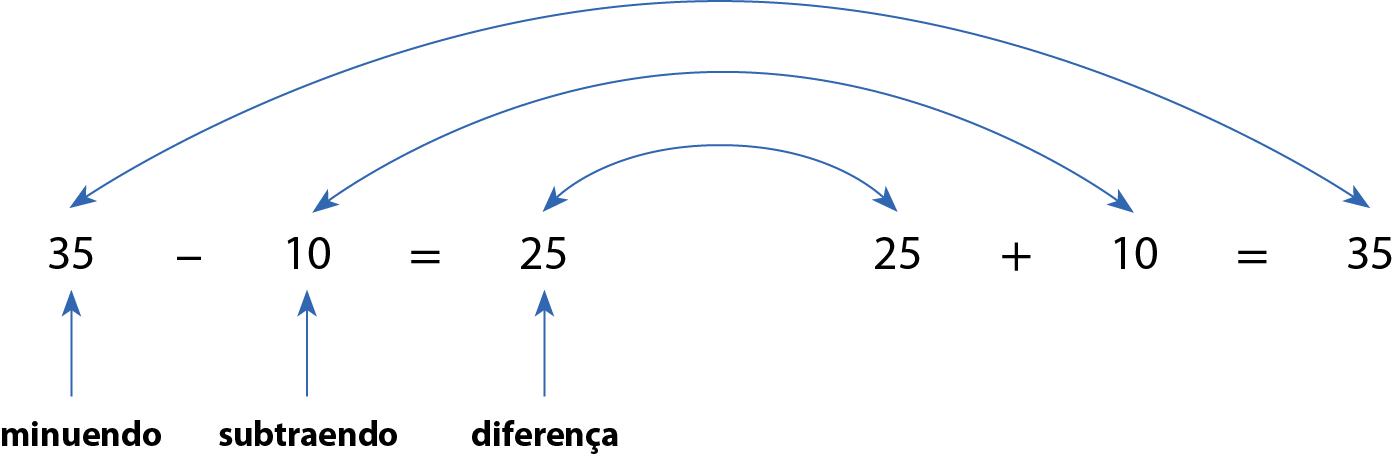
Observe as operações a seguir.

Acompanhe mais alguns exemplos.
a) 60 ‒ 20 = 40 porque 40 + 20 = 60,
e 40 + 20 = 60 porque 60 ‒ 20 = 40 ou porque 60 ‒ 40 = 20.
b) 125 ‒ 32 = 93 porque 93 + 32 = 125,
e 93 + 32 = 125 porque 125 ‒ 32 = 93 ou porque 125 ‒ 93 = 32.
Portanto, as sentenças 60 ‒ 20 = 40 e 40 + 20 = 60 são equivalentes, assim como as sentenças 125 ‒ 32 = 93 e 93 + 32 = 125.
Considerando os termos de uma subtração, percebemos que, ao adicionar a diferença com o subtraendo, obtemos o minuendo. Podemos verificar se uma dessas operações está correta por meio da outra. Dizemos, então, que a adição e a subtração são operações inversas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
17 Cristina saiu de casa com 5 cédulas de 10 reais, 3 moedas de 1 real e duas cédulas de 2 reais. Gastou 35 reais para pagar seu almoço.
a) Quanto dinheiro sobrou?
b) De que maneira Cristina pôde pagar a conta sem receber troco?
18

Use uma calculadora para determinar a diferença entre .67185 e .31846. Em seguida, verifique se você acertou, efetuando a operação inversa.
19 Efetue as subtrações e associe a cada uma delas a adição correspondente.
a) .5812 ‒ .4815
b) .72368 ‒ .25586
20 Efetue a adição 416 + 209 e associe a ela as duas subtrações correspondentes.
21

Considere a tabela a seguir.
|
Ano |
||
|---|---|---|
|
Regiões em desenvolvimento |
2005 |
2020 |
|
África |
195 |
282 |
|
Ásia |
554 |
418 |
|
América Latina e Caribe |
52 |
60 |
|
Oceania |
2 |
3 |
Dados obtidos em: THE STATE of Food Security and Nutrition in the World. fáo, Roma, 2021. Disponível em: https://oeds.link/Er8aSx. Acesso em: 18 mar. 2022.
Com o auxílio de uma calculadora, descubra a diferença, em milhões, entre as populações malnutridas, de 2005 e 2020, na Ásia e na América Latina e Caribe.
Respostas e comentários
17. a) 22 reais.
17. b) 3 notas de 10, uma nota de 2 e 3 moedas de 1 ou 3 notas de 10, duas notas de 2 e uma moeda de 1.
18. .35339
19. a) 997; 997 + .4815 = .5812
19. b) .46782; .46782 + .25586 = .72368
20. 625; 625 ‒ 209 = 416 e 625 ‒ 416 = 209
21. Ásia: 136 milhões de pessoas; América Latina e Caribe: 8 milhões de pessoas.
3. Adição e subtração
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico, tratamos da relação entre a adição e a subtração como operações inversas, ampliando o trabalho com a habilidade (ê éfe zero seis ême ah zero três).
Antes de apresentar a adição e a subtração como operações inversas, proponha aos estudantes, que em grupos, respondam à pergunta apresentada pela personagem. Peça a eles que pensem em diferentes números antes de apresentarem uma conclusão. Depois, peça-lhes que compartilhem com os demais colegas de turma.
Exercícios propostos
O bloco de exercícios que se inicia nesta página explora a subtração e suas relações com a adição.
As resoluções dos exercícios 17 a 20 estão no início deste Manual, nas orientações específicas do capítulo 2.
Aproveite o exercício 21, que apresenta alguns dados sobre a fome no mundo, para discutir com os estudantes a questão do desperdício de alimentos, por meio de uma discussão sobre o direito à alimentação, que, no caso do Brasil, é um direito constitucional. Incentive-os a pesquisar sobre o tema e mostre a eles o artigo correspondente da Constituição: “São direitos sociais [individuais e coletivos] a educação, a saúde, a alimentação, o trabalho, a moradia, o lazer, a segurança, a previdência social, a proteção à maternidade e à infância, a assistência aos desamparados, na fórma desta Constituição”. Assim, contribuímos para o desenvolvimento da competência geral 9 e ampliamos o trabalho com os Temas Contemporâneos Transversais educação em direitos humanos e direitos da criança e do adolescente.
Amplie este exercício explorando a interpretação dos dados da tabela questionando, por exemplo:
• Em que regiões houve aumento da população malnutrida de 2005 para 2020? (África, América Latina e Caribe, Oceania.)
• Em que regiões houve diminuição da população malnutrida de 2005 para 2020? (Ásia.)
Ainda é possível discutir com os estudantes fatores que expliquem o problema da fome na África. Eles podem fazer uma pesquisa prévia e trazer elementos para essa discussão, como os do texto a seguir.
É de conhecimento de todos que a África convive com o problema da fome, agora basta saber quais fatores desencadearam as diversas mazelas sociais que essa parte do mundo se sujeita.
Uma das causas da fome está ligada à fórma de ocupação do território e a extrema dependência econômica externa, herdada do período do colonialismo. Isso é agravado ainda mais com o acelerado crescimento populacional. reticências
FREITAS, E. As principais causas da fome na África. UOL Mundo Educação. Disponível em: https://oeds.link/CdkoMZ. Acesso em: 15 fevereiro 2022.
22 Nem sempre é possível efetuar uma subtração de dois números naturais. Nas subtrações indicadas a seguir, anote no caderno o resultado daquelas que podem ser realizadas.
a) 206 menos 48
b) 116 menos 116
c) 54 menos 75
d) 91 menos 91
e) 13 menos 23
f) 67 menos 49
23 Quando é possível efetuar uma subtração de dois números naturais?
24 Podemos dizer que para a subtração vale a propriedade comutativa? Dê um exemplo que justifique sua resposta.
25

Bruna conseguiu 27 figurinhas com um amigo. Ela já tinha 173 figurinhas em seu álbum e queria saber com quantas ficou. Para isso, ela fez a seguinte adição:

Converse com um colega sobre como Bruna resolveu o problema. Você conhece outra maneira de calcular o número de figurinhas? Explique como você resolveria.
26 Em uma subtração, a diferença é 26. Qual será o valor da nova diferença se aumentarmos 10 unidades no subtraendo? E se o minuendo aumentar em 4 unidades? E se o minuendo e o subtraendo aumentarem em 9 unidades?
27 Considere o texto de abertura deste capítulo. Se, nos Jogos Paralímpicos de Tóquio, em 2020, o Brasil conquistou 30 medalhas de bronze e 20 medalhas de prata, que operação matemática devemos fazer para obter o número de medalhas de bronze a mais que de prata que a delegação brasileira ganhou?
28 Ao fazer uma jarra de limonada, coloquei 100 gramas de açúcar. Depois, coloquei mais 50 gramas. Experimentei e não estava boa. Resolvi acrescentar 250 gramas de açúcar. A limonada ficou gostosa, mas muito doce. Cheguei à conclusão de que o último acréscimo de açúcar deveria ter sido de apenas 150 gramas.
a) Quantos gramas de açúcar coloquei no total?
b) Quantos gramas coloquei a mais que o ideal para meu paladar?
29 Lembrando que a adição e a subtração são operações inversas, descubra que número natural cada etiqueta (

) esconde.
a)

menos 12 = 20
b)

+ 36 = 75
c)

menos 15 = 25
d)

+ 98 = 231
30 De um número natural x de três algarismos, quero subtrair um número de dois algarismos e obter outro número natural de um algarismo.
a) Se x for 100, que números posso escolher?
b) E se x for 108?
c) E se x for 109?
31

Hora de criar ‒ Em duplas, cada integrante vai elaborar um problema que deve ser resolvido por meio da adição e da subtração com números naturais e que deve ter resultado final igual a 83. Depois, conversem sobre os problemas elaborados e verifiquem se atendem à proposta apresentada.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
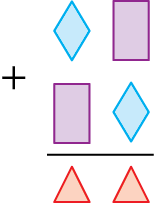
Descubra, em cada item, o valor de

,

e

, sabendo que representam, nessa ordem, números consecutivos formados por um algarismo.
a)
b)
Respostas e comentários
22. a) 158
22. b) 0
22. c) Impossível.
22. d) 0
22. e) Impossível.
22. f) 18
23. Só é possível quando o minuendo for maior ou igual ao subtraendo.
24. Não, pois 10 menos 5 ≠ 5 ‒ 10.
25. Resposta pessoal.
26. 16; 30; a diferença não se altera.
27. Subtração.
28. a) 400 gramas.
28. b) 100 gramas.
29. a) 32
29. b) 39
29. c) 40
29. d) 133
30. a) 99, 98, 97, 96, 95, 94, 93, 92, 91
30. b) Apenas 99.
30. c) Não é possível.
31. Resposta pessoal.
Pense mais um poucoreticências:
a)

= 1

= 2

= 3
b)

= 7

= 8

= 9
Exercícios propostos
As resoluções dos exercícios 22 a 31 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 25, espera-se que os estudantes percebam que, ao adicionar (7 ‒ 7), Bruna usou a propriedade do elemento neutro.
No exercício 26, a compreensão de certas propriedades das operações (no caso, da subtração) é um grande auxílio à ampliação do repertório para o cálculo e ao desenvolvimento da habilidade de resolver problemas. Após alguns testes, em que se aumentam o minuendo e o subtraendo da mesma maneira, os estudantes devem concluir que o resultado da subtração “original” vai permanecer. Essa ideia poderá ser empregada na realização de cálculos mentais quando modificamos/manipulamos os números dados no intuito de obter valores mais simples para a execução desses cálculos.
No exercício 28, como no item a os estudantes encontraram o total de açúcar utilizado, talvez alguns pensem em utilizar esse resultado (400 gramas) para chegar à resposta do item b:
• 100 + 50 + 150 = 300 (total de açúcar, em grama, caso tivesse colocado a quantidade correta)
• 400 menos 300 = 100 (diferença entre a quantidade de açúcar colocada e a quantidade ideal, em grama)
É interessante discutir que esses cálculos poderiam ser reduzidos, com alteração apenas na terceira vez em que o açúcar foi colocado, ou seja, só seria calculada a diferença nessa vez: 250 menos 150 = 100 (100 gramas).
Essa é uma boa oportunidade para integrar a Matemática com o cotidiano e fazer relações entre conhecimentos relativos tanto aos números e às operações quanto associados a grandezas e medidas.
Pense mais um poucoreticências
Este é um bom momento para trabalhar a habilidade de lidar com sistemas simbólicos. No item a, observando a primeira coluna da adição, é possível perceber que o único caso em que

+

=

é

= 1,

= 2 e

= 3, pois a soma de nenhum outro par de números consecutivos de um só algarismo resulta no consecutivo do maior número desse par: 2 + 3 = 5, 3 + 4 = 7, 4 + 5 = 9.
Ao resolver o item b por tentativa e erro, podem depreender da 1ª linha que os símbolos

e

representam números consecutivos, com

=

+ 1. Logo, as únicas possibilidades para a escrita de

e

são: 10, 21, 32, 43, 54, 65, 76, 87 e 89. Efetuando todas as subtrações correspondentes, a única que satisfaz a condição é

= 7,

= 8 e

= 9.
TRABALHANDO A INFORMAÇÃO
Construindo quadros e tabelas
A Medalha Internacional de Descobrimentos Proeminentes em Matemática, conhecida popularmente como Medalha Fields, é concedida a dois, três ou quatro matemáticos com idade máxima de 40 anos. É o prêmio mais importante dessa área, frequentemente comparado ao Prêmio Nobel.

Desde que foi instituída pelo matemático canadense John Charles Fields, em 1936, essa medalha tem sido entregue a cada quatro anos a jovens matemáticos que tenham grandes destaques em suas pesquisas.


Em 2018, os medalhistas foram Alessio Figalli (italiano), Ashkay Venkatesh (australiano de origem indiana), Caucher Birkar (britânico de origem curda) e Peter Scholze (alemão).
De maneira aleatória, as Medalhas Fields distribuídas até 2018 estão listadas a seguir, de acordo com os países de naturalidade dos condecorados.
|
EUA |
Reino Unido |
EUA |
EUA |
Reino Unido |
Irã |
|
Ucrânia |
França |
Japão |
Rússia |
França |
Nova Zelândia |
|
Japão |
Rússia |
Brasil |
EUA |
Reino Unido |
EUA |
|
Rússia |
EUA |
França |
Itália |
Alemanha |
Israel |
|
França |
França |
França |
EUA |
Austrália |
China |
|
Canadá |
Vietnã |
Rússia |
França |
França |
França |
|
EUA |
Noruega |
Japão |
Áustria |
Bélgica |
Itália |
|
Reino Unido |
EUA |
EUA |
Rússia |
Rússia |
Índia |
|
Bélgica |
Suécia |
França |
EUA |
EUA |
Irã |
|
Finlândia |
Rússia |
África do Sul |
Reino Unido |
Rússia |
Alemanha |
Observe que essa lista, com dados dispostos aleatoriamente, não oferece uma leitura prática para sabermos quantas Medalhas Fields foram concedidas a cada país. Organizando as informações em um quadro, a análise dos dados será mais fácil. Para isso, inicialmente, podemos percorrer a lista e atribuir um traço para cada vez que determinado país aparece.

Respostas e comentários
Trabalhando a informação
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah três dois e ê éfe zero seis ême ah três três.
Nesta seção, a compilação em quadro dos dados levantados por uma contagem da nacionalidade dos ganhadores de Medalhas Fields dá início aos processos de construção de quadros e tabelas, destacando as alternativas para sua organização e desafiando os estudantes, nas atividades subsequentes, a construir e interpretar novas tabelas, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah três dois).
É sempre bom lembrar quanto a vida moderna exige em relação à correta leitura de quadros ou tabelas, que dão suporte a muitas das informações veiculadas pelos meios de comunicação. Nessa seção, pode-se chamar a atenção para a participação dos brasileiros e das mulheres no desenvolvimento da Matemática, contribuindo para o trabalho com o Tema Contemporâneo Transversal ciência e tecnologia.
No caso de Artur Ávila, ele foi condecorado com a medalha por seu trabalho em sistemas dinâmicos. Já a iraniana mariam mirzacãni recebeu a medalha por descobrir como calcular o volume em espaços de superfícies hiperbólicas.
Caso julgue necessário, explique aos estudantes que o Reino Unido é constituído por Inglaterra, País de Gales, Escócia e Irlanda do Norte.
|
País de naturalidade |
Quantidade de Medalhas Fields conquistadas |
|---|---|
|
EUA |
12 |
|
Bélgica |
2 |
|
França |
10 |
|
Japão |
3 |
|
Reino Unido |
5 |
|
Rússia |
8 |
|
Outros (17 países) |
22 |
Dados obtidos em: INTERNATIONAL Mathematical Union. Disponível em: https://oeds.link/Ecy8tk. Acesso em:21 fevereiro. 2022.

Esse quadro tem o título Distribuição de Medalhas Fields por país de naturalidade dos matemáticos premiados até 2018, além de duas colunas (divisões na vertical) e oito linhas (divisões na horizontal).
Na 1ª linha, são apresentados:
• na coluna da esquerda, o assunto pesquisado (no caso, o país de naturalidade dos ganhadores das Medalhas Fields);
• na coluna da direita, o tipo de dado que se relaciona ao assunto (no caso, a quantidade de Medalhas Fields conquistadas por país).
Da 2ª à 8ª linha são especificados:
• na coluna da esquerda, alguns países de naturalidade dos ganhadores e a categoria “Outros”;
• na coluna da direita, a quantidade de medalhas correspondentes a cada país e à categoria “Outros”.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Cada estudante da turma de Enrico escreveu na lousa o nome de sua fruta preferida.

Com base nas informações na lousa, construa uma tabela. Dê um título à tabela e identifique a categoria dos dados e os dados obtidos. Depois, responda:
a) Quantos estudantes têm seriguela como fruta preferida?
b) Que fruta é apontada como a preferida dos estudantes da turma de Enrico?
c) Quantos estudantes preferem caju a outras frutas?
d) Que fruta tem a maior preferência: jabuticaba ou morango?
2 Faça uma pesquisa com os colegas da turma sobre o animal de estimação preferido e organize os dados obtidos em uma tabela. Compare a tabela construída por você com a de outros colegas. Há diferenças entre as tabelas construídas? Justifique.
Respostas e comentários
1. Construção de tabela.
1. a) 2 estudantes.
1. b) Maçã.
1. c) 5 estudantes.
1. d) Jabuticaba.
2. Respostas pessoais.
Agora quem trabalha é você!
Ao construir a tabela proposta na atividade 1, podem-se discutir as diversas fórmas de apresentação dos dados. É importante ressaltar também que, nessa construção, a tabela pode aparecer na horizontal ou na vertical.
Uma possível tabela para essa atividade é:
|
Fruta preferida |
Quantidade de estudantes |
|---|---|
|
kiwi |
2 |
|
manga |
2 |
|
maçã |
9 |
|
caju |
5 |
|
morango |
4 |
|
banana |
2 |
|
uva |
3 |
|
jabuticaba |
5 |
|
laranja |
3 |
|
pera |
2 |
|
goiaba |
1 |
|
seriguela |
2 |
Dados obtidos na turma de Enrico.
Ao analisar os dados da tabela, os estudantes podem responder às questões propostas, determinando:
a) 2 estudantes, pois a fruta foi citada somente duas vezes.
b) Maçã, que foi citada 9 vezes.
c) 5 estudantes escolheram caju.
d) Jabuticaba, que teve 5 votos. Já morango, teve 4 votos.
Aproveite para perguntar aos estudantes se conhecem ou se já experimentaram as frutas citadas. Comente sobre a importância do consumo de alimentos saudáveis como frutas, contribuindo para o trabalho com o Tema Contemporâneo Transversal educação alimentar e nutricional. Se tiver oportunidade, promova um dia da fruta, para que os estudantes possam levar para a escola e dividir com os colegas em um lanche comunitário.
Oriente os estudantes sobre as coletas das informações da pesquisa proposta na atividade 2. Sugira que os dados sejam coletados com todos os colegas da turma, deste modo, todos coletarão as mesmas informações e as tabelas só se diferenciarão pela disposição dos dados (vertical e horizontal). Por apresentar uma proposta de coletar dados em uma pesquisa, essa atividade contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah três três).
Adicionando e subtraindo mentalmente
Considere o número 25. Ele pode ser decomposto em parcelas de várias maneiras. Observe:

Outra maneira de decompor o número 25 é separando o maior número de dezenas das unidades. Observe.

Essa maneira de decompor um número ajuda no cálculo mental de algumas operações.
Acompanhe algumas estratégias para fazer o cálculo mentalmente.
a) Cálculo de 56 + 37, decompondo 37 em dezenas e unidades.
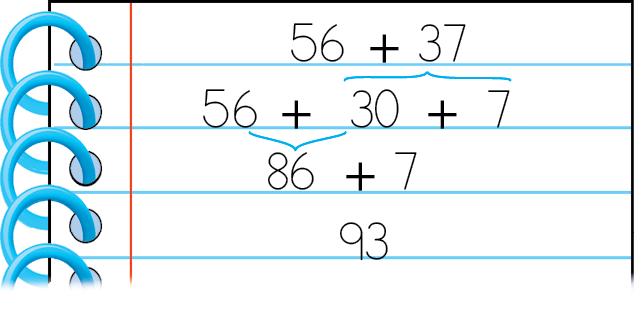
b) Para calcular 56 + 37, podemos também decompor os dois números em dezenas e unidades.
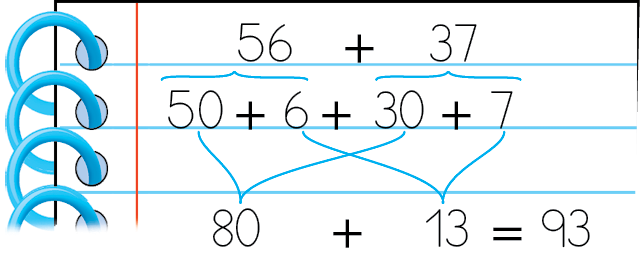
c) Cálculo de 45 ‒ 28, fazendo 45 menos 20 = 25 e 25 menos 8 = 17.
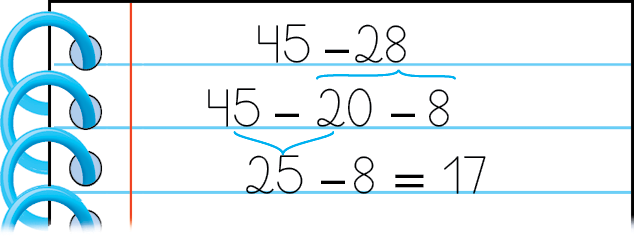
d) Para calcular 45 menos 28, também podemos usar a ideia de completar quantidades.
• 28 para 30 faltam 2.
• 30 para 45 faltam 15.
2 + 15 = 17
Assim, 45 menos 28 = 17.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
32


Calcule mentalmente as operações e, depois, registre como você fez o cálculo. Em seguida, junte-se a um colega e comparem os procedimentos usados.
a) 14 + 67
b) 74 + 28
c) 39 + 42
d) 77 + 23
e) 42 menos 14
f) 72 menos 56
g) 85 menos 26
h) 95 menos 36
33 Calcule: 12 + 25 + 18 + 15.
Agora, calcule: (12 + 18) + (25 + 15 ) .
Para você, qual das duas formas utilizadas é a mais simples? Por quê?
34

Resolva mentalmente as adições a seguir da maneira mais simples.
a) 11 + 37 + 9
b) 20 + 10 + 76
c) 54 + 23 + 7
d) 43 + 21 + 7 + 56 + 4
35

Podemos imaginar “saltos” em uma reta numérica para calcular mentalmente o resultado de adições. Observe.
• Para calcular 65 + 37:
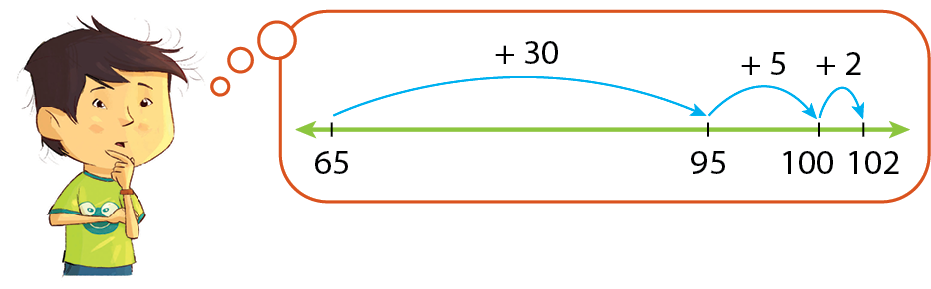
Logo, 65 + 37 = 102.
• Para calcular 135 + 98:
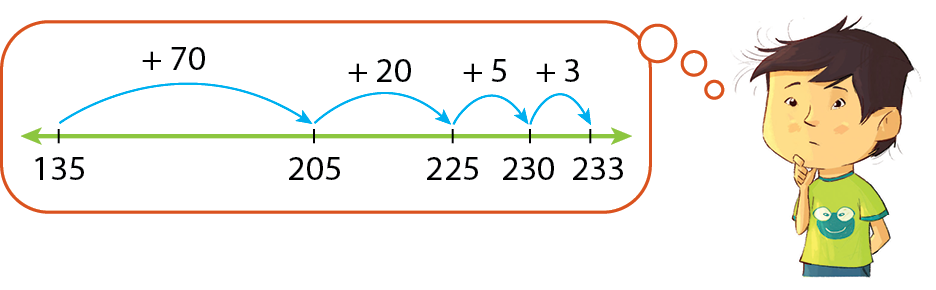
Logo, 135 + 98 = 233.
(Representações esquemáticas sem proporção.)
Respostas e comentários
32. a) 81
32. b) 102
32. c) 81
32. d) 100
32. e) 28
32. f) 16
32. g) 59
32. h) 59
33. 70; Respostas pessoais.
34. a) 57
34. b) 106
34. c) 84
34. d) 131
Adicionando e subtraindo mentalmente
Apresentamos algumas estratégias de cálculo mental. Aproveite este momento para perguntar aos estudantes se fariam essas operações de modo diferente do que foi apresentado. É possível que alguns estudantes utilizem os passos dos algoritmos estudados como estratégia de cálculo mental. Neste caso, é importante que compreendam que essas estratégias não se diferenciam somente pelo fato de um ser escrito e o outro não. Também deve ser considerado que as estratégias para o cálculo numérico devem variar conforme a operação e os valores envolvidos.
Exercícios propostos
Para a resolução do exercício 32, vale destacar que o “registro do pensamento” nem sempre é algo simples, especialmente para essa faixa etária. É provável que muitos estudantes argumentem que “não sabem explicar como fizeram”. Isso acontece pelo fato de os mecanismos de cálculo usados no registro escrito e no cálculo mental não serem necessariamente coincidentes. Espera-se aqui que os estudantes troquem opiniões e discutam modos de cálculos mentais sem, no entanto, a intenção de padronizar os registros, uma vez que podem adotar diferentes estratégias de desenvolvimento.
Usar “saltos” na reta numérica pode se tornar um bom recurso para o cálculo mental na medida em que o estudante precisa escolher o valor do “salto” que o conduza à solução, tanto na adição quanto na subtração, sendo esse valor de escolha individual. Assim, nos exercícios 35 e 36 (da página seguinte), os estudantes poderão apresentar diferentes procedimentos para solução, de acordo com os “saltos” escolhidos. Pode-se pedir a eles que apresentem seus procedimentos na lousa para os colegas perceberem outros caminhos para solução e, assim, ampliarem seu repertório.
Nesses exercícios, diga aos estudantes que as ilustrações dos “saltos” imaginados na reta numérica não estão em escala. Na primeira reta, por exemplo, os saltos mostram que 30 é maior que 5 e que 5 é maior que 2, mas sem escala.
As resoluções dos exercícios 33 e 34 estão no início deste Manual, nas orientações específicas do capítulo 2.
Agora, calcule mentalmente o resultado das adições imaginando “saltos” em uma reta numérica.
Os “saltos” podem ser de 10 em 10, de 20 em 20, de 100 em 100 etcétera e apenas com as unidades.
Em seguida, registre no caderno e verifique o resultado.
a) 49 + 27
b) 86 + 76
c) 125 + 148
d) 225 + 143
36

Também podemos subtrair mentalmente imaginando “saltos” em uma reta numérica. Observe.
• Para calcular 84 menos 46:
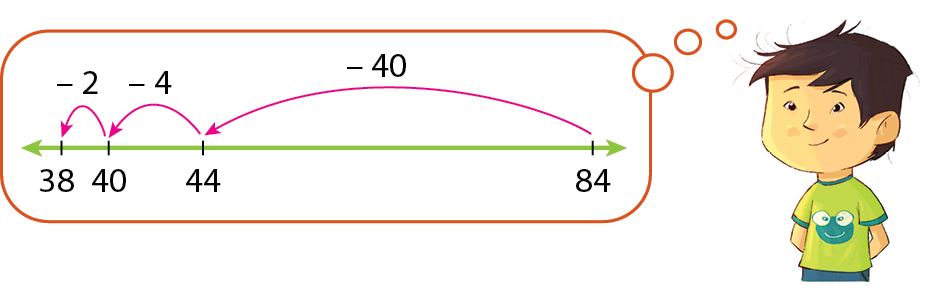
Então, 84 menos 46 = 38.
• Para calcular 123 menos 45
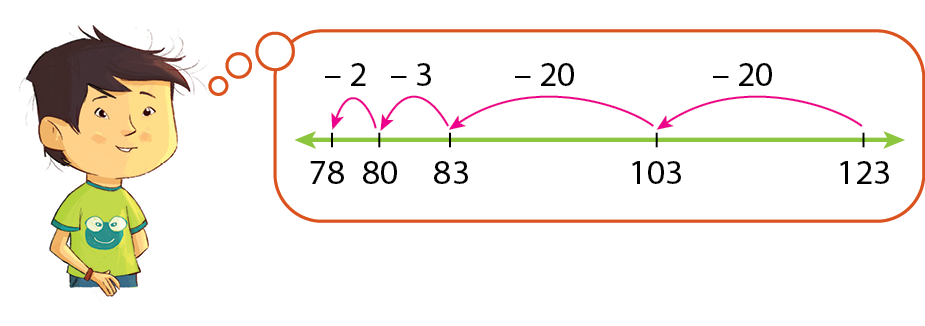
Então, 123 ‒ 45 = 78.
(Representações esquemáticas sem proporção.)
Agora, calcule mentalmente o resultado das subtrações imaginando “saltos” em uma reta numérica. Em seguida, faça o registro no caderno e verifique o resultado.
a) 57 menos 18
b) 65 menos 37
c) 74 menos 68
d) 196 menos 103
e) 346 menos 150
f ) 550 menos 206
37

Escreva um texto explicando como você faria para calcular mentalmente a adição 158 + 372 e a subtração 878 menos 269. Compartilhe sua resposta com o professor e os colegas de turma.
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO
Para adicionar dois números usando este quadro, basta fixar um número na primeira linha e outro na primeira coluna: na intersecção da linha com a coluna, obtemos a soma desses números.
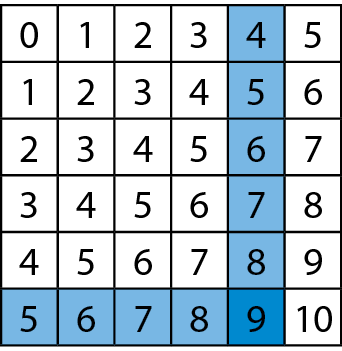
Como exemplo, se adicionarmos o número 4, que está na primeira linha (horizontal), e o número 5, que está na primeira coluna (vertical), obteremos soma 9, que está no cruzamento das duas.
Agora, faça o que se pede.
1 Com base no quadro apresentado, construa um quadro em que seja possível calcular 9 + 8. No mínimo, quantas linhas e quantas colunas o novo quadro terá?
2 Se colocarmos mais 5 linhas e 5 colunas no quadro construído na atividade anterior, continuando a sequência, será possível encontrar o número 23 como resultado da soma de dois números? Explique.
Expressões numéricas com adições e subtrações
Enquanto serve os últimos fregueses, Alberto pensa em como administrar o estoque de pães de hambúrguer da lanchonete.

Respostas e comentários
35. a) 76
35. b) 162
35. c) 273
35. d) 368
36. a) 39
36. b) 28
36. c) 6
36. d) 93
36. e) 196
36. f) 344
37. Resposta pessoal.
Pense mais um poucoreticências:
1. Construção de quadro; 9 linhas e 10 colunas ou 10 linhas e 9 colunas.
2. Não, pois a soma dos dois maiores números do novo quadro será 20.
Exercícios propostos
No exercício 37, os estudantes devem elaborar um texto explicando seus procedimentos de cálculos, assim como fizeram no exercício 32. Se tiverem dificuldades, oriente-os nesta escrita.
Pense mais um poucoreticências
Nesta seção, espera-se que os estudantes percebam que o quadro numérico para calcular 9 + 8 (na atividade 1) pode ser assim:
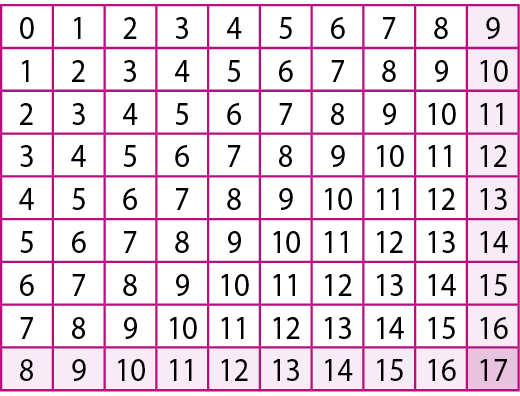
Ou seja, o quadro deve ter pelo menos 9 linhas e 10 colunas. Como a adição é comutativa, sabemos que 9 + 8 = 8 + 9, e assim o quadro também pode ter pelo menos 10 linhas e 9 colunas, obtendo-se 8 + 9.
Ao aumentar 5 linhas e 5 colunas no quadro apresentado (atividade 2), espera-se que os estudantes percebam que o maior número da primeira linha e da primeira coluna será o 10, ou seja, a maior soma será 20. Logo, não é possível aparecer soma 23.
Alberto resolve o problema da seguinte maneira:
200 menos 85 menos 98 + 120
Essa sequência de operações é um exemplo de expressão numérica. Ela pode ser representada por um único número, obtido quando efetuamos as operações.
Vamos calcular o valor da expressão numérica da situação apresentada:
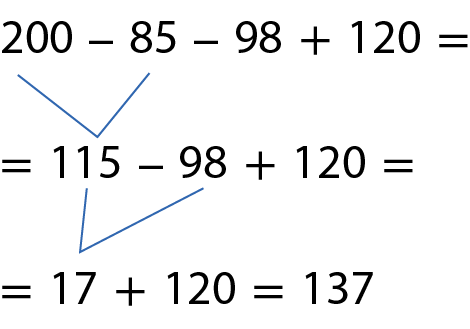
Portanto, Alberto iniciará o trabalho na quarta-feira com 137 pães.
Note que, para determinar o valor de uma expressão numérica que envolve adições e subtrações, efetuamos essas operações na ordem em que aparecem.
Em uma calculadora, fazemos esse cálculo da seguinte maneira:

Os sinais de associação em uma expressão numérica
Existem expressões numéricas que apresentam sinais de associação:
( ) parênteses [ ] colchetes { } chaves
Para exemplificar, observe estas expressões:
a) (12 menos 5) + 3
b) 12 menos (5 + 3)
Note que a posição dos parênteses é diferente nas duas expressões. Vamos calculá-las.
a)

b)

Repare que, por causa da posição dos parênteses, os valores das duas expressões são diferentes. Por isso, a posição dos parênteses e dos outros sinais de associação é muito importante. A presença desses sinais indica que devemos resolver as operações neles contidas seguindo uma ordem: primeiro, efetuam-se as operações entre parênteses; depois, as operações entre colchetes; finalmente, aquelas que estão entre chaves.
Observe mais alguns exemplos.
a) 2 + 5 + [7 menos (3 menos 1)] = = 2 + 5 + [7 menos 2] = = 2 + 5 + 5 = = 7 + 5 = 12
b) [2 + (5 + 7) menos 3] menos 1 = = [2 + 12 menos 3] menos 1 = = [14 menos 3] menos 1 = = 11 menos 1 = 10
c) 2 + [5 + (7 menos 3) menos 1] = = 2 + [5 + 4 menos 1] = = 2 + [9 menos 1] = = 2 + 8 = 10
Respostas e comentários
Expressões numéricas com adições e subtrações
No estudo das expressões numéricas, é importante os estudantes perceberem que expressões numéricas como 12 menos (5 + 3) e 12 menos 5 + 3 produzem resultados diferentes. Pode ser que alguns confundam essa situação com a propriedade associativa da adição. Esclareça a eles que, no caso de expressões numéricas, deve-se considerar a ordem das operações de acordo com os sinais de associação.
Deve-se ressaltar a importância do sinal de associação na primeira expressão, indicando que a primeira operação a ser efetuada é a adição. Já na segunda expressão, as operações de adição e subtração devem ser feitas na ordem em que aparecem:
• 12 menos (5 + 3) = 12 menos 8 = 4
• 12 menos 5 + 3 = 7 + 3 = 10
Pode ser discutido com os estudantes também o uso de calculadora simples e de calculadora científica (que podem ser encontradas no computador). É importante perceberem que uma calculadora simples sempre efetuará as operações na ordem em que forem digitadas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
38 Calcule o valor das expressões numéricas.
a) 36 ‒ 5 + 12 + 10
b) 36 ‒ (5 + 12) ‒ 10
c) 36 ‒ (12 + 10 ‒ 15)
d) (36 ‒ 5) ‒ (12 + 10)
39 Se Carlos tivesse mais 8 reais, poderia comprar um sorvete por 1 real, um sanduíche por 8 reais e ainda lhe sobraria 1 real. Quantos reais Carlos tem?
40 Na caixa de entrada de seu e-mail, Pedro acumulou seiscentas e cinquenta mensagens em um mês e deletou duzentas e oitenta e oito delas. No mês seguinte, ele recebeu setecentas e quarenta novas mensagens e apagou .1000 mensagens.
a) Determine a expressão que corresponde a essa situação.
b) Quantas mensagens ficaram na caixa de entrada de Pedro?
41 Um alpinista, depois de subir 455 metros de uma montanha, subiu mais 325 metros, porém escorregou e desceu 18 metros. Depois, ele tornou a subir 406 metros.
a) Determine a expressão correspondente a essa situação.
b) Qual é o valor dessa expressão?
c) A que altura da base da montanha se encontra esse alpinista?
42

Hora de criar – Pense em um número de três algarismos e escreva esse número como a soma de quatro números. Substitua dois desses quatro números pela diferença de outros dois números. Troque com um colega essas expressões numéricas criadas por vocês. Depois de cada um calcular o valor da expressão do outro, destroquem para corrigi-las.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Giovana achou um velho caderno com exercícios em uma caixa guardada por seu pai. Mas repare no que as traças fizeram!
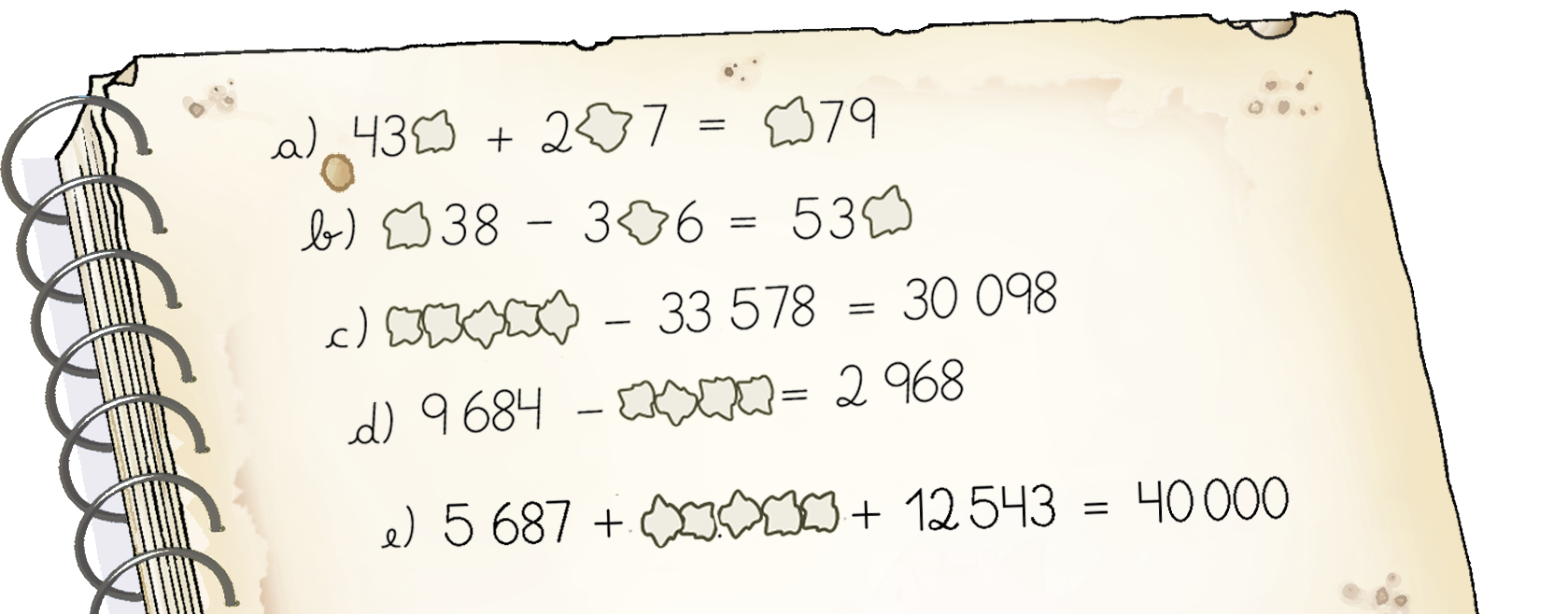
Descubra as contas que havia no caderno do pai de Giovana e escreva-as no caderno.
4. Multiplicação
Acompanhe as situações a seguir.
Situação 1
Bruna comprou um sofá, que pretende pagar em 10 parcelas de 230 reais cada uma. Qual será o valor total que Bruna pagará pelo sofá?

Podemos resolver esse problema usando uma adição de 10 parcelas iguais. Observe:

Respostas e comentários
38. a) 53
38. b) 9
38. c) 29
38. d) 9
39. 2 reais.
40. a) 650 menos 288 + 740 menos .1000
40. b) cento e duas mensagens.
41. a) 455 + 325 menos 18 + 406
41. b) .1168
41. c) .1168 metros.
42. Resposta pessoal.
Pense mais um poucoreticências:
a) 2, 4 e 6
b) 8, 0 e 2
c) .63676
d) .6716
e) .21770
Exercícios propostos
No exercício 38, incentive os estudantes a usarem o cálculo mental para descobrir o valor dessas expressões.
Lembre-os de priorizar as operações dentro dos parênteses, nos itens b, c e d.
a) 36 menos 5 + 12 + 10 = = 31 + 12 + 10 = = 43 + 10 = 53
b) 36 menos (5 + 12) menos 10 = = 36 menos 17 menos 10 = = 19 menos 10 = 9
c) 36 menos (12 + 10 menos 15) = = 36 menos (22 menos 15) = = 36 menos 7 = 29
d) (36 menos 5) menos (12 + 10) = = 31 menos 22 = 9
O exercício 39 apresenta uma situação interessante para os estudantes validarem as respostas após a resolução, ou seja, para conferirem se a solução encontrada está de acordo com o enunciado do problema.
Lembramos que a omissão ou má interpretação da informação inicial, “Se Carlos tivesse mais 8 reais”, pode levar a resultados errados, o que o próprio estudante tem a oportunidade de corrigir ao fazer a conferência da resposta.
Considerando o que Carlos gostaria de comprar, o valor de sua compra seria: 8 + 1 = 9, com 1 real de sobra, seriam 10 reais. Como ele tem 8 reais a menos, ele tem 1 menos 8 = 2 (2 reais).
As resoluções dos exercícios 40 a 42 estão no início deste Manual, nas orientações específicas do capítulo 2.
Pense mais um poucoreticências
Para resolver essa atividade, nos itens a e b, os estudantes devem decompor os números para analisar as ordens separadamente.
a) 43

+ 2

7 =

79 Unidades:

+ 7 = 9 → →

= 9 menos 7 = 2 Dezenas: 30 +

0 = 70 → →

= 7 menos 3 = 4 Centenas: 400 + 200 =

00 → →

= 4 + 2 = 6 Resposta: 2, 4 e 6, respectivamente.
b)

38 menos 3

6 = 53

Centenas:

00 menos 300 = 500 →

= 5 + 3 = 8 Dezenas: 30 menos

= 30 →

= 3 ‒ 3 = 0 Unidades: 8 menos 6 =

→ 8 menos 6 = 2 Resposta: 8, 0 e 2 respectivamente
Para os demais itens, obtemos:
c)




menos .33578 = .30098 .30098 + .33578 = .63676 Resposta: .63676
d) .9684 menos




= .2968. .9684 menos .2968 = .6716 Resposta: .6716
e) .5687 +





+ .12543 = .40000 .5687 +.12543 +





= .40000 .18230 +





= .40000 .40000 menos .18230 = .21770 Resposta: .21770
Podemos usar também a multiplicação de 10 por 230.

Logo, Bruna pagará .2300 reais pelo sofá.
Em uma calculadora, fazemos esse cálculo da seguinte maneira:
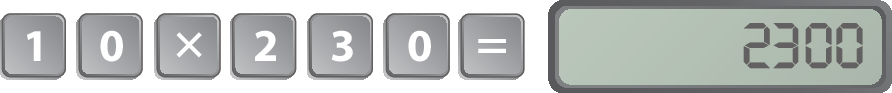
Situação 2
Em 2021, com a cidade de Paris em festa por receber os Jogos Paralímpicos de 2024, ao som da orquestra da França, houve uma apresentação coreográfica de um grupo de pessoas em cadeiras de rodas. Observe a imagem.

Para saber quantas pessoas sentadas participaram da coreografia não é necessário contar uma a uma. Como elas estão dispostas em uma formação retangular de 7 fileiras com 18 pessoas cada uma, basta efetuar a seguinte operação:

Logo, há 126 pessoas sentadas participando da coreografia.
Em uma calculadora, fazemos esse cálculo da seguinte maneira:

Situação 3
Ana e suas amigas estavam estudando juntas e resolveram preparar lanches naturais e suco de laranja. Sabendo que para fazer 1 copo de suco são necessárias 3 laranjas, quantas laranjas serão usadas para fazer 4 copos de suco?

Se, para 1 copo, são necessárias 3 laranjas, para 4 copos temos:

Portanto, para fazer 4 copos de suco de laranja, serão usadas 12 laranjas.
Nesse exemplo, está presente a ideia de proporção.
Em uma calculadora, fazemos esse cálculo da seguinte maneira:

As ideias de adição de parcelas iguais, formação retangular e proporção estão relacionadas à multiplicação.
Respostas e comentários
4. Multiplicação
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico, ao trabalhar com a multiplicação entre números naturais, retomando o conceito estudado nos anos iniciais do Ensino Fundamental, ampliamos o trabalho com a habilidade (ê éfe zero seis ême ah zero três).
No estudo da operação da multiplicação, apresentamos três situações desenvolvendo o significado de adição de parcelas iguais, com destaque para a organização retangular e a noção de proporcionalidade, ampliando e aprofundando o que já viram nos anos anteriores.
Proponha aos estudantes novas situações que envolvam multiplicação com essas ideias, para resolverem com ou sem o uso de calculadora. Em cada uma das multiplicações efetuadas, retome com eles os elementos de uma multiplicação: fatores e produto.
Na situação 2 apresentamos a imagem da coreografia realizada durante a apresentação de Paris como a cidade que iria receber os Jogos Paralímpicos de 2024. Comente com os estudantes que o grupo de pessoas vestiam preto e com o movimento dos braços formavam diferentes imagens, incluindo a palavra Paris representada na imagem. O coreógrafo francês Sadeck Waff foi o responsável por essa apresentação de “balé com as mãos” com 126 participantes, com e sem deficiência. O vídeo com essa apresentação está disponível em: https://oeds.link/kT1fSz. Acesso em: 22 abril 2022.
Se considerar adequado, proponha um trabalho com o professor de Arte, reproduzindo para os estudantes o vídeo com essa apresentação, contribuindo para o desenvolvimento da competência geral 3.
Na situação 3, lembre os estudantes de que ao conjunto de 12 elementos damos o nome dúzia.
Observações
▶ Podemos indicar uma multiplicação substituindo o sinal de vezes (×) por um ponto ( ⋅ ).
Observe alguns exemplos.
a) 13 × 5 ou 13 ⋅ 5
b) 4 × 5 ou 4 ⋅ 5
▶ O resultado de duas vezes um número é chamado dobro.
▶ O resultado de 3 vezes um número é chamado triplo.
▶ O resultado de 4 vezes um número é chamado quádruplo.
Assim:
• O dobro de 9 é 2 ⋅ 9, isto é, 18.
• O triplo de 14 é 3 ⋅ 14, isto é, 42.
• O quádruplo de 18 é 4 ⋅ 18, isto é 72 .
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
43 Em uma plantação, existem 118 fileiras com 84 pés de abacaxi em cada uma.
a) Para obter o número de pés de abacaxi, podemos fazer uma operação. Que operação é essa?
b) Que nome damos aos números 118 e 84 nessa operação? E ao resultado?
c) Quantos pés de abacaxi há nessa plantação?
44 Represente cada adição com uma multiplicação.
a) 5 + 5 + 5 + 5
b) 2 + 2 + 2 + 2 + 2
c) 7 + 7 + 7
d) a + a
45 Observe a figura a seguir.

Considerando essa figura, escreva:
a) a adição de 4 parcelas iguais que fornece o número de quadradinhos;
b) a adição de 7 parcelas iguais que fornece o número de quadradinhos;
c) a multiplicação de dois fatores que também fornece o número de quadradinhos.
46 Larissa mora no 13º andar, e os dois elevadores do prédio quebraram. De um pavimento a outro, são 18 degraus de escada. Quantos degraus Larissa terá de subir para chegar em casa, vindo do apartamento de sua amiga, que mora no 4º andar do mesmo prédio?
47 Em uma multiplicação, um dos fatores é zero. Qual é o produto?
48

Calcule mentalmente:
a) 5 ⋅ 10
b) 32 ⋅ 100
c) 74 ⋅ .1000
d) 42 ⋅ .10000
49

Continue calculando mentalmente:
a) 25 ⋅ 2
b) 25 ⋅ 200
c) 5 ⋅ 60
d) 5 ⋅ 600
e) 8 ⋅ 9
f) 80 ⋅ 90
50 Nosso coração bate, em média, 70 vezes por minuto. Quantas batidas nosso coração dá em 1 dia? Lembre-se de que uma hora é o mesmo que 60 minutos.
51 Responda às questões.
a) Quantos

existem na figura a seguir?

b) Quantos

e

existem na figura?
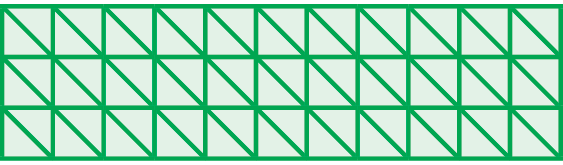
c) Quantos

,

,

,

existem?

Respostas e comentários
43. a) Multiplicação.
43. b) Fatores; produto.
43. c) .9912 pés de abacaxi.
44. a) 4 ⋅ 5
44. b) 5 ⋅ 2
44. c) 3 ⋅ 7
44. d) 2 ⋅ a
45. a) 7 + 7 + 7 + 7
45. b) 4 + 4 + 4 + 4 + 4 + 4 + 4
45. c) 4 ⋅ 7 ou 7 ⋅ 4
46. 162 degraus.
47. Zero.
48. a) 50
48. b) .3200
48. c) .74000
48. d) .420000
49. a) 50
49. b) .5000
49. c) 300
49. d) .3000
49. e) 72
49. f) .7200
50. .100800 batidas.
51. a) 33 quadradinhos.
51. b) 66 triângulos.
51. c) 132 triângulos.
Exercícios propostos
Neste bloco de exercícios, exploram-se a multiplicação associada à adição de parcelas iguais, à disposição retangular e à noção de proporcionalidade.
As resoluções dos exercícios 43 a 49 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 50, os estudantes devem considerar que o coração bate, em média, 70 vezes por minuto. Sabe-se que em uma hora há 60 minutos; logo, em um dia há: .1440 minutos (24 ⋅ 60 = .1440). Portanto, a quantidade de batidas do coração é dada por:
.1440 ⋅ 70 = .100800
Logo, o coração bate .100800 vezes por dia.
O exercício 51 oferece um momento para os estudantes buscarem relações entre as unidades de medida de área, ainda que apareçam de maneira apenas implícita no exercício. Para começar, no item a, eles devem relacionar a quantidade total de quadrinhos com a quantidade de quadrinhos em cada linha e em cada coluna do retângulo apresentado. Na resolução do item b, é importante observar se há estudantes fazendo a contagem dos triângulos; uma estratégia para lidar com o problema é pedir a outro estudante que tente explicar como resolver sem contar todos os triângulos. É fundamental destacar a ideia de que, cabendo dois triângulos em cada quadrinho, haverá o dobro de triângulos em relação ao número original de quadrinhos. De maneira similar, no item c, espera-se que os estudantes utilizem as relações:
• em cada quadrinho cabem dois “triângulos dos tipos do item b”, ou quatro “triângulos dos tipos do item c”;
• em cada “triângulo dos tipos do item b” cabem dois “triângulos dos tipos do item c”.
Discutindo essas relações, os estudantes observarão que não é mera coincidência ter encontrado os números 33, 66 e 132, ou seja, sempre o dobro do encontrado no item anterior. Ficará então mais natural verificar que, quando diminuímos a unidade de medida, mais vezes essa unidade de medida caberá em uma mesma superfície.
52 Leia as especificações que há no rótulo de uma embalagem de suco de uva. Depois, faça o que se pede.
|
Quantidade |
1 copo |
|---|---|
|
Água (mL) |
168 |
|
Quilocalorias |
155 |
|
Proteína (g) |
1 |
|
Gordura (g) |
Traços* |
|
Carboidrato (g) |
38 |
|
Cálcio (mg) |
23 |
|
Potássio (mg) |
334 |
|
Vitamina A (UI) |
20 |
* Nesse contexto, o termo traços significa quantidade mínima, algo que não se consegue quantificar.
a) Sabendo que essa embalagem contém 4 copos, copie o quadro acrescentando, à direita, uma coluna com os valores referentes ao total do conteúdo do recipiente.
b) Consta também no rótulo a informação de que, para cada porção de suco, devem ser acrescentadas 3 porções de água e açúcar a gôsto. Quantos copos de água devo usar para preparar todo o suco de uma embalagem? Quantas colheres de açúcar? Quantos copos de suco é possível preparar?
c)

Você já parou para observar as informações contidas nas embalagens de produtos que consome? Pesquise embalagens de produtos alimentícios e verifique se há informações que possibilitem identificar seus componentes, se há alertas para algum componente alergênico, entre outras informações. Reflita sobre a importância dessas informações e converse com o professor e os colegas.
53

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre multiplicação com números naturais. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Outra ideia associada à multiplicação
Considere as situações a seguir.
Situação 1
Bia tem duas calças de agasalho e quatro camisetas para treinar atletismo. De quantos modos diferentes ela pode se vestir para ir aos treinos?

Acompanhe como podemos combinar essas peças:
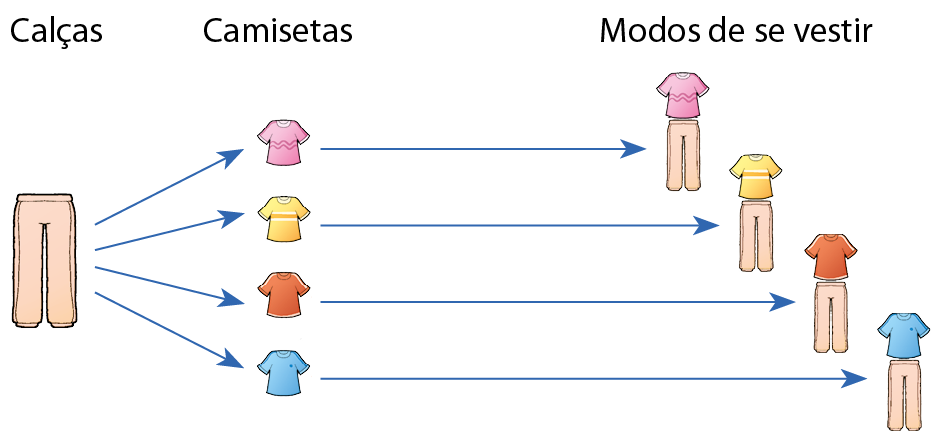
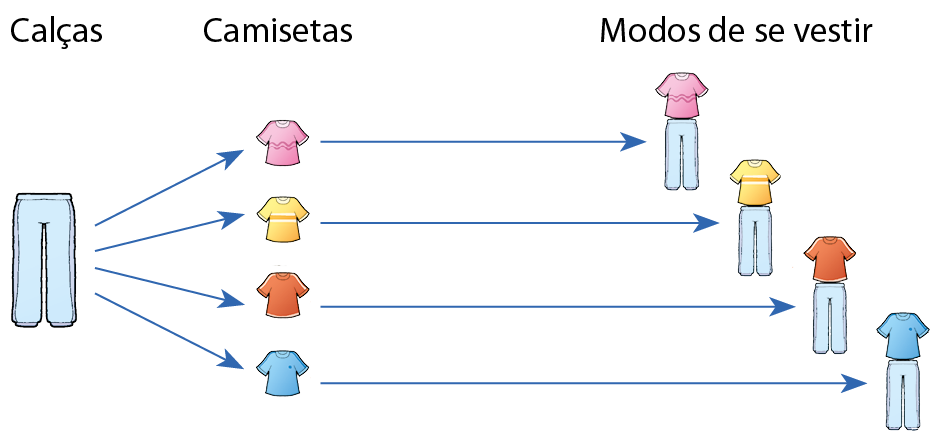
Observe que basta multiplicar 2 por 4 para encontrar o número de opções de vestimenta (2 ⋅ 4 = 8). O número 2 representa as duas possíveis escolhas de calças, e o número 4, as quatro possíveis escolhas de camisetas. Logo, existem 8 possibilidades diferentes para Bia se vestir.
Esse tipo de esquema, que leva à resposta de problemas envolvendo um raciocínio multiplicativo combinatório, é chamado árvore das possibilidades.
Respostas e comentários
52. a) 672; 620; 4; traços; 152; 92; .1336; 80
52. b) 12 copos de água; a gôsto; 16 copos de suco.
52. c) Resposta pessoal.
53. Resposta pessoal.
Exercícios propostos
No exercício 52, além da ideia de proporcionalidade em debate, à medida que os estudantes encontram as respostas, podem ser explorados os aspectos relacionados com alimentação e nutrição. Para isso, é possível promover um trabalho interdisciplinar com Ciências. As embalagens que os estudantes pesquisarem serão um importante objeto de estudo e discussão a esse respeito.
Uma ampliação interessante desse exercício é solicitar que coletem dados dos alimentos que mais consomem, para uma autoavaliação da alimentação. Mesmo não sendo especialistas em nutrição, é fundamental que todos tenham noções de alimentação e saúde, pois uma dieta desequilibrada é prejudicial à saúde.
Apresentamos a seguir o quadro solicitado no item a. A terceira coluna a ser acrescentada é equivalente a 4 vezes a quantidade presente na segunda coluna:
|
Quantidade |
1 copo |
4 copos |
|---|---|---|
|
Água (mL) |
168 |
672 |
|
Quilocalorias |
155 |
620 |
|
Proteína (g) |
1 |
4 |
|
Gordura (g) |
– |
– |
|
Carboidrato (g) |
38 |
152 |
|
Cálcio (mg) |
23 |
92 |
|
Potássio (mg) |
334 |
1.336 |
|
Vitamina A (UI) |
20 |
80 |
No item b, os estudantes devem considerar as informações apresentadas no enunciado e as do quadro. A embalagem contém o equivalente a 4 copos de suco e segundo o modo de preparo, para cada copo devem ser acrescentados 3 copos de água. Logo, para preparar o total de suco possível com uma garrafa seriam necessários 12 copos de água (3 ⋅ 4 = 12). A quantidade de açúcar é a gosto, e independe da quantidade de suco a ser preparado. Já para calcular a quantidade de suco preparado, os estudantes devem adicionar a quantidade de suco concentrado à quantidade de água, assim, serão 16 copos de suco preparado (4 + 12 = 16).
No item c, converse com os estudantes sobre a importância de lermos os rótulos de produtos que consumimos, pois neles constam informações sobre a validade e alertas a componentes alergênicos. Fale sobre o risco do consumo de produtos fóra da validade e da não identificação dos componentes para pessoas alérgicas, contribuindo para o trabalho com o Tema Contemporâneo Transversal educação alimentar e nutricional.
No exercício 53 apresentamos uma proposta de elaboração de problemas. Oriente os estudantes para que os problemas elaborados tenham os dados necessários para sua resolução. Pode-se organizá-los em uma lista para que sejam resolvidos como tarefa de casa ou como uma lista de estudo para os estudantes que ainda tiverem dificuldades com a operação de multiplicação.
Situação 2
Na lanchonete da escola de Manoela são oferecidas três opções de sanduíche (natural, frango e queijo), duas opções de suco (laranja e uva) e três opções de doce (brigadeiro, cajuzinho e bicho de pé).

Quantas são as possibilidades de Manoela escolher seu lanche, sabendo que ela vai comprar um sanduíche, um suco e um doce?
Vamos representar as opções no esquema a seguir.
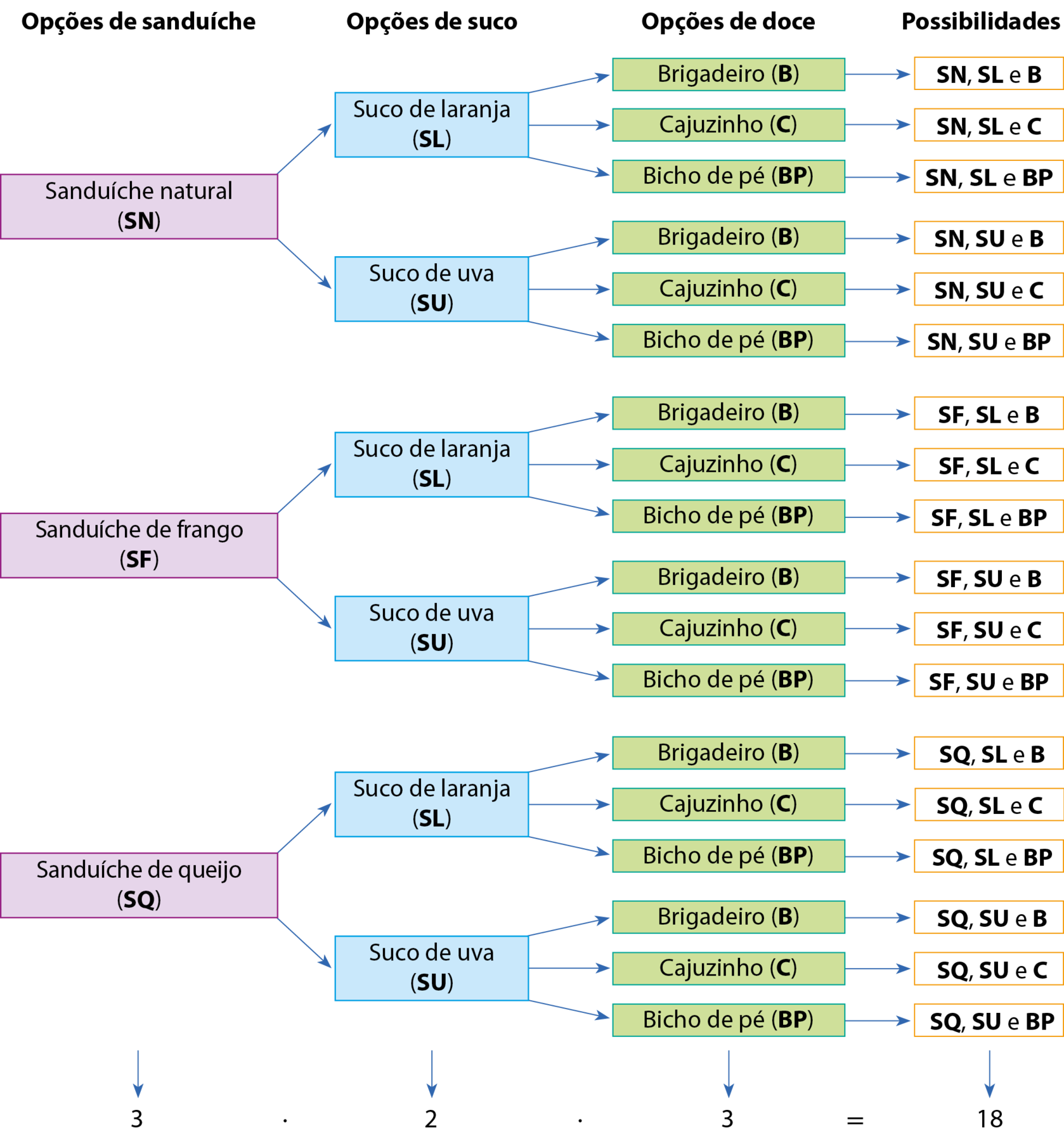
Respostas e comentários
Outra ideia associada à multiplicação
Apresentamos uma situação que trata do significado de combinatória associado à multiplicação, outro raciocínio a ser desenvolvido pelos estudantes. No cálculo de possibilidades, é importante eles desenvolverem estratégias de organização, como a árvore das possibilidades tratada nesse momento.
Converse com os estudantes sobre as duas situações e a organização das árvores das possibilidades que mostram a multiplicação associada à contagem. Proponha aos estudantes outras situações para fazerem a organização das possibilidades dessa maneira. Em seguida, alguns deles podem mostrar o que fizeram, discutindo cada esquema com a turma.
Ressalte o fato de que a representação das possibilidades, por esse tipo de esquema, para obter o total de possibilidades torna-se inviável para uma grande quantidade de opções. No entanto, o cálculo da multiplicação da quantidade de cada item sempre é possível.
Nesse caso, basta fazer uma multiplicação para encontrar quantas possibilidades Manoela tem de escolher seu lanche. Observe.

Logo, Manoela tem 18 possibilidades de escolher seu lanche.
Um esquema como esse é um instrumento útil para descrever todas as possibilidades de um evento, porém é inadequado quando a quantidade de opções e de itens é grande.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
54 Em um cinema, é possível comprar pipoca doce ou salgada em pacote pequeno, médio ou grande. Quantas são as possibilidades para a compra de um pacote de pipoca nesse cinema?

55 Rafael lança um dado e uma moeda ao mesmo tempo e observa as faces voltadas para cima. De quantos modos diferentes essas faces podem aparecer?
56 Tenho três lápis de cor nas cores azul, amarela e verde. Desejo pintar três faixas em uma figura com essas três cores, usando uma cor para cada faixa, conforme mostra a figura a seguir.

De quantas maneiras poderei fazê-lo? Desenhe todas as possibilidades.
57 De quantas maneiras posso calçar meus pés tendo três pares de tênis e cinco pares de meias diferentes?
58 Para fazer o trajeto de sua casa até a escola, Luciana tem de tomar duas conduções. Nem sempre ela usa os mesmos meios de transporte. Na primeira parte do percurso, Luciana toma trem ou ônibus; na segunda parte, metrô, carona no carro de uma amiga ou ônibus. De quantos modos diferentes Luciana pode fazer o trajeto de sua casa até a escola? E, supondo dispor dos mesmos meios para a volta da escola, de quantos modos diferentes poderá fazê-la?
59 Em uma lanchonete há 3 tipos de sanduíche, 2 tipos de suco e 2 tipos de sobremesa.

a) De quantas maneiras diferentes pode-se fazer uma refeição nessa lanchonete escolhendo 1 sanduíche, 1 suco e 1 doce?
b) Qual é a possibilidade de refeição mais barata que tenha um item de cada categoria?
60 Lucas está brincando com duas moedas. Ele lança as moedas e observa a face que fica virada para cima: cara ou coroa. Ao lançar duas moedas ao mesmo tempo, que faces poderá obter?

61

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre multiplicação com raciocínio combinatório. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Respostas e comentários
54. 6 possibilidades.
55. 12 modos diferentes.
56. 6 possibilidades.
57. 15 maneiras diferentes.
58. 6 modos diferentes: trem e ônibus, trem e metrô, trem e carona, ônibus e metrô, ônibus e carona, ônibus e ônibus. O mesmo vale para o trajeto de volta.
59. a) 12 maneiras diferentes.
59. b) Cachorro-quente, suco de limão e sorvete.
60. Cara e cara, cara e coroa, coroa e cara, coroa e coroa.
61. Resposta pessoal.
Exercícios propostos
Neste bloco de exercícios, que explora a ideia combinatória da multiplicação, a interpretação das situações envolvidas na resolução dos problemas é fundamental, já que o uso automático da multiplicação pode levar a um resultado correto, porém sem significado. Incentive os estudantes a exporem a um colega como entenderam cada problema e a procurarem juntos procedimentos para a resolução.
No exercício 54, solicite aos estudantes que façam cartões indicando o tipo de pipoca (doce ou salgada) e outros indicando separadamente o tamanho do pacote (pequeno, médio ou grande). Esses cartões podem ser usados para fazer as possíveis combinações. Com eles, os estudantes podem efetivamente verificar todas as possibilidades e representar no caderno a árvore das possibilidades.
Não é apropriado que os estudantes dessa faixa etária dependam da manipulação de materiais para solucionar problemas desse tipo, mas algumas simulações podem ser necessárias para que todos compreendam as generalizações esperadas.
Outra alternativa é a construção de um quadro, nesse caso de dupla entrada, que permita visualizar as combinações possíveis. Por exemplo:
|
Tamanho |
|||
|---|---|---|---|
|
Tipo |
Pequeno |
Médio |
Grande |
|
Doce |
|||
|
Salgada |
|||
Note que a construção do quadro permite verificar facilmente as 6 possibilidades de compra da pipoca, que também pode ser dada pela multiplicação: 2 ⋅ 3 = 6, em que 2 corresponde à quantidade de sabores, e 3, à quantidade de embalagens disponíveis.
No exercício 58, solicite aos estudantes que refaçam a proposta com base nos meios de transporte que eles costumam usar no lugar onde moram.
O exercício 60, de maneira sutil, desperta as ideias de possibilidades e de aleatoriedade. Caso tenham chegado às respostas com facilidade, desafie-os a encontrar a resposta para um lançamento de três moedas.
As resoluções dos exercícios 55 a 61 estão no início deste Manual, nas orientações específicas do capítulo 2.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
De quantas maneiras diferentes posso pintar as faixas de uma bandeira de 4 listras, usando as cores verde, azul, vermelha e amarela, sem repeti-las?
Observe uma das possibilidades na bandeira ilustrada.

PARA SABER MAIS

Multiplicação hindu
Os hindus desenvolveram vários métodos práticos para resolver problemas.
Para multiplicar dois números, criaram um método conhecido por vários nomes: “multiplicação em gelosia”, “em célula”, “em grade” ou “quadrilateral”.
Vamos efetuar algumas multiplicações aplicando esse método.
• 9 ⋅ 23
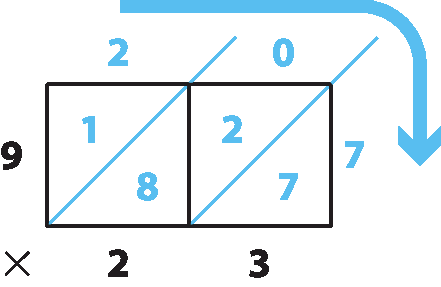
Produtos parciais:
9 ⋅ 3 = 27
9 ⋅ 2 = 18
Observe que o fator 9 está localizado à esquerda e o fator 23, abaixo, com os produtos parciais 27 e 18 ocupando as células interiores.
Os dígitos das fileiras diagonais são adicionados da direita para a esquerda:
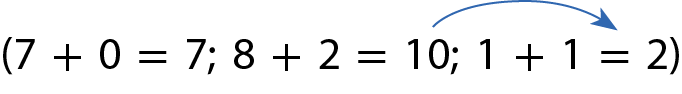
O produto 207, anterior, deve ser lido da esquerda para a direita.
Assim: 9 ⋅ 23 = 207
• 45 ⋅ 16
Procedendo da mesma maneira que no exemplo anterior, obtemos:
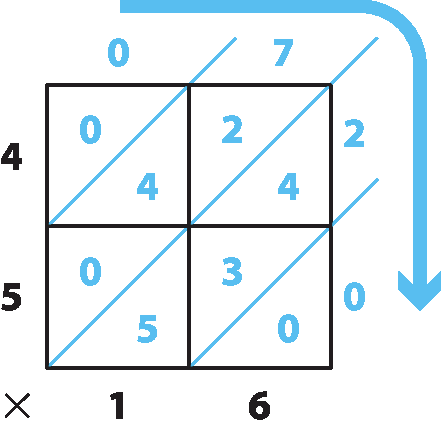
Assim: 45 ⋅ 16 = 720
O método utilizado pelos hindus funciona com multiplicações entre números com qualquer quantidade de algarismos. Observe:
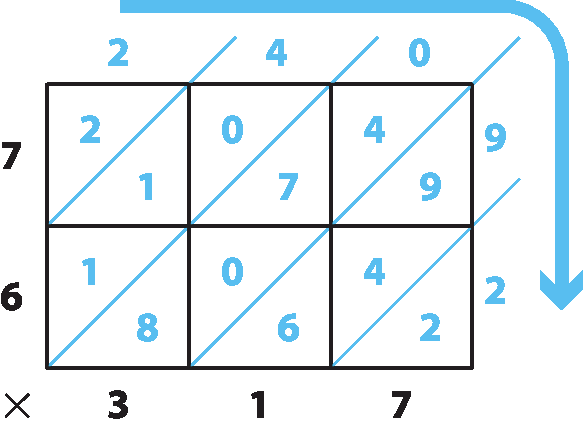
76 ⋅ 317 = .24092
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Aplicando o método hindu de multiplicação, calcule:
a) 37 ⋅ 43
b) 18 ⋅ 532
c) 125 ⋅ .9046
2 Escreva dois números e faça a multiplicação entre eles usando o método hindu e o algoritmo tradicional. Depois, responda: qual deles você acha mais fácil? Explique.
Respostas e comentários
Pense mais um poucoreticências:
24 maneiras diferentes.
Para saber mais:
1. a) .1591
1. b) .9576
1. c) ..1130750
2. Resposta pessoal.
Pense mais um poucoreticências
Apresentamos uma resolução possível para o desafio proposto nesta seção.
Usando a cor verde na primeira faixa, podemos combinar as outras cores de seis modos diferentes, como mostra o quadro a seguir.
|
1ª faixa |
2ª faixa |
3ª faixa |
4ª faixa |
|---|---|---|---|
|
Verde |
Azul |
Vermelho |
Amarelo |
|
Verde |
Azul |
Amarelo |
Vermelho |
|
Verde |
Vermelho |
Azul |
Amarelo |
|
Verde |
Vermelho |
Amarelo |
Azul |
|
Verde |
Amarelo |
Vermelho |
Azul |
|
Verde |
Amarelo |
Azul |
Vermelho |
O mesmo raciocínio pode ser usado com as outras cores na primeira faixa. Como são 4 cores, podemos pintar de 24 modos diferentes (6 ⋅ 4).
Para saber mais
Conhecer um pouco da história da Matemática é um dos meios mais convincentes para sua assimilação no corpo geral de conhecimentos. Mesmo que os estudantes já saibam fazer essas multiplicações, eles podem conhecer e aplicar algumas ideias surgidas ao longo da história. Ao trabalhar com essa temática, contribuímos para o desenvolvimento da competência geral 1. Comente com os estudantes a importância de estudarmos os conhecimentos históricos desenvolvidos por diferentes culturas, contribuindo para o trabalho com o Tema Contemporâneo Transversal diversidade cultural. Nesta seção, eles têm a oportunidade de aprender a multiplicação em gelosia.
Nos dois últimos exemplos, observe que as somas nas diagonais podem ocasionar o acréscimo de valores na casa decimal superior seguinte.
No caso do produto entre 125 e .9046 proposto no item c da atividade 1 do Agora é com você!, a configuração fica assim:
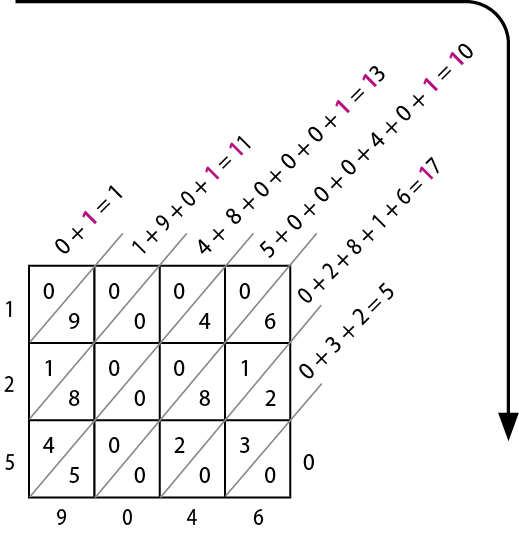
As resoluções das demais atividades da seção Para saber mais estão no início deste Manual, nas orientações específicas do capítulo 2.
Propriedades da multiplicação
Ana e Lúcio compraram o mesmo tipo de chocolate. Ela comprou duas caixas com 18 bombons em cada caixa, ele comprou 18 caixinhas com 2 bombons em cada uma. Quem comprou mais bombons?

Para saber, devemos multiplicar o número de caixas e o número de bombons em cada caixa:
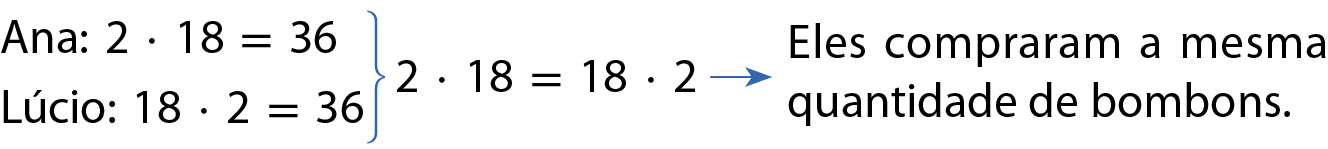
A ordem dos fatores não alterou o produto. Isso sempre ocorre quando multiplicamos dois números naturais quaisquer. Trata-se da propriedade comutativa da multiplicação.
Em uma multiplicação de dois números naturais, a ordem dos fatores não altera o produto.
Observe outros exemplos.
a) 24 ⋅ 2 = 2 ⋅ 24 = 48
b) 20 ⋅ 98 = 98 ⋅ 20 = .1960
Agora, observe dois modos de efetuar o produto 2 ⋅ 5 ⋅ 3.
1º modo
Efetua-se a multiplicação dos dois primeiros fatores e, depois, multiplica-se esse resultado pelo terceiro fator.

2º modo
Efetua-se a multiplicação dos dois últimos fatores e multiplica-se o primeiro fator pelo resultado obtido.

Ao associar os fatores de modos diferentes, o produto não se alterou. Esse fato sempre ocorre quando multiplicamos três ou mais números naturais quaisquer. Trata-se da propriedade associativa da multiplicação.
Em uma multiplicação de três ou mais números naturais quaisquer, podemos associar os fatores de modos diferentes sem alterar o produto.
Observe mais alguns exemplos.
a)

b)

Agora, considere as seguintes multiplicações:
• 1 ⋅ 18 = 18 ⋅ 1 = 18
• 22 ⋅ 1 = 1 ⋅ 22 = 22
• 1 ⋅ 327 = 327 ⋅ 1 = 327
Note que em todas essas multiplicações há um número (1) que, em qualquer posição, não influi no resultado. Esse número é o elemento neutro da multiplicação. A multiplicação de um número natural qualquer por 1 (ou vice-versa) é o próprio número. Trata-se de mais uma propriedade da multiplicação: a existência do elemento neutro.
O número 1 é o elemento neutro da multiplicação.
Respostas e comentários
Propriedades da multiplicação
Nesta página, trabalhamos as propriedades da multiplicação ampliando as noções que os estudantes já trazem de anos anteriores.
Proponha aos estudantes na lousa situações em que eles podem verificar como as propriedades da multiplicação, assim como as da adição, auxiliam no cálculo mental. Por exemplo, peça-lhes que obtenham o produto da seguinte multiplicação, identificando em cada passagem a propriedade utilizada.
15 ⋅ 1 ⋅ 7 ⋅ 5 ⋅ 2 =
= (15 ⋅ 1) ⋅ 7 ⋅ 5 ⋅ 2 = ➀
= 15 ⋅ 7 ⋅ 5 ⋅ 2 = ➁
= 15 ⋅ 2 ⋅ 7 ⋅ 5 = ➂
= (15 ⋅ 2) ⋅ (7 ⋅ 5) = ➃
= 30 ⋅ 35 =
= .1050
➀ (propriedade associativa da multiplicação)
➁ (existência do elemento neutro da multiplicação)
➂ (propriedade comutativa da multiplicação)
➃ (propriedade associativa da multiplicação)
A propriedade do fechamento não foi considerada aqui porque não estamos realizando um estudo axiomático da teoria dos conjuntos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
62 O produto 12 ⋅ 15 ⋅ 2 fica mais fácil de ser resolvido assim:
12 ⋅ (15 ⋅ 2) = 12 ⋅ 30 = 360
No caderno, mostre o modo mais fácil de calcular os seguintes produtos e determine-os.
a) 36 ⋅ 25 ⋅ 4
b) 5 ⋅ 45 ⋅ 2
c) 9 ⋅ 8 ⋅ 5
63 Efetue os produtos aplicando as propriedades da multiplicação.
a) 2 ⋅ 17 ⋅ 5
b) 2 ⋅ 15 ⋅ 36
c) 18 ⋅ 5 ⋅ 4
d) 2 ⋅ 38 ⋅ 5
e) 25 ⋅ 137 ⋅ 4
f) 12 ⋅ 0 ⋅ 1
g) 14 ⋅ 20 ⋅ 10
h) 12 ⋅ 1 ⋅ 10
i) 8 ⋅ 21 ⋅ 5
j) 75 ⋅ 1 ⋅ 4
64 Uma impressora faz 12 cópias por minuto. Outra imprime o triplo de cópias dos mesmos impressos em um minuto. Quantas cópias a segunda impressora faz em 15 minutos?
65 Uma loja vendeu 84 peças de roupas em outubro. Em novembro, vendeu o dobro de peças e, em dezembro, o triplo das peças vendidas em novembro. Quantas peças de roupa foram vendidas nesse trimestre?
66 Fábio tem trínta e duas bolinhas de gude, Fernanda tem o dobro das bolinhas de gude de Fábio, Ivone tem o triplo das bolinhas de gude de Fernanda e Francisco tem o quádruplo das bolinhas de gude de Ivone. Quantas bolinhas de gude tem cada um?

67

A calculadora de Fernando está com as teclas 6 e 8 quebradas. Para calcular o resultado da operação 16 ⋅ .4802, ele apertou a seguinte sequência de teclas:

a) O cálculo de Fernando está correto?
b) Redija uma explicação de como Fernando pensou para resolver esse problema.
c) Existe uma fórma de calcular o resultado dessa operação apertando-se um número menor de teclas? Justifique sua resposta.
d) Há uma maneira de fazer esse cálculo trocando-se uma operação de multiplicação por uma adição? Dê um exemplo.
A propriedade distributiva
Para entender a propriedade distributiva da multiplicação, vamos considerar as situações a seguir.
Situação 1
Mário é florista. Ele prepara suas mudas de girassol em pequenos vasos. Para atender a uma encomenda, Mário organizou os vasos sobre duas placas retangulares, conforme mostra a figura.
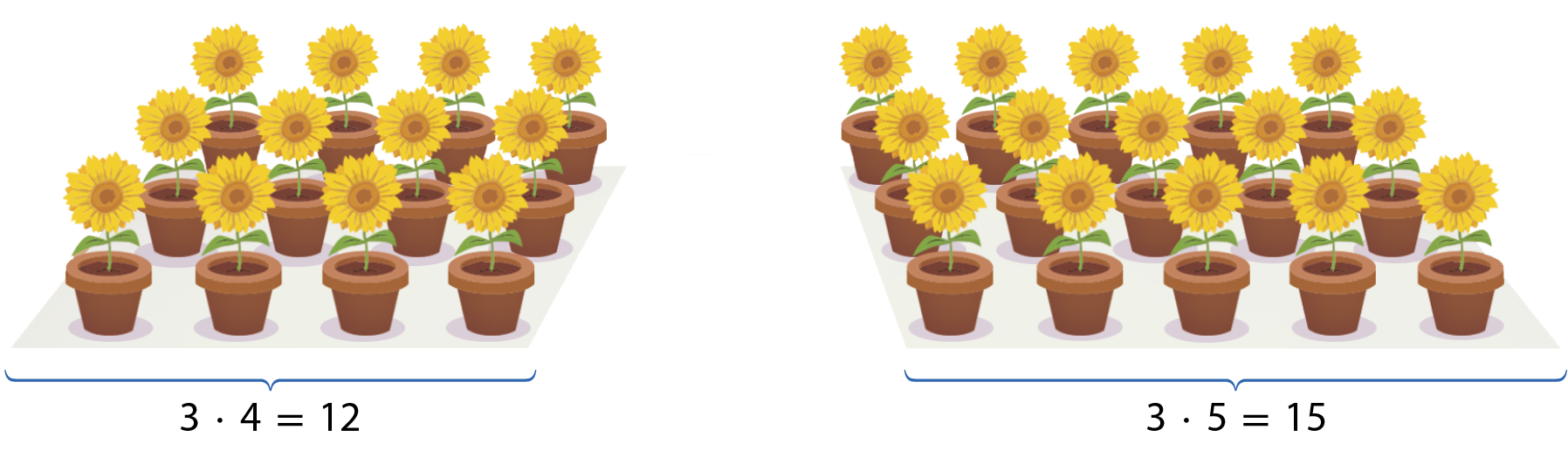
Quantos vasos de girassol foram vendidos nessa encomenda?
Respostas e comentários
62. Resposta pessoal.
62. a) .3600
62. b) 450
62. c) 360
63. a) 170
63. b) .1080
63. c) 360
63. d) 380
63. e) .13700
63. f) 0
63. g) .2800
63. h) 120
63. i) 840
63. j) 300
64. quinhentas e quarenta cópias.
65. setecentas e cinquenta e seis peças de roupa.
66. Fábio: trínta e duas bolinhas de gude; Fernanda: 64 bolinhas de gude; Ivone: cento e noventa e duas bolinhas de gude; Francisco: setecentas e sessenta e oito bolinhas de gude.
67. a) Sim.
67. b) Resposta possível: Ele substituiu 16 por 2 ⋅ 2 ⋅ 4 e .4802 por 2 ⋅ .2401.
67. c) Sim, por exemplo:

67. d) Sim; resposta possível:

Exercícios propostos
Este bloco de exercícios explora a aplicação das propriedades já estudadas da multiplicação. Observe se os estudantes associam de maneira conveniente, de modo que o cálculo seja facilitado. Compartilhe os diferentes procedimentos utilizados para que eles possam comparar o modo como fizeram com o de outro colega e, assim, reflitam sobre suas escolhas.
As resoluções dos exercícios 62 a 65 estão no início deste Manual, nas orientações específicas do capítulo 2.
Ao resolver o exercício 66, os estudantes podem se confundir, se não fizerem os registros das informações do enunciado. Para evitar equívocos, é importante que passem para o caderno as informações principais e que, chegando às respostas, voltem ao enunciado para conferi-las. Apresentamos a seguir uma sugestão para esse registro.
• Fábio tem trínta e duas bolinhas de gude → 32
• Fernanda tem o dobro de bolinhas de gude de Fábio → 2 ⋅ 32 = 64
• Ivone tem o triplo de bolinhas de gude de Fernanda → 3 ⋅ 64 = 192
• Francisco tem o quádruplo de bolinhas de gude de Ivone → 4 ⋅ 192 = 768
No exercício 67, os estudantes devem pensar em estratégias para calcular a multiplicação entre 16 e .4802, considerando que as teclas 6 e 8 não funcionam.
No item a, ao avaliar o cálculo eles podem efetuar as operações indicadas e concluir que o resultado obtido corresponde a .76832, que é o resultado de 16 ⋅ .4802.
Após responderem aos demais itens, peça aos estudantes que compartilhem as respostas dadas, pois esses itens admitem mais de uma resposta possível. O compartilhamento das diferentes estratégias contribui para o desenvolvimento dos estudantes em relação aos conteúdos estudados.
Calculando o número de vasos sobre cada placa e adicionando os resultados, temos:
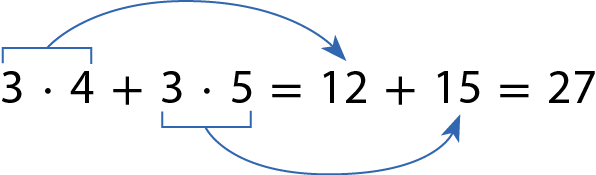
Contando como se fosse uma placa única, podemos escrever:
3 ⋅ (4 + 5) = 3 ⋅ 9 = 27
Observamos que 3 ⋅ (4 + 5) é o mesmo que 3 ⋅ 4 + 3 ⋅ 5.
Portanto, foram vendidos 27 vasos de girassol.
Situação 2
A figura a seguir representa o piso de duas salas. Quantas lajotas foram usadas nesses pisos?
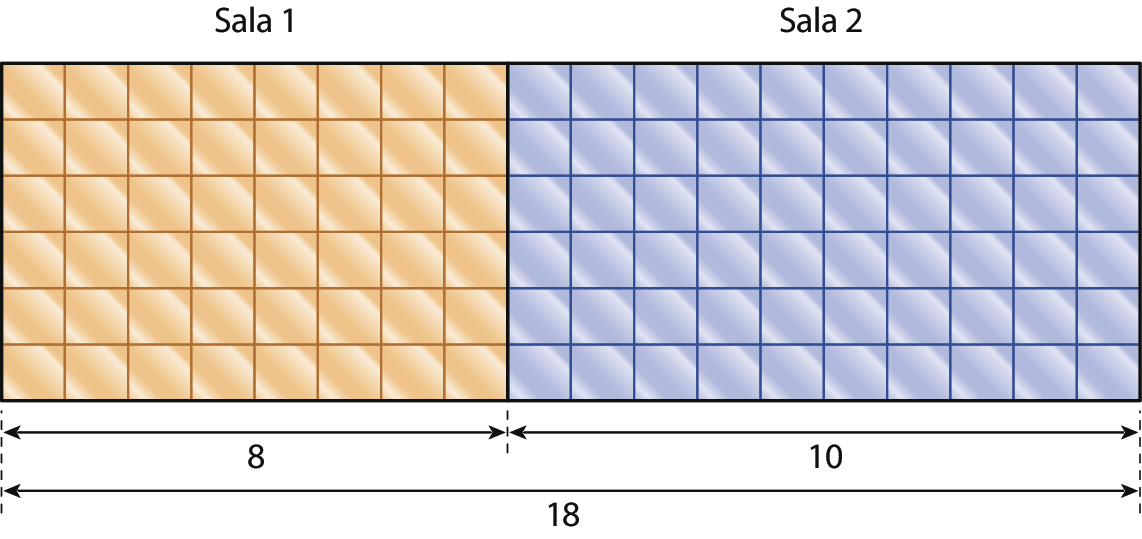
O número de lajotas da sala 1 é obtido calculando-se 6 ⋅ 8. O número de lajotas da sala 2, calculando-se 6 ⋅ 10.
Como o número total de lajotas é igual ao número de lajotas da sala 1 mais o número de lajotas da sala 2, temos:
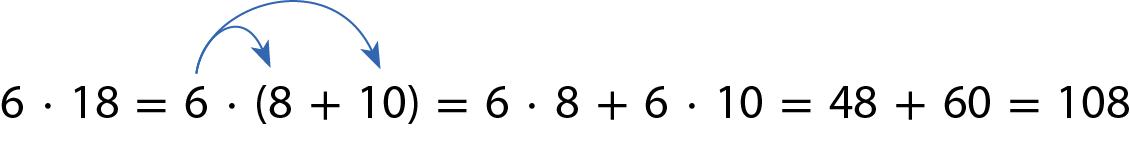
Logo, foram usadas 108 lajotas.
Assim, a multiplicação foi distribuída pelas parcelas de uma adição e, depois, os resultados foram adicionados, isto é, foi aplicada a propriedade distributiva da multiplicação em relação à adição.
Essa propriedade também pode ser aplicada em relação à subtração, como nos exemplos a seguir.
a)
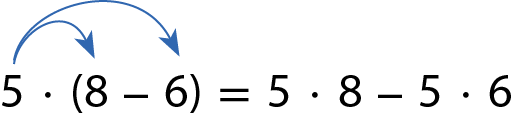
b)
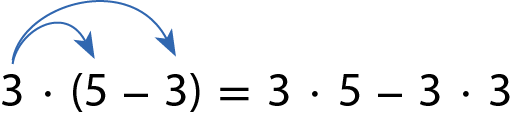
c)

d)
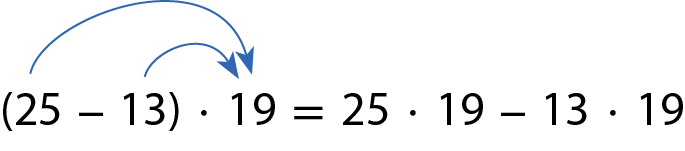
Observe nos exemplos a seguir como a propriedade distributiva pode ajudar a realizar cálculos mais rápidos ou mentalmente.
a)

b)

Respostas e comentários
A propriedade distributiva
Analise com os estudantes as situações propostas no livro, que possibilitam atribuir significado à propriedade distributiva da multiplicação em relação à adição. É fundamental que eles distingam a propriedade associativa.
Ressalte que a propriedade associativa envolve sempre a mesma operação (adição ou multiplicação), enquanto a propriedade distributiva envolve duas operações: multiplicação e adição (ou multiplicação e subtração).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
68 Calcule aplicando em cada caso a propriedade distributiva da multiplicação.
a) 8 ⋅ (9 + 4)
b) 10 ⋅ (7 ‒ 2)
c) (4 + 6) ⋅ 3
d) 4 ⋅ (6 ‒ 2)
e) (8 ‒ 3) ⋅ 8
f) (10 ‒ 4) ⋅ 8
69 Uma baleia-azul adulta pode pesar tanto quanto 26 elefantes africanos adultos, que têm aproximadamente .5000 quilogramas cada um. Calcule quantos quilogramas tem uma baleia-azul, aproximadamente.
70 Descubra e corrija as sentenças falsas, tornando-as verdadeiras.
a) 6 ⋅ 1 = 6
b) Se a é um número natural, então 5 ⋅ a = a ⋅ 5.
c) 6 ⋅ (7 + 4) = 6 ⋅ 4 + 6 ⋅ 7
d) 10 ⋅ (x + 1) = 10 ⋅ x
e) 5 ⋅ 0 = 5
71

Maria usa a decomposição para calcular mentalmente o resultado da multiplicação 6 ⋅ 35.
Observe.
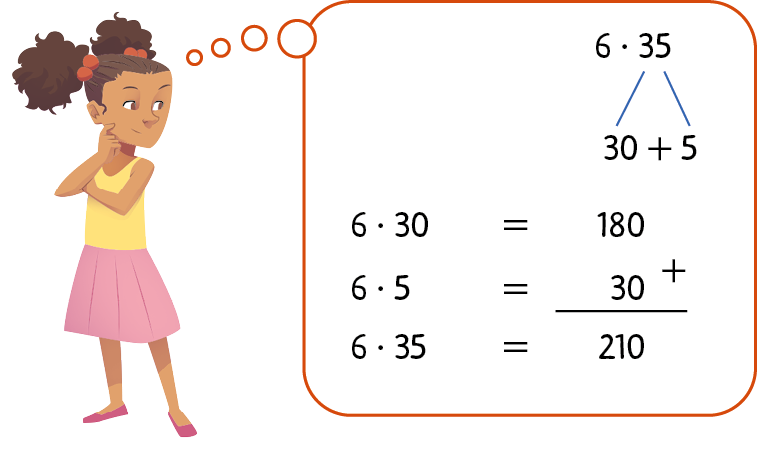
Calcule mentalmente o resultado das multiplicações a seguir, imaginando que um dos fatores é decomposto em dezenas e unidades.
a) 5 ⋅ 15
b) 7 ⋅ 42
c) 3 ⋅ 25
d) 4 ⋅ 13
e) 7 ⋅ 93
f) 6 ⋅ 58
72

Hora de criar – Em duplas, cada integrante vai elaborar um problema em que se empregue(m) propriedade(s) de multiplicação. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
73

Hora de criar – Escreva um número que seja o produto de três outros números naturais. Escreva esses três números multiplicados. Escreva-os novamente, agora substituindo-os por somas ou diferenças de três outros números. Troque com um colega essa última expressão numérica. Depois de cada um resolver a expressão elaborada pelo outro, destroquem para verificar se o colega chegou ao número inicialmente pensado.
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO

Junte-se a um colega e façam o que se pede.
1

Pensem em números de dois algarismos. Usando uma calculadora, multipliquem esses números por 101. Registrem cada multiplicação com o resultado obtido.

Agora, observando o que aconteceu com os produtos, calculem mentalmente:
a) 98 ⋅ 101
b) 89 ⋅ 101
2

Pensem em números de três algarismos. Usando uma calculadora, multipliquem esses números por .1001. Registrem cada multiplicação com o resultado obtido.

Agora, observando o que aconteceu com os produtos, calculem mentalmente:
a) 356 ⋅ .1001
b) 499 ⋅ .1001
3 Escrevam o produto de:
a) um número ab por 101;
b) um número abc por .1001.
Respostas e comentários
68. a) 104
68. b) 50
68. c) 30
68. d) 16
68. e) 40
68. f) 48
69. .130000 quilogramas.
70. a) Verdadeira.
70. b) Verdadeira.
70. c) Verdadeira.
70. d) Falsa: 10 ⋅ (x + 1) = 10 ⋅ x + 10 ⋅ 1
70. e) Falsa: 5 ⋅ 0 = 0
71. a) 75
71. b) 294
71. c) 75
71. d) 52
71. e) 651
71. f) 348
72. Resposta pessoal.
73. O estudante deve obter o número pensado pelo colega.
Pense mais um poucoreticências:
1. a) .9898
1. b) .8989
2. a) .356356
2. b) .499499
3. a) a.bab
3. b) á bê cê.á bê cê
Exercícios propostos
Neste bloco de exercícios, os estudantes podem aplicar os conhecimentos construídos sobre a propriedade distributiva.
Ao resolverem o exercício 68, os estudantes devem aplicar a propriedade distributiva da multiplicação. Deste modo, obtemos:
a) 8 ⋅ (9 + 4) = = 8 ⋅ 9 + 8 ⋅ 4 = = 72 + 32 = 104
b) 10 ⋅ (7 ‒ 2) = = 10 ⋅ 7 ‒ 10 ⋅ 2 = = 70 ‒ 20 = 50
c) (4 + 6) ⋅ 3 = = 4 ⋅ 3 + 6 ⋅ 3 = = 12 + 18 = 30
d) 4 ⋅ (6 ‒ 2) = = 4 ⋅ 6 ‒ 4 ⋅ 2 = = 24 ‒ 8 = 16
e) (8 ‒ 3) ⋅ 8 = = 8 ⋅ 8 ‒ 3 ⋅ 8 = = 64 ‒ 24 = 40
f) (10 ‒ 4) ⋅ 8 = = 10 ⋅ 8 ‒ 4 ⋅ 8 = = 80 ‒ 32 = 48
As comparações entre as medidas de massas, similares às propostas no exercício 69, são comuns no cotidiano e significativas para a compreensão de ordem de grandeza. Espera-se que os estudantes façam algumas estimativas, tendo em vista que a medida da massa dessa baleia equivale à medida da massa de 26 elefantes e que 1 elefante tem .5000 quilogramas. Logo, 26 ⋅ .5000 = .130000 (.130000 quilogramas).
O recurso à decomposição para o cálculo mental é muito comum. Assim, na resolução do exercício 71, incentive os estudantes a fazerem de acordo com o modo de Maria ou usando as suas estratégias pessoais.
No exercício 73, espera-se que os estudantes percebam que o quociente é o outro número dado.
As resoluções dos exercícios 70 a 73 estão no início deste Manual, nas orientações específicas do capítulo 2.
Pense mais um poucoreticências
Esta seção explora alguns padrões numéricos presentes em algumas multiplicações. Como se deseja que os estudantes observem os produtos obtidos e os relacionem, essa é uma situação propícia para efetuarem os cálculos usando uma calculadora. As atividades podem ser discutidas em duplas, o que enriquecerá o aprendizado.
As resoluções das atividades da seção Pense mais um poucoreticências estão no início deste Manual, nas orientações específicas do capítulo 2.
5. Divisão
Acompanhe as situações a seguir.
Situação 1

Em uma gincana promovida pelo Colégio Aprender, os estudantes arrecadaram oitocentas e quarenta latas de leite em pó, que foram doadas a instituições assistenciais. Para a doação, as latas de leite foram embaladas em caixas contendo 30 latas cada uma.
Para saber quantas caixas foram necessárias para embalar todas as latas, devemos procurar o número que, multiplicado por 30, resulte em oitocentas e quarenta.
Ao fazer isso, estamos realizando uma operação chamada divisão.
O número procurado é 28, pois: 28 ⋅ 30 = 840.
Vamos montar a divisão que nos dá esse resultado:
840 dividido por 30 = 28
Logo, foram necessárias 28 caixas.
Em uma calculadora, fazemos essa divisão da seguinte maneira:
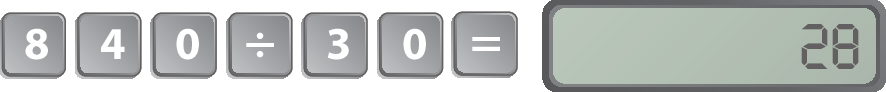
Nesse problema, ao dividir o total de latas de leite pela quantidade que cabe em cada caixa, fazemos uma repartição em partes iguais, uma distribuição equitativa do total dessas latas.
Situação 2
Os grilos são grandes saltadores. Um grilo chega a saltar uma distância de 90 centímetros, o que corresponde a 30 vezes o seu tamanho.

De acordo com as informações apresentadas, qual é o comprimento do grilo?
Para saber o comprimento do grilo, devemos fazer a seguinte divisão:
90 dividido por 30 = 3
Ao efetuar essa divisão, estamos calculando quantas vezes o número 30 cabe em 90. Essa é a ideia de medida, também associada a uma divisão.
Logo, de acordo com as informações apresentadas, o comprimento do grilo é 3 centímetros.
Em uma calculadora, fazemos essa divisão da seguinte maneira:

As ideias de distribuição equitativa (repartição em partes iguais) ou de medida (quantas vezes uma quantidade cabe em outra) estão relacionadas à divisão.
Respostas e comentários
5. Divisão
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
No estudo da operação divisão, ampliamos e aprofundamos o que os estudantes já viram nos anos anteriores, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah zero três). As duas situações desenvolvem os significados da divisão: distribuição equitativa e medida (quantas vezes cabe). Analise cada situação com os estudantes. Se julgar necessário, retome alguns procedimentos de cálculo de divisão com os quais eles já devem ter tido contato (decomposição, algoritmo usual, por exemplo) e incentive-os a utilizarem estratégias pessoais também.
Proponha aos estudantes novas situações que envolvam divisão, para serem resolvidas com ou sem o uso de calculadora. É importante destacar que o uso da calculadora para efetuar divisões entre números naturais pode gerar dificuldade nas divisões não exatas.
Nesse caso, discuta o significado do número que aparece no visor e a necessidade de se usar outros meios para descobrir todos os elementos de tais divisões. Nessas situações, a relação fundamental da divisão, apresentada mais adiante, poderá ser um recurso útil.
Na situação 1 apresentamos uma situação de uma gincana para arrecadação de alimentos para instituições assistenciais. Converse com os estudantes sobre o papel de instituições assistenciais e sua contribuição para a sociedade. As entidades e organizações de assistência social podem ser parceiras da administração pública no atendimento às famílias, indivíduos e grupos em situação de vulnerabilidade ou risco social. Pergunte se conhecem instituições desse tipo e caso conheçam, qual é o papel que exercem. Essa discussão contribui para o trabalho com o Tema Contemporâneo Transversal vida familiar e social.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
74 Uma granja tem .1944 ovos de codorna que devem ser acondicionados em caixas contendo 36 ovos cada uma. Quantas caixas serão necessárias para acondicionar todos os ovos?
75 Qual é o valor de:
a) 7 ⋅ 39? E de 273 dividido por 7? E de 273 dividido por 39?
b) 12 ⋅ 26? E de 312 dividido por 26? E de 312 dividido por 12?
c) 22 ⋅ 31? E de 682 dividido por 22? E de 682 dividido por 31?
d) 15 ⋅ 123? E de .1845 dividido por 15? E de .1845 dividido por 123?
76 Na produção de 800 carros iguais, foram usados ..1003200 parafusos. Quantos parafusos tem cada carro desse modelo?
77 Um atleta percorreu .10000 metros dando voltas em uma pista circular de 400 metros de comprimento. Quantas voltas o atleta deu nessa pista?
78 Ao entrar em um elevador, Pedro leu uma placa que informava a capacidade do elevador.

Quantos quilogramas, em média, o engenheiro que projetou esse elevador estimou para cada uma das 13 pessoas?
79 Para percorrer 352 quilômetros, um carro consumiu 32 litros de gasolina. Viajando nas mesmas condições, quantos litros esse carro vai gastar para percorrer 451 quilômetros?
80 Em uma festa de aniversário, foram preparados 3 saquinhos de doce para cada uma das 45 crianças convidadas. Entretanto, 5 delas não compareceram.

a) Quantos saquinhos de doce haviam sido preparados?
b) Tendo em vista que 5 crianças não compareceram, quantos saquinhos de doce sobraram?
c) É possível dar um saquinho de doce a mais para cada uma das crianças presentes? Se não, quantos saquinhos a mais deveriam ter sido preparados para que fosse possível dar 4 saquinhos para cada criança?
81

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre divisão com números naturais. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Propriedade fundamental da divisão
Considere as seguintes situações.
Situação 1
Um centro esportivo municipal tinha duzentas e vinte e cinco bolas de basquete para distribuir igualmente entre as 27 escolas de basquete mantidas pela prefeitura. Feita a distribuição, o responsável percebeu que foram dadas 8 bolas a cada escola e ainda sobraram 9 bolas:

Observe a igualdade que podemos escrever com os termos da divisão.

Respostas e comentários
74. 54 caixas.
75. a) 273; 39; 7
75. b) 312; 12; 26
75. c) 682; 31; 22
75. d) .1845; 123; 15
76. .1254 parafusos.
77. 25 voltas.
78. 70 quilogramas.
79. 41 litros.
80. a) 135 saquinhos.
80. b) 15 saquinhos.
80. c) Não; 25 saquinhos.
81. Resposta pessoal.
Exercícios propostos
No exercício 74 deve-se considerar que, como cada caixa contém 36 ovos, são necessárias 54 caixas (.1944 dividido por 36 = 54).
Os estudantes podem se reunir em trios para responder ao exercício 75. Eles devem ser desafiados a resolver fazendo o menor número possível de cálculos. Espera-se que, pela troca de ideias, os estudantes concluam que apenas a primeira operação de cada item precisa ser efetuada, pois as demais podem ser concluídas com base nela, uma vez que existem relações entre as operações de multiplicação e divisão.
No exercício 76 devem considerar que os carros são iguais; logo, têm o mesmo número de parafusos que são .1254 parafusos, pois
..1003200 dividido por 800 = .1254
O atleta, do exercício 77, deu 25 voltas na pista. Essa informação deve ser obtida ao efetuarem a divisão:
.10000 dividido por 400 = 25
A placa do elevador do exercício 78 indica capacidade: 13 pessoas ou 910 quilogramas. Com base na medida de massa máxima permitida é possível estimar a massa por pessoa fazendo 910 dividido por 13 = 70. O que corresponde a 70 quilogramas por pessoa.
O enunciado do exercício 79 apresenta a informação de que o carro consumiu 32 litros para percorrer 352 quilômetros, então o carro consumiu 1 litro para cada 11 quilômetros percorridos (352 dividido por 32 = 11). Isso significa que, para percorrer 451 quilômetros, ele deve consumir 41 litros (451 dividido por 11 = 41).
No exercício 80 deve-se considerar que foram convidadas 45 crianças, e preparados 3 saquinhos para cada uma. Assim, para cada item temos:
a) Foram preparados um total de 135 saquinhos (45 ⋅ 3 = 135).
b) Com o não comparecimento de 5 crianças, sobraram 15 saquinhos (3 ⋅ 5 = 15).
c) Foram convidadas 45 crianças e 5 faltaram, portanto compareceram 45 ‒ 5 = 40 (40 convidados). Como 15 é menor que 40, não é possível entregar um saquinho de doces a mais para cada criança, faltando 25 saquinhos (40 ‒ 15 = 25).
No exercício 81 cada estudante deverá elaborar um problema relacionado à divisão. Aproveite este momento para verificar se compreenderam o conceito de divisão e se conseguem elaborar um problema com dados suficientes para resolução.
Situação 2
Entre outros alimentos, uma creche recebeu 13 dúzias de maçãs para distribuir na merenda das 35 crianças matriculadas. É possível oferecer uma maçã para cada criança nos 5 dias da semana em que a creche funciona? Se não for possível, quantas maçãs faltarão?
Para responder a essa dúvida, devemos dividir o total de maçãs recebidas pelo total de crianças e verificar se dá 5, o número de dias úteis da semana.
Total de maçãs recebidas, 13 dúzias: 13 ⋅ 12 = 156 a serem divididas entre 35 crianças.
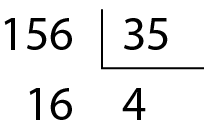
É possível dar uma maçã para cada estudante em apenas 4 dias e sobram 16 maçãs.
Observe que a relação entre esses números é: 156 = 4 ⋅ 35 + 16.
Isso significa que temos 4 grupos de 35 maçãs e 1 grupo de 16 maçãs, que é o que restou da divisão. Porém deveríamos ter 5 grupos de 35 maçãs, isto é, 5 ⋅ 35 = 175.
Para as 35 crianças receberem maçã no quinto dia, será necessário completar o que falta para o grupo de 16 chegar a 35, ou seja, 19 = 35 ‒ 16.
A divisão ficaria:

A relação entre esses números é 175 = 5 ⋅ 35 + 0, o que significa 5 grupos de 35 e resto 0.
Observe outros exemplos.
a)
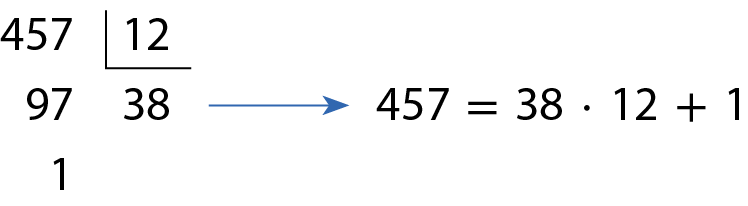
b)
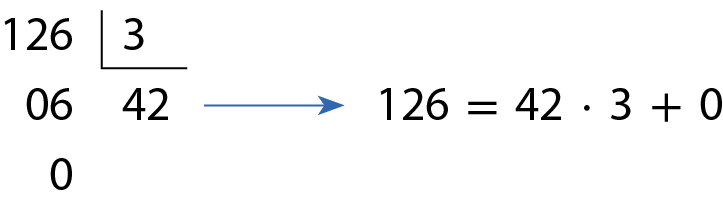
Essa é a propriedade fundamental da divisão, que podemos escrever assim:
dividendo = quociente ⋅ divisor + resto
Observações
▶ Não existe divisão por zero. Por exemplo, é impossível dividir 3 por zero, pois não existe um número que multiplicado por zero dê 3.
▶ Dizemos que uma divisão entre dois números naturais é exata quando o resto é zero.
Exemplo:
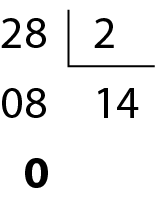
▶ Dizemos que uma divisão é não exata quando o resto é diferente de zero.
Exemplo:
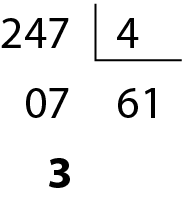
▶ O resto de uma divisão entre dois números naturais sempre é menor que o divisor. Observe.



▶ Em uma divisão exata, como há resto zero, temos: dividendo = quociente ⋅ divisor.
Assim, dizemos que a divisão exata e a multiplicação são operações inversas.
Respostas e comentários
Propriedade fundamental da divisão
Nas situações apresentadas, os estudantes podem verificar a relação fundamental da divisão, que relaciona todos os elementos envolvidos nessa operação.
Proponha a eles na lousa outras divisões para que indiquem a relação fundamental associada. Em cada uma das divisões efetuadas, incentive-os a identificar os elementos de uma divisão: dividendo, divisor, quociente e resto. Retome as noções de divisão exata e divisão não exata estudadas anteriormente. Ressalte que o resto sempre é menor que o divisor. A relação fundamental da divisão é um recurso para os estudantes comprovarem se efetuaram a operação corretamente.
Ressalte as observações, acerca da divisão, apresentadas nesta página. Ao longo do estudo da divisão, retome tais conclusões sempre que possível para que sejam assimiladas pelos estudantes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
82 Multiplique 34 por 56. Depois, divida o produto obtido por 34. O que aconteceu?
83 Pense em um número natural diferente de zero. Dê, se existir, o quociente e o resto na divisão:
a) de 0 por esse número;
b) desse número por zero;
c) desse número por 1;
d) desse número por ele mesmo.
84 Determine o número que falta em cada sentença a seguir.
a) 52 ⋅ 43 +

= .2257
b)

⋅ 32 + 4 = 580
c) 75 ⋅ 28 + 15 =

d) 26 ⋅

+ 3 = 341
85 Dividindo 42 por 6, o quociente é 7 e o resto é zero. Adicionando 1 ao dividendo e tornando a dividir por 6, o quociente continua sendo 7 e o resto passa a ser 1. Qual é o maior número que podemos adicionar a 42 para que a divisão por 6 continue tendo quociente 7?
86 Qual é o número que, dividido por 32, tem por quociente 21 e o resto é o maior possível?
87 O resto de uma divisão é 8 e é o maior resto possível; o quociente é igual ao divisor. Determine o dividendo.
88

A tecla

da calculadora de Ivo quebrou. Para saber quantas dúzias há em uma caixa com 83 laranjas, ele teclou:

Ele contou 6 toques na tecla

até aparecer no visor um número menor que 12. Concluiu que na caixa havia 6 dúzias e ainda restavam 11 laranjas. Com o auxílio de uma calculadora, faça o mesmo para efetuar as divisões e registre os resultados parciais (após cada toque da tecla

), o quociente e o resto.
a) 43 dividido por 12
b) 270 dividido por 49
c) 720 dividido por 94
d) 161 dividido por 23
Dividindo mentalmente
Decompor um número separando no dividendo as centenas das dezenas ajuda no cálculo mental de divisões. Como exemplo, vamos efetuar 236 dividido por 4.
• Para facilitar, separamos 236 em duas parcelas:
236 = 200 + 36
• Dividimos as parcelas por 4 e adicionamos os resultados:
200 dividido por 4 = 50 e 36 dividido por 4 = 9

50 + 9 = 59
• Portanto: 236 dividido por 4 = 59
Podemos indicar esses cálculos da seguinte maneira:

Outro modo de calcular mentalmente o quociente é decompondo o divisor em fatores.
Por exemplo, para efetuar a divisão de 90 por 6, o número 6 pode ser decomposto da seguinte maneira: 6 = 2 ⋅ 3.
Para dividir 90 por 6, dividimos 90 por um desses fatores e, depois, dividimos o resultado obtido pelo outro fator: 90 dividido por 2 = 45 e 45 dividido por 3 = 15
Então: 90 dividido por 6 = 90 dividido por (2 ⋅ 3) = (90 dividido por 2) dividido por 3 = 45 dividido por 3 = 15
Respostas e comentários
82. O quociente é 56.
83. c) O número pensado; 0.
83. a) 0; 0
83. b) Não existe.
83. d) 1; 0
84. a) 21
84. b) 18
84. c) .2115
84. d) 13
85. 5
86. 703
87. 89
88. a) 31; 19; 7; quociente 3; resto 7.
88. b) 221; 172; 123; 74; 25; quociente 5; resto 25.
88. c) 626; 532; 438; 344; 250; 156; 62; quociente 7; resto 62.
88. d) 138; 115; 92; 69; 46; 23; 0; quociente 7; resto 0.
Exercícios propostos
No exercício 82, espera-se que os estudantes percebam que o quociente é o outro número dado.
Para cada item do exercício 83 os estudantes devem perceber que:
a) Zero dividido por qualquer número natural diferente de zero é igual a 0 e tem resto 0.
b) Não é possível dividir nenhum número natural por 0.
c) Qualquer número natural dividido por 1 é igual ao próprio número e tem resto 0.
d) Qualquer número natural dividido por ele mesmo é igual a 1 e tem resto 0.
Ao resolver o exercício 84, devem relembrar a propriedade fundamental da divisão, que afirma: dividendo = quociente ⋅ divisor + resto.
a) 52 ⋅ 43 +

= .2257; logo,

é o resto da divisão de .2257 por 52, que é 21.
b)

⋅ 32 + 4 = 580; logo,

é o quociente da divisão de 580 por 32, que é 18.
c)

é o resultado da expressão: 75 ⋅ 28 + 15 = .2100 + 15 = .2115
d) 26 ⋅

+ 3 = 341; logo,

é o quociente da divisão de 341 por 26, que é 13.
É provável que resolvam o exercício 85 efetuando as divisões por 6 (de 43 até 48), o que não representa problema. Entretanto, após chegar à solução, eles podem experimentar o mesmo com outros números (como 35 dividido por 7) e verificar quanto podem adicionar a 35 para encontrar o mesmo quociente. É desejável que concluam que o máximo a adicionar é 1 unidade a menos que o divisor.
As resoluções dos exercícios 86 a 88 estão no início deste Manual, nas orientações específicas do capítulo 2.
Dividindo mentalmente
Neste tópico, destacamos estratégias de cálculo mental para uma divisão. Acompanhe os estudantes no desenvolvimento de suas estratégias de cálculo mental. Verifique se utilizam estratégias variadas ou se somente reproduzem o algoritmo mentalmente. Explique-lhes que as propriedades das operações e cálculos por aproximações são recursos que auxiliam as técnicas para cálculo mental.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
89

Calcule mentalmente estas divisões e registre como você fez os cálculos.
a) 108 dividido por 4
b) 309 dividido por 3
c) 312 dividido por 6
d) 448 dividido por 8
e) 530 dividido por 5
f) 981 dividido por 9
g) 350 dividido por 10
h) 350 dividido por 5
90

Reúna-se com um colega e escolham ao acaso seis números naturais que terminem em 0, 00 ou 000. Depois, dividam esses números por 10 e escrevam uma regra para efetuar mentalmente a divisão de números naturais, que terminem em zero, por 10.
91

Reúna-se com um colega e escolham ao acaso seis números naturais que terminem em 0 ou 5.
a) Dividam esses números por 5.
b) Multipliquem os números escolhidos por 2 e dividam os resultados por 10.
c) Comparem as respostas do item a com as do item b e escrevam uma regra para efetuar mentalmente a divisão por 5 de um número natural terminado em 0 ou 5.
92


Hora de criar – Elabore as operações solicitadas a seguir e registre o que você pensou. Depois, junte-se a um colega e, com uma calculadora, cada um confere o que o outro fez.
a) Uma adição cujo resultado seja .3240.
b) Uma multiplicação cujo resultado seja .5730.
c) Uma subtração cujo resultado seja .14270.
d) Uma divisão exata cujo resultado seja 450.
6. Expressões numéricas envolvendo as quatro operações
Em expressões numéricas que envolvem as quatro operações (adição, subtração, multiplicação e divisão), devemos efetuar essas operações na seguinte ordem:
• primeiro, efetuamos as multiplicações e as divisões na ordem em que aparecem;
• depois, efetuamos as adições e as subtrações, também na ordem em que aparecem.
Nas expressões numéricas com sinais de associação (parênteses, colchetes e chaves), resolvemos primeiro as operações neles contidas. Acompanhe alguns exemplos.
a)

b)
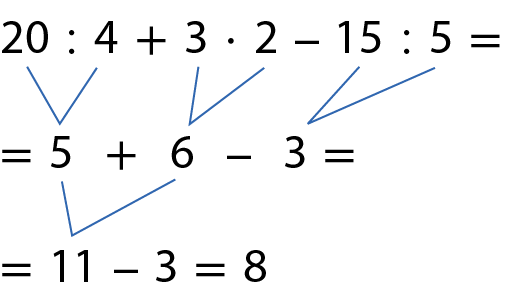
c)
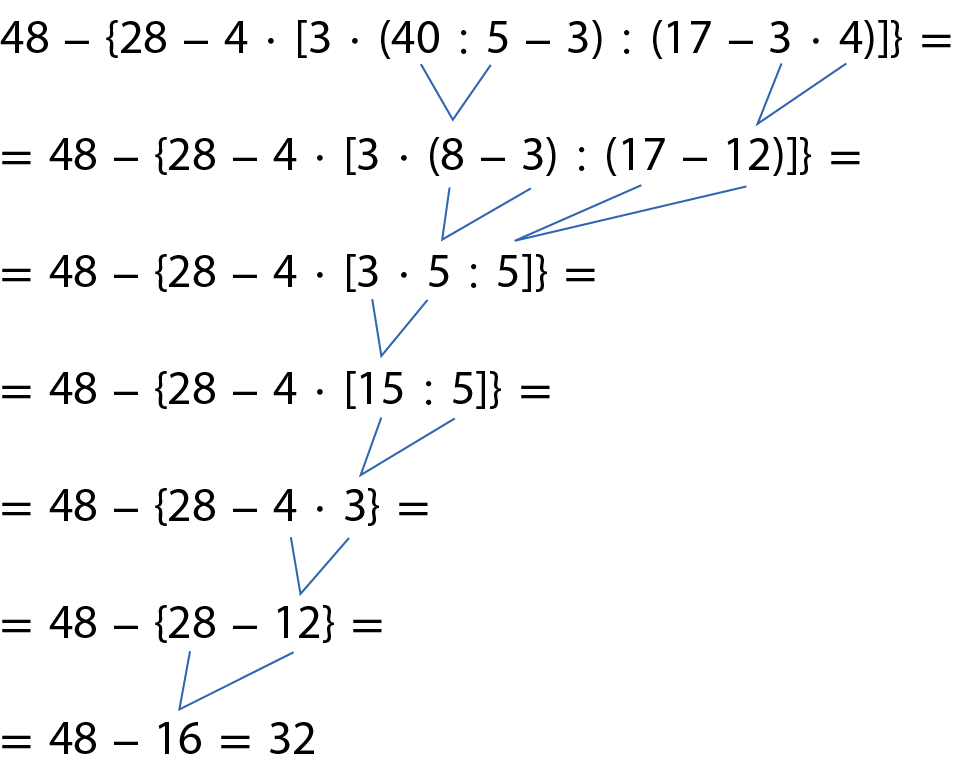
Respostas e comentários
89. a) 27
89. b) 103
89. c) 52
89. d) 56
89. e) 106
89. f) 109
89. g) 35
89. h) 70
90. Resposta pessoal.
91. Respostas pessoais.
92. Respostas pessoais.
Exercícios propostos
Após resolverem as operações propostas no exercício 89, peça aos estudantes que compartilhem as estratégias utilizadas; desse modo contribuem para a ampliação do repertório de cálculos mentais.
No exercício 90, espera-se que os estudantes concluam que, para dividir esses números por 10, basta excluir do dividendo o zero da casa das unidades.
Para a resolução do exercício 91, é interessante reunir os estudantes em duplas, circular entre eles e ouvir suas interpretações. A técnica de “multiplicar por 2 e dividir por 10” pode ser prática quando precisamos fazer uma divisão por 5; entretanto, é importante que os estudantes a compreendam, não a decorem simplesmente. Por isso, eles devem ficar livres para testar números e comparar resultados. A escrita da regra pode ser compartilhada e, no final, toda a turma escolhe a regra (ou formula mais uma) que ficou mais clara e fácil de compreender.
No item c, espera-se que os estudantes concluam que a divisão de números naturais, múltiplos de 5, por 5 é equivalente à multiplicação desses números por 2, seguida da divisão do resultado por 10.
Proponha aos estudantes que escrevam na lousa as diferentes operações elaboradas para o exercício 92, de modo a contribuir para a percepção de que diferentes cálculos possam ter o mesmo resultado.
6. Expressões numéricas envolvendo as quatro operações
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico, apresentamos expressões numéricas que envolvem as quatro operações estudadas até o momento: adição, subtração, multiplicação e divisão, e retomamos o uso de sinais de associação, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah zero três). É importante que os estudantes acompanhem passo a passo as operações efetuadas, identificando a ordem em que foram executadas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
93 O quadro mostra uma correspondência entre letras e números.
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
Associando o valor de cada expressão a seguir à letra correspondente no quadro, você vai descobrir uma palavra. Que palavra é essa?
a) 21 ‒ (32 ‒ 25)
b) 44 ‒ (4 ⋅ 9 ‒ 25) ‒ 12
c) 61 ‒ (54 ‒ 24 dividido por 4)
d) 25 ‒ {20 + [18 ‒ (13 + 10 dividido por 2)]}
e) 69 ‒ [26 + (67 ‒ 42)]
f) 4 + [(55 ‒ 2 ⋅ 9) ‒ (40 dividido por 2 + 6)]
94 A expressão 64 dividido por 8 dividido por 4 dividido por 2 pode ter diferentes resultados, dependendo do lugar onde forem colocados os sinais de agrupamento. Coloque os sinais de agrupamento para que a expressão tenha estes resultados:
a) 4
b) 16
95 Daniel deseja comprar uma van para transporte escolar que custa, à vista, .120000 reais. No pagamento a prazo, o preço dela passa a ser .145200 reais, sendo .24000 reais de entrada mais 50 prestações mensais iguais. Sabendo que Daniel vai comprar a prazo, determine:
a) uma expressão numérica que dê o valor de cada prestação;
b) o valor de cada prestação;
c)

a diferença entre o preço à vista e o total a prazo. Na sua opinião, essa diferença é pequena ou é grande? Se Daniel tivesse dinheiro para o pagamento à vista, essa opção seria a mais adequada? Justifique.
96

Hora de criar – A professora foi anotando na lousa o que cada estudante da fileira da janela falava. Todos falavam o mesmo número, mas, à medida que cada um o substituía por uma expressão, aumentavam as operações.

Copie a expressão de Dea, substituindo os números 36 e 15 por expressões numéricas com valores 36 e 15, respectivamente. Depois, troque sua nova expressão com um colega para que cada um efetue todas as operações indicadas e chegue ao número que Ana falou.
7. Potenciação
Acompanhe a situação a seguir.
Um grupo de amigos participará de um passeio ecológico. Cada um deverá usar um crachá no qual consta seu nome. Caio se encarregou de preparar os crachás. Para isso, elaborou estas etapas: cortou, com um tesoura sem pontas, uma folha de papel reciclado ao meio; cortou cada uma das duas partes ao meio; cortou novamente cada uma das partes ao meio; e, mais uma vez, cortou cada uma das partes ao meio. Com isso, obteve exatamente o número necessário de crachás.

Quantos crachás Caio fez?
Para calcular o número de crachás, podemos efetuar a multiplicação 2 ⋅ 2 ⋅ 2 ⋅ 2, na qual os quatro fatores são iguais a 2. Logo, são 16 crachás.
Ao efetuar uma multiplicação de fatores iguais, estamos realizando uma operação chamada potenciação.
Respostas e comentários
93. Número.
93. a) 14 (êne)
93. b) 21 (u)
93. c) 13 (ême)
93. d) 5 (ê)
93. e) 18 (érre)
93. e) 15 (óh)
94. a) 64 dividido por 8 dividido por (4 dividido por 2)
94. b) [64 dividido por (8 dividido por 4)] dividido por 2
95. a) (.145200 ‒ .24000) dividido por 50
95. b) .2424 reais.
95. c) .25200 reais. Resposta pessoal.
96. Resposta pessoal.
Exercícios propostos
Observe se, ao resolver os exercícios, os estudantes empregam corretamente as propriedades, se utilizam parênteses desnecessários e se estão conseguindo se expressar matematicamente. A construção da linguagem matemática inicia-se por situações simples como as de construir expressões numéricas, uma vez que elas oferecem oportunidade aos estudantes de mostrar a interpretação que estão dando aos símbolos e às propriedades.
O exercício 94 representa mais uma oportunidade para a realização de estimativas, pois, a cada teste com o lugar dos parênteses, os estudantes podem observar se o resultado é maior ou menor que o esperado. A ideia é notarem que, quando queremos um resultado maior, devemos fazer o dividendo ser o maior possível e o divisor, o menor possível, e vice-versa quando desejamos um resultado menor.
Para o exercício 95, devem considerar as seguintes informações do enunciado: preço à vista .120000 reais; preço a prazo .145200 reais; entrada .24000 reais; quantidade de prestações 50.
a) O valor de cada prestação é a quantidade que falta pagar além da entrada, dividido pela quantidade de prestações, ou seja, (.145200 ‒ .24000) : 50
b) o valor de cada prestação será a resolução da expressão do item a, ou seja: (.145200 ‒ .24000) dividido por 50 = .25200 dividido por 50 = .2424 (.2420 reais) A diferença é de .145200 ‒ .120000 = .25200
c) Após a resolução do item b, pode-se dar início a um debate sobre as vantagens e consequências de realizar compras a prazo, proposto no item c. É interessante lembrar aos estudantes que, na maioria das vezes, as taxas adicionais cobradas a prazo são tão altas que tornam mais vantajosa a compra à vista. Citar casos de produtos de maior custo, que, parcelados em muitas vezes, acabam tendo o custo final equivalente a dois desses produtos. Entretanto, nessa discussão devem ser consideradas também a situação do comprador e as circunstâncias da compra, que muitas vezes precisa ser realizada a prazo, ainda que matematicamente seja desfavorável para o comprador. Deste modo, contribui-se para o trabalho com o Tema Contemporâneo Transversal educação financeira.
As resoluções dos exercícios 93 e 96 estão no início deste Manual, nas orientações específicas do capítulo 2.
Observe.

Considerando o exemplo dado, temos:
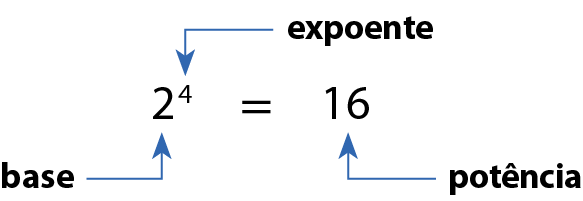
(Lemos 2elevado a 4 assim: “dois elevado à quarta potência” ou “dois elevado à quarta”.)
Em uma calculadora, efetuamos essa potência da seguinte maneira:

Observe outros exemplos.
a)

b)

c)

d)

Quadrado de um número
As potências de expoente 2 podem ser representadas geometricamente. Observe.
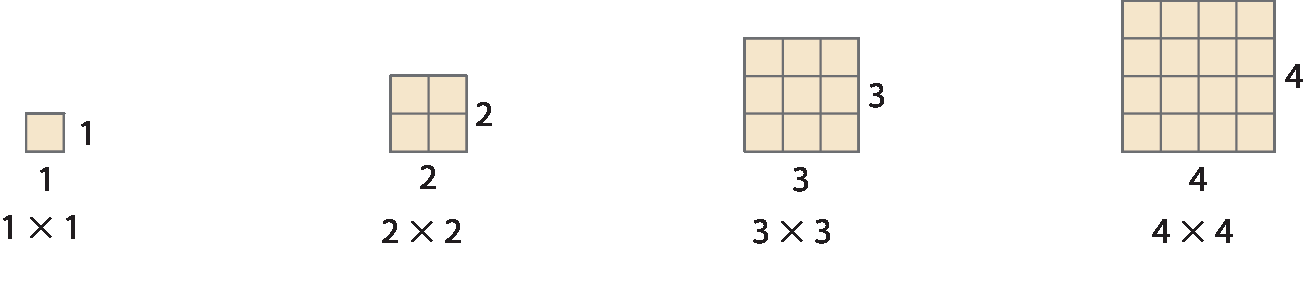
Pela associação com essas figuras, as potências de expoente 2 recebem nomes especiais:
• 1elevado a 2: “um ao quadrado”.
• 2elevado a 2: “dois ao quadrado”.
• 3elevado a 2: “três ao quadrado”.
• 4elevado a 2: “quatro ao quadrado”.
Cubo de um número
As potências de expoente 3 também podem ser representadas geometricamente. Observe.
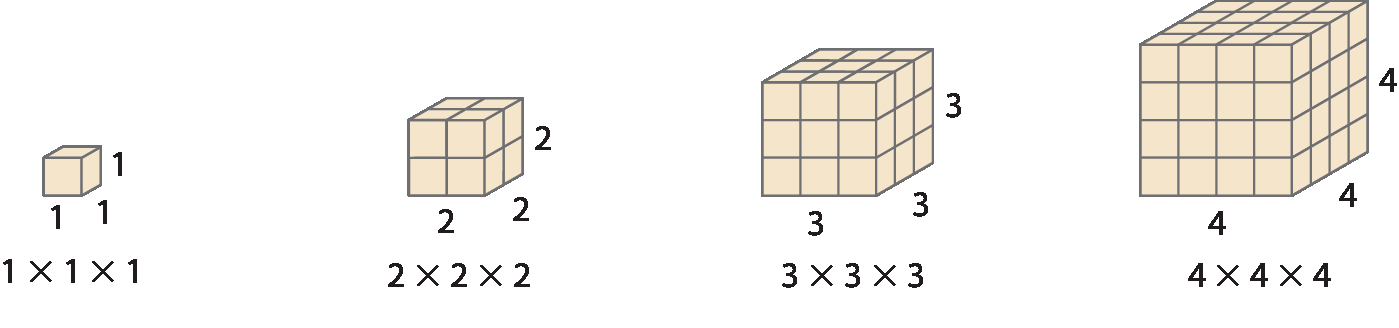
Da mesma maneira, essas potências recebem nomes especiais:
• 1elevado a 3: “um ao cubo”.
• 2elevado a 3: “dois ao cubo”.
• 3elevado a 3: “três ao cubo”.
• 4elevado a 3: “quatro ao cubo”.
Quando o expoente é 4, 5, 6, …, lemos: “quarta potência”, “quinta potência”, “sexta potência”, e assim por diante. Por exemplo:
• 9elevado a 4: “nove elevado à quarta potência”.
• 6elevado a 5: “seis elevado à quinta potência”.
Respostas e comentários
7. Potenciação
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico ampliamos o trabalho com a habilidade (ê éfe zero seis ême ah zero três) ao trabalhar com a potenciação com números naturais.
Explore com os estudantes a situação proposta para introduzir a potenciação. Se possível, leve calculadoras simples para a sala de aula, oferecendo aos estudantes a oportunidade de explorar procedimentos de uso de calculadora no cálculo de potências.
Ressalte que, para evitar equívocos no cálculo, eles devem interpretar corretamente cada potência. Por exemplo:
• 3elevado a 4 não deve ser interpretado como “4 vezes o número 3”, que acarretaria obter 12. A interpretação correta é “4 fatores 3”, o que demonstra que o cálculo é 3 ⋅ 3 ⋅ 3 ⋅ 3, resultando 81. Enfatize também a leitura das potências, como “três elevado à quarta”.
• 7elevado a 3 não deve ser interpretado como “3 vezes o número 7”, que acarretaria obter 21. A interpretação correta é “3 fatores 7”, o que demonstra que o cálculo é 7 ⋅ 7 ⋅ 7, resultando 343. Enfatize também a leitura, como “sete à terceira” ou, como será visto na página seguinte, “sete ao cubo”.
Destaque também os termos que compõem uma potenciação, para os estudantes se acostumarem com seus nomes e significados: base, expoente e potência.
Proponha aos estudantes que determinem os quadrados e os cubos de todos os números naturais de 0 a 10. Eles podem fazer quadros com tais potências para consultar em outros momentos.
Potências de expoente zero, de expoente 1 e de base 10
Observe os esquemas a seguir.
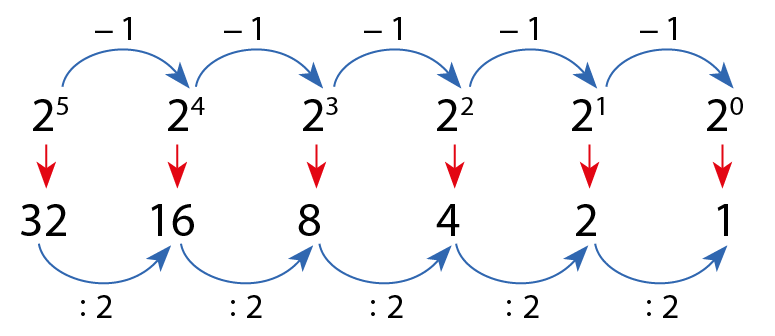
Nas potências de base 2, quando o expoente diminui uma unidade, a potência fica dividida por 2. Note que: 2elevado a 1 = 2 e 2elevado a 0 = 1.
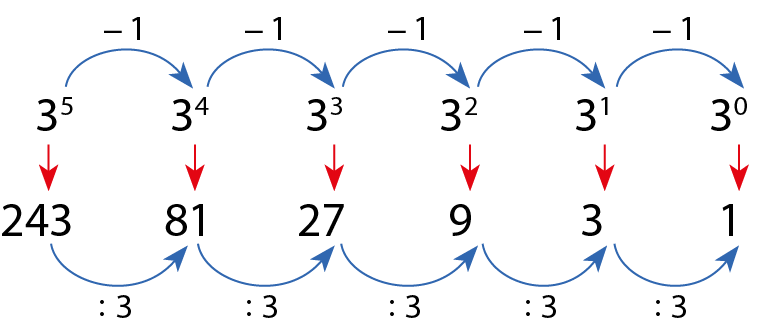
Nas potências de base 3, quando o expoente diminui uma unidade, a potência fica dividida por 3. Note que: 3elevado a 1 = 3 e 3elevado a 0 = 1.
Isso acontece sempre que a base for diferente de zero.
De modo geral, convencionamos que:
• Toda potência de expoente 1 é igual à base.
• Toda potência de expoente zero e base diferente de zero é igual a 1.
Agora, observe estas potências de base 10.
• 10elevado a 1 = 10

um zero
• 10elevado a 2 = 100

dois zeros
• 10elevado a 3 = .1000

três zeros
Toda potência de base 10 é igual ao número 1 seguido de tantos zeros quantas forem as unidades do expoente.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
97 Escreva no caderno as sentenças a seguir na fórma de potência.
a) 3 ⋅ 3
b) 7 ⋅ 7 ⋅ 7
c) 9 ⋅ 9 ⋅ 9 ⋅ 9
d) 1 ⋅ 1 ⋅ 1 ⋅ 1 ⋅ 1 ⋅ 1
98 Indique as potências na fórma de produto.
a) 10elevado a 3
b) 9elevado a 2
c) 8elevado a 4
d) 6elevado a 5
99 Como se lê cada potência?
a) 4elevado a 8
b) 13elevado a 3
c) 220elevado a 7
100 Calcule o valor das potências a seguir.
a) 5elevado a 3
b) 2elevado a 5
c) 3elevado a 5
d) 4elevado a 5
e) 10elevado a 2
f) 10elevado a 6
101 Identifique a regularidade presente e escreva o sexto termo da sequência: 3, 9, 27, 81, reticências
102 Por uma estrada, viajava a van de uma veterinária com sete caixas; em cada caixa havia sete compartimentos; e cada compartimento tinha sete embalagens de ração. Quantas embalagens de ração havia nas caixas?
103 Calcule cada uma das potências a seguir.
a) 1elevado a 4
b) 12elevado a 1
c) 20elevado a 1
d) .1996elevado a 0
e) 15elevado a 0
f) 100elevado a 1
g) 100elevado a 0
h) 1elevado a 10
i) 0elevado a 9
104 Calcule o valor do número natural x.
a) 6elevado a x = 36
b) 6elevado a x = 6
c) 6elevado a x = 1
105 Qual é o número maior:
a) 2elevado a 3 ou 3elevado a 2 ?
b) 10elevado a 0 ou 1elevado a 10 ?
c) 5elevado a 2 ou 2elevado a 5 ?
d) 1⁶ ou 1⁸ ?
e) 3elevado a 4 ou 4elevado a 3 ?
f) 10elevado a 2 ou 210 ?
Respostas e comentários
97. a) 3elevado a 2
97. b) 7elevado a 3
97. c) 9elevado a 4
97. d) 1elevado a 6
98. a) 10 ⋅ 10 ⋅ 10
98. b) 9 ⋅ 9
98. c) 8 ⋅ 8 ⋅ 8 ⋅ 8
98. d) 6 ⋅ 6 ⋅ 6 ⋅ 6 ⋅ 6
99. a) Quatro elevado à oitava potência.
99. b) Treze elevado ao cubo.
99. c) Duzentos e vinte elevado à sétima potência.
100. a) 125
100. b) 32
100. c) 243
100. d) .1024
100. e) 100
100. f) ..1000000
101. 729
102. trezentas e quarenta e três embalagens.
103. a) 1
103. b) 12
103. c) 20
103. d) 1
103. e) 1
103. f) 100
103. g) 1
103. h) 1
103. i) 0
104. a) 2
104. b) 1
104. c) 0
105. a) 3elevado a 2
105. b) São iguais.
105. c) 2elevado a 5
105. d) Iguais.
105. e) 3elevado a 4
105. f) 2elevado a 10
Potências de expoente zero, de expoente 1 e de base 10
Verifique se os estudantes entenderam o cálculo de potências de expoentes 1 e de expoente zero (para bases naturais diferentes de zero).
Proponha a eles algumas potências oralmente para responderem o valor também oralmente.
Como fórma de ampliação, pode-se fazer um ditado com resultados de potências de base 10 para os estudantes registrarem no caderno a potência de base 10 que originou tal resultado. Certifique-se de que todos entenderam o formato desse ditado. Por exemplo, podem ser ditados os seguintes números: .100000, 1, 10, ..1000000, .1000, .10000 e 100. Desse modo, espera-se que eles registrem, respectivamente, as seguintes potências: 10elevado a 5, 10elevado a 0, 10elevado a 1, 10elevado a 6, 10elevado a 3, 10elevado a 4 e 10elevado a 2.
Exercícios propostos
As resoluções dos exercícios 97 a 102 estão no início deste Manual, nas orientações específicas do capítulo 2.
Para responder ao exercício 103 os estudantes devem considerar que:
• O número 1 elevado a qualquer potência é 1.
• Qualquer número elevado a 1 é igual ao próprio número.
• Qualquer número elevado a 0 é igual a 1.
No exercício 104 devem analisar a igualdade para determinar o valor de x:
a) Deve-se considerar a que potência deve-se elevar o número 6 para obter 36:
6x = 36 = 6elevado a 2 ⇒ x = 2
b) Deve-se considerar a que potência deve-se elevar o número 6 para obter 6:
6x = 6 = 6elevado a 1 ⇒ x = 1
c) Neste caso, para que se obtenha 1, x deve ser igual a 0:
6x = 1 = 6elevado a 0 ⇒ x = 0
Para resolver o exercício 105, podem-se fazer alguns cálculos:
a) 2elevado a 3 = 2 ⋅ 2 ⋅ 2 = 8 e 3elevado a 2 = 3 ⋅ 3 = 9. Como 9 > 8 ⇒ 3elevado a 2 > 2elevado a 3.
b) 10elevado a 0 = 1 e 1elevado a 10 = 1, então 10elevado a 0 = 1elevado a 10.
c) 5elevado a 2 = 5 ⋅ 5 = 25 e 2elevado a 5 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 32. Como 32 > 25 ⇒ 2elevado a 5 > 5elevado a 2.
d) 1elevado a 6 = 1 e 18 = 1, então 1elevado a 6 = 1elevado a 8
e) 3elevado a 4 = 3 ⋅ 3 ⋅ 3 ⋅ 3 = 9 ⋅ 9 = 81 e 4elevado a 3 = 4 ⋅ 4 ⋅ 4 = 16 ⋅ 4 = 64. Como 81 > 64 ⇒ 3elevado a 4 > 4elevado a 3.
f) 10elevado a 2 = 10 ⋅ 10 = 100 e 2elevado a 10 = 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4 = 16 ⋅ 16 ⋅ 4 = 256 ⋅ 4 = .1024. Como .1024 > 100 ⇒ 2elevado a 10 > 10elevado a 2
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO

Com o auxílio de uma calculadora, determine as potências a seguir. a) 99elevado a 2 b) 999elevado a 2 c) .9999elevado a 2

Observando esses resultados, calcule mentalmente .99999elevado a 2.
Números quadrados perfeitos
Observe esta sequência de figuras.

Note que, conforme o número de quadradinhos, é possível construir quadrados, como no caso das figuras que têm 1, 4 e 9 quadradinhos. Nos demais casos, isso não é possível. Quando a quantidade de quadradinhos possibilita formar um quadrado, o número associado a ele é chamado número quadrado perfeito.
Um número natural é quadrado perfeito quando ele é quadrado de outro número natural.
Observe os números naturais que são quadrados perfeitos de 0 a 100:
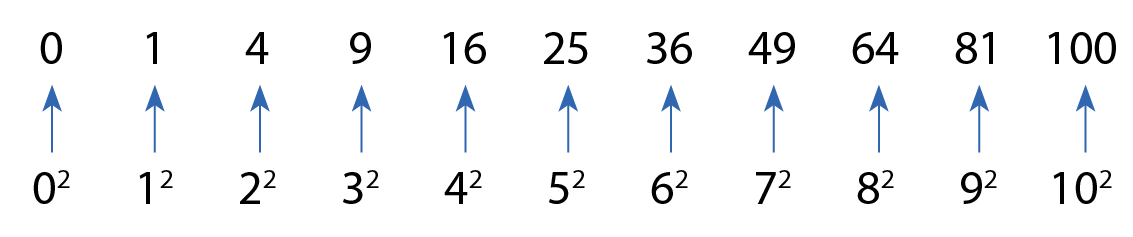
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
106 Descubra os números naturais quadrados perfeitos de 100 a 200.
107 Considere as centenas: 100, 200, 300, 400, 500, 600, 700, 800 e 900. Quais dessas centenas são quadrados perfeitos?
108 Escreva todos os números de três algarismos distintos formados por 1, 6 e 9. Em seguida, descubra quais desses números são quadrados perfeitos.
109

Hora de criar – Pense em um número natural e calcule o seu quadrado. A esse quadrado adicione o número pensado e mais o sucessor dele. Verifique se o número obtido é um quadrado perfeito. Em caso afirmativo, esse número obtido é quadrado de qual número? Verifique se um colega chegou à mesma conclusão.
Respostas e comentários
Pense mais um poucoreticências:
a) .9801
b) .998001
c) ..99980001
Resposta: ...9999800001
106. 100, 121, 144, 169 e 196.
107. 100, 400 e 900.
108. 169, 196, 619, 691, 916, 961; números quadrados perfeitos: 169, 196 e 961.
109. Sim, é quadrado do sucessor do número pensado.
Pense mais um poucoreticências
Esta seção pode ser realizada em duplas, propondo aos estudantes que discutam os padrões numéricos associados a cálculos de potências. Circule pela sala de aula e verifique se eles conseguem explicar o padrão observado. Utilizando uma calculadora, percebe-se que: 99elevado a 2 = .9801, 999elevado a 2 = .998001 e .9999elevado a 2 = ..99980001.
Então: .99999elevado a 2 = ...9999800001, pois:
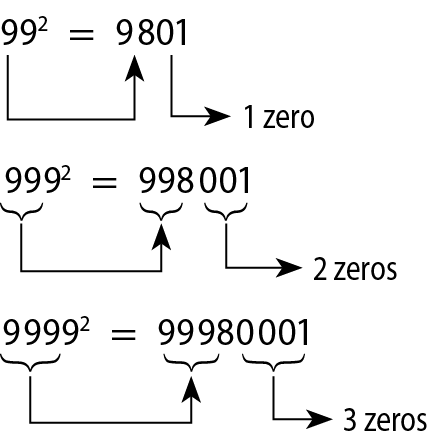
Seguindo o mesmo padrão, temos:
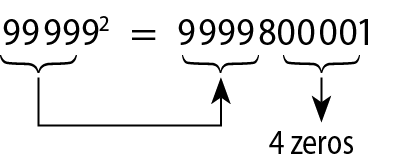
Números quadrados perfeitos
Tratamos aqui do conceito de quadrado perfeito, preparando os estudantes para o cálculo de raízes quadradas, que verão mais adiante.
Se julgar conveniente, apresente-lhes os cubos perfeitos e desenvolva de maneira similar à que foi usada com os quadrados perfeitos.
Exercícios propostos
No exercício 106, caso tenham dificuldade para encontrar os números que são quadrados perfeitos (e não estamos falando em extrair a raiz quadrada), pode-se sugerir que façam um quadro de quadrados perfeitos, usando a potenciação de base com um número natural qualquer e expoente sempre 2. O mesmo quadro será importante em estudos posteriores, especialmente no trabalho com radiciação. Assim, fazendo 10elevado a 2, 11elevado a 2, 12elevado a 2, 13elevado a 2 e 14elevado a 2, obtém-se a resposta deste exercício.
As resoluções dos exercícios 107 a 109 estão no início deste Manual, nas orientações específicas do capítulo 2.
8. Radiciação
Considere as questões propostas por Carla e Rodrigo.

Para responder a essas questões, usamos a operação inversa da potenciação, chamada radiciação, que indicamos pelo símbolo
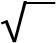
.
Na questão proposta por Carla, devemos encontrar a raiz quadrada de 25, ou seja, encontrar o número natural que elevado ao quadrado resulte em 25.
A resposta para essa questão é o número 5, porque 5elevado a 2 = 25.
Indicamos que a raiz quadrada de 25 é 5 escrevendo:
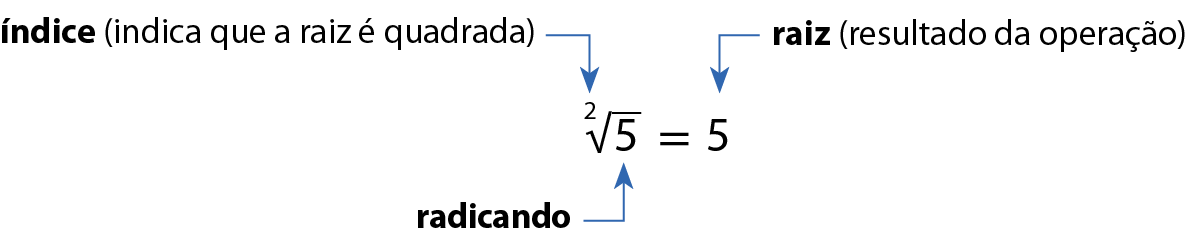
(Lemos: “a raiz quadrada de vinte e cinco é igual a cinco”.)
Em uma calculadora, podemos calcular essa raiz quadrada da seguinte maneira:

Observações
▶ Na indicação da raiz quadrada, não é preciso escrever o índice 2. Assim:
•
Raiz quadrada de 25 igual à 5pode ser indicada por
Raiz quadrada de 25 igual à 5•
Raiz quadrada de 36 igual à 6pode ser indicada por
Raiz quadrada de 36 igual à 6▶ Apenas os números quadrados perfeitos têm como raiz quadrada um número natural.
Na questão proposta por Rodrigo, devemos encontrar a raiz cúbica de 216, ou seja, encontrar o número que elevado ao cubo resulte em 216.
A resposta para essa questão é o número 6, porque 6elevado a 3 = 216.
Indicamos a raiz cúbica de 216 por:
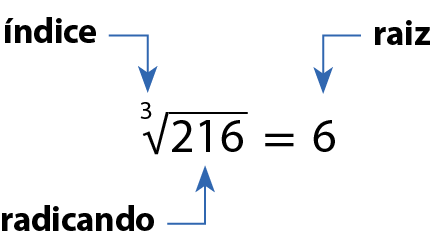
(Lemos: “a raiz cúbica de duzentos e dezesseis é igual a seis”.)
Respostas e comentários
8. Radiciação
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah zero três.
Neste tópico ampliamos o trabalho com a habilidade (ê éfe zero seis ême ah zero três) ao trabalhar com o cálculo radiciação de números naturais.
Explore com os estudantes a situação proposta para introduzir a radiciação. Se possível, leve calculadoras simples para a sala de aula, oferecendo aos estudantes a oportunidade de explorar procedimentos de uso desse instrumento para efetuar os cálculos solicitados, em especial o da raiz quadrada em que geralmente há uma tecla associada a essa operação.
Antes da introdução da operação radiciação, proponha aos estudantes que respondam às questões propostas pelos personagens e que depois, determinem, em duplas, os seguintes números:
• Qual é o número natural cujo quadrado é 400? (20)
• Qual é o número natural cuja quarta potência é 1? (1)
• Qual é o número natural cujo cubo é 27? (3)
Espera-se que eles percebam que na primeira situação devem buscar um número natural que multiplicado por ele mesmo resulte como produto o 400 e que se trata de um quadrado perfeito. Assim, podem verificar no quadro que fizeram (ou por tentativas) e obter o número 20. No entanto, para o cálculo por tentativas, é interessante terem uma pista para iniciar o processo, alguma estratégia para reduzir um pouco as opções. Por exemplo, no caso do 400, pode-se tomar algum quadrado perfeito conhecido, como o 100 = 10elevado a 2 e, assim, iniciar as tentativas com potências de bases maiores do que 10.
De maneira similar, é possível resolver as demais questões. Desse modo, os estudantes podem dar mais significado ao cálculo de raízes.
Ressalte os termos que compõem uma radiciação: índice, radicando e raiz.
Observe outros exemplos.
a)
Raiz quarta de 625 é igual a 5.= 5, porque 5elevado a 4 = 625 (Lemos: “a raiz quarta de seiscentos e vinte e cinco é igual a cinco”.)
b)
Raiz quinta de 243 é igual a 3.= 3, porque 3elevado a 5
= 243 (Lemos: “a raiz quinta de duzentos e quarenta e três é igual a três”.)
c)
Raiz sexta de 64 é igual a 2.= 2, porque 2elevado a 6
= 64 (Lemos: “a raiz sexta de sessenta e quatro é igual a dois”.)
Observação
▶ Nas calculadoras simples, não há teclas que possibilitem calcular raízes cúbicas, quartas, quintas, e assim por diante.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
110 Na operação
Raiz quadrada de 64 igual à 8pede-se:
a) o radicando;
b) a raiz;
c) o índice.
111 Justifique as igualdades.
a)
Raiz quadrada de 100 igual à 10b)
raiz cúbica de 343 igual a 7c)
Raiz quinta de 32 igual à 2d)
Raiz quarta de 1 igual à 1112 Encontre a raiz quadrada dos seguintes números quadrados perfeitos:
a) 49
b) 81
c) 121
d) 225
113 Para cada valor atribuído à letra a, calcule 2 ⋅ a, aelevado a 2 e
Raiz quadrada de a.a) a = 9
b) a = 25
c) a = 36
d) a = 100
114


Reúna-se com um colega e, com o auxílio de uma calculadora, descubram, primeiro, a soma dos quadrados e, depois, a raiz quadrada da soma de cada item a seguir.

a) 3elevado a 2 + 4elevado a 2
b) 6elevado a 2 + 8elevado a 2
c) 9elevado a 2 + 12elevado a 2
d) 12elevado a 2 + 16elevado a 2
e) 5elevado a 2 + 12elevado a 2
f) 10elevado a 2 + 24elevado a 2
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Observe o que acontece:
= 1
= 2
= 3
= 4
Agora, sem efetuar a operação, determine qual é a raiz quadrada de:
1 + 2 + 3 + 4 + 5 + 6 + 5 + 4 + 3 + 2 + 1

Depois, confira sua resposta com uma calculadora.
Respostas e comentários
110. a) 64
110. b) 8
110. c) 2
111. a)
Raiz quadrada de 100= 10, porque 10elevado a 2 = 100.
111. b)
Raiz cúbica de 343 é igual a 7.= 7, porque 7elevado a 3 = 343.
111. c)
Raiz quinta de 32 é igual a 2.= 2, porque 2elevado a 5 = 32.
111. d)
Raiz quarta de 1= 1, porque 1elevado a 4 = 1.
112. a) 7
112. b) 9
112. c) 11
112. d) 15
113. a) 18, 81 e 3, respectivamente.
113. b) 50, 625 e 5, respectivamente.
113. c) 72, .1296 e 6, respectivamente.
113. d) 200, .10000 e 10, respectivamente.
114. a) 25; 5
114. b) 100; 10
114. c) 225; 15
114. d) 400; 20
114. e) 169; 13
114. f) 676; 26
Pense mais um poucoreticências:
Resposta: 6
Radiciação
Antes dos Exercícios propostos, que exploram a radiciação, discuta com os estudantes o cálculo de raízes quadradas com uma calculadora simples. Peça a eles que efetuem na calculadora algumas raízes quadradas (exatas ou não). Converse com eles sobre o significado dos resultados que aparecem no visor que não são números naturais, como o caso da
Raiz quadrada de 2, na qual aparece 1,4142135. Espera-se que percebam que 2 não é um quadrado perfeito, isto é, não existe número natural que, elevado ao quadrado, dê 2; por isso, a raiz quadrada de 2 não é exata. Comente que neste momento estudaremos apenas os cálculos de radiciações que sejam exatas.
Exercícios propostos
As resoluções dos exercícios 110 a 113 estão no início deste Manual, nas orientações específicas do capítulo 2.
Como a intenção não é que os estudantes utilizem uma calculadora científica para resolver os itens do exercício 114, é importante verificar se não estão fazendo todos os cálculos de uma vez, o que os levará a resultados errados. Em uma calculadora comum, primeiro devem fazer registros parciais de cada potência, depois adicionar seus resultados e, só então, encontrar a raiz quadrada.
Os estudantes devem observar que, nesse exercício, a adição de dois números quadrados perfeitos resulta em um quadrado perfeito. Entretanto, também de fórma experimental, devem perceber que nem sempre isso ocorre, ou seja, há adições de dois números quadrados perfeitos que não resultam em um quadrado perfeito. Para mostrar-lhes isso, sugira a eles pelo menos uma adição, como 2elevado a 2 + 3elevado a 2.
Se julgar conveniente, aborde expressões numéricas envolvendo potenciação e radiciação, além das demais operações. Para isso, esclareça aos estudantes que devem primeiro calcular as potências e as raízes (na ordem em que aparecem) e, depois, seguir a ordem das demais operações (obedecendo aos sinais de associações, se houver).
Pense mais um poucoreticências
A seção pode ser feita em duplas. Incentive os estudantes a compararem com outras duplas o que fizeram. A regularidade a ser observada está na parcela central de cada expressão numérica que determina o radicando. Assim, a parcela central da expressão indicada é o 6.
TRABALHANDO A INFORMAÇÃO

Interpretando um gráfico de colunas
Os planetas e suas luas
Luas ou satélites naturais são corpos celestes que giram em torno de um planeta. A trajetória descrita pelos satélites, assim como a trajetória do planeta Terra em torno do Sol, é chamada órbita.


Dos planetas do Sistema Solar, apenas dois não possuem satélites naturais: Vênus e Mercúrio.
Note no gráfico a seguir a quantidade de satélites naturais, conhecida atualmente, dos demais planetas do Sistema Solar.
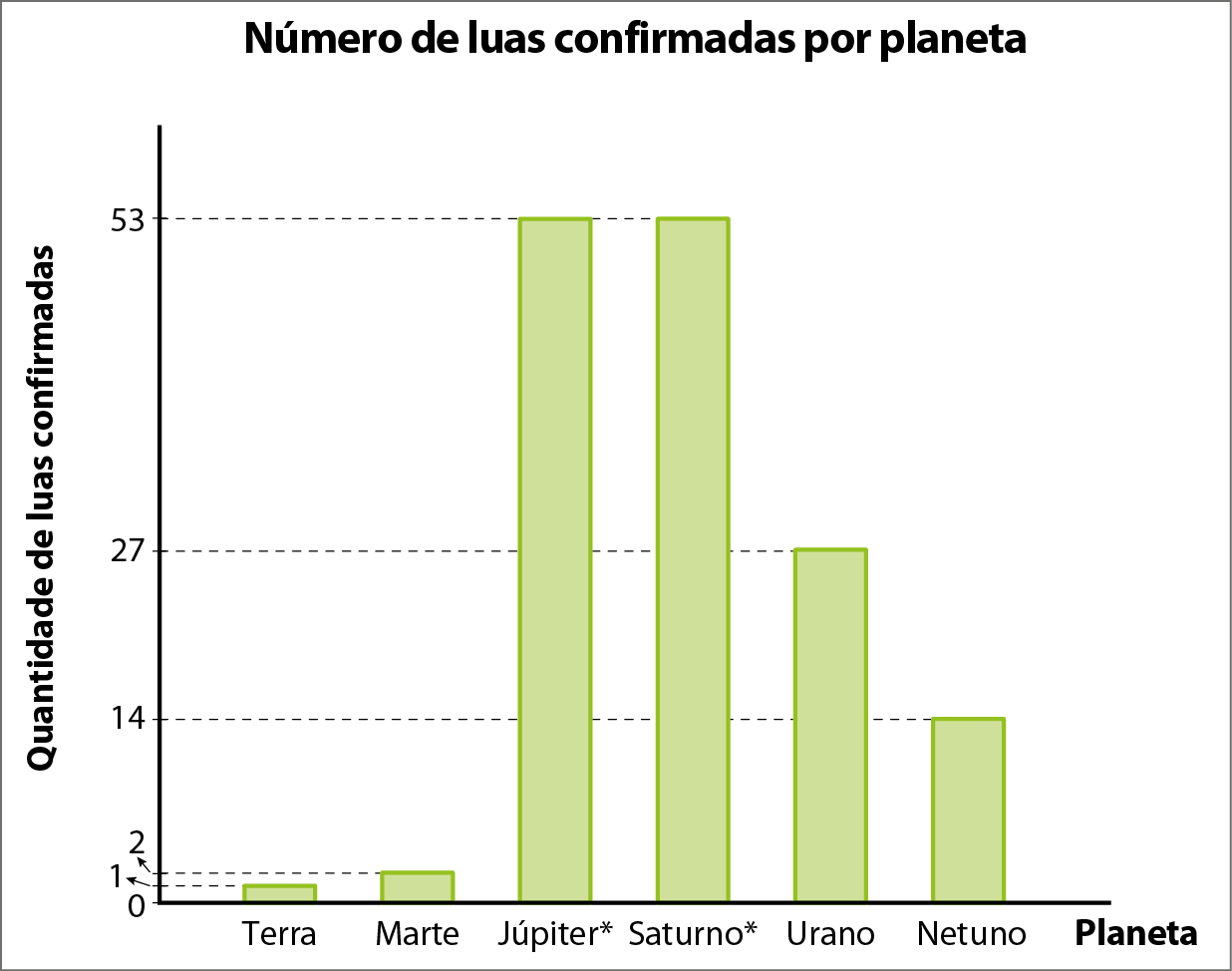

Essa figura é um exemplo de gráfico de colunas.
A primeira coluna, da esquerda para a direita, de altura 1, representa a quantidade de luas do planeta Terra: 1 lua. A segunda coluna, de altura 2, representa a quantidade de luas do planeta Marte: duas luas. E assim por diante.
Observe que as colunas referentes a Júpiter e Saturno têm alturas iguais, pois esses planetas têm o mesmo número de luas confirmadas, 53. Os asteriscos (*) chamam a atenção para uma informação. Nesse caso, assinalam que a quantidade de luas desses planetas ainda não é totalmente conhecida, uma vez que esses números representam o mínimo de luas confirmadas – é possível que haja mais. Além das 53 luas confirmadas, Saturno tem mais 29 luas provisórias, ainda não confirmadas, e Júpiter tem mais 26 luas provisórias que precisam de mais observações.
Respostas e comentários
Trabalhando a informação
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah três um e ê éfe zero seis ême ah três dois.
Esta seção introduz um conteúdo matemático muito importante para a compreensão do mundo atual: a interpretação de gráficos. A proposta aqui é estudar gráficos de colunas, recurso notadamente usual nas mídias contemporâneas, contribuindo para o desenvolvimento das habilidades (ê éfe zero seis ême ah três um) e (ê éfe zero seis ême ah três dois).
A interpretação de dados representados em fórma de gráfico (de colunas ou de qualquer outro tipo) envolve compreender cada elemento de tal gráfico. Nesse caso, uma questão simples, mas de extrema importância, é os estudantes compreenderem que a altura de cada coluna está relacionada ao número (no caso, o número de luas confirmadas por planeta) que queremos representar.
Aproveite esse momento para promover um trabalho com o professor de Ciências da Natureza sobre o estudo dos corpos celestes. Comente com os estudantes que muitos conceitos da Matemática foram importantes para esse estudo, seja para determinação de distâncias ou para o estudo das fórmas. Desse modo, contribui-se para o desenvolvimento das competências gerais 1 e 2.

Sugestão de leitura
Para apoiar essa proposta de trabalho, sugerimos a seguinte dissertação:
RODAS, H. F. A importância da Matemática no desenvolvimento da Astronomia. 2016. Dissertação (Mestrado Profissional em Matemática) – Universidade Federal de Alagoas, Maceió, 2016.
Este trabalho trata da fórma como a Astronomia se desenvolveu e a importância da Matemática nessa evolução.
Então, em um gráfico desse tipo, a altura de cada coluna corresponde à quantidade de vezes que a informação pesquisada foi observada naquele evento (acontecimento).
Em um gráfico de colunas, pode-se perceber rapidamente as colunas mais altas e as mais baixas, ou seja, as que representam maior ou menor número de observações segundo os dados em estudo.
Para fazer uma interpretação adequada de um gráfico, precisamos estabelecer comparações entre os dados apresentados e, às vezes, realizar alguns cálculos.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Com base no gráfico de colunas da página anterior, faça mais algumas interpretações.
a) Quantas luas confirmadas o planeta Netuno tem a mais que Marte?
b) Quantas luas confirmadas os planetas do Sistema Solar, excluindo Vênus e Mercúrio, têm no total?
2 Observe o gráfico a seguir e responda às questões.
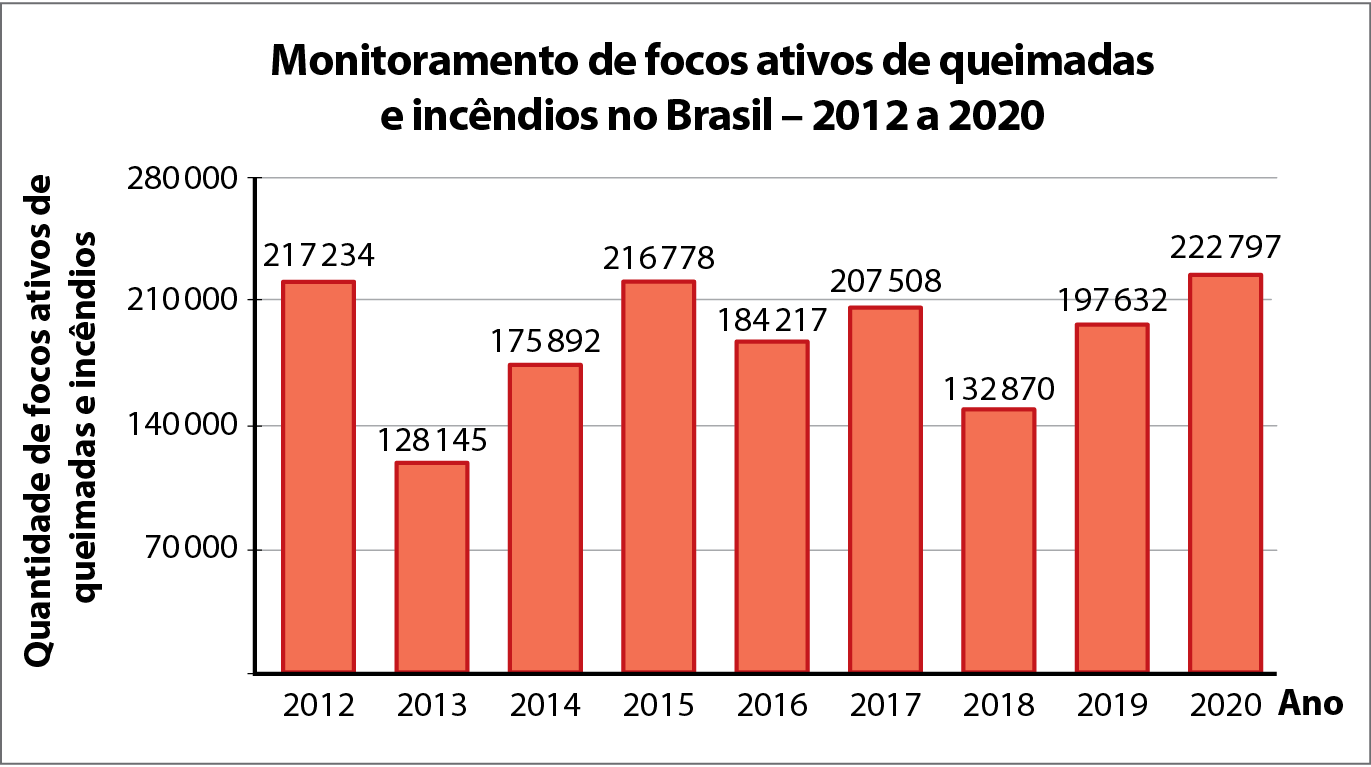

O gráfico apresenta a quantidade de focos ativos detectados por um satélite de referência, ou seja, os dados coletados diariamente por um mesmo satélite ao longo dos anos.
a) Em qual desses anos o número de focos ativos foi maior? Quantos focos?
b) Em que ano o número de focos ativos de queimadas foi menor? Quantos focos?
c) Qual foi a redução na quantidade de focos ativos de queimadas entre os anos 2013 e 2020?
d)

Em que ano ocorreu o maior aumento na quantidade de focos ativos de queimada em relação ao ano anterior? Arredonde para o milhar mais próximo e calcule mentalmente esse aumento.
Respostas e comentários
1. a) 12 luas.
1. b) 150 luas.
2. a) 2020; .222797 focos ativos.
2. b) 2013; .128145 focos ativos.
2. c) .94652 de focos ativos.
2. d) 2019; houve aumento de 65 mil focos ativos em relação a 2018.
Trabalhando a informação
Esta seção oferece uma oportunidade de discutir com os estudantes que interpretar dados não é simplesmente transcrever o que está no gráfico, mas comparar as informações, efetuar cálculos, enfim, dar tratamento aos dados.
Os temas escolhidos para este estudo abrem caminho para discussões relacionadas ao Sistema Solar e à preservação florestal, o que pode resultar em um trabalho interdisciplinar envolvendo professores de áreas como Geografia e Ciências e contribuir para o desenvolvimento dos Temas Contemporâneos Transversais ciência e tecnologia e educação ambiental.
Agora quem trabalha é você!
Os estudantes devem responder à atividade 1 com base no gráfico apresentado na página anterior.
a) Quantidade de luas confirmadas em Netuno: 14 luas; Quantidade de luas confirmadas em Marte: 2 luas. Assim, a diferença pedida é dada por: 14 ‒ 2 = 12 (12 luas).
b) Para este item, devem considerar as quantidades de luas representadas no gráfico e adicionar: 1 + 2 + 53 + 53 + 27 + 14 = 150 (150 luas).
Na atividade 2, considerando o gráfico apresentado, verificamos:
a) É o ano com a barra de maior altura, que é 2020, com .222797 focos de incêndio.
b) Em 2013, com a barra de menor altura, representando .128145 focos.
c) A diferença entre esses anos é de .222797 ‒ .128145 = .94652
d) Arredondando os valores do gráfico para o milhar mais próximo, anualmente, de 2012 até 2020, respectivamente, obtêm-se os seguintes totais de focos de queimadas: 217 mil; 128 mil; 176 mil; 217 mil; 184 mil; 208 mil; 133 mil; 198 mil; 223 mil.
Em relação ao ano anterior, houve aumento do total de focos de queimada em 2014, 2015, 2017, 2019 e 2020. O aumento nesses anos é dado, respectivamente, por: 176 ‒ 128 = 48; 217 ‒ 176 = 41; 208 ‒ 184 = 24; 198 ‒ 133 = 65; 223 ‒ 198 = 25. Portanto o maior aumento ocorreu em 2019, e foi de 65 mil focos.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1

Arredonde mentalmente os números e estime o valor das expressões a seguir.
a) 19 + 36 + 21
b) 26 + 38 + 84
c) 45 + 38 ‒ 15 + 22
d) 37 + 91 ‒ 63 ‒ 49
e) 55 ‒ 17 + 95 ‒ 33
2 No caixa do supermercado, dei uma nota de 50 reais para pagar uma compra de 37 reais. O caixa pediu 2 reais para facilitar o troco. Dando a ele os 2 reais, quanto recebo de troco?
3

De acordo com a estimativa do í bê gê É, em 2017 o estado do Amazonas tinha ..4063614 habitantes, dos quais ..1933350 não moravam na capital, Manaus. Com o auxílio de uma calculadora, descubra qual era a população de Manaus.

4 Que idade você terá no final de 2027? Em que ano você terá 33 anos?
5 A diferença entre dois números é 53. Determine a diferença entre seus sucessores. Justifique.
6 Substitua as figuras pelos algarismos 2, 3, 5 e 7 e encontre a diferença. (Dica: figuras iguais correspondem a algarismos iguais.)
7 Para pagar um livro de 32 reais e 50 centavos, Paulo usou uma nota de 50 reais. A atendente, porém, só tinha notas de 10 reais. Não tendo troco, ela pediu a Paulo que facilitasse o troco com moedas. Como ele pode ter feito isso?
8

O gráfico a seguir mostra a quantidade de matrículas feitas na Educação Profissional no Brasil.
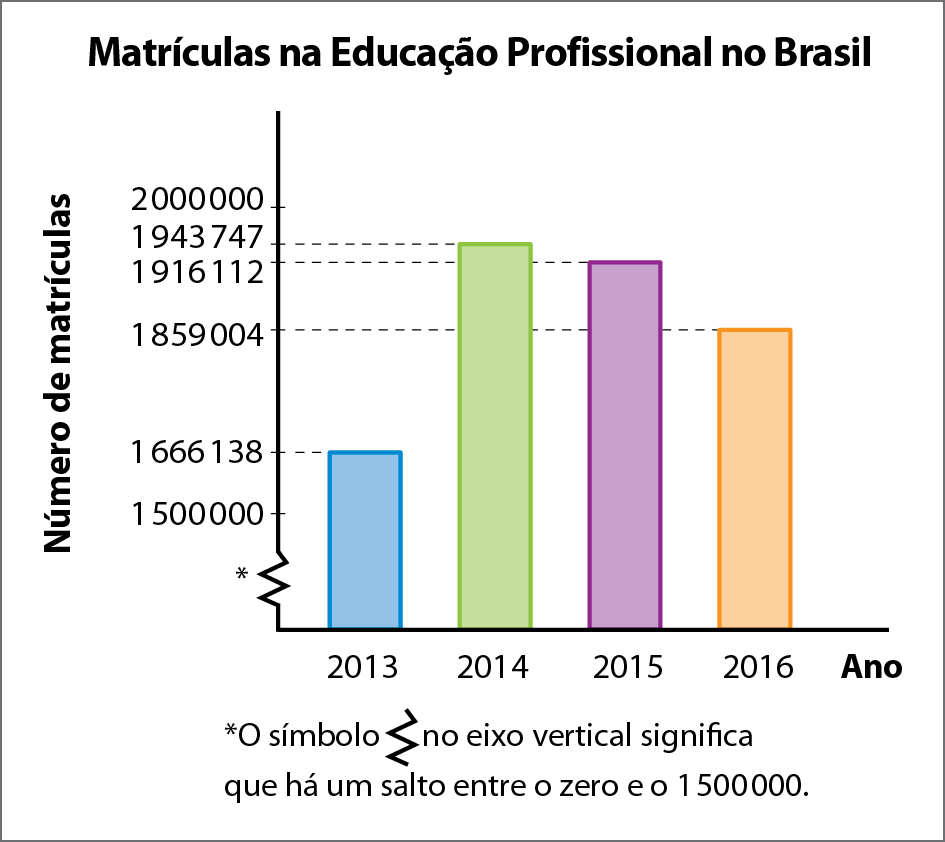
Com base no gráfico, use uma calculadora para responder a estas questões.
a) Em que ano houve mais estudantes matriculados?
b) De quanto foi a diminuição no número de matrículas de 2015 para 2016?
c) Arredonde o número de matrículas para unidade de milhar e calcule a diminuição pedida no item b.
9 Um número natural é expresso por:
9 + (21 ‒ 15) ⋅ 2
Qual é o valor do sucessor desse número?
10 Em um restaurante, são gastos mensalmente 43 litros de óleo. Sabendo que o dono do restaurante quer comprar esse óleo em latas de 6 litros, quantas dessas latas ele deve comprar por mês? Considerando as compras mensais, quantas latas ele deve comprar em um ano?
11 Isabel adquiriu um televisor, pagando uma entrada de 580 reais e mais três parcelas de 360 reais. À vista, ela teria pago .1590 reais. Qual é a diferença entre o preço a prazo e o preço à vista?
12 Quais números naturais compreendidos entre 200 e 500 são quadrados perfeitos?
Respostas e comentários
1. a) 80
1. b) 150
1. c) 90
1. d) 20
1. e) 110
2. 15 reais.
3. ..2130264 habitantes.
4. Respostas pessoais.
5. 53, pois, ao adicionar 1 ao minuendo e ao subtraendo, a diferença fica mantida.
6.

= 7;

= 5;

= 2;

= 3; A diferença é 52.
7. Paulo pode ter dado a ela 2 reais e 50 centavos para que devolvesse 20 reais de troco.
8. a) 2014
8. b) .57108 de matrículas.
8. c) 57 milhares.
9. 22
10. 8 latas; 86 latas.
11. 70 reais.
12. 225, 256, 289, 324, 361, 400, 441 e 484
Exercícios complementares
O bloco de exercícios é mais uma oportunidade de os estudantes revisitarem os principais conceitos tratados no capítulo e mobilizarem os conhecimentos construídos, identificando possíveis dúvidas.
As resoluções dos exercícios 1 a 5 estão no início deste Manual, nas orientações específicas do capítulo 2.
Uma estratégia comum para obter a solução do exercício 6 é a de tentativa e erro, destacando-se que, a cada tentativa malsucedida, os estudantes reflitam antes de fazer outra, pois o erro sempre dá uma pista em direção à solução. Converse com os estudantes e, considerando apenas os números naturais, verifique se compreendem que, para a subtração ser possível, o minuendo deverá ser maior do que o subtraendo.
Na resolução do exercício 7, pode-se conversar com a turma sobre a questão, comum em situações cotidianas, de facilitar o troco em compras que envolvam dinheiro em espécie. Explique aos estudantes que esse procedimento precisa ser compreendido tanto pelo responsável pelo caixa quanto pelo comprador. Sem essa compreensão, o comprador pode ficar intrigado por entregar mais dinheiro, embora já tenha dado o suficiente para pagar a compra. Pode-se também conversar sobre a vantagem de haver cédulas de 2 reais para facilitar trocos. Por exemplo, uma compra de 27 reais pode ser paga com três cédulas de 10 reais e uma cédula de 2 reais; nesse caso, apenas as três cédulas de 10 reais seriam suficientes, mas o caixa pode solicitar 2 reais para devolver uma só cédula de 5 reais como troco.
As resoluções dos exercícios 8 e 9 e dos exercícios 11 e 12 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 10, espera-se que os estudantes percebam que a compra de 8 latas em cada um dos 11 meses é suficiente para o gasto do ano, que é de 86 latas.
No exercício 12, é interessante discutir qual a maneira mais fácil de chegar aos números. Os estudantes podem consultar exercícios anteriores ou construir quadros como este:

VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Ao calcular o total de .1758 + .2439, considerando o arredondamento das parcelas para a centena mais próxima, obtêm-se
a) .4000.
b) .4100.
c) .4190.
d) .4200.
2 Considere a igualdade a seguir.
.1400 + 553 + 37 = .1400 +

+ 40
Nessa igualdade,

representa o número
a) 556.
b) 553.
c) 550.
d) 537.
3 Em determinado dia, o estoque do setor de informática de uma loja foi reposto com .5337 itens. Após a reposição, esse setor passou a ter .6473 itens. Quantos eram os itens do setor de informática dessa loja antes da reposição?
a) 136 itens.
b) .1136 itens.
c) .1144 itens.
d) .11810 itens.
4 A expressão 980 menos 75 + 36 equivale a
a) 905 + 36.
b) 980 + 39.
c) 980 + 111.
d) 905 + 111.
5 Um grupo de estudantes coletou quinhentas e dez latas de leite em pó para doar a uma instituição de caridade.

Sabendo que eles estão embalando essas latas em caixas com 15 unidades, a quantidade de caixas necessárias para embalar todas as latas será de:
a) 30 caixas.
b) trínta e duas caixas.
c) 34 caixas.
d) 36 caixas.
6 Considere a expressão numérica a seguir.
10 menos 10 + (10 menos 10 + 10) menos 10
O valor numérico dessa expressão é
a) 0.
b) 10.
c) 20.
d) 30.
7 Uma sorveteria oferece 36 sabores de sorvete de massa e 7 sabores para cobertura. Ao escolher apenas um sabor de sorvete e apenas um sabor de cobertura, é possível fazer
a) mais que 40 e menos que 45 combinações.
b) mais que 45 e menos que duzentas e cinquenta combinações.
c) mais que duzentas e cinquenta e menos que quatrocentas e cinquenta combinações.
d) mais que quatrocentas e cinquenta e menos que quinhentas combinações.
8 O número que deve ser multiplicado por 14 para obter 518 é
a) 27.
b) 32.
c) 36.
d) 37.
9 O número que elevado ao quadrado é igual a 144 é
a) 288.
b) 72.
c) 24.
d) 12.
10 Analise a igualdade a seguir.
(27 + 14) ⋅

= 369
Nessa igualdade, o valor de

é
a) 328.
b) 24.
c) 18.
d) 9.
11 Considere a seguinte expressão numérica.
Para que x seja igual a 23, o valor de a deve ser:
a) 9.
b) 8.
c) 4.
d) 3.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Você estudou diferentes operações com números naturais. Que ideias podemos associar à adição, à subtração, à multiplicação e à divisão?
b) Como você explicaria as duas propriedades da adição estudadas?
c) Que estratégia você utilizaria para subtrair mentalmente 98 de 200?
d) O resultado da expressão numérica (2 + 3) ⋅ 10 é o mesmo que o de 2 + (3 ⋅ 10)? Por quê?
e) Como você explicaria a vantagem de escrever uma adição de parcelas iguais como uma multiplicação? Dê um exemplo.
f) Explique, com exemplos, como é possível relacionar a divisão com a multiplicação.
Respostas e comentários
1. Alternativa d.
2. Alternativa c.
3. Alternativa b.
4. Alternativa a.
5. Alternativa c.
6. Alternativa a.
7. Alternativa c.
8. Alternativa d.
9. Alternativa d.
10. Alternativa d.
11. Alternativa c.
Organizando: As respostas a estas questões estão neste Manual.
Verificando
Nesta seção apresentamos questões que abrangem todo o capítulo sendo uma oportunidade para os estudantes validarem o entendimento do conteúdo estudado. Caso apresentem dúvidas em relação a alguma das atividades propostas, oriente-os a rever os conceitos apresentados no capítulo, assim também desenvolverão a autonomia no estudo.
As resoluções dos testes 1 a 11 estão no início deste Manual, nas orientações específicas do capítulo 2.
Organizando
a) Adição: ideias de juntar e de acrescentar.
Subtração: ideias de tirar, de comparar e de completar.
Multiplicação: ideias de adição de parcelas iguais, de disposição retangular e de proporção.
Divisão: ideias de distribuição equitativa (repartição em partes iguais) e de medida (quantas vezes uma quantidade cabe em outra).
b) Resposta pessoal. Espera-se que os estudantes comentem sobre a propriedade associativa e a comutativa da adição.
c) Resposta pessoal. Os estudantes podem considerar que 200 ‒ 98 equivale a 200 menos 100 + 2, por exemplo.
d) Não, pois, em uma expressão numérica, deve-se efetuar primeiro as operações entre parênteses.
Assim: (2 + 3) ⋅ 10 = 5 ⋅ 10 e 2 + (3 ⋅ 10) = 2 + 30.
e) Resposta pessoal. Espera-se que os estudantes comentem que, em adição de muitas parcelas, a multiplicação simplifica a escrita ou agiliza o cálculo. Exemplo: 73 + 73 + 73 + 73 + 73 + + 73 + 73 + 73 = 8 ⋅ 73.
f) Resposta pessoal. Espera-se que os estudantes expliquem a propriedade fundamental da divisão, relacionando o dividendo à multiplicação do quociente pelo divisor adicionada ao resto da divisão. Exemplo: 19 : 5 = 3 e resto 4, então 3 ⋅ 5 + 4 = 19.
DIVERSIFICANDO
Relações algébricas no quadrado mágico
Vamos considerar o quadrado mágico que vimos no início deste capítulo.


Podemos observar que:
• 4 é uma parcela comum às adições da 1ª linha e da 1ª coluna. 4 + 9 + 2 = 4 + 3 + 8 Cancelando a parcela comum, isto é, aplicando o Princípio Aditivo da Igualdade, temos: 9 + 2 = 3 + 8 Vamos pintar de amarelo as quadrículas dos números do 1º membro da igualdade e de vermelho as do 2º membro.
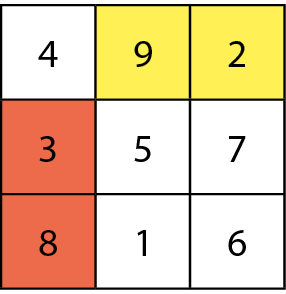
• 7 é uma parcela comum às adições da 2ª linha e da 3ª coluna. 3 + 5 + 7 = 2 + 7 + 6 Aplicando o Princípio Aditivo da Igualdade, cancelamos a parcela comum: 3 + 5 = 2 + 6 Vamos pintar de amarelo as quadrículas dos números do 1º membro da igualdade e de vermelho as do 2º membro.
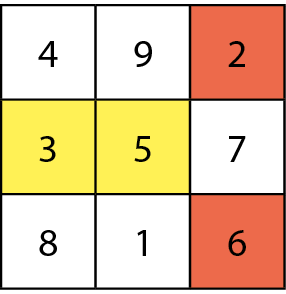
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Qual é a parcela comum às adições das diagonais desse quadrado mágico? Usando o mesmo critério das cores, reproduza o quadrado mágico do exemplo e pinte as quadrículas das diagonais.
2 A parcela comum às adições das diagonais também é comum a outras duas adições?
Em caso afirmativo, quais? Usando o mesmo critério das cores, reproduza novamente o quadrado mágico e pinte as quadrículas referentes a essas adições.
3 Cada quadrícula tem um número que é parcela comum a duas adições que têm a mesma soma? Aplicando o mesmo critério das cores, reproduza o quadrado mágico apresentado seis vezes em seu caderno. Para cada um, pinte as quadrículas referentes a duas adições que têm a mesma soma; excluindo a parcela comum. Cada um dos seis quadrados deve apresentar adições com somas diferentes um do outro.
4 Considere que o quadrado 4 × 4, a seguir, seja um quadrado mágico com números representados por letras. Qual das igualdades é verdadeira?
a) ê + F + G = C + K + óh
b) a + F + P = ih + J + éle
c) N + óh + P = M + ih + ê
d) a + F + K = H + K + N

Respostas e comentários
1. 5;
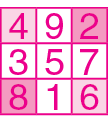
2. Sim;
9 + 5 + 1 = 3 + 5 + 7
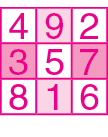
3. Sim;

4. Alternativa b.
Diversificando
A seção traz outros desafios envolvendo o quadrado mágico e padrões numéricos, com base no princípio aditivo da igualdade. Discuta o texto com os estudantes, antes de propor-lhes as questões, certificando-se de que entenderam todos os passos.
Agora é com você!
Sugerimos que as questões propostas sejam feitas em grupos. Ao final, cada grupo pode apresentar a solução de pelo menos uma atividade.
1. As adições das diagonais são 4 + 5 + 6 e 2 + 5 + 8, que têm a parcela comum 5. As cores iguais indicam as parcelas da adição que compõem um membro da igualdade 4 + 6 = 8 + 2.
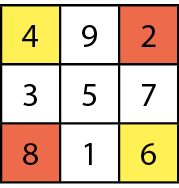
2. Sim, 5 é comum à coluna e à linha central desse quadrado, 9 + 5 + 1 e 3 + 5 + 7, respectivamente, que podemos representar com as cores da segunda tabela.
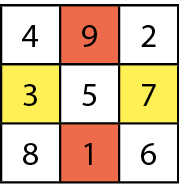
3. Sim, essa propriedade sempre é válida, pois a linha e a coluna daquela parcela comum sempre têm a mesma soma em um quadrado mágico.
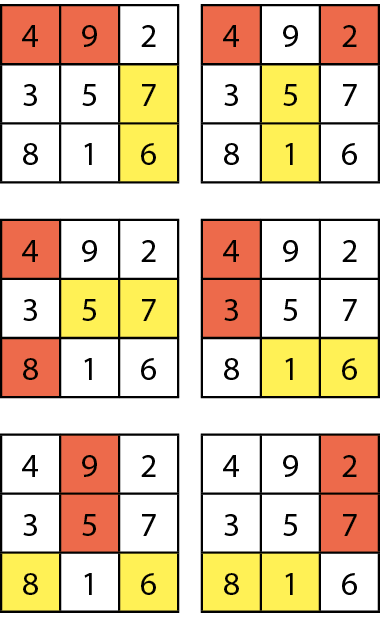
4. A diagonal da esquerda para a direita desse quadrado tem a soma a + F + K + P, e a terceira linha tem a soma ih + J + K + L, igualando e anulando a parcela comum, tem-se a + F + P = ih + J + L.
Alternativa b.