
CAPÍTULO 5 Um pouco de Álgebra

Observe, leia e responda no caderno.
a) Como você definiria algarismo? E algoritmo?
b) Supondo que você tenha de representar a adição de 2 com um número desconhecido, como você faria essa representação?
c) Uma professora de Matemática escreveu a seguinte expressão na lousa: x + 3 = 5. É possível encontrar um valor para x de modo que essa igualdade seja verdadeira. Que valor é esse?
d) Após a leitura do texto a seguir, você percebe que a Matemática é uma ciência construída em diferentes épocas, continuamente, e que atende às necessidades de diversas culturas?
As palavras algarismo e algoritmo, comuns nos livros de Matemática, têm origem no nome de Al-Khwārizmī, o maior matemático da época de ouro do islamismo, no século nove, em Bagdá (capital do atual Iraque, na Ásia).
Um dos mais importantes livros árabes da Idade Média, escrito por Al-Khwārizmī, cujo título é Hisab al-jabr al-muqabala (“Pequena obra sobre o cálculo da redução e da confrontação”), deu origem à palavra álgebra.
Trata-se de um livro sobre a resolução de equações (a ser estudada no próximo ano) com o auxílio de duas operações: al-jabr, que seria a “restauração” ou a “transposição de termos”, e al-muqabala, que seria a “redução de termos semelhantes”.
Respostas e comentários
a) Algarismos: símbolos usados para a representação de qualquer número no sistema de numeração indo-arábico. Algoritmo: conjunto de passos definidos e organizados para a execução de uma tarefa.
b) Exemplos de respostas: 2 + a; 2 +

c) x = 2
d) Resposta pessoal. Espera-se que os estudantes reconheçam essa característica da Matemática.
Capítulo 5 - Um pouco de Álgebra
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, cujo foco é a Unidade Temática Álgebra, tratamos do conceito de variável, da utilização de letras para representar números naturais quaisquer e da notação algébrica em diversas situações, como na demonstração de algoritmos de alguns critérios de divisibilidade de números naturais. Além disso, amplia-se o trabalho com gráficos, abordando a construção de um gráfico de colunas.
A abertura apresenta a origem das palavras algarismo, algoritmo e álgebra, destacando o matemático Al-Khwārizmī. Cabe, nesse momento, salientar a importância dos árabes no desenvolvimento da Matemática e na sua divulgação.
Converse com os estudantes sobre a percepção de que o desenvolvimento científico sempre dependeu da contribuição de diferentes povos e pessoas, deste modo se contribui para o desenvolvimento da competência geral 1.

Sugestão de leitura
Para enriquecer os assuntos abordados nesta página de abertura, sugerimos o artigo:
• Conheça a obra de Al-Khwārizmī, o Pai da Álgebra, Iqara Islam. Disponível em: https://oeds.link/5Y3Imr. Acesso em: 13 maio 2022.
Neste artigo apresentam-se diferentes contribuições de Al-Khwārizmī para o desenvolvimento da Matemática e da informática.
1. Apresentando a variável
Para começar a entender o que é a Álgebra, vamos considerar e resolver um problema do Exame Nacional do Ensino Médio (enêm - 2010).
Uma professora realizou uma atividade com seus alunos utilizando canudos de refrigerante para montar figuras, onde cada lado foi representado por um canudo. A quantidade (C ) de canudos depende da quantidade de quadrados (Q) que formam cada figura. A estrutura de formação das figuras está representada a seguir.
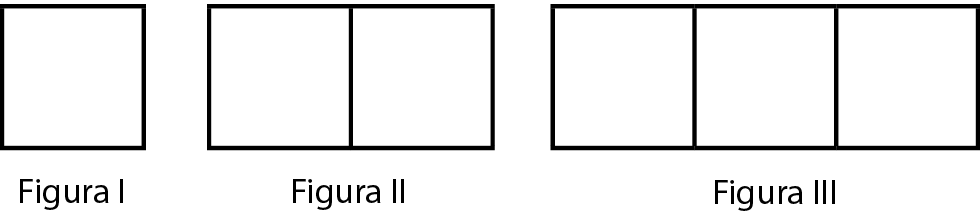
Que expressão fornece a quantidade de canudos em função da quantidade de quadrados?
a) C = 4Q
b) C = 3Q + 1
c) C = 4Q menos 1
d) C = Q + 3
• Compreendendo o problema
Descobrir qual das igualdades relaciona C (quantidade de canudos) com Q (quantidade de quadrados) corretamente em todas as figuras.
• Estabelecendo um plano de resolução
Uma maneira de resolver é testar as alternativas.
• Executando o plano
Na figura um, temos Q = 1 e C = 4. Substituindo esses valores nas alternativas, observamos que:
a) 4 = 4 ⋅ 1 (verdadeira);
b) 4 = 3 ⋅ 1 + 1 (verdadeira);
c) 4 = 4 ⋅ 1 menos 1 (falsa);
d) 4 = 1 + 3 (verdadeira).
Descartamos a alternativa c, pois ela é falsa para a figura um.
Na figura dois, temos Q = 2 e C = 7. Substituindo esses valores nas alternativas, observamos que:
a) 7 = 4 ⋅ 2 (falsa);
b) 7 = 3 ⋅ 2 + 1 (verdadeira);
d) 7 = 2 + 3 (falsa).
Descartamos as alternativas a e d. Basta testar a alternativa b na figura três, com Q = 3 e C = 10:
b) 10 = 3 ⋅ 3 + 1 (verdadeira).
• Refletindo sobre o que foi feito
Verificamos que a expressão da alternativa b satisfaz todas as figuras.
Portanto, C = 3Q + 1.
Respostas e comentários
1. Apresentando a variável
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah dois três.
Ao apresentar duas propostas de resolução de um exercício por meio de diferentes estratégias, este tópico contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah dois três).
Analise com os estudantes a situação apresentada na questão do Enem e proponha a eles a construção da sequência de figuras, ampliando com etapas além das apresentadas. Os estudantes devem perceber que existe uma relação entre a quantidade de canudos e a de quadrados que compõem cada figura da sequência. Para isso, eles podem montar um quadro como o mostrado a seguir (uma coluna com a quantidade de canudos e a outra com a quantidade de quadrados construídos).
|
Quantidade de canudos |
Quantidade de quadrados |
|---|---|
|
4 |
1 |
|
7 |
2 |
|
10 |
3 |
|
13 |
4 |
|
16 |
5 |
Após a observação do quadro, os estudantes podem procurar o padrão entre essas duas quantidades (das duas colunas) ou testar as alternativas que são apresentadas no problema.
Outra maneira de resolver esse problema é observar, nas figuras, que variação tem a quantidade C quando modificamos a quantidade Q. Para facilitar, vamos montar um quadro.
|
Figura |
Quadrado (Q) |
Canudo (C) |
Observação |
|---|---|---|---|
|
I |
1 |
4 |
4 = 3 ⋅ 1 + 1 |
|
II |
2 |
7 |
7 = 3 ⋅ 2 + 1 |
|
III |
3 |
10 |
10 = 3 ⋅ 3 + 1 |
Comparando as expressões numéricas da última coluna com as expressões algébricas das alternativas, percebemos que a alternativa b responde à questão.
Observe que, nesse problema, temos duas grandezas (quantidade de Quadrados e quantidade de Canudos) e que usamos símbolos (respectivamente, Q e C) para representá-las. Note que os valores de Q e de C variam, por isso chamamos cada uma das grandezas de variável.
Os números 4, 7 e 10 são os valores numéricos da expressão algébrica C = 3Q + 1 quando Q assume os valores 1, 2 e 3, respectivamente.
A Álgebra é a parte da Matemática que trabalha com grandezas cujos valores variam ou que são desconhecidos e, portanto, representados por símbolos (em geral, por letras).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Observe o padrão que existe na variação das figuras um a três da questão do Enem apresentada na página anterior e desenhe no caderno como seriam as figuras quatro e cinco. Depois, verifique se a expressão algébrica da alternativa b continua verdadeira para essas novas figuras.
2 As figuras a seguir representam o início de uma sequência infinita do que chamamos números triangulares. Observe.
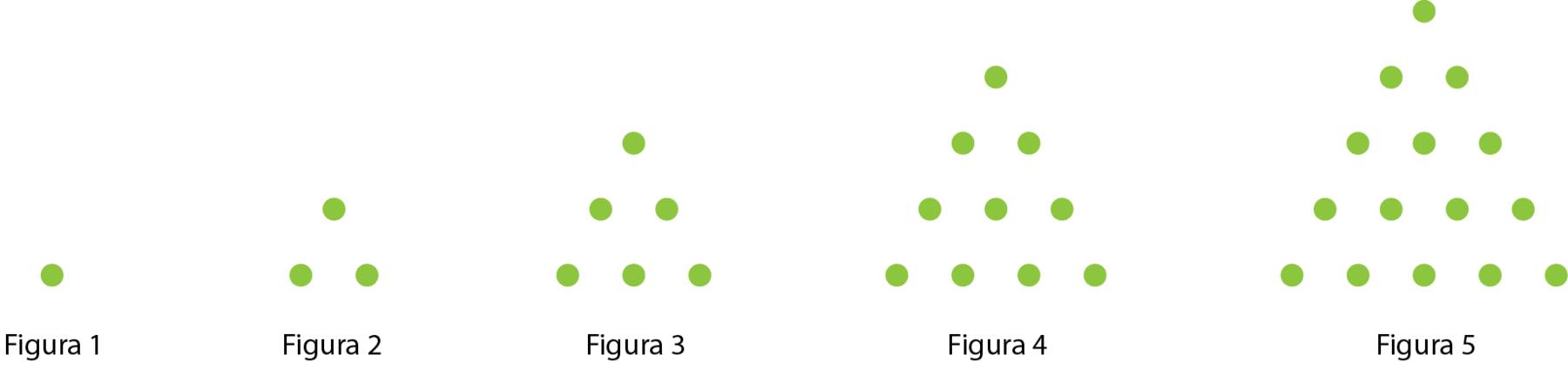
a) Quantas bolinhas tem cada uma das figuras?
b) Seguindo o padrão de formação das figuras, quantas bolinhas deve ter a figura 6? E a figura 10?
c) Calcule a soma das bolinhas das figuras: 1 e 2; 2 e 3; 3 e 4; 4 e 5. A sequência dessas somas apresenta um padrão? O que você pode dizer dessas somas?
d) Qual é a soma das bolinhas das figuras 9 e 10 da sequência? E das figuras 19 e 20?
e) Representando por n o número de uma figura qualquer de número triangular, o número da figura seguinte é (n + 1 ) . Escreva a soma das bolinhas das figuras n e (n + 1 ) .
3

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre sequência de números. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Respostas e comentários
1. Construção de figuras. A alternativa b continua verdadeira.
2. a) uma, 3, 6, 10 e 15 bolinhas.
2. b) vinte e uma bolinhas; 55 bolinhas.
2. c) 4, 9, 16 e 25; Sim; São quadrados perfeitos.
2. d) 100 bolinhas; quatrocentas bolinhas.
2. e) (n + 1)2
3. Resposta pessoal.
Apresentando a variável
O quadro apresentado mostra a relação entre as quantidades de quadrados e de canudos utilizados em cada figura da sequência. Essa relação será dada por uma expressão algébrica em que as grandezas envolvidas são representadas por letras.
Exercícios propostos
No exercício 1, os estudantes deverão considerar que a quantidade de quadrados corresponde à posição que a figura ocupa na sequência. Assim, a figura quatro terá 4 quadrados e a figura cinco, 5 quadrados. Apresentamos a seguir as figuras quatro e cinco:
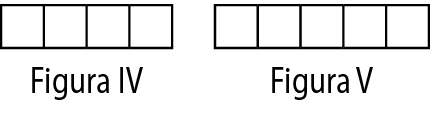
Para essas figuras, a alternativa b continua válida, pois:
13 = 3 ⋅ 4 + 1
16 = 3 ⋅ 5 + 1
Para ampliar o exercício 2, que apresenta a sequência de números triangulares, pode-se explorar a sequência de números quadrados.

Na sequência de quadrados, os estudantes podem observar que o número de bolinhas que cada figura tem é: 1, 4, 9, reticências (que são os números naturais quadrados perfeitos, com exceção do zero). Proponha a eles alguns questionamentos acerca dessa sequência, por exemplo:
• Quantas bolinhas terá a figura 6? (36 bolinhas.)
• Que figura é formada por 100 bolinhas? (A figura 10.)
A resolução do exercício 2 está no início deste Manual, nas orientações específicas do capítulo 5.
O exercício 3 apresenta uma proposta de elaboração de problemas sobre sequência numérica, permitindo avaliar como os estudantes expressam suas ideias e conhecimentos.
2. Generalizando conclusões
Em uma viagem, a família de Lizandra pagou duas tarifas de pedágio na ida: a primeira, de 23 reais, e a outra, de 19 reais. Na volta, o primeiro pedágio custou 19 reais e o segundo, 23 reais. Eles gastaram mais no pedágio na ida ou na volta?
Para responder à pergunta, adicionamos os valores:
• na ida: 23 + 19 = 42.
• na volta: 19 + 23 = 42.
Concluímos que o gasto foi igual, na ida e na volta, pois apenas a ordem dos valores mudou. Há infinitos pares de números naturais que verificam essa propriedade. Acompanhe as falas dos professores que generalizamglossário glossário essa situação.

Outra maneira de dizer o mesmo é com o uso da linguagem algébrica.

•

Sendo x e y dois números naturais quaisquer, as sentenças x + y = y + x também seriam verdadeiras?
Respostas e comentários
Orientações: Espera-se que os estudantes indiquem que sim e que percebam que a mudança das letras a e b para x e y não invalida a igualdade.
2. Generalizando conclusões
Neste item, desenvolve-se a noção de generalização. Analise com os estudantes a situação apresentada e retome a propriedade comutativa da adição, já estudada no capítulo 2.
Ressalte aos estudantes que, assim como foram usados a e b para indicar os dois números naturais quaisquer, poderia ter sido usado qualquer outro par de letras, ou seja, todas as sentenças a seguir expressam a propriedade comutativa da adição:
• a + b = b + a
• x + y = y + x
• a + z = z + a
Observe mais algumas sentenças com números naturais escritas na linguagem corrente e na linguagem algébrica.
|
Linguagem verbal |
Linguagem algébrica |
|---|---|
|
Em uma adição de três ou mais números, podemos associar as parcelas de modos diferentes sem alterar a soma. |
abre parêntese a mais b fecha parêntese mais c igual a mais abre parêntese b mais c fecha parêntese |
|
Em uma multiplicação de dois números, a ordem dos fatores não altera o produto. |
a vezes b igual b vezes a |
|
O número 1 é o elemento neutro da multiplicação. |
a vezes um igual um vezes a igual a |
|
Na multiplicação de um número pela soma de dois outros, podemos distribuir a multiplicação pelas parcelas. |
a vezes abre parêntese b mais c igual a vezes b mais a vezes c |
|
Toda potência de expoente zero e base diferente de zero é igual a 1. |
a elevado a zero igual um, sendo a diferente de zero |
|
O dobro de um número, mais 4. |
dois vezes a mais quatro igual dois a mais 4 |
|
O dobro da soma de um número com 4. |
dois vezes abre parêntese a mais quatro fecha parêntese igual dois abre parêntese a mais 4 fecha parêntese |
|
A diferença dos quadrados de dois números. |
a ao quadrado menos b ao quadrado |
|
O quadrado da diferença de dois números. |
abre parêntese a menos b fecha parêntese ao quadrado |
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
4 Escreva cada sentença dada a seguir em linguagem algébrica, para números naturais quaisquer.
a) O número zero é o elemento neutro da adição.
b) Em uma multiplicação de três ou mais números, podemos associar os fatores de modos diferentes sem alterar o produto.
c) Toda potência de expoente 1 é igual à base.
5 Nas expressões algébricas a seguir, substitua as letras por números naturais quaisquer e, após efetuar as operações indicadas, compare os valores obtidos. O que você conclui?
a) (a + b)elevado a 2 e aelevado a 2 + 2 ⋅ a ⋅ b + belevado a 2
b) (a ‒ b)elevado a 2 e aelevado a 2 ‒ 2 ⋅ a ⋅ b + belevado a 2
c) (a + b) ⋅ (a ‒ b) e aelevado a 2 ‒ belevado a 2

Agora, verifique com um colega se a conclusão dele é a mesma que a sua.
6

Hora de criar – Escreva uma sentença algébrica e elabore um problema sobre essa sentença. Proponha a um colega que o resolva e, depois, conversem sobre a solução apresentada.
3. Validando afirmações
Situação 1
Além de generalizar sentenças matemáticas, usamos a Álgebra para demonstrarglossário se as afirmações são verdadeiras ou não.


Respostas e comentários
Orientações: Organize a turma em dois grupos e promova um jogo entre eles. Peça a um deles que escreva na lousa sentenças em uma das linguagens verbal, como as do quadro a seguir, a fim de que o outro grupo “traduza” para a outra linguagem. Depois, invertem-se os papéis e os grupos.
4. a) a + 0 = 0 + a = a, sendo a um número natural.
4. b) (a ⋅ b) ⋅ c = a ⋅ (b ⋅ c ) , sendo a, b e c números naturais.
4. c) a elevado a 1 = a, sendo a um número natural qualquer.
5. As expressões são equivalentes para os valores testados.
6. Resposta pessoal.
Generalizando conclusões
Ao explorar o quadro, se necessário, recorde as propriedades da adição e da multiplicação de números naturais. Ressalte a diferenciação entre expressões do tipo:
• o dobro de um número menos 5 → 2 ⋅ x ‒ 5; o dobro da diferença entre um número e 5 → 2 ⋅ (x ‒ 5);
• o triplo do quadrado de um número → 3 ⋅ xelevado a 2; o quadrado do triplo de um número → (3 ⋅ x)elevado a 2.
Exercícios propostos
Nestes exercícios, alguns estudantes podem escrever suas respostas na lousa e comparar o que há de diferente e de similar entre elas.
As resoluções dos exercícios 4 a 6 estão no início deste Manual, nas orientações específicas do capítulo 5.
3. Validando afirmações
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um quatro.
Ainda nesta página, promova investigações antes de cada demonstração. É importante os estudantes constatarem que “se as duas parcelas de uma adição forem divisíveis por um número natural, então essa soma também será divisível por esse número”, o que contribuirá para o desenvolvimento da habilidade (ê éfe zero seis ême ah um quatro). Proponha a eles adições como: 99 = 9 + 90 e 108 = 81 + 27, de modo que reconheçam que 9, 90, 81 e 27 são divisíveis por 9, pois são múltiplos de 9. Caso haja dúvidas, sugira aos estudantes que escrevam cada um desses números como produto de dois fatores, sendo um deles o 9:
9 = 1 ⋅ 9; 90 = 10 ⋅ 9;
81 = 9 ⋅ 9; 27 = 3 ⋅ 9
As parcelas dessas adições são múltiplos de 9 e, portanto, divisíveis por 9.
Em seguida, devem verificar se 99 e 108 também são divisíveis por 9. São estratégias: efetuar a divisão desses números por 9, decompor cada número em um produto com fator 9 ou outro. Para qualquer estratégia, eles devem concluir que 99 e 108 são divisíveis por 9. Ressalte que 99 é a soma de dois números naturais divisíveis por 9 e ele próprio é divisível por 9; o mesmo ocorre com 108.
Comente que isso é sempre válido para qualquer adição desse tipo.

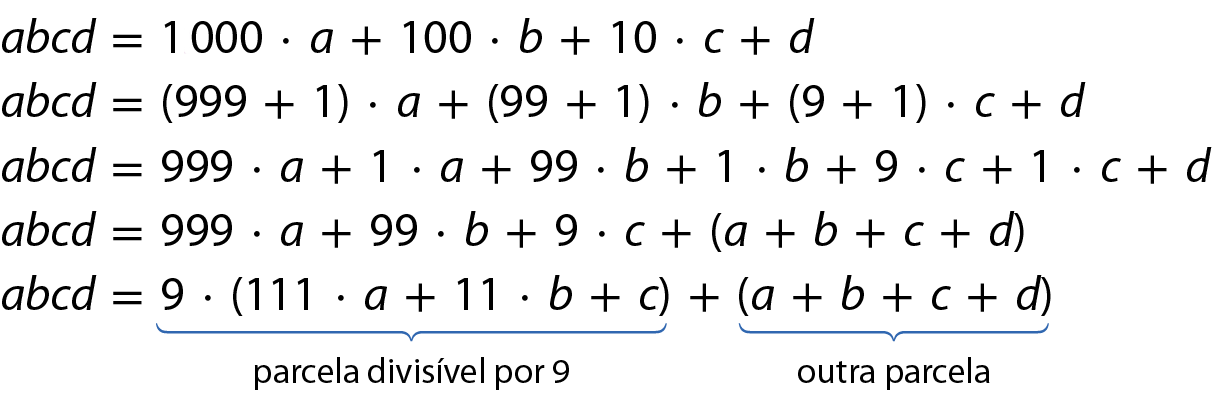
Para quaisquer valores de a, b, c e d, a primeira parcela é divisível por 9 porque ela é um número múltiplo de 9. Se a outra parcela (a + b + c + d ) , que é a soma dos valores absolutos dos algarismos, também for, então a soma delas, isto é, o número a bê cê dê, será divisível por 9.
Assim, fica demonstrado que:
Quando a soma dos valores absolutos dos algarismos de um número de quatro algarismos é divisível por 9, esse número é divisível por 9.
Para um número com mais ou com menos algarismos, o procedimento é o mesmo.
Por exemplo, .42507 é divisível por 9 porque 4 + 2 + 5 + 0 + 7 = 18, que é divisível por 9. Verifique efetuando a divisão de .42507 por 9.
Situação 2
O critério diz que um número natural qualquer é divisível por 6 somente quando ele é divisível por 2 e por 3. Vamos demonstrar a razão disso.
Antes de pensar em um número natural genérico representado por uma letra, vamos pensar, por exemplo, no número 114.
Verificamos que 114 é divisível por 2 porque termina em 4.
Então, existe um número (57) que, multiplicado por 2, dá 114, isto é, 114 = 2 ⋅ 57.
Por sua vez, 57 é divisível por 3 porque 5 + 7 = 12 e 12 é divisível por 3.
Então, existe um número (19) que, multiplicado por 3, dá 57, isto é, 57 = 3 ⋅ 19.

Na igualdade 114 = 2 ⋅ 57, podemos substituir 57 por 3 ⋅ 19 e ficamos com 114 = 2 ⋅ 57 = 2 ⋅ (3 ⋅ 19) = (2 ⋅ 3) ⋅ 19 = 6 ⋅ 19.
Como 114 = 6 ⋅ 19, concluímos que 114 é divisível por 6.
Agora, considerando um número natural qualquer, vamos generalizar. Para isso, representamos esse número por uma letra, por exemplo, x. Vamos supor que o número x seja divisível por 2 e por 3 e vamos proceder como fizemos com o número 114 para provar que x é divisível por 6.
Se x é divisível por 2, então existe um número natural y de modo que x = 2 ⋅ y.
Se o número x, ou seja, (2 ⋅ y) é divisível por 3, então o número y também é divisível por 3; logo, existe um número natural z de modo que y = 3 ⋅ z.
Na igualdade x = 2 ⋅ y, podemos substituir y por (3 ⋅ z ) .
Assim, temos x = 2 ⋅ y = 2 ⋅ (3 ⋅ z) ou (2 ⋅ 3) ⋅ z ou, ainda, x = 6 ⋅ z.
Como o número x é igual a 6 ⋅ z, ou seja, é múltiplo de 6, concluímos que x é divisível por 6.
Respostas e comentários
Validando afirmações
Para discutir a divisibilidade por 9, tomando um número de quatro algarismos, relembre também:
• a decomposição desse número segundo suas ordens: abcd = a ⋅ .1000 + b ⋅ 100 + c ⋅ 10 + d;
• a propriedade distributiva da multiplicação em relação à adição e sua aplicação em alguns exemplos:
a) 5 ⋅ (40 + 2) = 5 ⋅ 40 + 5 ⋅ 2
b) 10 ⋅ 2 + 5 ⋅ 3 + 15 ⋅ 7 = = (5 ⋅ 2) ⋅ 2 + 5 ⋅ 3 + (5 ⋅ 3) ⋅ 7 = = 5 ⋅ (2 ⋅ 2) + 5 ⋅ 3 + 5 ⋅ (3 ⋅ 7) = = 5 ⋅ 4 + 5 ⋅ 3 + 5 ⋅ 21 = = 5 ⋅ (4 + 3 + 21)
Converse com a turma sobre os passos da demonstração referente à divisibilidade por 9 apresentada no livro do estudante. Comente que esse procedimento é válido para qualquer número natural (não só para os que têm quatro algarismos), já que essa decomposição é possível para todo número natural.
Antes da justificativa do critério de divisibilidade por 6, sugerimos retomar os critérios de divisibilidade por 2 e por 3.
• Um número é divisível por 2 quando ele é par, ou seja, termina em 0, 2, 4, 6 ou 8. São divisíveis por 2, por exemplo: 126, 392, 798, .1354 (todos os números pares).
• Um número é divisível por 3 quando a soma de seus algarismos for divisível por 3. São divisíveis por 3, por exemplo: 396 (3 + 9 + 6 = 18; 18 é divisível por 3), .5349 (5 + 3 + 4 + 9 = 21; 21 é divisível por 3).
Ressalte que há números naturais divisíveis por 2 e por 3, como é o caso do 396. Em seguida, discuta o processo apresentado que justifica o critério de divisibilidade por 6.
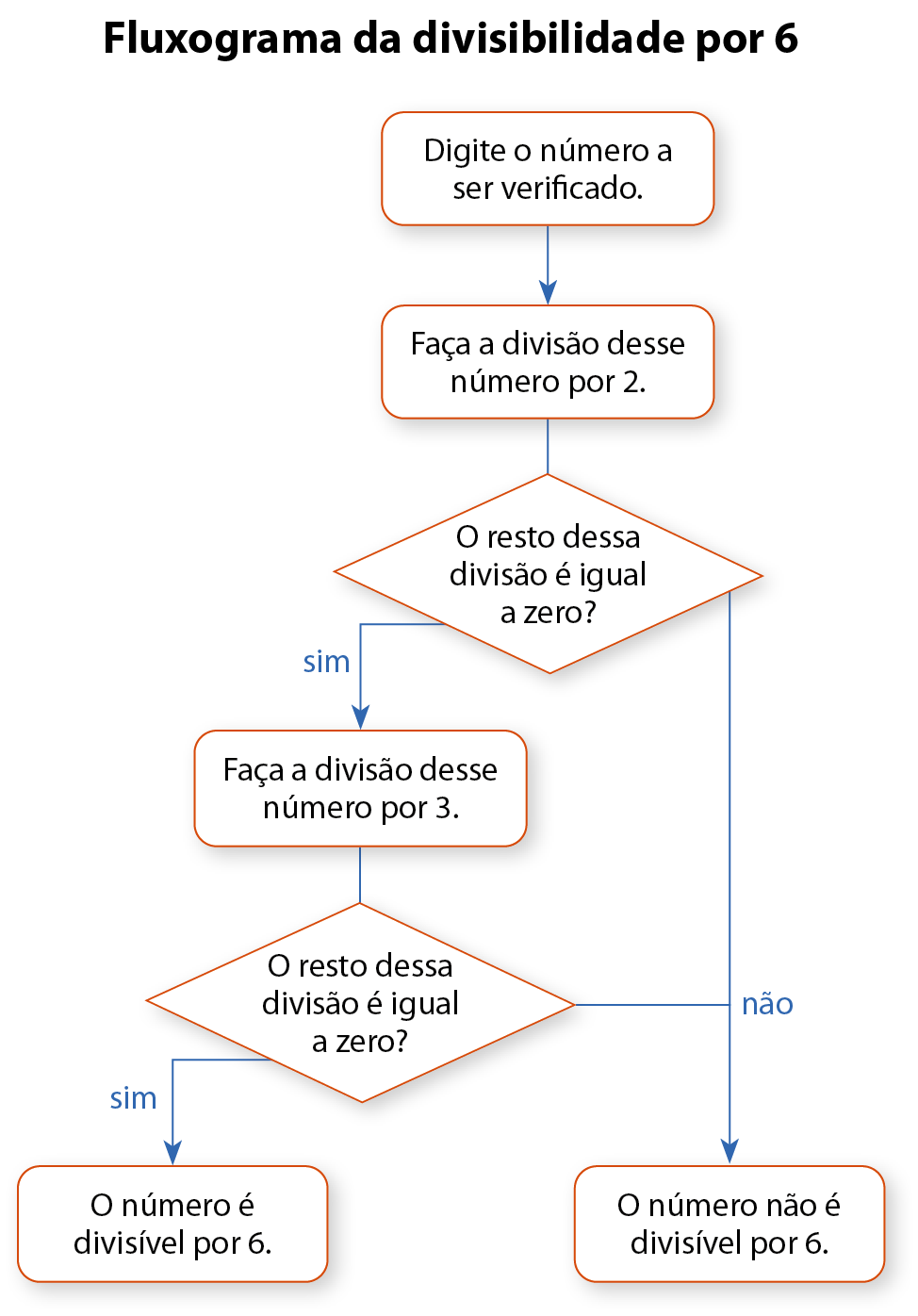
Com base na validação sobre a divisibilidade por 6, podemos montar um fluxograma. Vamos considerar que esse fluxograma serviria de base para programar uma máquina que verificaria se um número natural qualquer é ou não divisível por 6.

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
7 Responda às questões no caderno.
a) Todo número x divisível por 9 também é divisível por 3? Por quê?
b) Todo número x divisível por 8 também é divisível por 4? Por quê?
c) Todo número x divisível por 2 também é divisível por 4? Por quê?
8

Junte-se a um colega e demonstrem que um número de três algarismos á bê cê é divisível por 3 quando a soma (a + b + c) é divisível por 3.
9

Junte-se a um colega e demonstrem que um número do tipo á bê cê seis é divisível por 2.
10

Construa um fluxograma que possa ser usado para verificar se um número natural é divisível por 20. Depois, compare seu fluxograma com os de outros colegas da turma e verifique se há mais de uma possibilidade de realizar essa construção.
11

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre divisibilidade. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.
Respostas e comentários
7. a) Sim, porque x = 9 ⋅ y = 3 ⋅ (3 ⋅ y).
7. b) Sim, porque x = 8 ⋅ y = 4 ⋅ (2 ⋅ y).
7. c) Não; por exemplo, 6 é divisível por 2 e não é divisível por 4.
8. Demonstração.
9. Demonstração.
10. Construção de figura. Resposta pessoal.
11. Resposta pessoal.
Validando afirmações
Peça a cada estudante que leia uma etapa do fluxograma, e esclareça possíveis dúvidas, de modo a contribuir para o desenvolvimento da habilidade (ê éfe zero seis ême ah três quatro).
Exercícios propostos
No exercício 7, converse com os estudantes sobre o fato de que, para justificar a falsidade de uma afirmação, basta mostrar um contraexemplo (como para o item c), mas, para mostrar a veracidade, é necessário um argumento geral (como para os itens a e b).
No exercício 8 é solicitado aos estudantes uma demonstração relacionada à divisibilidade por 3. Acompanhe: Um número natural qualquer abc de três algarismos pode ser escrito como:
abc = 100 ⋅ a + 10 ⋅ b + c =
= (1 + 99) ⋅ a + (1 + 9) ⋅ b + c =
= a + 99 ⋅ a + b + 9 ⋅ b + c =
= 99 ⋅ a + 9 ⋅ b + (a + b + c) =
= 3 ⋅ 33 ⋅ a + 3 ⋅ 3 ⋅ b + (a + b + c) =
= 3 ⋅ (33 ⋅ a + 3 ⋅ b) + (a + b + c)
Para quaisquer valores de a, b e c, a primeira parcela é divisível por 3, pois é um número múltiplo de 3. Se a outra parcela (a + b + c), que é a soma dos algarismos do número abc, também for divisível por 3, ou seja, se a soma dos algarismos do número abc for divisível por 3, então o número abc será divisível por 3.
Para o exercício 9, um exemplo de resposta é que um número da fórma á bê cê seis termina em 6; logo, ele é par, garantindo que esse número é divisível por 2, para quaisquer valores de a, b e c.
A resolução do exercício 10 está no início deste Manual, nas orientações específicas do capítulo 5.
Oriente os estudantes na elaboração proposta no exercício 11. Se considerar adequado, organize-os em diferentes grupos para que cada grupo construa um fluxograma com base em determinado critério. Após as construções, solicite que compartilhem com os demais colegas de turma.
TRABALHANDO A INFORMAÇÃO
Construindo um gráfico de colunas
Na escola de música onde Cláudio é professor foi feita uma pesquisa de interesse para a formação de novas turmas que contou com 50 votos. Nessa pesquisa, os interessados podiam escolher entre os seguintes instrumentos: violão, acordeão, teclado ou flauta doce. Com o resultado da pesquisa, Cláudio formará duas turmas com os dois instrumentos mais votados.
Os votos foram registrados em uma folha de caderno, conforme mostrado a seguir.


(As imagens não respeitam as proporções reais entre os objetos.)
Com essas informações, Cláudio construiu um quadro. Elas também podem ser apresentadas em um gráfico de colunas.
|
Instrumentos |
Quantidade de interessados |
|---|---|
|
Violão |
17 |
|
Acordeão |
9 |
|
Teclado |
19 |
|
Flauta doce |
5 |
Dados obtidos pelo professor Cláudio.

Para construir esse gráfico, com o auxílio de uma régua, fazemos o seguinte:
• Traçamos uma linha vertical, na qual registramos a quantidade de interessados, e uma linha horizontal, na qual registramos os instrumentos.
• Escolhemos uma unidade de medida adequada para que os valores indicados na tabela caibam na linha vertical e outra para que as larguras das colunas caibam na linha horizontal. Para facilitar a leitura, convém que essas larguras sejam iguais.
• Traçamos as colunas. A coluna do violão deve ter 17 unidades de altura, pois há 17 interessados. A coluna do acordeão deve ser construída com 9 unidades de altura e, da mesma fórma, as colunas do teclado e da flauta doce devem ter 19 e 5 unidades de altura, respectivamente, correspondentes às escolhas dos interessados.
• Completamos o gráfico nomeando as linhas vertical e horizontal, chamadas eixos, dando um título ao gráfico e indicando a fonte dos dados.
Respostas e comentários
Trabalhando a informação
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah três um e ê éfe zero seis ême ah três dois.
Esta seção amplia a abordagem da Unidade Temática Probabilidade e estatística neste volume, aprofundando os conhecimentos que os estudantes já construíram acerca desse tipo de gráfico. O objetivo é levá-los a construir um gráfico de colunas com base em dados já tabulados em uma lista ou que eles mesmos possam tabular, contribuindo para o desenvolvimento das habilidades (ê éfe zero seis ême ah três um) e (ê éfe zero seis ême ah três dois). Essa atividade permite explorar:
• Duas fórmas de representação: quadro e gráfico de colunas.
• O conceito de escala – podem-se construir gráficos em diferentes escalas e discutir a escolha da escala.
• A construção das colunas – podem-se apresentar alguns gráficos de colunas nos quais a distância entre as colunas varie e promover uma discussão a fim de que os estudantes percebam que, para garantir a clareza na interpretação das informações, é conveniente que a distância entre as colunas e as barras seja sempre a mesma.
• A leitura e a interpretação de quadros e gráficos de colunas.
• A identificação dos elementos constitutivos de um gráfico.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 A professora Célia precisou classificar os participantes do coral segundo o tipo de voz e organizou os dados no quadro a seguir.
|
Tipo de voz |
Quantidade de alunos |
|---|---|
|
Tenor |
4 |
|
Barítono |
6 |
|
Baixo |
12 |
|
Soprano |
9 |
|
Contralto |
5 |
Dados obtidos pela professora Célia.
a) Pesquise o significado de cada tipo de voz que aparece no quadro.
b) Construa, em papel quadriculado, um gráfico de colunas para representar os tipos de voz dos alunos do coral.
c) Que tipo de voz masculina mais aparece nessa pesquisa? E feminina?
d) Entre os tipos de voz, há algum que tem o dobro de alunos de outra voz? Em caso afirmativo, qual?
e) Entre os tipos de voz, há algum que tem o triplo de alunos de outra voz? Em caso afirmativo, qual?
2

Seguindo as orientações do professor, os estudantes devem anotar no quadro de giz a localidade onde moram, ou seja, o bairro, sítio ou a comunidade, fazendo uma lista como a do exemplo a seguir.
Quando todos os estudantes já tiverem anotado, faça o que se pede.

a) Organize os dados em uma tabela e, com eles, construa um gráfico de colunas.
b) Compare o seu gráfico com o de um colega da turma para verificar se há diferenças. Se houver, explique por que isso ocorreu.
c) Há alguma localidade que se destaca na pesquisa pela quantidade de estudantes que lá vivem? Se houver, qual?
d) Apenas com os dados observados no gráfico, é possível descobrir quantos estudantes responderam à pesquisa? Em caso afirmativo, como?
Respostas e comentários
1. a) Tenor: voz masculina mais aguda; barítono: voz masculina mais grave que a do tenor; baixo: voz masculina mais grave que a do barítono; soprano: voz feminina mais aguda; contralto: voz feminina mais grave.
1. b) Construção de gráfico.
1. c) Baixo; soprano.
1. d) Sim, o número de baixos é o dobro do número de barítonos.
1. e) Sim, o número de baixos é o triplo do número de tenores.
2. a) Resposta pessoal.
2. b) Resposta pessoal.
2. c) Respostas pessoais.
2. d) Sim; basta adicionar os valores correspondentes a cada coluna.
Agora quem trabalha é você!
Na atividade 1, inicialmente proponha alguns questionamentos acerca do quadro apresentado:
• Quais são as variáveis envolvidas na tabela organizada pela professora Célia? (Resposta esperada: Tipo de voz e quantidade de alunos.)
• O que indica a quantidade de alunos nessa situação? (Resposta esperada: Determina a frequência (número de vezes) com que cada tipo de voz aparece nos participantes do coral.)
• Qual é a frequência dos sopranos? (Resposta esperada: 9.)
• Que tipo de voz teve frequência 6? O que isso significa? (Respostas esperadas: Barítono; isso significa que há 6 barítonos no grupo de participantes desse coral.)
• Ao adicionar todas as frequências, o que se obtém? (Resposta esperada: O total de participantes do coral.)
• Quantos alunos participam desse coral? (Resposta esperada: 36 alunos.)
Para o item b, questione:
• Que título você dará para seu gráfico? Por quê? (Espera-se que os estudantes coloquem o mesmo título da tabela, já que o gráfico será feito com base nela, mas isso não é obrigatório. O importante é analisar as justificativas para verificar como eles pensaram.)
• Qual é a fonte das informações que você colocará no seu gráfico? Por quê? (Espera-se que os estudantes considerem também a fonte da tabela.)
A resolução da atividade 1 está no início deste Manual, nas orientações específicas do capítulo 5.
Na atividade 2, é importante os estudantes terem a oportunidade de realizar uma pesquisa simples, como a sugerida, relativa à localidade onde moram. Também pode ter outra temática, como time de futebol para o qual torcem, lanche ou merenda favorita, desenho animado favorito ou uma pesquisa de interesse da turma.
4. Propriedades da igualdade
Letícia e Adriano são gêmeos e têm a mesma medida de altura. Em um parque de diversões, ao tentar entrar em um brinquedo, foram barrados pela altura. Não tiveram dúvida, tiraram os calçados e puderam entrar.
Representando a medida da altura de Letícia por x e a de Adriano por y, ambos calçados, e supondo que os tênis de cada um têm solado de 2 centímetros, podemos escrever:
Se x = y, então x ‒ 2 = y ‒ 2.
E vice-versa: se x ‒ 2 = y ‒ 2, então x = y.

Usamos aqui uma propriedade da igualdade que os matemáticos chamam princípio aditivo.
Adicionando ou subtraindo um mesmo número nos dois membros de uma igualdade, obtemos uma nova igualdade.
Observe alguns exemplos.
a) 3x ‒ 15 = x + 4 ‒ 15 equivale a 3x ‒ 15 + 15 = x + 4 ‒ 15 + 15, ou seja, a 3x = x + 4.
b) 8 + 2y = y + 13 equivale a 8 + 2y ‒ y = y + 13 ‒ y, ou seja, a 8 + y = 13.
Acompanhe agora esta outra situação.

Se, para um grupo x de pessoas, havia quantidades adequadas de pratos, de talheres, de cadeiras, ao duplicar o número de pessoas deve-se duplicar também o número de pratos, de talheres, de cadeiras.
Na situação anterior, temos outra propriedade da igualdade, chamada princípio multiplicativo.
Multiplicando os dois membros de uma igualdade por um mesmo número, ou dividindo-os por um mesmo número diferente de zero, obtemos uma nova igualdade.
Respostas e comentários
Orientações: Peça a um grupo de estudantes que faça uma breve dramatização dessa situação. A seguir, proponha uma discussão sobre procedimentos de sociabilidade, empatia e acolhimento.
4. Propriedades da igualdade
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um quatro.
Nesta página trabalhamos o princípio aditivo de uma igualdade, que está relacionado à habilidade (ê éfe zero seis ême ah um quatro). Espera-se que os estudantes compreendam que a aplicação desse princípio garante a obtenção de novas igualdades equivalentes à original, adicionando ou subtraindo um mesmo número nos dois membros da igualdade. Discuta a situação apresentada com os estudantes e amplie com outras.
Também apresentamos o princípio multiplicativo de uma igualdade, em que multiplicam-se ou dividem-se os dois membros de uma igualdade por um número diferente de zero para obter novas igualdades equivalentes entre si.
Discuta a situação apresentada com os estudantes e amplie com outras. Retome a notação simplificada da multiplicação, por exemplo: 2 ⋅ x pode ser indicado apenas por 2x, x ⋅ 2 por 2x também, a ⋅ b por ab, 2 ⋅ (5 + x) por 2(5 + x).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
12 A garagem da casa de meu vizinho tem 492 centímetros de medida de comprimento. Quando estaciona seu carro, ele sabe que sobram 77 centímetros. Qual é a medida do comprimento desse carro?
13 O total pago por Norma na compra de uma mesa e quatro cadeiras foi de .1220 reais. Ela lembra que o preço da mesa foi 580 reais, mas esqueceu quanto custou cada cadeira. Ajude Norma a calcular o preço de uma cadeira.
14 Para pagar a conta do supermercado, Marcela deu uma cédula de cinquenta reais. A funcionária do caixa pediu mais sete reais e disse que assim lhe devolveria vinte reais de troco. Quanto Marcela gastou nessa compra?

PARA SABER MAIS
A temperatura e a Álgebra
Você já imaginou viver em um lugar onde o trabalho dos bombeiros é incendiar, e não apagar? Viver em um mundo onde todo livro é considerado prejudicial ao ser humano e, por isso, deve ser queimado?
Esse mundo acontece no romance Fahrenheit 451, de rêi brédibâri, de 1953, que depois foi transformado em filme. O nome faz referência à temperatura 451, na escala Fahrenheit, em que os livros são queimados.

Há outras escalas de medida de temperatura, como a céucius e a Kelvin.
Quando imaginamos estar com febre, medimos a temperatura de nosso corpo com um termômetro que, no Brasil e na maioria dos países, é graduado na escala céucius. Colocamos o termômetro em contato com o corpo durante cêrca de dois minutos até que corpo e termômetro entrem em equilíbrio térmico e, então, lemos a medida da temperatura no termômetro.

A escala céucius lembra uma régua em que 0 °cê (lemos: “zero grau céucius”) corresponde à medida da temperatura em que a água congela (ponto de fusão da água) e 100 °cê (lemos: “cem graus céucius”) correspondem à medida da temperatura em que a água ferve (ponto de ebulição da água).
Na escala Kelvin, a água congela a 273 cá (lemos: “duzentos e setenta e três kelvin”) e ferve a 373 cá (lemos: “trezentos e setenta e três kelvin”).
Observe que, nas duas escalas, a diferença entre o ponto de ebulição e o ponto de fusão é igual a 100.
Podemos escrever uma expressão algébrica que relaciona as temperaturas medidas nessas duas escalas. Adotando TK e TC como as variáveis de temperatura, respectivamente, em kelvin e Celsius, temos:
TK = TC + 273 (um)
Respostas e comentários
12. 415 centímetros.
13. 160 reais.
14. 37 reais.
Exercícios propostos
No bloco de exercícios, proponha aos estudantes que realizem as atividades em duplas e discuta as situações com cada dupla, sempre que perceber a necessidade de sua intervenção.
Na resolução dos exercícios propostos oriente os estudantes a representar as situações por meio de uma expressão algébrica, mas outros caminhos de resolução devem ser validados.
No exercício 12, para determinar a medida x do comprimento do carro, pode-se fazer:
x + 77 = 492
x + 77 ‒ 77 = 492 ‒ 77
x = 415
Logo, a medida do comprimento do carro é de 415 centímetros.
Ao resolver o exercício 13, os estudantes podem considerar o preço de cada cadeira igual a x:
4x + 580 = .1220
4x + 580 ‒ 580 = .1220 ‒ 580
4x = 640
4x dividido por 4 = 640 dividido por 4
x = 160
Logo, o preço de cada cadeira é 160 reais.
Para o exercício 14, pode-se considerar o valor da compra de Marcela como x. Assim, obtemos:
x + 20 = 50 + 7
x + 20 = 57
x + 20 ‒ 20 = 57 ‒ 20
x = 37
Logo, Marcela gastou 37 reais.
Para saber mais
Nesta seção, explore a situação apresentada e verifique os conhecimentos que os estudantes já construíram acerca dessa nova grandeza – a temperatura –, se sabem como medi-la e qual instrumento é adequado para essa medição. póde-se propor um trabalho interdisciplinar com Ciências da Natureza.

Para fazer esse cálculo, basta substituir na expressão (um) TC por 37 °C. Assim, temos:
TK = TC + 273
TK = 37 + 273 = 310 (valor numérico da expressão TC + 273 quando TC é 37.)
Portanto, uma pessoa com 310 kélvin já está em estado febril.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Um cão pequeno sente-se bem a uma temperatura de medida de 38 a 39 graus céucius. E na escala Kelvin, qual seria o intervalo saudável para esse cão?
2 O manual de determinado computador informa que o processador trabalha bem a uma temperatura de medida igual a 333 kélvin. Isso corresponde a quantos graus céucius?
3 Sabe-se que o peixe acará-bandeira (Pterophyllum scalare) vive em águas com temperatura medindo 24 e 27 graus céucius.
Cauê mora em um local muito frio e precisa controlar a temperatura da água do aquário de seus peixinhos acarás-bandeiras. Para isso, ele comprou um termômetro importado que usa a escala Kelvin. Que medida de temperatura esse termômetro deve registrar para os peixes ficarem bem?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 As figuras a seguir representam o início de uma sequência infinita do que chamamos números quadrados. Cada um deles é igual à soma de dois números triangulares.

a) Mantendo o mesmo padrão de formação, qual será o número de bolinhas azuis da figura 5? E da figura 7? E da figura 9?
b) E qual será o número de bolinhas amarelas da figura 5? E da figura 7?
c) Seguindo o mesmo padrão, qual será o número quadrado da figura 5? E da figura 7? E da figura n?
d) Qual é o número da figura que terá, no total, 100 bolinhas? Quantas bolinhas azuis ela terá? E quantas bolinhas amarelas?
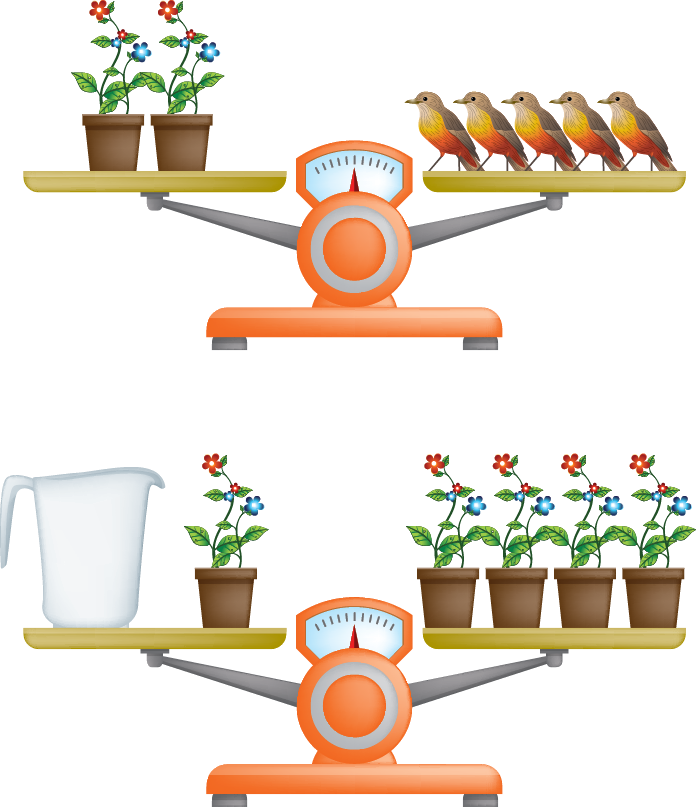
2 Nas figuras a seguir, as balanças estão equilibradas. Sabendo que a medida da massa de cada sabiá é igual a 90 gramas e que os vasos têm massas de mesma medida, qual é a medida da massa, em grama, de cada vaso com flor? E qual é a medida da massa da jarra?
Respostas e comentários
Para saber mais:
1. De 311 kélvin a 312 kélvin.
2. 60 °C.
3. De 297 kélvin a 300 kélvin.
Exercícios complementares:
1. a) 15, 28 e 45 bolinhas azuis.
1. b) vinte e uma e 36 bolinhas, respectivamente.
1. c) 36; 64; (n + 1) 2.
1. d) Figura 9, 45 bolinhas azuis e 55 bolinhas amarelas.
2. Cada vaso com flor: 225 gramas; jarra: 675 gramas.
Agora é com você!
Discuta as questões propostas, ressaltando a importância da linguagem algébrica para estabelecer relações e fórmulas que são usadas em muitas outras áreas do conhecimento, como Física, Química, Biologia, entre outras.
As resoluções e comentários sobre as atividades 1 a 3 estão no início deste Manual, nas orientações específicas do capítulo 5.
Exercícios complementares
Neste bloco de exercícios, os estudantes têm a oportunidade de retomar os principais conceitos tratados no capítulo e verificar possíveis dificuldades que ainda restem.
Sugerimos que os exercícios sejam desenvolvidos em duplas, o que ampliará e enriquecerá o repertório de estratégias que os estudantes já têm e consolidará os conhecimentos construídos.
Para responderem ao item a do exercício 1, eles devem identificar a regularidade presente na sequência apresentada. Eles devem perceber que a quantidade de bolinhas azuis é dada por:
n + (n ‒ 1) + (n ‒ 2) + reticências + (n ‒ n), em que n é maior que 1 e é o número da posição da figura na sequência.
Assim, o número de bolinhas azuis das figuras 5, 7 e 9 podem ser dadas por:
Figura 5: 5 + (5 ‒ 1) + (5 ‒ 2) + (5 ‒ 3) + (5 ‒ 4) + (5 ‒ 5) = = 5 + 4 + 3 + 2 + 1 + 0 = 15
Figura 7: 7 + (7 ‒ 1) + (7 ‒ 2) + (7 ‒ 3) + (7 ‒ 4) + (7 ‒ 5) + + (7 ‒ 6) + (7 ‒ 7) = 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 28
Figura 9: 9 + (9 ‒ 1) + (9 ‒ 2) + (9 ‒ 3) + (9 ‒ 4) + (9 ‒ 5) + (9 ‒ 6) + (9 ‒ 7) + (9 ‒ 8) + (9 ‒ 9) = 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 = 45
Para este caso, os estudantes também podem considerar que a partir da figura 4, a figura 5 terá uma fileira de 5 bolinhas azuis a mais, e assim sucessivamente; logo:
Figura 5 = 10 + 5 = 15
Figura 7 = 15 + 6 + 7 = 28
Figura 9 = 28 + 8 + 9 = 45
As resoluções dos demais itens do exercício 1 e do exercício 2 estão no início deste Manual, nas orientações específicas do capítulo 5.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Na linguagem algébrica, como podemos representar o triplo de um número mais a sua metade?
a)
3x mais um meiob)
x ao cubo mais fração x sobre 2c)
3x mais fração x sobre 2d)
x ao cubo mais um meio2 Observe a seguinte expressão:

A propriedade que está relacionada a essa expressão é:
a) propriedade comutativa da multiplicação.
b) propriedade distributiva da adição.
c) propriedade comutativa da adição.
d) propriedade distributiva da multiplicação.
3 Um número que é divisível por 15 precisa ser divisível por:
a) 3 e 5.
b) 3 e 10.
c) 5 e 10.
d) 10 e 15.
4 Adicionar ou subtrair um mesmo número nos dois membros de uma igualdade refere-se a qual propriedade?
a) Comutativa.
b) Distributiva.
c) Elemento neutro.
d) Princípio aditivo.
5 Ao subtrairmos 12 dos dois membros da igualdade 2x + 12 = 24 + x, obtemos:
a) 2x = 12 + x.
b) 2x = 24 + 12x.
c) 2x + 24 = 36 + x.
d) 2x ‒ 12 = 12 + x.
6 Ao multiplicarmos por 3 os dois membros da igualdade
x mais um terço igual a 6, obtemos:
a)
3x mais um nono igual a 18b) 3x + 1 = 18
c) 3x + 3 = 18
d) 3x + 9 = 18
7 A expressão que representa o triplo da diferença de um número com 7 é:
a) 3x ‒ 7
b) xelevado a 3 ‒ 7
c)
Um terço de x menos 7d) 3 ⋅ (x ‒ 7)
8 Observe a imagem.

Sabendo que a medida da massa de cada caixa é igual a 10 quilogramas e que os cachorros de pelúcia têm massas de mesma medida, que expressão representa essa situação?
a) 10 + 4y = 30 + 3y.
b) 40 + y = 30 + 3y.
c) 30 + y = 40 + 3y.
d) 40 + 4y = 30 + y.
9 No esquema a seguir, qual é o valor de R?
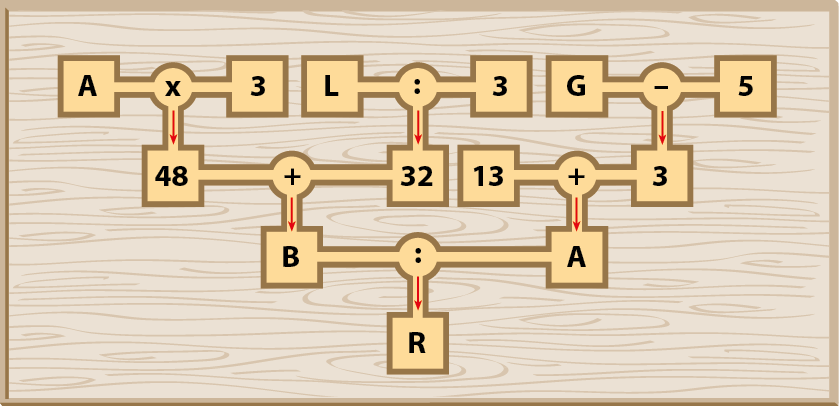
a) 5
b) 10
c) 16
d) 26
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões à seguir.
a) Escreva uma expressão algébrica e identifique as variáveis. Atribua números naturais às variáveis e calcule o valor numérico da expressão.
b) Escreva uma sentença com números naturais na linguagem verbal e na linguagem algébrica.
c) O que ocorre quando, em uma igualdade, adicionamos ou subtraímos um mesmo número em ambos os membros? Dê um exemplo.
d) E o que ocorre quando, em uma igualdade, multiplicamos ou dividimos ambos os membros por um mesmo número diferente de 0? Dê um exemplo.
Respostas e comentários
1. Alternativa c.
2. Alternativa c.
3. Alternativa a.
4. Alternativa d.
5. Alternativa a.
6. Alternativa b.
7. Alternativa d.
8. Alternativa b.
9. Alternativa a.
Organizando:
a) Resposta pessoal.
b) Resposta pessoal.
c) A igualdade se mantém. Resposta pessoal.
d) A igualdade se mantém. Resposta pessoal.
Verificando
Esses exercícios são mais uma oportunidade para os estudantes validarem o entendimento do conteúdo estudado neste capítulo. Oriente-os a reverem os conteúdos estudados caso alguma dúvida persista.
No teste 1 devem ler atentamente o comando da atividade e interpretar corretamente o significado de “o triplo de um número mais a sua metade”, deste modo, devem considerar que o triplo de um número deve ser representado por 3x e não por xelevado a 3, desconsiderando, as alternativas bê e d. A expressão “sua metade” deve ser entendida como a metade do número, ou seja,
x sobre 2e não o número
Um meio. Logo, a alternativa correta é a c. Para os estudantes que tiverem dificuldades com este teste, retome outros exemplos relacionando a linguagem escrita e falada com a linguagem algébrica, para que possam compreender e representar corretamente tais situações.
O teste 2 tem o objetivo de avaliar a compreensão dos estudantes em relação às propriedades das operações estudadas, no caso, a expressão ilustrada representa a propriedade comutativa da adição: em uma adição de dois números naturais, a ordem das parcelas não altera a soma. Logo, a alternativa correta é a c. Para os estudantes que não identificarem corretamente a propriedade, retome os exemplos estudados no capítulo 2 deste livro.
As resoluções dos testes 3 a 9 estão no início deste Manual, nas orientações específicas do capítulo 5.
Organizando
Ao retomarem os estudos para responder às questões propostas, incentive os estudantes a organizarem o aprendizado, fazendo resumos, quadros de destaque ou mapas conceituais para os conceitos que considerarem importantes.
As resoluções dos itens a a d estão no início deste Manual, nas orientações específicas do capítulo 5.
DIVERSIFICANDO
Desafiando a sua inteligência
Nas redes sociais, circula um desafio que pede às pessoas, com base em três igualdades consideradas válidas, que completem a quarta igualdade.
Nilza e Carlos enfrentaram o desafio.

Carlos respondeu: 8 + 11 = 40
Na sua opinião, ele acertou? Antes de prosseguir, tente resolver o desafio.
Qual é o padrão dessa sequência de igualdades, a lei de formação dela?
Vamos descobrir como Carlos chegou ao número 40.
Carlos observou cada linha isoladamente e percebeu que o resultado da 2ª linha (12) só seria obtido se ele fizesse uma adição entre o resultado da 1ª linha (5) aos números da esquerda da 2ª igualdade: [2 + 5] + 5 = 12.
Mas será que esse raciocínio também funcionava ao analisar a 3ª linha? Vejamos [3 + 6] + resultado anterior = 21 ? Sim, pois 3 + 6 + 12 = 21.
Então, Carlos repetiu o raciocínio para a linha seguinte, adicionando o resultado anterior para encontrar o próximo resultado: (8 + 11) + 21 = 40.
Observamos que Carlos usou um raciocínio por recorrência, pois para cada igualdade ele recorre à igualdade imediatamente anterior.
Já Nilza percebeu outro padrão de cálculo:
[1 + 4] = 1 + 1 ⋅ 4 = 5
[2 + 5] = 2 + 2 ⋅ 5 = 12
[3 + 6] = 3 + 3 ⋅ 6 = 21
Pensando assim, ela calculou: [8 + 11] = 8 + 8 ⋅ 11 = 8 + 88 = 96.
Como os dois conseguiram justificar o raciocínio que seguiram para obter sua resposta, podemos considerar que Carlos e Nilza estão corretos. Na Matemática, alguns problemas podem ter mais de uma resposta correta, e, quando isso ocorre, é importante justificar a resposta com argumentos válidos.
Note que Carlos teria chegado ao mesmo resultado de Nilza se tivesse seguido as etapas:
[4 + 7] = 4 + 7 + 21 = 32; [5 + 8] = 5 + 8 + 32 = 45; [6 + 9] = 6 + 9 + 45 = 60; [7 + 10] = 7 + 10 + 60 = 77; e [8 + 11] = 8 + 11 + 77 = 96.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Considerando a sequência dada nesse texto, calcule o valor de [13 + 16] utilizando o raciocínio de Nilza.
2 Explique como você faria para determinar o valor de [13 + 16] utilizando o raciocínio de Carlos.
3

Com alguns colegas, criem desafios parecidos com o de Nilza e Carlos e tentem resolvê-los. Depois, apresentem aos demais colegas da turma para que eles os resolvam.
Respostas e comentários
Orientações: Observe aos estudantes que o sinal “+”, escrito em vermelho no celular, não corresponde, de fato, ao sinal da adição de números naturais, mas a alguma operação hipotética com esses números. Esse tipo de desafio utiliza artifícios para criar uma dificuldade extra aos seguidores.
1. 221
2. A partir de [8 + 11] = 96, teria de obter [9 + 12] = 117; [10 + 13] = 140; [11 + 14] = 165; [12 + 15] = 192; e [13 + 16] = 221.
3. Resposta pessoal.
Diversificando
Nesta seção, os estudantes podem ter dificuldade para entender o uso dos colchetes. Comente que continuaremos a chamar de “parcelas” os elementos que estão sendo operados e de “soma” o resultado. Note que:
• [1 + 4] = 5
• [2 + 5] = 12 12 corresponde a 5 + 2 + 5.
• [3 + 6] = 21 21 corresponde a 12 + 3 + 6.
• [8 + 11] = ?
Não se pode obter diretamente esse resultado, pois houve um “pulo” na sequência das operações, cujas parcelas aumentavam de 1 em 1, ou seja, é preciso obter antes os valores de [4 + 7], [5 + 8], [6 + 9] e [7 + 10], cujos valores, seguindo esse padrão, devem ser, respectivamente, 32 (21 + 4 + 7), 45 (32 + 5 + 8), 60 (45 + 6 + 9) e 77 (60 + 7 + 10). Assim, o valor de [8 + 11] deve ser 77 + 8 + 11, ou seja, 96.
No raciocínio de Nilza não se depende da soma anterior, uma relação que pode ser aplicada em cada operação independentemente das demais, o que é vantajoso. Sugira aos estudantes que obtenham a próxima soma, depois de [8 + 11], pelo processo de Nilza.
A próxima soma é [9 + 12], que pelo processo dela é dada por: 9 + 9 ⋅ 12 = 9 + 108 = 117.
Agora é com você!
O exemplo apresentado anteriormente auxiliará na compreensão da questão 1. Neste caso, os estudantes deverão efetuar:
13 + 13 ⋅ 16 = 13 + 208 = 221
Na questão 2, sugira aos estudantes que observem as sequências das primeiras parcelas (1, 2, reticências) e das segundas parcelas (4, 5, reticências). O primeiro elemento da sequência das segundas parcelas (4) é 3 unidades maior do que o primeiro elemento das primeiras parcelas (1). Assim, se indicarmos por x um elemento da sequência das primeiras parcelas, deveremos indicar por x + 3 o elemento na posição correspondente na sequência das segundas parcelas.
Desse modo, eles podem concluir a relação: [x + (x + 3)] = x + x ⋅ (x + 3).
Oriente os estudantes na elaboração dos desafios propostos na questão 3. Aproveite para avaliar a capacidade de escrita e o conhecimento dos conceitos matemáticos envolvidos nos desafios elaborados. Se considerar adequado, monte uma lista com os desafios elaborados e proponha uma dinâmica em grupo para as resoluções.
Glossário
- Generalizar
- : estender determinada propriedade ou relação para mais casos.
- Voltar para o texto
- Demonstrar
- : ato de validar, com argumentação precisa, determinadas afirmações.
- Voltar para o texto