CAPÍTULO 10 Polígonos e poliedros

Observe, leia e responda no caderno.
a) Que figuras geométricas você identifica na obra de Victor Vasarely?
b) A obra foi produzida, em relevo, sobre madeira. Que efeitos, da imagem da obra, indicam sua tridimensionalidade? Explique.
c) Faça uma pesquisa sobre um artista que utilizou a Geometria em obras de arte. Apresente o resultado de sua pesquisa ao professor e aos colegas de turma.
Victor Vasarely se destacou na arte contemporânea ao criar uma nova tendência: a arte óptica. O artista nasceu em Pécs, Hungria, em 1906, e faleceu em Paris, França, em 1997.
A arte óptica ou op art, como é mais conhecida, tem como principal característica o uso de diferentes figuras geométricas, como polígonos, e em repetição exaustiva, passando a sensação de movimento, que resulta em um efeito ilusório para quem vê, dando a ideia de volume e de movimento.
Respostas e comentários
a) Quadriláteros, triângulos e círculos.
b) Espera-se que os estudantes indiquem que as sombras e as luzes presentes na imagem, permitem essa observação.
c) Resposta pessoal.
Capítulo 10 - Polígonos e poliedros
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Para complementar o estudo da Unidade Temática Geometria neste volume e ampliar os conhecimentos construídos em capítulos anteriores, tratamos de polígonos e poliedros associando essas figuras geométricas abstratas a objetos do cotidiano. Dessa maneira, os estudantes podem construir os conceitos com mais significado.
Na abertura, apresentamos uma obra de Victor Vasarely, conhecido como o pai da arte óptica ou Op Art e um dos fundadores da arte cinética. O seu fascínio por padrões lineares levou-o a desenhar diversos motivos por meio da utilização de linhas bicolores (pretas e brancas) e das deformações ondulantes, em que a sensação de profundidade e a multidimensionalidade dos objetos foram sempre uma preocupação constante. A introdução da cor nos seus trabalhos permitiu maior dinamismo, por meio do qual pretendeu retratar o universo inatingível das galáxias, a gigante pulsação cósmica e a mutação biológica das células. Os seus trabalhos são, então, essencialmente geométricos, policromáticos, multidimensionais, totalmente abstratos e intimamente ligados às ciências. Esta é uma boa oportunidade de mostrar aos estudantes como as figuras geométricas permitem essa sensação de multidimensionalidade.
As questões propostas permitem aos estudantes um olhar analítico sobre a produção artística apresentada, contribuindo para o desenvolvimento da competência geral 3, que propõe a valorização de manifestações artísticas. No item a, os estudantes devem identificar as diferentes figuras geométricas que o artista usou em sua obra. Neste caso, devem identificar o uso de círculos, triângulos e quadriláteros.
Para responder ao item b, espera-se que os estudantes relatem que as sombras identificadas em diferentes partes da imagem dessa obra indicam essa tridimensionalidade. Comente que há obras em que o efeito de luz e sombras é usado para dar a impressão de tridimensionalidade em superfícies planas.
Oriente os estudantes na pesquisa proposta no item c. Alguns artistas brasileiros, como Tarsila do Amaral, Luis Sacilotto e Rubem Valentim, fizeram uso de figuras geométricas em suas obras e podem fazer parte da pesquisa proposta.
1. Linhas poligonais
Observe agora a obra Curva dominante, do artista vaciíli candinsqui.
Para compor essa obra, que foi uma das mais representativas de sua fase parisiense, o artista usou diversas linhas.
•

Você identifica alguma figura geométrica representada nesta obra de arte?

Vamos destacar algumas das linhas utilizadas pelo artista em sua obra.

Quando uma linha é formada apenas por segmentos de reta consecutivos e não colineares, ela é chamada de linha poligonal.
Observe alguns exemplos.

As linhas poligonais podem ser abertas ou fechadas:


Respostas e comentários
Alguns estudantes podem identificar o uso de círculos e quadriláteros.
1. Linhas poligonais
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um oito.
Neste item, tratamos do conceito de linha poligonal, que será utilizado na conceituação de polígono contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah um oito). Aproveite a pergunta proposta para verificar se os estudantes reconhecem, com base no estudo em anos anteriores, círculos e quadriláteros como figuras geométricas. A proposta do trabalho com Arte pode ser ampliada ao comentar com os estudantes um pouco sobre a arte abstrata geométrica:
A arte abstrata tende a suprimir toda a relação entre a realidade e o quadro, entre as linhas e os planos, as cores e a significação que esses elementos podem sugerir ao espírito. Quando a significação de um quadro depende essencialmente da cor e da fórma, quando o pintor rompe os últimos laços que ligam a sua obra à realidade visível, ela passa a ser abstrata.
IMBROISI, M.; MARTINS, S. Abstracionismo Geométrico. História das Artes, 2022. Disponível em: https://oeds.link/KiuBbS. Acesso em: 13 março 2022.
Aproveite esse momento para propor à turma um trabalho interdisciplinar com o professor de Arte. Com base na pesquisa proposta na abertura deste capítulo, que servirá de referência, solicite aos estudantes que confeccionem uma representação artística utilizando linhas poligonais e não poligonais. Sob a orientação do professor de Arte, os estudantes poderão utilizar diferentes técnicas nessa produção.
Entre as linhas poligonais fechadas, há as linhas poligonais simples e as não simples:


Interior, exterior e convequicidade
O plano
Alfarepresentado a seguir é dividido pela linha poligonal fechada simples em duas regiões sem pontos comuns. Tais regiões são chamadas de região interior e região exterior.
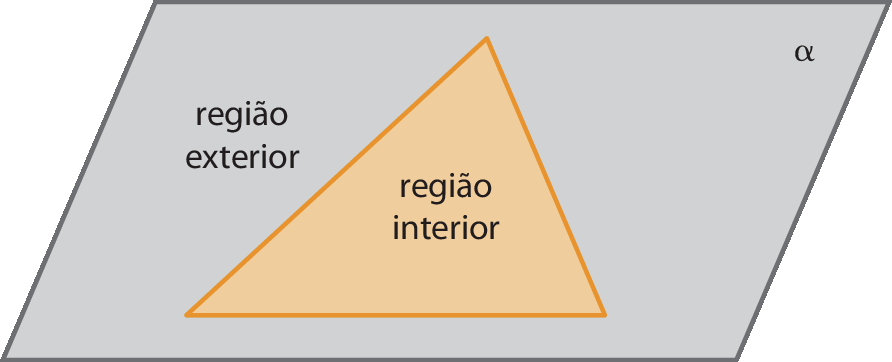
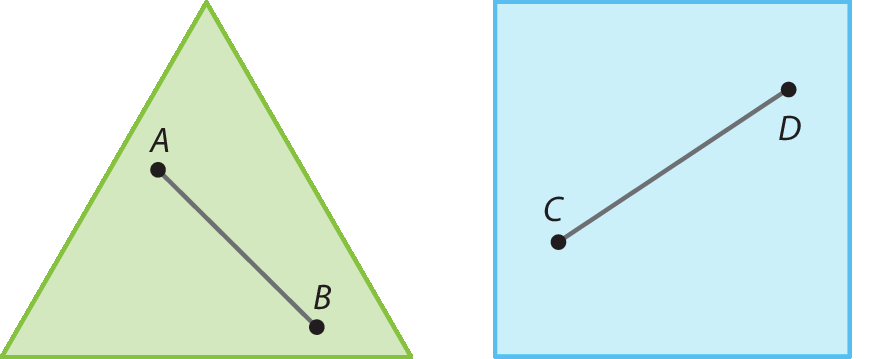
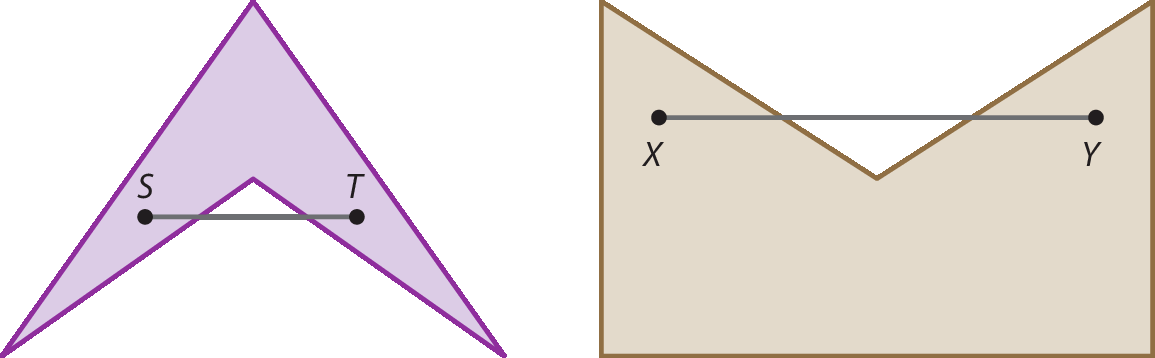
As regiões interiores, determinadas por uma linha poligonal fechada simples, podem ser classificadas em convexas ou não convexas.


Respostas e comentários
Interior, exterior e convexidade
Após a apresentação dos conteúdos, proponha aos estudantes uma dinâmica em que eles tenham de fazer algumas representações na lousa com base em algumas características predefinidas:
a) desenhe uma linha poligonal fechada e simples.
b) desenhe uma linha não poligonal aberta.
c) desenhe uma linha poligonal fechada e não simples.
d) desenhe uma região do plano não convéquica.
e) desenhe uma região do plano convéquica.
Esse tipo de atividade possibilitará aos estudantes refletir sobre os conceitos estudados.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Das figuras a seguir, verifique quais são linhas poligonais.
a)

b)

c)

d)

2 Classifique as linhas poligonais em aberta ou fechada. Entre as linhas poligonais fechadas, identifique a simples e a não simples.
a)

b)

c)

d)
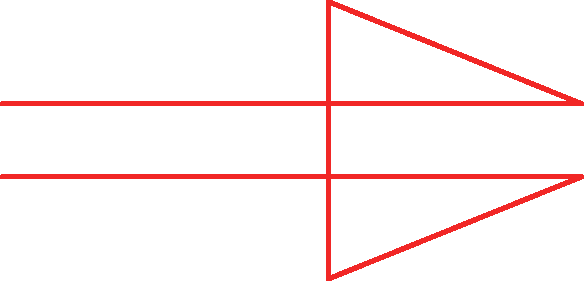
3 Classifique a região interior das linhas poligonais em convéquica ou não convéquica.
a)

b)

c)

d)

4

Hora de criar – Elabore um texto caracterizando as linhas poligonais abertas, fechadas, simples e não simples. Em seguida, compare seu texto com o de um colega e conversem sobre as diferenças entre eles.
2. Polígonos
Observe estas figuras.
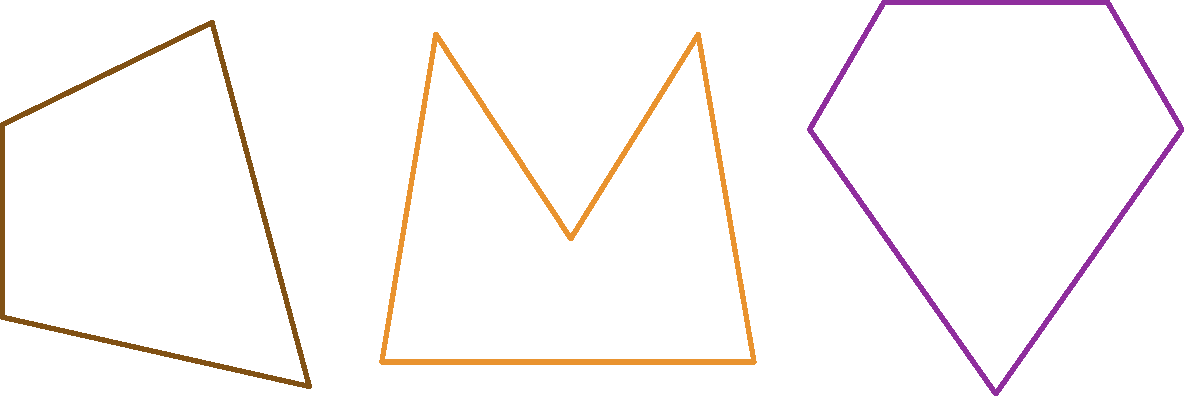

Toda linha poligonal fechada simples é denominada polígono.
Respostas e comentários
1. Alternativas b, c.
2. a) Fechada simples.
2. b) Fechada não simples.
2. c) Aberta.
2. d) Aberta.
3. a) Não convéquica.
3. b) convéquica.
3. c) Não convéquica.
3. d) convéquica.
4. Resposta pessoal.
Exercícios propostos
Neste bloco de exercícios, os estudantes podem aplicar os conceitos e as classificações vistos nas páginas anteriores.
As resoluções dos exercícios 1 a 3 estão no início deste Manual, nas orientações específicas do capítulo 10.
Como ampliação do exercício 3, entregue uma folha quadriculada aos estudantes e peça a eles que desenhem as figuras desse exercício nessa malha, apenas mantendo o formato delas, podendo variar o tamanho e marcando os extremos de cada segmento de reta que delimita cada figura nos cruzamentos das linhas da malha. Em seguida, que escolham dois pontos distintos do interior de cada figura e tracem o segmento de reta que tem esses pontos como extremos, de modo que parte desse segmento fique na região externa da figura.
Então, questione: “Você traçou tal segmento de reta em todas as figuras? Por quê?”. Espera-se que os estudantes percebam que só conseguem traçar um segmento dessa maneira nas figuras dos itens a e c, pelo fato de elas serem regiões não convexas. Nas figuras que são regiões convexas, como nos itens b e d, não é possível traçar um segmento de reta com essas características.
No exercício 4, não esperamos que os estudantes elaborem definições formais. Consideramos, nesse caso, que a redação é importante para promover a capacidade de argumentação, apreensão, caracterização e identificação das propriedades depreendidas visualmente.
2. Polígonos
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um oito.
Neste tópico apresentamos o conceito de polígonos, seus elementos e sua classificação quanto ao número de lados ou de ângulos internos, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah um oito).
Nesta coleção, assumimos a definição de polígono como linha poligonal fechada simples, em concordância com a definição de ângulo como reunião de duas semirretas de mesma origem. No entanto, para simplificar, podemos utilizar materiais manipuláveis como modelos, referindo-nos a uma região poligonal simplesmente como polígono. Combine essa linguagem com os estudantes, quando for o caso.
Vale destacar ainda que a classificação em polígono convexo ou polígono não convexo também toma por base a região plana por ele delimitada.
Os polígonos podem ser convéquiços ou não convéquiços.




EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
5 Entre as figuras representadas, verifique quais são polígonos.
a)

b)

c)

d)

e)

f)

6 Classifique os polígonos a seguir em convéquiço ou não convéquiço.
a)

b)

c)

d)

e)

f)

7 Logotipo é um símbolo que serve para identificar uma empresa, uma instituição, um produto, uma marca etcétera. Observe um exemplo.

a) Pesquise em jornais, revistas ou na internet logotipos em que seja possível identificar formas que lembram polígonos e reproduza seis deles.
b) Crie um logotipo para um brinquedo em que apareça uma figura que lembre um polígono.
Respostas e comentários
5. Alternativas a, d, ê.
6. a) Não convéquiço.
6. b) Não convéquiço.
6. c) Não convéquiço.
6. d) convéquiço.
6. e) convéquiço.
6. f) Não convéquiço.
7. a) Resposta pessoal.
7. b) Resposta pessoal.
Exercícios propostos
As alternativas a, d e e do exercício 5 apresentam polígonos, pois apresentam linhas poligonais simples e fechadas. Após a resolução desse exercício, para complementar a discussão a respeito da definição de polígono, pergunte aos estudantes por que as figuras b, c e f não são polígonos. Espera-se que eles identifiquem que a figura b é uma linha não simples e aberta, a figura c não é linha poligonal (além de ser aberta) e a figura f, apesar de ser uma linha poligonal fechada, é não simples.
No exercício 6, se considerar adequado, solicite aos estudantes que representem os polígonos em uma folha de papel quadriculado. Depois, peça-lhes que unam os vértices com segmentos de reta. Com base nessas representações, devem concluir que:
a) O polígono é não convéquiço.
b) O polígono é não convéquiço.
c) O polígono é não convéquiço.
d) O polígono é convéquiço.
e) O polígono é convéquiço.
f) O polígono é não convéquiço.
A pesquisa e a produção do exercício 7 é pessoal. Auxilie os estudantes nesse momento. Se possível, leve jornais e revistas para eles fazerem a pesquisa. Após as produções realizadas pelos estudantes, proponha a eles uma exposição com os logotipos criados e peça-lhes que falem sobre suas criações.

Sugestão de leitura
Para enriquecer o trabalho com o tema do capítulo, indicamos:
PEREIRA, M. D. Número de diagonais de um polígono: relato de uma experiência. Educação Matemática em Revista. Sociedade Brasileira de Educação Matemática, Ano. 15, número 29, página 43-50, 2010.
O autor apresentou uma possibilidade para a contagem das diagonais de um polígono, utilizando essa metodologia para desenvolver estratégias para resolver situações desafiadoras.
8 Cada sequência a seguir obedece a uma regra quanto ao número de canudinhos que formam um polígono. Descubra essa regra e, supondo que ela continue valendo, desenhe em seu caderno o próximo polígono, escrevendo o número de canudinhos que o formaram.
a)
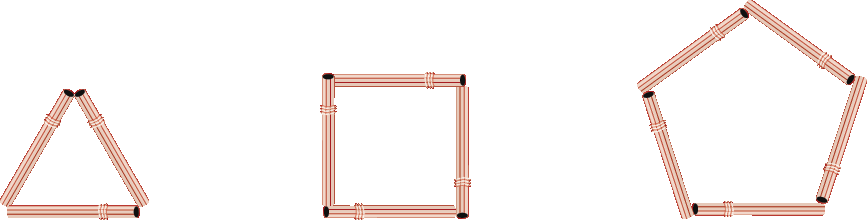
b)

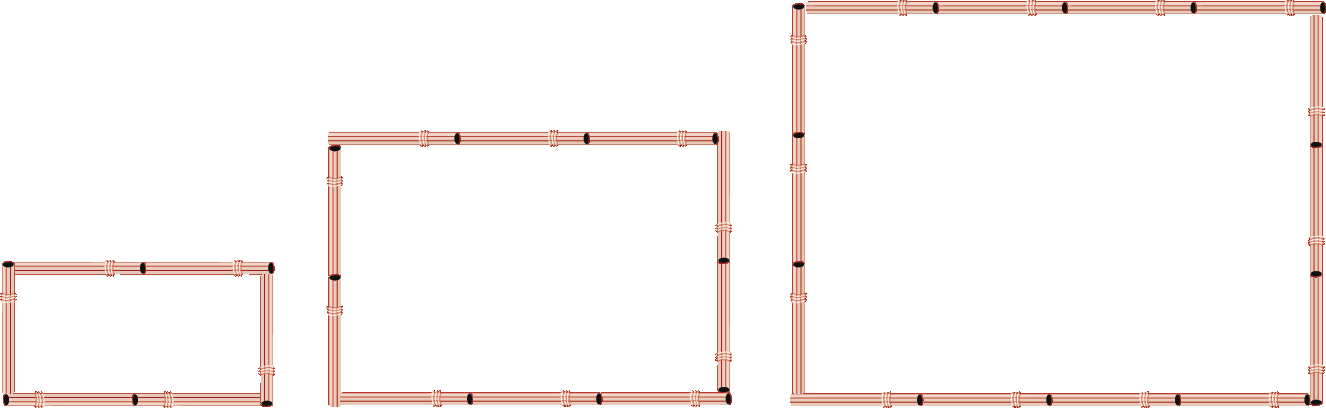
c)
Elementos de um polígono
Em um polígono qualquer, os segmentos que formam a linha poligonal são chamados de lados.
O ponto de encontro de dois lados consecutivos é chamado de vértice desse polígono.
Acompanhe um exemplo.
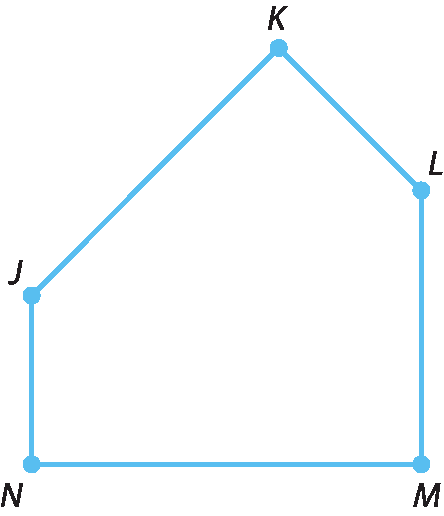
• Os vértices desse polígono são os pontos J, K, éle, M e N.
• Os lados do polígono são os segmentos
Segmento de reta JK,
Segmento de reta KL,
Segmento de reta LM,
Segmento de reta MNe
Segmento de reta NJ.
• Indicamos assim: polígono JKLMN.
• Os vértices J e K, K e éle, éle e M, M e N, N e J são consecutivos.
• Os vértices J e éle, J e M, K e M, K e N, éle e N são não consecutivos.
Respostas e comentários
8. Respostas possíveis:
8. a) a n = n + 2; construção de figura; 6.
8. b) a n = 3n; construção de figura; 12.
8. c) a n = 4n + 2; construção de figura; 18.
Exercícios propostos
O exercício 8 é uma oportunidade para a observação de regularidades em uma sequência de figuras. Para maior compreensão da regra que “gera” cada uma das sequências, incentive os estudantes a escrever a regra observada. Algumas explicações possíveis:
a) O número de canudinhos vai aumentando de 1 em 1; assim, a 4ª figura (um hexágono) pode ser composta de 6 canudinhos.
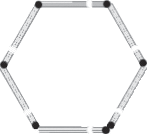
b) O número de canudinhos vai aumentando de 3 em 3; assim, a 4ª figura (um triângulo) pode ser composta de 12 canudinhos (9 + 3).
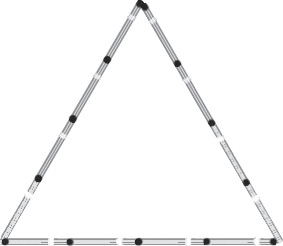
c) O número de canudinhos vai aumentando de 4 em 4; assim, a 4ª figura (um retângulo) pode ser composta de 18 canudinhos (14 + 4), sendo 5 no comprimento (ou base) e 4 na largura (ou altura).

Caso algum estudante apresente outra alternativa de resposta, cabe analisar também a justificativa, pois existem outras respostas possíveis.
Como ampliação prática desse exercício, podem-se levar para a sala de aula canudinhos de papel ou biodegradáveis, e montar as estruturas apresentadas nos itens com os estudantes.
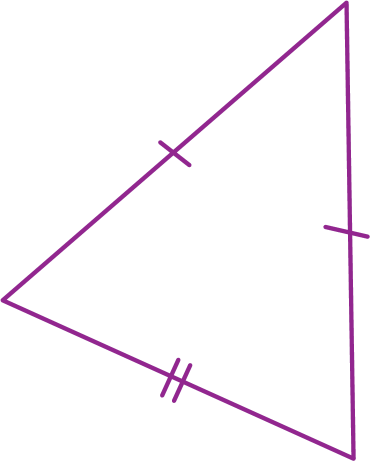
Para indicar os lados de mesma medida (lados congruentes) em um polígono, marcamos esses lados com o mesmo número de tracinhos.
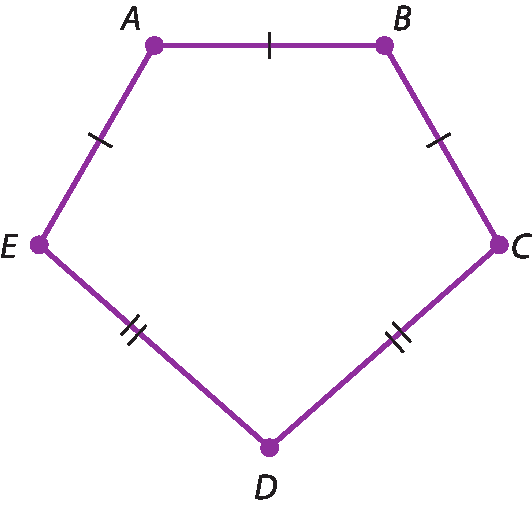
No polígono á bê cê dê é, os lados
Segmento de reta AB,
Segmento de reta BCe
Segmento de reta AEsão congruentes entre si. Os lados
Segmento de reta CDe
Segmento de reta DEtambém são congruentes entre si, mas têm medida diferente dos outros três lados.
Dois lados consecutivos de um polígono determinam um ângulo interno desse polígono.
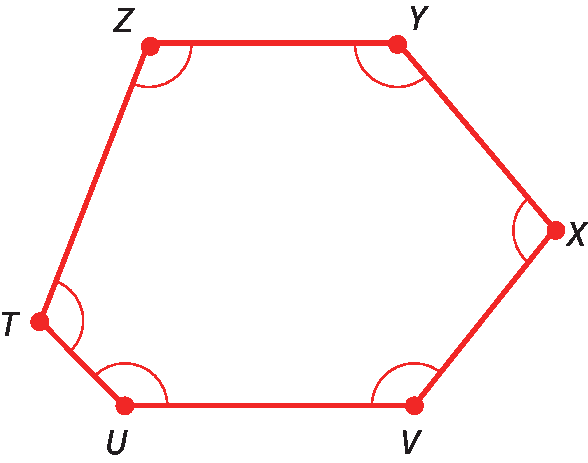
No polígono ZYXVUT, estão assinalados os ângulos internos, que indicamos por
ângulo Z,
ângulo Y,
ângulo X,
ângulo V,
ângulo Ue
ângulo T.
Os segmentos com extremos em dois vértices não consecutivos são chamados de diagonais do polígono.
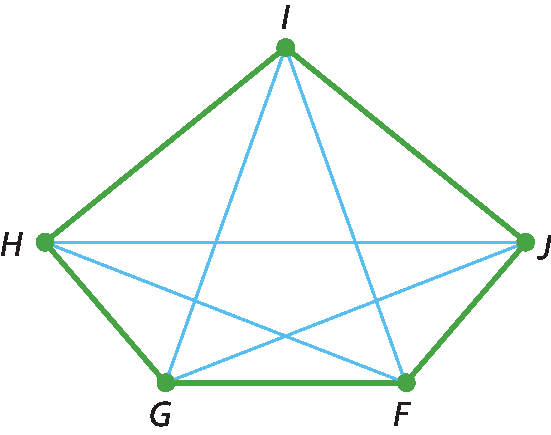
Os segmentos
Segmento de reta FI,
Segmento de reta FH,
Segmento de reta JG,
Segmento de reta JHe
Segmento de reta IGsão as diagonais do polígono éfe gê agá í jota.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
9 Desenhe um polígono de 7 lados, nomeie seus vértices e trace suas diagonais.
a) Quantos vértices tem esse polígono?
b) Identifique os lados desse polígono.
c) Quantos ângulos internos tem esse polígono? Identifique-os.
d) Quantas diagonais tem esse polígono? Identifique-as.
10 Desenhe um polígono que tenha 4 ângulos internos e nomeie seus vértices.
a) Quantos vértices tem esse polígono?
b) Identifique seus ângulos internos.
c) Quantos lados tem esse polígono? Identifique-os.
11 Desenhe um polígono de 3 lados e trace todas as suas diagonais. Quantas diagonais tem esse polígono?
12 Quantos vértices tem um polígono de 12 lados? E quantos ângulos internos?
Pense mais um pouco...
FAÇA A ATIVIDADE NO CADERNO
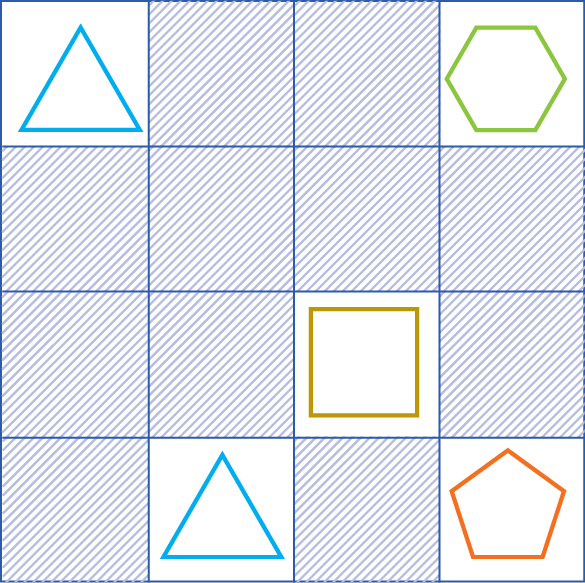
Copie o quadro e termine de preenchê-lo usando polígonos com a mesma fórma dos polígonos a seguir.
Mas atenção: não pode haver repetição de polígono em uma mesma linha nem em uma mesma coluna.

Respostas e comentários
9. a) 7 vértices.
9. b) Resposta pessoal.
9. c) 7 ângulos internos; Resposta pessoal.
9. d) 14 diagonais; Resposta pessoal.
10. a) 4 vértices.
10. b) Resposta pessoal.
10. c) 4 lados; Resposta pessoal.
11. Nenhuma.
12. 12 vértices; 12 ângulos internos.
Uma resposta possível da seção Pense mais um poucoreticências está neste Manual.
Elementos de um polígono
Os estudantes já viram em outro momento os elementos dos polígonos (lados, vértices, ângulos internos e diagonais) e suas representações. Para reforçar esse assunto desenhe na lousa alguns polígonos e peça a eles que localizem e identifiquem seus elementos.
Exercícios propostos
No exercício 9, os estudantes podem desenhar qualquer polígono de 7 lados. Eles devem perceber que, seja qual for o desenho desse polígono, ele deverá ter:
• 7 vértices;
• 7 lados;
• 7 ângulos internos;
• 14 diagonais.
A identificação (por meio de letras maiúsculas) dos vértices do polígono pode variar, pois é uma escolha pessoal. Para perceberem as semelhanças e diferenças em suas respostas, incentive os estudantes a trocá-las com pelo menos dois colegas.
As resoluções dos exercícios 10 e 12 estão no início deste Manual, nas orientações específicas do capítulo 10.
Após a resolução do exercício 11, é possível reforçar que, seja qual for o triângulo, nunca haverá diagonais. É importante que, após testarem em diferentes triângulos, os estudantes percebam que, ao unir dois de seus vértices, sempre estarão traçando um lado, nunca uma diagonal.
Pense mais um poucoreticências
O desafio proposto nesta seção pode ser realizado experimentalmente pelos estudantes. Organizados em duplas, eles podem recortar modelos desses polígonos feitos em papel sulfite e tentar montar o quadro. Oriente-os no manuseio da tesoura de ponta arredondada para a obtenção dos modelos de polígonos.
Uma possível solução seria:
Classificação dos polígonos
Em um polígono, o número de lados é igual ao número de ângulos internos. Alguns polígonos recebem nomes especiais, de acordo com o número de lados ou de ângulos internos. Observe.
|
Número de lados |
Número de ângulos |
Nome do polígono |
|---|---|---|
|
3 |
3 |
triângulo |
|
4 |
4 |
quadrilátero |
|
5 |
5 |
pentágono |
|
6 |
6 |
hexágono |
|
7 |
7 |
heptágono |
|
8 |
8 |
octógono |
|
9 |
9 |
eneágono |
|
10 |
10 |
decágono |
|
11 |
11 |
undecágono |
|
12 |
12 |
dodecágono |
|
15 |
15 |
pentadecágono |
|
20 |
20 |
icoságono |

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
13 Escreva o nome de cada polígono.
a)

b)

c)
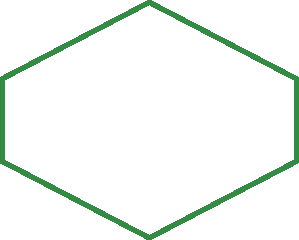
d)

e)

f)
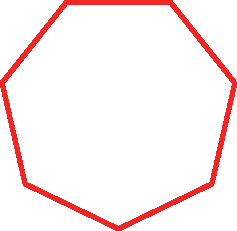
14 Responda às questões.
a) Quantos ângulos internos tem um hexágono?
b) Qual é o polígono que tem 12 vértices?
c) Quantos vértices, lados e ângulos internos tem o icoságono?
15 Em um colégio, foi disputado um torneio de tênis de mesa entre classes. Foram formadas 5 equipes e cada equipe jogou contra todas as outras uma única vez.

a) Quantas partidas foram disputadas ao todo?
b) Represente essa situação por meio de um polígono, dispondo cada equipe em um vértice do polígono. Que polígono você formou?
c) Que elementos desse polígono podem representar os jogos entre as equipes?
d) O que você precisa fazer para obter o total de partidas por meio do seu desenho?
Respostas e comentários
13. a) Quadrilátero.
13. b) Quadrilátero.
13. c) Hexágono.
13. d) Triângulo.
13. e) Octógono.
13. f) Heptágono.
14. a) 6 ângulos internos.
14. b) dodecágono.
14. c) 20 vértices; 20 lados; 20 ângulos internos.
15. a) 10 partidas.
15. b) Construção de figura; pentágono.
15. c) As diagonais e os lados.
15. d) Adicionar o número de diagonais com o número de lados.
Classificação dos polígonos
Essa é uma ótima oportunidade para incentivar os estudantes a usar o dicionário, para pesquisar sobre os prefixos penta-, hexa-, hepta- e as palavras pentágono, hexágono, heptágono, entre outras, usadas para nomear os polígonos.
Verifique quais polígonos os estudantes já conheciam pelo nome. Peça a eles que desenhem no caderno dois exemplares diferentes de cada polígono do quadro.
Exercícios propostos
Em um polígono, o número de lados é igual ao número de ângulos internos. Alguns polígonos recebem nomes especiais, de acordo com o número de lados ou de ângulos internos. Dessa maneira, no exercício 13, verificamos:
a) Tem 4 lados e 4 ângulos internos, é um quadrilátero.
b) Tem 4 lados e 4 ângulos internos, é um quadrilátero.
c) Tem 6 lados e 6 ângulos internos, é um hexágono.
d) Tem 3 lados e 3 ângulos internos, é um triângulo.
e) Tem 8 lados e 8 ângulos internos, é um octógono.
f) Tem 7 lados e 7 ângulos internos, é um heptágono.
As resoluções dos exercícios 14 e 15 estão no início deste Manual, nas orientações específicas do capítulo 10.
No exercício 15, espera-se que os estudantes observem a relação entre as combinações possíveis das cinco equipes de tênis de mesa com a situação do polígono e suas diagonais. Antes que estabeleçam qualquer relação, pode-se simular a situação com a participação de cinco estudantes, cada um representando uma equipe. À medida que se formarem os pares de equipes para representar as partidas, registre na lousa e, em seguida, faça um paralelo com o estudo das diagonais.
A título de exemplo, podemos acrescentar a clássica situação do encontro de um grupo de pessoas que trocam apertos de mãos, de maneira que ninguém deixe de cumprimentar ninguém e cada pessoa seja cumprimentada uma única vez. O número total de cumprimentos, nessas ocasiões, é calculado de modo similar ao exercício em questão. Esta atividade permite aos estudantes relacionar duas diferentes unidades temáticas da Matemática: Números e Geometria, trabalhando com as habilidades (ê éfe zero seis ême ah um oito) e (ê éfe zero seis ême ah zero três).
3. Triângulos
Diariamente nos deparamos com diversos objetos que nos dão a ideia de triângulo. Observe alguns objetos que podem ser relacionados a esse polígono de três lados.



(As imagens não respeitam as proporções reais entre os objetos.)
Elementos de um triângulo
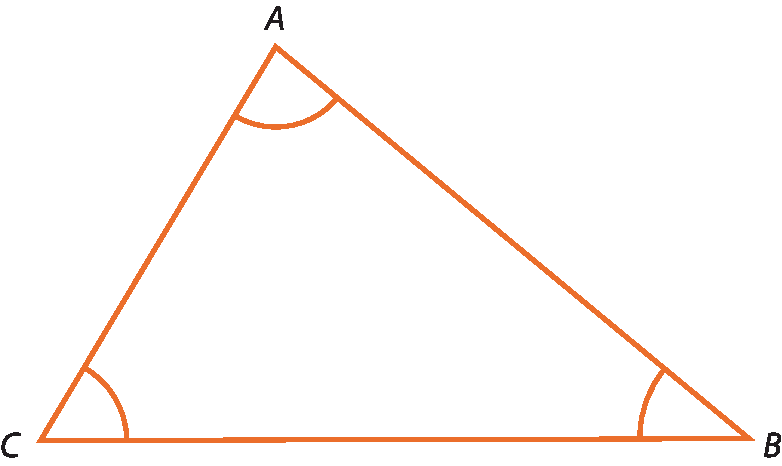
No triângulo á bê cê, destacamos seus elementos:
• a, B e C são os vértices.
•
Segmento de reta AB,
Segmento de reta BC, e
segmento de reta CAsão os lados.
•
Ângulo A,
Ângulo Be
ângulo Csão os ângulos internos.
Classificação dos triângulos
Os triângulos podem ser classificados quanto às medidas de seus lados e quanto às medidas de seus ângulos internos. Observe a seguir os dois tipos de classificação.
Classificação quanto às medidas dos lados
|
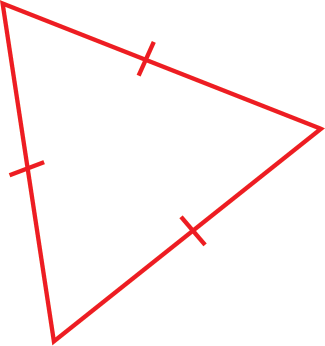
Triângulo isósceles |
Triângulo equilátero |
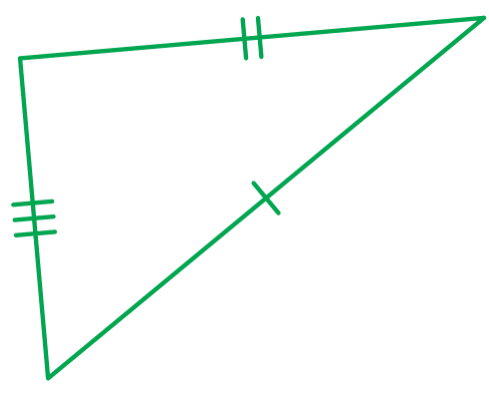
Triângulo escaleno |
|---|---|---|
|
|
|
|
Observe que, para ser classificado como isósceles, o triângulo deve ter pelo menos dois lados congruentes. Como os triângulos equiláteros têm três lados congruentes, eles também são classificados como triângulos isósceles.
Respostas e comentários
3. Triângulos
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah um nove, ê éfe zero seis ême ah dois dois e ê éfe zero seis ême ah dois três.
Os estudantes já devem conhecer o triângulo como um polígono de 3 lados. Neste estudo, pretendemos ampliar e aprofundar os conhecimentos já construídos acerca dessa figura, como conhecer e nomear todos os seus elementos: os 3 vértices, os 3 lados e os 3 ângulos internos.
Além disso, estudaremos dois tipos de classificação de triângulos: quanto às medidas de seus lados (tratada nesta página) e quanto às medidas de seus ângulos internos (tratada na página seguinte), contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah um nove).
Ao estudar a medida de segmento de reta, no capítulo 6 deste volume, os estudantes tiveram contato com a noção de segmentos congruentes. A classificação dos triângulos quanto às medidas de seus lados é feita com base nesse conceito: ter ou não lados congruentes e quantos. Espera-se que eles reconheçam:
• um triângulo que tem os três lados de medidas diferentes (aquele que não tem lados congruentes) como triângulo escaleno e aquele que tem pelo menos dois lados congruentes (de medidas iguais) como triângulo isósceles;
• um triângulo que tem todos os três lados congruentes como um caso particular de triângulo isósceles, ou seja, como triângulo equilátero.
Classificação quanto às medidas dos ângulos internos
|
Triângulo acutângulo |
Triângulo retângulo |
Triângulo obtusângulo |
|---|---|---|
|
|
|
|
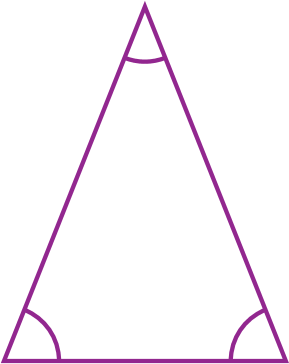
Um triângulo muito especial
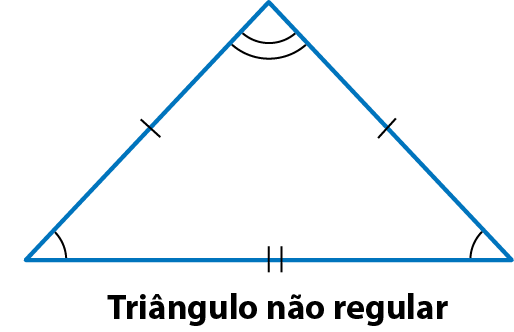
Todo triângulo equilátero (que tem três lados congruentes) também é um triângulo equiângulo (com três ângulos congruentes, ou seja, de mesma medida). Um polígono com essas características, lados congruentes e ângulos congruentes, é um polígono regular; neste caso, temos um triângulo regular.
Caso um lado tenha medida diferente dos outros ou um ângulo tenha medida diferente dos outros ângulos, o triângulo é não regular.

Construção de triângulos
Já aprendemos a construir ângulos usando o transferidor. Agora, vamos aprender a construir triângulos usando régua, compasso e transferidor.
Conhecendo a medida dos três lados de um triângulo, é possível construí-lo usando régua e compasso. Acompanhe o exemplo a seguir.
• Vamos construir o triângulo á bê cê, sabendo que as medidas de seus lados, em centímetro, são:
Medida do segmento AC.= 4,
Medida do segmento BC.= 4 e
Medida do segmento AB.= 3.
1º) Com o auxílio da régua, traçamos um segmento
Segmento de reta AC
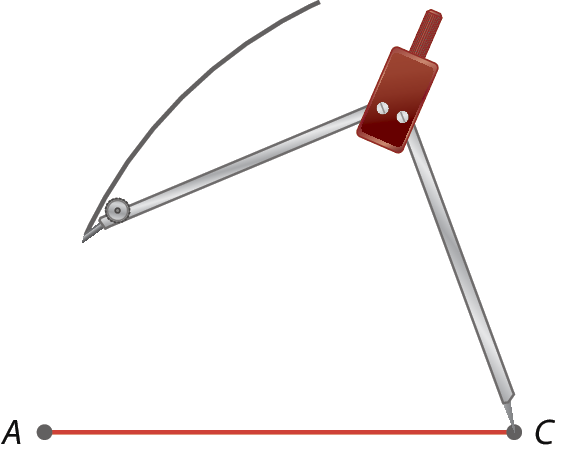
2º) Abrimos o compasso com a medida do segmento
Segmento de reta BC(4 centímetros) e traçamos um arco com a ponta-seca do compasso centrada em C.
Respostas e comentários
Classificação quanto às medidas dos ângulos internos
Ao classificar os triângulos de acordo com as medidas de seus ângulos internos, obtemos três classes: a dos triângulos que têm todos os ângulos internos agudos (triângulos acutângulos), a dos triângulos que têm um ângulo interno reto (triângulos retângulos), e a dos triângulos que têm um ângulo obtuso (triângulos obtusângulos).
Proponha aos estudantes uma atividade, em duplas, na qual cada integrante da dupla monta um triângulo com canudinhos de papel e, depois, faz a classificação do triângulo do outro. Mexendo na abertura e no tamanho dos canudinhos, eles podem perceber os vários tipos de triângulos.
Por meio dessa experimentação, os estudantes poderão verificar que, se o triângulo é equilátero, ele também será equiângulo, ou seja, tem os três ângulos internos de mesma medida.
Em seguida, proponha a eles que façam a combinação dessas duas classificações, registrando as conclusões no caderno. Espera-se que, ao combinar esses dois tipos de classificação, percebam que:
• triângulos acutângulos podem ser triângulos escalenos, isósceles ou, em particular, equiláteros (caso em que todos os ângulos internos medem 60graus);
• triângulos retângulos podem ser triângulos escalenos ou triângulos isósceles, mas não podem ser triângulos equiláteros, pois deveriam ter os três ângulos de mesma medida e não é possível um triângulo ter mais de um ângulo reto;
• triângulos obtusângulos podem ser triângulos escalenos ou triângulos isósceles, mas não podem ser triângulos equiláteros, já que um triângulo não pode ter mais do que um ângulo obtuso (entre 90graus e 180graus).
Discuta com os estudantes cada situação. Eles podem exemplificá-las construindo triângulos com os canudinhos e comparando os ângulos internos com um ângulo reto feito de papel.
Outro conceito que apresentamos é o de polígono regular. Peça a eles que identifiquem que tipo de triângulo pode ser um polígono regular. Espera-se que percebam que apenas o triângulo equilátero é um triângulo regular, pois é equiângulo também, ou seja, tem os três lados congruentes e os três ângulos internos de mesma medida.
3º) Repetimos o passo anterior para traçar outro arco, porém agora com a medida do segmento
segmento AB(3 centímetros) e a ponta-seca do compasso centrada em a. No encontro dos arcos, marcamos o ponto B.
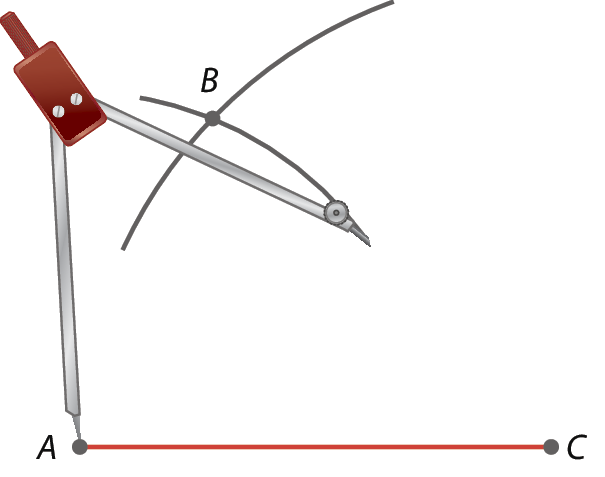
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
4º) Com o auxílio da régua, traçamos os segmentos
segmento BC e segmento AB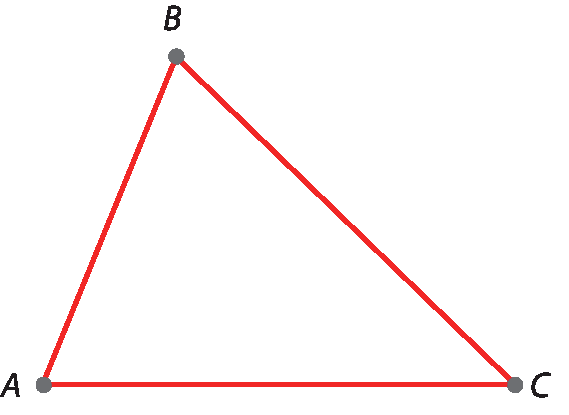
Também podemos construir um triângulo com régua, transferidor e compasso. Para isso, basta ter as medidas de dois lados e de um ângulo interno. Acompanhe o exemplo a seguir.
• Vamos construir o triângulo á bê cê, conhecendo as medidas de dois lados (em centímetro) e de um ângulo:
Medida do segmento de reta AC igual a 6. Medida do segmento de reta AB igual a 5.e
Medida do ângulo A igual a 60 graus.1º) Com o auxílio da régua, traçamos um segmento
Segmento de reta ACde 6 centímetros.

2º) Construímos um ângulo de 60graus, com lado
Semirreta AB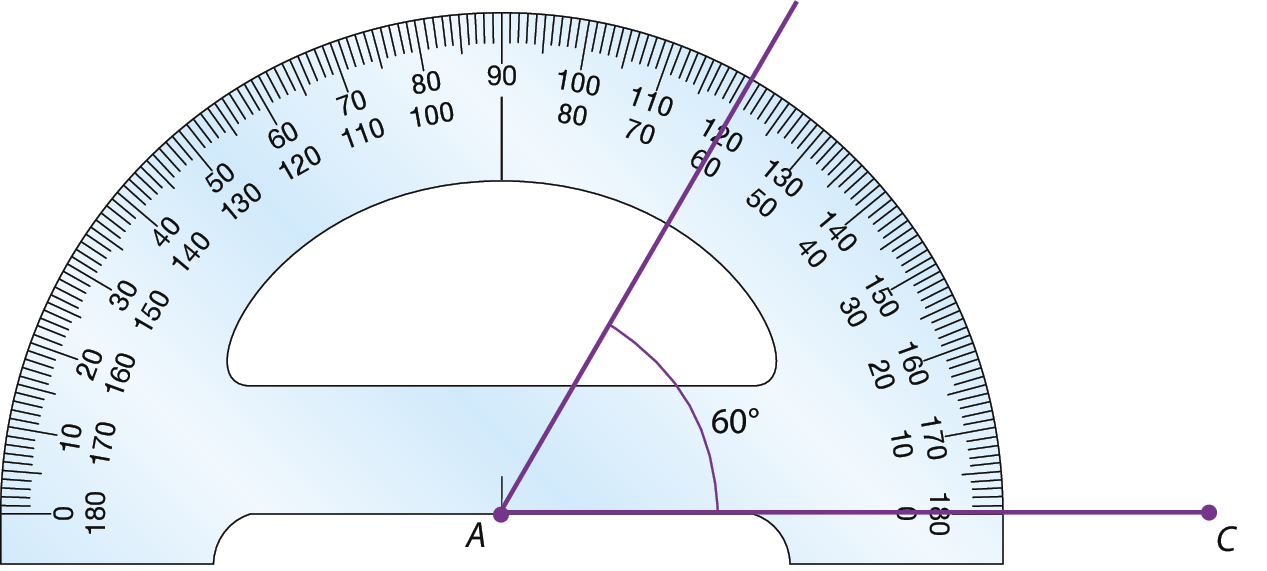
3º) Abrimos o compasso com a medida do segmento
Segmento de reta AB(5 centímetros) e, com a ponta‑seca em a, traçamos o arco para determinar o segmento
segmento AB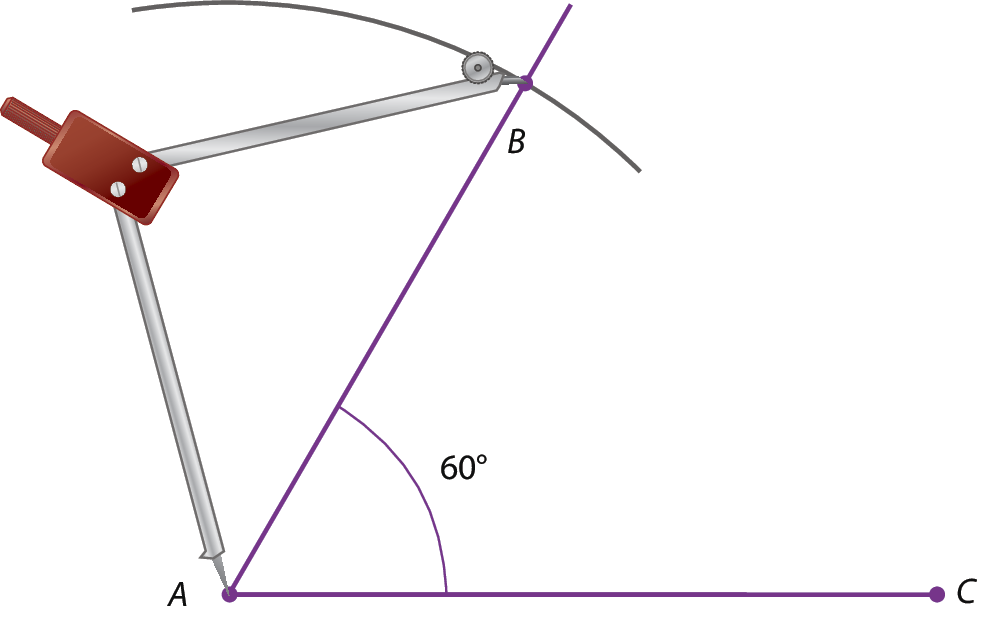
4º) Com o auxílio da régua, traçamos o segmento
Segmento de reta BC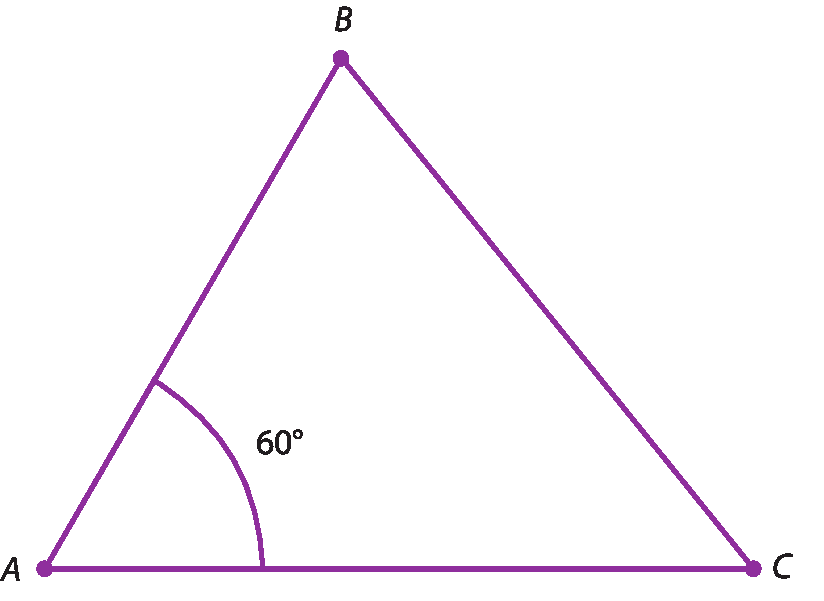
Respostas e comentários
Construção de triângulos
Apresentamos, neste momento, algumas construções de triângulos com o uso de instrumentos como régua, compasso e transferidor, o que contribui para o desenvolvimento das habilidades (ê éfe zero seis ême ah dois dois) e (ê éfe zero seis ême ah dois três).
Utilizando os instrumentos de desenho (régua, compasso e transferidor) para a lousa, solicite aos estudantes que construam triângulos seguindo passo a passo as etapas iniciadas na página anterior. Peça-lhes que registrem ao lado da figura o que foi feito, de modo que possam consultar como guia de estudo para construções propostas em outros momentos. Oriente-os sobre o uso do compasso para que tomem cuidado com a ponta-seca.
Proponha a eles que façam construções, caso seja possível, com base em alguns elementos dados (medidas dos três lados; medidas dos três ângulos internos, entre outros). Converse sobre alguns casos nos quais não é possível construir o triângulo indicado por falta de dados ou pela inexistência de um triângulo dessa natureza, como é o caso de um triângulo retângulo equilátero, que não existe.
Se tiver oportunidade, leve os estudantes à sala de informática para que possam fazer as construções por meio de um software. Para isso, podem usar ferramentas como as indicadas no capítulo 6 deste volume, em que foi apresentada a construção de retas paralelas e perpendiculares com o uso de um software. Deste modo, contribui-se para o desenvolvimento da competência geral 5.
PARA SABER MAIS
Uma propriedade importante dos triângulos
Estudamos que, em um polígono, o número de lados é igual ao número de ângulos.
Também é fato que as medidas dos lados, ou a soma das medidas dos lados, de um polígono não tem relação com o número de lados dele.

Com um mesmo pedaço de arame de um tamanho qualquer, podemos moldar um triângulo, ou um quadrilátero, ou um heptágono etcétera. A única relação que podemos estabelecer é que, quanto maior for o número de lados, menor será, em média, o tamanho dos lados.
Com esse arame, também podemos moldar vários tipos de triângulo. Neles, as medidas dos lados podem mudar, mas a soma das medidas não. Você saberia dizer por quê?
E a soma das medidas dos ângulos desses triângulos, será sempre a mesma?
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Pegue um pedaço de arame ou fio de cobre e experimente formar um triângulo com ele. Depois desmanche e forme outro, e outro, e outroreticências
a) Com uma régua, meça os lados de cada triângulo que você construiu com o fio e adicione essas medidas. As medidas dos perímetros deles são iguais?
b) Com um transferidor, meça também os ângulos desses triângulos e adicione essas medidas. As somas obtidas são iguais? Quantos graus?
(Faça a atividade com o auxílio de um adulto.)
2

Reúnam-se em dupla e façam o que se pede.
a) Em uma folha de papel sulfite, cada um deverá desenhar quatro triângulos quaisquer. Em seguida, trocarão as folhas para que meçam os ângulos internos e calculem, para cada triângulo, a soma dessas medidas. Mesmo sem ver os triângulos que seu colega desenhou, você pode prever a soma das medidas dos ângulos internos que ele obteve? Qual é essa soma?
b) Agora, desenhem outro triângulo, recortem-no e denominem as medidas dos ângulos internos de a, b e c. Depois, recortem o triângulo em três partes, de modo que cada parte fique com um dos vértices. Em seguida, juntem as partes, fazendo os três vértices coincidirem e os lados de um dos ângulos encostarem nos lados dos outros ângulos. Observem o esquema.

Vocês acham que a soma dos três ângulos assim obtida resulta em um ângulo de 180graus? Façam uma estimativa para o valor de a + b + c.
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
Respostas e comentários
Para saber mais. Resposta: Espera-se que o estudante conclua que a soma das medidas dos lados é a mesma porque o comprimento do fio permanece inalterado.
1. a) Descontadas imprecisões nas medidas, os perímetros são iguais.
1. b) Descontadas imprecisões nas medidas, sim; 180graus.
2. a) Espera-se que os estudantes respondam que sim; 180graus.
2. b) Espera-se que os estudantes obtenham somas iguais ou próximas de 180graus e concluam que os demais colegas também devem ter obtido esse valor.
Para saber mais
Esta seção aborda algumas experimentações com triângulos, como as propostas na atividade 1, na tentativa de mostrar uma importante propriedade: a soma das medidas dos ângulos internos de um triângulo é (sempre) 180graus, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah um nove).
O principal objetivo aqui é despertar a atenção dos estudantes e oferecer a eles condições de responderem à atividade 2.
a) Com uma medição precisa em qualquer triângulo é possível concluir que a soma dos ângulos internos dessa maneira é sempre 180graus.
b) A experimentação permite concluir de maneira visual que a soma das medidas dos ângulos é 180graus pois o recorte de todos os ângulos, quando unidos, sempre se apoia em uma reta, formando um ângulo raso.
Acompanhe os estudantes durante a resolução da atividade orientando-os no manuseio do arame ou fio de cobre e da tesoura de ponta arredondada.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
16 Com um compasso, compare as medidas dos lados e, com um transferidor, verifique se os ângulos internos são agudos, retos ou obtusos. Em seguida, classifique cada triângulo quanto aos lados e quanto aos ângulos.
a)
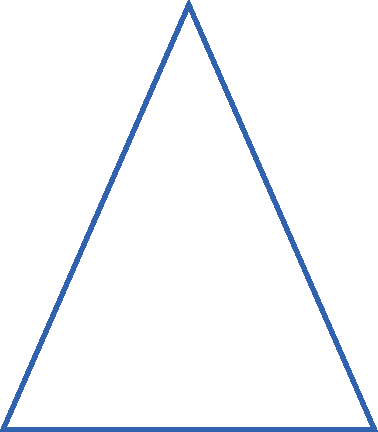
b)

c)

d)
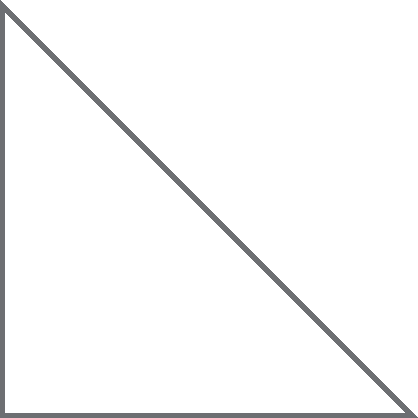
e)

f)

(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
17 Com três palitos iguais de sorvete, você pode construir um triângulo. Ele será um triângulo escaleno, isósceles ou equilátero? Justifique sua resposta.
18 Com 33 centímetros de um fio de arame, Renato construiu um triângulo equilátero. Com quantos centímetros ficou cada lado?
19 Construa triângulos (á bê cê ) em seu caderno usando régua e compasso. (As medidas dos lados são dadas em centímetro.)
a)
Medida do segmento AB.= 8,
Medida do segmento AC.= 6,
Medida do segmento CB.= 10
b)
Medida do segmento AB.= 8,
Medida do segmento AC.= 6,
Medida do segmento CB.= 6
c)
Medida do segmento AB.= 8,
Medida do segmento AC.= 5,
Medida do segmento CB.= 5
20 Classifique os triângulos dos itens a, b e c da atividade 19 quanto aos lados e, também, quanto aos ângulos internos.
21 Usando régua, transferidor e compasso, faça o que se pede. (As medidas dos lados são dadas em centímetro.)
a) Construa um triângulo ABC em que:
Medida do segmento AB.= 12,
Medida do segmento AC.= 6,
Medida do ângulo BAC= 60graus.
b) No triângulo obtido no item a, construa o ângulo
Ângulo BADde 30graus, sendo D um ponto pertencente ao segmento
Segmento de reta BC
c) A medida do lado
Segmento de reta CDé metade da medida do lado
Segmento de reta ADE a do lado
Segmento de reta ACé metade da medida do lado
Segmento de reta AB?
d) Meça os ângulos
Ângulo ACB,
Ângulo ABC,
Ângulo CAD,
Ângulo CDAe
Ângulo ADB
e) Classifique os triângulos á bê cê, á cê dê e á bê dê quanto aos lados e quanto aos ângulos internos.
22 Construa triângulos (á bê cê ) usando régua, transferidor e compasso. Se alguma das construções for impossível, explique o porquê. (As medidas dos lados são dadas em centímetro.)
a)
Medida do segmento AB.= 7,
Medida do ângulo BAC.= 40graus,
Medida do ângulo ABC.= 80graus.
b)
Medida do segmento AB.= 7,
Medida do ângulo BAC.= 40graus,
Medida do ângulo ABC.= 120graus.
c)
Medida do segmento AB.= 7,
Medida do ângulo BAC.= 40graus, =
Medida do ângulo ABC.= 140graus.
23

Hora de criar – Crie um fluxograma com os passos que devem ser seguidos para a construção de um triângulo usando régua e compasso.
Compare seu fluxograma com o de um colega. É possível simplificar ou complementar seu fluxograma?
Respostas e comentários
16. a) Isósceles e acutângulo.
16. b) Escaleno e acutângulo.
16. c) Equilátero e acutângulo.
16. d) Isósceles e retângulo.
16. e) Isósceles e obtusângulo.
16. f) Escaleno e retângulo.
17. O triângulo será equilátero, pois terá os três lados de mesma medida.
18. 11 centímetros.
19. Construção de figuras.
20. Escaleno e retângulo; isósceles e acutângulo; isósceles e obtusângulo.
21. a) Construção de figura.
21. b) Construção de figura.
21. c) Sim; sim.
21. d) 90graus; 30graus; 30graus; 60graus; 120graus
21. e) Os triângulos á bê cê e á cê dê são escalenos e retângulos, e o triângulo á bê dê é isósceles e obtusângulo.
22. Construção de figuras.
22. No item c a construção é impossível, pois um lado é paralelo ao outro.
23. Resposta pessoal.
Exercícios propostos
No exercício 16, circule pela sala de aula, verificando se os estudantes usam corretamente o compasso, tomando cuidado com a ponta-seca, para compararem as medidas dos lados dos triângulos, e o transferidor para fazer as medições dos ângulos.
Os estudantes deverão concluir para cada item a seguinte classificação:
a) Isósceles e acutângulo.
b) Escaleno e acutângulo.
c) Equilátero e acutângulo.
d) Isósceles e retângulo.
e) Isósceles e obtusângulo.
f) Escaleno e retângulo.
No exercício 17, a intenção é que os estudantes imaginem a figura formada e concluam que, se os palitos têm mesma medida de comprimento, o triângulo resultante é equilátero.
No exercício 18, o triângulo construído é equilátero. Logo, ele tem todos os lados congruentes. Assim, cada lado do triângulo mede 11 centímetros, pois 33 dividido por 3 = 11.
No exercício 19, é essencial que os estudantes disponham de material adequado para a construção de cada triângulo e sigam as orientações apresentadas e as recomendações sobre o manuseio do compasso. É importante compararem suas construções, em pequenos grupos, para identificar possíveis erros.
As construções dos itens a, b e c, estão no início deste Manual, nas orientações específicas do capítulo 10.
Ao classificar, no exercício 20, quanto às medidas dos lados e dos ângulos os triângulos construídos no exercício 19, obtemos:
a) Escaleno e retângulo.
b) Isósceles e acutângulo.
c) Isósceles e obtusângulo.
As resoluções dos exercícios 21 a 23 estão no início deste Manual, nas orientações específicas do capítulo 10.
Pense mais um pouco...
FAÇA A ATIVIDADE NO CADERNO
Desenhe duas retas paralelas, marque sobre uma delas dois pontos e, sobre a outra, três pontos.

a) É possível construir quantos triângulos tendo como vértices três desses pontos?
b) Explique o procedimento que você utilizou para contar os triângulos.
c)

Compare sua resposta com a de um colega. Vocês encontraram a mesma quantidade de triângulos? Comparem os procedimentos adotados.
4. Quadriláteros



Classificação dos quadriláteros
Os quadriláteros podem ser classificados quanto ao paralelismo de seus lados: podem não apresentar lados paralelos, podem apresentar apenas um par de lados paralelos ou, ainda, dois pares de lados paralelos.
|
Nenhum par de lados paralelos |
Somente um par de lados paralelos |
Dois pares de lados paralelos |
|---|---|---|
|
|
|
|
Respostas e comentários
Pense mais um poucoreticências:
a) 9 triângulos.
b) Resposta pessoal.
c) Resposta pessoal. Espera-se que as quantidades encontradas sejam as mesmas.
Resposta possível: Superfícies do livro e do caderno.
Pense mais um poucoreticências
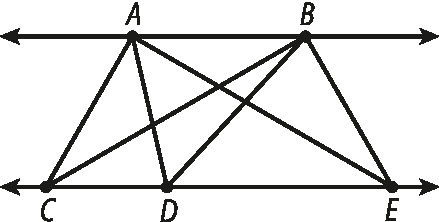
Nesta seção, o maior desafio é encontrar uma maneira organizada de traçar e contar os triângulos possíveis. Um possível procedimento é:
• Para facilitar a identificação, nomeamos os pontos. Primeiro, traçamos todos os triângulos possíveis de base
AB. Como o terceiro vértice deve ser um dos três pontos da outra reta, obteremos três triângulos: á bê cê, á bê dê e á bê é.
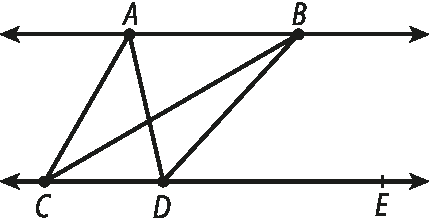
• Depois, traçamos todos os triângulos de base
CD: cê dê á e CDB, pois o terceiro vértice deve ser um dos dois pontos da outra reta.
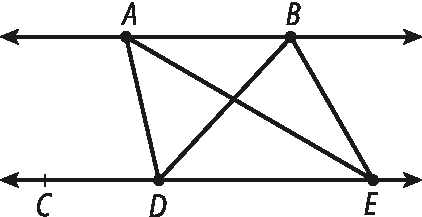
• Traçamos os dois triângulos de base
DE: dê ê á e DEB.
• Por fim, traçamos os dois triângulos de base
CE: cê ê á e cê ê bê.
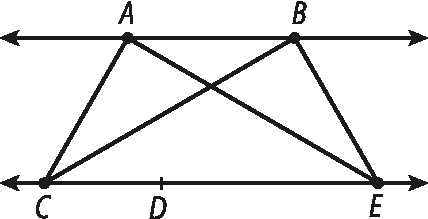
Logo, o total de triângulos é: 3 + 2 + 2 + 2 = 9.
4. Quadriláteros
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah dois zero e ê éfe zero seis ême ah dois dois.
Assim como nos triângulos, no estudo dos quadriláteros, destacamos a classificação quanto ao paralelismo dos lados e a verificação da presença de lados congruentes e de ângulos internos retos, o que contribui para o desenvolvimento da habilidade (ê éfe zero seis ême ah dois zero).
Após estudarem as classificações dos quadriláteros, proponha aos estudantes que, no caderno, organizem os tipos de quadriláteros em um diagrama de Venn. Ao final, verifique se todos organizaram corretamente.
Segue um exemplo:
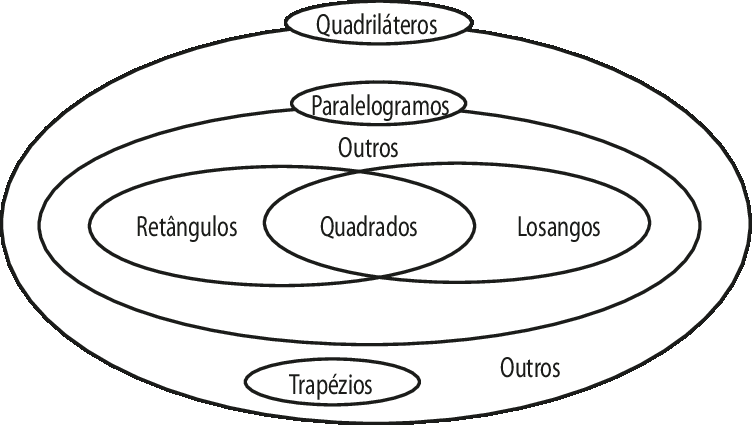
Entre os paralelogramos, vamos destacar o retângulo, o losango e o quadrado.
• Retângulo é um paralelogramo que tem os 4 ângulos internos retos.
• Losango é um paralelogramo que tem os 4 lados congruentes.
• Quadrado é um paralelogramo que tem os 4 ângulos internos retos e os 4 lados congruentes. Portanto, o quadrado é um polígono regular.
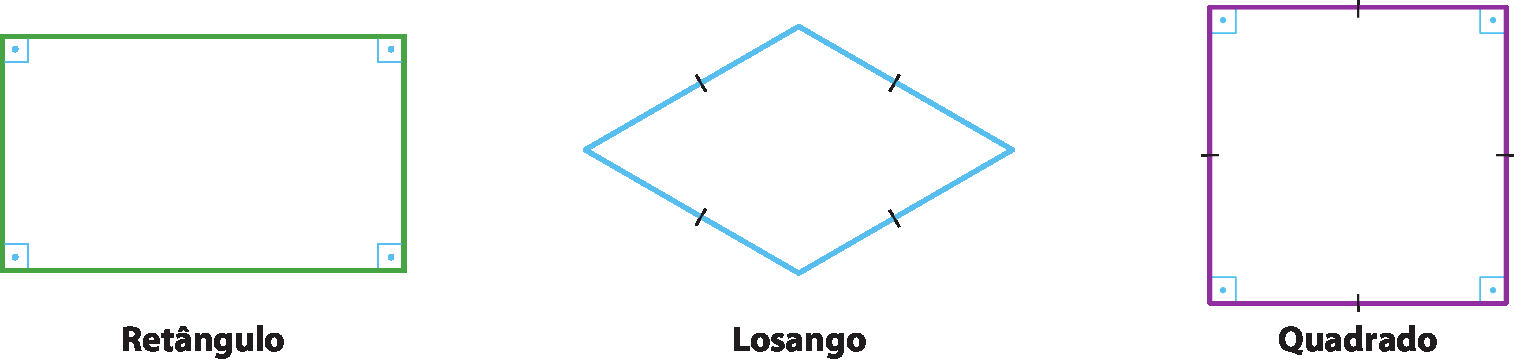
Observação
▶ O quadrado é ao mesmo tempo um retângulo e um losango, visto que tem os 4 ângulos internos retos e os 4 lados congruentes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
24 Classifique os quadriláteros em trapézio ou paralelogramo.
a)

b)
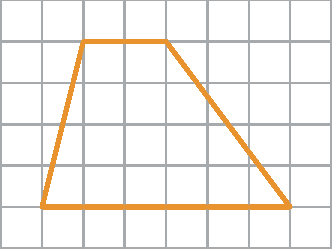
c)
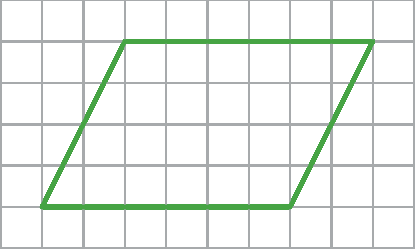
d)
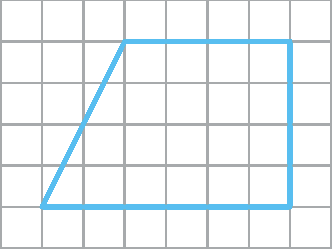
25 Desenhe em uma folha de papel quadriculado:
a) um losango que não seja quadrado;
b) um losango que seja quadrado;
c) um retângulo que não seja quadrado;
d) um retângulo que seja quadrado.
e) um paralelogramo que tenha diagonais de mesma medida;
f) um paralelogramo que não tenha diagonais de mesma medida.
26 Indique as afirmações verdadeiras. Depois, diga por que as demais são falsas.
a) Todo losango é um retângulo.
b) Todas as diagonais de um paralelogramo têm medidas iguais.
c) Todo quadrado é um losango.
d) Existem paralelogramos que têm todas as diagonais congruentes.
27

Reúna-se com um colega e construam um ângulo de 75graus e vértice B. Marquem um ponto a que diste 7 centímetros de B em um de seus lados e um ponto C que esteja a 4 centímetros de B no outro lado. Depois, tracem com o compasso dois arcos: um com a ponta-seca em a e 4 centímetros de abertura, outro com a ponta-seca em C e 7 centímetros de abertura, cortando o primeiro arco em um só ponto (D), de modo que
Segmento de reta CDe
Segmento de reta ABnão tenham ponto comum.
a) Que polígono vocês obtiveram?
b) Que polígono obteriam se substituísem as medidas 4 e 7 centímetros por 6 centímetros?
c) E se substituíssem a medida 75graus por 90graus?
d) E se substituíssem as medidas 4 e 7 centímetros por 6 centímetros e 75graus por 90graus?
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
28

Hora de criar – Escolha um quadrilátero e elabore uma afirmação verdadeira e uma falsa sobre ele. Depois, troque suas afirmações com um colega para que cada um possa identificar uma afirmação como verdadeira.
Respostas e comentários
24. a) Paralelogramo.
24. b) Trapézio.
24. c) Paralelogramo.
24. d) Trapézio.
25. Construção de figuras.
26. a) Falsa, pois há losangos cujos ângulos internos não são ângulos retos.
26. b) Falsa, pois um paralelogramo que não é retângulo tem diagonais com medidas diferentes.
26. c) Verdadeira.
26. d) Verdadeira.
27. a) Paralelogramo.
27. b) Losango.
27. c) Retângulo.
27. d) Quadrado.
28. Resposta pessoal.
Classificação dos quadriláteros
Se julgar conveniente, retome o conceito de polígono regular. Peça aos estudantes que identifiquem, dentre os quadriláteros estudados, que tipo de quadrilátero pode ser um polígono regular. Espera-se que percebam que apenas o quadrado é regular, pois é um quadrilátero equilátero e é um quadrilátero equiângulo também.
Exercícios propostos
As resoluções dos exercícios 24 e 26 a 28 estão no início deste Manual, nas orientações específicas do capítulo 10.
O exercício 25 propicia um momento para avaliar se os estudantes realmente compreenderam a classificação de quadriláteros. Seguem exemplos de resposta.
a)
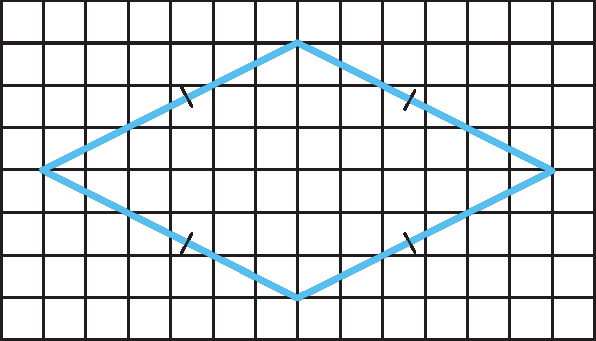
b)
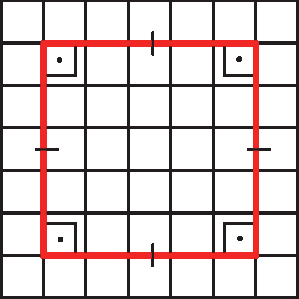
c)
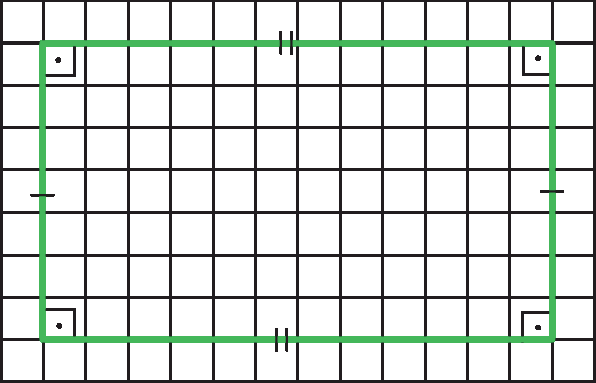
d)
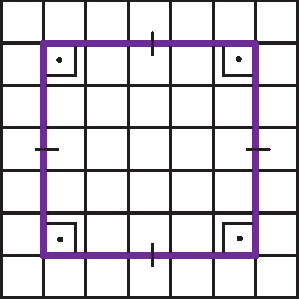
e)
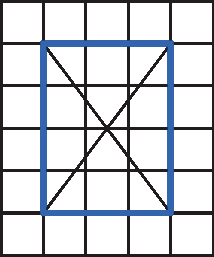
f)
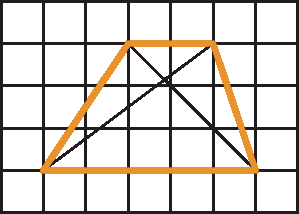
Proponha aos estudantes que respondam:
• Por que a figura a é um losango, mas não é um quadrado?
• Por que a figura b é um losango e também um quadrado?
• Por que a figura c é um retângulo, mas não é um quadrado?
• Por que a figura d é um retângulo e também um quadrado?
É importante comparar respostas entre colegas, para detectar equívocos e fazer ajustes.
No exercício 27, as duplas podem expor sua construção aos colegas para compararem as soluções. Por abordar a construção de quadriláteros, essa atividade permite o desenvolvimento da habilidade (ê éfe zero seis ême ah dois dois). Se tiver oportunidade, pode-se propor aos estudantes que a construção seja realizada com o uso de um software, o que propicia o trabalho com a competência geral 5. Durante o desenvolvimento da atividade oriente os estudantes no manuseio do compasso para que tomem cuidado com a ponta-seca.
5. O conceito de par ordenado
Considere as situações a seguir.
Situação 1
A figura a seguir representa um condomínio residencial formado por cinco prédios de apartamentos, cada um com cinco andares, sendo um apartamento por andar.
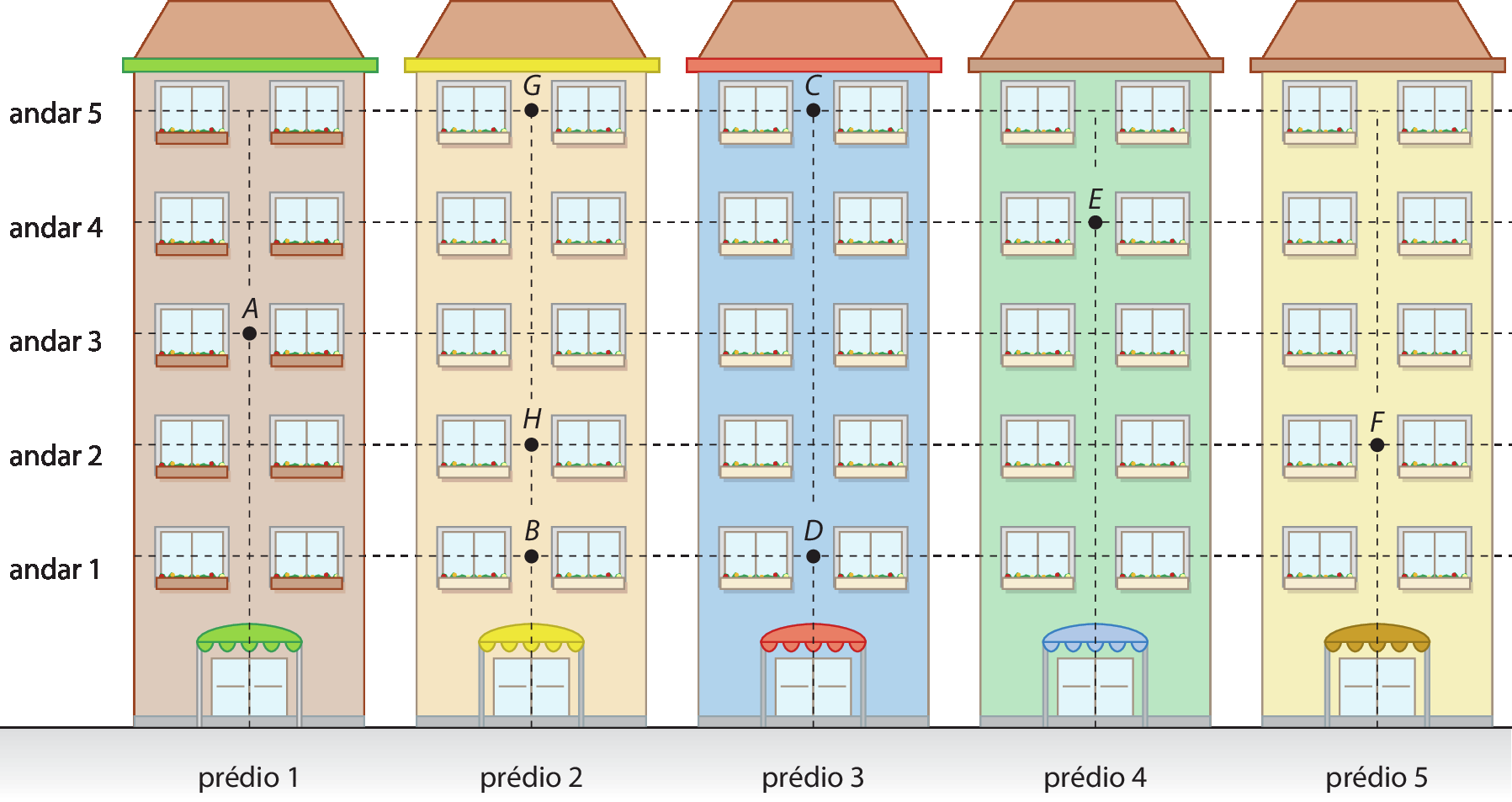
Podemos usar pares de números para identificar ou localizar cada apartamento do condomínio representado. Um dos números do par indicará o prédio, e o outro, o andar. Observe alguns exemplos no quadro.
|
Apartamento |
Prédio/Andar |
Par de números |
|---|---|---|
|
A |
prédio 1/andar 3 |
(1, 3) |
|
B |
prédio 2/andar 1 |
(2, 1) |
|
C |
prédio 3/andar 5 |
(3, 5) |
|
D |
prédio 3/andar 1 |
(3, 1) |
|
H |
prédio 2/andar 2 |
(2, 2) |
Observe que:
• os pares (1, 3) e (3, 1) indicam apartamentos diferentes: o primeiro par corresponde ao apartamento ei, enquanto o outro par corresponde ao apartamento D, o que nos faz perceber a importância da ordem nesses pares de números;
• os apartamentos B e H, que pertencem a um mesmo prédio, estão associados a pares de números em que o primeiro número é o mesmo (no caso, o número 2);
• os apartamentos B e D, situados no mesmo andar, estão associados a pares de números em que o segundo número é o mesmo (no caso, o número 1).
Os pares de números associados a situações em que a ordem dos elementos deve ser respeitada são chamados de pares ordenados.
Respostas e comentários
5. O conceito de par ordenado
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah um seis e ê éfe zero seis ême ah dois um.
Noções do conceito de par ordenado são abordadas desde os anos iniciais do Ensino Fundamental. Neste momento, pretendemos ampliar, consolidar e aprofundar essas noções, mas não esgotá-las, já que o assunto será retomado e aprofundado nos demais anos deste ciclo e no Ensino Médio. Deste modo, apresentamos situações e propomos atividades que contribuem para o desenvolvimento da habilidade (ê éfe zero seis ême ah um seis). O trabalho com a habilidade (ê éfe zero seis ême ah dois um) será realizado em duas propostas de exercícios, na seção de exercícios propostos.
Antes de ler a situação 1, explore com os estudantes apenas a ilustração do condomínio residencial. Peça-lhes opiniões sobre o modo como fariam para registrar as localizações dos apartamentos destacados. Aproveite para verificar conhecimentos que já construíram acerca desse tema.
Após essa atividade inicial, converse, com os estudantes, sobre o quadro apresentado e a maneira de registrar as localizações dos apartamentos do condomínio residencial, indicadas nele, por meio de pares ordenados. É fundamental que os estudantes percebam que pares do tipo (1, 3) e (3, 1) são diferentes e comunicam informações diferentes.
Se julgar conveniente, elabore questões nas quais é fornecido o par de números, e os estudantes têm de dizer, de acordo com a ilustração da situação 1, em que prédio e andar se localiza o apartamento.
Situação 2
Cruzando palavras
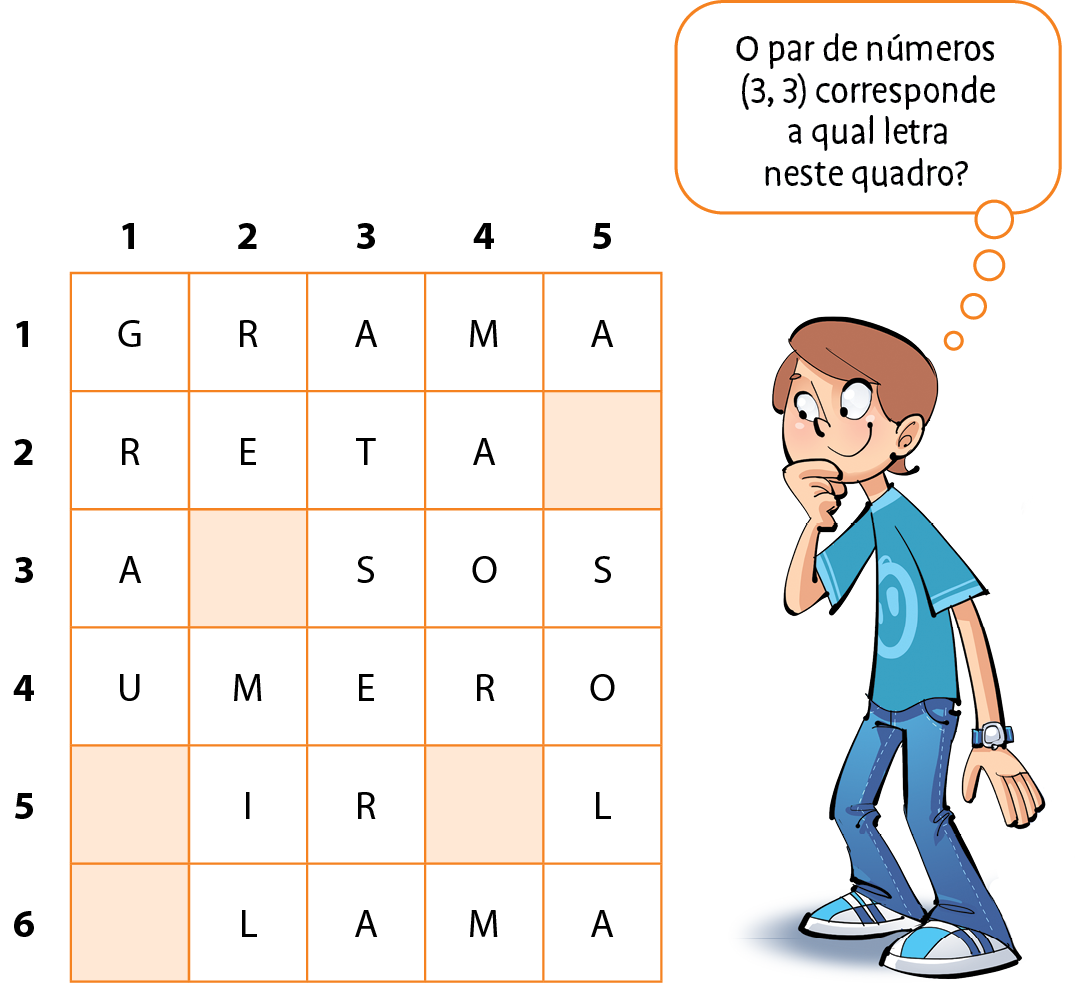
Horizontais
1. Unidade de medida de massa
2. Por dois pontos passa uma só
3. Socorro
4. Osso do esqueleto humano
5. Caminhar
6. Lodo
Verticais
1. Unidade de medida de ângulo
2. Nota musical/Dez centenas
3. Todo cubo tem (palavra invertida)
4. Faltou o ih para ser maior
5. Parte do sapato em contato com o solo
Considerando o quadro completo, podemos fazer algumas associações:
(2, 3)

T (4, 1)

U (5, 5)

L
Observações
▶ Dado o par ordenado (a, b), dizemos que a é o primeiro elemento do par e b, o segundo elemento. Exemplos:
• No par ordenado (4, 3), o primeiro elemento é 4 e o segundo é 3.
• No par ordenado (3, 4), o primeiro elemento é 3 e o segundo é 4.
▶ Dois pares ordenados (a, b) e (c, d ) são iguais se a = c e b = d. Exemplos:
• Se (a, b) = (4, 5), temos a = 4 e b = 5.
• Se (x, y) = (0, 3), temos x = 0 e y = 3.
▶ Dois pares ordenados (a, b) e (c, d ) são diferentes se a ≠ c ou b ≠ d. Exemplos:
• O par ordenado (7, 1) é diferente do par ordenado (1, 7).
• O par ordenado (2, 6) é diferente do par ordenado (6, 2).
Representação geométrica de pares ordenados
Para fazer a representação geométrica de pares ordenados, traçamos, em um plano, duas retas numéricas perpendiculares. Ao ponto de intersecção entre elas atribuímos o par ordenado (0, 0) e damos o nome de origem.
Chamamos a reta horizontal de eixo x e a reta vertical de eixo y.
Respostas e comentários
Resposta: Letra S.
O conceito de par ordenado
Analise com os estudantes a situação 2 e ressalte as noções de linha e coluna. Pergunte a eles qual foi a regra adotada para associar cada letra do quadro a um par de números. Com base nos exemplos, eles devem concluir que o primeiro número do par corresponde à linha em que a letra está no quadro, e o segundo número corresponde à coluna.
Ao trabalhar a representação geométrica de pares ordenados, explore a transposição das linhas e colunas de uma malha quadriculada para a ideia de plano cartesiano. Como os estudantes já têm trabalhado com a reta numérica, espera-se que associem cada eixo do plano cartesiano a uma reta numérica e, assim como já associaram números (naturais ou racionais positivos na fórma de fração ou na fórma decimal) a pontos de uma reta numérica, compreendam a associação de pares ordenados a pontos do plano cartesiano.
Cada par ordenado determina as coordenadas de um ponto do plano cartesiano, e cada ponto desse plano é a representação geométrica do par ordenado a ele associado. Nesse sentido, articulam-se duas Unidades Temáticas: Geometria e Álgebra, desenvolvendo noções de Geometria Analítica.
Nessa representação, os pares ordenados são associados a pontos; por isso, esses pares são chamados de coordenadas dos pontos, e a representação recebe o nome de sistema de coordenadas no plano cartesiano.
Observe a representação do ponto a(3, 4).
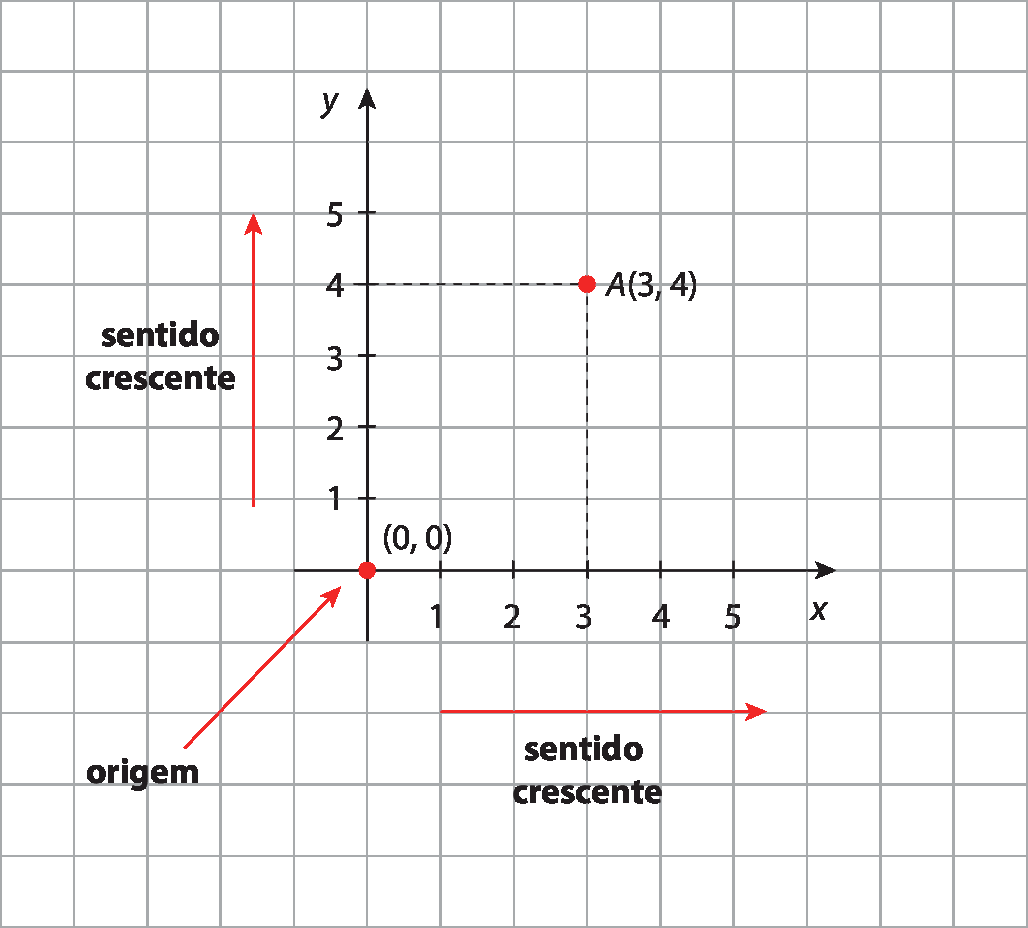
O primeiro elemento do par ordenado indica a posição em relação ao eixo horizontal, e o segundo elemento indica a posição em relação ao eixo vertical.
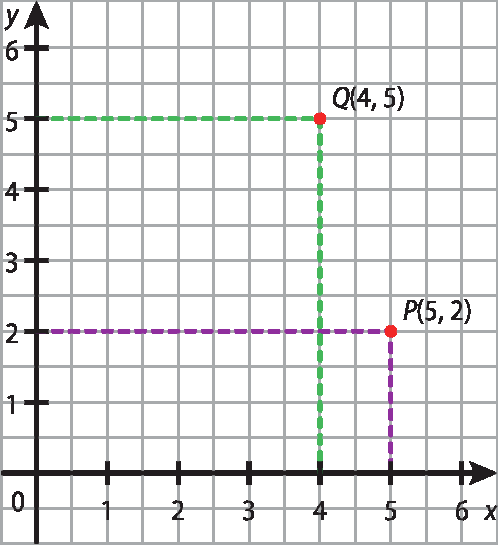
Acompanhe como podemos associar os pares ordenados a(1, 8), B(7, 6), C(9, 2) e D(3, 1) com os vértices de um polígono.
Traçando os segmentos
Segmentos AB,
Segmento de reta BC,
Segmentos CDe
Segmento de reta DA, obtemos o quadrilátero a bê cê dê.
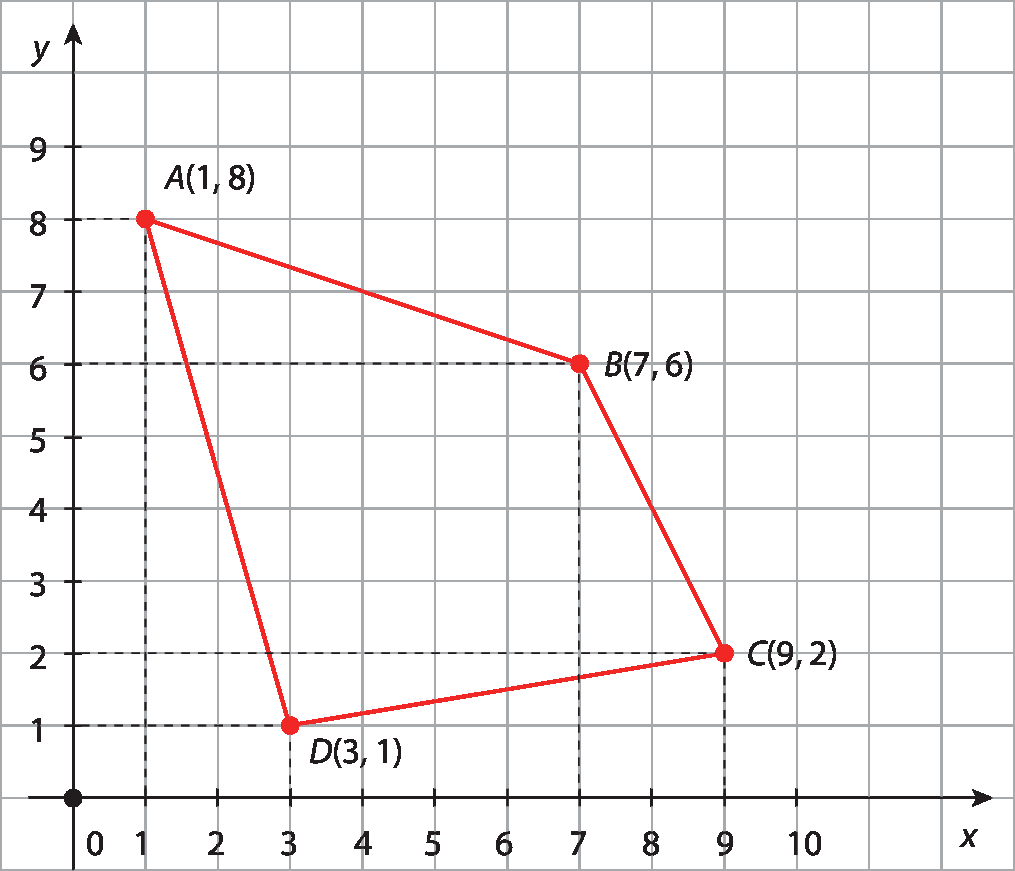
Respostas e comentários
Representação geométrica de pares ordenados
Providencie previamente planos cartesianos desenhados em malha quadriculada (considerando apenas o 1º quadrante) para que, em duplas, os estudantes explorem seus elementos, representem alguns pares ordenados neles (ou seja, localizem os pontos que têm essas coordenadas) e determinem as coordenadas de pontos destacados nesses planos cartesianos, como exemplifica a figura a seguir.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
29 Volte a observar a ilustração do condomínio residencial representado na situação 1. Usando um par de números em que o primeiro número indica o prédio e o segundo, o andar, dê a posição dos apartamentos:
a) E;
b) F;
c) G.
30 Observe o sistema de coordenadas com alguns pontos indicados.
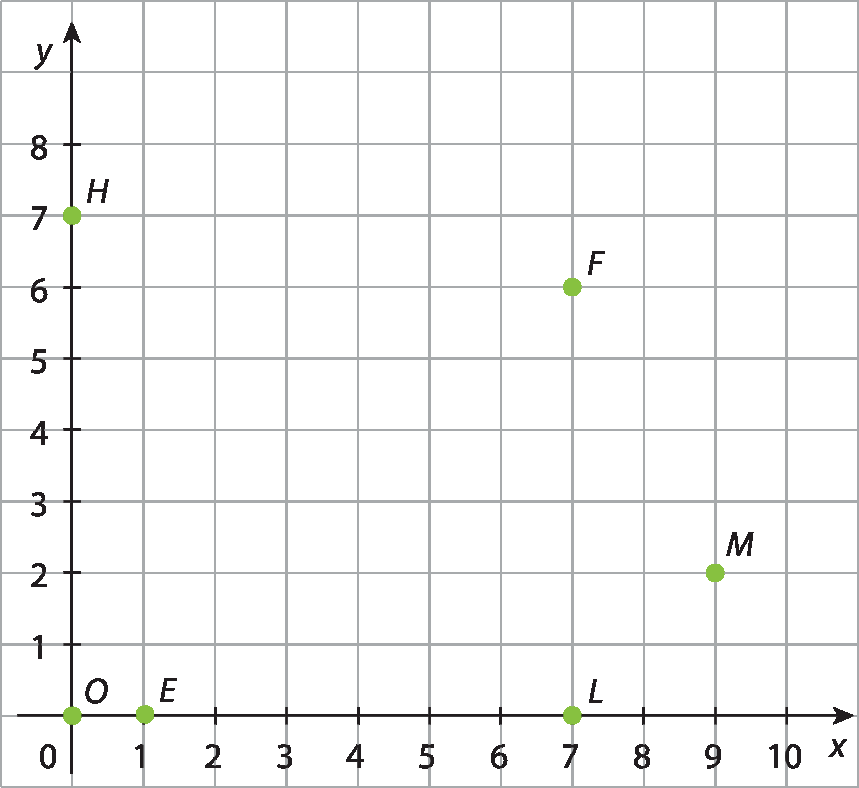
Agora, determine as coordenadas desses pontos.
31 Indique o valor de a e de b nos pares ordenados.
a) (3, 7) = (a, 7)
b) (a, b) = (0, 1)
c) (a, 2) = (3, b)
d) (a + 3, 8) = (5, b)
e) (3a, b + 4) = (9, 6)
32 Construa um sistema de coordenadas em uma folha de papel quadriculado e represente os seguintes pontos:
• a(0, 3)
• B (3, 0)
• C (6, 3)
• D (3, 6)
Se unirmos os pontos a, B, C, D e a, nessa ordem, por segmentos, obteremos um polígono. Que polígono é esse?
33 Em uma folha de papel quadriculado, construa um sistema de coordenadas e marque nele pontos que sejam vértices de um:
a) retângulo;
b) trapézio;
c) losango;
d) pentágono;
e) hexágono.
• Após a escolha dos pontos, construa para cada item o respectivo polígono.
34 Construa um sistema de coordenadas em uma folha de papel quadriculado e represente em um plano cartesiano três quadriláteros:
um) a bê cê dê, com vértices de coordenadas a(2, 4), B(4, 4), C(4, 2) e D(2, 2).
dois) ê éfe gê agá, que deve corresponder a uma redução do quadrilátero a bê cê dê, com lados medindo a metade das respectivas medidas dos lados de a bê cê dê.
três) í jota cá éle, que deve corresponder a uma ampliação do quadrilátero a bê cê dê, com lados medindo o dobro das respectivas medidas dos lados de a bê cê dê.
Depois, responda às questões:
a) Quais são as coordenadas dos vértices dos quadriláteros ê éfe gê agá e í jota cá éle?
b) O quadrilátero de vértices de coordenadas a(2, 4), bê linha(3, 4), cê linha(3, 3) e dê linha(2, 3) corresponde a uma ampliação ou a uma redução do quadrilátero a bê cê dê?
c) Como podemos classificar os quadriláteros representados quanto às medidas de seus lados e de seus ângulos? Justifique sua resposta.
35 Usando um programa de computador, Renato desenhou um retângulo em um plano cartesiano, conforme demonstrado na figura a seguir:
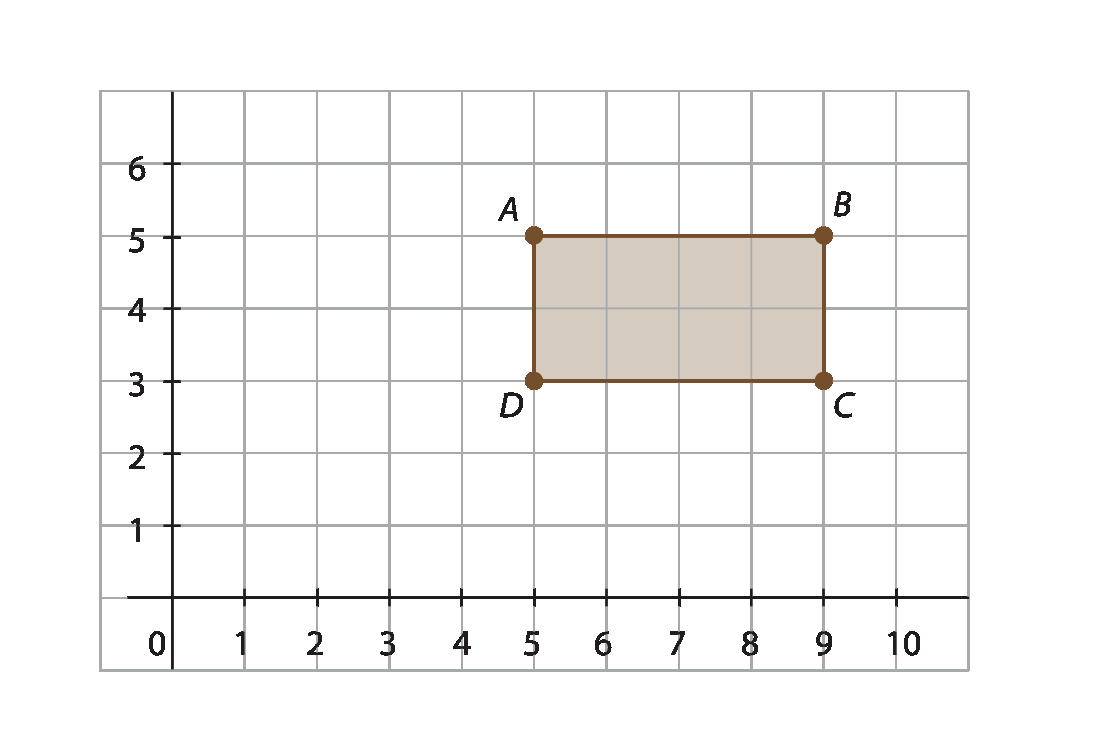
Renato queria ampliar esse retângulo e, então, deslocou o vértice B para bê linha(10, 5).
Para que Renato obtenha uma ampliação do retângulo a bê cê dê, de modo que as medidas dos segmentos
Segmento de reta A linha B linha,
Segmento de reta B linha C linha,
Segmento de reta C linha D linhae
Segmento de reta A linha D linhasejam, respectivamente, o dobro das medidas dos segmentos
Segmento de reta AB,
Segmento de reta BC,
Segmento de reta CDe
Segmento de reta AD, quais podem ser as coordenadas dos vértices á linha, cê linha e dê linha?
Respostas e comentários
29. a) (4, 4)
29. b) (5, 2)
29. c) (2, 5)
30. H(0, 7); óh(0, 0); F(7, 6); éle(7, 0); ê(1, 0); M(9, 2)
31. a) a = 3
31. b) a = 0 e b = 1
31. c) a = 3 e b = 2
31. d) a = 2 e b = 8
31. e) a = 3 e b = 2
32. Construção de sistema; um quadrado.
33. Respostas pessoais.
34. Construção de figuras.
34. a) Resposta pessoal.
34. b) Uma redução.
34. c) Quadrados, pois têm lados de mesma medida e ângulos internos retos.
35. Resposta possível: á linha(2, 5), cê linha(10, 1) e dê linha(2, 1).
Exercícios propostos
No exercício 29, deve-se retomar a ilustração do condomínio residencial para responder ao que se pede. No item a, pede-se a localização do apartamento ê; ele está no 4º andar do prédio 4; então, o par ordenado é (4, 4). No item b, pede-se a localização do apartamento F; ele está no 2º andar do prédio 5; então, o par ordenado é (5, 2). Por fim, no item c, pede-se a localização do apartamento G; ele está no 5º andar do prédio 2; logo, o par ordenado é (2, 5).
No exercício 30, os estudantes deverão indicar as coordenadas de pontos representados em um plano cartesiano. Se considerar adequado, faça a representação deste plano na lousa e faça a identificação dessas coordenadas junto com os estudantes. Depois, proponha a eles a localização de outros pontos e coordenadas de modo a fazer com que compreendam o funcionamento de um sistema de coordenadas. Ao resolver o exercício, eles devem perceber que o ponto M está 9 unidades à direita e duas unidades acima da origem; então, suas coordenadas são M(9, 2). De maneira semelhante, devem identificar as outras coordenadas: H(0, 7); óh(0, 0); F(7, 6); L(7, 0); ê(1, 0).
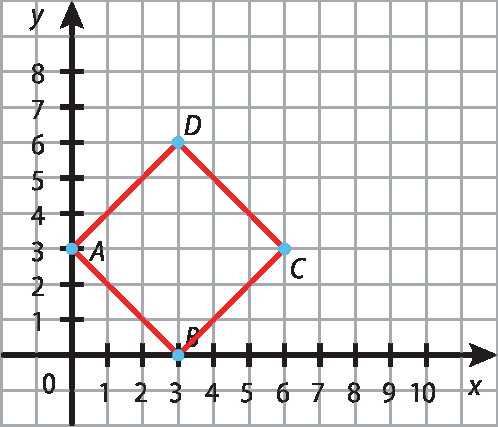
Para o exercício 32 sugerimos a construção de um sistema de coordenadas em uma malha quadriculada para facilitar a representação dos pontos e a identificação do polígono. Caso os estudantes tenham que fazer essa construção em outro tipo de folha, oriente-os no traçado dos eixos, que devem ser perpendiculares, e no posicionamento dos números, que devem ser equidistantes. Assim, conseguirão localizar os números e identificar corretamente o quadrado como o polígono a ser obtido, conforme indica a figura a seguir:
Nos exercícios 34 e 35, os estudantes deverão construir figuras planas semelhantes em situação de ampliação ou redução utilizando malha quadriculada e o sistema de coordenadas, contribuindo para o desenvolvimento da habilidade (ê éfe zero seis ême ah dois um). Caso eles tenham dificuldades, oriente-os na realização das cosntruções propostas.
As resoluções dos exercícios 31 e 33 a 35 estão no início deste Manual, nas orientações específicas do capítulo 10.
6. Planificação da superfície dos poliedros
Você já estudou que cada região plana da superfície de um poliedro é uma face do poliedro. Também viu que o encontro de duas faces determina um segmento de reta chamado aresta do poliedro e que o ponto de encontro de três ou mais arestas é denominado vértice do poliedro.
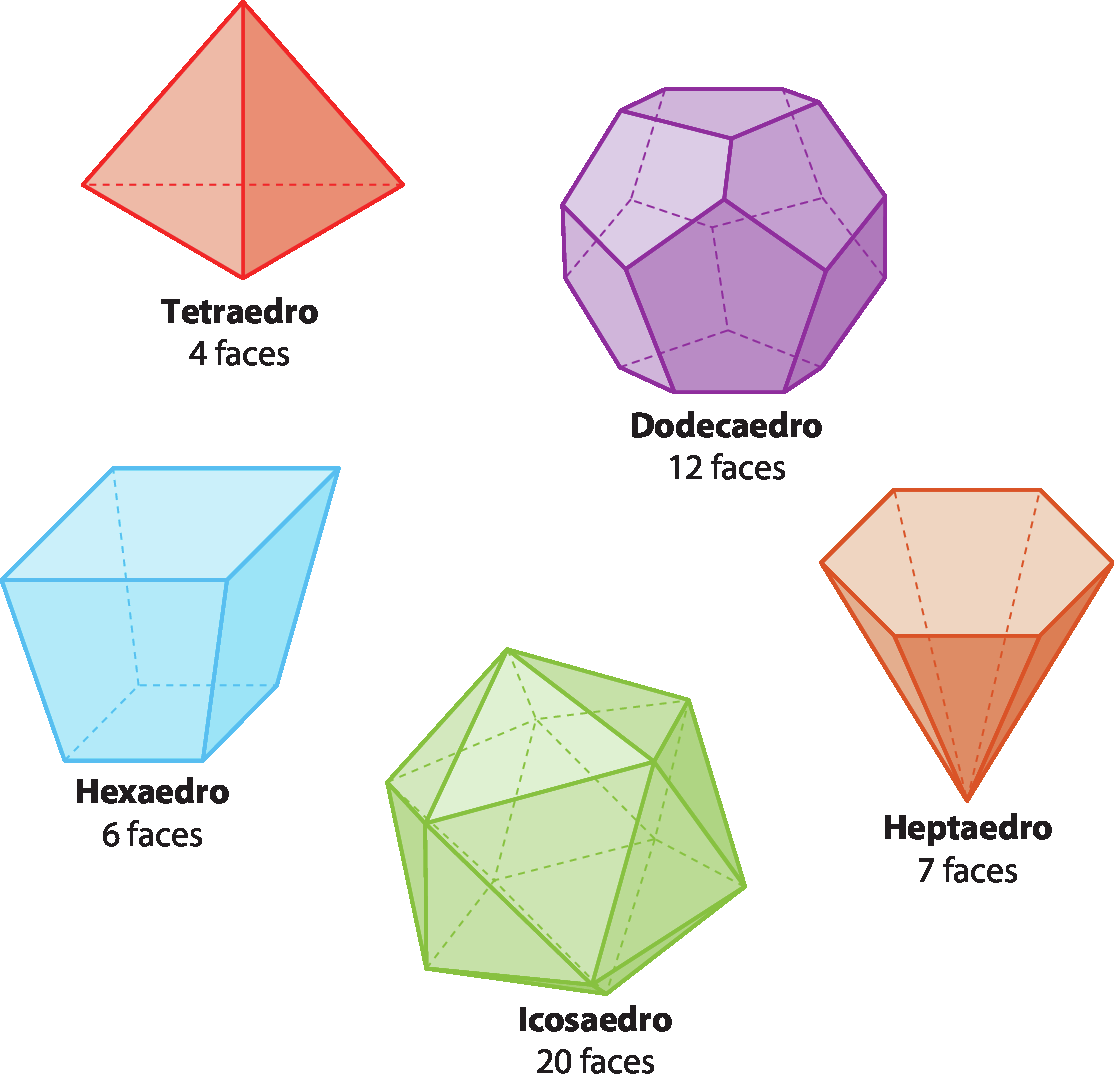
Classificação dos poliedros
Enquanto os polígonos podem ser nomeados de acordo com o número de lados, os poliedros recebem um nome de acordo com o número de faces. Observe o quadro a seguir.
|
Número de faces |
Nome do poliedro |
|---|---|
|
4 |
tetraedro |
|
5 |
pentaedro |
|
6 |
hexaedro |
|
7 |
heptaedro |
|
8 |
octaedro |
|
9 |
eneaedro |
|
10 |
decaedro |
|
12 |
dodecaedro |
|
15 |
pentadecaedro |
|
20 |
icosaedro |
Planificações
Considere a situação.
Antônio pegou um objeto com o formato de um poliedro e, apoiando-o sobre uma folha de papel em uma mesa, desenhou o contorno de todas as suas faces.
Depois, pintou a região interior desses contornos, obtendo 6 figuras.


As figuras obtidas por Antônio são regiões planas que representam as faces do poliedro, também denominadas regiões poligonais. Uma região poligonal é formada pelo polígono que a delimita e pela região interior desse polígono.
Nesse caso, Antônio obteve 6 regiões poligonais retangulares.
Respostas e comentários
6. Planificação da superfície dos poliedros
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um sete.
Neste tópico, vamos retomar e ampliar o estudo dos sólidos geométricos iniciado no capítulo 3, contribuindo para o trabalho com a habilidade (ê éfe zero seis ême ah um sete). Como trataremos apenas dos poliedros, se julgar necessário, retome as características desse grupo de sólidos, solicitando aos estudantes que refaçam algumas das atividades estudadas anteriormente.
Se possível, providencie antecipadamente modelos dos poliedros e moldes da planificação de sua superfície apresentados neste estudo, para que os estudantes possam manipulá-los, perceber seus elementos e contá-los (faces, vértices e arestas), decalcar suas faces e associá-las a regiões poligonais, montar e desmontar embalagens etcétera.
Sugerimos também que sejam fornecidos aos estudantes moldes de planificações de superfície de alguns poliedros (reproduzidas em tamanho grande), de modo que eles possam remontar esses sólidos.
Antônio recortou, com o auxílio de uma tesoura de pontas arredondadas, as figuras e uniu-as por um dos lados com fita adesiva, formando uma nova figura.

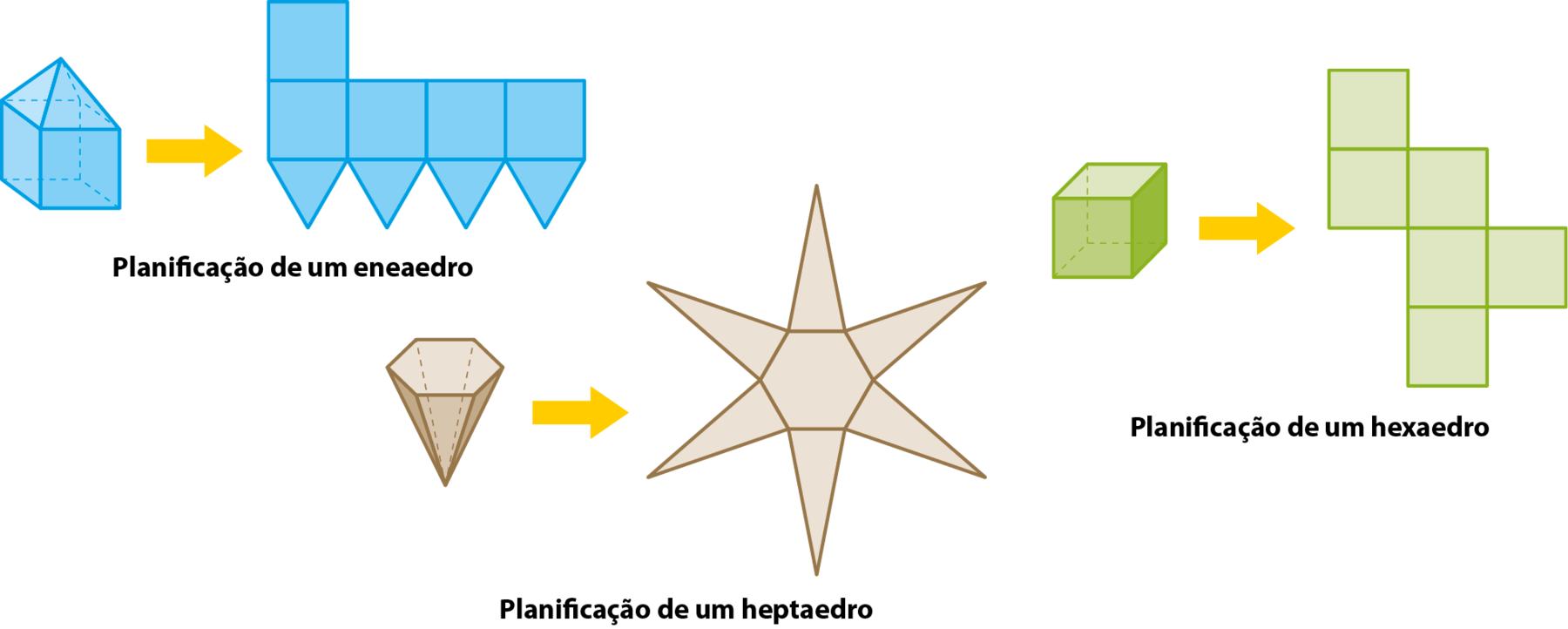
A figura obtida é chamada de planificação da superfície do poliedro ou, simplesmente, planificação do poliedro.
Com a planificação, é mais fácil visualizar quantas faces o poliedro tem. Observe alguns exemplos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
36

Observe as planificações de alguns poliedros. Em cada uma delas há um erro: há face a menos ou face a mais, ou então uma face errada ou fóra de lugar que não possibilita montar o poliedro com ela. Copie as planificações, corrigindo-as. Há só uma maneira de corrigi-las?
Compare sua resolução com a dos colegas.
a)
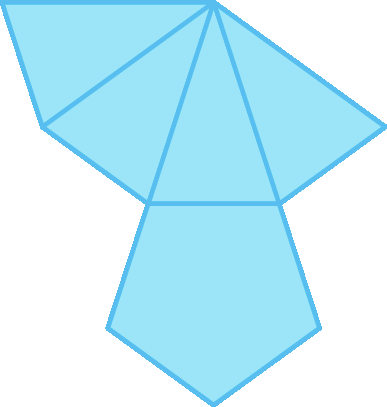
b)

c)

d)
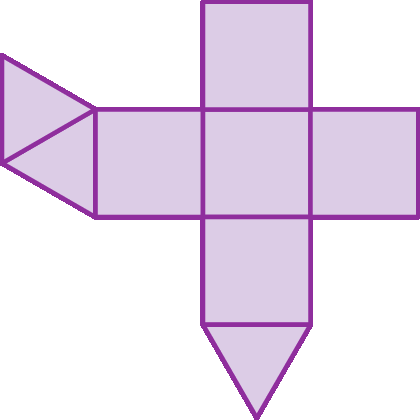
e)
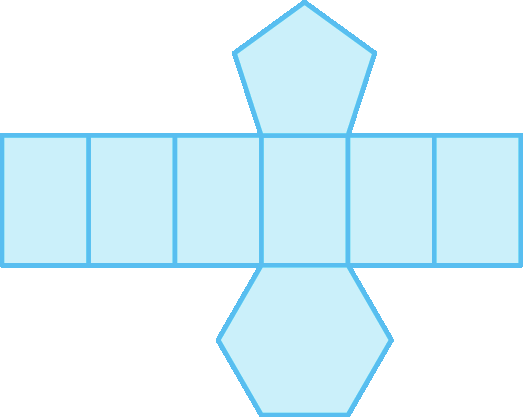
37 Considere os poliedros das planificações corrigidas na atividade anterior.
a) Quantas faces, arestas e vértices há em cada um deles?
b) Compare a soma dos números de vértices e faces com o número de arestas. O que você conclui?
Respostas e comentários
36. Construção de figuras; não.
37. a) Respostas possíveis, sendo f (faces), a (arestas) e v (vértices): figura a: 6 f, 10 a, 6 v; figura b: 6 f, 12 a, 8 v; figura c: 7 f, 12 a, 7 v; figura d: 9 f, 16 a, 9 v; figura ê: 8 f, 18 a, 12 v.
37. b) Espera-se que o estudante conclua que a soma dos números de vértices e de faces é igual ao número de arestas mais 2.

Sugestão de leitura
Para enriquecer o assunto, sugerimos o seguinte artigo:
SANTOS, K. S.; ARAÚJO, L. S. Uma breve abordagem histórica: Platão e os poliedros platônicos. In: ENCONTRO NACIONAL DE EDUCAÇÃO MATEMÁTICA, 12., 2016, São Paulo. Anaisreticências São Paulo: Sociedade Brasileira de Educação Matemática, 2016. Disponível em: https://oeds.link/I8NgN8. Acesso em: 27 maio 2022.
Este trabalho tem como objetivo apresentar, por meio da História da Matemática, uma evolução do tema Sólidos de Platão associada a personagens que contribuíram para seu desenvolvimento, associando Pitágoras, Teeteto, Euclides, Iorranes Kepler e Euler, sendo Platão considerado aqui o protagonista.
Exercícios propostos
Neste bloco de exercícios, os estudantes poderão ampliar seus conhecimentos acerca das planificações da superfície de poliedros.
No exercício 36, antes de reproduzirem as planificações no caderno, proponha a eles que tentem resolver o exercício apenas visualizando os poliedros montados, sem desenhá-los. Respostas possíveis para esse exercício:
a)
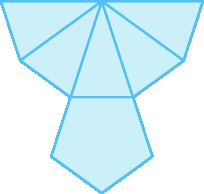
b)

c)

d)
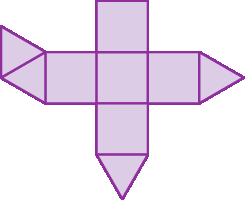
e)
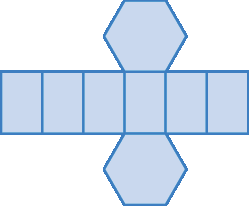
A resolução do exercício 37 está no início deste Manual, nas orientações específicas do capítulo 10.
PARA SABER MAIS
Ladrilhamento
Quando revestimos uma superfície plana com regiões poligonais sem deixar falhas ou sobrepô-las, dizemos que houve um ladrilhamento dessa superfície. Podemos ladrilhar uma superfície com um ou mais tipos de região poligonal.



Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Reproduza esta superfície poligonal na fórma de triângulo

e ladrilhe uma superfície retangular de 5 centímetros por 6 centímetrosponto
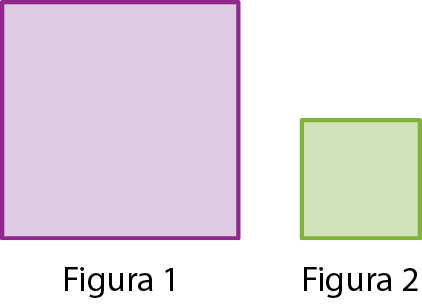
2 Ladrilhe uma superfície retangular de 7 centímetros por 4 centímetros, utilizando apenas superfícies quadrangulares iguais às apresentadas como figuras 1 e 2.
3 Copie em papel quadriculado o padrão a seguir e descubra quantas figuras quadradas verdes e quantas figuras alaranjadas faltam para completar uma superfície quadrada.
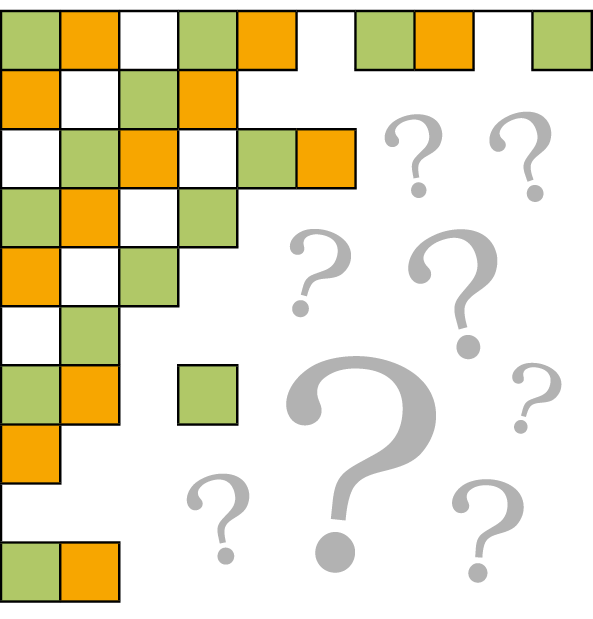
4 Utilizando uma superfície poligonal qualquer e uma única região poligonal por vez, descubra se é possível fazer um ladrilhamento utilizando regiões poligonais com a fórma de:
• triângulos equiláteros;
• octógonos;
• hexágonos;
• quadrados;
• pentágonos.
Respostas e comentários
1. Construção de figura.
2. Construção de figura.
3. Construção de figura; 20 verdes e 21 alaranjadas.
4. Respostas:
triângulos equiláteros: sim;
octógonos: não;
hexágonos: sim;
quadrados: sim;
pentágonos: não.
Para saber mais
Nesta seção, os estudantes devem mobilizar os conhecimentos já construídos sobre polígonos e desenvolver noções de área (utilizando conhecimentos de estudos anteriores, nos anos iniciais do Ensino Fundamental), assunto que será tratado no próximo capítulo. Desse modo, é possível avaliar o perfil de cada estudante com relação a esse aprendizado.
Agora é com você!
Veja possíveis figuras para as atividades 1 e 2.
Na atividade 1, há um retângulo de 5 centímetros de medida de largura por 6 centímetros de medida de altura composto de 6 retângulos menores, de 0,5 centímetro de medida de largura por 1 centímetro de medida de altura, idênticos (formados por dois triângulos azuis) na altura e 10 desses retângulos menores na base. Então, a superfície retangular tem lados de medidas 5 centímetros por 6 centímetros, utilizando cada triângulo azul com os dois lados menores medindo 1 centímetro e 0,5 centímetro.
A seguir, indicamos como a ilustração pode ser elaborada pelos estudantes. Nesta representação usamos medidas proporcionais a 5 e 6 centímetros.

Na atividade 2, os estudantes deverão cobrir uma superfície retangular, de lados medindo 7 centímetros por 4 centímetros, com figuras quadradas de lados medindo 2 centímetros (figura 1) e 1 centímetro (figura 2). Para isso, há diferentes possibilidades. Usando somente a figura 2, é possível cobrir toda a superfície maior com 7 figuras na base e 4 na altura, totalizando 28 figuras de 1 centímetro de medida de lado. Como cada grupo de duas figuras (2) na base e duas figuras (2) na altura formam uma figura 1, uma possível resposta seria a figura a seguir:

As resoluções das atividades 3 e 4 estão no início deste Manual, nas orientações específicas do capítulo 10.
TRABALHANDO A INFORMAÇÃO
A probabilidade das cores
As irmãs Neusa e Júlia fizeram uma experiência de jogar um dado cúbico e anotar a cor que ficava na face superior. Cada face é de uma cor diferente e elas sabem que a probabilidade de cada uma das cores estar na face superior é sempre a mesma, isto é,
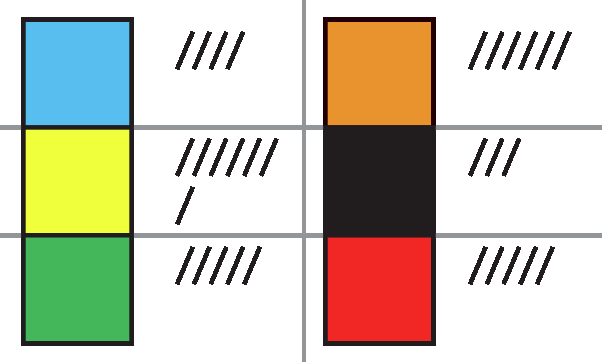
um sextoEnquanto uma delas jogava o dado, a outra anotava a cor da face superior, que podia ser azul, amarela, verde, laranja, preta ou vermelha, e colocava em um saquinho uma ficha colorida correspondente a cada jogada.

Depois de Júlia jogar o dado 30 vezes, Neusa verificou a frequência de cada cor, ou seja, quantas vezes cada cor ficou na face voltada para cima e organizou essas informações em uma tabela.
Observe as anotações e a tabela de frequência que ela fez:
|
Cor |
azul |
amarela |
verde |
laranja |
preta |
vermelha |
|---|---|---|---|---|---|---|
|
Frequência |
4 |
7 |
5 |
6 |
3 |
5 |
Dados obtidos por Neusa.
Neusa pediu à irmã que calculasse a probabilidade de retirar do saquinho uma ficha:
a) verde;
b) amarela;
c) preta.
Lembrando que a probabilidade é dada pela razão entre a frequência da cor e o total de jogadas do dado, Júlia calculou:
a) Probabilidade
igual cinco trinta avos igual um sextob) Probabilidade
igual sete trinta avosc) Probabilidade
igual três trinta avos igual um décimoConcluíram, então, que a probabilidade esperada, que seria
um sextose confirmou para a cor verde, mas não para a cor amarela nem para a preta.
Respostas e comentários
Trabalhando a informação
Habilidades da Bê êne cê cê: ê éfe zero seis ême ah um sete e ê éfe zero seis ême ah três zero.
Esta seção trata da observação de um experimento aleatório (lançar um dado de faces coloridas e observar a cor da face que fica voltada para cima), do levantamento da frequência de cores que saíram nesses lançamentos (registro em tabela de frequências) e do cálculo de probabilidade de eventos associados a esse experimento. Por explorar as características de um objeto que lembra a fórma de um poliedro e o cálculo de probabilidade, contribuímos para relacionar as Unidades Temáticas: Geometria e Probabilidade e estatística e as habilidades (ê éfe zero seis ême ah um sete) e (ê éfe zero seis ême ah três zero).
Converse com os estudantes a situação e o que as irmãs Neusa e Júlia fizeram para obter as probabilidades, ressaltando o significado da “frequência de cada cor” registrada na tabela. Proponha a eles alguns questionamentos em relação à interpretação dos dados da tabela feita por Neusa, por exemplo:
• “Qual é a frequência da cor verde? O que essa frequência significa?” (Espera-se que os estudantes identifiquem que a frequência da cor verde é 5, o que significa que, das 30 vezes que o dado foi lançado, em 5 vezes apareceu a face verde voltada para cima, 5 em 30.);
• “Que valor se obtém adicionando todas as frequências?” (Espera-se que os estudantes percebam que adicionando-se as frequências de cada cor deve-se obter o total de jogadas do dado, ou seja, 30. Verifique se eles respondem diretamente ou se fazem efetivamente a adição.).
Para o cálculo de cada probabilidade, os estudantes devem compreender que é preciso considerar a fração obtida da comparação entre a frequência da cor e o total de jogadas.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Calcule as probabilidades das outras cores no experimento das irmãs Neusa e Júlia.
2

Junte-se a um colega, construam um dado a partir da planificação de um hexaedro e pintem as faces com as mesmas cores do dado das irmãs. Depois, façam 60 lançamentos do dado e construam uma tabela de frequência. Para finalizar, calculem a probabilidade de cada cor ficar na face superior.
3

Discutam entre si se o aumento da quantidade de lançamentos favorece a possibilidade de as probabilidades das cores serem iguais.
4 Se as faces opostas do dado de Neusa e Júlia tivessem a mesma cor, a probabilidade de sair uma das cores continuaria igual a
um sexto? Justifique sua resposta.
5 Ao lançar uma moeda, qual é a probabilidade de sair cara? E de sair coroa? Com base no experimento de Júlia e Neusa e no resultado obtido por você na atividade 2, é correto afirmar que em dois lançamentos de uma moeda sairá cara em uma das vezes e coroa na outra vez? Justifique sua resposta.
7. Prismas
Nós já estudamos alguns poliedros. Agora, vamos conhecer melhor um grupo deles, fazendo novas apresentações.
Nos poliedros a seguir, estão destacadas duas faces. Essas duas faces são opostas, paralelas e idênticas. As demais têm fórma de paralelogramo.
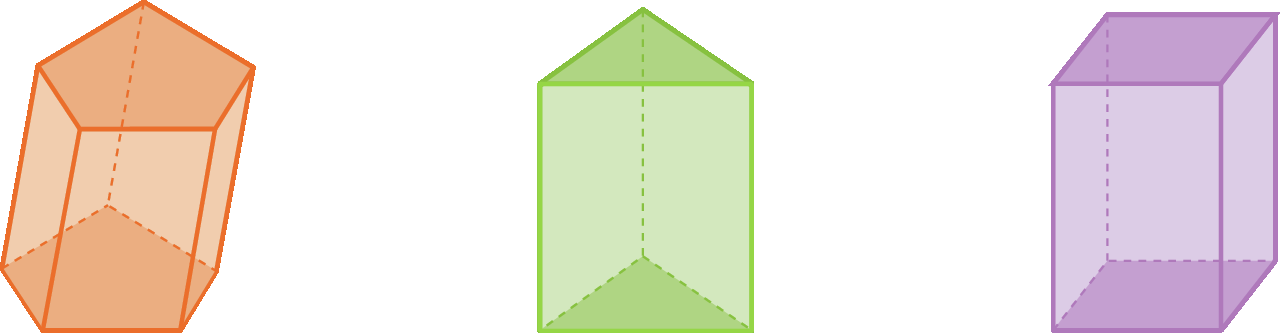
Esses poliedros são classificados como prismas. As duas faces opostas idênticas são chamadas de bases, e as outras, em fórma de paralelogramo, são as faces laterais.
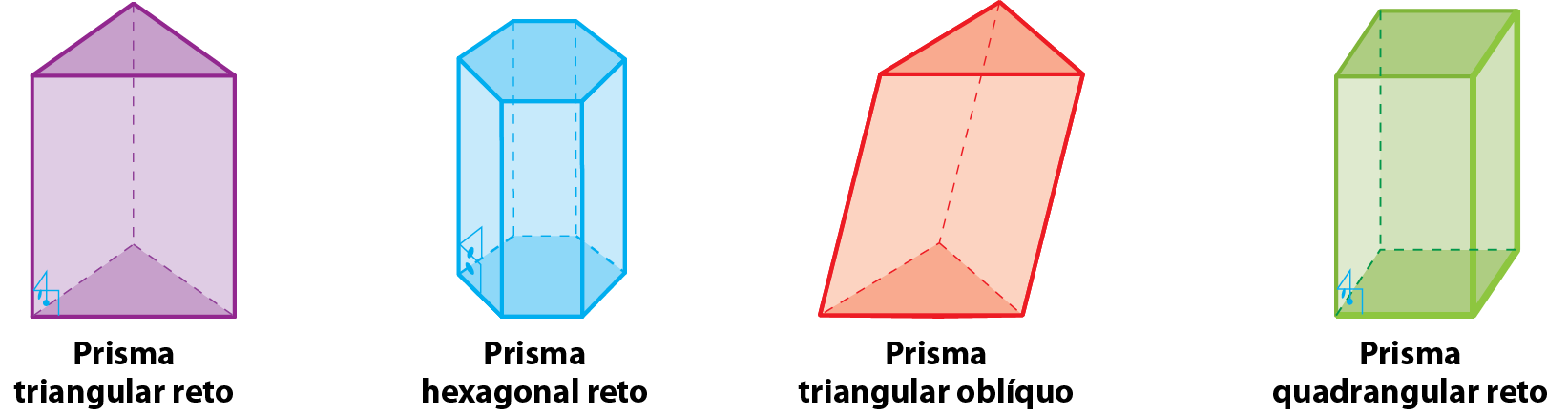
Classificação dos prismas
Os prismas podem ser nomeados de acordo com as bases e com a inclinação das arestas laterais em relação às bases.
Respostas e comentários
1. Azul:
Quatro trinta avos igual dois quinze avos; laranja:
Seis trinta avos igual um quinto; vermelha:
Cinco trinta avos igual um sexto.
2. Resposta pessoal.
3. Resposta pessoal.
4. Não, pois há 3 possibilidades de cores e, desse modo, a probabilidade de sair uma dessas cores será de
Fração 1 sobre 35. A probabilidade de sair cara ou coroa é de
um meioNão é correto afirmar que sairá cara em um lançamento e coroa no outro, pois, em cada lançamento, ambas as faces têm a mesma probabilidade de sair.
Agora quem trabalha é você!
As respostas das atividades 1 e 2 estão no início deste Manual, nas orientações específicas do capítulo 10.
Na atividade 3, é possível pensar em diversos argumentos. A princípio, o aumento da quantidade de lançamentos tende a tornar a diferença entre as frequências cada vez menos significativa, tornando as probabilidades bem próximas.
Não seria a mesma probabilidade na atividade 4, pois o dado teria apenas 3 cores diferentes; então, cada um terá probabilidade
Um terço.
Na atividade 5, a probabilidade de sair cara é a relação
Fração. Numerador: face cara; denominador: total de faces.que é igual a
Um meioIsso não significa que essa será a frequência observada em um número pequeno de repetições, como em duas rodadas, mas essa é a tendência.
7. Prismas
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um sete.
Para finalizar o desenvolvimento da Unidade Temática Geometria no 6º ano, aprofundamos o estudo de poliedros abordando as características de dois grupos importantes desse tipo de sólido: os prismas e as pirâmides, ampliando o trabalho com a habilidade (ê éfe zero seis ême ah um sete). No entanto, não temos a pretensão de esgotar o assunto, que será revisitado em outros anos do Ensino Fundamental e aprofundado no Ensino Médio.
Inicialmente, caracterizamos prismas e destacamos dentre suas faces aquelas que são suas duas bases e as demais que são as faces laterais.
Se possível, providencie modelos desses poliedros, de modo que os estudantes possam manuseá-los observando suas particularidades, identificar seus elementos (faces, vértices e arestas), suas bases e faces laterais.
É importante perceberem que, ao apoiar um prisma por uma de suas bases, observamos que metade de seus vértices fica sobre a superfície de apoio e metade deles fica fóra. Na manipulação dos modelos de prismas, é possível os estudantes comprovarem tal fato.
Observações
▶ Em um prisma reto, todas as faces laterais têm fórma de retângulo.
▶ Em um prisma oblíquo, nem todas as faces laterais têm fórma de retângulo.
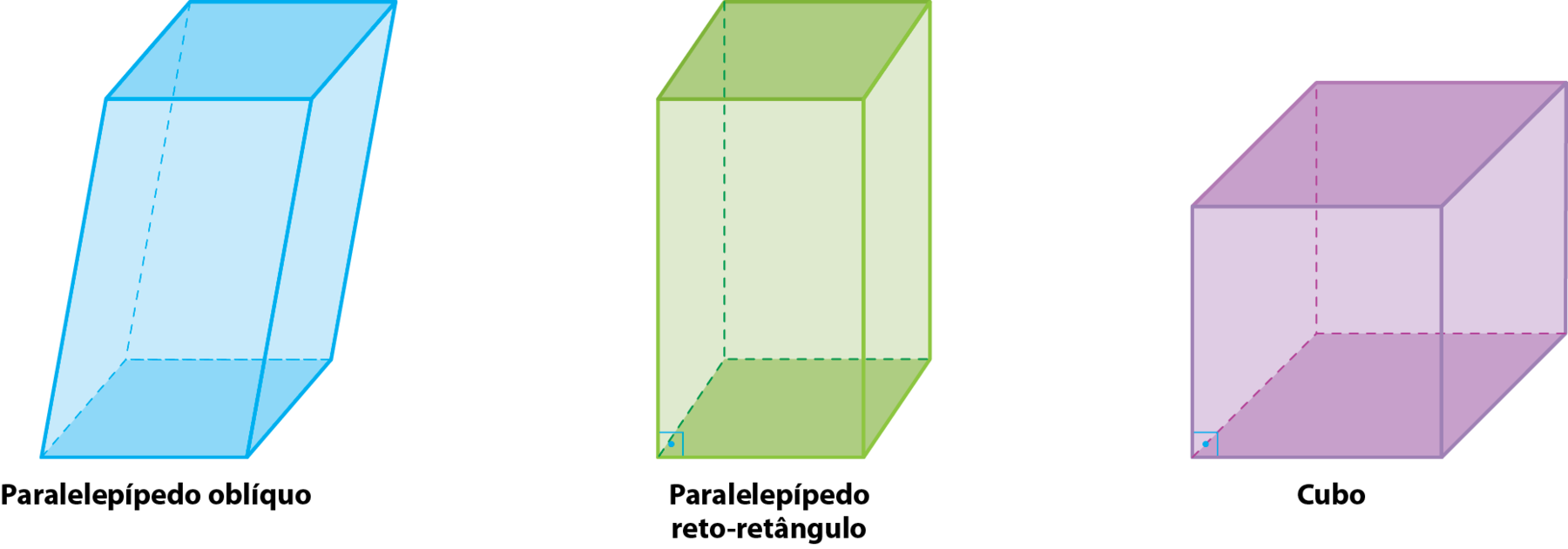
▶ Quando um prisma tem todas as faces em fórma de paralelogramos, ele é denominado paralelepípedo. Observe alguns exemplos de paralelepípedos:
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
38 Classifique os prismas a seguir em relação às bases.
a)

b)
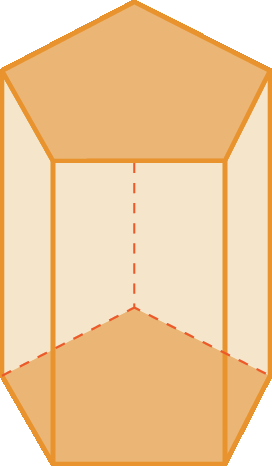
c)
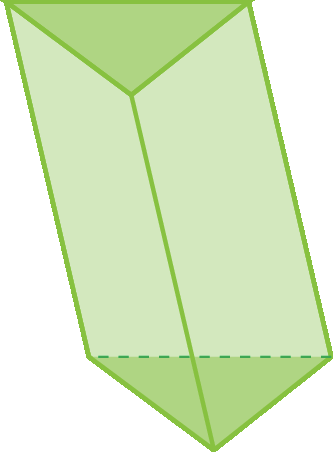
39 Classifique os prismas a seguir como prisma oblíquo ou prisma reto.
a)
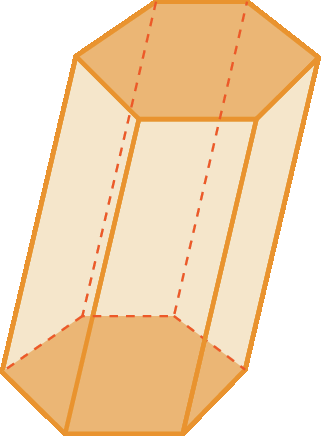
b)
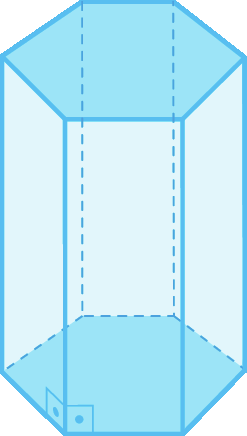
c)
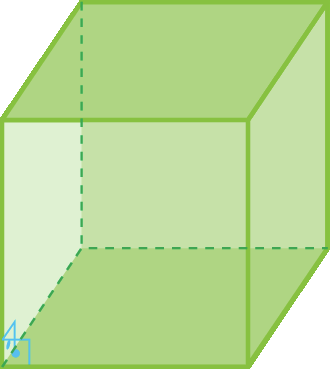
40 Quantas faces tem um prisma com 15 arestas? E um prisma com vinte e uma arestas?
41 Existe prisma com 39 arestas? E prisma com vinte e duas arestas? Justifique a sua resposta.
Respostas e comentários
38. a) Prisma quadrangular.
38. b) Prisma pentagonal.
38. c) Prisma triangular.
39. a) Oblíquo.
39. b) Reto.
39. c) Reto.
40. 7 faces; 9 faces.
41. Sim, pois 39 é múltiplo de 3. Não, pois 22 não é múltiplo de 3.
Classificação dos prismas
Abordamos a classificação quanto à inclinação das arestas laterais do prisma. Para isso, usando alguns modelos de prismas, destaque as arestas laterais e as arestas das bases. Espera-se que os estudantes percebam que um prisma é reto quando todas as suas arestas laterais são perpendiculares às arestas da base. Desse modo, todas as faces laterais de um prisma reto são retangulares. Caso contrário, o prisma é oblíquo, pois nem todas as faces laterais são retangulares.
Um tipo de prisma a destacar, provavelmente o mais comum que aparece nos formatos de objetos do cotidiano, é o paralelepípedo.
Os paralelepípedos são uma classe especial de prismas que têm todas as faces determinadas por paralelogramos. O sólido conhecido como bloco retangular, que é um prisma reto e tem todas as faces retangulares, é denominado paralelepípedo reto-retângulo. Um dos exemplares de paralelepípedo reto-retângulo é o cubo, com a particularidade de que todas as suas faces são quadradas.
Exercícios propostos
No exercício 38, os estudantes devem identificar a base do prisma para classificá-lo. No item a, o prisma é quadrangular, pois a base tem o formato de um quadrilátero; no item b, o prisma é pentagonal, pois a base tem o formato de um pentágono; no item c, o prisma é triangular, porque a base tem o formato de um triângulo. Pode-se ampliar a atividade solicitando aos estudantes que identifiquem o prisma oblíquo.
No exercício 39, caso algum estudante ainda tenha dúvida em classificar um prisma em oblíquo ou reto, diga-lhe que as faces laterais dos prismas retos têm o formato de retângulos. No item a, o prisma é oblíquo; no item b, o prisma é reto; no item c, o prisma é reto.
Como complemento ao exercício 40, questione os estudantes se faz diferença o prisma ser reto ou oblíquo, justificando a resposta.
As resoluções dos exercícios 40 e 41 estão no início deste Manual, nas orientações específicas do capítulo 10.
Paralelepípedo reto-retângulo: um sólido especial
No dia a dia, é possível observar objetos que possuem a fórma de prisma, com todas as faces retangulares, como é o caso de muitas embalagens, de muitos edifícios e de alguns objetos pessoais e utensílios, por exemplo.

(As imagens não respeitam as proporções reais entre os objetos.)
Quando um prisma tem todas as faces retangulares, ele é denominado paralelepípedo reto-retângulo ou bloco retangular.
Observe os exemplos.

Em todos eles, podemos contar: 6 faces, 8 vértices e 12 arestas.
Nos paralelepípedos da figura 1, observe que todas as faces são idênticas e têm a fórma de um quadrado.
Um paralelepípedo reto-retângulo é denominado cubo quando tem todas as faces na fórma de quadrado.
Respostas e comentários
Paralelepípedo reto‑retângulo: um sólido especial
Neste tópico, ampliamos o olhar para conhecer melhor os paralelepípedos reto-retângulos. Nesse momento, proponha aos estudantes que citem alguns exemplos de objetos ou estruturas que representam um paralelepípedo reto-retângulo. Eles podem citar vários tipos de embalagens e caixas, objetos de decoração, construções arquitetônicas famosas no mundo etcétera.
Pode ser interessante propor-lhes a observação de modelos de diferentes blocos retangulares. Organize a turma em grupos, distribua alguns modelos para cada grupo (é importante que os grupos tenham alguns modelos diferentes uns dos outros) e peça aos estudantes que determinem a quantidade de faces, de vértices e de arestas de cada modelo.
Ao final, cada grupo pode expor o que apurou, contribuindo para que todos percebam que os paralelepípedos reto-retângulos que têm em mãos têm 6 faces, 8 vértices e 12 arestas, independentemente do modelo considerado.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
42 Observe como uma parede pode ser construída com o empilhamento de tijolos:

Muitos objetos que usamos diariamente têm a fórma de paralelepípedo reto-retângulo. A que você atribui esse fato?
43 Grande parte das embalagens utilizadas atualmente tem a fórma de bloco retangular. Na sua opinião, por que isso ocorre?
44 Uma editora vai distribuir sua nova coleção de Matemática, composta de 4 volumes. Cada coleção foi amarrada conforme demonstrado na figura.
Quantas coleções há em cada um dos itens a seguir?
a)

b)

45 Tiago construiu vários cubos de cartolina com arestas de 1 centímetro.
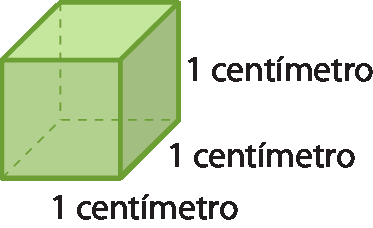
a) Quantos cubos iguais a esse Tiago precisa construir para formar um cubo com arestas de 2 centímetros?
b) Quantos desses cubos Tiago precisa construir para formar um cubo com arestas de 3 centímetros?
46

Reúna-se com um colega para copiar as planificações em uma cartolina. Após recortá-las e dobrá-las, com quais delas vocês conseguem montar um cubo?
a)
b)
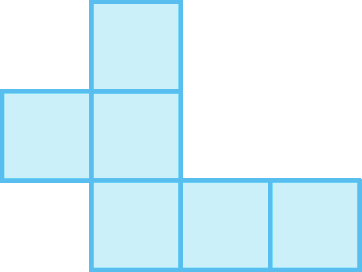
c)

(Use tesoura com ponta arredondada e a manuseie com cuidado!)
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
As figuras mostram o mesmo dado em três posições diferentes.

Qual é o símbolo que está na face oposta da

?
Respostas e comentários
42. Resposta possível: É fácil de manusear e empilhar.
43. Resposta possível: Embalagens com fórma de bloco retangular são mais fáceis de empilhar, armazenar e manusear.
44. a) 6 coleções.
44. b) 27 coleções.
45. a) 8 cubos.
45. b) 27 cubos.
46. Alternativas a e c.
Pense mais um poucoreticências:
A figura que tem a fórma de um quadrado verde.
Exercícios propostos
Uma possibilidade de resposta para o exercício 42 é que os paralelepípedos reto-retângulos são muito comuns no dia a dia, pois seus ângulos retos e faces facilitam o armazenamento, o empilhamento e a padronização de construções, por exemplo.
Para o exercício 43, combine antecipadamente com os estudantes que levem para a escola, no dia estipulado, embalagens vazias ou objetos que não tenham o formato de paralelepípedo. A intenção é experimentarem empilhar essas embalagens e verificar a dificuldade de fazer isso.
Uma possibilidade de resposta para esse exercício é que os paralelepípedos reto-retângulos são utilizados em embalagens, pois suas características facilitam o transporte e o armazenamento, nas fábricas e nos estabelecimentos comerciais.
As resoluções dos exercícios 44 a 46 estão no início deste Manual, nas orientações específicas do capítulo 10.
No exercício 45, vale destacar que a oportunidade de relacionar o volume de um recipiente com a contagem de cubos que cabem em seu interior dá mais significado à ideia de volume, o que contribuirá para outras situações relacionadas a esse conceito.
No exercício 46 oriente os estudantes na confecção das planificações para que tomem cuidado com o manuseio da tesoura de ponta arredondada.
Pense mais um poucoreticências
Neste desafio, estabeleça um tempo para os estudantes interpretarem e resolverem a situação individualmente. Em seguida, proponha a eles que, em duplas, cada um explique ao outro como obteve a resposta observando cada vista. Uma possível explicação:
Ao analisar apenas a primeira vista, podemos afirmar que qualquer um dos outros símbolos (círculo, quadrado ou triângulo) poderia estar na face oposta à da estrela. Ao analisar a segunda vista, podemos afirmar que o círculo e o triângulo não podem estar na face oposta à da estrela. Logo, só resta o quadrado como opção.
8. Pirâmides

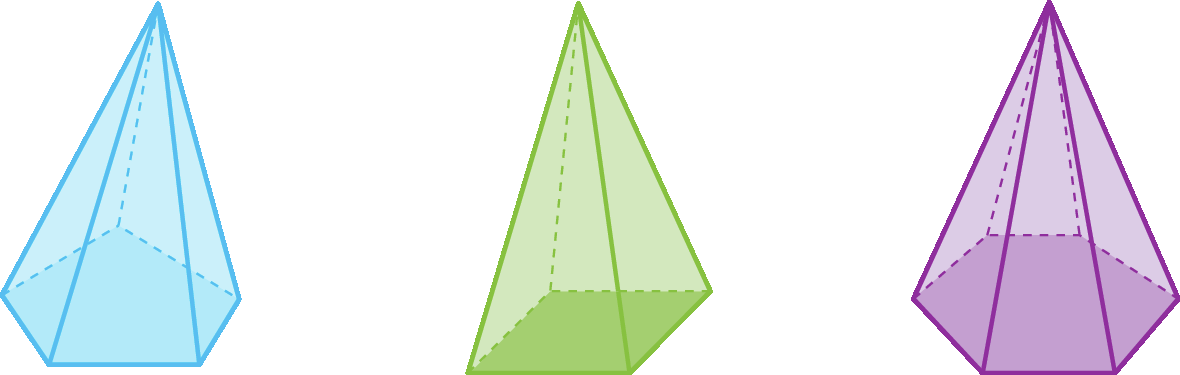
Todos são exemplos de pirâmides, possuem uma face que é uma região poligonal qualquer, chamada de base, e as demais faces são triangulares com um vértice comum, chamadas de faces laterais.
As arestas das faces laterais de uma pirâmide são chamadas de arestas laterais.
Classificação das pirâmides
As pirâmides podem ser nomeadas de acordo com a base. Observe.
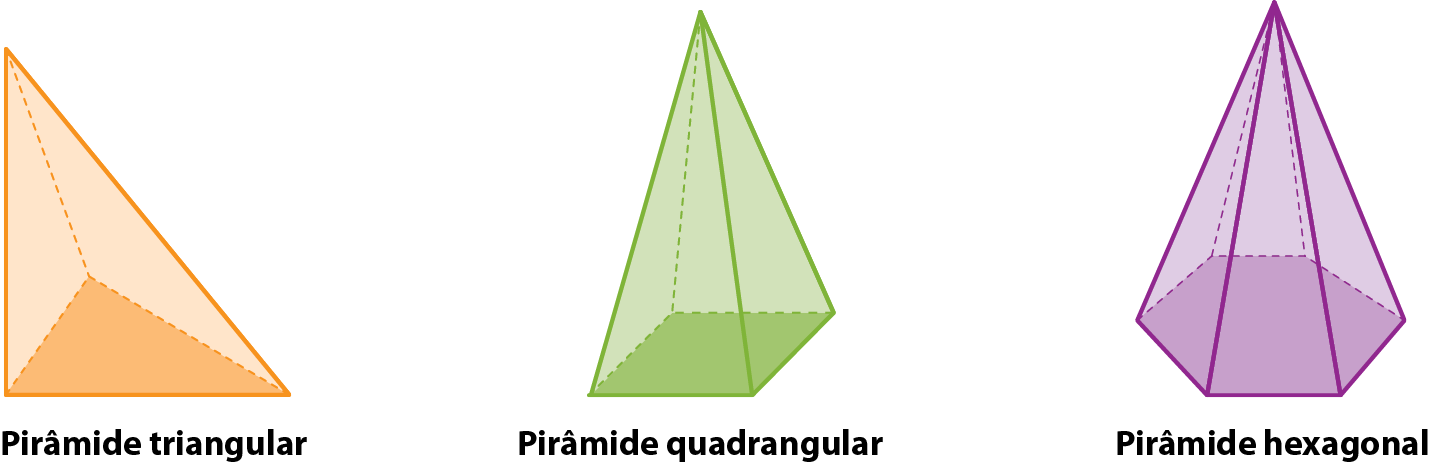
As pirâmides também podem ser classificadas como reta ou oblíqua:
• pirâmide reta – quando todas as arestas laterais são congruentes;
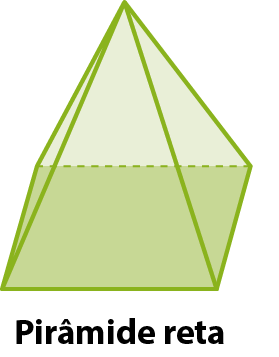
• pirâmide oblíqua – quando não é uma pirâmide reta.
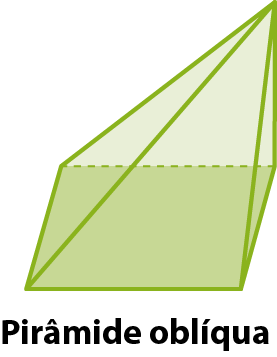
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
47 Classifique as pirâmides a seguir em relação à base e como pirâmide oblíqua ou pirâmide reta.
a)
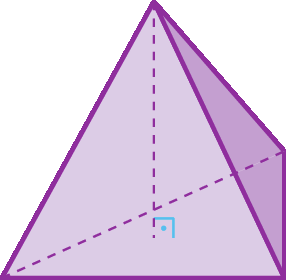
b)
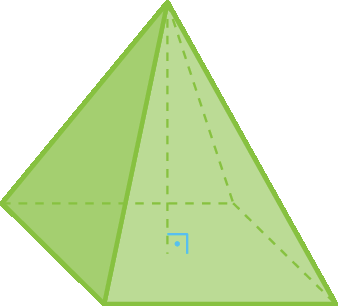
c)
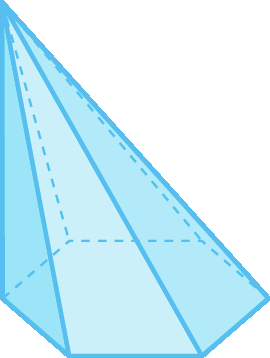
d)
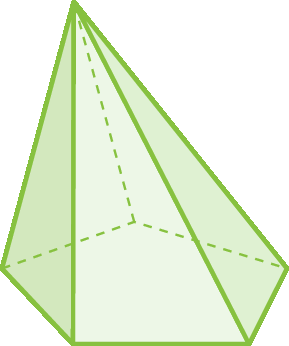
e)
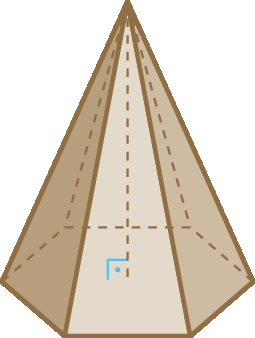
48 Quantos vértices tem uma pirâmide octogonal? E quantas arestas?
49 Quantas arestas e faces tem uma pirâmide de 10 vértices?
Respostas e comentários
47. a) Pirâmide triangular reta.
47. b) Pirâmide quadrangular reta.
47. c) Pirâmide hexagonal oblíqua.
47. d) Pirâmide pentagonal oblíqua.
47. e) Pirâmide hexagonal reta.
48. 9 vértices; 16 arestas.
49. 18 arestas e 10 faces.
8. Pirâmides
Habilidade da Bê êne cê cê: ê éfe zero seis ême ah um sete.
Neste tópico, também é importante a utilização de modelos variados de pirâmides, de modo que, ao manuseá-los, os estudantes observem suas particularidades, identifiquem seus elementos (faces, vértices e arestas), sua base e faces laterais.
Eles devem perceber que, ao apoiar uma pirâmide por sua base, observamos que apenas um vértice fica fóra da superfície de apoio na qual estão os demais vértices. Na manipulação dos modelos de pirâmides, é possível os estudantes comprovarem tal fato.
Do mesmo modo que fizemos para os prismas, para as pirâmides, também abordamos a classificação em reta ou oblíqua, ampliando o trabalho com a habilidade (EF06MA17). Para isso, novamente utilize alguns modelos de pirâmides e destaque as arestas laterais e as arestas da base. Espera-se que os estudantes percebam que uma pirâmide é reta quando todas as suas arestas laterais são congruentes entre si. Desse modo, todas as faces laterais de uma pirâmide reta são delimitadas por triângulos isósceles. Caso contrário, a pirâmide é oblíqua, pois nem todas as faces laterais são delimitadas por triângulos isósceles.
Exercícios propostos
No exercício 47, os estudantes devem verificar se as arestas laterais da pirâmide são congruentes e contar a quantidade de lados da base dela para responder à questão.
a) A pirâmide é reta e tem base em formato de triângulo. É triangular reta.
b) A pirâmide é reta e tem base em formato de quadrado. É quadrangular reta.
c) A pirâmide é oblíqua e tem base em formato de hexágono. É hexagonal oblíqua.
d) A pirâmide é oblíqua e tem base em formato de pentágono. É pentagonal oblíqua.
e) A pirâmide é reta e tem base em formato de hexágono. É hexagonal reta.
Como complemento ao exercício 48, pergunte aos estudantes se faz diferença a pirâmide ser reta ou oblíqua, justificando a resposta.
As resoluções dos exercícios 48 e 49 estão no início deste Manual, nas orientações específicas do capítulo 10.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Observe esta figura e responda às questões a seguir.
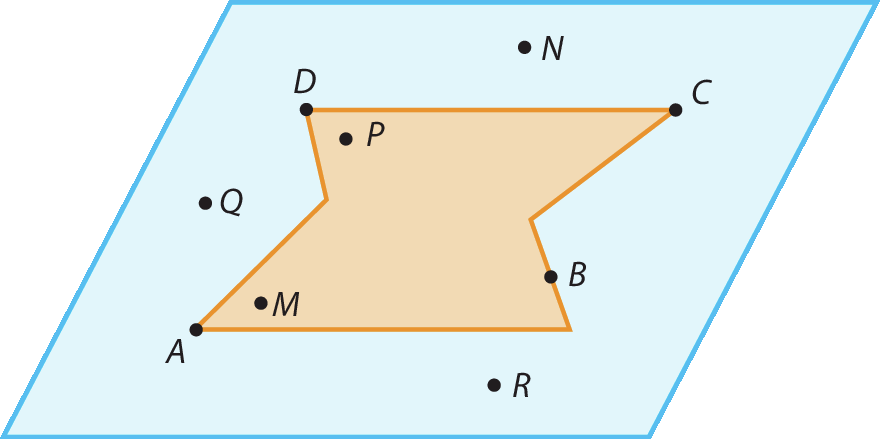
a) Dos pontos assinalados, quais pertencem à linha poligonal? E quais pertencem à sua região interior?
b) A região interior determinada pela linha poligonal é convéquica ou não convéquica? Justifique sua resposta.
2 Desenhe um polígono convéquiço com 4 lados e nomeie seus vértices.
a) Quantos ângulos internos tem esse polígono? Quais são?
b) Dê nome ao polígono que você desenhou.
3 Corrija as afirmações a seguir.
a) Quadriláteros que têm apenas um par de lados paralelos são chamados paralelogramos.
b) Um triângulo escaleno tem os três lados de mesma medida.
4 Copie a figura a seguir em uma folha de papel à parte e recorte-a. Em seguida, dobre-a no segmento
segmento AMfazendo o vértice C coincidir com o vértice B.
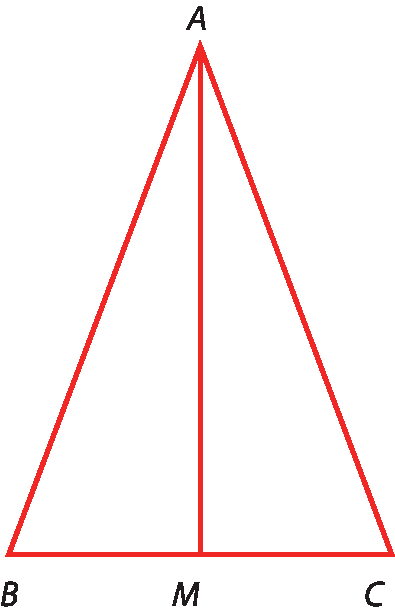
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
a) O que se verifica em relação aos lados
Segmento de reta ABe
Segmento de reta AC
b) E em relação aos ângulos
Ângulo B e Ângulo C?c) Como é classificado o triângulo á bê cê ?
d) O que se verifica em relação aos segmentos
Segmento de reta BMe
Segmento de reta MC
e) E em relação aos ângulos
Ângulo BMA Ângulo CMA
5 Responda:
a) Quantas arestas tem um prisma cuja base tem 9 lados? E se a base tiver 10 lados? E 11 lados? E se a base tiver um número n de lados?
b) Quantas arestas tem uma pirâmide cuja base tem 9 lados? E se a base tiver 10 lados? E 11 lados? E se a base tiver um número n de lados?
6 Represente em seu caderno um plano cartesiano e identifique os pontos:
a(3, 7) B(9, 7) C(11, 3)
D(1, 3) ê(6, 5) F(6, 1)
a) Ao traçar segmentos unindo os pontos a, B, C e D forma-se o quadrilátero a bê cê dê. Identifique esse quadrilátero e responda: Quais são suas características?
b) Considerando que três desses pontos correspondem aos vértices de um triângulo isósceles, quais são esses possíveis pontos?
c) Que pontos correspondem aos vértices de um losango?
7 Considere o trapézio representado no plano cartesiano a seguir.
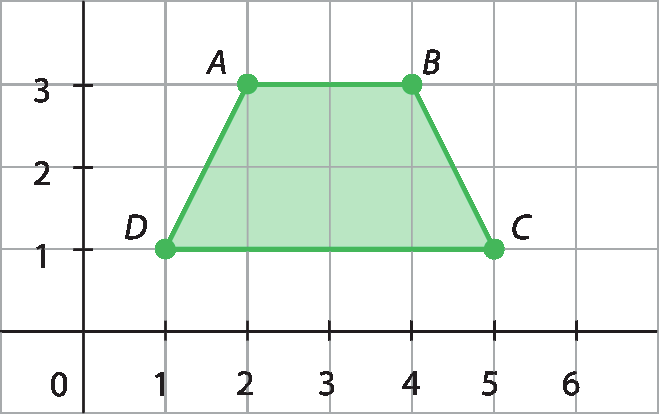
Otávio vai representar uma ampliação desse trapézio. Se ele pretende dobrar o tamanho dos lados desse polígono, quais devem ser as coordenadas de B′, sabendo que A′(3, 5).
Respostas e comentários
1. a) Linha poligonal: a, B, C, D; região interior: P, M.
1. b) É não convéquica, pois nem todo ponto do segmento
Segmento de reta PMpertence à região interior.
2. a) 4 ângulos; Resposta pessoal.
2. b) Resposta pessoal.
3. a) Resposta possível: Quadriláteros que têm apenas um par de lados paralelos são chamados trapézios.
3. b) Resposta possível: Um triângulo escaleno tem os três lados com medidas diferentes.
4. a) Eles têm a mesma medida.
4. b) Eles têm a mesma medida.
4. c) Isósceles.
4. d) Eles têm a mesma medida.
4. e) Eles são ângulos retos.
5. a) 27 arestas; 30 arestas; 33 arestas; 3n arestas.
5. b) 18 arestas; 20 arestas; vinte e duas arestas; 2n arestas.
6. Construção de figura.
6. a) Um trapézio; tem um par de lados paralelos.
6. b) Resposta possível: a, B e ê.
6. c) C, F, D e ê.
7. B′(7, 5)
Exercícios complementares
Neste bloco de exercícios, os estudantes têm a oportunidade de revisitar os principais conceitos tratados no capítulo. Verifique se ainda apresentam dificuldade em algum e, se for o caso, sugira a eles que refaçam algumas atividades referentes a tais assuntos.
No exercício 1, os estudantes deverão usar os conceitos aprendidos sobre região interior e exterior de uma linha poligonal, além do conceito de convexidade. Se tiverem dificuldades, retome o conteúdo com exemplos diferenciados para cada caso.
Após resolverem individualmente o exercício 2, peça a eles que respondam oralmente:
• Como cada um pode desenhar livremente o polígono?
• Que respostas podem ser diferentes e quais devem ser necessariamente iguais, de modo que estejam todas corretas?
Espera-se que os estudantes observem que, seja qual for o desenho, todos devem ter encontrado necessariamente 4 vértices e 4 ângulos internos. Porém, os vértices podem ter sido nomeados de maneiras diferentes, escolhendo-se quaisquer quatro letras maiúsculas. Além disso, o polígono desenhado é certamente um quadrilátero, mas, dependendo do desenho, poderá ser losango, retângulo etcétera.
O execício 3 propõe aos estudantes que analisem informações e apresentem argumentos para corrigi-las. No caso do item a, devem considerar que, para ser um paralelogramo, conforme definição apresentada, é preciso haver dois pares de lados paralelos. Quando há somente um par de lados paralelos, o quadrilátero é classificado como trapézio.
Para o item b, deverão considerar que o triângulo que tem os três lados de mesma medida é o equilátero. O triângulo escaleno tem os três lados de medidas diferentes.
Ao propor a resolução do exercício 4 oriente os estudantes no manuseio da tesoura de ponta arredondada ao recortarem a figura desenhada.
As resoluções dos exercícios 4 a 7 estão no início deste Manual, nas orientações específicas do capítulo 10.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 O ponto de encontro de dois lados consecutivos de um polígono é chamado de:
a) vértice.
b) lado.
c) diagonal.
d) ângulo interno.
2 Um polígono de 6 lados é denominado:
a) pentágono.
b) hexágono.
c) heptágono.
d) octógono.
3 Como é denominado um triângulo que tem os três lados de mesma medida?
a) escaleno
b) equilátero
c) isósceles
d) retângulo
4 Um trapézio é todo quadrilátero que tem:
a) dois pares de lados paralelos.
b) dois lados de mesma medida.
c) só um par de lados paralelos.
d) quatro ângulos retos.
5 Quantas diagonais tem um quadrilátero?
a) uma diagonal.
b) duas diagonais.
c) 3 diagonais.
d) 4 diagonais.
6 Em relação ao par ordenado (2, 6), podemos afirmar que:
a) é igual ao par ordenado (6, 2).
b) o 2 indica a posição em relação ao eixo horizontal.
c) o 2 indica a posição em relação ao eixo vertical.
d) corresponde à origem.
7 Um decaedro tem quantas faces?
a) 8 faces
b) 9 faces
c) 10 faces
d) 12 faces
8 Um dado com o formato de dodecaedro tem suas faces numeradas. Qual é a probabilidade de sair a face 2 no lançamento desse dado?
a)
um meiob)
Um sextoc)
um décimod)
um doze avos9 O prisma da imagem a seguir é denominado:
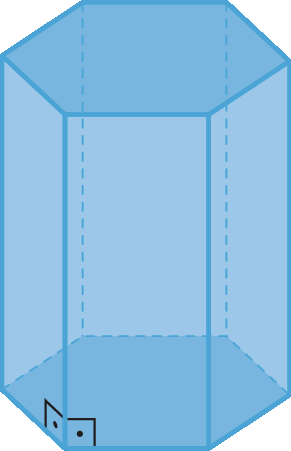
a) prisma pentagonal reto.
b) prisma pentagonal oblíquo.
c) prisma hexagonal reto.
d) prisma hexagonal oblíquo.
10 Uma pirâmide de base quadrangular tem quantas faces formadas por regiões triangulares?
a) 3 faces
b) 4 faces
c) 5 faces
d) 6 faces
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) O que é uma linha poligonal?
b) Qual é a definição de polígono?
c) Todo polígono é convexo? Justifique sua resposta.
d) Desenhe um polígono de 7 lados e identifique seus elementos.
e) Como os polígonos podem ser classificados? Dê dois exemplos.
f) Como os triângulos podem ser classificados em relação às medidas dos lados e em relação às medidas dos ângulos?
g) Com o auxílio de régua, compasso e esquadro, é possível desenhar um triângulo retângulo? Em caso afirmativo, descreva os passos para a construção.
h) Como os quadriláteros podem ser classificados em relação ao paralelismo de seus lados?
i) Quais são as características dos retângulos, quadrados e losangos?
j) Quais são as características dos prismas e das pirâmides?
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
Respostas e comentários
1. Alternativa a.
2. Alternativa b.
3. Alternativa b.
4. Alternativa c.
5. Alternativa b.
6. Alternativa b.
7. Alternativa c.
8. Alternativa d.
9. Alternativa c.
10. Alternativa b.
Organizando: As respostas a estas questões estão neste Manual.
Verificando
Essas atividades, propostas na fórma de testes, são mais uma oportunidade para o estudante consolidar a compreensão do conteúdo estudado neste capítulo. Instrua-os a retornarem às páginas anteriores caso alguma dúvida persista.
As resoluções dos testes 1 a 10 estão no início deste Manual, nas orientações específicas do capítulo 10.
Organizando
Incentive os estudantes a organizarem no caderno seu aprendizado, fazendo resumos, mapas conceituais ou aplicando destaques para conceitos importantes.
As questões propostas têm como objetivo fazer com que eles retomem os conteúdos aprendidos no capítulo e que reflitam sobre algumas temáticas. Após sua correção é importante pedir aos estudantes que compartilhem suas respostas; essa estratégia permitirá o compartilhamento de dúvidas e percepções, contribuindo para o aprendizado de todos.
a) Linha formada apenas por segmentos de reta consecutivos e não colineares.
e) Os polígonos podem ser classificados de acordo com o número de lados ou de ângulos internos. Exemplos: 4 lados e 4 ângulos internos: quadriláteros; 6 lados e 6 ângulos internos: hexágonos.
f) Lados:
• O triângulo isósceles tem pelo menos dois lados congruentes.
• O triângulo equilátero tem três lados congruentes.
• O triângulo escaleno tem três lados de medidas diferentes.
Ângulos:
• O triângulo acutângulo tem três ângulos agudos.
• O triângulo retângulo tem um ângulo reto e dois agudos.
• O triângulo obtusângulo tem um ângulo obtuso e dois ângulos agudos.
h) Nenhum par de lados paralelos: não recebe nome especial. Somente um par de lados paralelos: trapézios. Dois pares de lados paralelos: paralelogramos.
i) Retângulos: 4 ângulos retos. Quadrados: 4 ângulos retos e 4 lados congruentes. Losangos: 4 lados congruentes.
j) Os prismas têm duas faces opostas idênticas, que são chamadas de bases, e as outras, em formato de paralelogramo. As pirâmides têm uma face que é uma região poligonal qualquer, chamada de base, e as demais faces são triangulares com um vértice comum, chamadas de faces laterais.
As resoluções das questões b, c, d e g estão no início deste Manual, nas orientações específicas do capítulo 10.
DIVERSIFICANDO
Poliedros com massinha
Giovanna e Gabriela gostam de fazer modelos de poliedros usando massa de modelar.

Receita de massa de modelar
Ingredientes:
• 4 xícaras de farinha de trigo
• 1 xícara de sal
• 1 colher de sopa de óleo
• 1 xícara e meia de água
• Anilina suficiente para colorir
Misture tudo em uma vasilha.
Observe o modelo de tetraedro que uma fez e o de hexaedro (cubo) feito pela outra.
Depois de terminado seu tetraedro, Giovanna construiu um tetraedro truncado, cortando com planos seus quatro “bicos”. Ela obteve um poliedro com quatro faces triangulares e quatro faces hexagonais.
Observe o tetraedro truncado e sua planificação.
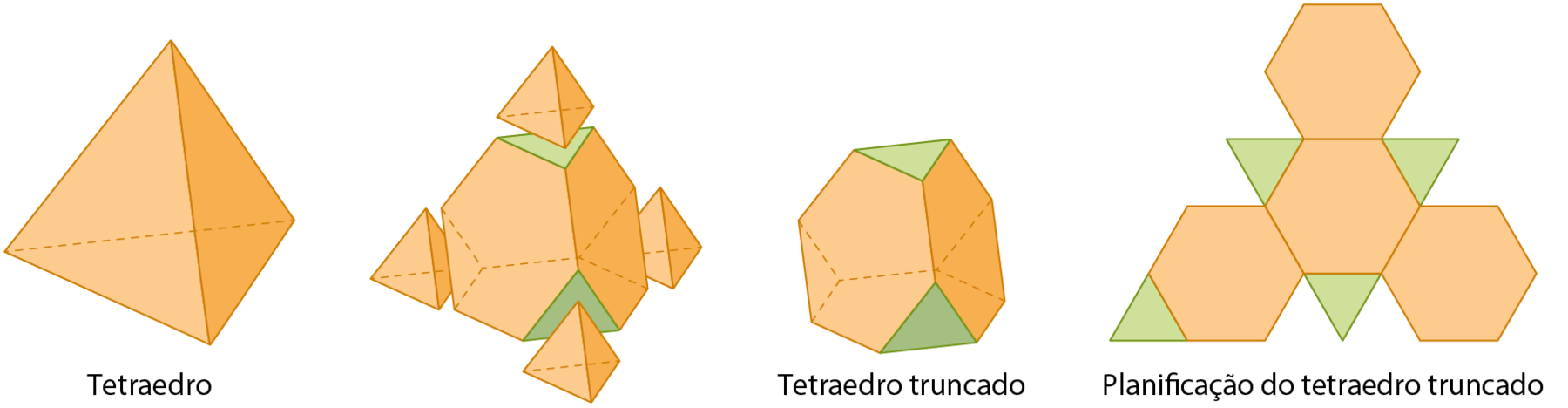
No dicionário Uáis da língua portuguesa, encontramos alguns significados para o verbo truncar:
1. separar do tronco, cortar;
2. retirar uma parte de, mutilar;
3. (rubrica: geometria) cortar (sólido geométrico) com um plano secante.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Em uma folha de papel sulfite, copie a planificação do tetraedro truncado apresentado anteriormente e monte um modelo desse poliedro.
2 Se Gabriela truncar o modelo de seu hexaedro do mesmo modo que Giovanna fez, quantas faces e que tipo ela obterá no novo modelo de poliedro? (Se quiser, antes de responder, você pode fazer sua própria massinha, construir um modelo de cubo e truncá-lo.)
3 Com massa de modelar, construa um modelo de pirâmide quadrangular reta e trunque-o com um só plano, de modo que obtenha um modelo de poliedro que contenha o vértice e outro que contenha a base da pirâmide.
a) O poliedro que contém o vértice é uma pirâmide? Em caso afirmativo, de que tipo?
b) Quantas faces terá o poliedro que contém o vértice? E o outro poliedro? Classifique essas faces.
(Faça a atividade com o auxílio de um adulto.)
Respostas e comentários
1. Construção do modelo.
2. 8 faces triangulares e 6 faces octogonais
3. a) Sim; uma pirâmide quadrangular.
3. b) o 1º: 4 faces triangulares e uma face quadrangular; o 2º: 6 faces quadrangulares.
Diversificando
Nesta seção, a referência ao trabalho com massa de modelar, independentemente da faixa etária, enriquece o aprendizado, pois requer mobilização dos conhecimentos já construídos sobre as características do sólido que se quer modelar e, assim, consolida e amplia esses conhecimentos.
Oriente os estudantes na execução da receita. Com a massinha, solicite-lhes que construam modelos de prismas e pirâmides. Ao manipular os moldes construídos, elabore duas tabelas, uma para prismas e outra para pirâmides, que organizem os nomes, os números de vértices, de arestas e de faces. Analisando as tabelas, eles devem estabelecer uma relação entre os elementos de cada uma delas.
As atividades do Agora é com você! podem ser feitas em duplas ou trios. A troca de experiências e a necessidade de expor o que pensa favorecem o aprendizado e promovem uma ampliação do repertório dos estudantes acerca do assunto.
Na atividade 1 oriente os estudantes a ampliarem o molde, com base na figura do livro, de modo proporcional. Para isso, oriente-os nesta tarefa.
Ao propor a tarefa, oriente os estudantes sobre o uso de tesouras de pontas arredondadas, que poderão ser utilizadas para o recorte da planificação do tetraedro truncado.
O uso de massinha poderá ser uma ferramenta para responderem às atividades 2 e 3. Oriente os estudantes no manuseio do material utilizado para a confecção da massinha e para modelar e truncar o tetraedro. Por ser um material maleável, não há necessidade de uso de objetos cortantes que possam oferecer algum risco aos estudantes.
As resoluções das atividades 2 e 3 estão no início deste Manual, nas orientações específicas do capítulo 10.