
CAPÍTULO 2 Números racionais

Observe a imagem, leia o texto e responda às questões no caderno.
a) Que números você identifica no texto?
b) Esses números podem ser escritos na fórma de fração?
c) Quais dos números apresentados no texto pertencem ao conjunto dos números racionais?
Em 2021, o estado do Piauí tinha aproximadamente ..3289290 habitantes; isso significa um aumento de 0,25% na população em relação a 2020, segundo o Instituto Brasileiro de Geografia e Estatística (í bê gê É).
Os residentes no Piauí representam cerca de 1,5% de toda a população brasileira, e de todos os habitantes do Piauí, cerca de 26,2% vivem em 160 municípios com menos de 10 mil habitantes, isso é equivalente a .861329 pessoas.
O município de São Raimundo Nonato está entre os 15 municípios mais populosos, com uma população aproximada de 35 mil habitantes em 2021.
1. Conhecendo um pouco mais os números racionais
No texto de abertura, que apresenta dados sobre o estado do Piauí, aparecem números como: 2021, ..3289290, 0,25 e 10 mil.
Você já aprendeu que esses números são exemplos de números racionais, pois também podem ser escritos na fórma de fração.
Neste capítulo, vamos estudar um pouco mais os números racionais e observar que números como ‒.4700, ‒314, 5 e ‒.33000 também são exemplos de números racionais. Considere a situação a seguir.
A tia de Ana pagou 180 reais pelo uniforme de basquete das 5 craques do time. Sabendo que o valor pago pela tia de Ana será dividido igualmente entre as 5 jogadoras, vamos descobrir quanto cada uma estava devendo, efetuando a divisão a seguir.
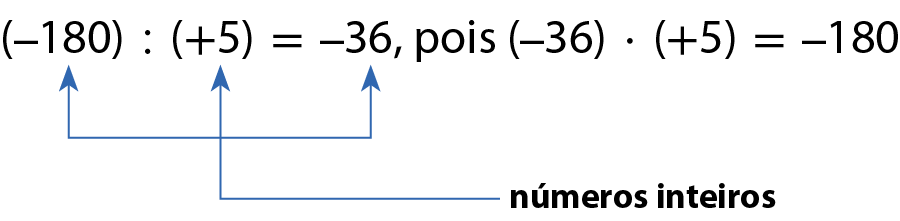
Cada uma delas estava devendo 36 reais para a tia de Ana.
Vemos que, nesse caso, o quociente de (‒180) : (+5) é um número inteiro negativo, uma vez que estamos dividindo números de sinais opostos, e pode ser expresso por uma fração, por exemplo:
Menos 180 sobre mais 5 igual a menos 36 sobre 1.Mais tarde, Ana lembrou que deviam também a inscrição no campeonato, o que elevou a dívida para 207 reais.
Então, Ana efetuou uma nova divisão (‒207) : (+5).
Ana observou que não existe nenhum número inteiro que multiplicado por +5 resulte em ‒207.
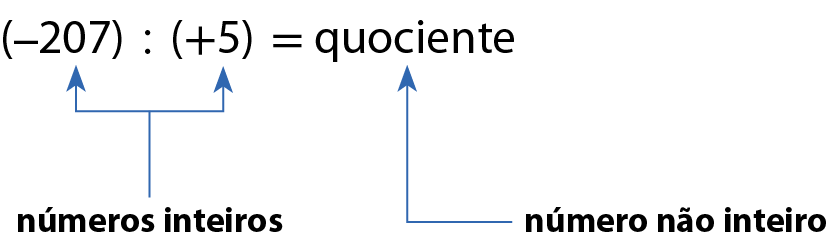
Ela sabe que o quociente de (‒207) : (+5) é um número não inteiro que pode ser expresso por uma fração, por exemplo,
menos 207 quintospor um número misto,
menos 41 inteiros e 2 quintosou, ainda, na fórma decimal:
menos 207 quintos igual menos 414 décimos igual menos 41,4=
menos 207 quintos igual menos 414 décimos igual menos 41,4= ‒41,4.
Então, as meninas descobriram que cada uma delas devia R$ 41,40quarenta e um reais e quarenta centavos para a tia de Ana.
Todo número que pode ser representado por uma fração
fração, numerador: a denominador: bem que a e b são números inteiros,
com b ≠ 0, é um número racional.
Acompanhe exemplos de números racionais.
a) ‒5
b)
9 meiosc) ‒0,75
d)
menos 1 terçoe) 3,2
f)
menos 20 quintosAlguns desses números já estão representados por frações:
9 meios, menos 1 terço, menos 20 quintosTambém podemos escrever os demais na fórma de fração. Observe.
–5 = –
menos 5 igual menos 5 sobre 1–0,75 = –
75 centésimos3,2 =
32 décimosAlém disso, todos esses números podem ser escritos na fórma decimal. Alguns já estão nessa fórma: ‒0,75 e 3,2. Vamos transformar os outros.
No caso das frações, basta dividir o numerador pelo denominador.
‒5 = ‒5,0
9 meios é igual a 4,5
menos 1 terço é igual a menos dízima 0,3, de período 3.
menos 20 quintos igual a menos 4 igual a menos 4,0
Os números ‒5; 4,5; ‒0,75; 3,2 e ‒4 podem ser representados por uma fração cujo denominador é uma potência de 10
menos 5 igual a menos 50 décimos; 4,5 igual a 45 décimos; menos 0,75 igual a 75 sobre 100; 3,2 igual a 32 décimos e menos 4 igual a menos 400 sobre 100.
No caso do número ‒0,333reticências, que é uma dízima periódica, a fórma de fração é
menos 1 terçoEle não pode ser transformado em uma fração decimal.
Observação
▶ Já vimos que podemos indicar uma dízima periódica por um traço sobre o período. Desse modo, o número ‒0,333reticências pode ser indicado por
menos 0 vírgula 3 com traço sobre o 3EXERCÍCIOS PROPOSTOS
Faça as atividades no caderno
1 Considere os quocientes de:
um (‒7) : ( + 4);
dois 5 : (‒9);
três (‒12) : ( + 2).
a) Escreva cada um desses quocientes na fórma de fração.
b) Qual é a fórma decimal desses quocientes?
c) Classifique cada quociente como número inteiro ou número não inteiro.
2 Determine a fórma decimal do número que representa o quociente de cada divisão. Desses números, quais não podem ser representados por frações decimais?
a) 11 : 4
b) (‒5) : 3
c) (‒9) : (‒2)
d) 22 : (‒15)
3 Associe cada número a uma das letras a, B, C ou D para mostrar em que local do quadro você os colocaria.
|
Número racional inteiro |
Número racional não inteiro |
|
|---|---|---|
|
Forma de fração |
A |
B |
|
Forma decimal |
C |
D |
a) 3,51
b) 351,0
c)
menos 18 meiosd) 4,111
e) 4,111reticências
f)
4 quintosg) ‒0, 5
h) ‒2,0
i)
menos 412 quintos4 Dados os números racionais 2,3;
menos 3 sétimos‒8,0;
1 sexto; 2,555reticências; 4,0; ‒1,6 e 0,222reticências, copie no caderno:
a) os números inteiros;
b) os números racionais na fórma de fração;
c) os números racionais na fórma decimal;
d) as dízimas periódicas.
5 Escreva um exemplo de número:
a) racional inteiro;
b) racional natural;
c) racional não inteiro;
d) natural não racional.
6 João calculou a medida do comprimento, em metro, do pátio da escola e a expressou da seguinte maneira: 12,3 métros. Para indicar essa medida por um número inteiro, João fará uma transformação de unidade de medida de comprimento. Como ele poderá fazer isso?

Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Considere uma fração cujo numerador é múltiplo do denominador, ambos números naturais.
Essa fração representa um número racional inteiro ou um número racional não inteiro? Justifique sua resposta.
2. Representação na reta numérica

Já sabemos que os números positivos ficam à direita do zero, e os negativos ficam à esquerda. Além disso, a medida da distância entre dois pontos que correspondem a números inteiros consecutivos é sempre a mesma (na reta a seguir, por exemplo, essa medida é 2 centímetros).

A seguir, vamos representar alguns números racionais na reta numérica.
Vamos marcar nessa reta o ponto que corresponde ao número
1 meio.Como esse número é positivo, o ponto correspondente a ele deve estar à direita da origem (ponto óh, que corresponde ao número zero). Assim, devemos dividir o segmento
segmento OAem duas partes iguais. O ponto M corresponde ao número
1 meio.
Para representar o número
menos 1 meionessa mesma reta, procedemos de modo semelhante, levando em conta, no entanto, que
menos 1 meioé negativo. Então,
menos 1 meiodeverá corresponder a um ponto da reta que fica à esquerda da origem. Assim, devemos dividir o segmento
OA linhaem duas partes iguais. O ponto ême linha corresponde ao número
menos 1 meio
O número
1 meio.é a abscissa do ponto M, e o número
menos 1 meioa abscissa do ponto ême linha.
Os pontos M e ême linha são chamados de pontos simétricos em relação a óh, pois estão à mesma distância de óh; porém um está à direita, e o outro, à esquerda. Dizemos que as abscissas
1 meio.e
Menos meio.são opostas.
Agora, vamos marcar os pontos P e pê linha de abscissas
11 quartos e menos 11 quartos.respectivamente. Como
11 quartos igual 2 inteiros e 3 quartos=
11 quartos igual 2 inteiros e 3 quartos=
2 mais 3 quartos., então
11 quartosé um número que está entre 2 e 3. De modo semelhante, podemos concluir que
Menos 11 quartos.está entre ‒3 e ‒2, pois:
menos 11 quartos=
menos 2 inteiros e 3 quartos=
menos 2 mais menos 3 quartos..
Vamos dividir os segmentos
BC e B linha C linhaem quatro partes iguais. Ao ponto P corresponde o número
11 quartos.e ao ponto pê linha, o número
menos 11 quartosOs pontos P e pê linha são simétricos em relação a óh.

Marquemos, ainda, os pontos de abscissas 1,3 e ‒1,3, ou seja,
13 décimos. Menos 13 décimos.Observe que 1,3 é maior que 1 e menor que 2, e ‒1,3 é menor que ‒1 e maior que ‒2.
Então, basta dividir os segmentos
AB e A linha B linhaem dez partes iguais para marcar os pontos em questão. Na reta, eles estão representados pelos pontos Q e Qʹ .

Observações
▶ Todo número racional pode ser associado a um ponto da reta numérica.
▶ Na reta numérica, dois pontos simétricos em relação à origem óh serão chamados apenas de pontos simétricos para simplificar a notação.
PARA SABER MAIS
Divisão de um segmento em partes iguais
Para dividir um segmento qualquer em determinado número de partes iguais (segmentos congruentes), podemos dividir sua medida por esse número de partes e, utilizando a escala da régua, marcar os pontos de divisão.
Também podemos dividir um segmento por meio de uma construção com régua e compasso. Essa construção geométrica é uma aplicação prática do Teorema de Tales, que será estudado no 9º ano.
Vamos dividir o segmento
segmento ABem sete partes de mesma medida.

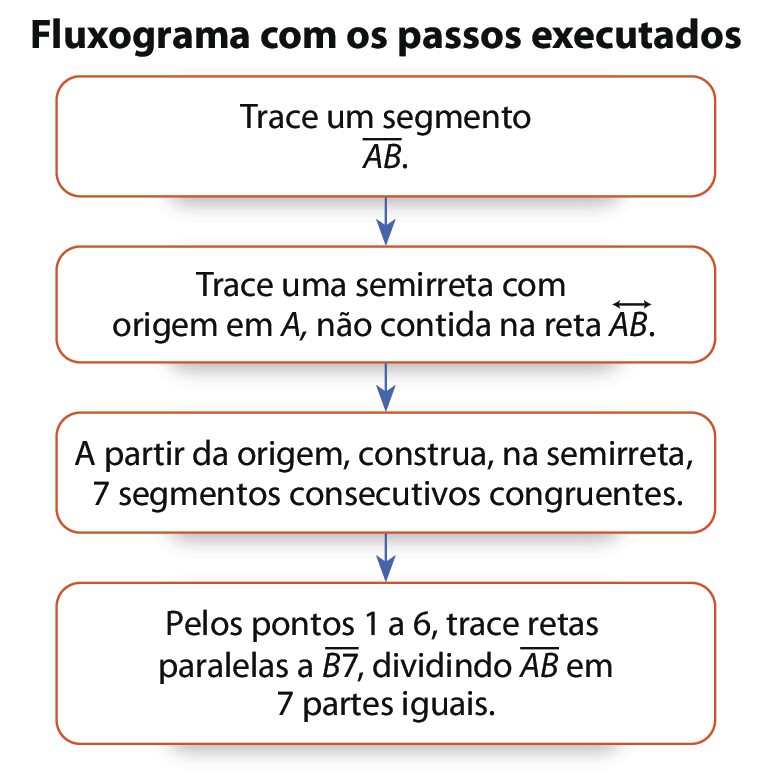
Acompanhe os passos.
1º Inicialmente, traçamos uma semirreta com origem a, conforme a figura a seguir. Nessa semirreta, a partir de a e com uma mesma abertura do compasso, marcamos sete segmentos consecutivos.
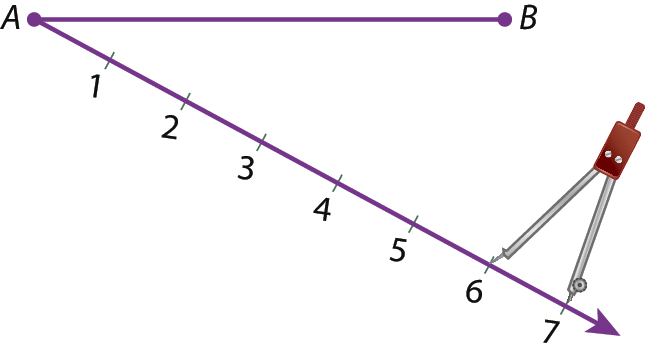
2º Depois, traçamos a reta
reta B 7e as retas paralelas a ela, que passam pelos pontos 1 a 6. Essas paralelas podem ser traçadas fazendo o esquadro deslizar junto à régua. Observe a figura.
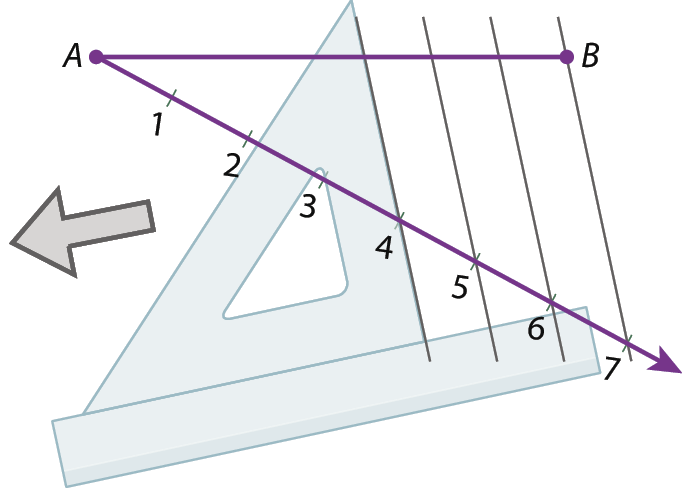
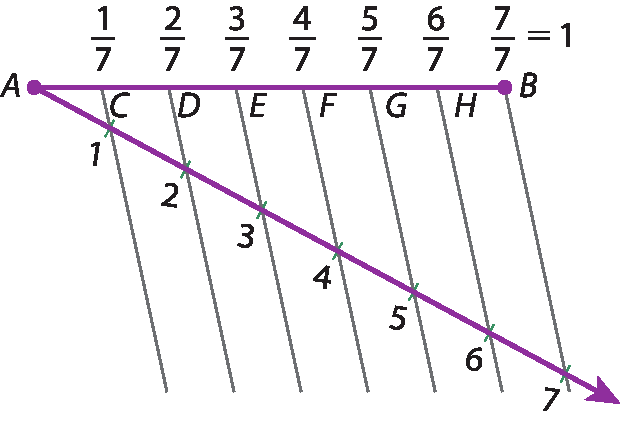
3º Os pontos C, D, ê, F, G e H dividem o segmento
segmento ABem sete partes de mesma medida.
Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
a) Usando régua, compasso e esquadro, trace um segmento qualquer e divida‑o em seis partes iguais.
b) É possível modificar o fluxograma da divisão de um segmento em partes iguais de modo que os passos sirvam para a divisão de qualquer segmento em um número natural n (n > 1) de partes iguais? Converse com o professor e os colegas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
7 Observe a reta numérica.
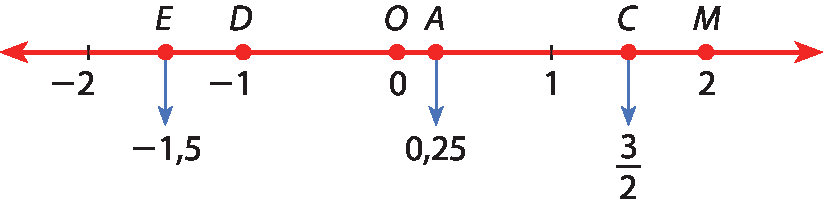
Determine as abscissas dos pontos a, M, D, ê e C.
8 Desenhe uma reta numérica e represente sobre ela os pontos:
• a, B, C e D de abscissas
2 quintos;
Menos 7 meios.;
5 meios.e
Menos 5 quartos, respectivamente;
• E, F, G e H de abscissas ‒2,5; 1,25; 3,5 e ‒0,4, respectivamente.
Descubra quais são os pares de pontos simétricos.
9 Em uma reta numérica, foram assinalados os pontos a, B, C, D e ê, que representam os números ‒1,5;
7 quintos.;
menos 1 quinto.; + 5,7 e ‒5,7, nessa ordem. Assim, é possível concluir que:
a) a está à direita de B ? Por quê?
b) a e C coincidem? Por quê?
c) D e E são simétricos? Por quê?
d) B está à direita dos demais pontos? Por quê?
3. Módulo de um número racional
Sabemos que, em uma reta numérica, é possível determinar a medida da distância do ponto de abscissa zero (origem) a outro ponto qualquer da reta.
A medida da distância de um ponto da reta numérica à origem é o módulo do número que corresponde a esse ponto.
Observe os exemplos a seguir.
a)
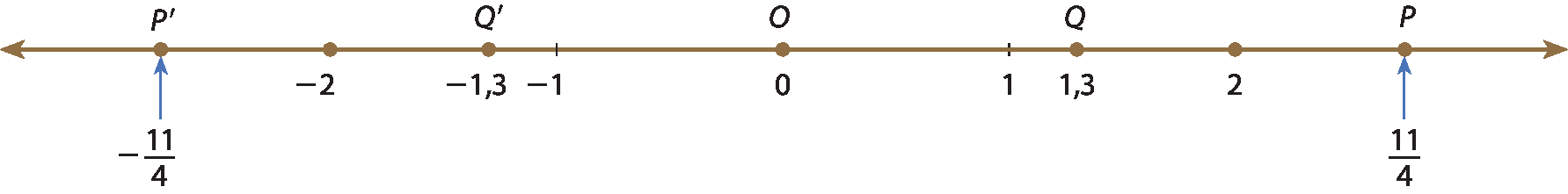
• O módulo de
Menos 11 quartos.(abscissa do ponto pê' ) é
11 quartos.(medida da distância do ponto pê' à origem). Então, como o módulo de
Menos 11 quartos.é indicado por
menos 11 quartospodemos escrever
barra vertical menos 11 quartos barra vertical• O módulo de 1,3 (abscissa do ponto Q) é 1,3 (medida da distância do ponto Q à origem). Então, |1,3| = 1,3.
• O módulo de ‒1,3 (abscissa do ponto Q' ) é 1,3 (medida da distância do ponto Q' à origem). Então, |‒1,3| = 1,3.
b) Se
5 terçosrepresenta a medida da distância de O a um ponto na reta numérica, então a abscissa desse ponto pode ser
menos 5 terços ou 5 terços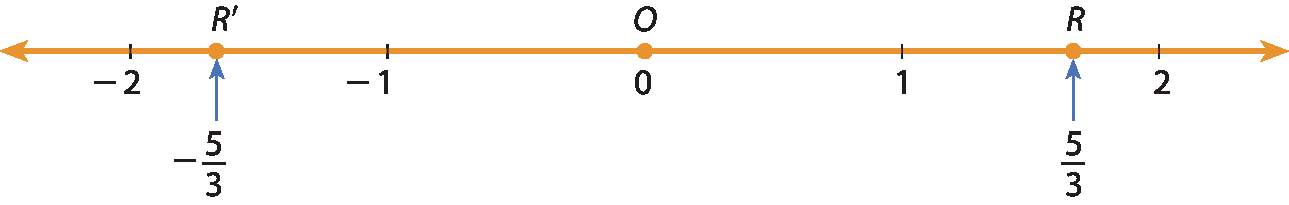
Números que têm o mesmo módulo, porém sinais diferentes, são opostos ou simétricos. Observe alguns números opostos:
•
1 meio.e
menos 1 meio• ‒0,4 e 0,4;
•
menos 2 inteiros e 1 quartoe
2 inteiros e 1 quarto• 3,717171reticências e ‒3,717171reticências
Podemos concluir que, se um número a é oposto de um número b, então b é oposto de a.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
10 Leia, pense e responda no caderno.
a) Qual é o módulo de
menos 3 quintosb) Quanto vale
módulo de menos 14,3c) Se |‒8| representa a medida da distância da origem O a T na reta numérica, qual é a abscissa do ponto T ?
d) Se
módulo de a igual 2 terçosquais são os possíveis valores de a?
e) Se |x | = 1,5, qual é a medida da distância do ponto de abscissa x até a origem?
11 Determine no caderno:
a) o oposto de
7 nonosb) o oposto de
menos 7 nonosc) o oposto de 5,4238;
d) o oposto do oposto de ‒6,72;
e) o oposto de |‒1, 555reticências|;
f) o oposto do oposto de
módulo de menos 6 quintos4. Comparação de números racionais
Já vimos como comparar números inteiros em uma reta numérica. Dados dois números inteiros diferentes, o menor é aquele que, na reta numérica, está à esquerda do outro.
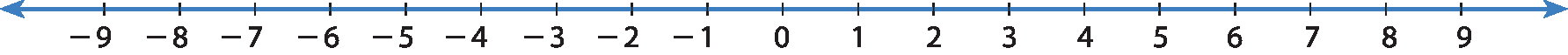
Observe alguns exemplos.
a) 6 > 3
b) 2 > ‒5
c) ‒4 < ‒1
d) ‒2 < 2
e) 0 > ‒8
f) 9 > 0
Agora, vamos aprender a comparar números racionais em uma reta numérica.
Dados dois números racionais diferentes, o menor é aquele que está à esquerda do outro na reta numérica.

Acompanhe os exemplos.
a)
menos 1 vírgula 8 é menor que menos 1 meiob)
menos 1 meio é menor que menos 2c)
3 meios menor que 2 inteiros e 1 terçod) ‒1,8 < 0
A seguir, veremos como comparar números racionais sem a reta numérica.
Comparando números racionais escritos na fórma de fração
Éverton e Lucas pegaram algumas laranjas do pomar e as usaram para fazer suco.
Para fazer o suco, Éverton espremeu 3 metades de uma laranja, e Lucas espremeu 5 metades.
Quem usou mais laranjas?
Quando os denominadores são iguais, basta comparar os numeradores. Como exemplo, vamos comparar os números
3 meios 5 meiosComo 3 < 5, ou seja, três metades são menores do que cinco metades, temos:
3 meios é menor que 5 meiosPortanto, Lucas usou mais laranjas do que Éverton.
Quando os denominadores são diferentes, reduzimos as frações ao mesmo denominador comum e então comparamos os numeradores, como no caso anterior.
Vamos comparar as frações
2 terços é menor que 3 quartosReduzindo‑as ao mesmo denominador, obtemos:
2 terços
=
oito 12 avose
3 quartos=
nove 12 avosComo
8 é menor que 9então
8 12 avos é menor que 9 12 avose, portanto,
2 terços é menor que 3 quartosDo mesmo modo, comparamos números racionais negativos escritos na fórma de fração.
Acompanhe os exemplos.
a)
menos 1 terço é maior que menos 3 quintospois ‒1 > ‒5.
b)
menos 2 terços é menor que menos 3 quintospois
menos 10 15 avos é menor que menos 9 15 avosComparando números racionais escritos na fórma decimal
Inicialmente, consideramos os sinais dos números dados: se eles forem diferentes, já sabemos que um número positivo é sempre maior que um número negativo; se os sinais forem iguais, comparamos a parte inteira. E se as partes inteiras forem iguais, comparamos a parte decimal.
Observe os exemplos.
a) 2,35 > ‒5,827 O primeiro número (2,35) é positivo, e o segundo (‒5,827) é negativo.
b) 2,35 < 2,6 A parte inteira é igual, mas o segundo número tem 6 décimos, enquanto o primeiro tem 3 décimos; portanto, 3 décimos < 6 décimos.
c) ‒2,35 > ‒2,6 A parte inteira é igual, mas o primeiro número tem 3 décimos negativos, e o segundo tem 6 décimos negativos; portanto, 3 décimos negativos > 6 décimos negativos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
12 Qual é maior, qual é menor? Responda usando os sinais > ou < .
a)
menos 5 terços menor que 2 nonosb)
2 terços 2sétimosc)
Menos 1 quarto Menos 5 sextosd)
Menos 1 oitavo Menos 1 meioe)
Menos 5 sextos Menos 2 quintosf)
1 inteiro e 1 quarto 3 inteiros e 1 quinto13 Identifique o maior número racional em cada caso.
a) ‒3,2 ou ‒5,4
b) ‒7,12 ou ‒7,10
c) 1,2 ou ‒10,6
d) ‒4,52 ou ‒4,5204
14 Papai fez o bolo preferido da família para a sobremesa de domingo. Para servi‑lo, repartiu-o em 24 pedaços iguais. Eu comi
1 12 avos.do bolo, minha irmã e papai comeram
1 oitavo.do bolo cada um, e mamãe comeu
1 sexto.do bolo. Quem comeu mais bolo?
15 Em cada item, compare os números racionais usando os sinais <, = ou >.
a)
módulo de menos zero vírgula 6 maior que módulo de menos 1 quintob)
módulo de menos 5 sextos módulo de 0,83 com período 3c)
módulo de menos meio módulo de menos 5 terçosd)
módulo de 5 quartos módulo de menos 3,2e)
módulo de menos 3 oitavos maior que módulo de zerof)
módulo de menos zero vírgula 6, com período 6, maior que módulo de zero vírgula 616 Escreva os números de cada item em ordem crescente.
a)
9 meios2,1; 0,65;
5 terçosb)
menos 11 meios 1 sexto0,1
c)
5 oitavos 7 terços módulo de menos 9 quartos módulo de menos 2,34 5 oitavos módulo de menos 9 quartos 7 terços módulo de menos 2,3417 Marina e Carolina foram mergulhar em Fernando de Noronha (Pernambuco). Em determinado momento, Marina se encontrava a ‒13,5 metros em relação ao nível do mar, e Carolina, por sua vez, estava a ‒11,6 metros.
a) Qual delas estava mais próxima da superfície?
b) Represente na fórma de fração a medida da profundidade em que cada uma se encontrava.
TRABALHANDO A INFORMAÇÃO


Gráficos e porcentagens

Queda em taxas de vacinação deve ‘ressuscitar’ doenças erradicadas do país
O índice de vacinação brasileiro regrediu, no ano passado [2020], a taxas de cobertura similares às dos anos 1980. A pandemia é apenas um dos fatores que explicam o fenômeno, já que a cobertura vacinal cai há pelo menos seis anos.
“Sem dúvida, a desinformação é a principal causa da queda da cobertura vacinal. As pessoas – incluindo aí vários profissionais de saúde – desconhecem os calendários vacinais para adolescentes, gestantes, adultos, idosos e imunodeprimidos. Some‑se a isso o desserviço prestado pelas fake news e eis o resultado desastroso que estamos vendo”, analisa Rosana Richtmann, infectologista e diretora do Comitê de Imunização da ésse bê í (Sociedade Brasileira de Infectologia). reticências
O melhor exemplo disso ocorreu com o retorno do sarampo, que reapareceu após anos de erradicação. “Ele voltou por causa das baixas coberturas vacinais”, afirma Renato Kfouri, diretor da ésse bê í ême (Sociedade Brasileira de Imunizações).
A proteção contra a doença está inclusa na vacina tríplice viral, que protege também contra caxumba e rubéola. Ela é dada de fórma gratuita em duas doses pelo sús (Sistema Único de Saúde) nos postos de saúde.
Fonte: MADEIRO, C. Queda em taxas de vacinação deve ‘ressuscitar’ doenças erradicadas do país. Portal VivaBem uól, 29 setembro 2021. Disponível em: https://oeds.link/MuK3zN. Acesso em: 17 maio 2022.
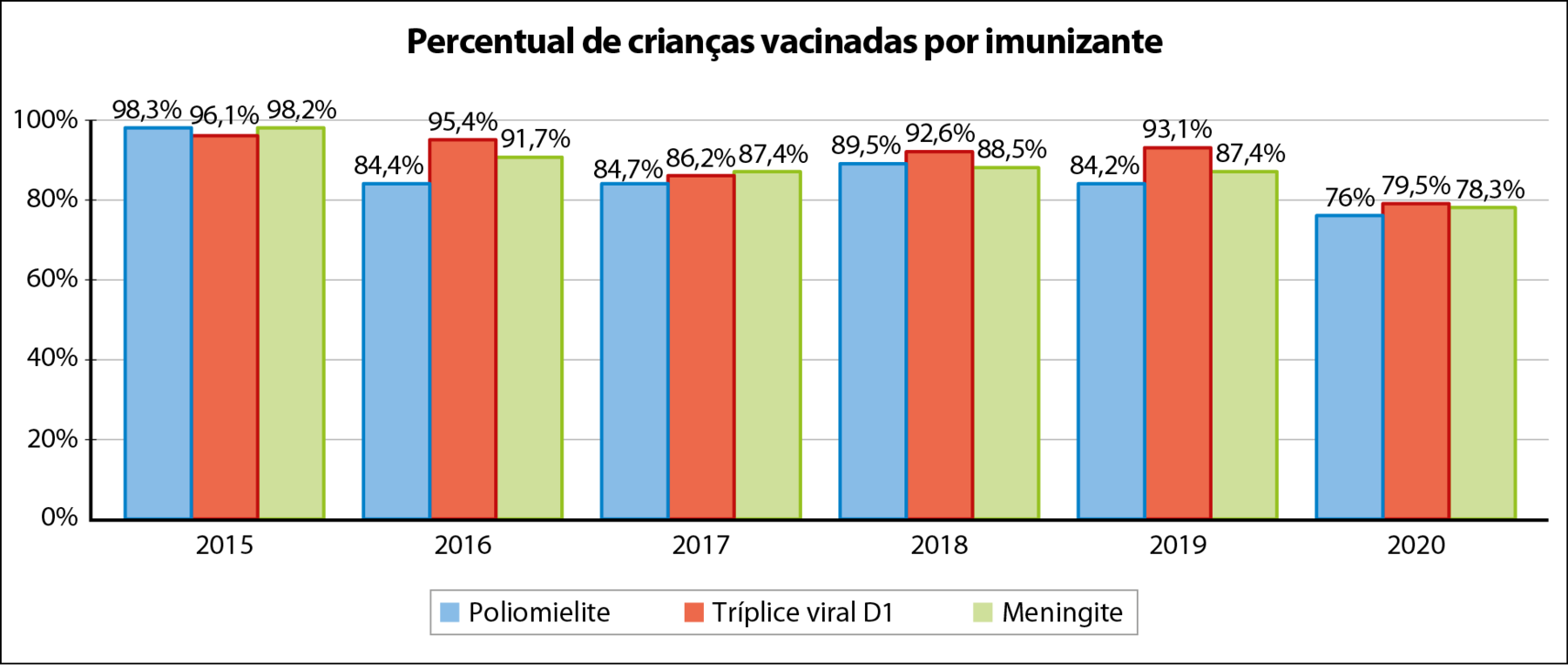
Observe no gráfico o percentual de crianças vacinadas em cada ano, por imunizante:
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Considerando a informação apresentada, responda às questões.
a) Qual é a importância da vacinação infantil?
b) Que ações podem ser tomadas por agentes de saúde para ampliar a cobertura vacinal infantil?
c) Qual foi a variação percentual da população vacinada em 2015 e em 2020 pelo imunizante da poliomielite?
d) E dos demais imunizantes, no mesmo período?
2 Faça uma pesquisa com seus colegas para saber qual foi a última vacina que eles tomaram e com quantos anos isso ocorreu.
• Para fazer sua pesquisa, estipule a quantidade de colegas que serão entrevistados.
• Elabore um questionário para que os colegas possam responder à sua pesquisa. Nesse questionário, você pode solicitar-lhes somente as informações necessárias à sua pesquisa.
• Após a coleta dos dados, organize as informações em uma tabela ou em um gráfico.
• Apresente o resultado obtido ao professor e aos colegas de turma.
5. O máximo divisor comum (ême dê cê)
A tabela mostra o número de livros encomendados pelas livrarias a, B e C a determinada editora.
|
Livraria |
Número de livros |
|---|---|
|
A |
96 |
|
B |
108 |
|
C |
132 |
Dados obtidos nas livrarias.
O encarregado de preparar as encomendas recebeu orientação de colocar o maior número possível de livros em cada pacote, de modo que todos os pacotes tivessem a mesma quantidade de livros.
Acompanhe o que o encarregado fez para determinar a quantidade de livros que deveria colocar em cada pacote.
Inicialmente, determinou os divisores naturais de cada um dos números da tabela:
• divisores de 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96;
• divisores de 108: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108;
• divisores de 132: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132.
Note que os números 1, 2, 3, 4, 6 e 12 são divisores de 96, de 108 e de 132, ou seja, eles são divisores comuns de 96, 108 e 132.
Assim, para que os pacotes tivessem a mesma quantidade de livros, o encarregado poderia colocar 1, 2, 3, 4, 6 ou 12 livros em cada pacote. Como foi determinado que cada pacote deveria ter o maior número possível de livros, então cada pacote deveria conter 12 livros.
O que o encarregado fez foi encontrar o maior divisor comum dos números 96, 108 e 132.
O maior divisor comum de dois ou mais números é chamado de máximo divisor comum e representado pelas iniciais ême dê cê.
Na situação descrita, o máximo divisor comum de 96, 108 e 132 é 12, que se indica por:
ême dê cê(96, 108, 132) = 12
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
18 Um marceneiro tem duas ripas de madeira, uma de 120 centímetros de medida de comprimento e outra de 180 centímetros, e deve cortá‑las em pedaços iguais para montar uma pequena estante. Sabendo que os pedaços devem ser do maior tamanho possível, qual deve ser a medida do comprimento de cada pedaço?

19 Determine:
a) os divisores de 60;
b) os divisores de 72;
c) os divisores comuns de 60 e 72;
d) o maior desses divisores comuns.
20 Determine:
a) ême dê cê(8, 10)
b) ême dê cê(40, 50)
c) ême dê cê(9, 12, 15)
d) ême dê cê(16, 56, 80)
21 Em uma classe há 28 meninos e vinte e uma meninas. A professora quer formar grupos só de meninas ou só de meninos, com a mesma quantidade de estudantes e com a maior quantidade possível.
a) Quantos estudantes terá cada um desses grupos?
b) Quantos grupos de meninas podem ser formados?
c) E quantos grupos de meninos?
22

Hora de criar – Elabore um problema envolvendo divisores comuns de 150 e 275. Troque de caderno com um colega para um resolver o problema do outro. Depois, destroquem para corrigi‑los.
Encontrando o ême dê cê pela decomposição em fatores primos
Vimos como calcular o ême dê cê de dois ou mais números naturais conhecendo seus divisores. Agora, vamos estudar como aplicar o processo da decomposição em fatores primos para o cálculo do ême dê cê de um número.
Como exemplo, vamos calcular o ême dê cê dos números 280 e 300. Inicialmente, decompomos cada número em fatores primos:
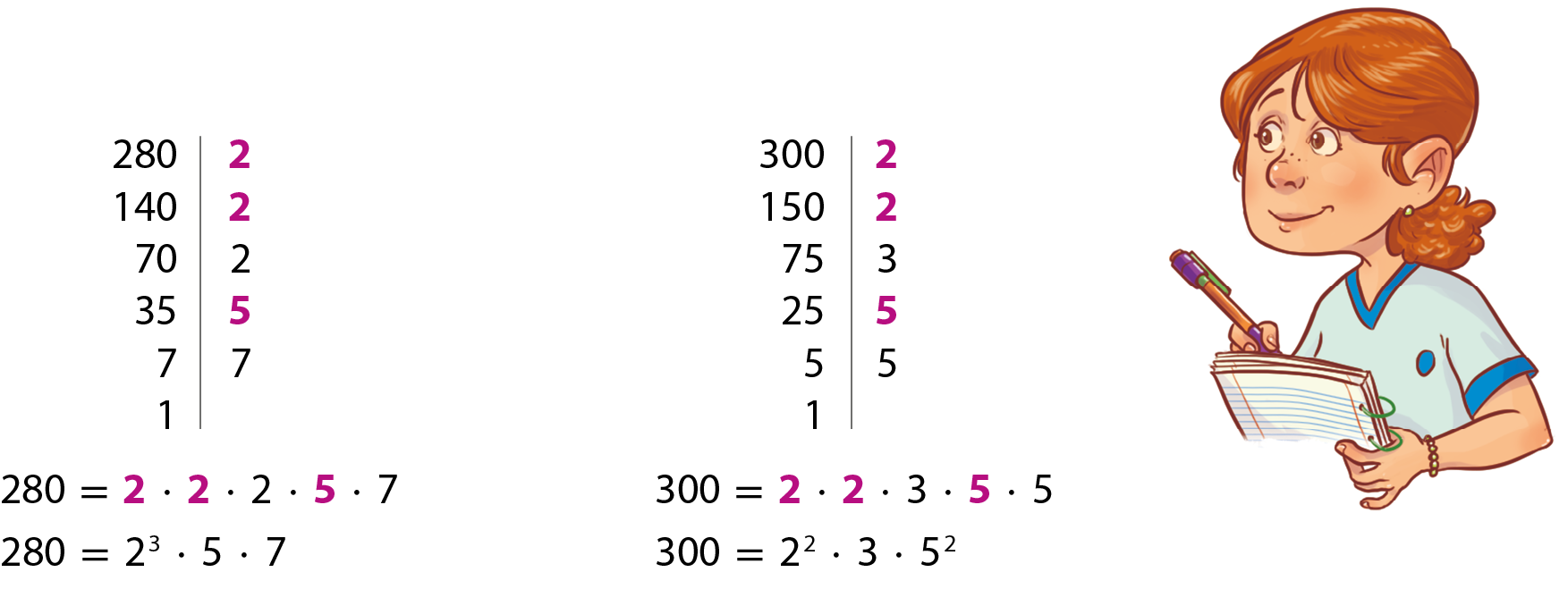
Os fatores primos comuns, destacados no exemplo, são 2 ⋅ 2 e 5, ou seja, 22 e 5 (é preciso considerar os fatores comuns que apresentem o menor expoente para que eles sejam divisores dos dois números). Multiplicando esses fatores, obtemos o mdc desses dois números. Então:
ême dê cê(280, 300) = 22 ⋅ 5 = 4 ⋅ 5 = 20
Ainda como exemplo, vamos calcular o ême dê cê dos números 120, 252 e 150.
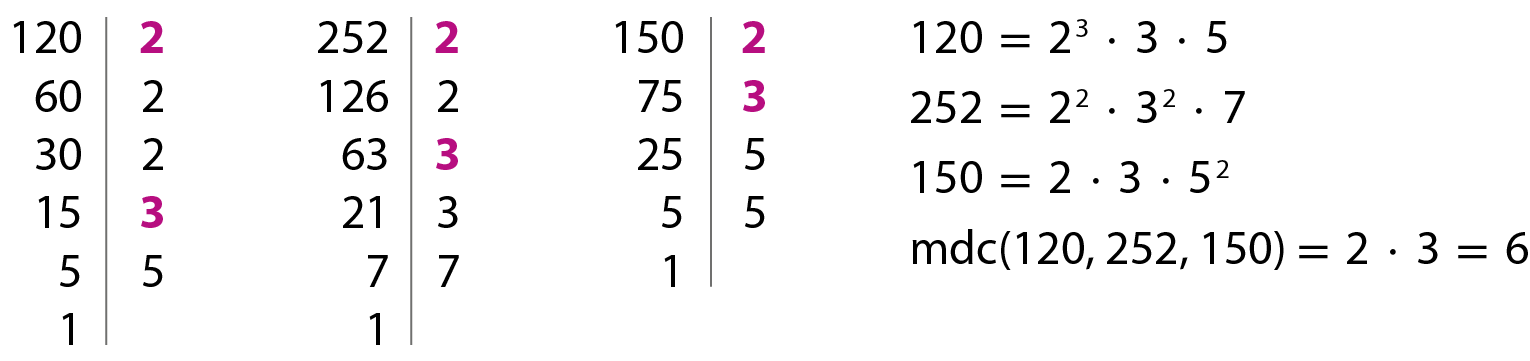
Observação
▶ Dois ou mais números que têm o máximo divisor comum igual a 1 são chamados de números primos entre si.
Por exemplo, 8 e 15 são primos entre si, pois o ême dê cê(8, 15) = 1. Observe:
• divisores de 8: 1, 2, 4, 8
• divisores de 15: 1, 3, 5, 15
Note que o único divisor comum desses números é o 1.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
23 Considerando a = 23 ⋅ 3 ⋅ 5, b = 22 ⋅ 32 ⋅ 7 e c = 24 ⋅ 32 ⋅ 7, calcule:
a) ême dê cê(a, b)
b) ême dê cê(a, c)
c) ême dê cê(b, c)
d) ême dê cê(a, b, c)
24 Aplicando a decomposição em fatores primos, determine o ême dê cê entre os números de cada item a seguir.
a) 32 e 48;
b) 60 e 72;
c) 75 e 125;
d) 70, 90 e 120;
e) 28, 70 e 84.
25 Em uma loja de tecidos, a balconista Carla conversa com o gerente Augusto:

Carla pensou e, em seguida, calculou com exatidão a medida do comprimento de cada retalho.
Determine essa medida.
26 Verifique se em cada caso os números são primos entre si. Justifique sua resposta.
a) 25 e 30
b) 40 e 21
c) 7 e 11
d) 28 e 35
27 Alexandre é o irmão mais velho de Regina e de Guilherme. Regina tem 12 anos, e Guilherme, 10. As idades dos três irmãos são números primos entre si. Determine a idade de Alexandre, sabendo que é um número múltiplo de 7 e menor que 25.
28

Junte‑se a um colega e façam o que se pede.
Cada um de vocês escolhe alguns números primos, repetidos ou não, e, multiplicando‑os, obtém três números compostos. A seguir, deve calcular o ême dê cê das três duplas de números compostos possíveis de formar com os números que o colega elaborou.
6. O mínimo múltiplo comum (ême ême cê)
Considere a seguinte situação.
Um feirante sempre leva para a feira a mesma quantidade de ovos de galinha para vender. Ele sabe que, colocando os ovos em embalagens para 12 ou para 18 ovos, não sobra nem falta ovo. Vamos calcular qual é o menor número de ovos que satisfaz essas condições.

Inicialmente, determinamos os múltiplos de cada um desses números:
• múltiplos de 12: 0, 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, reticências
• múltiplos de 18: 0, 18, 36, 54, 72, 90, 108, 126, reticências
Os números que são múltiplos de 12 e, também, de 18 são chamados de múltiplos comuns de 12 e 18. São eles: 0, 36, 72, reticências
Dos múltiplos comuns, diferentes de zero, o menor número é o 36. Assim, o menor número de ovos é 36.
O menor múltiplo comum de dois ou mais números, diferente de zero, é chamado de mínimo múltiplo comum e representado pelas iniciais ême ême cê.
Na situação apresentada, vimos que o mínimo múltiplo comum de 12 e 18 é 36, que se indica por:
ême ême cê(12, 18) = 36
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
29 Em certo país, as eleições para presidente ocorrem a cada 4 anos, e para senador, a cada 8 anos. Em 2022, essas eleições coincidiram. Determine os anos das quatro próximas vezes em que as eleições voltarão a coincidir.
30 Determine:
a) os múltiplos do número 6;
b) os múltiplos do número 9;
c) os múltiplos comuns dos números 6 e 9;
d) o menor desses múltiplos comuns, diferente de zero.
31 O dono da cantina da escola gosta de complicar as coisas. Quando lhe perguntaram sua idade, ele respondeu:
“Tenho mais de 40 anos, menos de 60 e minha idade é um múltiplo de 3 e de 8”. Qual é a idade dele?
32 Na fila em que entrei para comprar ingresso para assistir a um filme, havia 33 pessoas na minha frente. Notei que, a cada 3 pessoas, uma usava alguma peça de roupa branca; a cada 5 pessoas, uma usava óculos; e a cada 4, uma estava com um saquinho de pipoca nas mãos. Determine quantas pessoas dessa fila:
a) estavam com uma peça de roupa branca e usavam óculos.
b) estavam com uma peça de roupa branca e seguravam um saquinho de pipoca.
c) seguravam um saquinho de pipoca e usavam óculos.
d) estavam com uma peça de roupa branca, usavam óculos e seguravam um saquinho de pipoca.
Encontrando o mmc pela decomposição em fatores primos
Vimos como calcular o ême ême cê de dois ou mais números naturais conhecendo os múltiplos de cada um desses números. Existem, porém, outros processos que possibilitam calcular o ême ême cê entre dois ou mais números naturais. Vamos conhecer dois desses processos.
1º) Decompondo cada número separadamente
Esse processo consiste em decompor cada número em fatores primos.
Como exemplo, vamos determinar o ême ême cê dos números 280 e 300. Inicialmente, decompomos cada número em fatores primos:
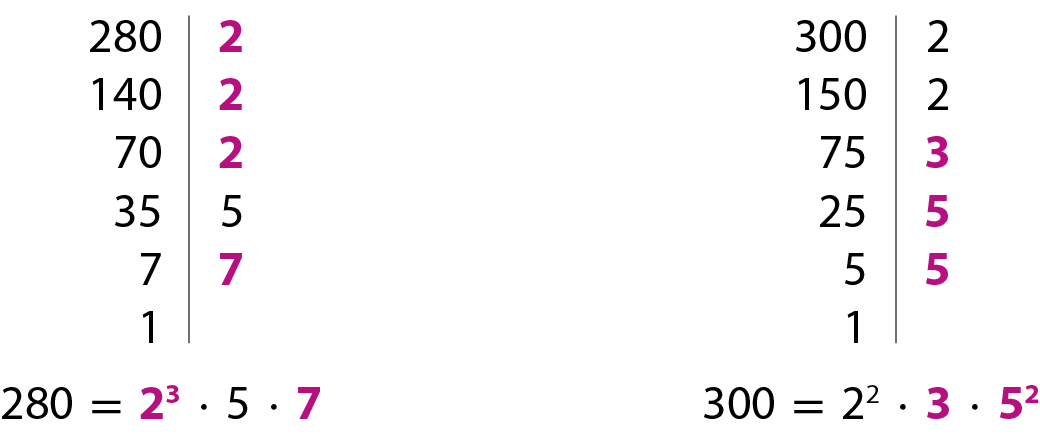
Multiplicamos os fatores primos comuns e não comuns e, entre os fatores de bases iguais, escolhemos aquele que apresenta maior expoente, pois procuramos o múltiplo de 280 e 300 ao mesmo tempo. Então: ême ême cê(280, 300) = 23 ⋅ 3 ⋅ 52 ⋅ 7 = 8 ⋅ 3 ⋅ 25 ⋅ 7 = .4200.
2º) Decomposição simultânea
Esse processo consiste em decompor simultaneamente os números em fatores primos.
Vamos determinar o ême ême cê dos números 280 e 300. Primeiro, decompomos simultaneamente os números em fatores primos:
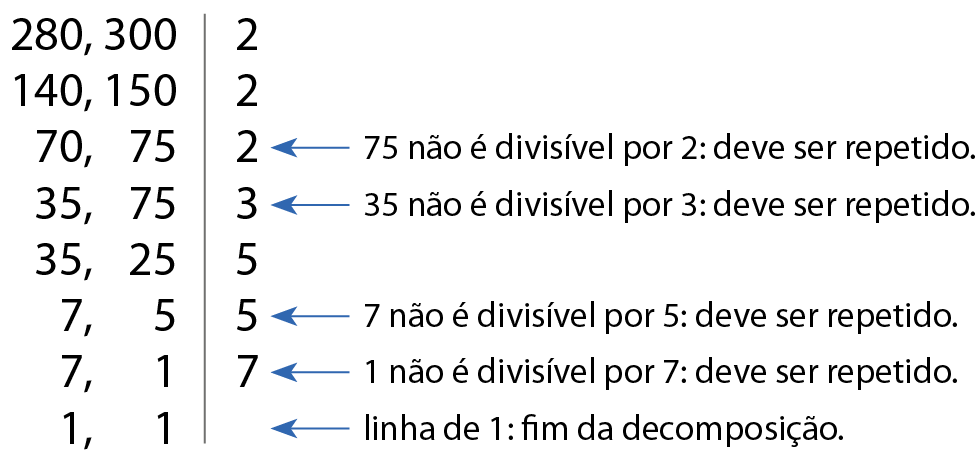
Em seguida, basta efetuar a multiplicação dos fatores obtidos.
Então, ême ême cê(280, 300) = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 7 = .4200.
Ainda como exemplo, vamos decompor simultaneamente os números 120, 252 e 300 em fatores primos:
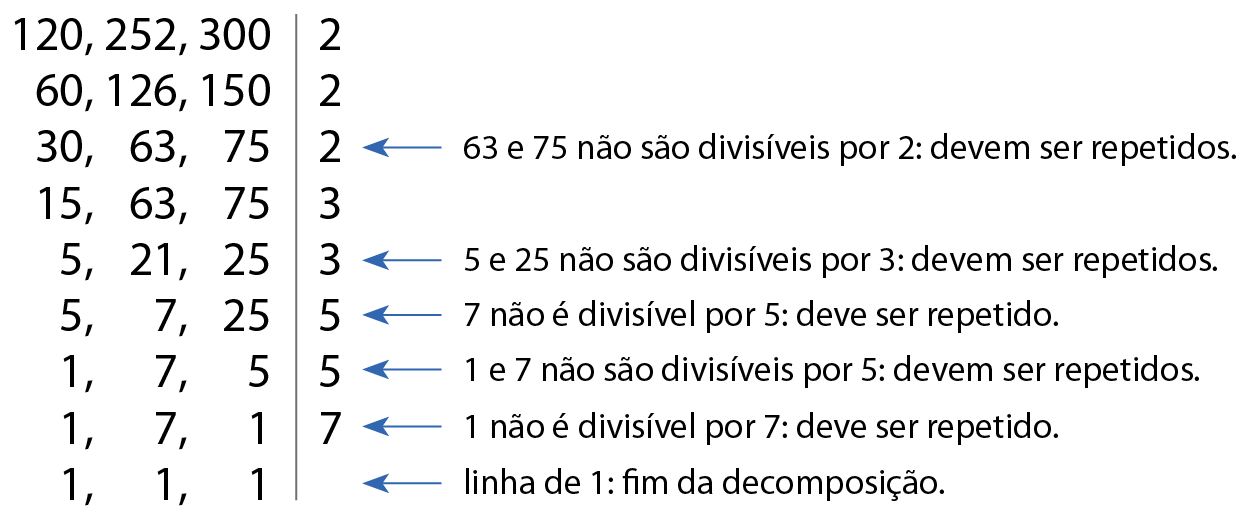
Em seguida, basta efetuar a multiplicação dos fatores obtidos. Assim:
ême ême cê(120, 252, 300) = 2 ⋅ 2 ⋅ 2 ⋅ 3 ⋅ 3 ⋅ 5 ⋅ 5 ⋅ 7 = .12600
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
33 Juliana dá uma volta em uma pista de atletismo em 4 minutos, e Marina em 5 minutos. Em determinado momento, após dar algumas voltas, as duas estarão correndo lado a lado. Depois de quantos minutos elas voltarão a se encontrar?
34 Considerando a = 23 ⋅ 32, b = 22 ⋅ 5 e c = 2 ⋅ 33, calcule:
a) ême ême cê(a, b)
b) ême ême cê(a, c)
c) ême ême cê(b, c)
d) ême ême cê(a, b, c)
35 Calcule pelo processo da decomposição em fatores primos o mínimo múltiplo comum dos números:
a) 25 e 30;
b) 22 e 99;
c) 36 e 48;
d) 150, 60 e 75.
36 Sônia trouxe de sua chácara uma cesta de laranjas para as irmãs Flávia e Fabiana. Flávia contou as laranjas de 6 em 6 e não sobrou nenhuma, e Fabiana as contou de 8 em 8 e, também, não sobrou nenhuma. Quantas laranjas continha a cesta, sabendo que o número delas era maior que 90 e menor que 100?
37 Usando o processo da decomposição simultânea em fatores primos, determine o mínimo múltiplo comum dos números:
a) 40 e 60;
b) 45 e 120;
c) 72, 45 e 54;
d) 15, 20 e 25.
38 De uma rodoviária, partem ônibus para João Pessoa (Paraíba) a cada 3 horas, para Natal (Rio Grande do Norte) a cada 6 horas e para Recife (Pernambuco) a cada 8 horas. Em determinado dia, às 7 horas da manhã, partiram, ao mesmo tempo, ônibus para essas três cidades. Após quantas horas essa coincidência voltou a ocorrer?
39 Em um sítio, há uma rua de laranjeiras e, ao seu lado, uma rua de limoeiros. Os pés de laranja são plantados a cada 4 metros, e os pés de limão, a cada 6 metros. No início das ruas, foi plantado um pé de laranja na frente de um pé de limão. De quantos em quantos metros isso acontece?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Escreva a representação decimal dos números
3 quartos 4 terços2 Dos números a seguir, qual deles pode indicar quantos irmãos uma pessoa tem? Por quê?
a)
menos 10 meiosb)
7 nonosc)
5 quartos.d)
fração, numerador: menos 5 denominador: 1e)
Menos 1 inteiro e 3 quartos3 Entre os números racionais 3,5;
Menos 2 terços.4,333reticências;
12 terços.3 e ‒4,5, escreva:
a) os números racionais inteiros;
b) os números racionais não inteiros;
c) os números que estão na fórma decimal;
d) as dízimas periódicas.
4 Observe a reta numérica a seguir.

Determine:
a) a abscissa do ponto M;
b) a abscissa do ponto N;
c) a abscissa do ponto Q;
d) a abscissa do ponto P que divide o segmento
segmento NQem duas partes iguais.
5 Responda.
a) Qual é o módulo de
Menos 1 quintob) Se |m| = 0,8, quais são os possíveis valores de m ?
6 Em cada item, compare os números racionais usando os sinais >, < ou =.
a) |‒2,5| e 2,5
b) 3,426 e 3,4181
c) ‒11,3 e ‒2,51
d)
Menos 3 oitavos Menos 1 meioe) 0,12 e
1 quinto.f)
Módulo de menos 2 vírgula 1e
Módulo de 0 vírgula 37 Responda.
a) Qual é o oposto do inverso de
Menos 2 quintos.b) Qual é o inverso do módulo de
menos 5 terçosc) Qual é o inverso do oposto de |‒2, 3| na fórma de fração?
8 Todos os quocientes a seguir são positivos, e os números a, b, c e d são diferentes de zero.

Descubra os sinais de a, b, c e d.
9 O número inteiro que pode ser colocado entre os pontos assinalados na reta numérica é:
a) 0.
b) ‒1.
c) ‒2.
d) ‒3.

10

Reúna-se com um colega e respondam ao que se pede.
a) Qual produto é maior: (28 ⋅ 42) ou ême dê cê(28, 42) ⋅ ême ême cê(28, 42)?
b) Qual produto é menor: (63 ⋅ 36) ou ême dê cê(63, 36) ⋅ ême ême cê(63, 36) ?
c) Comparem os produtos: (21 ⋅ 40) e ême dê cê(21, 40) ⋅ ême ême cê(21, 40) .
d) Escolham dois números naturais a e b não nulos e calculem os produtos: (ei ⋅ b) e ême dê cê(ei, b) ⋅ ême ême cê(ei, b) . O que se pode concluir sobre esses produtos?
e) Como vocês fariam para obter o ême dê cê(ei, b), com a e b não nulos, conhecendo os valores de ême ême cê(ei, b) e (ei ⋅ b)?
11 Fiz trezentas e trinta e seis balas de coco e duzentas e cinquenta e duas balas de mel. Quero separá‑las em pacotes, colocando em cada pacote o mesmo tipo e a mesma quantidade de balas. Qual é o maior número possível de balas em cada pacote? Quantos pacotes de bala obterei?
12 Hoje, Joana e Antônia se encontraram no cinema que costumam frequentar. Joana vai a cada 18 dias, e Antônia, a cada 24 dias. Daqui a quantos dias as duas amigas se encontrarão novamente nesse cinema?

VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Seja um número racional na fórma
fração, numerador: a denominador: bcom a e b inteiros. Se a for um número negativo, e b for positivo, então:
a)
fração, numerador: a denominador: bé positivo.
b)
fração, numerador: a denominador: bé negativo.
c)
fração, numerador: a denominador: bnão é positivo nem negativo.
d) não podemos afirmar nada sobre
fração, numerador: a denominador: b2 A mãe de Ana levou a filha e três amigos ao cinema. O valor total dos ingressos das crianças foi de R$ 62,80sessenta e dois reais e oitenta centavos. Qual foi o valor pago por ingresso, sabendo que todos tinham o mesmo preço?
a) R$ 15,00quinze reais
b) R$ 15,50quinze reais e cinquenta centavos
c) R$ 15,70quinze reais e setenta centavos
d) R$ 15,80quinze reais e oitenta centavos
3 Márcia representou alguns números na reta numérica, mas errou em uma dessas representações. Qual foi o número representado de modo incorreto?

a)
Menos 4 vírgula 1b)
Menos 2 vírgula 8c)
Menos 0 vírgula 5d)
3 vírgula 64 Que número corresponde ao oposto de 0,15?
a)
15 décimosb)
Menos 3 vinte avosc)
menos 3 quintosd) 0,015
5 Qual das desigualdades a seguir é verdadeira?
a)
5 oitavos Menos 1 meiob)
Menos 11 sétimos 15 sétimosc)
3 quintos. 3 meiosd)
Menos 1 meio Menos 1 quarto6 Amanda, Bruno, Camila e Denis foram mergulhar. Em certo momento, Amanda estava a ‒12,5 métros do nível do mar, Bruno estava a ‒10,2 métros, Camila, a ‒9,4 métros e Denis, a ‒13,9 métros.Quem estava mais próximo da superfície?
a) Amanda
b) Bruno
c) Camila
d) Denis
7 Rosa mora sozinha em uma cidade a 200 quilômetros de seus sobrinhos Roberto, Mário e Rosana. Para evitar que a tia Rosa fique muito tempo só, seus sobrinhos combinaram de visitá‑la da seguinte fórma: Roberto costuma visitá‑la a cada 12 dias, Mário, a cada 20 dias, e Rosana, a cada 18 dias. Supondo que eles se encontraram hoje na casa da tia Rosa, daqui a quantos dias será o próximo encontro dos três sobrinhos?
a) 120 dias
b) 150 dias
c) 180 dias
d) 200 dias
8 Quais são os fatores primos obtidos ao decompor o número 924?
a) 2, 3, 5 e 13
b) 3, 5, 7 e 11
c) 3, 7 e 19
d) 2, 3, 7 e 11
9 Dois números decompostos em fatores primos são expressos da seguinte maneira:
23 ⋅ 3 ⋅ 5 e 22 ⋅ 32 ⋅ 7
Qual é o produto de fatores primos que representa o mínimo múltiplo comum desses números?
a) 2 ⋅ 3 ⋅ 5 ⋅ 7
b) 22 ⋅ 3 ⋅ 5 ⋅ 7
c) 23 ⋅ 32 ⋅ 5 ⋅ 7
d) 25 ⋅ 33 ⋅ 5 ⋅ 7
10 Uma confeiteira tem 450 gramas de chocolate ao leite e 270 gramas de chocolate branco para fazer um doce. Qual é a quantidade máxima de doces que ela pode fazer, utilizando a mesma quantidade dos dois chocolates em cada doce?
a) 15
b) 90
c) 30
d) 270
11 Qual é o mínimo múltiplo comum entre os números 45, 15 e 60?
a) 5
b) 90
c) 15
d) 180
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir:
a) O que é um número racional? Dê 4 exemplos.
b) Construa uma reta numérica e represente os números: ‒3; ‒1,6; ‒0,5; 0;
1 quartoe 2,5.
c) Quando dois números racionais são opostos ou simétricos? O que há em comum entre eles?
d) Como você compara números racionais?
e) Qual estratégia você utiliza para calcular o ême dê cê entre dois números? E o ême ême cê? Você pode descrever passo a passo sua estratégia ou por meio de um fluxograma.
DIVERSIFICANDO
Corrida dos números primos
Número de participantes: 2, 3 ou 4 jogadores
Material:
• Tabuleiro a seguir, reproduzido ampliado em cartolina ou outro material.
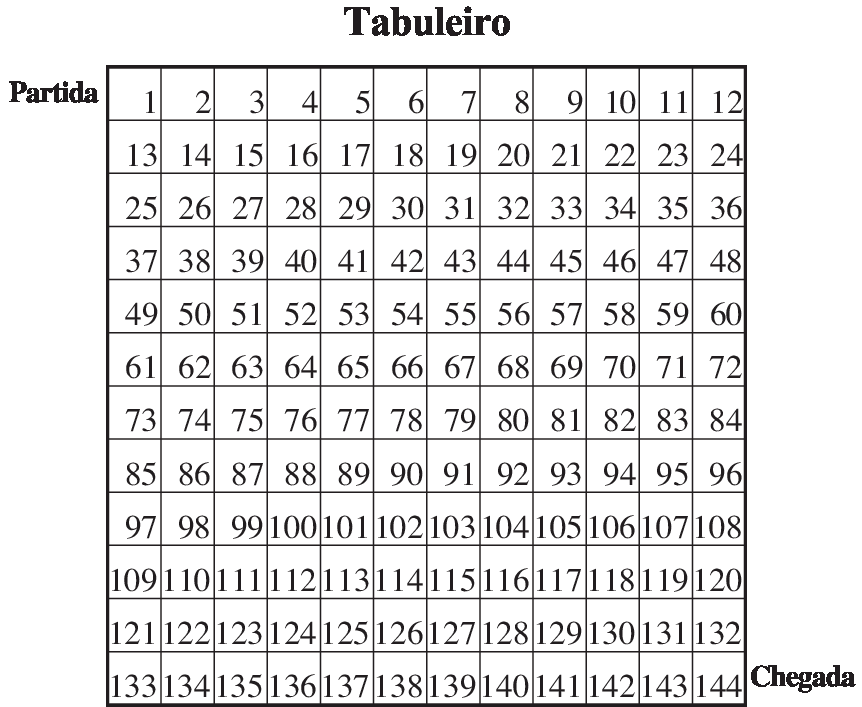
• Dois dados de 6 faces.
• Marcadores diferentes, um para cada jogador (podem ser miçangas, botões etcétera).

Regras:
• Cada jogador lança os dois dados. Quem conseguir a maior soma começa o jogo.
• Cada jogador, alternadamente, lança os dois dados. Marca no tabuleiro a casa correspondente à soma das faces viradas para cima.
• Da segunda jogada em diante, ao resultado dos dados deve ser adicionado o valor da casa onde o marcador se encontra.
• Quem cair em uma casa com um número primo deve levar seu marcador para a casa que apresenta o dobro desse número. Se o dobro do número não existir no tabuleiro, o jogador deve permanecer onde está.
• Se a soma das faces viradas para cima ultrapassar o que falta para chegar ao final, o jogador leva seu marcador para a última casa.
• Quem primeiro alcançar a última casa vence o jogo.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
• Com seu parceiro de jogo, analisem a situação a seguir.
Janaína e Carlos estão brincando de Corrida dos números primos, e o próximo a jogar é Carlos. O marcador de Carlos está na casa 68, e o de Janaína, na casa 123. Observem a ilustração que mostra como está o jogo e respondam à questão proposta.

Carlos ainda tem alguma chance de ganhar o jogo?