
CAPÍTULO 4 Ângulos

Observe, leia e responda no caderno.
a) Nesta fotografia, é possível associar a imagem das fitas com a ideia de ângulo. Quantos ângulos essas fitas determinam?
b) Todos os ângulos representados pelas fitas têm um vértice em comum. Qual é esse vértice?
c) Além dos ângulos mais fáceis de observar nas fitas, podemos destacar outros ângulos nessa imagem?
Na fotografia é possível analisar uma das coreografias realizada pelas atletas com a fita, em que podemos identificar a ideia de ângulo.
A fita é um aparelho composto por uma vareta presa a uma fita de seda ou material semelhante. [...]
Vista como o aparelho mais plástico da ginástica rítmica, a fita é usada para criar uma ampla gama de figuras no espaço durante os exercícios, como serpentinas, espirais e figuras em oito. [...]
Fonte: DICIONÁRIO Olímpico. Disponível em: https://oeds.link/KKY4jg. Acesso em: 9 junho 2022.
Mais do que aparecer nas fitas em um belo final de coreografia, ângulo é um conceito matemático de grande importância, empregado em exercícios obrigatórios da ginástica rítmica.
1. Ângulos e seus elementos
Inúmeras situações do dia a dia nos remetem à ideia de ângulo: quando viramos uma esquina, quando montamos uma tábua de passar roupas, quando olhamos as horas em um relógio de ponteiros ou quando observamos a inclinação do telhado de uma casa.
Nas fotografias a seguir, os destaques dão a ideia de ângulo.




Observe os exemplos.
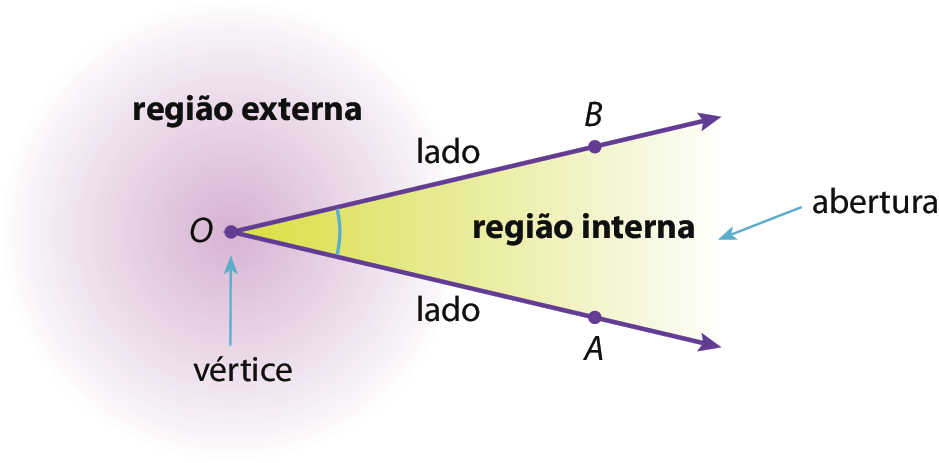
Ângulo
Símbolo. Ângulo AOB.de vértice óh e lados
Semirreta OAe
Semirreta OB.
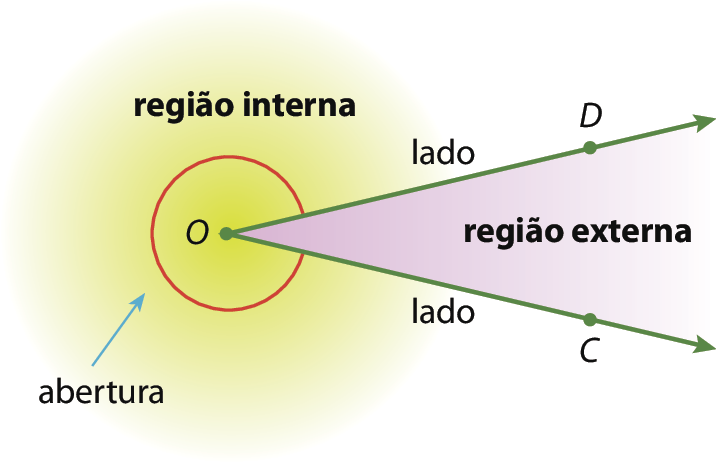
Ângulo
Símbolo. Ângulo COD.de vértice óh e lados
Semirreta OCe
Semirreta OD.
Note que a região interna é a região delimitada por semirretas, que contém a indicação de sua abertura. A outra região é a região externa.
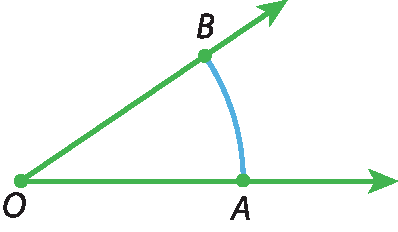
Ângulo nulo, ângulo de uma volta e ângulo raso
Considere o ângulo
Símbolo. Ângulo AOB..
Imagine o ponto B se deslocando sobre o arco
ABno sentido dos ponteiros do relógio (sentido horário). Ele se aproxima mais e mais do ponto a, até coincidir com o ponto a.
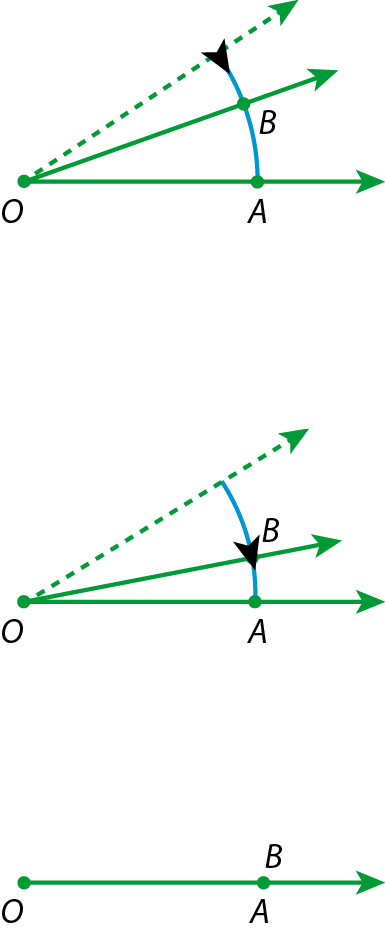
As duas semirretas têm todos os pontos em comum, ou seja, são coincidentes. Elas formam um ângulo nulo.
O ângulo nulo é formado por duas semirretas coincidentes.
Imagine o ponto B se deslocando sobre o arco
ABno sentido contrário ao dos ponteiros do relógio (sentido anti‑horário). Ele se move mais e mais até dar uma volta completa e coincidir com o ponto a.
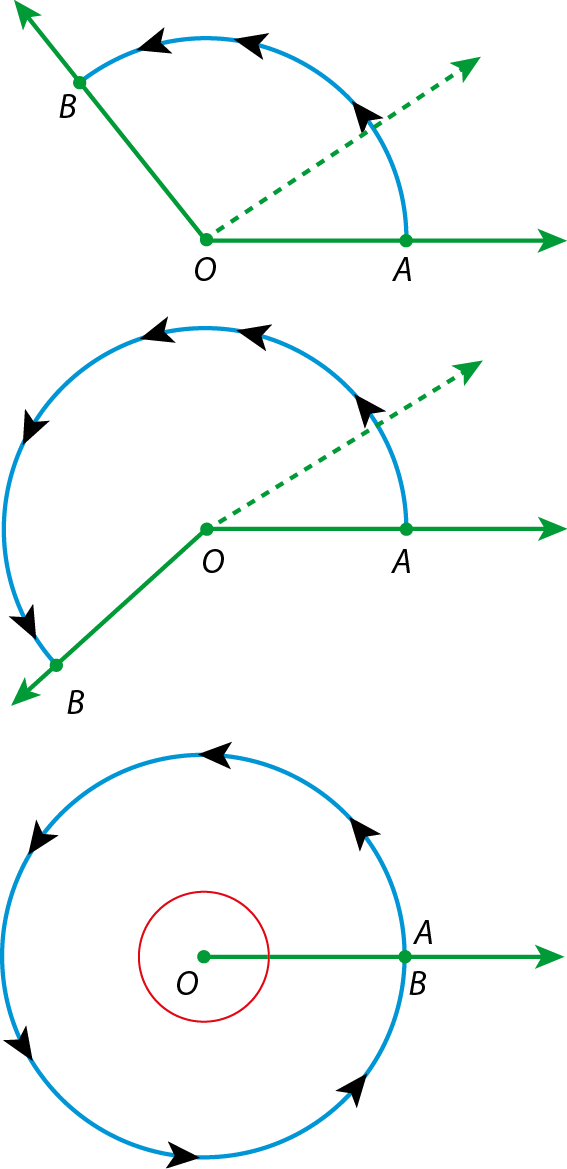
Quando
Semirreta OBcoincidir com
Semirreta OA, obteremos um ângulo de uma volta. Para diferenciá‑lo do ângulo nulo, assinalamos a abertura com um arco.
Observe o ângulo
Símbolo. Ângulo AOB.a seguir.
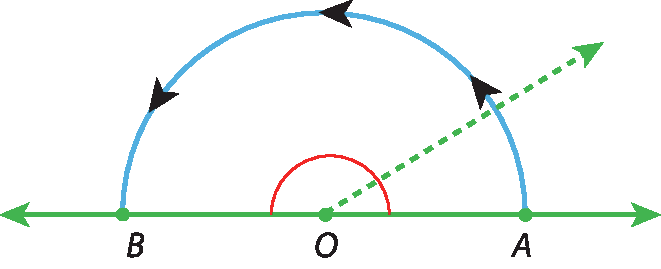
O ângulo raso ou ângulo de meia-volta formado por duas semirretas opostas.
2. Medida de um ângulo
Sabemos que um ângulo pode ser medido e que o grau, representado pelo símbolo pequeno círculo sobrescrito, é uma unidade de medida de ângulos.
Observe novamente a representação de um ângulo raso.

O ângulo
Símbolo. Ângulo AOB.tem medida igual a 180graus. Se dividirmos esse ângulo em 180 ângulos menores de mesma medida, cada ângulo obtido terá medida igual a 1grau.

Também vimos que o transferidor pode ser usado para medir ângulos e que ele está dividido em medidas de 1grau.
Vamos relembrar como proceder para medir ângulos usando um transferidor.
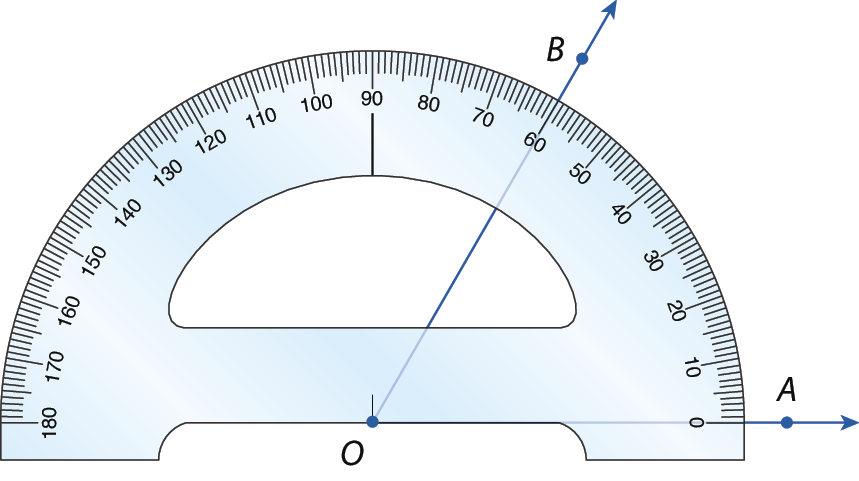
• O centro do transferidor deve ser disposto sobre o vértice do ângulo.
• Uma das semirretas (na figura,
Semirreta OA) que formam o ângulo deve ficar alinhada com o ponto central e com a indicação do ângulo de 0° do transferidor.
• A outra semirreta (na figura,
Semirreta OB) estará sob a marca do transferidor que indica a medida do ângulo.
A medida do ângulo
B O Aé 60graus, que indicamos da seguinte maneira:
A medida do ângulo B O A é igual a 60 graus.Os submúltiplos do grau são o minuto e o segundo. Indicamos 1 minuto por 1linha e 1 segundo por 1aspas.

Observe a relação entre o grau e seus submúltiplos:
• 1grau = 60minutos, ou seja, 1 minuto equivale a
Um sessenta avos.do grau;
• 1' = 60segundos, ou seja, 1 segundo equivale a
Um sessenta avos.do minuto.
Observação
▶ Lembre‑se de que, quanto à sua medida, um ângulo pode ser reto (medida igual a 90graus), agudo (medida entre 0grau e 90graus) ou obtuso (medida entre 90graus e 180graus).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Nesta figura, podemos observar três ângulos.
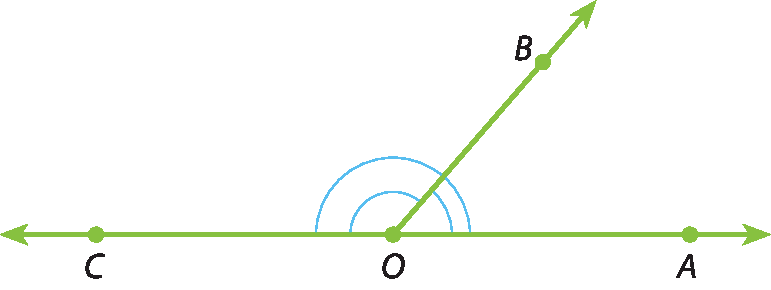
a) Quais são esses ângulos?
b) Com um transferidor, meça os ângulos da figura.
c) Qual deles é ângulo raso?
d) Qual deles é ângulo reto? Qual é obtuso? E qual é agudo?
2 O ângulo segundo o qual uma pessoa vê um objeto é chamado ângulo visual. Esse ângulo depende do tamanho do objeto e de sua distância em relação ao observador.
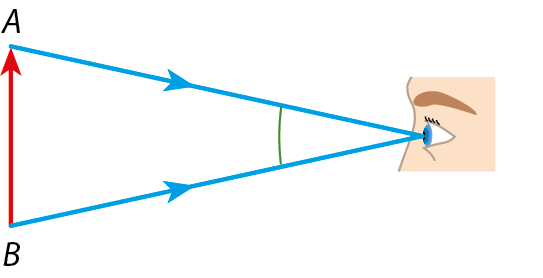
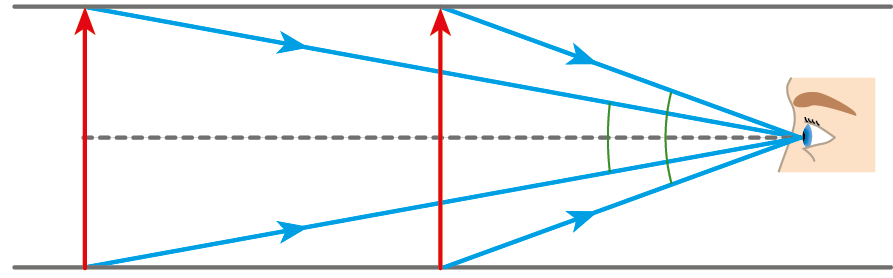
O ângulo visual pode ser um ângulo raso? Justifique sua resposta.
3 Trace uma reta e marque sobre ela dois pontos distintos, a e B. Use um transferidor para construir um ângulo de 42graus com vértice em a, com um dos lados sendo a semirreta
Semirreta AB, e outro ângulo de 42graus com vértice em B, com um dos lados sendo a semirreta
Semirreta BA, de modo que obtenha um polígono.
a) Que polígono você obteve?
b) Como é classificado esse polígono quanto aos lados?
4

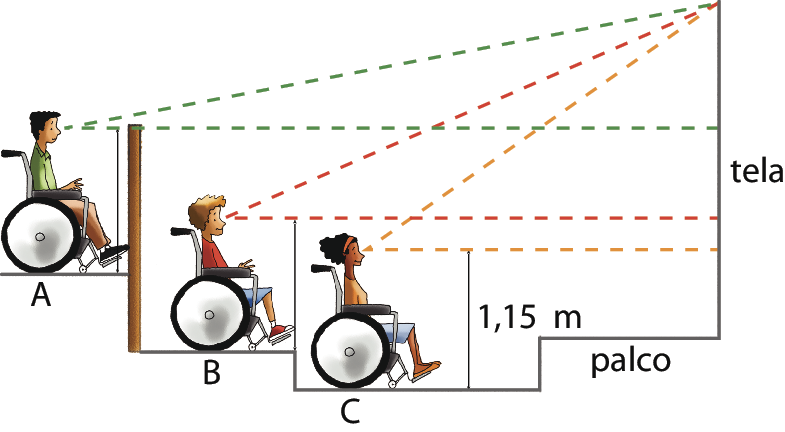
Segundo a Associação Brasileira de Normas Técnicas (á bê eni tê), os cinemas devem reservar lugares para pessoas usuárias de cadeira de rodas de acordo com a regra a seguir:
Pessoas em Cadeira de Rodas (pê cê érre) precisam de previsão de espaços onde possam estacionar convenientemente e acompanhar com conforto os eventos do auditório. Para tanto, os espaços devem atender à seguinte regra:
A localização dos espaços deve ser calculada traçando-se um ângulo visual de 30graus a partir do limite superior da boca de cena até a linha do horizonte visual (éle agá), com a altura de 1,15 métro do piso.
Quando existir anteparo em frente aos espaços para pê cê érre, sua altura e distância não podem bloquear o ângulo visual de 30graus, medido a partir da linha visual padrão, com altura de 1,15 métro do piso até o limite inferior da tela ou local do palco onde a atividade é desenvolvida.
Fonte: á bê eni tê êni bê érre 9050. Acessibilidade a edificações, mobiliário, espaços e equipamentos urbanos. Disponível em: https://oeds.link/b5svDJ. Acesso em: 19 maio 2022.
a) Entre as ilustrações a, B e C, qual delas está de acordo com essa regra? Justifique sua resposta.
b) Além da regra citada, há outras que os cinemas devem seguir para facilitar o acesso de pessoas em cadeira de rodas, como a instalação de rampas e a garantia de rotas de fuga acessíveis. Converse com os colegas de turma sobre o que mais é importante haver nos cinemas para facilitar o acesso das pessoas nessa condição.
c) Você costuma ir ao cinema? Em caso afirmativo, observe se essas regras são respeitadas. Depois, escreva um relato com suas observações.
5 Vitória está participando de uma brincadeira de caça ao tesouro e recebeu um mapa como o representado a seguir.
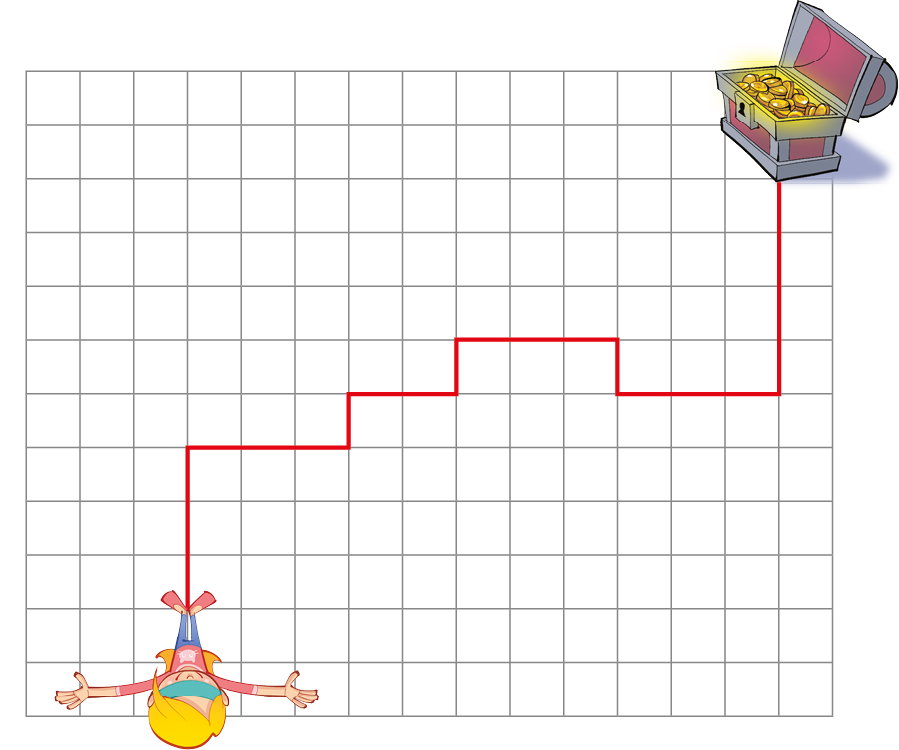
Sabendo que os lados de cada quadradinho da malha medem 1 métro, descreva o caminho que Vitória deverá seguir para encontrar o tesouro.
6

Hora de criar – Crie um mapa indicando uma trajetória como a do exercício anterior e represente‑a em uma folha de papel quadriculado. Junte‑se a um colega e, sem mostrar o mapa criado por você, descreva‑o para que o colega represente seu mapa em uma folha de papel quadriculado também. Em seguida, faça o mesmo com o mapa criado pelo seu colega. Comparem as representações e verifiquem se há diferença entre elas. Caso haja, expliquem por que vocês acham que elas ocorreram.
3. Ângulos congruentes
Observe uma fotografia de nado sincronizado, em que as atletas tentam formar ângulos congruentes com os braços.

Agora, atente para estes ângulos.
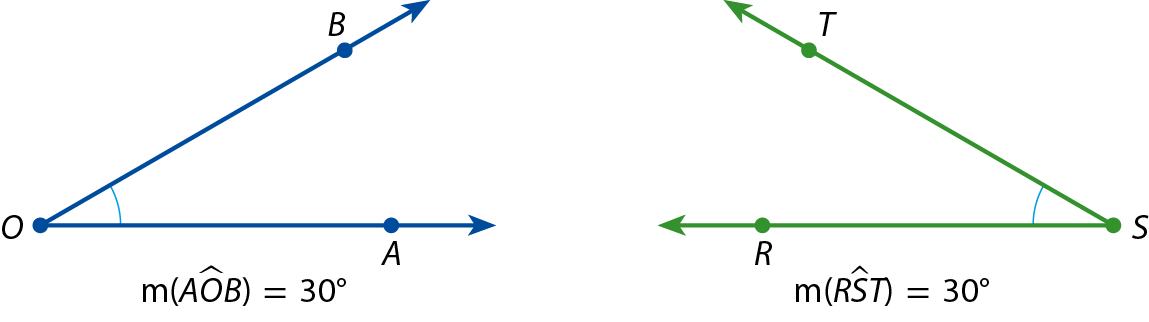
Como
Símbolo. Ângulo AOB.e
Símbolo. Ângulo RST.têm a mesma medida, dizemos que eles são ângulos congruentes. Indicamos que
Símbolo. Ângulo AOB.e
Símbolo. Ângulo RST.são ângulos congruentes da seguinte maneira:
(lemos: “o ângulo
Símbolo. Ângulo AOB.é congruente ao ângulo
RST”)
Dois ângulos são congruentes quando têm mesma medida.
Construção de ângulos congruentes

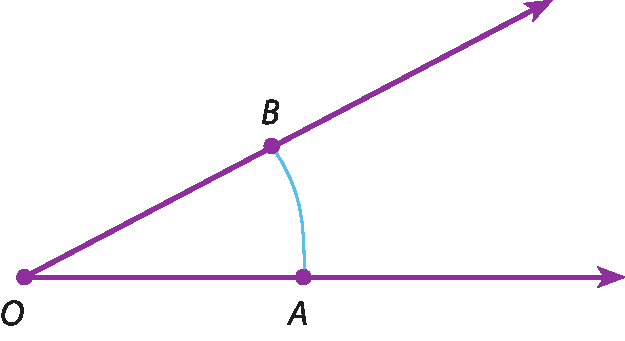
Acompanhe a construção do ângulo
Símbolo. Ângulo DEF.
Traçamos uma semirreta de origem E.
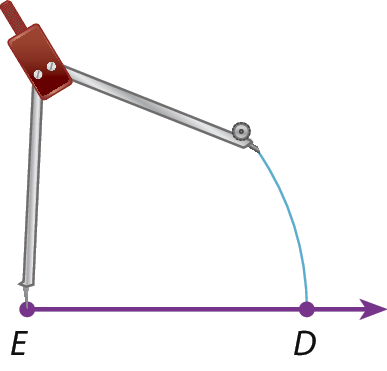
Colocamos a ponta‑seca do compasso em E e, com uma abertura de medida OA, traçamos um arco obtendo o ponto D.
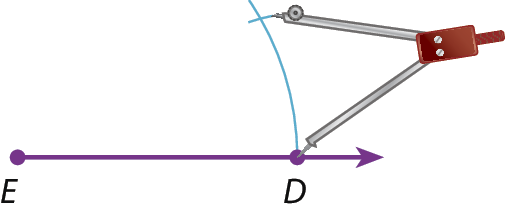
Colocamos a ponta‑seca do compasso em D e, com uma abertura de medida AB, marcamos F no arco traçado.
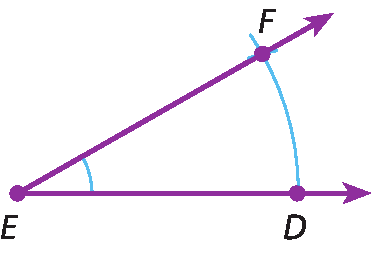
Traçamos a semirreta
Semirreta EFO ângulo
Símbolo. Ângulo DEF.construído é congruente ao ângulo
Símbolo. Ângulo AOB.dado.
Observe que o ponto éfe foi marcado de modo que a abertura de medida dê éfe fosse igual à abertura de medida A bê. Logo, os ângulos têm a mesma abertura e, portanto, são congruentes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
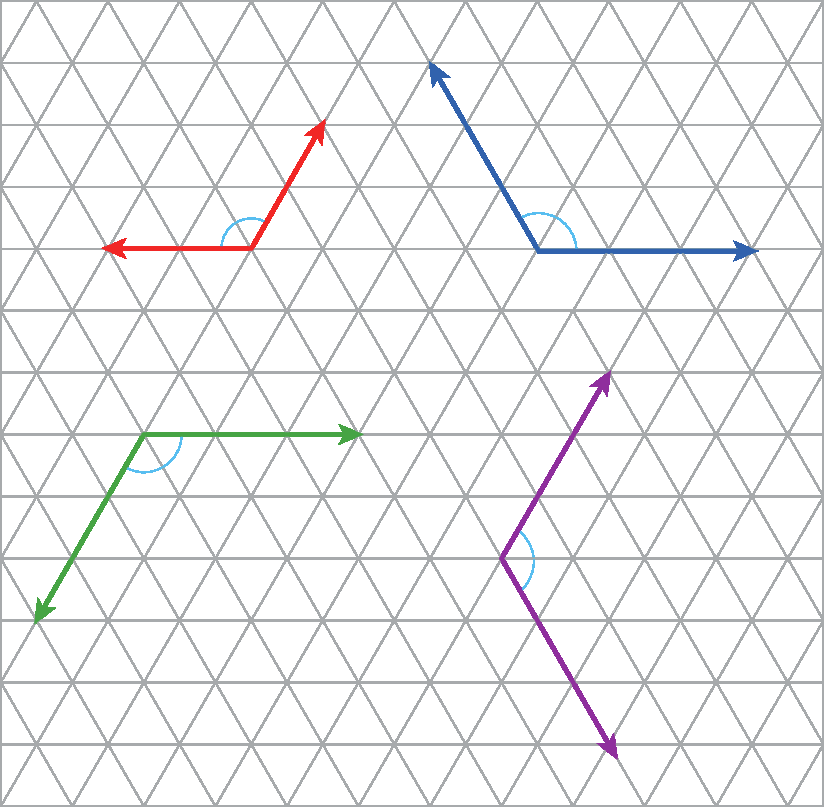
7 O que se pode dizer a respeito dos ângulos construídos na malha triangular?
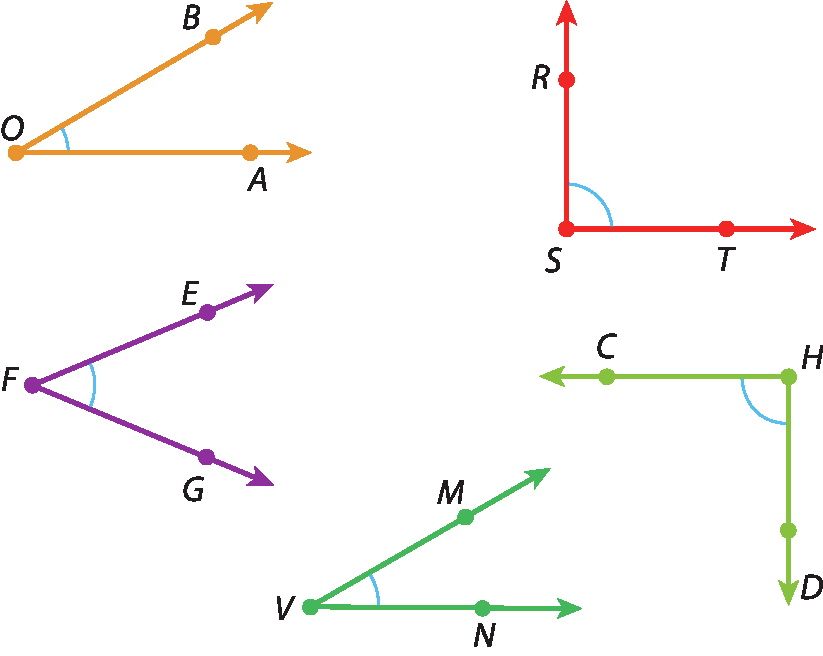
8 Verifique quais são os pares de ângulos congruentes. Registre a resposta no caderno.
9 Construa um fluxograma com os passos a serem seguidos para a construção de ângulos congruentes.
10 Na figura, o ângulo
Símbolo. Ângulo AOB.está dividido em seis ângulos congruentes.
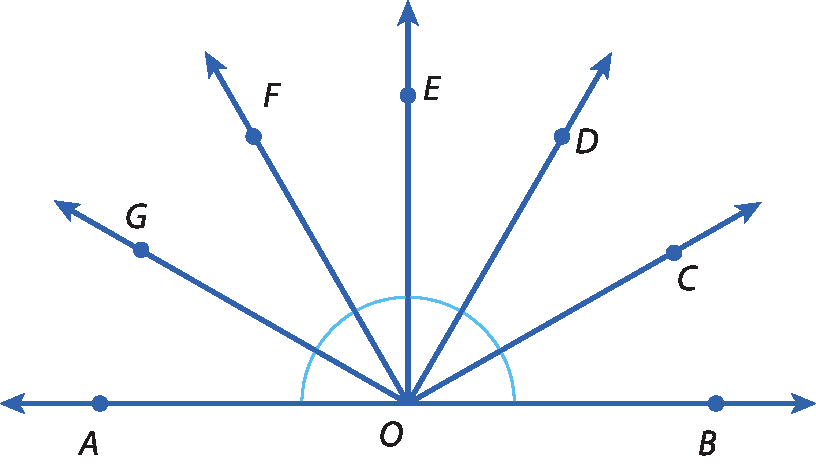
Nessas condições, no caderno, classifique as sentenças em falsas ou verdadeiras.
a)
Ângulo BOC, símbolo de congruência (sinal de igualdade e um símbolo de til em cima), ângulo CODb)
Ângulo BOD, símbolo de congruência (sinal de igualdade e um símbolo de til em cima), ângulo DOFc)
Ângulo COE, símbolo de congruência (sinal de igualdade e um símbolo de til em cima), ângulo AOFd)
Ângulo COD, símbolo de congruência (sinal de igualdade e um símbolo de til em cima), ângulo EOGe)
Ângulo COA, símbolo de congruência (sinal de igualdade e um símbolo de til em cima), ângulo BOGf)
Ângulo DOF, símbolo de congruência (sinal de igualdade e um símbolo de til em cima), ângulo AOE11 Construa, no caderno, com régua e compasso, um ângulo congruente ao ângulo dado em cada caso.
a)
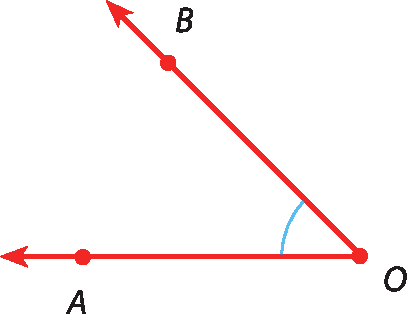
b)
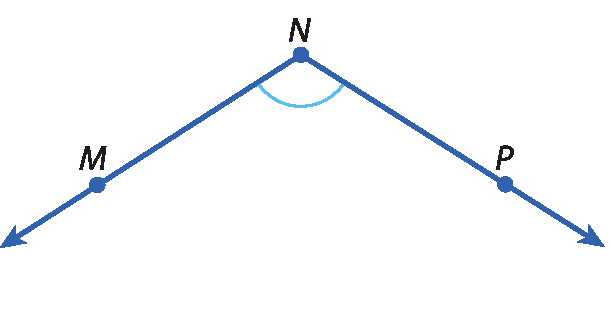
c)
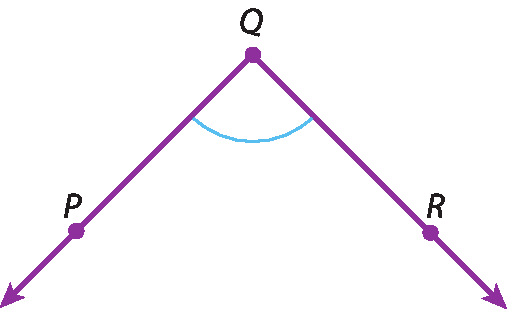
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
4. Operações com medidas de ângulos
Observe as situações a seguir.
Situação 1
Um esportista que utiliza cadeira de rodas saiu do mercado, passou pela escola, virou para a direita 90graus, foi em frente até atingir o ponto de táxi, virou para a direita 45graus e, finalmente, chegou ao ginásio de esportes.

Para saber quanto a direção do cadeirante mudou, desde que saiu do mercado até chegar ao ginásio de esportes, podemos montar um esquema, em que a linha vermelha representa o caminho percorrido por ele.
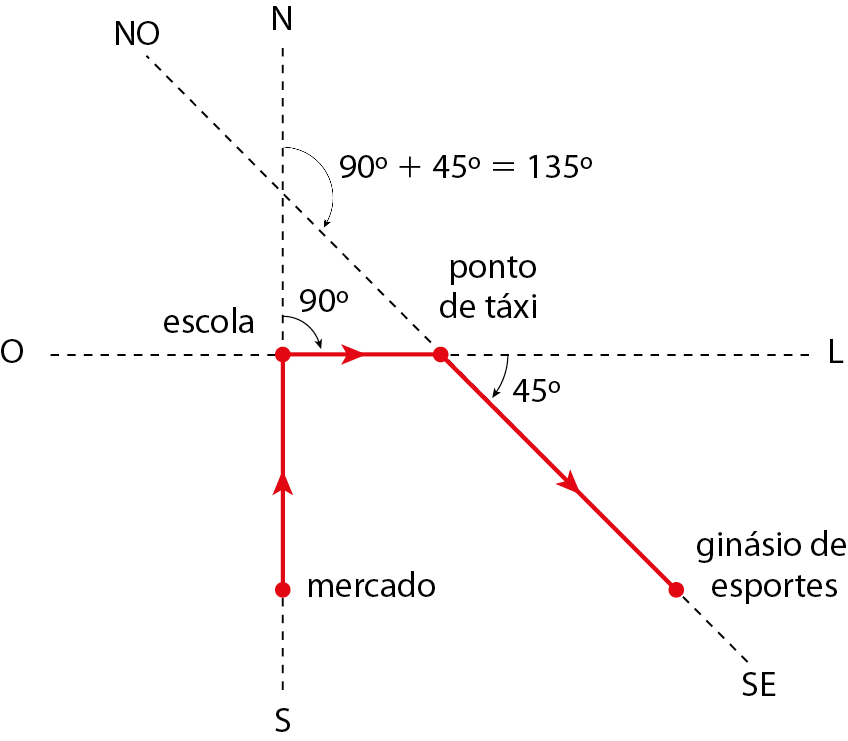
Observando os ângulos assinalados, podemos reparar que foram 90graus para a direita (na escola) e mais 45graus para a direita (no ponto de táxi). Nesse caso, dizemos que a direção inicial (Norte‑Sul) sofreu uma mudança para a direção final (Noroeste‑Sudeste) de 135graus para a direita, pois o esportista em cadeira de rodas virou 90graus para a direita e 45graus para a direita; portanto, 90graus + 45graus para a direita.
Situação 2
Considere agora uma nova situação em que a linha vermelha do esquema representa o caminho percorrido por um ciclista do ponto a até o ponto B.
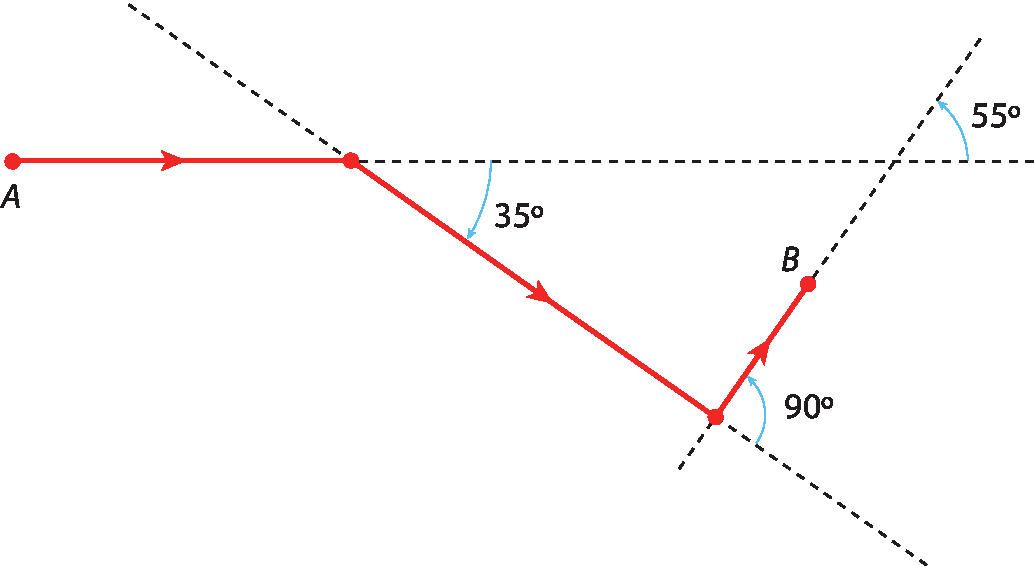
Observe as mudanças de direção do ciclista.
• 1ª mudança: 35graus para a direita;
• 2ª mudança: 90graus para a esquerda.
As mudanças de direção do ciclista (35graus para a direita e 90graus para a esquerda) equivalem a uma mudança de direção inicial de 55graus que é o mesmo que (90graus ‒ 35graus) para a esquerda.
Situações como essas, envolvendo mudança de direção, são comuns nas navegações aérea e marítima para localizar aviões, navios, cargas e até passageiros, no caso de queda ou de naufrágio, e nos dão uma ideia da importância de operar com medidas de ângulos.
Transformando unidades
Quando realizamos operações com medidas de ângulos, é possível aparecerem resultados com minutos e segundos maiores que 60 unidades.
Nesse caso, devemos transformar segundos em minutos e minutos em graus, ou seja, a cada 60 unidades, trocamos por uma unidade imediatamente superior. Acompanhe os exemplos.
a) Expressar 5graus20minutos em minutos.
5graus20minutos = 5 ⋅ 60minutos + 20minutos = 300minutos + 20minutos = 320minutos
b) Fazer a transformação de 150minutos em graus e minutos.
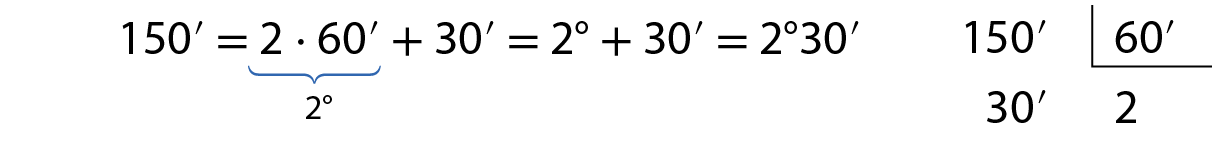

c) Expressar 80segundos em minutos e segundos.
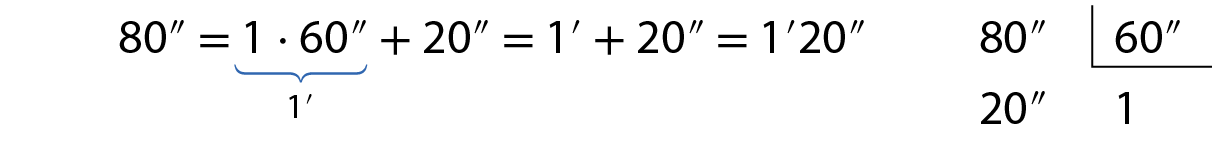
Adição e subtração de medidas de ângulos
A adição de medidas de ângulos é feita adicionando segundos com segundos, minutos com minutos e graus com graus. Da mesma fórma, a subtração é feita subtraindo segundos de segundos, minutos de minutos e graus de graus. Acompanhe os exemplos.
a) 38graus20minutos + 51graus40minutos

b) 90graus ‒ 40graus20minutos45segundos
90graus = 89graus60minutos = 89graus59minutos60segundos

Usando régua e compasso, podemos construir um ângulo cuja medida seja igual à soma das medidas de dois ângulos, ou um ângulo cuja medida seja igual à diferença entre as medidas de dois ângulos. Acompanhe os exemplos.
a) Dados os ângulos
A O Be
C O D, vamos construir, com régua e compasso, o ângulo
E O Fde medida:
medida do ângulo E O F.=
medida do ângulo A O B.+
medida do ângulo C O D.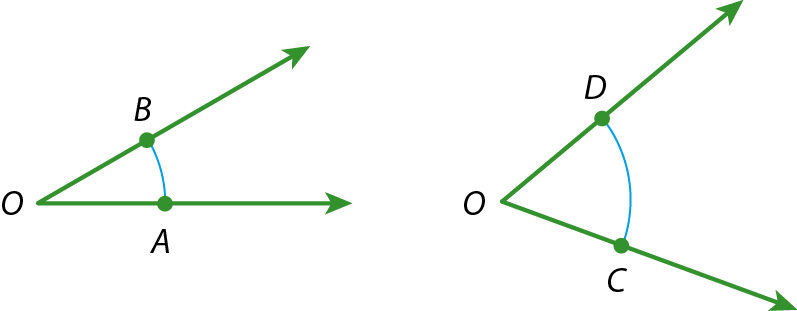

b) Dados os ângulos
G O He
Símbolo. Ângulo IOJ, vamos construir, com régua e compasso, o ângulo
K O Lde medida:
Medida do ângulo KOL=
Medida do ângulo IOJ‒
Medida do ângulo GOH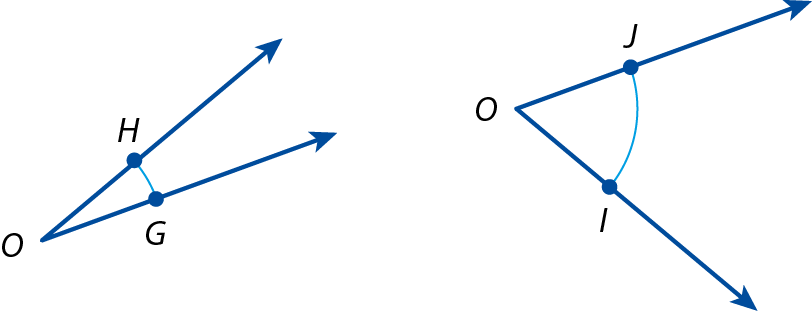

Ângulos adjacentes
Na figura a seguir destacamos os ângulos
Símbolo. Ângulo AOB.e
Símbolo. Ângulo BOC. Observe que esses ângulos têm mesmo vértice e um lado comum, mas não têm ponto em comum na região interna. Esses ângulos são chamados adjacentes.
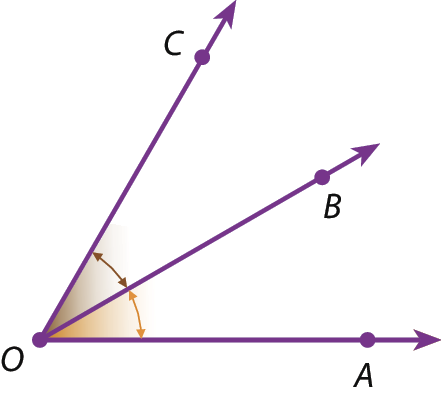

Ângulos complementares e ângulos suplementares
Dois ângulos que têm a soma de suas medidas igual a 90graus são ângulos complementares.
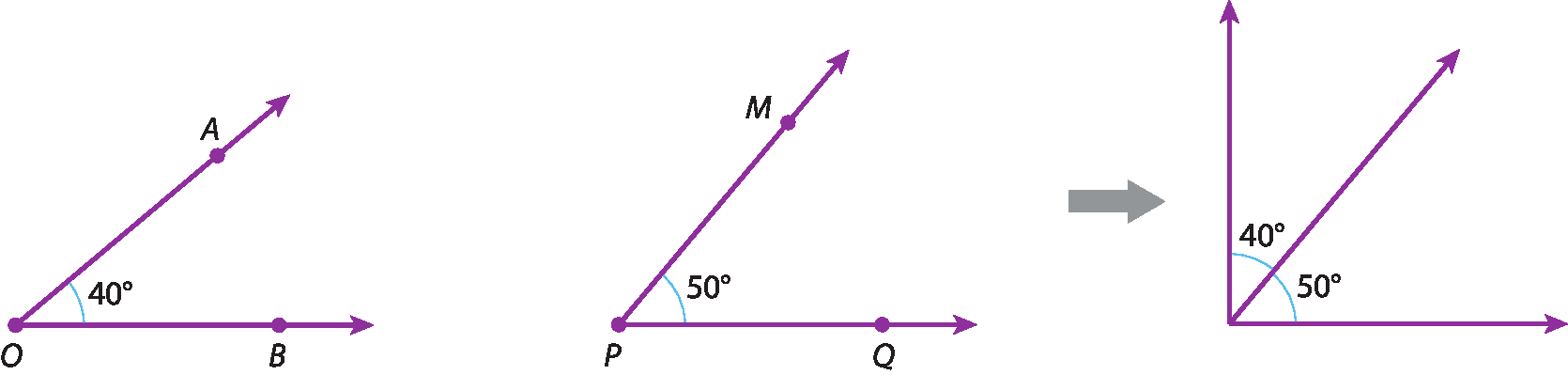
Os ângulos
Símbolo. Ângulo AOB.e
Símbolo. Ângulo MPQsão complementares, pois:
A medida do ângulo AOB mais a medida do ângulo MPQ é igual a 90 graus.ponto
Portanto, a medida do complemento de um ângulo agudo que mede x é (90graus ‒ x).
Dois ângulos que têm a soma de suas medidas igual a 180graus são ângulos suplementares.

Os ângulos
Símbolo. Ângulo AOB.e
Símbolo. Ângulo MPQsão suplementares, pois:
A medida do ângulo AOB mais a medida do ângulo MPQ é igual a 180 graus..
Logo, a medida do suplemento de um ângulo que mede y é (180graus ‒ y).
Ângulos opostos pelo vértice (ó pê vê)
Na figura, as semirretas
Semirreta OAe
Semirreta OBformam o ângulo
Símbolo. Ângulo AOB.e são opostas, respectivamente, às semirretas
Semirreta ODe
Semirreta OCque formam o ângulo
Símbolo. Ângulo CODAlém disso, os ângulos
Símbolo. Ângulo AOB.e
Símbolo. Ângulo CODtêm o vértice óh em comum.
Por esse motivo, dizemos que os ângulos
Símbolo. Ângulo AOB e ângulo CODsão opostos pelo vértice (ó pê vê).
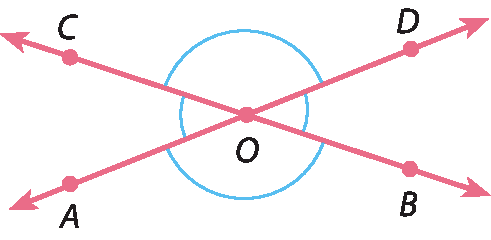
Os ângulos
Símbolo. Ângulo AOCe
Símbolo. Ângulo BODtambém são ângulos opostos pelo vértice.
Dois ângulos são opostos pelo vértice quando os lados de um são semirretas opostas aos lados do outro.
Uma propriedade importante dos ângulos opostos pelo vértice é:
Dois ângulos opostos pelo vértice são congruentes.
Vamos, então, demonstrar essa propriedade.
Considere as retas concorrentes r e s. Observe que elas formam quatro ângulos de medidas a, b, c e d.
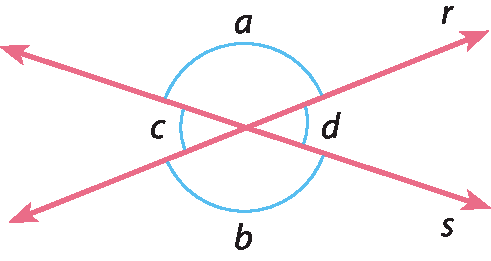
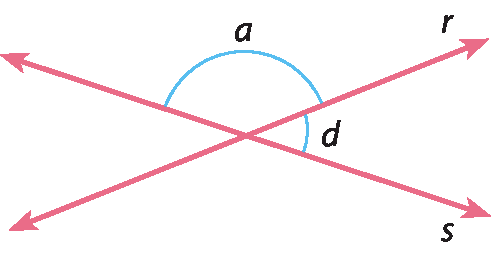
Agora, considere os ângulos de medidas a e d. Como esses ângulos são suplementares, temos: a + d = 180graus (um).
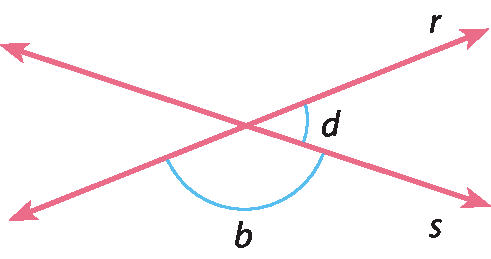
Observe que os ângulos de medidas d e b também são suplementares, então: d + b = 180graus (dois).
De (um) e (dois) podemos escrever a seguinte igualdade:
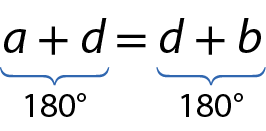
Subtraindo d de ambos os membros da igualdade, obtemos:
a = b
Se empregarmos esses mesmos argumentos para os ângulos de medidas d e c e seguirmos os mesmos passos, concluiremos que d = c.
Assim, demonstramos que dois ângulos opostos pelo vértice são congruentes.
Multiplicação e divisão da medida de um ângulo por um número natural
A multiplicação e a divisão da medida de um ângulo por um número natural são efetuadas multiplicando ou dividindo, respectivamente, os segundos, os minutos e os graus pelo número natural.
Em seguida, na multiplicação, reduzimos os segundos a minutos e os minutos a graus, quando resultarem em um número igual ou maior do que 60. Já na divisão, quando necessário, reduzimos graus a minutos e minutos a segundos.
Observe os exemplos.
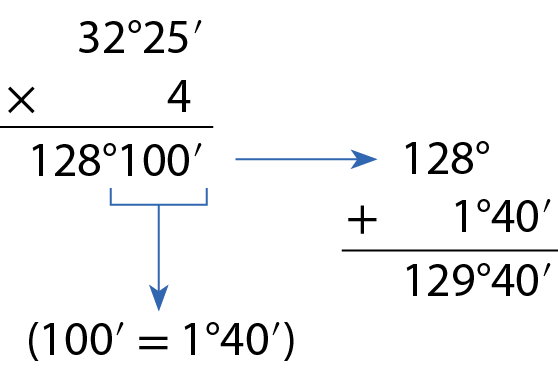
a) 32graus25minutos ⋅ 4
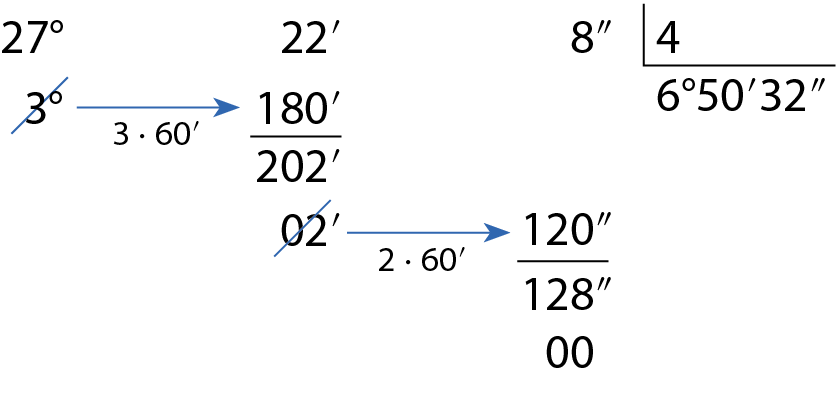
b) 27graus22minutos8segundos : 4
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
12 Converta em minutos.
a) 15graus
b) 10graus35minutos
c) 420segundos
d) .1020segundos
e) 4graus240segundos
f) 6graus360segundos
13 Estes quatro azulejos se ajustam perfeitamente. Quanto mede o ângulo formado por eles em torno do ponto O ?

14 A quantos segundos corresponde um ângulo que tem por medida 2graus10minutos30segundos?
15

Calcule mentalmente e expresse 94′ em graus e minutos.
16 Calcule.
a) 25graus12minutos + 40graus30minutos
b) 10graus45minutos45segundos + 20graus20minutos45segundos
c) 50graus40minutos ‒ 20graus35minutos
d) 45graus20minutos25segundos ‒ 30graus30minutos30segundos
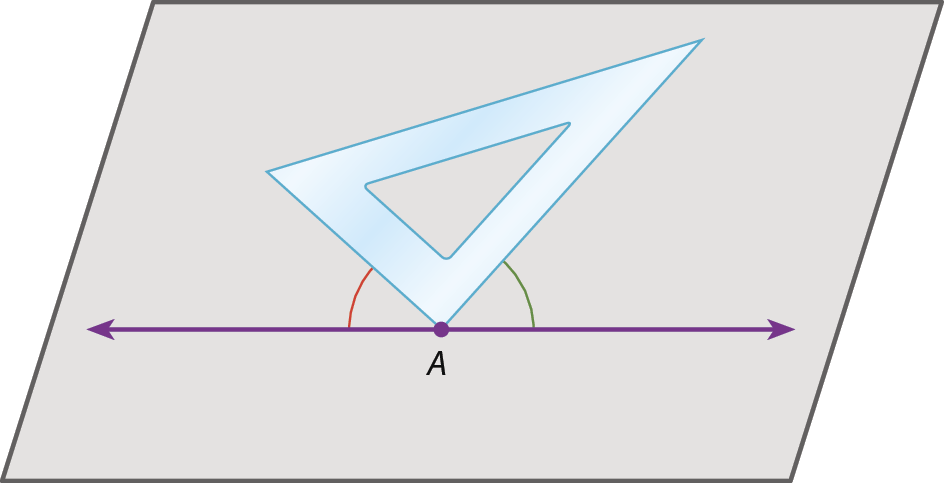
17 Nesta figura, um esquadro tem o vértice de seu ângulo reto apoiado no ponto a, e o ângulo indicado em vermelho mede 42°10′. Quanto mede o ângulo indicado em verde?
18 Determine:
a) a medida do complemento do ângulo de 17graus;
b) a medida do suplemento do ângulo de 40graus;
c) a medida do complemento do complemento do ângulo de 69graus.
19

Reúna‑se com um colega e respondam:
a) Escolham uma medida de um ângulo agudo qualquer. Qual é a soma da metade dessa medida com a metade da medida de seu suplemento?
b) A metade da medida de um ângulo obtuso mais a metade da medida de seu suplemento é igual a 90graus. Quanto mede esse ângulo?
20 O gráfico de setores a seguir apresenta o resultado de uma pesquisa feita com .1200 pré‑adolescentes de 10 a 13 anos do Colégio Estudebem.
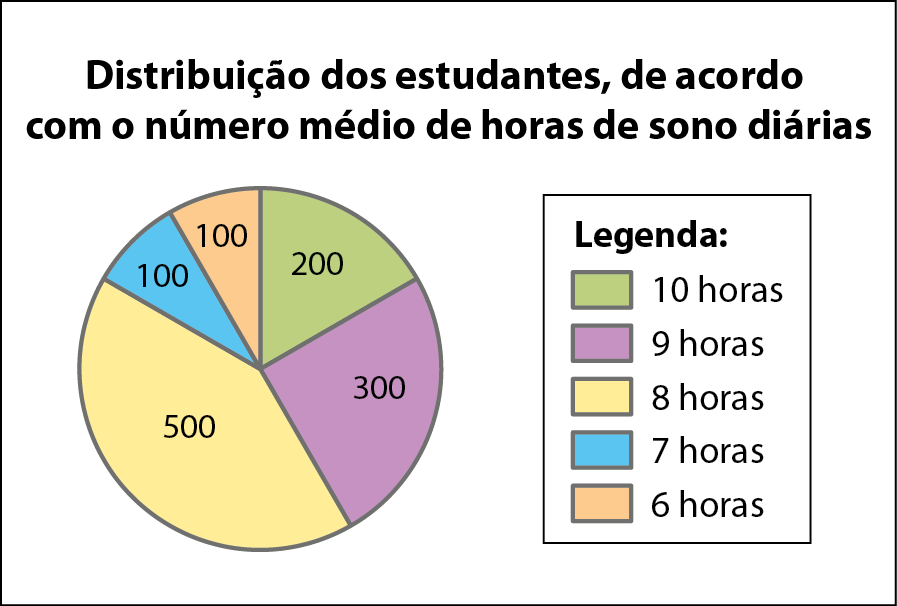
a) Qual é o número de horas de sono do maior grupo dos estudantes entrevistados?
b) É correto afirmar que mais da metade dos entrevistados dorme, em média, oito ou mais horas por dia?
c) Determine a medida dos ângulos centrais correspondentes a cada setor.
d) Classifique os ângulos de cada setor como reto, agudo ou obtuso.
21 Efetue.
a) 2 ⋅ 22graus30minutos
b) 5 ⋅ 25graus12minutos15segundos
c) 15graus20minutos : 4
d) 15graus10minutos24segundos : 4
22 Considere a figura a seguir, em que x, y e z são as medidas dos ângulos indicados.
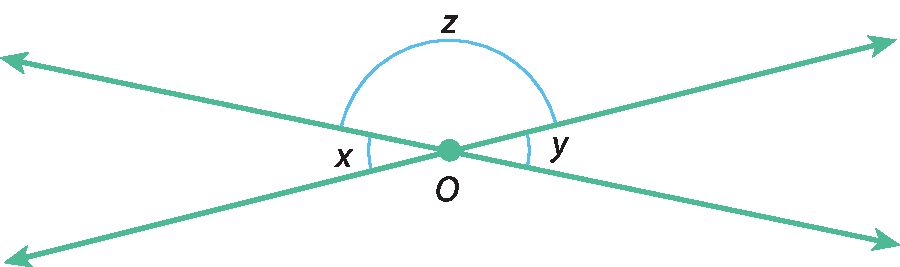
a) Quanto vale, em grau, x + z ? E z + y?
b) Qual é a relação entre x + z e z + y?
c) Qual é a relação entre x e y?
d) O que se pode concluir sobre as medidas de dois ângulos opostos pelo vértice quaisquer?
23 Considerando a figura do exercício 22, escreva um algoritmo, passo a passo, de como você faria uma demonstração da afirmação: quaisquer dois ângulos opostos pelo vértice são congruentes.
24 Calcule.
a)
2 terçosde 15graus
b)
3 quartosde 90graus
c)
2 quintosde 48graus30′
d)
5 sextosde 60graus18′6″
25 Em uma folha de papel, Pedro construiu dois ângulos: um medindo 42graus e outro 28graus. Em seguida, ele recortou as representações desses ângulos para usá‑las como moldes. Em outra folha, empregando somente os moldes, sem utilizar transferidor, ele construiu outros ângulos com estas medidas: 70graus, 14graus, 56graus e 126graus.
Explique como Pedro fez para construir cada um desses ângulos.
26 Com o auxílio de um transferidor, construa quatro ângulos de medidas 45graus, 90graus, 63graus e 104graus.
Agora, usando somente régua e compasso, construa ângulos de medidas:
a) 27graus;
b) 149graus;
c) 108graus;
d) 135graus;
e) 14graus;
f) 77graus.
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
27 A imagem mostra turbinas eólicas (de vento). Pela rotação de suas hélices, obtemos energia eólica, que é a energia obtida pelo movimento do vento.
Nesta fotografia, supondo que os três ângulos destacados tenham a mesma medida, calcule essa medida.

28

Hora de criar – Troque com um colega um problema que cada um de vocês criou sobre operações com medidas de ângulos. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi‑los.
Bissetriz de um ângulo
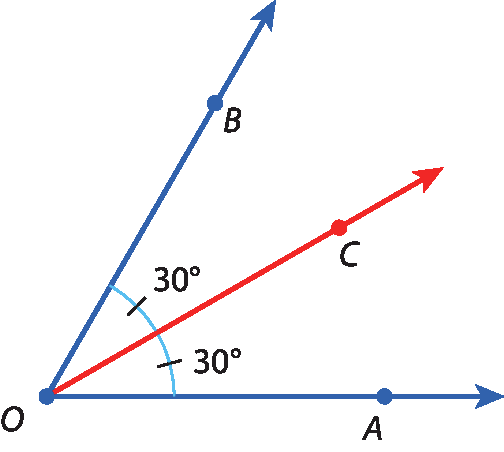
Na figura verificamos:
• m
abre parêntese, ângulo A O C, fecha parêntese.= 30graus e
medida do ângulo C O B igual 30 graus.Então,
ângulo A O C congruente ao Ângulo C O B.• A semirreta
Semirreta OCdivide o ângulo
Símbolo. Ângulo AOB.em dois ângulos congruentes.
Nesse caso, dizemos que
Semirreta OCé bissetriz de
Símbolo. Ângulo AOB.Bissetriz de um ângulo é a semirreta com origem no vértice desse ângulo e que o divide em dois outros ângulos congruentes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
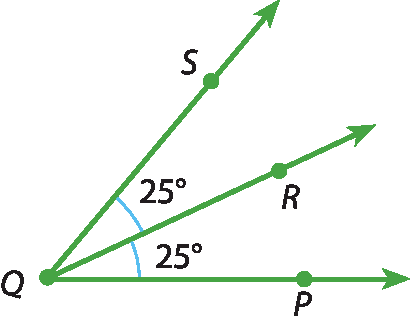
29 Observe a figura. Sabendo que
Medida do ângulo PQR é igual à medida do ângulo RQS, a semirreta
Semirreta QRé o que em relação a
Símbolo. Ângulo PQS?
30 Utilizando um transferidor, construa um ângulo de 115graus e trace sua bissetriz. Quais são as medidas dos ângulos obtidos?
31 Considere a figura e responda às questões a seguir no caderno, sabendo que
Semirreta ODé bissetriz de
Símbolo. Ângulo COEe
Semirreta OBé bissetriz de
Símbolo. Ângulo AOC.
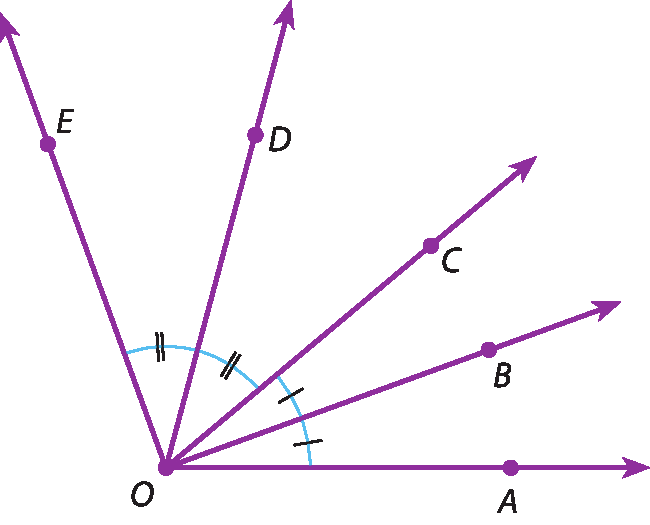
a) Se
Medida do ângulo AOB= 20graus, quanto mede
Símbolo. Ângulo AOC?
b) Se
Medida do ângulo COE= 70graus, quanto mede
Símbolo. Ângulo COD?
c) Se
Medida do ângulo AOB= 24graus e
Medida do ângulo COE= 82graus, quanto mede
Símbolo. Ângulo AOD?
32 Reproduza em uma folha de papel a figura e, em seguida, recorte‑a.
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
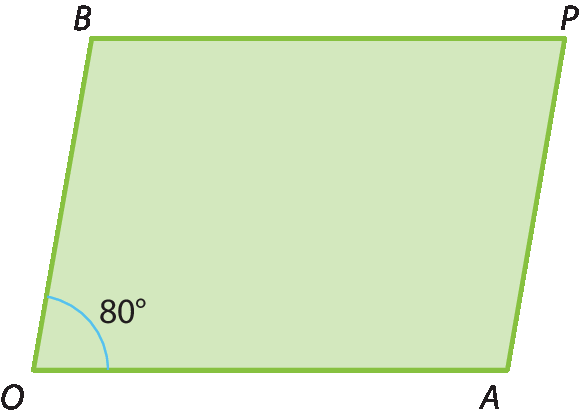
Agora, siga as instruções:
• Dobre a figura de modo que o lado
OAse sobreponha ao lado
OB.
• Desdobre a figura e trace
Semirreta OCsobre a marca da dobra feita no papel.
• Dobre a figura inicial de modo que o lado
OAse sobreponha a
Semirreta OC.
• Desdobre a figura e trace
Semirreta ODsobre a marca da nova dobra.
• Agora, calcule a medida dos ângulos
Símbolo. Ângulo AOD,
Símbolo. Ângulo AOCe
Símbolo. Ângulo BOD.
33

Hora de criar – Elabore um problema sobre medidas de ângulos formados pelas bissetrizes de dois ângulos suplementares. Troque‑o com um colega. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi‑los.
5. Ângulos formados por duas retas e por uma transversal
Na fotografia, observe a grade junto ao corrimão da escada. Podemos ver ângulos formados pelas barras paralelas ao corrimão com as barras verticais.

•

Considere dois pares quaisquer desses ângulos. Sem usar um transferidor, o que você diria a respeito das medidas deles?
Considere duas retas coplanares (retas que estão em um mesmo plano), r e s, cortadas por uma terceira reta t, chamada transversal. Essas retas determinam oito ângulos.
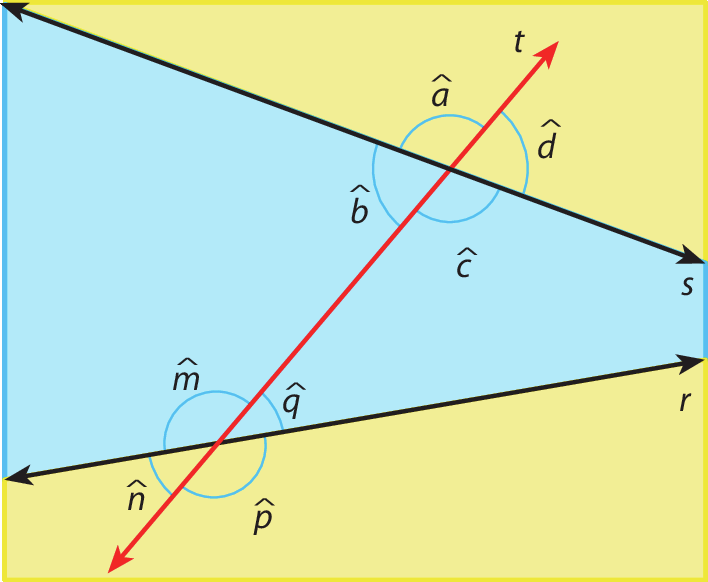
Na figura:
• os ângulos cujas indicações estão na faixa azul, entre as retas r e s, são chamados internos; assim, são internos os ângulos
b c me
qde medidas b, c, m e q ;
• os ângulos cujas indicações estão na região amarela são chamados externos; assim, são externos os ângulos
a d ne
pde medidas a, d, n e p.
Esses oito ângulos, combinados dois a dois, recebem nomes especiais, como veremos a seguir.
Ângulos correspondentes
Dois ângulos são correspondentes quando um é interno e o outro é externo, não têm o mesmo vértice e estão situados em um mesmo lado em relação à transversal. Os ângulos destacados nas figuras são correspondentes.

Observe a relação que existe entre ângulos correspondentes e retas paralelas. Para isso, vamos traçar uma reta s paralela a uma reta r usando régua e esquadro.
1. Vamos considerar a reta r e um ponto P fóra da reta.

2. Posicionamos um esquadro e uma régua como mostra a figura.
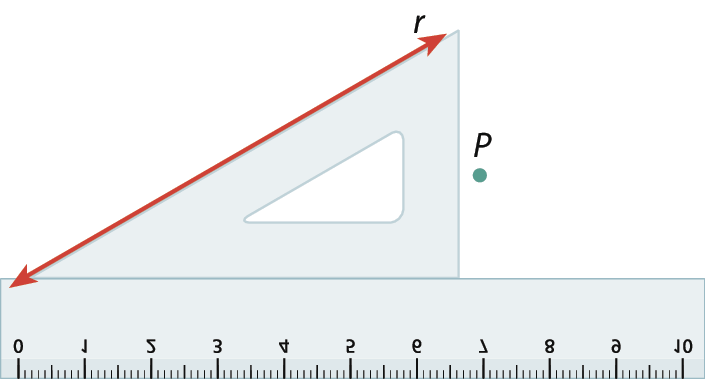
3. Deslizamos o esquadro apoiado na régua até chegar ao ponto P.
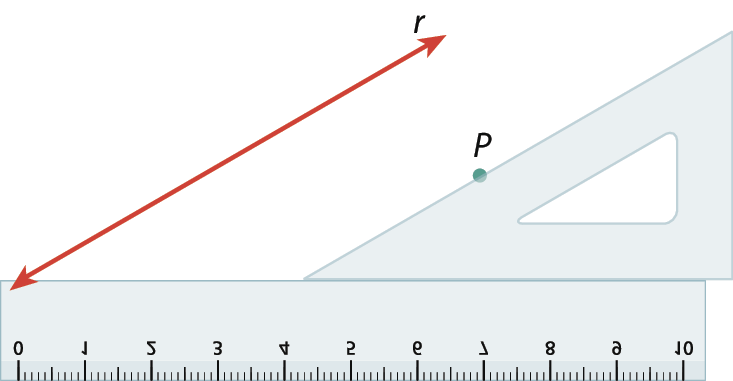
4. Traçamos a reta s, que é paralela à reta r. Mantendo a régua apoiada no papel, indicamos por a e b as medidas dos ângulos correspondentes determinados.
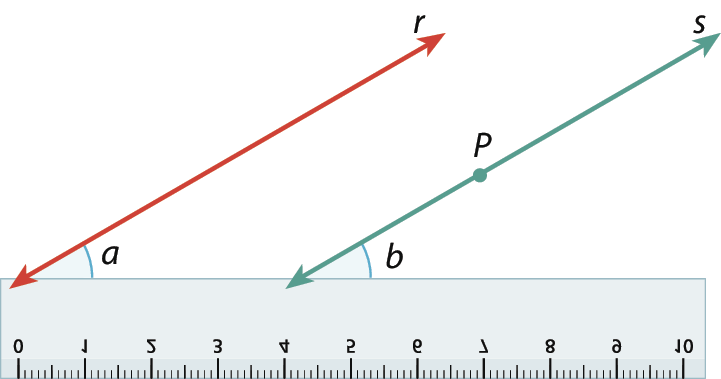
Note que construímos dois ângulos correspondentes congruentes (de medidas iguais, a = b) e obtivemos retas paralelas, visto que estão igualmente inclinadas sobre a régua.
Logo:
Se uma transversal corta duas retas formando ângulos correspondentes congruentes, então essas retas são paralelas.
O inverso também é verdadeiro:
Se duas retas são paralelas, então os ângulos correspondentes formados com uma transversal são congruentes.
Essa propriedade permite descobrir medidas de ângulos formados por duas retas paralelas cortadas por uma transversal conhecendo‑se a medida de apenas um dos ângulos. Acompanhe um exemplo.
Considerando a figura, em que r ⫽ s, vamos descobrir o valor de x para calcular a medida dos ângulos assinalados.
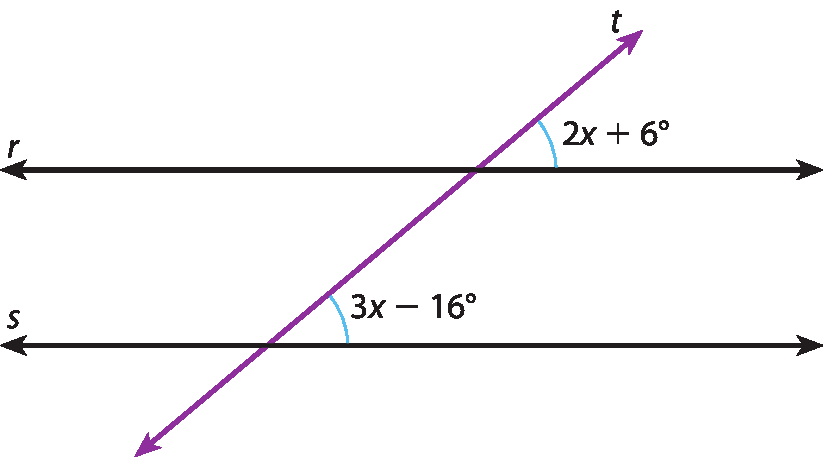
Os ângulos destacados são congruentes, pois são ângulos correspondentes formados por duas retas paralelas e uma transversal. Logo, devemos escrever a igualdade:
2x + 6graus = 3x ‒ 16graus
2x ‒ 3x = ‒16graus ‒ 6graus
‒x = ‒22graus
x = 22graus
Substituindo x por 22graus nas expressões 2x + 6graus e 3x ‒ 16graus, obtemos a medida dos ângulos assinalados, que devem ser iguais.
2x + 6graus = 2 ⋅ 22graus + 6graus = 44graus + 6graus = 50graus
3x ‒ 16graus = 3 ⋅ 22graus ‒ 16graus = 66graus ‒ 16graus = 50graus
Portanto, os ângulos assinalados na figura anterior medem 50graus.
Clique no play e acompanhe as informações do vídeo.
EXERCÍCIO PROPOSTO
FAÇA AS ATIVIDADES NO CADERNO
34 Nas figuras a seguir, r ⫽ s e t é transversal. Determine as medidas x e y dos ângulos destacados.
a)
b)
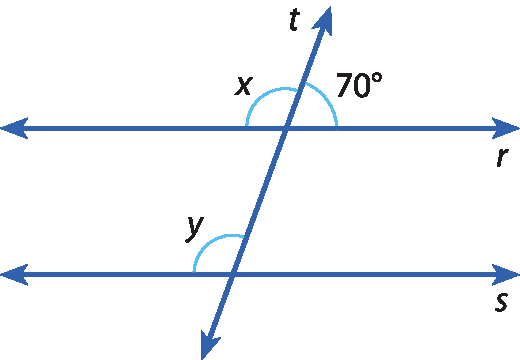
Ângulos alternos internos e ângulos alternos externos
Vamos considerar duas retas coplanares, r e s, e uma transversal, t.
Dois ângulos são alternos internos quando são internos, não têm o mesmo vértice e estão situados em lados opostos em relação à transversal. Os ângulos destacados nas figuras são alternos internos.

Dois ângulos são alternos externos quando são externos, não têm o mesmo vértice e estão situados em lados opostos em relação à transversal. Os ângulos destacados a seguir são alternos externos.
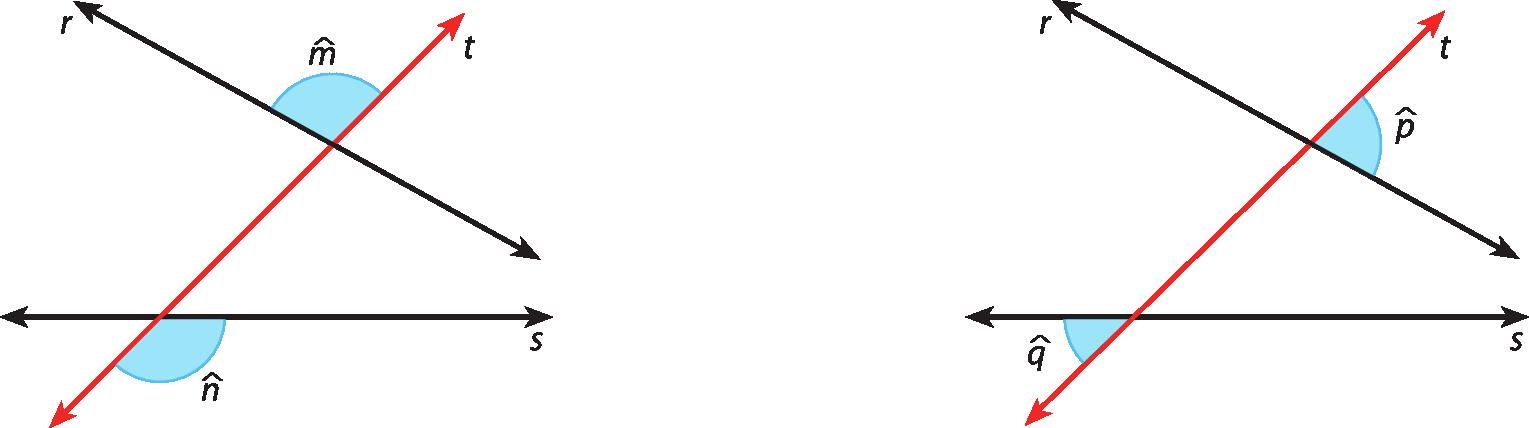
Vamos considerar as retas paralelas r e s cortadas pela transversal t na figura.
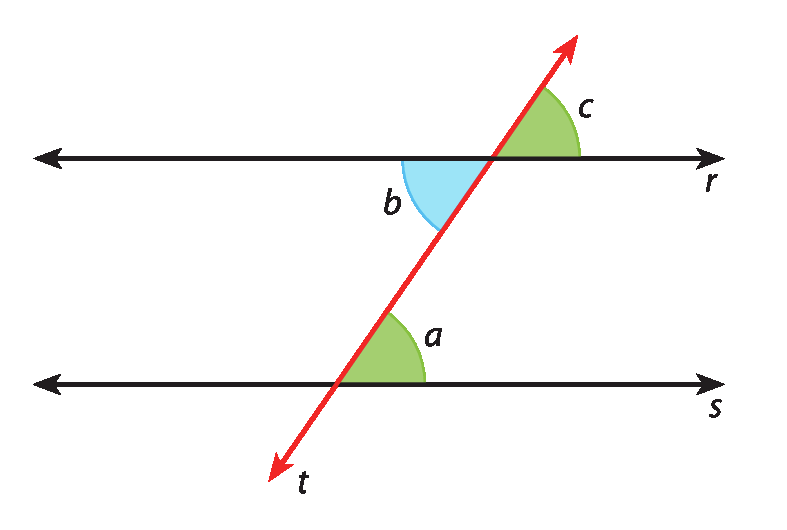
Os ângulos de medidas a e b são alternos internos.
Então, verificamos:
• a = c, pois são medidas de ângulos correspondentes formados pelas paralelas r e s com a transversal t;
• c = b, pois são medidas de ângulos opostos pelo vértice.
Logo, a = b, pois ambas as medidas são iguais a c.
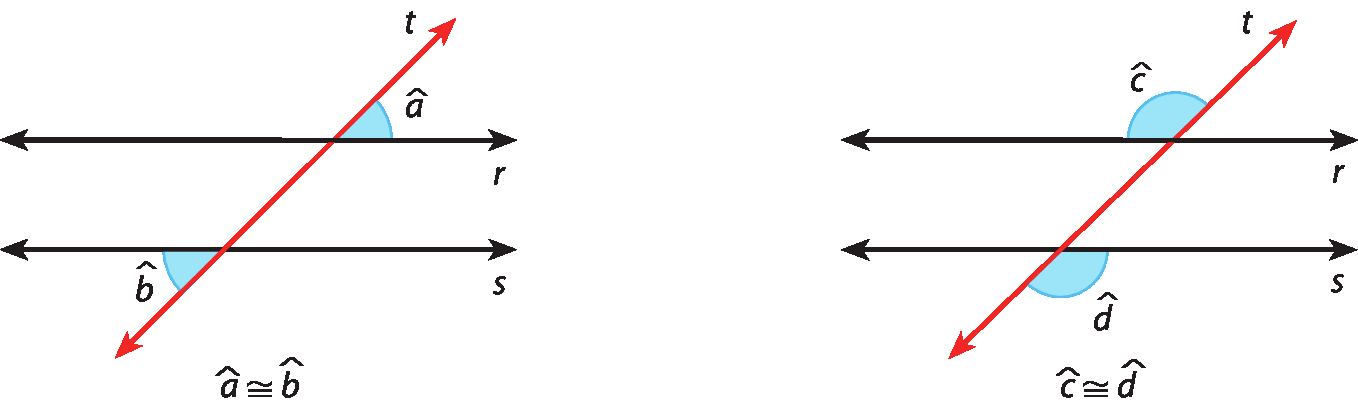
Isso significa que:
Se duas retas são paralelas, então os ângulos alternos internos formados com uma transversal são congruentes.

Essa propriedade também é válida para os ângulos alternos externos:
Se duas retas são paralelas, então os ângulos alternos externos formados com uma transversal são congruentes.
Conforme vimos, também podemos descobrir as medidas de ângulos formados por duas retas paralelas cortadas por uma transversal conhecendo a medida de apenas um dos ângulos.
Acompanhe o exemplo.
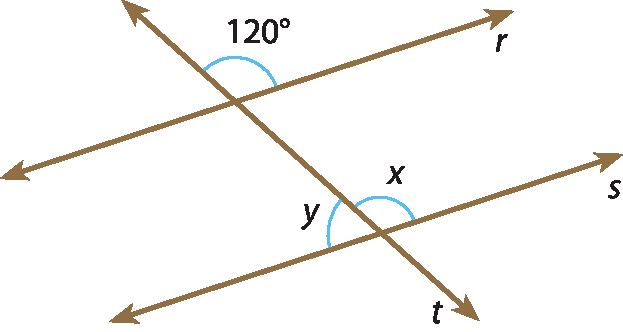
Na figura, r ⫽ s e t é transversal. Vamos calcular os valores de x, y e z.
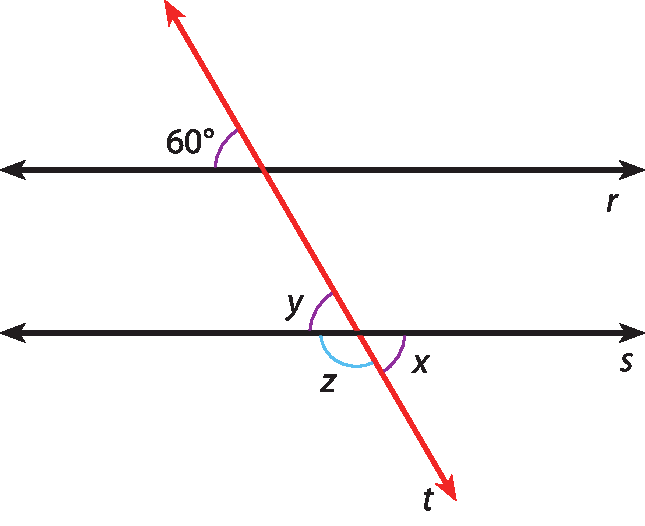
O ângulo de medida 60graus e o ângulo de medida x são alternos externos, formados por duas retas paralelas cortadas por uma transversal. Então, x = 60graus.
Sabemos também que y = 60graus, pois x e y são medidas de ângulos opostos pelo vértice.
Como x + z = 180graus, pois x e z são medidas de ângulos suplementares, obtemos:
60graus + z = 180graus
z = 120graus
Portanto, x = 60graus, y = 60graus e z = 120graus.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
35 Considere a figura, em que r ⫽ s e x, y e z são as medidas dos ângulos
x ye
zrespectivamente.
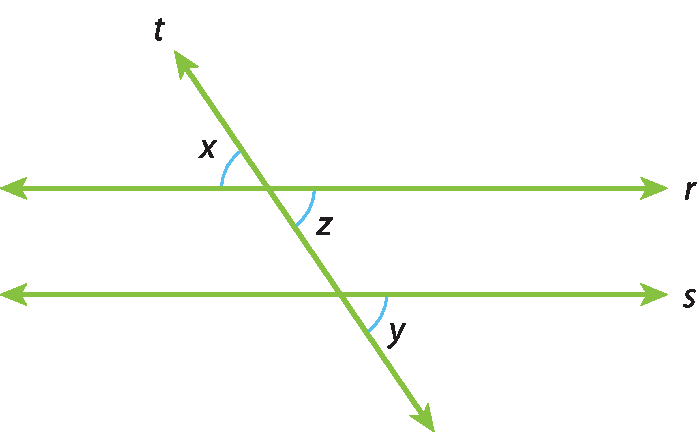
a) Os ângulos
x ysão ângulos alternos externos?
b) Os ângulos
x zsão ângulos complementares, suplementares ou opostos pelo vértice? Qual é a relação entre x e z?
c) Os ângulos
z ysão ângulos correspondentes? Qual é a relação entre z e y?
d) Comparando as respostas dos itens b e c, conclua qual é a relação entre x e y.
36 Trace uma linha reta representando uma estrada principal e marque nela os pontos a e D. Com régua e transferidor, trace o roteiro de um caminho, seguindo as indicações e usando a medida de 1 centímetro para representar 100 métros. Considerando o sentido de a para D, no ponto a da estrada principal, gire para a esquerda 58graus e ande 500 métros, marcando o ponto B. Gire para a esquerda 122graus e ande mais 300 métros, marcando o ponto C.
Agora responda: o segmento
BCé paralelo à estrada principal? Por quê?
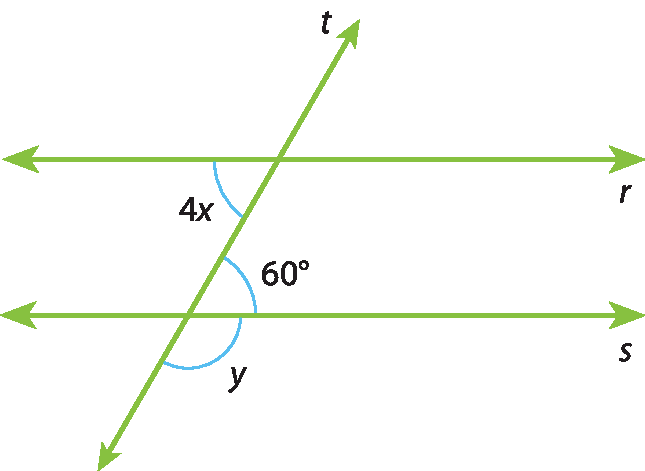
37 Determine as medidas x e y, considerando que r ⫽ s e que t é transversal.
38 Copie a figura a seguir, em que as retas
PQe
BCsão paralelas e a, b e c são medidas dos ângulos.
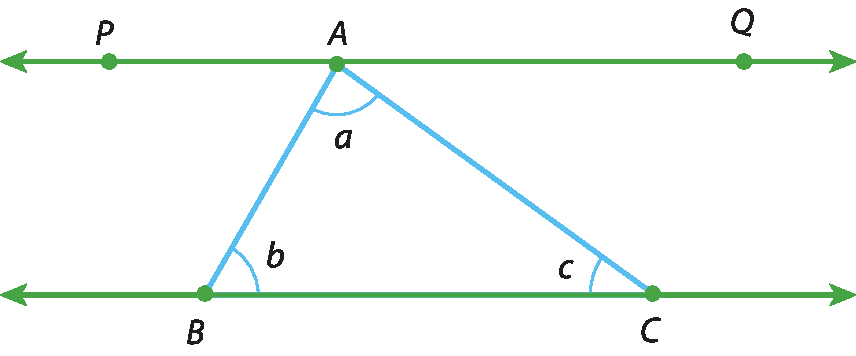
a) Qual é a medida de
ângulo PABE de
ângulo QACb) Qual é a soma das medidas dos ângulos
PAB BAC QACE a dos ângulos internos do triângulo á bê cê?
c) O resultado obtido no item b vale para a soma das medidas dos ângulos internos de qualquer triângulo?
Ângulos colaterais internos e ângulos colaterais externos
Vamos considerar duas retas coplanares, r e s, e uma transversal, t.
Dois ângulos são colaterais internos se são internos, não têm o mesmo vértice e estão situados no mesmo lado em relação à transversal. Observe em destaque nas figuras a seguir alguns ângulos colaterais internos.

Dois ângulos são colaterais externos se são externos, não têm o mesmo vértice e estão situados no mesmo lado em relação à transversal. Nas figuras a seguir, destacamos alguns ângulos colaterais externos.

Considere, na nova figura a seguir, as retas paralelas r e s, cortadas pela transversal t.
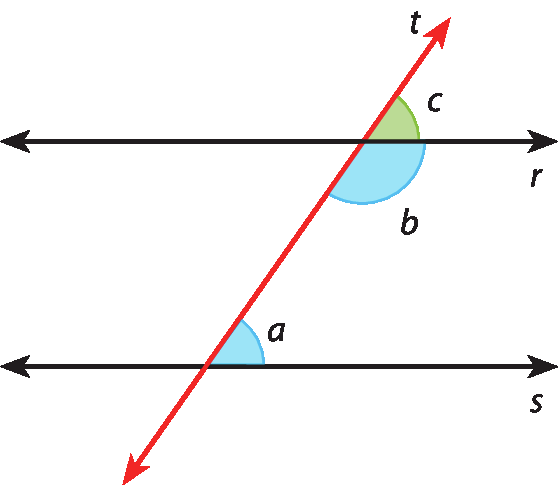
Os ângulos de medidas a e b são colaterais internos. Então, verificamos:
• a = c, pois são medidas de ângulos correspondentes formados pelas retas paralelas r e s com a transversal t ;
• c + b = 180graus, pois são medidas de ângulos suplementares.
Logo: a + b = 180graus.
Isso significa que:
Se duas retas são paralelas, então os ângulos colaterais internos formados com uma transversal são suplementares.
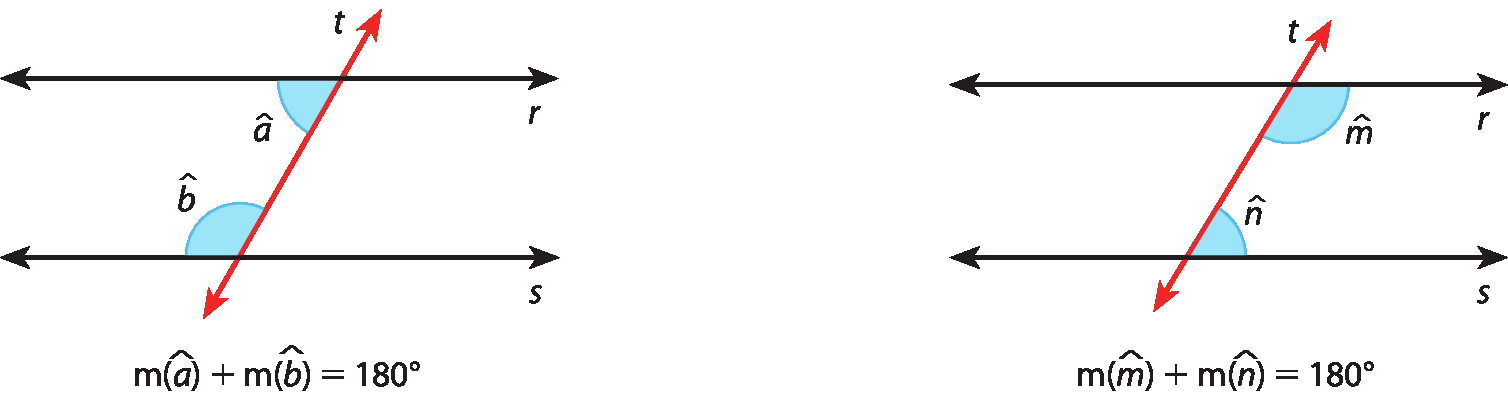
Essa propriedade também é válida para ângulos colaterais externos formados por duas paralelas cortadas por uma transversal:
Se duas retas são paralelas, então os ângulos colaterais externos formados com uma transversal são suplementares.
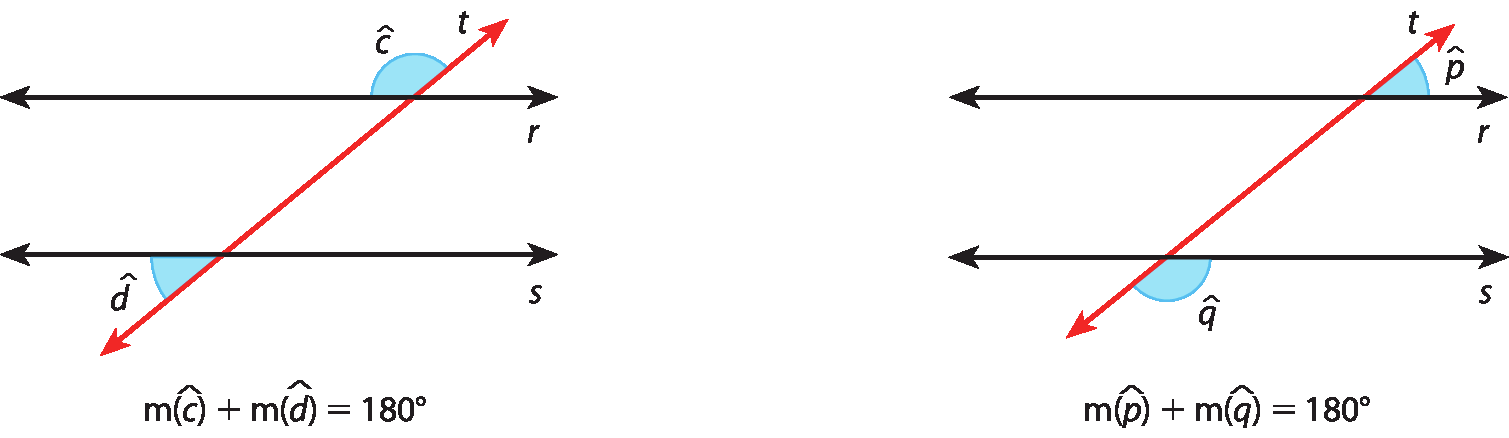
Com essas propriedades, podemos resolver problemas que envolvam medidas de ângulos formados por retas paralelas cortadas por uma transversal. Acompanhe um exemplo.
Vamos calcular a medida dos ângulos assinalados na figura, em que r ⫽ s.
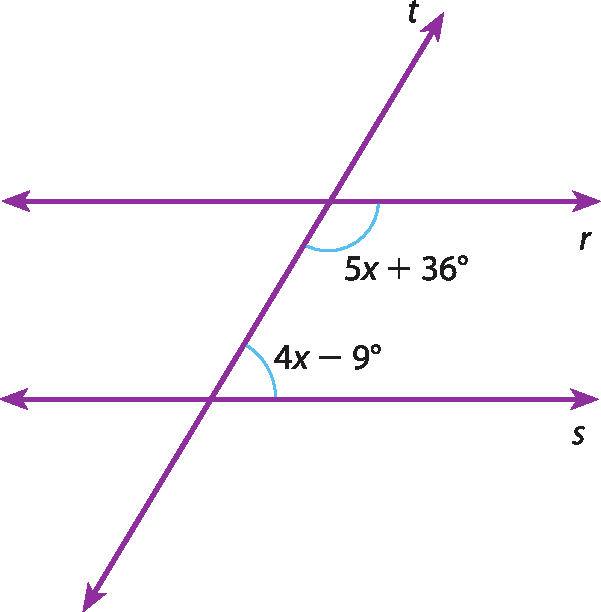
Os ângulos destacados são suplementares, pois são ângulos colaterais internos, formados por duas retas paralelas e uma transversal. Então:
(5x + 36graus) + (4x ‒ 9graus) = 180graus
5x + 4x = 180graus ‒ 36graus + 9graus
9x = 153graus
x = 17graus
Substituindo x por 17graus nas expressões 5x + 36graus e 4x ‒ 9graus, obtemos as medidas dos ângulos assinalados, cuja soma deve ser 180graus.
5x + 36graus = 5 ⋅ 17graus + 36graus = 121graus
4x ‒ 9graus = 4 ⋅ 17graus ‒ 9graus = 59graus
121graus + 59graus = 180graus
Portanto, os ângulos assinalados medem 121graus e 59graus.
Ângulos formados por duas retas paralelas e uma reta transversal com o uso de software
Podemos utilizar softwares matemáticos em uma série de situações, como verificar relações entre medidas de ângulos formados por duas retas paralelas e uma reta transversal.
1º passo
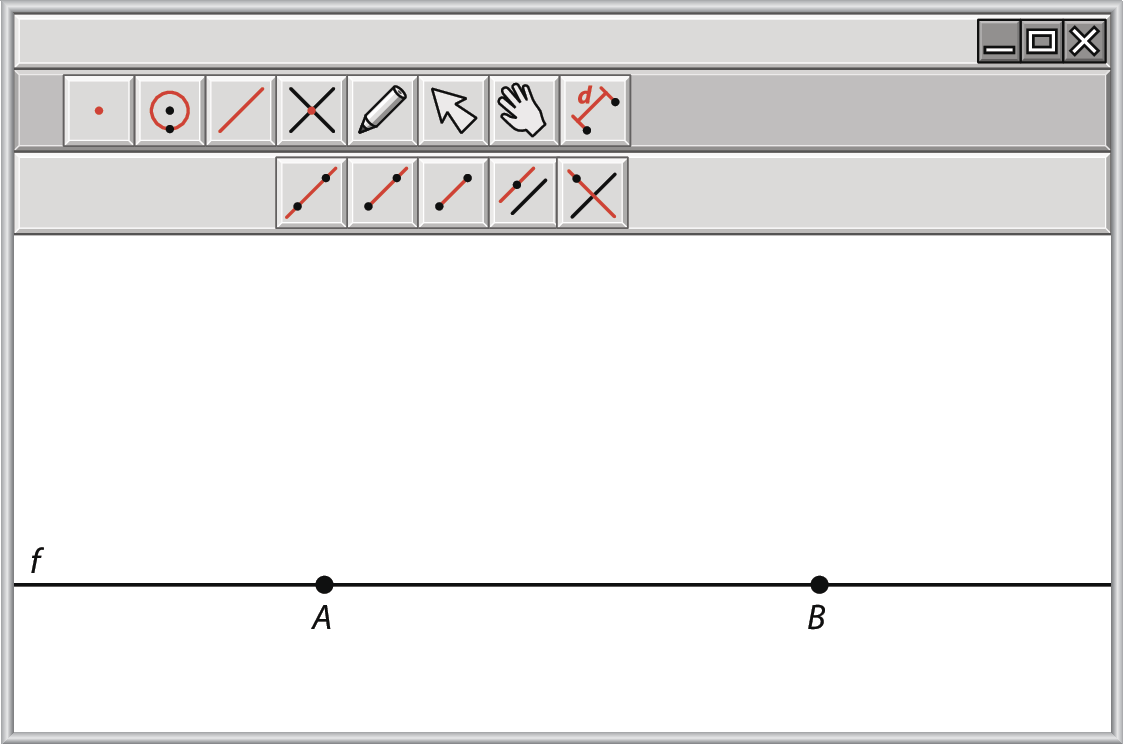
Em geral, as ferramentas ficam na parte superior da tela. Selecione a ferramenta “Reta” e clique em dois pontos quaisquer da tela para criar uma reta
AB2º passo
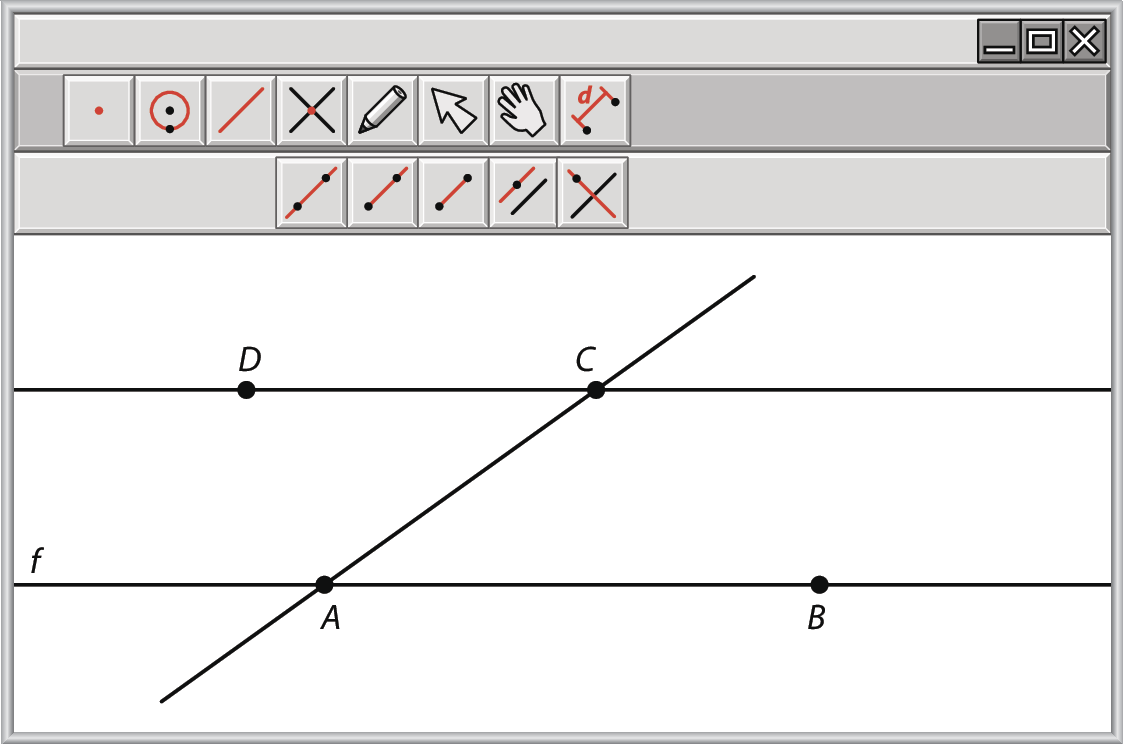
Repita o procedimento para obter as retas
CD e ACSelecionando a ferramenta “Mover”, é possível movimentar o ponto C ao longo da reta
CDe verificar que as congruências de vários pares de ângulos formados continuam valendo.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
39 Mostre que os ângulos colaterais externos formados por duas retas paralelas e uma transversal são suplementares.
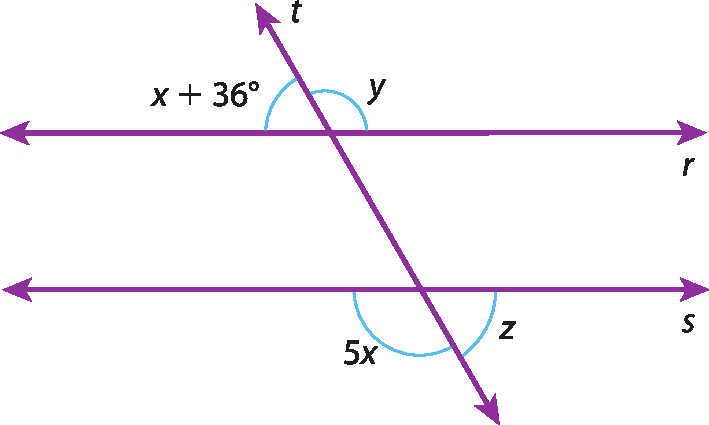
40 Sendo r ⫽ s, determine as medidas x, y e z.
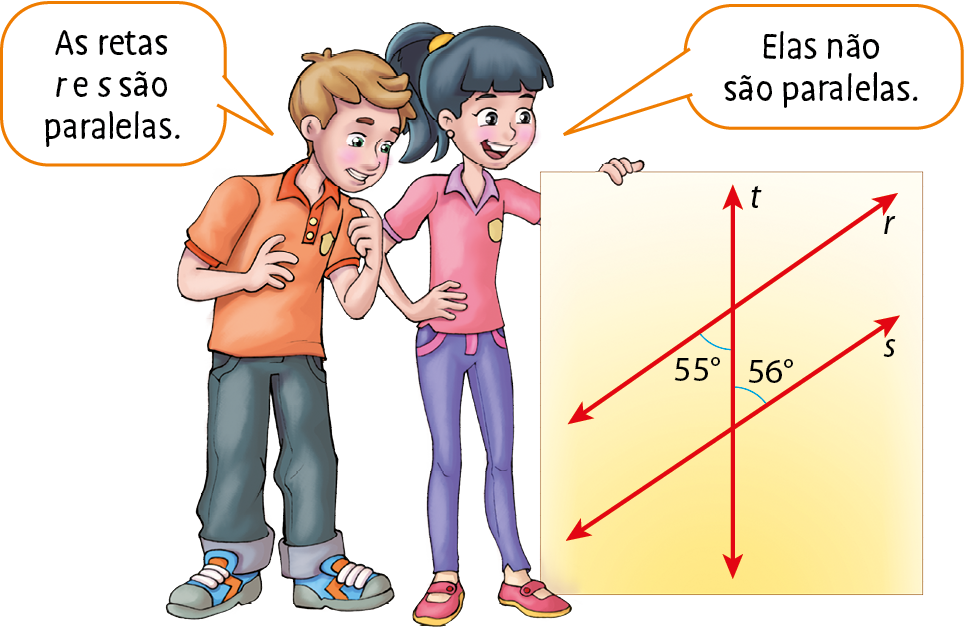
41 Quem tem razão na conversa a seguir, Mário ou Vilma? Justifique sua resposta.
42 Os ângulos mencionados a seguir são formados por duas retas paralelas e uma transversal. Identifique as sentenças falsas e corrija‑as. Os ângulos:
a) correspondentes são suplementares;
b) alternos internos são congruentes;
c) alternos externos são complementares;
d) colaterais internos são congruentes;
e) colaterais externos são suplementares.
43 Sendo r ⫽ s ⫽ t, calcule as medidas x e y dos ângulos destacados nas figuras.
a)
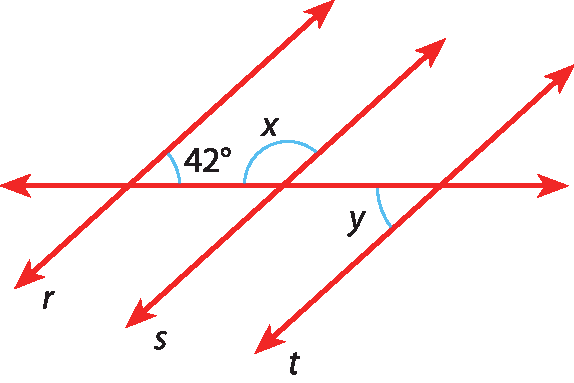
b)
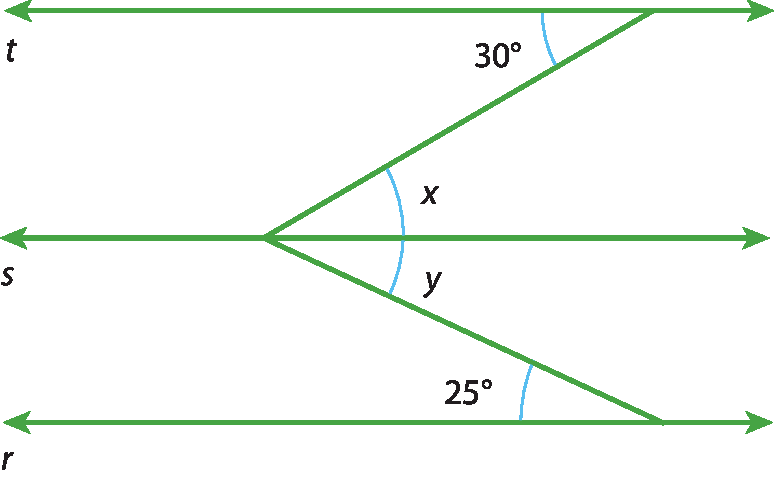
44 Sendo r ⫽ s e u ⫽ v, calcule as medidas a, x e y nas figuras.
a)
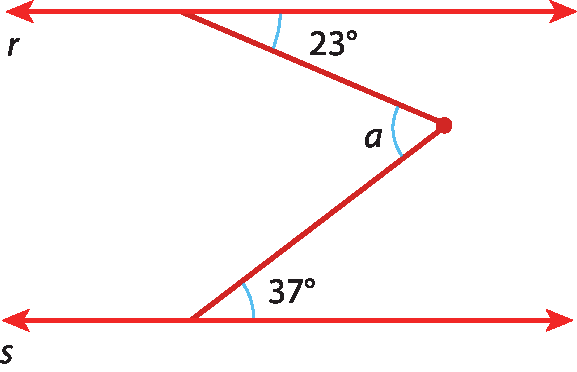
b)
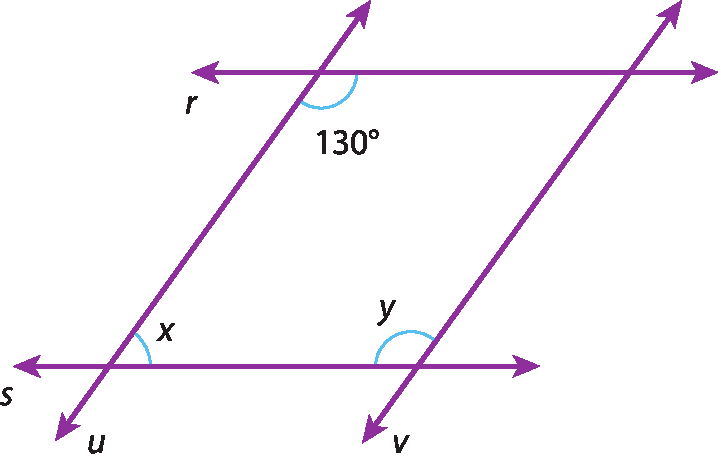
45 Na figura do triângulo á bê cê, foram traçadas duas retas paralelas ao lado
BC: uma reta pelo vértice a e a reta
MN. A medida do ângulo
Símbolo. Ângulo ABCé 38,5graus, e a medida do ângulo
Símbolo. Ângulo MNAé 64,5graus.
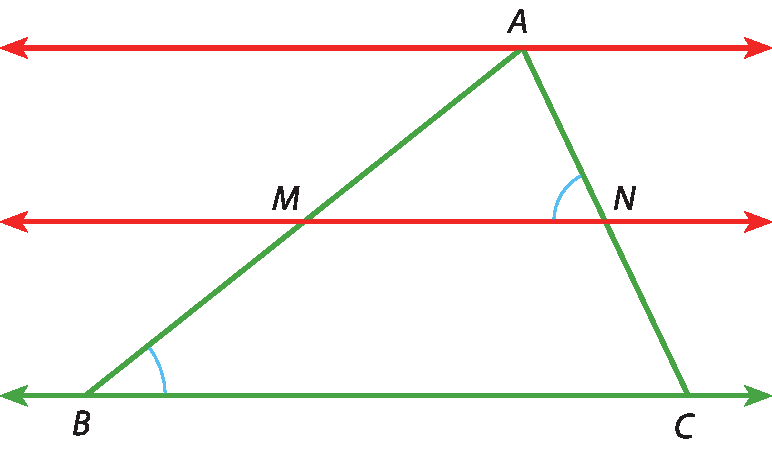
a) Qual é a medida do ângulo
ângulo AMNb) Qual é a medida do ângulo
ângulo BMNc) Qual é a medida do ângulo
ângulo BCATRABALHANDO A INFORMAÇÃO
Gráficos de setores
Gráficos de setores são usados principalmente quando se deseja relacionar entre si as partes do que está sendo representado, ou relacionar cada parte com o todo.
Vamos analisar a situação a seguir.
Um fabricante de jogos de videogame fez uma pesquisa para saber quais são os principais critérios de avaliação para determinar o interesse e a decisão de compra de um jogo voltado ao público infantojuvenil. O gráfico mostra o resultado da pesquisa feita com jovens de 10 a 15 anos. Observe como o gráfico ajuda a perceber a distribuição das opiniões por critério de avaliação.
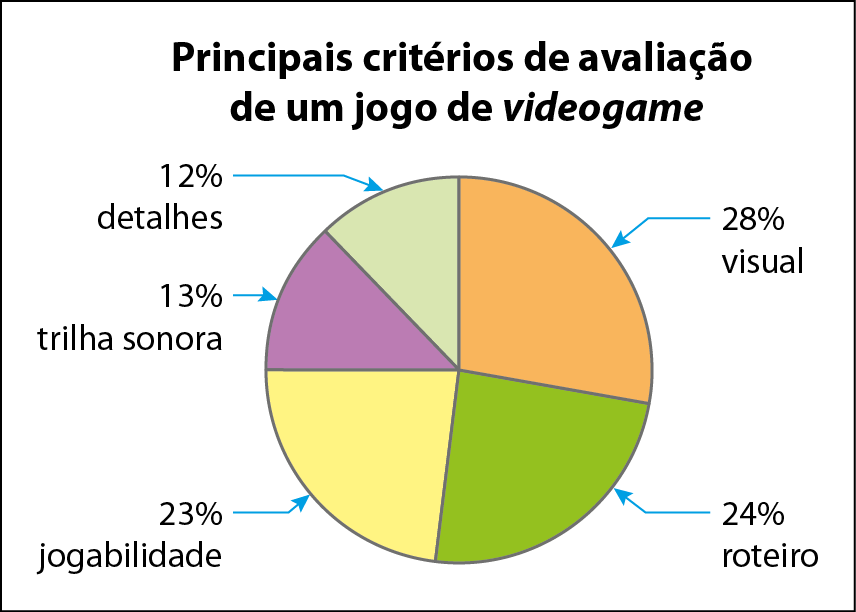

Se medirmos com um transferidor o ângulo do gráfico referente à jogabilidade, por exemplo, encontraremos aproximadamente 83graus. Se calcularmos 23% de 360graus, obteremos 82,8graus.
Com o transferidor, o setor relativo a roteiro medirá cêrca de 86graus, e 24% de 360graus é 86,4graus.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1

A tabela contém o resultado da mesma pesquisa, mas agora realizada com jovens de 16 a 18 anos. Copie essa tabela e complete‑a com as medidas em grau, obtidas com o uso de uma calculadora. Depois, meça os ângulos dos setores do gráfico com um transferidor e compare os resultados.

|
Categoria |
Porcentagem |
Grau |
|---|---|---|
|
trilha sonora |
10% |
|
|
detalhes |
18% |
|
|
visual |
41% |
|
|
roteiro |
19% |
|
|
jogabilidade |
12% |
Dados obtidos pelo fabricante de jogos.
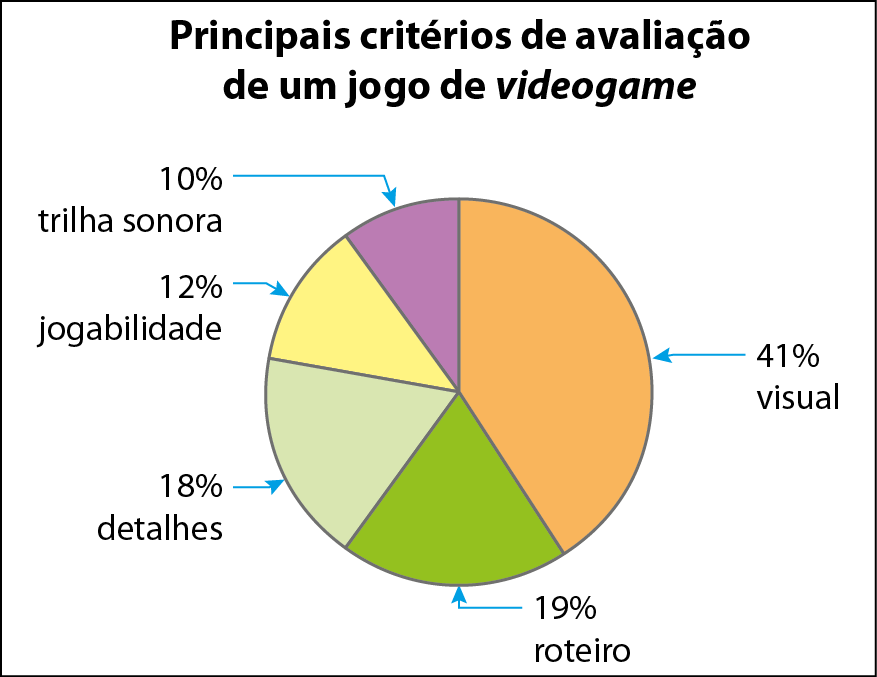
2 No gráfico da atividade 1, qual é a soma das porcentagens de todos os setores?
3 Os gráficos a seguir indicam a distribuição da população brasileira por cor de pele, em relação ao total de pessoas no Brasil em 2000 e em 2019. Calcule as medidas aproximadas dos setores e, depois, confira‑as com o transferidor.
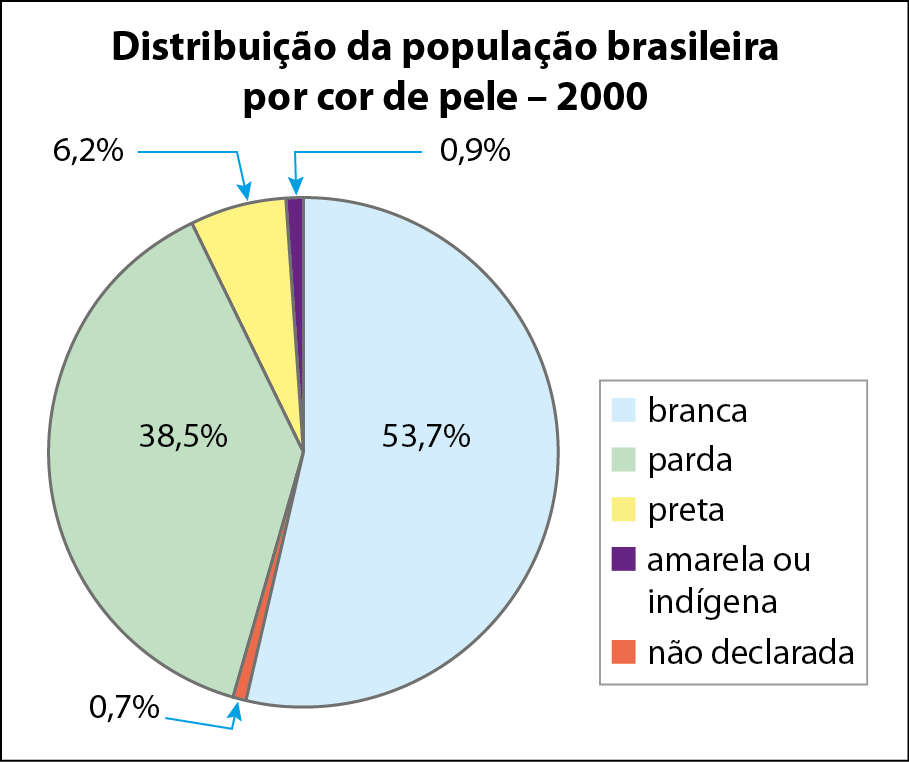
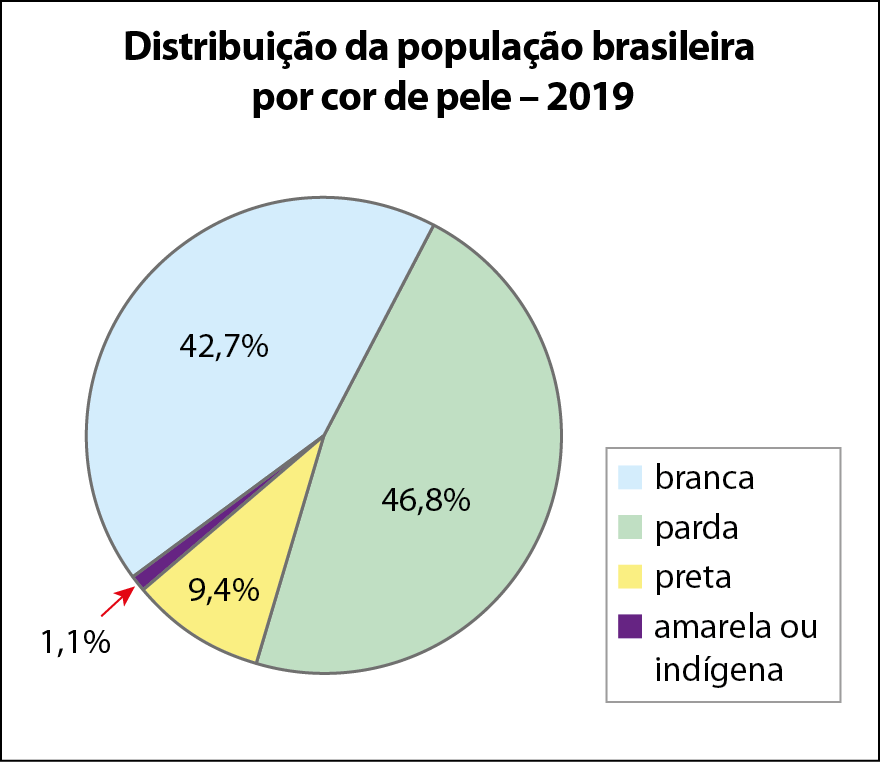
Agora, compare cada setor do gráfico de 2000 com o setor da respectiva cor de pele do gráfico de 2019 e escreva as alterações que ocorreram nesses dezenove anos.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Resolva a questão a seguir.
(ú éfe érre érre jota) A figura mostra a trajetória de uma bola de bilhar. Sabe‑se que, quando ela bate na lateral da mesa (retangular), fórma um ângulo de chegada que sempre é igual ao ângulo de saída. A bola foi lançada da caçapa a, formando um ângulo de 45graus com o lado
AD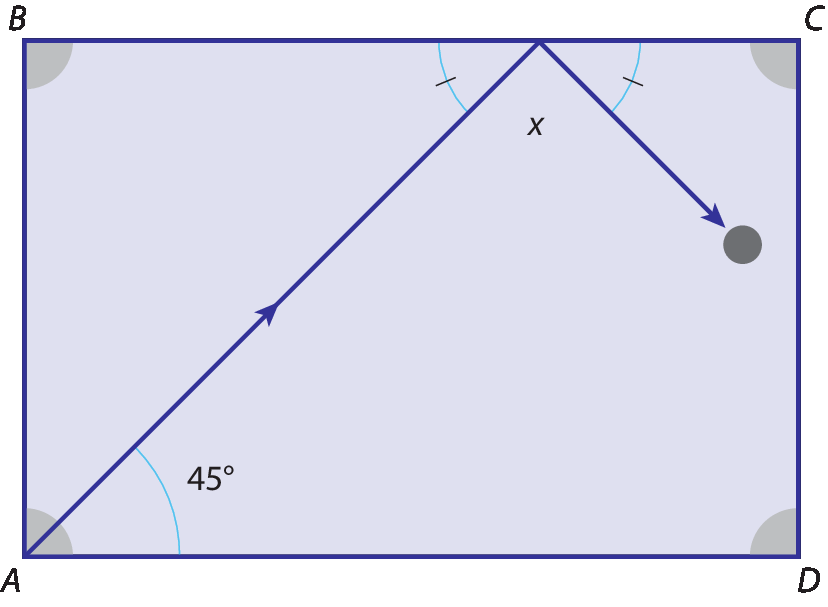
Sabendo‑se que o lado
ABmede duas unidades e
BCmede 3 unidades, a bola:
a) cairá na caçapa a.
b) cairá na caçapa B.
c) cairá na caçapa C.
d) cairá na caçapa D.
e) não cairá em nenhuma caçapa.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Usando régua e transferidor, construa um ângulo reto e, a partir dele, um ângulo de 45graus e um de 22graus30minutos.
2 Na figura a seguir, vista de cima, a cabeça de um parafuso tem a fórma de um hexágono com lados de mesma medida e com ângulos congruentes de 60graus.
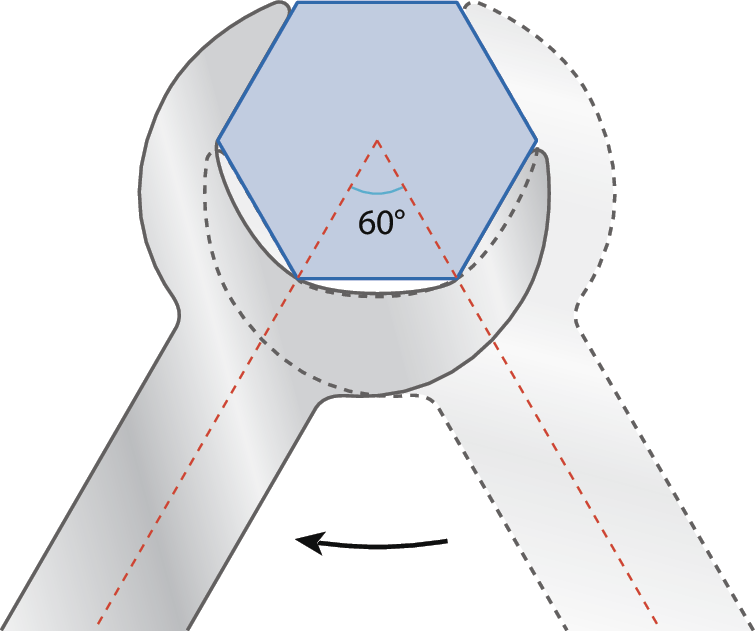
A cada movimento que um mecânico faz com a chave, o parafuso gira 60graus. Quantos movimentos iguais a esse o mecânico deve fazer para que o parafuso dê:
a) meia‑volta;
b) uma volta completa.
• Qual é a medida do ângulo interno desse hexágono? E a do ângulo externo?
3 Uma das manobras de skate chama‑se 900graus. Nessa manobra, o esqueitista dá um giro equivalente a quantas voltas?
4 Acompanhe a descrição do caminho que Ângela percorreu:
• Inicialmente, caminhei 10 métros em linha reta.
• Depois, girei 90graus à esquerda e avancei 10 métros novamente.
• Em seguida, girei 90graus à esquerda e avancei mais 20 métros.
Quantos graus Ângela deverá girar à esquerda para retornar ao ponto de partida em linha reta?
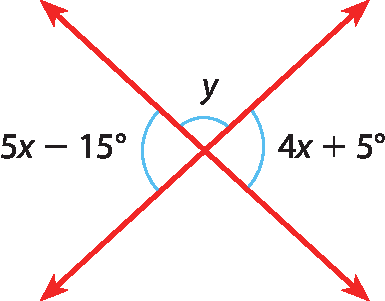
5 Determine as medidas x e y da figura.
6 No triângulo
MN⫽
BCCalcule as medidas xis e y.
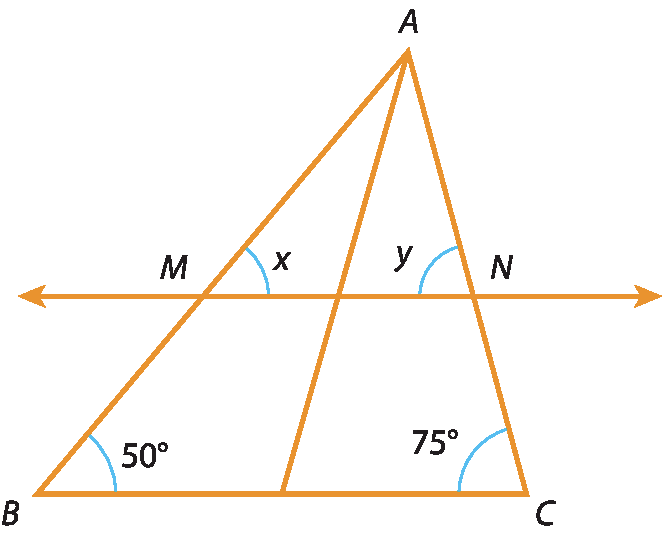
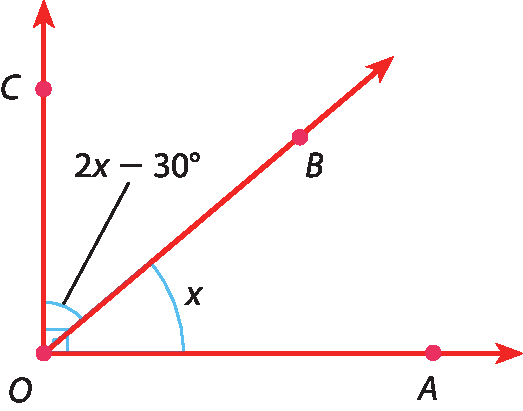
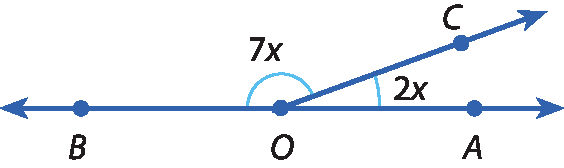
7 Calcule o valor de xis em cada figura.
a)
b)
8 Sendo r ⫽ s ⫽ t, calcule as medidas a, b, c, d, xis e y nas figuras.
a)
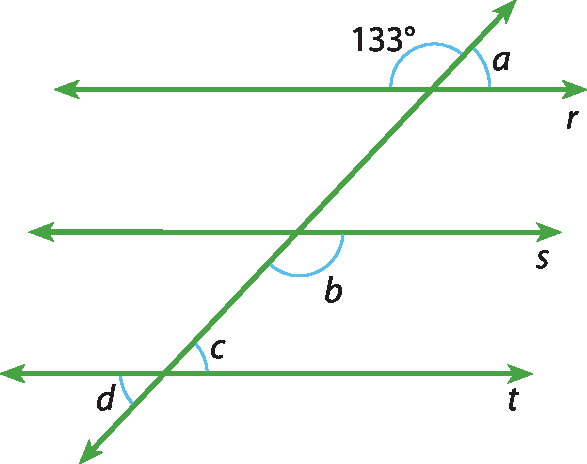
b)
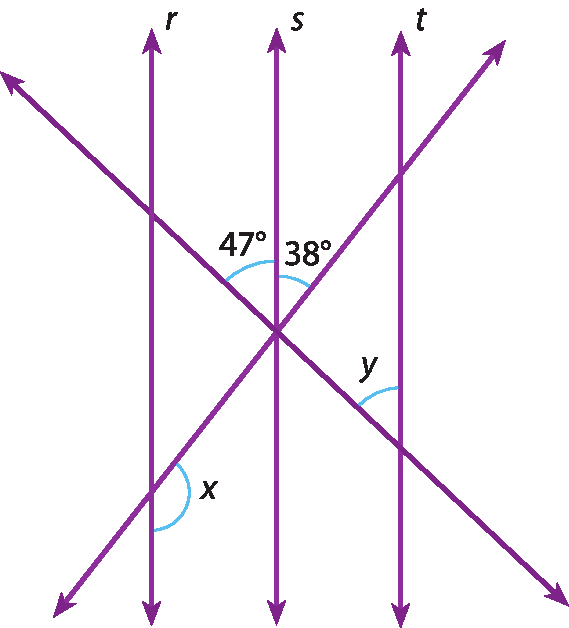
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Na imagem a seguir, supondo duas retas paralelas cortadas por duas transversais, são congruentes os ângulos:
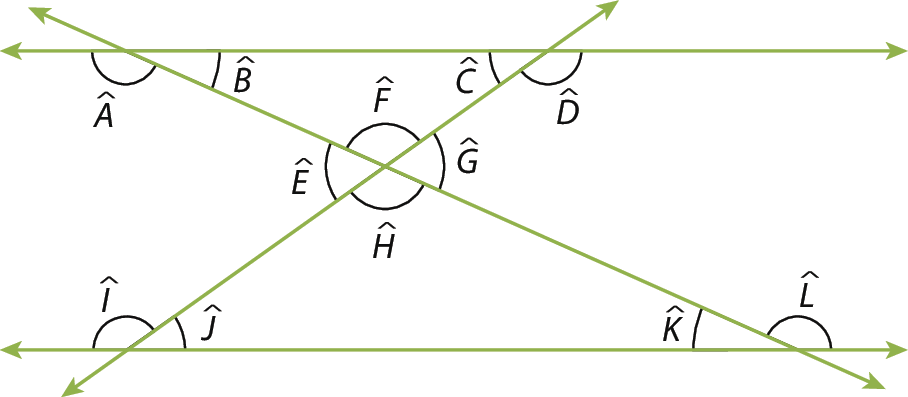
a)
ângulo A e ângulo D.b)
ângulo B e ângulo K.c)
ângulo E e ângulo H.d)
ângulo C e ângulo I.2 Na imagem da questão 1, os pares de ângulos
E e G e A e L.são congruentes pois são, respectivamente:
a) opostos pelo vértice e alternos externos.
b) opostos pelo vértice e alternos internos.
c) adjacentes e colaterais externos.
d) opostos pelo vértice e colaterais externos.
3 A representação correta de 5graus48minutos1segundos em segundo é:
a) .18000segundos
b) .20880segundos
c) .18481segundos
d) .20881segundos
4 Alguns aparelhos de GPS fornecem a medida da distância angular por meio da localização em grau, minuto e segundo. Qual é a medida da distância angular entre duas pessoas que estão na linha do Equador, sendo que uma está em 41graus20minutos5segundos Leste e a outra em 15graus53′58″ Oeste?
a) 57graus24segundos3segundos
b) 66graus14minutos3segundos
c) 57graus14minutos3segundos
d) 66graus24minutos3segundos
5
1 terçode 56graus28minutos15segundos equivale a:
a) 18graus49minutos25segundos
b) 28graus59minutos15segundos
c) 18graus19minutos25segundos
d) 28graus19minutos25segundos
6 A bissetriz de um ângulo divide‑o em dois ângulos:
a) adjacentes e correspondentes.
b) colaterais e alternos internos.
c) congruentes e opostos pelo vértice.
d) congruentes e adjacentes.
7 Dois ângulos são complementares se a soma de suas medidas for igual a:
a) 45graus.
b) 90graus.
c) 180graus.
d) 360graus.
8 Quais são, respectivamente, as medidas dos ângulos complementar e suplementar a um ângulo que mede 78graus22minutos?
a) 11graus38minutos e 101graus38minutos
b) 101graus38minutos e 11graus38minutos
c) 111graus48minutos e 21graus48minutos
d) 21graus48minutos e 111graus48minutos
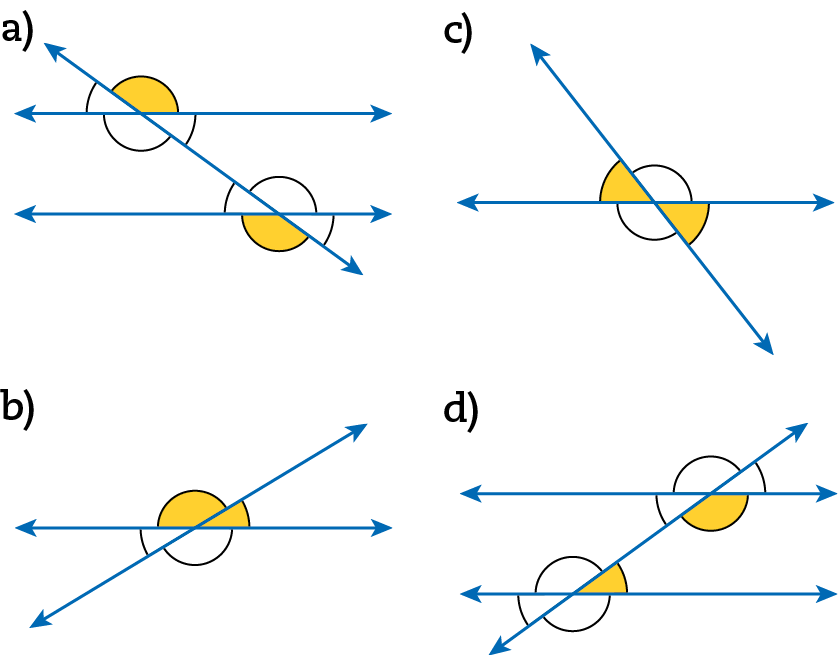
9 Assinale a alternativa que apresenta dois pares de ângulos opostos pelo vértice em destaque.
10 Na planta de uma obra, um engenheiro verificou que a rampa de acessibilidade, em desacordo com normas técnicas, apresentava um ângulo de inclinação de 9graus24minutos. Para corrigi-lo, decidiu traçar, na planta, a bissetriz desse ângulo. O ângulo da nova inclinação passou a medir:
a) 18graus48minutos
b) 4graus17minutos
c) 4graus42minutos
d) 4graus12minutos
11 Dois ângulos colaterais externos formados com uma transversal são:
a) complementares.
b) suplementares.
c) congruentes.
d) opostos pelo vértice.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, faça o que se pede.
a) Escreva, com suas palavras, o que é um ângulo.
b) Quais são os submúltiplos do grau? Escreva a relação entre o grau e seus submúltiplos.
c) Qual estratégia você usa para efetuar operações com medidas de ângulos em grau e seus submúltiplos?
d) Reflita sobre a afirmativa: dois ângulos podem ser complementares e também suplementares.
e) Em quais situações, estudadas neste capítulo, há pares de ângulos congruentes?