Página 108

CAPÍTULO 5 Equações

Fotografia. Vista do interior de um Museu com quadros de pinturas fixados em chapas de vidro. A frente estão 4 quadros sendo três de pinturas de mulheres e um de um homem. Abaixo, estão cubos na cor cinza que sustentam as chapas de vidro. Ao fundo há pessoas visitando o museu e mais quadros. — Obras do acervo permanente do Museu de Arte de São Paulo Assis Chateaubriand (maspi), São Paulo. (Fotografia de 2016.)

Observe, leia e responda no caderno.

a) Diferentes obras de arte, fotografias, gravuras e pinturas são frequentemente acompanhadas por molduras, de formas, cores e ornamentos diversos. Existem até museus e galerias que já dedicaram exposições especiais exclusivamente às molduras, destacando sua beleza e seu trabalho artesanal. Qual é a função da moldura de um quadro?

b) Faça uma pesquisa na internet e identifique o nome das pinturas de Amedeo Modigliani que aparecem na fotografia. O que essas obras de arte têm em comum?

c) Uma dessas telas tem 100 centímetros de medida de altura por 65 centímetros de medida de largura. Qual é a medida aproximada do perímetro dessa obra de arte?

O preço da moldura de um quadro depende do seu material e da medida do perímetro da pintura, isto é, da soma das medidas dos seus lados, e pode ser obtido por meio de uma equação. As quatro obras de arte que identificamos na imagem são do artista italiano Amedeo Modigliani (1884-1920) e foram pintadas entre os anos de 1916 a 1919. É possível notar que as quatro obras estão emolduradas.

A moldura, além de proteger uma obra de arte e de ter função decorativa, direciona o olhar, dá destaque à cena apresentada, delimita suas fronteiras. Ela pode atrair o espectador, mas também pode distraí-lo. Molduras podem ser consideradas obras de arte por si sós, mas há quem questione a importância da moldura em relação à pintura. No final, a combinação entre ambas é o que conta.

Página 109

1. Um pouco de História

Tradicionalmente, os textos de Matemática incluem problemas para os leitores resolverem. Os antigos textos de Matemática, como os egípcios, babilônicos, indianos, árabes e chineses, possuíam uma lista de problemas cujas soluções eram fornecidas posteriormente.

Os problemas tinham a função didática de ensinar Matemática, mas também refletiam as necessidades das sociedades e os diferentes aspectos da vida cotidiana da época.

Fotografia. Tábua retangular de argila com escritas cuneiformes. — Tábua babilônica, em escrita cuneiforme, datada entre 1800 antes de Cristo e 1600 antes de Cristo Nela estão registrados 25 problemas matemáticos.

Fotografia. Papiro retangular antigo com diversos hieróglifos. — Papiro de Rhind, cerca de 1650 antes de Cristo Esse papiro mede cerca de 33 centímetros de largura por 495 centímetros de comprimento e está escrito em hierático (que se lê da direita para a esquerda). O papiro contém uma coleção de 87 problemas, e seu nome refere-se ao escocês Alexander Henry Rhind, que o comprou por volta de 1858, em lúcsor, no Egito. É também designado como papiro de Ahmes, nome do escriba egípcio que o copiou.

Fotografia. Papel da página de um livro antigo, em tom marrom com texto em árabe. As bordas são adornadas com linhas curvadas. — Página do livro Hisab al-jabr al-muqabala – um tratado de Álgebra escrito pelo matemático Al-KhwāÁrīzmī, por volta de 825 Depois de Cristo

Fotografia. Papel da página de um livro amarelada. Nele, estão três colunas com textos em chinês. À direita das colunas há um círculo com quadrado dentro e letras em chinês dentro dele. Abaixo dessas figuras há um quadrado com um círculo dentro e letras em chinês dentro dele. — Página do Zhou bi suan jing ou Chou pei suan ching (entre 100 antes de Cristo e 100 Depois de Cristo), considerado o texto mais antigo da Matemática chinesa. Esta reprodução corresponde a uma edição de 1213, do acervo da Biblioteca de Xangai. O texto não é apresentado por meio de problemas e respostas, mas, sim, em fórma de diálogo.

(As imagens não respeitam as proporções reais entre os objetos.)

Página 110

Fotografia. Pedaço de papel antigo alaranjado com texto em língua hindi. — Fragmento do manuscrito Lilavati (A bela), escrito em 1150 d.C. pelo matemático indiano báscara. Lilavati é uma das quatro partes da obra Siddhanta siromani e contém 278 versos com problemas simples de Aritmética.

A seguir, destacamos dois problemas.

O primeiro faz parte da coleção do papiro de Rhind, e o segundo se baseia em uma das traduções do manuscrito Lilavati.

Ilustração. Pedaço de papel com as informações: Determinada quantidade e a sua quarta parte adicionadas dão 15. Qual é a quantidade? Ilustração. Pedaço de papel com as informações: … o colar do pescoço da esposa partiu-se. Um terço das pérolas caiu no chão, um quinto foi para debaixo da cama. A esposa apanhou um sexto, e seu amado, um décimo. Seis pérolas ficaram no fio original. Descubra o número total de pérolas no colar.

Você saberia resolver esses problemas?

Embora não seja fácil, é possível encontrar as respostas por meio de tentativas.

Neste capítulo, você vai aprender novos recursos que podem facilitar a resolução de problemas como esses.

2. Números representados por letras

Em algumas situações, você teve a oportunidade de trabalhar com expressões matemáticas.

Observe estas expressões, escritas na linguagem comum e na linguagem simbólica da Matemática.

a) Dois vezes cinco

Ilustração. Seta apontada para a direita.

2 ⋅ 5

b) Três vezes quatro mais um

3 ⋅ 4 + 1

c) O quadrado de dois sétimos adicionado a dois quintos

{(\frac{2}{7})}^{2} + \frac{2}{5}

Ilustração. Mulher branca de cabelo preto, liso e comprido e blusa lilás. Ela fala: Como você já deve ter estudado, a Álgebra é a parte da Matemática que trabalha com grandezas cujos valores variam (variáveis) ou que são desconhecidos (incógnitas) e que são representados por símbolos - em geral, por letras.

Página 111

Quando falamos de um número racional qualquer, podemos usar uma letra para representá-lo. Observe alguns exemplos.

a) O dobro de um número

2 ⋅ x

b) O triplo de um número mais quatro

3 ⋅ x + 4

c) A metade de um número menos um terço

\frac{x}{2} ‒ \frac{1}{3}

d) Um número mais seus três quintos

x +

\frac{3}{5}

⋅ x

e) A soma de dois números inteiros consecutivos

x + (x + 1)

Note que, em todos esses exemplos, a letra x pode ser qualquer número racional. Dizemos, então, que xis é uma variável. Conforme o valor assumido por x, há um valor para a expressão matemática.

As expressões 2 ⋅ x, 3 ⋅ x + 4,

\frac{x}{2} ‒ \frac{1}{3}

, x +

\frac{3}{5}

⋅ x e x + (x + 1) são exemplos de expressões algébricas. Em expressões como essas, a variável não precisa ser obrigatoriamente a letra x; ela pode ser representada por qualquer outra letra. Observe.

a) O dobro de um número

2 ⋅ y ou 2y (sem o sinal de multiplicação)

b) O triplo de um número menos dez

3z ‒ 10

c) O quadrado da metade de um número menos um terço desse número

{(\frac{t}{2})}^{2} ‒ \frac{1}{3} t

d) A soma de um número com o dobro de outro número

a + 2b

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Escolha uma letra para representar um número e traduza para a linguagem simbólica da Matemática cada expressão relativa a esse número.

a) O triplo desse número mais dez.

b) Esse número menos quatro.

c) O quádruplo desse número.

d) A terça parte desse número.

e) Três quartos desse número.

2 Leia e responda à questão.

Faltam apenas duas figurinhas para que meu amigo tenha o dobro do número de figurinhas que eu tenho.

Se indicarmos por y o número de figurinhas que eu tenho, como poderemos representar o número de figurinhas que meu amigo tem?

3 Sendo a e b dois números racionais, represente na linguagem simbólica da Matemática:

a) a soma desses números;

b) a diferença entre esses números;

c) o dobro de a menos o triplo de b;

d) o produto desses números.

4 Nas expressões a seguir, a letra x representa um número. Relacione cada expressão escrita na linguagem comum com a expressão algébrica correspondente, escrevendo no caderno o número romano e a letra a que está associado.

um. O dobro do quadrado de x .

dois. O quadrado do dobro de x.

três. A diferença entre o dobro de x e 3.

quatro. O dobro da diferença entre x e 3.

cinco. A divisão da soma de x com 3 por 2.

seis. A soma dos quadrados dos números x e 3.

sete. O quadrado da soma dos números x e 3.

a) 2x ‒ 3

b) x 2 + 32

c) (2x) 2

d) (x + 3) 2

e) 2x 2

\frac{x + 3}{2}

g) 2(x ‒ 3)

Página 112

5 Indique no caderno a expressão algébrica que se obtém com este comando:

Ilustração. Monitor de um computador com as informações: Considere um número racional xis; dobre esse número; adicione cinco ao resultado obtido; multiplique por três esse novo resultado.

6 Nas figuras, as letras x, y e z representam medidas de diferentes segmentos. Indique, no caderno, a expressão algébrica correspondente à medida do segmento

\overline{A B}

em cada caso.

Ilustração. Segmento de reta A e B e medidas entre os pontos: x, 2.

Ilustração. Segmento de reta A e B e medidas entre os pontos: y, y, 5.

Ilustração. Segmento de reta com pontos: A e B e medida de A até um ponto depois de B igual a 8. Entre o ponto B e esse ponto mede z.

Hora de criar – Crie três expressões que envolvam um número x qualquer e operações matemáticas. Escreva-as no caderno em linguagem comum e também represente-as por um fluxograma. Troque de caderno com um colega para que reescrevam essas expressões em linguagem simbólica. Depois destroquem para corrigi-las.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Junte-se a um colega para resolverem este problema de sequências numéricas.

Em uma brincadeira, Lucas falava um número e Lia dizia outro, segundo uma regra criada por ela. O objetivo da brincadeira era fazer Lucas descobrir a regra inventada por Lia. Acompanhem a sequência de números que eles falaram.

Lucas	1	2	3	4	5	9	15	20
Lia	4	5	6	7	8	12	18	23

a) Descubram a regra que Lia criou e escrevam essa regra na fórma de expressão algébrica.

b) Se Lucas falasse o número 25, que número Lia diria? E se ele falasse ‒3?

c) Que número Lucas deveria dizer para que Lia falasse o maior número possível?

Mais tarde, Lia passou a falar os números, e Lucas, segundo sua nova regra, dizia outro número. Acompanhem a nova sequência de números que eles falaram.

Lia	1	2	3	4	5	9	15	20
Lucas	7	9	11	13	15	23	35	45

d) Descubram a regra de Lucas e a escrevam na fórma de expressão algébrica.

e) Se Lia falasse o número zero, que número Lucas diria? E que número ela deveria dizer para que a resposta dele fosse o número 5?

f) Que número Lia deveria dizer para que Lucas falasse o maior número possível?

Página 113

3. Valor numérico de uma expressão algébrica

Retomamos aqui a situação da abertura deste capítulo sobre a moldura de quadros.

Observe o quadro retangular cuja moldura mede x centímetros por y centímetros de lado e custa α reais por centímetro.

Pintura. Homem de cabelo longo, preto e barba preta usa roupa clara com casaco vermelho. Com uma das mãos ele segura um papel enrolado e a outra mão está sobre um livro que está apoiado em uma mesa a frente do homem. — CIFRONDI, A. Euclide. cêrca de 1725. Óleo sobre tela, 133 por 95 centímetros. Fundação Cariplo, Milão, Itália.

Lembrando que a medida do perímetro de um polígono é dada pela soma das medidas de seus lados, temos:

x + x + y + y = 2 ⋅ x + 2 ⋅ y = 2x + 2y = 2 ⋅ (x + y)

Assim, podemos calcular o preço p da moldura a partir do cálculo da medida do perímetro do quadro:

p = 2 ⋅ (x + y) ⋅ α

Considerando que a medida da largura do quadro é 95 centímetros, que a medida de seu comprimento é 133 centímetros e supondo que cada centímetro da moldura custe R$ 2,75,dois reais e setenta e cinco centavos vamos obter o valor numérico de p substituindo x por 95, y por 133 e α por 2,75.

p = 2 ⋅ (95 + 133) ⋅ 2,75 = 2 ⋅ 228 ⋅ 2,75 = .1254

Portanto, o preço da moldura desse quadro é .1254 reais.

Quando trocamos as letras da expressão por números e efetuamos as operações indicadas, o número obtido é chamado de valor numérico.

No exemplo anterior, o número .1254 é o valor numérico da expressão 2 ⋅ (x + y) ⋅ α para x = 95, y = 133 e α = 2,75.

Considerando agora toda a superfície retangular do quadro e lembrando que a medida da área dessa superfície é o produto das medidas do comprimento e da largura, então a medida de sua área é dada pela expressão:

x ⋅ y ou xy

Como x = 95 e y = 133, medidas em centímetro, temos:

xy = 95 ⋅ 133 = .12635

O valor numérico da expressão xy, para x = 95 e y = 133, é .12635.

Portanto a medida da área do quadro é .12635 centímetros quadrados.

Página 114

Agora, acompanhe como calcular o valor numérico da expressão p2 + 2pq para p = ‒2 e q =

\frac{3}{5}

Substituindo na expressão a letra p por ‒2 e a letra q por

\frac{3}{5}

, temos:

p2 + 2pq = (‒2)2 + 2 ⋅ (‒2) ⋅

(\frac{3}{5}) = 4 ‒ \frac{12}{5} = \frac{8}{5}

Logo, o valor numérico da expressão p2 + 2pq, para p = ‒2 e q =

\frac{3}{5}

, é

\frac{8}{5}

ou 1,6.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

8 Sabendo que um triângulo é equilátero, determine uma expressão algébrica que indique a medida do perímetro desse triângulo.

9 Calcule o valor numérico das expressões.

a) 3x + 5, para x = ‒6

b) 2a + 7b, para a = ‒3 e b =

\frac{1}{7}

c) a2 + 3a, para a =

‒ \frac{1}{2}

d) a2 ‒ 2ab + b2, para a = ‒5 e b = 2

10 Esta região quadrada está dividida em 8 partes iguais.

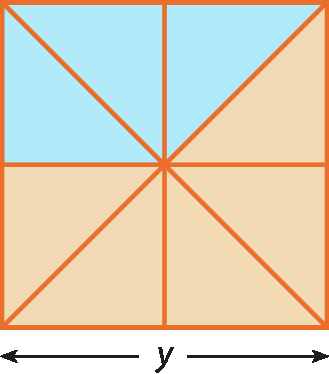
Ilustração. Quadrado dividido em 8 partes iguais com três partes pintadas de azul e 5 partes pintadas de laranja. A medida do lado do quadrado é y.

Determine a expressão algébrica que representa:

a) a medida da área da região quadrada;

b) a medida do perímetro do quadrado que delimita essa região;

c) a medida da área da parte laranja;

d) Agora, determine o valor numérico da medida da área da região quadrada para y = 2,1.

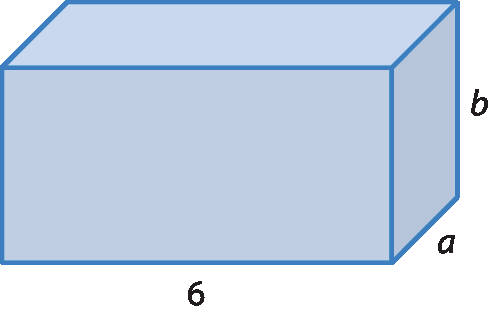
11 Considerando o bloco retangular, determine uma expressão algébrica que represente:

a) a medida do perímetro da face superior;

b) a medida da área da face superior;

c) a soma das medidas de todas as arestas;

d) a medida do volume do bloco retangular.

Ilustração. Bloco retangular com dimensões medindo 6, a e b.

12 Uma empresa de confecção assume um custo mensal fixo de R$ 10.000,00dez mil reais para o pagamento de algumas despesas com funcionários e impostos, além do custo de R$ 2,50dois reais e cinquenta centavos para cada camiseta produzida.

O custo mensal para essa empresa pode ser dado pela expressão algébrica:

C = .10000 + 2,5x,

em que C é o custo mensal, em real, e x é o número de camisetas produzidas.

Ilustração. À esquerda, homem sentado à frente de uma máquina de costura. Ele costura camisetas azuis e verdes. À direita, mulher sentada à frente de uma máquina de costura. Ela costura camisetas amarelas e laranjas. Ao fundo, móvel com tecidos, um bebedouro e ventilador no teto.

a) Determine o custo para a empresa no mês em que foram fabricadas .1000 camisetas.

b) Se cada camiseta for vendida a R$ 20,00vinte reais, a empresa terá lucro? Em caso afirmativo, de quanto?

13 O pacote de dados de uma operadora de celular, para o acesso à internet, com direito a 2 gigabytes, custa R$ 24,90vinte e quatro reais e noventa centavos por mês. Se o consumidor exceder esses 2 gigabytes, ele pagará R$ 5,00cinco reais por gigabyte excedente.

a) Escreva no caderno uma expressão algébrica que represente a situação em que o consumidor excede os 2 gigabytes.

b) Quanto um consumidor pagará, se usar 1 gigabyte em um mês? E se usar 5 gigabytes?

Hora de criar – Em duplas, criem um problema cada para obter o valor numérico de expressões algébricas. Criem problemas envolvendo situações do dia a dia. Troquem os problemas criados por vocês. Depois destroquem para corrigi-los.

Página 115

4. Termos algébricos

Observe as figuras.

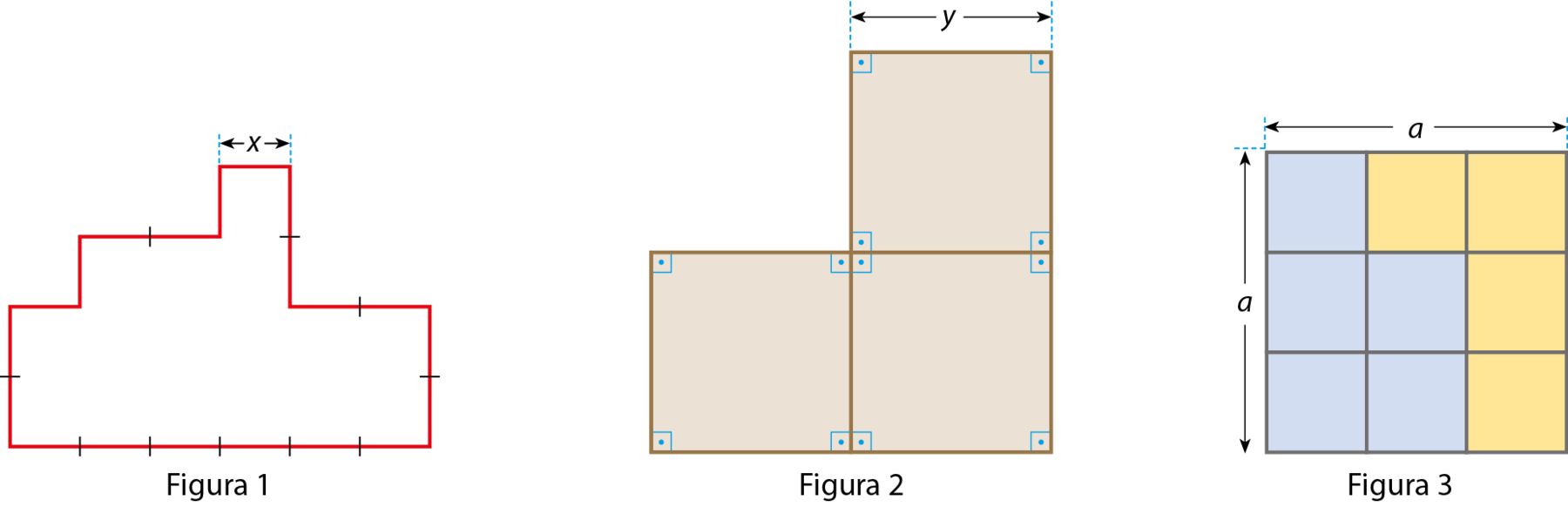
Ilustração. Figura composta por 10 lados em cada lado há indicações de divisões e cada divisão mede xis. Ilustração. Dois quadrados (um ao lado do outro) e acima do quadrado à direita um outro quadrado. A medida do lado de cada quadrado é y. Ilustração. Quadrado dividido em 9 quadradinhos de mesma medida. A medida do lado do quadrado é a. Há 4 quadradinhos pintados de amarelo e 5 de azul.

Os lados da figura 1 foram divididos em segmentos de mesma medida. Considerando a medida desses segmentos igual a x, dizemos que a medida do perímetro da figura é dada por 20x.

A figura 2 é formada por três superfícies quadradas de lados de mesma medida. Considerando a medida dos lados dessas superfícies igual a y, a medida da área da figura é dada pela expressão algébrica 3y 2.

Como as medidas dos lados da figura 3 valem a, a medida da sua área será dada por a2, enquanto a medida da área da região azul será dada por

\frac{5}{9} a^{2}

, e a medida da área da região amarela será dada por

\frac{4}{9}

a2.

As expressões 20x, 3y 2, a2,

\frac{5}{9} a^{2}

\frac{4}{9}

a2 são exemplos de termos algébricos.

Em um termo algébrico, distinguimos o coeficiente (parte numérica) e a parte literal (parte com letras). No quadro a seguir, mostramos alguns termos algébricos e destacamos, em cada um, o coeficiente e a parte literal.

Termo algébrico	Coeficiente	Parte literal
5x	5	x
‒m	‒1	m
$2 divisão de 3 sobre 4 x y elevado a 2$	$2 divisão de 3 sobre 4$	xy2
2 $divisão de abre parênteses a x fecha parênteses sobre 6$	$2 divisão de 1 sobre 6$	ax

Observe que um termo algébrico tem apenas um coeficiente e uma parte literal.

Agora, considere a expressão algébrica: 2a ‒ 5b. Essa expressão tem dois termos algébricos: 2a e ‒5b. O coeficiente do primeiro termo algébrico (2a) é 2, e o do segundo termo algébrico (‒5b) é ‒5.

Observações

▶ Um número racional é considerado “termo algébrico sem parte literal”.

Assim, a expressão x 2 ‒ 5x + 6 tem três termos algébricos: x 2, ‒5x e 6.

O coeficiente de x 2 é 1, o coeficiente de ‒5x é ‒5, e 6 é o termo algébrico sem parte literal.

▶ Note que a adição de termos algébricos resulta em uma expressão algébrica.

Por exemplo: x 2 + (‒5x) + 6 = x 2 ‒ 5x + 6

Página 116

Termos semelhantes

Observe as figuras a seguir.

A medida do segmento da figura 1 é dada por 3x.

A medida do perímetro do pentágono da figura 2 é dada por 5x.

Ilustração. Segmento de reta horizontal dividido em 3 partes em que cada parte mede xis. Ilustração. Pentágono com medida x em cada lado.

Os termos algébricos 3x e 5x têm a mesma parte literal (x); dizemos, então, que eles são termos semelhantes.

Acompanhe outros exemplos.

a) ‒2ax e 8ax são termos semelhantes, porque têm a mesma parte literal (ax).

b) 5ax 2 e 2a 2x não são termos semelhantes, porque as partes literais são diferentes (ax 2 ≠ a 2x), embora as variáveis, a e x, sejam as mesmas.

Simplificação de expressões algébricas

O triângulo da figura é equilátero, isto é, todos os lados têm mesma medida, que indicamos pela letra a.

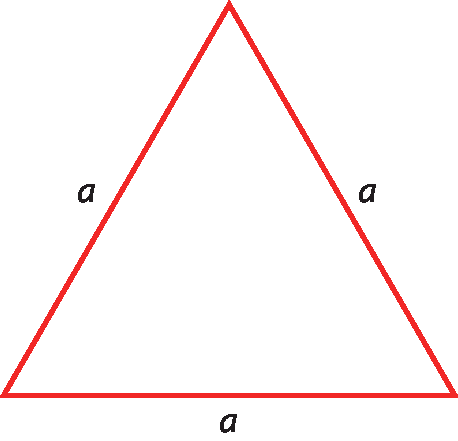
Ilustração. Triângulo com medida a em cada lado.

Então, a medida do perímetro desse triângulo é dada por: a + a + a.

Como esse triângulo é equilátero, a medida do seu perímetro é o triplo da medida do lado, ou seja, a medida do perímetro também é dada por: 3a.

É possível simplificar a expressão a + a + a escrevendo 3a. Assim, reduzimos a expressão a um único termo.

Acompanhe outros exemplos.

a) Vamos simplificar a expressão algébrica 2 ⋅ (x + 6) + x.

Para isso, vamos usar a propriedade distributiva da multiplicação:

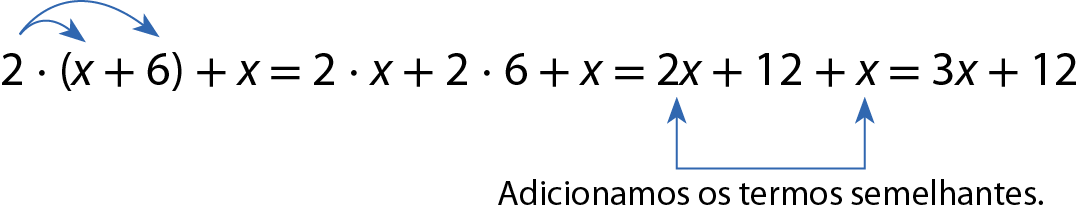
Esquema. 2 vezes abre parênteses xis mais 6, fecha parênteses (com setas apontando de 2 para xis e de 2 para 6), mais xis é igual a 2 vezes x mais 2 vezes 6 mais xis é igual a 2x mais 12 mais xis (com seta apontando em 2x e xis e texto: adicionamos os termos semelhantes) é igual a 3x mais 12.

b) Vamos simplificar a expressão

\frac{15 x + 9}{3}

+ x + 4.

Esquema. Fração, numerador: 15x mais 9; denominador: 3, fim da fração mais xis mais 4 é igual a 15x sobre 3, mais 9 sobre 3, mais xis mais 4 é igual a 5x mais 3 mais xis mais 4 é igual a 6x mais 7. Há uma seta que aponta de fração, numerador: 15x mais 9; denominador: 3, fim da fração, para a fração, 15x sobre 3, fim da fração, mais fração, 9 sobre 3, fim da fração e o texto abaixo da seta: Separamos em duas frações. Há setas apontando em 5x e x e em 3 e 4 com o texto: Adicionamos os termos semelhantes.

Página 117

Assim, reduzimos os termos semelhantes com a mesma parte literal x a 6x; reduzimos os termos semelhantes sem parte literal a 7.

Na prática, para reduzir termos semelhantes a um único termo, adicionamos algebricamente os coeficientes e conservamos a parte literal.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

15 Nesta figura, a medida da área de cada região quadrada é representada por 25x 2.

Ilustração. Retângulo dividido em 4 linhas e 6 colunas de quadradinhos amarelos e azuis intercalados.

a) Determine o termo algébrico que representa a medida da área da figura toda.

b) Indique o termo algébrico que representa a medida da área da parte pintada de verde.

c) Os dois termos obtidos são semelhantes? Justifique sua resposta.

d) Calcule o valor numérico de 25x 2 para x = 1,2.

16 Reduza os termos semelhantes das expressões algébricas a seguir.

a) ‒4x + 6y + 10x ‒ 2y ‒ x

b) x + 7x + 10y ‒ 3x

c) 2x ‒ 8y ‒ 6y ‒ y ‒ 9x

\frac{3}{2} x + \frac{1}{4} y ‒ \frac{1}{3} x + 2 y

17 Simplifique as expressões algébricas.

a) 4(x ‒ 1) + 3(x + 1)

b) ‒2(2x ‒ 4) + 5(‒2x ‒ 10)

\frac{2}{5} (x ‒ 0, 2) ‒ \frac{1}{2} (3 x ‒ \frac{4}{25})

18 Considere os polígonos a seguir e responda às questões.

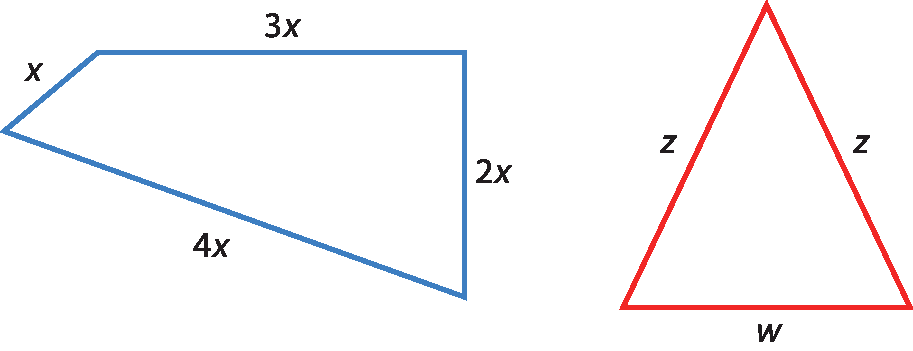
Ilustração. Quadrilátero com medidas: x, 4x, 2x e 3x. Ilustração. Triângulo com medidas: w, z, z.

a) Determine a expressão algébrica que representa a medida do perímetro de cada polígono.

b) Se x = 3,2 centímetros, qual é a medida do perímetro do quadrilátero?

c) Se z = 6 centímetros e w = 5 centímetros, qual é a medida do perímetro do triângulo?

19 No 1º semestre de 2021, os negócios de Alex tiveram o seguinte resultado: o lucro de fevereiro foi o dobro do lucro de janeiro; o lucro de março foi igual ao de janeiro; o de abril, igual ao de fevereiro; o de maio, o triplo do de janeiro; e o de junho, igual às quantias de janeiro e fevereiro juntas. Chamando de p o lucro do mês de janeiro, dê a expressão algébrica que indica:

a) o lucro de cada mês.

b) o lucro de todo o semestre.

20 Atribua à letra n os números naturais de 0 a 6. Depois, imaginando que se possa continuar atribuindo infinitamente os números naturais a n, considerando as duas expressões algébricas a seguir, quais regularidades numéricas são encontradas? Nomeie essas sequências numéricas.

a) 2n

b) 2n + 1

Considere a sequência de termos algébricos: a, a, 2a, 3a, 5a, 8a, 13a, 21a, 34a, reticências Junte-se a um colega e, fazendo o que se pede, descubram regularidades nas sequências numéricas.

a) Adicionem dois termos consecutivos quaisquer dessa sequência e comparem com o termo seguinte. O que acontece?

b) Adicionem a à soma dos quatro primeiros termos da sequência. O resultado é igual a algum outro termo da sequência? Em caso afirmativo, qual?

c) Adicionem a à soma, a partir do primeiro termo da sequência, de quantos termos quiserem dessa sequência. O resultado é igual a algum termo dessa sequência? Em caso afirmativo, qual?

d) Atribuindo 1 à letra a dessa sequência, temos a sequência de fibonáti. Escreva os dez primeiros números da sequência de fibonáti.

Página 118

5. Sentenças matemáticas e equações

Sentença é um conjunto de palavras com sentido completo. Algumas são consideradas ditados populares, por exemplo:

a) De poeta e de louco, todo mundo tem um pouco.

b) Mais difícil que encontrar uma agulha no palheiro é encontrar duas.

Quando uma sentença envolve números, ela é chamada sentença matemática. Observe alguns exemplos.

a) Cinco mais três é igual a oito.

b) Dois é menor que vinte.

c) Sete é diferente de nove.

d) Doze é o dobro de seis.

e) Dez é maior ou igual a dez terços.

Podemos escrever as sentenças matemáticas por extenso, como vimos anteriormente, ou na linguagem simbólica da Matemática. Observe.

a) 5 + 3 = 8

b) 2 < 20

c) 7 ≠ 9

d) 12 = 2 ⋅ 6

e) 10 ⩾

\frac{10}{3}

As sentenças matemáticas podem ser classificadas como verdadeiras ou falsas.

Verificamos facilmente que as sentenças 5 + 7 = 12 e

\frac{3}{4} \cdot \frac{4}{3} = 1

são verdadeiras, enquanto as sentenças 4 + 5 < 2 e 7 ‒ 2 = 4 são falsas.

A sentença 10 ⩾

\frac{10}{3}

é classificada como verdadeira, porque dez é maior ou igual a dez terços, e a conjunção ou liga duas afirmações:

• dez é maior que dez terços (verdadeira);

• dez é igual a dez terços (falsa).

Pelo fato de ou ser uma conjunção alternativa, basta uma dessas afirmações ser verdadeira para que a sentença também o seja.

Equações

Observe esta balança de dois pratos.

Perceba que ela está em equilíbrio e com os pratos na mesma altura, ou seja, a medida da massa total dos objetos colocados no prato 1 é igual à medida da massa total dos objetos colocados no prato 2.

Ilustração. Balança de dois pratos. No prato da esquerda, dois potes com mel e um peso de 50 gramas. No prato da direita, um pote com mel e um peso de 200 gramas. A balança está equilibrada.

Representando por x a medida da massa, em grama, de cada pote de mel, podemos escrever:

x + x + 50 = x + 200

Essa sentença matemática é expressa por uma igualdade e apresenta um elemento desconhecido. Ela é um exemplo de equação.

Equação é toda sentença matemática expressa por uma igualdade que apresenta letras representando números desconhecidos.

Página 119

Observe outros exemplos de equação.

a) 7x +

\frac{5}{2}

= 4

b) 2y 2 ‒ 3y + 7 = 0

c) 2x + 3y = 8

A expressão à esquerda do sinal de igual chama-se primeiro membro da equação, e a expressão à direita do sinal de igual, segundo membro da equação.

Acompanhe mais exemplos.

a) 2y ‒ 4 = 6, em que 2y ‒ 4 é o primeiro membro e 6 é o segundo membro.

b) 2z 2 + 4 = z ‒ 6, em que 2z 2 + 4 é o primeiro membro e z ‒ 6 é o segundo membro.

c) a + 1 =

\frac{b}{3}

, em que a + 1 é o primeiro membro e

\frac{b}{3}

é o segundo membro.

Em uma equação, os elementos desconhecidos (letras que representam números) cujos valores devem ser determinados são chamados de incógnitas.

Nos exemplos anteriores, podemos destacar que:

• na equação 2y ‒ 4 = 6, a incógnita é y ;

• na equação 2z 2 + 4 = z ‒ 6, a incógnita é z;

• na equação a + 1 =

\frac{b}{3}

, as incógnitas são a e b.

Observação

▶ Nem toda igualdade é uma equação. Por exemplo, 3 + 5 = 8 não é uma equação, porque não tem elemento desconhecido.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

22 Entre as sentenças a seguir, copie no caderno somente as equações.

a) 3x ‒ 9 = x + 6

b) 2y ‒ 9 = 21

c) 5 + 7 = 12

d) 3x ‒ 1 < 8

e) 92 ‒ 72 = 32

f) 9y 2 ‒ 7y = 0

23 Escreva a equação que tem por primeiro membro a expressão x 2 ‒ 2x e por segundo membro, 3x ‒ 6.

a) Na equação escrita, substitua x por 2 e calcule o valor numérico de cada membro. Faça o mesmo substituindo x por 3. O que aconteceu de comum nos dois casos?

b) Acontece o mesmo se você substituir x por 4?

24 Na equação 4y 2 ‒ 5y + 3 = 0, identifique o primeiro e o segundo membros. Se você trocar de lugar os membros dessa equação, ela tem seu significado alterado? Justifique sua resposta.

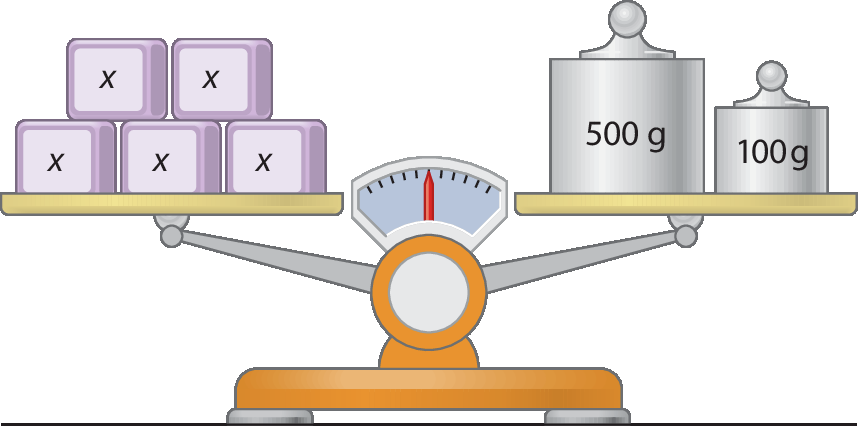
25 Indicando a medida da massa, em grama, de cada cubo por x, determine a equação sugerida pela balança em equilíbrio.

Ilustração. Balança de dois pratos. No prato à esquerda, cinco cubos de massa x cada um. No prato à direita, um peso de 500 gramas e 1 peso de 100 gramas. A balança está equilibrada.

Página 120

Raiz de uma equação

Observe outra balança em equilíbrio e com os pratos nivelados.

Ilustração. Balança de dois pratos. No prato à esquerda, três laranjas e um bloco de 50 gramas. No prato à direita, duas laranjas e um bloco de 200 gramas. A balança está equilibrada.

No prato da esquerda, há 3 laranjas e um bloco de 50 gramas. No prato da direita, temos duas laranjas e um bloco de 200 gramas. Vamos descobrir qual é a medida da massa de cada laranja.

Considerando cada laranja com x gramas, podemos representar essa situação pela equação:

3x + 50 = 2x + 200

O valor de x que torna a igualdade verdadeira é 150. Substituindo x por 150, temos:

3x + 50 = 2x + 200

3 ⋅ 150 + 50 = 2 ⋅ 150 + 200

Ilustração. Menino ruivo de boné azul e camiseta verde. Ele diz: Como foi que se chegou no número 150?

Ilustração. Mulher negra de cabelo castanho curto e blusa rosa. Ela diz: Calma, veremos adiante como se resolve uma equação.

450 + 50 = 300 + 200

500 = 500 (verdadeira)

Como x representa a medida da massa, em grama, de cada laranja, concluímos que cada laranja tem 150 gramas. O valor 150 é chamado de raiz da equação 3x + 50 = 2x + 200.

Um número é denominado raiz de uma equação quando, ao substituir a incógnita por ele, obtemos uma sentença verdadeira.

Esse procedimento de substituição da incógnita por um número serve para verificar se esse número é ou não raiz da equação.

Analise estes exemplos.

a) Para verificar se o número 5 é raiz da equação x + 2 = 7, substituímos x por 5. Assim, temos:

b) Para verificar se o número ‒3 é raiz da equação 2y + 15 = y + 12, substituímos y por ‒3. Dessa fórma, obtemos:

c) Para verificar se o número 4 é raiz da equação 3z + 2 = 5, substituímos z por 4. Assim, temos:

Página 121

Conjunto universo e solução de uma equação

Para conseguir resolver uma equação, precisamos saber quais são os valores que a incógnita pode assumir e quais são os valores que tornam a sentença verdadeira.

Vamos analisar as sentenças a seguir.

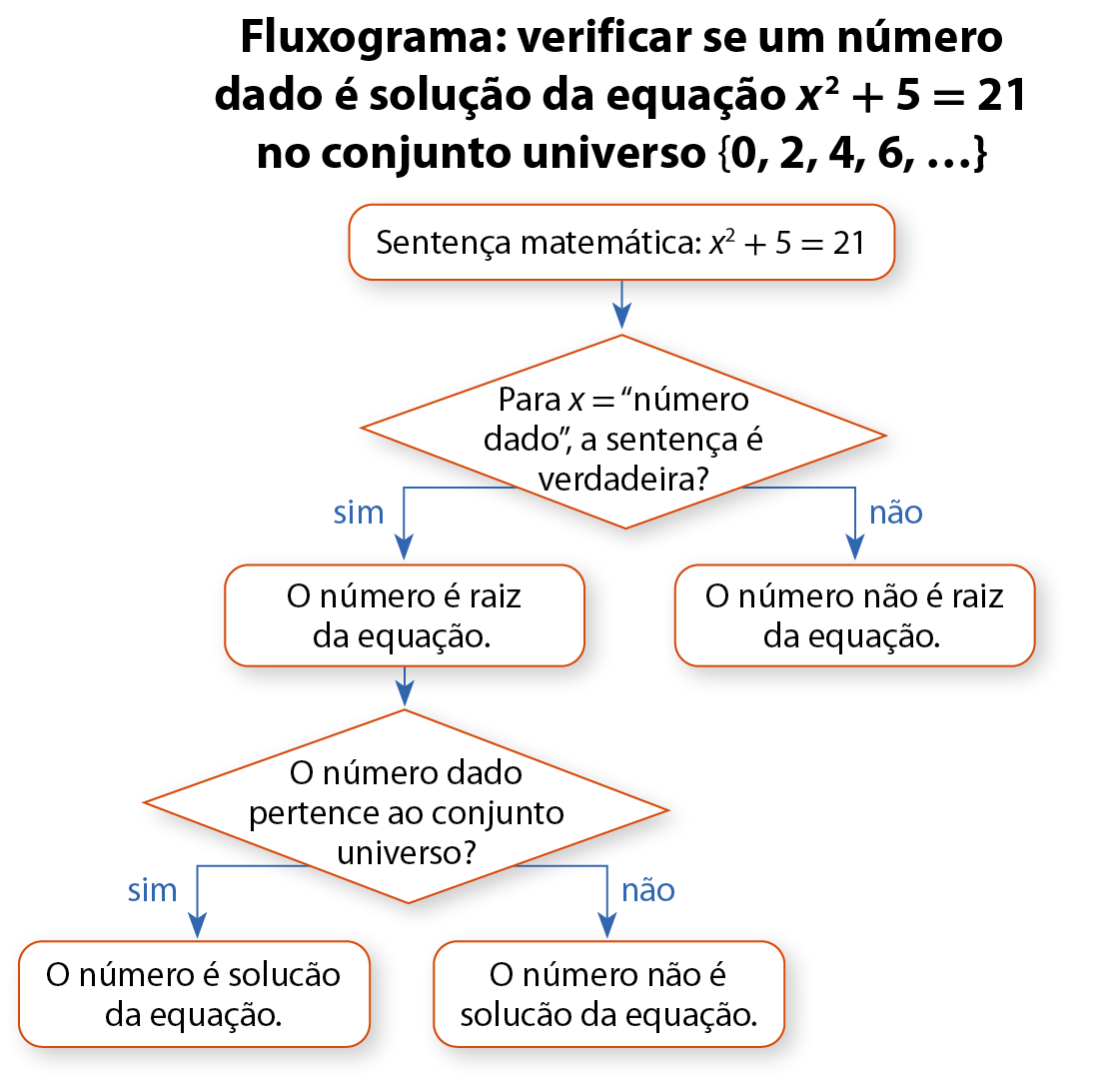
1ª) “Um número natural par elevado ao quadrado e adicionado a 5 é igual a 21.”

Escrevendo essa sentença na linguagem simbólica da Matemática, temos a equação:

x 2 + 5 = 21

Como x representa um número natural par, ele pode assumir qualquer valor do conjunto {0, 2, 4, 6, reticências}. Esse conjunto pode ser chamado de conjunto universo da equação dada.

Conjunto universo é aquele formado por todos os valores que a incógnita pode assumir.

Geralmente, o conjunto universo é representado pela letra U.

Fluxograma. Título Verificar se um número dado é solução da equação x ao quadrado mais 5 igual a 21 no conjunto universo zero, 2, 4, 6, reticencias.
Ação dentro de um retângulo: Sentença matemática: x elevado ao quadrado + 5 = 21.
Segue para a decisão dentro de um losango: Para xis igual a “número dado”, a sentença é verdadeira? Se não segue para a ação dentro de um retângulo: O número não é raiz da equação.
Se sim segue para a ação dentro de um retângulo: O número é raiz da equação. Depois segue para decisão dentro de um losango: O número dado pertence ao conjunto universo? Se sim segue para a ação dentro de um retângulo: O número é solução da equação.
Se não segue para a ação dentro de um retângulo: O número não é solução da equação.

Vamos verificar se os números ‒4 e 4 tornam a equação x 2 + 5 = 21 verdadeira.

• Para x = ‒4, temos: (‒4)2 + 5 = 21 16 + 5 = 21 (verdadeira)

• Para x = 4, temos: 42 + 5 = 21 16 + 5 = 21 (verdadeira)

Portanto, os números ‒4 e 4 são as raízes da equação. Note que ‒4 não é um número natural; então, ele não está no conjunto universo {0, 2, 4, 6, reticências}. Logo, ‒4 não é solução da equação.

A solução da equação x 2 + 5 = 21 no conjunto universo dado (números naturais pares) é 4.

2ª) “Um número inteiro par elevado ao quadrado e adicionado a 5 é igual a 21.”

Nessa sentença, ampliamos o conjunto universo da sentença anterior, considerando, agora, que o número seja inteiro e par.

A equação correspondente é x 2 + 5 = 21, e o conjunto universo é:

U = {reticências, ‒6, ‒4, ‒2, 0, 2, 4, 6, reticências}

Sabemos que as raízes dessa equação são ‒4 e 4. Como ambas pertencem ao conjunto universo, a solução é ‒4 e 4.

3ª) “Um número natural ímpar elevado ao quadrado e adicionado a 5 é igual a 21.”

A equação correspondente é x 2 + 5 = 21, e o conjunto universo é u = {1, 3, 5, 7, reticências}. As raízes dessa equação são ‒4 e 4. Como nenhuma delas está no conjunto universo (números naturais ímpares), dizemos que essa equação não tem solução no conjunto universo dado.

Soluções de uma equação são os valores do conjunto universo que tornam a sentença verdadeira.

Página 122

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

26 Em uma das fichas está impresso o número que é a raiz da equação 4y + 8 = y + 17.

Ilustração. Três fichas e cada uma com um número: menos 5, 3 e 5.

Que número é esse?

27 Verifique, no caderno, se 2 é raiz das equações:

a) x 2 = 4

b) ‒2x = 4

c) 2x = 4

d) xis ‒ 2 = 4

e) ‒x2 + 2 = x

28 Determine o conjunto universo e a solução da equação correspondente a cada sentença.

a) y é um número natural par que, dividido por 2, resulta em 3.

b) a é um número inteiro cujo módulo é 3.

c) x é um número natural que, dividido por ‒2, resulta em 3.

Hora de criar – Em duplas, cada um de vocês vai criar uma equação que tenha como raiz o número:

a) 8;

b) ‒8;

c) ‒0,8;

d) 0.

Depois, troquem as equações e as resolvam no caderno. Destroquem para corrigi-las. As equações criadas por vocês foram iguais? Os resultados obtidos foram os mesmos?

6. Equações do 1º grau com uma incógnita

Considere estas equações como exemplos.

a) 2x + 7 = 5

b) 3x + 2 = x ‒ 3

c) 5x 2 ‒ 8x + 7 = 0

d) x + y = 0

Apenas as duas primeiras equações têm uma só incógnita (letra x) com expoente 1 e são exemplos de equações do 1º grau com uma incógnita.

Ilustração. Mulher negra de cabelo comprido, liso e preto, e blusa amarela e jaleco. Ela diz: Neste capítulo, estudaremos apenas as equações do 1º grau com uma incógnita.

Equações equivalentes

A balança a seguir está em equilíbrio, com os pratos nivelados. No prato da esquerda, há 3 pacotes, cada um de x quilogramas, e 2 blocos de 1 quilograma. No prato da direita, há 8 blocos de 1 quilograma.

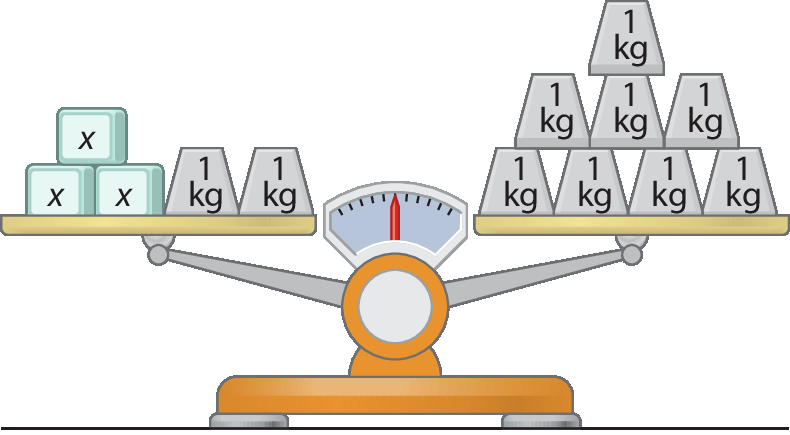
Ilustração. Balança de dois pratos. No prato à esquerda, três blocos com massa medindo x cada um e dois pesos de 1 quilograma cada. No prato à direita, 8 pesos de 1 quilograma cada. A balança está equilibrada.

Podemos representar essa situação pela equação

3x + 2 = 8.

Página 123

Retirando dois blocos de 1 quilograma de cada prato, a balança continua com os pratos nivelados, e a situação passa a ser esta:

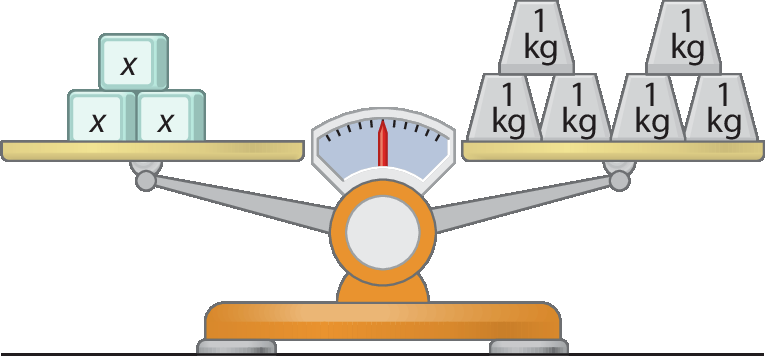
Ilustração. Balança de dois pratos. No prato à esquerda, três blocos de massa medindo x cada um. No prato à direita, 6 pesos de 1 quilograma cada. A balança está equilibrada.

Ilustração. Homem de cabelo ruivo e camisa vermelha. Ele diz: Observe que o que foi feito corresponde a subtrair 2 de cada membro da equação 3x + 2 = 8.

Deixando em cada prato a terça parte do que ele contém, a balança continua com os pratos nivelados. Passamos a ter a seguinte situação:

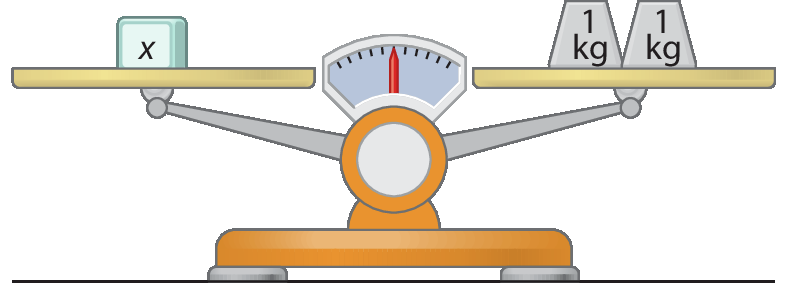
Ilustração. Balança de dois pratos. No prato à esquerda, um bloco de massa medindo x. No prato à direita, 2 pesos de 1 quilograma cada. A balança está equilibrada.

Ilustração. Homem de cabelo ruivo e camisa vermelha. Ele fala: Agora, o que foi feito corresponde a dividir por 3 os dois membros da equação 3x = 6.

Verificamos que o número 2 é solução das equações 3x + 2 = 8, 3x = 6 e x = 2.

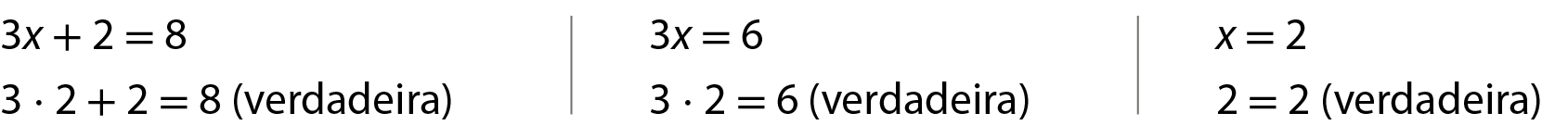
Esquema. Solução em duas linhas.
Primeira linha, 3x mais 2 igual a 8
Segunda linha, 3 vezes 2 mais 2 igual a 8, abre parênteses verdadeira fecha parênteses

Solução em duas linhas.
Primeira linha, 3x igual a 6
Segunda linha, 3 vezes 2 igual a 6, abre parênteses verdadeira fecha parênteses

Solução em duas linhas.
Primeira linha, x igual a 2
Segunda linha, 2 igual a 2, abre parênteses verdadeira fecha parênteses

Como 2 é a solução das três equações, dizemos que elas são equações equivalentes.

Quando duas ou mais equações do 1º grau têm a mesma solução, em um mesmo conjunto universo, são chamadas equações equivalentes.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

30 Verifique, em cada caso, se as equações são equivalentes ou não.

a) x ‒ 8 = 6 e x = 14

b) 2y ‒ 1 = y, 3y = ‒6 e y + 2 = 5

c) 4z + 1 = z + 7, 3z = 6 e z = 2

d) 2a + a = 12, 2a = 6 e a = 3

31 Observe as balanças a seguir, em que os blocos têm uma mesma unidade de medida.

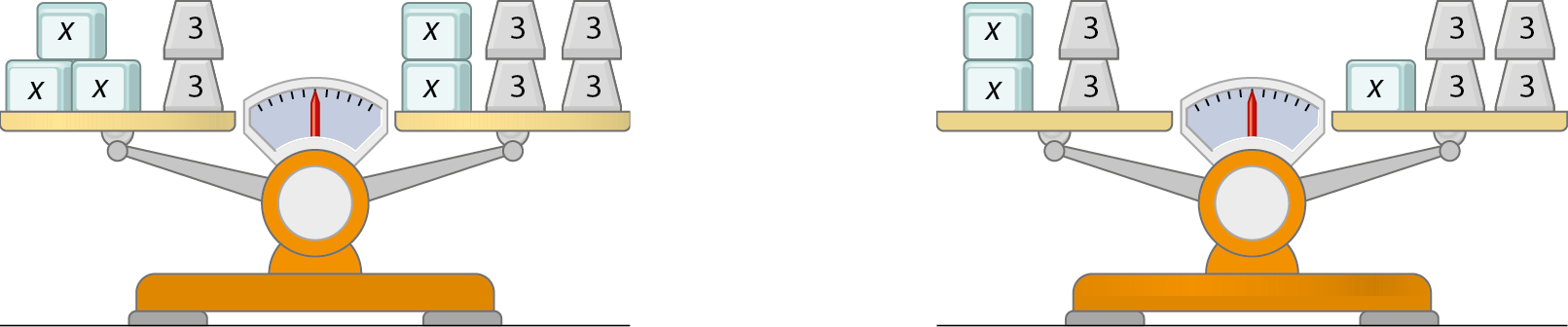
Ilustração. Balança de dois pratos. No prato à esquerda, três blocos de massa medindo x cada um e dois pesos de massa medindo 3 cada uma. No prato à direita, 2 blocos de massa medindo x cada um e 4 pesos de massa medindo 3 cada uma. A balança está equilibrada.
Ilustração. Balança de dois pratos. No prato à esquerda, dois blocos de massa medindo x cada um e dois pesos de massa medindo 3 cada. No prato à direita, 1 bloco de massa medindo x e 4 pesos de massa medindo 3 cada um. A balança está equilibrada.

a) O valor de x é o mesmo nas duas balanças? Justifique sua resposta.

b) Encontre, para cada situação, a equação que a representa. Essas equações são equivalentes?

Página 124

7. Resolução de equações

Na situação a seguir, vamos descobrir a medida da massa do cubo indicada pela letra x.

Ilustração. Balança de dois pratos. No prato à esquerda, dois cubos de massa medindo x cada um e um peso de 10 gramas. No prato à direita, um cubo de massa medindo x, um peso de 8 gramas e um peso de 10 gramas. A balança está equilibrada.

A balança está com os pratos nivelados. A equação correspondente é:

2x + 10 = x + 8 + 10

Vamos retirar um cubo de x gramas de cada prato.

Ilustração. Balança de dois pratos. No prato à esquerda, um cubo de massa medindo x e um peso de 10 gramas. No prato à direita, um peso de 8 gramas e um peso de 10 gramas. A balança está equilibrada.

A balança continua com os pratos nivelados. A equação correspondente é:

x + 10 = 8 + 10

Agora, vamos retirar um bloco de 10 gramas de cada prato.

Ilustração. Balança de dois pratos. No prato à esquerda, um cubo de massa medindo x. No prato à direita, um peso de 8 gramas. A balança está equilibrada.

Nessa situação, a balança continua com os pratos nivelados. A equação correspondente é:

x = 8

As equações obtidas em cada passo são equivalentes. Assim, a medida da massa de cada cubo é igual a 8 gramas.

A resolução de equações do 1º grau com uma incógnita é feita transformando-se cada equação em uma equação equivalente e mais simples, até que as soluções, elementos do conjunto universo, sejam obtidas.

Na resolução de equações, aplicaremos as propriedades que veremos a seguir.

Adicionando ou subtraindo um mesmo número aos dois membros de uma equação, obtemos uma equação equivalente à primeira.

Como exemplo, vamos resolver a equação 2x ‒ 1 = x + 5, cujo conjunto universo é

Ilustração. Conjunto dos números naturais.

Ilustração. Menina branca de cabelo curto e camiseta verde com os braços para cima. Ela fala: Já sei! Adicionamos adicionamos 1 aos dois membros e reduzimos os termos semelhantes. Depois subtraímos xis dos dois membros e reduzimos os termos semelhantes.

Página 125

Verificando:

2 ⋅ 6 ‒ 1 = 6 + 5

12 ‒ 1 = 11

11 = 11 (verdadeira)

Portanto, a solução da equação é 6.

Multiplicando ou dividindo os dois membros de uma equação por um mesmo número diferente de zero, obtemos uma equação equivalente à equação dada.

Como exemplo, vamos resolver a equação 5x = 20, cujo conjunto universo é

, utilizando a propriedade anterior.

Ilustração. Homem negro de cabelo castanho, óculos e camisa roxa. Ele diz: Como xis está sendo multiplicado por 5, dividimos os dois membros por 5.

Verificando:

5 ⋅ 4 = 20

20 = 20 (verdadeira)

Portanto, a solução da equação é 4.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

32 O esquema a seguir mostra uma balança com os pratos nivelados.

Ilustração. Balança de dois pratos. No prato à esquerda, quatro cubos de massa medindo x cada um e um peso de 5 gramas. No prato à direita, três cubos de massa medindo x cada um e 3 pesos de 5 gramas cada. A balança está equilibrada.

a) Determine a equação que representa essa situação.

b) Determine a equação que representa a situação quando se retiram de cada prato 3 cubos

e 1 bloco de

Ilustração. Peso de massa medindo 5 gramas.

c) Qual é a medida da massa de cada cubo?

33 Determine as raízes das equações aplicando as propriedades estudadas.

a) y + 9 = 3

b) x ‒ 12 = 15

c) y + 5 = ‒4

d) 3x = ‒12

e) 3x = 10

f) 5x = 90

34 Das equações da atividade anterior, se considerarmos como conjunto universo o conjunto dos números inteiros, todas as equações terão soluções?

E se considerarmos como conjunto universo o conjunto dos números naturais? Justifique suas respostas.

35 A raiz da equação

2x + 1 + 5(x ‒ 3) = 3(x + 1) + x é um número:

a) menor que ‒2.

b) maior que 30.

c) inteiro.

d) racional não inteiro.

e) negativo.

36 Com as 10 caixas que tenho, fiz duas pilhas de mesma altura, conforme mostra o desenho.

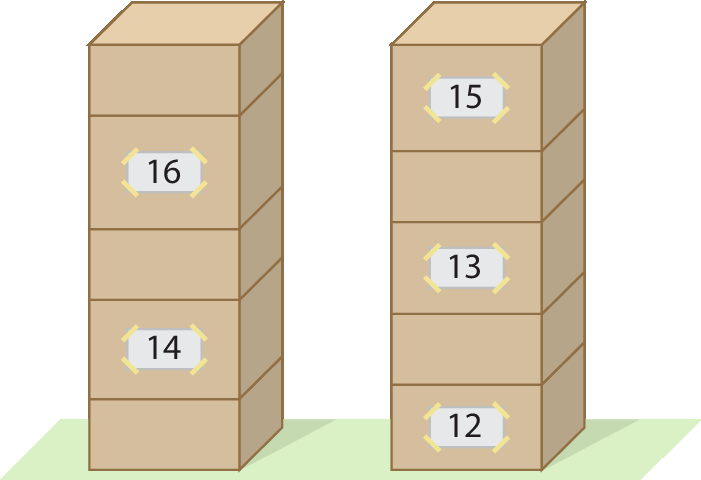
Ilustração. Duas pilhas de caixas de papelão de mesma altura. À esquerda, pilha com 5 caixas e em uma das caixas há uma etiqueta com o número 16 e outra caixa com uma etiqueta com o número 14. À direita, pilha de 5 caixas e em uma das caixas etiqueta com o número 15, em outra uma etiqueta com o número 13 e em outra uma etiqueta com o número 12.

Observe que, em algumas caixas, coloquei um adesivo com um número que representa a medida da sua altura em centímetro. As que estão sem adesivo têm a mesma altura.

a) Calcule a medida da altura das caixas sem adesivo.

b) Qual é a medida da altura de cada pilha de caixas?

Página 126

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Determine o valor de x no quadrado mágico a seguir, sabendo que a soma em cada linha, em cada coluna e nas diagonais é a mesma.

Ilustração. Lousa com um quadrado mágico desenhado nela composto por 3 linhas e 3 colunas. Primeira linha: 16, x + 4, x + 9. Segunda linha: 11, x + 8, 15. Terceira linha: x + 7, 17, 10. À esquerda do quadrado está escrito: xis é igual a ponto de interrogação. A frente da lousa uma mulher branca de cabelo loiro curto e camiseta azul. Ela está com uma das mãos aberta e a outra com o dedo indicador apontando para cima. Ao lado, menina negra de cabelo castanho encaracolado, tiara amarela e camiseta amarela. Ela segura um giz.

Equacionando problemas

O professor Paulo apresentou aos estudantes este problema:

Ilustração. Lousa com a informação: Em um estacionamento, cobram-se R$ 9,00 pela primeira hora e R$ 2,50 a cada hora excedente. Se um cliente pagou R$ 24,00, quanto tempo o carro dele permaneceu nesse estacionamento?

Lúcia resolveu o problema da seguinte maneira:

Ilustração. Caderno de espiral com as informações: Dos 24 reais eu subtraio os 9 reais da primeira hora. 24 menos 9 igual a 15 Sobraram 15 reais. Divido, então, 15 por 2,50 e encontro a quantidade de horas excedentes. Conta de divisão na chave. À esquerda, 15,0. Dentro da chave, 2,5. Abaixo de 15,0 número 0. Abaixo da chave, quociente 6. Adicionando a quantidade de horas excedentes encontradas com a primeira hora, o cliente deixou o carro por 7 horas no estacionamento.

Página 127

Marcos, por sua vez, resolveu o problema por tentativas.

E Jair apresentou o seguinte raciocínio:

Ilustração. Caderno espiral com as informações: Indicando por xis a quantidade de horas excedentes, temos: 9 + 2,5x = 24; 9 + 2,5x menos 9 = 24 menos 9. 2,5x sobre 2,5, é igual a 15 sobre 2,5. Xis = 6. Adicionando com a primeira hora, o total de horas que o carro permaneceu no estacionamento foi 7 horas.

Note que os três estudantes resolveram corretamente o problema, empregando diferentes métodos.

Com isso, você percebe que existem vários métodos para resolver um problema. O método da resolução por meio de uma equação, empregado por Jair, é um deles. Esse método, em muitos casos, facilita a resolução de problemas.

Acompanhe mais algumas situações.

Situação 1

As reproduções das telas a seguir são assinadas por Elza Bernardes. Eu as comprei por R$ 1.320,00mil trezentos e vinte reais. Pela tela a, paguei o dobro do que paguei pela tela B, e, pela tela C, paguei o triplo do que paguei pela B. Quanto paguei pela tela C?

Tela A

Pintura. Quadro retangular com um jarro de metal à esquerda e à direita uma cesta com frutas, com maçãs, peras e cacho de uvas verdes. Atrás da cesta há uma garrafa. — BERNARDES, E. Frutas à mesa. 1999. Óleo sobre tela, 54 por 77 centímetros. Coleção particular.

Tela B

Pintura. Quadro retangular com barcos parados na água próximos a um porto. À esquerda, construção e uma árvore. Ao fundo, morros. — BERNARDES, E. Vila de pescadores. 1987. Óleo sobre tela, 59 por 72 centímetros. Coleção particular.

Tela C

Pintura. Quadro retangular de uma casa com telhado triangular e árvores ao redor. Ao fundo, água e morros. — BERNARDES, E. Choupana no Tietê. 1990. Óleo sobre tela, 50 por 60 centímetros. Coleção particular.

Página 128

Indicando o valor da tela B por x, a tela a custou 2x, e a tela C, 3x.

Então, x + 2x + 3x = .1320.

Resolvendo a equação, temos:

xis + 2x + 3x = .1320

6x = .1320

\frac{6 x}{6} = \frac{1 320}{6}

xis = 220

O valor da tela C é 3x; logo:

3x = 3 ⋅ 220 = 660

Portanto, paguei R$ 660,00seiscentos e sessenta reais pela tela C.

Situação 2

Danilo e Diego são ciclistas e resolveram percorrer uma estrada que tem um trecho asfaltado e outro de terra.

Danilo percorreu o trecho asfaltado e mais 6 quilômetros do trecho de terra. Depois, retornou ao ponto de partida.

Diego percorreu o trecho asfaltado e mais 2 quilômetros do trecho de terra, depois voltou ao ponto de partida. Ele fez esse percurso duas vezes.

Quando fizeram as contas, descobriram que haviam percorrido a mesma distância. Quantos quilômetros tem o trecho asfaltado?

Vamos esquematizar a situação indicando a medida do comprimento do trecho asfaltado por x.

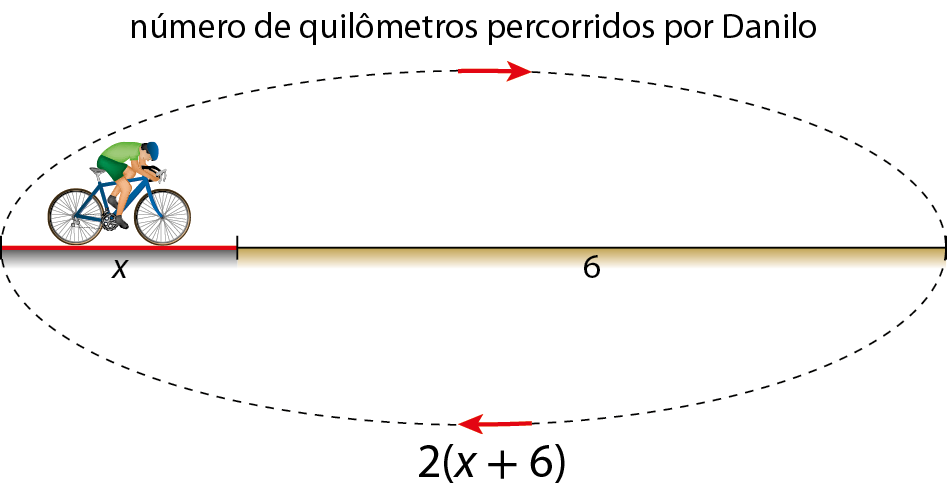
Ilustração. Trecho dividido em duas partes. À esquerda, ciclista sobre um pedaço do trecho de medida x. À direita, trecho de medida 6. Há uma linha tracejada da direita para esquerda ao redor da imagem com o texto: número de quilômetros percorridos por Danilo e a expressão 2, abre parênteses, xis mais 6, fecha parênteses.

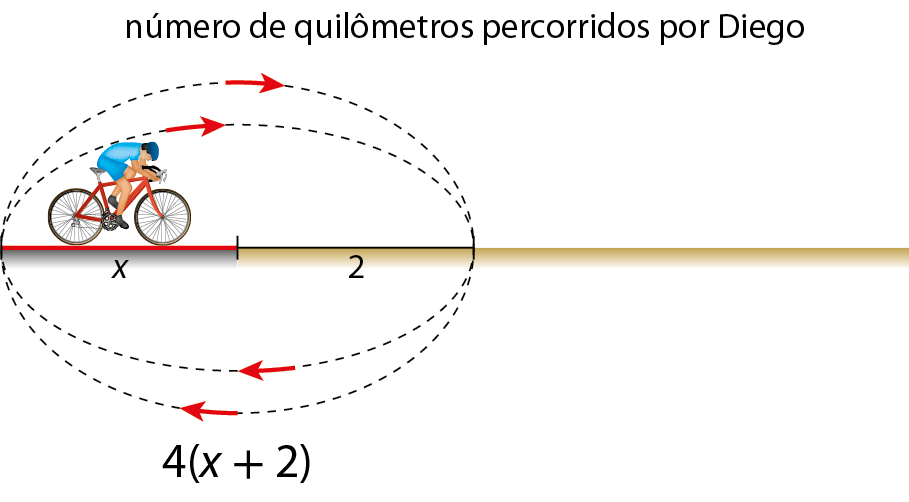
Ilustração. Trecho dividido em 3 partes. À esquerda, ciclista sobre trecho de medida x. À direita, trecho de medida 2. Duas linhas tracejadas da direita para esquerda ao redor do ciclista e da marca 2 com o texto: número de quilômetros percorridos por Diego e a expressão 4, abre parênteses, xis mais 2, fecha parênteses.

Como o número de quilômetros percorridos é o mesmo, escrevemos a seguinte equação:

2(x + 6) = 4(x + 2)

Vamos eliminar os parênteses aplicando a propriedade distributiva da multiplicação.

Página 129

Em seguida, continuamos a resolução:

Ilustração. Mulher de cabelo preto, camiseta roxa aponta para uma lousa ao seu lado com a informação: 2 abre parênteses, xis + 6, fecha parênteses é igual a 4, abre parênteses, xis + 2, fecha parênteses. Seta de 2 para x e para 6 e seta de 4 para x e 2. 2x + 12 = 4x + 8 2x + 12 menos 4x menos 12 = 4x + 8 menos 4x menos 12 2x menos 4x = 8 menos 12 menos 2x = menos 4. menos 2x sobre menos 2, é igual a menos 4 sobre menos 2. x é igual a 2.

Verificando:

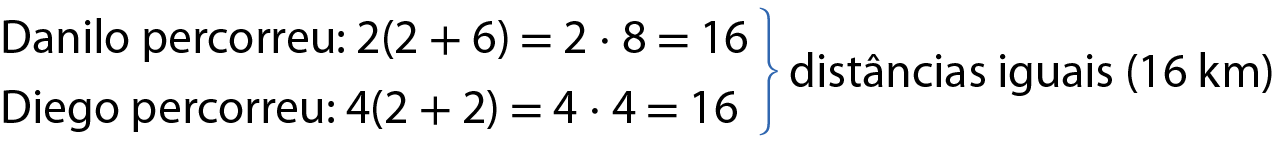
Esquema. Primeira linha. Danilo percorreu: 2 vezes, abre parênteses, 2 mais 6 fecha parênteses, igual a 2 vezes 8 igual a 16
Segunda linha. Diego percorreu: 4 abre parênteses 2 mais 2 fecha parênteses, igual a 4 vezes 4 igual a 16. Fecha chaves nas duas linhas para distâncias iguais abre parênteses 16 quilômetros fecha parênteses

Logo, o trecho asfaltado mede 2 quilômetros.

Clique no play e acompanhe a reprodução do Áudio.

Transcrição do áudio

Calculando o gasto de combustível

Duração: 4:48min. Página: 129.

>> [Locutor] Calculando o gasto de combustível

>> [Narrador] Júlia mora em Salvador, na Bahia, e acaba de entrar de férias. Neste ano, ela decidiu fazer uma viagem de carro e precisa calcular o custo do passeio.

>> [Narrador] O valor gasto por ela com combustível vai depender de vários fatores, como, por exemplo, a distância percorrida, o rendimento do automóvel, em quilômetro por litro, e o preço do combustível.

>> [Narrador] Em uma situação-problema, as grandezas cujos valores não são fixos são chamadas de variáveis.

>> [Narrador] Na viagem de carro de Júlia, as variáveis que determinam o valor gasto com combustível são: a distância percorrida, o preço do combustível e o rendimento [médio] do automóvel.

>> [Narrador] Agora, imagine que o carro de Júlia tem um consumo [médio] de 10 quilômetros por litro utilizando etanol. Ela vai para Alagoinhas, uma cidade a cerca de 120 quilômetros de distância de sua casa. Quantos litros de combustível vai gastar na viagem de ida e volta?

>> [Narrador] Somando o trajeto de ida e de volta, sabemos que a distância total percorrida por Júlia será de 240 quilômetros. Se o carro consome 1 litro a cada 10 quilômetros, podemos calcular o consumo para percorrer 240 quilômetros assim: 240 : 10 = 24. Ou seja, 24 litros.

>> [Narrador] Para saber o valor, em real, gasto na viagem, basta multiplicar o total de litros consumidos no percurso pelo preço do litro do combustível.

>> [Narrador] Podemos generalizar, escrevendo uma equação que relaciona o valor total a ser gasto com a viagem e o preço do combustível.

>> [Narrador] Chamando de y o gasto em real, e de x o valor do litro do combustível também em real, teremos: y = 24x.

>> [Narrador] Se o litro do etanol custa R$ 2,59, utilizando a equação y = 24x e substituindo x por 2,59, o gasto total da viagem será y = 24 · 2,59, ou seja, y = 62,16. Então, com 24 litros de etanol a R$ 2,59 o litro, o gasto será de R$62,16.

>> [Narrador] Supondo que, nessa viagem, o rendimento [médio] do carro com gasolina seja de 12 quilômetros por litro, e que o litro da gasolina custa R$ 3,99, qual será o custo total da viagem?

>> [Narrador] Se o carro consome 1 litro a cada 12 quilômetros, podemos calcular o consumo para percorrer 240 km assim: 240 : 12 = 20. Ou seja, 20 litros. Portanto, a relação entre y e x será dada agora por y = 20x.

>> [Narrador] Utilizando a equação y = 20x e substituindo x por 3,99, o gasto total da viagem com gasolina será y = 20 · 3,99, ou seja, y = 79,80. Então, com 20 litros de gasolina a R$ 3,99 o litro, o gasto será de R$79,80.

>> [Narrador] O custo da viagem utilizando etanol como combustível será de R$ 62,16. Já o custo da viagem, nas mesmas condições, utilizando gasolina, será de R$ 79,80.

>> [Narrador] A diferença entre os dois custos é de 79,80 – 62,16 = 17,64. Portanto, R$ 17,64.

>> [Narrador] Assim, podemos concluir que, variando o valor do combustível (x nas equações y = 24x e y = 20x), o custo da viagem também varia. E, com essas informações, Júlia consegue fazer uma boa estimativa de quanto gastará para passar as férias em Alagoinhas.

Créditos

Studio Spectrum

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

37 Maria tem o dobro da idade de Lúcia. Se Maria tivesse 8 anos a menos, e Lúcia, 4 anos a mais, elas teriam a mesma idade.

a) Representando a idade de Lúcia por y, como se representa a idade de Maria?

b) Determine a equação correspondente ao problema.

c) Qual é a idade de Lúcia?

d) Qual é a idade de Maria?

38 Uma mesa plástica custa o triplo de uma cadeira plástica. Duas dessas mesas e oito dessas cadeiras custam R$ 226,80duzentos e vinte e seis reais e oitenta centavos.

a) Qual é o preço de uma cadeira?

b) Qual é o preço de uma mesa?

c) Quanto custam 5 mesas e 20 cadeiras?

39 Sabendo que hoje a soma da idade de Guilherme e de Laura é 70 meses, há quantos meses a fotografia a seguir foi tirada?

Fotografia. Uma bebê sentada na grama. Ao lado, um bebê em pé segura a mão da bebê. — Guilherme, aos 18 meses, e Laura, aos 20 meses.

40 Em um jogo de basquete em cadeira de rodas, foram marcados 118 pontos. A equipe vencedora ganhou por uma diferença de 12 pontos. Quantos pontos marcou a equipe vencedora?

Fotografia. Destaque para dois homens em cadeira de rodas disputando uma bola de basquete. Ao fundo, arquibancada com pessoas. — Disputa pelo ouro nos Jogos Paralímpicos de Tóquio, no basquete feminino em cadeira de rodas. (Fotografia de 2021.)

41 Quatro candidatos disputavam a prefeitura de uma cidade. Após a apuração dos .5219 votos, foram obtidos os resultados: o primeiro candidato conseguiu 22 votos a mais que o segundo, 130 a mais que o terceiro e 273 votos a mais que o último. Quantos votos recebeu o candidato eleito?

42 Ricardo e Julinho subiram juntos em uma balança, e o ponteiro da balança marcou 80 quilogramas. Ricardo desceu, e Julinho pôde, então, verificar que ele tinha 6 quilogramas a mais que Ricardo. Quantos quilogramas tem Julinho?

Página 130

43 Observe o esquema das balanças e responda.

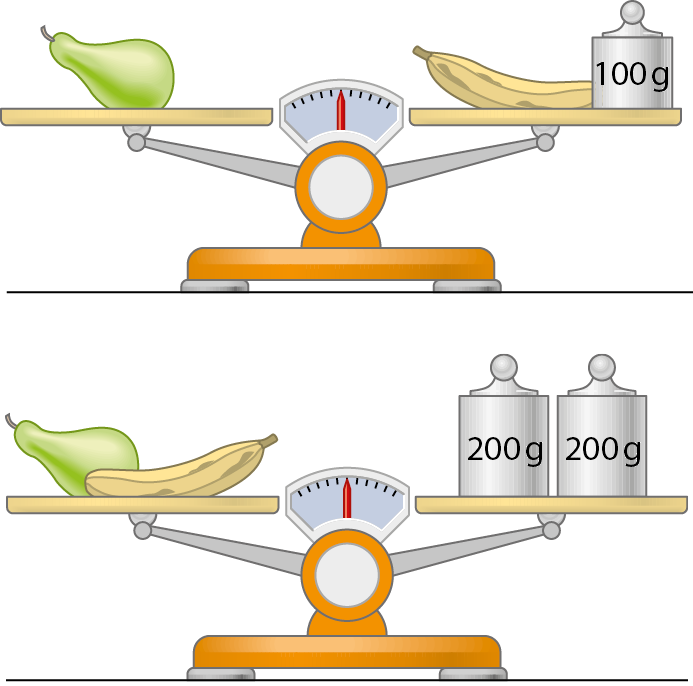
Ilustração. Balança de dois pratos. No prato à esquerda, uma pera. No prato à direita, uma banana e um peso de 100 gramas. A balança está equilibrada. Ilustração. Balança de dois pratos. No prato à esquerda, uma pera e uma banana. No prato à direita, dois pesos de 200 gramas. A balança está equilibrada.

De acordo com o que as balanças indicam, quantos gramas tem a pera? E a banana?

Na figura a seguir, está representada uma estrada com três postos de gasolina, a, B e C. A distância entre a e B é o triplo da distância de B a C. Calcule mentalmente qual é a medida da distância entre a e B.

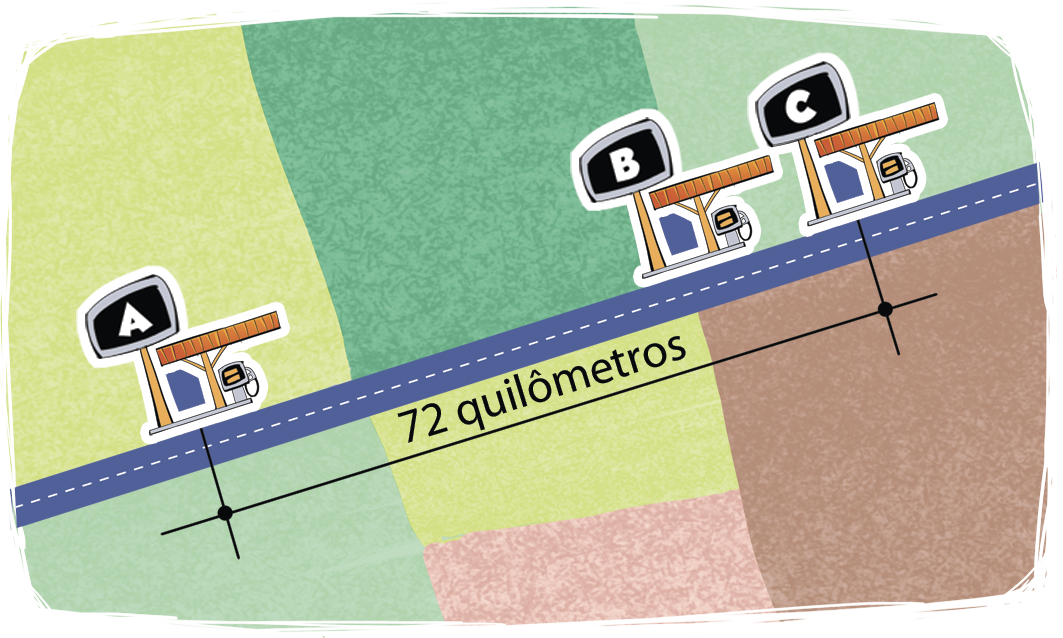
Ilustração. À esquerda, posto de gasolina A. À direita, postos de gasolina B e C. A distância do posto A até o C é 72 quilômetros.

(Representação fóra de escala.)

45 Hora de criar – Crie um problema que possa ser resolvido pelas equações:

a) 3x + 4 = 22

\frac{x}{2}

‒ 8 = 1

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

André gosta de impressionar as pessoas fazendo adivinhações. Ele consegue descobrir o número pensado por uma pessoa. Observe a conversa entre ele e Fernando.

André: Pense em um número.

Fernando: “5”

André: Dobre.

Fernando: “10”

André: Adicione 10.

Fernando: “20”

André: Multiplique por 4.

Fernando: “80”

André: Subtraia 40.

Fernando: “40”

André: Divida por 2.

Fernando: “20”

André: Quanto deu?

Fernando: 20

André: Você pensou no número 5.

Fernando: Como você adivinhou?

Junte-se a um colega para responderem às questões.

a) Descubram como André fez para adivinhar o número que Fernando pensou. Justifiquem a resposta.

b) Montem uma regra que possibilite adivinhar números, brinquem com outras duplas da classe e, em seguida, descubram as regras elaboradas pelas outras duplas.

Página 131

PARA SABER MAIS

A Matemática na História

A palavra álgebra deriva da palavra árabe al-jabr, presente no título do livro Hisâb al-jabr w’al-muqâ-balah, escrito em Bagdá, por volta do ano 825 Depois de Cristo, pelo matemático árabe Al-Khwārizmī.

A tradução literal do título desse livro é “Ciência da restauração ou reunião (al-jabr) e redução (w’al-muqâ-balah)”, que pode ser entendida matematicamente como a passagem de termos subtraídos para o outro membro de uma equação (al-jabr) e o cancelamento de termos semelhantes em membros opostos da equação (w’al-muqâ-balah).

A evolução do processo de resolução de equações abrange um período que vai de 1700 antes de Cristo até 1700 Depois de Cristo, caracterizando‑se principalmente pelo uso de abreviações e pela utilização de vários métodos.

Vamos tratar aqui de um método utilizado inicialmente pelos egípcios, conhecido mais tarde na Europa como “regra da falsa posição”, cuja notação era verbal.

A regra da falsa posição é um método de resolução de equações que atribui inicialmente um valor à incógnita. Ao se fazer a verificação, caso as condições dadas não forem satisfeitas, altera-se a estimativa inicial, multiplicando-a por um valor conveniente.

Atualmente, como temos à disposição um bom instrumental simbólico, pode parecer impossível que o uso da palavra tenha dificultado a resolução de uma equação. Mas observe como a equação x +

\frac{x}{7}

= 24 era representada com a notação verbal.

Ilustração. Quadro com a informação: Qual deve ser o valor de um número que, ao ter sua sétima parte adicionada, torna-se equivalente a 24?

Esse é um exemplo relativamente simples, que permite, entretanto, imaginar quanto se torna complicado o enunciado na notação verbal quando a equação é mais complexa.

Para resolver essa equação, vamos atribuir a x o valor 7. Então:

x +

\frac{x}{7}

= 7 +

\frac{7}{7}

= 8

Observe que o resultado obtido é diferente de 24. Precisamos multiplicar 8 por 3 para obter o resultado desejado (24). Assim, o valor procurado de x será o valor estimado inicialmente (7) multiplicado por 3, ou seja, 21 (7 ⋅ 3).

Verifique que 21 satisfaz a equação x +

\frac{x}{7}

= 24, pois:

Ilustração. Quadro com a informação: 21 mais 21 sobre 7, é igual a 21 mais 3, é igual a 24.

A regra da falsa posição tornou-se conhecida na Europa, na Idade Média, por meio dos árabes, aparecendo nas obras de Al-Khwārizmī – a mais antiga aritmética árabe – e de muitos outros, como o matemático italiano fibonáti (cêrca de 1170 a 1250), o matemático alemão Johannes Widmann (1462 a 1498) e o matemático inglês Robert Recorde (1510 a 1558).

Ilustração. Dois homens de turbantes e roupa branca seguram um papel desenrolado.

Página 132

Esse método desapareceu no decorrer do século dezesseis, com a descoberta de métodos mais sofisticados para a resolução de equações mais complexas.

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

1 Resolva pelo método da falsa posição a equação x +

\frac{x}{2}

= 21

2 Crie uma equação do 1º grau com uma incógnita e resolva-a pela regra da falsa posição.

Voltando aos problemas históricos

Agora podemos resolver os problemas propostos no início deste capítulo. Vamos começar com o problema do papiro de Rhind. Observe a ilustração.

Ilustração. Pedaço de papel desenrolado com o texto: Determinada quantidade e a sua quarta parte adicionadas resultam em 15. Qual é a quantidade?

Considerando a quantidade que queremos encontrar como x, podemos escrever a equação:

Ilustração. Homem de cabelo castanho, comprido e preso, óculos, cavanhaque e camiseta preta. Ele fala: Primeiro multiplicamos ambos os membros da equação por 4. Depois, dividimos ambos os membros da equação por 5.

Logo, a quantidade procurada é 12.

Agora vamos resolver o problema apresentado em Lilavati.

Ilustração. Pedaço de papel com as informações: … o colar do pescoço da esposa partiu-se. Um terço das pérolas caiu no chão, um quinto foi para debaixo da cama. A esposa apanhou um sexto, e seu amado, um décimo. Seis pérolas ficaram no fio original. Descubra o número total de pérolas no colar.

Considerando a quantidade total de pérolas do colar como xis, temos:

• Quantidade que caiu no chão:

\frac{1}{3} x

• Quantidade que foi para debaixo da cama:

\frac{1}{5} x

• Quantidade que a esposa apanhou:

\frac{1}{6} x

• Quantidade que o amado apanhou:

\frac{1}{10} x

• Quantidade que ficou no fio original: 6

Página 133

A quantidade de pérolas que saíram do fio é igual ao total de pérolas menos a quantidade de pérolas que ficaram no fio.

Portanto, a equação correspondente à situação descrita é:

\frac{1}{3} x + \frac{1}{5} x + \frac{1}{6} x + \frac{1}{10} x = x ‒ 6

Assim como na adição de frações, procuramos frações equivalentes de mesmo denominador; como ême ême cê (3, 5, 6, 10) = 30, temos:

\frac{10}{30} x + \frac{6}{30} x + \frac{5}{30} x + \frac{3}{30} x = x ‒ 6

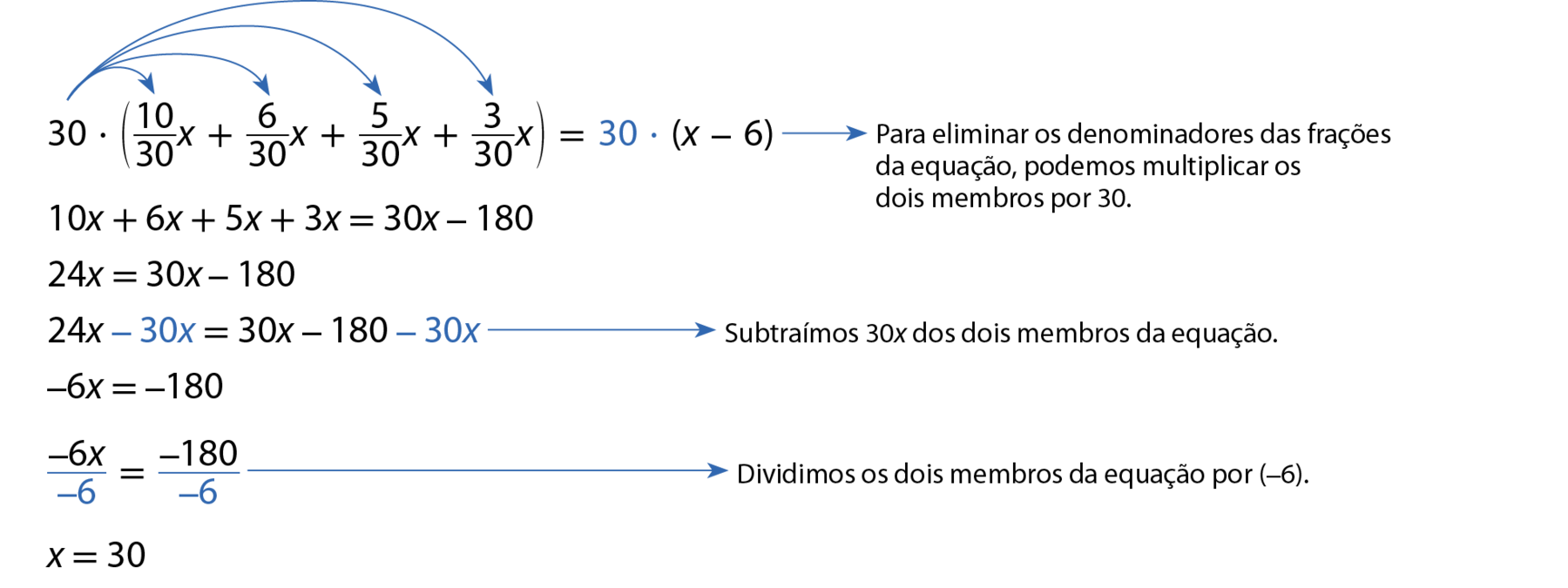
Esquema. 30 vezes abre parênteses, 10 sobre 30, vezes xis mais 6 sobre 30, vezes xis mais 5 sobre 30, vezes xis mais 3 sobre 30, vezes xis, fecha parênteses é igual a 30 vezes, abre parênteses, xis menos 6, fecha parênteses. Seta de 30 para a fração, 10 sobre 30, fim da fração. Seta de 30 para fração, 6 sobre 30, fim da fração. Seta de 30 para fração, 5 sobre 30, fim da fração. Seta de 30 para fração, 3 sobre 30, fim da fração. Seta apontando de abre parênteses, xis menos 6, fecha parênteses, para o texto: Para eliminar os denominadores das frações da equação, podemos multiplicar os dois membros por 30.

Logo, o número total de pérolas no colar era 30.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

46 Um número é adicionado a 10. Multiplica-se essa soma por 3, e o resultado é 72.

a) Qual das equações a seguir corresponde ao problema?

n + 10 ⋅ 3 = 72 ou (n + 10) ⋅ 3 = 72

b) Que número é esse?

47 A uma festa compareceram 43 convidados. Se tivessem ido mais dois jovens, eles seriam o quádruplo do número de adultos.

a) Indicando o número de adultos por x, represente o número de jovens.

b) Qual é a equação correspondente a essa situação?

c) Quantos adultos compareceram a essa festa? E quantos jovens?

Hora de criar – Em duplas, criem um problema cada que possa ser solucionado por meio da equação 4x ‒ 45 = 3. Troque seu problema com o do colega. Construa um fluxograma com o passo a passo para a resolução desse problema e resolva-o. Depois, destroquem para corrigi-los.

49 Um terreno retangular tem 100 métros de perímetro. A medida do seu comprimento é o triplo da medida da largura.

a) Indicando a medida da largura desse terreno por x, determine a medida do comprimento dele.

b) Determine a medida do perímetro desse terreno usando a letra x.

c) Escreva a equação associada ao problema.

d) Qual é a medida da largura do terreno? E qual é a medida do comprimento?

e) Calcule a medida da área do terreno.

50 Dentro de um ano, Ana Maria terá o triplo da idade que tinha há nove anos. Qual é a idade de Ana Maria hoje?

51 Determine o número inteiro mais próximo da solução da equação:

\frac{12 x ‒ 4}{6} ‒ \frac{8 x ‒ 3}{9}

x + \frac{2 x + 5}{3}

Página 134

52 Considerando conjunto universo o conjunto dos números racionais, calcule o valor de x nas equações a seguir.

a) 4(x + 3) = 20

b) 5(2x ‒ 1) = 2(x + 4)

c) 10 ‒ 2(x + 3) = 8 + 3(2x + 5)

\frac{3 x}{5} ‒ \frac{1}{2} = x ‒ \frac{2}{5}

\frac{x}{2} + \frac{3}{4} = \frac{2 x}{6} ‒ \frac{1}{3}

\frac{3 y}{2} ‒ 1 = \frac{3}{4} ‒ 2 y

53 Sonhei que no Pantanal Mato-Grossense uma arara pousou em uma árvore e cumprimentou os jaburus que lá se encontravam.

— Bom dia a todos os 57 jaburus amigos que se encontram nesta árvore.

Os jaburus responderam em coro:

— Bom dia!

Um jaburu comentou:

— Nós não somos tantos, dona Arara. Mas, se a senhora somar a nós

\frac{1}{3}

de nós e mais

\frac{1}{6}

de nós, aí, sim, seremos 57.

Quantos jaburus havia na árvore?

Fotografia. Dois jaburus, ave de cabeça preta e penas brancas no corpo. As pernas são finas e o bico é comprido e pontudo. Eles estão com os pés sobre a água e ao fundo há vegetação. — Os jaburus são aves de grande porte, que vivem em bandos e constroem ninhos coletivos. Pantanal Mato-Grossense.

54 Hoje, em uma classe, o número de meninos presentes foi igual ao número de meninas presentes, isso porque faltaram 5 meninas e 1 menino. Quantos estudantes há nessa classe, se o número de meninas é

\frac{5}{9}

do número de estudantes da classe?

55 Resolva o problema a seguir, que também está presente na obra Lilavati, de báscara.

Ilustração. Quadro com a informação: Um terço, um quinto e um sexto de uma quantidade de lótus foram oferecidos, respectivamente, ao Lorde Siva, ao Lorde Visnu e ao Sol; e um quarto foi oferecido a Parvati. Os seis lótus que sobraram
foram presenteados ao venerável preceptor. Diz depressa o número total de lótus.

Fotografia. Flor com pétalas na cor rosa e miolo amarelo. Ao redor, folhas verdes. — Lótus é uma flor aquática, muito comum na Índia.

56 Observe esta figura.

Ilustração. Uma garrafa, um copo e um recipiente com etiqueta escrito 4 litros. Os três objetos estão lado a lado.

Com três copos de água, enche-se totalmente a garrafa. Colocando-se no garrafão quatro garrafas de água e mais um copo de água, ainda assim falta 0,75 litro de água para encher o garrafão totalmente.

a) Quantos litros de água cabem nesse copo?

b) Quantos litros de água cabem nessa garrafa?

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

A partir do bloco de cima, cada número é a soma dos dois números que estão nos blocos imediatamente abaixo.

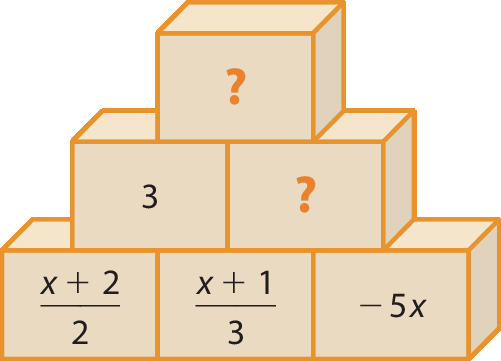
Ilustração. Pirâmide de blocos. De baixo para cima: Primeira fileira: fração, numerador: x + 2, denominador: 2, fim da fração; Fração, numerador: x + 1, denominador: 3, fim da fração; Menos 5 xis. Segunda fileira: 3, ponto de interrogação. Terceira fileira: ponto de interrogação.

a) Descubra o valor de x.

b) Escreva no seu caderno os números que devem ser colocados nos blocos com “?”.

Página 135

TRABALHANDO A INFORMAÇÃO

Média e estimativas

Quando algumas empresas fornecedoras de energia elétrica não conseguem fazer a leitura do consumo de uma residência, elas estimam o valor da próxima conta pela média do consumo dos últimos três meses. Vamos ver um exemplo.

Considere parte da conta de energia elétrica desta família.

Ilustração. Parte da conta de energia elétrica. Com as seguintes informações: HISTÓRICO DE CONSUMO. MÊS/ANO: abril/24. CONSUMO KWH: 192. MÊS/ANO: março/24. CONSUMO KWH: 185. MÊS/ANO: fevereiro/24. CONSUMO KWH: 178. MÊS/ANO: janeiro/24. CONSUMO KWH: 169. MÊS/ANO: dezembro/23. CONSUMO KWH: 186. MÊS/ANO: novembro/23. CONSUMO KWH: 188. MÊS/ANO: outubro/23. CONSUMO KWH: 175. MÊS/ANO: setembro/23. CONSUMO KWH: 175. MÊS/ANO: agosto/23. CONSUMO KWH: 145. MÊS/ANO: julho/23. CONSUMO KWH: 156. MÊS/ANO: junho/23. CONSUMO KWH: 150. MÊS/ANO: maio/23. CONSUMO KWH: 141. Ilustração. Parte superior de conta de energia com as informações: PARA CONTATO COM A COEMER INFORME ESTE NÚMERO DE IDENTIFICAÇÃO 99.9999-9 Leitura atual: 5604 Leitura anterior: 5421 Dias de consumo: 31 Resíduo kWh Classificação: RESIDENCIAL Ligação: BIFÁSICA Medidor kWh: 0000999999 Constante: 1.00000000 Média anual kWh: 170 Consumo médio em kWh: 185 CNPJ/CPF: 000.000.000–00 HISTÓRICO DE CONSUMO. MÊS/ANO: abril/24. CONSUMO KWH: 192. MÊS/ANO: março/24. CONSUMO KWH: 185. MÊS/ANO: fevereiro/24. CONSUMO KWH: 178. MÊS/ANO: janeiro/24. CONSUMO KWH: 169. MÊS/ANO: dezembro/23. CONSUMO KWH: 186. MÊS/ANO: novembro/23. CONSUMO KWH: 188. MÊS/ANO: outubro/23. CONSUMO KWH: 175. MÊS/ANO: setembro/23. CONSUMO KWH: 175. MÊS/ANO: agosto/23. CONSUMO KWH: 145. MÊS/ANO: julho/23. CONSUMO KWH: 156. MÊS/ANO: junho/23. CONSUMO KWH: 150. MÊS/ANO: maio/23. CONSUMO KWH: 141. CONTRIBUIÇÃO DE ILUMINAÇÃO PÚBLICA: 3,33 ATENDENDO A RESOLUÇÃO DA ANEEL 155/05, INFORMAMOS QUE A TARIFA DE ENERGIA ELÉTRICA É COMPOSTA DE:

Nos últimos três meses, temos:

Mês	Abril	Março	Fevereiro
Consumo	192 kWh	185 kWh	178 kWh

Calculando a média aritmética, temos:

\frac{192 + 185 + 178}{3}

\frac{555}{3}

= 185

A fornecedora estimou que o consumo do mês de maio dessa família foi 185 quilouótis hora.

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

1 Considerando a conta apresentada, responda às questões.

a) Supondo que a leitura não tivesse sido feita no mês de fevereiro, estime qual seria o consumo para esse mês com base no consumo dos 3 meses anteriores.

b) O valor que você encontrou foi igual ao consumido nesse mês? Qual foi a diferença?

c) Supondo que a fornecedora estime o valor cobrado para o mês com base na média de consumo dos 12 meses anteriores, qual seria a estimativa para o consumo de maio de 2024?

d) Que motivos podem ser levantados para a fornecedora considerar os últimos 3 meses, e não os últimos 12 meses, para fazer a estimativa de consumo de um mês? Converse com os colegas sobre isso.

2 Suponha que para uma residência tenham sido registradas as seguintes leituras:

Leitura de julho feita no dia 31 de julho: .8120 quilouótis hora

Leitura de agosto feita no dia 23 de agosto: .8396 quilouótis hora

Nesse caso, a fornecedora também faz uma estimativa para calcular o consumo de 31 dias.

Período entre uma leitura e outra: 23 dias

Consumo entre os 23 dias: .8396 ‒ .8120 = 276 (276 quilouótis hora)

A empresa calcula o consumo médio de um dia e, com base nesse valor, o de 31 dias.

Com essas informações, estime o consumo médio do mês de agosto.

Página 136

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Fernanda disse para José:

— Pense em um número. Já pensou? Então, dobre esse número, adicione 8, multiplique o resultado por 5, adicione 60 e subtraia 100. Quanto deu?

José respondeu para Fernanda:

— Deu 10.

a) Descubra o número em que José pensou e escreva a resposta no caderno.

b) Representando por x o número pensado e por y o resultado do cálculo proposto por Fernanda, escreva uma equação que relacione x com y.

c) Se você simplificar a equação do item b, o que se pode dizer de y e x ?

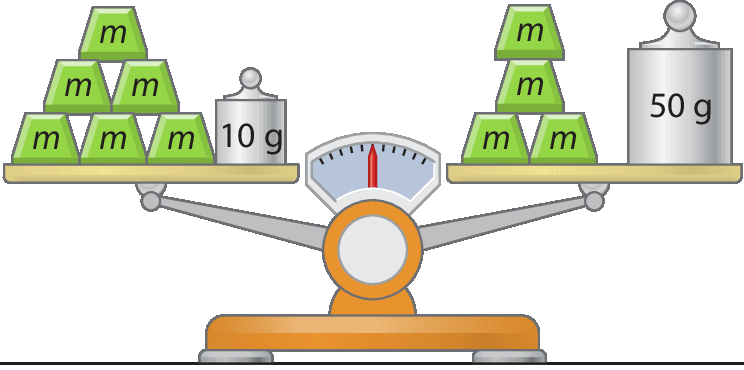
2 O esquema a seguir representa uma balança com os pratos nivelados. Calcule o valor de m.

Ilustração. Balança de dois pratos. No prato à esquerda, seis pesos de massa medindo m cada um e um peso de 10 gramas. No prato à direita, quatro pesos de massa medindo m cada um e 1 peso de 50 gramas. A balança está equilibrada.

3 Uma batedeira e um liquidificador custam, juntos, 291 reais. A batedeira custa 81 reais a mais que o liquidificador. Qual é o preço da batedeira?

4 Usando a regra da falsa posição, Juliana começou a resolver o seguinte problema:

“A quantidade e sua quarta parte adicionadas

resultam em 30. Qual é essa quantidade?”.

Observe o que Juliana já fez no caderno.

Ilustração. Caderno espiral com as informações: Quantidade: x. Equação: xis + fração, x sobre 4, fim da fração é igual a 30 Atribuo a xis o valor 4. Então: x mais x sobre 4 é igual a 4 mais 4 sobre 4, é igual a 5. O resultado deveria ser 30, e não 5. Devo multiplicar 5 por certo número para obter 30.

Calcule o número procurado por Juliana e termine a resolução desse problema.

5 Das equações a seguir, quais têm raiz igual a 5?

a) 5x + 4 ‒ 2x = 26 ‒ 3x

b) 3x ‒ 4 = 11

c) x ‒ (x + 1) = 12 ‒ (3x ‒ 2)

d) 4x + 9 = 3x + 5

e) 10x + 3 = 8x ‒ 2

6 Multiplicando as soluções das duas equações a seguir, encontraremos um número inteiro. Que número é esse?

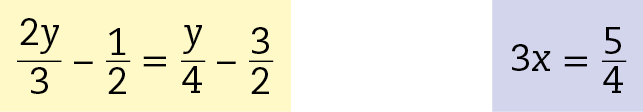
Ilustração. Fichas coloridas com expressões algébricas. Ficha amarela: 2y sobre 3, menos 1 sobre 2, é igual a y sobre 4, menos 3 sobre 2. Ficha azul: 3x é igual a 5 sobre 4.

7 Resolva as equações a seguir.

a) 7( y ‒ 1) = 2(3y + 1)

b) y + 4( y ‒ 1) = 9 ‒ 2( y + 3)

c) 4( y ‒ 2) + 3(2y ‒ 1) = 6(2y ‒ 3)

d) 8(y + 2) ‒ 5y + 7(2y ‒ 3) = 15 + 5y

8 Um número menos 12 é igual a

\frac{3}{4}

do mesmo número. Qual é esse número?

9 Leonardo tinha de dividir um número por 3, mas se enganou e multiplicou-o por 3. Com isso, encontrou 120 unidades a mais do que deveria ter encontrado. Qual é o número que Leonardo deveria dividir?

10 A medida do perímetro de um triângulo é igual a 72 centímetros. As medidas de seus lados são expressas por três números inteiros e consecutivos. Calcule essas medidas.

11 (éfe cê cê-Bahia) Um grupo de amigos quer dividir a despesa de uma lanchonete. Se cada um pagar R$ 20,00vinte reais, faltarão R$ 60,00sessenta reais; se cada um der R$ 30,00trinta reais, sobrarão R$ 90,00noventa reais. O número de pessoas nesse grupo é:

a) 10.

b) 12.

c) 14.

d) 15.

e) 18.

12 Responda: qual é a equação equivalente a

\frac{x ‒ 4}{5} ‒ \frac{x ‒ 5}{2} = \frac{x + 2}{10}

a) 4x = 15

b) 4x = ‒15

c) 4x = 35

d) 4x = ‒35

Página 137

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Ana e Bruno fazem aniversário no mesmo dia, mas a idade de Ana é igual ao dobro da idade de Bruno adicionada de três unidades. Se ei representa a idade de Ana e b representa a idade de Bruno, qual equação indica a situação descrita?

a) a = 3b + 2

b) a = 2b + 3

c) a + 3 = 2b

d) a =

\frac{b}{2}

+ 3

2 Uma marcenaria faz tampos de mesa retangulares de medidas x métros por y métros. Qual é a medida do perímetro e a medida da área do tampo de uma mesa com 1,2 métro de largura e 2 métros de comprimento?

a) x + y = 2,2 métros e x ⋅ y = 2,4 métros quadrados

b) 2 · x = 2,4 métros e 2 · y = 4,0 métros quadrados

c) 4(x + y) = 8,8 métros e x + y = 2,2 métros quadrados

d) 2(x + y) = 6,4 métros e x · y = 2,4 métros quadrados

3 Considere a expressão a seguir.

‒2ax + x +

\frac{8 ‒ 6 a}{2}

\frac{1}{2}

ax +

\frac{7}{3}

x ‒ 2(a + x)

Qual é a redução correta dessa expressão a termos semelhantes?

‒ \frac{3}{2}

ax +

\frac{4}{3}

x ‒ 5a + 4

\frac{5}{2}

ax +

\frac{16}{3}

x ‒ 5a + 8

\frac{5}{2}

ax +

\frac{1}{3}

x ‒ 5a + 4

‒ \frac{8}{3}

ax + 4

4 Identifique a alternativa que contém uma equação do 1º grau com uma incógnita.

a) a2 + b = 12

b) 5x + 8 < 1

c) 0 + 3 =

|‒ 3|

d) 27 = 2x + 1

5 Identifique a alternativa que contém a raiz da equação

\frac{20}{3}

x + 5 = 15.

a) 1,5

b) 3,0

c) 2,0

d) 6,0

6 Ao elevar ao quadrado um número natural múltiplo de 3, multiplicar esse resultado por 2 e, em seguida, subtrair 48, obtém-se como resultado final 114. Qual é o conjunto universo e solução da equação descrita por essa situação?

a) u = {..., ‒6, ‒3, 0, 3, 6, 9, 12, ...} e x = ‒9.

b) u = {..., ‒6, ‒3, 0, 3, 6, 9, 12, ...} e x = 9.

c) u = {0, 3, 6, 9, 12, ...} e x = 9.

d) u = {0, 3, 6, 9, 12, ...} e x = 81.

7 Um motorista particular cobra de seus clientes um valor fixo de R$ 5,90cinco reais e noventa centavos por corrida mais R$ 1,50um reais e cinquenta centavos por quilômetro rodado. Se a corrida de uma pessoa com esse motorista custou R$ 25,40vinte e cinco reais e quarenta centavos, quantos quilômetros foram percorridos?

a) 2,8 quilômetros

b) 18,0 quilômetros

c) 13,0 quilômetros

d) 19,5 quilômetros

8 Uma ceramista está produzindo kits com 3 vasos de cerâmica com alturas diferentes. Em cada kit, o primeiro vaso mede x centímetros de altura, o segundo mede 2x centímetros de altura e o terceiro mede 4x centímetros de altura. Um cliente comprou um kit e três suportes medindo 5 centímetros de altura cada para colocar os vasos em cima. Se a soma das medidas das alturas de todos os itens que esse cliente comprou é 1,06 métro, qual é a medida da altura de cada vaso em centímetro?

a) 30 centímetros; 60 centímetros; 120 centímetros

b) 15 centímetros; 30 centímetros; 60 centímetros

c) 13 centímetros; 26 centímetros; 52 centímetros

d) 6,5 centímetros; 13 centímetros; 26 centímetros

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões.

a) Qual é a diferença entre uma expressão algébrica, uma sentença matemática e uma equação?

b) O que é o coeficiente e o que é a parte literal de um termo algébrico?

c) Em qual situação podemos simplificar uma expressão algébrica?

d) O que é uma equação?

e) Como você explicaria para um amigo como ele deve fazer para encontrar a raiz de uma equação do 1º grau com uma incógnita?

f) Na sua opinião, qual é a importância de sabermos resolver equações?

g) Construa um fluxograma que permite calcular o valor numérico da expressão algébrica x2 + 5x + 3, para 0 < x < 10.

Página 138

DIVERSIFICANDO

Problemas de papiros e um pouco de “mágica”

Os conhecimentos que temos da Matemática egípcia provêm, essencialmente, de dois textos escritos em papiro: o papiro de Rhind e o papiro de Moscou. Nesses documentos, há problemas resolvidos, o que revela a preocupação pedagógica, pois muitos cálculos dos papiros são exercícios propostos para jovens estudantes.

Alguns problemas desses papiros não mencionam objetos concretos. Em vez disso, pedem o que equivale a soluções de equações, na fórma x + ax = b, em que a e b são conhecidos e x é desconhecido. A incógnita é chamada de “aha”.

Siga estes passos e tenha uma surpresa.

Ilustração. Folha amarela com as informações: • Pense em um número natural entre 1 e 5.• Multiplique-o por 2.• Adicione 8 ao resultado.• Divida por 2.• Subtraia o número que você pensou.• Associe esse resultado ao alfabeto. Por exemplo: se o resultado for 1, você escolherá a letra A; se for 2, escolherá a letra B; se for 3, escolherá a letra C; e assim por diante.• Agora, pense no nome de um país europeu iniciado com a letra escolhida.• Com a 5ª letra do nome desse país, pense no nome de um mamífero que voa. À direita do texto, cartola com uma varinha acima, estrelas e números de 1 a 5.

Você, por acaso, pensou no país Dinamarca e no animal morcego?

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

1 O problema 24 do papiro de Rhind, por exemplo, pede o valor de aha, informando que aha mais um sétimo de aha dá 19. Encontre o valor de aha.

2 Escolha uma das equações a seguir e crie um problema cuja resolução seja efetuada pela equação que você escolheu.

a) 2x + 3 = 5

b) 5 ‒ x = 1

c) x + 2x = 3

3 Repita o processo descrito na “mágica” apresentada, mas escolhendo o número racional

\frac{1}{2}

. Qual foi o resultado?

4 Aplicando o que você estudou nos capítulos anteriores, explique por que o resultado da conta que você fez na atividade 3 sempre será 4.

5 Se uma pessoa pensar em um número maior que 5, essa “mágica” funcionará? E se for um número racional qualquer? Justifique sua resposta.