
CAPÍTULO 6 Inequações

Observe a imagem e responda às questões no caderno.
a) Que sinal você usaria para comparar as medidas das massas das frutas dos pratos?
b) Como você escreveria a relação entre as medidas das massas dessas frutas?
c) Você já viu ou utilizou uma balança como a da fotografia? Converse com o professor e os colegas.
A balança é um dos instrumentos de medida mais antigos, que remonta à Antiguidade e às primeiras transações comerciais entre os povos, tendo sofrido ao longo do tempo, aperfeiçoamentos significativos, de modo a tornar-se mais eficiente, mais prática e sobretudo mais precisa.
Na fotografia, a massa dos morangos difere da massa das maçãs, pois o travessão que sustenta os dois pratos não está na posição horizontal e os pratos estão em alturas diferentes. Podemos descrever essa condição de duas maneiras, ambas verdadeiras: a medida da massa das maçãs é maior do que a dos morangos ou a medida da massa dos morangos é menor do que a das maçãs.
1. O que é inequação?
Nas situações a seguir, consideramos que a medida da massa de cada mamão em grama é a mesma, e, por ser desconhecida, vamos representá-la por x.
Situação 1

Na situação 1, a balança tem os pratos nivelados, o que indica uma igualdade da medida das massas, que pode ser expressa pela equação 3x + 100 = .1000.
Situação 2

Na situação 2, a balança tem os pratos desnivelados. Nesse caso, o conteúdo do prato da esquerda tem medida de massa menor que o conteúdo do prato da direita. Por isso, não podemos escrever uma igualdade que expresse a situação. Aqui, empregamos um sinal de desigualdade.
Toda sentença matemática em que aparece um destes sinais: ≠ (diferente), > (maior), < (menor), ⩾ (maior ou igual) ou ⩽ (menor ou igual), expressa uma desigualdade.
Observe alguns exemplos.
a) 5 + 3 ≠ 10
b) 83 ≠ 8 + 3
c) 7 > 5
d) 10 < 15
e) 2x ⩾ 100
f) y ⩽ ‒3
Considerando a desigualdade a ≠ b, verificamos:
a > b ou a < b
Nos exemplos a e b, obtemos:
5 + 3 < 10 e 83 > 8 + 3
Retomando a situação 2, a desigualdade que traduz a situação da balança é:

Observe que podemos escrever essa mesma desigualdade de outra fórma:
.1000 > 2x + 100
Note, ainda, que a letra x representa a massa desconhecida do mamão, ou seja, x é uma incógnita.
As sentenças 2x + 100 < .1000 e .1000 > 2x + 100 são exemplos de inequação.
Inequação é toda sentença matemática expressa por uma desigualdade que apresenta uma ou mais incógnitas.
Verifique outros exemplos de inequações.
a) x + 5 > 12
b) 2x ‒ 4 ⩽ x + 2
c) x 2 ‒ 5x ⩾ 0
d) x + y < 0
Observe que as inequações dos itens a e b têm uma só incógnita (a letra x) com expoente 1. Elas são exemplos de inequações do 1º grau com uma incógnita.
Já as duas últimas não são inequações do 1º grau com uma incógnita.
Assim como as equações, as inequações também têm dois membros. Vamos analisar isso, considerando a situação a seguir.
Em dezembro, Marly tirou 6 dias a mais de férias do que havia tirado em julho. No total (julho e dezembro), foram menos de 30 dias de férias.

Primeiro, indicaremos:

Sabendo que, no total, foram menos de 30 dias de férias, a quantidade de dias pode ser representada por esta inequação:
2y + 6 < 30
A expressão à esquerda do sinal de desigualdade é chamada de primeiro membro da inequação, e a expressão à direita do sinal de desigualdade, de segundo membro da inequação.
Portanto, na inequação 2y + 6 < 30:
• a incógnita é y;
• o primeiro membro é 2y + 6;
• o segundo membro é 30.

PARA SABER MAIS
Resolver problemas é uma arte!
No prefácio da primeira edição do livro A arte de resolver problemas, do matemático húngaro djêordji Polya (1887-1985), lemos:
Uma grande descoberta resolve um grande problema. O problema pode ser modesto, mas se ele desafiar a curiosidade e puser em jogo as faculdades inventivas, quem o resolver por seus próprios meios experimentará a tensão e gozará o triunfo da descoberta.
Fonte: POLYA, G. A arte de resolver problemas: um novo aspecto do método matemático. Rio de Janeiro: Interciência, 2006.
A proposta de Polya é fundamentada em um longo e sério estudo de métodos de resolução, conhecido por heurística, cuja definição é: arte de inventar, de fazer descobertas; ciência que tem por objeto a descoberta dos fatos; método educacional que consiste em fazer descobrir pelo estudante o que se lhe quer ensinar.
Para a resolução de problemas, Polya sugere uma abordagem em quatro etapas de procedimento.
1. Compreensão do problema
• Qual é a incógnita? Quais são os dados? Qual é a condicionante?
• Para determinar a incógnita, a condição é suficiente ou é insuficiente? É excessiva? É contraditória?
2. Estabelecimento de um plano
• Qual é a ligação entre os dados e a incógnita?
• Trace um caminho para a resolução: é possível descobrir algo para determinar a incógnita? E o que é preciso para descobrir esse algo?
• Já viu um problema parecido ou que corresponda a esse? Conhece um problema auxiliar?
• Conhece uma propriedade, um teorema, uma fórmula que seja útil para a resolução?
3. Execução do plano
• Verifique cada etapa da execução. É possível verificar se essa etapa está correta?
4. Reflexão sobre o que foi feito
• É possível verificar o resultado? E o argumento?
• É possível seguir um caminho diferente?
• O resultado obtido tem sentido no contexto do problema?
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
Ao folhear um livro antigo de enigmas, Carlos se deparou com estes:



a) Resolva esses três enigmas.
b) Carlos resolveu os três enigmas e afirmou que somente um deles tem solução. Ele está correto? Justifique sua resposta.
c) Redija um texto explicando como você fez para resolver cada um desses enigmas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Verifique, entre as sentenças, quais são inequações. Em seguida, identifique o primeiro e o segundo membro de cada inequação.
a) 3x ‒ 1 = 10
b) 7x < 10
c) x ‒ 5 ⩽ 0,25
d) 2x ‒ 5 < x + 6
e) 7 ‒ 2 < 10
f) 3x ‒ 2 < x + 4
g) x ‒ 15 = 20
h) 5x ‒ 3 ⩾ x + 10
i) 2 + 9 ≠
Menos 9 sétimos2 Hora de criar – Formule, em cada item, um problema que possa ser representado pela inequação apresentada.
a) 2x + 5 < 30
b) 3x + 12 > x ‒ 8
3 Escreva, usando o sinal <, a inequação que tem como primeiro membro 2x + 3 e como segundo membro x ‒ 2. Descubra um número inteiro negativo que torne essa sentença verdadeira.
4 Em um triângulo, a medida de um lado qualquer é menor que a soma das medidas dos outros dois.
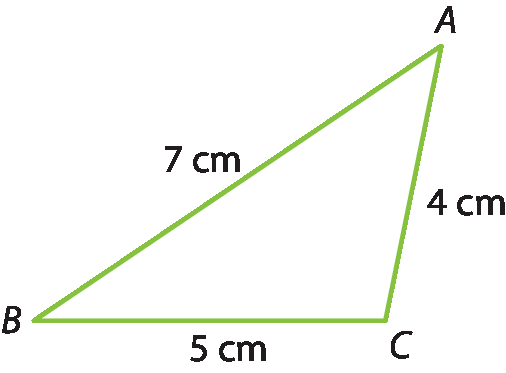
a) Escreva três desigualdades que relacionem as medidas dos lados do triângulo á bê cê ilustrado.
b) Verifique se é possível construir um triângulo com 6 centímetros, 8 centímetros e 12 centímetros de medidas de lado. Justifique sua resposta.
c) Em um triângulo, dois lados medem 5 centímetros e 8 centímetros, respectivamente. Qual é o maior número inteiro que pode representar a medida do terceiro lado? E o menor?
2. Solução de uma inequação
Para verificar se um número é solução de uma inequação, podemos substituir a incógnita pelo número considerado. Acompanhe o exemplo.
Vamos verificar se os números ‒5 e 2,5 são soluções da inequação 3x + 4 < 11,5.
• Substituindo x por ‒5, obtemos:

‒5 é uma solução da inequação dada.
• Substituindo x por 2,5, obtemos:

2,5 não é uma solução dessa inequação.
Acompanhe a situação a seguir.
O departamento de esportes de um clube comprou x pares de tênis a 100 reais cada par, além de outros materiais esportivos que custaram 600 reais. Foram gastos mais de .2000 reais e comprados menos de 20 pares de tênis. Determine as possíveis quantidades de pares de tênis encomendados.

Essa situação pode ser representada pela inequação: 100x + 600 > .2000
A quantidade de pares de tênis encomendados é um número natural, ou seja, o conjunto universo da inequação é o conjunto dos números naturais. Então, precisamos encontrar os números naturais que, colocados no lugar de x, tornam a sentença verdadeira.
• Para x = 10, obtemos:
100 ⋅ 10 + 600 > .2000
.1000 + 600 > .2000
.1600 > .2000 (falsa)
Por isso, dizemos que 10 não é uma solução da inequação dada.
• Para x = 12, obtemos:
100 ⋅ 12 + 600 > .2000
.1200 + 600 > .2000
.1800 > .2000 (falsa
Por isso, 12 também não é uma solução da inequação dada.
• Para x = 14, obtemos:
100 ⋅ 14 + 600 > .2000
.1400 + 600 > .2000
.2000 > .2000 (falsa
Então, 14 não é uma solução da inequação dada.
• Para x = 15, obtemos:
100 ⋅ 15 + 600 > .2000
.1500 + 600 > .2000
.2100 > .2000 (verdadeira)
Por isso, dizemos que 15 é uma solução da inequação dada.
Percebemos que qualquer número natural maior ou igual a 15 é solução dessa inequação. Portanto, os números naturais que satisfazem a inequação são: 15, 16, 17, 18, reticências
Porém, uma das condicionantes da situação-problema é a de que foram encomendados menos de 20 pares de tênis; portanto, x < 20. Assim, a quantidade de pares de tênis encomendados pode ter sido 15, 16, 17, 18 ou 19.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
5 Determine quais são os números inteiros negativos que são soluções da inequação 2x + 3 ⩾ x ‒ 1.
6 Considerando a inequação 4x ‒ 5 < 13 ‒ 2x, verifique entre os números a seguir quais são soluções dela.
a) 3
b) 1,5
c) 0
d) 4
e) ‒2
f)
menos 1 meio7 Sendo x > 20 e x ⩽ 21, com x racional, verifique entre as sentenças a seguir quais são verdadeiras.
a) x pode ser um número negativo.
b) x pode ser um número inteiro.
c) 20,1 pode ser um valor de x.
d) 21,1 pode ser um valor de x.
8 Um número é maior que ‒5 e menor que 4. Esse fato pode ser representado usando uma destas notações:
x > ‒5 e x < 4 ou ‒5 < x < 4
Agora, considerando ‒3 < x < 2, quais são os valores inteiros que x pode assumir?
9 Escreva uma inequação que corresponda a cada item.
a) Por questões econômicas, os produtos de uma indústria não devem ser embalados em menos de 20 unidades por caixa.
b) Para que esses produtos fiquem bem acondicionados, não devem ser embalados em mais de 30 unidades por caixa.
c) Cada caixa tem capacidade para 20 a 30 unidades desse produto.
10 Um feirante, após ter vendido x melões a R$ 9,00nove reais cada um, vendeu os restantes por um total de R$ 140,00cento e quarenta reais. Depois de vender todos os melões, ele obteve mais de R$ 500,00quinhentos reais.
a) Represente essa situação por meio de uma inequação.
b) 40 é solução dessa inequação? E 41?
c) Qual é a quantidade de melões que ele deve ter vendido a R$ 9,00nove reais?
3. Resolução de inequações
Na situação a seguir, vamos descobrir quais são as possibilidades para a medida da massa do pêssego, indicada pela letra x.
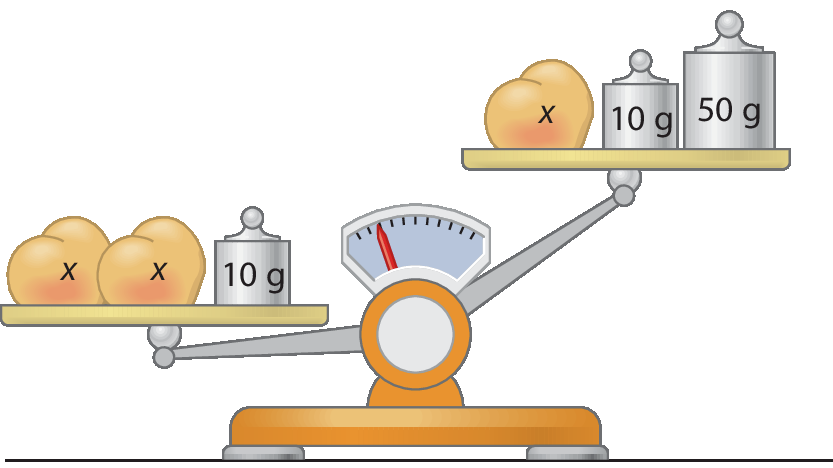
A balança, representada, não está nivelada: o prato da esquerda está com a maior medida de massa.
A inequação correspondente é:
2x + 10 > x + 10 + 50
• Vamos retirar um pêssego de xis gramas de cada prato.
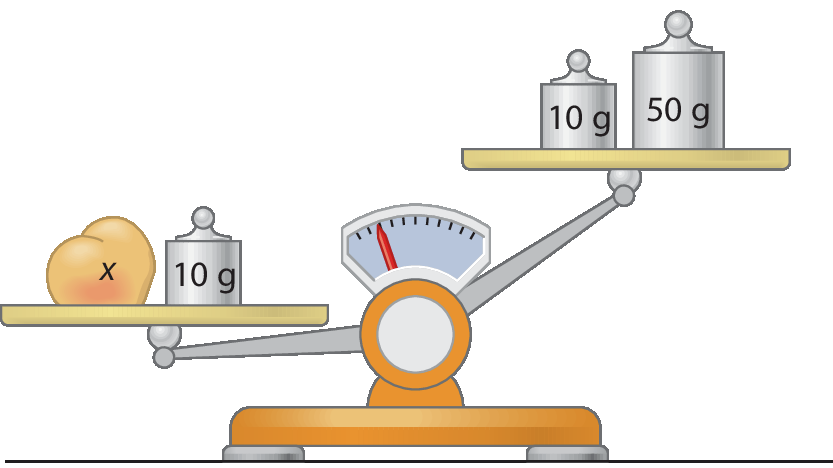
A balança continua desnivelada, mantendo a mesma elevação dos pratos, e o prato da esquerda ainda é o que tem maior medida de massa. A inequação correspondente é:
x + 10 > 10 + 50
• Agora, vamos retirar um peso de 10 gramas de cada prato.
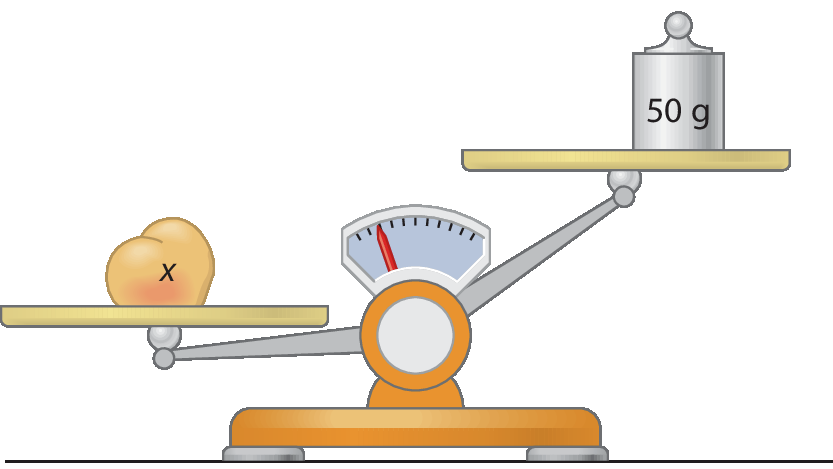
Observe que a balança continua desnivelada, mantendo a mesma elevação dos pratos. O prato da esquerda continua com maior medida de massa. A inequação correspondente é:
x > 50
As inequações obtidas em cada passo são equivalentes, ou seja, elas têm as mesmas soluções. Assim, concluímos que a medida da massa de cada pêssego é maior que 50 gramas.
A resolução de inequações do 1º grau com uma incógnita é feita de maneira semelhante à resolução de equações, ou seja, transformando-se cada inequação em uma inequação equivalente mais simples, até que sejam obtidas as possíveis soluções.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
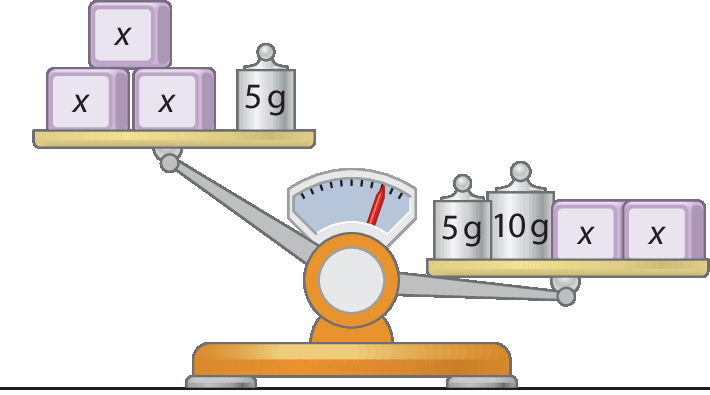
11 Desenhe cada etapa com os esquemas das balanças para encontrar a maior medida de massa possível de cada cubinho, em grama, expressa por um número inteiro.
12 Copie as afirmações falsas e, depois, modifique-as de modo que se tornem verdadeiras.
a) Se
9 meios> 2, então
9 meios+ 5 > 2 + 5.
b) Se
9 meios> 2, então
9 meios⋅ 2 < 2 ⋅ 2.
c) Se
9 meios> 2, então
9 meios‒ 2 < 2 ‒ 2.
d) Se ‒3 > ‒5, então ‒3 ⋅ (‒1) < (‒5) ⋅ (‒1).
e) Se 2x +
5 terços<
8 terçosentão 2x < 1.
13 Raquel e Muriel brincam em uma gangorra, cada uma em uma ponta. Raquel tem 31 quilogramas e, quando não impulsiona com os pés no chão para subir, Muriel não consegue descer.

a) Qual delas tem a maior medida de massa?
b) Sabendo que Muriel tem medida de massa m e que m é maior que 26 quilogramas, que valores inteiros m pode ter?
14

Hora de criar – Elabore um problema sobre inequação para um colega resolver. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Propriedades da desigualdade
Na resolução de inequações, aplicaremos as propriedades da desigualdade.
Inicialmente, vamos estabelecer que:
• os sinais < e < têm o mesmo sentido;
• os sinais < e > têm sentidos opostos;
• os sinais > e > têm o mesmo sentido;
• os sinais > e < têm sentidos opostos.
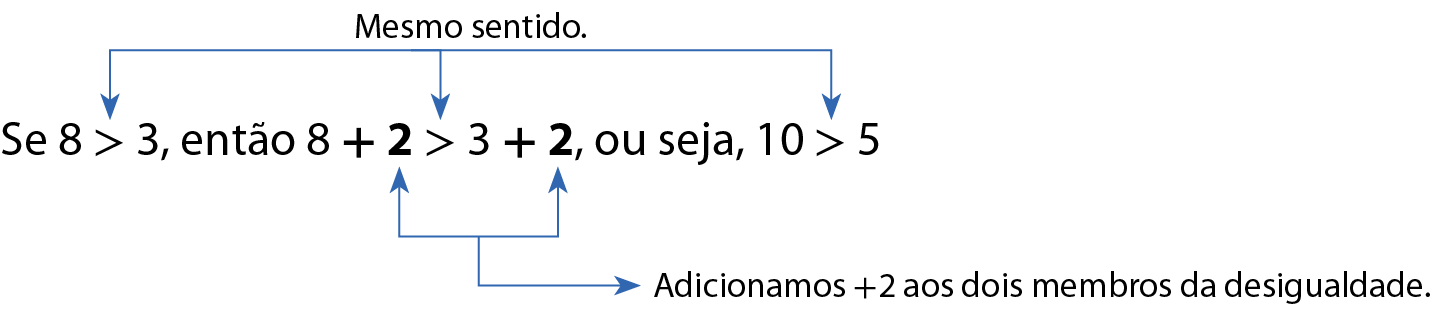
Verifique o que acontece com o sentido de uma desigualdade quando adicionamos um mesmo número a seus dois membros.
a)
b)
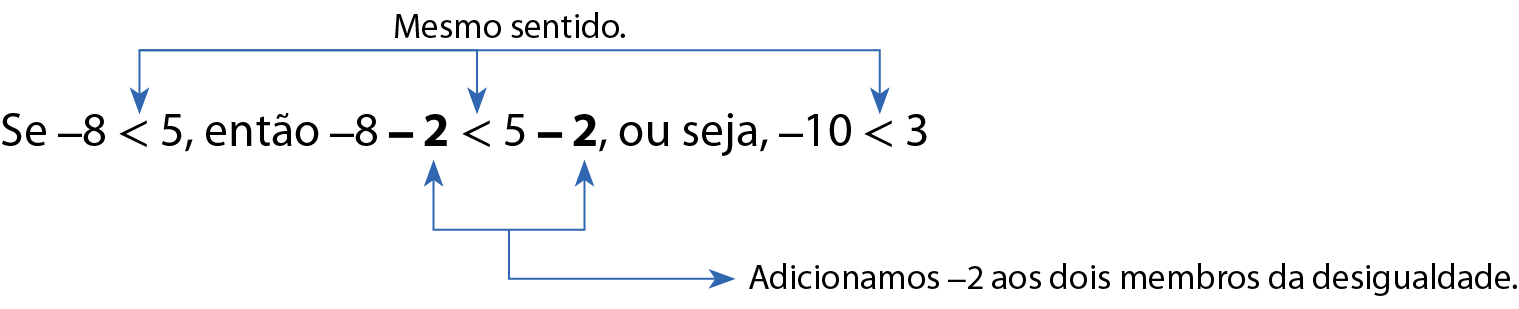
Note que o sentido das desigualdades não foi alterado.
Uma desigualdade não muda de sentido quando adicionamos ou subtraímos um mesmo número a seus dois membros.
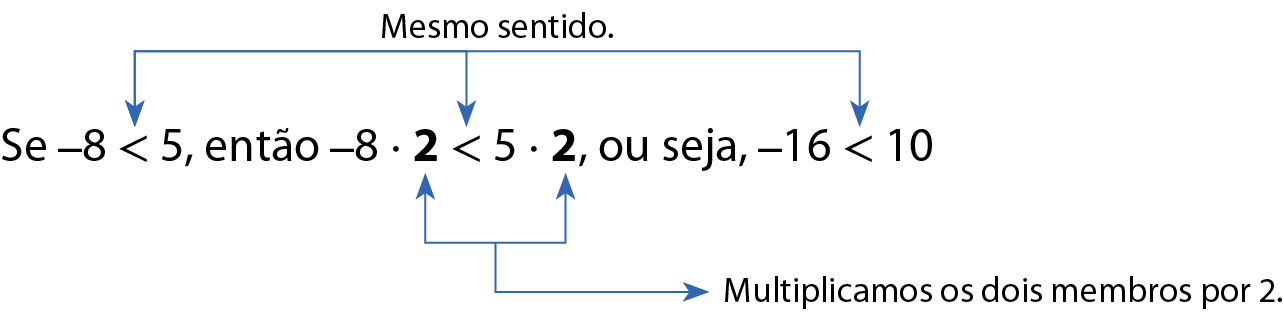
Agora, observe o que acontece quando multiplicamos ou dividimos os dois membros de uma desigualdade por um número positivo.
a)
b)
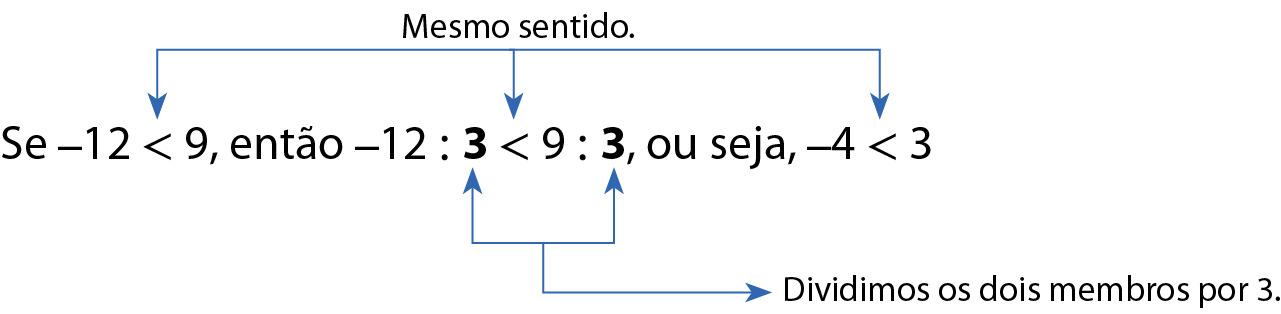
Repare que o sentido das desigualdades também não foi alterado.
Uma desigualdade não muda de sentido quando multiplicamos ou dividimos seus dois membros por um mesmo número positivo.
Verifique, ainda, o que acontece quando multiplicamos ou dividimos os dois membros de uma desigualdade por um número negativo.
a)
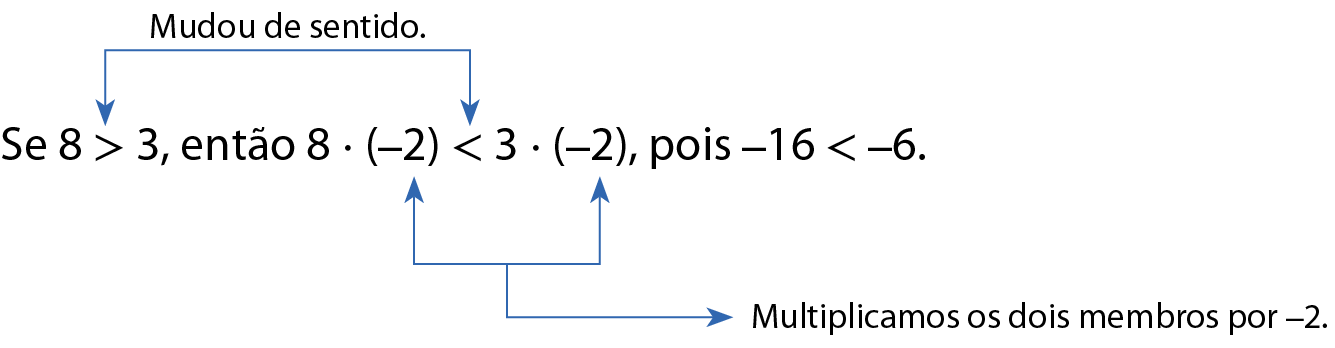
b)
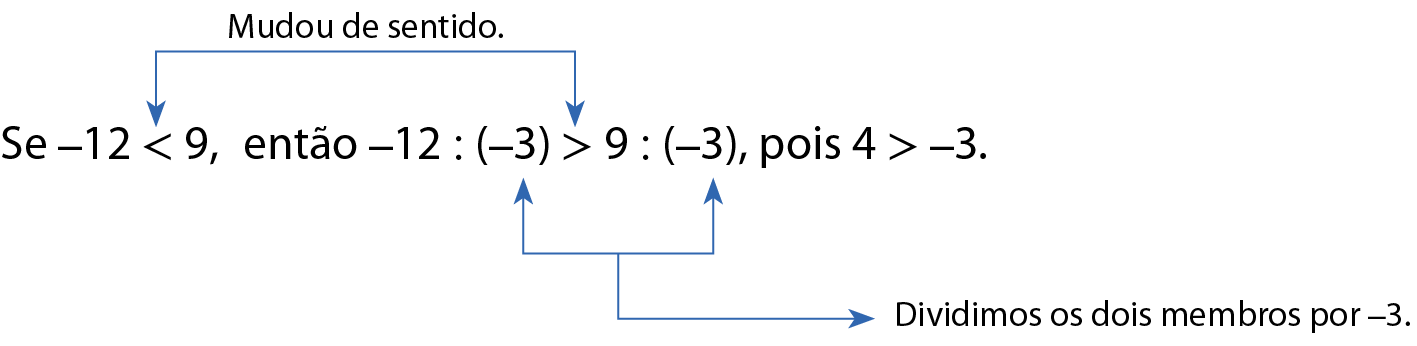
Nesse caso, podemos observar que a desigualdade mudou de sentido.
Uma desigualdade muda de sentido quando multiplicamos ou dividimos seus dois membros por um mesmo número negativo.
Para exemplificar, vamos resolver a inequação 5x + 3 > 2x ‒ 14, considerando x um número racional.
Aplicando as propriedades das desigualdades, obtemos:
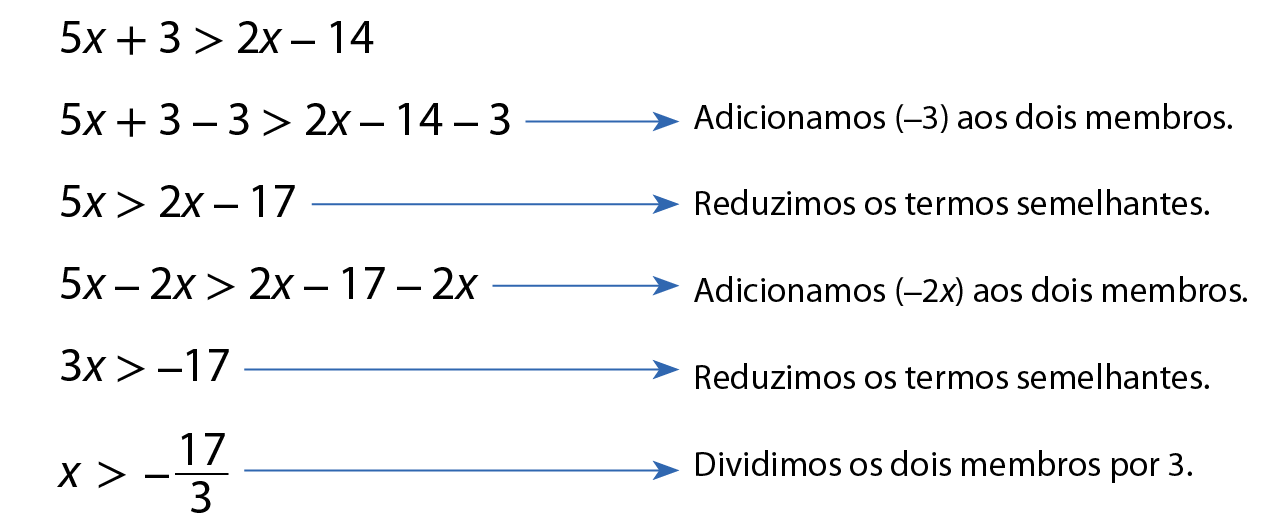
Logo, qualquer número racional maior que
menos 17 terçossatisfaz essa inequação.
Se quiséssemos determinar os números inteiros negativos que satisfazem a inequação dada, teríamos de encontrar todos os números inteiros negativos que são maiores que
menos 17 terços
Portanto, os números inteiros negativos maiores que
menos 17 terçossão ‒5, ‒4, ‒3, ‒2 e ‒1.
Resolvendo problemas com inequações
Acompanhe algumas situações de resolução de inequações.
Situação 1
Alex abrigou no tanque de piscicultura de seu sítio .2500 trutas e, com isso, ficou com uma quantidade maior que o triplo do que possuía. Antes disso, qual era o número máximo de trutas que havia no tanque?

Indicaremos por x a quantidade de trutas que havia inicialmente no tanque. Note que x tem de ser um número natural. Dessa fórma, podemos representar a situação pela inequação x + .2500 > 3x, sendo x um número natural.
Resolvendo essa inequação, podemos responder à questão.
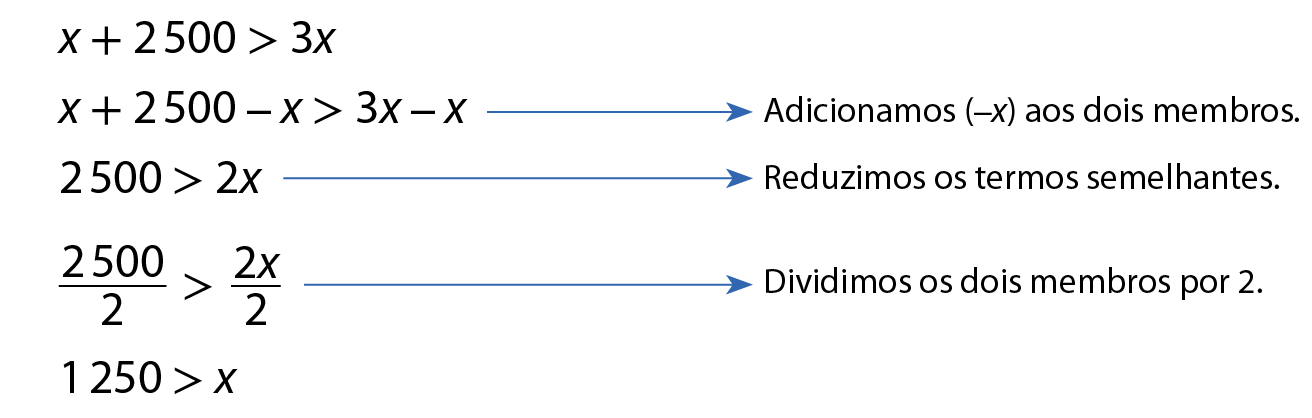
Como .1250 é maior que o número de trutas que havia inicialmente no tanque e x tem de ser um número natural, concluímos que havia, no máximo, .1249 trutas nesse tanque.
Situação 2
Vamos determinar os números inteiros que são soluções da inequação 2(x ‒ 5) ⩾ 3(x ‒ 4).
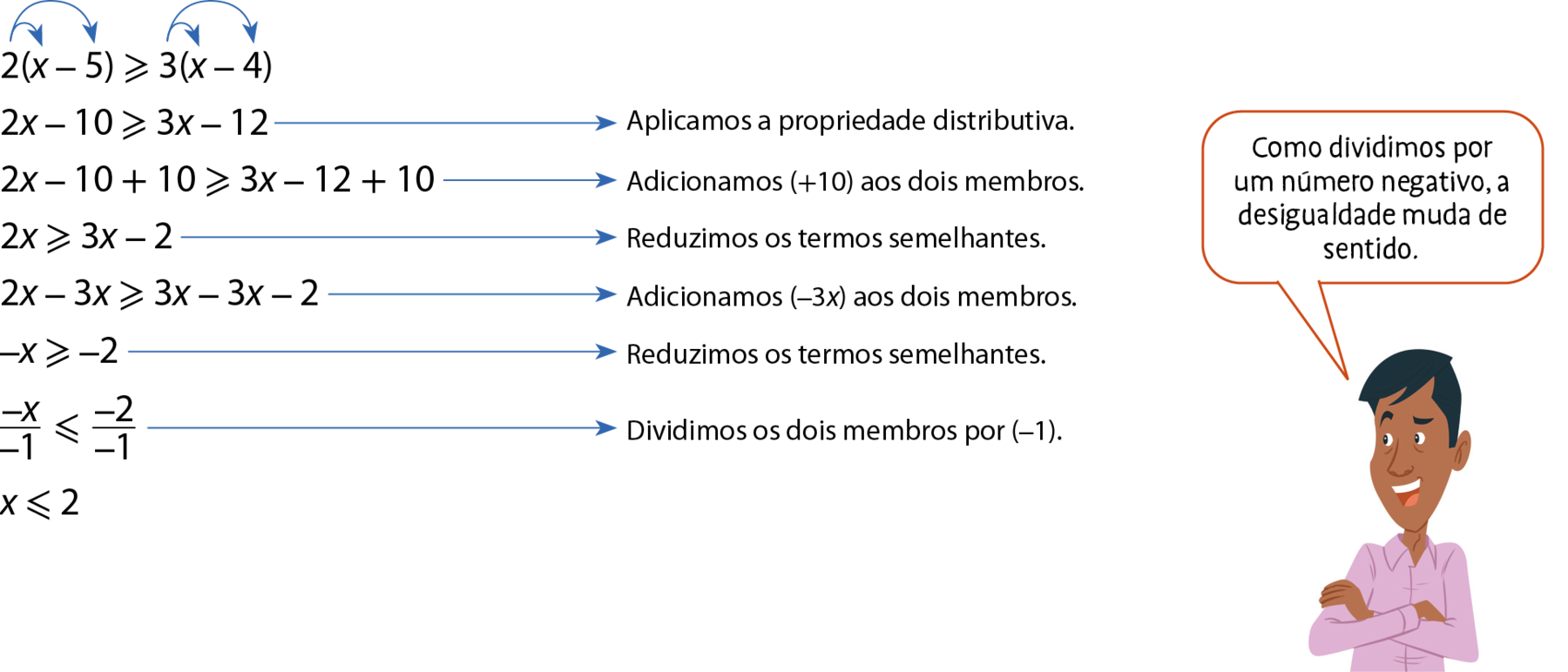
Logo, qualquer número inteiro menor ou igual a 2 é solução dessa inequação.
Situação 3
Sabendo que x é um número natural, vamos agora resolver a inequação
Fração, numerador x menos 3, denominador 3, mais, fração, numerador 2x menos 1, denominador 2 menor que 12.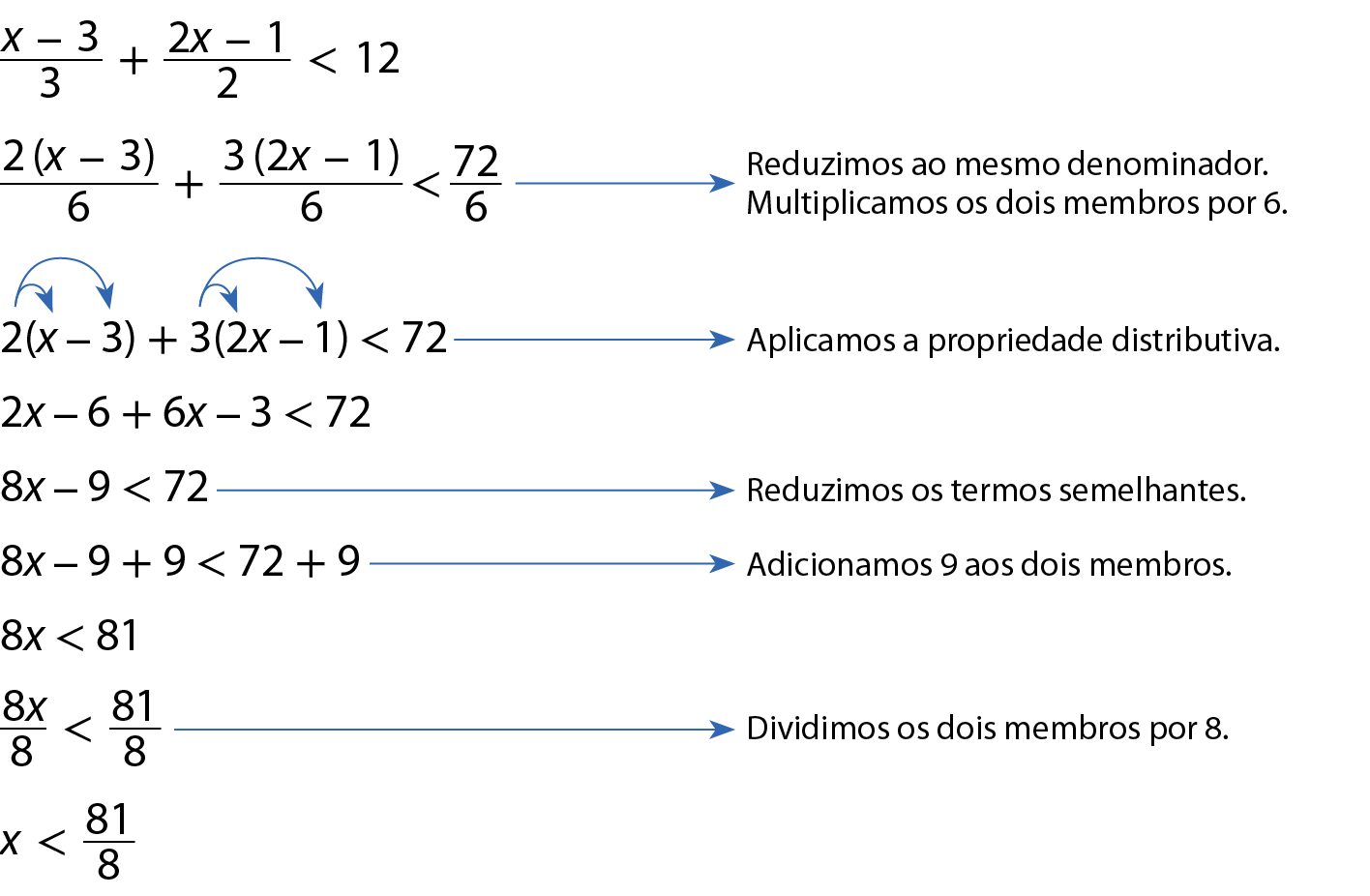
Dividindo 81 por 8, obtemos:
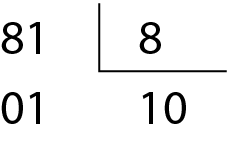
Então,
81 oitavosé um número entre 10 e 11. Logo, os números naturais menores que
81 oitavossão 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 e 10.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
15 Resolva as inequações a seguir.
a) x + 5 < 12, sendo x um número natural.
b) 2x ‒ 3 > 12, sendo x um número racional.
c) 3x ‒ 4 > 5x ‒ 10, sendo x um número inteiro.
d) 4x + 3 < x ‒ 18, sendo x um número natural.
16 Resolva as inequações, considerando x um número racional.
a) 4(x + 3) > 2(x ‒ 1)
b) 3(x + 2) > 2(2x + 4)
c) 5x ‒ (x ‒ 2) ⩽ 6
d) 7(x ‒ 2) < 2(3x + 4)
e) x ‒ 2(x ‒ 3) ⩽ x + 5
17 No polígono abaixo, sabe-se que xis é maior que 4 e que a medida de seu perímetro é menor que 32. Quais são os possíveis valores inteiros de xis?
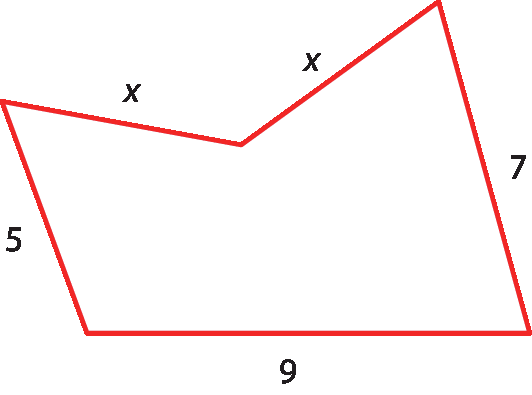
18 Dada a inequação 2(xis + 3) ⩽ 4(xis ‒ 1), encontre:
a) os números naturais menores que 8 que sejam soluções;
b) o menor número inteiro de três algarismos que seja solução.
19 De um garrafão contendo 10 litros de caldo de cana, até quantos copos com capacidade de 0,25 litro podem ser retirados de modo que restem mais de 3 litros?

20 Meu carro percorre 12 quilômetros com 1 litro de gasolina. Quantos litros de gasolina, no mínimo, preciso ter no tanque para percorrer mais de 700 quilômetros sem abastecer?
21 Meu pai tem 25 anos a mais que eu. Hoje, o triplo da minha idade mais a idade de meu pai é maior que a idade do meu avô. Sabendo que meu avô tem 65 anos, qual é a idade mínima de meu pai?
22 Considere
x menos 1 terço maior que, Fração, Numerador x denominador 2, mias 1 quarto.com x racional, e responda às questões no caderno.
a) O número 2 é solução? Por quê?
b) Existe algum número negativo que seja solução? Por quê?
23 Um bloco retangular mede 15 centímetros de comprimento, 12 centímetros de largura e 5 centímetros de altura. Paulo deseja construir outro bloco com a mesma medida de largura e a mesma medida de altura daquele, porém com mais de .1200 centímetros cúbicos de volume. Quantos centímetros, no mínimo, deve medir o comprimento desse outro bloco? (As medidas são expressas em números inteiros.)
24 Acompanhe como Joana resolveu a inequação
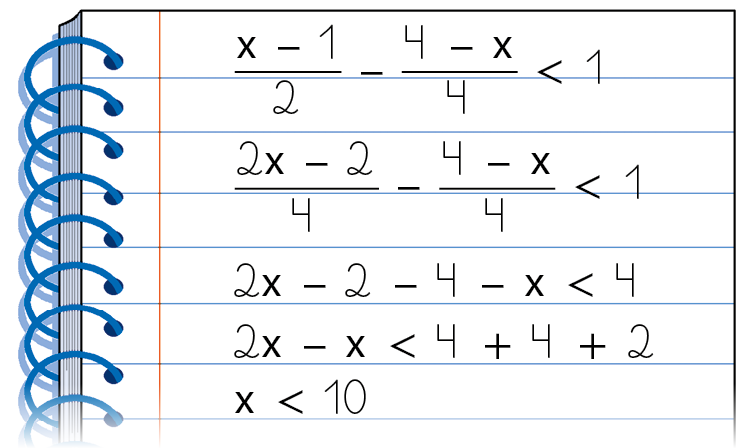
Ao conferir o resultado, ela percebeu que havia errado. Quando encontrou o erro, corrigiu-o e obteve a solução correta.
a) Que maneira ela pode ter escolhido para conferir o resultado?
b) Descubra qual foi o erro de Joana.
c) Qual foi a solução que Joana encontrou quando acertou?
25 Hora de criar ‒ Enuncie um problema que possa ser solucionado por meio da inequação 5x + 2 ⩽ 3x ‒ 15. Depois, resolva-o.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Digitei todo o trabalho do meu grupo no computador e imprimi as páginas sem usar o verso. Para isso, cada integrante do meu grupo deu 3 folhas, e ainda tive de colocar mais uma folha além das 3. Assim, usamos menos de 13 folhas no trabalho todo. Quantos eram os integrantes do meu grupo?
TRABALHANDO A INFORMAÇÃO

Alfabetizando com gráficos e tabelas
No dicionário, o verbete alfabetização é definido como:

O conceito de alfabetização pode ser ampliado para todo o tipo de aquisição das várias linguagens existentes, desde o “beabáglossário ” e a numeração até linguagens mais complexas como gráficos e tabelas. Um profissional da área médica, por exemplo, alfabetiza-se na leitura de um eletrocardiograma; um engenheiro, na leitura e escrita de um fluxograma; um músico, na leitura e escrita de uma partitura etcétera Podemos passar a vida toda nos alfabetizando em várias linguagens sem nunca chegar à totalidade delas.
A definição de um limite de aquisição do letramento, no início do Ensino Fundamental, é um tema polêmico que sempre volta ao debate: seria melhor no 2º ano ou no 3º ano?
Nos gráficos a seguir, observe qual era a situação dos estudantes do 3º ano de escolas públicas na leitura e na escrita, em 2016.
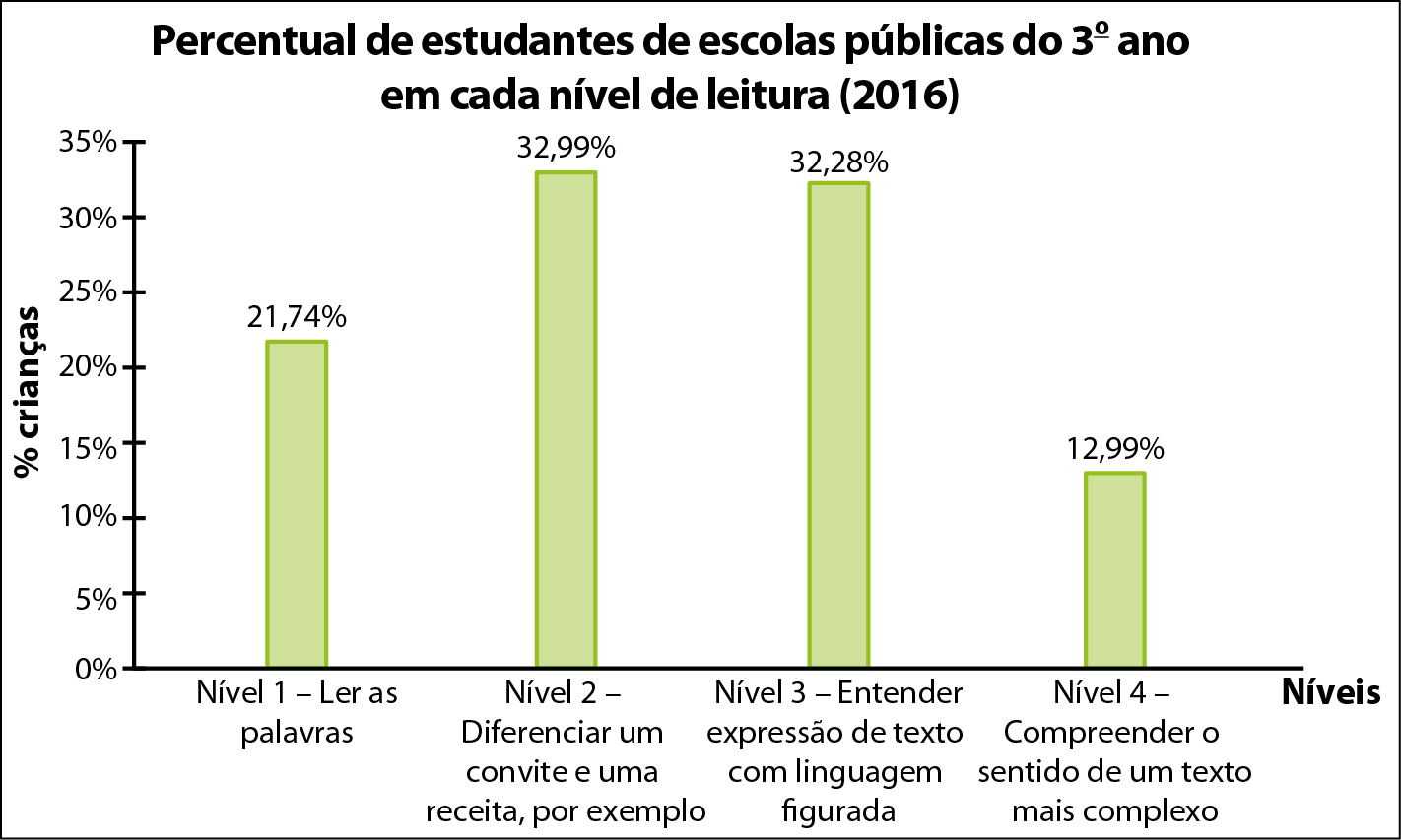
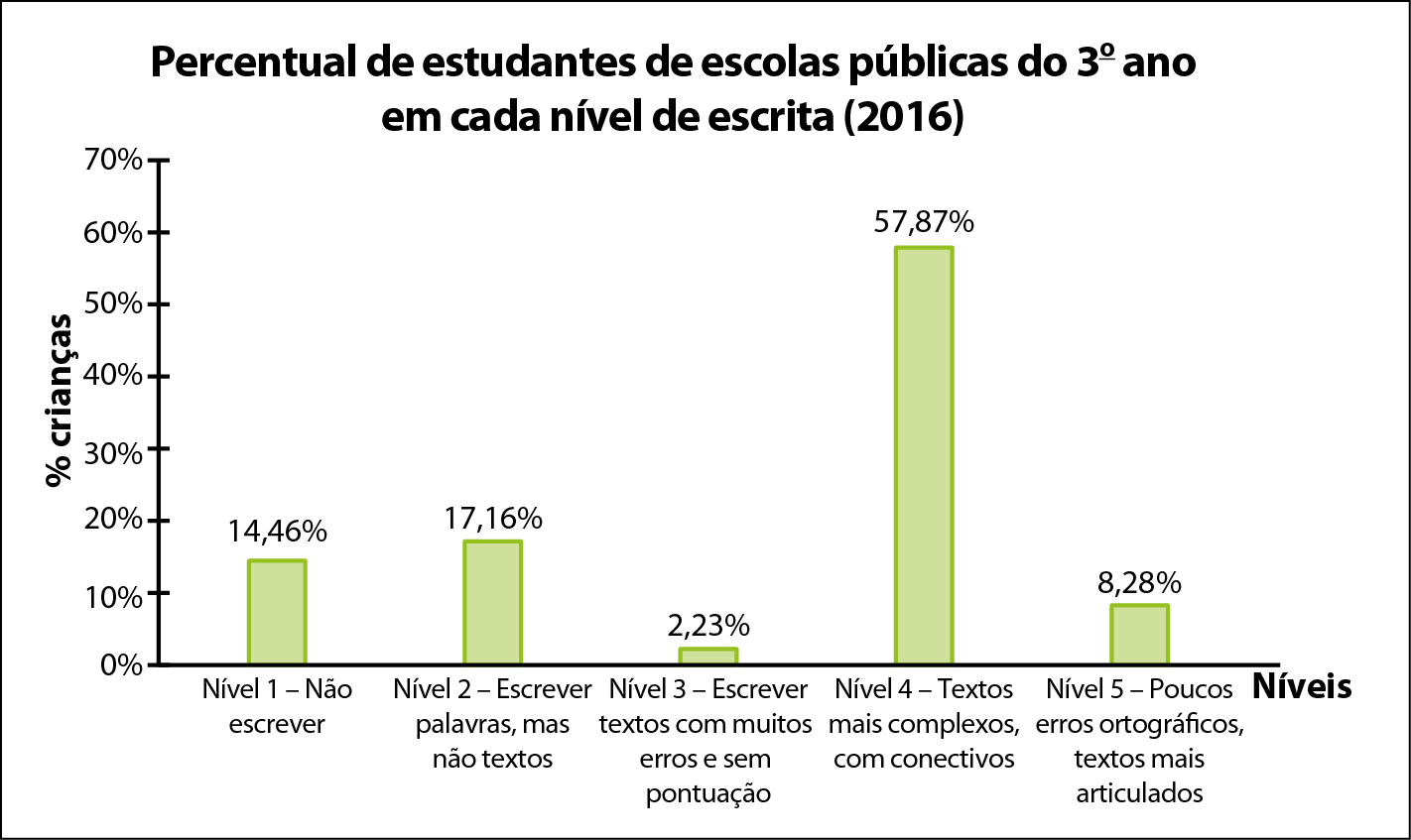
Você já aprendeu que os mesmos dados podem ser organizados de maneiras diferentes. Por exemplo, os dados apresentados nos gráficos poderiam ser organizados em fórma de tabela, de texto ou, ainda, em fórma de gráfico de barras.
Note como ficariam esses dados dispostos em fórma de tabela.
|
Nível |
1 |
2 |
3 |
4 |
5 |
|---|---|---|---|---|---|
|
Leitura |
Ler palavras (21,74%) |
Diferenciar textos (32,99%) |
Linguagem figurada (32,28%) |
Texto mais complexo (12,99%) |
— |
|
Escrita |
Não escrever (14,46%) |
Escrever palavras (17,16%) |
Muitos erros, sem pontuação (2,23%) |
Textos com conectivos (57,87%) |
Textos articulados (8,28%) |
BRASIL. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira (Inépi). Relatório do 3º ciclo de monitoramento das metas do Plano Nacional de Educação – 2020 [recurso eletrônico]. Brasília, Distrito Federal: Inépi, 2020.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Usando como referência os gráficos e a tabela anteriores, responda às perguntas.
a) Ao final do 3º ano, um pouco mais de 45% dos estudantes têm aprendizagem adequada em leitura. A quais níveis corresponde essa afirmação?
b) Ao final do 3º ano, quantos por cento dos estudantes têm aprendizagem adequada em escrita?
c) Nos anos de 2020 e 2021 muitos estudantes não tiveram acesso a aulas presenciais devido à pandemia de Covid-19. Se essa avaliação dos níveis de leitura e escrita fosse aplicada em 2022, o que você acha que aconteceria com esses níveis? Na sua opinião, o que os órgãos governamentais poderiam fazer para melhorar esses índices?
2 A mobilidade nas grandes cidades do mundo é um grande problema e um desafio para as respectivas administrações.
A mobilidade urbana é uma atividade essencial para a sociedade, já que se refere à locomoção das pessoas entre os espaços para atender às suas necessidades.
Ela é definida como qualquer tipo de movimento – a pé, de carro, ônibus, bicicleta, skate, cadeira de rodas, trem ou metrô – que tenha como finalidade o deslocamento de um ponto a outro em um espaço geográfico.
Um dos grandes desafios do nosso tempo é que a urbanização e o aumento da concentração de pessoas sem o planejamento adequado inviabiliza a mobilidade urbana.
A preferência pelo transporte individual e a escassez de ciclovias e transporte público nas cidades brasileiras são, com frequência, geradores de congestionamentos e gases do efeito estufa. Esse cenário afeta negativamente a qualidade de vida dos cidadãos.
Nesse contexto, é preciso buscar alternativas sustentáveis e estratégias para enfrentar o desafio da mobilidade urbana. A boa notícia é que já existem algumas possibilidades e exemplos a serem seguidos.
Fonte: Portal eCycle. Mobilidade urbana: desafios e ideias sustentáveis. Disponível em: https://oeds.link/5dmC6a. Acesso em: 18 fevereiro 2022.
a) Escolha 10 pessoas que você conheça e faça uma pesquisa sobre mobilidade urbana. Dependendo das pessoas que você escolher, poderá fazer perguntas como:
– Que meios de transporte você usa para se locomover de sua residência à escola?
– Que meios de transporte você usa para se locomover de sua residência ao trabalho?
– Para facilitar seu deslocamento, os órgãos públicos deveriam investir em quais meios de locomoção?
b) Após a coleta dos dados, organize as informações em tabelas e em gráficos.
c) Escreva um texto com uma conclusão de sua pesquisa e, depois, compartilhe-o com o professor e os demais colegas de turma.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Entre os números ‒3, 0 e 3, quais são soluções da inequação 5x ‒ 2 < 2x + 3?
2 Determine os números racionais que satisfazem as inequações a seguir.
a) 4(x + 3) > 2(x ‒ 1)
b) x ‒ 2(x ‒ 3) ⩽ x + 5
c) 2 + 5(3x + 1) > 0
3 A quantidade de CDs que eu tenho é o quádruplo da quantidade de CDs que meu irmão tem subtraída de 5. Juntos, temos, no máximo, 10 CDs. Quantos CDs pode ter meu irmão?
4 Emendando dois pedaços de barbante, obtém-se mais de 1 métro. A medida do comprimento do pedaço menor, em centímetro, é representado por um número inteiro. O pedaço maior tem 20 centímetros a mais que o menor. Qual é a medida do comprimento mínimo, em centímetro, do barbante menor?
5 Uma empresa tem a opção de embalar seu produto em dois tipos de caixa, a e B. Na caixa do tipo a, é possível embalar de 20 a 30 unidades, e na caixa do tipo B, de 15 a 20 unidades. Para este mês, a empresa usou 100 unidades de cada tipo de caixa.
a) Qual é a quantidade máxima de produtos que a empresa pode embalar neste mês? E qual é a quantidade mínima?
b) Represente por meio de uma inequação a quantidade de produtos que a empresa pode embalar neste mês.
c) A empresa poderá embalar .5001 produtos neste mês? E .4896 produtos? Justifique sua resposta.
6 Existe algum número racional maior que ‒4 que seja solução da inequação
Fração. Numerador x menos 2, denominador 3, fim da fração mais 2 x, maior igual que, Fração. Numerador 5x, denominador 2.Justifique sua resposta.
7 Quais números inteiros menores que 10 satisfazem a inequação
5 menos, Fração. Numerador x, denominador 2, menor igual que, Fração. Numerador x, denominador 3, mais 1.?
8 Um tonel contém 100 litros de azeite. Quantas garrafas de 0,9 litro é possível encher, no máximo, de modo que ainda sobrem mais de 10 litros no tonel?
9 Dois meninos faltaram à aula de informática. Ainda assim, nessa aula, o número de meninos era maior que o número de meninas. Sabendo-se que havia 10 meninas na sala de aula, qual é o menor número possível de estudantes dessa turma?
10 Ao final de uma prova de Matemática, realizada para selecionar os estudantes que participarão de uma Olimpíada de Matemática, Mariana comenta com seu amigo Rodrigo:
— Eu fui muito bem. Pelo gabarito que está afixado no quadro de avisos, acertei 75 questões. E você?
Rodrigo responde:
— Infelizmente não fui nada bem. Mesmo que tivesse acertado o dobro do que acertei, ainda precisaria de mais três acertos para superar o número de pontos que você obteve.
Qual foi a quantidade mínima de pontos que Rodrigo obteve?

11 Preciso cercar um terreno, que tem a fórma de um quadrilátero, para fazer uma horta. A medida do perímetro do terreno é maior que 120 metros. Dois dos lados têm a mesma medida. O terceiro lado mede a metade da medida dos lados que têm medidas iguais. O quarto lado mede 21 metros. Todos os lados têm medidas expressas por números inteiros. Nessas condições, qual é a quantidade mínima de metros de arame necessária para cercar esse terreno com seis voltas, que deve ter um portão que mede 1 metro de largura?
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Com um litro de gasolina, um automóvel percorre 12 quilômetros. O proprietário quer saber quantos litros de gasolina seriam necessários para que esse automóvel percorresse mais de 500 quilômetros. Qual é a inequação que descreve essa situação, sendo éle, a quantidade de litros?
a) 12éle > 500
b) 12éle < 500
c)
12 sobre l> 500
d)
12 sobre l< 12
2 Que inequação pode ser associada à balança?
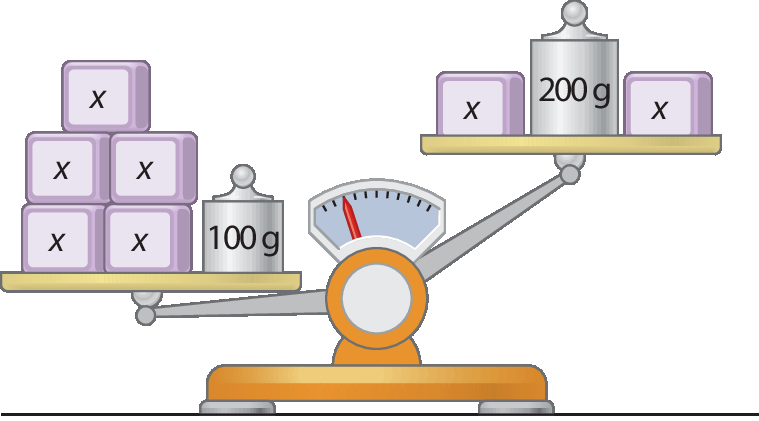
a) 5x + 100 < 2x + 200
b) 5x + 100 ⩽ 2x + 200
c) 5x + 100 > 2x + 200
d) 5x + 100 ⩾ 2x + 200
3 Carlos é ciclista e percorre 450 métros por minuto pedalando. De quanto tempo, no mínimo, ele precisa para percorrer mais de 36 quilômetros?
a) uma hora e 8 minutos
b) uma hora e 20 minutos
c) uma hora e 21 minutos
d) uma hora e 41 minutos
4 Se ‒3x < 18, então:
a) x < ‒6
b) x < 6
c) x > 6
d) x > ‒6
5 Quais números racionais satisfazem a inequação a seguir?
a) x <
Menos 8 quintosb) x >
8 dezenove avosc) x >
8 quintosd) x > 2
6 Qual é a solução de 5x + 12 ⩽ 3 (x ‒ 6)?
a) x ⩽
Menos 3 quartosb) x ⩾
3 quartosc) x ⩽ ‒15
d) x ⩾ ‒15
7 Elizete e Vinícius têm uma coleção de moedas. Elizete tem 10 moedas a menos que o dobro da quantidade de Vinícius e, juntos, eles têm menos de trezentas e oitenta moedas. Quantas moedas, no máximo, cada um tem?
a) Elizete tem, no máximo, trezentas e oitenta e oito moedas e Vinícius, 199.
b) Elizete tem, no máximo, duzentas e quarenta e oito moedas e Vinícius, 129.
c) Elizete tem, no máximo, duzentas e cinquenta moedas e Vinícius, 130.
d) Elizete tem, no máximo, duzentas e sessenta e oito moedas e Vinícius, 129.
8 A diferença entre as medidas x e y dos lados de um retângulo, dadas em centímetro, é igual a 2 centímetros. Quais devem ser os valores de x e de y para que a medida do perímetro do retângulo seja maior ou igual a 48 centímetros?

a) x ⩾ 12 centímetros e y ⩾ 10 centímetros
b) x ⩾ 13 centímetros e y ⩾ 11 centímetros
c) x > 13 centímetros e y > 11 centímetros
d) x ⩾ 25 centímetros e y ⩾ 23 centímetros
9 O custo de produção de doces em uma confeitaria é de R$ 3,00três reais por unidade mais um valor fixo de R$ 310,00trezentos e dez reais. Se a unidade é vendida por R$ 8,00oito reais, quantos doces, no mínimo, devem ser vendidos para que os ganhos cubram os gastos?
a) 61 doces.
b) 62 doces.
c) 28 doces.
d) 27 doces.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir:
a) O que é uma inequação?
b) Quantas soluções podem ter uma inequação?
c) Escreva dois exemplos de uma inequação do 1º grau com uma incógnita. Depois, identifique o primeiro e o segundo membro dessas inequações.
d) Em que circunstância o sentido de uma desigualdade muda?
e) Qual estratégia você usa para resolver uma inequação?
DIVERSIFICANDO
Pesagem de bolinhas
Considere 6 bolinhas, todas do mesmo tamanho e da mesma cor. Cinco delas têm a mesma massa, e uma delas é mais leve que as outras. O desafio é descobrir, em duas pesagens em uma balança de dois pratos, qual é a bolinha mais leve.

• Primeira pesagem: podemos descobrir isso dividindo as bolinhas em dois grupos de 3 bolinhas cada um e colocando cada grupo em um dos pratos da balança.
Observando a balança da figura a seguir, percebemos que, nesse caso, a bolinha mais leve está entre as que estão no prato da direita.
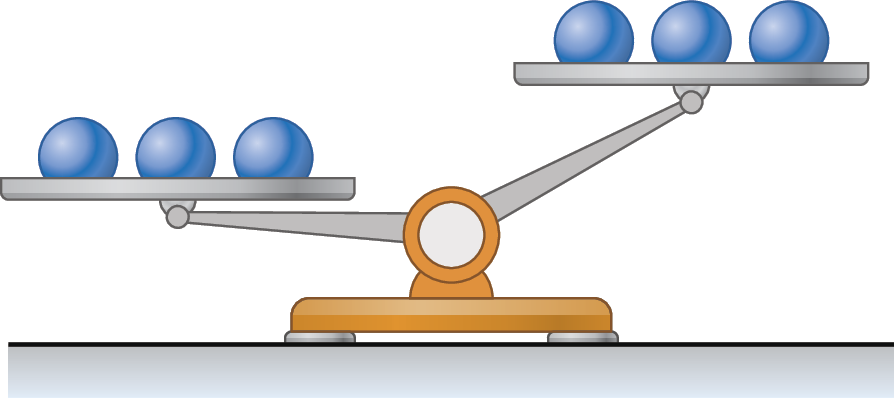
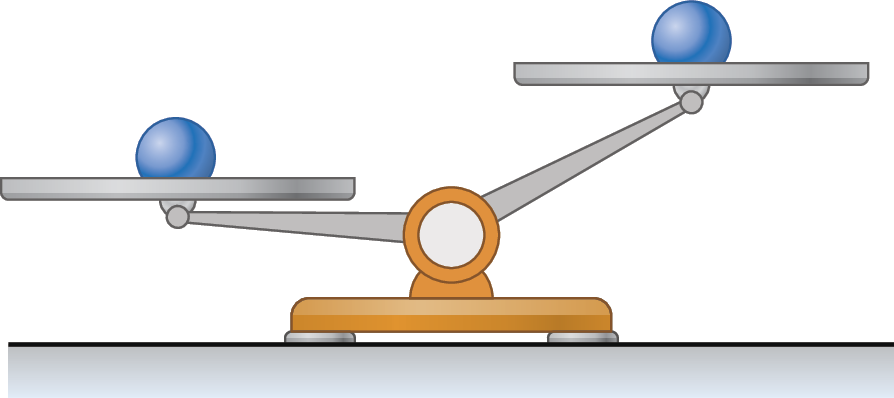
• Segunda pesagem: Agora, escolhemos duas das bolinhas que estavam no prato da direita e colocamos uma em cada prato.
Considerando o desnivelamento da balança da figura a seguir, percebemos que a bolinha mais leve está no prato da direita.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Resolva o desafio anterior dividindo as bolinhas em três grupos de duas bolinhas cada um.
2 São dadas 8 bolinhas, todas do mesmo tamanho e da mesma cor. Sete delas têm a mesma medida de massa, e uma delas é mais leve que as outras. Descubra, em duas pesagens em uma balança de dois pratos, qual é a bolinha mais leve.
3 São dadas 9 bolinhas, todas do mesmo tamanho e da mesma cor. Oito delas têm a mesma medida de massa, e uma delas é mais leve que as outras. Descubra, em duas pesagens em uma balança de dois pratos, qual é a bolinha mais leve.
4 São dadas 9 bolinhas, todas do mesmo tamanho e da mesma cor. Oito delas têm a mesma medida de massa, e uma delas é mais leve ou mais pesada que as outras. Descubra, em três pesagens em uma balança de dois pratos, qual delas tem massa diferente.
Glossário
- Beabá
- : reunião das letras que fazem parte do alfabeto; abecedário.
- Voltar para o texto