Página 156

CAPÍTULO 7 Sistemas de equações

Fotografia. Vista frontal de dois coelhos na cor cinza e um preto. Existem outros coelhos ao fundo da imagem, mas não é possível realizar a contagem. — Filhotes de coelhos da espécie Oryctolagus cuniculus em criadouro.

Observe, leia e responda no caderno.

a) A gestação de uma coelha dura quatro semanas, e em cada uma das seis ninhadas anuais nascem de quatro a oito filhotes. Supondo ocorrida essa situação, quais são os números mínimo e máximo de coelhos gestados em um ano por uma só coelha?

b) Considerando ême o número de machos e éfe o número de fêmeas de coelhos do sítio citado, escreva como se deve relacionar:

• ême e f com o total de coelhos;

• a diferença do dôbro de ême com éfe e o número 7.

Símbolo de fertilidade e prosperidade, a representação do coelho faz parte de crenças, literaturas, mitologias e folclores. Ele também pode estar presente em problemas de Matemática, como na seguinte situação:

Em um sítio, há 20 coelhos. A diferença entre o dôbro do número de machos e o número de fêmeas é igual a 7. Quantos coelhos machos há nesse sítio?

Página 157

1. Par ordenado e plano cartesiano

Par ordenado

Vamos recordar o conceito de par ordenado e sua representação geométrica em um plano, agora com números racionais.

Quem nunca brincou de palavras cruzadas? Dados os significados ou as dicas, as palavras devem ser escritas na horizontal e na vertical no quadro que também é dado. Acompanhe o exemplo.

Verticais

1. Cruzamento de duas retas distintas (palavra invertida)

2. Torne a unir

3. Aptidão inata

4. Fava‑de‑calabar (palavra invertida)

5. Fixes os olhos em

6. Triture com os dentes (palavra invertida)

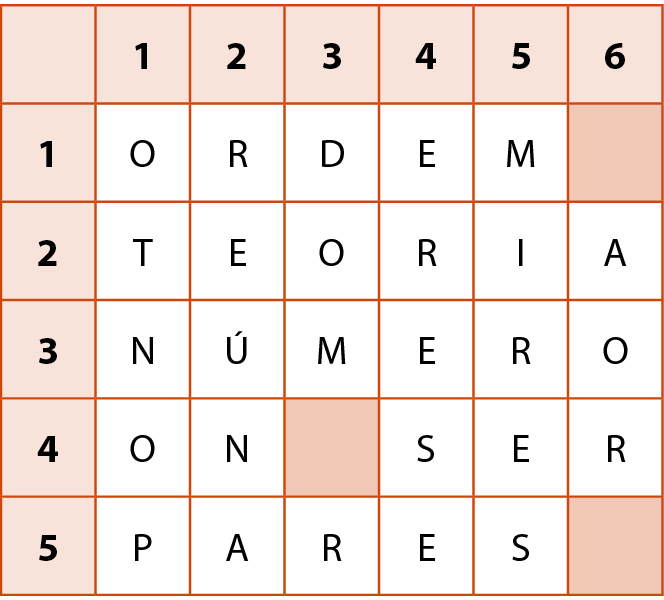
Imagem. Quadro de palavras cruzadas com seis linhas e sete colunas. Primeira linha: quadrado laranja 1, 2, 3, 4, 5, 6. Segunda linha: 1, O, R, D, E, M quadrado laranja escuro. Terceira linha: 2, T, E, O, R, I, A. Quarta linha: 3, N, Ú, M, E, R, O. Quinta linha: 4, O, N quadrado laranja escuro, S, E, R. Sexta linha: 5, P, A, R, E, S quadrado laranja escuro.

Horizontais

1. Organização metódica

2. Conjunto sistemático de ideias sobre determinado tema

3. Quantidade

4. Contração de (em + o) (palavra invertida); ente/criatura

5. Números múltiplos de dois

Cada letra desse passatempo tem um “endereço”, isto é, está em uma casa do quadro associada a um par de números. Convencionamos a ordem desse par: o primeiro é o das verticais, e o segundo é o das horizontais.

Assim, a letra D, que está no cruzamento da vertical 3 com a horizontal 1, é associada ao par ordenado (3, 1), e vice‑versa. A letra ih, que está no cruzamento da vertical 5 com a horizontal 2, está associada ao par ordenado (5, 2), e vice‑versa. Note que o par (1, 3) associa‑se à letra N da palavra NÚMERO e é diferente do par (3, 1); o par (2, 5) associa‑se à letra a da palavra PARES e é diferente do par (5, 2).

Plano cartesiano

Já estudamos o conceito de par ordenado com números racionais e sua representação geométrica em um plano. Vimos também que as soluções de uma equação do 1º grau com duas incógnitas são pares ordenados representados graficamente por pontos de um plano.

Um sistema cartesiano de coordenadas é formado por duas retas concorrentes, x e y, perpendiculares entre si, chamadas de eixos. Plano cartesiano é um plano que contém esse sistema.

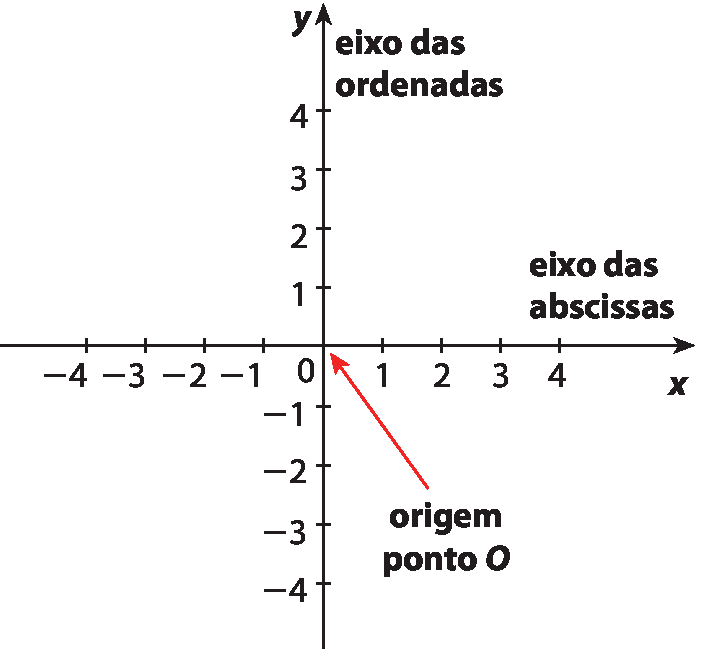
Ilustração. Eixo x (eixo das abcissas) com pontos de menos 4 a 4 e eixo y (eixo das ordenadas) com pontos de menos 4 a 4. Em 0, origem, ponto O.

• A reta horizontal é chamada de eixo das abscissas ou eixo dos x, que será representado por Ox.

• A reta vertical é chamada de eixo das ordenadas ou eixo dos y, que será representado por Oy.

• O ponto de cruzamento das duas retas é chamado de origem, que será representada por óh.

• Em intervalos iguais, cada eixo é numerado a partir da origem.

Página 158

Todo par ordenado (x, y) de números racionais, em que x é o primeiro elemento do par e y é o segundo elemento, pode ser representado em um plano cartesiano e corresponde a um ponto P desse plano.

Os números x e y recebem o nome de coordenadas do ponto P. Em particular, o número x é a abscissa do ponto P, e y é a ordenada do ponto P. Para simplificar a linguagem, vamos dizer que o ponto P é o par ordenado (x, y). O ponto origem é o par (0, 0).

Imagem. Como exemplo, vamos localizar no plano cartesiano o ponto P, abre parênteses, 3 vírgula 2, fecha parênteses. O número 3 é a abcissa e o número 2 é a ordenada.

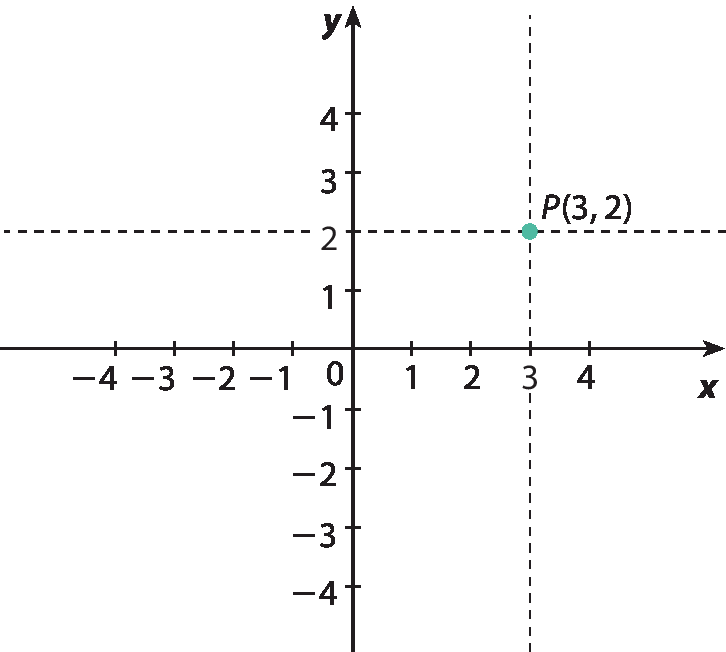
Ilustração. Eixo x com pontos de menos 4 a 4 e eixo y com pontos de menos 4 a 4. Ponto: P(3, 2).

• Pelo ponto do eixo dos x com abscissa 3, tracejamos uma linha paralela ao eixo dos y.

• Pelo ponto do eixo dos y com ordenada 2, tracejamos uma linha paralela ao eixo dos x.

• O ponto de cruzamento (ou ponto de intersecção) das linhas tracejadas é o ponto P(3, 2).

Observe a seguir a representação de outros pontos no plano cartesiano.

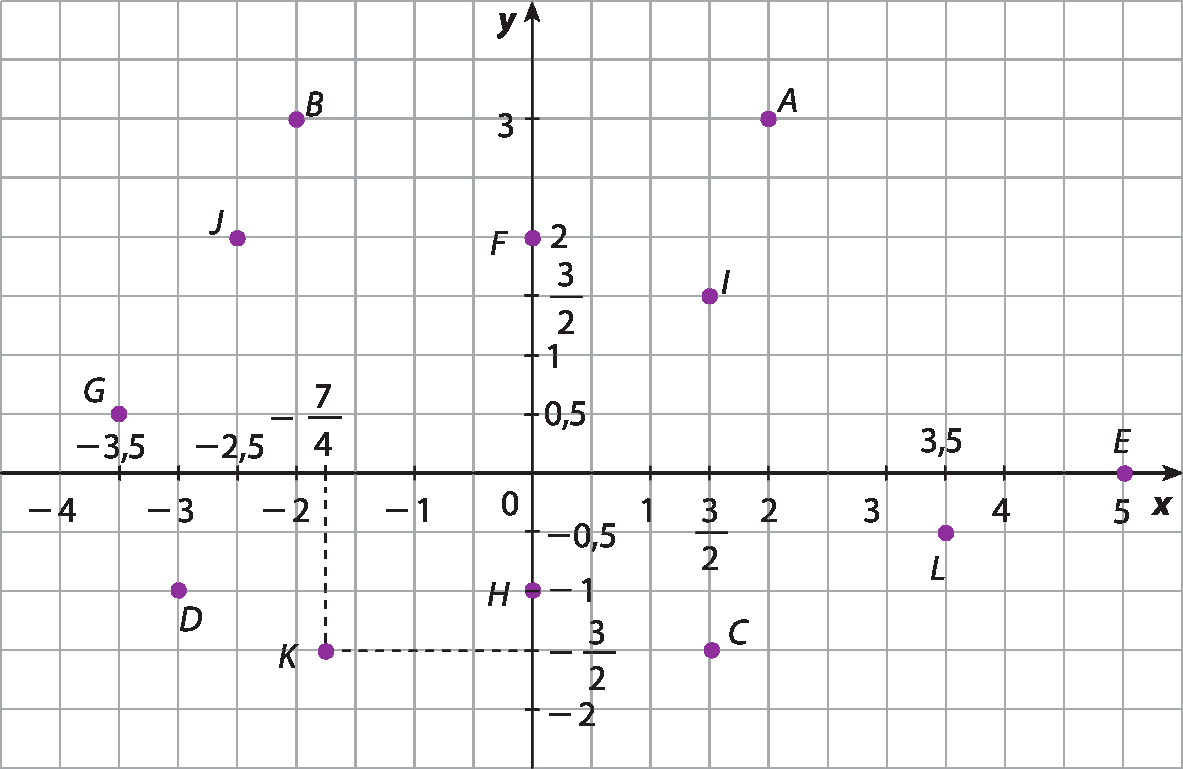
Ilustração. Malha quadriculada com um gráfico. Eixo x, pontos de menos 4 a 5 e eixo y, pontos de menos 2 a 3. Pontos: A(2, 3), B(menos 2, 3), C(três meios, menos três meios), D(menos 3, menos 1), E(5, 0), F(0, 2), G(menos 3,5, 0,5), H(0, menos 1), I(três meios, três meios), J(‒2,5, 2), K(menos sete quartos, menos três meios), L(3,5; menos 0,5).

Os pontos destacados no plano cartesiano são:

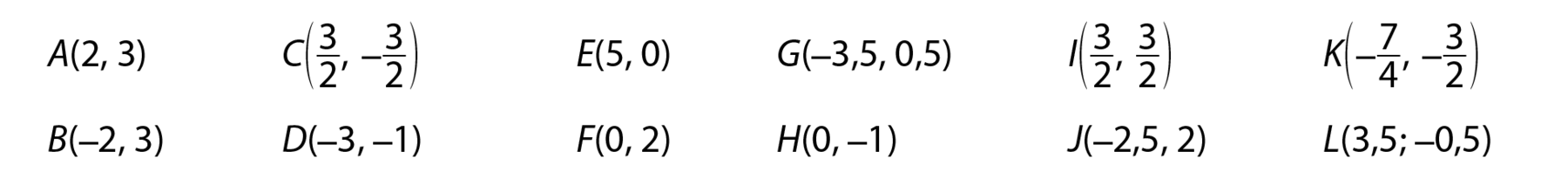
Ilustração. Doze pares ordenados distribuídos em duas linhas com seis pares em cada. Na primeira linha: A(2, 3), C(três meios, menos três meios), E(5, 0), G(menos 3,5, 0,5), I(três meios, três meios), K(menos sete quartos, menos três meios). Na segunda linha: B(menos 2, 3), D(menos 3, menos 1), F(0, 2), H(0, menos 1), J(‒2,5, 2), L(3,5; menos 0,5).

Observações

▶ Pontos do plano cartesiano representados por:

• pares ordenados com abscissas opostas e ordenadas iguais são chamados de pontos simétricos em relação ao eixo das ordenadas. Estão a igual distância de Oy. Exemplo: pontos a e B.

• pares ordenados com abscissas iguais e ordenadas opostas são chamados de pontos simétricos em relação ao eixo das abscissas. Estão a igual distância de Ox. Exemplo: pontos C e ih.

• pares ordenados com abscissas opostas e ordenadas opostas são chamados de pontos simétricos em relação à origem. Estão a igual distância da origem óh. Exemplo: pontos G e L.

Página 159

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

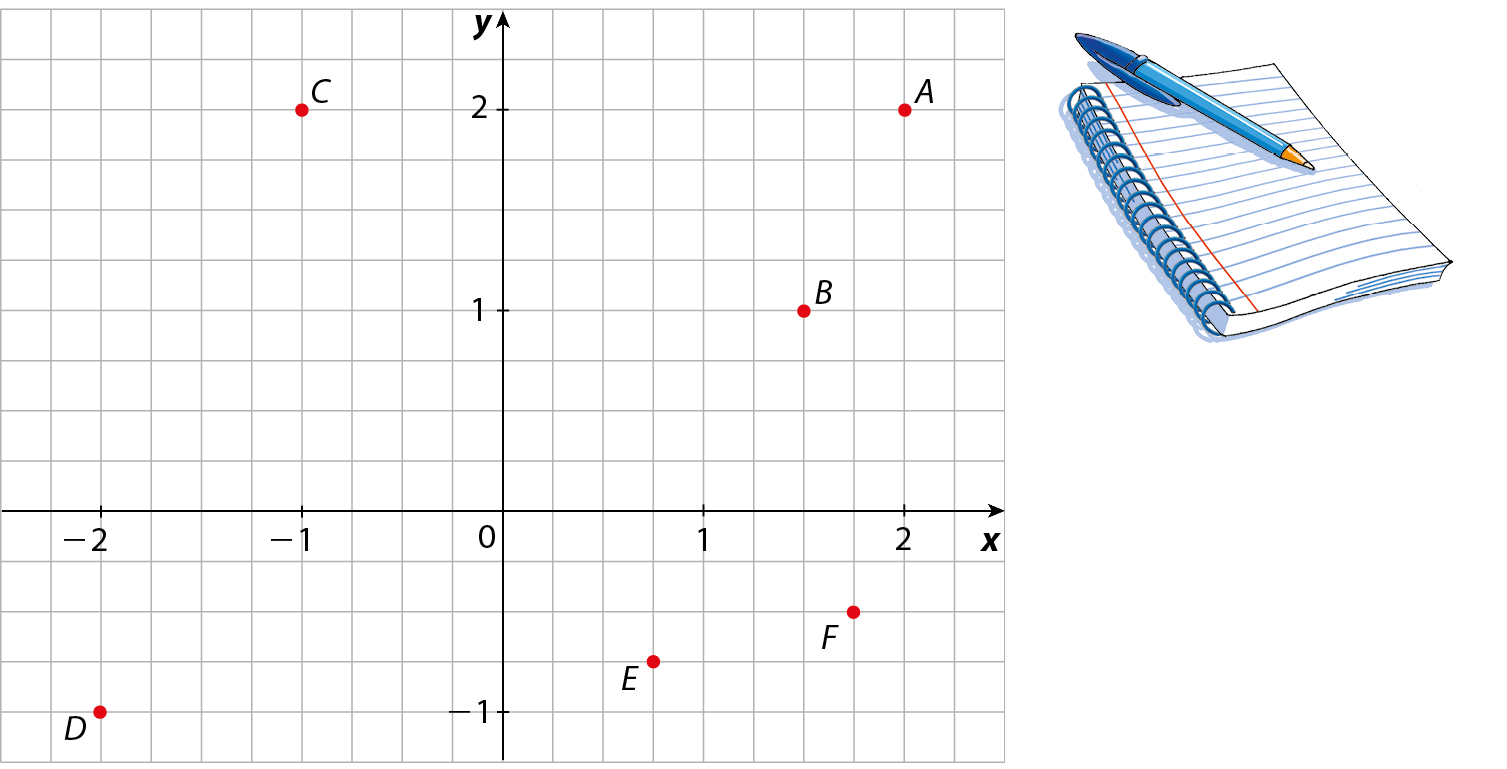
1 Escreva, no caderno, as coordenadas dos pontos localizados no plano cartesiano a seguir.

Ilustração. Malha quadriculada com gráfico. Eixo x, pontos de menos 2 a 2 e eixo y, pontos de menos 1 a 2. Pontos: A(2, 2); B (três meios, 1); C(menos 1, 2); D(menos 2, menos 1); E (três quartos, menos três quartos); F(sete quartos, menos um meio). Ilustração de caderno argolado branco com linhas e uma caneca azul

2 Construa um plano cartesiano em uma folha de papel quadriculado e localize os pontos indicados.

Ilustração. Nove pares ordenados distribuídos em duas linhas. Na primeira linha: A(-1, 3), C(4,-2), E(2, 0), G(0,5; 0,5), I(três meios, menos três meios. Na segunda linha: B(2, 4), D(-4,-3), F(-2,0), H(menos 3 quartos, menos e meios).

3 Construa um plano cartesiano em uma folha de papel quadriculado e desenhe o triângulo de vértices nos pontos A(‒2, 2), B(‒1, 5) e C(2, 2).

4 Construa em uma folha de papel quadriculado um plano cartesiano e localize os pontos a(5, ‒2); B(5, 2); C(2, 5); D(‒2, 5); ê(‒5, 2); F(‒5, ‒2); G(‒2, ‒5) e H(2, ‒5).

a) Traçando os segmentos

\overline{A B}

\overline{B C}

\overline{C D}

\overline{D E}

\overline{E F}

\overline{F G}

\overline{G H}

\overline{H A}

, qual é o polígono formado?

b) Quais desses pontos são simétricos em relação ao eixo Oy, ao eixo Ox, à origem?

5 Em uma folha de papel quadriculado, construa um plano cartesiano e assinale os pontos a(‒2, ‒1) e C (3, 4). Eles são os extremos da diagonal

\overline{A C}

de um quadrado.

a) Quais são os pontos extremos da outra diagonal desse quadrado?

b) Dê as coordenadas do ponto comum a essas duas diagonais.

c) Considerando u a unidade de medida do lado de cada quadradinho da malha quadriculada, determine a medida do perímetro desse quadrado.

Reúna‑se com um colega, providenciem papéis quadriculados e façam o que se pede.

a) Escolham oito números para x e assinalem em um plano cartesiano os pontos (x, y), em que y = 0,5x ‒ 1. Esses pontos pertencem à mesma reta?

b) Assinalem, em um plano cartesiano, os pontos M (‒2, ‒2) e N (2, 2). Tracem a reta que passa por esses pontos. Pelo traçado, é possível verificar outros pontos que pertencem à reta. Assinalem seis deles e escrevam suas coordenadas. Qual é a relação entre as coordenadas x e y dos pontos dessa reta? Os pontos M e N são simétricos em relação à origem?

c) Tracem a reta que passa pelos pontos a (‒4, 4) e B (4, ‒4). Assinalem outros seis pontos dessa reta e escrevam suas coordenadas. Qual é a relação entre as coordenadas x e y dos pontos da reta

\overset{\leftrightarrow}{A B}

? Os pontos a e B são simétricos em relação à origem?

Página 160

7 O plano cartesiano a seguir representa a tela de radar da tôrre de contrôle de um aeroporto. Os pontos representados correspondem às posições dos aviões.

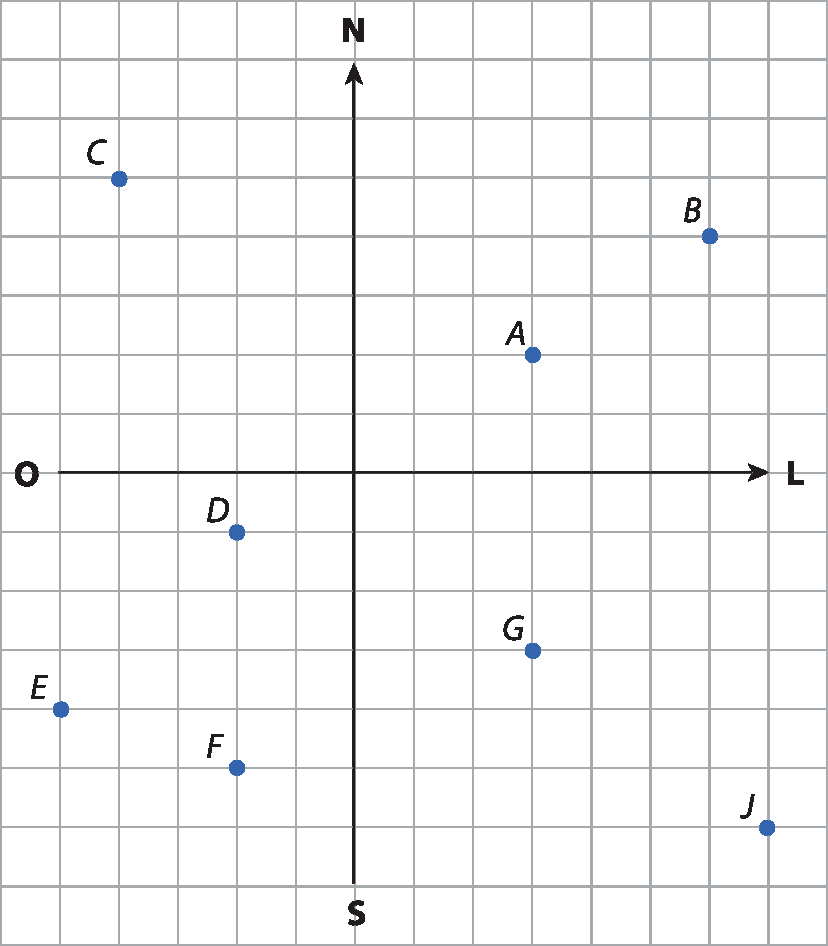
Ilustração. Malha quadriculada com gráfico. Eixo horizontal, extremidades O (oeste) e L (leste). Eixo vertical, extremidades N (norte) e S (sul). Pares ordenados: Acima de OL e À esquerda: C. À direita, A e B. Abaixo de OL à esquerda: D, E, F. À direita, G, J.

Suponha que a tôrre esteja situada na origem e que cada divisão dos eixos corresponda a 10 quilômetros. O norte está representado no sentido positivo do eixo dos y, e o leste, no sentido positivo do eixo dos xisponto

a) Quais são as coordenadas dos aviões B, C, E e G ?

b) Qual é a medida da distância entre os aviões a e G ? E entre os aviões F e D ?

c) O piloto do avião J se comunica com a tôrre, indicando sua posição, 70 quilômetros leste e 60 quilômetros sul, pedindo permissão para pousar no aeroporto. A informação do piloto está correta?

Fotografia. Vista parcial de um torre de controle aéreo. Algumas pessoas estão sentadas à frente de monitores com informações na tela. Ao fundo, pista de pouso e aviões.

2. Equações do 1º grau com duas incógnitas

Observe a seguinte manchete de jornal.

Fotografia. Manchete de jornal. Na última rodada do Campeonato Brasileiro de Futebol de 2021, o jogo entre Grêmio e Atlético Mineiro terminou com 7 gols marcados. Abaixo, jogador do Grêmio e do Atlético mineiro disputam a bola. Partida entre Grêmio e Atlético Mineiro na Arena do Grêmio em Porto Alegre (Rio Grande do Sul).

Página 161

Com a informação da manchete, não é possível saber quantos gols cada equipe marcou. Representando por xis a quantidade de gols marcados pelo Grêmio e por y a quantidade de gols marcados pelo Atlético Mineiro, podemos escrever a equação: xis + y = 7

Essa equação é uma equação do 1º grau com duas incógnitas.

Uma equação que pode ser escrita na fórma ax + by + c = 0, com a ≠ 0 e b ≠ 0, é chamada de equação do 1º grau com duas incógnitas.

Consideremos agora a equação 5x + 2y = 7, em que x e y são números racionais.

Essa é uma equação do 1º grau com duas incógnitas. Vamos ver um modo de obter uma das soluções dessa equação. Para isso, escolhemos um valor racional qualquer para x e, em seguida, substituímos esse valor na equação para determinar o valor de y. O par (x, y) será uma das soluções da equação.

Como exemplo, atribuiremos a x o valor ‒2 e o valor 1.

Ilustração. Resolução da equação 5x mais 2y igual a 7 na primeira linha. Na segunda linha, 5 vezes abre parênteses menos dois fecha parênteses mais 2y igual a 7. Terceira linha, menos 10 mais 2y igual a 7. Quarta linha, 2y igual a 7 mais 10. Quinta linha, 2y igual a 17. Sexta linha, 2y sobre dois igual 17 sobre dois. Sétima linha, y igual a 17 meios. No lado direito da resolução, uma menina de cabelo castanho e blusa verde fala: Atribuir a x o valor menos 2 quer dizer substituir x por menos 2.

Portanto, o par

(‒ 2, \frac{17}{2})

é uma solução da equação 5x + 2y = 7.

Ilustração. Resolução da equação 5x mais 2y igual a 7 na primeira linha. Na segunda linha, 5 vezes abre parênteses 1 fecha parênteses mais 2y igual a 7. Terceira linha, 5 mais 2y igual a 7. Quarta linha, 2y igual a 7 menos 5. Quinta linha, 2y igual a 2. Sexta linha, 2y sobre dois igual 2 sobre dois. Sétima linha, y igual a 1. No lado direito da resolução, uma menina de cabelo castanho e blusa verde diz: Aqui, substituímos x por 1.

Logo, o par (1, 1) é outra solução da equação 5x + 2y = 7.

Como podemos atribuir a x quaisquer números racionais, a equação 5x + 2y = 7 tem infinitas soluções.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

8 Entre os pares ordenados indicados a seguir, quais são soluções da equação 3x + 2y = 4?

a) (2, 1)

(\frac{1}{3}, \frac{3}{2})

c) (2, ‒1)

(‒ \frac{1}{3}, \frac{3}{4})

9 Considere a equação 4x ‒ 2y = 6 e responda:

a) Para que valor de x obtemos y = 7?

b) Para que valor de y obtemos x =

\frac{1}{2}

c) Se uma das soluções é o par (1,5; y), qual é o valor de y nesse caso?

d) Se uma das soluções é o par (x, ‒3), qual é o valor de x nesse caso?

10 Considerando a equação x + y = 4, calcule o valor de y quando se atribui a x o valor:

a) 9;

b) ‒3;

c) 2,5.

11 Considere novamente a equação x + y = 4. Multiplique cada membro dela por um mesmo número diferente de 0, à sua escolha. Se, na nova equação, você substituir x por 9, por ‒3, por 2,5, que valores de y espera obter? Seriam os mesmos valores de y obtidos no exercício anterior, ou seriam aqueles valores multiplicados pelo número que você escolheu?

Depois de responder no caderno, faça os cálculos e verifique a sua resposta.

Página 162

12 Expresse a situação representada na balança, com os pratos à mesma altura e em equilíbrio, por meio de uma equação do 1º grau com as incógnitas x e y, que representam as medidas das massas de cada cubo azul e de cada cubo verde, respectivamente.

Ilustração. Balança vermelha de dois pratos. no prato da esquerda, 3 cubos azuis de medida x cada e dois cubos verdes de medida y cada. No prato da direita, peso de 500 gramas. A balança em equilíbrio.

Agora, responda: qual é a medida da massa de cada cubo azul se a medida da massa de cada cubo verde for 70 gramas?

13 Joana brincava com dois dados de cores diferentes quando os deixou cair, simultaneamente, no chão. Observou o par de números obtidos e notou que a soma deles era 8. Indicando os números por x e y, descubra a equação correspondente a essa situação. Em seguida, determine todos os pares possíveis que podem ter saído nos dados.

Ilustração. Menina loira de camiseta azul. Ela está ajoelhada no chão e joga 2 dados um azul e um amarelo.

Hora de criar – Elabore um problema sobre equação do 1º grau com duas incógnitas que envolva as medidas das alturas de dois adolescentes. Troque com um colega e depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi‑los.

TRABALHANDO A INFORMAÇÃO

Possibilidades e probabilidades

Hugo está jogando trilha com sua irmã. Para andar o número de casas necessárias e vencer o jôgo na próxima rodada, ele precisa de uma soma de pelo menos 10 pontos ao lançar dois dados.

Ilustração. Menino de cabelo preto e camiseta listrada vermelha e branca está sentado no chão e segura dois dados cúbicos com a mão direita. Ao lado, menina de cabelo preto, camiseta vermelha e amarela listrada. Ela está deitada de bruços no chão. Entre eles, tapete com jogo de casas coloridas.

Qual é a probabilidade de Hugo vencer o jôgo na próxima rodada?

Para calcular essa probabilidade, devemos inicialmente descobrir todas as possibilidades de soma de números que ele pode tirar nos dados.

Ao lançar dois dados, Hugo pode tirar os seguintes pares de números:

Ilustração. Pares de números organizados em três linhas com doze pares em cada linha. Na primeira linha temos: par ordenado (1, 1), par ordenado (1, 4), par ordenado (2, 1), par ordenado (2, 4), par ordenado (3, 1), par ordenado (3, 4), par ordenado (4, 1), par ordenado (4, 4), par ordenado (5, 1), par ordenado (5, 4), par ordenado (6, 1), par ordenado (6, 4) com o par ordenado (6, 4) circulado. Na segunda linha temos: (1, 2), par ordenado (1, 5), par ordenado (2, 2), par ordenado (2, 5), par ordenado (3, 2), par ordenado (3, 5), par ordenado (4, 2), par ordenado (4, 5), par ordenado (5, 2), par ordenado (5, 5), par ordenado (6, 2), par ordenado (6, 5) com os pares ordenados (5, 5) e (6, 5) circulados. Na terceira linha temos: (1, 3), par ordenado (1, 6), par ordenado (2, 3), par ordenado (2, 6), par ordenado (3, 3), par ordenado (3, 6), par ordenado (4, 3), par ordenado (4, 6), par ordenado (5, 3), par ordenado (5, 6), par ordenado (6, 3), par ordenado (6, 6) com os pares ordenados (4, 6), (5, 6) e (6, 6) circulados.

Observe que há 36 pares diferentes de números, mas nem todos têm soma igual a 10 ou maior. Por isso, circulamos os pares de números que satisfazem essa condição. Então, entre as 36 possibilidades, há somente 6 pares cuja soma de números é igual a 10 ou maior.

Como há 6 possibilidades em 36 de Hugo obter uma soma igual a 10 ou maior, dizemos que a probabilidade de Hugo vencer o jôgo na próxima rodada é:

\frac{6}{36} = \frac{1}{6}

Página 163

Agora quem trabalha é você!

FAÇA A ATIVIDADE NO CADERNO

Considere o problema de Hugo e responda às questões a seguir.

a) Supondo que Hugo precise obter nos dados uma soma igual a 8 ou maior, a probabilidade de ele ganhar o jôgo aumenta? Justifique sua resposta.

b) Se a probabilidade de Hugo vencer o jôgo na próxima rodada fosse de 100%, quantas casas ele precisaria andar?

3. Sistemas de equações do 1º grau com duas incógnitas

Observe novamente a manchete apresentada no item anterior e uma segunda manchete, de outro jornal, sobre a mesma notícia.

Imagem. Manchete de jornal. Na última rodada do Campeonato Brasileiro de Futebol de 2021, o jogo entre Grêmio e Atlético Mineiro terminou com 7 gols marcados. Abaixo, fotografia do jogador do Grêmio e do Atlético mineiro disputam a bola com a legenda Partida entre Grêmio e Atlético Mineiro na Arena do Grêmio em Porto Alegre (Rio Grande do Sul).

Fotografia. Manchete de jornal. Campeonato Brasileiro de Futebol de 2021: Grêmio vence o Atlético Mineiro por 1 gol de diferença na Arena do Grêmio, em Porto Alegre (RS). À esquerda, brasão do Grêmio, composto por globo azul com preto e com três estrelas acima. No interior: 1903. GRÊMIO FBPA. Ao lado, brasão do Atlético mineiro de cor preta escrito CAM. Acima uma estrela.

Já vimos que somente com a informação da primeira manchete não é possível determinar a quantidade de gols marcados pelas equipes. O mesmo acontece se considerarmos apenas a informação da segunda manchete. Mas, se unirmos as informações apresentadas nas duas manchetes, poderemos resolver esse problema.

Para isso, vamos considerar x a quantidade de gols marcados pelo Grêmio e y a quantidade de gols marcados pelo Atlético Mineiro.

Já vimos que é possível associar à primeira manchete a seguinte equação:

x + y = 7, em que x e y são números naturais

Os pares ordenados (7, 0); (6, 1); (5, 2); (4, 3); (3, 4); (2, 5); (1, 6) e (0, 7) são soluções dessa equação.

Página 164

À segunda manchete, podemos associar a equação:

x = y + 1, em que x e y são números naturais

Observe, no quadro a seguir, alguns dos possíveis resultados desse jôgo, de acôrdo com a segunda manchete:

Gols marcados pelo Grêmio	1	2	3	4	5	6	7
Gols marcados pelo Atlético Mineiro	0	1	2	3	4	5	6
Pares ordenados	(1, 0)	(2, 1)	(3, 2)	(4, 3)	(5, 4)	(6, 5)	(7, 6)

Os pares ordenados (1, 0); (2, 1); (3, 2); (4, 3); (5, 4); (6, 5) e (7, 6) são, portanto, algumas das soluções da equação x = y + 1.

Note que o único par ordenado comum às duas situações é o par (4, 3), pois é o único em que a soma dos gols é igual a 7 e que representa a vitória do Grêmio por 1 gol de diferença. Logo, de acôrdo com essas informações, podemos afirmar que o Grêmio venceu o jôgo por 4 a 3.

As equações x + y = 7 e x = y + 1 também podem ser indicadas por:

\{\begin{cases} x + y = 7 \\ x = y + 1 \end{cases}

Elas constituem um exemplo de sistema de equações do 1º grau com duas incógnitas.

O par ordenado (4, 3), que verifica as duas equações, é a solução do sistema.

Note, na figura, o que acontece quando representamos, em um mesmo sistema de coordenadas, os pares ordenados que destacamos como soluções das duas equações.

Ilustração. Malha quadriculada com gráfico. Eixo x, pontos de menos 3 a 8 e eixo y, pontos de menos 3 a 8. Pares ordenados. Bolinhas roxas: 1 vírgula 0. 2 vírgula 1. 3 vírgula 2. 4 vírgula 3. 5 vírgula 2. 6 vírgula 1. 7 vírgula 0. Bolinhas azuis: 1 vírgula 6. 2 vírgula 5. 3 vírgula 4. 4 vírgula 3. 5 vírgula 2. 6 vírgula 1. 7 vírgula 6. Encontro das bolinhas: 4 vírgula 3. Segurando a malha, menino branco de cabelo preto e curto. Ele veste uma camiseta de manga comprida listrada de verde claro e verde escuro e uma calça azul.

Observe que, se traçássemos um segmento unindo os pontos que representam as soluções de uma mesma equação, obteríamos dois segmentos que se cruzariam no ponto de coordenadas (4, 3), que é a solução do sistema.

Resolução de sistemas

Existem vários métodos para resolver um sistema de equações do 1º grau com duas incógnitas. Aqui, estudaremos o método da substituição, que é um processo algébrico de resolução.

O método da substituição consiste em isolar uma das incógnitas em uma das equações e substituir na outra equação a expressão obtida.

Acompanhe as situações apresentadas na página seguinte.

Página 165

Situação 1

Em uma competição de esportes aquáticos, nas modalidades de natação e de saltos ornamentais, participaram trínta e duas equipes e 344 atletas. Cada equipe de natação inscreveu 12 atletas, e cada equipe de saltos ornamentais, 10 atletas. Quantas equipes de natação participaram da competição?

Ilustração. À esquerda, menino de sunga. À direita, dois meninos de sunga e uma menina de maiô. Todos estão em pé na frente de uma piscina com raias. Dentro da piscina, pessoas nadando. Ao fundo, mais pessoas em pé e outra piscina com um trampolim.

Indicando por x a quantidade de equipes de natação e por y a quantidade de equipes de saltos ornamentais, podemos montar o seguinte sistema de equações do 1º grau com duas incógnitas:

\{\begin{cases} x + y = 32 \\ 12 x + 10 y = 344 \end{cases}

Para resolver esse sistema pelo método da substituição, podemos escolher, por exemplo, a equação xis + y = 32 e isolar a incógnita x. Assim, obtemos:

Equação: x mais y é igual a 32. Abaixo outra equação: x mais y menos y é igual a 32 menos y
Abaixo a equação: x é igual a 32 menos y. Ao lado desta equação, cota: equação com duas incógnitas.

Agora, substituindo x por (32 ‒ y) na equação 12x + 10y = 344, obtemos:

Esquema. Expressão 12 x mais 10 y é igual a 344. Uma seta aponta para outra expressão, em que o termo x é substituído por 32 menos y. A expressão é: 12 vezes, abre parêntese, 32 menos y, fecha parêntese, mais 10 y é igual a 344. Uma seta à direita dessa expressão indica que ela corresponde a uma equação com uma incógnita.

Ao resolver essa equação, encontramos o valor de y:

384 ‒ 12y + 10y = 344

‒2y = ‒40

y = 20

Substituindo y por 20 na equação x + y = 32, encontramos o valor de x:

x + y = 32

x + 20 = 32

x = 12

Logo, a solução do sistema é o par ordenado (12, 20).

Portanto, 12 equipes de natação participaram da competição.

Página 166

Situação 2

Pavões e chinchilas são criados em um sítio. Ao todo são dezesseis cabeças e cinquenta e seis patas. Quantos pavões e quantas chinchilas há nesse sítio?

Indicando a quantidade de pavões por p e a de chinchilas por c, podemos reescrever as informações dadas por meio de equações do 1º grau com duas incógnitas.

Ao todo são dezesseis cabeças: p + c = 16.

Ao todo são cinquenta e seis patas: 2p + 4c = 56 (o pavão tem duas patas e a chinchila, 4 patas).

Assim, formamos o sistema de duas equações do 1º grau com duas incógnitas:

\{\begin{cases} p + c = 16 \\ 2 p + 4 c = 56 \end{cases}

Isolando a incógnita p na equação p + c = 16, obtemos:

p = 16 ‒ c (equação com duas incógnitas)

Substituindo p por (16 ‒ c) na equação 2p + 4c = 56, encontramos o valor de c:

Equação: 2p mais 4c é igual a 56. Abaixo a equação: 2 vezes, abre parêntese 16 menos c, fecha parêntese, mais 4c é igual a 56. Seta saindo de 2p da primeira equação e apontando para 16 menos c.
Ao lado desta equação, cota: equação com uma incógnita

32 ‒ 2c + 4c = 56

‒2c + 4c = 56 ‒ 32

2c = 24

\frac{2 c}{2} = \frac{24}{2}

c = 12

Substituindo c por 12 em p = 16 ‒ c, encontramos o valor de p:

p = 16 ‒ 12

p = 4

O par (4, 12) é a solução do sistema.

Portanto, nesse sítio há 4 pavões e 12 chinchilas.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

15 Verifique se o par ordenado (5, ‒3) é solução do sistema:

\{\begin{cases} x + y = 2 \\ 3 x + 2 y = 9 \end{cases}

16 A mesma balança manteve‑se nivelada em dois momentos:

Ilustração. Balança vermelha de dois pratos. No prato da esquerda, um mamão. No prato da direita, uma maçã e um peso de 100 gramas. A balança está em equilíbrio. Ilustração. Balança de dois pratos. No prato da esquerda, um mamão e uma maçã. No prato da direita, dois pesos de 200 gramas cada e dois pesos de 20 gramas cada. A balança está em equilíbrio.

a) Chame de xis a medida da massa do mamão e de y a medida da massa da maçã. Determine o sistema de equações correspondente a essa situação.

b) Resolva o sistema.

c) Quantos gramas tem o mamão?

17 Meu avô e meu pai foram pescar. Eles trouxeram 25 peixes de diversas espécies. Meu avô disse que pescou o quádruplo do número de peixes que meu pai. Quantos peixes cada um pescou?

Página 167

18 Para fazer duas alianças, foram usados 13 gramas de ouro. Uma das alianças tem 3 gramas a mais que a outra.

a) Escreva, no caderno, o sistema correspondente a essa situação.

Resolva mentalmente o sistema e diga quantos gramas tem a aliança maior.

19 Resolva os sistemas.

\{\begin{cases} x = 5 y \\ x + y = 12 \end{cases}

\{\begin{cases} x ‒ y = 10 \\ 2 x + 3 y = 10 \end{cases}

\{\begin{cases} x + y = 3 \\ 12 x ‒ 9 y = ‒ 20 \end{cases}

\{\begin{cases} 2 x + y = 7 \\ 5 x ‒ 2 y = ‒ 5 \end{cases}

20 Faça o que se pede em cada caso.

a) Encontre os valores de a, b e c, de maneira que os pares ordenados (1, a), (3, b) e (5, c)sejam soluções da equação x + y = 6.

b) Encontre os valores de éle, m e n, de modo que os pares ordenados (1, l ), (3, m) e (5, n) sejam soluções da equação x ‒ y = 2.

c) Construa um sistema de coordenadas em uma folha de papel quadriculado e represente os pares ordenados dos itens a e b.

d) Com base na representação do item c, estime o par ordenado que é solução do sistema de equações

\{\begin{cases} x + y = 6 \\ x ‒ y = 2 \end{cases}

e) Resolva esse sistema no caderno e verifique se sua estimativa estava correta.

21 O perímetro de um terreno retangular mede 84 métros. A medida do comprimento tem 18 métros a mais que a da largura. Quanto mede a área desse terreno?

22 Considere o sistema de equações:

\{\begin{cases} 2 x ‒ 2 y = 2 \\ x ‒ y = 23 \end{cases}

Agora faça o que se pede.

a) Encontre três pares ordenados que sejam soluções da 1ª equação.

b) Encontre três pares ordenados que sejam soluções da 2ª equação.

Procure, mentalmente, um par ordenado que seja solução das duas equações. O que você encontrou? Registre no caderno suas conclusões.

d) Resolva o sistema e confronte com suas conclusões. O que você observou?

23 Mauro e Laura colecionam figurinhas. Leia o diálogo entre eles.

Ilustração. Duas crianças com figurinhas sentadas uma de frente para a outra. À esquerda, menino branco de boné vermelho, camiseta branca e calça azul fala: Se você me der 3 figurinhas, ficaremos com quantidades iguais. À direita, menina negra de cabelo castanho, óculos, camiseta branca e calça azul fala: Se você me der 5 figurinhas, ficarei com o dobro das suas.

Quantas figurinhas cada um tem?

Hora de criar – Em duplas, cada integrante vai elaborar um problema sobre sistema de equações do 1º grau com duas incógnitas. Troquem de caderno para um resolver o problema do outro. Depois, destroquem para corrigi-los.

Pense mais um poucoreticências

FAÇA AS ATIVIDADES NO CADERNO

1 Vamos agora retomar a pergunta da abertura deste capítulo: “Em um sítio, há 20 coelhos. A diferença entre o dôbro do número de machos e o número de fêmeas é igual a 7.”

a) Quantos coelhos machos há nesse sítio?

b) Selecionando ao acaso um desses coelhos, qual é a probabilidade de selecionar uma fêmea?

2 Um rapaz está embalando algumas taças e observa que:

• após colocar 7 taças em cada caixa, restam 19 taças fóra das caixas;

• tentando colocar 10 taças em cada caixa, uma delas fica com 5 taças a menos do que as outras.

a) Quantas caixas esse rapaz está usando?

b) Quantas taças estão sendo embaladas?

Página 168

TRABALHANDO A INFORMAÇÃO

Interpretando um gráfico de linha

O desemprêgo é medido sistematicamente pelo Instituto de Pesquisa Econômica Aplicada (ipéa) em seis regiões metropolitanas do país: Recife, Salvador, Belo Horizonte, Rio de Janeiro, São Paulo e Porto Alegre. Ele é representado por um índice que mede a taxa de desocupação (ou desemprêgo aberto), isto é, considera apenas quem procurou emprêgo nos 30 dias anteriores à pesquisa e não exerceu nenhum tipo de trabalho – remunerado ou não – nos últimos sete dias.

Acompanhe na tabela a seguir os índices de novembro de 2020 a novembro de 2021.

Taxa de desocupação (em %)
Mês/ano	nov./20	dez.	jan./21	fev.	mar.	abr.	maio	jun.	jul.	ago.	set.	out.	nov.
Índice	14,4	14,2	14,5	14,6	14,9	14,8	14,7	14,2	13,7	13,1	12,6	12,1	11,6

Dados obtidos em: ipéa Data. Disponível em: https://oeds.link/f0zWJx. Acesso em: 15 fevereiro 2022.

Podemos representar os dados da tabela por um gráfico de colunas.

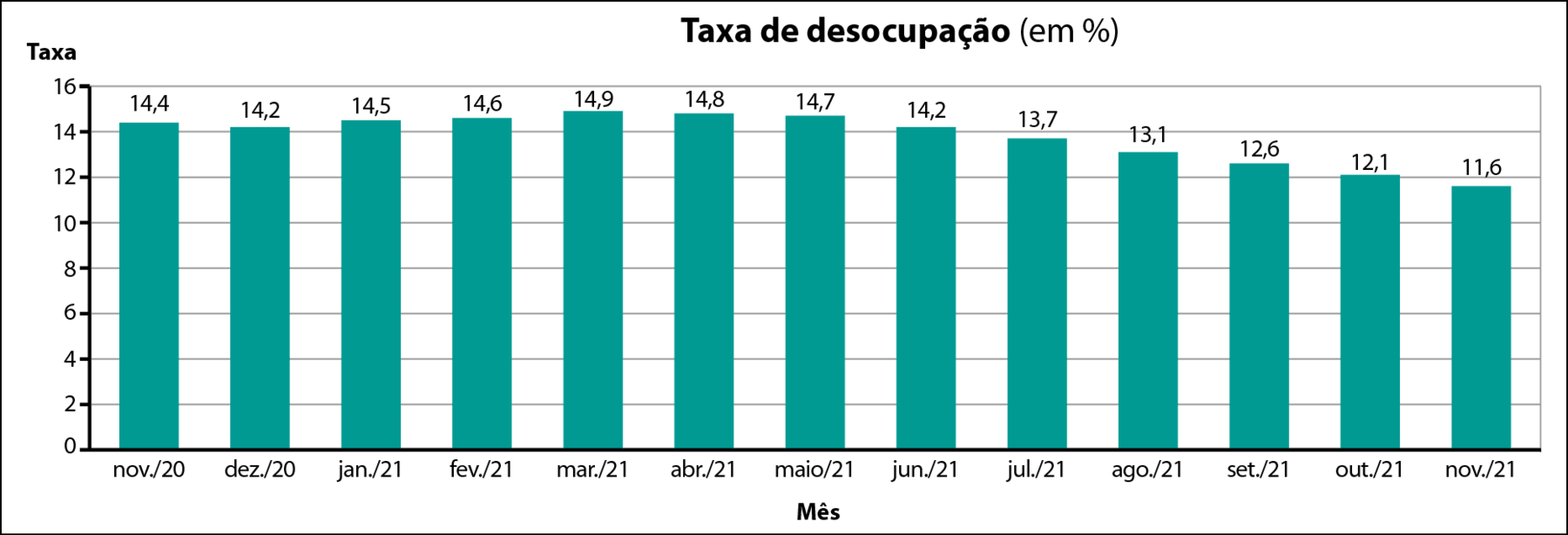
Gráfico em barras verticais. Taxa de desocupação (em %). No eixo x, mês. No eixo y, taxa. Os dados são: Mês: novembro de 2020. Taxa: 14,4. Mês: dezembro de 2020. Taxa: 14,2. Mês: janeiro de 2021. Taxa: 14,5. Mês: fevereiro de 2021. Taxa: 14,6. Mês: março de 2021. Taxa: 14,9. Mês: abril de 2021. Taxa: 14,8. Mês: maio de 2021. Taxa: 14,7. Mês: junho de 2021. Taxa: 14,2. Mês: julho de 2021. Taxa: 13,7. Mês: agosto de 2021. Taxa: 13,1. Mês: setembro de 2021. Taxa: 12,6. Mês: outubro de 2021. Taxa: 12,1. Mês: novembro de 2021. Taxa: 11,6. — Dados obtidos em: Instituto de Pesquisa Econômica Aplicada Data. Disponível em: https://oeds.link/f0zWJx. Acesso em: 15 fevereiro 2022.

Para perceber melhor a variação da taxa ao longo do tempo, usamos um gráfico de linha. Podemos construí‑lo, com base no gráfico anterior, marcando o ponto médio da parte superior de cada coluna. A seguir, apagamos as colunas e ligamos os pontos por segmentos de reta consecutivos.

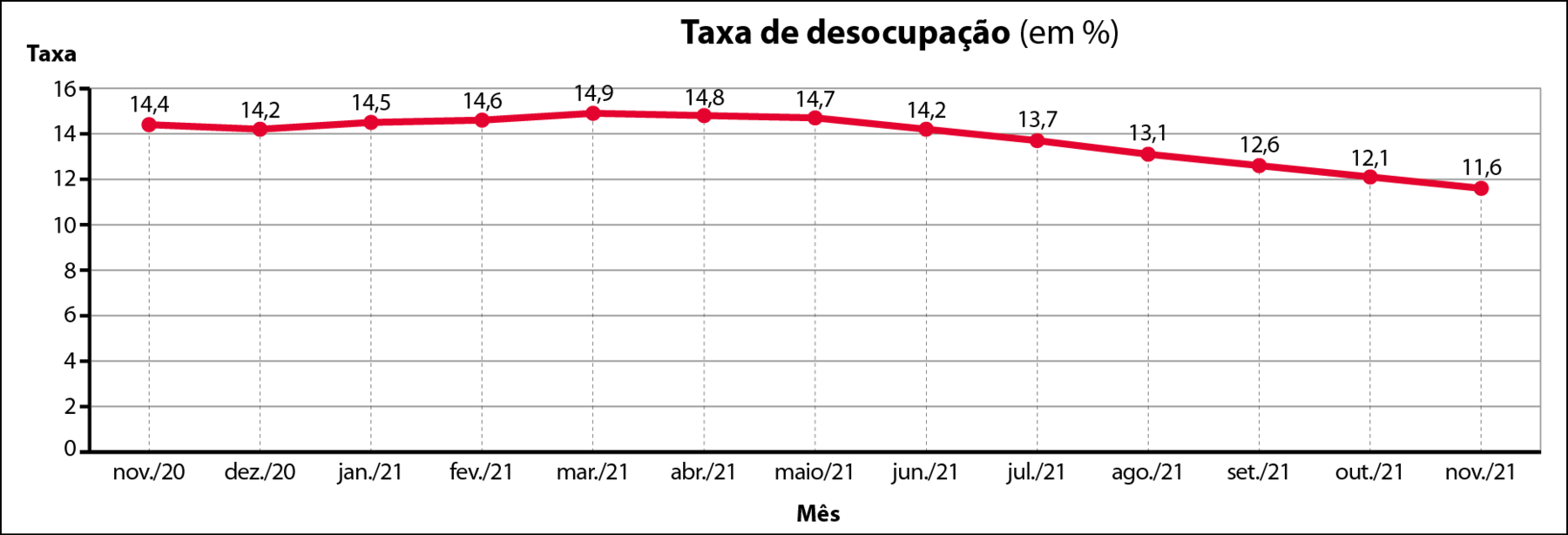
Gráfico em linha. Taxa de desocupação (em %). No eixo x, mês. No eixo y, taxa. Os dados são: Mês: novembro de 2020. Taxa: 14,4. Mês: dezembro de 2020. Taxa: 14,2. Mês: janeiro de 2021. Taxa: 14,5. Mês: fevereiro de 2021. Taxa: 14,6. Mês: março de 2021. Taxa: 14,9. Mês: abril de 2021. Taxa: 14,8. Mês: maio de 2021. Taxa: 14,7. Mês: junho de 2021. Taxa: 14,2. Mês: julho de 2021. Taxa: 13,7. Mês: agosto de 2021. Taxa: 13,1. Mês: setembro de 2021. Taxa: 12,6. Mês: outubro de 2021. Taxa: 12,1. Mês: novembro de 2021. Taxa: 11,6. — Dados obtidos em: Instituto de Pesquisa Econômica Aplicada Data. Disponível em: https://oeds.link/f0zWJx. Acesso em: 15 fevereiro 2022.

Página 169

Observe no gráfico que, nesse período, a taxa de desocupação subiu em 3 meses e caiu em 9 meses.

Note também que a variação da taxa pode ser maior em valor absoluto (segmento mais próximo da vertical, mais “em pé”) ou menor (segmento mais “deitado”), positiva (da esquerda para a direita, sobe) ou negativa (da esquerda para a direita, desce). Por exemplo, no período observado, no mês de agosto de 2021, cuja diminuição foi 0,6% (13,7% ‒ 13,1%), o segmento está mais “em pé” do que o do mês de abril, cuja queda foi de 0,1% (14,9% ‒ 14,8%), que está mais “deitado”. Ou seja, variação menor implica inclinação menor do segmento no gráfico.

Fotografia. Vista do alto de diversas pessoas aglomeradas ao lado de uma construção. — Pessoas aguardam em fila de emprêgo sob forte sol no Vale do Anhangabaú, região central de São Paulo (São Paulo). (Fotografia de 2019.)

Agora quem trabalha é você!

FAÇA A ATIVIDADE NO CADERNO

Observando o gráfico de linha da página anterior, responda às questões no caderno.

a) Dê dois períodos em que as inclinações de aumento são iguais. Neles, ocorreram aumentos iguais?

b) Dê um mês em que ocorreu menor aumento e um em que ocorreu maior queda, em relação ao mês anterior.

c) Tradicionalmente, em dezembro o desemprêgo diminui. A que você atribui isso?

Junte‑se a um colega e comentem a seguinte afirmação:

Se substituíssemos a linha poligonal do gráfico por um único segmento com extremidades no primeiro e no último ponto dessa linha, teríamos a variação total do período novembro de 2020 a novembro de 2021; porém não saberíamos que variações teriam ocorrido nos meses desse período.

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Verifique quais dos pares ordenados a seguir são soluções da equação 6x + 3y = 33.

a) (‒2, 7)

b) (7, ‒2)

c) (2, 7)

d) (5, 1)

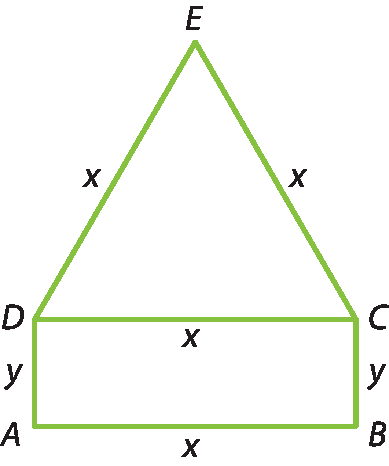
2 Com base na figura, enuncie um problema que possa ser solucionado por meio de um sistema de duas equações do 1º grau com duas incógnitas.

Resolva o problema que você elaborou.

Ilustração. Figura composta por um retângulo ABCD e por um triângulo CDE. AD e BC medem y, AB, CD, DE e CE medem x.

3 Carla gosta de natação e judô. Em uma academia, a natação exige um gasto médio, entre a mensalidade e a condução, de R$ 20,00vinte reais por aula, e o judô, de R$ 15,00quinze reais por aula. Carla pretende pagar R$ 200,00duzentos reais por mês e tem tempo disponível para praticar 12 aulas por mês entre os dois esportes. Quantas aulas Carla poderá fazer de cada um desses esportes?

Ilustração. Menina de touca, óculos e maiô nadando embaixo da água. Ilustração. Duas meninas de quimono praticando judô.

Página 170

4 (ú éfe ême gê) Uma prova de múltipla escolha com 60 questões foi corrigida assim: o estudante ganhava 5 pontos por questão que acertava e perdia 1 ponto por questão que errava ou deixava em branco. Se um estudante totalizou 210 pontos, o número de questões que ele acertou é:

a) 25.

b) 30.

c) 35.

d) 40.

e) 45.

5 Um clube ofereceu um baile a seus associados. Cada sócio titular pagou R$ 20,00vinte reais, e seus dependentes pagaram apenas metade. Com os .1200 participantes, o clube arrecadou R$ 18.000,00dezoito mil reais. Qual foi o número de dependentes presentes nesse baile?

6 Considere o cartaz que estava afixado em um teatro.

Ilustração. Cartaz em marrom. TEATRO. ADULTO: R$ 20,00. CRIANÇA (ATÉ 12 ANOS): R$ 12,00. Abaixo do texto, quatro máscaras.

Se, em uma apresentação teatral, foram vendidos 125 ingressos e arrecadados R$ 2.140,00dois mil cento e quarenta reais, quantas crianças assistiram a essa apresentação?

7 (Unifor‑Ceará) Um pacote tem 48 balas: algumas de hortelã e as demais de laranja. Se a terça parte do dôbro do número de balas de hortelã excede a metade do de laranjas em 4 unidades, então nesse pacote há:

a) 20 balas de hortelã.

b) 26 balas de laranja.

c) duas balas de laranja a mais que de hortelã.

d) igual número de balas dos dois tipos.

e) duas balas de hortelã a mais que de laranja.

8 Retome a resolução do sistema da Situação 2 da página 166, agora, isolando a incógnita c na equação p + c = 16. A solução do sistema é a mesma?

9 Resolva os sistemas:

\{\begin{cases} 2 x + y = 5 \\ 3 x ‒ y = 5 \end{cases}

\{\begin{cases} ‒ 2 x + 3 y = 1 \\ 4 x ‒ 5 y = 0 \end{cases}

\{\begin{cases} x = ‒ 2 y \\ x ‒ 3 y = 17, 5 \end{cases}

\{\begin{cases} 2 x + 5 y = 14 \\ x = y \end{cases}

\{\begin{cases} 2 x = 3 y \\ y = 2 x + 4 \end{cases}

\{\begin{cases} x + 2 y = 5 \\ 2 x + 3 y = 7 \end{cases}

10 Em uma sorveteria, os sorvetes são servidos em taças de 150 mililitros e de 200 mililitros. Em um dia, foram servidas setenta e duas taças e 12,8 litros de sorvete. Quantas taças de 200 mililitros foram servidas?

11 Uma pessoa fez uma compra de R$ 370,00trezentos e setenta reais e pagou com 11 cédulas: algumas de R$ 50,00cinquenta reais e outras de R$ 20,00vinte reais. Quantas cédulas de cada valor foram utilizadas para pagar essa compra?

12 Em um restaurante existem 60 mesas. Todas elas estão ocupadas, algumas por 4 pessoas e outras por 3 pessoas. No total são 195 pessoas. Quantas são as mesas ocupadas por 4 pessoas?

Ilustração. À esquerda, mesa com quatro pessoas sentadas. À direita, mesa com três pessoas sentadas. Ao fundo, mesas com pessoas sentadas.

13 Uma doceria vende em média .2000 doces por dia, entre brigadeiros de colhér e cocadas, obtendo com essa venda R$ 1.700,00mil setecentos reais. Sabendo que eles custam, respectivamente, R$ 0,80zero reais e oitenta centavos e R$ 1,00um reais, quantos doces de cada tipo são vendidos diariamente?

14 Um fazendeiro cria porcos e galinhas.

Quando um amigo lhe perguntou a quantidade desses animais, ele respondeu que havia contado 84 cabeças e 208 pés. Qual é a quantidade de porcos?

15 Eu tenho 25 cubos, uns com aresta medindo 5 centímetros e outros com aresta medindo 8 centímetros. Colocando uns sobre os outros, formo uma pilha com altura medindo 1,70 métro.

a) Quantos cubos de cada tamanho eu tenho?

b) Ao sortear, ao acaso, um desses cubos, qual é a probabilidade de sortear um cubo de aresta medindo 8 centímetros?

Página 171

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Se cada divisão dos eixos corresponde a 10 unidades, qual é o ponto que tem coordenadas (‒30, 10)?

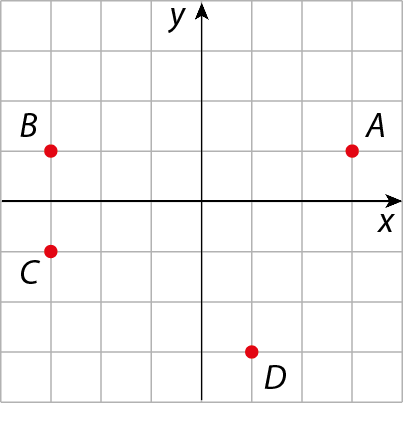
Ilustração. Malha quadriculada com gráfico. Eixo x e eixo y. À esquerda do eixo y e acima do eixo x, ponto B. À direita do eixo y e acimado eixo x, ponto A. Abaixo do eixo x e à esquerda do eixo y, ponto C e à direita do eixo y e abaixo do eixo x, ponto D.

a) A

b) B

c) C

d) D

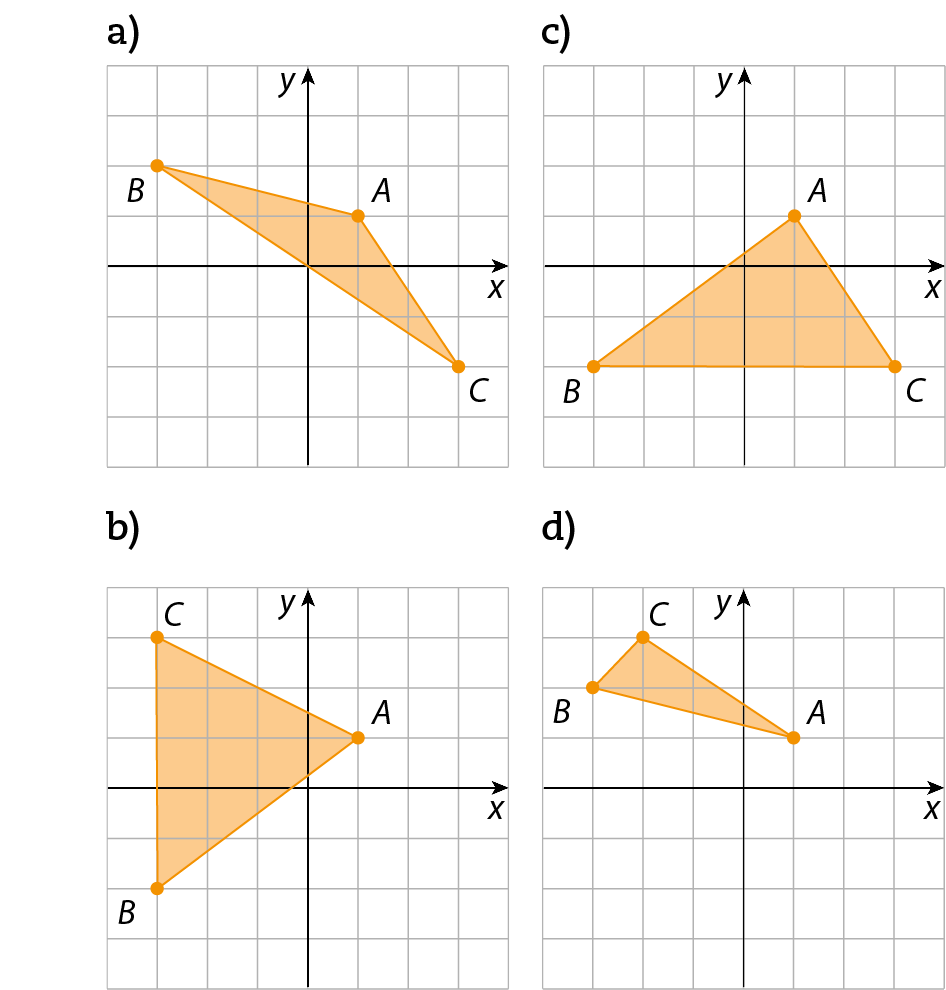
2 Qual dos triângulos a seguir tem vértices nos pontos a(1, 1), B(‒3, 2) e C(3, ‒2)?

Ilustração A. Malha quadriculada com gráfico. Eixo x e eixo y. Sobre o gráfico, triângulo ABC com a maior parte acima do eixo x. Ilustração B. Malha quadriculada com gráfico. Eixo x e eixo y. Sobre o gráfico, triângulo ABC com a maior parte à esquerda do eixo x. Ilustração C. Malha quadriculada com gráfico. Eixo x e eixo y. Sobre o gráfico, triângulo ABC com a maior parte abaixo do eixo x. Ilustração D. Malha quadriculada com gráfico. Eixo x e eixo y. Sobre o gráfico, triângulo ABC acima do eixo x.

3 Qual dos pares ordenados a seguir satisfaz a equação 3x + 5y = 18?

a) (0, 6)

b) (3, 1)

c) (‒11, 3)

d) (‒4, 6)

4 Em jogos de basquete, um time pode fazer x cestas, cada uma valendo 3 pontos, por um jogador atrás da linha de 3 pontos; e y cestas de 2 pontos por um jogador dentro dessa linha. Em um jôgo, um time fez um total de 113 pontos. Qual equação expressa essa situação? Se y = 34, qual é o valor de x?

a) 2x + 3y = 113 e x = 6

b) 2x + 3y = 113 e x = 5

c) 3x + 2y = 113 e x = 15

d) 3x + 2y = 113 e x = 16

5 Um padeiro faz uma quantidade ih de pão integral e uma quantidade s de pão sem glúten. O pão integral é vendido a R$ 15,00quinze reais, e o pão sem glúten, a R$ 22,00vinte e dois reais. Certo dia, ele vendeu R$ 696,00seiscentos e noventa e seis reais em pães e um total de 33 pães. Qual sistema de equações expressa essa situação?

\{\begin{cases} 22 i + 15 s = 33 \\ i + s = 696 \end{cases}

\{\begin{cases} 15 i + 22 s = 696 \\ i + s = 33 \end{cases}

\{\begin{cases} 22 i + 15 s = 696 \\ i + s = 33 \end{cases}

\{\begin{cases} 15 i + 22 s = 33 \\ i + s = 696 \end{cases}

6 Carlos foi à feira e comprou ême maçãs, que custavam R$ 1,00um reais a unidade, e c caixas de morangos, que custavam R$ 5,00cinco reais a caixa. Ele gastou R$ 29,00vinte e nove reais e voltou com 9 itens. Qual é o sistema de equações que modela essa situação?

\{\begin{cases} 5 m + 5 c = 29 \\ m + c = 9 \end{cases}

\{\begin{cases} 5 m + c = 29 \\ m + c = 9 \end{cases}

\{\begin{cases} 5 m + c = 9 \\ m + c = 29 \end{cases}

\{\begin{cases} m + 5 c = 29 \\ m + c = 9 \end{cases}

7 Maria tem R$ 25,00vinte e cinco reais em moedas de R$ 0,25zero reais e vinte e cinco centavos e R$ 0,10zero reais e dez centavos. Se ela tem 190 moedas no total, quantas são de 25 centavos e quantas são de 10 centavos, respectivamente?

a) 10 e 180

b) 50 e 140

c) 40 e 150

d) 90 e 100

8 Qual é a solução do sistema

\{\begin{cases} 3 x ‒ 2 y = 6 \\ x + y = 2 \end{cases}

a) x = 2 e y = 0

b) x = 0 e y = ‒3

c) x = 4 e y = ‒2

d) x = 0 e y = 2

9 Um terreno retangular tem lados de medidas x métros e y métros. Sabe‑se que x é o dôbro de y e que a medida do perímetro do terreno é 54 métros. Quais são os valores de x e de y?

a) 27 e 9

b) 27 e 13,5

c) 18 e 9

d) 28 e 14

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir:

a) Como você explicaria o plano cartesiano a um colega?

b) O que representa cada coordenada de um par ordenado associado a um ponto do plano cartesiano?

c) Quantos pares ordenados de números racionais uma equação do 1º grau com duas incógnitas pode ter como solução?

d) Como você explicaria a um colega a resolução de um sistema de equações do 1º grau com duas incógnitas?