Página 220

Parte 1

CAPÍTULO 10 Estudo dos polígonos

Fotografia. Recorte da representação gráfica da fachada de um museu em formato de triângulos grandes amarelos com outros menores dentro. — Representação gráfica de detalhe da fachada do museu.

Fotografia. Representação gráfica da fachada de um museu em formato de triângulos grandes amarelos com outros menores dentro. — Representação gráfica da fachada do Grande Museu Egípcio, no Cairo (Egito).

Observe, leia e responda no caderno.

a) A imagem retrata a aplicação da Matemática na Arquitetura. Qual figura geométrica você identifica na fachada do Grande Museu Egípcio?

b) Esse museu fica perto das Pirâmides de gizé. Pesquise e responda: quais são os nomes das três pirâmides mais famosas do Egito?

c) A figura dessa fachada é resultado de modificações repetidas em um triângulo inicial.

Ilustração. Sequência de 4 triângulos de mesmo tamanho. Triângulo 1: inteiro azul. Triângulo 2: dividido em 4 triângulos menores de mesmo tamanho, sendo 3 azuis e 1 branco. Triângulo 3: cada triângulo azul do triângulo 2 é dividido em 4 triângulos de mesmo tamanho, sendo 3 azuis e 1 branco. Triângulo 4: cada triângulo azul do triângulo 3 é dividido em 4 triângulos de mesmo tamanho, sendo 3 azuis e 1 branco.

Quantos triângulos escuros você vê na 1ª figura à esquerda? E na 2ª figura? E na 3ª figura? E na 4ª figura?

Titulo do carrossel

Gire o seu dispositivo para a posição vertical

A apenas 2 quilômetros de distância das pirâmides de gizé e considerado o maior museu do mundo dedicado a uma única civilização, o complexo cultural do Grande Museu Egípcio foi construído para abrigar uma coleção de aproximadamente .100000 artefatos antigos, cobrindo uma área total de .24000 métros quadrados.

Página 221

1. Polígonos

Já aprendemos que uma linha poligonal fechada simples é chamada de polígono.

Ilustração. Triângulos vermelhos e roxos intercalados. Na junção dos triângulos, um hexágono pequeno. Ao lado, homem de cabelo curto, camisa laranja e calça verde olha a imagem em um caleidoscópio, objeto que lembra uma luneta. — A imagem formada em um caleidoscópio reproduz e multiplica superfícies poligonais.

Agora, vamos recordar o que já sabemos sobre polígonos.

• Os polígonos dividem o plano em duas regiões sem pontos comuns: a interior e a exterior.

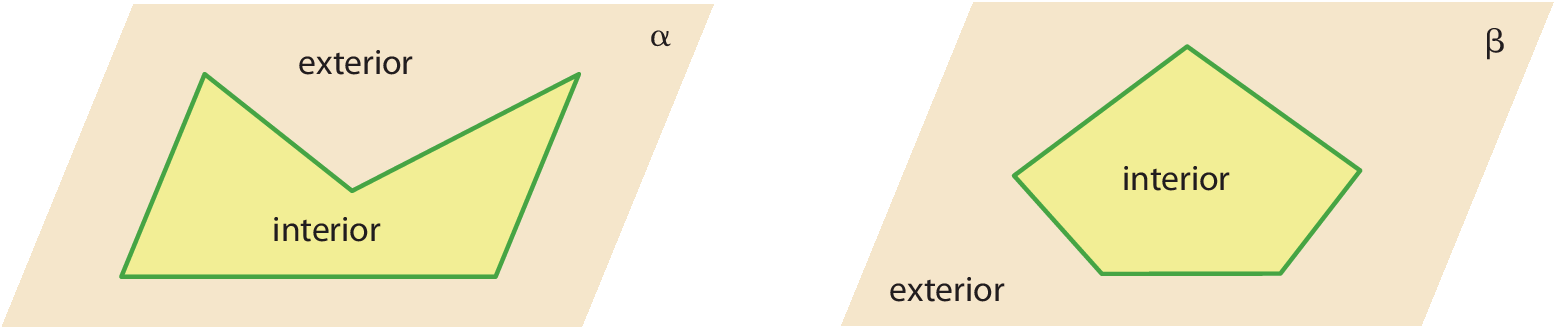
Ilustração. Plano alfa com polígono de 5 lados. Dentro do polígono escrito: interior. Fora do polígono, escrito: exterior. Ilustração. Plano beta com polígono de 5 lados. Dentro do polígono escrito: interior. Fora do polígono, escrito: exterior.

• Polígonos são denominados convéquiços quando o segmento que une quaisquer dois pontos de seu interior estiver contido nele. Caso contrário, são chamados de polígonos não convéquiços.

Ilustração. Polígono de 5 lados. Dentro, dois segmentos de reta. Ilustração. Estrela de quatro pontas. Segmento de reta passa parte dentro e parte fora da figura.

Neste e nos próximos capítulos, vamos trabalhar apenas com polígonos convéquiços, que chamaremos simplesmente de polígonos.

Página 222

Elementos de um polígono

Considere os elementos de um polígono. Alguns deles você já conhece.

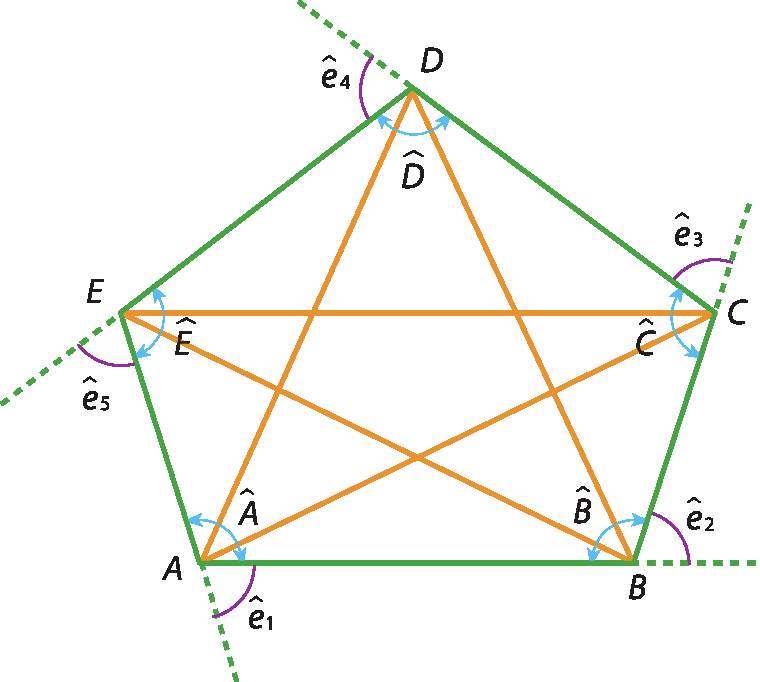
Ilustração. Pentágono A B C D E. Ângulos internos: A, B, C, D e E. Ângulos externos: e 1, e 2, e 3, e 4, e, e 5. As diagonais estão representadas.

• Lados: são os segmentos que formam o polígono. No polígono á bê cê dê é, os lados são

\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E} e \overline{E A} .

• Vértices: são os pontos de encontro de dois lados consecutivos de um polígono. No polígono á bê cê dê é, os vértices são os pontos a, B, C, D e ê.

• Ângulos internos: são os ângulos formados por duas semirretas com origem em um mesmo vértice. Cada uma contém um lado do polígono. No polígono á bê cê dê é, os ângulos internos são

\hat{A}, \hat{B}, \hat{C}, \hat{D} e \hat{E} .

• Ângulos externos: são os ângulos formados por duas semirretas com origem em um mesmo vértice. Uma contém um lado do polígono e a outra, o prolongamento do lado consecutivo a ele. No polígono á bê cê dê é, são ângulos externos:

{\hat{e}}_{1}, {\hat{e}}_{2}, {\hat{e}}_{3}, {\hat{e}}_{4}, e {\hat{e}}_{5}

• Diagonais: são os segmentos com extremidades em dois vértices não consecutivos do polígono. As diagonais do polígono á bê cê dê é são os segmentos

\overline{A C}, \overline{A D}, \overline{B D}, \overline{B E} e \overline{C E} .

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

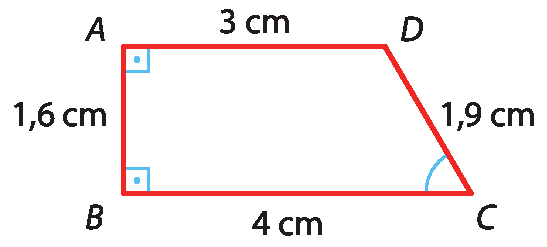
1 Calcule a medida do perímetro do trapézio a bê cê dê.

Ilustração. Trapézio ABCD com ângulo reto em A e B. ângulo agudo em C. A medida A B é 1,6 centímetro. C D é 1,9 centímetro, A D: 3 centímetros e B C: 4 centímetros.

2 Se os ângulos de um pentágono forem congruentes, e a soma das medidas deles for 540graus, quanto medirá cada um desses ângulos?

3 Desenhe um heptágono convexo e trace todas as diagonais. Essas diagonais determinam vários polígonos. Pinte a região interior de um desses polígonos que tenha:

a) 3 lados;

b) 4 lados;

c) 5 lados;

d) 6 lados;

e) 7 lados.

Considere três polígonos: um heptágono de lados medindo 2,5 centímetros, um octógono de lados medindo 2 centímetros e um eneágono de lados medindo 1,8 centímetro. Descubra, mentalmente, qual deles tem a maior medida de perímetro.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e resolvam este desafio. Copiem em uma folha de papel sulfite as figuras, nas quantidades indicadas, e recortem-nas.

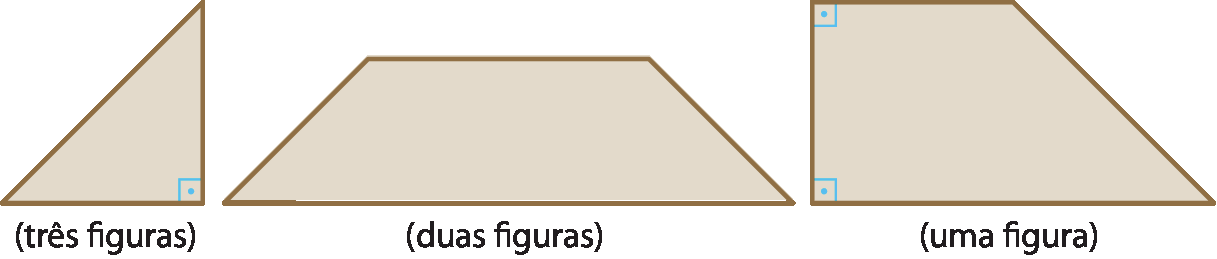
Ilustração. Triângulo retângulo: (três figuras). Trapézio: (duas figuras). Trapézio com dois ângulos retos: (uma figura).

(Use tesoura com ponta arredondada e a manuseie com cuidado!)

Depois, com as seis peças, construam uma cruz neste formato:

Página 223

2. Número de diagonais de um polígono

Considere o número de lados dos polígonos e o de diagonais traçadas por um de seus vértices.

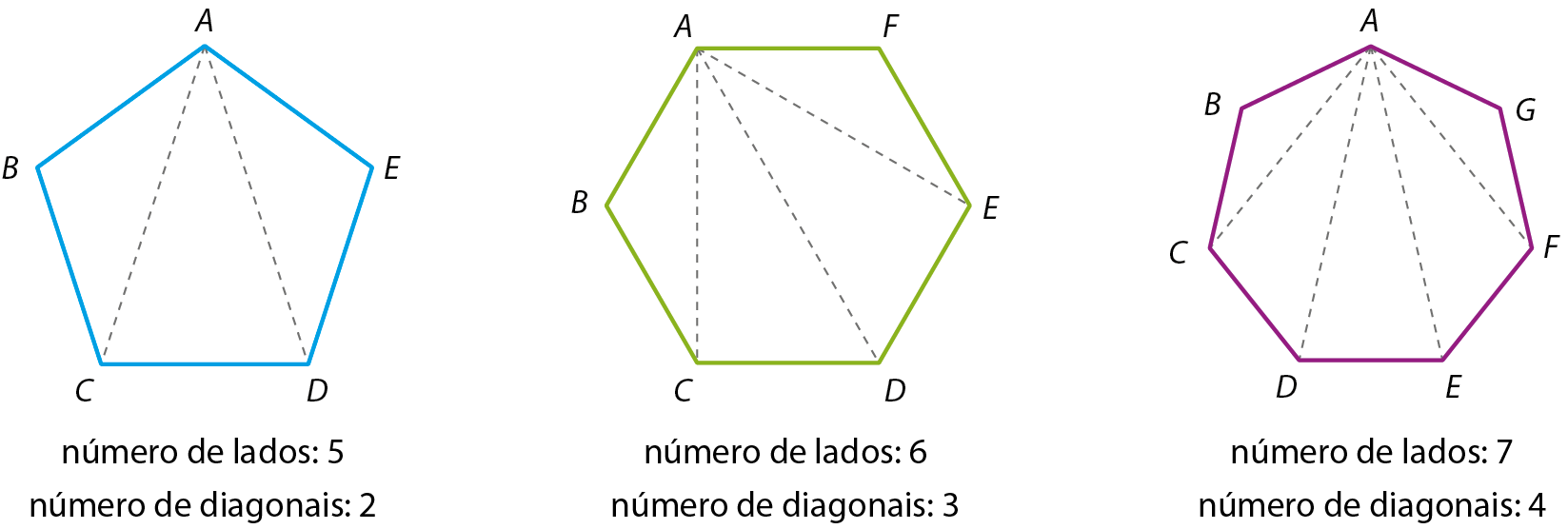
Ilustração. Pentágono A B C D E com duas diagonais traçadas partindo de A. Ilustração. Pentágono A B C D E com três diagonais traças partindo de A. Ilustração. Pentágono ABCDE com quatro diagonais traçadas partindo de A.

Note que o número de diagonais traçadas por um de seus vértices (o vértice a) é igual ao número de lados menos 3.

Em um polígono de n lados, podemos traçar, por um dos vértices, (n ‒ 3) diagonais.

Como o polígono tem n vértices, podemos traçar n ⋅ (n ‒ 3) diagonais.

Esse produto, porém, representa o dôbro do número de diagonais, pois cada diagonal foi contada duas vezes (por exemplo, a diagonal

\overline{A C}

e a diagonal

\overline{C A}

Então, para calcular o número total de diagonais d de um polígono de n lados, podemos empregar a fórmula:

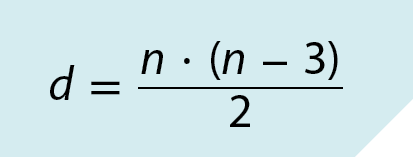
Sentença matemática. d igual a, fração, numerador n vezes, abre parênteses, n menos 3, fecha parênteses, denominador 2.

Acompanhe alguns exemplos.

a) Vamos calcular o número de diagonais de um octógono.

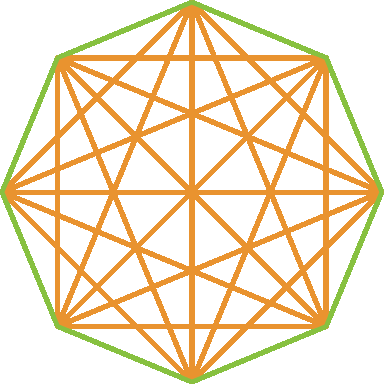
Ilustração.
Octógono com 5 diagonais partindo de cada vértice.

n = 8

d =

\frac{n \cdot (n ‒ 3)}{2}

\frac{8 \cdot (8 ‒ 3)}{2}

\frac{8 \cdot 5}{2}

\frac{40}{2}

= 20

Portanto, o octógono tem 20 diagonais.

b) Qual é o polígono cujo número de diagonais é igual ao número de lados?

Podemos escrever o sistema de equações:

\{\begin{cases} d = n \\ d = \frac{n \cdot (n ‒ 3)}{2} \end{cases}

Substituindo d por n, na segunda equação, obtemos:

n = \frac{n^{2} ‒ 3 n}{2}

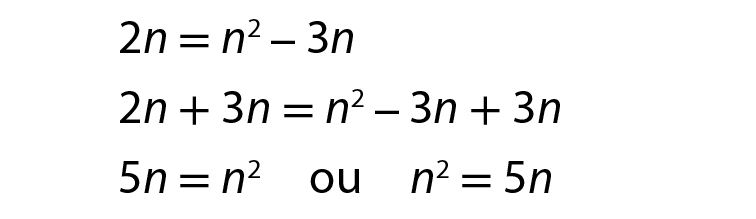
2n, igual a, n elevado ao quadrado, fim da potência, menos 3n.
2n mais 3n, igual a, n elevado ao quadrado, fim da potência, menos 3n mais 3n.
5n, igual a, n elevado ao quadrado ou n elevado ao quadrado, igual a, 5n.

Fração, numerador n elevado ao quadrado, denominador n, igual a, fração numerador 5n, denominador n. Ou seja, n igual a 5.

Logo, o polígono é o pentágono.

Ilustração. Menina de cabelo castanho, óculos, camiseta branca e calça. Ela está sentada no chão, escreve em um caderno e fala: Como n representa o número de lados de um polígono, com n diferente de 0, podemos dividir os dois membros por n.

Página 224

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

Calcule mentalmente:

a) Quantas diagonais podemos traçar a partir de um dos vértices de um hexágono?

b) Quantas diagonais tem um triângulo?

6 Desenhe um quadrado e trace suas diagonais.

a) Quantas diagonais ele tem?

b) Com uma régua, compare a medida das diagonais. O que é possível perceber?

7 Por um dos vértices de um polígono foi possível traçar até 4 diagonais. Que nome recebe esse polígono?

8 Quantas diagonais tem um polígono com:

a) 20 lados?

b) 16 lados?

c) 24 lados?

9 Quantos lados tem o polígono cujo número de diagonais é:

a) seis vezes o número de lados?

b) o quádruplo do número de lados?

10 Traçando todas as diagonais a partir de um vértice, quantos triângulos são formados em um:

a) quadrilátero?

b) pentágono?

c) hexágono?

d) heptágono?

e) decágono?

f) polígono de n lados?

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e façam o que se pede.

Cada um dos cinco cartões tem um número em uma face e uma figura na outra.

Ilustração. Cinco cartões contendo número ou figura. Primeiro cartão: 1 Segundo cartão: triângulo laranja Terceiro cartão: 2 Quarto cartão: losango verde, Quinto cartão: hexágono roxo.

Alguém afirmou: “Atrás de um número par há sempre um triângulo”.

Que procedimento devemos adotar para verificar se a afirmação é verdadeira, virando o menor número de cartões?

Conversem com outra dupla e comparem as respostas obtidas.

Elaborem outras afirmações sobre esses cartões para outra dupla fazer a verificação.

3. Estudando triângulos

Você já aprendeu que os triângulos são polígonos de três lados. Vamos relembrar quais são seus principais elementos.

Indicamos um triângulo á bê cê, como o da figura a seguir, por △ á bê cê.

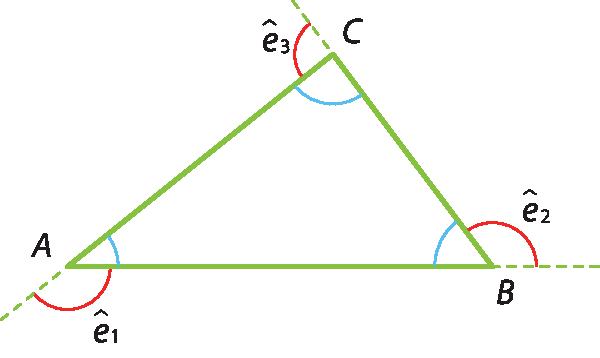
Ilustração.
Triângulo ABC.
Ângulos externos: e1, e2, e3.

Nesse triângulo, destacamos seus principais elementos:

• os vértices a, B e C;

• os lados

\overline{A B}, \overline{A C} e \overline{B C};

• os ângulos internos

B \hat{A} C o u \hat{A}, A \hat{B} C o u \hat{B}, e A \hat{C} B o u \hat{C}

• os ângulos externos

\hat{e}

₁,

\hat{e}

₂ e

\hat{e}

₃.

Página 225

Observe que cada lado é oposto ao ângulo interno determinado pelos outros dois lados:

•

\overline{B C}

é oposto ao ângulo

\hat{A}

;

•

\overline{A C}

é oposto ao ângulo

\hat{B}

;

•

\overline{A B}

é oposto ao ângulo

\hat{C}

Note, também, que cada ângulo externo é suplementar do ângulo interno adjacente:

• medida do(

\hat{A}

) + medida do(

\hat{e}

₁) = 180graus

• medida do(

\hat{B}

) + medida do(

\hat{e}

₂) = 180graus

• medida do(

\hat{C}

) + medida do(

\hat{e}

₃) = 180graus

Classificação de triângulos

Podemos classificar um triângulo de duas maneiras: pelas medidas dos lados ou pelas medidas dos ângulos internos.

Observação

▶ Indicamos os lados correspondentes em polígonos congruentes cortando esses lados com um mesmo número de tracinhos. Para indicar ângulos correspondentes, usamos um pequeno arco cortado por um mesmo número de tracinhos.

Classificação quanto às medidas dos lados

Quanto às medidas dos lados, os triângulos se classificam em isósceles, equilátero ou escaleno.

a) Triângulos isósceles são triângulos que têm dois lados congruentes. Em um triângulo isósceles:

• o ângulo formado pelos lados congruentes é chamado de ângulo do vértice;

• o lado oposto a esse ângulo é chamado de base;

• os ângulos adjacentes à base são chamados de ângulos da base.

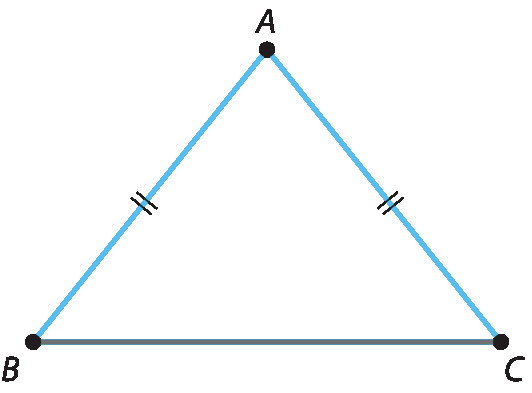
O △ á bê cê é isósceles, pois

\overline{A B} ≅ \overline{A C}

. Nesse triângulo, o ângulo do vértice é

\hat{A}

, a base é o lado

\overline{B C}

e os ângulos da base são

\hat{B} e \hat{C}

Ilustração.
Triângulo A B C com dois lados de mesma medida indicados.

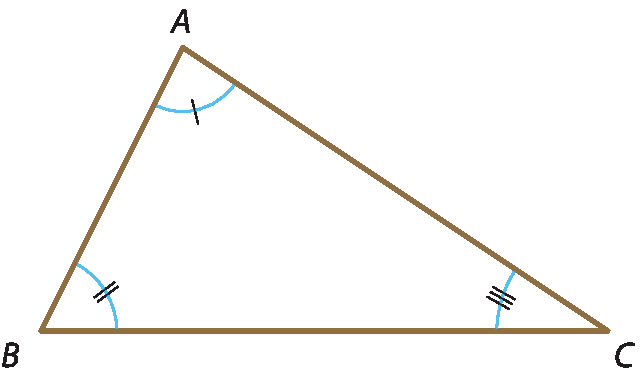
b) Triângulos equiláteros são triângulos que têm os três lados congruentes. Todo triângulo equilátero também é um triângulo isósceles. O △dê ê éfe é equilátero, pois

\overline{D E} ≅ \overline{D F} ≅ \overline{E F} .

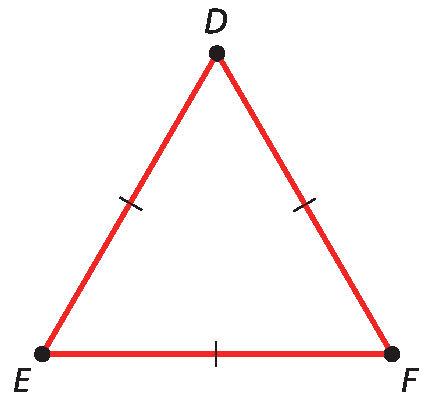
Ilustração.
Triângulo D E F com três lados de mesma medida.

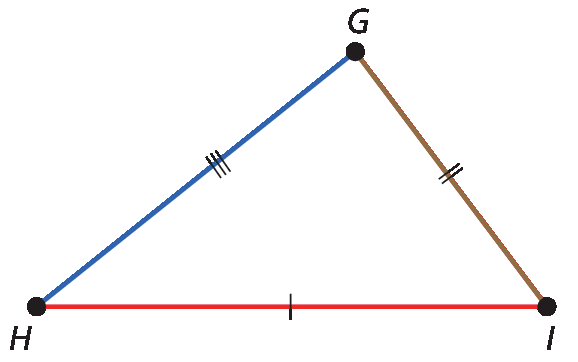
c) Triângulos escalenos são triângulos que não têm lados congruentes. O △ gê agá í é escaleno, pois não tem lados congruentes.

Ilustração.
Triângulo G H I com três lados com medidas diferentes.

Página 226

Classificação quanto às medidas dos ângulos

Quanto às medidas dos ângulos, os triângulos se classificam em acutângulo, obtusângulo ou retângulo.

a) Triângulos acutângulos são triângulos que têm os três ângulos internos agudos. O △ ABC é acutângulo, pois medida do(

\hat{A}

) < 90graus, medida do(

\hat{B}

) < 90graus e medida do(

\hat{C}

) < 90graus.

Ilustração.
Triângulo A B C com três ângulos internos de medidas diferentes.

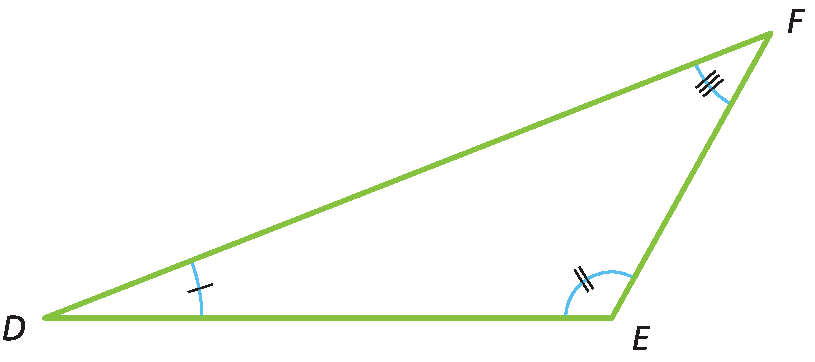
b) Triângulos obtusângulos são triângulos que têm um ângulo interno obtuso. O △ dê ê éfe é obtusângulo, pois medida do(

\hat{E}

) > 90graus.

Ilustração. Triângulo D E F com três ângulos internos com medidas diferentes.

c) Triângulos retângulos são triângulos que têm um ângulo interno reto. Em um triângulo retângulo, o lado oposto ao ângulo reto é chamado de hipotenusa, e os outros lados são chamados de catetos.

O triângulo á bê cê é retângulo, pois medida do(

\hat{B}

) = 90graus. Nesse triângulo, os catetos são

\overline{A B} e \overline{B C}

, e a hipotenusa é

\overline{A C} .

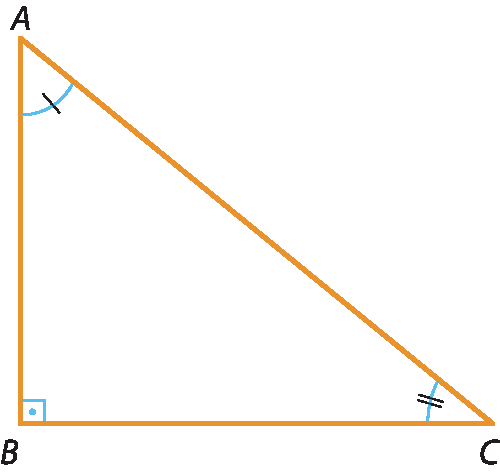
Ilustração.
Triângulo A B C com três ângulos internos diferentes, sendo um ângulo reto.

Ilustração. Menina de cabelo castanho e blusa azul pensa: Será que um triângulo pode ter dois ângulos internos obtusos? Ou dois ângulos internos retos?

Construção de triângulos

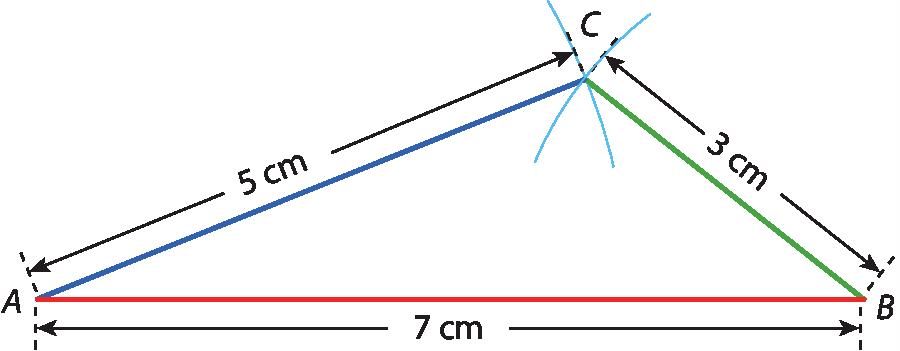
Vamos recordar a construção de um triângulo, com régua e compasso, quando são conhecidas as medidas de seus lados, por exemplo, 3 centímetros, 5 centímetros e 7 centímetros.

Ilustração. Segmento B C de 3 centímetros. Ilustração. Segmento A C de 5 centímetros. Ilustração. Segmento A B de 7 centímetros.

Acompanhe:

• Com o auxílio da régua, traçamos o segmento

\overline{A B}

de medida 7 centímetros.

• Com a ponta-sêca em A e abertura igual a á cê (5 centímetros), depois com a ponta-sêca em bê e abertura igual a bê cê (3 centímetros), traçamos arcos que se cruzam em cê.

• Com o auxílio da régua, traçamos os lados

\overline{A C} e \overline{B C}

Ilustração. Triângulo A B C. A medida A B é 7 centímetros. A medida B C é 3 centímetros. A medida A C é 5 centímetros. Intersecção de dois arcos no ponto C.

Fotografia. Destaque para a mãos de uma pessoa traçando três segmentos com uma régua. À esquerda, compasso e três segmentos de tamanhos diferentes. — Construção de um triângulo.

Página 227

Condição de existência de um triângulo

Nem sempre é possível construir um triângulo, mesmo sendo conhecidas as três medidas dos lados. Considere as situações a seguir.

Situação 1

Vamos tentar construir um triângulo de lados medindo 6 centímetros, 3 centímetros e 2 centímetros.

Ilustração. Três segmentos de tamanhos diferentes: 2 centímetros, 3 centímetros e 6 centímetros. Ao lado, figura aberta composta de 3 segmentos, sendo: À esquerda, 3 centímetros. Abaixo, 6 centímetros e à direita, 2 centímetros.

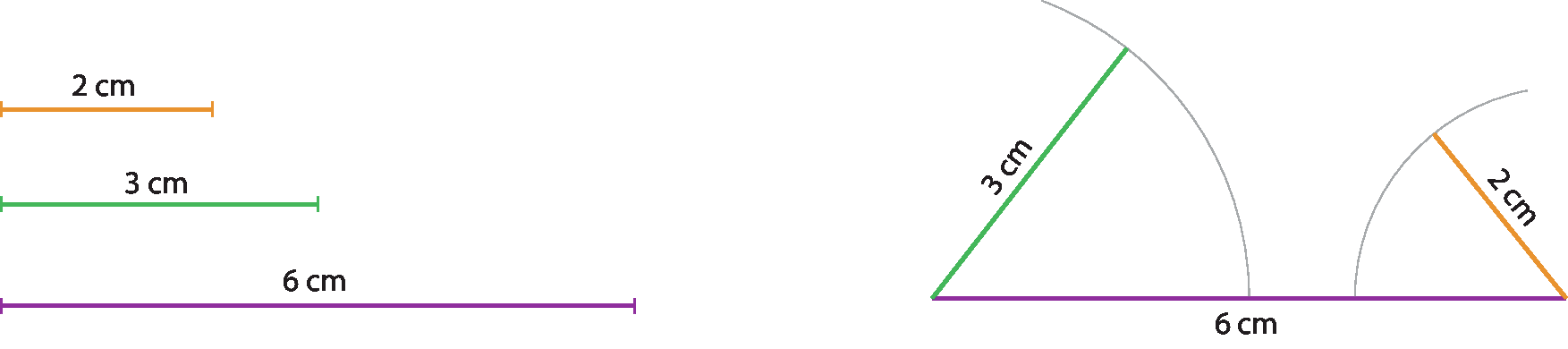
Perceba que não foi possível construir o triângulo com lados medindo 6 centímetros, 3 centímetros e 2 centímetros, pois os arcos traçados não se cruzam. Repare também que o maior segmento (de 6 centímetros) tem medida maior que a soma das medidas dos outros dois segmentos (3 centímetros + 2 centímetros = 5 centímetros). Isso significa que não existe um triângulo cujos lados medem 6 centímetros, 3 centímetros e 2 centímetros.

Situação 2

Vamos tentar construir um triângulo de lados medindo 7 centímetros, 4 centímetros e 3 centímetros.

Ilustração. Três segmentos de tamanhos diferentes: 3 centímetros, 4 centímetros e 7 centímetros. Ao lado, segmento de 4 centímetros e 3 centímetros sobrepostos ao segmento de 7 centímetros.

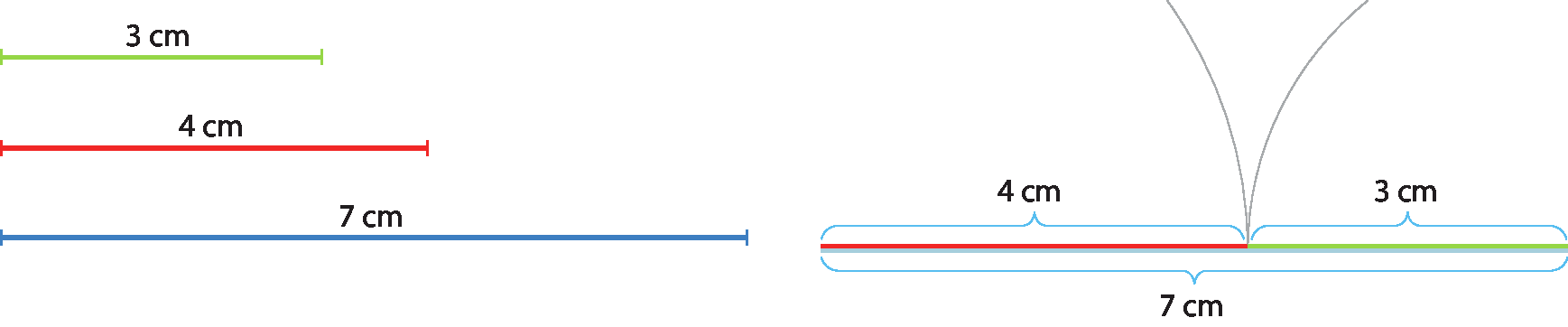
Perceba que também não foi possível construir o triângulo com lados medindo 7 centímetros, 4 centímetros e 3 centímetros. Repare que o maior segmento (de 7 centímetros) tem medida igual à soma das medidas dos outros dois segmentos (3 centímetros + 4 centímetros = 7 centímetros). Isso significa que não existe um triângulo cujos lados medem 7 centímetros, 4 centímetros e 3 centímetros.

Vimos que não foi possível construir o triângulo de medidas 6 centímetros, 3 centímetros e 2 centímetros, pois 6 > 2 + 3.

Também não foi possível construir o triângulo de medidas 7 centímetros, 4 centímetros e 3 centímetros, pois 7 = 4 + 3.

No entanto, é possível construir um triângulo de lados medindo 7 centímetros, 5 centímetros e 3 centímetros. Repare que o maior lado desse triângulo (7 centímetros) tem medida menor que a soma das medidas dos outros dois lados (5 centímetros + 3 centímetros = 8 centímetros). Isso também ocorre com os outros dois lados desse triângulo: a medida de cada um deles é menor que a soma das medidas dos outros dois:

• 5 centímetros < 3 centímetros + 7 centímetros

• 3 centímetros < 5 centímetros + 7 centímetros

Essa é a condição de existência de qualquer triângulo.

Em todo triângulo, a medida de qualquer lado é menor que a soma das medidas dos outros dois lados.

Página 228

Veja outros exemplos e o fluxograma da construção.

a) Vamos verificar se existe o triângulo cujos lados medem 12 centímetros, 9 centímetros e 8 centímetros. Basta verificar se a medida do lado maior é menor que a soma das medidas dos outros dois lados: 12 centímetros < 9 centímetros + 8 centímetros Logo, o triângulo existe.

b) Vamos verificar se existe o triângulo cujos lados medem 15 centímetros, 10 centímetros e 4 centímetros: 15 centímetros > 10 centímetros + 4 centímetros Logo, o triângulo não existe.

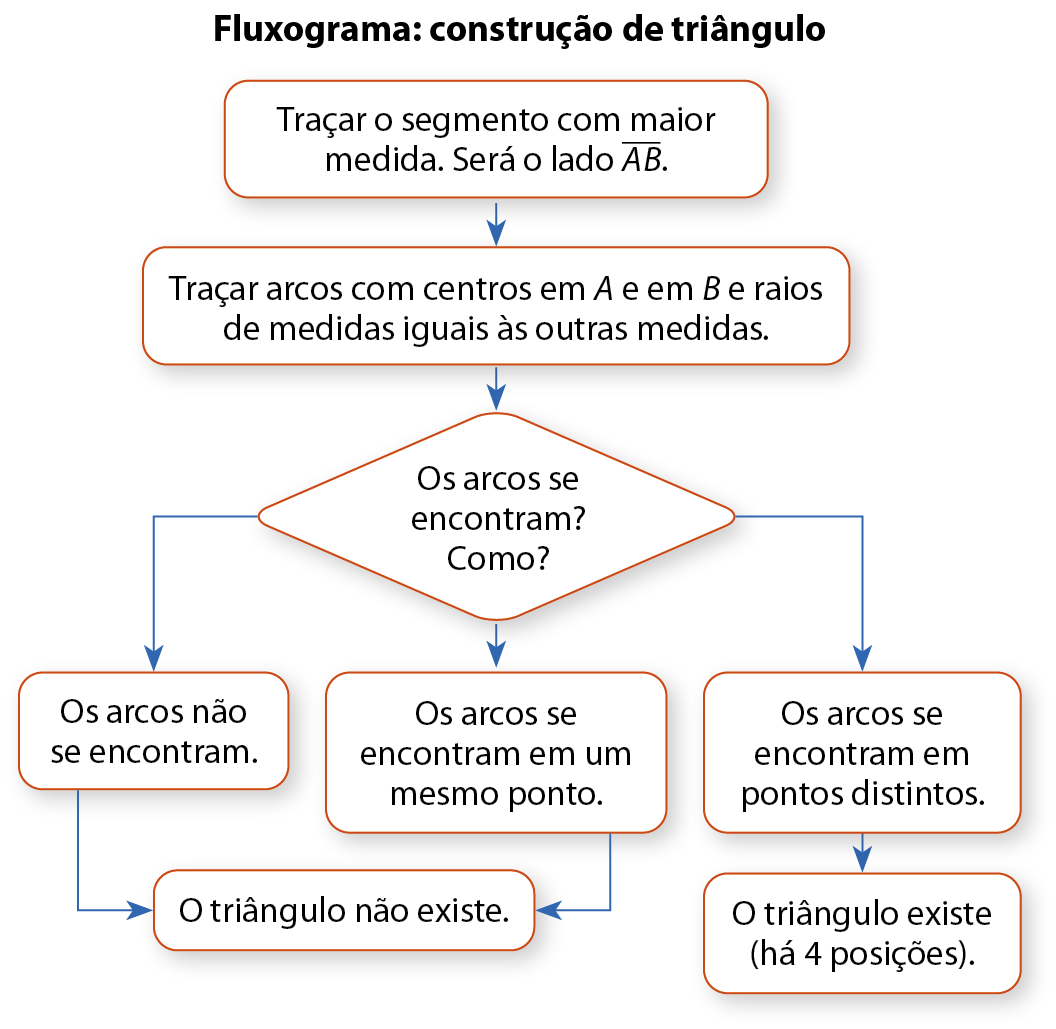
Fluxograma. A figura é um fluxograma com 8 caixas legendadas ligadas por setas. Em cada etapa, as setas apontam para a frente para uma caixa. Aqui, o fluxograma é descrito como listas nas quais os próximos passos possíveis são listados abaixo de cada legenda da caixa. 1. Traçar segmento com maior medida. Será o lado A B. a. Avança para Traçar os arcos com centros em A e em B e ralos de medida iguais às outras medidas. 2. Traçar os arcos com centros em A e em B e ralos de medida iguais às outras medidas. a. Avança para Os arcos se encontram? Como? 3. Os arcos se encontram? Como? a. Se não, avança para Os arcos não se encontram e avança para O triângulo não existe. b. Se sim em mesmo ponto, avança para Os arcos se encontram em um mesmo ponto, e avança para O triângulo não existe. c. Se sim em pontos distintos, avança para Os arcos se encontram em pontos distintos. 4. Os arcos se encontram em pontos distintos. a. Avança para O triângulo existe (há 4 posições).

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

11 Com régua e compasso, construa os triângulos:

a) isósceles; medida da base: 5 centímetros; lados congruentes: 4 centímetros;

b) equilátero; medida dos lados: 3 centímetros;

c) escaleno; medida dos lados: 6 centímetros, 4 centímetros e 3,5 centímetros.

(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)

12 Considere a figura a seguir.

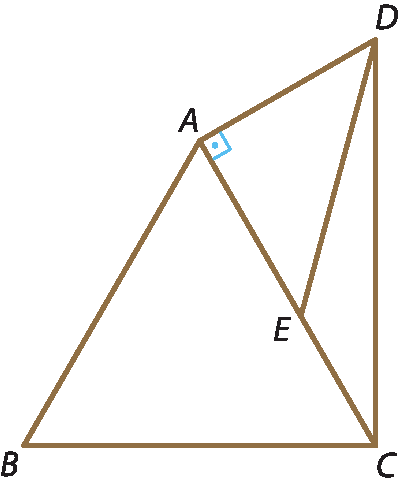
Ilustração. Quadriláterp composto de 3 triângulos. Triângulo A B C. Triângulo A D E Triângulo C D E. Ponto E está no segmento A C.

a) Quantos triângulos existem na figura?

b) Nomeie cada um deles.

c) Utilizando uma régua e um transferidor, classifique os triângulos á bê cê, á dê é e cê dê é quanto às medidas dos lados e quanto às medidas dos ângulos.

13 Desenhe um triângulo á bê cê, em que A bê = 5 centímetros, á cê = 3 centímetros e BC = 4 centímetros. Com um transferidor, meça o ângulo

A \hat{C} B

. Classifique esse triângulo quanto às medidas dos lados e dos ângulos.

14 Construa um triângulo retângulo e isósceles. Quanto medem seus ângulos agudos?

15 É possível a construção de um triângulo retângulo equilátero? Justifique sua resposta.

16 É possível a construção de um triângulo que tenha dois ângulos externos retos? E a de um triângulo que tenha dois ângulos externos obtusos?

17 Verifique se é possível construir, com régua e compasso, triângulos cujas medidas dos lados são:

a) a = 8 centímetros, b = 6 centímetros e c = 4 centímetros;

b) a = 8 centímetros, b = 5 centímetros e c = 4 centímetros;

c) a = 8 centímetros, b = 4 centímetros e c = 4 centímetros;

d) a = 8 centímetros, b = 3 centímetros e c = 4 centímetros;

e) a = 7 centímetros, b = 3 centímetros e c = 4 centímetros;

f) a = 6 centímetros, b = 3 centímetros e c = 4 centímetros;

(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)

18 Em quais itens do exercício 17 não foi possível construir o triângulo? Por que isso ocorreu?

Hora de criar – Troque com um colega um problema sobre triângulos criado por vocês. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Página 229

Pense mais um poucoreticências

FAÇA AS ATIVIDADES NO CADERNO

1 Construa uma figura conforme as indicações a seguir.

• Marque um ponto a.

• Desenhe o segmento

\overline{A B}

com 3 centímetros.

• Indo de a para B, faça um giro de 120graus em B para a esquerda. Trace

\overline{B C}

também com medida 3 centímetros.

• Indo de B para C, faça outro giro de 120graus em C para a esquerda e trace

\overline{A C}

a) Qual é a medida de

\overline{A C}

b) Qual é a medida do ângulo

C \hat{A} B

c) Que figura foi desenhada?

2 Renato quer construir um triângulo da seguinte maneira:

• um dos lados deve medir 30 centímetros;

• outro lado deve medir 20 centímetros;

• o terceiro lado deve ter como medida, em centímetro, um múltiplo de 15.

Ilustração. Homem de cabelo castanho, óculos e camisa amarela. ele está sentado de frente para uma bancada inclinada com uma folha e o desenho de um triângulo. Acima, luminária.

a) Dessa maneira, quantos triângulos diferentes Renato poderá construir?

b) Quais serão as medidas dos lados dos triângulos?

PARA SABER MAIS

Uma propriedade importante dos triângulos

Em toda estrutura que precisa ser rígida, pode verificar: existe um triângulo!

Essa propriedade do triângulo (rigidez) é aproveitada na construção de muitas estruturas, entre elas portões e armações de telhados, para conservá-las sem deformações.

Fotografia. Cerca retangular composta por tábuas horizontais e diagonais. Destaque para triângulo formado na cerca.

Fotografia. Telhado de madeira triangular. Destaque para triângulo formado na parte frontal do telhado.

Agora é com você!

As estruturas das figuras a seguir, feitas com canudinhos de papel presos por percevejos, representam polígonos diversos: triângulo (a), quadriláteros (B e C), pentágonos (D e ê) e hexágonos (F e G).

Com a ajuda de um adulto, você pode construí-las para descobrir uma das propriedades dos triângulos: ao tentar movimentar, com muito cuidado com o percevejo, um dos vértices de cada estrutura, você percebe que a única que permanece rígida é a que tem formato triangular.

Página 230

Ilustração. Sequência de sete figuras geométricas compostas por palitos de fósforos.
A. Triângulo composto por 3 palitos de fósforos. B. Quadrado composto por 4 palitos de fósforos. C. Paralelogramo composto por 4 palitos de fósforos. D. Pentágono composto por 5 palitos de fósforos. E. Pentágono composto por 5 palitos de fósforos. F. Hexágono composto por 6 palitos de fósforos. Ilustração. G. Hexágono composto por 6 palitos de fósforos.

4. Somas das medidas dos ângulos de um polígono

Soma das medidas dos ângulos internos de um triângulo

Considere um triângulo á bê cê qualquer e uma reta r paralela à reta

\overset{\leftrightarrow}{B C}

que passa por a. Indicamos por x e y as medidas dos ângulos formados pela reta r com os lados

\overline{A B}

\overline{A C}

, respectivamente.

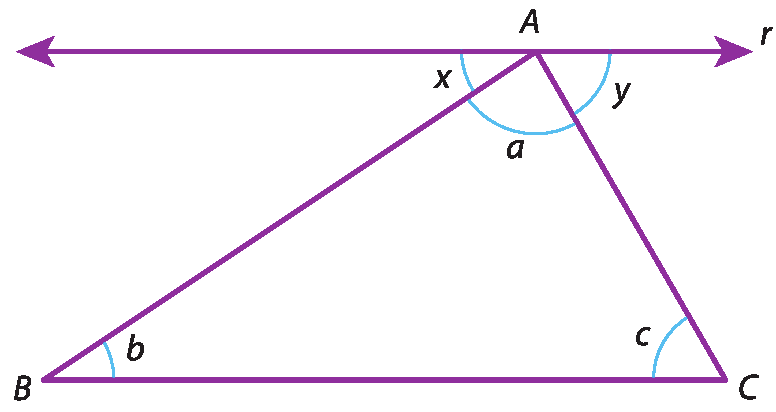
Ilustração. Triângulo A B C com reta r na horizontal sobre ponto A. Ângulos internos: a, b e c. Ângulos com a reta r, x e y.

Ângulos alternos internos formados por paralelas são congruentes; logo, x = b e y = c.

A soma das medidas dos três ângulos de vértice A fórma um ângulo raso com lados em r ; então, x + a + y = 180graus.

Substituindo x por b e y por c, obtemos: b + a + c = 180graus

Portanto:

A soma das medidas dos ângulos internos de um triângulo qualquer é igual a 180graus.

Página 231

Soma das medidas dos ângulos internos de um polígono de n lados

Considere os polígonos a seguir. Após traçar todas as diagonais por um vértice, obtivemos alguns triângulos que auxiliam no cálculo das somas S_i

das medidas dos ângulos internos.

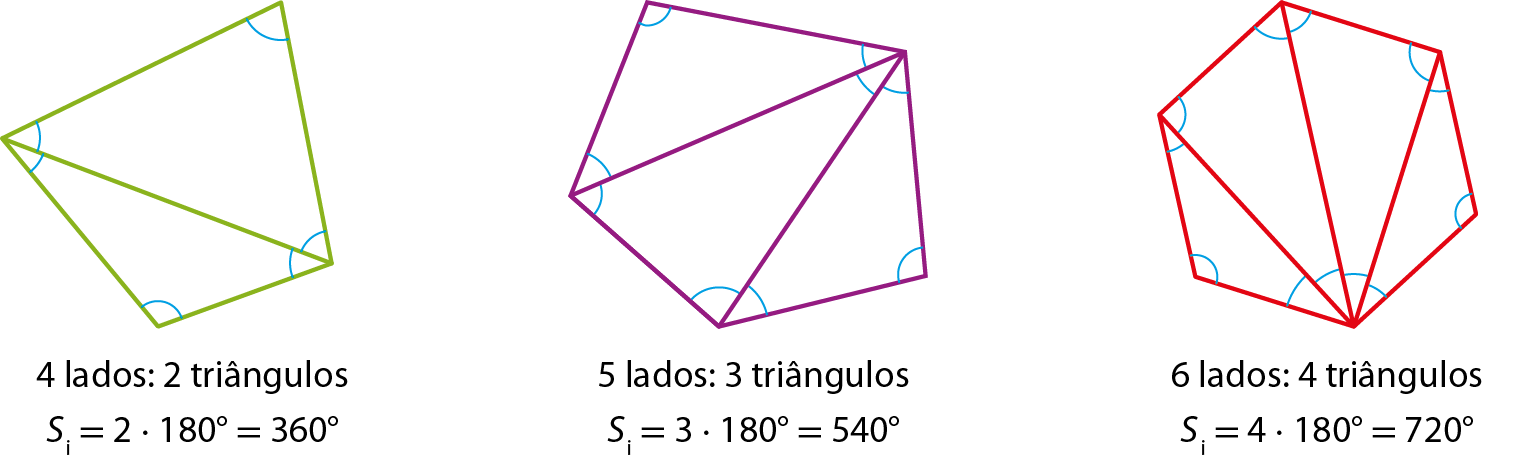
Ilustração. Quadrilátero com 1 diagonal traçada dividindo-o em 2 triângulos. Abaixo cotas: 4 lados: 2 triângulos, S i igual a 2 vezes 180 graus igual a 360 graus.
Ilustração. Pentágono com 2 diagonais traçadas a partir de um mesmo vértice dividindo o pentágono em 3 triângulos diferentes. Abaixo cotas: 5 lados: 3 triângulos, S i igual a 3 vezes 180 graus igual a 540 graus.
Ilustração. Hexágono com 3 diagonais traçadas a partir de um mesmo vértice dividindo o hexágono em 4 triângulos diferentes. Abaixo cotas: 6 lados: 4 triângulos, S i igual a 4 vezes 180 graus igual a 720 graus.

Agora, vamos considerar um polígono de n lados. Traçando todas as diagonais a partir de um dos vértices desse polígono, obtemos (n ‒ 2) triângulos.

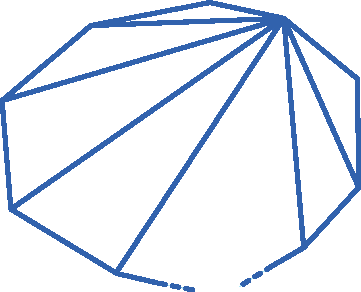
Ilustração. Vista de um polígono dividida em triângulos.

Sabendo que a soma das medidas dos ângulos internos de um triângulo é 180graus, a soma S_i das medidas dos ângulos internos de (n – 2) triângulos é:

Si = (n ‒ 2) ⋅ 180graus

A soma das medidas dos ângulos internos de um polígono de n lados é igual a: (n ‒ 2) ⋅ 180graus.

Acompanhe alguns exemplos.

a) Calcule a soma das medidas dos ângulos internos de um hexágono. n = 6 e Si

= (n ‒ 2) ⋅ 180graus Substituindo n por 6, obtemos:

Si = (6 ‒ 2) ⋅ 180graus

Si= 4 ⋅ 180graus = 720graus

Logo, a soma das medidas dos ângulos internos de um hexágono é 720graus.

b) Qual é o polígono cuja soma das medidas dos ângulos internos é .1080graus?

Si = (n ‒ 2) ⋅ 180graus e Si

= .1080graus

abre parênteses, n menos 2, fecha parênteses, vezes 180 graus, igual a mil e oitenta graus; duas setas azuis saem de 180 graus, uma vai até n e a outra até 2.

180graus ⋅ n ‒ 360graus = .1080graus

180graus ⋅ n = .1080graus + 360graus

180graus ⋅ n = .1440graus

n = 8

Portanto, o polígono é um octógono.

c) Calcule as medidas x e y indicadas na figura, sabendo que y ‒ x = 20graus.

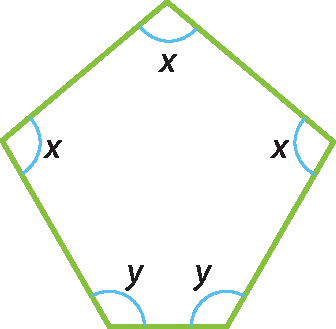
Ilustração.
Pentágono com 3 ângulos x e 2 ângulos y.

Na figura: n = 5 e Si

= 3x + 2y Como Si

= (n ‒ 2) ⋅ 180graus, temos: 3x + 2y = (5 ‒ 2) ⋅ 180graus 3x + 2y = 540graus

Ao resolver o sistema

\{\begin{cases} 3 x + 2 y = 540 ° \\ y ‒ x = 20 ° \end{cases}

, obtemos x = 100graus e y = 120graus.

Página 232

Soma das medidas dos ângulos externos de um polígono de n lados

A atividade a seguir nos permitirá perceber um resultado importante.

Desenhamos o polígono á bê cê dê é e seus ângulos externos

{\hat{e}}_{1}, {\hat{e}}_{2}, {\hat{e}}_{3}, {\hat{e}}_{4}, e {\hat{e}}_{5}

em uma folha de papel (fotografia 1). Com uma tesoura, recortamos a figura para destacar cada um dos ângulos externos, como sugere a fotografia 2.

Fotografia. Pentágono com ângulos externos e 1, e 2, e 3, e 4, e 5 destacados. Ao lado, lápis de cor, transferidor e régua. O pentágono é recortado com tesoura. Fotografia. Destaque para as mãos de uma pessoa recortando a figura.

Reunimos os cinco ângulos externos em tôrno de um dos vértices, de modo que se tornem adjacentes dois a dois (fotografia 3). Cada dois desses ângulos têm um lado comum, como mostra a fotografia 4; desse modo, podemos estimar que a soma das medidas desses ângulos é igual a 360graus.

Fotografia. Destaque para os ângulos do pentágono recortados. Fotografia. Destaque para os ângulos recortados do pentágono e que unidos formam um círculo colorido.

Para comprovar nossa estimativa, considere um polígono de n lados. Nele, vemos que em cada vértice a soma das medidas do ângulo interno com as do ângulo externo é igual a 180graus.

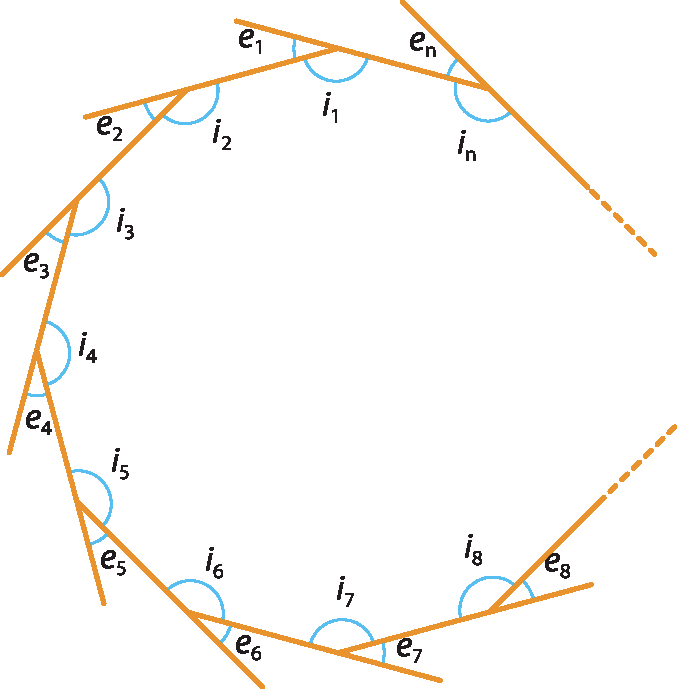
Ilustração. Figura com lado direito aberto e ângulos internos: i n, i1, i2, i3, i4, i5, i6, i8. ângulos externos: e 1, e 2, e 3, e 4, e 5, e 6, e 7, e 8.

Como o polígono de n lados tem n vértices, então a soma das medidas de todos os ângulos externos

(Se) com as de todos os ângulos internos (Si)

é igual a n ⋅ 180graus:

abre parênteses, e 1 mais i 1, fecha parênteses, mais, abre parênteses, e 2 mais i 2, fecha parênteses, mais, abre parênteses, e 3 mais i3, fecha parênteses, mais, abre parênteses, e 4 mais i4, fecha parênteses, mais, reticências, mais, abre parênteses, e n mais i n, fecha parênteses, igual a, n vezes 180 graus.
sendo que: e 1 mais i 1 corresponde a 180 graus, e 2 mais i 2 corresponde a 180 graus, e 3 mais i 3 corresponde a 180 graus, e 4 mais i 4 corresponde a 180 graus, e n mais i n corresponde a 180 graus.
Abre parênteses, e 1, mais, e 2, mais, e 3, mais, e 4, mais, reticências, mais, e n, fecha parênteses, mais abre parênteses, i 1, mais, i 2, mais i 3, mais, i 4, mais, reticências, mais, i n, fecha parênteses, igual a n vezes 180 graus.
S e mais S i igual a n vezes 180 graus.

Página 233

Substituindo Si

por (n ‒ 2) ⋅ 180graus, obtemos:

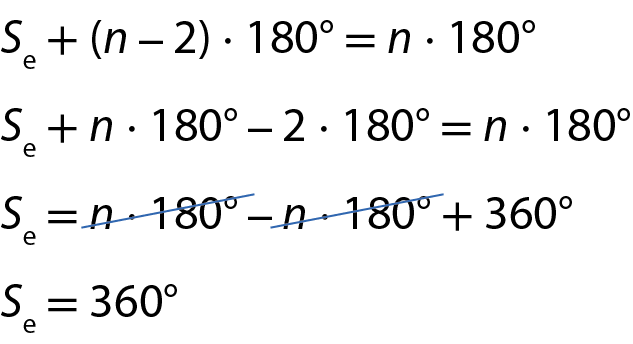
S e, mais, abre parênteses, n menos 2, fecha parênteses, vezes 180 graus, igual a, n vezes 180 graus.
S e, mais, n vezes 180 graus, menos 2 vezes 180 graus, igual a, n vezes 180 graus.
S e, igual a, n vezes 180 graus, menos n vezes 180 graus, mais, 360 graus.
S e, igual a 360 graus.

Portanto:

A soma das medidas dos ângulos externos de um polígono qualquer é 360graus.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

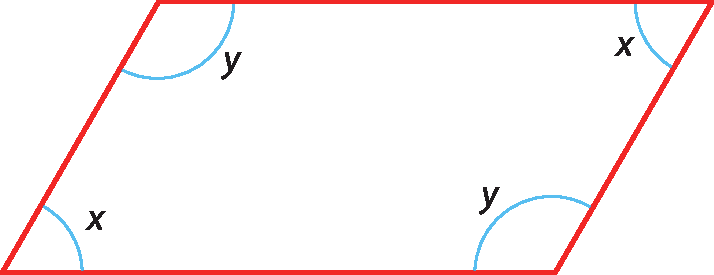
20 Determine a medida y do ângulo sabendo que, no quadrilátero, y = 2x.

Ilustração. Paralelogramo com dois ângulos x e dois ângulos y.

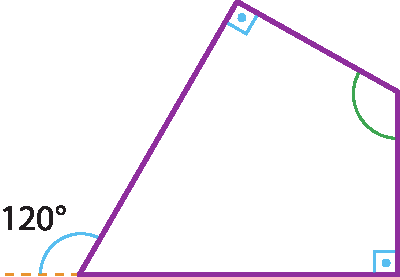
21 Determine a medida do ângulo destacado em verde.

Ilustração. Quadrilátero com 3 Ângulos internos em destaque e 1 ângulo externo. 1 ângulo interno é reto, o próximo é um ângulo em destaque verde, o seguinte é outros ângulo reto; o último ângulo interno não está em destaque, mas sim o ângulo externo corresponde a ele e que mede 120 graus.

22 A soma das medidas dos ângulos internos de um polígono é .1260graus.

a) Qual é o nome desse polígono?

b) Quantas diagonais ele tem?

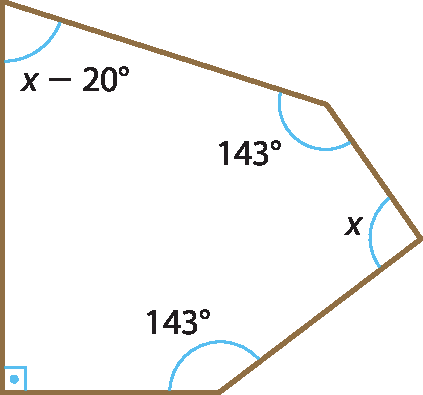
23 Calcule a medida xis do ângulo na figura.

Ilustração. Quadrilátero com ângulos internos: x menos 20 graus, 143 graus, x, 143 graus e 90 graus.

Descubra mentalmente a diferença entre a soma das medidas dos ângulos internos de um decágono e a de um octógono.

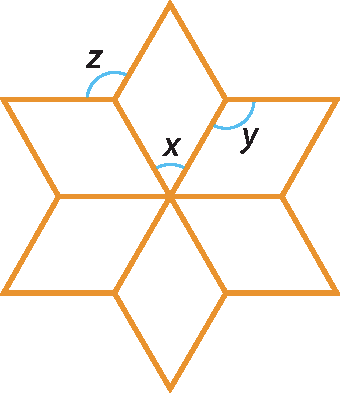
25 A figura é formada por seis paralelogramos congruentes. Sabendo que a medida y é o dôbro da medida x, qual é a medida z?

Ilustração. Figura semelhante a uma estrela composta por 6 paralelogramos unidos por um vértice em comum. Um ângulo interno do losango é x, o outro é y. A cada dois paralelogramos, os dois lados de mesma medida de cada um formam um ângulo z.

Reúna-se com um colega e façam o que se pede. Considerem a soma das medidas dos ângulos internos de um polígono de n lados como Si(n)

e a soma das medidas dos ângulos externos como Se(n)

e respondam.

Si(14) é o dôbro de Si(7)?

Se(14) é o dôbro de Se(7)

[Si(14) + Se(14)] é o dôbro de [Si(7) + Se(7)]

d) Existe algum valor para n de modo que Si(2n)

seja o dôbro de Si(n)

e) Existe algum valor para n de modo que Se(2n)

seja o dôbro de Se(n)

f) Existe algum valor para n de modo que [Se(2n) + Si(2n)]

seja o dôbro de [Se(n) + Si(n)]

Hora de criar – Escolha um polígono e elabore um problema sobre soma das medidas de ângulos internos e ou ou externos desse polígono. Troque com um colega e depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Página 234

5. Polígonos regulares

Já vimos que uma figura apresenta simetria em relação a um eixo quando ela pode ser dividida, por uma linha reta, em duas partes com mesmo formato e tamanho, como se fossem espelhadas.

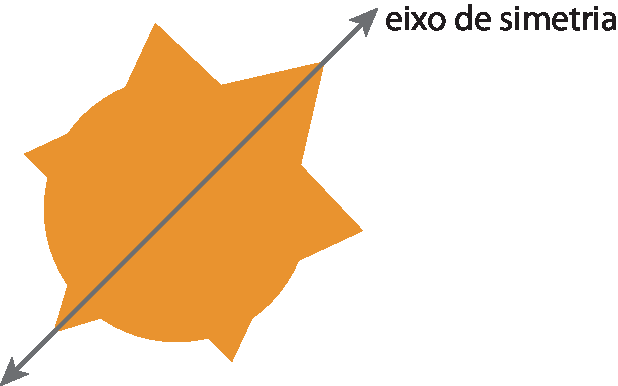
Ilustração. Figura laranja com três pontas triangulares acima e três menores abaixo. Reta (eixo de simetria) divide a figura ao meio em duas partes iguais.

A essa linha reta chamamos de eixo de simetria. Algumas figuras podem apresentar mais de um eixo de simetria.

Vimos também que um polígono é regular se tiver tantos eixos de simetria quantos forem os seus lados.

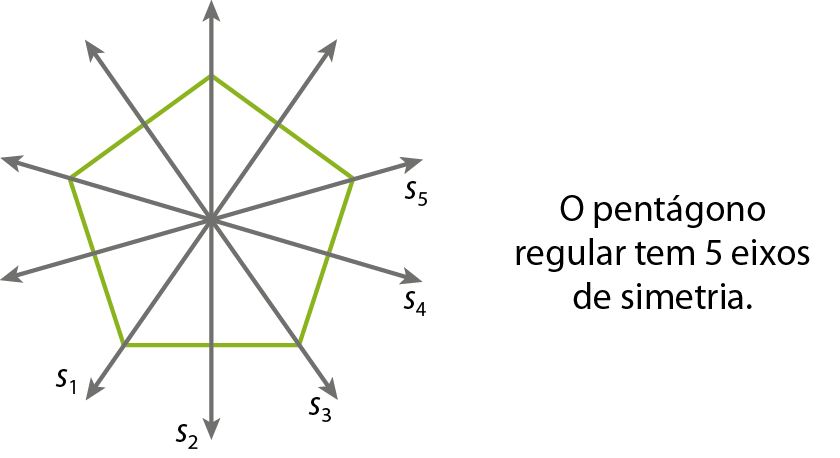
Ilustração.
Pentágono com 5 eixos de simetria: S1, S2, S3, S4 e S5. Ao lado cota: O pentágono regular tem 5 eixos de simetria.

Entretanto, é possível caracterizar um polígono regular de outro modo.

Um polígono é regular quando todos os seus lados são congruentes entre si e todos os seus ângulos internos são congruentes entre si.

Estas figuras são polígonos regulares.

Ilustração. Triângulo de lados e ângulos iguais. Ilustração. Quadrado. Ilustração.
Hexágono de lados e ângulos iguais. Ilustração.Octógono de lados e ângulos iguais.

Representando por a i a medida do ângulo interno de um polígono regular de n lados e por

a_{e}

a medida do ângulo externo, temos:

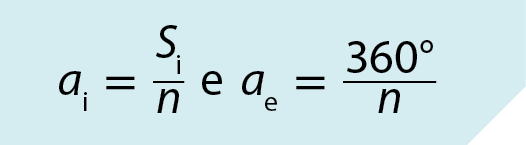
a i igual a, fração. numerador S subíndice i, denominador n e a e igual a, fração. numerador 360 graus, denominador n

Acompanhe os exemplos.

a) Vamos calcular a medida do ângulo interno e a medida do ângulo externo do octógono regular.

Ilustração.
Octógono de lados e ângulos iguais.

Si = (n – 2) · 180graus

Si = (8 – 2) · 180graus

Si = 6 · 180graus

Si = 6 · .1080graus

•

a_{i} = \frac{S_{i}}{n} = \frac{1080 °}{8} = 135 °

•

a_{e} = \frac{360 °}{n} = \frac{360 °}{8} = 45 °

Note que ai + ae = 135graus + 45graus = 180graus.

Logo, o ângulo interno mede 135graus, e o ângulo externo, 45graus.