
CAPÍTULO 12 Estudo da circunferência e do círculo

Observe a imagem e responda às questões no caderno.
a) Quantas pessoas cabem no máximo em um passeio de uma volta completa nessa roda-gigante?
b) A quantos graus corresponde o giro de deslocamento de uma cabine que está no ponto mais baixo até o ponto mais alto dessa roda-gigante?
c) Qual é a medida aproximada do menor ângulo com vértice no centro da roda-gigante e lados que passem no centro de duas cabines vizinhas?
Inaugurada em outubro de 2021, a Ain Dubai tem 250 metros de medida de altura. Está localizada na ilha artificial de Bluewaters, em Dubai. Ela tem 48 cabines de 30 métros2, com vista de 360graus, que podem levar até .1750 pessoas por vez. O passeio de uma volta completa pode durar até 38 minutos.
1. Circunferência
Observe a situação a seguir.
Para traçar o canteiro de uma praça, o jardineiro Luís usou uma corda presa a duas estacas de madeira, uma em cada ponta.

Com uma das estacas presa ao chão e mantendo a corda esticada, ele riscou a terra com a outra, dando uma volta completa.
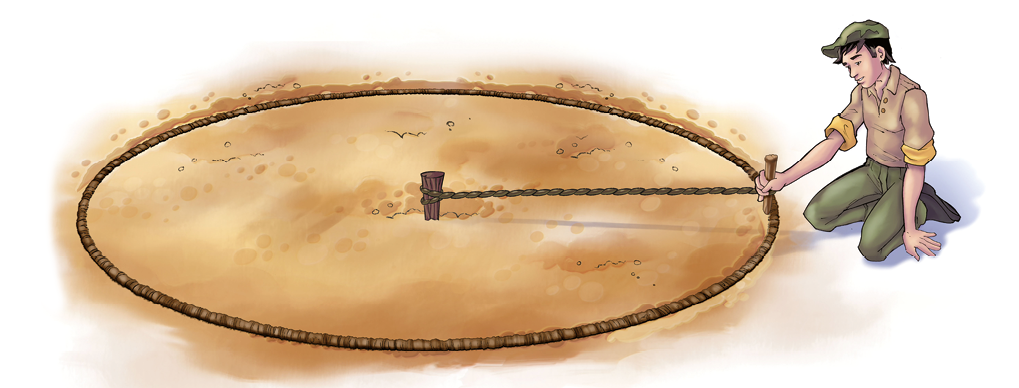
O traçado obtido pelo jardineiro dá a ideia de uma circunferência.
Circunferência é a linha formada por todos os pontos de um plano que estão à mesma distância de um ponto fixo desse plano.
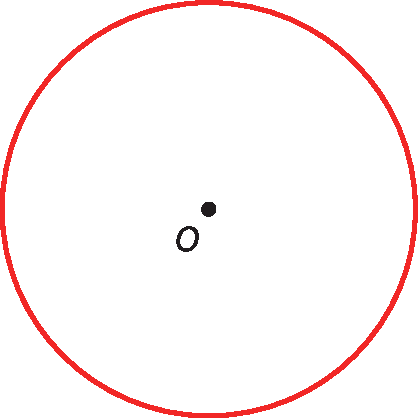
Considere a circunferência a seguir.
Todos os pontos de uma circunferência são equidistantes de um ponto fixo, chamado de centro da circunferência. Nessa circunferência, o centro é o ponto óh.
Destacamos alguns elementos em uma circunferência:
• Raio: segmento cujos extremos são o centro e um ponto qualquer da circunferência.
• Corda: segmento cujos extremos são dois pontos quaisquer de uma circunferência.
• Diâmetro: corda que passa pelo centro de uma circunferência. A medida do comprimento do diâmetro (D) é igual ao dôbro da medida do comprimento do raio (2r). Assim: D = 2r
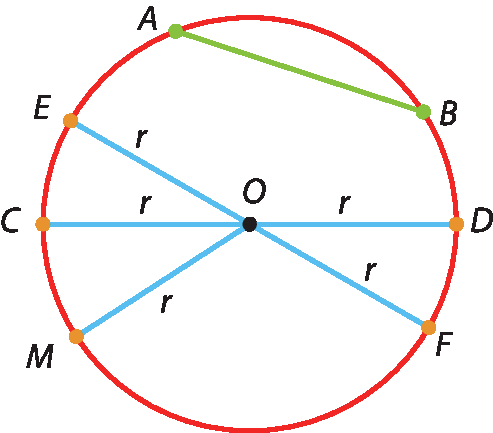
Na figura a seguir:
•
segmento de reta ABé uma corda;
•
segmento de reta CD e segmento de reta EFsão alguns dos diâmetros;
•
segmento de reta OM, segmento de reta OC e segmento de reta OFsão alguns dos raios.
Observação
▶ A palavra raio será usada tanto para designar um segmento como para indicar a medida desse segmento. Assim, por exemplo, quando dizemos que uma circunferência tem raio 3,8 centímetros, queremos dizer que os infinitos segmentos que são raios dessa circunferência medem 3,8 centímetros.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
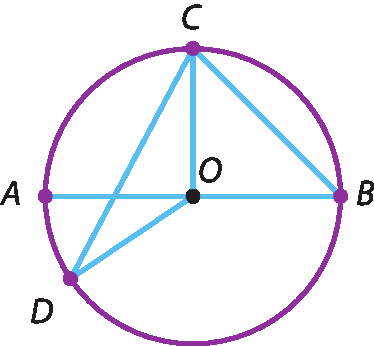
1 Observe a circunferência e classifique, no caderno, os segmentos em raio, diâmetro ou corda.
a)
segmento de reta OB
b)
o segmento de reta OC
c)
segmento de reta BC
d)
o segmento de reta AB
e)
Segmento de reta CD
f)
segmento de reta OD
2 Considere a figura a seguir, depois responda às questões no caderno.
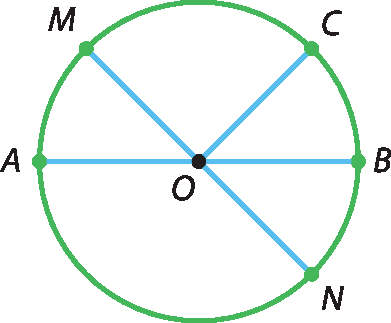
a) Se ó ême = 3 centímetros, quanto mede
Segmento de reta AB?
b) Se MN = 8 centímetros, quanto mede
segmento de reta OC?
c) Se ó cê = x, quanto mede
segmento de reta OB?
d) Se ó á = y, quanto mede
segmento de reta AB?
3 Com um compasso, trace três circunferências: uma de raio medindo 2 centímetros, outra de raio medindo 2,5 centímetros, e a terceira com a medida que você escolher. Em seguida, em cada uma delas, trace um diâmetro
ABuma corda
CDque não passe pelo centro óh, e um raio
OEConsiderando as possibilidades de suas escolhas para os pontos A, B, C, D e E, responda às questões no caderno.
a)
O segmento de reta CDpode ser maior que
O segmento de reta AB?
b)
O segmento de reta ABé sempre maior que
O segmento de reta CD?
c)
O segmento de reta CDpode ser maior que
O segmento de reta OE?
d)
o segmento de reta CDpode ser menor que
segmento de reta OE?
e)
o segmento de reta ABé sempre o dôbro de
OE?
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
4 Na figura, as expressões algébricas representam a medida dos raios da circunferência.
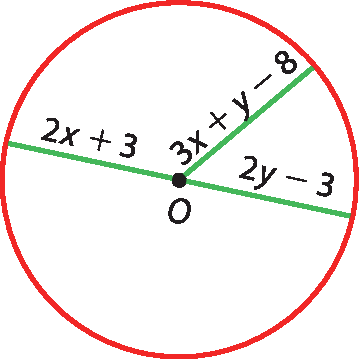
a) Escreva no caderno, com essas expressões, um sistema de duas equações com duas incógnitas.
b) Resolva o sistema do item a e calcule as medidas do raio e do diâmetro em unidades de comprimento (u).
5 Uma das maiores crateras conhecidas do nosso Sistema Solar está em Mercúrio, o planeta mais próximo do Sol. O diâmetro dessa cratera mede aproximadamente .1300 quilômetros. Determine, em metro, a medida aproximada do raio dessa cratera.

Superfície de Mercúrio. O Sol está a, aproximadamente, ..58000000 quilômetros de distância de Mercúrio, pouco mais de
um terçoda distância da Terra ao Sol.
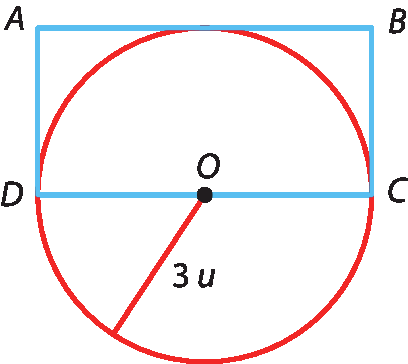
6 Calcule a medida do perímetro do retângulo ABCD.
7

Junte-se a um colega e façam o que se pede.
Na figura a seguir há duas circunferências de mesmo raio, e as medidas estão em uma mesma unidade de comprimento u.
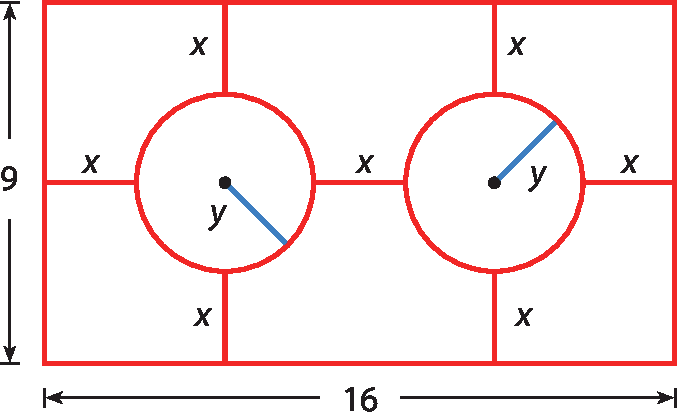
Escrevam e resolvam um sistema de duas equações com duas incógnitas para determinar a medida do raio das circunferências.
8

Hora de criar – Elabore um problema sobre circunferência. Troque-o com um colega e depois que cada um resolver o problema elaborado pelo outro, destroquem-nos para corrigi-los.
PARA SABER MAIS
Triângulos simétricos na circunferência
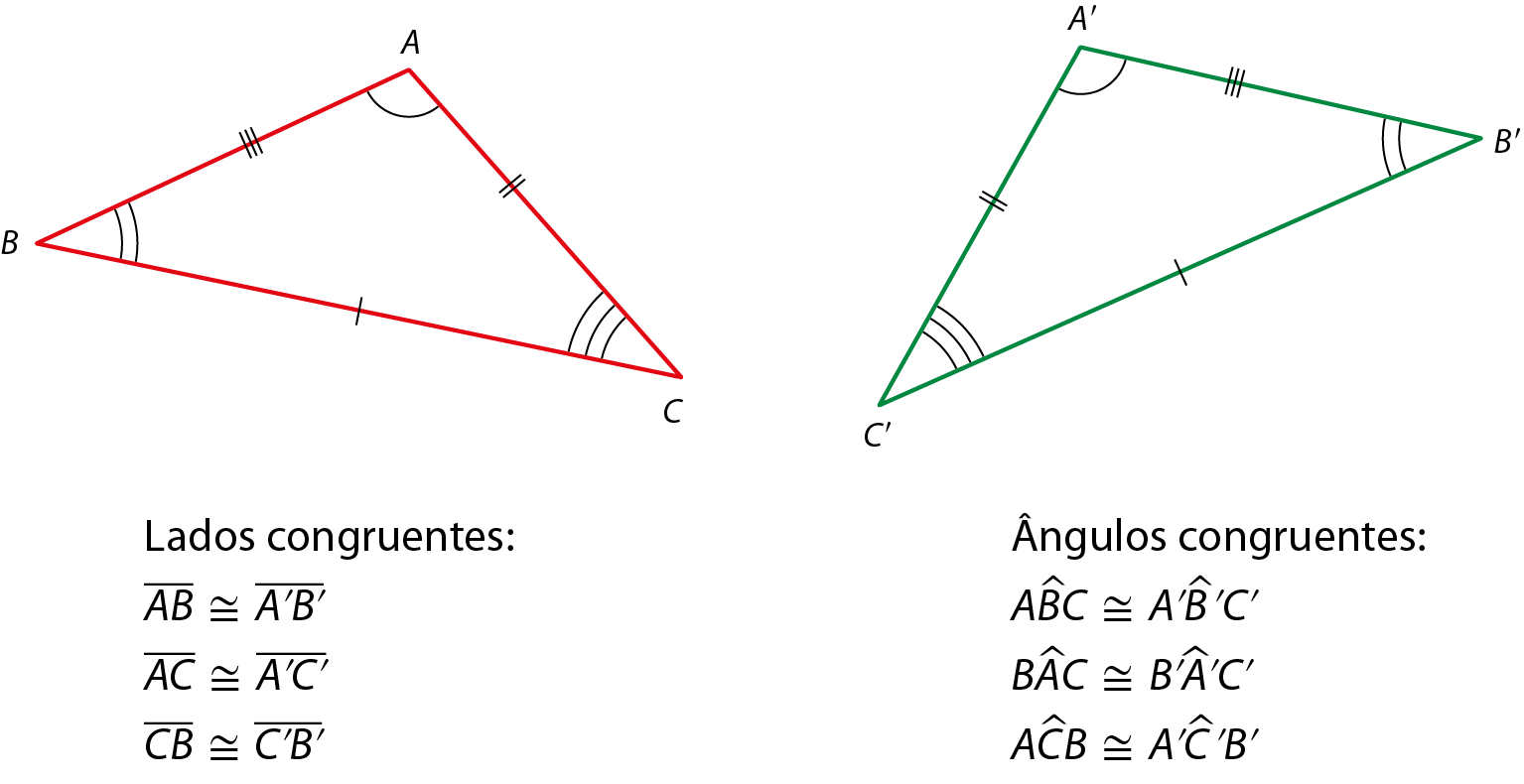
Já vimos que o conceito de congruência se aplica a elementos geométricos com medidas iguais. Por exemplo, segmentos congruentes têm medidas iguais; ângulos congruentes, também.
Podemos dizer que dois triângulos são congruentes quando as medidas de um deles são respectivamente iguais às medidas do outro: os lados de um são congruentes aos do outro e também os ângulos de um são congruentes aos ângulos do outro.
Observe a figura. A reta
CDé um eixo de simetria.
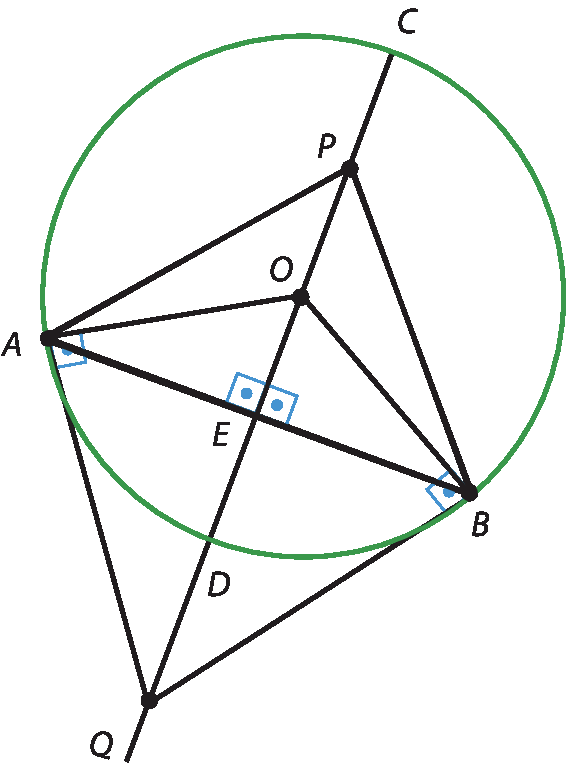
Dobrando a folha pela reta
CD, podemos perceber que há vários pares de triângulos que se sobrepõem; logo, são triângulos congruentes: △ô á ê ≅ △ó bê é, △pê á é ≅ △PBE, △QAE ≅ △QBE, △OAQ ≅ △OBQ, △PAQ ≅ △PBQ.
Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
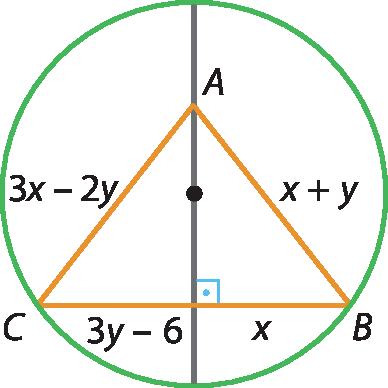
Considerando a figura a seguir, escreva e resolva um sistema de duas equações com duas incógnitas. Depois, calcule a medida do perímetro do triângulo ABC.
Círculo
Uma circunferência de centro óh, contida em um plano α, determina duas regiões: região interna e região externa.

Na figura a seguir:
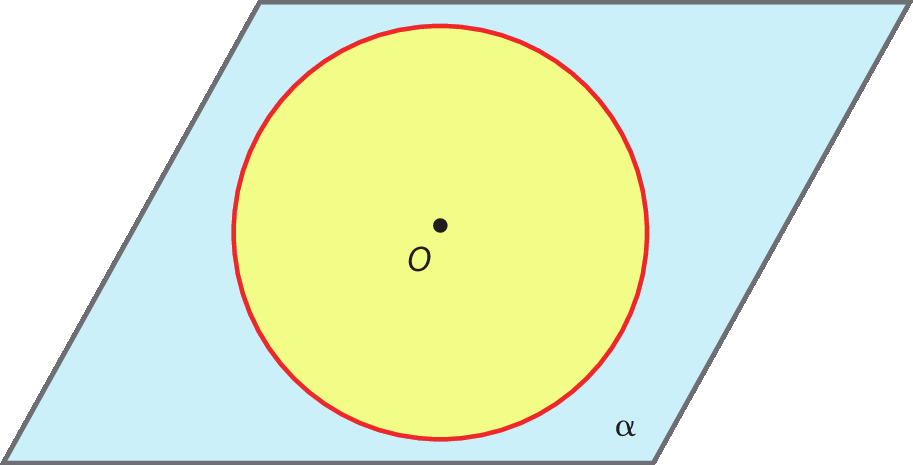
• a circunferência está desenhada em vermelho;
• a região interna à circunferência está pintada de amarelo e o centro pertence à região interna;
• a região externa está pintada de azul.
A região do plano formada por uma circunferência e pela região interna a ela é chamada de círculo.
Comprimento de uma circunferência
Vamos relembrar o exemplo do jardineiro Luís, apresentado anteriormente. Ele traçou o contôrno de um canteiro em uma praça com duas estacas de madeira e uma corda esticada.
Vimos que o traçado obtido por Luís dá a ideia de uma circunferência.
Após o traçado, Luís fez, com uma enxada, um sulco sobre a circunferência.

Desejando saber quantos metros de tela seriam necessários para cercar esse canteiro, ele esticou uma corda, acompanhando o sulco, e cortou-a ao final do contôrno.
Depois, com uma trena, mediu a corda e verificou que a medida da distância entre as duas estacas, com a corda esticada, era igual a 3 métros e que a medida do comprimento da circunferência era de 18,84 métros. Desse modo, concluiu que seriam necessários aproximadamente 19 métros de tela.

Considerando a distância entre as duas estacas, podemos dizer que ele traçou uma circunferência de 3 métros de medida de raio, ou seja, de 6 métros de medida de diâmetro.
Acompanhe outro exemplo.
Para determinar a medida do comprimento da circunferência de um pneu de bicicleta e a medida de seu diâmetro, podemos utilizar um barbante e uma fita métrica.


Suponha que contornemos com um barbante a circunferência a seguir. Esticando o barbante, ele teria a mesma medida do segmento
AB.
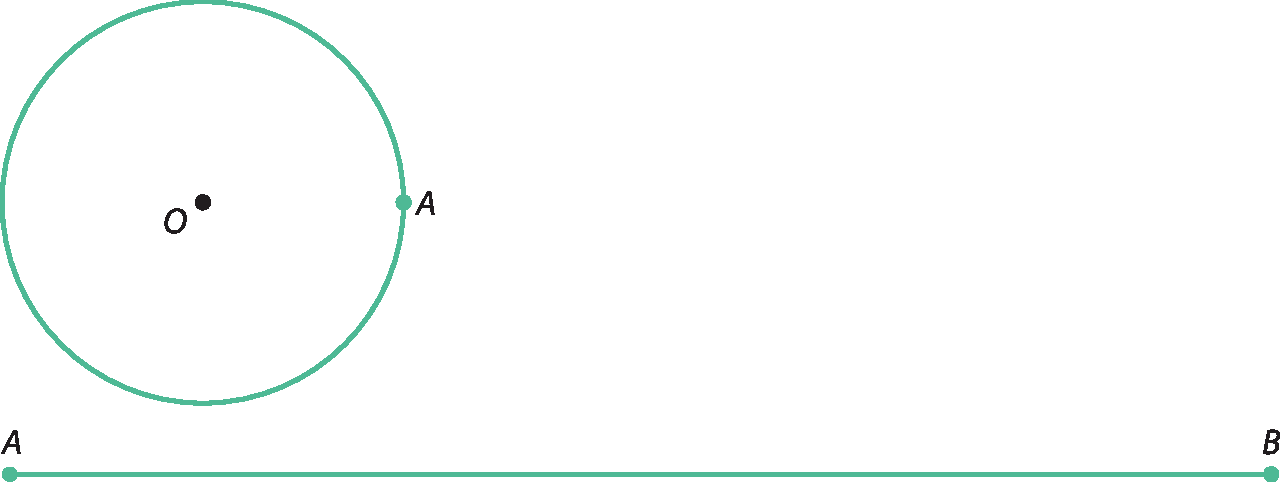
A medida do segmento
O segmento de reta ABé igual à medida do comprimento dessa circunferência.
A razão entre as medidas do comprimento da circunferência e do diâmetro é um número que, na fórma decimal, apresenta infinitas casas decimais não periódicas.
O avanço da tecnologia na área da informática tem validado, na prática, o que a teoria mostra: já é possível expressar esse número com milhões de casas decimais, e essa representação não apresenta nenhum período, pois trata-se de um número não racional. A esse tipo de número com infinitas casas decimais sem apresentar período, que estudaremos no próximo ano, chamamos de número irracional.
O número irracional, que representa a razão entre a medida do comprimento C de uma circunferência e a medida D de seu diâmetro, é representado pela letra grega π (lemos: “pi”).
Assim, podemos escrever:
Observe a representação decimal desse número com suas primeiras trinta casas decimais:
3,141592653589793238462643383279reticências
Como a medida D do diâmetro de uma circunferência é o dôbro da medida r de seu raio, podemos escrever:
Note que, no exemplo do jardineiro Luís, é possível chegar a um valor aproximado para π, pois a medida do comprimento da circunferência do canteiro, dividida pela medida de seu diâmetro, é: 18,84 : 6 = 3,14.
• Que tal fazer um experimento? Determine as medidas do comprimento da circunferência do pneu de uma bicicleta e do diâmetro dessa circunferência. Calcule a razão entre essas medidas. A que número você chegou?
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
9 Com uma régua, obtenha a medida r do raio da circunferência de centro óh, contida no plano α. Depois, meça as distâncias de cada um dos outros pontos da figura ao centro óh.
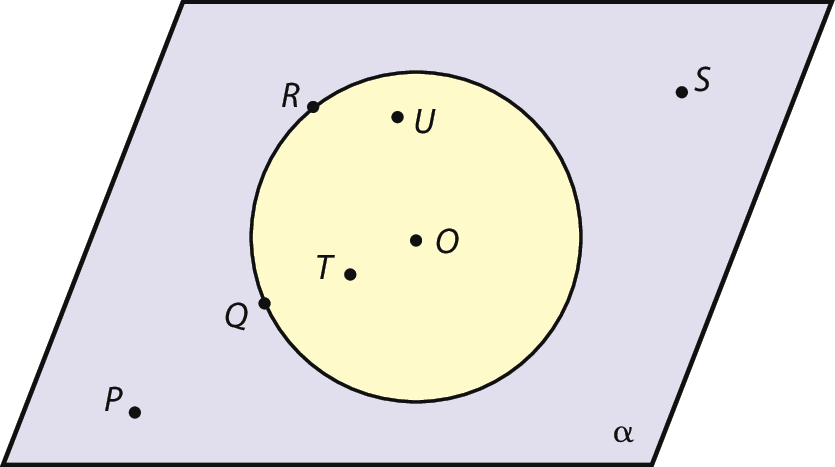
a) Compare com r as medidas das distâncias dos pontos destacados:
• da circunferência até óh;
• da região externa da circunferência até óh;
• da região interna da circunferência até óh.
b) No caderno, copie a figura e marque um ponto V, cuja medida da distância ao centro óh seja maior do que r, e um ponto W, cuja medida da distância a óh seja menor do que r. O ponto V pertence à circunferência, à região interna ou à região externa? E o ponto W ?
10 Uma roda de bicicleta tem 40 centímetros de medida raio. Calcule a medida aproximada do comprimento da circunferência dessa roda, considerando π = 3,14.
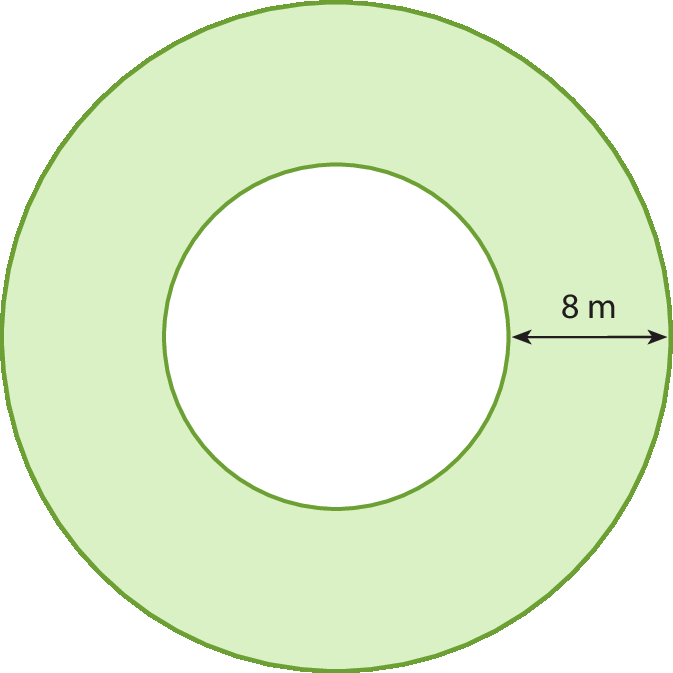
11 Uma pista circular tem 8 métros de medida de largura. O comprimento de sua margem interna mede .1570 métros. Determine a medida aproximada do comprimento de sua margem externa, considerando π = 3,14.
12 Marina e Paula estão na posição a de uma praça circular de 50 métros de medida de raio. Elas caminham em direção à posição B. Marina caminha segundo o traçado preto, e Paula, segundo o traçado vermelho.
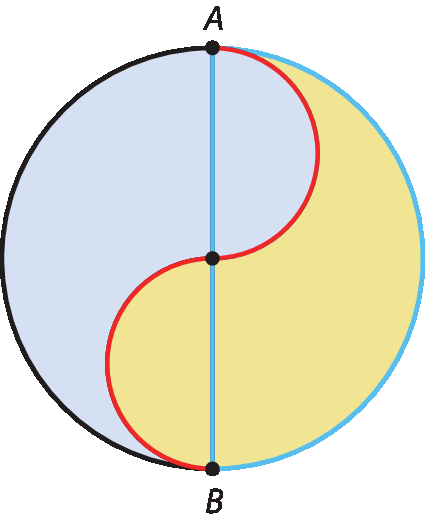
Considerando π = 3,14, faça o que se pede.
a) Sem fazer nenhum cálculo, responda: quem andou a maior distância? Justifique sua resposta.
b) Calcule quantos metros cada uma andou, aproximadamente, e verifique se você acertou o item anterior.
c) Agora, observe o trajeto feito por Andréa, conforme o traçado verde.
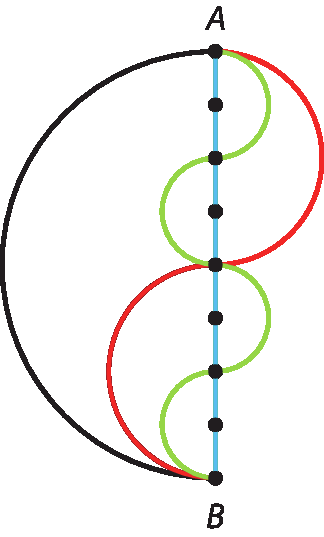
Sem fazer nenhum cálculo, é possível dizer que a distância percorrida por Andréa é maior ou menor do que as distâncias percorridas por Marina e Paula?
d) Calcule quantos metros Andréa andou, aproximadamente, e verifique se você acertou o item anterior.
e) Imagine que você caminhasse de a para B, fazendo um caminho sinuoso como o de Paula e o de Andréa; porém, percorrendo oito semicircunferências, cada uma delas de diâmetro de mesma medida que a do raio das semicircunferências percorridas por Andréa. Quantos metros você andaria?
13

Reúna-se com um colega para fazer algumas estimativas.
a) Desenhem o contôrno de uma moeda de 1 real. Estimem a medida do comprimento da circunferência desenhada, em centímetro, e tracem um segmento com esse comprimento.
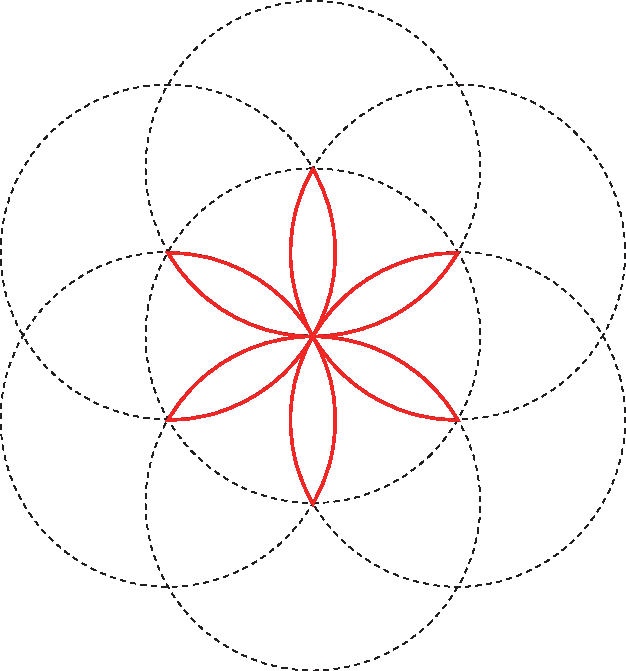
b) Estimem o comprimento do traçado vermelho da figura, em centímetro, feito com uma moeda de 1 real. Expliquem como fizeram essa estimativa.
14

Hora de criar – Elabore um problema sobre comprimento de circunferência. Troque-o com um colega e depois de cada um resolver o problema elaborado pelo outro, destroquem-nos para corrigi-los.
Trabalhando a informação

Limites do corpo humano
O professor Adelson passou um texto para motivar seus estudantes a fazerem uma pesquisa estatística sobre os limites do corpo humano. Acompanhe.
Corpo humano pode estar chegando ao limite, diz estudo
Cada geração é mais alta, forte e longeva que a geração anterior – mas isso está parando
Cientistas franceses e brasileiros analisaram os registros de longevidade, altura e fôrça física das pessoas em diversos países ao longo dos últimos 120 anos – e constataram que, mesmo com os avanços da medicina e a melhoria nas condições de vida, esses indicadores pararam de aumentar na década de 1980.
Fonte: isclárz, E. Corpo humano pode estar chegando ao limite, diz estudo. Superinteressante, São Paulo, edição 386, página 12, março 2018.
Orientação para grupos de trabalho
• Objetivo da pesquisa: comparar as alturas de jovens com as de seus pais, por gênero.
• População estatística (alvo): pessoas conhecidas, sendo uma de cada família.
• Coletar a altura (em centímetro) de 10 jovens (15 a 24 anos), sexo feminino, e a altura da respectiva mãe. Idem para sexo masculino e respectivo pai.
• Organizar os dados colhidos em duas tabelas (jovem – genitor ou genitora), incluindo a diferença de alturas e as respectivas médias de cada grupo.
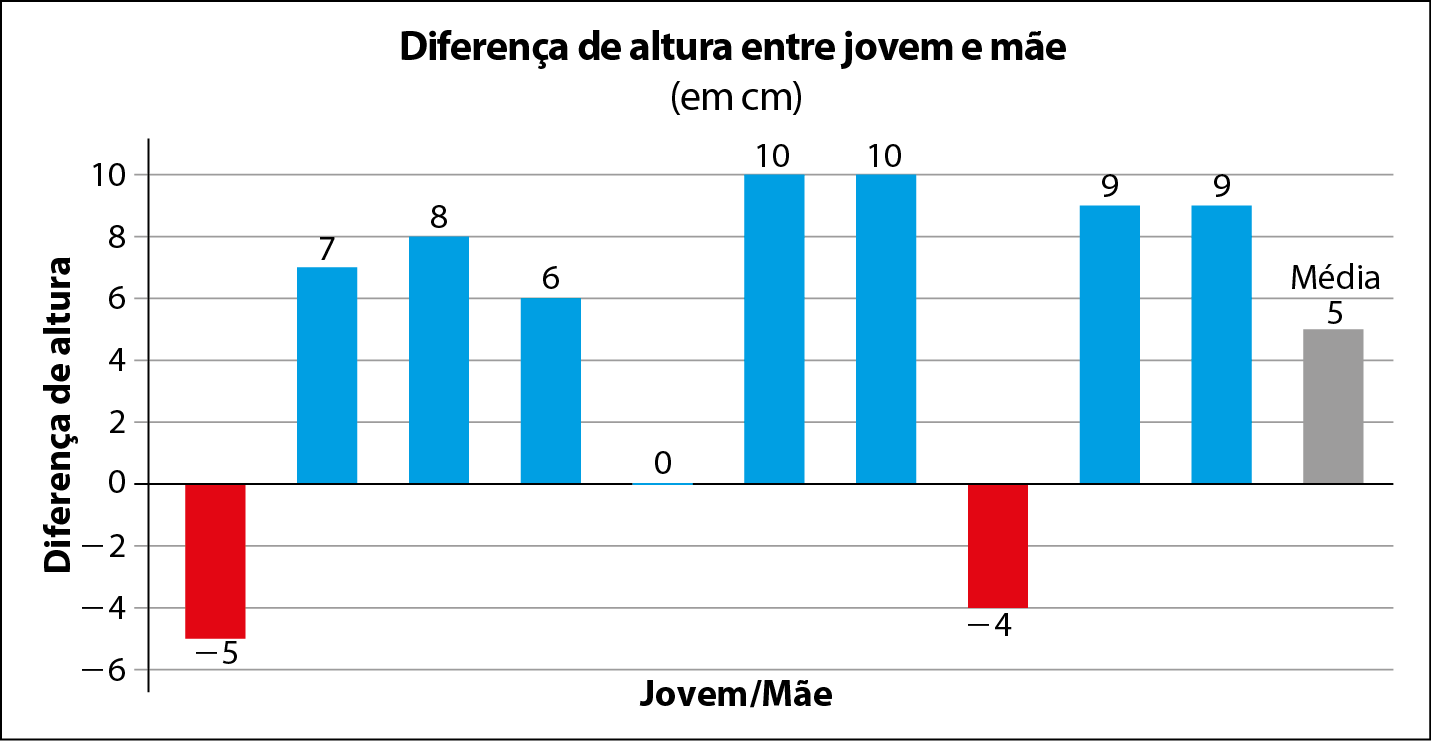
• Construir dois gráficos de colunas das diferenças de alturas (jovem/mãe; jovem/pai).
• Avaliar se a quantidade de pessoas pesquisadas (pesquisa amostral, isto é, pesquisa com uma parte da população estatística) é suficiente para chegar a conclusões seguras sobre as comparações das alturas das pessoas ou se seria necessário aumentar o número de pessoas pesquisadas até a totalidade da população (pesquisa censitária).
• Redigir relatório comparando as alturas de filhos e pais, por gênero, e verificar se a conclusão desse trabalho é compatível com a reportagem anterior.
Observe parte do trabalho de um dos grupos de estudantes de Adelson, com o gênero feminino.
|
Altura de jovem feminina (15-24 anos) e sua mãe (em cm) |
Média |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Jovem |
160 |
173 |
168 |
168 |
165 |
180 |
176 |
163 |
170 |
177 |
170 |
|
Mãe |
165 |
166 |
160 |
162 |
165 |
170 |
166 |
167 |
161 |
168 |
165 |
|
Diferença |
−5 |
7 |
8 |
6 |
0 |
10 |
10 |
−4 |
9 |
9 |
5 |
Dados obtidos pelos estudantes de Adelson.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 O mesmo grupo de estudantes do professor Adelson elaborou a seguinte tabela:
|
Altura de jovem masculino (15-24 anos) e seu pai (em cm) |
Média |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
Jovem |
170 |
188 |
173 |
168 |
173 |
180 |
176 |
175 |
180 |
177 |
176 |
|
Pai |
165 |
176 |
170 |
172 |
165 |
170 |
166 |
177 |
181 |
168 |
171 |
|
Diferença |
5 |
12 |
3 |
−4 |
8 |
10 |
10 |
−2 |
−1 |
9 |
5 |
Dados obtidos pelos estudantes de Adelson.
Construa o gráfico de colunas que representa os dados dessa tabela.
2

Junte-se a quatro colegas e façam uma pesquisa igual à proposta pelo professor Adelson, seguindo todas as etapas das orientações.
3

Agora o grupo do qual você faz parte deve juntar os dados de todos os outros grupos e fazer as tabelas, os gráficos e o relatório como se fosse uma só pesquisa. Com essa população estatística maior, a conclusão sobre a pesquisa é mais confiável?
2. Posições relativas
Posições relativas de um ponto em relação a uma circunferência
Se uma circunferência está contida em um plano α, então um ponto qualquer de α pode ser interno, externo ou pertencente à circunferência.
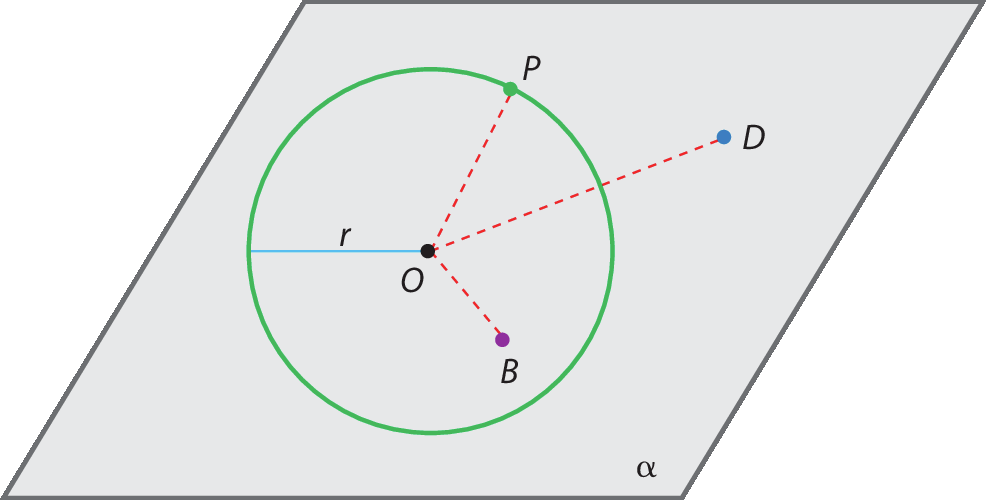
• Se a medida da distância de um ponto ao centro de uma circunferência é maior do que a medida do raio dessa circunferência, dizemos que esse ponto é externo a ela. Na figura, ó dê > r ; logo, o ponto D é externo à circunferência.
• Se a medida da distância de um ponto ao centro de uma circunferência é menor do que a medida do raio dessa circunferência, dizemos que esse ponto é interno a ela. Na mesma figura, ó bê < r ; logo, o ponto B é interno à circunferência.
• Se a medida da distância de um ponto ao centro de uma circunferência é igual à medida do raio dessa circunferência, dizemos que esse ponto pertence a ela. Na figura, ó pê = r ; logo, o ponto P pertence à circunferência.
Considerando essas três situações, concluímos que todos os pontos de uma circunferência têm a propriedade de estar à distância de medida r de óh. E só os pontos dessa circunferência têm essa propriedade.
Como estudamos anteriormente, dizemos que essa circunferência é o lugar geométrico dos pontos do plano que distam r de óh.
No próximo ano retomaremos o estudo deste e de outros lugares geométricos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
15 Considere a figura a seguir.
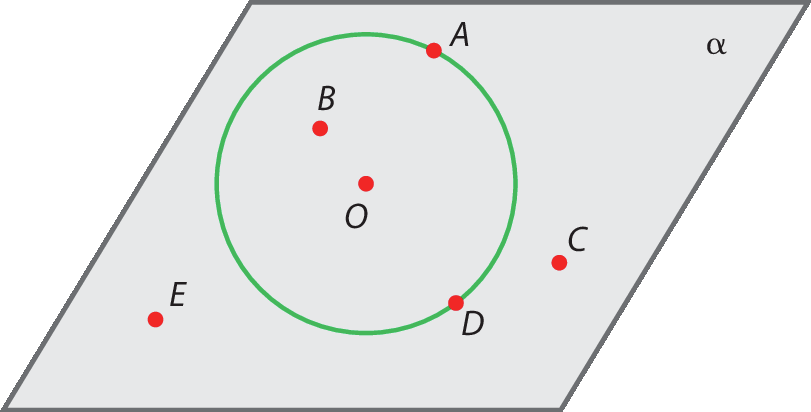
Agora, escreva no caderno os pontos:
a) internos à circunferência;
b) externos à circunferência;
c) pertencentes à circunferência.
Versão adaptada acessível
15. Represente, no caderno, uma circunferência e depois, indique:
a) 2 pontos internos à circunferência;
b) 2 pontos externos à circunferência;
c) 2 pontos pertencentes à circunferência.
16 Estabeleça uma relação de igualdade ou de desigualdade entre as medidas dos segmentos
OA OBe
OCcom o raio de medida r da circunferência do exercício anterior.
17 Com um compasso, trace uma circunferência de centro óh. Marque sobre ela dois pontos distintos, M e N, não colineares com o ponto óh. Como você classifica, quanto aos lados, o triângulo ême ó êne ?
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
18 No chão do pátio da escola onde Cristina estuda, há o desenho de uma circunferência que mede 6 métros de diâmetro. Certo dia, Cristina estava a 2 métros do centro dessa circunferência, e sua amiga Rosana, a 7 métros.
a) Qual é a posição de Cristina e de Rosana em relação à circunferência?
b) Determine a medida da distância entre elas, sabendo que Cristina, Rosana e o centro dessa circunferência estão sobre uma mesma reta.
19 Com um compasso, trace em uma folha avulsa uma circunferência de centro óh e marque sobre ela dois pontos distintos, a e B, não colineares com o ponto óh. Construa o triângulo á ó bê e, por dobradura, trace a bissetriz
ODdo ângulo
AOB, em que D seja ponto de
segmento AB.
a) Como são as medidas dos ângulos
OBAe
OAB?
b) Como são as medidas dos segmentos
ADe
BD?
c) Quanto aos ângulos, como se classifica o triângulo ODB ? E o triângulo ó dê á?
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
Posições relativas de uma reta em relação a uma circunferência
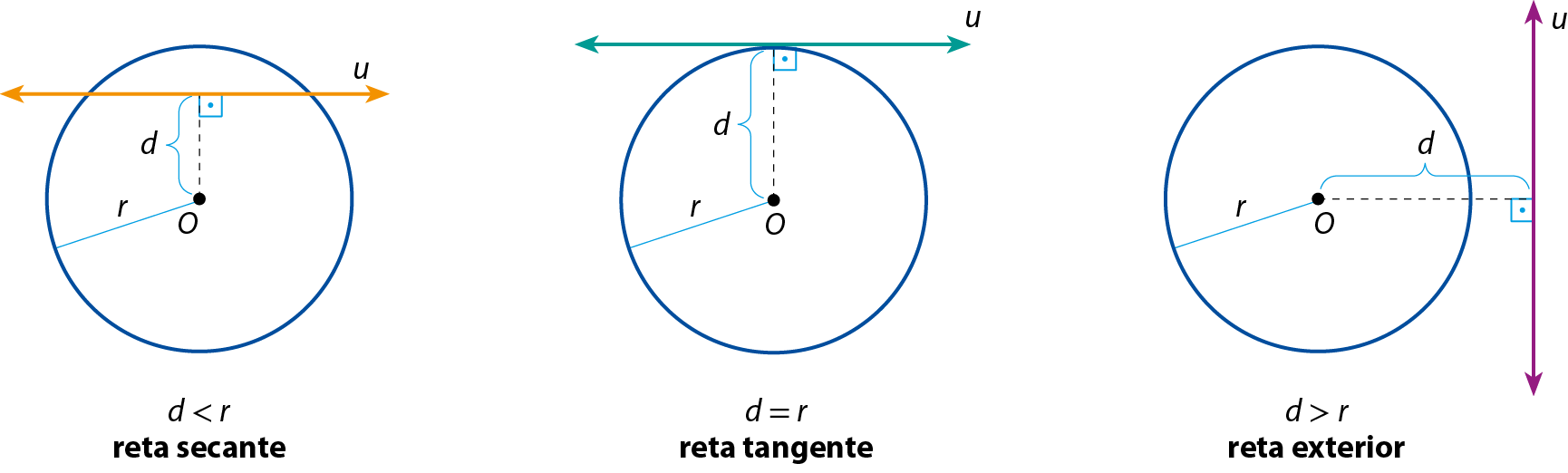
Em relação a uma circunferência, uma reta pode ser secante, tangente ou exterior.
• Secante: quando a reta tem dois pontos em comum com a circunferência.
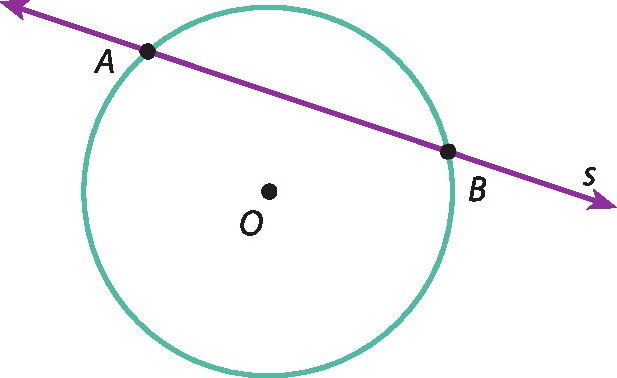
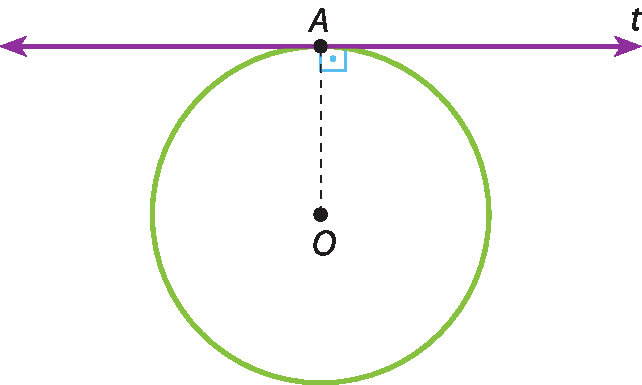
• Tangente: quando a reta tem só um ponto em comum com a circunferência.
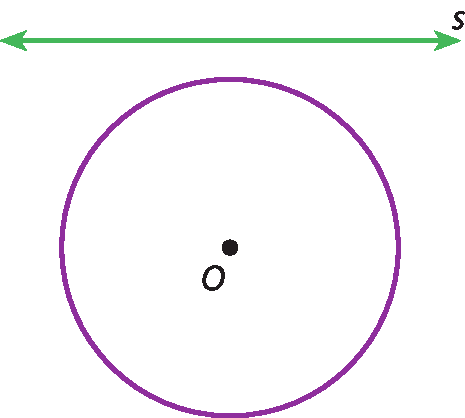
• Exterior (ou externa): quando a reta não tem ponto em comum com a circunferência.
Representando por d a medida da distância do centro da circunferência à reta e por r a medida do raio, temos:
Observação
▶ Toda reta tangente a uma circunferência é perpendicular ao raio traçado pelo ponto de tangência.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
20 Considere a figura a seguir.
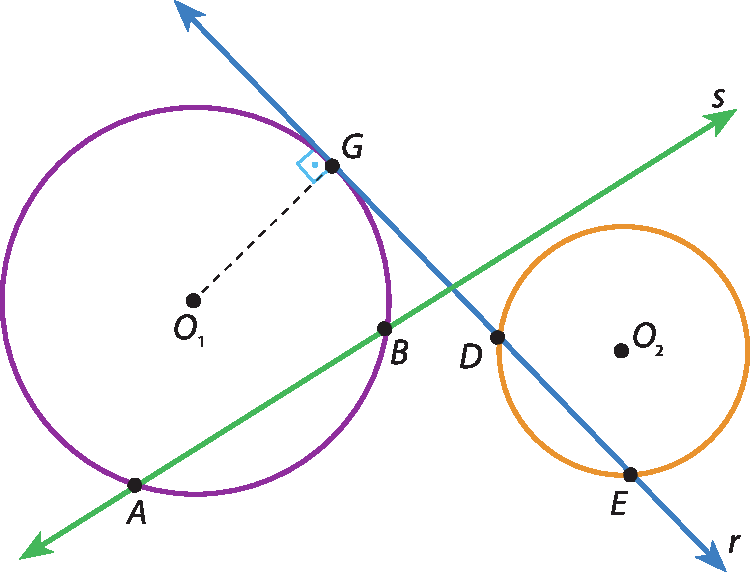
Agora, classifique:
a) a reta r em relação à circunferência de centro
O1;
b) a reta r em relação à circunferência de centro
O2;
c) a reta s em relação à circunferência de centro
O1;
d) a reta s em relação à circunferência de centro
O2.
21 Com régua e compasso, trace a circunferência de raio r e a reta s cuja medida da distância até o centro da circunferência é d. Depois, classifique a reta s em relação à circunferência.
a) r = 1,5 centímetro; d = 1 centímetro
b) r = 1,5 centímetro; d = 1,5 centímetro
c) r = 1,5 centímetro; d = 2 centímetros
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
22

Reúna-se com um colega e, em seguida, respondam às questões.
Uma metalúrgica produziu uma placa retangular de alumínio de medidas 20 centímetros por 15 centímetros. Os operários recortaram dois círculos dessa placa, como mostra a figura.
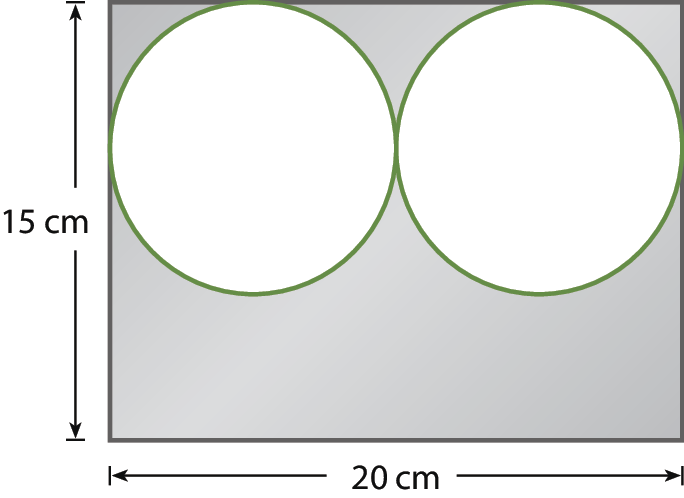
a) Com a sobra da placa, os operários recortaram outros quatro círculos idênticos e com raios de maior medida possível. Qual é a medida do raio desses círculos?
b) Considerando os círculos do item a, determine quantas placas serão necessárias para obter 120 desses círculos menores.
c) Se quiséssemos obter, com essas placas, novos círculos de raios cujas medidas fossem metade dos círculos menores do item a, quantas placas seriam necessárias para obter 48 desses círculos?
Posições relativas de duas circunferências
Vamos considerar a circunferência de centro
O1e raio de medida
r1e a circunferência de centro
O2e raio de medida
r2, com
r1 maior que r2. Além disso, vamos indicar por d a medida da distância entre os centros
O1 e O2De acôrdo com a posição relativa que apresentam, as circunferências podem ser secantes, tangentes exteriores, tangentes interiores, externas ou internas.
• Secantes: quando as circunferências têm dois pontos comuns, e a medida da distância entre seus centros é menor que a soma das medidas de seus raios e maior que a diferença entre elas.
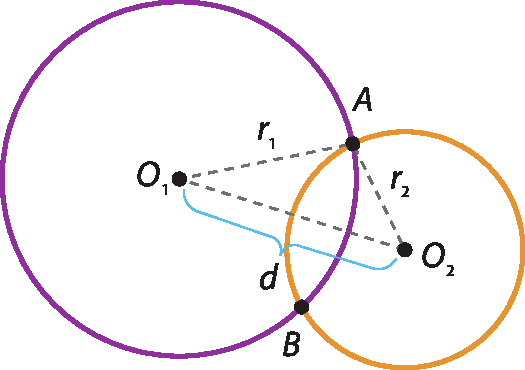
d <
r1 mais r2e d >
r1 menos r2• Tangentes exteriores: quando as circunferências têm um só ponto em comum, e a medida da distância entre seus centros é igual à soma das medidas de seus raios.
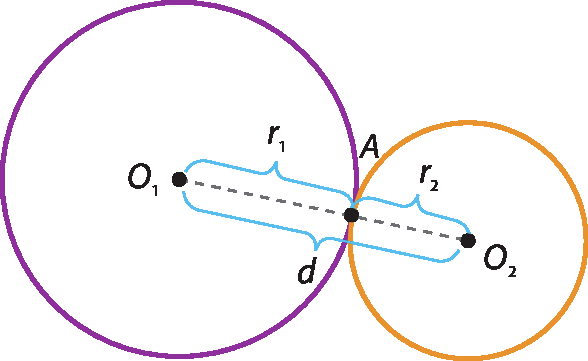
• Tangentes interiores: quando as circunferências têm um só ponto em comum, e a medida da distância entre seus centros é igual à diferença entre as medidas de seus raios.
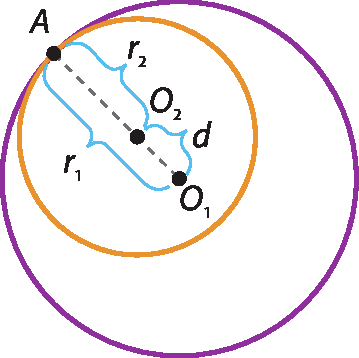
• Externas: quando as circunferências não têm ponto em comum, e a medida da distância entre seus centros é maior que a soma das medidas de seus raios.
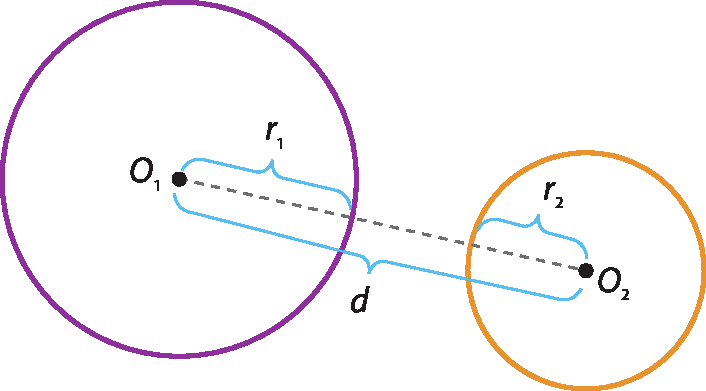
• Internas: quando as circunferências não têm ponto em comum, e a medida da distância entre seus centros é menor que a diferença entre as medidas de seus raios.
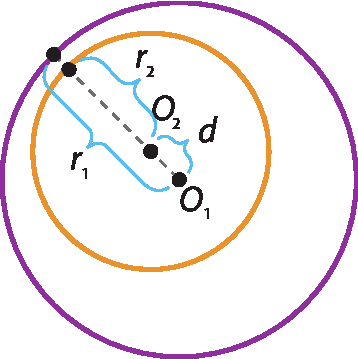
d < r1 ‒ r2
Acompanhe um exemplo.
Considere duas circunferências, uma de raio medindo r1 = 5 centímetros e outra de raio medindo r2 = 3 centímetros. Indicando por d a medida da distância entre os centros dessas circunferências, vamos determinar a posição relativa das circunferências nos seguintes casos:
a) d = 10 centímetros
b) d = 8 centímetros
c) d = 2 centímetros
d) d = 1 centímetro
e) d = 4 centímetros
Calculamos a soma das medidas dos raios e a diferença entre essas medidas.
• r1 + r2 = 5 centímetros + 3 centímetros = 8 centímetros
• r1 ‒ r2 = 5 centímetros ‒ 3 centímetros = 2 centímetros
a)
10 é maior que 8 abre parênteses d é maior que r1 mais r2 fecha parênteses

As circunferências são externas.
b)
8 é igual a 8 abre parênteses d é igual a r1 mais r2 fecha parênteses

As circunferências são tangentes exteriores.
c)
2 é igual a 2 abre parênteses d é igual a r1 menos r2 fecha parênteses

As circunferências são tangentes interiores.
d)
1 é menor que 2 abre parênteses d é menor que r1 menos r2 fecha parênteses

As circunferências são internas.
e) 4 > 2 e 4 < 8
abre parênteses d é maior que r1 menos r2 e d é menor que r1 mais r2 fecha parênteses

As circunferências são secantes.
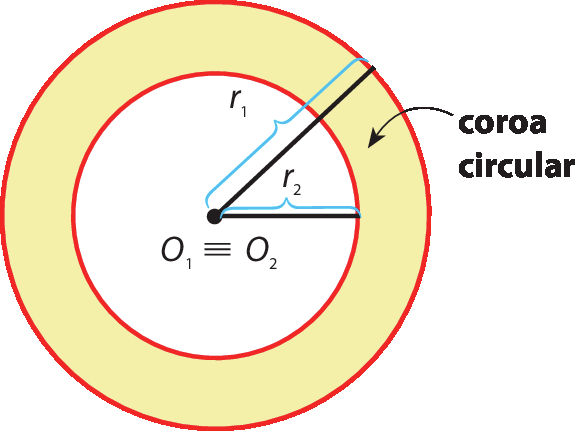
Circunferências concêntricas
Um caso particular de circunferências internas é aquele em que ambas têm o mesmo centro. Elas são chamadas de circunferências concêntricas, e a parte do plano compreendida entre elas recebe o nome de coroa circular.

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
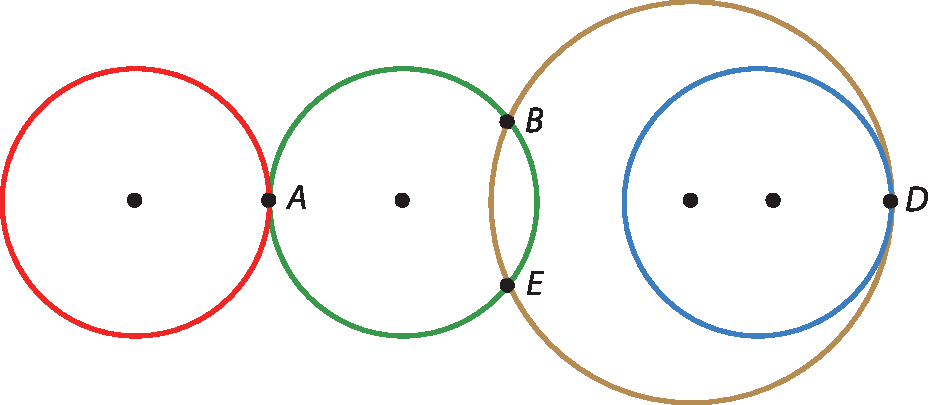
23 Dê a posição relativa das circunferências:
a) vermelha e verde;
b) vermelha e marrom;
c) verde e marrom;
d) marrom e azul.
Versão adaptada acessível
23. Represente 4 circunferências: C1, C2, C3 e C4, de modo que:
• C1 e C2 sejam tangentes exteriores;
• C2 e C3 sejam secantes;
• C1 e C3 sejam externas;
• C3 e C4 sejam tangentes exteriores.
24 Na figura, estão desenhados os aros olímpicos que representam a união dos cinco continentes.

Dê a posição relativa das circunferências das coroas circulares representadas pelas cores:
a) azul e amarela;
b) verde e vermelha;
c) preta e vermelha.
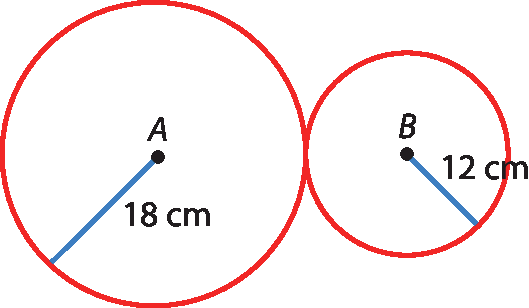
25 Determine a medida da distância entre os centros das seguintes circunferências:
a)
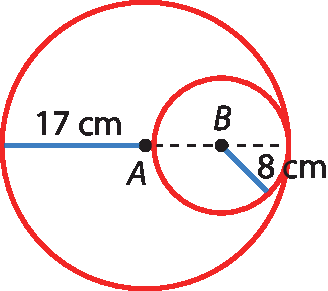
b)
c)
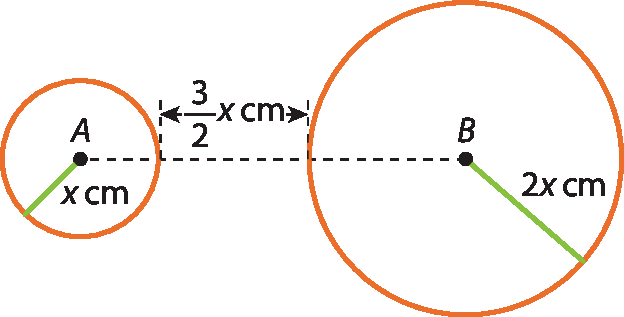
26 Indicando as medidas dos raios de duas circunferências por
r1 e r2e a medida da distância entre os centros por d, dê a posição delas quando:
a)
r1= 4 centímetros,
r2= 5 centímetros e d = 9 centímetros;
b)
r1= 3 centímetros,
r2= 5 centímetros e d = 10 centímetros;
c)
r1= 6 centímetros,
r2= 4 centímetros e d = 2 centímetros;
d)
r1= 6 centímetros,
r2= 4 centímetros e d = 8 centímetros;
e)
r1= 6 centímetros,
r2= 4 centímetros e d = 1 centímetro;
f)
r1= 7 centímetros,
r2= 5 centímetros e d = 0.
3. Segmentos tangentes a uma circunferência
Em seus projetos, a indústria automobilística enfrenta inúmeras questões para obter um produto com bom desempenho e sucesso. Uma questão importante é a medida da distância d entre eixos, por exemplo. Outra questão é sobre as medidas das distâncias
d1entre o eixo da roda e a frente do carro e
d2entre o eixo da roda e a traseira do carro.
Observe na figura que a soma
d1 mais d mais d2fornece a medida do comprimento do veículo.

Note que os triângulos cujos lados tangenciam as rodas no contato com o chão são triângulos retângulos, pois os raios nesses pontos são verticais e a linha do chão é horizontal. Os outros dois triângulos também são triângulos retângulos, pois são simétricos àqueles.
Vamos considerar a circunferência de centro óh e raio de medida r e um ponto P externo a ela.
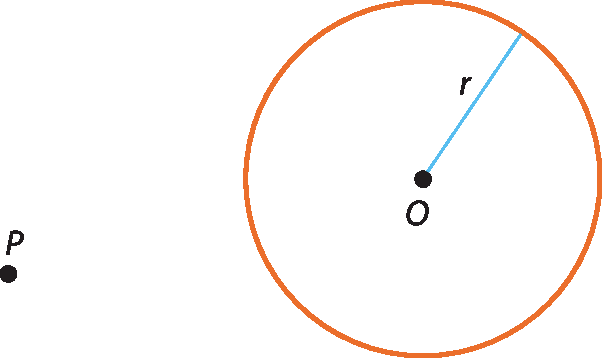
Vamos traçar por P os segmentos tangentes à circunferência:
segmento PAe
segmento PB.
Lembrando que, se a reta
PAé tangente à circunferência em A, então ela é perpendicular ao raio
OA. Do mesmo modo, a reta
PBé perpendicular ao raio
OB.
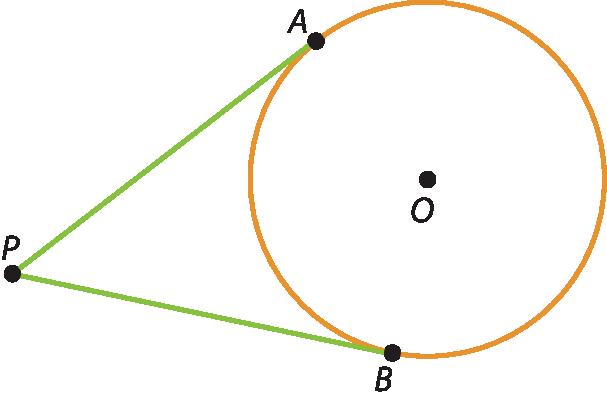
Com a régua, unimos os pontos a, B e P ao centro óh, obtendo os triângulos retângulos PAO e PBO. Como a reta
P Oé um eixo de simetria, esses triângulos são congruentes. Assim:
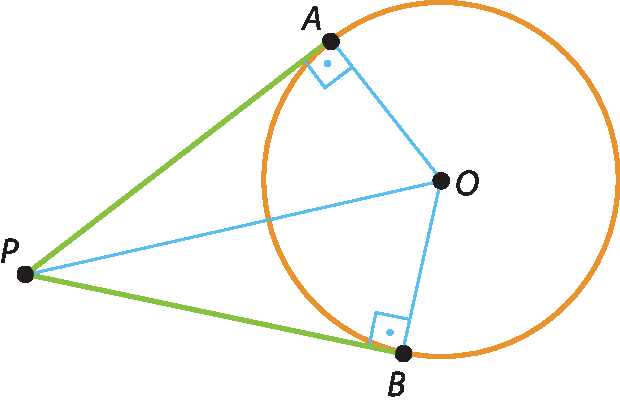
Os segmentos tangentes traçados de um mesmo ponto exterior a uma circunferência são congruentes.
Acompanhe alguns exemplos.
Vamos calcular o valor de xis em cada uma das figuras.
a)
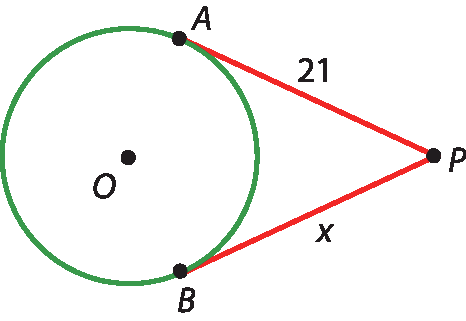
Como
segmento de reta P A é congruente ao segmento de reta PB, obtemos:
x = 21
b)
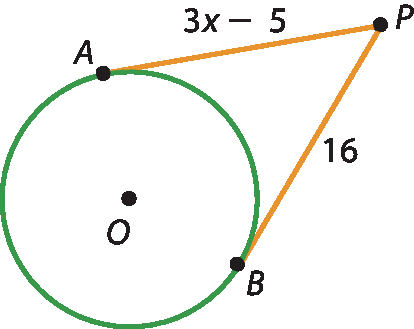
Como
segmento de reta P A é congruente ao segmento de reta PB, obtemos:
3x ‒ 5 = 16
3x = 21
x = 7
c)
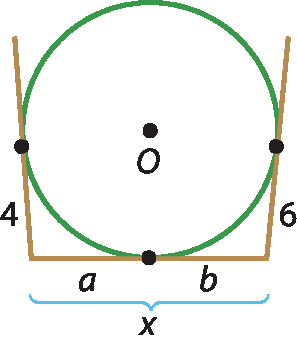
Como a = 4 e b = 6, obtemos:
x = 4 + 6
x = 10
Triângulo circunscrito
Um triângulo é circunscrito a uma circunferência quando seus lados são tangentes a ela. Nesse caso, dizemos que a circunferência é inscrita no triângulo.
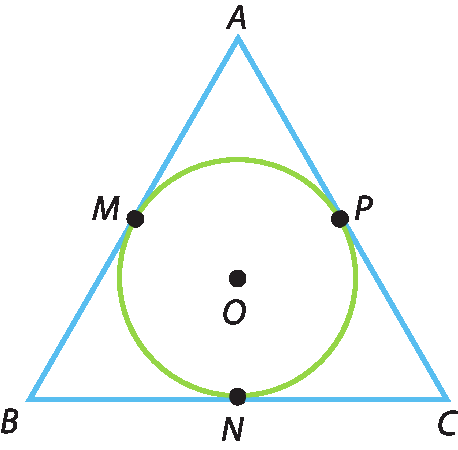
Na figura a seguir, o triângulo á bê cê é circunscrito à circunferência. Os pontos M, N e P são chamados de pontos de tangência.
Acompanhe um exemplo de aplicação.
Vamos calcular a medida do lado
ABdo triângulo ABC.
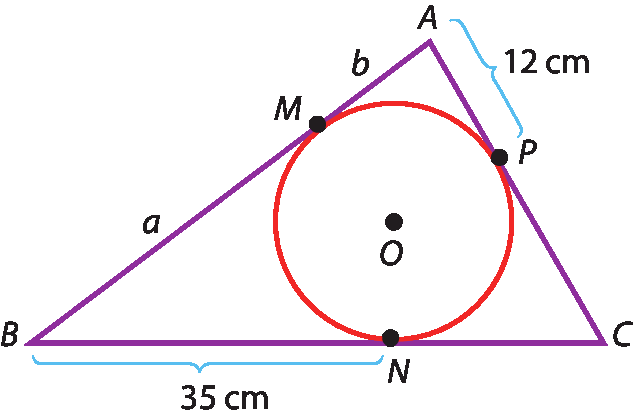
Como a = 35 centímetros e b = 12 centímetros, obtemos:
medida do(
AB) = 35 centímetros + 12 centímetros
medida do(
AB) = 47 centímetros
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
27 Calcule os valores de x, a e b.
a)
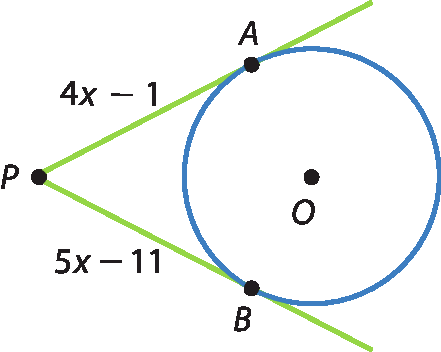
b)
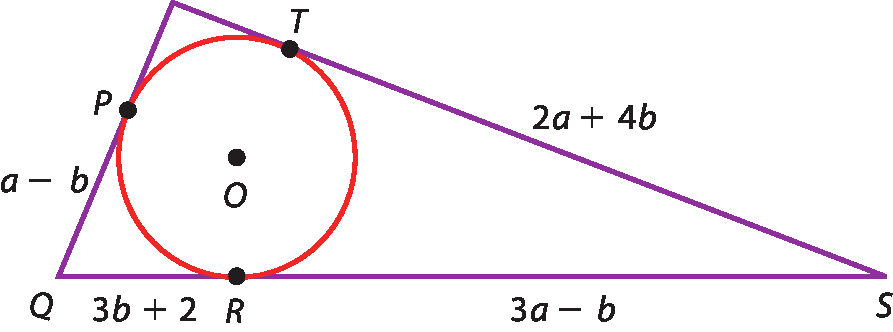
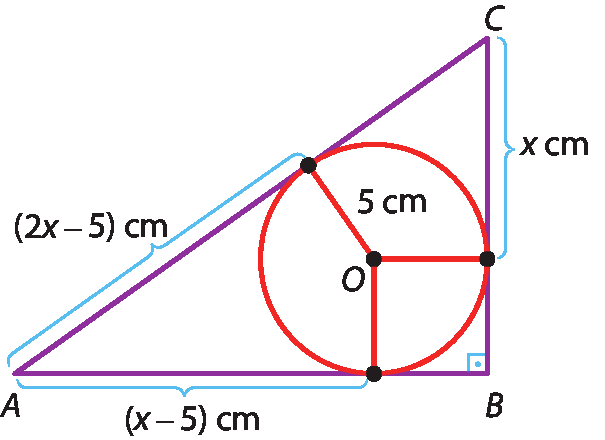
28 Determine o valor de xisponto
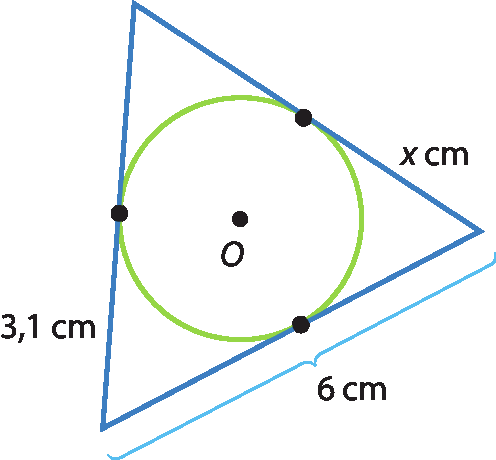
29 Calcule a medida do perímetro do triângulo.
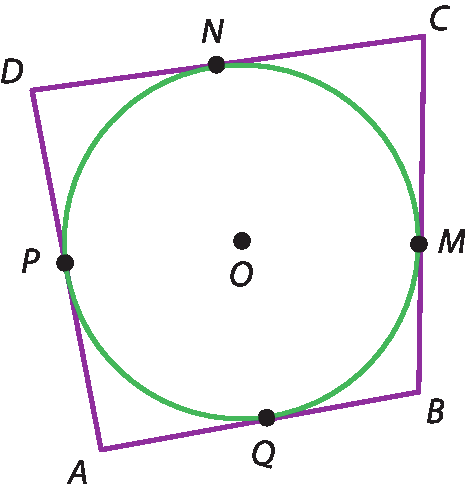
Quadrilátero circunscrito
Um quadrilátero é circunscrito a uma circunferência quando todos os seus lados são tangentes a ela. Nesse caso, dizemos que a circunferência é inscrita no quadrilátero.
Na figura, o quadrilátero a bê cê dê é circunscrito à circunferência.
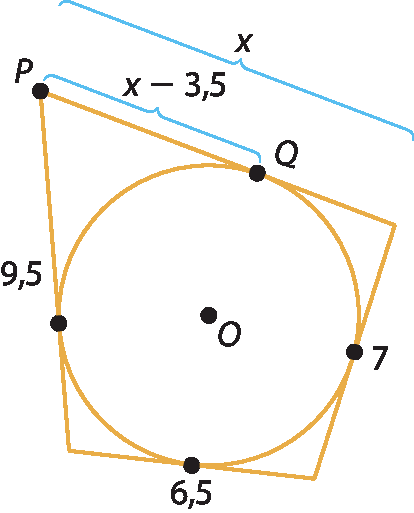
Considere a figura a seguir, que representa o quadrilátero a bê cê dê circunscrito à circunferência. Vamos calcular a soma das medidas dos lados opostos.
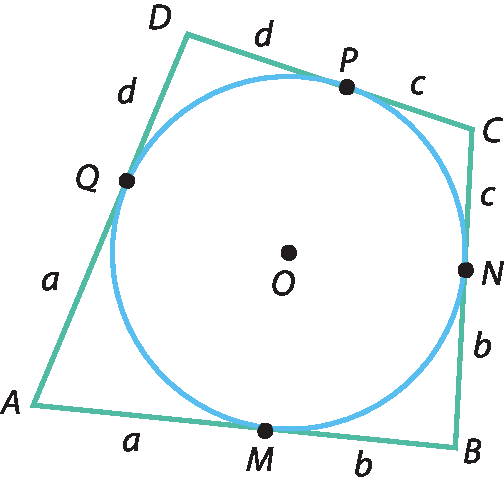
Logo: A bê + cedê = bê cê + á dê
Em todo quadrilátero circunscrito a uma circunferência, as somas das medidas dos lados opostos são iguais.
A propriedade recíproca, que não será demonstrada, também vale.
Se as somas das medidas dos lados opostos de um quadrilátero são iguais, então ele é circunscrito a uma circunferência.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
30 As medidas dos lados de um quadrilátero a bê cê dê são A bê = 4 centímetros, BC = 3 centímetros, cedê = 6 centímetros e á dê = 5 centímetros. Esse quadrilátero pode ser circunscrito a uma circunferência? Por quê?
31 Um trapézio isósceles é circunscrito a uma circunferência, e suas bases medem 11 centímetros e 7 centímetros. Quanto mede cada um dos outros dois lados?
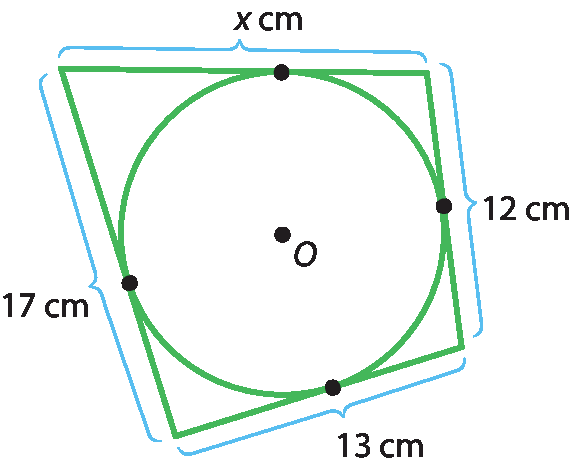
32 Calcule o valor de xis em cada figura.
a)
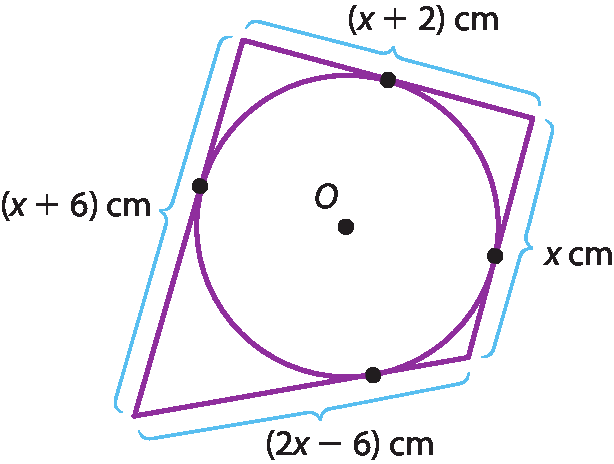
b)
33 José fez um esquema à mão livre de como gostaria que fosse construída uma piscina circular no terreno dele. Observe.
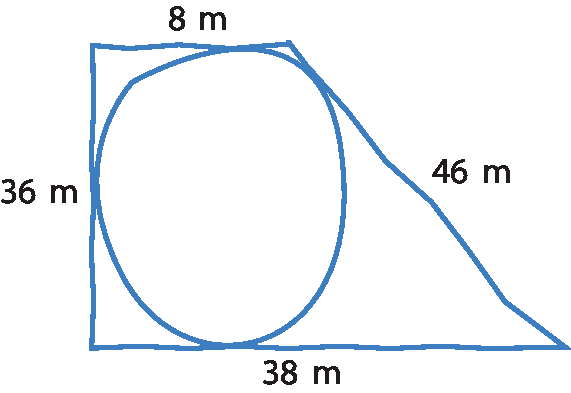
É possível construir a piscina de acôrdo com o esquema que José fez? Justifique sua resposta.
34 Um quadrilátero a bê cê dê é circunscrito a uma circunferência. As medidas de seus lados são á dê = 12 centímetros, dê cê = 9 centímetros, bê cê = (x + 7) centímetros e A bê = (2x + 1) centímetros. Calcule a medida do perímetro desse quadrilátero.
4. Arco de circunferência e ângulo central
Arco de circunferência
Dois pontos distintos de uma circunferência dividem-na em duas partes. Cada uma dessas partes é chamada de arco.
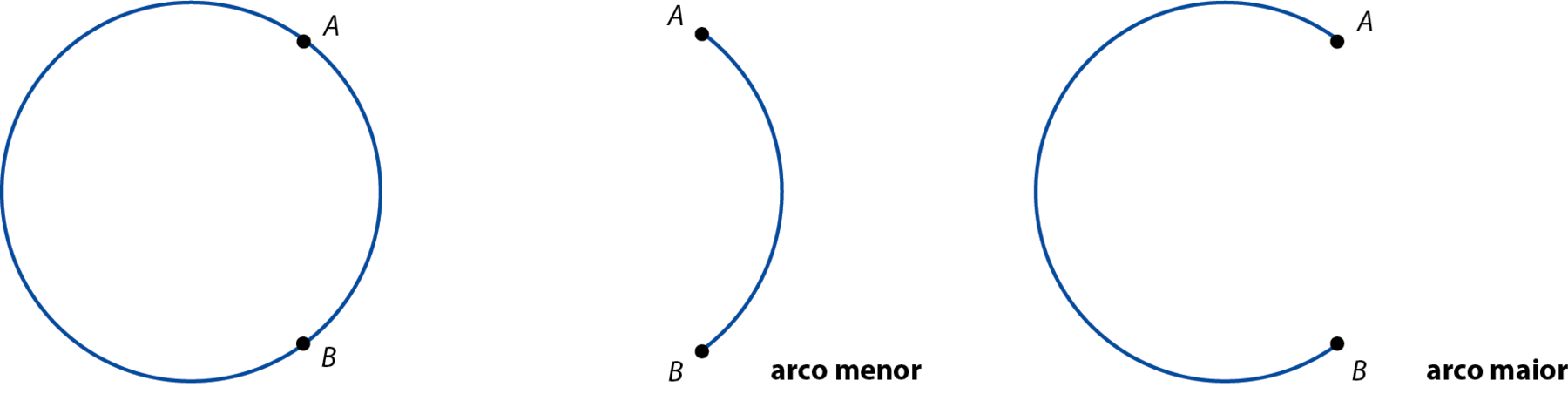

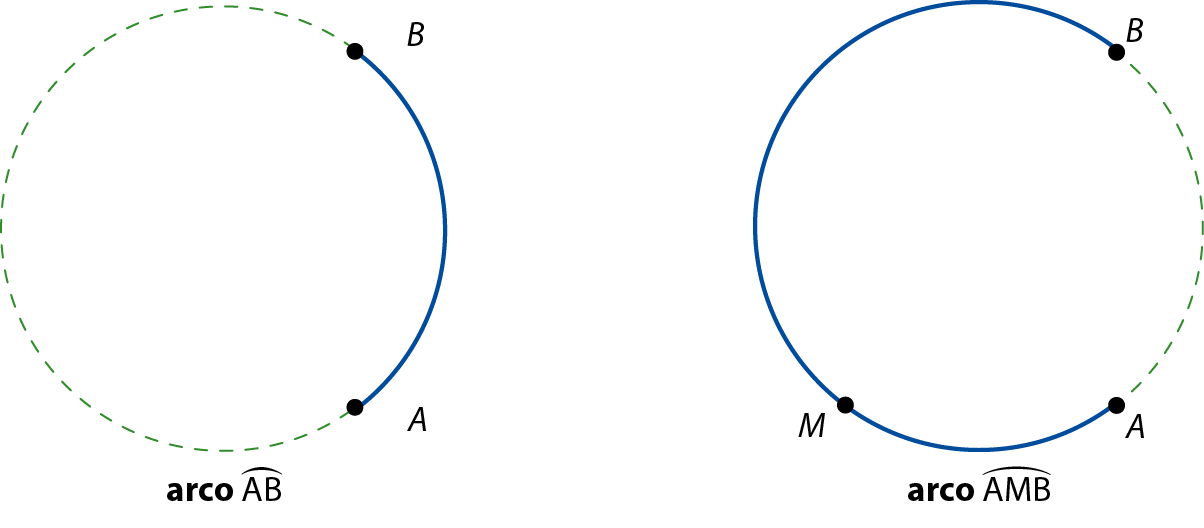
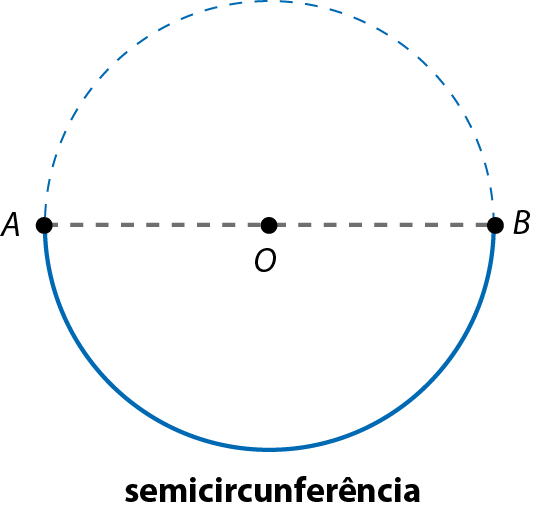
Quando os extremos a e bê coincidirem com os extremos de um diâmetro, cada um dos arcos será chamado de semicircunferência.
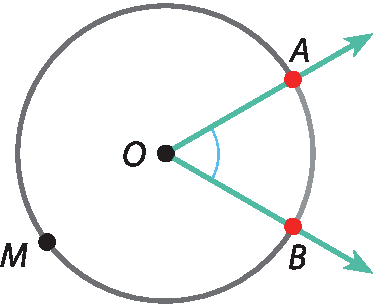
Ângulo central
Ângulo central é todo ângulo que tem seu vértice no centro de uma circunferência.
Na figura,
ângulo AOBé um ângulo central, e
arco ABé o arco correspondente a esse ângulo.
Dividindo uma circunferência em trezentas e sessenta partes de mesmo tamanho, determinamos 360 ângulos centrais, cada um deles de medida 1 grau (1pequeno círculo sobrescrito). A cada um desses ângulos centrais corresponde um arco cuja medida angular é 1 grau (1pequeno círculo sobrescrito). Assim, podemos afirmar que 1grau corresponde a
um trezentos e sessenta avosda circunferência, ou seja, a circunferência mede 360graus.
A medida angular de um arco de circunferência é igual à medida do ângulo central correspondente.
O sistema de medida de arcos é sexagesimal; portanto, são necessários 60 minutos (60linha) para obter 1grau, e 60 segundos (60aspas) para obter 1minutos. Acompanhe alguns exemplos.
a)
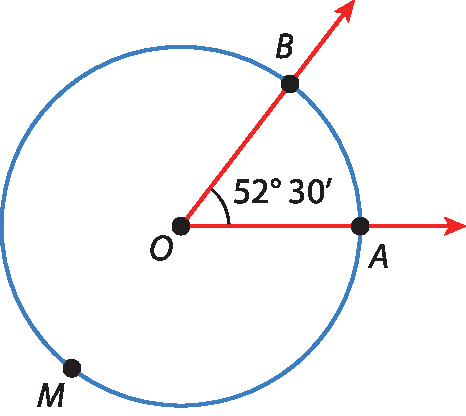
medida do(
arco AB) = 52graus 30linha
medida do(
arco AMB) = 360graus ‒ 52graus 30linha
medida do(
arco AMB) = 307graus 30linha
b)
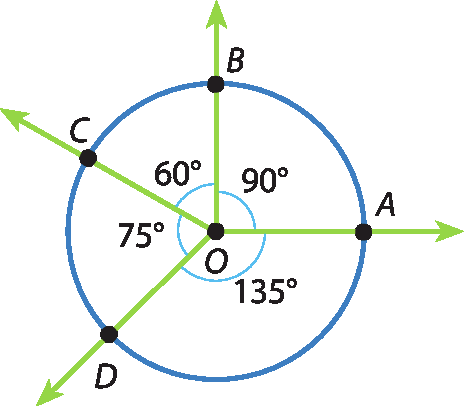
medida do(
arco AB) = 90graus
medida do(
arco BC) = 60graus
medida do(
arco CD) = 75graus
medida do(
arco AD) = 135graus
c)
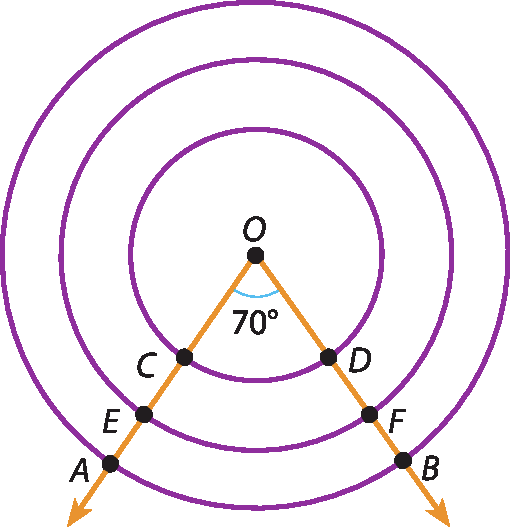
medida do(
arco AB) = 70graus
medida do(
arco CD) = 70graus
medida do(
arco EF) = 70graus

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
35 Observe as figuras a seguir.
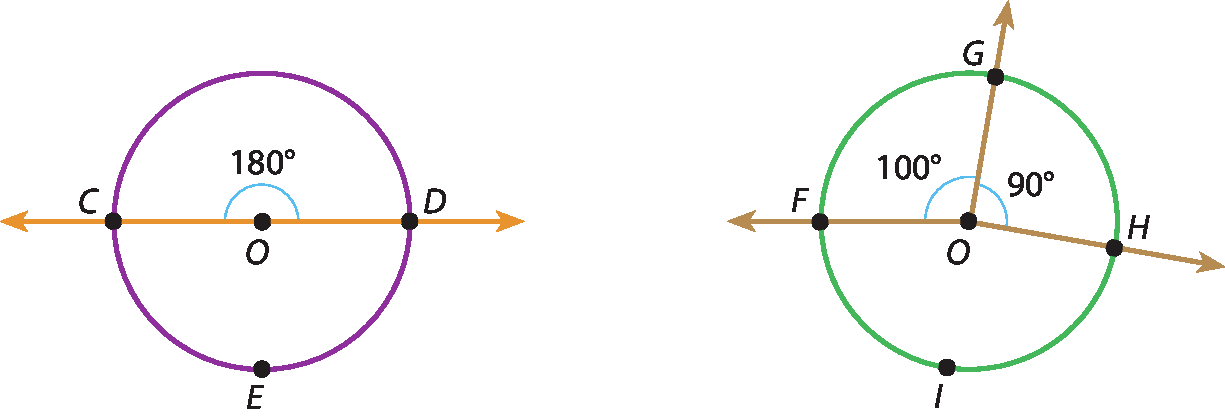
Agora, determine:
a) medida do(
arco CD)
b) medida do(
arco CED)
c) medida do(
arco HGF)
d) medida do(
arco FIH)
36 Determine, em grau, o valor de xis e de y nas figuras a seguir.
a)
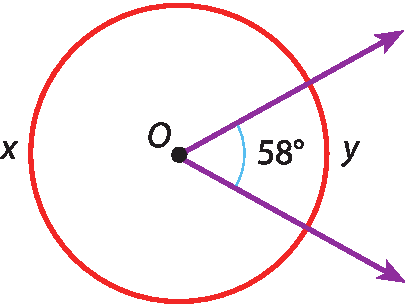
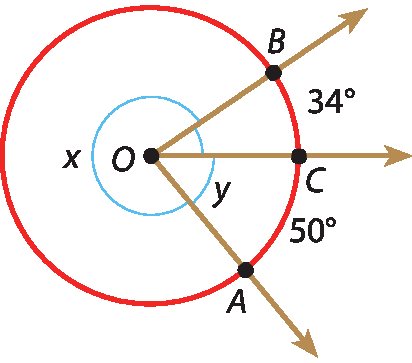
b)
37 Foi realizada uma pesquisa sobre a região de moradia de .1200 associados do Clube da Boa Viagem. Os resultados foram registrados no gráfico de setores.
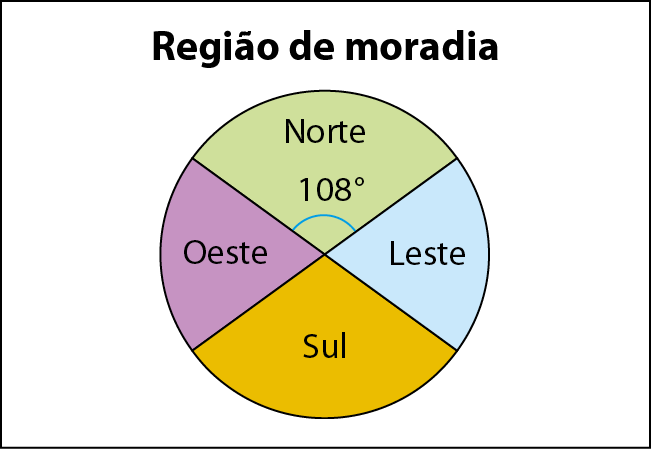
Agora, responda às questões.
a) Qual é a medida do ângulo central de cada setor?
b) Qual é a porcentagem de pessoas correspondente a cada setor?
c) Quais são as regiões de moradia que predominam nesse grupo de pessoas?
5. Ângulo inscrito
Ângulo inscrito é todo ângulo cujo vértice pertence à circunferência e cujos lados são semirretas secantes a ela.
Na figura,
ângulo ABCé um ângulo inscrito na circunferência.
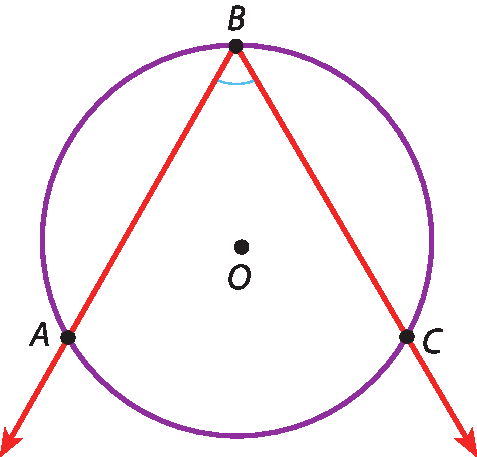
Vamos demonstrar o seguinte teorema:
A medida do ângulo inscrito é igual à metade da medida angular (em grau) do arco compreendido por seus lados.
Hipótese:
ângulo ABCé ângulo inscrito
Tese:
ângulo ABC igual a fração de arco AC sobre 2• Demonstração
Construção auxiliar: traçamos
semirreta BDpassando pelo centro O; traçamos também
segmento de reta OA e
segmento de reta OC.
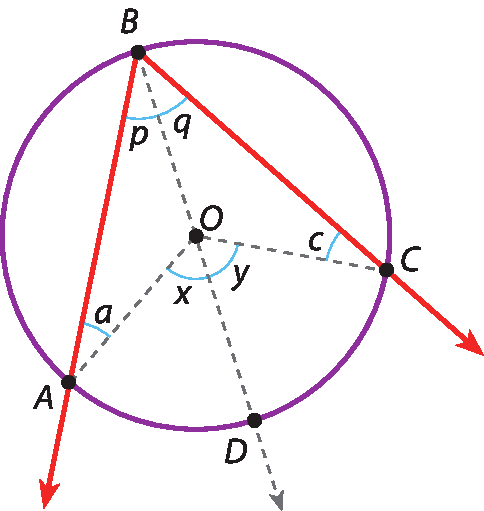
Assim, temos:

x = a + p e y = c + q (ângulos externos de um triângulo)

a = p e c = q (A bê ó e cê bê ó são triângulos isósceles)

x = 2p e y = 2q (substituindo a por p e c por q em

)

x + y = 2p + 2q (adicionando membro a membro)

x + y = 2( p + q ), ou seja,
p mais q é igual a fração, numerador: x + y, denominador: 2
x = m(
arco AD) e y = medida do(
arco DC) (medida do ângulo central)
Como p + q = medida do(
ângulo ABC) (por construção) e x + y = medida do(
ângulo AOC), então medida do(
ângulo ABC) =
medida do arco AC sobre 2EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
38 Determine, em grau, o valor de x nas figuras.
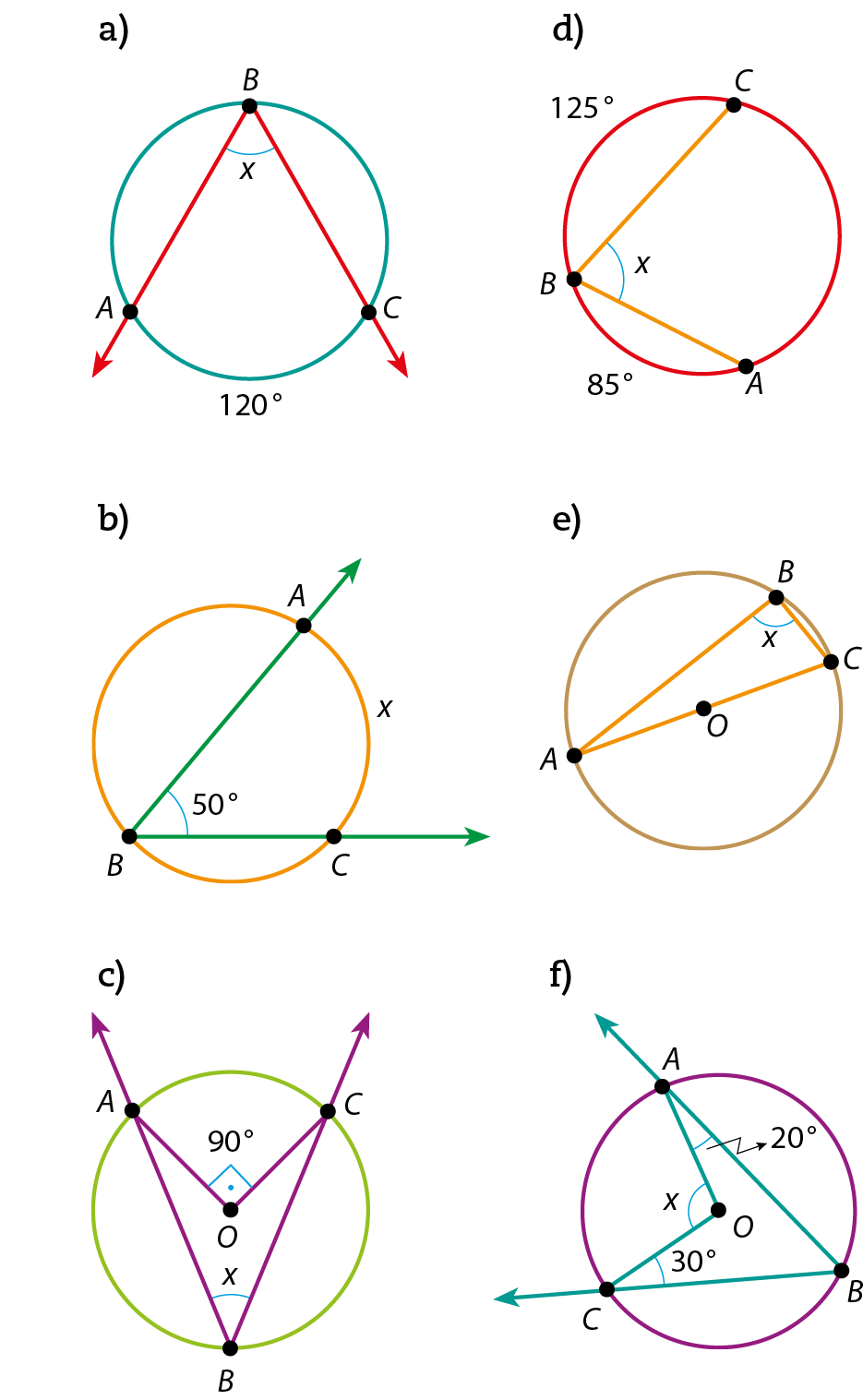
39 Observe as figuras e determine, em grau, o valor de x e de y.
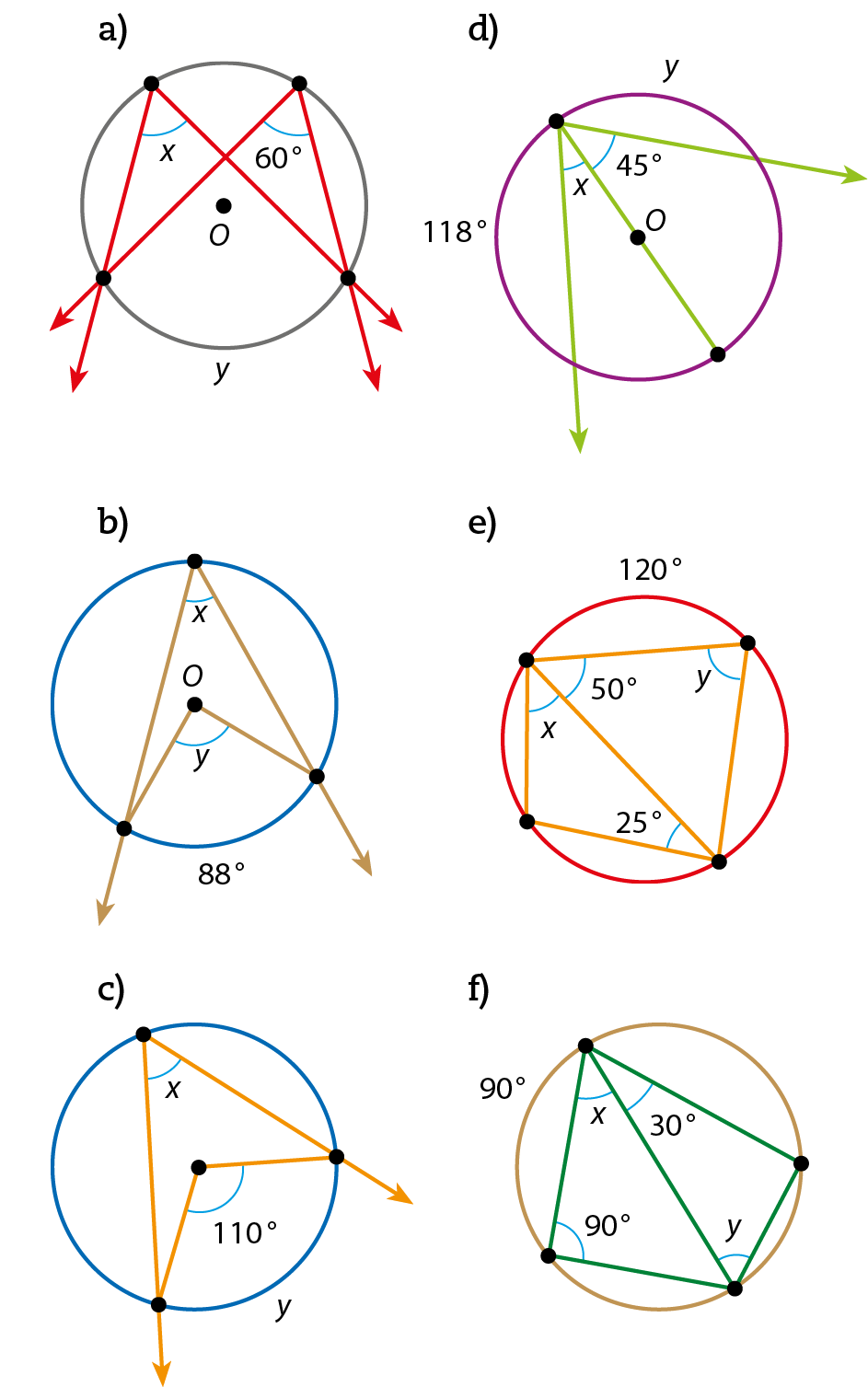
6. Ângulos cujos vértices não pertencem à circunferência
Já estudamos o ângulo central (com vértice coincidente com o centro da circunferência) e ângulos inscritos (com vértice na circunferência). Agora, vamos estudar os demais casos.
Considere a figura a seguir, em que M é um ponto interno à circunferência e x é a medida do ângulo
ângulo BMC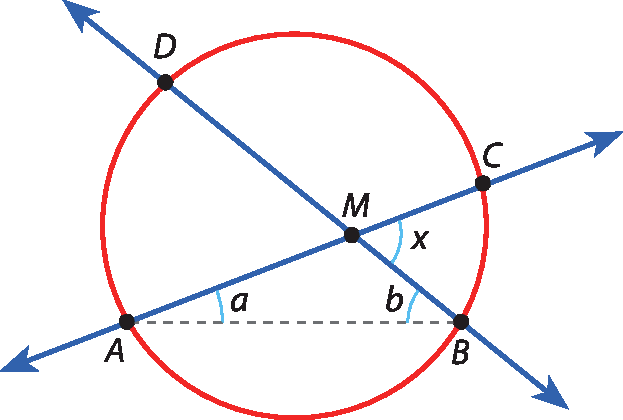
Vamos provar que:
x é igual a medida arco BC mais medida arco AD, tudo sobre 2Traçando o segmento
AB, obtemos o triângulo AMB. Como x é a medida de um ângulo externo não adjacente aos ângulos internos de medidas a e b, temos: x = a + b.
Como
a é igual a medida do arco BC sobre 2e
b é igual a medida do arco AD sobre 2, pois
ângulo ae
ângulo bsão ângulos inscritos, obtemos:
Agora, considere esta outra figura, em que M é um ponto externo à circunferência e x é a medida do ângulo
AMB.
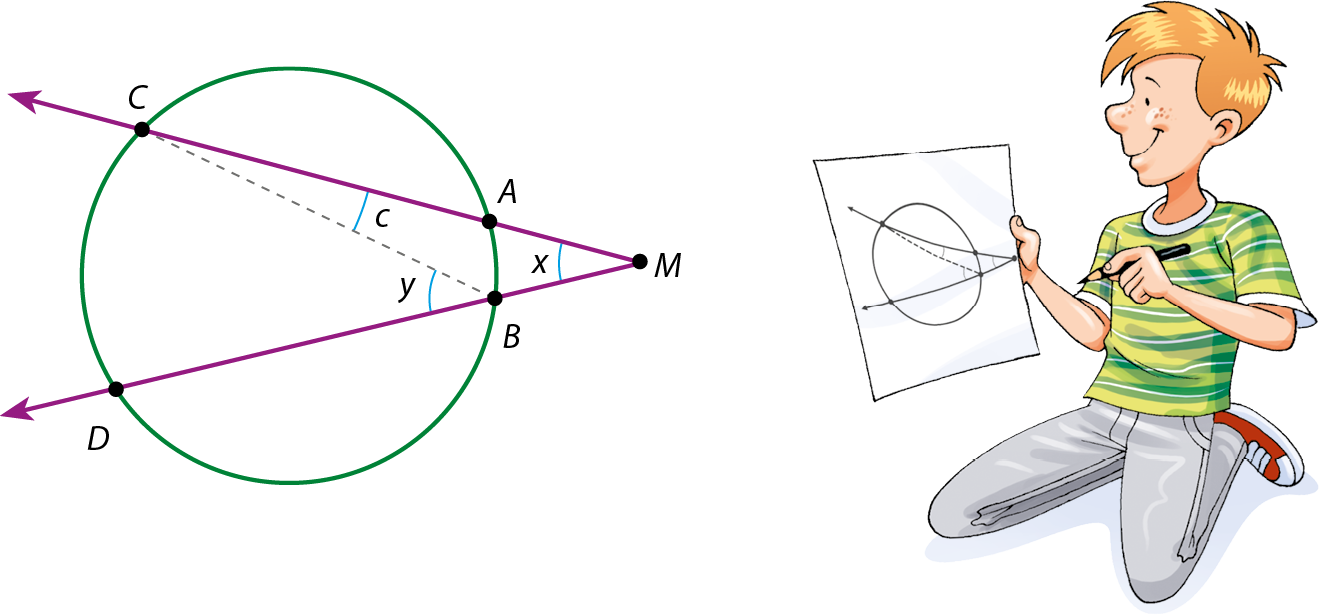
Vamos provar que:
x é igual a medida arco CD menos medida arco AB, tudo sobre 2Traçando o segmento
BC, obtemos o triângulo BMC. Como y é a medida de um ângulo externo não adjacente aos ângulos de medidas c e x, temos: y = c + x ou x = y ‒ c.
Como
y igual a medida do arco CD sobre 2e
c igual a medida do arco AB sobre 2, pois
ângulo ye
ângulo csão ângulos inscritos, obtemos:
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
40 Calcule, em grau, o valor de xis nas figuras.
a)
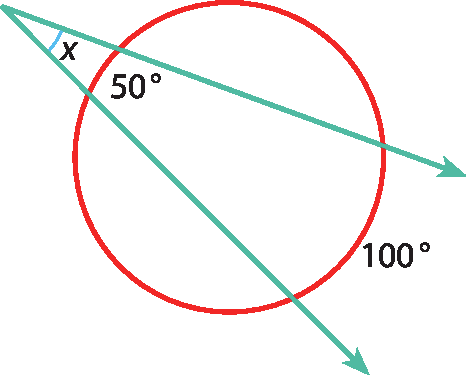
b)
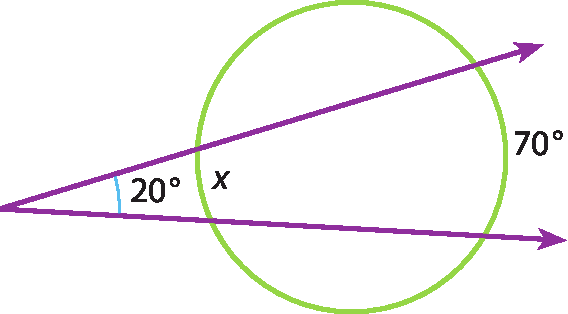
c)
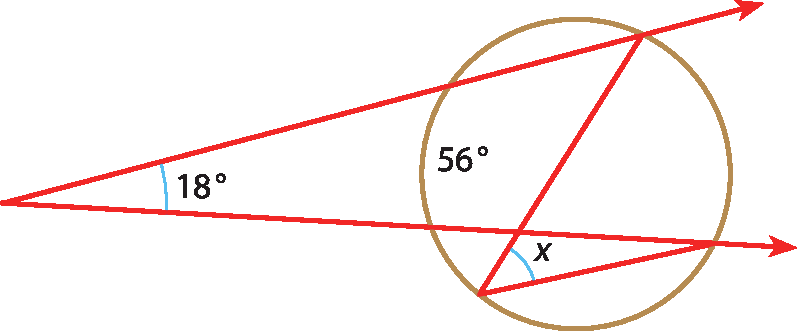
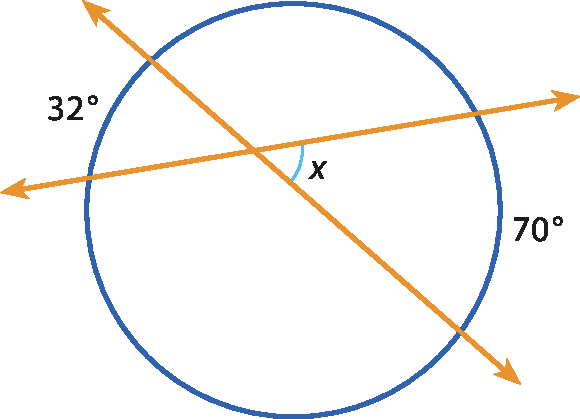
41 Calcule, em grau, o valor de xis nas figuras.
a)
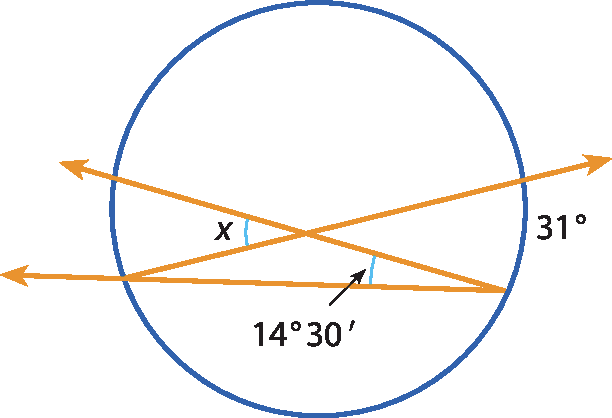
b)
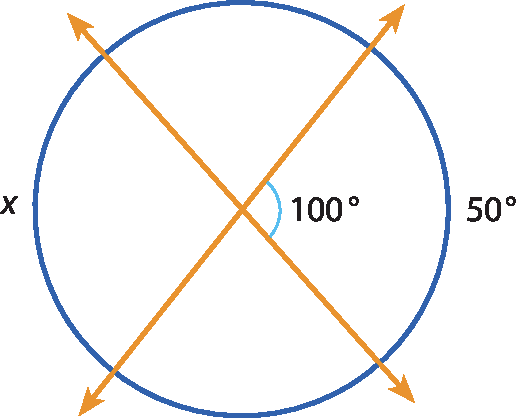
c)
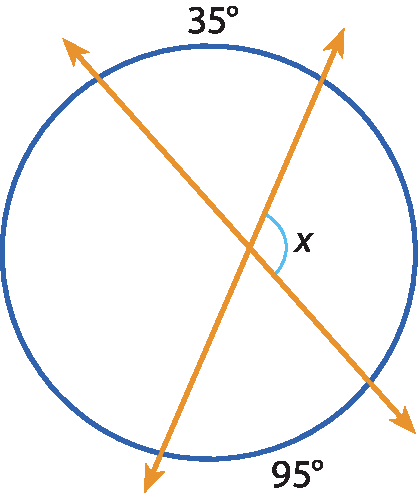
d)
42 (Cesgranrio-Rio de Janeiro) Se, na figura,
medida do arco AB é igual a 20 graus,
medida do arco BC é igual a 124 graus,
medida do arco CD é igual a 36 grause
medida do arco DE é igual a 90 graus, então o ângulo x mede:
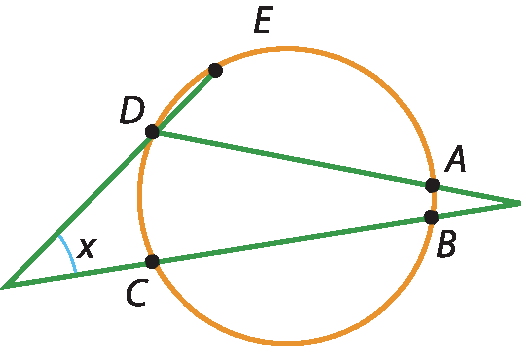
a) 34graus.
b) 35graus 30ʹ.
c) 37graus.
d) 38graus 30ʹ.
e) 40graus.
43 (univáli-Santa Catarina) Considere a figura a seguir.
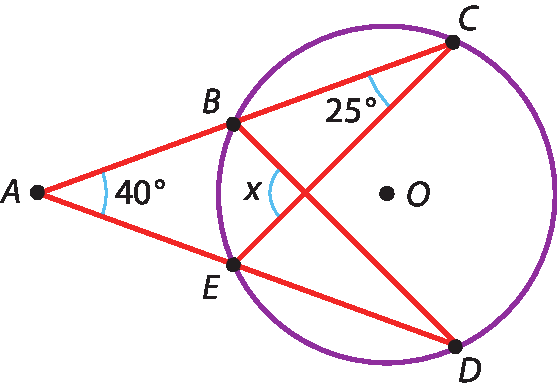
A medida x do ângulo assinalado é:
a) 90graus.
b) 85graus.
c) 80graus.
d) 75graus.
e) 70graus.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Reescreva as sentenças falsas, tornando-as verdadeiras.
a) Um polígono é circunscrito a uma circunferência se seus vértices pertencem à circunferência.
b) O centro de uma circunferência inscrita em um polígono é equidistante de seus lados.
c) As medidas dos segmentos tangentes traçados de um mesmo ponto exterior a uma circunferência são iguais.
d) A medida do ângulo inscrito em uma circunferência é igual à medida do arco compreendido pelos seus lados.
2 Considere que cada circunferência a seguir tem raio medindo 1 centímetro. Calcule a medida do perímetro do retângulo a bê cê dê, sabendo que seus lados são tangentes às circunferências e que elas são tangentes exteriores entre si.
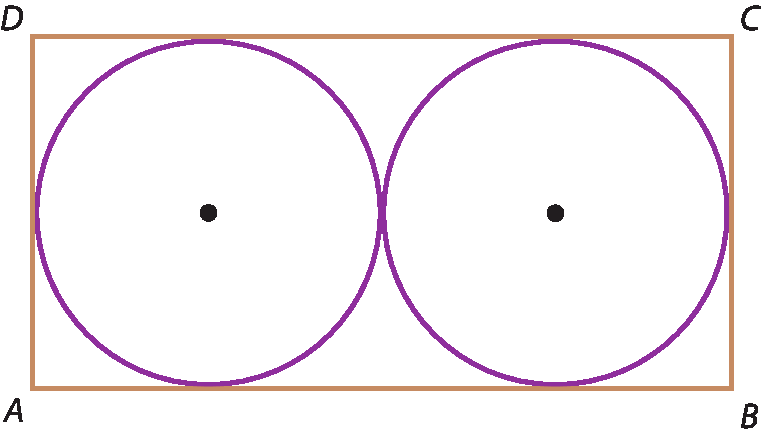
3 Sabendo que o retângulo tem 12 centímetros de medida de perímetro, calcule a medida do raio de cada circunferência.
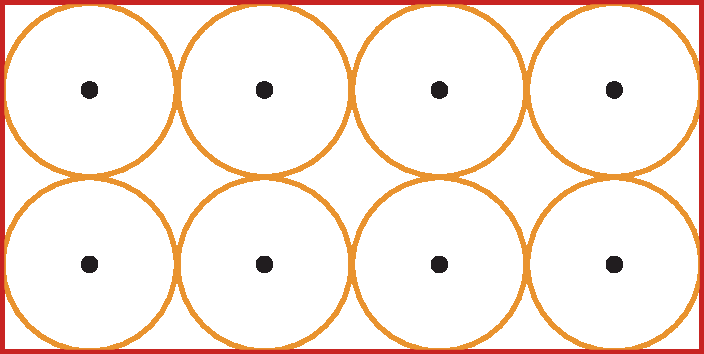
4 Dê a posição relativa das circunferências
C1, de centro
O1e raio de medida
r1, e
C2, de centro
O2e raio de medida
r2, nos seguintes casos:
a)
r1 igual 10 centímetros, r2 igual 4 centímetros e O1 O2 igual 6 centímetrosb)
r1 igual 8 centímetros, r2 igual 2 centímetros e O1 O2 igual 10 centímetrosc)
r1 igual 9 centímetros, r2 igual 6 centímetros e O1 O2 igual 7 centímetrosd)
r1 igual 8 centímetros, r2 igual 4 centímetros e O1 O2 igual 20 centímetrose)
r1 igual 7 centímetros, r2 igual 4 centímetros e O1 O2 igual 1 centímetro5 Calcule a medida do perímetro do quadrilátero circunscrito à circunferência.
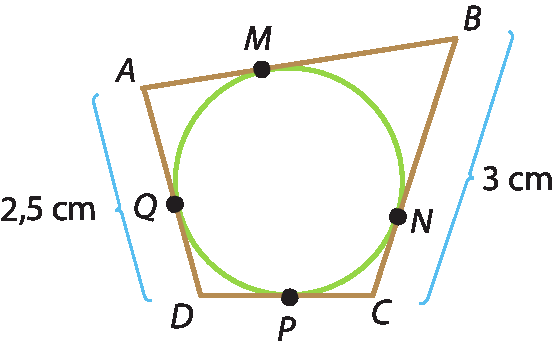
6 Na figura, o valor de xis, em grau, é:
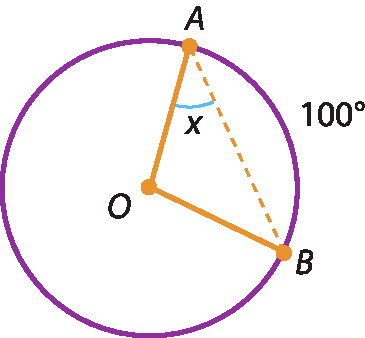
a) 50graus.
b) 80graus.
c) 100graus.
d) 40graus.
7 Na figura, o valor de xis, em grau, é:
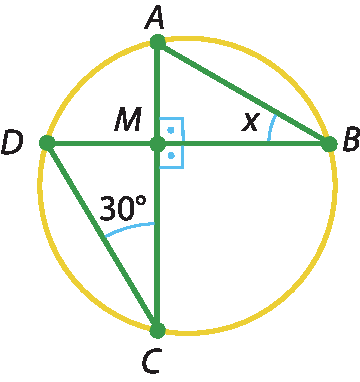
a) 30graus.
b) 60graus.
c) 120graus.
d) 15graus.
8 Calcule, em grau, o valor de x e de y nas figuras a seguir.
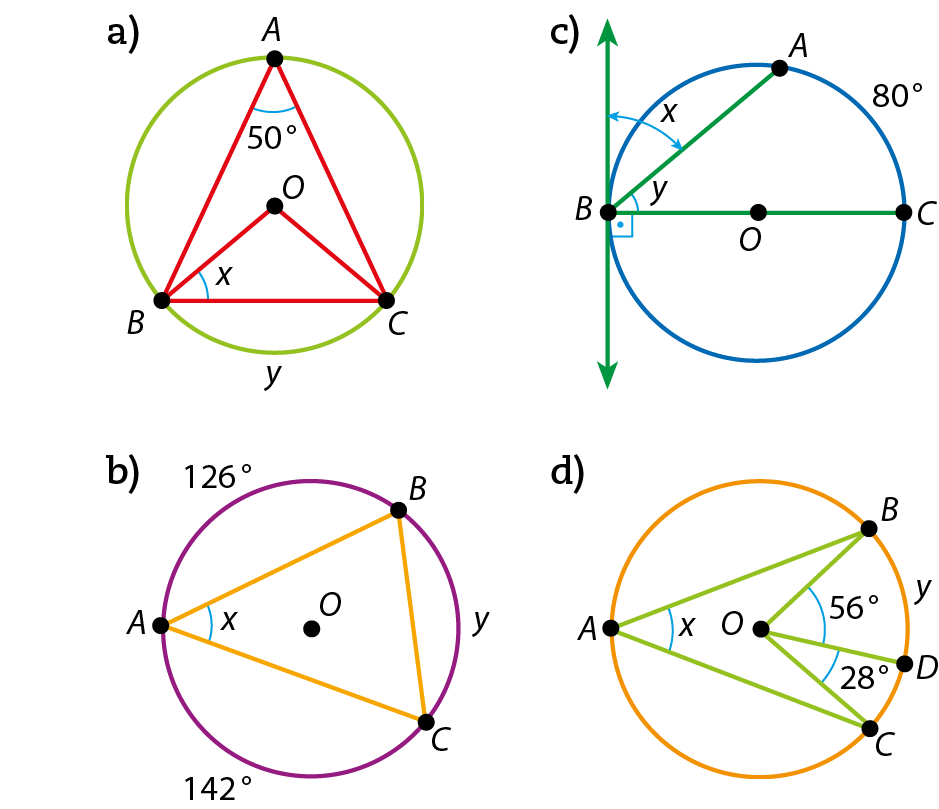
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Considere uma circunferência
C1de centro óh, sendo
segmento de reta ABuma corda, com AB = 2 centímetros. Sabendo que o diâmetro
segmento de reta EFtem medida igual ao triplo da medida de
segmento de reta AB, quais são as medidas de
segmento de reta EFe de
segmento de reta EO?
a) EF = 6 centímetros e EO = 3 centímetros
b) EF = 6 centímetros e EO = 2 centímetros
c) EF = 3 centímetros e EO = 4 centímetros
d) EF = 3 centímetros e EO = 6 centímetros
2 Seja um grupo de circunferências com medidas de diâmetros, em centímetro, dadas pela expressão 6x + 2. Para quais valores de x, em centímetro, as circunferências terão medidas de raio maior que 2 centímetros e menor que 13 cm?
a)
1 terço< x <
onze sextosb) 0 < x < 2
c)
um terço< x < 4
d) 0 < x < 6
3 Qual é a medida aproximada do comprimento de uma circunferência de diâmetro medindo 7 centímetros? (Considere π = 3,14.)
a) 10,99 centímetros
b) 21,98 centímetros
c) 32,97 centímetros
d) 43,96 centímetros
4 Um plano α, contém uma circunferência de centro O e os pontos P, Q e R. As medidas das distâncias desses pontos em relação ao centro O são: ó pê = 6 cm, ó quê = 8 centímetros e ó érre = 3 centímetros. Sabendo que o raio dessa circunferência mede 6 cm, quais são as posições dos pontos P, Q e R em relação à circunferência?
a) P pertence, Q é interno e R é externo.
b) P é interno, Q pertence e R é externo.
c) P é externo, Q pertence e R é interno.
d) P pertence, Q é externo e R é interno.
5 Considere as posições de r, s e t em relação a uma circunferência:
(um) nenhum ponto de r está contido na circunferência;
(dois) s tem dois pontos em comum com a circunferência;
(três) t tem um único ponto em comum com a circunferência.
Considerando as posições das retas r, s e t em relação à circunferência, temos:
a) r é externa, s é secante e t é tangente.
b) r é externa, s é tangente e t é secante.
c) r é secante, s é tangente e t é externa.
d) r é tangente, s é externa e t é secante.
6 Sejam duas circunferências,
C1de raio medindo 12 centímetros e
C2de raio medindo 8 centímetros. Se o centro de
C1está há uma distância de medida igual a 4 centímetros do centro da
C2, qual é a posição relativa entre
C1 e C2?
a) Secantes.
b) Tangentes exteriores.
c) Tangentes interiores.
d) Externas.
7 Considere a circunferência representada a seguir, com raio medindo 4 centímetros. Qual é a medida da área do triângulo pê ó quê?
a) 11 centímetros2
b) 13 centímetros2
c) 15 centímetros2
d) 17 centímetros2
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões.
a) Como você explicaria para um colega a diferença entre círculo e circunferência?
b) Quais são as posições relativas entre um ponto e uma circunferência, entre uma reta e uma circunferência e entre duas circunferências?
c) O que são circunferências concêntricas?
d) Quando um segmento é tangente à uma circunferência?
e) O que é possível afirmar sobre as somas das medidas dos lados opostos de qualquer quadrilátero circunscrito a uma circunferência?
f) Qual é a relação entre a medida angular de um arco de circunferência e a medida do ângulo central correspondente?