
CAPÍTULO 3 Estatística e probabilidade

Um mundo mais desigual é o legado imediato da pandemia [de Covid-19]. [reticências] No topo da pirâmide, um reduzido e seleto clube de multimilionários — 0,001% da população — viu suas fortunas crescerem 14%. Em uma amplíssima base, 100 milhões de pessoas a mais caíram na pobreza extrema. [reticências]
[reticências] [No Brasil,] os 10% mais ricos concentram 59% da renda nacional total, enquanto a metade [menos privilegiada] da população leva apenas cêrca de 10%. [reticências]
Fonte: PELLICER, L.; GRASSO, D. Os 10% mais ricos com 76% do patrimônio do planeta, o retrato da desigualdade na pandemia. El País, Madri, 7 dezembro 2021.
Na fotografia, grande parte de uma comunidade aparece refletida em um só edifício, ilustrando a desigualdade na distribuição de renda e riqueza no Brasil.
Observe, leia e responda no caderno.
a) Esta fotografia revela a desigualdade descrita nos dados estatísticos?
b) A população mundial era, no início de 2022, cêrca de 7,8 bilhões. Quantas pessoas correspondem a 0,001% dessa população?
c) A população brasileira era, no início de 2022, cêrca de 210 milhões. Quantas pessoas correspondem a 50% dessa população? E a 10%?
1. Origem da Estatística
A Estatística é o ramo da Matemática que possibilita coletar, descrever, organizar, analisar e comunicar dados a respeito de uma população ou de um fenômeno.
Os primeiros “dados estatísticos” apareceram há muito tempo, à medida que ocorria o desenvolvimento da escrita. Registros históricos (informações que encontramos em vestígios de civilizações anteriores à nossa) de mais de .2000 anos antes de Cristo apontam o uso de processos que hoje chamaríamos de estatísticos.
Grandes impérios da Antiguidade (como o sumério, o egípcio e o chinês) e da América pré-colombiana (maia, asteca e inca) fizeram uso do levantamento e do registro de dados quantitativos para obter informações sobre sua população e suas riquezas, especialmente para fins administrativos, tributários (relativos ao pagamento de impostos) e militares.

Talvez em virtude dessa aplicação, o termo estatística derive da palavra latina status, que significa “condição, situação”, ou, em sentido mais amplo, “Estado”.
O uso do termo para denominar esse campo de estudo é atribuído a Gottfried Achenwall (1719 a 1772), professor na Universidade de Göttingen, na Alemanha.
Na atualidade, a Estatística é essencial para o desenvolvimento de todas as ciências e está presente no cotidiano por meio de índices, tabelas e gráficos.
Neste capítulo, estudaremos alguns conceitos que esclarecem as mais diversas informações estatísticas, como: população e amostra, maneiras de obtenção e organização de dados em tabelas e gráficos e medidas de tendência central.
2. Coleta, organização e apresentação de dados
Coleta e organização
Uma bióloga fez uma pesquisa sobre a medida do comprimento da cauda dos leões adultos que vivem em determinada região. Durante o estudo, com sua equipe e em segurança, ela verificou o comprimento da cauda de 30 leões e, em seguida, anotou em um quadro as medidas aferidas.

Em Estatística, o conjunto de todos os elementos que contêm uma característica a ser estudada é chamado de população estatística. Na pesquisa realizada pela bióloga, a população estatística corresponde a todos os leões que vivem na região escolhida.
Quando uma pesquisa considera todos os elementos da população, ela é denominada censo. Porém nem sempre é possível pesquisar todos os elementos de uma população estatística, pois, em geral, a população a ser pesquisada é muito grande. Quando isso acontece, limitamos a pesquisa a uma parte da população, que chamamos de amostra.
No caso da pesquisa realizada pela bióloga, a amostra corresponde aos 30 leões que tiveram o comprimento de sua cauda medido. Ao escolher uma amostra, é necessário que ela represente a população. Isso significa que a amostra deve apresentar todas as características da população que representa e, também, deve ser imparcial, isto é, ela deve integrar, proporcionalmente, todos os elementos da população. Existem várias técnicas para escolher uma amostra de modo a garantir que ela represente, da melhor maneira possível, a população da qual foi retirada. Esse assunto será estudado em anos posteriores.
A coleta de dados pode ser feita por meio de observação, contagem, medida, questionário ou entrevista.
A medida do comprimento da cauda dos leões é a variável da pesquisa, ou seja, a característica que se quer estudar. Uma variável pode ser quantitativa (quando assume valor numérico associado a contagem ou medida) ou qualitativa (quando o valor da variável é expresso por um atributo). São exemplos de variáveis quantitativas: massa, idade, altura, entre outros. Já a côr dos olhos, a procedência, o tipo de pelo, entre outros, são exemplos de variáveis qualitativas.
Como já sabemos, após obter a medida do comprimento da cauda de cada leão, a bióloga anotou os dados em um quadro.

Os dados assim apresentados são denominados dados brutos. Essa apresentação não favorece a observação de regularidade ou tendência nos dados. Para isso, é conveniente organizá-los em ordem crescente ou decrescente, denominada rol. Com o rol de dados, podemos facilmente obter a amplitude da amostra, que é a diferença entre o maior e o menor valor. Também podemos verificar a frequência absoluta de cada medida, que corresponde à quantidade de vezes que cada valor aparece na amostra. Com os dados organizados dessa maneira, fica mais fácil apresentá-los em uma tabela de distribuição de frequências.

|
Medida da cauda (em centímetro) |
82 |
85 |
90 |
91 |
95 |
96 |
98 |
99 |
|---|---|---|---|---|---|---|---|---|
|
Frequência absoluta |
4 |
5 |
6 |
4 |
3 |
3 |
3 |
2 |
Dados obtidos pela bióloga.
Observando a tabela com os dados da distribuição da medida do comprimento da cauda dos leões, podemos chegar a diversas conclusões. Por exemplo:
• há 4 leões cujo comprimento da cauda mede 82 centímetros, ou seja, a medida 82 centímetros tem frequência 4;
• há 8 leões cujo comprimento da cauda mede 96 centímetros ou mais, pois as medidas 96 centímetros, 98 centímetros e 99 centímetros têm frequências 3, 3 e 2, respectivamente. E 3 + 3 + 2 = 8;
• há 15 leões cujo comprimento da cauda mede menos de 91 centímetros, pois 4 têm 82 centímetros de comprimento de cauda, 5 têm 85 centímetros e 6 têm 90 centímetros;
• a amplitude da amostra é 17 (99 ‒ 82).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 No caderno, classifique as variáveis a seguir em quantitativa ou qualitativa.
a) Salário.
b) Gênero.
c) Número de irmãos.
d) Opinião sobre a qualidade da água.
e) Número do sapato.
f) Escolaridade.
2 Dê dois exemplos de variável quantitativa e dois exemplos de variável qualitativa.
3 Em uma pesquisa referente à qualidade da coleta de lixo de determinado município que tem 10 bairros, o instituto responsável escolheu uma amostra formada por moradores de um mesmo bairro. Analisando a situação apresentada, pode-se afirmar que as conclusões obtidas por essa pesquisa são significativas para todo o município? Justifique.
4 Em um clube, a idade (em ano) dos participantes de um jôgo de vôlei era:
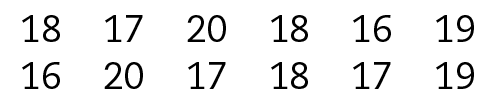
Com essas informações, elabore uma tabela de distribuição de frequência.
5 Gustavo fez uma pesquisa com alguns amigos para saber quantos animais de estimação cada um deles tinha em casa.

Observe os números que ele obteve:

Construa uma tabela de distribuição de frequência com esses dados.
6 Dos 120 estudantes do curso de Medicina, Cláudio registrou o número de batimentos cardíacos por minuto de 50 colegas de classe. Observe os números que ele registrou:
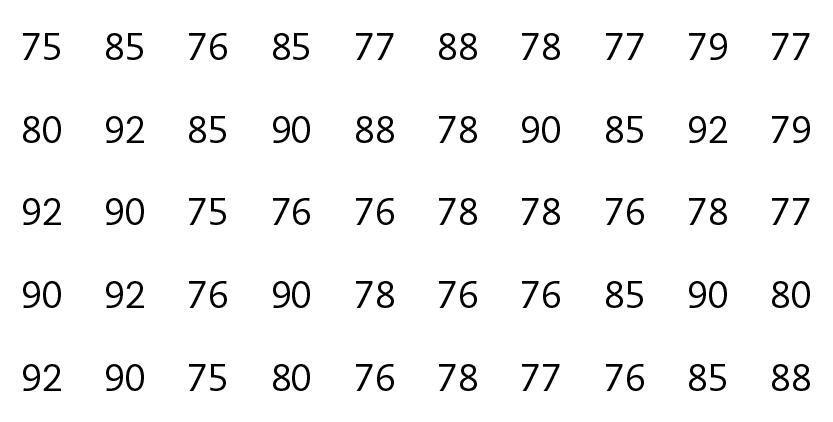
Com essas informações, construa uma tabela de distribuição de frequências e responda:
a) Quantos estudantes tem a população pesquisada? E quantos tem a amostra?
b) Qual é a amplitude dessa amostra?
c) Quantos estudantes apresentaram número de batimentos por minuto superior a 79?
d) Qual valor de batimentos por minuto aparece com maior frequência?
7

Hora de criar – Escolha uma variável quantitativa (idade, massa, altura, número de pessoas em casa etcétera) que possa ser pesquisada entre os colegas de classe. Faça a pesquisa, organize os dados em uma tabela de distribuição de frequências e, depois, apresente o resultado à turma.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Analise a tabela de distribuição de frequências que se refere às notas obtidas por todos os competidores em uma etapa classificatória para um torneio de saltos ornamentais.
|
Nota |
4,0 |
5,0 |
7,5 |
8,0 |
9,0 |
|---|---|---|---|---|---|
|
Frequência |
4 |
10 |
12 |
8 |
6 |
Dados obtidos pela organização do torneio.
a) Quantos atletas participaram da etapa classificatória?
b) Determine a porcentagem de atletas correspondente a cada nota e a soma das porcentagens.
c) Reproduza essa tabela acrescentando uma terceira linha para indicar as porcentagens.
d) Supondo que a nota para aprovação nessa competição seja 5,0, qual é a porcentagem de atletas reprovados nessa etapa?
Apresentação de resultados
Já aprendemos a interpretar e a organizar dados em tabelas e gráficos estatísticos. Essas representações são utilizadas tanto com o objetivo de organizar os dados obtidos em uma pesquisa a fim de observar padrões de comportamento das variáveis como para comunicar os resultados encontrados.
Vamos relembrar algumas dessas representações gráficas.
Gráfico de colunas
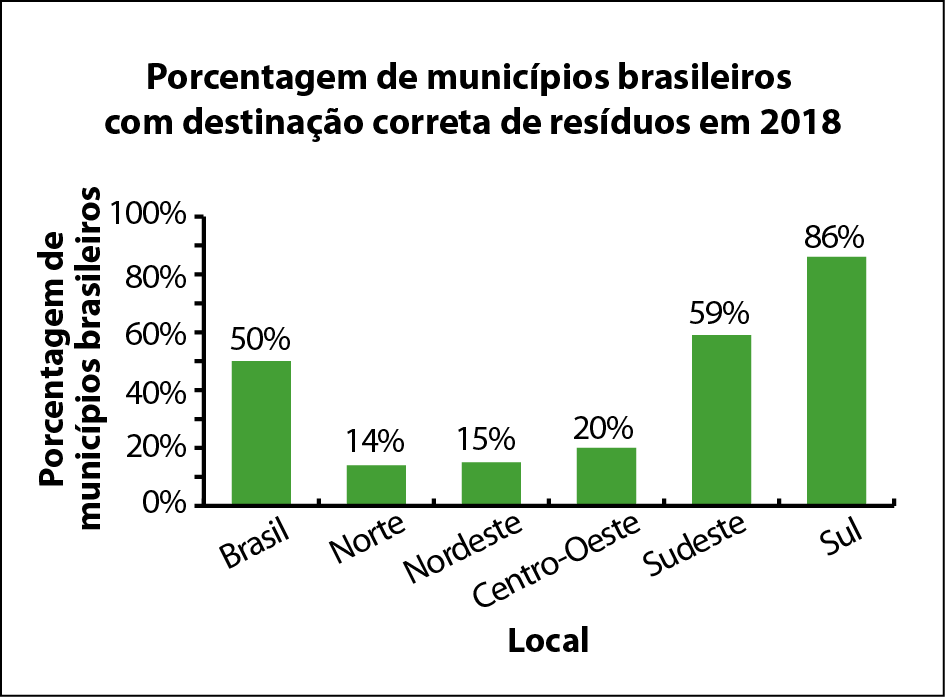
O gráfico de colunas é formado por retângulos de mesma medida de largura, com a base em um eixo horizontal e alturas correspondentes a valores em um eixo vertical.
Gráfico de barras
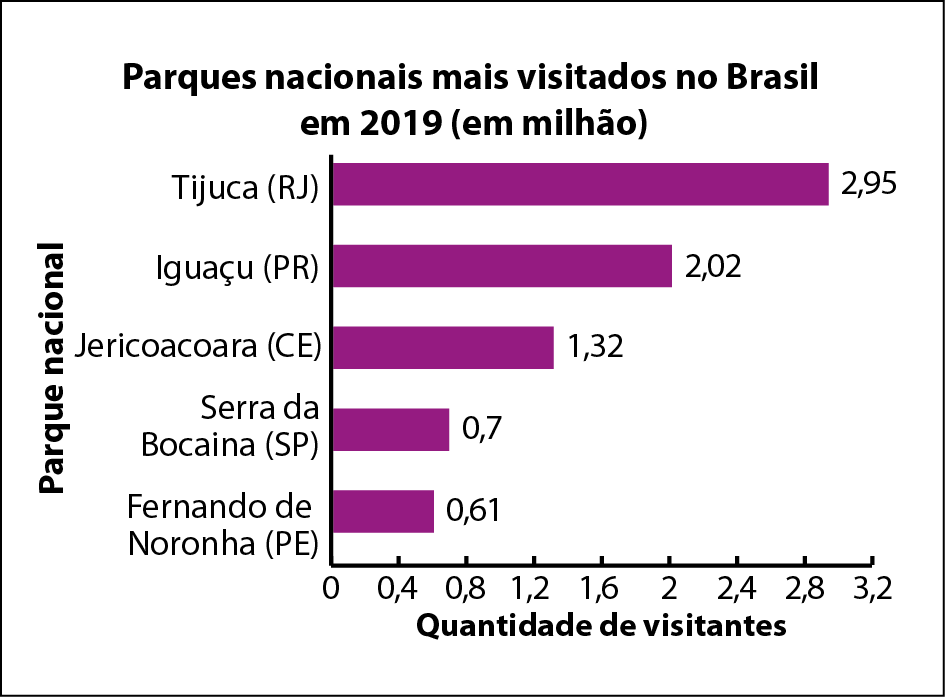
O gráfico de barras é parecido com o gráfico de colunas, só que a base dos retângulos que formam as barras fica apoiada no eixo vertical, e os valores ficam no eixo horizontal.
Tanto o gráfico de colunas quanto o de barras são muito utilizados, por causa da facilidade nas construções e da clareza na apresentação dos dados.
Gráfico de setores
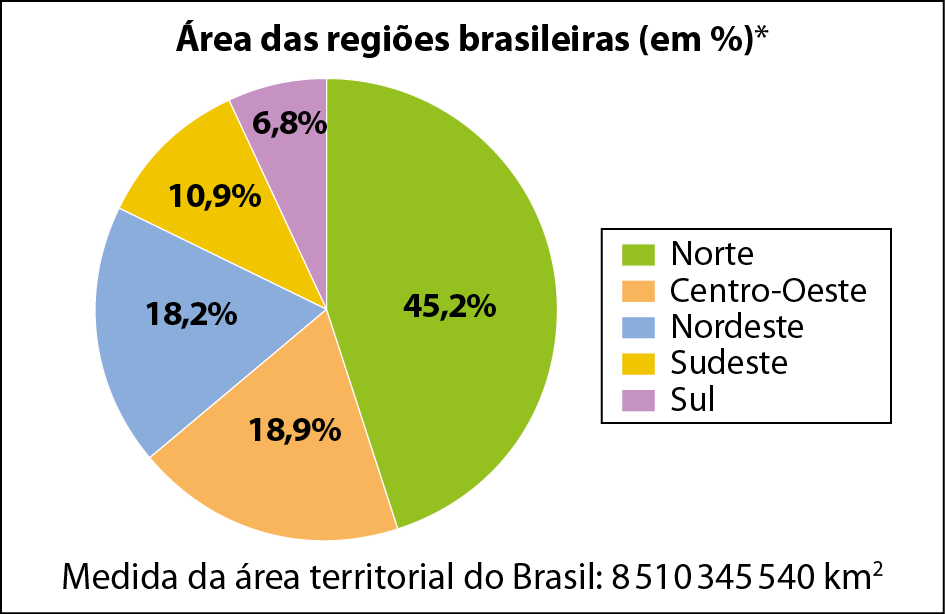
No gráfico de setores, a frequência de cada dado estatístico é representada por um setor (uma “fatia”) do círculo, cuja medida da área é proporcional à frequência. Ele é usado quando se deseja relacionar os dados estatísticos entre si ou com o todo. Nesse tipo de gráfico, a soma das porcentagens correspondentes às fatias deve ser 100%.
Gráfico de linha
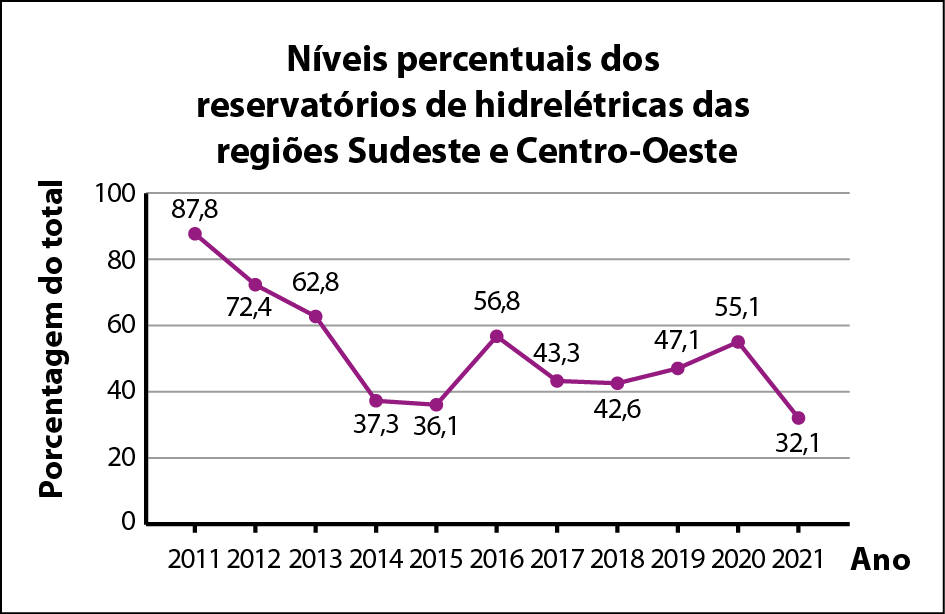
O gráfico de linha é usado principalmente para estudar um fenômeno no decorrer do tempo. Ele tem dois eixos: o horizontal, no qual, nesse exemplo, foram anotados os intervalos de tempo; e o vertical, em que foram marcadas frequências em determinada escala. Unindo os pontos obtidos no cruzamento das paralelas aos eixos pelos valores das variáveis, determinamos a linha do gráfico.
Gráficos de múltiplas entradas
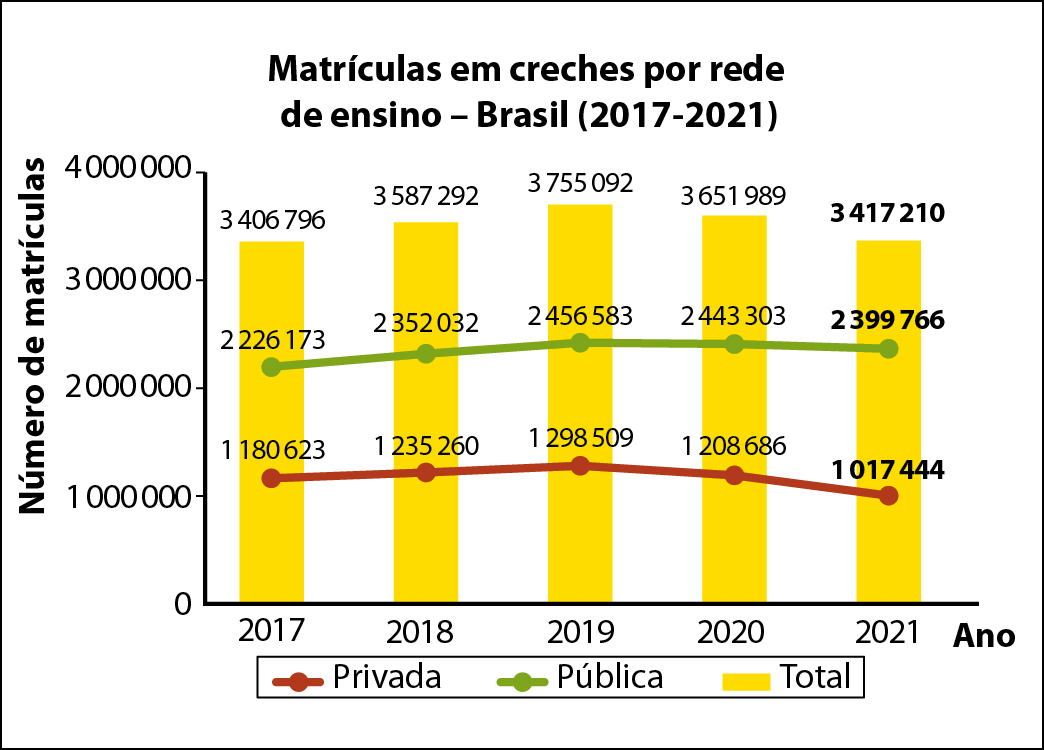
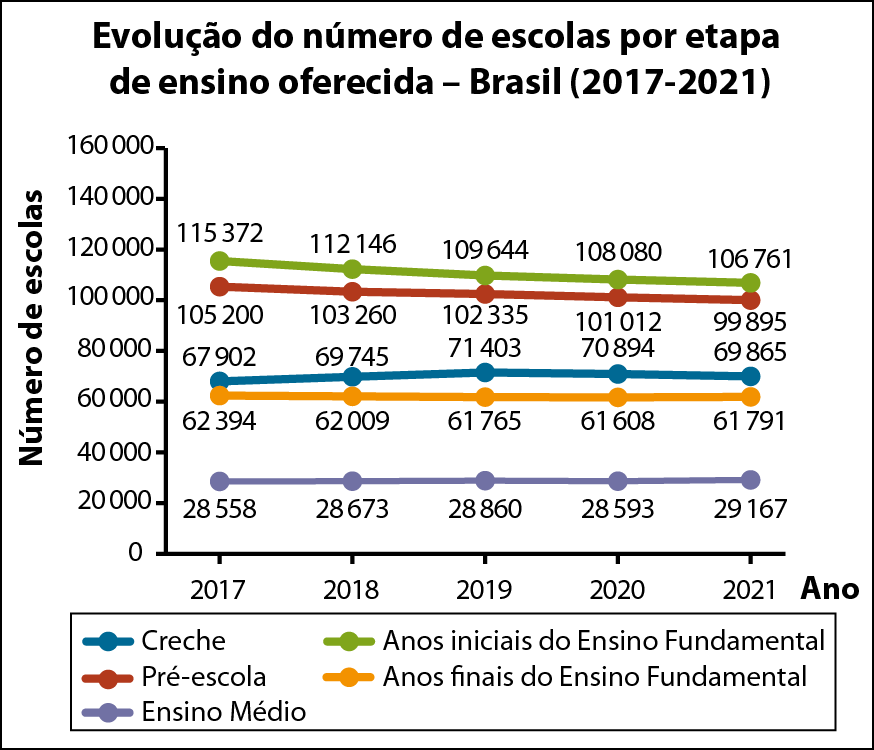
Um gráfico de múltiplas entradas pode ser de linha, de colunas, de barras, entre outros. Nele, representa-se uma mesma característica estudada para duas ou mais amostras, facilitando a comparação entre elas.
Pictograma


O pictograma é um gráfico formado por desenhos relacionados ao tema. Em alguns casos, as frequências/medidas da variável são representadas pela mesma figura em tamanhos proporcionais a essas frequências/medidas; às vezes, escolhe-se um ícone para representar determinada frequência/variável. Esse tipo de gráfico é muito usado em revistas e jornais.
Cartograma
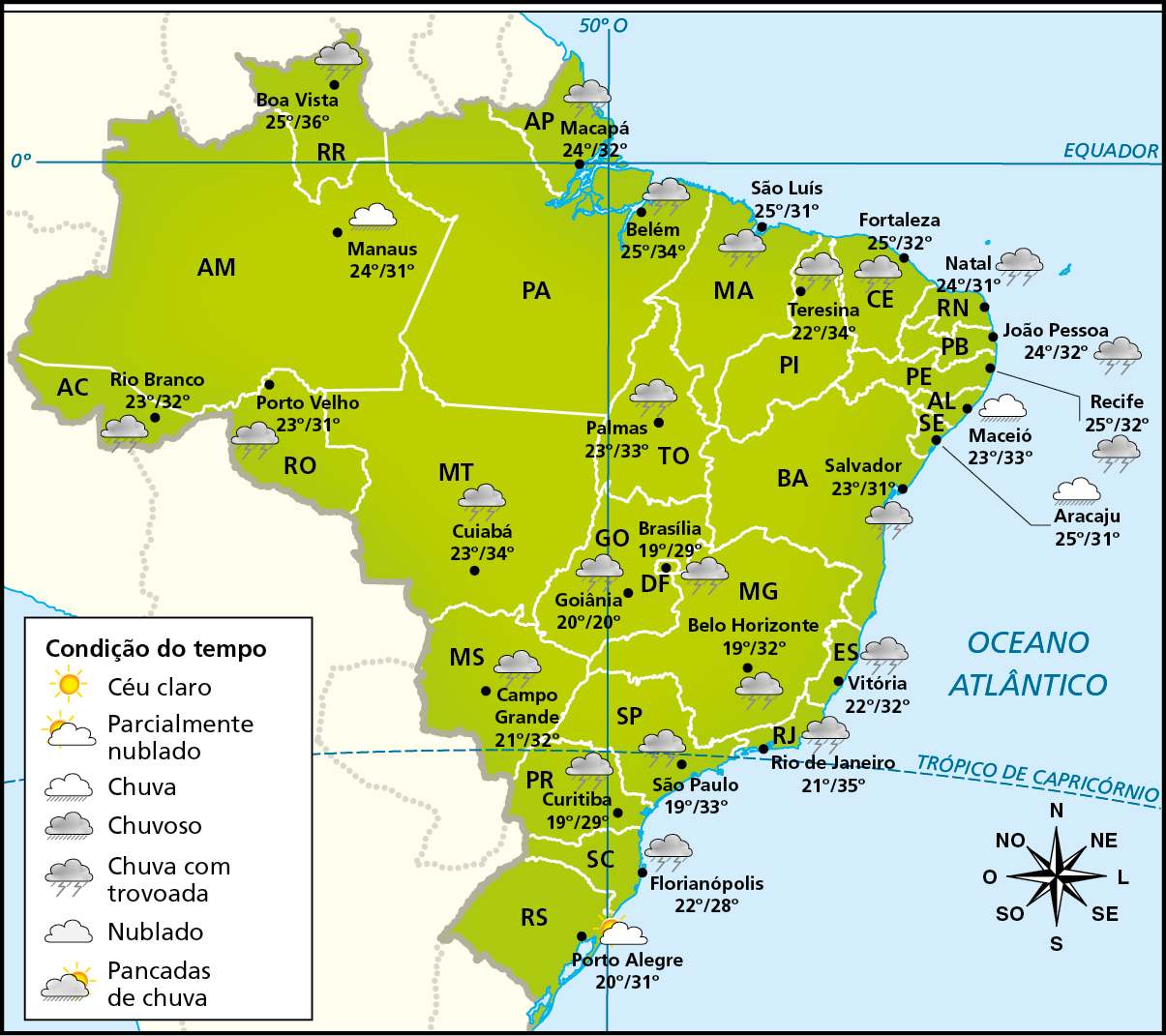
O cartograma é um mapa em que se representa, por meio de pontos, linhas e figuras, a ocorrência ou a intensidade de um fenômeno, como as condições do tempo.
É muito comum o uso de cartograma em revistas e jornais impressos, televisionados ou virtuais, para informar a previsão do tempo.
Os cartogramas também são usados para ilustrar e simplificar a comunicação de dados em reportagens e em estudos sobre determinadas variáveis características de um lugar.
Temperatura, em grauscélsius, e condições do tempo nas capitais em 22 de fevereiro de 2022
Infográfico
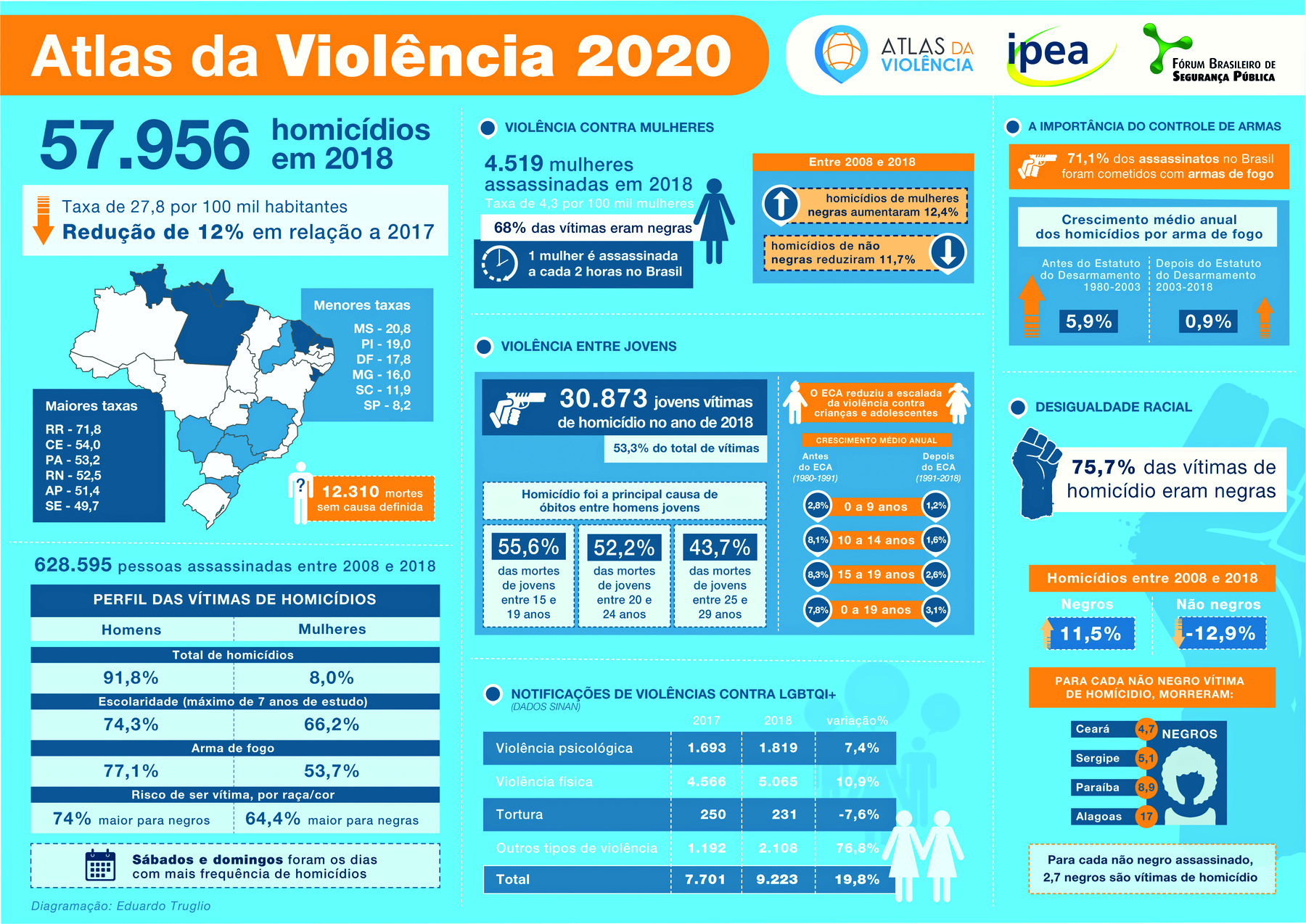
O infográfico é usado para apresentar informações por meio de recursos diversos, como gráficos, textos, ilustrações, fotografias, mapas etcétera. Atualmente, utilizam-se muitos infográficos em jornais, revistas e na internet.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
8 Observe o gráfico com dados do desmatamento da Mata Atlântica em 2020 e faça o que se pede.
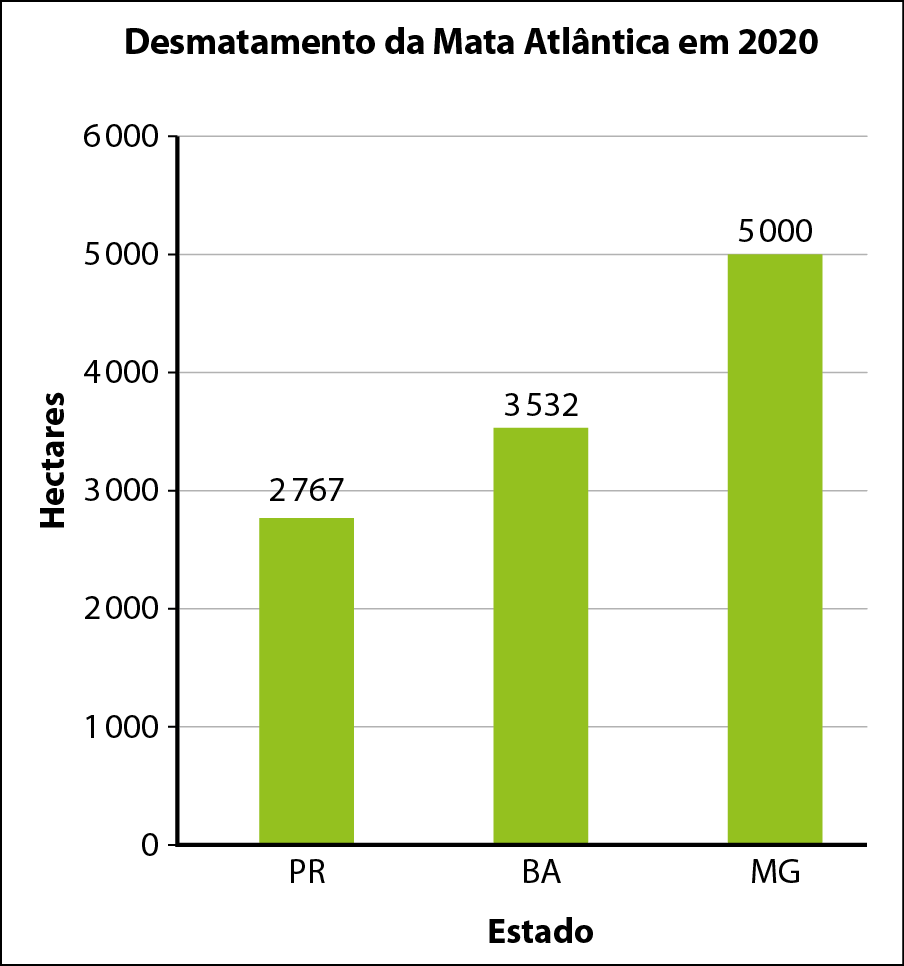
a) Considere que 1 hectare corresponde a .10000 métros quadrados e que a medida da área de um campo de futebol é .10800 métros quadrados. O equivalente a quantos campos de futebol, aproximadamente, foi desmatado em cada estado citado?
b) Construa um gráfico de barras com os dados obtidos no item a.
c) Pesquise em jornais, revistas ou na internet a atual situação do desmatamento da Mata Atlântica nos estados indicados no gráfico. Construa um novo gráfico de colunas com os dados obtidos com sua pesquisa e compare-o com este.
9 Observe a tabela a seguir.
|
Região do Brasil |
Medida da área (em milhões de km2)* |
|---|---|
|
Norte |
3,85 |
|
Nordeste |
1,55 |
|
Sudeste |
0,92 |
|
Sul |
0,58 |
|
Centro-Oeste |
1,61 |
*Valores aproximados. Dados obtidos em: í bê gê É. ÁREAS territoriais. Instituto Brasileiro de Geografia e Estatística. Disponível em: https://oeds.link/2YFZIy. Acesso em: 21 junho 2022.
a) Construa um gráfico de colunas que apresente a medida da área de cada região brasileira.
b) Construa um gráfico de barras horizontais que apresente a quantidade de estados de cada região brasileira.
c) Qual região brasileira tem maior medida de área?
d) É correto afirmar que a região de maior medida de área tem a maior quantidade de estados?
10 Observe no cartograma a previsão meteorológica para a região Centro-Oeste para o dia 2 de março de 2022.
Temperatura, em grauscélsius, e condições do tempo na região Centro-Oeste em 2 de março de 2022

a) Para qual local foi prevista a menor temperatura mínima?
b) E qual terá a menor temperatura máxima?
c) Qual foi a maior temperatura prevista?
11 Uma empresa de consultoria fez uma pesquisa para verificar o lucro de algumas empresas brasileiras que têm ações negociadas na bolsa de valores. Os dados obtidos foram registrados no gráfico de colunas a seguir.
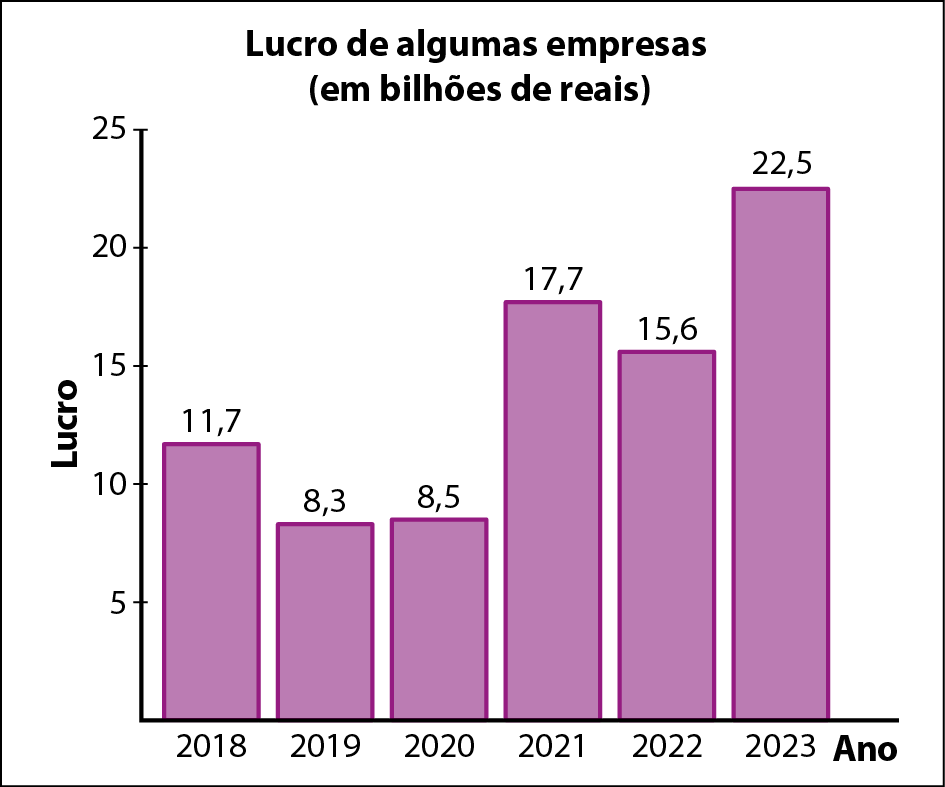
Agora, faça o que se pede.
a) Construa um gráfico de linha com as informações do gráfico de colunas apresentado.
b) Em que ano o lucro das empresas foi maior?
c) O que é possível observar em relação ao lucro dessas empresas nesse período?
12 O pictograma a seguir mostra a quantidade de funcionários em dois dos setores de uma empresa.

a) Quantos funcionários trabalham no departamento de produção dessa empresa?
b) Quantos funcionários trabalham no departamento de limpeza?
c) É possível construir um gráfico de setores para essa situação?
13 Hora de criar – Pesquise em jornais, revistas, atlas, internet e selecione dois gráficos de tipos diferentes sobre o tema que quiser. Elabore um texto que sintetize as informações apresentadas nesses gráficos.
TRABALHANDO A INFORMAÇÃO

Abordando um assunto com vários tipos de gráfico
Há tempos a dengue vem preocupando a população brasileira. Dados mostram que é necessário tomar todas as precauções para que essa doença não se dissemine ainda mais no Brasil. Observe a seguir os dados referentes a essa doença, organizados em diferentes tipos de gráfico.
Cartograma
Este cartograma mostra geograficamente o registro do número de casos por 100 mil habitantes da doença em 2021 nas regiões do Brasil.
Casos de dengue por 100 mil habitantes nas regiões brasileiras (2021)

Gráfico de linhas
Um gráfico de linhas é um bom instrumento para mostrar a evolução do número de casos de dengue no Brasil.
Segundo o Ministério da Saúde, os dados do início de janeiro até 7 de dezembro de 2019 apontam ..1527119 notificações de casos prováveis.
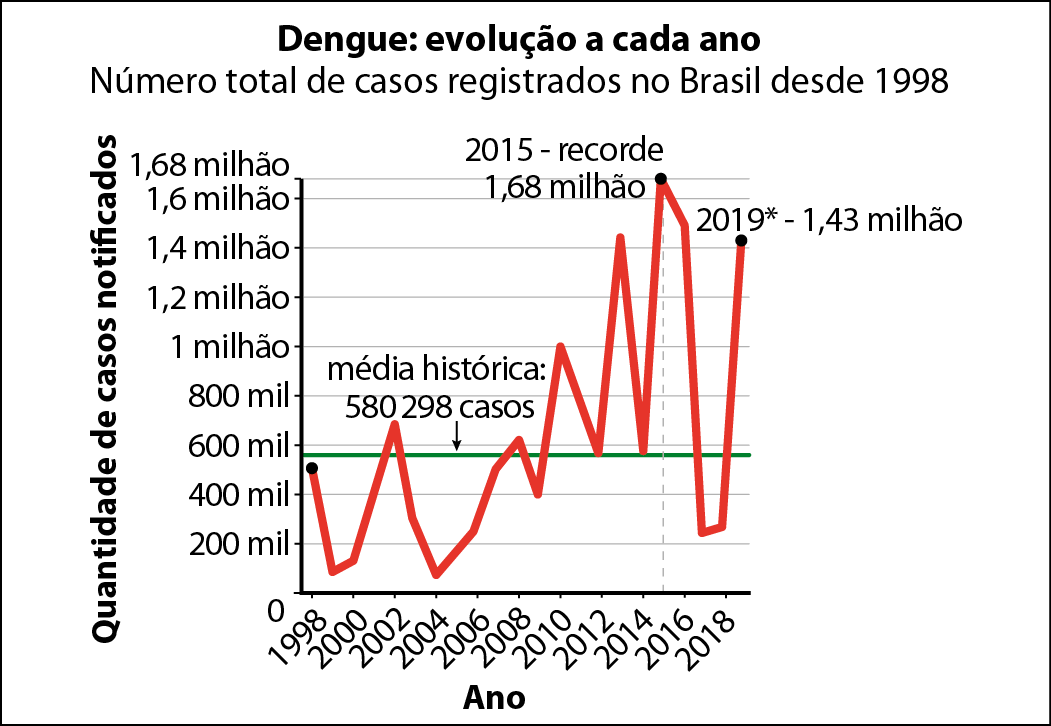
Gráfico de colunas
Em um gráfico de colunas, visualizamos a comparação da incidência da doença nos estados de Goiás, Minas Gerais e São Paulo em 2018 e 2019.

Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 A que é possível atribuir o aumento dos casos de dengue no Brasil em 2015 e 2019?
2 Considerando os anos de 2018 e 2019, quais foram os aumentos absoluto e percentual de casos de dengue no estado por 100 mil habitantes de São Paulo?
3

No gráfico de linha, lemos a seguinte informação: “A média histórica de casos, de 1998 a 2019, é .580298”. Discuta com um colega e escrevam o que vocês entendem que essa informação significa.
3. Frequência relativa
Para a festa de formatura do 9º ano de um colégio, a diretora elaborou uma pesquisa sobre o gênero musical preferido dos estudantes de duas turmas. Na turma a, há 26 estudantes, e, na turma B, 35 estudantes. O resultado obtido na pesquisa foi organizado na tabela a seguir.
|
Gênero |
Número de estudantes: turma A |
Número de estudantes: turma B |
|---|---|---|
|
Pop |
8 |
12 |
|
Funk |
5 |
8 |
|
Rap |
10 |
10 |
|
Indie |
1 |
1 |
|
Outros |
2 |
4 |
|
Total de estudantes |
26 |
35 |
Dados obtidos pela diretora do colégio.
Ao observar os resultados da tabela, é possível afirmar que os gêneros rap e indie têm a mesma preferência nas duas turmas?
O número de vezes que um dado se repete em uma pesquisa é chamado de frequência absoluta.
Apesar de os dois gêneros musicais apresentarem a mesma frequência absoluta (número de estudantes) nas duas turmas, a preferência de cada tipo de música não é a mesma, pois as turmas não têm a mesma quantidade de estudantes.
Vamos analisar os resultados em relação ao rap e ao indie, respectivamente:
• na turma a há 10 estudantes (rap) e 1 estudante (indie) em um total de 26 estudantes;
• na turma B há 10 estudantes (rap) e 1 estudante (indie) em um total de 35 estudantes.
Assim, percebemos que só é possível comparar a preferência de um gênero musical entre essas turmas se observarmos a razão entre o número de estudantes que preferem esse gênero e o total de estudantes da turma. Essa razão, em estatística, é chamada de frequência relativa.
A frequência relativa
F índice r, geralmente apresentada na fórma de porcentagem, é dada por:
frequência relativa =
frequência absoluta sobre total de elementosVamos calcular a frequência relativa para cada um dos gêneros musicais. Acompanhe.
Turma a:
• pop:
frequência relativa é igual a fração, 8 26 avos, fim da fração é aproximadamente igual a 0,31 que é igual a 31%.• funk:
frequência relativa é igual a fração, 5 26 avos, fim da fração, é aproximadamente igual a 0,19 que é igual a 19%.• rap:
frequência relativa é igual a fração, 10 26 avos, fim da fração, é aproximadamente igual a 0,38 que é igual a 38%.• indie:
frequência relativa é igual a fração, 1 26 avos, fim da fração, é aproximadamente igual a 0,04 que é igual a 4%.• outros:
frequência relativa é igual a fração, 2 26 avos, fim da fração, é aproximadamente igual a 0,08 que é igual a 8%.Turma B:
• pop:
frequência relativa é igual a fração, 12 35 avos, fim da fração, é aproximadamente igual a 0,34 que é igual a 34%.• funk:
frequência relativa é igual a fração, 8 35 avos, fim da fração, é aproximadamente igual a 0,23 que é igual a 23%.• rap:
frequência relativa é igual a fração, 10 35 avos, fim da fração, é aproximadamente igual a 0,29 que é igual a 29%.• indie:
frequência relativa é igual a fração, 1 35 avos, fim da fração, é aproximadamente igual a 0,03 que é igual a 3%.• outros:
frequência relativa é igual a fração, 4 35 avos, fim da fração, é aproximadamente igual a 0,11 que é igual a 11%.Podemos, então, montar a seguinte tabela:
|
Gênero |
Frequência relativa: turma A |
Frequência relativa: turma B |
|---|---|---|
|
Pop |
31% |
34% |
|
Funk |
19% |
23% |
|
Rap |
38% |
29% |
|
Indie |
4% |
3% |
|
Outros |
8% |
11% |
|
Total |
100% |
100% |
Dados obtidos pela diretora do colégio.
Notamos que, apesar de o rap apresentar a mesma frequência absoluta, a frequência relativa para esse gênero musical não foi a mesma nas duas turmas. O mesmo vale para o gênero indie. Com isso, concluímos que a preferência desses dois gêneros não é a mesma nas duas turmas.
Considere a situação a seguir.
O departamento de contrôle de qualidade de uma empresa testou a massa (em grama) de um lote de 50 pacotes de farinha, supostamente de 1 quilograma, e construiu o rol:
940; 945; 955; 955; 963; 970; 970; 972; 974; 988; 988; 988; 989; 990; 990; 991; 993; 993; 993; 996; 997; 997; 999; 999; .1000; .1000; .1000; .1000; .1000; .1002; .1002; .1004; .1005; .1005; .1005; .1008; .1009; .1009; .1012; .1016; .1016; .1019; .1019; .1020; .1023; .1023; .1024; .1025; .1025; .1028
Para ter uma ideia melhor da distribuição de frequência, a pesquisadora reuniu esses valores em grupos de amplitude igual a 25 gramas. A esses grupos chamamos “classe”. Nesse caso, cada classe constituía um conjunto de números de a até b, incluindo a e não incluindo b. Observe a tabela de distribuição de frequência em classes.
|
Classe (de a até b*) |
Frequência absoluta |
Frequência relativa |
|---|---|---|
|
De 925 até 950 |
2 |
4% |
|
De 950 até 975 |
7 |
14% |
|
De 975 até 1.000 |
15 |
30% |
|
De 1.000 até 1.025 |
23 |
46% |
|
De 1.025 até 1.050 |
3 |
6% |
|
Totais |
50 |
100% |
* O b não está incluído na classe. Dados obtidos pela empresa de farinha.
Analisando a tabela, em relação à marca estabelecida de 1 quilograma, podemos concluir que:
• em 76% dos pacotes, o êrro é menor ou igual a 25 gramas;
• 48% (4% + 14% + 30%) estão abaixo e 52% (46% + 6%) estão acima.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
14 Em uma pesquisa para saber o tempo, em hora, que os jovens gastam ouvindo música durante um dia, obtiveram-se os seguintes resultados:
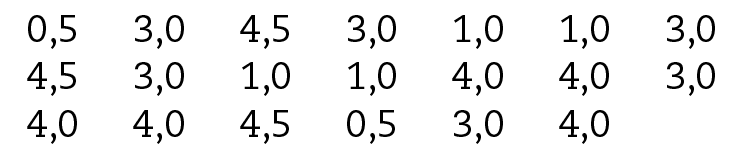
a) Construa uma tabela de distribuição de frequências absoluta e relativa em classes de números racionais de 0 a 1*, de 1 a 2*, de 2 a 3*, de 3 a 4 * e de 4 a 5*, em que * significa que o número final não está na classe.
b) Qual é a frequência absoluta dos jovens que gastam mais de 3 horas ouvindo música durante um dia?
c) Determine a frequência relativa dos jovens que gastam 3 horas ouvindo música durante um dia.
d) Analisando a tabela de distribuição de frequências construída, o que representam os 40%?
e) Podemos afirmar que mais de 50% dos jovens passam mais de 3 horas por dia ouvindo música? Justifique sua resposta.
15 Observe o gráfico a seguir.

Com base na análise do gráfico, faça o que se pede.
a) Construa uma tabela de distribuição de frequências com a frequência relativa em porcentagem.
b) Qual é a frequência relativa dos participantes do Enem com 18 anos nessa escola?
c) Qual é a porcentagem de participantes com idade superior a 17 anos?
d) O que é possível perceber, em relação ao número de estudantes que participam do Enem, à medida que a idade dos estudantes aumenta?
16 A tabela a seguir mostra o tempo, em hora, que os meninos e as meninas do 8º ano de um colégio acessam a internet semanalmente.
|
Tempo Classe (de a até b*) |
Frequência absoluta: meninos |
Frequência absoluta: meninas |
|---|---|---|
|
De 0 a 1 hora |
7 |
0 |
|
De 1 a 2 horas |
9 |
9 |
|
De 2 a 3 horas |
6 |
6 |
|
De 3 a 4 horas |
5 |
5 |
|
De 4 a 5 horas |
3 |
4 |
|
Total |
30 |
24 |
* O número b não está incluído na classe. Dados obtidos pelo colégio.
a) De acôrdo com os dados da tabela, é possível afirmar que, entre os estudantes do 8º ano, o percentual de meninos e o percentual de meninas que acessam a internet de 3 a 4 horas semanalmente são iguais? Justifique.
b) Construa a tabela de frequências relativas na fôrma percentual e verifique se sua resposta ao item a está correta.
4. Medidas estatísticas
Já aprendemos vários recursos e técnicas estatísticas para a descrição do grupo de valores que uma variável pode assumir. Observamos que as organizações de dados em tabelas de frequências e gráficos podem fornecer informações sobre o comportamento de uma variável, possibilitando verificar tendências e padrões.
Porém, às vezes, precisamos resumir ainda mais um conjunto de dados para expressar determinada característica da população pesquisada.
Para isso, estudaremos a seguir algumas medidas estatísticas de posição ou de tendência central: moda, média aritmética, média aritmética ponderada e mediana.
Moda
Paulo trabalha em uma empresa de roupas selecionando adolescentes para serem modelos comerciais. Ele escolheu 160 candidatos e anotou suas alturas nesta tabela.
|
Altura (em metro) |
1,50 |
1,55 |
1,56 |
1,58 |
1,60 |
1,62 |
1,68 |
1,70 |
1,72 |
1,75 |
|---|---|---|---|---|---|---|---|---|---|---|
|
Frequência absoluta |
10 |
15 |
22 |
23 |
25 |
35 |
12 |
10 |
5 |
3 |
Dados obtidos por Paulo.
Como a altura que aparece mais vezes, isto é, que apresenta a maior frequência (35) é 1,62 métro, dizemos que 1,62 métro é a moda desse conjunto de dados.

Paulo também registrou outra característica desse grupo, a idade, em uma tabela de distribuição das frequências absolutas.
|
Idade (em ano) |
12 |
13 |
14 |
15 |
16 |
17 |
|---|---|---|---|---|---|---|
|
Frequência absoluta |
11 |
34 |
34 |
32 |
31 |
18 |
Dados obtidos por Paulo.
Na tabela, as idades que apresentam a maior frequência (34) são 13 e 14 anos. Então, dizemos que nesse conjunto de dados existem duas modas (bimodal): 13 anos e 14 anos.
Nem sempre a moda é um número. Acompanhe outra situação.
A tabela a seguir apresenta o resultado de uma pesquisa realizada com clientes de uma empresa de tê vê por assinatura para conhecer melhor a preferência deles em relação a alguns canais.
|
Canal de TV |
Canal X |
Canal Y |
Canal Z |
Canal K |
Canal W |
|---|---|---|---|---|---|
|
Frequência absoluta: telespectadores |
420 |
600 |
500 |
280 |
200 |
Dados obtidos pela empresa de tê vê por assinatura.

Com base na tabela apresentada, percebemos que o canal de tê vê com maior frequência, 600 telespectadores, é o canal Y. Podemos dizer, então, que esse canal é a moda desse conjunto de dados.
Em um conjunto de dados, moda é o elemento, numérico ou não, que se destaca por apresentar a maior frequência absoluta. Se dois ou mais elementos desse conjunto tiverem a mesma frequência absoluta, maior do que os demais, esses elementos serão as modas do conjunto.
Observação
▶ Quando todos os valores de uma pesquisa tiverem a mesma frequência, dizemos que não há moda ou que o conjunto de dados é amodal. Por exemplo, na situação da pesquisa sobre a preferência de canais, se todos os canais tivessem a mesma preferência, o conjunto de canais seria amodal.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
17 Determine a moda de cada sequência.
a) 7, 7, 8, 10, 10, 13, 14, 7, 9, 7
b) 5, 5, 5, 5, 5, 5
c) 10, 12, 17, 12, 10, 18, 18, 20
d) 3,2; 4,3; 5,1; 7,8
18 Para avaliar a qualidade das lâmpadas produzidas por uma empresa, uma equipe técnica separou uma amostra com 20 lâmpadas e registrou sua vida útil, em dia:
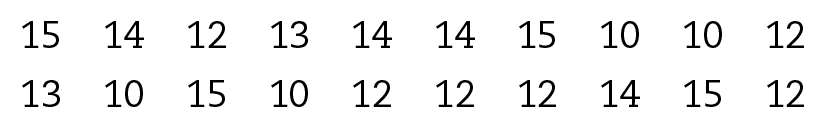
a) Construa uma tabela de distribuição de frequências absolutas para essa situação.
b) Determine a moda dessa distribuição de frequências.
19

Faça uma pesquisa com uma amostra de 10 colegas da classe e descubra qual é a moda dos esportes preferidos por vocês.
20 Hora de criar – Escreva uma situação de uma sequência de dados que seja bimodal e outra que seja amodal.
Média aritmética
Vamos relembrar como calcular a média de um conjunto de dados. Acompanhe a situação a seguir.
Alexandre, o professor de História, avisou aos estudantes que a média bimestral seria calculada conforme o seguinte critério: adicionam-se as notas obtidas no projeto individual, na prova e no trabalho em grupo e o resultado obtido é dividido por 3.
Laura é estudante na turma de Alexandre e calculou sua média bimestral desta maneira:
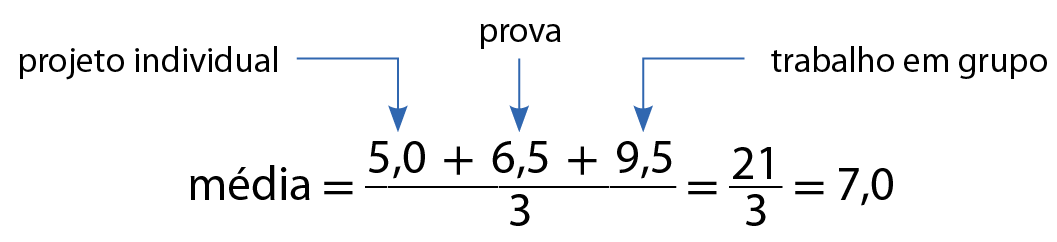
Portanto, nesse bimestre, Laura obteve média 7,0.
A média aritmética, ou simplesmente média, das notas de Laura é 7,0. Analisando o cálculo, é como se ela tivesse obtido notas 7,0 em todas essas avaliações.

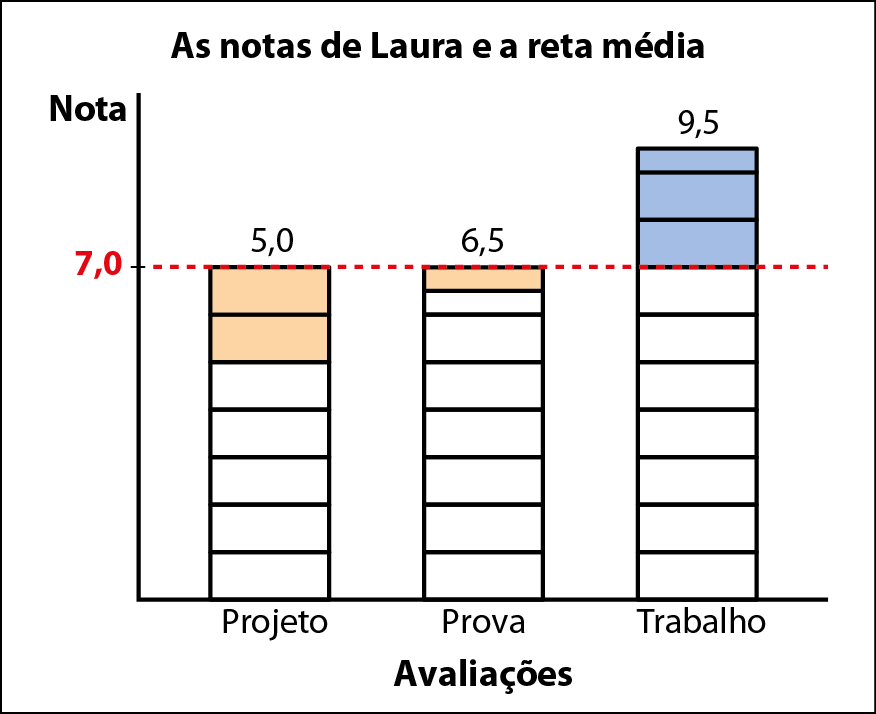
Observe que

= 1,0 e que

= 0,5.
Abaixo da reta média (

), há

e

em Projeto e

em Prova.
Acima da reta média, há

,

e

em Trabalho.
Como podemos notar, há duas vírgula cinco unidades acima (+2,5) e duas vírgula cinco unidades abaixo (‒2,5) da ordenada dos pontos da reta média.
A reta média ajuda a visualizar melhor a distribuição dos dados de um grupo de valores, se estão mais concentrados ou mais dispersos, isto é, mais espalhados.
O gráfico de colunas nos ajuda também a perceber o que os estatísticos chamam de amplitude, que é a diferença entre o maior e o menor valor da variável estudada. Nesse caso, a amplitude é 4,5 (9,5 ‒ 5).
No 9º ano, ampliaremos esse estudo da dispersão de um conjunto de valores por meio do cálculo do desvio médio.
Para calcular a média aritmética de dois ou mais números, basta dividir a soma desses números pela quantidade de números dados.
Média aritmética ponderada
Acompanhe as situações a seguir.
Situação 1
Durante o último mês, o número de atendimentos diários de uma clínica odontológica foi:

Para determinar a média diária de atendimentos feitos nessa clínica, podemos verificar a quantidade de atendimentos diários e calcular a média. Observe:
• 16 aparece 4 vezes;
• 17 aparece 3 vezes;
• 18 aparece 5 vezes;
• 19 aparece 5 vezes;
• 20 aparece 3 vezes.
Então:
média =
Expressão matemática. Média é igual à fração; numerador: 4 vezes 16 mais 3 vezes 17 mais 5 vezes 18 mais 5 vezes 19 mais 3 vezes 20; denominador: 4 mais 3 mais 5 mais 5 mais 3, fim da fração,=
fração: numerador: 64 mais 51 mais 90 mais 95 mais 60; denominador: 20=
fração, 360 20 avos= 18
Logo, a média diária de atendimentos feitos nessa clínica odontológica foi 18.
Situação 2
A prefeitura de um município brasileiro promoveu um concurso público para preencher algumas vagas. Na 1ª etapa do concurso, cada candidato realizou três provas: Matemática, Língua Portuguesa e Conhecimentos Gerais.
A média mínima para passar para a 2ª etapa do concurso era 6,0.
Observe o critério para o cálculo da média dos candidatos:
• prova de Matemática, peso 4;
• prova de Língua Portuguesa, peso 4;
• prova de Conhecimentos Gerais, peso 2.

Fernando era um dos candidatos. Assim que as notas foram publicadas no Diário Oficial do município, ele resolveu conferir sua média.
Como os pesos das provas são diferentes, para calcular sua média, Fernando precisou multiplicar cada nota pelo seu respectivo peso e, então, adicionar todos os resultados obtidos. Em seguida, dividiu o resultado pela soma de todos os pesos.
Observe como ele fez:
Dessa maneira, Fernando confirmou que sua média foi 6,2. Portanto, ele passou para a 2ª etapa do concurso público da prefeitura.
Note que, tanto na situação da clínica odontológica quanto na situação do concurso público, foi necessário considerar o peso de cada dado para calcularmos a média. Por esse motivo, ela é chamada de média aritmética ponderada.
Para obter a média aritmética ponderada de dois ou mais números, multiplicamos cada número por seu respectivo peso, adicionamos os produtos obtidos e dividimos o total pela soma dos pesos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
21 Lúcio comprou duas camisas; uma custou R$ 45,00quarenta e cinco reais, e a outra, R$ 39,00trinta e nove reais. Qual é o preço médio dessas camisas?
22 O quadro a seguir indica as temperaturas mínimas registradas na semana de 2 a 8 de julho em uma cidade da região Sul do Brasil. Encontre a média aritmética das temperaturas mínimas registradas nessa semana.
|
Dia |
Temperatura mínima (em °C) |
|---|---|
|
2 |
2 |
|
3 |
1 |
|
4 |
−6 |
|
5 |
−4 |
|
6 |
−4 |
|
7 |
−2 |
|
8 |
−1 |
23 O quadro a seguir apresenta o número de estudantes matriculados no 8º ano de uma escola entre os anos de 2020 e 2023.
|
2020 |
2021 |
2022 |
2023 |
|---|---|---|---|
|
193 |
209 |
216 |
210 |
a) Quantos estudantes foram matriculados no 8º ano dessa escola nesses quatro anos?
b) Qual foi o número médio de estudantes matriculados nos quatro anos indicados?
c) Em quais anos o número de matrículas foi inferior à média?
24 O número de automóveis vendidos em uma concessionária no primeiro trimestre do ano foi representado por um gráfico de barras.

a) Qual foi o número médio de automóveis vendidos na concessionária nesse trimestre?
b) Em março, quantos automóveis foram vendidos acima da média?
c) Considerando os três primeiros meses, faça uma estimativa de quantos automóveis devem ser vendidos no primeiro semestre do ano.
d) Mostre duas maneiras de chegar ao resultado do item anterior.
25 Para escolher um representante de sala, o 8º ano a fez uma votação. O resultado está representado na tabela a seguir.
|
Estudante |
Número de votos |
|---|---|
|
Adriana |
21 |
|
Vítor |
18 |
|
Mariana |
11 |
Dados obtidos pelo 8º ano a.
Faria sentido calcular a média para escolher o representante de sala do 8º ano?
26 Uma editora apresentou a quantidade de livros publicados no período de 2021 a 2023 no pictograma a seguir.

Calcule a média anual de livros produzidos por essa editora nesse período.
27 O salário mensal, em real, de cada um dos 10 funcionários de uma microempresa é:

a) Construa uma tabela de distribuição de frequências para essa situação.
b) Determine o salário modal (moda) desses funcionários.
c) Calcule o salário mensal médio desses funcionários.
d) Quantos funcionários recebem salário mensal menor que o salário mensal médio? Que porcentagem do total de funcionários eles representam?
e)

Discuta com um colega como é possível que o salário médio dos funcionários dessa empresa seja maior que o salário da maioria dos funcionários.
28 Em um concurso, a prova escrita tem peso 3, e a prova prática tem peso 2. Qual é a média de um candidato que obteve nota 8 na prova escrita e nota 5 na prova prática?
29 Catarina é professora de Matemática. Ela obtém a média bimestral dos estudantes propondo três atividades durante o bimestre: a nota da primeira atividade tem peso 1, a nota da segunda tem peso 2 e a da terceira tem peso 3. Calcule a média bimestral de um estudante de Catarina que obteve 4,0 na primeira atividade, 7,0 na segunda e 8,0 na terceira.
30 Uma imobiliária vendeu 5 terrenos a R$ 48.000,00quarenta e oito mil reais cada um e 10 terrenos a R$ 45.000,00quarenta e cinco mil reais cada um. Qual foi o valor médio dos terrenos vendidos pela imobiliária?
31

Hora de criar – Troque com um colega um problema, criado por vocês, sobre média aritmética ponderada. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Os gráficos a seguir representam pontos, de 0 a 100, que cada integrante das equipes a e B obteve na final da competição de saltos ornamentais promovida por um clube.
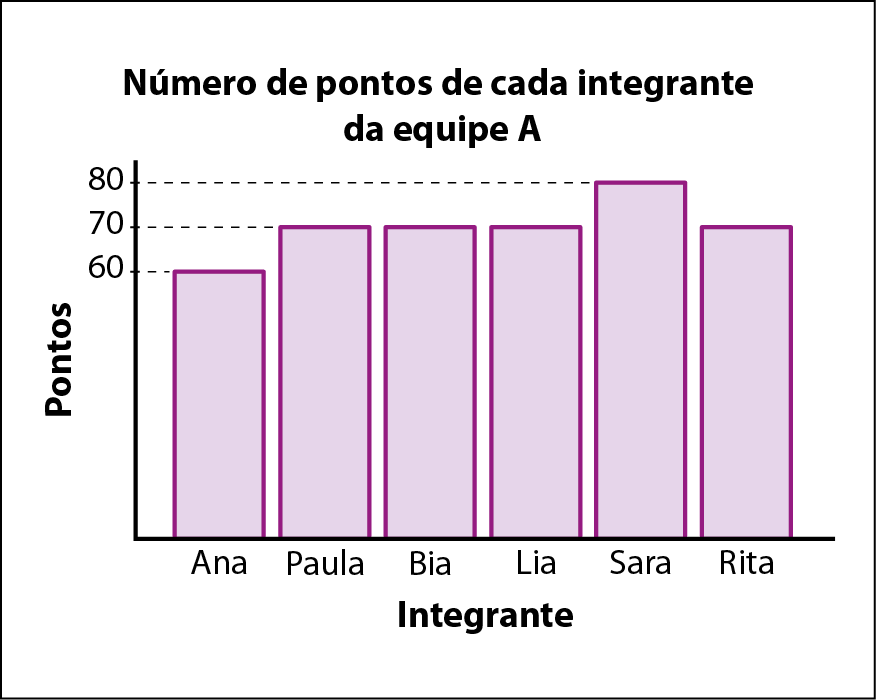
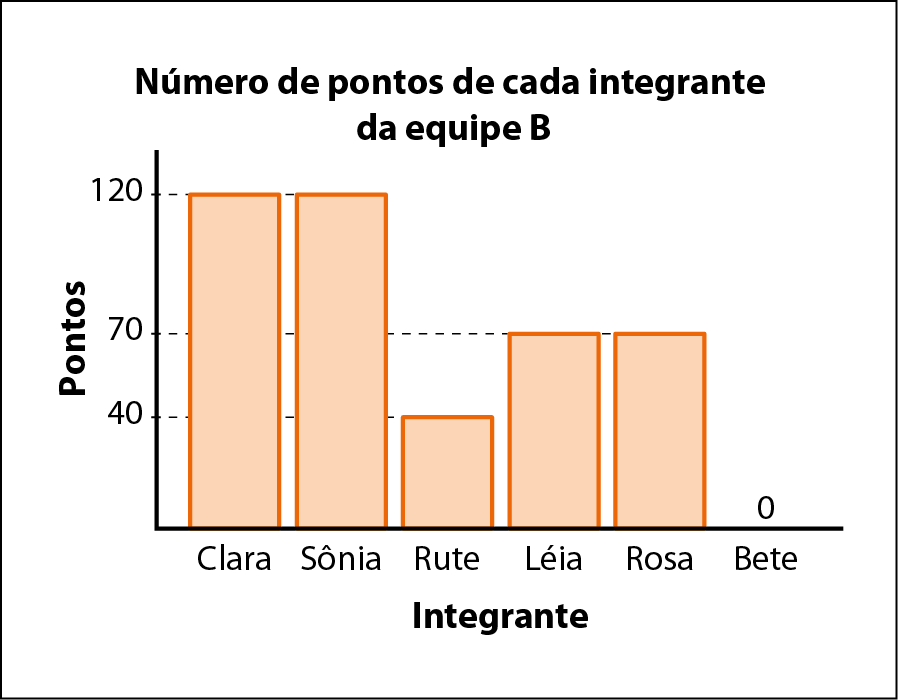
a) Quantos pontos cada equipe obteve?
b) Quantos integrantes tem cada equipe?
c) Calcule a média de pontos de cada equipe.
d) Qual equipe obteve maior média?
e) Nesse caso, a média aritmética traduz o perfil de cada equipe? Justifique.
Mediana
Acompanhe as situações a seguir.
Situação 1
Sete amigos se encontraram no fim de semana em um salão de jogos.

Após brincar em cada um dos jogos, eles obtiveram as seguintes pontuações finais: 160, 207, 177, 185, 175, 195 e 192.
O rol correspondente a essas pontuações é:

Como o conjunto de dados tem uma quantidade ímpar de termos, existe um termo que, após a ordenação, ocupa a posição central. Ele é chamado de termo central.

Observe que, nessa situação, o termo central ocupa a 4ª posição, que corresponde a 185 pontos. Então, dizemos que 185 é a mediana das pontuações finais obtidas pelo grupo de amigos.
Situação 2
Gabriela costuma participar de corridas de rua. Em um ano, ela participou de 8 corridas de 5 quilômetros e obteve os seguintes tempos, em minuto: 27, 32, 35, 29, 30, 25, 35 e 26.
O rol correspondente a esses tempos é:

Como o conjunto de dados tem uma quantidade par de termos, existem dois termos centrais.

Observe que, nessa situação, os termos centrais ocupam a 4ª e a 5ª posição, que correspondem aos tempos de 29 e 30 minutos, respectivamente.
Nesse caso, a mediana será a média aritmética desses dois valores.
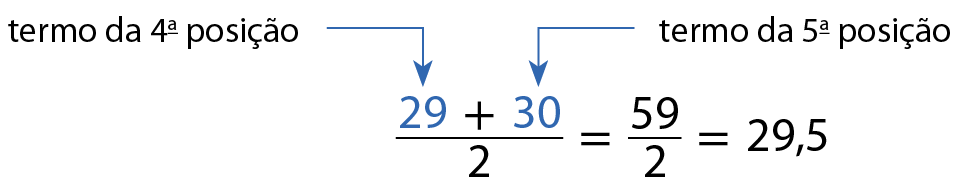
Ou seja, a mediana dos tempos obtidos por Gabriela é 29 minutos e 30 segundos.
Mediana de um grupo de valores ordenados, de modo crescente ou decrescente, é o termo que ocupa a posição central (com quantidade ímpar de termos) ou é o valor obtido pela média aritmética de seus dois termos centrais (com quantidade par de termos).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
32 Calcule a mediana dos seguintes grupos de valores:
a) 8, 4, 5, 3, 10
b) 1, 3, 6, 10, 13, 8, 5, 3
c) 0,2; 0,5; 0,1; 1,2; 1,5; 2,3; 0,7
d) 120, 142, 102, 101, 108, 150
33 Ana pesquisou o preço de um produto em 10 sites e encontrou os seguintes valores, em reais:

Determine o valor mediano (mediana) desses preços.
34 Observe o gráfico a seguir.
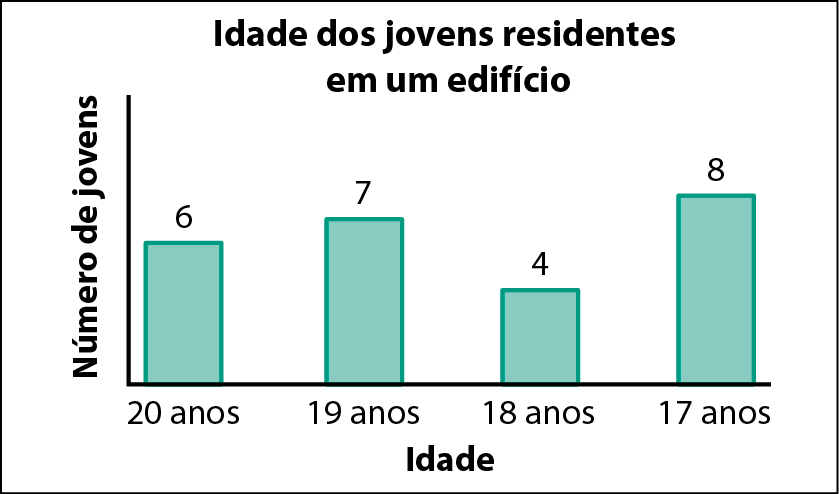
a) Quantos jovens residem nesse edifício?
b) Calcule a idade média desses jovens.
c) Determine a idade modal desses jovens.
d) Calcule a idade mediana desses jovens.
e) Se forem acrescentados a esses dados dois jovens de 16 anos, o que acontecerá com cada medida de tendência central calculada anteriormente?
35 Marta registrou o tempo, em minuto, que seus colegas gastam no percurso de casa à escola:

Determine:
a) a mediana desses valores;
b) a moda desses valores;
c) o tempo médio desse percurso;
d) a medida que, na sua opinião, caracteriza melhor esse grupo de dados. Justifique.
36 Uma empresa encomendou uma pesquisa sobre o chocolate preferido de alguns consumidores. O resultado obtido foi apresentado em uma tabela.
|
Tipo de chocolate |
Número de consumidores |
|---|---|
|
Meio amargo |
255 |
|
Ao leite |
765 |
|
Branco |
345 |
|
Amargo |
135 |
Dados obtidos pela empresa.
a) Determine qual das três medidas estatísticas (média, mediana e moda) caracteriza melhor essa pesquisa. Justifique sua resposta.
b) Calcule a porcentagem de cada tipo de chocolate em relação ao número total de consumidores.
c) Construa um gráfico de colunas com as porcentagens obtidas no item b.
TRABALHANDO A INFORMAÇÃO
Pesquisa amostral
Em anos anteriores, estudamos que, para fazer uma pesquisa estatística, por exemplo, para determinar qual é o esporte preferido dos estudantes de uma escola, é necessário planejá-la.
Assim, é preciso: definir o objetivo da pesquisa, isto é, o que se quer saber com a pesquisa – no exemplo, conhecer os esportes que mais interessam aos estudantes para organizar as aulas de Educação Física; determinar como será feita a coleta dos dados – por questionário, entrevista pessoal, rede social etcétera; definir com quem obter os dados a serem coletados, ou seja, definir o que os matemáticos chamam de população da pesquisa – no exemplo, estudantes de uma escola. Todos os estudantes serão contatados ou só uma parte?
Se todos os estudantes da população forem contatados, será uma pesquisa censitária. Se for só uma parte, uma amostra, será uma pesquisa amostral.
Na pesquisa amostral surge a questão: “Quais critérios empregar para escolher quem será pesquisado?”.

Definida a amostra, e obtidos os dados, estes devem ser organizados e apresentados em tabelas, em gráficos mais adequados a esses dados, sem se esquecer dos títulos e das fontes.
Finalmente, os dados organizados devem ser analisados. Alguns instrumentos que auxiliam na análise dos dados e na elaboração de um relatório conclusivo da pesquisa amostral são a obtenção da amplitude e das medidas de tendência central – moda, mediana, média aritmética ou ponderada – após selecionadas as mais adequadas a eles.
Agora quem trabalha é você!
FAÇA A ATIVIDADE NO CADERNO

Forme uma equipe com mais três colegas e planejem uma pesquisa amostral. Para isso, convém que discutam e decidam:
• a organização da equipe, ou seja, quem fará o quê;
• os objetivos da pesquisa e a elaboração de possíveis teses sobre o tema da pesquisa – sugestões: preferência de lazer, ou de profissão futura, ou de animais, ou de plantas, ou de filmes ou livros etcétera;
• a população e a amostra a serem pesquisadas;
• a maneira com que os dados serão obtidos;
• os recursos de organização dos dados mais adequados à pesquisa;
• a plataforma ou as plataformas em que o relatório será apresentado: caderno, cartaz, vídeo, mídia eletrônica etcétera
Também convém que, antes de passarem à parte prática, conversem com o professor sobre o projeto elaborado para realizar essa pesquisa.
PARA SABER MAIS
Estimativa de multidões
Leia a notícia a seguir.

Fonte: CARUARU. Prefeitura Municipal. Reuniões com segmentos culturais fortaleceram ações da Fundação de Cultura e Turismo de Caruaru em 2019. Caruaru: Prefeitura Municipal, 30 dez. 2019. Disponível em: https://oeds.link/wNdVCc. Acesso em: 4 mar. 2022.
Em cidades como Rio de Janeiro, São Paulo, Salvador e Recife, entre outras, têm ocorrido eventos que concentram públicos cada vez maiores. Estimar o número de pessoas de uma multidão é fundamental para qualquer organização responsável pelo planejamento ou mesmo pela avaliação posterior de um evento.
Para isso, os organizadores, a Polícia Militar e os órgãos de imprensa e de trânsito fazem uma estimativa, considerando que cada metro quadrado abriga até quatro pessoas. Por se tratar de uma norma internacional, esse método de estimativa é usado tanto pelos órgãos de segurança pública quanto pelos órgãos de imprensa de todo o mundo.
Outro método que fornece uma estimativa mais próxima do valor real é a fotografia aérea. Tiram-se fotografias aéreas da multidão, calcula-se a escala das fotografias e, em seguida, divide-se a fotografia em pequenas regiões quadradas, das quais se calcula a densidade média, para depois estimar a densidade da área toda.
Observe, nesta sequência de fotografias, diferentes densidades em uma mesma área.

Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 A imagem a seguir representa a fotografia aérea de um show. Faça uma estimativa do público desse evento.

2

Reúna-se com um colega e discutam a seguinte questão:
Para comemorar o título do campeonato nacional, torcedores de um time de futebol ocuparam a principal avenida da cidade. Estimativas indicaram que havia mais de 300 mil torcedores em toda a avenida. Sabendo que essa avenida tem 1 quilômetro de comprimento e 26 métros de largura, o que pode ser afirmado sobre essa estimativa? Justifique sua resposta.
3 Pesquise uma notícia sobre um grande evento na cidade onde você mora que tenha duas estimativas de participantes: uma da polícia e outra dos organizadores do evento. Em seguida, pesquise as dimensões do local e discuta qual estimativa possivelmente está correta.
5. Noções de probabilidade
Acompanhe as situações a seguir.
Situação 1
Uma loja fez uma promoção em que foram distribuídos .1000 números para o sorteio de uma bicicleta. Afonso tem 5 números e Geórgia, 1 número. Acompanhe como determinar a probabilidade de cada um deles ser sorteado.

Essa situação envolve a ideia de incerteza, pois sortear um número dentre os .1000 é um experimento no qual conhecemos os resultados possíveis, mas não podemos assegurar qual será o resultado final, ou seja, não é possível saber qual será o número sorteado. Esse tipo de experimento faz parte da Teoria das Probabilidades.
•

Você sabe quais são as regras determinadas pelo Ministério da Economia para realizar sorteios?
Na Teoria das Probabilidades, estudamos as leis que regem os fenômenos que dependem do acaso, isto é, fenômenos cujos resultados não podem ser previstos. Nesse caso, interessam a essa teoria os experimentos aleatórios, aqueles que podem ser repetidos nas mesmas condições tantas vezes quanto quisermos e cujos resultados possíveis são previamente conhecidos.

Na situação apresentada, os .1000 números do sorteio formam o espaço amostral, ou seja, o conjunto de todos os resultados possíveis do experimento.
O espaço amostral de um experimento aleatório é o conjunto de todos os resultados possíveis desse experimento.
O número adquirido por Geórgia fórma um evento desse experimento aleatório, do mesmo modo que os 5 números adquiridos por Afonso.
Qualquer conjunto de resultados possíveis de um experimento aleatório é chamado de evento.
Definidos o espaço amostral e o evento correspondente ao experimento aleatório, podemos determinar a probabilidade.
Probabilidade é a medida da chance de um evento acontecer.
No sorteio da bicicleta, cada número tem a mesma chance de ser sorteado. Nesse caso, para calcular a probabilidade, basta dividir o número de elementos do evento correspondente ao experimento aleatório pelo número de elementos do espaço amostral.
Probabilidade de ocorrência de um evento
igual à fração: número de elementos do evento sobre número de elementos do espaço amostral, fim da fração.Portanto, temos que:
• a probabilidade de Geórgia ser sorteada é
Fração. Um milésimo.ou 0,001 ou 0,1%;
• a probabilidade de Afonso ser sorteado é
Fração. Cinco milésimos.ou 0,005 ou 0,5%.
Situação 2
Qual é a probabilidade de sair a soma 6 no lançamento de dois dados comuns?
Antes de calcularmos a probabilidade, devemos definir o espaço amostral:


Observe que os casos favoráveis são:

Desse modo, a probabilidade de sair soma 6 nas faces dos dados é dada pela razão:
Observações
▶ A probabilidade de um evento é um número de 0 a 1.
▶ Quando a probabilidade é zero, dizemos que o evento é impossível.
▶ Quando a probabilidade é 1, dizemos que o evento é certo.
▶ A soma das probabilidades de todos os elementos do espaço amostral é 1.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
37 Sortear uma letra de um texto qualquer é um experimento aleatório? Por quê?
38 Em uma urna, há 9 bolas pretas, 5 bolas amarelas e 3 bolas vermelhas. Se retirarmos uma bola ao acaso, qual é a probabilidade de sair uma bola amarela?
39 A professora vai sortear, ao acaso, um estudante entre os 30 estudantes da sala. Sabendo que há 18 meninas na sala, qual é a probabilidade de ser sorteada uma menina? E de ser sorteado um menino? Qual é a soma das probabilidades?
40 Considerando o lançamento de dois dados comuns, determine a probabilidade de a soma das faces ser:
a) 8;
b) um número par;
c) maior que 10.
41 Quantos estudantes há na sua turma? Quantos são meninos? Calcule a probabilidade de que, ao sortear um estudante ao acaso, ele seja um menino.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Lucas inventou um jôgo com dados. O desafiante lança dois dados e, se em pelo menos um dos dados sair o número 1, Lucas ganha o jôgo. Se em pelo menos um dos dados sair como menor número o 2 ou o 3, o desafiante lança os dados novamente. E, se em pelo menos um dos dados não sair os números 1, 2 ou 3, o desafiante ganha o jôgo. Quem tem maior probabilidade de vencer o jôgo: Lucas ou seu desafiante?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 O pictograma a seguir mostra a quantidade de dê vê dês vendidos em uma loja durante a primeira semana de dezembro de 2023.
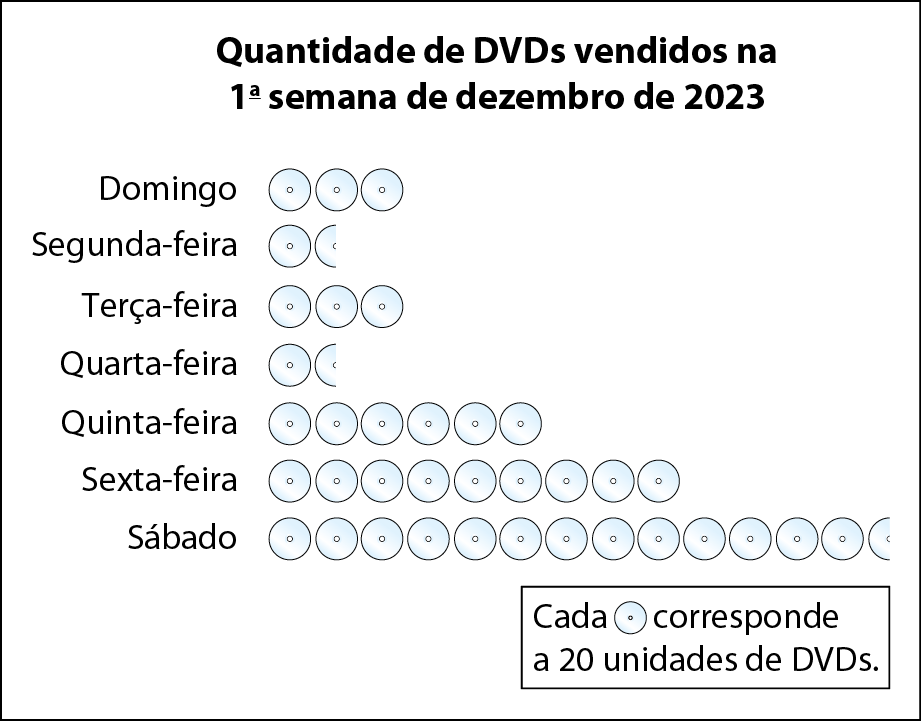
a) Construa uma tabela de distribuição de frequências, com a frequência relativa em porcentagem.
b) Sabendo que a meta de venda diária dessa loja é de 100 dê vê dês, em quantos dias a loja atingiu a meta?
c) Quantos dê vê dês foram vendidos nessa semana?
Use o enunciado seguinte para responder aos exercícios 2 e 3.
Em um escritório trabalham 40 pessoas cujas idades, em anos, são dadas em ordem crescente:
18 – 19 – 20 – 20 – 20 – 24 – 24 – 24
24 – 24 – 28 – 28 – 28 – 30 – 30 – 30
30 – 30 – 32 – 32 – 35 – 35 – 35 – 35
36 – 36 – 36 – 36 – 36 – 40 – 40 – 40
42 – 45 – 45 – 48 – 48 – 50 – 50 – 60
2 (saréspi) Relativamente ao total de funcionários desse escritório, a porcentagem dos que têm idades inferiores a 32 anos é:
a) 45%.
b) 38%.
c) 37,5%.
d) 25%.
3 (saréspi) Um prêmio vai ser sorteado entre os 40 funcionários do escritório. A probabilidade de que a pessoa sorteada tenha menos de 25 anos é:
a)
Fração, 1 oitavo..
b)
Fração, 2 oitavos..
c)
Fração, 3 oitavos..
d)
Fração, 5 oitavos..
4 (saréspi) Em uma chácara, há um total de 350 árvores frutíferas, assim distribuídas:
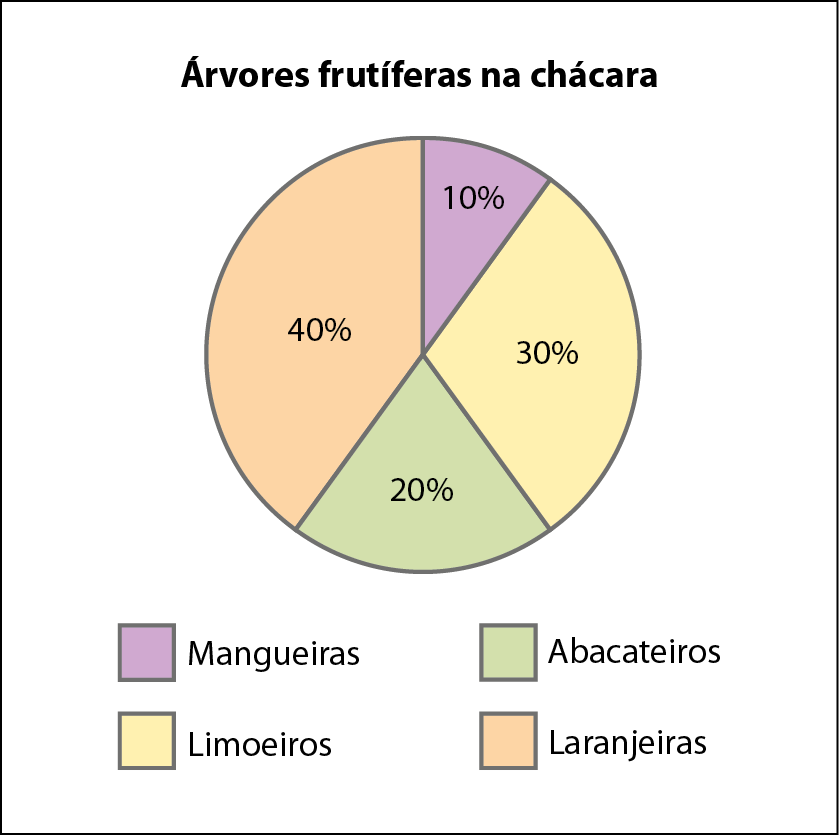
As quantidades de laranjeiras e mangueiras são, respectivamente:
a) 140 e 35.
b) 140 e 70.
c) 140 e 105.
d) 105 e 70.
5 (enêm) A permanência de um gerente em uma empresa está condicionada à sua produção no semestre. Essa produção é avaliada pela média do lucro mensal do semestre. Se a média for, no mínimo, de 30 mil reais, o gerente permanece no cargo; caso contrário, ele será despedido. O quadro mostra o lucro mensal em milhares de reais, dessa empresa, de janeiro a maio do ano em curso.
|
Janeiro |
Fevereiro |
Março |
Abril |
Maio |
|---|---|---|---|---|
|
21 |
35 |
21 |
30 |
38 |
Qual deve ser o lucro mínimo da empresa no mês de junho, em milhares de reais, para o gerente continuar no cargo no próximo semestre?
a) 26
b) 29
c) 30
d) 31
e) 35
6 Foi realizada uma pesquisa sobre o tempo que os 140 trabalhadores de uma empresa gastam no percurso entre a residência e o trabalho. Para tanto, foram selecionados, de modo imparcial, 40 trabalhadores.
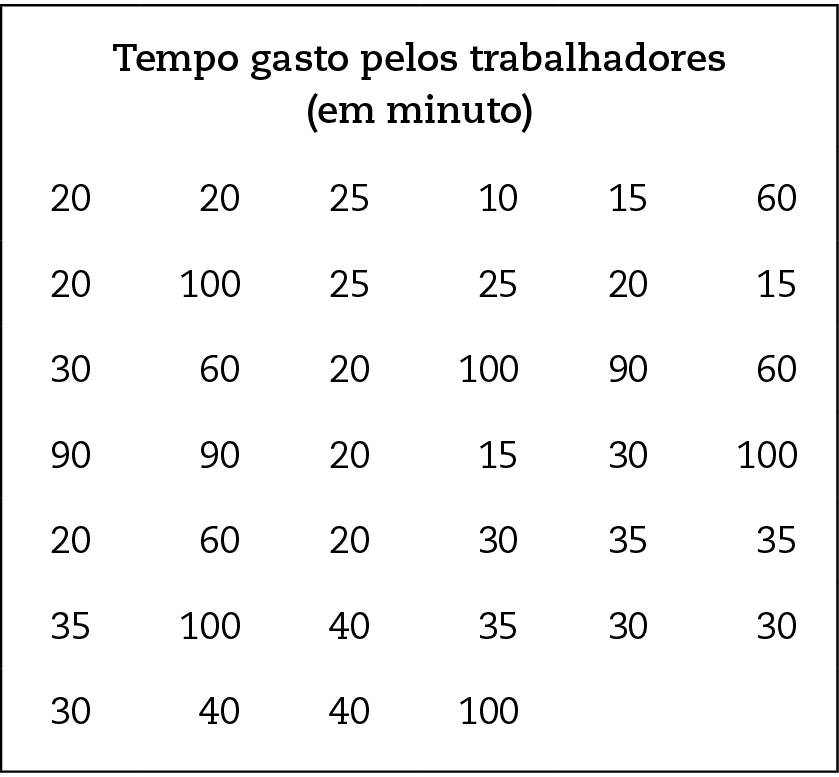
a) Construa uma tabela de distribuição de frequências com 5 classes, cada uma com amplitude igual a 20.
b) Calcule a média aritmética, a moda e a mediana do tempo gasto por esses trabalhadores.
c) Qual é a probabilidade de sortearmos, ao acaso, um trabalhador que gasta 90 minutos no percurso entre a residência e o trabalho?
7 A tabela a seguir mostra a idade das pessoas que se associaram a uma biblioteca pública durante o mês de julho.
|
Idade (em anos) |
Número de pessoas |
|---|---|
|
14 |
30 |
|
16 |
7 |
|
18 |
2 |
|
20 |
10 |
|
21 |
12 |
|
27 |
18 |
|
30 |
21 |
Dados obtidos pela bibliotecária.
Faça o que se pede.
a) Calcule a idade média dos associados.
b) Determine a idade modal e a idade mediana.
c) Construa um gráfico de colunas para essa situação.
d) Qual é a probabilidade de sortearmos, ao acaso, um associado que tenha mais de 21 anos?
8 Em uma pesquisa eleitoral para verificar a posição de três candidatos a prefeito de um município, 4.quinhentas pessoas foram consultadas. O resultado da pesquisa será organizado em um gráfico de setor circular. Sabendo que um certo candidato recebeu .1050 indicações de intenções de voto, qual é a medida do ângulo central correspondente ao setor do gráfico que representará as intenções de voto desse candidato?
a) 42graus
b) 84graus
c) 120graus
d) 276graus
9 Um paraquedista precisa pousar em uma região quadrada localizada em um terreno retangular, conforme o esquema a seguir. Sabendo que o comprimento do lado da região quadrada mede 8 metros e que o paraquedista certamente pousará no terreno retangular, calcule a probabilidade de o paraquedista pousar na região quadrada.
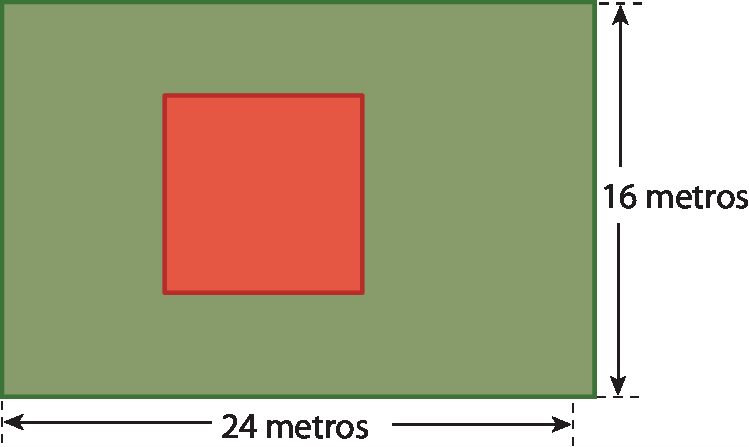
10 (ú éfe ême ésse) Uma empresa tem 18 funcionários. Um deles pede demissão e é substituído por um funcionário de 22 anos de idade. Com isso, a média das idades dos funcionários diminui 2 anos. A idade do funcionário que se demitiu é:
a) 50 anos.
b) 48 anos.
c) 54 anos.
d) 56 anos.
e) 58 anos.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Uma amostra representativa dos estudantes de uma escola deve conter:
a) somente estudantes do período da tarde.
b) estudantes de uma única turma.
c) estudantes das diferentes turmas e dos diferentes períodos.
d) todos os estudantes de um único período.
2 Uma pesquisa sobre jogos digitais foi realizada com .1000 participantes. O resultado referente ao dispositivo preferido para jogos digitais foi representado no gráfico a seguir.
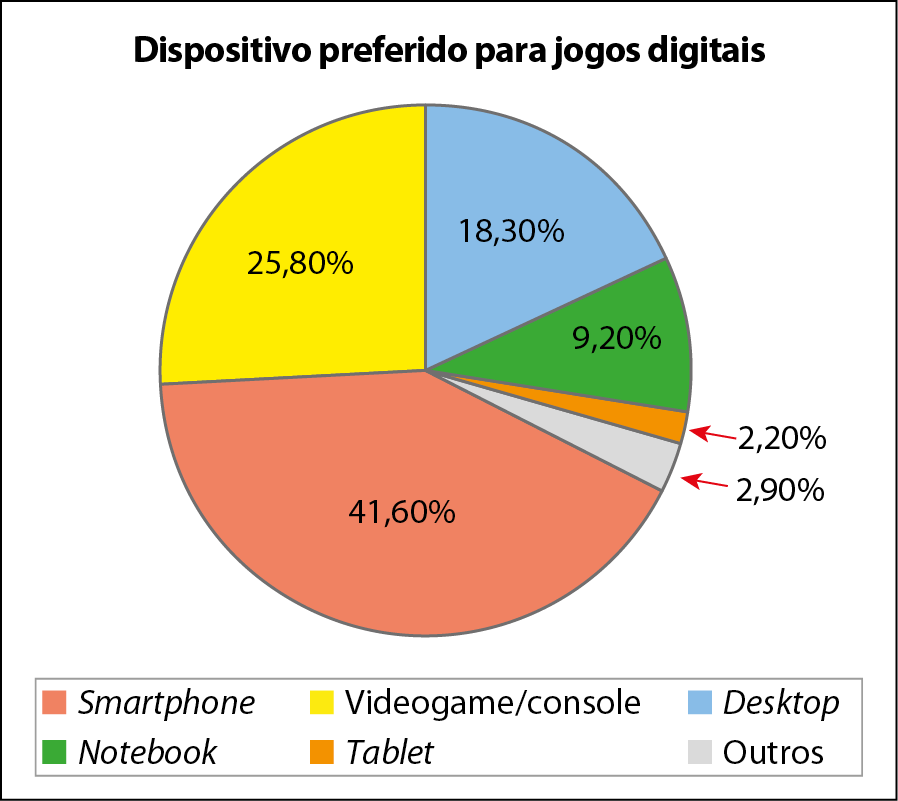
Com base nesses dados, é possível concluir que:
a) menos de quatrocentas pessoas preferem jogar em smartphone.
b) a opção que teve menos votos foi “Outros”.
c) aqueles que preferem computadores, desktop ou notebook, somam mais de 25% dos entrevistados.
d) o console foi a terceira opção mais votada.
3 Um supermercado fez uma pesquisa com os clientes sobre a preferência entre 3 marcas diferentes de sabonete.
|
Marca |
A |
B |
C |
|---|---|---|---|
|
Total de clientes |
205 |
103 |
92 |
Dados obtidos pelo supermercado.
A frequência relativa aproximada para cada marca de sabonete é, respectivamente:
a) 2,05; 1,03 e 0,92.
b) 0,68; 0,34 e 0,30.
c) 0,51; 0,26 e 0,23.
d) 0,21; 0,10 e 0,09.
4 A professora fez uma pesquisa com os estudantes sobre o tipo de livro preferido. Ela constatou que, dos 35 estudantes, 11 preferem quadrinhos, 10 suspense, 8 romance e os demais ficção. Qual é a moda desses dados?
a) Quadrinhos
b) Suspense
c) Romance
d) Ficção
5 Para fechar a nota bimestral dos estudantes, um professor utiliza a média aritmética ponderada. A nota máxima de todas as provas é 10 e a primeira prova tem peso 1, a segunda tem peso 2 e a terceira tem peso 3. Se um estudante tirou, respectivamente, 8, 5 e 7, qual foi a média bimestral desse estudante?
a) 6,5
b) 6,6
c) 6,8
d) 7,0
6 Os números a seguir representam os salários, em real, dos funcionários de uma empresa.
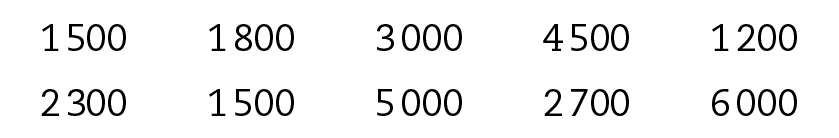
Qual é a mediana, em real, dos salários dos funcionários dessa empresa?
a) .2300
b) .2500
c) .2700
d) .2950
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Quais são as etapas de uma pesquisa estatística? Descreva, com as próprias palavras, cada uma delas.
b) Supondo que você faça uma pesquisa com um grupo de pessoas sobre o tempo que elas passam em redes sociais na internet todos os dias, explique como você faria para coletar e organizar os dados dessa pesquisa.
c) O que frequência absoluta e frequência relativa têm de diferente?
d) O que média, moda e mediana têm de diferente?
e) Quais são as informações necessárias para que seja possível calcular a probabilidade de um evento acontecer?