Página vinte e nove

ORIENTAÇÕES ESPECÍFICAS

Parte 1

O livro do 8º ano é composto de doze capítulos em que se desenvolvem as cinco Unidades Temáticas propostas pela Bê êne cê cê: Números, Álgebra, Geometria, Grandezas e medidas e Probabilidade e estatística, intercaladas e, sempre que possível, integradas, exploradas no corpo do texto explicativo e nas atividades.

A seguir, apresentamos sugestões de cronogramas para trabalhar com esses conteúdos em bimestre, trimestre e semestre com base nas organizações dos capítulos.

			Capítulos	Conteúdos	Habilidades e competências da BNCC
1º semestre	1º trimestre	1º bimestre	Capítulo 1 – Potências e raízes	• Potências com expoentes inteiros; • Potências de base 10; • Notação científica; • Raízes de números racionais; • Potências com expoente fracionário; • Problemas de contagem e o princípio multiplicativo; • Noção de juro simples; • Sequências numéricas.	Habilidades: (EF08MA01) (EF08MA02) (EF08MA03) (EF08MA04) (EF08MA09) (EF08MA11) Competências gerais: 1, 2, 4, 5, 9 e 10 Competências específicas: 1, 2, 4, 5 e 8
			Capítulo 2 – Construções geométricas e lugares geométricos	• Construções geométricas: segmentos congruentes, retas paralelas, retas perpendiculares, bissetrizes, ângulos; • Lugares geométricos: circunferência, mediatriz de um segmento e bissetriz de um ângulo; • Gráficos de setores.	Habilidades: (EF08MA15) (EF08MA17) (EF08MA23) (EF08MA27) Competências gerais: 1, 2, 3, 4, 5, 9 e 10 Competências específicas: 2, 3, 4, 5, 6 e 8
			Capítulo 3 – Estatística e probabilidade	• Pesquisas estatísticas: coleta, organização e apresentação de resultados; • Gráficos de barras, gráficos de colunas, gráficos de setores, gráficos de linha, pictogramas, cartogramas e infográficos; • Frequência absoluta e frequência relativa; • Medidas estatísticas de tendência central: moda, média aritmética e mediana; • Noções sobre pesquisas amostrais; • Estimativas; • Noções de probabilidade: espaço amostral, evento e probabilidade como medida.	Habilidades: (EF08MA04) (EF08MA22) (EF08MA23) (EF08MA24) (EF08MA25) (EF08MA26) (EF08MA27) Competências gerais: 1, 2, 4, 7, 8, 9 e 10 Competências específicas: 1, 2, 3, 4, 6, 7 e 8
		2º bimestre	Capítulo 4 – Cálculo algébrico	• Incógnita e variável; • Expressões algébricas; • Monômios; • Fração geratriz de uma dízima periódica; • Operações com monômios.	Habilidades: (EF08MA05) (EF08MA06) (EF08MA11) Competências gerais: 1, 2, 8, 9 e 10 Competências específicas: 2, 3, 5, 6 e 8

Página trinta

			Capítulos	Conteúdos	Habilidades e competências da BNCC
1º semestre	2º trimestre	2º bimestre	Capítulo 5 – Polinômios e frações algébricas	• Polinômios; • Operações com polinômios; • Frações algébricas; • Interpolação e extrapolação gráfica: gráficos de colunas duplas e gráficos de linhas duplas.	Habilidades: (EF08MA06) (EF08MA19) (EF08MA23) Competências gerais: 2, 4, 9 e 10 Competências específicas: 2, 3, 4, 5 e 8
1º semestre		2º bimestre	Capítulo 6 – Produtos notáveis e fatoração	• Produtos notáveis: quadrado da soma de dois termos, quadrado da diferença de dois termos, produto da soma pela diferença de dois termos e cubo da soma e da diferença de dois termos; • Fatoração de polinômios; • Aplicação de produtos notáveis e de fatoração para cálculo de valores numéricos; • Simplificação de frações algébricas; • Resolução de equações envolvendo frações algébricas; • Sequências numéricas recursivas e não recursivas; • Construção de gráfico de barras.	Habilidades: (EF08MA06) (EF08MA10) (EF08MA11) (EF08MA19) (EF08MA23) Competências gerais: 1, 2, 4, 9 e 10 Competências específicas: 3, 1, 3, 4, 5 e 8
2º semestre		3º bimestre	Capítulo 7 – Estudo dos triângulos	• Cevianas de um triângulo: mediana, bissetriz e altura; • Congruência de triângulos; • Estudo dos casos de congruência de triângulos; • Construção de um hexágono regular com descrição de procedimentos por escrito.	Habilidades: (EF08MA14) (EF08MA16) (EF08MA17) (EF08MA18) Competências gerais: 2, 3, 4, 7, 9 e 10 Competências específicas: 2, 5 e 8
	3º trimestre		Capítulo 8 – A Geometria demonstrativa	• Noções sobre Geometria demonstrativa: noções primitivas, postulados e teoremas; • Utilização de congruência de triângulos para demonstrações geométricas; • Propriedades do triângulo isósceles; • Propriedades de triângulos; • Aplicação dos conceitos de mediatriz e de bissetriz na resolução de problemas.	Habilidades: (EF08MA14) (EF08MA17) Competências gerais: 1, 2, 3, 4, 9 e 10 Competências específicas: 1, 2, 5 e 8
	3º trimestre		Capítulo 9 – Estudo dos quadriláteros	• Elementos dos quadriláteros; • Paralelogramos e suas propriedades; • Utilização de congruência de triângulos para demonstrações geométricas relativas a quadriláteros; • Trapézios; • Propriedade dos trapézios isósceles; • Propriedade da base média do triângulo e do trapézio; • Construção de quadriláteros com instrumentos de desenho geométrico.	Habilidades: (EF08MA12) (EF08MA13) (EF08MA14) (EF08MA15) (EF08MA17) (EF08MA19) Competências gerais: 2, 3, 6, 8, 9 e 10 Competências específicas: 2, 3, 5, 6, 7 e 8

Página trinta e um

			Capítulos	Conteúdos	Habilidades e competências da BNCC
2º semestre	4º trimestre	4º bimestre	Capítulo 10 – Sistemas de equação do 1º grau com duas incógnitas	• Métodos de resolução de sistemas de equações do 1º grau; • Grandezas proporcionais; • Representação gráfica de equações do 1º grau; • Classificação de um sistema de equações; • Solução gráfica de um sistema de duas equações do 1º grau • Composição de um gráfico de colunas a partir de outros gráficos.	Habilidades: (EF08MA06) (EF08MA07) (EF08MA08) (EF08MA09) (EF08MA12) (EF08MA13) (EF08MA23) (EF08MA26) (EF08MA27) Competências gerais: 2, 4, 5, 9 e 10 Competências específicas: 2, 3, 4, 5, 6 e 8
			Capítulo 11 – Área de regiões poligonais	• Área de paralelogramos: paralelogramos, retângulos, losangos e quadrados; • Área de triângulos; • Área de trapézios; • Construção de um losango com instrumentos de desenho geométrico; • Cálculo de área por decomposição em triângulos; • Interpretação e construção de pictogramas.	Habilidades: (EF08MA09) (EF08MA15) (EF08MA19) (EF08MA23) Competências gerais: 2, 4, 9 e 10 Competências específicas: 2, 3, 4, 6 e 8
			Capítulo 12 – Geometria e grandezas	• Polígonos regulares inscritos em uma circunferência; • Polígonos regulares circunscritos em uma circunferência; • Propriedades e elementos de polígonos regulares; • Área do círculo; • Volume de cilindros retos; • Volume de prismas retos; • Reconhecimento da relação entre um litro e um decímetro cúbico; • Resolução de problemas envolvendo medidas de volume e de capacidade.	Habilidades: (EF08MA15) (EF08MA16) (EF08MA19) (EF08MA20) (EF08MA21) Competências gerais: 1, 2, 4, 7, 9 e 10 Competências específicas: 1, 2, 3, 6 e 8

Considerações iniciais

Cada capítulo aborda objetos de conhecimento, entendidos como conteúdos, conceitos, processos, com a intenção de desenvolver as habilidades relacionadas a eles. Esses conhecimentos são articulados, retomados e ampliados a fim de proporcionar sua apropriação pelos estudantes, considerando a aprendizagem um processo contínuo e integrado.

Os conteúdos matemáticos são desenvolvidos de modo que as habilidades, as Unidades Temáticas, as competências e outras áreas do conhecimento se articulem e se relacionem, e são tratados na perspectiva das aprendizagens dos anos anteriores e posteriores. Assim, no livro do 8º ano do Ensino Fundamental, levamos em conta os objetivos de aprendizagem para o 7º ano, conforme proposto na Bê êne cê cê, visando preparar os estudantes para se apropriar dos conhecimentos previstos para o 9º ano.

A seguir, são feitas orientações didáticas sobre cada capítulo e o que se pretende que os estudantes desenvolvam neles.

Página trinta e dois

Capítulo 1 – Potências e raízes

• Objetivos do capítulo e justificativas

• Retomar cálculos de potenciação com base racional e expoente natural, ampliando para expoente negativo.

• Reconhecer e expressar valores em notação científica.

• Efetuar cálculo com raízes exatas.

• Resolver e elaborar problemas usando a relação entre potenciação e radiciação.

• Conceituar potência com expoente fracionário.

• Resolver e elaborar problemas de contagem envolvendo o princípio multiplicativo.

• Resolver problemas envolvendo cálculo de porcentagens e a ideia de juro.

• Resolver problemas que possam ser representados pela equação polinomial do 2º grau do tipo axelevado a 2 = b.

• Identificar regularidades em sequências numéricas recursivas.

• Utilizar a área de um quadrado no cálculo de raiz quadrada.

Ao retomar cálculos de potenciação ampliando para potências com expoentes inteiros e, associado a isso, ao possibilitar aos estudantes reconhecer e expressar valores em notação científica em diferentes situações, contribui-se para o desenvolvimento da competência específica 1 e da competência geral 1, pois eles poderão compreender que a Matemática é fruto das necessidades humanas e que contribui para analisar, descrever e solucionar problemas científicos e tecnológicos.

Calcular raízes exatas, associar a potenciação e a radiciação e explorar potências com expoentes fracionários favorece o desenvolvimento das competências gerais 2 e 4 e da competência específica 2, pois os estudantes poderão exercitar a curiosidade intelectual a fim de estabelecer as relações propostas, elaborar e testar hipóteses para verificar a pertinência de propriedades estudadas e, por isso, argumentar e defender ideias com base em fatos.

Ao resolver problemas envolvendo o princípio multiplicativo ou porcentagens e ideias de juro simples, os estudantes mobilizam e desenvolvem aspectos das competências específicas 4 e 5, pois precisam fazer observações sobre aspectos quantitativos e qualitativos de situações contextualizadas e significativas, investigando e organizando as informações a fim de interpretá-las adequadamente. Além disso, eles podem utilizar as ferramentas matemáticas para resolver esses problemas, inclusive por meio de tecnologias digitais, como a proposta de utilização de planilhas eletrônicas para organizar os dados sobre o cálculo de juro, favorecendo o desenvolvimento da competência geral 5.

Ainda em relação ao desenvolvimento da competência específica 1, os estudantes poderão desenvolvê-la ao explorar situações que possibilitam atribuir significados aos conhecimentos teóricos estudados, como a relação entre equações do tipo axelevado a 2 = b e o cálculo da medida da área de um quadrado, associados ao cálculo da raiz quadrada.

O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 são favorecidos com as diferentes atividades a serem realizadas em grupos, pois possibilitam aos estudantes exercitar diferentes habilidades socioemocionais ao trabalharem com a diversidade de aprendizagem entre os colegas, interagindo de fórma cooperativa.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah zero um) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.

(ê éfe zero oito ême ah zero dois) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.

(ê éfe zero oito ême ah zero três) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.

(ê éfe zero oito ême ah zero quatro) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo axelevado a 2 = b.

(ê éfe zero oito ême ah um um) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.

Neste capítulo, são desenvolvidos objetos de conhecimento da Unidade Temática Números. Nos conteúdos e atividades propostos foram consideradas as aprendizagens do 6º ano e do 7º ano relativas à potenciação de números naturais e ao reconhecimento e operações de números inteiros, desenvolvendo-se a habilidade (ê éfe zero oito ême ah zero um).

Esse é o momento de ampliação dos conhecimentos sobre potenciação com números naturais para abordar potências com expoente negativo e aprofundar radiciação, na perspectiva de que a continuidade desse processo conduza os estudantes a se apropriar da relação entre potenciação e radiciação com a apresentação da potência de expoente fracionário (ê éfe zero oito ême ah zero dois). Para isso, são trabalhados conceitos e atividades, além de se desenvolver também a notação científica que utiliza potências de base 10.

Ao ampliar os conhecimentos que os estudantes já têm sobre potenciação e radiciação, espera-se prepará-los para outros tipos de número e para a ampliação dos conjuntos numéricos que serão estudados no 9º ano do Ensino Fundamental (ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro).

Ainda na Unidade Temática Números, desenvolvem-se atividades envolvendo cálculos com porcentagens e problemas de contagem que tratam do princípio multiplicativo, possibilitando o desenvolvimento das habilidades (ê éfe zero oito ême ah zero três) e (ê éfe zero oito ême ah zero quatro).

A articulação com a Unidade Temática Álgebra é promovida ao apresentar expressões algébricas para o cálculo de juro, ao buscar regularidades em sequência que envolvem potências e ao resolver equações do tipo axelevado a 2 = b com o uso de potências e raízes, mobilizando aspectos das habilidades (ê éfe zero oito ême ah zero nove) e (ê éfe zero oito ême ah um um).

A articulação com a Unidade Temática Grandezas e medidas aparece pelo uso do conceito de área associada à noção de raiz quadrada. A conexão com Probabilidade e estatística se dá em atividade que explora a interpretação de gráfico de colunas, retomando conhecimentos construídos em anos anteriores.

Página trinta e três

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Abertura

a) Envolvem potências de 10 os seguintes dados: massa do sol = 1,989 ⋅ 1030 quilogramas; o número de vezes que esse valor corresponde à massa da terra = 333 ⋅ 103; temperatura do núcleo = 1,5 ⋅ 107 °C.

b) É maior: se observamos que 103 = 10 ⋅ 10 ⋅ 10 = .1000, o que o texto nos diz é que ela é 333 mil vezes maior.

c) Em 2012, o peso médio da humanidade era de 62 quilogramas. Para comparar, os estudantes devem dividir a massa de hidrogênio convertido em hélio, que é 6 ⋅ 1011 quilogramas, por essa medida de massa média, obtendo:

6 ⋅ 1011 : 62 = 6 ⋅ 1011 : 6,2 ⋅ 10 ≃ 0,97 ⋅ 1011 ‒ 1 ≃ 1 ⋅ 1010 = 1010

O importante é observar que, por estarmos considerando quantidades muito grandes, 0,97 pode ser aproximado por 1 sem prejuízo.

d) Sim, pois podem afetar sistemas eletrônicos e de comunicação. Professores podem mencionar a tempestade solar de 2003 que deixou a Suécia sem energia por uma hora.

Exercícios propostos

1. O número total de apartamentos pode ser calculado multiplicando-se o número de apartamentos por andar (6) pelo número de andares dos prédios (6) e pelo número de prédios (6), ou seja, 6 ⋅ 6 ⋅ 6 = 63.

2. a) Falsa. Pelas propriedades da potenciação, (4⁵)² = 45 ⋅ 2 = 410, enquanto 45² não pode ser simplificado além de 45² = 425.

Se julgar conveniente, refaça na lousa o exemplo apresentado no quadro Observações que antecede os exercícios, [(a³)2 ≠ a³2].

2. b) Verdadeira. Pelas propriedades da potenciação: (45)2 = 45 ⋅ 2 = 42 ⋅ 5 = (42)5.

2. c) Verdadeira. De acordo com a propriedade da potenciação (a ⋅ b)m = am ⋅ bm, considerando a = 2, b = 3 e m = 2.

2. d) Falsa. (2 + 3)2 = (5)2 = 25 e 22 + 32 = 4 + 9 = 13

2. e) Verdadeira. De acordo com a propriedade da potenciação (a : b)m = am : bm (com b ≠ 0), considerando a = 8, b = 4 e m = 3.

2. f) Falsa. (8 – 4)3 = 43 = 64 e 83 – 43 = 512 – 64 = 448

3. a) Pela propriedade da potenciação am · an = am + n:

(24 ⋅ 26) : (25 ⋅ 23) = (24 + 6) : (25 + 3) = 210 : 28

Pela propriedade da potenciação am : an = am ‒ n, assim:

210 : 28 = 210 ‒ 8 = 22

3. b) Pelas propriedades da potenciação:

(x4 ⋅ x2 ⋅ x3)2 : (x4)5 = (x4 + 2 + 3)2 : x4 ⋅ 5 =

= (x9)2 : x20 = x9 ⋅ 2 : x20 = x18 : x20 = x18 ‒ 20 = x ‒2

3. c)

\frac{2^{5 x - 1} · 2^{x + 2}}{2^{3 x - 2}} = \frac{2^{(5 x - 1) + (x + 2)}}{2^{3 x - 2}} = \frac{2^{6 x + 1}}{2^{3 x - 2}} =

= 2(6x + 1) : 2(3x ‒ 2) = 2(6x + 1) ‒ (3x ‒ 2) = 2(3x + 3)

3. d)

\frac{5^{2} \cdot 5^{3}}{5^{1} \cdot 5^{0}}

= (52 ⋅ 53) : (51 ⋅ 50)

É importante lembrar que 50 = 1. Assim:

(52 ⋅ 53 ) : (51 ⋅ 50 ) = (52 + 3) : (51 ⋅ 1) = 55 : 51 = 55 ‒ 1 = 54

5. a) Seguindo o raciocínio de Marina:

• a 5ª linha terá 2 ⋅ 2 ⋅ 2 ⋅ 2 macacos;

• a 6ª linha terá 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 macacos;

• a 7ª linha terá 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 macacos;

• a 8ª linha terá 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 macacos;

• a 9ª linha terá 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 macacos;

• a 10ª linha terá 512 macacos, pois

2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 ⋅ 2 = 29 = 512.

5. b) Lembrando que a1 = a e a0 = 1 (a ≠ 0), sendo a um número racional, o número de macacos da 1ª linha é 1 = 20, e o da segunda linha é 2 = 21.

5. c) O seguinte padrão pode ser observado.

• Número de macacos na 1ª linha: 20 = 21 – 1,

• Número de macacos na 2ª linha: 21 = 22 – 1,

• Número de macacos na 3ª linha: 2 ⋅ 2 = 22 = 23 ‒ 1,

e, assim por diante. Logo, o número de macacos na linha n é dado por 2n ‒ 1. Podemos usar o item a para reforçar esse raciocínio.

7. a) Como o denominador da fração pode ser escrito como uma potência de 10, 100 = 102, e o numerador é 1, da definição de potência com expoente negativo, temos:

\frac{1}{100} = \frac{1}{10^{2}}

= 10‒2

7. b) Analogamente, como .10000 = 104, temos:

\frac{1}{10 000} = \frac{1}{10^{4}}

= 10‒4

7. c) Como ..1000000 = 106, temos:

\frac{1}{1 000 000} = \frac{1}{10^{6}}

= 10‒6

7. d) O número 0,1 pode ser representado na fórma de fração, como nos itens anteriores.

0, 1 = \frac{1}{10} = \frac{1}{10^{1}} = 10^{- 1}

7. e) Analogamente:

0, 01 = \frac{1}{100} = \frac{1}{10^{2}} = 10^{– 2}

Página trinta e quatro

7. f)

0, 001 = \frac{1}{1 000} = \frac{1}{10^{3}} = 10^{- 3}

11.

m = {(\frac{4}{5} - \frac{1}{2})}^{- 3} = {(\frac{3}{10})}^{- 3} = {(\frac{10}{3})}^{3}

n = {(3 + \frac{1}{3})}^{2} = {(\frac{10}{3})}^{2}

Assim:

m : n = {(\frac{10}{3})}^{3} : {(\frac{10}{3})}^{2} = {(\frac{10}{3})}^{3 - 2} = \frac{10}{3}

12. a)

2^{- 8} = {(2^{- 1})}^{8} = {(\frac{1}{2})}^{8}

Com uma calculadora, determinamos que

\frac{1}{2} = 0, 5

(1 : 2 = 0,5). Portanto, 2‒8 = 0,58.

Multiplicando 0,5 por si mesmo 8 vezes na calculadora, obtemos 0,00390625.

12. b)

4^{‒ 5} = {(4^{‒ 1})}^{5} = {(\frac{1}{4})}^{5}

Com uma calculadora, determinamos que

\frac{1}{4} = 0, 25

(1 : 4 = 0,25). Portanto, 4‒5 = 0,255.

Multiplicando 0,25 por si mesmo 5 vezes na calculadora, obtemos 0,0009765625.

12. c)

0, 4^{‒ 3} = {(0, 4^{‒ 1})}^{3} = {(\frac{1}{0, 4})}^{3}

Com uma calculadora, determinamos que

\frac{1}{0, 4} = 2, 5

(1 : 0,4 = 2,5). Portanto, 0,4‒3 = 2,53.

Multiplicando 2,5 por si mesmo 3 vezes na calculadora, obtemos 15,625.

12. d)

0, 2^{‒ 6} = {(0, 2^{‒ 1})}^{6} = {(\frac{1}{0, 2})}^{6}

Com uma calculadora, determinamos que

\frac{1}{0, 2} = 5

(1 : 0,2 = 5). Portanto, 0,2‒6 = 56.

Multiplicando 5 por si mesmo 6 vezes na calculadora, obtemos .15625.

15. a) É preciso decompor 9 em fatores primos:

9 = 3 ⋅ 3 = 32

15. b) Note que 81 = 9 ⋅ 9 = 32 ⋅ 32 = 32 + 2 = 34. Alternativamente, podemos decompor 81 em fatores primos dividindo-o por 3 sucessivas vezes.

15. c) Como 27 = 3 ⋅ 3 ⋅ 3 = 33, logo:

\frac{1}{27} = \frac{1}{3^{3}}

\frac{1 · 1 · 1}{3 · 3 · 3}

\frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} = {(\frac{1}{3})}^{3}

= (3‒1)3 = 3‒1 ⋅ 3 = 3‒3

15. d) É preciso decompor 243 em fatores primos.

243 = 3 ⋅ 81 = 3 ⋅ 34 = 35.

Logo:

\frac{1}{243} = \frac{1}{3^{5}}

\frac{1 \cdot 1 \cdot 1 \cdot 1 \cdot 1}{3 \cdot 3 \cdot 3 \cdot 3 \cdot 3}

\frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} \cdot \frac{1}{3} = {(\frac{1}{3})}^{5}

= (3‒1)5 = 3‒1 ⋅ 5 = 3‒5

16. a) Primeiro, vamos escrever 4 e 8 como potências de base 2. Para isso, fazemos a decomposição em fatores primos:

4 = 2 ⋅ 2 = 22 e 8 = 2 ⋅ 4 = 23. Assim:

\frac{4^{2} \cdot 8^{3}}{2^{10}} = \frac{{(2^{2})}^{2} \cdot {(2^{3})}^{3}}{2^{10}}

\frac{2^{2 \cdot 2} \cdot 2^{3 \cdot 3}}{2^{10}}

\frac{2^{4} \cdot 2^{9}}{2^{10}}

\frac{2^{4^{+} 9}}{2^{10}}

\frac{2^{13}}{2^{10}}

= 213 ‒ 10 = 23

16. b) Primeiro, vamos escrever 9, 27 e 81 como potências de base 3. Para isso, fazemos a decomposição em fatores primos:

9 = 3 ⋅ 3 = 32, 27 = 3 ⋅ 9 = 33 e 81 = 9 ⋅ 9 = 34

Assim:

\frac{9^{3} \cdot 27^{2}}{81}

\frac{{(3^{2})}^{3} \cdot {(3^{3})}^{2}}{3^{4}}

\frac{3^{2 \cdot 3} \cdot 3^{3 \cdot 2}}{3^{4}}

\frac{3^{6} \cdot 3^{6}}{3^{4}}

\frac{3^{6^{+} 6}}{3^{4}} = \frac{3^{12}}{3^{4}}

= 312 ‒ 4 = 38

17. a) Para preencher a n-ésima linha da terceira coluna, é preciso multiplicar o número 10 por ele mesmo n vezes.

Expoente inteiro positivo (n)	Potência de base 10 (10n)	Valor da potência (resultado)	Número de zeros do resultado
1	101	10	1
2	102	100	2
3	103	1.000	3
4	104	10.000	4
5	105	100.000	5

17. b) 10n é o número consistindo em 1 seguido de n zeros.

17. c) Para preencher a terceira coluna, é preciso multiplicar 10‒1 =

\frac{1}{10}

= 0,1 por ele mesmo |n| vezes.

Expoente inteiro negativo (n)	Potência de base 10 (10n)	Valor da potência (resultado)	Número de casas decimais do resultado
−1	10−1	0,1	1
−2	10−2	0,01	2
−3	10−3	0,001	3
−4	10−4	0,0001	4
−5	10−5	0,00001	5

17. d) Para n inteiro e negativo, o valor da potência indicada por 10n é um número formado pelo algarismo 1 antecedido por |n| zeros, com uma vírgula entre o primeiro e o segundo algarismo, ou seja, é um número com |n| casas decimais.

Página trinta e cinco

18. Considerando que 10n é o número formado pelo algarismo 1 seguido de n zeros, para o número ....1000000000000, com 12 zeros, n = 12; portanto, a medida da distância média entre o planeta Saturno e o Sol é da ordem de 1012 métros.

19. a) 10‒1 =

\frac{1}{10}

= 0,1

19. b) 10‒2 = (10‒1)2 =

{(\frac{1}{10})}^{2}

= (0,1)2 = 0,01

19. c) 10‒3 = (10‒1)3 =

{(\frac{1}{10})}^{3}

= (0,1)3 = 0,001

19. d) 10‒5 = (10‒1)5 =

{(\frac{1}{10})}^{5}

= (0,1)5 = 0,00001

19. e) 10‒6 = (10‒1)6 =

{(\frac{1}{10})}^{6}

= (0,1)6 = 0,000001

20. Observando que 10‒n é um número com n casas decimais, com o algarismo 1 na última casa decimal e zero nas demais, para o número 0,0001, com 4 casas decimais, n = 4; portanto, a medida do diâmetro de um fio de cabelo fino é, aproximadamente, 10‒4 métro.

21. Espera-se que os estudantes construam um quadro como a seguir.

Prefixos das unidades de medida no SI
Nome	Símbolo	Fator de multiplicação da unidade
yotta	Y	1024 = 10.000.000.000.000.000.000.000.000
zetta	Z	1021 = 10.000.000.000.000.000.000.000
exa	E	1018 = 10.000.000.000.000.000.000
peta	P	1015 = 10.000.000.000.000.000
tera	T	1012 = 10.000.000.000.000
giga	G	109 = 10.000.000.000
mega	M	106 = 10.000.000
quilo	k	103 = 10.000
hecto	h	102 = 1.000
deca	da	101 = 100
nenhum	nenhum	100 = 1
deci	d	10−1 = 0,1
centi	c	10−2 = 0,01
mili	m	10−3 = 0,001
micro	μ	10−6 = 0,000001
nano	n	10−9 = 0,0000000001
pico	p	10−12 = 0,0000000000001
femto	f	10−15 = 0,0000000000000001
atto	a	10−18 = 0,0000000000000000001
zepto	z	10−21 = 0,0000000000000000000001
yocto	y	10−24 = 0,0000000000000000000000001

Dados obtidos em: Sistema Internacional de Unidades – ésse Í, tradução luso-brasileira da 9ª edição do BIPM, 2021. Disponível em: https://oeds.link/WK2qkY. Acesso em: 27 julho 2022.

22. a)

\frac{10^{3} \cdot 10^{2}}{10^{7}} = \frac{10^{3 + 2}}{10^{7}} = \frac{10^{5}}{10^{7}}

= 105 ‒ 7 = 10‒2 = 0,01

22. b)

\frac{10^{4} \cdot 10^{2}}{10^{9}} = \frac{10^{4 + 2}}{10^{9}} = \frac{10^{6}}{10^{9}}

= 106 ‒ 9 = 10‒3 = 0,001

22. c)

\frac{10^{‒ 16}}{10^{‒ 4} \cdot 10^{‒ 8}} = \frac{10^{‒ 16}}{10^{‒ 4 + (‒ 8)}}

\frac{10^{‒ 16}}{10^{‒ 4 ‒ 8}} = \frac{10^{‒ 16}}{10^{‒ 12}}

= 10‒16 ‒ (‒12) = 10‒16 + 12 = 10‒4 = 0,0001

22. d)

\frac{10^{‒ 4} \cdot 10^{‒ 8}}{10^{‒ 9}} = \frac{10^{‒ 4 + (‒ 8)}}{10^{‒ 9}}

\frac{10^{‒ 4 ‒ 8}}{10^{‒ 9}} = \frac{10^{‒ 12}}{10^{‒ 9}}

= 10‒12 ‒ (‒9) = 10‒12 + 9 = 10‒3 = 0,001

23. a) Deslocando a vírgula 4 casas para a direita, temos:

3,6 ⋅ 104 = .36000

23. b) Deslocando a vírgula duas casas para a direita, temos:

0,025 ⋅ 102 = 2,5

23. c) Deslocando a vírgula duas casas para a esquerda (pois o expoente é um número inteiro negativo), temos:

0,4 ⋅ 10‒2 = 0,004

23. d) Deslocando a vírgula 3 casas para a esquerda (pois o expoente é um número inteiro negativo), temos:

.3576 ⋅ 10‒3 = 3,576

24. Para simplificar o cálculo, vamos escrever os números na fórma de potência de base 10. Deslocando a vírgula para a direita cinco casas em 0,000025, obtemos: 0,000025 = 2,5 : 105 = 2,5 ⋅ 10‒5. Da mesma maneira, podemos concluir que 0,000000002 = 2 ⋅ 10‒9 (pois é preciso avançar 9 casas para obter 2). Logo:

0,000025 ⋅ 0,000000002 = (2,5 ⋅ 10‒5) ⋅ (2 ⋅ 10‒9) =

= 2,5 ⋅ 2 ⋅ 10‒5 ⋅ 10‒9 = 5 ⋅ 10‒5 ‒ 9 = 5 ⋅ 10‒14

Alternativa b.

25. Para fazer a adição, as potências de base 10 devem ter os mesmos expoentes. Então, considerando que 10‒23 = 10‒21 ‒ 2 = 10‒21 · 10‒2, temos:

5,24 ⋅10‒23 = 5,24 · 10‒21 · 10‒2 = 0,0524 · 10‒21 . Assim:

A = 5,24 · 10‒23 = 8,36 · 10‒21

A = 0,0524 · 10‒21 = 8, 36 · 10‒21

A = (8,36 – 0,0524) · 10‒21

A = 8,4124 · 10‒21

Alternativa c.

26. a) Para obter .567540 a partir de 56,754, é preciso deslocar a vírgula 4 casas para a direita, o que equivale a multiplicar por a = 104.

26. b) Para obter 30 a partir de 0,003, é preciso deslocar a vírgula 4 casas para a direita, o que equivale a multiplicar por a = 104.

26. c) Para obter 0,000023 a partir de 23, é preciso deslocar a vírgula 6 casas para a esquerda, o que equivale a multiplicar por a = 10‒6.

26. d) Para obter 0,00045 a partir de 4,5, é preciso deslocar a vírgula 4 casas para a esquerda, o que equivale a multiplicar por a = 10‒4.

Página trinta e seis

27. a) O prefixo “centi” equivale a um centésimo, ou 0,01 = = 10‒2. Logo, 1 centímetro = 10‒2 métro.

27. b) O prefixo “quilo” equivale a mil, ou .1000 = 103. Logo, 1 quilômetro = 103 métros; portanto, 100 quilômetros = (100 ⋅ 103) métros = (102 ⋅ 103) métros = 103 + 2 métros = 105 métros.

27. c) 1 quilograma equivale a .1000 gramas. Ou seja, 1 quilograma = .1000 gramas; portanto, 1 grama = (1 : .1000) quilograma = 10‒3 quilograma.

Logo: 10 gramas = 101 ⋅ 10‒3 quilograma = 101 + (‒3) = 10‒2 quilograma

27. d) Uma tonelada equivale a .1000 quilogramas = 103 quilogramas.

27. e) Como 1 centímetro = 10‒2 métro, temos:

1 centímetro quadrado = (1 centímetro) ⋅ (1 centímetro) = (10‒2 métro) ⋅ (10‒2 métro) = 10‒4 métros quadrados

Portanto, 10 centímetros quadrados = (10 ⋅ 10‒4) métros quadrados = 101 ‒ 4 métros quadrados = 10‒3 métros quadrados.

27. f) O prefixo “deci” equivale a um décimo.

Logo, 1 métro = 10 decímetros.

Como 1 centímetro = 10‒2 métro, temos que 1 centímetro = 10‒2 métro =

= 10‒2 ⋅ (10 decímetros) = (10‒2 ⋅ 10) decímetro = 10‒2 + 1 decímetro = 10‒1 decímetro.

Portanto: 1 centímetros cúbicos = (1 centímetro)³ = (10‒1 decímetro)³ = 10‒3 decímetro cúbico

28. Como 6,7 ⋅ 109 métros cúbicos corresponde a 37% da capacidade procurada, c, então, fazendo uma proporção:

\frac{37}{6, 7 \cdot 10^{9}} = \frac{100}{c}

c = \frac{100 \cdot 6, 7 \cdot 10^{9}}{37} = \frac{10^{2} \cdot 6, 7 \cdot 10 \cdot 10^{8}}{37}

c =

\frac{67}{37} \cdot 10^{10}

1, \bar{810}

⋅ 102 + 8 ≃ 1,811 ⋅ 1010

Logo, a capacidade total é de aproximadamente ...18110000000 métros cúbicos.

29. Precisamos determinar quanto de água o rio Amazonas lança no oceano em unidades compatíveis com a do volume do açude (metro cúbico). Por definição, 1 litro equivale a 1 decímetro cúbico.

Como 1 decímetro = 1 : 10 métro = 10‒1 métro, temos que 1 litro = 1 decímetro cúbico = (1 decímetro)³ = (1 ⋅ 10‒1 métro)³ = 10‒3 métro cúbico. Como um milhão é ..1000000 = 106, conclui-se que o rio Amazonas despeja 5 ⋅ 104 métros cúbicos por segundo no oceano, pois 50 milhões de litros correspondem a:

50 ⋅ 106 ⋅ 10‒3 métro cúbico = 5 ⋅ 10 ⋅ 106 ⋅ 10‒3 métro cúbico =

= 5 ⋅ 101 + 6 ‒ 3 métros cúbicos = 5 ⋅ 104 métros cúbicos

Fazendo uma proporção simples com a capacidade do açude Orós, determinamos o tempo t, em segundo, que o rio Amazonas leva para lançar o volume de água correspondente no oceano.

t = \frac{2 \cdot 10^{9}}{5 \cdot 10^{4}} = \frac{2}{5} \cdot \frac{10^{9}}{10^{4}}

= 0,4 ⋅ 105 = .40000

Ou seja, são necessários .40000 segundos para que o rio Amazonas lance no oceano Atlântico um volume de água igual à capacidade do açude Orós. Como uma hora tem .3600 segundos, isso equivale a

11, \bar{1}

horas.

\frac{40 000}{3 600} = \frac{400 \cdot 10^{2}}{36 \cdot 10^{2}}

\frac{400}{36} \cdot \frac{10^{2}}{10^{2}}

= 11,11111reticências

Ou seja, o tempo é maior do que 10 horas e menor do que 20 horas.

Alternativa d.

30. a) Para deslocar a vírgula uma casa para a esquerda, precisamos multiplicar por 101 e por 10‒1, obtendo:

12,6 = 12,6 ⋅ 10‒1 ⋅ 101 = 1,26 ⋅ 10

Como um milhão é ..1000000 = 106, 12,6 milhões correspondem a:

12,6 · 106 = 1,26 ⋅ 10 ⋅ 106 = 1,26 ⋅ 106 + 1 = 1,26 ⋅ 107

30. b) Para deslocar a vírgula duas casas para a esquerda, precisamos multiplicar por 102 e por 10‒2, obtendo:

361 = 361 ⋅ 10‒2 ⋅ 102 = 3,61 ⋅ 102

Logo: 361 ⋅ 106 = 3,61 ⋅ 102 ⋅ 106 = 3,61 ⋅ 106 + 2 = 3,61 ⋅ 108

30. c) Para deslocar a vírgula uma casa para a esquerda, precisamos multiplicar por 101 e por 10‒1, obtendo:

15 = 15 ⋅ 10‒1 ⋅ 101 = 1,5 ⋅ 10

Como um bilhão consiste em mil milhões, temos:

.1000 ⋅ ..1000000 = 103 ⋅ 106 = 109

Assim: 1,5 ⋅ 10 ⋅ 109 = 1,5 ⋅ 101 + 9 = 1,5 ⋅ 1010

30. d) Para deslocar a vírgula duas casas para a esquerda, precisamos multiplicar por 102 e por 10‒2, obtendo:

458,6 = 458,6 ⋅ 10‒2 ⋅ 102 = 4,586 ⋅ 102

Logo: 458,6 ⋅ 10‒5 = 4,586 ⋅ 102 ⋅ 10‒5 = 4,586 ⋅ 102 ‒ 5 = 4,586 ⋅ 10‒3

30. e) Para mudar a vírgula três casas para a esquerda, precisamos multiplicar por 103 e por 10‒3, obtendo: .3576 = .3576 ⋅ 10 ‒3 ⋅ 103 = 3,576 ⋅ 103

Logo: .3576 ⋅ 10‒3 = 3,576 ⋅ 103 ⋅ 10‒3 = 3,576 ⋅ 103 ‒ 3 = 3,576 ⋅ 100 = 3,576 ⋅ 1 = 3,576

30. f) Contamos 12 zeros depois da vírgula, seguidos do algarismo 1.

Logo: 0,0000000000001 = 1 ⋅ 10‒13

31. A configuração de menor distância possível é aquela na qual os dois planetas (a e B) estão alinhados com a estrela (ê) na ordem B, a, ê ou ê, a, B. Assim, distância entre os planetas é dada por:

é bê – ê á = 2,3 ⋅ 108 – 15 ⋅ 107 = (23 ⋅ 10‒1) ⋅ 108 – 15 ⋅ 107 =

= 23 ⋅ 107 – 15 ⋅ 107 = (23 – 15) ⋅ 107 = 8 ⋅ 107

Portanto, a medida da distância mínima entre a e B é 8 ⋅ 107 quilômetros.

Já a configuração de maior distância possível é aquela na qual os dois planetas (a e B) estão alinhados com a estrela (ê) na ordem B, ê, A ou a, ê, B. Nesse caso, a distância entre os planetas é dada por:

é bê + bê á = 2,3 ⋅ 108 + 15 ⋅ 107 = 2,3 ⋅ 108 + (1,5 ⋅ 10) ⋅ 107 =

= 2,3 ⋅ 108 + 1,5 ⋅ 108 = (2,3 + 1,5) ⋅ 108 = 3,8 ⋅ 108

Portanto, a medida da distância máxima entre a e B é 3,8 · 108 quilômetros.

32. a) Uma tonelada (1 t) equivale a:

.1000 quilogramas = 103 quilogramas

Assim:

2 ⋅ 1030 quilogramas = 2 ⋅ 1027 + 3 quilogramas = 2 ⋅ 1027 ⋅ 103 quilogramas = 2 ⋅ 1027 toneladas

Página trinta e sete

32. b) Montando uma proporção simples, determinamos a massa de medida ême, em quilograma, que é convertida em hélio por ano no núcleo do Sol. Considerando que a cada 1 segundo são convertidos cêrca de 6 ⋅ 1011 quilogramas de hidrogênio em hélio e que 1 ano tem aproximadamente 3 ⋅ 107 segundos.

\frac{m}{6 \cdot 10^{11}} = \frac{3 \cdot 10^{7}}{1}

m = (6 ⋅ 1011 ) ⋅ (3 ⋅ 107 ) = 3 ⋅ 6 ⋅ 1011 + 7

m = 18 ⋅ 1018 = 1,8 ⋅ 1019

Considerando que uma tonelada equivale a 10³ quilogramas, temos:

uma tonelada = 103 quilogramas ou 1 quilograma = 10‒3 tonelada

1,8 ⋅1019 quilogramas = 1,8 ⋅1019 ⋅ 10‒3 toneladas = 1,8 ⋅ 1019 ‒ 3 toneladas = 1,8 ⋅ 1016 toneladas

Portanto, 1,8 ⋅ 1016 toneladas de hidrogênio são convertidas em hélio por ano no núcleo do Sol.

33. Considerando que o prefixo mili corresponde a um fator de multiplicação de 10‒3, significa que 1 mililitro corresponde a 10‒3 litro, ou seja, 1 litro corresponde a 103 mililitros.

Portanto, 5,5 litros equivalem a 5,5 ⋅ 103 mililitros.

Se 1 mililitro contém 5 ⋅ 103 glóbulos vermelhos, 5,5 ⋅ 103 mililitros contêm 2,75 ⋅107 glóbulos vermelhos.

5,5 ⋅ 103 ⋅ 5 ⋅103 = 5, 5 ⋅ 5 ⋅ 103 + 3 = 27,5 ⋅ 106 = 2,75 ⋅107

34. a)

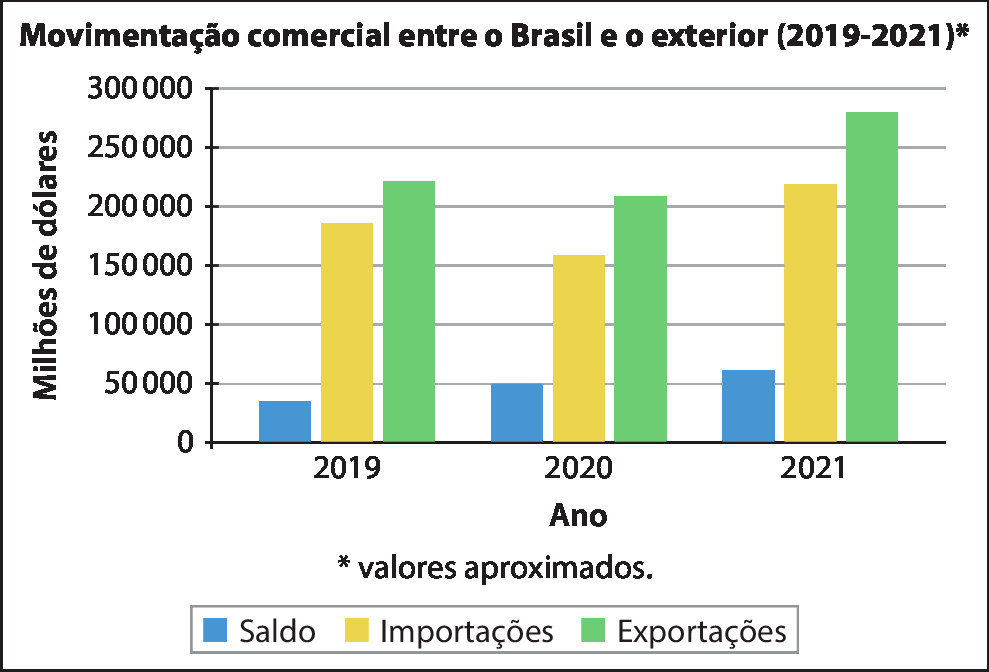
Estilo padrão; Gráfico em barras verticais. Movimentação comercial entre o Brasil e o exterior (2019 a 2021) *valores aproximados. Eixo x, ano. Eixo y, Milhões de dólares. Os dados são: 2019. Saldo: cerca de 40.000. Importações: cerca de 190.000. Exportações: cerca de 225.000. 2020. Saldo: 50.000. Importações: cerca de 160.000. Exportações: cerca de 210.000. 2021. Saldo: cerca de 60.000. Importações: cerca de 160.000. Exportações: cerca de 270.000. — Dados obtidos em: BRASIL. Resultados do comércio exterior brasileiro: dados consolidados. Disponível em: https://oeds.link/Mfafc2. Acesso em: 10 março 2022.

É importante observar que os dados estão em milhões de dólares. Logo, cada valor precisa ser multiplicado por 106 (..1000000 = 106) antes de ser escrito em notação científica.

Ano	Saldo (dólares)	Importações (dólares)	Exportações (dólares)
2019	3,5 ⋅ 1010	1,86 ⋅ 1011	2,21 ⋅ 1011
2020	5,0 ⋅ 1010	1,59 ⋅ 1011	2,09 ⋅ 1011
2021	6,1 ⋅ 1010	2,19 ⋅ 1011	2,80 ⋅ 1011

34. b) Para 2019:

2,21 ⋅ 1011 – 1,86 ⋅ 1011 = 0,35 ⋅ 1011 =

= 3,5 ⋅ 10‒1 ⋅ 1011 = 3,5 ⋅ 1010

Para 2020:

2,09 ⋅ 1011 – 1,59 ⋅ 1011 = 0,5 ⋅ 1011 =

= 5,0 ⋅ 10‒1 ⋅ 1011 = 5,0 ⋅ 1010

Para 2021:

2,80 ⋅ 1011 – 2,19 ⋅ 1011 = 0,61 ⋅ 1011 =

= 6,1 ⋅ 10‒1 ⋅ 1011 = 6,1 ⋅ 1010

34. c) Para calcular a média do saldo, adicionamos os valores dos três anos e dividimos por três:

\frac{3, 5 \cdot 10^{10} + 5, 0 \cdot 10^{10} + 6, 1 \cdot 10^{10}}{3}

\frac{14, 6 \cdot 10^{10}}{3}

\frac{14, 6}{3}

⋅ 1010 ≃ 4,9 ⋅ 1010

Analogamente, para a média das importações, temos:

\frac{5, 64 \cdot 10^{11}}{3}

\frac{5, 64}{3}

⋅ 1011 = 1,88 ⋅ 1011

Para a média das exportações, temos:

\frac{2, 21 . 10^{11} + 2, 09 . 10^{11} + 2, 80 . 10^{11}}{3}

\frac{7, 1 · 10^{11}}{3}

\frac{7, 1}{3}

⋅ 1011 ≃ 2,37 ⋅ 1011

34. d) Para a exportação atingir a média em 2019, faltaram 1,60 · 1010 dólares.

2,21 ⋅ 1011 – 2,37 ⋅ 1011 = – 0,16 ⋅ 1011 =

= –1,60 ⋅ 10‒ 1 ⋅ 1011 = – 1,60 ⋅ 1010

Para a exportação atingir a média em 2020, faltaram 2,80 · 1010 dólares.

2,09 ⋅ 1011 – 2,37 ⋅ 1011 = – 0,28 ⋅ 1011 =

= – 2,80 ⋅ 10‒ 1 ⋅ 1011 = – 2,80 ⋅ 1010

Em 2021, a exportação excedeu a média em 4,30 · 1010 dólares.

2,80 ⋅ 1011 – 2,37 ⋅ 1011 = 0,43 ⋅ 1011 =

= 4,30 ⋅ 10‒1 ⋅ 1011 = 4,30 ⋅ 1010

34. e)

Página trinta e oito

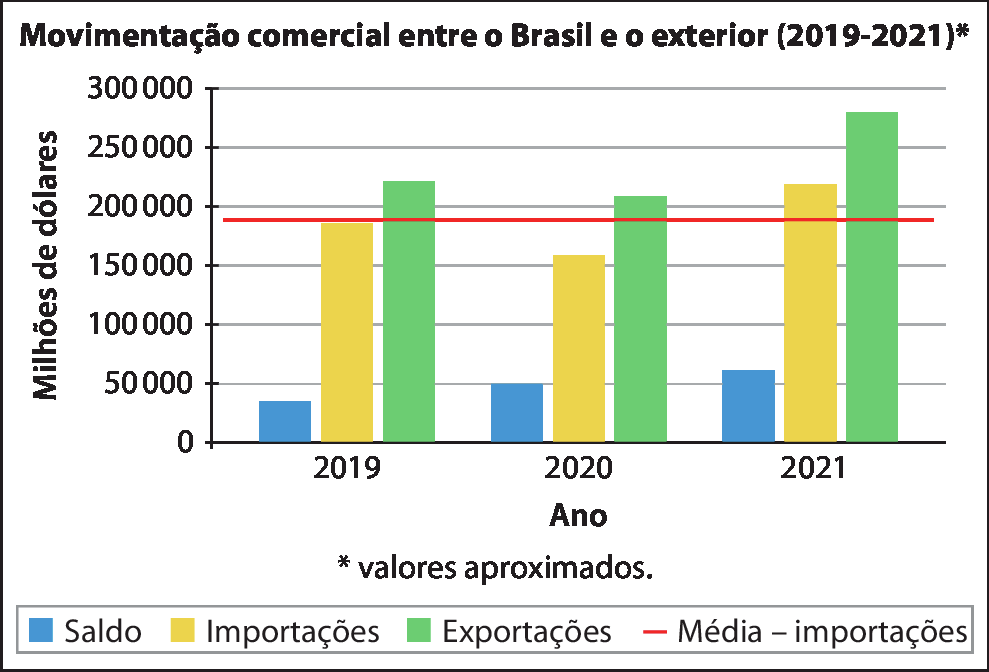
Sim. Se o gráfico tiver sido feito em escala no papel, pode-se medir os tamanhos. Analiticamente, pode-se observar que, em 2019, as importações foram quase iguais à média (1,86 ⋅ 1011 ≃ 1,88 ⋅ 1011), enquanto os valores de 2020 e 2021 diferem da média por cêrca de 3 ⋅ 1010 para mais e para menos, respectivamente (0,3 ⋅ 1011 = 3 ⋅ 1010).

35.

\frac{9, 0 · 10^{7}}{3, 0 · 10^{5}} = \frac{9}{3} · \frac{10^{7}}{10^{5}}

= 3 ⋅ 102

Ou seja, o raio de luz percorre essa distância em 300 segundos.

Como um minuto tem 60 segundos, são necessários 5 minutos (300 : 60 = 5).

Alternativa b.

38. a) Como observado, não existe número negativo cujo quadrado seja negativo. Portanto, a raiz quadrada de –25 não é um número racional.

38. b)

\frac{1}{16} = {(\frac{1}{4})}^{2}

Portanto,

\sqrt{\frac{1}{16}} = \frac{1}{4}

é um número racional.

38. c) O número

\frac{3}{4}

não é um quadrado perfeito. Portanto, sua raiz quadrada não é um número racional.

38. d) Como observado, não existe número negativo cujo quadrado seja negativo. Portanto, a raiz quadrada de

– \frac{1}{9}

não é um número racional.

38. e) O número

\frac{8}{10}

não é um quadrado perfeito. Portanto, sua raiz quadrada não é racional.

38. f)

\frac{25}{9} = {(\frac{5}{3})}^{2}

Portanto,

\sqrt{\frac{25}{9}} = \frac{5}{3}

é um número racional.

39. a) Do enunciado, concluímos que 352 ⋅ 352 = .123904. Assim:

– \sqrt{1 239, 04} = – \sqrt{\frac{123 904}{100}}

- \sqrt{\frac{352 \cdot 352}{10 \cdot 10}} =

= - \frac{352}{10} = - 35, 2

39. b)

\sqrt{12, 3904} = \sqrt{\frac{123 904}{10 000}}

\sqrt{\frac{352 \cdot 352}{100 \cdot 100}} =

= \frac{352}{100} = 3, 52

41. a) Escrevendo 100 = 10 ⋅ 10, vemos que 10 é um número que, elevado ao quadrado, resulta em 100. Porém, (–10) ⋅ (–10) = 100. Logo, –10 elevado ao quadrado também resulta em 100.

41. b) Convencionou–se que a

\sqrt{a}

representa a raiz quadrada positiva de a. Assim,

\sqrt{100}

= 10.

42. Um número negativo não pode ser o quadrado de um número racional. Logo, –49 não pode admitir uma raiz quadrada racional.

43. a) Como 441 = 21 ⋅ 21 = 212,

\sqrt{441}

= 21; portanto,

– \sqrt{441}

= –21.

43. b) Um número negativo não pode ser o quadrado de um número racional. Logo, –441 não pode admitir uma raiz quadrada racional. Deve-se enfatizar aqui a diferença entre o simétrico da raiz quadrada e a raiz quadrada de um número negativo.

44. a) Falsa, pois

\sqrt{10^{2}} = \sqrt{100}

= 10, enquanto

\sqrt{– 10^{2}} = \sqrt{– 100}

não é um número racional, pois um número negativo não pode ser o quadrado de um número racional.

44. b) Verdadeira, pois

\sqrt{10^{2}} = \sqrt{100} = 10

\sqrt{{(– 10)}^{2}} = \sqrt{(– 10) \cdot (– 10)} = \sqrt{100}

= 10.

44. c) Falsa, pois

\sqrt{{(– 7)}^{2}} = \sqrt{(– 7) \cdot (– 7)} = \sqrt{49} = 7

, que é diferente de –7.

44. d) Verdadeira, pois

\sqrt{{(– 7)}^{2}} = \sqrt{(– 7) \cdot (– 7)} = \sqrt{49} = 7

44. e) Falsa, pois

– \sqrt{10^{2}} = – \sqrt{100} = – 10

, enquanto

\sqrt{{(– 10)}^{2}} = \sqrt{(– 10) \cdot (– 10)} = \sqrt{100}

= 10.

44. f) Verdadeira, pois

– \sqrt{{(– 10)}^{2}}

– \sqrt{(– 10) \cdot (– 10)}

– \sqrt{100}

= –10.

44. g) Verdadeira, pois

\sqrt[3]{8} = 2

, já que 2 ⋅ 2 ⋅ 2 = 2³ = 8, e, como (–2)³ = (–2) ⋅ (–2) ⋅ (–2) = –8, temos

\sqrt[3]{– 8} = – 2

. Portanto,

– \sqrt[3]{– 8}

= –(–2) = 2.

44. h) Verdadeira. A raiz enésima de zero é zero, com êne natural não nulo. De fato, 0 vezes si mesmo êne vezes sempre resulta em zero, qualquer que seja n ⩾ 2.

45. a) 900 = 30 ⋅ 30 = 302. Portanto,

\sqrt{900}

= 30 e 2 ⋅

\sqrt{900}

= 2 ⋅ 30 = 60.

45. b) 2,56 =

\frac{256}{100} = \frac{16 \cdot 16}{10 \cdot 10}

\frac{16}{10} \cdot \frac{16}{10}

{(\frac{16}{10})}^{2}

= (1,6)2

Portanto,

\sqrt{2, 56}

= 1,6 e

\frac{3}{4} \cdot \sqrt{2, 56}

= 0,75 ⋅ 1,6 = 1,2.

45. c) Note que:

(–1)5 = (–1) ⋅ (–1) ⋅ (–1) ⋅ (–1) ⋅ (–1) =

= [(–1) ⋅ (–1)] ⋅ [(–1) ⋅ (–1)] ⋅ (–1) = 1 ⋅ 1 ⋅ (–1) =

= 1 ⋅ (–1) = –1

Logo,

\sqrt[5]{– 1}

= –1. Como

\sqrt{0} = 0

, temos:

\sqrt{0} - \sqrt[5]{– 1}

= 0 –(–1) = 0 + 1 = 1

Página trinta e nove

45. d) Começamos pela raiz cúbica:

– \frac{8}{27} = \frac{– 8}{27}

\frac{(– 2) \cdot (– 2) \cdot (– 2)}{3 \cdot 3 \cdot 3}

{(\frac{– 2}{3})}^{3}

Logo,

\sqrt[3]{– \frac{8}{27}} = – \frac{2}{3}

. Quanto à raiz quadrada,

\frac{25}{64} = \frac{5 \cdot 5}{8 \cdot 8} = {(\frac{5}{8})}^{2}

. Logo,

\sqrt{\frac{25}{64}} = \frac{5}{8}

Assim, temos:

\sqrt[3]{– \frac{8}{27}} - \sqrt{\frac{25}{64}}

– \frac{2}{3} - \frac{5}{8} = \frac{– 2 \cdot 8 – 5 \cdot 3}{24}

\frac{– 16 - 15}{24} = \frac{– 31}{24}

– \frac{31}{24}

46. Se agá representa a altura, temos h = 44,1 métros. Assim:

t =

\sqrt{\frac{h}{4, 9}} = \sqrt{\frac{44, 1}{4, 9}} = \sqrt{9}

= 3

Portanto, o objeto leva 3 segundos para atingir o solo.

47. Como 52 = 25, temos

\sqrt{25} = 5

. Logo:

\sqrt[3]{18 + \sqrt{84 - \sqrt{4 + \sqrt{25}}}}

\sqrt[3]{18 + \sqrt{84 - \sqrt{4 + 5}}}

= =

\sqrt[3]{18 + \sqrt{84 - \sqrt{9}}}

Como 32 = 9, temos

\sqrt{9}

= 3. Logo:

\sqrt[3]{18 + \sqrt{84 - \sqrt{9}}}

\sqrt[3]{18 + \sqrt{84 - 3}}

\sqrt[3]{18 + \sqrt{81}}

Como 92 = 81, temos

\sqrt{81}

= 9. Logo:

\sqrt[3]{18 + \sqrt{81}}

\sqrt[3]{18 + 9} = \sqrt[3]{27}

Por fim, como 3³ = 27, o valor da expressão é

\sqrt[3]{27}

= 3.

48. Fernanda acertou, pois tratou uma radiciação por vez. Daniel errou por cancelar as potências com os radicais antes de simplificar a expressão. Assim, deve-se enfatizar aqui a importância de se trabalhar gradualmente da expressão mais interna para a mais externa, aproveitando para destacar os riscos de simplesmente “cortar” os expoentes das potências e os índices.

49. a) Considerando que

a^{\frac{m}{n}} = \sqrt[n]{a^{m}}

, para

a = 2, m = 2 e n = 3, temos:

\sqrt[3]{2^{2}} = 2^{\frac{2}{3}}

49. b) Para a = 5, m = 3 e n = 4, temos:

\sqrt[4]{5^{3}} = 5^{\frac{3}{4}}

49. c) Para a = 10, m = 1 e n = 3, temos:

\sqrt[3]{10} = 10^{\frac{1}{3}}

50. a) Considerando que

a^{\frac{m}{n}} = \sqrt[n]{a^{m}}

, para

a = 2, m = 3 e n = 4, temos:

2^{\frac{3}{4}} = \sqrt[4]{2^{3}}

50. b) Para a = 9, m = 1 e n = 3, temos:

9^{\frac{1}{3}} = \sqrt[3]{9}

50. c) Para a = 8, m = 1 e n = 2, temos:

8^{\frac{1}{2}} = \sqrt[2]{8}

51. a) Como as propriedades da potenciação continuam válidas para expoentes fracionários, temos:

\sqrt{3^{6}} = 3^{\frac{6}{2}}

= 33 = 27

51. b)

512^{\frac{1}{3}} = \sqrt[3]{512}

Como 512 = 8 ⋅ 8 ⋅ 8 = 83, temos:

\sqrt[3]{512} = 8

51. c)

\sqrt[4]{2^{8}} = 2^{\frac{8}{4}}

= 22 = 4

53. Simplificando a expressão a:

A = [\frac{1}{2} – {(1 + \frac{1}{2})}^{2}] \cdot (\frac{6}{3} – \frac{2}{3})

[\frac{1}{2} – {(\frac{3}{2})}^{2}] \cdot (\frac{4}{3})

[\frac{2}{4} – \frac{9}{4}] . (\frac{4}{3}) = - \frac{7}{4} . \frac{4}{3} = - \frac{7}{3}

Simplificando a expressão B:

B = \frac{5}{7} : [2 - (\frac{2}{3} + 3)]

\frac{5}{7} : [2 - \frac{11}{3}]

\frac{5}{7} : [\frac{– 5}{3}]

\frac{5}{7} \cdot [\frac{3}{– 5}]

\frac{3}{– 7} = – \frac{3}{7}

Logo:

A \cdot B = - \frac{7}{3} \cdot (- \frac{3}{7}) = 1

Concluímos que os valores de a e B são números inversos.

54. De acordo com o item c:

\underset{= \frac{3}{4}, pelo item c}{\underset{⏟}{\frac{1}{1} · \frac{1}{2} + \frac{1}{2} · \frac{1}{3} + \frac{1}{3} · \frac{1}{4}}}

\frac{1}{4} \cdot \frac{1}{5} = \frac{3}{4} + \frac{1 \cdot 1}{4 \cdot 5} = \frac{3}{4} + \frac{1}{20} =

\frac{5 \cdot 3 + 1}{20} = \frac{15 + 1}{20} = \frac{16}{20} = \frac{4}{5}

55. É mais fácil começar trabalhando com frações e, apenas no final, escrever na fórma decimal. Vale recordar que a : bn = a ⋅ b‒n.

{(– 1 + \frac{1}{5})}^{2} : {(0, 4 – \frac{1}{5})}^{2} – 0, 7 \cdot \sqrt{\frac{36}{49}}

= =

{(– \frac{5}{5} + \frac{1}{5})}^{2} : {(\frac{4}{10} – \frac{1}{5})}^{2} – 0, 7 \cdot \sqrt{\frac{36}{49}}

{(– \frac{5}{5} + \frac{1}{5})}^{2} : {(\frac{2}{5} – \frac{1}{5})}^{2} – 0, 7 \cdot \sqrt{\frac{36}{49}}

{(– \frac{4}{5})}^{2} : {(\frac{1}{5})}^{2} – 0, 7 \cdot \sqrt{\frac{36}{49}}

{(– \frac{4}{5})}^{2} \cdot {(\frac{5}{1})}^{–2} - 0, 7 \cdot \sqrt{\frac{36}{49}}

{(– \frac{4}{5})}^{2} \cdot {(\frac{5}{1})}^{2} - 0, 7 \cdot \sqrt{\frac{36}{49}}

= =

\frac{16}{25} \cdot \frac{25}{1} – 0, 7 \cdot \sqrt{\frac{36}{49}}

\frac{16}{1} = 0, 7 \cdot \sqrt{{(\frac{6}{7})}^{2}}

16 - 0, 7 \cdot \frac{6}{7} = 16 - \frac{7}{10} \cdot \frac{6}{7} =

16 - \frac{6}{10} = 16 - 0, 6 = 15, 4