Página quarenta

Parte 2

56. Vale recordar as propriedades da potenciação com mesma base e que

a^{‒ n} = \frac{1}{a^{n}}

[{(- \frac{1}{2})}^{4} : {(- \frac{1}{2})}^{3}] \cdot {(- \frac{1}{2})}^{6} + 2^{‒ 7} =

= [{(- \frac{1}{2})}^{4 ‒ 3}] \cdot {(- \frac{1}{2})}^{6} + 2^{‒ 7} = {(- \frac{1}{2})}^{1} \cdot {(- \frac{1}{2})}^{6} + 2^{‒ 7} =

= {(- \frac{1}{2})}^{1 + 6} + 2^{‒ 7} = {(- \frac{1}{2})}^{7} + 2^{‒ 7} = (- 2^{‒ 1})^{7} + 2^{‒ 7} =

= –2‒7 + 2‒7 = 0

Alternativa c.

Pense mais um poucoreticências

Página 28

1. a) Como 400 = 20 ⋅ 20, concluímos que x = 20 é um valor que torna a sentença x2 = 400 verdadeira. Porém, como (–20) ⋅ (–20) = 400, x = –20 é outro valor possível.

Note que números menores do que 20, ao quadrado, resultam em valores menores do que 400; números maiores do que 20, ao quadrado, resultam em valores maiores do que 400.

1. b) Apenas 20, pois uma medida de comprimento precisa ter valor numérico positivo.

2. a) Como (4,8)2 = 23,04 e x2 = 23,04, podemos concluir que x = 4,8 é um valor que torna a igualdade verdadeira. Como (–4,8) ⋅ (–4,8) = 23,04, x = –4,8 é outro valor possível.

2. b) Apenas 4,8, pois a medida do comprimento dos lados precisa ter valor numérico positivo.

Trabalhando a informação

1. Conhecemos o capital C = .18000, a taxa de juros ih, de 8% ao ano, e o tempo t, de 2 anos.

Escrevendo ih na fórma decimal: i = 8% = 8 : 100 = 0,08

Assim, o rendimento para essa aplicação será:

j = C ⋅ i ⋅ t = .18000 ⋅ 0,08 ⋅ 2 = .2880.

Ou seja, R$ 2.880,00dois mil oitocentos e oitenta reais.

2. Neste caso, já sabemos que o rendimento foi de j = .2304, e o capital inicial C = .12000 e a taxa mensal ih = 1,6% = 0,016. Resta-nos determinar o tempo t correspondente.

j = C ⋅ i ⋅ t ⇒

t = \frac{J}{C \cdot i} = \frac{2 304}{12 000 \cdot 0, 016} = \frac{2 304}{192} = 12

É importante notar que a taxa dada foi mensal; então, o tempo é de 12 meses (ou 1 ano).

Para saber mais

Páginas 32

1. a) O computador calcula dois acento circunflexo três acento circunflexo três como (23)3 = 29 = 512.

1. b) Pela explicação dada no texto, o computador calcula primeiro dois acento circunflexo três como 2³ = 8; em seguida três acento circunflexo abre parênteses dois acento circunflexo três fecha parênteses = três acento circunflexo oito como 38 = .6561; e, por fim, dois acento circunflexo abre parênteses três acento circunflexo abre parênteses dois acento circunflexo três fecha parênteses fecha parênteses = 2^(6 561). Ou seja,

2^{(}^{3^{(2^{3})}}^{)}

= 2.6561

Note que esse número contém uma.novecentas e setenta e seis casas decimais; portanto, não pode ser calculado para além da fórma de potência com o auxílio de uma calculadora de mão, mas ele pode ser calculado utilizando uma calculadora científica, que fornecerá a resposta em notação científica.

1. c) Como a expressão dentro de parênteses é efetuada antes, o computador calcula primeiro dois acento circunflexo três como 2³, depois abre parênteses dois acento circunflexo fecha parênteses acento circunflexo quatro como (23)4 = 23 ⋅ 4 = 212 = .4096.

1. d) Neste caso, a expressão três acento circunflexo dois dentro dos primeiros parênteses é calculada como 32. Em seguida, essa expressão é elevada ao cubo; por fim, é elevada ao quadrado.

((32)3)2 = (32)3 ⋅ 2 = (32)6 = 32 ⋅ 6 = 312 = .531441

2. É importante que essa atividade seja corrigida na lousa para que os estudantes indiquem os pontos em que têm dificuldades e para que esclareçam as dúvidas de sintaxe.

3. Assim como na atividade anterior, é importante corrigir as expressões propostas pelos estudantes na lousa, para que eles percebam os equívocos de sintaxe.

Exercícios complementares

1. a) x ⋅ y ⋅ z = (22)3 ⋅ (23)2 ⋅ 23² = 22 ⋅ 3 ⋅ 23 ⋅ 2 ⋅ 29 = 26 ⋅ 26 ⋅ 29 =

= 26 + 6 + 9 = 221

1. b) x : y = (22)3 : (23)2 = 22 ⋅ 3 : 23 ⋅ 2 = 26 : 26 = 26 ‒ 6 = 20 = 1

x : z = (22)3 : 23² = 22 ⋅ 3 : 29 = 26 : 2 9 = 26 ‒ 9 = 2‒3 =

\frac{1}{2^{3}} = \frac{1}{8}

2. Observe que, passados 30 segundos, uma única célula se divide em duas. Passados mais 30 segundos, cada uma dessas duas células se divide em duas. Ou seja, após 2 ⋅ 30 segundos, temos 2 ⋅ 2 células = 22 células. Passados mais 30 segundos, cada uma dessas 22 células se divide em duas, totalizando 2³ células (2 ⋅ 22 = 22 + 1 = 2³). Ou seja, após 3 ⋅ 30 segundos, temos 2³ células. Extrapolando, após n ⋅ 30 segundos, temos 2n células. Logo, após 20 minutos = 20 ⋅ 2 ⋅ 30 segundos, temos 240 células.

5. a) Lembrando que qualquer número quando elevado a zero resulta 1, temos:

a = 50 – 2‒2 =

1 - \frac{1}{2^{2}} = 1 - \frac{1}{4} = \frac{4}{4} - \frac{1}{4} = \frac{3}{4}

b =

{(1 - \frac{1}{2})}^{‒ 1} = {(\frac{2}{2} - \frac{1}{2})}^{‒ 1} = {(\frac{1}{2})}^{‒ 1}

= (2‒1) ‒1 =

= 2‒1 ^⋅ (‒1) = 21 = 2

c = 120 – 3 = 1 – 3 = –2

Assim:

a^{b} = {(\frac{3}{4})}^{2} = \frac{3}{4} \cdot \frac{3}{4} = \frac{9}{16}

5. b) (b – a)c =

{(2 - \frac{3}{4})}^{‒ 2} = {(\frac{8}{4} – \frac{3}{4})}^{‒ 2}

= =

{(\frac{5}{4})}^{- 2} = {(\frac{4}{5})}^{2} = \frac{16}{25}

5. c)

{(\frac{a b}{c})}^{C} = {(\frac{\frac{3}{4} \cdot 2}{- 2})}^{- 2} = {(\frac{\frac{3}{4}}{– 1})}^{- 2} = {(– \frac{3}{4})}^{- 2}

{(- \frac{4}{3})}^{2} = \frac{16}{9}

Página quarenta e um

6. a)

{(2, 5)}^{- 2} = {(\frac{25}{10})}^{- 2} = {(\frac{10}{25})}^{2} = {(\frac{2}{5})}^{2} = \frac{4}{25}

6. b)

{(0, 15)}^{- 3} = {(\frac{15}{100})}^{- 3} = {(\frac{100}{15})}^{3} = {(\frac{20}{3})}^{3}

\frac{20^{3}}{3^{3}} = \frac{8 000}{27}

6. c)

{(0, 1)}^{- 4} = {(\frac{1}{10})}^{- 4} = {(\frac{10}{1})}^{4} = 10 000

6. d)

{(- 0, 01)}^{- 2} = {(- \frac{1}{100})}^{^{- 2}} = {(- \frac{100}{1})}^{2} = 10 000

7. a) Da relação 

a^{- n} = \frac{1}{a^{n}}

, para a = 10 e n = 2, temos:

\frac{1}{10^{2}} = 10^{- 2}

7. b)

\frac{1}{16} = \frac{1}{2^{4}} = 2^{- 4}

7. c)

(- \frac{1}{25}) = - (\frac{1}{25}) = - (\frac{1}{5^{2}}) = - (5^{‒ 2}) = - 5^{‒ 2}

7. d)

\frac{1}{125} = \frac{1}{5^{3}} = 5^{- 3}

7. e) Os divisores de 15 são 5 e 3, com 15 = 5 ⋅ 3. Portanto, 15 não pode ser decomposto em potências positivas de alguma base menor do que ele. Assim:

\frac{1}{15} = 15^{- 1}

7. f)

(- \frac{1}{100}) = - (\frac{1}{100}) = - (\frac{1}{10^{2}}) = - (10^{‒ 2}) = - 10^{‒ 2}

8. a) 57,8 milhões equivalem a 57,8 · 106 = 5,78 · 101 · 106 = 5,78 · 107

8. b) 8,5 bilhões equivalem a 8,5 · 109 e 9,7 bilhões equivalem a 9, 7 · 109

{[{(- \frac{1}{2})}^{2}]}^{- 3} : [(- \frac{1}{2}) \cdot {(- \frac{1}{2})}^{5} \cdot {(- \frac{1}{2})}^{- 3}] =

= {(- \frac{1}{2})}^{2 \cdot (- 3)} : [{(- \frac{1}{2})}^{1 + 5 + (- 3)}] = {(- \frac{1}{2})}^{- 6} : {(- \frac{1}{2})}^{3} =

= {(- \frac{1}{2})}^{- 6 - 3} = {(- \frac{1}{2})}^{- 9} = {(- \frac{2}{1})}^{9} = {(- 2)}^{9}

10. Pelas propriedades da potenciação:

(3‒1 ⋅ 3) – (5‒1 : 5) = 3‒1 + 1 – 5‒1 ‒ 1 = 30 – 5‒2 = 1 – 5‒2

Como 5‒2 =

\frac{1}{5^{2}} = \frac{1}{25}

= 0,04, essa expressão vale 1 – 0,04 = 0,96; um número racional maior que 0 e menor que 1.

Alternativa b.

11. Como x é um produto de potências de mesma base, podemos simplificar.

x = {(\frac{1}{3})}^{5} \cdot {(\frac{1}{3})}^{- 3} \cdot {(\frac{1}{3})}^{8} : {(\frac{1}{3})}^{9} = {(\frac{1}{3})}^{5 + (- 3) + 8} : {(\frac{1}{3})}^{9}

x = {(\frac{1}{3})}^{10} : {(\frac{1}{3})}^{9} = {(\frac{1}{3})}^{10 - 9} = \frac{1}{3}

L o g o, x^{3} = {(\frac{1}{3})}^{3} = \frac{1}{27} .

13. Como o prefixo “quilo” indica .1000 = 10³, temos: 1 quilograma = 10³ gramas. Então:

1,99 ⋅ 10‒26 quilograma = 1,99 ⋅ 10‒26 ⋅ 10³ grama = 1,99 ⋅ 10‒26 + 3 grama = 1,99 ⋅ 10‒23 grama

Então, a medida da massa é aproximadamente

1,99 ⋅ 10 ‒ 23 grama.

14. É importante lembrar que dividir por 100 equivale a deslocar a vírgula duas casas decimais para a esquerda.

\sqrt{\frac{81}{4}} - \sqrt{400} + \sqrt{2, 25} = \sqrt{\frac{81}{4}} - \sqrt{400} + \sqrt{\frac{225}{100}} =

= \sqrt{{(\frac{9}{2})}^{2}} - \sqrt{20^{2}} + \sqrt{{(\frac{15}{10})}^{2}} = \frac{9}{2} - 20 + \frac{15}{10} =

= \frac{45}{10} - \frac{200}{10} + \frac{15}{10} = - \frac{140}{10} = - 14

15. É preciso recordar a relação entre o número de casas decimais e potências de 10.

\frac{(0, 1) \cdot (0, 001) \cdot 10^{- 1}}{10 \cdot (0, 0001)} = \frac{10^{- 1} \cdot 10^{- 3} \cdot 10^{- 1}}{10 \cdot 10^{- 4}} =

= \frac{10^{- 1 - 3 - 1}}{10^{1 - 4}} = \frac{10^{- 5}}{10^{- 3}} = 10^{‒ 5 ‒ (‒ 3)} = 10^{‒ 2}

Mas x = 10‒3 = 10‒2 ‒ 1 = 10‒2 : 101. Assim, x =

\frac{10^{- 2}}{10}

, ou seja, 10‒2 = 10x. Como 10‒2 é o valor obtido para a expressão, conclui-se que a expressão é igual a 10x.

Alternativa b.

16. Recordando a relação entre o número de casas decimais e potências de 10, temos:

\frac{0, 000036}{80 000} = \frac{36 \cdot 10^{- 6}}{8 \cdot 10^{4}} = \frac{36}{8} \cdot \frac{10^{- 6}}{10^{4}}

= 4,5 ⋅ 10‒6 ‒ 4 = 4,5 ⋅ 10‒10

Como multiplicar por 10‒1 equivale a deslocar a vírgula uma casa para a esquerda, 4,5 = 45 ⋅ 10‒1. Assim:

4,5 ⋅ 10‒10 = 45 ⋅ 10‒1 ⋅ 10‒10 = 45 ⋅ 10‒1 ‒ 10 = 45 ⋅ 10‒11

Alternativa d.

17. Como a = 0,04 =

\frac{4}{100} = \frac{2 \cdot 2}{10 \cdot 10} = {(\frac{2}{10})}^{2}

, temos:

\sqrt{a} = \frac{2}{10}

= 0,2. Daí,

5 \sqrt{a}

= 5 ⋅ 0,2 = 1 e

2 a \sqrt{a}

= 2 ⋅ 0,04 ⋅ 0,2 = 0,016.

Página quarenta e dois

Verificando

1. Como repetições são permitidas, para a primeira casa, temos 10 algarismos possíveis. Para cada um desses algarismos, temos 10 escolhas para a segunda casa, totalizando 102 escolhas (10 ⋅ 10 = 102) para as duas primeiras casas. Prosseguindo com esse raciocínio, concluímos que há 104 distintas senhas possíveis (10 ⋅ 10 ⋅ 10 ⋅ 10 = 104).

Alternativa d.

2. Começamos decompondo os números que aparecem na expressão em potências de fatores primos, sempre que possível. Temos 4 = 2 ⋅ 2 = 22, 8 = 2 ⋅ 4 = 2 ⋅ 22 = 2³, 27 = 3 ⋅ 3 ⋅ 3 = 3³ e 49 = 7 ⋅ 7 = 72. Assim, substituindo e reordenando a expressão, temos:

\frac{2^{5} \cdot 3^{5} \cdot 4 \cdot 7^{2}}{8 \cdot 27 \cdot 49} = \frac{2^{5} \cdot 3^{5} \cdot 2^{2} \cdot 7^{2}}{2^{3} \cdot 3^{3} \cdot 7^{2}}

\frac{2^{5} \cdot 2^{2} \cdot 3^{5}}{2^{3} \cdot 3^{3}} = \frac{2^{5 + 2} \cdot 3^{5}}{2^{3} \cdot 3^{3}}

= \frac{2^{7}}{2^{3}} \cdot \frac{3^{5}}{3^{3}} = 2^{7 ‒ 3} \cdot 3^{5 ‒ 3} = 2^{4} \cdot 3^{2}

Alternativa b.

3. Observe que:

x = (0, 5)^{3} = {(\frac{5}{10})}^{3} = {(\frac{1}{2})}^{3} = \frac{1}{8}

y = {(\frac{1}{4})}^{- 2} = (4^{‒ 1})^{‒ 2} = 4^{2} = 16

Logo, x ⋅ y =

\frac{1}{8}

⋅ 16 = 2 e (x ⋅ y)2 = 22 = 4

Alternativa c.

4. Dividindo .3125 por 5 sucessivas vezes, notamos que .3125 = 5 ⋅ 5 ⋅ 5 ⋅ 5 ⋅ 5 = 55. Sendo

a^{- 1} = \frac{1}{a}

, para

a = \frac{1}{5}

, temos

{(\frac{1}{5})}^{- 1} = \frac{1}{\frac{1}{5}} = 5

. Logo:

3125 = 5^{5} = {({\frac{1}{5}}^{- 1})}^{5} = {(\frac{1}{5})}^{(- 1) \cdot 5} = {(\frac{1}{5})}^{- 5}

Alternativa a.

5. Recordando que 10‒n é o número com n casas depois da vírgula, sendo a última delas composta do algarismo 1 e as demais por 0, concluímos que 0,0001 métro = 10‒4 métro. Alternativa c.

6. Precisamos determinar uma medida de comprimento cujo produto por ela mesma resulte no valor numérico

\frac{121}{144}

\frac{121}{144} = \frac{11 \cdot 11}{12 \cdot 12} = \frac{11}{12} \cdot \frac{11}{12}

Logo, a medida do comprimento do lado é

\frac{11}{12}

métro.

Alternativa a.

7. Como 4 = 2 ⋅ 2 = 22,

\sqrt{4} = 2

Logo:

\sqrt[5]{245 – \sqrt[3]{6 + \sqrt{4}}}

\sqrt[5]{245 – \sqrt[3]{6 + 2}}

\sqrt[5]{245 – \sqrt[3]{8}}

Porém 8 = 2 ⋅ 2 ⋅ 2 = 2³. Portanto,

\sqrt[3]{8} = 2

. Assim:

\sqrt[5]{245 - \sqrt[3]{8}}

\sqrt[5]{245 - 2} = \sqrt[5]{243}

Como a raiz quinta de 243 não é evidente, decompomos 243 em fatores primos.

243 = 3 ⋅ 81 = 3 ⋅ 3 ⋅ 27 = 3 ⋅ 3 ⋅ 33 = 31 + 1 + 3 = 35

Se 243 = 35, significa que

\sqrt[5]{243}

= 3.

Alternativa b.

8. De

\sqrt[n]{a^{m}} = a^{\frac{m}{n}}

, para a = 18, n = 12 e m = 3, temos:

\sqrt[12]{18^{3}} = 18^{\frac{3}{12}} = 18^{\frac{1}{4}}

Alternativa c.

9. Considerando que 9 = 32 e 175 : 25 = 7, temos:

\sqrt[3]{9 \cdot 3} - [\frac{175}{25} + \frac{2^{5}}{2^{4}} \cdot {(0, 25)}^{- \frac{1}{2}}] =

= \sqrt[3]{3^{2} \cdot 3} - [7 + 2^{5 - 4} \cdot {(\frac{25}{100})}^{- \frac{1}{2}}] =

= \sqrt[3]{3^{2 + 1}} - [7 + 2^{1} \cdot {(\frac{1}{4})}^{- \frac{1}{2}}] =

= \sqrt[3]{3^{3}} - [7 + 2 \cdot 4^{\frac{1}{2}}] = 3 - [7 + 2 \cdot \sqrt{4}] =

= 3 – [7 + 2 ⋅ 2] = 3 – [7 + 4] = 3 – 11 = –8

Alternativa d.

10.

\frac{3^{2}}{3} - \frac{1}{4} \cdot [\sqrt{\frac{9}{36}} - (- 8 + \frac{1}{2})] =

= 3^{2 - 1} - \frac{1}{2^{2}} \cdot [\sqrt{\frac{3^{2}}{6^{2}}} - (- 2^{3} + 2^{- 1})] =

= 3^{1} - 2^{- 2} \cdot [\frac{3}{6} - (- 2^{3 \cdot (- 1)})] = 3^{1} - 2^{- 2} \cdot [\frac{3}{2 \cdot 3} - (- 2^{3 \cdot (- 1)})] =

= 3 - 2^{- 2} \cdot [\frac{1}{2} - (- 2^{- 3})] = 3 - 2^{- 2} \cdot [2^{- 1} + 2^{- 3}] =

= 3 – 2 ^–² ⋅ [2 ^–¹·⁽^–³⁾] = 3 – 2 ^–²⋅ ( 2 ³ ) =

= 3 – 2 ^–²+³ = 3 – 2¹ = 1

Alternativa a.

Diversificando

1. Na segunda linha, Rafael escreve – 24 como a diferença de dois números, de duas maneiras distintas.

Na terceira linha, Rafael decompõe os números em produtos de outros números.

Na quarta linha, Rafael completa os quadrados pela adição de 52 a ambos os membros.

Na quinta linha, Rafael identifica as diferenças de quadrados.

Na sexta linha, Rafael extrai a raiz quadrada.

Na sétima linha Rafael “cancela” o expoente 2 com o índice 2 da raiz.

Na oitava linha, Rafael adiciona 5 a ambos os membros, “cancelando” –5 e concluindo sua mágica.

Página quarenta e três

2. O erro foi cometido na passagem da sexta para a sétima linha, ao substituir

\sqrt{{(4 – 5)}^{2}}

por 4 – 5, pois 4 – 5 = –1, ou seja, é um número negativo e, por convenção, a raiz quadrada de um radicando resulta em um número positivo cujo quadrado equivale ao radicando.

3. a) Elevando ambas as potências à décima segunda potência, temos:

{(\sqrt[3]{3})}^{12} = 3^{\frac{12}{3}}

= 34 = 81

{(\sqrt[4]{4})}^{12} = 4^{\frac{12}{4}}

= 43 = 64

Como 81 é maior do que 64, então,

\sqrt[3]{3}

é maior do que

\sqrt[4]{4}

3. b) Como 4 = 22, temos:

\sqrt[4]{4} = \sqrt[4]{2^{2}} = 2^{\frac{2}{4}} = 2^{\frac{1}{2}} = \sqrt{2}

Logo, esses números são iguais.

Capítulo 2 – Construções geométricas e lugares geométricos

• Objetivos do capítulo e justificativas

• Fazer construções geométricas utilizando instrumentos de desenho.

• Construir segmentos congruentes, retas paralelas e retas perpendiculares com régua e compasso.

• Construir ângulos com o transferidor.

• Conceituar e construir lugares geométricos: circunferência, mediatriz, bissetriz, par de retas paralelas.

• Aplicar os lugares geométricos estudados na resolução de problemas.

• Construir, ler e interpretar gráficos de setores.

As propostas de construções geométricas apresentadas neste capítulo são importantes, pois favorecem o desenvolvimento da competência geral 2 e das competências específicas 2 e 6. Ao utilizar instrumentos de desenho geométrico para construir segmentos congruentes, retas paralelas, retas perpendiculares e ângulos e, ainda, ao compreender e aplicar o conceito de lugar geométrico, os estudantes mobilizam conhecimentos anteriores e os aplicam, ampliando a compreensão e desenvolvendo o raciocínio lógico, o espírito de investigação e a capacidade de produzir argumentos. Além disso, eles enfrentam situações-problemas imaginadas contribuindo para que utilizem diferentes tipos de registro e de linguagem. A competência geral 5 e a competência específica 5 são favorecidas no trabalho com as atividades envolvendo softwares de geometria dinâmica por meio dos quais os estudantes podem mobilizar e ampliar os conhecimentos de geometria. Essas tecnologias digitais favorecem, também, a verificação de hipótese apresentadas pelos estudantes e a validação de seus argumentos, pois facilitam a construção de situações imaginadas que possam ser testadas como contra-argumento, por exemplo.

Construir, ler e interpretar gráficos é um requisito importante para a participação ativa na sociedade atual e, ao estudar os gráficos de setores, os estudantes podem adquirir maior autonomia na análise de informações apresentadas dessa maneira e desenvolver as competências gerais 1 e 4 e as competências específicas 3 e 4, percebendo os conhecimentos matemáticos como ferramentas para compreender e explicar a realidade. A atividade proposta de pesquisa sobre um problema relacionado ao bairro em que os estudantes moram favorece o desenvolvimento da competência específica 8, pois, para realizá-la, os estudantes precisam interagir com os colegas e trabalhar de maneira cooperativa no planejamento e no desenvolvimento da pesquisa.

Para o desenvolvimento dos objetivos deste capítulo, as construções geométricas e a associação de necessidades práticas relacionadas ao aprimoramento de conceitos matemáticos, como a ideia de círculo e de circunferência, favorecem aos estudantes desenvolverem aspectos das competências gerais 3 e 4. Eles poderão fruir manifestações artísticas antigas e modernas e perceber a importância de valorizar esse tipo de linguagem, como o apresentado na obra do artista Wassily Kandinsky.

O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 são favorecidos com as diferentes atividades a serem realizadas em grupos, pois possibilitam aos estudantes exercitar diferentes habilidades socioemocionais ao trabalharem com a diversidade de aprendizagem entre os colegas, interagindo de forma cooperativa.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.

(ê éfe zero oito ême ah um sete) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

(ê éfe zero oito ême ah dois sete) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos de dados, destacando aspectos como as medidas de tendência central, a amplitude e as conclusões.

Neste capítulo, serão aprofundados os conhecimentos acerca das construções geométricas e dos lugares geométricos, com foco na Unidade Temática Geometria, ampliando conhecimentos do 7º ano (ê éfe zero sete ême ah dois dois e ê éfe zero sete ême ah dois quatro) e desenvolvendo aspectos relacionados às habilidades (ê éfe zero oito ême ah um cinco) e (ê éfe zero oito ême ah um sete) no que se refere à compreensão de mediatriz de um segmento e de bissetriz de um ângulo como lugares geométricos.

Esperamos que a diversidade de situações envolvendo tais conhecimentos possam subsidiar os assuntos que serão explorados no 9º ano, dentre eles determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer (ê éfe zero nove ême ah um seis).

Página quarenta e quatro

Este capítulo apresenta também articulação com temas das Unidades Temáticas Geometria, Números e Probabilidade e estatística na construção de gráficos de setores envolvendo construção de ângulos e cálculos com porcentagens, ampliando o estudo desse tipo de gráfico feito no 7º ano (ê éfe zero sete ême ah três sete) e possibilitando desenvolver aspectos da habilidade (ê éfe zero oito ême ah dois três). A atividade proposta para que os estudantes realizem uma pesquisa sobre problemas do bairro em que moram contribui para o desenvolvimento da habilidade (ê éfe zero oito ême ah dois sete).

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Abertura

a) Algumas linhas a se explorar: transporte (de bens e matérias-primas importantes para a sobrevivência das comunidades humanas), agricultura (arado, tração etc.) e mecanismos como moinhos.

b) O desenho que delimita uma roda representa uma circunferência.

Exercícios propostos

3. a) Reta que passa pelos pontos a e B.

3. b) Semirreta de origem a que passa por B.

3. c) Segmento de reta de extremidades a e B.

3. d) Semirreta de origem P que passa por Q.

3. e) Segmento de reta de extremidades P e Q.

4. a) Verdadeira. Como 800 centímetros = 8 ⋅ 100 centímetros e 100 centímetros = 1 métro, então, 800 centímetros = 8 métros, e ambos os segmentos têm a mesma medida de comprimento, o que significa que são congruentes.

4. b) Verdadeira. Se ambos os segmentos têm a mesma medida de comprimento 3 centímetros, significa que são congruentes.

4. c) Verdadeira. Para que

\bar{E F}

\bar{P Q}

sejam congruentes, a medida ê éfe deve ser igual à medida PQ.

4. d) Falsa. Visto que A bê = 5 centímetros = 5 ⋅ 10‒2 métro = 0,05 métro e CD = 5 decímetros = 5 ⋅ 10 ‒1 métro = 0,5 métro. Ou seja,

\bar{A B} e \bar{C D}

têm medidas diferentes e, portanto, não são congruentes.

5. a) Temos que XZ = XY + YZ, ou seja, 7,5 = XY + 5. Logo, XY = 7,5 – 5 = 2,5. Portanto,

\bar{X Y}

mede 2,5 centímetros.

5. b) Como a é ponto médio de

\bar{X Y}

, á ípsilon = XY : 2 = 1,25. Analogamente, YB = YZ : 2 = 2,5.

Então,

\bar{A B}

= AY + YB = 3,75; portanto, A bê = 3,75 centímetros.

Fluxograma com 5 caixas em sentido único. 1. Com a ferramenta Segmento de reta, construir segmento A B com medida de comprimento qualquer. a. avança para 2. 2. Com a ferramenta Reta, traçar uma reta qualquer e marcar um ponto qualquer C sobre a reta. a. avança para 3. 3. Com a ferramenta Circunferência, traçar uma circunferência com centro em C e raio de medida segmento AB. a. avança para 4. 4. Marcar um ponto D em uma das intersecções da circunferência com a reta desenhada. a. avança para 5. 5. Segmento CD é congruente segmento AB.

8. a) á dê = A bê + BC + CD

18 = 2 ⋅ CD + 3 ⋅ CD + CD = 6 ⋅ CD

Portanto, CD =

\frac{18}{6}

= 3. Como A bê = 2 ⋅ CD, temos que a medida de

\bar{A B}

é 6 centímetros.

8. b) BC = 3 ⋅ CD = 3 ⋅ 3 = 9

Então,

\bar{B C}

mede 9 centímetros.

8. c) CD =

\frac{18}{6}

= 3, ou seja,

\bar{C D}

mede 3 centímetros.

8. d) Como X é ponto médio de

\bar{A B}

, temos:

XB = A bê : 2 = 6 : 2 = 3

Como Y é ponto médio de BC, temos:

BY = BC : 2 = 9 : 2 = 4,5

Portanto, XY = XB + BY = 3 + 4,5 = 7,5, ou seja,

\bar{X Y}

mede 7,5 centímetros.

8. e) Como Y é ponto médio de BC, temos:

YC = BY = 4,5

Como Z é o ponto médio de CD, temos:

CZ = CD : 2 = 3 : 2 = 1,5

Portanto, ípsilon zê = YC + CZ = 4,5 + 1,5 = 6, ou seja,

\bar{Y Z}

mede 6 centímetros.

8. f) XZ = XB + BC + CZ

Recuperando os resultados dos itens anteriores, temos:

XZ = 3 + 9 + 1,5 = 13,5

Portanto,

\bar{X Z}

mede 13,5 centímetros.

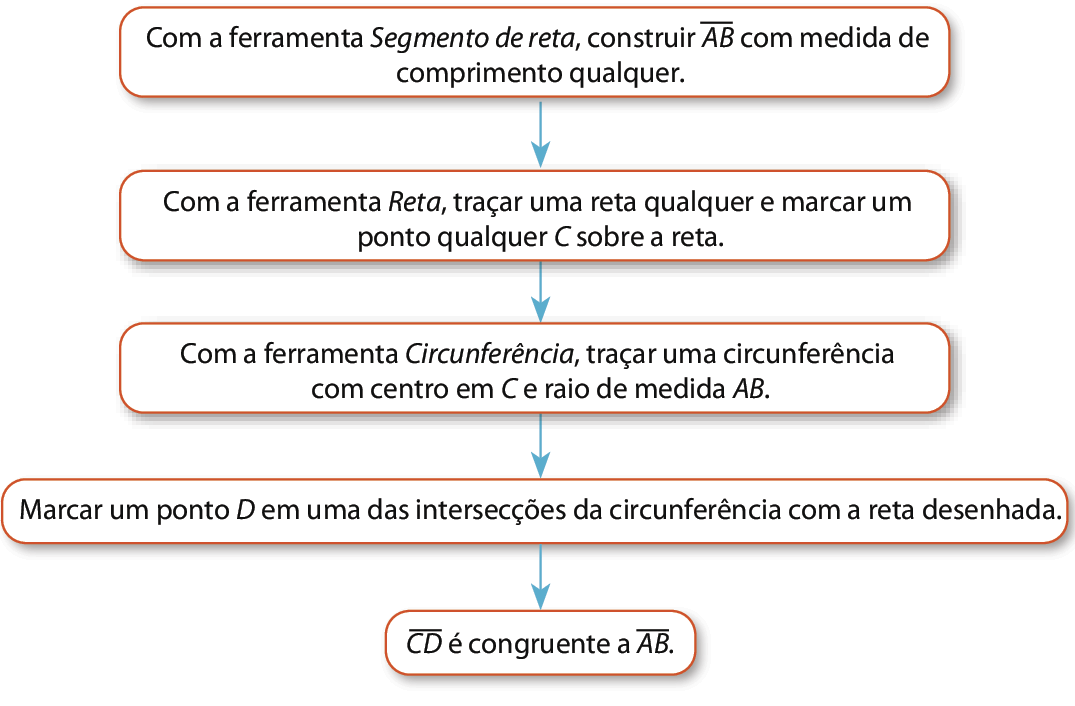
12. Considerando uma reta r e um ponto P fóra dela, para traçar em um software de Geometria dinâmica uma reta passando por P e paralela a r, é possível seguir estes passos.

Passo 1: Com a ferramenta Circunferência, traçar uma circunferência

C_{1}

com centro em P e que corte a reta r em dois pontos. Identificar um dos pontos como M.

Passo 2: Com a ferramenta Circunferência, traçar uma circunferência

C_{2}

, com mesmo raio

\bar{P M}

e centro em M, para, assim, encontrar R, a intersecção entre essa segunda circunferência

C_{2}

e a reta r.

Passo 3: Com a ferramenta Circunferência, traçar uma circunferência

C_{3}

, com mesmo raio

\bar{P M}

e centro em R, para, assim, encontrar Q, a intersecção entre essa terceira circunferência

C_{3}

e a circunferência

C_{2}

Página quarenta e cinco

Passo 4: Com a ferramenta Reta, traçar

\overset{\leftrightarrow}{P Q}

, que é a reta paralela à reta r.

13. a) O maior número possível de retas paralelas a m que podem ser traçadas passando por cinco pontos fóra de m é exatamente cinco, quando esses pontos, tomados três a três, são não colineares.

13. b) Não é possível, pois por cada ponto fóra de m passa exatamente uma reta paralela a m. Se são cinco pontos distintos, no máximo há cinco retas distintas (uma para cada ponto), mas não mais do que isso.

13. c) Sim, aqui se pode explorar os casos em que, por exemplo, mais do que um desses pontos estão sobre uma mesma reta. Nos casos em que os cinco pontos são colineares, há apenas uma reta paralela possível. Sugere-se apresentar na lousa algumas das soluções dos estudantes e, também, explorar outras possibilidades.

13. d) O menor número de retas paralelas que se pode traçar nessa situação é uma, quando os cinco pontos são todos colineares.

14. a) A figura obtida após as construções será como a imagem a seguir.

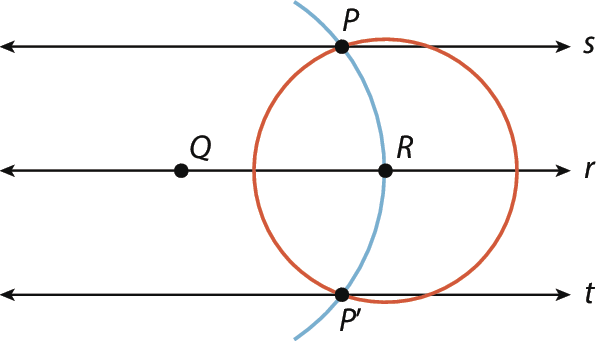
Ilustração. Circunferência com ponto R no centro. Três retas horizontais passam pela circunferência: Reta s na parte superior, r no centro e t na parte inferior. Ponto P na reta s e ponto P linha na reta t. Arco curvado para direita passa em P, R e P linha. P e P linha são pontos da circunferência

A reta t é paralela à reta s, pois estão ambas no mesmo plano e, como t não tem pontos em comum com r (por construção) e r não tem pontos em comum com s (por hipótese), t não tem pontos em comum com s, ou seja, as retas s e t também são paralelas.

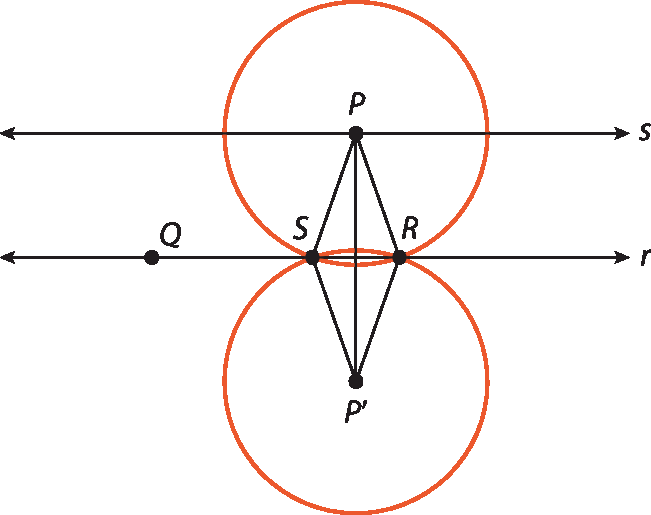
14. b) Ambas as distâncias têm mesma medida. Uma maneira de perceber isso intuitivamente é interpretar o segmento

\bar{P P ’}

como o lado comum a dois triângulos congruentes, △PSP’ e △PRP’; sendo S um quarto ponto sobre a reta r, na intersecção de duas circunferências de centros P e pê linha e raios

\bar{P R} e \bar{P ’ R}

, respectivamente.

Ilustração. Circunferência com ponto P no centro. Abaixo, circunferência com centro no ponto P linha. Duas retas horizontais passam pela circunferência de centro em P: Reta em p e reta r entre as circunferências com ponto Q à esquerda fora delas. Ponto S e R o encontro das circunferências, forma triângulo tracejado com P e triângulo tracejado com P linha.

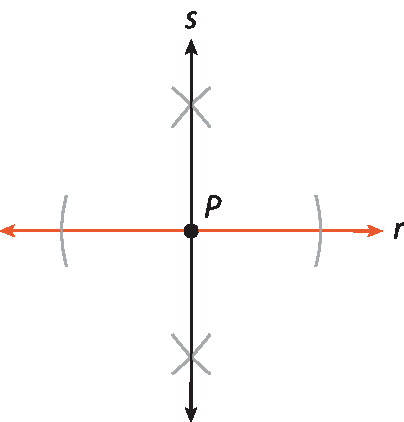
15. a) Espera-se que os estudantes sigam os passos descritos anteriormente para a construção das retas perpendiculares.

Ilustração. Reta horizontal r e reta vertical s que se cruzam em P.

15. b)

Ilustração. Reta horizontal r e reta vertical s que se cruzam no centro. Acima, em s, ponto P.

16.

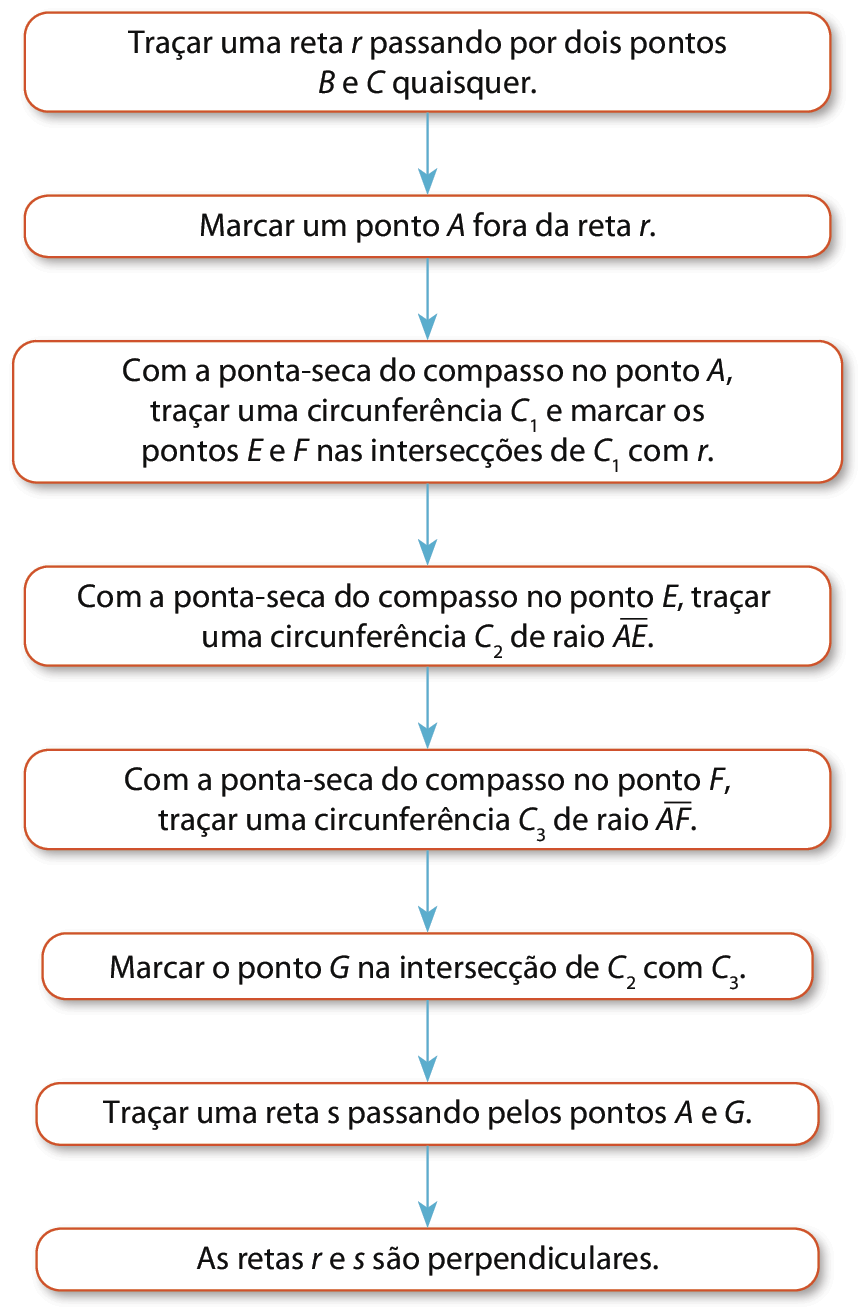
Fluxograma com 8 caixas em sentido único. 1. Traçar uma reta r passando por dois pontos B e C quaisquer. a. avança para 2. 2. Marcar um ponto A fora da reta r. a. avança para 3. 3. Com a ponta-seca do compasso no ponto A, traçar uma circunferência C1 e marcar os pontos E e F nas intersecções de C1 com r. a. avança para 4. 4. Com a ponta-seca do compasso no ponto E, traçar uma circunferência C2 de raio segmento AE. a. avança para 5. 5. Com a ponta-seca do compasso no ponto F, traçar uma circunferência C3 de raio segmento AF. a. avança para 6. 6. Marcar o ponto G na intersecção de C2 com C3. a. avança para 7. 7. Traçar uma reta s passando pelos pontos A e G. a. avança para 8. 8. As retas r e s são perpendiculares.

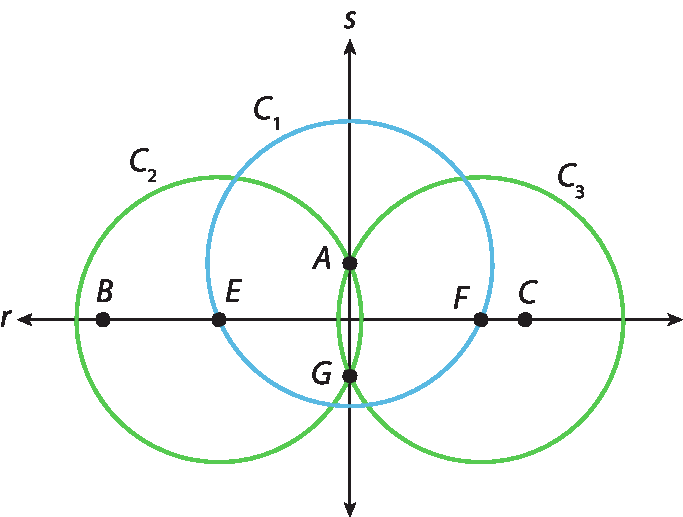
Ilustração. Reta horizontal r e reta vertical s que se cruzam no centro. Na reta r, ponto B, E, F e C. Na reta s, pontos A e G. No centro das retas, circunferência C1 passando em E e F e centro em A. À esquerda, circunferência C2 passa em A e G e tem centro em E. À direita, circunferência C3, passa em A e G e tem centro em F.

Página quarenta e seis

17. Sem requisitos adicionais, como medidas prescritas para os lados, pode-se fazer assim: selecionar a ferramenta Segmento de reta e clicar em dois pontos, a e B, para traçar um lado do retângulo; utilizar a ferramenta Reta perpendicular para traçar as retas r e s perpendiculares ao segmento

\bar{A B}

e passando por a e B, respectivamente; demarcar um ponto C sobre a reta s, que será o terceiro vértice do retângulo; utilizar a ferramenta Reta perpendicular para traçar uma reta t perpendicular à reta s e passando pelo ponto C; marcar o quarto vértice D na intersecção das retas t e r.

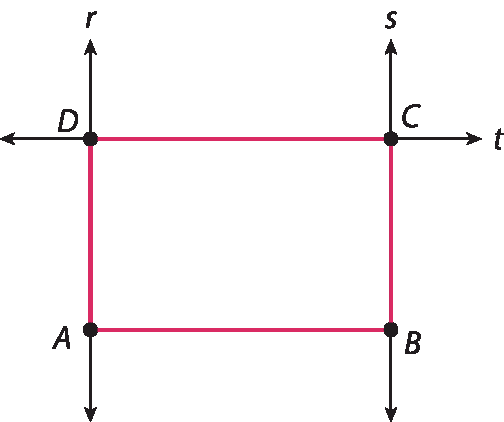
Ilustração. Retas verticais paralelas. Reta r com ponto D e abaixo, ponto A. Reta s com ponto C e abaixo, ponto B. Reta t na horizontal passa em C e D. Segmento de reta de A até B. Destacado o retângulo A B C D

18. Se o desenho tiver sido feito cuidadosamente, com a precisão de uma régua de mão, os estudantes devem obter 10 centímetros para a medida do segmento

\bar{C D}

. Pelo teorema de Pitágoras, é possível verificar que essa é a medida exata. O julgamento quanto à adequação do uso do teorema fica a cargo do professor.

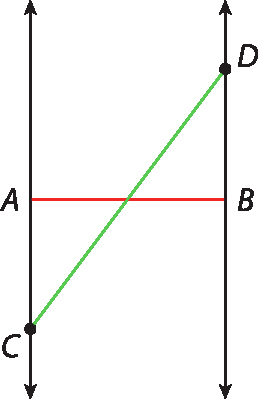
Ilustração. Retas verticais paralelas. No centro, segmento de reta horizontal A B e segmento de reta diagonal C D, sendo C na parte inferior e D na parte superior.

20. a) O importante, neste exercício, é retomar que o lugar geométrico dos pontos que distam d de um ponto a dado é a circunferência de centro em a e raio d.

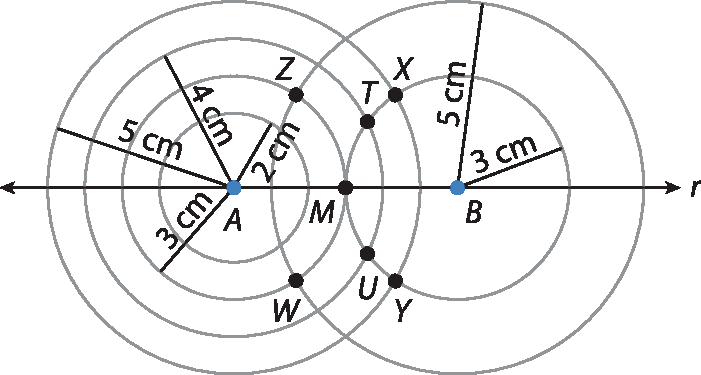
Esquema. Reta horizontal r com ponto A e ponto B. Com centro no ponto A, quatro circunferências concêntricas de raios 2 centímetros, 3 centímetros, 4 centímetros e 5 centímetros. Com centro no ponto B, duas circunferências concêntricas com raios medindo 3 centímetros 5 centímetros. As circunferências com centro em A e raio de 3 centímetros tem pontos em comum com a circunferência com centro em B e raio 3 centímetros, sendo eles os pontos W, U, Y, Z, M, T, X.

Os pontos X e Y na figura estão a 5 centímetros de a e 3 centímetros de B.

20. b) Os pontos Z e W na figura estão a 3 centímetros de a e 5 centímetros de B.

20. c) Os pontos T e u na figura estão a 4 centímetros de a e 3 centímetros de B.

20. d) O ponto M na figura está a 3 centímetros de A e 3 centímetros de B.

20. e) Não é possível obter esse ponto, pois, como vemos na figura, as circunferências de centro em a e raio medindo 2 centímetros e centro em B e raio medindo 3 centímetros não se cruzam.

21. a) Para construir os triângulos, traçamos uma reta r qualquer e marcamos sobre ela dois vértices (a e B) a uma distância igual a uma das medidas indicadas para os lados do triângulo. Em seguida, traçamos uma circunferência centrada em a e outra centrada em B, cada uma delas com raio igual a uma das outras medidas indicadas para os lados. Os possíveis terceiros vértices (C) estarão sobre a intersecção dessas circunferências, se existirem. Para classificar os triângulos quanto aos ângulos, os estudantes podem, por exemplo, medir a abertura dos ângulos com um transferidor ou comparar com um modelo de ângulo reto.

O triângulo a seguir é isósceles e obtusângulo.

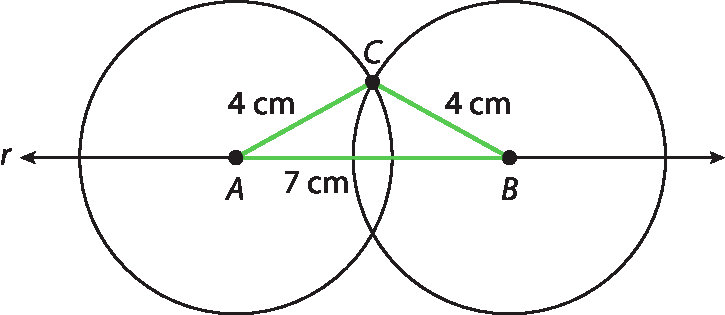
Esquema. Reta horizontal r com ponto A e ponto B. Circunferência com centro em A. Circunferência com centro em B. Essas circunferências se encontram em C onde formam um triângulo com A e B com medida de 4 centímetros cada até C. A medida A B é 7 centímetros.

21. b) O triângulo é equilátero e acutângulo.

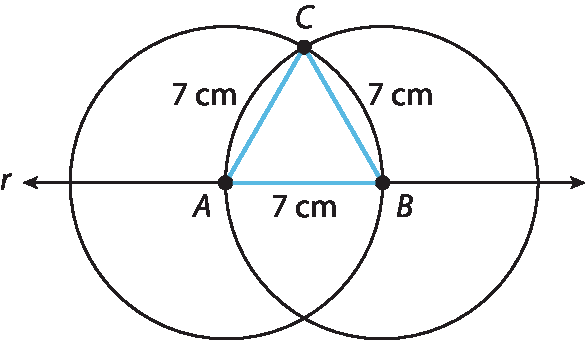
Esquema. Reta horizontal r com ponto A e ponto B. Ponto A é centro de uma circunferência. Ponto B é centro de outra circunferência. Elas se encontram em C onde formam um triângulo com A e B com medida de 7 centímetros cada até C. A medida A B é 7 centímetros.

21. c) O triângulo é isósceles e acutângulo.

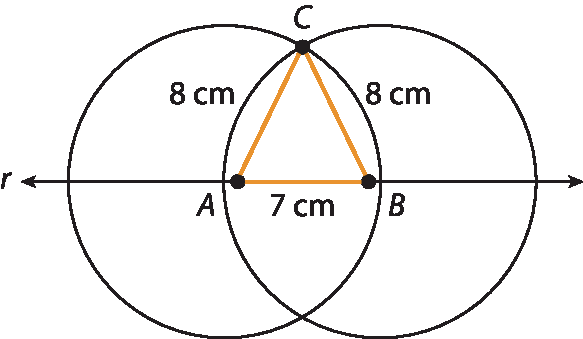
Esquema. Reta horizontal r com ponto A e ponto B. Com centro no ponto A há uma circunferência. Com centro no ponto B, há outra circunferência. Elas se encontram em C onde formam um triângulo com A e B com medida de 8 centímetros cada até C. A medida AB é 7 centímetros.

21. d) O triângulo é escaleno e retângulo.

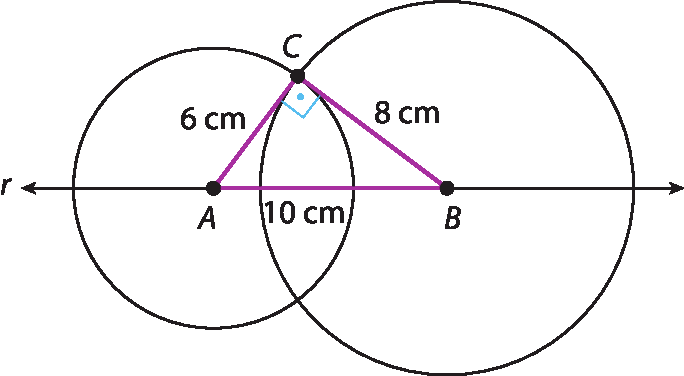
Esquema. Reta horizontal r com ponto A e ponto B. Com centro no ponto A tem uma circunferência. Com centro no ponto B, tem outra circunferência. Elas se encontram em C onde formam um triângulo retângulo com A e B com medida de 6 centímetros em AC e 8 centímetros em BC. A medida AB é 10 centímetros. O triângulo é retângulo em C.

22. a) Para construir os segmentos de reta

\bar{P Q}, \bar{P R}, \bar{P S} e \bar{P T}

, fixamos a ponta-seca do compasso no ponto P e, com uma abertura igual a A bê, traçamos uma circunferência de centro P e raio de medida A bê. O polígono obtido é um retângulo. Para mostrar que esse polígono, é de fato, um retângulo, pode-se decompô-lo em quatro triângulos isósceles para concluir que seus quatro ângulos são iguais a 90°, o que caracteriza os paralelogramos que são retângulos.

Página quarenta e sete

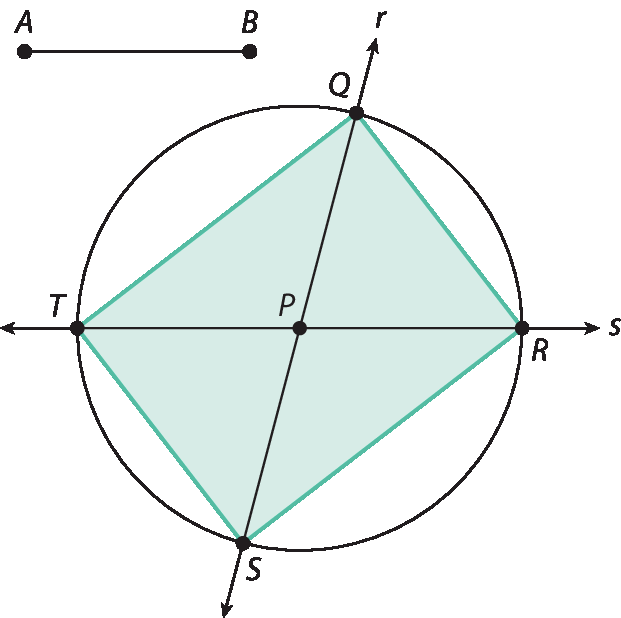
Ilustração. Circunferência com retângulo dentro. Reta r com ponto Q e S e reta s com ponto T e R se cruzam no centro da circunferência no ponto P.
Os pontos Q R S T pertencem à circunferência

22. b) Como

\bar{P Q} = \bar{P S} e \bar{P T} = \bar{P R}

, pois todos esses segmentos são raios de uma mesma circunferência, vemos que, de fato,

\bar{Q S}

\bar{R T}

se cruzam em seus respectivos pontos médios, que são ambos o ponto P.

24. a) Sejam a, B e C os vértices do triângulo, traçamos as mediatrizes de

\bar{A B}

\bar{B C}

. Assim, ao traçar a circunferência pedida a partir do ponto de encontro D, vemos que de fato ela contém os três vértices.

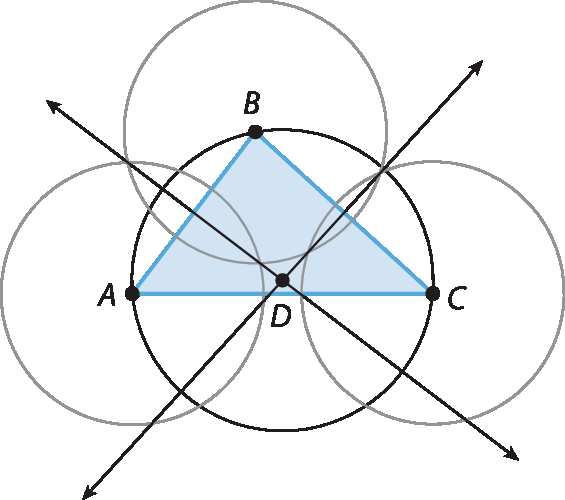
Ilustração. Circunferência com triângulo ABC dentro. Duas retas diagonais se cruzam em D, no centro da circunferência, parte inferior do triângulo. Ao redor, mais três círculos.

24. b) Ao construir a mediatriz do lado

\bar{A C}

, vemos que as três mediatrizes se encontram em um único ponto, D.

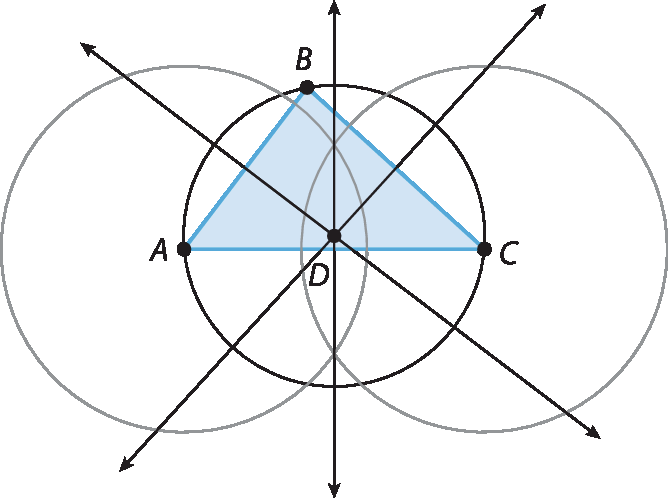
Ilustração. Circunferência com triângulo ABC dentro. Duas retas diagonais e uma reta vertical se cruzam em D, no centro da circunferência, parte inferior do triângulo. Ao redor, outras duas circunferências, uma com centro em A, outra em C. Os pontos A B C pertencem à circunferência com centro em D.

33. Como o lugar geométrico dos pontos equidistantes de r e t é uma reta v, paralela a r, e o lugar geométrico dos pontos equidistantes de s e u é uma reta w, paralela a s, o lugar geométrico dos pontos equidistantes das quatro retas simultaneamente é aquele constituído por pontos simultaneamente em v e w. Mas, como v e w são ambas retas paralelas a um par de retas originalmente concorrentes, elas também serão concorrentes. Portanto, seu cruzamento consistirá em um único ponto óh.

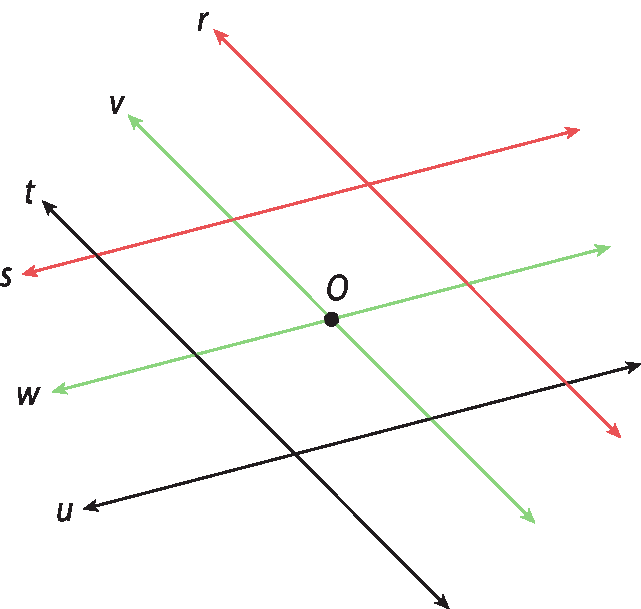
Ilustração. Feixe de retas paralelas. Três retas paralelas diagonais: r, v, t. Três retas paralelas s, w e u. Reta v cruza com reta w no ponto O.

34. É importante comentar com os estudantes que a abertura a ser utilizada no compasso não deve ser igual a ó pê, na figura a seguir, mas sim à medida A bê. É interessante realizar a construção em um software para utilizar a ferramenta de ampliação e variar os ângulos entre as retas concorrentes.

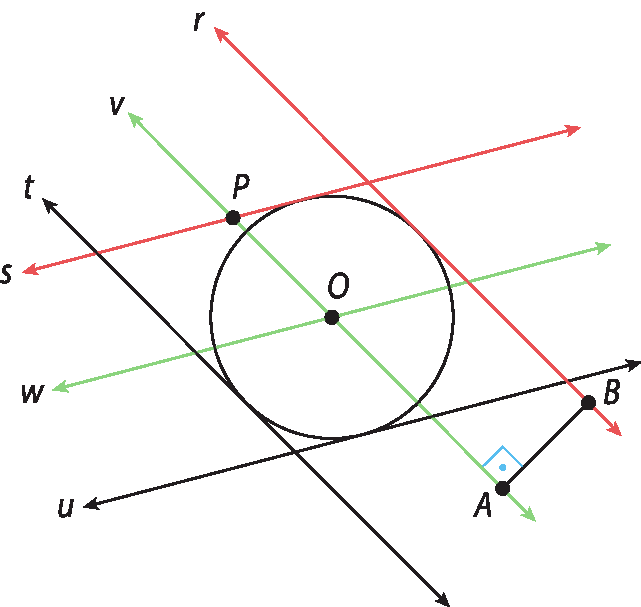
Ilustração.
Três retas paralelas diagonais: r, v, t. Sobre elas, três retas s, w e u. Reta v cruza com reta w no, ponto O.
Circunferência ao redor de O tangencia retas r, s, t e u. Ponto P na reta v e s. Segmento A B sendo ponto B da reta v e ponto A da reta r com ângulo reto em A.

Pense mais um pouco…

Página 57

Após fazer alguns experimentos, os estudantes devem perceber que as bissetrizes se cruzam todas em um mesmo ponto.

Para saber mais

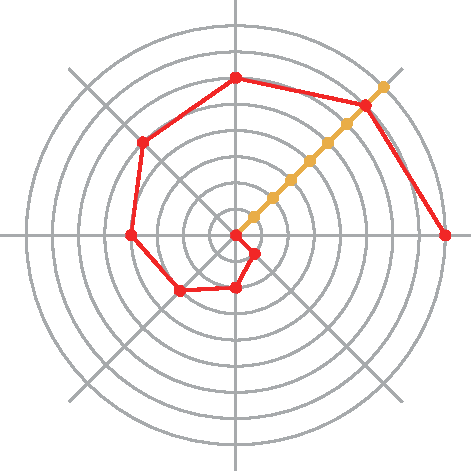
Esta construção é análoga à apresentada. Porém deve-se observar que agora os raios devem ser demarcados de 1 centímetro em 1 centímetro, visto que devemos fazer uma subdivisão em 8 partes iguais, em vez de 16.

Ilustração. Oito circunferências, concêntricas com duas retas diagonais, uma reta vertical e uma reta horizontal que se cruzam no centro das circunferências. Reta laranja do centro até a última circunferência. Linha vermelha em forma que lembra uma espiral.

Página quarenta e oito

Exercícios complementares

6. O triângulo em questão pode ser desenhado de acordo com os passos a seguir.

Passo 1: Traça-se um segmento

\bar{A B}

de 4 centímetros.

Passo 2: Com o compasso, traçam-se duas circunferências de raio 4 centímetros, uma centrada no ponto a e a outra centrada no ponto B. Os pontos a e B serão dois vértices do triângulo. O ponto C, na intersecção dessas circunferências, é o terceiro vértice do triângulo.

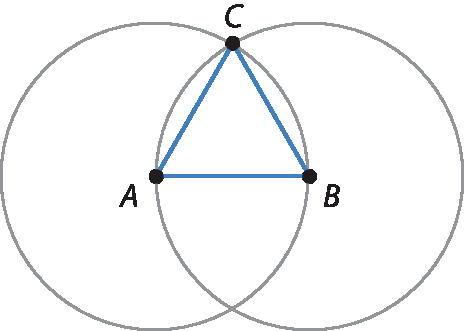
Ilustração do passo 2. Duas circunferências uma com centro em A outra em B. Na intersecção, ponto C. Triângulo ABC está representado.

Passo 3: Agora, para cada par de lados, o lugar geométrico dos pontos que equidistam das respectivas retas suportes é dado pelo par de retas que contém as bissetrizes dos ângulos entre eles. Então, para cada vértice, traçamos as bissetrizes correspondentes. Por exemplo, para o vértice a:

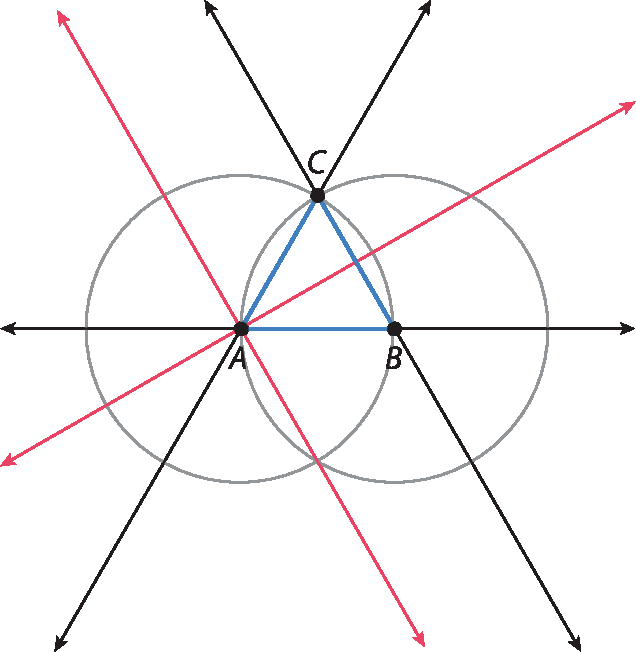
Ilustração.
Na ilustração do passo 2, são acrescentadas duas retas diagonais vermelhas que se cruzam em A. Reta preta passa em C e A e outra reta preta passa em C e B.

Passo 4: Ao fazermos isso para todos os vértices, obtemos os pontos D, ê, F e G, que equidistam das três retas suportes dos lados do triângulo.

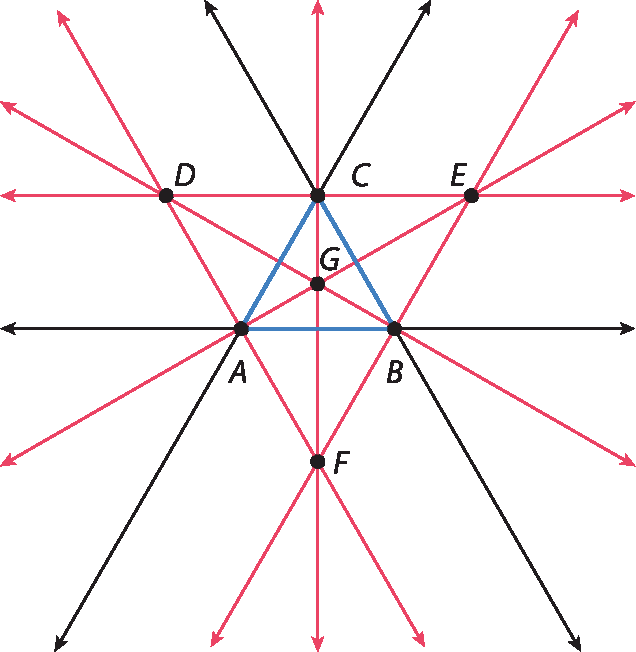
Ilustração do passo 4. Na ilustração do passo 3 são suprimidas as circunferências e adicionadas retas D E, E F, F C, D B, E A,

7. O raio de cada circunferência deve ser a distância do respectivo centro ao lado mais próximo do triângulo, dado pelo segmento de bissetriz que cruza tal lado perpendicularmente.

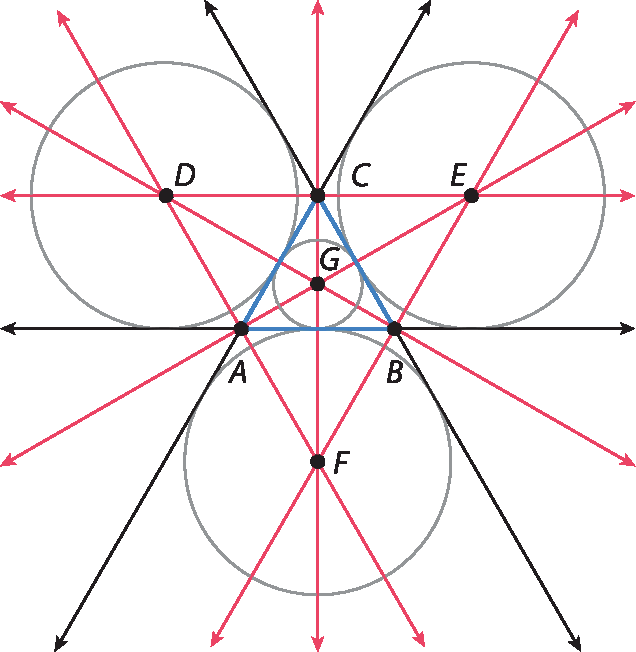
Ilustração. Duas retas paralelas horizontais: uma superior e uma inferior. Na reta superior, pontos D, C e E. Na reta inferior, pontos A e B. Abaixo da reta inferior, ponto F. Entre as retas, triângulo A B C e circunferência inscrita a ele com centro no ponto G. Retas inclinadas A C e B C. Reta vertical C G que passa pelo ponto F. Retas inclinadas A D e B E que passam pelo ponto F. Retas inclinadas A E e B D que passam pelo ponto G. Circunferências de centro D. Circunferência de centro E. Circunferência de centro F.

8. a) Como os dois ângulos mostrados formam um ângulo reto, a soma de suas medidas deve ser 90°. Assim:

(x + 15°) + (3x – 5°) = 90°

4x + 10° = 90°

4x = 90° – 10° = 80°

x =

\frac{80 °}{4}

= 20°

8. b) Como os dois ângulos mostrados formam um ângulo raso, a soma de suas medidas deve ser 180°. Assim:

(3x + 20°) + x = 180°

4x + 20° = 180°

4x = 180° – 20° = 160°

x =

\frac{160 °}{4}

= 40°

Verificando

5. Essas duas circunferências terão exatamente um ponto em comum, pois a soma das medidas de seus raios é exatamente igual a A bê.

Alternativa b.

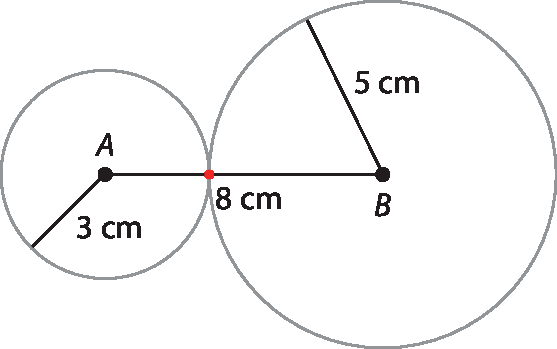
Ilustração. À esquerda, circunferência de centro em A e com raio de 3 centímetros. À direita, circunferência de centro em B com raio de 5 centímetros. A distância do centro da circunferência A até B é 8 centímetros.

\vec{O P}

precisa conter a bissetriz do ângulo

A \hat{O} B

, o que significa que

A \hat{O} P

B \hat{O} P

são congruentes. Logo:

2x + 5° = 3x

3x – 2x = 2x + 5° – 2x

x = 5°

Assim:

medida do(

A \hat{O} P

) = 2 ⋅ 5° + 5° = 15° = medida do(

B \hat{O} P

)

medida do(

A \hat{O} B

) = medida do(

A \hat{O} P

) + medida do(

B \hat{O} P

) = 15° + 15° = 30°

Alternativa c.

Página quarenta e nove

7. A primeira divisória de raia é uma reta paralela a dois lados da piscina – que são paralelos – e cujos pontos são equidistantes dos lados. As próximas divisórias, por sua vez, são retas equidistantes de um dos lados e da divisória instalada anteriormente. Assim, o professor considerou pontos equidistantes de duas retas paralelas.

Alternativa a.

Capítulo 3 – Estatística e probabilidade

• Objetivos do capítulo e justificativas

• Trabalhar com coleta, organização e apresentação de dados.

• Reconhecer uma variável estatística e classificá-la como qualitativa ou quantitativa.

• Resolver problemas envolvendo cálculo de porcentagens.

• Determinar a frequência absoluta e a frequência relativa de dados coletados em uma pesquisa.

• Interpretar e organizar tabelas de distribuição de frequências.

• Explorar e avaliar diferentes tipos de gráfico: de colunas, de barras, de setores, de linha, pictograma.

• Organizar dados de uma variável contínua em classes.

• Utilizar a noção de área do quadrado para estimativa de quantidade de pessoas por metro quadrado.

• Conceituar e calcular medidas estatísticas: moda, média aritmética (simples ou ponderada) e mediana.

• Conceituar espaço amostral e evento de um experimento aleatório.

• Conceituar e determinar a probabilidade de eventos de um experimento aleatório.

Os objetivos deste capítulo se justificam à medida que favorecem o desenvolvimento da competência geral 4 e da competência específica 4. Ao mobilizar conceitos sobre variáveis quantitativas e qualitativas e aprofundar conhecimentos sobre pesquisas estatísticas, os estudantes utilizam diferentes linguagens para coletar, analisar e comunicar os dados coletados em pesquisas desse tipo. Além disso, são apresentados aspectos históricos sobre Estatística, possibilitando desenvolver a competência geral 1 e a competência específica 1. Em relação a essas competências, os estudantes poderão valorizar os conhecimentos matemáticos envolvidos neste capítulo, ao perceber que eles são construídos e podem ser utilizados sobre o mundo social para entender e explicar a realidade e para contribuir com uma sociedade justa, inclusiva e democrática.

Ao compreender como trabalhar com coleta, organização e apresentação de dados, reconhecer variáveis estatísticas, determinar frequência absoluta e frequência relativa e, ainda, compreender e utilizar medidas estatísticas, os estudantes desenvolvem as competências específicas 2, 3 e 4 e a competência geral 2, pois tornam-se cada vez mais capazes de fazer observações sistemáticas, relacionando aspectos quantitativos e qualitativos de diferentes práticas sociais, ampliam a autonomia para investigar, organizar, representar e comunicar informações relevantes e podem expressar suas respostas ou conclusões utilizando diferentes registros e linguagens, especificamente, gráficos e tabelas. Nesse mesmo aspecto, colaboram com o desenvolvimento dessas competências a resolução de problemas envolvendo porcentagens, a interpretação de gráficos de distribuição de frequências, o conhecimento e uso de diferentes tipos de gráfico e a compreensão sobre o cálculo de probabilidades.

Em diferentes momentos do capítulo, apresentam-se atividades para serem realizadas em duplas ou grupos, o que favorece o desenvolvimento das competências gerais 9 e 10 e da competência específica 8, pois os estudantes precisam trabalhar com os colegas de maneira cooperativa, exercitar o diálogo e a resolução de conflitos. Além disso, a proposta de realização de uma pesquisa possibilita aos estudantes planejar e desenvolver, coletivamente, as etapas envolvidas para a coleta e apresentação de dados.

Entre as diferentes situações apresentadas, destacamos o trabalho com os dados sobre o desmatamento e com os dados sobre a dengue, temáticas que contribuem para o desenvolvimento das competências gerais 7 e 8 e as competências específicas 6 e 7.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah zero quatro) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.

(ê éfe zero oito ême ah dois dois) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

(ê éfe zero oito ême ah dois quatro) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.

(ê éfe zero oito ême ah dois cinco) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.

(ê éfe zero oito ême ah dois seis) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).

Os conceitos e atividades envolvendo o estudo de Estatística e de Probabilidade são o foco deste capítulo, desenvolvendo a Unidade Temática Probabilidade e estatística. No campo da Estatística, são trabalhadas a origem da Estatística, coleta e organização de dados, variáveis, tabela de distribuição de frequências com frequências absolutas e frequências relativas e tipos variados de gráfico (de colunas, de barras, de setores, de linha, pictograma), além de cartograma e infográfico, possibilitando o desenvolvimento das habilidades (ê éfe zero oito ême ah dois três), (ê éfe zero oito ême ah dois quatro), (ê éfe zero oito ême ah dois seis) e (ê éfe zero oito ême ah dois sete).