Página sessenta e três

Parte 5

Capítulo 5 – Polinômios e frações algébricas

• Objetivos do capítulo e justificativas

• Conceituar polinômios e operar com eles.

• Conceituar fração algébrica.

• Resolver problemas envolvendo o cálculo de valor numérico de polinômios e frações algébricas.

• Utilizar o conceito de perímetro de polígonos e de área de retângulos para compor expressões algébricas.

• Explorar gráficos de colunas duplas e de linhas duplas.

• Aplicar os conceitos de interpolação e de extrapolação gráfica.

Neste capítulo, amplia-se o estudo de conteúdos da unidade temática Álgebra e são explorados problemas envolvendo polinômios e frações algébricas. Os objetivos relacionados a esses conteúdos se justificam à medida que são trabalhados de maneira a associar Geometria, Números e Álgebra, a fim de que os estudantes assimilem os procedimentos e operações envolvendo polinômios. Deste modo, a competência específica 3 é desenvolvida. Além disso, os objetivos desse capítulo, principalmente os relacionados ao estudo de polinômios, contribuem para mobilizar e desenvolver a competência específica 5, pois os estudantes poderão adquirir mais autonomia para modelar e resolver situações e problemas do cotidiano, por meio de expressões algébricas.

Desenvolvem-se, ainda, as competências gerais 2 e 4 e a competência específica 2, pois os estudantes são incentivados a exercitar a curiosidade intelectual, a argumentar e a desenvolver o raciocínio lógico à medida que precisam expressar situações-problema, por meio de polinômios.

Ao possibilitar que os estudantes explorem e apliquem conceitos relacionados à interpolação e extrapolação gráficas, analisando gráficos de colunas duplas e gráficos de linhas duplas, eles desenvolvem a competência específica 4.

O contexto utilizado para explorar pesquisas censitárias e pesquisas amostrais, neste capítulo, favorece o desenvolvimento das competências gerais 9 e 10 e a competência específica 8, pois os estudantes deverão, em grupos, pesquisar e discutir sobre a importância de agir e tomar decisões com base em princípios democráticos, solidários e inclusivos.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah zero seis) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.

(ê éfe zero oito ême ah um nove) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

Na Unidade Temática Álgebra, situações que exploram o pensamento algébrico também são o foco deste capítulo, em que são abordados polinômios e suas operações e frações algébricas e que desenvolve a habilidade (ê éfe zero oito ême ah zero seis), ampliando e aprofundando os conhecimentos abordados no capítulo anterior.

As Unidades Temáticas Grandezas e medidas e Probabilidade e estatística articulam-se, respectivamente, com a presença do conceito de área de retângulos associados a expressões algébricas, mobilizando a habilidade (ê éfe zero oito ême ah um nove) e na seção Trabalhando a informação, com a interpretação de gráficos de colunas duplas e de linhas duplas e noções de interpolação e extrapolação gráfica que desenvolve aspectos da habilidade (ê éfe zero oito ême ah dois três).

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Exercícios propostos

3. a) Como o lucro é a diferença entre o valor de venda e o valor de compra, conclui-se que o lucro por caderno pode ser expresso algebricamente por: y – x. E o lucro, por uma quantidade z de cadernos, que pode ser expresso por: z ⋅ (y – x) ou z ⋅ y – z ⋅ x

3. b) Substituindo x = 3,2, y = 8,7 e z = 24, temos:

24 ⋅ (8,7 – 3,2) = 24 ⋅ 5,5 = 132

O lucro é de R$ 132,00cento e trinta e dois reais.

4. a) Como a medida da área do retângulo é igual ao produto entre as medidas de largura e altura, a medida da área do ladrilho é expressa algebricamente por a ⋅ b ou ab.

4. b) Basta multiplicar a medida da área de um ladrilho pela quantidade de ladrilhos; portanto, 120 ⋅ ab ou 120ab.

4. c) Considerando a = 15 centímetros = 0,15 métro e b = 20 centímetros = 0,2 métro, temos: 120 ⋅ 0,15 ⋅ 0,20 = 3,6.

Então, a medida da área é 3,6 métros quadrados.

6. b) Como cada espelho fica abaixo de um degrau ou do patamar, o número total de espelhos é 14 + 1 = 15. Portanto, a medida da altura da escada é expressa por: 15 ⋅ ê. Então, com ê = 17 centímetros, conclui-se que a altura da escada mede 2,55 métros, pois: 15 ⋅ ê = 15 ⋅ 17 = 255 e 255 centímetros = 2,55 métros.

6. c) Com um patamar de 65 centímetros e 14 degraus, tem-se que o comprimento horizontal da escada mede: 14 ⋅ P + 65. A medida do comprimento é calculada fazendo P = 30 ⇒ 14 ⋅ 30 + 65 = 485; e como 485 centímetros = 4,85 métros, a medida do comprimento horizontal–lateral é 4,85 métros.

7. a) (2x + y + 3) + (–5x + y – 1) = 2x + y + 3 – 5x + y – 1 = 2x – 5x + y + 3 – 1 = –3x + 2y + 2

7. b)

(\frac{7 a}{5} - 2 a b + \frac{b^{2}}{3})

(4 a b - \frac{b^{2}}{3})

\frac{7 a}{5}

– 2ab +

\frac{b^{2}}{3}

+ 4ab

- \frac{b^{2}}{3} = \frac{7 a}{5}

– 2ab + 4ab

+ \frac{b^{2}}{3} – \frac{b^{2}}{3} = \frac{7 a}{5} + 2 a b

7. c) 3ab – 6a2 + a2 – 4ab + 2b2 + 5a2 – 3b2 = (3ab – 4ab) + (–6a2 + a2 + 5a2) + (2b2 – 3b2) = –ab + 0a2 + (–b2) = –ab – b²

7. d)

\frac{x^{2}}{3} + \frac{2 x}{5} - \frac{1}{4} + \frac{2 x^{2}}{3} - \frac{1}{4}

(\frac{x^{2}}{3} + \frac{2 x^{2}}{3}) + (\frac{2 x}{5}) +

+ (\frac{2 x}{5}) + (– \frac{1}{4} - \frac{1}{4})

\frac{3 x^{2}}{3} + \frac{2 x}{5} - \frac{2}{4}

x^{2} + \frac{2 x}{5} - \frac{1}{2}

Página sessenta e quatro

8. a) (x2 – 3x + 5) + (x2 + 2x – 4) = x2 – 3x + 5 + x2 + 2x – 4 = = x2 + x2 – 3x + 2x + 5 – 4 = 2x2 – x + 1

8. b) (x2 – 3x + 5) + (x2 + 2x – 4) + (x2 + 5x – 1) =

= x2 – 3x + 5 + x2 + 2x – 4 + x2 + 5x – 1 =

= x2 + x2 + x2 – 3x + 2x + 5x + 5 – 4 – 1 = 3x2 + 4x

8. c) (x2 – 3x + 5) + (x2 + 5x – 1) = x2 – 3x + 5 + x2 + 5x – 1 = x2 + x2 – 3x + 5x + 5 – 1 = 2x2 + 2x + 4

8. d) (x2 + 2x – 4) + (x2 + 5x – 1) = x2 + 2x – 4 + x2 + 5x – 1 = x2 + x2 + 2x + 5x – 4 – 1 = 2x2 + 7x – 5

9. a) (5x2 – 3x + 4) – (2x2 + 4x – 3) = 5x2 – 3x +

+ 4 – 2x2 – 4x + 3 = 5x2 – 2x2 – 3x – 4x + 4 + 3 =

= 3x2 – 7x + 7

9. b) (2x2 + 4x – 3) – (5x2 – 3x + 4) = 2x2 + 4x – 3 – 5x2 + + 3x – 4 = 2x2 – 5x2 + 4x + 3x – 3 – 4 = –3x2 + 7x – 7

9. c) (5x2 – 3x + 4) + (x2 – 3x) – (2x2 + 4x – 3) = 5x2 – 3x + + 4 + x2 – 3x – 2x2 – 4x + 3 = 5x2 + x2 – 2x2 – 3x – 3x – – 4x + 4 + 3 = 4x2 – 10x + 7

9. d) (5x2 – 3x + 4) – (x2 – 3x) + (2x2 + 4x – 3) = 5x2 – 3x + 4 – x2 + 3x + 2x2 + 4x – 3 = 5x2 – x2 + 2x2 +

+ 3x + 3x + 4x + 4 – 3 = 6x2 + 4x + 1

10. Como em uma adição de duas parcelas, a soma menos uma das parcelas é igual à outra, temos:

(–3x + 2y + 2) – (2x + y + 3) = –3x + 2y + 2 – 2x – y – 3 = –3x – 2x + 2y – y + 2 – 3 = –5x + y – 1

11. Como em uma subtração, o minuendo menos o resto é igual ao subtraendo, temos:

(2x3 – 3x2 + x – 4) – (–3x3 – 5x2 + 4x + 1) = 2x3 – 3x2 + x – 4 + 3x3 + 5x2 – 4x – 1 =

= 2x3 + 3x3 – 3x2 + 5x2 + x – 4x – 4 – 1 =

= 5x3 + 2x2 – 3x – 5

12. a) 10x2 – (5x + 6) – [2x – (3x2 – 2)] =

= 10x2 – 5x – 6 – [2x + 3x2 + 2] =

= 10x2 – 5x – 6 – 2x + 3x2 – 2 =

= 10x2 + 3x2 – 5x – 2x – 6 – 2 = 13x2 – 7x – 8

12. b) 5a – [3b + 7 – (4a – 5b) + (2 – a)] = 5a – [3b + 7 – 4a +

+ 5b + 2 – a] = 5a – 3b – 7 + 4a – 5b – 2 + a = 5a +

+ 4a + a – 3b – 5b – 7 – 2 = 10a – 8b – 9

12. c)

x^{2} + (\frac{1}{2} x - 2) - (– \frac{1}{2} + x + \frac{1}{3} x^{2})

x^{2} + \frac{1}{2} x - 2 +

+ \frac{1}{2} - x - \frac{1}{3} x^{2}

x^{2} - \frac{1}{3} x^{2} + \frac{1}{2} x - x - 2 + \frac{1}{2}

= =

\frac{3 - 1}{3} x^{2} + \frac{1 - 2}{2} x + \frac{- 4 + 1}{2}

\frac{2}{3} x^{2} - \frac{1}{2} x - \frac{3}{2}

13. Do enunciado é possível encontrar algumas informações e preencher o seguinte quadro:

		Quantidade de moedas de x centavos	Quantidade de moedas de y centavos	Quantidade de moedas de z centavos	Total em centavos
a)	Início	18	30	40	18x + 30y + 40z
b)	1º mês	18 + 8 = 26	30 + 10 = 40	40	26x + 40y + 40z
c)	mês seguinte	26	40 ‒ 12 = 28	40 ‒ 8 = 32	26x + 28y + 32z

14. a) (2x + 1) + (3x – 2) = 2x + 3x + 1 – 2 = 5x – 1

14. b) (3x – 2) + (2x) = 3x + 2x – 2 = 5x – 2

14. c) (2x + 1) + (3x – 2) + (2x) = 2x + 3x + 2x + 1 – 2 = 7x – 1

16. a) 7x ⋅ (2x – 5) = 7x ⋅ 2x – 7x ⋅ 5 = 14x2 – 35x

16. b) (3a2 – 2a – 1) ⋅ 5a = 3a2 ⋅ 5a – 2a ⋅ 5a – 1 ⋅ 5a =

= 15a3 – 10a2 – 5a

16. c) –3x ⋅ (4x2 – 3x + 1) = –3x ⋅ 4x2 – 3x ⋅ (–3x) – 3x ⋅ 1 =

= –12x3 + 9x2 – 3x

16. d)

\frac{2}{5} a \cdot (a - \frac{1}{4}) = \frac{2}{5} a \cdot a – \frac{2}{5} \cdot \frac{1}{4} \cdot a = \frac{2}{5} a^{2} - \frac{1}{10} a

16. e) (0,3x2 – 1,4x) ⋅ (–0,2x3) = 0,3x2 ⋅ (–0,2x3) – 1,4x ⋅ (–0,2x 3) = –0,06x5 + 0,28x4

16. f)

(\frac{1}{3} y^{2} + \frac{4}{7} y^{3}) \cdot (- 3 y) = \frac{1}{3} y^{2} \cdot (- 3 y) + \frac{4}{7} y^{3} \cdot (- 3 y) =

- y^{3} - \frac{12}{7} y^{4}

17. a) A soma das medidas das áreas é (6x2 + x), pois:

(2x + 1) ⋅ x + 2x ⋅ 2x = 2x ⋅ x + 1 ⋅ x + 4x2 =

= 2x2 + x + 4x2 = 6x2 + x

17. b) Com x = 5, temos: 6x2 + x = 6 ⋅ 5 (5)2 + (5) = 6 ⋅ 25 + 5 =

= 150 + 5 = 155

Então, esse é o valor numérico do binômio.

17. c) Como 100 = 10 ⋅ 10, tem-se que o lado do quadrado mede 10. Então: 2x = 10 ⇒

\frac{2 x}{2} = \frac{10}{2}

⇒ x = 5

19. a) (5x – 1) ⋅ (5x + 1) = 5x ⋅ 5x + 5x ⋅ 1 – 1 ⋅ 5x – 1 ⋅ 1 =

= 25x2 + 5x – 5x – 1 = 25x2 – 1

19. b) (a + b) ⋅ (a + b) = a ⋅ a + a ⋅ b + b ⋅ a + b ⋅ b =

= a2 + 2ab + b2

19. c) (2x2 – 3x – 6) ⋅ (5x – 2) =

= 2x2 ⋅ 5x – 2x2 ⋅ 2 – 3x ⋅ 5x + 3x ⋅ 2 – 6 ⋅ 5x + 6 ⋅ 2 =

= 10x3 – 4x2 – 15x2 + 6x – 30x + 12 =

= 10x3 – 19x2 – 24x + 12

19. d)

(2 a + \frac{3}{5} b) · (a - \frac{1}{2} b)

= 2 a \cdot a - 2 a \cdot \frac{1}{2} b + \frac{3}{5} b \cdot a - \frac{3}{5} b \cdot \frac{1}{2} b

= 2 a^{2} - a b + \frac{3}{5} a b - \frac{3}{10} b^{2}

= 2 a^{2} + \frac{- 5 + 3}{5} a b - \frac{3}{10} b^{2}

= 2 a^{2} - \frac{2}{5} a b - \frac{3}{10} b^{2}

21. a) A ⋅ B = (x2 + 3x – 2)( x + 2) =

= x2 ⋅ x + x2 ⋅ 2 + 3x ⋅ x + 3x ⋅ 2 – 2 ⋅ x – 2 ⋅ 2 =

= x3 + 2x2 + 3x2 + 6x – 2x – 4 = x3 + 5x2 + 4x – 4

A ⋅ C = (x2 + 3x – 2)(x – 3) =

= x2 ⋅ x – x2 ⋅ 3 + 3x ⋅ x – 3x ⋅ 3 – 2 ⋅ x + 2 ⋅ 3 =

= x3 – 3x2 + 3x2 – 9x – 2x + 6 = x3 – 11x + 6

A ⋅ B + A ⋅ A = (x3 + 5x2 + 4x – 4) + (x3 – 11x + 6) =

= x3 + x3 + 5x2 + 4x – 11x – 4 + 6 = 2x3 + 5x2 – 7x + 2

Página sessenta e cinco

21. b) B + C = (x + 2) + (x – 3) = x + x + 2 – 3 = 2x – 1

= x2 ⋅ 2x – x2 ⋅ 1 + 3x ⋅ 2x – 3x ⋅ 1 – 2 ⋅ 2x + 2 ⋅ 1 =

= 2x3 – x2 + 6x2 – 3x – 4x + 2 = 2x3 + 5x2 – 7x + 2

22. a) 3x ⋅ (2x – 3) ⋅ ( x + 2) = (3x ⋅ 2x – 3x ⋅ 3) ⋅ (x + 2) =

= (6x2 – 9x) ⋅ ( x + 2) = 6x2 ⋅ x + 6x2 ⋅ 2 – 9x ⋅ x – 9x ⋅ 2 =

= 6x3 + 12x – 9x2 – 18x = 6x3 + 3x2 – 18x

22. b) –2x ⋅ ( x + 5) ⋅ (2x – 5) = (–2x ⋅ x – 2x ⋅ 5) ⋅ (2x – 5) =

= (–2x2 – 10x) ⋅ (2x – 5) = –2x2 ⋅ 2x + 2x2 ⋅ 5 – 10x ⋅ 2x + 10x ⋅ 5 =

= –4x3 + 10x2 – 20x2 + 50x = –4x3 – 10x2 + 50x

22. c) (a – 2b) ⋅ (a + 2b) ⋅ (a – b) =

= (a ⋅ a + a ⋅ 2b – 2b ⋅ a – 2b ⋅ 2b) ⋅ (a – b) =

= (a2 + 4ab – 4ab – 4b2) ⋅ (a – b) = (a2 – 4b2) ⋅ (a – b) =

= a2 ⋅ a – a2 ⋅ b – 4b2 ⋅ a + 4b2 ⋅ b = a3 – a2b – 4ab2 + 4b3

22. d) (a – b) ⋅ (a + b) ⋅ (3a – b) =

= (a ⋅ a + a ⋅ b – b ⋅ a – b ⋅ b) ⋅ (3a – b) =

= (a2 + ab – ab – b2) ⋅ (3a – b) = (a2 – b2) ⋅ (3a – b) =

= a2 ⋅ 3a – a2 ⋅ b – b2 ⋅ 3a + b2 ⋅ b = 3a3 – a2b – 3ab2 + b3

22. e)

\frac{x}{2} (x + \frac{1}{3}) \cdot (2 x - \frac{1}{2})

(\frac{x}{2} \cdot x + \frac{x}{2} · \frac{1}{3}) \cdot (2 x - \frac{1}{2})

(\frac{x^{2}}{2} + \frac{x \cdot 1}{2 \cdot 3}) \cdot (2 x - \frac{1}{2})

(\frac{x^{2}}{2} + \frac{x}{6}) \cdot (2 x - \frac{1}{2})

= =

\frac{x^{2}}{2} \cdot 2 x + \frac{x}{6} \cdot 2 x – \frac{x^{2}}{2} \cdot \frac{1}{2} - \frac{x}{6} \cdot \frac{1}{2}

x^{3} + \frac{x^{2}}{3} - \frac{x^{2}}{4} - \frac{x}{12}

x^{3} + \frac{4 x^{2}}{12} - \frac{3 x^{2}}{12} - \frac{x}{12}

x^{3} + \frac{x^{2}}{12} - \frac{x}{12}

24. a) (8x5 + 6x3) : (+2x2 ) = 8x5 : (+2x2) + 6x3 : (+2x2) =

= (8 : 2) x5 ‒ 2 + (6 : 2) x3 ‒ 2 = 4x3 + 3x

24. b) (12ab + 15a2b + 9ab2) : (3ab) =

= 12ab : (3ab) + 15a2b : (3ab) + 9ab2 : (3ab) = 4 + 5a + 3b

24. c) (20x – 10x2) : (–5x) = 20x : (–5x) – 10x2 : (–5x) = –4 + 2x

24. d) (a3 + a2 + a) : (a) = a3 : a + a2 : a + a : a = a2 + a + 1

24. e) (x5 + x2): (–x2) = x5 : (–x2) + x2 : (–x2) = –x3 – 1

24. f) (7x2 – 8x + 5) : (–1) = 7x2 : (–1) – 8x : (–1) + 5 : (–1) =

= –7x2 + 8x – 5

25. (21x3 – 28x2 + 14x) : (–7x) = 21x3 : (–7x) – 28x2 : (–7x) + 14x : (–7x) = –3x2 + 4x – 2

26. (–8xy + 9x2y – 6xy2) : (–4xy) =

= –8xy : (–4xy) + 9x2y : (–4xy) – 6xy2 : (–4xy) = 2 – 2,25x + 1,5y

27.

(\frac{7}{3} x^{2} + \frac{1}{4} x) : (– \frac{1}{2} x)

\frac{7}{3} x^{2} : (– \frac{1}{2} x) + \frac{1}{4} x : (– \frac{1}{2} x)

– \frac{7}{3} · \frac{2}{1} x - \frac{1}{4} · \frac{2}{1}

– \frac{14}{3} x + \frac{1}{2}

28. [(25x2 – 15x) : (–5x)] ⋅ (5x + 3) =

= [25x2 : (–5x) – 15x : (–5x)] ⋅ (5x + 3) = [–5x + 3] ⋅ (5x + 3) =

= –5x ⋅ 5x + (–5x) ⋅ 3 + 3 ⋅ 5x + 3 ⋅ 3 =

= –25x2 – 15x + 15x + 9 = –25x2 + 9

32. M ⋅ (2x – 1) = 6x2 – 7x + 2

M = (6x2 – 7x + 2) : (2x – 1) = 3x – 2, pois:

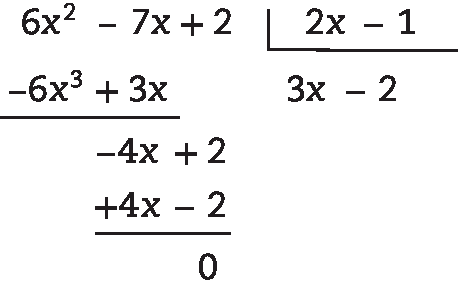
Algoritmo da divisão.
Na chave: 2 x menos 1

Fora da chave: 6 x ao quadrado menos 7 x mais 2; abaixo, menos 6 x ao cubo mais 3 x; abaixo menos 4 x mais 2; abaixo mais 4 x menos 2; abaixo 0.

Quociente: 3 x menos 2

33. a) x + 4, pois:

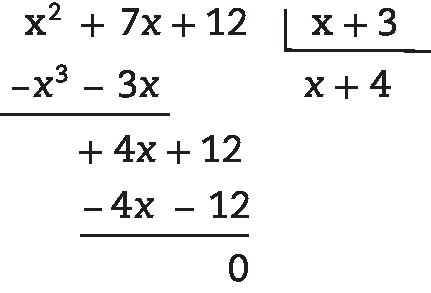
Algoritmo da divisão.
Na chave: x mais 3

Fora da chave: x ao quadrado mais 7 x mais 12; abaixo, menos x ao cubo menos 3 x; abaixo mais 4 x mais 12; abaixo, menos 4 x menos 12; abaixo resto zero.

Quociente: x mais 4

33. b) 2x – 5, pois:

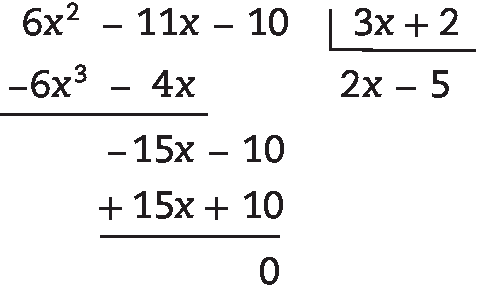
Algoritmo da divisão.
Na chave:3 x mais 2

Fora da chave: 6 x ao quadrado menos 11 x menos 10; abaixo, menos x ao cubo menos 4 x; abaixo menos 15 x menos 10; abaixo mais 15 x mais 10; abaixo, resto zero.

Quociente: 2 x menos 5

33. c) 2x2 – 3x, pois:

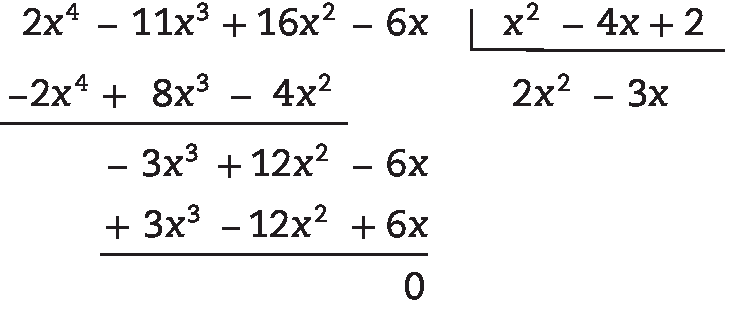
Algoritmo da divisão.
Na chave: x ao quadrado menos 4 x mais 2

Fora da chave: 2 x à quarta menos 11 x ao cubo mais 16 x ao quadrado menos 6 x; abaixo menos 2 x à quarta mais 8 x ao cubo menos 4 x ao quadrado; abaixo menos 3 x ao cubo mais 12 x ao quadrado menos 6 x; abaixo mais 3 x ao cubo menos 12 x ao quadrado mais 6 x; abaixo resto 0.

Quociente: 2 x ao quadrado menos 3 x

34. a) O quociente é 2x2 – 5x – 7 e o resto é –20, pois:

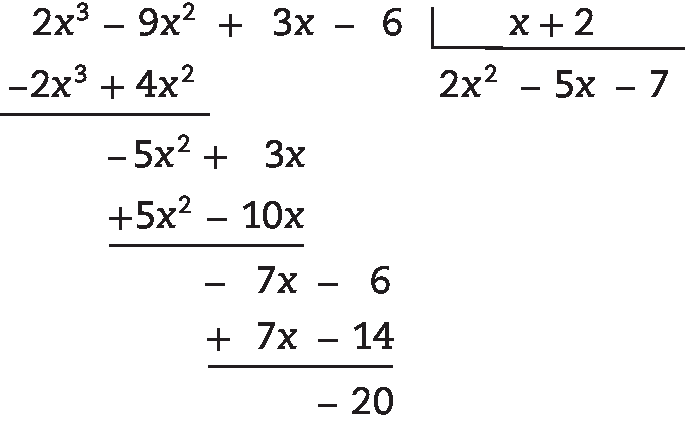
Algoritmo da divisão.
Na chave: x mais 2

Fora da chave: 2 x ao cubo menos 9 x ao quadrado mais 3x menos 6, abaixo menos 2 x ao cubo mais 4 x ao quadrado, abaixo menos 5 x ao quadrado mais 3 x, abaixo mais 5 x ao quadrado menos 10 x, abaixo menos 7 x menos 6, abaixo mais 7 x menos 14, abaixo resto 20.

Quociente: 2 x ao quadrado menos 5 x menos 7

34. b) O quociente é 2a + 1 e o resto é a – 2, pois:

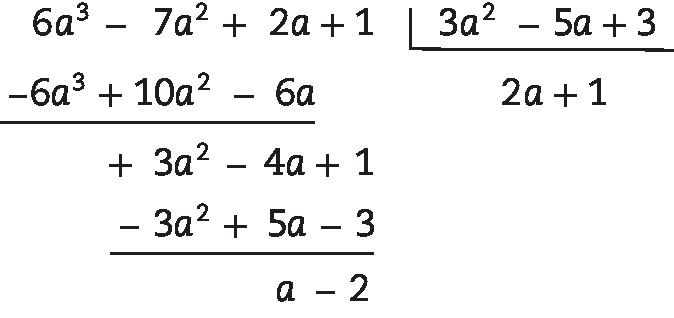
Algoritmo da divisão.
Na chave:3 a ao quadrado menos 5 a mais 3

Fora da chave: 6 a ao cubo menos 7 a ao quadrado mais 2 a mais 1, abaixo menos 6 a ao cubo mais 10 a ao quadrado menos 6 a, abaixo mais 3 a ao quadrado menos 4 a mais 1, abaixo menos 3 a ao quadrado mais 5 a menos 3, abaixo resto a menos 2

Quociente: 2 a mais 1

35. O polinômio a desejado é tal que:

A ⋅ (a2 + 2a – 5) = 3a3 + 2a2 – 23a + 20

Portanto, a = (3a3 + 2a2 – 23a + 20) : (a2 + 2a – 5) = 3a – 4, pois:

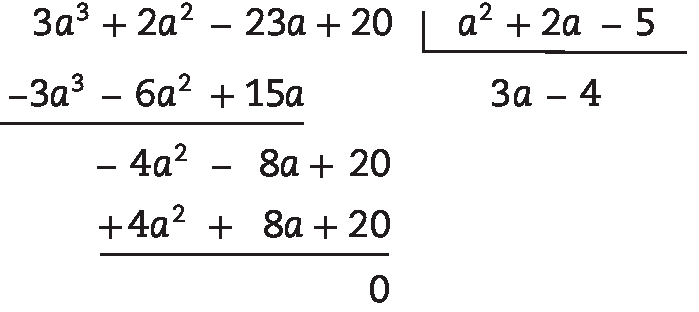
Algoritmo da divisão.
Na chave: a ao quadrado mais 2 a menos 5

Fora da chave: 3 a ao cubo mais 2 a ao quadrado menos 23 a mais 20, abaixo menos 3 a ao cubo menos 6 a ao quadrado mais 15 a, abaixo menos 4 a ao quadrado menos 8 a mais 20, abaixo mais 4 a ao quadrado mais 8 a mais 20, abaixo zero

Quociente: 3 a menos 4

Página sessenta e seis

36. O polinômio que representa a medida da altura é tal que pode ser calculado da maneira apresentada a seguir.

(5x2 + 2x – 3) : (5x – 3) = x + 1, pois:

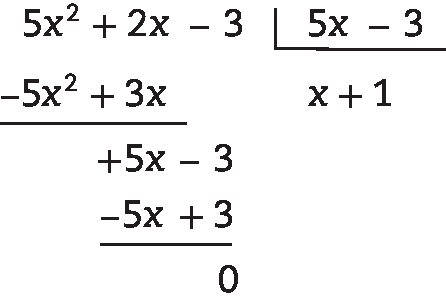
Algoritmo da divisão.

Na chave: 5 x menos 3

Fora da chave: 5 x ao quadrado mais 2 x menos 3, abaixo menos 5 x ao quadrado mais 3 x, abaixo mais 5 x ao quadrado mais 3 x, abaixo mais 5 x menos 3, abaixo menos 5 x mais 3, abaixo resto zero.

Quociente: x mais 1

38. a) Se a largura mede x, o dobro da medida da largura, em metro, é 2x e, com 15 métro, tem-se que a medida do comprimento do terreno fica algebricamente expressa por 2x + 15. Portanto, a razão entre as medidas é

\frac{2 x + 15}{x}

38. b) Como x = 12, temos:

\frac{2 x + 15}{x} = \frac{2 \cdot 12 + 15}{12} = \frac{24 + 15}{12} = \frac{39}{12} = \frac{13}{4}

39. a) Como o consumo é a razão entre a medida da distância percorrida e a medida de volume de combustível, conclui-se que essa razão, em quilômetro por litro, é algebricamente expressa por

\frac{x}{y}

39. b) O dobro da medida da distância percorrida pela primeira moto é 2x e, como a segunda moto percorreu essa medida de distância com (y + 5) litros de gasolina, a razão na segunda moto é expressa por

\frac{2 x}{y + 5}

40. O polinômio do denominador deve ser zero. A condição y – 6 = 0 implica y = 6.

41. Só não podem ser atribuídos valores para x que façam o valor numérico do denominador ser zero. A condição 2x – 3 ≠ 0 implica 2x ≠ 3, que, por sua vez, implica x ≠

\frac{3}{2}

(ou x ≠ 1,5).

42. A condição b – 2a ≠ 0 implica b ≠ 2a.

43. Sendo x o saldo da poupança ontem, então o depósito do meu avô foi 4 ⋅ x + 200 e a razão pedida é:

\frac{x}{x + (4 x + 200)} = \frac{x}{5 x + 200}

Pense mais um poucoreticências

Resposta pessoal. Observe se os estudantes percebem que, como todo número pode ser decomposto em suas ordens utilizando potências de 10, então essa decomposição pode ser usada para efetuar operações, como a divisão, de modo que essa maneira de dividir se assemelha ao método da divisão de polinômios.

Trabalhando a informação

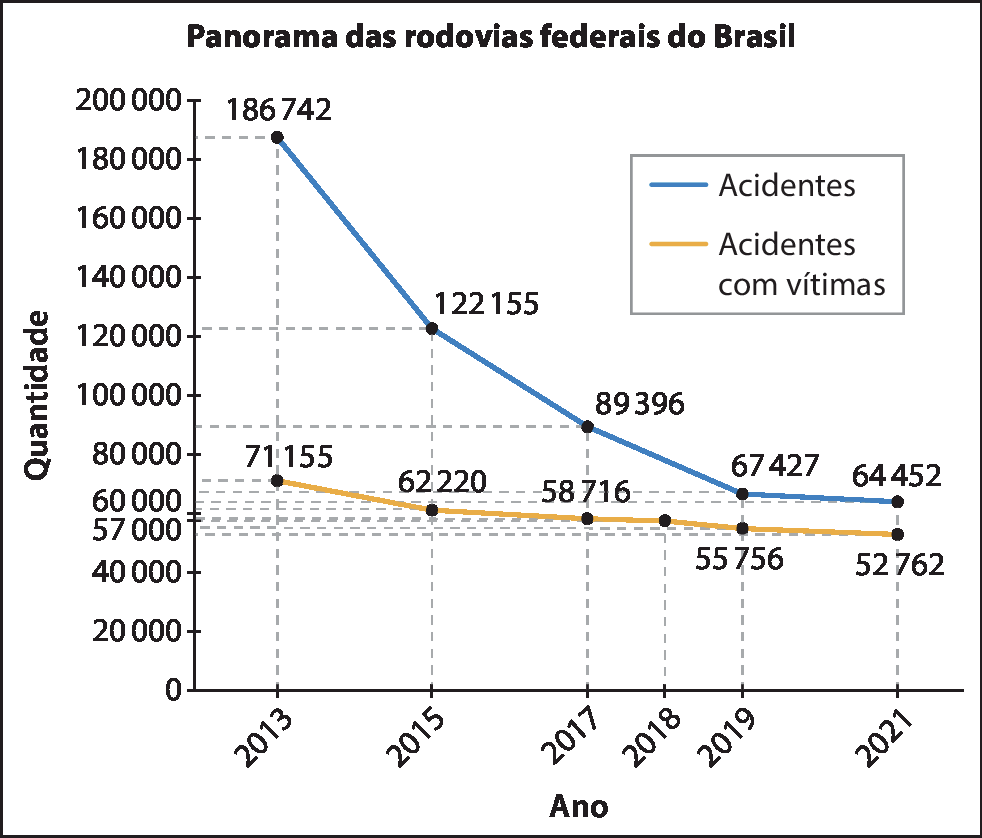
a) O gráfico de colunas é primeiro nessa seção Trabalhando a informação, o que fornece dados panorâmicos sobre ocorrências nas rodovias federais do Brasil; portanto, a resposta esperada é o segundo gráfico dessa seção, com os mesmos dados, porém representados utilizando um gráfico de linhas duplas.

d) Podemos aproximar essa quantidade fazendo uma média, ou seja, pegando o valor intermediário entre o número de acidentes de 2017 e o de 2019; portanto, será aproximadamente 78 mil acidentes, pois:

\frac{89 396 + 67 427}{2} = \frac{156 823}{2}

= .78411,5 ≃ .78000

e) O procedimento descrito por interpolação gráfica é traçar duas retas como as observadas na figura a seguir, concluindo que a quantidade aproximada de acidentes com vítimas em 2018 é de .57000.

Gráfico em linha. Panorama das rodovias federais do Brasil. Eixo x, ano. Eixo y. quantidade. Os dados são: Acidentes: 2013: 186.742. 2015: 122.155. 2017: 89.396. 2019: 67.427. 2021: 64.452. Acidentes com vítimas: 2013: 71.155. 2015: 62.220. 2017: 58.716. 2018: 57.000. 2019: 55.756. 2021: 52.762. — Dados obtidos em: CONFEDERAÇÃO Nacional do Transporte. Painel cê êne tê de acidentes rodoviários. Brasília, Distrito Federal: cê êne tê, dezembro 2021. Disponível em: https://oeds.link/8jwrqr. Acesso em: 23 junho 2022.

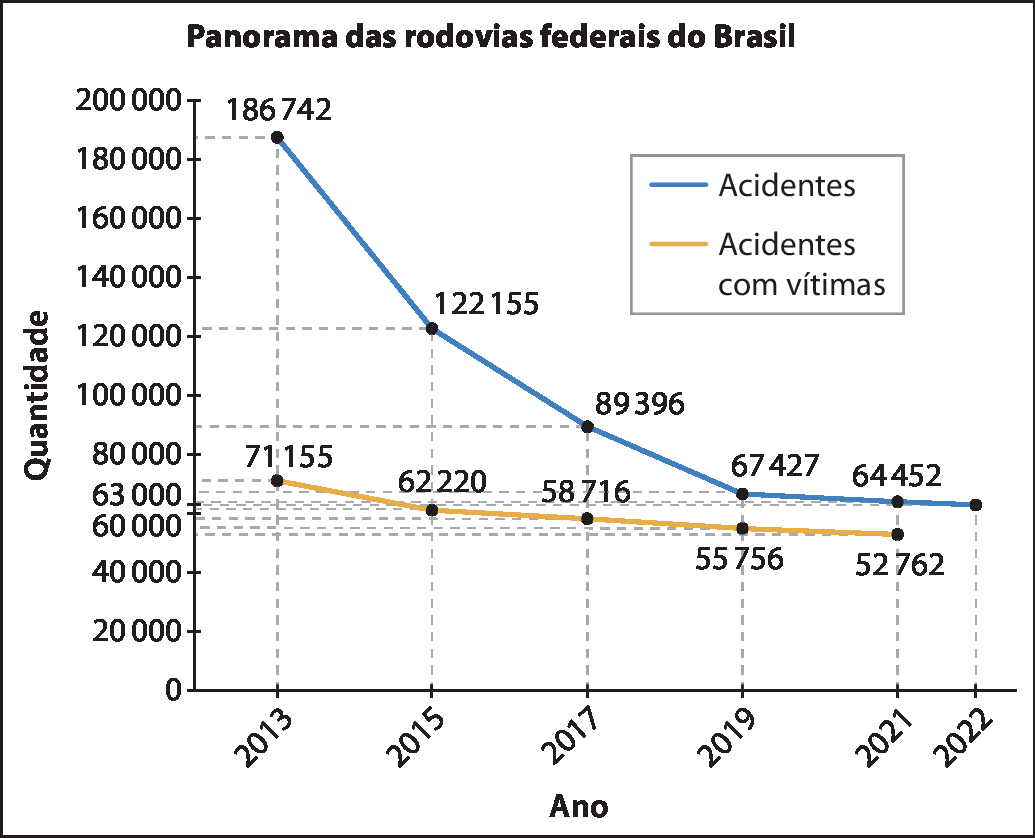
f) Uma estimativa para a quantidade total de acidentes em 2022 é .63000. Observe a seguir o prolongamento da linha.

Página sessenta e sete

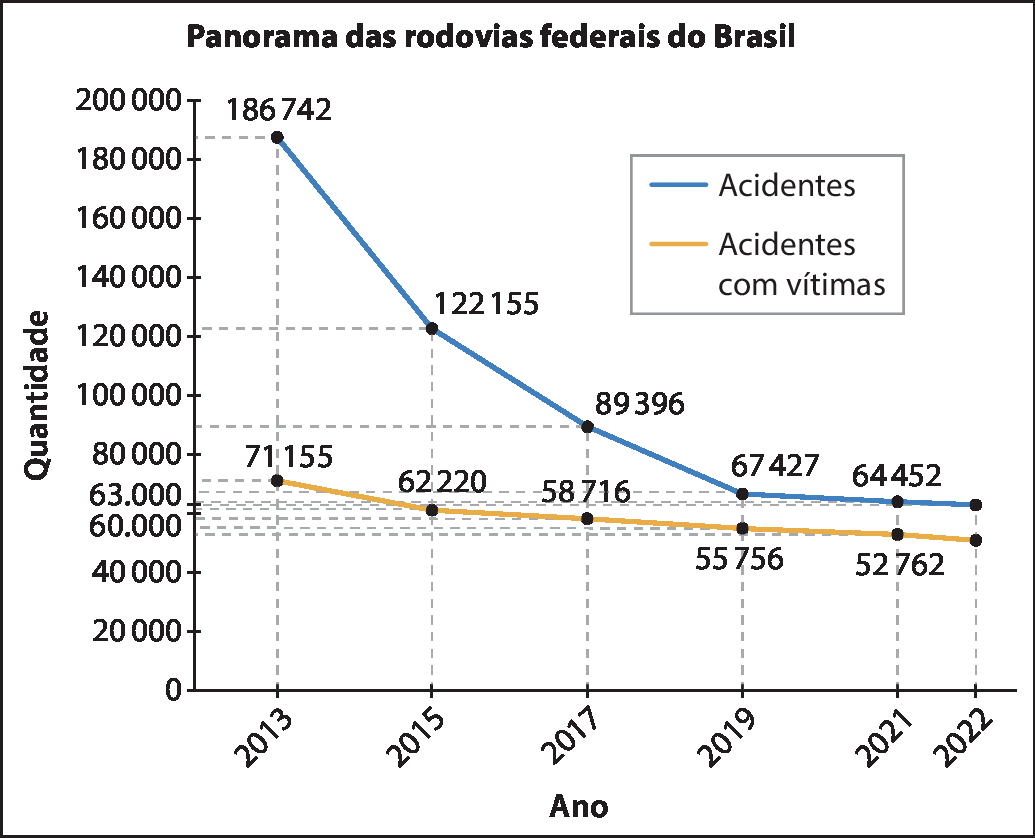
g) Uma estimativa para acidentes com vítimas para 2022 é .51000 acidentes.

Exercícios complementares

1. a) a = 1, b = 1 e c = 2, então:

a + 2b – 4c = 1 + 2 ⋅ 1 – 4 ⋅ 2 = 1 + 2 – 8 = –5

1. b) Para a expressão a + 2b – 4c assumir seu valor máximo, as parcelas a e 2b devem ser as maiores possíveis, enquanto o subtraendo 4c deve ser o menor possível. Assim, atribuindo a = 2, b = 2 e c = 0, temos:

a + 2b – 4c = 2 + 2 ⋅ 2 – 4 ⋅ 0 = 2 + 4 – 0 = 6

1. c) Fazendo um quadro com as 6 possibilidades:

a	b	c	a + 2b − 4c
0	1	2	0 + 2 ⋅ 1 − 4 ⋅ 2 = 0 + 2 − 8 = −6
0	2	1	0 + 2 ⋅ 2 − 4 ⋅ 1 = 0 + 4 − 4 = 0
1	0	2	1 + 2 ⋅ 0 − 4 ⋅ 2 = 1 + 0 − 8 = −7
1	2	0	1 + 2 ⋅ 2 − 4 ⋅ 0 = 1 + 4 − 0 = 5
2	0	1	2 + 2 ⋅ 0 − 4 ⋅ 1 = 2 + 0 − 4 = −2
2	1	0	2 + 2 ⋅ 1 − 4 ⋅ 0 = 2 + 2 − 0 = 4

Da última linha do quadro obtêm-se: a = 2 , b = 1 e c = 0

2. a) (3a2 – 5b) + (5a2 + 5b) = 3a2 + 5a2 – 5b + 5b = 8a2

2. b) (3x2 – 5x + 2) – (x2 + 6x – 4) + (5x – 7) =

= 3x2 – 5x + 2 – x2 – 6x + 4 + 5x – 7 =

= 3x2 – x2 – 5x – 6x + 5x + 2 + 4 – 7 = 2x2 – 6x – 1

2. c) (a2 – ab) + (b2 – ab) – (a2 + b2) =

= a2 – ab + b2 – ab – a2 – b2 =

= a2 – a2 – ab – ab + b2 – b2 = –2ab

2. d)

(- \frac{1}{2} a - 2 b) - (\frac{3}{5} b + 2 a)

- \frac{1}{2} a - 2 b - \frac{3}{5} b - 2 a

= - \frac{1}{2} a - \frac{4}{2} a - \frac{10}{5} b - \frac{3}{5} b

\frac{- a - 4 a}{2} + \frac{- 10 b - 3 b}{5}

= \frac{- 5}{2} a - \frac{13}{5} b

3. a) 3a – (b – a) + (5b – 2a) = 3a – b + a + 5b – 2a =

= 3a + a – 2a – b + 5b = 2a + 4b

3. b) x2 – {3x – [(x + 3) +(x2 – 1)]} =

= x2 – {3x – [x + 3 + x2 – 1]} =

= x2 – {3x – [x2 + x + 2]} =

= x2 – {3x – x2 – x – 2} =

= x2 – {–x2 + 2x – 2} =

= x2 + x2 – 2x + 2 =

= 2x2 – 2x + 2

3. c) 2y –[–3xy + (–2x + 5y) – (–4xy + x)] =

= 2y – [–3xy – 2x + 5y + 4xy – x] =

= 2y – [–3xy + 4xy – 2x – x + 5y] =

= 2y – [+xy – 3x + 5y] = 2y – xy + 3x – 5y =

= –xy + 3x – 3y

5. a) (x – 2) ⋅ (x + 5) = x ⋅ x + x ⋅ 5 – 2 ⋅ x – 2 ⋅ 5 =

= x2 + 5x – 2x – 10 = x2 + 3x – 10

5. b) (2x – 4) ⋅ (3x + 1) = 2x ⋅ 3x + 2x ⋅ 1 – 4 ⋅ 3x – 4 ⋅ 1 =

= 6x2 + 2x – 12x – 4 = 6x2 – 10x – 4

5. c) (x – 1) ⋅ (x2 + x + 1) =

= x ⋅ x2 + x ⋅ x + x ⋅ 1 – 1 ⋅ x2 – 1 ⋅ x – 1 ⋅ 1 =

= x3 + x2 – x2 + x – x – 1 = x3 – 1

5. d) (a – 1) ⋅ (a2 – 1)(a + 1) =

= [a ⋅ a2 + a ⋅ (–1) – 1 – a2 – 1 ⋅ (–1)] (a + 1) =

= [a3 – a2 – a + 1] (a + 1) =

= a3 ⋅ a + a3 ⋅ 1 – a2 ⋅ a – a2 ⋅ 1 – a ⋅ a – a ⋅ 1 + 1 ⋅ a + 1 ⋅ 1 =

= a4 + a3 – a3 – a2 – a2 – a + a + 1 = a4 – 2a2 + 1

6. O polinômio é tal que será (quociente) ⋅ (divisor) + (resto), portanto:

(5x2 – 3x + 1) ⋅ (x2 + 2x – 3) + (–5x + 2) =

= 5x2 ⋅ x2 + 5x2 ⋅ 2x + 5x2 ⋅ (–3) – 3x ⋅ x2 – 3x ⋅ 2x –

– 3x ⋅ (–3) + 1 ⋅ x2 + 1 ⋅ 2x + 1⋅ (–3) – 5x + 2 =

= 5x4 + 10x3 – 15x2 – 3x3 – 6x2 + 9x + x2 + 2x – 3 – 5x + 2 = 5x4 + 10x3 – 3x3 – 15x2 – 6x2 + x2 + 9x + 2x – 5x – 3 + 2 = 5x4 + 7x3 – 20x2 + 6x – 1

7. O polinômio que satisfaz

A ⋅ (2x – 1) = (8x3 – 14x + 11x – 3) é tal que:

A = (8x3 – 14x +11x – 3) : (2x – 1) = 4x2 – 5x + 3, pois:

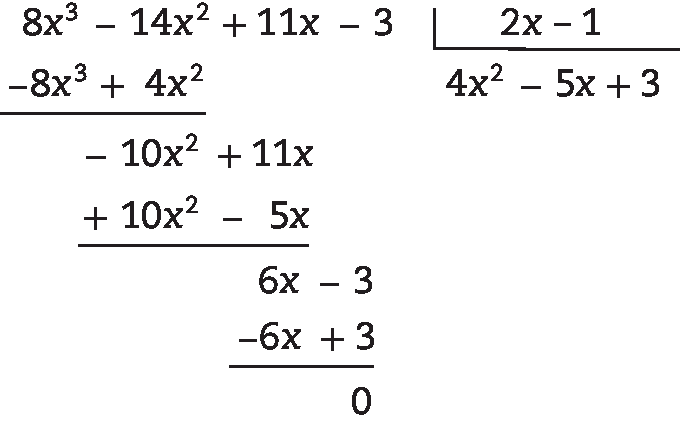
Algoritmo da divisão.

Na chave: 2 x menos 1

Fora da chave: 8 x ao cubo menos 14 x ao quadrado mais 11 x menos 3, abaixo menos 8 x ao cubo mais 4 x ao quadrado, abaixo menos 10 x ao quadrado mais 11 x, abaixo mais 10 x ao quadrado menos 5 x, abaixo 6 x menos 3, abaixo menos x mais 3, abaixo resto zero

Quociente: 4 x ao quadrado menos 5 x mais 3.

8. a) B ⋅ C = (2x2 + 5x – 12) ⋅ (2x – 3) =

= 2x2 ⋅ 2x + 2x2 ⋅ (–3) + 5x ⋅ 2x + 5x ⋅ (–3) – 12 ⋅ 2x – 12 ⋅ (–3) =

= 4x3 – 6x2 + 10x2 –15x – 24x + 36 =

= 4x3 + 4x2 – 39x + 36

8. b) D2 = (x + 4) ⋅ (x + 4) = x ⋅ x + x ⋅ 4 + 4 ⋅ x + 4 ⋅ 4 =

= x2 + 8x + 16

Página sessenta e oito

8. c) B : C = x + 4, pois:

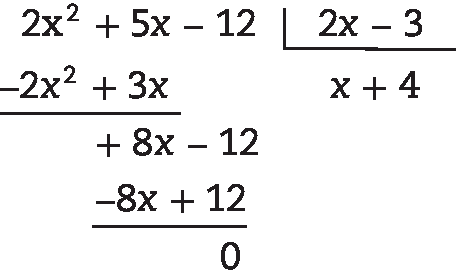
Algoritmo da divisão.

Na chave: 2 x menos 3

Fora da chave: 2 x ao quadrado mais 5 x menos 12, abaixo menos 2 x ao quadrado mais 3 x, abaixo mais 8 x menos 12, abaixo menos 8 x mais 12, abaixo resto zero.

Quociente: x mais 4

8. d) ([6x2 – 5x – 6 ] + [ 2x2 + 5x – 12]) ⋅ (2x – 3) =

= (6x2 + 2x2 – 5x + 5x – 6 – 12) ⋅ (2x – 3) =

= (8x2 – 18) ⋅ (2x – 3) = 8x2 ⋅ 2x + 8x2 ⋅ (–3) – 18 ⋅ 2x – 18 ⋅ ( – 3) = 16x3 – 24x2 – 36x + 54

9. Como 5x ⋅ (x – 3) = 5x ⋅ x + 5x ⋅ (–3) = 5x2 – 15x então a divisão é (5x3 + 5x2 – 60x) : (5x2 – 15x) = x + 4, pois:

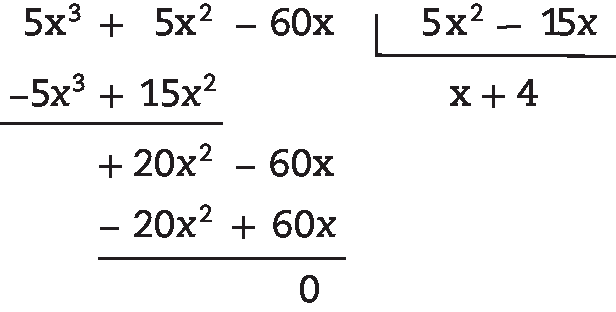
Algoritmo da divisão.

Na chave: 5 x ao quadrado menos 15 x

Fora da chave: 5 x ao cubo mais 5 x ao quadrado menos 60 x, abaixo menos 5 x ao cubo mais 15 x ao quadrado, abaixo mais 20 x ao quadrado menos 60 x, abaixo menos 20 x ao quadrado mais 60 x, abaixo resto 0

Quociente: x mais 4

10. (x3 – 2x2 – x + 2) : (x2 – 1) = (x – 2); como é uma divisão exata, o resto é zero. Considere a divisão a seguir.

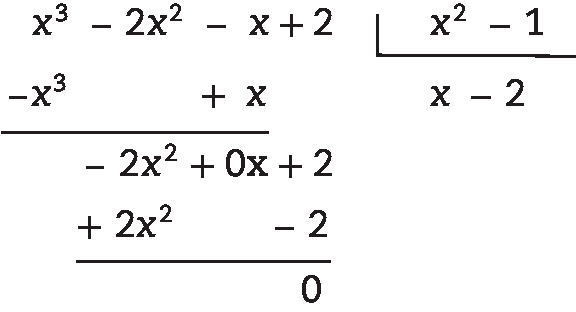
Algoritmo da divisão.

Na chave: x ao quadrado menos 1

Fora da chave: x ao cubo menos 2 x ao quadrado menos x mais 2, abaixo menos x ao cubo mais x, abaixo menos 2 x ao quadrado mais 0 x mais 2, abaixo mais 2 x ao quadrado menos 2, abaixo 0.

Quociente: x menos 2

11. Para que a fração

\frac{E}{P}

seja mínima, o numerador ê deve ser mínimo, enquanto o denominador P deve ser máximo. Assim, o menor valor de

\frac{E}{P}

\frac{16}{30} = \frac{8}{15}

≃ 0,53.

Para que a fração

\frac{E}{P}

seja máxima, o numerador ê deve ser máximo, enquanto o denominador P deve ser mínimo. Assim, o menor valor de

\frac{E}{P}

\frac{18}{25}

= 0,72.

Verificando:

2. A medida do perímetro é 4a + 4b, pois:

a + b + a + b + a + b + a + b = a + a + a + a + b + b + b + b = 4a + 4b

Alternativa c.

3. A medida da área é 2x2 + 4x, pois:

2x ⋅ (x + 2) = 2x ⋅ x + 2x ⋅ 2 = 2x2 + 4x

Alternativa d.

4. (a3 – a2 + a) ⋅ (a + 1) = a3 ⋅ a – a2 ⋅ a + a ⋅ a + a3 ⋅ 1 – a2 ⋅ 1 + + a ⋅ 1 = a4 – a3 + a2 + a3 – a2 + a =

= a4 – a3 + a3 + a2 – a2 + a = a4 + a

Alternativa a.

5. Efetuando a divisão:

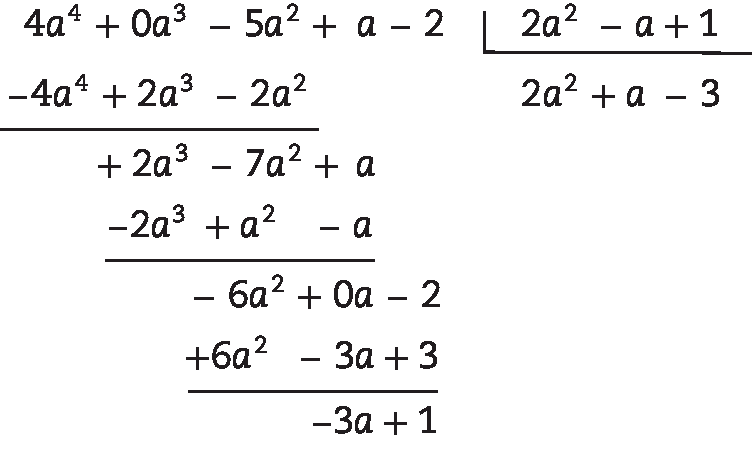
Algoritmo da divisão.

Na chave: 2 a ao quadrado menos a mais 1

Fora da chave: 4 a elevado à quarta mais 0 a ao cubo menos 5 a ao quadrado mais a menos 2, abaixo menos 4 a elevado à quarta mais 2 a ao cubo menos 2 a ao quadrado, abaixo 2 a ao cubo menos 7 a ao quadrado mais a, menos 2 a ao cubo mais a ao quadrado menos a, abaixo menos 6 a ao quadrado mais 0 a menos 2, abaixo 6 a ao quadrado menos 3 a mais 3, abaixo menos 3 a mais 1

Quociente: 2 a ao quadrado mais a menos 3

Então R = –3a + 1. Com

a = \frac{1}{3}

, tem-se:

R = –3a + 1 = –3 ⋅

\frac{1}{3}

+ 1 = –1 + 1 = 0.

Alternativa a.

6. Com quociente exato, verifica-se que o resto é zero. Portanto, o polinômio procurado é:

(5a2 – 2a – 3) ⋅ (3a – 4) =

= 5a2 ⋅ 3a – 5a2 ⋅ 4 – 2a ⋅ 3a + 2a ⋅ 4 – 3 ⋅ 3a + 3 ⋅ 4 =

= 15a3 – 20a2 – 6a2 + 8a – 9a + 12 = 15a3 – 26a2 – a + 12

Alternativa a.

7. Contando 10 vezes os juros de 80 reais, conclui-se que o total gasto é expresso pela soma do valor à vista com o total de juros pago: x + 10 ⋅ 80 = x + 800. Dividindo o valor da entrada em 10 partes iguais, obtemos cada parcela, expressa por

\frac{x}{10} + 80

Alternativa c.

8. Como medida da área = medida da base ⋅ medida da altura, então a medida da altura é obtida dividindo-se a expressão que determina a medida da área pela da medida da base. O quociente é a expressão da medida da altura. Portanto, x + 3.

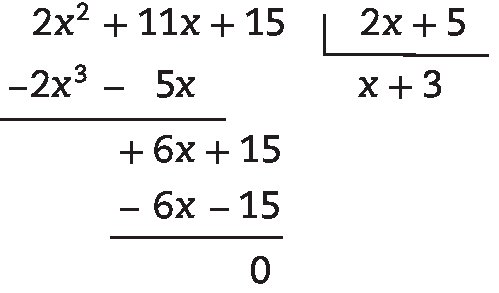
Algoritmo da divisão.

Na chave: 2 x mais 5

Fora da chave: 2 x ao quadrado mais 11 x mais 15, abaixo menos 2 x ao cubo menos 5 x, abaixo mais 6 x mais 15, abaixo menos 6 x menos 15, abaixo resto 0.

Quociente: x mais 3

Alternativa a.

Capítulo 6 – Produtos notáveis e fatoração

• Objetivos do capítulo e justificativas

• Ampliar o cálculo algébrico com os processos de produtos notáveis e fatoração.

• Reconhecer e aplicar os produtos notáveis e os casos de fatoração estudados.

• Resolver equações do tipo ax2 = b por meio de fatoração.

• Simplificar expressões envolvendo frações algébricas.

• Resolver equações envolvendo frações algébricas.

• Identificar regularidades em sequências recursivas e em sequências não recursivas.

• Analisar e construir fluxograma que permite indicar os números seguintes em determinada sequência numérica.

Página sessenta e nove

• Utilizar as noções de área de retângulos e de volume de blocos retangulares no estudo de produtos notáveis e fatoração.

• Interpretar e construir gráfico de barras.

Dando continuidade ao trabalho dos capítulos anteriores, a Unidade Temática Álgebra é foco neste capítulo e favorece a mobilização e aprofundamento do desenvolvimento da competência específica 5. Ao apresentar aos estudantes novas ferramentas e conceitos algébricos, como produtos notáveis e fatoração e sua utilização em simplificação de expressões algébricas ou de equações, bem como o estudo de sequências recursivas e de sequências não recursivas, contribuímos para que eles mobilizem conhecimentos que os favoreçam a modelar e resolver situações do cotidiano.

O trabalho com áreas de retângulos e volume de blocos retangulares favorece a compreensão do estudo de produtos notáveis e de fatoração e possibilitam aos estudantes estabelecer conexões e relações com as Unidades Temáticas Álgebra e Geometria. Dessa maneira, eles desenvolvem a competência específica 3.

O estudo sobre gráficos de barras e ressaltando a importância de que as barras sejam proporcionais aos valores numéricos que indicam, desenvolve a competência específica 4 e as competências gerais 2 e 4, pois os estudantes podem adquirir mais autonomia na leitura e interpretação de informações que são veiculadas no dia a dia nos diferentes meios de comunicação, analisando aspectos qualitativos e quantitativos de cada contexto. Também é mobilizada e ampliada a capacidade de argumentar com base em dados e informações precisas.

Em diferentes momentos do capítulo, como na abertura ou na primeira seção Para saber mais apresentamos conteúdos que favorecem o desenvolvimento da competência geral 1 e a competência específica 1, à medida em que os estudantes podem compreender os conhecimentos matemáticos como historicamente construídos e que podem ser aplicados para resolver situações reais.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah zero seis) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo ax² = b.

(ê éfe zero oito ême ah um zero) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.

(ê éfe zero oito ême ah um um) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

Este capítulo amplia e aprofunda os conhecimentos acerca das expressões algébricas trabalhados em capítulos anteriores, tratando de produtos notáveis e de fatoração relativos à Unidade Temática Álgebra e desenvolvendo a habilidade (ê éfe zero oito ême ah zero seis).

Os conhecimentos deste capítulo constituem subsídios para a compreensão dos estudos a serem desenvolvidos no 9º ano (ê éfe zero nove ême ah zero nove). Além disso, ainda relacionado à Unidade Temática Álgebra, o capítulo desenvolve aspectos da habilidade (ê éfe zero oito ême ah zero nove) ao tratar da resolução de equações do tipo ax² = b por meio de fatoração e, desenvolve também, as habilidades (ê éfe zero oito ême ah um zero) e (ê éfe zero oito ême ah um um) ao explorar sequências recursivas e sequências não recursivas.

A articulação com a Unidade Temática Grandezas e medidas é promovida por meio da associação de noções de área de retângulos e volume de blocos retangulares a expressões algébricas mobilizando, assim, a habilidade (ê éfe zero oito ême ah um nove).

Com a Unidade Temática Probabilidade e estatística, a articulação se dá na seção Trabalhando a informação, que trata da construção de gráfico de barras e favorece o desenvolvimento de aspectos da habilidade (ê éfe zero oito ême ah dois três), que é trabalhada em diferentes situações neste volume.

• Comentários e resoluções

Abertura

c) Como s é a medida do semiperímetro, nesse triângulo será:

s = \frac{a + b + c}{2} = \frac{3 + 4 + 5}{2} = \frac{12}{2} = 6

Portanto, pela fórmula de Heron temos:

A = \sqrt{s (s - a) (s - b) (s - c)}

\sqrt{6 (6 - 3) (6 - 4) (6 - 5)}

\sqrt{6 \cdot 3 \cdot 2 \cdot 1}

\sqrt{36}

= 6

A medida da área é 6.

Exercícios propostos

3. a) O lado do quadrado maior mede 9 unidades de comprimento; então, sua área mede oitenta e uma unidades de área (9 ⋅ 9 = 81); o lado do quadrado menor mede a, pois sua área mede a² e a ⋅ a = a2; então, as regiões um e dois são retângulos de lados de medidas 9 e a; portanto, cada um tem área de medida 9a (9 ⋅ a = 9a).

3. b) A medida da área total pode ser calculada pela soma das medidas das áreas de cada parte. Assim:

a2 + 9a + 9a + 81 = a2 + 18a + 81

3. c) A medida do lado do quadrado maior é dada pela soma das medidas dos lados dos dois quadrados coloridos, isto é, a + 9.

Página setenta

3. d) (a + 9)2 = (a)2 + 2 ⋅ a ⋅ 9 + 92 = a2 + 18a + 81

Essa é a mesma expressão para a medida da área total da figura determinada no item b.

4. a) Falsa. (x + 8)2 = (x)2 + 2 ⋅ x ⋅ 8 + 82 = x2 +16x + 64

4. c) Falsa. (x + 3y)2 = (x)2 + 2 ⋅ x ⋅ 3y + (3y)2 = x2 + 6xy + 9y2

5. a) (3x + y)2 = (3x)2 + 2 ⋅ 3x ⋅ y + y2 = 9x2 + 6xy + y2

5. b) (3a + 2)2 = (3a)2 + 3a ⋅ 2 + 22 = 9a2 +12a + 4

5. c) (4a + y3)2 = (4a)2 + 2 ⋅ 4a ⋅ y³ + (y³)2 =

= 16a2 + 8ay3 + y6

5. d)

{(\frac{3}{4} x + \frac{2}{5} y)}^{2} + {(\frac{3}{4} x)}^{2} + 2 \cdot \frac{3}{4} x \cdot \frac{2}{5} y + {(\frac{2}{5} y)}^{2} = \frac{9}{16} x^{2} + \frac{3}{5} x y + \frac{4}{25} y^{2}

6. a) a (5a –1) + (a + 2)2 =

= a ⋅ 5a – a ⋅ 1 + a2 + 2 ⋅ a ⋅ 2 + 22 =

= 5a2 – a + a2 + 4a + 4 = 6a2 + 3a + 4

6. b) (2x + 3)2 – x(x – 4) =

= (2x)2 + 2 ⋅ 2x ⋅ 3 + 32 – x ⋅ x – x ⋅ (–4) =

= 4x2 + 12x + 9 – x2 + 4x = 3x2 + 16x + 9

6. c) (y – 3)(y + 2) – (y + 1)2 =

= y ⋅ y + y ⋅ 2 – 3 ⋅ y – 3 ⋅ 2 – (y2 + 2 ⋅ y ⋅ 1 + 12) =

= y2 + 2y – 3y – 6 – (y2 + 2y + 1) =

= – y – 6 – 2y – 1 = – 3y – 7

6. d) (9y + 1)2 – (y + 9)2 =

= (9y)2 + 2 ⋅ 9y ⋅ 1 + 12 – (y2 + 2 ⋅ y ⋅ 9 + 92) =

= 81y2 + 18y + 1 – (y2 + 18y + 81) =

= 81y2 + 18y + 1 – y2 – 18y – 81 = 80y2 – 80

6. e) (2a + 3b)2 – 4a(a + 3b) =

= (2a)2 + 2 ⋅ 2a ⋅ 3b + (3b)2 – 4a ⋅ a – 4a ⋅ 3b =

= 4a2 + 12ab + 9b2 – 4a2 – 12ab = 9b2

6. f) (1 + 5a)2 + 25(1 – a2) =

= 12 + 2 ⋅ 1 ⋅ 5a + (5a)2 + 25 ⋅ 1 + 25 ⋅ (–a2) =

= 1 + 10a + 25a2 + 25 – 25a2 = 10a + 26

8. a) (–x + 6)2 = (–x)2 + 2 ⋅ (–x) ⋅ 6 + 62 = x2 – 12x + 36

8. b)

{(- \frac{x}{2} + \frac{y}{3})}^{2}

{(\frac{- x}{2})}^{2} + 2 \cdot (\frac{- x}{2}) \cdot \frac{y}{3} + {(\frac{y}{3})}^{2}

= =

\frac{x^{2}}{4} - \frac{x y}{3} + \frac{y^{2}}{9}

10. a) (3a – 5)2 = (3a)2 – 2 ⋅ 3a ⋅ 5 + 52 = 9a2 – 30a + 25

10. b) (3x – 2y)2 = (3x)2 – 2 ⋅ 3x ⋅ 2y + (2y)2 = 9x2 – 12xy + 4y2

10. c) (3a2 – 1)2 = (3a2)2 – 2 ⋅ 3a2 ⋅ 1 + 12 = 9a4 – 6a2 + 1

10. d)

{(x - \frac{1}{2})}^{2} = x^{2} - 2 \cdot x \cdot \frac{1}{2} + {(\frac{1}{2})}^{2}

x^{2} - x + \frac{1}{4}

11. a) (2x + 1)2 + (x – 5)2 =

= (2x)2 + 2 ⋅ 2x ⋅ 1 + 12 + x2 – 2 ⋅ x ⋅ 5 + 52 =

= 4x2 + 4x + 1 + x2 – 10x + 25 = 5x2 – 6x + 26

11. b) (x – 1)2 – (x + 1)2 =

= x2 – 2 ⋅ x ⋅ 1 + 12 – [x2 + 2 ⋅ x ⋅ 1 + 12] =

= x2 – 2x + 1 – [x2 + 2x + 1] =

= x2 – 2x + 1 – x2 – 2x – 1 = –4x

11. c) x(x – 3)2 – 4

{(x + \frac{1}{2})}^{2}

= x[x2 – 2 ⋅ x ⋅ 3 + 32] – 4 ⋅

[x^{2} + 2 \cdot x \cdot \frac{1}{2} + {(\frac{1}{2})}^{2}]

= x ⋅ [x2 – 6x + 9] – 4 ⋅

[x^{2} + x + \frac{1}{4}]

= x3 – 6x2 + 9x – 4x2 – 4x – 1 = x3 – 10x2 + 5x – 1

12. a)

{(x + \frac{1}{x})}^{2} = x^{2} + 2 \cdot x \cdot \frac{1}{x} + {(\frac{1}{x})}^{2}

x^{2} + 2 + \frac{1}{x^{2}}

(x^{2} + \frac{1}{x^{2}})

+ 2 = 5 + 2 = 7

12. b)

{(x - \frac{1}{x})}^{2} = x^{2} - 2 \cdot x \cdot \frac{1}{x} + {(\frac{1}{x})}^{2}

x^{2} - 2 + \frac{1}{x^{2}}

(x^{2} + \frac{1}{x^{2}})

– 2 = 5 – 2 = 3

15. 4x2 – 4x + 1 = (2x)2 – 2 ⋅ 2x ⋅ 1 + (1)2 = (2x – 1)2

Portanto o lado do quadrado mede 2x – 1; assim, a medida do perímetro é dada por:

4(2x – 1) = 4 ⋅ 2x – 4 ⋅ 1 = 8x – 4

16. b) Falsa. (4a2 + 7b) ⋅ (4a2 – 7b) = (4a2)2 – (7b)2 =

= 42 a4 – 72b7 = 16a4 – 49b2

16. c) Falsa. (0, 3x + 0, 4y) ⋅ (0, 3x – 0, 4 y) = (0, 3x)2 – (0, 4y)2 = 0, 09x2 – 0,16 y²

17. a) (x + 11) ⋅ (x – 11) = x2 – 112 = x2 – 121

17. b) (5 – a3) ⋅ (5 + a3) = 52 – (a3)2 = 25 – a6

17. c) (a2 – 5) ⋅ (a2 + 5) = (a2)2 – 52 = a4 – 25

17. d)

(\frac{3}{4} x + y)

⋅

(\frac{3}{4} x - y) = {(\frac{3}{4} x)}^{2} - y^{2} = \frac{9}{16} x^{2} - y^{2}

18. a) (3x + 2) ⋅ (3x – 2) + (x + 2)2 =

= (3x)2 – 22 + x2 + 2 ⋅ x ⋅ 2 + 22 =

= 9x2 – 4 + x2 + 4x + 4 = 10x2 + 4x

18. b) (5x – 6)2 – (5x + 4)(5x – 4) =

= (5x)2 – 2 ⋅ 5x ⋅ 6 + 62 – [(5x)2 – 42] =

= 25x2 – 60x + 36 – 25x2 + 16 = –60x + 52

18. c) 32m2 + 16m – 2 ⋅ (4m + 1)2 =

= 32m2 + 16m – 2 ⋅ [(4m)2 + 2 ⋅ 4m ⋅ 1 + 12] =

= 32m2 + 16m – 2 ⋅ [16m2 + 8m + 1] =

= 32m2 + 16m – 32m2 – 16m – 2 = –2

19. b) O antecessor de x é x – 1 e o sucessor de x é x + 1, portanto a multiplicação será (x + 1) ⋅ (x – 1).

19. c) Ao adicionar 1 ao resultado, temos:

(x + 1) ⋅ (x – 1) + 1 = x2 – 1 ⋅ x + 1 ⋅ x – 1 ⋅ 1 + 1 =

= x2 – x + x – 1 + 1 = x2

A raiz quadrada será

\sqrt{x^{2}}

= x, de fato o número pensado.

Página setenta e um

20. a) (25 + 1) ⋅ (25 – 1) = 252 – 12 = 625 – 1 = 624

Portanto: (25 + 1) ⋅ (25 – 1) = 624

20. b) 21 ⋅ 19 = (20 + 1) ⋅ (20 – 1) = 202 – 12 = 400 – 1 = 399

Portanto: 202 – 12 = 399

20. c) Os dois números x e y são tais que x + y = 28 e x – y =

= 10. Procura–se x2 – y2. Aplicando o produto da soma pela diferença, temos:

x2 – y2 = ( x + y ) ⋅ (x – y)

Então: x2 – y2 = 28 ⋅ 10 = 280

Ou seja, a diferença entre os quadrados é 280. Também podemos testar hipóteses para os valores de x e y.

x	y	x + y	x − y	Conclusão
5	5	5 + 5 = 10	5 − 5 = 0
18	10	18 + 10 = 28	18 − 10 = 8	só x + y = 28
20	10	20 + 10 = 30	20 − 10 = 10	só x − y = 10
19	9	19 + 9 = 28	19 − 9 = 10	x − y = 10 e x + y = 28 ✓

Então, x + y = 28 e x – y = 10 é verdadeiro para x = 19 e y = 9; portanto, esses são os números procurados.

20. d) Os dois números são x + y = 30 e x – y = 20; procura-se x2 – y2 = (x + y)(x – y) = 30 ⋅ 20 = 600.

20. f) m + h = 4 e m2 – h2 = 80

m2 – h2 = (m + h)(m – h) ⇒ 80 = 4 ⋅ (m – h) ⇒

⇒ m – h =

\frac{80}{4}

= 20

22. a) (x + 1)3 = x3 + 3 ⋅ x2 ⋅ 1 + 3 ⋅ x ⋅ 12 + 13 = x3 + 3x2 + 3x + 1

22. b) (2a + 3)3 = (2a)3 + 3 ⋅ (2a)2 ⋅ 3 + 3 ⋅ 2a ⋅ 32 + 33 =

= 8a3 + 3 ⋅ 4a2 ⋅ 3 + 3 ⋅ 2a ⋅ 9 + 27 =

= 8a3 + 36a2 + 54a + 27

22. c) (1 – x)3 = 13 – 3 ⋅ 12 ⋅ x + 3 ⋅ 1 ⋅ x2 – x3 = 1 – 3x + 3x2 – x3

22. d) (3a – 2)3 = (3a)3 – 3 ⋅ (3a)2 ⋅ 2 + 3 ⋅ 3a ⋅ 22 – 23 =

= 27a3 – 3 ⋅ 9a2 ⋅ 2 + 3 ⋅ 3a ⋅ 4 – 8 =

= 27a3 – 54a2 + 36a – 8

23. (4a – b)3 = (4a)3 – 3 ⋅ (4a)2 ⋅ b + 3 ⋅ 4a ⋅ b2 – b3 =

= 64a3 – 48a2b + 12a2b – b3 4a + b) é: (4a + b)3 =

= (4a)3 + 3 ⋅ (4a)2 ⋅ b + 3 ⋅ 4a ⋅ b2 + b3 =

= 16a3 + 48a2 + 12ab2 + b3

Portanto, 16a3 – 48a2b + 12a2b – b3 – [64a3 + 48a2 +

+ 12ab2 + b3 ] = 64a3 – 48a2b + 12a2b – b3 – 64a3 – 48a2 – 12ab2 – b3 = –96a2b – 2b3

24. a) (2a + 1)3 – 6a(2a + 1) = (2a)3 + 3 ⋅ (2a)2 ⋅ 1 + 3 ⋅ 2a ⋅ 12 +

+ 13 – 6a ⋅2a – 6a ⋅ 1 = 8a3 + 12a2 + 6a + 1 – 12a2 – 6a = 8a3 + 1

24. b) (a – b)3 – 3ab(b – a) = a3 – 3a2b + 3ab2 – b3 – 3ab2 + 3a2b = a3 – b3

24. c) (x – 2y)3 + 6xy(x – 2y) =

= x3 – 6x2y + 12xy2 – 8y3 + 6x2y – 12xy2 = x3 – 8y3

25. (a + 5)3 = a3 + 3 ⋅ a2 ⋅ 5 + 3 ⋅ a⋅ 52 + 53 =

= a3 + 15a2 + 75a + 125

26. a) Os fatores do 1º termo são: 3, 5, a, x e x; os fatores do 2º termo são: 2, 5, a, a e x; portanto, os fatores comuns são 5, a e x, ou 5ax.

26. b) Como 15ax2 : 5ax = 3x e 10a2 x: 5ax = 2a, então:

15ax2 – 10a2x = 5ax (3x – 2a)

27. a) O fator comum aos termos é a, então:

\{\begin{cases} a b : a = b \\ a c : a = c \end{cases}

⇒ ab + ac = a(b + c)

27. b) O fator comum aos termos é x, então:

\{\begin{cases} x^{2} : x = x \\ 3 x : x = 3 \end{cases}

⇒ x2 + 3x = x(x + 3)

27. c) O fator comum aos termos é a, então:

\{\begin{cases} a^{2} : a = a \\ a : a = 1 \end{cases}

⇒ a2 + a = a(a + 1)

27. d) O fator comum aos termos é 5, então:

\{\begin{cases} 5 x : 5 = x \\ 20 : 5 = 4 \end{cases}

⇒ 5x + 20 = 5(x + 4)

27. e) O fator comum aos termos é 7ab, então:

\{\begin{cases} 14 a^{2} b : 7 a b = 2 a \\ 21 a b^{3} : 7 a b = 3 b^{2} \end{cases}

⇒ 14a2b + 21ab3 = 7ab(2a + 3b2)

27. f) O fator comum aos termos é 5x², então:

\{\begin{cases} 15 x^{3} : 5 x^{2} = 3 x \\ 10 x^{2} : 5 x^{2} = 2 \end{cases}

⇒ 15x3 – 10x2 = 5x2(3x – 2)

28. a) Representando o número por x, do enunciado obtém-se a equação 2x2 = 3x, que equivale a 2x2 – 3x = 0. Observando que x é o fator comum aos termos do polinômio 2x2 – 3x, na fórma fatorada, temos:

\{\begin{cases} 2 x^{2} : x = 2 x \\ 3 x : x = 3 \end{cases}

⇒ 2x2 – 3x = x(2x – 3) = 0

Como o produto é nulo, então um dos seus fatores também deve ser. Assim, ou x = 0 ou 2x – 3 = 0. Resolvendo a segunda equação:

2x – 3 = 0 ⇒ 2x = 3 ⇒

\frac{2 x}{2} = \frac{3}{2}

⇒ x =

\frac{3}{2}

Portanto, o número procurado é 0 ou

\frac{3}{2}

Página setenta e dois

28. b) Nesse caso, se o número é y, então 3y2 = 2y, que equivale a 3y2 − 2y = 0, em cujo 1º membro y é fator comum aos termos.

\{\begin{cases} 3 y^{2} : y = 3 y \\ 2 y : y = 2 \end{cases}

⇒ 3y2 = 2 y ⇒ 3y2 – 2y = 0 ⇒

y(3y – 2) = 0 ⇒

\{\begin{cases} y = 0 ou \\ 3 y - 2 = 0 \end{cases}

Como y ≠ 0, temos y =

\frac{2}{3}

, pois:

3y – 2 = 0 ⇒ 3y = 2 ⇒

\frac{3 y}{3} = \frac{2}{3}

⇒

y = \frac{2}{3}

28. c) A medida da área da figura 1 é dada por:

2 ⋅ (x2) = 2x2

A medida da área da figura 2 é dada por:

5 ⋅ x = 5x

Como as medidas são iguais, logo:

2x2 = 5x ⇒ 2x2 – 5x = 0.

Fatorando o 1º membro, cujo fator comum é x:

\{\begin{cases} 2 x^{2} : x = 2 x \\ 5 x : x = 5 \end{cases}

⇒ 2x2 – 5x = 0 ⇒ x(2x – 5) = 0 ⇒

\{\begin{cases} x = 0 \\ 2 x - 5 = 0 \end{cases}

Como x é a medida do lado de um quadrado, então x ≠ 0; portanto, a única solução é x = 2,5.

2x – 5 = 0 ⇒ 2x = 5 ⇒ x =

\frac{5}{2}

= 2,5

29. a) O fator comum aos termos é a, então:

\{\begin{cases} a^{3} : a = a^{2} \\ a^{2} : a = a \\ a : a = 1 \end{cases}

⇒ a3 + a2 + a = a(a2 + a + 1)

29. b) O fator comum aos termos é 3, então:

\{\begin{cases} 6 x^{2} : 3 = 2 x^{2} \\ 9 x : 3 = 3 x \\ 12 : 3 = 4 \end{cases}

⇒ 6x2 – 9x + 12 = 3(2x2 – 3x + 4)

29. c) O fator comum aos termos é 3x, então:

\{\begin{cases} 3 x : 3 x = 1 \\ 6 x^{2} : 3 x = 2 x \\ 9 x^{3} : 3 x = 3 x^{2} \end{cases}

⇒ 3x + 6x2 + 9x3 = 3x(1 + 2x + 3x2)

29. d) O fator comum aos termos é 5x, então:

\{\begin{cases} 10 x^{3} : 5 x = 2 x^{2} \\ 15 x^{2} : 5 x = 3 x \\ 20 x : 5 x = 4 \end{cases}

⇒ 10x3– 15x2+ 20x = 5x(2x2 – 3x + 4)

29. e) O fator comum aos termos é

\frac{a}{2}

, então:

\{\begin{cases} \frac{a}{2} : \frac{a}{2} = \frac{a}{2} \cdot \frac{2}{a} = 1 \\ \frac{a^{2}}{4} : \frac{a}{2} = \frac{a^{2}}{4} \cdot \frac{2}{a} = \frac{a}{2} \\ \frac{a^{3}}{6} : \frac{a}{2} = \frac{a^{3}}{6} \cdot \frac{2}{a} = \frac{a^{2}}{3} \end{cases}

⇒

\frac{a}{2} + \frac{a^{2}}{4} – \frac{a^{3}}{6} = \frac{a}{2} (1 + \frac{a}{2} – \frac{a^{2}}{3})

29. f) O fator comum aos termos é

\frac{m}{3}

, então:

\{\begin{cases} \frac{m}{12} : \frac{m}{3} = \frac{m}{12} \cdot \frac{3}{m} = \frac{3}{12} = \frac{1}{4} \\ \frac{5 m^{2}}{6} : \frac{m}{3} = \frac{5 m^{2}}{6} \cdot \frac{3}{m} = \frac{5 m}{2} \Rightarrow \\ \frac{2 m^{3}}{9} : \frac{m}{3} = \frac{2 m^{3}}{9} . \frac{3}{m} = \frac{2 m^{2}}{3} \end{cases}

⇒

\frac{m}{12} - \frac{5 m^{2}}{6} + \frac{2 m^{3}}{9} = \frac{m}{3} (\frac{1}{4} - \frac{5 m}{2} + \frac{2 m^{2}}{3})

30.

\{\begin{cases} x (y - 2) : (y - 2) = x \\ 7(y - 2) : (y - 2) = 7 \\ a (y - 2) : (y - 2) = a \end{cases}

⇒

⇒ x(y – 2) – 7(y – 2) + a(y – 2) = (y – 2)(x – 7 + a)

31. 2xy é o fator comum dos dois termos, então:

\{\begin{cases} 6 x^{2} y : 2 x y + 3 x \\ - 2 x y^{2} : 2 x y = - y \end{cases}

⇒

⇒ 6x2y – 2xy2 = 2xy ⋅ (3x – y) = 12 ⋅ 3 = 36

33. a) 5x – xy + 15 – 3y = x(5 – y) + 3(5 – y) = (5 – y)(x + 3)

33. b) 2ax + 3a + 4bx + 6b = a(2x + 3) + 2b(2x + 3) = (2x + 3)(a + 2b)

33. c) ax – 2a + x – 2 = a(x – 2) +1(x – 2) = (x – 2)(a +1)

33. d) x3 + 3x2 + 2x + 6 = x2 (x + 3) + 2(x + 3) = (x + 3)(x2 + 2)

33. e) 10x² – 15xy – 4x + 6 y = 5x(2x – 3y) – 2(2x – 3y) = (2x – 3y)(5x – 2)

33. f) a3 – a2 + a – 1 = a2 (a – 1) + 1(a – 1) = (a – 1)(a2 + 1)

34. a) As medidas das áreas dos quatro retângulos que compõem a figura são:

3 ⋅ x = 3x (superior esquerdo)

3 ⋅ 2 = 6 (inferior esquerdo)

x ⋅ y = xy (superior direito)

2 ⋅ y = 2y (inferior direito)

Portanto, a medida da área da figura toda é expressa por:

3x + 6 + xy + 2y

34. b) Outra maneira de calcular a medida da área é por meio da multiplicação (x + 2) ⋅ (3 + y).

Página setenta e três

34. c) 3x + 6 + xy + 2y = 3(x + 2) + y(x + 2) = (x + 2)(3 + y)

35. a) mx – my + nx – ny = m(x – y) + n(x – y) = (x – y)(m + n) = 2 ⋅ 10 = 20

37. a) x2 – 4 = x2 – 22 = (x + 2)(x – 2)

37. b) a2 – 36 = a2 – 62 = (a + 6)(a – 6)

37. c) y2 – 1 = y2 – 12 = (y + 1)(y – 1)

37. d) 25x2 – 4 = (5x)2 – 22 = (5x + 2)(5x – 2)

37. e)

\frac{1}{100} a^{2} - \frac{1}{49} = {(\frac{1}{10} a)}^{2} – {(\frac{1}{7})}^{2}

(\frac{1}{10} a + \frac{1}{7}) = (\frac{1}{10} a - \frac{1}{7})

37. f)

x^{2} y^{2} – \frac{1}{9} = {(x y)}^{2} – {(\frac{1}{3})}^{2}

(x y + \frac{1}{3}) (x y - \frac{1}{3})

38. a) Como o fator comum aos dois termos é 3x, temos:

\{\begin{cases} 15 x y : 3 x = 5 y \\ 9 x : 3 x = 3 \end{cases}

⇒ 15xy + 9x = 3x(5y + 3)

38. b) 15xy + 9x + 10y + 6 = 3x (5y + 3) + 2(5y + 3) =

= (5y + 3)(3x + 2)

38. c) 100x2 – 1 = (10x)2 – 12 = (10x + 1)(10x – 1)

38. d) Como o fator comum aos dois termos é 12ab, temos:

\{\begin{cases} 36 a^{2} b : 12 a b = 3 a \\ - 48 a b^{2} : 12 a b = - 4 b \end{cases}

⇒ 36a2b – 48ab2 = 12ab(3a – 4b)

38. e) (x – 1)2 – 1 = (x – 1)(x – 1) – 1 =

= x2 – 1x – 1x + (–1)2 – 1 = x2 – 2x = x(x – 2)

38. f) (x + 5)2 – 9 = (x + 5)2 – 32 = (x + 5 + 3)(x + 5 – 3) =

= (x + 8)(x + 2)

38. g) 25 – (x + y)2 = 52 – (x + y)2 = [5 + (x + y)] · [5 – (x + y)] = (5 + x + y)(5 – x – y)

38. h) 9a2 – (a – 5)2 = (3a)2 – (a– 5)2 = [3a + (a – 5)] · [3a – (a – 5)] = (3a + a – 5)(3a – a + 5) = (4a – 5)(2a + 5)

39. a) a3 – a = a(a2 – 1) = a(a + 1)(a – 1)

39. b) 12x3 – 3xy2 = 3x(4x2 – y2) = 3x(2x + y)(2x – y)

39. c) a2b – b3 = b(a2 – b2) = b(a + b)(a – b)

39. d) a3 – 9a = a(a2 – 9) = a(a + 3)(a – 3)

40. a) x2 – 25 = 0 ⇒ (x + 5)(x – 5) = 0 ⇒

\Rightarrow \{\begin{cases} x + 5 = 0 \Rightarrow x = - 5 \\ x – 5 = 0 \Rightarrow x = 5 \end{cases}

40. b) x2– 64 = 0 ⇒ (x + 8)(x – 8) = 0

\Rightarrow \{\begin{cases} x + 8 = 0 \Rightarrow x = - 8 \\ x - 5 = 0 \Rightarrow x = 8 \end{cases}

40. c) 81x2 – 49 = 0 ⇒ (9x + 7)(9x – 7) = 0

⇒

\{\begin{cases} 9 x + 7 = 0 \Rightarrow 9 x = - 7 \Rightarrow x = - \frac{7}{9} \\ 9 x - 7 = 0 \Rightarrow 9 x = 7 \Rightarrow x = \frac{7}{9} \end{cases}

40. d) 25x2 – 36 = 0 ⇒ (5x + 6)(5x – 6) = 0

⇒

\{\begin{cases} 5 x + 6 = 0 \Rightarrow 5 x = - 6 \Rightarrow x = - \frac{6}{5} \\ 5 x - 6 = 0 \Rightarrow 5 x = 6 \Rightarrow x = \frac{6}{5} \end{cases}

40. e) 9x2 – 1 = 0 ⇒ (3x + 1)(3x – 1) = 0

⇒

\{\begin{cases} 3 x + 1 = 0 \Rightarrow 3 x = - 1 \Rightarrow x = - \frac{1}{3} \\ 3 x - 1 = 0 \Rightarrow 3 x = 1 \Rightarrow x = \frac{1}{3} \end{cases}

40. f)

x^{2} – \frac{9}{16} = 0

⇒

(x + \frac{3}{4}) (x – \frac{3}{4}) = 0

⇒

\{\begin{cases} x + \frac{3}{4} = 0 \Rightarrow x = - \frac{3}{4} \\ x - \frac{3}{4} = 0 \Rightarrow x = \frac{3}{4} \end{cases}

41. a) Como a área do quadrado maior mede m², pois m ⋅ m = m2, e a área do quadrado menor mede n², pois n ⋅ n = n2, tem-se que a área da parte pintada mede m2 – n2.

41. b) Como a região um é um retângulo de base m e altura (m – n), a medida de sua área pode ser expressa por m(m – n).

41. c) Como a região dois é um retângulo de base (m – n) e altura n, a medida de sua área pode ser expressa por (m – n)n.

41. d) A expressão que dá a soma das medidas das áreas das regiões um e dois é:

m(m − n) + (m − n)n

41. e) Como m – n é o fator comum:

\{\begin{cases} m (m - n) : (m - n) = m \\ n (m - n) : (m - n) = n \end{cases}

⇒

⇒ m(m – n) + n(m – n) = (m + n)(m – n)

43. a) Sim, pois o dobro do produto das raízes dos termos extremos é 2 ⋅ x ⋅ 2, que coincide com o termo central 4x.

43. b) Não é, pois o dobro do produto das raízes dos termos extremos é 2 ⋅ y ⋅ 10 = 20y, diferente do termo central 5y. Uma possível modificação para formar um quadrado perfeito é y2 + 20y +100.

43. c) Sim, pois o dobro do produto das raízes dos termos extremos é 2 ⋅ a ⋅ 5, que coincide com o termo central 10a.

43. d) Não é, pois, o dobro do produto das raízes dos termos extremos é 2 ⋅ 4a ⋅ 3b = 24ab, diferente do termo central 36ab. Uma possível modificação para formar um quadrado perfeito é 16a2 + 24ab + 9b2.

Página setenta e quatro

43. e) Sim, reescrevendo a expressão como m2 + 2mm + n2, verifica-se que o dobro do produto das raízes dos termos extremos é 2 ⋅ m ⋅ n, que coincide com o termo central 2mn.

43. f) Sim, pois o dobro do produto das raízes dos termos extremos é 2 ⋅ x ⋅

\frac{1}{2}

, que coincide com o oposto do termo central –x.

44. a) x2 + 6x + 9 = x2 + 2 ⋅ x ⋅ 3 + 32 = (x + 3)2

44. b) 4x2 + 12xy + 9y2 = (2x)2 + 2 ⋅ 2x ⋅ 3y + (3y)2 = (2x + 3y)2

44. c) x4 – 4x2 + 4 = (x2)2 – 2 ⋅ x2 ⋅ 2 + 22 = (x2 – 2)2

44. d) x2y2 – 10xy + 25 = (xy)2 – 2⋅ xy ⋅ 5 + 52 = (xy – 5)2

44. e)

\frac{4}{9} x^{2} + \frac{4}{21} x + \frac{1}{49}

{(\frac{2}{3} x)}^{2} + 2 \cdot \frac{2}{3} x \cdot \frac{1}{7} + {(\frac{1}{7})}^{2}

= =

{(\frac{2}{3} x + \frac{1}{7})}^{2}

44. f) 0,25a2 – 0,30a + 0,09 = (0,5a)2 – 2 ⋅ 0,5a ⋅ 0,3 + 0,32 =

= (0,5a – 0,3)2

45. Como 81 + 90a + 25a2 = 92 – 2 ⋅ 9 ⋅ 5a + (5a)2 = (9 + 5a), obtemos o binômio 9 + 5a.

46. A = y2 + 14ya + 49a2 = y2 + 2 ⋅ y ⋅ 7a + (7a)2 = (y + 7a)2

A medida A da área é o quadrado da medida do lado, então o lado mede y + 7a.

49. a) De (a + b)2 = 64, tem-se:

a2 + 2ab + b2 = 64 ⇒ a2 + b2 + 2ab = 64

Substituindo ab por 12 nessa equação:

a2 + b2 + 2 ⋅ 12 = 64 ⇒ a2 + b2 = 64 – 24 ⇒ a2 + b2 = 40

49. b) De (a + b)2 = 81 tem-se:

a2 + 2ab + b2 = 81 ⇒ a2 + b2 + 2ab = 81

Substituindo a2 + b2 por 53 nessa equação:

53 + 2ab = 81 ⇒ 2ab = 28 ⇒ ab =

\frac{28}{2}

⇒ ab = 14

49. c) (a = b)2 = a2 + b3 = 2ab

Substituindo a2 + b2 por 13 e ab por 12, tem-se:

13 + 2 ⋅ 12 = 13 + 24 = 37

52. a) a3 – 1 = a3 – 13 = (a – 1)(a2 + a ⋅ 1 + 12 ) =

= (a – 1)(a2 + a + 1)

52. b) 8a3 + 1 = (2a)3 + 13 = (2a + 1)[(2a)2 – 2a ⋅ 1 + 12] =

= (2a + 1)(4a2 – 2a + 1)

52. c) x3 – 27 = x3 – 33 = (x – 3)(x2 + x ⋅ 3 + 32) =

= (x – 3)(x2 + 3x + 9)

52. d) x3 + 64 = x3 + 43 = (x + 4)(x2 – x ⋅ 4 + 42) =

= (x + 4)(x2 – 4x +16)

52. e) 1 – x3 = 13 – x3 = (1 – x)(12 + 1 ⋅ x + x2 ) =

= (1 – x)(1 + x + x2)

52. f) 27a3 + 8y3 = (3a)3 + (2y)3 =

= (3a + 2y)[(3a)2 – 3a ⋅ 2y + (2y)2] =

= (3a + 2y)(9a2 – 6ay + 4y2)

53. a) Falsa. a3 +b3 = (a + b)(a2 – ab +b2)

53. b) Verdadeira. (a + b)(a2 – ab + b2) = (a2 – ab + b2)(a + b)

53. c) Falsa. a3 – b3 = (a – b)(a2 + ab + b2)

53. d) Verdadeira. (a – b)(a2 + ab + b2) = (a2 + ab + b2)(a – b)

54. a)

\frac{x^{2} + 1}{x^{2} + 1} = 1

54. b)

\frac{4 x + 2}{– 4 x - 2} = \frac{4 x + 2}{- (4 x + 2)} = - \frac{4 x + 2}{4 x + 2} = - 1

55. a)

\frac{a^{2} - a}{a} = \frac{a (a - 1)}{a} = a - 1

55. b)

\frac{x^{2} - 16}{x + 4} = \frac{(x + 4) (x - 4)}{x + 4} = x - 4

55. c)

\frac{3 x^{2} + 6 x + 3}{x + 1} = \frac{3 (x^{2} + 2 x + 1)}{x + 1}

\frac{3 {(x + 1)}^{2}}{x + 1}

= =

\frac{3 (x + 1) (x + 1)}{(x + 1)}

= 3(x + 1) = 3x + 3

55. d)

\frac{5 a^{2} - 20}{a - 2} = \frac{5 (a^{2} - 4)}{a - 2}

\frac{5 (a + 2) (a – 2)}{(a – 2)}

= = 5(a + 2) = 5a + 10

56.

\frac{10 a + 5 b}{2 a + b} = \frac{5 (2 a + b)}{(2 a + b)} = \frac{5}{1} = 5

57. a)

\frac{15 a^{5} b}{4 a^{2} b^{3}} = \frac{15 a^{5 – 2}}{4 b^{3 – 1}} = \frac{15 a^{3}}{4 b^{2}}

57. b)

\frac{15 {(– 2)}^{3}}{4 {(2)}^{2}} = \frac{15 · (– 8)}{4 \cdot 4} = \frac{– 15}{2}

57. c) Como não existe divisão por zero, para existir é necessário verificar: 4b2 ≠ 0 ⇒ b2 ≠ 0 ⇒ b ≠ 0. Portanto, com b = 0, a fração não representa número real.

58. a)

\frac{10 x y}{10 x^{2} + 20 x y} = \frac{10 x y}{10 x (x + 2 y)} = \frac{y}{x + 2 y}

(cartão azul)

58. b)

\frac{x^{2} - 2 x y + y^{2}}{3 x - 3 y} = \frac{{(x - y)}^{2}}{3 (x - y)} = \frac{x - y}{3}

(cartão verde)

58. c)

\frac{x - 2}{x^{2} - 4} = \frac{(x - 2)}{(x + 2) (x - 2)} = \frac{1}{x + 2}

(cartão vermelho)

58. d)

\frac{x^{2} - 10 x + 25}{2 x - 10} = \frac{{(x - 5)}^{2}}{2 (x - 5)} = \frac{x - 5}{2}

(cartão amarelo)

59. a) É 3x – 2, pois:

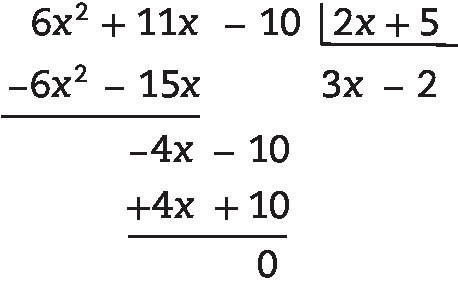
Algoritmo da divisão

Na chave: 2 x mais 5

Fora da chave: 6 x ao quadrado mais 11 x menos 10, abaixo menos 6 x ao quadrado menos 15 x, abaixo menos 4 x menos 10, abaixo mais 4 x mais 10, abaixo zero

Quociente: 3 x menos 2

59. b) x = 0 ⇒ 3x – 2 = 3 ⋅ 0 – 2 = –2

59. c) x =

\frac{2}{3}

⇒ 3x – 2 = 3 ⋅

\frac{2}{3}

– 2 = 2 – 2 = 0

Página setenta e cinco

59. d) Pode assumir qualquer valor racional desde que 2x + 5 ≠ 0 ⇒ 2x ≠ –5 ⇒ x ≠ –

\frac{5}{2}

60. A simplificação correta seria:

\frac{x^{2} + x}{x} = \frac{x (x + 1)}{x}

= x + 1

61. a) x ≠ 0

61. b) x – 2 ≠ 0 ⇒ x ≠ 2

61. c) x ≠ 0

61. d) x + 1 ≠ 0 ⇒ x ≠ –1

62. a) Simplificando os numeradores por 4, temos:

\frac{3}{x} = \frac{1}{x - 2}

Considerando x ≠ 0 e x ≠ 2, multiplicamos os termos da equação por x(x – 2), obtendo:

(\frac{3}{x}) \cdot x (x - 2) = (\frac{1}{x - 2})

⋅ x(x – 2) ⇒ 3(x – 2) = x ⇒

⇒ 3x – 6 = x ⇒ 3x – x = 6 ⇒ 2x = 6 ⇒

⇒ x =

\frac{6}{2}

⇒ x = 3

Portanto, 3 é a solução da equação.

62. b) Simplificando os numeradores por 4, temos:

\frac{– 1}{x} = \frac{1}{x - 2}

Considerando x ≠ 0 e x ≠ 2, multiplicamos os termos da equação por x(x – 2), obtendo:

\frac{- 1}{x} \cdot x (x - 2) = \frac{1}{x - 2}

⋅ x(x – 2) ⇒ x = –(x – 2) ⇒ x = –x + 2 ⇒ x + x = 2 ⇒ 2x = 2 ⇒

⇒ x =

\frac{2}{2}

⇒ x = 1

Portanto, 1 é a solução da equação.

63. a) Sendo x o número de famílias inicialmente previsto, então

40 = \frac{720}{x – 2}

. Considerando x ≠ 2, multiplicamos os termos da equação por x (x – 2), obtendo:

40 \cdot (x - 2) = (\frac{720}{x - 2})

⋅ (x – 2) ⇒ 40(x – 2) = 720 ⇒ 40x – 80 = 720 ⇒ 40x = 720 + 80 ⇒

⇒ 40x = 800 ⇒ x =

\frac{800}{40}

⇒ x = 20

Portanto, o número inicial era 20 famílias.

63. b) Compareceram 18 famílias.

x – 2 = 20 – 2 = 18

63. c) Cada família teria recebido 36 quilogramas, pois 720 : 20 = 36.

64. a) Sendo x o número pensado, o enunciado sugere a equação

\frac{x + 4}{x - 2} = \frac{x - 6}{x - 9}

. Considerando x ≠ 2 e x ≠ 9, multiplicamos os termos da equação por (x – 2)(x – 9), obtendo:

(\frac{x + 4}{x - 2})

⋅ (x – 2)(x – 9) ⋅

(\frac{x - 6}{x - 9})

⋅ (x – 2)(x – 9) ⇒

⇒ (x + 4) ⋅ (x – 9) = (x – 6)(x – 2) ⇒

⇒ x2 + 4x – 9x – 36 = x2 –6x – 2x + 12 ⇒ –5x – 36 = –8x + 12 ⇒ 8x – 5x = 36 + 12 ⇒

⇒ 3x = 48 ⇒ x =

\frac{48}{3}

⇒ x = 16

Lúcia pensou no número 16.

64. b) Substituindo x = 16 em um dos membros da equação do item anterior, temos:

\frac{x + 4}{x - 2}

\frac{16 + 4}{16 - 2} = \frac{20}{14} = \frac{10}{7}

65. a) Sendo x o número de lotes da chácara menor e y a medida de área de cada lote, temos:

\{\begin{cases} y = \frac{2 880}{x} \\ y = \frac{5 040}{2 x – 2} \end{cases}

Comparando as expressões de y, temos:

\frac{2 880}{x} = \frac{5 040}{2 x - 2}

Simplificando os numeradores por mdc(.2880, .5040) = 144, temos:

20 = \frac{35}{2}

Considerando x ≠ 0 e x ≠ 1, multiplicamos os termos da equação por x(2x – 2), obtendo:

(\frac{20}{x})

⋅ x (2x – 2) =

(\frac{35}{2 x - 2})

⋅ x (2x – 2) ⇒

⇒ 20 (2x – 2) = 35x ⇒ 40x – 40 = 35x ⇒

⇒ 40x – 35x = 40 ⇒ 5x = 40 ⇒ x =

\frac{40}{5}

= 8

Portanto a chácara menor ficou dividida em 8 lotes.

65. b) A chácara maior ficou dividida em 14 lotes.

2 ⋅ 8 – 2 = 16 – 2 = 14

65. c) 360 métro quadrado, pois .2880 : 8 = 360.

66. Resposta pessoal. Um exemplo de sequência não recursiva são esses números quaisquer que foram escolhidos sem critério específico: 3, 56, 546, 65, 60, 960, 18. Uma sequência recursiva são os primeiros múltiplos de 3: 0, 3, 6, 9, 12, 15, 18.

67. x = 1, y = 2, 9x + y = 9 ⋅ 1 + 2 = 11

x = 2, y = 3, 9x + y = 9 ⋅ 2 + 3 = 21

x = 3, y = 4, 9x + y = 9 ⋅ 3 + 4 = 31

x = 4, y = 5, 9x + y = 9 ⋅ 4 + 5 = 41

x = 5, y = 6, 9x + y = 9 ⋅ 5 + 6 = 51

x = 6, y = 7, 9x + y = 9 ⋅ 6 + 7 = 61

x = 7, y = 8, 9x + y = 9 ⋅ 7 + 8 = 71

x = 8, y = 9, 9x + y = 9 ⋅ 8 + 9 = 81

x = 9, y = 10, 9x + y = 9 ⋅ 9 + 10 = 91

Sim, é uma sequência recursiva.

69. a) Considerando n um número natural, temos:

(n + 1)2 – n2 = [(n + 1) + n] ⋅ [(n + 1) – n] = (n + 1) + n

Note que (n + 1) + n é um número ímpar.

69. b) (n + 1)2 – n2 = n2 + 2n + 1 – n2 = 2n + 1

Note que 2n + 1 é um número ímpar.

Página setenta e seis

Pense mais um poucoreticências

Página 130

a) 12 = (10 + 2)2 = 102 + 2 ⋅ 10 ⋅ 2 + 22 = 100 + 40 + 4 = 144

b) 24 = (20 + 4)2 = 202 + 2 ⋅ 20 ⋅ 4 + 42 = 400 + 160 + 16 = 576

c) 35 = (30 + 5)2 = 302 + 2 ⋅ 30 ⋅ 5 + 52 = 900 + 300 + 25 = .1225

d) 52 = (50 + 2)2 = 502 + 2 ⋅ 50 ⋅ 2 + 22 = .2500 + 200 + 4 = .2704

Página 133

a) 29 = (30 – 1)2 = 302 – 2 ⋅ 30 ⋅ 1 + 12 = 900 – 60 + 1 = 841

b) 38 = (40 – 2)2 = 402 – 2 ⋅ 40 ⋅ 2 + 22 = .1600 – 160 + 4 = .1444

c) 99 = (100 – 1)2 = 1002 – 2 ⋅ 100 ⋅ 1 + 12 = .10000 – 200 + 1 = .9801

d) 57 = (60 – 3)2 = 602 – 2 ⋅ 60 ⋅ 3 + 32 = .3600 – 360 + 9 = .3249

Página 152

Sendo x o número de filhos de José, conclui-se que o número de filhos de Luís é (x + 1), pelas informações do enunciado. Pelo diálogo entre os irmãos,

\frac{960}{x + 1} = \frac{720}{x}

. Simplificando os numeradores por ême dê cê(720, 960) = 240, então

\frac{4}{x + 1} = \frac{3}{x}

. Considerando x ≠ 0 e x ≠ –1, multiplicamos os termos da equação por x (x +1), obtendo:

(\frac{4}{x + 1})

⋅ x ( x + 1) =

(\frac{3}{x})

⋅ x (x + 1) ⇒ 4x = 3(x + 1) ⇒

⇒ 4x = 3x + 3 ⇒ 4x – 3x = 3 ⇒ x = 3

Então, José tem 3 filhos, e cada um ficou com um terreno de medida 240 métros quadrados, pois 720 : 3 = 240.

Para saber mais

Páginas 138 e 139

2. 0,21 ⋅ 7 + 0,21 ⋅ 3 = 0,21 ⋅ (7 + 3) = 0, 21 ⋅ 10 = 2,1

3. a) 15 ⋅ 18 + 15 ⋅ 2 = 15 ⋅ (18 + 2) = 15 ⋅ 20 = 300

3. b) 5,4 ⋅ 13 – 5,4 ⋅ 3 = 5,4 ⋅ (13 – 3) = 5,4 ⋅10 = 54

3. c)

12 \cdot \frac{7}{13} + 12 \cdot \frac{6}{13} = 12 \cdot (\frac{7}{13} + \frac{6}{13})

12 \cdot \frac{13}{13} = 12

3. d) 4,5 ⋅ 8 + 4,5 ⋅ 7 – 4,5 ⋅ 5 = 4,5 ⋅ (8 + 7 – 5) = 4,5 ⋅ 10 = 45

3. e) 3,8 ⋅ 4,2 + 3,8 ⋅ 4,6 + 3,8 ⋅ 1,2 = 3,8 ⋅ (4,2 + 4,6 + 1,2) = 3,8 ⋅ 10 = 38

3. f)

10 \cdot \frac{17}{11} - 10 \cdot \frac{6}{11} = 10 (\frac{17}{11} - \frac{6}{11})

10 \cdot \frac{11}{11} = 10

Trabalhando a informação

1. Considerando as informações do enunciado sobre os anos de nascimento de cada geração, é possível calcular a idade das pessoas de cada geração conforme o ano em que se realiza a atividade.

3. A medida da maior barra (que representa 97) deve ser menor do que a medida de comprimento de uma folha A4 (297 milímetros = 29,7 centímetros) para que o gráfico fique adequado. A escala escolhida precisa ser tal que a menor barra fique visível.

Exercícios complementares

1. a) (3a– 2b)2 = (3a)2 – 2 ⋅ 3a ⋅ 2b + (2b)2 = 9a2 – 12ab + 4b2

1. b) (5a + 7)(5a – 7) = (5a)2 – 72 = 25a2 – 49

1. c) (3x2 + y3)2 = (3x2)2 + 2 ⋅ 3x2 ⋅ y3 + (y3)2 = 9x4 + 6x2y3 + y6

1. d) (–5 – 2y)2 = (–5)2 + 2 ⋅ (–5) ⋅ (–2y) + (–2y)2 = 25 + 20y + 4y2

2. (5a + 9b)(5a – 9b) = (5a)2 – (9b)2 = 25a2 – 81b2

3. A2 – B + C = (x – 3)2 –(x2 + 3) + 9x = x2 – 6x + 9 – x2 – 3 + 9x = 3x + 6 = 3(x + 2)

Alternativa c.

4. Fazendo a operação inversa para descobrir:

(x + 10)2 – (x2 + 5x + 70) = x2 + 20x + 100 – x2 – 5x – 70 = 15x + 30

5. Como 9x2 + 24x + 16 = (3x + 4)2, tem-se a = 3 e b = 4. Portanto: a + b = 3 + 4 = 7

6. a) Como (a2 + b2) – (a – b)2 = a2 + b2 – a2 + 2ab – b2 = 2ab, deve-se subtrair a expressão 2ab.

6. b) (a + b)2 – (a2 + 2ab) = a2 + 2ab + b2 – a2 – 2ab = b2

Portanto, deve-se adicionar b².

6. c) (a + b)2 = a2 + 2ab + b2 = (a2 + b2) + 2 ⋅ (ab) = 34 + 2 ⋅ 15 = 34 + 30 = 64

6. d) Para (a + b)2 = 196, temos:

a2 + 2ab + b2 = 196 ⇒ a2 + b2 + 2ab = 196

Substituindo (a2 + b2) por 100 nessa equação, temos:

100 + 2ab = 196 ⇒ 2ab = 196 –100 ⇒ 2ab = 96 ⇒ ab =

\frac{96}{2}

⇒ ab = 48

7. 3752 – 3742 = (375 + 374)(375 – 374) = 749 ⋅ 1 = 749

A soma dos algarismos do resultado é 20 (7 + 4 + 9 = 20). Alternativa c.

8. a) 3x2 – 75 = 3(x2 – 25) = 3(x + 5)(x – 5)

8. b) a3 – ab2 = a(a2 – b2) = a(a + b)(a – b)

8. c) x4 – 16 = (x2 + 4)(x2 – 4) = (x2 + 4)(x + 2)(x – 2)

8. d) a2 – x2 + a + x = (a + x)(a – x) + 1 ⋅ (a + x) = (a + x) ⋅ [(a – x) + 1] = (a + x) ⋅ (a – x + 1)

8. e) x2 – y2 + 2x + 2y = (x + y)(x – y) + 2 ⋅ (x + y) = (x + y) ⋅ [(x – y) + 2] = (x + y) ⋅ (x – y + 2)

8. f) 2x2 – 12x + 18 = 2(x2 – 6x + 9) = 2(x – 3)2

9. a) (a + b)2 = 182 = 324

9. b) (a – b)2 = 22 = 4

9. c) a2 – b2 = (a + b)(a – b) = 18 ⋅ 2 = 36

10. a) (x + y)2 = 142 = 196

10. b) Para x2 + 2xy + y2 = (x + y)2, temos:

(x2 + y2 ) + 2xy = 142

Então, substituindo (x2 + y2) por 116, temos:

116 + 2xy = 142 ⇒ 2xy = 196 – 116 ⇒ 2xy = 80 ⇒

⇒ xy =

\frac{80}{2}

⇒ xy = 40

10. c) Como (x – y)2 = x2 – 2xy + y2 = (x2 + y2)– 2(xy), substituindo os resultados dos itens anteriores, tem-se: (x – y)2 = 116 – 2 ⋅ 40 = 116 – 80 = 36