Página setenta e sete

Parte 6

11. a) x2 + 12x = 0 ⇒ x (x + 12) = 0 ⇒

⇒

\{\begin{cases} x = 0 \\ x + 12 = 0 \Rightarrow x = - 12 \end{cases}

As soluções da equação são 0 e –12.

11. b) 6x2 – 5x = 0 ⇒ x (6x – 5) = 0 ⇒

⇒

\{\begin{cases} x = 0 \\ 6 x - 5 = 0 \Rightarrow 6 x = 5 \Rightarrow x = \frac{5}{6} \end{cases}

As soluções da equação são 0 e

\frac{5}{6}

11. c) 4x2 – 14x + 1 = 0 ⇒ (2x – 1)2 = 0 ⇒ 2x – 1 = 0 ⇒

⇒ 2x = 1 ⇒ x =

\frac{1}{2}

11. d) 9x2 + 6x + 1 = 0 ⇒ (3x + 1)2 = 0 ⇒ 3x + 1 = 0 ⇒

⇒ 3x = –1 ⇒ x = –

\frac{1}{3}

13. (3a – 2b)2 = (3a)2 – 2 ⋅ 3a ⋅ 2b + (2b)2 = 9a2 – 12ab + 4b2

A soma dos coeficientes da expressão desenvolvida é:

9 + (–12) + 4 = 1

Alternativa c.

14. 2(x2 + 3y)(x2 – 3y) = 2[(x2)2 – (3y)2] = 2(x4 – 9y2) = 2x4 – 18y2

Alternativa b.

15. (2x + 9y)2 – 36xy = (2x)2 + 2 ⋅ 2x ⋅ 9y + (9y)2 – 36xy = = 4x2 + 36xy + 81y2 – 36xy = 4x2 + 81y2

Então, com x = –1 e y = 1, tem-se:

4x2 + 81y2 = 4 ⋅ (–1)2 + 81 ⋅ (1)2 = 4 + 81 = 85

Alternativa c.

16. x2 + 6xy + y2 = x2 + 2xy + y2 + 4xy = (x + y)2 + 4xy

Então, com x + y = 8 e xy = 15, tem-se:

(x + y)2 + 4xy = 82 + 4 ⋅ 15 = 64 + 60 = 124

Alternativa d.

17. (x + 3)(x – 3) – x2 = x2 – 9 – x2 = –9

Alternativa b.

18. y4 – 4y2 + 4 = (y2 – 2)2

Alternativa a.

19. ab + 2b – 3a – 6 = b(a + 2) – 3(a + 2) = (a + 2) ⋅ (b – 3)

Alternativa b.

20. a)

\frac{x^{2} + x}{x^{2} - 1} = \frac{x (x + 1)}{(x - 1) (x + 1)} = \frac{x}{x - 1}

20. b)

\frac{b - a}{a^{2} - b^{2}} = \frac{– 1 (a - b)}{(a + b) (a - b)} = \frac{– 1}{a + b}

Verificando

1. (x + 4)2 – (2x – 3)2 =

x2 + 2 ⋅ x ⋅ 4 + 42 – [(2x)2 – 2 ⋅ 2x ⋅ 3 + 32] =

= x2 + 8x + 16 – 4x2 + 12x – 9 = –3x2 + 20x + 7

Alternativa b.

2. A medida da área do pedaço inicial é 122 centímetros2, pois é um quadrado de lado medindo 12 centímetros. A medida da área do pedaço retirado é x2 centímetro2, pois o lado mede x centímetro. Portanto, a medida da área que sobrou é 122 – x2 = 144 – x2.

Alternativa d.

3. (5x – 3)3 = (5x)3 – 3 ⋅ (5x)2 ⋅ 3 + 3 ⋅ 5x ⋅ 32 – 33 = = 125x3 – 225x2 + 135x – 27

Alternativa a.

4. O fator comum é 4xy, portanto:

24x2y + 32xy2 – 12xy = 4xy(6x + 8y – 3)

Alternativa d.

5. 3ab + 3ac – 5b – 5c = 3a(b + c) – 5(b + c) =

= (b + c) ⋅ (3a – 5) = (3a – 5)(b + c)

Alternativa b.

6. Como a área media x2 métros quadrados, o lado do terreno quadrado media x métro. Após a alteração, sua nova área pode ser fatorada como x2 – 4a2 = (x + 2a) ⋅ (x – 2a), então uma possibilidade é que um dos lados tenha aumentado 2a metros e o outro tenha diminuído 2a metros. Alternativa a.

7. 25x2 – 60xy + 36 y2 = (5x)2 – 2 ⋅ 5x ⋅ 6 y + (6 y )2 = (5x – 6 y )2

Alternativa b.

\frac{(3 a + 2 b) {(3 a - 2 b)}^{2}}{18 a^{2} - 8 b^{2}}

\frac{(3 a + 2 b) {(3 a - 2 b)}^{2}}{2 (9 a^{2} - 4 b^{2})}

= =

\frac{(3 a + 2 b) (3 a - 2 b) (3 a - 2 b)}{2 (3 a + 2 b) (3 a - 2 b)}

\frac{3 a - 2 b}{2}

Alternativa d.

9. Sendo n um número natural, a expressão 2n representa necessariamente um número par; logo, a expressão 2n + 1 representa necessariamente um número ímpar. Então, a sequência formada será a dos números ímpares. Alternativa d.

Capítulo 7 – Estudo dos triângulos

• Objetivos do capítulo e justificativas

• Conceituar cevianas de um triângulo: mediana, bissetriz e altura.

• Estudar e aplicar as cevianas de um triângulo.

• Conceituar e estudar os casos de congruência de triângulos.

• Aplicar congruência de triângulos em demonstrações de propriedades geométricas.

• Analisar a construção de um hexágono regular com descrição do procedimento por escrito.

• Construir um dodecaedro regular a partir da medida do ângulo central associado a ele.

• Identificar simetria em figuras obtidas por composição de transformações geométricas.

Os objetivos desse capítulo, que aborda os elementos do triângulo e dos casos de congruência de triângulos, são importantes para desenvolver as competências gerais 2, 4 e 7 e a competências específicas 2 e 5, pois são apresentadas atividades em que os estudantes devem exercitar a curiosidade intelectual, o espírito de investigação, aplicar métodos lógico-dedutivos para demonstrar propriedades e argumentar sobre a validade deles.

Do mesmo modo, essas competências são mobilizadas e desenvolvidas nas atividades de construção geométrica propostas, pois os estudantes são incentivados a justificar os procedimentos envolvidos nas construções geométricas, além de utilizar diferentes ferramentas para concretizá-las.

A competência geral 3 também é desenvolvida neste capítulo, pois eles têm a oportunidade de fruir uma manifestação artística envolvendo triângulos, nas situações apresentadas na página de Abertura e na seção Para saber mais que explora o grafite.

Página setenta e oito

Diferentes atividades e contextos, neste capítulo, favorecem o desenvolvimento das competências gerais 9 e 10 e a competência específica 8, pois os estudantes deverão, em grupos, pesquisar, discutir e interagir com os colegas a fim de comunicar respostas ou comentar estratégias de resoluções.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah um quatro) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.

(ê éfe zero oito ême ah um seis) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.

(ê éfe zero oito ême ah um sete) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

(ê éfe zero oito ême ah um oito) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

Objetos de conhecimento da Unidade Temática Geometria são estudados com a ampliação do estudo dos triângulos, visando a preparar os estudantes para a continuidade desse estudo ao apresentar-lhes conteúdos que desenvolverão a habilidade (ê éfe zero oito ême ah um quatro) em capítulos seguintes e, ainda, no 9º ano (ê éfe zero nove ême ah um dois, ê éfe zero nove ême ah um três e ê éfe zero nove ême ah um quatro).

Os conteúdos e atividades propostos exploram, inicialmente, as cevianas (mediana, bissetriz e altura) de um triângulo e suas aplicações em situações diversas e favorecem o desenvolvimento da habilidade (ê éfe zero oito ême ah um sete). Em seguida, aborda-se a congruência de triângulos, conteúdo base para a demonstração de várias propriedades geométricas. Também neste capítulo, são descritos procedimentos por escrito da construção de um hexágono regular em uma seção Para saber mais e que favorece o desenvolvimento da habilidade (ê éfe zero oito ême ah um seis). Na seção Diversificando, exploram-se aspectos da habilidade (ê éfe zero oito ême ah um oito) ao abordar a identificação de simetria em figuras obtidas por composição de transformações geométricas.

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Abertura

a) Os triângulos são retângulos, pois apresentam um ângulo reto.

Exercícios propostos

1. a) Altura: é a ceviana que une perpendicularmente um dos vértices ao seu lado oposto (ou ao seu prolongamento.

1. b) Bissetriz: é a ceviana que divide um dos ângulos internos do triângulo em dois ângulos congruentes.

1. c) Mediana, bissetriz e a altura: segmento de reta que une um vértice ao ponto médio do lado oposto a ele, divide um dos ângulos interno do triângulo em dois ângulos congruentes e une perpendicularmente um dos vértices ao seu lado oposto, portanto, a ceviana coincide com as três definições.

1. d) Bissetriz: é a ceviana que divide um dos ângulos internos do triângulo em dois ângulos congruentes.

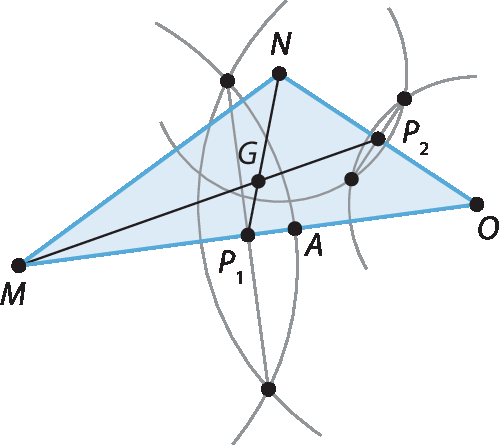
2. a) O ponto formado pela intersecção das medianas é chamado de baricentro. Para traçar a mediana, liga-se um vértice ao ponto médio do lado oposto; observe um esboço a seguir.

Ilustração. Triângulo M N O. No centro do triângulo, ponto G indica o baricentro.
Ponto médio P 1 de segmento M O e ponto médio P 2 de segmento N O.

Dois pontos fora do triângulo indicam a construção de um segmento perpendicular ao segmento M O passando por P 1.

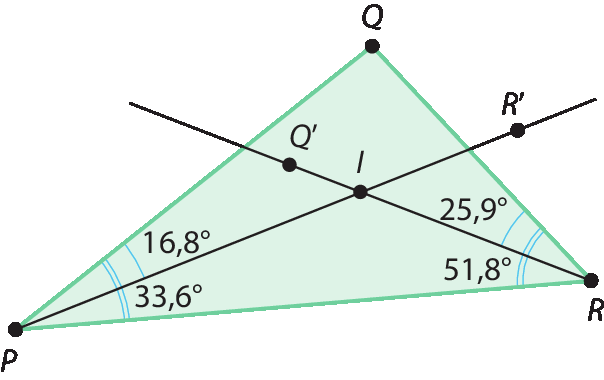
2. b) O ponto obtido pela intersecção das bissetrizes é chamado de incentro. Para traçar uma bissetriz, basta medir o ângulo com transferidor e dividir sua medida pela metade, então encontrar o ponto por onde passa a semirreta desejada, de fórma a traçar um ângulo com metade da medida do original.

Ilustração. Triângulo P Q R. No centro do triângulo, ponto I indica o incentro. Reta de r até lado P Q com o ponto Q; essa reta divide o ângulo R em 25,9 graus e 51,8 em R. Reta de P até lado QR com ponto R linha, divide o ângulo P em: 33,6 graus e 16,8 graus. As retas se cruzam no centro em I.

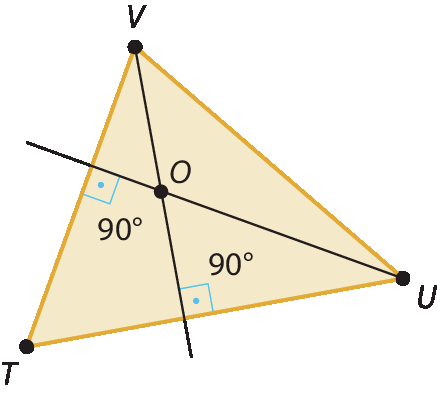
2. c) O ponto formado pela intersecção das alturas é chamado de ortocentro. Para traçar, com o esquadro, posicionar de modo que um lado dele passe por um vértice (por exemplo V) e o lado perpendicular da ferramenta acompanhe o lado oposto (nesse exemplo,

\bar{T U}

Ilustração. Triângulo T U V com diagonal de U até lado V T e reta de V até lado T U. As retas se cruzam no centro em O.

3. Para traçar a bissetriz de um ângulo

\hat{A}

em um triângulo á bê cê, deve-se fixar a ponta-seca do compasso no ponto a, traçar um arco de circunferência intersectando os lados

\bar{A B}

\bar{A C}

, respectivamente, no ponto M e no ponto N; determina-se o ponto médio do segmento

\bar{M N}

e obtém-se a reta suporte da bissetriz que passa por a e por esse ponto médio. O ponto a e o ponto de intersecção dessa reta suporte com o lado oposto a

\hat{A}

determinam a bissetriz desse vértice.

Página setenta e nove

Para traçar a mediatriz do lado

\bar{A B}

, deve-se determinar o ponto médio M desse lado e traçar um segmento partindo de M até o vértice C do triângulo.

4. Como o segmento

\bar{A M}

é a mediana, M é ponto médio do segmento

\bar{B C}

. Assim, os segmentos

\bar{B M}

\bar{M C}

têm a mesma medida. Portanto, a medida BC é 3,8 centímetros (1,9 + 1,9 = 3,8). Assim, obtemos o perímetro do triângulo á bê cê, que mede 9,5 centímetros (2,2 + 3,8 + 3,5 = 9,5).

Ilustração. Circunferência. No centro, ponto O. Dentro, triângulo R S T, tal que os pontos R S T pertencem à circunferência.
Duas diagonais retas e uma vertical formam ponto A no lado R T e B no lado R S. Há um ângulo de 90 graus nos pontos A, B e C com as retas.

6. A maior altura será a altura relativa ao menor lado. O triângulo escaleno acutângulo, á bê cê pode ser qualquer e a conclusão será a mesma.

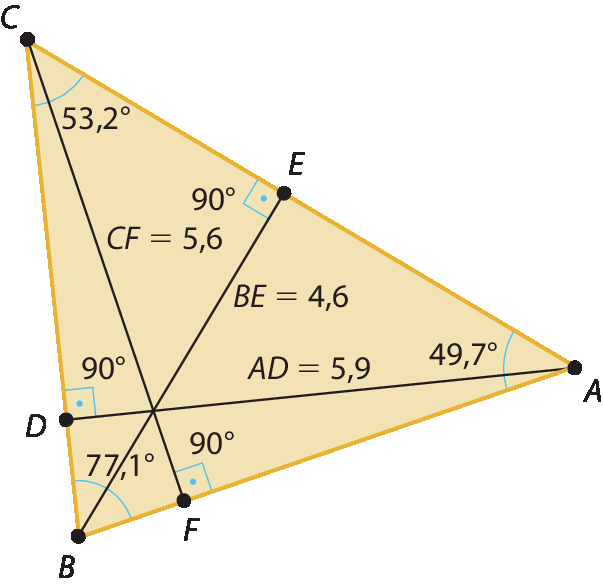
Ilustração. Triângulo A B C. De A, segmento de reta até o lado BC, chegando no ponto D. De B, segmento de reta até o lado A C, encontrando o ponto E. De C, segmento de reta até lado A B, encontrando o ponto F. OS ângulos são: A: 49,7 graus. B: 77,1 graus. C: 53,2 graus. As medidas são: AS: 5,9. BE: 4,6. CF: 5,6. ângulo de 90 graus em E, D e F.

8. O triângulo á bê cê é um triângulo retângulo, portanto, os lados

\bar{B A}

\bar{B C}

também são alturas relativas aos seus respectivos lados e têm o ponto B em comum. Deste modo, construindo a altura relativa ao lado

\bar{A C}

, verificamos que o ortocentro coincide com o vértice B.

9. Como é afirmado que em cada item os triângulos são congruentes, então:

9. a) Os lados

\bar{A B}

\bar{E D}

são congruentes, pois são lados opostos aos ângulos congruentes

\hat{C}

; os lados

\bar{A C}

\bar{C D}

são congruentes, pois são lados opostos aos ângulos congruentes

\hat{E} e \hat{B}

; os lados

\bar{B C}

\bar{C D}

são congruentes, pois são lados opostos aos ângulos congruentes

\hat{A} e \hat{D}

9. b) Os lados

\bar{A B}

\bar{Q P}

são congruentes, pois são lados opostos aos ângulos congruentes,

\hat{C} e \hat{R}

; os lados

\bar{A C}

\bar{Q R}

são congruentes, pois são lados opostos aos ângulos congruentes,

\hat{B} e \hat{P}

; os lados

\bar{B C}

\bar{P R}

são congruentes, pois são lados opostos aos ângulos congruentes

\hat{A} e \hat{Q}

10. a) Os ângulos

\hat{A} e \hat{D}

são congruentes, pois são ângulos opostos aos lados congruentes,

\bar{C E}

\bar{C B}

; os ângulos

\hat{B} e \hat{E}

são congruentes, pois são ângulos opostos aos lados congruentes,

\bar{A C}

\bar{C D}

; os ângulos

{\hat{C}}_{1} e {\hat{C}}_{2}

são congruentes, pois são ângulos opostos aos lados congruentes

\bar{A B}

\bar{D E}

10. b) Os ângulos

\hat{A} e \hat{M}

são congruentes, pois são ângulos opostos aos lados congruentes

\bar{B C}

\bar{N P}

; os ângulos

\hat{C} e \hat{N}

são congruentes, pois são ângulos opostos aos lados congruentes,

\bar{A B}

\bar{M P}

; os ângulos

\hat{B} e \hat{P}

são congruentes, pois são ângulos opostos aos lados congruentes

\bar{A C}

\bar{M N}

11. Os triângulos são congruentes, então os lados

\bar{A B}

\bar{M N}

são congruentes, assim, 5x + 13 = 7x – 3. Então, 7x – 5x = 13 + 3, resultando em 2x = 16 e, por fim, x = 8. Pela congruência de

\bar{A C}

\bar{P M}

, temos x + 12y = 6x + 4y, portanto (8) + 12y = 6(8) + 4y, resultando em 12y – 4y = 48 – 8, logo 8y = 40, y = 5.

12. Os triângulos são congruentes e então, os ângulos

\hat{T} e \hat{C}

são congruentes, assim 3y = 45; logo, y = 15graus. Como 7x + 2y = 58, temos 7x + 2 ⋅ (15) = 58. Então, 7x = 58 – 30 = 28 ⇒ x = 4°. Portanto, as medidas são x = 4° e y = 15°.

13. a) Os lados

\bar{A D}

\bar{A B}

são congruentes. O ângulo

\hat{A}

é congruente em ambos os triângulos e o lado

\bar{A C}

é comum aos dois triângulos. O caso de congruência é lado ângulo lado.

13. b) Como as retas r e s são paralelas, o ângulo

\hat{O}

é congruente em ambos os triângulos, bem como o ângulo

\hat{P}

\hat{N}

são congruentes (ângulos alternos internos) e, ainda, M e Q são congruentes (alternos internos); então, os triângulos são congruentes pelos casos ângulo-lado-ângulo ou

L A A_{O}

13. c) Os lados

\bar{T R}

\bar{S U}

são congruentes. O lado

\bar{R S}

é comum aos dois triângulos; portanto, como os ângulos

\hat{R} e \hat{S}

são congruentes, o caso de congruência é o lado ângulo lado.

14. a) Pelo caso de congruência lado ângulo lado, temos que x = 78° e y = 40°.

14. b) Pelo caso de congruência ângulo-lado-ângulo, temos que y = 20 e x = 15.

14. c) Pelo caso de congruência ângulo-lado-ângulo, temos que y + 7 = 13, y = 6 e x + y = 9 ⇒ x + 6 = 9 ⇒ x = 3.

15. Sabemos que os lados

\bar{B A}

\bar{A D}

\bar{C A}

\bar{A E}

são congruentes; além disso, o ângulo

\hat{A}

é congruente em ambos os triângulos, pois são ângulos opostos pelo vértice. Desse modo, os triângulos dê á cê e bê á é são congruentes.

16. a) A mediana (segmento

\bar{A M}

) é comum aos dois triângulos. Os lados

\bar{B M}

\bar{M C}

são congruentes, pois M é o ponto médio do segmento

\bar{B C}

. Além disso, o triângulo á bê cê é equilátero, portanto os lados

\bar{A B}

\bar{A C}

são congruentes. O caso de congruência é lado lado lado.

16. b) A bissetriz (segmento

\bar{A D}

) divide o

\hat{A}

em dois ângulos congruentes; além disso, o segmento

\bar{A D}

é comum aos dois triângulos. Os lados

\bar{A B}

\bar{A C}

são congruentes, pois o triângulo á bê cê é equilátero. O caso de congruência é lado ângulo lado.

Página oitenta

16. c) A altura (segmento

\bar{A H}

) é comum aos dois triângulos, além disso os ângulos

{\hat{H}}_{1}

{\hat{H}}_{2}

são retos. Os lados

\bar{A B}

\bar{A C}

e os ângulos

\hat{B}

\hat{C}

são congruentes, pois o triângulo á bê cê é equilátero. O caso de congruência é

L A A_{o}

16. d) Sim, pois em triângulos equiláteros a altura, mediana e bissetriz são segmentos que coincidem.

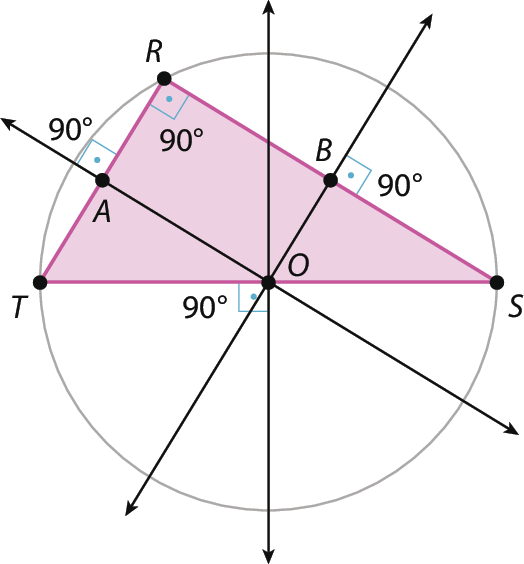
17. a) O segmento

\bar{C D}

é o diâmetro da circunferência de centro óh. Assim, os segmentos

\bar{A E}

\bar{E B}

são congruentes, pois o ponto ê é ponto médio do segmento

\bar{A B}

(o diâmetro corta perpendicularmente uma corda passando por seu ponto médio). Os segmentos

\bar{B O}

\bar{A O}

são congruentes, pois são raios da circunferência de centro óh. Desse modo, pelo caso de congruência entre triângulos retângulos, os triângulos ô á ê e ó bê é são congruentes. Outro caso possível é lado ângulo lado, uma vez que o segmento ó é é comum aos dois triângulos.

17. c) óh é o centro da circunferência, portanto x + 3y = 2x + 4, reduzindo em x = 3y – 4. Além disso, x + y = 2x – y, reduzindo em 2y = x. Assim, pela igualdade 2y = 3y – 4 ⇒ y = 4 e, então, x = 2 ⋅ 4 = 8. Portanto, o diâmetro é 40, pois x + 3y + 2x + 4 = 8 + 3 ⋅ (4) + 2 ⋅ (8) + 4 = 40. O raio equivale a 20 (pois 40 : 2 = 20) e a corda

\bar{A B}

equivale a 24, pois 2(x + y) = 2 ⋅ 12 = 24.

Para saber mais

Páginas 172 e 173

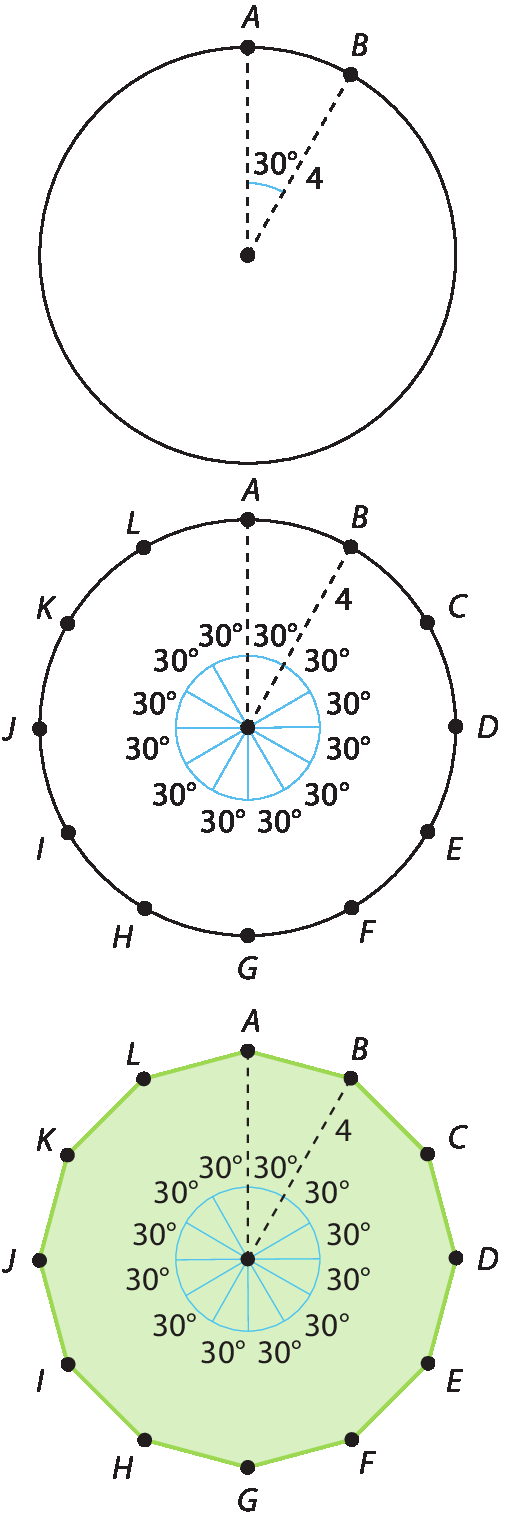
2. Traçando ângulos centrais de 30°, é possível encontrar os 12 vértices do dodecágono procurado.

Ilustração. Circunferência com ponto A e B na parte superior formando ângulo de 30 graus no centro com raios indicados por linhas tracejadas. Medida DO RAIO: 4. Ilustração. Circunferência com 12 pontos em evidência: A B C D E F G H I J K L. No centro, ponto com 12 ângulos de 30 graus cada. Medida da reta tracejada AB: 4. Ilustração. Polígono regular A B C D E F G H I J K L. No centro, ponto com 12 ângulos de 30 graus cada. Distância de B ao centro é igual a 4.

Exercício complementares

1. a) Falsa. Resposta possível: o ponto de encontro da medianas de um triângulo chama-se baricentro.

1. d) Falsa. Resposta possível: o lado oposto ao ângulo reto de um triângulo retângulo chama-se hipotenusa.

2. O triângulo é equilátero; portanto, as medianas, alturas e bissetrizes se coincidem. Desse modo, a intersecção formada pelas cevianas são o ortocentro, o baricentro e o incentro.

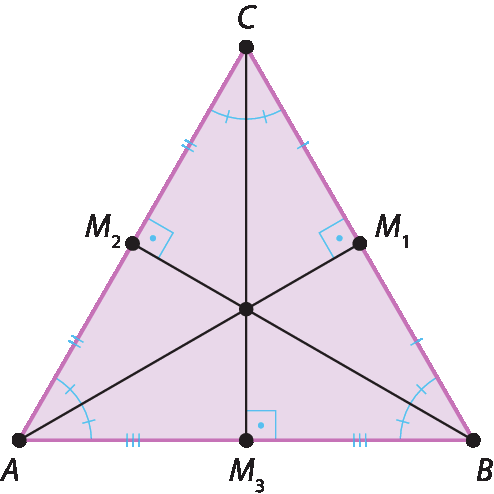
Ilustração. Triângulo A B C. De A, segmento de reta até o lado B C, encontrando ponto M 1 e formando 90 graus com lado B C. De B, segmento de reta até o lado A C, encontrando o ponto M 3 e formando 90 graus com lado A B. De C, segmento de reta até lado A B, encontrando ponto M 2 e formando 90 graus com lado A C. Todos esses segmentos se intersectam em um ponto.

3. Construção da figura; por exemplo, no caso das bissetrizes, a figura a seguir. O ponto ê encontrado é baricentro, incentro e ortocentro desse triângulo, porque á bê cê é equilátero por construção.

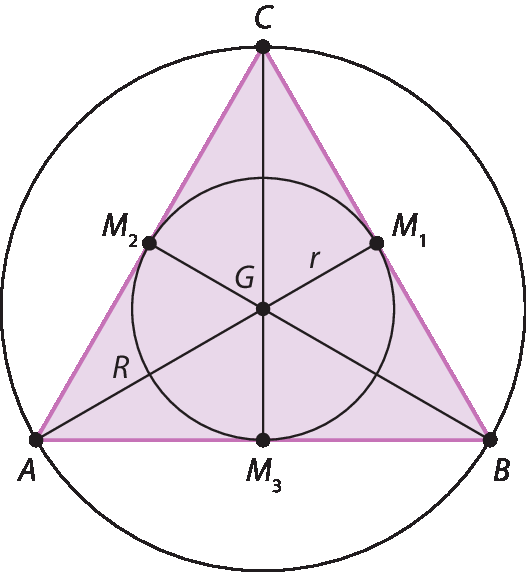
Ilustração. Circunferência. No centro, ponto G. Triângulo A B C tal que pontos A B C pertencem à circunferência. Dentro desse triângulo há uma circunferência cujos pontos M 1, M 2 e M 3 são a intersecção dela com o triângulo. Segmentos de reta indicados: A M 1, B M 2, C M 3.
De G a M 1 está indicado a medida r.

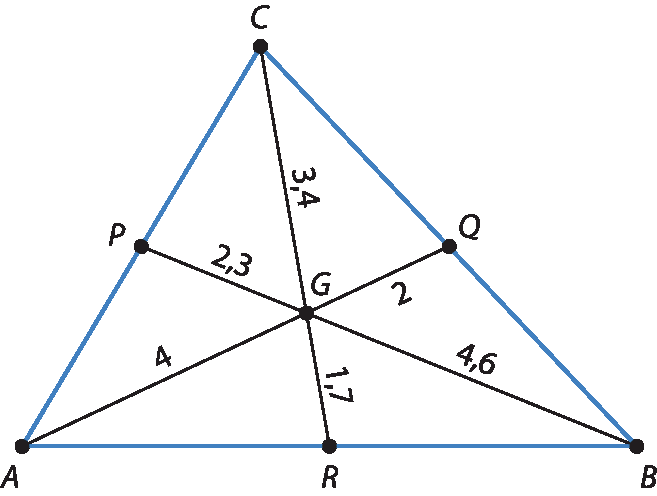
4. Construindo conforme a descrição e medindo os segmentos, conforme representado na imagem a seguir, é possível concluir que, sempre, o segmento de extremos no ponto médio e no baricentro (por exemplo,

\bar{P G}

) cabe duas vezes no respectivo segmento de extremos no baricentro e no vértice (por exemplo,

\bar{G B}

Ilustração. Triângulo A B C. No centro, ponto G. De A, segmento de reta até lado BC, encontrando ponto Q. De B, segmento de reta até lado A C, encontrando ponto P. De C, segmento de reta até lado A B, encontrando ponto R. Medidas: De G até C: 3,4. De G até R: 1,7. De G até Q: 23: 2. De G até P: 2,3. De G até A: 4.

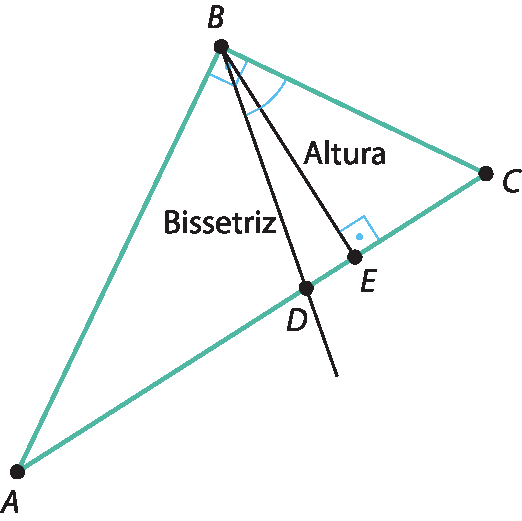
5. Alternativa e. A bissetriz do ângulo reto divide o ângulo em dois ângulos que medem 45°. O ângulo formado entre a bissetriz e a altura é 25°; desse modo, a situação descrita está representada a seguir.

Ilustração. Triângulo A B C. De B, bissetriz até lado A C, encontrando ponto D; de B, segmento de reta até lado A C com ângulo reto e encontrando o ponto E, esse segmento é a altura.

Página oitenta e um

O ângulo

E \hat{B} C

mede 20°, pois é a diferença entre os ângulos

D \hat{B} C

D \hat{B} E

e 45 – 25 = 20. Como a soma dos ângulos internos de um triângulo é 180°, em ê bê cê, se

m (B \hat{C} A) = x

; logo, 90 + 20 + x = 180 ⇒ x = 180 – 110 = 70, então

m (B \hat{C} A)

= 70°. Então, pela mesma propriedade, 90° + 70° +

m (B \hat{A} C)

= 180°, portanto

m (B \hat{A} C)

= 180° – 160° = 20°. Alternativa e.

6. As bissetrizes dividem os ângulos, respectivamente em 25° e 45°. Assim, no triângulo ABC, com

m (A \hat{B} C)

= 90° e

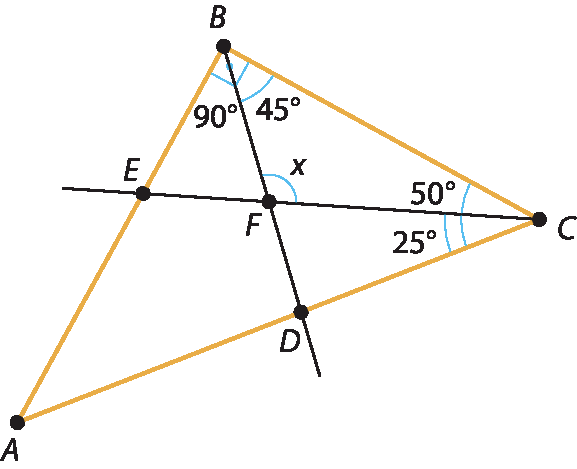
m (B \hat{C} A)

= 50°, se o ponto de encontro entre as bissetrizes é F, o triângulo BCF possui ângulos de 25°, 45° e x, que é a medida do ângulo procurado. Como soma das medidas dos ângulos internos de um triângulo é 180°, então: 25° + 45° + x = 180° ⇒ x = 180° – 70° = 110°

Ilustração. Triângulo A B C. De C, segmento de reta até lado A B, encontrando ponto E. De B, segmento de reta até lado A C, encontrando o ponto D. No centro, ponto F, de interseção entre os segmentos de reta que partem dos vértices B e C. Ângulo B C F com medida 50 graus. Ângulo C B F com medida 45 graus. Ângulo B F C com medida x grau. Ângulo A B C com medida 90 graus. Ângulo D C F com medida 25 graus.

Verificando

1. Alternativa d. O é o baricentro; desse modo, incide no lado pelo ponto médio, então o segmento

\bar{B C}

mede 36 centímetros,

\bar{A C}

mede 30 centímetros e

\bar{B A}

mede 24 centímetros. Assim, o perímetro tem medida 90 centímetros, pois: 36 + 30 + 24 = 90

2. Alternativa b. O baricentro é o centro de gravidade do triângulo, pois é formado pelo encontro das medianas.

3. Alternativa b. O ângulo

\hat{B}

mede 32°, pois

\bar{A D}

é a bissetriz do ângulo

\hat{B}

. Pela soma das medidas dos ângulos internos de um triângulo, temos que 32 + 90 +

m (\hat{C})

= 180 ⇒

m (\hat{C})

= 58. Logo, o ângulo

\hat{C}

mede 58°.

4. Alternativa c. O incentro é o ponto equidistante dos vértices do triângulo.

5. Alternativa a. O segmento

\bar{A E}

é a altura relativa à base

\bar{C B}

, pois a ceviana

\bar{A E}

fórma um ângulo reto com a reta suporte da base

\bar{C B}

6. Alternativa d. O ortocentro é formado pela intersecção das retas suporte das alturas dos triângulos; portanto, se esse triângulo for obtusângulo, ou seja, um dos ângulos do triângulo medir mais que 90°, a intersecção das alturas relativas aos seus respectivos lados estará na região externa do triângulo.

7. Alternativa a. Os triângulos são congruentes, portanto,

\hat{C}

é congruente a

\hat{F}

, que mede 36°. Pela soma das medidas dos ângulos internos de um triângulo, o ângulo

\hat{D}

, que é congruênte ao ângulo

\hat{A}

, mede 54°, pois 54 + 36 + 90 = 180. Pelo mesmo argumento, os lados

\bar{E F}

\bar{B C}

são congruentes; logo, o perímetro mede 14,8 centímetros, pois 5 + 3,6 + 6,2 = 14,8

8. Alternativa c. Considerando somente um lado e um ângulo ou somente as medidas dos ângulos, não é possível afirmar que dois triângulos são congruentes.

Diversificando

1. É interessante questionar, por exemplo, qual seria o menor e o maior caminho que o robô poderia percorrer.

2. O labirinto não apresenta simetria, pois, construindo o eixo de simetria no centro da figura, não é possível obter um caminho que seja simétrico. Por outro lado, existem caminhos que são simétricos, por exemplo, o caminho mais curto. Dê 1 passo e vire 90° à direita. Dê 3 passos e vire 90° à esquerda. Dê 12 passos e vire 90° a esquerda. Dê 3 passos e vire 90° à direita. Dê um passo à frente.

3. Em ambos os casos, existem duas combinações. Os dois desenhos são formados apenas com dois tipos de azulejo: um inteiro branco e outro com metade azul e metade branco.

4. A primeira combinação não possui eixo de simetria, pois as partes não são simétricas. Já na segunda combinação, é possível obter quatro eixos de simetria, todos passando pelo centro da figura: um no eixo vertical, um no eixo horizontal e dois eixos nas diagonais do quadrado.

Capítulo 8 – A Geometria demonstrativa

• Objetivos do capítulo e justificativas

• Compreender o que são demonstrações geométricas.

• Aplicar congruência de triângulos em demonstrações geométricas.

• Resolver problemas com base no conceito de mediatriz e bissetriz como lugares geométricos.

• Construir reta perpendicular a uma reta dada.

• Reconhecer figuras obtidas por composições de transformações geométricas.

As demonstrações geométricas apresentadas neste capítulo e os problemas envolvendo as demonstrações de propriedades de triângulos, mobilizam conhecimentos sobre mediatriz de um segmento e bissetriz de ângulo e favorecem o desenvolvimento das competências gerais 2 e 4 e da competência específica 2, pois os estudantes devem investigar a validade de propriedades e apresentar argumentos que justifiquem as demonstrações. As demonstrações das propriedades também mobilizam aspectos da competência específica 5, já que os estudantes devem utilizar procedimentos e ferramentas matemáticas nas demonstrações.

Além disso, desenvolvem-se a competência geral 1 e a competência específica 1, ao explorar aspectos históricos sobre a geometria empírica e a geometria demonstrativa, o que contribui para os estudantes perceberem que os conhecimentos matemáticos são fruto das necessidades e preocupações de diferentes culturas em diferentes momentos históricos.

Ao trabalhar com obras de arte como a proposta na abertura ou com noções sobre fractais, os estudantes têm a oportunidade de fruir diferentes manifestações artísticas e podem desenvolver a competência geral 3.

Página oitenta e dois

O contexto utilizado para explorar pesquisas censitárias e pesquisas amostrais, neste capítulo, favorece o desenvolvimento das competências gerais 9 e 10 e a competência específica 8, pois os estudantes deverão, em grupos, pesquisar e discutir sobre a importância de agir e tomar decisões com base em princípios democráticos, solidários e inclusivos.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah um quatro) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.

(ê éfe zero oito ême ah um sete) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

Este capítulo dá continuidade ao capítulo anterior, aplicando os conceitos de mediatriz de um segmento e bissetriz de um ângulo e a congruência de triângulos em demonstrações de algumas propriedades e na resolução das atividades, vinculadas à Unidade Temática Geometria; dessa maneira, os estudantes antecipam aspectos relacionados ao desenvolvimento da habilidade (ê éfe zero oito ême ah um quatro) e aplicam os conhecimentos associados ao desenvolvimento da habilidade (ê éfe zero oito ême ah um sete).

A articulação com a Unidade Temática Álgebra é feita na seção Diversificando, que aborda a regularidade existente nos fractais. O trabalho com este capítulo visa embasar os conhecimentos que serão construídos no 9º ano relativo a demonstrações (ê éfe zero nove ême ah um zero e ê éfe zero nove ême ah um três).

• Comentários e resoluções

Exercícios propostos

1. Medindo com uma régua ou usando outro instrumento, como um barbante ou tira de papel, é possível concluir que os segmentos são congruentes e, por isso, nenhum deles é maior.

2. b) Falso, pois há aves que não são galos, como os patos.

3. Os teoremas são propriedades que podem ser demonstradas, um teorema é composto de duas partes: hipótese é a parte que se supõe conhecida, e tese é a parte que se deseja provar.

3. a) Hipótese: um número é múltiplo de 3 e de 5; tese: esse número é múltiplo de 15.

3. b) Hipótese: uma altura de um triângulo é bissetriz; tese: esse triângulo é isósceles.

3. c) Hipótese: duas retas cortadas por uma reta transversal são paralelas; tese: essas retas determinam ângulos alternos internos de mesma medida.

4. a) Falsa. O triângulo pode ser equilátero.

4. b) Verdadeira, pois triângulos retângulos têm um ângulo interno de medida 90°, e todos os ângulos internos dos triângulos equiláteros medem 60°.

4. c) Falsa. As bissetrizes formam um ângulo de medida 120°.

10. Como os ângulos da base de um triângulo isósceles são congruentes, sendo x a medida dos ângulos

\hat{B}

\hat{C}

x + x + 72° = 180° ⇒ 2x = 180° – 72° ⇒ x =

\frac{108 °}{2}

⇒ x = 54°

11. Como

\bar{A B} ≅ \bar{A C}

, conclui-se que

ABC é isósceles de base

\bar{B C}

11. a) Como a altura relativa à base de um triângulo isósceles coincide com sua mediana, tem-se que

\bar{B H} ≅ \bar{C H}

. Portanto:

m (\bar{C H}) = m (\bar{B H}) = 2

m (\bar{B C}) = m (\bar{B H}) + m (\bar{C H})

= 2 + 2 = 4 (4 centímetros)

11. b) Como a altura relativa à base de um triângulo isósceles coincide com sua bissetriz interna, conclui-se que

m ({\hat{A}}_{1})

= 40°.

11. c) Como os ângulos da base de um triângulo isósceles são congruentes, sendo x =

m (\hat{B}) = m (\hat{C})

, no

á bê cê tem-se:

(40° + 40°) + x + x = 180° ⇒ 2x = 180° – 80° ⇒

⇒

x = \frac{100 °}{2} \Rightarrow x = 50 °

12. Com as informações do enunciado, e como a altura relativa à base de um triângulo isósceles coincide com sua mediana, tem-se que

\bar{B H} ≅ \bar{H C}

. Portanto:

m (\bar{H C})

m (\bar{B H}) = 3, 5 c m

13. a) No triângulo maior: 2x + 2x + 62° = 180° ⇒ ⇒ 4x = 180° – 62° ⇒

x = \frac{118 °}{4} \Rightarrow x = {(\frac{59}{2})}^{o} = 29 ° 30 ’

E no triângulo menor: x + x + y = 180° ⇒ 2x + y = 180°

Então, substituindo x por

{(\frac{59}{2})}^{o}

nessa última equação:

2 ⋅

{(\frac{59}{2})}^{o}

+ y = 180° ⇒ 59° + y = 180° ⇒ ⇒ y = 180° – 59° ⇒ y = 121°

13. b) No triângulo maior: 75° + 62° + y = 180° ⇒ 137° + y = 180° ⇒ y = 180° – 137° ⇒ y = 43°

Como o triângulo menor é isósceles, com seus ângulos da base medindo y, então: x + y + y = 180° ⇒ x + 2y = 180°

Então, substituindo y por 43° nessa última equação: x + 2 ⋅ 43° = 180° ⇒ x + 86° = 180° ⇒ x = 180° – 86° ⇒ x = 94°

13. c) Como o triângulo maior possui dois ângulos de mesma medida, esse triângulo é isósceles. Então, comparando os lados congruentes, opostos a cada ângulo de 65°, tem-se:

5x – 3° = 12° ⇒ 5x = 12° + 3° ⇒

x = \frac{15 °}{3} \Rightarrow x = 3 °

Como a altura relativa à base de um triângulo isósceles coincide com sua mediana, então

y = \frac{3 x + 1}{2}

. Com x = 3°, temos:

y = \frac{3 \cdot 3 ° + 1 °}{2} = \frac{10 °}{2} \Rightarrow y = 5 °

16. a) Os ângulos internos da base do triângulo isósceles maior medem 75°, pois 180 – 105 = 75. Portanto, nesse triângulo maior verifica-se que a soma de seus ângulos internos é:

3x + 75 + 75 = 180 ⇒ 3x = 180 – 150 ⇒

x = \frac{30}{3} \Rightarrow x = 10

Página oitenta e três

Então, como os ângulos internos da base do triângulo menor que é isósceles medem y, e o ângulo do vértice oposto mede x = 10°, nesse triângulo tem-se:

10 + y + y = 180 ⇒ 2 y = 180 –10 ⇒ y =

\frac{170}{2}

⇒ y = 85

Logo, a medida y é 85°.

16. b) Os ângulos internos da base do triângulo isósceles medem x, e o ângulo do vértice oposto mede 120°; então, nesse triângulo tem-se:

120 + x + x = 180 ⇒ 2x = 180 – 120 ⇒ x =

\frac{60}{2}

⇒ x = 30

Logo, x = 30°; assim, conclui-se que o triângulo maior tem os ângulos medindo 80°, x e x + y, ou seja:

80 + x + (x + y) = 180 ⇒ 80 + 30 + (30 + y) = 180 ⇒

⇒ 140 + y = 180 ⇒ y = 180 – 140 ⇒ y = 40

Logo, y = 40°.

17. Incentive os estudantes a elaborarem situações-problema envolvendo diferentes contextos, inclusive geométricos; depois, solicite-lhes que compartilhem com os colegas os problemas elaborados. Desenvolva a resolução de alguns deles na lousa.

19. a) O lado de maior medida opõe-se ao ângulo de maior medida. O ângulo interno de vértice B do triângulo mede 90°, por isso ele é o maior ângulo interno do triângulo. Logo,

\bar{A C}

é o maior lado, e

\bar{A B}

, o menor lado.

19. b) O ângulo interno de vértice B do triângulo mede 120°, pois 180 – 60 = 120, por isso ele é o maior ângulo interno do triângulo. Logo,

\bar{A C}

é o maior lado, e

\bar{B C}

, o menor lado.

20. Como o maior lado é o que mede 5,5 centímetros, conclui–se que o maior ângulo interno é o do vértice oposto B, mesmo que a figura não aparente esse resultado. Como o menor lado é o que mede 3 centímetros, conclui–se que o menor ângulo interno é o do vértice oposto a, mesmo que a figura não aparente esse resultado.

21. O ângulo de 100° é obtuso e, portanto, o maior dos três ângulos internos do triângulo. Assim, o lado oposto a esse ângulo é o maior lado do triângulo, que mede 5,5 centímetros.

22. Como 60 > 40, o lado oposto ao ângulo de 60° é maior que o lado oposto ao ângulo de 40°. Portanto, Ana mora mais longe da lanchonete do que Renata.

23. a) Não é possível, pois ao ângulo de maior medida deve se opor o lado de maior medida, e isso não ocorreu.

23. b) Não é possível, pois a soma das medidas dos ângulos internos de um triângulo é 180°, e isso não ocorreu.

24. No vértice onde está Marcos, o ângulo interno do triângulo mede 75°, pois 180 – 105 = 75, e sendo y a medida do ângulo interno no vértice onde está Daniel:

y + 75 + 60 = 180 ⇒ y + 135 = 180 ⇒ y = 180 – 135 ⇒ y = 45

Portanto, x = 75° e y = 45°.

25. a) O ângulo interno de vértice D do

cê dê é mede 60°, pois 180 – 120 = 60. Então, y = 60°, pois y + 60 + 60 = 180 ⇒ y + 120 = 180 ⇒ y = 180 – 120 ⇒ y = 60

Como as retas A bê e CD são paralelas, o ângulo x corresponde ao ângulo interno de vértice D do triângulo cê dê é. Logo, x = 60°.

25. b) Como as retas A bê e CD são paralelas, o ângulo x é alterno interno em relação ao ângulo dado de medida 48°. Portanto, x = 48°. Do mesmo paralelismo, o ângulo interno de vértice D do triângulo cê dê é é correspondente ao ângulo interno de vértice B do triângulo á bê é, que mede 80°. Assim, y = 52°, pois: y + 48 + 80 = 180 ⇒ y + 128 = 180 ⇒ y = 180 – 128 ⇒ y = 52°

Exercícios complementares

1. Os ângulos internos do lado oposto ao ângulo b do triângulo medem:

• 180° – a = 180° – 105° = 75°

• 180° – x

Portanto, nesse triângulo, a soma dos ângulos internos é dada por

40 + 75 + 180 – x = 180

115 – x = 0

x = 115

Portanto, x = 115°.

Alternativa ê.

2. Sejam z igual a metade do ângulo reto e w igual à metade do ângulo agudo desconhecido do triângulo maior. No vértice do ângulo reto tem-se:

z + z = 90 ⇒ 2z = 90 ⇒ z =

\frac{90}{2}

⇒ z = 45

No triângulo maior: 90 + 50 + 2w = 180 ⇒ 140 + 2w = = 180 ⇒ 2w = 180 – 140 ⇒ w =

\frac{40}{2}

⇒ w = 20

Logo, z = 45° e w = 20°.

No triângulo menor, verificamos que a soma dos ângulos internos é dada por: x + z + w = 180 ⇒ x + 45 + 20 = 180 ⇒ x = 180 – 65 ⇒ x = 115

Finalmente, no vértice do ângulo agudo da base:

w + w + y = 180 ⇒ 20 + 20 + y = 180 ⇒ y = 180 – 40 ⇒ y = 140

Logo, x = 115° e y = 140°.

3. Os ângulos internos do do triângulo cujos vértices são as intersecções entre as retas t e u, entre as retas s e u e entre as retas s e t medem: 35° (oposto pelo vértice ao ângulo dado); 70° (oposto pelo vértice ao ângulo dado); 180° – x (suplementar de x). Assim, nesse triângulo:

35 + 70 + (180 – x) = 180 ⇒ 105 + 180 – x = 180 ⇒

⇒ 105 – x = 0 ⇒ 105 = x

Logo, x = 105°. Alternativa ê.

4. O triângulo bêá’ê é isósceles, pois, do enunciado,

\bar{B E} ≅ \bar{B A} ’

. Sendo x a medida dos ângulos congruentes internos da base

\bar{E A ’}

, como B é vértice de um ângulo reto:

90 + x + x = 180 ⇒ 2x = 180 – 90 ⇒ x =

\frac{90}{2}

⇒ x = 45

Logo, a medida do ângulo é 45°.

Página oitenta e quatro

6. Sendo x a medida do ângulo procurado,

m (D \hat{E} C) = x

, e y as medidas dos ângulos determinados pelas bissetrizes dos ângulos da base do triângulo á bê cê, então

m (D \hat{C} E)

= m (E \hat{C} B) = y

; como triângulo á bê cê é isósceles, então

m (A \hat{C} B)

= m (A \hat{B} C) = 2 y

; e como

\bar{B D}

é bissetriz, tem-se que

m (A \hat{B} D)

= m (D \hat{B} C)

\frac{m (A \hat{B} C)}{2} = \frac{2 y}{2} = y

. A figura a seguir indica todos esses ângulos.

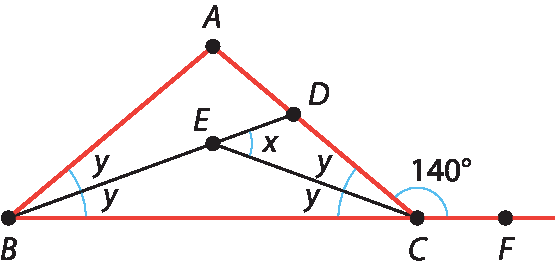
Ilustração. Triângulo A B C. No centro, ponto E. Segmento de reta de B até lado A C, passando por E, encontrando ponto D. Segmento de reta de C até E. De B, semirreta B C horizontal com ponto F externo ao triângulo. A medida do ângulo A B D é y grau. A medida do ângulo E B C é y grau. A medida do ângulo E C B é y grau. A medida do ângulo D E C é x grau. A medida do ângulo D C E é y grau. A medida do ângulo D C F é 140 graus.

Do vértice C, conclui-se que y = 20°, pois: 2y + 140 = 180 ⇒ 2y = 180 – 140 ⇒ y =

\frac{40}{2}

⇒ y = 20. Notando que o ângulo de medida x é externo do triângulo bê cê é no vértice ê, tem-se: x = y + y = 20 + 20 = 40. Logo, x = 40°. Alternativa c.

7. Como x é a medida de um ângulo externo do

á bê cê

vértice B: x = 33° + 45° = 78°. Como as retas

\overset{\leftrightarrow}{D E}

\overset{\leftrightarrow}{B C}

são paralelas, os ângulos agudos de vértices D e C se correspondem. Portanto: y + 45° = 180° ⇒ y = 180° – 45° ⇒ y = 135°.

8. Como á cê = BC, então

á bê cê é isósceles de base

\bar{A B}

e, portanto, os ângulos de sua base têm a mesma medida de 25°. Como BC = BD, então

BCD é isósceles de base

\bar{C D}

e, portanto, os ângulos de sua base têm a mesma medida y. Como o ângulo de medida y no vértice C é ângulo externo do

á bê cê, tem-se: y = 25° + 25° = 50°. Como o ângulo de medida x no vértice B é ângulo externo do

á bê dê, tem-se: x = 25° + y = 25° + 50° = 75°. Alternativa d.

9. Supondo que as linhas pontilhadas sejam paralelas, os ângulos de medidas α e 150° são colaterais internos, então: α +150° = 180° ⇒ α = 180° – 150° ⇒ α = 30°. Substituindo α por 30° na equação dada pelo enunciado: α + β = 135° ⇒ 30° + β = 135° ⇒ β = 135° – 30° ⇒ β = 105°. Como os ângulos de medida θ e α + β = 135° também são colaterais internos em relação às retas pontilhadas: θ + 135° = 180° ⇒ θ = 180° – 135° ⇒ θ = 45°. Alternativa c.

10. Sendo x a medida do ângulo procurado, como os dois trechos têm o mesmo comprimento, o triângulo na figura é isósceles e, portanto, possui 2 ângulos internos de medida (x + 18)°. Então, prolongando a trajetória do primeiro trecho, obtemos um ângulo correspondente ao de 18° entre a primeira trajetória do avião e a direção norte, conforme a figura a seguir:

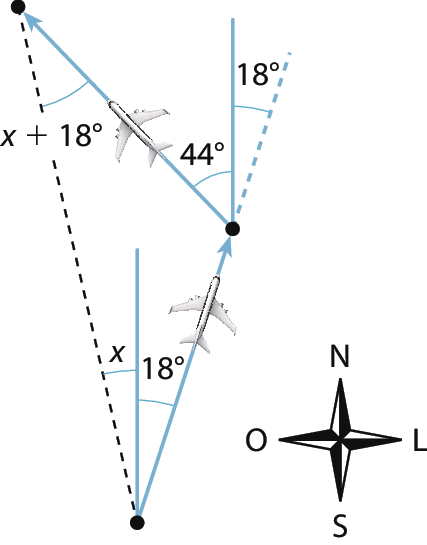
Esquema. 3 pontos não colineares formando triângulo. O ângulo indicado no ponto 1 é dividido em dois outros ângulos, sendo um de medida x grau, outro de medida 18 graus. O ângulo no ponto 2 mede x mais 18 graus. O ângulo externo no ponto 3 é dividido em dois ângulos cujas medidas são 44 graus e 28 graus. Ilustração de um avião sobre o lado definido pelo ponto 3 e o ponto 2, em direção ao ponto 2. Há uma representação de uma rosa dos ventos.

Como o ângulo de medida 62° (44 + 18 = 62) é ângulo externo do triângulo isósceles:

(x + 18) + (x + 18) = 62 ⇒ 2x + 36 = 62 ⇒ 2x = 62 – 36 ⇒ ⇒ x =

\frac{26}{2}

⇒ x = 13. Assim, x = 13°. Alternativa b.

Verificando

1. Triângulos congruentes têm elementos correspondentes de medidas iguais. Alternativa d.

2. Do enunciado constrói-se a figura:

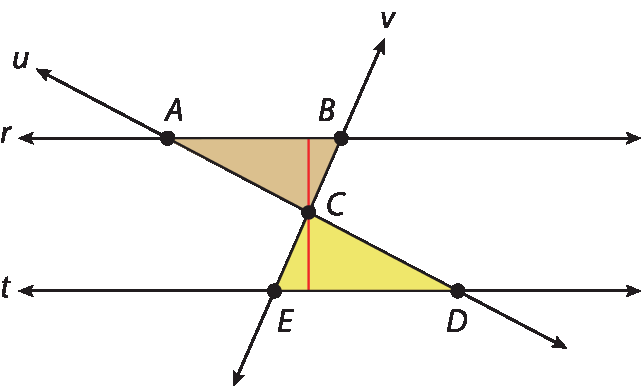
Ilustração. Duas retas horizontais paralelas, r e t. Sobre elas, duas retas diagonais cruzadas, u e v, no centro das retas paralelas, em um ponto C, formando um triângulo bege A B C (pontos A e B sobre a reta r) e triângulo amarelo C D E (pontos D e E sobre a reta t). Uma linha vermelha liga as retas r e t, passando pelo ponto C.

Como

á bê cê ≅

dê cê é, as alturas relativas ao vértice C de ambos os triângulos têm a mesma medida. Assim, o ponto C é equidistante das retas r e t. Alternativa a.

3. Como os triângulos equiláteros são triângulos isósceles em que qualquer lado pode ser considerado como sendo a base, a propriedade da coincidência entre bissetriz interna, altura e mediana relativas à base dos triângulos isósceles vale para todos os lados dos triângulos equiláteros. Alternativa c.

á bê cê e

á dê cê são congruentes pelo caso ângulo-lado-ângulo, pois:

C \hat{A} B

≅

C \hat{A} B

(

\bar{A C}

é bissetriz de

B \hat{A} D

)

\bar{A C} ≅ \bar{A C}

(lado comum aos triângulos)

A \hat{C} B ≅ A \hat{C} D

(

\bar{A C}

é bissetriz de

B \hat{A} D

)

Alternativa d.

5. Sendo θ a medida do ângulo interno de vértice a do triângulo á bê cê, obtemos

á bê cê:

θ + α + β = 180° ⇒ θ + 82° + 69° = 180° ⇒ θ = 180° –151° ⇒ θ = 29°

Como

m (\bar{A D}) = m (\bar{D E})

, o

á dê é é isósceles de base

\bar{A E}

, então

m (D \hat{A} E) = m (D \hat{E} A) = θ

; assim: γ + θ + θ = 180° ⇒

⇒ γ + 29° + 29° = 180° ⇒ γ + 58° = 180° ⇒ γ = 180° – 58° ⇒ γ = 122°.

Alternativa d.

6. Assim como nos triângulos isósceles, a altura de um triângulo equilátero coincide com sua mediana e com sua bissetriz interna. Portanto:

m (\bar{C D}) = 25 cm

, pois o lado mede 50 centímetros e 50 : 2 = 2;

m (D \hat{A} C) = 30 °

, pois a medida do ângulo interno de um triângulo equilátero é 60° e 60 : 2 = 30. Alternativa c.

7. Como o triângulo é isósceles de base

\bar{A C}

, obtemos

m (\hat{A})

= m (\hat{C})

= 22°. Então, como α é a medida do ângulo externo oposto à base do triângulo, α = 22° + 22° = 44°.

Alternativa b.