Página oitenta e cinco

Parte 7

Capítulo 9 – Estudo dos quadriláteros

• Objetivo do capítulo e justificativas

• Utilizar congruência de triângulos para demonstrações de propriedades de quadriláteros.

• Construir quadriláteros utilizando instrumentos de desenho.

• Reconhecer que a soma das medidas dos ângulos internos (e a dos ângulos externos) e o número de lados de um polígono não são grandezas proporcionais.

• Resolver problemas com base no conceito de mediatriz e de bissetriz como lugares geométricos.

• Resolver problemas envolvendo o conceito de área e de volume.

• Analisar informações contidas em rótulos de embalagens.

Neste capítulo, o estudo de quadriláteros se apoia, principalmente, no desenvolvimento da competência geral 2 e das competências específicas 2 e 5. Ao explorar os elementos e propriedades dos quadriláteros, mobilizam-se conhecimentos e conteúdos trabalhados anteriormente a fim de validar ou de demonstrar tais propriedades. Os estudantes também enfrentam situações-problemas em diferentes contextos e em situações imaginadas e, ao expor seus argumentos ou conclusões aos colegas, desenvolvem a competência específica 6.

O contexto do capítulo possibilita apresentar obras de arte e desenvolver a competência geral 3, pois os estudantes podem fruir diferentes manifestações artísticas.

Os problemas envolvendo medidas de ângulos, medidas de área e medidas de comprimento, associados às propriedades de quadriláteros, possibilitam desenvolver aspectos da competência específica 3, de maneira que os estudantes podem relacionar conhecimentos da Unidade Temática Grandezas e Medidas e de Geometria.

O Trabalho com a análise de informações em rótulos de embalagens na seção Trabalhando a informação possibilita aos estudantes refletir sobre as diferentes informações apresentadas em rótulos de produtos alimentícios, o que favorece o desenvolvimento da competência geral 8 e da competência específica 7.

Na seção Para saber mais, ao trabalhar com a aplicação de conteúdos matemáticos no ramo da construção, contribuímos para o desenvolvimento da competência geral 6.

O contexto utilizado para explorar pesquisas censitárias e pesquisas amostrais, neste capítulo, favorece o desenvolvimento das competências gerais 9 e 10 e a competência específica 8, pois os estudantes deverão, em grupos, pesquisar e discutir sobre a importância de agir e tomar decisões com base em princípios democráticos, solidários e inclusivos.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah um dois) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.

(ê éfe zero oito ême ah um três) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.

(ê éfe zero oito ême ah um quatro) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.

(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.

(ê éfe zero oito ême ah um sete) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

(ê éfe zero oito ême ah um nove) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

O foco deste capítulo é a Unidade Temática Geometria, em que ampliamos os temas abordados em capítulos anteriores deste livro, a fim de consolidar e aprofundar os conhecimentos construídos e visando dar subsídios para o que será estudado no 9º ano (ê éfe zero nove ême ah um dois e ê éfe zero nove ême ah um três).

Desenvolvem-se atividades com novas construções geométricas e novas aplicações da congruência de triângulos para demonstrações de propriedades de quadriláteros, o que se relaciona ao desenvolvimento da habilidade (ê éfe zero oito ême ah um quatro) e mobiliza conhecimentos relativos às habilidades (ê éfe zero oito ême ah um cinco) e (ê éfe zero oito ême ah um sete). A aplicação de expressões de cálculo de medidas de área de figuras geométricas e a resolução e elaboração de problemas envolvendo medidas de área possibilitam o desenvolvimento da habilidade (ê éfe zero oito ême ah um nove).

A relação entre o número de lados de um polígono e a soma das medidas dos ângulos internos exemplifica a não proporcionalidade, o que, por contraposição, reforça o desenvolvimento das habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três).

Articulam-se as Unidades Temáticas Álgebra, com a identificação de grandezas não proporcionais na seção Para saber mais (Polígonos e proporcionalidade), Grandezas e medidas, na resolução de atividades que envolvem a noção de área e volume, e Probabilidade e estatística, com a análise de informações em rótulos de embalagens na seção Trabalhando a informação.

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Exercícios propostos

2. a) No quadrilátero MNPQ, tem-se:

80° + 108° + 105° + x = 360° ⇒ 293° + x = 360°

x = 360° ‒ 293° ⇒ x = 67°

2. b) No vértice Q, tem-se:

y = 180° ‒ 108° = 72°

Página oitenta e seis

3. a)

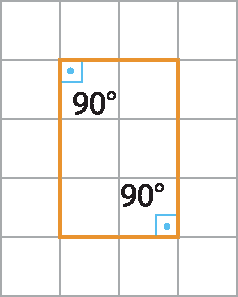
Ilustração. Em malha quadriculada, de 5 linhas e 4 colunas de quadrados, um retângulo composto por 3 linhas e duas colunas, com indicação de 2 ângulos retos.

3. b)

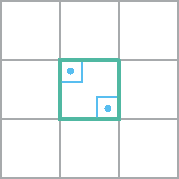
Ilustração. Em malha quadriculada, de 3 linhas e 3 colunas de quadrados, um quadrado no centro, com indicação de 2 ângulos retos.

3. c)

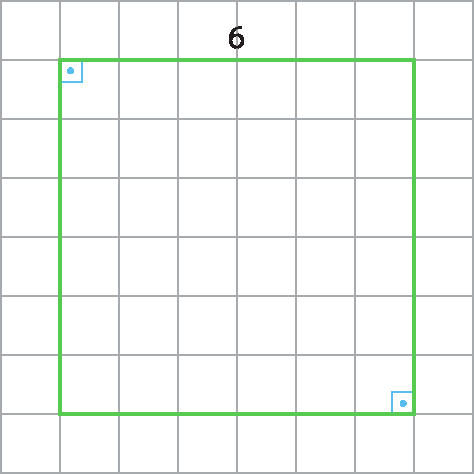
Ilustração. Em malha quadriculada, de 8 linhas e 8 colunas de quadrados, um quadrado composto por 6 linhas e 6 colunas, com indicação de 2 ângulos retos e lado de medida 6.

4. Sendo x a medida do quarto ângulo:

104° + 97° + 53° + x = 360° ⇒ x = 360° ‒ 254° = 106°

5. Como a soma das medidas dos ângulos internos é igual a 360°, tem-se:

x + (x + 40°) + (x + 80°) + 3x = 360°

6x + 120° = 360° ⇒ 6x = 240° ⇒ x = 40°

6. Sendo

x = m (\hat{C})

, tem-se:

m (\hat{D})

2 x e m (\hat{A})

m (\hat{B}) = 3 x .

Assim:

3x + 3x + x + 2x = 360° ⇒ 9x = 360° ⇒ x =

\frac{360 °}{9}

⇒ x = 40°

Portanto: m(

\hat{C}

) = 40° e m(

\hat{A}

) = 120° (3 ⋅ 40° = 120°).

7. Sendo x a medida do ângulo de vértice D:

108° + 76° + 92° + x = 360° ⇒ 276° + x = 360° ⇒

⇒ x = 360° ‒ 276° ⇒ x = 84°

Então, sendo y a medida do ângulo formado pelas duas bissetrizes:

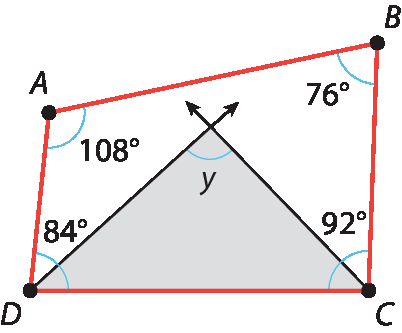
Ilustração. Quadrilátero A B C D. Bissetrizes dos ângulos relativos aos vértices D e de C se cruzam na parte interna do quadrilátero em um ponto com ângulo de medida y grau, formando um triângulo em destaque. O ângulo relativo ao vértice A mede 108 graus. O ângulo relativo ao vértice B mede 76 graus. O ângulo relativo ao vértice C mede 92 graus. O ângulo relativo ao vértice D mede 84 graus.

Para o triângulo em destaque:

\frac{84 °}{2} + y + \frac{92 °}{2}

= 180° ⇒ 42° + y + 46° = 180° ⇒

⇒ 88° + y = 180° ⇒ y = 180° ‒ 88° ⇒ y = 92°

Portanto, o ângulo formado pelas bissetrizes dos ângulos

\hat{C}

\hat{D}

mede 92°.

8. a)

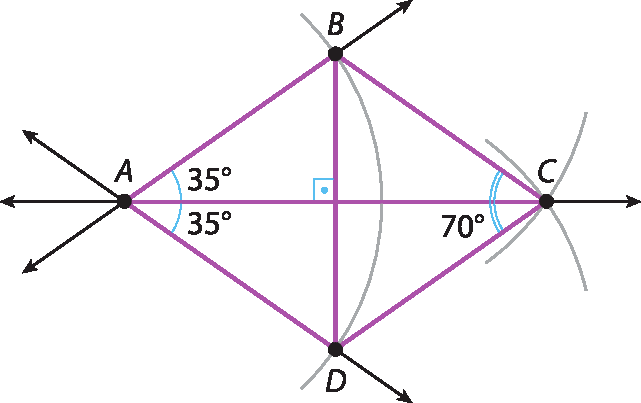
Ilustração. Reta horizontal com pontos A e C, e reta vertical com pontos B e D. Quadrilátero A B C D, de modo que: o ângulo entre os segmento A C e B D é reto; o ângulo B C D mede 70 graus; o ângulo entre os segmento A C e B D é reto; B A D está dividido pela metade e cada parte mede 35 graus.

Ao construir um quadrilátero com todos os lados congruentes e um dos ângulos medindo 70°, os estudantes obterão um quadrilátero com mais um ângulo de medida 70°. Sendo os outros dois ângulos de medidas e considerando que a soma das medidas dos ângulos internos é igual a 360°, temos:

70° + 70° + x + x = 360° ⇒ 2x = 360° ‒ 140° ⇒ x = 110°

8. b) Ao traçar as diagonais, formam-se quatro triângulos congruentes. Tomando um deles, por exemplo,

á bê ême, tem-se:

m (B \hat{A} M)

= 55°;

m (A \hat{B} M)

= 35°. Sabendo que a soma das medidas dos ângulos internos de um triângulo é 180graus, temos:

m (A \hat{M} B)

= 180° ‒ 90° = 90°

10. Sendo x a medida dos ângulos obtusos do paralelogramo, temos:

74° + x + 74° + x = 360° ⇒ 148° + 2x = 360° ⇒ 2x = 212° ⇒ x = 106°

11. Sendo x a medida dos ângulos agudos do losango, temos:

125° + x + 125° + x = 360° ⇒ 250° + 2x = 360° ⇒

⇒ 2x = 360° ‒ 250° ⇒ 2x = 110° ⇒ x = 55°

12. a) Como os ângulos opostos de um paralelogramo são congruentes, então:

5x – 20° = 4x + 10° ⇒ 5x ‒ 4x = 30° ⇒ x = 30°

Assim, os ângulos obtusos medem 130°, pois:

4 ⋅ 30° + 10° = 130°

Sabendo que a soma das medidas dos ângulos internos é igual a 360°, temos:

130° + y + 130° + y = 360° ⇒ 2y = 360° ‒ 260° ⇒

⇒ 2y = 100° ⇒ y = 50°

12. b) y + 30° + 83° = 180° ⇒ y + 113° = 180° ⇒ ⇒ y = 180° ‒ 113° ⇒ y = 67°

Como os ângulos de medidas x e y são alternos internos, x = y = 67°.

13. O ângulo suplementar adjacente ao ângulo externo de medida 108° é o ângulo interno de medida 72° (180° ‒ 108° = 72°). Assim, sendo os dois ângulos agudos do paralelogramo de medidas 72° e os dois ângulos obtusos de medidas iguais a x, considerando que a soma das medidas dos ângulos internos é igual a 360°, temos:

72° + x + 72° + x = 360° ⇒ 2x = 360° ‒ 144° ⇒

⇒ 2x = 216° ⇒ x = 108°

Portanto, no paralelogramo há dois ângulos internos de medida 108° e dois ângulos internos de medida 72°.

Página oitenta e sete

19. a) As diagonais de um retângulo são congruentes e, como os retângulos também são paralelogramos, suas diagonais interceptam-se em seus pontos médios. Então, x = 5 centímetros e y = 10 centímetros (y = 5 centímetros + 5 centímetros = 10 centímetros).

19. b) Como os losangos também são paralelogramos, os lados

\bar{A B}

\bar{C D}

são paralelos; portanto, os ângulos de medidas y e 50° são alternos internos. Logo, y = 50°. As diagonais do paralelogramo são perpendiculares entre si e o

á cê dê é isósceles de base

\bar{A C}

. Então, como a altura de um triângulo isósceles coincide com sua bissetriz interna, tem-se que

m (B \hat{D} C)

= x. Sendo M o ponto de interseção das diagonais do losango, no

DMC:

x + 90° + 50° = 180° ⇒ x = 180° ‒ 140° = 40°

19. c) Como os quadrados também são losangos, x = 90°. Como as diagonais de um losango também são bissetrizes de seus ângulos internos, y = 45°, pois y = 90° : 2 = 45°.

20. Sendo x a medida do ângulo desconhecido e, como as diagonais de um retângulo determinam quatro triângulos isósceles em seu interior, considerando que a soma das medidas dos ângulos internos de um triângulo é igual a 180°, temos:

x + x + 100° = 180° ⇒ 2x = 180° ‒ 100° ⇒

⇒ 2x = 80° ⇒ x = 40°

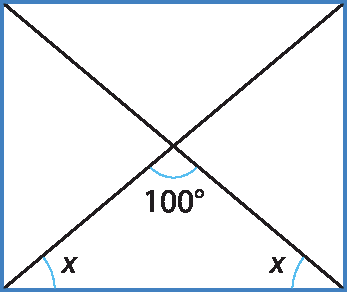
Ilustração. Retângulo com as suas duas diagonais destacadas. Na triângulo inferior, os ângulo internos da base medem x grau cada um e o outro ângulo interno mede 100 graus.

22. As diagonais do losango são bissetrizes de seus ângulos internos, então dois dos ângulos desse losango medem 70°, pois 2 ⋅ 35° = 70°. Então, sendo x a medida dos outros dois ângulos internos:

x + 70° + x + 70° = 360° ⇒ 2x = 360° ‒ 140° ⇒

⇒ 2x = 220° ⇒ x = 110°

Portanto, no losango há dois ângulos de medida 70° e dois ângulos de medida 110°.

23. Ao construir um quadrado com duas diagonais de medida 5,6 centímetros, serão formados lados de aproximadamente 4 centímetros, ou 40 milímetros.

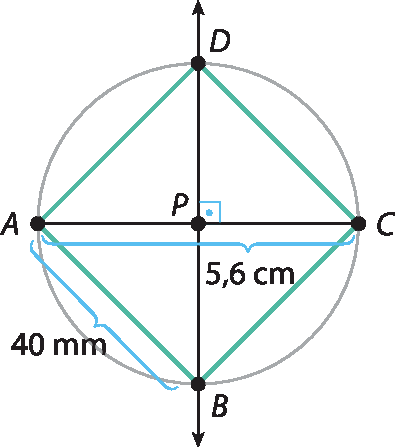
Ilustração. Quadrado A B C D, com suas diagonais destacadas, que se intersectam no ponto P, formando um ângulo reto entre si. Fora do quadro, uma circunferência passa pelos pontos A, B, C e D, e tem centro em P. A medida do segmento A B é 40 milímetros. A medida do segmento A C é 5,6 milímetros.

Assim, a área será 16 centímetros quadrados (4 ⋅ 4 = 16). Como 1 centímetro quadrado = 100 milímetros quadrados, então 16 centímetros quadrados = .1600 milímetros quadrados.

25.

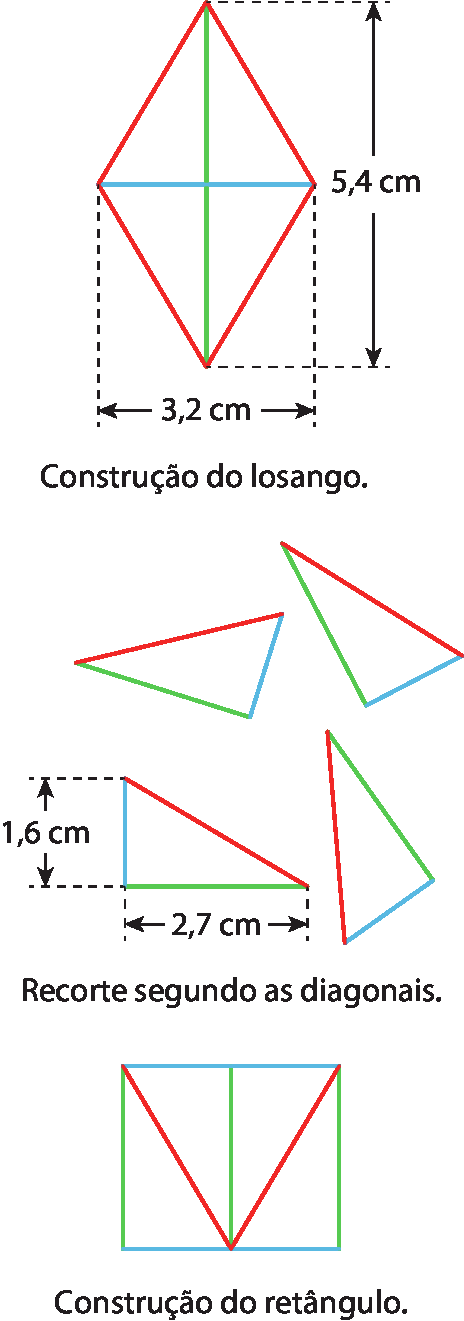
Ilustração. Losango, em vermelho, com sua diagonal maior destacada em verde e sua diagonal menor destacada em azul. A diagonal mede 5,4 centímetros. A diagonal menos mede 3,2 centímetros. Ilustração. Quatro triângulos congruentes. Em um desses triângulos, a altura (em azul) mede 1,6 centímetros; a base (em verde) mede 2,7 centímetros. O outro lado é destacado em vermelho. Ilustração. Retângulo composto por 4 triângulos congruentes, com seus lados destacados nas cores azul, verde e vermelho. Dois lados opostos do retângulo estão coloridos de azul, e os outros dois lados estão coloridos de verde. Há um segmento em verde dividindo o retângulo ao meio, pela base. Há dois segmentos em vermelho dividindo cada retângulo menor em dois triângulos congruentes.

As áreas do losango e do retângulo têm a mesma medida, pois são formadas pelas mesmas partes. Como a medida da área do losango é igual à medida da área do retângulo de lados medindo 3,2 centímetros (uma diagonal menor) e 2,7 centímetros (metade da diagonal maior), temos:

A = 3,2 ⋅ 2,7 = 8,64

Portanto, a área do losango mede 8,64 centímetros quadrados.

26. a)

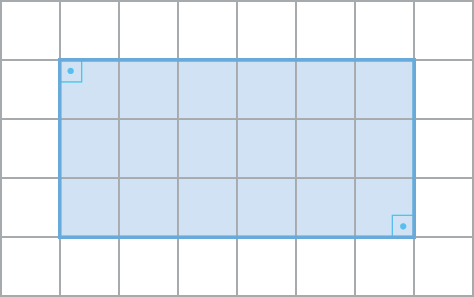
Ilustração. Malha quadriculada com retângulo composto por 3 linhas e 6 colunas de quadradinhos azuis.

26. b)

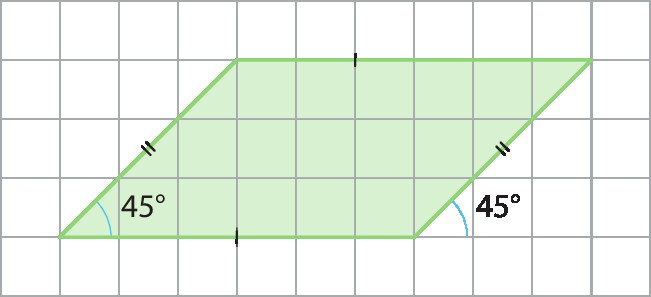
Ilustração. Malha quadriculada com paralelogramo composto por 15 quadradinhos inteiros e 6 quadradinhos pela metade na cor verde. Há indicação de que dois lados opostos do paralelogramo são congruentes. Há também indicação de que um dos ângulos internos do paralelogramo mede 45 graus.

26. c) Não é possível construir esse quadrilátero.

Página oitenta e oito

29.

Ilustração. Retângulo A B C D. Reta horizontal P Q abaixo de B C.

Por se tratar de um retângulo,

\bar{A D} ∥ \bar{B C}

. Como, por construção,

\bar{P Q} ∥ \bar{A D}

, teremos

\bar{P Q} ∥ \bar{B C} .

30. a) Como a soma das medidas dos ângulos internos de um quadrilátero é igual a 360°, temos:

x + 4x + 3x + 2x = 360° ⇒ 10x = 360° ⇒ x =

\frac{360 °}{10}

⇒ x = 36°

No vértice superior direito do trapézio, por se tratar de ângulos suplementares, 3x + y = 180°. Então:

3 ⋅ 36° + y = 180° ⇒ 108° + y = 180° ⇒

⇒ y = 180° ‒ 108° ⇒ y = 72°

30. b) Como os ângulos da base maior são congruentes e o ângulo interno do vértice inferior esquerdo é alterno interno do ângulo de medida 70°, concluímos que a medida de x é 70°. O ângulo de medida x é suplementar ao ângulo de medida y, então:

x + y = 180° ⇒ 70° + y = 180° ⇒ y = 180° ‒ 70° ⇒ y = 110°

31. a) Seja x a medida do ângulo agudo do trapézio, como a soma das medidas dos ângulos internos é igual a 360°, temos:

x + 3x + 90° + 90° = 360° ⇒ 4x = 360° ‒ 180° ⇒ x = 45°

Desse modo, o ângulo obtuso medirá 135°

(3 ⋅ 45° = 135°).

31. b) O ângulo agudo mede 45°.

35. Sendo x a medida do ângulo agudo do trapézio, temos:

x + 2x + 90° + 90° = 360° ⇒ 3x = 180° ⇒ x = 60°

Portanto, os ângulos medem 90°, 90°, 60° e 120°

(2x = 2 ⋅ 60° = 120°).

36. É preciso recordar que os paralelogramos têm os lados opostos paralelos. Quando Fabiana escreve “pelo menos dois”, isso implica que podem ser mais de dois; portanto, Fabiana inclui os paralelogramos em sua definição, que não está de acordo com a definição apresentada no capítulo.

39. a)

\frac{5, 4 + 8, 6}{2} = \frac{14}{2} = 7

Então, x = 7 centímetros.

39. b)

\frac{x + 9}{2}

= 6 ⇒ x + 9 = 2 ⋅ 6 ⇒ x = 12 ‒ 9 ⇒ x = 3

Logo, x = 3 centímetros.

39. c)

\frac{x + 4, 8}{2}

= 5,6 ⇒ x + 4,8 = 2 ⋅ 5,6 ⇒ x = 11,2 ‒ 4,8 ⇒ x = 6,4

Logo, x = 6,4 centímetros.

40. a. Os lados do

MNP medem: MN = 4,5 centímetros (9 : 2 = 4,5); MP = 5 centímetros (10 : 2 = 5); NP = 3 centímetros (6 : 2 = 3). Portanto, o perímetro do

MNP mede 12,5 centímetros, pois 4,5 + 5 + 3 = 12,5.

40. b. BC = 11 centímetros (2 ⋅ 5,5 = 11); AB = 7 centímetros (2 ⋅ 3,5 = 7); BC = 8 centímetros (2 ⋅ 4 = 8). Portanto, o perímetro do

á bê cêmede 26 centímetros (11 + 7 + 8 = 26).

41. a) Traçando a diagonal

\bar{A C}

do quadrilátero, tem-se que

\bar{M N}

é base média relativa à base

\bar{A C}

bê á cê. Portanto:

\bar{M N}

‖

\bar{P Q}

41. b) Traçando a diagonal

\bar{B D}

do quadrilátero, tem-se que

\bar{Q M}

é base média relativa à base

\bar{B D}

BCD. Portanto:

\bar{Q M}

‖

\bar{P N}

41. c) Como PQ é base média relativa à base á cê do

bê á cê, tem-se: PQ

‖

\bar{A C}

‖

\bar{M N}

. Como

\bar{P N}

é base média relativa à base

\bar{B D}

BCD, tem-se:

\bar{P N}

‖

\bar{B D}

‖

\bar{Q M}

Como

\bar{P Q}

‖

\bar{M N}

\bar{P N}

‖

\bar{Q M}

, o quadrilátero MNPQ é um paralelogramo.

41. d) Neste caso, MN = 6 centímetros, pois 12 : 2 = 6.

41. e) Neste caso, QM = 8 centímetros, pois 16 : 2 = 8.

41. f) Neste caso, BD = 40 centímetros, pois 2 ⋅ 20 = 40.

44. a) Sendo x e y as medidas das bases do trapézio, temos:

\frac{x + y}{2}

= 20 ⇒ x + y = 2 ⋅ 20 = 40

A medida do perímetro do trapézio é 64 centímetros (12 + 12 + x + y = 24 + 40 = 64).

44. b) Sendo x < y, temos:

y = 32 centímetros (8 + y = 40 ⇒ y = 32)

Para saber mais

Página 195

Soma das medidas dos ângulos de polígonos
Polígono	n	Si	Se
Triângulo	3	Si3 = (3 − 2) ⋅ 180° = 180°	Se3 = 360°
Quadrilátero	4	Si4 = (4 − 2) ⋅ 180° = 360°	Se4 = 360°
Pentágono	5	Si5 = (5 − 2) ⋅ 180° = 540°	Se5 = 360°
Hexágono	6	Si6 = (6 − 2) ⋅ 180° = 720°	Se6 = 360°
Heptágono	7	Si7 = (7 − 2) ⋅ 180° = 900°	Se7 = 360°
Octógono	8	Si8 = (8 − 2) ⋅ 180° = 1.080°	Se8 = 360°
Eneágono	9	Si9 = (9 − 2) ⋅ 180° = 1.260°	Se9 = 360°
Decágono	10	Si10 = (10 − 2) ⋅ 180° = 1.440°	Se10 = 360°

2. a)

2 \cdot S_{i 3} = 2 \cdot 180 ° = 360 ° = S_{i 4}

, ou seja, o polígono é um quadrilátero.

2 \cdot S_{e 3} = 2 \cdot 360 ° = 720 °

, ou seja, nenhum polígono.

Página oitenta e nove

2. b)

2 \cdot S_{i 3} = 3 \cdot 180 ° = 540 ° = S_{i 5}

, ou seja, o polígono é um pentágono.

3 ⋅ Se₃ = 3 ⋅ 360° = .1080°, ou seja, nenhum polígono.

3. a)

2 \cdot S_{i 3} = 2 \cdot 180 ° = 360 ° = S_{i 4}

2 \cdot S_{e 3} = 2 \cdot 360 ° = 720 °; S_{e 6} = 360 °

3. b)

2 \cdot S_{i 4} = 2 \cdot 360 ° = 720 ° = S_{i 6}

2 \cdot S_{e 4} = 2 \cdot 360 ° = 720 °; S_{e 8} = 360 °

3. c)

2 \cdot S_{i 5} = 2 \cdot 540 ° = 1 080 ° = S_{i 8}

2 \cdot S_{e 5} = 2 \cdot 360 ° = 720 °; S_{e 10} = 360

3. d) Dois lados não são suficientes para compor um polígono.

3. e)

3 \cdot S_{i 3} = 3 \cdot 180 ° = 540 ° = S_{i 5}

3 \cdot S_{e 3} = 3 \cdot 360 ° = 1 080 °; S_{e 9} = 360 °

4. Espera-se que os estudantes concluam que nem as grandezas

S_{i} e n

, nem as grandezas

S_{e} e n

formam proporções.

Trabalhando a informação

1. Resposta possível: sabor uva, não contém glúten, ingredientes, zero de açúcar, 15 gramas, código de barras, modo de preparo, validade, lote.

2. Sim, a gelatina não contém glúten.

3. A resposta depende da data em que a atividade é realizada.

4. Ela usou três caixinhas de 15 gramas, o que equivale a 45 gramas, pois 3 ⋅ 15 = 45. Na caixinha, informa-se que não é necessário usar açúcar, então Valentina não usou açúcar.

5. Para cada caixinha, é necessário usar 250 mililitros de água, então Valentina precisou de 750 mililitros de água (3 ⋅ 250 = 750). Ao todo, Valentina precisa de .1500 mililitros de água (750 + 750 = .1500), ou 1,5 litro.

6. Espera-se que os estudantes respondam que sim, no contorno das imagens da uva.

7. Medida do comprimento: 6,0 centímetros; medida da altura: 5,0 centímetros; medida da largura: 1,5 centímetro.

8. 8 retângulos e 5 trapézios.

9. Espera-se que os estudantes respondam que ela deve separar para reciclagem.

10. Resposta pessoal.

Exercícios complementares

1. a) Retângulo.

1. b) Trapézio isósceles.

1. c) Trapézio retângulo.

1. d) Quadrado.

2. 90° + 50° + x + 2x + 10° = 360° ⇒ 3x + 150° = 360° ⇒ 3x = 210° ⇒ x = 70°

3. a bê cê dê é um paralelogramo, porque suas diagonais se intersectam nos respectivos pontos médios.

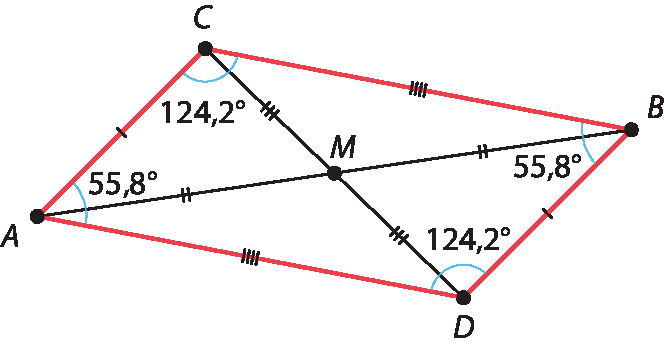
Ilustração. Paralelogramo ABCD com duas diagonais que se cruzam no centro, em M. ângulos: A: 55,8 graus. B: 55,8 graus. C: 124,2 graus e D: 124,2 graus.

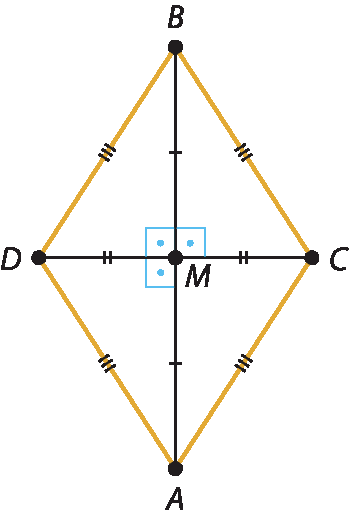
Ilustração. Losango ABCD. Duas retas, sendo AB e CD se cruzam no centro, em M.

Como suas diagonais são perpendiculares entre si, então seus quatro lados são congruentes. Desse modo, trata-se de um losango.

5. a) Como os ângulos opostos de um paralelogramo são congruentes:

5x – 56° = 3x + 16° ⇒ 5x –3x = 16° + 56° ⇒

⇒ x = 72° : 2 ⇒ x = 36°

5. b) Os ângulos adjacentes a um mesmo lado do paralelogramo são suplementares. Assim:

5x + 12° + 2x = 180° ⇒ 7x = 180° ‒ 12° ⇒

⇒ 7x = 168° ⇒ x = 168° : 7 ⇒ x = 24°

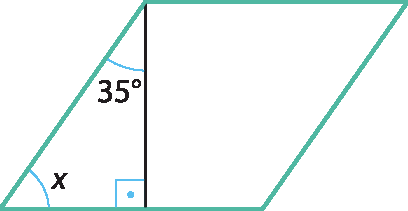
Ilustração. Paralelogramo com um segmento que parte de um vértice de um dos lados para o lado oposto, formando um triângulo retângulo. O ângulo interno, não reto, na base do triângulo mede x grau. O outro ângulo interno do triângulo mede 35 graus.

Sendo x a medida dos ângulos agudos desse paralelogramo, no vértice superior esquerdo do paralelogramo, seus ângulos obtusos medem 125° (35° + 90° = 125°).

Do triângulo retângulo indicado na figura, temos:

x + 35° + 90° = 180° ⇒ x + 125° = 180° ⇒ x = 55°

7. Como as diagonais de um losango são bissetrizes de seus ângulos internos, seus dois ângulos agudos medem 56°, pois 2 ⋅ 28° = 56°. Como os ângulos adjacentes a um mesmo lado de um losango são suplementares, seus dois ângulos obtusos medem 124°, pois 180° ‒ 56° = 124°.

8. a) Como os ângulos da base de um trapézio isósceles são congruentes, então suas medidas são iguais; assim:

3x + 10° = x + 40° ⇒ 3x – x = 40° ‒ 10° ⇒

⇒ 2x = 30° ⇒ x = 15°

Página noventa

8. b) Como os ângulos adjacentes a um mesmo lado não paralelo de um trapézio são suplementares, então:

2x + 7° + 2x ‒ 27° = 180° ⇒ 4x = 200° ⇒ x = 50°

9. Considere x a medida do ângulo pedido.

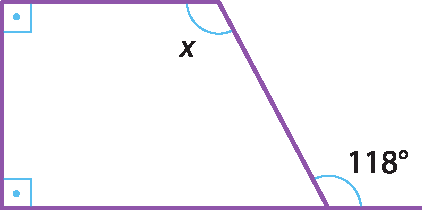
Ilustração. Trapézio retângulo, com dois ângulos retos e um ângulo obtuso, acima, com medida de x grau. No canto inferior direito, ângulo externo de medida 118 graus.

Por x ser alterno interno ao ângulo externo de medida 118°, a medida de x é igual a 118°.

11. Como a base média mede 30 centímetros,

\frac{x + y}{2}

= 30 ⇒ x + y = 60.

Então, para a medida do perímetro, temos:

x + y + 10 + 10 = 60 + 20 = 80

Portanto, a medida do perímetro do trapézio é 80 centímetros.

12.

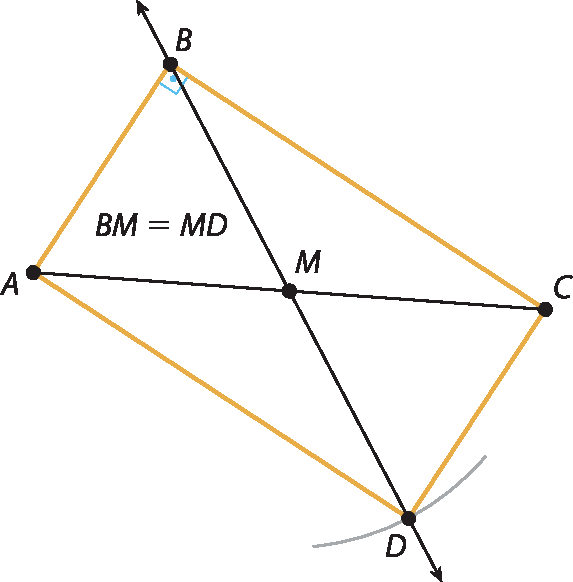
Ilustração. Retângulo A B C D com duas diagonais que se cruzam no centro, em M. Há indicação que a medida do segmento B M é igual à medida do segmento M D.

dê ême ah pelo caso éle á éle, pois:

•

\bar{B M}

≅

\bar{M D}

(D é simétrico de B em relação a M)

•

B \hat{M} C

≅

D \hat{M} A

(opostos pelo vértice)

•

\bar{A M}

≅

\bar{M C}

(M é ponto médio de

\bar{A C}

)

Então, os ângulos

C \hat{B} M e A \hat{D} M

são congruentes e, como eles também são alternos internos, conclui-se que os lados

\bar{A D} e \bar{B C}

são paralelos.

O mesmo raciocínio aplicado aos lados

\bar{A B} e \bar{C D}

garante que o quadrilátero a bê cê dê é um paralelogramo.

Verificando

1. Sendo x a medida do ângulo obtuso do trapézio, temos:

x + 55° + 90° + 90° = 360° ⇒ x + 235° = 360° ⇒ x = 125°

Alternativa c.

2. Como os ângulos adjacentes a um mesmo lado de um paralelogramo são suplementares, no paralelogramo laranja, tem-se:

a + 70° = 180° ⇒ a = 180° ‒ 70° ⇒ a = 110°

Como os paralelogramos amarelo e azul são congruentes, em torno do vértice do ângulo de medida 70° tem-se:

c + c + 70° = 360° ⇒ 2c = 360° ‒ 70° ⇒ c = 190° : 2 ⇒ c = 145°

b + 145° = 180° ⇒ b = 35°

Alternativa b.

3. Como as diagonais de um paralelogramo interceptam-se nos seus pontos médios,

m (\bar{C M}) = m (\bar{A M})

= 5 centímetros e

m (\bar{D M}) = m (\bar{B M})

= 7 centímetros.

Assim,

m (\bar{A C})

= 10 centímetros, pois

m (\bar{A C}) = m (\bar{A M}) + m (\bar{C M}

) = = 5 centímetros + 5 centímetros = 10 centímetros, e

m (\bar{B D})

= 14 centímetros, pois

m (\bar{B D})

m (\bar{B M}) + m (\bar{D M})

= 7 centímetros + 7 centímetros = 14 centímetros. Então, a soma das medidas dessas diagonais é 24 centímetros (10 + 14 = 24).

Alternativa c.

4. Todo retângulo tem diagonais congruentes.

Apenas os losangos que são quadrados têm diagonais congruentes.

Apenas os paralelogramos que são retângulos têm diagonais congruentes.

Alternativa b.

5. Como

m (\bar{C E}) = m (\bar{A E})

= 6,5 centímetros, conclui-se que

m (\bar{A C})

= 13 centímetros, pois

m (\bar{A C})

m (\bar{A E})

m (\bar{C E})

= 6,5 centímetros + 6,5 centímetros = 13 centímetros. Sabendo que

m (\bar{B C}) = m (\bar{D A})

= 20 centímetros;

m (\bar{C D})

m (\bar{A B})

= 12 centímetros, conclui-se que a medida do perímetro do triângulo á cê dê é 45 centímetros:

m (\bar{C D}) + m (\bar{D A}) + m (\bar{A C})

= 12 centímetros + 20 centímetros + 13 centímetros = 45 centímetros

Alternativa c.

6. Os ângulos adjacentes à mesma base de um trapézio isósceles são congruentes.

Os trapézios isósceles têm dois ângulos agudos e dois ângulos obtusos.

As bases de todo trapézio são paralelas e têm medidas diferentes; portanto, os lados de um trapézio não são todos congruentes.

Alternativa a.

7. Sendo x a medida da base maior:

\frac{x + 5}{2}

= 10 ⇒ x + 5 = 2 ⋅ 10 ⇒ x = 20 ‒ 5 ⇒ x = 15

Logo, a base maior mede 15 centímetros.

Alternativa b.

8. Sendo x e y as medidas das bases, do valor da base média tem-se:

\frac{x + y}{2}

= 24 ⇒ x + y = 2 ⋅ 24 ⇒ x + y = 48

Sendo z a medida dos lados não paralelos, da medida do perímetros tem-se:

x + y + z + z = 88 ⇒ 48 + 2z = 88 ⇒ 2z = 88 ‒ 48 ⇒

⇒ z =

\frac{40}{2}

⇒ z = 20

Portanto, cada um dos lados não paralelos do trapézio mede 20 centímetros.

Alternativa b.

Diversificando

1. Três tipos: retângulo (B, D, ê, F e H, sendo D e F quadrados) e trapézio (a, C, G e ih).

Página noventa e um

2. a) Se os livros ficarem totalmente dentro da caixa, caberão nela 10 livros (20 : 2 = 10). Se Gabriela deixar uma parte de cada livro para fóra, caberão 13 livros (26 : 2 = 13).

2. b) 13 ⋅ 20 centímetros ⋅ 2 centímetros ⋅ (26 centímetros ‒ 20 centímetros) = 520 centímetros quadrados ⋅ 6 centímetros = .3120 centímetros cúbicos

3. Resposta possível: Sim, basta imaginar um prisma de base triangular sem uma das bases.

4. a) Sim, o triângulo terá cada lado composto de 4 palitos de sorvete.

4. b) O retângulo. O retângulo de maior medida de área é o quadrado cujo lado é formado por 3 palitos de sorvete.

Capítulo 10 — Sistemas de equações do 1º grau com duas incógnitas

• Objetivos do capítulo e justificativas

• Conceituar e resolver sistemas de equações do 1º grau com duas incógnitas.

• Resolver problemas envolvendo valor numérico de expressões algébricas.

• Reconhecer e aplicar os métodos de resolução de um sistema de equações do 1º grau.

• Representar geometricamente uma equação linear do 1º grau com duas incógnitas, associando-a a uma reta do plano cartesiano.

• Obter graficamente a solução de um sistema de equações do 1º grau representando suas equações lineares no plano cartesiano.

• Classificar um sistema de equações do 1º grau como sistema determinado, indeterminado ou impossível.

• Resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau do tipo ax² = b.

• Identificar a natureza da variação de duas grandezas expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.

• Interpretar gráfico de setores e gráfico de colunas compostas.

• Analisar gráfico para representar dados envolvendo a média aritmética.

Neste capítulo, a Unidade Temática Álgebra é ampliada e aprofundada com conteúdos que retomam a modelagem de situações por meio de expressões algébricas, a resolução de equações e de sistemas de equações de 1º grau que favorecem o desenvolvimento da competência geral 2 e competência específica 5, pois, mais uma vez, os estudantes utilizam ferramentas matemáticas para modelar e resolver problemas.

O estudo da representação geométrica de equação do 1º grau com duas incógnitas e a de sistemas de equações desse mesmo tipo possibilita aos estudantes desenvolverem a competência geral 4 e as competências específicas 3 e 6, pois são feitas inter-relações entre Álgebra e Geometria e podem-se enfrentar situações-problema que permitem aos estudantes utilizarem diferentes registros e linguagens.

De maneira semelhante, os objetivos que envolvem interpretação de gráficos se justificam à medida que possibilitam desenvolver a competência geral 4 e a competência específica 4, pois os estudantes se apropriam de diferentes maneiras para divulgar informações e adquirem condições de observar e analisar aspectos qualitativos e quantitativos em diferentes situações.

Propomos em algumas atividades o uso de software para representações gráficas, com o objetivo de observarem padrões e regularidades entre as variáveis, o que contribui para o desenvolvimento da competência geral 5 e da competência específica 2.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah zero seis) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.

(ê éfe zero oito ême ah zero sete) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano.

(ê éfe zero oito ême ah zero oito) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-lo, utilizando, inclusive, o plano cartesiano como recurso.

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo ax2 = b.

(ê éfe zero oito ême ah um três) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

(ê éfe zero oito ême ah dois seis) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).

(ê éfe zero oito ême ah dois sete) Planejar e executar pesquisa amostral, selecionando uma técnica de amostragem adequada, e escrever relatório que contenha os gráficos apropriados para representar os conjuntos

Os conceitos e as atividades ligados à Unidade Temática Álgebra, foco deste capítulo, utilizam como base os conhecimentos já construídos nos capítulos 4, 5 e 6 deste livro e aqueles trazidos do 7º ano (ê éfe zero sete ême ah um três e ê éfe zero sete ême ah um oito). Exploram-se situações e resoluções de problemas que envolvem sistemas de equações do 1º grau com duas incógnitas e os métodos de resolução desses sistemas (método da substituição e da adição) retomando e mobilizando a habilidade (ê éfe zero oito ême ah zero seis) e desenvolvendo as habilidades (ê éfe zero oito ême ah zero sete) e (ê éfe zero oito ême ah zero oito).

Página noventa e dois

São abordadas também a representação gráfica de uma equação do 1º grau com duas incógnitas, a solução gráfica de um sistema de duas equações do 1º grau e a classificação desses sistemas. Além disso, exploram-se ideias sobre grandezas diretamente proporcionais e grandezas inversamente proporcionais, associadas a gráficos no plano cartesiano mobilizando as habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três).

Desse modo, espera-se que esses conteúdos constituam embasamento necessário, entre outros assuntos, ao estudo de funções, durante o 9º ano (ê éfe zero nove ême ah zero seis). Ainda na Unidade Temática Álgebra, este capítulo trata da resolução de equações do tipo ax2 = b, por exemplo, na seção Para saber mais com o tema “Raiz quadrada ou diferença de dois quadrados”, contribuindo para a mobilização da habilidade (ê éfe zero oito ême ah zero nove).

Algumas das atividades vinculam-se também à Unidade Temática Probabilidade e estatística, caso da seção Trabalhando a informação, que apresenta a “Composição de um gráfico de colunas formadas a partir de outros gráficos”, que explora gráficos de setores e gráfico de colunas compostas e desenvolve a habilidade (ê éfe zero oito ême ah dois três); na última seção Trabalhando a informação do capítulo, desenvolvem-se as habilidades (ê éfe zero oito ême ah dois seis) e (ê éfe zero oito ême ah dois sete), ao propor a realização de uma pesquisa.

• Comentários e resoluções

Exercícios propostos

2. a) Pelo método da substituição, isolando x na 2ª equação temos: x ‒ 3y = ‒5 ⇒ x = 3y – 5. Substituindo x por (3y ‒ 5) na 1ª equação, temos:

3 ⋅ (3y ‒ 5) + 2y = 40 ⇒ 9y – 15 + 2y = 40 ⇒

⇒ 11y = 55 ⇒ y = 5

Substituindo y por 5 na equação em que x está isolado, temos:

x = 3 ⋅ 5 ‒ 5 ⇒ x = 10

Portanto, o par ordenado (10, 5) é a solução do sistema.

Pelo método da adição, multiplicando a 2ª equação por (‒3) e adicionando, membro a membro, as duas equações, obtemos:

\{\begin{cases} 3 x + 2 y = 40 \\ - 3 x + 9 y = 15 \end{cases}

⇒ 11y = 55 ⇒

\frac{11 y}{11} = \frac{55}{11}

⇒ y = 5

Substituindo y por 5 na 1ª equação, obtemos:

3x + 2 ⋅ 5 = 40 ⇒ 3x + 10 = 40 ⇒ 3x = 30 ⇒ x = 10

Portanto, o par (10, 5) é a solução do sistema.

2. b) Pelo método da substituição, isolando x na 2ª equação, obtendo:

5x = 2y + 29 ⇒ x =

\frac{2 y + 29}{5}

⇒ x = 0,4y + 5,8

Substituindo x por (0,4y + 5,8) na 1ª equação, obtemos:

4 ⋅ (0,4y + 5,8) + 3y = 14 ⇒ 1,6y + 23,2 + 3y = 14 ⇒ 4,6y = ‒9,2 ⇒ y = ‒2

Substituindo y por ‒2 na equação em que x está isolado, obtemos:

x = 0,4 ⋅ (‒2) + 5,8 ⇒ x = ‒0,8 + 5,8 ⇒ x = 5

Portanto, o par (5, ‒2) é a solução do sistema. Pelo método da adição, multiplicando a 1ª equação por 2 e a 2ª equação por 3, obtemos:

\{\begin{cases} 4 x + 3 y = 14 \cdot (2) \\ 5 x - 2 y = 29 \cdot (3) \end{cases}

⇒

\{\begin{cases} 8 x + 6 y = 28 \\ 15 x - 6 y = 87 \end{cases}

Adicionando, membro a membro, as equações, obtemos:

23x = 115 ⇒ x = 5

Substituindo x por 5 na 1ª equação, temos:

4 ⋅ 5 + 3y = 14 ⇒ 3y = 14 ‒ 20 ⇒ y = ‒2

Portanto, o par (5, ‒2) é a solução do sistema.

3. a) Subtraindo a 1ª equação da 2ª equação, teremos:

‒y = ‒5 + 1 = ‒4

Logo, y = 4.

Substituindo o valor de y na segunda equação, temos:

x = 2 ⋅ 4 + 1 ⇒ x = 9

Logo, o par (9, 4) é solução do sistema.

3. b) Como y = x ‒ 5, temos:

x + x ‒ 5 = 9 ⇒ 2x = 14 ⇒ x = 7

Assim, y = 7 ‒ 5 = 2. Logo, o par (7, 2) é solução do sistema.

4. Sendo p e f as idades atuais do pai e do filho, respectivamente, hoje, temos: p = 20 + f. Daqui a 5 anos, p + 5 = 2(f + 5). Substituindo p por (20 + f) na 2ª equação, obtemos:

(20 + f) + 5 = 2(f + 5) ⇒ 25 + f = 2f + 10 ⇒ f = 15

Substituindo f por (15) na 1ª equação, obtemos:

p = 20 + 15 ⇒ p = 35

Assim, a idade do filho é 15 anos e a idade do pai é 35 anos.

5. Sendo d o algarismo das dezenas e u o algarismo das unidades, o número considerado fica expresso por:

10d + u

Então, temos o sistema:

\{\begin{cases} u = 5 + d \\ 10 d + u = 3 (d + u) \end{cases}

Substituindo u por (5 + d) na 2ª equação, obtemos:

10d + 5 + d = 3(d + 5 + d) ⇒ 11d + 5 = 6d + 15 ⇒

⇒ 5d = 10 ⇒ d = 2

Substituindo d por 2 na 1ª equação, obtemos:

u = 5 + 2 ⇒ u = 7

Portanto, trata-se do número 27, pois (10 ⋅ 2) + 7 = 27.

6. a) Efetuando a propriedade distributiva e isolando os termos literais das equações, obtemos:

\{\begin{cases} 2 (x - 2) + 3 y = - 7 \\ 3 x - 2 (y - 4) = - 3 \end{cases} \Rightarrow \{\begin{cases} 2 x - 4 + 3 y = - 7 \\ 3 x - 2 y + 8 = - 3 \end{cases} \Rightarrow

\Rightarrow \{\begin{cases} 2 x + 3 y = - 3 \\ 3 x - 2 y = - 11 \end{cases}

Multiplicando a 1ª equação por 2 e a 2ª equação por 3, obtemos:

\{\begin{cases} 2 x + 3 y = - 3 \\ 3 x - 2 y = - 11 \end{cases} \Rightarrow \{\begin{cases} 4 x + 6 y = - 6 \\ 9 x - 6 y = - 33 \end{cases}

Fazendo a adição das duas equações, obtemos:

13x + 0y = ‒39 ⇒ x = ‒3

Substituindo x por ‒3 na 1ª equação, temos:

2 ⋅ (‒3) + 3y = ‒3 ⇒ ‒6 + 3y = ‒3 ⇒ 3y = 3 ⇒ y = 1

Portanto, o par ordenado (‒3, 1) é a solução do sistema.

Página noventa e três

6. b)

\{\begin{cases} 2, 4 x - 0, 6 y = 2, 4 \\ 3, 6 x + y = 7, 4 \end{cases}

Isolando y na 2ª equação, temos:

y = 7,4 ‒ 3,6x

Substituindo y por 7,4 ‒ 3,6x na 1ª equação, obtemos:

2,4x ‒ 0,6(7,4 ‒ 3,6x) = 2,4 ⇒ 2,4x ‒ 4,44 + 2,16x = 2,4 ⇒

⇒ 4,56x = 2,4 + 4,44 ⇒ 4,56x = 6,84 ⇒ x = 1,5

Substituindo x por 1,5 na equação em que y está isolado, obtemos:

y = 7,4 ‒ 3,6 ⋅ 1,5 ⇒ y = 7,4 ‒ 5,4 ⇒ y = 2

Portanto, o par ordenado (1,5; 2) é a solução do sistema.

7. Sendo b a medida da base e h a medida da altura do retângulo, em centímetro, dos dados do enunciado, podemos montar o seguinte sistema.

\{\begin{cases} 2 b + 2 h = 22 \\ b - \frac{h}{2} = 5 \end{cases}

Multiplicando a 2ª equação por 4, obtém-se:

\{\begin{cases} 2 b + 2 h = 22 \\ 4 b - 2 h = 20 \end{cases}

Adicionando, membro a membro, obtemos:

6b = 42 ⇒

\frac{6 b}{6} = \frac{42}{6}

⇒ b = 7

Substituindo b por 7 na 1ª equação, obtemos:

2 ⋅ 7 + 2h = 22 ⇒ 14 + 2h = 22 ⇒ 2h = 8 ⇒ h = 4

Portanto, a medida da área do retângulo é 28 centímetros quadrados (7 ⋅ 4 = 28).

9. Sendo x a quantidade de notas de 5 reais e y a quantidade de notas 2 reais, pelas informações do enunciado podemos montar o seguinte sistema de equações:

\{\begin{cases} 5 x + 2 y = 89 \\ x + y = 22 \end{cases}

Multiplicando a 2ª equação por ‒2, obtemos:

\{\begin{cases} 5 x + 2 y = 89 \\ - 2 x - 2 y = - 44 \end{cases}

Adicionando, membro a membro, obtemos:

3x + 0y = 45 ⇒ x = 15

Substituindo x por 15 na 2ª equação, obtemos:

15 + y = 22 ⇒ y = 7

Portanto, foram 15 notas de R$ 5,00cinco reais e 7 notas de R$ 2,00dois reais.

13. a) Resposta possível:

\{\begin{cases} y = x \\ y = - x \end{cases}

Solução: (0, 0)

13. b) Resposta possível:

\{\begin{cases} 2 x - 2 y = 0 \\ x - y = - 1 \end{cases}

Não há par ordenado que seja solução do sistema.

14. a) O par ordenado (3, 4) é a solução do sistema.

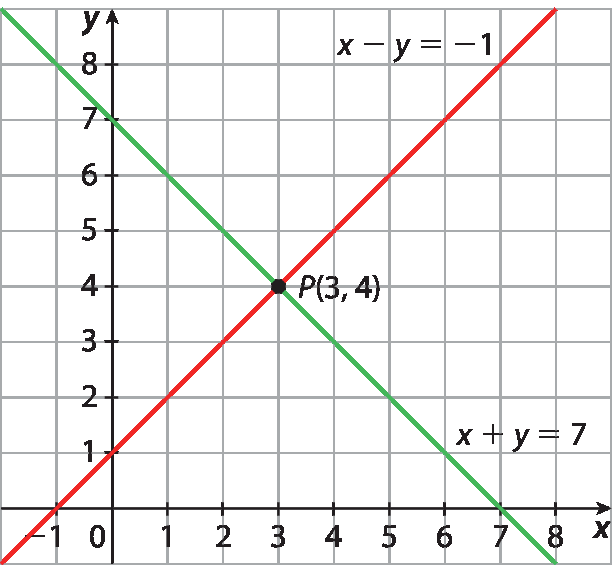
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 1 e 8. Eixo vertical y, com marcações de valores entre 0 e 8. Reta vermelha inclinada para cima, passando pelos pontos de coordenadas (menos 1, 0) e P (3, 4). Ela tem equação: x menos y igual a menos 1. Reta verde inclinada para baixo, passando pelos pontos de coordenadas (0, 7) e P (3, 4). Ela tem equação: x mais y igual a 7. As retas se cruzam no ponto P.

14. b) O par ordenado (3, ‒1) é a solução do sistema.

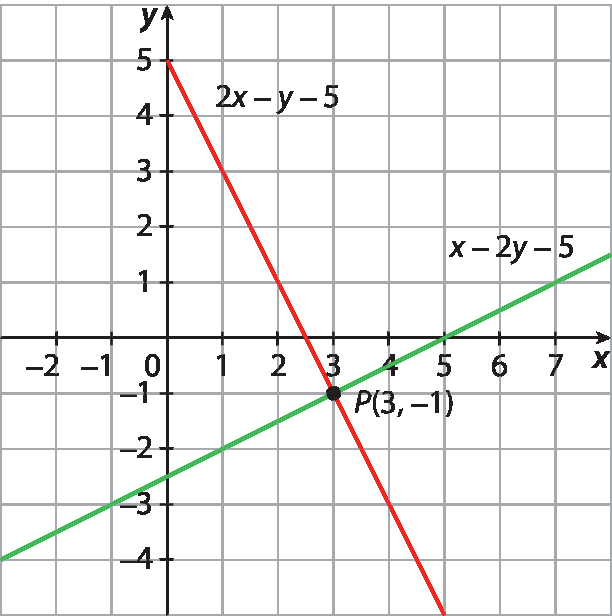
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 2 e 7. Eixo vertical y, com marcações de valores entre menos 4 e 5. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas (0, 5) e P (3, menos 1). Ela tem equação: 2 x menos y igual a 5. Reta verde inclinada para cima, passando pelos pontos de coordenadas P (3, 4) e (5, 0). Ela tem equação: x menos 2 y igual a 5. As retas se cruzam no ponto P.

14. c) O par ordenado (‒3, 2) é a solução do sistema.

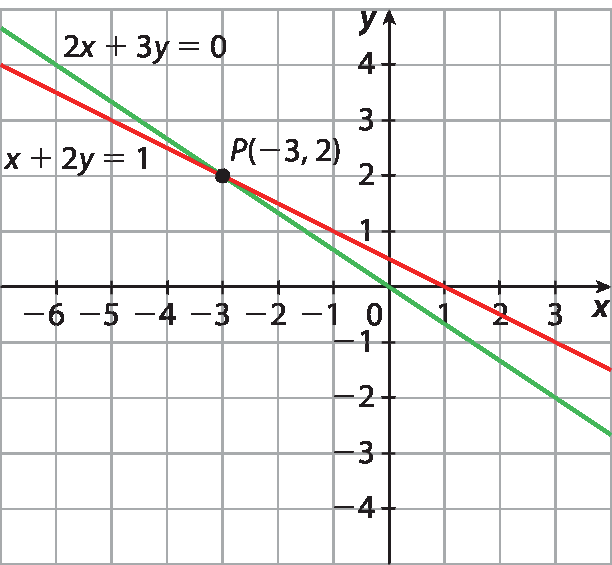
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 6 e 3. Eixo vertical y, com marcações de valores entre menos 4 e 4. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas P (menos 3, 2) e (1, 0). Ela tem equação: x mais 2 y igual a 1. Reta verde inclinada para baixo, passando pelos pontos de coordenadas P (menos 3, 2) e (0, 0). Ela tem equação: 2 x mais 3 y igual a 0. As retas se cruzam no ponto P.

14. d) O par ordenado (‒1, 1) é a solução do sistema.

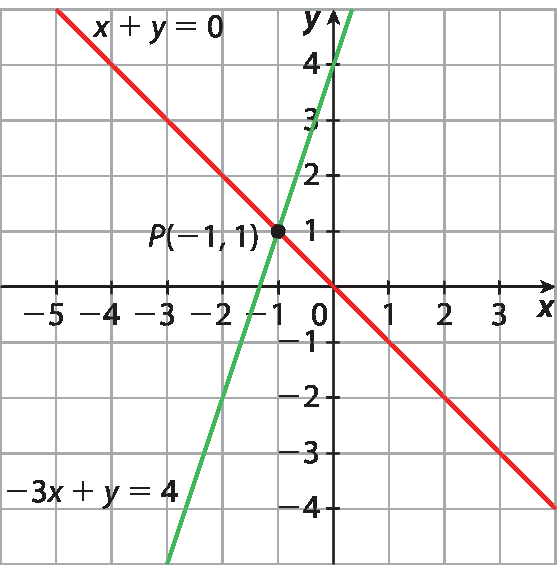
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 5 e 3. Eixo vertical y, com marcações de valores entre menos 4 e 4. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas P (menos 1, 1) e (0, 0). Ela tem equação: x mais y igual a 0. Reta verde inclinada para cima, passando pelos pontos de coordenadas P (menos 1, 1) e (0, 4). Ela tem equação: menos 3 x mais y igual a 4. As retas se cruzam no ponto P.

Página noventa e quatro

15. a) Observando que as retas são concorrentes, conclui-se que o sistema é determinado. O par ordenado (4, 3) é a solução do sistema.

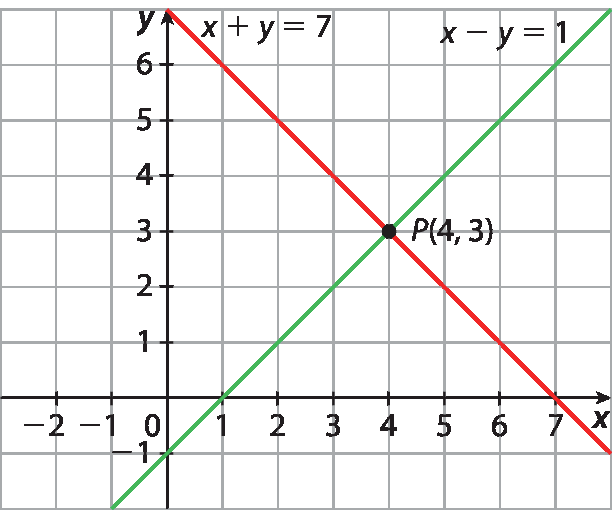
15. b) Observando que as retas são paralelas, conclui-se que o sistema é impossível.

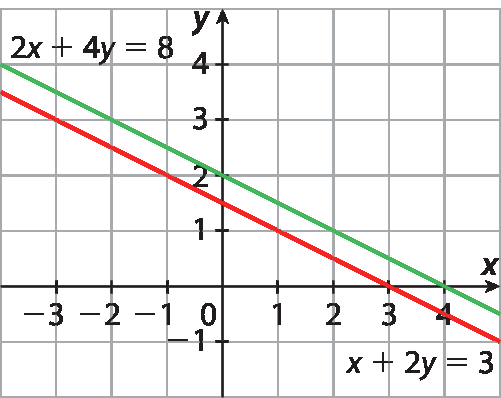
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 3 e 4. Eixo vertical y, com marcações de valores entre menos 1 e 4. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas (0, um meio) e (3, 0). Ela tem equação: x mais 2 y igual a 3. Reta verde com a mesma inclinação da reta vermelha, passando pelos pontos de coordenadas (0, 2) e (4, 0). Ela tem equação: 2 x mais 4 y igual a 8. As retas não se interceptam.

15. c) Observando que as retas são concorrentes, conclui-se que o sistema é determinado. O par ordenado (‒2, 4) é a solução do sistema.

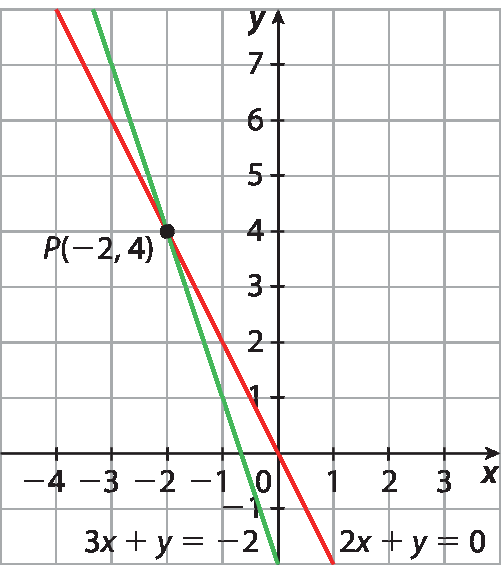
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 4 e 3. Eixo vertical y, com marcações de valores entre menos 2 e 7. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas P (menos 2, 4) e (0, 0). Ela tem equação: 2 x mais y igual a 0. Reta verde inclinada para baixo, passando pelos pontos de coordenadas P (menos 2, 4) e (0, menos 2). Ela tem equação: 3 x mais y igual a menos 2. As retas se cruzam no ponto P.

15. d) Observando que as retas são coincidentes, conclui-se que o sistema é indeterminado.

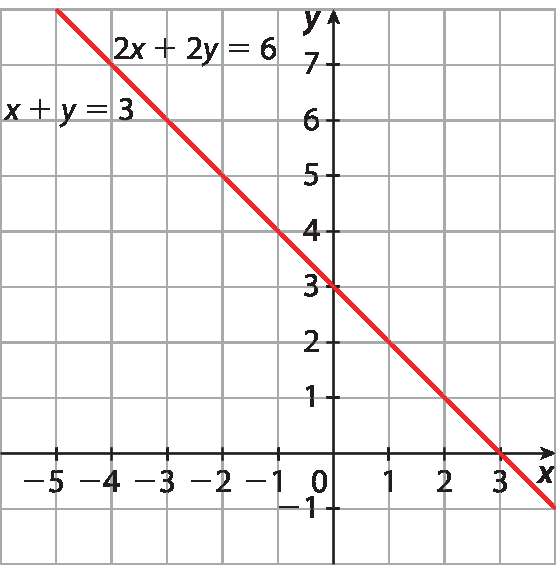
15. e) Observando que as retas são paralelas, conclui-se que o sistema é impossível.

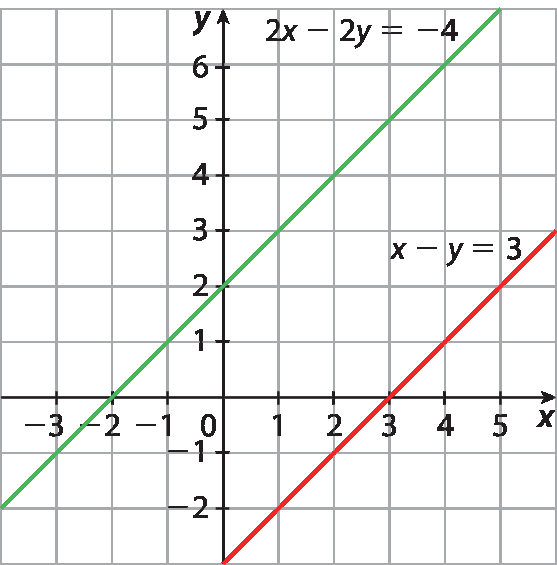
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 3 e 5. Eixo vertical y, com marcações de valores entre menos 3 e 6. Reta vermelha inclinada para cima, passando pelos pontos de coordenadas (0, menos 3) e (3, 0). Ela tem equação: x menos y igual a 3. Reta verde com a mesma inclinação da reta vermelha, passando pelos pontos de coordenadas (menos 2, 0) e (0, 2). Ela tem equação: 2 x menos 2 y igual a 4. As retas não se interceptam.

15. f) Observando que as retas são coincidentes, conclui-se que o sistema é indeterminado.

Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 1 e 6. Eixo vertical y, com marcações de valores entre menos 2 e 5. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas (0, 5) e (2,5, 0). Ela representa a equação: 4 x mais 2 y igual a 10, e a equação: 2 x mais y igual a 5.

Exercícios complementares

1. Sendo x a quantidade de notas de 50 reais e y a quantidade de notas de 100 reais, podemos escrever o seguinte sistema de equações.

\{\begin{cases} 50 x + 100 y = 700 \\ x + y = 10 \end{cases}

Dividindo a 1ª equação por 50 e multiplicando a 2ª equação por ‒1, obtemos:

\{\begin{cases} 50 x + 100 y = 700 \\ x + y = 10 \end{cases}

⇒

\{\begin{cases} x + 2 y = 14 \\ - x - y = - 10 \end{cases}

Adicionando, membro a membro, obtemos y = 4. Substituindo y por 4 na 2ª equação do sistema original, obtemos:

x + 4 = 10 ⇒ x = 10 ‒ 4 ⇒ x = 6

Portanto, Cristina retirou 6 notas de R$ 50,00cinquenta reais e 4 notas de R$ 100,00cem reais.

2. Seja x o número de moças e y o número de rapazes, com os dados informados no enunciado podemos escrever o seguinte sistema de equações.

\{\begin{cases} y = 4 x + 3 \\ y - 1 = 5 x \end{cases}

Substituindo y por (4x + 3) na 2ª equação, obtemos:

4x + 3 ‒ 1 = 5x ⇒ 2 = 5x ‒ 4x ⇒ x = 2

Substituindo x por 2 na 1ª equação, obtemos:

y = 4 ⋅ 2 + 3 ⇒ y = 11

Portanto, a quantidade total de jovens é 13, pois:

x + y = 2 + 11 = 13

Página noventa e cinco

4. a)

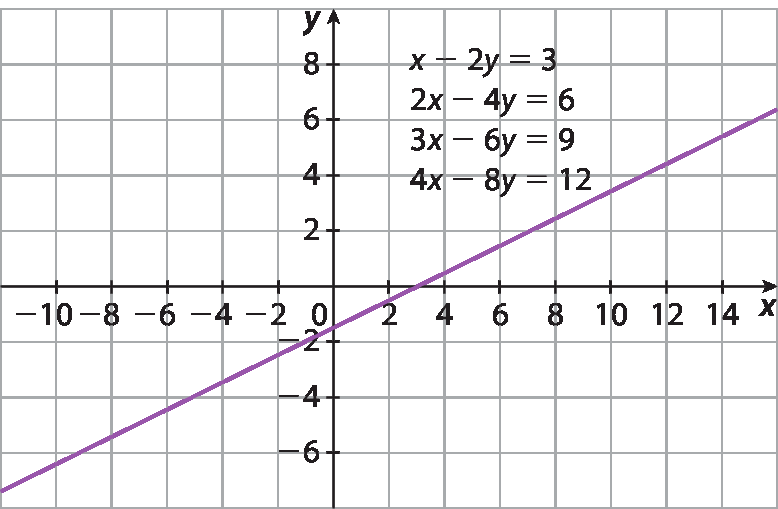
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 10 e 14. Eixo vertical y, com marcações de valores entre menos 6 e 8. Reta inclinada para cima, passando pelo eixo x entre os valores 2 e 4, e pelo eixo y entre os valores menos 2 e 0. Ela representa as equações: x menos 2 y igual a 3; 2 x menos 4 y igual a 6; 3 x menos 6 y igual a 9; e 4 x menos 8 y igual a 12.

4. b) Da representação no plano cartesiano, percebemos que as retas são coincidentes.

4. c) Ao multiplicar ambos os membros da equação x ‒ 2y = 3 por 2, ou por 3 ou por 4, obtemos, respectivamente:

2x ‒ 4y = 6

3x ‒ 6y = 9

4x ‒ 8y = 12

5. a) Observando que as retas são concorrentes, conclui-se que o sistema é determinado. Assim, o par ordenado (7, 5) é a solução do sistema.

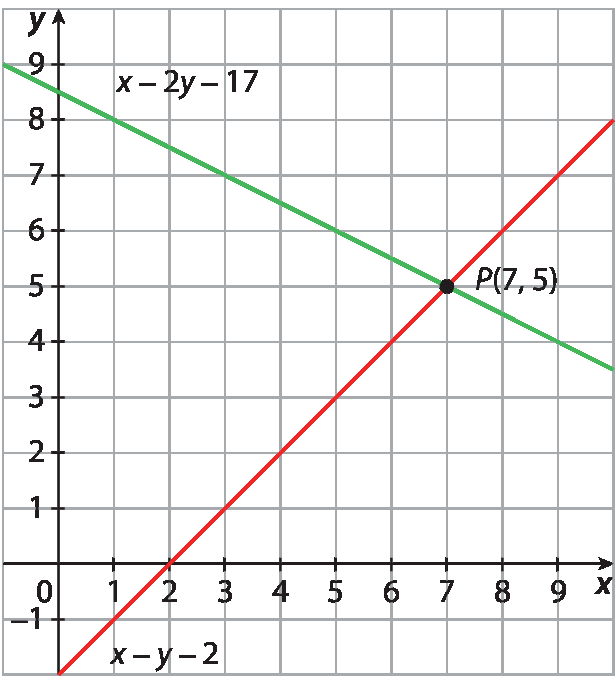
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre 0 e 7. Eixo vertical y, com marcações de valores entre menos 0 e 9. Reta vermelha inclinada para cima, passando pelos pontos de coordenadas (2, 0) e P (7, 5). Reta verde inclinada para baixo, passando pelos pontos de coordenadas (3, 7) e P (7, 5). Ela tem equação: x menos 2 y igual a 17. As retas se cruzam no ponto P.

5. b) Observando que as retas são concorrentes, conclui-se que o sistema é determinado. Assim, o par ordenado (‒5, 1) é a solução do sistema.

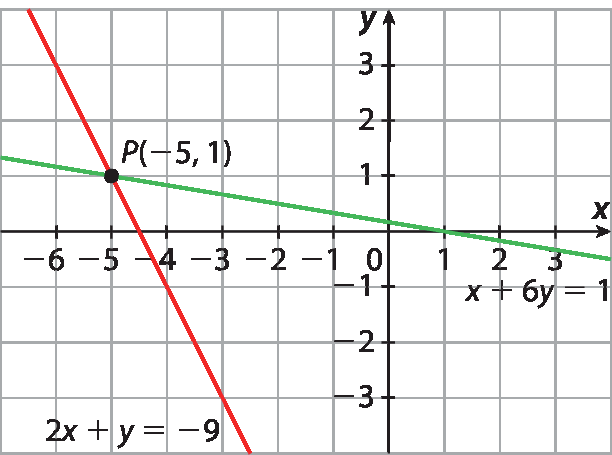
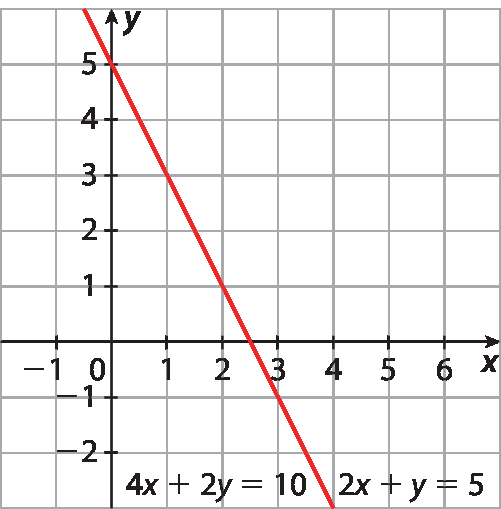
5. c) Observando que as retas são paralelas, conclui-se que o sistema é impossível.

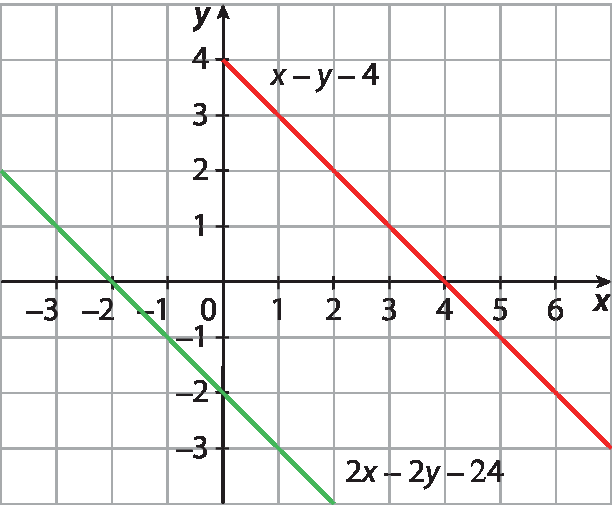
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 3 e 6. Eixo vertical y, com marcações de valores entre menos 3 e 4. Reta vermelha inclinada para baixo, passando pelos pontos de coordenadas (0, 4) e (4, 0). Ela tem equação: x menos y igual a 4. Reta verde com a mesma inclinação da reta vermelha, passando pelos pontos de coordenadas (menos 2, 0) e (0, menos 2). Ela tem equação: 2 x menos 2 y igual a menos 2.. As retas não se interceptam.

5. d) Observando que as retas são coincidentes, conclui-se que o sistema é indeterminado.

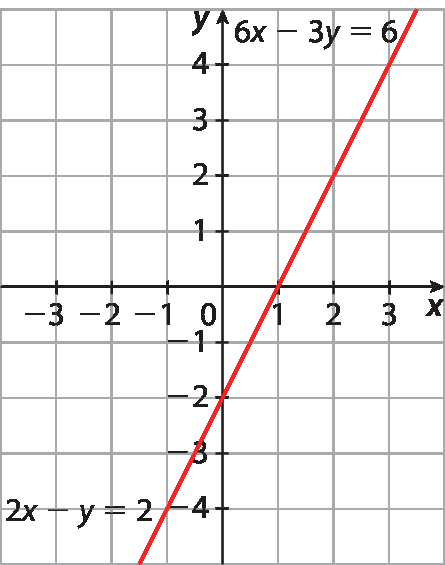
Gráfico. Plano cartesiano x y desenhado em malha quadriculada. Eixo horizontal x com marcações de valores entre menos 3 e 3. Eixo vertical y, com marcações de valores entre menos 4 e 4. Reta vermelha inclinada para cima, passando pelos pontos de coordenadas (0, menos 2) e (1, 0). Ela representa a equação: 6 x menos 3 y igual a 6, e a equação: 2 x menos y igual a 2.

6. Multiplicando a 1ª equação por 6, e a 2ª equação por 15 e simplificando as frações, obtemos:

\{\begin{cases} \frac{x}{2} + \frac{y}{3} = \frac{4}{3} \\ \frac{2 x - y}{3} - \frac{x + 3 y}{5} = 0 \end{cases}

⇒

\{\begin{cases} \frac{6 x}{2} + \frac{6 y}{3} = \frac{24}{3} \\ \frac{15 (2 x - y)}{3} - \frac{15 (x + 3 y)}{5} = 0 \end{cases}

⇒

\{\begin{cases} 3 x + 2 y = 8 \\ 5 (2 x - y) - 3 (x + 3 y) = 0 \end{cases}

Aplicando a propriedade distributiva, obtemos:

\{\begin{cases} 3 x + 2 y = 8 \\ 10 x - 5 y - 3 x - 9 y = 0 \end{cases}

⇒

\{\begin{cases} 3 x + 2 y = 8 \\ 7 x - 14 y = 0 \end{cases}

Multiplicando a 1ª equação por 7 e adicionando as duas equações membro a membro, obtemos:

28x = 56 ⇒ x =

\frac{56}{28}

⇒ x = 2

Substituindo x por 2 na equação: 3x + 2y = 8, temos:

3 ⋅ 2 + 2y = 8 ⇒ 6 + 2y = 8 ⇒ 2y = 8 ‒ 6 ⇒ 2y = 2 ⇒ y = 1

Assim, x : y = 2, pois 2 : 1 = 2.

7. Sendo a a quantidade de grampos dos processos de André e C a quantidade de grampos dos processos de Carlos, com os dados do problema podemos escrever o seguinte sistema de equações.

\{\begin{cases} A + C = 78 \\ A + 2 C = 110 \end{cases}

Multiplicando a 1ª equação por ‒1 e adicionando as equações membro a membro, obtemos C = 32. Assim, a quantidade de processos de Carlos é igual a 32.

Alternativa d.

8. O problema apresentado pode ser descrito pelo seguinte sistema de equações.

\{\begin{cases} x + y = 84 \\ 3 x = 4 y \end{cases} \Rightarrow \{\begin{cases} x + y = 84 \\ x = \frac{4}{3} y \end{cases}

Substituindo x por

\frac{4}{3} y

na equação x + y = 84, temos:

\frac{4}{3} y + y = 84 \Rightarrow \frac{7}{3} y = 84 \Rightarrow 7 y = 84 \cdot 3 \Rightarrow y = \frac{252}{7} \Rightarrow y = 36

Página noventa e seis

Substituindo y por 36 na equação x + y = 84, temos:

x + 36 = 84 x = 48

Como o viaduto mede 84 metros, o centro do viaduto está a 42 metros de cada uma das extremidades (pois 84 : 2 = 42); portanto, Eduarda e Carlos se encontraram a 6 metros do centro do viaduto (48 – 42 = 6).

Verificando

1. Substituindo x por y + 30 na 2ª equação, temos:

y + 30 + 5 = 2(y + 10) ⇒ y + 35 = 2y + 20 ⇒ 35 ‒ 20 = 2y – y ⇒ y = 15

Substituindo y por 15 na 1ª equação, obtemos:

x = 15 + 30 ⇒ x = 45

Alternativa d.

2. Sejam x a quantidade de embalagens de coco ralado e y a quantidade de caixas de chocolate em pó. Com os dados do problema, podemos escrever o seguinte sistema de equações.

\{\begin{cases} 4 x + 5 y = 54 \\ 100 x + 200 y = 1 800 \end{cases}

Multiplicando a 1ª equação por ‒1 e dividindo a 2ª equação por 25, obtemos:

\{\begin{cases} - 4 x - 5 y = - 54 \\ 4 x + 8 y = 72 \end{cases}

Adicionando as equações, membro a membro, temos:

3y = 18 ⇒ y = 6

Substituindo y por 6 na 1ª equação, obtemos:

4x + 5 ⋅ 6 = 54 ⇒ 4x + 30 = 54 ⇒ 4x = 54 ‒ 30 ⇒ 4x = 24 ⇒ x = 6

Então, Jorge comprou 6 embalagens de coco ralado e 6 caixas de chocolate em pó.

Alternativa b.

3. Sendo x a quantidade de cédulas de R$ 50,00cinquenta reais e y a quantidade de cédulas de R$ 100,00cem reais, com os dados do problema obtemos o seguinte sistema:

\{\begin{cases} 50 x + 100 y = 9 450 \\ x + y = 120 \end{cases}

Dividindo a 1ª equação por 50 e multiplicando a 2ª equação por ‒1, obtemos:

\{\begin{cases} x + 2 y = 189 \\ - x - y = - 120 \end{cases}

Adicionando as equações, membro a membro, obtemos y = 69. Substituindo y por 69 na 2ª equação, obtemos:

x + 69 = 120 ⇒ x = 51

Assim, a quantidade de cédulas de R$ 100,00cem reais é 69 e a quantidade de cédulas de R$ 50,00cinquenta reais é 51.

Alternativa c.

4. Vamos testar os pontos dados em cada alternativa nas equações: (um) 2x ‒ 4y = 10 e (dois) x ‒ 2y = 5

4. a) (um) 2 ⋅ 7 ‒ 4 ⋅ 1 = 10 ⇒ 10 = 10

(dois) 7 ‒ 2 ⋅ 1 = 5 ⇒ 5 = 5

Então (7, 1) é solução.

(um) 2 ⋅ 3 ‒ 4 ⋅ (‒1) = 10 ⇒ 10 = 10

(dois) 3 ‒ 2 ⋅ (‒1) = 5 ⇒ 5 = 5

Então (3, ‒1) é solução.

4. b) (um) 2 ⋅ 5 ‒ 4 ⋅ 0 = 10 ⇒ 10 = 10

(dois) 5 ‒ 2 ⋅ 0 = 5 ⇒ 5 = 5

Então (5, 0) é solução.

(um) 2 ⋅ 9 ‒ 4 ⋅ 2 = 10 ⇒ 10 = 10

(dois) 9 ‒ 2 ⋅ 2 = 5 ⇒ 5 = 5

Então (9, 2) é solução.

4. c) (um) 2 ⋅ 0 ‒ 4 ⋅ (‒2,5) = 10 ⇒ 10 = 10

(dois) 0 ‒ 2 ⋅ (‒2,5) = 5 ⇒ 5 = 5

Então (0, ‒2,5) é solução.

(um) 2 ⋅ 11 ‒ 4 ⋅ 3 = 10 ⇒ 10 = 10

(dois) 11 ‒ 2 ⋅ 3 = 5 ⇒ 5 = 5

Então (11, 3) é solução.

4. d) (um) 2 ⋅ ‒4 ‒ 4 ⋅ (‒3) = 10 ⇒ 4 ≠ 10

(dois) ‒4 ‒ 2 ⋅ (‒3) = 5 ⇒ 2 ≠ 5

Então (‒4, ‒3) não é solução.

(um) 2 ⋅ (‒3) ‒ 4 ⋅ (‒1) = 10 ⇒ ‒2 ≠ 10

(dois) ‒4 ‒ 2 ⋅ (‒3) = 5 ⇒ 2 ≠ 5

Então (‒3, ‒1) não é solução.

Alternativa d.

5. Os pontos (‒1, 0) e (0, 1) pertencem à reta de equação y = x + 1. Os pontos (‒1, 0) e (0, ‒1) pertencem à reta de equação y = ‒x ‒ 1. Os pontos (0, 0) e (1, 2) pertencem à reta de equação y = 2x. Portanto, a equação y = ‒2x – 2 não está representada no gráfico.

Alternativa b.

6. A reta de equação y = 2x passa pelos pontos (0, 0) e (1, 2) e a reta de equação y = x + 1 passa pelos pontos (‒1, 0) e (0, 1).

Alternativa a.

Capítulo 11 — Área de regiões poligonais

• Objetivos do capítulo e justificativas

• Determinar expressões para o cálculo da área de figuras planas poligonais: área de paralelogramo, de triângulo, de losango e de trapézio.

• Retomar e aplicar a área de retângulos (quadrados ou não).

• Resolver problemas envolvendo valor numérico de expressões algébricas.

• Resolver e elaborar problemas envolvendo o cálculo de áreas.

• Reconhecer o cálculo de área por meio da decomposição em triângulos.

• Aplicar congruência de triângulos em demonstrações geométricas.

• Analisar a construção de um losango e explorar suas características.

• Reconhecer transformações geométricas: reflexão, translação e rotação.

• Interpretar e construir pictogramas.

Neste capítulo, os estudantes retomam, ampliam e aplicam diferentes conteúdos trabalhados nos capítulos anteriores explorando a Unidade Temática Geometria associada à Álgebra e, assim, desenvolvendo a competência específica 3. São propostas atividades em que é necessário argumentar, exercitar a curiosidade intelectual e o raciocínio lógico, a fim de demonstrar a validade de expressões algébricas para o cálculo da medida de área de algumas figuras planas e, dessa maneira, desenvolvem-se as competências gerais 2 e 4 e as competências específicas 2 e 6.