Página noventa e sete

Parte 8

Ao explorar pictogramas, os estudantes podem ampliar a compreensão de diferentes tipos de representações gráficas e, portanto, desenvolver a competência geral 4 e a competência específica 4, à medida que utilizam diferentes linguagens para se expressar ou comunicar informações e que analisam aspectos qualitativos e quantitativos nos contextos apresentados. Além disso, ao desenvolver pesquisas, os estudantes precisam interagir entre si de maneira cooperativa e mobilizam a competência específica 8.

A contextualização na abertura do capítulo possibilita desenvolver as competências gerais 9 e 10 e a competência específica 8, pois os estudantes podem exercitar a empatia, dialogar em respeito a situações que tratam sobre a saúde e a importância de bancos de transplante de órgãos, por exemplo.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo ax² = b.

(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou sófitiuérs de geometria dinâmica, mediatriz, bissetriz, ângulos de 90°, 60°, 45° e 30° e polígonos regulares.

(ê éfe zero oito ême ah um nove) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

Neste capítulo, serão aprofundados os estudos relativos à Unidade Temática Grandezas e medidas envolvendo a grandeza área, levando-se em conta os conhecimentos desenvolvidos nos anos anteriores, em especial no 7º ano (ê éfe zero sete ême ah dois nove, ê éfe zero sete ême ah três um e ê éfe zero sete ême ah três dois), aportes para a compreensão dos temas aqui tratados. Os conhecimentos que abrangem medidas de área promovem o estabelecimento de expressões algébricas de cálculo de área de regiões poligonais: paralelogramo, triângulo, losango e trapézio; dessa maneira, desenvolvem a habilidade (ê éfe zero oito ême ah um nove).

A Unidade Temática Números também está presente neste capítulo com atividades que abordam áreas e cálculo de porcentagens. A conexão com a Unidade Temática Álgebra se concretiza pela resolução de problemas que envolvem o cálculo do valor numérico das expressões que determinam a área das regiões poligonais estudadas mobilizando, por vezes, a habilidade (ê éfe zero oito ême ah zero nove).

Com a Unidade Temática Geometria, a conexão se concretiza por meio de atividades da seção Para saber mais, que mobiliza a habilidade (ê éfe zero oito ême ah um cinco) e promove a aplicação da congruência de triângulos para demonstrações de propriedades de quadriláteros e a construção de um losango. A seção Trabalhando a informação, cujo tema é pictogramas, promove a articulação com a Unidade Temática Probabilidade e estatística e desenvolve a habilidade (ê éfe zero oito ême ah dois três).

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Exercícios propostos

1. Como

A_{paralelogramo} = b \cdot h = x \cdot y

e a ordem dos fatores não altera o produto, as áreas dos dois paralelogramos têm a mesma medida, ou seja,

A_{paralelogramo} = y \cdot x = 80 m ²

2. Sendo h a medida da altura do paralelogramo, temos:

A_{paralelogramo} = b \cdot h \Rightarrow 56 = 8 \cdot h \Rightarrow h = 56 : 8 \Rightarrow h = 7

Assim, a medida da altura é 7 centímetros.

4. Então, podemos dividir a altura total do mosaico em três partes iguais a 2,12 centímetros, que corresponde à medida de altura de um paralelogramo verde. Desse modo, a área de cada um desses paralelogramos mede 10,6 centímetros quadrados, pois:

A_{paralelogramo} = b \cdot h \Rightarrow A_{paralelogramo} = 5 \cdot 2, 12 = 10, 6

A área do quadrado mede 9 centímetros quadrados, pois:

A_{q u a d r a d o} = b \cdot h \Rightarrow A_{q u a d r a d o} = 3 \cdot 3 = 9

Então, podemos concluir que a medida total da área da superfície do mosaico corresponde à soma das medidas da áreas de todas as figuras, ou seja,

A_{t o t a l} =

3 · 10,6 + 2 · 9 = 49,8. Assim, a área da superfície do mosaico mede 49,8 centímetros quadrados.

5. a) De acôrdo com a figura, os paralelogramos têm bases e alturas de medidas iguais; portanto, as medidas de suas áreas também são iguais. Desse modo, a área de cada paralelogramo mede 6 centímetros quadrados (4 · 1,5 = 6) e a área total da figura mede 12 centímetros quadrados (2 · 6 = 12).

5. b) De acôrdo com a figura, os paralelogramos têm bases e alturas de medidas iguais; portanto, as medidas de suas áreas também são iguais. Desse modo, a área de cada paralelogramo mede 4 centímetros quadrados (2 · 2 = 4) e a área total da figura mede 8 centímetros quadrados (2 · 4 = 8).

6. a)

A_{p a r a l e log r a m o} = b \cdot h \Rightarrow 34, 2 = 7, 6 \cdot h \Rightarrow

⇒ h  =  34,2 : 7,6  ⇒ h  = 4,5

Assim, a altura mede 4,5 centímetros.

6. b)

A_{paralelogramo} = b \cdot h \Rightarrow 27, 3 = b \cdot 3 \Rightarrow

⇒ h = 27,3 : 3 ⇒ b = 9,1

Assim, a base mede 9,1 centímetros.

7. Supondo que a figura central azul seja um quadrado sobreposto pelos quadrados amarelos, precisamos obter a parte que está faltando para completar o quadrado. Pela leitura da figura, os quadrados amarelos estão posicionados de modo que os pontos médios de seus lados interceptam o lado do quadrado azul. Desse modo, pode-se concluir que o lado do suposto quadrado azul mede 2 centímetros (1 + 0,5 + 0,5 = 2) e, portanto, sua área mede 4 centímetros quadrados

(A_{q u a d r a d o} = 2 \cdot 2 = 4)

Agora, é preciso descontar a quantidade adicionada que equivale a um quadrado amarelo, de área medindo 1 centímetro quadrado. Assim, a área da região pintada de azul mede 3 centímetros quadrados (4 ‒ 1 = 3).

Página noventa e oito

9. A área do dormitório mede 10,5 métros quadrados (3,5 · 3,0 = 10,5). A sala tem lados de medida 5,5 métros (lado₁ = 3,5 + 2 = 5,5; lado₂ = 3,0 + 2,5 = 5,5). Desse modo, a área da sala mede 26,25 métros quadrados [(5,5 · 5,5) ‒ 4 = 26,25]. Assim, o carpete será colocado sobre uma área de 36,75 métros quadrados (26,25 + 10,5 = 36,75) . Portanto, o dono do apartamento deverá gastar R$ 1.764,00 mil setecentos e sessenta e quatro reais(48 · 36,75 = .1764).

15. A base e a altura do triângulo verde coincidem com a base e a altura do paralelogramo. Desse modo, a área da região pintada de verde tem a mesma medida da área do triângulo de base medindo 4,5 métros e altura medindo 2,4 métros, ou seja, 5,4 métros quadrados.

A = \frac{4, 5 · 2, 4}{2} = 5, 4

16. A medida da área da região pintada de azul é igual à medida da área do paralelogramo subtraída da medida da área do triângulo branco. As bases e alturas das duas figuras têm mesmas medidas.

A área do triângulo mede 6 centímetros quadrados.

A_{t r i â n g u l o} = \frac{b \cdot h}{2} \Rightarrow A_{t r i â n g u l o} = \frac{4 · 3}{2} = 6

A área do paralelogramo mede 12 centímetros quadrados.

A_{paralelogramo} = b \cdot h \Rightarrow A_{paralelogramo} = 3 \cdot 4 = 12

Então, a área da região pintada de azul mede 6 centímetros quadrados (12 ‒ 6 = 6).

17. O hexágono é formado por 6 triângulos iguais. A área de cada um desses triângulos mede 1,7 centímetro quadrado.

A_{t r i â n g u l o} = \frac{2, 0 \cdot 1, 7}{2} = 1, 7

Portanto, a área do hexágono mede 10,2 centímetros quadrados (6 ⋅ 1,7 = 10,2).

18. a) A medida da área da figura é dada pela soma das medidas das áreas do retângulo e do triângulo. A medida da área do retângulo é 9 centímetros quadrados (6 ⋅ 1,5 = 9). A medida da área do triângulo é 4,5 centímetros quadrados.

A_{t r i â n g u l o} = \frac{6, 0 · 1, 5}{2} = 4, 5

Assim, a área da figura mede 13,5 centímetros quadrados (9 + 4,5 = 13,5).

18. b) A figura é formada por três triângulos congruentes. Assim, as áreas dos três triângulos têm a mesma medida; portanto, a área da figura mede aproximadamente 22,31 centímetros quadrados.

3 \cdot (\frac{4, 25 \cdot 3, 5}{2}) = 3 \cdot 7, 4375 ≃ 22, 31

20. A área do triângulo á bê cê mede 31,15 centímetros quadrados.

A_{t r i â n g u l o} = \frac{7 · 8, 9}{2} = 31, 15

A medida do lado

\bar{B C}

é dada por:

\frac{B C \cdot 6, 2}{2} = 31, 15 \Rightarrow B C = \frac{2 · 31, 15}{6, 2} \Rightarrow B C ≃ 10

Logo, o lado

\bar{B C}

mede aproximadamente 10 centímetros.

Usando o mesmo raciocínio, sendo h a altura relativa ao lado

\bar{A B}

, h mede aproximadamente 6,9 centímetros.

\frac{9 · h}{2}

= 31,15 ⇒ h = 62,3 : 9 ⇒ h ≃ 6,9

21. A área do losango mede 97,2 centímetros quadrados.

A_{l o s a n g o} = \frac{D \cdot d}{2} \Rightarrow A_{l o s a n g o} = \frac{14, 4 \cdot 13, 5}{2} = 97, 2

23. A medida da base do retângulo coincide com a medida da diagonal maior do losango (D) e a medida da altura do retângulo coincide com a medida da diagonal menor do losango (d).

Portanto, a área do losango mede 27,9 métros quadrados.

A_{l o s a n g o} = \frac{12, 4 · 4, 5}{2} = 27, 9

24. a) A medida da área do losango é quatro vezes a medida da área do triângulo em destaque. Portanto, a área do losango mede 48 centímetros quadrados.

A_{l o s a n g o} = 4 \cdot 12 = 48

24. b) Juntas, as duas regiões pintadas de verde têm a mesma medida de área de um quarto do losango, que corresponde à medida da área do triângulo retângulo; assim, a medida da área do losango é quatro vezes a medida da área do triângulo em destaque. Portanto, a área do losango mede 48 centímetros quadrados (4 ⋅ 12 = 48).

25.

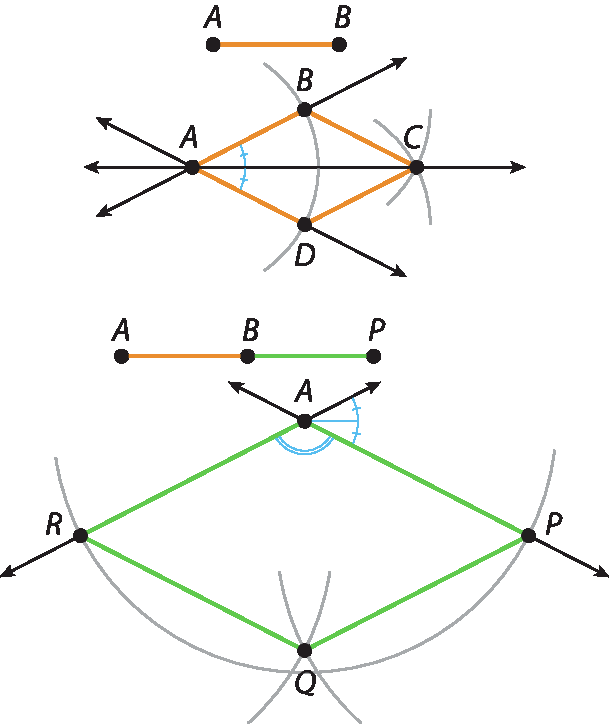
Ilustração. Figura 1. Segmento de reta A B. Figura 2. Reta horizontal A C. Segmento de reta A B, fora da reta que passa por C. Segmento de reta A D, fora da reta que passa por B e por C. Arco B D traçado, com centro em A. Dois arcos passando pelo ponto C. A figura A B C D forma um losango, destacado. O ângulo interno A é dividido pela bissetriz A C. Ilustração. Figura 1. Segmento de reta A B e segmento B P consecutivos, tais que A B P são pontos colineares. Figura 2. Losango A P Q R. Um arco R P com centro em A. Um arco passando por Q, com centro em P. Um arco passando por Q, com centro em R. Ângulo P A R destacado. Ângulo externo ao ângulo P A R, passando pela reta A R, destacado e dividido em dois.

A medida da área do primeiro losango é quatro vezes menor que a medida da área do segundo losango; logo, ele caberá 4 vezes dentro do segundo losango.

26. Como a área do losango tem medida igual a 48 centímetros quadrados, precisamos obter dois números que multiplicados resultem em 96, uma vez que a medida da área do losango é calculada por:

A_{l o s a n g o} = \frac{D \cdot d}{2} \Rightarrow 48 \cdot 2 = D \cdot d \Rightarrow D \cdot d = 96

Página noventa e nove

Como D e d são números naturais, podemos decompor o número 96, obtendo as seguintes possibilidades para D e d: 1 centímetro e 96 centímetros, 2 centímetros e 48 centímetros, 3 centímetros e 32 centímetros, 4 centímetros e 24 centímetros, 6 centímetros e 16 centímetros, 8 centímetros e 12 centímetros.

27. Os lados do quadrado a bê cê dê coincidem com as diagonais do losango éfe gê agá é. Assim, a área do losango éfe gê agá é mede 72 centímetros quadrados.

A_{l o s a n g o} = \frac{D \cdot d}{2} \Rightarrow \frac{12 · 12}{2} = 72

Para o losango éfe linha, gê linha, agá linha, é linha, o lado maior do retângulo coincide com a diagonal maior do losango, ou seja, eles têm mesma medida.

A_{l o s a n g o} = \frac{D · d}{2} \Rightarrow 72 = \frac{16 · d}{2} \Rightarrow d = 9

Logo, a diagonal menor do losango éfe linha, gê linha, agá linha, é linha mede 9 centímetros. De 12 centímetros para 9 centímetros foram reduzidos 3 centímetros (12 ‒ 9 = 3).

28. Oriente os estudantes na elaboração dos problemas.

29. a) Como (B + b) = 15,5, a medida da área do trapézio é 96,1 centímetros quadrados.

A_{t r a p é z i o} = \frac{(B + b) · h}{2} \Rightarrow A_{t r a p é z i o} = \frac{15, 5 · 12, 4}{2} = 96, 1

29. b) Seja S a soma das medidas das bases do trapézio, temos:

\frac{S · 12, 4}{2} = 155 \Rightarrow S = \frac{155 · 2}{12, 4} = 25

Então a soma das medidas das bases do trapézio é 25 centímetros.

30. A medida da área é dada por:

A_{t r a p é z i o} = \frac{(B + b) · h}{2} \Rightarrow A_{t r a p é z i o} \frac{(5 + 3) · 2}{2} = 8

Portanto, a área mede 8 centímetros quadrados.

31. A figura é formada por dois trapézios equivalentes, pois as medidas de seus lados são iguais. Desse modo, a medida da área total é 88 métros quadrados. Portanto, serão necessários 88 métros quadrados de grama para cobrir esse terreno.

A_{t r a p é z i o} = 2 \cdot \frac{(13 + 9) \cdot 4}{2} = 44

A_{t o t a l} = 2 \cdot 44 = 88

32. A medida do perímetro do trapézio é 22 centímetros e os lados não paralelos medem 5 centímetros; então, a soma das medidas das bases tem que ser 12 centímetros.

5 + 5 + b + B = 22 ⇒ B + b = 22 ‒ 10 ⇒ B + b = 12

Portanto, a área desse trapézio isósceles mede 24 centímetros quadrados.

\frac{12 · 4}{2}

= 24

33. A medida da área do paralelogramo é 400 centímetros quadrados.

20 ⋅ 20 = 400

A medida da área do triângulo é 200 centímetros quadrados.

\frac{20 · 20}{2}

= 200

A medida da área do trapézio é 400 centímetros quadrados.

\frac{(27 + 13) \cdot 20}{2}

= 400

34.

A_{t r a p é z i o} = \frac{(B + b) · h}{2} \Rightarrow 260 = \frac{(B + 12) · 10}{2} \Rightarrow

⇒ 10B + 120 = 520 ⇒ B =

\frac{400}{10}

⇒ B = 40

Logo, a base maior mede 40 cmétros.

35. O escritório pode ser dividido em um trapézio e um triângulo. No trapézio, a medida da base maior é 3,10 métros, da base menor é 2,70 métros e da altura é 3,10 métros. No triângulo retângulo, a base mede 2,50 métros e a altura mede 1,90 métro.

A medida da área do trapézio pode ser estimada em 9 métros quadrados.

A_{t r a p é z i o} = \frac{(3, 10 + 2, 70) · 3, 10}{2} = 8, 99

A medida da área do triângulo pode ser estimada em 2,5 métros quadrados.

A_{t r i â n g u l o} = \frac{2, 50 · 1, 90}{2} = 2, 375

Portanto, a área total mede 11,365 métros quadrados (2,375 + 8,99 = 11,365).

A área total estimada mede aproximadamente 11,5 métros quadrados (9 + 2,5 = 11,5). O erro de aproximação depende da estimativa. Comparando o valor aproximado de 11,5 métros quadrados com o valor calculado de 11,365 métros quadrados, temos uma diferença de 0,135 métro quadrado, o que representa aproximadamente 1,2% da medida da área total de 11,365 métros quadrados.

36. a) A medida da área do terreno a é dada por:

A_{t r a p é z i o A} = \frac{(34 + 30) · 25}{2} = 800

Logo, a área do terreno A mede 800 métros quadrados.

36. b) A medida das áreas dos terrenos a e B são iguais. Então, temos:

A_{trapézio B} = \frac{(30 + 20) \cdot x}{2} \Rightarrow 800 = 25 x \Rightarrow x = 32

A medida do lado representado por x é 32 métros.

Pense mais um poucoreticências

Página 236

1. a) Sim, pois os triângulos foram obtidos do recorte da diagonal do mesmo retângulo, consequentemente, as áreas deles têm medidas iguais.

1. b) A medida da área do triângulo corresponde à metade da medida da área do retângulo; portanto, sua área mede 9 unidades de medida de área (18 : 2 = 9).

Página cem

1. c) Será 2x, pois a medida da área do retângulo será o dobro da medida da área do triângulo.

2. a) Sim, pois foram obtidos a partir da diagonal do mesmo paralelogramo; portanto, são equivalentes.

2. b) Sim, pois foram obtidos a partir da diagonal do mesmo paralelogramo; portanto, são equivalentes.

2. c) Não, pois o triângulo de um foi obtido do córte pela diagonal menor do paralelogramo um, e o triângulo de dois foi obtido pelo córte da diagonal maior do paralelogramo dois.

2. d) Se a área de um mede x, a área de dois também mede x. A medida da área será a mesma, pois, mesmo que os triângulos sejam obtidos por córtes de diagonais diferentes, os triângulos de um e de dois têm medida de área que é igual à metade da medida da área do paralelogramo. Como as áreas dos paralelogramos têm medidas iguais, as metades das medidas das áreas (área dos triângulos) também são iguais. Desse modo, a medida da área equivale à metade, ou seja,

\frac{x}{2}

2. e) Pela definição de equivalência, as medidas das áreas devem ser iguais, então um e dois são equivalentes.

Página 243

Para obter a medida da área da parte verde, basta calcular a medida da área do retângulo e subtrair a medida da área do losango.

A área do retângulo mede 25,20 centímetros quadrados (4,20 ⋅ 6,00 = 25,20).

No losango, a diagonal maior mede 4,98 centímetros (6 ‒ 2 ⋅ 0,51 = 4,98) e a diagonal menor mede 3,18 centímetros (4,20 ‒ 2 ⋅ 0,51 = 3,18).

Assim, a medida da área do losango é aproximadamente 7,92 centímetros quadrados.

A_{l o s a n g o} = \frac{4, 98 · 3, 18}{2} = 7, 92

Concluímos que a área da parte verde mede aproximadamente 17,28 centímetros quadrados.

25,20 ‒ 7,92 = 17,28.

Trabalhando a informação

1. De acôrdo com o texto, a cada 100 habitantes, 45 viviam em áreas rurais (campo), o que representa 45%; portanto, aproximadamente 3,4 bilhões dos 7,6 bilhões de habitantes viviam no campo.

2. De acôrdo com o texto, uma em cada 160 crianças são autistas; portanto, de 2 bilhões de crianças, aproximadamente 12,5 milhões são autistas.

...2000000000 : 160 = ..12500000

3. São 120 estudantes no total; 40 preferem vôlei, o que representa um terço da quantidade total, ou seja, aproximadamente 33,3%.

4. A resposta depende da pesquisa realizada pelos estudantes.

Exercícios complementares

3. A área de um losango mede 600 centímetros quadrados.

\frac{D · d}{2} = \frac{40 · 30}{2} = 600

A área de um triângulo mede 300 centímetros quadrados.

\frac{b · h}{2} = \frac{30 · 20}{2} = 300

A área total mede .6000 centímetros quadrados (6 ⋅ 600 + 8 ⋅ 300 = .6000).

4. A medida da área do trapézio é 70 centímetros quadrados.

\frac{(18 + 10) · 5}{2} = 70

5. A medida da área do losango é 4 centímetros quadrados.

\frac{4 · 2}{2} = 4

Os quatro paralelogramos são congruentes. Assim, a área da região cinza mede 24 centímetros quadrados (4 ⋅ 6 = 24). Desse modo, o preço da parte composta de ouro é R$ 360,00 trezentos e sessenta reais(90 ⋅ 4 = 360), e o preço da parte composta de prata é R$ 96,00noventa e seis reais, (4 · 24 = 96,00). Logo, o preço da placa é R$ 456,00 quatrocentos e cinquenta e seis reais(360 + 96 = 456).

6. A medida da área do losango é 54,4 centímetros quadrados.

\frac{12, 8 · 8, 5}{2} = 54, 4

Como as medidas da área do losango e do triângulo são iguais, sendo h a altura relativa à base do triângulo, temos h = 8,0 centímetros.

\frac{13, 6 · h}{2} = 54, 4 \Rightarrow h = \frac{54, 4 · 2}{13, 6} \Rightarrow h = 8

8. Temos um retângulo de base medindo 12 centímetros e altura medindo 10 centímetros. Também é possível identificar dois triângulos de bases medindo 12 centímetros e alturas medindo x centímetro e (10 – x) centímetros.

A medida da área do quadrilátero é dada por A₁ + A₂.

A_{1} = \frac{12 \cdot x}{2}

A_{2} = \frac{12 \cdot (10 – x)}{2}

A_{1} + A_{2} = \frac{12 x + 120 - 12 x}{2} = \frac{120}{2} = 60

Portanto, a medida da área do quadrilátero é 60 centímetros quadrados.

Alternativa b.

9. Do quadrilátero á bê dê é, podemos obter dois triângulos traçando o segmento

\bar{D A}

. Assim, podemos calcular a medida da área do quadrilátero á cê dê éfe pela soma das medidas das áreas dos triângulos á dê éfe e á cê dê. O triângulo á dê éfe tem área de medida 21 u²

(\frac{6 \cdot 7}{2} = 21)

. A base do triangulo á cê dê mede 2 u; e sua altura mede 10 u, portanto, sua área medirá 10 u²

(\frac{2 \cdot 10}{2} = 10)

. Logo, a área do quadrilátero á cê dê éfe mede 31 u² (21 + 10 = 31).

Alternativa c.

Página cento e um

Verificando

3. Vamos considerar que a medida da área dessa face seja igual à medida da área de um triângulo de base medindo 36 centímetros e altura medindo 18 centímetros, subtraído da medida da área de um triângulo cuja base mede 20 centímetros e a altura mede 10 centímetros. Assim:

A = \frac{36 · 18}{2} – \frac{20 · 10}{2} \Rightarrow A = 324 ‒ 100 \Rightarrow A = 224

A área mede 224 centímetros quadrados.

Alternativa a.

4. O triângulo é retângulo, então um dos seus lados coincide com sua altura. Precisamos descartar a medida de lado 5 centímetros, pois a maior medida de um triângulo é a hipotenusa. Assim, a área mede 6 centímetros quadrados.

\frac{3 · 4}{2} = 6

Alternativa c.

5. Sendo D a diagonal maior do losango, a medida da área do losango é dada por:

\frac{D · 7, 0}{2} = 45, 5 \Rightarrow D = 91 : 7 \Rightarrow D = 13

Assim, a diagonal mede 13 centímetros.

Alternativa b.

6. A área da tela mede 576 centímetros quadrados.

A_{l o s a n g o} = \frac{D · d}{2} \Rightarrow A_{l o s a n g o} = \frac{4 8 \cdot 24}{2} = 576

Alternativa a.

7. A medida da área total é dada pela soma das medidas das áreas de cada trapézio lateral, da medida da área da base quadrada e da medida da área da tampa da urna. Assim:

A_{t o t a l} = 4 \cdot \frac{(18 + 10) · 30}{2} + 18 \cdot 18 + 10 \cdot 10 \Rightarrow

\Rightarrow A_{t o t a l} = 1 680 + 324 + 100 = 2 104

Logo, a área total do papelão usado para a construção da urna mede .2104 centímetros quadrados.

Alternativa b.

8. A figura tem a fórma de um trapézio. A medida da área do quadrado é 16 centímetros quadrados (4 ⋅ 4 = 16). Como o triângulo retângulo é isósceles, um de seus lados coincide com sua altura; portanto, a medida de sua área é 8 centímetros quadrados

(\frac{4 \cdot 4}{2} = 8)

. Consequentemente, a medida da área do trapézio formado é 24 centímetros quadrados (16 + 8 = 24).

Alternativa b.

Capítulo 12 – Geometria e grandezas

• Objetivos do capítulo e justificativas

• Reconhecer polígono regular e suas propriedades: ser inscritível em uma circunferência e ser circunscritível a uma circunferência.

• Reconhecer os elementos de um polígono regular.

• Analisar a descrição de procedimentos para construção de um polígono regular.

• Construir polígonos regulares.

• Determinar a área de um círculo.

• Resolver e elaborar problemas envolvendo a área de um círculo.

• Estabelecer uma expressão para o cálculo do volume de um cilindro circular reto.

• Relacionar volume e capacidade.

• Reconhecer a relação entre um litro e um decímetro cúbico.

• Resolver problemas envolvendo medidas de volume e de capacidade.

Este capítulo aborda conteúdos de Álgebra, Geometria e Grandezas e Medidas, possibilitando aos estudantes aplicar conhecimentos trabalhados anteriormente e perceber a relação entre eles; assim, desenvolvem a competência específica 3.

Reconhecer os elementos dos polígonos regulares e suas propriedades e estabelecer expressões algébricas para a medida da área de um círculo ou para a medida do volume de prisma e cilindro retos favorecem o desenvolvimento das competências gerais 2 e 4 e da competência específica 2, pois os estudantes precisam argumentar, defender ideias e justificar procedimentos nas diferentes atividades propostas no capítulo.

Para determinar a expressão que relaciona a medida da área ao raio de um círculo, exploram-se elementos da história da Matemática, favorecendo o desenvolvimento da competência geral 1 e da competência específica 1.

O exercício 24 da seção Exercícios propostos explora o uso consciente da água, propondo aos estudantes que reflitam sobre ações que podem ser planejadas para evitar o aumento no uso de água e não gerar uma crise hídrica no país, contribuindo para o trabalho com a competência geral 7 e a competência específica 6.

Diferentes atividades propostas no decorrer do capítulo favorecem o desenvolvimento das competências gerais 9 e 10 e da competência específica 8, pois os estudantes deverão, em grupos, pesquisar e discutir diferentes estratégias de resolução de problemas, bem como expor opiniões e ideias e respeitar as dos colegas, interagindo com eles.

• Habilidades trabalhadas no capítulo

(ê éfe zero oito ême ah um seis) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.

Página cento e dois

(ê éfe zero oito ême ah dois zero) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.

(ê éfe zero oito ême ah dois um) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.

Os conhecimentos abordados neste capítulo também se referem à Unidade Temática Grandezas e medidas, oportunidade para ampliar o trabalho com medidas de área (com a área do círculo) e as ideias que envolvem medidas de volume e de capacidade, destacando a relação entre um decímetro cúbico e um litro, além de apresentar o volume de um cilindro reto; dessa maneira, desenvolvem-se as habilidades (ê éfe zero oito ême ah um nove), (ê éfe zero oito ême ah dois zero) e (ê éfe zero oito ême ah dois um). Os conhecimentos acerca de medida de volume e de capacidade estão embasados nos anos anteriores, em especial no 7º ano (ê éfe zero sete ême ah três zero), que, por sua vez, visam preparar o estudante para o conhecimento acerca de medidas de volume a ser desenvolvido no 9º ano (ê éfe zero nove ême ah um nove).

As conexões com outras Unidades Temáticas estão presentes nas diversas atividades propostas que compreendem medidas. A relação com a Unidade Temática Álgebra aparece quando as propostas envolvem o cálculo de valor numérico de expressões algébricas tratadas no capítulo; e a articulação com a Unidade Temática Geometria ocorre por meio de atividades que promovem o reconhecimento de polígono regular, seus elementos e a relação entre a soma das medidas de seus ângulos (internos ou externos) e a quantidade de lados do polígono, na descrição de procedimentos para a construção de polígono regular e em construções de polígonos inscritos ou circunscritos a uma circunferência mobilizando as habilidades (ê éfe zero oito ême ah um cinco) e (ê éfe zero oito ême ah um seis).

• Comentários e resoluções

Exercícios propostos

1. Lembrando que um polígono inscrito tem todos os seus vértices pertencentes à circunferência, e um polígono circunscrito tem uma circunferência que tangencia todos os lados do polígono em seus pontos médios.

1. a) Os quatro vértices pertencem à circunferência, portanto o polígono é inscrito.

1. b) Apenas quatro dos cinco vértices pertencem à circunferência, portanto ele não é inscrito nem circunscrito.

1. c) A circunferência tangencia todos os lados do polígono, portanto, o polígono é circunscrito.

1. d) Apenas dois dentre os quatro vértices do polígono pertencem à circunferência, portanto ele não é inscrito nem circunscrito.

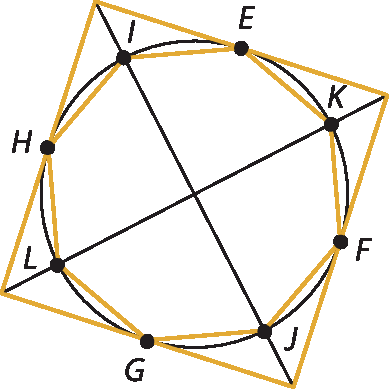
Ilustração. Quadrado com circunferência dentro. No interior da circunferência, octógono E K F J G L H I. A circunferência passa pelos pontos E K F J G L H I. As duas diagonais do quadrado estão destacadas e uma delas passa pelos pontos I e J, a outra passa pelos pontos K e L.

O polígono (octógono) será inscrito.

3. b) Não é polígono regular, pois não tem todos os ângulos congruentes.

3. d) Não é polígono regular, pois não tem todos os lados congruentes.

4. Uma sugestão de resposta é um fluxograma como o que segue.

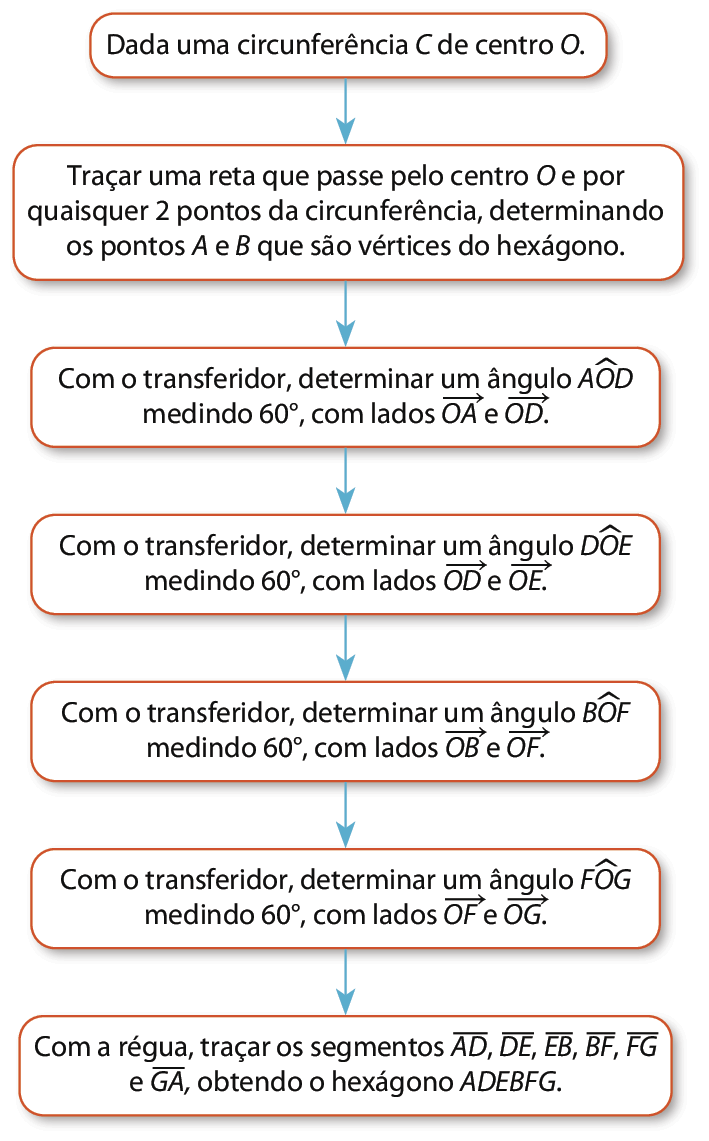
Fluxograma com 7 caixas relacionadas por setas de direção única. O procedimento está indicado pelos tópicos a seguir. 1. Dada uma circunferência C de centro O. Seta para 2. 2. Traçar uma reta que passe pelo centro O e por quaisquer 2 pontos da circunferência, determinando os pontos A e B que são vértices do hexágono. Seta para 3. 3. Com o transferidor, determinar um ângulo A O D medindo 60 graus, com lados O A e O D. Seta para 4. 4. Com o transferidor, determinar um ângulo D O E medindo 60 graus, com lados O D e O E. Seta para 5. 5. Com o transferidor, determinar um ângulo B O F medindo 60 graus, com lados O B e O F. Seta para 6. 6. Com o transferidor, determinar um ângulo F O G medindo 60 graus, com lados O F e O G. Seta para 7. 7. Com a régua, traçar os segmentos A D, D E, E B, B F, F G e G A, obtendo o hexágono A D E B F G.

5. Em um triângulo equilátero, temos:

a_{c} = \frac{360}{n} \Rightarrow a_{c} = \frac{360}{3} \Rightarrow a_{c} = 120

Assim, o ângulo central mede 120°.

6. Para que o ângulo interno (a_i) seja igual ao ângulo externo (a_e) é necessário que a_i = a_e = 90° (pois juntos eles medem 180°). Para que o ângulo central também tenha medida 90°, temos a_c =

\frac{360}{n}

⇒ 90 =

\frac{360}{n}

⇒ n = 4, ou seja, o número de lados tem de ser igual a 4. Desse modo, o polígono tem de ser um quadrado.

7. a)

a_{c} = \frac{360}{n} \Rightarrow a_{c} = \frac{360}{20} \Rightarrow a_{c} = 18

Assim, o ângulo central mede 18°.

Página cento e três

7. b)

a_{i} = \frac{S_{i}}{n} \Rightarrow a_{i} = \frac{(n – 2) · 180}{n} \Rightarrow a_{i} = \frac{(20 – 2) · 180}{20} \Rightarrow

⇒ a_i = 162

Portanto, o ângulo interno mede 162°. Agora, considerando que o ângulo interno a_i e o ângulo externo a_e são ângulos suplementares, temos a relação:

a_i + a_e = 180 ⇒ a_e = 180 ‒ 162 ⇒ a_e = 18

Portanto, o ângulo externo mede 18°.

8. a)

a_{i} = \frac{S_{i}}{n} \Rightarrow 144 = \frac{(n - 2) · 180}{n} \Rightarrow 144 = \frac{180 n – 360}{n} \Rightarrow

⇒ 144n = 180n ‒ 360 ⇒ 36n = 360 ⇒ n = 10

Portanto, o polígono tem 10 lados.

8. b) Como a_i e a_e são suplementares, temos:

a_i = 180 ‒ a_e ⇒ a_i = 180 ‒ 30 ⇒ a_i = 150

Assim, o ângulo interno mede 150°. Usando a propriedade dos ângulos internos:

a_{i} = \frac{(n – 2) · 180}{n} \Rightarrow 150 = \frac{180 n – 360}{n} \Rightarrow

⇒ 150n = 180n ‒ 360 ⇒ 30n = 360 ⇒ n = 12

Portanto, o polígono tem 12 lados.

8. c) Para encontrarmos o número de lados n, podemos usar a relação entre o ângulo central e o número de lados de um polígono, assim:

a_{c} = \frac{360}{n} \Rightarrow 10 = \frac{360}{n} \Rightarrow n = \frac{360}{10} \Rightarrow n = 36

Assim, o polígono tem 36 lados.

11. A partir dos dados do exercício, por tratar-se de um hexágono regular, concluímos que n = 6. Desse modo, podemos usar a relação entre o ângulo central e o número de lados:

a_{c} = \frac{360}{n} \Rightarrow a_{c} = \frac{360}{6} \Rightarrow a_{c} = 60

O ângulo central mede 60°. Assim, a medida do ângulo interno é dada por:

a_{i} = \frac{S_{i}}{n} \Rightarrow a_{i} = \frac{(n – 2) \cdot 180}{n} \Rightarrow a_{i} = \frac{(6 – 2) · 180}{6} \Rightarrow a_{i} = \frac{720}{6}

⇒ a_i = 120

Ou seja, o ângulo interno mede 120°. Como a_e e a_i são suplementares, podemos usar a relação a_e = 180 ‒ 120 ⇒ a_e = 60, ou seja, o ângulo externo mede 60°.

13. As respostas dependem do total de lados do polígono escolhido. Considerando n = 8 como exemplo, temos:

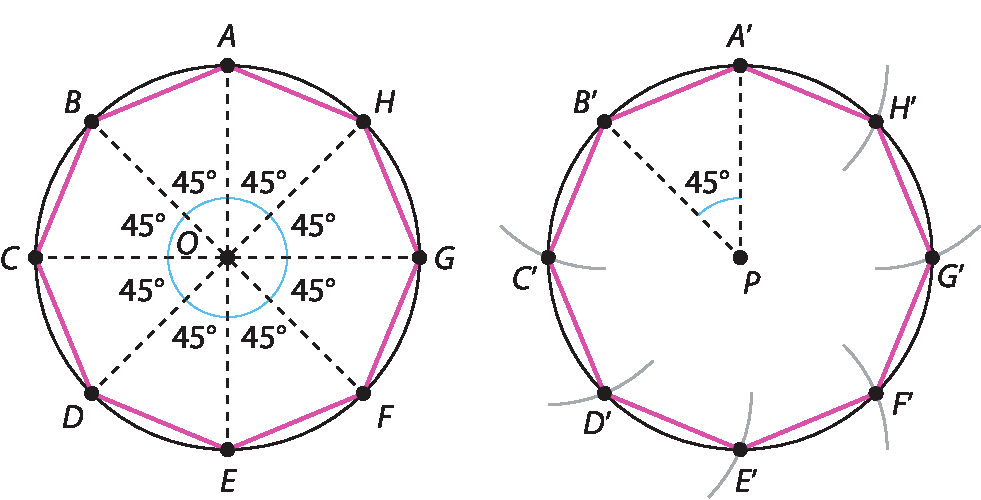
Ilustração. Octógono regular, A B C D E F G H, interno a uma circunferência, com oitos ângulos centrais medindo 45 graus indicados. No centro, ponto O. Circunferência com centro em O passando por A B C D E F G H. Ao lado, octógono regular, interno a uma circunferência de centro P, com vértices: A linha, B linha, C linha, D linha, E linha, F linha, G linha, H linha. No centro, ponto P. Segmentos de reta tracejados de P até A linha e B linha. Ângulo A linha, P, B linha medindo 45 graus.

14. a) O raio de um polígono regular tem a mesma medida do raio da circunferência circunscrita a ele. Além disso, um hexágono regular á bê cê dê é éfe, com centro no ponto óh, pode ser decomposto em 6 triângulos equiláteros, congruentes ao triângulo á ó bê. Assim, á ó = ó bê = A bê = 9; portanto, o raio mede 9 centímetros.

14. b) C = 2πr ⇒ C = 2 ⋅ 3,14 ⋅ 9 ⇒ C = 56,52

Portanto, o comprimento da circunferência mede 56,52 centímetros.

14. c) Vamos encontrar a área do círculo usando a aproximação π ≃ 3,1416. Assim:

A = πr² ⇒ A = π ⋅ 9² ⇒ A = 3,1415 ⋅ 81 ≃ 254,47

Portanto, a área dessa circunferência mede aproximadamente 254,47 centímetros quadrados.

15. Sejam x e 2r, respectivamente, as medidas do comprimento e do raio da circunferência maior. Assim:

x = 2π(2r) = 2 ⋅ (2πr) = 2 ⋅ C

Portanto, alternativa c.

18. Oriente os estudantes na realização da atividade incentivando-os a elaborar problemas contextualizados. Após realizarem a atividade, solicite aos estudantes que apresentem o problema elaborado aos demais colegas e, se possível, que resolvam na lousa alguns deles.

20. A resposta dependerá das embalagens pesquisadas pelos estudantes. Ressalte que, por imprecisão dos instrumentos utilizados, as medidas de volume obtidas serão aproximadas.

22. a) Como 1 litro = 1 decímetro cúbico, temos que:

12 decímetros cúbicos = 12 litros

22. b) Como 1 métro cúbico = .1000 litros, temos que:

5,4 métros cúbicos = (5,4 ⋅ .1000) litros = .5400 litros

22. c) Como 1 decímetro cúbico = .1000 centímetros cúbicos, temos que:

30 centímetros cúbicos = (30 : .1000) litro = 0,03 litro

22. d) Como 1 decímetro cúbico = .1000 centímetros cúbicos, temos que:

30 centímetros cúbicos = (30 : .1000) decímetros cúbicos = 0,03 decímetro cúbico

Como 1 decímetro cúbico = 1 litro, temos que:

0,03 decímetro cúbico = 0,03 litro

Agora, como 1 litro = .1000 mililitros, temos que:

0,03 litro = (0,03 ⋅ .1000) mililitros = 30 mililitros

Página cento e quatro

22. e) Como 1 métro cúbico = ...1000000000 milímetros cúbicos, temos que:

500 milímetros cúbicos = (500 : ...1000000000) métros cúbicos = 0,0000005 métro cúbico

Agora, como 1 métro cúbico = .1000 L, temos que:

0,0000005 métro cúbico = (0,0000005 ⋅ .1000) litro = 0,0005 litro

Finalmente como 1 litro = .1000 mililitros, temos que:

0,0005 litro = (0,0005 ⋅ .1000) mililitro = 0,5 mililitro.

22. f) Como 1 métro cúbico = .1000 litros, temos que:

0,25 métro cúbico = (0,25 ⋅ .1000) litros = 250 litros

23. Como a caixa é cúbica e tem arestas medindo 0,80 métro, vamos determinar a medida de seu volume (V):

V = 0,8 ⋅ 0,8 ⋅ 0,8 ⇒ V = 0,512

Assim, a medida do volume é 0,512 métro cúbico.

Como 1 métro cúbico = .1000 litros, então:

0,512 métro cúbico = (0,512 ⋅ .1000) litros = 512 litros

Portanto, a medida da capacidade é 512 litros.

25. Se o consumo mensal foi de 22 métros cúbicos, e sabendo-se que 1 métro cúbico equivale a .1000 litros, teremos:

22 métros cúbicos = (22 ⋅ .1000) litros = .22000 litros

Portanto, foram gastos .22000 litros de água.

26. A resposta depende do número de habitantes da cidade, mas, para esboçar uma resolução generalizada, usaremos n para designar o número de habitantes do município. Então,

q = \frac{n}{2, 9}

é a quantidade média de domicílios, ou seja, quantidade média de caixas-d’água desse município. A medida de tempo para encher uma caixa-d’água, visto que uma caixa-d’água tem 500 litros (0,5 métro cúbico), será dada, em segundo, por:

t = 0,5 : 56 ⇒ t ≃ 0,009

Então, basta fazer t = 0,009 ⋅ q para obter a medida de tempo que o sistema levaria para encher todas as caixas-d’água da cidade, considerando que, inicialmente, todas estejam vazias.

28. Inicialmente, a piscina contém 48 métros cúbicos de água, ou seja, .48000 litros de água (pois 8 ⋅ 4 ⋅ 1,5 = 48).

Ao entrarem as 10 pessoas, o nível de água sobe 2 centímetros, então, a nova medida de volume é 48,64 métros cúbicos (pois 8 ⋅ 4 ⋅ 1,52 = 48,64). Como 1 métro cúbico = .1000 litros, a medida do volume é .48640 litros. Ou seja, o volume aumentou 640 litros (.48640 ‒ .48000 = 640). Como 1 litro = 1 decímetro cúbico, então a medida do volume aumentou 640 decímetros cúbicos. Como 640 : 10 = 64, temos que a medida do volume médio do corpo de cada pessoa é 64 decímetros cúbicos.

29. Como foram 3 etapas por 10 dias, a quantidade total de etapas foi 30 (3 ⋅ 10 = 30). Visto que, em cada uma dessas etapas, foram acrescentados 3 mililitros, a medida total acrescentada foi 90 mililitros (30 ⋅ 3 = 90). Como 1 centímetro cúbico = 1 mililitro, então 90 mililitros correspondem a 90 centímetros cúbicos.

30. A medida de tempo que essa quantidade de água seria suficiente para uma pessoa beber é 75 dias (pois 150 : 2 = 75).

31. a) Basta fazer a medida do volume de álcool produzido com a cana-de-açúcar dividida pela medida do volume de álcool produzido com o milho, ficando .7500 : .3000 = 2,5. Assim, cana-de-açúcar rende 2,5 vezes mais etanol que o milho.

31. b) A partir da leitura do texto, é dado que 1 hectare de cana-de-açúcar rende 7,5 mil litros de etanol, portanto 4,3 milhões de hectares renderá

...32250000000 litros, pois: ..4300000 ⋅ .7500 = ...32250000000

Pense mais um poucoreticências

Página 266

a) Seja

V_{m}

a medida do volume (em litro) de água despejada a cada m minuto, então, para m > 1, m natural, e com

V_{1} = 1

, temos:

Vm = 2 ⋅ (Vm – 1)

V5 = 2⋅ V4 = 2 ⋅ 8 = 16

V6 = 2 ⋅ V5 = 2 ⋅ 16 = 32

V7 = 2 ⋅ V6 = 2 ⋅ 32 = 64

V8 = 2 ⋅ V7 = 2 ⋅ 64 = 128

b) Em

V_{8}

, o tanque fica pela metade. Nesse momento, a medida do volume é a soma das medidas de volumes despejados até então, logo, 255 litros, pois:

128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255

c) Se 255 é a metade do tanque, então a medida da capacidade do tanque é de 510 litros, pois 2 ⋅ 255 = 510. Note que

V_{9}

= 2 ⋅

V_{8}

= 2 ⋅ 128 = 256. Logo, o tanque ficará cheio apenas um minuto depois.

Exercícios complementares

1. a) Sabendo o valor de

S_{i}

podemos descobrir o número de lados n, fazendo:

Si = (n ‒ 2) ⋅ 180 ⇒ .2520 = (n ‒ 2) ⋅ 180 ⇒

⇒ .2520 = 180n ‒ 360 ⇒ n = 16

Portanto, o polígono tem 16 lados.

Agora, podemos usar a relação

a_{c} = \frac{360}{n}

e substituir n por 16 para encontrar o ângulo central. Assim,

a_{c} = \frac{360}{16}

= 22,5. Portanto, o ângulo central mede 22,5°.

1. b) Como se trata de um polígono regular, temos a relação:

a_{i} = \frac{S_{i}}{n} = \frac{2 520}{16}

= 157,5

Logo, os ângulos internos medem 157,5°.

1. c) Como

a_{i} e a_{e}

são suplementares, temos:

a_i + a_e = 180 ⇒ a_e = 22,5

Portanto, o ângulo externo mede 22,5°.

2. a) Usando a relação

a_{c} = \frac{360}{n}

e substituindo

a_{c}

por 9, teremos: 9 =

\frac{360}{n}

⇒ n = 40. O polígono tem 40 lados.

Página cento e cinco

2. b) Com os dados do problema, usaremos a relação

a_{i} = \frac{S_{i}}{n}

, e substituiremos

a_{i}

por 30. Assim, obtemos:

30 =

\frac{(n – 2) · 180}{n}

⇒ 30 =

\frac{180 n – 360}{n}

⇒

⇒ 30n = 180n ‒ 360 ⇒ 150n = 360 ⇒ n = 2,4

Como n tem de ser um número natural, esse polígono não existe.

2. c) Pelo enunciado, o ângulo interno mede 10°. Assim, concluímos que o ângulo externo mede 170° (pois são suplementares); usando a relação do ângulo interno de um polígono regular inscrito, obtemos:

a_i =

\frac{(n – 2) · 180}{n}

⇒ 170 =

\frac{180 n – 360}{n}

⇒

⇒ 170n = 180n ‒ 360 ⇒ 10n = 360 ⇒ n = 36

Assim, o polígono tem 36 lados.

3. Considerando a_i =

\frac{S_{i}}{n}

, temos que (n ‒ 2) ⋅ 180 = 180n ‒ 360 deve ser o menor possível. Como (180n ‒ 360) tem de ser o menor possível, mas diferente de zero, então n tem de ser maior que 2; logo, n tem de ser igual a 3. Desse modo, trata-se de um triângulo e a soma das medidas de seus ângulos internos resulta 180°. Então,

S_{i}

tem de medir 180°. Assim,

a_{i} = \frac{S_{i}}{n} \Rightarrow a_{i} = \frac{180}{3} = 60

. Desse modo, para o ângulo interno ser o menor possível, ele tem de medir 60°. Já para ser o maior possível, não é possível determinar, pois 180n ‒ 360 tem de ser o maior possível, mas n pode ser qualquer natural maior do que 3.

4. A partir da planificação, podemos perceber que a base do paralelogramo tem 2,5 centímetros de medida de largura por 1,3 centímetro de medida de comprimento; e a altura do paralelogramo tem medida 2 centímetros. Assim, V = 2,5 ⋅ 1,3 ⋅ 2 ⇒V = 6,5. Como 1 centímetro cúbico equivale a .1000 milímetros cúbicos, a medida do volume do paralelepípedo é .6500 milímetros cúbicos (6,5 ⋅ .1000 = .6500).

5. A medida do volume da argila é dada por .1000 vezes a medida do volume de cada tijolo. Chamando

V_{a}

a medida de volume de argila, e

V_{t}

a medida do volume de cada tijolo, então

V_{a}

= .1000 ⋅

V_{t}

. Agora, para descobrir a medida do volume de cada tijolo:

V_{t}

= 22 ⋅ 10 ⋅ 5 ⇒

V_{t}

= .1100. Como .1000 centímetros cúbicos = 1 decímetro cúbico, o volume de cada tijolo mede 1,1 decímetro cúbico. Assim, o volume de argila terá medida .1100 decímetros cúbicos, pois 1,1 ⋅ .1000 = .1100.

6. a) O problema nos fornece os dados:

r = 25 centímetros e h = 100 centímetros

Podemos calcular a medida do volume dessa caixa cilíndrica, em centímetros cúbicos:

Vc = πr² h ⇒ Vc = 3,14 ⋅ 25² ⋅ 100 ⇒ Vc = .196250

Portanto, a medida do volume é 196,25 litros (pois 1 centímetro cúbico equivale a 1 mililitro e .1000 mililitros equivale a 1 litro).

6. b) A massa de água contida na caixa tem medida .196250 gramas, pois 1 centímetro cúbico = 1 grama.

7. No recipiente 2 mantém-se a medida da área da base em toda secção que se faça na altura h. Desse modo, ao dobrar o volume de água no recipiente, a altura h dobrará. Alternativa c.

8. Discuta com os estudantes o significado de economia nesse contexto do problema, considerando que a caixa-d'água é a mesma, ou seja, a medida do volume total é a mesma. Se considerarmos que a caixa-d'água tem volume de medida x, então eram gastos

\frac{2}{5} x

. Com a troca por descargas econômicas, o gasto passou a ser

\frac{1}{4} x

. Então, a economia é calculada pela diferença entre os consumos de água, ou seja, a fração da caixa-d'água economizada é

\frac{3}{20}

, pois:

\frac{2}{5} - \frac{1}{4} = \frac{8 - 5}{20} = \frac{3}{20}

Alternativa b.

Verificando

5. Como o polígono regular tem 8 lados, a soma dos ângulos internos é dada por: (8 – 2) ⋅ 180 = .1080

Portanto, a soma dos ângulos internos desse polígono é .1080°.

Alternativa a.

6. A área que a fonte ocupará na praça corresponde à área da base dessa fonte. Pelo enunciado, sabemos que o raio mede 3,5 métros. Então, a área mede 38,5 métros quadrados (S = π ⋅ r² ⇒ S = 3,14 ⋅ 3,5² ⇒ S ≃ 38,5).

O comprimento da circunferência da fonte mede 21,98 métros (C = 2 ⋅ π ⋅ r = 2 ⋅ 3,14 ⋅ 3,5 ≃ 2).

Alternativa a.

7. A medida da área da base desse copo é 28,26 centímetros quadrados, pois S = π ⋅ r² ⇒ S = 3,14 ⋅ 3³ = 28,26. Pelos dados do exercício, pelo fato de esse copo estar com água pela metade, a altura h₂ = 6 centímetros. Portanto, o volume de água mede 169,56 mililitros (V = π ⋅ r² ⋅ h₂ ⇒ V = 28,26 ⋅ 6 = 169,56).

Alternativa b.

8. O volume de suco foi distribuído em 5 copos, pois:

.2000 : 400 = 5; e 1 centímetro cúbico = 1 mililitro

Alternativa c.

Organizando

a) É todo polígono cujos lados são congruentes e os ângulos internos têm a mesma medida.

b) Os pontos de tangência são os respectivos pontos médios dos lados do polígono.

c) A medida do ângulo central corresponde à divisão de 360° pelo número de lados do polígono.

a_{i} = \frac{S_{i}}{n} = \frac{(n – 2) · 180}{n}

e) A medida do comprimento da circunferência é dada por: π ⋅ r²

f) A medida do volume do cilindro é dada por: π ⋅ r² ⋅ h

g) Resposta pessoal. Espera-se que os estudantes considerem que volume é o espaço que determinado objeto ocupa, e a capacidade é o espaço interno de um recipiente que pode ser preenchido ‒ ou, ainda, quanto de líquido ou gás cabe no espaço interno de um recipiente.