Parte 9
Sugestão de avaliação diagnóstica
Atividade 1
(ê éfe zero sete ême ah zero um) Resolver e elaborar problemas com números naturais, envolvendo as noções de divisor e de múltiplo, podendo incluir máximo divisor comum ou mínimo múltiplo comum, por meio de estratégias diversas, sem a aplicação de algoritmos.
Uma empresa produz embalagens plásticas formadas por um recipiente e por sua tampa. Os recipientes são produzidos e colocados em caixas com 48 peças, enquanto as tampas são colocadas em caixas com 60 peças. Em seguida, eles são enviados ao setor que deve receber caixas com recipientes e caixas com tampas para fazer a montagem das embalagens. Considerando que deve ser entregue o mesmo número de recipientes e tampas, quantas caixas de cada tipo, no mínimo, devem ser enviadas?
Resposta: No mínimo 5 caixas de recipientes e 4 caixas de tampas.
Resolução e comentários
Para resolver esta atividade , os estudantes precisam compreender que, como as caixas com recipientes vêm com 48 peças cada, à medida que chegam mais caixas, a quantidade de recipientes é sempre um múltiplo de 48. De modo similar, a quantidade de tampas é sempre um múltiplo de 60. Para obter o mínimo múltiplo comum, eles podem escrever os múltiplos de cada um dos valores e observar quando os valores são iguais.
Múltiplos de 48: 0, 48, 96, 144, 192, 240, 288, reticências
Múltiplos de 60: 0, 60, 120, 180, 240, 300, reticências
Assim, para montar duzentas e quarenta embalagens, são necessárias, no mínimo, 5 caixas com 48 recipientes cada (240 : 48 = 5) e 4 caixas com 60 tampas cada (240 : 60 = 4).
A respeito dos múltiplos de um número natural, é importante que os estudantes compreendam que os múltiplos de 48 não são necessariamente os números que “aumentam de 48 em 48”. Por exemplo, a sequência 1, 49, 97, 145, reticências, “aumenta de 48 em 48”, mas deixa resto 1 quando os números dela são divididos por 48; logo, os números dessa sequência não são múltiplos de 48.
Atividade 2
(ê éfe zero sete ême ah zero dois) Resolver e elaborar problemas que envolvam porcentagens, como os que lidam com acréscimos e decréscimos simples, utilizando estratégias pessoais, cálculo mental e calculadora, no contexto de educação financeira, entre outros.
Um produto que era vendido por R$ 40,00quarenta reais teve um aumento de 20% em seu preço. Qual é o novo preço desse produto?
Resposta: R$ 48,00quarenta e oito reais
Resolução e comentários
Os problemas envolvendo aumentos e decréscimos simples restringem-se basicamente a dois tipos: aqueles em que são dados um valor, a taxa de acréscimo ou de decréscimo e pede-se o novo valor; e aqueles em que são dados a taxa de acréscimo ou de decréscimo, o valor final obtido e pede-se o valor inicial. Em geral, o primeiro tipo, abordado nesta atividade, é considerado mais simples pelos estudantes, e pode ser resolvido por meio da aplicação da ideia de proporcionalidade. Observe, a seguir, algumas resoluções possíveis.
• 20% é um quinto de 100% (100% : 5 = 20%). Portanto, basta dividir o valor inicial por 5 para determinar o valor do aumento do preço do produto (R$ 40,00quarenta reais : 5 = R$ 8,00oito reais) e, em seguida, adicionar o valor obtido ao valor inicial (R$ 8,00oito reais + R$ 40,00quarenta reais = R$ 48,00quarenta e oito reais).
• 20% pode ser escrito na forma decimal como 0,20. Assim, para determinar o valor do aumento do preço do produto, basta fazer 0,20 ⋅ R$ 40,00quarenta reais = R$ 8,00oito reais. Em seguida, basta adicionar o valor obtido ao valor inicial (R$ 8,00oito reais + R$ 40,00quarenta reais = R$ 48,00quarenta e oito reais).
• É possível primeiro calcular qualquer outra porcentagem do valor inicial, por exemplo, 10%, para depois aplicar a ideia de proporcionalidade. 10% de R$ 40,00quarenta reais são R$ 4,00quatro reais (R$ 40,00quarenta reais · 0,10 = R$ 4,00quatro reais). Portanto, 20% de R$ 40,00quarenta reais são R$ 8,00oito reais (2 · R$ 4,00quatro reais = R$ 8,00oito reais). Assim, adicionado o valor obtido para o aumento ao valor inicial, concluímos que o novo preço do produto é de R$ 48,00quarenta e oito reais (R$ 8,00oito reais + R$ 40,00quarenta reais = R$ 48,00quarenta e oito reais).
• Como o preço inicial corresponde a 100% do valor, após um aumento de 20%, o produto passará a custar 120% daquele valor. 120% pode ser escrito na forma decimal como 1,20; então, 120% de R$ 40,00quarenta reais é igual a R$ 48,00quarenta e oito reais (R$ 40,00quarenta reais · 1,20 = R$ 48,00quarenta e oito reais).
Atividade 3
(ê éfe zero sete ême ah zero três) Comparar e ordenar números inteiros em diferentes contextos, incluindo o histórico, associá-los a pontos da reta numérica e utilizá-los em situações que envolvam adição e subtração.
A temperatura máxima adequada para a conservação de carne de aves congelada mede 18 graus Celsius negativos, enquanto a temperatura máxima adequada para a conservação de carne de aves refrigerada mede 4 graus Celsius positivos. Uma câmara fria registra 8 graus Celsius positivos. Quanto a medida da temperatura deve diminuir para chegar à medida de temperatura máxima adequada em cada caso?
Resposta: Deve diminuir 26 °C para atingir a medida de temperatura máxima adequada para o congelamento e 4 °C para atingir a medida de temperatura máxima adequada para a refrigeração.
Resolução e comentários
Um modo de resolver a atividade é realizar os cálculos por meio dos procedimentos usuais.
Considerando a diferença entre a medida de temperatura da câmara fria (+8 °C) e a medida de temperatura recomendada para carnes refrigeradas (+4 °C), determinamos quanto a temperatura deve diminuir para chegar à medida de temperatura máxima adequada para a refrigeração.
8 °C ‒ 4 °C = 4 °C
Considerando a diferença entre a medida de temperatura da câmara fria (+8 °C) e a medida de temperatura recomendada para carnes congeladas (‒18 °C), determinamos quanto a temperatura deve diminuir para chegar à medida de temperatura máxima adequada para o congelamento.
8 °C ‒ (‒18 °C) = 26 °C
Caso os estudantes utilizem a reta numérica para a resolução, eles precisam localizar corretamente os números nela e calcular a distância entre os valores pedidos.
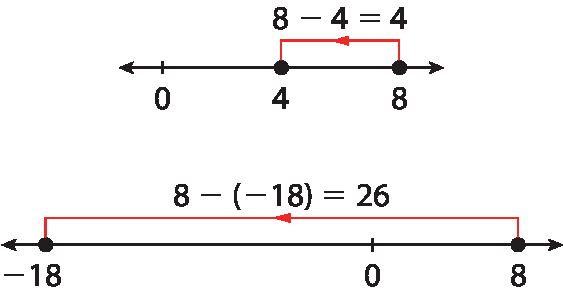
A representação visual possibilita aos estudantes observar que, no primeiro caso, a diferença entre as medidas 8 °C e 4 °C é igual a 4 °C (8 ‒ 4 = 4). No segundo caso, de ‒18 °C a 0 °C a diferença é igual a 18 °C; a diferença de 0 °C a 8 °C é igual a 8 °C; portanto, a diferença entre as medidas 8 °C e ‒18 °C é igual a 26 °C [8 °C ‒ (‒18 °C) = 26 °C].
Atividade 4
(ê éfe zero sete ême ah zero quatro) Resolver e elaborar problemas que envolvam operações com números inteiros.
Marcelo tinha R$ 84,00oitenta e quatro reais em sua conta corrente. Ele pagou uma conta no valor de R$ 112,00cento e doze reais e, em seguida, depositou R$ 75,00setenta e cinco reais. Qual é o saldo final da conta de Marcelo?
Resposta: R$ 47,00quarenta e sete reais
Resolução e comentários
Ao resolver a atividade, os estudantes podem realizar as operações na sequência em que são apresentadas (84 ‒ 112 + 75) ou adicionar os valores positivos (84 + 75) e, depois, adicionar o resultado a (‒112).
No primeiro caso, ao fazer 84 ‒ 112, os estudantes devem reconhecer que o resultado será negativo, pois o valor absoluto de ‒112 é maior do que o valor absoluto de 84. Adicionando essas parcelas, temos 84 ‒ 112 = ‒28. Em seguida, como +75 tem maior valor absoluto do que ‒28, conclui-se que o resultado será positivo: ‒28 + 75 = 47.
O segundo procedimento facilita os cálculos porque, após adicionar os dois valores positivos, 84 + 75 = 159, compara-se com o valor negativo ‒112 e observa-se que o resultado será positivo: 159 ‒ 112 = 47.
Atividade 5
(ê éfe zero sete ême ah zero cinco) Resolver um mesmo problema utilizando diferentes algoritmos.
Flávio quer calcular o resultado de (‒18 + 33). Qual dos procedimentos mostrados a seguir não permite obter a resolução correta?
a)

b)

c)
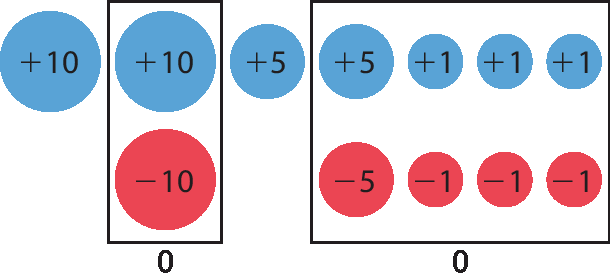
d) ‒18 + 33 = –(33 ‒ 18) = ‒15
Resposta: Alternativas a e d.
Resolução e comentários
As duas primeiras alternativas enfatizam o uso da reta numérica para a realização da operação. Na alternativa a foi representado o deslocamento de –18 até 33, o que representa uma adição de valores: –(–18) + 33 = 51. Portanto, essa alternativa está incorreta. Já na alternativa b foi representada a subtração 33 – 18 = 15. Observe se os estudantes entendem a representação em cada caso. Se tiverem dificuldades, apresente outros exemplos com operações envolvendo números positivos e negativos. A alternativa c utiliza a ideia de cancelamento ao se fazer a adição de números opostos: as 18 unidades positivas, representadas em azul, se anulam com as 18 unidades negativas, representadas em vermelho; restam, então, 15 unidades positivas. A alternativa d está incorreta, pois considera que o sinal resultante da adição dos dois valores é negativo.
Atividade 6
(ê éfe zero sete ême ah zero seis) Reconhecer que as resoluções de um grupo de problemas que têm a mesma estrutura podem ser obtidas utilizando os mesmos procedimentos.
(ê éfe zero sete ême ah zero sete) Representar por meio de um fluxograma os passos utilizados para resolver um grupo de problemas.
Acompanhe o fluxograma a seguir.
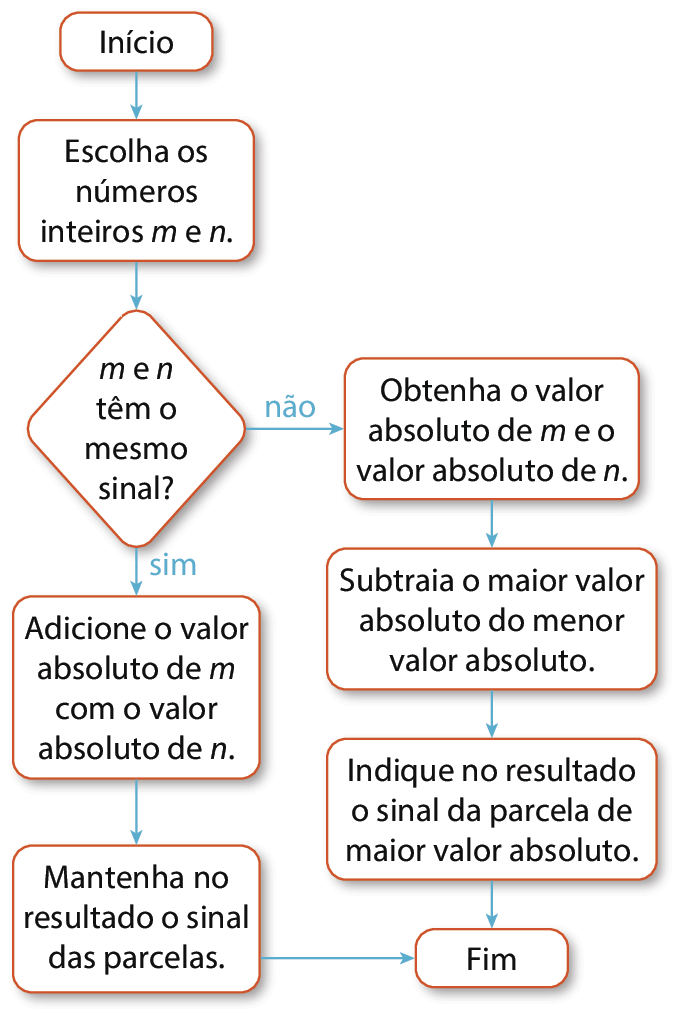
Qual é o tipo de problema que a aplicação desse fluxograma permite resolver?
a) A comparação entre dois números inteiros.
b) A subtração de dois números inteiros.
c) A adição de dois números inteiros.
d) A multiplicação de dois números inteiros.
Resposta: Alternativa c.
Resolução e comentários
Esta atividade tem por objetivo avaliar se os estudantes reconhecem que os fluxogramas podem representar as diversas etapas para resolver uma categoria de problemas similares. Como os números designados por m e n são inteiros, é possível que ambos tenham o mesmo sinal ou sinais opostos, o que é verificado no bloco de tomada de decisão. No caso da resposta ser “sim”, adicionar dois números positivos resulta em outro número positivo e adicionar dois números negativos resulta em outro número negativo; assim, como o sinal da soma não se altera, basta adicionar o valor absoluto ou módulo das parcelas e manter o sinal das parcelas envolvidas na adição. Por outro lado, se os sinais das parcelas são opostos, prevalece o sinal daquela de maior valor absoluto e, em seguida, deve-se subtrair a menor parcela da maior. Portanto, o fluxograma apresenta as etapas para a realização de uma adição qualquer de dois números inteiros.
Atividade 7
(ê éfe zero sete ême ah zero oito) Comparar e ordenar frações associadas às ideias de partes de inteiros, resultado da divisão, razão e operador.
André, Beatriz, Carlos e Denise estavam no mesmo restaurante para comer pizza. Considerando que as pizzas consumidas eram de mesmo tamanho, analise as situações:
• André comeu uma fatia de uma pizza dividida em 4 partes iguais;
• Beatriz estava em um grupo de 5 amigos que dividiram igualmente 2 pizzas entre si;
• Carlos comeu 2 dos 8 pedaços de uma pizza;
• Denise comeu um sexto de 2 pizzas.
Ordene em ordem crescente a fração de pizza que cada um deles comeu.
Resposta:
Fração. 1 quarto. Fração. 2 oitavos. Fração. 2 sextos. Fração. 2 quintos.Resolução e comentários
Esta atividade avalia a compreensão dos estudantes sobre as diferentes ideias de fração e a comparação entre os valores de frações representadas por meio de diferentes denominadores. No caso de André, a ideia envolvida é a parte de um todo dividido em partes iguais, em que uma parte de um total de 4 corresponde a
Fração. 1 quarto.. Ao dizer que Carlos comeu 2 de cada 8 pedaços, a ideia é a de razão, no caso,
Fração. 2 oitavos.. Por fim, o consumo de Denise é descrito por meio da ideia de operador, ou seja,
Fração. 1 sexto.de 2
Abre parêntese, fração 1 sexto, vezes 2, igual fração 2 sextos, fecha parêntese..
Para comparar as frações, os estudantes podem fazer uso da divisão do numerador pelo denominador.
1 : 4 = 0,25
2 : 5 = 0,40
2 : 8 = 0,25
2 : 6 = 0,33reticências
Outra possibilidade é por meio de frações equivalentes:
ême ême cê(4, 8, 6, 5) = 120
Em qualquer caso, a ordenação obtida por meio da comparação das frações deve ser:
Atividade 8
(ê éfe zero sete ême ah zero nove) Utilizar, na resolução de problemas, a associação entre razão e fração, como a fração
2 terçospara expressar a razão de duas partes de uma grandeza para três partes da mesma ou três partes de outra grandeza.
Vítor e Patrícia colheram maçãs em um pomar e, ao final, Vítor percebeu que colheu 3 de cada 5 maçãs obtidas por eles. Se Vítor colheu 18 maçãs, quantas foram colhidas por Patrícia?
Resposta: 12 maçãs
Resolução e comentários
Os estudantes podem ter dificuldades para resolver atividades que envolvem a divisão em partes proporcionais. Isso pode ocorrer devido à falta de compreensão do conceito envolvido ou da linguagem utilizada. Há diferentes modos de resolução.
• Por meio de representação em diagramas.
Como a referência dada é a de que Vítor colheu 3 de cada 5 maçãs, pode-se representar a situação como na figura a seguir.
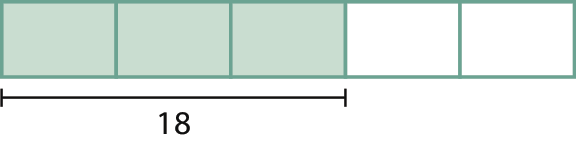
Como as 3 partes colhidas por Vítor correspondem a 18 maçãs, conclui-se que cada parte contém 6 maçãs (18 : 3 = 6). Portanto, as duas partes de Patrícia correspondem a 12 maçãs (2 · 6 = 12).
• Por meio de equação.
Se Vítor colheu
3 quintosdas maçãs, então essa fração do total x corresponde a 18.
Portanto, a parte colhida por Patrícia corresponde a
2 quintosde 30, ou seja, 12 maçãs (30 ‒ 18 = 12).
Atividade 9
(ê éfe zero sete ême ah um zero) Comparar e ordenar números racionais em diferentes contextos e associá-los a pontos da reta numérica.
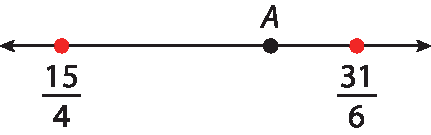
Assinale a alternativa que apresenta o número associado ao ponto A, cuja localização na reta numérica fica entre
15 quartose
31 sextos.
a)
28 quintosb)
19 quartosc)
22 sextosd)
26 quintosResposta: Alternativa b.
Resolução e comentários
A atividade apresenta a comparação de frações por meio de sua localização na reta numérica,
31 sextos>
15 quartos, e pede aos estudantes que identifiquem a fração localizada entre elas. Um modo de resolver a atividade é por meio da ideia de fração como divisão, não sendo necessário realizar o cálculo até a obtenção de todas as suas ordens decimais, bastando, apenas, um valor aproximado. Como 15 : 4 = 3,75 e 31 : 6 ≃ 5,167; conclui-se que a alternativa correta deve indicar uma fração cujo valor situa-se entre esses dois valores. Essa fração é
19 quartos.
• 28 : 5 = 5,6
• 19 : 4 = 4,75
• 22 : 6 = 3,67
• 26 : 5 = 5, 2
Atividade 10
(ê éfe zero sete ême ah um um) Compreender e utilizar a multiplicação e a divisão de números racionais, a relação entre elas e suas propriedades operatórias.
Acompanhe como Ricardo realizou o cálculo 2,4 : 0,08.
• Primeiro, ele igualou o número de casas decimais acrescentando um algarismo zero em 2,4 e eliminou as vírgulas:
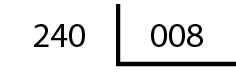
• Em seguida, ele fez a divisão 240 : 8, obtendo o quociente 30.
Indique a alternativa que justifica de forma correta o processo executado por Ricardo.
a) Acrescentar o algarismo zero equivale a dividir 2,4 por 10. Eliminar as vírgulas equivale a multiplicar 2,4 e 0,08 pelo mesmo valor.
b) O algarismo zero foi acrescentado porque 2,4 é o mesmo que 2,40. Ao eliminar as vírgulas, significa que tanto 2,4 quanto 0,08 foram multiplicados por 100, não alterando o resultado da divisão original.
c) Acrescentar o algarismo zero equivale a multiplicar 2,4 por 100. Eliminar as vírgulas equivale a multiplicar 2,4 por 10 e multiplicar 0,08 por 100.
d) Acrescentar o algarismo zero equivale a multiplicar 2,4 por 10. Eliminar as vírgulas equivale a multiplicar 2,4 por 100 e 0,08 por 10.
Resposta: Alternativa b.
Resolução e comentários
O objetivo desta atividade é avaliar se os estudantes reconhecem os princípios por meio dos quais o algoritmo utilizado por Ricardo é válido. É importante que os estudantes compreendam os procedimentos empregados no cálculo, e não somente reproduzam uma sequência de passos de forma mecânica, pois isso permite desenvolver as habilidades relacionadas ao uso dos princípios de uma igualdade, além de desenvolver ferramentas que podem ser úteis para o cálculo mental e a resolução de problemas. É esperado que eles reconheçam que o acréscimo do algarismo zero à direita da parte decimal do número não o altera, o que pode ser mostrado fazendo:
A etapa seguinte, na qual as vírgulas são retiradas, exige que os estudantes compreendam que, em uma igualdade, a multiplicação dos dois membros pelo mesmo número não nulo preserva a igualdade. É esperado que os estudantes tenham sido expostos a situações em que tenham aplicado essa propriedade, que pode ser observada em exemplos simples.
30 : 6 = 5
300 : 60 = 5
.3000 : 600 = 5
.30000 : .6000 = 5
Assim, na divisão 2,4 : 0,08, ao multiplicar o dividendo e o divisor por 100; 2,4 torna-se 240 e 0,08 torna-se 8, o que equivale a “eliminar as vírgulas”.
Atividade 11
(ê éfe zero sete ême ah um dois) Resolver e elaborar problemas que envolvam as operações com números racionais.
Use as informações a seguir, complete-as com outras de modo a elaborar um problema que faça sentido e resolva-o.
• Com metade do que restou, Fernanda pagou R$ 20,00vinte reais em um ingresso para o cinema.
• Fernanda gastou
1 terçodo que tinha na compra de um par de sapatos.
Exemplo de resposta: Fernanda gastou
1 terçodo que tinha na compra de um par de sapatos. Com metade do que restou, Fernanda pagou R$ 20,00vinte reais em um ingresso para o cinema. Quantos reais ela tinha no início? Resposta: Fernanda tinha R$ 60,00sessenta reais.
Resolução e comentários
Ao serem apresentados a informações incompletas, os estudantes devem mobilizar diversas habilidades desenvolvidas ao longo de sua escolarização e reuni-las de modo que texto e encadeamento lógico das condições fornecidas façam sentido no problema a ser criado, o que envolve, também, a compreensão dos procedimentos associados ao cálculo com frações. O modo como as informações foram escritas restringe, por exemplo, a ordem em que as duas frases devem se suceder no texto, pois, ao afirmar que ela pagou R$ 20,00vinte reais usando metade do que restou, sugere-se que houve um gasto anterior, que pode se referir à frase em que aparece a menção à personagem Fernanda ou à inclusão de outros gastos intermediários que os estudantes podem inserir a seu critério. No caso do exemplo de resposta apresentado, os estudantes podem representar a situação por meio de um esquema.

Como Fernanda gastou
1 terçodo que tinha com a compra do par de sapatos, restaram
2 terçosdo total. Então, como ela gastou metade do que sobrou, ou seja,
1 terçodo total, com a compra do ingresso, conclui-se que cada terço corresponde a R$ 20,00vinte reais e que no início Fernanda tinha 3 · R$ 20,00vinte reais = R$ 60,00sessenta reais.
Atividade 12
(ê éfe zero sete ême ah um três) Compreender a ideia de variável, representada por letra ou símbolo, para expressar relação entre duas grandezas, diferenciando-a da ideia de incógnita.
No retângulo a seguir, a medida da altura é uma unidade maior do que a medida n da base.
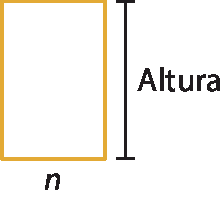
Considerando essa informação, complete corretamente o quadro a seguir.
|
Medida da base (n) |
Medida da altura |
Medida do perímetro |
|---|---|---|
|
1 |
||
|
2 |
||
|
3 |
||
|
n |
Resposta:
|
Medida da base (n) |
Medida da altura |
Medida do perímetro |
|---|---|---|
|
1 |
2 |
1 + 2 + 1 + 2 = 6 |
|
2 |
3 |
2 + 3 + 2 + 3 = 10 |
|
3 |
4 |
3 + 4 + 3 + 4 = 14 |
|
n |
n + 1 |
n + n + 1 + n + n + 1 = 4n + 2 |
Resolução e comentários
Nesta atividade, os estudantes devem compreender que a partir da variável n é possível obter uma expressão algébrica para a medida da altura do retângulo e para a medida do perímetro. Espera-se que o uso de um quadro seja familiar aos estudantes, pois as variações sugeridas para n na coluna correspondente auxiliam no reconhecimento de seu caráter “variável”, em contraposição à ideia de incógnita, que decorre de uma igualdade e, portanto, não se altera. Essa característica do uso de uma letra para representar tanto a ideia de uma incógnita quanto de uma variável pode trazer algumas dificuldades aos estudantes durante o processo de aprendizado, mas seu uso em diferentes contextos e aplicações contribui para que adquiram mais experiência e familiaridade com essa distinção. Por esse motivo, é importante observar o significado que eles atribuem à letra n e como eles manipulam os símbolos durante as operações, a fim de esclarecer eventuais equívocos que podem se repetir durante a realização de outras atividades que exigem o uso da álgebra.
Atividade 13
(ê éfe zero sete ême ah um quatro) Classificar sequências em recursivas e não recursivas, reconhecendo que o conceito de recursão está presente não apenas na matemática, mas também nas artes e na literatura.
Observe a figura a seguir, composta de quadrados.

Considerando as medidas dos lados desses quadrados, qual sequência numérica poderia representá-las?
a) 2, 4, 8, 16, 32, reticências
b) 1; 1,5; 3; 3,5; 4; 4,5; reticências
c) 2, 5, 10, 17, 26, reticências
d) 5, 10, 15, 20, 25, 30, reticências
Resposta: Alternativa d.
Resolução e comentários
Nesta atividade, os estudantes devem reconhecer que as medidas dos lados dos quadrados, a partir do centro, aumentam linearmente, ou seja, por meio de acréscimos constantes. No caso da alternativa a, a sequência numérica pode ser descrita por meio da expressão
a n, igual, 2 elevado a n., de modo que os acréscimos não são sempre os mesmos. Na alternativa b, os termos, a partir do terceiro, podem ser obtidos por meio de adições. Nesse caso, os acréscimos também não são sempre os mesmos. Na alternativa c, os termos são obtidos por meio da expressão
a n, igual, n elevado a 2, fim do expoente, mais 1.. Os acréscimos, nessa sequência, não são sempre os mesmos. Na alternativa d, os acréscimos são os mesmos e iguais a 5, o que corresponde à situação descrita.
Atividade 14
(ê éfe zero sete ême ah um cinco) Utilizar a linguagem algébrica para expressar regularidades encontradas em sequências numéricas.
Observe a sequência de figuras.
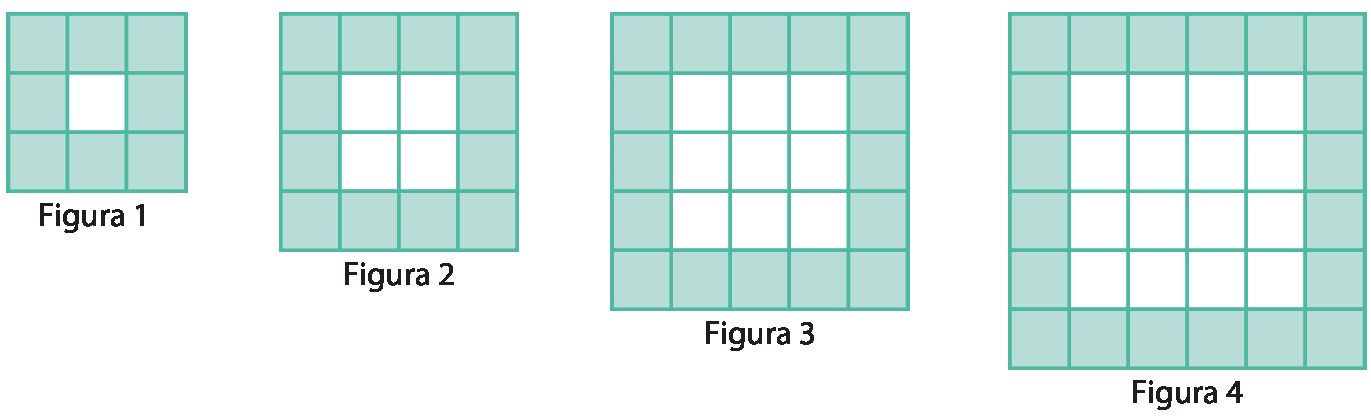
Assinale a expressão algébrica que relaciona a posição n da figura na sequência à quantidade Q de quadradinhos pintados de verde.
a) Q = 3 ⋅ n
b) Q = n + 4
c) Q = 4 ⋅ n + 4
d) Q = n² ‒ n
Resposta: Alternativa c.
Resolução e comentários
Para responder a esta atividade, os estudantes podem recorrer ao teste das alternativas substituindo o número correspondente à posição da figura em n e, por meio de cálculo, verificar os resultados obtidos. Assim, ao testar a alternativa a para a figura 1 obtém-se Q = 3 ⋅ 1 = 3, o que está incorreto, pois a quantidade de quadradinhos é 9. A alternativa b também mostra-se incorreta para n = 1, pois, nesse caso, Q = 1 + 4 = 5. De modo análogo pode-se testar as alternativas seguintes das quais apenas a c mostra-se correta. Entretanto, os estudantes podem obter a expressão algébrica por diferentes processos de construção das figuras. Por exemplo, eles podem observar que os quadradinhos coloridos podem ser obtidos partindo do quadrado central, em branco. Considerando a medida do lado do quadrado central como n, a quantidade de quadradinhos que tocam suas laterais é igual a 4n. Acrescentando os 4 quadradinhos dos cantos da figura, temos 4n + 4.
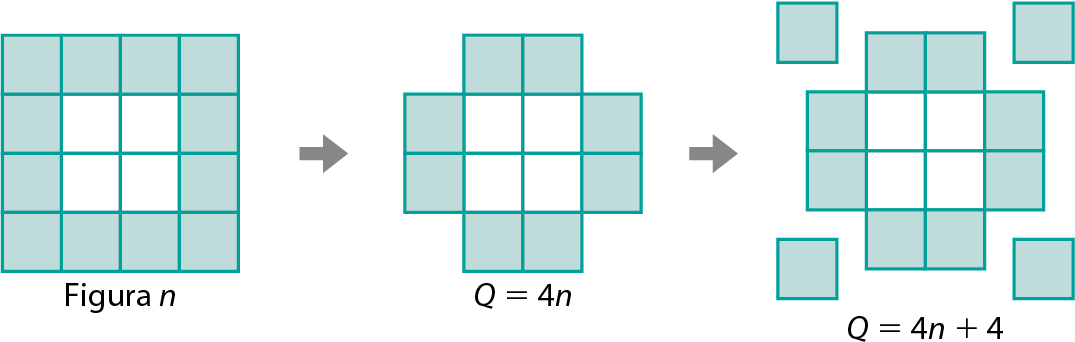
Atividade 15
(ê éfe zero sete ême ah um seis) Reconhecer se duas expressões algébricas obtidas para descrever a regularidade de uma mesma sequência numérica são ou não equivalentes.
Considere a sequência numérica: 5, 8, 11, 14, reticências
Essa sequência corresponde à quantidade de quadradinhos que compõem cada uma das figuras a seguir.
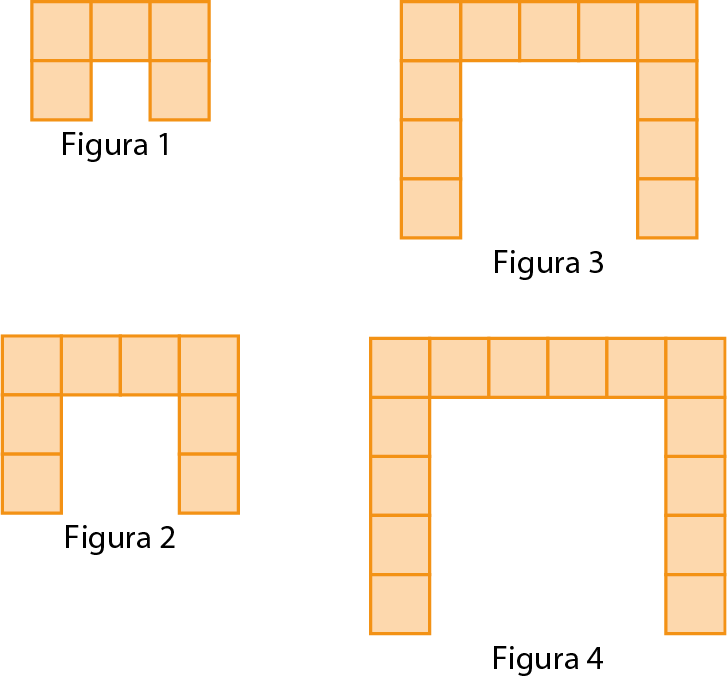
Indique a alternativa cuja expressão algébrica não corresponde à sequência numérica apresentada.
a) (n + 2) + 2n
b) 3n + 2
c) 3n ‒ 2
d) (n + 2)² ‒ n² ‒ (n + 2)
Resposta: Alternativa c.
Resolução e comentários
Caso os estudantes já tenham adquirido maior vivência com o uso da linguagem algébrica, eles podem observar que as alternativas a e b são equivalentes, pois, ao adicionar as partes literais n + 2n, obtém-se 3n, de modo que n + 2 + 2n = 3n + 2. Como há apenas uma alternativa incorreta, e a alternativa c é obviamente diferente de 3n + 2, conclui-se que ela é a alternativa que mostra uma expressão não equivalente. Entretanto, espera-se que os estudantes, ao analisarem as alternativas, busquem pistas do processo de sua obtenção, a fim de obter a conclusão correta de forma direta.
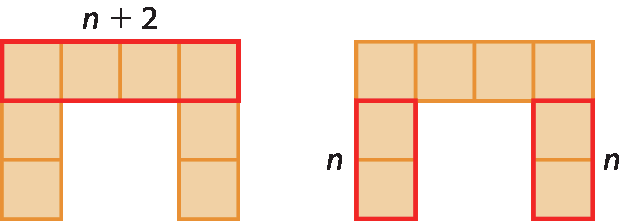
a) A expressão n + 2 representa o número de quadradinhos da fileira horizontal de cada figura. Como cada uma das duas laterais tem o mesmo número n de quadradinhos, conclui-se que o total de quadradinhos é n + 2 + 2n.
b) A expressão 3n representa os 3 grupos de n quadradinhos da figura. O termo 2 adicionado corresponde aos 2 quadradinhos dos cantos.
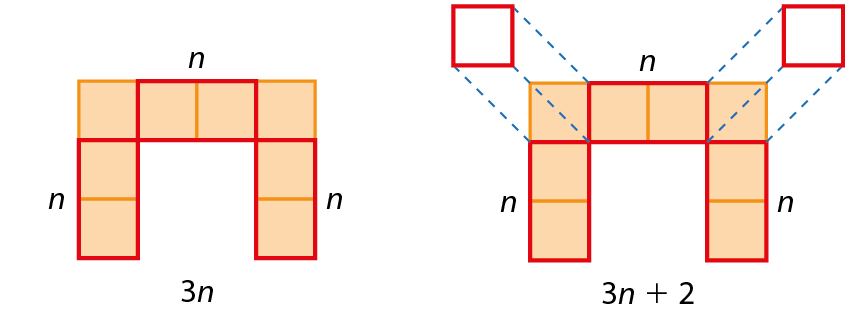
d) A expressão (n + 2)² representa a quantidade de quadradinhos do quadrado não completo de lado n + 2, o qual, subtraído do número de quadradinhos no centro da figura, dado por n², e subtraído de (n + 2), resulta no número de quadradinhos da figura: (n + 2)² ‒ n² ‒ (n + 2). Caso os estudantes saibam realizar a multiplicação de termos algébricos, pode-se fazer: (n + 2) ⋅ (n + 2) ‒ n² ‒ n ‒ 2 = n² + 2n + 2n + 4 ‒ n² ‒ n ‒ 2 = 3n + 2
Atividade 16
(ê éfe zero sete ême ah um sete) Resolver e elaborar problemas que envolvam a variação de proporcionalidade direta e de proporcionalidade inversa entre duas grandezas, utilizando sentença algébrica para expressar a relação entre elas.
Para uma festa foi comprada uma quantidade de suco de frutas suficiente para encher 40 copos de 250 mililitros cada. Entretanto, como foram convidadas mais pessoas, essa mesma quantidade de suco teve de ser transferida para copos de 200 mililitros. Quantos copos foram cheios com suco de fruta?
Resposta: 50 copos.
Resolução e comentários
Os problemas envolvendo a proporcionalidade direta ou a inversa podem ser resolvidos como problemas simples de aritmética, por meio do raciocínio proporcional, usando regras práticas que automatizam o processo, como a conhecida “regra de três”, ou usando a linguagem algébrica para expressar a relação entre as grandezas.
• Uso da aritmética. O volume total de suco nos 40 copos de 250 mililitros é .10000 mililitros (40 ⋅ 250 = .10000). Se essa quantidade for distribuída em copos de 200 mililitros cada, serão necessários 50 copos (.10000 : 200 = 50).
• Raciocínio proporcional.
A razão entre a capacidade do copo menor e a do copo maior é
fração 200 sobre 250.=
4 quintos. Como as grandezas são inversamente proporcionais, temos:
Capacidade de cada copo (mililitro) Número de copos

• Regra de três.

200 ⋅ x = 250 ⋅ 40 → x =
fração: 10 mil, 200 avos= 50 (50 copos)
• Linguagem algébrica.
As grandezas capacidade c e número de copos n são inversamente proporcionais, então o produto de seus valores é igual a uma constante k (c ⋅ n = k).
Para c = 250 e n = 40, temos que k = 250 ⋅ 40 ou k = .10000.
Substituindo o valor de k novamente na igualdade, com c = 200, temos:
200 ⋅ n = .10000 ⇒ n =
fração: 10 mil, 200 avos= 50
Atividade 17
(ê éfe zero sete ême ah um oito) Resolver e elaborar problemas que possam ser representados por equações polinomiais de 1º grau, redutíveis à forma ax + b = c, fazendo uso das propriedades da igualdade.
A idade de Renata há 3 anos era a metade da idade que ela terá daqui a 4 anos. Qual é a idade de Renata?
Resposta: Renata tem 10 anos.
Resolução e comentários
Um dos maiores desafios no desenvolvimento do pensamento algébrico é a etapa em que os estudantes devem traduzir enunciados de problemas para a linguagem algébrica. Esse desenvolvimento ocorre de forma gradativa e exige a exposição dos estudantes a uma grande variedade de problemas e a discussão detalhada de cada etapa da transposição do texto, de modo que os estudantes consigam atribuir significado às ações executadas.
Nesta atividade, espera-se que os estudantes reconheçam que a incógnita é a idade atual de Renata, que será designada por x. Assim, há 3 anos, ela tinha 3 anos a menos do que tem atualmente, ou seja, x ‒ 3. A idade dela em 4 anos será 4 anos a mais do que a idade atual, ou seja, x + 4. De acôrdo com o texto, a idade dela 3 anos atrás (x ‒ 3) corresponde à metade da idade que ela terá em 4 anos.
Após a obtenção da equação polinomial de 1º grau, os estudantes devem aplicar as propriedades da igualdade para determinar o valor de x.
2 ⋅ (x ‒ 3) = 2 ⋅
Abre parêntese, fração: numerador: x mais 4; denominador: 2, fecha parêntese.⇒ 2x ‒ 6 = x + 4 ⇒ 2x ‒ 6 ‒ x = x + 4 ‒ x ⇒ x ‒ 6 = 4 ⇒ x = 10
Portanto, Renata tem 10 anos de idade.
Atividade 18
(ê éfe zero sete ême ah um nove) Realizar transformações de polígonos representados no plano cartesiano, decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro.
Observe o quadrilátero a bê cê dê no plano cartesiano a seguir. Desenhe a figura obtida ao multiplicar cada coordenada dos pontos que formam esse quadrilátero por (‒2).
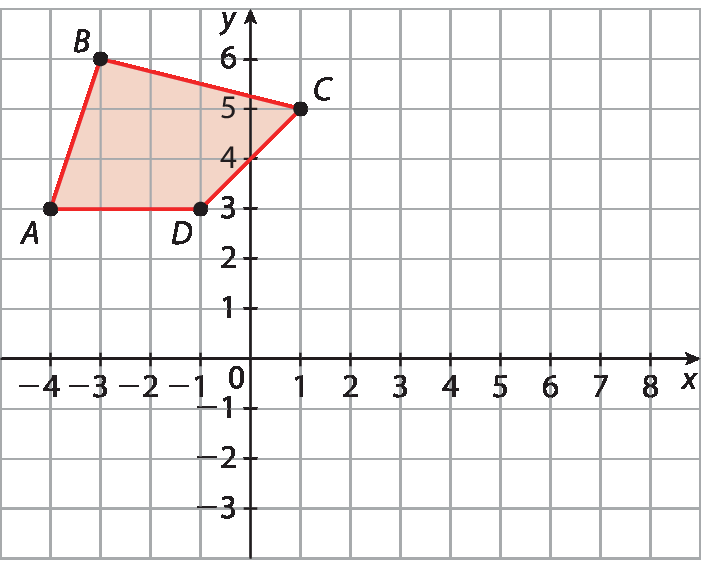
Resposta:
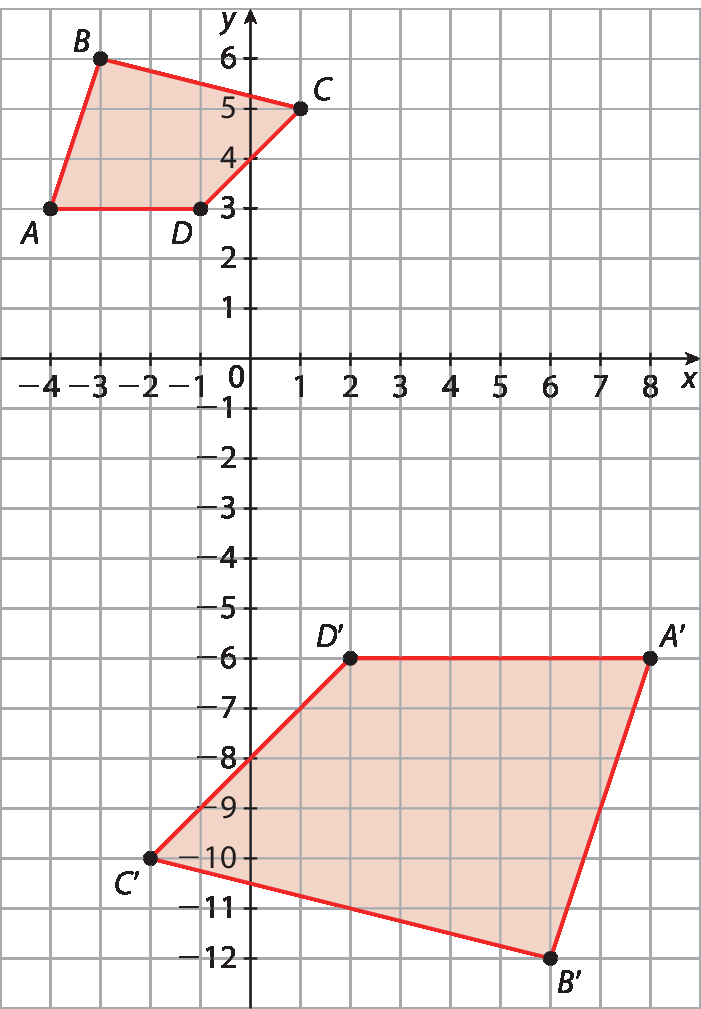
Resolução e comentários
Transformações de polígonos como ampliação/redução, com a obtenção do simétrico em relação a uma reta ou um ponto, podem ser estudadas por meio de transformações aplicadas a suas coordenadas no plano cartesiano. Nesta atividade, a multiplicação de uma coordenada por ( ‒2) pode ser compreendida por meio de duas ações:
• a multiplicação das coordenadas de cada ponto do polígono por 2 equivale a ampliá-lo por um fator 2, ou seja, dobrar as medidas de seus lados;
• a multiplicação das coordenadas por (‒1), ou simplesmente “trocar o sinal” das coordenadas, equivale a “inverter” a figura (observe que, na figura original, o vértice a está à esquerda do vértice D, e, na nova figura, o vértice divisores de ’ está à esquerda de á’).
Atividade 19
(ê éfe zero sete ême ah dois zero) Reconhecer e representar, no plano cartesiano, o simétrico de figuras em relação aos eixos e à origem.
Construa o simétrico do retângulo a bê cê dê em relação ao eixo vertical.
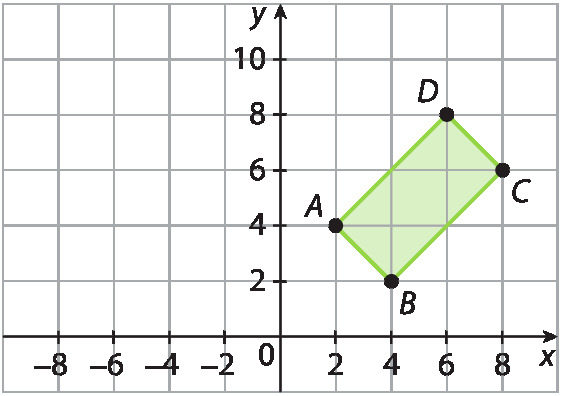
Resposta:
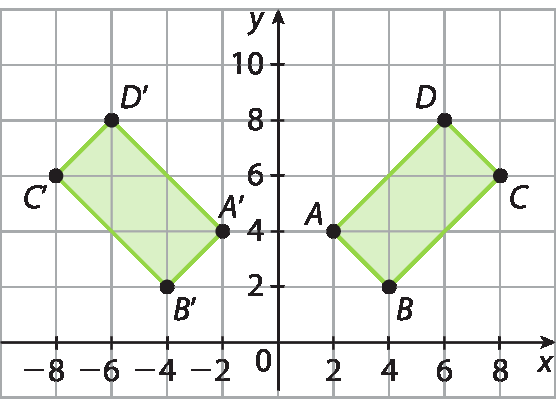
Resolução e comentários
Para desenhar o simétrico de um polígono em relação ao eixo y, os estudantes devem reconhecer que as coordenadas y dos pontos não se alteram, mas as coordenadas x trocam de sinal, nesse caso, têm sinal negativo.
a(2, 4) → á linha(‒2, 4)
B(4, 2) → bê linha(‒4, 2)
C(8, 6) → cê linha(‒8, 6)
D(6, 8) → dê linha(‒6, 8)
Entretanto, é mais provável que os estudantes tenham obtido os pontos simétricos de cada vértice medindo a distância de cada vértice ao eixo y. Por exemplo, o ponto a tem coordenada x = 2, de modo que de a até a origem, desloca-se duas unidades, então essa é a distância entre o ponto a e o eixo y. Assim, para obter o simétrico á linha, desloca-se o ponto a(0, 4) duas unidades para a esquerda a partir do eixo y, chegando a á linha(‒2, 4). Raciocínio similar permite obter os demais vértices, bê linha, cê linha e dê linha.
Atividade 20
(ê éfe zero sete ême ah dois um) Reconhecer e construir figuras obtidas por simetrias de translação, rotação e reflexão, usando instrumentos de desenho ou softwares de geometria dinâmica, e vincular esse estudo a representações planas de obras de arte, elementos arquitetônicos, entre outros.
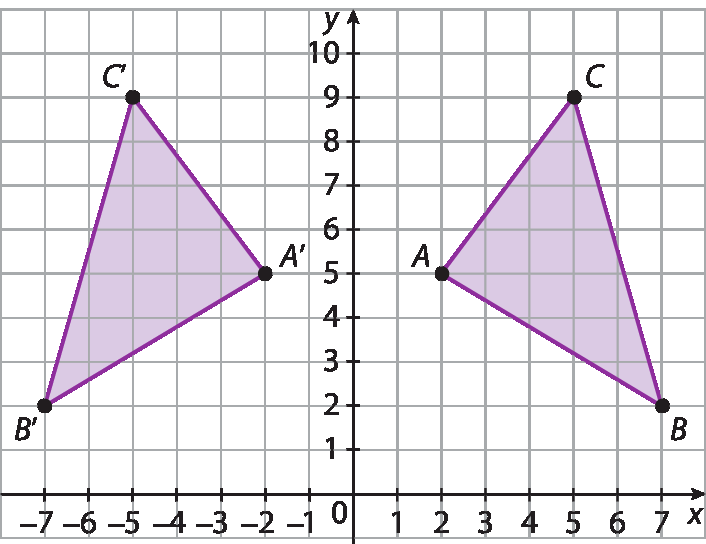
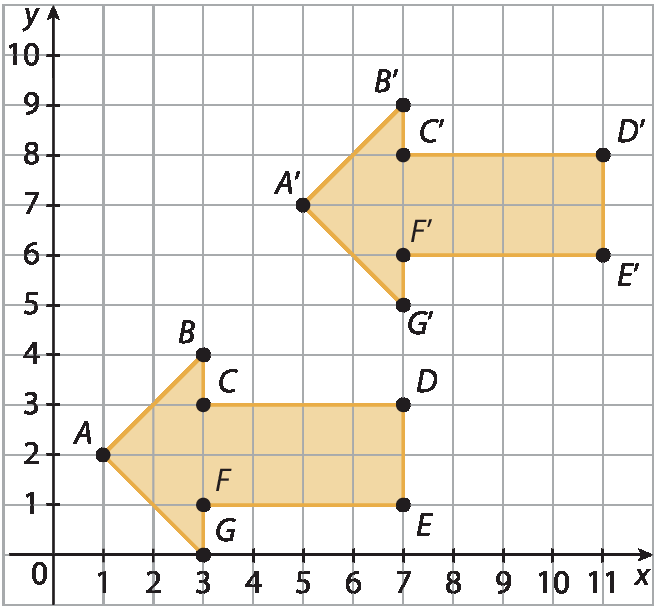
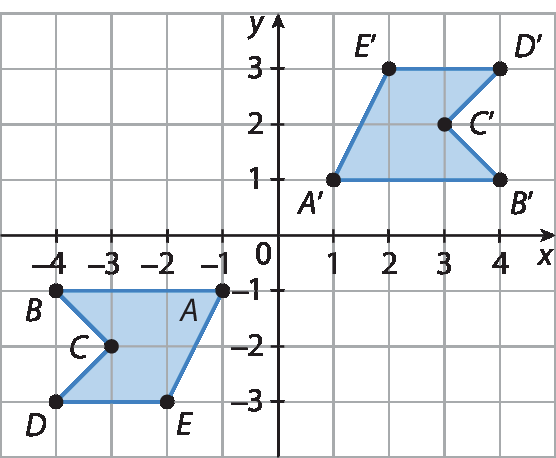
Indique a alternativa que mostra uma figura simétrica da outra, obtida por meio de uma rotação de 180° em relação à origem (0, 0).
a)
b)
c)
d)
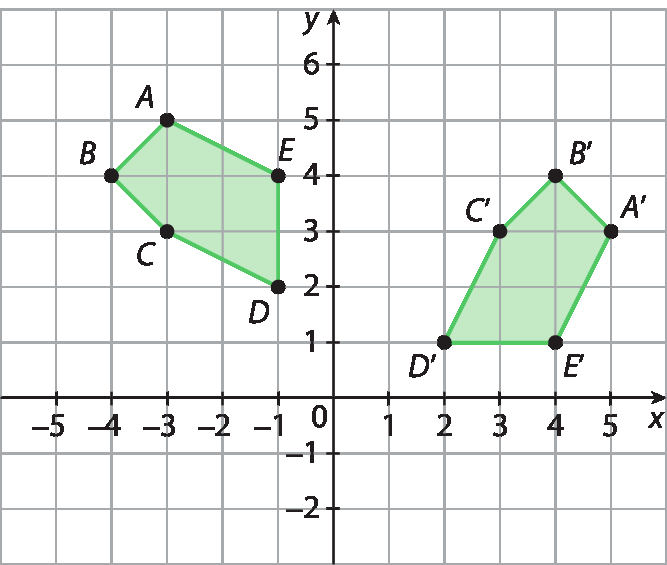
Resposta: Alternativa a.
Resolução e comentários
Uma rotação de 180°, ou meia-volta, em torno da origem dos eixos coordenados pode ser reconhecida considerando que ela faz com que a figura obtida pareça espelhada em relação à figura original, levando em conta o centro da rotação. Entretanto, os estudantes podem ser levados ao erro e assinalar a alternativa c, considerando apenas o fato de que uma figura fica espelhada em relação à outra, o que não corresponde ao conceito de rotação. A alternativa b apresenta uma translação da figura e a alternativa d apresenta uma rotação com um ângulo diferente de 180°.
Atividade 21
(ê éfe zero sete ême ah dois dois) Construir circunferências, utilizando compasso, reconhecê-las como lugar geométrico e utilizá-las para fazer composições artísticas e resolver problemas que envolvam objetos equidistantes.
Na figura a seguir, as circunferências de centro P e Q têm raios de medida 5 centímetros.
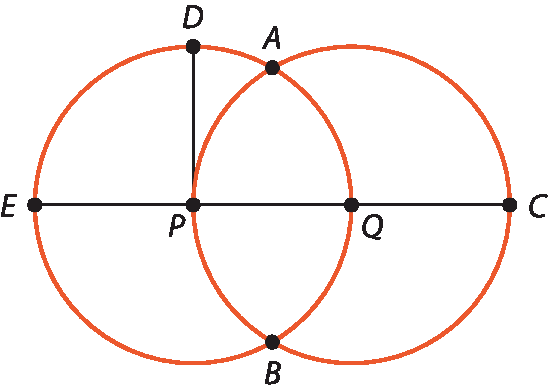
Os pontos que estão à mesma distância de P e de Q são:
a) C e ê.
b) D e C.
c) a e D.
d) a e B.
Resposta: Alternativa d.
Resolução e comentários
O objetivo desta atividade é avaliar se os estudantes compreendem a propriedade comum aos pontos de uma circunferência, aqueles que estão à mesma distância de seu centro. Para que o ponto esteja à mesma distância dos dois centros P e Q, ele deve ser um ponto da circunferência de centro P e também pertencer à circunferência de centro Q, ou seja, pode ser o ponto a ou o ponto B. Além de avaliar o conhecimento dos estudantes sobre a definição de circunferência, esta atividade permite que esse raciocínio sirva de base para a compreensão do método empregado na construção da mediatriz de um segmento
P Q.
Atividade 22
(ê éfe zero sete ême ah dois três) Verificar relações entre os ângulos formados por retas paralelas cortadas por uma transversal, com e sem uso de softwares de geometria dinâmica.
Na figura a seguir, as retas r e s são paralelas e cortadas por uma reta t transversal a elas. Ao usar um transferidor, Rita verificou que os pares de ângulos correspondentes, como
ângulo de
ângulo h, têm a mesma medida, 130°. Em seguida, ela verificou experimentalmente que os pares de ângulos opostos pelo vértice, como
ângulo de
ângulo b, também são congruentes.
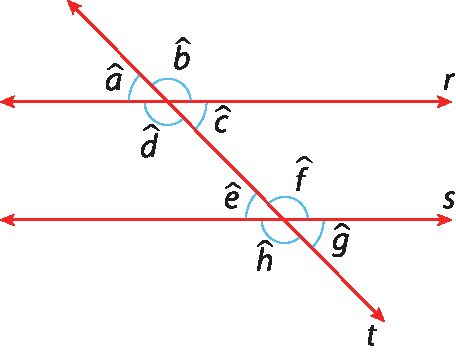
O raciocínio que permite concluir, com base nessas informações, que os ângulos alternos internos
ângulo de
ângulo ftêm a mesma medida é:
a)
ângulo fé o suplemento de
ângulo h; portanto, também tem a mesma medida que
ângulo he
ângulo d.
b)
ângulo fé oposto pelo vértice em relação a
ângulo h; portanto, tem a mesma medida que
ângulo he, consequentemente, também é congruente a
ângulo d.
c)
ângulo fé o complemento de
ângulo h; portanto, também tem a mesma medida que
ângulo he
ângulo d.
d)
ângulo fe
ângulo dsão alternos internos; portanto, são congruentes.
Resposta: Alternativa b.
Resolução e comentários
Esta atividade avalia o conhecimento dos estudantes sobre a nomenclatura usada para identificar pares de ângulos em retas paralelas cortadas por uma transversal e, também, o encadeamento lógico que permite deduzir que ângulos alternos internos são congruentes. Espera-se que a informação fornecida pelo enunciado sobre a congruência de ângulos correspondentes tenha sido verificada empiricamente pelos estudantes por meio de softwares de geometria dinâmica ou por meio de medições diretas com auxílio do transferidor; isso favorece o entendimento de que, em Geometria, tais resultados aceitos como evidentes (chamados postulados ou axiomas) são necessários para que, a partir deles, outros resultados possam ser demonstrados por meio da aplicação do raciocínio lógico aos demais elementos em estudo.
Atividade 23
(ê éfe zero sete ême ah dois quatro) Construir triângulos, usando régua e compasso, reconhecer a condição de existência do triângulo quanto à medida dos lados e verificar que a soma das medidas dos ângulos internos de um triângulo é 180°.
Luís quer construir um triângulo com lados de medida 6 centímetros, 3 centímetros e 2 centímetros. Para isso, ele desenhou com a régua um segmento medindo 6 centímetros de comprimento e, em seguida, posicionou o compasso da forma indicada na figura a seguir para construir dois arcos de circunferência.
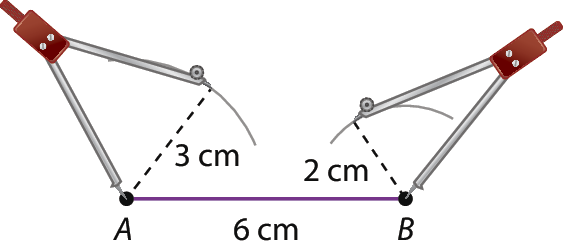
Observando o procedimento utilizado por ele, é possível concluir que:
a) os dois arcos traçados com o compasso se interceptam, marcando o 3º vértice do triângulo; assim, os outros dois lados do triângulo podem ser construídos com auxílio de uma régua.
b) os dois arcos traçados com o compasso se interceptam sobre o lado
A B; portanto, como os três pontos estão alinhados, não é possível construir o triângulo.
c) os arcos não se cruzam, pois 6 > 3 + 2; portanto, o triângulo não pode ser construído.
d) os arcos se cruzam em mais de um ponto; portanto, não é possível determinar qual é o 3º vértice do triângulo.
Resposta: Alternativa c.
Resolução e comentários
Nesta atividade é avaliada a compreensão dos estudantes sobre a condição de existência de um triângulo: a medida de um lado deve ser menor do que a soma das medidas dos outros dois lados. A figura que mostra o procedimento de construção de um triângulo com régua e compasso favorece a compreensão dessa condição, mesmo que os estudantes não se recordem dela, pois, nesse caso, a soma das medidas dos raios (2 + 3 = 5) é menor do que 6; portanto, os arcos não se cruzam e não é possível determinar o terceiro vértice do triângulo.
Atividade 24
(ê éfe zero sete ême ah dois cinco) Reconhecer a rigidez geométrica dos triângulos e suas aplicações, como na construção de estruturas arquitetônicas (telhados, estruturas metálicas e outras) ou nas artes plásticas.
A figura a seguir mostra estruturas com formatos que lembram um quadrado, um losango e um triângulo. Essas estruturas são construídas com palitos de sorvete presos por percevejos. Observe que a estrutura que lembra um losango é obtida com a aplicação de uma fôrça em um dos vértices da estrutura que lembra um quadrado. Se fizermos o mesmo com a estrutura que lembra um triângulo, ela não se deformará.
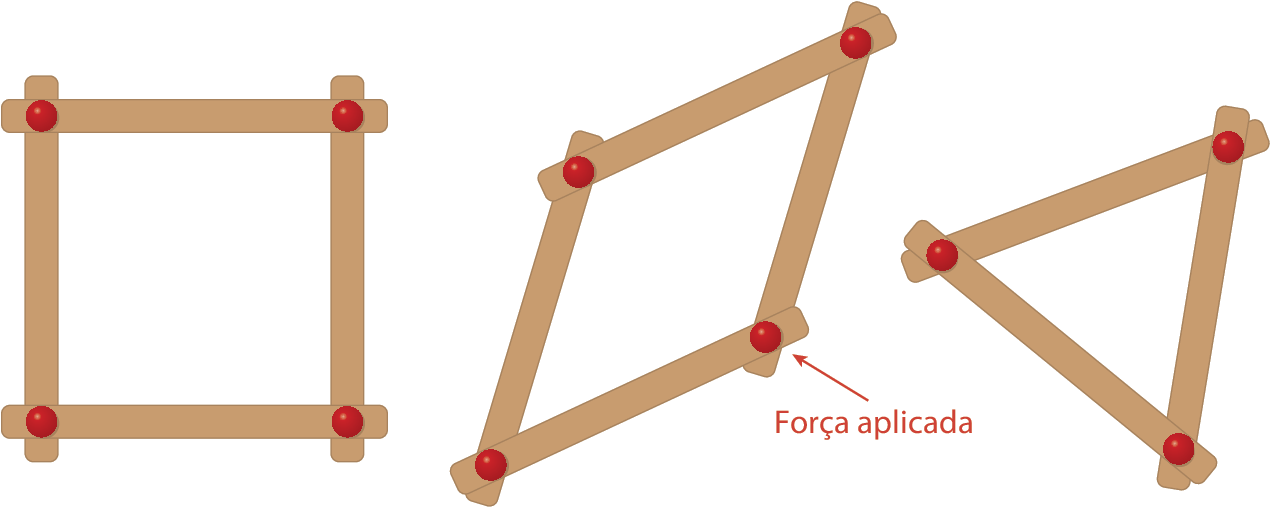
Indique a alternativa que apresenta uma explicação para esse fato.
a) Os vértices do triângulo estão mais próximos entre si do que os vértices do quadrado.
b) O triângulo tem três vértices; como três é um número ímpar, não é possível deformar o triângulo.
c) Com as medidas dos três lados definidas, só é possível construir um único triângulo e, por isso, não é possível deformá-lo.
d) Os ângulos internos de um triângulo têm sempre medida menor do que os ângulos internos de um quadrilátero.
Resposta: Alternativa c.
Resolução e comentários
A rigidez dos triângulos é uma propriedade com diversas aplicações práticas na Engenharia. Ela pode ser aplicada, por exemplo, na construção de treliças e de tesouras em telhados. Ela pode ser compreendida em associação com a atividade anterior, que mostra o procedimento para a construção de um triângulo. Como os arcos traçados sobre um lado determinado, com centros nas extremidades desse lado, só têm um único ponto de intersecção, conclui-se que existe apenas um triângulo com as medidas dadas, de modo que as medidas dos ângulos internos não mudam; assim, a estrutura triangular não pode mudar de forma.
Atividade 25
(ê éfe zero sete ême ah dois seis) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um triângulo qualquer, conhecidas as medidas dos três lados.
O fluxograma a seguir mostra um algoritmo para a construção de um triângulo a partir das medidas de seus lados, representadas por a, b e c. Entretanto, um dos passos indicados foi apagado e não é possível ver a instrução que ele continha.
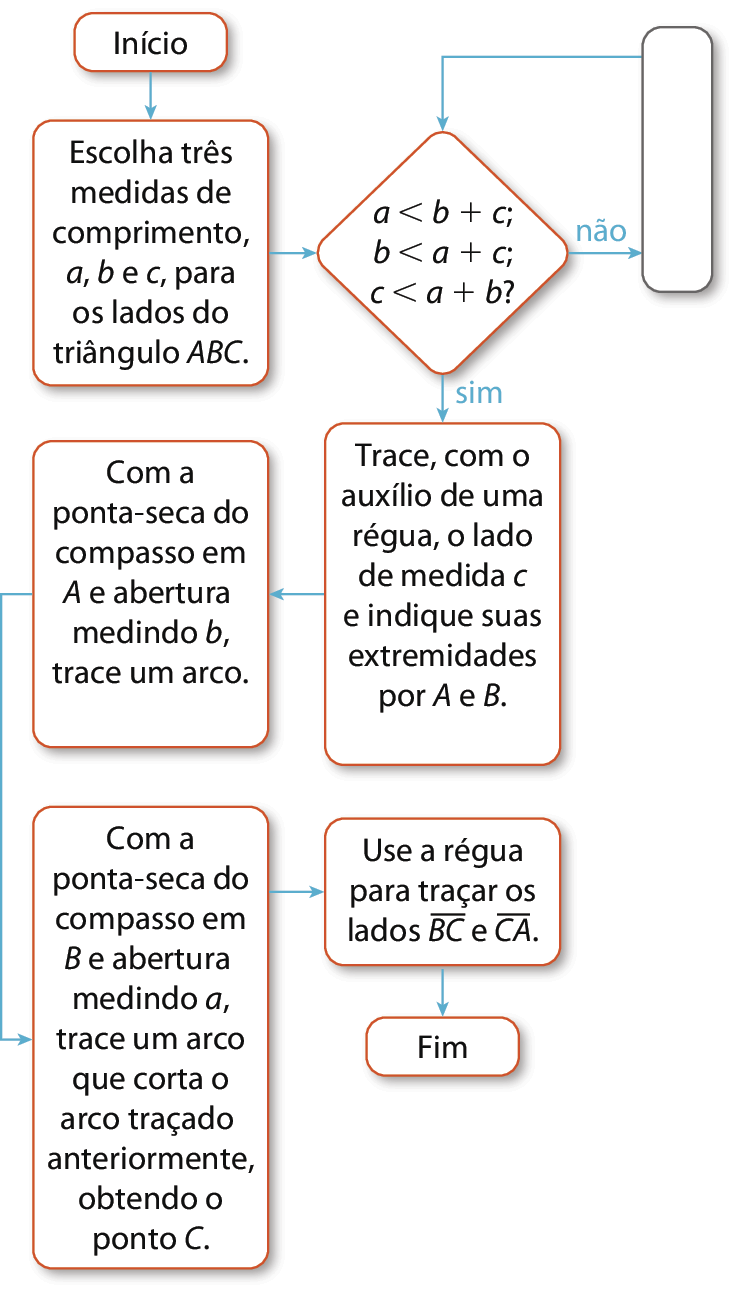
Qual das alternativas a seguir apresenta o conteúdo apagado?
a) Escolha outras medidas de comprimento para os lados a, b e c.
b) Multiplique cada uma das medidas dos lados a, b e c por 2.
c) Divida cada uma das medidas dos lados a, b e c por 2.
d) Substitua as medidas de a, b e c por potências de 10 consecutivas.
Resposta: Alternativa a.
Resolução e comentários
Ao analisar o fluxograma apresentado, espera-se que os estudantes reconheçam que um algoritmo para a construção de um triângulo só pode ser executado caso as medidas dos seus lados satisfaçam a condição de existência: a soma das medidas de dois lados sempre deve ser maior do que a medida do terceiro lado. Assim, os estudantes devem compreender que, como a parte apagada do fluxograma corresponde ao não atendimento à condição de existência de um triângulo, as medidas dos lados devem ser alteradas e novamente submetidas à verificação da condição até que ela seja satisfeita.
Atividade 26
(ê éfe zero sete ême ah dois sete) Calcular medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, e estabelecer relações entre ângulos internos e externos de polígonos, preferencialmente vinculadas à construção de mosaicos e de ladrilhamentos.
Para preencher uma superfície plana, é possível utilizar ladrilhos de formato quadrado, pois eles se encaixam sem deixar espaços vazios, como mostra a figura a seguir.
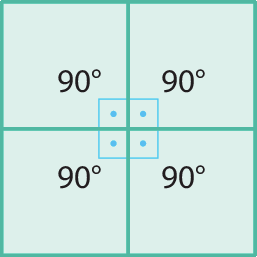
Indique a alternativa que apresenta o polígono regular que, ao ser encaixado repetidas vezes, não preenche uma superfície plana sem deixar espaços vazios.
a) Triângulo equilátero.
b) Pentágono regular (5 lados).
c) Hexágono regular (6 lados).
Resposta: Alternativa b.
Resolução e comentários
Para responder a esta atividade, os estudantes devem compreender que a medida do ângulo interno de um polígono deve ser um divisor de 360°. Em seguida, eles devem calcular a medida de cada ângulo interno dos diferentes polígonos apresentados nas alternativas e verificar se o valor obtido é um divisor de 360.
Os ângulos internos de um triângulo equilátero medem 60°. Como 60 é um divisor de 360 (360 : 60 = 6), um triângulo equilátero, ao ser encaixado repetidas vezes, preenche uma superfície plana sem deixar espaços vazios.
Os ângulos internos de um pentágono regular medem 108° (540° : 5 = 108°). Como 108 não é um divisor de 360 (360 : 108 = 3,33reticências), um pentágono regular, ao ser encaixado repetidas vezes, não preenche uma superfície plana sem deixar espaços vazios.
Os ângulos internos de um hexágono regular medem 120° (720° : 6 = 120°). Como 120 é um divisor de 360 (360 : 120 = 3), um hexágono regular, ao ser encaixado repetidas vezes, preenche uma superfície plana sem deixar espaços vazios.
Atividade 27
(ê éfe zero sete ême ah dois oito) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular (como quadrado e triângulo equilátero), conhecida a medida de seu lado.
Bruna fazia um fluxograma descrevendo um procedimento para construir um quadrado. A parte inicial e a final do fluxograma estão prontas, mas falta ela descrever os passos para completar os blocos intermediários do fluxograma: a obtenção dos quatro pontos igualmente espaçados sobre a circunferência, a, B, C e D, que serão os vértices do quadrado. Descreva um procedimento para a obtenção desses quatro pontos, completando o fluxograma de Bruna.
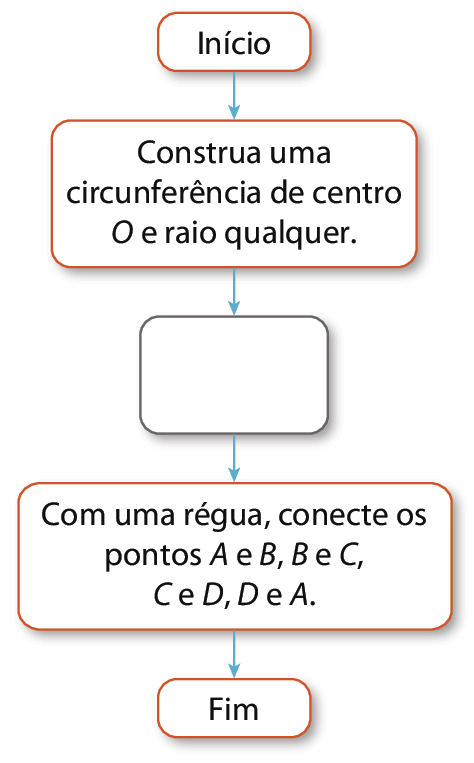
Resposta possível: Escolha um ponto a qualquer da circunferência e trace um diâmetro passando por a, determinando o ponto B da circunferência; construa uma reta perpendicular a
A B, passando por óh, determinando os pontos C e D na intersecção com a circunferência.
Resolução e comentários
Nesta atividade, espera-se que os estudantes reconheçam que um polígono regular pode ser obtido dividindo a circunferência em n partes iguais, neste caso, um quadrado, em 4 partes iguais. Daí a possibilidade de pedir a construção de dois diâmetros perpendiculares entre si, pois a medida do ângulo central será 360° : 4 = 90°. De modo geral, a construção de qualquer polígono regular a partir de uma circunferência dada exige a construção de ângulos centrais consecutivos de medida 360° : n.
A seguir, apresentamos um exemplo em que n = 8 (octógono regular). Assim, como 360° : 8 = 45°, basta construir 8 ângulos centrais cujas medidas sejam 45°.
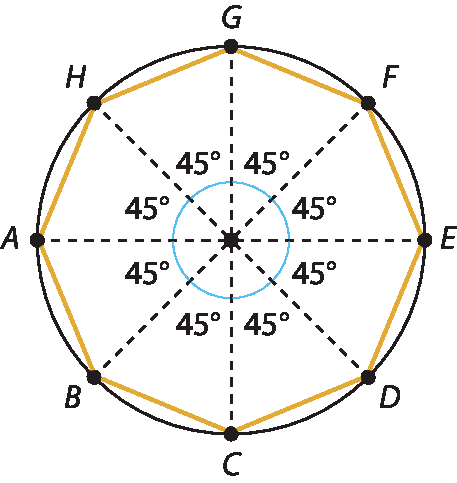
Atividade 28
(ê éfe zero sete ême ah dois nove) Resolver e elaborar problemas que envolvam medidas de grandezas inseridos em contextos oriundos de situações cotidianas ou de outras áreas do conhecimento, reconhecendo que toda medida empírica é aproximada.
O departamento de contrôle de qualidade de uma empresa que produz embalagens plásticas mediu a espessura, em milímetro, de 10 peças do mesmo produto. A espessura esperada para as peças é de 3,0 milímetros. Os resultados das medidas, em milímetro, são apresentados no quadro a seguir.

Para saber a variação média das medidas obtidas em relação à espessura esperada, Heitor calculou a diferença entre cada valor e 3,0, considerando o resultado sempre positivo; em seguida, adicionou todos os valores obtidos e dividiu a soma pelo número de medições efetuadas. Que valor ele encontrou para a variação média das medidas obtidas em relação à espessura esperada?
Resposta: 0,12 milímetro
Resolução e comentários
Um dos aspectos inerentes à ação de medir uma grandeza com um instrumento de medida é a ocorrência de erro. Nesta atividade, é avaliada a habilidade do estudante interpretar e acompanhar a realização de uma sequência de cálculos que levam ao desvio absoluto médio de um conjunto de medidas, cuja denominação formal não precisa ser apresentada aos estudantes. Espera-se que eles sigam as etapas descritas no enunciado para obter o resultado. Para as diferenças, temos:
3,0 ‒ 3,0 = 0,0
3,0 ‒ 2,9 = 0,1
3,0 ‒ 2,9 = 0,1
3,2 ‒ 3,0 = 0,2
3,3 ‒ 3,0 = 0,3
3,2 ‒ 3,0 = 0,2
Para a soma, temos:
0,0 + 0,1 + 0,3 + 0,0 + 0,0 + 0,1 + 0,2 + 0,2 + 0,1 + 0,2 = 1,2
Para o resultado da divisão, temos: 1,2 : 10 = 0,12
Então, a variação média das medidas obtidas em relação à espessura esperada é 0,12 milímetro.
Atividade 29
(ê éfe zero sete ême ah três zero) Resolver e elaborar problemas de cálculo de medida do volume de blocos retangulares, envolvendo as unidades usuais (metro cúbico, decímetro cúbico e centímetro cúbico).
O aquário de Isabel tem as medidas indicadas na figura a seguir.
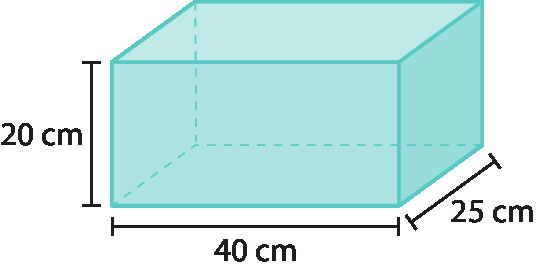
Quantos litros de água cabem nesse aquário?
Resposta: 20 litros.
Resolução e comentários
Para responder a esta atividade, os estudantes precisam compreender que a medida do volume de um bloco retangular é dada pelo produto das medidas de comprimento, largura e altura. Eles também precisam lembrar que 1 litro equivale a .1000 centímetros cúbicos ou .1000 mililitros. Assim, devem concluir que no aquário cabem .20000 centímetros cúbicos de água.
20 ⋅ 40 ⋅ 25 = .20000
Como .1000 centímetros cúbicos = 1 litro, conclui-se que .20000 centímetros cúbicos = 20 litros.
Ao discutir a resolução da atividade com os estudantes, converse com eles sobre a importância prática de saber calcular o volume ou a capacidade de um bloco retangular para determinar a medida aproximada do volume ou da capacidade de objetos com formatos irregulares, por exemplo, uma pedra. Proponha a resolução do seguinte problema aos estudantes: Se o aquário da atividade estiver com água até a altura de medida 10 centímetros e, ao mergulhar uma pedra em seu interior, o nível da água sobe para 10,5 centímetros, como é possível calcular o volume da pedra com base nessas informações? Espera-se que os estudantes compreendam que, ao mergulhar a pedra na água, o aumento no nível da água está relacionado à medida de seu volume. Assim, a medida do volume da pedra seria igual à medida do volume de um bloco retangular de medidas 25 centímetros × 40 centímetros × 0,5 centímetros (10,5 centímetros ‒ 10 centímetros = 0,5 centímetro). Portanto, a medida do volume da pedra é 500 centímetros cúbicos, ou meio litro (25 ⋅ 40 ⋅ 0,5 = 500).
Atividade 30
(ê éfe zero sete ême ah três um) Estabelecer expressões de cálculo de área de triângulos e de quadriláteros.
Observe no losango a seguir as indicações das medidas de suas duas diagonais: a diagonal maior de medida D e a diagonal menor de medida d. Pedro decompôs esse losango em quatro triângulos equivalentes e reagrupou os dois triângulos da parte inferior do losango, colocando-os na parte superior, obtendo o retângulo em amarelo.
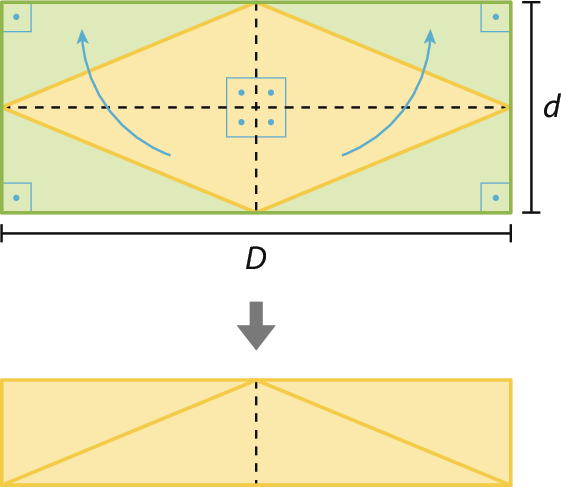
Com base nesse raciocínio, é possível concluir que a área de um losango é dada por:
a) A = D + d
b) A = D ⋅ d
c) A =
fração de numerador: D maiúsculo vezes d minúsculo, e denominador: 2.d) A = D² + d²
Resposta: Alternativa c.
Resolução e comentários
O objetivo desta atividade é avaliar se os estudantes compreendem um raciocínio empregado para o cálculo da área de um losango, utilizando a ideia de equivalência de áreas e o procedimento para o cálculo da área de um retângulo. O desenvolvimento do pensamento geométrico e algébrico dos estudantes deve incorporar a habilidade de acompanhar um raciocínio constituído de várias etapas com o apoio de imagens que sugerem padrões, propriedades e relações existentes entre os elementos que compõem o objeto em estudo. Assim, as medidas do retângulo cuja área é equivalente à do losango não são apresentadas para que os estudantes reconheçam que a medida da base não se alterou (D), enquanto a da altura foi reduzida à metade
Fração. Numerador d minúsculo. Denominador 2.. Outro raciocínio comumente apresentado para a obtenção da área de um losango é considerar que cada triângulo retângulo destacado em amarelo no interior do losango é congruente a um triângulo em verde, de modo que a área do retângulo formado por 8 triângulos é igual a D ⋅ d. Como a área do losango corresponde à metade da área desse retângulo, a medida de sua área é dada por
fração de numerador: D maiúsculo vezes d minúsculo, e denominador: 2..
Atividade 31
(ê éfe zero sete ême ah três dois) Resolver e elaborar problemas de cálculo de medida de área de figuras planas que podem ser decompostas por quadrados, retângulos e/ou triângulos, utilizando a equivalência entre áreas.
O terreno de Regina tem o formato de um trapézio, ou seja, de um quadrilátero que tem dois lados paralelos. O esquema a seguir mostra as medidas desse terreno. Qual é a medida de sua área, em metro quadrado?
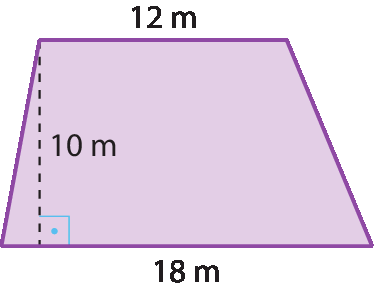
Resposta: 150 métros quadrados
Resolução e comentários
Os estudantes podem utilizar diferentes estratégias para obter medida da área da figura. Por exemplo, com base em sua decomposição e no rearranjo de suas partes ou aplicando a ideia de adicionar áreas de modo a formar um retângulo e, depois, subtrair a área adicionada, como mostram as figuras a seguir.
Decompõe-se o trapézio em dois triângulos e um retângulo de base medindo 12 métros e altura medindo 10 métros. Os dois triângulos são reunidos de modo a formar um novo triângulo de base medindo 6 métros (18 ‒ 12 = 6) e altura medindo 10 métros.
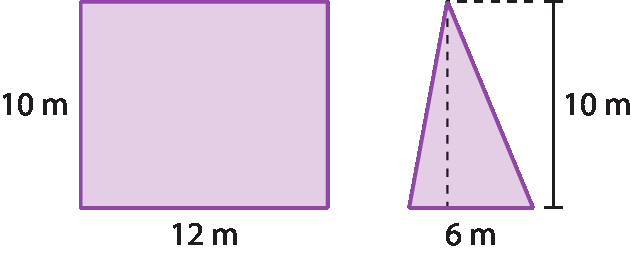
Calculando as áreas e adicionando-as, obtém-se:
(12 ⋅ 10) +
Abre parêntese, fração de numerador 6 vezes 10, denominador 2, fecha parêntese.= 120 + 30 = 150
Prolonga-se a base menor do trapézio, formando um retângulo de base medindo 18 métros e altura medindo 10 métros; em seguida, subtraem-se as medidas de área dos dois triângulos adicionados.
(18 ⋅ 10) ‒
Abre parêntese, fração de numerador 6 vezes 10, denominador 2, fecha parêntese.= 180 ‒ 30 = 150
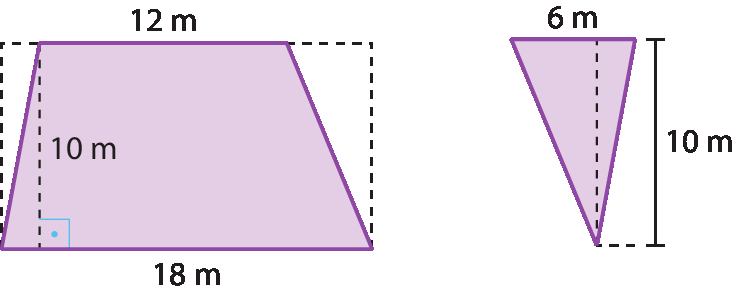
Note que, utilizando qualquer uma das estratégias, a medida encontrada para a área do terreno é a mesma, 150 métros quadrados.
Atividade 32
(ê éfe zero sete ême ah três três) Estabelecer o número π como a razão entre a medida de uma circunferência e seu diâmetro, para compreender e resolver problemas, inclusive os de natureza histórica.
A roda de certo modelo de automóvel mede 45 centímetros de diâmetro. Qual é a medida da distância percorrida por ele quando a roda dá duzentas voltas completas? Considere π = 3,1.
Resposta: 279 métros
Resolução e comentários
Para resolver esta atividade, os estudantes precisam compreender que a medida do comprimento da circunferência corresponde à medida da distância percorrida por ela a cada volta completa, assim:
π =
fração, numerador: medida do comprimento da circunferência; denominador: medida do diâmetro
3,1 =
Fração de numerador: C, denominador: 0,45.⇒ C = 3,1 ⋅ 0,45 = 1,395 (1,395 métros)
Assim, para saber a medida da distância percorrida pelo automóvel após duzentas voltas completas da roda, basta fazer 200 ⋅ 1,395 = 279. Logo, a distância mede 279 métros.
Atividade 33
(ê éfe zero sete ême ah três quatro) Planejar e realizar experimentos aleatórios ou simulações que envolvem cálculo de probabilidades ou estimativas por meio de frequência de ocorrências.
Em uma caixa há 5 bolas, sendo 3 delas azuis e as outras duas vermelhas. Os estudantes da turma de Letícia calcularam a probabilidade de, ao sortear uma bola dessa caixa, sair uma bola azul. Em seguida, diversos grupos de estudantes da turma fizeram uma simulação realizando 500 sorteios de modo aleatório e registrando os resultados obtidos na tabela a seguir. Qual dos grupos obteve o resultado mais próximo do que era esperado?
|
Grupo |
Número de vezes em que a bola sorteada foi azul |
|---|---|
|
A |
178 |
|
B |
380 |
|
C |
190 |
|
D |
281 |
Dados obtidos pelos grupos.
Resposta: O grupo D.
Resolução e comentários
A resolução desta atividade envolve o conhecimento dos conceitos de probabilidade e frequência relativa. A probabilidade de sair uma bola azul é dada por:
=
3 quintos= 0,60
Assim, é esperado que
3 quintosdos 500 sorteios tenham como resultado bolas azuis, ou seja:
⋅ 500 = 300
Comparando esse valor teórico com os resultados das simulações, observa-se que o grupo D, com 281 sorteios de bolas azuis, foi aquele que mais se aproximou do valor esperado. Outra forma de fazer a comparação entre a previsão (0,60) e os resultados das simulações é calcular a frequência relativa do resultado obtido por cada grupo.
Grupo a:
Fração 178 500 avos≃ 0,36
Grupo B:
Fração 380 500 avos= 0,76
Grupo C:
Fração 190 500 avos= 0,38
Grupo D:
Fração 281 500 avos≃ 0,56
Como o valor mais próximo de 0,60 obtido pelos grupos é 0,56, conclui-se que a resposta é o grupo D.
Atividade 34
(ê éfe zero sete ême ah três cinco) Compreender, em contextos significativos, o significado de média estatística como indicador da tendência de uma pesquisa, calcular seu valor e relacioná-lo, intuitivamente, com a amplitude do conjunto de dados.
Os salários dos jogadores de duas equipes de basquete são apresentados na tabela a seguir.
|
Salário dos jogadores da equipe A |
Salário dos jogadores da equipe B |
|---|---|
|
R$ 3.500,00 |
R$ 2.500,00 |
|
R$ 4.500,00 |
R$ 3.500,00 |
|
R$ 5.000,00 |
R$ 2.000,00 |
|
R$ 3.500,00 |
R$ 2.000,00 |
|
R$ 3.500,00 |
R$ 10.000,00 |
Dados obtidos pelas equipes de basquete.
Considerando a média dos salários dos jogadores de cada equipe, é correto afirmar que:
a) como os salários dos jogadores da equipe a não são os mesmos dos jogadores da equipe B, as médias de salários são diferentes.
b) as médias são iguais e na equipe B os salários de cada jogador estão mais próximos desse valor médio.
c) os salários da equipe B não têm um valor médio, porque R$ 5.000,00cinco mil reais não corresponde ao salário de nenhum dos jogadores.
d) as médias são iguais e na equipe a os salários de cada jogador estão mais próximos desse valor médio.
Resposta: Alternativa d.
Resolução e comentários
Esta atividade tem por objetivo avaliar a compreensão dos estudantes sobre o conceito de média aritmética e abordar informalmente a ideia de variabilidade dos dados em torno da média. A alternativa a sugere uma resposta equivocada, em que valores diferentes resultam em médias aritméticas diferentes. Espera-se que os estudantes reconheçam que, se dois conjuntos de dados têm o mesmo número de elementos e as somas são iguais, eles apresentam o mesmo valor para a média aritmética. Neste caso, ambas as somas equivalem a R$ 20.000,00vinte mil reais; dividindo esse valor por 5 temos uma média igual a R$ 4.000,00quatro mil reais. Na alternativa b, espera-se que os estudantes observem que o valor médio R$ 4.000,00quatro mil reais está mais distante dos salários individuais dos jogadores da equipe B do que dos salários individuais dos jogadores da equipe A; logo, essa alternativa está incorreta. Como a alternativa d corresponde à sua negativa, ela é a resposta correta.
Ao discutir a correção dessa alternativa com os estudantes, enfatize o fato de que os quatro primeiros salários dos jogadores da equipe B estão próximos entre si, mas a inclusão de um valor extremo (R$ 10.000,00dez mil reais) fez com que a média aumentasse e os valores se distanciassem do valor médio. Esse fato ilustra como a média aritmética é sensível a valores extremos, sejam eles muito inferiores ou superiores aos demais valores do conjunto de dados.
Atividade 35
(ê éfe zero sete ême ah três seis) Planejar e realizar pesquisa envolvendo tema da realidade social, identificando a necessidade de ser censitária ou de usar amostra, e interpretar os dados para comunicá-los por meio de relatório escrito, tabelas e gráficos, com o apoio de planilhas eletrônicas.
(ê éfe zero sete ême ah três sete) Interpretar e analisar dados apresentados em gráfico de setores divulgados pela mídia e compreender quando é possível ou conveniente sua utilização.
Em outubro de 2021, a prefeitura de um município noticiou que ocorreram trínta e duas mortes por covíd-19 de pessoas vacinadas contra a doença (com uma ou duas doses da vacina). No mesmo período, ocorreram 20 mortes por covíd-19 de pessoas não vacinadas. Com base nessa notícia, Natália construiu o seguinte gráfico de setores.
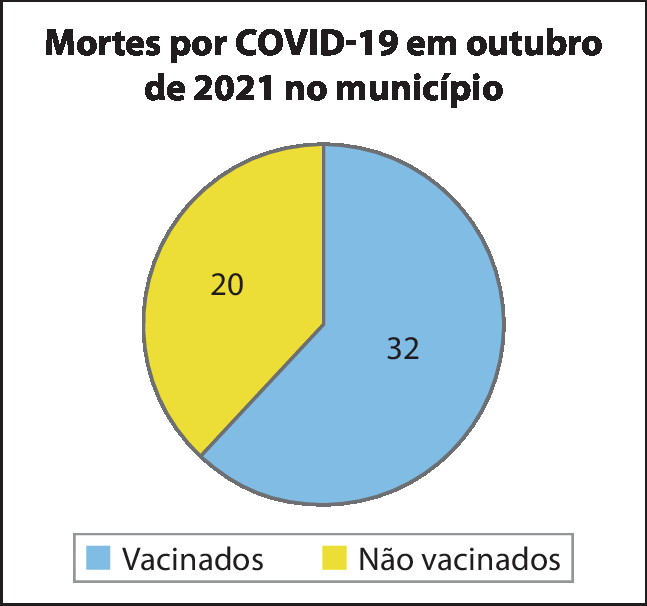
Dados fornecidos pela prefeitura do município.
Entretanto, pesquisando um pouco mais, Natália verificou que os 32 óbitos ocorreram dentre um grupo formado por 3.quinhentas pessoas vacinadas, e os 20 óbitos ocorreram dentre quatrocentas pessoas não vacinadas. Assim, ela calculou as seguintes razões.
Vacinados:
Fração. 32, três mil e quinhentos avos≃ 0,009 ou 0,9%
Não vacinados:
Fração. 20, 400 avos= 0,05 ou 5%
Com base nessas informações, indique a alternativa que melhor representa a situação.
a) O gráfico de setores apresentado é suficiente para a compreensão de que não tomar vacina torna a pessoa vulnerável à covíd-19.
b) O gráfico de setores não representa corretamente a situação, pois, em termos proporcionais, o número de óbitos dentre as pessoas não vacinadas é cêrca de 5,5 vezes maior do que o número de óbitos dentre as pessoas vacinadas
Abre parêntese, fração de numerador 5, e denominador 0,9. É aproximadamente igual a 5,5. Fecha parêntese..
c) O gráfico de setores está incorreto porque ele só pode ser construído para representar valores percentuais.
d) O gráfico que representaria corretamente a situação seria um gráfico de barras que utiliza os mesmos dados do gráfico de setores sem utilizar as informações apresentadas sobre o total de pessoas em cada um dos grupos.
Resposta: Alternativa b.
Resolução e comentários
O objetivo desta atividade é possibilitar aos estudantes refletir sobre a conveniência de usar um gráfico de setores para representar um conjunto de dados. Espera-se que eles percebam que gráficos como esse, quando construídos fóra de contexto, podem não fornecer um panorama adequado para obter uma conclusão válida e que representa corretamente a situação analisada. Os estudantes também devem reconhecer que, apesar de à primeira vista os dados do gráfico indicarem que tomar vacina pode tornar a pessoa mais vulnerável à doença, os dados posteriores mostram o contrário. Ao analisar os novos dados, percebe-se que o motivo pelo qual há mais mortes dentre pessoas vacinadas é que elas formam a imensa maioria da população em estudo e, mesmo as pessoas não vacinadas sendo uma parcela muito pequena da população, ainda assim o número de mortes entre essas pessoas é expressivo. É importante a discussão desses aspectos relacionados à leitura e à interpretação de dados para a formação cidadã dos estudantes.