Página 9

CAPÍTULO 1 Potências e raízes

Fotografia. Fundo escuro com o Sol redondo e vermelho com manchas mais claras. — Uma das maiores erupções solares já observadas foi detectada em fevereiro de 2022 por uma sonda não tripulada da ESA/NASA.

O Sol é a estrela mais próxima da Terra e é essencial para a manutenção da vida no planeta por ser fonte de calor e de luz. Segundo estimativas da Náza (National Aeronautics and Space Administration), a medida da massa do Sol é cêrca de 1,989 ⋅ 1030 quilogramas, aproximadamente 333 ⋅ 103 vezes a medida da massa da Terra, e a temperatura em seu núcleo, a região mais quente do Sol, mede cêrca de 1,5 ⋅ 107 graus Célsius, mais de quatrocentas.000 vezes a temperatura média do corpo humano.

Erupções solares são comuns durante o ciclo de atividade do Sol e, nos períodos de alta atividade solar, as chamadas tempestades solares podem afetar sistemas eletrônicos e de comunicação na Terra e no espaço.

Observe, leia e responda no caderno.

a) Identifique os diferentes dados numéricos apresentados no texto e indique quais deles foram expressos por meio de potência de base 10.

b) De acôrdo com os dados apresentados no texto, a medida da massa do Sol é maior ou menor do que a medida da massa da Terra? Aproximadamente quantas mil vezes?

c) O Sol é como um grande reator termonuclear, realizando em seu núcleo a fusão de cêrca de 6 ⋅ 1011 quilogramas de hidrogênio (agá) em hélio (agá ê) por segundo. Como a medida da massa de hidrogênio convertida em hélio por segundo no núcleo do Sol se compara com a medida da massa média de um humano adulto?

d) As tempestades solares têm algum impacto na vida na Terra? Faça uma pesquisa na internet, em livros ou revistas e compartilhe as informações com a turma.

Respostas e comentários

a) Expressos por meio de potência de base 10: 1,989 ⋅ 1030 quilogramas (1030); 333 ⋅ 103 (103) e 1,5 ⋅ 107 graus Célsius (107). Expresso sem o uso de potência de base 10: .400000.

b) Aproximadamente trezentas e trinta e três mil vezes maior.

c) Considerando 65 quilogramas a medida da massa média de um humano adulto, espera-se que os estudantes concluam que a medida da massa de hidrogênio convertida em hélio por segundo no núcleo do Sol é cêrca de ...10000000000 vezes (1010 vezes) a medida da massa média de um humano adulto.

d) Comente com os estudantes que as tempestades solares podem afetar indiretamente a vida humana na Terra, ao interferir em sistemas eletrônicos e de comunicação na Terra e no espaço.

Capítulo 1 – Potências e raízes

Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.

Este capítulo retoma e amplia o trabalho com as operações potenciação e radiciação, abordando potências de base racional e expoente natural e estendendo o cálculo para potências de expoente negativo; potências de base 10 e a introdução da notação científica; raízes quadradas e raízes cúbicas exatas de números racionais, estendendo para índice n natural maior do que 1.

O trabalho com o tema da abertura, que apresenta números expressos em notação científica, pode ser feito com o intuito de levar os estudantes a avaliar os números que aparecem no texto. Isso possibilita verificar os conhecimentos que já possuem acerca de potências e o entendimento que eles têm desse tipo de notação.

Além disso, o tema proposto nesta abertura possibilita desenvolver atividades interdisciplinares com Ciências, abordando aspectos do Tema Contemporâneo Transversal ciência e tecnologia. Por exemplo, pode-se propor aos estudantes que realizem pesquisas a fim de descrever a composição da estrutura do Sistema Solar, a localização desse Sistema na Galáxia (a Via Láctea) e a dela no Universo. Para complementar, eles podem utilizar softwares que possibilitem visualizar o céu simulando planetários.

Sugestão de leitura

Para ampliar o trabalho com o tema, sugerimos:

LONGHINI, M. D.; MENEZES, L. D. D. Objeto virtual de aprendizagem no ensino de Astronomia: algumas situações-problema propostas a partir do software Stellarium. Caderno Brasileiro de Ensino de Física, volume 27, número 3, 2010. Disponível em: https://oeds.link/sBBdpG. Acesso em: 28 julho 2022.

O trabalho apresenta uma discussão sobre a utilização de objetos virtuais de aprendizagem no ensino de Ciências e algumas propostas de atividades no istelárium, um programa computacional de uso livre.

Página 10

1. Potências

Conta-se que o jôgo de xadrez foi inventado há mais de .1500 anos, como um jôgo de estratégia militar.

Uma das muitas lendas para a origem do xadrez é conhecida como o mito de Sessa. De acôrdo com esse mito, o sábio Sessa apresentou o jôgo a um rei da Índia, que ficou tão entusiasmado com o jôgo que ofereceu a Sessa a liberdade de escolher o que ele desejasse como recompensa por tão notável invento. Toda a côrte esperava que Sessa fosse pedir grandes riquezas, mas ele surpreendeu a todos com o seguinte pedido:

Ilustração. Folha de papel marrom, que lembra um papiro, com as informações: 1 grão de trigo pela primeira casa do tabuleiro; 2 grãos de trigo pela segunda casa; 4 grãos de trigo pela terceira casa; 8 grãos de trigo pela quarta casa; 16 grãos de trigo pela quinta casa; ... e assim por diante, sempre dobrando o número de grãos da casa anterior até a sexagésimo quarta casa (o tabuleiro de xadrez tem 64 casas).

Fotografia. Vista superior de um tabuleiro de xadrez com peças brancas em pé e pretas na derrubadas.

Seu pedido provocou risos. Um invento tão brilhante e um pedido tão simples. O rei e toda a côrte ficaram decepcionados. Você não ficaria?

Respostas e comentários

1. Potências

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero um.

Este tópico trabalha a habilidade (ê éfe zero oito ême ah zero um), pois os estudantes poderão explorar diferentes situações envolvendo potências.

Para introduzir o trabalho com este tópico, providencie um tabuleiro de xadrez e objetos para representar os grãos de trigo (como pequenas bolinhas de papel amassado ou arroz cru) e solicite aos estudantes que façam uma simulação da lenda de Sessa para as primeiras casas. Provavelmente, quando chegarem à 7ª ou à 8ª casa do tabuleiro, perceberão que a quantidade de grãos aumenta de modo considerável, se comparada à quantidade inicialmente colocada na 1ª casa. Trabalhe com eles a regularidade presente nesse aumento antes de apresentar o texto que relaciona essa regularidade com potências de base 2.

Página 11

Mas palavra de rei é palavra de rei, e ele pediu a seus criados que entregassem a Sessa um pequeno saco de grãos de trigo. Sessa recusou a oferta, dizendo que queria receber exatamente o que havia pedido. Nem um grão a mais, nem um grão a menos.

Ilustração. À esquerda, homem de cabelo comprido escuro, bigode com coroa dourada, roupa branca, colar e pulseiras douradas (rei). Ao lado, homem em pé com roupa branca segura um saco em direção a um homem de roupa branca ajoelhado na frente do rei.

O rei pediu então a seus calculistas que efetuassem as contas. Depois de muitas horas de trabalho, eles chegaram a este número:

Ilustração. Folha de papel marrom, que lembra um papiro, com o número: 18.446.744.073.709.551.615.

Ou seja, o que Sessa esperava receber eram dezoito quintilhões, quatrocentos e quarenta e seis quatrilhões, setecentos e quarenta e quatro trilhões, setenta e três bilhões, setecentos e nove milhões, quinhentos e cinquenta e um mil, seiscentos e quinze grãos de trigo.

É um número tão grande que seriam necessários muitos anos para produzir tanto trigo!

De que maneira o rei cumpriria sua promessa? Que situação difícil a dele. Mas como ele poderia imaginar que daquele pedido tão simples resultaria tamanha quantidade de trigo?

Entendendo a aflição do monarca por não poder cumprir sua promessa, Sessa perdoou a dívida. Afinal, seu objetivo fora atingido: chamar a atenção do rei para que tomasse mais cuidado com suas promessas e seus julgamentos.

O final não poderia ser mais feliz: Sessa foi nomeado conselheiro do rei.

Ilustração. À esquerda, homem de cabelo comprido escuro, bigode com coroa dourada, roupa branca, colar e pulseiras douradas (rei). À frente dele, homem de roupa branca em pé com a mão estendida na direção do rei.

Respostas e comentários

Potências

Antes de apresentar o total de grãos de trigo obtido pelos calculistas, peça aos estudantes que estimem essa quantidade e a anotem no caderno. Depois, proponha que comparem a estimativa com as de dois colegas e conversem sobre os valores estimados.

Continue a leitura do texto com os estudantes e peça a eles que verifiquem se fizeram uma boa estimativa. O que se espera é que o valor estimado seja muito menor do que o valor real. Para incentivar a curiosidade intelectual e favorecer o desenvolvimento da competência geral 2, proponha aos estudantes descobrir quantos anos seriam necessários para produzir essa quantidade de grãos. A produção mundial anual de trigo no início dos anos 1990 era cêrca de 500 milhões de toneladas, e, atualmente, são produzidos cêrca de 750 milhões de toneladas.

Se necessário, oriente-os a pesquisar estimativas de quantos grãos de trigo há em 1 quilograma de trigo para determinar o total de anos necessários para produzir a quantia de trigo pedida por Sessa.

Incentive os estudantes a justificar o procedimento e as estimativas adotadas de maneira que desenvolvam, também, a competência geral 7.

Considerando, por exemplo, que um saco com 60 quilogramas de trigo contém cêrca de ..1380000 grãos de trigo, isto é, cêrca de 14 · 105 grãos, e que a quantidade pedida por Sessa é cerca de 18 · 1018 grãos de trigo, seriam necessários cêrca de 1,3 · 1013 sacos (18 · 1018 : 14 · 105 = 1,3 · 1013), que equivale a cêrca de 7,8 · 1011 t de trigo (1,3 · 1013 · 60 : .1000 = 7,8 · 1011). Considerando a atual produção de trigo no mundo, de 750 milhões de toneladas ao ano, seriam necessários cêrca de .1040 anos (7,8 · 1011 : ..750000000 = .1040) para quitar a dívida do rei com Sessa.

Sugestão de leitura

Para ampliar o assunto, sugerimos:

ÁVILA, G. O jôgo de xadrez. Revista do Professor de Matemática, número 25, 1994. Disponível em: https://oeds.link/fLexBu. Acesso em: 19 julho 2022.

Neste material, o autor aborda diversas considerações sobre o prêmio pedido por Sessa na lenda do xadrez.

Página 12

O que acabamos de ler é um interessante exemplo de aplicação de potenciação, pois a quantidade de grãos de trigo de cada casa do tabuleiro pode ser expressa por uma potência. Observe:

61ª casa ………………………..………. 2elevado a 0

62ª casa ………………………..………. 2elevado a 1

63ª casa ………………………..………. 2elevado a 2

⋮

64ª casa ………………………..………. 2elevado a 63

Ilustração. Homem de cabelo escuro curto, óculos e camisa vermelha. Ele fala: Este também é um exemplo de sequência, chamada sequência recursiva, em que qualquer número pode ser obtido recorrendo à sua posição na sequência ou ao número anterior por meio de uma regra ou fórmula de recorrência. Assim, o elemento n da enésima casa é 2 elevado a n menos 1.

Agora, vamos recordar o que sabemos sobre potências.

Revendo conhecimentos sobre potências

Você deve se lembrar do significado de 3elevado a 2 e de 3elevado a 3:

• 3elevado a 2 = 3 ⋅ 3 = 9

• 3elevado a 3 = 3 ⋅ 3 ⋅ 3 = 27

De modo geral, sendo a um número racional, temos:

• a elevado a 2 = a ⋅ a

• aelevado a 3 = a ⋅ a ⋅ a

Considerando um expoente genérico n, em que n é um número inteiro, definimos aelevado a n assim:

• se n > 1, então:

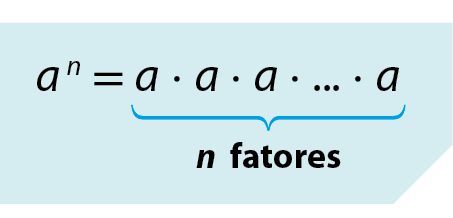
Esquema. a elevado a n igual a vezes a vezes a vezes reticências vezes a. abaixo dos a após o igual está escrito n fatores.

• se n = 1, então:

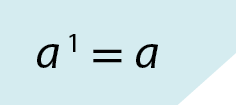
• se n = 0 e a ≠ 0, então:

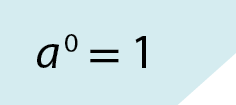
Propriedades das potências

Para a resolução de um trabalho escolar, Mércia, Nilza e Norma precisaram calcular o valor da expressão: (7elevado a 4 ⋅ 7elevado a 2)elevado a 3 : 7elevado a 15.

Acompanhe como cada uma delas fez.

• Mércia indicou as potenciações como multiplicações de fatores iguais e depois simplificou a fração, assim:

7elevado a 4 = 7 ⋅ 7 ⋅ 7 ⋅ 7

7elevado a 2 = 7 ⋅ 7

7elevado a 4 ⋅ 7elevado a 2 = 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7

(7elevado a 4 ⋅ 7elevado a 2)elevado a 3 = (7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7)elevado a 3 = (7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7) ⋅ (7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7) ⋅ (7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7)

fração, numerador abre parênteses, 7 elevado a 4 vezes 7 ao quadrado, fecha parênteses, elevado a 3; denominador: 7 elevado 15, igual a fração; 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7; denominador: 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7 vezes 7; 15 números 7 do numerador foram cancelados com 15 números 7 do denominador; igual a 7 vezes 7 vezes 7, igual, 343

Respostas e comentários

Potências

Proponha aos estudantes que verifiquem alguma regularidade na contagem de grãos de trigo de cada casa do tabuleiro de xadrez e registrem no caderno. Se julgar necessário, dê a dica de que podem usar potências de base 2. Depois, peça a alguns deles que mostrem na lousa o que fizeram no caderno e discuta com toda a turma cada situação. Se necessário, reproduza a sequência apresentada no livro (número de grãos de cada casa do tabuleiro expresso em potências de base 2) e explore-a com os estudantes.

Retome a potenciação com base natural antes de ampliar para os números racionais maiores ou iguais a 0 (zero).

Página 13

• Nilza calculou os produtos parciais, depois calculou os produtos dos produtos e, em seguida, calculou o quociente:

7elevado a 4 = 7 ⋅ 7 ⋅ 7 ⋅ 7 = .2401

7elevado a 2 = 7 ⋅ 7 = 49

7elevado a 4 ⋅ 7elevado a 2 = .2401 ⋅ 49 = .117649

(7elevado a 4 ⋅ 7elevado a 2)elevado a 3 = (.117649)elevado a 3 = .117649 ⋅ .117649 ⋅ .117649 = .....1628413597910449

7elevado a 15 = 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 ⋅ 7 = ....4747561509943

\frac{{(7^{4} \cdot 7^{2})}^{3}}{7^{15}} = \frac{1 628 413 597 910 449}{4 747 561 509 943} = 343

• E Norma calculou o valor da expressão aplicando as propriedades da potenciação estudadas no ano anterior:

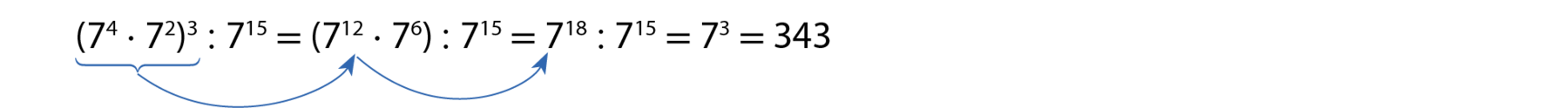
abre parênteses 7 elevado a 4, vezes, 7 ao quadrado, fecha parenteses, elevado a três, dividido 7 elevado a 15, igual, abre parênteses, 7 elevado a 12, vezes 7 elevando a 6, fecha parênteses, dividido por 7 elevado a 15, igual, 7 elevado a 18, dividido 7 elevado a 15, igual, 7 ao cubo, igual, 343. Do traço abaixo de abre parênteses 7 elevado a 4, vezes, 7 ao quadrado, fecha parenteses, elevado a três, parte uma seta para abre parênteses, 7 elevado a 12, vezes 7 elevando a 6, De 7 elevado a 12 parte uma seta para 7 elevado a18

Ilustração. mulher de cabelo na altura dos ombros, blusa rosa e casaco roxo. Ela fala: Não há somente uma maneira de calcular o valor da expressão. Qual delas você acha mais simples? Ilustração. mulher de cabelo na altura dos ombros, blusa rosa e casaco roxo. Ela diz: Observe como Norma transformou a 'potência de um produto' no 'produto de uma potência'

A expressão (13 ⋅ 8)elevado a 4 é a potência de um produto.

(13 ⋅ 8)elevado a 4 = (13 ⋅ 8) ⋅ (13 ⋅ 8) ⋅ (13 ⋅ 8) ⋅ (13 ⋅ 8) = 13 ⋅ 8 ⋅ 13 ⋅ 8 ⋅ 13 ⋅ 8 ⋅ 13 ⋅ 8 = 13elevado a 4 ⋅ 8elevado a 4

A expressão 13elevado a 4 ⋅ 8elevado a 4 é o produto de uma potência.

(13 ⋅ 8)elevado a 4 = 13elevado a 4 ⋅ 8elevado a 4

Esta é mais uma propriedade da potenciação.

Considere outros exemplos:

• (‒7 ⋅ 2,3)elevado a 3 = (‒7)elevado a 3 ⋅ (2,3)elevado a 3

•

{(\frac{2}{13} \cdot \frac{4}{5})}^{6} = {(\frac{2}{13})}^{6} \cdot {(\frac{4}{5})}^{6}

• (5elevado a 2 ⋅ xelevado a 3)elevado a 5 = 5elevado a 10 ⋅ xelevado a 15

Resumindo e generalizando as propriedades da potenciação, dados os números racionais a e bê ê os números naturais m e n, obtemos:

aelevado a m ⋅ aelevado a n = aelevado a m ⁺ ⁿ

aelevado a m : aelevado a n = aelevado a m ⁻ ⁿ (com a ≠ 0)

(aelevado a m )elevado a n = aelevado a m ^⋅ ⁿ

(a ⋅ b)elevado a m = aelevado a m ⋅ belevado a m

(a : b)elevado a m = aelevado a m : belevado a m (com b ≠ 0)

Respostas e comentários

Propriedades das potências

Trabalhe as propriedades da potenciação com os estudantes. Retome as potências de base negativa para verificar o grau de familiaridade que a turma apresenta com o assunto. É importante que os estudantes façam a distinção de potências de mesma base nesse caso para aplicarem as propriedades corretamente. Por exemplo, espera-se que eles percebam que (‒3)elevado a 2 · 3elevado a 4 ou (‒3)elevado a 3 · 3elevado a 4 não são casos de produtos de potências de mesma base, visto que as bases são diferentes (‒3 e 3). Assim, para efetuar (‒3)elevado a 2 · 3elevado a 4, deve-se, primeiro, verificar que (‒3)elevado a 2 = 3elevado a 2, visto que o expoente é par, e então obter:

(‒3)elevado a 2 · 3elevado a 4 = 3elevado a 2 · 3elevado a 4 = 3elevado a 6

Já no caso de (‒3)elevado a 3 · 3elevado a 4, como (‒3)elevado a 3 = ‒3elevado a 3, verificamos que (‒3)elevado a 3 · 3elevado a 4 = ‒3elevado a 3 · 3elevado a 4 = ‒3elevado a 7, enquanto 3elevado a 3 · 3elevado a 4 = 3elevado a 7, o que obviamente resulta em produtos distintos, pois um é negativo e o outro é positivo.

Página 14

Acompanhe mais um exemplo de aplicação das propriedades da potenciação.

\frac{a^{5 x ‒ 2} \cdot a^{2 + x}}{{(a^{x ‒ 1})}^{2}}

\frac{a^{5 x ‒ 2 + 2 + x}}{a^{2 x ‒ 2}}

\frac{a^{6 x}}{a^{2 x ‒ 2}}

= a elevado a 6ˣ ⁻ ⁽²ˣ ⁻ ²⁾ = a elevado a 6ˣ ⁻ ²ˣ ⁺ ² = a elevado a 4ˣ ⁺ ², em que a ≠ 0.

Observações

▶ Note que, para a ≠ 0, aelevado a 0 = 1 é compatível com a propriedade: aelevado a m : aelevado a n = aelevado a m ⁻ⁿ (se a ≠ 0).

Por exemplo:

aelevado a 2 : aelevado a 2 =

\frac{a \cdot a}{a \cdot a}

= 1 e aelevado a 2 menos 2 = aelevado a 0 = 1

▶ É importante observar que, em geral, (aelevado a 3)elevado a 2 ≠

a^{3^{2}}

. Entenda por quê.

• (aelevado a 3)elevado a 2 = aelevado a 3 ⋅ aelevado a 3 = aelevado a 3 mais 3 = aelevado a 6 ou (aelevado a 3)elevado a 2 = aelevado a 3^⋅elevado a 2 = aelevado a 6

• aelevado a 3elevado a 2 = a (elevado a 3elevado a 2) = a elevado a 9

▶ Em (aelevado a 3)elevado a 2, o que está elevado ao quadrado é aelevado a 3.

▶ Em a elevado a 3elevado a 2, o que está elevado ao quadrado é o expoente 3.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Em um condomínio há 6 prédios. Em cada prédio há 6 andares e, em cada andar, 6 apartamentos. Expresse na fórma de potência o número de apartamentos desse condomínio.

Ilustração. Condomínio com seis prédios lado a lado com seis andares cada um.

2 Classifique as expressões a seguir em verdadeiras ou falsas. Justifique sua resposta.

a) (4elevado a 5)elevado a 2 =

4^{5^{2}}

b) (4elevado a 5)elevado a 2 = (4elevado a 2)elevado a 5

c) (2 ⋅ 3)elevado a 2 = 2elevado a 2 ⋅ 3elevado a 2

d) (2 + 3)elevado a 2 = 2elevado a 2 + 3elevado a 2

e) (8 dividido por 4)elevado a 3 = 8elevado a 3 dividido por 4elevado a 3

f) (8 menos 4)elevado a 3 = 8elevado a 3 menos 4elevado a 3

3 Simplifique as expressões a seguir, obtendo uma única potência.

a) (2elevado a 4 ⋅ 2elevado a 6) dividido por (2elevado a 5 ⋅ 2elevado a 3)

b) (xelevado a 4 ⋅ x elevado a 2 ⋅ x elevado a 3)elevado a 2 dividido por (x elevado a 4)elevado a 5, com x ≠ 0

\frac{2^{5 x ‒ 1} \cdot 2^{x + 2}}{2^{3 x ‒ 2}}

\frac{5^{2} \cdot 5^{3}}{5^{1} \cdot 5^{0}}

4 Sendo a = 3x elevado a 2 + 5x menos 6, determine o valor de a para:

a) x = menos2

b) x =

\frac{1}{2}

5 Considere o desenho que Marina fez.

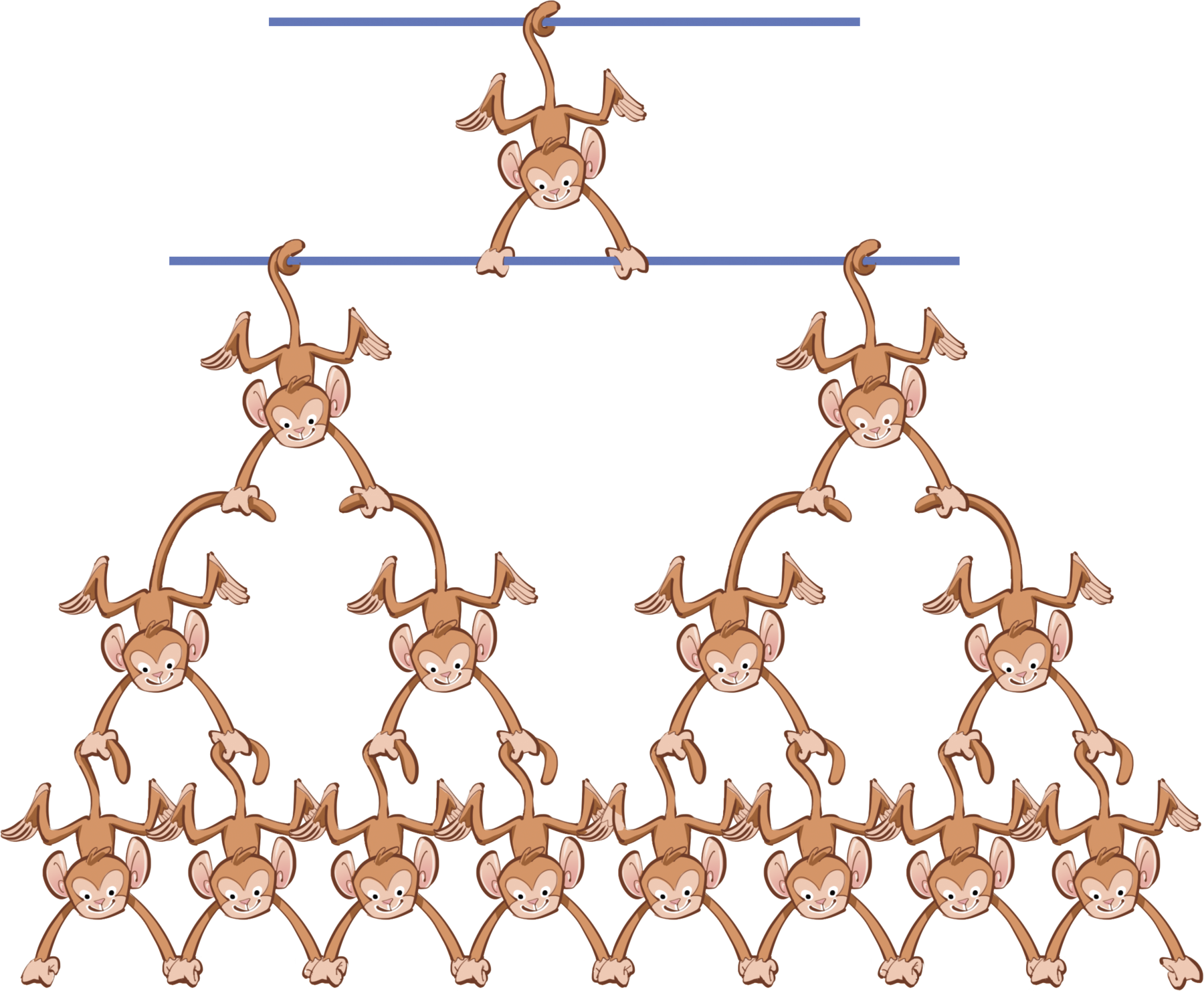
Ilustração. Pilha com macacos. De baixo para cima: fileira com 6 macacos. Acima, quatro macacos. Acima, dois macacos segurando uma barra pela cauda. Acima, um macaco segura uma barra com as mãos e a outra com a cauda.

Observe que o número de macacos dobra a cada linha.

1ª linha

2ª linha

3ª linha

2 ⋅ 2

4ª linha

2 ⋅ 2 ⋅ 2

Suponha que Marina continue desenhando dessa fórma – dobrando a cada linha a quantidade de macacos da linha anterior.

a) Qual será o número de macacos da 10ª linha?

b) Represente o número de macacos da 1ª e da 2ª linha por uma potência de base 2.

c) Escreva uma fórmula de recorrência para essa sequência.

Respostas e comentários

1. 6elevado a 3 apartamentos.

2. a) Falsa, pois (4elevado a 5)elevado a 2 = 4elevado a 10 e 4elevado a 5elevado a 2 = 4elevado a 25.

2. b) Verdadeira, pois (4elevado a 5)elevado a 2 = 4elevado a 10 e (4elevado a 2)elevado a 5 = 4elevado a 10.

2. c) Verdadeira, pois (2 ⋅ 3)elevado a 2 = (2 ⋅ 3) ⋅ (2 ⋅ 3) = 2elevado a 2 ⋅ 3elevado a 2.

2. d) Falsa, pois (2 + 3)elevado a 2 = 25 e 2elevado a 2 + 3elevado a 2 = 13.

2. e) Verdadeira, pois (8 dividido por 4)elevado a 3 = 8 e 8elevado a 3 dividido por 4elevado a 3 = 8.

2. f ) Falsa, pois (8 menos 4)elevado a 3 = 64 e 8elevado a 3 menos 4elevado a 3 = 448.

3. a) 2elevado a 2

3. b) x elevado a menos 2

3. c) 2elevado a 3ˣ ⁺ ³

3. d) 5elevado a 4

4. a) menos4

4. b)

‒ \frac{11}{4}

5. a) 512 macacos.

5. b) 1 = 2elevado a 0 e 2 = 2elevado a 1

5. c) 2elevado a nmenos 1, em que n é o número da linha.

Exercícios propostos

No exercício 1, se julgar necessário, solicite aos estudantes que façam um esquema similar a uma árvore de possibilidades a fim de visualizarem com maior facilidade a relação com potência. É possível fazer algumas “ramificações” e, então, generalizar e observar como a potência 6elevado a 3 pode representar a quantidade total de apartamentos desse condomínio.

As resoluções dos exercícios 2, 3 e 5 estão no início deste Manual, nas orientações específicas do capítulo 1.

Ao trabalhar o item b do exercício 3, chame a atenção dos estudantes para o fato de que há restrição para o valor de x. Essa é uma boa oportunidade para pedir a eles que justifiquem a presença dessa e de outras restrições verificando se percebem que x deve ser diferente de zero, pois a divisão por zero é uma indeterminação matemática.

No exercício 4, no item a, como x = menos2, obtemos:

A = 3 · (menos2)elevado a 2 + 5 · (menos2) menos 6 = 3 · 4 menos 10 menos 6 = menos4

Já no item b, com x =

\frac{1}{2}

, obtemos:

A = 3 ·

{(\frac{1}{2})}^{2}

+ 5 ·

\frac{1}{2}

menos 6 =

\frac{3}{4}

\frac{5}{2}

menos 6 = menos

\frac{11}{4}

Com a intenção de buscar a melhor estratégia de resolução para o exercício 5, peça aos estudantes que formem trios. Alguns podem tentar resolvê-lo por meio de desenhos, mas devem perceber que é mais trabalhoso. Nesse caso, oriente-os a verificar se há relação do exercício com o conteúdo em estudo: potências. Aproveite o momento e faça-lhes outras perguntas, como: Quantos macacos haverá na 7ª linha? E na 11ª? (Respostas: respectivamente, 2elevado a 6 macacos e 2elevado a 10 macacos).

Ao final, devem perceber que na enésima linha haverá 2elevado a n menos 1 macacos. Essa generalização colabora com o desenvolvimento das habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três). Se possível, explore outras situações como essa e solicite aos estudantes que indiquem uma generalização para cada situação.

Página 15

PARA SABER MAIS

Novo modêlo de placa para veículos

Placas com padrão do Mercosúl entram em vigor em todo o país

detrân que ficar fora do padrão não conseguirá emplacar novos veículos

Fotografia. Placa de um veículo. Na parte superior, ao centro, a palavra Brasil e ao lado direito a bandeira do país. Na parte de baixo o código QRCode e a placa: FKJ6F08. Entre os números, ondas sinusoidais. No canto inferior esquerdo, BR (distintivo do Brasil). — Novo modêlo de placa veicular do Mercosul.

Após sucessivos adiamentos, começa a valer nesta sexta-feira (31) o prazo para que os Departamentos de Trânsito (Detrans) de todos os estados concluam os procedimentos para implantar a nova placa do Mercosúl. reticências

[O novo modêlo apresenta o padrão com três letras, um número, uma letra e dois números (éfe cá jota seis éfe zero oito), diferente] do modêlo atualmente adotado no país, com três letras e quatro números. O novo modêlo permite mais de 450 milhões de combinações, o que, considerando o padrão de crescimento da frota de veículos no Brasil, pode levar mais de 100 anos.

“Atualmente são quase 5 milhões de veículos emplacados com a nova [placa de identificação veicular]. O govêrno federal estima que, até o fim de 2023, o Brasil já esteja com quase toda sua frota circulando com a nova placa”, informou a assessoria do Ministério da Infraestrutura.

Fonte: NASCIMENTO, L. Placas com padrão do Mercosúl entram em vigor em todo o país. AgênciaBrasil, Brasília, Distrito Federal, 31 janeiro 2020. Disponível em: https://oeds.link/HyybWj. Acesso em: 20 junho 2022.

Mais de 450 milhões de combinações diferentes! Será que a reportagem não exagerou? Para conferir a veracidade da informação sobre o número total de placas possíveis com o novo modêlo, podemos fazer um cálculo combinatório.

Devemos considerar todas as possibilidades para cada uma das sete posições (casas) a serem preenchidas pelas 26 letras do alfabeto e pelos algarismos de 0 a 9.

Esquema com 7 campos.
primeiro campo: letra;
segundo campo: letra;
terceiro campo: letra;
quarto campo: algarismo;
quinto campo: letra;
sexto campo: algarismo;
sétimo campo: algarismo;

A primeira casa pode ser preenchida de 26 maneiras diferentes; para cada uma dessas maneiras podemos preencher a segunda casa de outras 26 maneiras diferentes, o que resulta, para as duas primeiras casas, em um total de 26 ⋅ 26, isto é, 676 combinações diferentes.

Esquema com 7 campos. primeiro campo: 26; segundo campo: 26; Demais campos estão vazios.

Para cada uma dessas 676 combinações, a terceira casa pode ser preenchida por 26 letras diferentes, o que resulta, para as três primeiras casas, em um total de 26 ⋅ 26 ⋅ 26, ou seja, .17576 combinações.

Esquema com 7 campos. primeiro campo: 26; segundo campo: 26; terceiro campo: 26; Demais campos estão vazios.

Respostas e comentários

Para saber mais

Essa seção possibilita aos estudantes desenvolver a habilidade (ê éfe zero oito ême ah zero três), pois é trabalhada uma situação envolvendo problemas de contagem e a aplicação do princípio multiplicativo. Se julgar necessário, apresente aos estudantes outras situações mais simples para eles aplicarem o princípio multiplicativo. Por exemplo, quantos números de 3 algarismos é possível formar com os algarismos 3, 5 e 7? (3 · 3 · 3 = 27; 27 números). E se os algarismos não puderem se repetir? (3 · 2 · 1 = 6; 6 números).

No caso das placas, os estudantes devem compor as letras e os algarismos, considerando que pode haver repetição. Por isso, devem obter: 26 · 26 · 26 · 10 · 26 · 10 · 10 (compondo cada placa com 4 letras e 3 algarismos), ou seja, 26elevado a 4 · 10elevado a 3 = .456976 · .1000, determinando desse modo ..456976000 placas.

Este contexto possibilita trabalhar atividades que desenvolvem o Tema Contemporâneo Transversal educação para o trânsito e, ainda, realizar um trabalho interdisciplinar com Geografia. Pode-se propor, por exemplo, que os estudantes pesquisem sobre o Mercosúl e analisem a atuação desse bloco econômico em relação à mobilidade nos países que o integram.

Página 16

Continuando a aplicar esse raciocínio, que os matemáticos dão o nome de princípio fundamental da contagem, para as sete casas obtemos o total de combinações possíveis.

Esquema com 7 campos.
primeiro campo: 26;
segundo campo: 26;
terceiro campo: 26;
quarto campo: 10;
quinto campo: 26;
sexto campo: 10;
sétimo campo: 10.

26 · 26 · 26 · 10 · 26 · 10 · 10 = 456 976 000

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

Use uma calculadora para responder ao que se pede.

1 Quantas placas diferentes poderíamos obter se fossem usados apenas algarismos de 0 a 9 em todas as casas?

2 Quantas placas diferentes poderíamos obter se fossem usadas apenas letras em todas as casas?

3 Lúcia e Lucas são investigadores e precisam identificar um carro com placa de modêlo com três letras e quatro números. Lúcia conhece apenas as letras da placa procurada; Lucas conhece apenas os números dessa placa. Qual deles tem maior probabilidade de determinar a placa desse carro primeiro? Por quê?

Potência com expoente inteiro negativo

Aprendemos a efetuar operações com potências que têm por base um número racional e por expoente um número natural.

Agora, vamos interpretar o significado de potências que tenham por base um número racional e por expoente um número inteiro negativo.

Considere o quociente 52 : 55. Pela propriedade do quociente de potências de mesma base, obtemos:

5 elevado a 2, dividido 5 elevado 5, igual, 5 elevado ao expoente 2 menos 5, fim do expoente, igual 5 elevado a menos 3 5 elevado ao quadrado dividido 5 elevado a 4, igual a fração: numerado 5 ao quadrado, denominado 5 elevado a 5, igual a fração, numerador 5 vezes 5, denominados 5 vezes 5 vezes 5 vezes 5 vezes 5, igual, a fração: numerador 1, denominador 5 ao cubo, igual a fração : 1 ao cubo, denominador 5 ao cubo, igual a fração, um quinto ao cubo

Logo,

5^{‒ 3} = {(\frac{1}{5})}^{3} .

Note ainda que:

primeira linha: 5 elevado a menos 3, igual, 5 elevado ao expoente 3 vezes menos 1, fim do expoente. segunda linha: 5 elevado a menos 3, igual, um quinto elevado 3, igual, fração: numerado 1, denominador 5 ao cubo. uma chave ligando a primeira e a segunda linha , aponta, para abre parênteses 5 elevado a 3, fecha parênteses elevado a menos 1, igual fração: numerado 1, denominador 5 ao cubo

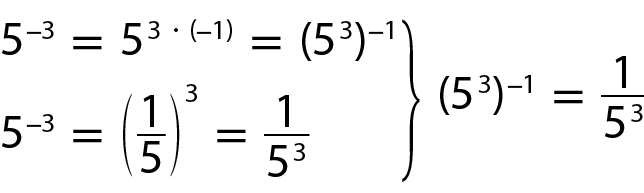
Isso significa que (53)‒1 pode ser interpretado como o inverso de 53 ou, ainda, que 5‒3 é o inverso de 53.

A potência com expoente negativo de um número racional diferente de zero é igual a outra potência que tem a base igual ao inverso da base anterior e o expoente igual ao oposto do expoente anterior, ou seja, um expoente positivo.

Respostas e comentários

1. 107 ou ..10000000 placas.

2. 267 ou ...8031810176 placas.

3. Lúcia, porque ela terá de descobrir cada um dos números entre .10000 possíveis, enquanto Lucas terá de descobrir cada uma das letras entre .17576 possíveis combinações.

Agora é com você!

Na atividade 1, espera-se que os estudantes notem que, como são 10 algarismos possíveis (0 a 9) para cada casa e são sete casas, obtemos no total 10..000000 números distintos, pois: 10 · 10 · 10 · 10 · 10 · 10 · 10 = 107 = ..10000000

O mesmo raciocínio da atividade anterior se aplica na atividade 2. Porém, agora são 26 opções para cada casa, totalizando ...8031810176 placas diferentes, pois:

26 · 26 · 26 · 26 · 26 · 26 · 26 = 267 = ...8031810176

Na atividade 3, espera-se que os estudantes respondam que Lúcia tem mais chance de determinar a placa do carro primeiro, já que ela precisa descobrir cada um dos números entre .10000 possíveis (104 = .10000), enquanto Lucas precisa descobrir cada uma das letras entre .17576 possíveis (263 = 26 · 26 · 26 = .17576).

Potência com expoente inteiro negativo

A potência de base racional não nula estendida para expoente negativo usa como pontos de partida a divisão de potências de mesma base e a noção de número inverso. É importante que os estudantes relacionem as potências de expoente ‒1 como o inverso da base. Assim:

• 7 ‒1 =

\frac{1}{7}

• 100‒1 =

\frac{1}{100}

• (0,5)‒1 =

\frac{1}{0, 5} = \frac{1}{\frac{1}{2}}

= 2 (o inverso de meio é 2)

•

{(\frac{1}{3})}^{‒ 1}

= 3 (o inverso de um terço é 3)

• (1,01)‒1 =

{(\frac{101}{100})}^{‒ 1} = \frac{100}{101}

• (‒3)‒1 = ‒

\frac{1}{3}

Página 17

Acompanhe alguns exemplos.

a) 3‒2 =

{(\frac{1}{3})}^{2} = (\frac{1}{3}) \cdot (\frac{1}{3}) = \frac{1}{9}

10^{‒ 3} = {(\frac{1}{10})}^{3} = \frac{1^{3}}{10^{3}} = \frac{1}{1000}

c) (‒5)‒2 =

{(‒ \frac{1}{5})}^{2} = (‒ \frac{1}{5}) \cdot (‒ \frac{1}{5}) = \frac{1}{25}

{(\frac{2}{14})}^{‒ 1} = {(\frac{14}{2})}^{1} = 7

e) (0,25)‒2 =

{(\frac{25}{100})}^{‒ 2} = {(\frac{1}{4})}^{‒ 2} = {(\frac{4}{1})}^{2}

= 42 = 16

Observação

▶ Todas as propriedades da potenciação já estudadas também são válidas para potências com expoente inteiro negativo.

Generalizando, podemos escrever:

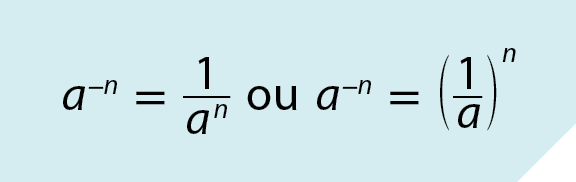
a elevado menos n, igual fração: numerador 1, denominador a elevado n, ou, a elevado menos n igual abre parênteses fração: numerador 1 e denominador a, fecha parênteses elevado a n

, para a ≠ 0 e sendo n um número natural.

Assim, para n = 1 e a ≠ 0, temos:

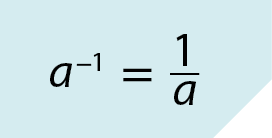
a elevado menos 1 , igual, fração: numerador 1, denominador a.

Isso significa que a ‒1 é o inverso de a, pois

\frac{1}{a}

é o inverso de a.

Assim, se a ‒1 é o inverso de a, também a é o inverso de a ‒1.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

6 Calcule as potências.

{(\frac{3}{4})}^{‒ 2}

{(‒ \frac{5}{4})}^{‒ 3}

c) 10‒3

d) 2‒1

e) (‒6)‒2

{(\frac{1}{9})}^{‒ 2}

7 Escreva na fórma de potência de base 10.

\frac{1}{100}

\frac{1}{10 000}

\frac{1}{1 000 000}

d) 0,1

e) 0,01

f) 0,001

8 Aplicando as propriedades de potenciação, reduza a uma só potência.

{(\frac{2}{3})}^{‒ 5} \cdot {(\frac{2}{3})}^{2}

{(‒ \frac{5}{4})}^{‒ 1} : {(‒ \frac{5}{4})}^{‒ 6}

{[{(‒ \frac{3}{2})}^{2}]}^{‒ 3}

d) [(‒2)0]‒3

9 Sabendo que

a = {(\frac{2}{3})}^{‒ 1}

b = ‒ \frac{5}{2},

calcule o que se pede.

a) a ‒ b

b) a : b

c) a ⋅ b 2

d) (a + b)2

Respostas e comentários

6. a)

\frac{16}{9}

6. b)

‒ \frac{64}{125}

6. c)

\frac{1}{1 000}

6. d)

\frac{1}{2}

6. e)

\frac{1}{36}

6. f) 81

7. a) 10‒2

7. b) 10‒4

7. c) 10‒6

7. d) 10‒1

7. e) 10‒2

7. f) 10‒3

8. a)

{(\frac{2}{3})}^{‒ 3}

8. b)

{(‒ \frac{5}{4})}^{5}

8. c)

{(‒ \frac{3}{2})}^{‒ 6}

8. d) (‒2)0

9. a) 4

9. b)

‒ \frac{3}{5}

9. c)

\frac{75}{8}

9. d) 1

Potência com expoente inteiro negativo

Peça aos estudantes que exemplifiquem na lousa a generalização a‒n =

\frac{1}{a^{n}}

, para a ≠ 0 e sendo n um número natural.

Possíveis respostas:

• 7‒4 =

\frac{1}{7^{4}} = \frac{1}{2 401}

• 10‒3 =

\frac{1}{10^{3}} = \frac{1}{1 000}

• (0,25)‒2 =

\frac{1}{{(0, 25)}^{2}} = \frac{1}{{(\frac{1}{4})}^{2}}

= =

\frac{1}{\frac{1}{16}}

= 16

Exercícios propostos

Para resolver o exercício 6, pode-se considerar que, para determinar potências cujos expoentes são números racionais negativos, invertemos a base e trocamos o sinal do expoente. Assim:

{(\frac{3}{4})}^{‒ 2} = {(\frac{4}{3})}^{2} = \frac{16}{9}

{(‒ \frac{5}{4})}^{‒ 3} = {(‒ \frac{4}{5})}^{3} = ‒ \frac{4^{3}}{5^{3}} =

‒ \frac{64}{125}

10^{‒ 3} = {(\frac{1}{10})}^{3} = \frac{1}{1 000}

2^{‒ 1} = {(\frac{1}{2})}^{1} = \frac{1}{2}

{(‒ 6)}^{‒ 2} = {(‒ \frac{1}{6})}^{2} = \frac{1}{6^{2}} = \frac{1}{36}

{(\frac{1}{9})}^{‒ 2} = 9^{2} = 81

A resolução do exercício 7 está no início deste Manual, nas orientações específicas do capítulo 1.

Para resolver o exercício 8, podem-se aplicar as propriedades de potenciação. Assim, obtemos:

{(\frac{2}{3})}^{‒ 5} \cdot {(\frac{2}{3})}^{2} = {(\frac{2}{3})}^{‒ 5 + 2}

{(\frac{2}{3})}^{‒ 3}

{(‒ \frac{5}{4})}^{‒ 1} : {(‒ \frac{5}{4})}^{‒ 6} =

{(‒ \frac{5}{4})}^{‒ 1 ‒ (‒ 6)} = {(‒ \frac{5}{4})}^{5}

{[{(‒ \frac{3}{2})}^{2}]}^{‒ 3} = {(‒ \frac{3}{2})}^{2 \cdot (‒ 3)} =

{(‒ \frac{3}{2})}^{‒ 6}

d) [(‒2)0]‒3 = (‒2)0 · (‒3) = (‒2)0

Para resolver o exercício 9, fazemos a =

{(\frac{2}{3})}^{‒ 1} = \frac{3}{2}

e b =

‒ \frac{5}{2}

. Assim, obtemos:

a) a ‒ b =

\frac{3}{2} ‒ (‒ \frac{5}{2}) = \frac{3}{2} + \frac{5}{2} = \frac{8}{2}

= 4

b) a : b =

\frac{\frac{3}{2}}{‒ \frac{5}{2}} = ‒ \frac{6}{10} = ‒ \frac{3}{5}

c) a · b2 =

\frac{3}{2} \cdot {(‒ \frac{5}{2})}^{2} = \frac{3}{2} \cdot \frac{25}{4} = \frac{75}{8}

d) (a + 2)2 =

{(\frac{3}{2} + (‒ \frac{5}{2}))}^{2} = {(\frac{3}{2} ‒ \frac{5}{2})}^{2} = {(‒ \frac{2}{2})}^{2}

= = (‒1)2 = 1

Página 18

10 Sendo

x = {(2 ‒ \frac{1}{2})}^{‒ 2}

y = {(1 + \frac{1}{3})}^{‒ 1}

, calcule x ⋅ y.

11 Considerando

m = {(\frac{4}{5} ‒ \frac{1}{2})}^{‒ 3}

n = {(3 + \frac{1}{3})}^{2},

encontre o valor de m : n.

Utilizando uma calculadora, obtenha o valor das potências a seguir.

a) 2‒8

b) 4‒5

c) 0,4‒3

d) 0,2‒6

• Quando são elevados a um expoente negativo, o que acontece com os números maiores que 0 e menores que 1? E o que acontece com os números maiores que 1?

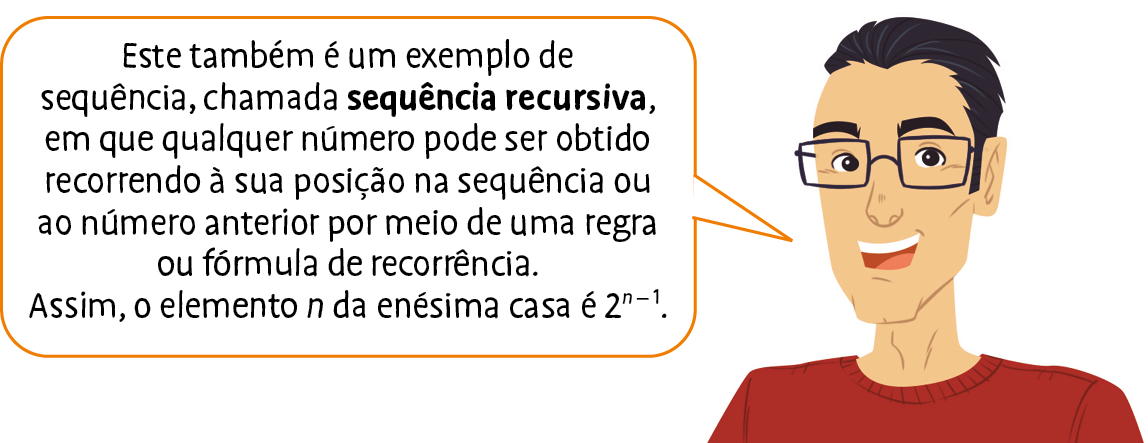
Hora de criar – Em duplas, criem um problema cada um envolvendo uma sequência recursiva em que os elementos da sequência podem ser escritos como uma potência de base 3. Troque de caderno com o colega, resolvam o problema um do outro e escrevam a fórmula de recorrência da sequência. Depois de cada um resolver o problema elaborado pelo outro, destroquem os cadernos para corrigi-los.

Como escrever um número como potência de uma base dada

Conhecendo o significado de uma potência e as propriedades de potências de mesma base, em certos casos podemos escrever um número na fórma de potência de determinada base.

Por exemplo, vamos escrever:

a) 32 como potência de base 2.

Decompondo 32 em fatores primos, obtemos 32 = 25.

\frac{1}{8}

como potência de base

\frac{1}{2}

\frac{1}{8} = \frac{1^{3}}{2^{3}} = \frac{1 \cdot 1 \cdot 1}{2 \cdot 2 \cdot 2} = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = {(\frac{1}{2})}^{3}

Portanto:

\frac{1}{8} = {(\frac{1}{2})}^{3}

\frac{1}{8}

como potência de base 2.

\frac{1}{8} = {(\frac{1}{2})}^{3} = \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} = 2^{‒ 1} \cdot 2^{‒ 1} \cdot 2^{‒ 1} = 2^{‒ 3}

Portanto:

\frac{1}{8} = 2^{‒ 3}

\frac{8}{27}

como potência de base

\frac{3}{2}

\frac{8}{27} = \frac{2^{3}}{3^{3}} = {(\frac{2}{3})}^{3} = \frac{2}{3} \cdot \frac{2}{3} \cdot \frac{2}{3} = {(\frac{3}{2})}^{‒ 1} \cdot {(\frac{3}{2})}^{‒ 1} \cdot {(\frac{3}{2})}^{‒ 1} = {(\frac{3}{2})}^{‒ 3}

Portanto:

\frac{8}{27} = {(\frac{3}{2})}^{‒ 3}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

14 Escreva os números a seguir como potência de base 2.

a) 256

b) .1024

\frac{1}{64}

\frac{1}{128}

15 Escreva os números a seguir como potência de base 3.

a) 9

b) 81

\frac{1}{27}

\frac{1}{243}

Respostas e comentários

10.

\frac{1}{3}

11.

\frac{10}{3}

12. a) 0,00390625

12. b) 0,0009765625

12. c) 15,625

12. d) .15625

12. Conclusões: Ficam maiores que 1; ficam menores que 1 e maiores que 0.

13. Resposta pessoal.

14. a) 28

14. b) 210

14. c) 2‒6

14. d) 2‒7

15. a) 32

15. b) 34

15. c) 3‒3

15. d) 3‒5

Exercícios propostos

Para resolver o exercício 10, podemos determinar o valor numérico de x e de y para depois obter o produto entre esses números. Assim:

x =

{(2 ‒ \frac{1}{2})}^{‒ 2} = {(\frac{3}{2})}^{‒ 2} = \frac{4}{9}

y =

{(1 + \frac{1}{3})}^{‒ 1} = {(\frac{4}{3})}^{‒ 1} = \frac{3}{4}

x · y =

\frac{4}{9} \cdot \frac{3}{4} = \frac{3}{9} = \frac{1}{3}

Pelos itens c e d do exercício 12, percebemos que números entre 0 e 1 ficam maiores do que 1 ao serem elevados a expoentes negativos. Por outro lado, pelos itens a e b, percebemos que números maiores do que 1 ficam menores do que 1 ao serem elevados a expoentes negativos. Sugerimos abordar com os estudantes outros casos numéricos, aplicando a verificação desse fato. Para auxiliá-los, podem-se utilizar os recursos de uma planilha eletrônica para obter automaticamente a potência de números entre 0 e 1 elevados a um expoente negativo e a potência de números maiores do que 1 elevados a um expoente negativo. Dessa maneira, desenvolvem-se a competência geral 2 e a competência geral 7, pois os estudantes exercitam a curiosidade intelectual ao buscar experimentar o resultado e, ainda, podem aprimorar a justificativa e os argumentos para explicar por que a propriedade é válida.

No exercício 13, relembre com os estudantes o que é uma sequência recursiva, escrevendo alguns exemplos na lousa. Ao final deste exercício, se possível, deixe-os compartilhar entre si alguns problemas elaborados. A seguir indicamos um exemplo de sequência recursiva para esse exercício, considerando a1 = 3 e n natural tal que n > 1.

an = 3 · an ‒ 1

Cujos termos são: 3, 9, 27, 81reticências

Destaque com os estudantes que essa mesma sequência numérica poderia ser dada de maneira não recursiva, com n natural tal que n > 0, por:

an = 3n

Como escrever um número como potência de uma base dada

Se julgar necessário, retome com os estudantes a decomposição em fatores primos para números naturais. Além disso, caso eles ainda tenham alguma dificuldade na aplicação das propriedades da potenciação, peça-lhes que refaçam algumas atividades anteriores sobre esse assunto.

Exercícios propostos

No exercício 14, devemos decompor em fatores primos a base dada em cada item, a fim de determinar uma maneira de escrevê‑la como potência. Assim:

a) 256 = 2 · 2 · 2 · 2 · 2 · 2 · 2 · 2 = 28

b) .1024 = 256 · 2 · 2 = 28 · 2 · 2 = 28 + 1 + 1 = 210

\frac{1}{64} = \frac{1}{2^{6}} = 2^{‒ 6}

\frac{1}{128} = \frac{1}{2^{7}} = 2^{‒ 7}

A resolução do exercício 15 está no início deste Manual, nas orientações específicas do capítulo 1.

Página 19

16 Simplifique as expressões obtendo uma única potência.

\frac{4^{2} \cdot 8^{3}}{2^{10}}

\frac{9^{3} \cdot 27^{2}}{81}

Reúna-se com um colega e façam o que se pede.

a) Reproduzam o quadro a seguir no caderno e completem-na, atribuindo a n os números inteiros de 1 a 5.

Quadro de 4 colunas e com apenas a primeira linha indicada. Coluna 1: Expoente inteiro positivo n Coluna 2: Potência de base 10 10 elevado a n Coluna 3: Valor da potência (resultado) Coluna 4: Número de zeros do resultado

b) Comparando a primeira e a última coluna do quadro do item a, escrevam uma regra para obter, sem fazer cálculos, o valor da potência indicada por 10ⁿ.

c) Reproduzam no caderno o quadro a seguir e completem-na atribuindo a n os números inteiros de ‒1 a ‒5.

Quadro de 4 colunas e com apenas a primeira linha indicada. Coluna 1: Expoente inteiro negativo n Coluna 2: Potência de base 10 10 elevado a n Coluna 3: Valor da potência (resultado) Coluna 4: Número de zeros do resultado

d) Comparando a primeira e a última coluna do quadro do item c, escrevam uma regra para obter, sem fazer cálculos, o valor da potência indicada por 10ⁿ.

18 A medida da distância média entre o planeta Saturno e o Sol é da ordem de ....1000000000000 métros. Expresse essa medida como uma potência de base 10.

Fotografia. Fundo escuro com planeta Saturno, composto por esfera e elipse ao redor. — Fotografia do planeta Saturno feita pelo telescópio espacial Hubble em 2021.

19 Escreva a representação decimal das potências de base 10 a seguir.

a) 10‒1

b) 10‒2

c) 10‒3

d) 10‒5

e) 10‒6

20 O diâmetro de um fio de cabelo fino mede aproximadamente 0,0001 métro. Escreva essa medida como uma potência de base 10.

21 No Sistema Internacional de Unidades (ésse Í), para formar um múltiplo ou um submúltiplo de uma unidade de medida, é preciso colocar o prefixo desejado na frente do nome dessa unidade de medida. Esse mesmo procedimento também é usual para os símbolos.

Por exemplo:

• 1 megawatt = 1 ême dáblio = ..1000000 uáts = 106 uáts

• 1 nanossegundo = 1 êne ésse = 0,000000001 segundo = 10‒9 segundo

Pesquise os vinte prefixos estabelecidos pelo Sistema Internacional de Unidades e complete o quadro a seguir.

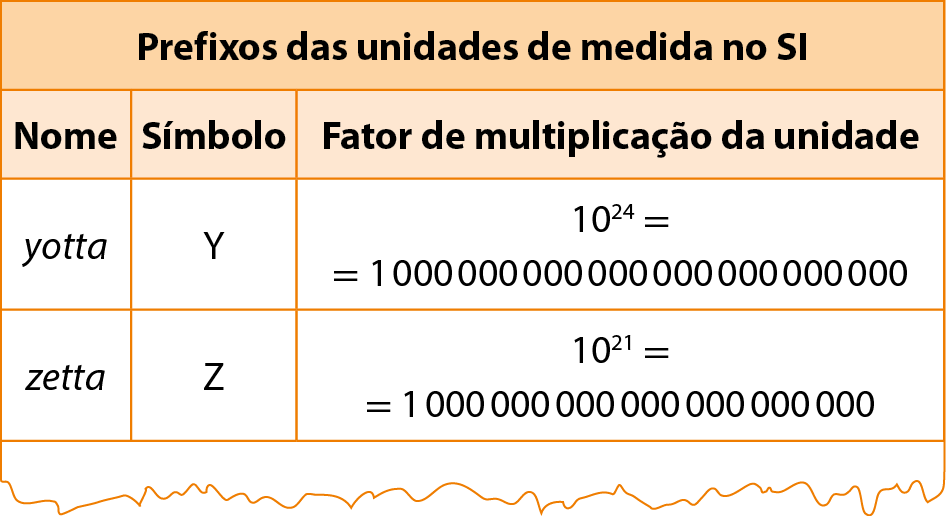
Quadro; Prefixos das unidades de medida no SI. Coluna 1: nome; coluna 2: símbolo; coluna 3 Fator de multiplicação da unidade. Linha 1 coluna 1: yotta Linha 1 coluna 2: Y Linha 1 coluna 3: 10 elevado a 24 igual 1.000.000.000.000.000.000.000.000. Linha 2 coluna 1: zetta Linha 2 coluna 2: Z Linha 2 coluna 3: 10 elevado a 21 igual 1.000.000.000.000.000.000.000.

22 Reduza cada uma das expressões a seguir a uma única potência de base 10 e represente essa potência na fórma decimal.

\frac{10^{3} \cdot 10^{2}}{10^{7}}

\frac{10^{4} \cdot 10^{2}}{10^{9}}

\frac{10^{‒ 16}}{10^{‒ 4} \cdot 10^{‒ 8}}

\frac{10^{‒ 4} \cdot 10^{‒ 8}}{10^{‒ 9}}

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Mostre que multiplicar 3 por 10⁴ é o mesmo que dividir 3 por 10^‒4.

Respostas e comentários

16. a) 23

16. b) 38

17. a) Construção de tabela.

17. b) Espera-se que os estudantes concluam que, para n inteiro e positivo, o valor da potência 10ⁿ é o número formado por 1 seguido de n zeros.

17. c) Construção de tabela.

17. d) Espera-se que os estudantes concluam que, para n inteiro e negativo, o valor da potência 10ⁿ é o número formado por 1 antecedido por |n | zeros, com uma vírgula entre o primeiro e o segundo algarismo.

18. 1012 métros

19. a) 0,1

19. b) 0,01

19. c) 0,001

19. d) 0,00001

19. e) 0,000001

20. 10‒4 métro

21. Construção de tabela.

22. a) 10‒2 e 0,01

22. b) 10‒3 e 0,001

22. c) 10‒4 e 0,0001

22. d) 10‒3 e 0,001

Pense mais um poucoreticências: 3 ⋅ 104 = .30000

3 : 10‒4 =

\frac{3}{10^{‒ 4}} = \frac{3}{\frac{1}{10^{4}}} = 3 \cdot \frac{10^{4}}{1}

= 3 ⋅ 104 = .30000

Exercícios propostos

As resoluções dos exercícios 16 a 22 estão no início deste Manual, nas orientações específicas do capítulo 1.

Após os estudantes responderem ao exercício 17, solicite a alguns deles que registrem na lousa suas resoluções para todos discutirem a objetividade das redações das regras obtidas e para as compararem com suas próprias soluções. O exercício de redação leva os estudantes a ampliar e a diversificar o vocabulário, além de desenvolver a habilidade de organização do pensamento e de argumentação.

Nos exercícios 18 e 20, os estudantes lidarão com situações que envolvem medidas muito grandes ou muito pequenas. Vale a pena solicitar-lhes que, após a resolução do exercício 20, façam uma relação entre os dois exercícios, respondendo, por exemplo: Quantas vezes 1012 contém 10‒4? (Resposta: 1016, pois 1012 : 10‒4 = 1016).

O exercício 21 oferece novamente a possibilidade de trabalhar com unidades de medida. Pergunte aos estudantes que outras unidades de medida eles conhecem que usam os prefixos estabelecidos pelo Sistema Internacional (ésse Í). Informações sobre esse sistema podem ser consultadas em: Sistema Internacional de Unidades: ésse Í. Duque de Caxias, Rio de Janeiro: in metro/CICMA/SEPIN, 2012. Disponível em: https://oeds.link/v1HYMb. Acesso em: 19 julho 2022.

Página 20

TRABALHANDO A INFORMAÇÃO

Trabalhando com juro

Ilustração. Mesa com duas pessoas sentadas. À direita, mulher de cabelo escuro e blusa branca. À esquerda, homem de cabelo castanho e camisa azul listrada. Eles estão sentados. Sobre a mesa, computador e placa gerente.

Quando fazemos um empréstimo de dinheiro em um banco, pagamos uma espécie de aluguel por ele. Esse “aluguel” é chamado de juro ( jóta ).

Nas compras a prazo também pagamos juro. Do mesmo modo, recebemos juro quando fazemos uma aplicação financeira, por exemplo, na caderneta de poupança.

O que pagamos ou recebemos de juro é uma porcentagem sobre o dinheiro emprestado ou aplicado durante determinado tempo (tê ). Essa porcentagem é chamada de taxa de juro ( ih ).

A quantia que se empresta ou se aplica é chamada de capital (cê ). A soma do capital com o juro é denominada montante (ême ).

Quando um capital é aplicado por certo tempo a determinada taxa de juro, o montante pode crescer de acôrdo com dois regimes de capitalização (processo de formação do juro): o juro simples ou o juro composto. Aqui veremos o juro simples.

Dada uma aplicação de R$ 500,00quinhentos reais com taxa de juro de 10% ao mês, em 3 meses, quanto essa aplicação renderá, se o juro for calculado sempre sobre os R$ 500,00quinhentos reais?

A cada mês, o juro é dado por:

10% de 500 =

\frac{10}{100}

⋅ 500 = 50

Ao final dos 3 meses, o capital de R$ 500,00quinhentos reais renderá R$ 150,00cento e cinquenta reais de juro.

O juro assim calculado é chamado de juro simples. Nesse caso, o montante é igual a R$ 650,00seiscentos e cinquenta reais.

Agora, vamos chegar a uma fórmula para calcular juro simples.

Ilustração. homem de cabelo curto, cavanhaque e camiseta azul. Ele fala: Note que o juro simples é calculado apenas sobre o capital inicial.

Sendo cê o capital, ih a taxa de juro (expressa na fórma decimal), tê o tempo de aplicação ou de empréstimo (na mesma unidade de medida da taxa) e jóta o juro, obtemos:

Tempo (t)	Juro (j)
primeiro mês	C ⋅ i
segundo mês	C ⋅ i + C ⋅ i
terceiro mês	C ⋅ i + C ⋅ i + C ⋅ i
...	...
t-ésimo mês

Assim, o cálculo do juro simples pode ser feito do seguinte modo:

j = C ⋅ i ⋅ t

Respostas e comentários

Trabalhando a informação

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero quatro.

Esta seção apresenta a noção de juro simples e juro composto e aborda cálculos de porcentagem, possibilitando o desenvolvimento da habilidade (ê éfe zero oito ême ah zero quatro) e do Tema Contemporâneo Transversal educação financeira.

Sugestão de leitura

Para ampliar o trabalho com esta seção, sugerimos o material:

SOUZA, H. J. C. Matemática financeira: uma aplicação direta no cotidiano. Dissertação (mestrado), Universidade Federal da Paraíba, 2013. Disponível em: https://oeds.link/SlTS5E. Acesso em: 19 julho 2022.

Nesta dissertação, o autor apresenta os principais tópicos de Matemática Financeira e explora o uso de planilhas eletrônicas para sistematizar algumas aplicações dessa área.

Página 21

Como exemplo, vamos considerar que um capital de R$ 2.000,00dois mil reais seja aplicado a uma taxa de juros de 2,5% ao mês, no regime de juro simples. Pelos dados, obtemos: C = R$ 2.000,00dois mil reais e i = 2,5% = 0,025.

Podemos expressar o juro em função do tempo t por:

j = C ⋅ i ⋅ t, ou seja, j = .2000,00 ⋅ 0,025 ⋅ t, ou, ainda, j = 50t

Assim, após 3 meses, por exemplo, essa aplicação rende R$ 150,00cento e cinquenta reais de juro, pois j = 50 ⋅ 3 = 150.

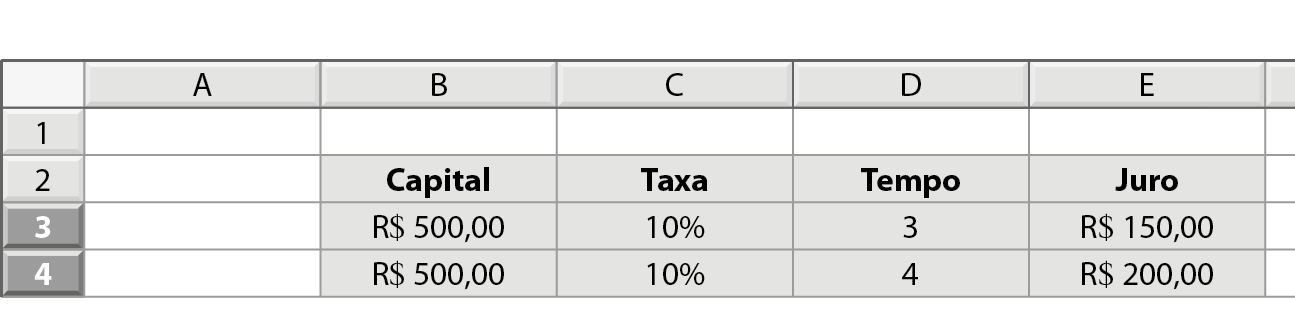
Você sabia que pode programar uma planilha eletrônica para calcular o juro simples utilizando uma fórmula? Observe a planilha a seguir. Nela, na coluna Juro ( jóta), podemos digitar a fórmula do juro simples (j = C ⋅ i ⋅ t) relacionando os valores das colunas Capital (cê), Taxa (ih) e Tempo (tê).

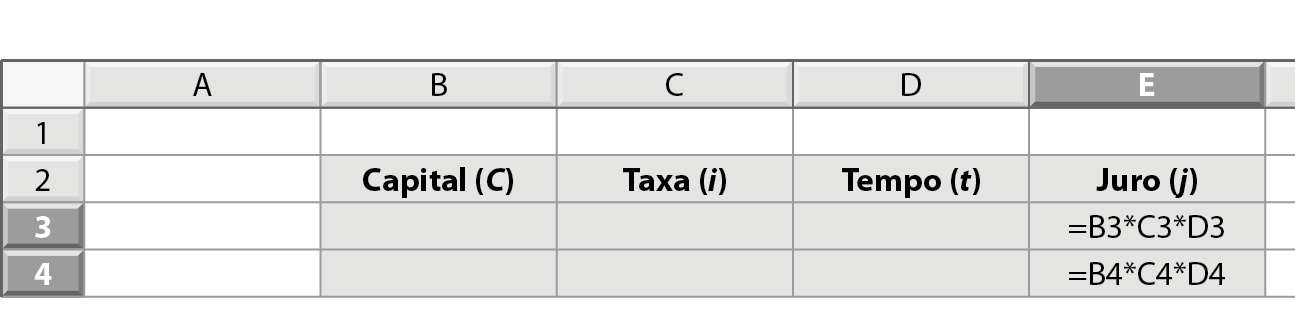
Ilustração. Planilha eletrônica. Acima, coluna de A até E. À esquerda, linha 1 a 4. B2: Capital (C). C2: taxa (i). D2: tempo (i). E2: Juro (i). E3: =B3*C3*D3. E4: =B4*C4*D4

Perceba que, na célula que indicará o valor do juro, temos o capital multiplicado pela taxa multiplicado pelo tempo, assim como na fórmula que deduzimos anteriormente.

Assim, para saber o valor total do juro de uma aplicação, como no exemplo da página anterior, basta digitar os dados do problema e a planilha calculará o juro automaticamente.

Ilustração. Planilha eletrônica. Acima, coluna de A até E. À esquerda, linha 1 a 4. B2: Capital (C). C2: taxa (i). D2: tempo (i). E2: Juro (i). B3: R$ 500,00. C3: 10%. D3: 3. E3: R$ 150,00. B4: R$ 500,00. C3: 10%. D3: 4. E3: R$ 200,00.

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

1 Um capital de R$ 18.000,00dezoito mil reais é aplicado à taxa de 8% ao ano no regime de juro simples. Determine o rendimento para uma aplicação de 2 anos.

2 Por quanto tempo o capital de R$ 12.000,00doze mil reais esteve aplicado à taxa de juro simples de 1,6% ao mês para render R$ 2.304,00dois mil trezentos e quatro reais de juro?

Multiplicação e divisão por potências de base 10

Para multiplicar, de maneira prática, um número por uma potência de base 10 com expoente inteiro positivo, como 101, 102, 103, reticências, basta deslocar a vírgula uma, duas, três, reticências casas para a direita. Isso é possível porque, nesse caso, o valor de cada uma dessas potências (resultado) tem um, dois, três, reticências zeros.

Observe alguns exemplos.

a) 5,126 ⋅ 101 = 51,26

b) 0,0028 ⋅ 102 = 0,28

c) 12,0 ⋅ 103 = .12000

d) 8,56 ⋅ 104 = .85600

Já para multiplicar um número por uma potência de base 10 com expoente inteiro negativo, como 10⁼¹, 10⁼², 10⁼³, reticências, deslocamos a vírgula uma, duas, três, reticências casas para a esquerda, o que equivale a dividir esse número por 101, 102, 103, reticências ou por 10, 100, .1000, reticências

Respostas e comentários

1. R$ 2.880,00dois mil oitocentos e oitenta reais

2. 12 meses (ou 1 ano).

Trabalhando a informação

Este pode ser um bom momento para utilizar as planilhas eletrônicas como ferramenta para auxiliar os cálculos e organizar as informações. Se houver possibilidade, proponha aos estudantes a utilização de planilhas eletrônicas como exemplificado na seção.

As resoluções das atividades do Agora quem trabalha é você! estão no início deste Manual, nas orientações específicas do capítulo 1.

Ressalte a importância de observar o período de aplicação da taxa de juro e o tempo, pois sempre devem estar expressos na mesma unidade de medida. Por exemplo, na atividade 1, se a taxa fosse 8% ao mês e o tempo continuasse a ser 2 anos, deveríamos expressar o tempo em meses, ou seja, usar 24 meses nos cálculos.

Além disso, comente que devemos utilizar nos cálculos o valor da taxa expresso na fórma decimal (ou de fração). Se julgar adequado, incentive os estudantes a obter taxas percentuais na fórma decimal, calculando mentalmente. Por exemplo: 10% = 0,1; 50% = 0,5; 12% = 0,12; 2% = 0,02; 0,5% = 0,005.

Multiplicação e divisão por potências de base 10

Para retomar e, posteriormente, aplicar operações envolvendo potências de base 10, sugerimos que proponha multiplicações e divisões por 10, 100, .1000 etcétera na lousa para alguns estudantes resolverem e a turma avaliar e fazer a validação. Espera-se que eles utilizem os conhecimentos que já construíram em anos anteriores.

Página 22

Observe alguns exemplos.

a) 356 ⋅ 10‒2 = 3,56

b) .25678,2 ⋅ 10‒3 = 25,6782

c) 0,5 ⋅ 10‒1 = 0,05

d) 2,45 ⋅ 10‒3 = 0,00245

Nos exemplos anteriores, efetuamos multiplicações por potências de base 10, mas também é possível efetuar divisões. Acompanhe, a seguir, duas dessas multiplicações transformadas em divisões.

8,56 vezes 10 elevado a 4, igual 8,56, vezes fração numerador 1, denominador 10 elevado a menos 4, igual, fração; numerador 8,56, denominador 10 elevado a menos 4, igual 8,56 dividido 10 elevado menos 4, igual 85.600. Acima, uma seta aponta para o expoente da primeira parcela 10 elevado a 4 e para o ultimo divisor 10 elevado a menos 4, indicando que os sinais dos expoentes são opostos.

0,5 vezes 10 elevado a menos 1, igual 0,5, vezes fração numerador 1, denominador 10 elevado a 1, igual, fração; numerador 0,5, denominador 10 elevado a 1, igual 0,5 dividido 10 elevado a 1, igual 0,05.
Acima, uma seta aponta para o expoente da primeira parcela 10 elevado a menos 1 e para o ultimo divisor 10 elevado a 1, indicando que os sinais dos expoentes são opostos.

Observe que, na divisão por uma potência de base 10 com expoente inteiro negativo, como 10‒4, deslocamos a vírgula para a direita. Já na divisão por uma potência de base 10 com expoente inteiro positivo, como 101, deslocamos a vírgula para a esquerda.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

23 Efetue as multiplicações por potências de base 10.

a) 3,6 ⋅ 104

b) 0,025 ⋅ 102

c) 0,4 ⋅ 10‒2

d) .3576 ⋅ 10‒3

24 O produto 0,000025 ⋅ 0,000000002 é igual a:

a) 50 ⋅ 10‒14

b) 5 ⋅ 10‒14

c) 5 ⋅ 10‒40

d) 5 ⋅ 10‒4

e) 50 ⋅ 10‒13

25 O valor da expressão

A = 5,24 ⋅ 10‒23 + 8,36 ⋅ 10‒21 é:

a) 5,62 ⋅ 10‒21

b) 5,62 ⋅ 10‒23

c) 8,4124 ⋅ 10‒21

d) 8,4124 ⋅ 10‒23

e) 8,4124 ⋅ 10‒44

26 Descubra a potência de base 10 que deve ser colocada no lugar de a para que se obtenha:

a) 56,754 ⋅ a = .567540

b) 0,003 ⋅ a = 30

c) a ⋅ 23 = 0,000023

d) a ⋅ 4,5 = 0,00045

27 Converta as medidas a seguir usando potências de base 10.

a) 1 centímetro em métro.

b) 100 quilômetros em métro.

c) 10 gramas em quilograma.

d) uma tonelada em quilograma.

e) 10 centímetros quadrados em métros quadrados.

f) 1 centímetro cúbico em decímetros cúbicos.

28 O açude Castanhão, no Ceará, com 325 quilômetros quadrados de área inundada, é o maior açude da América Latina. Ele tem capacidade de armazenamento de 6,7 ⋅ 109 métros cúbicos de água, que corresponde a cêrca de 37% de toda a capacidade de armazenamento dos reservatórios cearenses. Determine a capacidade total de armazenamento dos reservatórios cearenses.

Fotografia. À esquerda, região com água. À direita, estrutura com ponte. Ao fundo, morros e nuvens. — O açude Castanhão, localizado no município de Jaguaribara (Ceará), é formado pela barragem das águas do rio Jaguaribe. (Fotografia de 2021.)

29 (ú éfe ême gê) O açude Orós, um dos maiores reservatórios do Brasil, tem capacidade para armazenar 2 ⋅ 109 métros cúbicos de água. Sabe-se que o rio Amazonas lança no oceano Atlântico 50 milhões de litros de água por segundo.

Com base nesses dados, é correto afirmar que o tempo que o rio Amazonas leva para lançar no oceano Atlântico um volume igual à capacidade do açude Orós é:

a) maior que 20 horas.

b) menor que 5 horas.

c) maior que 5 horas e menor que 10 horas.

d) maior que 10 horas e menor que 20 horas.

Respostas e comentários

23. a) .36000

23. b) 2,5

23. c) 0,004

23. d) 3,576

24. Alternativa b.

25. Alternativa c.

26. a) 104

26. b) 104

26. c) 10‒6

26. d) 10‒4

27. a) 10‒2 métro

27. b) 105 métros

27. c) 10‒2 quilograma

27. d) 103 quilogramas

27. e) 10‒3 métros quadrados

27. f) 10‒3 decímetros cúbicos

28. Aproximadamente ...18110000000 métros cúbicos.

29. Alternativa d.

Multiplicação e divisão por potências de base 10

Trabalhe os exemplos apresentados sobre multiplicação e divisão de números racionais por potências de base 10, de modo a garantir que os estudantes associem a multiplicação por uma potência de base 10 com expoente negativo à divisão, por exemplo:

• 5 · 10‒3 = 5 : 103 = 5 : .1000 = 0,005

• 12 : 102 = 12 · 10‒2 = 0,12

Exercícios propostos

As resoluções dos exercícios 23 ao 29 estão no início deste Manual, nas orientações específicas do capítulo 1.

No exercício 26, antes de calcular os valores exatos de cada item, peça aos estudantes que estimem os expoentes, visto que têm condições de prever, em primeiro lugar, se os expoentes serão positivos ou negativos.

Aproveite os exercícios 28 e 29 e verifique se os estudantes sabem o que é um açude (o mesmo que represa; construção para represar a água dos rios visando a utilizá-la na agricultura, no abastecimento de cidades e na indústria). Sugira que busquem mais informações sobre os açudes Castanhão e Orós e pesquisem quais são as principais represas que abastecem a região onde moram.

Página 23

Notação científica

O uso das potências é bastante comum em áreas da Ciência como Medicina, Biologia, Astronomia, Geologia, entre muitas outras.

ilustração. Homem de cabelo castanho, óculos e jaleco branco. Ao lado de um microscópio ele diz: A medida do diâmetro de uma bactéria, que é um organismo unicelular, varia de 10 elevado a menos 4 m a 2 vezes 10 elevado a menos 6 m.

Ilustração. Mulher de cabelo preto e curto, jaleco branco, fala: A medida do raio do Sol é aproximadamente 6,96 vezes 10 elevado a 8 m.

Esse tipo de registro é chamado de notação científica. Ele fornece uma ideia precisa da ordem de grandeza (bilhões, milhões, milésimos etcétera) de uma medida e é fundamental para trabalhar com números “muito grandes” ou “muito pequenos”, isto é, muito próximos de 0. A ordem de grandeza de uma medida é dada pela potência de base 10.

Em notação científica, os números são escritos como produto de dois fatores, em que um deles é uma potência de base 10 com expoente inteiro (positivo ou negativo), e o outro é um número igual a 1 ou maior que 1 e menor que 10.

Observe os exemplos.

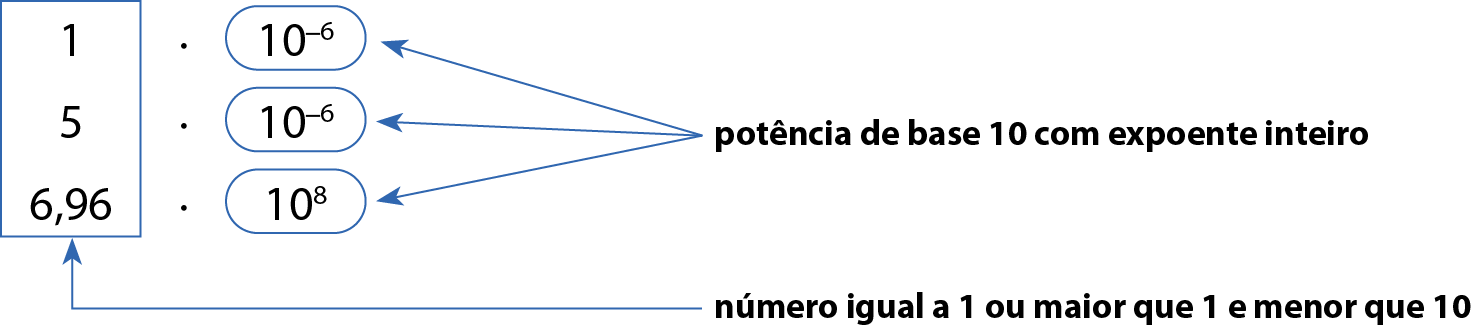
primeira linha: uma vez 10 elevado a menos 6 segunda linha: 10 elevado a menos 6 terceira linha : 6,96 vezes, 10 elevado 8. As 3 linhas estão centralizadas pelo sinal de vezes. Abaixo , uma seta que parte da frase : número igual a 1 ou maior que 1 e menor que 10, uni-se a a uma retângulo que contem a primeira parcela de cada linha. À esquerda das multiplicações, Três setas parte, da frase: potência de base 10 com expoente inteiro e uni-se a cada uma da segunda parcela de cada linha. setas par

Observe outros exemplos de números escritos em notação científica.

a) 5,2 ⋅ 106

b) 8,1 ⋅ 1012

c) 1,25 ⋅ 10elevado a menos 3

d) 2,236 ⋅ 10elevado a menos 9

Agora, vamos escrever alguns números em notação científica.

a) .3265

Para escrever esse número como produto de dois fatores, um deles uma potência de base 10, vamos multiplicá-lo por 10elevado a menos 3 e por 103, pois 10elevado a menos 3 ⋅ 103 = 100 = 1. Assim, obtemos:

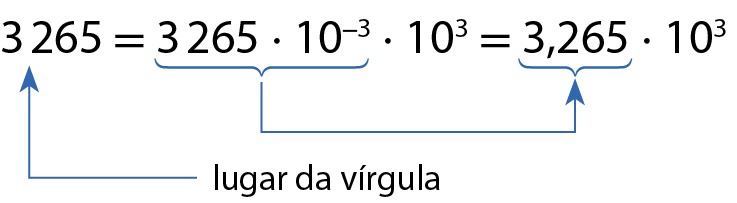
3mil 265, igual, 3 mil 265 vezes 10 elevado a menos 3 vezes 10 elevado a 3, igual, 3,265 vezes 10 ao cubo . Abaixo, uma seta parte da frase: lugar da vírgula e aponta para o números 3 mil 265. De um traço, abaixo de 3 mil 265 vezes 10 elevado a menos 3, parte uma seta que aponta para 3 ,265

Respostas e comentários

Notação científica

Espera-se que os estudantes utilizem os conhecimentos que já construíram acerca de potências de base 10 e da multiplicação (ou divisão) por potências de 10 para aplicar no registro de um número (ou medida) em notação científica.

Aproveite o momento e comente o uso dos prefixos gregos (como nano-, micro-, mili-, quilo-, mega- e giga-) na designação das diferentes potências de base 10. Por exemplo, 1 miligrama corresponde a 10elevado a menos 3 grama, 1 micrograma, a 10elevado a menos 6 grama, e 1 nanograma, a 10elevado a menos 9 grama.

Amplie perguntando aos estudantes se conhecem mais palavras com esses prefixos. Podem surgir palavras como: nanotecnologia, microbiologia, microscópio, microcomputador, micróbio, milímetro, mililitro, quilograma, quilômetro e megalomania. A nanotecnologia, por exemplo, pode ser considerada um conjunto de atividades ou mecanismos que ocorrem em uma escala extremamente pequena, mas que tenham implicações no mundo real.

Pode-se propor aos estudantes que pesquisem as implicações da nanotecnologia no bem-estar das pessoas, desenvolvendo-se uma atividade interdisciplinar com Ciências.

Página 24

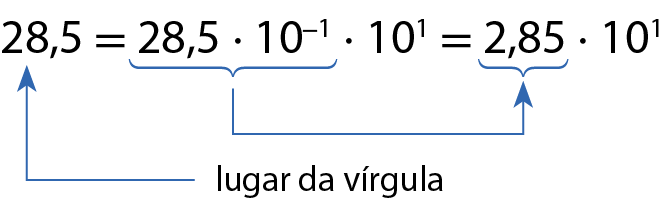
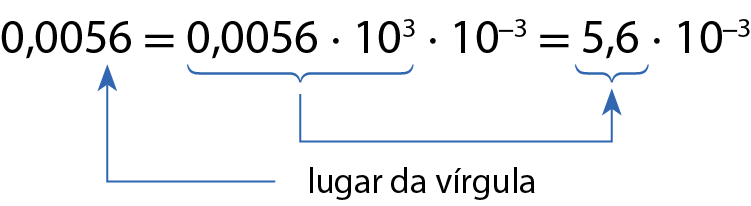
c) 0,0056

Quando o número é menor que 1, devemos multiplicá-lo por uma potência de base 10 com expoente positivo e, para não mudar o valor, multiplicar o resultado pela potência de base 10 com expoente oposto ao da primeira multiplicação, ou seja, expoente negativo.

0,0056, igual, 0,0056 vezes 10 elevado ao cubo vezes 10 elevado a menos 3, igual, 5,6 vezes 10 elevado a menos 3. Abaixo, uma seta parte da frase: lugar da vírgula e aponta para o número 0,0056. De um traço, abaixo de 0,0056 vezes 10 ao cubo, parte uma seta que aponta para 5,6.

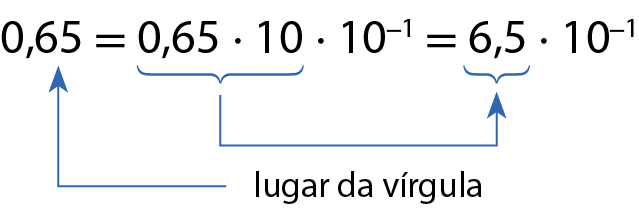
0,65, igual, 0,65 vezes, 10 vezes ,10 elevado a menos 1, igual, 6,5 vezes 10 elevado a menos 1. Abaixo, uma seta parte da frase: lugar da vírgula e aponta para o numero 0,65. De um traço, abaixo de 0,65 vezes 10, parte uma seta que aponta para 2,85.

Verifique agora como a notação científica é usada para expressar:

a) a medida da distância da Terra até o Sol;

..150000000 quilômetros = 1,5 ⋅ 108 quilômetros

Ilustração. Sistema solar. À esquerda, o sol. à direita, elipses com os planetas: Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano, Netuno. — Representação esquemática do Sistema Solar. O Sol, os planetas e as órbitas não estão representados nas proporções reais nem com cores reais.

b) a medida da massa do átomo de hidrogênio.

0,00000000000000000000000166 grama = 1,66 ⋅ 10‒24 grama

Ilustração. Próton, representado por esfera azul. Ao redor, elipse com esfera vermelha menor (elétron). — Representação esquemática do átomo de hidrogênio. O próton, o elétron e sua órbita não estão representados nas proporções reais nem com cores reais.

Respostas e comentários

Notação científica

Aborde com os estudantes as situações apresentadas, as quais envolvem números muito grandes ou muito pequenos, e verifique se eles conhecem outros exemplos. Sugira que façam uma pesquisa de notícias ou reportagens veiculadas pela mídia e cujo contexto apresente números expressos na notação científica (ou que poderiam ser mais bem expressados na notação científica) e, depois, registrem os valores encontrados em notação científica. É possível realizar um trabalho interdisciplinar com Ciências, por exemplo, propondo aos estudantes que façam a representação do Sol e dos planetas do Sistema Solar em escala (considerando o diâmetro médio de cada planeta e do Sol). Se possível, pode-se compor em escala, também, a representação das distâncias médias entre os planetas e o Sol, se na escola houver espaço suficiente. Uma alternativa seria posicionar a representação do Sol em um espaço comum da escola e determinar em que locais ao redor da escola deveriam ficar os demais planetas (considerando a distância média deles até o Sol).

Sugestão de leitura

Para ampliar e enriquecer seu trabalho com esse tema, sugerimos:

SILVA, E. M. E. O Sistema Solar. PLANETÁRIO ú éfe ésse cê. Disponível em: https://oeds.link/rWdxPJ. Acesso em: 19 julho 2022.

Neste texto, a autora apresenta informações sobre planetas e outros corpos do Sistema Solar, por exemplo, a distância média deles até o Sol e o diâmetro equatorial dos principais componentes do Sistema Solar.

Página 25

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

30 Escreva em notação científica cada um dos números a seguir.

a) 12,6 milhões

b) 361 ⋅ 106

c) 15 bilhões

d) 458,6 ⋅ 10‒5

e) .3576 ⋅ 10‒3

f) 0,0000000000001

31 Dois planetas, a e B, giram em tôrno de uma estrela ê em órbitas praticamente circulares e no mesmo plano.

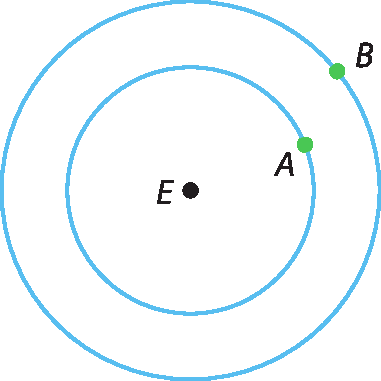
Ilustração. duas circunferências concêntricas de centro E, a menor contém o ponto A, a maior contém o ponto B.

A medida da distância de a até a estrela ê é 15 ⋅ 107 quilômetros, e a medida da distância de B até a estrela E é 2,3 ⋅ 108 quilômetros. Desprezando os diâmetros desses astros, calcule a medida da distância máxima e a medida da distância mínima entre a e B e expresse-as em notação científica.

32 Na abertura do capítulo, vimos que:

a) a medida da massa do Sol é aproximadamente 2 ⋅ 1030 quilogramas. Expresse, em notação científica, essa medida em tonelada.

b) reações de fusão nuclear no núcleo do Sol convertem cêrca de 6 ⋅ 1011 quilogramas de hidrogênio (agá) em hélio (agá ê) por segundo. Sabendo que 1 ano tem aproximadamente 3 ⋅ 107 segundos, quantas toneladas de hidrogênio são convertidas em hélio por ano no núcleo do Sol? Dê sua resposta em notação científica.

33 Cada mililitro de sangue humano contém, em média, 5 ⋅ 103 glóbulos vermelhos. No corpo de um ser humano adulto circulam cêrca de 5,5 litros de sangue. De acôrdo com esses dados, qual é o número médio, em notação científica, de glóbulos vermelhos que há no corpo de um adulto?

Fotografia. Glóbulos vermelhos em formato arredondado. Eles estão aglomerados. — Glóbulos vermelhos (hemácias) do sangue humano em fotomicrografia eletrônica de varredura, colorida artificialmente. (Ampliação de 2.400 vezes.)

A tabela a seguir mostra os dados da movimentação comercial entre o Brasil e o exterior de 2019 a 2021. Reúna-se com um colega e construam um gráfico de colunas com os dados da tabela. Lembrem-se de indicar os valores em milhões de dólares no eixo vertical, os anos no eixo horizontal, e de dar um título ao gráfico. Note que cada um dos dados da movimentação comercial (Saldo, Importações, Exportações), por ano, corresponde a uma coluna no gráfico, ou seja, para cada um dos três anos no gráfico, deve haver três colunas.

Movimentação comercial entre o Brasil e o exterior (2019-2021)*
Ano	Saldo (milhões de dólares)	Importações (milhões de dólares)	Exportações (milhões de dólares)
2019	35.000	186.000	221.000
2020	50.000	159.000	209.000
2021	61.000	219.000	280.000

* Valores aproximados. Dados obtidos em: BRASIL. Resultados do comércio exterior brasileiro: dados consolidados. Disponível em: https://oeds.link/Mfafc2. Acesso em: 10 mar. 2022.

Respostas e comentários

30. a) 1,26 ⋅ 107

30. b) 3,61 ⋅ 108

30. c) 1,5 ⋅ 1010

30. d) 4,586 ⋅ 10‒3

30. e) 3,576 ⋅ 100

30. f) 1 ⋅ 10‒13

31. 3,8 ⋅ 108 quilômetros; 8 ⋅ 107 quilômetros

32. a) 2 ⋅ 1027 toneladas.

32. b) 1,8 ⋅ 1016 toneladas.

33. 2,75 ⋅ 107 glóbulos vermelhos.

34. Construção de gráfico.

Exercícios propostos

As resoluções dos exercícios 30 ao 34 estão no início deste Manual, nas orientações específicas do capítulo 1.

No exercício 32, há novamente a oportunidade de trabalhar com transformações entre unidades de medida de massa em situações contextualizadas. Nesse exercício, os estudantes poderão utilizar a relação existente entre duas unidades de massa: o quilograma e a tonelada, além de escrever tal medida em notação científica.

Amplie as discussões com os estudantes fazendo-os refletir sobre o gráfico do exercício 34, com questões como:

• Por que não é conveniente, neste caso, colocar os números “completos” no gráfico? (Possível resposta: Porque são formados por muitos algarismos, o que dificultaria a organização das informações.)

• O que aconteceria se esquecessem de escrever a informação ”milhões de dólares” no eixo vertical do gráfico? (Resposta possível: A ordem de grandeza dos valores monetários seria alterada, ficaria “milhares” de dólares em vez de “milhões”.)

Ao trabalhar com saldos, importações e exportações nesse exercício, abordamos o Tema Contemporâneo Transversal educação financeira.

Página 26

Com base no gráfico que vocês construíram, façam o que se pede.

a) Expressem em notação científica os valores, em dólares, apresentados no gráfico.

b) Para cada ano, verifiquem se a diferença entre os valores das exportações e os das importações é igual ao saldo.

c) Qual foi a média aproximada das exportações nesse período? E das importações? E do saldo?

d) Para cada ano, escrevam, com um número negativo, o quanto falta para a exportação atingir a média ou, com um número positivo, em quanto a exportação excedeu a média.

e) No gráfico, tracem uma reta horizontal pelo valor da média das importações. Façam uma estimativa para responder à questão: a parte da coluna da importação de 2021 que ficou acima da reta traçada é equivalente à soma das partes das outras duas colunas que ficaram abaixo da reta?

35 (ú éfe ésse é) Um raio de luz, propagando-se no vácuo, desloca-se com velocidade de 3,0 ⋅ 105 quilômetros por segundo aproximadamente. Se a distância entre dois planetas mede 9,0 ⋅ 107 quilômetros, então o tempo, em minuto, que o raio de luz levará para cobrir essa distância é:

a) 5,2.

b) 5.

c) 4,5.

d) 4.

e) 3,8.

Hora de criar – Em duplas, cada um de vocês vai elaborar um problema utilizando a notação científica. Para o problema, considerem situações do dia a dia que envolvam números que podem ser escritos em notação científica, como a velocidade da conexão da internet, o consumo de energia elétrica de um equipamento, o pacote de dados de um plano de uma operadora de celular, entre outros. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

2. Calculando com raízes

Raiz quadrada de números racionais

Acompanhe algumas situações nas quais desejamos calcular a raiz quadrada de números racionais.

Situação 1

Observe o quadrado alaranjado na figura. Considerando a medida da área do quadrado maior igual a 1 centímetro quadrado, e a medida do comprimento de seu lado igual a 1 centímetro, podemos dizer que:

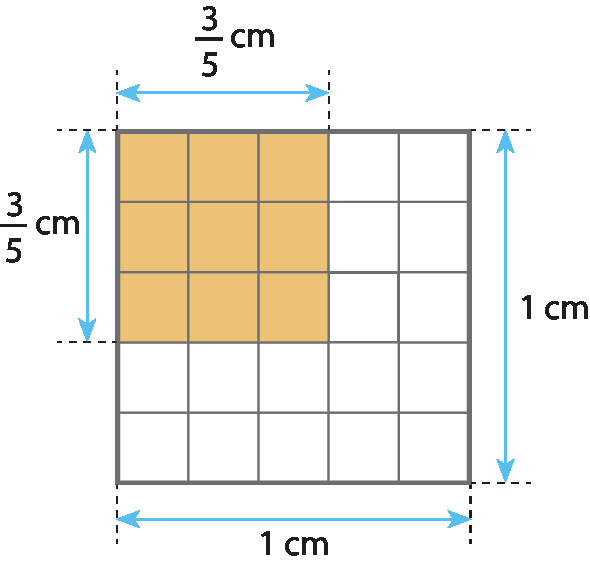
Ilustração. Quadrado composto por 25 quadradinhos. Dentro do quadrado maior, no canto esquerdo superior um quadrado formado por 9 quadradinhos laranja. Do lado externo, direito e inferior, do quadrado maior, a indicação do comprimento de 1 centímetro, Do lado externo, esquerdo e superior, do quadrado laranja, a indicação do comprimento de 3 quintos centímetro.

• a medida da área de cada quadradinho é

\frac{1}{25}

centímetro quadrado;

• a medida da área do quadrado alaranjado é

\frac{9}{25}

centímetro quadrado;

• a medida do comprimento do lado do quadrado alaranjado é

\frac{3}{5}

centímetro.

Note que a área do quadrado alaranjado pode ser obtida da seguinte fórma:

\frac{3}{5}

⋅

\frac{3}{5}

{(\frac{3}{5})}^{2}

\frac{9}{25}

, ou seja,

\frac{9}{25}

centímetro quadrado

Nesse caso, o número

\frac{3}{5}

é chamado de raiz quadrada de

\frac{9}{25}

, que indicamos por

\sqrt{\frac{9}{25}} = \frac{3}{5}

(lemos: “a raiz quadrada de nove vinte e cinco avos é três quintos”).

O número

\frac{9}{25}

é um número racional quadrado perfeito.

Respostas e comentários

34. a) Exportações: 2,21 ⋅ 1011 (2019); 2,09 ⋅ 1011 (2020); 2,80 ⋅ 1011 (2021)

Importações: 1,86 ⋅ 1011 (2019); 1,59 ⋅ 1011 (2020); 2,19 ⋅ 1011 (2021)

Saldo: 3,5 ⋅ 1010 (2019); 5,0 ⋅ 1010 (2020); 6,1 ⋅ 1010 (2021)

34. b) Sim.

34. c) Exportações: 2,37 ⋅ 1011; importações: 1,88 ⋅ 1011; saldo: 4,9 ⋅ 1010

34. d) 2019: ‒1,60 ⋅ 1010; 2020: ‒2,80 ⋅ 1010; 2021: +4,30 ⋅ 1010

34. e) Sim.

35. Alternativa b.

36. Resposta pessoal.

Exercícios propostos

A resolução do exercício 35 está no início deste Manual, nas orientações específicas do capítulo 1.

2. Calculando com raízes

Habilidade da Bê êne cê cê: EF08MA02.

Este tópico possibilita explorar a habilidade (ê éfe zero oito ême ah zero dois) ao associar a potenciação à radiciação. Retome o cálculo de raiz quadrada, propiciando aos estudantes mobilizarem conhecimentos já construídos em anos anteriores.

Retomamos o uso do conceito de área de quadrado como base para o cálculo de raiz quadrada por ser um facilitador para a compreensão dos estudantes, além de tornar o aprendizado mais significativo. Ressaltamos a conexão das Unidades Temáticas Números, Geometria e Grandezas e medidas.

Explore a figura da situação 1. Peça aos estudantes que justifiquem as afirmações feitas em relação às áreas:

• Nas condições expostas, por que a área de cada quadradinho que compõe o quadrado maior (de lado de 1 centímetro) mede

\frac{1}{25}

centímetro quadrado? (Resposta: Espera-se que percebam que, se o quadrado maior tem área medindo 1 centímetro quadrado e é composto de 25 quadradinhos idênticos, a medida da área de cada quadradinho corresponde a

\frac{1}{25}

da medida da área do quadrado grande, ou seja:

\frac{1}{25}

de 1 centímetro quadrado =

\frac{1}{25}

centímetro quadrado )

• Por que a área do quadrado alaranjado mede

\frac{9}{25}

centímetro quadrado? (Resposta esperada: Porque o quadrado alaranjado é composto de 9 quadradinhos de área medindo

\frac{1}{25}

centímetro quadrado cada um.)

• Além disso, os estudantes podem perceber pela figura que a medida do lado do quadrado alaranjado é

\frac{3}{5}

da medida do lado do quadrado maior, ou seja:

\frac{3}{5}

de 1 centímetro =

\frac{3}{5}

centímetro.

Página 27

Situação 2

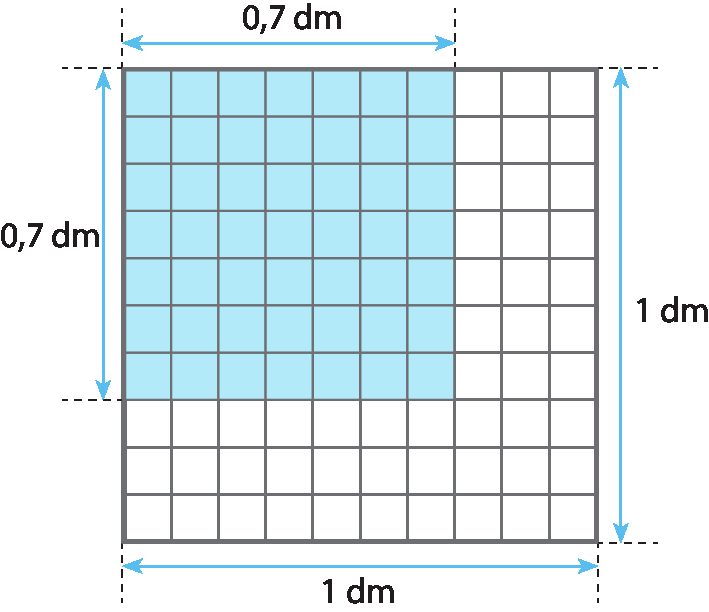
Ilustração. Quadrado composto por 100 quadradinhos. Dentro do quadrado maior, no canto esquerdo superior um quadrado formado por 49 quadradinhos azul. Do lado externo, direito e inferior, do quadrado maior, a indicação do comprimento de 1 decímetro , Do lado externo, esquerdo e superior, do quadrado azul, a indicação do comprimento de 0,7 decímetro

A medida da área do quadrado azul da figura pode ser obtida do seguinte modo:

0,7 ⋅ 0,7 = 0,49, ou seja, 0,49 decímetro quadrado

O número 0,7 é a raiz quadrada de 0,49, que indicamos por

\sqrt{0, 49}

Assim, obtemos:

\sqrt{0, 49}

\sqrt{\frac{49}{100}}

\frac{7}{10}

= 0,7

Observe que, para calcular o valor da raiz quadrada de 0,49, precisamos determinar o número racional que, multiplicado por ele mesmo, resulta em 0,49. Esse número é 0,7.

0,7 ⋅ 0,7 =

{0, 7}^{2}

{(\frac{7}{10})}^{2}

\frac{49}{100}

= 0,49

Assim, obtemos:

\sqrt{0, 49}

= 0,7, visto que 0,72 = 0,49

Dizemos que o número 0,49 é um número racional quadrado perfeito.

Dado um número racional quadrado perfeito, a sua raiz quadrada é um número racional positivo ou nulo cujo quadrado é o número dado.

Observe outros exemplos.

\sqrt{\frac{81}{256}} = \frac{9}{16}

\sqrt{\frac{4}{225}} = \frac{2}{15}

\sqrt{0, 01}

\sqrt{\frac{1}{100}}

\frac{1}{10}

= 0, 1

Observações

▶ Quando queremos considerar o oposto de uma raiz quadrada, fazemos a indicação colocando o sinal de menos à esquerda da raiz. Por exemplo:

‒ \sqrt{\frac{9}{25}}

indica o oposto de

\sqrt{\frac{9}{25}} .

‒ \sqrt{0, 49}

indica o oposto de

\sqrt{0, 49} .

▶ Todo número racional, quando elevado ao quadrado, resulta no número 0 ou em um número racional positivo. Logo, não existe um número racional que seja a raiz quadrada de um número racional negativo.

Por exemplo, a raiz quadrada do número

‒ \frac{100}{9}

não é um número racional, pois não existe número racional que, elevado ao quadrado, resulte em

‒ \frac{100}{9} .

▶ A raiz quadrada de um número racional positivo será um número racional somente se esse número for um quadrado perfeito.

Por exemplo, a raiz quadrada do número

\frac{2}{3}

não é racional, pois não existe número racional que, elevado ao quadrado, resulte em

\frac{2}{3} .

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

37 Calcule:

\sqrt{0, 04}

\sqrt{\frac{36}{49}}

\sqrt{0, 81}

‒ \sqrt{\frac{64}{100}}

\sqrt{\frac{25}{9}}

‒ \sqrt{\frac{49}{4}}

Respostas e comentários

37. a) 0,2

37. b)

\frac{6}{7}

37. c) 0,9

37. d)

‒ \frac{4}{5}

37. e)

\frac{5}{3}

37. f)

‒ \frac{7}{2}

Calculando com raízes

A situação 2 pode ser trabalhada de maneira análoga ao que foi feito com a primeira situação.

Se julgar adequado, proponha aos estudantes que efetuem, utilizando uma calculadora simples, a raiz quadrada de alguns números racionais. Podem verificar, por exemplo, o que aparece no visor da calculadora quando efetuam a raiz quadrada de:

• 0,25 → aparece no visor 0,5; ou seja,

\sqrt{0, 25}

= 0,5;

• 2 → aparece no visor 1,4142135;

•

\frac{3}{5}

(ou 3 : 5 = 0,6) → aparece no visor 0,7745966.

Proponha aos estudantes que usem números negativos para tentar obter a raiz quadrada na calculadora e verifiquem se será indicado “êrro” no visor. Além disso, se julgar oportuno, comente que alguns números racionais não apresentam raízes racionais, como acontece com a raiz quadrada de 2 ou de 5 e que, nesses casos, consideramos aproximações ao utilizar a potência expressa como número decimal.

Exercícios propostos

Acompanhe uma resolução para o exercício 37:

\sqrt{0, 04} = \sqrt{\frac{4}{100}}

\frac{4}{100} = \frac{2}{10} \cdot \frac{2}{10} = {(\frac{2}{10})}^{2}

\sqrt{\frac{4}{100}} = \frac{2}{10} = 0, 2

\frac{36}{49} = \frac{6 \cdot 6}{7 \cdot 7} = \frac{6}{7} \cdot \frac{6}{7} = {(\frac{6}{7})}^{2}

\sqrt{\frac{36}{49}} = \frac{6}{7}

\sqrt{0, 81} = \sqrt{\frac{81}{100}}

\frac{81}{100} = \frac{9}{10} \cdot \frac{9}{10} = {(\frac{9}{10})}^{2}

\sqrt{\frac{81}{100}} = \frac{9}{10} = 0, 9

\frac{64}{100} = \frac{8 \cdot 8}{10 \cdot 10} = \frac{8}{10} \cdot \frac{8}{10} = {(\frac{8}{10})}^{2}

‒ \sqrt{\frac{64}{100}} = ‒ \frac{8}{10} = ‒ \frac{4}{5}

\frac{25}{9} = \frac{5 \cdot 5}{3 \cdot 3} = \frac{5}{3} \cdot \frac{5}{3} = {(\frac{5}{3})}^{2}

\sqrt{\frac{25}{9}} = \frac{5}{3}

\frac{49}{4} = \frac{7 \cdot 7}{2 \cdot 2} = \frac{7}{2} \cdot \frac{7}{2} = {(\frac{7}{2})}^{2}

‒ \sqrt{\frac{49}{4}} = ‒ \frac{7}{2}

Página 28

38 Identifique os números cuja raiz quadrada é um número racional.

a) ‒25

\frac{1}{16}

\frac{3}{4}

‒ \frac{1}{9}

\frac{8}{10}

\frac{25}{9}

39 Sabendo que

\sqrt{123 904} = 352,

calcule mentalmente:

‒ \sqrt{1 239,04}

\sqrt{12,3904}

40 Descubra a medida do lado de cada região quadrada representada a seguir, considerando a medida da área de cada uma delas.

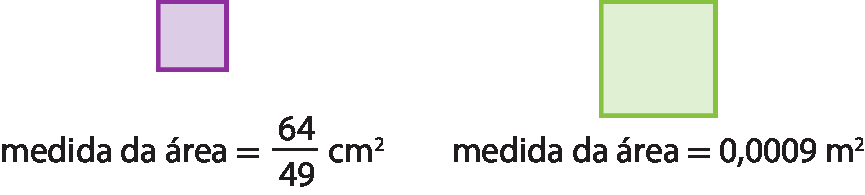
Ilustração. Quadrado. Ilustração. Quadrado maior. medida da área, igual a, 64, 49 avos centímetros quadrados

Pense mais um poucoreticências

FAÇA AS ATIVIDADES NO CADERNO

1 Sendo x 2 = 400, responda às perguntas a seguir.

Ilustração. Área verde com uma região quadrangular medindo x de lado. No centro da região, informação: medida de área = 400 metros quadrados.

a) Quais são os valores de x que tornam essa sentença verdadeira?

b) Qual é o valor que x pode assumir se ele representa, em metro, a medida do comprimento do lado de um terreno quadrado?

2 Sabendo que (4,8)2 = 23,04, responda às perguntas.

a) Quais são os valores de x que tornam verdadeira a igualdade x 2 = 23,04?

b) Das respostas ao item a, qual é o valor que x pode assumir se 23,04 representa a medida da área de um quadrado?

Outras raízes

Observe a imagem do cubo.

Ilustração. Cubo composto por 125 cubos pequenos.

Tomando o cubinho

como unidade de medida de volume, podemos dizer que a medida do volume do cubo maior – cuja medida da aresta é 5 unidades de medida de comprimento – é 125

(53 = 125).

A situação inversa seria calcular a medida da aresta do cubo maior sabendo que a medida do seu volume é 125

e que a medida da aresta de um cubinho é 1 unidade de medida de comprimento.

Assim, a medida da aresta do cubo maior corresponde a um número que, elevado ao cubo, resulta em 125. Esse número é a raiz cúbica de 125.

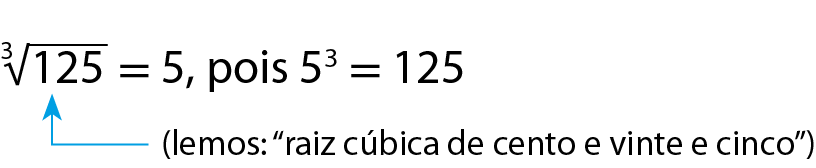
Então, a aresta do cubo maior mede 5 unidades de medida de comprimento.

Respostas e comentários

38. Alternativas b e f.

39. a) ‒35,2

39. b) 3,52

40. Área menor:

\frac{8}{7} cm

40. Área maior: 0,03 métro ou 3 centímetros

Pense mais um poucoreticências:

1. a) ‒20 e 20.

1. b) 20

2. a) ‒4,8 e 4,8.

2. b) 4,8

Exercícios propostos

As resoluções dos exercícios 38 e 39 estão no início deste Manual, nas orientações específicas do capítulo 1.

No exercício 40, verifique se os estudantes associam corretamente o fato de que a medida da área de um quadrado é dada pelo quadrado da medida do lado. Assim, para um quadrado cuja área é

\frac{64}{49}

centímetros quadrados, seu lado será

\frac{8}{7}

centímetros (pois

\sqrt{64}

= 8 e

\sqrt{49}

= 7). Sugira aos estudantes que escrevam 0,0009 em notação científica antes de determinar sua raiz quadrada:

0,0009 = 9 · 10‒4 = 32 · (10‒2)2 = (3 · 10‒2)2

Desse modo, eles podem verificar que 0,0009 pode ser expresso pelo quadrado de (3 · 10‒2). Portanto, a raiz quadrada de 0,0009 é o número que, elevado ao quadrado, resulta em 0,0009, ou seja,

\sqrt{0, 0009}

= 3 · 10‒2 = 0,03. Podem concluir que o lado da região quadrada cuja área mede 0,0009 métro quadrado mede 0,03 métro (ou 3 centímetros).

Pense mais um poucoreticências

Para explorar a atividade 1, incentive os estudantes a observar o significado da igualdade x2 = 400 e, assim, determinar o valor de x, desenvolvendo a habilidade (ê éfe zero oito ême ah zero nove). Espera-se que eles percebam que devem procurar um número que, elevado ao quadrado, resulte em 400 e verifiquem haver dois números nessas condições: 20 e ‒20.

Pergunte a eles se podemos afirmar que x =

\sqrt{400}

. Espera-se que observem que, desse modo, não conseguimos o valor ‒20, que também satisfaz a igualdade dada. Logo, nesse caso, o cálculo da raiz quadrada nos fornece apenas o valor positivo de x. Ressalte que, se x indicasse alguma medida (como o comprimento do lado de um quadrado), no entanto, ele não poderia assumir valores negativos, e assim a raiz quadrada equivaleria ao valor de x.

Página 29

Acompanhe outros exemplos.

raiz quarta de 1, 81 avos , igual um terço, pois 1 terço elevado a 4, igual, 1, 81 avos.
Abaixo, uma seta que parte da frase: (lemos: raiz quarta de um oitenta e um avos) e aponta para raiz quarta de 1,81 avos.

Raiz quinta de menos 32, igual, menos 2, pois abre parênteses menos 2 fecha parênteses elevado a cinco. Abaixo, uma seta que parte da frase (lemos: 'raiz quinta de menos trinta e dois') e aponta para raiz quinta de menos 32.

De modo geral, para determinar

\sqrt[n]{a}

(lemos: “raiz enésima de a”), sendo n um número natural diferente de 0 e a um número racional, verificamos dois casos:

• para n par e a ⩾ 0:

\sqrt[n]{a}

é o número racional b (com b ⩾ 0), tal que b ⁿ = a;

• para n ímpar:

\sqrt[n]{a}

é o número racional b, tal que b ⁿ = a.

Essa operação é chamada radiciação, a operação inversa da potenciação.

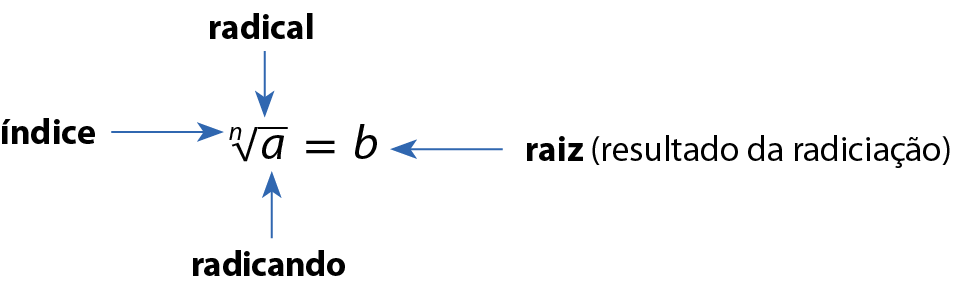
Esquema. raiz enésima de a, igual b Acima a palavra radical indica o simbolo da raiz. À esquerda a palavra índice indica o número pequeno que a esquerda e na parte superior do radical. abaixo a palavra radicando que indica o número dentro do radical. do lado direito a raiz (resultado da radiciação que indica o b

O símbolo

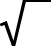
Imagem. Símbolo que lembra a letra V com um traço horizontal na extremidade do canto superior direito.

é chamado de radical. Se esse símbolo não estiver acompanhado de um índice, indica a raiz quadrada de um número a.

Acompanhe alguns exemplos de cada um dos dois casos gerais.

• 1º caso: n é um número natural não nulo par, e a é um número racional não negativo.

Como exemplo, vamos calcular a raiz quadrada de 25.

Há dois números racionais que, elevados ao quadrado, resultam em 25: ‒5 e +5, pois (‒5)2 = 25 e (+5)2 = 25.

Devemos, então, dizer que a raiz quadrada de 25 é 5 ou ‒5? Para garantir um resultado único, convencionou-se que

\sqrt{a}

representa a raiz quadrada positiva de a. Assim,

\sqrt{25} = 5 .

Observe outros exemplos.

\sqrt{36} = 6

\sqrt[4]{\frac{16}{81}} = \frac{2}{3}

\sqrt{1,44} = 1,2

\sqrt[8]{0,00000001}

= 0,1

Note que o número 0,00000001 é a representação decimal de (0,1)8. Assim:

\sqrt[8]{{(0,1)}^{8}} = 0,1

Com o auxílio de uma calculadora, também podemos calcular

\sqrt[8]{0,00000001}

digitando:

Ilustração. Teclas: 0 ponto 00000001, raiz, raiz, raiz. Visor: 0.1.

Observação

▶ Note que, se a é um número racional negativo (a < 0), sendo n par, não é possível definir

\sqrt[n]{a}

como um número racional.

Como exemplo, vamos mostrar que

\sqrt{‒ 4}

não é um número racional. De fato, se

\sqrt{‒ 4}

fosse um número racional m, deveríamos ter m² = ‒4, o que é impossível, pois o quadrado de qualquer número racional é sempre um número não negativo. Logo,

\sqrt{‒ 4}

não é um número racional.

Respostas e comentários

Outras raízes

Na introdução de raízes de outros índices, naturais maiores que 2, iniciada na página anterior, o uso do conceito de volume do cubo para dar significado à raiz cúbica pode ser abordado como foi feito anteriormente com o uso da área do quadrado para o cálculo da raiz quadrada.

Se possível, providencie calculadoras simples para os estudantes efetuarem o cálculo de algumas raízes, conforme mostrado para

\sqrt[8]{0,00000001}

Página 30

• 2º caso: n é um número natural não nulo ímpar, e a é um número racional.

Acompanhe, a seguir, alguns exemplos de raízes de índice ímpar.

\sqrt[3]{64}

= 4, pois 43 = 64

\sqrt[5]{\frac{243}{32}} = \frac{3}{2}

, pois

{(\frac{3}{2})}^{5} = \frac{243}{32}

\sqrt[3]{‒ 64}

= ‒ 4, pois (‒ 4)3 = ‒64

\sqrt[5]{‒ \frac{243}{32}} = ‒ \frac{3}{2}

, pois

{(‒ \frac{3}{2})}^{5} = ‒ \frac{243}{32}

Quando n for ímpar, a raiz enésima terá o mesmo sinal do radicando.

Observação

▶ A raiz enésima de zero é zero, com n natural não nulo. Ou seja:

\sqrt[n]{0} = 0

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

41 Responda às questões a seguir.

a) Dois números, elevados ao quadrado, resultam em 100. Quais são eles?

b) Qual é a raiz quadrada de 100?

42 Por que não existe a raiz quadrada de ‒ 49 quando trabalhamos com números racionais?

43 Calcule, se for um número racional, o valor de:

‒ \sqrt{441}

\sqrt{‒ 441}

44 Classifique cada sentença em verdadeira ou falsa.

\sqrt{10^{2}} = \sqrt{‒ 10^{2}}

\sqrt{10^{2}} = \sqrt{{(‒ 10)}^{2}}

\sqrt{{(‒ 7)}^{2}} = ‒ 7

\sqrt{{(‒ 7)}^{2}} = 7

‒ \sqrt{10^{2}} = \sqrt{{(‒ 10)}^{2}}

‒ \sqrt{{(‒ 10)}^{2}} = ‒ 10

\sqrt[3]{8} = ‒ \sqrt[3]{‒ 8}

\sqrt[n]{0} = 0,

para n ⩾ 2

45 Calcule:

a) 2 ⋅

\sqrt{900}

\frac{3}{4} \cdot \sqrt{2, 56}

\sqrt{0} ‒ \sqrt[5]{‒ 1}

\sqrt[3]{‒ \frac{8}{27}} ‒ \sqrt{\frac{25}{64}}

46 Um objeto solto de determinada altura leva certo tempo para atingir o solo.

Esse tempo é dado pela relação

t = \sqrt{\frac{h}{4, 9}} .

Nessa relação, t representa o tempo, em segundo, e h representa a altura, em metro.

Calcule quanto tempo um objeto leva para atingir o solo caindo de uma altura que mede 44,1 métros.

Ilustração. à esquerda, morro. Pedra cai de altura de 44,1 metros.

47 Calcule o valor da expressão a seguir.

\sqrt[3]{18 + \sqrt{84 ‒ \sqrt{4 + \sqrt{25}}}}

48 A professora pediu aos estudantes que calculassem o valor da expressão a seguir.

\sqrt[3]{1^{3} + \sqrt[3]{1^{3} ‒ \sqrt[3]{1^{3} + \sqrt{7^{2}}}}}

Daniel fez deste modo:

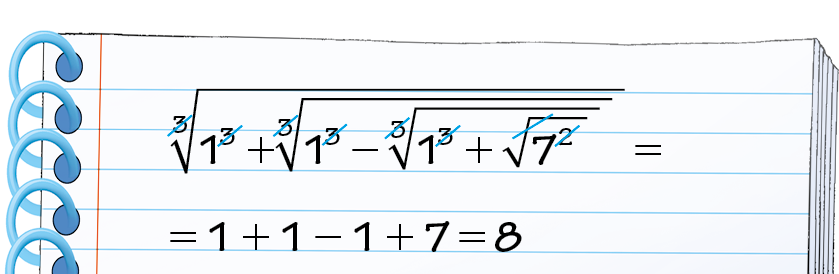
Ilustração. Caderno com a expressão. Na primeira linha: raiz cúbica de radicando; 1 ao cubo, mais raiz cúbica de radicando: 1 ao cubo, menos raiz cubica de radicando 1 ao cubo mais raiz quadrada de 7 ao quadrado, igual.. Todos os índices das raízes e os expoentes estão cortados, com um traço azul, indicando que foram cancelados . Na segunda linha: igual, 1 mais 1 mais 1 menos 1 mais 7, igual 8

Fernanda fez desta maneira:

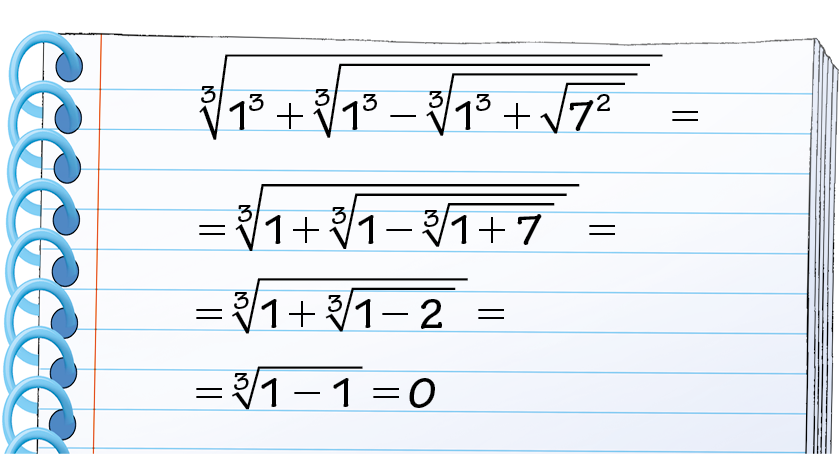
lustração. Caderno com expressão. Na primeira linha: raiz cúbica de radicando; 1 ao cubo, mais raiz cúbica de radicando: 1 ao cubo, menos raiz cubica de radicando 1 ao cubo mais raiz quadrada de 7 ao quadrado, igual. Na segunda linha: raiz cúbica de radicando; 1, mais raiz cúbica de radicando: 1 mais 7 Na terceira linha: raiz cúbica de radicando; 1, mais raiz cúbica de radicando: 1 menos 2 Na quarta linha: raiz cúbica de radicando; 1 menos 1, igual a zero

Algum deles acertou? Em caso afirmativo, quem?

Respostas e comentários

41. a) ‒10 e 10

41. b) 10

42. Porque nenhum número racional elevado ao quadrado resulta em ‒49.

43. a) ‒21

43. b) Não é um número racional.

44. a) Falsa.

44. b) Verdadeira.

44. c) Falsa.

44. d) Verdadeira.

44. e) Falsa.

44. f) Verdadeira.

44. g) Verdadeira.

44. h) Verdadeira.

45. a) 60

45. b) 1,2

45. c) 1

45. d)

‒ \frac{31}{24}

46. 3 segundos.

47. 3

48. Sim; Fernanda.

Exercícios propostos

As resoluções dos exercícios 41 a 48 estão no início deste Manual, nas orientações específicas do capítulo 1.

Verifique como os estudantes procedem na resolução do exercício 46 e compartilhe as diferentes estratégias que surgirem. Espera-se que eles retomem conhecimentos construídos em anos anteriores, que serão sistematizados e ampliados ainda neste volume.

Um procedimento esperado é observarem que, considerando o valor de h = 44,1, devem efetuar a divisão de 44,1 por 4,9 (obtendo 9) e, em seguida, calcular a raiz quadrada do valor obtido, ou seja,

\sqrt{9}

, que fornecerá o valor de t procurado.

O exercício 48 possibilita discutir os critérios de ordem das operações a serem efetuadas em uma expressão numérica, assim como chama a atenção para o uso indevido do cálculo que será formalizado no estudo das propriedade dos radicais, assunto que será tratado no 9º ano.

Página 31

3. Potências com expoente fracionário

Até aqui, estudamos potências com expoente inteiro. Agora, vamos estudar as potências com expoente fracionário, relacionando potenciação com radiciação.

Já vimos que, se bⁿ = a, então

b = \sqrt[n]{a}

, com n natural não nulo e b ⩾ 0.

Como exemplo, vamos considerar a potência (73)2 = 76.

De acôrdo com a definição de raiz quadrada, verificamos que 73 é a raiz quadrada de 76, pois (73)2 = 76.

Assim, podemos escrever:

Raiz quadrada de sete elevado a seis, igual, sete ao cubo ou raiz quadrado de sete elevado a 6 , igual a 7 elevado seis meios . Da frase numerador: expoente do radicando parte uma seta que aponta para o 6, numerador da fração do expoente Da frase: denominador: índice do radical parte uma seta que aponta para o 2, denominador da fração do expoentes

Toda expressão com radical de radicando positivo pode ser escrita como uma potência em que a base é o radicando e o expoente é expresso por uma fração que tem, no numerador, o expoente do radicando e, no denominador, o índice do radical.

Acompanhe, por exemplo, as expressões a seguir.

\sqrt[8]{5^{3}} = 5^{\frac{3}{8}}

Observe que:

{(5^{\frac{3}{8}})}^{8} = 5^{\frac{3}{8} \cdot 8} = 5^{3}

\sqrt[7]{3^{2}} = 3^{\frac{2}{7}}

Observe que:

{(3^{\frac{2}{7}})}^{7} = 3^{\frac{2}{7} \cdot 7} = 3^{2}

\sqrt[3]{{(\frac{1}{8})}^{2}} = {(\frac{1}{8})}^{\frac{2}{3}}

Observe que:

{[{(\frac{1}{8})}^{\frac{2}{3}}]}^{3}

{(\frac{1}{8})}^{\frac{2}{3} \cdot 3}

{(\frac{1}{8})}^{2}

Se a é um número racional positivo, m é um número inteiro e n é um número natural não nulo, temos:

a^{\frac{m}{n}} = \sqrt[n]{a^{m}}

Verifique outros exemplos.

\sqrt[3]{5^{2}} = 5^{\frac{2}{3}}

\sqrt[3]{2^{15}}

2^{\frac{15}{3}}

= 2 ⁵

\sqrt{10} = 10^{\frac{1}{2}}

7^{\frac{4}{3}} = \sqrt[3]{7^{4}}

9^{‒ \frac{1}{2}}

{(\frac{1}{9})}^{\frac{1}{2}}

\sqrt{\frac{1}{9}}

\frac{1}{3}

0, 25^{\frac{1}{2}}

\sqrt{0, 25}

= 0,5

Observação

▶ As propriedades válidas para as potências de expoente inteiro também são válidas para as potências de expoente fracionário que tenham base positiva.

Por exemplo:

três elevado a um quinto, vezes, três elevado a dois terços, igual, 3 elevado ao expoente um quinto mais 2 terços, fim do expoente, igual, 3 elevado a 13, 15 avos. Da frase: para determinar o produto de potências de mesma base, conservamos a base e adicionamos os expoentes., parte um seta que aponta para o expoente 13,15 avos

Respostas e comentários

3. Potências com expoente fracionário

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero dois.

Se julgar necessário, retome a propriedade “potência de potência” da potenciação e comente com os estudantes que, ao estender o cálculo de potências para expoentes racionais, é pressuposto que todas as propriedades continuem válidas.

Identifique na lousa os elementos do exemplo dado para que eles percebam o que ocorre.

• Pela propriedade de potência de potência, obtemos: (73)2 = 76

Assim podemos escrever que, se (73)2 = 76, então 73 =

\sqrt{7^{6}}

7^{\frac{6}{2}}

, pois

7^{\frac{6}{2}}

= 73.

Forneça outros exemplos, como:

• Verificamos que: (54)3 = 512

Como (54)3 = 512, então 54 =

\sqrt[3]{5^{12}}

5^{\frac{12}{3}}

, pois:

5^{\frac{12}{3}}

= 54

Página 32

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

49 Represente na fórma de potência com expoente fracionário.

\sqrt[3]{2^{2}}

\sqrt[4]{5^{3}}

\sqrt[3]{10}

50 Escreva a expressão com radical que corresponda a cada potência a seguir.

2^{\frac{3}{4}}

9^{\frac{1}{3}}

8^{\frac{1}{2}}

51 Calcule:

\sqrt{3^{6}}

512^{\frac{1}{3}}

\sqrt[4]{2^{8}}

52 Reduza a uma só potência, usando as propriedades das potências.

2^{\frac{1}{3}} \cdot 2^{\frac{1}{4}}

2^{\frac{1}{3}} : 2^{\frac{1}{4}}

{(12^{\frac{1}{2}})}^{\frac{4}{3}}

3^{{(\frac{1}{16})}^{\frac{1}{2}}}

PARA SABER MAIS

A linguagem das máquinas

Ilustração. Vista de lado de menino de cabelo vermelho, camiseta azul sentado na frente de um computador sobre a mesa.

Os softwares são programados com uma sintaxe, isto é, os comandos são digitados seguindo um conjunto de regras que definem a estrutura e as expressões corretas para determinada linguagem de programação. Isso faz com que a máquina entenda corretamente a operação que deve efetuar ao receber cada comando.

Para calcular 23 em seu computador, Paulo precisava digitar a sequência dois acento circunflexo três.

Quando Paulo digitava dois acento circunflexo três e, em seguida, pedia o resultado, a resposta que aparecia era 8.

Para calcular potências de potências, era necessário acrescentar parênteses.

Ou seja, se ele digitasse dois acento circunflexo abre parênteses três acento circunflexo dois fecha parênteses, a máquina calculava 23² = 29 = 512, mas, se digitasse dois acento circunflexo três acento circunflexo dois, o computador calculava (23)2 = 82 = 64.

Para garantir resultados corretos em seus cálculos, utilizando ferramentas computacionais e até uma simples calculadora, é fundamental prestar atenção às regras e propriedades das operações e escrever as expressões corretamente. Isso também é importante quando você faz cálculos no papel: o uso adequado dos parênteses nas expressões, por exemplo, precisa ser respeitado.

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

1 Paulo digitou as informações de cada item no software de computador. Descubra e efetue as expressões que ele queria calcular. Escreva os resultados na fórma de potência.

a) dois acento circunflexo três acento circunflexo três

b) dois acento circunflexo abre parênteses três acento circunflexo abre parênteses dois acento circunflexo três fecha parênteses fecha parênteses

c) abre parênteses dois acento circunflexo fecha parênteses acento circunflexo quatro

d) abre parênteses abre parênteses três acento circunflexo dois fecha parênteses acento circunflexo três fecha parênteses acento circunflexo dois

2 A importância dos parênteses não é uma novidade. De fato, você já deve ter observado, por exemplo, que:

(a + b)2 ≠ a + b2

Escreva como você digitaria as expressões a seguir, considerando que, no caso da divisão, o comando para a máquina é “/”.

a) (a + b)2

b) a + b 2

\frac{1}{a + b}

\frac{1}{a}

+ b

\frac{a + b}{c + d}

\frac{a}{c + d}

+ b

Respostas e comentários

49. a)

2^{\frac{2}{3}}

49. b)

5^{\frac{3}{4}}

49. c)

10^{\frac{1}{3}}

50. a)

\sqrt[4]{2^{3}}

50. b)

\sqrt[3]{9}

50. c)

\sqrt{8}

51. a) 27

51. b) 8

51. c) 4

52. a)

2^{\frac{7}{12}}

52. b)

2^{\frac{1}{12}}

52. c)

12^{\frac{2}{3}}

52. d)

3^{\frac{1}{4}}

Para saber mais:

1. a) (2³)3 = 29

1. b) 23²³ = 23⁸ = 2.6561

1. c) (23)4 = 212

1. d) ((32)3)2 = 312

2. a) (amaisbê)^2

2. b) amaisbê^2

2. c) 1/(a + b)

2. d) 1/a + b

2. e) (a + b)/(c + d)

2. f) a/(c + d) + b

Exercícios propostos

As resoluções dos exercícios 49 ao 51 estão no início deste Manual, nas orientações específicas do capítulo 1.

No exercício 52, é interessante que os estudantes comparem com outros colegas não apenas a solução encontrada em cada item, mas também as resoluções, pois aqui o uso de propriedades poderá facilitar os cálculos.

Uma possível resolução para esse exercício é a seguinte:

2^{\frac{1}{3}} \cdot 2^{\frac{1}{4}} = 2^{\frac{1}{3} + \frac{1}{4}} = 2^{\frac{4 + 3}{12}} = 2^{\frac{7}{12}}

2^{\frac{1}{3}} : 2^{\frac{1}{4}} = 2^{\frac{1}{3} ‒ \frac{1}{4}} = 2^{\frac{4 ‒ 3}{12}} = 2^{\frac{1}{12}}

{(12^{\frac{1}{2}})}^{\frac{4}{3}} = 12^{\frac{1}{2} \cdot \frac{4}{3}} = 12^{\frac{1 \cdot 4}{2 \cdot 3}} =

= 12^{\frac{4}{6}} = 12^{\frac{2}{3}}

3^{{(\frac{1}{16})}^{\frac{1}{2}}} = 3^{\sqrt{\frac{1}{16}}} = 3^{\sqrt{{(\frac{1}{4})}^{2}}} = 3^{\frac{1}{4}}

Para saber mais

Se houver disponibilidade na escola, leve os estudantes à sala de informática para experimentarem diferentes usos de comandos em planilhas eletrônicas. O mesmo pode ser feito com o uso de calculadoras científicas.

Este trabalho possibilita desenvolver o Tema Contemporâneo Transversal ciência e tecnologia.

As resoluções das atividades 1 a 3 estão no início deste Manual, nas orientações específicas do capítulo 1.

Página 33

3 Dependendo da máquina ou do software utilizado, o comando para calcular a raiz quadrada de um número pode ser a tecla

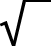
, a tecla

\sqrt[2]{x}

ou a sequência ésse quê érre tê (sigla do termo em inglês square root, que significa “raiz quadrada”). Para obter a raiz cúbica, não existindo a tecla apropriada, você pode digitar o seguinte: a^(1/3), que equivale a

\sqrt[3]{a}

Do mesmo modo, para obter a raiz quadrada, você também pode digitar: a^(1/2), que equivale a

\sqrt{a}

. Dependendo da máquina, não é necessário colocar os parênteses na fração

\frac{1}{2}

. Na dúvida, entretanto, é melhor colocá-los.

Como você digitaria as expressões a seguir? Lembre-se de que o comando de divisão da máquina é “/” e tome o devido cuidado com os parênteses.

\sqrt{a + b}

a + \sqrt{b}

\frac{1}{\sqrt{a + b}}

\frac{1}{\sqrt{a}} + b

4. Expressões numéricas com números racionais

Já vimos que muitas vezes precisamos calcular o valor de expressões numéricas para resolver problemas. Aprendemos também que:

• Quando a expressão tem sinais de associação, eles devem ser eliminados na seguinte ordem: primeiro calculam-se as expressões que estão entre parênteses, depois as expressões entre colchetes, e, finalmente, as expressões entre chaves.

• As operações devem ser efetuadas nesta ordem:

a) potenciação e radiciação, na ordem em que aparecem;

b) multiplicação e divisão, na ordem em que aparecem;

c) adição e subtração, na ordem em que aparecem.

Vamos calcular o valor de algumas expressões numéricas com números racionais.

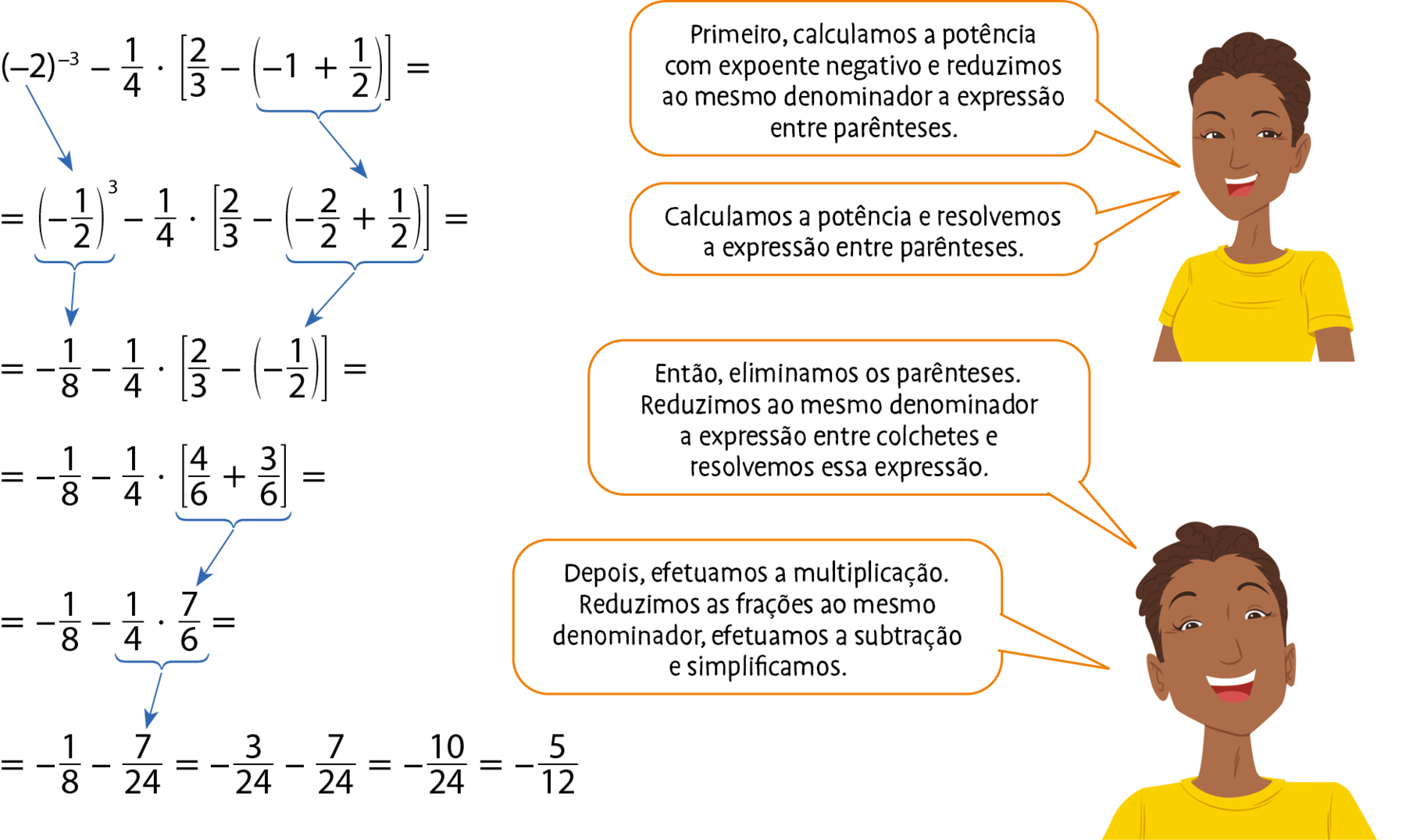
Primeira linha: menos 2 elevado a menos 3, menos um quarto, vezes, abre colchetes dois terços, menos, abre parênteses menos 1 mais um meio, fecha parênteses, fecha colchetes , igual Do cubo do menos 2, da primeira linha , parte uma seta para menos um meio da segunda linha . Do traço abaixo do menos 1 mais um meio, da primeira linha parte uma seta apontando para menos dois meios mais um meio, da segunda linha. Segunda linha: igual, cubo de menos um meio, menos um quarto, vezes abre colchetes dois terços menos abre parênteses menos dois meios mais um meio, fecha parênteses, fecha colchetes , igual Do cubo de menos um meio, da segunda linha, parte um seta para menos um oitavo da terceira linha. Do traço abaixo de menos 2 meios mais um meio, da segunda linha , parte uma seta apontando para menos um meio da da terceira linha. Terceira linha: igual, menos um oitavo, menos um quarto , vezes, abre colchetes 4 sextos mais 3 sextos, fecha colchetes, igual Quarta linha: igual, menos um oitavo, menos um quarto, vezes abre colchetes quatro sextos mais três sextos, fecha parênteses, igual Do traço abaixo de 4 sextos mais 3 sextos , da quarta linha, parte uma seta apontando para sete sexto da quinta linha. Quinta linha: igual, menos um oitavo, menos um quarto vezes sete sextos. Do traço abaixo de menos um quarto vezes sete sextos , da quinta linha, parte uma seta que aponta para sete ,24 avos da sexta linha. Sexta linha: igual, menos um oitavo, menos 7, 24 avos igual menos 3 , 24 avos, igual menos 10, 24 avos, igual menos 5 ,12 avos.Ilustração. Mulher de cabelo curto e camiseta amarela. Ela fala: Primeiro, calculamos a potência com expoente negativo e reduzimos ao mesmo denominador a expressão entre parênteses. Depois fala: Calculamos a potência e resolvemos a expressão entre parênteses. Ilustração. Mulher de cabelo curto e camiseta amarela. Ela diz: Então, eliminamos os parênteses. Reduzimos ao mesmo denominador a expressão entre colchetes e resolvemos essa expressão. Depois, efetuamos a multiplicação. Reduzimos as frações ao mesmo denominador, efetuamos a subtração e simplificamos.

Respostas e comentários

3. a) (a + b)^(1/2)

3. b) a + b^(1/2)

3. c) 1/(a + b)^(1/2)

3. d) 1/a^(1/2) + bê

4. Expressões numéricas com números racionais

Se julgar necessário, escreva na lousa alguns exemplos de expressões numéricas envolvendo apenas operações com números inteiros. Em seguida, trabalhe com os estudantes os exemplos apresentados de expressões numéricas envolvendo números racionais. Nas resoluções dessas expressões, retome as operações com números racionais na fórma de fração.

Amplie os exemplos com outras expressões numéricas envolvendo números racionais expressos na fórma decimal.

Página 34

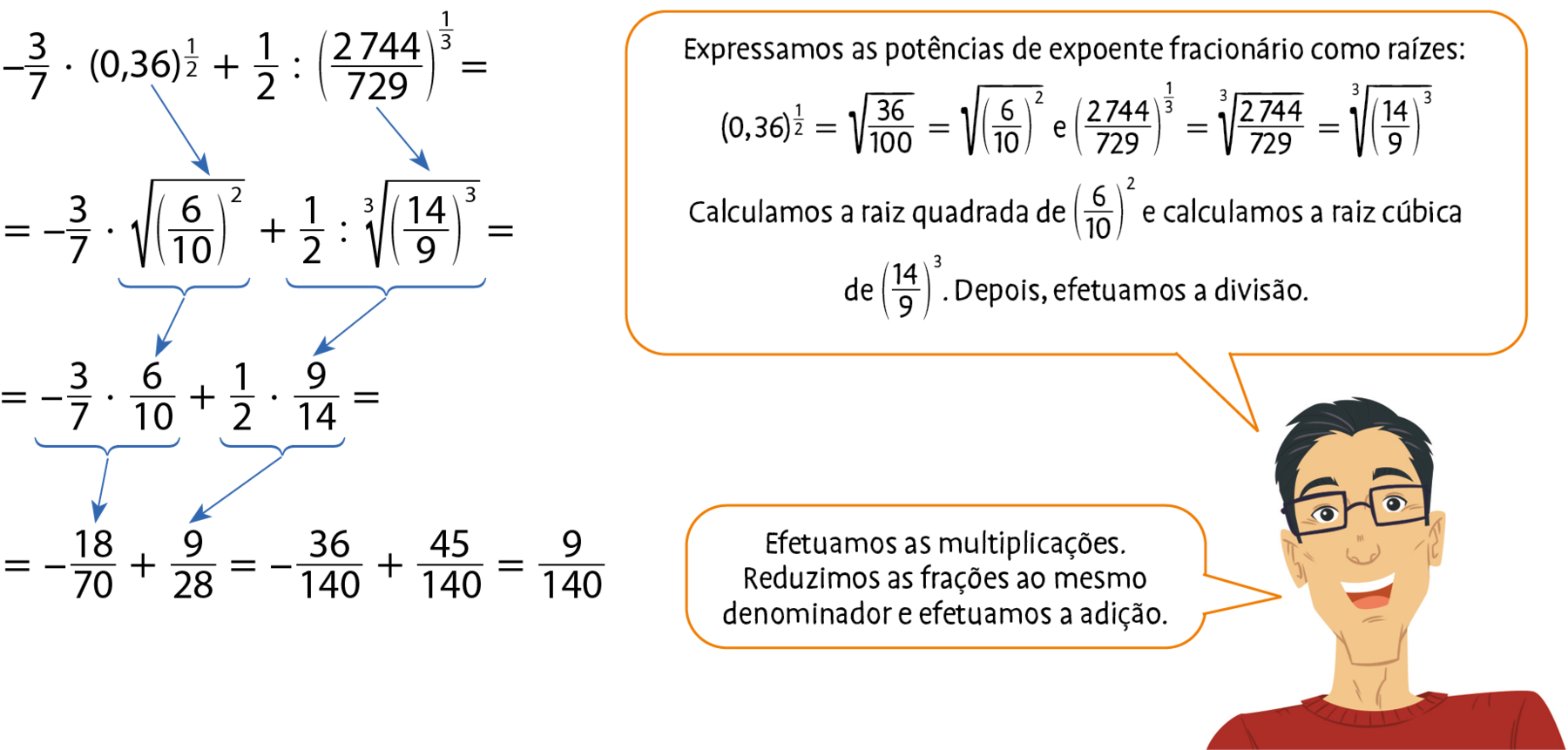
Ilustração. Homem de cabelo preto, óculos e camisa vermelha, fala: Expressamos as potências de expoente fracionário como raízes: abre parênteses 0,36 fecha parênteses elevado a um meio igual raiz quadrada da fração 36 centésimos igual raiz quadrada de abre parênteses fração 6 décimos, fecha parênteses elevado a 2 e abre parênteses 2.744 , 729 avos fecha parênteses elevado a um terço igual raiz cúbica de abre parênteses 2.744, 729 avos, igual, raiz quadrada de abre parênteses 14 nonos, fecha parênteses elevado a 3. Calculamos a raiz quadrada de abre parênteses fração 6 décimos fecha parênteses elevado a 2 e calculamos a raiz cúbica de abre parênteses 14 nonos, fecha parênteses elevado a 3. Depois, efetuamos a divisão. Efetuamos as multiplicações. Reduzimos as frações ao mesmo denominador e efetuamos a adição.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

53 Considere as expressões.

A = [\frac{1}{2} ‒ {(1 + \frac{1}{2})}^{2}] \cdot (2 ‒ \frac{2}{3})

B = \frac{5}{7} : [2 ‒ (\frac{2}{3} + 3)]

Determine o produto A ⋅ B. O que se pode concluir sobre os valores de a e de B?

Note que as seguintes igualdades são verdadeiras e têm uma regularidade.

\frac{1}{1} \cdot \frac{1}{2} = \frac{1}{2}

\frac{1}{1} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{3} = \frac{2}{3}

\frac{1}{1} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{3} + \frac{1}{3} \cdot \frac{1}{4} = \frac{3}{4}

Observando a sequência dessas igualdades, determine mentalmente o valor da expressão a seguir. Verifique, em seguida, se seu resultado está correto, efetuando os cálculos no caderno.

\frac{1}{1} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{3} + \frac{1}{3} \cdot \frac{1}{4} + \frac{1}{4} \cdot \frac{1}{5}

55 Escreva, na fórma decimal, o número que representa o valor da expressão:

{(‒ 1 + \frac{1}{5})}^{2} : {(0, 4 ‒ \frac{1}{5})}^{2} ‒ 0, 7 \cdot \sqrt{\frac{36}{49}}

56 (UPF-Rio Grande do Sul) O valor da expressão

[{(‒ \frac{1}{2})}^{4} : {(‒ \frac{1}{2})}^{3}] \cdot {(‒ \frac{1}{2})}^{6} + 2^{‒ 7}

é:

a) ‒2.

b) ‒1.

c) 0.

\frac{1}{2}

57 (unifór-Ceará) Qual é o valor de x?

x = \frac{1}{2} ‒ 0, 8 + \frac{3}{4} ‒ \sqrt{\frac{1}{4}}

\frac{19}{20}

‒ \frac{1}{20}

‒ \frac{1}{10}

‒ \frac{19}{10}

Hora de criar – Em dupla, cada um cria uma expressão numérica que contenha adição, subtração, multiplicação, divisão, potenciação e raiz quadrada. Troquem de caderno e, depois de cada um calcular o valor da expressão elaborada pelo outro, destroquem para corrigi-las.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e respondam às questões a seguir.

a) A raiz cúbica de um número a é 4. Qual é a raiz sexta de a?

b) A raiz sexta de um número a é 3. Qual é a raiz quadrada de a?

Respostas e comentários

53. O produto é 1. Os valores de a e B são números inversos.

54.

\frac{4}{5}

55. 15,4

56. Alternativa c.

57. Alternativa b.

58. Resposta pessoal.

Pense mais um poucoreticências:

a) 2

b) 27

Exercícios propostos

As resoluções dos exercícios 53 ao 56 estão no início deste Manual, nas orientações específicas do capítulo 1.

Amplie o exercício 54 propondo aos estudantes que escrevam no caderno a quinta igualdade da sequência. Espera-se que eles apresentem a seguinte resposta:

\frac{1}{1} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{3} + \frac{1}{3} \cdot \frac{1}{4} +

+ \frac{1}{4} \cdot \frac{1}{5} + \frac{1}{5} \cdot \frac{1}{6} = \frac{5}{6}

Uma possível resolução para o exercício 57 é a seguinte:

x = \frac{1}{2} ‒ 0, 8 + \frac{3}{4} ‒ \sqrt{\frac{1}{4}} =

= \frac{1}{2} ‒ \frac{8}{10} + \frac{3}{4} ‒ \sqrt{{(\frac{1}{2})}^{2}} =

= \frac{1}{2} ‒ \frac{8}{10} + \frac{3}{4} ‒ \frac{1}{2} =

= ‒ \frac{8}{10} + \frac{3}{4} = ‒ \frac{16}{20} + \frac{15}{20} = ‒ \frac{1}{20}

Alternativa b.

Pense mais um poucoreticências

Esta é mais uma oportunidade para os estudantes exercitarem suas estratégias pessoais de cálculo envolvendo radiciação. Os diferentes procedimentos que surgirem na resolução devem ser apresentados à turma. Como estratégia adquirida ao longo do Ensino Fundamental, eles podem perceber que, se

\sqrt[3]{a}

= 4, então 43 = a, ou seja, a = 64. Assim,

\sqrt[6]{a}

\sqrt[6]{64}

= 2.

Da mesma maneira, se

\sqrt[6]{a}

= 3, então 36 = a, ou seja, a = 729 e, assim,

\sqrt{a}

\sqrt{729}

= 27.

Página 35

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Sendo x = (22)3, y = (23)2 e z = 23², calcule:

a) x ⋅ y ⋅ z na fórma de uma potência.

b) x : y

c) x : z

2 Em determinadas condições, uma célula divide-se em duas a cada 30 segundos. Partindo-se de uma única célula, quantas células existirão no vigésimo minuto? Escreva a resposta na fórma de potência.

3 (Vunéspi) O valor da expressão

4 \cdot {(\frac{1}{2})}^{4} + {(\frac{1}{4})}^{\frac{1}{2}}

é:

\frac{3}{4} .

\frac{4}{3} .

\frac{1}{3} .

\frac{1}{4} .

e) 5.

4 (ú éfe ésse ême-Rio Grande do Sul) O valor da expressão

\frac{16^{\frac{3}{4}}}{8^{\frac{1}{3}}} : \frac{2^{4}}{8^{2}}

é igual a:

a) 2elevado a menos 1.

b) 20.

2^{\frac{1}{2}}

d) 24.

e) 26.

5 Sendo a = 50 menos 2elevado a menos 2, b =

{(1 ‒ \frac{1}{2})}^{‒ 1}

e c = 120 menos 3, calcule:

a) a^b

b) (b menos a)c

{(\frac{a b}{c})}^{c}

6 Escreva cada potência a seguir na fórma de fração.

a) (2,5)elevado a menos 2

b) (0,15)elevado a menos 3

c) (0,1)elevado a menos 4

d) (menos0,01)elevado a menos 2

7 Escreva as frações a seguir na fórma de potência com expoente inteiro negativo.

\frac{1}{10^{2}}

\frac{1}{16}

(‒ \frac{1}{25})

\frac{1}{125}

\frac{1}{15}

(‒ \frac{1}{100})

8 Escreva as informações a seguir em notação científica.

a) No dia 31 de julho de 2018, Marte esteve a 57,8 milhões de quilômetros da Terra.

b) As últimas projeções das Nações Unidas indicam que a população mundial deve chegar a 8,5 bilhões em 2030 e a 9,7 bilhões em 2050.

9 Reduza a uma só potência.

{[{(‒ \frac{1}{2})}^{2}]}^{‒ 3} : [(‒ \frac{1}{2}) \cdot {(‒ \frac{1}{2})}^{5} \cdot {(‒ \frac{1}{2})}^{‒ 3}]

10 O valor da expressão (3elevado a menos 1 ⋅ 3) menos (5elevado a menos 1 dividido por 5) é um número racional:

a) maior que menos1 e menor que 0.

b) maior que 0 e menor que 1.

c) menor que 0.

d) maior que 1.

11 Sabendo que

x = {(\frac{1}{3})}^{5} \cdot {(\frac{1}{3})}^{‒ 3} \cdot {(\frac{1}{3})}^{8} : {(\frac{1}{3})}^{9}

calcule o valor de x 3.

12 Resolva as expressões e apresente os resultados em notação científica.

\frac{3, 6 \cdot 10^{4}}{10^{‒ 2} \cdot 1, 2}

\frac{2, 1 \cdot 10^{‒ 2}}{10^{‒ 3} \cdot 0, 7}

13 A massa de um átomo de carbono é de aproximadamente 1,99 ⋅ 10 elevado a menos 26 quilograma. Expresse esse valor em grama e usando notação científica.

Ilustração. Duas linhas com três símbolos cada. Primeira linha: BORO, B. CARBONO, C. NITROGÊNIO, N. Segunda linha: ALUMÍNIO, Al. SILÍCIO, Si. FÓSFORO, P. Acima das colunas, 3A, 4A, 5A.

14 Calcule o valor da expressão a seguir.

\sqrt{\frac{81}{4}} ‒ \sqrt{400} + \sqrt{2, 25}

15 (Vunéspi) Se x = 10elevado a menos 3, então

\frac{(0, 1) \cdot (0, 001) \cdot 10^{‒ 1}}{10 \cdot (0, 0001)}

é igual a:

a) 100x.

b) 10x.

c) x.

\frac{x}{10} .

\frac{x}{100} .

16 (éfe cê cê) A expressão

\frac{0, 000036}{80000}

é equivalente a:

a) 0,45 ⋅ 10 elevado a menos 12.

b) 4,5 ⋅ 10 elevado a menos 12.

c) 4,5 ⋅ 10 elevado a menos 11.

d) 45 ⋅ 10 elevado a menos 11.

e) 45 ⋅ 10 elevado a menos 10.

17 A letra a representa o número racional 0,04. Determine os valores de

\sqrt{a},

5 \sqrt{a}

2 a \sqrt{a}

Respostas e comentários

1. a) 221

1. b) 1 ou 20

1. c)

\frac{1}{8}

\frac{1}{2^{3}}

2. 240 células.

3. Alternativa a.

4. Alternativa d.

5. a)

\frac{9}{16}

5. b)

\frac{16}{25}

5. c)

\frac{16}{9}

6. a)

\frac{4}{25}

6. b)

\frac{8000}{27}

6. c) .10000

6. d) .10000

7. a) 10elevado a menos 2

7. b) 2elevado a menos 4

7. c) menos5elevado a menos 2

7. d) 5elevado a menos 3

7. e) 15elevado a menos 1

7. f) menos10elevado a menos 2

8. a) 5,78 ⋅ 107 quilômetros.

b) 8,5 ⋅ 109 em 2030 e 9,7 ⋅ 109 em 2050.

{(‒ \frac{1}{2})}^{‒ 9}

10. Alternativa b.

11.

\frac{1}{27}

12. a) 3,0 ⋅ 106

12. b) 3,0 ⋅ 101

13. 1,99 ⋅ 10elevado a menos 23 grama

14. menos14

15. Alternativa b.

16. Alternativa d.

17. 0,2; 1 e 0,016

Exercícios complementares

Nesta seção são oferecidas novas oportunidades para os estudantes retomarem e aplicarem os principais conceitos trabalhados no capítulo.

As resoluções dos exercícios 1, 2, 5 a 11 e 13 a 17 estão no início deste Manual, nas orientações específicas do capítulo 1.

Pode-se resolver o exercício 3 da seguinte maneira:

4 \cdot {(\frac{1}{2})}^{4} + {(\frac{1}{4})}^{\frac{1}{2}} =

= 2^{2} \cdot {(2^{‒ 1})}^{4} + \sqrt{\frac{1}{4}} =

= 2^{2} \cdot 2^{‒ 4} + \sqrt{{(\frac{1}{2})}^{2}} = 2^{2 ‒ 4} + \frac{1}{2} =

= 2^{‒ 2} + \frac{1}{2} = \frac{1}{2^{2}} + \frac{1}{2} =

= \frac{1}{4} + \frac{1}{2} = \frac{1}{4} + \frac{2}{4} = \frac{3}{4}

Portanto, a alternativa a é a correta.

No exercício 4 é importante os estudantes perceberem que é necessário reduzir todos os números à potências de mesma base 2 para efetuar os cálculos:

\frac{16^{\frac{3}{4}}}{8^{\frac{1}{3}}} : \frac{2^{4}}{8^{2}} = \frac{{(2^{4})}^{\frac{3}{4}}}{{(2^{3})}^{\frac{1}{3}}} : \frac{2^{4}}{{(2^{3})}^{2}} = \frac{2^{4 \cdot \frac{3}{4}}}{2^{3 \cdot \frac{1}{3}}} : \frac{2^{4}}{2^{3 \cdot 2}} = \frac{2^{3}}{2^{1}} : \frac{2^{4}}{2^{6}} =

= 2elevado a 3 menos 1 dividido por 2 elevado a 4 menos 6 = 2elevado a 2 dividido por 2elevado a menos 2 = 2elevado a 2 · 2elevado a menos, abre parênteses, menos 2, fecha parênteses =

= 22 · 22 = 2(2 + 2) = 24

Assim, a alternativa d é a correta.

Apresentamos a seguir uma possível resolução para o exercício 12.

\frac{3, 6 \cdot 10^{4}}{10^{‒ 2} \cdot 1, 2} = \frac{3, 6}{1, 2} \cdot \frac{10^{4}}{10^{‒ 2}}

= =

\frac{36}{12}

· 104 · 102 = 3 · 106

\frac{2, 1 \cdot 10^{‒ 2}}{10^{‒ 3} \cdot 0, 7} = \frac{2, 1}{0, 7} \cdot \frac{10^{‒ 2}}{10^{‒ 3}}

= =

\frac{21}{7}

· 10elevado a menos 2 · 103 = 3 · 101

Esse exercício pode ser enriquecido solicitando aos estudantes que formulem expressões numéricas envolvendo os conteúdos deste capítulo e troquem entre si para cada um resolver o que o colega criou. Ao final, faça uma correção coletiva das expressões numéricas elaboradas pelos estudantes.

Página 36

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Apesar de não ser a opção mais segura, é possível criar a senha de desbloqueio de celular de 4 dígitos com um ou mais algarismos repetidos. Nesse caso, quantas são as possibilidades de senhas?

a) 49

b) 94

c) 410

d) 104

2 Indique a alternativa que contém o valor da expressão a seguir.

\frac{2^{5} \cdot 3^{5} \cdot 4 \cdot 7^{2}}{8 \cdot 27 \cdot 49}

a) 22 ⋅ 3

b) 24 ⋅ 32

c) 27 ⋅ 35 ⋅ 72

d) 23 ⋅ 33 ⋅ 72

3 Se x = (0,5)3 e y =

{(\frac{1}{4})}^{‒ 2}

, quanto vale z = (x ⋅ y)2?

a) 1

b) 2

c) 4

d) 64

4 Escreva o número .3125 como uma potência de base

\frac{1}{5}

{(\frac{1}{5})}^{‒ 5}

{(\frac{1}{5})}^{5}

{(\frac{1}{5})}^{‒ 4}

{(\frac{1}{5})}^{4}

5 Uma folha de papel sulfite tem espessura medindo 0,0001 métro. Escreva essa medida em notação científica.

a) 1 ⋅ 10 ‒3 métro

b) 10 ⋅ 10 ‒3 métro

c) 1 ⋅ 10 ‒ 4 métro

d) 10 ⋅ 10 ‒ 4 métro

6 Maria é marceneira e, para fazer um móvel, ela cortou um pedaço de madeira em formato quadrado com área medindo

\frac{121}{144}

métros quadrados. Qual é a medida do comprimento dos lados desse pedaço de madeira?

\frac{11}{12}

métro

\frac{12}{11}

métros

c) 1 métro

d) 11 métros

7 Calcule o valor da expressão a seguir e indique a alternativa que apresenta o resultado correto.

\sqrt[5]{245 ‒ \sqrt[3]{6 + \sqrt{4}}}

a) 2

b) 3

c) 5

d) 9

8 Das potências a seguir, qual é equivalente a

\sqrt[12]{18^{3}}

12^{\frac{1}{3}}

18^{\frac{1}{3}}

18^{\frac{1}{4}}

d) 184

9 Qual é o resultado da expressão numérica a seguir?

\sqrt[3]{9 \cdot 3} ‒ [\frac{175}{25} + \frac{2^{5}}{2^{4}} \cdot {(0, 25)}^{‒ \frac{1}{2}}]

a) 14

b) ‒2

c) ‒5

d) ‒8

10 Indique a alternativa que contém o resultado da expressão numérica a seguir.

\frac{3^{2}}{3}

‒

\frac{1}{4}

\cdot

[\sqrt{\frac{9}{36}} ‒ (‒ 8 + \frac{1}{2})]

a) 1

\frac{9}{4}

c) 5

\frac{11}{4}

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões.

a) Quais são os elementos que compõem a expressão de uma potência?

b) Ao dividirmos duas potências de mesma base, como obtemos os expoentes? E ao multiplicarmos duas potências de mesma base?

c) Qual é a potência equivalente a uma dada potência de expoente negativo?

d) Como obtemos a raiz equivalente a uma dada potência de expoente fracionário?

e) Quais são os elementos que compõem a expressão de uma raiz?

f) Como você explicaria a um colega o que é notação científica?

Respostas e comentários

1. Alternativa d.

2. Alternativa b.

3. Alternativa c.

4. Alternativa a.

5. Alternativa c.

6. Alternativa a.

7. Alternativa b.

8. Alternativa c.

9. Alternativa d.

10. Alternativa a.

Organizando:

a) A base e o expoente.

b) Devemos subtrair do expoente do dividendo o expoente do divisor. No caso da multiplicação, devemos adicionar os expoentes.

c) É a potência cujo expoente é o oposto do expoente da potência dada e cuja base é o inverso da base da potência dada. No caso do expoente fracionário, por exemplo,

\frac{a}{c}

e base b,

b^{\frac{a}{c}}

, o denominador da fração torna-se o índice da raiz, e o numerador, o expoente do radicando:

\sqrt[c]{b^{a}}

d) Escrevendo a raiz cujo índice é o denominador do expoente da potência dada e cujo radicando é a potência de mesma base e expoente igual ao numerador do expoente da potência dada.

e) O índice, o radical e o radicando.

f) Resposta pessoal.

Verificando

Os testes desta seção podem ser utilizados a fim de preparar os estudantes para exames e avaliações. Sugerimos que eles resolvam os testes individualmente. Depois, realize coletivamente a correção deles e, em outro momento, proponha aos estudantes que os resolvam novamente, solicitando-lhes, contudo, que registrem os cálculos necessários para obter as respostas.

Alternativamente, podem-se reunir os estudantes em duplas ou trios, propondo-lhes que resolvam os testes e, em outro momento, retomando os testes, propondo-lhes que os resolvam individualmente.

As resoluções dos testes 1 a 10 estão no início deste Manual, nas orientações específicas do capítulo 1.

Organizando

Os itens propostos nesta seção possibilitam compor uma autoavaliação. Os estudantes podem responder a cada item no caderno. Depois, coletivamente, eles discutem as respostas dadas, corrigindo ou complementando a própria resposta.

Página 37

DIVERSIFICANDO

Um truque de mágica?

Em um espetáculo, o grande mágico Rafael deixou para o final a mágica dos números. O truque consistia em mostrar que 4 é igual a 6. Acompanhe como o mágico fez os cálculos nesse truque, criando a ilusão de que 4 = 6.

Ilustração. Homem de cabelo curto, camisa, gravata e terno preto com faixa vermelha na cintura. Ele usa luvas brancas e segura uma varinha próxima a uma lousa com a informação: menos 24 = menos 24. 16 menos 40 = 36 menos 60. 4 vezes 4 menos 2 vezes 4 vezes 5 = 6 vezes 6 menos 2 vezes 6 vezes 5. 4 elevado ao quadrado menos 2 vezes 4 vezes 5 + 5 elevado ao quadrado = 6 elevado ao quadrado menos 2 vezes 6 vezes 5 + 5 elevado ao quadrado. Fração, numerador abre parênteses 4 menos 5 fecha parênteses elevado ao quadrado, denominador raiz quadrada de abre parênteses 4 menos 5 fecha parênteses elevado ao quadrado = fração, numerador abre parênteses 6 menos 5 fecha parênteses elevado ao quadrado, denominador raiz quadrada abre parênteses 6 menos 5 fecha parênteses elevado ao quadrado. 4 menos 5 = 6 menos 5. 4 = 6.

O que é maior?

Ao arrumar o quarto, Tiago encontrou o caderno de Matemática de seu irmão. Lá, havia um exercício que não estava resolvido. Observe o exercício e a resolução de Tiago a seguir.

(As imagens não respeitam as proporções reais entre os objetos.)

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

Formem grupos de 3 a 4 colegas, discutam os cálculos feitos pelo mágico Rafael e expliquem cada passagem que foi realizada na conta feita por ele.

2 Qual foi o êrro cometido no cálculo?

3 Usando o mesmo raciocínio de Tiago, indique o que é maior.

\sqrt[3]{3} ou \sqrt[4]{4}

\sqrt[4]{4} ou \sqrt{2}

Respostas e comentários

1. Espera-se que os estudantes percebam que, na terceira linha, Rafael escreve os mesmos números da segunda linha, mas fatorados. Depois de adicionar 52 a ambos os membros dessa igualdade, ele obtém o quadrado da diferença de dois termos.

2. Espera-se que os estudantes percebam que o êrro do cálculo está na passagem da sexta para a sétima linha, pois

\sqrt{{(4 ‒ 5)}^{2}} = \sqrt{{(‒ 1)}^{2}} = \sqrt{1} = 1 \neq 4 ‒ 5

; portanto, 1 = 1, não 4 = 6.

3. a)

{(\sqrt[3]{3})}^{12}

= 34 = 81 e

{(\sqrt[4]{4})}^{12}

= 43 = 64; como 81 > 64, então

\sqrt[3]{3} > \sqrt[4]{4}

3. b)

{(\sqrt[4]{4})}^{4}

= 4 e

{(\sqrt{2})}^{4}

= 22 = 4; como 4 = 4, então

\sqrt[4]{4} = \sqrt{2}

Diversificando

Com os estudantes reunidos em duplas, proponha-lhes que analisem as resoluções apresentadas para cada situação desta seção. Para a resolução do “O que é maior?”, por exemplo, pergunte a eles se conseguem justificar o cálculo das duas potências envolvendo raízes. Espera-se que utilizem o expoente fracionário e propriedades da potenciação:

•

{(\sqrt[6]{26})}^{6}

{(26^{\frac{1}{6}})}^{6}

26^{\frac{1}{6} \cdot 6}

= 261

•

{(\sqrt{3})}^{6}

{(3^{\frac{1}{2}})}^{6}

3^{\frac{1}{2} \cdot 6}

= 33