
CAPÍTULO 2 Construções geométricas e lugares geométricos

Observe a imagem e responda às questões no caderno.
a) Em sua opinião, o que a invenção da roda possibilitou no desenvolvimento da humanidade?
b) Que figura geométrica plana pode representar um desenho da roda?

Não há consenso sobre a origem da roda, talvez a mais importante construção geométrica humana, mas sabe-se que a percepção de sua existência é remota. Data de cêrca de 3500 antes de Cristo o registro mais antigo da representação da roda, encontrado nas ruínas da cidade de Ur, atual Iraque.
Em discussões polêmicas, é comum ironizar afirmando que alguém está “reinventando a roda”, insinuação de que sua fala não acrescenta nada à discussão.
Em Pedagogia, “reinventar a roda” tem sentido positivo: significa dar ao estudante condições para que ele faça suas próprias descobertas. Vamos reinventar a roda?
Respostas e comentários
a) Resposta pessoal.
b) Possíveis respostas: circunferência, círculo ou coroa circular.
Capítulo 2 - Construções geométricas e lugares geométricos
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, a retomada de conceitos geométricos já estudados em conjunto com as construções geométricas propiciam aos estudantes a consolidação de conceitos de Geometria plana.
É importante explorar as construções geométricas propostas neste capítulo utilizando materiais de desenho geométrico como esquadro, transferidor, régua e compasso e, ainda, softwares de Geometria dinâmica.
Explore a fotografia e proponha aos estudantes que comentem os detalhes do Estandarte de Ur. Após ler o texto, trabalhe os itens a e b e converse sobre a importância da roda, por exemplo, no desenvolvimento da agricultura e dos meios de transporte e o fato de ela poder ser representada por um círculo (ou circunferência, dependendo do contexto).
Pode-se desenvolver um trabalho interdisciplinar com Geografia de maneira a propor análises de aspectos representativos da dinâmica de fluxos imigratórios na América Latina. Espera-se que os estudantes percebam que a possibilidade de criar tecnologias na agricultura e para os meios de transporte, no decorrer da história, impactou os fluxos migratórios.
Além disso, para desenvolver o Tema Contemporâneo Transversal educação para o multiculturalismo nas matrizes históricas e culturais brasileiras, a pesquisa pode ser ampliada de maneira que eles possam compreender os fluxos migratórios relacionados à região em que vivem e estudar a história das populações indígenas que há (ou havia) nessa região.

Sugestões de leitura
Para ampliar, sugerimos os materiais:
INSTITUTO Brasileiro de Geografia e Estatística. Indígenas. í bê gê É, Rio de Janeiro (Rio de Janeiro), [a partir do ano de 2020]. Disponível em: https://oeds.link/Q59bhw. Acesso em: 6 junho 2022.
Neste site do í bê gê É há informações sobre a população indígena no Brasil.
ZORZETTO, R. Ascensão e declínio dos Tupi. PESQUISA fapésp. edição 311, janeiro 2022. Disponível em: https://oeds.link/zUD1rR. Acesso em: 6 junho 2022.
Neste trabalho, apresentam-se considerações acadêmicas e dados sobre os falantes da língua indígena tupi no decorrer da história.
1. Construções geométricas
As ideias e os conceitos da Geometria relacionados a retas e ângulos estão entre os conhecimentos matemáticos mais antigos da humanidade, como indicam algumas tabletas de argila dos sumérios, alguns papiros egípcios e documentos escritos de gregos e romanos.
Retas e ângulos também aparecem nas artes plásticas, seja em pinturas antigas, seja em obras contemporâneas, como as dos mestres abstracionistas. A obra do artista vaciíli candinsqui (1866 a 1944) reproduzida a seguir é um exemplo de aplicação desses conceitos nas artes plásticas.

A preocupação em organizar todo o conhecimento geométrico acumulado começou com os gregos. Eles transformaram a Geometria que resolvia cada caso particular em uma Geometria que tratava das propriedades das figuras de maneira generalizada.
Como estudado em anos anteriores, ponto, reta e plano são noções primitivas, isto é, são aceitas sem definição.
Para dar continuidade ao nosso estudo, vamos rever alguns conceitos referentes a esses elementos geométricos.
Respostas e comentários
1. Construções geométricas
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um cinco.
O início deste tópico traz uma obra do artista russo vacíli Kandinsky, que introduziu a abstração no campo das artes visuais.
Proponha aos estudantes uma pesquisa de obras de arte concreta desse artista e de artistas nacionais, como Waldemar Cordeiro, Geraldo Barros, Lygia Clark, Lygia Pape, Hélio Oiticica e Amílcar de Castro, com as quais poderá motivá-los no estudo da Geometria e a desenvolver a competência geral 3, pois com a pesquisa eles poderão usufruir desse tipo de de manifestação artística.

Sugestão de leitura
Para ampliar e enriquecer o trabalho sobre candinsqui, sugerimos o material:
QUINTÃO, B. P. A abstração entre Wassily candinsqui e grafismos indígenas. Trabalho de conclusão de curso (Bacharelado em Teoria, Crítica e História da Arte) – Universidade de Brasília, Brasília, 2018. Disponível em: https://oeds.link/TTgmIn. Acesso em: 6 junho 2022.
Nesta pesquisa, a autora investiga obras do período do Der Blaue Reiter do artista russo vaciíli candinsqui (1866 a 1944) e grafismos indígenas amazônicos como fórmas abstratas.
Retas, semirretas e segmentos de reta
Acompanhe a seguir um resumo de elementos que fazem parte de uma reta.
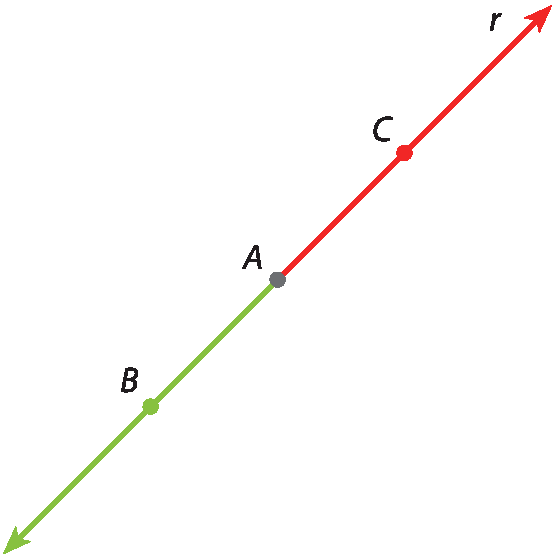
A semirreta
a semirreta ABde origem a que passa por B está pintada de verde. As semirretas
a semirreta ABe
a semirreta ACsão opostas: têm a mesma origem A e estão na mesma reta r.
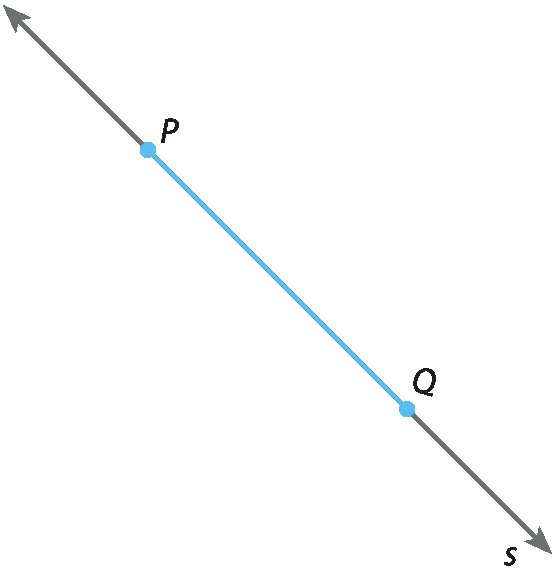
A parte pintada de azul é o segmento de reta
PQde extremidades P e Q, formado pelos pontos P, Q e por todos os demais pontos da reta s que estão entre P e Q.
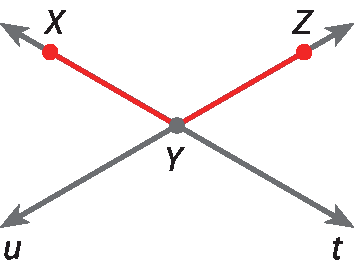
Os segmentos
XYe
YZsão consecutivos, pois têm uma extremidade comum: o ponto Y.
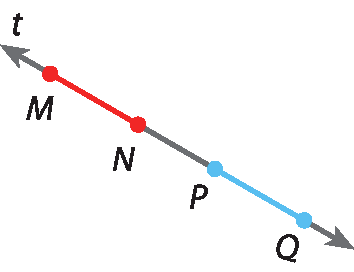
Os segmentos
MNe
PQsão colineares, pois estão na mesma reta t.
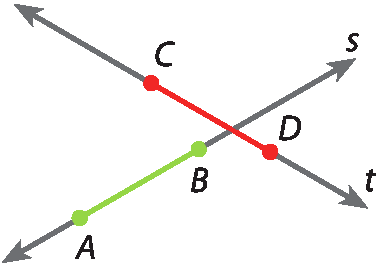
Os segmentos
CDe
ABtêm a mesma medida de comprimento. São segmentos congruentes. Indicamos:
segmento AB≅
CD.
Agora, observe esta figura:
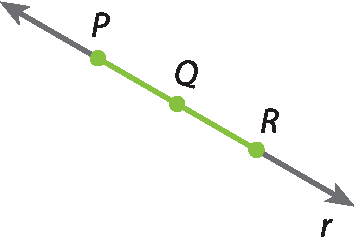
O ponto Q divide o segmento
PRem dois segmentos congruentes:
PQe
QR. O ponto Q é o ponto médio de
PR.
Respostas e comentários
Retas, semirretas e segmentos de reta
Como base para as construções geométricas que serão propostas, retomamos conceitos de Geometria plana. Esperamos que os estudantes possam mobilizar os conhecimentos já estudados em anos anteriores e consolidá-los nessa retomada.
Ressalte os conceitos de segmentos de reta consecutivos, segmentos de reta congruentes e ponto médio de um segmento de reta. Os estudantes podem fazer cartazes criando figuras que envolvam esses conceitos com diversos materiais (palitos de madeira, linha, arame etcétera). Se julgar conveniente, faça uma exposição desses trabalhos.
Construindo segmentos congruentes com régua e compasso
Com o auxílio de régua e compasso, observe os passos para a construção de um segmento
CDcongruente a um segmento dado
AB.

1. Com uma régua, traçamos uma reta r qualquer e sobre ela marcamos um ponto C.
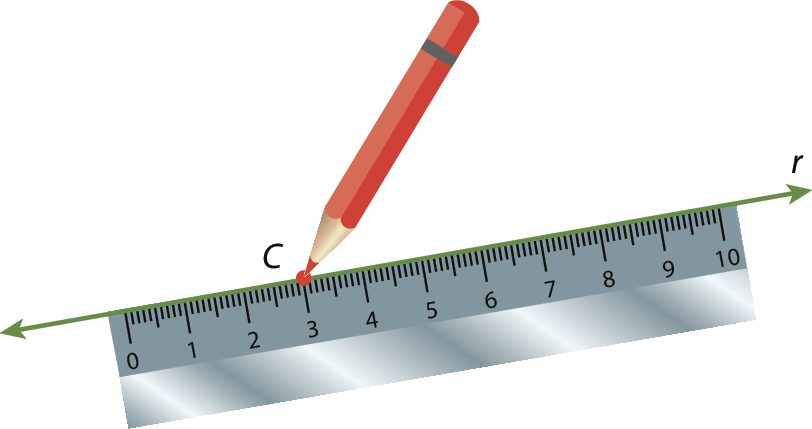
2. Com a ponta-sêca do compasso em a, abrimos o compasso até o ponto B.
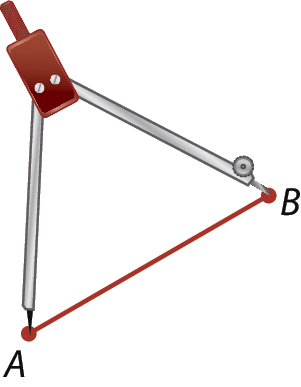
3. Com a ponta-sêca do compasso em C e abertura igual a A bê, traçamos um arco que intersecta a reta r no ponto D. Os pontos C, D e todos os pontos da reta r que estão entre C e D formam o segmento
CD, que é congruente ao segmento
AB.
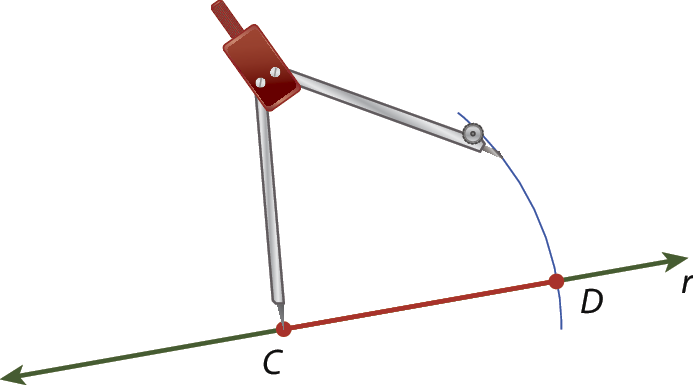
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Nessa construção, o segmento
CDé congruente ao segmento
AB, pois ambos têm a mesma medida, dada pela abertura do compasso.
Utilizando um software de Geometria dinâmica também é possível construir segmentos congruentes. Nesse recurso há ferramentas de compasso e de construção de segmentos, que possibilitam seguir os passos 1, 2 e 3 explicitados para essa construção.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Escreva no caderno os pares de segmentos consecutivos que aparecem na figura a seguir.
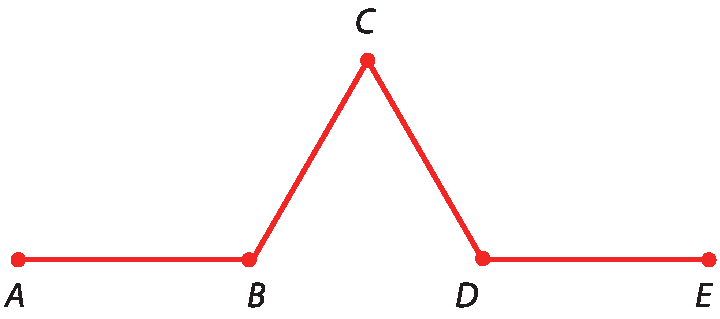
2 Copie a figura do exercício 1 e acrescente o segmento
BD.
Além dos segmentos consecutivos já identificados naquele exercício, que outros segmentos consecutivos a nova figura apresenta?
3 Registre no caderno o significado de cada indicação a seguir: reta, semirreta ou segmento de reta.
a)
AB com um traço em cima com seta em ambos os sentidosb)
AB com um traço em cima com seta à direitac)
AB com um traço em cimad)
PQ com um traço em cima com seta à direitae)
PQ com um traço em cimaRespostas e comentários
1.
1. Segmentos AB e BC, segmentos BC e CD, segmentos CD e DE..
2.
AB e BD;
AB e BE;
AD e DE;
AD e BD;
AB e AE;
AB e AD;
AD e DC;
BD e DC;
BC e BD;
o segmento BC e o segmento BE.
3. a) Reta.
3. b) Semirreta.
3. c) Segmento de reta.
3. d) Semirreta.
3. e) Segmento de reta.
Construindo segmentos congruentes com régua e compasso
Para realizar as construções geométricas propostas, é importante que os estudantes providenciem previamente os materiais de desenho necessários: régua, compasso, esquadros, lápis etcétera.
Reproduza na lousa a construção apresentada para que eles acompanhem cada etapa. Em seguida, entregue a cada estudante uma folha de papel sulfite preparada com segmentos traçados. Peça a eles que construam dois segmentos de reta distintos entre si e congruentes a cada segmento dado. Depois, devem marcar o ponto médio de cada um desses segmentos de reta. Espera-se que, para isso, utilizem a escala da régua; entretanto, se julgar apropriado, pode ser realizada uma atividade investigativa a fim de que os estudantes identifiquem um procedimento para determinar, apenas com régua e compasso (sem usar as marcações de medida da régua), o ponto médio de um segmento. Por exemplo, para determinar o ponto M, ponto médio de
A B, pode-se:
• com centro em a, traçar uma circunferência de raio r, tal que r é maior que a metade de A bê;
• com centro em B e raio r, traça-se outra circunferência;
• traçar o segmento
segmento OP, em que os pontos óh e P são intersecção das circunferências anteriormente construídas;
• marcar o ponto M em
AB, tal que M é o ponto de intersecção de
ABcom
segmento OP;
• M é o ponto médio de
AB.
Os estudantes podem organizar em fluxogramas as etapas das construções geométricas utilizadas e apresentar aos demais colegas da turma a fim de validar as etapas para determinar o ponto médio de um segmento.
Sempre que necessário, relembre os estudantes de terem cuidado no manuseio do compasso, a fim de evitar que se machuquem com a ponta-sêca.
Exercícios propostos
Para resolver o exercício 1, deve-se aplicar a definição de segmentos consecutivos, que são aqueles que têm uma extremidade em comum. Assim, são segmentos consecutivos:
e
BC, pois B é extremidade de ambos.
e
CD, pois C é extremidade de ambos.
e
DE, pois D é extremidade de ambos.
No exercício 2, também serão consecutivos os segmentos:
e
BD, pois B é extremidade de ambos.
e
DE, pois D é extremidade de ambos.
Para resolver o exercício 3, deve-se considerar que a notação para reta é um traço com seta em ambos os sentidos; de semirreta, o traço com uma seta; de segmento, apenas o traço.
4 Identifique a sentença falsa e justifique sua resposta.
a) Se AB = 8 métros e CD = 800 centímetros, então
segmento AB≅
segmento CDb) Se MN = 3 centímetros e XY = 3 centímetros, então
o segmento MN é congruente ao segmento XY≅
o segmento MN é congruente ao segmento XYc) Se
EF≅
PQ, então EF = PQ.
d) Se AB = 5 centímetros e CD = 5 decímetros, então
AB≅
CD.
5 Na figura a seguir, a é o ponto médio de
XYe B é o ponto médio de
YZ, que mede 5 centímetros.
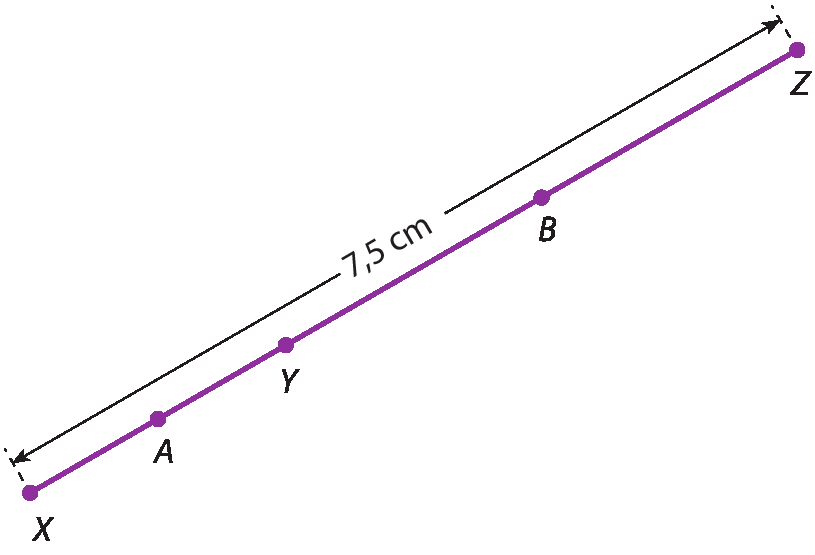
a) Quanto mede o segmento
XY?
b) Qual é a medida do segmento
AB?
6. Um software de Geometria dinâmica tem as seguintes ferramentas:
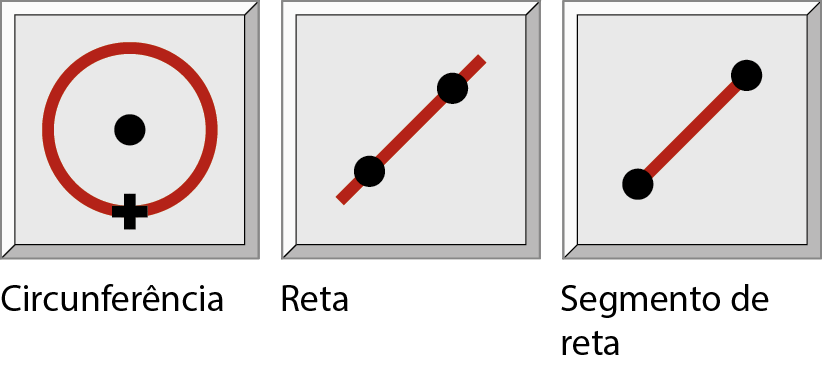
Construa um fluxograma com os passos que devem ser seguidos para a construção de 2 segmentos congruentes usando essas 3 ferramentas do software.
7 Observe os pontos destacados no segmento
AFrepresentado a seguir.

• B é o ponto médio de
segmento AC;
• C é o ponto médio de
segmento AD;
• D é o ponto médio de
segmento BE;
• E é o ponto médio de
segmento DF.
Sabendo que BC = 0,5 centímetro, determine:
a) a medida do segmento
AF;
b) a medida do segmento
CE.
8 Considere que a figura a seguir representa um segmento
ADde medida 18 centímetros, sendo X o ponto médio de
AB, Y o ponto médio de
BCe Z o ponto médio de
CD.

Sabendo que a medida de
ABé o dôbro da medida de
segmento cde que
segmento BCmede o triplo de
segmento CD, determine a medida dos segmentos:
a)
AB;
b)
BC;
c)
CD;
d)
XY;
e)
YZ;
f )
XZ.
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO

Reúna-se com um colega e façam o que se pede.
1 a, B, C e D são pontos de uma mesma reta r, de tal maneira que A bê = 6 centímetros, BC = 2 centímetros, á cê = 8 centímetros e BD = 1 centímetros.
Nessas condições, representem, no caderno, a reta r e esses pontos.
2 Considerem o segmento
segmento ADrepresentado a seguir, em que á dê = 8 centímetros e BC = 2,5 centímetros.

a) É possível calcular a medida A bê ? E a medida BD ?
b) A medida CD pode valer 6 centímetros? Justifiquem a resposta.
c) Quais são os possíveis valores da medida á cê ?
Respostas e comentários
4. Alternativa d, pois A bê ≠ CD.
5. a) 2,5 centímetros
5. b) 3,75 centímetros
6. Construção de figura.
7. a) 5 centímetros
7. b) 2,5 centímetros
8. a) 6 centímetros
8. b) 9 centímetros
8. c) 3 centímetros
8. d) 7,5 centímetros
8. e) 6 centímetros
8. f) 13,5 centímetros
Pense mais um poucoreticências
1. Construção de figura.
2. a) Não; não.
2. b) Não, pois: á dê ‒ BC = A bê + CD
8 ‒ 2,5 = A bê + 6
A bê = 5,5 ‒ 6
Logo, para CD valer 6 centímetros, A bê deveria ser negativa.
2. c) 2,5 < á cê < 8
Exercícios propostos
As resoluções dos exercícios 4 a 6 e do exercício 8 estão no início deste Manual, nas orientações específicas do capítulo 2. No exercício 4, há uma articulação do conceito de congruência com a transformação de unidades de medida, relacionando as Unidades Temáticas Geometria e Grandezas e medidas.
No exercício 7, se BC = 0,5 centímetro e B é o ponto médio de
segmento ACentão A bê = 0,5 centímetro. Continuando, á cê = 1,0 centímetro e, sendo C o ponto médio de
segmento ADentão CD = á cê = 1,0 centímetro. Como D é ponto médio de
segmento BEé possível determinar o comprimento de
segmento BDescrevendo-se:
BD = BC + CD = 0,5 + 1,0
BD = 1,5 centímetro
Portanto, DE = 1,5 centímetro.
Como ê é ponto médio de
segmento DFentão
o segmento DEé congruente a
o segmento EFlogo, EF = 1,5 centímetro. Agora, basta efetuar a adição:
á éfe = á cê + CD + dê ê + ê éfe
á éfe = 1,0 + 1,0 + 1,5 + 1,5
á éfe = 5 centímetros
No item b, temos: como C é ponto médio de
segmento AD, CD = á cê = 1. Logo, cê é = CD + dê ê = 1 + 1,5 = 2,5. A medidade de
segmento CEé 2,5 centímetros.
No exercício 8, trabalhe essa atividade por meio de questionamentos, induzindo os estudantes à conclusão de que a distância entre os dois pontos médios X e Y é a semissoma das medidas dos dois segmentos
ABe
BCObserve que a distância de X a Z não é a semissoma das medidas dos segmentos
ABe
CDpois estes não são consecutivos.
A resolução do exercício 8 propicia a inter-relação das Unidades Temáticas Geometria e Álgebra. Representando por x a medida CD, o equacionamento é imediato. Proponha aos estudantes que experimentem outras atribuições para x, como x = A bê ou x = ZD para verificarem que as medidas dos segmentos são as mesmas.
Pense mais um poucoreticências
Na atividade 1, os estudantes são levados a considerar mais de uma possibilidade na construção da figura. Exemplos de resposta:
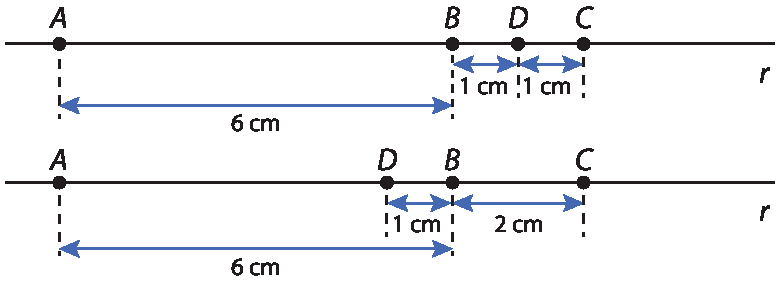
Na atividade 2, itens a e c, a indeterminação da medida pedida decorre da possibilidade de haver infinitos valores para á cê entre os números racionais 2,5 e 8, que tornam plausível a situação proposta.
Posição relativa de retas
Aqui também vamos rever alguns conceitos referentes às retas.
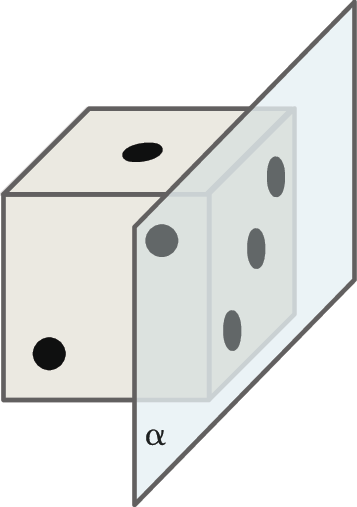
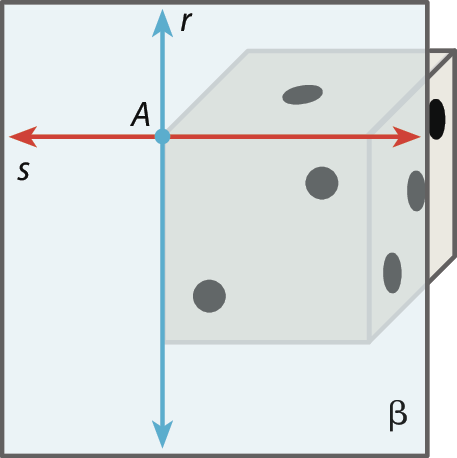
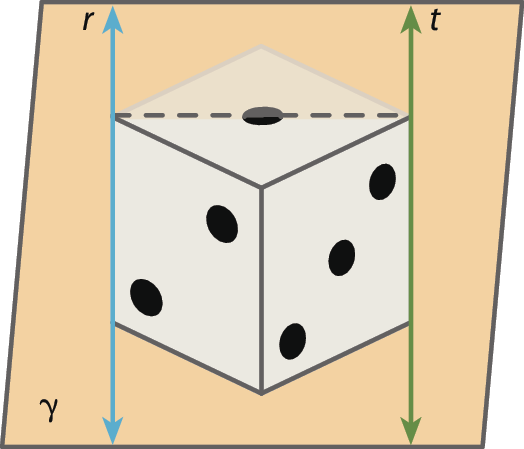
Duas retas de um plano são coincidentes quando têm todos os pontos em comum. Indicamos que as retas c e d são coincidentes por: c ≡ d.

Dadas duas retas, s e t, caso não exista um plano que as contenha, chamamos s e t de retas reversas.
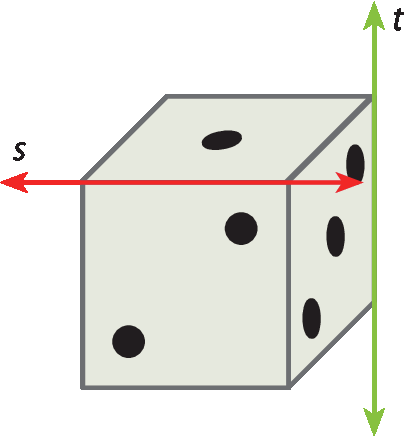
Observação
▶ Para que duas retas sejam paralelas ou concorrentes, elas devem, necessariamente, estar em um mesmo plano, isto é, deve existir um plano que as contenha. Nesse caso, dizemos que elas são retas coplanares.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
9 Escreva a posição relativa das retas coplanares r e s quando:
a) elas não têm ponto em comum;
b) elas têm apenas um ponto em comum.
10 Identifique qual é a sentença falsa e justifique no caderno.
a) Se a e B são dois pontos de um plano α, então a reta
ABestá contida nesse plano.
b) Se duas retas, r e s, não têm ponto em comum, então elas são paralelas.
c) Se duas retas são coplanares e não têm ponto em comum, então elas são paralelas.
Respostas e comentários
9. a) Paralelas.
9. b) Concorrentes.
10. a) Verdadeira.
10. b) Falsa, pois r e s podem ser reversas.
10. c) Verdadeira.
Posição relativa de retas
Neste item, tratamos das posições relativa entre duas retas, seja no plano, seja no espaço. As arestas de um cubo podem ser associadas a segmentos de retas e, assim, podem-se associá-los às suas respectivas retas suporte explorando as posições relativas entre as retas de maneira menos abstrata.
Exercícios propostos
Para resolver estes exercícios, é necessário recorrer às definições sobre posições relativas entre retas.
No exercício 9, quando duas retas são coplanares e não têm pontos em comum, elas são paralelas e, ainda, quando duas retas coplanares têm apenas um ponto em comum, elas são concorrentes. Logo, as retas do item a são paralelas, e as do item b, concorrentes.
No exercício 10, discutimos a relação entre pontos, retas e planos. No item a, pelo axioma da determinação de reta, consideramos que existe apenas uma reta que passa por a e por bê. Assim, se A e B estão no mesmo plano, todos os pontos da reta
ABtambém pertencem a esse plano.
No item b, mostre aos estudantes que as retas reversas não têm ponto comum, assim como as paralelas. A diferença é o fato de que retas paralelas são coplanares, e as retas reversas não são. Logo, precisamos de duas informações para saber se as retas são paralelas.
No item c, temos as duas informações necessárias para saber se duas retas são paralelas ou não.
11 Considere o bloco retangular ilustrado a seguir.
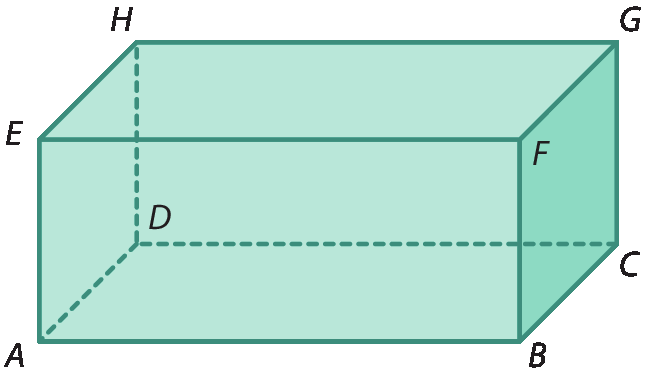
Classifique como paralelas, concorrentes ou reversas as retas que contêm os pares de arestas:
a)
AB e BC.
b)
CD e HG.
c)
AB e CG.
d)
BF e AE.
e)
AD e BF.
f)
HG e AB.
Construindo retas paralelas com régua e compasso
Considere uma reta r e um ponto P não pertencente a r. Vamos construir, com o auxílio de régua e compasso, uma reta paralela à reta r e que passe pelo ponto P.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
1. Com a ponta-sêca do compasso em P, traçamos um arco que corta r, obtendo o ponto M.
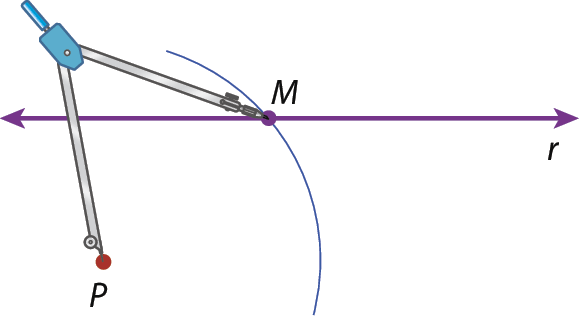
2. Com a mesma abertura PM e a ponta-sêca do compasso em M, traçamos um arco que intersecta r, obtendo o ponto R.
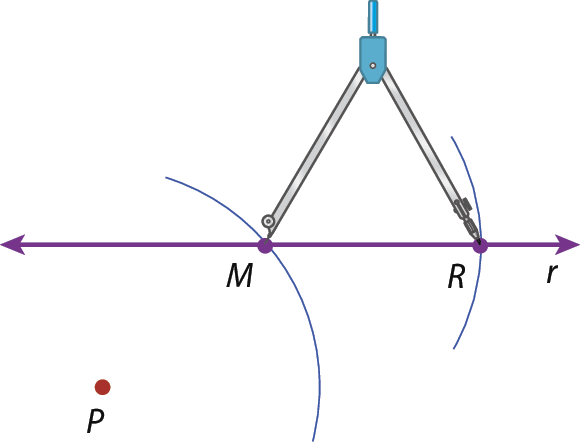
3. Com a mesma abertura MR e a ponta-sêca do compasso em R, traçamos um arco que intersecta o primeiro arco, obtendo o ponto Q.
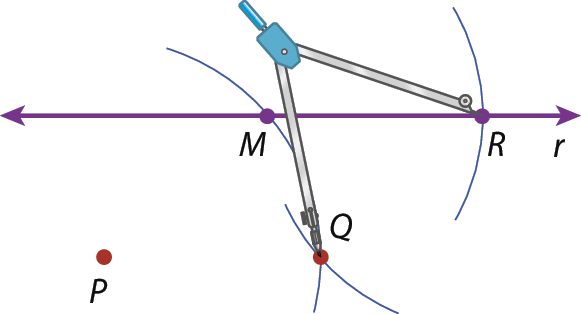
4. Com a régua, traçamos a reta
PQ, que é paralela à reta r.
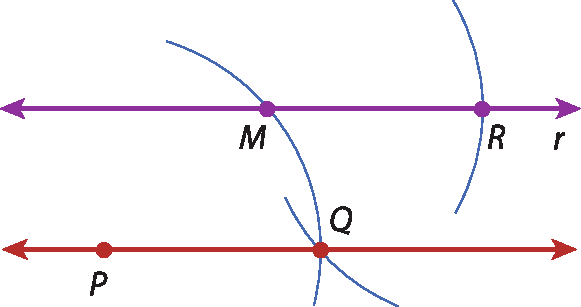
Observe que
os segmentos PM,
os segmentos MR,
os segmentos RQe
os segmentos QPtêm mesma medida, que é a da abertura PM do compasso. Então, a figura PMRQ é um losango.
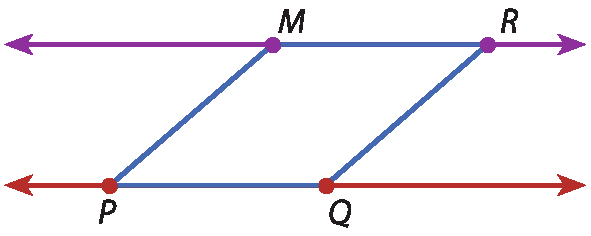
Como os lados opostos de um losango são paralelos, então
a reta P Q⫽
a reta M R.
Respostas e comentários
11. a) Concorrentes.
11. b) Paralelas.
11. c) Reversas.
11. d) Paralelas.
11. e) Reversas.
11. f) Paralelas.
Exercícios propostos
Para facilitar a resolução, no exercício 11, se possível, associe a sala de aula com o bloco retangular. Considerando que os segmentos são arestas de um bloco retangular, verificamos que:
a) como
os segmentos ABe
os segmentos BCsão consecutivos, as retas que os contêm são concorrentes em B.
b) como
os segmentos CDe
os segmentos HGsão arestas opostas de uma mesma face, as retas que os contêm são paralelas.
c) como
os segmentos ABe
os segmentos CGsão perpendiculares a planos não paralelos e arestas de duas faces opostas, as retas que as contêm são reversas.
d) como
os segmentos BFe
os segmentos AEsão arestas opostas de uma mesma face, as retas que os contêm são paralelas.
e) como
Segmento ADe
Segmento BFsão perpendiculares a planos não paralelos e arestas de duas faces opostas, as retas que os contêm são reversas.
f) como
Segmento HGe
ABsão arestas de duas faces opostas e paralelas a
o segmento DC, as retas que os contêm são paralelas.
Construindo retas paralelas com régua e compasso
Apresente a construção das retas paralelas passo a passo na lousa para os estudantes acompanharem todo o procedimento. Espera-se que eles mobilizem conhecimentos sobre paralelogramos já estudados em anos anteriores.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
12 Usando um software de Geometria dinâmica, desenhe uma reta e um ponto fora dela. Construa uma reta paralela a essa reta que passe por esse ponto. Indique os passos que você seguiu para fazer essa construção.
13 Desenhe uma reta m e cinco pontos que não pertençam a ela. Depois, construa retas paralelas a m por esses pontos e responda às questões.
a) Qual é o maior número de retas paralelas à reta m que podem ser traçadas passando por esses cinco pontos?
b) É possível deslocar os cinco pontos a fim de obter mais de cinco retas paralelas a m?
c) É possível trocar a posição de algum desses cinco pontos e traçar menos de cinco retas paralelas a m?
d) Qual é o menor número de retas paralelas que podem ser traçadas?
14 Em uma folha de papel transparente, copie a figura a seguir.
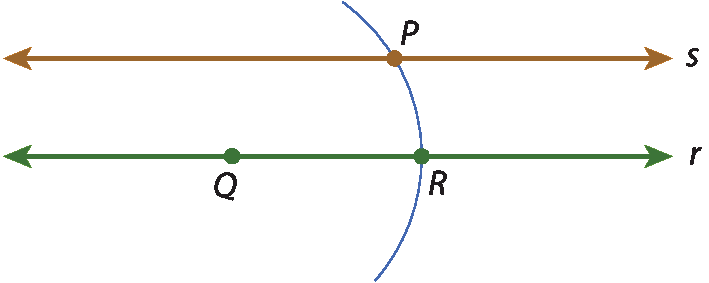
Com a ponta-sêca do compasso em R e abertura RP, obtenha no arco da figura o ponto pê linha, simétrico de P em relação a r. Em seguida, trace por pê linha a reta t paralela à reta r.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Considerando que s é paralela a r, r é paralela a t e P e pê linha são pontos simétricos em relação a r, o que você conclui sobre:
a) a posição das retas s e t ?
b) as distâncias de P a r e de pê linha a r ?
2. Ângulos
O ângulo é uma figura que você já conhece e com a qual tem trabalhado em muitas situações. Vamos retomar a definição de ângulo e algumas de suas características.
Ângulo é a figura geométrica formada por duas semirretas de mesma origem.
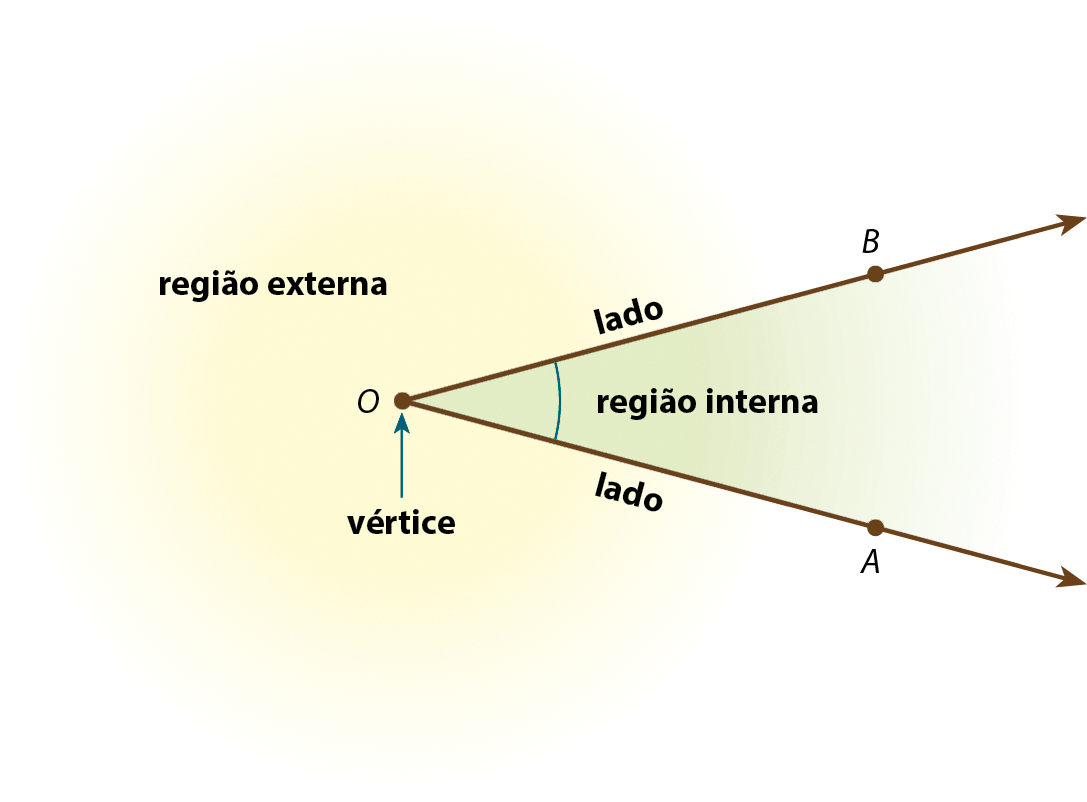
Nessa figura, o ponto O é o vértice do ângulo, e as semirretas
OAe
OBsão os lados. Indicamos esse ângulo por
Símbolo. Letra A, letra Ó com acento circunflexo (chapéu), letra B.(lemos: “ângulo á ó bê” ).
A unidade de medida de ângulo mais utilizada é o grau, que é obtido quando dividimos o ângulo de uma volta em 360 ângulos iguais. À abertura de um desses ângulos associa-se a medida unitária 1grau. De acôrdo com suas medidas, os ângulos recebem nomes especiais.
Respostas e comentários
12. Construção de figura.
13. a) 5 retas paralelas.
13. b) Não.
13. c) Sim.
13. d) 1 reta paralela.
14. a) b) Espera-se que os estudantes concluam que s ⫽ t e que as distâncias de P a r e de pê linha a r são iguais.
Exercícios propostos
As resoluções dos exercícios 12 a 14 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 13, convém organizar um painel com os diferentes desenhos dos estudantes em relação ao posicionamento dos pontos e, depois, discutir as respostas. Aborde as possibilidades de posicionamento desses pontos, desde a situação em que todos estão alinhados (quando há uma única reta paralela a m) até os cinco pontos, tomados a diferentes distâncias de m, ou se cada par desses pontos a igual distância de m forem simétricos em relação a m (quando há cinco retas distintas paralelas a m).
2. Ângulos
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um cinco.
Neste tópico, retomamos o conceito de ângulo e seus principais elementos e são trabalhadas construções geométricas de retas perpendiculares, desenvolvendo aspectos da habilidade (ê éfe zero oito ême ah um cinco) e preparando os estudantes para o estudo sobre bissetriz de ângulo formado por dois segmentos de reta consecutivos (lados consecutivos de um polígono) e mediatriz de um segmento de reta.
O arco marcado na figura indica a abertura do ângulo que estamos considerando. Observe.

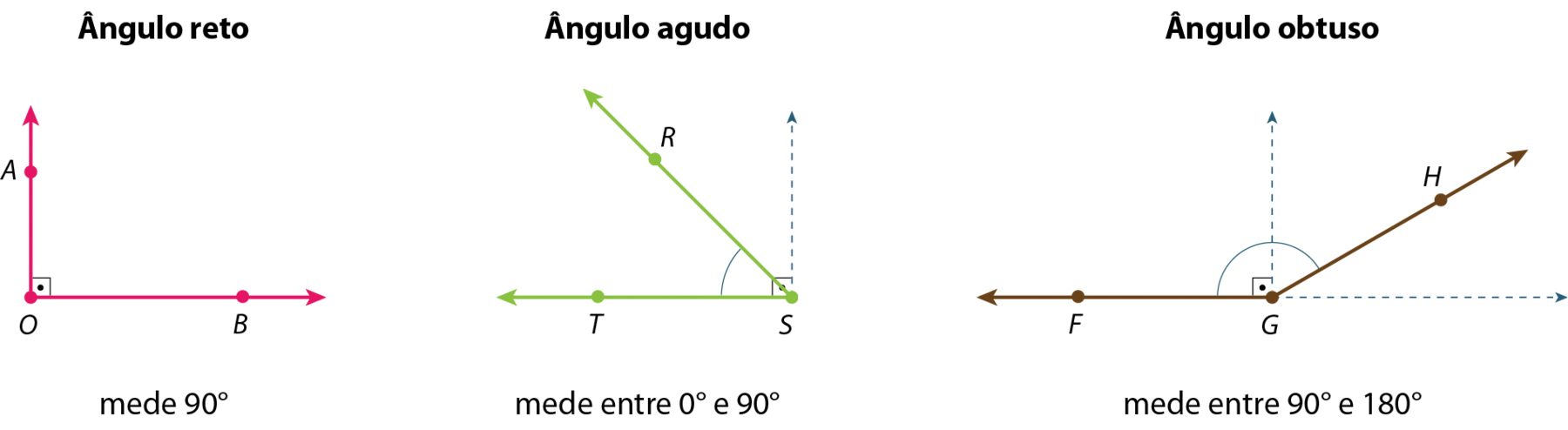
Observações
▶ Indicamos a medida de um ângulo
ângulo AOBpor: m(
ângulo AOB).
▶ Dois ângulos são congruentes quando têm a mesma medida. Acompanhe um exemplo.
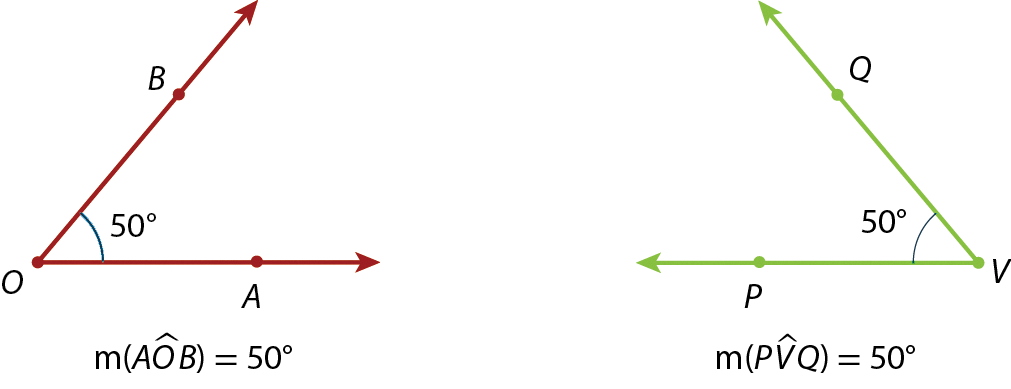
Os ângulos
AOBe
PVQ, nas figuras apresentadas, têm a mesma medida (50graus). Dizemos, então, que
AOBe
PVQsão ângulos congruentes e escrevemos
ângulo AOB≅
ao ângulo PVQ.
▶ Duas retas concorrentes são denominadas perpendiculares se formarem quatro ângulos retos entre si.
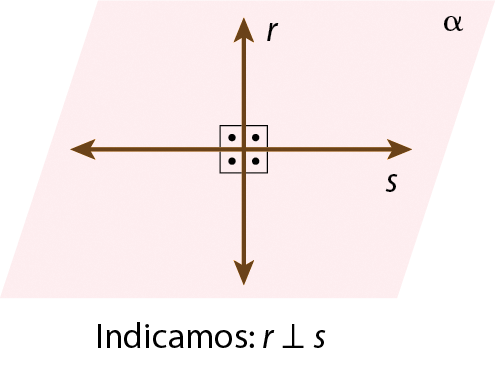
▶ Quando duas retas são concorrentes, mas não formam ângulos retos entre si, são denominadas retas oblíquas.
Respostas e comentários
Ângulos
Retomamos os tipos de ângulo, apresentando ângulo de 0grau, de 360graus, de 180graus e de 90graus e sua classificação como nulo, ângulo de meia volta, ângulo de uma volta, reto, agudo ou obtuso. São retomados ainda os conceitos de ângulos congruentes, retas perpendiculares e retas oblíquas. Esses conteúdos também serão base para novas construções geométricas.
Se julgar conveniente, prepare previamente atividades para os estudantes retomarem o uso do transferidor: medindo ângulos fornecidos e construindo ângulos solicitados. Essa retomada é importante para aplicarem esses procedimentos na medição e na construção dos setores de um gráfico circular, assunto que será apresentado adiante neste capítulo.
Construindo retas perpendiculares com régua e compasso
Já vimos, em anos anteriores, como construir retas perpendiculares com régua e transferidor e, também, com régua e esquadro. Agora, acompanhe a construção semelhante empregando régua e compasso.
Considere uma reta s e um ponto P. Vamos traçar uma perpendicular r à reta s, por esse ponto. Observe dois exemplos.
• Quando o ponto está na reta
1. Traçamos uma reta s e marcamos um ponto P.

2. Com qualquer abertura do compasso e ponta-sêca em P, marcamos dois pontos a e B em s.
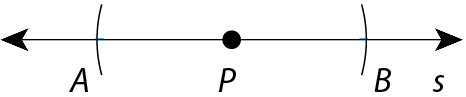
3. Com a abertura do compasso maior que
APe ponta-sêca em a, depois em B, traçamos dois arcos marcando dois pontos, C e D, na intersecção entre eles.

4. A reta
CDé a reta r, perpendicular à reta s.
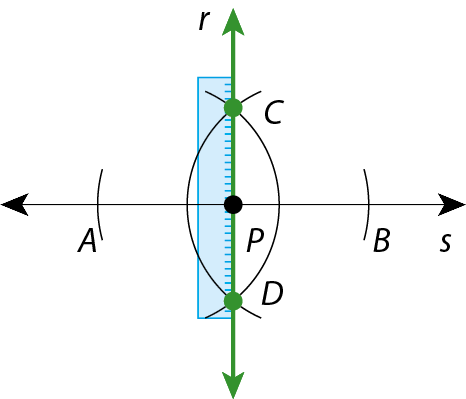
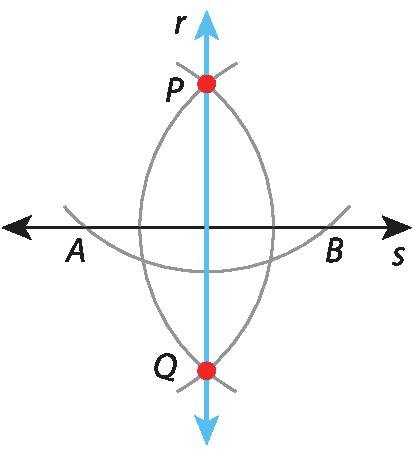
• Quando o ponto não está na reta
1. Traçamos uma reta s e marcamos um ponto P.
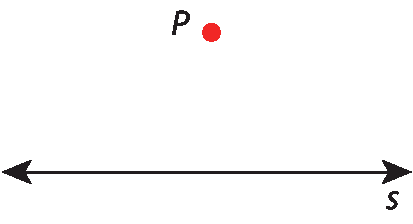
2. Traçamos um arco com centro em P e marcamos os pontos a e B em s.
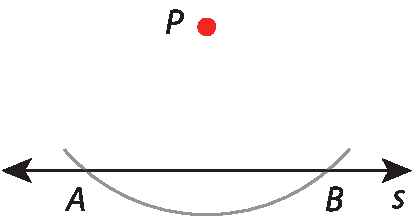
3. Traçamos arcos com centro em a e B e com abertura á pê, obtendo o ponto Q.
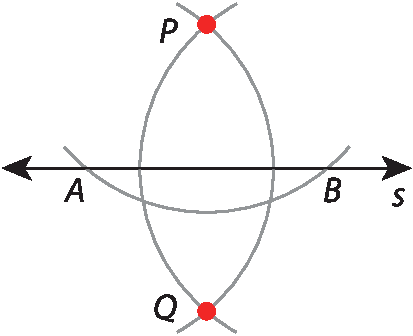
4. Traçamos a reta r, que contém os pontos P e Q e é perpendicular à reta s.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Essas construções também podem ser realizadas por meio de um software de Geometria dinâmica. Para isso, podem-se utilizar ferramentas como as indicadas a seguir.

•

Como você construiria duas retas perpendiculares com essas ferramentas? Converse com o professor e os colegas.
Respostas e comentários
Converse com os estudantes sobre as ferramentas apresentadas. Alguns poderão indicar a construção por meio das ferramentas de construção de reta, de ponto e de compasso, e outros poderão indicar a ferramenta de reta perpendicular. Comente que, a partir de uma reta e um ponto dados, essa ferramenta traça a reta perpendicular que passa por esse ponto.
Construindo retas perpendiculares com régua e compasso
Essa construção deve ser realizada passo a passo na lousa para que os estudantes a acompanhem com facilidade. Em seguida, peça-lhes que tracem uma reta qualquer em uma folha de papel e, depois, troquem o papel com um colega para traçarem uma reta perpendicular à reta traçada. Proponha que decidam se essa construção será feita por um ponto da reta traçada ou por um ponto fora dela. Ao final, discuta com eles essas possibilidades.
Lembre os estudantes de utilizarem o compasso com cuidado, a fim de que não se machuquem com a ponta-sêca.
Após realizarem a construção com régua e compasso, se possível, reserve uma aula para que possam utilizar um software de Geometria dinâmica a fim de fazerem as construções de retas perpendiculares por meio das ferramentas desse software. Caso perceba estudantes com dificuldade nessa atividade, oriente-os a tomarem como referência o fluxograma para a construção de reta paralela a uma reta dada, da página seguinte.
Ao explorar o uso de tecnologias digitais, os estudantes podem desenvolver a competência geral 5, pois adquirem mais autonomia para produzir conhecimentos.
Para a construção de uma reta s perpendicular a uma reta r, passando por um ponto a pertencente a r, pode-se seguir o conjunto de passos do fluxograma e obter a seguinte construção:
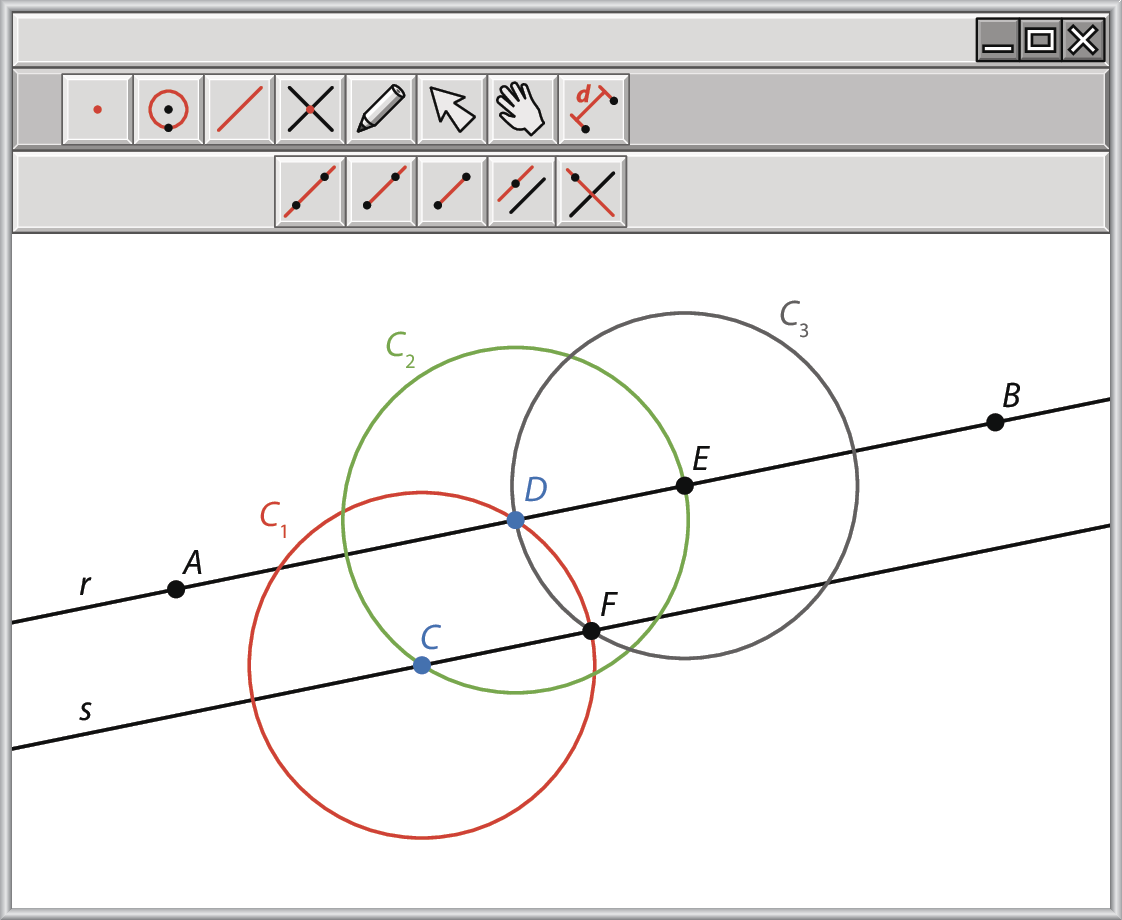
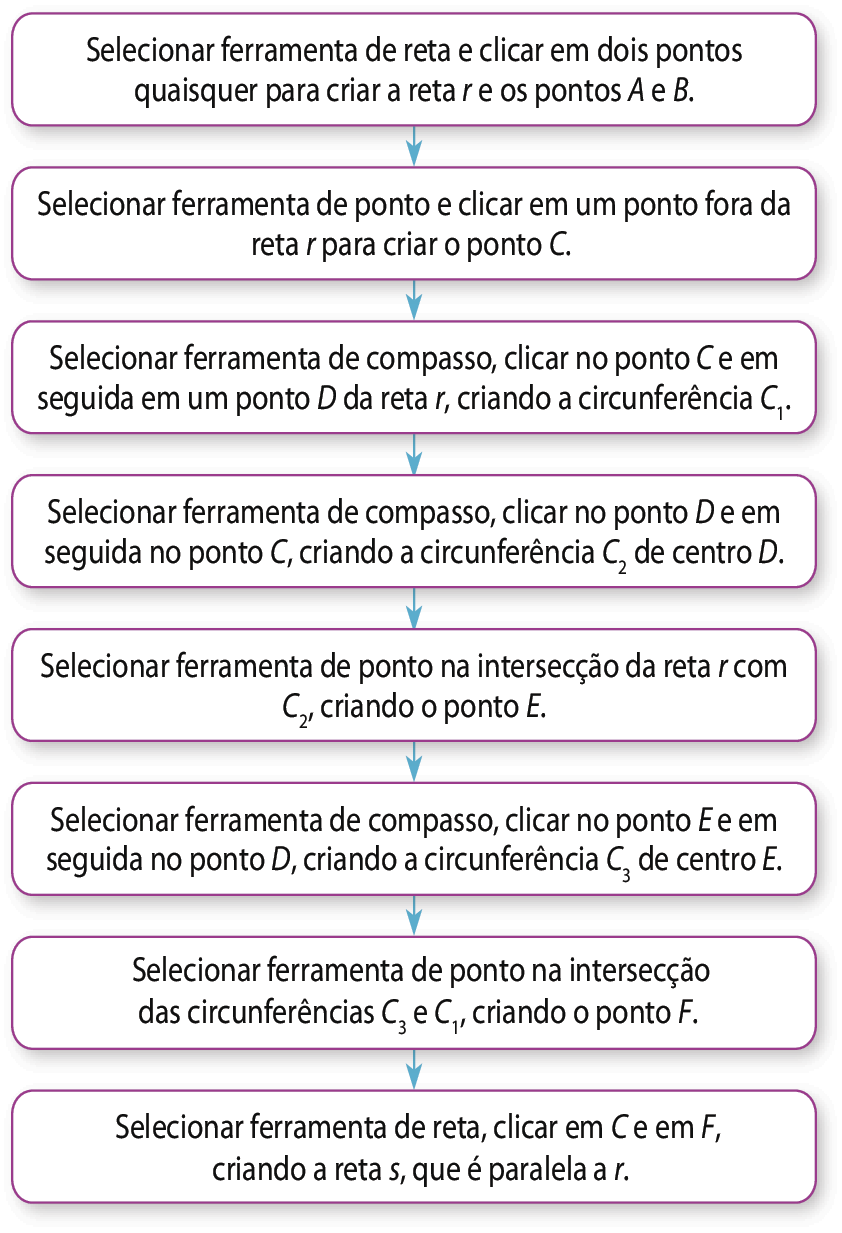
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
15 Desenhe uma reta e trace, por um ponto, uma reta perpendicular a essa reta, nas seguintes condições:
a) o ponto está na reta;
b) o ponto não está na reta.
16 Elabore, no caderno, um fluxograma com as etapas para a construção de uma reta s, perpendicular a r, passando por um ponto a que não pertence à reta.
17 Considerando as ferramentas disponíveis em um software de Geometria dinâmica, explique a sequência de etapas que você seguiria para a construção de um retângulo.

18

Reúna-se com um colega e desenhem um segmento horizontal
Segmento ABmedindo 6 centímetros. Em cada extremidade do segmento, tracem uma reta perpendicular a ele. Marquem, sobre a reta perpendicular traçada pelo ponto a e abaixo de
Segmento AB, um ponto C, de modo que á cê = 4 centímetros. Depois marquem, sobre a reta perpendicular traçada pelo ponto B e acima de
Segmento AB, um ponto D, tal que BD = 4 centímetros.
a) Discutam e estimem a medida para o segmento
CD.
b) Unam os pontos C e D e meçam com uma régua o segmento
CD. Qual é essa medida? Vocês fizeram uma boa estimativa?
19

Hora de criar – Elabore um problema sobre retas paralelas ou sobre retas perpendiculares. Troque com um colega e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Respostas e comentários
15. Construção de figura.
16. Construção de figura.
17. Resposta pessoal.
18. a) Resposta pessoal.
18. b) 10 centímetros. Resposta pessoal.
19. Resposta pessoal.
Exercícios propostos
As resoluções dos exercícios 15 a 18 estão no início deste Manual, nas orientações específicas do capítulo 2.
O exercício 18 é uma atividade que pode ser feita em dupla. Envolve construção geométrica de retas perpendiculares, medida de segmento e construção de triângulo, em particular do triângulo retângulo de medidas 3 centímetros, 4 centímetros e 5 centímetros. Avalie se convém pedir aos estudantes que comparem o quadrado da medida da hipotenusa com a soma dos quadrados das medidas dos catetos, antecipando, assim, uma verificação particular do teorema de Pitágoras.
Para o exercício 19, se possível, proponha aos estudantes utilizarem um software de Geometria dinâmica como ferramenta para elaborar e resolver o problema.
PARA SABER MAIS
Construção da espiral de Arquimedes
Arquimedes (cêrca de 287 antes de Cristo-212 antes de Cristo), o maior matemático e físico da Antiguidade, viveu e morreu em Siracusa, cidade da Sicília (na época ainda uma colônia da Magna Grécia), que por dois anos resistiu ao cerco dos romanos graças às suas engenhosas invenções.
Embora não fosse feita apenas com o uso de régua e compasso, dos três famosos problemas de Geometria – a duplicação do cubo, a trissecção do ângulo e a quadratura do círculo –, a espiral de Arquimedes forneceu soluções para os dois últimos.
A espiral é definida como o lugar geométrico no plano de um ponto que se move uniformemente, partindo de um raio, ao longo do raio, enquanto esse raio, por sua vez, gira uniformemente em tôrno de sua origem.
Acompanhe os passos de um procedimento para a obtenção de alguns pontos de uma espiral.
1. Traçamos uma circunferência de raio medindo 8 centímetros e duas retas perpendiculares que passem pelo seu centro. Com um transferidor, vamos traçar bissetrizes dividindo-a em 16 partes iguais.
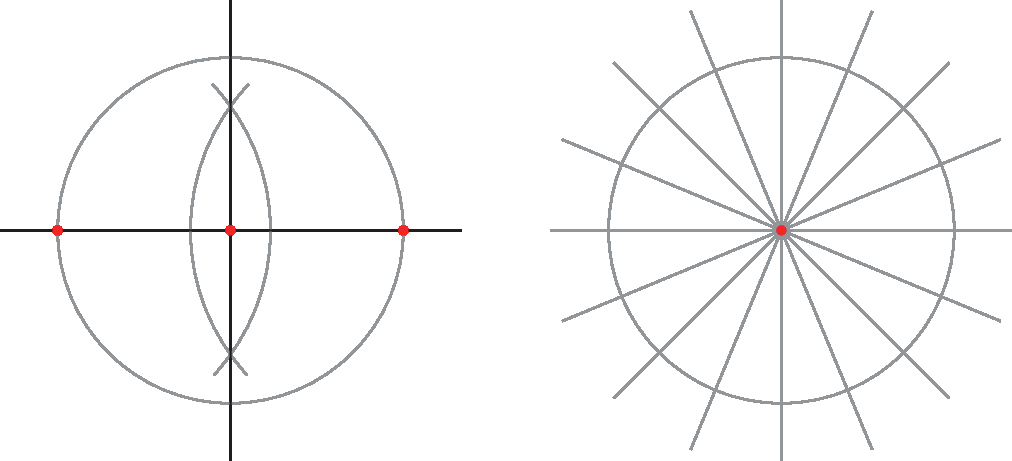
2. Usando uma régua, vamos marcar em um dos raios traçados, a partir do centro, pontos de 0,5 em 0,5 centímetro. Traçamos circunferências concêntricas que passem por esses pontos.
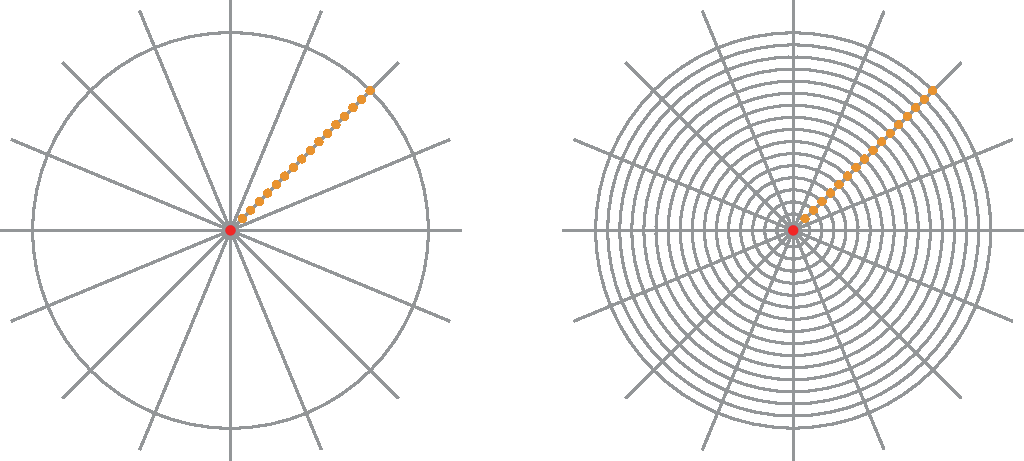
3. Com uma côr diferenciada, partindo do centro, marcamos uma sequência de pontos que são intersecção de um raio com uma circunferência – apenas um ponto por circunferência e por raio.
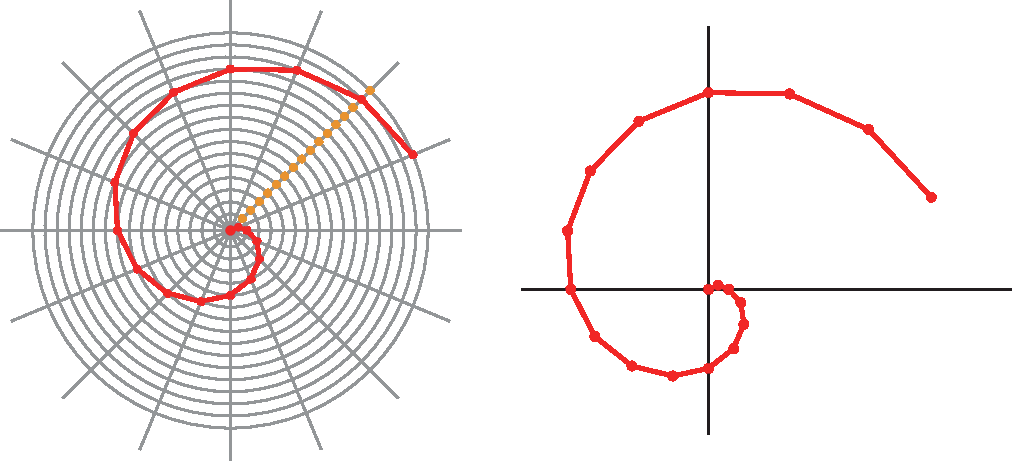
Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
No caderno, trace uma circunferência com raio medindo 8 centímetros, divida-a em 8 partes iguais e construa uma espiral semelhante à espiral apresentada.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Respostas e comentários
Construção de figura.
Para saber mais
Nesta seção, apresentamos a construção da espiral de Arquimedes. Comente com os estudantes que, ainda neste capítulo, o conceito de lugar geométrico será aprofundado.
Neste momento, eles utilizarão o conceito de bissetriz de ângulo – semirreta que divide um ângulo em dois ângulos congruentes entre si. Para facilitar as construções, sugere-se que eles utilizem transferidor. Se julgar conveniente, proponha uma apresentação das construções feitas. Eles podem realizar essas construções utilizando os recursos de softwares de Geometria dinâmica e, depois, expor as construções em um blog ou página web da escola. Desse modo, eles desenvolvem a competência geral 5 e, ainda, a competência geral 4, pois podem utilizar os recursos tecnológicos para produzir e para comunicar conhecimentos.
Incentive os estudantes a pesquisar mais informações sobre Arquimedes e suas contribuições para a Matemática, desenvolvendo, assim, a competência geral 1 e levando-os a perceber que a Matemática é um conjunto de saberes historicamente construídos.
A resolução da atividade do Agora é com você! está no início deste Manual, nas orientações específicas do capítulo 2.
TRABALHANDO A INFORMAÇÃO
Construindo gráfico de setores
A serra da Mantiqueira é uma cadeia montanhosa com área medindo aproximadamente .4350 quilômetros quadrados que se estende ao longo de três estados brasileiros: São Paulo, Minas Gerais e Rio de Janeiro. Essa região atrai muitos turistas em busca da tranquilidade das montanhas e do clima mais ameno.
Para planejar suas campanhas publicitárias em certo ano, uma agência de turismo fez uma pesquisa buscando conhecer melhor o perfil dos turistas da serra da Mantiqueira. Considere o resultado dessa pesquisa de acôrdo com a estação do ano.
|
Grupos de pessoas |
Inverno (em %) |
Demais estações do ano (em %) |
|---|---|---|
|
Grupos familiares com crianças |
42 |
|
|
Amigos ou casais de 18 a 25 anos |
15 |
|
|
Amigos ou casais de 26 a 50 anos |
26 |
16 |
|
Amigos ou casais acima de 50 anos |
12 |
13 |
|
Participantes de eventos empresariais |
43 |
Dados obtidos pela agência.
Apesar de ter havido lacunas na elaboração da tabela referente a essa pesquisa, em relação ao período de inverno foi possível construir um gráfico de setores.
Para representar o perfil dos turistas da serra da Mantiqueira no inverno por um gráfico de setores, procedemos assim:
• Calculamos a medida, em grau, do setor referente a cada uma das partes:
• 42% de 360graus = 0,42 ⋅ 360graus = 151,2graus ≃ 151graus
• 15% de 360graus = 0,15 ⋅ 360graus = 54graus
• 26% de 360graus = 0,26 ⋅ 360graus = 93,6graus ≃ 94graus
• 12% de 360graus = 0,12 ⋅ 360graus = 43,2graus ≃ 43graus

• Traçamos um círculo e nele construímos, com um transferidor, a partir de um raio qualquer, a sequência dos setores cujas medidas calculamos.
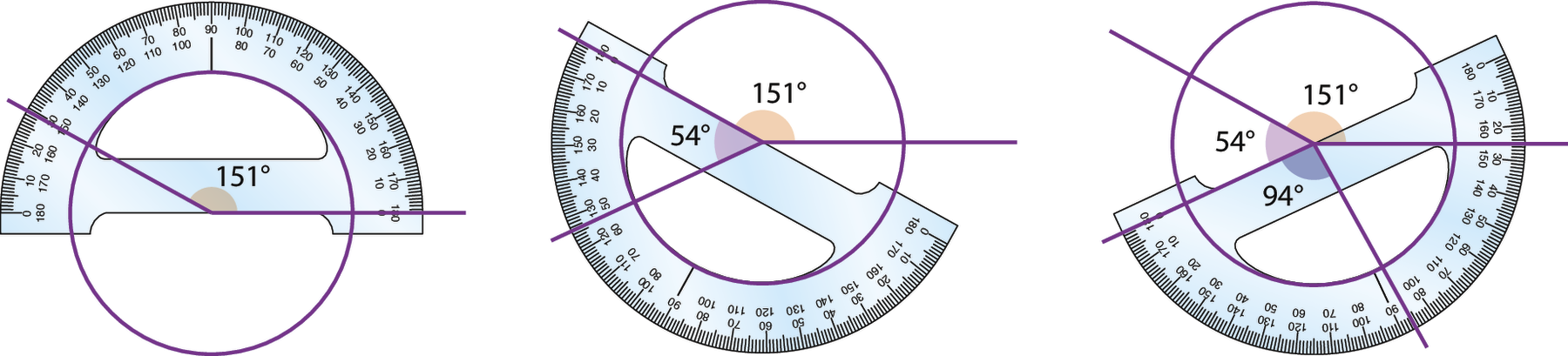
Respostas e comentários
Trabalhando a informação
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah dois três.
Esta seção possibilita aos estudantes construir um gráfico de setores e, assim, trabalhar de maneira que entendam melhor fatos importantes que afetam seu cotidiano, o que desenvolve a habilidade (EF08MA23).
Apresente aos estudantes a construção dos setores do gráfico na lousa, de modo que acompanhem e reproduzam cada etapa no caderno. Após a construção, ressalte com eles algumas considerações importantes:
• Como o gráfico é circular, reunindo todos os setores obtemos o círculo todo, ou seja, adicionando as medidas de todos os ângulos dos setores obtemos 360graus, assim como a soma das porcentagens de todos os setores representa 100%.
• Setores de mesmo ângulo representam regiões de mesmo tamanho no gráfico, ou seja, correspondem ao mesmo valor associado a eles (ou mesmos percentuais).
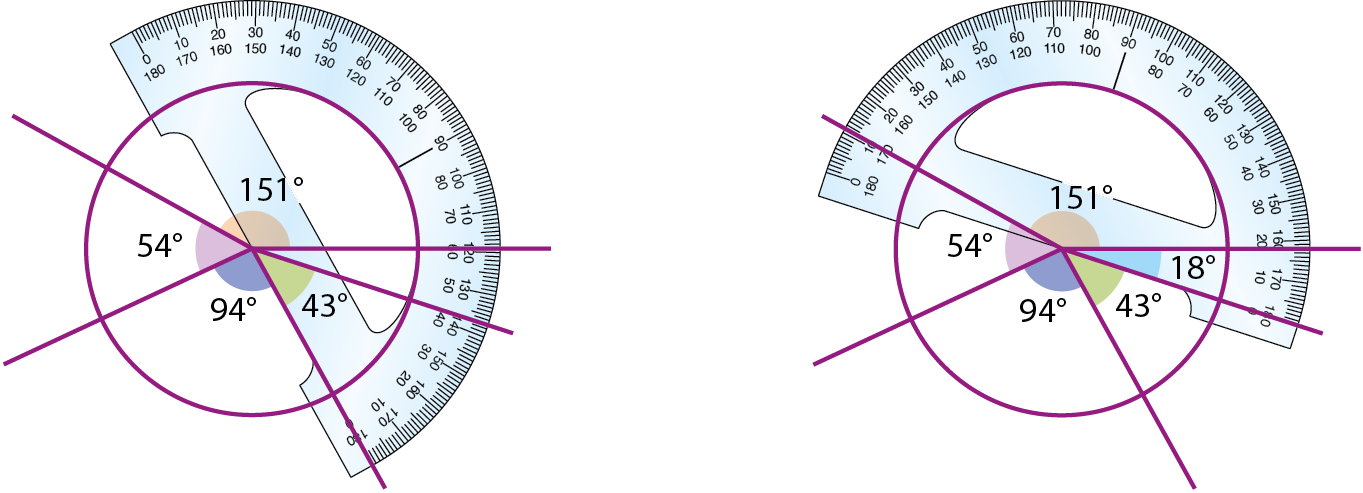
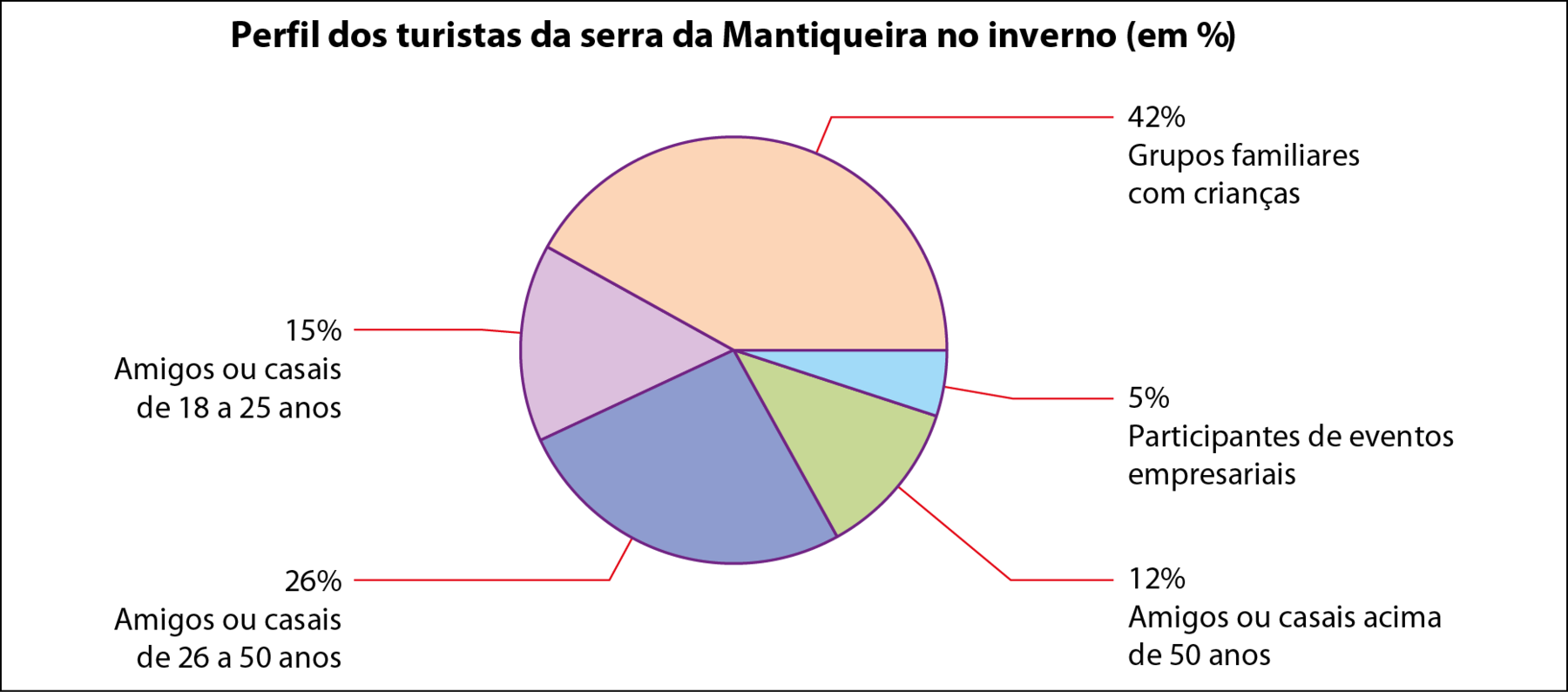
Note que a falta do último dado não impediu a construção do gráfico. O setor que falta para completar o círculo é o setor correspondente aos “Participantes de eventos”, referente, na tabela, à diferença entre 100% e a soma das outras porcentagens, isto é, 5%. Apenas para confirmar, podemos comparar a medida desse ângulo (18graus) com o cálculo:
5% de 360graus = 0,05 ⋅ 360graus = 18graus
• Identificamos e registramos cada setor com o nome e com a respectiva porcentagem.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
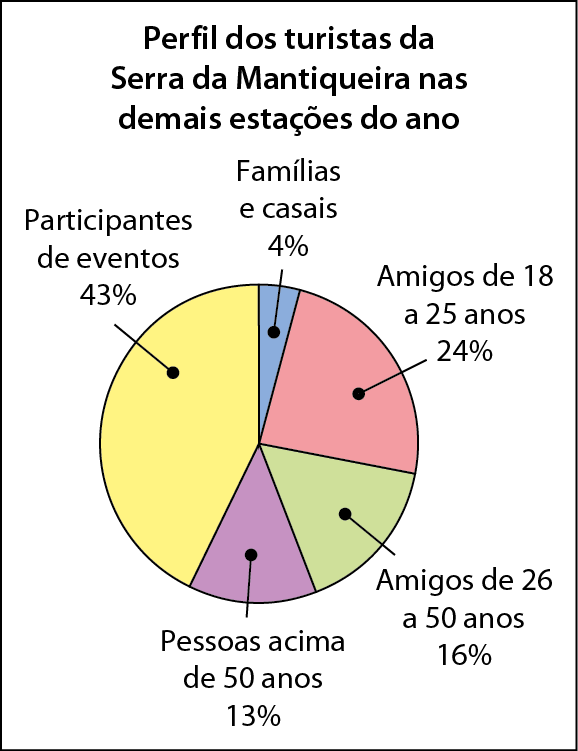
1 Sabendo que a porcentagem do grupo “Amigos ou casais de 18 a 25 anos” é seis vezes a de “Grupos familiares com crianças”, construa o gráfico que representa o perfil dos turistas nas demais estações do ano.
2 Compare os dois gráficos e escreva uma frase sobre o perfil dos turistas no inverno e nas demais estações do ano.
3

Com dois colegas, façam uma pesquisa com suas famílias e vizinhos (no mínimo 20 pessoas) sobre qual problema do seu bairro (água, cultura, educação, luz, moradia, saúde, segurança, transporte etcétera) eles consideram o mais urgente a ser resolvido pela gestão municipal. Registre os dados em uma tabela com as quantidades absolutas em uma coluna e com as respectivas porcentagens em outra coluna. Com base nessa tabela, construam um gráfico de setores. Apresente os dados obtidos ao professor e aos colegas.
Respostas e comentários
1. Construção de gráfico.
2. Respostas possíveis:
– No inverno, a maior parte dos turistas viaja em família, e a menor parte é para participar de eventos empresariais.
– Nas duas épocas pesquisadas há uma porcentagem parecida de turistas com mais de 50 anos.
3. Construção de gráfico.
Agora quem trabalha é você!
Na atividade 1, como a soma das porcentagens indicadas na tabela para as categorias “Demais estações do ano” é 72% (16 + 13 + 43 = 72), verificamos que a soma da porcentagem de “Famílias e casais” e “Amigos de 18 a 25 anos” é 28% (100 ‒ 72 = 28). Assim, sendo x a porcentagem relativa a “Famílias e casais”, obtemos x + 6x = 28; portanto, x = 4.
Assim, os estudantes devem concluir que 4% são do grupo “Famílias e casais”, e 24% são do grupo “Amigos de 18 a 25 anos”. Apresentamos um exemplo de gráfico de setores para essa questão:
Na atividade 2, compartilhe com toda a turma as frases criadas pelos estudantes.
Na atividade 3, o gráfico depende dos dados coletados pelos estudantes.
3. Lugares geométricos
Em anos anteriores, mesmo sem nos preocupar com uma definição formal, já trabalhamos com lugares geométricos (éle gê). Neste tópico, vamos estudar um pouco mais alguns lugares geométricos.
Lembra-se da abertura deste capítulo, quando leu “Vamos reinventar a roda?”? A roda é um objeto que, ao ser representado no plano, sem perspectiva, é limitado por uma circunferência, que é um lugar geométrico.
Em Geometria plana, estabelecemos a seguinte definição:
Um conjunto de pontos é um lugar geométrico se, e apenas se, atende a duas condições:
• todos os pontos desse conjunto têm uma propriedade;
• só os pontos desse conjunto de pontos têm essa propriedade.
A circunferência como um lugar geométrico
Observe como é simples verificar que a circunferência é um lugar geométrico.
Em um plano α, considere a circunferência de centro óh e de raio medindo r e a propriedade “pontos de α que estão à distância de medida r do ponto óh ”.
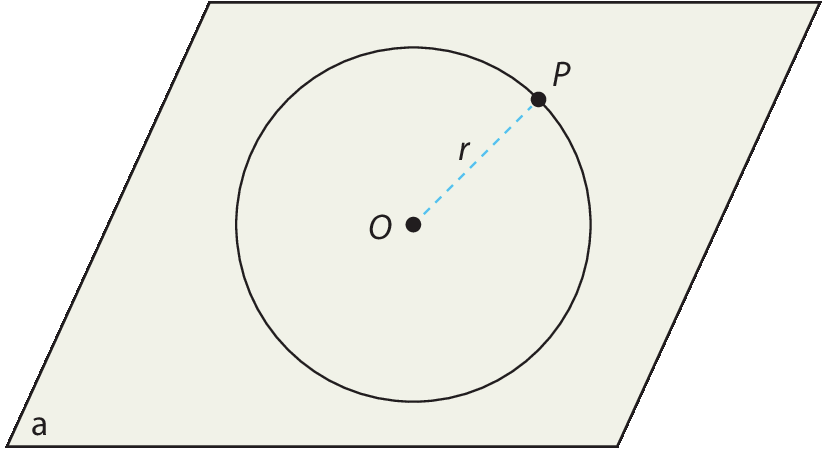
• Todos os pontos P dessa circunferência estão à distância de medida r do ponto óh.
• Só os pontos dessa circunferência estão à distância de medida r do ponto óh.
O lugar geométrico dos pontos de um plano que estão a uma distância fixa de um ponto fixo do plano é a circunferência de centro nesse ponto e raio de medida igual a essa distância.
Como você já estudou, para traçar uma circunferência de centro óh e raio de medida r, basta usar o compasso com abertura igual a r e fixar a ponta-sêca no ponto óh.
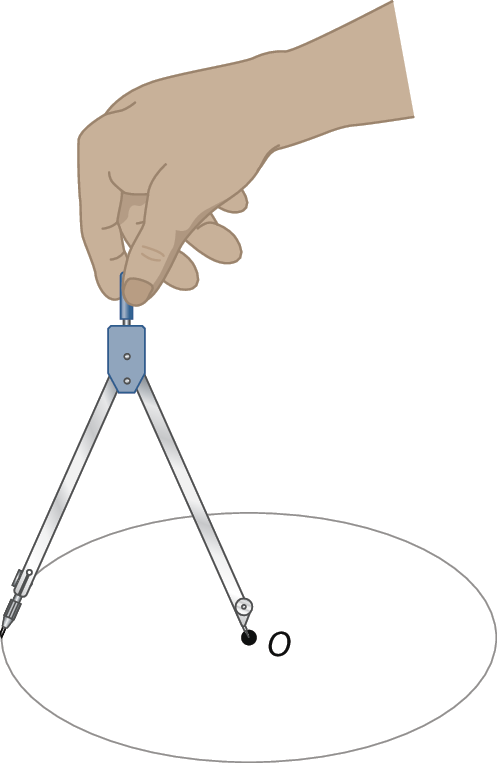
Ao girar o compasso com a volta completa, sem mexer na sua abertura, fica garantido que todos os pontos marcados pela grafite estão à distância de medida r de óh. E, exceto os pontos da circunferência, não há outro ponto do plano que esteja à distância de medida r de óh.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Respostas e comentários
3. Lugares geométricos
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um sete.
Neste tópico, serão apresentadas as definições de lugar geométrico, bissetriz de ângulos formados por duas retas concorrentes e mediatriz de um segmento, desenvolvendo-se a habilidade (ê éfe zero oito ême ah um sete). Ressalte aos estudantes as duas condições que definem um lugar geométrico.
O primeiro lugar geométrico a ser apresentado é a circunferência, cuja construção os estudantes já devem conhecer. Peça a cada estudante que desenhe uma circunferência em uma folha de papel avulsa. Depois, compartilhe os desenhos para perceberem que o raio da circunferência não estava definido, por isso surgiram circunferências de raios distintos; mas, apesar disso, em cada circunferência os pontos delas estão sempre à mesma distância de seu centro.
Em seguida, entregue aos estudantes uma folha de papel avulsa com um ponto marcado e peça a eles que desenhem a circunferência cujo centro seja esse ponto.
Determine uma medida para o raio e peça que desenhem novamente uma circunferência de centro no mesmo ponto demarcado, com a medida do raio indicado, determinando, assim, duas circunferências concêntricas.

Sugestão de leitura
Para ampliar e enriquecer o trabalho com esse tema, sugerimos:
OLIVEIRA, M. R. Explorando lugares geométricos através da resolução de problemas. Dissertação (Mestrado Profissional em Matemática na Rede Nacional), Instituto de Ciências Matemáticas e Computação, USP, 2016. Disponível em: https://oeds.link/LzsLQp. Acesso em: 6 junho 2022.
Esta dissertação tem o objetivo de resgatar a importância do ensino do desenho geométrico aplicado à resolução de problemas de construção geométrica plana.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
20 No caderno, trace uma reta r qualquer e marque em r dois pontos, a e B, distantes 6 centímetros. Obtenha pontos distantes:
a) 5 centímetros de a e 3 centímetros de B;
b) 3 centímetros de a e 5 centímetros de B;
c) 4 centímetros de a e 3 centímetros de B;
d) 3 centímetros de a e 3 centímetros de B;
e) 2 centímetros de a e 3 centímetros de B.
21 Construa, quando possível, e depois classifique quanto aos lados e quanto aos ângulos um triângulo com lados medindo:
a) 7 centímetros, 4 centímetros e 4 centímetros;
b) 7 centímetros, 7 centímetros e 7 centímetros;
c) 7 centímetros, 8 centímetros e 8 centímetros;
d) 10 centímetros, 6 centímetros e 8 centímetros.
Pontos equidistantes dos extremos de um segmento
Mediatriz de um segmento
A palavra equidistante significa “a igual distância”.
Vamos considerar um segmento
ABmedindo 4 centímetros e obter pontos que estão a uma mesma distância de a e de B.
Por exemplo:
• pontos C e D à distância 4 centímetros de a e de B;
• pontos ê e F à distância 3,5 centímetros de a e de B;
• pontos G e H à distância 3 centímetros de a e de B;
• pontos ih e J à distância 2,5 centímetros de a e de B.
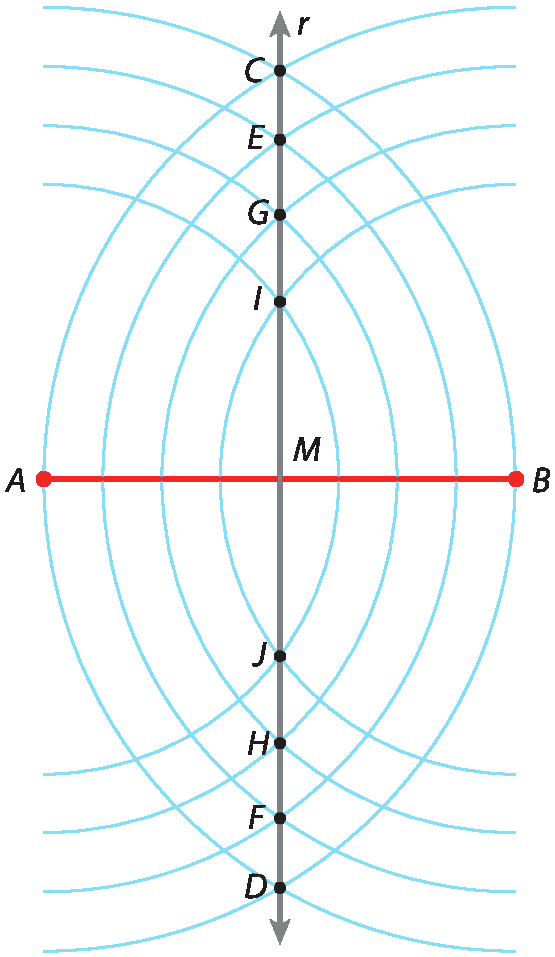
Os pontos C, D, ê, F, G, H, ih e J estão alinhados e pertencem à reta r que passa pelo ponto médio M de
AB, pois M também é equidistante de a e de B.
A reta r é a mediatriz do segmento
AB.
O lugar geométrico dos pontos de um plano equidistantes dos extremos de um segmento
segmento ABé a mediatriz desse segmento.
Dado um segmento
AB, para traçar sua mediatriz basta obter dois pontos equidistantes de a e de B e traçar a reta que passa por eles. Note que essa reta é perpendicular ao segmento
AB, no qual a intersecção determina o seu ponto médio M.
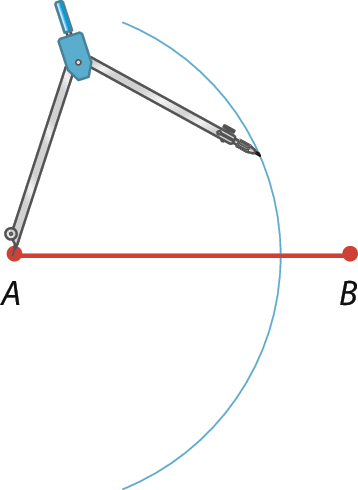
Acompanhe os passos para construir com régua e compasso a reta mediatriz ao segmento
AB1. Com a ponta-sêca do compasso em a e abertura maior que a metade de A bê, traçamos um arco.
Respostas e comentários
20. a) b) c) d) Construção de figura.
20. e) Não é possível obter ponto.
21. a) Isósceles; obtusângulo.
21. b) Equilátero; acutângulo.
21. c) Isósceles; acutângulo.
21. d) Escaleno; retângulo.
Exercícios propostos
As resoluções dos exercícios 20 e 21 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 20, os estudantes devem aplicar o conceito de circunferência como lugar geométrico para determinar os pontos solicitados.
Pontos equidistantes dos extremos de um segmento
Para desenvolver esse conteúdo, proponha aos estudantes que representem um segmento
A Bem uma folha de papel sulfite e, em seguida, façam uma circunferência com centro em a e raio m um pouco maior que a metade de
segmento A Be, depois, uma circunferência com raio m e centro em B. Eles devem marcar os pontos de intersecção dessas circunferências. Em seguida, com raio n um pouco maior que m, devem traçar uma circunferência com centro em a e outra com centro em B e, por fim, destacar os pontos de intersecção entre elas. Eles devem repetir esse procedimento até perceberem que os pontos marcados são colineares, isto é, determinam uma reta.
2. Com a ponta-sêca do compasso em B e com a mesma abertura, traçamos outro arco, que intersecta o primeiro. Obtemos, assim, os pontos P e Q.
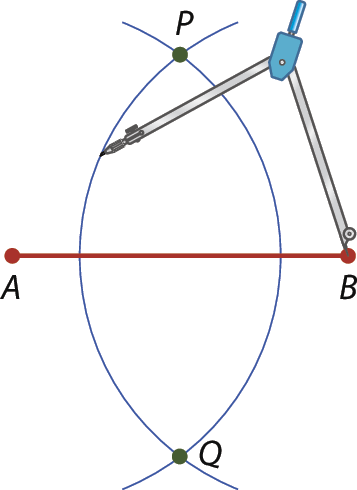
3. Traçamos a reta
PQ, perpendicular a
AB, que intersecta o segmento
ABem M. Assim, determinamos o ponto médio do segmento
AB.
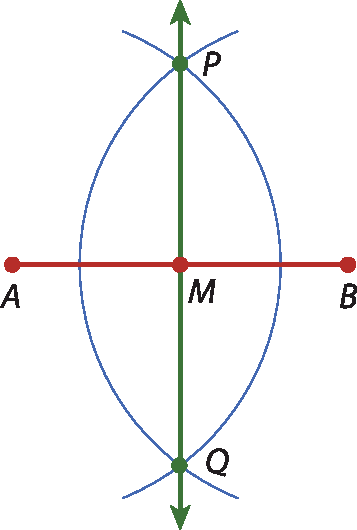
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Observe que, nessa construção, o polígono APBQ é um losango, já que
AP≅
PB≅
BQ≅
QA(a abertura do compasso é a mesma). Então,
PQe
ABsão as diagonais desse losango. Essas diagonais dividem o losango em quatro triângulos retângulos e isósceles congruentes, o que pode ser verificado por meio de dobradura. Dessa fórma, M é o ponto médio de
AB.
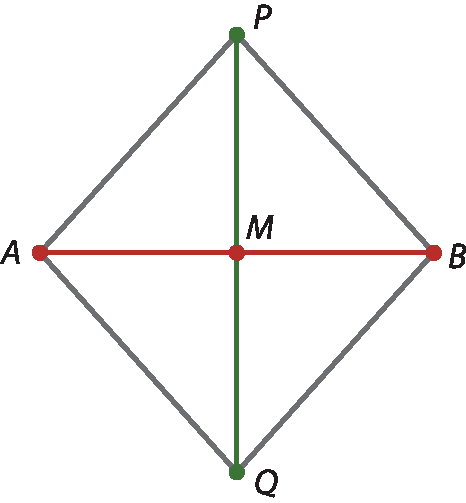
Assim, as diagonais de um losango são perpendiculares entre si e se cortam no ponto médio.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
22 Desenhe no caderno duas retas, r e s, concorrentes em um ponto P e um segmento de reta
ABqualquer, fora de r e de s. Em seguida, com régua e compasso, construa em r e s quatro segmentos de reta,
PQ,
PR,
PSe
PT, com Q e S pertencentes a r, e R e T pertencentes a s, todos congruentes a
PT.
a) Traçando os segmentos
QR,
RS,
STe
TQ, que polígono obtemos?
b) Os segmentos
QSe
RTsão as diagonais desse polígono. Essas diagonais se intersectam no ponto médio? Que ponto é esse?
23 Releia os passos para obter o ponto médio de um segmento e responda: por que, no primeiro passo, a abertura do compasso deve ser maior que a metade da medida do segmento dado?
24 No caderno, desenhe um triângulo qualquer e trace as mediatrizes de dois de seus lados. Com a ponta-sêca do compasso no ponto de encontro dessas mediatrizes e abertura dele até um dos vértices, trace uma circunferência.
a) A circunferência passa pelos três vértices?
b) Trace a mediatriz do outro lado do triângulo. As três mediatrizes se encontram em um único ponto?
25 Decalque em uma folha de papel transparente o paralelogramo a bê cê dê representado a seguir.
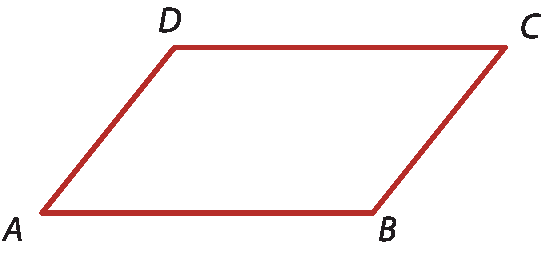
Em seguida, com régua e compasso, obtenha o ponto médio da diagonal
ACe o ponto médio da diagonal
BD. Esses pontos médios coincidem? O que você pode concluir sobre a intersecção das diagonais de um paralelogramo?
26

Hora de criar – Elabore um problema sobre as construções geométricas com o apôio de um software de Geometria dinâmica e lugar geométrico. Troque com um colega e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Respostas e comentários
22. a) Retângulo.
22. b) Sim; o ponto P.
23. Porque, caso contrário, os dois arcos não se cruzariam nos pontos que determinam a reta que passa pelo ponto médio.
24. a) Sim.
24. b) Sim.
25. Construção de figura. Sim. Espera-se que os estudantes concluam que as diagonais de um paralelogramo se intersectam no ponto médio.
26. Resposta pessoal.
Pontos equidistantes dos extremos de um segmento
Apresente aos estudantes a construção da mediatriz de um segmento na lousa. Ao final, peça-lhes que a construam no caderno.
Espera-se que percebam que essa construção determina retas perpendiculares que passam pelo ponto médio do segmento considerado. Lembre-os de terem cuidado no manuseio do compasso, a fim de que não se machuquem com a ponta-sêca.
Exercícios propostos
As resoluções dos exercícios 22 e 24 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 23, espera-se que os estudantes percebam que, caso a medida de abertura do compasso seja menor do que a metade do segmento dado, não se determinam pontos de intersecção entre as circunferências construídas.
No exercício 25, em que os estudantes têm de decalcar a figura, eles devem traçar uma diagonal
A Ce determinar seu ponto médio construindo a mediatriz dessa diagonal. Em seguida, devem traçar a outra diagonal
B De determinar seu ponto médio.
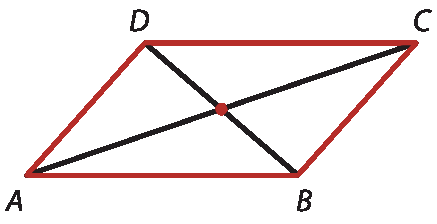
Para resolver o exercício 26, sugere-se primeiro apresentar aos estudantes alguns exemplos de problemas que possam ser elaborados e discutir sua resolução com eles. Em seguida, os estudantes podem criar outros problemas envolvendo a definição de lugar geométrico de circunferência e de mediatriz.
Pontos equidistantes de duas retas concorrentes
Bissetriz de um ângulo
Outro conceito referente a lugar geométrico que já estudamos é a bissetriz de um ângulo.
Lembrando: bissetriz de um ângulo é a semirreta com origem no vértice desse ângulo e que o divide em dois outros ângulos congruentes.
Nas figuras a seguir, a semirreta
O Cdivide o ângulo
A O Bem dois ângulos congruentes, ou seja, em dois ângulos de mesma medida. Logo,
a semirreta OCé bissetriz do ângulo
o ângulo AOBem cada caso.
Uma propriedade importante de qualquer ponto da bissetriz de um ângulo é que ele está a igual distância dos lados desse ângulo.
Observe que os segmentos
CAe
CB, que indicam a distância de C aos lados do ângulo, são congruentes. Fazendo uma dobradura pela bissetriz, verificamos que o ponto B e o ponto a se sobrepõem.
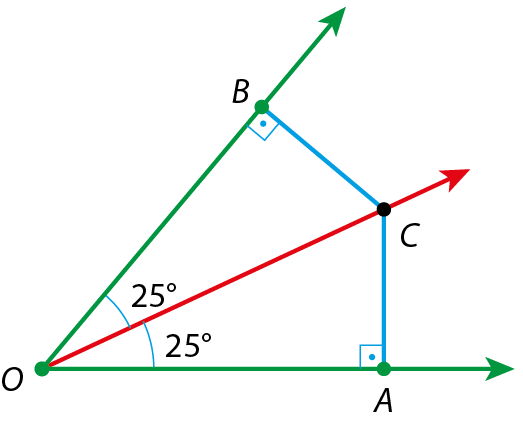
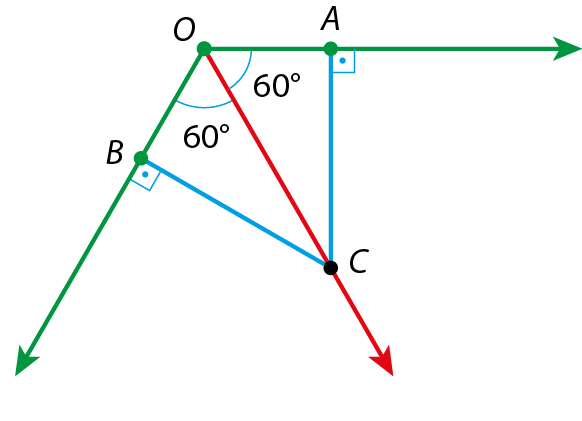
Como estudamos anteriormente, a bissetriz de um ângulo
A O Bpode ser obtida por dobradura de modo que um lado se sobreponha ao outro lado.
A bissetriz também pode ser traçada com régua e transferidor ou com régua e compasso. Acompanhe os passos da construção.
1. Com a ponta-sêca do compasso em óh, traçamos um arco determinando M e N.
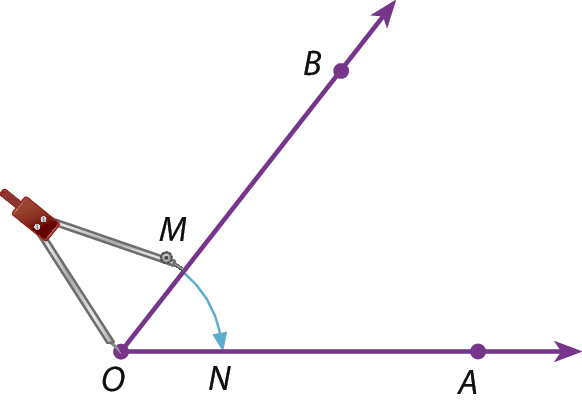
2. Com a ponta-sêca do compasso em N e depois em M, traçamos com a mesma abertura do compasso os arcos que se intersectam em D.
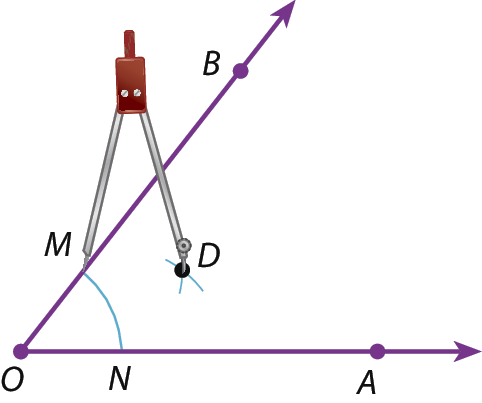
3. Traçamos a semirreta
a semirreta OD, que é a bissetriz do ângulo
A O B.
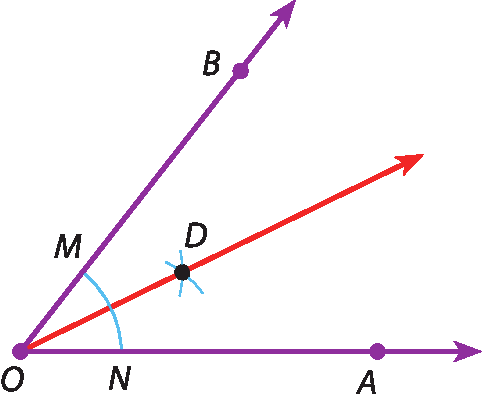
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)


Respostas e comentários
Pontos equidistantes de duas retas concorrentes
Neste tópico, abordamos a bissetriz de um ângulo como lugar geométrico e os passos para sua construção com régua e compasso. Apresente aos estudantes a construção na lousa e peça-lhes que façam o mesmo no caderno. Em seguida, para verificar, proponha a eles que meçam com o transferidor os ângulos formados e confirmem que têm mesma medida.
Prepare folhas de papel avulsas com ângulos de medidas inteiras, de modo que suas bissetrizes também determinem dois ângulos de medidas inteiras, e entregue-as aos estudantes. Eles devem construir as bissetrizes com régua e compasso e, em seguida, verificar os ângulos obtidos medindo com o transferidor.
Como aplicação da bissetriz como lugar geométrico, apresentamos outro lugar geométrico: o par de retas que contém as bissetrizes dos ângulos formados por duas retas concorrentes.
Lembre os estudantes de utilizar o compasso com cuidado, a fim de que não se machuquem com a ponta-sêca.
Considere a situação a seguir.
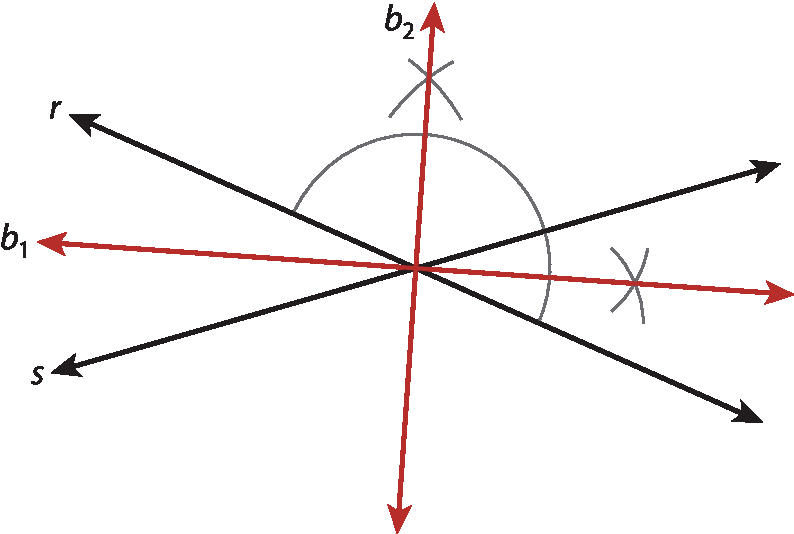
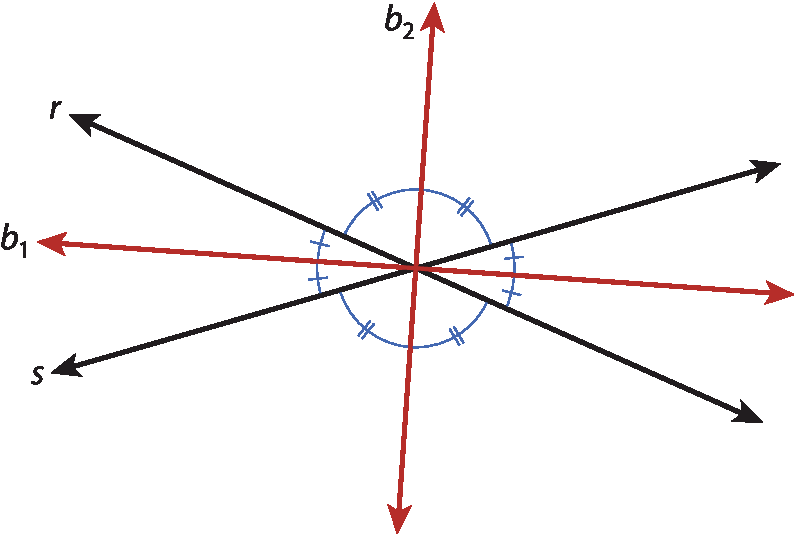
Dadas duas retas concorrentes r e s, obter o lugar geométrico dos pontos cuja propriedade é “estar à mesma distância dessas retas”.
Duas retas r e s concorrentes formam quatro ângulos, dois a dois, opostos pelo vértice.
O lugar geométrico dos pontos do plano equidistantes de duas retas concorrentes é o par de retas que contém as bissetrizes dos ângulos formados por essas retas.
Dadas duas retas r e s, concorrentes, para obter esse lugar geométrico basta construir as bissetrizes de dois ângulos adjacentes formados por elas e prolongá-las.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
27 Nas figuras a seguir,
semirreta O Mé bissetriz de
ângulo AOB. Determine:
a) m(
ângulo MOB), sabendo que m(
ângulo AOB) = 60graus.
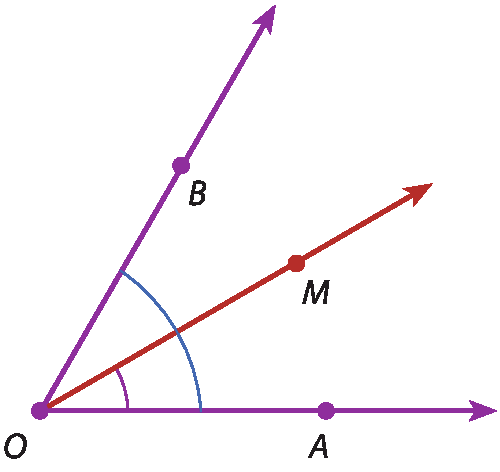
b) m(
ângulo AOB), sabendo que m(
o ângulo AOM) = 40graus.
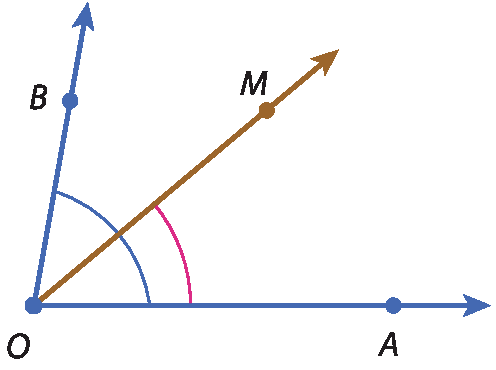
28 Nesta figura, m(
ângulo AOB) = 30graus e m(
ângulo BOC) = 70graus,
A semirreta OMé bissetriz de
ângulo AOBe
A semirreta ONé bissetriz de
ângulo BOC.
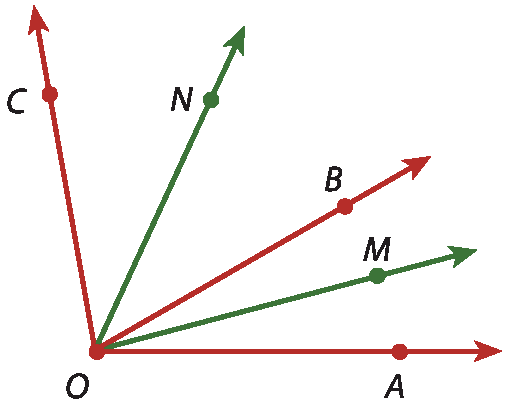
Calcule:
a) m(
ângulo AOC);
b) m(
ângulo AOM);
c) m(
o ângulo NOC);
d) m(
ângulo MON).
29 Copie no caderno a figura a seguir.
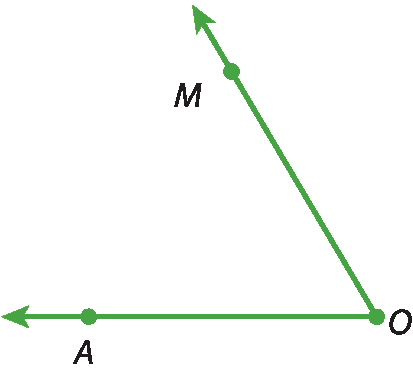
Sabendo que
A semirreta OMé a bissetriz do ângulo
ângulo AOBconstrua a semirreta
OB
Respostas e comentários
27. a) 30graus
27. b) 80graus
28. a) 100graus
28. b) 15graus
28. c) 35graus
28. d) 50graus
29. Construção de figura.
Exercícios propostos
No exercício 27, ao aplicar a definição de bissetriz, podem-se resolver os itens a e b.
No item a, como a medida de
ângulo A O Bé 60graus e como
semirreta O Mé bissetriz, verificamos que a medida de
ângulo A O Me de
ângulo M O Bé 30graus (pois 60 : 2 = 30). Já no item b, como a medida de
ângulo A O Mé 40graus, verificamos que a medida de
ângulo A O Bé 90graus (pois 2 · 40 = 80).
Para o exercício 28, verificamos:
a) a medida de
ângulo A O Cé 100graus, pois é a soma das medidas dos ângulos
A O Be
B O Cou seja, 30 + 70 = 100.
b) como a medida de
ângulo A O Mé igual à de
ângulo M O B, pois
semirreta O Mé bissetriz de
ângulo A O Bcuja medida é 30graus, verificamos que a medida desses ângulos é 15graus (30 : 2 = 15).
c) a medida de
ângulo N O Cé igual à metade da medida de
ângulo B O Cpois
semirreta O Né bissetriz desse ângulo; assim,
ângulo N O Cmede 35graus.
d) a medida de
ângulo M O Nequivale à soma das medidas dos ângulos
M O Be
B O N; dos itens anteriores, verificamos que
ângulo B O Nmede 35graus (pois é congruente a
ângulo N O C) e
ângulo M O Bmede 15graus (pois é congruente a
ângulo A O M). Assim,
ângulo M O Bmede 50graus (35 + 15 = 50).
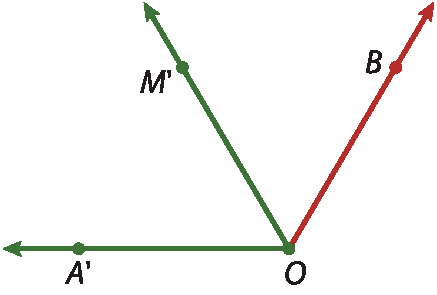
A seguir, apresentamos a figura obtida na construção solicitada no exercício 29. Nessa construção, os estudantes devem aplicar o conceito de bissetriz como lugar geométrico e a definição de ângulos congruentes.
Para obter essa construção basta seguir os passos:
• Com centro em óh, traçar uma circunferência e marcar os pontos á linha e ême linha que são intersecção da circunferência com os lados do ângulo
A O M.
• Com centro em ême linha e raio
segmento A linha M linha, traçar um arco que intersecte a circunferência, determinando o ponto B.
• Traçar a semirreta
semirreta OB.
30 Sendo x a medida de um ângulo, observe a figura em que
semirreta O Ae
semirreta O Fsão semirretas opostas.
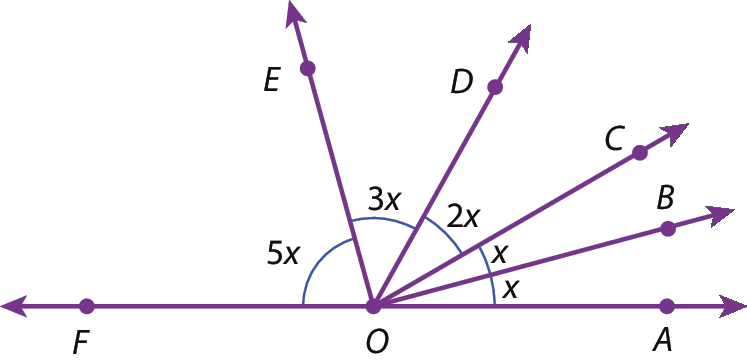
a) Qual é o ângulo congruente a
ângulo AOBE a
ângulo AOC
b) Qual é o ângulo congruente a
ângulo BODE a
ângulo COE
c) Qual é o valor de x ?
d)
OBé bissetriz de algum dos ângulos destacados? De qual? E
OCE
ODE
OE31 Copie a figura a seguir, em que x e y representam as medidas de
ângulo AOBe
ângulo BOC, respectivamente, e os pontos a e C são colineares.
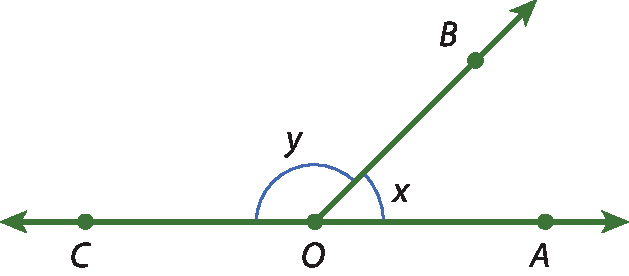
Com régua e compasso, construa as bissetrizes
OMde
ângulo AOBe
ONde
ângulo BOCe, em seguida, responda às questões.
a) Quanto vale x + y ?
b) Qual é a medida de
ângulo MOB? E de
ângulo BON?
c) Qual é a medida de
ângulo M O N?
d) O que você pode dizer a respeito das retas
OMe
ON?
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Desenhe um triângulo qualquer e trace as bissetrizes de seus ângulos internos. O que você observa a respeito da intersecção dessas bissetrizes?
Pontos equidistantes de duas retas paralelas

Considere a situação a seguir.
Dadas duas retas paralelas r e s, obter o lugar geométrico dos pontos cuja propriedade é “estar à mesma distância dessas retas”.
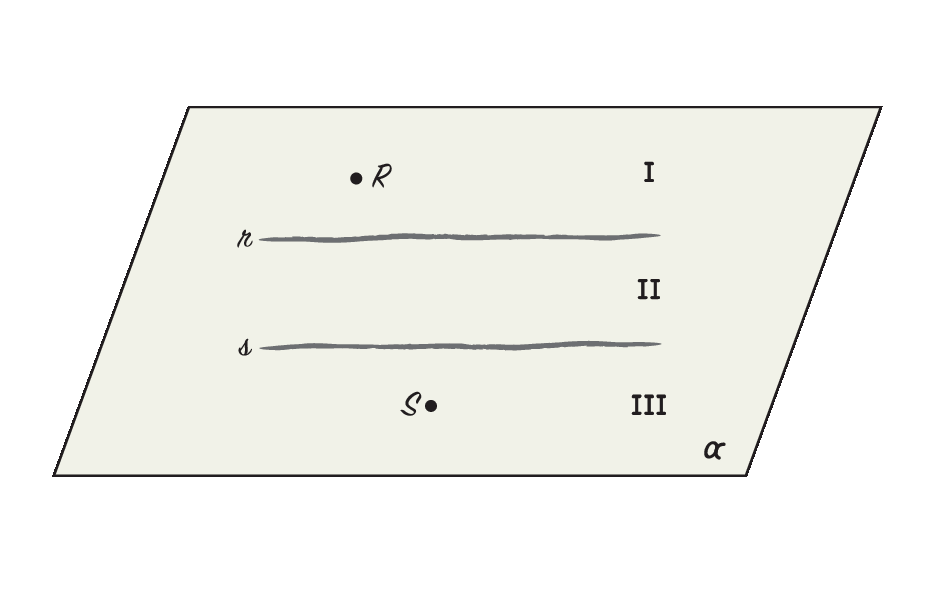
Vamos raciocinar elaborando um esbôço à mão livre. Traçamos duas retas supostamente paralelas. Elas dividem o plano em três regiões. Os pontos procurados necessariamente devem estar na região dois, entre as retas. Note que um ponto qualquer R da região um está mais próximo de r e que um ponto qualquer S da região três está mais próximo de s.
Respostas e comentários
30. a)
ângulo BOC e COD.
30. b)
ângulos D O E; E O F.
30. c) 15graus
30. d) Sim,
ângulo A O C. Sim,
ângulo A O D. Sim,
ângulo B O E. Sim,
ângulo C O F.
31. Construção de figura.
31. a) 180graus
31. b)
x sobre y; y sobre 2.
31. c) 90graus
31. d) São perpendiculares.
Pense mais um poucoreticências: As três bissetrizes intersectam-se em um único ponto.
Exercícios propostos
No exercício 30, verificamos:
a) O ângulo congruente a
A O Bé
B O Cpois ambos apresentam medida x. O ângulo congruente a
A O C é C O D, pois ambos apresentam medida 2x.
b) O ângulo congruente a
B O Dé
D O E, pois ambos apresentam medida 3x. O ângulo congruente a
C O E é E O F, pois ambos apresentam medida 5x.
c) Como
O A e O Fsão semirretas opostas, formam um ângulo raso
A O F. Portanto, a soma das medidas dos ângulos mostrados na figura deve ser 180graus: x + x + 2x + 3x + 5x = 180graus, o que implica 12x = 180graus; portanto, x = 15graus.
d)
semirreta O Bé bissetriz do ângulo
A O C,pois o divide em dois ângulos congruentes
A O B e B O C, ambos de medida x.
semirreta OCé bissetriz do ângulo
A O D, pois o divide nos ângulos congruentes
A O C e C O D, ambos de medida 2x.
semirreta ODé bissetriz do ângulo
B O E, pois o divide nos ângulos congruentes
B O De
D O E,ambos de medida 3x.
semirreta O Eé bissetriz do ângulo
C O F, pois o divide nos ângulos congruentes
C O E e E O F, ambos de medida 5x.
No exercício 31, verificamos:
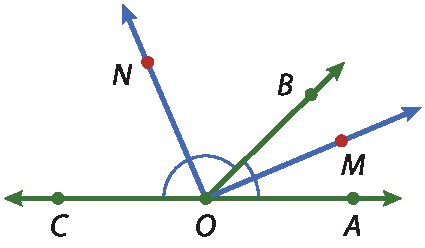
a) Como os pontos a, óh e C são colineares, as semirretas
A O e O Csão opostas. Portanto,
A O Cé um ângulo raso; assim, sua medida é 180graus. Além disso, a semirreta
O Bdivide este ângulo em
A O B e B O C; logo, x + y = 180graus.
b) Como
semirreta OMé bissetriz de
A O B, divide esse ângulo em dois ângulos congruentes, um deles sendo
M O B. Portanto, a medida de
M O Bé metade da medida x de
A O B; assim, m(
ângulo M O B) =
x sobre 2. Como
semirreta ONé bissetriz de B
OC, divide esse ângulo em dois ângulos congruentes, um deles sendo
B O N. Portanto, a medida de
B O Né metade da medida y de
B O C; assim, m
ângulo B O N=
y sobre 2.
c) A semirreta
O Bdivide o ângulo
M O Nem
M O Be
B O N; logo, m(
ângulo M O N) = m(
ângulo M O B) + m(
ângulo B O N). Pelo item b, m(
ângulo M O N) =
x sobre 2+
y sobre 2=
meio(x + y). Pelo item a, m(
ângulo M O N) =
meio· (x + y) =
meio· 180graus= 90graus. Ou seja,
M O Né um ângulo reto.
d) Pelo item c, podemos afirmar que as retas são perpendiculares, pois duas semirretas suas determinam um ângulo reto.
Pense mais um poucoreticências
A resolução da atividade está no início deste Manual, nas orientações específicas do capítulo 2.
Vamos imaginar um ponto P qualquer da região dois, que está à mesma distância de r e de s. A distância de P a r é indicada no esbôço pela medida do segmento perpendicular a r com extremidades em P e em um ponto a de r.
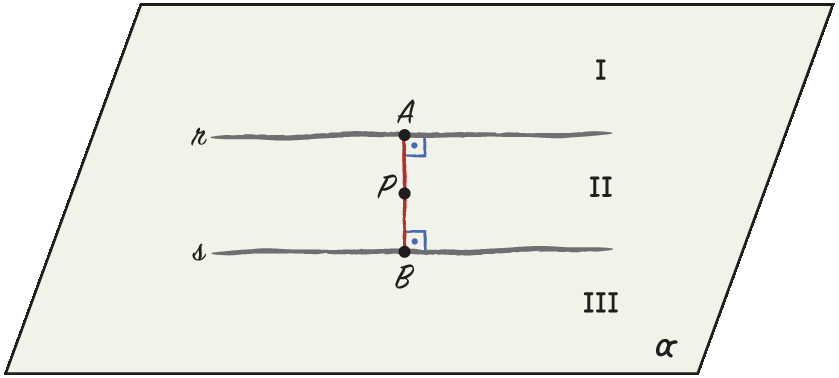
Analogamente, a distância de P a s é indicada pela medida do segmento perpendicular a s com extremidades em P e em um ponto B de s.
Então, P é o ponto médio do segmento
segmento AB, perpendicular a r e a s.
A mediatriz do segmento
segmento AB, sendo perpendicular a ele, é paralela às retas r e s, e todos os seus pontos, assim como o ponto P, são equidistantes de r e de s.
O lugar geométrico dos pontos equidistantes de duas retas paralelas r e s é a reta paralela a elas, que é mediatriz de qualquer segmento
AB, perpendicular a ambas, com a em r e com B em s.
A construção com régua e compasso desse lugar geométrico segue os passos seguintes.
1. Marcamos um ponto a qualquer em r e traçamos a perpendicular a r por a, obtendo B em s.
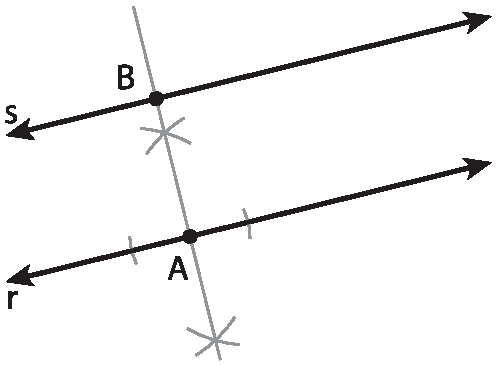
2. Traçamos a mediatriz do segmento
segmentos AB, obtendo a reta m.
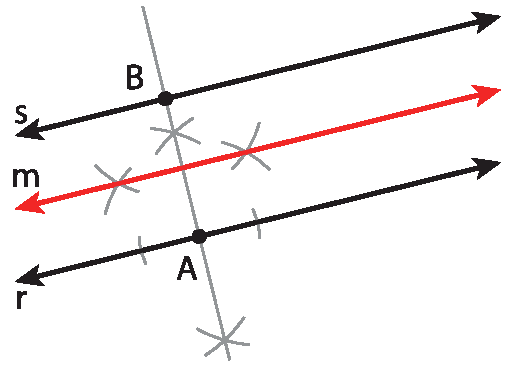
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
32 Fixando a régua no caderno, trace duas retas r e s, paralelas, uma em cada borda da régua. A seguir, obtenha o lugar geométrico dos pontos equidistantes dessas retas.
33 No caderno, trace duas retas r e s, concorrentes. Alinhando uma borda da régua em r, trace a reta t, paralela a r pela outra borda da régua. Da mesma maneira, trace a reta u, paralela a s. A seguir, obtenha o lugar geométrico dos pontos equidistantes dessas quatro retas.
34 O lugar geométrico obtido no exercício anterior é constituído de apenas um ponto óh. Com a ponta-sêca do compasso em óh e com abertura igual à distância dele até qualquer uma das retas, trace uma circunferência. Essa circunferência é tangente às quatro retas?
35 Considere a construção obtida no exercício 34 e responda:
a) Qual é o polígono obtido cujos vértices são intersecções das retas r, s, t e u? Quais são as características desse polígono?
b) Qual é a relação entre o ponto óh e esse polígono?
36

Hora de criar – Em dupla, elaborem um problema cada um sobre construções de lugares geométricos com o apôio de um software. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Respostas e comentários
32. Construção de figura.
33. Construção de figura.
34. Construção de figura. Sim.
35. a) Paralelogramo; possui lados paralelos, com lados e ângulos opostos congruentes.
35. b) Espera-se que os estudantes percebam que o ponto óh é o centro do polígono, que corresponde ao ponto de encontro de suas diagonais.
36. Resposta pessoal.
Pontos equidistantes de duas retas paralelas
Neste tópico, tratamos de outro lugar geométrico determinado pelos pontos equidistantes de duas retas paralelas.
Apresente a construção na lousa para os estudantes acompanharem todos os passos. Em seguida, peça-lhes que reproduzam essa construção no caderno. Se julgar adequado, proponha a eles que discutam a construção em duplas, o que enriquecerá o aprendizado.
Exercícios propostos
Seguindo os procedimentos 1 e 2 indicados, no exercício 32, obtemos:
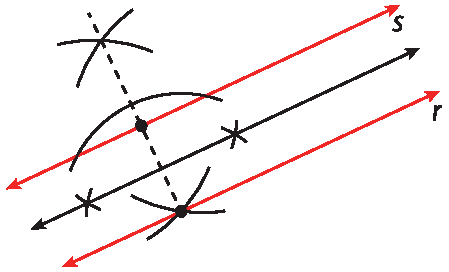
As resoluções dos exercícios 33 a 35 estão no início deste Manual, nas orientações específicas do capítulo 2.
Para o exercício 36, incentive os estudantes a elaborar os problemas e verificar sua resolução antes de trocarem com os colegas. Se possível, solicite a alguns estudantes que apresentem na lousa o problema elaborado.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 A figura a seguir é uma composição com peças do tangram. Faça uma cópia no caderno e destaque retas que passem pelos lados dos polígonos que sejam:
a) paralelas;
b) concorrentes;
c) concorrentes perpendiculares;
d) coincidentes.
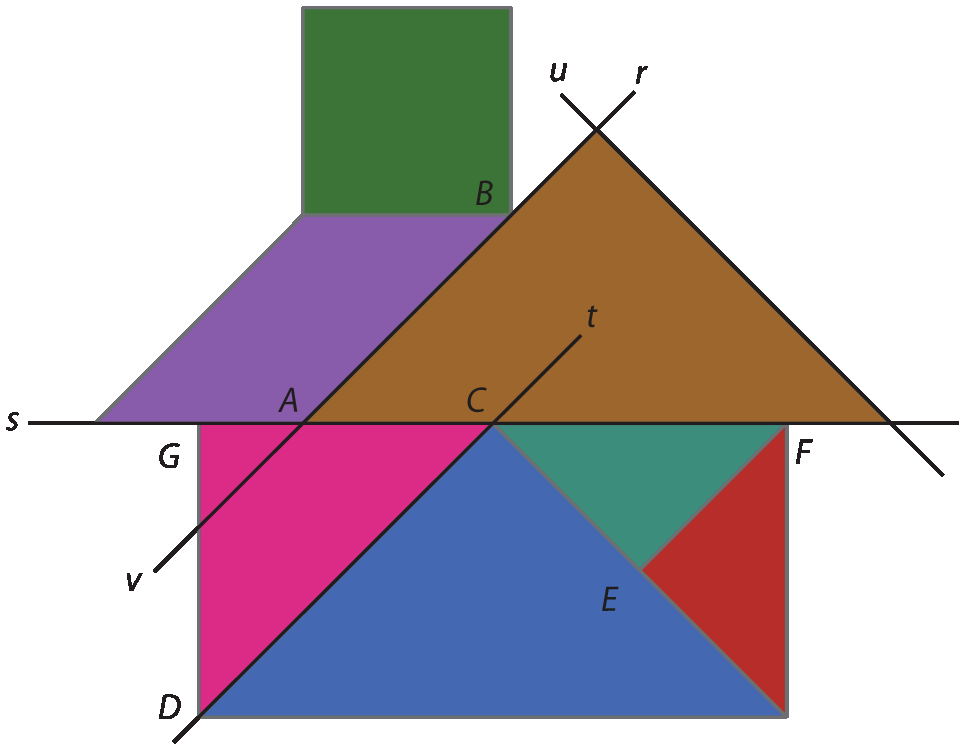
2 Ainda na cópia da figura do exercício anterior, use letras para nomear os vértices dos polígonos. Depois, escreva:
a) três pares de segmentos paralelos;
b) três pares de segmentos consecutivos;
c) três pares de segmentos colineares;
d) três pares de segmentos congruentes.
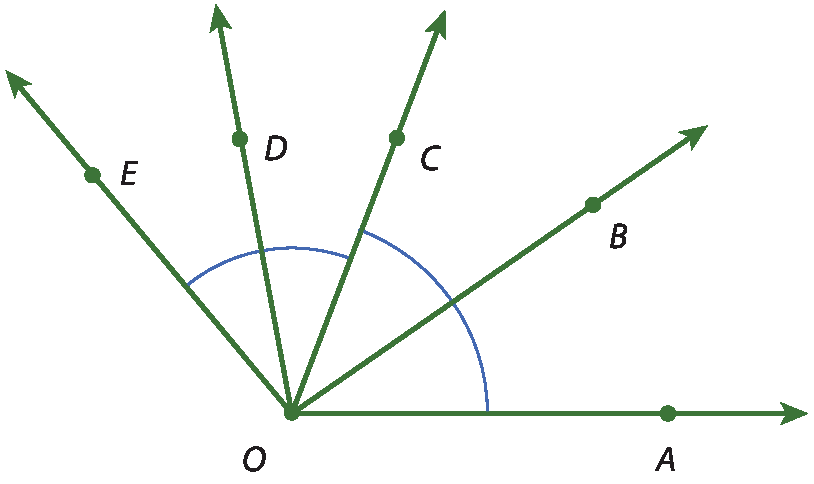
3 Considere medida do(
o ângulo AOC) = 70graus, medida do(
o ângulo COE) = 60graus,
a semirreta OBé bissetriz de
o ângulo AOCe
a semirreta ODé bissetriz de
a semirreta COECalcule a medida de
a semirreta BOD.
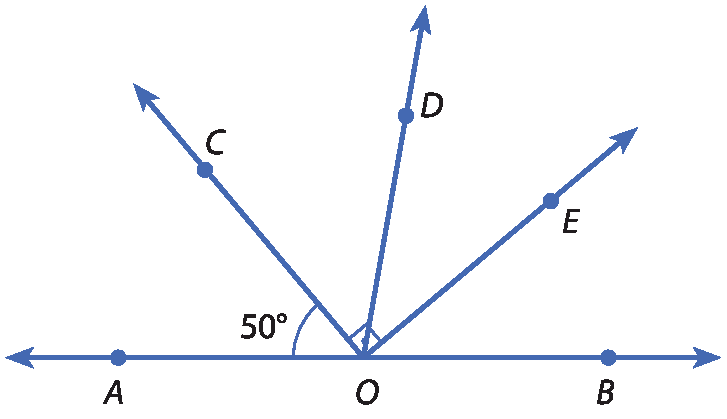
4 Na figura a seguir,
a semirreta OCé bissetriz de
ângulo AOD. Explique por que
a semirreta OEé bissetriz de
o ângulo BOD.
5 No caderno, decalque a figura do arco
ABa seguir e, com régua e compasso, obtenha o lugar geométrico dos pontos que equidistam dos extremos a e B.

6 Com régua e compasso, desenhe um triângulo equilátero de lados medindo 4 centímetros. A seguir, obtenha os quatro pontos que formam o lugar geométrico dos pontos que equidistam das três retas suportes dos lados do triângulo.
7 Na figura da resolução do exercício anterior, trace quatro circunferências, cada uma delas com centro em um dos pontos obtidos e tangentes às três retas suportes dos lados do triângulo.
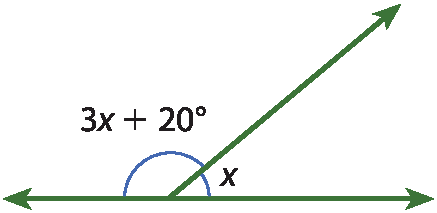
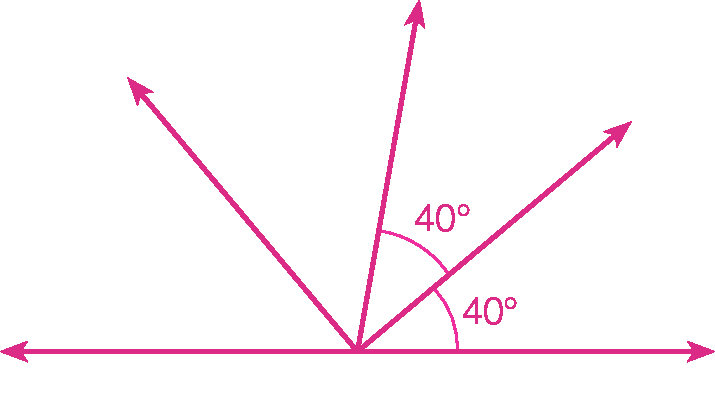
8 Calcule a medida x nas figuras a seguir.
a)
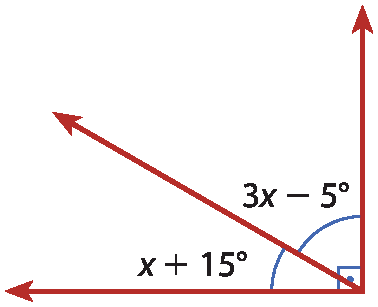
b)
Respostas e comentários
1. Respostas possíveis:
1. a) r e t.
1. b) r e s.
1. c) r e u.
1. d) r e v.
2. Respostas possíveis:
2. a)
Segmentos AB e CD;
segmentos AB e EF;
segmentos CD e EF.
2. b)
segmentos AB e AC.;
segmentos AB e AF.;
segmentos AC e CE..
2. c)
segmentos AC e AG;
segmentos AC e CF.;
segmentos GC e CF..
2. d)
segmentos GC e GD.;
segmentos GC e CF.;
segmentos CD e EF..
3. 65graus
4.
a semirreta OEé bissetriz de
ângulo BODporque divide o ângulo
ângulo BODem dois ângulos congruentes.
5. Construção de figura (mediatriz de
segmento AB).
6. Construção de figura.
7. Construção de figura.
8. a) x = 20graus
8. b) x = 40graus
Exercícios complementares
Este bloco de exercícios é mais uma oportunidade de os estudantes revisarem os principais conceitos tratados no capítulo e utilizarem os conhecimentos construídos, identificando possíveis dúvidas.
No exercício 1, verificamos:
a) r e t formam um par de retas paralelas já em destaque, mas os estudantes podem ainda identificar s e os prolongamentos da base do triângulo maior azul ou dos lados horizontais do quadrado verde. Também u e
reta CEsão paralelas, entre outras possibilidades.
b) r e s, s e t, u e r, u e v são alguns exemplos de pares de retas concorrentes. Há outros, se considerarmos também os prolongamentos dos lados cujos vértices não estão nomeados.
c) Como os triângulos do tangram são todos triângulos retângulos, em particular identificamos u e r como um par de retas perpendiculares.
d) Como r = v =
AB, essas retas são coincidentes.
As resoluções dos exercícios 6 a 8 estão no início deste Manual, nas orientações específicas do capítulo 2.
No exercício 3, como
a semirreta OBé bissetriz de
ângulo AOC, divide esse ângulo em dois ângulos congruentes, um deles sendo
o ângulo BOC. Portanto, a medida de
o ângulo BOCé metade da medida medida do(
o ângulo AOC) = 70graus; assim, medida do(
o ângulo BOC) = 35graus. Como
a semirreta ODé bissetriz de
o ângulo COEdivide esse ângulo em dois ângulos congruentes, um deles sendo
o ângulo CODPortanto, a medida de
o ângulo CODé metade da medida medida do(
o ângulo COE) = 60graus; assim, medida do(
o ângulo COD) = 30graus. Como
a semirreta OCé uma semirreta entre
a semirreta OBe
a semirreta ODo ângulo
o ângulo BODdecompõe-se nos ângulos
os ângulos BOC e COD; portanto, medida do(
o ângulo BOD) = medida do(
o ângulo BOC) + medida do(
o ângulo COD) = 35graus + 30graus = 65graus.
No exercício 4, sendo
a semirreta OCbissetriz de
ângulo AOD, divide esse ângulo em dois ângulos congruentes,
ângulo AOC e ângulo COD; logo, medida do(
ângulo COD) = medida do(
ângulo AOC) = 50graus. Como
ângulo COEé um ângulo reto, então medida do(
ângulo COE) = 90graus; além disso,
a semirreta ODé uma semirreta entre
a semirreta OCe
a semirreta OC, o ângulo
ângulo COEdecompõe-se nos ângulos
ângulo DOEe
ângulo COD; portanto, medida do(
ângulo COE) + medida do(
ângulo COD) = medida do(
ângulo DOE). Substituindo as medidas conhecidas, obtemos 90graus = 50graus + medida do(
ângulo DOE). Segue que medida do(
ângulo DOE) = 40graus. Sabendo que B
ângulo OE é suplemento de A
ângulo OE, logo: medida do(
ângulo BOE) = 180graus – 50graus – 90graus= 40graus. Portanto,
ângulo DOEe
ângulo BOEsão congruentes, pois têm mesma medida, 40graus. Como
a semirreta OEdivide
ângulo BODem
ângulo BOEe
ângulo DOE, então
OEé bissetriz de
ângulo BOD.
No exercício 5, deve-se observar que o arco é um mero artefato: o conjunto dos pontos equidistantes de a, B é a mediatriz de
segmento ABe só depende desses extremos. Assim, basta construir a mediatriz do segmento
segmento ABde acôrdo com as instruções da página 53.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Na construção a seguir, podemos afirmar que:
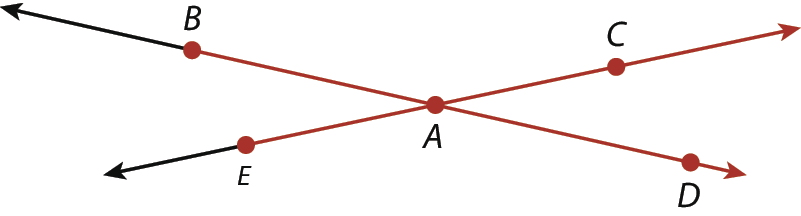
a) as semirretas
A semirreta ECe
A semirreta BDsão consecutivas.
b) os segmentos
segmento ABe
segmento AEsão consecutivos.
c) os segmentos
segmento BDe
segmento CEsão congruentes.
d) os segmentos
segmento ABe
segmento ACsão colineares.
2 No cubo ilustrado a seguir, as retas r e s são:
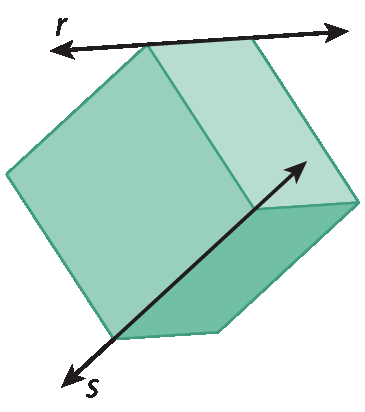
a) concorrentes.
b) coincidentes.
c) paralelas.
d) reversas.
3 Na planta de ruas vemos representações que nos dão ideia de retas paralelas e perpendiculares.
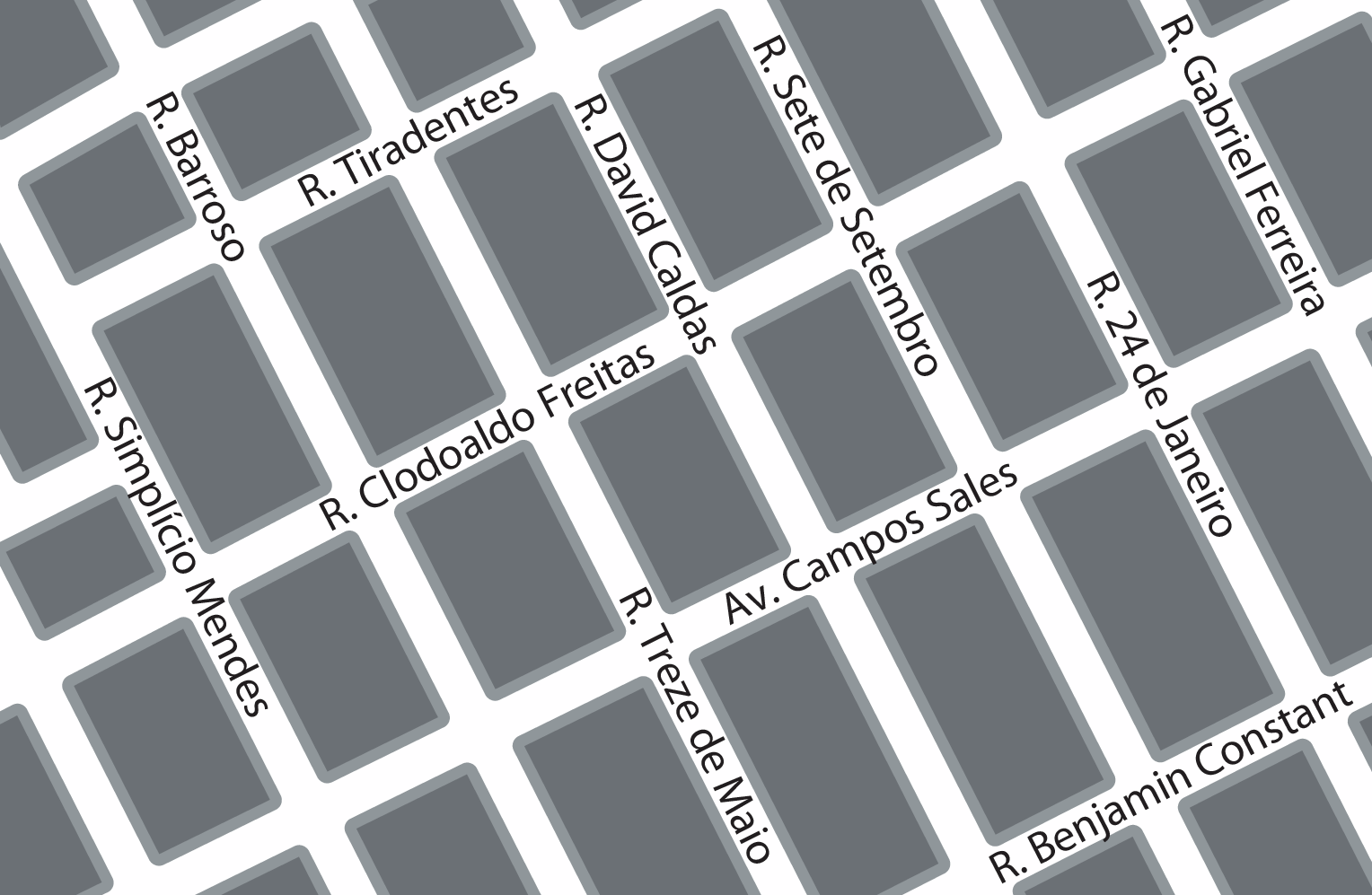
Quais ruas dão ideia de retas perpendiculares?
a) Rua Clodoaldo Freitas e Rua Tiradentes.
b) Rua Sete de Setembro e Rua Treze de Maio.
c) Rua Tiradentes e Rua Benjamin Constant.
d) avenida Campos Sales e Rua 24 de Janeiro.
Versão adaptada acessível
3. Faça a representação de um mapa de ruas que contenha: duas ruas perpendiculares e duas ruas paralelas. Quais são os nomes dessas ruas?
Orientação para acessibilidade
Se considerar adequado, forneça um geoplano para que o estudante possa fazer a representação.
4 Na figura a seguir, se
COBmede 30graus, então ao traçar a bissetriz de
AOB, obteremos dois ângulos de medida igual a:
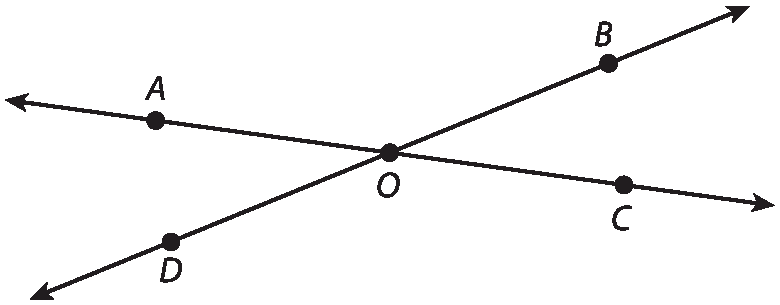
a) 150graus.
b) 75graus.
c) 30graus.
d) 15graus.
5 Dois pontos a e B distam 8 centímetros. Se traçarmos duas circunferências, uma de centro a e raio medindo 3 centímetros e uma de centro B e raio medindo 5 centímetros, quantos pontos as circunferências terão em comum?
a) 0
b) 1
c) 2
d) Infinitos.
6 Se a semirreta
A semirreta OPé composta dos pontos equidistantes de
A semirreta OAe de
A semirreta OB, medida do(
ângulo AOB) é:
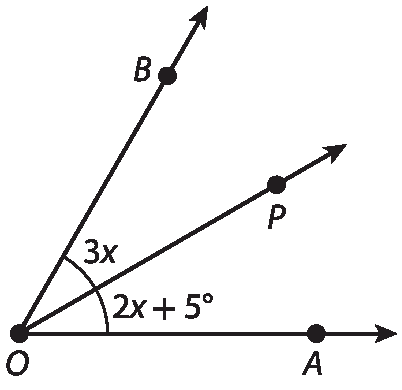
a) 5graus
b) 15graus
c) 30graus
d) 60graus
7 Um professor de natação instalou uma divisória de raias no centro de uma piscina retangular e, em seguida, outras duas, cada uma no centro das raias criadas anteriormente. A ideia de lugar geométrico utilizada pelo professor de natação nessa instalação foram os pontos equidistantes de:
a) duas retas paralelas.
b) duas retas concorrentes.
c) um ponto central.
d) duas retas perpendiculares.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Que instrumentos você utilizou para fazer as construções geométricas propostas?
b) Que posições duas retas podem assumir? Descreva-as.
c) Defina circunferência e bissetriz de um ângulo como um lugar geométrico.
d) Construa um fluxograma com os passos para a construção da mediatriz de um segmento de reta.
Respostas e comentários
1. Alternativa b.
2. Alternativa d.
3. Alternativa d.
4. Alternativa b.
5. Alternativa b.
6. Alternativa c.
7. Alternativa a.
Organizando:
a) Compasso, régua, lápis e software de Geometria dinâmica.
b) Paralelas: quando não têm ponto comum e são coplanares; concorrentes: quando têm um ponto em comum; coincidentes: quando têm todos os pontos em comum; e reversas: quando não têm ponto comum e não são coplanares.
c) Circunferência de centro óh e raio medindo r é o lugar geométrico dos pontos de um plano que estão à distância r de óh. O lugar geométrico dos pontos do plano equidistantes de duas retas concorrentes é o par de retas que contém as bissetrizes dos ângulos formados por essas retas.
d) Construção de figura.
Verificando
Esta seção pode ser utilizada para propor aos estudantes exercícios como treino para avaliações de larga escala.
No teste 1, analisando cada alternativa, verificamos:
a) Falso, pois essas semirretas não têm extremidade comum.
b) Verdadeiro, pois esses segmentos têm o ponto a como extremidade comum.
c) Falso, nada garante que os segmentos considerados tenham a mesma medida.
d) Falso, pois ambos os segmentos estão contidos em retas concorrentes.
No teste 2, a alternativa d é a correta; as retas r e s são reversas, pois não estão contidas em um mesmo plano.
No teste 3, os pares apresentados nas alternativas a, b e c são de ruas paralelas. Já a avenida Campos Sales e a Rua 24 de Janeiro encontram-se em uma esquina de ângulo reto, transmitindo a ideia de retas perpendiculares; assim, a alternativa d é a correta.
No teste 4, medida do(
o ângulo AOC) = 180graus, pois A
o ângulo OC é um ângulo raso. Como
a semirreta OBdivide esse ângulo nos ângulos
o ângulo AOBe
o ângulo COB, obtemos: medida do(
o ângulo AOB) + medida do(
o ângulo COB) = 180graus, o que nos leva a medida do(
o ângulo AOB) + 30graus = 180graus ou a medida do(
o ângulo AOB) = 180graus ‒ 30graus = 150graus. A bissetriz de
segmento ABdivide esse ângulo em dois ângulos de medida igual a
fração 150 graus sobre 2= 75graus, e a alternativa b é a correta.
As resoluções dos testes 5 a 7 estão no início deste Manual, nas orientações específicas do capítulo 2.
Organizando
As perguntas propostas nessa seção possibilitam aos estudantes retomar os principais conteúdos trabalhados neste capítulo. Sugerimos propor a eles que façam resumos, mapas conceituais e produzam outros esquemas que possam ser utilizados como recursos para estudar os conteúdos abordados.
No item d, o fluxograma pode conter os seguintes passos:
1) Dado o segmento
segmento AB, com a ponta-sêca do compasso em a, e depois em B, traçar arcos com abertura maior do que metade da distância AB.
2) Traçar a reta definida pelos dois pontos de intersecção dos arcos do passo 1.
DIVERSIFICANDO
Texto do Infografico

Gire o seu dispositivo para a posição vertical
Matemática na Arqueologia

Em uma escavação de um sítio arqueológico, Daniel encontrou alguns objetos antigos, entre os quais pedaços da roda de uma carroça.
Para recuperar informações a respeito desse achado arqueológico, como a medida do raio da roda, Daniel procedeu da seguinte maneira:
• riscou um arco no chão, contornando o pedaço da roda com cuidado para não danificá-lo;
• marcou os pontos a, B e C no desenho do arco e traçou os segmentos
segmento ABe
segmento bC;
• desenhou as mediatrizes dos segmentos
segmento ABe
segmento BC, obtendo, no cruzamento delas, o ponto D, no qual estaria o centro da roda;
• depois mediu a distância á dê com uma fita métrica e obteve a medida do raio da roda.

Como o desenho foi feito na terra e com instrumentos precários, Daniel obteve apenas um valor aproximado, fato que deve ser considerado pelo arqueólogo.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Se Daniel tivesse marcado apenas os pontos a e B no desenho do arco, ele conseguiria encontrar a medida do raio da roda? Justifique sua resposta.
2 Explique por que o procedimento de Daniel funcionou, ou seja, que propriedades matemáticas aplicadas ao desenho justificam a conclusão de que o ponto D é o centro da circunferência.
3 Imagine a roda inteira, sem o centro, como se fosse um anel gigante. Como você encontraria a medida do raio? Compare sua resposta com a de um colega.
Respostas e comentários
1. Resposta possível: Não, pois o centro da circunferência é obtido pela intersecção de duas mediatrizes e, nesse caso, com os pontos a e B, ele poderia construir somente uma mediatriz.
2. Resposta possível: Como D pertence à mediatriz de
segmento AB, está a igual distância de a e de B. Analogamente, está à mesma distância de B e de C. Como a, B e C são pontos quaisquer do arco, concluímos que D dista igualmente de todos os pontos do arco; logo, D é centro do arco e, por extensão, da circunferência.
3. Respostas possíveis: Repetir o procedimento de Daniel. Contornar a roda com um barbante para obter a medida do comprimento da circunferência e dividi-lo por 6,28 (aproximação de 2π), pois a medida do comprimento da circunferência é igual a 2πr, em que r é a medida do raio.
Diversificando
Nesta seção, retome a definição da circunferência e da mediatriz como lugares geométricos:
• O lugar geométrico dos pontos de um plano que estão a uma mesma distância fixa de um ponto dado do plano é a circunferência de centro nesse ponto e raio de medida dada por essa distância.
• O lugar geométrico dos pontos de um plano equidistantes dos extremos de um segmento de reta é a mediatriz desse segmento (reta perpendicular ao segmento que passa pelo seu ponto médio).
Antes de propor aos estudantes as questões do Agora é com você!, converse com eles o que garante que o encontro das mediatrizes de duas cordas de uma circunferência determina o seu centro.
Comente com os estudantes que, assim como dois pontos distintos determinam uma única reta, três pontos distintos e não alinhados determinam uma única circunferência que passa por esses três pontos.
Desse modo, espera-se que eles percebam que todos os pontos equidistantes de a e B estão na mediatriz da corda
ABe todos os pontos equidistantes de B e C estão na mediatriz da corda
BCAssim, D é um ponto equidistante de a, de B e de C, por isso é o centro da circunferência determinada por esses três pontos, cuja medida do raio é a distância entre quaisquer desses pontos até D.