Página 91

CAPÍTULO 4 Cálculo algébrico

Fotografia. Grande nuvem de explosão nuclear com bomba de hidrogênio em uma ilha. Ao fundo, céu azul. — Imagem de uma das maiores explosões nucleares com bomba de hidrogênio, realizada nas Ilhas márchal, que destruiu completamente a ilha Elugelab. (Fotografia de 1952.)

Observe a imagem e responda às questões no caderno.

a) Na equação ê = mc2, a medida de massa pode assumir valores negativos? Justifique sua resposta.

b) Quantos valores ê, m e c podem assumir?

A equação E = mc2 (energia de um sistema é igual à medida de massa multiplicada pelo quadrado da velocidade da luz no vácuo) sintetiza parte da teoria da relatividade de ainstain, considerada um divisor de águasglossário entre a Física clássica e a Física moderna. Ela sugere que é possível transformar matéria em energia, e vice-versa. Em explosões nucleares, ocorre a transformação de matéria em energia.

O cálculo algébrico é a estrada pela qual transitam ideias fundamentais do conhecimento humano.

Respostas e comentários

a) Espera-se que os estudantes respondam que não, pois massa é uma grandeza sempre positiva.

b) Espera-se que os estudantes respondam que a energia do sistema (E) e a medida de massa (m) podem assumir infinitos valores positivos não nulos, e a velocidade da luz no vácuo (c), um um único valor.

Capítulo 4 – Cálculo algébrico

Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.

Neste capítulo, ampliamos o trabalho com Álgebra, relacionando-o, sempre que possível, a elementos da Geometria ou a situações do cotidiano. O foco será o trabalho com as expressões algébricas. Nesta abertura, apresentamos a equação, que estabelece a relação geral entre energia e massa ligada à teoria da relatividade, de Albert Einstein.

Converse com os estudantes sobre os itens a e b propostos, destacando o significado das “letras” em E = mc 2. Eles devem compreender que ê e m são variáveis e c é uma constante. Além disso, como m expressa a medida de massa, m é um valor positivo não nulo; assim, a quantidade de energia expressa por E será positiva e não nula (pois c 2 é positivo). Esse contexto favorece a interdisciplinaridade com Ciências e o desenvolvimento do Tema Contemporâneo Transversal ciência e tecnologia. Sugerimos propor aos estudantes atividades em que possam identificar e classificar diferentes fontes e tipos de energia (renováveis e não renováveis) com destaque para a energia nuclear. Eles podem pesquisar esse tipo de energia e debater com os colegas o fato de que qualquer avanço tecnológico sempre pode ser utilizado para fins pacíficos ou bélicos.

Nesse sentido, podem desenvolver a competência geral 10, discutindo e percebendo a necessidade de agir pessoal e coletivamente tomando decisões com base em princípios éticos, solidários e sustentáveis. A competência geral 9 também pode ser desenvolvida, pois poderão discutir e perceber a importância de exercitar a empatia e a resolução de conflitos de maneira a respeitar a diversidade e os direitos humanos.

Sugestões de leitura

Para enriquecer a discussão sobre esse tema, sugerimos:

GONÇALVES, O. D.; ALMEIDA, I. P. S. A energia nuclear e seus usos na sociedade. Ciência Hoje, volume 37, número 220, outubro 2005. Disponível em: https://oeds.link/dLEaGj. Acesso em: 7 junho 2022.

Este artigo trata dos tipos de radiação e suas aplicações na saúde, na indústria, na pesquisa, no ambiente e como geração de energia.

GOLDEMBERG, J. O futuro da energia nuclear. Revista úspi, número 91, página seis a quinze, 2011. Disponível em: https://oeds.link/L8emjS. Acesso em: 7 junho 2022.

Este artigo discute a estagnação da energia nuclear no mundo e apresenta possíveis causas, como movimentos sociais, elevados custos econômicos ou os riscos ambientais.

Página 92

1. Incógnita e variável

Clique no play e acompanhe a reprodução do Áudio.

Transcrição do áudio

Por que x?

Duração: 4:01min. Página: 92.

>> [Locutora] Por que x?

>> [Luciana] Oi, tudo bem? Eu sou a professora Luciana Moura e vou contar para vocês a origem das palavras “álgebra” e “algarismo”. Ambas têm origem em uma cultura muito antiga, que contribuiu muito para o desenvolvimento da humanidade: a cultura árabe.

>> [Luciana] Os árabes se dedicaram ao estudo de antigos textos de diversas origens – hindu, grega, romana, mesopotâmica... –, traduzindo, aprimorando e propagando esses conhecimentos pela Europa.

>> [Luciana] A palavra “álgebra” tem sua origem na tradução do termo al-jabr, presente no título do livro Kitab al-Jabr wa-l-Muqabala, escrito por um dos mais importantes matemáticos do século IX, Muhammad ibn Musa al-Khwarizmi. E não é por acaso que o sobrenome al-Khwarizmi lembra a palavra [tom enfático] “algarismo”! Esse pensador árabe produziu notáveis trabalhos sobre Matemática e Astronomia.

>> [Luciana] O livro em questão tratava de problemas de restauração e redução em situações que envolviam álgebra, geometria e partilhas de heranças. Para explicar o que significa restauração e redução, vamos pensar no seguinte problema: 2 coisas, isto é, 2 quantidades desconhecidas adicionadas a 5 têm resultado igual a 9.

>> [Luciana] Primeiro, considere “coisas” como [tom enfático] números. Agora, vamos supor que essas quantidades desconhecidas sejam números naturais. Em seguida, utilizando a operação inversa da adição, vamos subtrair 5 unidades dos 2 membros da igualdade para garantir o balanceamento da equação. Com isso, obtemos uma sentença reduzida e equivalente à anterior: “duas quantidades desconhecidas cuja soma é igual a 4”.

>> [Luciana] Agora, vamos pensar em todas as possibilidades que satisfazem a essa igualdade. Se um dos valores desconhecidos for 1, o outro valor será 3, para que a soma seja igual a 4; e se um dos valores for 2, o outro também será 2.

>> [Luciana] Repare que, se voltarmos à primeira sentença, “a soma de 2 quantidades desconhecidas a 5 resulta em 9”, podemos dizer que uma das quantidades vale 1 e a outra vale 3; ou que ambas são iguais a 2.

>> [Luciana] Alguns séculos mais tarde, começaram a ser utilizadas letras para representar as quantidades desconhecidas dos problemas, ou seja, suas incógnitas.

>> [Luciana] A letra x é usualmente a mais empregada para representar incógnitas. Uma das possíveis explicações para isso vem da letra árabe sheen, componente do termo al-shalan, “coisa desconhecida” em árabe. Essa letra, muito presente nos textos matemáticos árabes, inclusive os escritos por al-Khwarizmi, tem o som de SH e, ao ser traduzida para o espanhol, seu som foi substituído pelo som da letra grega chi, que, por sua vez, tem a grafia muito semelhante ao xis maiúsculo do alfabeto latino.

>> [Luciana] [Tom enfático] Interessante, não é? Espero que vocês tenham gostado. Até a próxima!

Créditos

Studio Spectrum

Em anos anteriores, você estudou um ramo da Matemática que trabalha com grandezas cujos valores variam, de modo proporcional ou não, ou que são desconhecidos e, por isso, são representados por símbolos ‒ em geral, por letras. Essa parte da Matemática é chamada de Álgebra.

Ao prescrever determinados remédios, é comum que os pediatras recorram à Matemática, principalmente à Álgebra.

Fotografia. Médica pediatra de cabelo preto, jaleco branco e estetoscópio no pescoço está com as mãos no pescoço de uma menina de cabelo preto e camiseta azul sentada em uma maca. — Pediatra atendendo uma paciente.

Para calcular a dose que devem administrar a uma criança, com base na dose indicada a adultos, os pediatras aplicam a chamada fórmula de iãng:

d o s e infantil = \frac{i d a d e d a c r i a n ç a (e m a n o) \cdot d o s e p a r a a d u l t o}{i d a d e d a c r i a n ç a (e m a n o) + 12 a n o s}

Por exemplo, para uma criança de 8 anos de idade, um médico calcula a dose infantil ( x ) de um medicamento, cuja dose para adultos é 250 miligramas, resolvendo a equação:

x = \frac{8 \cdot 250}{8 + 12}

No estudo das equações, representamos o termo desconhecido por uma letra chamada de incógnita.

Na equação

x = \frac{8 \cdot 250}{8 + 12}

, a incógnita é a letra x; efetuando os cálculos, obtemos seu valor, que é 100. Isso significa que a dose de medicamento a ser administrada à criança é 100 miligramas.

Acompanhe agora outra situação.

Márcio e seus filhos foram a um pesqueiro, onde são cobrados R$ 8,00oito reais de entrada e R$ 10,00dez reais por quilograma de peixe pescado. Dessa maneira, se Márcio pescar:

• 1 quilograma, deverá pagar, em real:

8,00 + 10,00 = 18,00;

• 1,5 quilograma, deverá pagar, em real:

8,00 + 10,00 ⋅ 1,50 = 8,00 + 15,00 = 23,00;

• 2 quilogramas, deverá pagar, em real:

8,00 + 10,00 ⋅ 2 = 8,00 + 20,00 = 28,00, e assim por diante.

Não sabemos quanto Márcio vai pescar, mas podemos determinar o valor que ele deve pagar por n quilogramas de peixe pescado: 8,00 + 10,00 ⋅ n.

Nesse caso, a letra n pode assumir o valor 3, ou 3,2, ou 12,5, ou qualquer outro valor não negativo. Por isso, essa letra é chamada de variável.

O uso de letras para representar grandezas de valores variáveis ou desconhecidos dá origem a uma linguagem com expressões próprias da Matemática, a linguagem algébrica. Nesse campo, estudamos generalizações de conceitos e de operações da Aritmética.

Respostas e comentários

1. Incógnita e variável

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero seis.

Para introduzir os conceitos de incógnita e variável, importantes para o desenvolvimento da habilidade (EF08MA06) utilizamos a fórmula de iãng, usada por pediatras para calcular a dosagem de remédio a ser administrada a uma criança, e uma situação do cálculo do valor a ser pago em um pesqueiro.

Para trabalhar as habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três), aborde com os estudantes algumas situações em que as grandezas são diretamente proporcionais ou que são inversamente proporcionais. Esse conteúdo será desenvolvido no decorrer deste volume, de maneira que eles possam utilizá-lo em diferentes momentos de aprendizagem. No capítulo 10, apresentaremos os gráficos que podem ser associados a grandezas desses tipos.

Assim, a Álgebra aparece como um instrumento necessário que deve ser entendido, dominado e exercitado pelos estudantes para que seja aplicado na resolução de diversos problemas do dia a dia e de outras áreas do conhecimento, como a Biologia e a Física. Pode-se propor a eles que pesquisem e discutam a importância de tomar remédios apenas quando indicados por médicos e nas doses recomendadas por eles; dessa maneira, os estudantes podem adquirir mais autonomia no cuidado com a saúde e desenvolver a competência geral 8.

Página 93

2. Expressões algébricas

Neste capítulo, ampliaremos nosso estudo a respeito de expressões algébricas.

Expressão algébrica é aquela que tem apenas letras, ou números e letras.

Analise os seguintes exemplos:

Ilustração. Retângulo com o comprimento a e largura b.

a) A expressão algébrica que representa a medida da área do retângulo apresentado é ab.

b) A expressão algébrica que representa a medida do perímetro desse retângulo é 2a + 2b.

O uso de letras para representar números facilita a tradução de sentenças da linguagem verbal escrita para a linguagem algébrica.

Acompanhe alguns exemplos.

a) O oposto do dôbro de um número x adicionado a um número y

‒2x + y

b) A diferença entre a terça parte de um número x e o oposto de 5

\frac{x}{3} - (‒ 5)

c) O inverso do dôbro de um número x não nulo

\frac{1}{2 x}, c o m x \neq 0

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Orlando, dono de uma quitanda, colocou 5 maçãs em um dos pratos de uma balança e nivelou-a colocando no outro prato um bloco de massa medindo 500 gramas e dois blocos de massa medindo 200 gramas cada um.

Ilustração. Balança de dois pratos. No prato à esquerda, cinco maçãs. No prato à direita, dois pesos de 200 gramas e um peso de 500 gramas. A balança está equilibrada.

Indicando a massa média de cada maçã por x, represente no caderno essa situação por meio de uma equação.

2 Represente no caderno, usando símbolos:

a) a diferença entre o número x e o número y;

b) a soma do número m com o triplo do número n;

c) o quociente do número a pelo número b (com b ≠ 0);

d) a ordem das parcelas da adição de a e b não altera a soma;

e) a diferença entre os quadrados dos números c e d;

f) o quadrado da diferença dos números c e d;

g) o cubo do número y.

3 O número 574, decomposto em centenas, dezenas e unidades, pode ser escrito da seguinte maneira:

5 ⋅ 102 + 7 ⋅ 10 + 4

Agora, considere um número qualquer de quatro algarismos ( a b c d ).

a) Determine a ordem de cada algarismo desse número.

b) Decomponha o número a b c d de acôrdo com a ordem de seus algarismos.

4 Em uma divisão com números naturais, o divisor é x, o quociente é y e o resto é o maior possível. Qual é a expressão do dividendo?

Respostas e comentários

1. 5x = 900

2. a) x ‒ y

2. b) m + 3n

2. c)

\frac{a}{b}

2. d) a + b = b + a

2. e) c 2 ‒ d 2

2. f) (c ‒ d)2

2. g) y 3

3. a) a → algarismo das unidades de milhar;

b → algarismo das centenas;

c → algarismo das dezenas;

d → algarismo das unidades.

3. b) a ⋅ 103 + b ⋅ 102 + c ⋅ 10 + d

4. xy + x ‒ 1

2. Expressões algébricas

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero seis.

É importante os estudantes compreenderem o conceito de expressão algébrica, desenvolvendo a habilidade (EF08MA06), pois com base nele são feitas as generalizações, o estudo de equações e o de funções, tão importantes no desenvolvimento de diferentes conceitos e conteúdos em Matemática. Embora já tenham lidado com equações do 1º grau em anos anteriores, esta é a primeira vez que tratam as expressões a fim de estudá-las em si mesmas, isto é, independentemente se vão ou não atribuir valores às variáveis e incógnitas.

Neste momento, apresentamos como traduzir para a linguagem algébrica situações matemáticas apresentadas na língua materna. Fazer um paralelo com a Aritmética pode ajudar em muitas situações com as quais os estudantes vão se deparar. Por exemplo, eles já sabem que o dôbro de um número é obtido fazendo duas vezes esse número, o que facilita o entendimento de que, ao indicar o número por x, representamos o dôbro de um número por 2 · x.

Exercícios propostos

Neste bloco, os exercícios desenvolvem o uso da linguagem matemática por meio das expressões algébricas.

As resoluções dos exercícios 1 a 4 estão no início deste Manual, nas orientações específicas do capítulo 4.

No exercício 2, queremos que os estudantes inicialmente exercitem a relação entre a Matemática e a língua materna, percebendo, por exemplo, o que há de diferente entre os itens ê e f. No item ê, temos a diferença entre os quadrados de dois números (c 2 ‒ d 2); no item f, o quadrado da diferença entre dois números (c ‒ d)2.

No exercício 3, temos um exemplo de articulação das Unidades Temáticas Álgebra e Números. O número 574 decomposto em ordens é escrito: 5 · 102 + 7 · 10 + 4, e um número de quatro algarismos, representado por a bê cê dê, decomposto é: a · 103 + b · 102 + c · 10 + d.

Este é um bom momento para promover uma discussão com os estudantes a respeito da condição de que a não pode representar o algarismo zero, visto que o número deve ser de quatro algarismos.

Essa discussão pode ser motivadora para a apresentação do valor numérico de uma expressão algébrica.

Página 94

Valor numérico de uma expressão algébrica

Vamos recordar o cálculo do valor numérico de uma expressão algébrica. Para isso, considere a situação a seguir.

Ilustração. Vista do alto de loja de brinquedos com patinetes, skates e prateleira com brinquedos.

Em uma loja de brinquedos, encontram-se x patinetes e y skates. A expressão que representa o número total de rodas é 2x + 4y.

Se houver 12 patinetes e 15 skates, o número total de rodas será:

2 ⋅ (12) + 4 ⋅ (15) = 24 + 60 = 84

Então, dizemos que o valor numérico da expressão algébrica 2x + 4y para x = 12 e y =15 é 84.

Acompanhe outra situação.

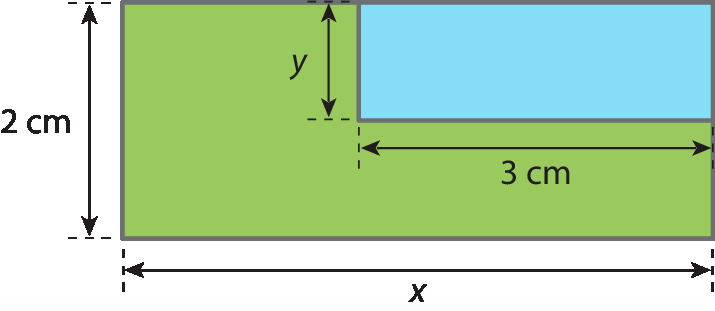
Ilustração. Retângulo verde com medida 2 centímetros por x. Dentro, retângulo azul medindo 3 centímetros por y. Um vértice do retângulo azul coincide com um vértice do retângulo verde no canto superior direito. — Figura 1

Vamos calcular a medida da área da região pintada de verde da figura 1, considerando x = 5 centímetros e y = 1 centímetro.

Para calcular a medida da área pedida, basta obter o valor numérico da expressão 2x ‒ 3y para x = 5 e y = 1.

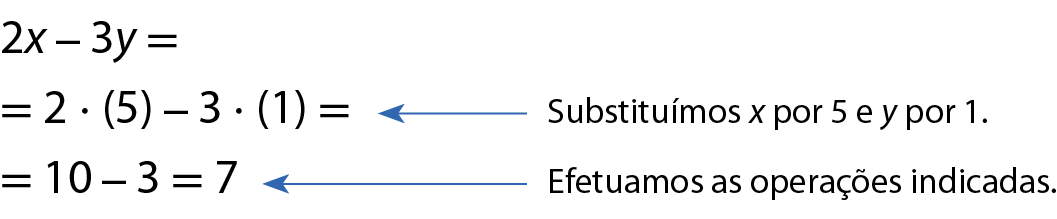
Sentença matemática. Primeira linha: 2x menos 3y igual. Segunda linha: igual, 2 vezes, abre parênteses, 5, fecha parênteses, menos 3 vezes, abre parênteses, 1, fecha parênteses, igual. Terceira linha: igual 10 menos 3, igual, 7. Do lado direito da segunda linha, flecha para esquerda dizendo: Substituímos x por 5 e y por 1. Do lado direito da terceira linha, Flecha para esquerda dizendo: Efetuamos as operações indicadas.

Então, dizemos que 7, que é o valor numérico da expressão algébrica 2x ‒ 3y para x = 5 e y = 1, é a medida da área da região da figura pintada de verde, em centímetro quadrado.

O valor numérico de uma expressão algébrica é o número que se obtém ao substituir as variáveis por números e efetuar as operações indicadas.

Analise outros exemplos.

a) Vamos calcular o valor numérico da expressão a2 ‒ b2 para

a = \frac{1}{2}

b = \frac{2}{3}

a^{2} ‒ b^{2} = {(\frac{1}{2})}^{2} ‒ {(\frac{2}{3})}^{2}

\frac{1^{2}}{2^{2}} ‒ \frac{2^{2}}{3^{2}} = \frac{1}{4} ‒ \frac{4}{9}

\frac{9 ‒ 16}{36} = ‒ \frac{7}{36}

Portanto, o valor numérico da expressão algébrica a2 ‒ b2 para

a = \frac{1}{2}

b = \frac{2}{3}

‒ \frac{7}{36}

b) Vamos calcular o valor numérico da expressão

\frac{3 x^{2} ‒ 5 x}{x + 3}

para x = 4.

\frac{3 x^{2} ‒ 5 x}{x + 3} = \frac{3 \cdot {(4)}^{2} ‒ 5 \cdot (4)}{4 + 3}

\frac{3 \cdot 16 ‒ 20}{7}

\frac{48 ‒ 20}{7} = \frac{28}{7} = 4

Portanto, o valor numérico da expressão algébrica

\frac{3 x^{2} ‒ 5 x}{x + 3}

para x = 4 é 4.

Respostas e comentários

Valor numérico de uma expressão algébrica

Ressalte aos estudantes o fato de que expressões que apresentam variáveis (ou incógnitas) nos denominadores têm uma condição de existência: o denominador não pode se anular. Por isso, as variáveis não podem assumir valores que anulem o denominador.

Apresente na lousa outros exemplos de expressões algébricas dadas por frações em que há variáveis no denominador para os estudantes buscarem os valores que elas não podem assumir.

Página 95

Ilustração. Homem de cabelo preto e camisa laranja diz: Uma expressão que apresenta letra no denominador não tem valor numérico quando os valores atribuídos às variáveis anulam o denominador. Vamos examinar um exemplo.

Considerando que 300 estudantes são distribuídos em grupos e sabendo que há x estudantes em cada grupo, o número de grupos formados é dado por

\frac{300}{x}

. Se cada grupo tiver dois estudantes a menos, então o número de grupos será representado por

\frac{300}{x ‒ 2}

Nessa situação, x representa um número natural não nulo no primeiro caso (não há grupo com 0 estudante) e, no segundo caso, x representa um número natural maior que 2. Além disso, observe que:

• para x = 0, a expressão

\frac{300}{x}

não tem valor numérico definido;

• para x = 2, a expressão

\frac{300}{x ‒ 2}

não tem valor numérico definido.

Note que obtemos o valor da variável para o qual a expressão não tem valor numérico igualando o denominador a 0 e resolvendo a equação encontrada.

Analise outros exemplos.

a) Para que valor de x a expressão

\frac{3 x ‒ 1}{2 x ‒ 5}

não tem valor numérico definido? Essa expressão não tem valor numérico definido quando o denominador é igual a zero, ou seja, quando 2x ‒ 5 = 0. Resolvendo essa equação, obtemos

x = \frac{5}{2}

. Logo, a expressão

\frac{3 x ‒ 1}{2 x ‒ 5}

não tem valor numérico definido para

x = \frac{5}{2}

b) Que relação deve existir entre x e y para que a expressão

\frac{3 x + 2 y}{x ‒ 2 y}

não tenha valor numérico definido? A expressão não terá valor numérico definido quando o denominador for igual a zero; nesse caso, quando x ‒ 2y = 0. Assim, x = 2y.

Portanto, a relação procurada é x = 2y.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

5 Aplique a fórmula de iãng, descrita no início deste capítulo, para calcular no caderno a dose para uma criança de 6 anos, medida em miligrama, de um remédio cuja dose indicada para adulto é:

a) 150 miligramas;

b) 210 miligramas;

c) 300 miligramas.

6 Com base nos resultados do exercício anterior, é possível concluir que a dose de um remédio para uma criança de 6 anos é a quarta parte da dose desse remédio indicada para um adulto? Por quê?

Respostas e comentários

5. a) 50 miligramas.

5. b) 70 miligramas.

5. c) 100 miligramas.

6. Não, pois é a terça parte.

Exercícios propostos

Retomamos no exercício 5 a contextualização da introdução do capítulo sobre a fórmula de iãng.

Assim, em cada item, calculamos a dose x, em miligrama.

x = \frac{6 \cdot 150}{6 + 12} = \frac{6 \cdot 150}{18} = 50

x = \frac{6 \cdot 210}{6 + 12} = \frac{6 \cdot 210}{18} = 70

x = \frac{6 \cdot 150}{6 + 12} = \frac{6 \cdot 300}{18} = 100

Dando continuidade a essa problemática, no exercício 6, os estudantes são levados a analisar e aplicar a fórmula para uma criança de 6 anos, concluindo que a dose de um remédio, para essa idade, é sempre igual à terça parte da dose para um adulto.

Página 96

7 Considere a figura a seguir. Ela é formada por quadrados idênticos.

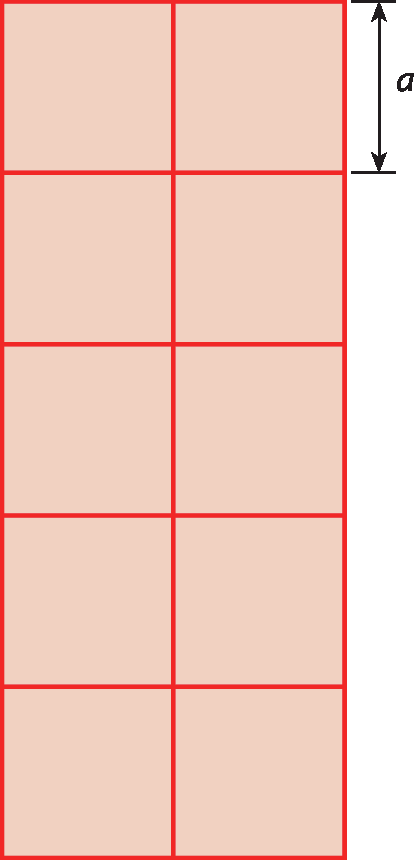
Ilustração. Retângulo vertical dividido em 5 linhas e duas colunas, formando 10 quadrados. A medida do lado de cada quadrado é a.

Agora, no caderno, faça o que se pede.

a) Determine a expressão que representa a medida do perímetro dessa figura.

b) Calcule o valor numérico da expressão da medida do perímetro para a = 3,6.

c) Encontre a expressão que representa a medida da área dessa figura.

d) Determine o valor numérico da expressão da medida da área para a = 5.

8 Calcule no caderno o valor numérico das expressões:

a) 2a + 3b, para

a = \frac{5}{2}

b = \frac{2}{3}

;

b) x 2 + 2x, para x = ‒5;

\frac{x + y}{x ‒ y}

, para x = 4 e y = 2;

- \frac{2 b + \sqrt{b^{2} ‒ 4 a c}}{2 a}

, para a = 2, b = ‒10 e c = 12.

9 Se 0 é o valor numérico da expressão x2 ‒ y, dê exemplos de valores inteiros que x e y podem assumir.

10 Para que valores de a as expressões a seguir não têm valor numérico?

\frac{a ‒ 4}{a + 5}

\frac{a + 3 b}{2 a ‒ 4}

11 Que relação deve existir entre a e b para que as expressões a seguir não tenham valor numérico?

\frac{a ‒ 1}{a ‒ b}

\frac{3 x}{2 a + 3 b}

12 Considere a, B e C números naturais e a equação:

A = B · C

a) Para A = 1, que valores B e C devem assumir para que a equação seja verdadeira?

b) Para A = 0, que valores B e C devem assumir para que a equação seja verdadeira?

13 José faz pequenos fretes urbanos com seu caminhão, cobrando uma taxa inicial de R$ 50,00cinquenta reais e mais R$ 6,00seis reais por quilômetro rodado.

a) Indicando por x o número de quilômetros rodados, qual é a expressão que representa o preço cobrado por José?

b) Quanto ele cobra por um frete de 6 quilômetros?

14 Um relógio registra o consumo de energia elétrica de uma residência em quilouát-hora (cá dáblio agá). Nas lâmpadas e nos aparelhos elétricos, aparece indicada, entre outras coisas, a quantidade de energia elétrica consumida em cada unidade de tempo, chamada de potência e expressa em watt (dáblio).

Ilustração. Lâmpada escrito nela: 100 watts, 127 volts. Ao lado, 1 quilowatt igual 1000 watt.

Para calcular o consumo mensal de energia elétrica ∁ (em quilowatts-hora), pode-se aplicar a fórmula em que ∁ é o consumo de energia, p é a potência do aparelho, h é o tempo de uso por dia (em hora) e d é o número de dias de uso por mês:

∁ = \frac{p \cdot h \cdot d}{1000}

Aplicando essa fórmula, calcule o consumo de energia elétrica, relativo a 30 dias, de:

a) uma lâmpada de 100 uáts que fica acesa durante 3 horas por dia;

b) um chuveiro de .4000 uáts que é utilizado durante uma hora por dia.

Reunindo-se com um colega, retomem a situação das patinetes e dos skates da página 94 e respondam à questão a seguir.

• É possível que o valor numérico da expressão algébrica que representa o número total de rodas seja um número ímpar? Por quê?

Respostas e comentários

7. a) 14a

7. b) 50,4

7. c) 10a2

7. d) 250

8. a) 7

8. b) 15

8. c) 3

8. d)

‒ \frac{9}{2}

9. Respostas possíveis: x = y = 1; x = y = 0; x = ‒1 e y = 1.

10. a) a = ‒5

10. b) a = 2

11. a) a = b

11. b) 2a = ‒3b

12. a) B = C = 1

12. b) Ou B = 0, ou C = 0 ou B = C = 0.

13. a) 50 + 6x

13. b) R$ 86,00oitenta e seis reais

14. a) 9 quilouótis hora

14. b) 120 quilouótis hora

15. Não, pois x e y estão sendo multiplicados por números pares.

Exercícios propostos

As resoluções dos exercícios 7 a 9 e dos exercícios 12 a 15 estão no início deste Manual, nas orientações específicas do capítulo 4.

No exercício 10, as expressões não têm valor numérico quando os denominadores são nulos; desta maneira, isso ocorre quando:

a) a + 5 = 0 a = ‒5

b) 2a ‒ 4 = 0 2a = 4 a = 2

De maneira similar, no exercício 11, temos:

a) a ‒ b = 0 a = b

b) 2a + 3b = 0

2a = ‒3b

Página 97

Ainda reunido com o colega, façam o que se pede.

Dada a expressão

\frac{3 x^{2} ‒ 12}{(x + 2) \cdot (x ‒ 2)}

a) calculem o valor numérico para x = 6, x = ‒4, x =

\frac{2}{3}

e x =

‒ \frac{3}{2}

;

b) calculem os valores de x para os quais não existe o valor numérico da expressão;

c) cada um escolhe um número para x, diferente da resposta do item b, para que o outro calcule o valor numérico da expressão, depois corrija o cálculo feito pelo colega;

d) se forem escolhidos outros números para x, o valor numérico da expressão continua o mesmo?

Hora de criar ‒ Com um colega, elaborem um problema cada um sobre expressão algébrica ou valor numérico de expressão algébrica. Troque seu problema com o do colega e, depois de cada um resolver o problema do outro, destroquem para corrigi-los.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e respondam às questões a seguir.

Com uma calculadora, resolvam as expressões:

Ilustração. 4 quadros com expressões.
Primeiro quadro: 9 vezes 1 mais 2.
Segundo quadro: 9 vezes 12 mais 3.
Terceiro quadro: 9 vezes 123 mais 4.
Quarto quadro: 9 vezes mil 234 mais 5.

b) Agora, sem a calculadora, resolvam a expressão: 9 ⋅ .12345 + 6, observando o padrão das expressões numéricas do item a.

c) Calculem o valor numérico da expressão 9x + y para x = .123456 e y = 7.

d) Escolham um número para x e outro para y para que se tenha 9x + y = ..11111111.

e) Os números escolhidos no item d são os únicos números possíveis?

3. Monômios

Considere as expressões algébricas: ‒2a,

\frac{x}{3}

, 3x 2 e ‒3y.

Observe que elas não apresentam operação de adição ou de subtração, que os expoentes das letras são números naturais (não têm letra em um radical) e que não há letra no denominador. Nessas condições, as expressões algébricas são chamadas de monômios.

Em um monômio, distinguimos o coeficiente (parte numérica) e a parte literal (parte com letras).

O quadro a seguir mostra os coeficientes e as partes literais de alguns monômios.

Monômio	Coeficiente	Parte literal
5x 3y 2	5	x 3y2
$menos 2 sétimos$ ab3m	$menos 2 sétimos$	ab3m
$raiz quadrada de 2$	$raiz quadrada de 2, fim da raiz, vezes x$	x
ab5	1	ab5

Observações

▶ Todo número não nulo é um monômio sem parte literal. Exemplos: 5; ‒10;

\frac{5}{6}

; 0,51;

\sqrt{3}

▶ O número 0 é chamado de monômio nulo.

▶ Costuma-se omitir os coeficientes 1 e ‒1 dos monômios. Exemplos: 1z = z; ‒1a2c = ‒a2c

Respostas e comentários

16. a) 3; 3; 3; 3

16. b) x = 2; x = ‒2

16. c) O valor numérico calculado deve ser 3 para ambos, quaisquer que sejam os números escolhidos, desde que diferentes de 2 e de ‒2.

16. d) Sim.

17. Resposta pessoal.

Pense mais um poucoreticências:

a) 11; 111; .1111; .11111

b) .111111

c) ..1111111

d) Espera-se que os estudantes escolham x = ..1234567 e y = 8.

e) Embora os estudantes tenham sido induzidos pelos itens anteriores a dar a resposta adequada ao item d, espera-se que eles percebam que existem infinitos pares de números x e y, tal que o valor numérico de 9x + y seja ..11111111.

Exercícios propostos

O exercício 16 estimula a curiosidade dos estudantes quanto ao fato de o valor numérico da expressão ser constante para todos os valores possíveis atribuídos a x. Como motivação à continuidade do estudo de Álgebra, comente com eles que isso será esclarecido no estudo de produtos notáveis. Se julgar conveniente, aplique a propriedade distributiva na expressão do denominador a fim de evidenciar que, para x diferente de ‒2 e de 2, a expressão é simplificada para 3.

A resolução do exercício 16 está no início deste Manual, nas orientações específicas do capítulo 4.

O exercício 17 pode ser resolvido em pequenos grupos ou duplas. Cada grupo discute e elabora um problema e, em seguida, troca com o de outro grupo para o resolverem. Essa dinâmica possibilita aos estudantes discutir o assunto e as estratégias para elaborar o problema.

Pense mais um poucoreticências

A seção trabalha uma curiosidade numérica com o uso da calculadora. Os estudantes, em grupo, devem identificar o padrão das expressões numéricas propostas e relacioná-lo com a expressão algébrica 9x + y.

No item d, induzidos pela sequência dos resultados anteriores, eles podem obter x = ..1234567 e y = 8, raciocinando aritmeticamente. No entanto, podem obter outro par de valores (existem infinitos) para x e y que contemplem a igualdade.

O item ê desperta o senso crítico dos estudantes para evitar que caiam nos enganos a que os padrões podem levar. Retome esse exercício quando estudarem equação do 1º grau com duas incógnitas e discuta com eles a importância do espírito crítico nos procedimentos de indução. Neste momento, contudo, eles podem procurar outros pares de valores para x e y, por tentativa e êrro, que satisfaçam a igualdade.

3. Monômios

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero seis.

Neste tópico, prosseguimos com o desenvolvimento da habilidade (ê éfe zero oito ême ah zero seis) iniciando o estudo de um tipo especial de expressão algébrica ‒ os monômios ‒, base para o estudo dos polinômios. Destaque as características principais que envolvem esse tipo de expressão algébrica.

Página 98

Monômios semelhantes

Considere os polígonos a seguir.

Ilustração. Triângulo de lados iguais com medida a em cada lado. Ilustração. Quadrado de lados iguais com medida a em cada lado. Ilustração. Pentágono de lados iguais com medida a em cada lado. Ilustração. Hexágono de lados iguais com medida a em cada lado.

A medida do perímetro desses polígonos pode ser indicada por monômios. Observe:

Polígono	Triângulo	Quadrado	Pentágono	Hexágono
Medida do perímetro	3a	4a	5a	6a

Note que os monômios 3a, 4a, 5a e 6a têm a mesma parte literal (a).

Então, dizemos que eles são monômios semelhantes ou termos semelhantes.

Termos semelhantes ou monômios semelhantes são aqueles que têm a mesma parte literal. Monômios que não têm parte literal são semelhantes entre si.

Acompanhe outros exemplos.

a) Os monômios 9a2x e ‒2a2x têm a mesma parte literal (a2x). Portanto, são termos semelhantes.

b) Os monômios

‒ \frac{1}{4} y

, 0,5y e ‒3y têm a mesma parte literal (y). Logo, são termos semelhantes.

c) Os monômios 12a2c e 12ac2 não têm a mesma parte literal (a2c ≠ ac2). Portanto, não são termos semelhantes.

d) 3 e

\sqrt{2}

são dois números não nulos e, portanto, são monômios semelhantes, apesar de não terem parte literal.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

18 Explique por que as expressões a seguir não são monômios.

a) 2x + 5

2 \frac{a}{b}

4 \sqrt{5 x}

19 Dê o coeficiente de cada monômio.

a) ‒2xy

\frac{3}{5} a

c) x

d) ‒y

\frac{x y^{2}}{5}

‒ \frac{a}{3}

20 João coleciona selos. Indicando por x a quantidade de selos de João, represente com um monômio a quantidade de selos de cada colecionador a seguir.

a) Glaucia tem a metade da quantidade de selos de João.

b) Ricardo tem o dôbro da quantidade de selos de João.

c) Gabriel tem

\frac{2}{3}

da quantidade de selos de João.

Respostas e comentários

18. a) Porque envolve a operação de adição.

18. b) Porque tem letra no denominador.

18. c) Porque tem letra no radicando.

19. a) ‒2

19. b)

\frac{3}{5}

19. c) 1

19. d) ‒1

19. e)

\frac{1}{5}

19. f)

‒ \frac{1}{3}

20. a)

\frac{x}{2}

20. b) 2x

20. c)

\frac{2}{3} x

Monômios semelhantes

No estudo dos monômios, muitas vezes recorreremos a conceitos geométricos para embasar as situações, mostrando mais uma vez a correlação entre as Unidades Temáticas Álgebra, Geometria e Grandezas e medidas. Esse é o caso da apresentação de monômios semelhantes (ou termos semelhantes), na qual utilizamos a noção de perímetro de polígonos regulares.

Exercícios propostos

No exercício 18, os estudantes devem aplicar a definição de monômios. No item c, pode-se reescrever a expressão de maneria a evidenciar que x tem expoente fracionário,

\frac{1}{2}

A resolução do exercício 18 está no início deste Manual, nas orientações específicas do capítulo 4.

No exercício 19, a resolução é imediata da definição de parte literal e coeficiente de monômios; relembre aos estudantes que, quando o coeficiente for 1 ou ‒1, pode ser “ocultado” como ocorre nos itens c e d.

No exercício 20, os estudantes devem escrever como expressão algébrica termos que já são conhecidos deles, como dôbro de uma quantidade, triplo, metade, terça parte etcétera Incentive-os a escrever outras sentenças na linguagem verbal para, depois, registrarem uma expressão algébrica, como feito neste exercício. Aproveite para destacar que as situações envolvem grandezas diretamente proporcionais. Questione os estudantes se grandezas inversamente proporcionais, como a relação entre velocidade média e tempo

(v = \frac{d}{t})

para percorrer uma distância d determinada, representa um monômio; espera-se que comentem que não, pois v + d ‒ t ‒1, com d fixo e t variável, o expoente de t não é natural. Isso antecipa o desenvolvimento de aspectos das habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três).

Página 99

21 Um pintor cobra R$ 30,00trinta reais por metro quadrado de parede pintada. Francisco quer calcular quanto vai gastar para pintar as paredes da casa onde ele mora. Para isso, decidiu usar um monômio e indicou a medida da área das paredes por y (em metro quadrado). Que monômio Francisco usou para fazer esse registro?

22 Observe a figura.

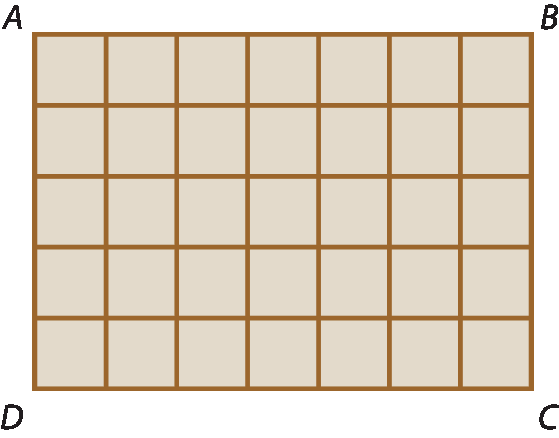
Ilustração. Retângulo A B C D dividido em 5 linhas e 7 colunas, formando 35 quadrados.

Indicando por x a medida do lado de cada quadradinho que forma essa figura, determine:

a) o monômio que representa a medida do perímetro do retângulo a bê cê dê;

b) o valor numérico da medida desse perímetro para x = 1,2;

c) o monômio que representa a medida da área desse retângulo;

d) o valor numérico da medida dessa área para x = 4,5.

23 Entre as alternativas a seguir, quais apresentam monômios semelhantes?

a) 4x e ‒7x

b) 5ab, 3ab e 2ab

\frac{a}{3}

e 5a

d) 2a e 2b

e) 8a2 e ‒5a

f) ‒6, ‒2 e 10,4

g) 7x2y e 9xy2

h) 12xy e ‒21yx

24 Considere o quadrado e sua região interna.

Ilustração. Quadrado azul com medida 3x cada lado.

a) Escreva um monômio que represente a medida do perímetro e outro que represente a medida da área desse quadrado.

b) Esses monômios são semelhantes? Justifique sua resposta.

Hora de criar ‒ Com um colega, elaborem um problema cada um em que as quantidades sejam representadas com monômios e as soluções dos problemas sejam os valores numéricos dos monômios. Troque seu problema com o do colega e, depois de cada um resolver o problema do outro, destroquem para corrigi-los.

PARA SABER MAIS

Cálculo algébrico e dízima periódica

Já sabemos que podemos escrever qualquer fração na fórma decimal. Por exemplo:

\frac{5}{4}

= 1,25, pois 5 : 4 = 1,25

\frac{4}{50}

= 0,08, pois 4 : 50 = 0,08

\frac{17}{1 000}

= 0,017, pois 17 : .1000 = 0,017

\frac{962}{100}

= 9,62, pois 962 : 100 = 9,62

Também podemos escrever números decimais como frações:

• 8,3 =

\frac{83}{10}

• 20,14 =

\frac{2 014}{100}

• 4,012 =

\frac{4 012}{1 000}

• ‒0,0068 = ‒

\frac{68}{10 000}

Basta contar a quantidade de casas decimais e o denominador será o número 1 seguido dessa quantidade de zeros.

E quando o número decimal for uma dízima periódica, por exemplo, 0,3333reticências?

Para contar a quantidade de casas após a vírgula, vamos recorrer ao notável matemático alemão David Hilbert (1862 a 1943). Conta-se que ele narrava uma história sobre um gerente de hotel onde havia infinitos quartos, todos ocupados. Desafiado a acomodar um novo hóspede, o gerente resolveu o problema transferindo cada hóspede antigo para o quarto de número imediatamente superior: o do quarto 1 foi para o quarto 2, o do quarto 2 foi para o quarto 3, o do 3 foi para o 4, e assim fez infinitamente (no infinito não há o último). No quarto 1, que ficou vago, ele acomodou o novo hóspede.

Representando 0,3333reticências por x, vamos calcular o valor de 10x.

Respostas e comentários

21. 30y

22. a) 24x

22. b) 28,8

22. c) 35x2

22. d) 708,75

23. Alternativas a, b, c, f, h.

24. a) Medida do perímetro: 12x; medida da área: 9x2.

24. b) Não, pois eles não têm a mesma parte literal.

25. Resposta pessoal.

Exercícios propostos

No exercício 21, o preço cobrado pelo pintor por metro quadrado é 30 reais, entregando a pintura pronta. Indicando a área a ser pintada por y (em métros quadrados), o monômio que representa o custo dessa obra é 30y.

Uma sugestão para ampliação desse exercício é atribuir valores a y e, com esses valores, compor um quadro que mostre o custo de acôrdo com a área.

Área	Custo (em reais)
100	30 ⋅ (100) = 3.000
150	30 ⋅ (150) = 4.500
200	30 ⋅ (200) = 6.000

Desse modo, os estudantes podem perceber que o custo da obra depende da área a ser pintada, pois essas grandezas são diretamente proporcionais.

As resoluções dos exercícios 22 a 25 estão no início deste Manual, nas orientações específicas do capítulo 4.

Para saber mais

Os estudantes já operaram com números racionais na fórma de fração e na fórma decimal, já associaram a ideia de quociente a uma fração e, também, já trabalharam quocientes decimais. Todo esse conhecimento construído em anos anteriores dá suporte ao tema tratado nesta seção, que explora a dízima periódica.

Ao se depararem com frações que indicam quocientes decimais não exatos, os estudantes obtêm dízimas periódicas, notações decimais que, embora tenham uma representação decimal infinita, apresentam uma repetição na parte decimal (um período). É o caso de

\frac{1}{3}

, que indica o quociente da divisão 1 : 3, cuja notação decimal é a dízima periódica 0,3333reticências, em que o período é 3. Pelo fato de o período já aparecer logo depois da vírgula, dizemos que é uma dízima periódica simples. No caso em que há algarismos depois da vírgula que não façam parte do período, como em 2,1044444reticências, dizemos que a dízima periódica é composta.

Página 100

Se x = 0,3333reticências, então temos 10x = 10 ⋅ 0,3333reticências = 3,3333reticências

Considerando 0,3333reticências e 3,3333reticências e lembrando da história apresentada, notamos que é como se cada um dos infinitos 3 do primeiro número tivesse se transferido para a casa imediatamente à esquerda. Agora, vamos calcular o valor de (10x ‒ x).

10x ‒ x = 3,333reticências ‒ 0,3333reticências

(As infinitas casas após a vírgula são iguais, então elas se anulam.)

9x = 3,0000reticências ou

x = \frac{3}{9} = \frac{1}{3}

Podemos verificar

\frac{1}{3}

dividindo 1 por 3 com a calculadora, que dá 0,3333reticências

A fração

\frac{1}{3}

, que gera a dízima periódica, chama-se fração geratriz da dízima.

Para obter a fração geratriz da dízima 5,181818reticências de período 18, por exemplo, seguimos o procedimento apresentado a seguir.

Como o período tem duas casas, devemos transferir cada período 18 duas casas para a esquerda. Fazemos isso multiplicando x por 100, isto é, vamos calcular o valor de 100x.

Se x = 5,181818reticências, então 100x = 100 ⋅ 5,181818reticências = 518,181818reticências (o 1º período “saltou” para a esquerda da vírgula).

100x ‒ x = 518,181818reticências ‒ 5,181818reticências

(As infinitas casas após a vírgula são iguais, então se anulam.)

99x = 513,000000reticências ou

x = \frac{513}{99}

Com uma calculadora, verifique que

\frac{513}{99}

é a fração geratriz da dízima periódica 5,181818reticências

Agora é com você!

FAÇA A ATIVIDADE NO CADERNO

Determine a fração geratriz das seguintes dízimas:

a) 0,7777reticências

b) 7,7777reticências

c) 0,525252reticências

d) 52,525252reticências

4. Operações com monômios

Ao trabalhar com números, você aprendeu a efetuar as operações de adição, subtração, multiplicação, divisão, potenciação e radiciação. Agora, vamos realizar essas mesmas operações com expressões algébricas. Chamamos esse estudo de cálculo algébrico.

Adição algébrica de monômios

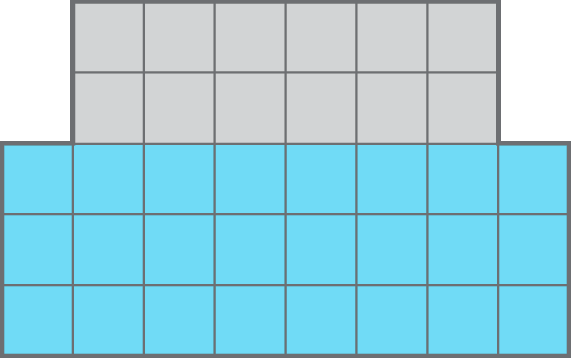
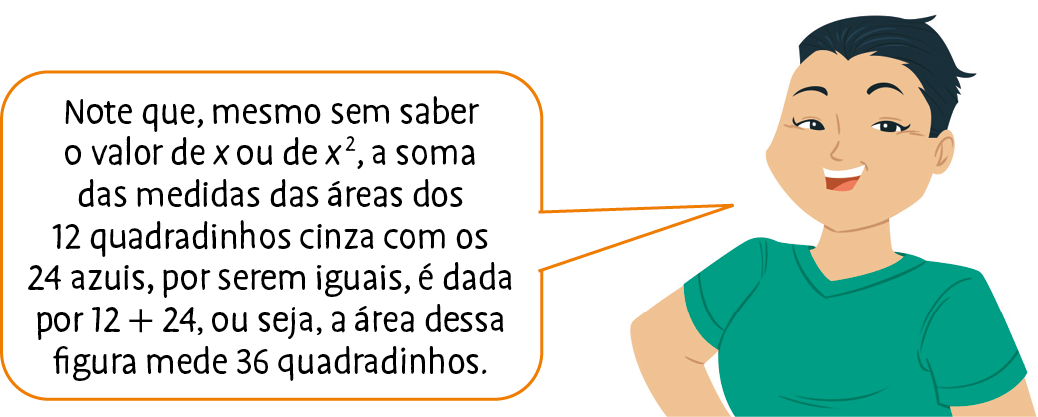
Na figura, a medida da área de cada quadradinho é x2. A medida da área da parte azul é 24x2, e a da parte cinza é 12x2.

Ilustração. Três linhas e oito colunas de quadradinhos azuis. Acima, duas linhas e 6 colunas de quadradinhos cinzas.

Ilustração. Mulher de cabelo curto e camiseta verde fala:
Note que, mesmo sem saber o valor de x ou de x ao quadrado, a soma das medidas das áreas dos 12 quadradinhos cinza com os 24 azuis, por serem iguais, é dada por 12 mais 24, ou seja, a área dessa figura mede 36 quadradinhos.

Respostas e comentários

\frac{7}{9}

\frac{70}{9}

\frac{52}{99}

\frac{5 200}{99}

Para saber mais

O processo algébrico de determinação de uma fração geratriz de uma dízima periódica (fração que origina a dízima) foi utilizado para dízimas periódicas simples. Os estudantes podem reconhecer e utilizar os procedimentos para a obtenção de uma fração geratriz para uma dízima periódica desenvolvendo, assim, a habilidade (ê éfe zero oito ême ah zero cinco).

Apresente aos estudantes uma dízima periódica composta e desafie-os a determinar sua dízima algebricamente. Faça intervenções que os incentivem a elaborar e testar hipóteses, fornecendo dicas para continuarem o trabalho com o processo. Por exemplo, considerando a dízima periódica 0,23333reticências, os estudantes podem verificar que, se fizermos x = 0,23333reticências e multiplicarmos membro a membro a igualdade por 10 ou por 100, não obteremos partes decimais iguais à parte decimal de x:

• 10x = 10 · 0,23333reticências 10x = 2,3333reticências

• 100x = 100 · 0,23333reticências 100x = 23,3333reticências

Nesse caso, em vez de utilizar o x na subtração, devemos observar que 10x e 100x têm partes decimais iguais:

100x ‒ 10x = 23,3333reticências ‒ 2,3333reticências

90x = 21,0000reticências

90x = 21

x = \frac{21}{90} = \frac{7}{30}

Logo, a fração irredutível que gera a dízima periódica 0,23333reticências é

\frac{7}{30}

. A fração

\frac{21}{90}

também gera a mesma dízima. Peça aos estudantes que efetuem a divisão e comprovem que essas frações realmente geram essa dízima periódica.

As resoluções dos itens do Agora é com você! estão no início deste Manual, nas orientações específicas do capítulo 4.

4. Operações com monômios

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero seis.

Iniciamos o estudo das operações com monômios dando destaque para a adição de monômios. Os estudantes podem desenvolver a habilidade (ê éfe zero oito ême ah zero seis) à medida que ampliam a compreensão sobre operações envolvendo monômios. Para a compreensão dos procedimentos, eles devem perceber que podem associar propriedades aritméticas às operações algébricas.

Página 101

A medida da área da figura é obtida pela contagem de todos os quadradinhos ou pela adição das medidas das áreas das duas partes, isto é, pela adição dos monômios 24x 2 e 12x 2.

24x 2 + 12x 2 = 36x 2

Assim, a área total da figura mede 36x 2.

Uma expressão em que aparecem apenas adições e subtrações de monômios é chamada de adição algébrica de monômios.

Acompanhe alguns exemplos.

a) (‒5ab) + (‒2ab) ‒ (‒3ab) = ‒5ab ‒ 2ab + 3ab = ‒4ab

(‒ \frac{3}{4} x^{3} y)

‒

(\frac{1}{3} x^{3} y)

‒ \frac{3}{4} x^{3} y

‒

\frac{1}{3} x^{3} y

\frac{‒ 9 x^{3} y ‒ 4 x^{3} y}{12}

\frac{‒ 13 x^{3} y}{12}

A adição algébrica de monômios semelhantes é obtida adicionando-se algebricamente os coeficientes e conservando-se a parte literal.

Esse processo de cálculo também é chamado de redução dos monômios (ou termos) semelhantes.

Observe alguns exemplos em que ocorre redução de monômios semelhantes.

Sentença matemática. Menos 2x ao quadrado vezes y mais 3x ao quadrado vezes y menos 5x ao quadrado vezes y, igual, menos 4x ao quadrado vezes y. Abaixo, abre parênteses, menos 2 mais 3 menos 5, igual, menos 4, fecha parênteses. Seta azul saindo dessa conta e apontando para menos 4x ao quadrado vezes y.

Sentença matemática. 5 meios vezes a vezes b ao quadrado menos 2 terços vezes a vezes b ao quadrado mais 1 quarto vezes a vezes b ao quadrado, igual, 25, 12 avos, vezes a vezes b ao quadrado. Abaixo, abre parênteses, 5 meios menos 2 terços mais 1 quarto, igual, 30 menos 8 mais 3, tudo sobre 2, igual 25 sobre 12, fecha parênteses. Seta azul saindo dessa conta e apontando para menos 25, 12 avos, vezes a vezes b ao quadrado.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

26 Determine a fração geratriz de:

a) 0,354354354reticências

b) 6,88888reticências

c) 7,878787reticências

27 Efetue os cálculos algébricos a seguir no caderno.

a) (‒10x) + (+6x)

b) (0,8x 2y) + (‒3,5x 2y)

(‒ \frac{2}{5} a b) + (‒ \frac{3}{10} a b)

d) (‒9ay) ‒ (‒3ay)

e) (

0, \overline{2} a^{3}

) ‒ (

‒ 0, \overline{5} a^{3}

)

28 Determine o monômio que representa a medida do segmento

\overline{A B}

Ilustração. Segmento AB. Entre eles, pontos C, D e E. Entre A e C, y. Entre C e D, 2y. Entre D e E, 2 terços vezes y. Entre E e B, 5 quartos vezes y.

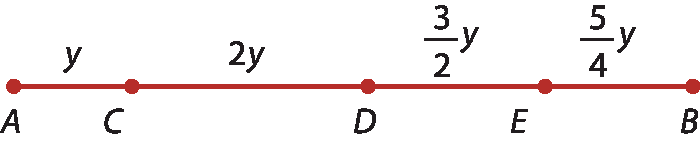
29 Uma empresa de software lançou um novo programa no mercado. No primeiro mês, ela vendeu determinada quantidade desse novo programa. No segundo mês, foi vendido o dôbro do que se vendeu no primeiro mês. No terceiro mês, foi vendido o triplo do que se vendeu nos meses anteriores. Represente a quantidade de unidades vendidas nos três primeiros meses.

30 Represente a medida do segmento

\overline{M P}

, sabendo que a medida do segmento

\overline{M N}

é 6,5x.

Ilustração. Segmento M N. Entre eles, ponto P. Entre P e N, 2,3 x.

Respostas e comentários

26. a)

\frac{118}{333}

26. b)

\frac{62}{9}

26. c)

\frac{780}{99}

27. a) ‒4x

27. b) ‒2,7x 2y

27. c)

‒ \frac{7}{10} a b

27. d) ‒6ay

27. e)

\frac{7}{9} a^{3}

28.

\frac{23}{4} y

29. 12x

30. 4,2x

Adição algébrica de monômios

Ao operar com monômios, o intuito é trabalhar tomando como base as operações estudadas com números inteiros e com números racionais.

A adição algébrica entre monômios será efetuada quando eles apresentarem mesma parte literal, ou seja, quando forem termos semelhantes.

Desenvolva os exemplos na lousa, retomando a adição entre números racionais sempre que necessário, observando o que ocorre com os sinais e retomando adição e subtração de números racionais na fórma de fração. Amplie os exemplos utilizando também coeficientes racionais expressos na fórma decimal para que os estudantes mobilizem todos os conhecimentos já construídos com as operações envolvendo números racionais.

Exercícios propostos

No exercício 26, uma maneira de determinar as frações geratrizes de cada item é considerar diferentes números com a mesma parte decimal.

a) Seja x = 0,354354354reticências .1000x = 354,354354354reticências Logo: .1000x ‒ x = 354 ‒ 0 999x = 354

x = \frac{354}{999}

x = \frac{118}{333}

b) Seja x = 6,8888reticências 10x = 68,8888reticências Então: 10x ‒ x = 68 ‒ 6 9x = 62

x = \frac{62}{9}

c) Seja x = 7,878787reticências 100x = 787,878787reticências Então: 100x ‒ x = 787 ‒ 7 99x = 780

x = \frac{780}{99}

As resoluções dos exercícios 27 a 30 estão no início deste Manual, nas orientações específicas do capítulo 4.

No exercício 27, item ê, observe a conveniência de recordar a notação de dízima periódica.

Página 102

31 Reduza os monômios semelhantes.

a) ‒ 4xy + 6xy ‒ 5xy

b) 5a 3 + 7a 3 ‒ 9a 3 + 3a 3

c) ‒3x ‒ 5x + 2x ‒ x + 4x

\frac{3}{2} x^{2} + \frac{2}{3} x^{2} ‒ \frac{7}{6} x^{2}

m^{3} n^{2} + \frac{4}{5} m^{3} n^{2} ‒ \frac{5}{3} m^{3} n^{2} ‒ \frac{1}{9} m^{3} n^{2}

32 Durante um campeonato de basquetebol promovido em uma escola, o time do 8º ano ganhou x partidas, perdeu (x ‒ 2) partidas e empatou

\frac{x}{2}

partidas.

a) Determine a expressão algébrica que representa o número de partidas que esse time jogou. Essa expressão é um monômio? Por quê?

b) Sabendo que para cada vitória o time ganha 3 pontos, para cada empate ganha 1 ponto e nas derrotas o time não ganha nem perde pontos, qual é o total de pontos obtidos por esse time? O total de pontos é representado por um monômio?

Multiplicação e divisão de monômios

Vamos recordar as multiplicações de potências de bases iguais considerando dois exemplos.

a) 23 ⋅ 22 = 23 + 2 = 25

b) a ⋅ a2 ⋅ a4 = a1 + 2 + 4 = a7

Com base nesses exemplos, observe o cálculo dos produtos a seguir.

Sentença matemática. Primeira linha: abre parênteses, 3a ao quadrado, fecha parênteses, vezes, abre parênteses, 5ab, fecha parênteses, igual. Segunda linha: igual, abre parênteses, 3 vezes 5, fecha parênteses, vezes, abre parênteses, a ao quadrado vezes ab, fecha parênteses, igual. Terceira linha: igual 15 vezes a elevado a 2 mais 1, fim do expoente, vezes b, igual, 15 vezes a ao cubo vezes b. Do lado direito da segunda linha, flecha para esquerda dizendo: Aplicamos as propriedades comutativa e associativa da multiplicação. Do lado direito da terceira linha, Flecha para esquerda dizendo: Efetuamos as operações.

b) (+4xy2) ⋅ (‒9a3x2y) = 4 ⋅ (‒9) ⋅ (x ⋅ y2 ⋅ a3 ⋅ x2 ⋅ y) = ‒36a3x3y3

O produto de dois monômios é obtido da seguinte maneira:

• primeiro, multiplicam-se os coeficientes;

• em seguida, multiplicam-se as partes literais.

Agora, vamos recordar as divisões de potências de bases iguais, considerando dois exemplos.

a) 27 : 22 = 27 ‒ 2 = 25

b) a 4 : a = a 4 ‒ 1 = a 3, com a ≠ 0.

Agora, com base nesses exemplos, observe o cálculo dos quocientes a seguir, considerando o monômio divisor diferente de zero.

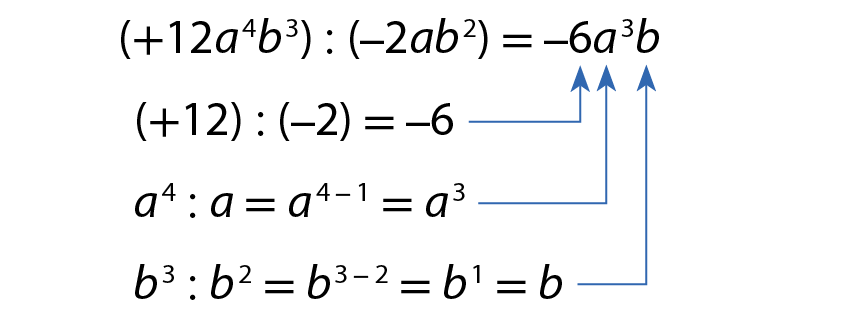
mais 12 a à quarta b ao cubo. Dividido por menos 2 a b ao quadrado igual a menos 6 a ao cubo b. Setas relacionam: mais 12 dividido por menos 2 ao coeficiente numérico menos 6. a à quarta dividido por a igual a elevado, a 4 menos 1, ao coeficiente literal a ao cubo b ao cubo dividido por b ao quadrado igual a b elevado a, 3 menos 2, igual a b elevado a 1 igual a b ao coeficiente literal b

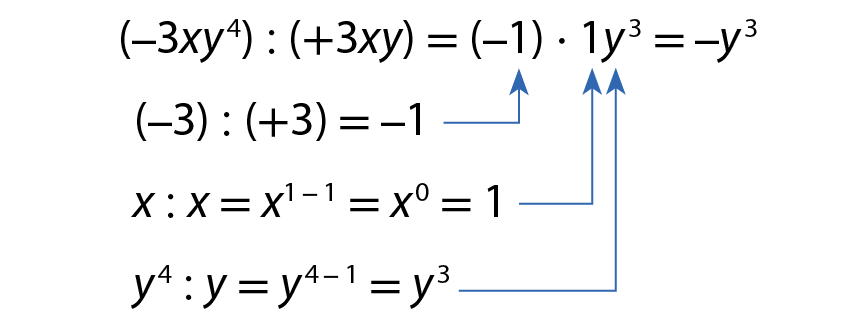
menos 3 x y à quarta. dividido por mais 3 x y, igual a menos 1 vezes 1 y ao cubo igual a menos y ao cubo. setas relacionam menos 3 dividido por mais 3 ao coeficiente numérico menos 1; x dividido por x igual a X elevado a, 1 menos 1. Igual x elevado a zero igual 1 a ao coeficiente numérico 1. y à quarta dividio por y igual a y elevado a, 4 menos 1, igual y ao cubo ao coeficiente literal y ao cubo.

O quociente de dois monômios é obtido da seguinte maneira:

• primeiro, dividem-se os coeficientes;

• em seguida, dividem-se as partes literais.

Respostas e comentários

31. a) ‒3xy

31. b) 6a 3

31. c) ‒3x

31. d) x 2

31. e)

\frac{1}{45}

m 3n 2

32. a)

\frac{5 x ‒ 4}{2}

. Não, porque envolve uma subtração.

32. b)

\frac{7 x}{2}

. Sim.

Exercícios propostos

A resolução do exercício 31 está no início deste Manual, nas orientações específicas do capítulo 4.

Para o exercício 32, apresentamos a seguinte resolução:

ganhou: x partidas

perdeu: (x ‒ 2) partidas

empatou:

\frac{x}{2}

partidas

a) Por meio da expressão algébrica x + (x ‒ 2) +

\frac{x}{2}

, obtemos uma expressão algébrica para o número de partidas que esse time disputou:

x + (x - 2) + \frac{x}{2} =

\frac{2 x + 2 x ‒ 4 + x}{2}

= \frac{5 x ‒ 4}{2}

Assim, o número de partidas é representado pelo binômio:

\frac{5 x ‒ 4}{2}

Essa expressão não é um monômio, pois apresenta uma subtração no numerador.

b) A expressão algébrica que representa o total de pontos desse time é:

3 \cdot x + 1 \cdot \frac{x}{2} + 0 \cdot (x - 2) = 3 x + \frac{x}{2} = \frac{6 x ‒ x}{2} = \frac{7 x}{2}

Logo,

\frac{7 x}{2}

corresponde ao total de pontos obtidos por esse time. Essa expressão, que pode ser escrita na fórma

\frac{7}{2} x

, é um monômio, pois é formada de um único produto (sem adição nem subtração) no qual não há letras em denominador nem em radical. A antecipação da multiplicação do número 3 com o monômio x está ao alcance dos estudantes, que já escreveram algebricamente expressões do tipo “o triplo de x”.

Multiplicação e divisão de monômios

A multiplicação e a divisão de monômios tem base nas propriedades da potenciação. A multiplicação entre monômios sempre resulta em outro monômio, mas a divisão entre eles nem sempre terá um quociente que também é um monômio; por exemplo, x : x2 equivale a

x^{\frac{1}{2}}

, cujo expoente não é natural, assim como a divisão de dois números inteiros nem sempre resulta em quociente inteiro.

Desenvolva os exemplos na lousa, pedindo aos estudantes que indiquem as propriedades de potenciação utilizadas em cada passo.

Página 103

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

33 Calcule no caderno os produtos a seguir.

a) (4a 2x 3) ⋅ (‒5ax 2)

b) (‒6xy) ⋅ (‒3y)

c) (0,5x) ⋅ (2,4x 2)

(‒ \frac{7}{11} a)

⋅ (+2ab) ⋅ (‒11a)

e) (‒2ax) ⋅

(\frac{3}{2} a x^{2}) \cdot (‒ \frac{1}{2} a)

34 Calcule os quocientes a seguir, supondo que o monômio divisor seja diferente de zero.

a) (16x5) : (‒ 4x2)

b) (36xy 4) : (‒6xy)

c) (‒35a) : (+7a)

d) (+3ab2) :

(‒ \frac{10}{5})

(‒ \frac{4}{5} x^{5} y) : (+ \frac{4}{3} x^{2} y)

35 Multiplicando (5ax2 ‒ 2ax2 ‒ 7ax2) por

(\frac{1}{2} x + \frac{1}{4} x)

, obtemos um monômio. Efetue a multiplicação e calcule o valor numérico desse monômio para a = 2 e x = ‒2.

36 O quociente de

(\frac{3}{4} x^{3} y + \frac{2}{3} x^{3} y ‒ \frac{1}{6} x^{3} y)

por

\frac{3}{2} x

é um monômio. Qual é seu valor numérico se x = ‒3 e y = 6?

37 Considere as figuras e faça o que se pede.

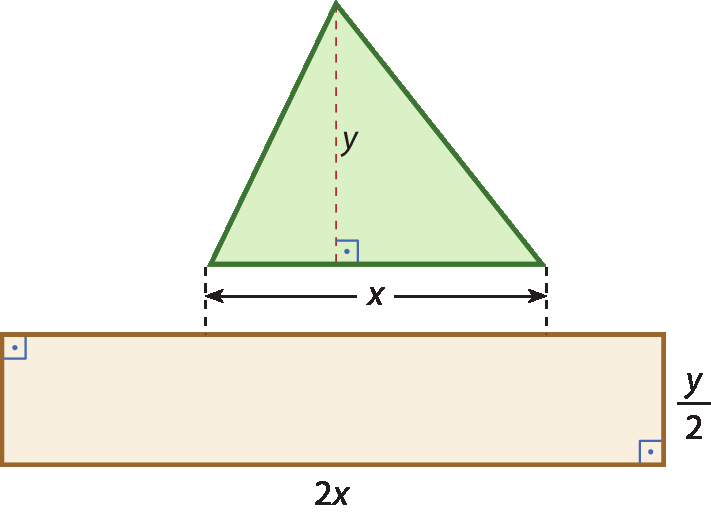
Ilustração. Triângulo de lado com medida x. Reta vertical tracejada com medida y indicando sua altura.
Abaixo, retângulo com medida de comprimento 2 x e medida da altura igual a fração y sobre 2.

a) Sabendo que a medida da área de um triângulo é dada pelo semiproduto das medidas da altura e da base, determine o monômio que representa a soma das medidas das áreas das duas figuras.

b) Obtenha o valor numérico desse monômio para x = 0,5 e y = 1,2.

38 Marcelo separou uma parte retangular de um terreno para construir uma piscina retangular e, em volta dela, um gramado.

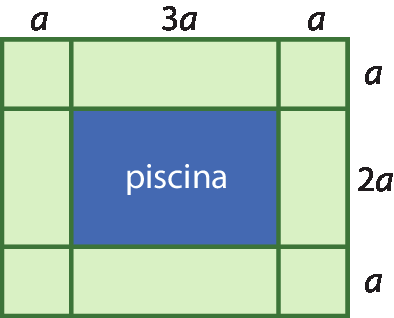
Ilustração. Retângulo verde com um retângulo azul no centro, representando uma piscina. A região visível do retângulo verde é tal que, acima e abaixo da piscina, temos: 2 quadrados verdes de lado a nas extremidades e 1 retângulo verde de lado a por 3a entre eles; à direita e à esquerda da piscina, temos: 2 quadrados verdes de lado a nas extremidades e 1 retângulo verde de lado 2a por a entre eles.

a) Determine a medida da área destinada à piscina.

b) Determine a medida da área destinada ao gramado.

c) Sendo a = 3,2 métros, calcule a quantidade de grama utilizada, em metro quadrado.

Potenciação de monômios

Vamos recordar duas propriedades da potenciação:

• (a 2)3 = a 2 ⋅ 3 = a 6

• (a 2 ⋅ b)3 = (a 2)3 ⋅ b 3 = a 6 ⋅ b 3

Os exemplos a seguir mostram como aplicar essas propriedades a monômios.

a) (‒2a 3x) 2 = (‒2)2 ⋅ (a 3)2 ⋅ x 2 = 4a6x 2

{(‒ \frac{2}{3} m^{2} x)}^{3} = {(‒ \frac{2}{3})}^{3} \cdot (m^{2})^{3} \cdot x^{3} = ‒ \frac{8}{27} m^{6} x^{3}

A potência de um monômio é obtida da seguinte maneira:

• eleva-se o coeficiente à potência indicada;

• em seguida, eleva-se a parte literal à potência indicada.

Observe outros exemplos.

a) (‒5a)2 = 25a 2

{(+ \frac{3}{5} x^{2} y)}^{3} = \frac{27}{125} x^{6} y^{3}

Respostas e comentários

33. a) ‒20a3x 5

33. b) 18xy 2

33. c) 1,2x 3

33. d) 14a3b

33. e)

\frac{3}{2} a^{3} x^{3}

34. a) ‒4x 3

34. b) ‒6y 3

34. c) ‒5

34. d)

‒ \frac{3}{2} a b^{2}

34. e)

‒ \frac{3}{5} x^{3}

35. O valor numérico é 48.

36. O valor numérico é 45.

37. a)

\frac{3}{2} x y

37. b) O valor numérico é 0,9.

38. a) 6a2

38. b) 14a2

38. c) 143,36 métros2

Exercícios propostos

As resoluções dos exercícios 33 a 38 estão no início deste Manual, nas orientações específicas do capítulo 4.

Na resolução dos exercícios 37 e 38, espera-se que os estudantes retomem os conhecimentos construídos no ano anterior a respeito de áreas de triângulos e de retângulos.

Além das operações de multiplicação e divisão entre monômios, eles também aplicarão nesses exercícios a adição algébrica entre monômios e a determinação do valor numérico de expressões algébricas.

Revisitar conceitos já trabalhados é também uma maneira de ampliar e consolidar os conhecimentos construídos e de acompanhar o aprendizado dos estudantes, o que possibilita fazer intervenções mais específicas para que as dúvidas não persistam por muito tempo.

Potenciação de monômios

Neste tópico, tratamos da potenciação de monômios, com base na multiplicação e nas propriedades de potências numéricas. Se necessário, incentive os estudantes a compor um resumo no caderno sobre as propriedades da potenciação e a utilizá-lo sempre que necessário na resolução de exercícios envolvendo operações com monômios.

Página 104

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

39 Calcule.

a) (+2x)2

b) (‒3a 2)3

c) (+2x 2y)3

d) (‒xy 2)4

e) (‒5x 4y)1

{(‒ \frac{1}{2} a)}^{2}

40 A medida do lado de um quadrado é dada por

\frac{5}{3} a

. Qual é medida da área desse quadrado?

41 Considere o cubo representado a seguir.

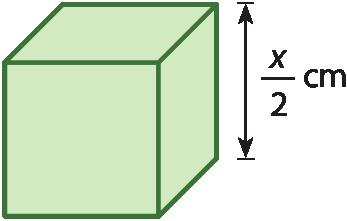
Ilustração. Cubo com medida de lado x sobre 2 centímetros.

a) Expresse a medida do volume do cubo.

b) Qual é a medida da área da superfície desse cubo?

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Sequências recursivas de molduras e de quadrados

Nesta composição de quadrados, as unidades de medida de comprimento são dadas em centímetro. O quadrado central foi contornado com uma moldura branca, formando um segundo quadrado. O novo quadrado foi contornado com uma moldura vermelha, chegando-se a um terceiro quadrado, e assim por diante, até obter o quadrado com a moldura cinza.

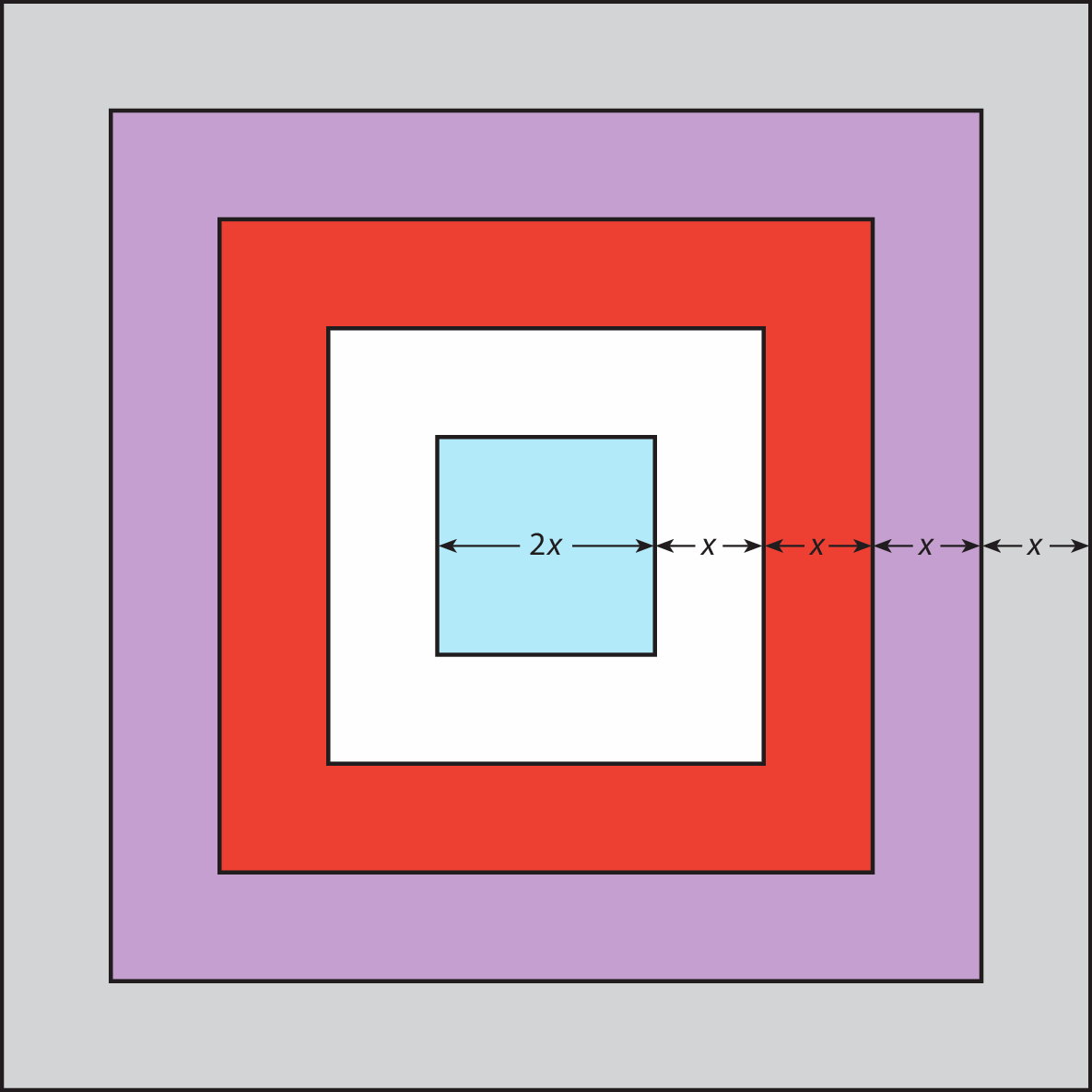
Ilustração. Cinco quadrados, um dentro do outro de maneira que o centro deles coincidem. Primeiro quadrado. Cor azul: lado mede 2 x. Segundo quadrado. Cor branca: medida x é acrescentada à direita do quadrado azul. Terceiro quadrado. Cor vermelha: medida x é acrescentada à direita do quadrado branco. Quarto quadrado. Cor roxa: medida x é acrescentada à direita do quadrado vermelho. Quinto quadrado. Cor cinza: medida x é acrescentada à direita do quadrado roxo.

a) Forme, a partir da medida da área do quadrado central, a sequência recursiva dos monômios que representam as medidas das áreas das molduras, dadas em centímetros quadrados.

b) Uma dessas molduras tem a mesma medida de área de um dos quadrados construídos. Qual é o monômio que representa essa medida?

c) Qual é o valor numérico do monômio obtido no item b para x = 2,4 centímetros?

d) Considerando a sequência de resultados obtidos no item a, faça uma extrapolação e estime a medida da área da próxima moldura a ser formada.

Respostas e comentários

39. a) 4x 2

39. b) ‒27a 6

39. c) 8x 6y 3

39. d) x 4y 8

39. e) ‒5x 4y

39. f)

\frac{1}{4} a^{2}

40.

\frac{25 a^{2}}{9}

41. a)

\frac{x^{3}}{8}

centímetros cúbicos

41. b)

\frac{3}{2} x^{2}

centímetros quadrados

Pense mais um poucoreticências: a) Moldura branca: 12x 2; moldura vermelha: 20x 2; moldura lilás: 28x 2; moldura cinza: 36x 2.

b) 36x 2

c) 207,36

d) 44x2 centímetros quadrados

Exercícios propostos

As resoluções dos exercícios 39 a 41 estão no início deste Manual, nas orientações específicas do capítulo 4.

Pense mais um poucoreticências

Nesta seção, os estudantes poderão desenvolver a habilidade (ê éfe zero oito ême ah um zero) ao identificar a regularidade da sequência associada à situação proposta.

Apresentamos resoluções para os itens desta seção.

a) Sejam:

A_{a}

= medida da área do quadrado azul

A_{b}

= medida da área do quadrado branco

A_{v}

= medida da área do quadrado vermelho

A_{l}

= medida da área do quadrado lilás

A_{c}

= medida da área do quadrado cinza Então:

A_{a}

= (2x)2 = 4x2

A_{b}

= (4x)2 = 16x2

A_{v}

= (6x)2 = 36x2

A_{l}

= (8x)2 = 64x2

A_{c}

= (10x)2 = 100x2 Logo, a medida da área da moldura branca é:

A_{b} ‒ A_{a}

= 16x 2 ‒ 4x 2 = 12x 2 A medida da área da moldura vermelha é:

A_{v} ‒ A_{b}

= 36x 2 ‒ 16x 2 = 20x 2 A medida da área da moldura lilás é:

A_{l} ‒ A_{v}

= 64x 2 ‒ 36x 2 = 28x 2 A medida da área da moldura cinza é:

A_{c} ‒ A_{l}

= 100x 2 ‒ 64x 2 = 36x 2 A sequência é: 12x 2, 20x 2, 28x 2, 36x 2

b) Do item anterior, percebe-se que a medida da área da moldura cinza é igual à medida da área do quadrado vermelho.

c) 36 · (2,4)2 = 36 · 5,76 = 207,36

Logo, o valor numérico do monômio é 207,36.

d) Considerando da mais central para a mais externa, cada moldura acrescentada tem a medida de sua área igual à medida da área da moldura anterior mais 8x 2. Assim, a medida da área da próxima moldura a ser formada será 44x 2.

Página 105

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 (enêm) A expressão “Fórmula de iãng” é utilizada para calcular a dose infantil de um medicamento, dada a dose do adulto:

dose de criança, igual a, abre parenteses, Fração. Numerador idade da criança (em anos), denominador idade da criança (em anos) mais 12, fecha parenteses, vezes dose de adulto.

Uma enfermeira deve administrar um medicamento X a uma criança inconsciente, cuja dosagem de adulto é de 60 miligramas. A enfermeira não consegue descobrir onde está registrada a idade da criança no prontuário, mas identifica que, algumas horas antes, foi administrada a ela uma dose de 14 miligramas de um medicamento Y, cuja dosagem de adulto é 42 miligramas. Sabe-se que a dose da medicação Y administrada à criança estava correta.

Então, a enfermeira deverá ministrar uma dosagem do medicamento X, em miligramas, igual a:

a) 15.

b) 20.

c) 30.

d) 36.

e) 40.

2 Considere o retângulo formado por quadrados de lado medindo y, em centímetro.

Ilustração. Retângulo dividido em duas linhas de 10 quadradinhos cada. Há 7 quadradinhos pintados de amarelo. A medida de cada lado do quadradinho é y.

Faça o que se pede.

a) Determine a medida do perímetro desse retângulo.

b) Determine a medida da área desse retângulo.

c) Qual é a medida da área da parte pintada de amarelo?

3 Efetue as adições algébricas.

a) (‒3x) + (‒8x)

b) (‒12y) + (+6y)

c) (+5ab) ‒ (‒7ab)

d) (+2xy) + (+13xy)

4 Efetue as operações e escreva o resultado na fórma de fração irredutível.

a) 13,75 +

\frac{3}{4}

‒ 12,833reticências

b) (14,1666reticências) ⋅

\frac{7}{3} : \frac{5}{3}

5 Reduza os monômios semelhantes.

a) ‒12a + 9a + 5a

b) 15y ‒ 10y ‒ 6y

‒ \frac{3}{4} a x + \frac{1}{3} a x ‒ \frac{1}{2} a x

6 Calcule os produtos a seguir.

a) (+2x) ⋅ (+3x 2)

b) (‒3y) ⋅ (4y 2)

c) (‒4x 2y) ⋅ (‒3xy 2)

d) (‒5ab) ⋅ (+3a)

7 Calcule os quocientes a seguir, considerando que as variáveis do divisor sejam diferentes de zero.

a) (‒20a 5) : (+4a 2)

b) (+3xy 3) : (4y)

c) (‒24a 3b 2) : (4ab)

d) (‒3,2a 3b) : (0,5a)

8 Calcule as potências a seguir.

a) (‒3x 2y 3)2

{(\frac{6}{3} a^{2} b^{4})}^{3}

{(‒ \frac{2}{5} x)}^{2}

d) (‒0,4a)3

9 Em 1787, o cientista francês Jacques Charles observou que os gases se dilatam quando aquecidos e se contraem quando resfriados.

Ilustração. Figura 1: garrafa em temperatura ambiente. Garrafa com bico maleável na parte superior. — Figura 1: garrafa em temperatura ambiente

Ilustração. Figura 2: garrafa resfriada em contato com gelo. Garrafa dentro de recipiente com gelo. — Figura 2: garrafa resfriada em contato com gêlo

A fórmula

V = \frac{5}{3} \cdot T + 455

relaciona a medida do volume V de certo gás (em centímetro cúbico) com a medida de sua temperatura T (em grau Celsius). Calcule a medida do volume desse gás a 21 graus Célsius.

Respostas e comentários

1. Alternativa b.

2. a) 24y centímetros

2. b) 20y 2 centímetros quadrados

2. c) 7y 2 centímetros quadrados

3. a) ‒11x

3. b) ‒6y

3. c) 12ab

3. d) 15xy

4. a)

\frac{5}{3}

4. b)

\frac{119}{6}

5. a) 2a

5. b) ‒y

5. c)

‒ \frac{11}{12} a x

6. a) 6x 3

6. b) ‒12y 3

6. c) 12x 3y 3

6. d) ‒15a 2b

7. a) ‒5a 3

7. b)

\frac{3}{4} x y^{2}

7. c) ‒6a 2b

7. d) ‒6,4a 2b

8. a) 9x 4y 6

8. b) 8a 6b 12

8. c)

\frac{4}{25} x^{2}

8. d)‒0,064a 3

9. 490 centímetros cúbicos

Exercícios complementares

Este bloco de exercícios amplia as oportunidades de os estudantes retomarem e aplicarem os conceitos desenvolvidos no capítulo.

As resoluções dos exercícios 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 4.

No exercício 9, trabalhe o cálculo da medida do volume do gás em questão para outras medidas de temperatura. Peça aos estudantes, por exemplo, que organizem um quadro no qual registram as medidas do volume V para medidas de temperatura T, em grau Celsius, iguais a 3, 6, 9, 12, 15, 18, 21, reticências e pergunte a eles: Quando os valores de T aumentam 3 unidades, que variações experimentam os valores de V? Aumentam ou diminuem? Quanto?

Espera-se que os estudantes percebam que, nesse caso, os valores de V aumentam 5 unidades. Desse modo, de maneira intuitiva, trabalhamos a ideia de função. Neste exercício, ao substituir T = 21 graus Célsius na equação dada, obtemos:

V = \frac{5}{3} \cdot 21 + 455

V = \frac{105}{3} + 455

V = 35 + 455

V = 490

Ou seja, para T = 21 graus Célsius, temos V = 490 centímetros cúbicos.

Página 106

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 A expressão algébrica 15x + 3 pode representar qual situação a seguir?

a) A idade de Bruna, que é 3 anos mais velha que sua irmã, que tem 15 anos.

b) O valor da refeição com suco em um restaurante que cobra 15 reais a refeição e 3 reais o suco.

c) Carlos tem 15 canecas, que é o triplo da quantidade de canecas de Gabi.

d) A distância percorrida por Otávio ao dar 3 voltas em uma pista de 15 quilômetros.

2 Considere os números reais a, b, c e d. Ao multiplicar a soma de a e b pelo oposto de c, obtém-se o inverso de d. Qual é a expressão algébrica que descreve essa situação?

a) (a + b) ⋅

\frac{1}{c}

= ‒d

b) a + b ⋅

\frac{1}{c}

= ‒d

c) (a + b) ⋅ (‒c) =

\frac{1}{d}

d) a + b ⋅ c =

\frac{1}{d}

3 Para qual valor de x a expressão algébrica

\frac{x^{2} ‒ 4}{2 x + 8}

não tem valor numérico?

a) 2

b) ‒2

c) ‒8

d) ‒ 4

4 Qual é o coeficiente do monômio

‒ \frac{2 a x^{2}}{5}

‒ \frac{2 a}{5}

b) ‒2

‒ \frac{2}{5}

\frac{2}{5}

5 Ao reduzir os termos semelhantes da expressão algébrica a seguir

‒2x2 + 8xy ‒ 3y2 + y2 + 2x2 ‒ 5xy + x2y

obtemos:

a) x2 ‒ 2y2 + 3xy + x2y

b) 2y2 + 4xy

c) ‒2y2 + 3xy + x2y

d) 2x2y2

6 Identifique a alternativa que contém dois monômios semelhantes.

\frac{1}{2}

a2b e ‒2a2b

b) 18ab e ‒18b

c) 5x3 e 5x

d) ‒9m2n3 e ‒9m3n2

7 Uma quadra poliesportiva tem as medidas das dimensões indicadas na ilustração, dadas em centímetro.

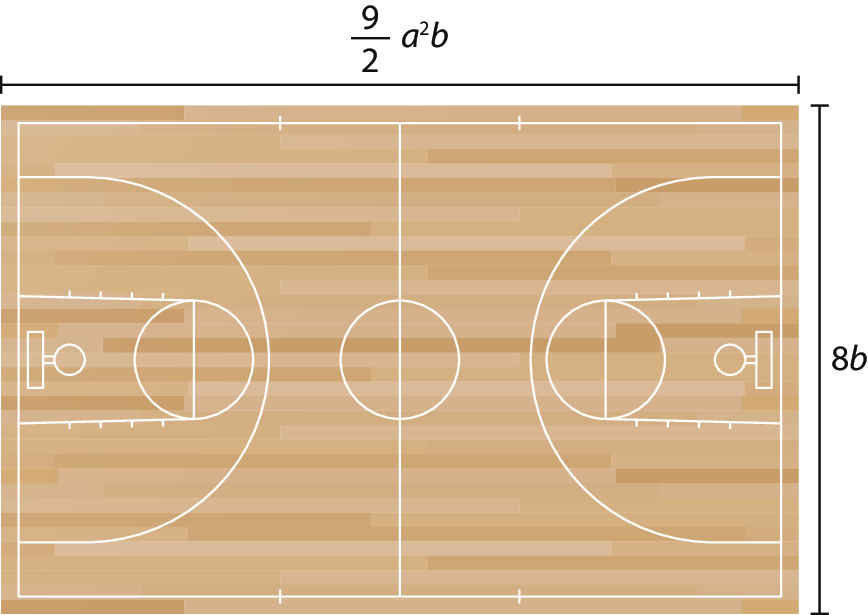
Ilustração. Quadra poliesportiva na horizontal com medidas: 9 meios, vezes a ao quadrado vezes b, por 8 b.

Qual é o monômio que expressa a medida da área dessa quadra, em centímetros quadrados?

a) 36a2b 2

\frac{8}{2}

a2b

c) 72ab2

d) 36a2b

8 Ao elevarmos o monômio

\frac{2}{3} x y^{3}

à 5ª potência, o que obtemos como resultado?

\frac{2}{3} x^{5} y^{15}

\frac{32}{243} x^{5} y^{15}

\frac{32}{243} x^{5} y^{8}

\frac{10}{3} x^{5} y^{8}

9 Um prisma de base quadrada tem volume de medida igual a

\frac{3}{16}

a2 b4 c 7 centímetros3 e aresta da base medindo

\frac{1}{2}

abc3 centímetros. Qual é a medida da altura do prisma, em centímetro?

\frac{1}{4} a^{2} b^{2} c^{2}

\frac{3}{8} a^{2} b^{2} c

\frac{3}{4} b^{2} c

\frac{3}{2} b^{4} c

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.

a) Qual é a diferença entre incógnita e variável?

b) Como você explicaria para um colega o que é um monômio?

c) Quais são as informações que precisamos ter para encontrar o valor numérico de uma expressão algébrica?

d) Na sua opinião, por que é importante estudarmos expressões algébricas?

Respostas e comentários

1. Alternativa b.

2. Alternativa c.

3. Alternativa d.

4. Alternativa c.

5. Alternativa c.

6. Alternativa a.

7. Alternativa a.

8. Alternativa b.

9. Alternativa c.

Organizando:

a) A incógnita é um ou mais valores que é preciso determinar em uma equação; variável é um valor que pode variar dentro das delimitações algébricas e/ou de uma situação.

b) Resposta pessoal. Espera-se que os estudantes considerem que um monômio é uma expressão algébrica que não envolve operações de adição ou subtração, que apresenta uma parte literal, composta de variáveis e seus respectivos expoentes, e um número como coeficiente.

c) Precisamos da expressão algébrica e dos valores das incógnitas ou variáveis.

d) Resposta pessoal. Espera-se que os estudantes considerem que o estudo de expressões algébricas é útil na resolução de problemas e de situações do cotidiano.

Verificando

No teste 1, cada alternativa pode ser relacionada a diferentes expressões algébricas.

a) Sendo a idade da irmã de Bruna igual a x, em anos, a idade de Bruna é x + 3.

b) Seja x a quantidade, em quilograma, então o total é dado por 15x + 3.

c) Seja x a quantidade de canecas de Gabi, então a de Carlos é 15x.

d) A distância que Otávio percorreu, em quilômetro, é dada por 15 · 3, ou seja, 45 quilômetros.

No teste 2, devemos considerar a multiplicação de a + b pelo oposto de c, isto é, por ‒c. Assim, temos (a + b) · (‒c). Com isso, obtemos o inverso de d, ou seja,

\frac{1}{d}

. Logo:

(a + b) · (‒c) =

\frac{1}{d}

No teste 3, temos uma fração algébrica cujo denominador é 2x + 8. Assim, 2x + 8 não deve assumir valor nulo. Isso acontece quando 2x + 8 = 0, ou seja, quando

x = ‒ \frac{8}{2} = ‒ 4

. Assim, x não deve assumir o valor ‒4.

A resolução do teste 4 é imediata à definição de coeficiente de monômio. Em

‒ \frac{2 a x^{2}}{5}

, a parte literal é ax2; portanto,

‒ \frac{2}{5}

é o coeficiente.

As resoluções dos testes 5 a 9 estão no início deste Manual, nas orientações específicas do capítulo 4.

Organizando

Esta seção pode ser utilizada como uma autoavaliação, em que os estudantes respondem às questões propostas e, depois, comparam com as respostas dos colegas. Proponha a eles que respondam no caderno a cada item e, depois, faça uma roda de conversa de maneira a possibilitar que os estudantes corrijam e complementem as respostas dadas.

Página 107

DIVERSIFICANDO

Troca de e-mails

Leia com atenção a troca de e-mails que ocorreu em 2011 entre Fábio e Rita.

Ilustração. Rapaz de cabelo castanho e camisa azul. Ele está sentado de frente para uma mesa com computador. Ilustração. Moça de cabelo castanho preso, camiseta amarela e calça. Ela está sentada em um sofá com um notebook apoiado sobre as coxas.

De: Fábio [mailto: fabio@exemplo.com.br]

Enviada em: sábado, 31 de dezembro de 2011, 12:01

Para: Rita

Assunto: NOTE QUE ESTRANHO

Rita, você reparou que neste ano de 2011 tivemos 4 datas bem interessantes?

1/1/11, 1/11/11, 11/1/11, 11/11/11

Tente entender istoreticências separe os dois últimos dígitos do ano em que você nasceu e adicione esse número à idade que você fez neste ano de 2011. O TOTAL SERÁ 111reticências (para os nascidos no período de 1900 a 1999).

POR EXEMPLO: nasci em 1992 (os dois últimos dígitos formam: 92);

92 mais a minha idade no meu aniversário em 2011: 92 + 19 = 111.

Agora, tente você, não dá para entender; algum matemático explica isso???

De: Rita [mailto: rita@exemplo.com.br]

Enviada em: sábado, 31 de dezembro de 2011, 12:30

Para: Fábio

Assunto: Re: NOTE QUE ESTRANHO

Olá, Fábio.

Matemática e brincadeira às vezes estão juntas! Mas não noto nada de estranho nisso.

• Sejam x e y dois algarismos; vamos representar por xy o número formado pelos dois últimos algarismos do ano de nascimento (para os nascidos no período de 1900 a 1999).

• No ano 2000, a idade de quem nasceu em 19xy era (100 ‒ xy), e a idade dessa pessoa em 2011 é (100 ‒ xy) + 11, porque de 2000 a 2011 passaram-se 11 anos.

• Adicionamos o número formado pelos dois últimos algarismos do ano de nascimento à idade em 2011, isto é: xy + (100 ‒ xy) + 11.

• Como xy adicionado a ‒xy resulta em 0, a expressão xy + (100 ‒ xy) + 11 é igual a 100 + 11, isto é, 111, qualquer que seja o valor de xy.

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

Brincando com números, Rita percebeu algumas curiosidades. Tente descobri-las.

1 Calcule:

a) 11 × 12 e 11 × 21

b) 11 × 13 e 11 × 31

c) 11 × 14 e 11 × 41

d) 11 × 24 e 11 × 42

2 O que acontece com os produtos obtidos na atividade 1?

3 Agora, calcule:

a) 11 × 35 e 11 × 53

b) 11 × 36 e 11 × 63

c) 11 × 37 e 11 × 73

4 A resposta dada na atividade 2 pode ser generalizada?

Respostas e comentários

1. a) 132 e 231.

1. b) 143 e 341.

1. c) 154 e 451.

1. d) 264 e 462.

2. Cada par de números obtidos em cada um dos itens da atividade 1 tem os mesmos algarismos, mas em ordem invertida.

3. a) 385 e 583.

3. b) 396 e 693.

3. c) 407 e 803.

4. Não. De modo geral, para que o padrão se mantenha, é necessário que a soma dos algarismos do número de dois dígitos que é multiplicado por 11 seja maior que 1 e menor que 10.

Diversificando

O trabalho com curiosidades numéricas é um campo amplo e farto para aplicações da Álgebra.

Proponha à turma a brincadeira da idade, de modo que ela seja feita considerando as idades dos adultos que vivem com os estudantes. Deixe que eles formulem hipóteses acerca da razão pela qual o “truque” dá certo.

Depois, discuta com os estudantes o procedimento apresentado. Ao representar o ano do nascimento por 19xy (nascidos no século vinte), verifique se eles realmente compreenderam o significado de xy, que, neste caso, não é a multiplicação entre x e y, mas o número formado pelos dois últimos algarismos do ano do nascimento. Por exemplo, nascidos em 1954, xy = 54; nascidos em 1904, xy = 04 = 4 etcétera Desse modo, a idade no ano 2000 dessas pessoas era:

• .2000 ‒ .1954 = 46

.2000 ‒ .1900 = 100

100 ‒ 54 = 46

• .2000 ‒ .1904 = 96

.2000 ‒ .1900 = 100

100 ‒ 4 = 96

• .2000 ‒ 19xy = ?

.2000 ‒ .1900 = 100

(100 ‒ xy) corresponde à idade no ano .2000 de quem nasceu em 19xy

Ressalte que “a idade hoje” se refere à data do e-mail, que é 31 de dezembro de 2011, ou seja, 11 anos depois de 2000. Por isso, adicionamos 11 às idades obtidas em 2000:

• 46 + 11 (nascida em 1954)

• 96 + 11 (nascida em 1904)

• (100 ‒ xy) + 11 (nascida em 19xy)

Adicionando o número formado pelos dois últimos algarismos do ano do nascimento da pessoa (nascida no século vinte) à expressão da idade obtida em 2011 e efetuando os cálculos, temos:

• (46 + 11) + 54 = 111

• 96 + 11 + 4 = 111

• (100 ‒ xy) + 11 + xy = = 100 ‒ xy + 11 + xy = = 100 + 11 = 111

A exemplificação numérica amplia o grau de compreensão das expressões algébricas pelos estudantes.

Glossário

Divisor de águas: : acontecimento, fato ou situação que serve de referência temporal.; Voltar para o texto