Página 108

CAPÍTULO 5 Polinômios e frações algébricas

Fotografia. Vista do alto de escadaria com partes curvadas em região de rochas com pouca vegetação e o mar abaixo. — Escadaria com cêrca de 230 degraus em San Juan de Gaztelugatxe, País Basco (Espanha). (Fotografia de 2017.)

Grandiosa, como a da imagem, ou em residências, monumentos, morros e prédios públicos, escadas fixas ou rolantes fazem parte do meio em que vivemos.

Escadas fixas têm piso de medida x (medida da profundidade do degrau) e espelho de medida y (medida da altura do degrau) e são construídas conforme a legislação. O desenho de uma escada segue uma equação polinomial, garantindo o conforto dos usuários ao subir ou descer.

Observe, leia e responda no caderno.

a) Pesquise na internet, em livros, atlas etcétera a história da ilha Gaztelugatxe, situada na península Ibérica, e da escadaria que lhe dá acesso. Elabore um texto com um resumo dessa pesquisa.

b) Considerando que essa escadaria tenha exatamente 230 degraus cada um com piso medindo x e espelho medindo y, que medida teria o comprimento de um tapete que recobrisse todos esses degraus?

Respostas e comentários

a) Resposta pessoal.

b) 230 · (x + y)

Capítulo 5 – Polinômios e frações algébricas

Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.

Neste capítulo, desenvolvemos o conceito de polinômios e frações algébricas. Tratamos também de valor numérico de um polinômio e das operações entre polinômios. É uma ampliação do cálculo algébrico tratado no capítulo 4. Além disso, o capítulo aborda a interpolação e a extrapolação gráfica.

A abertura apresenta como motivação uma grandiosa escadaria na ilha Gaztelugatxe, Espanha, cuja história ficcional remonta ao século doze, com os cavaleiros templários, e ao século dezesseis, com o corsário Francis Drêic. Outro exemplo bastante conhecido é a escadaria da muralha da China. O enfoque é o cálculo algébrico presente na construção de escadas, segundo a legislação vigente.

Sugira aos estudantes que utilizem diferentes meios para realizar a pesquisa proposta no item a; por exemplo, após obterem dados gerais e informações ou curiosidades sobre o local, eles podem observar em mapas o continente em que a ilha se situa, o país ao qual pertence, além de analisar o mapa da própria ilha, observando diferentes elementos, como o relevo, vias públicas, trajetos até a ilha etcétera

No item b, considerando as dimensões indicadas, tem-se que o comprimento de tapete para cobrir um degrau é (x + y); assim, para cobrir 230 degraus é necessário um tapete de comprimento de medida 230 · (x + y), em unidade de comprimento.

Página 109

1. Polinômios

Considere estes retângulos e o trapézio.

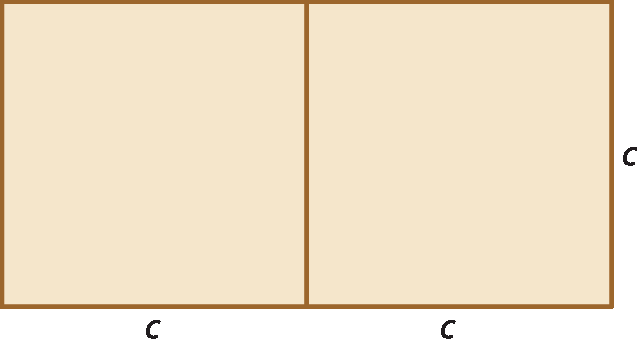
Ilustração. Retângulo dividido em 2 quadrados de laco c cada um. — Figura 1

Ilustração. Trapézio com as medidas: x, x, x, y, em que y é a medida da base maior. — Figura 2

Ilustração. Quadrado composto por 2 retângulos e 2 quadrados. 1 retângulo com medidas a por b, 1 quadrado com medidas b por b, 1 quadrado com medidas a por a e 1 retângulo com medidas b por a. — Figura 3

A figura 1 é formada por dois quadrados, e cada quadrado tem lado de medida c e área de medida c 2. A expressão que representa a medida da área dessa figura é 2c 2.

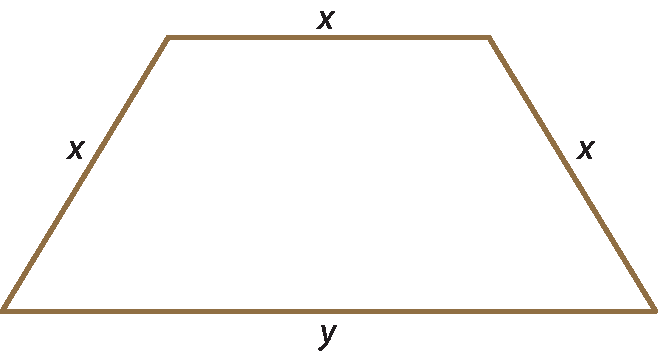
A figura 2 é um trapézio com um lado de medida y e três lados de medida x. A expressão que representa a medida do perímetro dessa figura é 3x + y.

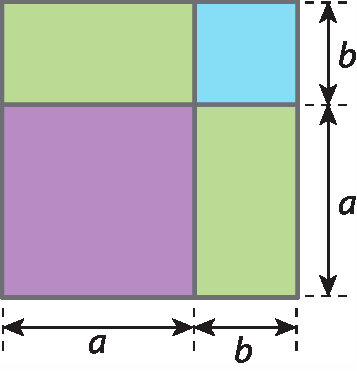
A figura 3, por sua vez, é formada por:

• um quadrado com região interna roxa de lado medindo a e área medindo a 2;

• dois retângulos com regiões internas verdes de medida de área ab;

• um quadrado com região interna azul de lado medindo b e área medindo b 2.

Uma expressão que representa a medida da área dessa figura é a 2 + 2ab + b 2.

As expressões 2c 2, 3x + y e a 2 + 2ab + b 2 são exemplos de polinômios.

Polinômio é toda expressão algébrica que representa um monômio ou uma soma algébrica de monômios.

Observações

▶ Os polinômios de um só termo são chamados monômios, os de dois termos, binômios, e os de três termos, trinômios. Os polinômios com mais de três termos não recebem denominação específica.

▶ O polinômio formado por monômios nulos é o polinômio nulo. Exemplo: 0x 2 + 0mn + 0.

▶ O termo do polinômio que não apresenta variável (letra) é chamado de termo independente.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Classifique como monômio, binômio ou trinômio as expressões algébricas a seguir.

a) 2x 2 ‒ 3x

b) 5a 2 ‒ 3a + 7

c) x

d) 7x ‒ 5y

e) ‒5

f) a 5 ‒ 3

g) x 3 ‒ y 3

h) x 2 ‒ 2xy + y 2

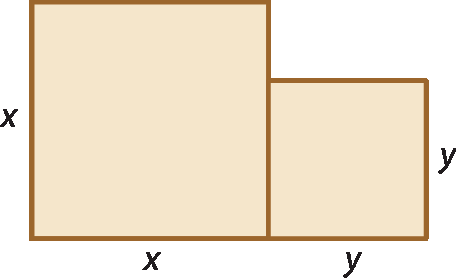
2 Determine o polinômio que corresponde à medida da área da figura a seguir, formada por dois quadrados. Em seguida, calcule a medida da área para x = 4,5 centímetros e y = 2,5 centímetros.

Ilustração. Quadrado com medidas x por x. Encostado nele, quadrado menor com medidas y por y. Ambos têm a parte inferior alinhadas.

Respostas e comentários

1. a) Binômio.

1. b) Trinômio.

1. c) Monômio.

1. d) Binômio.

1. e) Monômio.

1. f) Binômio.

1. g) Binômio.

1. h) Trinômio.

2. x 2 + y 2; 26,5 centímetros quadrados

1. Polinômios

Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero seis e ê éfe zero oito ême ah um nove.

Neste tópico, ao retomar a ideia de medida de área de figuras poligonais e resolver e elaborar problemas que possam ser representados por expressões algébricas, além de efetuar o cálculo numérico dessas expressões, os estudantes desenvolvem as habilidades (ê éfe zero oito ême ah zero seis) e (ê éfe zero oito ême ah um nove).

Conceituamos polinômios utilizando como recurso de contexto o cálculo de medidas de área e de perímetro de figuras poligonais.

Reproduza as figuras apresentadas no início da página e explore seus elementos. Ressalte o que um monômio e um polinômio têm de diferente, de modo que os estudantes compreendam que nem todo polinômio é um monômio, mas todo monômio é um polinômio de um único termo.

Exercícios propostos

No exercício 1, os polinômios são apresentados com os termos semelhantes reduzidos, pois esse conceito ainda não foi tratado. Logo, espera-se que os estudantes classifiquem os polinômios por meio dos significados dos prefixos mono, bi e tri.

Comente com eles que a figura do exercício 2 é uma composição de dois quadrados justapostos e que, portanto, a medida da área da figura é dada pela adição das medidas das áreas das partes.

A medida da área do quadrado maior é x2.

A medida da área do quadrado menor é y2.

A medida da área da figura é x2 + y2.

Para x = 4,5 centímetros e y = 2,5 centímetros, obtemos:

x2 + y2 = (4,5)2 + (2,5)2 = 26,5

Logo, a área mede 26,5 centímetros quadrados.

Página 110

3 Cláudia é dona de uma papelaria. Ela compra um caderno por x reais e o revende por y reais.

Fotografia. Vista superior de uma bancada com diversos cadernos coloridos. Ao fundo, prateleiras com objetos.

a) Qual é a expressão algébrica que representa o lucro de Cláudia por caderno vendido? E por z cadernos vendidos?

b) Qual foi o lucro de Cláudia na venda de 24 cadernos, comprados por R$ 3,20três reais e vinte centavos e vendidos por R$ 8,70oito reais e setenta centavos cada um?

4 O piso da cozinha da casa de Ana é revestido por ladrilhos retangulares, como o ladrilho da figura, em que a e b são dados em metro.

Ilustração. Retângulo com dois losangos, um dentro do outro e 4 triângulos, um em cada canto. A medida do retângulo é a por b.

a) Represente com um monômio a medida da área do ladrilho, em metro quadrado.

b) Indique a medida da área do piso da cozinha, em metro quadrado, sabendo que foram necessários 120 desses ladrilhos para forrá-lo.

c) Calcule a medida da área, em metro quadrado, da cozinha de Ana, sabendo que cada ladrilho mede 15 centímetros por 20 centímetros.

5 Em um estacionamento estão x motos e y carros. Encontre o binômio que representa:

a) o número de veículos;

b) o número de rodas;

c) o valor arrecadado, sabendo que cada moto paga R$ 12,00doze reais pela diária e cada carro paga R$ 18,00dezoito reais.

6 Em arquitetura, os projetos de escadas fixas usam a chamada fórmula de Blondel: 2E + P ≃ 64, na qual ê é a medida do espelho e P é a medida do piso. A escada da casa de Carlos tem 14 degraus com pisos de 30 centímetros e espelhos de 17 centímetros, mais um patamar de 65 centímetros.

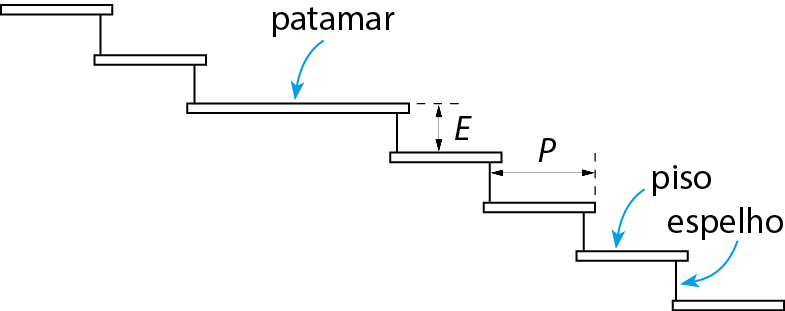
Ilustração. Projeto de uma escada, onde a altura de cada degrau é E, a largura é P, o topo do degraus é chamado de piso, e a lateral de espelho. Um dos degraus é chamado de patamar e é mais largo.

a) Essa escada está de acôrdo com a fórmula de Blondel? Por quê?

b) Qual é o monômio que representa o cálculo da medida da altura dessa escada? Qual é a medida da altura dela?

c) Qual é o polinômio que representa o cálculo da medida do comprimento horizontal lateral dessa escada? Qual é a medida do comprimento horizontal lateral dela?

2. Operações com polinômios

Adição de polinômios

Para representar estes dois polígonos foram usados ao todo 6 canudinhos de medida a, 3 canudinhos de medida b e 2 canudinhos de medida c, todas dadas em centímetro.

Ilustração. Polígono com 5 lados e medidas: a, a, b, c, b. Ilustração. Polígono com 6 lados e medidas: b, a, a, c, a, a.

Respostas e comentários

3. a) y ‒ x; z(y ‒ x)

3. b) R$ 132,00cento e trinta e dois reais

4. a) ab

4. b) 120ab

4. c) 3,6 métros quadrados

5. a) x + y

5. b) 2x + 4y

5. c) 12x + 18y

6. a) Sim, porque 2 ⋅ 17 + 30 = 64.

6. b) 15E; 2,55 métros

6. c) 14P + 65; 4,85 métros

Exercícios propostos

As resoluções dos exercícios 3, 4 e 6 estão no início deste Manual, nas orientações específicas do capítulo 5.

Para a resolução do exercício 5, os estudantes devem atentar para o fato de que motocicletas têm duas rodas, e carros, quatro rodas. Assim, o número de veículos é representado por x + y (item a) e o número de rodas, por 2x + 4y (item b).

Por fim, se cada moto paga diária de R$ 12,00doze reais e cada carro R$ 18,00dezoito reais, aplicando o conceito de proporcionalidade, x motos pagam 12x reais e y carros pagam 18y reais, o que nos leva ao binômio 12x + 18y (item c).

Aproveite a situação do exercício 6 para propor aos estudantes uma pesquisa sobre a construção de escadas.

Na resolução desse exercício, ressalte que para aplicar a fórmula de Blondel é necessário ter as medidas do espelho (E) e do piso (P).

Caso o prédio da escola tenha escadas fixas, acompanhe os estudantes até uma dessas escadas. Munidos de trena, eles devem determinar a medida do espelho (que deve ser a mesma em todos os degraus) e a medida do piso (que deve ser a mesma em todos os degraus). E, se possível, medir a altura e o comprimento total da escada para confrontar com o resultado da multiplicação do número de degraus pelas medidas do espelho e do piso, respectivamente. Lembre os estudantes de que devem medir os patamares também, se eles existirem, e considerar suas medidas. Peça a eles que respondam oralmente à questão “Que problemas pode apresentar uma escada em que a medida da altura dos degraus não é uniforme? E se a medida do piso não for uniforme?”. Espera-se que eles concluam que, nesse caso, a segurança da escada estaria comprometida, e transitar por ela poderia ocasionar acidentes e quedas.

Finalmente, os estudantes devem verificar se a escada está de acôrdo com a fórmula de Blondel.

2. Operações com polinômios

Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero seis e ê éfe zero oito ême ah um nove.

Com exemplos numéricos, recorde brevemente com a turma as quatro operações fundamentais com números racionais.

Neste tópico, ao retomar a ideia de medida de área de figuras poligonais e resolver e elaborar problemas que possam ser representados por expressões algébricas, além de efetuar o cálculo numérico dessas expressões, aprofundamos o trabalho com as habilidades (ê éfe zero oito ême ah zero seis) e (ê éfe zero oito ême ah um nove).

Página 111

Em centímetro, a medida do perímetro do polígono 1 é representada pelo polinômio 2a + 2b + c e a medida do perímetro do polígono 2 é representada pelo polinômio 4a + b + c, ambos os polígonos nas variáveis a, b e c.

Na construção dos dois polígonos, empregamos os 6 canudinhos de medida a, os 3 canudinhos de medida b e os 2 canudinhos de medida c, ou seja, construímos linhas cuja soma das medidas dos comprimentos é dada, em centímetro, por:

6a + 3b + 2c

O polinômio 6a + 3b + 2c é a soma dos polinômios 2a + 2b + c e 4a + b + c.

Esse resultado poderia ter sido obtido da seguinte maneira:

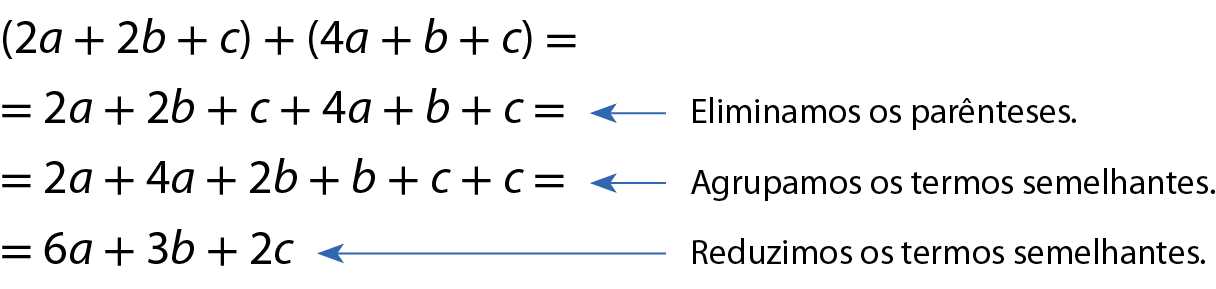
Esquema. abre parêntese 2a mais 2b mais c fecha parêntese mais abre parêntese 4a mais b mais c fecha parêntese igual
igual 2a mais 2b mais c mais 4a mais b mais c igual seta azul apontando para essa expressão com a indicação eliminamos os parênteses.
igual 2a mais 4a mais 2b mais b mais c mais c igual seta azul apontando para essa expressão com a indicação agrupamos os termos semelhantes.
igual 6a mais 3b mais 2c seta azul apontando para essa expressão com a indicação reduzimos os termos semelhantes.

Ilustração. Mulher de cabelo curto castanho, óculos, blusa rosa e camisa amarela. Ela fala: Para adicionar dois polinômios, devemos agrupar os termos semelhantes e depois reduzi-los.

Acompanhe outros exemplos.

a) Vamos calcular (4x2 ‒ 7x + 2) + (3x2 + 3).

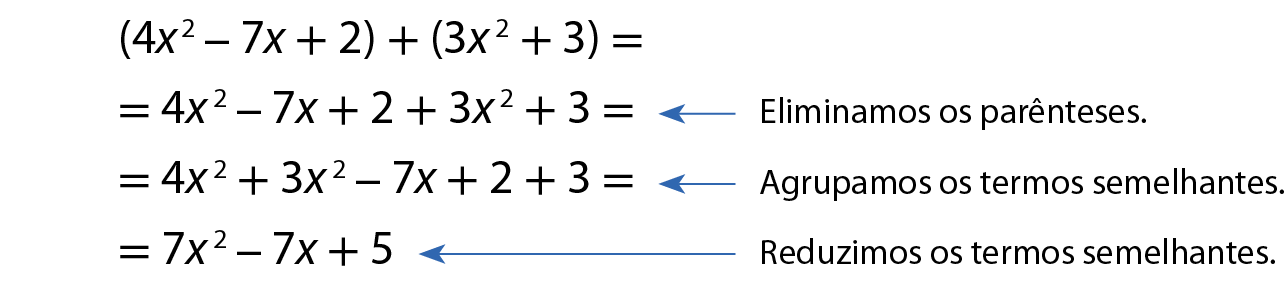
Esquema. abre parêntese 4 x ao quadrado menos 7x mais 2 fecha parêntese mais abre parêntese 3 x ao quadrado mais 3 fecha parêntese igual igual 4 x ao quadrado menos 7x mais 2 mais 3 x ao quadrado mais 3 igual seta azul apontando para essa expressão com a indicação eliminamos os parênteses. igual 4 x ao quadrado mais 3 x ao quadrado menos 7x mais 2 mais 3 igual seta azul apontando para essa expressão com a indicação agrupamos os termos semelhantes. igual 7 x ao quadrado menos 7x mais 5 seta azul apontando para essa expressão com a indicação reduzimos os termos semelhantes

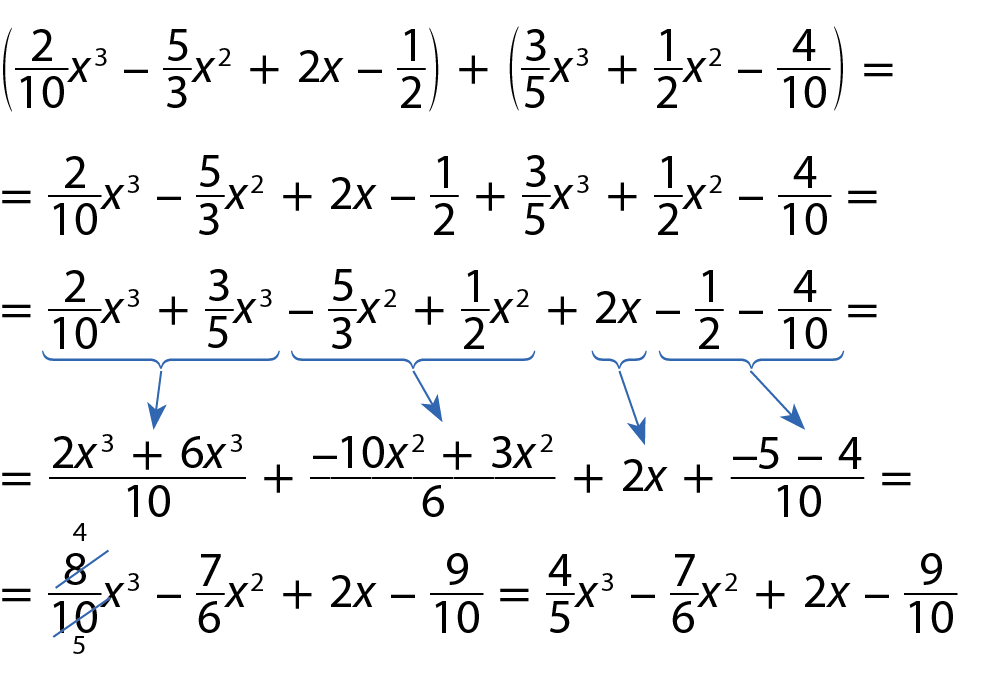
b) Dados os polinômios a = 0,2x 3 ‒

\frac{5}{3}

x 2 + 2x ‒

\frac{1}{2}

B = \frac{3}{5} x^{3} + \frac{1}{2} x^{2} ‒ 0, 4

, vamos calcular a + B.

Abre parenteses, 2 décimos vezes x ao cubo, menos 5 terços vezes x ao quadrado, mais 2x menos 1 meio, Fecha parenteses. Mais. Abre parenteses, 3 quintos vezes x ao cubo, mais, 1 meio vezes x ao quadrado, menos 4 décimos, Fecha parenteses, igual a. Igual a, 2 décimos, vezes x ao cubo, menos, 5 terços vezes x ao quadrado, mais 2x, menos 1 meio, mais, 3 quintos vezes x ao cubo, mais, 1 meio vezes x ao quadrado, menos 4 décimos, igual a. Igual a, 2 décimos vezes x ao cubo, mais, 3 quintos vezes x ao cubo, menos, 5 terços vezes x ao quadrado, mais, 1 meio vezes x ao quadrado, mais 2x, menos 1 meio, menos 4 décimos, igual a. Igual a, fração, numerador 2 vezes x ao cubo, mais 6 vezes x ao cubo, denominador 10, fim da fração mais, fração, numerador menos 10, vezes x ao quadrado, mais 3 vezes x ao quadrado, denominador 6, fim da fração mais 2x, mais, fração, numerador menos 5 menos 4, denominador 10, igual a. Igual a, 8 décimos, vezes x ao cubo, menos, 7 sextos vezes x ao quadrado, mais, 2x menos 9 décimos, igual a, 4 quintos vezes x ao cubo, menos 7 sextos vezes x ao quadrado, mais 2x, menos 9 décimos.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

7 Calcule:

a) (2x + y + 3) + (‒5x + y ‒ 1)

(\frac{7 a}{5} ‒ 2 a b + \frac{b^{2}}{3}) + (4 a b ‒ \frac{b^{2}}{3})

c) (3ab ‒ 6a 2) + (a 2 ‒ 4ab + 2b 2) + (5a 2 ‒ 3b 2)

(\frac{x^{2}}{3} + \frac{2 x}{5} ‒ \frac{1}{4}) + (\frac{2 x^{2}}{3} ‒ \frac{1}{4})

8 Dados os polinômios a = x 2 ‒ 3x + 5, B = x 2 + 2x ‒ 4 e C = x 2 + 5x ‒ 1, calcule:

a) A + B

b) A + B + C

c) A + C

d) B + C

Respostas e comentários

7. a) ‒3x + 2y + 2

7. b)

\frac{7 a}{5} + 2 a b

7. c) ‒ab ‒ b2

7. d)

x^{2} + \frac{2 x}{5} ‒ \frac{1}{2}

8. a) 2x 2 ‒ x + 1

8. b) 3x 2 + 4x

8. c) 2x 2 + 2x + 4

8. d) 2x 2 + 7x ‒ 5

Adição de polinômios

Para introduzir a adição de polinômios, utilizamos um contexto envolvendo medidas de perímetro de polígonos. Se julgar necessário, retome a adição com números racionais e relembre que a adição de monômios é efetuada apenas entre termos semelhantes, ou seja, termos que têm a mesma parte literal.

Exercícios propostos

As resoluções dos exercícios 7 e 8 estão no início deste Manual, nas orientações específicas do capítulo 5.

No exercício 8, oriente os estudantes a primeiro efetuar o cálculo mentalmente, com base na adição de números inteiros.

Página 112

Subtração de polinômios

Nas figuras a seguir, o polígono 1 foi representado com 4 canudinhos de medida a, 4 canudinhos de medida b e 2 canudinhos de medida c, e o polígono 2 foi representado com 4 canudinhos de medida a e 2 canudinhos de medida b, todas as medidas dadas em centímetro.

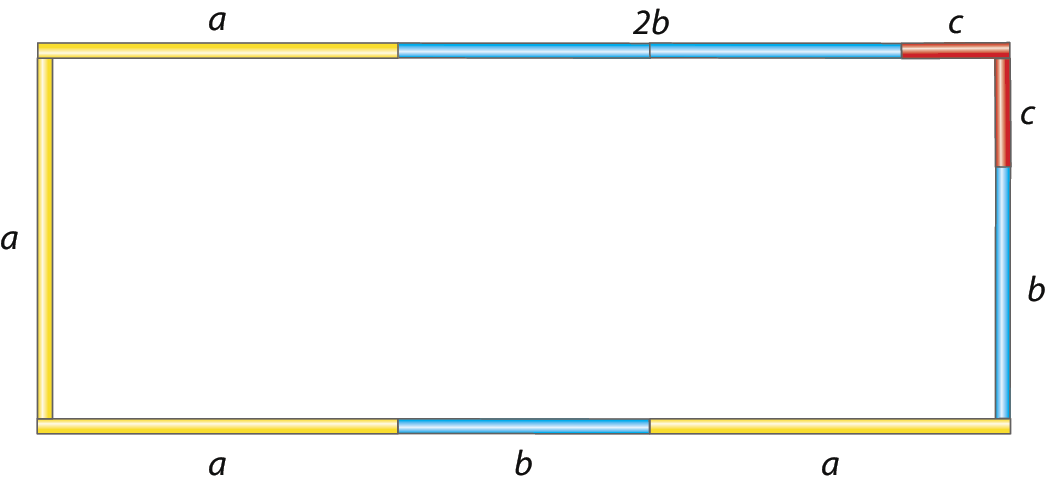
Ilustração. Retângulo composto por canudinhos. As medidas dos canudinhos são: lado esquerdo: a, lado superior: a, 2b, c, lado direito: c, b, lado inferior: a, b, a. — Polígono 1

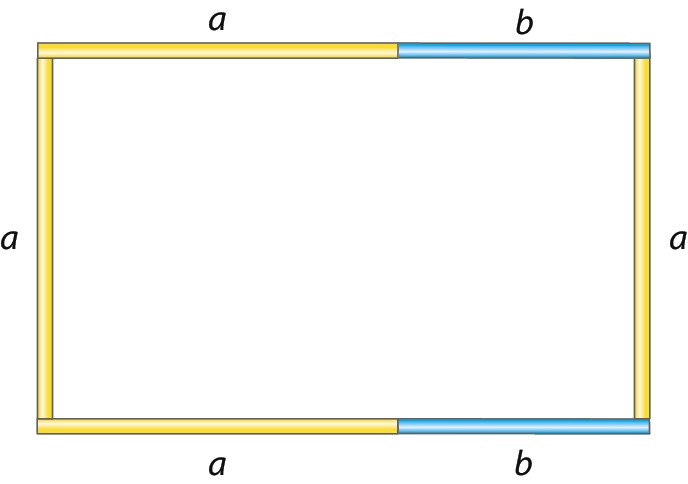
Ilustração. Retângulo composto por canudinhos. As medidas dos canudinhos são: lado direito: a, lado superior: a, b, lado esquerdo: a, lado inferior: a, b. — Polígono 2

O polinômio que representa, em centímetro, a medida do perímetro do polígono 1 é 4a + 4b + 2c, e o polinômio que representa a medida do perímetro do polígono 2 é 4a + 2b.

Na construção do polígono 1, empregamos 2 canudinhos de medida b e 2 canudinhos de medida c a mais que no polígono 2, ou seja, construímos linhas cuja diferença das medidas de comprimento, em centímetro, é dada por:

2b + 2c

O polinômio 2b + 2c é a diferença entre os polinômios 4a + 4b + 2c e 4a + 2b.

Esse resultado poderia ter sido obtido da seguinte maneira:

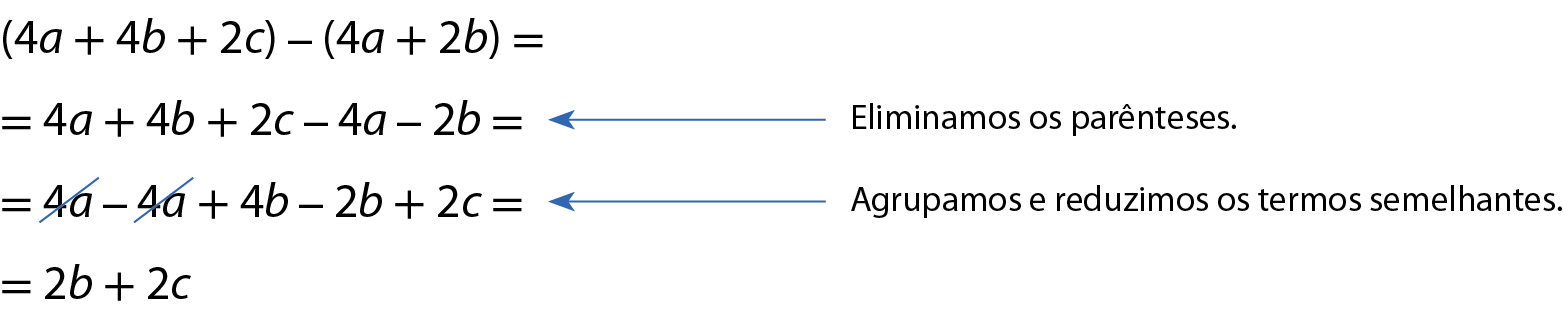
Esquema. abre parêntese 4a mais 4b mais 2c fecha parêntese menos abre parêntese 4a mais 2b fecha parêntese igual. igual 4a mais 4b mais 2c menos 4a menos 2b igual seta azul apontando para essa expressão com a indicação eliminamos os parênteses. igual 4a, cortado com um traço, menos 4a, cortado com um traço, mais 4b menos 2b mais 2c igual seta azul apontando para essa expressão com a indicação agrupamos e reduzimos os termos semelhantes. igual 2b mais 2c.

Acompanhe outros exemplos.

Esquema. 2x menos abre parêntese 4y menos 3x fecha parêntese 5x menos y fecha parêntese igual. igual 2x menos 4y mais 3x mais 5x menos y igual seta azul apontando para essa expressão com a indicação eliminamos os parênteses. igual 10x menos 5y seta azul apontando para essa expressão com a indicação reduzimos os termos semelhantes.

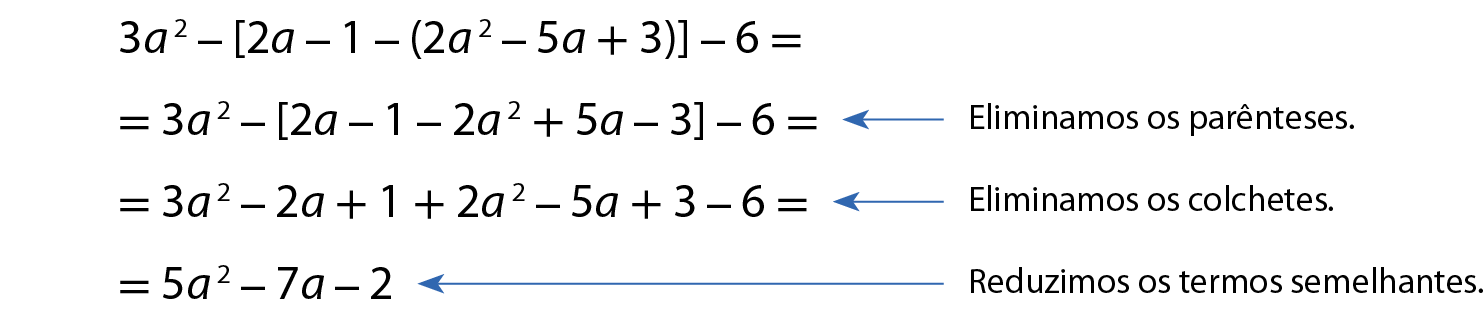
Esquema. 3 a ao quadrado menos abre colchete 2a menos 1 menos abre parêntese 2 a ao quadrado menos 5a mais 3 fecha parêntese fecha colchete menos 6 igual. igual 3 a ao quadrado menos abre colchete 2a menos 1 menos 2 a ao quadrado mais 5a menos 3 fecha colchete menos 6 igual seta azul apontando para essa expressão com a indicação eliminamos os parêntese. igual 3 a ai quadrado menos 2a mais 1 mais 2 a ao quadrado menos 5a mais 3 menos 6 igual seta azul apontando para essa expressão com a indicação eliminamos os colchetes. igual 5 a ao quadrado menos 7a menos 2 seta azul apontando para essa expressão com a indicação reduzimos os termos semelhantes.

Respostas e comentários

Subtração de polinômios

A comparação da quantidade de canudinhos utilizada na construção de dois polígonos e a utilização das medidas de seus perímetros possibilitam aos estudantes atribuir significado à subtração de polinômios.

Comente com eles que a adição e a subtração de polinômios podem ser tratadas como a adição algébrica entre eles, como ocorre no cálculo com números racionais. Essa analogia remete ao entendimento das ordens e classes numéricas dos números racionais na fórma decimal. Isso confere aos estudantes maior autonomia e confiança no trato com essa operação.

Página 113

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

9 Dados os polinômios a = 5x 2 ‒ 3x + 4, B = 2x 2 + 4x ‒ 3 e C = x 2 ‒ 3x, calcule:

a) A ‒ B

b) B ‒ A

c) A + C ‒ B

d) A ‒ C + B

10 Qual polinômio devemos adicionar ao polinômio 2x + y + 3 para obter o polinômio ‒3x + 2y + 2?

11 Qual polinômio devemos subtrair do polinômio 2x 3 ‒ 3x 2 + x ‒ 4 para obter o polinômio ‒3x 3 ‒ 5x 2 + 4x + 1?

12 Reduza os termos semelhantes.

a) 10x 2 ‒ (5x + 6) ‒ [2x ‒ (3x 2 ‒ 2)]

b) 5a ‒ [3b + 7 ‒ (4a ‒ 5b) + (2 ‒ a)]

x^{2} + (\frac{1}{2} x ‒ 2) ‒ (‒ \frac{1}{2} + x + \frac{1}{3} x^{2})

13 Ângela tinha um cofre com 18 moedas de x centavos, 30 moedas de y centavos e 40 moedas de z centavos. Durante o mês, depositou 8 moedas de x centavos e 10 moedas de y centavos. No mês seguinte, retirou 12 moedas de y centavos e 8 moedas de z centavos.

Ilustração. Menina de cabelo castanho e blusa amarela está com moedas na frente de um porquinho rosa.

Determine o polinômio que representa o total de centavos no cofre:

a) no início das operações;

b) no final do mês anterior;

c) no mês seguinte.

14 Observe a figura a seguir.

Ilustração. Reta A D. Entre ela, pontos B e C. Entre A e B, medida de 2x mais 1. Entre B e C, medida de 3x menos 2. Entre C e D, medida de 2x.

Com base na figura, determine:

a) a medida do segmento

\overline{A C}

;

b) a medida do segmento

\overline{B D}

;

c) a medida do segmento

\overline{A D}

Hora de criar – Elabore, e passe para um colega, um problema sobre adição ou subtração de polinômios que envolva as medidas de perímetro de dois polígonos regulares. Depois de cada um resolver o problema do outro, destroquem para corrigi-los.

Multiplicação de polinômio por monômio

Ilustração. Homem de cabelo liso preto e camisa verde. Ele fala: Observe as figuras a seguir, formadas por retângulos, e suas respectivas medidas dos lados, em centímetro.

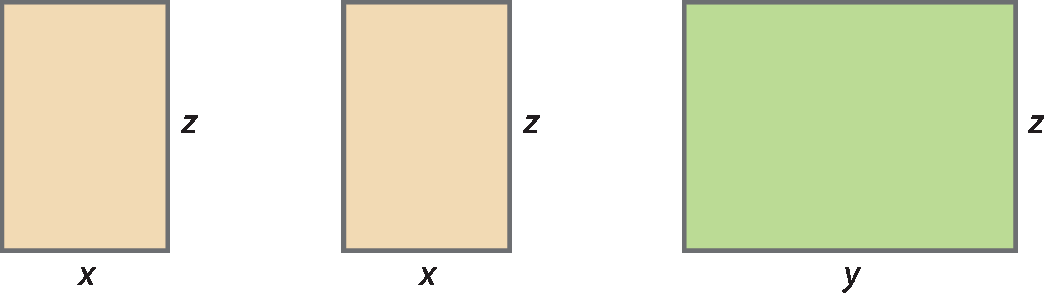
Ilustração. Retângulo x por z. Ilustração. Retângulo x por z. Ilustração. Retângulo y por z.

A adição das medidas das áreas dessas figuras resulta, em centímetros quadrados, na soma:

xz + xz + yz = 2xz + yz

Agrupando as três figuras, formamos um retângulo maior.

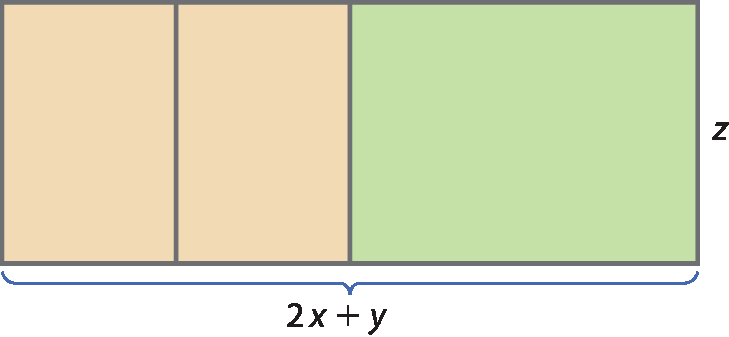
Ilustração. Retângulo composto por três partes, sendo dois retângulos iguais com medidas x e z e um retângulo maior com medidas y e z. A medida total do retângulo é 2x mais y por x.

Respostas e comentários

9. a) 3x 2 ‒ 7x + 7

9. b) ‒ 3x 2 + 7x ‒ 7

9. c) 4x 2 ‒ 10x + 7

9. d) 6x 2 + 4x + 1

10. ‒5x + y ‒ 1

11. 5x 3 + 2x 2 ‒ 3x ‒ 5

12. a) 13x 2 ‒ 7x ‒ 8

12. b) 10a ‒ 8b ‒ 9

12. c)

\frac{2}{3} x^{2} ‒ \frac{1}{2} x ‒ \frac{3}{2}

13. a) 18x + 30y + 40z

13. b) 26x + 40y + 40z

13. c) 26x + 28y + 32z

14. a) 5x ‒ 1

14. b) 5x ‒ 2

14. c) 7x ‒ 1

15. Resposta pessoal.

Exercícios propostos

As resoluções dos exercícios 9 a 12 e dos exercícios 14 e 15 estão no início deste Manual, nas orientações específicas do capítulo 5.

No exercício 13, espera-se que os estudantes compreendam que, ao tomar 18 moedas de x centavos, obtemos 18x centavos. Do mesmo modo, obteríamos 30y centavos e 40z centavos; e assim para todos os demais casos. Para efetuar os cálculos, eles devem estar atentos às ações indicadas (tinha, depositou, retirou).

Para o item a, que representa a situação inicial, estão envolvidas as representações das quantias que Ângela tinha: 18x centavos, 30y centavos e 40z centavos. Assim, ao todo ela tinha (18x + 30y + 40z) centavos.

Para o item b, os estudantes devem determinar a quantia total depositada e acrescentar ao que Ângela já tinha. Assim, obtemos como a representação do total depositado (8x + 10y) centavos, que, acrescentados a (18x + 30y + 40z) centavos que Ângela já tinha, nos fornecem a seguinte quantia:

(18x + 30y + 40z) + (8x + 10y) = 18x + 30y + 40z + 8x + 10y = 26x +40y + 40z

Ou seja, ao final do mês anterior, Ângela ficou com (26x + 40y + 40z) centavos.

Finalmente, para o item c, da quantia obtida no item b devemos subtrair a quantia retirada no mês seguinte.

(26x + 40y + 40z) ‒ (12y + 8z) = 26x + 40y + 40z ‒ 12y + 8z = 26x + 28y + 32z

Assim, no mês seguinte, Ângela ficou com (26x + 28y + 32z) centavos no cofre.

Página 114

Em centímetro, a base desse retângulo mede 2x + y, e a altura mede z. Portanto, a medida da área desse retângulo é (2x + y) ⋅ z, em centímetros quadrados. No entanto, a medida dessa área é igual à soma das medidas das áreas dos três retângulos que formaram o retângulo maior. Logo:

(2x + y) ⋅ z = 2xz + yz

Observe que a expressão 2xz + yz também resulta da aplicação da propriedade distributiva em (2x + y) ⋅ z:

Esquema. abre parêntese 2x mais y fecha parêntese vezes z igual 2xz mais yz. Na expressão há uma seta azul saindo do 2x e chegando no z e uma seta azul saindo y e chegando no z.

Acompanhe outros exemplos.

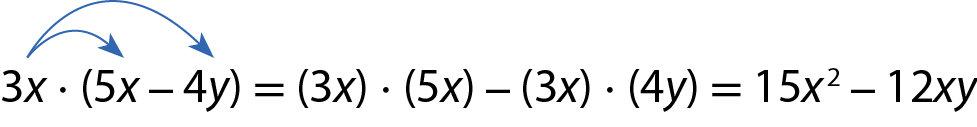
Esquema. 3x vezes abre parêntese 5x menos 4y fecha parêntese igual abre parêntese 3x fecha parêntese vezes abre parêntese 5x fecha parêntese menos abre parêntese 3x fecha parêntese vezes abre parêntese 4y fecha parêntese igual 15 x ao quadrado menos 12xy. Na expressão há duas setas azuis saindo do 3x e chegando no 5x e no menos 4y.

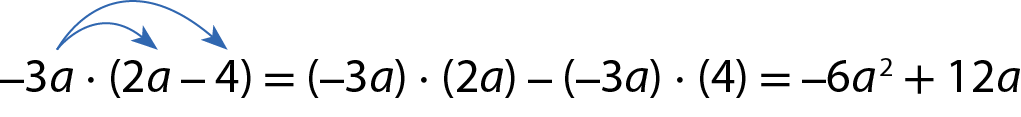
Esquema. menos 3a vezes abre parêntese 2a menos 4 fecha parêntese igual abre parêntese menos 3a fecha parêntese vezes abre parêntese 2a fecha parêntese menos abre parêntese menos 3a fecha parêntese vezes abre parêntese 4 fecha parêntese igual menos 6 a ao quadrado mais 12a.
Na expressão há duas setas azuis saindo do menos 3a e chegando no 2a e no menos 4.

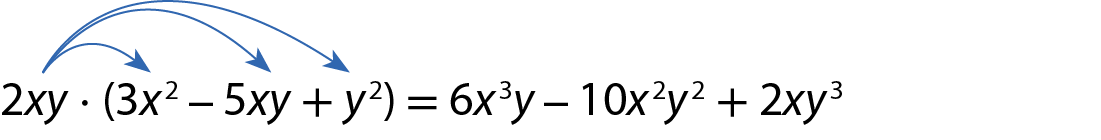
Esquema. 2xy vezes abre parêntese 3x ao quadrado menos 5xy menos y ao quadrado fecha parêntese igual 6 x ao cubo y ao quadrado mais 2x y ao cubo. Na expressão há três setas azuis saindo do 2xy e chegando no 3 x ao quadrado, menos 5xy e y ao quadrado.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

16 Calcule:

a) 7x ⋅ (2x ‒ 5)

b) (3a 2 ‒ 2a ‒ 1) ⋅ 5a

c) ‒3x ⋅ (4x 2 ‒ 3x + 1)

\frac{2}{5} a \cdot (a ‒ \frac{1}{4})

e) (0,3x 2 ‒ 1,4x) ⋅ (‒0,2x 3)

(\frac{1}{3} y^{2} + \frac{4}{7} y^{3}) \cdot (‒ 3 y)

17 Observe as figuras 1 e 2.

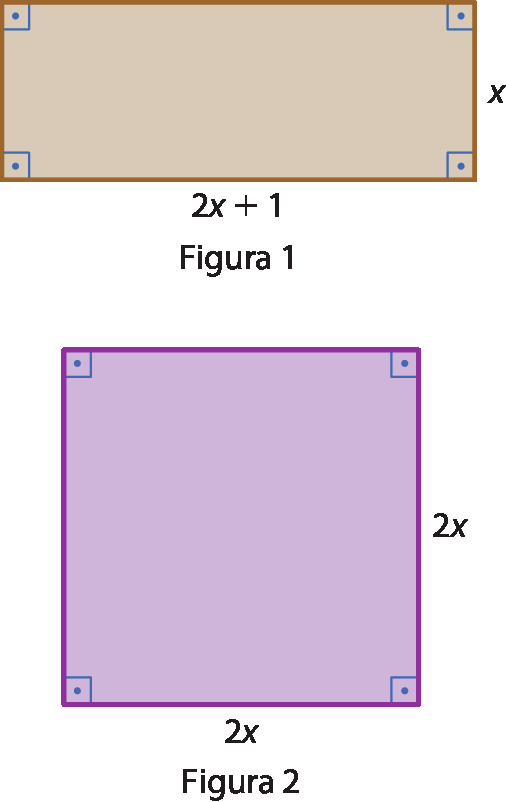
Ilustração. Retângulo com lados de medida x e 2x mais 2. Legenda: Figura 1. Quadrado com lados de medida 2x. Legenda: Figura 2.

a) Qual é o binômio que expressa a soma da medidas das áreas das duas figuras?

b) Qual é o valor numérico do binômio obtido no item a, se x = 5?

c) Qual é o valor numérico de x, se a área do quadrado da figura 2 mede 100?

18 Em uma sala retangular, foi colocado um tapete quadrado, como mostra a figura a seguir, cujas medidas são dadas em centímetro.

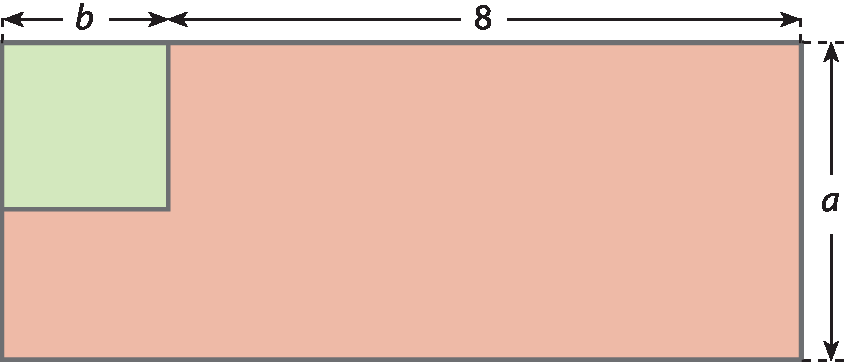
Ilustração. Retângulo com um lado medindo b mais 8 e o outro medindo a. Dentro, na parte superior, quadrado de lados medindo b. O quadrado e tem o vértice superior esquerdo coincidente ao vértice do retângulo e os lados que determinam esse vértice estão sobre os lados do retângulo.

Faça o que se pede.

a) Que expressão algébrica representa, em centímetro quadrado, a medida da área da sala não coberta pelo tapete?

b) Se a = 4 e b = 2,1, calcule a medida da área da sala que ficou descoberta.

Respostas e comentários

16. a) 14x 2 ‒ 35x

16. b) 15a 3 ‒ 10a 2 ‒ 5a

16. c) ‒12x 3 + 9x 2 ‒ 3x

16. d)

\frac{2}{5} a^{2} ‒ \frac{1}{10} a

16. e) ‒0,06x 5 + 0,28x 4

16. f)

‒ y^{3} ‒ \frac{12}{7} y^{4}

17. a) 6x 2 + x

17. b) 155

17. c) x = 5

18. a) 8a + ab ‒ b2

18. b) 35,99 métros quadrados

Multiplicação de polinômio por monômio

A multiplicação de polinômio por um monômio, assim como a multiplicação entre polinômios, tem por base a propriedade distributiva da multiplicação. Se julgar necessário, desenvolva algumas atividades envolvendo essa propriedade com multiplicações de números racionais.

Reproduza na lousa as figuras apresentadas na situação que inicia esse tópico e trabalhe as medidas das áreas dos três retângulos e a do quarto, que foi obtido com a justaposição dos primeiros três retângulos. Essa situação possibilita aos estudantes atribuírem significado à multiplicação de polinômio por um monômio.

Exercícios propostos

As resoluções dos exercícios 16 e 17 estão no início deste Manual, nas orientações específicas do capítulo 5.

No exercício 18, os estudantes devem estabelecer inicialmente uma estratégia de cálculo da medida da área da região não coberta pelo tapete quadrado. Espera-se que eles percebam que a medida da área procurada (item a) é obtida pela medida da área da sala retangular, cujas dimensões são a por (b + 8), subtraída da medida da área do tapete quadrado (de lado b).

medida da área procurada = a · (b + 8) ‒ b2 = ab + 8a ‒ b2

O item b trabalha o valor numérico de uma expressão algébrica, ou seja, quando a = 4 métros e b = 2,1 métros, a medida da área da região da sala não coberta pelo tapete é:

medida da área procurada = ab + 8a ‒ b2 = 4 · 2,1 + 8 · 4 ‒ (2,1)2

medida da área procurada = 8,4 + 32 ‒ 4,41 = 35,99

Logo, a área procurada nesse caso mede 35,99 métros quadrados.

Página 115

Multiplicação de polinômio por polinômio

Ilustração. Mulher de cabelo vermelho e blusa roxa. Ela fala: As figuras 1 e 2 são compostas de retângulos, e as respectivas medidas de seus lados são dadas em centímetro.

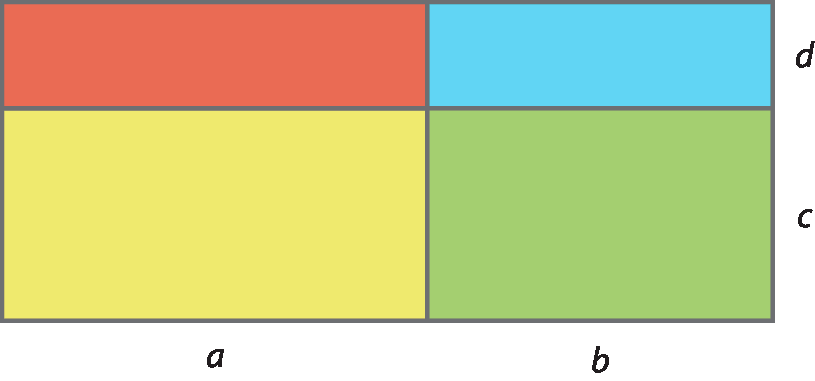
Figura 1. Retângulo composto de 4 retângulos coloridos. Acima no lado esquerdo retângulo vermelho e, à direita dele, retângulo azul. Abaixo do retângulo vermelho, retângulo amarelo e à direita deste, retângulo verde. Retângulo vermelho tem lados medindo a e d; retângulo azul lados medindo b e d; retângulo amarelo lados medindo a e c; retângulo verde lados medindo b e c. — Figura 1

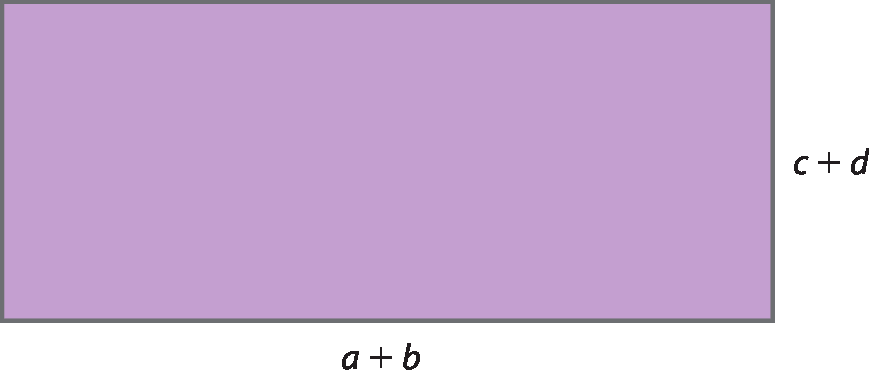
Figura 2. Retângulo com um lado medindo a mais b e outro lado mede c mais d. — Figura 2

Podemos determinar a medida da área da figura 1, em centímetro quadrado, calculando separadamente a medida da área de cada retângulo de que ela é formada e adicionando os resultados obtidos: ac + ad + bc + bd.

A medida da área da figura 2, em centímetros quadrados, é dada por: (a + b) ⋅ (c + d).

Como as duas figuras (1 e 2) são determinadas por dois retângulos de mesmas dimensões, elas têm áreas de mesma medida. Logo:

(a + b) ⋅ (c + d ) = ac + ad + bc + bd

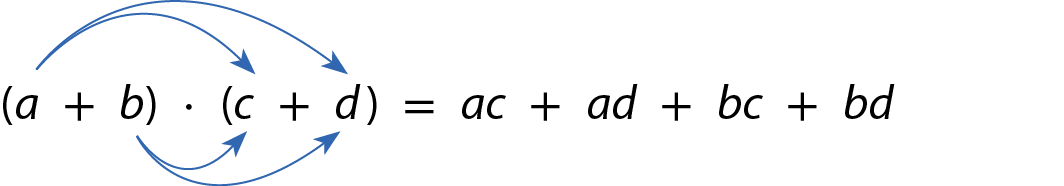
Esquema. abre parêntese a mais b fecha parêntese vezes abre parêntese c mais d fecha parêntese igual ac mais ad mais bc mais bd. Na expressão há duas setas azuis saindo do a e chegando no c e no d e duas setas azuis saindo do b e chegando no c e no d.

Ilustração. Mulher de cabelo vermelho e blusa roxa. Ela fala: Note que, para multiplicar dois polinômios, aplicamos a propriedade distributiva, multiplicando cada termo de um deles por todos os termos do outro. Depois reduzimos os termos semelhantes obtidos.

Acompanhe outros exemplos.

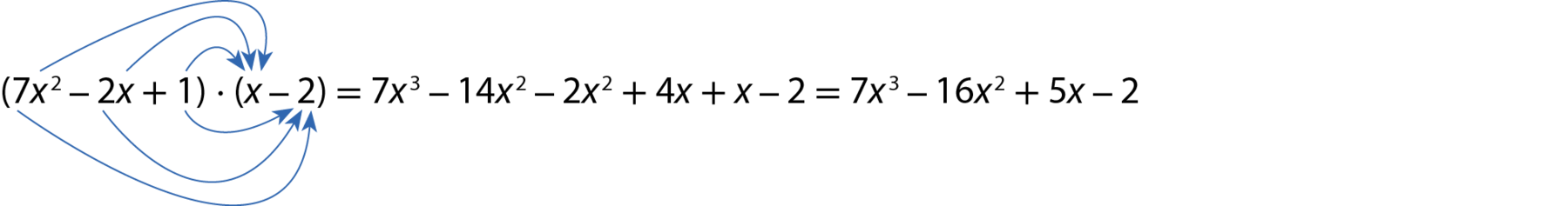
Esquema. abre parêntese 7 x ao quadrado menos 2x mais 1 fecha parêntese vezes abre parêntese x menos 2 fecha parêntese igual 7 x ao cubo menos 14 x ao quadrado menos 2 x ao quadrado mais 4x mais x menos 2 igual 7 x ao cubo menos 16 x ao quadrado mais 5x menos 2. Na expressão há duas setas azuis saindo do 7 x ao quadrado e chegando no x e no menos 2, duas setas azuis do menos 2x e chegando no x e no menos 2 e duas setas saindo do 1 e chegando no x e n menos 2.

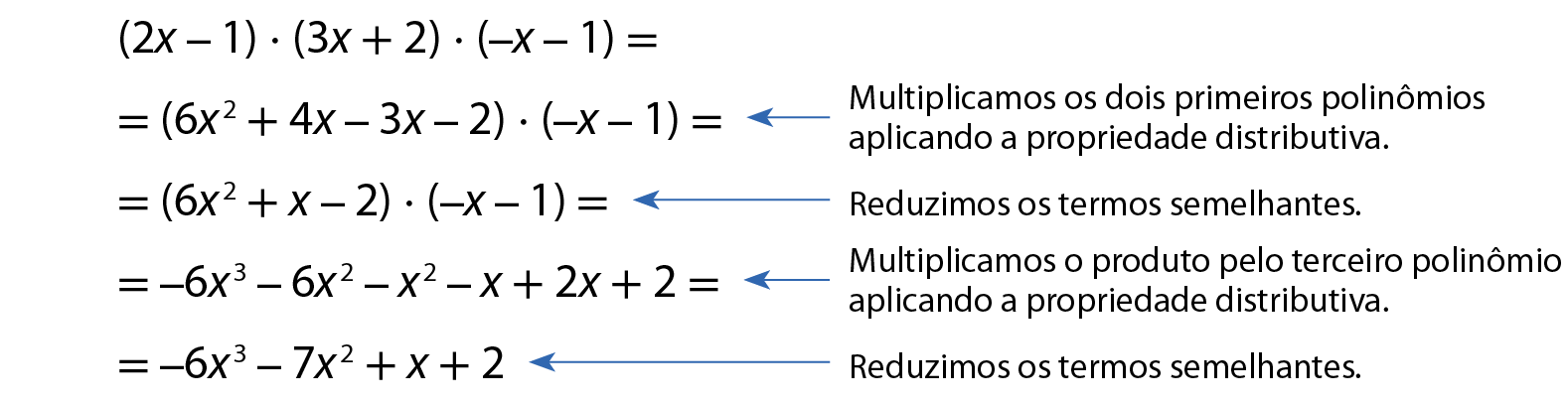
Esquema. abre parêntese 2x menos 1 fecha parêntese vezes abre parêntese 3x mais 2 fecha parêntese vezes abre parêntese menos x menos 1 fecha parêntese igual.
igual abre parêntese 6 x ao quadrado mais 4x menos 3x menos 2 fecha parêntese vezes abre parêntese menos x menos 1 fecha parêntese igual seta apontando para essa expressão com a indicação multiplicamos os dois primeiros polinômios aplicando a propriedade distributiva.
igual abre parêntese 6 x ao quadrado mais x menos 2 fecha parêntese vezes abre parêntese menos x menos 1 fecha parêntese igual seta azul apontando para essa expressão com a indicação multiplicamos o produto pelo terceiro polinômio aplicando a propriedade distributiva.
igual menos 6 x ao cubo menos 7 x ao quadrado mais x mais 2 seta apontando para essa expressão com a indicação reduzimos os termos semelhantes.

Respostas e comentários

Multiplicação de polinômio por polinômio

Uma atividade a ser feita, antes de desenvolver o conteúdo deste tópico, é solicitar a um grupo de estudantes que trace ao acaso, de ponta a ponta da lousa, uma linha horizontal e uma linha vertical. A outro grupo, solicite que meça com uma trena e registre as alturas e larguras dos quatro retângulos delimitados pelo contôrno da lousa e pelas duas linhas representadas, como na figura 1, e, também, da própria lousa. A seguir, outro grupo deve escrever o cálculo das medidas das áreas de cada retângulo e da área da lousa.

Finalizando a atividade, peça aos estudantes que comparem a medida da área da lousa com a soma das medidas das áreas dos quatro retângulos. Caso o formato da lousa não seja retangular, a atividade pode ser feita considerando outra superfície com esse formato ou, ainda, representando um retângulo na lousa.

Explore as figuras que possibilitam aos estudantes atribuir significado à multiplicação de dois polinômios.

• medida da área do retângulo vermelho = ad

• medida da área do retângulo amarelo = ac

• medida da área do retângulo azul = bd

• medida da área do retângulo verde = bc

Como o retângulo maior da figura 1 tem as mesmas dimensões do retângulo da figura 2, podemos concluir que a medida da área da figura 2 é igual à medida da área da figura 1.

(a + b) · (c + d) = ac + ad + bc + bd

Comente com os estudantes que esse resultado é o mesmo quando aplicamos a propriedade distributiva ao produto indicado.

Antes de apresentar a resolução dos exemplos desta página, proponha que resolvam cada um deles.

Página 116

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

19 Calcule:

a) (5x ‒ 1) ⋅ (5x + 1)

b) (a + b) ⋅ (a + b)

c) (2x 2 ‒ 3x ‒ 6) ⋅ (5x ‒ 2)

(2 a + \frac{3}{5} b) \cdot (a ‒ \frac{1}{2} b)

20 Observe o retângulo.

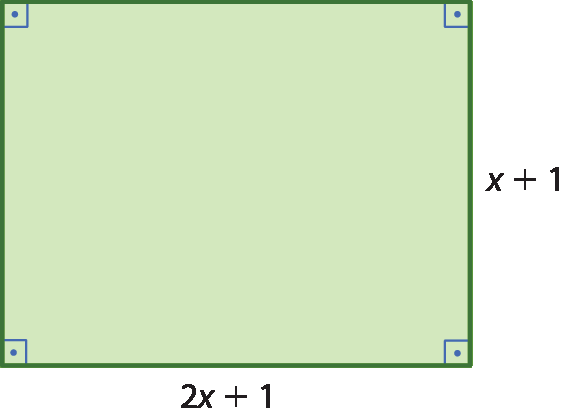
Ilustração. Retângulo com lados medindo 2x mais 1 por x mais 1.

a) Determine o trinômio que representa a medida da área do retângulo.

b) Calcule o valor numérico desse trinômio para x = 0,4.

21 Dados a = x 2 + 3x ‒ 2, B = x + 2 e C = x ‒ 3, calcule:

a) a ⋅ B; a ⋅ C e a ⋅ B + a ⋅ C

b) B + C e a ⋅ (B + C )

22 Calcule os produtos a seguir.

a) 3x ⋅ (2x ‒ 3) ⋅ (x + 2)

b) ‒2x ⋅ (x + 5) ⋅ (2x ‒ 5)

c) (a ‒ 2b) ⋅ (a + 2b) ⋅ (a ‒ b)

d) (a ‒ b) ⋅ (a + b) ⋅ (3a ‒ b)

\frac{x}{2} (x + \frac{1}{3}) \cdot (2 x ‒ \frac{1}{2})

Hora de criar – Elabore um problema que envolva a medida da área de um quadrado e a medida x de seu lado, que deve ser um número natural. Troque o problema com o de um colega. Depois de cada um resolver o problema do outro, destroquem para corrigi-los.

Divisão de polinômio por monômio

A medida da área do retângulo a seguir é dada em centímetro quadrado e representada pelo polinômio 6x 2 + 9x, e a medida da altura é dada em centímetro e representada pelo monômio 3x, com x ≠ 0.

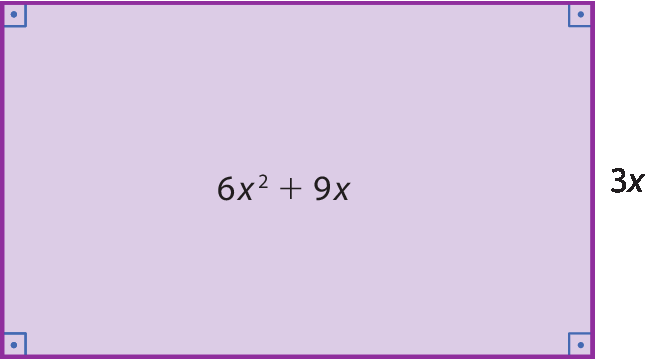
Ilustração. Retângulo medindo 3x de altura. Dentro, sua área é indicada como 6 vezes x ao quadrado mais 9 x.

Vamos determinar o polinômio que representa a medida da base do retângulo.

Para isso, devemos dividir o polinômio 6x 2 + 9x pelo monômio 3x, ou seja, encontrar o polinômio que, multiplicado por 3x, resulta em 6x 2 + 9x.

Esse polinômio é 2x + 3, pois 3x ⋅ (2x + 3) = 6x 2 + 9x. Observe que o polinômio 2x + 3 pode ser obtido dividindo-se cada um dos termos de 6x 2 + 9x por 3x:

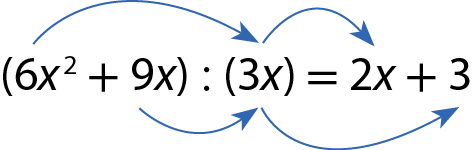
Esquema. abre parêntese 6 x ao quadrado mais 9 x fecha parêntese dividido por abre parêntese 3x fecha parêntese igual 2x mais 3. Na expressão seta azul saindo do 6 x ao quadrado e chegando no 3x, seta azul saindo do 3x e chegando no 2x. Há também uma seta azul saindo do 9x e chegando no 3x e uma seta azul saindo do 3x e chegando no 3.

Respostas e comentários

19. a) 25x 2 ‒ 1

19. b) a 2 + 2ab + b 2

19. c) 10x 3 ‒ 19x 2 ‒ 24x + 12

19. d)

2 a^{2} ‒ \frac{2}{5} a b ‒ \frac{3}{10} b^{2}

20. a) 2x 2 + 3x + 1

20. b) 2,52

21. a) x 3 + 5x 2 + 4x ‒ 4; x 3 ‒ 11x + 6; 2x 3 + 5x 2 ‒ 7x + 2

21. b) 2x ‒ 1; 2x 3 + 5x 2 ‒ 7x + 2

22. a) 6x 3 + 3x 2 ‒ 18x

22. b) ‒4x 3 ‒ 10x 2 + 50x

22. c) a 3 ‒ a 2b ‒ 4ab 2 + 4b 3

22. d) 3a 3 ‒ 3ab 2 ‒ a 2b + b 3

22. e)

x^{3} + \frac{x^{2}}{12} ‒ \frac{x}{12}

23. Resposta pessoal.

Orientação: Espera-se que o estudante responda: 5 centímetros; divisão (10 : 2).

Exercícios propostos

As resoluções dos exercícios 19, 21 e 22 estão no início deste Manual, nas orientações específicas do capítulo 5.

No exercício 20, a medida da área do retângulo é dada por (2x + 1) · (x + 1). Efetuando a multiplicação desses dois polinômios, obtemos a expressão da medida da área do retângulo.

(2x + 1) · (x + 1) = 2x2 + 2x + x + 1 = 2x2 + 3x + 1

Portanto, 2x2 + 3x + 1 é o trinômio que representa a medida da área do retângulo (item a).

No item b, calculamos o valor numérico desse trinômio para x = 0,4, que indica a medida da área do retângulo.

2x2 + 3x + 1 = 2 · (0,4)2 + 3 · 0,4 + 1 =

= 2 · 0,16 + 1,2 + 1 = 0,32 + 1,2 + 1 = 2,52

Acompanhe a resolução do exercício 23 verificando e auxiliando os estudantes em eventuais dúvidas tanto na criação de polinômios quanto na aplicação da propriedade distributiva da multiplicação.

Divisão de polinômio por monômio

Verifique se a proposta de atividade, que envolve a relação intrínseca entre as operações multiplicação e divisão, apresentada pelo personagem, foi compreendida. Caso contrário, proponha outras duplas de números para que os estudantes respondam oralmente.

Ainda neste tópico, introduzimos a divisão de polinômio por monômio (não nulo), dividindo cada termo do polinômio pelo monômio dado.

Página 117

Acompanhe outros exemplos.

Ilustração. Homem de cabelo ruivo e camisa vermelha diz: Admitimos para as variáveis apenas valores que não anulam o divisor.

Esquema. abre parêntese 18 x ao cubo menos 12 x ao quadrado mais 3x fecha parêntese dividido por abre parêntese menos 3x fecha parêntese igual menos 6 x ao quadrado mais 4x menos 1. Na expressão, seta azul saindo do 18 x ao cubo e chegando no menos 3x, seta azul saindo do menos 12 x ao quadrado e chegando no menos 3x e seta azul saindo do 3x e chegando no menos 3x.

Esquema. abre parêntese 7 x ao cubo y ao quadrado menos 5 x ao quadrado y elevado a 4 fecha parêntese dividido por menos 3 x ao quadrado y fecha parêntese igual menos 7 terços xy mais 5 terços y ao cubo.
Na expressão, seta azul saindo do 7 x ao cubo y ao quadrado e chegando no menos 3 x ao quadrado y e seta azul saindo do 5 x ao quadrado y elevado a 4 e chegando no menos 3 x ao quadrado y.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

24 Calcule os quocientes a seguir.

a) (8x 5 + 6x 3) : (+2x 2)

b) (12ab + 15a 2b + 9ab 2) : (3ab)

c) (20x ‒ 10x 2) : (‒5x)

d) (a 3 + a 2 + a) : (a)

e) (x 5 + x 2) : (‒x 2)

f) (7x 2 ‒ 8x + 5) : (‒1)

25 Determine o polinômio que, multiplicado por ‒7x, resulta em 21x 3 ‒ 28x 2 + 14x.

26 Multiplicando-se o monômio ‒4xy pelo polinômio a, encontra-se o polinômio ‒8xy + 9x 2y ‒ 6xy 2.

Determine o polinômio A.

27 Qual é o quociente de

(\frac{7}{3} x^{2} ‒ \frac{1}{4} x)

por

(‒ \frac{1}{2} x)

28 Calcule o valor da expressão:

[(25x 2 ‒ 15x) : (‒5x)] ⋅ (5x + 3)

29 Caio gosta de elaborar desafios matemáticos. Leia o desafio que ele propôs ao amigo Tiago.

Ilustração. Caderno com as informações: O produto da idade de dois irmãos é representado pela expressão algébrica x ao quadrado mais 10x. Sabendo que x representa a idade do irmão mais novo, descubra a expressão algébrica que representa a idade do irmão mais velho e determine a diferença de idade entre eles.

Supondo que Tiago esteja raciocinando corretamente, qual é a resposta que ele dará a Caio?

Polinômios com uma só variável

Observe estes polinômios:

• x 2 ‒ 8x + 12

Ele apresenta somente a variável x, cujo maior expoente é 2; dizemos que é um polinômio do 2º grau na variável x, ou que tem grau 2.

• 2y 4 ‒ 3y 2 + 5y ‒ 6

Ele apresenta somente a variável y, cujo maior expoente é 4; dizemos que é um polinômio do 4º grau na variável y, ou que tem grau 4.

• z 3 ‒ 1

Ele apresenta somente a variável z, cujo maior expoente é 3; dizemos que é um polinômio do 3º grau na variável z, ou que tem grau 3.

Polinômios desse tipo são chamados de polinômios com uma variável.

Respostas e comentários

24. a) 4x 3 + 3x

24. b) 4 + 5a + 3b

24. c) ‒4 + 2x

24. d) a 2 + a + 1

24. e) ‒x 3 ‒ 1

24. f) ‒7x 2 + 8x ‒ 5

25. ‒3x 2 + 4x ‒ 2

26. 2 ‒ 2,25x + 1,5y

27.

‒ \frac{14}{3} x + \frac{1}{2}

28. ‒25x 2 + 9

29. x + 10; 10 anos é a diferença de idade entre eles.

Exercícios propostos

As resoluções dos exercícios 24 a 28 estão no início deste Manual, nas orientações específicas do capítulo 5.

Note que o exercício 26 pressupõe a aplicação da relação entre a multiplicação e divisão como operações inversas.

No exercício 29, o produto entre os dois fatores que representam as idades dos irmãos é dado pelo binômio x2 + 10x. Se um dos fatores é x (idade do irmão mais novo), temos que a idade do irmão mais velho é dada por:

idade do mais velho = (x2 + 10x) : x

idade do mais velho = x2 : x + 10x : x

idade do mais velho = x + 10

Desse modo, espera-se que os estudantes percebam que a diferença entre as idades é 10 anos (ou seja, quantos anos o irmão mais velho tem a mais do que o irmão mais novo). Eles também podem calcular essa diferença.

diferença entre as idades = (x + 10) ‒ x

diferença entre as idades = x + 10 ‒ x = 10

Logo, a resposta de Tiago deve ser: a expressão algébrica que representa a idade do irmão mais velho é x + 10, e a diferença entre as idades é 10 anos.

Página 118

Em geral, os termos de um polinômio com uma variável são apresentados segundo as potências decrescentes dessa variável.

Observe alguns exemplos.

a) 5x 2 ‒ 4x + 2

b) x 3 ‒ 2x 2 + x ‒ 1

c) 2x 4 ‒ 3x 2 + 2

Observação

▶ Se em um polinômio de grau n ordenado segundo as potências de x faltar uma ou mais potências de x com expoente menor do que n, então os coeficientes desses termos serão 0, e o polinômio será chamado de polinômio incompleto. Acompanhe alguns exemplos.

a) x 2 ‒ 4 é um polinômio incompleto e pode ser escrito como x 2 + 0x ‒ 4. x 2 + 0x ‒ 4 é a fórma geral do polinômio x 2 ‒ 4.

b) 2x 4 ‒ 3x 2 + 2 é um polinômio incompleto e pode ser escrito como 2x 4 + 0x 3 ‒ 3x 2 + 0x + 2. 2x 4 + 0x 3 ‒ 3x 2 + 0x + 2 é a fórma geral do polinômio 2x 4 ‒ 3x 2 + 2.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

30 Ordene os polinômios de acôrdo com as potências decrescentes de x.

a) 2x + 3x 2 ‒ 4

b) ‒6 + x 4 ‒ 5x 2 + 4x 3 ‒ 2x

c) 4x + 5x 3 ‒ 1

d) 5x 2 ‒ 3x + 2x 3 ‒ 4

e) 2 + 7x + 9x 2

31 Escreva os polinômios a seguir na fórma geral.

a) x 3 + 2x 2 ‒ 5

b) x 3 + 1

c) y 4 ‒ 8y 2 + 15

d) z 4 ‒ 16

e) m 4 ‒ 2m 2

Divisão de polinômio por polinômio

Ilustração. Homem de cabelo liso e camisa verde diz: Vamos recordar, por meio de um exemplo, o algoritmo da divisão entre dois números e perceber o que há em comum entre ele e o procedimento para a divisão entre dois polinômios.

Esquema. Sequência indicando 3 passos de divisão. Passo 1. Algoritmo de divisão. Na chave, 4. Fora da chave, 905. Abaixo do 905, sinal de menos e número 8. Linha. Número 1. Abaixo da chave, número 2. Passo 2. Algoritmo de divisão. Na chave, 4. Fora da chave, 905. Abaixo do 905, sinal de menos e número 8. Linha. Número 10, Abaixo, sinal de menos e número 8. Linha. Abaixo, número 2. Abaixo da chave, número 22. Passo 3. Esquema. Algoritmo de divisão. Na chave, 4. Fora da chave, 905. Abaixo do 905, sinal de menos e número 8. Linha. Número 10, Abaixo, sinal de menos e número 8. Linha. Abaixo, número 25. Abaixo, sinal de menos e número 24. Linha. Abaixo, número 1. Abaixo da chave, número 226.

Podemos confirmar o resultado da divisão verificando a igualdade:

quociente ⋅ divisor + resto = dividendo

Nesse caso, obtemos: 226 ⋅ 4 + 1 = 905

Respostas e comentários

30. a) 3x 2 + 2x ‒ 4

30. b) x 4 + 4x 3 ‒ 5x 2 ‒ 2x ‒ 6

30. c) 5x 3 + 4x ‒ 1

30. d) 2x 3 + 5x 2 ‒ 3x ‒ 4

30. e) 9x 2 + 7x + 2

31. a) x 3 + 2x 2 + 0x ‒ 5

31. b) x 3 + 0x 2 + 0x + 1

31. c) y 4 + 0y 3 ‒ 8y 2 + 0y + 15

31. d) z 4 + 0z 3 + 0z 2 + 0z ‒ 16

31. e) m 4 + 0m 3 ‒ 2m 2 + 0m + 0

Polinômios com uma só variável

Destaque as ideias tratadas no boxe Observação e proponha aos estudantes que façam uma lista de polinômios incompletos e troquem com um colega. Cada um escreve a fórma geral de cada polinômio criado pelo colega. Faça uma correção coletiva, socializando o trabalho de cada dupla.

Exercícios propostos

Para a resolução do exercício 30, os estudantes devem ordenar os polinômios dados de acôrdo com os expoentes decrescentes.

Completando os polinômios dados no exercício 31 com os termos nulos dos expoentes faltantes, obtemos:

a) x3 + 2x2 + 0x ‒ 5

b) x3 + 0x2 + 0x + 1

c) y4 + 0y3 ‒ 8y2 + 0y + 15

d) z4 + 0z3 + 0z2 + 0z ‒ 16

e) m4 + 0m3 ‒ m2 + 0m + 0

Divisão de polinômio por polinômio

Neste tópico, introduzimos divisão de dois polinômios fazendo um paralelo com a divisão entre dois números naturais e usando como base a relação fundamental da divisão.

Avalie se a turma necessita de outros exemplos. Em caso afirmativo, solicite aos estudantes que escolham três números naturais, representados por a, b e c (sendo a com 3 dígitos, b e c com 1 dígito e c < b). Em seguida, eles devem obter d = a · b + c. Por fim, devem efetuar a divisão entre d e b para obter o quociente a e o resto c, de modo que a e c sejam menores que o divisor b.

Página 119

A divisão de um polinômio por outro polinômio não nulo será efetuada apenas entre polinômios com uma variável só.

Para facilitar essas divisões, devemos escrever os polinômios considerando a ordem decrescente das potências da variável, e o polinômio dividendo deve ser escrito na fórma geral.

Aprenderemos com exemplos como se calcula o quociente de um polinômio por outro polinômio. O processo que vamos utilizar visa a construir gradativamente um polinômio quociente que, multiplicado pelo polinômio divisor e adicionado ao resto, resulte no polinômio dividendo.

a) Vamos calcular o quociente de 8x 2 ‒ 10x + 5 por 2x + 1. Começamos dividindo o primeiro termo do dividendo (8x 2) pelo primeiro termo do polinômio divisor (2x), obtendo o primeiro termo do quociente: 4x.

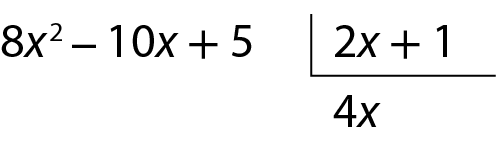
Esquema. Algoritmo de divisão. Na chave, 2x mais 1. Fora da chave, 8 vezes x ao quadrado, menos 10 vezes x, mais 5. Embaixo da chave, 4 vezes x.

Multiplicamos o quociente obtido (4x) pelo divisor 2x + 1, obtendo o produto 8x 2 + 4x. Subtraímos esse produto do dividendo, assim como ocorre na divisão entre números.

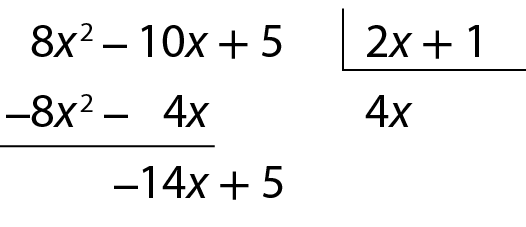
Esquema. Algoritmo de divisão. Na chave, 2x mais 1. Fora da chave, 8 vezes x ao quadrado, menos 10 vezes x, mais 5. Abaixo, menos 8 vezes x ao quadrado, menos 4 vezes x. Linha. Abaixo, menos 14 vezes x, mais 5. Embaixo da chave, 4x.

Repetimos as etapas anteriores para calcular o quociente de ‒14x + 5 por 2x + 1. Dividimos ‒14x por 2x, obtendo o segundo termo do quociente, ‒7. Multiplicamos ‒7 por 2x + 1, obtendo ‒14x ‒ 7. Subtraímos esse produto de ‒14x + 5 e obtemos o resto 12.

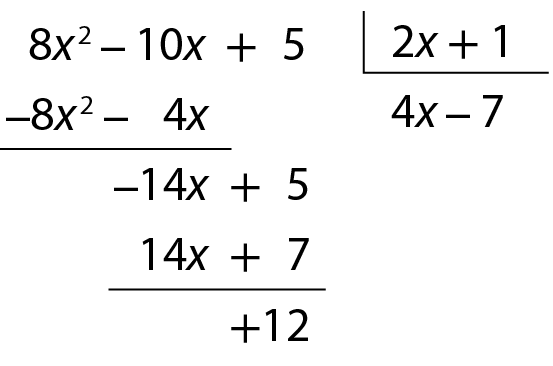
Fazendo a verificação:

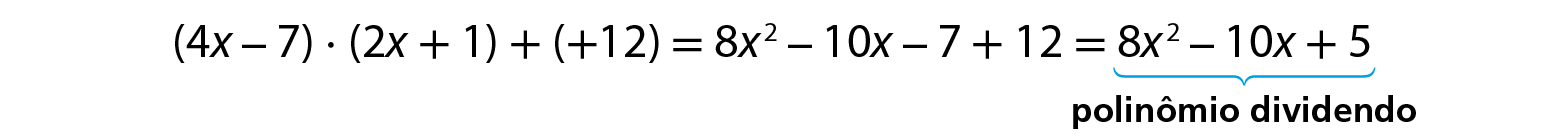
Esquema. abre parêntese 4x menos 7 fecha parêntese vezes abre parêntese 2x mais 1 fecha parêntese mais abre parêntese mais 12 fecha parêntese igual 8 x ao quadrado menos 10x menos 7 mais 12 igual 8 x ao quadrado menos 10x mais 5. Na expressão, há uma chave horizontal selecionando o termo depois do último símbolo de igual com a indicação polinômio dividendo

b) Vamos calcular o quociente de 12x 4 ‒ 17x 3 ‒ 3x 2 ‒ 11x ‒ 3 por 3x 2 ‒ 2x ‒ 3.

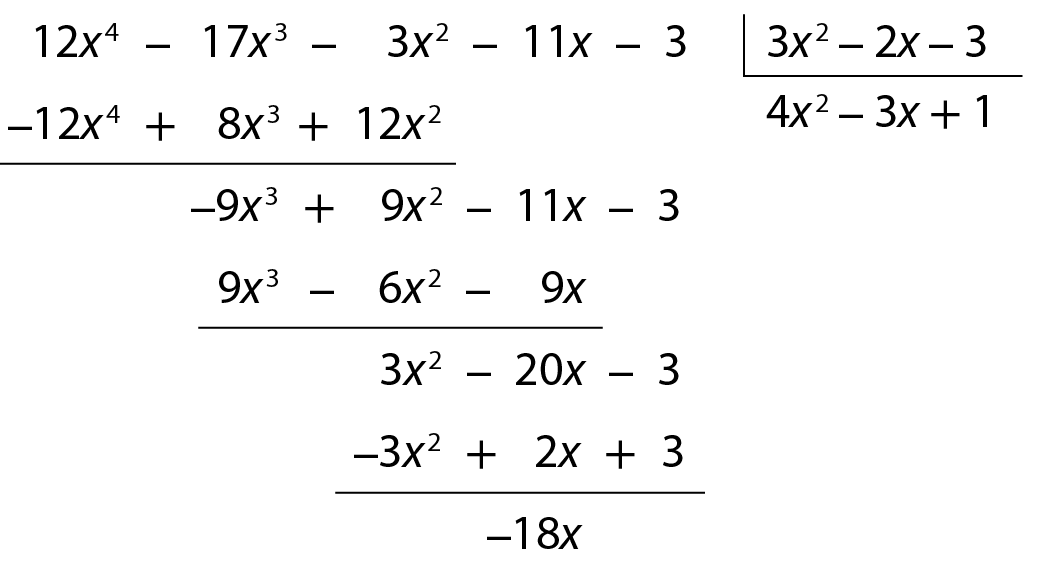
Esquema. Algoritmo de divisão. Na chave, 3 vezes x ao quadrado, menos 2 vezes x, menos 3. Fora da chave, 12 vezes x a quarta, menos 17 vezes x ao cubo, menos 3 vezes x ao quadrado, menos 11 vezes x, menos 3. Abaixo, Sinal de menos, 12 vezes x a quarta, mais 8 vezes x ao cubo, mais 12 vezes x ao quadrado. Linha. Abaixo, menos 9 vezes x ao cubo, mais 9 vezes x ao quadrado, menos 11 vezes x, manos 3. Abaixo, 9 vezes x ao cubo, menos 6 vezes x ao quadrado, menos 9 vezes x. Linha. Abaixo, 3 vezes x ao quadrado, menos 20 vezes x, menos 3. Abaixo, menos 3 vezes x ao quadrado, mais 2 vezes x, mais 3. Linha. Abaixo, menos 18 vezes x. Abaixo da chave, como resultado: 4 vezes x ao quadrado, menos 3 vezes x, mais 1. Quociente: 4 vezes x ao quadrado, menos 3 vezes x, mais 1. Resto: menos 18 x.

Quociente: 4x 2 ‒ 3x + 1

Resto: ‒18x

Respostas e comentários

Divisão de polinômio por polinômio

Antes de apresentar aos estudantes o exemplo da divisão dos polinômios, proponha na lousa mais alguns polinômios de uma variável e incompletos para que os escrevam no caderno na fórma geral e ordenados.

Em seguida, reproduza na lousa os passos da divisão dos exemplos a e b para que eles os acompanhem e desenvolvam as etapas da divisão.

Para auxiliá-los a atribuir significados às operações com polinômios estudadas, pode-se sugerir que testem os resultados obtidos trocando a incógnita por alguns valores numéricos.

Por exemplo, para a divisão de 8x2 ‒ 10x + 5 por 2x ‒ 1, cujo quociente é dado por 4x ‒ 7 e o resto é 12 (como realizado no exemplo a), sabemos que:

(8x2 ‒ 10x + 5) = (2x + 1) · (4x ‒ 7) + 12

Assim, podemos atribuir um valor a x (desde que não anule o divisor) e verificar a igualdade. Fazendo x = 1, obtemos:

(8 · 12 ‒ 10 · 1 + 5) = (2 · 1 + 1) · (4 · 1 ‒ 7) + 12

(8 · 1 ‒ 10 + 5) = (4 ‒ 7) · (2 + 1) + 12

(8 ‒ 10 + 5) = (4 ‒ 7) · 3 + 12

3 = ‒3 · 3 + 12

3 = ‒9 + 12

3 = 3 (verdadeiro)

Atribuindo outros valores numéricos a x, obtemos sempre uma igualdade verdadeira do tipo a = a, em que a é um número real, e x é diferente de ‒

\frac{1}{2}

Se possível, os estudantes podem utilizar recursos como planilhas eletrônicas para fazer essa verificação de maneira automática; para isso, eles podem digitar em uma célula a um o valor de x, em uma célula B1 a expressão do dividendo em função do valor de a um , em uma célula C1 a expressão que relacione o dividendo ao divisor, ao quociente e ao resto. Assim, quando variar o valor da célula a um , automaticamente pode-se verificar que o valor de B1 e de C1 serão iguais.

Esse trabalho com tecnologias digitais favorece o desenvolvimento da competência geral 5, pois os estudantes podem desenvolver estratégias que lhes possibilitem resolver problemas e produzir conhecimentos com mais autonomia.

Página 120

c) Vamos calcular o quociente de 8x 3 ‒ 1 por 2x ‒ 1. Como o polinômio dividendo é incompleto, vamos escrevê-lo na fórma geral: 8x 3 + 0x 2 + 0x ‒ 1

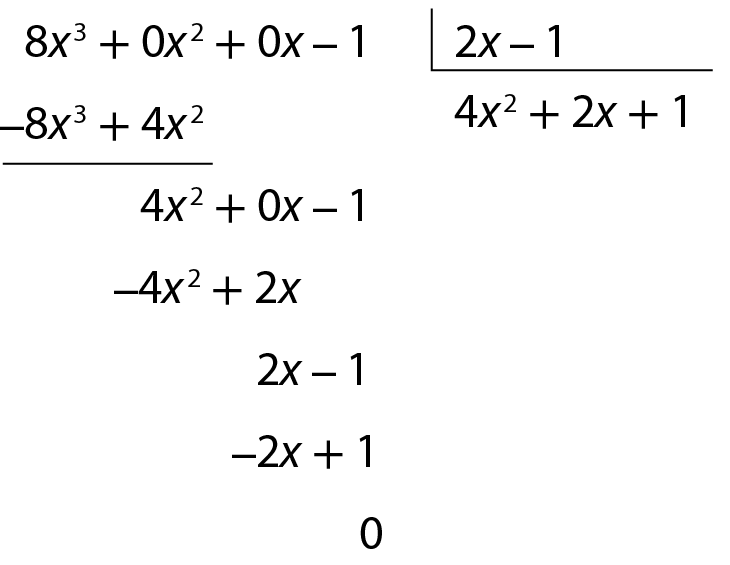
Esquema. Algoritmo de divisão. Na chave, 2x menos 1. Fora da chave, 8 vezes x ao cubo, mais 0 x ao quadrado, mais 0 x menos 1. Abaixo, menos 8 vezes x ao cubo, mais 4 vezes x ao quadrado. Linha. Abaixo, 4 vezes x ao quadrado, mais 0 x menos 1. Abaixo, menos 4 vezes x ao quadrado, mais 2 vezes x. Linha. Abaixo, 2 vezes x menos 1. Abaixo, menos 2 vezes x mais 1. Linha. Abaixo, 0 Embaixo da chave, 4 vezes x ao quadrado, mais 2 vezes x, mais 1. Quociente: 4 vezes x ao quadrado, mais 2 vezes x, mais 1. Resto: 0

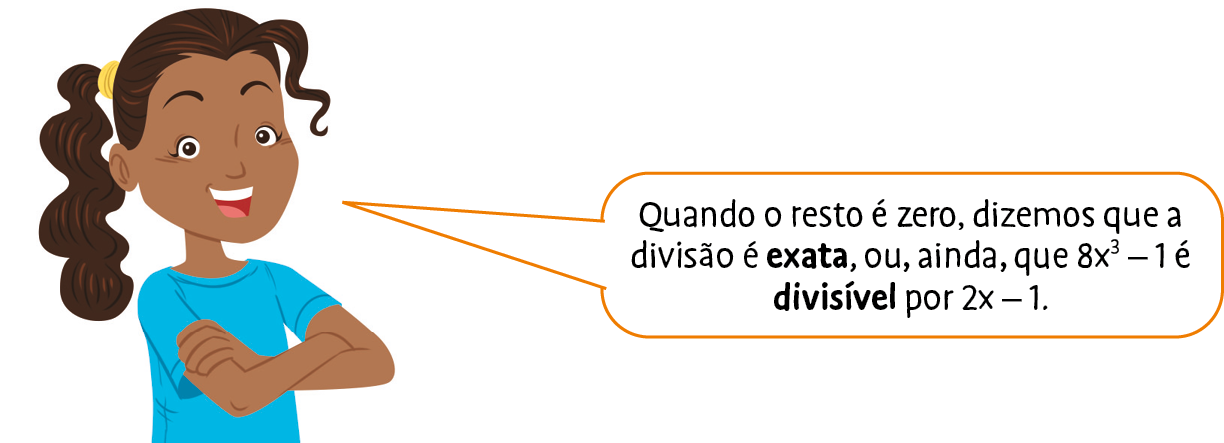
Quociente: 4x 2 + 2x + 1

Resto: 0

Ilustração. Menina de cabelo castanho e camiseta azul. Ela fala: Quando o resto é zero, dizemos que a divisão é exata, ou, ainda, que 8x elevado ao cubo menos 1 é divisível por 2x menos 1.

Ilustração. Homem de cabelo liso e camisa verde diz: Faça a verificação dos resultados dos exemplos b e c usando a igualdade: quociente vezes divisor mais resto igual ao dividendo.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

32 Determine o polinômio M que, multiplicado por 2x ‒ 1, resulta em 6x 2 ‒ 7x + 2. Verifique sua resposta.

33 Calcule o quociente.

a) (x 2 + 7x + 12) : (x + 3)

b) (6x 2 ‒ 11x ‒ 10) : (3x + 2)

c) (2x 4 ‒ 11x 3 + 16x 2 ‒ 6x) : (x 2 ‒ 4x + 2)

34 Determine o quociente e o resto das divisões.

a) (2x 3 ‒ 9x 2 + 3x ‒ 6) : (x ‒ 2)

b) (6a 3 ‒ 7a 2 + 2a + 1) : (3a 2 ‒ 5a + 3)

35 Qual é o polinômio que, multiplicado por a 2 + 2a ‒ 5, dá 3a 3 + 2a 2 ‒ 23a + 20?

36 A medida da área do retângulo a seguir, em métro quadrado, é dada pela expressão 5x 2 + 2x ‒ 3. Calcule o polinômio que representa a medida da altura desse retângulo, em metro.

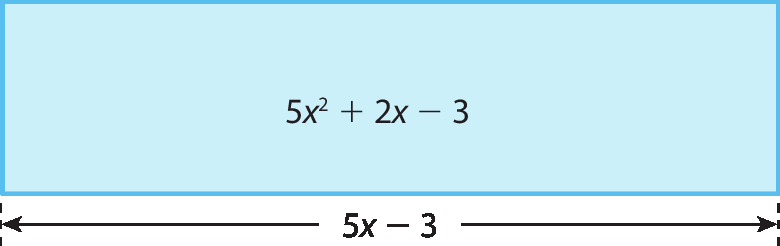
Ilustração. Retângulo com lado maior medindo 5x menos 3 . Dentro, sua área é indicada como 5 x ao quadrado mais 2x menos 3.

Hora de criar – Elabore, e depois passe para um colega, um problema sobre divisão de polinômios com uma só variável, sendo o dividendo um polinômio incompleto. Depois de cada um resolver o problema do outro, destroquem para corrigi-los.

Respostas e comentários

32. 3x ‒ 2

33. a) x + 4

33. b) 2x ‒ 5

33. c) 2x 2 ‒ 3x

34. a) 2x 2 ‒ 5x ‒ 7; ‒20

34. b) 2a + 1; a ‒ 2

35. 3a ‒ 4

36. x + 1

37. Resposta pessoal.

Exercícios propostos

As resoluções dos exercícios 32 a 35 estão no início deste Manual, nas orientações específicas do capítulo 5.

Note que o exercício 35, assim como o exercício 36, pressupõe a aplicação da relação fundamental entre a multiplicação e a divisão.

Como a medida da área do retângulo é dada pelo produto da medida da base pela medida da altura, no exercício 36, temos:

medida da área do retângulo = (medida da base) · (medida da altura)

5x2 + 2x ‒ 3 = (5x ‒ 3) · (medida da altura)

medida da altura = (5x2 + 2x ‒ 3) : (5x ‒ 3)

Efetuando a divisão desses dois polinômios, obtemos o quociente (x + 1) e resto zero. Podemos verificar esse resultado por meio da relação fundamental da divisão. Assim, temos:

quociente · divisor + resto = (x + 1) · (5x ‒ 3) + 0 =

= 5x2 ‒ 3x + 5x ‒ 3 + 0 = 5x2 + 2x ‒ 3 (que é o dividendo)

Para o exercício 37, incentive os estudantes a utilizarem contextos que os auxiliem na elaboração dos problemas, como a área de retângulos, triângulos e outras figuras geométricas cujas medidas de comprimento (dos lados, da altura etcétera) sejam dadas por meio de polinômios.

Página 121

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Podemos efetuar a divisão de números inteiros escritos na fórma polinomial. Por exemplo, para efetuar .2753 : 21, podemos fazer as seguintes representações:

.2753 = 2 ⋅ 103 + 7 ⋅ 102 + 5 ⋅ 10 + 3 e 21 = 2 ⋅ 10 + 1

Esquema. Algoritmo de divisão. Na chave, 2 vezes 10 mais 1. Fora da chave, 2 vezes 10 ao cubo, mais 7 vezes 10 ao quadrado, mais 5 vezes 10, mais 3. Abaixo, menos 2 vezes 10 ao cubo, menos 1 vezes 10 ao quadrado. Linha. Abaixo, 6 vezes 10 ao quadrado, mais 5 vezes 10. Abaixo, menos 6 vezes 10 ao quadrado, menos 3 vezes 10. Linha. Abaixo, 2 vezes 10 mais 3. Abaixo, menos 2 vezes 10 menos 1. Linha. Abaixo, 2. Embaixo da chave, 1 vezes 10 ao quadrado, mais 3 vezes 10 mais 1.

Quociente: 1 ⋅ 102 + 3 ⋅ 10 + 1 = 131

Resto: 2

Ilustração. Menina de cabelo castanho e camiseta azul. Ela fala: Essa divisão com números na forma polinomial lembra a divisão entre dois polinômios com uma só variável.

Agora, explique como foi efetuada essa divisão.

TRABALHANDO A INFORMAÇÃO

Interpolação e extrapolação gráfica

As rodovias federais brasileiras somam mais de .76000 quilômetros de extensão. A manutenção da malha rodoviária é dispendiosa e, em geral, deixa a desejar, o que afeta a sua qualidade e compromete a segurança dos usuários. No entanto, atitudes que deveriam ser evitadas, como ultrapassagem indevida, ingestão de álcool, desobediência à sinalização e excesso de velocidade, também contribuem para a imensa quantidade de acidentes.

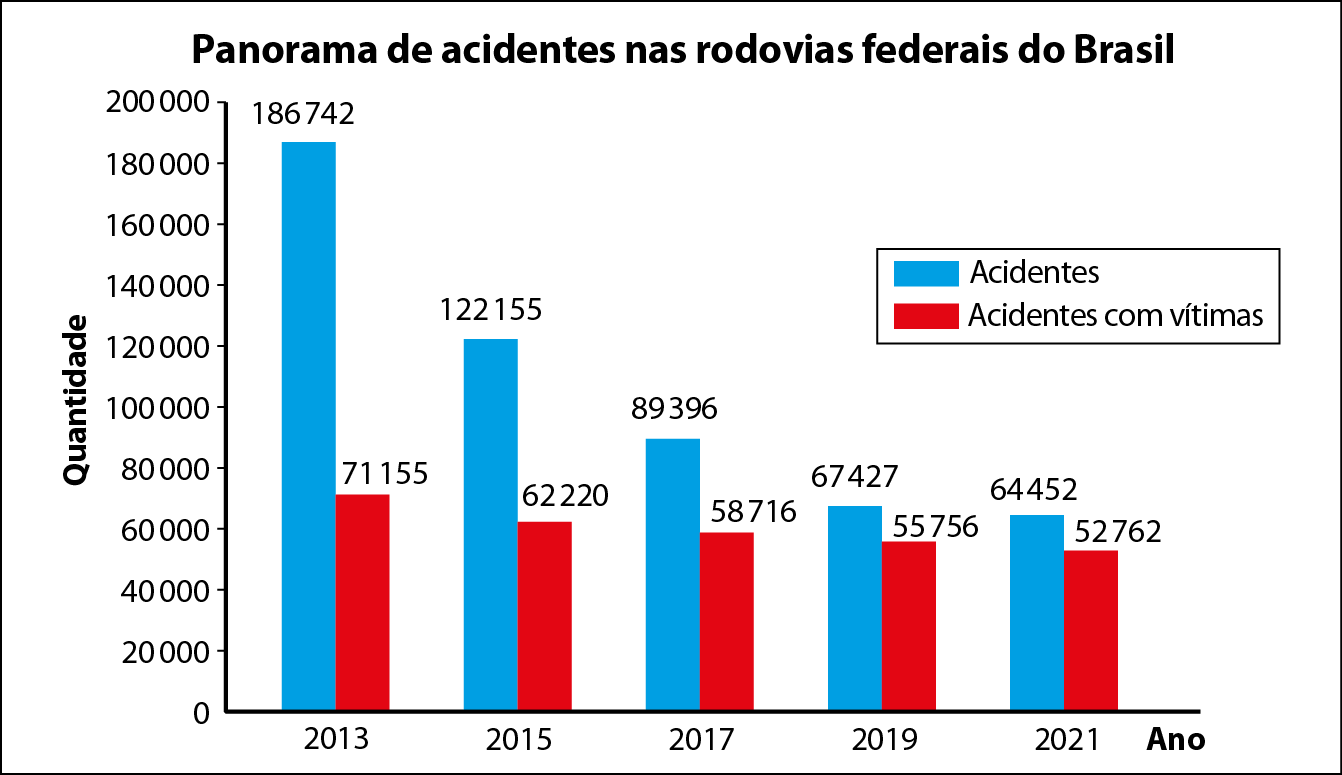
Observe a seguir o gráfico de colunas duplas, que informa a quantidade de acidentes e de acidentes com vítimas em rodovias federais brasileiras entre 2013 e 2021.

Gráfico em barras verticais. Título: Panorama de acidentes nas rodovias federais do Brasil. Eixo x, ano de 2013 a 2021. Eixo y, quantidade de 0 a 200.000. Os dados são: 2013. Acidentes: 186.742. Acidentes com vítimas: 71.155. 2015. Acidentes: 122.155. Acidentes com vítimas: 62.220. 2017. Acidentes: 89.396. Acidentes com vítimas: 58.716. 2019. Acidentes: 67.427. Acidentes com vítimas: 55.756. 2021. Acidentes: 64.452. Acidentes com vítimas: 52.762. — Dados obtidos em: CONFEDERAÇÃO Nacional do Transporte. Painel cê êne tê de acidentes rodoviários. Brasília, Distrito Federal: CNT, dezembro 2021. Disponível em: https://oeds.link/8jwrqr. Acesso em: 23 junho 2022.

Respostas e comentários

Pense mais um poucoreticências: Resposta pessoal.

Pense mais um poucoreticências

Retomamos na seção a escrita de um número natural na forma polinomial.

Aqui, espera-se que os estudantes consigam explicar com suas próprias palavras um exemplo dado do algoritmo da divisão euclidiana, com o qual estão familiarizados. Novamente, promovemos uma oportunidade de discutir e identificar uma analogia entre a Álgebra e a Aritmética.

Trabalhando a informação

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah dois três.

Nesta seção, trabalhamos com diferentes tipos de gráfico para representar um conjunto de dados de uma pesquisa, possibilitando, assim, o desenvolvimento da habilidade (ê éfe zero oito ême ah dois três).

Abordando gráficos de colunas duplas e de linhas duplas, a seção trata da interpolação e da extrapolação, que são processos de obtenção dos valores de uma função mediante o conhecimento de seu comportamento em um dado intervalo numérico.

Esse é um instrumento importante no tratamento da informação e na análise de gráficos que, em jornais e revistas, ilustram e fundamentam matérias e textos sobre assuntos diversos. Também o poder público, nas esferas municipal, estadual e nacional, utiliza esse instrumento para construir novos projetos e acompanhar a execução de outros que estiverem em andamento.

O contexto possibilita explorar o Tema Contemporâneo Transversal educação para o trânsito, por meio da ampliação da discussão sobre a importância da direção defensiva e do respeito à sinalização e à legislação. Peça aos estudantes que levem para a sala de aula matérias de jornais com gráficos para analisar as informações e dar base para a argumentação da importância da atuação das esferas governamentais na manutenção das vias públicas e das ações individuais quanto à direção defensiva.

Página 122

Com os dados desse gráfico de colunas, vamos construir um gráfico que chamamos de gráfico de linhas duplas. Para isso, representamos as colunas do gráfico anterior por linhas tracejadas verticais (sem largura). Em seguida, marcamos o ponto superior de cada coluna referente ao número de acidentes e unimos esses pontos com segmentos de reta, em azul. Depois, fazemos o mesmo com as colunas referentes ao número de acidentes com vítimas; marcamos o ponto superior de cada coluna e unimos esses pontos com segmentos de reta, em vermelho.

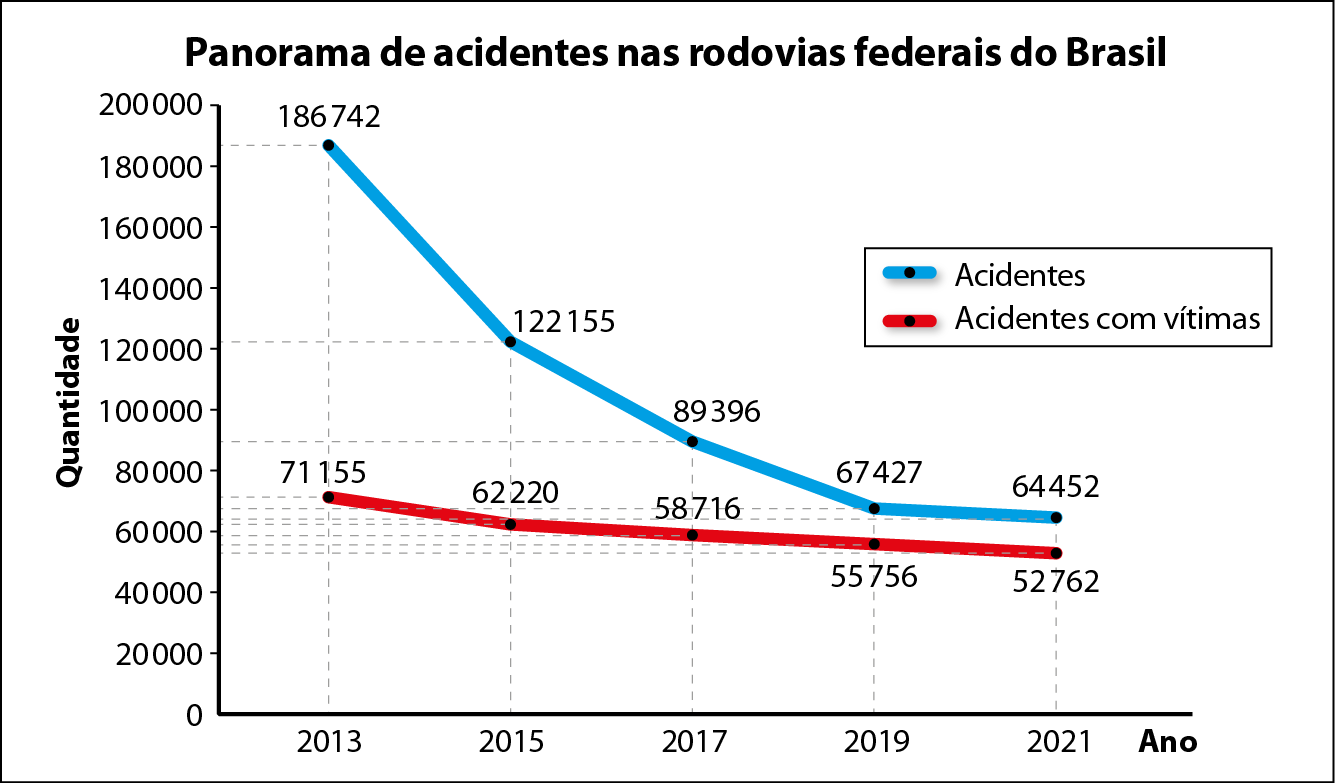
Gráfico em linhas. Título: Panorama de acidentes nas rodovias federais do Brasil. Eixo x, ano de 2013 a 2021. Eixo y, quantidade de 0 a 200.000. Os dados são: 2013. Acidentes: 186.742. Acidentes com vítimas: 71.155. 2015. Acidentes: 122.155. Acidentes com vítimas: 62.220. 2017. Acidentes: 89.396. Acidentes com vítimas: 58.716. 2019. Acidentes: 67.427. Acidentes com vítimas: 55.756. 2021. Acidentes: 64.452. Acidentes com vítimas: 52.762. Linha azul passa pelos dados de acidentes e linha vermelha passa pelos dados de acidentes com vítimas. — Dados obtidos em: CONFEDERAÇÃO Nacional do Transporte. Painel cê êne tê de acidentes rodoviários. Brasília, Distrito Federal: CNT, dezembro 2021. Disponível em: https://oeds.link/8jwrqr. Acesso em: 23 junho 2022.

Com esse gráfico, percebemos mais facilmente a variação da quantidade de acidentes e de acidentes com vítimas entre 2013 e 2021.

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

Com base nos dados estatísticos apresentados, faça o que se pede.

a) Copie o gráfico de colunas em uma folha de papel quadriculado e, seguindo o procedimento descrito, construa o gráfico de linhas correspondente.

b) Em que ano o total de acidentes foi maior? E em que ano foi menor?

c) Em que ano o número de acidentes com vítimas foi maior? E em que ano foi menor?

d) Tomando por base o total de acidentes dos anos 2017 e 2019 no gráfico de linhas, faça uma estimativa do total de acidentes de 2018.

e) Quando obtemos um valor de um intervalo gráfico tomando por base os valores dos extremos desse intervalo, fazemos o que chamamos de interpolação gráfica. Para fazer a interpolação gráfica, em sua cópia do gráfico, trace uma reta vertical por 2018 até intersectar a linha de acidentes, em seguida trace uma reta horizontal por esse ponto de intersecção até o eixo vertical. Agora, faça uma estimativa da quantidade aproximada de acidentes com vítimas em 2018.

f) Considerando os valores do total de acidentes indicados no gráfico de linhas, imagine como seria o prolongamento desse gráfico e faça uma estimativa desse total em 2022.

g) Quando obtemos um valor de um gráfico por meio de seu prolongamento, fazemos o que chamamos de extrapolação gráfica. Em sua cópia do gráfico, prolongue a linha que representa a quantidade de acidentes com vítimas. Para fazer a extrapolação gráfica, trace uma reta vertical por 2022 até intersectar o prolongamento da linha de acidentes com vítimas, em seguida trace uma reta horizontal por esse ponto de intersecção até o eixo vertical. Assim, faça uma extrapolação gráfica para obter a quantidade aproximada de acidentes com vítimas em 2022.

Respostas e comentários

a) Construção de gráfico.

b) Maior: 2013; menor: 2021.

c) Maior: 2013; menor: 2021.

d) Aproximadamente .78000 acidentes.

e) Aproximadamente .57000 acidentes com vítimas.

f) Aproximadamente .63000 acidentes.

g) Aproximadamente .51000 acidentes com vítimas.

Agora quem trabalha é você!

As resoluções dos itens a a g estão no início deste Manual, nas orientações específicas do capítulo 5.

Comente com os estudantes que a leitura e interpretação de um gráfico é tão importante quanto a de um texto e que a interpolação e a extrapolação são procedimentos que, embora não deem resultados exatos, auxiliam no entendimento das informações do gráfico.

Página 123

3. Frações algébricas

Acompanhe a situação a seguir.

Considere um ônibus que percorre 640 quilômetros em x  horas, com x > 2 e velocidade constante. Em média, esse ônibus desenvolve a velocidade constante de

\frac{640}{x}

quilômetros por hora. Vamos admitir que um carro percorra os mesmos 640 quilômetros em (x ‒ 2) horas, com velocidade constante. Nesse caso, a velocidade média, em quilômetro por hora, seria representada pelo quociente

\frac{640}{x ‒ 2}

Ilustração. Quatro pessoas dentro de um automóvel azul em uma estrada. Ao redor, vegetação e arbustos.

Expressões como a da situação apresentada, que indicam o quociente entre dois polinômios, são chamadas de frações algébricas. Chamaremos de numerador o polinômio dividendo e chamaremos de denominador o polinômio divisor.

Fração algébrica é o quociente de dois polinômios indicado na fórma de fração cujo denominador seja uma expressão algébrica.

O denominador de uma fração numérica é sempre diferente de zero. No caso das frações algébricas, a ou as variável ou variáveis do polinômio que representa ou representam o denominador não pode ou podem assumir valores que o anulem. Acompanhe os exemplos.

a) Na fração algébrica

\frac{640}{x ‒ 2}

, devemos ter x ‒ 2 ≠ 0, ou seja, x ≠ 2.

b) Na fração algébrica

\frac{b + 2 a}{2 b + 3 a}

, devemos ter 2b + 3a ≠ 0, ou seja, b ≠

‒ \frac{3 a}{2}

ou a ≠

‒ \frac{2 b}{3}

Valor numérico de fração algébrica

Imagine que o ônibus da situação anterior gaste 12 horas para fazer o percurso, ou seja, que x seja igual a 12. Qual seria a sua velocidade média? E a velocidade média do carro? Qual dos dois veículos é mais veloz considerando todo o percurso? Essas velocidades estariam compatíveis com a velocidade máxima permitida para esse trecho da estrada, de 60 quilômetros por hora?

Para responder a todas essas questões, iniciamos atribuindo o número 12 para x nas frações algébricas e calculando as velocidades, em quilômetros por hora.

• Ônibus:

v_{o}

\frac{640}{12}

= 53,3

• Carro:

v_{c}

\frac{640}{12 ‒ 2}

\frac{640}{10}

= 64

Ilustração. Garota de cabelo preto liso e camiseta branca. Ela fala: 53,3 é o valor numérico aproximado da primeira fração algébrica, e 64 é o valor numérico da segunda fração algébrica para x igual a 12. Como a velocidade do carro é maior do que a velocidade do ônibus, o carro é mais veloz. A velocidade do ônibus está compatível com a velocidade máxima (60 quilômetro por hora) permitida nesse trecho da estrada, mas a velocidade do carro não está! Que conselho você daria para o condutor desse carro?

Respostas e comentários

Orientação: Espera-se que o conselho seja: diminuir a velocidade para 60 quilômetros por hora.

3. Frações algébricas

Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero seis.

Neste tópico, ao resolver e elaborar problemas que possam ser representados por expressões algébricas, além de efetuar o cálculo numérico dessas expressões, os estudantes têm a oportunidade de desenvolver a habilidade (EF08MA06).

Assim como a divisão entre dois números inteiros pode ter como quociente um número racional, que pode ser dado na fórma de fração, a divisão não exata entre dois polinômios pode ser indicada na fórma de fração algébrica.

Trabalhe com os estudantes a situação apresentada. Eles devem perceber que, como em uma fração algébrica existe variável no denominador, essa expressão deve ter condição de existência, pois sabemos que o denominador não pode se anular.

O valor numérico de uma fração algébrica é obtido como foi feito para as expressões algébricas; apenas devemos observar se o valor indicado não anula o denominador. Nesse caso, a variável (ou variáveis) do denominador não pode ou podem assumir valores que anulem o denominador.

O conteúdo deste tópico traz uma abordagem prévia do que será desenvolvido no 9º ano sobre razões com grandezas de naturezas diferentes, entre as quais a velocidade.

Página 124

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

38 Um terreno é retangular, e seu comprimento mede 15 métros a mais do que o dôbro de sua largura x, dada em metro.

a) Escreva a razão entre as medidas do comprimento e da largura.

b) Qual é o valor numérico dessa razão, se a largura medir 12 métros?

39 Uma moto percorreu x quilômetros com y litros de gasolina. Uma segunda moto percorreu o dôbro dessa distância com ( y + 5) litros de gasolina. Escreva o consumo médio de gasolina, dado em quilômetro por litro:

a) da primeira moto;

b) da segunda moto.

40 Para que valor de y a expressão

\frac{12 + y}{y ‒ 6}

não representa uma fração algébrica?

41 Quais são os valores racionais que podem ser atribuídos à letra x na fração algébrica

\frac{x + 5}{2 x ‒ 3}

42 Que relação deve existir entre b e a para que a fração algébrica

\frac{2 a + b}{b ‒ 2 a}

represente um número racional?

43 Ontem, eu tinha em minha conta poupança certa quantia em real. Hoje, meu avô depositou nessa conta o quádruplo do que eu tinha ontem mais R$ 200,00duzentos reais. Represente por uma fração algébrica a razão entre o saldo que minha conta poupança tinha ontem e o saldo depois do depósito feito por meu avô.

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Na expressão a + 2b ‒ 4c, as variáveis só podem assumir os números 0, 1 ou 2.

a) Qual é o valor numérico da expressão para a = 1, b = 1 e c = 2?

b) Qual é o maior valor numérico possível?

c) Determine a, b e c, com a ≠ b ≠ c, de modo que o valor numérico da expressão seja 4.

2 Calcule:

a) (3a 2 ‒ 5b) + (5a 2 + 5b)

b) (3x 2 ‒ 5x + 2) ‒ (x 2 + 6x ‒ 4) + (5x ‒ 7)

c) (a 2 ‒ ab) + (b 2 ‒ ab) ‒ (a 2 + b 2)

(‒ \frac{1}{2} a ‒ 2 b) ‒ (\frac{3}{5} b + 2 a)

3 Elimine parênteses, colchetes e chaves e reduza os termos semelhantes.

a) 3a ‒ (b ‒ a) + (5b ‒ 2a)

b) x 2 ‒ {3x ‒ [(x + 3) + (x 2 ‒ 1)]}

c) 2y ‒ [‒3xy + (‒2x + 5y) ‒ (‒4xy + x)]

4 Do polinômio a subtraí o polinômio 4x ‒ 3y + 4, o que resultou em ‒4x ‒ 6y ‒ 9. Qual é o polinômio a?

5 Calcule os produtos dos polinômios a seguir.

a) (x ‒ 2) ⋅ (x + 5)

b) (2x ‒ 4) ⋅ (3x + 1)

c) (x ‒ 1) ⋅ (x 2 + x + 1)

d) (a ‒ 1)(a 2 ‒ 1)(a + 1)

6 Determine o polinômio que dividido por 5x 2 ‒ 3x + 1 tem por quociente x 2 + 2x ‒ 3 e resto ‒5x + 2.

7 Determine o polinômio A que multiplicado por 2x ‒ 1 tem por produto 8x 3 ‒ 14x 2 + 11x ‒ 3.

8 Dados: A = 6x 2 ‒ 5x ‒ 6, B = 2x 2 + 5x ‒ 12,C = 2x ‒ 3 e D = x + 4, calcule:

a) B ⋅ C

b) D 2 = D ⋅ D

c) B : C

d) (A + B) ⋅ C

9 Qual é o resultado da divisão de 5x 3 + 5x 2 ‒ 60x por 5x (x ‒ 3)?

10 (FESPSão Paulo) Qual é o resto da divisão do polinômio x 3 ‒ 2x 2 ‒ x + 2 por x 2 ‒ 1?

11 A inclinação de uma escada fixa é dada pela fração

\frac{E}{P}

, em que ê é a medida do espelho e P é a medida do piso (degrau). Quanto maior é o valor numérico da fração, mais inclinada é a escada. O piso de uma escada comum varia de 25 centímetros a 30 centímetros, e o espelho, de 16 centímetros a 18 centímetros. Qual é a menor e qual é a maior inclinação que uma escada com essas medidas pode ter?

Respostas e comentários

38. a)

\frac{2 x + 15}{x}

38. b)

\frac{13}{4}

39. a)

\frac{x}{y}

39. b)

\frac{2 x}{y + 5}

40. y = 6

41. Qualquer número racional diferente de

\frac{3}{2}

42. b ≠ 2a

43.

\frac{x}{5 x + 200}

1. a) ‒5

1. b) 6

1. c) a = 2, b = 1 e c = 0.

2. a) 8a 2

2. b) 2x 2 ‒ 6x ‒ 1

2. c) ‒2ab

2. d)

‒ \frac{5}{2} a ‒ \frac{13}{5} b

3. a) 2a + 4b

3. b) 2x 2 ‒ 2x + 2

3. c) 3x ‒ 3y ‒ xy

4. ‒9y ‒ 5

5. a) x 2 + 3x ‒ 10

5. b) 6x 2 ‒ 10x ‒ 4

5. c) x 3 ‒ 1

5. d) a 4 ‒ 2a 2 + 1

6. 5x 4 + 7x 3 ‒ 20x 2 + 6x ‒ 1

7. A = 4x 2 ‒ 5x + 3

8. a) 4x 3 + 4x 2 ‒ 39x + 36

8. b) x 2 + 8x + 16

8. c) x + 4

8. d) 16x 3 ‒ 24x 2 ‒ 36x + 54

9. x + 4

10. 0

11. Menor:

\frac{16}{30}

≃ 0,53; maior:

\frac{18}{25}

≃ 0,72.

Exercícios propostos

As resoluções do exercício 38 e dos exercícios 40 a 43 estão no início deste Manual, nas orientações específicas do capítulo 5.

No exercício 39, é possível explorar condições como “Para que valor de y e de x os consumos das duas motos são iguais?”. Ao resolver a equação dada pela igualdade das frações algébricas que representam os consumos, obtidas no item a

(\frac{x}{y})

e no item b

[\frac{2 x}{(y + 5)}]

, os estudantes devem chegar ao valor 5 para y e concluir que o valor de x pode, consideradas as limitações de uma situação real, ser qualquer um.

Exercícios complementares

Neste bloco de exercícios, os estudantes têm a oportunidade de retomar os principais conceitos tratados no capítulo e verificar possíveis dificuldades que ainda tenham.

Sugerimos que eles se organizem em duplas para que resolvam exercícios, o que ampliará e enriquecerá o repertório de estratégias que eles já têm e consolidará os conhecimentos construídos.

Proponha que refaçam alguns exercícios dos tópicos anteriores desse capítulo sobre os quais ainda tenham dúvida. Revisitar conceitos e estratégias já estudadas pode contribuir para o aprendizado.

As resoluções dos exercícios 1 a 3 e dos exercícios 5 a 10 estão no início deste Manual, nas orientações específicas do capítulo 5.

No exercício 4, retratamos a situação descrita:

A ‒ (4x ‒ 3y + 4) = ‒4x ‒ 6y ‒ 9

Desse modo, verificamos que o polinômio A é dado por:

A = ‒4x ‒ 6y ‒ 9 + (4x ‒ 3y + 4)

A = ‒4x ‒ 6y ‒ 9 + 4x ‒ 3y + 4

A = ‒9y ‒ 5

O exercício 11 retoma o tema da arquitetura de uma escada que deve contemplar determinados limites quanto às medidas do espelho e do piso, o que implica limites na inclinação da escada. Comente com os estudantes que essas exigências arquitetônicas atendem necessidades de segurança e de preservação da saúde dos usuários das escadas e são reguladas por leis específicas. Para resolver o exercício, deve-se considerar que a menor inclinação é dada pela razão entre a menor medida do espelho e a maior medida do piso; também deve-se considerar que a maior inclinação é dada pela razão entre a maior medida do espelho e a menor medida do piso. A título de curiosidade, informe que a menor inclinação (0,53) corresponde a um ângulo de medida aproximada 28graus e que a maior inclinação (0,72) corresponde a um ângulo de medida aproximada 35graus.

Página 125

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Os trinômios são:

a) polinômios de um único termo.

b) polinômios de dois termos.

c) polinômios de três termos.

d) polinômios do terceiro grau.

2 Em metro, qual é a medida do perímetro da figura a seguir, composta de retângulos e cujas medidas dos lados são dadas em metro?

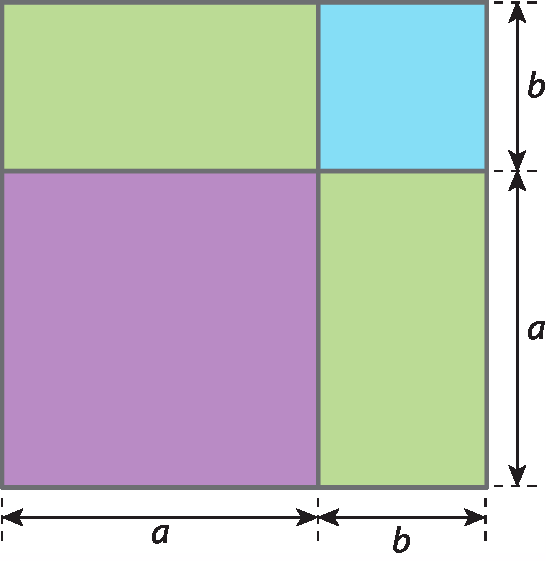
Ilustração. Retângulo composto de 2 retângulos iguais e 2 quadrados. Retângulo verde à esquerda de quadrado azul. Abaixo deles, quadrado roxo à esquerda e retângulo verde à direita. Retângulo verde tem lados com medidas a por b. Quadrado azul tem lados com medidas b. Quadrado roxo tem lados com medidas a. Retângulo verde tem lados com medidas b por a.

a) a + b

b) 2a + 2b

c) 4a + 4b

d) aelevado a 2 + 2ab + belevado a 2

3 Determine a medida da área do retângulo a seguir, cujas medidas dos lados são dadas em centímetro e a área, em centímetro quadrado.

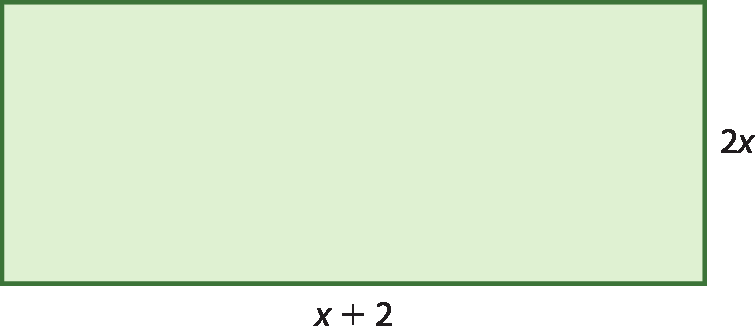
Ilustração. Retângulo com lados medindo x mais 2 por 2 vezes x.

a) 3x + 2

b) 6x + 4

c) 2xelevado a 2 + 2

d) 2xelevado a 2 + 4x

4 Determine o produto dos polinômios a seguir.

(aelevado a 3 menos aelevado a 2 + a) ⋅ (a + 1)

a) aelevado a 4 + a

b) aelevado a 4 + aelevado a 2

c) aelevado a 3 menos aelevado a 2 + a

d) aelevado a 4 menos aelevado a 3 + aelevado a 2

5 Dividindo-se 4aelevado a 4 menos 5aelevado a 2 + a menos 2 por 2aelevado a 2 menos a + 1, encontra-se um resto R. Calcule o valor numérico de R para

a = \frac{1}{3} .

a) R = 0

b) R = 1

c) R = 3

d) R = a

6 Qual é o polinômio que, dividido por 5aelevado a 2 menos 2a menos 3, tem por quociente exato 3a menos 4?

a) 15aelevado a 3 menos 26aelevado a 2 menos a + 12

b) 15aelevado a 3 menos 26aelevado a 2 + 17a + 12

c) 15aelevado a 3 menos 26aelevado a 2 menos a menos 12

d) 15aelevado a 3 + 14aelevado a 2 menos a + 12

7 Márcia comprou uma televisão, que estava sendo vendida à vista por x reais, e pagará em 10 prestações de mesmo valor. Cada prestação corresponde a

\frac{1}{10}

do valor à vista, acrescido de 80 reais de juro. Que expressão algébrica representa, em real, o valor total pago por Márcia e o valor de cada prestação, respectivamente?

a) 10x + 800 e x + 80

b) 10x + 80 e

\frac{x}{10} + 80

c) x + 800 e

\frac{x}{10} + 80

d) x + 80 e

\frac{x}{10}

8 A medida da área do retângulo a seguir é expressa pelo polinômio 2xelevado a 2 + 11x + 15 e dada em métro quadrado. Que polinômio representa a medida da altura desse retângulo, em metro?

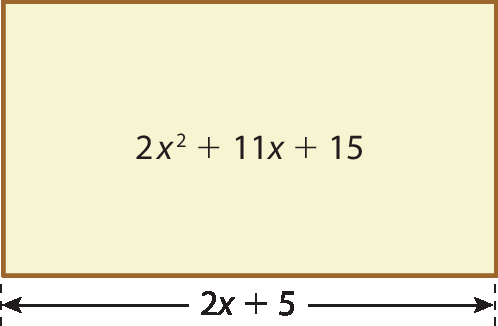
Ilustração. Retângulo com lado maior medindo 2 vezes x mais 5. Dentro, sua área é indicada como 2 vezes x ao quadrado, mais 11 vezes x, mais 15.

a) x + 3

b) 2x + 5

c) 4xelevado a 2 + 25

d) 2xelevado a 2 + 9x + 10

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões.

a) O que é um polinômio?

b) Explique como se deve proceder para adicionar dois polinômios.

c) Para calcular o produto entre dois polinômios, aplica-se a propriedade distributiva. Explique como essa propriedade é aplicada.

d) O que é fração algébrica?

Respostas e comentários

1. Alternativa c.

2. Alternativa c.

3. Alternativa d.

4. Alternativa a.

5. Alternativa a.

6. Alternativa a.

7. Alternativa c.

8. Alternativa a.

Organizando: Veja as resposta neste Manual.

Verificando

As resoluções dos testes 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 5.

Sugerimos que esses testes sejam utilizados, entre outros objetivos pedagógicos, para preparar os estudantes para realizar avaliações de larga escala. Eles podem resolver os testes e, depois, em duplas ou pequenos grupos, compartilhar as estratégias de resolução com os colegas.

Organizando

Esta seção possibilita retomar os principais conteúdos trabalhados neste capítulo.

Incentive os estudantes a compartilhar as respostas com os colegas e, se julgar adequado, a compor um mapa conceitual de maneira coletiva, explicitando os conteúdos do capítulo e apresentando informações relevantes sobre eles.

a) Polinômio é toda expressão algébrica que representa um monômio ou uma soma algébrica de monômios.

b) Para adicionar dois polinômios, agrupamos os termos semelhantes e, depois, os reduzimos.

c) Para multiplicar dois polinômios, a propriedade distributiva é aplicada da seguinte maneira: multiplicando cada termo de um deles por todos os termos do outro; depois reduzimos os termos semelhantes obtidos.

d) Fração algébrica é o quociente entre dois polinômios indicado na fórma de fração cujo denominador é uma expressão algébrica.