
CAPÍTULO 6 Produtos notáveis e fatoração

Observe, leia e responda no caderno.
a) Pesquise na internet, em livros, enciclopédias etcétera, junto a um colega, a história e os inventos de Arquimedes. Elaborem um texto com um resumo dessa pesquisa.
b) Pesquise também a participação de Arquimedes na Segunda Guerra Púnica no cêrco da República Romana a Siracusa.
c) Calcule a medida da área de um triângulo com lados de medidas 3, 4 e 5 usando a fórmula de Heron.
Arquimedes (cêrca de 287 antes de Cristo-212 antes de Cristo), natural da cidade de Siracusa, foi um dos maiores matemáticos, físicos e inventores do século três antes de Cristo
A fórmula para a medida da área de um triângulo com lados medindo a, b e c, conhecida como fórmula de Heron,
A é igual a raiz quadrada da seguinte multiplicação: s vezes abre parênteses s menos a fecha parênteses, vezes abre parênteses s menos b fecha parênteses, vezes abre parênteses s menos c fecha parênteses, fim da raiz., em que s é a medida do semiperímetro, era conhecida por Arquimedes vários séculos antes de Heron ter nascido.
A bomba de água em parafuso para retirar água de porões de navios, irrigar campos e drenar charcos é a invenção mecânica de Arquimedes mais conhecida. Ainda hoje é utilizada no Egito, nos Países Baixos e até no Rio de Janeiro.
Respostas e comentários
a) Resposta pessoal.
b) A cidade de Siracusa resistiu ao cerco de Roma por anos, pois era protegida por armas desenvolvidas por Arquimedes. Conta-se que Arquimedes foi morto por um soldado romano, que violou as instruções do general romano Marcelo para poupar sua vida.
c) 6 unidades de área.
Capítulo 6 – Produtos notáveis e fatoração
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas. Inicialmente, são considerados os produtos notáveis, cuja frequência no cálculo algébrico justifica um estudo sistematizado sobre o desenvolvimento dessas expressões na fórma de polinômios.
Trabalhamos também uma expressão algébrica escrita na fórma fatorada. Para isso, além da aplicação da propriedade distributiva da multiplicação, é importante que os estudantes percebam a aplicação dos produtos notáveis estudados no início do capítulo.
Finalizando o capítulo, tratamos de simplificação de expressões algébricas como uma aplicação do que foi estudado e apresentamos investigações em sequências recursivas e em sequências não recursivas com base no cálculo algébrico já desenvolvido.
O texto da abertura deste capítulo possibilita o desenvolvimento do Tema Contemporâneo Transversal ciência e tecnologia. Comente e discuta com os estudantes que a produção de conhecimento em diferentes áreas, como a Matemática, estimula o desenvolvimento de tecnologias que podem ser aplicadas em outras áreas, como Medicina, Economia, Engenharia, entre tantas outras.
Ao realizarem as pesquisas indicadas nos itens a e b, os estudantes desenvolvem a competência geral 1, pois podem perceber a evolução dos conceitos matemáticos e a Matemática como um conjunto de conhecimentos historicamente construídos, influenciados ou inspirados em diferentes contextos do cotidiano.
No item c, como o semiperímetro é 6 (pois 5 + 4 + 3 = 12 e 12 : 2 = 6), obtemos que:
A =
Raiz quadrada de seis· (6 ‒ 3) · (6 ‒ 4) · (6 ‒ 5)
A =
Raiz quadrada de 36A = 6

Sugestão de leitura
Para ampliar o trabalho com o tema proposto nesta abertura, sugerimos:
SÁ, I. P. Arquimedes de Siracusa e o seu método da exaustão: uma atividade didática para o cálculo de π. Revista Eletrônica Teccen, Vassouras, volume 4, número 3, página 15-24, maio/agosto, 2011. Disponível em: https://oeds.link/etkDpU. Acesso em: 9 junho 2022.
Esse artigo apresenta um período da vida e da obra de Arquimedes de Siracusa e trata das possibilidades da história da Matemática como metodologia de ensino.
1. Os produtos notáveis
Vimos como calcular o produto de polinômios aplicando a propriedade distributiva da multiplicação. Agora, vamos estudar alguns produtos de binômios que aparecem com bastante frequência no cálculo algébrico, os chamados produtos notáveis.
Quadrado da soma de dois termos
Usando como unidade de medida o comprimento do segmento

, vamos construir:
• um quadrado com lado medindo 4u ;
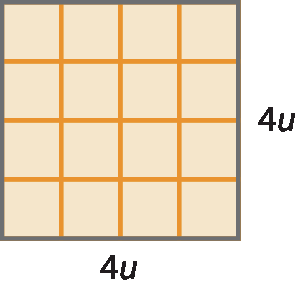
• dois retângulos com lados medindo 4u e 3u ;
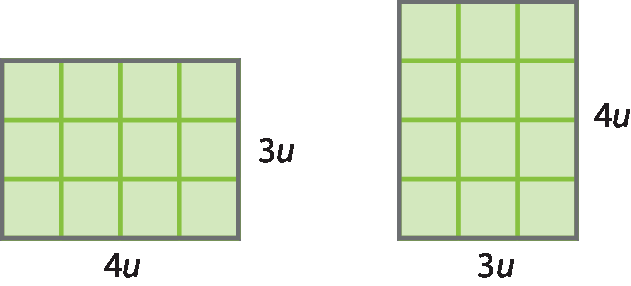
• um quadrado com lado medindo 3u.
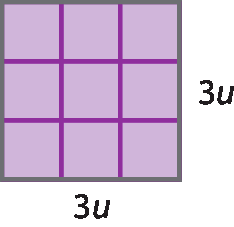

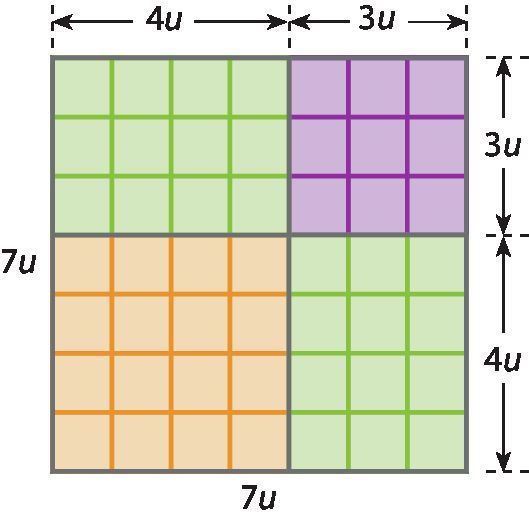
Jairo e Vanessa concluíram que a medida da área do quadrado montado é 49u2. Acompanhe como eles fizeram os cálculos.

Respostas e comentários
1. Os produtos notáveis
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero seis e ê éfe zero oito ême ah um nove.
Ao trabalhar o desenvolvimento de produtos notáveis, os estudantes podem desenvolver a habilidade (ê éfe zero oito ême ah zero seis) ao ampliar conteúdos e estratégias que podem ser utilizados na resolução de problemas. Além disso, a medida de área de figuras planas é associada frequentemente ao conteúdo algébrico, a fim de lhe atribuir significados e, desta maneira, os estudantes utilizam a habilidade (ê éfe zero oito ême ah um nove). Convém lembrar que, para simplificar a linguagem, nos referimos à área da região poligonal simplesmente como área do polígono. Por exemplo, a área de uma região retangular será denominada área do retângulo.
Explore com os estudantes as figuras dos quadrados apresentados. A fim de que ampliem a compreensão do produto notável quadrado da soma de dois termos, escreva na lousa alguns exemplos para que eles construam as figuras que os auxiliem a atribuir significado a tais produtos. Depois, alguns estudantes podem mostrar à turma como os resolveram, justificando as etapas.
Um quadrado de lado medindo ℓ tem área de medida ℓ 2.
Agora, considere um quadrado de lado medindo a + b.
A medida da área desse quadrado é (a + b)2.
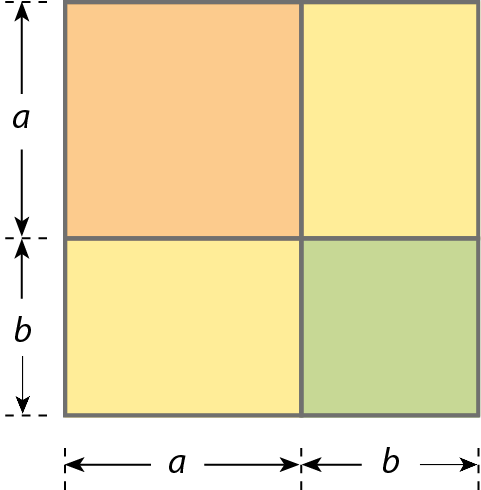
Vamos separar as quatro partes em que o quadrado está dividido e indicar a expressão que representa a medida da área de cada uma delas.
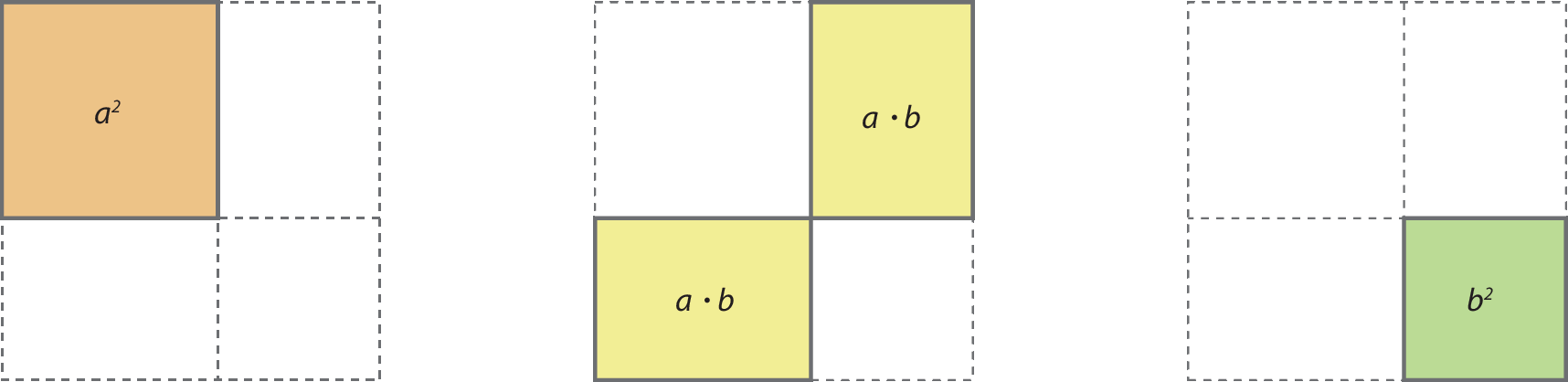
Adicionando as medidas das áreas em destaque, obtemos: a 2 + 2 ⋅ ab + b 2
Logo: (a + b)2 = a 2 + 2ab + b 2
Esse resultado poderia ter sido obtido da seguinte maneira:
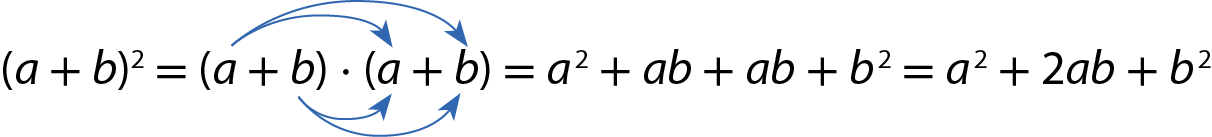
Portanto:
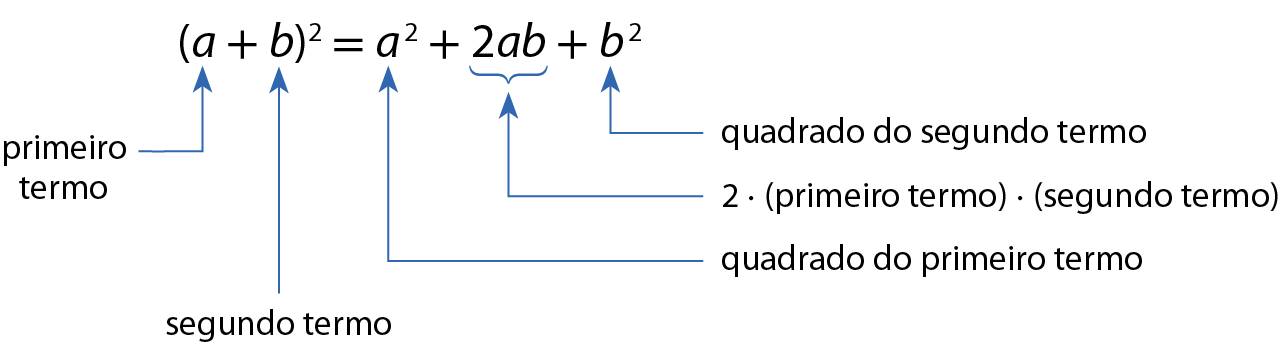
O quadrado da soma de dois termos é igual ao quadrado do primeiro termo mais duas vezes o produto do primeiro pelo segundo termo mais o quadrado do segundo termo.
Acompanhe a aplicação desse produto notável em alguns exemplos.
a) Efetue:

Respostas e comentários
Quadrado da soma de dois termos
Encerre a apresentação do quadrado da soma de dois termos com a turma explorando as figuras desta página. Se julgar conveniente, peça aos estudantes que reproduzam as figuras no caderno e destaquem quais são o primeiro e o segundo termo nos produtos para os quais fizeram as figuras.
Proponha a cada um que descreva o trinômio obtido em relação a esses termos. Por exemplo, se o produto for: (2x + 3y)(2x + 3y), ou seja, (2x + 3y)2, espera-se que os estudantes identifiquem 2x como primeiro termo e 3y como segundo termo. Assim, eles devem obter:
• quadrado do primeiro termo: (2x)2 = 4x2
• quadrado do segundo termo: (3y)2 = 9y2
• duas vezes o primeiro termo vezes o segundo termo: 2 · 2x · 3y = (2 · 2 · 3) · x · y = 12xy
Logo:
(2x + 3y)2 = 4x2 + 12xy + 9y2

b) Calcule:
• (‒3a + 5)2 = = (‒3a)2 + 2 ⋅ (‒3a) ⋅ 5 + 52 = = 9a 2 ‒ 30a + 25
• (‒5x ‒ 2y)2 = = [(‒5x) + (‒2y)]2 = = (‒5x)2 + 2 ⋅ (‒5x) ⋅ (‒2y) + (‒2y)2 = = 25x 2 + 20xy + 4y 2
c) Simplifique a expressão 4x 2(x + 2) ‒ x(2x + 3)2.
Aplicando a propriedade distributiva da multiplicação, obtemos:


EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Reproduza, em uma folha de papel sulfite, as figuras a seguir. Depois, recorte-as e monte um quadrado com elas.
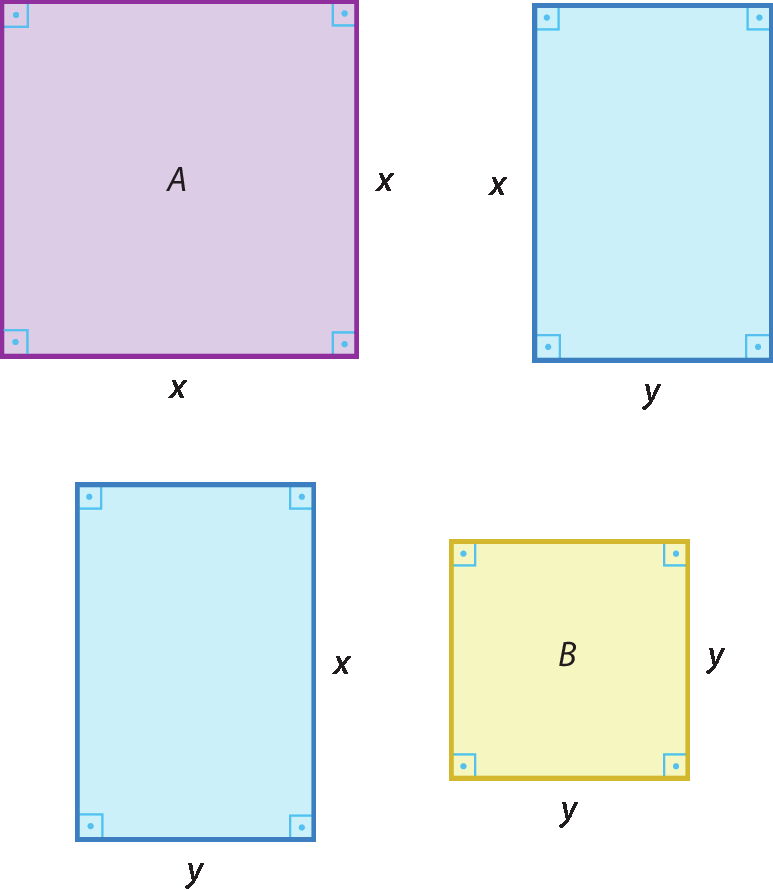
Agora, escreva a medida:
a) da área do quadrado a;
b) da área de cada retângulo;
c) da área do quadrado B;
d) de cada lado da figura construída;
e) da área da figura construída.
2 Considerando a figura a seguir, faça o que se pede.
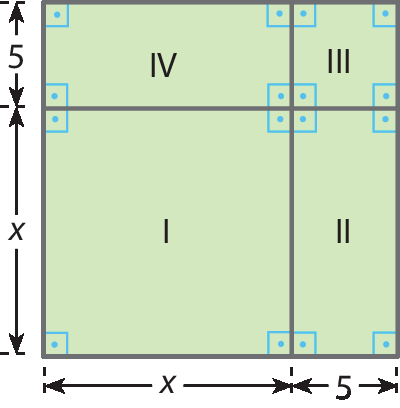
a) Determine as medidas das áreas um, dois, três e quatro.
b) Determine a medida da área da figura toda.
c) Calcule (x + 5)2 e compare com a medida da área da figura.
Respostas e comentários
1. Construção de figura.
1. a) x 2
1. b) xy
1. c) y 2
1. d) x + y
1. e) x 2 + 2xy + y 2
2. a) um: x 2; dois: 5x; três: 25; quatro: 5x.
2. b) x 2 + 10x + 25
2. c) (x + 5)2 = x 2 + 10x + 25. São iguais.
Exercícios propostos
Com base no desenvolvimento teórico, este bloco de exercícios mantém o vínculo entre as Unidades Temáticas Álgebra e Geometria.
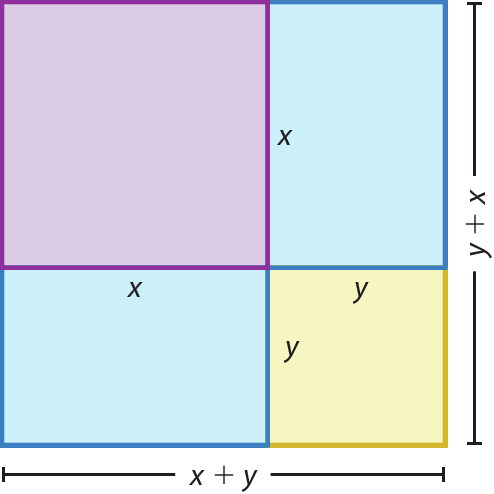
No exercício 1, lembre aos estudantes que devem utilizar tesouras de pontas arredondadas e manuseá-las com cuidado. Apresentamos a seguir um exemplo de quadrado que se obtém com as figuras recortadas, cuja área é dada por: (x + y)2 = x2 + 2xy + y2
No exercício 2, é importante que os estudantes comparem a medida da área da figura com o desenvolvimento do produto notável para verificar a igualdade. No item a, a resposta decorre diretamente da definição de área de retângulos, isto é, a medida da área das figuras será dada pelo produto entre as medidas de dois lados consecutivos dela. No item b, a medida da área do quadrado composto das figuras um, dois, três e quatro será a soma das medidas das áreas das figuras um, dois, três e quatro, dada por x2 + 5x + 25 + 5x, que equivale a x2 + 10x + 25. Além disso, no item c, pode-se considerar que o quadrado tem lados de medida x + 5 e que, portanto, a medida de sua área é dada por (x + 5)2; logo:
(x + 5)2 = x2 + 10x + 25
De fato:
(x + 5)2 = (x + 5) · (x + 5) =
= x2 + 10x + 25
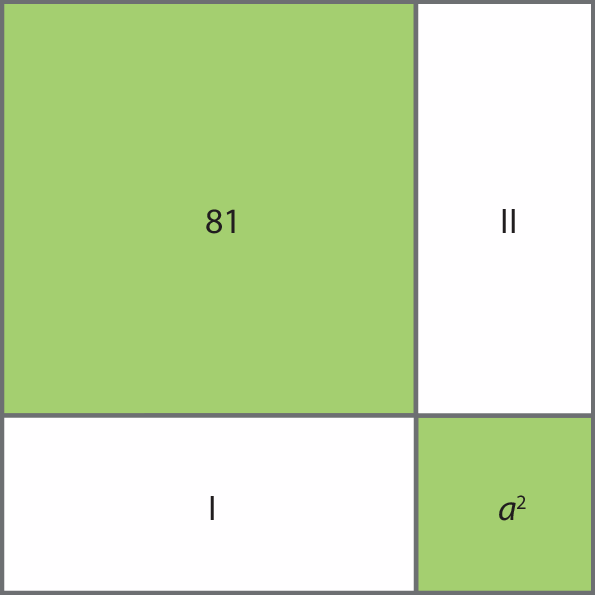
3 A figura a seguir representa um quadrado. As partes pintadas de verde também são quadradas, cujas medidas das áreas são as indicadas.
Faça o que se pede.
a) Determine as medidas das áreas um e dois.
b) Determine a medida da área da figura toda.
c) Determine a medida do lado do quadrado maior.
d) Calcule (a + 9)2 e compare com a medida da área da figura.
4 Corrija as sentenças falsas.
a) (x + 8)2 = x 2 + 64
b) (3x + 5)2 = (3x)2 + 2 ⋅ (3x ) ⋅ 5 + 52 = = 9x 2 + 30x + 25
c) (x + 3y)2 = x 2 + 3xy + (3y)2 = = x 2 + 3xy + 9y 2
5 Calcule o quadrado da soma em cada item.
a) (3x + y)2
b) (3a + 2)2
c) (4a + y3)2
d)
Expressão algébrica. Abre parênteses, 3 quartos de x, mais 2 quintos de y, fecha parênteses, elevado a 2.
6 Simplifique as expressões a seguir.
a) a(5a ‒ 1) + (a + 2)2
b) (2x + 3)2 ‒ x(x ‒ 4)
c) ( y ‒ 3)( y + 2) ‒ ( y + 1)2
d) (9y + 1)2 ‒ ( y + 9)2
e) (2a + 3b)2 ‒ 4a(a + 3b)
f) (1 + 5a)2 + 25(1 ‒ a2)
7 As medidas dos lados de um jardim quadrado foram aumentadas em 3 metros.

Considerando x a medida do lado do jardim antes do aumento, dê o polinômio que representa:
a) a nova medida da área desse jardim;
b) o aumento verificado na medida da área do jardim.
8 Desenvolva.
a) (‒x + 6)2
b)
Expressão algébrica. Abre parênteses, menos x sobre 2, mais, y sobre 3, fecha parênteses, elevado a 2.
9

Hora de criar – Elabore três expressões que representem o quadrado de uma soma, sendo uma delas apenas com números conhecidos, isto é, sem letras. Troque-as com um colega para que cada um desenvolva as expressões do outro. Em seguida, desfaçam a troca e corrijam as expressões.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO

Podemos aplicar o quadrado da soma para fazer cálculos mais rápidos, até mesmo mentalmente.
Acompanhe.
452 = (40 + 5)2 = 402 + 2 ⋅ 40 ⋅ 5 + 52 = .1600 + 400 + 25 = .2025
812 = (80 + 1)2 = 802 + 2 ⋅ 80 ⋅ 1 + 12 = .6400 + 160 + 1 = .6561
Agora, ao aplicar o quadrado da soma, calcule mentalmente as potências. Em seguida, registre o resultado no caderno.
a) 122
b) 242
c) 352
d) 522
Respostas e comentários
3. a) um: 9a; dois: 9a.
3. b) a2 + 18a + 81
3. c) a + 9
3. d) (a + 9)2 = a2 + 18a + 81. São iguais.
4. a) x 2 + 16x + 64
4. b) Verdadeira.
4. c) x 2 + 2 ⋅ x ⋅ 3y + (3y)2 = x 2 + 6xy + 9y 2
5. a) 9x 2 + 6xy + y 2
5. b) 9a2 + 12a + 4
5. c) 16a2 + 8ay 3 + y 6
5. d)
Expressão algébrica. 9 16 avos de x ao quadrado, somado com 3 quintos de xy, mais 4 25 avos de y ao quadrado.6. a) 6a2 + 3a + 4
6. b) 3x 2 + 16x + 9
6. c) ‒3y ‒ 7
6. d) 80y 2 ‒ 80
6. e) 9b2
6. f) 26 + 10a
7. a) (x 2 + 6x + 9) métros quadrados
7. b) (6x + 9) métros quadrados
8. a) x 2 ‒ 12x + 36
8. b)
Expressão algébrica. x ao quadrado sobre 4, menos xy sobre 3, mais y ao quadrado sobre 9.
9. Resposta pessoal.
Pense mais um poucoreticências:
a) 144
b) 576
c) .1225
d) .2704
Exercícios propostos
As resoluções dos exercícios 3 a 6 e do exercício 8 estão no início deste Manual, nas orientações específicas do capítulo 6.
No exercício 3, assim como no exercício 2, os estudantes devem comparar a medida da área da figura com o desenvolvimento do produto notável para verificar a igualdade.
A resolução do exercício 7 leva à generalização do cálculo da medida da área de um jardim quadrado cuja ampliação é pedida, tendo como parâmetro a medida anterior do lado desse quadrado. Esse tipo de procedimento pode ser útil na elaboração de projetos. Outras questões propostas ao longo do capítulo promovem a percepção desse vínculo, que pode ainda ser reforçado por outras atividades elaboradas como complemento.
Uma possível resolução para o exercício é:
a) Indicando por x a medida do lado do quadrado original, se aumentamos em 3 metros cada lado, a medida da área do quadrado obtido, em métro quadrado, é dada por (x + 3)2. Utilizando o produto notável, obtemos (x2 + 6x + 9).
b) Inicialmente, o jardim tem área dada pela expressão x2. Para obter o aumento na área, basta subtrair essa área inicial da área obtida no item a.
Assim, o aumento da medida da área, em métro quadrado, é dado por: (x2 + 6x + 9) ‒ x2 =
= x2 + 6x + 9 ‒ x2 = 6x + 9
Pense mais um poucoreticências
A seção mostra a associação entre Aritmética e Álgebra, que também aparecerá em outros momentos deste capítulo. Aqui, os estudantes verificam a aplicação do produto notável quadrado da soma de dois termos para calcular potências numéricas de uma maneira mais rápida e até mentalmente. Faça outros exemplos na lousa e promova uma dinâmica em que os estudantes devem determinar o quadrado de alguns números por meio desse método.
As resoluções dos itens a a d desta seção estão no início deste Manual, nas orientações específicas do capítulo 6.
PARA SABER MAIS
A Matemática na História
O conceito de produtos notáveis apareceu na Grécia nos estudos de álgebra geométrica, ferramenta bastante empregada pelos gregos para lidar com situações que envolviam números irracionais.
A álgebra geométrica grega chegou até nós principalmente por meio do livro dois da obra Os elementos, de Euclides (cêrca de 325 antes de Cristo-265 antes de Cristo). Entretanto, é muito provável que a álgebra dos primeiros gregos – desde os pitagóricos (século seis antes de Cristo ao século três antes de Cristo) até Euclides, Arquimedes (cêrca de 287 antes de Cristo-212 antes de Cristo) e Apolônio (cêrca de 262 antes de Cristo-190 antes de Cristo) – já fosse geométrica, o que estabeleceu uma tradição na representação de situações essencialmente algébricas, bem como daquelas que envolviam números irracionais.
Vários fatores podem ser associados a essa tradição, por exemplo, a dificuldade de lidar na época com números irracionais e números racionais, a inexistência de uma notação algébrica satisfatória (que surgiu somente no século dezesseis) e o grande avanço da Geometria (que naturalmente empregaria a álgebra geométrica sempre que possível na representação de situações matemáticas). Portanto, era natural para os matemáticos gregos desse período adotar um estilo geométrico para o qual tinham habilidade.
No livro dois de Os elementos, são encontradas algumas identidades algébricas, como:
(a + b)2 = a 2 + 2ab + b 2
(a + b)(a ‒ b) = a2 ‒ b 2
4ab + (a ‒ b)2 = (a + b)2
Entretanto, essas identidades não eram apresentadas dessa maneira, pois não havia essas notações naquela época. Os gregos, desde os pitagóricos até Euclides, pensavam nessas situações geometricamente.
Por exemplo, o produto ab era visto como um retângulo com medidas de base a e altura b. Assim, a identidade (a + b)2 = a 2 + 2ab + b 2 era representada como o diagrama da figura a seguir.
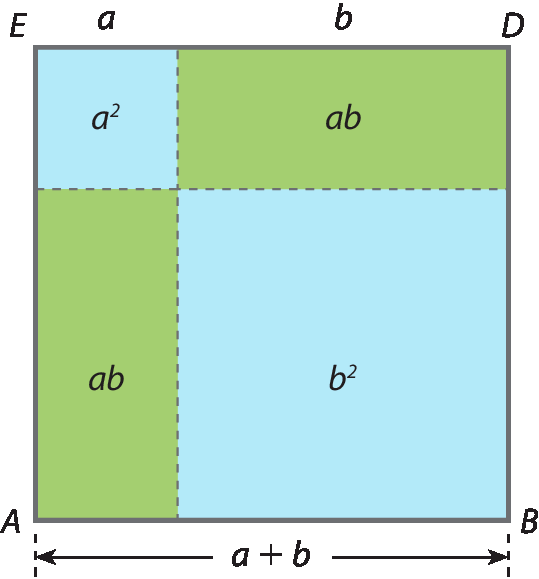
E enunciada da seguinte maneira:

Euclides registrou esse resultado pitagórico na proposição 4 do livro dois de Os elementos e a prova é dada diretamente pela interpretação geométrica da situação.
Na figura, “o quadrado sobre a linha toda” é o quadrado á bê dê é; “aos quadrados sobre as duas partes” são os quadrados de medidas de áreas a 2 e b 2 (em azul); e “duas vezes o retângulo que as partes contêm” são os dois retângulos de medidas de área ab (em verde).
A proposição 4 é representativa da maneira como os problemas que envolvem álgebra eram concebidos e apresentados. Seguramente, as tentativas de expressão de todas as situações algébricas surgidas naquela época, segundo a álgebra geométrica, podiam levar a construções muito complicadas. Em virtude disso, a álgebra geométrica necessita de mais do que um texto escrito para que seja bem entendida, por isso o uso de figuras.
Respostas e comentários
Para saber mais
Trabalhar a história da Matemática, tema desta seção, é mais uma maneira de possibilitar aos estudantes que atribuam significado aos conteúdos matemáticos e desenvolvam a competência geral 1 e a competência específica 1.
Proponha a eles uma leitura com a turma, organizada em grupos, para que a discussão entre eles facilite a interpretação do texto e enriqueça a sua compreensão. Em seguida, peça a um representante de cada grupo que exponha as dificuldades encontradas pelo grupo e as eventuais dúvidas que ainda apresentem. Ao final, encerre o tema desta seção discutindo com a turma as dificuldades e as dúvidas que surgirem.
Quadrado da diferença de dois termos
Considere a figura a seguir.
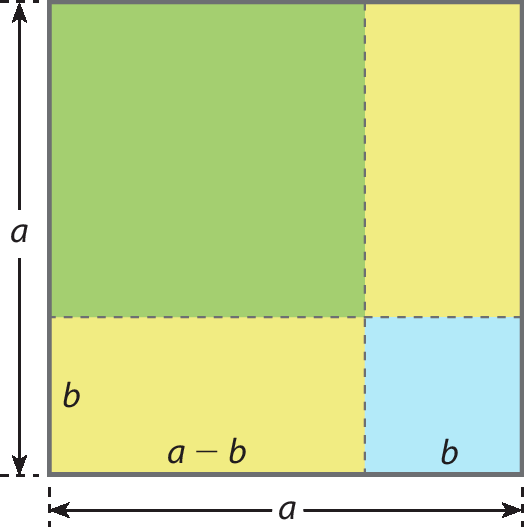
Analisando a figura, sabemos que o lado do quadrado verde mede a ‒ b. Assim, chegamos ao polinômio que representa a medida da área desse quadrado, ou seja, (a ‒ b)2.
Vamos separar as quatro partes em que o quadrado maior está dividido e indicar a expressão que representa a medida da área de cada uma delas.
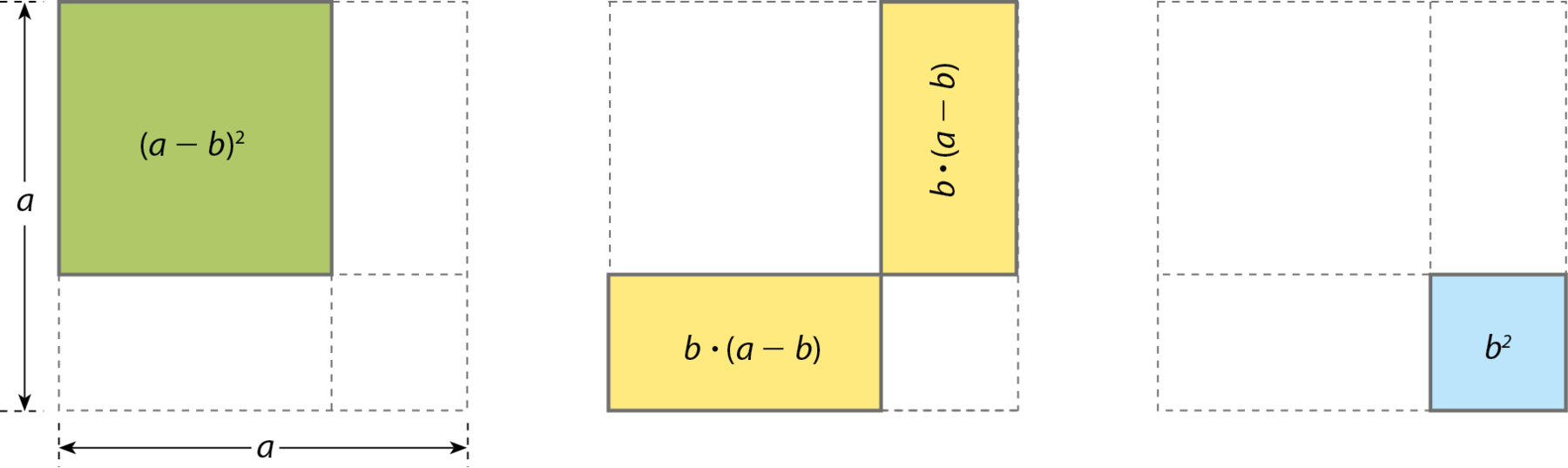
Observe que a medida da área do quadrado verde é igual às medidas das áreas do quadrado cujo lado mede a menos as das duas áreas dos retângulos amarelos e menos a da área do quadrado azul, cujo lado mede b, ou seja:
(a ‒ b)2 = a 2 ‒ 2 ⋅ b ⋅ (a ‒ b) ‒ b 2
(a ‒ b)2 = a 2 ‒ 2ab + 2b 2 ‒ b 2
(a ‒ b)2 = a 2 ‒ 2ab + b 2
Também podemos calcular o quadrado de a ‒ b aplicando a propriedade distributiva da multiplicação:
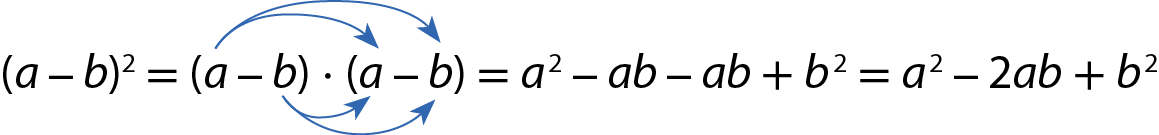
Portanto:
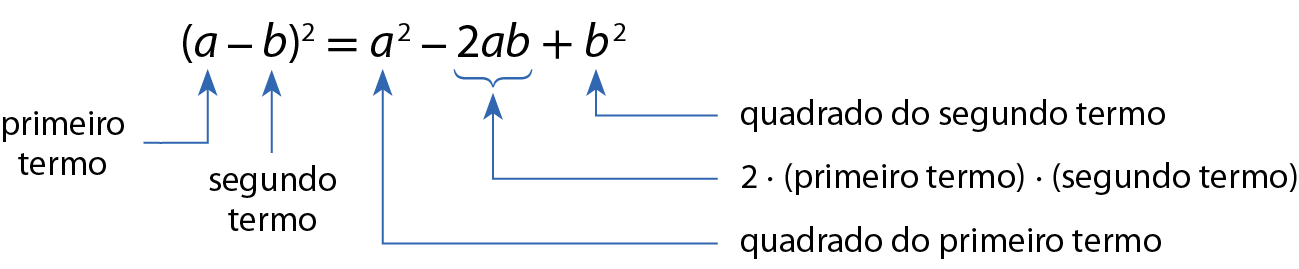
O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo menos duas vezes o produto do primeiro pelo segundo termo mais o quadrado do segundo termo.
Respostas e comentários
Quadrado da diferença de dois termos
De modo análogo ao que foi feito com o quadrado da soma, explore com os estudantes as figuras apresentadas.
Amplie também com outros exemplos do produto notável quadrado da diferença de dois termos e peça a eles que construam as figuras; assim, podem-se atribuir significado geométrico a tais produtos.
Acompanhe alguns exemplos.
a) Desenvolva:
• (x ‒ 3)2 = x 2 ‒ 2 ⋅ x ⋅ 3 + 32 = x 2 ‒ 6x + 9
• (3a ‒ b)2 = (3a)2 ‒ 2 ⋅ (3a) ⋅ b + b 2 = 9a 2 ‒ 6ab + b 2
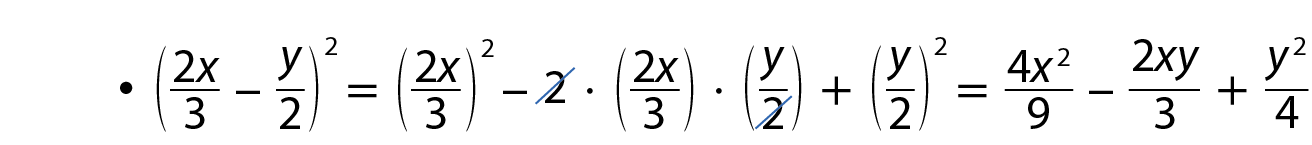
b) Simplifique a expressão (x ‒ 2) ⋅ (x ‒ 5)2 ‒ x ⋅ (x ‒ 6)2.

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
10 Desenvolva os quadrados da diferença.
a) (3a ‒ 5)2
b) (3x ‒ 2y)2
c) (3a 2 ‒ 1)2
d)
Expressão algébrica. Abre parênteses x menos um meio fecha parênteses elevado a 2.11 Simplifique cada expressão.
a) (2x + 1)2 + (x ‒ 5)2
b) (x ‒ 1)2 ‒ (x + 1)2
c) x(x ‒ 3)2 ‒
4 vezes abre parênteses x mais um meio fecha parênteses elevado a 2
12 Sendo x2 +
Fração 1 sobre x ao quadrado= 5, calcule o valor de:
a)
Expressão algébrica. Abre parênteses x mais fração 1 sobre x fecha parênteses elevado a 2.
b)
Expressão algébrica. Abre parênteses x menos fração 1 sobre x fecha parênteses elevado a 2.
13

Hora de criar – Elabore três expressões que representem o quadrado de uma diferença ou de uma soma, sendo uma delas apenas com números conhecidos, isto é, sem letras. Troque-as com um colega para que cada um desenvolva as expressões do outro. Em seguida, desfaçam a troca e façam as correções.
14 Na figura a seguir, as medidas são dadas em uma mesma unidade. O lado do quadrado a bê cê dê mede 10 e o lado de cada quadrado azul, 2x. Para que valor de x a soma das medidas das áreas dos quadrados azuis é igual à medida da área do quadrado vermelho?
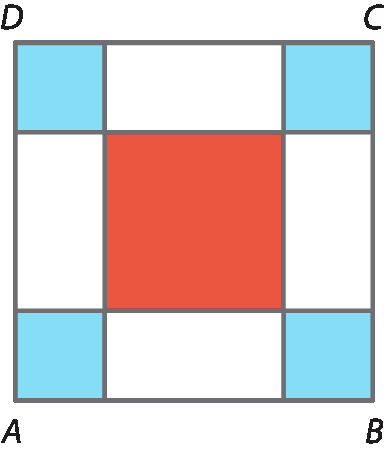
Nesse caso, quanto vale a soma das medidas das áreas dos quatro retângulos brancos?
15 Determine a medida do perímetro de um quadrado cuja área mede 4x 2 ‒ 4x + 1.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO

Podemos aplicar o quadrado da diferença para realizar cálculos com mais rapidez, até mesmo mentalmente. Acompanhe.
392 = (40 ‒ 1)2 = 402 ‒ 2 ⋅ 40 ⋅ 1 + 12 = .1600 ‒ 80 + 1 = .1521
482 = (50 ‒ 2)2 = 502 ‒ 2 ⋅ 50 ⋅ 2 + 22 = .2500 ‒ 200 + 4 = .2304
Agora, aplicando o quadrado da diferença, calcule mentalmente as potências. Em seguida, registre o resultado no caderno.
a) 292
b) 382
c) 992
d) 572
Respostas e comentários
10. a) 9a 2 ‒ 30a + 25
10. b) 9x 2 ‒ 12xy + 4y 2
10. c) 9a 4 ‒ 6a 2 + 1
10. d)
Expressão algébrica. x ao quadrado, menos x, mais 1 quarto.11. a) 5x 2 ‒ 6x + 26
11. b) ‒4x
11. c) x 3 ‒ 10x 2 + 5x ‒ 1
12. a) 7
12. b) 3
13. Resposta pessoal.
14. Para x = 1,25; 50.
15. 8x ‒ 4
Pense mais um poucoreticências:
a) 841
b) .1444
c) .9801
d) .3249
Exercícios propostos
As resoluções dos exercícios 10 a 13 e do exercício 15 estão no início deste Manual, nas orientações específicas do capítulo 6.
Observe a resolução do exercício 14, no qual a medida do lado de cada quadrado azul é dada por 2x; logo, a medida da área de cada um desses quadrados é dada por 4x2, e a medida da área desses quatro juntos é dada por 16x2. A medida do lado do quadrado vermelho é dada por (10 ‒ 4x); logo, a medida de sua área é dada por:
(10 ‒ 4x)2 = 100 ‒ 2 · 10 · 4x + 16x 2 = 100 ‒ 80x + 16x 2
Para obter o valor de x de modo que a soma das medidas das áreas dos quadrados azuis seja igual à medida da área do quadrado vermelho, basta impor a seguinte igualdade:
16x 2 = 100 ‒ 80x + 16x 2
80x = 100
x = 1,25
Portanto, o valor de x é igual a 1,25.
Nesse caso, a medida da área de cada retângulo branco é dada por:
2x · (10 ‒ 4x) = 20x ‒ 8x 2
Como x = 1,25, então a medida da área desses retângulos é dada por:
20 · 1,25 ‒ 8 · (1,25)2 = 25 ‒ 8 · 1,5625 = 25 ‒ 12,5 = 12,5
Assim, a área dos quatro retângulos mede 50 unidades de área, pois 4 · 12,5 = 50.
Pense mais um poucoreticências
Esta seção tem como objetivo levar os estudantes a perceber uma aplicação do produto notável quadrado da diferença de dois termos para calcular potências numéricas mentalmente.
Faça outros exemplos na lousa e promova uma dinâmica em que os estudantes devem determinar o quadrado de alguns números por meio desse método. Além disso, incentive-os a discutir quando é conveniente usar o quadrado da diferença entre dois termos em relação ao uso do quadrado da soma de dois termos.
As resoluções dos itens a a d desta seção estão no início deste Manual, nas orientações específicas do capítulo 6.
Produto da soma pela diferença de dois termos
Observe a figura a seguir.
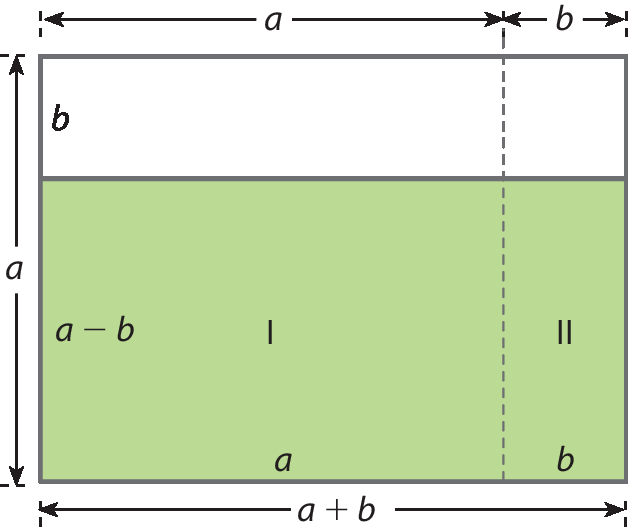
Por meio dela, podemos conhecer o polinômio que representa a medida da área do retângulo verde.
A base desse retângulo mede a + b, e a altura dele mede a ‒ b.
Portanto, a medida da área do retângulo verde é igual a (a + b) ⋅ (a ‒ b).
A medida da área do retângulo um é dada por a ⋅ (a ‒ b), e a do retângulo dois, por b ⋅ (a ‒ b).
Observe, na figura, que a medida da área do retângulo verde é dada pela soma das medidas das áreas de um e de dois, ou seja:
(a + b) ⋅ (a ‒ b) = a(a ‒ b) + b(a ‒ b)
(a + b) ⋅ (a ‒ b) = a 2 ‒ ab + ab ‒ b 2
(a + b) ⋅ (a ‒ b) = a 2 ‒ b 2
Também podemos calcular o produto (a + b) ⋅ (a ‒ b) aplicando a propriedade distributiva da multiplicação:

Portanto:

O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
Acompanhe alguns exemplos.
a)
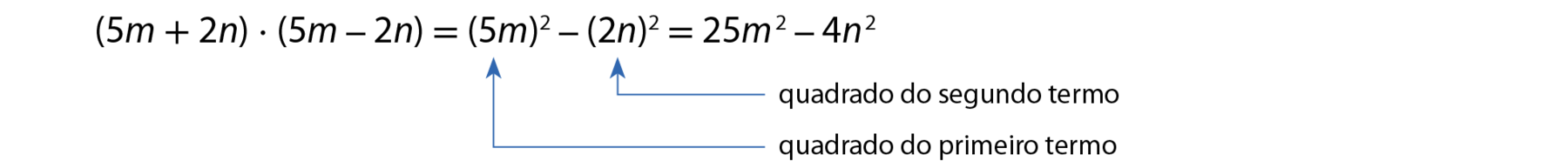
b)
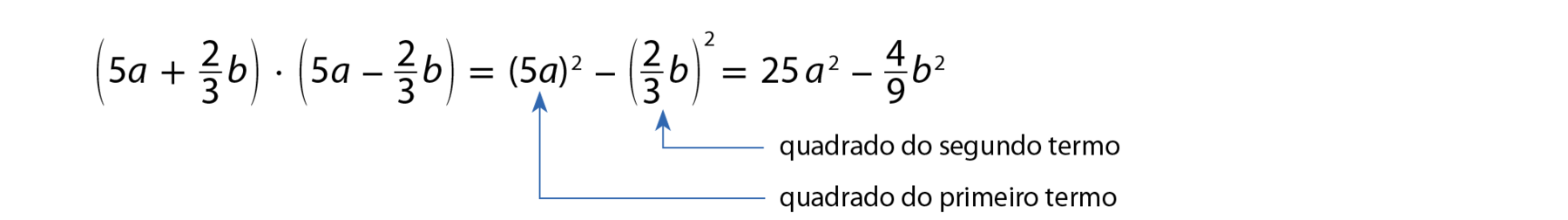
Respostas e comentários
Produto da soma pela diferença de dois termos
Este é outro produto notável que, posteriormente, com o estudo de fatoração, aplicaremos na resolução de um tipo especial de equação do 2º grau.
Proponha a um estudante que explique a figura apresentada para discussão com a turma.
Para ampliar a compreensão pelos estudantes dos produtos notáveis apresentados neste capítulo, sugerimos atividades investigativas envolvendo materiais manipuláveis, como o Algeplan, ou recursos digitais que representem geometricamente os produtos notáveis.

Sugestões de leitura
SILVA,R. C. M. Utilizando o algeplan como recurso didático para a compreensão de expressões algébricas. Monografia (graduação), ú éfe pê bê/CCAE, 2014. Disponível em: https://oeds.link/wVQrfC. Acesso em: 9 junho 2022.
Nesse trabalho, avaliam-se potencialidades e limitações do uso do Algeplan na compreensão da escrita e na representação de expressões algébricas.
MASSANTE, K. A. S. C. C.; BARBOSA, A. C. M.; GONÇALVES, I. M. Atividades utilizando o Algeplan no software GeoGebra. décimo segundo Encontro Nacional de Educação Matemática – minicurso, 2016. Disponível em: https://oeds.link/i0Ym5v. Acesso em: 9 junho 2022.
Nesse material, apresenta-se o desenvolvimento de uma sequência de tarefas utilizando o Algeplan virtual e o GeoGebra.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
16 Corrija as sentenças que forem falsas.
a) (5x ‒ 2) ⋅ (5x + 2) = (5x)2 ‒ 22 = 25x 2 ‒ 4
b) (4a 2 + 7b) ⋅ (4a 2 ‒ 7b) = = (4a 2)2 ‒ (7b)2 = 16a 2 ‒ 49b
c) (0,3x + 0,4y) ⋅ (0,3x ‒ 0,4y) = = (0,3x)2 ‒ (0,4y)2 = 0,9x 2 ‒ 1,6y 2
17 Calcule.
a) (x + 11) ⋅ (x ‒ 11)
b) (5 ‒ a 3) ⋅ (5 + a 3)
c) (a 2 ‒ 5) ⋅ (a 2 + 5)
d)
Abre parênteses fração 3 quartos de x, fim da fração, mais y fecha parênteses, vezes abre parênteses fração 3 quartos de x, fim da fração, menos y fecha parênteses.
18 Simplifique as expressões.
a) (3x + 2) ⋅ (3x ‒ 2) + (x + 2)2
b) (5x ‒ 6)2 ‒ (5x + 4) ⋅ (5x ‒ 4)
c) 32m 2 + 16m ‒ 2 ⋅ (4m + 1)2
19 Existem certas “adivinhações” em Matemática que podem ser comprovadas por meio de processos algébricos. Acompanhe uma delas.


d) Justifique, algebricamente, essa “adivinhação”.
20

Junte-se a um colega e resolvam os problemas a seguir. Para isso:
• leiam atentamente o enunciado e identifiquem o que é dado e o que é pedido;
• transformem em linguagem matemática (sentenças numéricas ou algébricas, esquemas, construções geométricas etc.) as informações dadas;
• com base nas relações estabelecidas no item anterior, formulem e executem um plano de resolução;
• façam, finalmente, a verificação das respostas obtidas.
a) Sabendo que 252 = 625, calculem (25 + 1) ⋅ (25 ‒ 1).
b) Sabendo que 202 = 400, calculem o produto 21 ⋅ 19.
c) A soma de dois números é 28 e a diferença, 10. Calculem a diferença entre os quadrados desses números. Em seguida, determinem os dois números e verifiquem a solução.
d) Se dois números têm por soma 30 e por diferença 20, então qual é a diferença entre os quadrados desses números?
e) Deem o valor de 26 ⋅ 28, sabendo que 272 = 729.
f) Sabendo que (m + h) = 4 e que m 2 ‒ h 2 = 80, calculem m ‒ h.
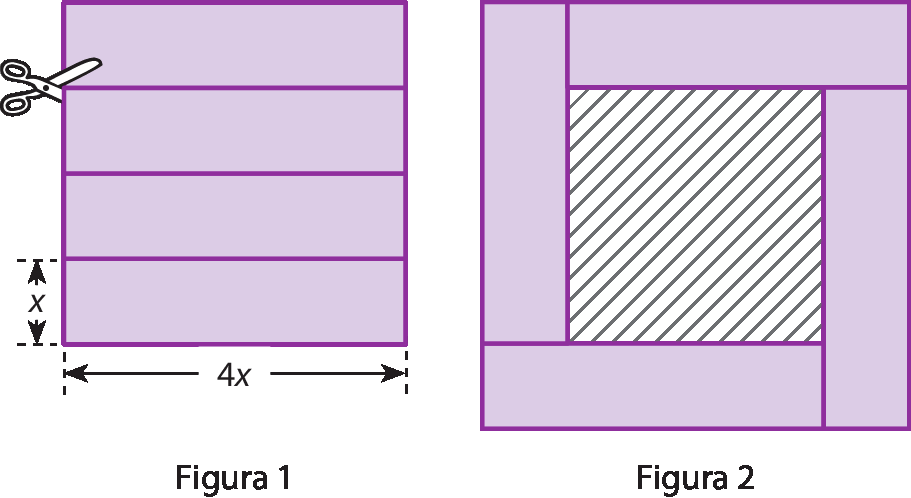
g) Cortando uma folha com formato de um quadrado em quatro retângulos iguais, pode-se montar a figura 2. Determinem a medida da área da parte hachurada.
21

Em duplas, façam o que se pede.
a) Escolham quatro números naturais consecutivos.
b) Determinem o quadrado dos números escolhidos.
c) Obtenham a diferença entre o quadrado do quarto número e o do terceiro.
d) Obtenham a diferença entre o quadrado do terceiro número e o do segundo.
e) Obtenham a diferença entre o quadrado do segundo número e o do primeiro.
• Observem os números obtidos nos itens c, d e ê. O que vocês podem perceber?
Respostas e comentários
16. a) Verdadeira.
16. b) 16a 4 ‒ 49b 2
16. c) 0,09x 2 ‒ 0,16y 2
17. a) x 2 ‒ 121
17. b) 25 ‒ a 6
17. c) a 4 ‒ 25
17. d)
Fração 9 16 avos de x ao quadrado, fim da fração, menos y ao quadrado.18. a) 10x 2 + 4x
18. b) ‒60x + 52
18. c) ‒2
19. a) x
19. b) (x + 1) ⋅ (x ‒ 1)
19. c)
Expressão algébrica. Raiz quadrada da expressão: x ao quadrado menos 1 mais 1, fim da raiz; é igual a: raiz quadrada de x ao quadrado.19. d) Como x é um número natural, obtemos
Expressão algébrica. Raiz quadrada de x ao quadrado é igual a x.20. a) 624
20. b) 399
20. c) 280; 19 e 9
20. d) 600
20. e) 728
20. f) 20
20. g) 9x 2
21. Respostas pessoais.
21. Espera-se que os estudantes percebam que as diferenças entre os quadrados formam uma sequência de números ímpares consecutivos.
Exercícios propostos
Nesta série de exercícios, os estudantes aplicarão cálculo algébrico e os produtos notáveis estudados.
As resoluções dos exercícios 16 a 20 estão no início deste Manual, nas orientações específicas do capítulo 6.
A seguir apresentamos a resolução dos itens ê e g do exercício 20.
No item ê, como 26 = 27 ‒ 1 e 28 = 27 + 1, obtemos:
26 · 28 = (27 ‒ 1) · (27 + 1) = 272 ‒ 12 = 729 ‒ 1 = 728
No item g, analisando a figura (e as medidas fornecidas), os estudantes podem verificar que a parte hachurada é um quadrado de lado de medida (4x ‒ x), ou seja, 3x. Logo, a área da parte hachurada é dada por 9x2.
Eles também podem efetuar o cálculo da seguinte maneira.
A medida da área da parte hachurada é dada pela diferença entre as medidas das áreas das figuras 2 e 1
Abre parêntese, A índice 2 menos A índice 1, fecha parêntese.A medida da área da figura 1 é dada por:
A medida da área da figura 2 é dada por:
Portanto:
No exercício 21, há infinitas possibilidades de escolha de quatro números naturais consecutivos. Após fazer os cálculos, é importante que as duplas registrem suas respostas, pois isso ajudará os estudantes a perceber que a diferença entre os quadrados fórma uma sequência de números ímpares consecutivos. Vamos apresentar aqui o caso genérico, no qual são escolhidos quatro números naturais consecutivos quaisquer. Nesse caso, as respostas são:
a) x, x + 1, x + 2, x + 3
b) x2, (x + 1)2, (x + 2)2, (x + 3)2
c) (x + 3)2 ‒ (x + 2)2 = x2 + + 6x + 9 ‒ (x2 + 4x + 4) = = x2 + 6x + 9 ‒ x2 ‒ 4x ‒ ‒ 4 = 2x + 5
d) (x + 2)2 ‒ (x + 1)2 = x2 + 4x + + 4 ‒ (x2 + 2x + 1) = 2x + 3
e) (x + 1)2 ‒ x2 = x2 + 2x + 1 ‒ x2 = = 2x + 1
• Os números obtidos nos itens c, d e ê formam uma sequência decrescente de números ímpares consecutivos: 2x + 5, 2x + 3 e 2x + 1.
Cubo da soma e da diferença de dois termos
Considere um cubo cuja aresta mede a + b, como mostra a figura a seguir.
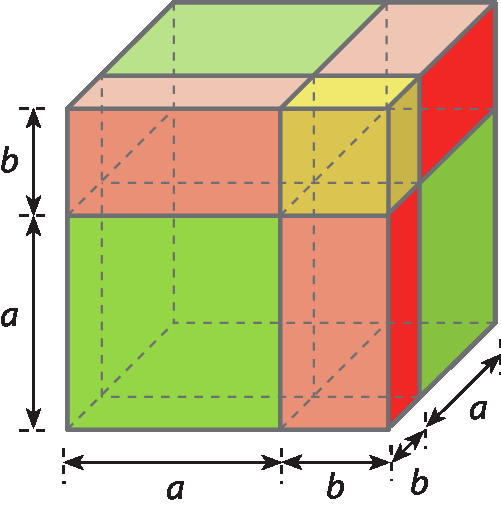
A medida do volume desse cubo é dada por (a + b)3.
Vamos separar as partes em que o cubo está dividido.
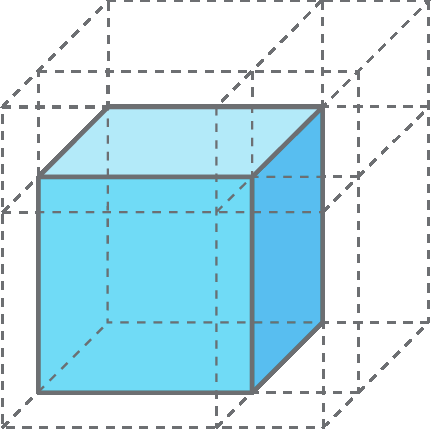
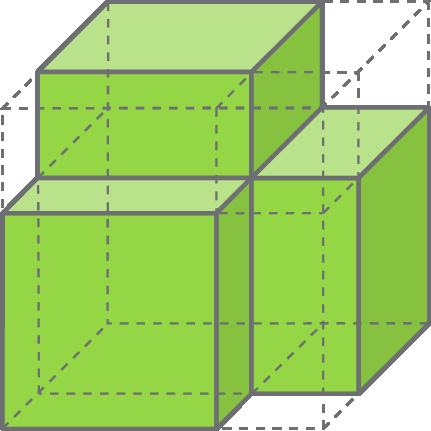
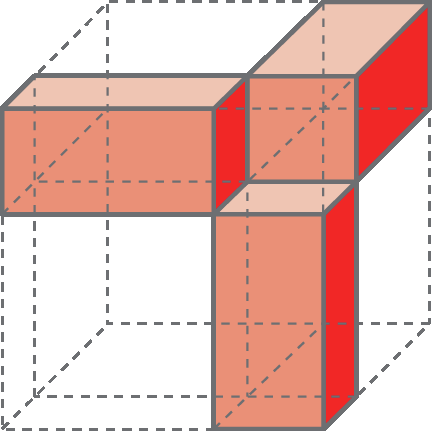
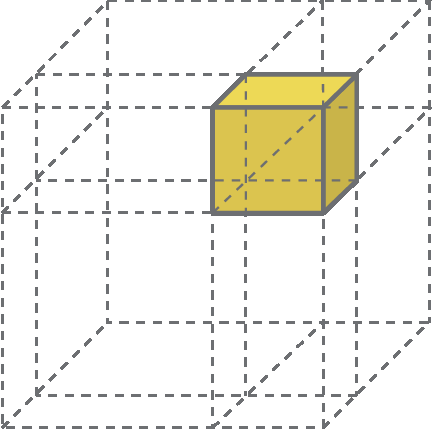
Adicionando as medidas de todos esses volumes, obtemos a 3 + 3a 2b + 3ab 2 + b 3.
A medida do volume do todo é igual à soma das medidas dos volumes das partes, logo:
(a + b) 3 = a 3 + 3a 2b + 3ab 2 + b 3
Esse mesmo resultado pode ser obtido aplicando a propriedade distributiva da multiplicação:

Respostas e comentários
Cubo da soma e da diferença de dois termos
Neste tópico, para introduzir o produto notável, utilizamos paralelepípedos e cubos que formam um cubo maior. Se possível, providencie modelos desses sólidos para que os estudantes observem a montagem e manuseiem as peças.
Portanto:

Observe também o cubo da diferença de dois termos.

Portanto:

Acompanhe alguns exemplos.
a) (x + 2)3 = x 3 + 3 ⋅ x 2 ⋅ 2 + 3 ⋅ x ⋅ 22 + 23 = = x 3 + 6x 2 + 12x + 8
b) (2x + y)3 = (2x)3 + 3 ⋅ (2x)2 ⋅ y + 3 ⋅ (2x) ⋅ y 2 + y 3 = = 8x 3 + 3 ⋅ (4x 2 ) ⋅ y + 3 ⋅ (2x) ⋅ y 2 + y 3 = = 8x 3 + 12x 2y + 6xy 2 + y 3
c) (5x ‒ 2)3 = (5x)3 ‒ 3 ⋅ (5x)2 ⋅ 2 + 3 ⋅ (5x) ⋅ 22 ‒ 23 = = 125x 3 ‒ 150x 2 + 60x ‒ 8

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
22 Desenvolva.
a) (x + 1)3
b) (2a + 3)3
c) (1 ‒ x)3
d) (3a ‒ 2)3
23 Calcule a diferença entre o cubo de (4a ‒ b) e o cubo de (4a + b).
24 Simplifique as expressões a seguir.
a) (2a + 1)3 ‒ 6a(2a + 1)
b) (a ‒ b)3 ‒ 3ab(b ‒ a)
c) (x ‒ 2y)3 + 6xy ⋅ (x ‒ 2y)
25 Determine o polinômio que representa a medida do volume do cubo a seguir.
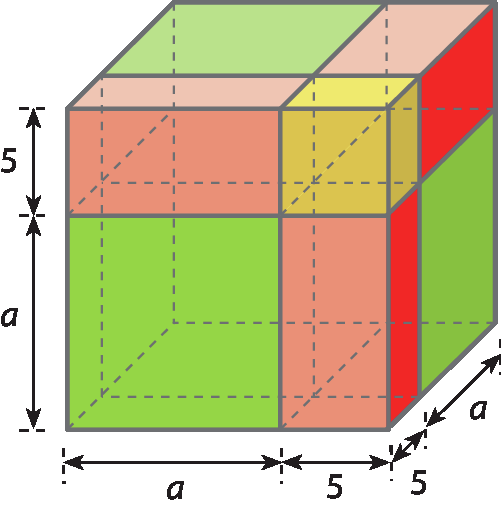
Respostas e comentários
22. a) x 3 + 3x 2 + 3x + 1
22. b) 8a 3 + 36a2 + 54a + 27
22. c) 1 ‒ 3x + 3x 2 ‒ x 3
22. d) 27a3 ‒ 54a2 + 36a ‒ 8
23. ‒96a2b ‒ 2b3
24. a) 8a3 + 1
24. b) a3 ‒ b3
24. c) x 3 ‒ 8y 3
25. a3 + 15a2 + 75a + 125
Cubo da soma e da diferença de dois termos
Para ampliar o estudo do cubo da soma de dois termos, peça aos estudantes que representem geometricamente outros exemplos com figuras. Se possível, podem construir modelos das peças em isopor ou montá-las em cartolina.
Sugira a eles que escrevam o cubo da diferença de dois termos como se fosse soma e, depois, calculem usando o cubo da soma de dois termos. Por exemplo:
• (a ‒ b)3 = [a + (‒b)]3
Nesse caso, os estudantes devem identificar os dois termos que serão utilizados no cubo da soma:
primeiro termo: a;
segundo termo: (‒b).
• (a ‒ b)3 = [a + (‒b)]3 = a3 + 3a2(‒b) + 3a(‒b)2 + (‒b)3 = a3 ‒ 3a2b + 3ab2 ‒ b3
Essa é a expressão do cubo da diferença de dois termos.
Exercícios propostos
As resoluções dos exercícios 22 a 25 estão no início deste Manual, nas orientações específicas do capítulo 6.
2. Fatoração de polinômios
Sabemos que um número natural pode ser decomposto em um produto de dois ou mais fatores. Esse procedimento é chamado de fatoração. Existem várias maneiras de fatorar um número natural. Observe alguns exemplos de fatoração do número 72.
72 = 8 ⋅ 9
72 = 6 ⋅ 12
72 = 2 ⋅ 2 ⋅ 18
72 = 23 ⋅ 32
Assim como os números naturais, alguns polinômios podem ser fatorados.
Fatorar um polinômio, quando possível, significa escrevê-lo como produto de polinômios mais simples.
Considere a figura e acompanhe como Bruno e Letícia determinaram a medida da área dessa figura.


Logo:

A expressão (a + b) ⋅ c é a fórma fatorada do polinômio ac + bc.
A seguir, vamos estudar diferentes casos de fatoração de polinômios: fator comum em evidência, agrupamento, diferença de dois quadrados, trinômio quadrado perfeito, soma ou diferença de dois cubos.
PARA SABER MAIS
Fatorando expressões numéricas
Assim como os números, as expressões numéricas podem ser fatoradas.
Já sabemos que, pela propriedade distributiva da multiplicação, é possível desenvolver uma expressão numérica escrita na fórma fatorada. Acompanhe.


Respostas e comentários
2. Fatoração de polinômios
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero seis e ê éfe zero oito ême ah um nove.
Neste tópico, são retomados conhecimentos sobre áreas de figuras planas e desenvolvidas operações envolvendo expressões algébricas, particularmente, a fatoração de polinômios, contribuindo para o trabalho com as habilidades (EF08MA06) e (ê éfe zero oito ême ah um nove). Ao iniciar o estudo da fatoração de uma expressão algébrica, retome a fatoração de um número natural. Os estudantes devem compreender que fatorar um número ou uma expressão algébrica é decompor esse número ou expressão algébrica em um produto de dois ou mais fatores. Explore com eles a figura e a situação apresentadas.
Para saber mais
Nesta seção, propomos aos estudantes mais uma aplicação de cálculo mental envolvendo números, agora com a fatoração. Ao apropriar-se de técnicas de cálculo mental, eles agilizam seus procedimentos e adquirem autoconfiança, o que deve ser incentivado.
Agora, vamos fazer o inverso, ou seja, escrever na fórma fatorada expressões desenvolvidas pela aplicação da propriedade distributiva da multiplicação.
• 5 ⋅ 3 + 5 ⋅ 11 Trata-se de uma adição na qual cada parcela é um produto de dois fatores, em que o número 5 é um fator comum.

• 2,4 ⋅ 7 ‒ 2,4 ⋅ 2 Cada parcela tem em comum o fator 2,4.

Esse procedimento nos ajuda a calcular de maneira mais fácil, ou até mesmo mentalmente, o valor de algumas expressões numéricas.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1

Calcule mentalmente: 0,21 ⋅ 7 + 0,21 ⋅ 3.
2 Explique como você pensou para fazer o cálculo na atividade 1.
3 Calcule o valor de cada expressão.
a) 15 ⋅ 18 + 15 ⋅ 2
b) 5,4 ⋅ 13 ‒ 5,4 ⋅ 3
c) 12 ⋅
Fração, 7 13 avos+ 12 ⋅
Fração, 6 13 anos
d) 4,5 ⋅ 8 + 4,5 ⋅ 7 ‒ 4,5 ⋅ 5
e) 3,8 ⋅ 4,2 + 3,8 ⋅ 4,6 + 3,8 ⋅ 1,2
f) 10 ⋅
Fração, 17 11 avos‒ 10 ⋅
Fração 6 11 avosFatoração colocando em evidência um fator comum
Considere a figura formada por três retângulos com base medindo 2.

A medida A da área dessa figura pode ser dada pela soma das medidas das áreas dos três retângulos:
A = 2x + 2y + 2z
Podemos também obter a medida da área considerando o retângulo maior, cuja altura mede (x + y + z) e a base, comum aos três retângulos, mede 2:
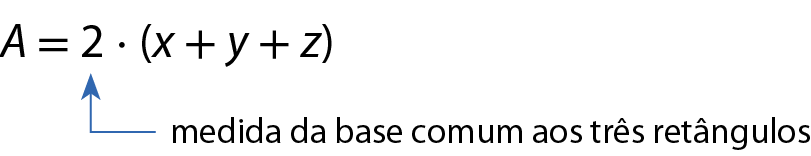
Logo: 2x + 2y + 2z = 2 ⋅ (x + y + z)
Nesse caso, dizemos que 2(x + y + z) é a fórma fatorada do polinômio 2x + 2y + 2z e, também, que colocamos em evidência o fator comum a todos os termos (2).
Respostas e comentários
1. 2,1
2. Resposta possível:
0,21 ⋅ 7 + 0,21 ⋅ 3 = 0,21 ⋅ (7 + 3) = 0,21 ⋅ 10 = 2,1
3. a) 300
3. b) 54
3. c) 12
3. d) 45
3. e) 38
3. f) 10
Agora é com você!
As resoluções das atividades 1 a 3 estão no início deste Manual, nas orientações específicas do capítulo 6.
Fatoração colocando em evidência um fator comum
Instigue os estudantes a perceber que este caso de fatoração utiliza a propriedade distributiva da multiplicação partindo do resultado para o produto indicado (ou seja, faz o caminho inverso daquele percorrido ao aplicar a propriedade distributiva).
Explore os exemplos orientando os estudantes a verificar que esse tipo de fatoração auxilia na resolução de equações do 2º grau do tipo ax2 + bx = 0 (para a ≠ 0). Nesse tipo de equação, no primeiro membro o fator x é comum. Então:
ax2 + bx = 0
x · (ax + b) = 0
x = 0 ou ax + b = 0
x = 0 ou ax = ‒b
x = 0 ou
x é igual à: menos fração; numerador: b, denominador: a.Acompanhe alguns exemplos.
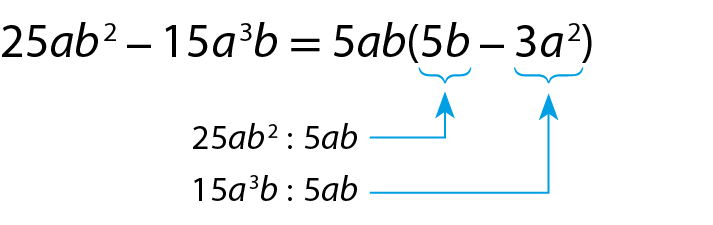
a) Fatore o polinômio 25ab 2 ‒ 15a 3b. 25ab 2 = 5 ⋅ 5 ⋅ a ⋅ b ⋅ b 15a 3b = 3 ⋅ 5 ⋅ a ⋅ a ⋅ a ⋅ b O fator comum é 5ab. Portanto:
b) Calcule o valor numérico do polinômio x 2y ‒ xy 2, sabendo que xy = 21 e x ‒ y = 4. Inicialmente, vamos fatorar o polinômio: x 2y ‒ xy 2 = xy ⋅ (x ‒ y) Agora, substituímos xy por 21 e (x ‒ y) por 4 na expressão fatorada: xy ⋅ (x ‒ y) = 21 ⋅ 4 = 84
c) Resolva a equação 2x 2 ‒ 35x = 0, em que x é um número racional. O fator comum aos termos do polinômio 2x 2 ‒ 35x é x. Portanto: 2x 2 ‒ 35x = 0 ou x(2x ‒ 35) = 0 Como o produto é nulo, então um dos dois fatores é obrigatoriamente nulo, ou seja: x = 0 ou 2x ‒ 35 = 0 ⇒ 2x = 35 ⇒
Fração 2 x sobre 2 é igual à fração 35 meios⇒ x = 17,5 Logo, as soluções da equação são 0 e 17,5.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
26 Considere o binômio 15ax 2 ‒ 10a 2x e responda:
a) Quais são os fatores comuns a esses termos?
b) Qual é a fórma fatorada desse binômio?
27 Fatore os binômios colocando os fatores comuns em evidência.
a) A bê + á cê
b) x 2 + 3x
c) a 2 + a
d) 5x + 20
e) 14a 2b + 21ab 3
f) 15x 3 ‒ 10x 2
28

Reúna-se com um colega e resolvam os problemas a seguir. Para isso:
• leiam atentamente o enunciado e identifiquem o que é dado e o que é pedido;
• transformem em linguagem matemática (sentenças numéricas ou algébricas, esquemas, construções geométricas etcétera) as informações dadas;
• com base nas relações estabelecidas no item anterior, formulem e executem um plano de resolução;
• façam a verificação das respostas obtidas.
a) Qual é o número cujo dôbro de seu quadrado é igual ao seu triplo?
b) Qual é o número diferente de zero cujo triplo de seu quadrado é igual ao seu dôbro?
c) Observem as figuras a seguir.
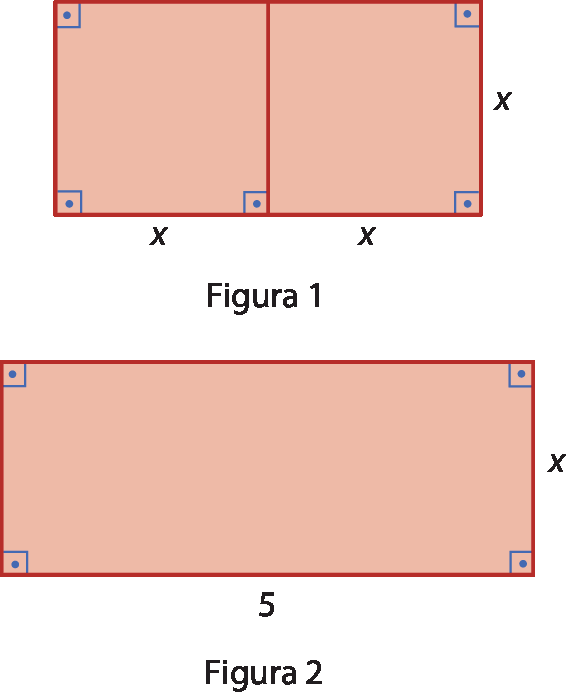
Na figura 1, há dois quadrados com lados medindo x e, na figura 2, um retângulo com lados medindo x e 5. Obtenham o valor de x que satisfaça a relação: as medidas das áreas da figura 1 e da figura 2 são iguais.
29 Fatore os polinômios a seguir.
a) a 3 + a 2 + a
b) 6x 2 ‒ 9x + 12
c) 3x + 6x 2 + 9x 3
d) 10x 3 ‒ 15x 2 + 20x
e)
Fração: a sobre 2, fim da fração; mais fração: a ao quadrado sobre 4, fim da fração; menos fração: a ao cubo sobre 6, fim da fração.f)
Fração: m sobre 12, fim da fração; menos fração: 5 m ao quadrado sobre 6, fim da fração; mais fração: 2 m ao cubo sobre 9, fim da fração.Respostas e comentários
26. a) 5ax
26. b) 5ax(3x ‒ 2a)
27. a) a(b + c)
27. b) x(x + 3)
27. c) a(a + 1)
27. d) 5(x + 4)
27. e) 7ab(2a + 3b2)
27. f) 5x 2(3x ‒ 2)
28. a) 0 ou
Fração, 3 meios28. b)
Fração, dois terços28. c) 2,5
29. a) a(a 2 + a + 1)
29. b) 3(2x 2 ‒ 3x + 4)
29. c) 3x(1 + 2x + 3x 2 )
29. d) 5x(2x 2 ‒ 3x + 4)
29. e)
Fração; numerador a, denominador 2, fim da fração, vezes abre parênteses 1 mais fração; numerador a, denominador 2, fim da fração, menos fração; numerador a ao quadrado, denominador 3, fim da fração, fecha parênteses29. f)
Fração; numerador m, denominador 3, fim da fração, vezes abre parênteses fração 1 quarto, menos fração numerador 5 m, denominador 2, fim da fração, mais fração numerador 2 m ao quadrado, denominador 3, fim da fração, fecha parêntesesExercícios propostos
As resoluções dos exercícios 26 a 29 estão no início deste Manual, nas orientações específicas do capítulo 6.
30 Fatore a expressão x( y ‒ 2) ‒ 7( y ‒ 2) + a( y ‒ 2), colocando o fator ( y ‒ 2) em evidência.
31 Sabendo que 2xy = 12 e 3x ‒ y = 3, quanto vale 6x 2y ‒ 2xy 2?
32 Resolva cada equação.
a) x 2 + 7x = 0
b) m 2 ‒ 5m = 0
c) 3y 2 ‒ 18y = 0
d) 2x 2 ‒ 9x = 0
e) x 2 = x
f) 4x 2 = ‒3x
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Sejam m e n dois números naturais quaisquer. Então, 2m e 2n são dois números pares.
Lembrando que o consecutivo de um número par é um número ímpar, prove que a soma de dois números ímpares quaisquer sempre é um número par.
Fatoração por agrupamento
Considere a figura a seguir.
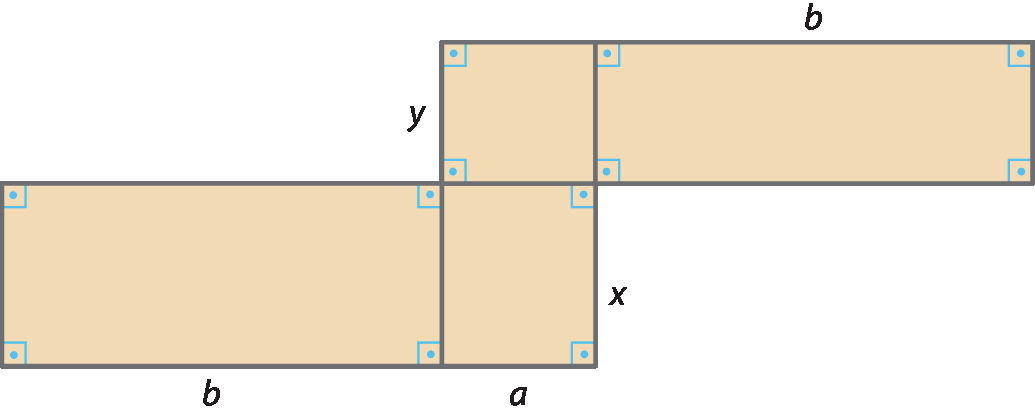
A expressão que representa a medida da área dessa figura é o polinômio:
á xis + á ípsilon + bx + by
Observe que não há fatores comuns a todos os termos desse polinômio, mas é possível agrupá-los de modo que cada grupo tenha um fator comum. Nesse caso, o polinômio é fatorado por agrupamento. Acompanhe.
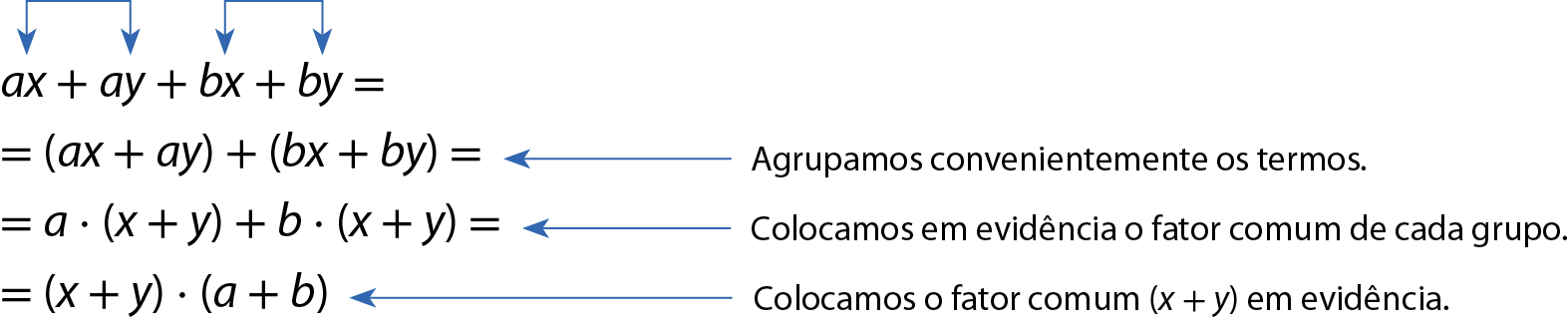
Agora, acompanhe como podemos obter uma fórma fatorada do polinômio xy + 2x + 4y + 8.

O produto ( y + 2) ⋅ (x + 4) é a fórma fatorada do polinômio xy + 2x + 4y + 8.
Respostas e comentários
30. ( y ‒ 2)(x ‒ 7 + a)
31. 36
32. a) 0 ou ‒7.
32. b) 0 ou 5.
32. c) 0 ou 6.
32. d) 0 ou
Fração, nove meios.
32. e) 0 ou 1.
32. f) 0 ou
Fração, menos três quartos.
Pense mais um poucoreticências: (2m + 1) + (2n + 1) = 2m + 2n + 2 = 2(m + n + 1)
Exercícios propostos
As resoluções dos exercícios 30 e 31 estão no início deste Manual, nas orientações específicas do capítulo 6.
O exercício 32 aproveita o caso de fatoração estudado e aplica na resolução de equações. Neste momento, não é necessário que os estudantes saibam que a equação é de 2º grau; o objetivo é que utilizem a fatoração para determinar o valor de x.
a) x 2 + 7x = 0 x · (x + 7) = 0 ➀ x = 0 ou x + 7 = 0 ➁ x = 0 ou x = ‒7 ➂ Convém ressaltar para os estudantes as etapas de resolução: ➀ Colocando o fator comum x em evidência. ➁ Como o produto é zero, então ao menos um dos fatores é zero. ➂ Esses são os valores de x que satisfazem a equação.
Para os demais itens, o procedimento é similar.
b) m 2 ‒ 5m = 0 m · (m ‒ 5) = 0 m = 0 ou m ‒ 5 = 0 m = 0 ou m = 5
c) 3y 2 ‒ 18y = 0 3y · (y ‒ 6) = 0 3y = 0 ou y ‒ 6 = 0 y = 0 ou y = 6
d) 2x 2 ‒ 9x = 0 x · (2x ‒ 9) = 0 x = 0 ou 2x ‒ 9 = 0 x = 0 ou
Equação. x é igual a 9 meiose) x 2 = x x 2 ‒ x = 0 x · (x ‒ 1) = 0 x = 0 ou x ‒ 1 = 0 x = 0 ou x = 1
f) 4x 2 = ‒3x 4x 2 + 3x = 0 x · (4x + 3) = 0 x = 0 ou 4x + 3 = 0 x = 0 ou 4x = ‒3 x = 0 ou x =
Fração, menos 3 quartosPense mais um poucoreticências
Nesta seção é trabalhada novamente a inter-relação entre a Álgebra e a Aritmética. A demonstração do fator aritmético pode ser feita usando argumentos algébricos, como segue.
Se 2m e 2n são números pares, então 2m + 1 e 2n + 1 são números ímpares. Adicionando esses números ímpares, obtemos:
(2m + 1) + (2n + 1) = 2m + 2n + 2 = 2(m + n + 1)
Assim, mostramos que a soma de dois números ímpares é um número par.
Janaína obteve a mesma fórma fatorada para o polinômio xy + 2x + 4y + 8, agrupando os termos de maneira diferente. Acompanhe como ela fez.
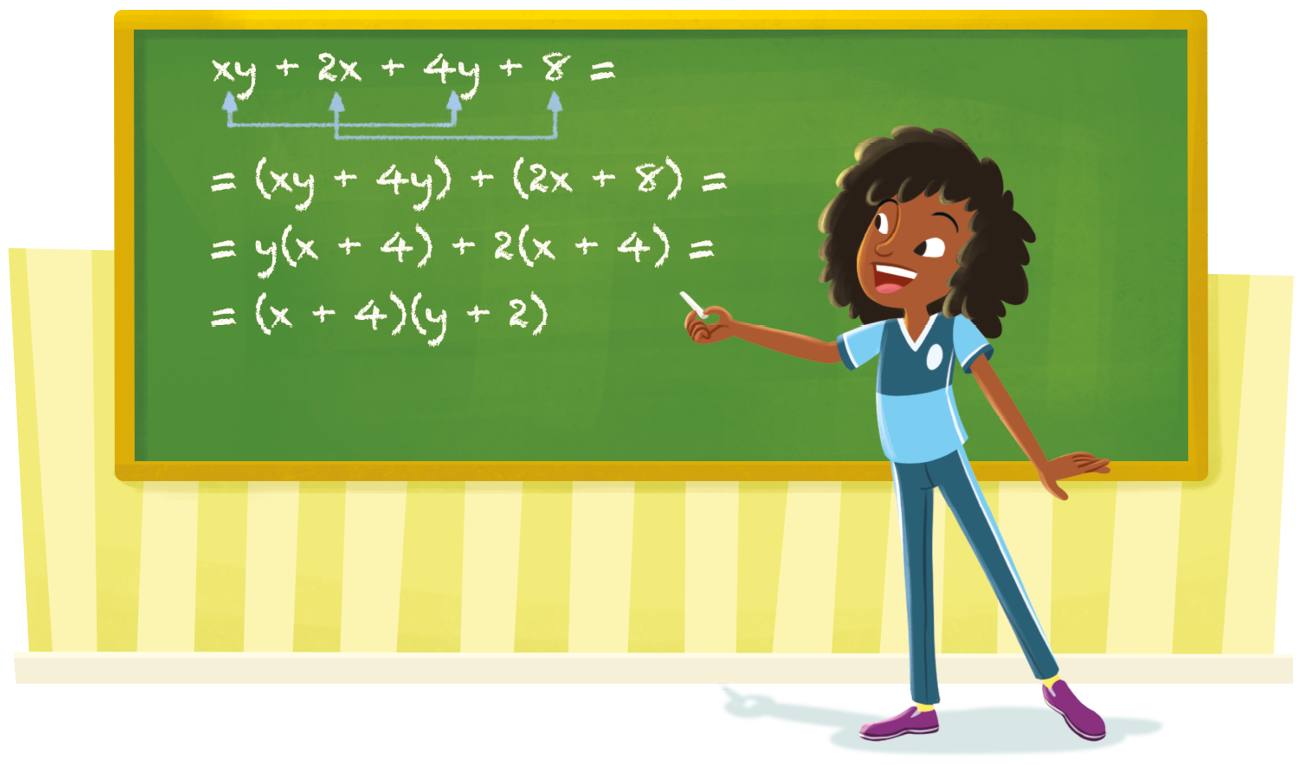
Acompanhe alguns exemplos.
a) ax ‒ bx + 2a ‒ 2b = = (ax ‒ bx) + (2a ‒ 2b) = = x(a ‒ b) + 2(a ‒ b) = (a ‒ b) ⋅ (x + 2) O produto (a ‒ b) ⋅ (x + 2) é a fórma fatorada do polinômio ax ‒ bx + 2a ‒ 2b.
b) xy + 2x ‒ 3y ‒ 6 = = (xy + 2x) ‒ (3y + 6) = = x( y + 2) ‒ 3( y + 2) = ( y + 2) ⋅ (x ‒ 3) O produto ( y + 2) ⋅ (x ‒ 3) é a fórma fatorada do polinômio xy + 2x ‒ 3y ‒ 6.
c) Sabendo que 3a ‒ b = 10 e a + c = 3, calcule o valor da expressão 3a 2 + 3ac ‒ ab ‒ bc. Fatorando a expressão, obtemos:
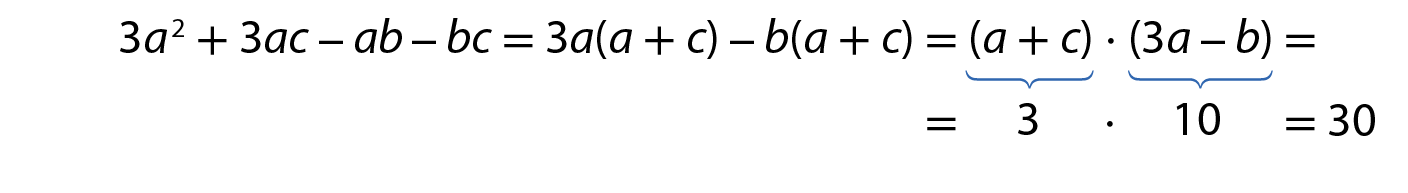
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
33 Fatore cada polinômio.
a) 5x ‒ xy + 15 ‒ 3y
b) 2ax + 3a + 4bx + 6b
c) ax ‒ 2a + x ‒ 2
d) x 3+ 3x 2 + 2x + 6
e) 10x 2 ‒ 15xy ‒ 4x + 6y
f) a 3 ‒ a 2 + a ‒ 1
34 Considere a figura a seguir e faça o que se pede.
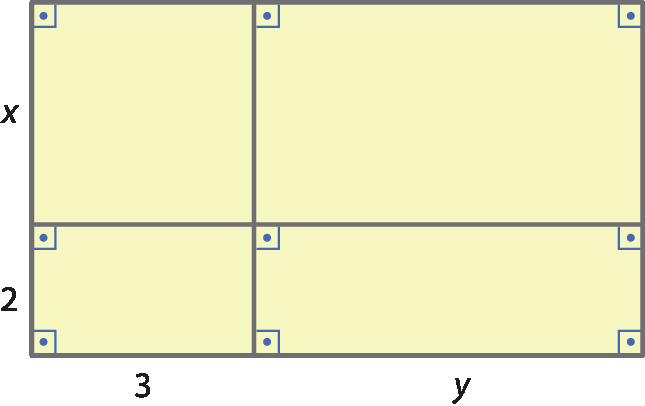
a) Determine a medida da área da figura adicionando as medidas das áreas das partes que a compõem.
b) Determine a medida da área da figura indicando o produto da medida da base pela medida da altura.
c) Fatore a expressão obtida no item a.
d) Escreva a igualdade entre os resultados obtidos nos itens a e b.
35 Considerando a expressão mx ‒ my + nx ‒ ny, faça o que se pede.
a) Sabendo que m + n = 10 e x ‒ y = 2, determine o valor da expressão dada.
b) Faça uma figura cuja medida da área possa ser representada pela expressão dada.
c) Escreva a medida da área da figura indicando o produto das medidas da base pela medida da altura.
Respostas e comentários
33. a) (5 ‒ y)(x + 3)
33. b) (2x + 3)(a + 2b)
33. c) (x ‒ 2)(a + 1)
33. d) (x + 3)(x 2 + 2)
33. e) (2x ‒ 3y)(5x ‒ 2)
33. f) (a ‒ 1)(a 2 + 1)
34. a) 3x + 6 + xy + 2y
34. b) (3 + y)(x + 2)
34. c) (x + 2)(3 + y)
34. d) 3x + 6 + xy + 2y = (3 + y)(x + 2)
35. a) 20
35. b) Construção de figura.
35. c) (m + n)(x ‒ y)
Fatoração por agrupamento
Este caso de fatoração utiliza duas ou mais vezes o caso anterior, colocando em evidência um fator comum. A dificuldade pode aparecer na escolha dos termos que devem ser agrupados para que a fatoração seja completada até o final. Ressalte esse fato para os estudantes.
Exercícios propostos
As resoluções dos exercícios 33 e 34 estão no início deste Manual, nas orientações específicas do capítulo 6.
No exercício 35, no item a, ao fatorarmos mx ‒ my + nx ‒ ny obtemos:
(x ‒ y)(m + n)
Assim, considerando que m + n = 10 e x ‒ y = 2, obtemos que:
mx ‒ my + nx ‒ ny = (x ‒ y)(m + n) = 10 ⋅ 2 = 20
No item b, uma possível resposta é a figura a seguir.
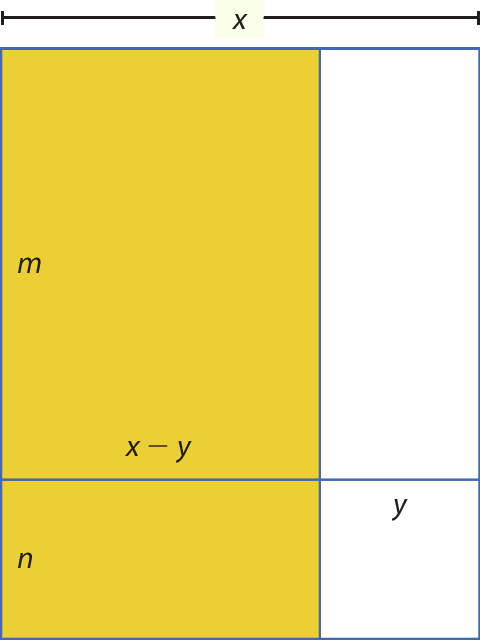
No item c, podemos notar que a medida da área da região amarela dessa figura é dada pela expressão mx ‒ my + nx ‒ ny. Vamos obtê-la de duas maneiras:
(expressão dada)
ou
(fórma fatorada da expressão dada)
Vamos fatorar a expressão dada para comprovar:
mx ‒ my + nx ‒ ny =
= m(x ‒ y) + n(x ‒ y) =
= (x ‒ y)(m + n)
36

Hora de criar – Escreva dois binômios e multiplique-os. Troque com um colega apenas o produto elaborado por cada um, sem que um saiba dos binômios do outro, para que o outro fatore. Depois destroquem para corrigi-los.
Fatoração da diferença de dois quadrados
Já sabemos que, ao desenvolver o produto (a + b)(a ‒ b), obtemos a 2 ‒ b 2. Assim, quando obtemos (a + b)(a ‒ b) a partir de a 2 ‒ b 2, estamos fatorando o binômio a 2 ‒ b 2. Acompanhe a representação geométrica dessa situação.
A medida da área da figura 1 é dada por a 2 ‒ b 2.
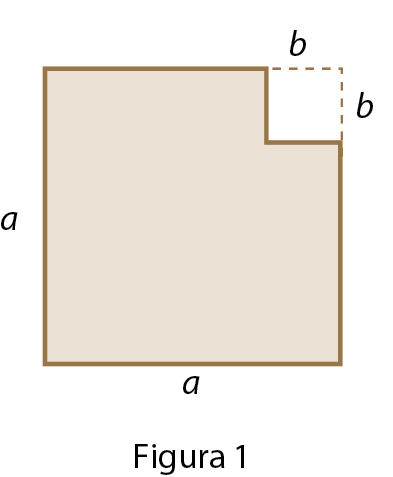
Observe o que acontece quando recortamos e deslocamos a região um, conforme mostram as figuras 2 e 3.
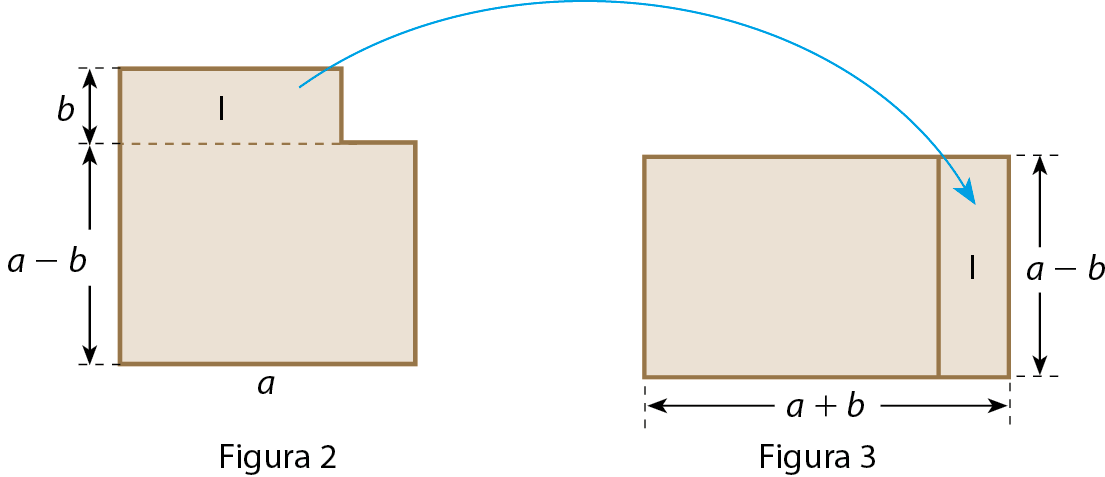
Obtemos um retângulo cujos lados medem (a + b) e (a ‒ b). A medida da área é dada por:
(a + b) ⋅ (a ‒ b)
Como a medida da área da figura 1 é igual à da área da figura 3, obtemos:

Acompanhe alguns exemplos.
a) Fatore:


• (a + b)2 ‒ c 2 = [(a + b) + c] ⋅ [(a + b) ‒ c] = (a + b + c)(a + b ‒ c)
• 36 ‒ (x ‒ 2)2 = 62 ‒ (x ‒ 2)2 = [6 + (x ‒ 2)] ⋅ [6 ‒ (x ‒ 2)] = = (6 + x ‒ 2)(6 ‒ x + 2) = (4 + x)(8 ‒ x)


Respostas e comentários
36. Resposta pessoal.
Exercícios propostos
A elaboração de problemas pelos estudantes, como o exercício 36 propõe, é uma importante estratégia para levá-los a criar, desenvolver o senso crítico, aprender a pesquisar e a ensinar.
Fatoração da diferença de dois quadrados
Trabalhe com as figuras que introduzem esse caso de fatoração, que está ligado ao produto notável produto da soma pela diferença de dois termos. Espera-se que os estudantes percebam que, quando fatoramos um binômio desse tipo por esse caso, recaímos nesse produto notável. Por exemplo:

• 49x2 ‒ 144b4z6 = = (7x + 12b2z3)(7x ‒ 12b2z3)
Se julgar necessário, retome a potenciação de monômios e as propriedades de potências estudadas.
b) Fatore completamente a expressão 5a 2 ‒ 20. Colocando o fator comum (5) em evidência, obtemos:

c) Resolva a equação x 2 ‒ 4 = 0, sendo x um número racional. Ao fatorar o binômio x 2 ‒ 4, obtemos:
(x + 2)(x ‒ 2) = 0 O produto é nulo; logo, um dos fatores é nulo. x + 2 = 0 ou x ‒ 2 = 0 x = ‒2 x = 2
Portanto, as soluções da equação são ‒2 e 2.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
37 Fatore as diferenças de dois quadrados a seguir.
a) x 2 ‒ 4
b) a 2 ‒ 36
c) y 2 ‒ 1
d) 25x 2 ‒ 4
e)
Expressão algébrica. Um centésimo de a ao quadrado, menos fração 1 49 avos.f)
Expressão algébrica. x ao quadrado vezes y ao quadrado, menos fração um nono.38 Fatore as expressões a seguir.
a) 15xy + 9x
b) 15xy + 9x + 10y + 6
c) 100x 2 ‒ 1
d) 36a 2b ‒ 48ab 2
e) (x ‒ 1)2 ‒ 1
f) (x + 5)2 ‒ 9
g) 25 ‒ (x + y)2
h) 9a 2 ‒ (a ‒ 5)2
39 Fatore completamente as expressões.
a) a 3 ‒ a
b) 12x 3 ‒ 3xy 2
c) a 2b ‒ b 3
d) a 3 ‒ 9a
40 Considerando x um número racional, resolva cada equação.
a) x 2 ‒ 25 = 0
b) x 2 ‒ 64 = 0
c) 81x 2 ‒ 49 = 0
d) 25x 2 ‒ 36 = 0
e) 9x 2 ‒ 1 = 0
f) x 2 ‒
Fração. 9 16 avos= 0
41 Na figura a seguir, o lado do quadrado a bê cê dê mede m e o lado do quadrado cê é éfe gê mede n.
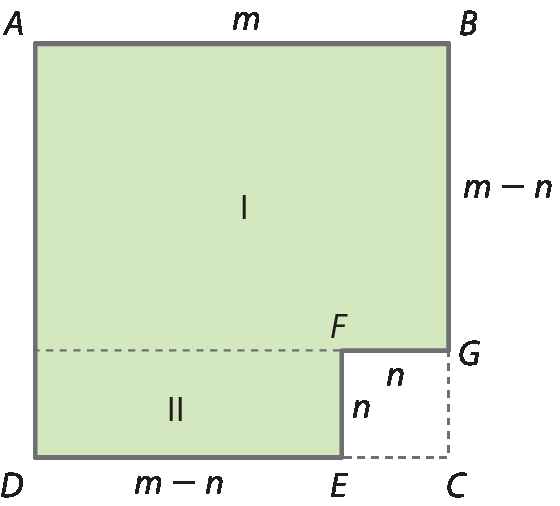
a) Escreva a medida da área da parte pintada como diferença de dois quadrados.
b) Determine a expressão que fornece a medida da área da região um.
c) Determine a expressão que fornece a medida da área da região dois.
d) Determine a expressão da soma das medidas das áreas das regiões um e dois.
e) Fatore o polinômio obtido no item d.
f) Escreva a igualdade entre os resultados obtidos nos itens a e ê.
42 Mário e Vítor descobriram que suas idades hoje correspondem a dois números ímpares consecutivos.
Eles verificaram ainda que a diferença entre os quadrados de suas idades é 40. Quais são as idades dos dois amigos?
Respostas e comentários
37. a) (x + 2)(x ‒ 2)
37. b) (a + 6)(a ‒ 6)
37. c) (y + 1)(y ‒ 1)
37. d) (5x + 2)(5x ‒ 2)
37. e)
Expressão algébrica. Abre parênteses um décimo de a, mais um sétimo, fecha parênteses, abre parênteses um décimo de a, menos um sétimo fecha parênteses.
37. f)
Expressão algébrica. Abre parênteses x y mais um terço, fecha parênteses, abre parênteses x y menos um terço fecha parênteses.
38. a) 3x(5y + 3)
38. b) (3x + 2)(5y + 3)
38. c) (10x + 1)(10x ‒ 1)
38. d) 12ab(3a ‒ 4b)
38. e) x(x ‒ 2)
38. f) (x + 8)(x + 2)
38. g) (5 + x + y)(5 ‒ x ‒ y)
38. h) (4a ‒ 5)(2a + 5)
39. a) a(a + 1)(a ‒ 1)
39. b) 3x(2x + y)(2x ‒ y)
39. c) b(a + b)(a ‒ b)
39. d) a(a + 3)(a ‒ 3)
40. a) 5 ou ‒5
40. b) 8 ou ‒ 8
40. c)
Fração, 7 nonosou
Fração, menos 7 nonos40. d)
Fração, menos 6 quintosou
Fração, 6 quintos40. e)
Fração. menos 1 terçoou
Fração, um terço40. f)
Fração, menos três quartosou
Fração, três quartos41. a) m 2 ‒ n 2
41. b) m(m ‒ n)
41. c) n(m ‒ n)
41. d) m(m ‒ n) + n(m ‒ n)
41. e) (m ‒ n)(m + n)
41. f) m 2 ‒ n 2 = (m ‒ n)(m + n)
42. Um tem 9 anos e o outro, 11.
Exercícios propostos
As resoluções dos exercícios 37 a 41 estão no início deste Manual, nas orientações específicas do capítulo 6.
No exercício 42, dois amigos, cujas idades hoje correspondem a dois números ímpares consecutivos, sabem que a diferença entre os quadrados dessas idades é igual a 40. Para determiná-las, observamos que, se 2x representa um número par, podemos afirmar que o sucessor e o antecessor de 2x são dois números ímpares consecutivos. Então, as idades desses amigos podem ser representadas por 2x ‒ 1 e 2x + 1, e vale a igualdade:
(2x + 1)2 ‒ (2x ‒ 1)2 = 40
Aplicando a fatoração da diferença de dois quadrados, obtemos:
[(2x + 1) + (2x ‒ 1)] · [(2x + 1) ‒ (2x ‒ 1)] = 40
[2x + 1 + 2x ‒ 1] · [2x + 1 ‒ 2x + 1] = 40
[4x] · [2] = 40
x = 5
Assim:
2x + 1 = 2 · 5 + 1 = 10 + 1 = 11
2x ‒ 1 = 2 · 5 ‒ 1 = 10 ‒ 1 = 9
Portanto, as idades são 9 anos e 11 anos.
Comente com os estudantes que, embora saibamos quais são as idades, sem saber qual dos amigos é o mais velho, não conseguimos identificar qual é a idade de cada um.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Faça o que se pede.
a) Fatore a expressão numérica 762 ‒ 752.
b) Dê o resultado da expressão do item a.
c) Compare o resultado do item b com a adição (76 + 75).
d) Fatore a expressão 1382 ‒ 1372, calcule seu valor numérico e compare-o com a adição (138 + 137).
e)

Calcule mentalmente o valor numérico da expressão 2212 ‒ 2202 e, em seguida, escreva como procedeu a esse cálculo.
Fatoração do trinômio quadrado perfeito
Trinômio quadrado perfeito: a2 + 2ab + b2
A medida da área da figura apresentada pode ser obtida adicionando as medidas das áreas de suas partes: a2 + 2ab + b 2.
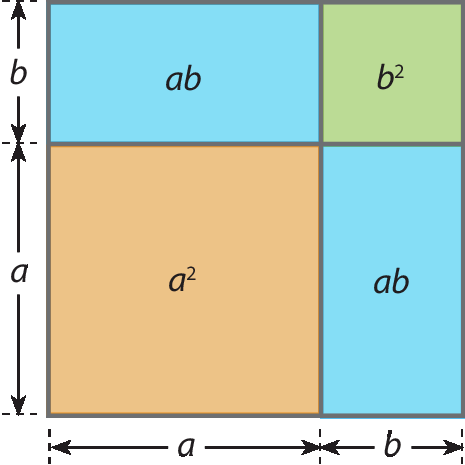
Como se trata de um quadrado, a medida da sua área também pode ser calculada elevando a medida do lado ao quadrado: (a + b)2.
Portanto:

Trinômio quadrado perfeito: a2 ‒ 2ab + b2
Observe a figura a seguir.
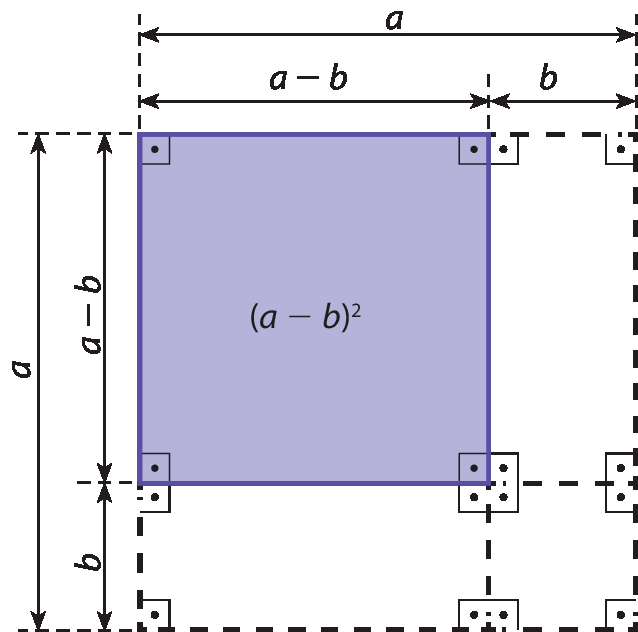
Analisando-a, percebe-se que a medida da área da parte roxa pode ser obtida da seguinte maneira:
a 2 ‒ 2 ⋅ b(a ‒ b) ‒ b 2 =
= a 2 ‒ 2ab + 2b 2 ‒ b 2 =
= a 2 ‒ 2ab + b 2
Como a parte roxa é uma figura quadrada, a medida da sua área também pode ser calculada elevando a medida do lado ao quadrado: (a ‒ b)2.
Logo:
a 2 ‒ 2ab + b 2 = (a ‒ b)2
Portanto, a fórma fatorada de a 2 ‒ 2ab + b 2 é (a ‒ b)2.
Respostas e comentários
Pense mais um poucoreticências:
a) (76 + 75) ⋅ (76 ‒ 75)
b) 151
c) São iguais.
d) (138 + 137) ⋅ (138 ‒ 137) = 275. São iguais.
e) 441. Espera-se que os estudantes percebam que a diferença dos quadrados de dois números consecutivos é a soma desses números.
Pense mais um poucoreticências
Para esta seção, apresentamos a seguinte resolução:
a) 762 ‒ 752 = (76 + 75) · (76 ‒ 75)
b) (76 + 75) · (76 ‒ 75) = 151 · 1 = 151
d) Fazemos: 1382 ‒ 1372 = (138 + 137) · (138 ‒ 137) = = 275 · 1 = 275 Agora, 138 + 137 = 275; portanto, o resultado de (1382 ‒ 1372) é igual ao resultado de (138 + 137).
e) 2212 ‒ 2202 = (221 + 220) = 441
Espera-se que os estudantes percebam que a diferença entre os quadrados de dois números consecutivos é a soma desses números.
Fatoração do trinômio quadrado perfeito
Trabalhe com as figuras nos dois casos, reproduzindo-as na lousa e mostrando as etapas aos estudantes. Essa fatoração está ligada aos produtos notáveis quadrado da soma e quadrado da diferença de dois termos.

Acompanhe alguns exemplos.
a)

2 ⋅ x ⋅ 3 = 6x x2 + 6x + 9 = (x + 3)2
b)
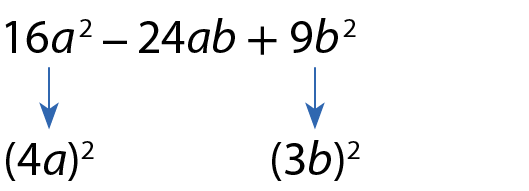
2 ⋅ 4a ⋅ 3b = 24ab 16a 2 ‒ 24ab + 9b 2 = (4a ‒ 3b)2
Acompanhe, agora, outros exemplos.
a) Verifique se o seguinte trinômio é quadrado perfeito:
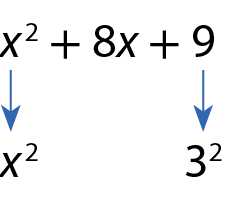
O dôbro do produto das raízes é: 2 ⋅ x ⋅ 3 = 6x ≠ 8x. Logo, x 2 + 8x + 9 não é um trinômio quadrado perfeito. Ele não pode ser escrito como o quadrado de um binômio.
b) Fatore:
a 3+ 2a 2b + ab 2 Colocando a em evidência, obtemos:

c) Sabendo que a 2 + b 2 = 234 e ab = 45, calcule o valor de (a + b)2.
Como (a + b)2 = a 2 + 2ab + b 2, obtemos:
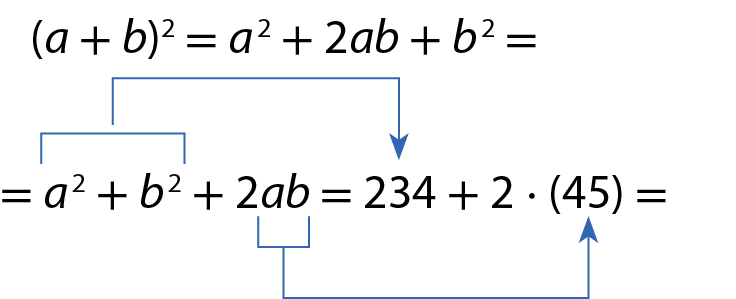

= 234 + 90 = 324
Respostas e comentários
Fatoração do trinômio quadrado perfeito
Após trabalhar os exemplos propostos, é importante discutir com os estudantes situações nas quais temos expressões algébricas cujo caso de fatoração não pode ser aplicado. É o que acontece com os trinômios, que não correspondem a quadrados perfeitos, e com os binômios que não configuram diferença de dois quadrados.
d) Resolva a equação 4x 2 ‒ 4x + 1 = 0, sabendo que x é um número racional.
O primeiro membro dessa equação é um trinômio quadrado perfeito. Ao fatorar esse trinômio, obtemos (2x ‒ 1)2 = 0. Uma potência só é nula quando a base também é nula. Assim, temos:
2x ‒ 1 = 0 ou, ainda, x =
Fração. 1 meioLogo, a solução da equação 4x 2 ‒ 4x + 1 é o número
Fração. 1 meio.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
43 Identifique os trinômios que são quadrados perfeitos e modifique os demais para que passem a ser também.
a) x 2 + 4x + 4
b) y 2 + 5y + 100
c) a 2 + 10a + 25
d) 16a 2 + 36ab + 9b 2
e) m 2 + n 2 + 2mn
f) x 2 ‒ x +
Fração, 1 quarto44 Fatore os trinômios quadrados perfeitos a seguir.
a) x 2 + 6x + 9
b) 4x 2 + 12xy + 9y 2
c) x 4 ‒ 4x 2 + 4
d) x 2y 2 ‒ 10xy + 25
e)
Polinômio. 4 nonos de x ao quadrado, mais 4 21 avos de x, mais 1 49 avos.
f) 0,25a 2 ‒ 0,30a + 0,09
45 Escreva o binômio que, elevado ao quadrado, dá o trinômio 81 + 90a + 25a 2.
46 A medida da área de um quadrado é representada pelo trinômio y 2 + 14ya + 49a 2. Determine a medida do lado desse quadrado.
47 Fatore completamente:
a) 2x 3 + 4x 2 + 2x
b) 5a 2 ‒ 20a + 20
c) 3x 3 + 18x 2 + 27x
d) 7x 2y 2 ‒ 14xy + 7
e) 9a 3 ‒ 25a
f) 16x 4 ‒ 8x 2 + 1
48

Hora de criar – Elabore duas expressões que sejam quadrado de uma soma e duas que sejam quadrado de uma diferença. Desenvolva-as como trinômios do quadrado perfeito. Em seguida, troque com um colega os trinômios desenvolvidos para que cada um fatore e obtenha os quadrados da soma e da diferença daquilo que o outro elaborou. Depois, desfaçam a troca e verifiquem se as fatorações estão corretas.
49 Calcule os valores pedidos nas expressões.
a) Sabendo que (a + b)2 = 64 e A bê = 12, calcule o valor de a 2 + b 2.
b) Se (a + b)2 = 81 e a 2 + b 2 = 53, calcule o valor de A bê.
c) Sendo a 2 + b 2 = 13 e A bê = 12, calcule o valor de (a + b)2.
50 Obtenha os números que são soluções das equações a seguir.
a) x 2 + 18x + 81 = 0
b) y 2 ‒ 2y + 1 = 0
c) 4a 2 ‒ 12a + 9 = 0
51 A professora do 8º ano propôs o jôgo dos polinômios escondidos. Acompanhe.
Número de participantes: 2 jogadores
Regras:
• A partir de dois polinômios, cada jogador deve determinar o produto e formar um novo polinômio, sem que o outro jogador saiba.
• Os dois polinômios iniciais devem ser do 1º grau com uma única variável.
• Cada jogador apresenta para seu oponente apenas o polinômio que formou.
• Vence aquele que descobrir primeiro dois polinômios cujo produto resulte no polinômio apresentado.
Pensando na estrutura do jôgo, responda:
a) Roberto apresentou para Juvenal o polinômio 3x 2 + 9x ‒ 30, que ele formou com o produto dos polinômios (3x ‒ 6) e (x + 5). É possível obter outro par de polinômios cujo produto dê o polinômio formado por Roberto? Justifique sua resposta.
b) Juvenal apresentou para Roberto o polinômio x 2 ‒ 2x + 1. Determine um par de polinômios que Roberto pode encontrar.
c) O polinômio formado por Juvenal segue as regras do jôgo? Justifique.
Respostas e comentários
43. São quadrados perfeitos os trinômios dos itens a, c, ê, f.
Respostas possíveis: b) y 2 + 20y + 100; d) 16a 2 + 24ab + 9b 2.
44. a) (x + 3)2
44. b) (2x + 3y)2
44. c) (x 2 ‒ 2)2
44. d) (xy ‒ 5)2
44. e)
Expressão algébrica. A expressão: 2 terços de x, mais um sétimo, entre parênteses, elevado a 2.
44. f) (0,5a ‒ 0,3)2
45. 9 + 5a
46. y + 7a
47. a) 2x(x + 1)2
47. b) 5(a ‒ 2)2
47. c) 3x(x + 3)2
47. d) 7(xy ‒ 1)2
47. e) a(3a + 5)(3a ‒ 5)
47. f) (2x + 1)2(2x ‒ 1)2
48. Resposta pessoal.
49. a) 40
49. b) 14
49. c) 37
50. a) ‒9
50. b) 1
50. c)
Fração, 3 meios51. a) Sim. Observe: 3x 2 + 9x ‒ 30 = (3x ‒ 6)(x + 5) = 3(x ‒ 2)(x + 5) = (x ‒ 2)(3x + 15)
51. b) Fatorando o trinômio, obtemos os polinômios (x ‒ 1) e (x ‒ 1), cujo produto dá o polinômio apresentado por Juvenal.
51. c) Sim, pois Juvenal obteve o polinômio como produto de dois polinômios do 1º grau com uma única variável. Não foi exigido que os polinômios fossem diferentes.
Exercícios propostos
Nesta série de exercícios, os estudantes aplicarão mais de um caso de fatoração em uma expressão para fatorá-la completamente.
As resoluções dos exercícios 43 a 46 e dos exercícios 48, 49 e 51 estão no início deste Manual, nas orientações específicas do capítulo 6.
No exercício 47, a fatoração dos polinômios deve ser feita em duas etapas. Convém lembrar aos estudantes que nem sempre é conveniente colocar o fator comum em evidência como primeira fatoração.
a) 2x 3 + 4x 2 + 2x = = 2x · (x 2 + 2x + 1) = = 2x · (x + 1)2
b) 5a 2 ‒ 20a 2 + 20 = = 5 · (a 2 ‒ 4a + 4) = = 5 · (a ‒ 2)2
c) 3x 3 + 18x 2 + 27x = = 3x · (x 2 + 6x + 9) = = 3x · (x + 3)2
d) 7x 2y 2 ‒ 14xy + 7 = = 7 · (x 2y 2 ‒ 2xy + 1) = = 7 · (xy ‒ 1)2
e) 9a 3 ‒ 25a = = a · (9a 2 ‒ 25) = = a · [(3a)2 ‒ (5)2] = = a · [(3a + 5) · (3a ‒ 5)] = = a(3a + 5) · (3a ‒ 5)
f) 16x 4 ‒ 8x 2 + 1 = = (4x 2)2 ‒ 2 · 4x 2 · 1 + 12 = = (4x 2 ‒ 1)2 = = [(2x)2 ‒ 12]2 = = [(2x + 1) · (2x ‒ 1)]2 = = (2x + 1)2 · (2x ‒ 1)2
No exercício 50, para obter os números que são soluções das equações, precisamos escrever cada polinômio do primeiro membro na fórma fatorada:
a) x 2 + 18x + 81 = 0 (x + 9)2 = 0 (x + 9) · (x + 9) = 0 ➀ x + 9 = 0 ou x + 9 = 0 ➁ x = ‒9 ou x = ‒9 ➂ Convém destacar aos estudantes as etapas de resolução: ➀ Como o produto é zero, então um dos fatores é nulo. ➁ Temos o mesmo binômio. ➂ Logo, a solução é a mesma. Portanto, x é igual a ‒9.
Para os demais itens, o procedimento é similar.
b) y 2 ‒ 2y + 1 = 0 ⇒ (y ‒ 1)2 = 0 ⇒ y ‒ 1 = 0 ⇒ y = 1
c) 4a 2 ‒ 12a + 9 = 0 ⇒ (2a ‒ 3)2 = 0 ⇒ 2a ‒ 3 = 0 ⇒ a =
Fração, três meiosPense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega, leiam o texto e façam o que se pede.
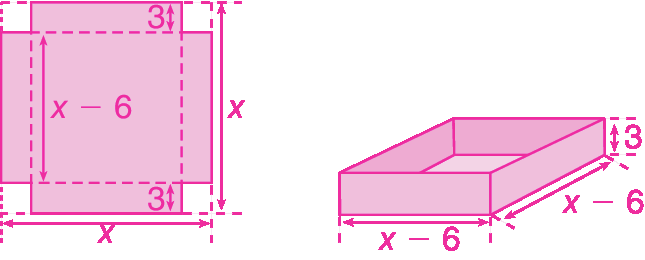
De uma folha de cartolina quadrada de x centímetro de lado, foram recortados quatro quadrados iguais, um em cada canto. Dobrando essa cartolina e colando os lados, obtém-se uma caixa aberta, conforme mostram as figuras a seguir.
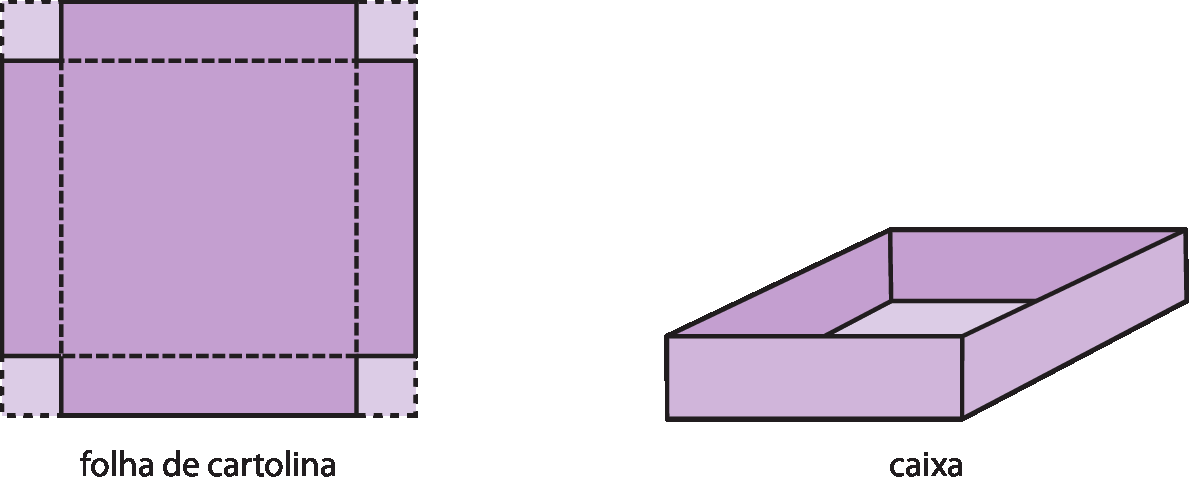
A medida da capacidade da caixa montada com a folha de cartolina é dada pela expressão 3x 2 ‒ 36x + 108.
Fatorem completamente essa expressão, reproduzam as figuras e identifiquem todas as medidas, observando a expressão fatorada que vocês encontraram.
Fatoração da diferença e da soma de dois cubos

Diferença de dois cubos


Soma de dois cubos


Acompanhe alguns exemplos.
a) a 3 ‒ 8 = (a ‒ 2) ⋅ (a 2 + 2a + 4)
b) 8x 3 + 27 = (2x + 3) ⋅ (4x 2 ‒ 6x + 9)
Respostas e comentários
Pense mais um poucoreticências: 3(x ‒ 6)2
Pense mais um poucoreticências
Incentive os estudantes a discutir o problema e a comentar como a fatoração pode auxiliar na resolução da situação proposta. Como a caixa tem formato que pode ser associado a um bloco retangular, seu volume é dado pelo produto da medida de três arestas que têm um vértice em comum (que correspondem às medidas da largura, do comprimento e da altura da caixa).
Fatorando a expressão dada, obtemos:
3x 2 ‒ 36x + 108 =
= 3(x 2 ‒ 12x + 36) =
= 3(x 2 ‒ 2 · 6x + 62) =
= 3(x ‒ 6)2
Se julgar conveniente, construa com os estudantes a caixa descrita na atividade. Para sua construção, lembre-os de que devem utilizar tesouras de pontas arredondadas e manuseá-las com cuidado.
Fatoração da diferença e da soma de dois cubos
Neste tópico, apresentamos a fatoração da diferença e da soma de dois cubos, ligadas aos produtos notáveis cubo da soma e da diferença de dois termos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
52 Fatore os binômios.
a) a 3 ‒ 1
b) 8a 3 + 1
c) x 3 ‒ 27
d) x 3 + 64
e) 1 ‒ x 3
f) 27a 3 + 8y 3
53 Classifique como verdadeira ou falsa cada sentença.
a) a3 + b 3 = (a + b)3
b) a3 + b 3 = (a 2 ‒ ab + b 2)(a + b)
c) a3 ‒ b 3 = (a ‒ b)(a 2 ‒ ab + b 2)
d) a3 ‒ b 3 = (a 2 + ab + b 2)(a ‒ b)
3. Simplificando frações algébricas
Já vimos que simplificar uma fração numérica significa determinar outra com termos mais simples e que seja equivalente à fração dada. Um dos modos de fazer isso é decompor o numerador e o denominador em fatores primos e cancelar os fatores comuns.
Acompanhe alguns exemplos.
a)

b)


Acompanhe outros exemplos.
a)

b)

c)

d)

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
54 Dê um exemplo de fração algébrica em que o numerador e o denominador sejam iguais.
a) Qual é o valor dessa fração?
b) Faça o mesmo para uma fração algébrica na qual o numerador e o denominador sejam opostos.
55 Reduza cada fração algébrica a um polinômio.
a)
Fração algébrica. Fração com numerador a ao quadrado menos a, e denominador a.
b)
Fração algébrica. Fração com numerador x ao quadrado menos 16, e denominador x mais 4.c)
Fração algébrica. Fração com numerador 3 x ao quadrado, mais 6 x, mais 3, e denominador x mais 1.d)
Fração algébrica. Fração com numerador 5 a ao quadrado menos 20, e denominador a menos 2.56 A fração algébrica
Fração algébrica. No numerador: 10 a mais 5 b, e denominador: 2 a mais b.pode ser reduzida a um número inteiro. Que número é esse?
57 O quociente do monômio 15a5b pelo monômio 4a2b3 não é um monômio.
a) Determine na fórma reduzida a fração que representa esse quociente.
b) Dê o valor numérico dessa fração para a = ‒2 e b = 2.
c) Para que valor de b essa fração não representa um número racional?
Respostas e comentários
52. a) (a ‒ 1)(a 2 + a + 1)
52. b) (2a + 1)(4a 2 ‒ 2a + 1)
52. c) (x ‒ 3)(x 2 + 3x + 9)
52. d) (x + 4)(x 2 ‒ 4x + 16)
52. e) (1 ‒ x)(1 + x + x 2 )
52. f) (3a + 2y)(9a 2 ‒ 6ay + 4y 2 )
53. a) Falsa.
53. b) Verdadeira.
53. c) Falsa.
53. d) Verdadeira.
54. a) Resposta pessoal. 1.
54. b) Resposta pessoal. ‒1.
55. a) a ‒ 1
55. b) x ‒ 4
55. c) 3x + 3
55. d) 5a + 10
56. 5
57. a)
Fração algébrica. Fração com numerador 15 a ao cubo, e denominador 4 b ao quadrado.
57. b)
Fração, menos 15 meios
57. c) b = 0
Exercícios propostos
As resoluções dos exercícios 52 e 53 estão no início deste Manual, nas orientações específicas do capítulo 6.
3. Simplificando frações algébricas
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah zero seis.
O trabalho com a simplificação de frações algébricas tem por base a aplicação das técnicas de fatoração e, assim, permite o desenvolvimento da habilidade (ê éfe zero oito ême ah zero seis).
Converse com os estudantes sobre um tipo de êrro muito comum: o cancelamento do denominador com apenas uma das parcelas do numerador. É importante destacar também a condição de existência da fração algébrica, que não pode ter seu denominador anulado.
Exercícios propostos
As resoluções dos exercícios 54 a 57 estão no início deste Manual, nas orientações específicas do capítulo 6.
58 Observe estes cartões coloridos.
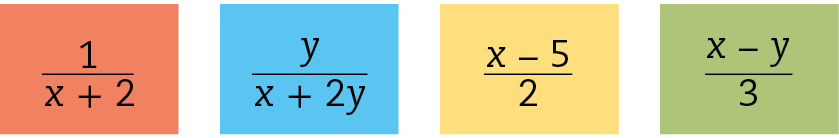
Cada cartão corresponde à simplificação de uma das frações a seguir. Efetue os cálculos e indique a côr do cartão que corresponde a cada uma delas.
a)
Fração algébrica. Numerador: 10 x y. Denominador: 10 x ao quadrado, mais 20 x y.b)
Fração algébrica. Numerador: x ao quadrado, menos 2 x y, mais y ao quadrado. Denominador: 3 x menos 3 y.c)
Fração algébrica. Numerador: x menos 2. Denominador: x ao quadrado, menos 4.d)
Fração algébrica. Numerador: x ao quadrado, menos 10 x, mais 25. Denominador: 2 x menos 10.59 Dividindo o numerador pelo denominador da fração algébrica obtém-se um binômio.
a) Determine esse binômio.
b)

Calcule mentalmente o valor numérico desse binômio para x = 0.
c) Determine o valor numérico desse binômio para x =
Fração. 2 terços.
d) Que valores racionais x pode assumir nessa fração algébrica?
60

Reúna-se com um colega e observem como Marta e Cláudio fizeram a simplificação da fração algébrica
Fração, numerador x ao quadrado mais x, denominador x..
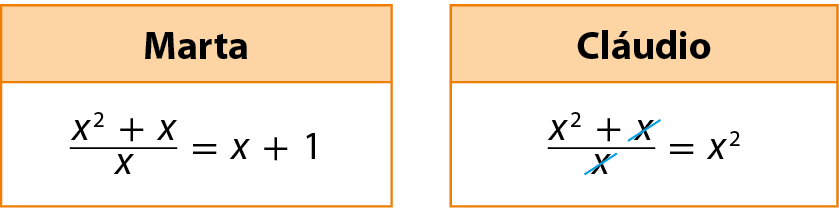
a) Quem acertou? Como vocês chegaram a essa conclusão?
b) Comentem o modo como cada um deles fez a simplificação e identifiquem qual foi o êrro.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Acompanhe o diálogo entre Felipe e Vanda.




Escrevendo uma sentença algébrica, explique por que Felipe disse que basta subtrair 2.
Respostas e comentários
58. Amarelo: d; vermelho: c; azul: a; verde: b.
59. a) 3x ‒ 2
59. b) ‒2
59. c) Zero.
59. d) Qualquer número racional diferente de
Fração, menos 5 meios.
60. a) Marta. Resposta possível: fizemos a simplificação para conferir.
60. b) Marta colocou x em evidência, visto que ele é fator comum em x2 + x. Assim, pôde efetuar a simplificação com o x do denominador. Cláudio errou ao simplificar a parcela x do numerador com o x do denominador.
Avalie a conveniência de pedir aos estudantes que atribuam algum valor para x e verifiquem quais das simplificações resultam em mesmo valor.
Pense mais um poucoreticências:
Fração: Numerador: abre parênteses x mais 5 fecha parênteses, x, menos 3 x. Denominador: x, fim da fração.=
Fração com numerador: x ao quadrado, mais 2 x. Denominador: x, fim da fração=
Fração com numerador: x, abre parênteses x mais 2 fecha parênteses. Denominador: x, fim da fração= x + 2, com x ≠ 0
Exercícios propostos
As resoluções dos exercícios 58 a 60 estão no início deste Manual, nas orientações específicas do capítulo 6.
Pense mais um poucoreticências
O lúdico e o desafio têm presença nesta seção, com texto apresentado em fórma de história em quadrinhos.
A atividade pode ser desenvolvida em duplas ou trios. Depois que os estudantes discutirem a questão e perceberem a justificativa algébrica, proponha a cada grupo que crie um desafio desse tipo para trocar com outro grupo: um resolve o desafio do outro.
Ao final, um representante da dupla (ou trio) deve mostrar na lousa o desafio e como foi resolvido. Valide com a turma os desafios criados e suas resoluções.
Problemas e equações
Considere o problema a seguir.

Um projeto social distribuiria 160 bolas entre algumas escolas de certo município. No dia da partilha, houve duas novas inscrições no projeto. Por isso, cada escola recebeu
Fração, 4 quintosdo número de bolas que teria recebido se não tivesse havido novas inscrições.
Quantas escolas estavam inscritas inicialmente no projeto?
Vamos indicar por x o número de escolas inscritas inicialmente.
• Número de bolas que cada escola recebeu:
Fração: numerador 160; denominador x mais 2• Número de bolas que cada escola teria recebido:
Fração: numerador 160; denominador xPortanto:
ou
Fração: numerador 160; denominador x mais 2; fim da fração. É igual à fração: 4 quintos, vezes a fração: numerador 160; denominador x, fim da fraçãoPara resolver essa equação, em primeiro lugar, devemos observar que x não pode assumir os valores ‒2 e 0, pois anularia os denominadores.
Multiplicando os termos da equação por (x + 2)(5x), obtemos:
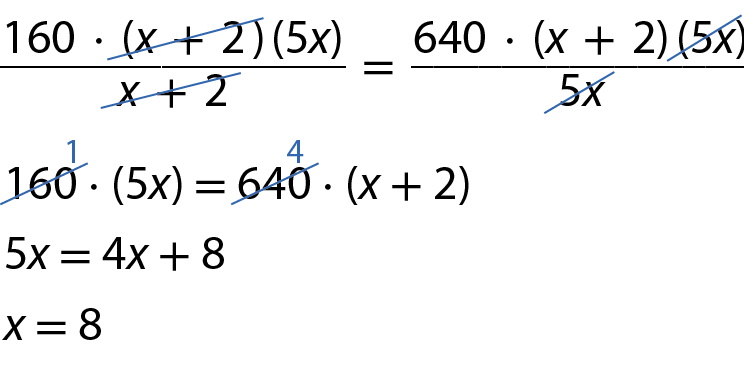
O número 8 não anula nenhum dos denominadores.
Portanto, foram inscritas inicialmente 8 escolas.
Acompanhe outro exemplo.
Vamos resolver a equação
Fração; numerador 2, denominador x mais 3, fim da fração. É igual a fração; numerador 5, denominador x, fim da fração., para x racional, sendo x ≠ ‒3 e x ≠ 0.
Multiplicando os termos da equação por x(x + 3), múltiplo de todos os denominadores, obtemos:

2x = 5x + 15
2x ‒ 5x = 15
‒3x = 15
x = ‒5
O número ‒5 não anula nenhum dos denominadores.
Portanto, a raiz e solução da equação é ‒5.
Respostas e comentários
Problemas e equações
Neste tópico, apresentamos alguns problemas que podem ser resolvidos com equações envolvendo frações algébricas e o uso de fatoração. Tais equações recaem em equações do 1º grau; entretanto, é necessário discutir a condição de existência e eliminar das possibilidades de solução os valores que anulam os denominadores das frações algébricas envolvidas.
Explore os exemplos com os estudantes, reproduzindo-os na lousa e pedindo a eles que justifiquem as etapas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
61

Determine mentalmente o valor que x não pode assumir nas seguintes equações:
a)
Equação. Fração 5 sobre x é igual à fração 10 meios.
b)
Equação. Fração, numerador 2, denominador x menos 2; é igual a 1.c)
Equação. 3 sobre x, é igual à 3.
d)
Equação. Fração, numerador 5 x, denominador x mais 1; é igual à 4.62 Resolva as equações a seguir.
a)
Equação. Fração, numerador 12, denominador x; é igual a fração, numerador 4, denominador x menos 2, sendo x diferente de 0 e x diferente de 2., sendo x ≠ 0 e x ≠ 2
b)
Equação. Fração, numerador menos 4, denominador x; é igual a fração, numerador 4, denominador x menos 2, sendo x diferente de 0 e x diferente de 2., sendo x ≠ 0 e x ≠ 2
63 Em uma distribuição de 720 quilogramas de alimentos, duas famílias não compareceram, o que possibilitou a cada uma das outras famílias receber 40 quilogramas de alimentos.
a) Quantas famílias deveriam receber os alimentos?
b) Quantas famílias compareceram?
c) Se todas as famílias tivessem comparecido, quantos quilogramas de alimento cada uma teria recebido?
64 Lúcia pensou em um número, adicionou 4 unidades e dividiu o resultado pela diferença entre o número pensado e 2. Em seguida, subtraiu 6 unidades do número pensado e dividiu o resultado pela diferença entre esse número e 9. Ao obter a resposta, Lúcia percebeu que os dois quocientes eram iguais.
a) Em que número Lúcia pensou?
b) Qual foi o quociente obtido?
65 Uma chácara de .5040 métros quadrados e outra de .2880 métros quadrados foram divididas em lotes de mesma área. A chácara maior teve o dôbro de lotes da chácara menor menos 2 lotes.
a) Em quantos lotes foi dividida a chácara menor?
b) E a chácara maior?
c) Quantos metros quadrados tem cada lote?
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega, leiam o texto e, depois, façam o que se pede.
José e Luís são irmãos. Luís tem um filho a mais que José.
Acompanhem o diálogo entre eles.



Descubram quantos filhos tem José e quantos metros quadrados couberam a cada filho.
Respostas e comentários
61. a) x ≠ 0
61. b) x ≠ 2
61. c) x ≠ 0
61. d) x ≠ ‒1
62. a) 3
62. b) 1
63. a) 20 famílias.
63. b) 18 famílias.
63. c) 36 quilogramas.
64. a) 16
64. b)
Fração. 10 sétimos
65. a) 8 lotes.
65. b) 14 lotes.
65. c) 360 métros quadrados
Pense mais um poucoreticências: 3 filhos; 240 métros quadrados.
Exercícios propostos
As resoluções dos exercícios 61 a 64 estão no início deste Manual, nas orientações específicas do capítulo 6.
Apresentamos a seguir a resolução do exercício 65, destacando inicialmente algumas considerações sobre as informações do enunciado.
• A área da chácara menor mede .2880 métros quadrados.
• O número de lotes da chácara menor é dado por x.
• A área da chácara maior mede .5040 métros quadrados.
• O número de lotes da chácara maior é dado por 2x ‒ 2.
Dividindo a medida da área de cada chácara pela quantidade de lotes em que ela foi igualmente repartida, obtemos a medida da área de cada lote; no caso, todos têm áreas de mesma medida (seja a da chácara maior, seja a da chácara menor). Assim:
Fatorando os denominadores, obtemos:
Simplificando:
Observando a condição de existência dos denominadores, concluímos que x ≠ 0 e x ≠ 1 (valores que anulam algum dos denominadores).
Agora, vamos multiplicar membro a membro por um múltiplo de todos os denominadores, assumindo a condição de existência de cada fração algébrica:
· x · (x ‒ 1) =
=
Fração, numerador 2520, denominador x menos 1.· x · (x ‒ 1)
.2880 · (x ‒ 1) = .2520 · x
.2880x ‒ .2880 = .2520x
360x = .2880
x = 8 (que é diferente de 0 e de 1)
Logo, a chácara menor foi dividida em 8 lotes (item a).
Desse modo, substituindo x por 8 na expressão 2x ‒ 2, determinamos a quantidade de lotes da chácara maior:
2x ‒ 2 = 2 · 8 ‒ 2 = 16 ‒ 2 = 14
Portanto, a chácara maior foi dividida em 14 lotes (item b).
Finalmente, para determinar a medida da área de cada lote, podemos utilizar
Fração. Numerador 2880, denominador x.ou
Fração. Numerador 5040, denominador 2 x menos 2.e substituir x por 8. Assim:
Portanto, concluímos que a área de cada lote mede 360 métros quadrados (item c).
Pense mais um poucoreticências
A resolução da atividade desta seção está no início deste Manual, nas orientações específicas do capítulo 6.
TRABALHANDO A INFORMAÇÃO
Construindo um gráfico de barras
Você já ouviu falar em gerações X, Y e Z?
Há estudos que nomeiam as gerações de acôrdo com a época de seu nascimento, porém com datas não consensuais:
• de 1960 até 1979

Geração X
• de 1980 até 1990

Geração Y
• de 1991 até 2010

Geração Z
A época em que uma pessoa nasce influencia diretamente seus hábitos e gostos, sobretudo devido aos recursos disponíveis em cada momento histórico.
Buscando encontrar semelhanças e diferenças entre as gerações, uma revista de psicologia entrevistou trezentas pessoas, sendo 100 de cada geração. Cada entrevistado respondeu a 5 perguntas e chegou-se a estes números:
|
Número de respostas positivas (por geração) |
|||
|---|---|---|---|
|
X |
Y |
Z |
|
|
Pratica atividade física? |
33 |
41 |
54 |
|
Lê jornal impresso? |
51 |
34 |
8 |
|
Tem animal de estimação? |
18 |
10 |
3 |
|
Tem perfil em rede social? |
32 |
86 |
97 |
|
Troca mensagens via celular? |
9 |
21 |
58 |
Dados obtidos pela revista de psicologia.
Esses mesmos dados podem ser representados por meio de um gráfico de barras, tomando-se alguns cuidados:
• escolher uma escala adequada, ou seja, um tamanho que caiba no papel e, ao mesmo tempo, que não seja tão pequena a ponto de dificultar a leitura dos dados;
• elaborar uma legenda que possibilite a leitura e a interpretação desses dados;
• escrever nos locais corretos o título do gráfico e o que cada eixo representa.
Por exemplo, pode-se começar um gráfico assim:
• Para cada pergunta feita, devem ser associadas 3 barras, cada uma representando uma geração. Para diferenciá-las, usamos cores diferentes e as respectivas legendas: geração X em roxo, geração Y em laranja e geração Z em verde.
• O maior valor a ser representado é 97, e o menor é 3; então precisamos pensar em uma escala que inclua e deixe visíveis esses valores, assim como os que completam esse intervalo. Se, por exemplo, a barra que representa o maior valor medir 12 centímetros, então, considerando que a razão entre as respostas positivas deve ser igual à razão entre as medidas dos comprimentos das barras, ou seja, essas grandezas devem ser proporcionais, podemos calcular a medida do comprimento das outras barras. Acompanhe a seguir.
Respostas e comentários
Trabalhando a informação
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah dois três.
Para a construção de um gráfico de barras, como citado nesta seção, é necessário estabelecer qual escala será usada.
Oriente os estudantes a primeiro analisar os dados a serem representados, em particular o maior e o menor valor, e assim escolherem uma unidade mais adequada ao espaço de que dispõem para a construção do gráfico. Definida a unidade, basta aplicar a noção de proporcionalidade para calcular o comprimento das barras. Aproveite para discutir a adequação de gráficos de barras para a representação de determinados conjuntos de dados, apresentando aos estudantes exemplos de gráficos de barras que não utilizam escala adequada, desenvolvendo a habilidade (ê éfe zero oito ême ah dois três).
|
Pergunta |
Número de respostas positivas |
Medida do comprimento da barra |
|---|---|---|
|
Tem perfil...? |
97 |
12 cm |
|
Pratica atividade...? |
33 |
a |
As razões são iguais:
97a = 396
a =
Fração. 396 97 avos≃ 4,1
|
Pergunta |
Número de respostas positivas |
Medida do comprimento da barra |
|---|---|---|
|
Tem perfil...? |
97 |
12 cm |
|
Pratica atividade...? |
41 |
b |
As razões são iguais:
97b = 492
b =
Fração. 492 97 avos≃ 5,1
Assim, um possível esbôço do gráfico seria:
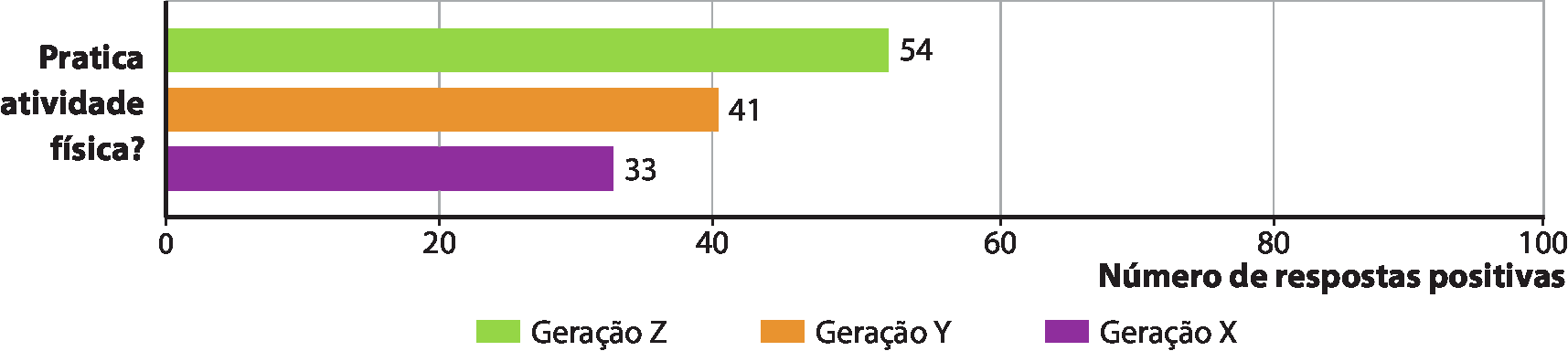
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
Considere o gráfico iniciado e as informações apresentadas anteriormente.
1 Em que faixa etária encontram-se hoje pessoas da geração X? E as da geração Y? E da geração Z?
2 O que falta no gráfico iniciado para ele ficar completo?
3 Para caber em uma folha a4, qual deve ser o comprimento máximo da maior barra a ser representada? E o da menor barra?
4 Escolha uma escala e faça o gráfico de barras que representa a situação.
5 Compare o seu gráfico com o dos colegas. Há diferenças entre eles? Justifique.
Respostas e comentários
1. As respostas dependem do ano corrente.
2. Além do título, faltam as barras correspondentes às demais perguntas feitas na pesquisa e a fonte: revista de psicologia.
3. É preciso estar atento aos maiores e aos menores valores a serem representados: 97 e 3, respectivamente. Dessa maneira, deve-se buscar uma escala apropriada para que “97” caiba na folha (297 milímetros × 210 milímetros) e “3” fique visível.
4. Construção de gráfico.
5. Resposta pessoal.
Agora quem trabalha é você!
Para a atividade 1, sendo x um ano, tal que x > 2010, temos que as faixas etárias de cada geração são dadas por:
• geração X: de (x ‒ 1979) a (x ‒ 1960);
• geração Y: de (x ‒ 1990) a (x ‒ 1980);
• geração Z: de (x ‒ 2010) a (x ‒ 1991).
Para a atividade 4, apresentamos um possível gráfico relativo à tabela Número de respostas positivas (por geração), apresentada anteriormente.
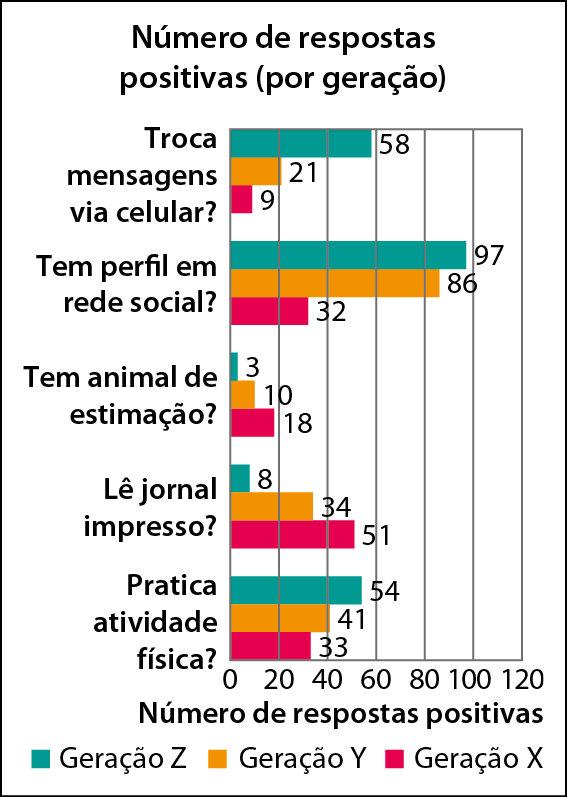
Proponha aos estudantes que elaborem algumas perguntas sobre o gráfico para trocar com um colega: cada um responde às questões do outro. Exemplos de questões que podem ser criadas:
• Qual geração das pessoas entrevistadas pratica mais atividade física? (Resposta: Geração Z.)
• Qual geração tem menos perfis em rede social? (Resposta: Geração X.)
• Em qual geração mais de 50% dos entrevistados têm animal de estimação? (Resposta: Em nenhuma delas.)
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Fibonacci e sequências recursivas
Duração: 5:11min. Página: 155.
[Locutora] Fibonacci e sequências recursivas
Vinheta.
>> [Luciana Moura] Oi, tudo bem? Eu sou a professora Luciana Moura e vou falar com vocês sobre Leonardo de Pisa, ou Leonardo Fibonacci, um dos principais matemáticos europeus da Idade Média.
>> [Luciana Moura] Ele nasceu por volta de 1170, na cidade de Pisa, Itália, um importante centro comercial daquela época.
>> [Luciana Moura] Por conta das inúmeras viagens de seu pai, um [tom enfático] renomado mercador, Fibonacci pôde conhecer diversas culturas e estudar a Matemática praticada nos países árabes.
>> [Luciana Moura] Em seu primeiro livro, Liber abaci, livro dos ábacos ou livro dos cálculos, ele apresenta o sistema de numeração indo-arábico, além de resolver problemas com base nesse sistema.
>> [Luciana Moura] Um dos problemas apresentados no Liber abaci acabou deixando Fibonacci muito famoso, pois a sequência de números que representa sua solução recebeu o nome de sequência de Fibonacci, em sua homenagem, já no século XIX.
>> [Luciana Moura] O problema era: um homem colocou um casal de filhotes de coelho recém-nascidos em um lugar cercado. Ele supôs que esses filhotes procriariam logo no segundo mês de vida, quando em geral se tornam férteis, gerando outro casal. Esse novo casal, por sua vez, também procriaria com dois meses de idade, e assim por diante.
>> [Luciana Moura] Considere que nenhum animal tenha morrido no período de um ano. Quantos casais de coelhos nasceram, contando com o primeiro casal?
>> [Luciana Moura] A solução para esse problema é um termo da sequência numérica que encontramos ao escrever a quantidade de casais mês a mês: 1, 1, 2, 3, 5, 8, 13, 21...
>> [Luciana Moura] Um fato interessante dessa sequência é que, a partir do terceiro termo, todos os outros são determinados pela soma dos dois termos imediatamente anteriores.
>> [Luciana Moura] Observe: o primeiro e o segundo termos são iguais a 1. O terceiro termo é 2, que é igual à soma de seus dois antecessores: 1 + 1. O quarto termo é 3, igual a 1 + 2. O quinto termo é 5, igual a 2 + 3, e assim por diante.
>> [Luciana Moura] Agora, é fácil descobrir a resposta para a questão acima.
>> [Luciana Moura] Quando esse tipo de regularidade acontece com números, chamamos de sequência recursiva.
>> [Luciana Moura] Em Computação, o uso de sequências recursivas permite a redução de um problema em outros mais simples, até que seja possível sua resolução, ou até atingir determinado valor da sequência.
>> [Luciana Moura] Para compreender melhor, considere a ação de subir uma escada até chegar a um andar específico. Enquanto não se chega a esse andar, devemos subir mais um degrau e, a cada degrau que subimos, o ponto final estará mais próximo.
>> [Luciana Moura] Seguindo esse modelo, conseguimos facilmente projetar quais serão os anos em que as próximas copas do mundo de futebol serão realizadas, já que esses torneios acontecem a cada 4 anos. A última copa foi em 2018; logo, as próximas serão em 2022, 2026, 2030, e assim por diante, bastando somar 4 anos à data anterior.
>> [Luciana Moura] Nesse caso, cada termo da sequência é sempre determinado pela adição de um valor fixo ao termo precedente. Esse valor fixo é chamado de razão.
>> [Luciana Moura] Para finalizar, imagine que você tenha enviado uma mensagem virtual com uma piada a 10 amigos, e cada um desses 10 amigos compartilhou a mensagem com outras 10 pessoas, e assim sucessivamente.
>> [Luciana Moura] A quantidade de pessoas que compartilharam a mensagem pode ser obtida adicionando-se os termos da sequência 1, 10, 100, 1 000 etc.
>> [Luciana Moura] Perceba que, agora, cada termo da sequência é sempre determinado pela multiplicação do termo precedente por um valor fixo, também chamado razão. Observe que o valor dos termos cresce muito rapidamente!
Vinheta.
Créditos
Todos os áudios inseridos neste conteúdo são da Free Sound.
4. Sequências numéricas
Situação 1
Observe o fluxograma a seguir.
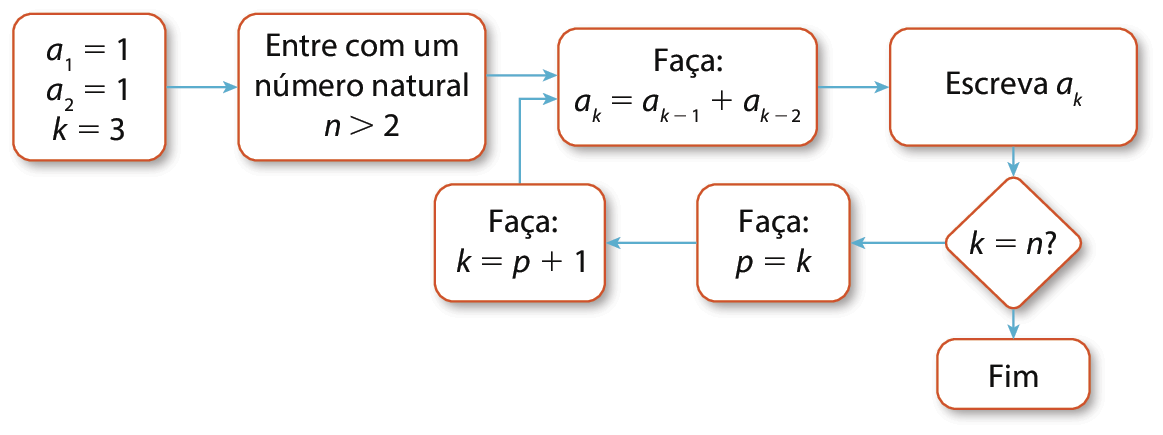
Esse fluxograma pode ser utilizado para obtermos, de maneira recursiva, os números da sequência de Fibonacci. Essa sequência é dada da seguinte maneira: o 1º termo
Abre parênteses, a índice 1, fecha parênteses.é 1, o 2º termo
Abre parênteses, a índice 2, fecha parênteses.é 1 e, a partir do 3º termo
Abre parênteses, a índice 3, fecha parênteses., o valor numérico é dado pela adição dos dois termos anteriores. Assim, temos:
•
•
A índice 2 é igual a 1•
A índice 3 é igual a, a índice 2 mais a índice 1 é igual a, 1 mais 1 é igual a 2•
A índice 4 é igual a, a índice 3 mais a índice 2 é igual a, 2 mais 1 é igual a 3•
A índice 5 é igual a, a índice 4 mais a índice 3 é igual a, 3 mais 2 é igual a 5•
A índice 6 é igual a, a índice 5 mais a índice 4 é igual a, 5 mais 3 é igual a 8⋮
•
A índice n é igual a, a índice n menos 2, mais a índice n menos 1
A sequência obtida pode ser indicada por:
1, 1, 2, 3, 5, 8, ...
Seguindo este raciocínio, para determinar o milésimo termo da sequência de Fibonacci, precisaríamos calcular todos os termos que o antecedem a fim obter de
Termo. a índice 999 e a índice 998, pois:
A índice 1000 é igual a, a índice 999 mais a índice 998.
Por esse motivo, podemos dizer que a sequência de Fibonacci é uma sequência recursiva.
Sequências recursivas são aquelas em que os primeiros termos são dados e os termos seguintes são determinados com base no valor de termos anteriores e de uma expressão algébrica que define uma lei de formação da sequência.
Situação 2
De acôrdo com a lenda do xadrez, apresentada no capítulo 1, a quantidade de trigo em cada casa do tabuleiro segue a sequência numérica:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, reticências , ......9223372036854775808
E esses números são obtidos a partir do dôbro do número anterior, com o primeiro deles sendo o número 1 (1 grão de trigo na primeira casa do tabuleiro). Assim, podemos determinar essa sequência recursivamente, da seguinte maneira:
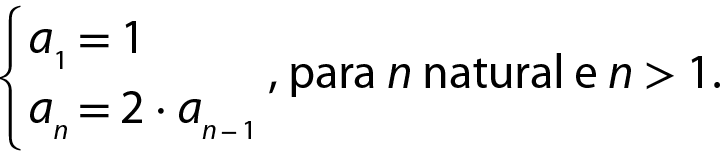
No entanto, neste caso, também poderíamos determinar a mesma sequência numérica de maneira não recursiva, considerando apenas a posição (n) do termo na sequência e uma lei de formação, dada pela expressão algébrica:
A índice n é igual a, 2 elevado a n menos 1, para n natural e n > 0.
Assim, se quisermos saber o valor do 64º termo dessa sequência, basta fazermos:
A índice 64 é igual a, a elevado a, 64 menos 1 que é igual a 2 elevado a 63Respostas e comentários
4. Sequências numéricas
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah um zero e ê éfe zero oito ême ah um um.
Este tópico explora a associação entre sequências numéricas e expressões algébricas para descrevê-las, desenvolvendo, assim, as habilidades (ê éfe zero oito ême ah um zero) e (EF08MA11).
O fluxograma apresentado na situação 1 é utilizado para determinar os n primeiros termos da sequência de fibonáti que é definida recursivamente. Incentive os estudantes a determinar alguns termos dessa sequência utilizando o fluxograma. Por exemplo, questione-os quais são os valores obtidos quando n = 8; eles devem obter a sequência numérica: 1, 1, 2, 3, 5, 8, 13, 21.
Ressalte para os estudantes que uma sequência numérica recursiva pode ser definida ao explicitar seu primeiro termo (ou primeiros termos), fornecendo uma regra para obter os termos seguintes a partir de termos anteriores. Por exemplo, na situação 2, a sequência 1, 2, 4, 8, 16, 32, reticências das potências de 2 com expoente natural correspondente a 20, 21, 22, 23, 24, 25, reticências, dada de maneira não recursiva por
A índice n é igual a, 2 elevado a, n menos 1, para n natural não nulo (n = 1, 2, 3, 4, 5, reticências), também poderia ser dada recursivamente a partir do 1º termo a1 = 1 e de uma regra para obter um termo qualquer da sequência a partir do anterior:
Obtemos alguns elementos e verificamos que essa é a sequência das potências de base 2:
•
quando n é igual à 1, o valor de a índice 1 é 1.•
quando n é igual à 2, o valor de a índice 2 é 2 vezes a índice resultado de: 2 menos 1, igual à 2 vezes a índice 1.•
quando n é igual a 3, o valor de a índice 3 é 2 vezes a índice resultado de: 3 menos 1, igual a 2 vezes a índice 2.•
quando n é igual à 4, o valor de a índice 4 é 2 vezes a índice resultado de: 4 menos 1, igual à 2 vezes a índice 3.•
Quando n é igual a 5, o valor de a índice 5 é 2 vezes a índice resultado de: 5 menos 1, igual a 2 vezes a índice 4.
• o enésimo termo →
o enésimo termo será a índice n, que é igual a 2 vezes a índice resultado de: n menos 1, para n igual a 2, 3, 4, 5, etc.(para n = 2, 3, 4, 5, reticências)
Observe que, desta maneira, não precisamos saber todos os termos anteriores ao 64º termo para calculá-lo.
As sequências não recursivas são aquelas que não dependem de termos anteriores para determinar o próximo termo, pode-se determinar o valor de um elemento da sequência apenas pela sua posição. Exemplo: an = 2n – 1 é não recursiva, enquanto an = 2na – 1 com a1 = 1 é recursiva (e ambas tratam da mesma sequência numérica, para n natural e n > 0).
Representamos, por meio de um fluxograma, como um computador faria para imprimir a sequência dos totais de grãos de trigo, de maneira não recursiva.
um) Inicia o procedimento atribuindo 1 à variável n.
dois) Calcula e imprime o valor numérico de
Termo. a índice n é igual a 2 elevado a n menos 1..
(No 1º cálculo fica
Termo a índice 2 é igual a 2 elevado à diferença 2 menos 1, que é igual a 2..)
três) Pergunta se n é igual a 64.
quatro) Em caso negativo, adiciona 1 a n e volta ao passo dois.
(No 2º cálculo fica a2 = 22 ‒ 1 = 2; no 3º fica
Cálculo numérico. Termo a índice 3 é igual a 2 elevado à diferença 3 menos 1, que é igual a 4.; etcétera)
cinco) Em caso afirmativo, termina o procedimento.
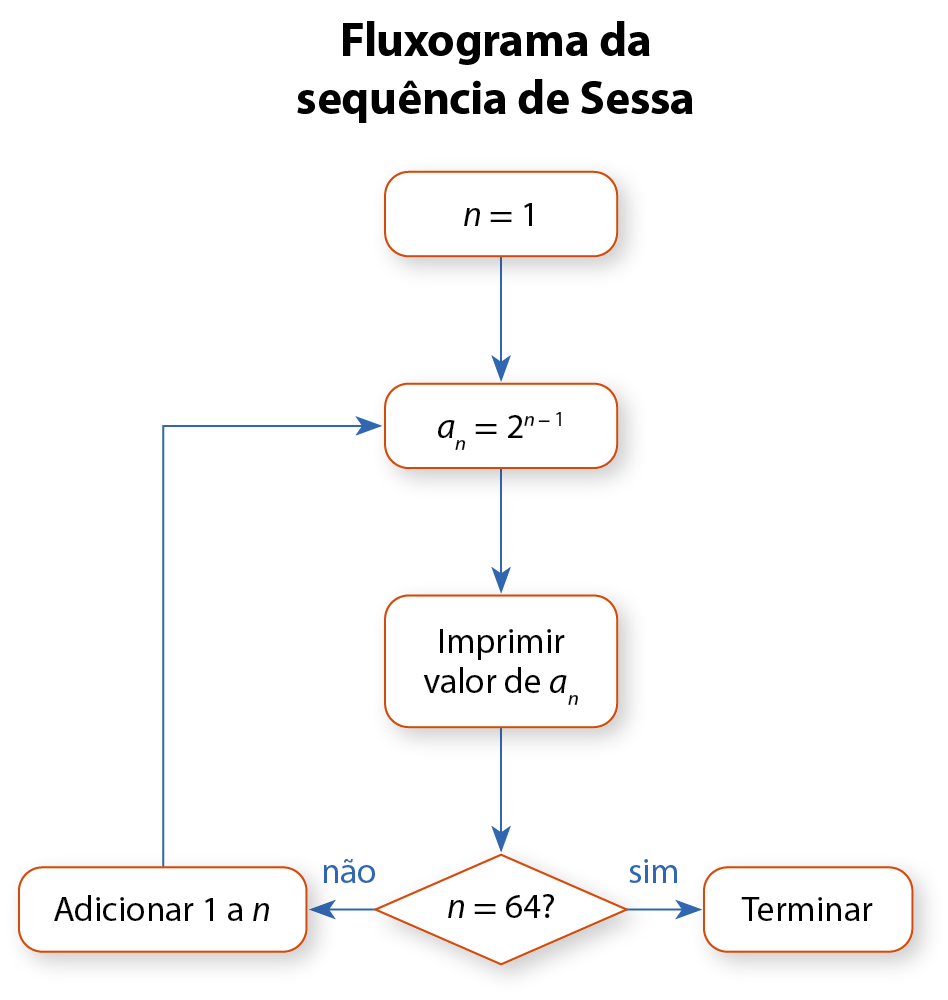
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
66 Dê um exemplo de sucessão recursiva e um de sucessão não recursiva.
67 A atividade “Pense mais um poucoreticências” da página 97 traz uma sequência numérica obtida pela expressão 9x + y para x assumindo um número formado pelos algarismos de 1 a no máximo 9, em ordem crescente de valor absoluto, e y assumindo o valor absoluto do sucessor do último algarismo de x. Escreva os cálculos e os respectivos resultados dos nove primeiros termos dessa sequência.
68 Qual é o número de bolinhas de uma das diagonais da enésima caixa desta sequência?
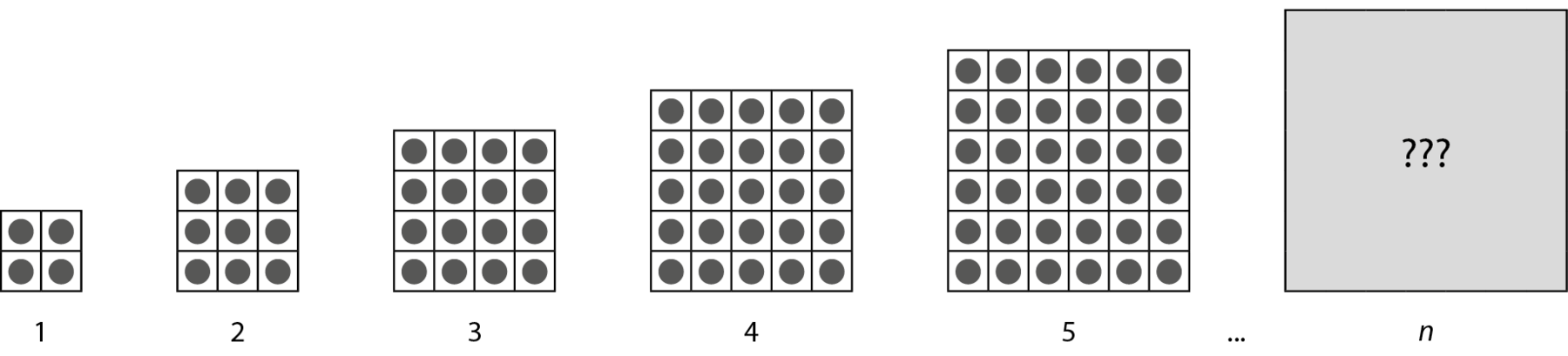
69 Em cada item, escreva os 10 primeiros termos da sequência numérica dada pela lei de formação indicada, considerando n natural e n ⩾ 0.
• O que você pode afirmar sobre as leis de formação dessas sequências numéricas?
a) (n + 1) + n
b) 2n + 1
Respostas e comentários
66. Resposta pessoal.
67. 9 ⋅ 1 + 2 = 11; 9 ⋅ 12 + 3 = 111; 9 ⋅ 123 + 4 = .1111; 9 ⋅ .1234 + 5 = .11111; 9 ⋅ .12345 + 6 = .111111; 9 ⋅ .123456 + 7 = ..1111111; 9 ⋅ ..1234567 + 8 = ..11111111; 9 ⋅ ..12345678 + 9 = ..111111111; 9 ⋅ ..123456789 + 10 = ...1111111111.
68. n + 1
69. São equivalentes.
69. a) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
69. b) 1, 3, 5, 7, 9, 11, 13, 15, 17, 19
Sequências numéricas
Reproduza o fluxograma na lousa e analise cada etapa com os estudantes. Eles devem perceber que, enquanto o valor de n não atinge 64, o processo é retomado adicionando-se 1 ao valor anterior de n.
Exercícios propostos
No exercício 66, incentive os estudantes a produzir diferentes sequências numéricas e a compartilhar com os colegas. Incentive-os também a discutir quais são sequências recursivas e quais são sequências não recursivas.
No exercício 68, verificamos que em uma das diagonais:
• na 1ª caixa há 2 bolinhas (2 = 1 + 1);
• na 2ª caixa há 3 bolinhas (3 = 2 + 1);
• na 3ª caixa há 4 bolinhas (4 = 3 + 1);
• na 4ª caixa há 5 bolinhas (5 = 4 + 1);
• na 5ª caixa há 6 bolinhas (6 = 5 + 1);
• na enésima caixa há (n + 1) bolinhas.
No exercício 69, pode-se perceber que as sequências numéricas obtidas serão equivalentes, pois, em ambas, n varia de 0 a 9 e, ainda:
(n + 1) + n = n + 1 + n =
= n + n + 1 = 2n + 1
Assim, com base em 2n + 1 e fazendo n variar de 0 a 9, obtemos:
2 ⋅ 0 + 1 = 1
2 ⋅ 1 + 1 = 3
2 ⋅ 2 + 1 = 5
2 ⋅ 3 + 1 = 7
2 ⋅ 4 + 1 = 9
2 ⋅ 5 + 1 = 11
2 ⋅ 6 + 1 = 13
2 ⋅ 7 + 1 = 15
2 ⋅ 8 + 1 = 17
2 ⋅ 9 + 1 = 19
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Desenvolva.
a) (3a ‒ 2b)2
b) (5a + 7) ⋅ (5a ‒ 7)
c) (3x 2 + y 3 )2
d) (‒5 ‒ 2y)2
2 Determine o binômio obtido por meio de:
(5a + 9b)(5a ‒ 9b).
3 (ulbra-Rio Grande do Sul) Sendo A = x ‒ 3, B = x 2 + 3 e C = 9x, o valor de A2 ‒ B + C é:
a) 3(x + 4).
b) x + 4.
c) 3(x + 2).
d) x + 2.
e) 3.
4 Que binômio devemos adicionar à expressão x 2 + 5x + 70 para obter o quadrado de (x + 10)?
5 Elevando um binômio da fórma ax + b ao quadrado, obtém-se 9x 2 + 24x + 16. Calcule o valor de a + b, com a e b positivos.
6 Resolva as questões a seguir.
a) Que expressão devemos subtrair de a 2 + b 2 para obter o quadrado de (a ‒ b)?
b) Que expressão devemos adicionar a a 2 + 2ab para obter o quadrado de (a + b)?
c) Se a 2 + b 2 = 34 e ab = 15, qual é o valor de (a + b)2 ?
d) Se a 2 + b2 = 100 e (a + b)2 = 196, qual é o valor de ab?
7 (éfe gê vê-São Paulo) Seja N o resultado da operação 3752 ‒ 3742. A soma dos algarismos de N é:
a) 18.
b) 19.
c) 20.
d) 21.
e) 22.
8 Fatore completamente as expressões a seguir.
a) 3x 2 ‒ 75
b) a 3 ‒ ab 2
c) x 4 ‒ 16
d) a 2 ‒ x 2 + a + x
e) x 2 ‒ y 2 + 2x + 2y
f) 2x 2 ‒ 12x + 18
9 Sabendo que a + b = 18 e a ‒ b = 2, calcule o valor de:
a) (a + b)2;
b) (a ‒ b)2;
c) a 2 ‒ b 2.
10 Sabendo que x + y = 14 e x 2 + y 2 = 116, calcule o valor de:
a) (x + y)2;
b) xy ;
c) (x ‒ y)2.
11 Determine os valores que são soluções das equações a seguir.
a) x 2 + 12x = 0
b) 6x 2 ‒ 5x = 0
c) 4x 2 ‒ 4x + 1 = 0
d) 9x 2 + 6x + 1 = 0
12 (ó bê ême) Os números naturais x e y são tais que x 2 ‒ xy = 23. Qual é o valor de x + y?
a) 24
b) 30
c) 34
d) 35
e) 45
13 A soma dos coeficientes do desenvolvimento da expressão (3a ‒ 2b)2 é:
a) 5.
b) 22.
c) 1.
d) 2.
14 A expressão 2(x 2 + 3y)(x 2 ‒ 3y) é igual a:
a) x 4 ‒ 9y 2.
b) 2x 4 ‒ 18y 2.
c) 2x 4 ‒ 9y 2.
d) 4x 4 ‒ 9y 2.
15 O valor da expressão (2x + 9y)2 ‒ 36xy, para x = ‒1 e y = 1, é:
a) 13.
b) ‒5.
c) 85.
d) 65.
16 (ó bê ême) Se x + y = 8 e xy = 15, qual é o valor de x 2 + 6xy + y 2 ?
a) 64
b) 109
c) 120
d) 124
e) 154
17 A expressão (x + 3) ⋅ (x ‒ 3) ‒ x 2 é igual a:
a) 2x ‒ 9 ‒ x 2.
b) ‒9.
c) ‒6x ‒ 9.
d) 6x ‒ 9.
18 Fatorando a expressão y 4 ‒ 4y 2 + 4, obtemos:
a) ( y2 ‒ 2)2.
b) ( y + 2)2.
c) ( y2 + 2)2.
d) n.d.a.
19 Fatorando a expressão ab + 2b ‒ 3a ‒ 6, obtemos:
a) (a ‒ 2) ⋅ (b + 3).
b) (a + 2) ⋅ (b ‒ 3).
c) (a ‒ 2) ⋅ (b ‒ 3).
d) n.d.a.
20 Simplifique as frações algébricas.
a)
Fração algébrica. Numerador: x ao quadrado, mais x. Denominador: x ao quadrado, menos 1.
b)
Fração algébrica. Numerador: b menos a. Denominador: a ao quadrado, menos b ao quadrado.
Respostas e comentários
1. a) 9a 2 ‒ 12ab + 4b 2
1. b) 25a 2 ‒ 49
1. c) 9x 4 + 6x 2y 3 + y 6
1. d) 25 + 20y + 4y 2
2. 25a 2 ‒ 81b 2
3. Alternativa c.
4. 15x + 30
5. 7
6. a) 2ab
6. b) b 2
6. c) 64
6. d) 48
7. Alternativa c.
8. a) 3(x + 5)(x ‒ 5)
8. b) a(a + b)(a ‒ b)
8. c) (x 2 + 4)(x + 2)(x ‒ 2)
8. d) (a + x)(a ‒ x + 1)
8. e) (x + y)(x ‒ y + 2)
8. f) 2(x ‒ 3)2
9. a) 324
9. b) 4
9. c) 36
10. a) 196
10. b) 40
10. c) 36
11. a) 0 ou ‒12
11. b) 0 ou
Fração. 5 sextos11. c)
Fração. 1 meio11. d)
Fração, menos um terço12. Alternativa e.
13. Alternativa c.
14. Alternativa b.
15. Alternativa c.
16. Alternativa d.
17. Alternativa b.
18. Alternativa a.
19. Alternativa b.
20. a)
Fração algébrica. Numerador: x . Denominador: x menos 1.20. b)
Fração algébrica. Numerador: menos 1. Denominador: a mais b.Exercícios complementares
Esta série de exercícios retoma os principais conceitos tratados no capítulo, possibilitando aos estudantes retomar e aplicar os conhecimentos construídos.
As resoluções dos exercícios 1 a 11 e dos exercícios 13 a 20 estão no início deste Manual, nas orientações específicas do capítulo 6.
A seguir, apresentamos a resolução do exercício 12.
x 2 ‒ xy = 23
x(x ‒ y) = 23
Como 23 é primo, a única decomposição possível de 23 como um produto de dois fatores é
23 = 1 · 23 (ou 23 = 23 · 1).
Assim, obtemos duas possibilidades para x e y:
• x = 23 e x ‒ y = 1
x ‒ y = 1
x ‒ 1 = y
y = 22
Logo: x + y = 23 + 22 = 45
• x = 1 e x ‒ y = 23
x ‒ y = 23
x ‒ 23 = y
1 ‒ 23 = y
y = ‒22
Mas x e y são números naturais; logo, essa solução não convém.
Portanto, x + y = 45 (alternativa e).
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 A expressão
(x + 4)elevado a 2 menos (2x menos 3)elevado a 2
é igual a:
a) menos3xelevado a 2 menos 4x + 25.
b) menos3xelevado a 2 + 20x + 7.
c) menos4xelevado a 2 + 20x + 5.
d) 5xelevado a 2 menos 4x + 25.
2 Carlos pegou uma placa quadrada de madeira com lado medindo 12 centímetros e cortou dela, para descarte, outra placa quadrada com lado medindo x centímetro. Que expressão fornece a medida da área da superfície de madeira que sobrou?
a) 144 menos 2x
b) 144 menos 24x + xelevado a 2
c) 24 menos 12x + xelevado a 2
d) 144 menos xelevado a 2
3 Uma fábrica de brinquedos produz cubos mágicos com aresta medindo 5x centímetros. Para construir um modêlo míni, projeta-se diminuir 3 centímetros de cada aresta. Qual seria a medida do volume do cubo míni?
a) 125xelevado a 3 ‒ 225xelevado a 2 + 135x menos 27
b) 125xelevado a 3 + 225xelevado a 2 + 135x + 27
c) 27 menos 135x + 225xelevado a 2 ‒ 125xelevado a 3
d) 25xelevado a 2 menos 30x + 9
4 Colocando em evidência o fator comum de 24xelevado a 2y + 32xyelevado a 2 menos 12xy, obtém-se:
a) 12xy(2xy + 4xy menos 1).
b) 4xelevado a 2yelevado a 2(6x + 8y menos 3).
c) 12xy(2x + 4y menos 1).
d) 4xy(6x + 8y menos 3).
5 Fatorando por agrupamento a expressão 3ab + 3ac menos 5b menos 5c, obtemos:
a) (menos2)(ab + c).
b) (3a menos 5)(b + c).
c) (3a + 5)(b menos c).
d) (a menos 5)(b + 3c).
6 Uma horta foi construída em um terreno quadrado que tinha área medindo xelevado a 2 métros quadrados. Após um replantio, passou a ser retangular e teve sua área alterada para (xelevado a 2 menos 4aelevado a 2) métros quadrados. Indique uma possível alteração nas medidas dos lados do quadrado original.
a) Adição de 2a métros em uma dimensão e subtração de 2a métros em outra.
b) Subtração de 2a métros nas duas dimensões do quadrado.
c) Adição de 4a métros em uma dimensão e subtração de 4a métros em outra.
d) Subtração de 4a métros nas duas dimensões do quadrado.
7 A fórma fatorada de 25xelevado a 2 menos 60xy + 36yelevado a 2 é:
a) (25x menos 36y)elevado a 2.
b) (5x menos 6y)elevado a 2.
c) (6x menos 5y)elevado a 2.
d) (5x + 6y)elevado a 2.
8 Simplificando a fração algébrica
Fração algébrica. Numerador: O produto da expressão 3 a mais 2 b pelo quadrado de 3 a menos 2 b. Denominador: 18 a ao quadrado, menos 8 b ao quadrado.obtemos:
a) 3a menos 2b.
b)
Fração algébrica. Numerador: 3 a mais 2 b. Denominador: 2.c) 3a + 2b.
d)
Fração algébrica. Numerador: 3 a menos 2 b. Denominador: 2.9 O enésimo termo de uma sequência numérica é dado pela expressão
termo de índice n é igual a 2 vezes n mais 1., onde n é um número inteiro. Assim, temos uma sequência de números:
a) inteiros terminados em 1.
b) inteiros pares.
c) naturais ímpares.
d) inteiros ímpares.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Quais foram os produtos notáveis estudados? Escolha um deles e, com suas palavras, descreva-o.
b) Quais foram as fatorações estudadas? Escolha uma delas e, com suas palavras, descreva-a.
c) Com base no que você estudou, estabeleça, por meio de um texto ou de um esquema, a relação entre o produto notável e a fatoração.
d) O que classifica uma sequência numérica como não recursiva?
Respostas e comentários
1. Alternativa b.
2. Alternativa d.
3. Alternativa a.
4. Alternativa d.
5. Alternativa b.
6. Alternativa a.
7. Alternativa b.
8. Alternativa d.
9. Alternativa d.
Organizando:
a) Quadrado da soma de dois termos, quadrado da diferença de dois termos, produto da soma pela diferença de dois termos e cubo da soma e cubo da diferença de dois termos. Resposta pessoal.
b) Fatoração pela evidência de fator comum, fatoração por agrupamento, diferença de dois quadrados, trinômio quadrado perfeito e diferença e soma de dois cubos. Resposta pessoal.
c) Resposta pessoal. Espera-se que os estudantes considerem que os procedimentos de desenvolvimento dos produtos notáveis são opostos aos respectivos casos de fatoração.
d) Uma sequência é dita não recursiva quando é possível obter uma lei de formação da sequência que não dependa de nenhum valor de seus termos.
Verificando
Os testes propostos nesta seção podem ser utilizados para preparar os estudantes para avaliações de larga escala.
Pode-se propor que resolvam individualmente cada um deles e, depois, realizar a correção na lousa, deixando-os compartilhar as estratégias de resolução utilizadas.
As resoluções dos testes 1 a 9 estão no início deste Manual, nas orientações específicas do capítulo 6.
Organizando
As questões desta seção possibilitam retomar com os estudantes os principais conceitos trabalhados no capítulo. Elas também podem orientá-los ao fazerem uma autoavaliação.
É interessante que cada estudante responda individualmente e, depois, comente com os colegas as respostas, corrigindo-as ou complementando-as.
DIVERSIFICANDO
A Álgebra explica a Aritmética
Em um almanaque de curiosidades, Inês leu um “truque” para calcular o quadrado de um número natural n terminado em 5.

Acompanhe alguns exemplos.
• 352 é calculado da seguinte maneira: 3 ⋅ (3 + 1) ⋅ 100 = .1200; .1200 + 25 = .1225; então, 352 = .1225
• 1652 é calculado da seguinte maneira: 16 ⋅ (16 + 1) ⋅ 100 = .27200; .27200 + 25 = .27225; então, 1652 = .27225
Inês achou interessante e quis entender o porquê disso, pois sabe que em Matemática não há truques. Depois de pesquisar, chegou às igualdades:
• 352 = 3 ⋅ (3 + 1) ⋅ 100 + 25 352 = 3 ⋅ 4 ⋅ 100 + 25 352 = 30 ⋅ 40 + 52 352 ‒ 52 = (35 ‒ 5) ⋅ (35 + 5)
• 1652 = 16 ⋅ (16 + 1) ⋅ 100 + 25 1652 = 16 ⋅ 17 ⋅ 100 + 25 1652 = 160 ⋅ 170 + 52 1652 ‒ 52 = (165 ‒ 5) ⋅ (165 + 5)
Assim, ela percebeu que esse procedimento pode ser explicado pelo produto da soma pela diferença e que, pelo menos para números de dois algarismos, favorece o cálculo mental.
Ao generalizar o que fez com alguns números e usando D para representar um algarismo, Inês fez o caminho inverso ao das expressões dos exemplos dados e anotou no caderno. Acompanhe na imagem.

Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO

Reúna-se com um colega e façam o que se pede.
1

Calculem mentalmente as potências e, em seguida, expliquem como fizeram.
a) 152
b) 452
c) 752
d) 952
2

Usem uma calculadora para verificar os cálculos a seguir.
a) 1152 = 11 ⋅ 12 ⋅ 100 + 25 = .13225
b) 1452 = 14 ⋅ 15 ⋅ 100 + 25 = .21025
c) 2152 = 21 ⋅ 22 ⋅ 100 + 25 = .46225
d) .37852 = 378 ⋅ 379 ⋅ 100 + 25 = ..14326225
Respostas e comentários
1. a) 1 ⋅ 2 ⋅ 100 + 25 = 225
1. b) 4 ⋅ 5 ⋅ 100 + 25 = .2025
1. c) 7 ⋅ 8 ⋅ 100 + 25 = .5625
1. d) 9 ⋅ 10 ⋅ 100 + 25 = .9025
2. Verificação de cálculos utilizando uma calculadora.
Diversificando
A inter-relação entre os diversos campos da Matemática dá coesão ao estudo, aspecto que deve ser realçado para os estudantes, e sua busca deve ser incentivada. Esta seção é mais um exemplo do que pode ser trabalhado nesse sentido, em que mostramos como a Álgebra explica “truques” da Aritmética.
Além do aspecto lúdico e curioso, é possível encontrar mais um caso de cálculo mental. Em um segundo momento, é pedido aos estudantes que verifiquem a validade desse procedimento no cálculo de algumas potências, fazendo uso de uma calculadora.