
CAPÍTULO 7 Estudo dos triângulos

Composta de desenhos feitos com azulejos de 15 centímetros por 15 centímetros e elaborados com a combinação de quatro cores, esta é a imagem da obra Tempestade de triângulos, de Alexandre Mancini.
Essa combinação lembra um problema matemático histórico, formulado na Inglaterra em 1852: Serão suficientes quatro cores para pintar um mapa plano de maneira que dois países vizinhos não partilhem a mesma côr?
Apenas em 1976, com o uso de computador, o teorema das quatro cores foi demonstrado.
Observe a imagem e responda às questões no caderno.
a) Com relação aos ângulos, que tipos de triângulo podemos identificar nesta obra?
b) Com relação aos lados, que tipos de triângulo podemos identificar nesta obra?
c) Faça um desenho de algum lugar ou de algum objeto utilizando apenas triângulos na composição dele.
Respostas e comentários
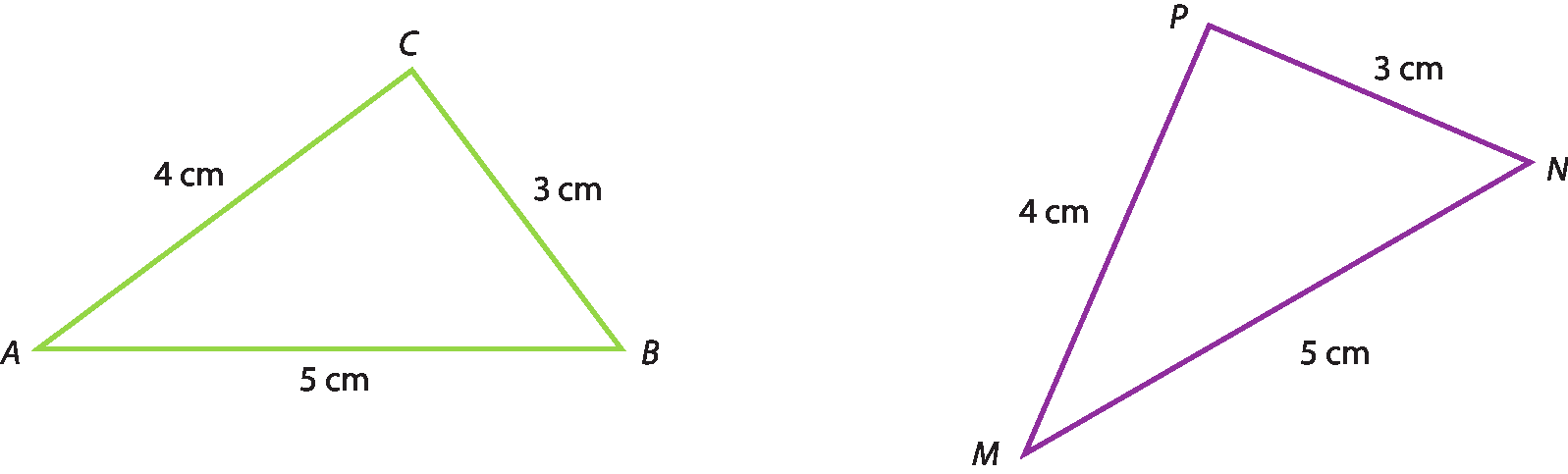
a) Resposta possível: triângulo retângulo.
b) Resposta possível: triângulo isósceles.
c) Construção de figura.
Capítulo 7 – Estudo dos triângulos
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, ampliamos o estudo dos triângulos, já desenvolvido em anos anteriores, apresentando outros elementos do triângulo conhecidos como cevianas. Para cada tipo de ceviana aqui estudada – mediana, bissetriz e altura – há três segmentos de reta (cada um com uma extremidade em um vértice), cuja intersecção constitui um ponto característico do triângulo: baricentro, incentro e ortocentro, respectivamente.
O estudo da congruência de triângulos dá continuidade ao que foi explorado para os polígonos e fornece subsídios para trabalhar, posteriormente, demonstrações de propriedades dos triângulos.
Nesta fase do aprendizado, os estudantes já devem compreender e reproduzir a abordagem dos conceitos e das ideias da Matemática de maneira mais sistematizada e axiomática.
Na abertura, apresentamos uma obra do artista plástico Alexandre Mancini, que apresenta triângulos. Verifique os conhecimentos que os estudantes já possuem sobre essa figura. Proponha a eles que façam uma composição com triângulos, podendo usar malhas triangulares. Antes de compor as produções, eles podem pesquisar outras manifestações artísticas e culturais que utilizem triângulos e, assim, podem desenvolver a competência geral 3, pois podem fruir diferentes manifestações artísticas para compor sua própria produção. Depois, exponha os trabalhos na sala de aula.
1. Cevianas de um triângulo
Já estudamos que uma importante característica do triângulo é sua rigidez. Ela pode ser observada ao se construir um triângulo com três canudinhos e linha. Não é possível deformá-lo, a não ser cortando os canudos ou a linha.
Essa característica dos triângulos é usada, principalmente, nas estruturas metálicas de pontes e torres ou no madeiramento dos telhados das casas. Observe as imagens a seguir.


O triângulo tem outras características interessantes e úteis para serem estudadas. Um exemplo é o baricentro, um dos centros geométricos definidos pelas cevianas, que veremos a seguir.
Uma laje triangular pode ser apoiada em um único ponto sem correr o risco de cair. Esse ponto é o baricentro, que tem a propriedade física de ser o centro de massa do triângulo.
Chamamos de ceviana de um triângulo todo segmento de reta que tem como extremidades um vértice e um ponto da reta suporte do lado oposto.
Pela definição, um triângulo tem infinitas cevianas, porém há três tipos especiais: as medianas, as bissetrizes e as alturas, que serão estudadas a seguir.
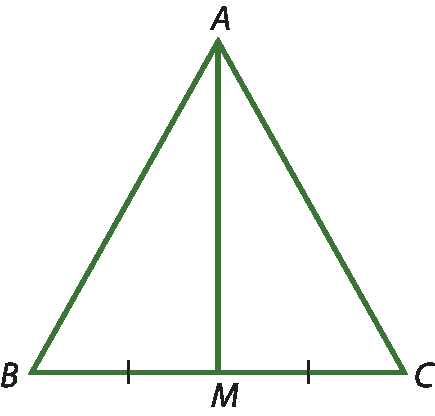
Mediana
Considerando um triângulo á bê cê qualquer, podemos determinar o ponto médio M do lado
BC.
O segmento
AMé chamado de mediana relativa ao lado
BC.
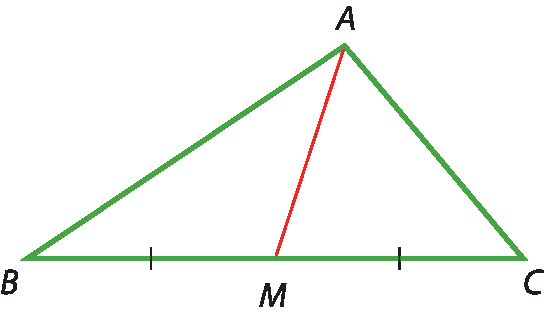
Mediana de um triângulo é toda ceviana que une um vértice ao ponto médio do lado oposto a ele.
Todo triângulo tem três medianas, que se encontram em um ponto chamado de baricentro.
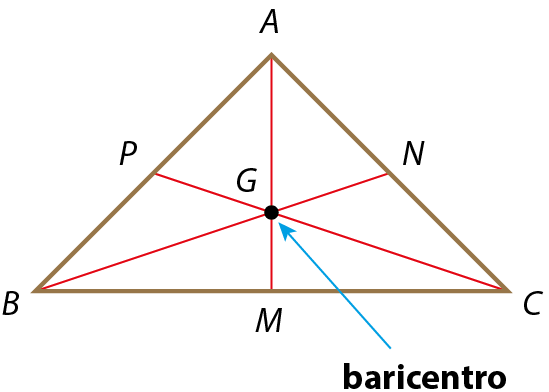
No triângulo á bê cê, temos:
•
AMé a mediana relativa ao lado
BC;
•
BNé a mediana relativa ao lado
AC;
•
CPé a mediana relativa ao lado
AB.
As três medianas se encontram no ponto G, que é o baricentro do △á bê cê.
Respostas e comentários
1. Cevianas de um triângulo
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um sete.
Esse tópico possibilita retomar os conceitos de mediatriz e de bissetriz como lugares geométricos, mobilizando a habilidade (EF08MA17), antes de explorar o conceito de cevianas de um triângulo. Se julgar necessário, relembre com os estudantes as principais características de um triângulo e suas classificações. Para isso, faça um cartaz e deixe-o afixado para consulta pelos estudantes ao longo do desenvolvimento do capítulo. Isso pode contribuir para a consolidação de tais conceitos. Algumas sugestões de informações são:
• Triângulo é um polígono de 3 lados, 3 vértices e 3 ângulos internos.
• Triângulo isósceles tem dois lados de mesma medida. O terceiro lado é chamado de base do triângulo isósceles, e o vértice oposto é denominado vértice do triângulo isósceles.
• Triângulo equilátero tem os três lados de mesma medida. Seus três ângulos internos medem 60graus.
• Triângulo retângulo tem um ângulo interno reto.
• Triângulo acutângulo tem os três ângulos internos agudos.
• Triângulo obtusângulo tem um ângulo interno obtuso.
Na apresentação da mediana, retome ponto médio de um segmento de reta. Ressalte aos estudantes que cada segmento que é mediana relativa a algum lado do triângulo passa pelo ponto médio desse lado, assim como a reta mediatriz desse segmento. Podem-se desenvolver atividades investigativas, com régua e compasso ou com softwares de geometria dinâmica, envolvendo a construção de triângulos com o objetivo de obter um triângulo tal que a mediatriz de um de seus lados contenha a mediana relativa a esse lado. Essa atividade pode ser retomada após o estudo dos casos de congruência de triângulos, por exemplo, pedindo aos estudantes que demonstrem que, quando a mediatriz de um lado contém a mediana relativa a esse lado, o triângulo é isósceles.
De fato, seja um triângulo qualquer ABC, tal que M é o ponto médio do lado
ACe
BMseja perpendicular a esse lado. Assim, o segmento
BMé a mediana relativa a
AC, e a reta
BMé mediatriz de
AC. Além disso, os triângulos á ême bê e CMB serão congruentes (pelo caso éle á éle); portanto,
ABe
BCsão congruentes e, assim, o triângulo ABC é isósceles.
Ao incentivar investigações e demonstrações, possibilita-se que os estudantes desenvolvam a competência geral 2, pois exercitam a curiosidade intelectual e recorrem à imaginação e à criatividade para elaborar e testar hipóteses. Além disso, a competência geral 7 também é utilizada pelos estudantes, ao argumentarem e demonstrarem os fatos matemáticos.
Propriedade do baricentro
Podemos construir um triângulo em uma cartolina e determinar seu baricentro.
Para isso, recortamos esse triângulo e passamos um barbante pelo baricentro.

Segurando o triângulo suspenso, como mostra a fotografia, ele se manterá na posição horizontal. Isso ocorre porque o baricentro é o ponto de equilíbrio, ou centro de gravidade, do triângulo.
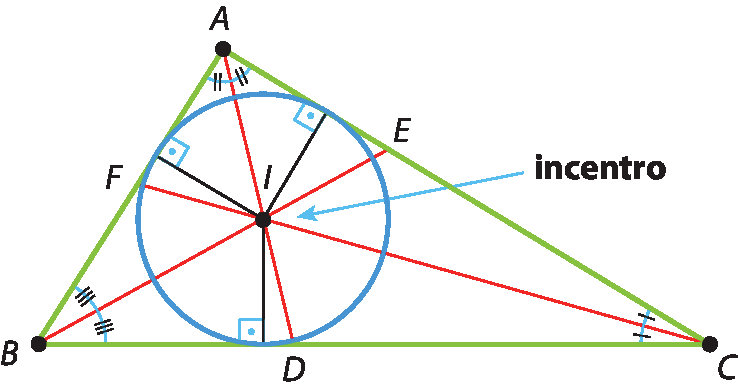
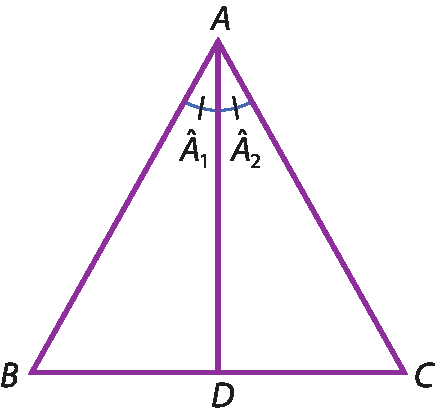
Bissetriz
Considerando um triângulo ABC qualquer, podemos traçar a bissetriz do ângulo interno
A.
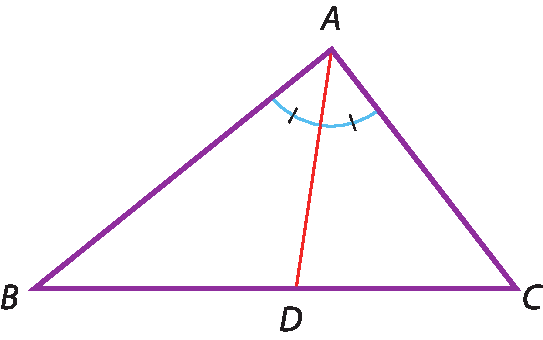
O segmento
ADé a bissetriz do triângulo relativa ao ângulo
A.
Bissetriz de um triângulo é toda ceviana que divide ao meio um dos ângulos internos do triângulo.
Todo triângulo tem três bissetrizes, que se encontram em um ponto chamado de incentro.
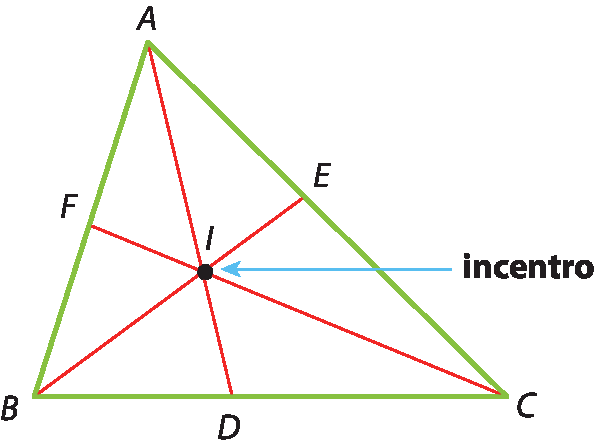
No triângulo á bê cê, temos:
•
Segmento A Dé a bissetriz relativa ao ângulo
A;
•
Segmento B Eé a bissetriz relativa ao ângulo
B;
•
Segmento C Fé a bissetriz relativa ao ângulo
C.
As três bissetrizes se encontram no ponto ih, que é o incentro do △á bê cê.
Conforme já estudamos, a bissetriz é o lugar geométrico dos pontos que estão à mesma distância das retas que formam o ângulo. Logo, o incentro está à mesma distância dos três lados do triângulo, ou seja, ele é o centro da circunferência inscrita no triângulo.

Respostas e comentários
Orientação: Espera-se que os estudantes respondam que não, pois os raios da circunferência nos pontos de tangência são perpendiculares aos lados do triângulo.
Propriedade do baricentro
O baricentro, intersecção das três medianas de um triângulo, é um ponto de propriedades especiais. Se julgar conveniente, comente que, em cada mediana, a distância do vértice ao baricentro é igual ao dôbro da distância do baricentro ao ponto médio do lado oposto a esse vértice.
Proponha, ainda, aos estudantes que realizem a experimentação descrita para verificarem que o baricentro é o ponto de equilíbrio do triângulo (como mostrado na fotografia).
Bissetriz
Na apresentação da bissetriz de um triângulo, retome o conceito de bissetriz de um ângulo.
Comente que cada segmento que é bissetriz do triângulo está contido na semirreta que é a bissetriz do ângulo considerado. Nesse caso, o ponto a ser destacado é o incentro, intersecção das três bissetrizes de um triângulo, que é o centro da circunferência inscrita no triângulo.
Possibilite aos estudantes realizar atividades em que determinam a circunferência inscrita de alguns triângulos, utilizando régua e compasso e, se possível, também utilizando recursos de algum software de Geometria Dinâmica. Advirta-os quanto a terem cuidado no manuseio do compasso, a fim de que não se machuquem com a ponta-sêca.
Clique no play e acompanhe as informações do vídeo.
Observação
▶ A mediatriz de um lado de um triângulo é a reta perpendicular a esse lado que passa pelo seu ponto médio. Todo triângulo tem três mediatrizes, que se encontram em um único ponto denominado circuncentro.
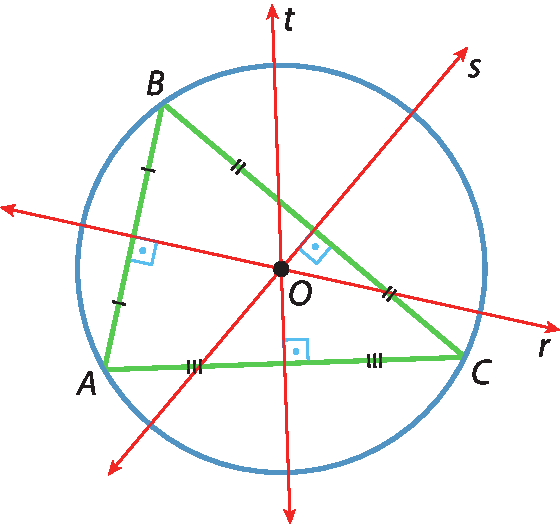
O circuncentro é o centro da circunferência que circunscreve o triângulo. Na figura, o ponto óh é o circuncentro do triângulo á bê cê.
Altura
Considerando um triângulo á bê cê qualquer, podemos traçar, pelo ponto a, um segmento perpendicular à reta suporte do lado
BC.
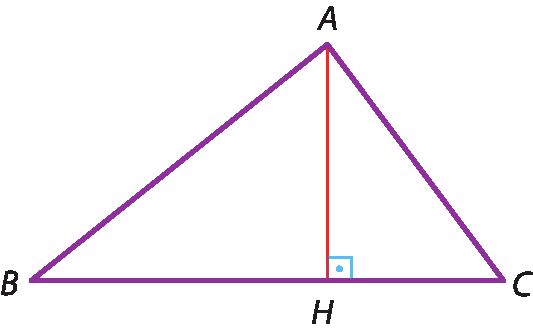
O segmento
AHé a altura relativa ao lado
BC.
Altura de um triângulo é a ceviana que une perpendicularmente um dos vértices ao seu lado oposto (ou ao seu prolongamento).
No triângulo anterior, o ponto H é chamado de “pé da altura” relativa ao lado
BC.
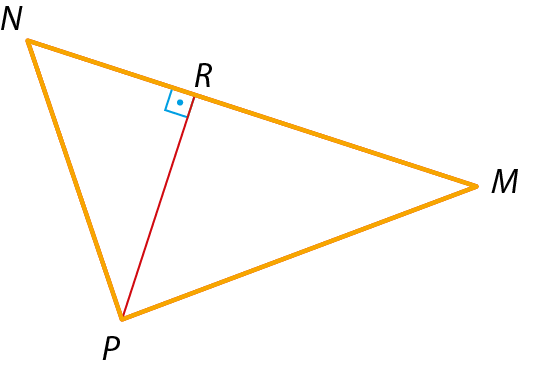
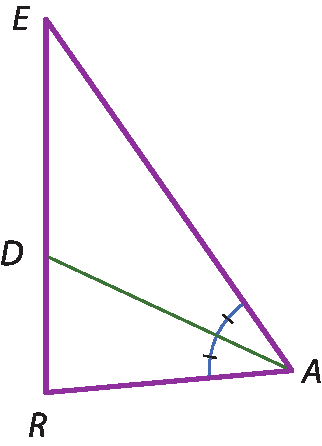
Observe a altura
P Rrelativa ao lado
segmento de reta MNem cada um dos triângulos a seguir.
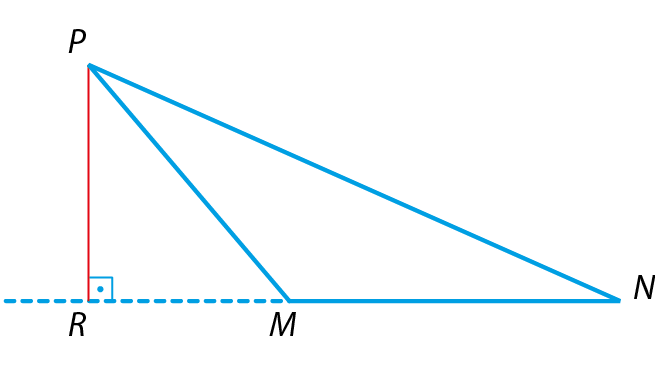
Todo triângulo tem três alturas. O ponto de encontro das retas que contêm as alturas é chamado de ortocentro.
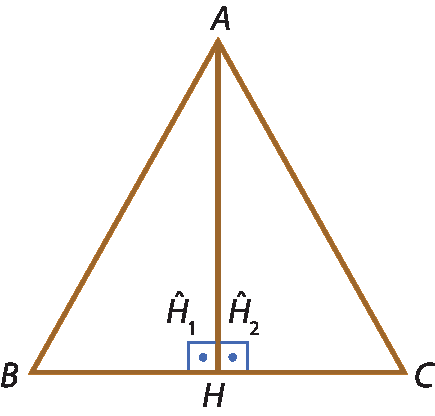
Considere o triângulo acutângulo á bê cê a seguir.
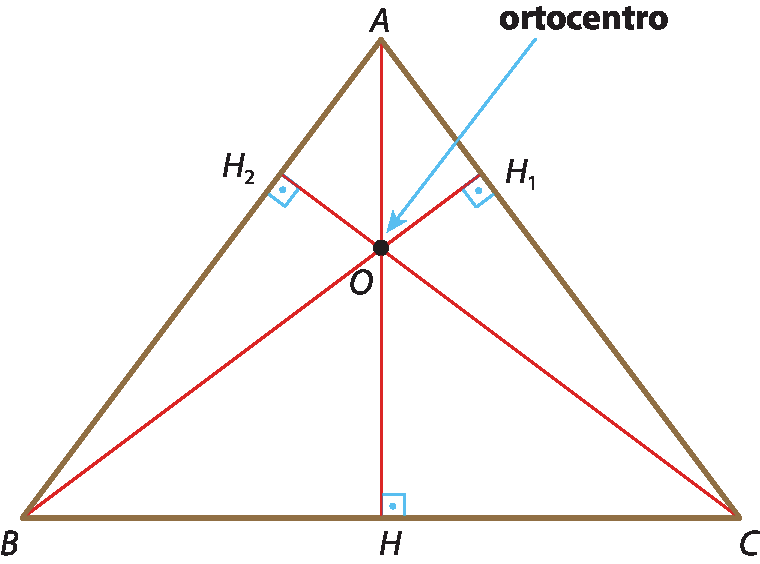
Nesse triângulo, temos:
•
AHé a altura relativa ao lado
BC;
•
Segmento B H1é a altura relativa ao lado
AC;
•
Segmento C H2é a altura relativa ao lado
segmento de reta AB.
As três alturas se encontram no ponto óh, que é o ortocentro do △á bê cê.
Observe que, neste caso, o ortocentro se localiza no interior do triângulo. Isso acontece em todos os triângulos acutângulos.
Respostas e comentários
Altura
Das três cevianas, provavelmente a mais conhecida é a altura, por estar presente no cálculo da área do triângulo. Ela também é a única das cevianas que pode ficar fora da região interna do triângulo, neste caso, sendo determinada considerando o prolongamento do lado. Trabalhe com exemplos nos quais isso ocorre.
O ortocentro é o ponto de intersecção das retas suporte das três alturas de um triângulo e pode ficar fora da região interna do triângulo. Apresente exemplos aos estudantes e proponha que representem diferentes triângulos e determinem as alturas relativas a cada lado dos triângulos representados.
Peça que verifiquem onde se encontra o ortocentro no caso de um triângulo retângulo. Espera-se que eles percebam que, nesse caso, o ortocentro coincide com o vértice do ângulo reto.
Agora, considere o triângulo obtusângulo á bê cê.
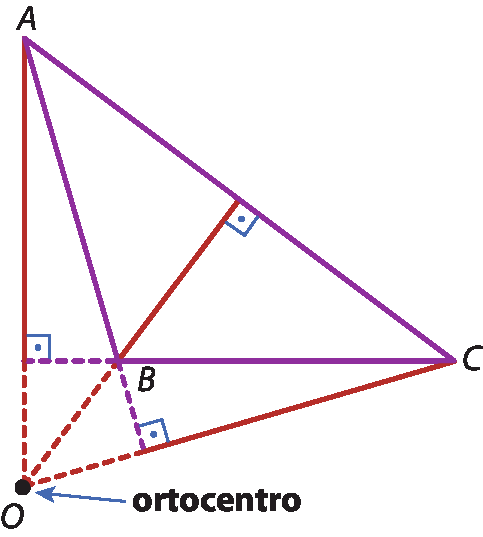
Nesse triângulo, o ortocentro encontra-se na região externa ao triângulo.
Isso acontece em todos os triângulos obtusângulos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Em cada um dos triângulos a seguir, o segmento
A Dé mediana, bissetriz ou altura?
a)
b)
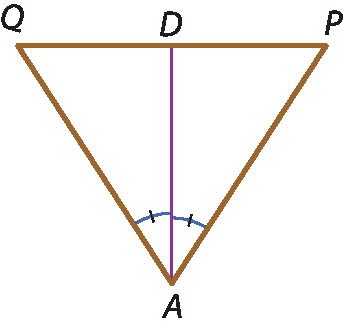
c)
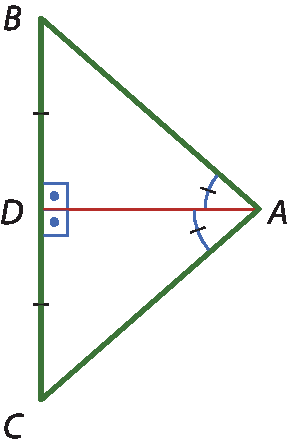
d)
2 No caderno, desenhe os triângulos pedidos em cada caso e responda às questões.
a) Triângulo ême êne ó qualquer. Trace, com régua e compasso, as medianas relativas aos lados
M Oe
N O. Como se chama o ponto em que elas se encontram?
b) Triângulo PQR qualquer. Trace, usando transferidor e régua, as bissetrizes dos ângulos
Pe
R. Como se chama o ponto em que elas se encontram?
c) Triângulo tê ú vê qualquer. Trace, com régua e esquadro, as alturas relativas aos lados
T Ue
T V. Como se chama o ponto em que as retas suporte delas se encontram?
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)
3 No caderno, desenhe um triângulo á bê cê qualquer e trace a bissetriz relativa ao ângulo
Be a mediatriz relativa ao lado
BC. Explique como você traçou a bissetriz e a mediatriz desse triângulo.
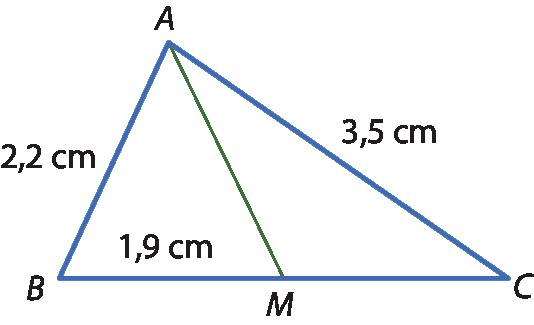
4 No triângulo á bê cê a seguir,
AMé a mediana. Determine a medida do perímetro desse triângulo.
5 No caderno, desenhe um triângulo retângulo érre ésse tê. E trace as mediatrizes dos lados desse triângulo, que se encontram no ponto óh. Depois, com o auxílio de um compasso, trace uma circunferência de centro O e raio
O R.
Explique como você determinou as mediatrizes.
6 Construa, no caderno, um triângulo á bê cê que seja escaleno e acutângulo. Com esquadro e régua, trace as três alturas do triângulo. Qual delas é a maior?
7 Construa, no caderno, um triângulo á bê cê isósceles não equilátero.
a) Trace a mediana relativa à base
BC.
b) Trace a bissetriz do ângulo do vértice a.
c) A bissetriz coincidiu com a mediana?
d) Trace a altura relativa à base. O que aconteceu com a altura e com a mediana?
8

Hora de criar – Construa um triângulo á bê cê, retângulo em B, qualquer. Troque com um colega para que cada um trace as três alturas no triângulo construído pelo outro e obtenha o ortocentro H.
O que você pode falar sobre os pontos H e B? Acontece o mesmo com o ortocentro obtido por seu colega? Verifique se aconteceu o mesmo com os outros colegas da turma.
Respostas e comentários
1. a) Altura.
1. b) Bissetriz.
1. c) Mediana, bissetriz e altura.
1. d) Bissetriz.
2. a) Construção de figura; baricentro.
2. b) Construção de figura; incentro.
2. c) Construção de figura; ortocentro.
3. Construção de figura; resposta pessoal.
4. 9,5 centímetros
5. Construção de figura; resposta pessoal.
6. Altura relativa ao lado menor.
7. a) Construção de figura.
7. b) Construção de figura.
7. c) Sim.
7. d) Elas coincidiram.
8. Os pontos H e B coincidem para todos os triângulos retângulos em B.
Exercícios propostos
As resoluções dos exercícios 1 e 2, dos exercícios 4 a 6 e do exercício 8 estão no início deste Manual, nas orientações específicas do capítulo 7.
Para os exercícios 3 e 5, por exemplo, os estudantes podem registrar passo a passo as construções utilizando fluxogramas; assim, aprimoram aspectos importantes para o desenvolvimento posterior da habilidade (ê éfe zero oito ême ah um seis).
Para o exercício 3, uma possível construção da bissetriz:
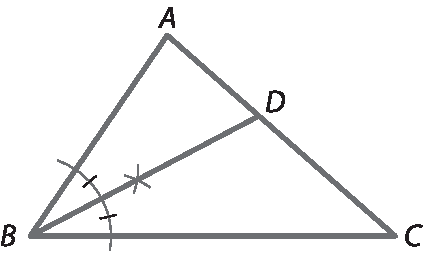
Possível construção da mediatriz:
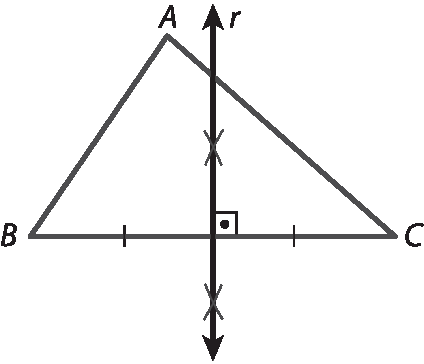
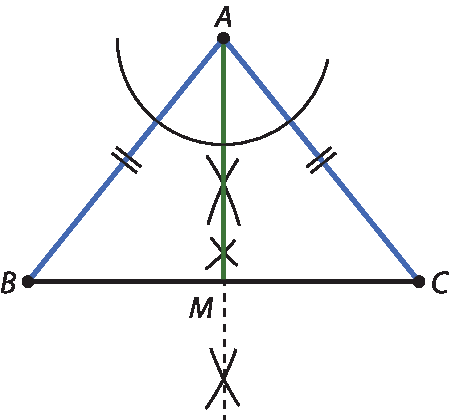
No exercício 7, a particularidade do triângulo leva a outra propriedade do triângulo isósceles: a mediana, a altura e a bissetriz, todas relativas à base do triângulo isósceles, são coincidentes. Segue a possível construção para os itens a, b e d.
PARA SABER MAIS


Geometria e grafite
O trabalho de um artista urbano, diferente das outras fórmas de compor arte, está disponível até aos desinteressados. O poeta Paulo Leminski pichavaglossário nas ruas de Curitiba em 1980 um poema curto que dizia: “palpite/ o grafite não tem limite”. O significado desse poema impresso na pele da cidade faz relação com o caráter espontâneo da arte urbana. É impossível não notar um grafite ao trafegar pelas ruas de uma cidade. [reticências]
Fonte: GEOMETRIA da cidade nas alturas. Diário da manhã, Goiânia, 28 junho 2017. Seção Cultura. Disponível em: https://oeds.link/vXBTt3. Acesso em: 12 julho 2022.
O grafite surgiu no Brasil no final da década de 1970, influenciado pelo movimento hip-hop vindo dos Estados Unidos. Para esse movimento, o grafite é a maneira de expressar toda a opressão que a humanidade vive, principalmente os menos favorecidos, ou seja, o grafite reflete a realidade das ruas. No entanto, se não tiverem autorização, a pichação e o grafite em espaços públicos ou privados podem ser considerados crimes.
Com o passar do tempo, diferentes técnicas de grafite surgiram, e muitos artistas brasileiros tornaram-se reconhecidos mundialmente pelo trabalho realizado. Entre eles, o artista Eduardo Kobra, que tem seu trabalho representado em diferentes murais pelo mundo.

Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 O artista utilizou triângulos na composição da obra Ellis Island. Como esses triângulos podem ser classificados?
2 Antes de realizar trabalhos como esse, os artistas costumam fazer um planejamento, no papel, dividindo a superfície em áreas menores, que servirá de orientação para o trabalho final. Suponha que você tenha de compor um mural de formato retangular com um grafite composto de figuras geométricas. Faça a representação, em um papel, de como seria esse grafite e apresente-o aos colegas.
Respostas e comentários
1. Espera-se que os estudantes identifiquem triângulos que podem ser associados a triângulos isósceles e a triângulos isósceles retângulos.
2. Resposta pessoal.
Para saber mais
Nesta seção é apresentado o grafite como uma fórma de levar a arte ao acesso de todos, além de atuar como instrumento de crítica social, chamando a atenção para problemas sociais atuais, como desigualdade social, desigualdade de gênero, preconceito, criminalidade, escassez de moradia, entre outros. Ao abordar esse tema é possível trabalhar com os estudantes o Tema Contemporâneo Transversal vida familiar e social. Converse com eles sobre como esse tipo de arte urbana tem papel importante nas transformações sociais.
Comente que o grafite é uma fórma de manifestação cultural e artística presente em diversos países e que costuma retratar o dia a dia, os diversos pontos de vista, as experiências e os valores de diferentes pessoas das mais variadas culturas. Essa discussão favorece o desenvolvimento da competência geral 3 e o trabalho com o Tema Contemporâneo Transversal diversidade cultural.
A respeito da legalidade do grafite, comente que, desde 2011, de acôrdo com a Lei número 12.408, a prática do grafite “[reticências] realizada com o objetivo de valorizar o patrimônio público ou privado mediante manifestação artística, desde que consentida pelo proprietário [reticências]” deixou de ser considerada crime.
O exercício 2 do Agora é com você! possibilita que os estudantes desenvolvam a competência geral 4, ao propor que eles utilizem a linguagem visual e conhecimentos das linguagens artística e matemática para expressar experiências, ideias e sentimentos na criação de um mural. Incentive-os a trabalharem com temas relacionados ao seu contexto social.
2. Congruência de triângulos
Já estudamos congruência de polígonos. Como qualquer polígono pode ser dividido ou decomposto em triângulos, o estudo da congruência de triângulos pode nos auxiliar em problemas mais complicados que envolvam a congruência de polígonos.
Agora, vamos estudar, em particular, os triângulos congruentes.
Dois triângulos são congruentes quando os lados correspondentes e os ângulos correspondentes forem congruentes.
Observe as figuras a seguir.
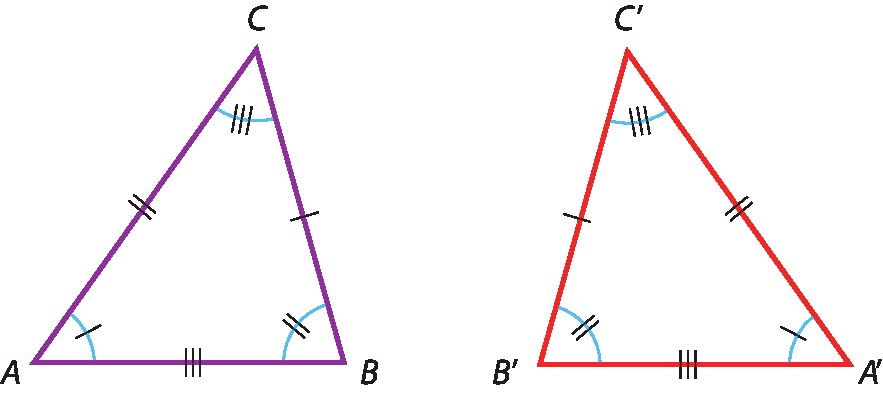
Nessas figuras, o △á bê cê ≅ △á linha bê linha cê linha (lemos “o triângulo á bê cê é congruente ao triângulo á linha bê linha cê linha ”), ou seja:
Ângulo A congruente ângulo a linha
e
Ângulo B congruente ao ângulo B linhaÂngulo C congruente ao ângulo C linha
Observe que, se dois triângulos são congruentes, então:
• os lados correspondentes opostos a ângulos congruentes são congruentes;
• os ângulos correspondentes opostos a lados congruentes são congruentes.
Acompanhe os exemplos.
a) Sabendo que △á bê cê ≅ △ême êne pê, vamos indicar os lados congruentes.
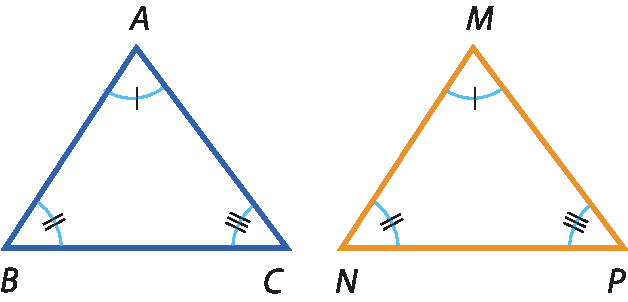
Nesses triângulos, temos:
•
Segmento de reta AB congruente ao segmento de reta MN(lados opostos a ângulos congruentes:
Ângulo C congruente ângulo P•
Segmento de reta BC congruente ao segmento e reta NP(lados opostos a ângulos congruentes:
Ângulo A congruente ângulo M•
Segmento de reta AC congruente ao segmento de reta MP(lados opostos a ângulos congruentes:
Ângulo B congruente ângulo Nb) Sabendo que △á bê cê ≅ △ême êne pê, vamos indicar os ângulos congruentes.
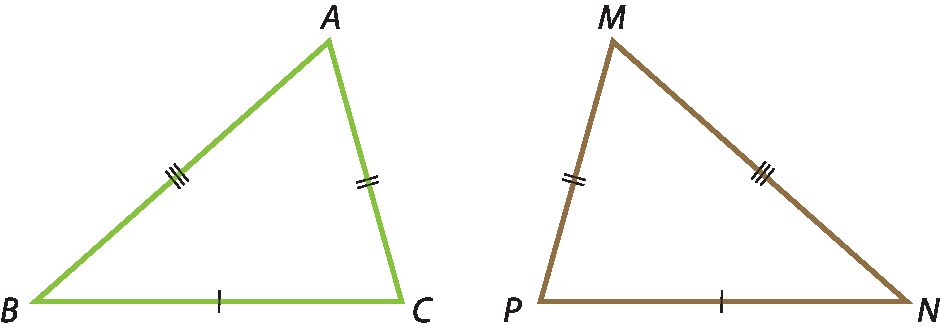
Nesses triângulos, temos:
•
Ângulo A congruente ângulo M(ângulos opostos a lados congruentes:
Segmento de reta BC congruente ao segmento de reta PN);
•
ângulo B congruente ângulo N(ângulos opostos a lados congruentes:
Segmento de reta AC congruente ao segmento de reta MP);
•
Ângulo C congruente ângulo P(ângulos opostos a lados congruentes:
Segmento de reta AB congruente ao segmento de reta MN).
Respostas e comentários
2. Congruência de triângulos
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um quatro.
Este tópico aborda os casos de congruência de triângulos; assim, prepara os estudantes para, posteriormente, desenvolverem a habilidade (ê éfe zero oito ême ah um quatro).
Retome a congruência de polígonos e a notação própria utilizada para a congruência.
Pode-se propor aos estudantes que, em uma folha de papel, com régua e transferidor, representem determinado triângulo, dadas as medidas de dois lados e do ângulo formado entre eles. Depois, eles recortam o triângulo representado e comparam com as produções dos demais colegas, a fim de verificar que todos os triângulos produzidos são congruentes.
Solicite a eles que façam outros triângulos dessa maneira para os compararem novamente, mas utilizando outras informações, por exemplo, dada a medida de um dos segmentos e a medida de cada ângulo formado entre esse segmento e os demais lados do triângulo.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
9 Em cada item, os pares de triângulos são congruentes. Indique no caderno a congruência entre os lados desses triângulos.
a)
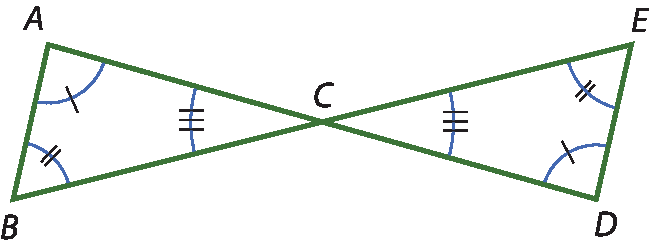
b)
10 Em cada item, os pares de triângulos são congruentes. Indique no caderno a congruência entre os ângulos desses triângulos.
a)
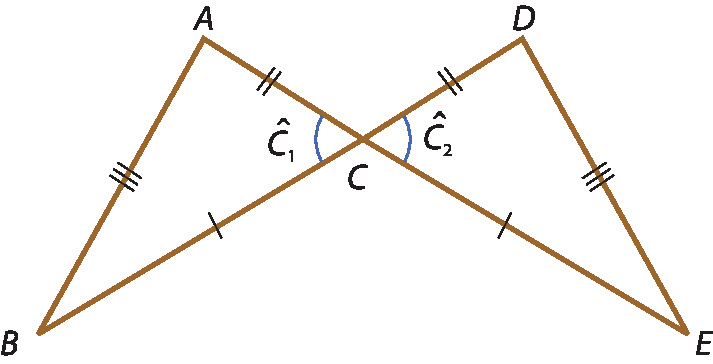
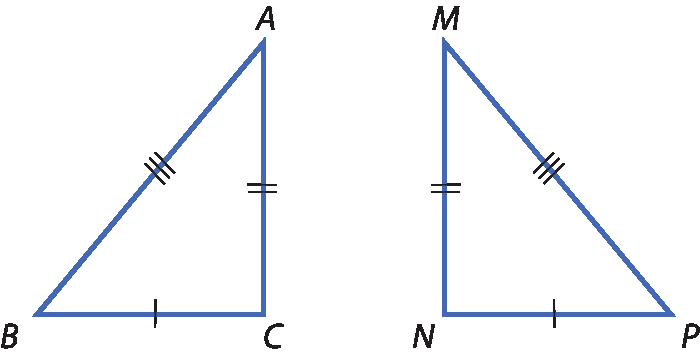
b)
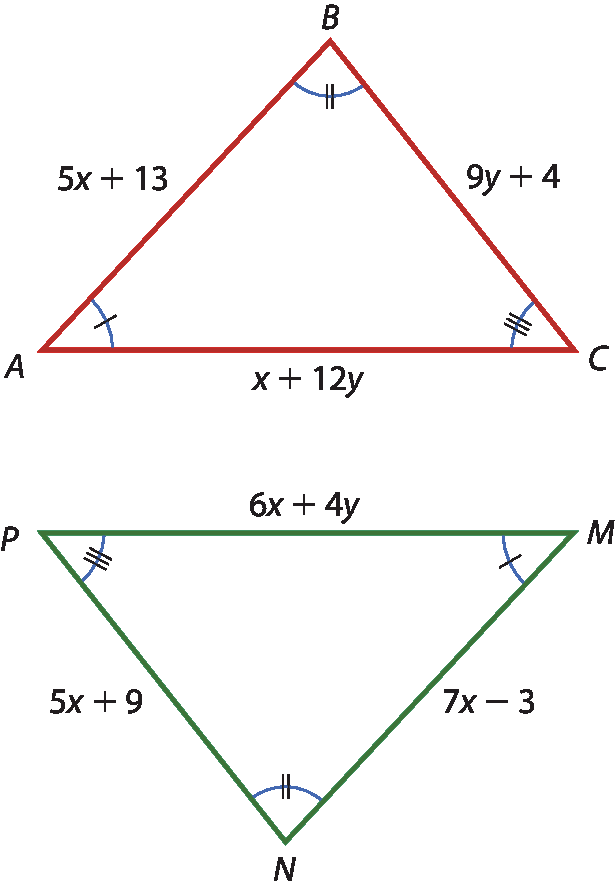
11 Sabendo que △á bê cê ≅ △ême êne pê, calcule x e y.
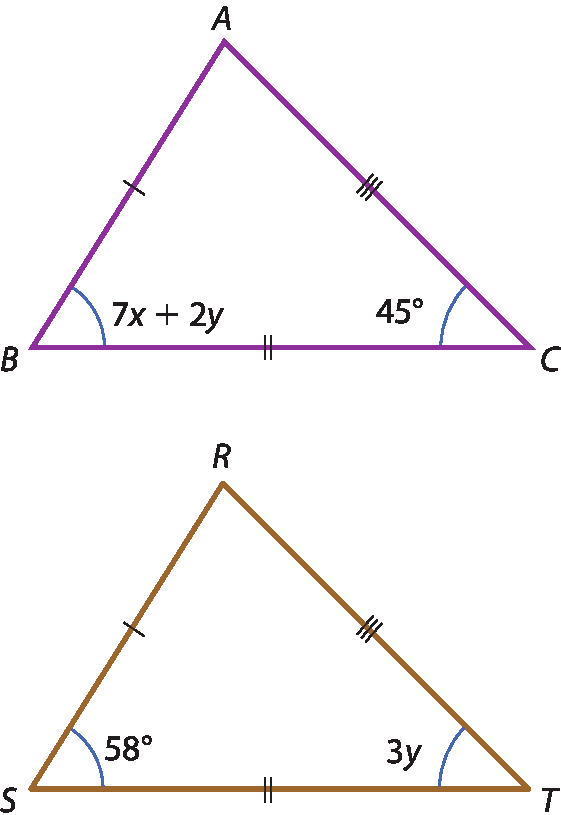
12 Calcule x e y, em grau, sabendo que △á bê cê ≅ △érre ésse tê.
Casos de congruência de triângulos
Vimos que dois triângulos são congruentes quando os lados correspondentes e os ângulos correspondentes são, respectivamente, congruentes e, assim, podemos sobrepô-los. Isso significa que, para concluir que dois triângulos são semelhantes, devemos verificar seis congruências, com três pares de lados e com três pares de ângulos.
No entanto, em algumas situações, é possível reconhecer a congruência de dois triângulos quando são conhecidos apenas três de seus elementos. Isso é feito por meio dos casos de congruência, que vamos estudar a seguir.
Respostas e comentários
9. a)
Segmento de reta AB congruente ao segmento de reta DESegmento de reta AC congruente ao segmento de reta DC
Segmento de reta BC congruente ao segmento de reta EC
9. b)
Segmento de reta AC congruente ao segmento de reta QRSegmento de reta BC congruente ao segmento de reta PR
Segmento de reta AB congruente ao segmento de reta QP
10. a)
Ângulo A congruente ângulo DÂngulo B congruente ângulo E
ângulo C1 congruente ângulo C2
10. b)
ângulo A congruente ângulo MAngulo B congruente ângulo P
Ângulo C congruente ângulo N
11. x = 8; y = 5
12. x = 4graus; y = 15graus
Exercícios propostos
Neste bloco de exercícios, os estudantes aplicarão o conceito de congruência de triângulos.
Ressalte a importância de tomar na ordem correta os elementos correspondentes entre os dois triângulos considerados para determinar a congruência (ou não) desses triângulos.
As resoluções dos exercícios 9 a 12 estão no início deste Manual, nas orientações específicas do capítulo 7.
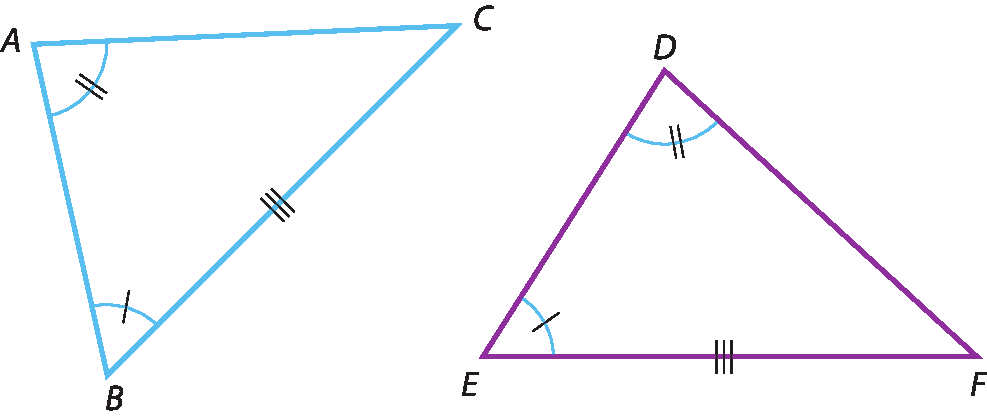
Caso lado-lado-lado (éle éle éle)
Dois triângulos são congruentes quando têm os três lados respectivamente congruentes.
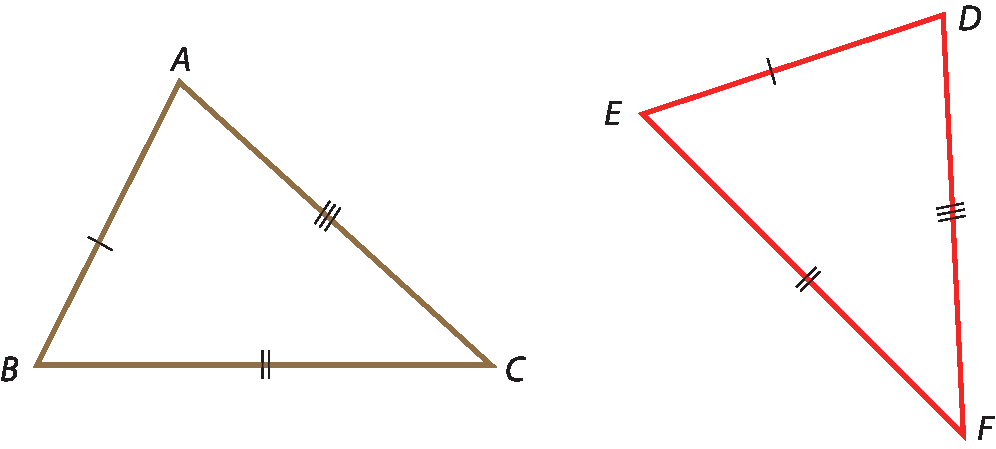
Como exemplo, considere os triângulos a seguir.
Note que esses triângulos têm os três lados correspondentes com medidas iguais, ou seja, são congruentes (
Segmento de reta AB congruente ao segmento de reta MN,
Segmento de reta BC congruente ao segmento e reta NPe
Segmento de reta AC congruente ao segmento e reta MP). Isso garante, pelo caso lado lado lado, que os triângulos á bê cê e ême êne pê sejam congruentes.

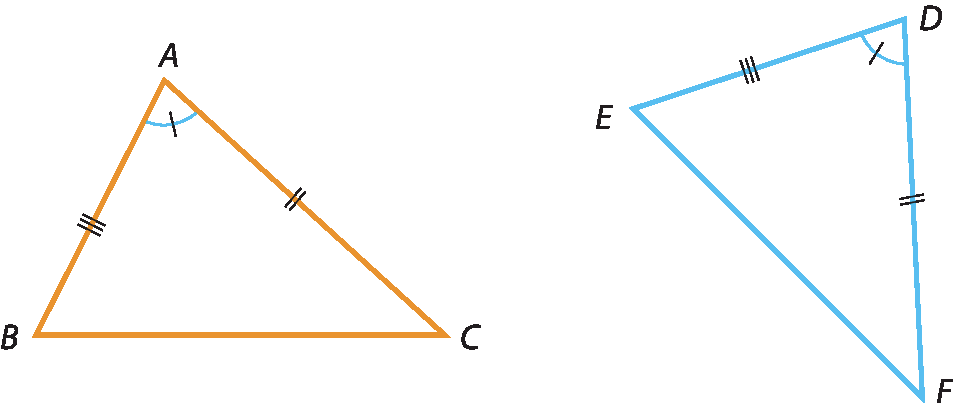
Caso lado-ângulo-lado (éle á éle)
Dois triângulos são congruentes quando têm dois lados e o ângulo compreendido entre eles respectivamente congruentes.
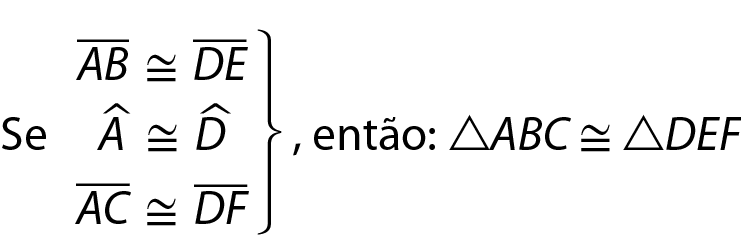
Respostas e comentários
Caso lado-lado-lado (LLL)
Incentive os estudantes a realizarem a experimentação proposta: decalcar o triângulo ême êne pê em uma folha de papel de seda (solicitada previamente) e sobrepor o decalque ao triângulo á bê cê, fazendo coincidir os lados correspondentes.
É importante comentar com eles que cada congruência entre lados correspondentes dos dois triângulos considerados deve ser justificada para que possamos utilizar o caso lado lado lado de congruência de triângulos. Por exemplo, considere o triângulo isósceles á bê cê a seguir, em que M é ponto médio do lado
BC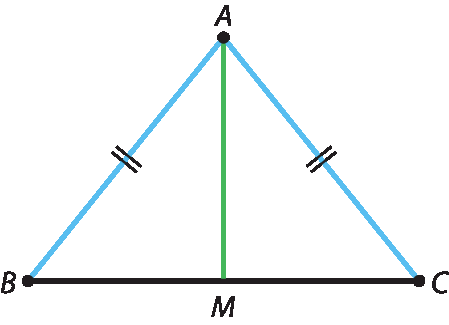
Podemos concluir a congruência dos triângulos á bê ême e á cê ême pelo caso lado lado lado da seguinte maneira:
•
Segmento de reta AB congruente ao segmento de reta AC(lados de mesma medida em triângulo isósceles)
•
Segmento de reta AM congruente ao segmento de reta AM
(lado comum)
•
Segmento de reta BM congruente ao segmento de reta CM
(M é ponto médio de
BC)
Como exemplo, considere os triângulos a seguir.
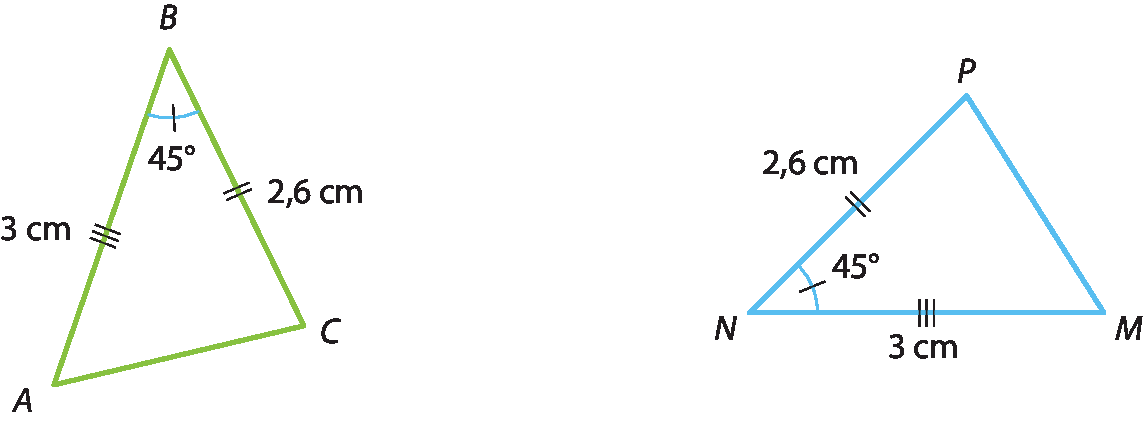
Esses triângulos têm dois lados correspondentes congruentes (
Segmento de reta AB congruente ao segmento e reta MNe
Segmento de reta BC congruente ao segmento e reta NP), e os ângulos compreendidos por esses lados também são congruentes (
Ângulo B congruente ângulo N). Isso garante, pelo caso lado ângulo lado, que os triângulos á bê cê e ême êne pê sejam congruentes.
Observação
▶ No caso lado ângulo lado, assim como nos casos que vamos estudar a seguir, a ordem dos elementos deve ser respeitada para verificar a congruência entre os triângulos.
Para exemplificar, considere os triângulos á bê cê e dê ê éfe.
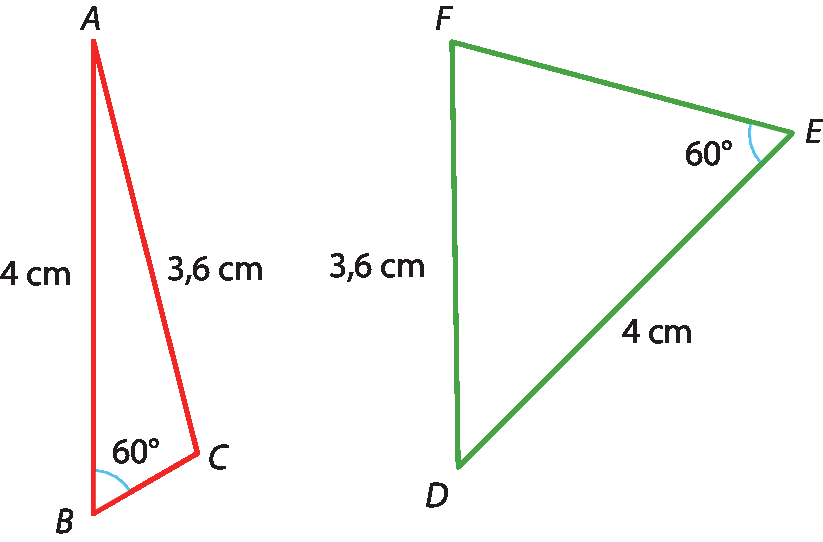
Com régua e transferidor, verifique que os triângulos á bê cê e dê ê éfe têm dois lados congruentes e um ângulo congruente, mas não são triângulos congruentes.
Caso ângulo-lado-ângulo (á éle á )
Dois triângulos são congruentes quando têm dois ângulos e o lado adjacente a esses ângulos respectivamente congruentes.
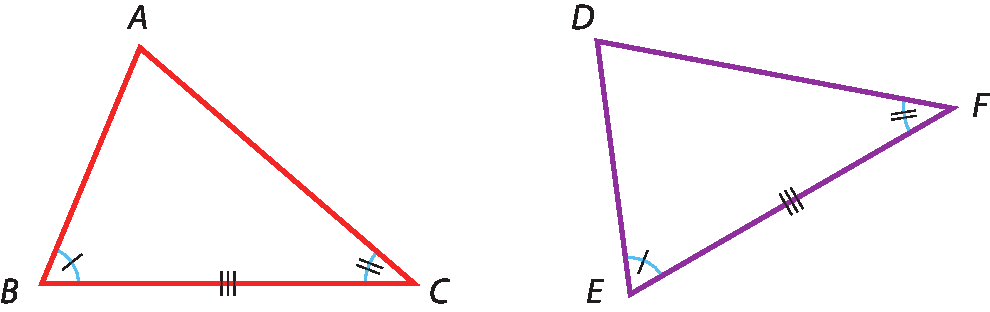
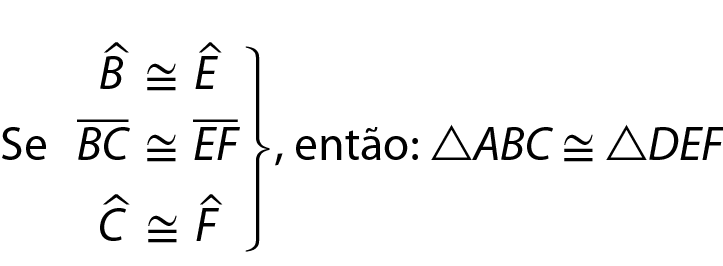
Como exemplo, considere os triângulos a seguir.
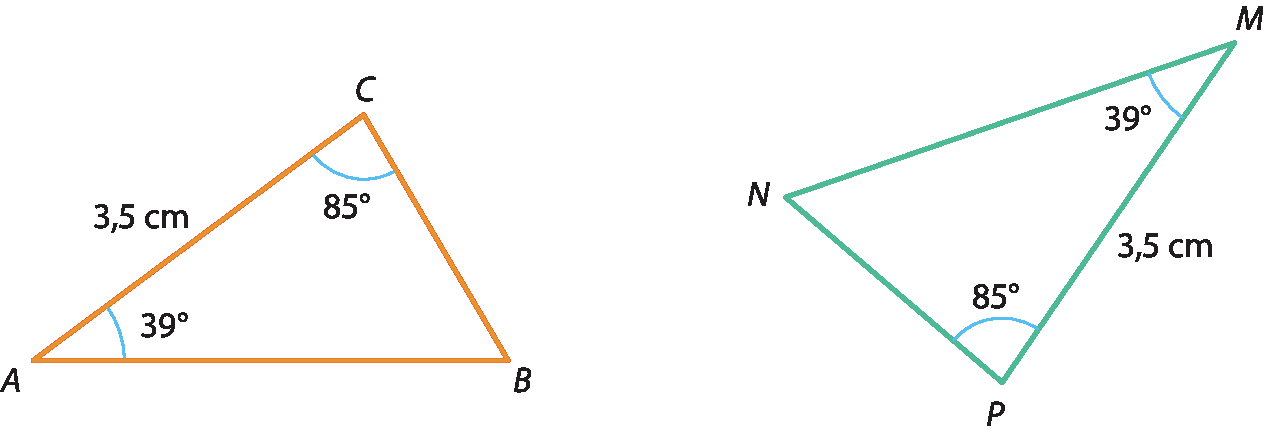
Esses triângulos têm dois ângulos correspondentes congruentes (
Ângulo A congruente ângulo Me
Ângulo C congruente ângulo P), e os lados adjacentes a esses ângulos também são congruentes (
Segmento de reta AC congruente ao segmento de reta MP). Isso garante, pelo caso ângulo-lado-ângulo, que os triângulos á bê cê e ême êne pê sejam congruentes.
Respostas e comentários
Caso lado‑ângulo‑lado (éle á éle) e caso ângulo‑lado‑ângulo (á éle á )
Para explorar os casos de congruência lado ângulo lado e ângulo-lado-ângulo, forneça aos estudantes pares de triângulos congruentes envolvendo esses dois casos para que os identifiquem. Além disso, sugerimos retomar a construção de triângulos para cada um desses casos, de maneira que cada estudante represente o triângulo cujas medidas de dois lados e a do ângulo entre eles sejam dadas para, depois, comparar as produções e perceber que ocorre a congruência. De maneira análoga, eles representam o triângulo cujas medidas de um lado e dos dois ângulos que ele determina (com os demais lados) sejam dadas.
Esse tipo de atividade em que os estudantes verificam que ocorre uma propriedade pode desenvolver a competência geral 2, pois exercitam a curiosidade intelectual, podendo ser, também, incentivados a justificar ou demonstrar as propriedades observadas ou hipóteses.
Caso lado-ângulo-ângulo oposto (éle á áo)
Dois triângulos são congruentes quando têm um lado, o ângulo adjacente a esse lado e um ângulo oposto a esse lado respectivamente congruentes.
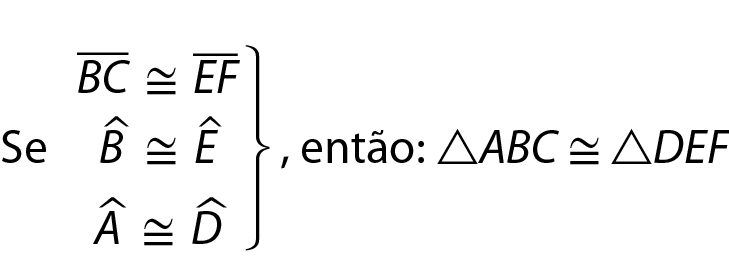
Como exemplo, considere os triângulos a seguir.
Esses triângulos têm, respectivamente, congruentes: um lado (
Segmento de reta BC congruente ao segmento e reta NP), um ângulo adjacente a esse lado (
Ângulo B congruente ângulo N) e o ângulo oposto ao lado congruente (
Ângulo A congruente ângulo M). Desse modo, pelo caso lado-ângulo-ângulo opostoo , garantimos que os triângulos á bê cê e ême êne pê sejam congruentes.

Observação
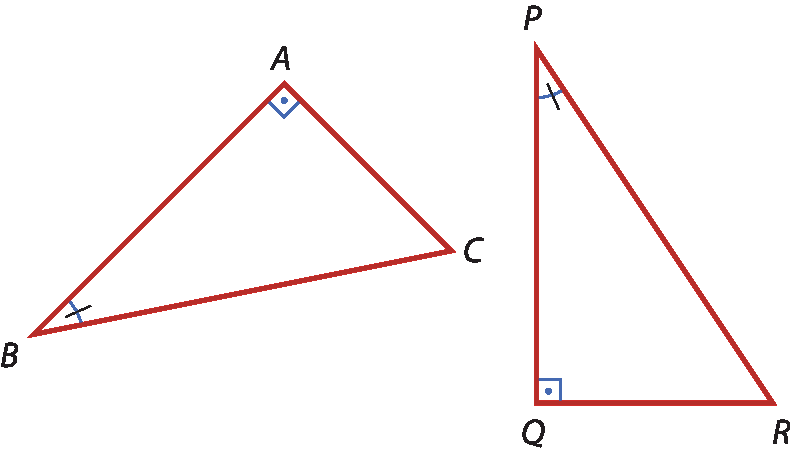
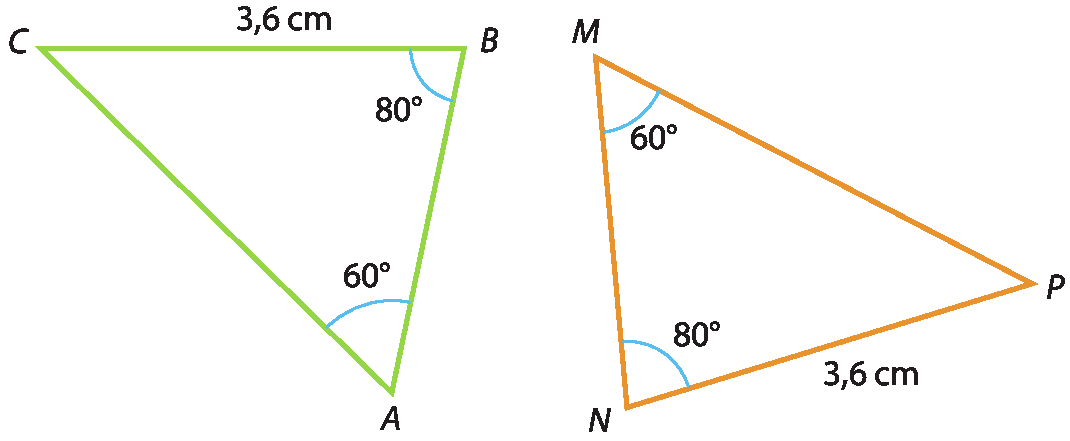
▶ Além dos quatro casos de congruência de triângulos estudados, vamos conhecer um caso válido somente para os triângulos retângulos, o caso cateto-hipotenusa (cê agá).
Dois triângulos retângulos são congruentes quando têm a hipotenusa e um cateto respectivamente congruentes.
Considere os triângulos retângulos á bê cê e ême êne pê, com
Segmento de reta AC congruente ao segmento de reta MPe
Segmento de reta AB congruente ao segmento de reta MN.
Então, pelo caso cateto-hipotenusa, os triângulos á bê cê e ême êne pê são congruentes.
Respostas e comentários
Caso lado-ângulo-ângulo oposto (éle á áO)
Antes de tratar do caso lado-ângulo-ângulo opostoo, represente alguns triângulos na lousa e peça aos estudantes que identifiquem ângulos opostos a determinados lados desses triângulos, de modo que não fiquem dúvidas quanto a essa nomenclatura.
Apresente-lhes o caso lado-ângulo-ângulo opostoo e, em seguida, forneça a eles pares de triângulos congruentes envolvendo esse caso para que os identifiquem.
Se julgar pertinente, incentive os estudantes a demonstrarem o caso cateto-hipotenusa. Considerando dois triângulos retângulos, á bê cê e ême êne pê, tais que
segmento de reta ABe
segmento de reta MNsejam congruentes e
segmento de reta ACe
segmento de reta MPsejam suas hipotenusas e congruentes, pode-se transladar o triângulo ême êne pê de maneira que
segmento de reta ACe
segmento de reta MPcoincidam, obtendo o quadrilátero á bê cê êne. Como os ângulos internos em B e em N são retos, os lados opostos do quadrilátero são paralelos, ou seja, tal quadrilátero é um paralelogramo. Assim, os lados opostos são congruentes; portanto, os triângulos que o compõem são congruentes.
Ao trabalhar demonstrações, os estudantes desenvolvem a competência geral 7, pois precisam argumentar e justificar a validade das informações consideradas na demonstração.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
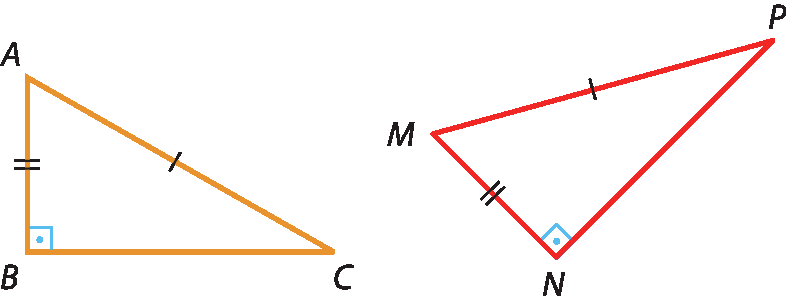
13 Verifique em cada item quais são os pares de triângulos congruentes e escreva no caderno o caso pelo qual são congruentes.
a)
b)
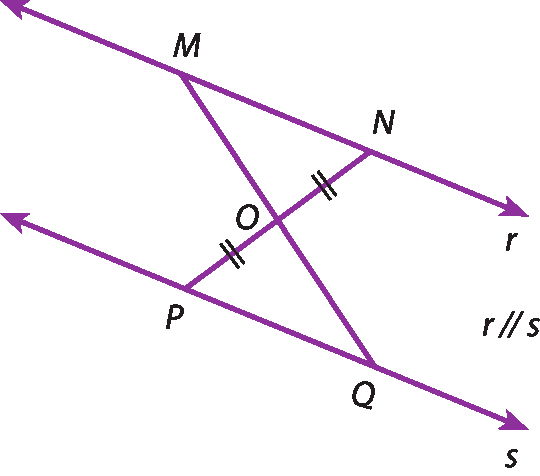
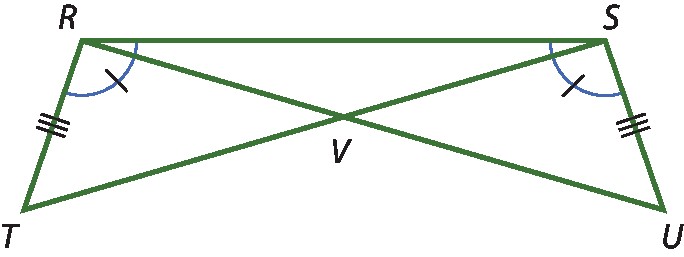
c)
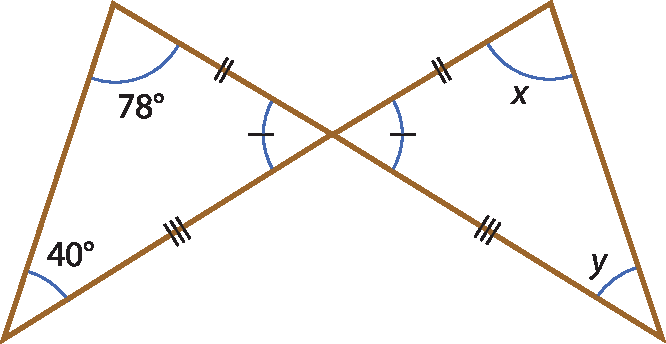
14 Calcule os valores de x e y nas figuras a seguir.
a)
b)
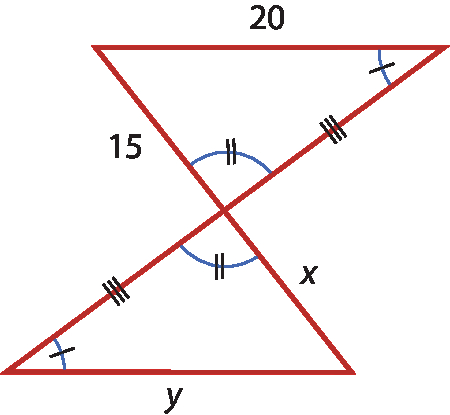
c)
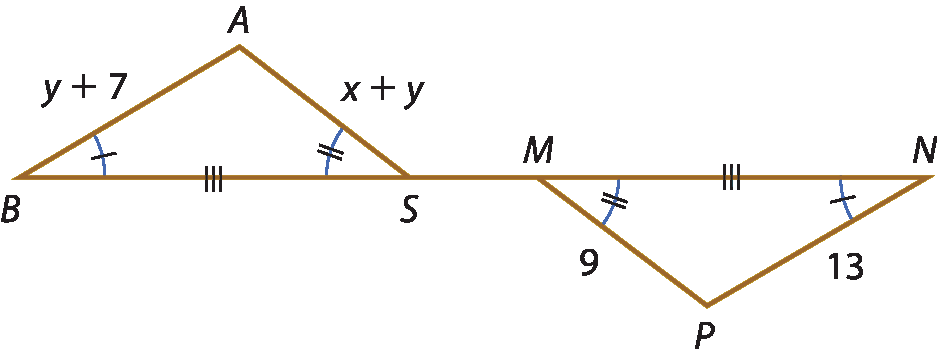
15 Observe a figura a seguir.
Sabendo que as marcas iguais indicam lados de mesma medida, explique por que podemos afirmar que
Segmento de reta EB congruente ao segmento de reta DC.
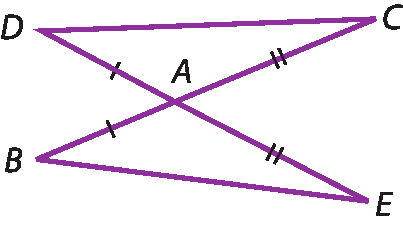
16 Considere um triângulo á bê cê equilátero.
a) Ao traçar a mediana
AM, obtemos dois triângulos: △á ême bê e △á ême cê. Esses triângulos são congruentes? Justifique sua resposta.
b) Ao traçar a bissetriz
A D, obtemos dois triângulos: △á dê bê e △á dê cê. Esses triângulos são congruentes? Justifique sua resposta.
c) Ao traçar a altura
AH, também obtemos dois triângulos: △a agá bê e △á agá cê. Esses triângulos são congruentes? Justifique sua resposta.
d) Todos os triângulos obtidos nos itens anteriores são congruentes? Justifique sua resposta.
Respostas e comentários
13. a) △á bê cê ≅ △á dê cê; caso lado ângulo lado.
13. b) △ême ó êne ≅ △quê ó pê; caso á éle á ou lado-ângulo-ângulo opostoo.
13. c) △érre tê ésse ≅ △ésse ú érre; caso lado ângulo lado.
14. a) x = 78graus; y = 40graus
14. b) x = 15; y = 20
14. c) x = 3; y = 6
15.
Segmento de reta EB congruente ao segmento de reta DCporque os triângulos á dê cê e á bê é são congruentes pelo caso lado ângulo lado.
16. a) Sim, pelo caso lado lado lado.
Segmento de reta BM congruente ao segmento de reta MC
Segmento de reta AM congruente ao segmento e reta AM
Segmento de reta AB congruente ao segmento e reta AC
16. b) Sim, pelo caso lado ângulo lado.
Segmento de reta AD congruente ao segmento de reta AD
Ângulo A1 congruente ângulo A2
Segmento de reta AB congruente ao segmento e reta AC
16. c) Sim, pelo caso lado-ângulo-ângulo opostoo.
Segmento de reta AH congruente ao segmento de reta AH
Ângulo H1 congruente ao ângulo H2
Ângulo B congruente ângulo C
16. d) Sim; resposta pessoal.
Exercícios propostos
As resoluções dos exercícios 13 a 15 estão no início deste Manual, nas orientações específicas do capítulo 7.
O exercício 16 pode ser ampliado perguntando aos estudantes se todos os triângulos obtidos nos itens a, b e c são congruentes. Espera‑se que reconheçam que sim.
É interessante observar com eles que essa pergunta sintetiza o que foi abordado nos itens desse exercício e que, portanto, em um triângulo equilátero, a mediana, a altura e a bissetriz relativas a um mesmo lado são congruentes.
17

Reúna-se com um colega e façam o que se pede.
Na figura a seguir, a corda
ABé perpendicular ao diâmetro
CD.
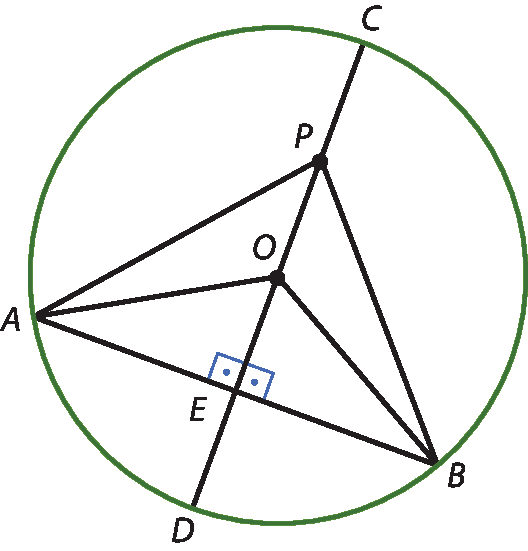
a) Qual é o caso de congruência de triângulos que assegura que △ô á ê ≅ △ó bê é ?
b) Considerando os triângulos pê á é e pê bê ê, demonstrem que
Segmento de reta AP congruente ao segmento de reta BP.
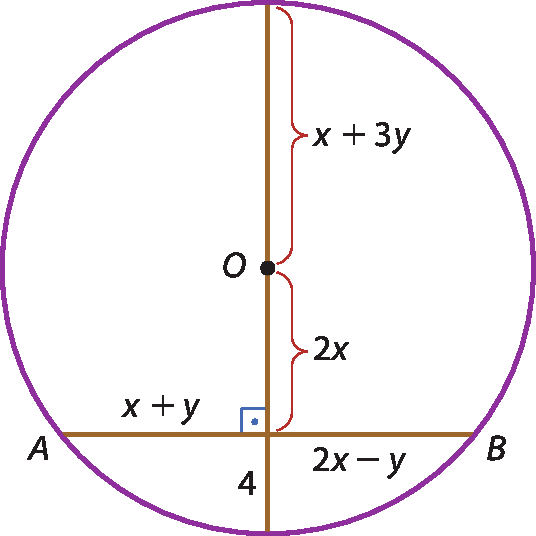
c) Considerem a figura a seguir, em que as expressões representam as medidas dos segmentos. No caderno, calculem as medidas do raio, do diâmetro e da corda
AB.
PARA SABER MAIS
Construindo um hexágono regular com uma moeda
Com uma moeda de 1 real, Márcia e Mílton inicialmente traçaram uma circunferência de centro óh. Depois, cada um deles construiu o desenho da figura 1, dividindo a circunferência em 6 arcos congruentes.
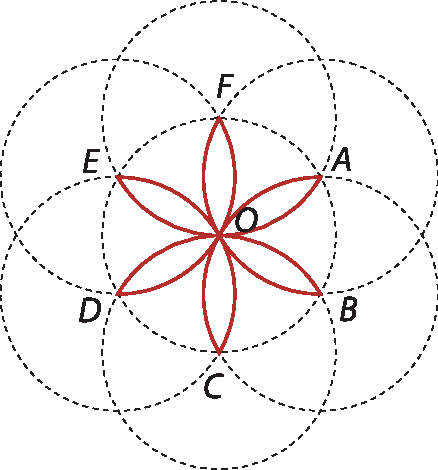
Examinando bem o desenho, eles perceberam que os pontos a, B, C, D, ê e F são os centros das seis circunferências que passam por óh e, também, são vértices consecutivos de um hexágono regular inscrito na circunferência de centro óh.
Então, cada um completou o desenho traçando o seu polígono. Note, na figura 2, como ficou o hexágono á bê cê dê é éfe.
Com um transferidor, Márcia verificou que os ângulos centrais
Ângulo A O B,
Ângulo B O C,
Ângulo C O D,
Ângulo D O E,
Ângulo E O Fe
Ângulo F O Amedem 60graus.
Para fazer a mesma verificação, Mílton foi mais prático e usou o ângulo de 60graus de um esquadro de 30graus e 60graus. Observe, na figura 3, como ele fez para verificar a medida do ângulo
Ângulo B O CDa mesma fórma, ele fez com os demais ângulos centrais.
Respostas e comentários
17. a) Caso Chile.
17. b) Demonstração.
17. c) Medida do raio: 20; medida do diâmetro: 40; A bê = 24.
Exercícios propostos
O exercício 17 pode ser resolvido com os estudantes organizados em duplas, o que enriquecerá o aprendizado. No item a, ó á = ó bê, pois são a medida do raio da circunferência; ó é = ó é, pois são as medidas dos lados comuns aos triângulos; como essas medidas correspondem às medidas da hipotenusa e de um dos catetos; pelo caso Chile, os triângulos são congruentes. A seguir, apresentamos um exemplo de demonstração para o item b.
Considerando os triângulos pê á é e pê bê ê, verificamos:
•
Segmento de reta AE congruente ao segmento de reta BE
(pela congruência citada no item a)
•
Ângulo AEO congruente ao ângulo BEO
(ângulos retos)
•
Segmento de reta PE congruente ao segmento de reta PE
(lado comum)
Logo, pelo caso lado ângulo lado, os triângulos pê á é e pê bê ê são congruentes.
Portanto,
Segmento de reta AP congruente ao segmento de reta BP, pois são lados correspondentes em triângulos congruentes.
A resolução do item c está no início deste Manual, nas orientações específicas do capítulo 7.
Para saber mais
A seção desenvolve a construção de polígonos regulares, em particular a construção de um hexágono regular. Reproduza as figuras na lousa e refaça com os estudantes cada etapa da construção descrita nessa seção.
Além disso, solicite que elaborem um fluxograma descrevendo as etapas para construir, com régua e compasso, um hexágono regular, favorecendo o desenvolvimento da habilidade (EF08MA16).
A partir dessa experiência, Márcia e Mílton verificaram que é possível construir hexágonos regulares traçando arcos ou ângulos centrais de 60graus e apresentaram um trabalho escolar descrevendo um algoritmo com os passos a seguir.
Márcia
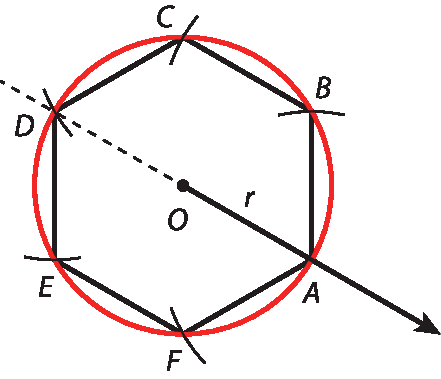
• Traçar uma circunferência de centro óh e raio r.
• Traçar uma semirreta qualquer de origem óh, que corta a circunferência no ponto a.
• Com a ponta-sêca do compasso em ae abertura igual ao raio, traçar um arco obtendo B e F na circunferência.
• Repetir o traçado do arco com centros em B, C e D, obtendo na circunferência, respectivamente, C, D e ê.
• Traçar
Segmento de reta AB,
Segmento de reta BC,
Segmento de reta CD,
Segmento de reta DE,
Segmento de reta EFe
Segmento de reta FA.
Mílton
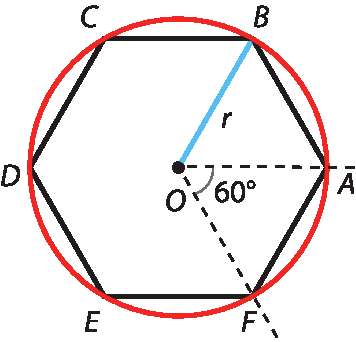
• Traçar uma circunferência de centro óh e raio r.
• Encostar em óh a ponta (vértice do ângulo de 60graus) do esquadro e traçar um ângulo de 60graus que corta a circunferência nos pontos a e F.
• Ainda com a ponta do esquadro em óh, traçar ângulos de 60graus adjacentes a
Ângulo A O Fobtendo B e ê.
• Repetir o passo anterior, traçando ângulos de 60graus adjacentes a
Ângulo A O Be
Ângulo F O Eobtendo C e D.
• Traçar
Segmento de reta AB,
Segmento de reta BC,
Segmento de reta CD,
Segmento de reta DE,
Segmento de reta EFe
Segmento de reta FA.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
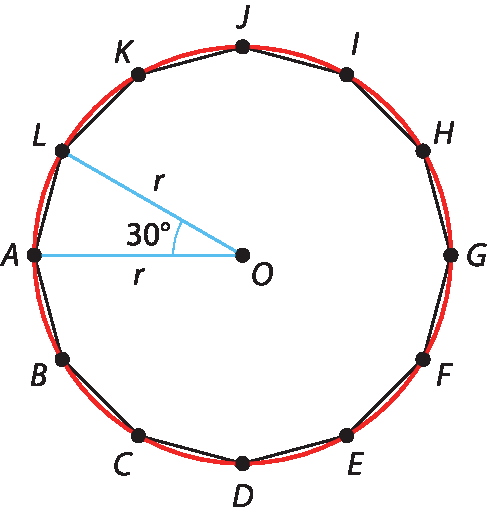
1 Construa dois hexágonos regulares com lados de 4 centímetros, um pelo algoritmo de Márcia e o outro pelo de Mílton.
2 Em uma circunferência de raio de 4 centímetros, construa um dodecágono regular traçando ângulos centrais de 30graus com um esquadro.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 No caderno, corrija as sentenças falsas.
a) O ponto de encontro das mediatrizes de um triângulo chama-se ortocentro.
b) Todo triângulo equilátero é isósceles.
c) Se um triângulo é equilátero, então cada um de seus ângulos internos mede 60graus.
d) O lado oposto ao ângulo reto de um triângulo retângulo chama-se cateto.
2 Com régua e compasso, construa no caderno um triângulo equilátero á bê cê de lados com 7 centímetros. A seguir, escolha entre traçar as bissetrizes dos ângulos internos, as alturas e as medianas. O ponto de intersecção das cevianas que você escolheu é o baricentro de á bê cê ? Ele é o incentro de á bê cê ? Ele é o ortocentro de á bê cê ?
3 No triângulo á bê cê do exercício anterior, com a ponta-seca do compasso no ponto de intersecção obtido, trace as circunferências inscrita e circunscrita ao triângulo.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)
4 Com régua e compasso, construa um triângulo á bê cê de lados A bê = 8 centímetros, á cê = 6 centímetros e bê cê = 7 centímetros e obtenha o seu baricentro G. Depois, usando o compasso em cada mediana, verifique quantas vezes a medida do segmento com extremidades no baricentro e no ponto médio do lado do triângulo cabe no segmento com extremidades no baricentro e no vértice.
5 (unébi-Bahia) Num triângulo retângulo, a altura e a bissetriz relativas à hipotenusa formam um ângulo de 25graus. Os ângulos agudos desse triângulo medem:
a) 35graus e 55graus.
b) 40graus e 50graus.
c) 30graus e 60graus.
d) 15graus e 75graus.
e) 20graus e 70graus.
6 Em um triângulo retângulo, a medida de um dos ângulos agudos é 50graus. Calcule a medida do ângulo obtuso formado pela sua bissetriz com a bissetriz do ângulo reto.
Respostas e comentários
Para saber mais:
1. Construção de figura.
2. Construção de figura.
Exercícios complementares
1. a) Falsa. Resposta possível: o ponto de encontro das mediatrizes de um triângulo chama-se circuncentro.
1. b) Verdadeira.
1. c) Verdadeira.
1. d) Falsa. Resposta possível: o lado oposto ao ângulo reto de um triângulo retângulo chama-se hipotenusa.
2. Construção de figura.
3. Construção de figura.
4. Cabe duas vezes em cada mediana.
5. Alternativa ê.
6. 110graus.
Agora é com você!
Reúna os estudantes em duplas ou trios e peça a eles que leiam a descrição do algoritmo de Márcia e de Mílton para resolverem a atividade 1.
Exemplo das construções descritas pelos algoritmos de Márcia e de Mílton, respectivamente:
Na atividade 2, espera-se que os estudantes transfiram os conhecimentos da construção do hexágono regular para a construção do dodecágono regular. Para isso, eles podem considerar o algoritmo de Márcia e, no 3º passo, aplicar uma abertura do compasso igual à metade da medida do raio; dessa maneira, eles irão obter os pontos de B a L, que são os vértices do dodecágono assim com o ponto A.
Exercícios complementares
Este bloco de exercícios retoma os principais conceitos tratados no capítulo, possibilitando que os estudantes retomem os conhecimentos construídos e identifiquem possíveis dúvidas que ainda tenham.
As resoluções dos exercícios 1 a 6 estão no início deste Manual, nas orientações específicas do capítulo 7.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Sabendo que o ponto óh é o baricentro do triângulo á bê cê, determine a medida do perímetro desse triângulo.
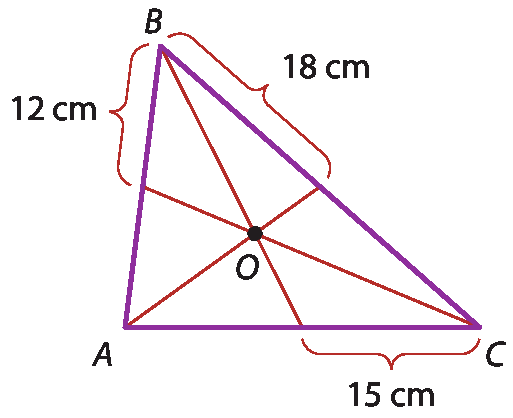
a) 45 centímetros
b) 72 centímetros
c) 75 centímetros
d) 90 centímetros
2 Um malabarista está treinando para um truque de equilíbrio. Ele precisa equilibrar uma tábua de vidro triangular não equilátera em uma vara de madeira. Para que ele consiga realizar o truque, a extremidade da vara deve estar posicionada no:
a) circuncentro do triângulo.
b) baricentro do triângulo.
c) incentro do triângulo.
d) ortocentro do triângulo.
3 Sabendo que
ADé a bissetriz do ângulo
B, determine a medida do ângulo
C.
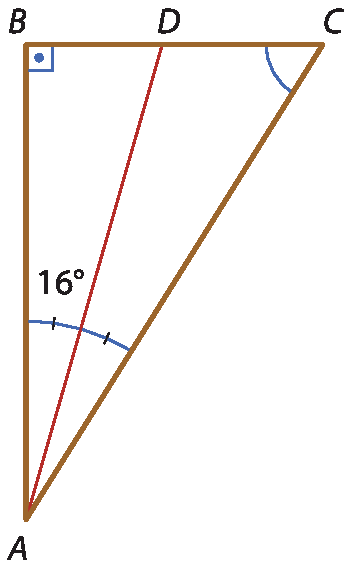
a) 32graus
b) 58graus
c) 74graus
d) 90graus
4 Em um jardim, há uma praça triangular onde se deseja instalar uma fonte que fique equidistante das laterais da praça. Desse modo, a fonte deve ser instalada no:
a) circuncentro do triângulo.
b) baricentro do triângulo.
c) incentro do triângulo.
d) ortocentro do triângulo.
5 Que segmento indica a altura do triângulo á bê cê em relação à base
CB?
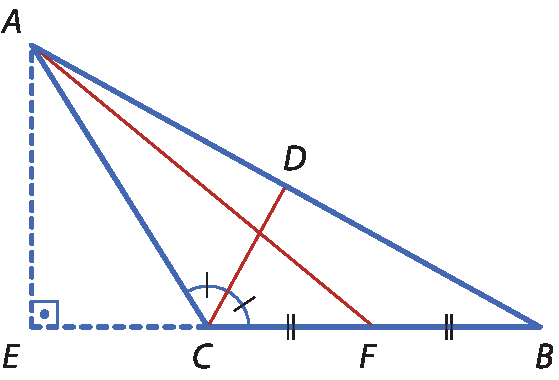
a)
Segmento AEb)
ACc)
CDd)
Segmento de reta AF6 Como deve ser classificado um triângulo para que seu ortocentro se encontre na região externa?
a) Equilátero
b) Acutângulo
c) Retângulo
d) Obtusângulo
7 Sabendo que os triângulos á bê cê e dê ê éfe a seguir são congruentes, determine as medidas do ângulo
Ae do perímetro pê do triângulo dê ê éfe.
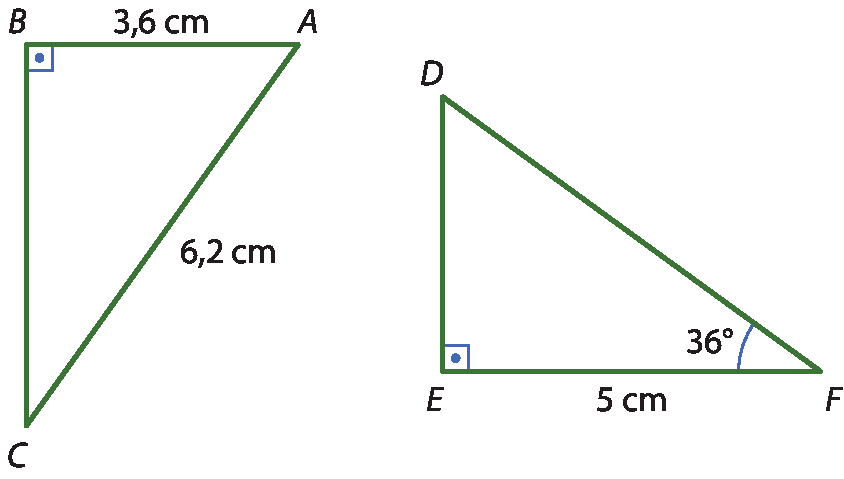
a) medida do(
A) = 54graus e p = 14,8 centímetros
b) medida do(
A) = 36graus e p = 14,8 centímetros
c) medida do(
A) = 54graus e p = 12,2 centímetros
d) medida do(
A) = 36graus e p = 12,2 centímetros
8 Quais dos casos a seguir não estão relacionados à congruência de triângulos ?
a) lado lado lado e lado ângulo lado
b) lado ângulo lado e ângulo-lado-ângulo
c) lado-ângulo e ângulo-ângulo-ângulo
d) Chile e lado-ângulo-ângulo opostoo
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Na sua opinião, por que as cevianas estudadas no capítulo merecem destaque?
b) Qual é a condição para que o trio bissetriz, mediatriz e altura referente a cada um dos ângulos ou dos lados de um triângulo seja o mesmo segmento?
c) Quando dois triângulos são congruentes?
d) Quais são os casos de congruência entre dois triângulos?
Respostas e comentários
1. Alternativa d.
2. Alternativa b.
3. Alternativa b.
4. Alternativa c.
5. Alternativa a.
6. Alternativa d.
7. Alternativa a.
8. Alternativa c.
Organizando:
a) Resposta pessoal.
b) A condição é que o triângulo deve ser equilátero. Nos casos em que o triângulo é isósceles, apenas o trio referente à base é o mesmo segmento.
c) Quando os lados correspondentes e os ângulos correspondentes tiverem a mesma medida.
d) Lado-ângulo-lado, ângulo-lado-ângulo, lado-ângulo-ângulo oposto e lado-lado-lado. Para triângulos retângulos, há o caso cateto-hipotenusa.
Verificando
Os testes propostos nessa seção podem ser utilizados para preparar os estudantes para avaliações de larga escala.
Pode-se solicitar a eles que resolvam cada teste individualmente e, depois, corrigi-los na lousa, possibilitando que os estudantes compartilhem as estratégias de resolução utilizadas.
As resoluções dos testes 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 7.
Organizando
As questões apresentadas nessa seção possibilitam retomar com os estudantes os principais conceitos trabalhados no capítulo. Elas também podem orientar uma autoavaliação dos estudantes.
É interessante que cada um responda e, depois, comente com os colegas as respostas, corrigindo-as ou complementando-as.
DIVERSIFICANDO
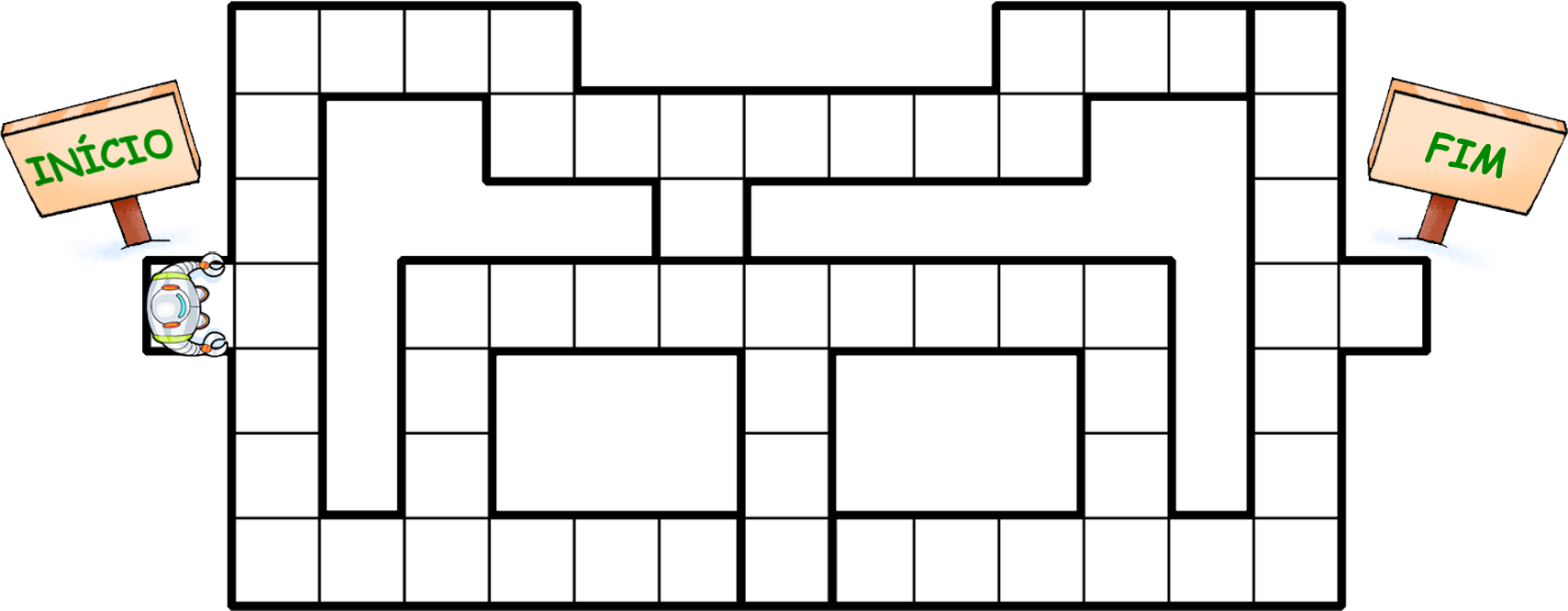
Ângulos e simetria
Vanessa vai participar do campeonato “O labirinto dos robôs”. Cabe a ela escrever as informações corretas do caminho que o robô deve fazer. O objetivo é fazer o robô chegar ao final do percurso sem que ele bata nas paredes do labirinto.
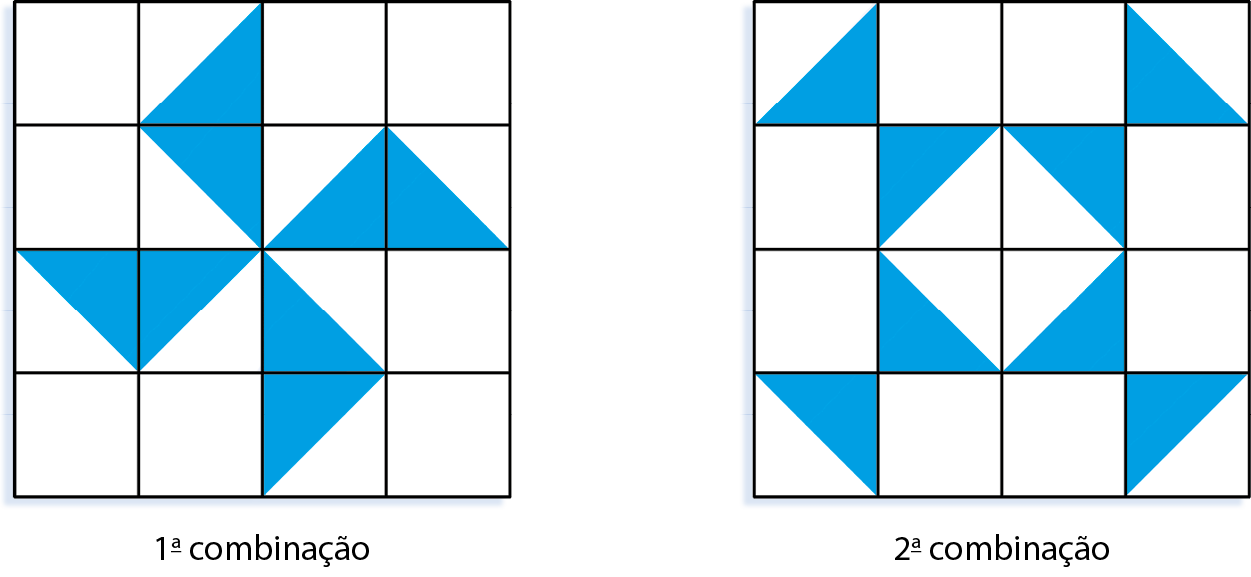
Azulejos
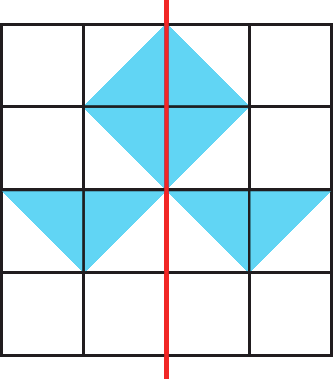
Pedro conseguiu juntar dinheiro para colocar azulejos novos em sua cozinha. Na loja de material para construção, ele resolveu combinar alguns azulejos. Observe as combinações que ele fez.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Com o auxílio da ilustração de “O labirinto dos robôs”, escreva todos os passos que o robô deve dar para completar o percurso sem bater nas paredes. Por exemplo: “Dê 1 passo e vire 90graus à esquerda”. Cada passo corresponde a um quadrado.
2 O labirinto apresenta simetria? E o caminho que o robô deve fazer para chegar ao final do percurso? Justifique suas respostas.
3 Quantos tipos de azulejo Pedro usou para fazer a primeira combinação? E a segunda?
4 Entre essas combinações, qual apresenta uma figura com eixo de simetria? Quantos eixos de simetria essa combinação tem?
5

Formem grupos e, considerando os azulejos representados, façam uma nova combinação que apresente uma figura com eixo de simetria. Escolham um representante do grupo para desenhar a combinação na lousa e outro representante para explicá-la e mostrar o eixo de simetria.
Respostas e comentários
1. Resposta possível: Dê 1 passo e vire 90graus à direita. Dê 3 passos e vire 90graus à esquerda. Dê 2 passos e vire 90graus à esquerda. Dê 3 passos e vire 90graus à direita. Dê 8 passos e vire 90graus à direita. Dê 3 passos e vire 90graus à esquerda. Dê 2 passos e vire 90graus à esquerda. Dê 3 passos e vire 90graus à direita. Dê 1 passo à frente.
2. Espera-se que os estudantes percebam que o labirinto não apresenta simetria e que o caminho que o robô deve fazer apresenta simetria. O eixo de simetria seria uma linha vertical localizada no centro.
3. 1ª combinação: 2 tipos; 2ª combinação: 2 tipos.
4. A segunda; 4 eixos de simetria.
5. Construção de figura.
Diversificando
Nesta seção, os estudantes poderão trabalhar a ideia de transformações geométricas na resolução das atividades propostas, desenvolvendo a habilidade (ê éfe zero oito ême ah um oito).
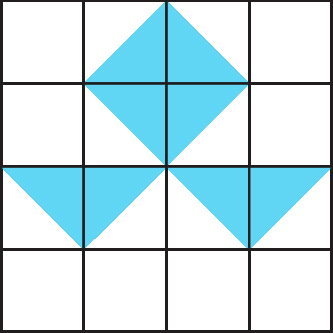
A seguir, um exemplo de figura construída para a atividade 5 do Agora é com você! e a mesma figura construída com eixo de simetria.
Glossário
- Pichar
- : escrever ou rabiscar em muros ou paredes.
- Voltar para o texto