
CAPÍTULO 8 A Geometria demonstrativa

O cubo impossível de Escher nos faz pensar que nem tudo é o que parece ser. Um falso silogismoglossário também pode nos alertar sobre o cuidado que devemos ter com conclusões apressadas:
Todos os cavalos raros são caros. Verdade.
Os cavalos baratos são raros. Verdade.
Então, os cavalos baratos são caros! Verdade?
Por isso, a Matemática, apoiada nas regras da Lógica e em um mínimo de postulados, não dispensa demonstrações rigorosas.
Observe, leia e responda no caderno.
a) Você já ouviu falar de Mauríts Cornélis Éscher? Pesquise, em dupla, a obra desse artista gráfico. Depois, elaborem um painel com imagens e texto com o material da pesquisa.
b) Como você classifica a frase “Cavalos baratos são caros”? Verdadeira? Falsa?
c) Avalie o silogismo a seguir como falso ou verdadeiro. “Todos os gatos são mamíferos. Há mamíferos que são ratos. Logo, há gatos que são ratos!”
Respostas e comentários
a) Resposta pessoal.
b) Espera-se que os estudantes percebam que os adjetivos “baratos” e “caros” são antônimos; logo, a frase é falsa.
c) Falso.
Capítulo 8 – A Geometria demonstrativa
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Este capítulo dá continuidade ao estudo iniciado no capítulo anterior, mostrando como a congruência de triângulos pode ser utilizada em demonstrações geométricas, justificando propriedades de triângulos e de quadriláteros ou outros polígonos.
Espera-se que os estudantes desenvolvam cada vez mais o raciocínio lógico dedutivo fundamental para a continuidade de seus estudos em Matemática, em particular na Unidade Temática Geometria.
Para desenvolverem a pesquisa proposta no item a, podem-se sugerir sites e materiais com informações relevantes para, a partir deles, os estudantes realizarem novas pesquisas.
A proposta nos itens b e c, e no texto de abertura, possibilita aos estudantes discutirem sobre fake news e as conclusões resultantes de falso silogismo.
É comum tomar premissas verdadeiras, como as do item c, e desenvolver uma conclusão falsa. O fato de alguns mamíferos serem gatos e de alguns mamíferos serem ratos não nos permite concluir que alguns gatos sejam ratos. Esse tipo de raciocínio está presente em muitas falsas informações disseminadas em massa nas redes sociais. Dessa maneira, sugerimos um trabalho interdisciplinar com Língua Portuguesa, a fim de que os estudantes analisem diferentes práticas que realizam em redes sociais (curtir, compartilhar, comentar etcétera) e textos associados a diferentes gêneros da cultura digital (meme, gif, comentário, charge digital etcétera) que contenham algum tipo de falso silogismo. Assim os estudantes podem perceber a importância da análise crítica das informações publicadas em diferentes mídias e a importância de uma atitude ética ao usar redes sociais, desenvolvendo, assim, a competência geral 5.

Sugestões de leitura
GOMES, S. F.; PENNA, J. C. B. O. ARROIO, A. Fake news científicas: percepção, persuasão e letramento. Ciência & Educação, Bauru, volume 26, e20018, 2020. Disponível em: https://oeds.link/Ylxb0B. Acesso em: 8 junho 2022.
Neste artigo, os autores trabalham a compreensão de quais elementos influenciam na credibilidade de notícias científicas.
COELHO, A. modêlo lógico matemático com apontamentos à teoria dos jogos e teoria econômica do crime para combate a fake news. Revista Humanidades e Inovação, volume 7, número 9, 2020. Disponível em: https://oeds.link/sMknwZ. Acesso em: 8 junho 2022.
Neste artigo, é analisado o fenômeno da fake news sob a ótica da Teoria dos Jogos e Teoria Econômica do Crime. Também se propõe um modêlo lógico matemático aplicável ao combate dessa prática.
1. Demonstrações geométricas
Muitas das propriedades geométricas já estudadas foram consideradas verdadeiras com base em medições experimentais ou na simples observação. Porém, nem sempre chegamos a conclusões corretas efetuando medições, considerando que a medida está sujeita a erros decorrentes de, por exemplo, um desenho impreciso ou um instrumento defeituoso. A simples observação também pode levar a conclusões erradas, pois, muitas vezes, as aparências enganam.
Um observador descuidado, ao observar a figura a seguir, poderá concluir que cedê > A bê, quando, de fato, A bê = cedê. (Verifique!)
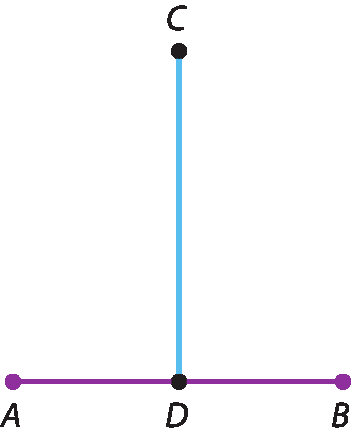
Isso nos faz pensar que nem sempre a medição ou a simples observação são suficientes para confirmar se uma propriedade geométrica é verdadeira ou falsa. Por mais evidente que pareça, uma propriedade só pode ser considerada verdadeira depois de provada.
Noções primitivas e postulados
Já estudamos que, em Geometria, pontos, retas e planos são noções aceitas sem definição; por isso são chamadas de noções primitivas.
Além das noções primitivas, na Geometria, estabelecemos algumas verdades iniciais aceitas sem demonstração: os postulados.
A seguir, vamos estudar alguns postulados que foram estabelecidos como propriedades fundamentais das noções primitivas.
Postulados
• Uma reta tem infinitos pontos.

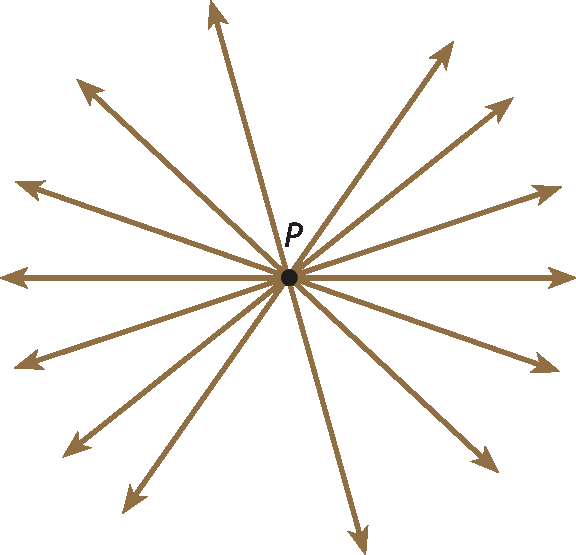
• Por um ponto, passam infinitas retas.
Respostas e comentários
1. Demonstrações geométricas
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um quatro.
Este tópico possibilita aos estudantes demonstrar diferentes propriedades de triângulos utilizando, principalmente, a congruência de triângulos e, assim, contribui para o posterior desenvolvimento da habilidade (ê éfe zero oito ême ah um quatro), ampliando as demonstrações para outras figuras geométricas planas. Discuta com os estudantes a importância de retratar criteriosamente uma situação, destacando as informações dadas e, se for o caso, representar por meio de figuras que se aproximem o máximo possível dos dados fornecidos pela situação. Apenas o desenho não resolverá o problema proposto, mas uma figura com muitas imperfeições pode atrapalhar a estratégia ou até mascarar resultados e levar a conclusões inadequadas. Por exemplo, se o problema indica que o triângulo é equilátero, não é conveniente representar essa situação com um triângulo retângulo.
Outra discussão importante é a consideração de casos particulares quando queremos um resultado generalizado. Por exemplo, se devemos tomar um triângulo qualquer, desenhar um triângulo equilátero pode induzir a obter conclusões de resultados válidos apenas para esse tipo de triângulo, não para um triângulo qualquer.
• Dois pontos distintos determinam uma única reta.
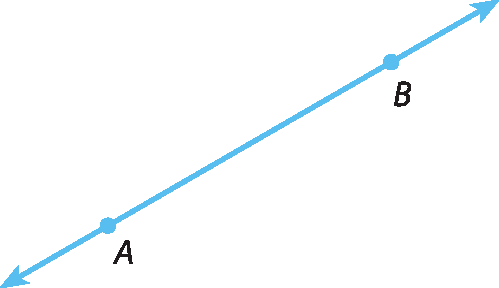
• Entre dois pontos distintos quaisquer de uma reta, sempre existe outro ponto dessa reta.

• Quaisquer três pontos não colineares determinam um, e somente um, plano.
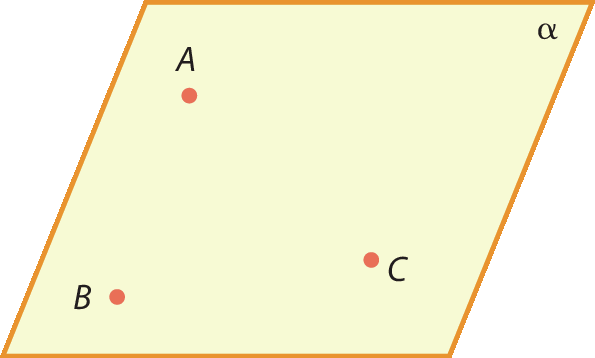
• Por um ponto P qualquer situado fora de uma reta r, passa uma única reta paralela à reta dada.

Teoremas
Os teoremas são propriedades que podem ser demonstradas com base nos postulados ou em propriedades anteriormente demonstradas.
Um teorema é composto de duas partes:
• a parte que se supõe conhecida, chamada de hipótese;
• a parte que se deseja provar, chamada de tese.
Acompanhe alguns exemplos.
a) Se duas retas paralelas são cortadas por uma transversal, então os ângulos correspondentes são congruentes.
Hipótese: duas retas paralelas são cortadas por uma transversal.
Tese: os ângulos correspondentes são congruentes.
b) Se um triângulo é isósceles, então os ângulos da base são congruentes.
Hipótese: um triângulo é isósceles.
Tese: os ângulos da base são congruentes.
Respostas e comentários
Demonstrações geométricas
Ao longo do estudo de Geometria, os estudantes já devem ter se deparado com noções primitivas e suas representações. Retomamos esses conceitos para apresentar-lhes os postulados e teoremas, aprofundando e sistematizando o estudo desse tópico de Geometria plana.
Converse com eles e incentive-os a diferenciar postulado de teorema, de maneira que percebam que um postulado é uma informação tida como verdadeira, sem necessidade de demonstração, enquanto um teorema é uma informação que deve ser provada verdadeira.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Qual dos segmentos é maior,
segmento ABou
segmento CD?

2 Indique falso ou verdadeiro para cada silogismo a seguir.
a) Toda estrela brilha com luz própria.
Nenhum planeta brilha com luz própria.
Então, nenhum planeta é estrela.
b) Todos os galos são aves.
Algumas aves são patos.
Então, todos os patos são galos.
3 Identifique a hipótese e a tese em cada caso.
a) Se um número é múltiplo de 3 e de 5, então esse número é múltiplo de 15.
b) Se uma altura de um triângulo é bissetriz, então esse triângulo é isósceles.
c) Se duas retas cortadas por uma reta transversal são paralelas, então elas determinam ângulos alternos internos de mesma medida.
4 Verifique se as sentenças a seguir são verdadeiras ou falsas e dê um exemplo que justifique o fato de as sentenças serem falsas, caso haja alguma.
a) Se um triângulo é isósceles, então ele tem dois lados congruentes e um de medida diferente.
b) Se um triângulo é retângulo, então ele não pode ser equilátero.
c) Se um triângulo é equilátero, então as bissetrizes de dois ângulos internos determinam apenas ângulos agudos.
PARA SABER MAIS
Da Geometria empírica à demonstrativa
A Geometria teve início em tempos remotos e desenvolveu-se lentamente até atingir a amplitude atual. Nesse trajeto, passou por diferentes papéis.
De modo geral, a Geometria inicial tratava somente de problemas geométricos concretos, apresentados isoladamente, e entre os quais não se observava nenhuma ligação.
Com o tempo, começaram-se a detectar propriedades e relações gerais com base em certo número de observações relativas a fórmas, tamanhos e relações espaciais de objetos físicos específicos, que passaram a ser casos particulares. Tais descobertas favoreceram a ordenação de problemas geométricos práticos em grupos de mesmo tipo, cada qual solucionável por meio de um mesmo procedimento geral.
Não se sabe quantos séculos foram necessários para a Geometria adquirir státus de ciência; entretanto, historiadores acreditam que o início desse processo ocorreu ao longo do vale do rio Nilo, no Egito antigo, bem como nas bacias de outros grandes rios, como o Tigre e o Eufrates, na Mesopotâmia.
Quanto ao vale do rio Nilo, vale lembrar a importância da agrimensura como possível origem para a palavra geometria, que significa “medida da terra”. Além disso, as bacias desses rios foram berços de fórmas avançadas de sociedade, conhecidas por sua habilidade em engenharia na drenagem de pântanos, irrigação, obras de defesa contra inundações e construção de grandes edifícios e estruturas, projetos que requeriam muita geometria prática.
A Geometria da Mesopotâmia e a do Egito eram, portanto, basicamente experimentais, derivadas de regras usadas pelos técnicos dessas civilizações, o que lhes possibilitou calcular medidas de áreas e muitos resultados bem antes dos gregos, porém não de maneira dedutiva.
Respostas e comentários
1. Nenhum deles, pois são congruentes.
2. a) Verdadeiro.
2. b) Falso.
3. a) Hipótese: um número é múltiplo de 3 e de 5; tese: esse número é múltiplo de 15.
3. b) Hipótese: uma altura de um triângulo é bissetriz; tese: esse triângulo é isósceles.
3. c) Hipótese: duas retas cortadas por uma reta transversal são paralelas; tese: essas retas determinam ângulos alternos internos de mesma medida.
4. a) Falsa. O triângulo pode ser equilátero.
4. b) Verdadeira.
4. c) Falsa. As bissetrizes formam um ângulo de 120graus.
Exercícios propostos
Esta série de exercícios pode ser desenvolvida com os estudantes em duplas, o que enriquecerá o aprendizado, já que eles deverão expor o que pensam e compreender o pensamento do colega, para depois debater, refletir e esboçar uma conclusão com argumentos mais bem elaborados.
As resoluções dos exercícios 1 a 4 estão no início deste Manual, nas orientações específicas do capítulo 8.
No exercício 2, se julgar conveniente, o uso de diagramas que representem a situação pode ser uma boa estratégia.
A seguir, a representação da situação do item a, em que o conjunto representado pelo retângulo B é o conjunto dos astros e corpos celestes que brilham com luz própria.
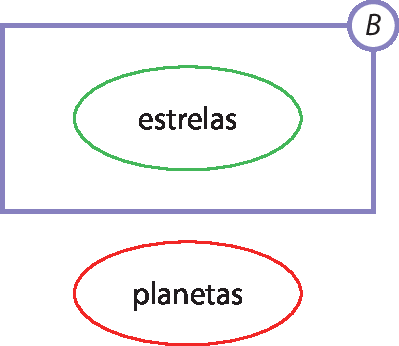
Se toda estrela brilha com luz própria, todas as estrelas estão contidas no conjunto B.
Se nenhum planeta brilha com luz própria, não há planeta algum nesse conjunto, ou seja, nenhum planeta pertence ao conjunto B.
Logo, podemos concluir que nenhum planeta é estrela. Pode-se ampliar a atividade propondo à turma um trabalho interdisciplinar com Ciências, de maneira que os estudantes listem outros corpos celestes que pertençam ao conjunto B e outros que não pertençam a esse conjunto.
As modificações político-econômicas dos últimos séculos do segundo milênio antes de Cristo resultaram na diminuição do poder do Egito e da Babilônia. Tal mudança propiciou o florescimento de novas culturas.
Os gregos transformaram a Geometria empírica, ou científica, dos antigos egípcios e babilônios no que se poderia chamar de Geometria demonstrativa. Segundo esta, todas as verdades geométricas deveriam ser demonstradas por raciocínios dedutivos, com base em princípios chamados de axiomas ou postulados, não por processos experimentais.
A Geometria demonstrativa começou, provavelmente, com o trabalho do matemático grego Tales de Mileto (624 a 547 antes de Cristo), considerado um dos sete sábios da Antiguidade. Tales foi a primeira pessoa conhecida a utilizar métodos dedutivos em Geometria. Viveu no Egito, de onde levou a Geometria para a Grécia, começando a aplicar a essa ciência, pela primeira vez, procedimentos dedutivos da Filosofia grega.
No campo da Matemática, o primeiro pensamento dedutivo ocorreu na área da Geometria, e a fórma de pensamento dedutivo estabeleceu um modêlo e determinou uma tradição que perduram até nossos tempos no procedimento de validação das verdades matemáticas.

Congruência de triângulos nas demonstrações geométricas
Acabamos de aprender que é possível provar que alguns fatos matemáticos são verdadeiros usando como base outros fatos já comprovados e em uma sequência de conclusões lógicas, sem usar instrumento de medida. É o que chamamos de fazer uma “prova” ou “demonstração” matemática.
Os casos de congruência de triângulos podem ser utilizados para demonstrar a validade de algumas propriedades geométricas. Nas situações a seguir, vamos considerar que os casos de congruência de triângulos são verdades já demonstradas.
a) Na figura, temos:
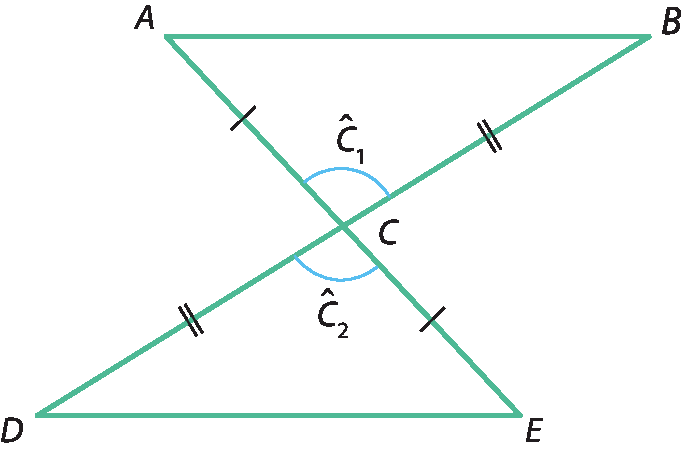
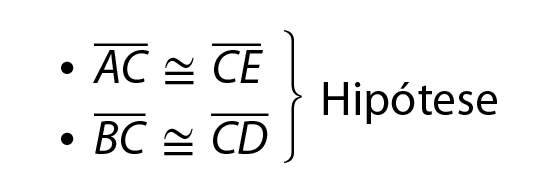
Vamos provar que:
segmento A B é congruente ao segmento D E. Chave à direita. Tese.Respostas e comentários
Para saber mais
Esta seção enriquece e dá significado ao aprendizado do tema abordado, fazendo sua contextualização com a história da Matemática.

Sugestão de leitura
Para ampliar o trabalho, sugerimos:
JESUS, D. L. S. O papel demonstrativo dos diagramas na geometria euclidiana. Dissertação (Mestrado em Filosofia), Universidade Federal da Bahia, Salvador, 2017. Disponível em: https://oeds.link/byq9qt. Acesso em: 8 junho 2022.
Nesse trabalho, resgatam-se algumas das principais discussões sobre a maneira como se pode obter conhecimento por meio de justificativas diagramáticas, apresentando-se uma defesa de um modêlo de prova matemática parcialmente fundamentado em diagramas. Na investigação, tratam-se algumas características e demonstrações que constam na obra Os elementos, de Euclides.
Para verificar se os segmentos
A Be
D Esão congruentes, poderíamos medi-los com o auxílio de uma régua ou usar um compasso com a medida do segmento
A Bpara conferir se essa medida coincide com a do segmento
D E. Em qualquer desses casos, sempre haveria a possibilidade de êrro de medição ou mesmo um defeito do instrumento.
Então, vamos provar que
segmento A B é congruente ao segmento D E.
• Demonstração

Considerando os triângulos á bê cê e é dê cê, temos:
1.
Segmento A C é congruente ao segmento C E(por hipótese)
2.
Ângulo C1 ≅
Ângulo C2 (ângulos opostos pelo vértice)
3.
Segmento B C é congruente ao segmento C D(por hipótese)
Logo, pelo caso lado ângulo lado, os triângulos á bê cê e é dê cê são congruentes. Portanto,
segmento A B é congruente ao segmento D E, pois são lados correspondentes em triângulos congruentes.
b) Dada a figura a seguir, em que
Segmento A B é paralelo ao segmento P Ne
segmento A C é paralelo ao segmento M N, vamos provar que
Segmento A C é congruente ao segmento N M.
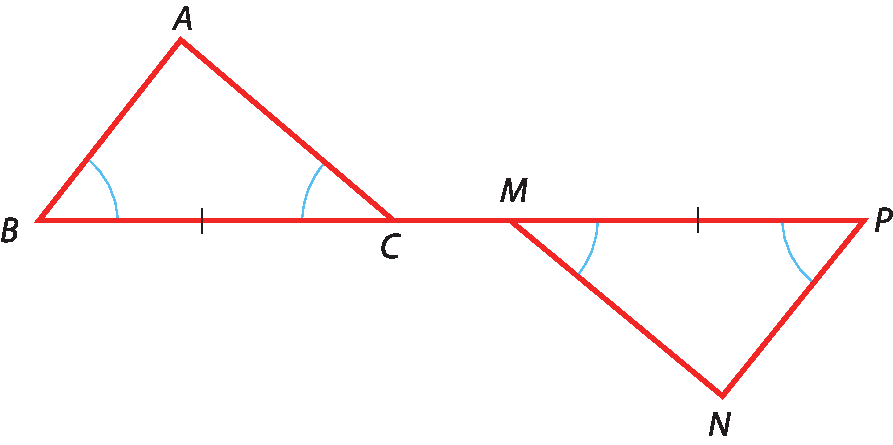
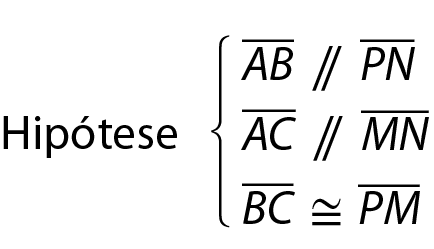
Tese {
segmento A C é congruente ao segmento N M• Demonstração
Considerando os triângulos á bê cê e NPM, temos:
1.
Ângulo A C com origem em B, congruente com ângulo N M com origem em P(ângulos alternos internos)
2.
segmento B C é congruente ao segmento P M(por hipótese)
3.
Ângulo ACB é congruente ao ângulo NMP(ângulos alternos externos)
Logo, pelo caso ângulo-lado-ângulo, os triângulos á bê cê e NPM são congruentes. Portanto,
segmento A C é congruente ao segmento N M., pois são lados correspondentes em triângulos congruentes.
c) Vamos usar a congruência de triângulos para justificar a validade da seguinte construção geométrica: bissetriz de um ângulo.
• Construção
1º) Com a ponta-séca do compasso em O, traçamos um arco determinando os pontos M e N.
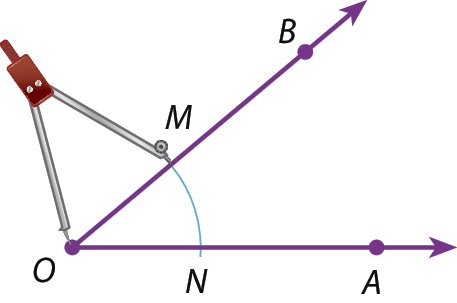
(Ao usar o compasso, atenção para não se machucar com a ponta-séca!)
2º) Com a mesma abertura do compasso e a ponta-séca em M e, em seguida, em N, traçamos os arcos que se intersectam em D.
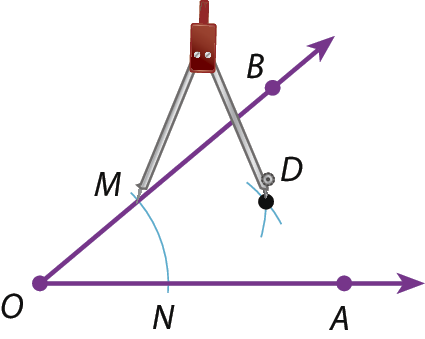
Respostas e comentários
Congruência de triângulos nas demonstrações geométricas
Assumindo sem demonstração os casos de congruência, apresentamos aos estudantes alguns exemplos de demonstrações e de justificativas para construções geométricas. Apresentamos, também, a justificativa da construção da bissetriz de um ângulo.
Incentive os estudantes a escreverem no caderno a definição de bissetriz de um ângulo. Revisitar conceitos e retomar conhecimentos já construídos são passos indispensáveis para que eles consolidem e ampliem conceitos e procedimentos.
3º) Traçamos a semirreta
O D, que é a bissetriz do ângulo
ângulo A O B.
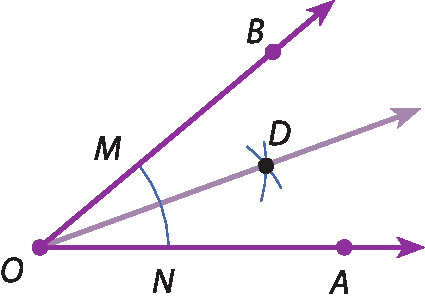
• Justificativa Entenda por que essa construção é válida.
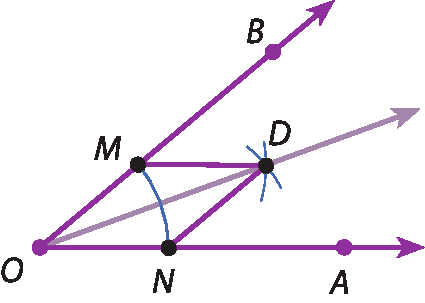
Considerando os triângulos ó ême dê e ó êne dê, temos:
1.
Segmento O M é congruente ao segmento O N(mesma abertura do compasso)
2.
Segmento M D é congruente ao segmento N D(mesma abertura do compasso)
3.
Segmento O D é congruente ao segmento O D(lado comum)
Logo, pelo caso lado lado lado, os triângulos ó ême dê e ó êne dê são congruentes. Portanto,
Ângulo M D com origem em O, congruente com ângulo N D com origem em O, pois são ângulos correspondentes em triângulos congruentes. Assim,
semirreta O Dé bissetriz do ângulo
ângulo A O B.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
5 Em cada caso, faça o que se pede.
a) Prove que
segmento A C é congruente ao segmento C D.
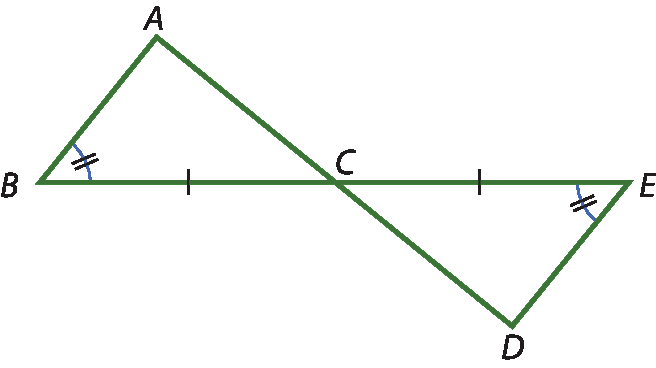
Considere:
segmento B C é congruente ao segmento C E;
ângulo B é congruente ao ângulo Eb) Prove que
segmento A C é congruente ao segmento C E.
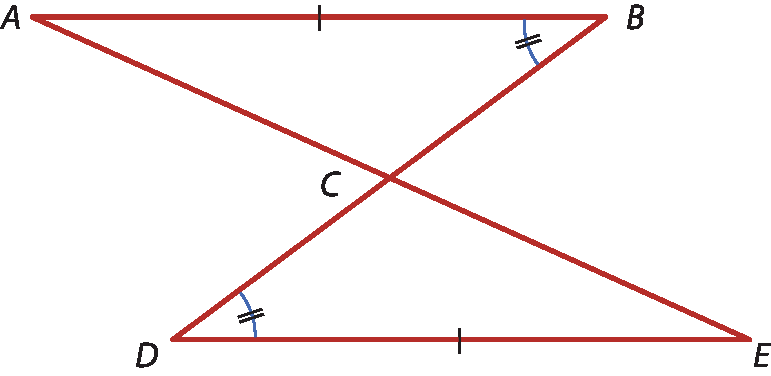
Considere:
segmento A B é congruente ao segmento D E, ponto e vírgula, ângulo B é congruente ao ângulo Dc) Dado o quadrilátero á bê dê cê, prove que
ângulo A é congruente ao ângulo D.
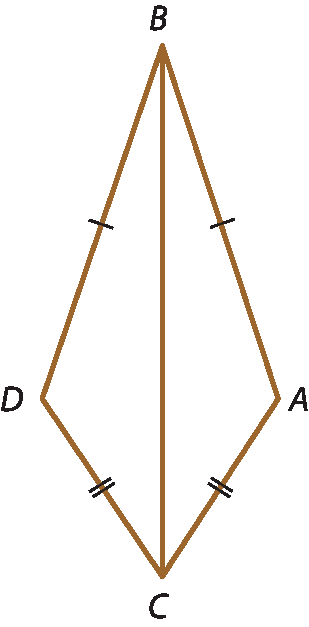
Considere:
segmento B A é congruente ao segmento B D;
segmento A C é congruente ao segmento D Cd) Dado o quadrilátero á bê dê cê, prove que
segmento A C é congruente ao segmento D C.
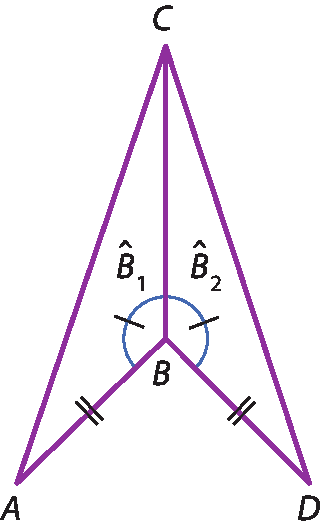
Considere:
segmento A B é congruente ao segmento D B;
Ângulo B11 ≅
Ângulo B22
Respostas e comentários
5. Demonstrações.
5. a) Caso ângulo-lado-ângulo.
5. b) Caso lado-ângulo-ângulo opostoo.
5. c) Caso lado lado lado.
5. d) Caso lado ângulo lado.
Exercícios propostos
Apresentamos a seguir uma possível resolução para o exercício 5.
a) Considerando os triângulos ABC e Dê ê cê, verificamos:
•
Ângulo B congruente ao ângulo E(dado)
•
segmento B C é congruente ao segmento C E(dado)
•
ângulo A C B é congruente ao ângulo D C E(ângulos opostos pelo vértice)
Logo, pelo caso ângulo-lado-ângulo, os triângulos á bê cê e Dê ê cê são congruentes. Portanto,
segmento A C é congruente ao segmento C Dpois são lados correspondentes em triângulos congruentes.
b) Considerando os triângulos á bê cê e é dê cê, verificamos:
•
segmento A B é congruente ao segmento D E(dado)
•
Ângulo B congruente com ângulo D(dado)
•
ângulo A C B é congruente ao ângulo E C D(ângulos opostos pelo vértice)
Logo, pelo caso lado-ângulo-ângulo opostoo, os triângulos á bê cê e é dê cê são congruentes. Portanto,
o segmento AC é congruente ao segmento CEpois são lados correspondentes em triângulos congruentes.
c) Considerando os triângulos á bê cê e dê bê cê, verificamos:
•
o segmento BA é congruente ao segmento BD(dado)
•
o segmento AC é congruente ao segmento DC(dado)
•
segmento B C é congruente ao segmento B C(lado comum)
Logo, pelo caso lado lado lado, os triângulos á bê cê e dê bê cê são congruentes. Portanto,
Ângulo A congruente com ângulo Dpois são ângulos correspondentes em triângulos congruentes.
d) Considerando os triângulos á bê cê e dê bê cê, verificamos:
•
segmento A B é congruente ao segmento D B(dado)
•
ângulo A M C é congruente ao ângulo B M C(dado)
•
segmento B C é congruente ao segmento B C(lado comum)
Logo, pelo caso lado ângulo lado, os triângulos á bê cê e dê bê cê são congruentes. Portanto,
o segmento A C é congruente ao segmento D Cpois são lados correspondentes em triângulos congruentes.
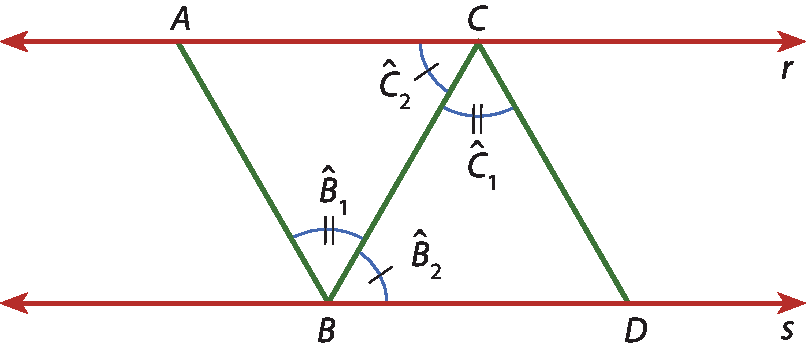
6 Na figura, temos r ⫽ s,
segmento A B é paralelo ao segmento C D,
Ângulo B1 congruente ao ângulo C1e
Ângulo B2 congruente ao ângulo C2Prove que
segmento A C é congruente ao segmento B D.
7 Faça o que se pede.
a) Dados
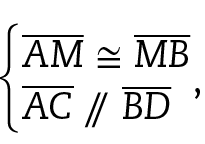
prove que
segmento A C é congruente ao segmento B D.
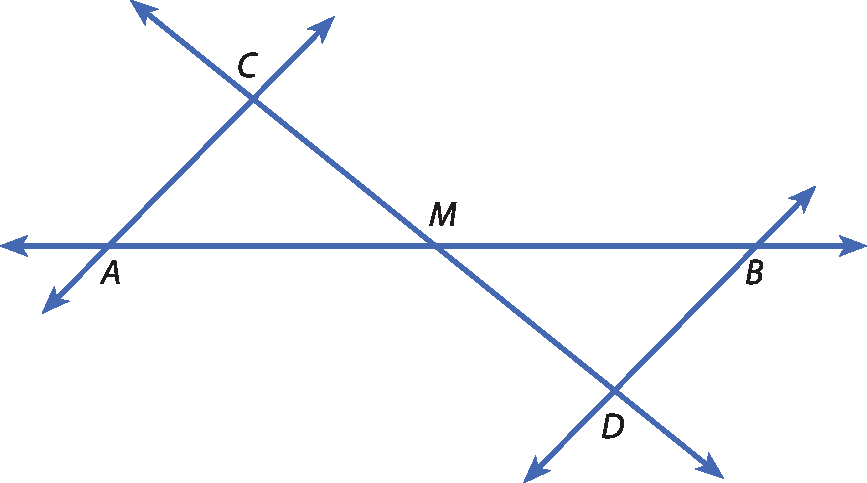
b) Dado o quadrilátero ABCD, em que
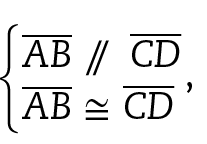
prove que
ângulo A é congruente ao ângulo C.
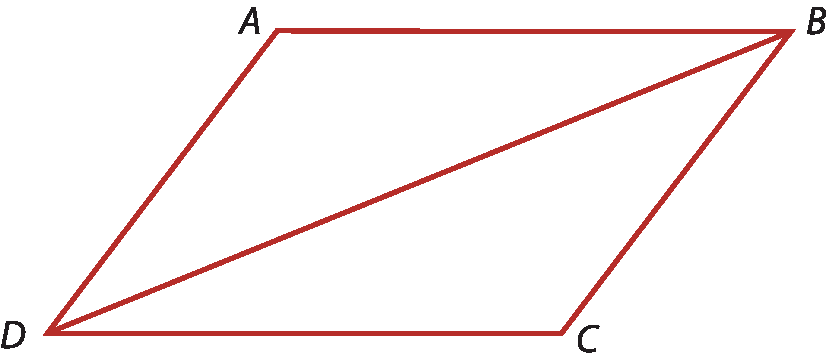
8 Vamos rever a construção de uma perpendicular a uma reta r que passa por um ponto P dessa reta, dados P e r.
1º) Com a ponta-séca do compasso em P e uma abertura qualquer, traçamos um arco que intersecta r nos pontos M e N.
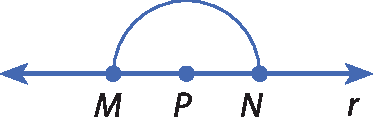
2º) Com a ponta-séca do compasso em M e em N, traçamos dois arcos, com a mesma abertura (maior que PM) do compasso, que se intersectam em a.
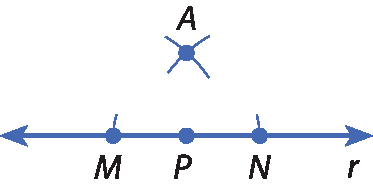
3º) A reta
A Pé perpendicular à reta r. O ponto P é chamado “pé da perpendicular” de
reta A Psobre r.
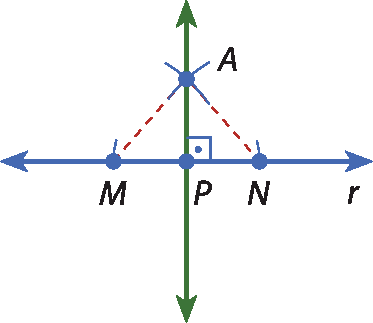
• Justifique por que essa construção é válida.
9 Vamos rever a construção de uma perpendicular a uma reta r que passa por um ponto P que não está na reta, dados P e r.
1º) Com a ponta-sêca do compasso em P, traçamos um arco que intersecta r nos pontos M e N.
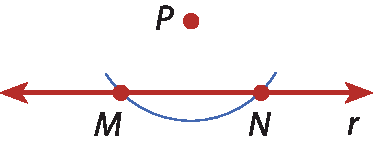
2º) Com a ponta-séca do compasso em M e em N, traçamos dois arcos de mesmo raio que se intersectam em B.
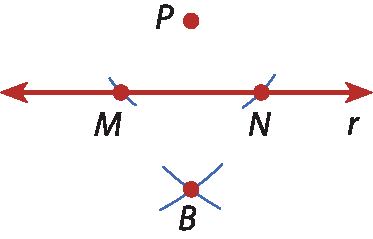
3º) A reta
P Bé perpendicular à reta r e intersecta r no ponto X.
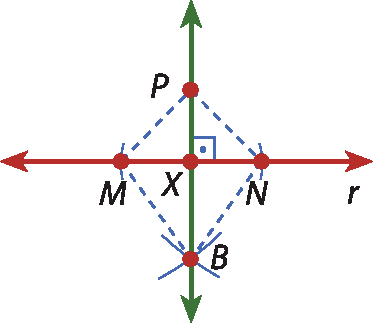
• Justifique por que essa construção é válida.
Respostas e comentários
6. Demonstração (caso ângulo-lado-ângulo).
7. a) Demonstração (caso lado-ângulo-ângulo opostoo).
7. b) Demonstração (caso lado ângulo lado).
8. Demonstração (caso lado lado lado).
9. Demonstração (caso lado lado lado).
Exercícios propostos
No exercício 6, considerando os triângulos á bê cê e dê cê bê:
•
ângulo A C B é congruente ao ângulo C B D(ângulos alternos internos)
•
segmento B C é congruente ao segmento B C(lado comum)
•
ângulo A B C é congruente ao ângulo B C Dângulos alternos internos)
Pelo caso ângulo-lado-ângulo, os triângulos são congruentes. Portanto,
segmento A C é congruente ao segmento B Dpois são lados correspondentes em triângulos congruentes.
No exercício 7, uma resolução possível:
a) Considerando os triângulos á ême cê e bê ême dê:
•
ângulo C é congruente ao ângulo D(ângulos alternos internos)
•
segmento A M é congruente ao segmento M B(dado)
•
Ângulo A C com origem em M, congruente com ângulo B D com origem em M(ângulos opostos pelo vértice)
Pelo caso lado-ângulo-ângulo opostoo, os triângulos são congruentes. Portanto,
segmento A C é congruente ao segmento B D, pois são lados correspondentes em triângulos congruentes.
b) Considerando os triângulos á bê dê e cê dê bê:
•
segmento A B é congruente ao segmento C D(dado)
•
Ângulo A D com origem em B, congruente com ângulo C B com origem em D(ângulos alternos internos)
•
segmento B D é congruente ao segmento B D(lado comum)
Pelo caso lado ângulo lado, os triângulos são congruentes. Portanto,
ângulo A é congruente ao ângulo C, pois são ângulos correspondentes em triângulos congruentes.
No exercício 8, considerando os triângulos ême pê a e êne pê á:
•
segmento P M é congruente ao segmento P N(mesma abertura do compasso)
•
segmento M A é congruente ao segmento N A(mesma abertura do compasso)
•
segmento A P é congruente ao segmento A P(lado comum)
Os triângulos são congruentes pelo caso lado lado lado. Logo,
ângulo M P A é congruente ao ângulo N P A, pois são ângulos correspondentes em triângulos congruentes.
Como são ângulos adjacentes e suplementares:
Concluímos que a reta
A Pé perpendicular à reta r pelo ponto P.
No exercício 9, considerando os triângulos pê ême bê e pê êne bê:
•
segmento P M é congruente ao segmento P N(mesma abertura do compasso)
•
segmento M B é congruente ao segmento N B(mesma abertura do compasso)
•
segmento P B é congruente ao segmento B P(lado comum)
Assim, os triângulos são congruentes pelo caso lado lado lado. Logo,
ângulo M P B é congruente ao ângulo N P B, pois são ângulos correspondentes em triângulos congruentes.
Logo,
ângulo M X P é congruente ao ângulo N X Ppois são ângulos correspondentes em triângulos congruentes. Como são ângulos adjacentes e suplementares, concluímos que são ângulos retos e, portanto,
Reta P B⟂ r.
2. Propriedades do triângulo isósceles
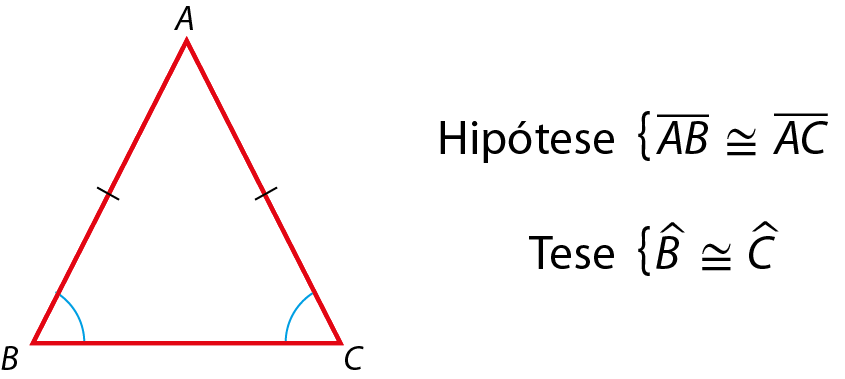
1ª propriedade
Em todo triângulo isósceles, os ângulos da base são congruentes.

• Demonstração Construção auxiliar: vamos traçar a bissetriz
A D.
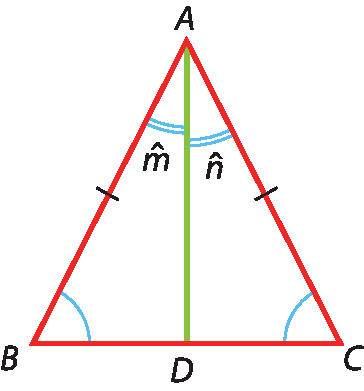
Comparando os triângulos á dê bê e á dê cê, temos:
1.
segmento A B é congruente ao segmento A C(por hipótese)
2.
ângulo m é congruente ao ângulo n(
segmento ADé bissetriz)
3.
segmento A D é congruente ao segmento A D(lado comum)
Logo, pelo caso lado ângulo lado, os triângulos á dê bê e á dê cê são congruentes. Portanto,
ângulo B é congruente ao ângulo C, pois são ângulos correspondentes em triângulos congruentes.
Como exemplo, vamos calcular o valor de x, em grau, no triângulo é éfe gê, sabendo que
segmento E F é congruente ao segmento E G.

x + 55graus + 55graus = 180graus
x + 110graus = 180graus
x = 180graus ‒ 110graus
x = 70graus
2ª propriedade
Em todo triângulo isósceles, a mediana, a altura e a bissetriz relativas à base coincidem.

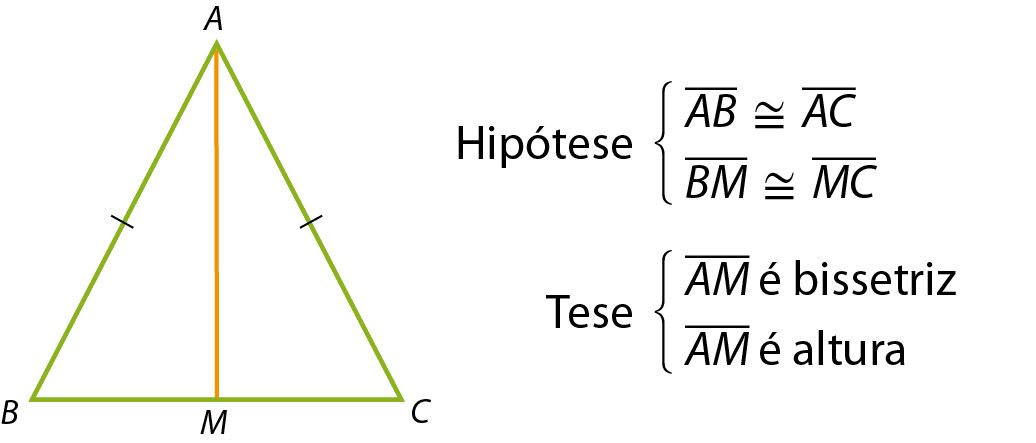
Respostas e comentários
2. Propriedades do triângulo isósceles
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um sete.
Neste tópico, os estudantes podem retomar os conceitos de mediatriz e de bissetriz e de congruência para explorar as propriedades do triângulo isósceles, mobilizando aspectos da habilidade (EF08MA17).
Apresentamos a demonstração da propriedade que trata da congruência dos ângulos da base de um triângulo isósceles. Ressalte que ela é válida também para triângulos equiláteros.
Incentive os estudantes a acompanharem as demonstrações das propriedades. Proponha a eles que façam a leitura das demonstrações das propriedades indicadas neste tópico e, depois, alguns deles a expliquem aos demais, realizando a demonstração na lousa.
• Demonstração
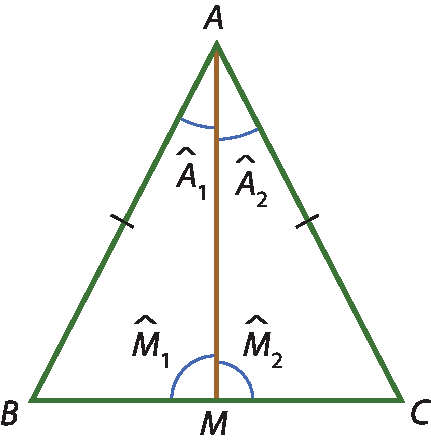
Comparando os triângulos á ême bê e á ême cê, temos:
1.
segmento A B é congruente ao segmento A C(por hipótese)
2.
segmento B M é congruente ao segmento M C(
segmento A Mé mediana relativa ao lado
B C)
3.
segmento A M é congruente ao segmento A M
(lado comum)
Logo, pelo caso lado lado lado, os triângulos á ême bê e á ême cê são congruentes. Portanto:
•
Ângulo A1 ≅
Ângulo A2, o que prova que
segmento A Mé a bissetriz relativa ao ângulo
Ângulo A.
•
Ângulo M1 ≅
Ângulo M2 e, por serem adjacentes e suplementares, cada um deles é um ângulo reto, o que prova que
Ângulo Mé a altura relativa ao lado
Ângulo M.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
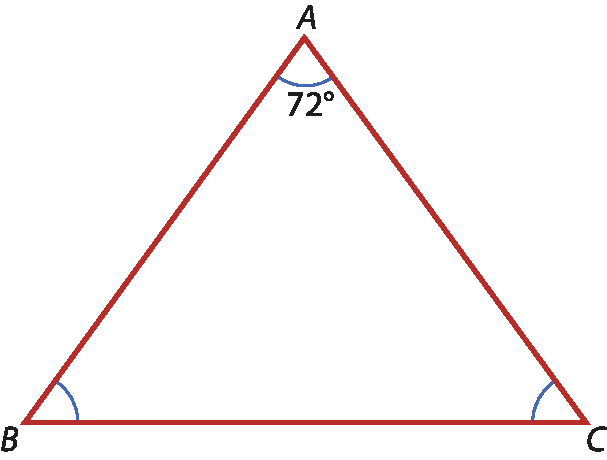
10 O triângulo á bê cê é isósceles de base
B C.
Calcule:
a) a medida do ângulo
Ângulo B;
b) a medida do ângulo
Ângulo C.
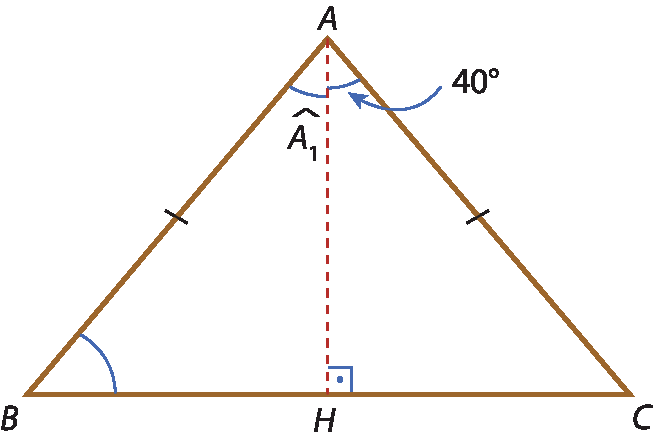
11 Do triângulo á bê cê, pede-se:
a) medida do(
segmento B C), sabendo que medida do(
segmento B H) = 2 centímetros;
b) medida do(
Ângulo A1);
c) medida do(
Ângulo B).
12 Em um triângulo isósceles á bê cê,
segmento A Hé a altura relativa à base
B C. Sendo medida do(
segmento B H) = 3,5 centímetros, calcule medida do(
segmento H C).
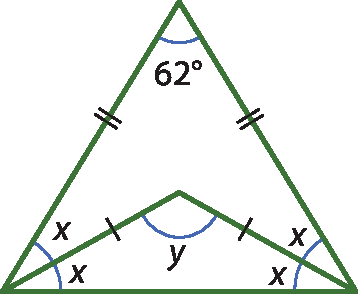
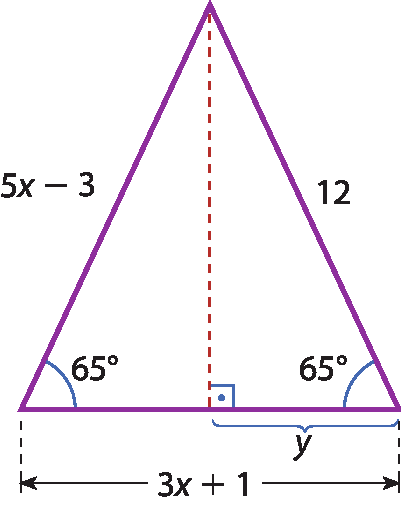
13 Calcule x e y nas figuras a seguir.
a)
b)
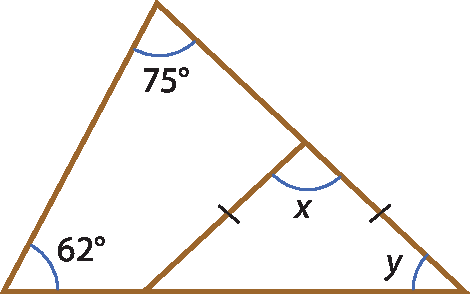
c)
14 Calcule as medidas dos ângulos de um triângulo isósceles no qual cada ângulo da base mede o quádruplo da medida do ângulo do vértice.
15 Calcule a medida de cada ângulo obtuso determinado por duas bissetrizes de um triângulo equilátero.
Respostas e comentários
10. a) 54graus
10. b) 54graus
11. a) 4 centímetros
11. b) 40graus
11. c) 50graus
12. medida do(
segmento H C) = 3,5 centímetros
13. a) x = 29graus 30minutos
y = 121graus
13. b) x = 94graus
y = 43graus
13. c) x = 3
y = 5
14. 20graus, 80graus e 80graus.
15. 120graus
Exercícios propostos
Neste bloco de exercícios, os estudantes aplicarão as propriedades demonstradas e também utilizarão conhecimentos sobre outras propriedades geométricas já estudadas e sobre equações do 1º grau para obter as medidas solicitadas.
As resoluções dos exercícios 10 a 13 estão no início deste Manual, nas orientações específicas do capítulo 8.
Na resolução do exercício 14, como os ângulos da base medem o quádruplo do ângulo do vértice no triângulo isósceles em questão, indiquemos por x a medida do ângulo do vértice. Assim, os ângulos da base medem 4x cada um. Sabendo que a soma das medidas dos ângulos internos de um triângulo é 180graus, obtemos:
x + 4x + 4x = 180
9x = 180
x = 20
E, portanto: 4x = 80
Logo, esse triângulo tem ângulos internos de medidas 20graus, 80graus e 80graus.
Na resolução do exercício 15, incentive os estudantes a representarem a situação por meio de uma figura, por exemplo:
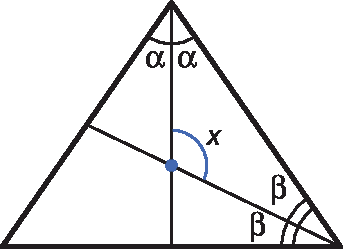
Indicamos por x a medida do ângulo obtuso determinado pelas bissetrizes de dois ângulos internos de um triângulo equilátero. Como o triângulo é equilátero, todos os seus ângulos internos medem 60graus. Como tomamos as bissetrizes de dois desses ângulos internos, α = β = 30graus. Verificamos também que α + β + x = 180graus. Assim:
30 + 30 + x = 180
x = 180 ‒ 60 = 120
Ou seja, a medida de cada ângulo obtuso determinado por duas bissetrizes de um triângulo equilátero mede 120graus.
16 Calcule as medidas x e y, em grau, nas figuras a seguir.
a)
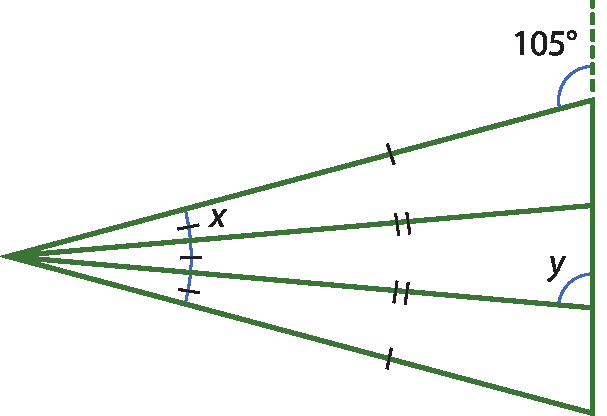
b)
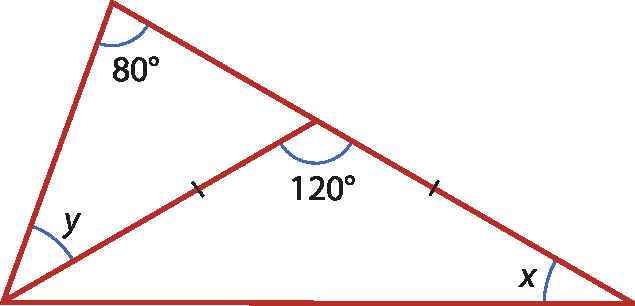
17

Hora de criar – Em dupla, cada um cria um problema sobre triângulo isósceles. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
18 A figura representa a construção da mediatriz do segmento
AB.
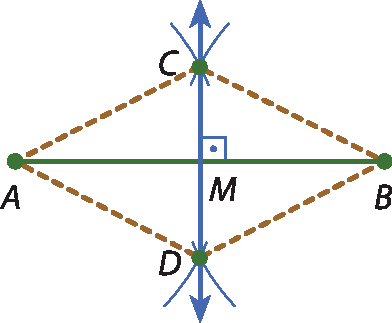
a) Observando a figura, justifique por que essa construção é válida.
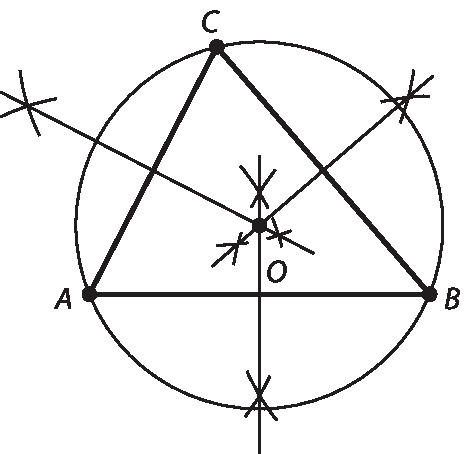
b) Desenhe um triângulo qualquer e trace as mediatrizes de seus lados. Depois, trace a circunferência de centro na intersecção das mediatrizes e que passa pelos vértices do triângulo.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
3. Propriedades de um triângulo qualquer
1ª propriedade
A medida do ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não adjacentes a ele.
Considere o triângulo á bê cê a seguir.
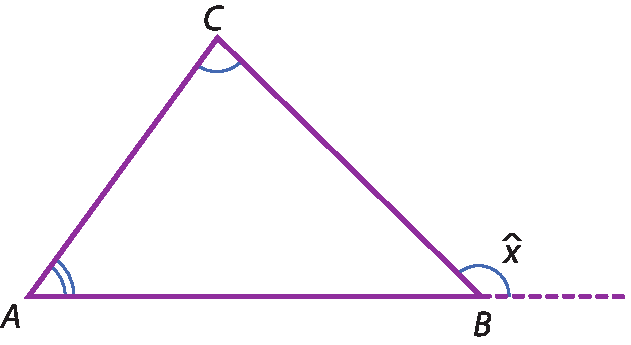

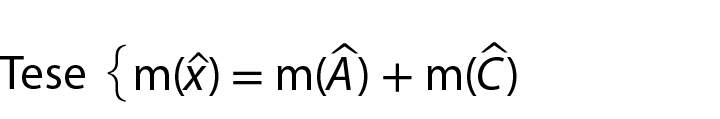
• Demonstração
No triângulo á bê cê, temos:
1. medida do(
Ângulo x) + medida do(
ângulo B) = 180graus (
Ângulo xe
ângulo Bsão adjacentes e suplementares)
2. medida do(
ângulo A) + medida do(
ângulo B) + medida do(
ângulo C) = 180graus (
ângulo A,
ângulo Be
ângulo Csão ângulos internos de um triângulo)
Logo:

Como exemplo de aplicação, vamos calcular x, em grau, nos triângulos a seguir.
a)
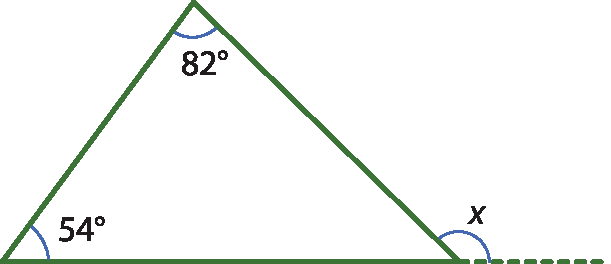
x = 54 + 82
x = 136
b)
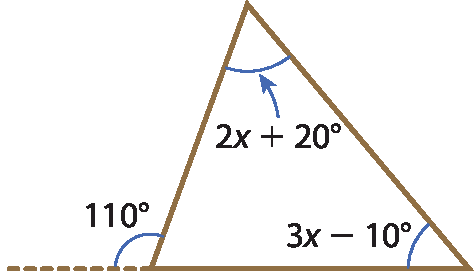
2x + 20 + 3x ‒ 10 = 110
5x = 100 ⇒ x = 20
Respostas e comentários
16. a) x = 10graus
y = 85graus
16. b) x = 30graus
y = 40graus
17. Resposta pessoal.
18. a) Demonstração.
18. b) Construção de figura.
Exercícios propostos
As resoluções dos exercícios 16 e 17 estão no início deste Manual, nas orientações específicas do capítulo 8.
A seguir, indicamos uma resolução para o exercício 18.
a) Sejam C e D pontos quaisquer da mediatriz. Considerando os triângulos á cê ême e BCM, verificamos:
•
segmento A M é congruente ao segmento B M(M é ponto médio)
•
ângulo A M C é congruente ao ângulo B M C(ângulo reto)
•
segmento M C é congruente ao segmento M C(lado comum)
Logo, pelo caso lado ângulo lado, os triângulos á cê ême e BCM são congruentes. Desse modo, verificamos
segmento A C é congruente ao segmento B C(lados correspondentes em triângulos congruentes), ou seja, C é equidistante dos pontos a e B e é ponto da reta que passa por C e D, perpendicular ao segmento
A B.
De modo análogo, provamos que os triângulos ADM e BDM são congruentes e que
segmento A D é congruente ao segmento B D, o que garante que D é equidistante dos pontos a e B e é ponto da reta que passa por C e D. Logo, a reta que passa por C e D é a mediatriz do segmento
A B.
b) Exemplo de figura:
2ª propriedade
Se dois lados de um triângulo são desiguais, então ao lado de maior medida opõe-se o ângulo de maior medida.
Considere o triângulo á bê cêa seguir.
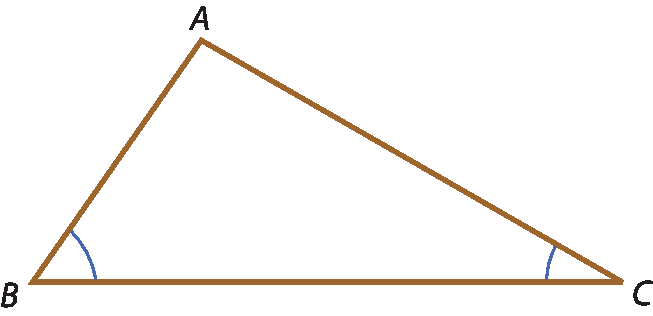
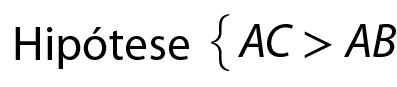
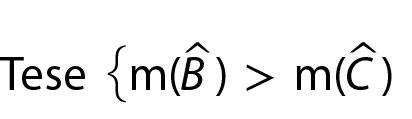
• Demonstração
Construção auxiliar: marcamos sobre
segmento A Cum ponto D tal que
segmento A D é congruente ao segmento A B.
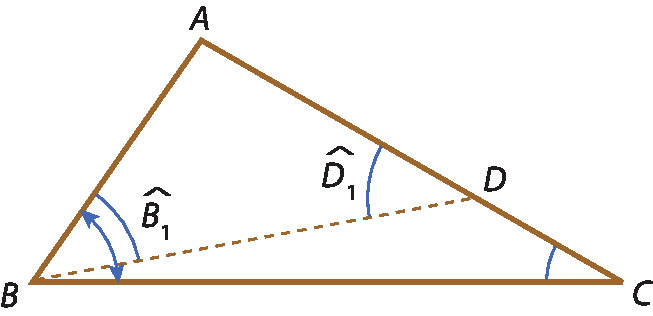
1. O triângulo á bê dê é isósceles (por construção)
2. medida do(
ângulo B1) ≅ medida do(
ângulo D1) (propriedade do triângulo isósceles)
3. medida do(
ângulo D1) > medida do(
ângulo C) (pela propriedade do ângulo externo)
4. medida do(
ângulo B1) > medida do(
ângulo C) (substituindo
ângulo D1por
ângulo B1)
5. medida do(
ângulo B) > medida do(
ângulo B1) (pela construção auxiliar)
6. medida do(
ângulo B) > medida do(
ângulo C) (pois medida do(
ângulo B) > medida do(
ângulo B1) > medida do(
ângulo C))
Vamos admitir, sem demonstração, que a recíproca dessa propriedade seja verdadeira, isto é, se dois ângulos de um triângulo são desiguais, então ao ângulo de maior medida opõe-se o lado de maior medida.
Acompanhe alguns exemplos.
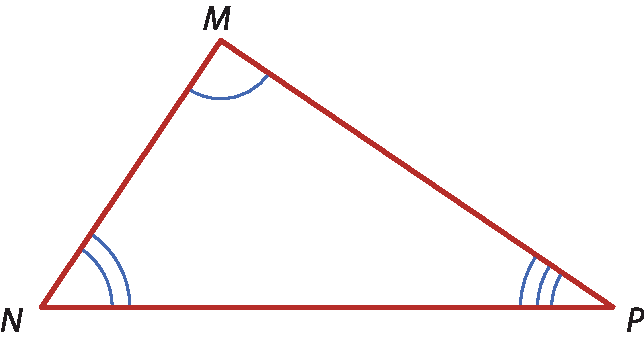
a) No triângulo ême êne pê, temos medida do(
ângulo M) > medida do(
ângulo N). Que relação existe entre
segmento N Pe
segmento M P?

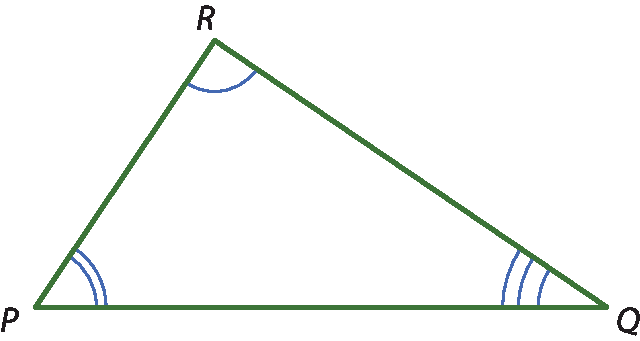
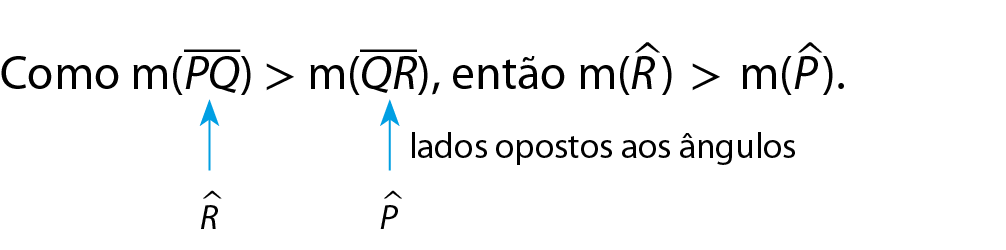
b) No triângulo pê quê érre, temos medida do(
segmento P Q) > medida do(
segmento Q R). Que relação existe entre
ângulo Re
ângulo P?
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
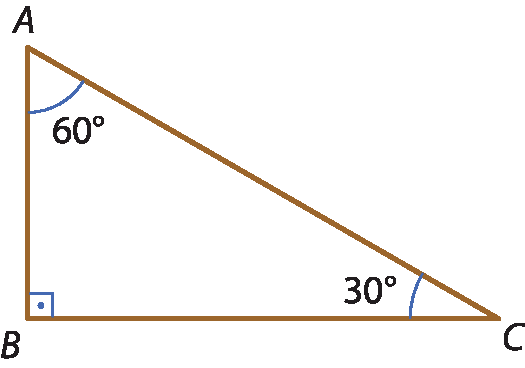
19 Observe o triângulo e determine o lado de maior medida e o de menor medida. Justifique.
a)
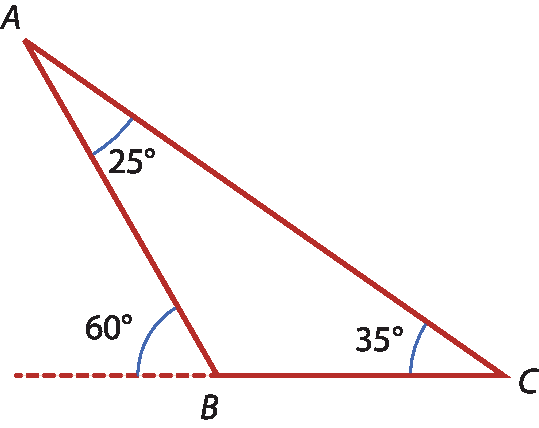
b)
Respostas e comentários
19. a) Maior lado:
segmento A C; oposto ao ângulo de maior medida. Menor lado:
segmento A B; oposto ao ângulo de menor medida.
19. b) Maior lado:
segmento A C; oposto ao ângulo de maior medida. Menor lado:
segmento B C; oposto ao ângulo de menor medida.
3. Propriedades de um triângulo qualquer
Abordamos neste tópico duas propriedades válidas para triângulos quaisquer: a primeira é a que relaciona a medida de um ângulo externo com as medidas dos dois ângulos internos não adjacentes; a segunda, aquela que relaciona lados e ângulos (ao maior lado opõe-se o maior ângulo, para triângulos que tenham lados de medidas desiguais).
Apresente cada demonstração na lousa e peça aos estudantes que justifiquem cada etapa. Reproduza os exemplos na lousa para eles resolverem coletivamente, antes de apresentar as resoluções.
Exercícios propostos
A resolução do exercício 19 está no início deste Manual, nas orientações específicas do capítulo 8.
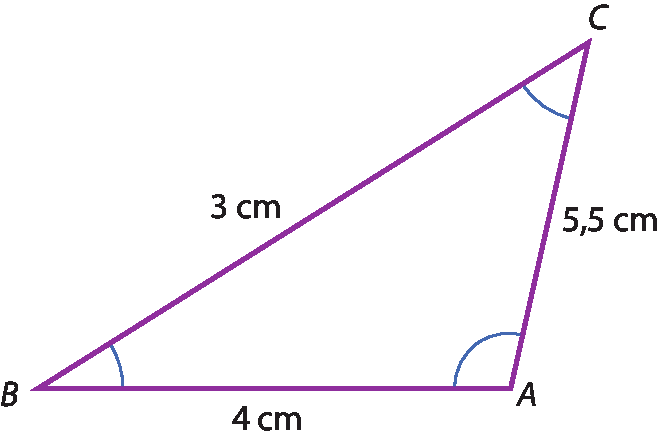
20 Neste triângulo, os comprimentos dos lados não estão proporcionais às medidas indicadas. Determine o maior ângulo e o menor ângulo.
21 Dois lados de um triângulo medem, respectivamente, 5,5 centímetros e 4 centímetros. O terceiro lado mede aproximadamente 3 centímetros. Um de seus ângulos mede 100graus. Quanto mede o lado oposto a ele?
22 Ana e Renata moram perto de uma lanchonete, conforme mostra o esquema a seguir.
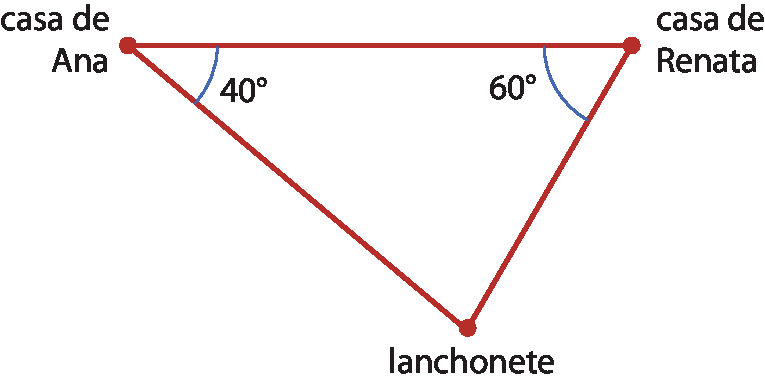
Qual delas mora mais distante da lanchonete? Justifique.
23 Em cada caso, as medidas estão indicadas em uma mesma unidade. Verifique que casos são possíveis. Quando for impossível, justifique.
a)
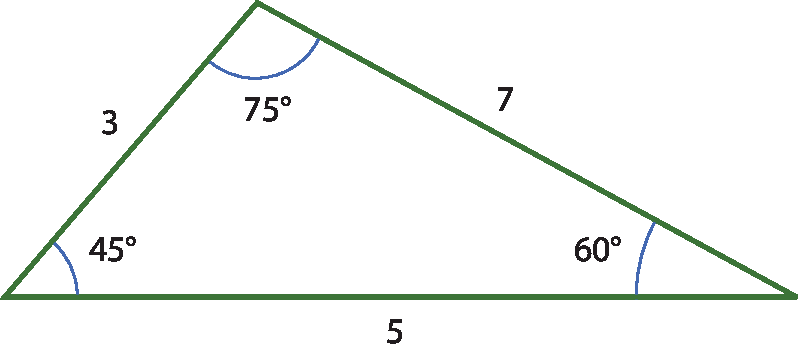
b)
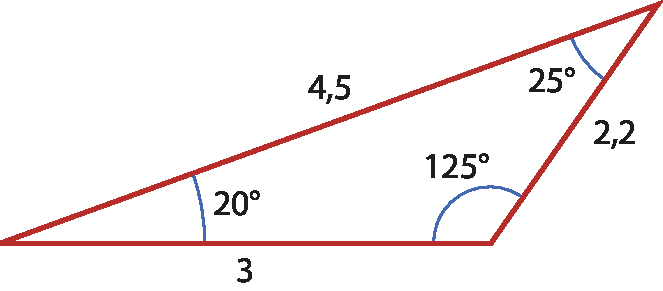
24 Em um jôgo de futebol, Paulo cobra uma falta jogando a bola para Marcos, que a joga para Daniel. A trajetória da bola está representada na figura a seguir. Determine as medidas x e y, em grau.
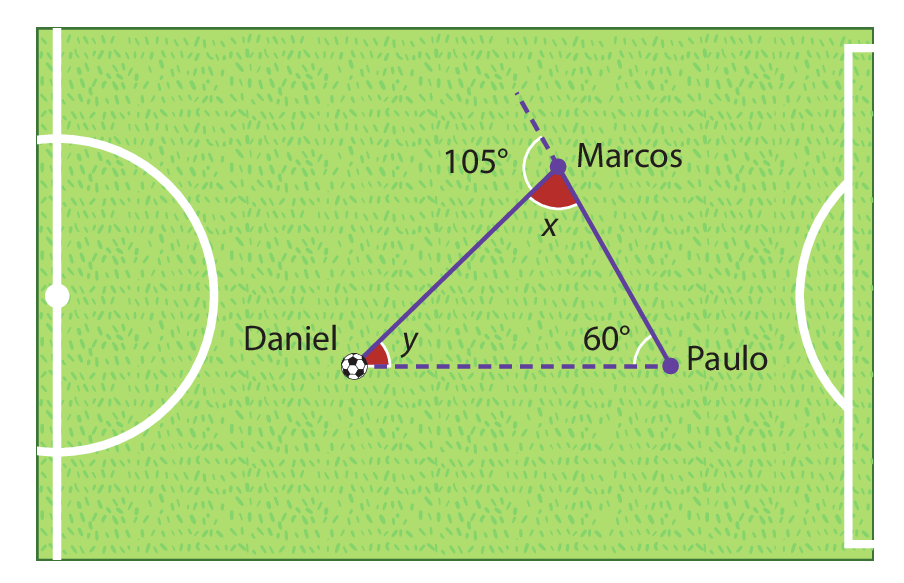
25 Sabendo que
segmento A B é paralelo a segmento C D, calcule o valor de x e de y, em grau, nos triângulos a seguir.
a)
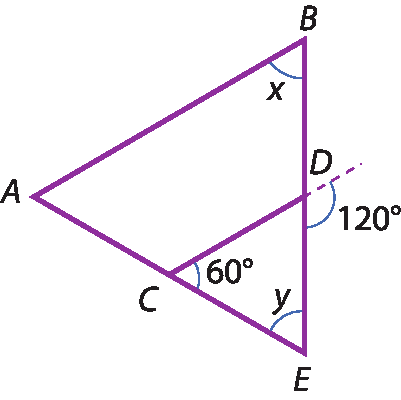
b)
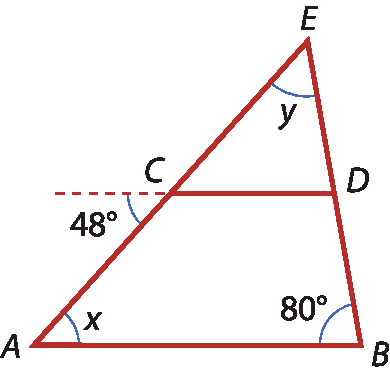
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Considere que a = 105graus e b = 40graus; qual é a medida x do ângulo indicado na figura?
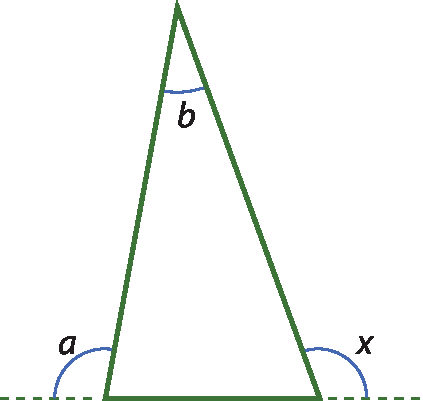
a) 35graus
b) 40graus
c) 65graus
d) 75graus
e) 115graus
2 Calcule as medidas x e y no triângulo.
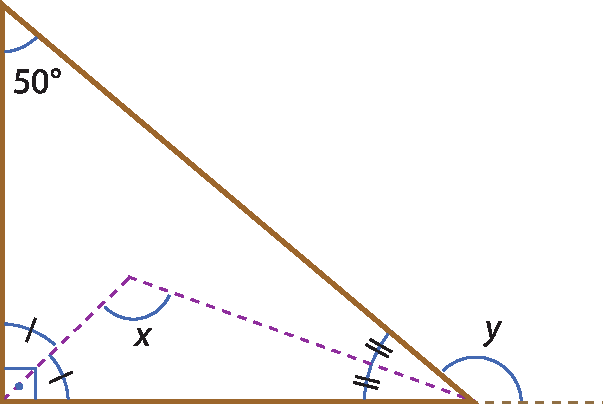
Respostas e comentários
20. Maior ângulo:
Ângulo B; menor ângulo:
Ângulo A.
21. 5,5 centímetros
22. Ana, pois ao maior ângulo se opõe o maior lado do triângulo.
23. a) Não é possível, pois ao ângulo de maior medida deve se opor o lado de maior medida, e isso não ocorreu.
23. b) Não é possível, pois a soma das medidas dos ângulos internos de um triângulo é 180graus, e isso não ocorreu.
24. x = 75graus
y = 45graus
25. a) x = 60graus
y = 60graus
25. b) x = 48graus
y = 52graus
1. Alternativa ê.
2. x = 115graus
y = 140graus
Exercícios propostos
As resoluções dos exercícios 20 a 25 estão no início deste Manual, nas orientações específicas do capítulo 8.
Exercícios complementares
Este bloco de exercícios retoma os principais conteúdos estudados no capítulo, possibilitando que os estudantes utilizem os conhecimentos construídos e identifiquem possíveis dúvidas que ainda tenham.
Proponha a eles, por exemplo, que se reúnam em duplas e organize-as de maneira que algumas duplas resolvam os exercícios pares e as outras, os ímpares. Em seguida, as duplas são reorganizadas de maneira que em cada uma tenha um estudante que resolveu os exercícios pares, e o outro, os ímpares.
Essa dinâmica possibilita a eles trocarem estratégias de resolução e explicarem a um colega como resolveram o exercício, ampliando a compreensão sobre os conteúdos.
As resoluções dos exercícios 1 e 2 estão no início deste Manual, nas orientações específicas do capítulo 8.
3 (éfe cê cê) Na figura a seguir, as retas r e s são paralelas. A medida x do ângulo assinalado é:
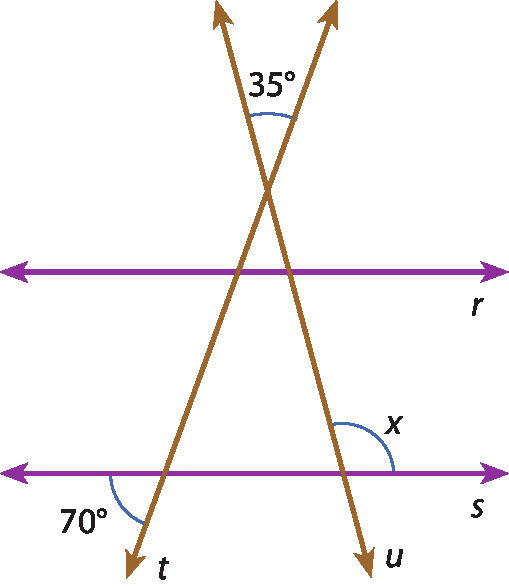
a) 135graus.
b) 120graus.
c) 115graus.
d) 110graus.
e) 105graus.
4 (saréspi) O vértice a de uma folha de papel retangular será dobrado sobre o lado
B Cde fórma que as medidas bê ê e BA' sejam iguais, como mostra a figura.
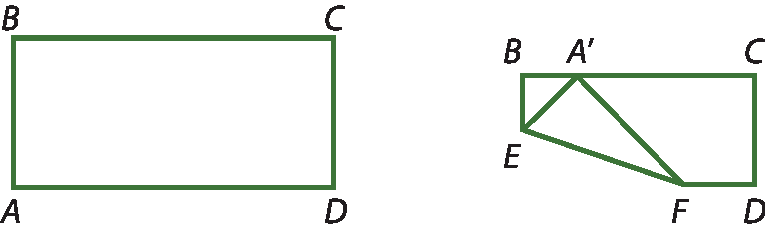
Nas condições dadas, a medida do ângulo, que é um dos ângulos internos do triângulo BA'E, é:
a) 45º.
b) 60º.
c) 100º.
d) 120º.
5 (univáli-Santa Catarina) O peso da figura está suspenso por duas cordas de mesma medida e presas no teto.
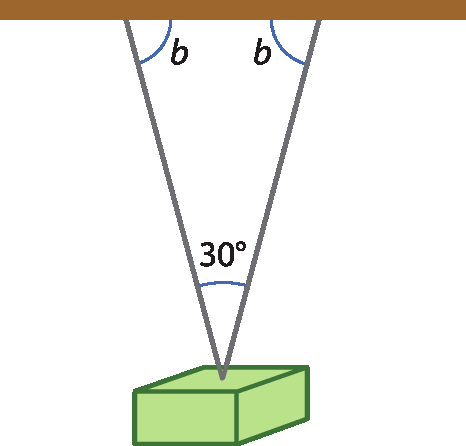
Se o ângulo entre as cordas é de 30graus, então o ângulo
Ângulo b, formado pela corda e o teto, mede:
a) 105graus.
b) 100graus.
c) 90graus.
d) 75graus.
e) 60graus.
6 (ú éfe ême gê) Nesta figura,
segmento A B é congruente ao segmento A C,
segmento B Dé bissetriz de
Ângulo A B C,
segmento C Ebissetriz de
Ângulo B C De a medida do ângulo
Ângulo A C Fé 140graus.
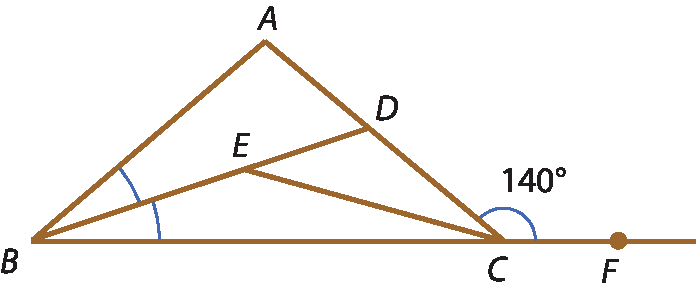
A medida do ângulo
Ângulo D E C, em grau, é:
a) 20
b) 30
c) 40
d) 50
e) 60
7 No triângulo á bê cê da figura, temos:
RETA D Ee
RETA B Csão paralelas, medida do(
Ângulo A) = 33graus e medida do(
Ângulo C) = 45graus. Calcule x e y.
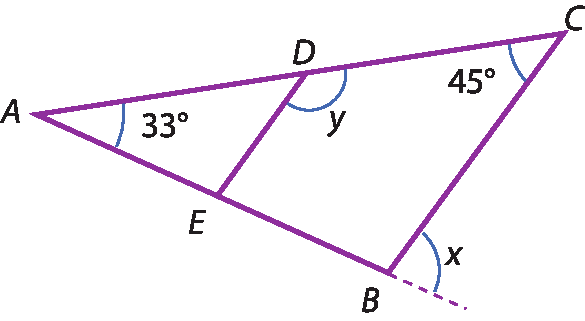
8 (ú éfe ême gê) Na figura, á cê = cê bê = bê dê e medida do(
Ângulo A) = 25graus.
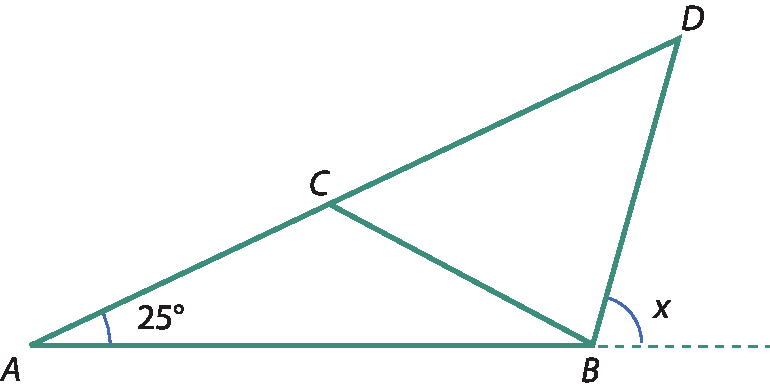
O valor de x é:
a) 50graus.
b) 60graus.
c) 70graus.
d) 75graus.
e) 80graus.
9 (ufáque) Considere a figura a seguir.
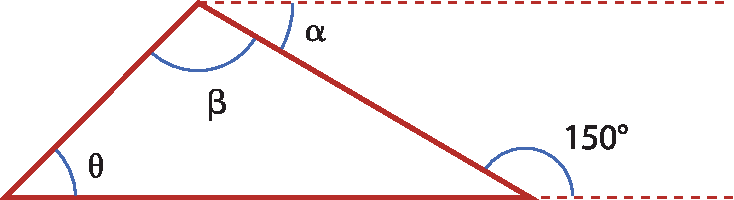
Sabendo-se que α + β = 135graus, temos que α, β e θ medem, respectivamente:
a) 30graus, 45graus e 105graus.
b) 30graus, 115graus e 35graus.
c) 30graus, 105graus e 45graus.
d) 45graus, 105graus e 30graus.
e) α = β = 45graus e θ = 90graus.
10 (ó bê mépi) A figura mostra dois trechos de 300 quilômetros cada um percorridos por um avião. O primeiro trecho faz um ângulo de 18graus com a direção norte, e o segundo, um ângulo de 44graus, também com a direção norte. Se o avião tivesse percorrido o trecho assinalado em pontilhado, qual seria o ângulo desse trecho com a direção norte?
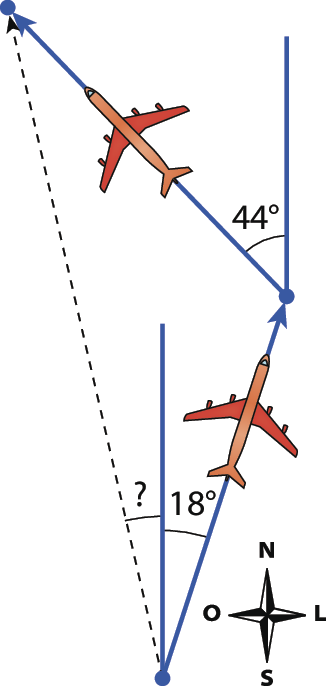
a) 12graus
b) 13graus
c) 14graus
d) 15graus
e) 16graus
Respostas e comentários
3. Alternativa e.
4. Alternativa a.
5. Alternativa d.
6. Alternativa c.
7. x = 78graus
y = 135graus
8. Alternativa d.
9. Alternativa c.
10. Alternativa b.
Exercícios complementares
Procure incentivar os estudantes a compartilhar as respostas obtidas, certificando-se de que o debate não se concentre apenas na resposta final, mas também na resolução dos exercícios. Os estudantes podem ter percorrido caminhos diferentes mas, com a explanação e o intercâmbio de estratégias, os procedimentos ganharão mais significado e riqueza.
As resoluções dos exercícios 3 e 4 e dos exercícios 6 a 10 estão no início deste Manual, nas orientações específicas do capítulo 8.
Apresentamos a seguir uma possível resolução para o exercício 5.
30 + b + b = 180
2b = 180 ‒ 30
2b = 150
b = 75
Ou seja, a medida b é 75graus (alternativa d).
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Se dois triângulos á bê cê e dê ê éfe são congruentes, então:
a) as medidas de todos os lados são iguais;
b) ambos devem ser retângulos;
c) seus vértices são coincidentes;
d) as medidas de seus respectivos lados são iguais.
2 Duas retas r e t paralelas são cortadas por duas retas transversais u e v, que se intersectam entre r e t, no ponto C, formando os triângulos á bê cê e dê cê é congruentes. a e B pertencem a r, D e ê pertencem a t. O que podemos afirmar sobre C ?
a) É um ponto equidistante de r e t.
b) Pertence às retas r e t.
c) Está mais distante de r do que de t.
d) Pertence a apenas uma das retas citadas.
3 Das sentenças a seguir, identifique a verdadeira.
a) Se traçarmos a diagonal em um quadrado, então os triângulos gerados não serão congruentes.
b) Se a bissetriz de um ângulo de medida α o divide ao meio, então a bissetriz de um desses novos ângulos gerará dois ângulos de medida
Fração. Numerador alfa, denominador 3..
c) Se um triângulo é equilátero, então a bissetriz, a mediana e a altura referentes a um mesmo lado coincidem.
d) Se um dos ângulos externos de um triângulo mede 60graus, então o triângulo é acutângulo.
4 No quadrilátero a seguir, o fato de
segmento A Cser a bissetriz de
Ângulo D A Be de
Ângulo B C Dfaz com que os triângulos ABC e ADC sejam:
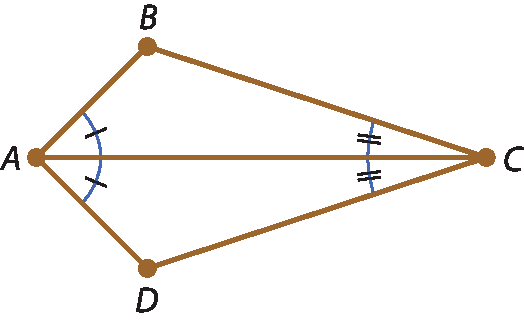
a) isósceles.
b) diferentes.
c) equiláteros.
d) congruentes.
5 Na imagem a seguir,
segmento A D é congruente ao segmento D E, α = 82graus e β = 69graus. Qual é a medida γ?
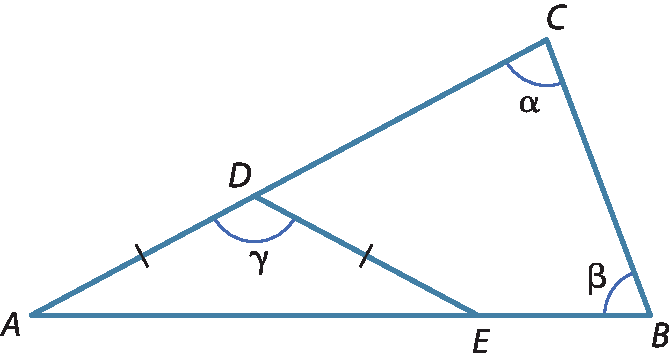
a) 29graus
b) 58graus
c) 100graus
d) 122graus
6 Um Dizáiner projetou uma janela em formato de triângulo equilátero com lados medindo 50 centímetros, conforme a imagem. O segmento
A Dé a altura da janela e representa uma viga de sustentação.
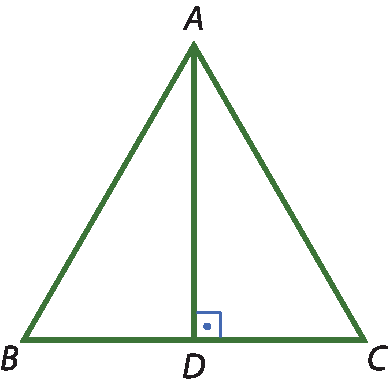
A que distância a extremidade C está da viga de sustentação e qual é a medida do ângulo
Ângulo D A C?
a) 50 centímetros e 30graus
b) 25 centímetros e 30graus
c) 50 centímetros e 60graus
d) 25 centímetros e 15graus
7 Na imagem a seguir,
segmento A B é congruente ao segmento B Ce medida do(BÂC) = 22graus. Determine a medida α do ângulo externo com vértice em B.
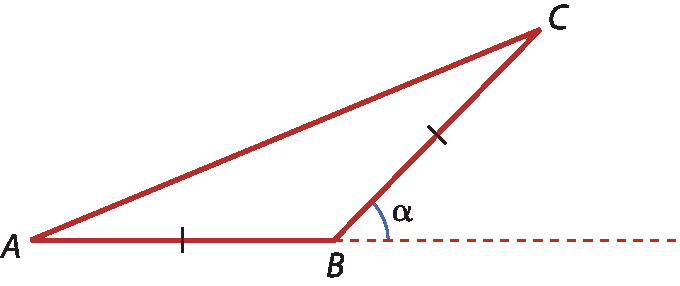
a) α = 22graus
b) α = 44graus
c) α = 136graus
d) α = 180graus
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Como você explicaria a um colega o que é Geometria demonstrativa?
b) Em um teorema, o que é a hipótese e o que é a tese?
c) Liste três postulados descritos neste capítulo.
d) Qual é a relação que podemos estabelecer entre a medida do lado de um triângulo e a medida do ângulo oposto a esse lado?
Respostas e comentários
1. Alternativa d.
2. Alternativa a.
3. Alternativa c.
4. Alternativa d.
5. Alternativa d.
6. Alternativa c.
7. Alternativa b.
Organizando:
a) Geometria demonstrativa é aquela que comprova todas as proposições geométricas com base em raciocínios dedutivos.
b) A hipótese é aquilo que se sabe e a tese é aquilo que se deseja provar.
c) Resposta possível:
• Uma reta tem infinitos pontos.
• Por um ponto, passam infinitas retas.
• Dois pontos distintos determinam uma única reta.
d) O lado de maior medida é oposto ao ângulo de maior medida, e o lado de menor medida é oposto ao ângulo de menor medida.
Verificando
Os testes propostos nessa seção podem contribuir para preparar os estudantes para exames de larga escala. Sugerimos que eles se reúnam em pequenos grupos para resolver os testes e, depois, resolvam-nos novamente de maneira individual.
Essa prática possibilita que eles apreendam estratégias e ampliem a compreensão dos conteúdos, além de favorecer a compreensão da avaliação individual como uma etapa do ensino que deve ser encarada com mais naturalidade. Ao resolver os mesmos testes, os estudantes podem adquirir maior segurança nesse tipo de avaliação.
As resoluções dos testes 1 a 7 estão no início deste Manual, nas orientações específicas do capítulo 8.
Organizando
Sugerimos que essas questões sejam utilizadas em uma aula a fim de revisar o conteúdo. Primeiro, os estudantes podem fazer uma autoavaliação pautada nessas questões e em outras que julgar relevantes. Depois, em uma discussão coletiva, conversam sobre as respostas dadas a cada uma delas.
DIVERSIFICANDO
Fractais
Considere o segmento
A B, dividido em três partes iguais.
Construímos sobre
segmento C Dum triângulo equilátero e, em seguida, apagamos o segmento
segmento C D.
Em cada um desses quatro segmentos, repetimos o mesmo procedimento.
Prosseguindo assim, obtemos a figura a seguir.

Essa figura, formada por repetições de padrões, é um exemplo de fractal. Ela conserva todas as propriedades da figura inicial.
Observe, a seguir, algumas imagens de fractais construídos com o uso do computador.


Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
Uma das figuras mais elementares da geometria fractal é o triângulo de Sierpinski. Para sua construção, partimos de um triângulo equilátero.
Unindo os pontos médios desse triângulo, obtemos quatro triângulos menores e desconsideramos aquele que não tem vértice coincidindo com um dos vértices do triângulo original.

Repetindo esse procedimento, obtemos:

Descubra qual é a quarta figura do triângulo de Sierpinski.


Respostas e comentários
Diversificando
O tema proposto nesta seção possibilita o desenvolvimento de um trabalho interdisciplinar com Arte. Sugerimos propor aos estudantes que façam uma pesquisa sobre artistas que utilizam a geometria fractal para construir suas obras. Proponha que pesquisem também obras de arte em que é possível notar fórmas que lembram fractais.
Apresentamos uma resolução para a atividade do Agora é com você!.
Observando o padrão, concluímos:
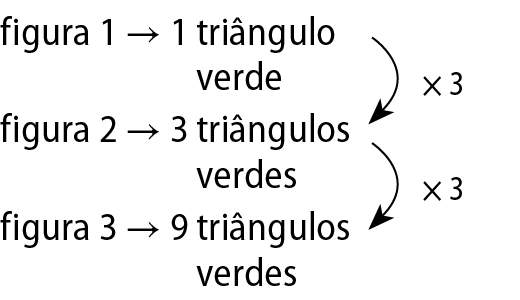
Prosseguindo na construção, a figura seguinte terá 27 triângulos verdes (alternativa c).

Sugestão de leitura
Para ampliar o trabalho com esse tema, sugerimos:
FARIA, R. W. S.; MALTEMPI, M. V. Padrões Fractais: conectando Matemática e Arte. écos : Revista Científica, São Paulo, número 27, página 33-53, janeiro/abril 2012. Disponível em: https://oeds.link/Lc5yDw. Acesso em: 8 junho 2022.
Nesse artigo, apresenta-se o conceito de fractal e seu potencial no processo de ensino e aprendizagem de conteúdos matemáticos, com ênfase em aspectos visuais e artísticos.
Glossário
- Silogismo
- : raciocínio dedutivo estruturado formalmente com base em duas proposições (premissas), das quais se obtém por inferência uma terceira (conclusão).
- Voltar para o texto