
CAPÍTULO 9 Estudo dos quadriláteros

Observe a imagem e responda às questões no caderno.
a) Que figuras geométricas planas você identifica nessa obra de Luiz Sacilotto?
b) É possível dizer que nessa obra há retângulos? E losangos?
c) Faça um desenho utilizando apenas quadriláteros.
Luiz Sacilotto (1924 a 2003) foi um pintor, escultor e desenhista brasileiro abstracionista, embora muitas de suas obras também tenham forte relação com o movimento Op Art, caracterizado pelos efeitos visuais e pelo uso de ilusões de óptica.
O artista buscava utilizar em suas obras figuras geométricas planas para dar a quem as observa a sensação de movimento e dinamismo, gerando ilusões de curvas, dobras e profundidade.
Respostas e comentários
a) Resposta possível: trapézio, quadrado, retângulo e triângulo.
b) Espera-se que os estudantes respondam que sim, pois todo quadrado é também retângulo e losango.
c) Construção de figura.
Capítulo 9 – Estudo dos quadriláteros
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, retomamos e ampliamos o estudo dos quadriláteros. Iniciamos com uma breve revisão dos elementos que constituem um quadrilátero. Avançamos o estudo sobre a classificação dos quadriláteros, tendo como critérios os lados serem ou não paralelos, serem ou não perpendiculares, serem ou não congruentes. Aprofundamos o estudo sobre as propriedades decorrentes das características de classificação dos quadriláteros, demonstrando propriedades com base na congruência de triângulos, assunto já trabalhado em capítulos anteriores.
A abertura destaca a relação entre Matemática e Arte, apresentando uma obra de Luiz Sacilotto para explorar a conexão entre essas duas áreas de conhecimento. Esse contexto possibilita o desenvolvimento da competência geral 3, pois estimula os estudantes a apreciar e usufruir diferentes manifestações artísticas. Incentive-os a pesquisar exposições culturais regionais.
Além disso, essa é uma ótima oportunidade para um projeto interdisciplinar com Arte. Solicite aos estudantes um trabalho sobre Luiz Sacilotto e sua obra. Organize grupos de três integrantes e cada grupo, à sua escolha, deve fazer a reprodução de uma das obras do artista. O conjunto dessas reproduções pode compor uma exposição a ser agendada com a direção da escola.

Sugestão de leitura
GUIA das Artes. Luiz Sacilotto. São Lourenço, [2015?]. Disponível em: https://oeds.link/TD0vCr. Acesso em: 10 junho 2022.
O portal de conteúdo especializado em Arte apresenta a biografia do artista Luiz Sacilotto e a cronologia de suas obras.
1. Quadriláteros
Podemos perceber os quadriláteros em muitas situações que vivenciamos, por exemplo, ao ler um livro ou ler um texto na tela do computador, na bandeirada final de uma corrida, em um jôgo de xadrez.


(As imagens não respeitam as proporções reais entre os objetos.)
Quadriláteros são polígonos de quatro lados.

Elementos dos quadriláteros
Considere os quadriláteros a seguir.
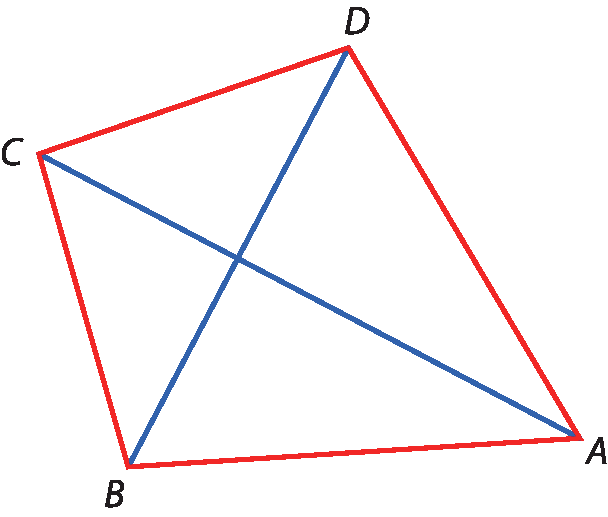
No quadrilátero a bê cê dê, destacamos:
• os vértices a, B, C e D;
• os lados
Segmento de reta AB. Segmento de reta BC.,
Segmento de reta BC.,
Segmento de reta CD.e
Segmento de reta DA.;
• as diagonais
Segmento de reta AC.e
Segmento de reta BD.;
• os lados consecutivos
Segmento de reta AB e segmento de reta BC,
Segmento de reta BC e segmento de reta CD,
Segmento de reta CD e segmento de reta DA,
Segmento de reta DA e segmento de reta AB;
• os lados opostos
Segmento de reta AB e segmento de reta CD,
Segmento de reta BC e segmento de reta AD.
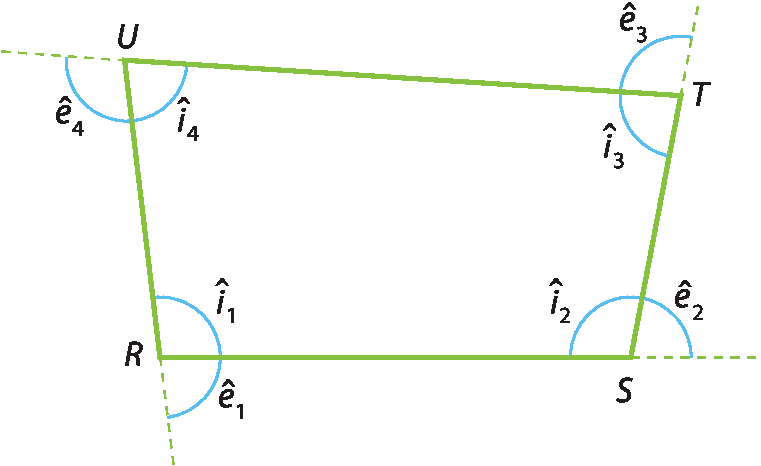
No quadrilátero érre ésse tê ú, destacamos:
• os ângulos internos
Ângulo i.1 ,
Ângulo i.2 ,
ângulo i3 e
ângulo i4 ;
• os ângulos consecutivos
ângulo i1 e
ângulo i2 ,
ângulo i2 e
ângulo i3 ,
ângulo i3 e
ângulo i4 ,
ângulo i4 e
ângulo i1;
• os ângulos opostos
ângulo i1 e
ângulo i3 ,
Ângulo i.2 e
Ângulo i.4;
• os ângulos externos
ângulo e1 ,
ângulo e2 ,
ângulo e3 e
ângulo e4.
Respostas e comentários
1. Quadriláteros
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um quatro.
Trabalhar demostração de propriedades dos quadriláteros por meio da congruência de triângulos possibilita ao estudante o desenvolvimento da habilidade (ê éfe zero oito ême ah um quatro).
Inicialmente, proponha aos estudantes que, em grupos, confeccionem cartazes nos quais apresentem:
• o que são quadriláteros, com desenhos de exemplos;
• os principais elementos de um quadrilátero;
• o que são quadriláteros convexos, com desenhos de exemplos e de contraexemplos (quadriláteros não convexos).
Em seguida, um representante de cada grupo apresenta o cartaz do grupo. Registre na lousa as conclusões da turma, ressaltando os temas que mais geraram dúvidas. Desse modo, espera-se que os estudantes ampliem e consolidem os conhecimentos construídos acerca de quadriláteros:
• Quadrilátero é um polígono de 4 lados. Tem 4 vértices, 4 ângulos internos e 4 ângulos externos.
• A convexidade de um quadrilátero pode ser verificada constatando que existem quadriláteros cujo prolongamento dos lados não cruza seu interior; nesse caso, os quadriláteros são convexos. Quando há lados cujo prolongamento cruza o interior do quadrilátero, ele é não convexo.
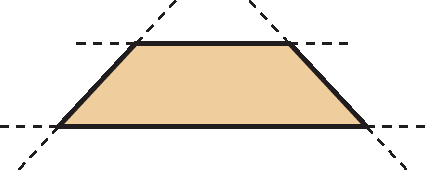
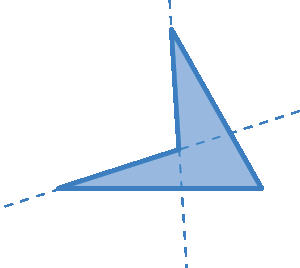
• A diagonal de um quadrilátero é todo segmento de reta cujas extremidades são vértices não consecutivos do quadrilátero (ou seja, não é um de seus lados). Todo quadrilátero tem duas diagonais.
Reproduza na lousa o quadrilátero RSTU apresentado nesta página e destaque os ângulos internos e os ângulos externos. Explique aos estudantes que o nosso estudo será feito considerando sempre quadriláteros convexos.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Desenhe um quadrilátero qualquer em uma folha de papel. Marque os ângulos internos desse quadrilátero, cada um com uma côr diferente. Recorte o quadrilátero separando os quatro ângulos internos.

Reúna os ângulos internos em tôrno de um dos vértices do quadrilátero, justapondo seus lados de modo que se obtenha um único ângulo, cuja medida será a soma das medidas dos quatro ângulos internos.
Qual é o valor dessa soma? Justifique.
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Sabendo que a soma das medidas dos ângulos internos de um triângulo é 180graus, demonstre que a soma das medidas dos ângulos internos de um quadrilátero é 360graus.
2 Considere o quadrilátero ême êne pê quê.
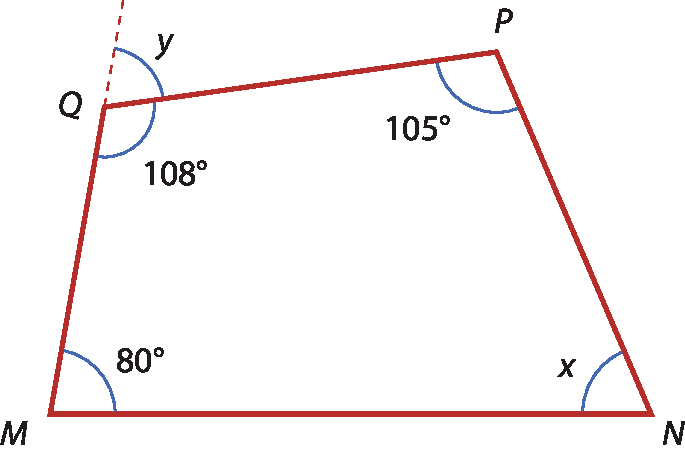
Calcule no caderno:
a) a medida x do ângulo
N;
b) o valor de y.
3 Com o auxílio de régua e transferidor, desenhe no caderno um quadrilátero que tenha:
a) dois ângulos internos opostos congruentes medindo 90graus;
b) dois ângulos internos opostos congruentes, medindo 90graus, e quatro lados congruentes;
c) dois ângulos internos opostos congruentes, medindo 90graus, e quatro lados congruentes de 6 centímetros.
Em cada item, quantos quadriláteros diferentes com essas características é possível construir?
4 Três dos ângulos internos de um quadrilátero medem, respectivamente, 104graus, 97graus e 53graus. Calcule a medida do quarto ângulo desse quadrilátero.
5 Em um quadrilátero, os ângulos internos medem, respectivamente, x, x + 40graus, x + 80graus e 3x. Calcule o valor de x, em grau.
6 Em um quadrilátero ABCD, medida do(
ângulo A) = medida do(
ângulo B), medida do(
ângulo B) = 3 ⋅ medida do(
ângulo C) e medida do(
ângulo D) = 2 ⋅ medida do(
ângulo C). Calcule a medida dos ângulos
Ce
A.
7 Em um quadrilátero a bê cê dê, temos:
• medida do(
ângulo A) = 108graus
• medida do(
ângulo B) = 76graus
• medida do(
ângulo C) = 92graus
Calcule a medida do ângulo formado pelas bissetrizes dos ângulos
Ce
D.
8 Com o auxílio de régua, transferidor e compasso, desenhe um quadrilátero a bê cê dê que tenha os quatro lados congruentes (com a medida que você quiser) e um ângulo de 70graus.
a) Qual é a medida dos outros ângulos internos?
b) Trace as diagonais que se intersectam no ponto M. Qual é a medida do ângulo que elas formam?
c) Meça
segmento de reta AM,
Segmento de reta BM.,
Segmento de reta CM.e
Segmento de reta DM.e responda: qual é a relação do ponto M com a diagonal maior? E com a diagonal menor?
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)
Respostas e comentários
Pense mais um poucoreticências: O valor é 360graus. Resposta possível: Ao juntar os quatro ângulos em torno de um dos vértices do quadrilátero, obtemos o giro de uma volta completa, que corresponde a 360graus.
1. Demonstração. Espera-se que os estudantes iniciem traçando uma das diagonais do quadrilátero.
2. a) x = 67graus
2. b) y = 72graus
3. a) Construção de figura. Resposta possível: quadrado.
3. b) Construção de figura. Quadrado.
3. c) Construção de figura. Com quatro ângulos medindo 90graus e quatro lados medindo 6 centímetros, existe um único quadrado.
4. 106graus
5. x = 40graus
6. medida do(
ângulo C) = 40graus e medida do(
ângulo A) = 120graus.
7. 92graus
8. a) 70graus; 110graus e 110graus.
8. b) 90graus
8. c) M é ponto médio da diagonal maior e da diagonal menor.
Pense mais um poucoreticências
Uma boa maneira de iniciar o estudo de um conceito é com uma atividade na qual os estudantes manipulem modelos concretos. Esta seção contempla esse tipo de abordagem, pois explora uma propriedade importante de um quadrilátero: a soma das medidas dos ângulos internos de um quadrilátero é 360graus.
Nesta atividade, os estudantes recortam os ângulos internos de um quadrilátero desenhado em papel e, analogamente ao que já foi feito para a soma das medidas dos ângulos internos de um triângulo, justapõem as partes em tôrno de um vértice com o objetivo de verificar o valor da soma das medidas desses ângulos.
Exercícios propostos
Uma possível demonstração para o exercício 1 é dada a seguir. Nela é utilizada apenas uma diagonal para dividir o quadrilátero em dois triângulos, resultando diretamente na verificação de que a soma das medidas dos ângulos internos do quadrilátero é igual à soma das medidas dos ângulos internos desses dois triângulos (2 · 180graus = 360graus).
Observe a resolução:
Hipótese: ABCD é um quadrilátero
Tese: medida do(
ângulo A) + medida do(
ângulo B) + medida do(
ângulo C) + medida do(
ângulo D) = 360graus
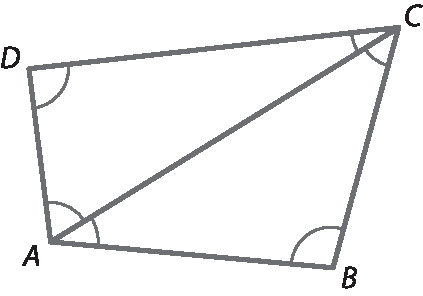
• Demonstração
Tomemos o quadrilátero a bê cê dê e tracemos sua diagonal
AC.
No triângulo á bê cê, temos: medida do(B
AC) + medida do(A
BC) + medida do(A
CB) = 180graus
No triângulo ACD, temos: medida do(D
AC) + medida do(A
CD) + medida do(C
DA) = 180graus
Logo, [medida do(B
AC) + medida do(A
BC) + medida do(A
CB)] + [medida do(D
AC) + medida do(A
CD) + medida do(C
DA)] = 180graus + 180graus
[medida do(B
AC) + medida do(D
AC)] + [medida do(A
CB) + medida do(A
CD)] + medida do(A
CC) + medida do(C
DA) = 360graus
medida do(B
AD) + medida do(A
BC) + medida do(B
CD) + medida do(C
DA) = 360graus
As resoluções dos exercícios 2 a 8 estão no início deste Manual, nas orientações específicas do capítulo 9.
PARA SABER MAIS
Polígonos e proporcionalidade
Já conhecemos as fórmulas da soma Si das medidas dos ângulos internos e da soma Se das medidas dos ângulos externos de um polígono de n lados.


Vamos examinar se existe proporcionalidade entre essas grandezas (Si e Se ) e o número n de lados dos polígonos. Em outras palavras, vamos verificar se, dobrando o número de lados, também dobra o valor de Si e o valor de Se ; se, triplicando o número de lados, também triplica o valor de Si e o valor de Se etcétera Enfim, se as grandezas Si e n formam proporções e se as grandezas Se e n formam proporções.
Observe a seguir o quadro das somas das medidas dos ângulos internos e dos ângulos externos de um polígono.
|
Polígono |
n |
Si |
Se |
|---|---|---|---|
|
Triângulo |
3 |
= (3 − 2) ⋅ 180° = 180° |
= 360° |
|
Quadrilátero |
4 |
= (4 − 2) ⋅ 180° = 360° |
= 360° |
|
Pentágono |
5 |
||
|
Hexágono |
|||
|
Heptágono |
|||
|
Octógono |
|||
|
Eneágono |
|||
|
Decágono |
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Copie no caderno o quadro apresentado e complete-o.
2 Considerando o quadro que você completou, responda às questões a seguir.
a) Qual polígono tem Si igual ao dôbro de Si3? Qual polígono tem Se igual ao dôbro de Se3?
b) Qual polígono tem Si igual ao triplo de Si3? Qual polígono tem Se igual ao triplo de Se3?
3 Comparando dois polígonos, um de n lados e outro de 2n lados, responda às questões.
a) Si6 é o dôbro de Si3? E Se6 é o dôbro de Se3?
b) Si8 é o dôbro de Si4? E Se8 é o dôbro de Se4?
c) Si10 é o dôbro de Si5? E Se10 é o dôbro de Se5?
d) Si6 é o triplo de Si2? E Se6 é o triplo de Se2?
e) Si9 é o triplo de Si3? E Se9 é o triplo de Se3?
4 Considerando as suas respostas às atividades 2 e 3, você diria que as grandezas Si e n formam proporções? E as grandezas Se e n formam proporções?
Respostas e comentários
1. Construção de quadro.
2. a) Quadrilátero; nenhum.
2. b) Pentágono; nenhum.
3. a) Não; não.
3. b) Não; não.
3. c) Não; não.
3. d) Não; não.
3. e) Não; não.
4. Espera-se que os estudantes concluam que nem as grandezas ésse minúsculoi e n, nem as grandezas ésse minúsculoe e n formam proporções.
Para saber mais
Esta seção trata de uma situação na qual analisamos se as grandezas envolvidas são ou não proporcionais, trabalhando com a soma das medidas dos ângulos de polígonos.
A relação entre o número de lados de um polígono e a soma das medidas dos ângulos internos exemplifica a não proporcionalidade, o que, por contraposição, reforça o desenvolvimento das habilidades (ê éfe zero oito ême ah um dois) e (EF08MA13).
Apresentar aos estudantes situações em que não há proporcionalidade é mais uma maneira de compreenderem grandezas proporcionais. É como apresentar-lhes o avesso para que entendam o direito.
As resoluções das atividades 1 a 4 do Agora é com você! estão no início deste Manual, nas orientações específicas do capítulo 9.
2. Paralelogramos
Para compor a obra reproduzida a seguir, o artista brasileiro Hélio Oiticica (1937-1980) usou diferentes figuras que dão a ideia de paralelogramos. Observe-as.

Paralelogramos são quadriláteros que têm os lados opostos paralelos.
Na figura a seguir,
segmento AB é paralelo ao segmento CDe
segmento AD é paralelo ao segmento BC. Logo, o quadrilátero a bê cê dê é um paralelogramo.

O lado
ABé uma base do paralelogramo, e o segmento
DHé uma altura do paralelogramo relativa a essa base.
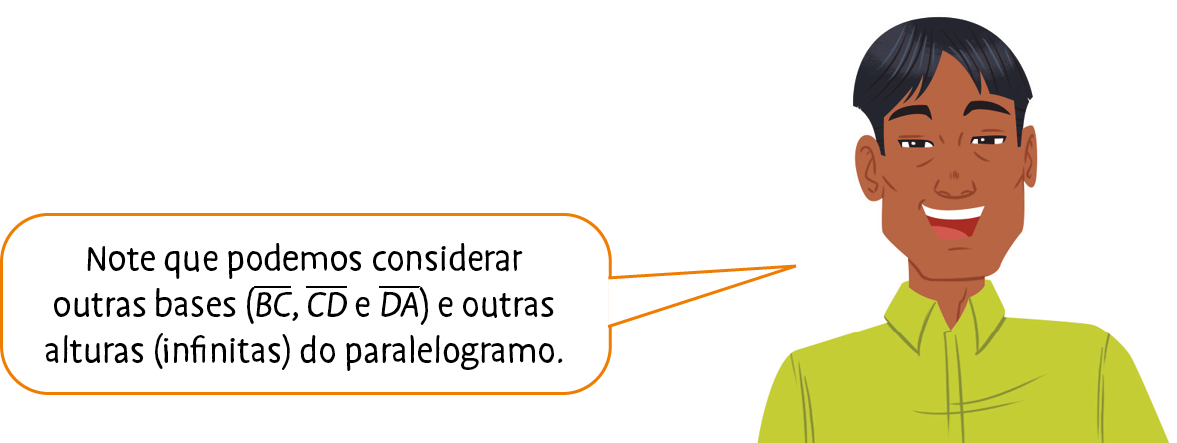
Entre os paralelogramos, destacam-se três casos particulares.
Retângulos: paralelogramos que têm os quatro ângulos congruentes (retos).

Losangos: paralelogramos que têm os quatro lados congruentes.
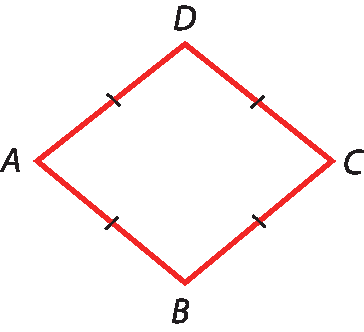
Quadrados: paralelogramos que têm os quatro lados congruentes e os quatro ângulos congruentes (retos).
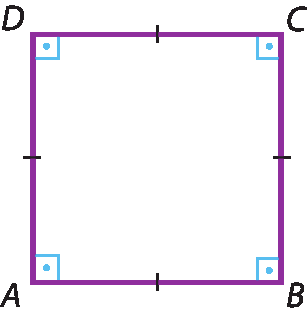
Assim, todo quadrado é um retângulo e, também, é um losango.
Respostas e comentários
2. Paralelogramos
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah um quatro, ê éfe zero oito ême ah um cinco, ê éfe zero oito ême ah um sete e ê éfe zero oito ême ah um nove.
Ao trabalhar a demostração de propriedades dos quadriláteros por meio da congruência de triângulos, o estudante desenvolve a habilidade (ê éfe zero oito ême ah um quatro). Ao construir mediatriz, bissetriz e aplicar esses conceitos na resolução de problemas, favorece o desenvolvimento das habilidades (ê éfe zero oito ême ah um cinco) e (EF08MA17). A aplicação de expressões para o cálculo de medidas de área de figuras geométricas e a resolução e elaboração de problemas envolvendo medidas de área possibilitam o desenvolvimento da habilidade (ê éfe zero oito ême ah um nove).
A primeira classe de quadriláteros que vamos estudar é a dos paralelogramos. Inicialmente, é importante retomar com os estudantes a classificação dos quadriláteros quanto ao paralelismo de seus lados:
• paralelogramos: quadriláteros que têm dois pares de lados paralelos (ou seja, têm os lados opostos paralelos);
• trapézios: quadriláteros que têm apenas dois pares de lados paralelos (ou seja, têm dois lados paralelos e dois lados não paralelos);
• quadriláteros que não são nem trapézios nem paralelogramos: aqueles que não têm lados paralelos.
Peça a alguns estudantes que desenhem na lousa exemplos de paralelogramos observando a característica que fórma esse grupo de quadriláteros. Espera-se que surjam diferentes tipos de paralelogramo. Em cada um deles, destaque uma base e a altura relativa a essa base. Ressalte o ângulo reto determinado ao traçar cada altura.
Faça desenhos de paralelogramos na lousa, destacando retângulos, losangos e quadrados. Peça aos estudantes que descrevam as características de cada um. Desse modo, eles expõem o que já sabem sobre essas figuras. Complemente, então, com as características que não surgirem.

Sugestão de leitura
Para ampliar e enriquecer a discussão com os estudantes, sugerimos:
NUNES, K. R. A. Tecendo Matemática com Arte. Associação Nacional dos Professores de Matemática na Educação Básica. Disponível em: https://oeds.link/GqnXGR. Acesso em: 10 junho 2022.
O artigo discute algumas relações entre Matemática e Arte e apresenta propostas para o trabalho de conceitos matemáticos por meio do estudo e da análise de obras de arte, fazendo com que a sala de aula se transforme em um ambiente de argumentação, pesquisa e construção de conhecimentos, e estimulando a criatividade dos estudantes.
Propriedades dos paralelogramos
1ª propriedade

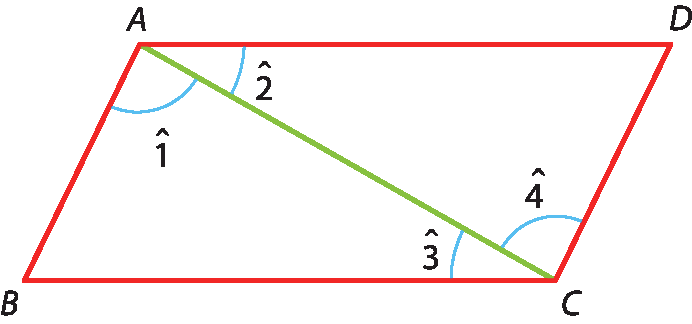
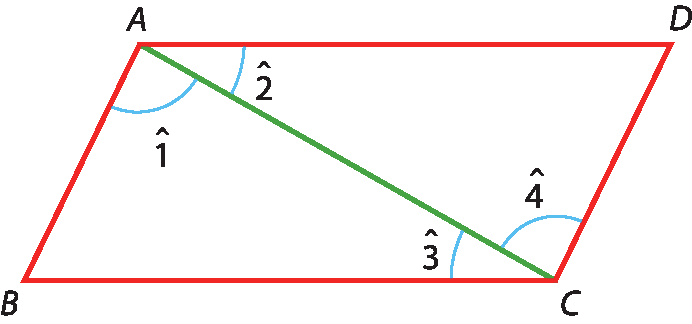
• Demonstração
Traçando a diagonal
Segmento de reta AC., decompomos o paralelogramo a bê cê dê nos triângulos á bê cê e cê dê á. Analisando os elementos desses triângulos, temos:
•
O ângulo 1 congruente ao ângulo 4.(ângulos alternos internos formados pelos segmentos paralelos
Segmento de reta ABe
Segmento de reta CDcom a diagonal
Segmento de reta AC.);
•
O segmento de reta AC é congruente ao segmento de reta AC.(lado comum);
•
O ângulo 3 congruente ao ângulo 2.(ângulos alternos internos formados pelos segmentos paralelos
Segmento de reta ADe
Segmento de reta BCcom a diagonal
Segmento de reta AC).
Pelo caso ângulo-lado-ângulo, os triângulos á bê cê e cê dê á são congruentes. Portanto:
e
O segmento de reta BC é congruente ao segmento de reta AD.2ª propriedade

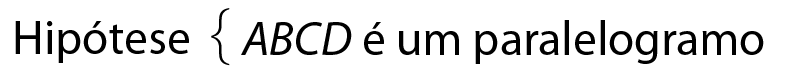
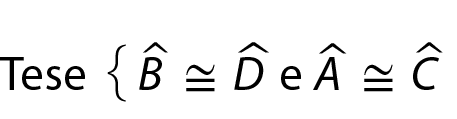
Respostas e comentários
Propriedades dos paralelogramos
Ressalte a inclusão dos tipos especiais de paralelogramos antes de iniciar o estudo de suas propriedades.
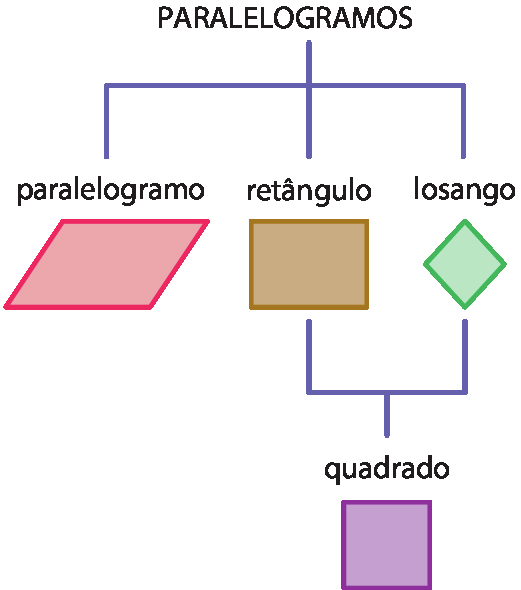
Analise o diagrama com os estudantes, de modo que reconheçam que retângulos, losangos e quadrados são paralelogramos e que quadrados são retângulos e também losangos. Registre em um cartaz o que caracteriza cada tipo de paralelogramo e afixe-o na sala de aula, possibilitando que os estudantes o consultem quando necessário.
• Paralelogramo: quadrilátero que tem os lados opostos paralelos.
• Retângulo: paralelogramo que tem 4 ângulos internos retos.
• Losango: paralelogramo que tem 4 lados de mesma medida.
• Quadrado: paralelogramo que tem os 4 ângulos internos retos e os 4 lados de mesma medida (é um retângulo e é um losango).
Ressalte para os estudantes que toda propriedade válida para paralelogramos é válida também para retângulos, losangos e quadrados, pois estes também são paralelogramos.
A primeira propriedade tratada é: “Os lados opostos de um paralelogramo são congruentes”. Reproduza na lousa a demonstração, fazendo cada etapa com os estudantes.
• Demonstração
Traçando a diagonal
Segmento de reta AC., decompomos o paralelogramo a bê cê dê nos triângulos á bê cê e cê dê á. Por raciocínio análogo à demonstração da 1ª propriedade, analisando os elementos dos triângulos obtidos, á bê cê e cê dê á, concluímos, pelo caso ângulo-lado-ângulo, que os triângulos á bê cê e cê dê á são congruentes. Portanto,
O ângulo B congruente ao ângulo D.. Se traçarmos a diagonal
Segmento de reta BD., demonstraremos que
O ângulo A congruente ao ângulo C..
3ª propriedade

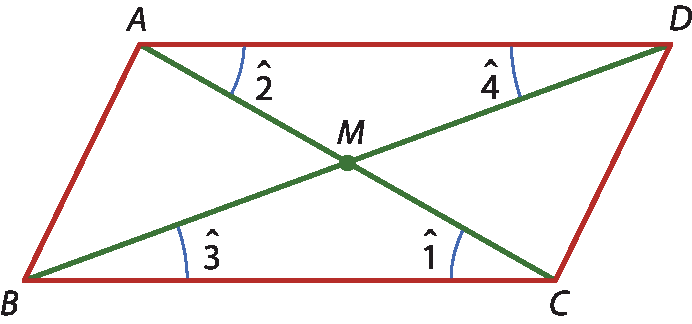
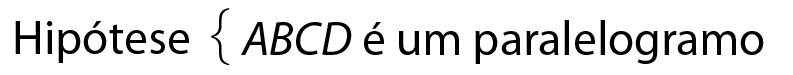
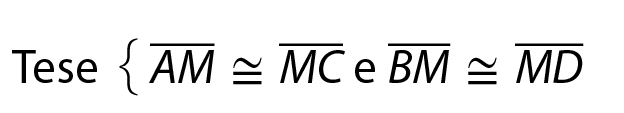
• Demonstração
Comparando os elementos dos triângulos bê ême cê e dê ême ah, temos:
•
O ângulo 1 congruente ao ângulo 2.(ângulos alternos internos formados pelos segmentos paralelos
Segmento de reta AD.e
Segmento de reta BC.com a diagonal
Segmento de reta AC.);
•
O segmento de reta AD é congruente ao segmento de reta BC.(lados opostos de um paralelogramo demonstrado na 1ª propriedade);
•
O ângulo 3 congruente ao ângulo 4.(ângulos alternos internos formados pelos segmentos paralelos
Segmento de reta AD.e
Segmento de reta BC.com a diagonal
Segmento de reta BD.).
Logo, pelo caso ângulo-lado-ângulo, os triângulos bê ême cê e dê ême ah são congruentes. Portanto:
e
O segmento de reta BM é congruente ao segmento de reta MD.EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
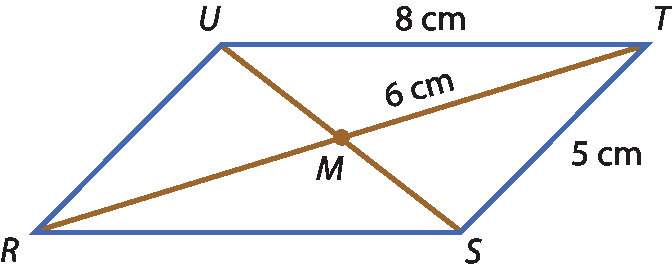
9 Observe os paralelogramos e, considerando as propriedades estudadas, determine:
a) x e y;
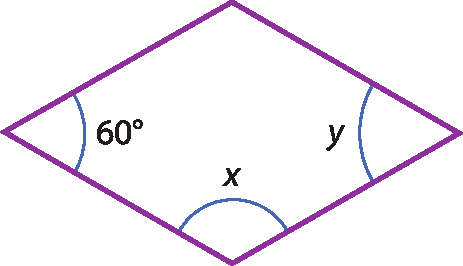
b) Érre ésse, érre ú, MR e RT.
10 Um dos ângulos agudos de um paralelogramo mede 74graus. Calcule a medida de um dos ângulos obtusos desse paralelogramo.
Respostas e comentários
9. a) x = 120graus e y = 60graus.
9. b) 8 centímetros, 5 centímetros, 6 centímetros, 12 centímetros.
10. 106graus
Propriedades dos paralelogramos
Nesta página, demonstramos outras duas propriedades dos paralelogramos:
• Os ângulos internos opostos de um paralelogramo são congruentes.
• As diagonais de um paralelogramo se cruzam nos respectivos pontos médios.
Antes de apresentar aos estudantes as demonstrações, organize-os em duplas e peça que demonstrem cada propriedade. Com base no que já estudaram da primeira propriedade e em estudos anteriores, é esperado que eles desenvolvam tais demonstrações. Depois, discuta com a turma o que cada dupla fez e, se julgar necessário, reproduza na lousa a demonstração do livro.
Exercícios propostos
Apresentamos aqui uma possível resolução do exercício 9.
a) Pela 2ª propriedade, obtemos y = 60graus. Pelo fato de os lados de um paralelogramo serem paralelos, os ângulos de medidas x e y são ângulos colaterais internos, portanto suplementares; assim, x = 120graus.
b) Aplicando a 3ª propriedade, obtemos: MR = MT = 6 centímetros RT = RM + MT = 12 centímetros Aplicando a 1ª propriedade, obtemos: érre ú = ésse tê = 5 centímetros Érre ésse = ú tê = 8 centímetros
A resolução do exercício 10 está no início deste Manual, nas orientações específicas do capítulo 9.
11 Em um losango, um dos ângulos mede 125graus. Determine a medida de um dos ângulos agudos desse losango.
12 Nos paralelogramos a seguir, calcule x e y.
a)
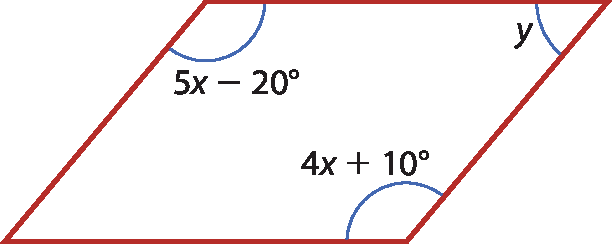
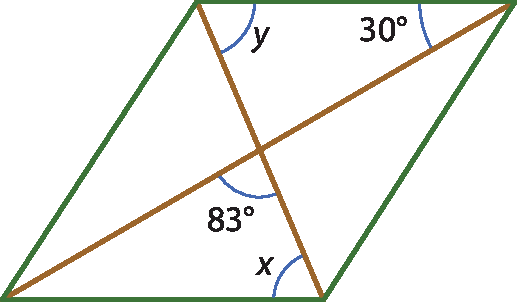
b)
13 Em um paralelogramo, um dos ângulos externos mede 108graus. Calcule as medidas dos ângulos internos desse paralelogramo.
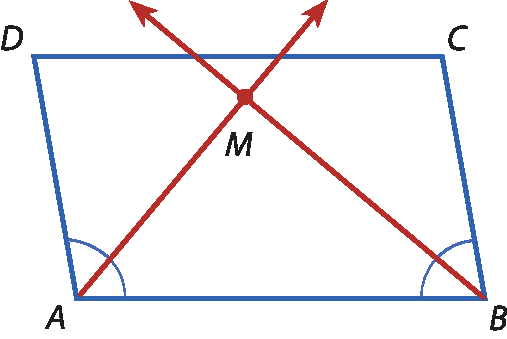
14 No paralelogramo a seguir, medida do(
ãngulo B) = 80graus,
Semirreta BM.é bissetriz do ângulo
Be
Semirreta AM.é bissetriz do ângulo
A. Calcule a medida do ângulo
A M B.
15 Construa um paralelogramo cujas diagonais meçam 4,2 centímetros e 5,6 centímetros e formem entre si um ângulo de 110graus.
16 Considere os paralelogramos a bê cê dê e ê éfe gê agá a seguir.
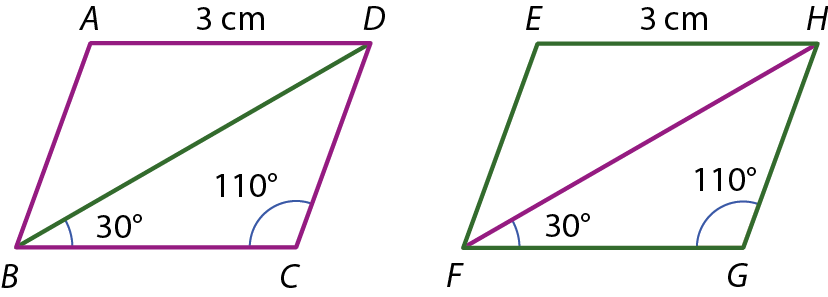
Esses paralelogramos são congruentes? Justifique sua resposta.
17 Agora, considere os paralelogramos éle ême êne ó e PQRS a seguir.
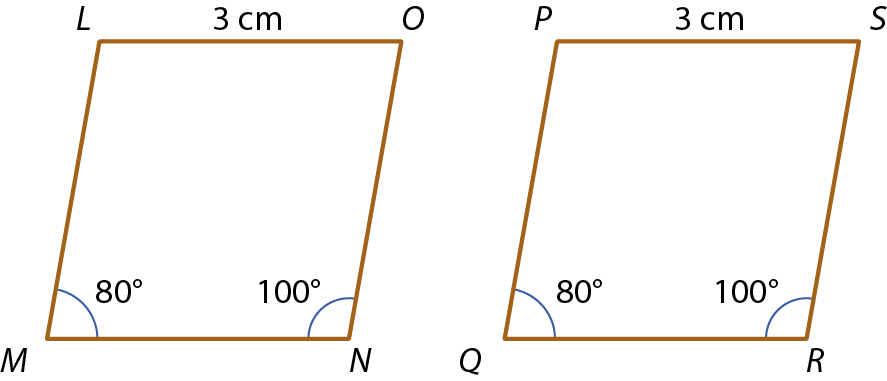
Podemos afirmar que esses paralelogramos são congruentes? Justifique sua resposta.
18

Hora de criar – Em dupla, cada um cria um problema sobre uma das propriedades do paralelogramo. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
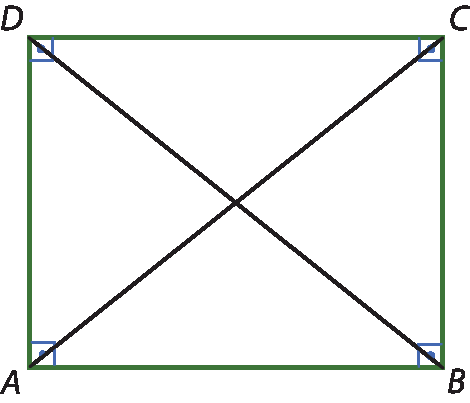
Propriedade dos retângulos

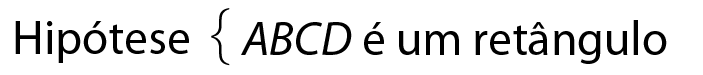
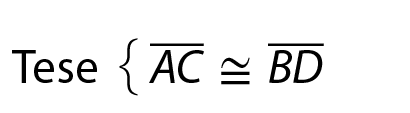
Respostas e comentários
11. 55graus
12. a) x = 30graus
y = 50graus
12. b) x = 67graus
y = 67graus
13. 72graus, 72graus, 108graus, 108graus.
14. 90graus
15. Construção de figura.
16. Sim, pois △bê cê dê ≅ △éfe gê agá pelo caso ângulo-lado-ângulo. Consequentemente,
O segmento de reta DC é congruente ao segmento de reta HG..
17. Não, pois não temos as medidas de
Segmento de reta ON.e
Segmento de reta SR..
18. Resposta pessoal.
Exercícios propostos
As resoluções dos exercícios 11 a 13 e dos exercícios 16 a 18 estão no início deste Manual, nas orientações específicas do capítulo 9.
No exercício 14, a medida do ângulo A
MB independe da medida dada (80graus) para o ângulo
B. Explore esse exercício pedindo aos estudantes que repitam a resolução, inicialmente, atribuindo a medida 70graus ao ângulo, depois 60graus e depois uma medida qualquer a ser escolhida por eles. Apresente a demonstração da proposição a seguir ou solicite a eles que a apresentem.
As bissetrizes de dois ângulos consecutivos de um paralelogramo formam, com o lado comum a esses ângulos, um triângulo retângulo, sendo esse lado a hipotenusa.
Hipótese:
Tese: O triângulo á ême bê é um triângulo retângulo com hipotenusa
A B• Demonstração
Tomemos o paralelogramo a bê cê dê e tracemos as bissetrizes dos ângulos B
AD e A
BC.
Vamos representar medida do(B
AD) por x. Então:
medida do(A
BC) = (180graus ‒ x)
medida do(B
AM) =
x sobre denominador 2
medida do(A
BM) =
fração, numerador 180 graus menos x, denominador 2, fim da fração
Como a soma das medidas dos ângulos internos de um triângulo é 180graus, obtemos:
medida do(B
AM) + medida do(A
BM) + medida do(A
MB) = 180graus
+
fração, numerador 180 graus menos x, denominador 2, fim da fração+ medida do(A
ângulo MB) = 180graus
+ medida do(A
MB) = 180graus 90graus + medida do(A
MB) = 180graus medida do(A
MB) = 90graus
Portanto, o triângulo á ême bê é retângulo em M, ou seja,
o segmento de reta A Bé a hipotenusa.
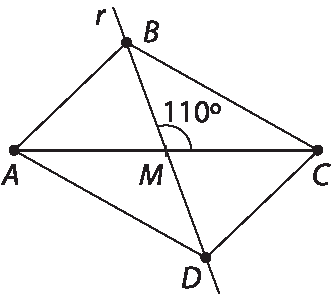
Para o exercício 15, segue uma possível resolução.
Usando uma régua, traçamos um segmento
A Ccuja medida é 5,6 centímetros e marcamos o seu ponto médio M.
Com um transferidor, construímos um ângulo de 110graus, com vértice em M, e traçamos uma reta r. Nela, marcamos os pontos B e D, de modo que BD = 4,2 centímetros, com M seu ponto médio.
Os pontos a, B, C e D são os vértices do paralelogramo.
• Demonstração
Traçando as diagonais
Segmento de reta AC.e
Segmento de reta BD.no retângulo a bê cê dê, ele pode ser decomposto nos triângulos á bê dê e bê á cê.
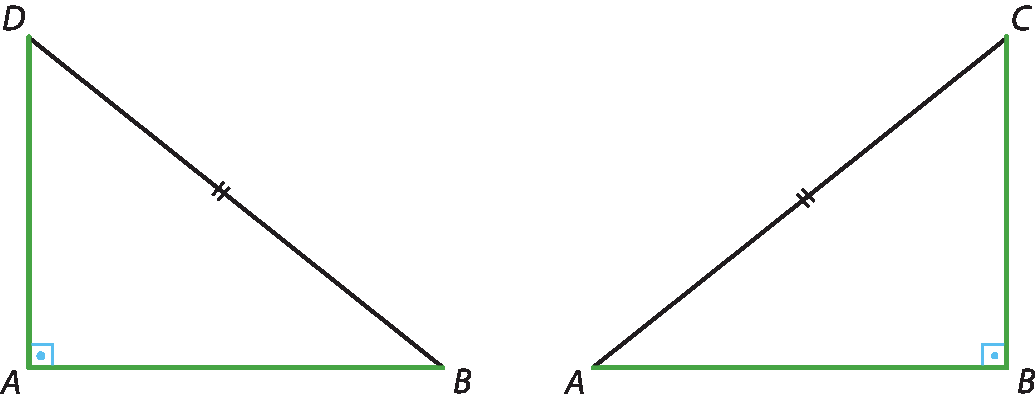
Comparando os elementos desses triângulos, temos:
•
O segmento de reta AD é congruente ao segmento de reta BC.(lados opostos de um paralelogramo);
•
O ângulo A congruente ao ângulo B.(ângulos retos);
•
O segmento de reta AB é congruente ao segmento de reta AB.(lado comum).
Logo, pelo caso lado ângulo lado, os triângulos á bê dê e bê á cê são congruentes. Portanto,
O segmento de reta AC é congruente ao segmento de reta BD..
Propriedade dos losangos

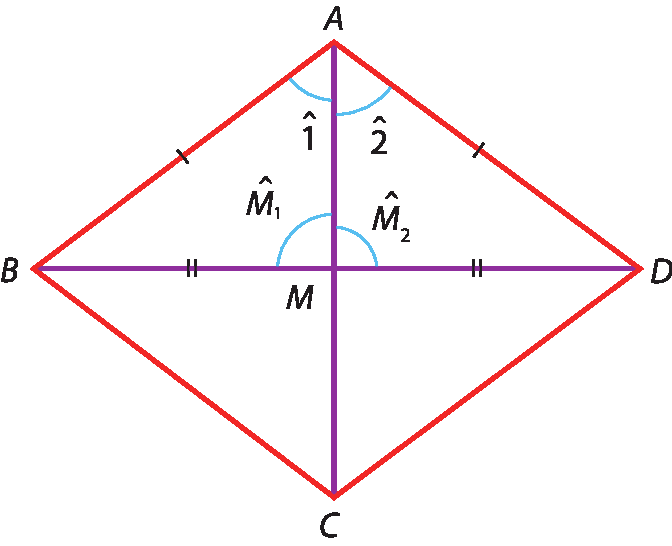
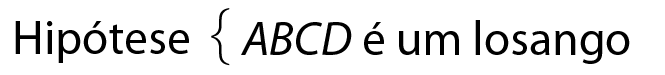
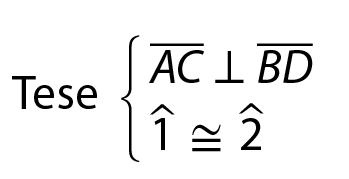
• Demonstração
Analisando os elementos dos triângulos á ême bê e á ême dê, obtidos ao traçarmos as diagonais no losango a bê cê dê, temos:
•
segmento de reta A B é congruente ao segmento de reta A D(lados de um losango);
•
segmento de reta B M é congruente ao segmento de reta M D(M é ponto médio de
B D);
•
segmento de reta A M é congruente ao segmento de reta A M(lado comum);
Logo, pelo caso lado lado lado, os triângulos á ême bê e á ême dê são congruentes. Portanto:
•
ângulo 1 é congruente ao ângulo 2., o que prova que
Semirreta AC.é bissetriz do ângulo
A;
•
ângulo M1 ≅
ângulo M2, que, por serem suplementares, são retos, o que prova que
o segmento A C⟂
a segmento B D.
Por raciocínio análogo, prova-se que
Semirreta CA.é bissetriz do ângulo
C,
Semirreta BD.é bissetriz do ângulo
ãngulo B.e
Semirreta DB.é bissetriz do ângulo
D.
Respostas e comentários
Propriedade dos retângulos e propriedade dos losangos
Na sequência, apresentamos propriedades específicas de retângulos e de losangos:
• As diagonais de um retângulo são congruentes.
• As diagonais de um losango são perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos.
Ressalte que essas propriedades também são válidas para um quadrado, visto que todo quadrado pode ser classificado como retângulo e como losango.
As demonstrações dessas propriedades estão apresentadas de maneira compreensível e bem fundamentada. No entanto, os estudantes podem fazer verificações por meio de modelos desenhados em papel, recortados e convenientemente dobrados segundo suas diagonais, suas bissetrizes, suas mediatrizes; ou por superposição de seus elementos (lados e ângulos). Solicite aos estudantes que levem para a sala de aula vários paralelogramos, retângulos, losangos e quadrados recortados em papel. Lembre-os de que devem usar tesouras de pontas arredondadas e manuseá‑las com cuidado. Programando-se dessa maneira, é suficiente usar parte de uma aula para essas verificações. Convém observar aos estudantes que verificação não é o mesmo que demonstração.
Propriedades dos quadrados
O quadrado é, ao mesmo tempo, um retângulo e um losango, portanto apresenta as propriedades desses dois paralelogramos.

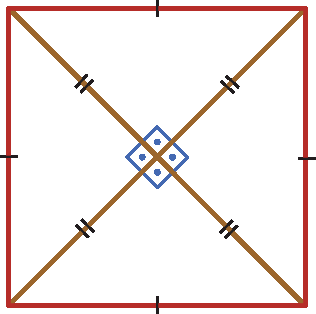
Observação
▶ Um paralelogramo que não é retângulo tem diagonais não congruentes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
19 Nos quadriláteros a seguir, determine x e y.
a)
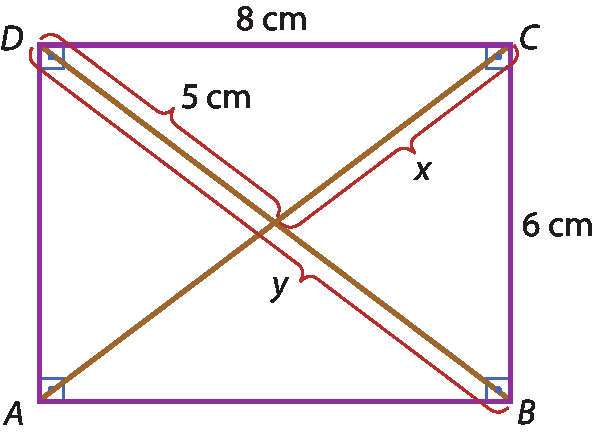
b)
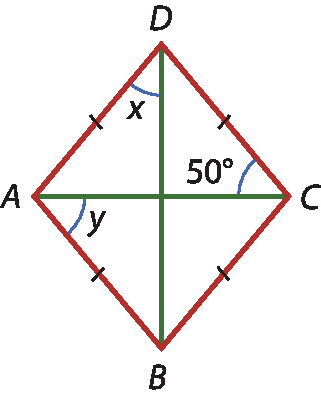
c)
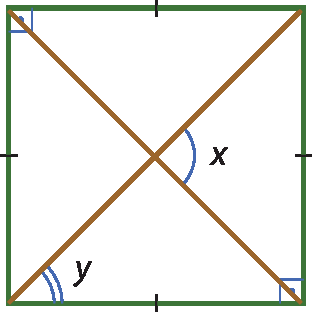
20 As diagonais de um retângulo cortam-se formando um ângulo de 100graus. Determine a medida do menor ângulo que uma dessas diagonais fórma com um dos lados.
21 Corrija no caderno as sentenças falsas.
a) Em apenas alguns retângulos, as diagonais são congruentes.
b) As diagonais de um losango são perpendiculares entre si.
c) As diagonais dos retângulos são perpendiculares entre si.
d) As diagonais de um quadrado não formam, entre si, ângulo de 90graus.
e) As diagonais de um quadrado formam com os lados ângulos de 45graus.
22 A diagonal de um losango fórma, com um dos lados, um ângulo de medida igual a 35graus. Calcule as medidas dos ângulos desse losango.
23 Usando régua e compasso, construa um quadrado cujas diagonais meçam 5,6 centímetros. Com a régua, determine a medida do lado, em milímetro.
Calcule a medida da área desse quadrado, em milímetro quadrado.
(Ao usar o compasso, atenção para não se machucar com a ponta-seca.)
24 Cada diagonal de um retângulo mede 5 centímetros. Elas cortam-se formando um ângulo de medida igual a 60graus. Usando régua, transferidor e compasso, construa esse retângulo, meça seus lados e determine a medida aproximada de sua área, em milímetro quadrado.
(Ao usar o compasso, atenção para não se machucar com a ponta-seca.)
Respostas e comentários
19. a) x = 5 centímetros
y = 10 centímetros
19. b) x = 40graus
y = 50graus
19. c) x = 90graus;
y = 45graus.
20. 40graus
21. a) Falsa. Em todos os retângulos, as diagonais são congruentes.
21. b) Verdadeira.
21. c) Falsa. As diagonais de alguns retângulos são perpendiculares entre si.
21. d) Falsa. As diagonais de um quadrado sempre formam, entre si, ângulo de 90graus.
21. e) Verdadeira.
22. 70graus, 70graus, 110graus, 110graus.
23. Aproximadamente .1600 milímetros quadrados (considerando que a medida aproximada do lado seja 40 milímetros).
24. Aproximadamente .1075 milímetros quadrados.
Propriedades dos quadrados
Para os quadrados, basta considerar todas as propriedades anteriores:
• As diagonais de um quadrado são congruentes, perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos.
Exercícios propostos
As resoluções dos exercícios 19 a 23 estão no início deste Manual, nas orientações específicas do capítulo 9.
Para a resolução do exercício 24, oriente os estudantes a fazerem uma figura construída à mão livre que contenha as informações do enunciado. Assim, eles percebem, por exemplo, que as diagonais do retângulo formam, com os lados menores, triângulos equiláteros; logo, o lado menor mede 2,5 centímetros, metade da medida da diagonal.
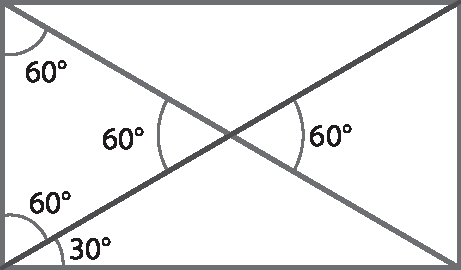
Esse procedimento facilita e encaminha adequadamente a construção do retângulo com régua e compasso.
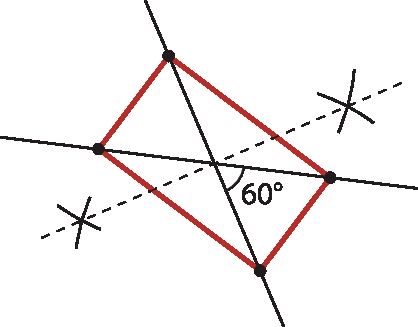
Medindo com a régua o retângulo construído, o estudante encontrará 43 milímetros para a medida da base e 25 milímetros para a medida da altura (aproximadamente). Assim:
Aretângulo ≃ 43 · 25
Aretângulo ≃ .1075
Portanto, a área desse retângulo mede aproximadamente .1075 milímetros quadrados.
25 Em uma folha avulsa, com o auxílio de régua e de compasso, construa um losango cujas diagonais meçam 5,4 centímetros e 3,2 centímetros. Depois, recorte o contôrno dele e córte-o segundo as diagonais. Com os quatro triângulos obtidos, monte um retângulo e determine a medida de sua área. A medida da área do losango inicial é igual à medida da área do retângulo obtido? Determine a medida da área desse losango.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca. Use tesoura com ponta arredondada e a manuseie com cuidado!)
26 Desenhe os quadriláteros descritos a seguir e, depois, responda às perguntas.
a) Um quadrilátero cujos ângulos opostos sejam congruentes, pelo menos um deles sendo reto. Como você classifica esse quadrilátero?
b) Um quadrilátero em que pelo menos um dos ângulos não seja reto, sendo os lados opostos paralelos e congruentes. Como você classifica esse quadrilátero?
c) Um quadrilátero em que somente dois lados sejam paralelos e somente um dos ângulos seja reto.
27 Com base nas respostas do exercício anterior, faça o que se pede.
a) Você conseguiu desenhar um quadrilátero em todos os itens? Em caso negativo, em que item não conseguiu?
b) Compare suas respostas com as dos colegas. Houve divergências? Se sim, em quais itens? Como você explicaria?
28

Hora de criar – No caderno, faça um desenho com quadriláteros e redija instruções de modo que um colega possa construir o mesmo desenho. Troque seu texto com o de um colega e tentem fazer o desenho descrito pelo outro. Depois, comparem os desenhos.
Se houver divergências, analisem o caso e tentem descobrir o que poderia ter ocorrido.
29 Considere um retângulo a bê cê dê. Seja P um ponto de
segmento A B. Trace por P uma reta paralela a
segmento A D. Chame de Q o ponto em que essa reta intersecta
segmento C D. Demonstre que
segmento P Q⫽
segmento B C.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Alberto pinta painéis como este.
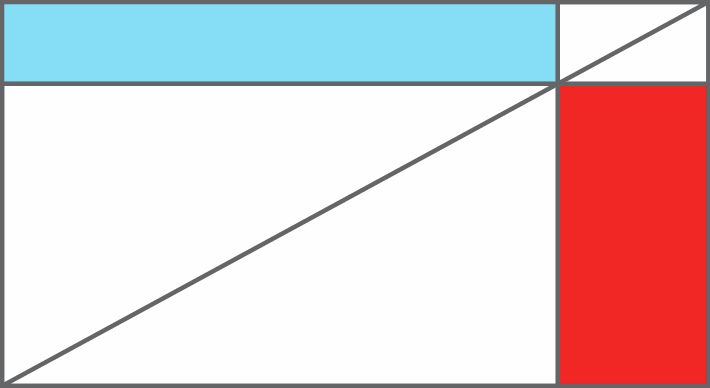

(As imagens não respeitam as proporções reais entre os objetos.)
Para pintar o painel apresentado, Alberto gastou mais tinta azul ou vermelha? Justifique sua resposta.
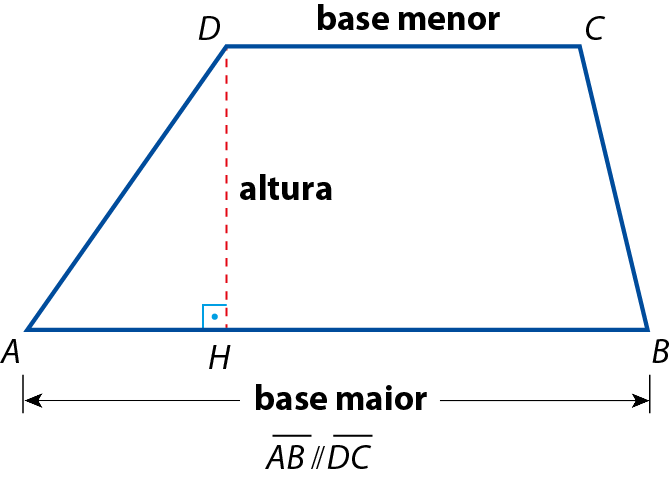
3. Trapézios

Os lados paralelos são chamados de bases do trapézio. Todo segmento que tem extremidades em uma base e na reta suporte da outra, perpendicular a elas, chama-se altura do trapézio.
Respostas e comentários
25. Sim. A área do losango mede 8,64 centímetros quadrados.
26. a) Respostas possíveis: retângulo ou quadrado.
26. b) Resposta possível: losango.
26. c) Não é possível construir esse quadrilátero.
27. a) Item c.
27. b) Respostas pessoais.
28. Resposta pessoal.
29.
segmento PQ é paralelo ao segmento ADe
segmento AD é paralelo ao segmento BC; logo,
segmento PQ é paralelo ao segmento BC.
Pense mais um poucoreticências: Alberto gastou quantidades iguais de tinta azul e tinta vermelha. Demonstração.
Exercícios propostos
As resoluções dos exercícios 25 a 29 estão no início deste Manual, nas orientações específicas do capítulo 9.
Os exercícios 26 e 27 exigem reflexão e aplicação das propriedades do paralelogramo, do retângulo, do losango e do quadrado nas tentativas de construção das figuras pedidas com base nas instruções do enunciado.
O exercício 28 propõe uma situação contrária à dos exercícios 26 e 27. Nele, é o estudante quem estabelece as condições. Essa é uma boa oportunidade para constatar possíveis dificuldades na aprendizagem dos conceitos estudados.
Pense mais um poucoreticências
Apresentamos uma possível justificativa para o fato de as medidas das áreas da região azul e da região vermelha serem iguais. Para isso, consideremos o seguinte esquema:
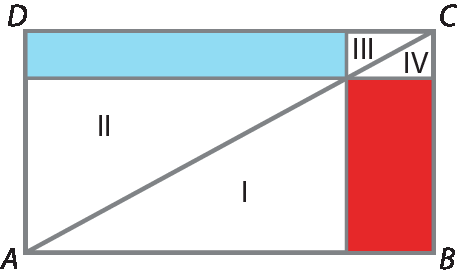
Pode-se afirmar que o triângulo á bê cê é equivalente ao triângulo á dê cê, com medidas de área igual a m. Além disso, as regiões indicadas como um e dois são equivalentes e indicamos a medida da área delas como n e, ainda, as regiões três e quatro também são equivalentes e indicamos a medida da área delas como k.
Sejam x a medida da área em azul e y a da área em vermelho. Obtemos que:
x = m ‒ n ‒ k e y = m ‒ n ‒ k; logo, x = y.
Portanto, Alberto gastou quantidades iguais de tinta azul e de tinta vermelha para pintar o painel apresentado.
No trapézio a bê cê dê, verificamos que os ângulos
Ae
D, assim como os ângulos
Be
C, são colaterais internos formados pelas bases
ABe
CDcom os lados não paralelos.
Logo:
• medida do(
ângulo A) + medida do(
ângulo D) = 180graus
• medida do(
ângulo B) + medida do(
ângulo C) = 180graus
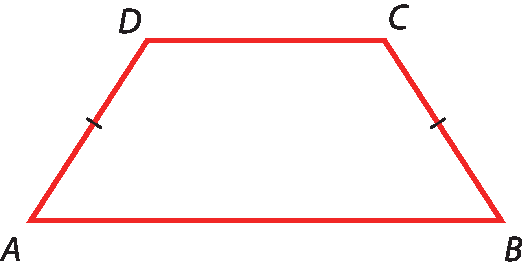
Destacamos três tipos de trapézio.
Trapézios isósceles: aqueles em que os lados opostos não paralelos são congruentes.
Trapézios retângulos: aqueles que têm dois ângulos internos retos.
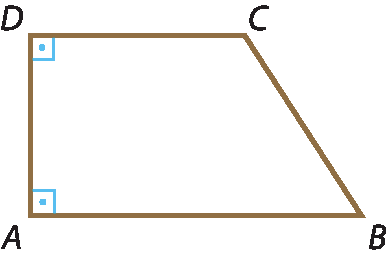
Trapézios escalenos: aqueles que não têm ângulo reto e em que os lados opostos não paralelos não são congruentes.
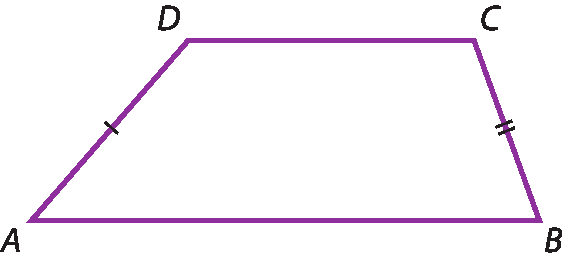
Propriedades dos trapézios isósceles
1ª propriedade

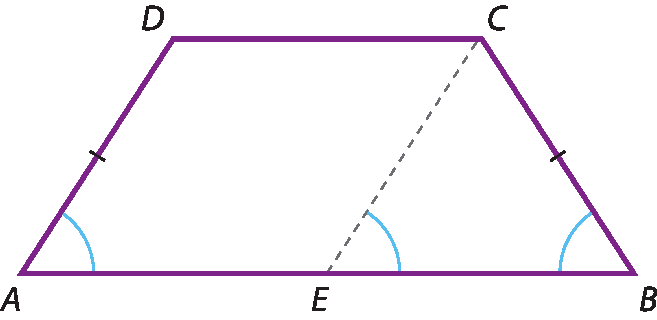

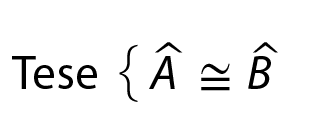
• Demonstração
Traçando pelo ponto C um segmento paralelo a
Segmento de reta AD., determinamos o ponto ê em
segmento AB. Assim, temos:
•
O segmento de reta AD é congruente ao segmento de reta CE.(são lados opostos de um paralelogramo);
•
O segmento de reta AD é congruente ao segmento de reta BC.(pela hipótese);
•
O segmento de reta CE é congruente ao segmento de reta BC(
O segmento de reta CE é congruente ao segmento de reta AD que é congruente ao segmento de reta BC.).
Logo, ECB é um triângulo isósceles e, portanto,
O ângulo B congruente ao ângulo E.. Como
O ângulo E congruente ao ângulo A.(ângulos correspondentes), temos
O ângulo A congruente ao ângulo B.(
O ângulo B é congruente ao ângulo E que é congruente ao ângulo A.). Como medida do(
ãngulo D) = 180graus ‒ medida do(
ãngulo A.), medida do(
ãngulo C.) = 180graus ‒ medida do(
ãngulo B) e medida do(
ãngulo A.) = medida do(
ãngulo B), temos medida do(
ãngulo D) = medida do(
ãngulo C.). Logo,
O ângulo D congruente ao ângulo C..
Respostas e comentários
3. Trapézios
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um quatro.
Neste tópico desenvolvemos um trabalho com a habilidade (EF08MA14) ao demonstrar propriedades de quadriláteros aplicando a congruência de triângulos.
Pergunte à turma em que os trapézios diferem dos paralelogramos. Assim, poderá verificar se os estudantes compreenderam a classificação dos quadriláteros discutida anteriormente. Desenhe na lousa quadriláteros diversos, dentre eles paralelogramos e trapézios de vários tipos. Em seguida, peça aos estudantes que identifiquem os trapézios, justificando suas escolhas.
Proponha a eles também que, entre os trapézios identificados, identifiquem as duas bases (maior e menor) e tracem uma altura de cada trapézio. Depois, podem classificá-los como trapézio isósceles, trapézio retângulo e trapézio escaleno.
Discuta com a turma a 1ª propriedade para trapézios isósceles: “Em um trapézio isósceles, os ângulos internos adjacentes à mesma base são congruentes”. Reproduza a demonstração na lousa e peça aos estudantes que justifiquem cada etapa.
2ª propriedade
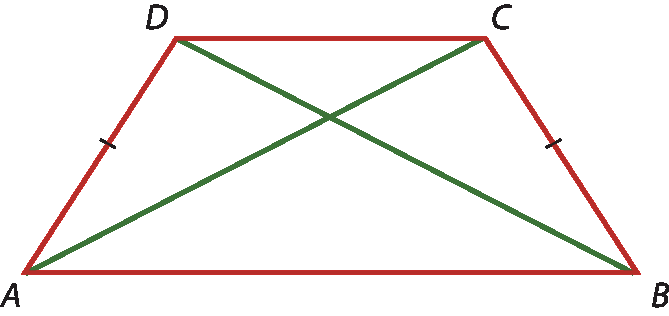

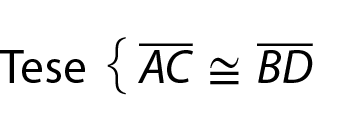
• Demonstração
Vamos destacar do trapézio a bê cê dê os triângulos á bê cê e bê á dê.
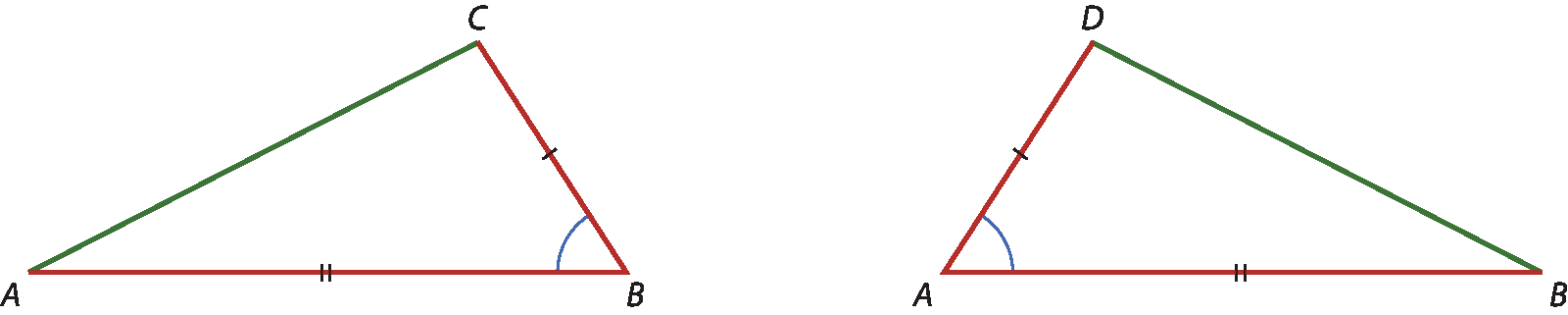
Assim, temos:
•
O segmento de reta AB é congruente ao segmento de reta AD(pela hipótese);
•
O ângulo B congruente ao ângulo A.(ângulos adjacentes à base
Segmento de reta AB.do trapézio isósceles);
•
O segmento de reta AB é congruente ao segmento de reta AB.(lado comum).
Logo, pelo caso lado ângulo lado, os triângulos á bê cê e bê á dê são congruentes. Portanto,
O segmento de reta AC é congruente ao segmento de reta BD..
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
30 Calcule os valores de x e y, em grau, nos trapézios a seguir e classifique-os em escaleno, isósceles ou retângulo.
a)

b)

31 Em um trapézio retângulo, a medida do ângulo obtuso é igual ao triplo da medida do ângulo agudo. Determine:
a) a medida do ângulo obtuso;
b) a medida do ângulo agudo.
32 No trapézio a seguir, temos
O segmento de reta AD é congruente ao segmento de reta BC..
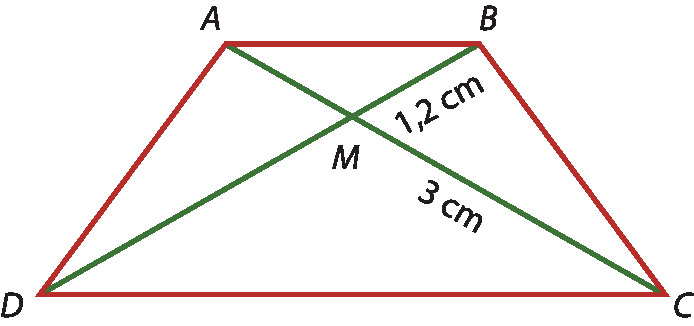
a) Como podemos classificar esse trapézio?
b) Como podemos classificar os triângulos á bê ême e cê dê ême?
c) Calcule a medida de cada diagonal.
Respostas e comentários
30. a) x = 36graus; y = 72graus; escaleno.
30. b) x = 70graus; y = 110graus; isósceles.
31. a) 135graus
31. b) 45graus
32. a) Trapézio isósceles.
32. b) Os triângulos são isósceles.
32. c) 4,2 centímetros
Propriedades dos trapézios isósceles
Nesta página, tratamos da 2ª propriedade para trapézios isósceles: “Em um trapézio isósceles, as diagonais são congruentes”.
Organize os estudantes em duplas e proponha a eles que demonstrem essa propriedade. Em seguida, peça-lhes que compartilhem o que fizeram com outra dupla e comparem as estratégias utilizadas.
Exercícios propostos
Neste bloco de exercícios, além de aplicar as propriedades e a classificação de trapézios, os estudantes devem mobilizar seus conhecimentos sobre equações para determinar medidas desconhecidas.
As resoluções dos exercícios 30 e 31 estão no início deste Manual, nas orientações específicas do capítulo 9.
A seguir, apresentamos uma possível resolução do exercício 32. Como os lados não paralelos
Segmento de reta AD.e
segmento de reta BCsão congruentes, podemos concluir que se trata de um trapézio isósceles (item a). Acompanhe a seguir:
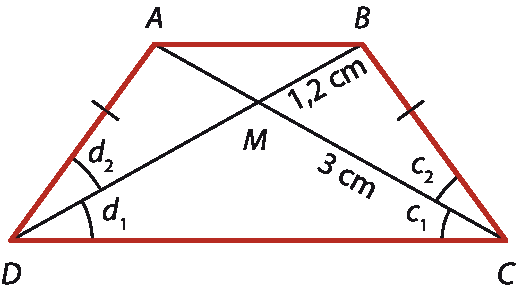
Os triângulos á dê cê e bê cê dê são congruentes pelo caso lado lado lado:
1.
Segmento de reta AD.≅
segmento de reta BC(hipótese do exercício)
2.
segmento de reta DC≅
segmento de reta DC(lado comum)
3.
Segmento de reta AC.≅
Segmento de reta BD.(diagonais em trapézio isósceles)
Então, os ângulos internos correspondentes desses dois triângulos são congruentes entre si. Desse modo, o ângulo de medida c₁ oposto ao lado
Segmento de reta AD.no triângulo á dê cê é congruente ao ângulo de medida d₁ oposto ao lado
BCno triângulo BCD (ângulos internos opostos a lados congruentes em triângulos congruentes). Assim: c₁ = d₁.
Logo, o triângulo cê dê ême é isósceles de base
Segmento de reta DC., pois tem os ângulos dessa base congruentes.
De maneira análoga, provamos que o triângulo á bê ême é isósceles de base
AB. Portanto, á bê ême e cê dê ême são triângulos isósceles (item b).
Como os triângulos ABM e CDM são isósceles, temos DM = MC = 3 centímetros e ei ém = MB = 1,2 centímetro. Assim:
cê á = DB = DM + MB = 3 centímetros + 1,2 centímetro
cê á = DB = 4,2 centímetros (item c)
33 As diagonais de um trapézio isósceles medem 6 centímetros. O ponto de encontro dessas diagonais fica a 2 centímetros dos vértices da base menor, e elas formam entre si um ângulo de medida igual a 60graus. Faça um desenho desse trapézio.
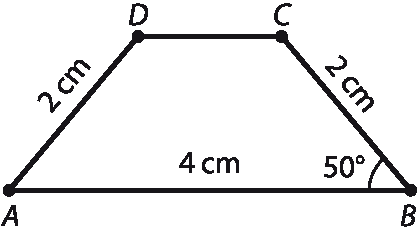
34 Considere a seguinte descrição de um trapézio isósceles: a base maior mede 4 centímetros, cada um dos lados não paralelos mede 2 centímetros e fórma com a base maior um ângulo medindo 50graus. Construa esse trapézio.
35 O maior ângulo interno de um trapézio retângulo tem o dobro da medida de seu menor ângulo interno. Calcule as medidas dos ângulos internos desse trapézio.
36 Fabiana definiu trapézio da seguinte maneira:

A definição de Fabiana está de acôrdo com a definição apresentada neste capítulo? Justifique sua resposta.
37

Hora de criar – Em dupla, cada um cria um problema sobre trapézio. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi‑los.
TRABALHANDO A INFORMAÇÃO
Rotulando informações
Valentina desmontou uma caixinha de gelatina para descartá-la com o material reciclável. Observe como essa caixinha ficou.
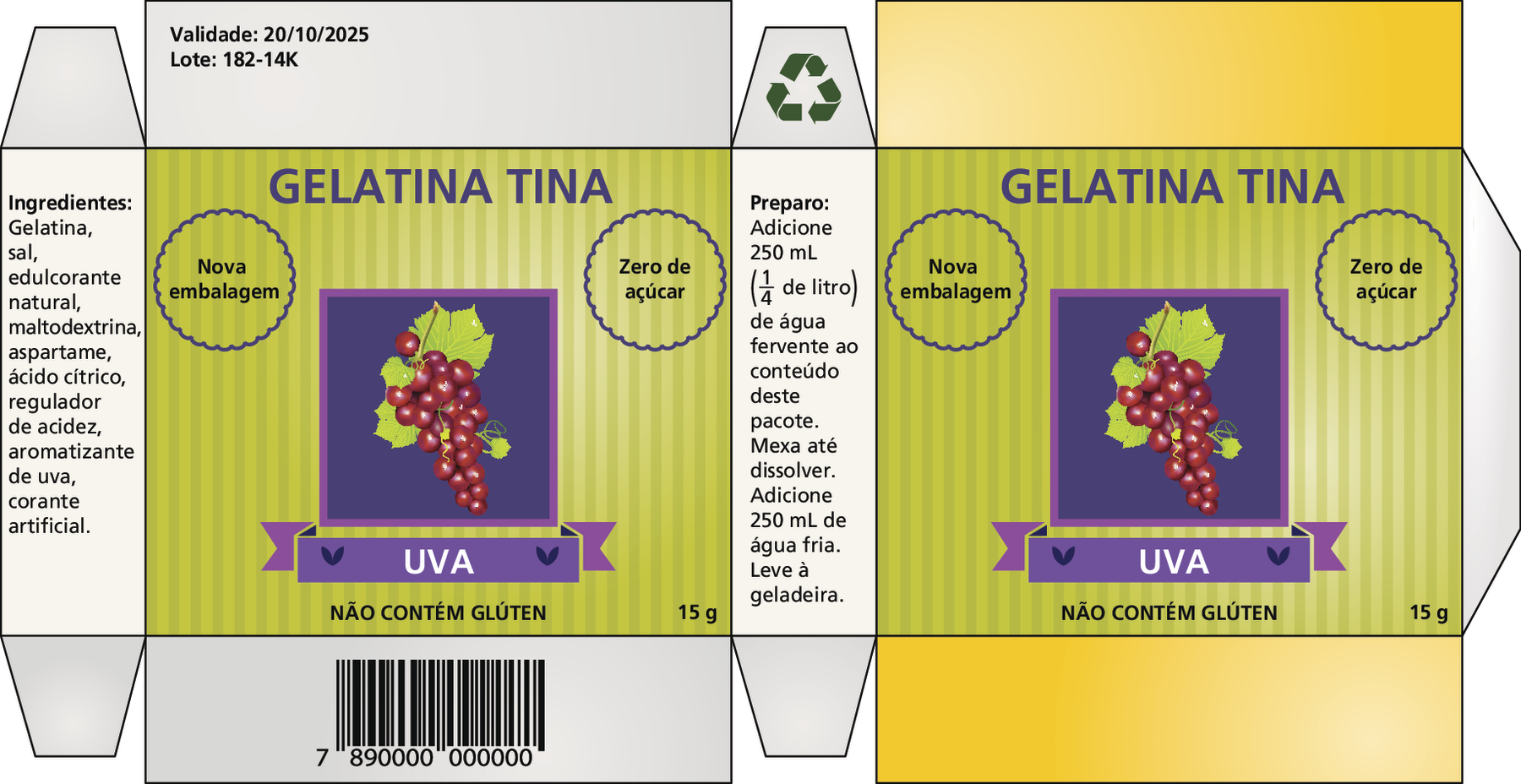
Quantas informações importantes e necessárias o rótulo de uma embalagem traz!
Em um rótulo assim, podemos identificar o produto, seu código de barras, saber a data de validade, o lote, o tipo de embalagem, a medida da massa, os ingredientes, as orientações de uso etcétera
Esse rótulo traz orientações de preparo e ainda contém o selo indicando que a embalagem é reciclável.
Respostas e comentários
33. Construção de figura; há duas construções possíveis.
34. Construção de figura.
35. 60graus, 90graus, 90graus, 120graus.
36. Não. Espera-se que os estudantes percebam que, ao dizer que pelo menos dois dos lados opostos são paralelos, Fabiana incluiu, além dos trapézios, os paralelogramos nessa definição.
37. Resposta pessoal.
Exercícios propostos
No exercício 33, sugira aos estudantes que façam à mão livre um esbôço da situação. Depois, iniciem a construção pelas diagonais do trapézio. Assim, traçamos duas retas concorrentes, r e s, formando um ângulo de 60graus. Vamos chamar de P o ponto de intersecção dessas retas. Essas retas conterão as diagonais do trapézio em construção.
Na reta r, marcamos os pontos ae C, de modo que á cê = 6 centímetros e pê á = 2 centímetros. Da mesma maneira, na reta s, marcamos os pontos B e D, de modo que bê dê = 6 centímetros e pê bê = 2 centímetros.
Os pontos a, B, C e D são os vértices do trapézio.
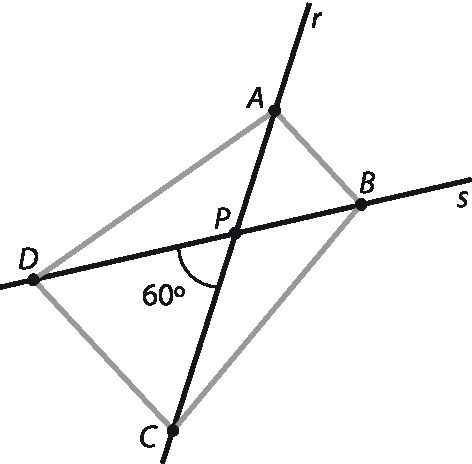
Segue uma possível figura para o exercício 34. Demarcamos em uma reta os pontos a e B, com A bê = 4 centímetros. Com o transferidor, construímos um ângulo de 50grausde vértice B, na base maior. Com a ponta-sêca do compasso em B e abertura de 2 centímetros, determinamos o ponto C, distante 2 centímetros de B, e traçamos a reta paralela à base maior passando por C. Com a ponta-sêca em a e abertura de 2 centímetros, traçamos um arco que cruza essa reta paralela em D. O quadrilátero a bê cê dê obtido é o trapézio solicitado.
Lembre os estudantes de que devem tomar muito cuidado para não se machucarem com a ponta-sêca ao usar o compasso.
As resoluções dos exercícios 35 a 37 estão no início deste Manual, nas orientações específicas do capítulo 9.
No exercício 37, incentive os estudantes a representarem um trapézio antes de elaborar o problema. Depois, com base no trapézio representado, será mais prático elaborar uma situação-problema.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Que informações você pode destacar nessa imagem da embalagem?
2 Valentina tem intolerância a glúten. Ela pode comer essa gelatina?
3 Esse produto pode ser consumido na data de hoje? Por quê?
4 Para fazer gelatina para a família, Valentina usa três caixinhas como essa. Quantos gramas de pó de gelatina Valentina usa? E de açúcar?
5 Quantos mililitro de água fervente Valentina deve adicionar ao pó para preparar três caixinhas de gelatina? E quantos litros de água ao todo?
6 Sem realizar medições, você identifica figuras que lembram quadrados na imagem da embalagem? Em caso afirmativo, onde?
7 Com uma régua, obtenha as medidas das três dimensões da caixinha de gelatina.
8 Quantos e quais tipos de quadrilátero compõem as faces e as abas dessa embalagem?
9 Após fazer a gelatina, o que Valentina deve fazer com as caixinhas?
10 Em papel de seda, faça um decalque do contôrno da imagem da embalagem e cole-o em papel-cartão. Depois, recorte essa figura, vinque os lados comuns entre faces e entre faces e abas. Cole as abas, monte a caixinha e crie um rótulo do produto que quiser.
(Use tesoura com ponta arredondada e a manuseie com cuidado!)
4. Propriedades da base média do triângulo e do trapézio
Base média do triângulo

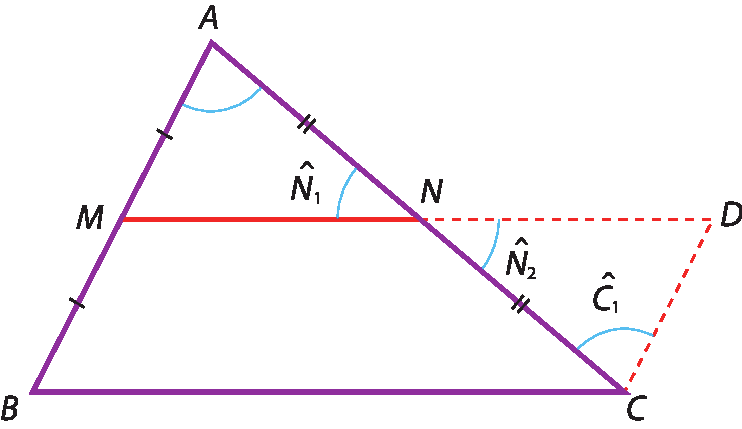
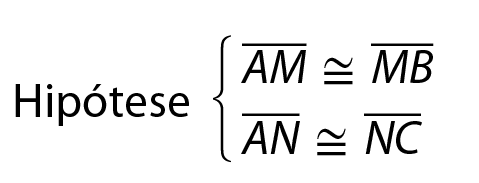
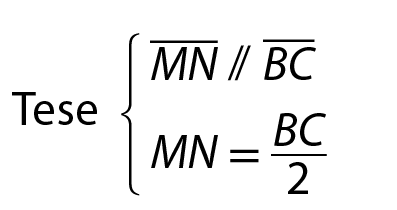
• Demonstração
Construção auxiliar: traçamos pelo vértice C uma reta paralela a
segmento AB, que intersecta
Semirreta MN.no ponto D. Assim, temos:
•
O ângulo A congruente ao ângulo C.1 (ângulos alternos internos formados por duas retas paralelas e uma transversal);
•
O segmento de reta AN é congruente ao segmento de reta NC.(pela hipótese);
•
ângulo N1 ≅
ângulo N2 (ângulos opostos pelo vértice);
• △AMN ≅ △CDN (pelo caso ângulo-lado-ângulo);
Respostas e comentários
1. Resposta possível: sabor uva, não contém glúten, ingredientes, zero de açúcar, 15 gramas, código de barras, modo de preparo, validade, lote.
2. Sim.
3. A resposta depende da data em que a atividade é realizada.
4. Pó de gelatina: 45 gramas; açúcar: 0 grama.
5. Volume de água fervente: 750 mililitros; volume total de água: 1,5 litro ou
3 meioslitro.
6. Espera-se que os estudantes respondam que sim, no contôrno das imagens da uva.
7. Comprimento: 6,0 centímetros; altura: 5,0 centímetros; largura: 1,5 centímetro.
8. 8 retângulos e 5 trapézios.
9. Espera-se que os estudantes respondam que ela deve separar para reciclagem.
10. Resposta pessoal.
Trabalhando a informação
As resoluções das atividades 1 a 10 do Agora quem trabalha é você! estão no início deste Manual, nas orientações específicas do capítulo 9.
Sobre a atividade 7, sugerimos que discuta com os estudantes quais seriam essas três dimensões, antes de fazerem as medições. Proponha a eles que imaginem a caixa montada ou leve para a sala de aula modelos dela para que as manuseiem. Espera-se que eles identifiquem a largura, a altura e o comprimento da caixa.
Explore figuras de uma dimensão, como o segmento de reta (lado de algum quadrilátero), e figuras de duas dimensões, como a superfície de regiões poligonais, estimulando os estudantes a perceberem as dimensões estudadas e solicitando a eles que façam comparações com as dimensões de figuras tridimensionais.
4. Propriedades da base média do triângulo e do trapézio
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um quatro.
Neste tópico desenvolvemos um trabalho com a habilidade (EF08MA14) ao demonstrar propriedades de quadriláteros aplicando a congruência de triângulos.
•
O segmento de reta MN é congruente ao segmento de reta ND.(lados correspondentes de triângulos congruentes);
•
O segmento de reta CD é congruente ao segmento de reta AM.(lados correspondentes de triângulos congruentes);
•
O segmento de reta AM é congruente ao segmento de reta MB.(pela hipótese);
•
O segmento de reta CD é congruente ao segmento de reta MB.(
O segmento de reta CD é congruente ao segmento de reta AM que é congruente ao segmento de reta MB.);
• BCDM é paralelogramo.
Logo,
segmento de reta MD⫽
segmento de reta BC.ou
segmento de reta MN.⫽
O segmento de reta BCe
O segmento de reta MD é congruente ao segmento de reta BC.ou, ainda, MN + ND = BC. Como
O segmento de reta ND é congruente ao segmento de reta MN., temos 2 ⋅ MN = BC; portanto, MN =
fração: numerador o comprimento do segmento BC, denominador 2, fim da fração.
Base média do trapézio

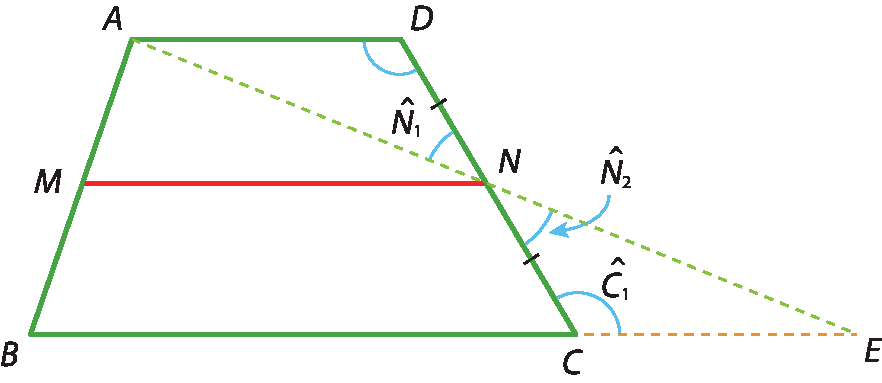
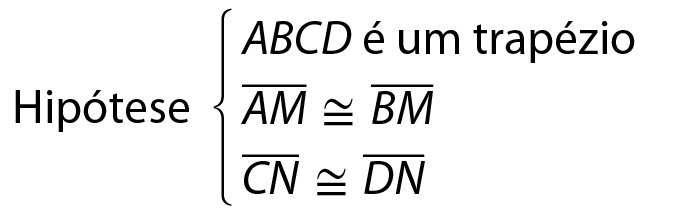
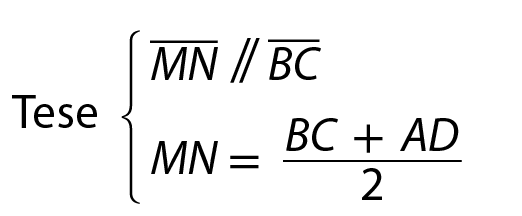
• Demonstração Construção auxiliar:
Semirreta AN.e
Semirreta BC., que se cruzam no ponto ê. Assim, temos:
•
O ângulo D congruente ao ângulo C.1 (ângulos alternos internos formados por duas retas paralelas e uma transversal);
•
O segmento de reta CN é congruente ao segmento de reta DN.(pela hipótese);
•
N1 ≅
N2 (ângulos opostos pelo vértice).
Logo, pelo caso ângulo-lado-ângulo, os triângulos A dê êne e ECN são congruentes. Portanto,
O segmento de reta AN é congruente ao segmento de reta NE.e
Segmento de reta AD é congruente ao segmento de reta CE.. Sabemos que MN =
fração: numerador o comprimento do segmento BE, denominador 2, fim da fraçãoe
segmento MN⫽
O segmento de reta BC(propriedade da base média do triângulo). Pela construção da figura, temos: bê ê = BC + cê é Sendo
O segmento de reta CE é congruente ao segmento de reta AD, podemos escrever: bê ê = BC + á dê Substituindo bê ê por BC + á dê em MN =
fração: numerador o comprimento do segmento BE, denominador 2, fim da fração, obtemos: MN =
fração: numerador: o comprimento do segmento BC mais o comprimento do segmento AD, denominador 2, fim da fraçãoRespostas e comentários
Base média do triângulo e base média do trapézio
Discuta com a turma os conceitos de base média de um triângulo e de um trapézio.
Prepare antecipadamente, em folha separada, várias figuras de diferentes tipos de triângulos e de trapézios para que os estudantes identifiquem nelas a base média desses polígonos (determinando os pontos médios dos lados envolvidos) e façam medições para comprovar as propriedades apresentadas.
Transcreva as demonstrações na lousa e peça aos estudantes que justifiquem cada etapa.
PARA SABER MAIS
O trapézio no telhado
Na edificação de casas, desde a fundação até o telhado, importantes conceitos matemáticos se expressam de maneira relativamente simples em procedimentos rotineiros de construtores, empreiteiros e pedreiros, como levantar paredes, instalar um sistema hidráulico e montar e cobrir um telhado.
Na construção do madeirame que suporta os telhados, são necessários cálculos matemáticos que possibilitam determinar com exatidão as medidas de todos os elementos que o compõem.
Nos telhados em formato de trapézio, por exemplo, os cálculos empregados para determinar as medidas das vigas (que são paralelas às bases do trapézio) baseiam-se na propriedade da base média do trapézio: se, pelo ponto médio de cada um dos lados não paralelos de um trapézio, traçarmos um segmento de reta, esse segmento será paralelo às bases, e a medida dele será a média aritmética das medidas dessas bases.
Por exemplo, em um trapézio cujas bases medem 6 métros e 10 métros, a medida da base média é dada por
Fração, numerador: 6 mais 10, denominador: 2, fim da fraçãométros, ou seja, 8 métros.
Assim, se um telhado em formato de trapézio tiver somente 3 vigas paralelas, a maior medindo 10 métros de comprimento e a menor medindo 6 métros, a viga que for colocada entre elas, nos pontos médios dos lados não paralelos, deverá medir 8 métros de comprimento.

Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
Um telhado trapezoidal tem 5 vigas paralelas e igualmente espaçadas. A menor delas (a superior) mede 2 métros de comprimento, e a maior (a inferior) mede 12 métros de comprimento. Calcule no caderno a medida do comprimento das outras 3 vigas.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
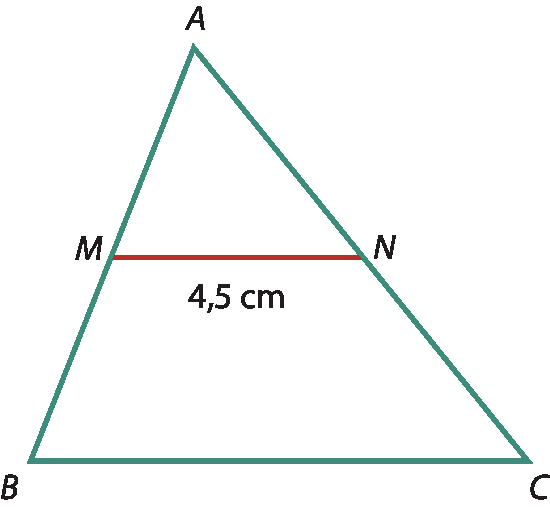
38 Nas figuras, M e N são pontos médios de
segmento de reta ABe
Segmento de reta AC., respectivamente. Determine:
a) MN
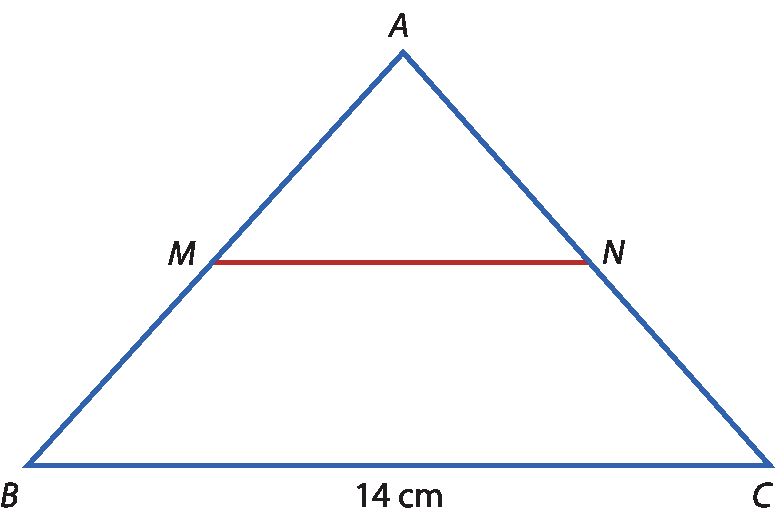
b) BC
Respostas e comentários
Para saber mais: 7 métros; 4,5 métros; 9,5 métros.
38. a) 7 centímetros
38. b) 9 centímetros
Para saber mais
No Agora é com você!, sugira aos estudantes que façam um esbôço da situação.
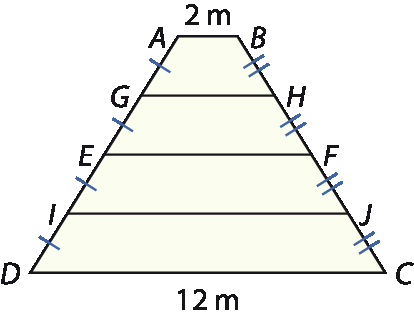
•
segmento de reta EFé a base média do trapézio a bê cê dê:
EF = (2 + 12) : 2 = 14 : 2 = 7
•
segmento de reta GH.é a base média do trapézio á bê éfe é:
GH = (2 + 7) : 2 = 9 : 2 = 4,5
•
segmento de reta IJ.é a base média do trapézio é éfe cê dê:
í jota = (7 + 12) : 2 = 19 : 2 = 9,5
Logo, as outras três vigas têm comprimentos de medidas: 4,5 métros, 7 métros, 9,5 métros.
Exercícios propostos
Apresentamos a seguir uma possível resolução para o exercício 38.
a) Aplicando a propriedade da base média do triângulo, obtemos: MN =
fração: numerador o comprimento do segmento BC, denominador 2, fim da fraçãoMN =
fração: 14 meios, fim da fração= 7 Logo, MN mede 7 centímetros.
b) Aplicando a propriedade da base média do triângulo, obtemos: MN =
fração: numerador o comprimento do segmento BC, denominador 2, fim da fração4,5 =
fração: numerador o comprimento do segmento BC, denominador 2, fim da fraçãoBC = 2 · 4,5 Logo, BC mede 9 centímetros.
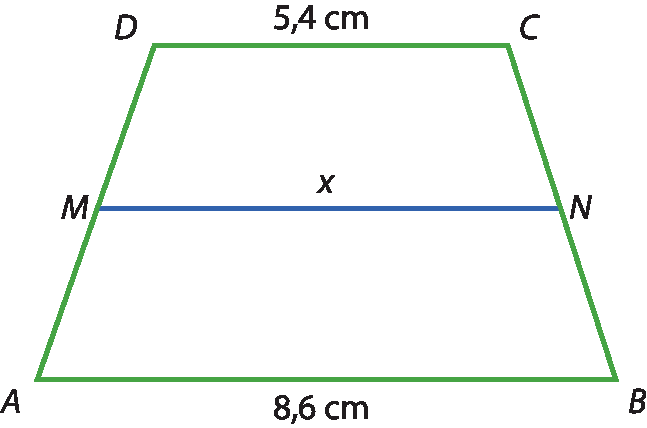
39 Nos trapézios a seguir, M e N são, respectivamente, os pontos médios de
segmento de reta ADe
segmento de reta BC. Calcule o valor de x.
a)
b)
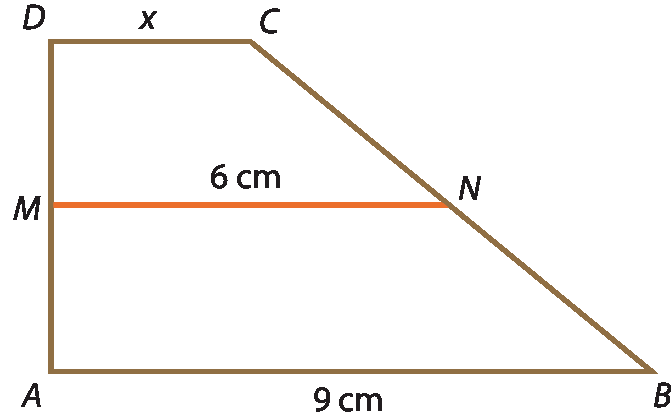
c)
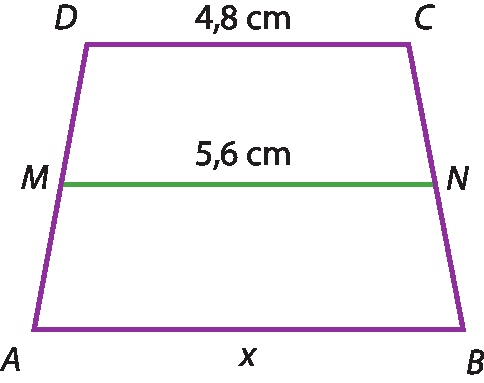
40 Nas figuras, M, N e P são, respectivamente, os pontos médios de
segmento de reta AB,
Segmento de reta AC.e
Segmento de reta BC.. Determine:
a) a medida do perímetro do △MNpê;
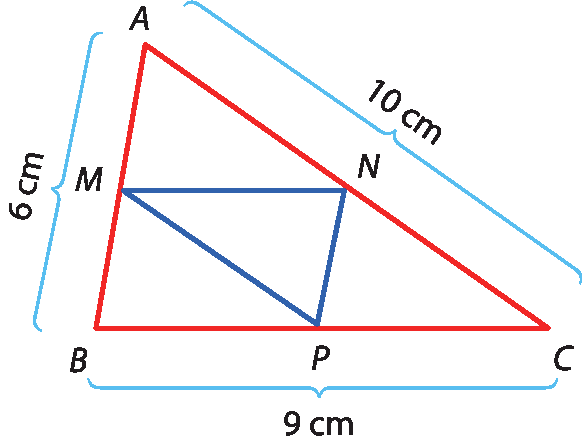
b) a medida do perímetro do △á bê cê.
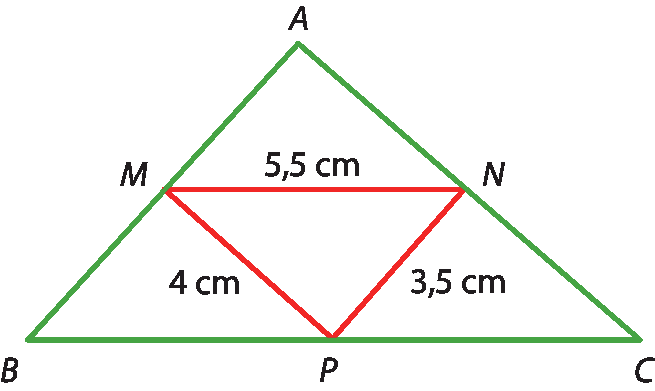
41 Na figura a seguir, M, N, P e Q são, respectivamente, os pontos médios de
segmento de reta AB,
segmento de reta BC,
segmento de reta CDe
segmento de reta AD.
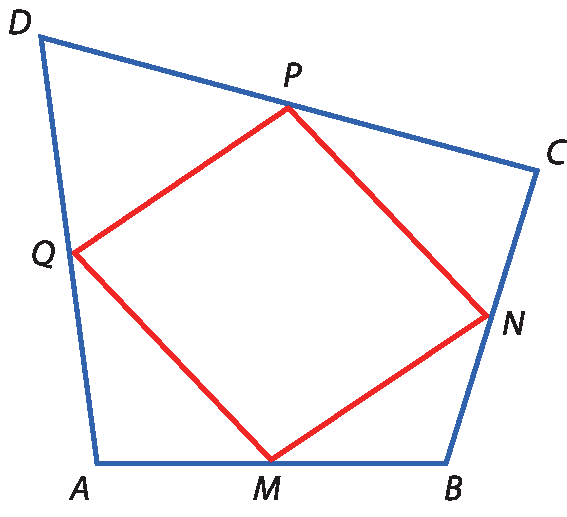
a) Prove que
segmento de reta MN⫽
Segmento de reta PQ..
b) Prove que
Segmento de reta QM.⫽
Segmento de reta PN..
c) Como podemos classificar o quadrilátero MNPQ?
d) Se AC = 12 centímetros, quanto mede o segmento
segmento de reta MN?
e) Se BD = 16 centímetros, quanto mede
Segmento de reta QM.?
f) Se PN = 20 centímetros, quanto mede
Segmento de reta BD.?
42 O lado do triângulo equilátero vermelho mede 6 centímetros. Desenhamos um segundo triângulo equilátero (verde) unindo os pontos médios dos lados do triângulo vermelho. Unindo os pontos médios dos lados do triângulo verde, desenhamos um terceiro triângulo equilátero (azul). Qual é a medida do perímetro do triângulo azul?
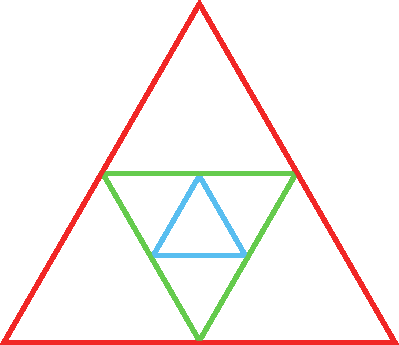
43 Considere um trapézio cujas bases meçam 10 centímetros e 5 centímetros.
a) Quanto mede o segmento de reta que une os pontos médios dos lados não paralelos?
b) Prolongando os lados não paralelos, obtêm-se dois triângulos equiláteros. Qual é a medida do perímetro desse trapézio?
44 Em um trapézio isósceles, os lados não paralelos medem 12 centímetros, e a base média, 20 centímetros.
a) Calcule a medida do perímetro desse trapézio.
b) Se a base menor mede 8 centímetros, quanto mede a base maior desse trapézio?
Respostas e comentários
39. a) x = 7 centímetros
39. b) x = 3 centímetros
39. c) x = 6,4 centímetros
40. a) 12,5 centímetros
40. b) 26 centímetros
41. a) Demonstração.
41. b) Demonstração.
41. c) Paralelogramo.
41. d) 6 centímetros
41. e) 8 centímetros
41. f) 40 centímetros
42. 4,5 centímetros
43. a) 7,5 centímetros
43. b) 25 centímetros
44. a) 64 centímetros
44. b) 32 centímetros
Exercícios propostos
As resoluções dos exercícios 39 a 41, e dos exercícios 44 e 46 estão no início deste Manual, nas orientações específicas do capítulo 9.
Apresentamos a seguir uma possível resolução para o exercício 42. Cada lado do triângulo verde é a base média do triângulo vermelho relativo a um lado de 6 centímetros. Logo, a medida de cada lado do triângulo verde é 3 centímetros (metade da medida do lado de 6 centímetros). Cada lado do triângulo azul é a base média do triângulo verde relativo a um lado que mede 3 centímetros. Logo, a medida de cada lado do triângulo azul é 1,5 centímetro (metade da medida do lado de 3 centímetros). Portanto, a medida do perímetro do triângulo azul é 4,5 centímetros (3 · 1,5 centímetro).
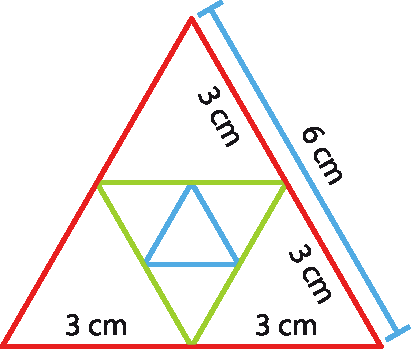
Apresentamos uma possível resolução para o exercício 43, com um esbôço da situação:
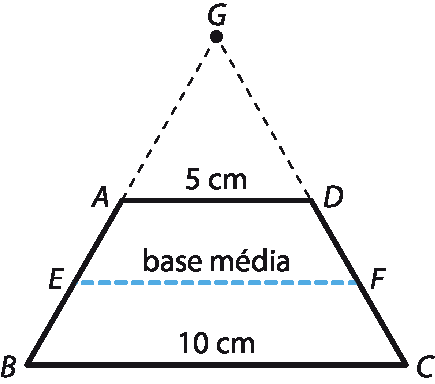
a) A base média desse trapézio mede [(10 + 5) : 2] centímetros, ou seja, 7,5 centímetros.
b) O triângulo gê á dê é equilátero (dado do enunciado). Logo, á gê = gê dê = 5 centímetros.
O triângulo gê é éfe é equilátero (dado do enunciado).
Logo, é gê = éfe gê = 7,5 centímetros.
Como é gê = ê á + AG, obtemos:
7,5 centímetros = ê á + 5 centímetros
Ou seja: ê á = 2,5 centímetros.
Analogamente, obtemos:
éfe dê = 2,5 centímetros
Como ê e F são pontos médios dos lados não paralelos desse trapézio, consideramos:
bê ê = ê á = 2,5 centímetros
cê éfe = éfe dê = 2,5 centímetros
Logo, podemos concluir que bê á = cedê = 5 centímetros. Portanto, a medida do perímetro desse trapézio é 25 centímetros (5 + 10 + 5 + 5 = 25).
45 Em um trapézio, a base média fórma, com um dos lados não paralelos, um ângulo medindo 45graus e, com o outro lado, fórma um ângulo de 60graus. Calcule as medidas dos ângulos desse trapézio.
46

Hora de criar – Em dupla, cada um cria um problema sobre base média de um trapézio. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Classifique os quadriláteros da figura.
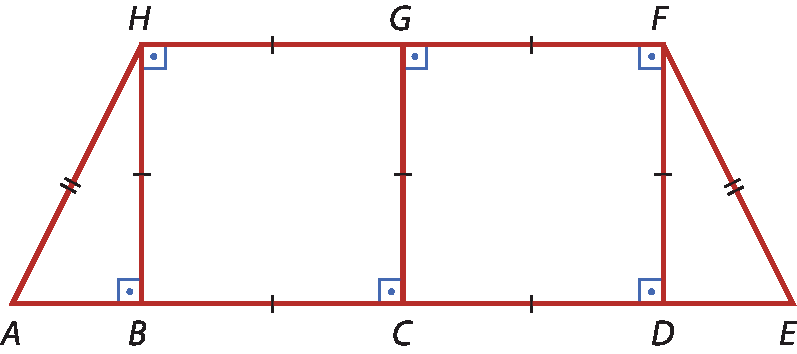
a) bê dê éfe agá
b) á é éfe agá
c) á cê gê agá
d) bê cê gê agá
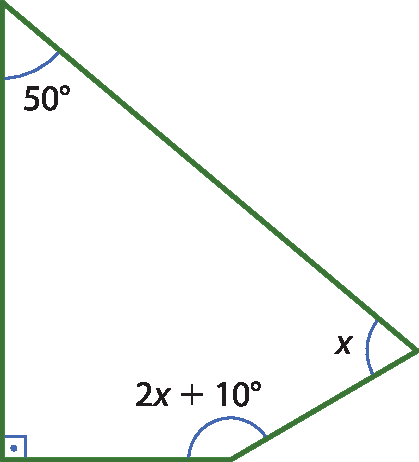
2 Calcule o valor de x.
3 Desenhe dois segmentos,
segmento de reta ABe
segmento de reta CD, que se intersectem nos seus respectivos pontos médios. Que tipo de quadrilátero você obtém traçando os segmentos
AC,
CB,
Segmento de reta BD.e
DA? Justifique sua resposta.
4 Desenhe dois segmentos não congruentes,
segmento de reta ABe
segmento de reta CD, perpendiculares entre si, que se cruzem nos respectivos pontos médios. Que tipo de paralelogramo você obtém traçando os segmentos
AC,
CB,
Segmento de reta BD.e
DA? Justifique sua resposta.
5 Calcule o valor de x em cada paralelogramo a seguir.
a)
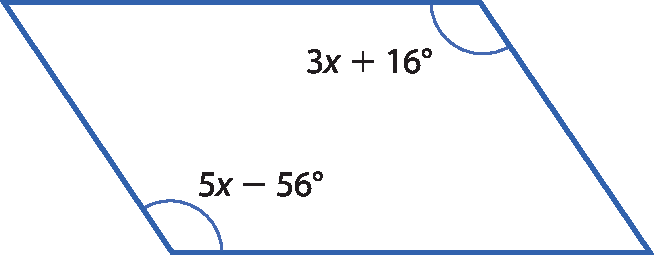
b)
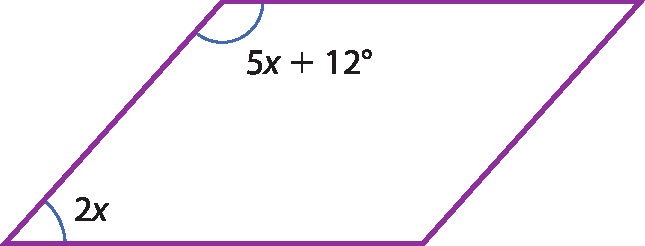
6 Uma altura de um paralelogramo fórma, com um dos lados, um ângulo medindo 35graus. Calcule as medidas dos ângulos desse paralelogramo.
7 Uma das diagonais de um losango fórma, com um dos lados, um ângulo medindo 28graus. Calcule as medidas dos ângulos desse losango.
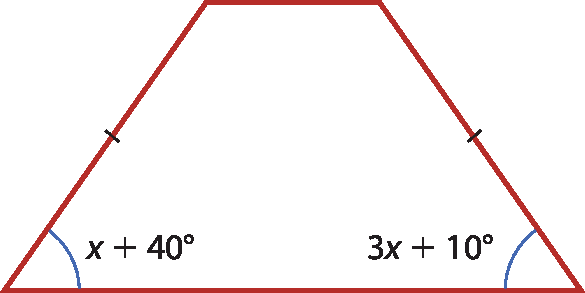
8 Calcule o valor de x em cada trapézio a seguir.
a)
b)
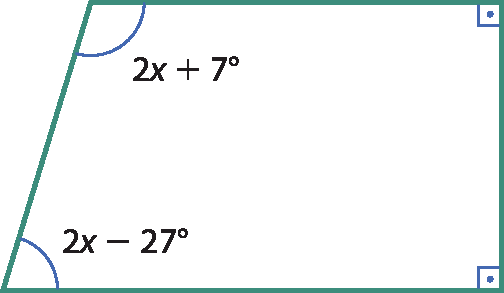
9 Um dos ângulos externos de um trapézio retângulo mede 118graus. Calcule a medida do ângulo obtuso desse trapézio.
10 A medida do perímetro de um trapézio isósceles é 66 centímetros. A base média mede 20 centímetros. Faça o cálculo e responda: quanto mede cada um dos lados não paralelos?
11 A base média de um trapézio isósceles mede 30 centímetros. Cada um dos lados congruentes mede 10 centímetros. Calcule a medida do perímetro desse trapézio.
12 Construa um triângulo retângulo á bê cê, reto em B. Marque o ponto M médio, de
segmento de reta AC, e o ponto D, simétrico de B em relação a M. Prove que a bê cê dê é um paralelogramo.
Respostas e comentários
45. 45graus, 60graus, 120graus, 135graus.
46. Resposta pessoal.
1. a) Retângulo.
1. b) Trapézio isósceles.
1. c) Trapézio retângulo.
1. d) Quadrado.
2. x = 70graus
3. a bê cê dê é um paralelogramo, porque suas diagonais se intersectam nos respectivos pontos médios.
4. Losango, porque as diagonais são perpendiculares entre si e se intersectam nos respectivos pontos médios.
5. a) x = 36graus
5. b) x = 24graus
6. 55graus, 55graus, 125graus, 125graus.
7. 56graus, 56graus, 124graus, 124graus.
8. a) x = 15graus
8. b) x = 50graus
9. 118graus
10. 13 centímetros
11. 80 centímetros
12. Construção de figura. Demonstração.
Exercícios propostos
A seguir uma possível resolução para o exercício 45.
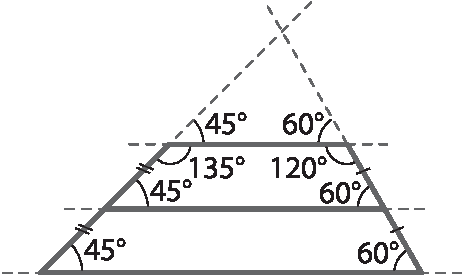
Logo, os ângulos internos do trapézio são 45graus, 60graus, 120graus e 135graus.
No exercício 46, possibilite aos estudantes discutir situações em que eles observam estruturas que possam ser associadas a trapézios; incentive-os a considerarem um dos contextos apresentados para elaborar a situação-problema.
Exercícios complementares
Este bloco de exercícios propicia aos estudantes revisitarem o trabalho com quadriláteros desenvolvido, ampliando e consolidando os conhecimentos que já construíram. Além disso, podem perceber possíveis dúvidas que ainda persistam e elucidá-las com o auxílio do professor e dos colegas.
As resoluções dos exercícios 1 a 9 e dos exercícios 11 e 12 estão no início deste Manual, nas orientações específicas do capítulo 9.
Apresentamos a seguir uma possível resolução para o exercício 10. Indicamos por B a medida da base maior, por b a medida da base menor e por x a medida dos lados não paralelos (uma vez que o trapézio é isósceles). Como a medida do perímetro do trapézio (P) é 66 centímetros, obtemos a seguinte expressão:
P = 2x + B + b
66 = 2x + B + b
66 ‒ 2x = B + b
=
Fração, numerador B+b, denominador 2, fim da fração
Como a base média mede 20 centímetros, obtemos:
= 20
· 2 = 20 · 2
66 ‒ 2x = 40
‒2x = ‒26
=
Fração, numerador menos 26, denominador menos 2, fim da fraçãox = 13
Portanto, cada lado não paralelo desse trapézio mede 13 centímetros.
Para o exercício 12, por simetria de construção, os triângulos retângulos á bê cê e cê dê á são congruentes; então, o quadrilátero a bê cê dê é um retângulo, que também é um paralelogramo.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
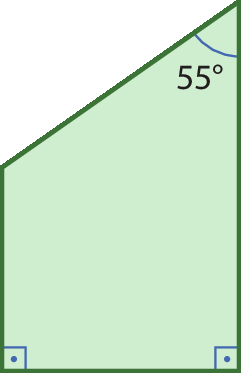
1 Este quadrilátero representa um dos vidros que Carlos precisou cortar para a janela de uma casa. Qual é a medida do maior ângulo interno do quadrilátero?
a) 100graus
b) 90graus
c) 125graus
d) 135graus
2 Para fazer um mosaico, uma artista usou dois tipos de paralelogramo. O ângulo agudo de um desses polígonos, o paralelogramo laranja, mede 70graus, conforme indicação na figura.
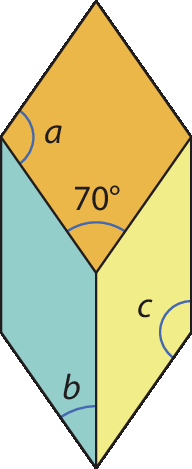
As medidas a, b e c dos ângulos destacados nesses paralelogramos são, respectivamente:
a) 90graus, 35graus e 145graus.
b) 110graus, 35graus e 145graus.
c) 110graus, 45graus e 145graus.
d) 140graus, 70graus e 290graus.
3 Seja um paralelogramo a bê cê dê e M o ponto de intersecção de suas diagonais. Sabendo que ei ém = 5 centímetros e BM = 7 centímetros, qual é a soma das medidas das diagonais desse quadrilátero?
a) 10 centímetros
b) 15 centímetros
c) 24 centímetros
d) 30 centímetros
4 Ter diagonais congruentes é uma característica:
a) de todos os losangos.
b) de todos os retângulos.
c) de todos os trapézios.
d) de todos os paralelogramos.
5 No paralelogramo a bê cê dê, a seguir, o ponto ê é o ponto de intersecção das diagonais,
ABmede 12 centímetros,
BCmede 20 centímetros e
Segmento de reta AE.mede 6,5 centímetros.
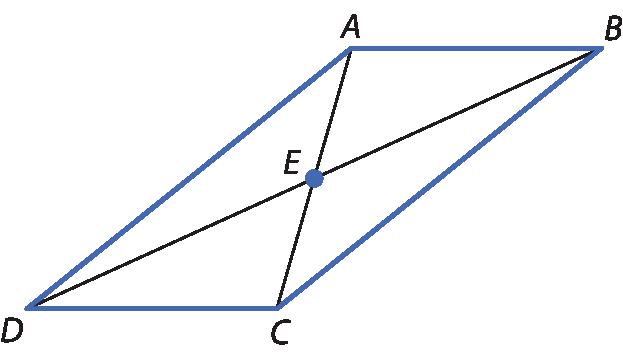
Qual é a medida do perímetro do triângulo á cê dê?
a) 37 centímetros
b) 38,5 centímetros
c) 45 centímetros
d) 46,5 centímetros
6 Todo trapézio isósceles tem:
a) ângulos da base congruentes.
b) todos os ângulos congruentes.
c) lados paralelos congruentes.
d) todos os lados congruentes.
7 No trapézio a bê cê dê, M e N são, respectivamente, os pontos médios de
Segmento de reta AD.e
segmento de reta BC. A base menor,
AB, mede 5 centímetros e a paralela
Segmento de reta MN.mede 10 centímetros.
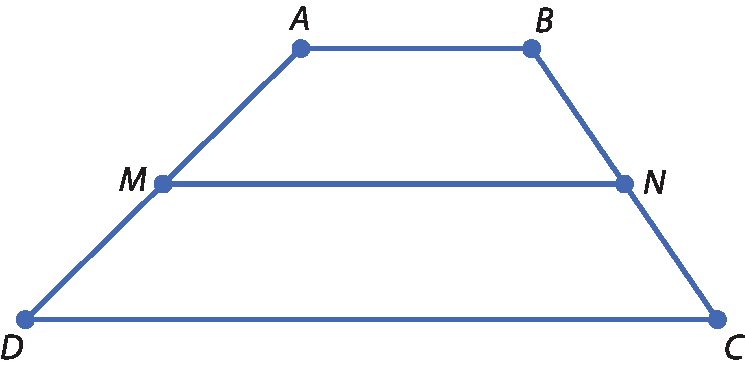
Qual é a medida da base maior
Segmento de reta DC.?
a) 10 centímetros
b) 15 centímetros
c) 20 centímetros
d) 25 centímetros
8 A medida do perímetro de um trapézio isósceles é igual a 88 centímetros e a base média mede 24 centímetros. Quanto mede cada um dos lados não paralelos desse trapézio?
a) 15 centímetros
b) 20 centímetros
c) 24 centímetros
d) 32 centímetros
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Qual é a definição de paralelogramo?
b) Quais são as propriedades relacionadas a todos os paralelogramos?
c) Quais são as propriedades das diagonais dos retângulos e das diagonais dos losangos?
d) Defina trapézio isósceles e indique duas propriedades relacionadas a esse tipo de trapézio.
e) O que é a base média de um triângulo? Como se calcula sua medida?
f) O que é a base média de um trapézio? Como se calcula sua medida?
Respostas e comentários
1. Alternativa c.
2. Alternativa b.
3. Alternativa c.
4. Alternativa b.
5. Alternativa c.
6. Alternativa a.
7. Alternativa b.
8. Alternativa b.
Organizando:
a) Paralelogramo é todo quadrilátero que tem os lados opostos paralelos.
b) Os lados opostos de um paralelogramo são congruentes, os ângulos opostos são congruentes e as diagonais se intersectam no ponto médio.
c) Retângulos: são congruentes; losangos: são perpendiculares entre si e estão contidas nas bissetrizes dos ângulos internos.
d) São trapézios em que os lados opostos não paralelos são congruentes. Propriedades: os ângulos adjacentes à base são congruentes e as diagonais são congruentes.
e) É o segmento que une os pontos médios de dois lados de um triângulo. Sua medida é igual à metade da medida do terceiro lado.
f) É o segmento que une os pontos médios dos lados não paralelos de um trapézio. Sua medida é igual à metade da soma das medidas das bases.
Verificando
Nesta seção são propostos testes que abordam os conteúdos apresentados ao longo deste capítulo, sendo uma oportunidade para os estudantes validarem o entendimento do conteúdo estudado. Caso eles apresentem dúvidas em relação a algum dos testes propostos, oriente-os a rever os conceitos apresentados no capítulo.
As resoluções dos testes 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 9.
Organizando
No item a, espera-se que o estudante tenha percebido que as definições são pontos de partida para o desenvolvimento do estudo em questão. No caso, o próprio nome do polígono – paralelogramo – indica aquilo que o caracteriza: lados paralelos.
No item b, espera-se que o estudante descreva as três propriedades dos paralelogramos (lados opostos congruentes, ângulos opostos congruentes e diagonais se intersectam no ponto médio).
No item c, caso o estudante tenha dificuldade de lembrar as propriedades das diagonais de um retângulo e de um losango, oriente-o a esboçar esses quadriláteros e traçar as diagonais. Tal esbôço, se bem-feito, lhe dará pistas das propriedades.
No item d, verifique se o estudante faz um analogia entre as classificações do triângulo isósceles e do trapézio isósceles.
Nos itens ê e f, o estudante pode fazer uma analogia como um instrumento de aquisição mnemônica atentando para o significado das palavras média (para o cálculo numérico) e médio (para o ponto médio). Assim, também ficará mais fácil obter a resposta à segunda pergunta: as medidas da base média são a metade da medida da base do triângulo e a média aritmética das medidas das bases do trapézio.
DIVERSIFICANDO
Quadriláteros na caixa
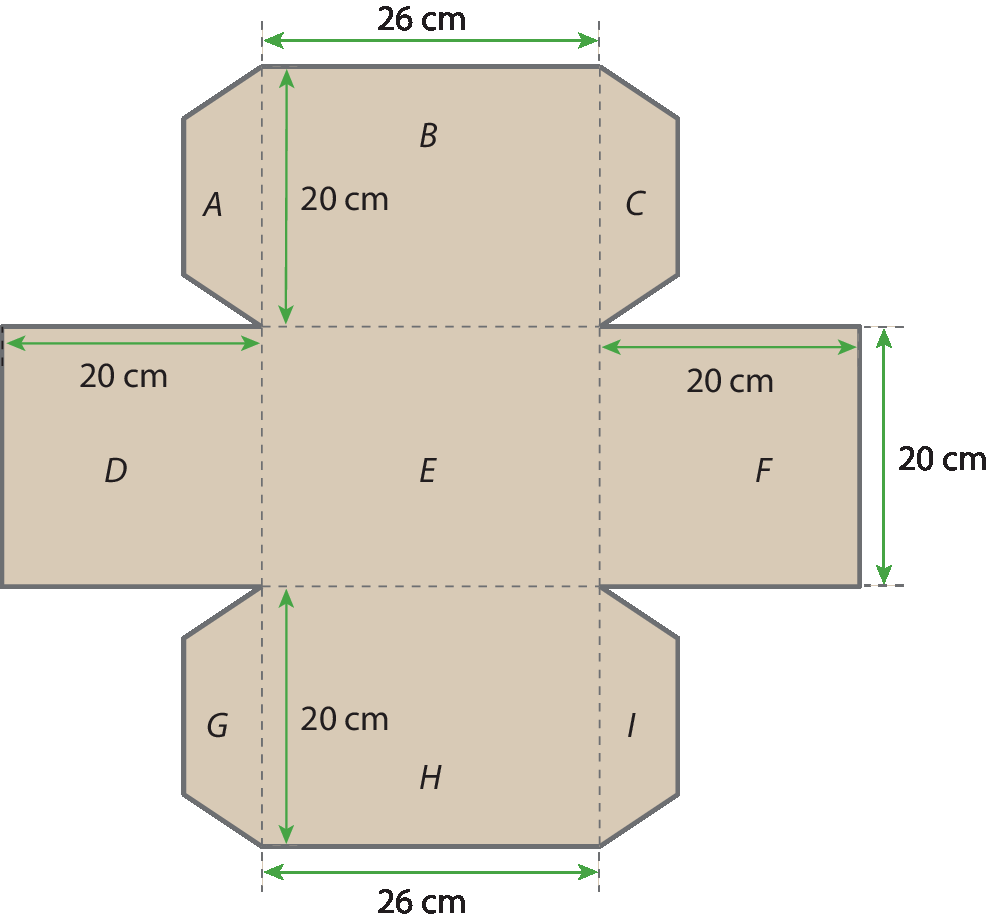
Gabriela guarda sua coleção de livros na estante da sala, mas uma das prateleiras quebrou. Como seu pai só poderá consertar a estante no fim de semana, pediu a ela que guardasse os livros em uma caixa. Então, Gabriela desenhou a planificação da superfície de uma caixa em uma folha de papelão. Depois, com cuidado, recortou e montou-a. Observe a planificação a seguir.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Quantos tipos de quadrilátero podemos identificar nessa planificação? Classifique os quadriláteros que você identificou.
2 Os livros de Gabriela têm as medidas indicadas na figura.

a) Determine quantos deles cabem na caixa se ela os guardar de modo que nenhuma parte deles fique fora da caixa e se ela os guardar de modo que uma das faces de área menor fique em contato com a base da caixa.
b) Calcule a medida do volume que ocupariam os livros que, no segundo modo do item anterior, ficariam fora da caixa.
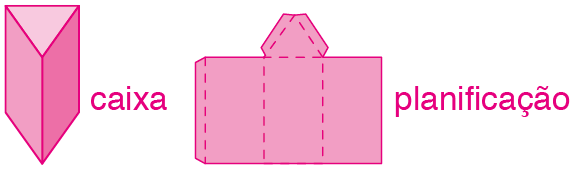
3 É possível ter uma caixa cuja planificação não seja composta apenas de quadriláteros? Explique por quê. Em caso afirmativo, desenhe uma dessas caixas.
4 Usando apenas 12 palitos de sorvete iguais, construa um retângulo de tal modo que ele tenha a maior medida de área possível. Depois, responda às questões.

a) Podemos construir um triângulo equilátero com esses 12 palitos?
b) Qual dessas figuras construídas com os 12 palitos tem maior medida de área: o retângulo ou o triângulo?
Respostas e comentários
1. Três tipos: retângulo (B, D, ê, F e H, , sendo D e F quadrados) e trapézio (a, C, G e ih ).
2. a) 10 livros; 13 livros.
2. b) .3120 centímetros cúbicos
3. Resposta possível: Sim, basta imaginar um prisma de base triangular sem uma das bases. Uma possibilidade de desenho:
4. O retângulo de maior medida de área é o quadrado cujo lado é formado por 3 palitos de sorvete.
4. a) Sim, o triângulo terá cada lado composto de 4 palitos de sorvete.
4. b) O retângulo.
Diversificando
Esta seção aborda triângulos, quadriláteros e prismas. Reproduza em cartolina a planificação apresentada, em tamanho maior, de modo que os estudantes possam trabalhar em grupos, montando e desmontando a caixa.
As resoluções e comentários das atividades 1 a 4 do Agora é com você! estão no início deste Manual, nas orientações específicas do capítulo 9.
Providencie palitos de sorvete ou similar para que os estudantes realizem a atividade 4.