
CAPÍTULO 10 Sistemas de equações do 1º grau com duas incógnitas

O Havaí é um estado americano composto de 137 ilhas e conhecido por suas belas praias, vulcões e competições internacionais de surfe. A cidade de Honolulu, situada na costa sul da ilha de Oahu, é a capital do estado e tem uma diferença de fuso horário de 7 horas em relação ao fuso horário de Brasília, que determina a hora oficial do Brasil.
Sabendo que a soma de determinado horário x em Brasília com determinado horário correspondente y em Honolulu é igual a 24 horas, como podemos determinar o horário nessas duas cidades? Conhecendo a diferença de fuso horário entre as cidades, é possível construir um sistema de equações do 1º grau com duas incógnitas para determinar o horário em Honolulu e o horário correspondente em Brasília nessa situação.
Sistemas de equações do 1º grau com duas incógnitas podem ser utilizados para a resolução de problemas em diversas situações cotidianas como essa.
Leia e responda no caderno.
a) Pesquise, em dupla com um colega, a história do surfe. Depois, elaborem um painel com imagens e texto, organizando as informações obtidas com a pesquisa.
b) Representando por x o horário em Brasília e por y o horário em Honolulu, escreva uma equação que traduza a frase:
• A diferença de fuso horário entre Brasília e Honolulu é de 7 horas.
• A soma da hora x (Brasília) com a hora y (Honolulu) é igual a 24 horas.
c) Aplicando o método da substituição, estudado no ano anterior, resolva um sistema com as equações do item b e descubra o horário correspondente em Brasília e em Honolulu.
Respostas e comentários
a) Resposta pessoal.
b) Diferença: x ‒ y = 7; soma: x + y = 24
c) Em Brasília: 15 horas 30 minutos; em Honolulu: 08 horas 30 minutos.
Capítulo 10 – Sistemas de equações do 1º grau com duas incógnitas
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Avançamos na Unidade Temática Álgebra retomando e ampliando o estudo dos sistemas de equações do 1º grau com duas incógnitas. Destacamos a representação gráfica e, com ela, classificamos e analisamos a existência e o número de soluções.
Ampliando o estudo de gráficos, trabalhamos a construção de um gráfico de colunas a partir de gráficos de setores.
Na abertura, a situação apresentada envolve sistemas de equações e fusos horários. A informação de que a soma da hora x (Brasília) com a hora y (Honolulu) é igual a 24 horas pode ser representada pela equação x + y = 24 (item b). E a informação de que a diferença de fuso horário entre Brasília e Honolulu é de 7 horas pode ser representada por x ‒ y = 7 (item b).
Logo, o sistema obtido é:
Da segunda equação, obtemos que x = 7 + y. Assim, tomando a primeira equação, temos:
x + y = 24
7 + y + y = 24
2y = 24 ‒ 7
2y = 17
y = 8,5
Portanto o horário em Honolulu correspondente às 15 horas e 30 minutos e em Brasília são 8 horas e 30 minutos (item c).
1. Revisão e desenvolvimento da resolução de sistemas do 1º grau
Pedro e Maria gostam de pescar. Analise o diálogo a seguir.


•

Analisando as grandezas, quantidade de peixes pescados e medida da massa total de peixes pescados, podemos dizer que elas são proporcionais? Por quê?proporcionais? Por quê?
Considerando que Maria fez todos os cálculos corretamente, é possível determinar quantos quilogramas tem o peixe de Pedro.
Indicando por x a medida da massa, em quilograma, do peixe de Pedro, e por y a medida da massa total dos peixes de Maria, podemos escrever as seguintes equações:

Essas equações formam um sistema de equações do 1º grau com duas incógnitas.
Um sistema de equações do 1º grau com duas incógnitas pode ter uma, nenhuma ou infinitas soluções. Se tiver solução, cada uma será um par ordenado (x, y), que é solução de cada uma das equações.
No sistema
Sistema de duas equações com duas incógnitas. A equação de cima é y igual a x mais 3 e a de baixo é y igual a 1 vírgula 5x., a solução é o par ordenado (6, 9), pois, ao substituir x por 6 e y por 9 nas duas equações, obtemos sentenças verdadeiras:
• 9 = 6 + 3 (sentença verdadeira)
• 9 = 1,5 ⋅ 6 (sentença verdadeira)
Observe que cada uma das equações do sistema tem mais de uma solução, mas o sistema formado por essas duas equações tem apenas uma solução. Por exemplo:
• (0, 3) é solução de y = x + 3, mas não é de y = 1,5x; logo, (0, 3) não é solução do sistema.
• (0, 0) é solução de y = 1,5x, mas não é de y = x + 3; logo, (0, 0) não é solução do sistema.
A seguir, vamos recordar o método da substituição de resolução de um sistema de duas equações do 1º grau com duas incógnitas e estudar o método da substituição e o método da adição.
Respostas e comentários
Não, pois, por exemplo ao dobrar, triplicar ou quadruplicar a quantidade de peixes, a massa total não é duplicada, triplicada ou quadruplicada.
1. Revisão e desenvolvimento da resolução de sistemas do 1º grau
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero seis e ê éfe zero oito ême ah zero oito.
Neste tópico, retomamos a resolução e elaboração de problemas que envolvem o cálculo numérico das expressões algébricas, favorecendo o desenvolvimento da habilidade (ê éfe zero oito ême ah zero seis), e a resolução de sistemas de equações do 1º grau com duas incógnitas, possibilitando o desenvolvimento da habilidade (ê éfe zero oito ême ah zero oito).
O contexto da história em quadrinhos tem como objetivo descontrair e diversificar a linguagem, auxiliando na contextualização dos conceitos apresentados.
Antes de desenvolver a situação resolvendo-a por meio de um sistema de equações do 1º grau, converse com os estudantes sobre o fato de a quantidade de peixes pescados e a massa total de peixes pescados serem grandezas não proporcionais.
Incentive-os a justificar esse fato, sendo válidas respostas como “Cada peixe tem uma massa diferente de outro.”; solicite também que deem outros exemplos de grandezas que não sejam proporcionais, como a idade e a altura de uma pessoa, entre outros. Este trabalho favorece o desenvolvimento de aspectos das habilidades (ê éfe zero oito ême ah um dois) e (EF08MA13).
Na retomada do conceito de um sistema de equações do 1º grau com duas incógnitas, peça aos estudantes que identifiquem cada equação e as incógnitas que compõem o sistema. Proponha a eles que reescrevam o mesmo sistema apresentando as equações de fórma diferente, o que mostrará a familiaridade deles com Álgebra. Uma possível resposta é:
Verifique se os estudantes compreendem o que é uma solução para cada equação do sistema. Estimule-os a apresentar outras soluções possíveis para cada equação.
Método da substituição

Em um escritório trabalham 33 pessoas. Sílvio percebeu que, se forem demitidos 3 homens e admitidas 4 mulheres, o número de homens e de mulheres passará a ser igual. Quantos homens e quantas mulheres trabalham nesse escritório?
Indicando por h a quantidade de homens e por m a quantidade de mulheres, o sistema a ser resolvido é:
Isolando a incógnita h na equação h ‒ m = 7, temos:
h ‒ m = 7
h ‒ m + m = 7 + m
h = 7 + m

Substituindo h por (7 + m) na equação h + m = 33, determinamos o valor de m.
(7 + m) + m = 33
7 + 2m = 33
7 + 2m ‒ 7 = 33 ‒ 7
Fração, numerador 2m, denominador 2, fim da fração, é igual a fração, 26 meios.
m = 13
Substituindo m por 13 na equação h = 7 + m, determinamos o valor de h.
h = 7 + m
h = 7 + 13
h = 20
Logo, a solução do sistema é h = 20 e m = 13.
Portanto, nesse escritório trabalham 20 homens e 13 mulheres.
De maneira geral, podemos considerar que a resolução de um sistema de equações do 1º grau com duas incógnitas pelo método da substituição consiste em:
• isolar uma das incógnitas de uma das equações;
• substituir, na outra equação, a expressão determinada, obtendo uma equação com uma única incógnita;
• resolver a equação de uma incógnita obtida e substituir o valor, em uma das equações do sistema, para obter o valor da outra incógnita.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO

Durante um mês, Júlia guardou em um cofre moedas de 25 e de 10 centavos. Ao abri-lo, constatou que tinha duzentas e dez moedas, em um total de R$ 35,70trinta e cinco reais e setenta centavos. Quantas moedas de cada tipo Júlia guardou?
Respostas e comentários
Pense mais um poucoreticências: 98 moedas de 25 centavos e 112 de 10 centavos.
Método da substituição
Pergunte aos estudantes quais métodos conhecem para a resolução de um sistema de equações do 1º grau com duas incógnitas. Verifique se sabem dizer em que consiste o método da substituição.
Pergunte a eles também o que representa cada uma das equações que formam o sistema na situação apresentada.
Comente com os estudantes que convém fazer a verificação, substituindo no sistema original os valores encontrados para as incógnitas. Caso uma das igualdades não seja verdadeira, é preciso rever a resolução.
Pense mais um poucoreticências
Uma possível resolução é dada a seguir. Indicando por x a quantidade de moedas de 25 centavos e por y a quantidade de moedas de 10 centavos, concluímos que:
• x + y = 210 (quantidade total de moedas)
• x · 0,25 + y · 0,10 = 35,70 (quantia total de dinheiro) Assim formamos o sistema:
Esquema. Sistema de equações. Primeira equação: x mais y igual a 210. Segunda equação: 0,25x mais 0,1y igual a 35,7.⇒
Símbolo de implicação para outro sistema de equações. Primeira equação: y igual a 210 menos x. Segunda equação: 0,25x mais 0,1y igual a 35,7.Resolvendo esse sistema pelo método da substituição, encontramos o valor de x substituindo y por (210 ‒ x) na equação 0,25x + 0,1y = 35,7. Assim:
0,25x + 0,1 · (210 ‒ x) = 35,7
0,25x ‒ 0,1x = 35,7 ‒ 21
0,15x = 14,7
0 vírgula 15x sobre 0 vírgula 15
=
14 vírgula 7 sobre 0 vírgula 15x = 98
Então, substituímos x por 98 em y = 210 ‒ x e obtemos:
y = 210 ‒ 98 = 112
Logo, Júlia guardou 98 moedas de 25 centavos e 112 moedas de 10 centavos.
Método da adição
Diego entrou em uma sorveteria para comprar picolés e água.

Nessa sorveteria, o preço de três picolés e uma garrafa de água é R$ 12,00doze reais.
Diego pagou R$ 15,00quinze reais por dois picolés e três garrafas de água.
Qual é o preço do picolé e da garrafa de água?
Indicando por p o preço do picolé e por g o preço da garrafa de água, o sistema a ser resolvido é:
O método da adição consiste em adicionar membro a membro as duas equações visando obter uma nova equação que tenha apenas uma das incógnitas. Para isso, é necessário que o coeficiente de uma das incógnitas seja oposto ao coeficiente correspondente à mesma incógnita da outra equação, pois, assim, esses termos serão anulados quando adicionados.
Porém, no sistema do exemplo apresentado, as equações não satisfazem essa condição. Por isso, vamos obter um sistema equivalente a esse multiplicando por ‒3 ambos os membros da equação 3p + g = 12.
Adicionando membro a membro as equações, obtemos o valor de p:
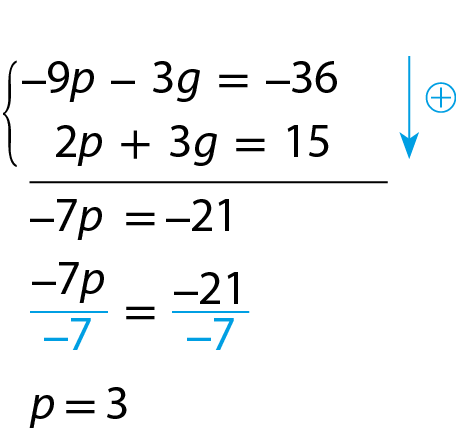
Substituindo p por 3 em uma das equações, por exemplo, 3p + g = 12, obtemos:
3p + g = 12
3 ⋅ 3 + g = 12
9 + g = 12
9 + g ‒ 9 = 12 ‒ 9
g = 3
Logo, a solução do sistema é p = 3 e g = 3.
Portanto, o preço tanto do picolé quanto da garrafa de água é R$ 3,00três reais.

Observe:
Respostas e comentários
Método da adição
Converse com os estudantes para avaliar se eles entenderam o que representa cada uma das equações que formam o sistema na situação apresentada.
Pergunte a eles em que consiste o método da adição para resolver sistemas de equações. Estimule-os a perceber que, neste caso e em muitos outros, precisamos determinar alguma equação equivalente a uma das apresentadas no sistema (ou a ambas) de modo que, ao adicionar membro a membro as duas equações do sistema, uma das incógnitas seja anulada. Para isso, eles devem se lembrar da seguinte propriedade de uma igualdade:
• A relação de igualdade existente entre dois termos (ou duas expressões) permanece quando se multiplica por um mesmo número não nulo cada um desses termos (ou cada uma dessas expressões).
Proponha à turma fazer a verificação das soluções encontradas.
Comente que, conforme o sistema, basta aplicar a propriedade citada em apenas uma das suas equações. Há sistemas, entretanto, nos quais é necessário aplicar a propriedade nas duas equações para conseguir anular uma das incógnitas.
A resolução de um sistema de equações do 1º grau com duas incógnitas pelo método da adição consiste em:
• multiplicar, quando necessário, ambos os membros de uma (ou das duas) equações por um número conveniente, de modo que se obtenham coeficientes opostos em uma das incógnitas;
• adicionar membro a membro as duas equações, obtendo uma equação com uma única incógnita;
• resolver a equação de uma incógnita e substituir o valor obtido em uma das equações do sistema para determinar o valor da outra incógnita.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 (saréspi) Em um campeonato de futebol, os times ganham 3 pontos em cada vitória, 1 ponto por empate e 0 ponto por derrota. O time Cruzadão participou de 50 jogos e fez 54 pontos, tendo perdido 12 jogos. Chame de v o número de jogos que Cruzadão venceu; de d, o número de jogos em que foi derrotado e de e, os jogos em que houve empate.
Assinale a alternativa que mostra corretamente o sistema de equações que representa essa situação:
a)
Esquema. Sistema de equações. Primeira equação: v mais e igual a 50. Segunda equação: 3v mais 1e igual a 54.b)
Esquema. Sistema de equações. Primeira equação: v mais ê, mais 12, igual a 50. Segunda equação: 3v mais 1e igual 54.c)
Esquema. Sistema de equações. Primeira equação: v mais ê, mais d igual a 54. Segunda equação: 3v mais ê, mais 0d igual a 50.d)
Esquema. Sistema de equações. Primeira equação: v mais ê mais 0,12 igual a 50. Segunda equação: 3v mais 1e igual a 54.2 Usando o método da substituição e da adição, resolva os sistemas a seguir e verifique a solução obtida.
a)
Esquema. Sistema de equações. Primeira equação: 3x mais 2y igual a 40. Segunda equação: x menos 3y igual a menos 5.b)
Esquema. Sistema de equações. Primeira equação: 4x mais 3y igual a 14. Segunda equação: 5x menos 2y igual a 29.3

Resolva mentalmente.
a)
Esquema. Sistema de equações. Primeira equação: x menos y igual a 5. Segunda equação: x igual a 2y mais 1.
b)
Esquema. Sistema de equações. Primeira equação: x mais y igual a 9. Segunda equação: y igual a x menos 5.
4 Um pai tem 20 anos a mais do que o filho. Calcule a idade de cada um, sabendo que daqui a 5 anos o pai terá o dôbro da idade do filho.
5 Um número tem dois algarismos. O algarismo das unidades tem 5 unidades a mais que o algarismo das dezenas. O número considerado é o triplo da soma do valor absoluto de seus algarismos. Determine esse número.
6 Resolva os sistemas a seguir pelo método que você julgar mais conveniente e verifique as soluções obtidas.
a)
Esquema. Sistema de equações. Primeira equação: 2 vezes abre parênteses x menos 2 fecha parênteses mais 3y igual a menos 7. Segunda equação: 3x menos 2 vezes abre parênteses y menos 4 fecha parênteses igual a menos 3.
b)
Esquema. Sistema de equações. Primeira equação: 2,4x menos 0,6y igual a 2,4. Segunda equação: 3,6x mais y igual a 7,4.
7 Calcule a medida da área de um retângulo cujo perímetro mede 22 centímetros e a diferença entre a medida da base e a metade da medida da altura seja de 5 centímetros.
8 Um supermercado apresentou as seguintes ofertas:
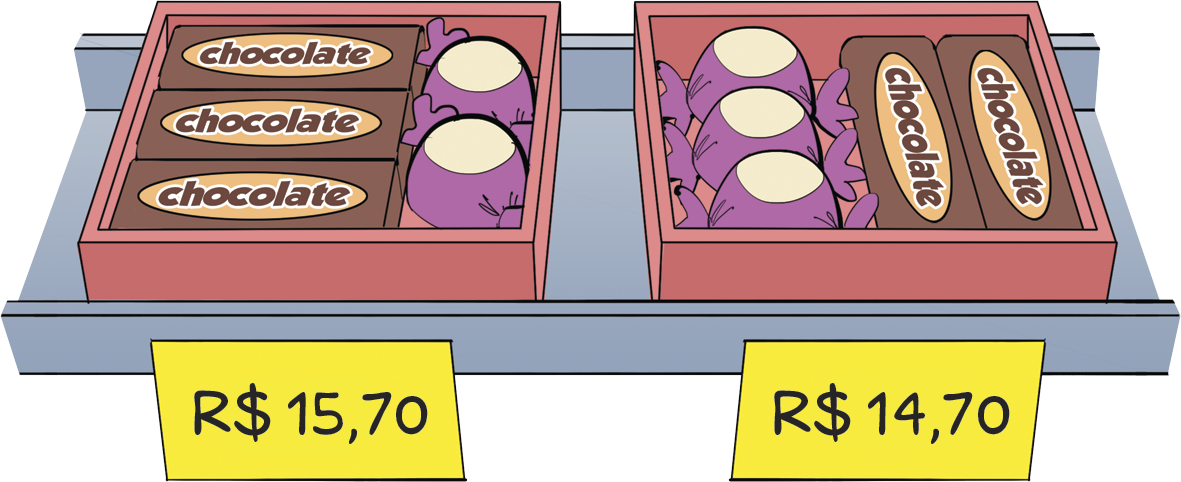
Nessa promoção, a quanto está sendo vendido cada bombom?
9 Luís pagou uma dívida de R$ 89,00oitenta e nove reais com notas de R$ 5,00cinco reais e de R$ 2,00dois reais. Ao todo, ele usou 22 notas. Quantas notas eram de R$ 5,00cinco reais e quantas eram as notas de R$ 2,00dois reais?
10

Hora de criar – Reúna-se com um colega e façam o que se pede.
Cada um pensa em um par ordenado de números e escreve duas equações do 1º grau, com duas incógnitas que tenham o par imaginado como solução de cada uma das equações. Troquem entre si os sistemas formados pelas duas equações escritas para que o colega resolva o sistema por um dos métodos revistos. Desfaçam a troca para que cada um faça a verificação da resposta, resolvendo o sistema pelo outro método.
Respostas e comentários
1. Alternativa b.
2. a) (10, 5)
2. b) (5, ‒2)
3. a) (9, 4)
3. b) (7, 2)
4. Pai: 35 anos; filho: 15 anos.
5. O número é 27.
6. a) (‒3, 1)
6. b) (1,5; 2)
7. 28 centímetros quadrados
8. R$ 2,54dois reais e cinquenta e quatro centavos
9. 15 notas de R$ 5,00cinco reais e 7 notas de R$ 2,00dois reais.
10. Resposta pessoal.
Exercícios propostos
As resoluções dos exercícios 2 a 7 e do exercício 9 estão no início deste Manual, nas orientações específicas do capítulo 10.
Neste bloco de exercícios, os estudantes aplicarão as técnicas de resolução de sistemas de equações do 1º grau com duas incógnitas e resolverão problemas do cotidiano.
No exercício 1, aparentemente, a situação apresenta três incógnitas vê, ê e d. Porém, como é atribuído à derrota 0 ponto e é informada a quantidade de derrotas (12), a derrota d deixa de configurar uma incógnita. Assim, a adição do número de jogos que o time Cruzadão venceu (vê) com o número de jogos em que houve empate (ê) e o número de jogos que ele perdeu (12) resulta em 50 jogos (v + e + 12 = 50).
Como em cada vitória os times ganham 3 pontos e em cada empate eles ganham 1 ponto, a equação que relaciona o número de pontos obtidos pelo time Cruzadão (54) no campeonato com o número de jogos que ele venceu (vê) e o número de jogos em que houve empate (ê) é 3v + 1e = 54.
Portanto a alternativa b mostra corretamente o sistema de equações que representa a situação descrita.
No exercício 3, peça aos estudantes que expliquem a um colega seu raciocínio para resolver mentalmente os sistemas.
Apresentamos uma possível resolução para o exercício 8. Representando o preço do chocolate por c e o do bombom por b, a leitura da imagem leva ao sistema de equações:
Multiplicando a 1ª equação por ‒2 e a 2ª por 3, obtemos:
Adicionando, membro a membro, as equações, obtemos:
5b = 12,70 ou b = 2,54
Logo, cada bombom custa R$ 2,54dois reais e cinquenta e quatro centavos.
Destacamos também o exercício 10, no qual os estudantes, em duplas, elaboram sistemas partindo da solução, trocam com o colega, resolvem e depois avaliam e corrigem a resolução do outro. Oriente-os para que os coeficientes das equações não sejam múltiplos uns dos outros.
PARA SABER MAIS
Grandezas proporcionais

Reúna-se com um colega e leiam o diálogo entre Ricardo e Cristina.

Quando duas grandezas estão relacionadas de maneira que a variação de uma implica na variação da outra na mesma razão, dizemos que elas são grandezas diretamente proporcionais. Se a variação de uma implicar na variação da outra a uma razão inversa, dizemos que elas são grandezas inversamente proporcionais.
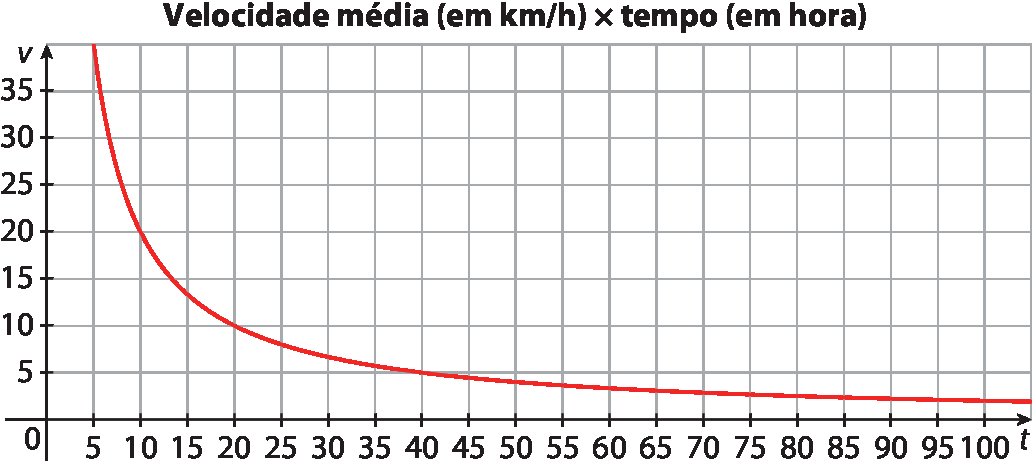
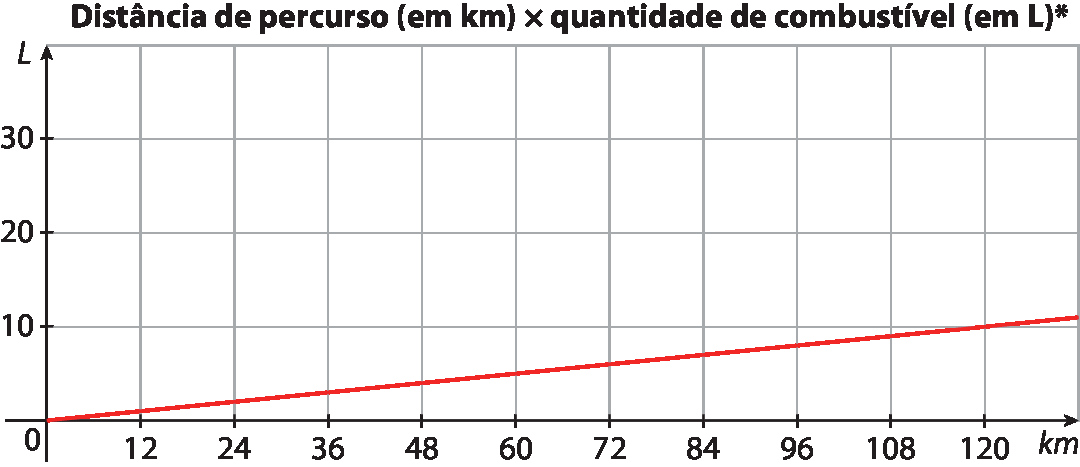
Em relação à situação do diálogo entre Ricardo e Cristina, observem os gráficos construídos com ferramentas de um software de Geometria dinâmica.
Agora é com você!
FAÇAM AS ATIVIDADES NO CADERNO
a) Elaborem dois problemas: um envolvendo grandezas diretamente proporcionais e outro envolvendo grandezas inversamente proporcionais.
b) Em uma folha de papel quadriculado, façam um esbôço do gráfico que representa a situação de cada problema elaborado.
c) Em um software de Geometria dinâmica, obtenham cada gráfico e os comparem com os apresentados nessa seção. O que os gráficos têm em comum e o que têm de diferente?
Respostas e comentários
Veja as respostas neste Manual.
Para saber mais
Essa atividade possibilita desenvolver as habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três), pois os estudantes podem analisar o gráfico de duas grandezas inversamente proporcionais. Para explorar o contexto, incentive-os a compor um quadro relacionando a velocidade e o tempo do percurso. Por exemplo:
|
Tempo (t) em hora |
Velocidade (v) em km/h |
|---|---|
|
1 |
200 |
|
2 |
100 |
|
4 |
50 |
|
8 |
25 |
|
16 |
12,5 |
Explore que, ao dobrar o tempo (de uma hora para duas horas ou de 8 horas para 16 horas, por exemplo) a velocidade cai à metade (de 200 quilômetros por hora para 100 quilômetros por hora ou de 25 quilômetros por hora para 12,5 quilômetros por hora, respectivamente).
Para facilitar, oriente-os a determinar a distância do percurso que será percorrido pelos personagens; como a uma velocidade média de 50 quilômetros por hora são necessárias 4 horas de percurso, então, a distância a ser percorrida é 200 quilômetros. Assim, se v é a velocidade média e t é o tempo, respectivamente, em quilômetro por hora e em hora, então:
Pergunte aos estudantes se t pode assumir valores negativos ou nulo; espera-se que percebam que não, pois no contexto o tempo deve ser positivo e maior do que zero.
Incentive e oriente os estudantes a representar em um plano cartesiano os pontos obtidos. Sugerimos deixar que eles se expressem sobre o gráfico verificando, por exemplo, se compreendem que, neste caso, o gráfico não será uma reta. Para ampliar a compreensão, indicamos que seja feita uma atividade utilizando softwares de geometria dinâmica para obter o gráfico que representa a relação entre v e t; lembre os estudantes de limitar os valores de t ao usar o software, isto é, de que t > 0. No Agora é com você!, para o item a, espera-se que os estudantes criem problemas que possam ser expressos algebricamente por:
• y =
y igual a fração, numerador a, denominador x, fim da fração.; com x ≠ 0; a um número real.
• h = a · z; com a um número real.
Para os item b e c, oriente-os a produzir gráficos como os apresentados nessa página. Espera-se que percebam que os gráficos envolvendo grandezas diretamente proporcionais apresentam retas que passam pela origem e, ainda, que os gráficos que envolvem grandezas inversamente proporcionais apresentam uma “curva”. Para este tipo de gráfico, sugerimos trabalhar com softwares de geometria dinâmica ou representar alguns na lousa para os estudantes os analisarem.
TRABALHANDO A INFORMAÇÃO
Composição de um gráfico de colunas formadas a partir de outros gráficos
Estudantes dos cursos de Comunicação, Economia, Psicologia, Engenharia e Medicina fizeram uma prova de Língua Portuguesa para descobrir quais eram as principais dificuldades nessa área.
Após a correção da prova, foi feito um levantamento do índice de erros cometidos, que foram representados nos gráficos a seguir.
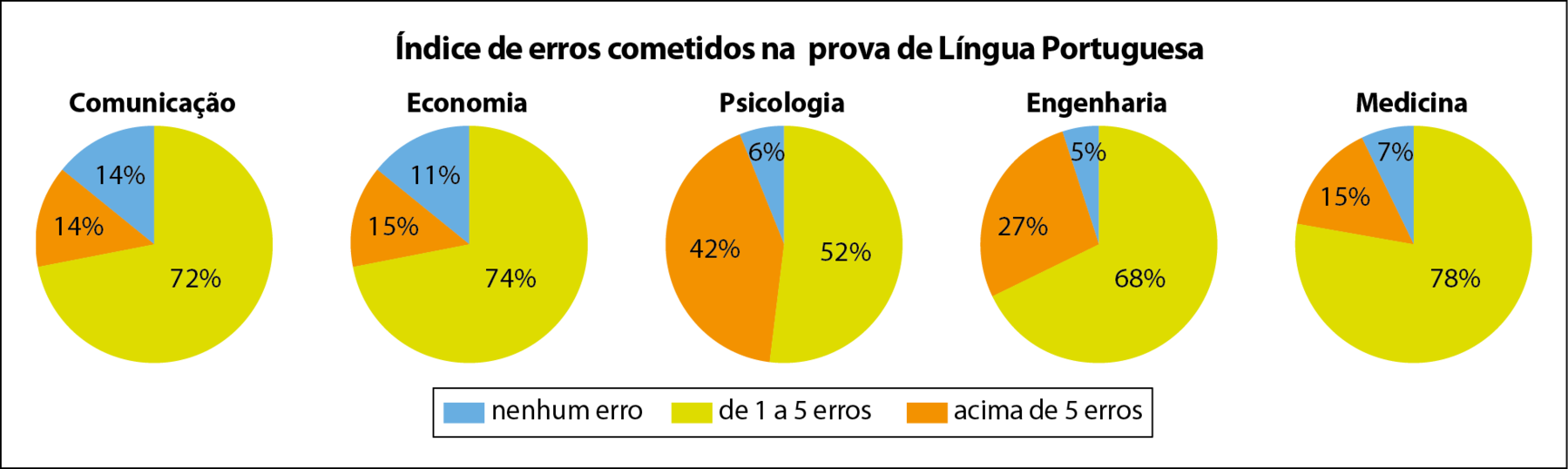
Esses dados também podem ser organizados em um único gráfico de colunas compostas. Para isso, haverá uma coluna para cada curso no eixo horizontal; no eixo vertical, serão indicados os intervalos de erros em porcentagem e, por isso, em uma escala de 0 a 100.
Observe atentamente o gráfico e compare-o com os anteriores.
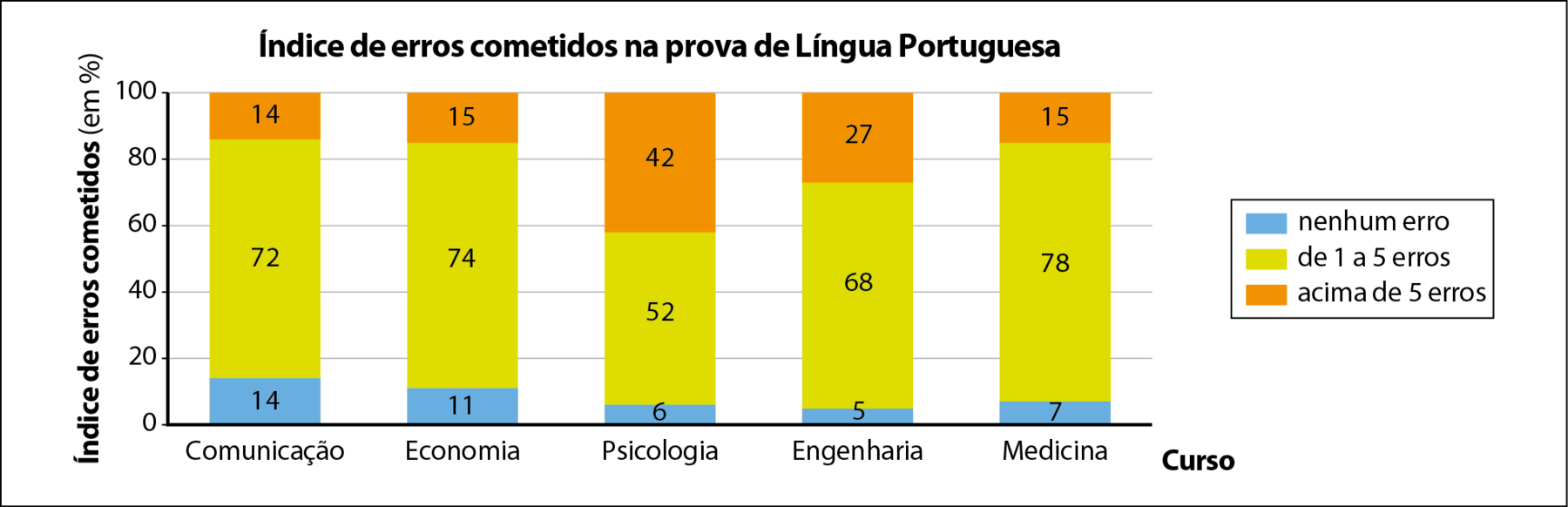
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Com base nos dados apresentados, responda:
a) Os estudantes de que curso tiveram maior quantidade de provas sem erros? E quais tiveram menor quantidade?
b) Que gráfico você usou para responder ao item a? Justifique sua resposta.
2 Considerando que, em todos os cursos, o mesmo número de estudantes foi submetido a essa prova, faça um novo gráfico de setores, por meio das médias aritméticas de cada categoria indicada pela côr na legenda, que mostre de modo geral (não por curso) os índices de erros dessa prova.
Respostas e comentários
1. a) Curso de Comunicação; curso de Engenharia.
1. b) É possível usar tanto os gráficos de setores como o gráfico de colunas, porém o gráfico de colunas é mais sintético e possibilita uma comparação visual mais rápida.
2. Construção de gráfico.
Trabalhando a informação
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah dois três.
Ampliando a compreensão da leitura de gráficos, a seção apresenta a construção de um gráfico de colunas compostas de dados obtidos de outros gráficos, no caso, gráficos de setores, possibilitando, assim, o desenvolvimento da habilidade (EF08MA23).
Peça aos estudantes que pesquisem exemplos de gráficos utilizados em diferentes meios de comunicação para analisarem e comporem os mesmos dados em gráficos de colunas compostas.
Para resolver a atividade 2 do Agora quem trabalha é você!, os estudantes devem primeiro calcular as médias de cada um dos índices de erros (nenhum êrro, de 1 a 5 erros e acima de 5 erros) considerando os cinco cursos. Como em cada curso há o mesmo número de estudantes, é possível adicionar diretamente as porcentagens para cada um dos três índices de erros e dividir o total obtido por 5 (número de colunas ou número de cursos). Com as médias aritméticas dos valores de cada categoria descrita na legenda, é construído o gráfico de setores solicitado.

2. Representações gráficas
Soluções de uma equação do 1º grau com duas incógnitas
Dada uma equação do 1º grau com duas incógnitas, existem infinitos pares de números que são soluções dessa equação.
Como exemplo, vamos considerar a equação x + y = 3. Como x + y = 3 e y = 3 ‒ x são equações equivalentes, os pares ordenados que satisfazem a equação considerada são da forma:

Para determinar alguns desses pares, atribuímos a x qualquer valor e determinamos o valor correspondente de y. O quadro a seguir mostra alguns desses pares.
|
x |
−1 |
0 |
0,5 |
1 |
2 |
2,5 |
3 |
4 |
|---|---|---|---|---|---|---|---|---|
|
y = 3 − x |
4 |
3 |
2,5 |
2 |
1 |
0,5 |
0 |
−1 |
|
Par obtido |
(−1, 4) |
(0, 3) |
(0,5; 2,5) |
(1, 2) |
(2, 1) |
(2,5; 0,5) |
(3, 0) |
(4, −1) |
Os pares ordenados (‒1, 4), (0, 3), (0,5; 2,5), (1, 2), (2, 1), (2,5; 0,5), (3, 0) e (4, ‒1) são algumas soluções da equação x + y = 3.
Vamos representar esses pares ordenados em um plano cartesiano.

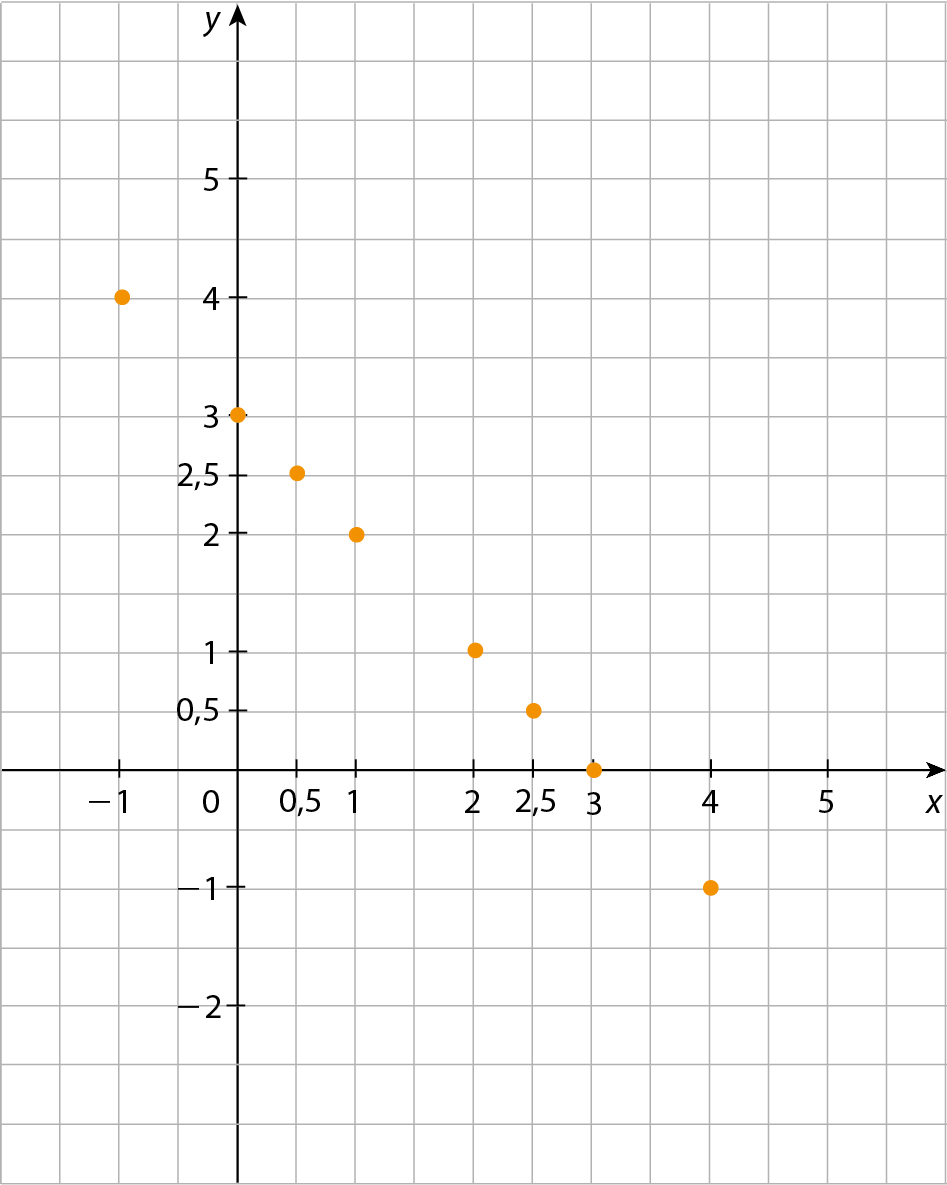

Respostas e comentários
2. Representações gráficas
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero sete e ê éfe zero oito ême ah zero oito.
Neste tópico, avançamos na representação de uma equação do 1º grau com duas incógnitas, agora utilizando o plano cartesiano e relacionando suas soluções a retas, ou seja, cada solução da equação (par ordenado) corresponde a um ponto da reta; os infinitos pares ordenados obtidos como solução correspondem aos infinitos pontos de uma mesma reta, o que favorece o desenvolvimento da habilidade (EF08MA07). A resolução de sistemas de equações do 1º grau com duas incógnitas também passa a ser gráfica e possibilita o desenvolvimento da habilidade (EF08MA08). Duas equações correspondem a duas retas do plano cartesiano que podem ser concorrentes, paralelas ou coincidentes.
Retome o trabalho inicial feito com os estudantes, quando foi proposto a eles buscar soluções a cada equação do sistema trabalhado. Faça o mesmo neste momento, de modo que eles percebam que uma equação com duas incógnitas tem infinitas soluções. Ressalte também que os pares ordenados que são soluções da equação x + y = 3, por exemplo, podem ser representados por (x, 3 ‒ x) ou (3 ‒ y, y).
Trabalhe a representação dos pares ordenados no plano cartesiano. É importante que os estudantes reconheçam e localizem pontos. Proponha a eles, por exemplo, uma brincadeira de batalha naval em grupo.
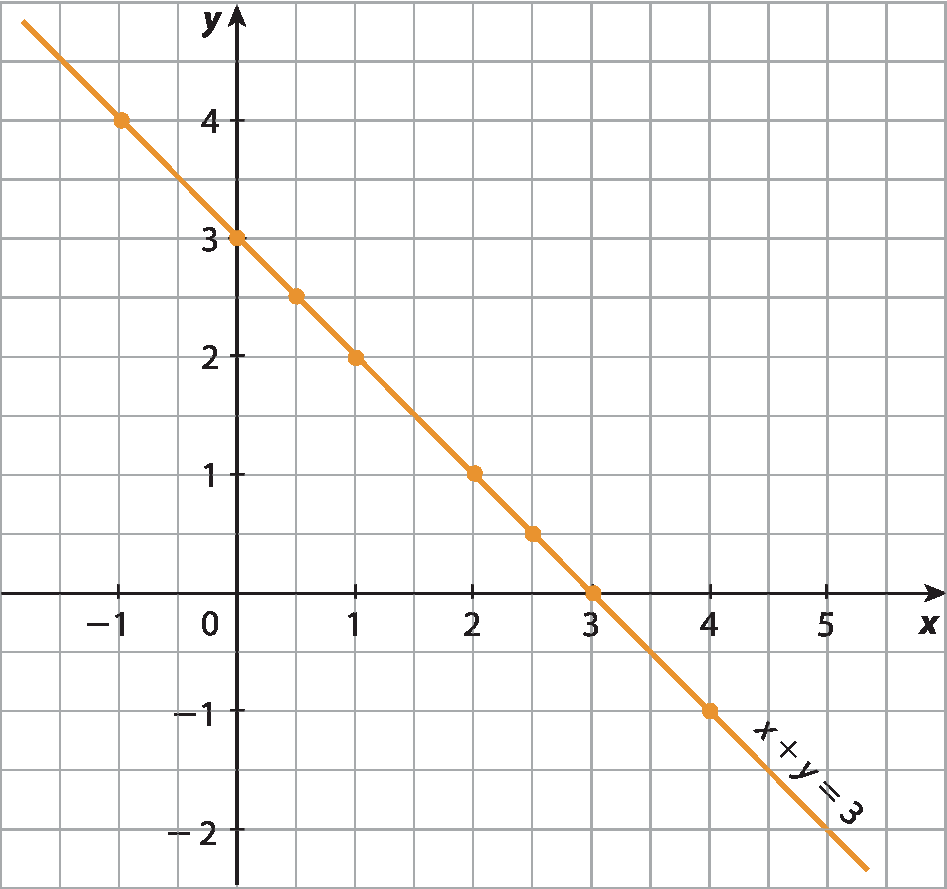

• A reta que contém esses pontos é a solução gráfica da equação x + y = 3.
• Qualquer ponto que pertença a essa reta será solução da equação x + y = 3.
• Nenhum ponto fora dessa reta é solução da equação x + y = 3.
Sabemos que por dois pontos passa uma única reta; então, para representar graficamente as soluções de uma equação do 1º grau com duas incógnitas, é suficiente:
• determinar dois pontos que sejam solução da equação;
• localizar esses pontos no plano cartesiano;
• traçar a reta determinada por esses pontos.
•

Considere que o salário de uma pessoa que planta feijão dependa diretamente da quantidade de feijões, em quilograma, que ela vende em um mês. Se ela ganha R$ 3,00três reais por quilograma de feijão vendido, como poderíamos representar essa situação em um gráfico? R$ 3,00três reais por quilograma de feijão vendido, como poderíamos representar essa situação em um gráfico?
Acompanhe outro exemplo de representação gráfica de uma equação:
Vamos representar graficamente soluções da equação 2x + y = 5.
Para isso, determinamos dois pares ordenados que sejam solução dessa equação.
• Para x = 1, temos: 2 ⋅ 1 + y = 5 y = 3 Logo, obtemos o par (1, 3).
• Para x = ‒1, temos: 2 ⋅ (‒1) + y = 5 y = 7 Logo, obtemos o par (‒1, 7).
Portanto, os pares (1, 3) e (‒1, 7) são soluções da equação 2x + y = 5. Em seguida, localizamos no plano cartesiano os pontos que representam esses pares ordenados e traçamos a reta que os contém.
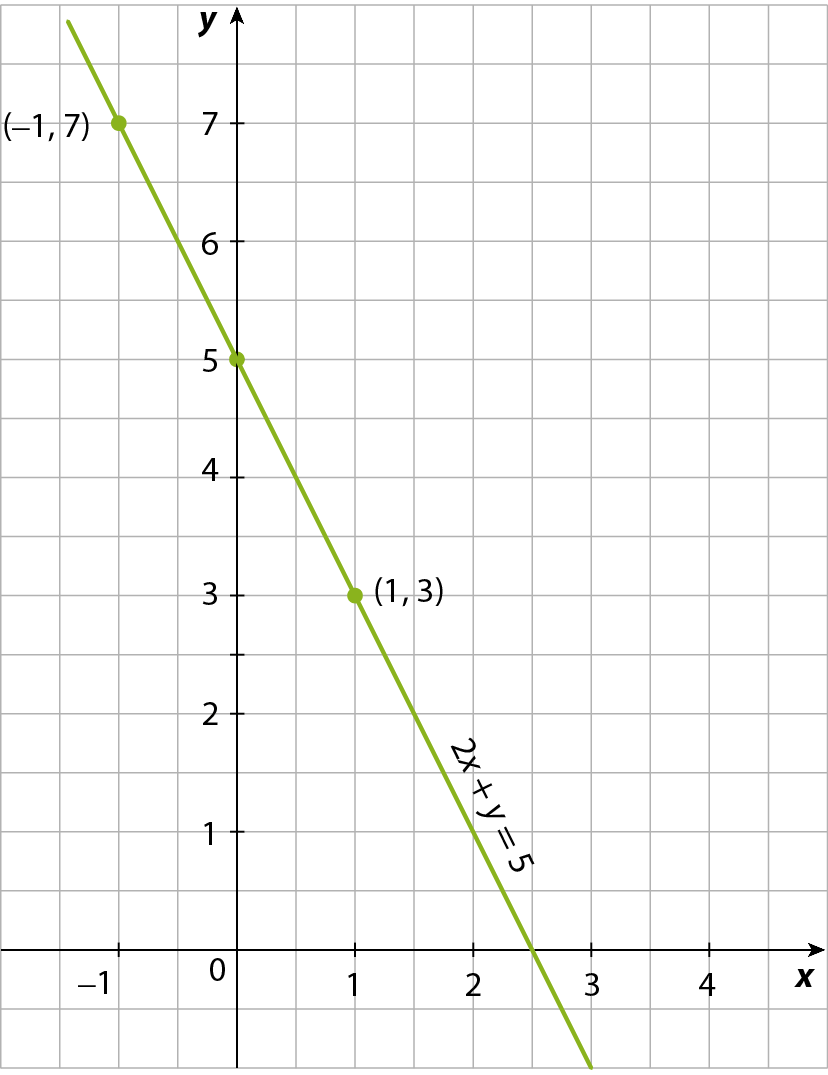
A reta obtida representa graficamente as soluções da equação 2x + y = 5.
Respostas e comentários
Espera-se que os estudantes indiquem que podem representar os pontos (0, 0) e (2, 6), por exemplo, e traçar a reta que liga esses dois pontos. Incentive-os a representar esse gráfico e discutirem sobre a proporcionalidade envolvida na situação.
Representações gráficas
Em concordância com a Bê êne cê cê, o conjunto dos números reais é objeto de estudo contido no livro do 9º ano desta coleção; portanto, se julgar conveniente, sugerimos utilizar softwares de geometria dinâmica como ferramentas auxiliares para representar as equações sem a necessidade de justificar que, em princípio, a variável independente pode assumir qualquer valor real.
Explore os exemplos apresentados. Se julgar necessário, reproduza-os na lousa para ampliar a discussão com a turma. Retome o fato de que dois pontos determinam uma única reta, permitindo que eles se apropriem do fato de que é suficiente representar apenas dois pontos cujas coordenadas satisfazem a equação dada.
Mostre aos estudantes que outros pares ordenados podem ser escolhidos, pois, desde que satisfaçam a equação, eles pertencem à mesma reta e a determinam.
Para desenvolver as habilidades (ê éfe zero oito ême ah um dois) e (ê éfe zero oito ême ah um três), aborde o fato de que a situação proposta para ser discutida oralmente é um exemplo de variação diretamente proporcional e pode ser generalizada por y = 3x, em que y é o salário em reais e x é o total de feijão, em quilograma. Incentive os estudantes a darem outros exemplos de situações em que as grandezas envolvidas são diretamente proporcionais e proponha que comparem os gráficos nessas situações, a fim de que percebam que são da fórma y = ax, em que a é um número real diferente de 0. O gráfico será sempre uma reta que passa pela origem.
Solicite que escolham, cada um, outro valor para substituir x na equação 2x + y = 5, obtenham o valor correspondente de y, localizem o ponto de coordenadas (x, y) no plano cartesiano e constatem que ele é um ponto da reta representada por essa equação.
Em seguida, explore a resolução de sistemas de equações do 1º grau, conduzindo os estudantes a perceberem que a solução do sistema é dada pelas coordenadas do ponto de intersecção das retas que representam as equações do sistema.
Solução de um sistema de equações do 1º grau com duas incógnitas
Agora, vamos considerar o sistema
Esquema. Sistema de equações. Primeira equação: x mais y igual a 3. Segunda equação: 2x mais y igual a 5.formado pelas equações x + y = 3 e 2x + y = 5.
Resolvendo-o por qualquer um dos métodos estudados, obtemos como solução o par ordenado (2, 1). Podemos obter graficamente essa solução. Para isso, é necessário traçar em um mesmo plano cartesiano as duas retas que representam as soluções das equações que formam o sistema.
Como, para traçar uma reta, basta conhecer dois de seus pontos, atribuímos dois valores a uma das incógnitas e calculamos os valores correspondentes da outra. Assim, obtemos pares ordenados que são coordenadas de dois dos pontos da reta.
x + y = 3
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
3 |
(0, 3) |
|
3 |
0 |
(3, 0) |
2x + y = 5
|
x |
y |
(x, y) |
|---|---|---|
|
0 |
5 |
(0, 5) |
|
2,5 |
0 |
(2,5; 0) |
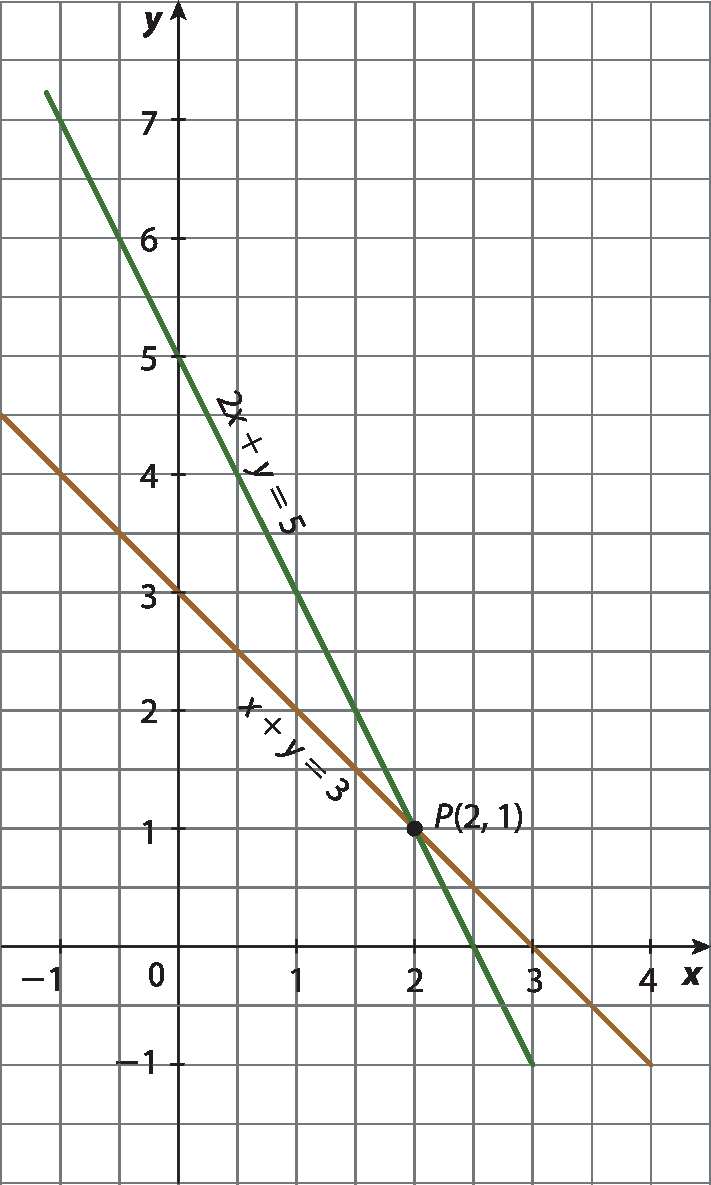
Observe que, nesse plano cartesiano, traçamos as retas que representam soluções das equações que formam o sistema. Como o ponto P, e só ele, pertence às duas retas, suas coordenadas satisfazem as duas equações; logo, o par ordenado (2, 1), intersecção das duas retas, é a solução do sistema.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
11 Usando papel quadriculado, represente graficamente as soluções de cada equação a seguir.
a) 3x + y = 8
b) x ‒ y = ‒3
c) 2x ‒ 3y = 4
d) 2x + y = ‒2
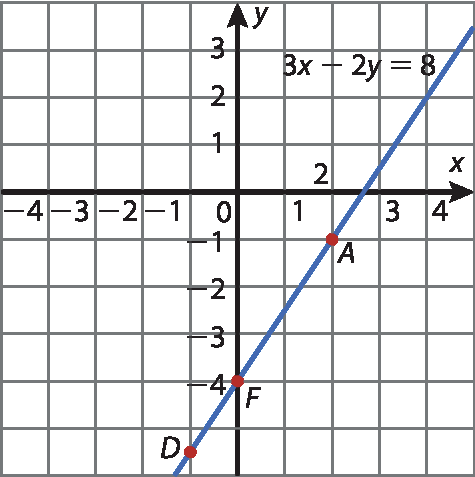
12 Dos pontos a(2, ‒1), B(‒2, 1),
C (menos um meio, 4) D(menos 1, menos onze meios)ê(0, 4) e F(0, ‒4), quais pertencem à reta cuja equação é 3x ‒ 2y = 8? Localize esses pontos em um plano cartesiano e trace essa reta.
13

Hora de criar – Crie um sistema de equações correspondente a cada representação gráfica. Depois, discuta com um colega qual par ordenado seria solução de cada sistema.
a)
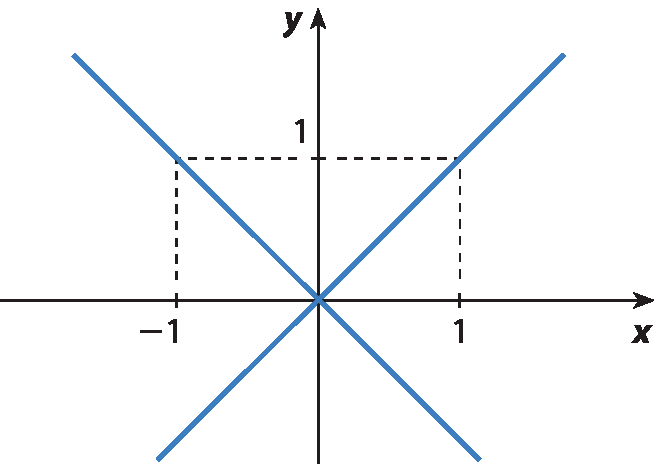
b)
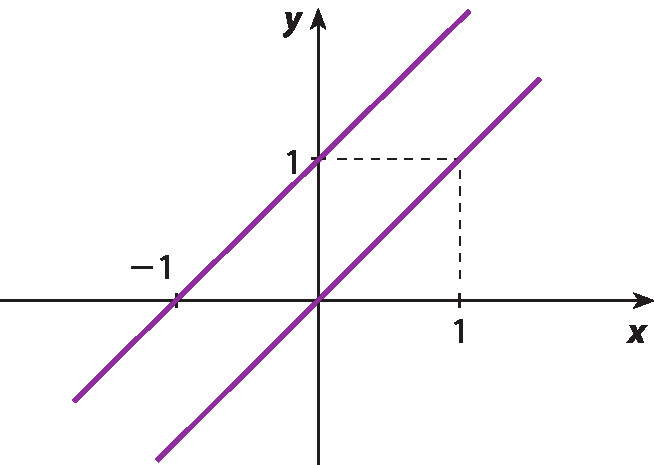
Respostas e comentários
11. Construção de gráficos.
12. Pontos a, D e F. Construção de gráfico.
13. a) Resposta possível:
Solução: (0, 0)
13. b) Resposta possível:
Não há par ordenado que seja solução do sistema.
Exercícios propostos
As resoluções dos exercícios 13 e 14 estão no início deste Manual, nas orientações específicas do capítulo 10.
Para o exercício 11, temos as seguintes representações gráficas.
a)
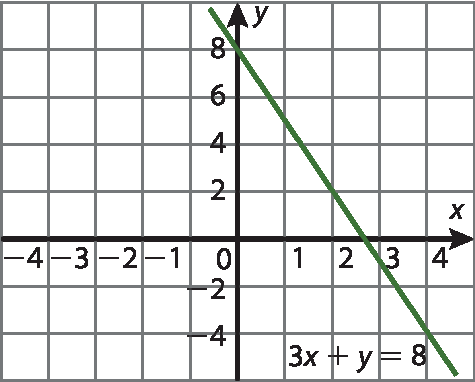
b)
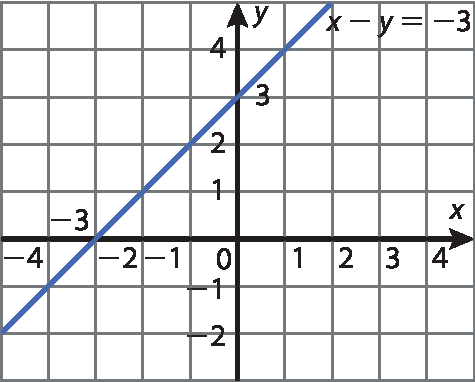
c)
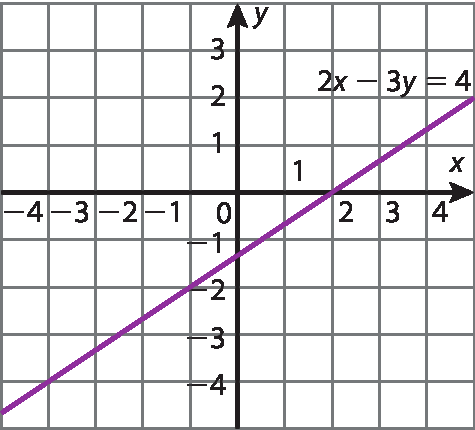
d)
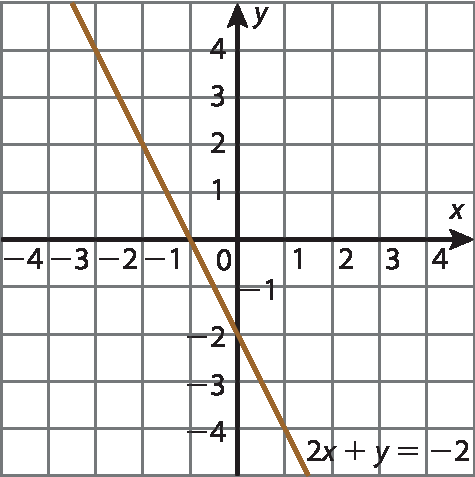
Para o exercício 12, a representação dos pontos e da reta no plano cartesiano é dada a seguir.
14 Usando uma folha de papel quadriculado, resolva graficamente os sistemas a seguir.
a)
Esquema. Sistema de equações. Primeira equação: x mais y igual a 7. Segunda equação: x menos y igual a menos 1.b)
Sistema de duas equações com duas incógnitas. A equação de cima é 2x mais y igual a 5 e a de baixo é x menos 2y igual a 5c)
Sistema de duas equações com duas incógnitas. A equação de cima é x mais 2y igual a 1 e a de baixo é 2x menos 3y igual a zerod)
Esquema. Sistema de equações. Primeira equação: x mais y igual a 0. Segunda equação: menos 3x mais y igual a 4.PARA SABER MAIS
Raiz quadrada ou diferença de dois quadrados?
Até agora trabalhamos com a resolução de equações do 1º grau. Porém, aplicando o que já estudamos sobre o conceito de raiz quadrada, podemos resolver algumas equações do 2º grau.
Vamos ajudar Luís a resolver o seu problema.
Luís quer montar uma granja em seu terreno de 90 métros quadrados. Mas a legislação do município exige uma medida de área mínima de 414 métros quadrados para essa atividade. Para ter exatamente essa medida de área mínima, o corretor de imóveis ofereceu a Luís um terreno quadrado, que faz divisa com o dele, cujo lado mede x metros. Luís quer saber qual é a metragem do terreno oferecido pelo corretor. Vamos calcular a medida x, em metro, do lado do terreno em formato quadrangular.
Considerando a figura a seguir como uma representação do novo terreno de Luís, temos:
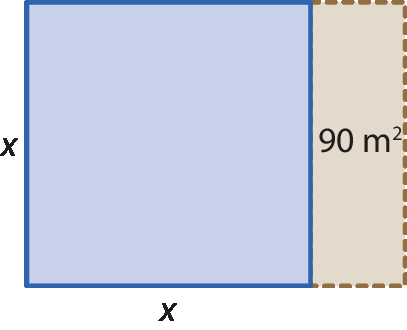
x 2 + 90 = 414
x 2 = 414 ‒ 90
x 2 = 324
x = ±
Raiz quadrada de 324x = ±18
Usando a calculadora:

Como a medida do lado deve ser um número positivo, o lado do terreno mede 18 métros.
Outra maneira de resolver a equação do problema de Luís é aplicando o produto notável “diferença de dois quadrados”.
x 2 + 90 = 414
x 2 + 90 ‒ 414 = 0
x 2 ‒ 324 = 0
x 2 ‒ 182 = 0
(x ‒ 18) ⋅ (x + 18) = 0 (Fatorando a diferença de dois quadrados)
Um produto é zero quando um de seus fatores for zero. Então:
x ‒ 18 = 0 ⇒ x = 18 ou x + 18 = 0 ⇒ x = ‒18
Como a medida do lado deve ser um número positivo, o lado do terreno mede 18 métros.
Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
Considere a figura e faça o que se pede.
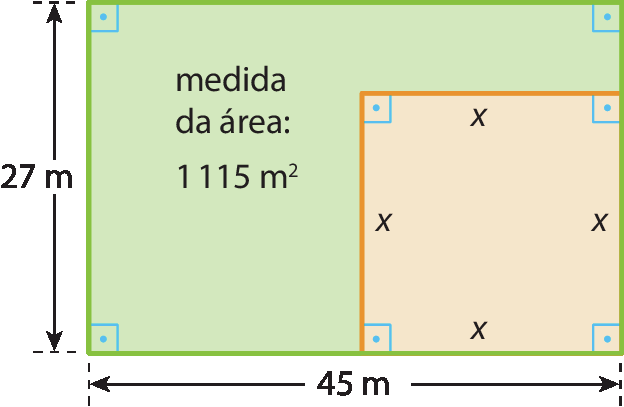
a) Escreva uma equação que relacione a medida da área da figura verde com a medida da área total.
b) Determine as raízes dessa equação.
c) Determine o valor de x, correspondente à medida do lado do quadrado.
Respostas e comentários
14. a) (3, 4)
14. b) (3, ‒1)
14. c) (‒3, 2)
14. d) (‒1, 1)
Para saber mais:
a) Resposta possível: .1115 = 45 ⋅ 27 ‒ x 2
b) x₁ = ‒10 e x₂ = 10
c) x = 10 métros
Para saber mais
A seção trabalha o tema “Raiz quadrada ou diferença de dois quadrados?” para resolver equações do 2º grau dos tipos ax 2 = b e x2 ‒ b2 = 0, que possibilitam utilizar a habilidade (ê éfe zero oito ême ah zero nove).
Reproduza os exemplos na lousa para que os estudantes acompanhem cada etapa. Explore também a figura.
A seguir, apresentamos a resolução dos itens propostos no Agora é com você!.
a) A figura composta da região verde com a região quadrada é um retângulo de dimensões que medem 27 métros por 45 métros. Desse modo, a medida da área dessa figura pode ser dada pela soma das medidas das áreas das regiões que a compõem. Afigura = Afigura verde + Aquadrado Afigura verde = Afigura ‒ Aquadrado Afigura verde = 27 · 45 ‒ x2 .1115 = 27 · 45 ‒ x2 .1115 = .1215 ‒ x2
b) Podemos resolver desta maneira: .1115 = .1215 ‒ x2 x 2 = .1215 ‒ .1115 x 2 = 100 x =
Raiz quadrada de 100
x = ±10 Logo, as raízes da equação são 10 ou ‒10. No entanto, considerando a situação proposta, x é a medida do lado de um quadrado, ou seja, x não pode assumir valores negativos.
c) Pelo exposto no item anterior, o lado do quadrado é 10 métros.
3. Classificação de um sistema de equações
Um sistema de equações, conforme a quantidade de soluções, pode ser classificado em determinado, impossível ou indeterminado.
Pela resolução gráfica, fica mais simples entender a classificação dada a um sistema. No entanto, nem sempre é possível chegar à solução exata, quando existe, do sistema por esse método.
Sistema determinado
Um sistema de equações do 1º grau com duas incógnitas é determinado quando apresenta uma única solução. Acompanhe um exemplo.
Vamos resolver o sistema:
Esquema. Resolução de um sistema de equações pelo método da adição. Primeira equação: x mais y igual a 7. Segunda equação: x menos y igual a 3.• Resolução algébrica
Pelo método da adição, temos:
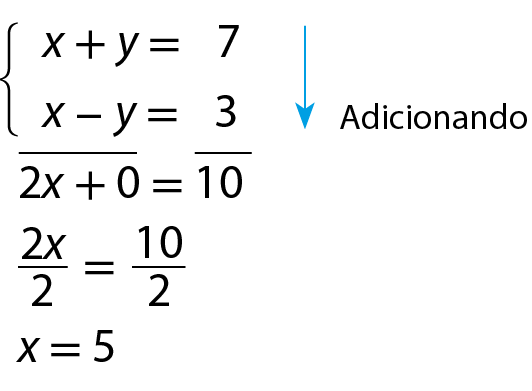
Substituindo x por 5 na equação x + y = 7, temos:
x + y = 7
5 + y = 7
y = 7 ‒ 5
y = 2
Logo, o par (5, 2) é a solução desse sistema.
• Resolução gráfica Vamos construir em um mesmo plano cartesiano as retas que representam as soluções gráficas de cada equação.
x + y = 7
|
x |
y |
(x, y) |
|---|---|---|
|
7 |
0 |
(7, 0) |
|
0 |
7 |
(0, 7) |
x + y = 3
|
x |
y |
(x, y) |
|---|---|---|
|
3 |
0 |
(3, 0) |
|
−2 |
−5 |
(−2, −5) |
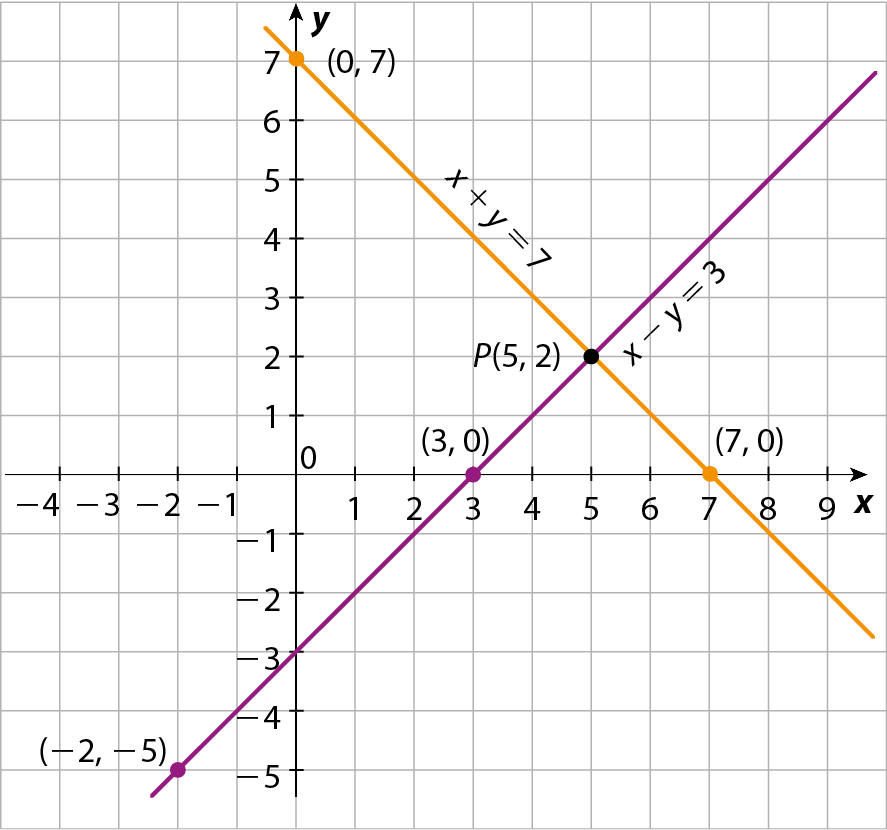
Observe que:
• as retas são concorrentes no ponto P ;
• as coordenadas do ponto P determinam o par ordenado (5, 2), que é a única solução do sistema.
Se um sistema de equações do 1º grau com duas incógnitas é determinado, então as retas que representam as soluções das duas equações no plano cartesiano são retas concorrentes.
Respostas e comentários
3. Classificação de um sistema de equações
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah zero seis, ê éfe zero oito ême ah zero sete e ê éfe zero oito ême ah zero oito.
Dando continuidade ao desenvolvimento das habilidades (EF08MA06), (EF08MA07) e (EF08MA08), neste tópico amplia-se o trabalho com a representação gráfica das soluções de equações do 1º grau no plano cartesiano (retas) e de sistemas de equações do 1º grau com duas incógnitas, agora com a classificação dos sistemas vinculada à posição relativa entre as duas retas: concorrentes, paralelas ou coincidentes.
Para tratar da classificação de um sistema de equações do 1º grau com duas incógnitas de acôrdo com o número de soluções desse sistema, ressalte que:
• Se o sistema tem uma única solução, ele é um sistema possível e determinado. Nesse caso, ele é associado a duas retas concorrentes cujas coordenadas do ponto de intersecção são a solução do sistema.
• Se o sistema não tem solução, o que significa que não há solução comum às duas equações do sistema, ele é um sistema impossível. Nesse caso, ele é associado a duas retas paralelas (que não têm pontos em comum).
• Se o sistema é possível, mas é indeterminado, ou seja, tem infinitas soluções, ele é um sistema possível e indeterminado. Nesse caso, o sistema é associado a duas retas coincidentes (que têm todos os pontos em comum).
Trabalhe o exemplo dado, que se refere a um sistema determinado. Peça aos estudantes que verifiquem que as coordenadas do ponto de intersecção P(5, 2) das duas retas concorrentes satisfazem as duas equações do sistema.
Sistema impossível
Um sistema de equações do 1º grau com duas incógnitas é impossível quando não existe par ordenado que seja solução das duas equações simultaneamente. Acompanhe um exemplo.
Vamos resolver o sistema:
Esquema. Sistema de equações. Primeira equação: 2x mais 6y igual a 10. Segunda equação: x mais 3y igual a menos 1.• Resolução algébrica Vamos resolver o sistema pelo método da substituição. Isolando x em x + 3y = ‒1, temos:
x = ‒1 ‒ 3y
Substituindo x por ‒1 ‒ 3y em 2x + 6y = 10, temos:
2(‒1 ‒ 3y) + 6y = 10
‒2 ‒ 6y + 6y = 10
‒6y + 6y = 10 + 2
0y = 12
Não existe valor de y de modo que 0y = 12. Portanto, não existe um par (x, y) que satisfaça as duas equações. Dizemos, então, que o sistema é impossível.
• Resolução gráfica Vamos construir, em um mesmo plano cartesiano, as retas que representam as soluções gráficas de cada equação.
2x + 6y = 10
|
x |
y |
(x, y) |
|---|---|---|
|
−1 |
2 |
(−1, 2) |
|
2 |
1 |
(2, 1) |
x + 3y = ‒1
|
x |
y |
(x, y) |
|---|---|---|
|
−1 |
0 |
(−1, 0) |
|
2 |
−1 |
(2, −1) |
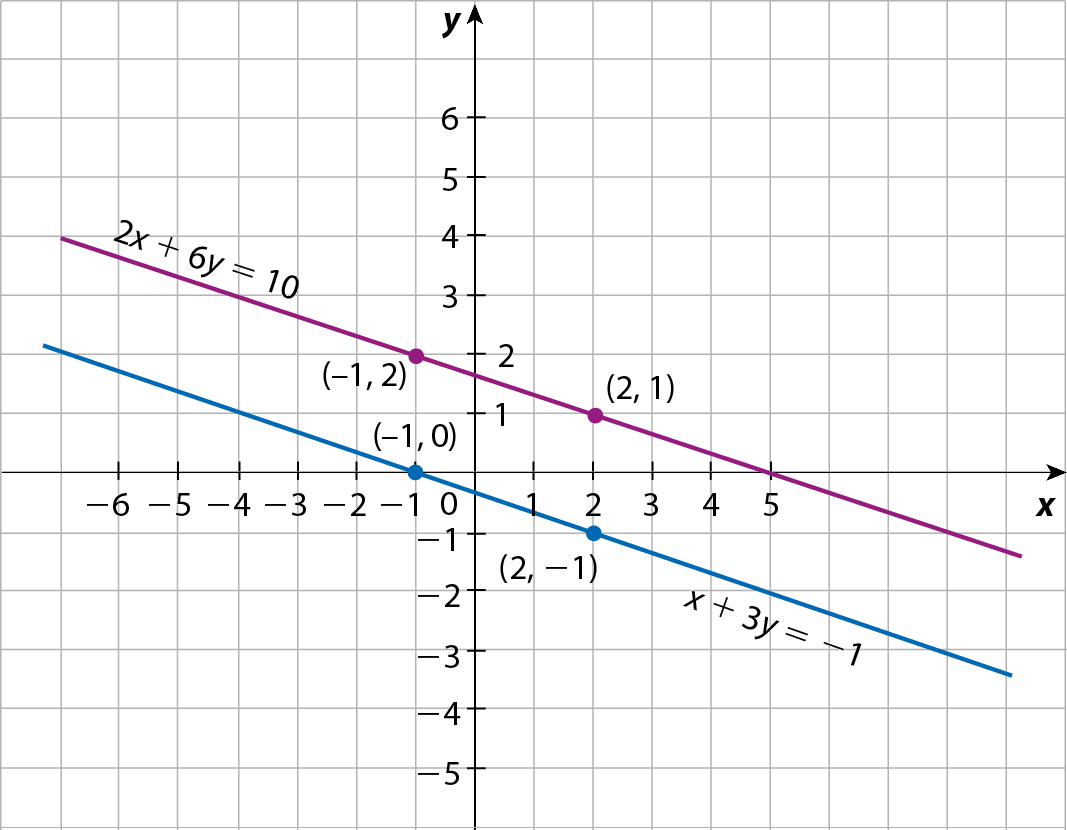
Observe que:
• as retas são distintas e paralelas;
• não existe par ordenado que seja solução do sistema.
Se um sistema de equações do 1º grau com duas incógnitas é impossível, então as retas que representam as soluções das duas equações no plano cartesiano são retas paralelas.
Respostas e comentários
Sistema impossível
Nesta página, tratamos do sistema impossível. Isso significa que não há solução comum entre as duas equações que o compõem; portanto, não pode haver ponto comum às duas retas, ou seja, as retas que retratam essa situação são retas paralelas.
Ressalte à turma que, na resolução algébrica de um sistema que não tem solução, ocorrerá alguma igualdade falsa, como é o caso de 0y = 12, o que gera 0 = 12 (falso).
Para ampliar, proponha aos estudantes que, em duplas, criem sistemas impossíveis. Depois, cada dupla apresenta para a turma o seu sistema e sua resolução na lousa.
Peça aos estudantes que verifiquem, no sistema usado como exemplo, se há algum número multiplicando o 1º membro (a₁x + b₁y) de uma das equações que resulta no 1º membro (a₂x + b₂y) da outra equação. E, depois, se há um número que, multiplicado pelo 2º membro da 1ª equação (c₁), resulta no 2º membro da outra equação (c₂). Por fim, peça a eles que verifiquem se esses fatores obtidos são iguais. Espera-se que concluam que não, não são iguais. Destacamos que, para realizar essas comparações, é conveniente que as equações estejam na fórma ax + by = c, com a, b e c números reais.
Sistema indeterminado
Um sistema de equações do 1º grau com duas incógnitas é indeterminado quando tem infinitas soluções.

Como exemplo, vamos resolver o sistema:
Sistema de duas equações com duas incógnitas. A equação de cima é 2x mais 6y igual a 8 e a de baixo é x mais 3y igual a 4• Resolução algébrica Aplicando o método da substituição, isolamos x em x + 3y = 4. Assim: x = 4 ‒ 3y Substituindo x por 4 ‒ 3y em 2x + 6y = 8, temos:
2 ⋅ (4 ‒ 3y) + 6y = 8
8 ‒ 6y + 6y = 8
‒6y + 6y = 8 ‒ 8
0y = 0
Como qualquer número multiplicado por zero é igual a zero, existem infinitos valores de y, de modo que 0y = 0. O sistema apresenta infinitas soluções. A seguir, são apresentados alguns dos infinitos pares (x, y) que verificam as duas equações do sistema dado.
Em x = 4 ‒ 3y, atribuindo a y, por exemplo, 1, 2 e 3, temos, para x, os valores 1, ‒2 e ‒5.
a) (1, 1)
Na primeira equação, temos: 2x + 6y = 8 2 ⋅ (1) + 6 ⋅ (1) = 8 2 + 6 = 8 8 = 8 (verdadeiro)
Na segunda equação, temos: x + 3y = 4 1 + 3 ⋅ (1) = 4 1 + 3 = 4 4 = 4 (verdadeiro)
b) (‒2, 2) Na primeira equação, temos: 2x + 6y = 8 2 ⋅ (‒2) + 6 ⋅ (2) = 8 ‒4 + 12 = 8 8 = 8 (verdadeiro) Na segunda equação, temos: x + 3y = 4 (‒2) + 3 ⋅ (2) = 4 ‒2 + 6 = 4 4 = 4 (verdadeiro)
c) (‒5, 3)
Na primeira equação, temos: 2x + 6y = 8 2 ⋅ (‒5) + 6 ⋅ (3) = 8 ‒10 + 18 = 8 8 = 8 (verdadeiro) Na segunda equação, temos: x + 3y = 4 (‒5) + 3 ⋅ (3) = 4 ‒5 + 9 = 4 4 = 4 (verdadeiro)
Os pares (1, 1), (‒2, 2) e (‒5, 3) são algumas das infinitas soluções do sistema.
Respostas e comentários
Sistema indeterminado
Algebricamente, ao resolver um sistema indeterminado, aparecerá uma igualdade sempre verdadeira, independentemente dos valores atribuídos à incógnita, como é o caso de 0y = 0, o que gera 0 = 0 (sempre verdadeira, qualquer que seja y).
Nesses casos, a solução é dada de maneira genérica por um par ordenado que depende de uma das incógnitas, que será uma variável. Dependendo dos valores atribuídos a essa variável, obtemos soluções distintas para o sistema.
Comente com a turma que a representação gráfica de um sistema possibilita sua resolução graficamente, assim como a sua classificação em sistema determinado, sistema indeterminado ou sistema impossível.
Peça aos estudantes que verifiquem, no sistema usado como exemplo, se há um número que, multiplicado pelo 1º membro (a₁x + b₁y) de uma das equações, resulta no 1º membro (a₂x + b₂y) da outra equação. E, depois, se há um número que, multiplicado pelo 2º membro da 1ª equação (c₁), resulta no 2º membro da outra equação (c₂). Por fim, peça a eles que verifiquem se esses fatores obtidos são iguais. Espera-se que concluam que sim, são iguais.
• Resolução gráfica
2x + 6y = 8
|
x |
y |
(x, y) |
|---|---|---|
|
1 |
1 |
(1, 1) |
|
4 |
0 |
(4, 0) |
x + 3y = 4
|
x |
y |
(x, y) |
|---|---|---|
|
−2 |
2 |
(−2, 2) |
|
7 |
−1 |
(7, −1) |
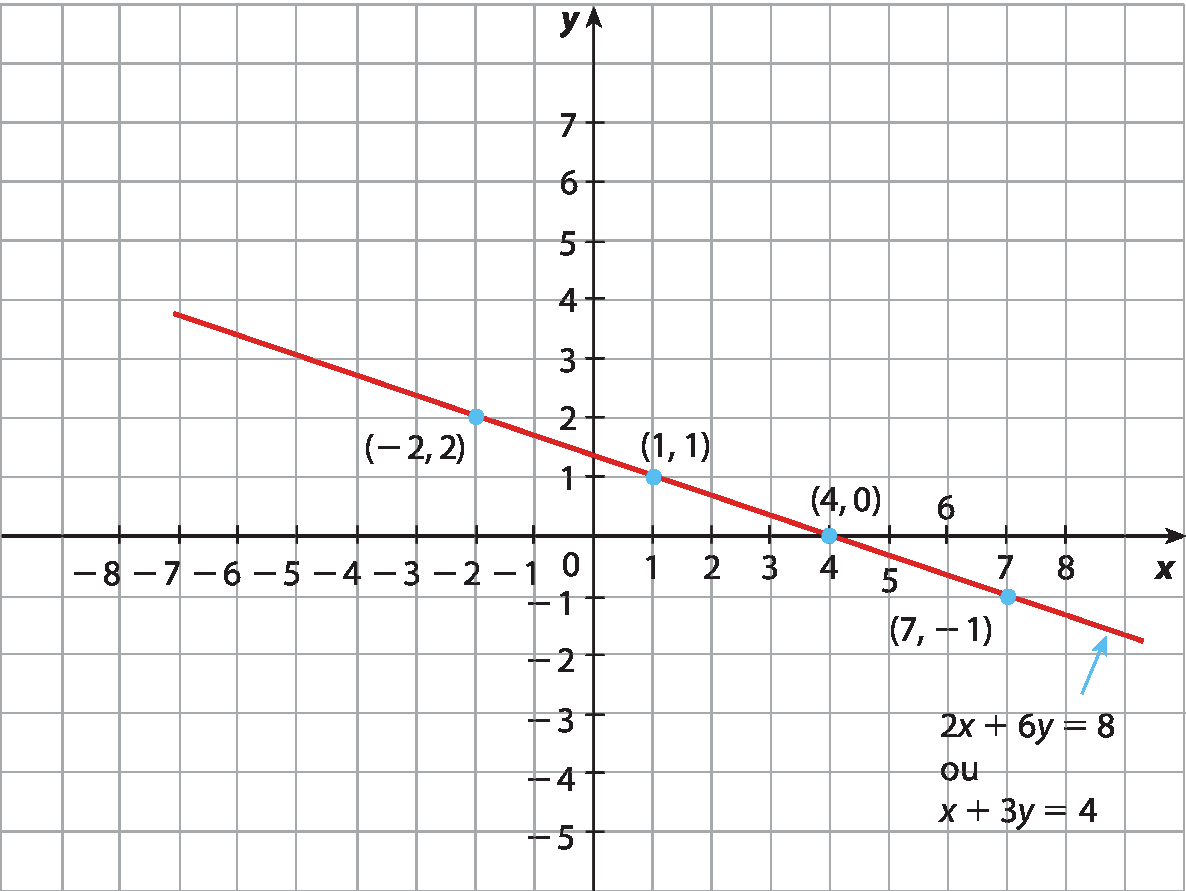
Observe que:
• as retas são coincidentes;
• existem infinitos pontos cujas coordenadas são soluções do sistema.
Se um sistema de equações do 1º grau com duas incógnitas é indeterminado, as retas que representam as soluções das duas equações no plano cartesiano são retas coincidentes. Resumindo:
Sistema determinado: tem uma única solução e as retas que representam as soluções das equações do sistema são concorrentes.
Sistema impossível: não tem solução e as retas que representam as soluções das equações do sistema são paralelas.
Sistema indeterminado: tem infinitas soluções e as retas que representam as soluções das equações do sistema são coincidentes.
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Problemas com sistemas de equações
Duração: 5:53min. Página: 227.
>> [Locutor] Problemas com sistemas de equações
>> [Narrador] Numa tarde ensolarada, as amigas Bruna e Mirela conversam em frente à escola, enquanto esperam a mãe de Bruna vir buscá-las.
Som de pessoas falando ao fundo.
>> [Mirela] Bruna, ontem fui à nova lanchonete do meu bairro. Comprei um sanduíche e um suco de laranja. Ou melhor, minha mãe comprou. [Risos]
>> [Bruna] E você comeu sanduíche de quê?
>> [Mirela] De queijo branco com tomate. Estava delicioso!
>> [Bruna] Hum... devia estar mesmo! E quanto custou o sanduíche?
>> [Mirela] Dez reais! Bem... o suco e o sanduíche custaram 10 reais. Não lembro quanto custou cada um.
>> [Bruna] Vamos pensar. Será que a gente consegue descobrir quanto custou cada um só com essa informação? Já temos uma pista: sabemos que o sanduíche e o suco custaram, juntos, 10 reais.
>> [Mirela] Se a gente sabe o preço total e temos apenas dois produtos, é só calcular 10 dividido por 2. É fácil! Cinco reais cada um. Custou 5 reais o sanduíche e 5 reais o suco. [Tom animado] Matei a charada!
>> [Bruna] [Tom de dúvida] Acho que desse modo não dá para saber o valor certo, Mirela! [Tom de questionamento] Como você pode ter certeza de que o sanduíche e o suco têm o mesmo preço? Se o sanduíche custasse 9 reais e o suco, 1 real, o total também seria 10 reais.
>> [Mirela] [Tom de confirmação do raciocínio] É mesmo... E se o sanduíche custasse 7 reais e o suco, 3 reais, o total também seria 10 reais!
>> [Bruna] [Tom explicativo] Pois é! Se a gente só tiver a informação do valor total que foi gasto, não conseguiremos calcular o valor individual de cada produto consumido. É como a professora de Matemática disse na aula: temos duas incógnitas, o valor do sanduíche, que pode ser x, e o valor do suco, que pode ser y, mas temos apenas uma informação, ou melhor, equação. Precisamos de pelo menos mais uma equação para descobrir o valor das duas incógnitas. Com uma apenas, não vai dar para resolver o problema!
>> [Mirela] Dez reais menos o preço do suco é igual ao preço do sanduíche. [Riso]
>> [Bruna] Verdade, mas, ainda assim, todos os valores que citamos continuam servindo como resposta. Não vamos deixar o preço correto se tivermos várias respostas válidas. Há diversos valores que, somados, resultam 10.
>> [Mirela] Seria, neste caso, um sistema de equações possível e indeterminado, justamente porque existem várias soluções possíveis. [Tom de desafio] Precisamos de mais pistas!
>> [Bruna] [Tom de elogio] Acertou de novo! Você se lembra de mais alguma informação importante para a gente calcular os valores de x e de y? Tente se lembrar de alguma informação que nos ajude a calcular com certeza o valor do suco e do sanduíche. Por enquanto, só sabemos que o valor do sanduíche x, somado ao valor do suco y , é igual a 10 reais.
>> [Mirela] [Tom animado] Ah, lembrei de uma coisa importantíssima! Minha mãe comentou que o sanduíche era somente 2 reais mais caro que o suco. É isso mesmo! O valor do sanduíche era somente 2 reais mais caro.
>> [Bruna] [Tom de descoberta] Opa, essa parece ser uma pista valiosa! [Tom explicativo] Vejamos: a gente já sabia que o valor do sanduíche x mais o valor do suco y era igual a 10 reais. Agora, sabemos que o valor do sanduíche x é igual ao valor do suco y mais 2 reais. Ou seja, x é igual a y mais 2 reais. Essa seria a segunda equação do nosso sistema, concorda?
>> [Mirela] Sim! E agora a gente consegue calcular o preço de cada um.
>> [Bruna] [Tom de confirmação de raciocínio] Agora sim! [Tom explicativo] Vamos ver: quando só sabíamos que a soma dos dois itens era 10 reais, tínhamos várias alternativas para o preço de cada um. Mas agora, com essa nova pista, sabemos que não pode ser qualquer um daqueles valores que achamos antes.
>> [Mirela] Agora, temos duas equações e duas incógnitas.
>> [Bruna] [Tom de confirmação de raciocínio] Exatamente! Qual é o preço de cada um, se o sanduíche é 2 reais mais caro que o suco e o preço dos dois juntos é 10 reais? Esse seria o nosso sistema de equações.
>> [Mirela] [Tom pensativo] Vamos ver... [Tom explicativo] Resolvendo o sistema, temos que x é igual a 6 e y é igual a 4. Portanto, a resposta é 6 e 4: 6 mais 4 é igual a 10, e 6 é 2 a mais que 4. Então, os valores 6 e 4 atendem às duas equações que temos, certo?
>> [Bruna] [Tom de confirmação de raciocínio] Certíssimo! Os únicos valores que satisfazem as duas equações ao mesmo tempo são 6 e 4. Então, o sanduíche custa 6 reais e o suco de laranja custa 4 reais. Essa segunda equação nos permitiu ter um sistema de equações possível e determinado, ou seja, um sistema de equações que possui apenas uma única resposta correta. Nesse caso, o par de valores 6 e 4 é a única resposta possível.
>> [Mirela] [Tom contente] Agora, não temos mais dúvidas! O sanduíche de queijo branco custa 6 reais e o suco de laranja custa 4 reais!
>> [Bruna] E descobrimos isso usando os sistemas de equações aprendidos hoje na aula de Matemática! [Riso] Lembrando que, se nosso sistema não tivesse nenhuma resposta que satisfizesse as duas equações, teríamos um sistema impossível.
>> [Mirela] [Tom animado] Muito legal isso! [Tom de questionamento] Bem, mas agora estou com outro problema, Bruna. Será que, com toda a sua esperteza, você consegue me ajudar a resolvê-lo?
>> [Bruna] [Tom animado] Claro, ajudo sim!
>> [Mirela] Essa conversa sobre sanduíche de queijo me deu uma fome gigantesca! [Risos]
>> [Bruna] Estou com fome também! [Risos, tom empolgado] Vamos juntas à lanchonete comer um maravilhoso sanduíche de queijo branco?
Vinheta.
Créditos
Todos os áudios inseridos neste conteúdo são da Free Sound.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
15 Resolva graficamente os sistemas a seguir, usando uma folha de papel quadriculado. Em seguida, classifique-os em determinado, indeterminado ou impossível.
a)
Esquema. Sistema de equações. Primeira equação: x mais y igual a 7. Segunda equação: x menos y igual a 1.b)
Esquema. Sistema de equações. Primeira equação: x mais 2y igual a 3. Segunda equação: 2x mais 4y igual a 8.c)
Esquema. Sistema de equações. Primeira equação: 2x mais y igual a 0. Segunda equação: 3x mais y igual a menos 2.d)
Esquema. Sistema de equações. Primeira equação: x mais y igual a 3. Segunda equação: 2x mais 2y igual a 6.e)
Esquema. Sistema de equações. Primeira equação: x menos y igual a 3. Segunda equação: 2x menos 2y igual a menos 4.f)
Esquema. Sistema de equações. Primeira equação: 2x mais y igual a 5. Segunda equação: 4x mais 2y igual a 10.16 Acompanhe o diálogo entre João e Pedro.

Quantas figurinhas tem cada um?
Respostas e comentários
15. a) (4, 3); sistema determinado.
15. b) Sistema impossível.
15. c) (‒2, 4); sistema determinado.
15. d) Sistema indeterminado.
15. e) Sistema impossível.
15. f) Sistema indeterminado.
16. Pedro tem trezentas figurinhas; João, 420.
Exercícios propostos
A resolução do exercício 15 está no início deste Manual, nas orientações específicas do capítulo 10.
Para o exercício 16, apresentamos a seguir uma possível resolução.
Considerando a quantidade de figurinhas de Pedro x e a quantidade de figurinhas de João y, pela informação de João, temos:
y mais um quinto vezes x, é igual a 2 vezes abre parênteses x menos um quinto vezes x fecha parênteses
Pela informação de Pedro, temos:
y ‒ 60 = x + 60
Assim, obtemos o seguinte sistema:
⇒
⇒
Símbolo de implicação para outro sistema de equações. Primeira equação: 5y menos 7x igual a 0. Segunda equação: y menos x igual a 120.Multiplicando a equação y ‒ x = 120 por ‒7, temos:
Então:
‒2y = ‒840
fração; numerador: menos 2y, denominador: menos 2, fim da fração; é igual a fração; numerador: menos 840, denominador: menos 2
y = 420
Substituindo y por 420 em y ‒ x = 120, obtemos:
420 ‒ x = 120
420 ‒ 120 = x
x = 300
Portanto, Pedro tem trezentas figurinhas e João tem quatrocentas e vinte figurinhas.
Solicite aos estudantes que validem a solução do problema substituindo, nas falas de João e de Pedro, os valores obtidos e efetuando os cálculos descritos.
TRABALHANDO A INFORMAÇÃO
Censo Demográfico
A primeira contagem da população brasileira foi realizada em 1872, ainda durante o Império, mas foi a partir de 1890, já sob a República, que os censos se tornaram decenais. O Brasil mantém um excelente retrospecto dos censos regulares e inovadores; foi, por exemplo, o primeiro país a incluir o tema fecundidade e o único da América Latina a colhêr informações sobre renda.
Os Censos Demográficos são a única fórma de informação sobre a situação de vida da população em cada um dos municípios e localidades do País. As demais pesquisas domiciliares são levantamentos por amostragem, que não são representativas para todos esses níveis geográficos.
Fonte: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. í bê gê É – População: censo demográfico. Comitê de Estatísticas Sociais. Rio de Janeiro: Instituto Brasileiro de Geografia e Estatística, [2021?]. Disponível em: https://oeds.link/HQcmp1. Acesso em: 13 julho 2022.
Diferentes características da população são avaliadas no Censo Demográfico, por exemplo, questões relacionas a saúde, moradia, trabalho, educação e raça.
A cada Censo, novas características populacionais podem ser acrescentadas, por exemplo, até o Censo 2010, a população que se considera quilombola não era identificada, mas perguntas sobre isso passaram a ser foco das discussões e devem ser incluídas nos próximos censos. O Instituto Brasileiro de Geografia e Estatística (í bê gê É) não tem uma estimativa dessa população, mas calcula que o Brasil tenha 5.novecentas e setenta e duas localidades quilombolas, divididas em .1672 municípios brasileiros.

Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Faça uma pesquisa sobre o Censo Demográfico realizado no Brasil pelo í bê gê É e responda às questões a seguir.
a) Qual é a diferença entre pesquisa censitária e pesquisa amostral?
b) Qual é a importância da realização de um Censo Demográfico para a população de um país?
c) Qual foi o último Censo realizado? Selecione alguns dos resultados dessa pesquisa e apresente aos colegas.
2 Qual é a origem das comunidades quilombolas? Qual é a característica atual da população dessas comunidades?
3 Forme um grupo com cinco ou mais colegas para fazer uma pesquisa. Escolham um tema a ser pesquisado. Essa pesquisa deverá ser realizada de fórma censitária com os colegas de turma. Organizem as informações coletadas em tabelas e em gráficos. Façam uma análise dos resultados e arpesentem-nos à turma.
Respostas e comentários
1. a) Na pesquisa censitária, consideramos todos os elementos de uma população, já na amostral, consideramos uma parcela representativa da população.
1. b) Identificar as características da população, produzindo informações para a definição de políticas públicas, em qualquer nível governamental, e de investimentos, pela iniciativa privada.
1. c) A resposta depende do momento em que a atividade for realizada.
2. Segundo a Secretaria Especial do Desenvolvimento Social, do govêrno federal, as comunidades quilombolas são grupos com identidade cultural própria e se formaram por meio de um processo histórico que começou nos tempos da escravidão no Brasil. Elas simbolizam a resistência a diferentes fórmas de dominação. Essas comunidades mantêm forte ligação com sua história e trajetória, preservando costumes e cultura trazidos por seus antepassados.
Sobre as características atuais dessas comunidades, solicite aos estudantes que pesquisem em sites governamentais para obter as informações e compartilhar com os colegas.
3. Resposta pessoal.
Trabalhando a informação
Habilidades da Bê êne cê cê: ê éfe zero oito ême ah dois três e ê éfe zero oito ême ah dois seis.
Esta seção apresenta o Censo Demográfico e discute sua importância, distinguindo pesquisas censitárias de pesquisas por amostragem.
Ao propor aos estudantes que pesquisem a diferença entre pesquisa censitária e pesquisa amostral, a atividade 1 do Agora quem trabalha é você! favorece o desenvolvimento da habilidade (EF08MA26). Peça aos estudantes que citem situações em que as pesquisas amostrais são mais adequadas que as pesquisas censitárias.
Na atividade 3, ao organizar as informações coletadas em tabelas e gráficos, os estudantes devem avaliar a adequação dos diferentes tipos de gráfico que conhecem para representar o conjunto de dados de sua pesquisa, desenvolvendo, assim, a habilidade (EF08MA23).
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Cristina retirou R$ 700,00setecentos reais de um banco, em 10 notas, sendo algumas de R$ 100,00cem reais e outras de R$ 50,00cinquenta reais. Quantas notas de R$ 50,00cinquenta reais e de R$ 100,00cem reais Cristina recebeu?
2 Leia o que Luís diz. Depois, descubra quantos jovens estavam reunidos.

3 O perímetro do trapézio a seguir mede 39 centímetros. Sabe-se que y é igual a 60% de x.
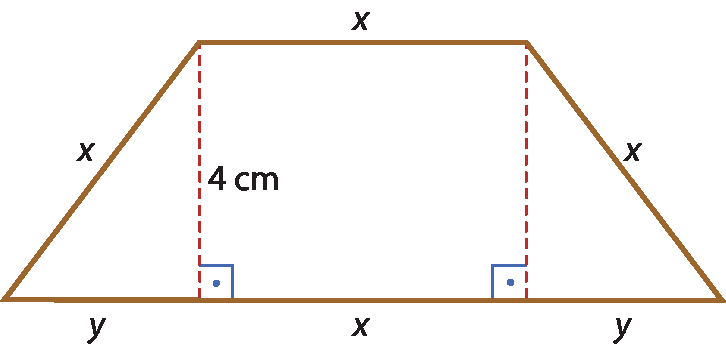
Determine as medidas x e y, em centímetro.
4 Faça o que se pede.
a) Represente, no plano cartesiano, as soluções das seguintes equações:
• x ‒ 2y = 3
• 2x ‒ 4y = 6
• 3x ‒ 6y = 9
• 4x ‒ 8y = 12
b) Qual é a posição relativa das retas que representam as soluções dessas equações?
c) Qual é a relação entre os coeficientes da segunda equação e os da primeira equação? E a relação entre os coeficientes da terceira equação e os da primeira equação? E a relação entre os coeficientes da quarta equação e os da primeira equação?
5 Usando uma folha de papel quadriculado, resolva graficamente os sistemas e classifique-os como determinado, indeterminado ou impossível.
a)
Esquema. Sistema de equações. Primeira equação: x menos y igual a 2. Segunda equação: x mais 2y igual a 17.b)
Esquema. Sistema de equações. Primeira equação: 2x mais y igual a menos 9. Segunda equação: x mais 6y igual a 1.c)
Esquema. Sistema de equações. Primeira equação: x mais y igual a 4. Segunda equação: 2x mais 2y igual a menos 4.d)
Esquema. Sistema de equações. Primeira equação: 2x menos y igual a 2. Segunda equação: 6x menos 3y igual a 6.6 Sabendo que o par (x, y) é a solução do sistema a seguir, determine x : y.
7 (unirrio-Rio de Janeiro) Em um escritório de advocacia, trabalham apenas dois advogados e uma secretária. Como Doutor André e Doutor Carlos sempre advogam em causas diferentes, a secretária Cláudia coloca 1 grampo em cada processo de Doutor André e 2 grampos em cada processo de Doutor Carlos, para diferenciá-los facilmente no arquivo. Sabendo-se que ao todo são 78 processos, nos quais foram usados 110 grampos, podemos concluir que o número de processos de Doutor Carlos é igual a:
a) 64.
b) 46.
c) 40.
d) 32.
e) 28.
8 Eduarda estava em uma das pontas de um viaduto, que mede 84 metros de comprimento. Na outra ponta estava seu irmão Carlos. Eles caminharam até se encontrar. A cada 3 metros percorridos por Eduarda, Carlos percorreu 4 metros. A quantos metros do centro do viaduto eles se encontraram?
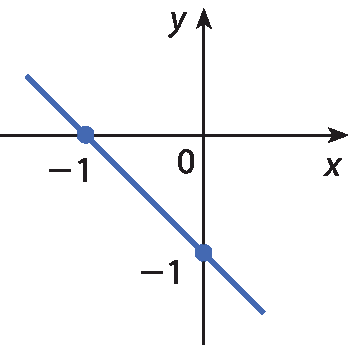
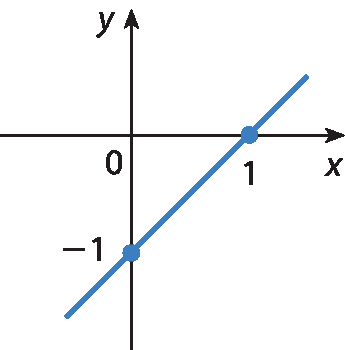
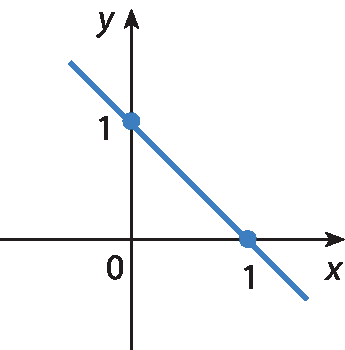
9 Que representação gráfica apresenta as soluções da equação x ‒ y = 1?
a)
b)
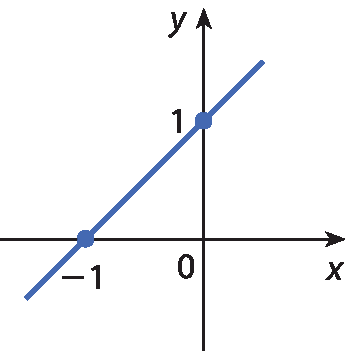
c)
d)
Respostas e comentários
1. Seis notas de R$ 50,00cinquenta reais e quatro notas de R$ 100,00cem reais.
2. 13 jovens.
3. x = 7,5 centímetros e y = 4,5 centímetros.
4. a) Construção de gráficos.
4. b) Coincidentes.
4. c) Dobro; triplo; quádruplo.
5. a) (7, 5); sistema determinado.
5. b) (‒5, 1); sistema determinado.
5. c) Sistema impossível.
5. d) Sistema indeterminado.
6. x : y = 2
7. Alternativa d.
8. 6 métros
9. Alternativa c.
Exercícios complementares
As resoluções dos exercícios 1 e 2 e dos exercícios 4 a 8 estão no início deste Manual, nas orientações específicas do capítulo 10.
Neste bloco, os estudantes têm a oportunidade de revisitar os principais conceitos trabalhados no capítulo.
No exercício 3, eles revisitam também os conhecimentos que já construíram acerca de trapézios, articulando as Unidades Temáticas Álgebra, Números, Geometria e Grandezas e medidas. Uma possível resolução é apresentada a seguir.
A medida do perímetro é 39 centímetros.
y é igual a 60% de x, ou seja, y = 0,6x.
Da figura, temos:
4x + 2y = 39
Assim, obtemos o sistema:
Os estudantes podem resolver esse sistema pelo método que desejarem. Nesse caso, como já temos a incógnita y isolada na primeira equação, o método da substituição pode ser o mais conveniente.
Assim, vamos substituir y por 0,6x na segunda equação:
4x + 2y = 39
4x + 2 · 0,6x = 39
5,2x = 39
x = 7,5
Voltando à equação y = 0,6x, obtemos:
y = 0,6 · 7,5 = 4,5
Logo, x = 7,5 centímetros e y = 4,5 centímetros.
No exercício 9, espera-se que os estudantes percebam que um modo de resolver é tomar dois pontos de cada reta e verificar se suas coordenadas satisfazem a equação. Outro modo é construir a representação gráfica da equação x ‒ y = 1 e comparar com as alternativas.
Quando x = 0, temos ‒y = 1 e, portanto, y = ‒1; logo, o ponto (0, ‒1) pertence à reta.
Além disso, quando y = 0, temos que x = 1; logo, o ponto (1, 0) pertence à reta.
Dessa maneira, a reta dada na alternativa c é a representação gráfica das soluções da equação.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Resolva o sistema de equações a seguir pelo método de substituição.
Qual é a solução desse sistema de equações?
a) x = 42, y = 12
b) x = 35, y = 10
c) x = 40, y = 10
d) x = 45, y = 15
2 Para fazer um doce, Jorge comprou embalagens de 100 gramas de coco ralado, a R$ 4,00quatro reais cada uma, e caixas com 200 gramas de chocolate em pó, a R$ 5,00 cinco reaiscada. Ele gastou R$ 54,00cinquenta e quatro reais e comprou .1800 gramas desses produtos. Quantas unidades Jorge comprou de cada produto?
a) duas embalagens de coco ralado e 10 caixas de chocolate em pó.
b) 6 embalagens de coco ralado e 6 caixas de chocolate em pó.
c) 5 embalagens de coco ralado e 7 caixas de chocolate em pó.
d) 10 embalagens de coco ralado e duas caixas de chocolate em pó.
3 Joana recebeu uma premiação de R$ 9.450,00nove mil quatrocentos e cinquenta reais em 120 cédulas de 50 e 100 reais. Quantas cédulas de cada valor Joana recebeu?
a) 59 cédulas de 50 reais e 65 de 100 reais.
b) setenta e uma cédulas de 50 reais e 59 de 100 reais.
c) cinquenta e uma cédulas de 50 reais e 69 de 100 reais.
d) quarenta e uma cédulas de 50 reais e 74 de 100 reais.
4 Entre as alternativas a seguir, qual não contém uma solução para o sistema apresentado?
a) (7, 1) e (3, ‒1)
b) (5, 0) e (9, 2)
c) (0, ‒2,5) e (11, 3)
d) (‒4, ‒3) e (‒3, ‒1)
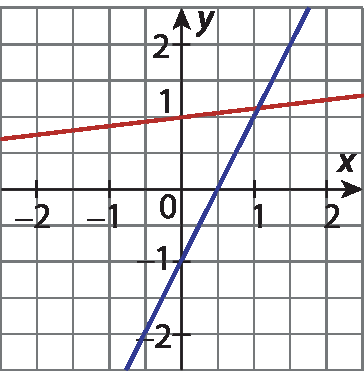
5 Os gráficos apresentados não representam a solução de qual equação?
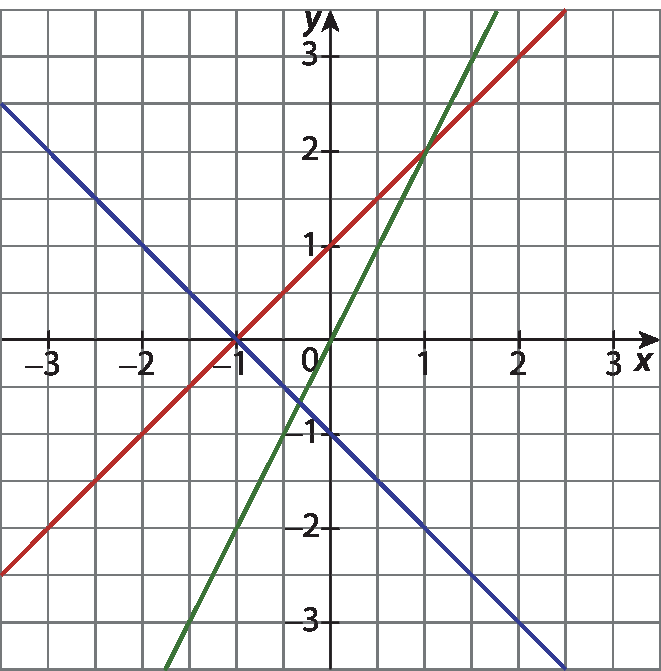
a) y = x + 1
b) y = ‒2x ‒ 2
c) y = ‒x ‒ 1
d) y = 2x
6 Determine qual dos gráficos a seguir representa a solução do sistema:
a)
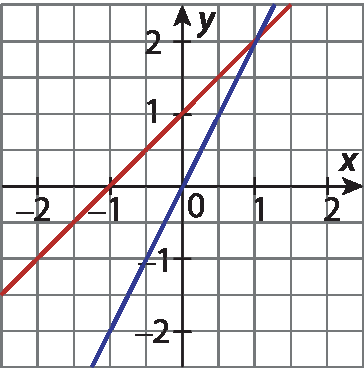
b)
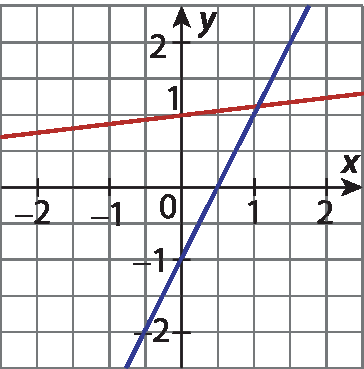
c)
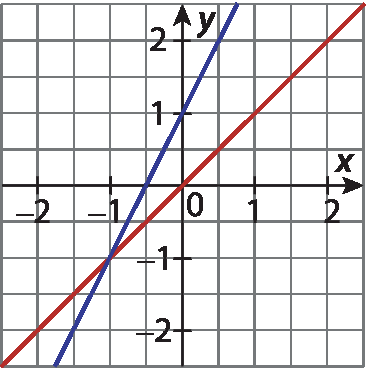
d)
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Que métodos de resolução de sistemas de equações você aprendeu neste capítulo?
b) Qual é a solução gráfica obtida de uma equação de 1º grau?
c) Para obter a solução gráfica de uma equação de 1º grau, pelo menos quantos pares ordenados devem ser obtidos?
d) Qual é a solução gráfica obtida na resolução de um sistema de equações de 1º grau?
e) Quais são as classificações possíveis de um sistema e como são suas soluções?
Respostas e comentários
1. Alternativa d.
2. Alternativa b.
3. Alternativa c.
4. Alternativa d.
5. Alternativa b.
6. Alternativa a.
Organizando:
a) Método da substituição e da adição.
b) É uma reta.
c) 2 pares ordenados.
d) O par ordenado que é a intersecção das duas retas que são soluções das equações que o sistema contém.
e) Determinado: tem uma única solução; impossível: não existe par ordenado que seja solução; indeterminado: apresenta infinitas soluções.
Verificando
Nesta seção são propostos testes que abordam os conteúdos apresentados ao longo deste capítulo, sendo uma oportunidade para os estudantes validarem o entendimento do conteúdo estudado. Caso eles apresentem dúvidas em relação a algum dos testes propostos, oriente-os a rever os conceitos apresentados no capítulo; assim, também desenvolverão a autonomia no estudo.
As resoluções dos testes 1 a 6 estão no início deste Manual, nas orientações específicas do capítulo 10.
Organizando
No item a, dos métodos de resolução de sistemas de equações do 1º grau com duas incógnitas, foram trabalhados o método da substituição e o método da adição.
No item b, a solução gráfica de uma equação do 1º grau com duas incógnitas é uma “reta” representada no plano cartesiano.
No item c, para encontrar a solução gráfica de uma equação do 1º grau com duas incógnitas basta obter as coordenadas de dois de seus pontos, localizá-los no plano cartesiano e traçar a reta que os contenha.
No item d, a solução gráfica de um sistema de equações do 1º grau com duas incógnitas é dada pelo par ordenado que é a intersecção das duas retas que são soluções das equações que o sistema contém.
No item ê, um sistema de equações do 1º grau com duas incógnitas pode ser: possível e determinado, a solução é constituída de um único ponto, que é a intersecção das retas soluções de cada equação; impossível, a solução não existe, pois as retas de cada equação são paralelas (não há pontos de intersecção entre elas); possível e indeterminado, a solução é o conjunto dos infinitos pontos das retas soluções de cada equação, que são coincidentes.
DIVERSIFICANDO
Onde está o êrro?
Rogério encontrou em um jornal antigo uma brincadeira matemática e ficou curioso para saber a resposta, mas o jornal estava rasgado justamente na parte da solução. Observe o recorte do jornal.

Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Encontre o êrro cometido no cálculo desenvolvido no recorte de jornal.
2 Fernanda descobriu o êrro cometido no jornal e fez uma brincadeira parecida em uma folha de caderno, seguindo o mesmo raciocínio. Analise as operações de Fernanda e descubra onde está o êrro.
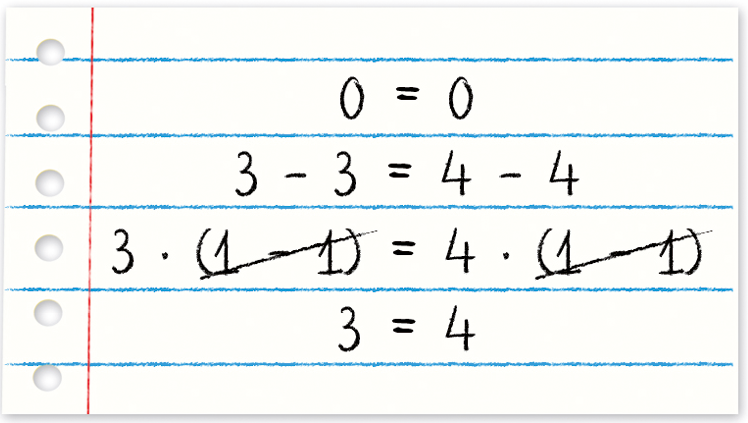
Respostas e comentários
1. Espera-se que os estudantes percebam dois erros: a2 ‒ b2 = a2 ‒ a ⋅ b só vale se b = 0 ou se a = b; na multiplicação de ambos os membros por
1 sobre, abre parênteses. a menos b, fecha parêntesescomo a = 1 e b = 1, temos a ‒ b = 0, e não é possível dividir por zero.
2. O êrro cometido foi semelhante ao do jornal, pois, após colocar em evidência os números 3 e 4, ela cortou os membros comuns entre parênteses. Ao fazer esse córte, Fernanda dividiu por zero, o que não é possível.
Diversificando
Nesta seção, apresentamos técnicas algébricas usadas de maneira inadequada para mascarar e obter igualdades numéricas absurdas.
Incentive os estudantes a buscar o êrro em cada situação. Essa atividade pode ser feita em duplas, o que enriquecerá as observações e a elaboração de hipóteses. Ao final, promova uma roda de conversa com a turma para que todos exponham o que concluíram e ampliem o repertório de estratégias, propiciando aos estudantes reavaliar e corrigir seus erros.