
CAPÍTULO 12 Geometria e grandezas

A natureza, produtora de espécimes exuberantes, é generosa em oferecer fórmas que encantam e que possibilitam desenvolver o sentido da estética nas pessoas.
Por meio da observação do objeto real, o ser humano apreende a beleza e projeta fórmas ideais, como as que estudaremos nos polígonos regulares.
Observe, leia e responda no caderno.
a) A superfície do botão da flor-de-cera lembra um polígono. Que polígono é esse?
b) As marcas nas superfícies nos dão a ideia de uma divisão em 5 partes. Essas partes lembram o formato de outro polígono. Qual é o nome desse polígono?
c) Você conhece outras fórmas na natureza que nos dão ideia de figuras geométricas? Que fórmas são essas? Converse com o professor e os colegas.
Respostas e comentários
a) Um pentágono.
b) Triângulo.
c) Resposta pessoal.
Capítulo 12 – Geometria e grandezas
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, estudaremos os polígonos regulares, seus elementos e suas propriedades. Trataremos ainda da medida da área de um círculo e da medida do volume de um cilindro circular reto.
Ao iniciar o estudo deste capítulo, converse com os estudantes sobre os padrões geométricos observáveis na flora, na fauna e em diversos fenômenos naturais. São exemplos desses padrões: favos hexagonais de uma colmeia, espirais nas conchas de moluscos e na flor do girassol, fórmas regulares das teias de aranha e da casca do abacaxi, simetrias em borboletas, corujas e algumas plantas, como a flor-de-cera da fotografia de abertura.
Ao responder às questões propostas na abertura, é provável que os estudantes notem que os botões da flor-de-cera têm cinco lados, mas não se lembrem como nomear o polígono que a superfície dos botões faz lembrar. Incentive-os a associar os nomes dos polígonos ao número de lados para que concluam que a superfície em questão lembra um pentágono. De maneira análoga, os estudantes devem notar que cada uma das cinco partes que compõem a superfície de um botão da flor-de-cera tem três lados e lembra um triângulo.
Após a discussão com os estudantes sobre as outras fórmas na natureza que eles conhecem que dão ideia de figuras geométricas, proponha-lhes uma atividade para que relacionem padrões geométricos encontrados na natureza com padrões geométricos encontrados em obras de arte e arquitetônicas. Para isso, organize a turma em dois grupos e proponha a um deles que pesquise os padrões geométricos encontrados na natureza e ao outro que pesquise os padrões encontrados nas Artes plásticas e na Arquitetura. Organize uma exposição das imagens desses diferentes padrões em um mural construído pelos estudantes e converse com eles sobre as relações entre os padrões geométricos pesquisados pelos dois grupos, mostrando que muitas obras de arte e arquitetônicas são inspiradas na natureza.
Atividades como essa proporcionam uma ótima oportunidade para o desenvolvimento da competência geral 9.
Durante a pesquisa em grupo e a construção do mural, estimule a cooperação e o diálogo entre os estudantes e ajude-os a resolver possíveis conflitos que possam surgir, destacando a importância do respeito mútuo.
1. Polígonos regulares inscritos e circunscritos em uma circunferência
Na abertura deste capítulo, lemos que a observação de objetos reais é assimilada pelo ser humano. A partir daí, ele imagina e elabora os correspondentes objetos ideais e, assim, promove novos conhecimentos.
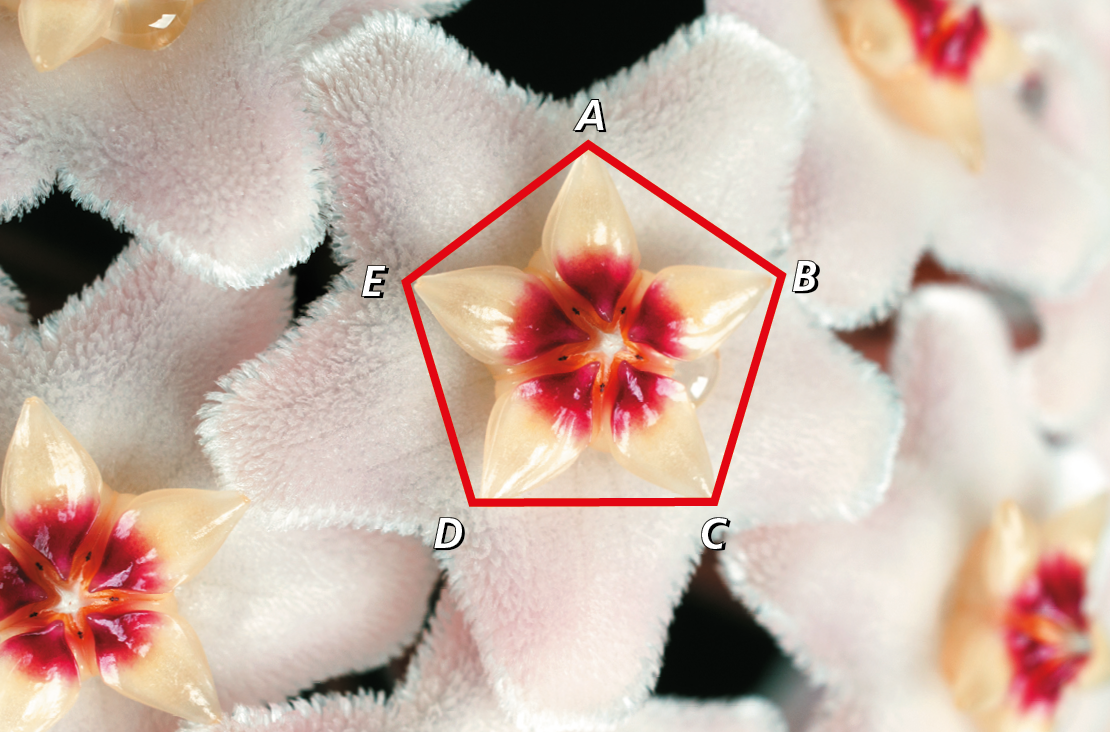
No pentágono regular á bê cê dê é destacado na fotografia da flor-de-cera (Hoya carnosa), temos:
•
Segmento A B≅
Segmento B C≅
Segmento C D≅
Segmento D E≅
Segmento E A
•
Ângulo A≅
Ângulo B≅
Ângulo C≅
Ângulo D≅
Ângulo EObserve que o alvéolo de um favo de mel também nos faz lembrar um polígono, que é o hexágono regular.
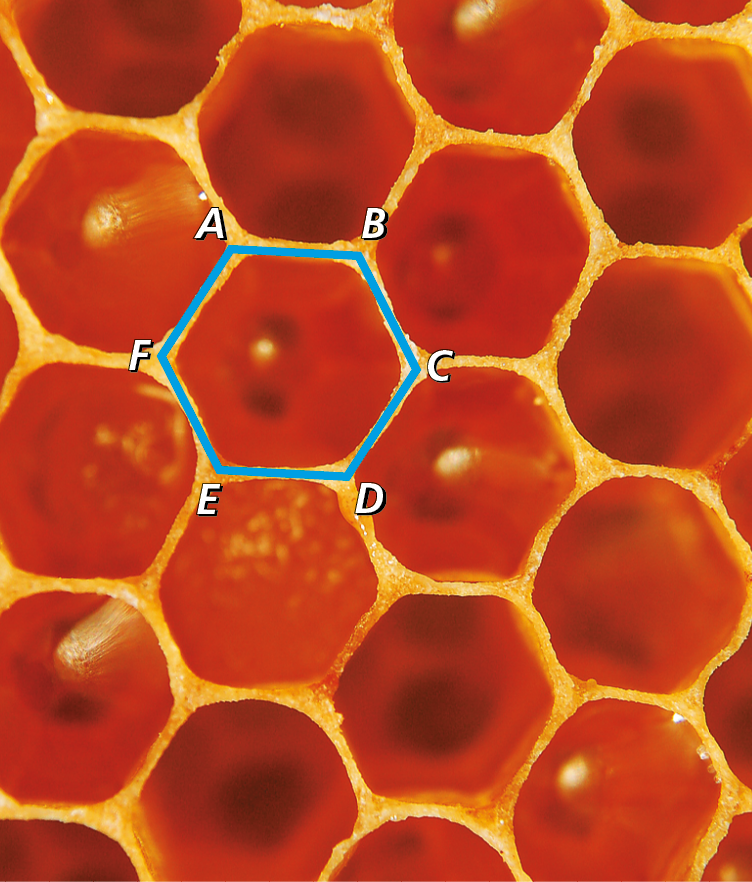
No hexágono regular á bê cê dê é éfe destacado na fotografia, temos:
•
Segmento A B≅
Segmento B C≅
Segmento C D≅
Segmento D E≅
Segmento E F≅
Segmento F A•
Ângulo A≅
Ângulo B≅
Ângulo C≅
Ângulo D≅
Ângulo E≅
Ângulo F(As imagens não respeitam as proporções reais entre os objetos.)
Os polígonos regulares também são bastante usados nas artes plásticas, especialmente em algumas obras de tendências modernistas. Observe a reprodução de uma obra do pintor paulista Luiz Sacilotto (1924 a 2003), cujo formato lembra um quadrado.

No quadrado a bê cê dê indicado na reprodução da obra, temos:
•
Segmento A B≅
Segmento B C≅
Segmento C D≅
Segmento D A•
Ângulo A≅
Ângulo B≅
Ângulo C≅
Ângulo DRespostas e comentários
1. Polígonos regulares inscritos e circunscritos em uma circunferência
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um cinco.
Este tópico possibilita ampliar a compreensão dos estudantes quanto à construção de polígonos regulares e de ângulos de 90graus, 60graus, 45graus e 120graus, desenvolvendo, assim, a habilidade (ê éfe zero oito ême ah um cinco).
Pergunte a eles que formatos observados na natureza associam a polígonos regulares. Espera-se que identifiquem pelo menos os favos hexagonais de uma colmeia.
Aproveite esse momento para verificar os conhecimentos que os estudantes já têm sobre polígonos regulares. Peça-lhes exemplos desse tipo de polígono: quadrado, triângulo equilátero, hexágono regular etcétera
Em seguida, retome com eles o conceito de polígono regular: “Todo polígono convexo que tem todos os lados de mesma medida e todos os ângulos internos congruentes entre si é um polígono regular”.
Se julgar conveniente, comente com os estudantes que os ângulos externos de um polígono regular também são congruentes entre si. Por exemplo:
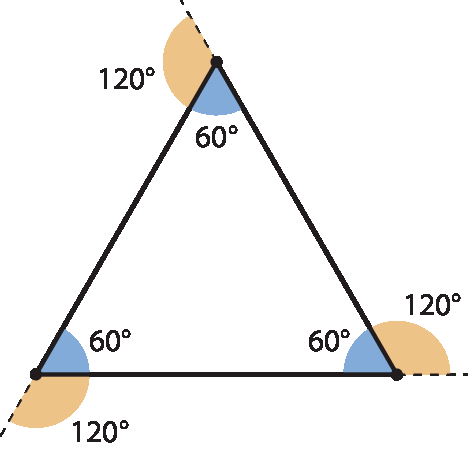
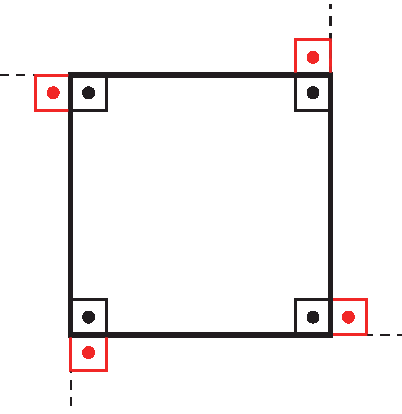
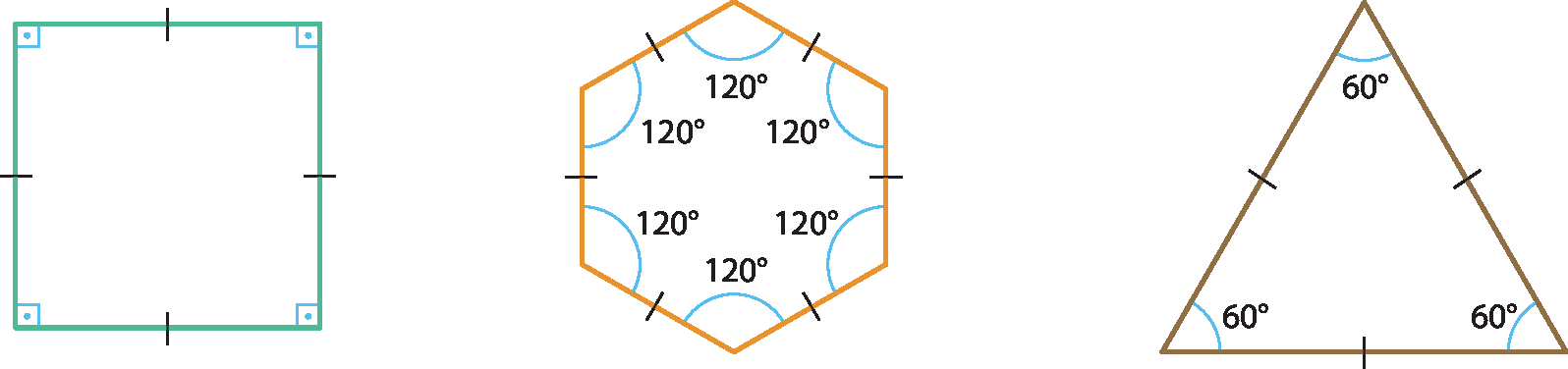
Observe alguns exemplos de polígonos regulares.

Propriedades dos polígonos regulares
Considere alguns objetos.

A moeda de 25 centavos cunhada no biênio 1994 a 1995 tem ao fundo o desenho que lembra um heptágono regular. Essa situação sugere um polígono cujos vértices estão sobre uma circunferência. Nesse caso, dizemos que o polígono está inscrito na circunferência.
A porca representada na imagem a seguir tem uma parte com o formato circular e a outra parte com o formato de um hexágono regular. Essa situação sugere um polígono cujos lados são tangentes a uma circunferência. Nesse caso, dizemos que o polígono está circunscrito à circunferência.

(As imagens não respeitam as proporções reais entre os objetos.)
Podemos dizer que, se um polígono é regular, então existe uma circunferência que passa por todos os seus vértices e outra que tangencia todos os seus lados.
Enunciamos as propriedades a seguir.
Todo polígono regular é inscritível em uma circunferência.
Todo polígono regular é circunscritível a uma circunferência.
Observe os exemplos.
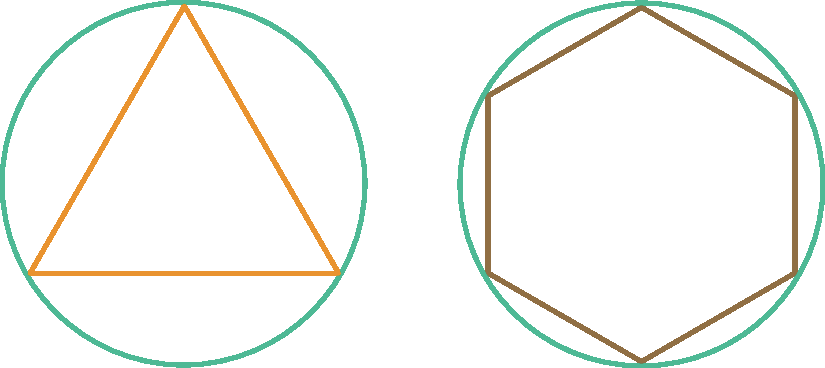
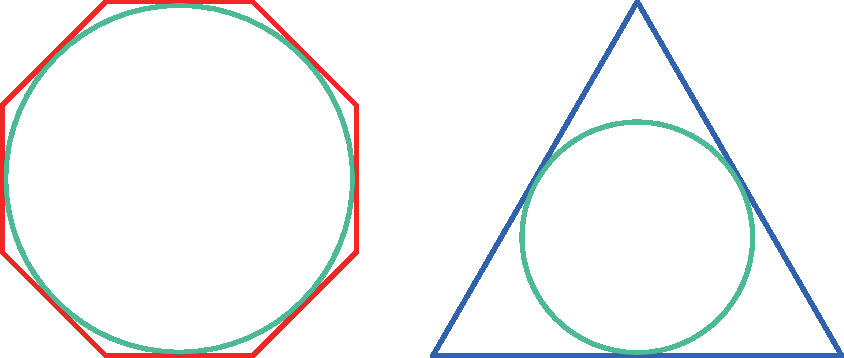
Respostas e comentários
Propriedades dos polígonos regulares
Destaque para os estudantes que um polígono é inscritível em uma circunferência quando todos os seus vértices pertencem a essa circunferência. Nesse caso, a circunferência se diz circunscrita ao polígono.
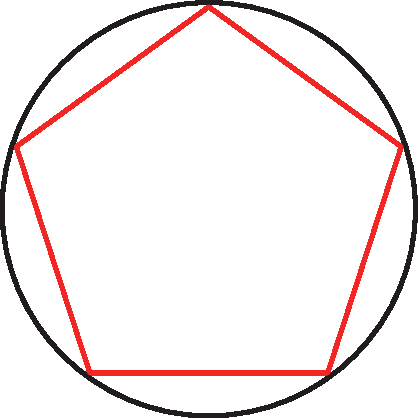
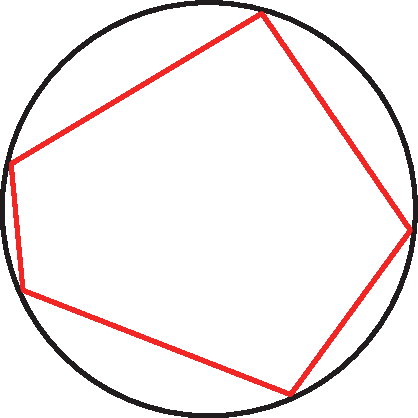
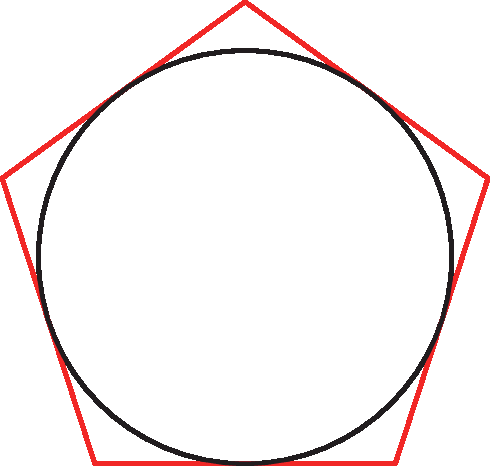
Comente também que um polígono é circunscritível a uma circunferência quando todos os seus lados são tangentes a ela. Nesse caso, a circunferência se diz inscrita no polígono.
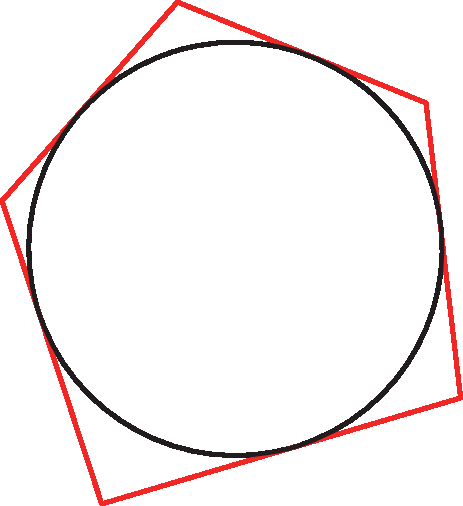
Acompanhe, a seguir, como inscrever e como circunscrever um quadrado.
• Nesta circunferência, vamos traçar um diâmetro qualquer e a sua mediatriz, obtendo o diâmetro perpendicular a ele. Observe que a circunferência ficou dividida em quatro arcos congruentes de 90graus.
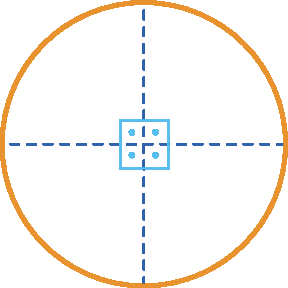
• As cordas determinadas pelos pontos consecutivos de divisão formam um quadrado inscrito na circunferência.
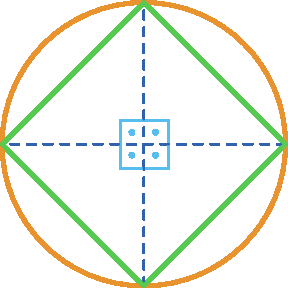
• As tangentes determinadas pelos pontos de divisão formam um quadrado circunscrito à circunferência.
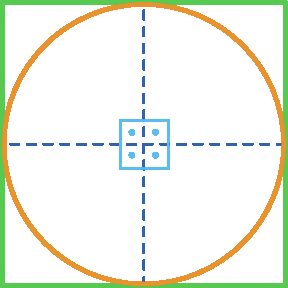
Generalizando, dizemos que:
• se uma circunferência é dividida em três ou mais arcos congruentes, então as cordas determinadas pelos pontos consecutivos de divisão formam um polígono regular inscrito na circunferência;
• se uma circunferência é dividida em três ou mais arcos congruentes, então as tangentes aos pontos consecutivos de divisão formam um polígono regular circunscrito à circunferência.
Com base no que estudamos, podemos construir o fluxograma a seguir, que verifica se um quadrado é inscrito ou circunscrito a uma circunferência.
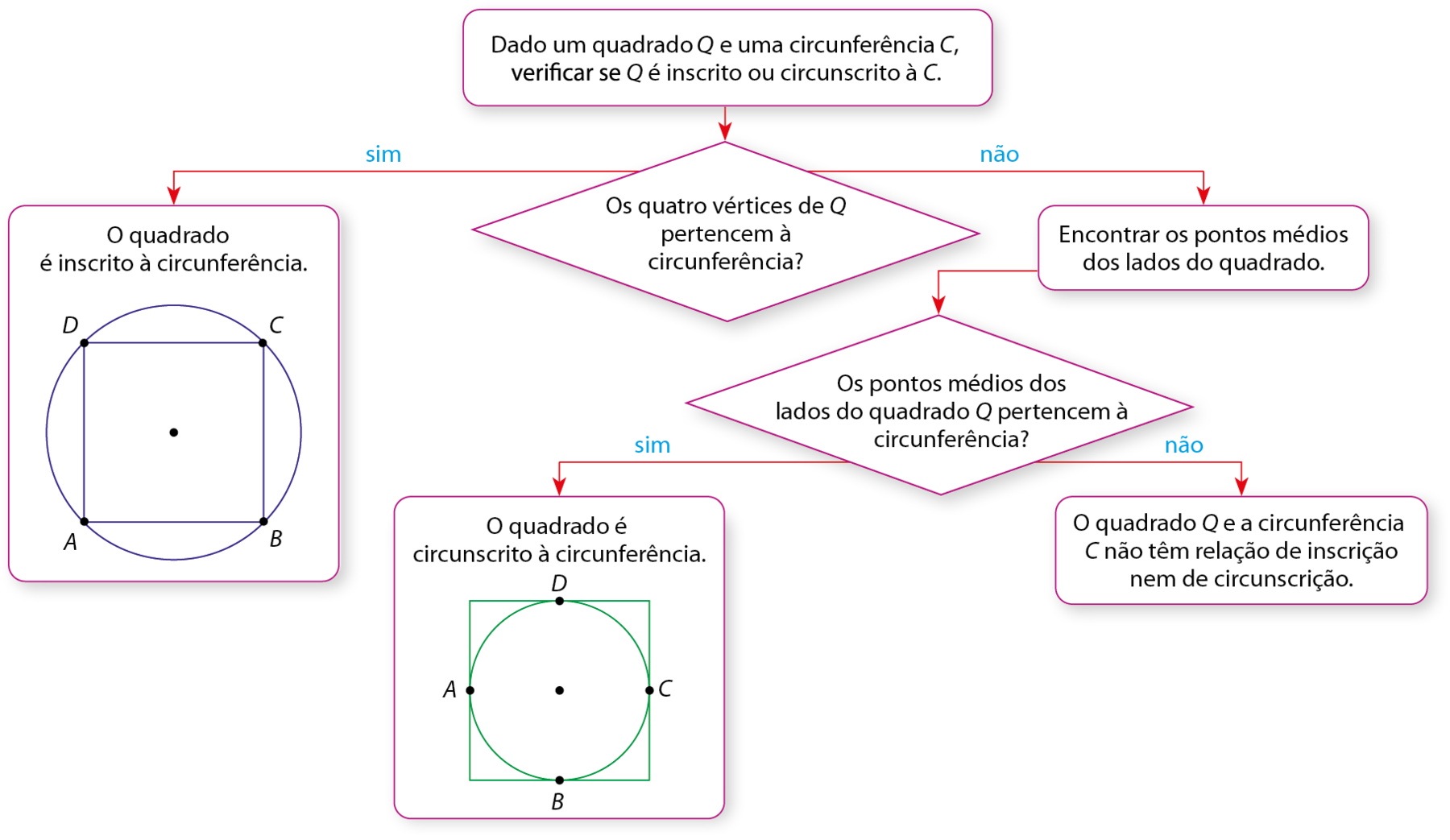
Observação
▶ A circunferência inscrita em um polígono regular tangencia os lados desse polígono nos seus respectivos pontos médios.
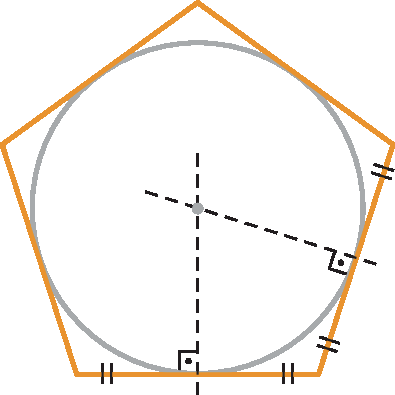
Respostas e comentários
Propriedades dos polígonos regulares
Se julgar necessário, retome os conceitos de corda, diâmetro e raio de uma mesma circunferência.
• Corda: todo segmento de reta cujas extremidades são pontos de uma mesma circunferência.
• Diâmetro: toda corda que passa pelo centro da circunferência (a maior das cordas).
• Raio: todo segmento de reta cujas extremidades são um ponto da circunferência e o seu centro (a medida do comprimento de um raio é a metade da medida do comprimento de um diâmetro).
Reproduza na lousa a construção dos quadrados inscrito e circunscrito para os estudantes acompanharem cada etapa. Então, seguindo passo a passo a descrição do fluxograma, mostre a eles como verificar qual dos quadrados é inscrito e qual é circunscrito à circunferência. Depois, pergunte como seriam os passos da construção de um triângulo equilátero inscrito em uma circunferência e de um triângulo equilátero circunscrito a uma circunferência. Espera-se que eles percebam que devem dividir a circunferência em três arcos congruentes de 120graus.
Se julgar conveniente, demonstre para a turma a afirmação do boxe Observação.
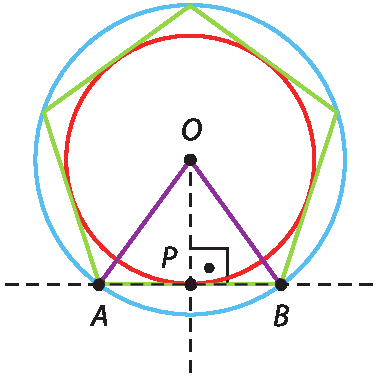
Os triângulos á pê ó e bê pê ó são triângulos retângulos. Como as hipotenusas
Segmento A Oe
Segmento B Osão congruentes (raios da circunferência maior) e
Segmento O P(lado comum) é cateto dos dois triângulos, então os triângulos á pê ó e BPO são congruentes. Portanto,
Segmento A Pe
Segmento B Psão congruentes. Logo, P é o ponto médio de
Segmento A B, congruente com segmento B C, congruente com segmento C D, congruente com segmento D E, congruente com segmento E A.(lado do polígono).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
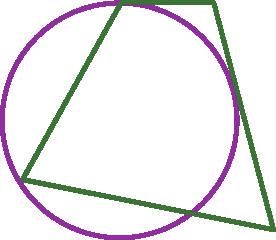
1 Indique se o polígono é inscrito na circunferência, circunscrito a ela ou se nenhum dos casos se aplica ao item.
a)
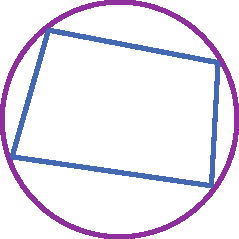
b)

c)

d)
Versão adaptada acessível
1. Faça a representação de:
a) um polígono inscrito em uma circunferência;
b) um polígono circunscrito em uma circunferência;
c) um polígono interno a uma circunferência, que não seja inscrito.
Orientação para acessibilidade
Oriente os estudantes na construção das circunferências e dos polígonos, fornecendo materiais adequados para a construção. Uma sugestão é usar o apoio de objetos circulares e linhas para a representação.
2 Considere um quadrado circunscrito e suas diagonais. A tangência entre essas figuras e as intersecções das diagonais do quadrado com a circunferência determinam 8 pontos. Ao unir esses pontos com segmentos de reta, obtemos um polígono. Faça um esbôço dessa construção e indique se o polígono será inscrito ou circunscrito à circunferência.
3 Indique os itens que não apresentam polígonos regulares. Em seguida, justifique.
a)
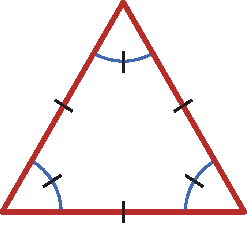
b)
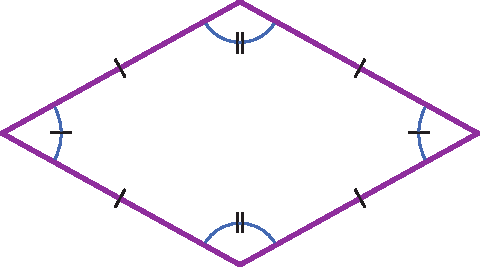
c)
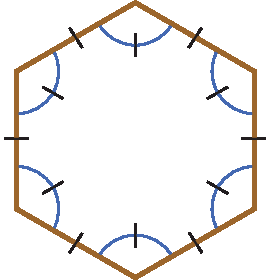
d)
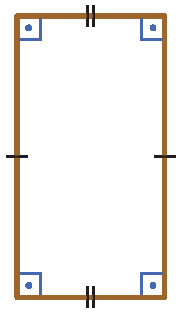
4 Para a construção de um hexágono regular inscrito, usando compasso, régua e transferidor, quais são os passos a serem seguidos? Construa um fluxograma com esses passos e compartilhe com o professor e os colegas.
PARA SABER MAIS
Determinando aproximações do número pi
Muitos matemáticos gregos da Antiguidade preocuparam-se com medidas de comprimento e de área, sobretudo Eudoxo de Cnido (408 a 355 ? antes de Cristo) e, depois, Arquimedes de Siracusa (287 a 212 ? antes de Cristo).
Arquimedes foi um dos maiores matemáticos da Antiguidade, embora o centro da Matemática no período em que viveu, chamado de Idade Helenística, estivesse em Alexandria (no Egito).
Esse sábio — que era matemático, físico e inventor — nasceu no início do século três antes de Cristo, em Siracusa (cidade localizada na atual ilha da Sicília, na Itália), e morreu em 212 antes de Cristo, durante um ataque dos romanos à cidade.
Sempre muito engenhoso, mesmo durante o cerco à cidade pelas tropas romanas, Arquimedes inventou catapultas para lançar pedras, assim como polias e ganchos para espatifar navios romanos. Com essas e outras invenções, ele conseguiu manter o inimigo distante por, pelo menos, três anos. Contudo, durante o massacre que sucedeu a tomada de Siracusa, Arquimedes foi assassinado por um soldado romano, apesar das ordens expressas do general Marcelo para que preservassem a vida do grande sábio.

Respostas e comentários
1. a) Inscrito.
1. b) Nenhum dos casos.
1. c) Circunscrito.
1. d) Nenhum dos casos.
2. Construção de figura. O polígono (octógono) será inscrito na circunferência.
3. b) Não é polígono regular, pois não tem todos os ângulos congruentes.
3. d) Não é polígono regular, pois não tem todos os lados congruentes.
4. Construção de fluxograma.
Exercícios propostos
No exercício 1, peça aos estudantes que justifiquem suas respostas. No item b, espera-se que eles percebam que um dos vértices do quadrilátero não pertence à circunferência. Aproveite o item d para questionar se é possível um polígono ser inscrito ou circunscrito tendo um vértice na parte interna e outro na parte externa da circunferência.
As resoluções dos exercícios 1 a 4 estão no início deste Manual, nas orientações específicas do capítulo 12.
Para saber mais
O intuito desta seção é apresentar o número π como um exemplo de número irracional, descrevendo uma de suas aproximações, obtida por Arquimedes.
Comente com os estudantes que todo número racional pode ser expresso por uma fração cujos termos são dois números inteiros (com denominador não nulo). Desse modo, os números racionais ou são inteiros (dados por frações aparentes), ou têm fórma decimal exata
Entre parênteses: como 2 quintos, que é igual a zero vírgula 4, ou têm fórma decimal infinita e periódica
Entre parênteses: dízimas periódicas, como zero vírgula 33333 reticências, cuja fração geratriz é 1 terço.
No entanto, há números cuja fórma decimal é infinita e não periódica, como 0,023002300023reticências; tais números não são racionais.
Desse modo, os estudantes podem perceber que há outros tipos de número. Os números irracionais são números que têm a notação decimal infinita e não periódica (como as raízes quadradas não exatas; por exemplo,
Raiz quadrada de 2).
O número π é outro exemplo de número irracional; ele é definido pela razão entre a medida do comprimento de uma circunferência e a medida de seu diâmetro.
No livro do 9º ano, trataremos desses dois tipos de número (números racionais e números irracionais), ao abordar o conjunto dos números reais.
Proponha aos estudantes que determinem experimentalmente aproximações de π para 3,14 usando diferentes latas cilíndricas, barbante, fita métrica e calculadora. Eles podem calcular a razão entre a medida do comprimento da circunferência que delimita o cilindro pela medida de seu diâmetro.
Entre as obras escritas por esse matemático grego, aproximadamente dez tratados foram preservados até hoje. No que diz respeito à medida de comprimentos e de áreas, destacamos um tratado de Geometria plana denominado A medida do círculo. Nele, Arquimedes faz uma aproximação para a medida do comprimento da circunferência, estabelecendo, pela primeira vez, um método para o cálculo de valores aproximados de um número não racional, o número irracional hoje denominado π, que é a razão entre as medidas do comprimento e do diâmetro da circunferência.
O comprimento da circunferência fica entre o perímetro de qualquer polígono regular inscrito e qualquer polígono regular circunscrito, como sugerem as figuras a seguir.
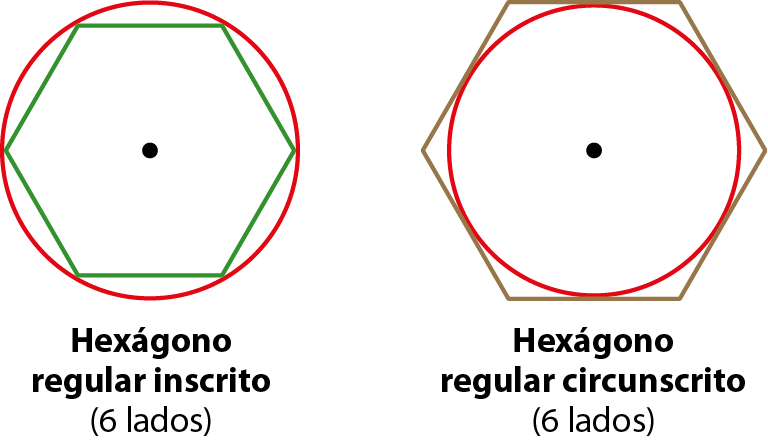

Para calcular a medida do comprimento da circunferência de raio de medida 1, em unidade de comprimento, Arquimedes considerou, inicialmente, a medida do perímetro dos hexágonos regulares inscrito e circunscrito à circunferência. Depois, ele comparou o comprimento dela com o perímetro de outros polígonos regulares inscritos e circunscritos, dobrando o número de lados a cada comparação. Ao calcular a medida do perímetro dos polígonos inscrito e circunscrito de 12, 24, 48 e 96 lados, Arquimedes obteve resultados que se aproximavam cada vez mais de 2π.
Foi assim que Arquimedes obteve a primeira aproximação historicamente conhecida para a medida do comprimento da circunferência, bem como para o número π. Ele chegou à conclusão de que π era um número entre
223, 71 avose
22 sétimos, ou seja, 3,140reticências e 3,142reticências Assim, Arquimedes obteve uma aproximação para π com duas casas decimais. Esse método é conhecido como método clássico para o cálculo de π.
Elementos de um polígono regular
Em um polígono regular, temos:
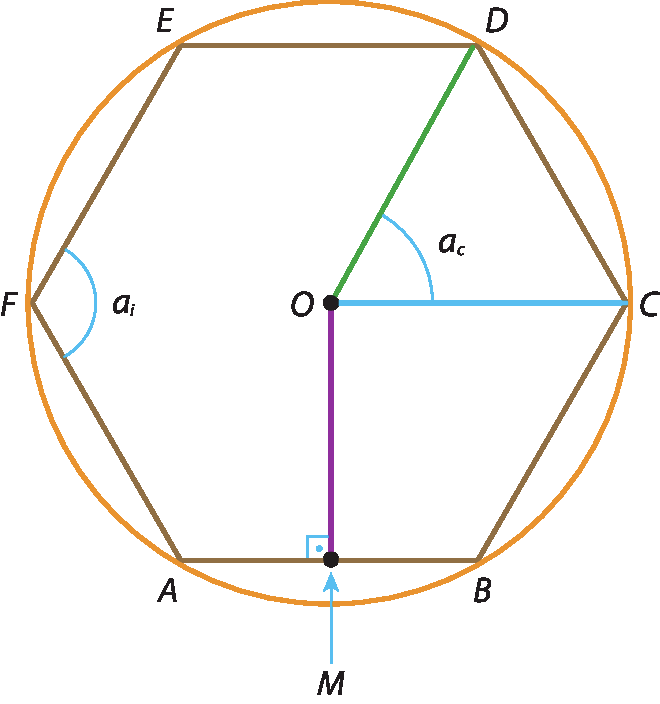
• centro do polígono: centro da circunferência circunscrita a ele (na figura, o ponto óh );
• raio do polígono: raio da circunferência circunscrita a ele (na figura,
Segmento O Ce
Segmento O D);
• apótema do polígono: segmento que une o centro do polígono ao ponto médio de um de seus lados (na figura,
Segmento O M);
• ângulo central: aquele cujo vértice é o centro do polígono e cujos lados são semirretas que contêm dois vértices consecutivos do polígono (na figura,
Ângulo C O D).
Respostas e comentários
Elementos de um polígono regular
Chame a atenção dos estudantes para o fato de que o apótema do polígono é o raio da circunferência nele inscrita.
Prepare antecipadamente folhas de papel sulfite com desenhos de vários tipos de polígono regular e entregue uma a cada estudante. Peça a eles que destaquem os elementos desses polígonos regulares.
Depois, em duplas, solicite aos estudantes que comparem os elementos destacados, fazendo os acertos que julgarem necessários.
Ao final, faça a análise de cada uma das figuras com toda a turma, verificando se eles indicaram os elementos dos polígonos corretamente. Certifique-se de que os estudantes compreenderam o conceito de apótema e de ângulo central de um polígono regular.
Representando por ac a medida do ângulo central de um polígono regular de n lados, por ai a medida do ângulo interno e por Si a soma das medidas dos ângulos internos, temos:
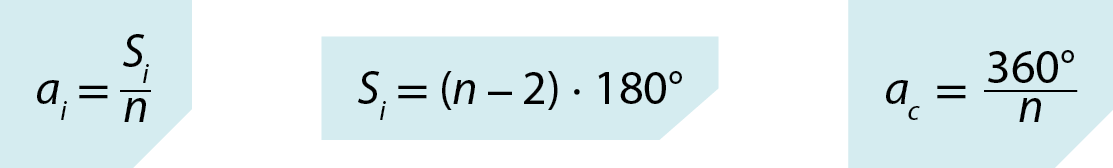
Como exemplo, vamos considerar este octógono regular.
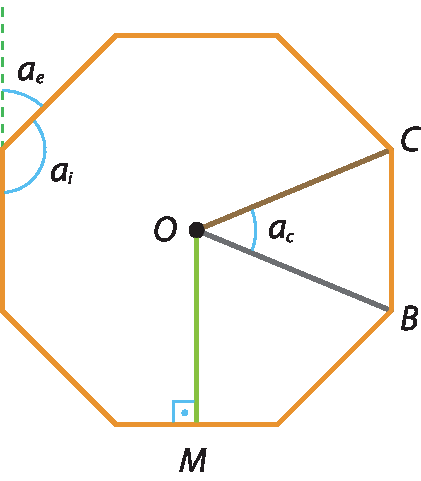
• O ponto óh é o centro do octógono.
• Os segmentos
O C e O Bsão raios.
• O segmento
O Mé um dos apótemas.
• O ângulo
C O Bé um ângulo central.
A medida ac de um ângulo central desse polígono é dada por:
ac igual a, fração, numerador 360 graus, denominador n
Assim, como n = 8, temos:
ac igual a, fração, numerador 360 graus, denominador 8= 45graus
A medida ai de um ângulo interno desse polígono é dada por:
ai igual a, fração, numerador Si, denominador n, igual a, fração, numerador n menos 2, vezes 180 graus, denominador n
Assim, como n = 8, temos:
ai igual a, fração, numerador abre parênteses, 8 menos 2, fecha parênteses, vezes 180 graus, denominador 8.= 135graus
Uma maneira de obter a medida ae de um ângulo externo desse polígono é utilizando a fórmula ai + ae = 180graus. Assim, 135graus + ae = 180graus, ou seja, ae = 45graus.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
5 Calcule a medida do ângulo central de um triângulo equilátero.
6 Qual é o polígono regular em que as medidas do ângulo central, do ângulo interno e do ângulo externo são todas iguais? Qual é o valor delas?
7 Um polígono regular tem 20 lados.
a) Quanto mede seu ângulo central?
b) Quanto mede seu ângulo interno? E seu ângulo externo?
8 Quantos lados tem um polígono regular em que:
a) o ângulo interno mede 144graus?
b) o ângulo externo mede 30graus?
c) o ângulo central mede 10graus?
9 A figura central do tampo de uma mesa foi formada a partir de um dodecágono regular, como indicado na figura a seguir. Determine a medida do ângulo central desse dodecágono.
10 A soma das medidas dos ângulos internos de um polígono regular é .3240graus.
Determine:
a) a medida do ângulo central desse polígono;
b) a medida do ângulo externo desse polígono.
Respostas e comentários
5. 120graus
6. Quadrado; ac = 90graus; ai = 90graus; ae = 90graus.
7. a) 18graus
7. b) 162graus; 18graus.
8. a) 10 lados.
8. b) 12 lados.
8. c) 36 lados.
9. 30graus
10. a) ac = 18graus
10. b) ae = 18°
Exercícios propostos
No exercício 9, chame a atenção dos estudantes para observarem que, quanto maior for o número de lados de um polígono regular, menor será a medida de seu ângulo central. Nesse caso, há um polígono regular de 12 lados; logo, para obter a medida de seu ângulo central, podemos efetuar:
ac =
ac igual a, fração, numerador 360 graus, denominador 12ac = 30°
Para a resolução do item a do exercício 10, lembre os estudantes de que a medida de um ângulo central (ac ) de um polígono regular é dada por ac =
Fração. Numerador 360 graus, denominador n.; portanto, é necessário determinar o número de lados (n) desse polígono.
Como a soma das medidas dos ângulos internos (Si ) desse polígono regular é conhecida, é possível determinar o número de lados (n) do polígono pela relação Si = (n ‒ 2) · 180graus e, assim, obtemos:
Si = .3240graus = (n ‒ 2) · 180graus
.3240graus = 180graus · n ‒ 360graus
.3240graus + 360graus = 180graus · n
.3600graus = 180graus · n
n = 20
ac =
ac igual a, fração, numerador 360 graus, denominador 20, igual a 18 graus.= 18graus
Assim, o ângulo central desse polígono mede 18graus.
Para a resolução do item b do exercício 10, lembre os estudantes de que a medida de um ângulo externo (ae ) de um polígono regular é dada pela relação ai + ae = 180graus e que a medida de um ângulo interno (ai) de um polígono regular é dada por ai =
fração, numerador Si, denominador n. Assim:
ai =
Fração, numerador 3240 graus, denominador 20.= 162graus
162graus + ae = 180graus
ae = 180graus ‒ 162graus = 18graus
Portanto, o ângulo externo desse polígono mede 18graus.
As resoluções dos exercícios 5 a 8 estão no início deste Manual, nas orientações específicas do capítulo 12.
11 A figura a seguir é um selo comemorativo dos 50 anos de fundação de um colégio.

Sabendo que o hexágono desenhado nesse selo é regular, determine as medidas do ângulo central, do ângulo externo e do ângulo interno desse hexágono.
12

Reúna-se com um colega e façam o que se pede.
Copiem no caderno a figura a seguir. Nela, temos parte de um polígono regular de n lados e de uma circunferência de centro O circunscrita a esse polígono.
Indicamos por ac, ae e x as medidas dos ângulos central, externo e
Ângulo O A B, respectivamente.
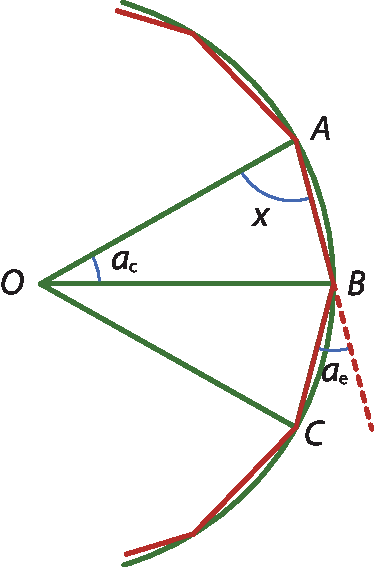
a) Classifiquem, quanto às medidas dos lados, os triângulos ó á bê e ó bê cê. Esses triângulos são congruentes?
b) Representem, em função de x, as medidas do ângulo
O B Ae do ângulo central.
c) Representem, em função de x, as medidas do ângulo
A B Ce do ângulo externo.
d) Qual é a relação entre as medidas do ângulo central e do ângulo externo?
13

Hora de criar – Ainda em dupla, façam o que se pede.
Cada um deve traçar duas circunferências de raio medindo 4 centímetros e escolher um polígono regular com n lados, n ⩾ 6, para ser construído pelo outro de duas maneiras.
I. Traçam-se n ângulos centrais adjacentes de medida
Fração. Numerador 360 graus, denominador ncujos lados determinam, na circunferência, os n vértices do polígono. Em seguida, traçam-se os lados do polígono.
II. Traça-se um só ângulo central de medida
Fração. Numerador 360 graus, denominador n., determinando, na circunferência, os vértices a e B. Usando um compasso com abertura igual a A bê, marcam-se na circunferência, a partir de B, os demais vértices. Em seguida, traçam-se os lados do polígono.
Depois de cada um construir o polígono das duas maneiras, discutam e escolham qual delas é a melhor. Justifiquem a escolha.
(Ao usarem o compasso, atenção para não se machucarem com a ponta-sêca!)
2. Cálculo intuitivo da medida da área do círculo
Em Matemática, a tentativa de resolução de problemas, sendo ou não insolúveis, como o da quadratura do círculo com régua e compasso, em geral, leva à criação de novos conceitos e ideias. Para os gregos, obter a medida do comprimento do lado do quadrado de mesma área que um círculo significava calcular a medida da área de um círculo.
O método clássico ou método de exaustão criado por Eudoxo e Arquimedes também foi aplicado para calcular a medida da área do círculo.
De maneira simples, podemos dizer que eles pensaram assim: sabiam que todo polígono pode ser decomposto em triângulos e sabiam calcular a medida da área de um triângulo; logo, podiam calcular a medida da área de qualquer polígono regular, inscrito ou circunscrito em um círculo, com um número n de lados cada vez maior, aproximando-se cada vez mais da medida da área do círculo.
Arquimedes começou por calcular a medida do perímetro (e, consequentemente, da área) de um hexágono regular inscrito, depois foi dobrando o número de lados até chegar ao polígono de 96 lados. Aqui, vamos simplificar iniciando com um quadrado inscrito e dobrando o número de lados por duas vezes, apenas para ilustrar a ideia.
Respostas e comentários
11. 60graus, 60graus, 120graus.
12. a) Isósceles, isósceles; sim.
12. b) x; 180graus ‒ 2x.
12. c) 2x; 180graus ‒ 2x.
12. d) São iguais.
13. Construção de figura. Respostas pessoais.
Exercícios propostos
O exercício 12 é uma atividade procedimental na qual os estudantes, com base nos conceitos aprendidos, resolvem itens cuidadosamente dirigidos para ajudá-los na construção de um novo conhecimento.
Para a resolução do item a, é importante observar que ó á = ó bê = ó cê (medidas de raios dessa circunferência), o que comprova que os triângulos ó á bê e ó bê cê são isósceles.
No item b, o ângulo
O B Aé um dos ângulos da base do triângulo OAB, e o outro ângulo dessa mesma base é o de medida x. Assim: medida do(
Ângulo O B A) = x. Portanto, a medida ac do ângulo central é dada por:
ac + 2x = 180graus
ac = 180graus ‒ 2x
No item c, o triângulo isósceles OBC também tem ângulos da base medindo x cada um, pois o ângulo do vértice desse triângulo também é o ângulo central de medida ac = 180graus ‒ 2x do polígono regular considerado. Como o ângulo
A B Cé obtido pela soma de um ângulo da base de cada triângulo isósceles (OAB e OBC), sua medida é dada por:
medida do(
Ângulo A B C) = x + x = 2x
Como a soma do ângulo
Medida do ângulo A B Ccom o ângulo externo de medida ae é um ângulo raso, obtemos:
medida do(
Ângulo A B C) + ae = 180graus
2x + ae = 180graus
ae = 180graus ‒ 2x
Então, no item d, as medidas do ângulo central e do ângulo externo são iguais: ac = ae.
O exercício 13 é uma boa oportunidade de conversar com a turma sobre o uso de diferentes estratégias para a resolução de problemas.
As resoluções dos exercícios 11 e 13 estão no início deste Manual, nas orientações específicas do capítulo 12.
Agora, observe na figura 1 que a medida da área do quadrado de lado ℓ₄ é igual à medida da área SP4 do paralelogramo de base medindo 2ℓ₄ e altura medindo h₄, que é menor do que a medida da área Sc do círculo.
Note que 2ℓ₄ é a medida do semiperímetro p₄ do quadrado e que podemos escrever:
= p₄ ⋅ h₄ < Sc ,
em que
S índice i índice 4.é a medida da área do polígono regular inscrito de 4 lados, p₄ é a medida do semiperímetro do quadrado e h₄ é a medida da altura de cada triângulo da divisão.
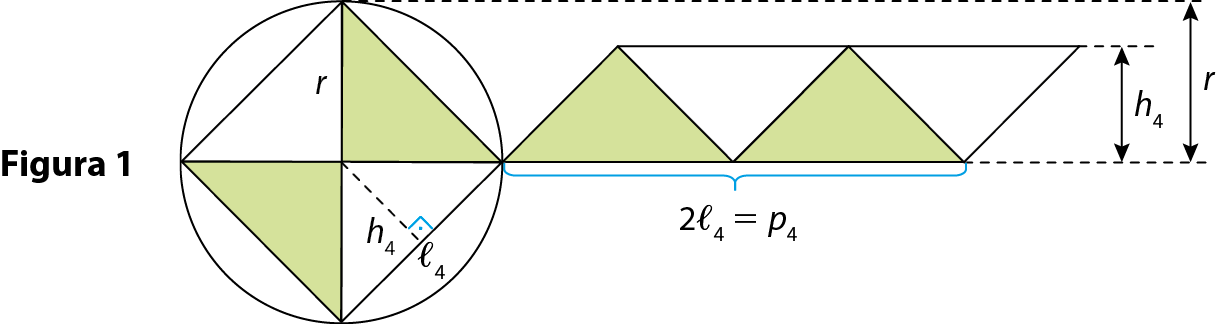
Na figura 2, a medida da área do octógono de lado medindo ℓ₈ é igual à medida da área SP8 do paralelogramo de base medindo 4ℓ₈ e altura medindo h₈, que é menor do que a medida da área Sc do círculo.
Note que 4ℓ₈ é a medida do semiperímetro p₈ do octógono e que podemos escrever:
= p₈ ⋅ h₈ < Sc ,
em que
S índice i índice 8.é a medida da área do polígono regular inscrito de 8 lados, p₈ é a medida do semiperímetro do octógono e h₈ é a medida da altura de cada triângulo da divisão.
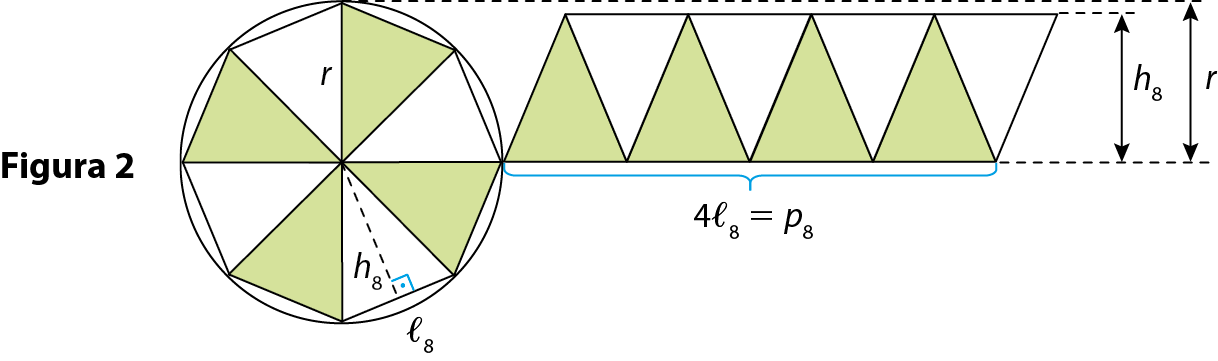
Na figura 3, a medida da área do hexadecágonoglossário de lado medindo ℓ₁₆ é igual à medida da área SP16 do paralelogramo de base medindo 8ℓ₁₆ e altura medindo h₁₆, que é menor do que a medida da área Sc do círculo.
Note que 8ℓ₁₆ é a medida do semiperímetro p₁₆ do hexadecágono e que podemos escrever:
= p₁₆ ⋅ h₁₆ < Sc ,
em que
S índice i índice 16.é a medida da área do polígono regular inscrito de 16 lados, p₁₆ é a medida do semiperímetro do hexadecágono e h₁₆ é a medida da altura de cada triângulo da divisão.
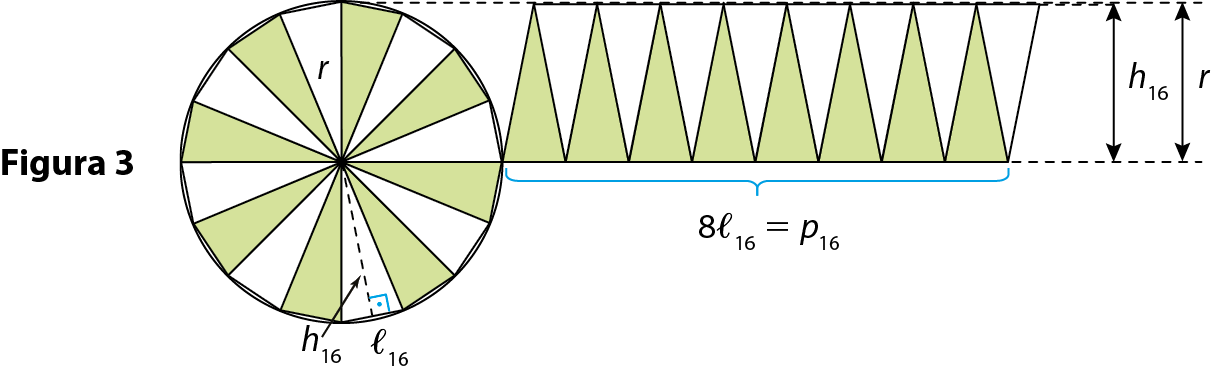
Temos uma sequência de medidas de áreas crescentes
S índice i índice n.= pn ⋅ hn, isto é, cada vez maiores, mas que têm um limite, que é a medida da área Sc do círculo. Os valores da sequência se aproximam da medida da área do círculo sem nunca alcançá-la.
<
S índice i índice 8.<
S índice i índice 16.< ... < Sc

Respostas e comentários
2. Cálculo intuitivo da medida da área do círculo
Habilidade da Bê êne cê cê: ê éfe zero oito ême ah um nove.
Este tópico possibilita ampliar a compreensão dos estudantes quanto à resolução de problemas que envolvam cálculos de medidas de área de triângulos e de círculos, desenvolvendo, assim, a habilidade (ê éfe zero oito ême ah um nove).
Reproduza na lousa as figuras de cada etapa apresentada e discuta com os estudantes o procedimento para a obtenção da medida da área de um círculo por aproximações das áreas de polígonos regulares inscritos no círculo, de modo que eles compreendam todas as etapas.
Ressalte que a medida do semiperímetro é a metade da medida do perímetro. Por exemplo, a medida do perímetro de um quadrado de lado ℓ é 4ℓ. Por isso, a medida do seu semiperímetro é 2ℓ.
Ao discutir os exemplos apresentados com os estudantes, comente que, em geral, usamos π = 3,14 como aproximação nos cálculos.
Como, ao aumentar o número n de lados dos polígonos, as medidas dos semiperímetros pn se aproximam da medida do semicomprimento πr da circunferência do círculo e as medidas das alturas hn se aproximam de r, medida do raio do círculo, obtemos a medida da área Sc do círculo substituindo hn por r e pn por πr na igualdade
S índice i índice n.= pn ⋅ hn:
= pn ⋅ hn = (πr) ⋅ r = πr2
Assim, temos:
Sc = πr 2
Acompanhe alguns exemplos.
a) Os valores aproximados da medida do comprimento C da circunferência e da medida da área S do círculo de raio medindo 5 centímetros são dados por: C ≃ 2 ⋅ 3,14 ⋅ 5 = 31,4 S ≃ 3,14 ⋅ 52 = 3,14 ⋅ 25 = 78,5
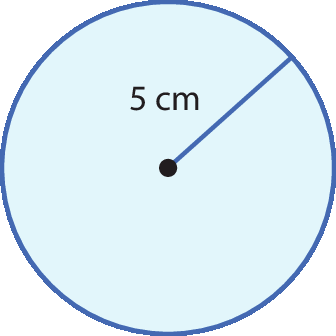
A circunferência de raio medindo 5 centímetros tem comprimento medindo aproximadamente 31,4 centímetros e o seu círculo tem medida de área aproximadamente igual a 78,5 centímetros quadrados.
b) A lona lateral do picadeiro (em vermelho) de um circo foi montada sobre uma circunferência de comprimento medindo 78,5 métros.

Qual é a medida do raio desse picadeiro? C = 2πr 78,5 ≃ 2 ⋅ 3,14 ⋅ r r ≃
r é aproximadamente, fração, numerador 78,5, denominador 2 vezes 3,14, igual a, fração, numerador 78,5, denominador 6,28, igual a 12,5.= 12,5 O picadeiro do circo tem raio medindo aproximadamente 12,5 metros.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
14 Sabendo que o hexágono inscrito na circunferência é regular e tem lado medindo 9 centímetros, calcule a medida:
a) do raio da circunferência;
b) do comprimento da circunferência;
c) da área do círculo delimitado pela circunferência.
15 (saréspi) O desenho representa um brinco formado por duas circunferências tangentes. A medida do diâmetro da maior é o dôbro da medida do diâmetro da menor. Se a medida do comprimento da circunferência menor é igual a C, então a medida do comprimento da maior é:

a) 2πC.
b) πC.
c) 2C.
d) C.
16 (Saresp) As rodas de uma bicicleta têm 70 centímetros de medida do diâmetro. Assinale a alternativa que mostra a medida da distância, em metro, percorrida pela bicicleta após 100 voltas das rodas. (Considere π = 3,14.)
a) 109,9
b) 219,8
c) .3846,5
d) .15386
17 Um ralo circular de chão de medida de 10 centímetros de diâmetro, feito em alumínio, foi projetado com 12 buracos circulares, sendo 6 buracos com 2 centímetros de medida de diâmetro e 6 com 1 centímetro de medida de diâmetro. Qual é a medida aproximada da área, em centímetros quadrados, ocupada pelo alumínio?
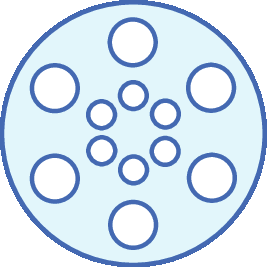
a) 25π
b) 19π
c) 7,5π
d) 17,5π
18

Hora de criar – Em dupla, cada um cria um problema sobre área de círculo. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Respostas e comentários
14. a) 9 centímetros
14. b) Aproximadamente 56,52 centímetros.
14. c) Aproximadamente 254,47 centímetros quadrados.
15. Alternativa c.
16. Alternativa b.
17. Alternativa d.
18. Resposta pessoal.
Exercícios propostos
No exercício 16, lembre aos estudantes que a medida do comprimento C de uma circunferência é dada por C = 2πr e que a medida do raio de uma circunferência é igual à metade da medida do seu diâmetro.
Assim, considerando que a medida do diâmetro das rodas de uma bicicleta é 70 centímetros, com π = 3,14, a medida do comprimento da circunferência das rodas é 219,8 centímetros.
C = 2πr = 2 · 3,14 · 35
C = 219,8
Então, após 100 voltas das rodas, a bicicleta percorreu .21980 centímetros.
219,8 · 100 = .21980
Lembre aos estudantes que 1 metro equivale a 100 centímetros; portanto, após 100 voltas das rodas, a bicicleta percorreu 219,8 métros.
= 219,8
Alternativa b.
Apresentamos a seguir uma resolução possível para o exercício 17.
Considerando que o diâmetro do ralo mede 10 centímetros, o diâmetro de 6 buracos mede 2 centímetros e os dos outros 6 buracos medem 1 centímetro, obtemos, em centímetros quadrados:
• Sralo sem buracos = π ·
abre parênteses, 10 sobre 2, fecha parênteses, elevado ao quadrado.Sralo sem buracos = 25π
• Sburaco maior = π ·
abre parênteses, dois sobre 2, fecha parênteses, elevado ao quadradoSburaco maior = π
• Sburaco menor = π ·
um meio elevado ao quadradoSburaco menor =
35 vezes pi, menos 6 vezes pi, menos 6 vezes, fração, numerador pi, denominador 4.
Então, a medida da área do ralo com os buracos, em centímetros quadrados, é dada por:
Sralo com buracos = 25π ‒ 6 · π ‒ 6 ·
fração, numerador pi, denominador 4Sralo com buracos = 25π ‒ 6π ‒ 1,5π
Sralo com buracos = 25π ‒ 7,5π
Sralo com buracos = 17,5π
Alternativa d.
As resoluções dos exercícios 14, 15 e 18 estão no início deste Manual, nas orientações específicas do capítulo 12.
Sralo sem buracos = 25π
3. Relação entre volume e capacidade
Volume do cilindro circular reto
No 6º ano, você deve ter estudado os corpos redondos, aqueles que têm pelo menos uma parte da superfície com fórma arredondada.
Observe algumas fotografias de objetos e os respectivos corpos redondos que eles lembram.

Por ora, vamos voltar a atenção para o cilindro reto, destacando alguns de seus elementos.
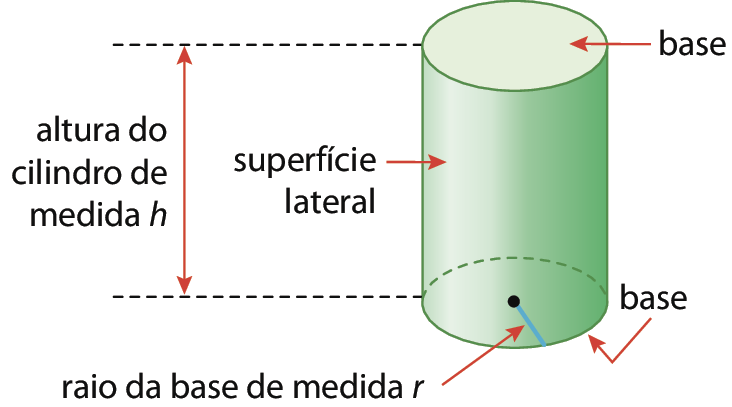
A maneira como observamos os objetos pode nos fornecer ou omitir informações sobre eles.
Observe como poderiam ser representadas algumas vistas de uma pilha de bolachas com o formato cilíndrico, cujas medidas r e h são dadas em centímetro.

Na vista superior, notamos apenas uma superfície circular e podemos calcular a medida da área dessa superfície, em centímetros quadrados, que é uma base do cilindro: Sb = πr 2
Na vista frontal, percebemos apenas a altura de medida h da pilha de bolachas.
Se h = 1, a medida do volume do cilindro é Vc = πr 2; se h = 2, a medida do volume do cilindro é Vc = πr 2 ⋅ 2; se h = 3, a medida do volume do cilindro é Vc = πr 2 ⋅ 3, e assim por diante, com as medidas de volume sempre dadas em centímetros cúbicos.
A medida do volume dessa pilha cilíndrica de bolachas é dada pelo produto entre as medidas da área da base e da altura.
Vc = πr 2h
Respostas e comentários
3. Relação entre volume e capacidade
Discuta com os estudantes o procedimento realizado para o cálculo da medida do volume de um cilindro circular reto.
Se julgar adequado, aproveite esse momento para apresentar a eles o cálculo das medidas das áreas lateral e total desse cilindro. Para isso, providencie vários modelos desse tipo de cilindro para que os estudantes possam manipulá‑los.
Ao observar a planificação da superfície desse sólido, eles poderão calcular as medidas da área lateral e da área de cada base do cilindro.
Acompanhe um exemplo.
Vamos calcular a medida aproximada do volume de um pacote de bolachas recheadas que tem 25 bolachas circulares com 4 centímetros de medida de diâmetro e altura medindo 8 milímetros cada uma.
A medida do raio, em centímetro, é metade da medida do diâmetro; logo, r = 4 : 2 = 2.
A medida da área, em centímetros quadrados, da base é aproximadamente igual a Sb ≃ 3,14 ⋅ 22 = 12,56.
Devemos escrever a medida da altura com a mesma unidade de medida dos outros elementos. A altura de cada bolacha mede 8 milímetros, ou seja, 0,8 centímetro.
Logo, a altura do pacote de bolachas, em centímetro, é dada por: h = 25 ⋅ 0,8 = 20.
Agora, podemos calcular a medida do volume do pacote de bolachas, em centímetros cúbicos:
Vb ≃ 12,56 ⋅ 20 = 251,2
O pacote de bolachas tem aproximadamente 251,2 centímetros cúbicos de volume.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
19 Dadas as medidas do raio e da altura, qual é o cilindro reto de volume com maior medida, C₁ ou C₂?
C₁: raio r₁ medindo 3 centímetros e altura h₁ medindo 5 centímetros
C₂: raio r₂ medindo 5 centímetros e altura h₂ medindo 3 centímetros
20 Pesquise três embalagens cilíndricas de tamanhos diferentes, obtendo, com uma régua, as medidas aproximadas do raio e da altura. Depois, calcule as medidas aproximadas dos volumes dessas embalagens.
Sugestão: lata de óleo comestível, lata de milho ou ervilha, lata de atum, galão de tinta etcétera
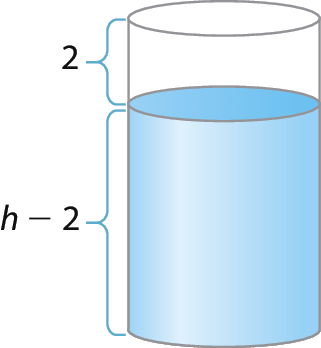
21 Bruno é poceiro e costuma utilizar uma máquina para fazer poços com diâmetro medindo 1 métro. Ele sabe que em um terreno a água começa a aflorar com 2 métros de medida de profundidade e quer um poço que, depois de pronto, tenha cêrca de 8 métros cúbicos de água. Ao todo, Bruno terá de cavar um poço de aproximadamente quantos metros de medida de profundidade?
Volume e capacidade
Respostas e comentários
19. C2, pois V1 = 45π e V2 = 75π.
20. Resposta pessoal.
21. 12 métros
Exercícios propostos
Para a resolução do exercício 19, lembre aos estudantes que a medida do volume de um cilindro reto é dada por Vc = πr2h. Assim, para o cilindro C1, de raio medindo 3 centímetros e altura medindo 5 centímetros, obtemos:
VC1 = π · 32 · 5
VC1 = π · 9 · 5
VC1 = 45π
Para o cilindro C₂, de raio medindo 5 centímetros e altura medindo 3 centímetros, obtemos:
VC2 = π · 52 · 3
VC2 = π · 25 · 3
VC2 = 75π
Portanto, o cilindro C₂ é o cilindro reto de maior medida de volume.
A resolução e comentários do exercício 20 estão no início deste Manual, nas orientações específicas do capítulo 12.
No exercício 21, a figura pode auxiliar a compreensão do texto do enunciado. Ressalte esse fato para os estudantes e, se necessário, analise com eles as características da figura.
Eles devem perceber que 8 métros cúbicos é a medida do volume correspondente a um cilindro de altura de medida (h ‒ 2) e diâmetro da base medindo 1 métro, resultando em um raio que mede 0,5 métro. Assim:
Vcilindro = (medida da área da base) · (medida da altura do cilindro)
8 = π · (0,5)2 · (h ‒ 2)
8 =
8 igual a, fração, numerador pi, denominador 4, vezes, h menos 2· (h ‒ 2)
8 ·
8 vezes, fração, numerador pi, denominador 4, igual a, fração, numerador pi, denominador 4, vezes, h menos 2, vezes, fração, numerador pi, denominador 4.=
8 vezes, fração, numerador pi, denominador 4, igual a, fração, numerador pi, denominador 4, vezes, h menos 2, vezes, fração, numerador pi, denominador 4.· (h ‒ 2) ·
8 vezes, fração, numerador pi, denominador 4, igual a, fração, numerador pi, denominador 4, vezes, h menos 2, vezes, fração, numerador pi, denominador 4.fração, numerador 32, denominador pi, igual a, h menos 2
= h ‒ 2
fração, numerador 32, denominador pi, mais 2, igual a, h menos 2 mais 2
+ 2 = h ‒ 2 + 2
h =
h igual a, fração, numerador 32, denominador pi, mais 2, aproximadamente, 10 mais 2+ 2 ≃ 10 + 2
h ≃ 12
Portanto, deve-se cavar um poço de aproximadamente 12 métros de profundidade.
Já estudamos que o litro corresponde à medida da capacidade de um recipiente cúbico com 1 decímetro de medida de aresta, ou seja, a medida do volume ocupado por 1 litro de líquido é 1 decímetro cúbico.
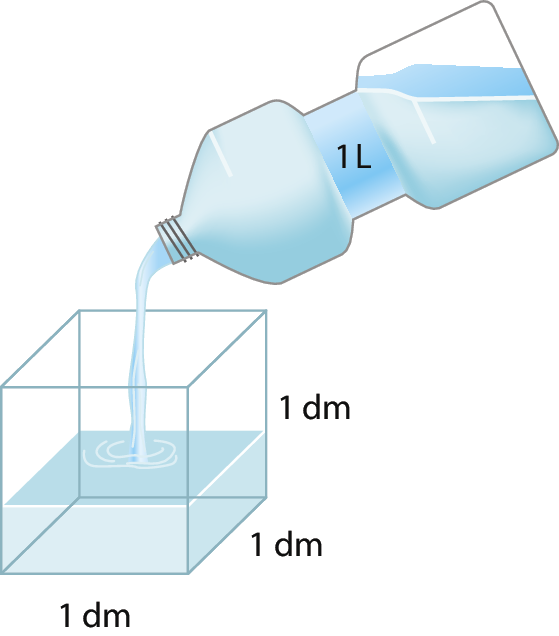
1 litro = 1 decímetro cúbico

Então, podemos escrever as seguintes relações:
• 1 litro = 1 decímetro cúbico .1000 mililitros = .1000 centímetros cúbicos
1 mililitro = 1 centímetro cúbico

• 1 litro = 1 decímetro cúbico .1000 litros = .1000 decímetros cúbicos
.1000 litros = 1 métro cúbico

(As imagens não respeitam as proporções reais entre os objetos.)
Acompanhe dois exemplos de conversão de unidades de medida de volume em unidades de medida de capacidade.
a) 1,2 métro cúbico em litro.
Como 1 métro cúbico = .1000 litros, temos: 1,2 métro cúbico = .1200 litros
b) .3200 centímetros cúbicos em centilitro.
Inicialmente, transformamos .3200 centímetros cúbicos em decímetros cúbicos: .3200 centímetros cúbicos = 3,2 decímetros cúbicos Como 1 decímetro cúbico = 1 litro, temos: .3200 centímetros cúbicos = 3,2 litros = 320 centilitros
Respostas e comentários
Volume e capacidade
Promova uma discussão sobre os conceitos de capacidade e volume, comparando os dois conceitos. Assim, os estudantes expõem o que sabem acerca deles. Trabalhe com eles algumas relações entre as unidades de medida de capacidade e de volume, promovendo o desenvolvimento da habilidade (EF08MA20).
Se julgar conveniente, faça a experiência de utilizar uma caixa cúbica de 1 decímetro cúbico de capacidade para preenchê-la com a areia contida em uma garrafa de 1 litro, o que evidenciará a relação 1 litro = 1 decímetro cúbico.
O cálculo da medida do volume da caixa cúbica promove o desenvolvimento da habilidade (EF08MA21).
Partindo da relação linear 1 decímetro = 10 centímetros, é interessante mostrar aos estudantes como obter esta outra relação:
.1000 mililitros = .1000 centímetros cúbicos
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
22 Escreva a conversão de:
a) 12 decímetros cúbicos em litro;
b) 5,4 métros cúbicos em litro;
c) 30 centímetros cúbicos em litro;
d) 30 centímetros cúbicos em mililitro;
e) 500 milímetros cúbicos em mililitro;
f) 0,25 métro cúbico em litro.
23 Qual é a medida da capacidade, em litro, de uma caixa cúbica com 0,80 métro de aresta?
24 Leia o texto e responda às questões.

Evolução das demandas de água no Brasil
A demanda de água no Brasil vem crescendo continuamente ao longo dos anos, com destaque para o abastecimento das cidades, a indústria e a agricultura irrigada. A retirada para irrigação aumentou de 640 para 965 métros cúbicos por segundonas últimas duas décadas e representa aproximadamente 50% da retirada total pelos usos consuntivosglossário setoriais de água em 2020 — esse setor tem grande potencial de expansão e continuará liderando o crescimento das retiradas.
Estima-se um aumento de 42% das retiradas de água nos próximos 20 anos (até 2040), passando de .1947 métros cúbicos por segundo para .2770 métros cúbicos por segundo, um incremento de 26 trilhões de litros ao ano extraídos de mananciais. Esses dados reforçam a necessidade de ações de planejamento para que os usos se desenvolvam com segurança hídrica, evitando crises hídricas e proporcionando os usos múltiplos da água, principalmente quando considerados os efeitos das mudanças climáticas no ciclo da água.
[reticências] As mudanças climáticas tendem a acelerar alguns usos, especialmente na agropecuária e na agroindústria. A demanda para a irrigação, por exemplo, pode ter um acréscimo de 15% em 2040 em relação à demanda tendencial (com base no clima médio atual). Nas regiões de irrigação mecanizada (excluindo o arroz sob inundação), a demanda pode ter um acréscimo de 20% em um cenário mais crítico de mudança do clima.
Fonte: AGÊNCIA Nacional de Águas e Saneamento Básico (ANA). Conjuntura dos Recursos Hídricos no Brasil 2021: Relatório Pleno. Disponível em: https://oeds.link/l2oZAF. Acesso em: 20 março 2022.
a) De anos anteriores para 2020, de quantos métros cúbicos por segundo foi o aumento no uso consuntivo de água?
b) Segundo o texto, ao passar de .1947 métros cúbicos por segundo para .2770 métros cúbicos por segundo, há um aumento de 26 trilhões de litros de água extraídos de mananciais ao ano. Se esse aumento fosse de 100 métros³/s, aproximadamente, quantos litros de água seriam extraídos de mananciais em um ano? Essa quantidade equivale a quantos metros cúbicos de água?
c) Sabendo que, em 2020, a irrigação foi responsável por uma retirada de 942 métros³/s de água, se a previsão de acréscimo para 2040 for entre 15% e 20%, como o estimado, de quanto será a retirada de água pela irrigação neste ano?
d) O que pode causar o aumento desenfreado do consumo da água?
e) Converse com o professor e os colegas sobre ações que podem ser planejadas para evitar o aumento no uso de água e não gerar uma crise hídrica no país.
25 Em determinado mês, um hidrômetro registrou o consumo mensal de água de uma casa de 22 métros cúbicos. Quantos litros de água foram gastos nessa residência?
26

Reúna-se com um colega e pesquisem o número estimado de habitantes do município em que vocês vivem. Depois, façam uma estimativa da quantidade de domicílios que existem nele. Para fazerem a estimativa, utilizem 2,9 como o número médio de moradores em uma residência. Em seguida, resolvam a questão.
Supondo que, em média, os domicílios tenham uma caixa-d’água com capacidade de 500 litros, calculem quanto tempo um sistema com vazão de 56 métros³/s levaria para encher todas as caixas-d’água.
Leiam com atenção as informações a seguir.
Respostas e comentários
22. a) 12 litros
22. b) .5400 litros
22. c) 0,030 litro
22. d) 30 mililitros
22. e) 0,5 mililitro
22. f) 250 litros
23. 512 litros
24. a) 325 métros cúbicos por segundo
24. b) 3,16 trilhões de litros de água ou 3,16 bilhões de metros cúbicos de água.
24. c) De .1083,3 métros cúbicos por segundo a .1130,4 métros cúbicos por segundo.
24. d) Mudanças climáticas.
24. e) Resposta pessoal.
25. .22000 L
26. A resposta depende da população da cidade.
Exercícios propostos
O exercício 24 pode ser feito em duplas. Caso julgue necessário, analise o texto com os estudantes. Ao final, peça a cada dupla que crie outras questões sobre esse texto e troquem-nas com outra dupla: cada uma responde às questões elaboradas pela outra. Compartilhe todas as questões e as respostas, fazendo uma correção coletiva com a turma. Essa é mais uma oportunidade para o desenvolvimento da competência geral 9. O trabalho em grupo valoriza a diversidade de ideias e propicia o exercício da empatia, do diálogo e da cooperação, com o objetivo de chegar a um resultado em comum.
Ao apresentar aos estudantes dados sobre as demandas de água no Brasil, converse com eles sobre o impacto dessas demandas no meio ambiente e a necessidade de ações de planejamento para que ocorra o consumo consciente e para evitar crises hídricas, cada vez mais comuns no Brasil nos últimos anos. Esse exercício possibilita o trabalho com o Tema Contemporâneo Transversal meio ambiente. Converse com os estudantes sobre a demanda de água na cidade ou região onde residem. Pergunte a eles se já ouviram falar em crise hídrica em sua região e se sabem quais são os possíveis impactos dessa crise em seu dia a dia e no meio ambiente. Converse também sobre as atitudes que podem ser tomadas para evitar o aumento na demanda de água e evitar uma crise hídrica (item ê).
Para o item a, temos:
965 métros cúbicos por segundo ‒ 640 métros cúbicos por segundo = 325 métros cúbicos por segundo
Logo, o aumento no uso consuntivo de água foi de 325 métros cúbicos por segundo.
No item b, temos:
.2770 métros cúbicos por segundo ‒ .1947 métros cúbicos por segundo = 823 métros cúbicos por segundo
E 823 métros3/s corresponde a um aumento de 26 trilhões de litros de água extraídos de mananciais ao ano. Se esse aumento fosse de 100 métros cúbicos por segundo, obteríamos:
≃ ....3159173754556
Portanto aproximadamente 3,16 trilhões de litros de água seriam extraídos de mananciais em um ano, que equivale a 3,16 bilhões de métros cúbicos.
A resolução do item c possibilita o desenvolvimento da habilidade (EF08MA04). Para essa resolução é preciso determinar 15% de 942 métros cúbicos por segundo e 20% de 942 métros cúbicos por segundo.
· 942 =
15 centésimos vezes 942, igual a 14130 centésimos, igual a 141,3= 141,3
· 942 =
20 centésimos vezes 942, igual a 18840 centésimos, igual a 188,4= 188,4
Assim, a retirada de água pela irrigação em 2040 será entre .1083,3 métros³/s (942 + 141,3 = .1083,3) e .1130,4 métros cúbicos por segundo (942 + 188,4 = .1130,4).
No item d, de acôrdo com o texto, o aumento desenfreado do consumo da água pode ser causado por mudanças climáticas.
As resoluções e comentários dos exercícios 22, 23, 25 e 26 estão no início deste Manual, nas orientações específicas do capítulo 12.
27

Junte-se a um colega e façam o que se pede.
Aquífero Guarani
O Aquífero Guarani encontra-se sob área de quatro países: Brasil, Uruguai, Argentina e Paraguai. [reticências] Com uma extensão calculada em mais de 1 milhão de quilômetros quadrados, somente no estado de São Paulo abastece total ou parcialmente [reticências] cêrca de 200 cidades. Só a área de recarga tem .46211 quilômetros quadrados que equivale a 4,6 milhões de hectares. É considerado um dos maiores reservatórios de água subterrânea do planeta, com .37000 quilômetros cúbicos de água de capacidade e um volume anual de 163 quilômetros cúbicos de fluxo de recarga. [reticências]
[reticências] Desde 2009 o Aquífero Guarani entrou no estado que se chama “rebaixando”, ou seja, seu volume de recarga é inferior ao volume de água retirado. Em Ribeirão Preto, por exemplo, a taxa de retirada já foi 30 vezes o volume de recarga. [reticências]
Fonte: GIGANTE Guarani. Aquífero Guarani. Site Gigante Guarani. Botucatu, [2015?]. Disponível em: https://oeds.link/DffyjW. Acesso em: 14 julho 2022.
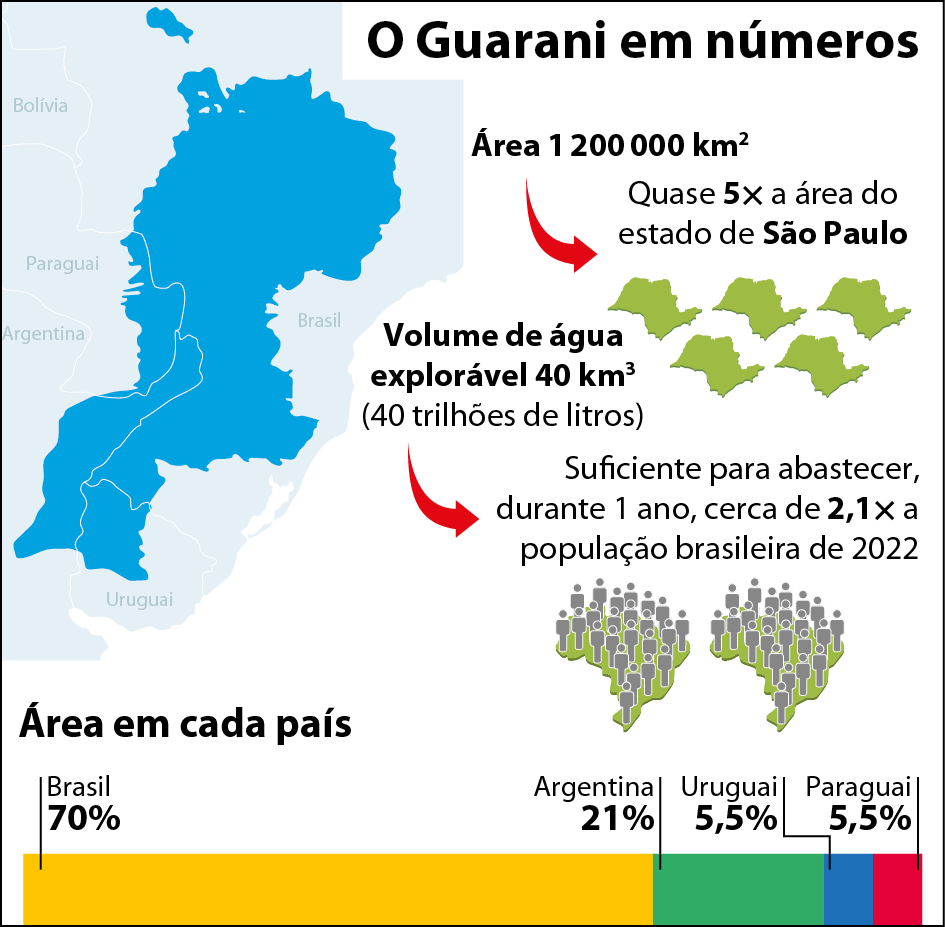
Agora, respondam às questões.
a) Quantos metros cúbicos de água são exploráveis no Aquífero Guarani?
b) Considerando o infográfico qual seria a medida de área aproximada do estado de São Paulo?
c) Segundo o texto, o município de Ribeirão Preto já chegou a retirar um volume de água 30 vezes maior que o volume reposto no sistema. Para uma reposição de .10000 litros de água, quantos metros cúbicos teriam sido retirados?
28 Uma piscina tem 8 métros de medida de comprimento, 4 métros de medida de largura e 1,60 métro de medida de profundidade. Ela está com água ao nível de 1,50 métro.
Se 10 pessoas mergulhassem nessa piscina e o nível da água subisse 2 centímetros, qual seria a medida do volume médio do corpo de cada uma dessas pessoas em decímetro cúbico?
29 Durante uma pesquisa, um cientista precisou realizar várias etapas. Foram três etapas diárias durante 10 dias. Em cada etapa, eram acrescentados 3 mililitros de um fármaco em uma solução. Quantos centímetros cúbicos desse fármaco foram acrescentados na solução durante a pesquisa?
30 Os médicos recomendam que uma pessoa beba pelo menos 2 litros de água por dia. Uma única goteira pode desperdiçar 150 litros de água por dia. Determine o tempo, em dia, que essa quantidade de água seria suficiente para uma pessoa beber, atendendo à recomendação médica mínima.
31 Leia o texto a seguir e responda às questões.
![Ilustração. Folha de papel com a informação: O etanol ou álcool etílico pode ser produzido a partir de matérias-primas, como milho, beterraba ou cana-de-açúcar. No Brasil, o modelo mais utilizado é o da cana. Essa opção tem algumas vantagens, pois é mais produtiva do que o combustível extraído do milho e causa um impacto menor ao meio ambiente. Se um hectare de milho rende 3 mil litros de etanol, a mesma área equivale a 7,5 mil litros no caso da cana. [...]](../resources/images/im_251_267_mb8_c12_f2_lp_g24_digital_group_52561.png)
a) Quantas vezes mais etanol rende a cana-de-açúcar em relação ao milho?
b) Em 2020 ou 2021, o estado de São Paulo colheu cêrca de 4,3 milhões de hectares de cana-de-açúcar, sendo o maior produtor nacional. Se toda essa cana fosse destinada à produção de etanol, quantos litros seriam obtidos?
Respostas e comentários
27. a) 40 bilhões de metros cúbicos.
27. b) .240000 quilômetros quadrados
27. c) 300 métros cúbicos
28. 64 decímetros cúbicos
29. 90 centímetros cúbicos
30. 75 dias.
31. a) duas vírgula cinco vezes.
31. b) ...32250000000 litros
Exercícios propostos
O exercício 27 possibilita ampliar a compreensão dos estudantes quanto à relação entre litro e metro cúbico e sua aplicação na resolução de problemas que envolvem o cálculo de medidas de capacidade e de volume, desenvolvendo, assim, a habilidade (EF08MA20).
Para responder às questões, os estudantes devem buscar informações nos textos apresentados e no infográfico. Por isso, caso eles ainda tenham dificuldades em interpretação de texto, é importante fazer a leitura com a turma, apontando os dados mais importantes do texto e perguntando aos estudantes sobre seus significados.
No item a, o infográfico mostra que o volume de água explorável no Aquífero Guarani mede 40 trilhões de litros, que equivale a 40 bilhões de metros cúbicos. Lembre aos estudantes que 1 métro cúbico = .1000 litros ou 1 litro =
1 milésimométros cúbicos, assim:
....40000000000000 litros = =
40000000000000 milésimosmétros cúbicos = = ...40000000000 métros cúbicos
No item b, de acôrdo com o infográfico, ..1200000 quilômetros quadrados correspondem a cinco vezes a medida da área do estado de São Paulo; portanto, essa área deve medir .240000 quilômetros quadrados (..1200000 : 5 = .240000).
No item c, como o volume de água retirado é 30 vezes maior que o volume reposto no sistema, para uma reposição de .10000 litros de água, obtemos:
.10000 · 30 = .300000
Como 1 métro cúbico = .1000 litros, .300000 : .1000 = 300; portanto, 300 metros cúbicos de água teriam sido retirados.
As resoluções dos exercícios 28 a 31 estão no início deste Manual, nas orientações específicas do capítulo 12.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
O cano de alimentação de um tanque despeja água no ritmo que mostra o quadro.
|
Tempo |
Medida do volume de água despejada |
|---|---|
|
1º minuto |
1 L |
|
2º minuto |
2 L |
|
3º minuto |
4 L |
|
4º minuto |
8 L |
Considerando que, inicialmente, o tanque está vazio, responda às questões.
a) Quantos litros de água o cano de alimentação despeja no tanque no 5º minuto? E no 6º? E no 7º? E no 8º?
b) Após 8 minutos, esse tanque fica com água até a metade. Quantos litros de água ele contém nesse momento?
c) Após 8 minutos, aproximadamente quantos minutos ainda serão necessários para o tanque ficar cheio?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Um polígono regular tem a soma das medidas dos seus ângulos internos igual a .2520graus. Determine a medida do ângulo:
a) central desse polígono;
b) interno desse polígono;
c) externo desse polígono.
2 Quantos lados tem, se existir, um polígono regular em que o ângulo:
a) central mede 9graus?
b) interno mede 30graus?
c) externo mede 10graus?
3 Qual é a menor medida do ângulo interno de um polígono regular? E a maior?
4 A figura a seguir é a planificação da superfície de um paralelepípedo retângulo. Calcule a medida do volume, em milímetro cúbico, desse paralelepípedo.
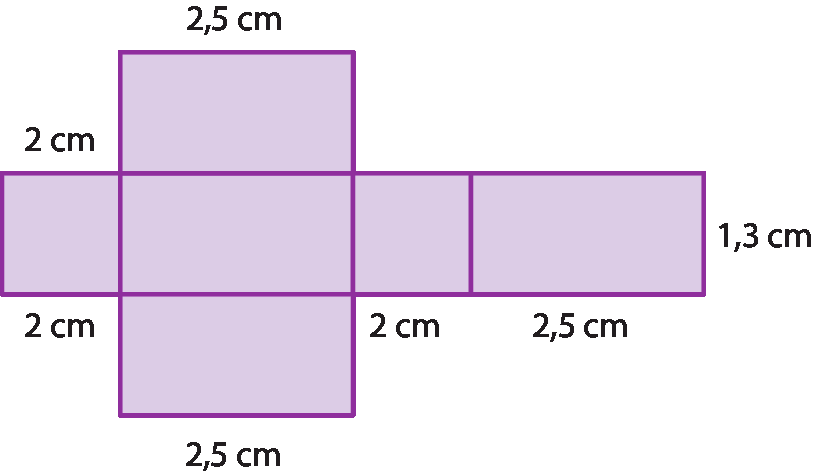
5 Qual é a medida do volume de argila necessária para fabricar .1000 tijolos com as seguintes medidas: 22 centímetros de comprimento, 10 centímetros de largura e 5 centímetros de altura?
6 Uma caixa cilíndrica tem 25 centímetros de medida de raio, 100 centímetros de medida de altura e está cheia de água. Considere π = 3,14.
a) Calcule a medida da capacidade dessa caixa em litro.
b) Calcule a medida da massa da água contida nessa caixa. (Considere que a massa de 1 centímetro cúbico equivale a 1 grama.)
7 (saréspi) Se dobrarmos o volume de água contida em cada um dos recipientes indicados na figura, a altura h da água dobrará apenas no(s) recipiente(s):
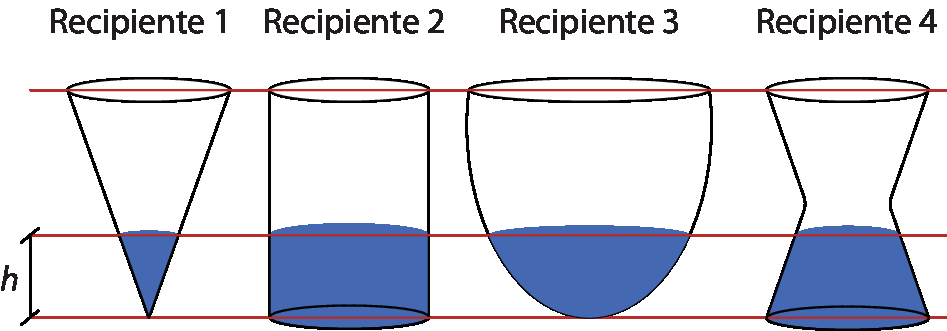
a) 4.
b) 3.
c) 2.
d) 1.
8 (saréspi) Na casa de Mariana o gasto diário de água com descargas correspondia a
2 quintosda capacidade da caixa-d’água. Com a troca por descargas mais econômicas, esse consumo passou a ser de
1 quartoda capacidade da mesma caixa-d’água. Logo, a fração da caixa-d’água economizada com essa troca foi de:
a)
1, 20 avosb)
3, 20 avosc)
2 quartosd)
1 quintoRespostas e comentários
Pense mais um poucoreticências: a) 16 litros; 32 litros; 64 litros; 128 litros.
b) 255 litros
c) 1 minuto.
1. a) 22,5graus
1. b) 157,5graus
1. c) 22,5graus
2. a) 40 lados.
2. b) Não existe.
2. c) 36 lados.
3. 60graus. Não é possível determinar a maior medida do ângulo interno de um polígono regular.
4. .6500 milímetros cúbicos
5. .1100 decímetros cúbicos
6. a) 196,25 litros
6. b) .196250 g
7. Alternativa c.
8. Alternativa b.
Pense mais um poucoreticências
Verifique se os estudantes percebem a regularidade apresentada no quadro: a cada minuto, o volume de água despejada dobra, originando a sequência:
1, 2, 4, 8, 16, 32, 64, 128, reticências
Espera-se que eles percebam que essa é a sequência das potências de base 2 com expoente natural.
20 → 1º termo
21 → 2º termo
22 → 3º termo
23 → 4º termo
24 → 5º termo
25 → 6º termo
26 → 7º termo
27 → 8º termo
⋮ ⋮ ⋮
Desse modo, eles podem identificar que o enésimo termo dessa sequência é dado por 2n ‒ 1, em que n é a posição do termo na sequência, ou seja, n é um número natural maior que zero; dessa maneira, mobilizam a habilidade (ê éfe zero oito ême ah um zero).
Considerando que essa sequência continue indefinidamente, pergunte a eles qual é a medida do volume de água despejada no 12º minuto. Eles devem perceber que o valor procurado corresponde ao 12º termo da sequência, ou seja, é dado por
2n ‒ 1, para n = 12.
Assim: 212 ‒ 1 = 211 = .2048, ou seja, no 12º minuto foram despejados .2048 litros de água.
No item b, os estudantes devem perceber que precisam adicionar as medidas dos volumes despejados do 1º ao 8º minuto.
As resoluções das atividades estão no início deste Manual, nas orientações específicas do capítulo 12.
Exercícios complementares
Este bloco de exercícios trabalha os principais conceitos estudados no capítulo. Espera-se que os estudantes utilizem os conhecimentos construídos, percebendo se ainda têm alguma dificuldade.
No exercício 7, peça a eles que justifiquem a resposta dada. Ao expor suas ideias, os estudantes podem detectar possíveis equívocos no procedimento que utilizaram ou auxiliar colegas que não entenderam o enunciado.
No exercício 8, espera-se que eles percebam que devem comparar as frações dadas (pois são referentes à mesma capacidade) e determinar a diferença entre elas.
As resoluções dos exercícios 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 12.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Qual dos polígonos a seguir não é regular?
a)
b)
c)
d)
2 Um hexágono circunscrito terá quantos pontos em comum com a circunferência?
a) 4
b) 5
c) 6
d) 7
3 Um pingente de colar tem uma estrutura de prata triangular e uma pedra circular de quartzo verde, de diâmetro medindo 1,1 centímetro, conforme a figura a seguir.
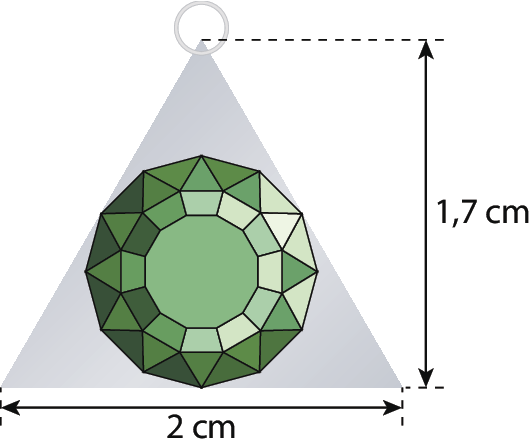
Qual é a medida aproximada da área da superfície da estrutura triangular que fica visível nesse pingente?
a) 2,8 centímetros quadrados
b) 1,7 centímetros quadrados
c) 0,95 centímetros quadrados
d) 0,75 centímetros quadrados
4 Qual é a medida do ângulo interno de um polígono regular de 20 lados?
a) 180graus
b) 162graus
c) 150graus
d) 130graus
5 Um polígono regular tem 8 lados. Qual é a soma das medidas de seus ângulos internos?
a) .1080graus
b) .1260graus
c) .1440graus
d) .1800graus
6 A prefeitura de um município irá instalar uma fonte circular em uma praça pública. O diâmetro da fonte mede 7 métros, conforme indica a figura a seguir.
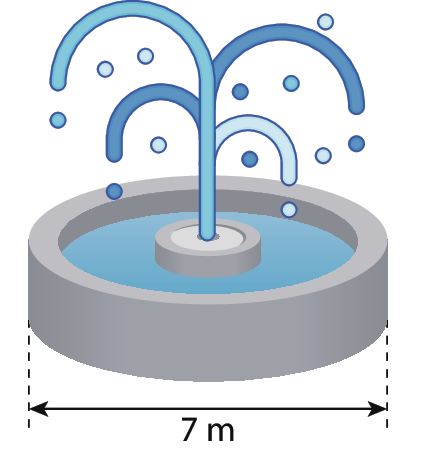
As medidas aproximadas da área que a fonte ocupará na praça e do comprimento da circunferência da fonte são, respectivamente:
a) 38,5 métros quadrados e 22 métros.
b) 38,5 métros quadrados e 11 métros.
c) 76,9 métros quadrados e 22 métros.
d) 153,9 métros quadrados e 43 métros.
7 Um copo cilíndrico tem altura de medida igual a 12 cm e raio da base medindo 3 cm. Ele está com água até a metade de sua capacidade. Quantos mililitros de água há no copo?
a) 113,04 mililitros
b) 169,56 mililitros
c) 339,12 mililitros
d) 678,64 mililitros
8 Uma garrafa de 2 litros de suco teve seu conteúdo inteiramente distribuído em copos de 400 centímetros cúbicos. A quantidade de copos totalmente preenchidos de suco foi:
a) 3 copos.
b) 4 copos.
c) 5 copos.
d) 8 copos.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) O que caracteriza um polígono como regular?
b) Considere uma circunferência inscrita em um polígono regular. Qual é a relação entre os lados desses polígonos e os pontos de tangência?
c) Qual é a relação entre a medida do ângulo central de um polígono regular e a quantidade de lados desse polígono?
d) Escreva a fórmula que relaciona a medida do ângulo interno de um polígono regular e a soma das medidas de seus ângulos internos.
e) Qual é a medida da área de um círculo de raio de medida r?
f ) Qual é a medida do volume de um cilindro circular reto com raio de medida r e altura de medida h?
g) Como você explicaria para um colega a diferença entre volume e capacidade?
Respostas e comentários
1. Alternativa d.
2. Alternativa c.
3. Alternativa d.
4. Alternativa b.
5. Alternativa a.
6. Alternativa a.
7. Alternativa b.
8. Alternativa c.
Organizando: As respostas para estas questões estão no Manual.
Verificando
Esses testes são mais uma oportunidade para o estudante validar o entendimento do conteúdo estudado neste capítulo. Instrua-os a retornar às páginas anteriores caso alguma dúvida persista.
No teste 1, lembre-os das características dos polígonos regulares. Dos polígonos apresentados, o único que não tem todos os seus lados congruentes entre si e todos os seus ângulos congruentes entre si é o octógono da alternativa d.
No teste 2, lembre aos estudantes que um polígono circunscrito tem todos os seus vértices pertencentes à circunferência. Um hexágono tem 6 vértices; logo, tem 6 pontos em comum com a circunferência; portanto, a alternativa c é a correta.
Para a resolução do teste 3, lembre os estudantes do cálculo da medida da área de uma superfície triangular
St igual a, fração, numerador b vezes h, denominador 2e do cálculo da medida da área de uma superfície circular (Sc = πr elevado a 2).
A medida da área do triângulo é 1,7 centímetros quadrados
Fração, numerador 2 vezes 1,7, denominador 2, igual a 1,7.
A medida da área circular da pedra de raio medindo r = 0,55 centímetro é aproximadamente 0,95 centímetro quadrado (π · 0,55elevado a 2 = 0,9485 ≃ 0,95).
Portanto, a área da superfície da estrutura triangular do pingente mede aproximadamente 0,75 centímetro quadrado (1,7 menos 0,95 = 0,75), e a alternativa d é a correta.
Para a resolução do teste 4, lembre os estudantes do cálculo da medida do ângulo interno de um polígono regular:
Assim, para n = 20, obtemos:
ái =
ai igual a, fração, numerador 20 menos 2, vezes 180 graus, denominador 20, igual a 162 graus.= 162°
Logo, a alternativa b é a correta.
As resoluções dos exercícios 5 a 8 estão no início deste Manual, nas orientações específicas do capítulo 12.
Organizando
Incentive os estudantes a organizar seus aprendizados no caderno, fazendo resumos, mapas conceituais, fluxogramas ou aplicando destaques em conceitos importantes.
As questões propostas têm como objetivo fazer com que eles retomem os conteúdos estudados no capítulo e reflitam sobre algumas temáticas. Após sua correção é importante pedir aos estudantes que compartilhem suas respostas. Essa estratégia permitirá o compartilhamento de dúvidas e percepções sobre o conteúdo, contribuindo para o aprendizado de todos.
As resoluções das questões estão no início deste Manual, nas orientações específicas do capítulo 12.
Glossário
- Hexadecágono
- : polígono de 16 lados.
- Voltar para o texto
- Usos consuntivos
- : usos que consomem água.
- Voltar para o texto