Página 38

Parte 1

CAPÍTULO 2 Operações com números reais

Fotografia. Pintura. Ao fundo, construção de cor clara com pessoas em pé, entre homens e mulheres. À frente, pessoas sentadas nos degraus da construção. Um homem calvo de barba, camisa vermelha escreve em um livro. Ao lado, homem de cabelo escuro, barba, blusa laranja está com um livro aberto e mostra para um homem atrás dele. À direita, homem de cabelo preto sentado com a cabeça baixa e a mão sobre papéis. — SANZIO, R. Detalhe da obra Escola de Atenas. 1509 a 1510. Pintura em reboco, 5 por 7,7 métros. Na imagem, Pitágoras, sentado à esquerda, é observado por Parmênides, em pé, e Hipatia, ao fundo.

Reza a lenda que a descoberta dos irracionais causou tanto escândalo entre os gregos que o pitagórico responsável por ela, Hípaso, foi expulso da escola e condenado à morte. Não se sabe de onde veio essa história, mas parece pouco provável que seja verídica. reticências

Na verdade, a descoberta da incomensurabilidade representou uma nova situação que motivou novos desenvolvimentos matemáticos.

ROQUE , T. História da Matemática: uma visão crítica, desfazendo mitos. Rio de Janeiro: zarrár, 2012. página 124 a 126.

Observe, leia e responda no caderno.

a) Você se lembra de algum fato da história da Matemática sobre números? Se sim, descreva-o. Se não, faça uma pesquisa, escolha um que ache interessante e relate.

b) Com uma fita métrica, meça o contorno e o diâmetro de algumas rodas com tamanhos diferentes. Depois, divida a medida do contorno pela medida do diâmetro, ambas na mesma unidade de medida.

c) Verifique se os quocientes obtidos no item b são próximos do número irracional “pi”.

Página 39

1. Potências nas medidas astronômicas, subatômicas e informáticas

O Sistema Internacional de Unidades (ésse Í) tem uma história recente se comparada à histórica necessidade humana de medir, que vem desde a origem das civilizações. Antes, cada povo tinha seu próprio sistema de medidas, muitas vezes com unidades imprecisas, tendo por base o corpo humano (palmo, pé, cúbito, jarda, passo etcétera), o que criava muitos problemas, principalmente para o comércio.

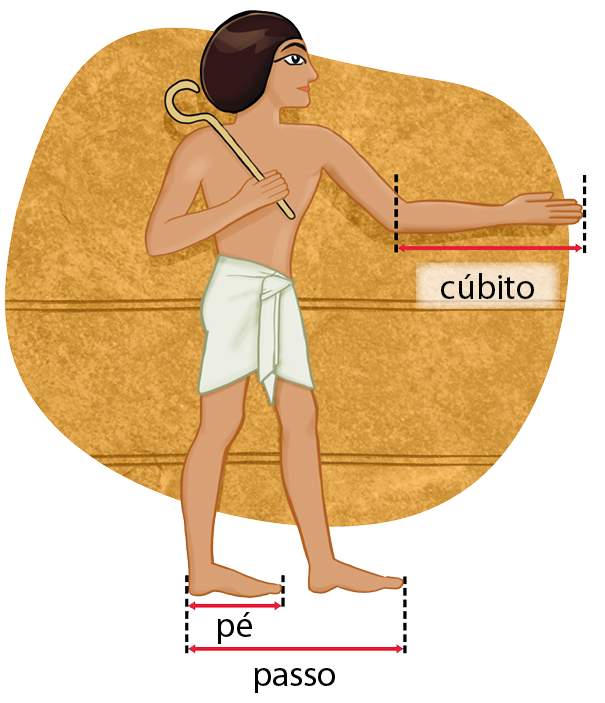
Ilustração. Homem em pé virado para direita. Ele está com um braço esticado. Do cotovelo até a ponta do dedo: cúbito. A medida do pé: pé. Medida de um pé a outro: passo.

O ésse Í, sistema atual desenvolvido com base no Sistema Métrico Decimal (ésse ême dê, França, 1799) e consolidado apenas em 1960, com suas sete unidades de base, é mais complexo e diversificado do que o ésse ême dê.

Visando atender a uma extensa gama de medidas para várias grandezas, há muitos prefixos no ésse Í. Observe o quadro a seguir.

Fotografia.
Metro graduado. — Metro padrão.

Nome	Símbolo	Fator pelo qual a unidade é multiplicada
yotta	Y	1024 = 1.000.000.000.000.000.000.000.000
zetta	Z	1021 = 1.000.000.000.000.000.000.000
exa	E	1018 = 1.000.000.000.000.000.000
peta	P	1015 = 1.000.000.000.000.000
tera	T	1012 = 1.000.000.000.000
giga	G	109 = 1.000.000.000
mega	M	106 = 1.000.000
quilo	k	103 = 1.000
hecto	h	102 = 100
deca	da	10
deci	d	10−1 = 0,1
centi	c	10−2 = 0,01
mili	m	10−3 = 0,001
micro	µ	10−6 = 0,000001
nano	n	10−9 = 0,000000001
pico	p	10−12 = 0,000000000001
femto	f	10−15 = 0,000000000000001
atto	a	10−18 = 0,000000000000000001
zepto	z	10−21 = 0,000000000000000000001
yocto	y	10−24 = 0,000000000000000000000001

Dados obtidos em: in metro. Disponível em: https://oeds.link/0SWA3H. Acesso em: 26 março 2022.

Fotografia. Medidor digital virado para a direita. — Quando apontado para determinado ponto ou objeto, o medidor digital calcula a medida da distância até ele.

Página 40

O tema medidas é muito amplo; por isso, vamos nos restringir à medida de comprimento cuja unidade de base é o metro (ême).

Ilustração. Fundo escuro com estrelas. À direita, astronauta aponta objeto para direita e diz: O metro é definido como a medida do comprimento do trajeto percorrido pela luz no vácuo durante um intervalo de tempo que mede 1, 299792458 avos de segundo.

O metro, como as demais unidades de base, tem múltiplos e submúltiplos dados por prefixos. Por exemplo: “quilo-” (do grego khílioi,ai,ei, mil, milhar): um quilômetro (1 cá ême) = mil metros (103 ême); “mili-” (do francês millième, milésimo): um milímetro (1 ême ême) = um milésimo de metro (10^‒3 ême).

No entanto, os prefixos da tabela conjugados com as unidades de base ainda são insuficientes ou inconvenientes para determinadas situações.

Na Astronomia, o estudo do Universo indica a necessidade de outras unidades de medida fóra do ésse Í, que são:

• Unidade Astronômica (U A): a medida da distância média entre a Terra e o Sol, uma unidade astronômica ≃ 1,5 ⋅ 1011 métros;

• ano-luz: a medida da distância que a luz percorre em 1 ano, 1 ano-luz ≃ 9,5 ⋅ 1015 métros ≃ 63.duzentas e quarenta e uma unidades astronômicas;

• parsec (pc): a medida da distância em que uma unidade astronômica (perpendicular à linha de visão) subtende um ângulo de 1 segundo de arco; 1 parsec ≃ 3,26 anos-luz ≃ .206265 unidades astronômicas.

Os Exoplanetas

Assim como o Sol, outras grandes estrelas se formaram. Será que essas estrelas poderiam também ter planetas em sua órbita? A resposta é sim! Esses planetas que se encontram fóra do nosso Sistema Solar, na órbita de outras estrelas, são chamados de exoplanetas.

Um exemplo de estrela que se formou como o nosso Sol é a anã vermelha Proxima Centauri. Ela é a estrela fóra do Sistema Solar que está mais próxima da Terra, podendo ser identificada no céu na constelação do Centauro, a uma distância de aproximadamente 4,2 anos-luz (cêrca de 40 trilhões de quilômetros) do nosso planeta.

Fotografia. Estrela arredondada vermelha luminosa em fundo escuro. — Esta ilustração da NASA mostra uma estrela anã vermelha orbitada por um exoplaneta hipotético. As anãs vermelhas tendem a ser magneticamente ativas, exibindo proeminências de arco e uma variedade de manchas escuras.

Fonte: RIOGA, L. Os exoplanetas. In: Blog Espaço do conhecimento UFMG. Belo Horizonte, [data provável: 2019]. Disponível em: https://oeds.link/ltYYdt. Acesso em: 24 março 2022.

Página 41

Na outra ponta das atividades científicas está a nanotecnologia.

Certa vez, o físico Eric Drexler disse: “A próxima grande revolução na ciência será tão pequena que você não vai enxergá-la nem com microscópio. Os efeitos, porém, serão devastadores”. Na nanotecnologia, como o próprio nome sugere, são trabalhadas medidas extremamente pequenas para o desenvolvimento de produtos com tamanho inferior a 100 nanômetros.

Observe o prefixo nano na tabela da página 39: 1 nanômetro é a unidade de medida de comprimento equivalente à bilionésima parte de um metro, ou 10‒9 métros (símbolo: êne ême).

Diferentemente da Astronomia, a nanotecnologia não criou novas unidades de medida.

Nanocápsulas feitas de polímeros naturais causam menos impactos ao meio ambiente

Cientistas da Embrapa e da Universidade Estadual Paulista (Unésp) testaram o impacto, em ambientes aquáticos, de dois compostos envoltos em nanocápsulas feitas de polímeros. Polímeros são macromoléculas formadas por unidades estruturais menores que podem ser naturais ou artificiais. No estudo, os pesquisadores verificaram que polímeros naturais causam menos impactos ambientais. reticências

Fotografia. Formas arredondadas transparentes em fundo azul. — O uso da nanotecnologia para fins agroalimentares é considerado mais sustentável ambientalmente do que formulações convencionais.

Fonte: TORDIN, C. Nanocápsulas feitas de polímeros naturais causam menos impactos ao meio ambiente. Embrapa. 14 dezembro 2021. Disponível em: https://oeds.link/Dq4tw0. Acesso em: 24 março 2022.

Hoje vivemos no mundo da informática. O byte é a menor unidade de armazenamento de dados, correspondente à codificação de um caractere (letra, algarismo, símbolo de pontuação).

Fotografia. Linhas coloridas com números e códigos. — Composição que remete a um código de programação de software.

A estrutura numérica de sistemas de informática é fundamentada no código binário, que representa os dados usando um sistema de dois símbolos, frequentemente “0” e “1”, chamado sistema binário. Por isso, os múltiplos das unidades de medida da informática são escritos considerando potências de base 2, e os prefixos utilizados para identificá-los têm nomenclatura própria. São os prefixos binários: kibi (cá í), mebi (ême í), gibi (gê I), tebi (tê Í), pebi (pê í), exbi (ê í), zebi (zê í) e yobi (ípsilon í). Note que esses prefixos derivam dos prefixos do ésse Í e são todos acompanhados da contração da palavra binário, "bi".

• byte (bê) é a menor unidade de armazenamento;

• kibibyte (cá í bê) equivale a 210 bytes ou .1024 bytes; 1 kibi báite = 210 báites;

• mebibyte (ême í bê) equivale a 220 bytes ou .1024 kibibytes; 1 mebi báite = 210 kibi báites = 220 báites;

• gibibyte (gê í bê) equivale a 230 bytes ou .1024 mebibytes; 1 gibi báite = 210 mebi báites = 230 báites;

• tebibyte (tê í bê) equivale a 240 bytes ou .1024 gibibytes; 1 tebi báite = 210 gibi báites = 240 báites;

• pebibyte (pê i bê) equivale a 250 bytes ou .1024 tebibytes; 1 pebi báite = 210 tebi báites = 250 báites;

• exbibyte (é í bê) equivale a 260 bytes ou .1024 pebibytes; 1 exbi báite = 210 pebi báites = 260 báites;

• zebibyte (zê í bê) equivale a 270 bytes ou .1024 exbibytes; 1 zebi báite = 210 exbi báites = 270 báites;

• yobibyte (ípsilon é bê) equivale a 280 bytes ou .1024 zebibytes; 1 yobi báite = 210 zebi báites = 280 báites.

Página 42

Os fatores de conversão que definem os prefixos no SI são potências de 10:

• 10 ou 10‒1 para os três primeiros múltiplos e para os três primeiros submúltiplos.

Por exemplo:

a) para transformar 75 métros em decâmetro, fazemos 75 métros = 75 ⋅ 10‒1 decâmetros = 7,5 decâmetros;

b) para transformar 75 centímetros em milímetro, fazemos 75 centímetros = 75 ⋅ 10 milímetros = 750 milímetros.

• 103 (.1000) ou 10‒3 (0,001) para os demais prefixos.

Por exemplo:

a) para transformar .41852 metros em terâmetro (tê ême), fazemos:

.41852 métros = .41852 ⋅ 10‒3 ⋅ 10‒3 ⋅ 10‒3 ⋅ 10‒3 terâmetro = 4,1852 ⋅ 10‒8 terâmetro;

b) para transformar 0,29 metro em nanômetro, fazemos:

0,29 métro = 0,29 ⋅ 103 ⋅ 103 ⋅ 103 nanômetros = 0,29 ⋅ 109 nanômetros = ..290000000 nanômetros = 2,9 ⋅ 108 nanômetros.

Os fatores de conversão que definem os prefixos binários são potências de base 2:

• 210 (.1024) para transformar uma unidade para a unidade imediatamente inferior;

• 2‒10 (.1024‒1) para transformar uma unidade para a unidade imediatamente superior.

Popularmente, os prefixos do ésse Í são utilizados para indicar múltiplos de unidades de medida da informática, quando deveriam ser utilizados os prefixos binários; por exemplo, é comum o uso de 50 ême bê ou 50 megabytes, no lugar de 50 ême í bê ou 50 mebibytes. Note que mega e mebi são prefixos que indicam múltiplos com fatores diferentes: 106 ≠ 220 , pois 106 = ..1000000 e 220 = ..1048576. Portanto, 50 megabytes não correspondem ao mesmo número de bytes que 50 mebibytes.

No entanto, potências de 10 são usadas em situações específicas na informática. Os fabricantes de discos rígidos, por exemplo, usam potências de 10 para identificar capacidades de armazenamento. Quando o fabricante indica que um disco rígidoglossário tem capacidade de armazenamento de 500 gigabáites, por exemplo, isso quer dizer que o disco rígido pode armazenar até 500 bilhões de bytes ou 500 × 109 báites, o que corresponde a aproximadamente 466 gibi báites.

Note que arredondar .1024 para .1000 e considerar que 1 quilo báite é aproximadamente 1 kibi báite é razoável, mas observe que, quando tratamos de múltiplos cada vez maiores, arredondamentos acumulados geram erros grandes de aproximação.

Por exemplo, ao considerar 1 yotta báite = 1 yobi báite, o erro de aproximação é de quase 21%.

1 yotta báite = 1024 báites =........1000000000000000000000000 báites

1 yobi báite = 280 báites = ........1208925819614629174706176 báites

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Disco de vidro pode guardar arquivos com até 360 térabáites “para sempre”

Pesquisadores da Universidade de Southampton, no Reino Unido, anunciaram uma unidade de disco que pode armazenar dados, como documentos e obras de arte, “para sempre”. O dispositivo, que consiste em um pequeno vidro nanoestruturado e tem gravação a laser, é capaz de guardar 360 térabáites por até 13,8 bilhões de anos.

Fotografia. Destaque para a mão de uma pessoa segurando um círculo pequeno de vidro transparente. — Disco digital criado na Universidade de Southampton, no Reino Unido. (Fotografia de 2017.)

Fonte: TECHTUDO. Disco de vidro pode guardar arquivos com até 360 térabáites “para sempre”. Portal de notícias Techtudo, [Rio de Janeiro],17 fevereiro 2016. Disponível em: https://oeds.link/F2Dga0. Acesso em: 23 março 2022.

Com base nas informações apresentadas na notícia, determine a capacidade de armazenamento do disco de vidro considerando potências de base 2 e utilizando os prefixos binários.

Página 43

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

Usando uma calculadora, dê a medida da distância aproximada, em quilômetro, entre a Terra e o exoplaneta GJ 1214b, que está fora do Sistema Solar, a 40 anos-luz.

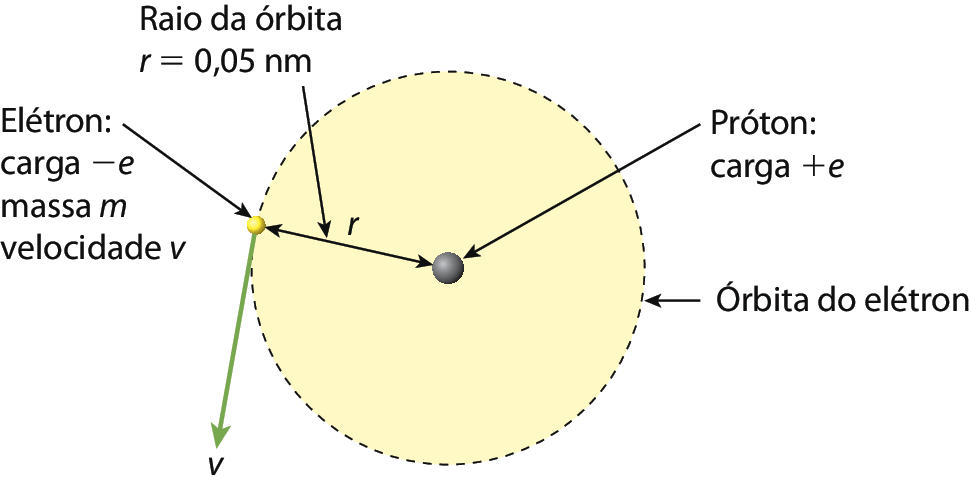
2 No átomo de hidrogênio de Bór, o elétron anda ao redor de um próton central, em uma órbita circular com o raio medindo aproximadamente 0,05 nanômetro. Qual é a medida dêsse raio, em metro?

Ilustração. Circunferência chamada órbita do elétron. No centro, esfera pequena chamada de próton: carga positiva e. Da esfera até a extremidade, medida r, chamada de Raio da órbita, r igual a 0,05 nanômetro. Seta verde v para baixo na diagonal da esfera amarela na extremidade do raio, chamada Elétron: carga negativa e massa m velocidade v.

3 Até quantos megabytes um disco de vidro pode guardar? Esse valor corresponde a quantos mebibytes?

4 Considere o erro cometido ao se praticar arredondamentos da base 2 para a base 10 nas unidades usadas na informática.

a) Qual é o erro percentual que se comete ao arredondar 1 kibi báite para .1000 báites, substituindo 210 por 103?

b) Qual é o erro percentual que se comete, substituindo-se 280 por 1024, ao arredondar 1 yobi báite para ........1000000000000000000000000 báites?

“A constelação em que vivemos, a Via Láctea, [reticências] tem a fórma de espiral achatada com cêrca de 100 mil a éle de diâmetro e 200 bilhões de estrelas [reticências], faz parte do Grupo Local. Três das galáxias do Grupo Local são visíveis a olho nu:

• Andrômeda – 220 mil a éle de diâmetro e a uma distância de 2,9 milhões a éle.

• Grande Nuvem de Magalhães – 70 mil a éle de diâmetro e a uma distância de 200 mil a éle.

• Pequena Nuvem de Magalhães – 14 mil a éle de diâmetro e a uma distância de 168 mil a éle.”

Fonte: ALMANAQUE Abril 2015. São Paulo: Abril, 2015. página 171.

Fotografia. Céu escuro com uma forma em espiral achatada de cor escura no centro e mais clara nas laterais com diversas estrelas. — Fotografia de trecho da Via Láctea. (Fotografia de 2015.)

Use uma calculadora e escreva em notação científica, na unidade quilômetro e na Unidade Astronômica, as medidas aproximadas descritas no texto anterior, em que a éle corresponde à unidade ano-luz.

Hora de criar – Após pesquisar, na internet, em livros, em jornais ou em revistas, medidas de comprimento usadas na Astronomia ou na nanotecnologia, troque com um colega um problema, criado por vocês. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Hora de criar – Agora, faça o mesmo que no exercício 6, após pesquisar medidas de armazenamento no campo da informática. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi‑los.

Página 44

2. Potência com expoente fracionário e radicais

Já estudamos potência com expoente fracionário tendo por base números racionais, em que relacionamos potenciação e radiciação.

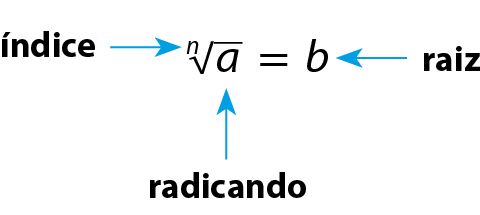
Consideremos a definição: se bn = a, então b =

\sqrt[n]{a}

, com n natural não nulo e b ⩾ 0.

Ilustração. Homem de cabelo castanho e camiseta preta fala: Esta é uma boa hora para recordar a nomenclatura. Em outras palavras, dizemos que um número b, não negativo, é igual à raiz enésima de um número a quando esse número b elevado a n, número natural e não nulo, é igual ao número a.

Observações

▶ Dando nome aos símbolos:

Esquema.
Raiz enésima de a, igual a b.
Uma flecha aponta para n, dizendo "índice".
Uma flecha aponta para a, dizendo "radicando".
Uma flecha aponta para b, dizendo "raiz".

▶

\sqrt[n]{a} = b

(lemos: “raiz enésima de a é igual a b”)

▶ O símbolo

\sqrt{}

é chamado de radical. Usamos esse mesmo símbolo para indicar a raiz quadrada de um número a.

Como já estudamos, (73)2 = 76. Então, pela definição dada, podemos dizer que 73 é a raiz quadrada de 76, isto é, 73 =

\sqrt[2]{7^{6}}

. Como

3 = \frac{6}{2}

, temos

7^{\frac{6}{2}} = \sqrt[2]{7^{6}}

Também observamos que (72)3 = 76. Portanto, podemos dizer que 72 é a raiz cúbica de 76, isto é, 72 =

\sqrt[3]{7^{6}}

. Como 2 =

\frac{6}{3}

, temos

7^{\frac{6}{3}} = \sqrt[3]{7^{6}}

Ilustração. Mulher de cabelo enrolado castanho e camiseta amarela. Ela fala: As relações que estabelecemos nos exemplos anteriores se referem apenas aos expoentes das potências e aos índices das raízes, ou seja, no lugar da base 7, podemos considerar qualquer número real positivo.

Assim, podemos ampliar este estudo para potência com expoente fracionário tendo por base números reais. Acompanhe.

• (π3)2 = π6

Aplicando a definição para raiz quadrada, π3 =

\sqrt[2]{π^{6}}

π^{\frac{6}{2}} = \sqrt[2]{π^{6}}

•

{[{(\sqrt{5})}^{3}]}^{4} = {(\sqrt{5})}^{12}

Aplicando a definição para raiz quarta, temos

{(\sqrt{5})}^{3} = \sqrt[4]{{(\sqrt{5})}^{12}}

{(\sqrt{5})}^{\frac{12}{4}}

= \sqrt[4]{{(\sqrt{5})}^{12}}

Se a é um número real positivo, m é um número inteiro e n é um número natural não nulo, temos:

a^{\frac{m}{n}} = \sqrt[n]{a^{m}}

Página 45

Observação

▶ As propriedades válidas para as potências de expoente inteiro são válidas para as potências de expoente fracionário que tenham base positiva. Por exemplo:

•

π^{\frac{2}{3}} \cdot π^{\frac{1}{4}} = π^{\frac{2}{3} + \frac{1}{4}} = π^{\frac{11}{12}}

•

{[{(\sqrt[3]{2})}^{\frac{2}{3}}]}^{\frac{3}{5}} = {(\sqrt[3]{2})}^{\frac{2}{3} \cdot \frac{3}{5}} = {(\sqrt[3]{2})}^{\frac{2}{5}}

•

{(\sqrt{10})}^{\frac{3}{2}} : {(\sqrt{10})}^{5} = {(\sqrt{10})}^{\frac{3}{2} - 5} = {(\sqrt{10})}^{- \frac{7}{2}}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

8 Escreva na fórma de potência com expoente fracionário.

\sqrt[5]{8, 1^{4}}

\sqrt{π^{3}}

\sqrt[6]{{(\frac{1}{7})}^{4}}

\sqrt[9]{{(\sqrt{8})}^{3}}

9 Represente na fórma de radical.

π^{\frac{1}{2}}

ϕ^{\frac{6}{5}}

{(\sqrt{3})}^{\frac{1}{4}}

d) (5)0,5

10 Reduza a uma só potência, usando as propriedades das potências.

{(\sqrt{7})}^{\frac{1}{3}} \cdot {(\sqrt{7})}^{\frac{1}{4}}

{(\sqrt{7})}^{\frac{1}{3}} : {(\sqrt{7})}^{\frac{1}{4}}

{[{(\sqrt{10})}^{\frac{1}{3}}]}^{\frac{9}{2}}

π^{{(\frac{1}{16})}^{\frac{1}{2}}}

11 Calcule.

{(\sqrt{\sqrt{2}})}^{4}

{0, 512}^{\frac{1}{3}}

\sqrt[5]{π^{10}}

{(\sqrt{27})}^{\frac{2}{3}}

Reúna-se com um colega e façam o que se pede.

• Representem cada radical a seguir na fórma de potência com expoente fracionário.

• Simplifiquem, se possível, a fração do expoente da potência obtida.

• Representem a potência com expoente simplificado na fórma de radical.

• Comparem cada radical dado com o respectivo radical obtido. Escrevam uma regra prática para simplificar um radical, quando possível.

\sqrt[12]{π^{6}}

\sqrt[14]{{1,7}^{7}}

\sqrt[6]{{(\frac{13}{5})}^{9}}

\sqrt[18]{ϕ^{12}}

\sqrt[24]{{(\frac{π}{2})}^{8}}

\sqrt[12]{π^{18}}

PARA SABER MAIS

A história dos números irracionais

O conceito de número real passou por transformações significativas até chegar à fórma como o entendemos hoje. Em sentido mais prático, pode-se dizer que a ideia de medida implica noção de número real. Para tentar compreender a motivação que desencadearia a noção de número real, precisamos pensar em quando surgiu a necessidade da ideia de números irracionais (números que não podem ser expressos na fórma

\frac{p}{q}

, com pê e quê inteiros e q ≠ 0).

Essa ideia teve origem, provavelmente, em contextos geométricos na Grécia antiga. Para os pitagóricos, o conceito de número era o que para nós são os números naturais, e as razões eram, então, somente estabelecidas entre números naturais.

Não se tem certeza da descoberta de números irracionais, mas é certo que, para os gregos clássicos, foi muito difícil aceitá-los.

Página 46

O filósofo grego Aristóteles (384 a 322 antes de Cristo) provou que a diagonal do quadrado com seu lado estão relacionados de tal modo que a medida da diagonal ou do lado é um número irracional. Essa é a prova mais antiga que se conhece para a característica irracional da diagonal do quadrado em relação ao seu lado quando a medida deste é dada por um número natural. Ela envolve, teoricamente, números irracionais e, portanto, amplia a ideia original grega de número.

Do ponto de vista geométrico, dois segmentos estabelecerão uma razão, representada por um número racional, se for possível encontrar um pequeno segmento que meça ambos os segmentos dados, ou seja, que caiba um número inteiro de vezes em cada um dos segmentos dados originalmente.

Por exemplo, considere os segmentos

\overline{A B}

\overline{C D}

\overline{E F}

a seguir.

Ilustração. Segmento de reta A B dividido em 8 partes. Cada parte representa u. Abaixo. Segmento de reta C D dividido em 3 partes. Cada parte representa u. À direita. Segmento de reta E F que corresponde a u.

Note que o segmento

\overline{E F}

cabe 8 vezes no segmento

\overline{A B}

e 3 vezes no segmento

\overline{C D}

, o que implica que os segmentos

\overline{A B}

\overline{C D}

estabeleçam uma razão de 8 para 3 ou, em termos numéricos, o número racional

\frac{8}{3}

Inicialmente, os gregos não concebiam a existência de segmentos para os quais tal medida não existisse, o que resultaria numericamente em números irracionais, como no quadrado a bê cê dê, em que a razão entre as medidas da diagonal e de seu lado é

\sqrt{2}

Ilustração. Quadrado ABCD com medida do lado: AB: 1 e BC: 1. De A até C, diagonal com medida raiz quadrada de 2
Em B ângulo reto.

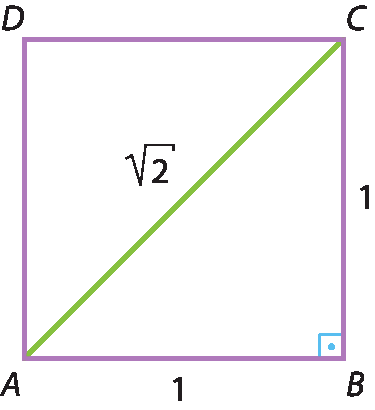
Essas medidas envolvendo números irracionais foram percebidas provavelmente por algum pitagórico, entre 500 antes de Cristo e 375 antes de Cristo Uma vez que na escola pitagórica os números naturais e suas razões formavam a essência de todas as coisas, uma descoberta dessa natureza deve ter gerado grande crise.

Tudo isso constituiu um importante passo na formação do número real, refletindo, posteriormente, no que viriam a ser os números irracionais, ampliando o conceito de número na Grécia e contribuindo para a construção da ideia de número real, que foi sendo gradualmente estabelecida.

3. Propriedades dos radicais

1ª propriedade

Considerando o radical

\sqrt[3]{5^{3}}

, temos:

\sqrt[3]{5^{3}} = 5^{\frac{3}{3}} = 5^{1} = 5

Da mesma maneira:

\sqrt[4]{5^{4}} = 5

\sqrt[3]{{(‒ 5)}^{3}}

= ‒5, mas

\sqrt[4]{{(‒ 5)}^{4}}

= 5, pois:

(‒5)4 = (‒5) ⋅ (‒5) ⋅ (‒5) ⋅ (‒5) = 625 e

\sqrt[4]{625}

= 5.

Ao calcular

\sqrt[3]{{(‒ 5)}^{3}}

, extraímos uma raiz de índice ímpar de um número negativo, ou seja,

\sqrt[3]{‒ 125} .

O resultado é um número negativo, ‒5, pois (‒5)3 = ‒125.

Página 47

Entretanto, ao calcular

\sqrt[4]{{(‒ 5)}^{4}}

, extraímos a raiz de índice par de um número positivo, isto é,

\sqrt[4]{625},

que é 5, pois 54 = 625.

De modo geral:

se n é um número natural ímpar, então

\sqrt[n]{a^{n}}

= a, sendo a um número real;

se n é um número natural par não nulo, então

\sqrt[n]{a^{n}}

|a|

, sendo a um número real.

Observe alguns exemplos.

\sqrt[3]{2^{3}}

= 2

\sqrt[3]{{(‒ 2)}^{3}}

= ‒2

\sqrt{5^{2}} = |5| = 5

\sqrt{{(‒ 5)}^{2}} = |‒ 5| = 5

Observação

▶ Quando o radicando for uma potência de expoente par que tenha na base uma expressão literal que represente um número real, vamos admitir que o radicando assume apenas valores reais iguais a zero ou maiores do que zero.

Assim:

\sqrt[4]{x^{4}} = x

Admitindo que x ⩾ 0.

\sqrt{{(3 x ‒ 5)}^{2}}

= 3x ‒ 5

Admitindo que 3x ‒ 5 ⩾ 0, ou seja, x ⩾

\frac{5}{3}

2ª propriedade

Observe o cálculo a seguir.

Esquema. Raiz 12 de 3 elevado a 8, flecha inclinada indo até o resultado seguinte, dizendo Escrevemos a expressão na forma de potência, igual a, 3, elevado a 8, 12 avos, flecha inclinada indo até o resultado seguinte, dizendo Simplificamos a fração do expoente, igual a, 3 elevado a 2 terços, flecha inclinada até o resultado seguinte, dizendo Escrevemos a expressão na forma de raiz, igual a, raiz cúbica de 3 ao quadrado.

Assim:

\sqrt[12]{3^{8}} = \sqrt[12 : 4]{3^{8 : 4}} = \sqrt[3]{3^{2}}

Dividindo-se o índice e o expoente do radicando por um mesmo número natural maior do que zero, o valor do radical não se altera, ou seja:

\sqrt[n]{a^{m}} = \sqrt[n : p]{a^{m : p}}

sendo a um número real positivo, m um número inteiro, n um número natural não nulo e p divisor de m e n.

Essa propriedade nos possibilita simplificar certos radicais, isto é, transformá-los em radicais mais simples e equivalentes aos radicais dados.

Página 48

Como exemplo, vamos simplificar os radicais a seguir.

\sqrt[12]{{(\frac{1}{2})}^{9}} = \sqrt[12 : 3]{{(\frac{1}{2})}^{9 : 3}} = \sqrt[4]{{(\frac{1}{2})}^{3}}

Dividimos o índice e o expoente por 3, que é divisor de 12 e de 9.

\sqrt[20]{3, 7^{15}} = \sqrt[20 : 5]{3, 7^{15 : 5}} = \sqrt[4]{3, 7^{3}}

Dividimos o índice e o expoente por 5, que é divisor de 20 e de 15.

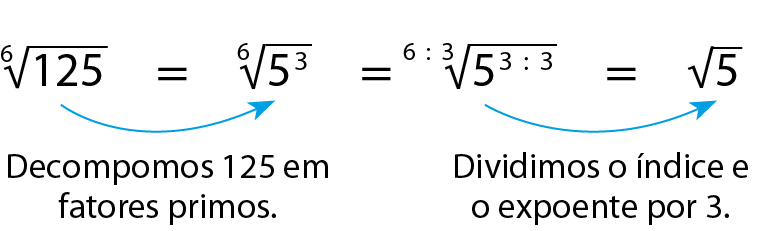
Esquema. Raiz sexta de 125, igual a, raiz sexta de 5 cubos, igual a, raiz de índice 6 dividido por 3, de 5 elevado a 3 dividido por 3, igual a, raiz quadrada de 5.
De Raiz sexta de 125 para raiz sexta de 5 cubos, seta azul indicando: Decompomos 125 em fatores primos.
De raiz de índice 6 dividido por 3, de 5 elevado a 3 dividido por 3 para raiz quadrada de 5, seta azul indicando: Dividimos o índice e o expoente por 3.

3ª propriedade

Observe os cálculos a seguir.

\sqrt{3 \cdot 5} = {(3 \cdot 5)}^{\frac{1}{2}} = 3^{\frac{1}{2}} \cdot 5^{\frac{1}{2}} = \sqrt{3} \cdot \sqrt{5}

\sqrt[4]{\frac{7}{3} \cdot 6, 5}

{(\frac{7}{3} \cdot 6, 5)}^{\frac{1}{4}}

{(\frac{7}{3})}^{\frac{1}{4}}

⋅

{(6, 5)}^{\frac{1}{4}}

\sqrt[4]{\frac{7}{3}}

⋅

\sqrt[4]{6, 5}

Em geral, sendo a e b números reais positivos e n um número natural não nulo, temos:

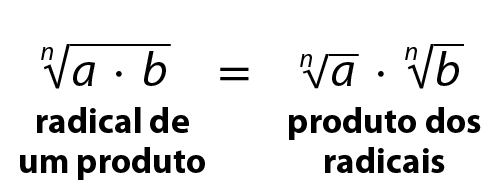
Esquema. Raiz enésima de a vezes b, igual a raiz enésima de a vezes raiz enésima de b.
Abaixo de Raiz enésima de a vezes b indicação: radical de um produto.
Abaixo de a raiz enésima de a vezes raiz enésima de b indicação: produto dos radicais.

Observe os exemplos.

\sqrt[3]{5, 8 \cdot 3} = \sqrt[3]{5, 8} \cdot \sqrt[3]{3}

\sqrt[5]{7 \cdot \frac{5}{4}} = \sqrt[5]{7} \cdot \sqrt[5]{\frac{5}{4}}

4ª propriedade

Observe o cálculo a seguir.

\sqrt{\frac{2}{3}} = {(\frac{2}{3})}^{\frac{1}{2}} = \frac{2^{\frac{1}{2}}}{3^{\frac{1}{2}}} = \frac{\sqrt{2}}{\sqrt{3}}

Em geral, sendo a e b números reais positivos (note que b ≠ 0) e n um número natural não nulo, temos:

Esquema. Raiz enésima de a sobre b. Igual a, fração, numerador Raiz enésima de a, denominador Raiz enésima de b.
Abaixo de Raiz enésima de a sobre b indicação: radical de um quociente.
Abaixo de fração, numerador Raiz enésima de a, denominador Raiz enésima de b indicação: quociente de radicais.

Observe os exemplos.

\sqrt{\frac{2}{7}} = \frac{\sqrt{2}}{\sqrt{7}}

\sqrt[3]{\frac{3}{5}} = \frac{\sqrt[3]{3}}{\sqrt[3]{5}}

Página 49

Com base nas propriedades que acabamos de estudar, é possível simplificar certos radicais tirando fatores do radicando.

Como exemplo, vamos simplificar os radicais a seguir.

\sqrt{50} = \sqrt{2 \cdot 5^{2}} = \sqrt{2} \cdot \sqrt{5^{2}} = \sqrt{2} \cdot 5 = 5 \sqrt{2}

\sqrt{24} = \sqrt{2^{3} \cdot 3} = \sqrt{2^{2} \cdot 2 \cdot 3} = \sqrt{2^{2}} \cdot \sqrt{2 \cdot 3} = 2 \cdot \sqrt{6} = 2 \sqrt{6}

\sqrt[3]{\frac{625}{64}} = \frac{\sqrt[3]{625}}{\sqrt[3]{64}} = \frac{\sqrt[3]{5^{3} \cdot 5}}{\sqrt[3]{2^{6}}} = \frac{\sqrt[3]{5^{3}} \cdot \sqrt[3]{5}}{2^{2}} = \frac{5 \sqrt[3]{5}}{4}

Da mesma fórma que podemos tirar fatores do radicando, podemos inserir fatores externos no radicando. Acompanhe alguns exemplos.

2 \sqrt{5} = \sqrt{2^{2} \cdot 5}

3 \sqrt[3]{5} = \sqrt[3]{3^{3} \cdot 5}

2 \sqrt[4]{18} = \sqrt[4]{2^{4} \cdot 18}

7 \sqrt[3]{7^{2}} = \sqrt[3]{7^{3} \cdot 7^{2}} = \sqrt[3]{7^{5}}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

13 Calcule.

\sqrt[3]{10^{3}}

\sqrt[4]{1, 7^{4}}

\sqrt{{(\frac{5}{6})}^{2}}

\sqrt[4]{2^{4}}

14 Simplifique os radicais.

\sqrt[9]{5^{6}}

\sqrt[15]{3^{20}}

\sqrt[6]{11^{3}}

\sqrt[18]{7^{2}}

15 Decomponha o radicando em fatores primos e simplifique os radicais.

\sqrt[10]{32}

\sqrt[6]{27}

\sqrt[4]{0, 36}

\sqrt[6]{0, 216}

16 Simplifique os radicais, sabendo que a ⩾ 0, x ⩾ 0, y ⩾ 0 e m ⩾ 0.

\sqrt[6]{a^{3}}

\sqrt[20]{x^{15}}

\sqrt[9]{y^{6}}

\sqrt[12]{m^{10}}

17 Transforme em um produto de radicais.

\sqrt{4 \cdot 5}

\sqrt[3]{2 \cdot 3}

\sqrt[4]{7 \cdot 10}

18 Represente como um quociente de radicais.

\sqrt{\frac{2}{5}}

\sqrt[3]{\frac{18}{5}}

\sqrt[5]{\frac{2}{9}}

19 Simplifique os radicais.

\sqrt{8}

\sqrt[3]{27 \cdot 5}

\sqrt[5]{2^{7}}

\sqrt[4]{2^{7} \cdot 3^{5} \cdot 5^{4}}

\sqrt[3]{162}

\sqrt[6]{3^{3} \cdot 4^{12}}

20 Introduza nos radicais os fatores externos em cada caso.

2 \sqrt{5}

3 \sqrt[3]{2}

‒ 2 \cdot 3 \cdot \sqrt[3]{10}

\frac{2}{3} \sqrt{5}

0, 2 \sqrt[3]{2}

2 \sqrt[4]{3}

Glossário

Disco rígido: : dispositivo usado para armazenar os dados em computadores, popularmente chamado de agá dê (do inglês hard disk).; Voltar para o texto